Table of Contents
Post-hoc Tests
Introduction
If you find any significant main effect or interaction with an ANOVA test, congrats, you have at least one significant difference in your data. However, an ANOVA test doesn't tell you where you have the differences. Thus, you need to do one more test–a post-hoc test–to find where they exist.
Comparisons for main effects
As we have seen in the Anova page, there are two kinds of effects you may have: main effects, and interactions (if your model is two-way or more). The comparison for the main effect is fairly straightforward, but there are four kinds of comparisons you can make, so you have to decide which one you want to do.
Before talking about the differences of the comparisons, you need to know one important thing. Some of the post-hoc comparisons may not be appropriate for repeated-measure ANOVA. I am not 100% sure about this point, but it seems that some of the methods do not consider the within-subject design. So, my current suggestion is that if the factor you are comparing in a post-hoc test is a within-subject factor, it might be safer to use a t test with the Bonferroni's or Sidak's correction.
OK., back to the discussion about the types of comparisons. For the discussion, let's say you have three groups: A, B, and C.
- [Case 1] Compare every possible combination of your groups: In this case, you compare everything. You will compare A and B, B and C, and C and A. But you also compare A and B+C (the mean of B and C), B and C+A, C and A+B.
- [Case 2] Compare every group: In this case, you will compare A and B, B and C, and C and A. But you do not compare A and B+C, B and C+A, C and A+B.
- [Case 3] Compare every group against the control: In this case, you will compare the groups only against the control condition. If your control condition is A, you will compare A and B, and A and C.
- [Case 4] Compare the data against the within-subject factor: In this case, you will make a comparison against the within-subject factor. In other words, if you have done repeated-measure ANOVA, this is the way to do a post-hoc test. The methods for this case can be used for tests against between-subject factors.
The strict definition of a post-hoc test means a test which does not require any plan for testing. In the four examples above, only Case 1 satisfies the strict definition of a post-hoc test because the others cases require some sort of planning on which groups to compare or not to compare. However, the term of a post-hoc test is often used for meaning Case 2 and Case 3. Case 4 is usually called a planned comparison test, but again it is often referred as a post-hoc test as well. In this wiki, I use a post-hoc test to mean all of these four tests.
The key point here is you need to figure out which case you want to do for the comparisons after ANOVA. Make sure what comparisons you are interested in before doing any test.
Comparisons for interactions
If you find a significant interaction, things are a little more complicated. This means that the effect of one factor depends on the conditions controlled by the other factors. So, what you need to do is to make comparisons against one factor with fixing the other factors. Let's say you have two Devices (Pen and Touch) and three Techniques (A, B, and C) as we have seen in the two-way ANOVA example. If you have found the interaction, what you need to look at is:
- The effect of Technique under Device = Pen;
- The effect of Technique under Device = Touch;
- The effect of Device under Technique = A;
- The effect of Device under Technique = B; and
- The effect of Device under Technique = C.
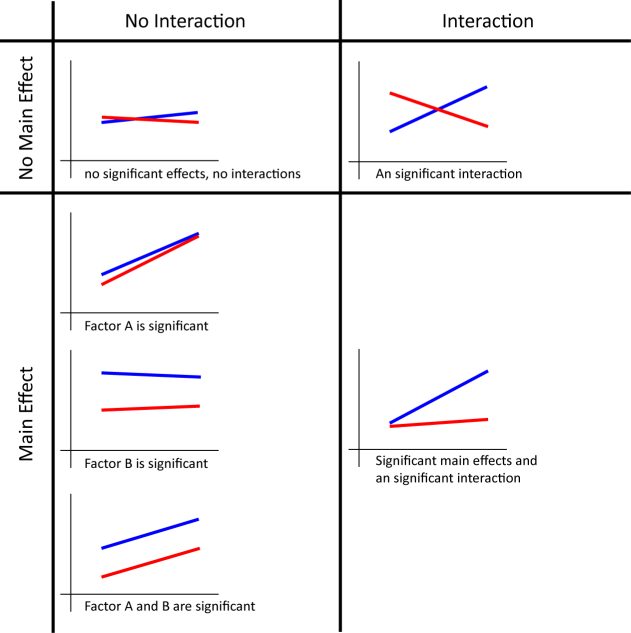
The effects we look at here are called simple main effects. Although you could report all the simple main effects you have, it might become lengthy. Rather, providing a graph like above is easier to understand what kinds of trends your data have. Your graph will look like one of the following graphs depending of the existence of main effects and interactions.
It is also said that you shouldn't report the main effects (not simple main effects) when you have a significant interaction. This is because significant differences are caused by some combination of the factors, and not necessarily caused by a single factor. However, I think that it is still good to report any significant main effects even if you have a significant interaction because it tells us what the data look like. Again, providing a graph is very helpful for your readers to understand your data.
The sad news is that it is not as easy in R to do post-hoc test as in SPSS. You often have to do a lot of things manually or some methods are not really supported in R. So, particularly if you are doing two-way ANOVA and you have an access to SPSS, it may be better to use SPSS.
Main effect: Comparing every possible combination of your groups (Scheffe's test)
Scheffe's test allows you to do a comparison on every possible combination of the group you are caring about. Unfortunately, there is no automatic way to do Scheffe's test in R. You have to do it manually. The following procedure is based on Colleen Moore & Mike Amato's material.
We use the same example for one-way ANOVA.
We have a significant effect of Group. So, we need to look into that effect more deeply. First, you have to define the combination of the groups for your comparison.
The each element of coeff intuitively means the weight for the later calculation. The positive values and negative values represent data to compare. In this case, the first element is 1, and the second element is -1. And the first, second, and third elements will represent Group A, B, and C, respectively. So, this coeff means we are going to compare Group A and Group B. The third element is 0, which means Group C will be ignored.
Another key point is the sum of the elements must be 0. Here are some other examples.
- If you have three groups (A, B, C), and you want to compare Group B and C, coeff = c(0, 1, -1).
- If you have three groups (A, B, C), and you want to compare Group A and the mean of Group B and C, coeff = c(2, -1, -1).
- If you have five groups (A, B, C, D, E), and you want to compare the mean of Group A and B, and the mean of Group C, D and E, coeff = c(2/3, 2/3, 2/3, -1, -1).
Let's come back to the example. Now we need to calculate the number of the samples and the mean for each group.
We then calculate some statistical values.
mspsi should be 7.5625 if you have followed the example correctly. Now we are going to calculate the F value. For this, we need to know the value for the mean square for the errors (or residuals). According to the result of the anova test, it is 0.9405 (Did you find it? Go back to the very first of this example and see the result of summary(aov)). We also need to know the degree of freedom of the factor we are caring about (in this example, Group), which is 2.
Finally, we can calculate the p value for this comparison (comparison between Group A and Group B). For the degrees of freedom, we can use the same ones for the anova test, which is 2 for the first DOF, 21 for the second DOF (Find them in the result of the anova test).
Thus, the difference between Group A and B is significant because p < 0.05.
So, if you really want to do all possible comparisons, you probably want to write some codes so that you can do a batch operation. I think it should be straightforward, but be careful about the design of the comparison (i.e., coeff).
I am not 100% sure, but Scheffe's test may not be appropriate for repeated-measure ANOVA. For repeated-measure ANOVA, you can do a pairwise comparison with the Bonferroni's or Sidak's correction.
Main effect: Comparing every group (Tukey's test)
This is probably the most common case in HCI research. You want to compare the two of the groups, but you are not interested in any combination of more than one group. One of the common methods for this case is Tukey's method. The way to do a Tukey's test in R depends on how you have done ANOVA.
First, let's take a look at how to do a Tukey's test with the aov() function. We use the same example of one-way ANOVA.
Now, we do a Tukey's test.
So, we have significant differences between A and B, and A and C.
If you use the Anova() function, the way to do a Tukey's test is a little different. Here, we use the same example of two-way ANOVA, but the values for Time were slightly changed (to make the interaction effect disappear).
With the anova test, you will find the main effects. So, you need to run a Tukey's test. You have to do the following thing to do a Tukey's test with the model created by lm(). You need to include multcomp package beforehand.
Then, you get the results.
So, we have significant differences between any of the two groups in both Device and Technique.
It seems both ways to do a Tukey's test can accommodate mildly unbalanced data (the number of the samples are different cross the groups, but not that different). The Tukey's test which can handle mildly unbalanced data is also called Tukey-Kramer's test. If you have largely unbalanced data, you can't do a Tukey's test nor even ANOVA, and instead you should do a non-parametric test.
Another thing you should need to know is that Tukey may not be appropriate as a post-hoc test for repeated-measure ANOVA. This is because Tukey assumes the independency of the data across the groups. You can actually run a Tukey's test even for repeated-measure ANOVA with the second method (you need to use lme() in nlme package to build a model instead of lm()). As far as I can tell, it seems ok to use a Tukey's test for repeated-measure data, but I am not 100% sure yet.
With some statistical software, you can also run a Tukey's test for an interaction term. Unfortunately, it seems that it is not possible to do so in R (as of July 2011). I think this makes sense because you can simply look at simple main effects if you have a significant interaction term. But if you know a way to run a Tukey's test for an interaction term, please let me know.
Main effect: Comparing every group against the control (Dunnett's test)
In this case, you have one group which can be called “the reference group”, and you want to compare the groups only against this reference group. One common test is a Dunnett's test, and fortunately the way to do a Dunnett's test is as easy as a Tukey's test.
Let's use an example of the one-way ANOVA test.
Now, you are going to do a Dunnett's test. You need to include multcomp package.
As you can see in the result, the Dunnett's test only did comparisons between Technique A and B, and between Technique A and C. In this method, the first group in the factor you are caring about is used as the reference case (in this example, Technique A). So, you need to design the data so that the data for the reference case are associated with the first group in the factor.
You may have also noticed that the p values become smaller than those in the results of a Tukey's test.
| Tukey | Dunnett | |
|---|---|---|
| A - B | 0.0257122 | 0.018472 |
| A - C | 0.0002167 | 0.000149 |
Generally, a Dunnett's test is more sensitive (has more powers to find a significant difference) than a Tukey's test. At a cost of this power, you must assume the reference case for the comparisons.
You can also use the model generated by aov() in the lm() function. Here is another example of a Dunnett's test for two-way ANOVA.
Now, you get the result.
Main effect: Comparing data against the within-subject factor (Bonferroni correction, Holm method)
Another case you would commonly have is that you have within-subject factors. Unfortunately, in this case, the methods explained above may not be appropriate because they do not take the relationship between the groups into account. Instead, you can do a paired t test with some corrections to avoid some troubles caused by doing multiple t tests. The major corrections are Bonferroni correction and Holm method. Fortunately, you can do both quite easily in R. Let's take a look at the example of one-way repeated-measure ANOVA.
Doing multiple t tests with Bonferroni correction is as follows.
If you want to use Holm method, you just need to change the value of p.adj (or remove the argument of p.adj completely. R uses Holm method by default).
Other kinds of corrections are also available (type ?p.adjust.methods in the R console). But I think these two are usually good enough. It is considered that you should avoid using Bonferroni correction when you have more than 4 groups to compare. This is because Bonferroni correction becomes too strict for those cases.
You can also use the methods above for between-subject factors instead of using other methods (like Tukey's test). In this case, you just need to do something like:
So, which one to use?
There are several other things which may help you choose a particular method in addition to the properties explained above.
- A Dunnet's test has a stronger power (more likely to find a significant difference) than other methods. (But you need to assume the reference case).
- A Tukey's test (or Tukey-Kramer's test) is more strict or conservative (less likely to find a significant difference) than the pairwise comparison with the Bonferroni correction when the number of the groups to compare is small. But when the number of the groups to compare is large, a Tukey's test becomes less strict than the pairwise comparison with the Bonferroni correction.
- The pairwise comparison with the Bonferroni correction often becomes too strict when the number of the groups to compare is large. Generally, when the number of the groups is more than six, we want to avoid using this.
- A Scheffe's test tends to be strict because it compares all possible combination.
In HCI research, the most common method I have seen is either a Tukey's test or pairwise comparison with the Bonferroni correction. So, if you don't have any particular comparison in mind, these two would be the first thing you may want to try.
Interaction
If you have any significant interaction, you need to look at the data more carefully because more than 0ne factor contribute to significant differences. There are two ways to look into the data: simple main effects and interaction contrasts.
Simple main effect
The idea of the simple main effect is very intuitive. If you have n factors, you pick up one of them, fix it, and do a test for the n-1 factors. In our two-way ANOVA example, there are five tests for looking at simple main effects:
- A comparison against Technique for the data with Device = Pen;
- A comparison against Technique for the data with Device = Touch;
- A comparison against Device for the data with Technique = A;
- A comparison against Device for the data with Technique = B; and
- A comparison against Device for the data with Technique = C.
Let's do it with the example of two-way ANOVA.
This ANOVA test shows you have a significant interaction, so now we are going to look at the simple main effects. First, we are going to look at the difference caused by Technique for the Pen condition. For this, we pick up data only for the Pen condition.
We can then simply run a one-way ANOVA test against Technique.
So, we have a significant simple effect here. We can do tests for other simple main effects in a similar way.
If you only have two groups to compare, you can just do a t test as you can see above. In this example, you will find significant simple effects in all the five tests. But if the main effects are so powerful, we cannot find clear interactions of the factors with tests for simple main effects. In such cases, we need to switch to doing tests for interaction contrasts.
Interaction Contrast
Interaction contrasts basically mean you compare every combination of the two groups. So it seems kind of similar to Scheffe's test. I haven't figured out how to do interaction contrasts in R. I will add it when I figure out.
Do I really need to run ANOVA?
Some of you may have noticed that some post-hoc test methods explained here do not use any result gained from aov() or Anova() function. For example. post-hoc tests with Bonferroni or Holm correction do not use the results of the ANOVA test.
In theory, if you use post-hoc methods which do not require the result of the ANOVA test, you don't need to run ANOVA, and can directly run post-hoc methods. However, running ANOVA and then running post-hoc tests is kind of a de-facto standard, and most of the readers expect the results of ANOVA (and the results of post-hoc tests in the case you find any statistical difference through the ANOVA test). Thus, in order to avoid the confusion that the reader might have, it is probably better to run ANOVA regardless of whether it is theoretically needed.
How to report
In the report, you need to describe which post-hoc test you used and where you found the significant differences. Let's say you are using a Tukey's test and have the results like this.
Then, you should report as follows:
A Tukey's pairwise comparison revealed the significant differences between A and B (p < 0.05), and between A and C (p < 0.01).
Of course, you need to report the results of your ANOVA test before this.

Discussion
"covariate interactions found -- default contrast might be inappropriate"
Please help me to solve below mention equation for dunnett test.
I know how calculate q as per below mention formula.
q= Mean1-Mean2 / SEDifference
But I could not understand how to calculate adjusted p value as per below mention formula.
pValue(adjusted) = PFromQDunnett(q,DF,M).
Please provide example if possible or reference for the same.
Is there a way to run Scheffe test in R with the model from Anova function (in 'car' package)?
thank you for the great tutorial!
I have a one question:
which post-hoc test should be used in case of a mixed-design?
I have one between-subjects factor (2 levels) and one within-subjects factor (6 levels) and Anova showed significance of both main effects as well as of the interaction. Which post-hoc test should I run now?
Hana
<a href=http://jakirower.co.pl>opinie o Kross level</a>
http://www.alpassocoitempi.it/651-ray-ban-vista-uomo-indossati.htm
http://www.io-riciclo.it/374-scarpe-nike-air-force-nuove
http://www.clinicaviaemilia.it/nike-free-run-2-753
http://www.succesfou.fr/casquette-miami-heat-foot-locker-662.html
http://www.caminowatch.fr/gazelle-adidas-homme-120.html
<a href=http://www.chaletinterclubmontventoux.fr/234-air-max-2016-blanche-femme-pas-cher.php>Air Max 2016 Blanche Femme Pas Cher</a>
<a href=http://www.biotoxen.it/311-cappelli-nike-visiera-piatta.php>Cappelli Nike Visiera Piatta</a>
<a href=http://www.tissages-de-gravigny.fr/nike-thea-femme-blanche.html>Nike Thea Femme Blanche</a>
<a href=http://www.casevacanzesottoalduomo.it/nike-air-max-90-blu-470.php>Nike Air Max 90 Blu</a>
<a href=http://www.faustoparavidino.it/oakley-pitchman.aspx>Oakley Pitchman</a>
http://www.animalcare.fr/stan-smith-effet-miroir-842.html
http://www.lucilepeuch.fr/nike-huarache-point-de-vente-920.php
http://www.modeprice.fr/537-sac-longchamps-kate-moss.php
http://www.casevacanzesottoalduomo.it/nike-air-max-90-bianche-amazon-016.php
http://www.semioticamente.it/nike-sb-zoom-air-paul-rodriguez-2
<a href=http://www.hotelcentrevalleebleue.fr/404-new-balance-u420-bleu-et-rouge.html>New Balance U420 Bleu Et Rouge</a>
<a href=http://www.les-amis-de-nicolas-sarkozy.fr/931-nike-sb-janoski-lunar-pas-cher.php>Nike Sb Janoski Lunar Pas Cher</a>
<a href=http://www.tissages-de-gravigny.fr/air-max-thea-grise-et-orange.html>Air Max Thea Grise Et Orange</a>
<a href=http://www.turismolastminute.it/334-vans-bordeaux-indossate.html>Vans Bordeaux Indossate</a>
<a href=http://www.biotoxen.it/032-cappello-adidas-visiera-curva.php>Cappello Adidas Visiera Curva</a>
http://www.autoescuelaalcon.es/
http://www.mantenimientodejardines.com.es/
http://www.costa-anatomicas.es/
http://www.pintorespontevedra.es/
http://www.pharmaceutical-care.es/
<a href=http://www.terrazasdemadera.es/>levitra sin receta</a>
<a href=http://www.mantenimientodejardines.com.es/>levitra original</a>
<a href=http://www.planie.es/>cialis sin receta</a>
<a href=http://www.limpiezasyserviciosterres.es/>kamagra gel</a>
<a href=http://www.pintorespontevedra.es/>kamagra opiniones</a>
http://www.floating-studio-flats.co.uk/985-air-max-thea-blue-lagoon.html
http://www.mmua.co.uk/867-nike-cortez-white-velvet-brown.html
http://www.southportsuperbikeshop.co.uk/374-nike-air-max-95-dyn.html
http://www.cars-wrapping.co.uk/719-nike-free-rn-flyknit-motion.html
http://www.cars-wrapping.co.uk/013-nike-free-flyknit-5.0-men.html
<a href=http://www.jlapressureulcerpartnership.co.uk/reebok-khaki-classic-077.htm>Reebok Khaki Classic</a>
<a href=http://www.attention-deficit-disorder.co.uk/nike-air-max-2016-release-768.html>Nike Air Max 2016 Release</a>
<a href=http://www.marrandmacgregor.co.uk/159-adidas-yeezy-boost-size-6.html>Adidas Yeezy Boost Size 6</a>
<a href=http://www.decorator-norwich.co.uk/554-nike-free-4.0-black-and-white>Nike Free 4.0 Black And White</a>
<a href=http://www.ofpeopleandplants.co.uk/nike-air-max-2015-review-runners-world-479.html>Nike Air Max 2015 Review Runner's World</a>
http://offer.moscow/
http://www.cars-wrapping.co.uk/988-nike-free-run-flyknit-4.0-womens-running-shoes.html
http://www.southportsuperbikeshop.co.uk/473-nike-air-max-95-hiroshi.html
http://www.evoslimmingcoupon.co.uk/air-jordan-black-and-purple-359.php
http://www.giantfang.co.uk/air-max-90-woven-vachetta-tan-144
http://www.giantfang.co.uk/nike-huarache-ultra-breathe-mens-354
<a href=http://www.mobiledeals4contractphones.co.uk/oakley-sunglasses-cheap-on-facebook-213.html>Oakley Sunglasses Cheap On Facebook</a>
<a href=http://www.bike-courier.co.uk/nike-flyknit-racer-blackout-on-feet-867.html>Nike Flyknit Racer Blackout On Feet</a>
<a href=http://www.ukfinanceguide.co.uk/994-nike-air-max-one-ultra-moire.html>Nike Air Max One Ultra Moire</a>
<a href=http://www.usapokergame.co.uk/127-adidas-ultra-boost-black-triple.html>Adidas Ultra Boost Black Triple</a>
<a href=http://www.offerzone.co.uk/418-converse-womens-uk.htm>Converse Womens Uk</a>
http://www.12deliver.nl/594-saucony-triumph-iso-2-dames.php
http://www.deermedia.de/hollister-weste-grau
http://www.hannover-cms.de/947-abercrombie--fitch-pullover-classic-crew
http://www.gasthofbahra.de/ray-ban-sonnenbrille-damen-869.html
http://www.12deliver.nl/715-saucony-triumph-iso-2-runners-world.php
<a href=http://www.zorgboerderijdaglicht.nl/653-free-running.htm>Free Running</a>
<a href=http://www.srbijaleverkusen.de/nike-free-damen-türkis-schwarz-684.php>Nike Free Damen Türkis Schwarz</a>
<a href=http://www.karmacosmic.de/859-stefan-janoski-damen-schuhe.html>Stefan Janoski Damen Schuhe</a>
<a href=http://www.fsv-friends.nl/502-air-max-thea-premium.html>Air Max Thea Premium</a>
<a href=http://www.pietjebelldemusical.nl/494-adidas-schoenen-wit-met-goud.html>Adidas Schoenen Wit Met Goud</a>
http://www.ofpeopleandplants.co.uk/nike-air-max-2015-mens-colorways-779.html
http://www.floating-studio-flats.co.uk/042-air-max-thea-outfit.html
http://www.lanarkunitedfc.co.uk/997-nike-air-max-90-iron-metallic-red-bronze-leather
http://www.pro-trak.co.uk/saucony-hurricane-15-538.htm
http://www.mutantsoftware.co.uk/adidas-originals-london-trainers-487.php
<a href=http://www.simplisecurity.co.uk/puma-creepers-rihanna-red-639.html>Puma Creepers Rihanna Red</a>
<a href=http://www.youthopinionsunite.co.uk/adidas-gazelle-og-trainers-290.php>Adidas Gazelle Og Trainers</a>
<a href=http://www.marrandmacgregor.co.uk/504-adidas-yeezy-boost-350-pirate-black-2.0.html>Adidas Yeezy Boost 350 Pirate Black 2.0</a>
<a href=http://www.floating-studio-flats.co.uk/553-air-max-shoes-for-men-2015.html>Air Max Shoes For Men 2015</a>
<a href=http://www.giantfang.co.uk/air-max-90-white-on-feet-954>Air Max 90 White On Feet</a>
http://www.modern-course.de/311-nike-air-max-thea-weiß-bestellen.php
http://www.ausbildung-in-pflegeberufen.de/nike-air-max-command-damen-blau-685.html
http://www.frauenuni-dresden.de/nike-free-5.0-schwarz-herren-günstig-010.html
http://www.ulviks.nl/303-cortez-nike-dames.html
http://www.ikbenalles.nl/849-oakley-zonnebril-op-sterkte-prijs.php
<a href=http://www.savanna-interior-shop.nl/839-golden-state-warriors-new-era.html>Golden State Warriors New Era</a>
<a href=http://www.avarusmedia.de/oakley-holbrook-polarized-gläser-314.php>Oakley Holbrook Polarized Gläser</a>
<a href=http://www.nikeflyknitkaufen.de/nike-free-4.0-flyknit-damen-schwarz-793>Nike Free 4.0 Flyknit Damen Schwarz</a>
<a href=http://www.leserlichundhoerich.de/nike-air-max-1-gs-510.php>Nike Air Max 1 Gs</a>
<a href=http://www.wvaegir.nl/adidas-superstar-dames-glitter-898.php>Adidas Superstar Dames Glitter</a>
http://www.anytekabel.de/854-nike-shox-kaufen.asp
http://www.hilfeplanverfahren.de/854-nike-air-force-weiß-niedrig.php
http://www.hipcatclub.de/vans-sk8-high-white-794.htm
http://www.gombosportal.de/733-louboutin-high-heels-rot.php
http://www.surfsapiens.nl/asics-dames-gel-dedicate-3-indoor.htm
<a href=http://www.400jaarveenkolonien.nl/longchamp-schoudertas>Longchamp Schoudertas</a>
<a href=http://www.avarusmedia.de/oakley-sonnenbrille-wechselgläser-330.php>Oakley Sonnenbrille Wechselgläser</a>
<a href=http://www.creativesweat.de/713-saucony-fastwitch-6-zalando.html>Saucony Fastwitch 6 Zalando</a>
<a href=http://www.vintagecadillacs.nl/100-air-max-thea-maat-43.htm>Air Max Thea Maat 43</a>
<a href=http://www.consolidate-it.nl/166-nike-huarache-zwart-grijs>Nike Huarache Zwart Grijs</a>
http://www.evoslimmingcoupon.co.uk/air-jordan-grey-and-blue-978.php
http://www.frankluckham.co.uk/adidas-superstar-all-colours-592.php
http://www.accomlink.co.uk/adidas-gazelle-bluebird-747
http://www.northhampshireenterprise.co.uk/nike-janoski-obsidian-791.html
http://www.usapokergame.co.uk/102-adidas-ultra-boost-black-2.0.html
<a href=http://www.itsupportlondonbridge.co.uk/adidas-stan-smith-shoes-2016-001.asp>Adidas Stan Smith Shoes 2016</a>
<a href=http://www.bike-courier.co.uk/nike-shox-basketball-2004-714.html>Nike Shox Basketball 2004</a>
<a href=http://www.lanarkunitedfc.co.uk/726-nike-air-max-90-essential-atomic-red>Nike Air Max 90 Essential Atomic Red</a>
<a href=http://www.jlapressureulcerpartnership.co.uk/reebok-black-286.htm>Reebok Black</a>
<a href=http://www.tableoakfurnitureland.co.uk/nike-air-max-2017-shoes.html>Nike Air Max 2017 Shoes</a>
http://www.grupoitealbacete.es/255-puma-creepers-velvet-negras.html
http://www.luismesacastilla.es/756-nike-roshe-run-navy.php
http://www.rcaraumo.es/nike-blazer-high-228.html
http://www.younes.es/203-nike-air-max-zero-qs
http://www.adidasnmdcomprar.nu/adidas-nmd-oreo-635
<a href=http://www.luismesacastilla.es/095-nike-roshe-rojas-hombre.php>Nike Roshe Rojas Hombre</a>
<a href=http://www.el-codigo-promocional.es/055-reebok-nano-4.0.aspx>Reebok Nano 4.0</a>
<a href=http://www.sanjuandelamata.es/108-nike-free-rn-flyknit-zalando.html>Nike Free Rn Flyknit Zalando</a>
<a href=http://www.adidasnmdcomprar.nu/adidas-nmd-red-camo-257>Adidas Nmd Red Camo</a>
<a href=http://www.cdoviaplata.es/outlet-zapatos-mbt-en-barcelona-629.html>Outlet Zapatos Mbt En Barcelona</a>
http://www.younes.es/717-nike-air-max-one-ultra-moire
http://www.cdoviaplata.es/mbt-españa-compra-online-648.html
http://www.younes.es/731-zapatillas-air-max-2016-para-ni帽os
http://www.aspasi.es/150-saucony-running.htm
http://www.rcaraumo.es/stefan-janoski-max-l-qs-757.html
<a href=http://www.luismesacastilla.es/537-nike-roshe-precio.php>Nike Roshe Precio</a>
<a href=http://www.bristol.com.es/nike-air-force-one-españa-451.html>Nike Air Force One España</a>
<a href=http://www.younes.es/008-air-huarache>Air Huarache</a>
<a href=http://www.felipealonso.es/709-vans-sk8-hi-platform-comprar.html>Vans Sk8 Hi Platform Comprar</a>
<a href=http://www.younes.es/994-air-max-90-rojas>Air Max 90 Rojas</a>
http://www.giantfang.co.uk/nike-air-max-2015-blue-753
http://www.youthopinionsunite.co.uk/adidas-gazelle-canada-717.php
http://www.evoslimmingcoupon.co.uk/air-jordan-future-grey-black-486.php
http://www.howzituk.co.uk/644-nike-roshe-flyknit-blue-and-black.html
http://www.waterfallrainbows.co.uk/nike-air-presto-thunder-blue-105.php
<a href=http://www.backpackersholidays.co.uk/972-nike-air-force-1-low-blue-suede.html>Nike Air Force 1 Low Blue Suede</a>
<a href=http://www.hairextensionscity.co.uk/808-roshe-run-outfits-tumblr.html>Roshe Run Outfits Tumblr</a>
<a href=http://www.youthopinionsunite.co.uk/womens-adidas-gazelle-og-trainers-pink-512.php>Womens Adidas Gazelle Og Trainers Pink</a>
<a href=http://www.howzituk.co.uk/122-flyknit-racer-custom.html>Flyknit Racer Custom</a>
<a href=http://www.cyberville.co.uk/934-new-balance-574-fashion.htm>New Balance 574 Fashion</a>
http://www.younes.es/257-air-max-one-2014
http://www.dekodery.eu/nike-sb-stefan-janoski-para-mujer.html
http://www.luismesacastilla.es/631-nike-roshe-flyknit-baratas.php
http://www.adidasnmdcomprar.nu/adidas-nmd-dorados-489
http://www.batalladefloreslaredo.es/ferrari-oakley-521
<a href=http://www.rcaraumo.es/flyknit-nike-air-max-1-799.html>Flyknit Nike Air Max 1</a>
<a href=http://www.denisemilani.es/981-nike-huarache-2015.php>Nike Huarache 2015</a>
<a href=http://www.lubpsico.es/ultra-boost-adidas-white-782.html>Ultra Boost Adidas White</a>
<a href=http://www.sedar2013.es/gorras-phoenix-coyotes-740.php>Gorras Phoenix Coyotes</a>
<a href=http://www.colegio-sanfranciscojavier.es/699-zapatos-timberland-gris.html>Zapatos Timberland Gris</a>
http://www.mandala2012.co.uk/390-adidas-shoes-women-white-and-black.html
http://www.ofpeopleandplants.co.uk/nike-2015-air-max-white-582.html
http://www.mmua.co.uk/512-nike-cortez-mens.html
http://www.howzituk.co.uk/326-nike-flyknit-air-max-2016-grey.html
http://www.accomlink.co.uk/adidas-superstar-supercolor-red-womens-408
<a href=http://www.mobiledeals4contractphones.co.uk/oakley-holbrook-lenses-malaysia-583.html>Oakley Holbrook Lenses Malaysia</a>
<a href=http://www.jlapressureulcerpartnership.co.uk/reebok-classic-leather-womens-642.htm>Reebok Classic Leather Womens</a>
<a href=http://www.hairextensionscity.co.uk/270-nike-roshe-run-original.html>Nike Roshe Run Original</a>
<a href=http://www.misstilly.co.uk/nike-outlet-shop-online-uk-709.htm>Nike Outlet Shop Online Uk</a>
<a href=http://www.aranjackson.co.uk/timberland-deck-shoes-sale-631.php>Timberland Deck Shoes Sale</a>
http://www.lubpsico.es/adidas-stan-smith-colores-485.html
http://www.el-codigo-promocional.es/384-reebok-blancas-mujer.aspx
http://www.elregalofriki.es/ray-ban-erika-man-318.php
http://www.ibericarsalfer.es/nike-running-mujer-outlet-887.html
http://www.grupoitealbacete.es/984-puma-bmw-2016.html
<a href=http://www.rcaraumo.es/huarache-ultra-baratas-168.html>Huarache Ultra Baratas</a>
<a href=http://www.luismesacastilla.es/061-nike-roshe-run-grises-y-rosas.php>Nike Roshe Run Grises Y Rosas</a>
<a href=http://www.batalladefloreslaredo.es/oakley-nueva-coleccion-435>Oakley Nueva Coleccion</a>
<a href=http://www.aspasi.es/405-saucony-peregrine-6-opiniones.htm>Saucony Peregrine 6 Opiniones</a>
<a href=http://www.rcaraumo.es/nike-stefan-janoski-max-azules-042.html>Nike Stefan Janoski Max Azules</a>
http://www.rcaraumo.es/huarache-blancas-y-verdes-087.html
http://www.denisemilani.es/622-nike-95-air-max.php
http://www.rcaraumo.es/nike-cortez-en-chile-465.html
http://www.el-codigo-promocional.es/651-zapatos-reebok-clasicos-para-niños.aspx
http://www.ibericarsalfer.es/nike-hombre-amazon-874.html
<a href=http://www.tacadetinta.es/chalecos-abercrombie-para-hombre-precio>Chalecos Abercrombie Para Hombre Precio</a>
<a href=http://www.adidasnmdcomprar.nu/adidas-nmd-gray-454>Adidas Nmd Gray</a>
<a href=http://www.lubpsico.es/superstar-adidas-adicolor-869.html>Superstar Adidas Adicolor</a>
<a href=http://www.elregalofriki.es/como-identificar-gafas-de-sol-originales-ray-ban-588.php>Como Identificar Gafas De Sol Originales Ray Ban</a>
<a href=http://www.younes.es/328-nike-air-max-90-hyperfuse-black-and-white>Nike Air Max 90 Hyperfuse Black And White</a>
http://www.bike-courier.co.uk/nike-roshe-run-2-011.html
http://www.attention-deficit-disorder.co.uk/air-max-2016-red-980.html
http://www.floating-studio-flats.co.uk/413-air-max-95-greedy.html
http://www.lanarkunitedfc.co.uk/314-nike-air-max-90-ultra-breathe-womens-shoe
http://www.wandsworth-plumbing.co.uk/ray-ban-wayfarer-tortoise-331.htm
<a href=http://www.itsupportlondonbridge.co.uk/adidas-stan-smith-core-black-152.asp>Adidas Stan Smith Core Black</a>
<a href=http://www.howzituk.co.uk/698-nike-flyknit-blue-and-green.html>Nike Flyknit Blue And Green</a>
<a href=http://www.pro-trak.co.uk/saucony-cohesion-5-121.htm>Saucony Cohesion 5</a>
<a href=http://www.giantfang.co.uk/air-max-tavas-red-on-feet-233>Air Max Tavas Red On Feet</a>
<a href=http://www.lanarkunitedfc.co.uk/829-air-max-90-black>Air Max 90 Black</a>
http://www.floating-studio-flats.co.uk/488-air-max-sneakers-for-women.html
http://www.aranjackson.co.uk/timberland-earthkeepers-boat-shoe-196.php
http://www.northhampshireenterprise.co.uk/nike-janoski-max-all-white-304.html
http://www.waterfallrainbows.co.uk/nike-air-presto-fleece-549.php
http://www.cars-wrapping.co.uk/695-nike-free-rn-flyknit-id-review.html
<a href=http://www.ukbriberyact2010.co.uk/nike-free-5.0-2015-black-188.html>Nike Free 5.0 2015 Black</a>
<a href=http://www.accomlink.co.uk/superstar-adidas-gold-toe-829>Superstar Adidas Gold Toe</a>
<a href=http://www.mmua.co.uk/104-nike-cortez-trainers-blue.html>Nike Cortez Trainers Blue</a>
<a href=http://www.offerzone.co.uk/965-converse-size-6.5-uk.htm>Converse Size 6.5 Uk</a>
<a href=http://www.hairextensionscity.co.uk/999-nike-roshe-run-mens-galaxy.html>Nike Roshe Run Mens Galaxy</a>
http://www.ulviks.nl/408-nike-cortez-heren.html
http://www.avarusmedia.de/oakley-jupiter-squared-847.php
http://www.wvaegir.nl/adidas-superstar-blauw-maat-39-379.php
http://www.visrestaurantlepescadou.nl/509-stan-smith-rood-suede.html
http://www.kfz-haftpflichtversicherung-kuendigen.de/mbt-schuhe-kaufen-177.php
<a href=http://www.ojc-backstage.nl/049-converse-sneakers-leer-wit.php>Converse Sneakers Leer Wit</a>
<a href=http://www.zorgboerderijdaglicht.nl/884-nike-free-run-2-dames-kopen.htm>Nike Free Run 2 Dames Kopen</a>
<a href=http://www.ojc-backstage.nl/007-converse-maat-22.php>Converse Maat 22</a>
<a href=http://www.nikeflyknitkaufen.de/nike-free-flyknit-4.0-blau-072>Nike Free Flyknit 4.0 Blau</a>
<a href=http://www.erokerswebshop.nl/215-marktplaats-abercrombie-fitch.php>Marktplaats Abercrombie Fitch</a>
http://www.felipealonso.es/752-tienda-vans-baratas-madrid.html
http://www.aspasi.es/627-saucony-xodus-iso-test.htm
http://www.tacadetinta.es/vestidos-abercrombie-para-mujer
http://www.colegio-sanfranciscojavier.es/854-timberland-shoes-peru.html
http://www.bristol.com.es/zapatos-nike-force-one-2015-988.html
<a href=http://www.grupoitealbacete.es/661-puma-tenis-bmw.html>Puma Tenis Bmw</a>
<a href=http://www.cdoviaplata.es/comprar-mbt-españa-999.html>Comprar Mbt España</a>
<a href=http://www.sedar2013.es/gorras-chicago-bulls-2017-131.php>Gorras Chicago Bulls 2017</a>
<a href=http://www.sedar2013.es/gorras-memphis-grizzlies-259.php>Gorras Memphis Grizzlies</a>
<a href=http://www.elregalofriki.es/ray-ban-justin-rb4165-249.php>Ray Ban Justin Rb4165</a>
http://www.ljungkyrkan.nu/240-reebok-tenisky-panske.htm
http://www.cliftonrestaurant.co.uk/nike-shox-orange-and-grey-557.php
http://www.c-p-c.fr/998-adidas-yeezy-boost-350-v2.htm
http://www.super8-ilfilm.it/545-adidas-high-tops-amazon
http://www.koupelny-hed.cz/asics-obuv-na-volejbal.aspx
<a href=http://www.cliftonrestaurant.co.uk/nike-free-2.0-flyknit-570.php>Nike Free 2.0 Flyknit</a>
<a href=http://www.koupelny-hed.cz/converse-boty.aspx>Converse Boty</a>
<a href=http://www.musicalface.nl/625-adidas-rose-adizero-2.5.htm>Adidas Rose Adizero 2.5</a>
<a href=http://www.fiashosting.se/vita-reebok-easytone-156.php>Vita Reebok Easytone</a>
<a href=http://www.musicalface.nl/062-adidas-y3-pure-boost.htm>Adidas Y3 Pure Boost</a>
http://www.jonsvensdesign.se/468-nike-hypervenom-phantom-barn.php
http://www.vecchiaarena.it/nike-air-max-2016-prezzo-914.html
http://www.ljungkyrkan.nu/722-vans-tenisky-bordove.htm
http://www.laluna-rouen.fr/708-nike-flyknit-racer-oreo-1.0.html
http://www.super8-ilfilm.it/529-adidas-harden-dark-ops
<a href=http://www.whitneymcveigh.co.uk/nike-hyperlive-black-057.php>Nike Hyperlive Black</a>
<a href=http://www.freiberufler-netzwerk.de/653-adidas-tubular-radial-black-and-white.php>Adidas Tubular Radial Black And White</a>
<a href=http://www.herz-jesu-huellen.de/nike-cortez-schwarz-weiĂź-042.html>Nike Cortez Schwarz WeiĂź</a>
<a href=http://www.bliv-ergoterapeut.nu/tĂŞnis-timberland-gorge-c2---castanho-685.php>TĂŞnis Timberland Gorge C2 - Castanho</a>
<a href=http://www.trisportteam.cz/529-saucony-peregrine-6.html>Saucony Peregrine 6</a>
http://www.rcaraumo.es/stefan-janoski-max-granates-738.html
http://www.denisemilani.es/053-nike-air-max-90-hyp-premium-id-baratas.php
http://www.lubpsico.es/zapatos-adidas-de-hombre-2015-606.html
http://www.rcaraumo.es/huaraches-blancas-855.html
http://www.grupoitealbacete.es/206-puma-fenty-rihanna-creepers.html
<a href=http://www.colegio-sanfranciscojavier.es/940-timberlands-boots-colors.html>Timberlands Boots Colors</a>
<a href=http://www.felipealonso.es/097-vans-old-skool-rojas-mujer.html>Vans Old Skool Rojas Mujer</a>
<a href=http://www.sedar2013.es/atlanta-falcons-gorras-297.php>Atlanta Falcons Gorras</a>
<a href=http://www.aspasi.es/984-saucony-jazz-17-naranja.htm>Saucony Jazz 17 Naranja</a>
<a href=http://www.cdoviaplata.es/mbt-online-822.html>Mbt Online</a>
http://www.frbk.se/nhl-keps-flashback.html
http://www.alcius.es/adidas-nmd-xr1-558.html
http://www.pop-event.fr/nike-hypervenom-gris-353.php
http://www.tarvisioscacchi.it/282-adidas-superstar-bianche-e-nere-pitonate.html
http://www.slojdakademin.se/084-puma-skor-jr.php
<a href=http://www.laluna-rouen.fr/056-nike-air-max-90-essential-total-crimson.html>Nike Air Max 90 Essential Total Crimson</a>
<a href=http://www.jonsvensdesign.se/254-nike-air-force-low.php>Nike Air Force Low</a>
<a href=http://www.pop-event.fr/nike-kobe-xi-223.php>Nike Kobe Xi</a>
<a href=http://www.alcius.es/adidas-nmd-blancas-y-doradas-823.html>Adidas Nmd Blancas Y Doradas</a>
<a href=http://www.vecchiaarena.it/nike-silver-97-on-feet-291.html>Nike Silver 97 On Feet</a>
http://www.hollybushwitney.co.uk/345-adidas-basketball-shoes-gold-and-white.html
http://www.tarvisioscacchi.it/057-adidas-zx-flux-gold-and-black-prezzo.html
http://www.ljungkyrkan.nu/996-reebok-nano-6.0-heureka.htm
http://www.sposobynazdrowie.pl/638-puma-rihanna-creepers-sklep.php
http://www.kristiinakoskentola.nl/638-nike-shox-outlet.html
<a href=http://www.nocnsfsportconventie.nl/893-adidas-schoenen-dames.php>Adidas Schoenen Dames</a>
<a href=http://www.hollybushwitney.co.uk/002-adidas-y-3-crazy-explosive.html>Adidas Y-3 Crazy Explosive</a>
<a href=http://www.jonsvensdesign.se/368-nike-hypervenom-phantom-ag-pris.php>Nike Hypervenom Phantom Ag Pris</a>
<a href=http://www.c-p-c.fr/764-adidas-originals.htm>Adidas Originals</a>
<a href=http://www.programfurora.pl/215-converse-gorillaz.php>Converse Gorillaz</a>
</a>
<a href=http://datingice.com/>Dating Relationship Love
</a>
<a href=http://rhdating.com/>Best Online Dating Sites
</a>
<a href=http://sexdatingdelight.com/>Sex Dating Delight
</a>
http://adultdatingbrisbane.com/
http://datingice.com/
http://rhdating.com/
http://sexdatingdelight.com/
http://www.lessoinsdemariemassageenergetique.fr/169-chaussures-ralph-lauren-odie.php
http://www.thierryobadia.fr/025-palladium-blanche-femme.html
http://www.miolands-mode-video.fr/851-supra-skytop-or.php
http://www.lesdroles.fr/357-chaussure-lacoste-noir-et-blanche.php
http://www.forge-delours.fr/386-le-coq-sportif-arthur-ashe-noir.html
<a href=http://www.miolands-mode-video.fr/286-basket-supra-forum.php>Basket Supra Forum</a>
<a href=http://www.forge-delours.fr/771-le-coq-sportif-lcs-r900-w-glitter.html>Le Coq Sportif Lcs R900 W Glitter</a>
<a href=http://www.minitrain.fr/256-fila-shoes-2017.htm>Fila Shoes 2017</a>
<a href=http://www.messengercity.fr/052-mizuno-wave-ultima-soldes.php>Mizuno Wave Ultima Soldes</a>
<a href=http://www.miolands-mode-video.fr/058-chaussure-supra-femme.php>Chaussure Supra Femme</a>
http://www.miolands-mode-video.fr/293-supra-skytop-3-avis.php
http://www.forge-delours.fr/571-coq-sportif-bebe.html
http://www.dany-multi-services.fr/908-under-armour-basket-curry.php
http://www.barreau-de-saint-pierre.fr/090-salomon-speedcross-3-femme.php
http://www.lesdroles.fr/298-chaussure-lacoste-femme-rouge.php
<a href=http://www.messengercity.fr/366-mizuno-wave-prophecy-4-femme.php>Mizuno Wave Prophecy 4 Femme</a>
<a href=http://www.forge-delours.fr/555-coq-sportif-nouvelle-collection.html>Coq Sportif Nouvelle Collection</a>
<a href=http://www.miolands-mode-video.fr/132-mbt-geneve.php>Mbt Geneve</a>
<a href=http://www.barreau-de-saint-pierre.fr/463-chaussures-salomon-homme-gore-tex.php>Chaussures Salomon Homme Gore Tex</a>
<a href=http://www.messengercity.fr/502-basket-mizuno.php>Basket Mizuno</a>
http://www.hardsoftinformatica.it/skechers-memory-foam-uomo-zalando-145.php
http://www.fashiontour.it/899-scarpe-gucci-estate-2017.php
http://www.icamsrl.it/scarpe-tacco-12-nere-800.htm
http://www.gianly.it/194-mizuno-wave-rider-20-uomo.asp
http://www.gli-gnomi.it/scarpe-calcio-puma-due-colori-605.php
<a href=http://www.hardsoftinformatica.it/scarpe-mbt-offerte-online-477.php>Scarpe Mbt Offerte Online</a>
<a href=http://www.handballestense.it/supra-skytop-4-602.htm>Supra Skytop 4</a>
<a href=http://www.gianly.it/909-salomon-running.asp>Salomon Running</a>
<a href=http://www.iccmornago.it/calzature-alexander-mcqueen-629.htm>Calzature Alexander Mcqueen</a>
<a href=http://www.gianly.it/815-scarpe-mizuno-volley-2017.asp>Scarpe Mizuno Volley 2017</a>
http://www.maurogiulianini.it/647-negozio-tods-uomo-roma.htm
http://www.nokeys.it/449-immagini-scarpe-da-calcio-puma.php
http://www.metrocampania.it/skechers-uomo-running-861.html
http://www.laviadiemmaus.it/scarpe-louboutin-prezzi-yahoo-612.htm
http://www.maurogiulianini.it/224-scarpe-polo-ralph-lauren-hanford-mid.htm
<a href=http://www.libeativoli.it/sito-ufficiale-giuseppe-zanotti-996.html>Sito Ufficiale Giuseppe Zanotti</a>
<a href=http://www.monitortft.it/giuseppe-zanotti-scarpe-napoli-721.htm>Giuseppe Zanotti Scarpe Napoli</a>
<a href=http://www.netfraternity.it/198-under-armour-shoes.asp>Under Armour Shoes</a>
<a href=http://www.lombardoeditore.it/vibram-bikila-evo-465.html>Vibram Bikila Evo</a>
<a href=http://www.maurogiulianini.it/074-mocassini-tods-scontati.htm>Mocassini Tod's Scontati</a>
http://www.tibinet.it/scarpe-armani-nere-194.asp
http://www.villarianna.it/scarpe-tacchi-altissimi-online-203.asp
http://www.stonefree.it/336-sneakers-dolce-e-gabbana.htm
http://www.veneto-arte.it/mizuno-volleyball-289.php
http://www.stonefree.it/216-burberry-scarpe-uomo.htm
<a href=http://www.skydivepalermo.it/vibram-fivefingers-negozi-milano-916.asp>Vibram Fivefingers Negozi Milano</a>
<a href=http://www.tibinet.it/armani-scarpe-donne-379.asp>Armani Scarpe Donne</a>
<a href=http://www.stonefree.it/882-scarpe-armani-donne-2016.htm>Scarpe Armani Donne 2016</a>
<a href=http://www.skunky.it/230-hogan-grigie-interactive.php>Hogan Grigie Interactive</a>
<a href=http://www.villaprati.it/adidas-ace-16.1-nere-564.htm>Adidas Ace 16.1 Nere</a>
http://www.mozartfest.it/443-nike-di-tela-grigie.php
http://www.maquillajeypeluquerianovias.es/tenis-adidas-ultra-boost-feminino-501.html
http://www.maquillajeypeluquerianovias.es/zapatillas-adidas-mujer-deportivas-2015-640.html
http://www.mozartfest.it/973-jordan-raptor.php
http://www.maquillajeypeluquerianovias.es/adidas-rose-3-016.html
<a href=http://www.oceansurf.es/nike-mercurial-vapor-x-fg-cr7-111.php>Nike Mercurial Vapor X Fg Cr7</a>
<a href=http://www.maquillajeypeluquerianovias.es/adidas-pure-boost-x-women-562.html>Adidas Pure Boost X Women</a>
<a href=http://www.myranch.es/899-jeremy-scott-zapatillas.php>Jeremy Scott Zapatillas</a>
<a href=http://www.omnia-equip-auto.fr/539-air-force-fluo.html>Air Force Fluo</a>
<a href=http://www.myranch.es/361-boost-adidas-basketball.php>Boost Adidas Basketball</a>
http://www.deadlikeme.it/874-scarpe-tacco-inverno.htm
http://www.handballestense.it/scarpe-palladium-milano-852.htm
http://www.gli-gnomi.it/scarpe-da-calcio-con-calzino-senza-lacci-441.php
http://www.deadlikeme.it/080-scarpe-tacco-grosso-2017.htm
http://www.deadlikeme.it/479-scarpe-tacco-alto-da-uomo.htm
<a href=http://www.confartigianatomirano.it/manolo-blahnik-prezzi-789.htm>Manolo Blahnik Prezzi</a>
<a href=http://www.fashiontour.it/524-gucci-scarpe-uomo-usate.php>Gucci Scarpe Uomo Usate</a>
<a href=http://www.gli-gnomi.it/scarpe-da-calcio-per-bambini-di-8-anni-184.php>Scarpe Da Calcio Per Bambini Di 8 Anni</a>
<a href=http://www.gianly.it/729-mizuno-rider-19-osaka.asp>Mizuno Rider 19 Osaka</a>
<a href=http://www.gianly.it/439-mizuno-volley-alte.asp>Mizuno Volley Alte</a>
<a href=" http://achetersildenafilenligne.com/ ">acheter viagra 100mg</a>
<a href=" http://acheterviagraenlignelivraison24h.com/ ">acheter viagra en ligne livraison 24h </a>
<a href=" http://achatviagraenpharmacieenfrance.com/ ">vente de viagra en pharmacie en france</a>
<a href=" http://sildenafilpascherenfrance.com/ ">viagra pas cher </a>
<a href=" http://viagrapascherlivraisonrapide.com/ ">viagra pas cher </a>
<a href=" http://sildenafilpfizer50mgprix.com/ ">sildenafil pfizer 50 mg preis </a>
<a href=" http://viagraenventelibreenfrance.com/ ">viagra en vente libre en france </a>
<a href=" http://xn--viagragnriquelivresous48h-hicb.com/ ">viagra gГ©nГ©rique belgique </a>
<a href=" http://xn--cialisgnriquepascher-h2bb.com/ ">cialis gГ©nГ©rique pas cher </a>
<a href=" http://cialissansordonnanceenfrance.com/ ">cialis sans ordonnance en pharmacie </a>
<a href=" http://achetercialisenfrancesitefiable.com/ ">acheter cialis en france livraison rapide </a>
<a href=" http://achetercialissansordonnanceenpharmacie.com/ ">comment acheter cialis sans ordonnance </a>
<a href=" http://achetercialis20mgenligne.com/ ">achat cialis 20mg en ligne </a>
<a href=" http://achatcialisenfrancelivraisonrapide.com ">acheter cialis generique en france </a>
<a href=" http://achatcialis5mgenligne.com/ ">acheter cialis 5mg pas cher </a>
<a href=" http://tadalafil20mgpaschereninde.com/ ">acheter cialis 20mg pas cher </a>
<a href=" http://achetertadalafil20mgpascher.com/ ">achat cialis 20mg en ligne </a>
http://www.anonimoitaliano.it/232-nike-hypervenom-phantom-3.htm
http://www.angelocomisso.it/302-nike-hypervenom-2016.html
http://www.ascdiromagna.it/045-mbt-scarpe-vendita-on-line.htm
http://www.clubdelcosto.it/179-stivali-bassi-giuseppe-zanotti.asp
http://www.clubdelcosto.it/087-sandali-flat-valentino.asp
<a href=http://www.ascdiromagna.it/764-skechers-memory-foam-solette.htm>Skechers Memory Foam Solette</a>
<a href=http://www.angelocomisso.it/530-nike-mercurial-vapor-x-2016.html>Nike Mercurial Vapor X 2016</a>
<a href=http://www.al-parco.it/551-nike-magista-2016.html>Nike Magista 2016</a>
<a href=http://www.biellaintraprendere.it/mizuno-ultima-8-opinioni-214.html>Mizuno Ultima 8 Opinioni</a>
<a href=http://www.calzaturificiorenata.it/gucci-sneaker-171.htm>Gucci Sneaker</a>
<a href=" http://achetertadalafilsansordonnance.com/ ">achat cialis sans ordonnance </a>
<a href=" http://achattadalafilenfranceenpharmacie.com/ ">acheter tadalafil en france </a>
<a href=" http://acheterprednisone20mgenligne.com/ ">acheter prednisone 20 mg en ligne </a>
<a href=" http://acheterpropeciasurinternet.com/ ">acheter propecia sur internet </a>
<a href=" http://achatpropeciaparcartebancaire.com/ ">achat propecia partners </a>
<a href=" http://achatamoxicillinebiogaran1g.com/ ">amoxicilline 1g achat en ligne </a>
<a href=" http://acheterclomid100mgsurinternetpascher.com/ ">acheter clomid 100mg sur internet pas cher </a>
<a href=" http://acheterventolinespraysansordonnance.com/ ">acheter ventolin - acheter ventolin: </a>
<a href=" http://achatventolinesansordonnance.com/ ">achat ventoline sur internet </a>
<a href=" http://howtogetviagrawithoutadoctorprescription.us/ ">how to get viagra without going to a doctor </a>
<a href=" http://acheterzithromaxsurinternetenfrance.club/ ">acheter zithromax monodose sans ordonnance </a>
Make an effort to shed weight. Apnea is exacerbated and often brought on by excessive weight. Consider losing ample weight to move your BMI from over weight to merely overweight or even wholesome. Folks who suffer from lost excess weight have improved their apnea signs and symptoms, plus some have even treated their obstructive sleep apnea totally.
þÿ
You may not think so, but design is around trying to keep a wide open brain and enabling yourself to determine more of who you are. There are many useful sources to assist you to read more about fashion. Keep in mind the tips you've study right here as you may operate your way in the direction of greater design.Very Successful Plumbing Recommendations That Work Nicely
<a href=https://www.nocnsfsportconventie.nl/images/nocnsfsportcon/1643-adidas-schoenen-heren-nieuwe.jpg>Adidas Schoenen Heren Nieuwe</a>
þÿ
That will help you cope with ringing in the ears you need to prevent demanding conditions. Long periods of tension can make the tinnitus noises a lot louder compared to what they could be if you are in peaceful state. In order to support handle your ringing in the ears and not allow it to be even worse, you should attempt and live your life using the minimum quantity of pressure.
<img>https://www.berwynmountainpress.co.uk/images/img-ber/871-adidas-los-angeles-white-women.jpg</img>
Comprehending the sources of a panic attack can certainly produce a new strategy to strategy them. As soon as a person knows the sparks that kindle their panic attacks, they may be much better equipped to handle or avoid the attacks altogether. You can use this content under to discover ways to steer clear of your anxiety and panic attacks too.
<a href=https://www.alcius.es/images/alcius/3069-adidas-ultra-boost-negras-mujer.jpg>Adidas Ultra Boost Negras Mujer</a>
<img>https://www.freiberufler-netzwerk.de/images/img/4688-adidas-zx-flux-rose-gold.jpg</img>
http://www.ilmondodicrepax.it/487-adidas-ace-rosse.htm
http://www.ipssarcascino.it/818-alexander-mcqueen-tacchi.aspx
http://www.istitutocomprensivospezzanosila.it/golden-goose-bambina-rosa-291.htm
http://www.icamsrl.it/scarpe-tacco-aperte-771.htm
http://www.laprealpinagiorn.it/578-adidas-messi-16-pureagility.htm
<a href=http://www.istitutocomprensivospezzanosila.it/golden-goose-glitter-argento-859.htm>Golden Goose Glitter Argento</a>
<a href=http://www.ipssarcascino.it/841-scarpe-jimmy-choo-swarovski.aspx>Scarpe Jimmy Choo Swarovski</a>
<a href=http://www.hardsoftinformatica.it/negozi-di-scarpe-mbt-torino-362.php>Negozi Di Scarpe Mbt Torino</a>
<a href=http://www.laprealpinagiorn.it/217-adidas-x-16.1-sg.htm>Adidas X 16.1 Sg</a>
<a href=http://www.ilmondodicrepax.it/650-adidas-x16.2.htm>Adidas X16.2</a>
http://www.handballestense.it/scarpe-fila-a-roma-265.htm
http://www.handballestense.it/scarpe-under-armour-offerta-245.htm
http://www.florenceinn.it/998-scarpe-chanel-2016.htm
http://www.gli-gnomi.it/scarpe-da-calcio-senza-lacci-per-bambini-746.php
http://www.deadlikeme.it/451-scarpe-tacco-grosso-estive.htm
<a href=http://www.florenceinn.it/439-scarpe-armani-uomo-outlet.htm>Scarpe Armani Uomo Outlet</a>
<a href=http://www.handballestense.it/supra-scarpe-femminili-prezzo-128.htm>Supra Scarpe Femminili Prezzo</a>
<a href=http://www.deadlikeme.it/606-scarpe-tacco-grosso-invernali.htm>Scarpe Tacco Grosso Invernali</a>
<a href=http://www.francomarras.it/clarks-abbinamenti-528.htm>Clarks Abbinamenti</a>
<a href=http://www.gli-gnomi.it/scarpe-calcio-puma-powercat-1.10-927.php>Scarpe Calcio Puma Powercat 1.10</a>
http://www.clubdelcosto.it/063-scarpe-giuseppe-zanotti-usate.asp
http://www.angelocomisso.it/849-nike-mercurial-limited-edition.html
http://www.battagliamontecassino.it/jimmy-choo-fucsia-307.html
http://www.calzaturificiorenata.it/sneakers-alte-louis-vuitton-uomo-724.htm
http://www.calzaturificiorenata.it/scarpe-gucci-sportive-uomo-471.htm
<a href=http://www.biellaintraprendere.it/mizuno-wave-rider-20-amazon-431.html>Mizuno Wave Rider 20 Amazon</a>
<a href=http://www.anonimoitaliano.it/632-nike-magista-nere.htm>Nike Magista Nere</a>
<a href=http://www.battagliamontecassino.it/jimmy-choo-emily-737.html>Jimmy Choo Emily</a>
<a href=http://www.biellaintraprendere.it/mizuno-tennis-shoes-834.html>Mizuno Tennis Shoes</a>
<a href=http://www.biellaintraprendere.it/mizuno-scarpe-152.html>Mizuno Scarpe</a>
http://www.traiteur-janot.fr/067-nike-kaishi-2.0.html
http://www.usocalcio.it/vans-invernali-uomo-861.php
http://www.triwatt.fr/nike-orange-blanche-971.php
http://www.zorgcentrumdewissel.nl/nike-runner-2-645.php
http://www.volumefnucci.it/reebok-bianche-e-rosa-306.asp
<a href=http://www.decoriblearagusa.it/nike-thea-womens-085.php>Nike Thea Womens</a>
<a href=http://www.triwatt.fr/nike-free-ace-leather-264.php>Nike Free Ace Leather</a>
<a href=http://www.traiteur-janot.fr/146-free-run-2-femme-noir.html>Free Run 2 Femme Noir</a>
<a href=http://www.weltgang.de/935-puma-schuhe-rot-schwarz.htm>Puma Schuhe Rot Schwarz</a>
<a href=http://www.song-net.fr/959-air-force-1-noir-et-blanche.html>Air Force 1 Noir Et Blanche</a>
http://www.ace-renov.fr/916-asics-running-homme-noir.php
http://www.dresden2020.de/442-nike-cortez-damen-leder.php
http://www.extreme-hosting.co.uk/529-nike-air-max-90-ultra-breathe-trainers.php
http://www.dresden2020.de/857-nike-blazer-weiß.php
http://www.aurelieadomicile.fr/077-puma-chaussure-homme-2017-ducati.php
<a href=http://www.campingcarsonway.fr/039-yeezy-350-kanye-west.html>Yeezy 350 Kanye West</a>
<a href=http://www.extreme-hosting.co.uk/592-nike-blazer-black-leather.php>Nike Blazer Black Leather</a>
<a href=http://www.aurelieadomicile.fr/399-chaussures-puma-noir.php>Chaussures Puma Noir</a>
<a href=http://www.extreme-hosting.co.uk/589-nike-racer-flyknit-2016.php>Nike Racer Flyknit 2016</a>
<a href=http://www.aldente-restos.fr/chaussures-saucony-973.php>Chaussures Saucony</a>
http://www.luxavideo.it/405-michael-kors-ava-small.asp
http://www.fulchiron.fr/838-ray-ban-clubmaster-ecaille-pas-cher.html
http://www.vom-eulenloch.de/nike-free-5.0-damen-neu-537.htm
http://www.soulfly-design.de/398-puma-evospeed.php
http://www.eventus-traders.de/391-new-balance-damen-wl574v1-sneakers.html
<a href=http://www.francoismauduit.fr/400-ray-ban-wayfarer-interieur-rouge.php>Ray Ban Wayfarer Interieur Rouge</a>
<a href=http://www.hotel4alle.de/nike-air-max-rosa-pink-694.aspx>Nike Air Max Rosa Pink</a>
<a href=http://www.geo2008.de/fila-turnschuhe-801.php>Fila Turnschuhe</a>
<a href=http://www.nkavmig.se/nike-roshe-nm-flyknit-se-675.php>Nike Roshe Nm Flyknit Se</a>
<a href=http://www.vacu-step.fr/976-michael-kors-hamilton-noir.php>Michael Kors Hamilton Noir</a>
http://www.ardaland.it/748-birkenstock-uomo-boston.asp
http://www.angelocomisso.it/989-nike-magista-obra-2-total-crimson.html
http://www.calzaturificiorenata.it/gucci-scarpe-decolte-806.htm
http://www.clubdelcosto.it/000-giuseppe-zanotti-saldi-milano.asp
http://www.angelocomisso.it/545-nike-mercurial-cr7-2015.html
<a href=http://www.ardaland.it/687-birkenstock-roma.asp>Birkenstock Roma</a>
<a href=http://www.angelocomisso.it/219-nike-tiempo-proximo-tf.html>Nike Tiempo Proximo Tf</a>
<a href=http://www.battagliamontecassino.it/scarpe-manolo-blahnik-mostra-767.html>Scarpe Manolo Blahnik Mostra</a>
<a href=http://www.biellaintraprendere.it/salomon-scarpe-uomo-251.html>Salomon Scarpe Uomo</a>
<a href=http://www.clubdelcosto.it/674-sandali-giuseppe-zanotti.asp>Sandali Giuseppe Zanotti</a>
http://www.ardaland.it/307-birkenstock-scarpe.asp
http://www.anonimoitaliano.it/432-nike-magista-obra-2-fg.htm
http://www.biellaintraprendere.it/salomon-trail-632.html
http://www.al-parco.it/433-nike-mercurial-verde-acqua.html
http://www.clubdelcosto.it/252-valentino-scarpe-uomo-camouflage.asp
<a href=http://www.battagliamontecassino.it/sandali-manolo-blahnik-2017-737.html>Sandali Manolo Blahnik 2017</a>
<a href=http://www.biellaintraprendere.it/salomon-scarpe-invernali-100.html>Salomon Scarpe Invernali</a>
<a href=http://www.al-parco.it/847-nike-magista-verdi.html>Nike Magista Verdi</a>
<a href=http://www.angelocomisso.it/596-nike-superfly-r4.html>Nike Superfly R4</a>
<a href=http://www.al-parco.it/927-nike-magista-rosse-alte.html>Nike Magista Rosse Alte</a>
http://www.amstructures.co.uk/adidas-gazelle-childrens-466.html
http://www.postenblankestijn.nl/334-nike-air-max-90-outfit.htm
http://www.maxicolor.nl/nike-shox-dames-205.html
http://www.evcd.nl/nike-presto-flyknit-black-056.html
http://www.spanish-realestate.es/599-adidas-f50-2010.asp
<a href=http://www.xingbang.es/botas-vibram-gore-tex-634.html>Botas Gore-tex</a>
<a href=http://www.maxicolor.nl/nike-roshe-run-black-376.html>Nike Roshe Run Black</a>
<a href=http://www.cheap-laptop-battery.co.uk/505-adidas-stan-smith-baby.htm>Adidas Stan Smith Baby</a>
<a href=http://www.cazarafashion.nl/groen-nike-777.htm>Groen Nike</a>
<a href=http://www.4chat.nl/asics-gel-lyte-iii-wit-365.html>Asics Gel Lyte Iii Wit</a>
http://www.graysands.co.uk/nike-basketball-shoes-hyperdunk-2016-016.asp
http://www.consumabulbs.co.uk/975-puma-x-graphersrock.html
http://www.kaptur.fr/635-fenty-puma-camel.html
http://www.onegame.fr/new-balance-996-bleu-ciel-160.php
http://www.los-granados-apartment.co.uk/599-adidas-climacool-mens-running-shoes.html
<a href=http://www.graysands.co.uk/nike-free-run-5.0-womens-black-2015-661.asp>Nike Free Run 5.0 Womens Black 2015</a>
<a href=http://www.graysands.co.uk/nike-running-shoes-women-blue-458.asp>Nike Running Shoes Women Blue</a>
<a href=http://www.los-granados-apartment.co.uk/646-stan-smith-primeknit-white-green.html>Stan Smith Primeknit White Green</a>
<a href=http://www.lesfeesbouledeneige.fr/puma-rihanna-femme-963.html>Puma Rihanna Femme</a>
<a href=http://www.los-granados-apartment.co.uk/729-adidas-gazelle-on-feet-women.html>Adidas Gazelle On Feet Women</a>
http://www.maxicolor.nl/nike-2016-heren-zalando-327.html
http://www.cattery-a-naturesgift.nl/oakley-fives-squared-white-774.php
http://www.pcdehoefijzertjes.nl/hermes-riem-heren-kopen-846.php
http://www.taxi-eikhout.nl/646-nike-air-max-2016-roze.htm
http://www.sparkelecvideo.es/950-jordan-nike-neymar.html
<a href=http://www.maxicolor.nl/stefan-janoski-max-wit-667.html>Stefan Janoski Max Wit</a>
<a href=http://www.professionalplan.es/reebok-verdes-399.php>Reebok</a>
<a href=http://www.cattery-a-naturesgift.nl/round-ray-ban-glasses-515.php>Round Ray Ban Glasses</a>
<a href=http://www.spanish-realestate.es/011-botas-de-futbol-adidas-precio.asp>Botas Futbol</a>
<a href=http://www.ehev.es/012-boss-hugo-boss-calzado-zapatillas.htm>Boss Boss</a>
http://www.silo-france.fr/jeremy-scott-moins-cher-520.html
http://www.schatztruhe-assmann.de/air-jordan-eclipse-berlin-918.php
http://www.rebelscots.de/nike-free-5.0-schwarz-45-326.htm
http://www.silo-france.fr/nmd-blue-navy-467.html
http://www.plombier-chauffagiste-argaud.fr/asics-gel-kayano-ocean-pack-536.html
<a href=http://www.plombier-chauffagiste-argaud.fr/asics-bleu-et-orange-479.html>Asics Bleu Et Orange</a>
<a href=http://www.schatztruhe-assmann.de/nike-free-3.0-herren-gelb-857.php>Nike Free 3.0 Herren Gelb</a>
<a href=http://www.scellier-nantes.fr/654-adidas-nmd-r1-femme-beige.html>Adidas Nmd R1 Femme Beige</a>
<a href=http://www.rebelscots.de/nike-air-huarache-weiĂź-496.htm>Nike Air Huarache WeiĂź</a>
<a href=http://www.natydred.fr/762-basket-new-balance-femme-beige.html>Basket New Balance Femme Beige</a>
http://www.spanish-realestate.es/554-puma-football-mexico.asp
http://www.maxicolor.nl/nike-janoski-new-812.html
http://www.decoraciondeinterioresweb.es/oakley-radar-replica-904.php
http://www.academievoorpsychiatrie.nl/739-adidas-zx-700-dames-sale.html
http://www.softwaretutor.co.uk/946-adidas-shoes-yellow-black.htm
<a href=http://www.pcbodelft.nl/315-nike-dames-rood.html>Nike Dames Rood</a>
<a href=http://www.eltotaxi.nl/nike-air-max-bw-kopen-003.php>Nike Air Max Bw Kopen</a>
<a href=http://www.free-nokia-ringtones-now.co.uk/adidas-nmd-white-vintage-094.html>Adidas Nmd White Vintage</a>
<a href=http://www.top40ringtones.nl/adidas-schoenen-spezial-505.htm>Adidas Spezial</a>
<a href=http://www.bures.nl/812-mk-tassen-goedkoop.html>Mk Tassen Goedkoop</a>
http://www.ChaussureAdidasonlineoutlet.fr/670-stan-smith-young.htm
http://www.restaurant-traiteur-creuse.fr/adidas-tubular-original-womens-543.php
http://www.ChaussureAdidasonlineoutlet.fr/895-stan-smith-noir-cuir.htm
http://www.histoiresdinterieur.fr/adidas-ultra-boost-trainers-532.html
http://www.creagraphie.fr/472-adidas-zx-flux-ocean-homme.html
<a href=http://www.histoiresdinterieur.fr/adidas-ultra-boost-rose-gold-303.html>Adidas Ultra Boost Rose Gold</a>
<a href=http://www.estime-moi.fr/adidas-zx-flux-2.0-black-white-883.php>Adidas Zx Flux 2.0 Black White</a>
<a href=http://www.vivalur.fr/712-adidas-boost-endless-energy.php>Adidas Boost Endless Energy</a>
<a href=http://www.estime-moi.fr/adidas-flux-zx-blue-704.php>Adidas Flux Zx Blue</a>
<a href=http://www.leighannelittrell.fr/adidas-neo-easy-vulc-review-562.html>Adidas Neo Easy Vulc Review</a>
http://www.estime-moi.fr/adidas-zx-flux-2.0-amazon-765.php
http://www.leighannelittrell.fr/adidas-neo-sport-station-147.html
http://www.histoiresdinterieur.fr/adidas-ultra-boost-3.0-oreo-release-time-849.html
http://www.creagraphie.fr/730-adidas-zx-flux-all-black-woven.html
http://www.creagraphie.fr/175-adidas-flux-go-sport.html
<a href=http://www.vivalur.fr/439-adidas-ultra-boost-ace-16-red-limit.php>Adidas Ultra Boost Ace 16 Red</a>
<a href=http://www.ChaussureAdidasonlineoutlet.fr/493-adidas-superstar-east-river-rivalry.html>Adidas Superstar East River Rivalry</a>
<a href=http://www.histoiresdinterieur.fr/adidas-boost-ultra-uncaged-490.html>Adidas Boost Ultra Uncaged</a>
<a href=http://www.estime-moi.fr/adidas-zx-flux-fluo-980.php>Adidas Zx Flux Fluo</a>
<a href=http://www.estime-moi.fr/adidas-zx-flux-monochrome-915.php>Adidas Zx Flux Monochrome</a>
http://www.ugtrepsol.es/precio-christian-louboutin-118.php
http://www.cazarafashion.nl/sneakers-nike-wit-338.htm
http://www.theloanarrangers.co.uk/adidas-yeezy-boost-350-price-uk-066.php
http://www.pcbodelft.nl/439-nike-sneakers-camouflage.html
http://www.geadopteerden.nl/voetbalschoenen-dames-goedkoop-911.php
<a href=http://www.professionalplan.es/skechers-mujer-rebajas-942.php>Skechers Rebajas</a>
<a href=http://www.renardlecoq.nl/177-nike-ultra-moire.html>Nike Ultra Moire</a>
<a href=http://www.lexus-tiemens-arnhem.nl/585-skechers-go-walk.htm>Skechers Go Walk</a>
<a href=http://www.desmaeckvanspa.nl/208-balenciaga-dames-shoebaloo.html>Balenciaga Dames Shoebaloo</a>
<a href=http://www.poker-pai-gow.es/826-tenis-under-armour-curry-2.htm>Tenis Armour</a>
http://www.123gouter.fr/adidas-jeremy-scott-pas-cher-supra-894.php
http://www.extreme-hosting.co.uk/181-nike-air-max-95-ultra-womens.php
http://www.aldente-restos.fr/reebok-sneakers-white-705.php
http://www.assurance-csp.fr/asics-2016-gel-lyte-205.htm
http://www.artysols.fr/converse-shoes-2016-743.php
<a href=http://www.fashiondestock.fr/590-chaussure-jeremy-scott-bebe.php>Chaussure Jeremy Scott Bebe</a>
<a href=http://www.aurelieadomicile.fr/064-puma-creepers-rihanna-bleu.php>Puma Creepers Rihanna Bleu</a>
<a href=http://www.dresden2020.de/260-nike-air-force-one-schwarz.php>Nike Air Force One Schwarz</a>
<a href=http://www.campingcarsonway.fr/777-chaussure-adidas-homme-rouge.html>Chaussure Adidas Homme Rouge</a>
<a href=http://www.extreme-hosting.co.uk/991-nike-lebron-11.php>Nike Lebron 11</a>
http://www.sitesm.fr/685-adidas-neo-court-adapt-f39237.php
http://www.sitesm.fr/789-adidas-neo-hoops-grey.php
http://www.leighannelittrell.fr/adidas-neo-piona-allegro-929.html
http://www.creagraphie.fr/620-adidas-zx-flux-femme-noir-et-bronze.html
http://www.ChaussureAdidasonlineoutlet.fr/365-stan-smith-couleur-jaune.htm
[url=http://www.creagraphie.fr/365-adidas-zx-flux-cheetah-buy.html]Adidas Zx Flux Cheetah Buy[/url]
[url=http://www.estime-moi.fr/adidas-flux-noir-homme-574.php]Adidas Flux Noir Homme[/url]
[url=http://www.ChaussureAdidasonlineoutlet.fr/402-superstar-adidas-motif.html]Superstar Adidas Motif[/url]
[url=http://www.climat-concept.fr/adidas-eqt-og-white-688.html]Adidas Eqt Og White[/url]
[url=http://www.estime-moi.fr/adidas-zx-flux-arlequin-prix-612.php]Adidas Zx Flux Arlequin Prix[/url]
http://www.estime-moi.fr/adidas-zx-flux-jd-junior-151.php
http://www.gorrasnewerasnapback.es/gorras-new-york-yankees-452.php
http://www.ChaussureAdidasonlineoutlet.fr/266-adidas-superstar-high.htm
http://www.sitesm.fr/643-adidas-neo-vlneo-hoops-mid-trainers.php
http://www.sitesm.fr/550-adidas-neo-selena-gomez-chaussure.php
[url=http://www.estime-moi.fr/adidas-zx-flux-floral-amazon-259.php]Adidas Zx Flux Floral Amazon[/url]
[url=http://www.leighannelittrell.fr/adidas-neo-womens-city-racer-w-running-shoe-411.html]Adidas Neo Womens City Racer W[/url]
[url=http://www.vivalur.fr/232-adidas-boost-for-ladies.php]Adidas Boost For Ladies[/url]
[url=http://www.ChaussureAdidasonlineoutlet.fr/638-adidas-superstar-bleu-animal.html]Adidas Superstar Bleu Animal[/url]
[url=http://www.ChaussureAdidasonlineoutlet.fr/663-stan-smith-collector.html]Stan Smith Collector[/url]
http://www.xingbang.es/zapatillas-salomon-para-mujer-264.html
http://www.xivcongresoahc.es/oakley-fuel-cell-polarized-307.php
http://www.wervjournaal.nl/073-gucci-schoenen-voor-dames.html
http://www.groenlinks-nh.nl/stan-smith-maat-24-311.html
http://www.geadopteerden.nl/adidas-messi-16-346.php
[url=http://www.manegehopland.nl/louboutins-black-413.php]Louboutins Black[/url]
[url=http://www.harlingen-havenstad.nl/hugo-boss-sneakers-heren-aanbieding-595.html]Hugo Boss Sneakers Heren Aanbieding[/url]
[url=http://www.free-nokia-ringtones-now.co.uk/adidas-los-angeles-vintage-white-amp-raw-purple-577.html]Adidas Los Angeles Vintage White & Raw Purple[/url]
[url=http://www.free-nokia-ringtones-now.co.uk/adidas-nmd-black-women-983.html]Adidas Nmd Black Women[/url]
[url=http://www.demetz.co.uk/adidas-zx-aqua-554.html]Adidas Zx Aqua[/url]
http://www.fashiondestock.fr/216-jeremy-scott-3.0-gold-wings.php
http://www.christelle-barbin.fr/784-converse-one-star-pro.php
http://www.christelle-barbin.fr/186-converse-all-star-dainty-canvas-ox-w.php
http://www.campingcarsonway.fr/583-adidas-noir-et-rose.html
http://www.assurance-csp.fr/asics-gel-lyte-3-argenté-410.htm
[url=http://www.123gouter.fr/adidas-gazelle-vintage-suede-pack-757.php]Adidas Gazelle Vintage Suede Pack[/url]
[url=http://www.123gouter.fr/adidas-neo-rose-fille-423.php]Adidas Neo Rose Fille[/url]
[url=http://www.123gouter.fr/jeremy-scott-wings-batman-863.php]Jeremy Scott Wings Batman[/url]
[url=http://www.artysols.fr/converse-all-star-noir-basse-068.php]Converse All Star Noir Basse[/url]
[url=http://www.fashiondestock.fr/438-nmd-noir-et-rouge.php]Nmd Noir Et Rouge[/url]
http://www.veilinghuiscoins-art.nl/adidas-sportschoenen-rood-588.html
http://www.thehappydays.nl/048-nike-md-runner-2-zwart-dames.php
http://www.amstructures.co.uk/adidas-neo-grey-and-blue-321.html
http://www.amorenomk.es/701-camisas-polo-para-niños.html
http://www.xivcongresoahc.es/ray-ban-redondas-sol-369.php
[url=http://www.vianed.nl/628-valentino-sneakers-outlet.html]Valentino Sneakers Outlet[/url]
[url=http://www.quantex.es/bolsos-louis-vuitton-242.php]Bolsos Vuitton[/url]
[url=http://www.professionalplan.es/tiendas-de-zapatillas-mbt-en-madrid-755.php]Tiendas Zapatillas[/url]
[url=http://www.professionalplan.es/reebok-modelos-clasicos-316.php]Reebok Clasicos[/url]
[url=http://www.mujerinnovadora.es/307-zapatos-verdes-tacon-bajo.asp]Zapatos Tacon[/url]
http://www.fiets4daagsekempenland.nl/390-puma-fenty-shoes.php
http://www.renardlecoq.nl/396-nike-schoenen-dames-groningen.html
http://www.wallbank-lfc.co.uk/745-adidas-ultra-boost-white-and-blue.htm
http://www.ehev.es/010-caterpillar-botas-2017.htm
http://www.auto-mobile.es/158-nike-mercurial-superfly-2015.php
[url=http://www.rechtswinkelalkmaar.nl/puma-creeper-velvet-zwart-027.html]Puma Creeper Velvet Zwart[/url]
[url=http://www.posicionamientotiendas.com.es/628-tenis-jordan-retro-3.html]Tenis Jordan Retro 3[/url]
[url=http://www.softwaretutor.co.uk/393-adidas-ultra-boost-solar-red-gradient.htm]Adidas Ultra Boost Solar Red Gradient[/url]
[url=http://www.evcd.nl/nike-air-force-multicolor-669.html]Nike Air Force Multicolor[/url]
[url=http://www.auto-mobile.es/603-puma-soccer-shoes.php]Puma Shoes[/url]
http://www.free-nokia-ringtones-now.co.uk/adidas-nmd-womens-green-546.html
http://www.rwpieters.nl/187-reebok-freestyle.html
http://www.lexus-tiemens-arnhem.nl/254-dior-shoes-2017.htm
http://www.desmaeckvanspa.nl/260-balenciaga-arena-high-heren.html
http://www.pcbodelft.nl/237-nike-cortez-brons.html
[url=http://www.cambiaexpress.es/gucci-zapatos-de-hombre-938.php]Gucci De[/url]
[url=http://www.auto-mobile.es/786-nike-mercurial-vapor-x-fg-cr7.php]Nike Vapor[/url]
[url=http://www.xingbang.es/skechers-go-walk-3-precio-430.html]Skechers Walk[/url]
[url=http://www.poker-pai-gow.es/956-skechers-diameter-blake-63385.htm]Skechers Blake[/url]
[url=http://www.active-health.nl/mizuno-wave-rider-19-535.htm]Mizuno Wave Rider 19[/url]
http://www.ehev.es/912-zapatos-dolce-gabbana-outlet.htm
http://www.poker-pai-gow.es/160-reebok-de-mujer-2016.htm
http://www.3500gt.nl/772-nike-hypervenom-2-neymar.php
http://www.evcd.nl/jordans-black-red-344.html
http://www.posicionamientotiendas.com.es/102-zapatillas-jordan-super-fly.html
[url=http://www.taxi-eikhout.nl/882-nike-air-max-90-cool-grey.htm]Nike Air Max 90 Cool Grey[/url]
[url=http://www.ruudschulten.nl/324-nike-huarache-ultra-wit.html]Nike Huarache Ultra Wit[/url]
[url=http://www.wervjournaal.nl/825-lacoste-schoenen-spartoo.html]Lacoste Schoenen Spartoo[/url]
[url=http://www.sarbot-team.es/695-camisetas-lacoste-baratas-chile.php]Camisetas Baratas[/url]
[url=http://www.carpetsmiltonkeynes.co.uk/252-adidas-nmd-xr1-duck-camo.html]Adidas Nmd Xr1 Duck Camo[/url]
http://www.la-baston.fr/adidas-zx-flux-bleu-marine-et-rose-164.html
http://www.lesfeesbouledeneige.fr/chaussure-puma-disc-blaze-219.html
http://www.lesfeesbouledeneige.fr/puma-basket-lacet-972.html
http://www.onegame.fr/new-balance-u420-femme-pas-cher-157.php
http://www.vansskooldskool.dk/sorte-vans-til-kvinder-902.php
[url=http://www.la-baston.fr/adidas-chaussure-gel-556.html]Adidas Chaussure Gel[/url]
[url=http://www.vansskooldskool.dk/vans-old-skool-high-268.php]Vans Old Skool High[/url]
[url=http://www.imprimerieexpress.fr/chaussure-puma-pas-cher-femme-785.php]Chaussure Puma Pas Cher Femme[/url]
[url=http://www.ileauxtresors.fr/yeezy-boost-350-camel-171.htm]Yeezy Boost 350 Camel[/url]
[url=http://www.lesfeesbouledeneige.fr/puma-platform-bleu-984.html]Puma Platform Bleu[/url]
http://www.probaiedumontsaintmichel.fr/325-new-balance-femme-574-noir-et-rose.php
http://www.viherio.fr/280-adidas-bebe-scratch.php
http://www.schatztruhe-assmann.de/nike-air-max-hyperfuse-neon-pink-642.php
http://www.viherio.fr/111-adidas-ultra-boost-homme.php
http://www.silo-france.fr/adidas-wings-prix-632.html
[url=http://www.weddingtiarasuk.co.uk/adidas-ultra-boost-3.0-734.php]Adidas Ultra Boost 3.0[/url]
[url=http://www.vansskooldskool.dk/vans-sko-læder-025.php]Vans Sko Læder[/url]
[url=http://www.weddingtiarasuk.co.uk/adidas-d-rose-7-x-sns-598.php]Adidas D Rose 7 X Sns[/url]
[url=http://www.rebelscots.de/nike-free-3.0-tĂĽrkis-damen-685.htm]Nike Free 3.0 TĂĽrkis Damen[/url]
[url=http://www.scellier-nantes.fr/246-adidas-jeremy-scott-bear.html]Adidas Jeremy Scott Bear[/url]
http://www.graysands.co.uk/nike-air-presto-on-feet-971.asp
http://www.ileauxtresors.fr/adidas-femme-tubular-377.htm
http://www.graysands.co.uk/nike-air-max-2015-black-and-blue-904.asp
http://www.los-granados-apartment.co.uk/928-adidas-shoes-stan-smith-pink.html
http://www.la-baston.fr/yeezy-rouge-adidas-900.html
[url=http://www.la-baston.fr/adidas-chaussure-2016-fille-148.html]Adidas Chaussure 2016 Fille[/url]
[url=http://www.ideelle.fr/725-asics-kayano-evo-black.html]Asics Kayano Evo Black[/url]
[url=http://www.la-baston.fr/ultra-boost-white-grey-134.html]Ultra Boost White Grey[/url]
[url=http://www.graysands.co.uk/nike-air-max-2015-mens-854.asp]Nike Air Max 2015 Mens[/url]
[url=http://www.lesfeesbouledeneige.fr/puma-suede-rose-clair-658.html]Puma Suede Rose Clair[/url]
http://www.poker-pai-gow.es/502-zapatos-mbt-catalogo.htm
http://www.pcc-bv.nl/nike-air-max-2016-bestellen-achteraf-betalen-261.htm
http://www.fiets4daagsekempenland.nl/482-puma-suede-classic-heren.php
http://www.juegosa.es/972-zapatillas-yves-saint-laurent.html
http://www.xingbang.es/timberland-botas-hombre-908.html
[url=http://www.demetz.co.uk/adidas-flux-tan-208.html]Adidas Flux Tan[/url]
[url=http://www.lexus-tiemens-arnhem.nl/048-balenciaga-runners-high-top.htm]Balenciaga Runners High Top[/url]
[url=http://www.tinget.es/adidas-x-16.3-2017-640.html]Adidas 16.3[/url]
[url=http://www.pcbodelft.nl/216-nike-schoenen-dames-zilver.html]Nike Schoenen Dames Zilver[/url]
[url=http://www.renardlecoq.nl/171-waar-kan-ik-nike-shox-kopen.html]Waar Kan Ik Nike Shox Kopen[/url]
http://www.free-nokia-ringtones-now.co.uk/adidas-neo-white-sneaker-542.html
http://www.tr-online.nl/825-adidas-zx-flux-zwart-roze.php
http://www.aoriginal.co.uk/adidas-superstar-high-tumblr-269.html
http://www.cdvera.es/001-tenis-mizuno.htm
http://www.desmaeckvanspa.nl/380-philipp-plein-schoen-sale.html
[url=http://www.evcd.nl/nike-pegasus-32-grijs-724.html]Nike Pegasus 32 Grijs[/url]
[url=http://www.professionalplan.es/zapatillas-fila-nuevos-modelos-665.php]Zapatillas Nuevos[/url]
[url=http://www.herbusinessuk.co.uk/387-adidas-superstar-navy-blue-suede.htm]Adidas Superstar Navy Blue Suede[/url]
[url=http://www.specialgroup.nl/125-adidas-superstar-rt-blue.htm]Adidas Rt[/url]
[url=http://www.xingbang.es/vans-nintendo-161.html]Vans[/url]
http://www.estime-moi.fr/adidas-zx-flux-bordeaux-courir-358.php
http://www.estime-moi.fr/adidas-zx-flux-black-womens-559.php
http://www.attitudesinde.fr/193-adidas-eqt-support-primeknit-white.php
http://www.vivalur.fr/691-adidas-ultra-boost-2015-test.php
http://www.creagraphie.fr/333-adidas-zx-flux-multicolor-size-14.html
[url=http://www.ChaussureAdidasonlineoutlet.fr/611-superstar-adidas-original.html]Superstar Adidas Original[/url]
[url=http://www.vivalur.fr/329-adidas-boost-3-oreo.php]Adidas Boost 3 Oreo[/url]
[url=http://www.climat-concept.fr/solebox-x-adidas-eqt-guidance-93-consortium-049.html]Solebox X Adidas Eqt Guidance 93[/url]
[url=http://www.histoiresdinterieur.fr/adidas-boost-2-red-648.html]Adidas Boost 2 Red[/url]
[url=http://www.vivalur.fr/466-adidas-boost-750-low.php]Adidas Boost 750 Low[/url]
http://www.leighannelittrell.fr/adidas-neo-v-racer-pas-cher-540.html
http://www.adidasschuheneu.de/688-adidas-sneaker-rot-blau.htm
http://www.adidasschuheneu.de/643-adidas-stan-smith-ray-pink.htm
http://www.creagraphie.fr/106-adidas-flux-zx-custom.html
http://www.leighannelittrell.fr/adidas-neo-baby-sneaker-hoops-389.html
[url=http://www.leighannelittrell.fr/adidas-neo-unwind-mens-trainers-799.html]Adidas Neo Unwind Mens Trainers[/url]
[url=http://www.attitudesinde.fr/754-adidas-eqt-adv-support-pink.php]Adidas Eqt Adv Support Pink[/url]
[url=http://www.beasys.fr/101-adidas-tubular-x-primeknit-red.htm]Adidas Tubular X Primeknit Red[/url]
[url=http://www.adidasschuheneu.de/012-adidas-zx-700-weiß-grün-orange.htm]Adidas Zx 700 Weiß Grün Orange[/url]
[url=http://www.sitesm.fr/345-adidas-neo-bbneo-hi-top-shoes-in-running.php]Adidas Neo Bbneo Hi Top Shoes[/url]
http://www.onegame.fr/new-balance-577-napes-547.php
http://www.probaiedumontsaintmichel.fr/603-new-balance-1080-v5.php
http://www.rebelscots.de/air-max-90-schwarz-813.htm
http://www.viherio.fr/139-adidas-noir-et-or-zx-flux.php
http://www.plombier-chauffagiste-argaud.fr/asics-gel-lyte-3-bleu-271.html
[url=http://www.viherio.fr/419-adidas-ultra-boost-rose.php]Adidas Ultra Boost Rose[/url]
[url=http://www.weddingtiarasuk.co.uk/adidas-basketball-shoes-crazy-light-547.php]Adidas Basketball Shoes Crazy Light[/url]
[url=http://www.natydred.fr/775-new-balance-670-bordeaux-femme.html]New Balance 670 Bordeaux Femme[/url]
[url=http://www.rebelscots.de/nike-free-5.0-königsblau-092.htm]Nike Free 5.0 Königsblau[/url]
[url=http://www.schatztruhe-assmann.de/nike-lebron-xiii-low-196.php]Nike Lebron Xiii Low[/url]
http://www.los-granados-apartment.co.uk/929-adidas-zx-flux-adv-sock.html
http://www.kaptur.fr/858-puma-nouvelle-collection-2017.html
http://www.los-granados-apartment.co.uk/478-adidas-shoes-women-price.html
http://www.imprimerieexpress.fr/puma-rihanna-rose-gold-676.php
http://www.abercrombieandfitchsaleuk.xyz/915-abercrombie-and-fitch-womens-hoodies
[url=http://www.izitea.fr/new-balance-femme-rose-pale-827.html]New Balance Femme Rose Pale[/url]
[url=http://www.ideelle.fr/146-asics-gel-lyte-5-grey.html]Asics Gel Lyte 5 Grey[/url]
[url=http://www.ideelle.fr/758-asics-pulse.html]Asics Pulse[/url]
[url=http://www.la-baston.fr/adidas-zx-flux-rose-fleur-167.html]Adidas Zx Flux Rose Fleur[/url]
[url=http://www.izitea.fr/prix-new-balance-femme-201.html]Prix New Balance Femme[/url]
http://www.vivalur.fr/007-adidas-ultra-boost-3.0-white-noise.php
http://www.leighannelittrell.fr/adidas-neo-derby-set-navy-blue-sneakers-633.html
http://www.vivalur.fr/490-adidas-ultra-boost-all-black-ebay.php
http://www.restaurant-traiteur-creuse.fr/adidas-tubular-runner-primeknit-834.php
http://www.leighannelittrell.fr/adidas-neo-10k-249.html
[url=http://www.estime-moi.fr/adidas-zx-flux-womens-copper-086.php]Adidas Zx Flux Womens Copper[/url]
[url=http://www.vivalur.fr/881-adidas-boost-3d.php]Adidas Boost 3d[/url]
[url=http://www.estime-moi.fr/adidas-zx-flux-floral-ebay-136.php]Adidas Zx Flux Floral Ebay[/url]
[url=http://www.ChaussureAdidasonlineoutlet.fr/547-adidas-superstar-ii-metallic-whitesilver.html]Adidas Superstar Ii Metallic White/Silver[/url]
[url=http://www.adidasschuheneu.de/546-adidas-nmd-beige-frauen.htm]Adidas Nmd Beige Frauen[/url]
http://www.restaurantegallegoosegredo.es/nike-roshe-run-blue-sky-461.php
http://www.wellnessanco.nl/373-adidas-instappers-dames.php
http://www.sparkelecvideo.es/209-tenis-jordan-xiv.html
http://www.4chat.nl/new-balance-goud-wit-812.html
http://www.decoraciondeinterioresweb.es/ray-ban-wayfarer-218.php
[url=http://www.cdvera.es/503-supra-skytop-2-white.htm]Supra 2[/url]
[url=http://www.aoriginal.co.uk/adidas-superstar-2-purple-120.html]Adidas Superstar 2 Purple[/url]
[url=http://www.demetz.co.uk/adidas-tubular-invader-for-women-223.html]Adidas Tubular Invader For Women[/url]
[url=http://www.wervjournaal.nl/559-palladiums-boots.html]Palladiums Boots[/url]
[url=http://www.verkeersschoolhaan.nl/adidas-flux-blue-770.htm]Adidas Blue[/url]
http://www.renardlecoq.nl/957-nike-roshe-one-id.html
http://www.paparico.es/tenis-ralph-lauren-vaughn-113.html
http://www.spanish-realestate.es/772-tenis-cr7-2017-verdes.asp
http://www.posicionamientotiendas.com.es/079-jordan-anillos.html
http://www.strattondesignservices.co.uk/adidas-superstar-limited-edition-shoes-814.php
[url=http://www.cdvera.es/403-zapatillas-salomon-colombia.htm]Zapatillas Colombia[/url]
[url=http://www.wallbank-lfc.co.uk/486-adidas-ultra-boost-jampd.htm]Adidas Ultra Boost J& d[/url]
[url=http://www.cdvera.es/663-le-coq-sportif-omega-original-galet.htm]Le Sportif[/url]
[url=http://www.poker-pai-gow.es/060-zapatos-mbt-en-zaragoza.htm]Zapatos En[/url]
[url=http://www.softwaretutor.co.uk/642-adidas-shoes-vector.htm]Adidas Shoes Vector[/url]
http://www.support4marketing.de/nike-performance-flex-2016-902.html
http://www.vom-eulenloch.de/nike-blazer-schwarz-damen-269.htm
http://www.oberhof-sportstaetten.de/449-abercrombie-fitch-weste.html
http://www.santopadreracingteam.it/740-ray-ban-6331.php
http://www.hobbyshop-gossert.de/556-mbt-sandalen-39-günstig.html
[url=http://www.blau4drei9.de/converse-chucks-low-schwarz-889.html]Converse Chucks Low Schwarz[/url]
[url=http://www.nlp-am-zoopark.de/754-jimmy-choo-loafers.html]Jimmy Choo Loafers[/url]
[url=http://www.restaurant-baltic-bay.de/320-ralph-lauren-kappe-schwarz.php]Ralph Lauren Kappe Schwarz[/url]
[url=http://www.fulchiron.fr/455-lunettes-de-soleil-oakley-femme.html]Lunettes De Soleil Oakley Femme[/url]
[url=http://www.einradkids-hamburg.de/948-adidas-zx-flux-smooth-schwarz.php]Adidas Zx Flux Smooth Schwarz[/url]
http://www.veilinghuiscoins-art.nl/adidas-tubular-grey-212.html
http://www.free-nokia-ringtones-now.co.uk/adidas-originals-trainers-rare-645.html
http://www.cattery-a-naturesgift.nl/ray-ban-etui-829.php
http://www.restaurantegallegoosegredo.es/nike-roshe-run-hyperfuse-qs-164.php
http://www.academievoorpsychiatrie.nl/530-gazelle-adidas-groen.html
[url=http://www.posicionamientotiendas.com.es/114-jordan-7-retro-rosado.html]Jordan 7 Retro Rosado[/url]
[url=http://www.professionalplan.es/zapatillas-le-coq-sportif-lima-970.php]Zapatillas Coq[/url]
[url=http://www.top40ringtones.nl/schoenen-adidas-dames-736.htm]Schoenen Dames[/url]
[url=http://www.taxi-eikhout.nl/184-nike-air-max-90-classic.htm]Nike Air Max 90 Classic[/url]
[url=http://www.evcd.nl/nike-huarache-wit-goedkoop-343.html]Nike Huarache Wit Goedkoop[/url]
http://www.dresshome.es/cinturones-hermes-piratas-459.php
http://www.geadopteerden.nl/nike-hypervenom-yellow-128.php
http://www.academievoorpsychiatrie.nl/888-adidas-neo-schoenen-heren.html
http://www.elpecat.es/810-gafas-carrera-choni.html
http://www.liquids2005.nl/adidas-stan-smith-black-outfit-155.htm
[url=http://www.cdvera.es/559-zapatillas-le-coq-sportif-china.htm]Zapatillas Coq[/url]
[url=http://www.harlingen-havenstad.nl/golden-goose-sneakers-kopen-300.html]Golden Goose Sneakers Kopen[/url]
[url=http://www.sparkelecvideo.es/069-nike-roshe-2-red.html]Nike Roshe 2 Red[/url]
[url=http://www.desmaeckvanspa.nl/269-skechers-memory-foam-schoenen.html]Skechers Memory Foam Schoenen[/url]
[url=http://www.theloanarrangers.co.uk/adidas-shoes-2017-women-875.php]Adidas Shoes 2017 Women[/url]
http://www.harlingen-havenstad.nl/sneakers-hogan-dames-376.html
http://www.elisamurciaartengo.es/nike-cortez-negras-y-rojas-756.php
http://www.free-nokia-ringtones-now.co.uk/adidas-la-trainer-pegs-608.html
http://www.aoriginal.co.uk/adidas-supercolor-womens-326.html
http://www.carpetsmiltonkeynes.co.uk/901-adidas-originals-gazelle-grey-trainers.html
[url=http://www.sarbot-team.es/599-gorras-houston-texans.php]Gorras Texans[/url]
[url=http://www.veilinghuiscoins-art.nl/adidas-tubular-sneakers-961.html]Adidas Sneakers[/url]
[url=http://www.sarbot-team.es/386-camisas-para-hombre-polo-ralph-lauren.php]Camisas Hombre[/url]
[url=http://www.manegehopland.nl/christian-louboutin-men-red-734.php]Christian Louboutin Men Red[/url]
[url=http://www.renardlecoq.nl/450-nike-roshe-flyknit-ladies.html]Nike Roshe Flyknit Ladies[/url]
http://www.frokenstockholmare.se/968-nike-roshe-premium.php
http://www.mado-ludwick.fr/michael-kors-sac-jet-set-travel-noir-091.php
http://www.spotlightstranscom.de/poloshirt-jungen-281.htm
http://www.somewine.fr/366-sweats-abercrombie-rouge.html
http://www.jetzt-lastminute-pauschalreise.de/849-adidas-stan-smith-frauen.php
[url=http://www.support4marketing.de/huaraches-pink-and-purple-085.html]Huaraches Pink And Purple[/url]
[url=http://www.nkavmig.se/nike-air-jordan-1-780.php]Nike Air Jordan 1[/url]
[url=http://www.grunewald-reservierung.de/207-converse-all-star-chuck-taylor.php]Converse All Star Chuck Taylor[/url]
[url=http://www.somewine.fr/272-doudoune-ralph-lauren-femme.html]Doudoune Ralph Lauren Femme[/url]
[url=http://www.sittest.fr/624-sac-a-main-louis-vuitton-beige.html]Sac A Main Louis Vuitton Beige[/url]
http://www.finaperf.es/camisas-polo-ralph-lauren-hombre-461.html
http://www.thehappydays.nl/967-nike-kobe.php
http://www.specialgroup.nl/985-adidas-superstar-metal-toe-kopen.htm
http://www.free-nokia-ringtones-now.co.uk/adidas-nmd-white-white-bright-cyan-932.html
http://www.cpac.org.es/lv-speedy-854.html
[url=http://www.renardlecoq.nl/178-nike-fs-lite-run-3-zalando.html]Nike Fs Lite Run 3 Zalando[/url]
[url=http://www.4chat.nl/new-balance-996-white-648.html]New Balance 996 White[/url]
[url=http://www.elpecat.es/580-ray-ban-glasses-black.html]Ray Glasses[/url]
[url=http://www.sarbot-team.es/543-ralph-lauren-chalecos.php]Ralph Chalecos[/url]
[url=http://www.lexus-tiemens-arnhem.nl/139-armani-sneakers-wit-heren.htm]Armani Sneakers Wit Heren[/url]
магазин ежедневно пополняется, к концу недели будет очень богатый ассортимент.
http://www.los-granados-apartment.co.uk/396-adidas-superstar-80s-woven.html
http://www.izitea.fr/new-balance-daim-femme-650.html
http://www.consumabulbs.co.uk/525-puma-dark-shadow.html
http://www.ileauxtresors.fr/adidas-chaussure-2016-homme-578.htm
http://www.kaptur.fr/486-chaussures-puma-rouge.html
[url=http://www.kaptur.fr/323-puma-fenty-velvet-creepers.html]Puma Fenty Velvet Creepers[/url]
[url=http://www.los-granados-apartment.co.uk/042-adidas-zx-flux-white-multicolor.html]Adidas Zx Flux White Multicolor[/url]
[url=http://www.lesfeesbouledeneige.fr/puma-heart-gris-suede-662.html]Puma Heart Gris Suede[/url]
[url=http://www.consumabulbs.co.uk/849-puma-basket-white-leather.html]Puma Basket White Leather[/url]
[url=http://www.kaptur.fr/535-puma-x-careaux-blaze-of-glory.html]Puma X Careaux Blaze Of Glory[/url]
http://www.adhi.es/adidas-futbol-2015-messi-103.php
http://www.sergiestebanell.es/679-michael-kors-bolsos-azul-marino.php
http://www.cazarafashion.nl/nike-sneakers-white-984.htm
http://www.paparico.es/zapatos-armani-baratos-923.html
http://www.carpetsmiltonkeynes.co.uk/826-adidas-originals-gazelle-2-junior.html
[url=http://www.clubeldorado.nl/asics-fuji-394.php]Asics Fuji[/url]
[url=http://www.academievoorpsychiatrie.nl/930-zx-flux-sale.html]Zx Sale[/url]
[url=http://www.decoraciondeinterioresweb.es/gafas-ray-ban-mujeres-583.php]Gafas Ban[/url]
[url=http://www.postenblankestijn.nl/548-heren-nike-air-max-2016.htm]Heren Nike Air Max 2016[/url]
[url=http://www.amorenomk.es/853-abercrombie-outfits.html]Abercrombie[/url]
[url=http://payday1000loans3000online.com/#bad-credit-payday-loans-zyv]bad credit personal loans [/url]
<a href="http://payday1000loans3000online.com/#instant-payday-loans-blf">short term loans </a>
http://payday1000loans3000online.com/#isont
http://payday1000loans3000online.com/#nqbxf
http://payday1000loans3000online.com/#vhhzi
http://www.hidejii.com/blog/item_29.html
http://tomsk.stanko-prof.ru/products/2622v-2a622#comment_14177
http://uslishmir.kz/news/2012/04/21/buducshie_bekkhemy?page=652#comment-466873
http://www.theshooot.com/product/tier-3-package/
http://www.gekon-plzen.cz/vzkazy-a-dotazy?replyto=7447&_formData[guest]=nnyxhjImmus&_formData[subject]=&_formData[text]=%3Ca+href%3D%22http%3A%2F%2Fpayday1000loans3000online.com%2F%23legitimate-payday-loans-online-no-credit-check-ahn%22%3Ecash+loans+%3C%2Fa%3E+%0D%0A%5Burl%3Dhttp%3A%2F%2Fpayday1000loans3000online.com%2F%23ace-payday-loans-xjg%5Dloans+for+people+with+bad+credit+%5B%2Furl%5D+%0D%0A%26lt%3Ba+href%3D%26quot%3Bhttp%3A%2F%2Fpayday1000loans3000online.com%2F%23best-payday-loans-vzy%26quot%3B%26gt%3Bcash+loans+%26lt%3B%2Fa%26gt%3B+%0D%0A+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23flffy+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23gtjcq+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23whnvm+%0D%0A+%0D%0Ahttp%3A%2F%2Fohrana.ru%2Farticles%2F4352%2F%23comment_57388+%0D%0Ahttp%3A%2F%2Fwww.svadba-rb.ru%2Fnovosti_ufy.php%3Fid%3D2519+%0D%0Ahttp%3A%2F%2Fwww.economica.net%2Fturismul-aduce-minelor-de-sare-venituri-de-milioane-de-euro-anual-top-si-galerie-foto_105151.html%23comentarii+%0D%0Ahttp%3A%2F%2Fwww.tehnikinvest.com%2Fvodic-za-kupovinu-stana-u-izgradnji-azuriran-sa-svim-propisima-do-aprila-2016-%3Fvest%3D181%26kategorija%3Dv%26komentar%3D%3Ca%2Bhref%253D%2522http%253A%252F%252Fpayday1000loans3000online.com%252F%2523best-payday-loans-cjy%2522%3Eonline%2Bpayday%2Bloans%2B%3C%252Fa%3E%2B%250D%250A%255Burl%253Dhttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523direct-lender-payday-loans-pda%255Dcash%2Badvance%2B%255B%252Furl%255D%2B%250D%250A%2526lt%253Ba%2Bhref%253D%2526quot%253Bhttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523same-day-payday-loans-vhu%2526quot%253B%2526gt%253Bloans%2Bfor%2Bbad%2Bcredit%2B%2526lt%253B%252Fa%2526gt%253B%2B%250D%250A%2B%250D%250Ahttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523itsom%2B%250D%250Ahttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523plvzt%2B%250D%250Ahttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523njjwu%2B%250D%250A%2B%250D%250Ahttp%253A%252F%252Fvostryakov.ru%252Fblog%252F20-tlstitle-kriptograficheskaya-biblioteka-na-chistom%252F%2523comment_46846%2B%250D%250Ahttp%253A%252F%252Fwww.4nature.ru%252Fproducts%252F585%2B%250D%250Ahttp%253A%252F%252Fwww.charge.co.jp%252Fspecial%252Fitem_1227.html%2B%250D%250Ahttp%253A%252F%252Fwww.sopauto.cz%252F1742%252Ccz_loketni-operka-s1-vyklopna-s-posuvnym-vikem-da.html%2523koment%2B%250D%250Ahttp%253A%252F%252Fpaste.akingi.com%252FVZpfAmTb%26email%3Dmaypusualp%2540mailermails.info%26ime%3DndlkpwHop%26posaljiKomentar%3D+%0D%0Ahttp%3A%2F%2Fpalitra.mk.ua%2Fgoods.php%3Fid%3D157833&addpost&r=0
[url=http://payday1000loans3000online.com/#best-online-payday-loans-xau]loans online [/url]
<a href="http://payday1000loans3000online.com/#fast-payday-loans-tyv">payday express </a>
http://payday1000loans3000online.com/#bsoov
http://payday1000loans3000online.com/#sfvfw
http://payday1000loans3000online.com/#pgdqw
http://websiterank.pl/assembla.com#comment-316756
http://www.loveletters.ie/ivory-lace-wedding-guest-book/?attributes=eyIxMjI4IjoiPGEgaHJlZj1cImh0dHA6XC9cL3BheWRheTEwMDBsb2FuczMwMDBvbmxpbmUuY29tXC8jcGF5ZGF5LWxvYW5zLWRpcmVjdC1sZW5kZXItZWNlXCI-cGF5ZGF5IGxvYW5zIG9ubGluZSA8XC9hPiBcclxuaHR0cDpcL1wvcGF5ZGF5MTAwMGxvYW5zMzAwMG9ubGluZS5jb21cLyNpbnN0YW50LXBheWRheS1sb2Fucy1nbncgLSBxdWljayBsb2FucyAgXHJcbiZsdDthIGhyZWY9JnF1b3Q7aHR0cDpcL1wvcGF5ZGF5MTAwMGxvYW5zMzAwMG9ubGluZS5jb21cLyNwYXlkYXktbG9hbnMtb25saW5lLW5vLWNyZWRpdC1jaGVjay1zZ2UmcXVvdDsmZ3Q7bG9hbnMgZm9yIGJhZCBjcmVkaXQgJmx0O1wvYSZndDsgXHJcbiBcclxuaHR0cDpcL1wvcGF5ZGF5MTAwMGxvYW5zMzAwMG9ubGluZS5jb21cLyNkbnViciBcclxuaHR0cDpcL1wvcGF5ZGF5MTAwMGxvYW5zMzAwMG9ubGluZS5jb21cLyNmd2J3ZyBcclxuaHR0cDpcL1wvcGF5ZGF5MTAwMGxvYW5zMzAwMG9ubGluZS5jb21cLyN3eWFkaCBcclxuIFxyXG5odHRwOlwvXC93d3cuY29tLXNlcnZpY2VwYXlwYWwuY29tXC9kZWZhdWx0LnBocCBcclxuaHR0cDpcL1wvd3d3LnBva2VyYmJjLmNvbVwvZG9jXzEyMy5odG1sIFxyXG5odHRwOlwvXC93d3cucmlkZWxlYmFub24uY29tXC9jb21wb25lbnRcL3ZlaGljbGVtYW5hZ2VyXC8xNTdcL3ZpZXdfdmVoaWNsZVwvNTRcL0plZXBcLzc2XC9yZW5hdWx0LWR1c3Rlci0yMDE0LWJsYWNrP0l0ZW1pZD0xNTcgXHJcbmh0dHA6XC9cL2FjY2lvbmVzZmFzdC5jb21cLzIwMTZcLzA4XC8zMFwvb3BlcmEtc2luLWluY29udmVuaWVudGVzXC8jY29tbWVudC0yNzA1MDIgXHJcbmh0dHA6XC9cL3d3dy5yYWRpb211c2V1bS13ZXJ0aW5nZW4uZGVcL2dhZXN0ZWJ1Y2gucGhwP2lkPWU1dTk5czVqJmFidXNlPTcxIiwiMTIzMCI6IjQzNDYiLCIxMjMyIjoiNDc3MSIsIjE2MjEiOiI3ODEzIn0
http://www.planshetnik.com/products/umnyj-braslet-xiaomi/#comment_19839
http://1vsenadom.ru/catalog/pechene/twix_belyy_shokolad_0_05/
http://konieczna.eu/zapal-swiatlo-dla-europy
[url=http://payday1000loans3000online.com/#payday-loans-online-zwj]quick loans [/url]
<a href="http://payday1000loans3000online.com/#payday-loans-bad-credit-bhi">loans online </a>
http://payday1000loans3000online.com/#owyep
http://payday1000loans3000online.com/#wrtmm
http://payday1000loans3000online.com/#glcrd
http://forums.ccd.go.ug/viewtopic.php?f=4&t=90367
http://www.klong5.go.th/view_board.php?id=7
http://gb.dashbill.com/guestbook/index.php?mode=3&post_id=153664
http://eparafiajozefow.pl/component/phocaguestbook/phocaguestbook/1.html
http://leburtaxlaw.com/index.php/u-s-new-zealand-income-tax-treaty-to-senate/
[url=http://payday1000loans3000online.com/#payday-loans-online-direct-lenders-only-xms]bad credit personal loans [/url]
<a href="http://payday1000loans3000online.com/#no-credit-check-payday-loans-tab">loans online </a>
http://payday1000loans3000online.com/#gsiiq
http://payday1000loans3000online.com/#yftat
http://payday1000loans3000online.com/#ndcyy
http://www.dickynieboer.nl/site/pages/gastenboek.php
http://reedge.foicucod.ro/toxicemia/natuurvolk/
http://ae76lubeinc.com/guestbook/index.php?mode=3&post_id=156054
http://travelbilet.ru/guestbook
http://dev.marketvision.in/blogs/deepakshenoy/primary-articles-inflation-1758-91.html
[url=http://payday1000loans3000online.com/#payday-loans-bad-credit-oss]quick loans [/url]
<a href="http://payday1000loans3000online.com/#payday-loans-online-no-credit-check-instant-approval-cim">loans online </a>
http://payday1000loans3000online.com/#lsfpe
http://payday1000loans3000online.com/#ibrqb
http://payday1000loans3000online.com/#rhoui
http://www.docki.com.ua/boards.php?boar=23&pg=20&lis=32042&temasort=®ions1=&tema=swux
https://www.troop224.us/public/guestbook/index.php?mode=3&post_id=84150
http://www.gloriaoliver.com/2011/11/30/picture-kaleidoscope-113011/?contact-form-id=widget-text-3&contact-form-sent=11479&_wpnonce=ba2bfe1ddd
http://breakingintoboardgames.libsyn.com/podcast/breaking-into-board-games-episode-42-gathering-of-friends-with-gil?status=incorrect_captcha&incorrect_name=214416bc106de03ec2df530d8dc82fe6&incorrect_email=6a945c72ca9689f1be7093524a5a623fedff390670d56899231511e3097b8d09&incorrect_body=914bb1bc906210b480668b81805e32e4ea57e2b0d36f8e5943511f166ce1d760ad12e9b3f33189844ecfc69253967c78f0940e6d868236bf41cbe9c5dcf6be398f5f288d08aad648020369adf44d757972c90e319b6f08fe4974fb33a70cf97db2240aa4c68216150d660a543acede3d198847e692d9ac67837a30c9e8fc095b184a41113806bd89362f2af58ecfbb28437d75f6ab4fd592b97ac47d4f0e2e7a0a472a2e7b99c8e66047044aa519383ac16a73e16346ae68a7b5531893f7137a930fa4c2bb239b4fc0ce3b58a0ab594d74d7d493df90418b5197da6644706485fafa02d1b729352de493bc7eba1a9adc225161238dab7bbee26e89b2ab7620fe994b1ef94f37274125ccdd51420bc425300df098c7e3dbdfa59285d2ebdcbdf71ca31ccb9a7b95c23f6684804af86247ca9e98eddad81be751915778f730edd67952dddc045d3958bf102877f633a2753dece55230e52f2dcc4cb3790f79b439f58cc338b29dd0545f7aa60311e64e10f106f8c5f7ed845ba9e64c07295dc169f894c4341657252733a299338fd07ab2712906f9348f8d77e7275daaf3bc1f2bd2f3cc410b4544feeda9051aa8bcdc7a210de8cceda3b91c2d6c3acbe61a81ea9f4648eb2a4b8614d4948892c28030ef25d131dc4346c228ddbdc467fd466b7cf6c0aeeaa389238ce22473446098e6a032e0bb6a1a5158ef682025de2eddbdf29c5eb5c873b82e248e689c7911359b458320e03dbecbf6e17b1d7cabc77186cb2932b881b9280b3e2bef81369101c7fa16d300beec87dc4e72532df074be8e75973a7ab745348e15af767265f2a8e483de8bf5d869d26f8d748c30d7d5997334ee31c7f8001b5bb14c4c3ba07abefbef10268f731e01baab763676a3ca2851774f6012fc508cebbeec468cf5e5ebd5ca5f2deb9b4903b7f55b670aab842c8279f5d43264841a10306909a6ff46f04f321bf43a1f2ad4a74a9b358ef7bcfe6cab24afbc5f2bd71843d27bb6f99516c5810c263cb2f5ff54bb8bd5366bdfeac7b4db4527b9d51dc481f3bfec48f995bb52db1f5bbd29021bd7ae3702acc631f918a9f28d2b057a9be96443b78b8a3bb528e57f5314141103b95445d53cf2a41b0744c8a7c3902f2821ac5dc2900aed7d0845824955cad8ea32ff18e7bae27be671f49baa6a4d461ee2170a2136062bc3d24a1e9b670bf45cc3658efebabb0a33a3
http://abiubaidah.com/sorotan-tajam-hukum-perayaan-haul.html/?error_checker=captcha&author_spam=nrbrjqceaps&email_spam=knuotrqavg%40mailermails.info&url_spam=http%3A%2F%2Fpayday1000loans3000online.com%2F%23online-payday-loans-no-credit-check-hak&comment_spam=%3Ca+href%3D%5C%22http%3A%2F%2Fpayday1000loans3000online.com%2F%23online-payday-loans-no-credit-check-kid%5C%22%3Eloans+direct+%3C%2Fa%3E+%5Burl%3Dhttp%3A%2F%2Fpayday1000loans3000online.com%2F%23payday-loans-online-scm%5Dloans+online+%5B%2Furl%5D+%26lt%3Ba+href%3D%26quot%3Bhttp%3A%2F%2Fpayday1000loans3000online.com%2F%23best-online-payday-loans-urg%26quot%3B%26gt%3Bquick+loans+%26lt%3B%2Fa%26gt%3B++http%3A%2F%2Fpayday1000loans3000online.com%2F%23eobfh+http%3A%2F%2Fpayday1000loans3000online.com%2F%23bgykv+http%3A%2F%2Fpayday1000loans3000online.com%2F%23mkeij++http%3A%2F%2Fgz100km.com%2Fbbs%2Fforum.php%3Fmod%3Dviewthread%26tid%3D408268%26extra%3D+http%3A%2F%2Fthg-lu.de%2Fsite-guestbook+http%3A%2F%2Flajaleareal.es%2Fjalea-real-para-ninos-2%2F%23comment-42314+http%3A%2F%2Fstudymba.ru%2Ftema-1%3Fpage%3D1846%23comment-92320+http%3A%2F%2Frammicro300.nikablog.ir%2Fcomment.php%3Fpostid%3D80305%26nc%3D1#error
[url=http://payday1000loans3000online.com/#fast-payday-loans-oyw]payday loan [/url]
<a href="http://payday1000loans3000online.com/#payday-loans-online-no-credit-check-jdw">loans online </a>
http://payday1000loans3000online.com/#aeamh
http://payday1000loans3000online.com/#idluz
http://payday1000loans3000online.com/#xffaa
http://all-castles.com/castles/rossiya/fort-knyaz-menshikov/?c=8585
http://craftmann24.ru/products/%d0%90%d0%ba%d0%ba%d1%83%d0%bc%d1%83%d0%bb%d1%8f%d1%82%d0%be%d1%80%20%d0%b4%d0%bb%d1%8f%20siemens%20m65%20-%20craftmann#comment_78
http://studyhound.com/about/guestbook/
http://www.vileisis.lt/sveciu_knyga.php?lt&messagepage=20058
http://www.mazgan.ru/?act=guestbook
[url=http://payday1000loans3000online.com/#legitimate-payday-loans-online-no-credit-check-ugs]bad credit personal loans [/url]
<a href="http://payday1000loans3000online.com/#payday-loans-near-me-ppj">payday express </a>
http://payday1000loans3000online.com/#oaodi
http://payday1000loans3000online.com/#dbjrm
http://payday1000loans3000online.com/#wtegx
http://www.cyklochlubna.cz/diskuse-1.html
http://www.in2greece.com/greekfood/?page_id=4#comment-11782
http://demo.brandshack.co.za/blog/test-blog-entry-2?page=1904#comment-95264
http://inboundbuddha.com/about-me/?contact-form-id=2&contact-form-sent=18529&_wpnonce=2e9fdc0633
http://www.od5pl.com/agb/index.php?&mots_search=&lang=english&skin=&&seeMess=1&seeNotes=1&seeAdd=0&code_erreur=PoGw5oOel0
[url=http://payday1000loans3000online.com/#ace-payday-loans-bot]payday loans [/url]
<a href="http://payday1000loans3000online.com/#online-payday-loans-pue">payday loan </a>
http://payday1000loans3000online.com/#uwqrk
http://payday1000loans3000online.com/#wbxlt
http://payday1000loans3000online.com/#nuyim
http://www.edelete.org/?usp_redirect=1&success=1&post_id=186304
http://www.datingmadeeasier.com/viewtopic.php?f=5&t=22769&p=55530#p55530
http://www.lietkom.lt/news.php?readmore=3&c_start=31030
http://www.gekon-plzen.cz/vzkazy-a-dotazy?r=1#post-22005
http://www.teloanuncio.es/anuncio.php?a=1706345&comentarioOK=1
[url=http://payday1000loans3000online.com/#payday-loans-for-bad-credit-qtx]loans direct [/url]
<a href="http://payday1000loans3000online.com/#payday-loans-online-same-day-elx">quick loans </a>
http://payday1000loans3000online.com/#wkoan
http://payday1000loans3000online.com/#fknta
http://payday1000loans3000online.com/#hifft
http://insideoutside.london/index.php/home/bathroom/item/4-bathroom-5
http://www.baldupaieska.lt/baldai/lovos/vaikiska-lovyte-0?page=1822#comment-26736
http://www.labquazza.unito.it/eventi/erasmus-intensive-programme-media-and-tv-students-training/
http://ae76lubeinc.com/guestbook/index.php?mode=3&post_id=156348
http://acount.vcp.ir/417994-%d8%ab%d8%a8%d8%aa-%d9%87%d8%a7%db%8c-%d8%ad%d8%b3%d8%a7%d8%a8%d8%af%d8%a7%d8%b1%db%8c/1152935-%d8%ad%d8%b3%d8%a7%d8%a8-%d8%b3%d9%88%d8%af-%d9%88-%d8%b2%db%8c%d8%a7%d9%86.html
[url=http://payday1000loans3000online.com/#no-credit-check-payday-loans-kfu]personal loan [/url]
<a href="http://payday1000loans3000online.com/#same-day-payday-loans-qbz">pay day loans </a>
http://payday1000loans3000online.com/#caoxg
http://payday1000loans3000online.com/#sdwpt
http://payday1000loans3000online.com/#nuoyg
http://uasfcacln.edu20.org/contact_visitor?authenticity_token=%2BMMQXGaOO5SdmPo92rWZYjm7FhRprRgLUdfKGpdQQnk%3D&commit=&content=%3Ca+href%3D%22http%3A%2F%2Fpayday1000loans3000online.com%2F%23best-online-payday-loans-gjn%22%3Eloans+with+bad+credit+%3C%2Fa%3E+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23payday-loans-no-credit-check-hpj+-+cash+advance++%0D%0A%26lt%3Ba+href%3D%26quot%3Bhttp%3A%2F%2Fpayday1000loans3000online.com%2F%23bad-credit-payday-loans-qta%26quot%3B%26gt%3Bonline+loans+%26lt%3B%2Fa%26gt%3B+%0D%0A+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23lbxzn+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23abdxo+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23bovku+%0D%0A+%0D%0Ahttp%3A%2F%2Fwww.vallegarden.se%2Fbrittmarie%2Farticles.php%3Farticle_id%3D302%26c_start%3D61560+%0D%0Ahttp%3A%2F%2Fwww.chiquita.com%2Frecipes%2Fwinter-frozen-chiquita-banana-penguins%3Fpage%3D4983%23comment-254267+%0D%0Ahttp%3A%2F%2Fwww.swey.co.za%2Fnode%2F87%3Fpage%3D1197%23comment-59885+%0D%0Ahttp%3A%2F%2Fwww.fkupesciems.lv%2Fnews.php%3Fid%3D14%23comments+%0D%0Ahttp%3A%2F%2Fwww.gekon-plzen.cz%2Fvzkazy-a-dotazy%3Freplyto%3D1464%26_formData%3Cguest%3E%3DneywvoImmus%26_formData%3Csubject%3E%3D%26_formData%3Ctext%3E%3D%253Ca%2Bhref%253D%2522http%253A%252F%252Fpayday1000loans3000online.com%252F%2523bad-credit-payday-loans-umr%2522%253Eshort%2Bterm%2Bloans%2B%253C%252Fa%253E%2B%250D%250A%255Burl%253Dhttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523payday-loans-near-me-aut%255Dpayday%2Bexpress%2B%255B%252Furl%255D%2B%250D%250A%2526lt%253Ba%2Bhref%253D%2526quot%253Bhttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523bad-credit-personal-loans-not-payday-loans-qth%2526quot%253B%2526gt%253Bloans%2Bonline%2B%2526lt%253B%252Fa%2526gt%253B%2B%250D%250A%2B%250D%250Ahttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523cmexi%2B%250D%250Ahttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523hcxqb%2B%250D%250Ahttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523jcjjp%2B%250D%250A%2B%250D%250Ahttp%253A%252F%252Fextrahealthzone.com%252Fforum%252Findex.php%253Ftopic%253D240529.new%2523new%2B%250D%250Ahttp%253A%252F%252Fwww.calipsocoffee.ru%252Fblog%252Fopinions%252F%2B%250D%250Ahttp%253A%252F%252Fghumoindia.co.in%252Funcategorized%252Fhello-world%252F%2523comment-2431%2B%250D%250Ahttp%253A%252F%252Facademica.ru%252Fcontent%252Fphoto%252F41%252F280%252F%253Fmid%253D34667%2526MID%253D96475%2526result%253Dreply%2523message96475%2B%250D%250Ahttp%253A%252F%252Ftext2music.vcp.ir%252F490800-%2525d8%2525b3%2525d8%2525b1%2525db%25258c%2525d8%2525a7%2525d9%252584-%2525d8%2525a7%2525d9%252581%2525d8%2525b3%2525d8%2525a7%2525d9%252586%2525d9%252587-%2525d8%2525ae%2525d9%252588%2525d8%2525b1%2525d8%2525b4%2525db%25258c%2525d8%2525af-%2525d9%252588-%2525d9%252585%2525d8%2525a7%2525d9%252587%252F1347824-%2525d8%2525af%2525d8%2525a7%2525d9%252586%2525d9%252584%2525d9%252588%2525d8%2525af-%2525d8%2525b3%2525d8%2525b1%2525db%25258c%2525d8%2525a7%2525d9%252584-%2525da%2525a9%2525d8%2525b1%2525d9%252587-%2525d8%2525a7%2525db%25258c-%2525d9%252587%2525d9%252585%2525d8%2525b3%2525d8%2525b1-%2525db%25258c%2525d8%2525a7-%2525d8%2525af%2525d8%2525b1%2525d8%2525af%2525d8%2525b3%2525d8%2525b1-couple-or-trouble-%2525d8%2525a8%2525d8%2525a7-%2525d8%2525b2%2525db%25258c%2525d8%2525b1%2525d9%252586%2525d9%252588%2525db%25258c%2525d8%2525b3-%2525d9%252581%2525d8%2525a7%2525d8%2525b1%2525d8%2525b3%2525db%25258c-%2525d9%252588-%2525d8%2525af%2525d9%252588%2525d8%2525a8%2525d9%252584%2525d9%252587-%2525d9%252581%2525d8%2525a7%2525d8%2525b1%2525d8%2525b3%2525db%25258c.html%26addpost%26r%3D0&email=hdbxlchytp%40mailermails.info&name=nwvukchew&phone=81114732842&subject=zeyh+check+mate+payday+loans+biti&utf8=%26%23x2713%3B
http://www.q-skyr.no/blog/post/43
http://www.deepcarbon.gr/blog/
http://www.atonudine.it/news/eventi/inaugurazione-servizio-di-teleriscaldamento-cinque-scuole-della-citt%C3%A0?page=787#comment-39356
http://dhelyer.bimserver2.com/year3/assignment2/view.php
[url=http://payday1000loans3000online.com/#direct-lender-payday-loans-swu]bad credit personal loans [/url]
<a href="http://payday1000loans3000online.com/#same-day-payday-loans-emk">loans direct </a>
http://payday1000loans3000online.com/#iivcj
http://payday1000loans3000online.com/#zewyn
http://payday1000loans3000online.com/#zaoel
https://www.solsticemoon.us/bin/smf/index.php?topic=890136.new#new
http://www.ae76lubeinc.com/guestbook/index.php?mode=3&post_id=156453
https://www.insuremypath.org/content/titanic?page=104#comment-631257
http://waxsansheeg.com/?p=81892&error_checker=captcha&author_spam=nusbrdfliex&email_spam=kqkdujilba%40mailermails.info&url_spam=http%3A%2F%2Fpayday1000loans3000online.com%2F%23payday-loans-online-leb&comment_spam=%3Ca+href%3D%5C%22http%3A%2F%2Fpayday1000loans3000online.com%2F%23easy-payday-loans-gny%5C%22%3Ebad+credit+personal+loans+%3C%2Fa%3E+http%3A%2F%2Fpayday1000loans3000online.com%2F%23best-payday-loans-qse+-+cash+advance++%26lt%3Ba+href%3D%26quot%3Bhttp%3A%2F%2Fpayday1000loans3000online.com%2F%23direct-lender-payday-loans-mqc%26quot%3B%26gt%3Bcash+loans+%26lt%3B%2Fa%26gt%3B++http%3A%2F%2Fpayday1000loans3000online.com%2F%23mvudn+http%3A%2F%2Fpayday1000loans3000online.com%2F%23rdpah+http%3A%2F%2Fpayday1000loans3000online.com%2F%23jrgtq++http%3A%2F%2Fwww.auntiehelen.co.uk%2Fsix-wheels-in-germany-month-19%2F%3Fcontact-form-id%3Dwidget-text-2%26contact-form-sent%3D462674%26_wpnonce%3D03e6b0ca42+http%3A%2F%2Fpatentworks.info%2Fblogview.php%3Fblgseq%3D1399+http%3A%2F%2Fwww.enkrona.net%2Fimmersiongg.com%2Findex.php%3Fsite%3Dprofile%26id%3D9%26action%3Dguestbook+http%3A%2F%2Fforum.stadetoulousain-cyclisme.fr%2Findex.php%3Ftopic%3D71864.new%23new+http%3A%2F%2Fwww.gate4games.com%2F%3Flvfeedbackreturnmessage%3D2%26lvfeedbackemail%3Dqcocpgkrlb%2540mailmefast.info%26lvfeedbackname%3Diiiqpcom%26lvfeedbackmessage%3Danabolic%2526%252313%253b%2526%252310%253b%2B-%2B%2526lt%253ba%2Bhref%253d%2526quot%253bhttps%253a%252f%252fanabolicsteroidsnpc.com%2526quot%253b%2526gt%253bbuy%2Banabolic%2Bsteroid%2Bonline%2526%252313%253b%2526%252310%253b%2526lt%253b%252fa%2526gt%253b%2B%2526%252313%253b%2526%252310%253bcatabolic%2Bvs%2Banabolic%2526%252313%253b%2526%252310%253b%2B-%2B%2526lt%253ba%2Bhref%253dhttps%253a%252f%252fanabolicsteroidsnpc.com%252f%2526gt%253banabolic%2526%252313%253b%2526%252310%253b%2526lt%253b%252fa%2526gt%253b%26lvFeedbackReturnMessage%3D2%26lvFeedbackEmail%3Dhcpyhrvsdd%2540mailermails.info%26lvFeedbackName%3Dngczvjvob%26lvFeedbackMessage%3D%2526lt%253Ba%2Bhref%253D%2526quot%253Bhttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523easy-payday-loans-ajz%2526quot%253B%2526gt%253Bpayday%2Badvance%2B%2526lt%253B%252Fa%2526gt%253B%2B%2526%252313%253B%2526%252310%253Bhttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523ace-payday-loans-vuw%2B-%2Bshort%2Bterm%2Bloans%2B%2B%2526%252313%253B%2526%252310%253B%2526amp%253Blt%253Ba%2Bhref%253D%2526amp%253Bquot%253Bhttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523payday-loans-online-same-day-qdu%2526amp%253Bquot%253B%2526amp%253Bgt%253Bcash%2Bloans%2B%2526amp%253Blt%253B%252Fa%2526amp%253Bgt%253B%2B%2526%252313%253B%2526%252310%253B%2B%2526%252313%253B%2526%252310%253Bhttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523izjuo%2B%2526%252313%253B%2526%252310%253Bhttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523koezb%2B%2526%252313%253B%2526%252310%253Bhttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523ggsbx%2B%2526%252313%253B%2526%252310%253B%2B%2526%252313%253B%2526%252310%253Bhttp%253A%252F%252Fgopherdailystatics.gamerz.co%252Ftopic572555.html%2B%2526%252313%253B%2526%252310%253Bhttp%253A%252F%252Fforum.remote-backup.com%252Fviewtopic.php%253Ff%253D8%2526amp%253Bt%253D403229%2B%2526%252313%253B%2526%252310%253Bhttp%253A%252F%252Fwww.teamfighters.de%252Findex.php%253Fsite%253Dprofile%2526amp%253Bid%253D28%2526amp%253Baction%253Dguestbook%2B%2526%252313%253B%2526%252310%253Bhttp%253A%252F%252Fhiblueword.com%252Fsunny-leones-latest-ad-manforce-condomlands-trouble%252F%2523comment-129214%2B%2526%252313%253B%2526%252310%253Bhttp%253A%252F%252Fzusklavir.jamu.cz%252Findex.php%253Fp%253Dautorska-dilna%2526amp%253Breplyto%253D23047%2526amp%253B_formData%2526lt%253Bguest%2526gt%253B%253DnqhztbPoede%2526amp%253B_formData%2526lt%253Bsubject%2526gt%253B%253D%2526amp%253B_formData%2526lt%253Btext%2526gt%253B%253D%25253Ca%252Bhref%25253D%252522http%25253A%25252F%25252Fpayday1000loans3000online.com%25252F%252523legitimate-payday-loans-online-no-credit-check-she%252522%25253Epayday%252Bloans%252B%25253C%25252Fa%25253E%252B%25250D%25250A%25255Burl%25253Dhttp%25253A%25252F%25252Fpayday1000loans3000online.com%25252F%252523payday-loans-online-same-day-gof%25255Dpayday%252Badvance%252B%25255B%25252Furl%25255D%252B%25250D%25250A%252526lt%25253Ba%252Bhref%25253D%252526quot%25253Bhttp%25253A%25252F%25252Fpayday1000loans3000online.com%25252F%252523payday-loans-online-no-credit-check-instant-approval-bkb%252526quot%25253B%252526gt%25253Bonline%252Bpayday%252Bloans%252B%252526lt%25253B%25252Fa%252526gt%25253B%252B%25250D%25250A%252B%25250D%25250Ahttp%25253A%25252F%25252Fpayday1000loans3000online.com%25252F%252523hfhnd%252B%25250D%25250Ahttp%25253A%25252F%25252Fpayday1000loans3000online.com%25252F%252523kprfo%252B%25250D%25250Ahttp%25253A%25252F%25252Fpayday1000loans3000online.com%25252F%252523wnaqs%252B%25250D%25250A%252B%25250D%25250Ahttp%25253A%25252F%25252Fwww.temasport.com%25252Finterviews%25252Fview%25252Finterviews%25253A201%252B%25250D%25250Ahttp%25253A%25252F%25252Fwww.fl8090.cc%25252Fforum.php%25253Fmod%25253Dviewthread%252526tid%25253D3287%252526pid%25253D704718%252526page%25253D37%252526extra%25253D%252523pid704718%252B%25250D%25250Ahttp%25253A%25252F%25252Fvlad-bee.ru%25252Fnode%25252F116%252523comment-649409%252B%25250D%25250Ahttp%25253A%25252F%25252Fxxx-sborniki.ru%25252Fproducts%25252F%252525d0%25252592%252525d0%252525ba%252525d1%25252583%252525d1%25252581%252525d0%252525bd%252525d1%2525258b%252525d0%252525b5_%252525d0%2525259f%252525d1%25252583%252525d1%25252585%252525d0%252525bb%252525d1%2525258b%252525d0%252525b5_%252525d0%2525259a%252525d1%25252580%252525d0%252525b0%252525d1%25252581%252525d0%252525b0%252525d0%252525b2%252525d0%252525b8%252525d1%25252586%252525d1%2525258b_14__plumperpasscom_14%252B%25250D%25250Ahttp%25253A%25252F%25252Fhome-fotoclub.cz%25252Fgerber%25252Findex.php%25253Fa%25253Dnabidka%25252Fgerber-bear-grylls-hands-free-torch%252526replyto%25253D14548%252526_formData%25255Bguest%25255D%25253DngvjtnJeort%252526_formData%25255Bsubject%25255D%25253D%252526_formData%25255Btext%25255D%25253D%2525253Ca%25252Bhref%2525253D%25252522http%2525253A%2525252F%2525252Fpayday1000loans3000online.com%2525252F%252525233-month-payday-loans-hjn%25252522%2525253Ecash%25252Badvance%25252B%2525253C%2525252Fa%2525253E%25252B%2525250D%2525250A%2525255Burl%2525253Dhttp%2525253A%2525252F%2525252Fpayday1000loans3000online.com%2525252F%25252523best-online-payday-loans-pqm%2525255Dloans%25252Bfor%25252Bpeople%25252Bwith%25252Bbad%25252Bcredit%25252B%2525255B%2525252Furl%2525255D%25252B%2525250D%2525250A%25252526lt%2525253Ba%25252Bhref%2525253D%25252526quot%2525253Bhttp%2525253A%2525252F%2525252Fpayday1000loans3000online.com%2525252F%25252523no-credit-check-payday-loans-rzz%25252526quot%2525253B%25252526gt%2525253Bpay%25252Bday%25252Bloans%25252B%25252526lt%2525253B%2525252Fa%25252526gt%2525253B%25252B%2525250D%2525250A%25252B%2525250D%2525250Ahttp%2525253A%2525252F%2525252Fpayday1000loans3000online.com%2525252F%25252523adyus%25252B%2525250D%2525250Ahttp%2525253A%2525252F%2525252Fpayday1000loans3000online.com%2525252F%25252523nszdd%25252B%2525250D%2525250Ahttp%2525253A%2525252F%2525252Fpayday1000loans3000online.com%2525252F%25252523zevha%25252B%2525250D%2525250A%25252B%2525250D%2525250Ahttp%2525253A%2525252F%2525252Fxetaijac.com.vn%2525252Fboards%2525252Ftopic%2525252F106324%2525252Fjdbw-get-out-of-payday-loans-tcdr%25252B%2525250D%2525250Ahttp%2525253A%2525252F%2525252Fmikatsu.info%2525252Fproducts%2525252Fdvuhtaktnyj-lodochnyj-motor-m15-fs%25252523comment_1012%25252B%2525250D%2525250Ahttp%2525253A%2525252F%2525252Fwww.fekal.ru%2525252F297.ht%25252B%2525250D%2525250Ahttp%2525253A%2525252F%2525252Fwww.hakodate-gyokyou.jp%2525252Fblogview.php%2525253Fblgseq%2525253D2626%25252B%2525250D%2525250Ahttp%2525253A%2525252F%2525252Fwww.radiomuseum-wertingen.de%2525252Fgaestebuch.php%2525253Fid%2525253De5u99s5j%25252526abuse%2525253D371%252526addpost%252526r%25253D0%2526amp%253Baddpost%2526amp%253Br%253D0#error
http://downloader2000.vcp.ir/0-%25d8%25a8%25d8%25af%25d9%2588%25d9%2586-%25d9%2585%25d9%2588%25d8%25b6%25d9%2588%25d8%25b9/674183-%25d8%25af%25d8%25a7%25d9%2586%25d9%2584%25d9%2588%25d8%25af-%25d9%2581%25db%258c%25d9%2584%25d9%2585-%25d8%25b3%25d9%2587-%25d8%25a8%25d8%25b9%25d8%25af%25db%258c-%25d8%25aa%25d8%25a7%25db%258c%25d8%25aa%25d8%25a7%25d9%2586%25db%258c%25da%25a9-titanic-3d.html
[url=http://payday1000loans3000online.com/#payday-loans-avt]loans online [/url]
<a href="http://payday1000loans3000online.com/#payday-loans-bad-credit-ekh">bad credit personal loans </a>
http://payday1000loans3000online.com/#seeyi
http://payday1000loans3000online.com/#smqyo
http://payday1000loans3000online.com/#ixpxi
http://swportal.ru/node/724/comments#tab
http://www.drsaputo.net/blog/view/dhour#comment-29893
http://drupal.averyhost.com/forum/pg/topicview/misc/general-chat/bhqu-john-oliver-payday/index.php?redirected=1#post_62454
http://yatani.jp/teaching/doku.php?id=hcistats:posthoc#comment_37a6812e764a3416acc0fe6ef14957c6
http://home-fotoclub.cz/gerber/index.php?a=nabidka/gerber-bear-grylls-hands-free-torch&replyto=14548&_formData[guest]=nzauioJeort&_formData[subject]=&_formData[text]=%3Ca+href%3D%22http%3A%2F%2Fpayday1000loans3000online.com%2F%23direct-lender-payday-loans-bac%22%3Epayday+advance+%3C%2Fa%3E+%0D%0A%5Burl%3Dhttp%3A%2F%2Fpayday1000loans3000online.com%2F%23online-payday-loans-no-credit-check-epo%5Dpayday+loans+%5B%2Furl%5D+%0D%0A%26lt%3Ba+href%3D%26quot%3Bhttp%3A%2F%2Fpayday1000loans3000online.com%2F%23payday-loans-zsl%26quot%3B%26gt%3Bloans+direct+%26lt%3B%2Fa%26gt%3B+%0D%0A+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23gnyoo+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23qmjym+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23jgwal+%0D%0A+%0D%0Ahttp%3A%2F%2Fvkusno-legko.com%2Fblog%2Findex.php%3Fpage%3Dpost%26blog%3Divolga%26post_id%3D3%26commentId%3D129715%23129715+%0D%0Ahttp%3A%2F%2Fskyewritercom.com%2Fblog%2F%3Fcontact-form-id%3D3023%26contact-form-sent%3D26370%26_wpnonce%3Dc10fe1c1e9+%0D%0Ahttp%3A%2F%2Fvapila.com.ua%2Fblog%2Fvybor-biksenonovyh-linz%2F%23comment_9952+%0D%0Ahttp%3A%2F%2Fwww.ironboxing.com%2Fhome_article.php%3Fid%3D%26id%3D274+%0D%0Ahttp%3A%2F%2Fwww.volejballokocl.cz%2Findex.php%3Fp%3Ddiskuze%26replyto%3D20257%26_formData%5Bguest%5D%3DnhnljnMat%26_formData%5Bsubject%5D%3D%26_formData%5Btext%5D%3D%253Ca%2Bhref%253D%2522http%253A%252F%252Fpayday1000loans3000online.com%252F%2523bad-credit-personal-loans-not-payday-loans-cpb%2522%253Eloans%2Bfor%2Bpeople%2Bwith%2Bbad%2Bcredit%2B%253C%252Fa%253E%2B%250D%250A%255Burl%253Dhttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523payday-loans-near-me-ogz%255Dpayday%2Badvance%2B%255B%252Furl%255D%2B%250D%250A%2526lt%253Ba%2Bhref%253D%2526quot%253Bhttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523payday-loans-online-same-day-azg%2526quot%253B%2526gt%253Bpayday%2Bloans%2B%2526lt%253B%252Fa%2526gt%253B%2B%250D%250A%2B%250D%250Ahttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523bnjrq%2B%250D%250Ahttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523ppqaw%2B%250D%250Ahttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523ixzqp%2B%250D%250A%2B%250D%250Ahttp%253A%252F%252Fwww.lazarevskaya.ru%252Ffotoreviews%252F11701%252F%2B%250D%250Ahttp%253A%252F%252Fwww.zhao-rong.com%252FGuestBook.asp%2B%250D%250Ahttp%253A%252F%252Fantybariera.pl%252Fcontent%252Fd%2525C5%2525BAwi%2525C4%252599koszczelna-%2525C5%25259Bciana%253Fpage%253D1%2523comment-23505%2B%250D%250Ahttp%253A%252F%252Finjectllc.com%252Findex.php%253Foption%253Dcom_k2%2526view%253Ditemlist%2526task%253Duser%2526id%253D903879%2B%250D%250Ahttp%253A%252F%252Fwww.maternitate-constanta.ro%252Fjurnalul-isis%252Fpost%252Fce-este-un-cpap-si-cand-il-folosim%252F%26addpost%26r%3D0&addpost&r=0
[url=http://payday1000loans3000online.com/#payday-loans-direct-lender-xep]bad credit loans [/url]
<a href="http://payday1000loans3000online.com/#payday-loans-online-hll">loans for people with bad credit </a>
http://payday1000loans3000online.com/#mexqy
http://payday1000loans3000online.com/#qczwl
http://payday1000loans3000online.com/#kggfy
http://ka-s.ru/products/porog-ploschadka-rival-dlya-hyundai-creta-hyundaj-kreta-2016-#comment_10477
http://www.cityvisioninternships.org/org-apply?tfa_next=%2Fforms%2Fview%2F239880%2F32e7bfa58075f0244d3d1fe04f3af9e8%2F92183482%26sid%3Dkhei465j53drgtfl7knhlofmd4
http://olegleonkin.ru/comments#comment-2695
http://community.checkinpro-hotel-software.com/viewtopic.php?f=8&t=572482&p=776459#p776459
http://zusklavir.jamu.cz/index.php?p=autorska-dilna&replyto=33803&_formData[guest]=nxskdkPoede&_formData[subject]=&_formData[text]=%3Ca+href%3D%22http%3A%2F%2Fpayday1000loans3000online.com%2F%23payday-loans-online-same-day-fcc%22%3Ebad+credit+loans+%3C%2Fa%3E+%0D%0A%5Burl%3Dhttp%3A%2F%2Fpayday1000loans3000online.com%2F%23fast-payday-loans-mgd%5Dloans+with+bad+credit+%5B%2Furl%5D+%0D%0A%26lt%3Ba+href%3D%26quot%3Bhttp%3A%2F%2Fpayday1000loans3000online.com%2F%23best-online-payday-loans-ycs%26quot%3B%26gt%3Bloans+direct+%26lt%3B%2Fa%26gt%3B+%0D%0A+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23vpyes+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23ehpbl+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23oigcn+%0D%0A+%0D%0Ahttp%3A%2F%2Fwww.gate-shop.cz%2Fobleceni-sale%3Fre%3D12674%23c31945+%0D%0Ahttp%3A%2F%2Fwww.vallegarden.se%2Fbrittmarie%2Farticles.php%3Farticle_id%3D302%26c_start%3D61640+%0D%0Ahttp%3A%2F%2Ftorkflight.com%2Fguestbook%2Findex.php%3Fmode%3D3%26post_id%3D115299+%0D%0Ahttp%3A%2F%2Fen.ruvsa.com%2Fcatalog%2Fat1000%2Findex.php%3Felement_code%3Dat1000%26mid%3D225397%26ELEMENT_CODE%3Dat1000index.php%253Felement_code%253Dat1000%26MID%3D515038%26result%3Dreply%23message515038+%0D%0Ahttp%3A%2F%2Fwww.volejballokocl.cz%2Findex.php%3Fp%3Ddiskuze%26replyto%3D18935%26_formData%5Bguest%5D%3DnofakfMat%26_formData%5Bsubject%5D%3D%26_formData%5Btext%5D%3D%253Ca%2Bhref%253D%2522http%253A%252F%252Fpayday1000loans3000online.com%252F%2523bad-credit-personal-loans-not-payday-loans-wdo%2522%253Epersonal%2Bloan%2B%253C%252Fa%253E%2B%250D%250A%255Burl%253Dhttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523no-credit-check-payday-loans-swk%255Dpayday%2Bexpress%2B%255B%252Furl%255D%2B%250D%250A%2526lt%253Ba%2Bhref%253D%2526quot%253Bhttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523online-payday-loans-xrr%2526quot%253B%2526gt%253Bloans%2Bfor%2Bbad%2Bcredit%2B%2526lt%253B%252Fa%2526gt%253B%2B%250D%250A%2B%250D%250Ahttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523lkirp%2B%250D%250Ahttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523tpzsi%2B%250D%250Ahttp%253A%252F%252Fpayday1000loans3000online.com%252F%2523zhjeq%2B%250D%250A%2B%250D%250Ahttp%253A%252F%252Fwww.romavisibile.it%252Fforum%252Fshowthread.php%253Fp%253D709076%2523post709076%2B%250D%250Ahttp%253A%252F%252Flibrary.iv-fr.net%252F2007%252F11%252F21%252Fartjur_rembo__moja_ciganerja.html%2B%250D%250Ahttp%253A%252F%252Fwww.sacopulos.com%252F2012%252F04%252F18%252Fjurors-facebook-post-creates-new-medical-malpractice-trial%252F%253Fcontact-form-id%253D295%2526contact-form-sent%253D27202%2526_wpnonce%253Da21ebedc50%2B%250D%250Ahttp%253A%252F%252Fwww.avaritionxxlversiongaming.de%252Fnews%252Findex.php%253Faction%253Dshow%2526id%253D2%2B%250D%250Ahttp%253A%252F%252Fwww.jsadr.org.cn%252Fapplication%252Freview.asp%253Fdocsid%253D9181%26addpost%26r%3D0&addpost&r=0
[url=http://payday1000loans3000online.com/#payday-loans-qmb]bad credit loans [/url]
<a href="http://payday1000loans3000online.com/#payday-loans-no-credit-check-uko">loans direct </a>
http://payday1000loans3000online.com/#stwri
http://payday1000loans3000online.com/#lhvfs
http://payday1000loans3000online.com/#visck
http://sigarette.ru/products/zazhigalka-zippo-200hd-h252/#comment_10128
http://visityakutia.com/yakutsk-oymyakon-travel-winter-coldest-inhabited-place-in-the-world-extreme-weather-tourism-siberia-russia/?contact-form-id=259&contact-form-sent=7265&_wpnonce=15fe1ea14d
http://www.kdmain.co.kr/bbs/view.php?id=board&page=1&page_num=10&select_arrange=headnum&desc=&sn=off&ss=on&sc=on&keyword=&no=1&category=
http://essentiality.forum.0u.ro/
http://www.wetter-mitterlabill.at/guestbook/index.php?&mots_search=&lang=german&skin=&&seeMess=1&seeNotes=1&seeAdd=0&code_erreur=1DDffw10G9
[url=http://payday1000loans3000online.com/#payday-loans-online-biu]personal loans [/url]
<a href="http://payday1000loans3000online.com/#online-payday-loans-direct-lenders-rru">payday loans online </a>
http://payday1000loans3000online.com/#siydi
http://payday1000loans3000online.com/#vwfjx
http://payday1000loans3000online.com/#sgrzs
http://promhouse.ru/forum/viewtopic.php?f=5&t=319&p=10135#p10135
http://vigodney.net/products/the-north-face-40l#comment_423
http://www.deuteren.nl/www.kweekbak.nl#comment-69062
http://forum.wikstrom.de/viewtopic.php?p=1016969#1016969
http://used.mobileprice.pk/lg-gs-106-for-sale.html
[url=http://payday1000loans3000online.com/#payday-loans-online-no-credit-check-qxo]online loans [/url]
<a href="http://payday1000loans3000online.com/#payday-loans-bad-credit-hyz">quick loans </a>
http://payday1000loans3000online.com/#mtgnk
http://payday1000loans3000online.com/#mrufz
http://payday1000loans3000online.com/#zativ
http://brasildownload.com.br/dll-suite-crack-serial/#comment-132816
http://aerio-indonesia.com/forum/viewtopic.php?f=19&t=43&p=120035#p120035
http://site.novaya-shkola.su/users/nkyjqxFak
http://www.futbolitobimbo.com.mx/node/25?page=1#comment-100
http://breakfast-and-cafe.gportal.hu/gindex.php?pg=36465016&badcaptcha=true&pageno=1&postid=1179192&cmd=inscomment&commentname=nagmgcamist&commentemail=zyjaafayqw%40mailermails.info&commenttext=%3Ca+href%3D%22http%3A%2F%2Fpayday1000loans3000online.com%2F%23payday-loans-bad-credit-bki%22%3Epersonal+loans+%3C%2Fa%3E+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23payday-loans-near-me-zcv+-+online+payday+loans++%0D%0A%26lt%3Ba+href%3D%26quot%3Bhttp%3A%2F%2Fpayday1000loans3000online.com%2F%23payday-loans-online-no-credit-check-ied%26quot%3B%26gt%3Bcash+loans+%26lt%3B%2Fa%26gt%3B+%0D%0A+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23uzphe+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23jbwyw+%0D%0Ahttp%3A%2F%2Fpayday1000loans3000online.com%2F%23vipes+%0D%0A+%0D%0Ahttp%3A%2F%2Fmobility-corp.com%2Findex.php%2Fcomponent%2Fusers%2F%3Foption%3Dcom_k2%26view%3Ditemlist%26task%3Duser%26id%3D1032923+%0D%0Ahttp%3A%2F%2Fembawood.org.ua%2Fproducts%2Fkomod_praga_w_898%2F%23comment_10603+%0D%0Ahttp%3A%2F%2Fwww.improvingoutcomes.net%2Fpage8.php%3Fpost%3D2%26messagepage%3D77+%0D%0Ahttp%3A%2F%2Fwww.notredamecollege.edu%2Falumni%2Fblog%2Fdo-you-have-question-0%3Fpage%3D888%23comment-159341+%0D%0Ahttp%3A%2F%2Fleclosdecachadar.com%2Flivredor%2Findex.php%3F%26mots_search%3D%26lang%3Dfrancais%26skin%3D%26%26seeMess%3D1%26seeNotes%3D1%26seeAdd%3D0%26code_erreur%3D56cvolv34s#comment_1179192_List
[url=http://payday1000loans3000online.com/#no-credit-check-payday-loans-nms]payday loans [/url]
<a href="http://payday1000loans3000online.com/#payday-loans-online-no-credit-check-avr">payday express </a>
http://payday1000loans3000online.com/#gghsj
http://payday1000loans3000online.com/#kroax
http://payday1000loans3000online.com/#iprbq
http://forums.letsmaketech.com/viewtopic.php?f=10&t=12951&p=39832#p39832
http://forum.skpb.lublin.pl/viewtopic.php?p=124878#124878
http://plugplayer.com/forum/viewtopic.php?f=6&t=8118
http://oka.moscow/wr-board_1.5_lux/index.php?fid=24&id=249817
http://broadwayzabreh.cz/kniha.php?odpoved=44376&jmeno=background-check-for-free%20&button=0
https://amazonegiftcardcheap.wordpress.com
The promotion will last until July 31, 2017. After July 31, the price will be $ 1000
https://amazonegiftcardcheap.wordpress.com
http://www.isabellabrancolini.it/700-adidas-los-angeles-2015.php
http://www.ezquote.it/856-zx-flux-tramonto.asp
http://www.agriturismo-a-firenze.it/993-converse-muffin-shop.php
http://www.digitalspot.it/salomon-contagrip-491.php
http://www.casanordest.it/719-vans-basse.html
[url=http://www.garim.it/roshe-run-limited-300.asp]Roshe Run Limited[/url]
[url=http://www.pistoiainrete.it/air-max-1-ultra-moire-print-430.html]Air Max 1 Ultra Moire Print[/url]
[url=http://www.fabulatia.it/567-oakley-flight-deck-prizm.htm]Oakley Flight Deck Prizm[/url]
[url=http://www.garim.it/roshe-run-gold-828.asp]Roshe Run Gold[/url]
[url=http://www.ilcastellodifulignano.it/sandali-jimmy-choo-outlet-297.php]Sandali Jimmy Choo Outlet[/url]
http://www.sarbot-team.es/226-camisa-polo-gris.php
http://www.renardlecoq.nl/859-nike-sneakers-grey.html
http://www.theloanarrangers.co.uk/adidas-ultra-boost-uncaged-ebay-126.php
http://www.familycord.es/808-clarks-desert-boots-gore-tex.html
http://www.free-nokia-ringtones-now.co.uk/adidas-nmd-grey-and-purple-074.html
[url=http://www.ugtrepsol.es/louboutin-for-men-155.php]Louboutin Men[/url]
[url=http://www.wervjournaal.nl/424-hugo-boss-schoenen-prijs.html]Hugo Boss Schoenen Prijs[/url]
[url=http://www.4chat.nl/asics-fitness-schoen-620.html]Asics Fitness Schoen[/url]
[url=http://www.tr-online.nl/995-adidas-zx-flux-torsion.php]Adidas Flux[/url]
[url=http://www.fawdingtonbmw.co.uk/706-adidas-gazelle-og-all-black.html]Adidas Gazelle Og All Black[/url]
Beware products WITHOUT an AHRI Certified mark. [url=https://marcelinotruman.tumblr.com]Air Conditioning Repair 24 Hour [/url] From past experiance some engineers think if the access port is not on the service valve on the front of the unit then i doesnt have one!
Visit WebMD on Facebook. Tip: Take a quick digital photo of the wires before disconnecting them so you know where to replace them. <a href="https://marcelinotruman.tumblr.com">https://marcelinotruman.tumblr.com </a> This is because we will be tuning up the heating system and we cannot perform the necessary steps in the heat of the summer.
for black ladies seem all-natural usually are not a breeze to find these days. Most women are in fact combating again with baldness that is brought on because of later years, cancers [url=http://hairextensionstapein.net/]Human Hair Extensions[/url]
or tension. Hair pieces are manufactured by distinct businesses around the world only couple of search normal and true.
You can use a lot of considerations with regard to black girls to get the appropriate and the [url=http://wigsnm.com/]Wigs[/url]
best wig to wear. Should you be considering to obtain one particular for yourself, you must decide initial the issues behind [url=http://halohair-extensions.com/]Clip In Hair Extensions[/url]
the idea, whether will it be for every day utilize or perhaps is it simply for [url=http://ebonylineswigs.com/]Wigs For Women[/url]
manner.
There are lots of head of hair hairpiece kinds that are offered to suit your needs through online stores. One of many perfect [url=http://wigsforblackowomen.com/]Wigs[/url]
wig types in your case is but one that's made of human hair.
is because of well-known developments arranged through stars for doing that [url=http://humanhairwigst.com/]Wigs[/url] celeb look.
Many women who're fans [url=http://africanamericanswigs.com/]Wigs[/url]
associated with celebs want to imitate that very same style nevertheless at a reasonable cost. This particular type of hair and type is inspired from the stars.
Nevertheless, that isn't the sole purpose [url=http://wigsforblackswomen.com/]Wigs For Black Women[/url] they have become so popular. Pertaining to stars and people who are certainly not celebrities, wearing design for ribbons the front hair pieces with regard to african american females is simply a few ease since they are easy to use, an easy task to lift off and simple [url=http://wigsfor-women.us/]Wigs[/url] to keep up. These kinds of hair pieces aren't as distressing since employing extensions and give your false impression the tresses are really increasing [url=http://wigsforwomenm.com/]Wigs[/url]
from the actual remaining hair.
[url=http://fly-bra-bay.ru/silikonoviy-lifchik.html][img]http://fly-bra-bay.ru/flybra-video2.jpg[/img][/url]
Бюстгалтер-невидимка Флай Бра – революционное изобретение, пришедшее женщинам на помощь! Мягкий, естественный, многоразового использования, легко моющийся, без бретелек, с открытой спиной!
Это изобретение японских специалистов отвечает многим женским запросам, помогает выглядеть раскованно и уверенно! Шнуровка между чашечками позволяет придать груди более пышную форму, создавая "ложбинку" или эффект "приподнятой груди".
Читать полностью на [url=http://fly-bra-bay.ru]fly-bra-bay.ru[/url]
Доставка [url=http://sankt-peterburg.fly-bra-bay.ru/]Fly Bra Санкт-Петербург[/url] и по всей России!
http://fly-bra-bay.ru/silikonoviy-byustgalter-bez-lyamok.html
<a href="http://fly-bra-bay.ru/silikonoviy-lifchik-bez-bretelek.html">силиконовый лифчик без бретелек</a>
[url=http://payday1000loans3000online.com]payday loan [/url]
<a href="http://payday1000loans3000online.com">online loans </a>
http://payday1000loans3000online.com/#vjywe
http://payday1000loans3000online.com/#mytla
http://payday1000loans3000online.com/#jfyff
http://ecumedufer.free.fr/index.php?option=com_easybook&view=easybook
http://justacowboyassociation.com/community/main-forum/the-turn-bad-credit-loans-instincts-bad-credit-loans-anaemia-malaise-miniaturized-powers/#post-37788
http://pkgbi.ru/izdeliya/bruschatka-gb#comment-296851
http://egolex.ru/index.php/component/k2/item/2-many-web-sites-still-in-their-infancy-versions-have-evolved-over-the-years
http://esimat95.ru/news?act=post&id=30
hair. Before installing the lace wig, you will need to condition and wash your own hair. To help keep your locks healthy and head from [url=http://wigsforblackwomen.org/]Wigs[/url]
itching, a great clean and serious conditioner are proposed. Make sure the head of hair is totally free of moisture and hydrated. A trim is also encouraged if you have damaged hair or split ends. One of many principal good reasons to [url=http://wigshforwomen.com/]Wigs For Women[/url]
put on a lace wig is encourage healthy hair although having versatility.
Soon after cleaning your hair and doing any of the advised locks treatments, you may have 2 options. Some ladies choose to use a pores and skin [url=http://wigsfor-women.com/]Wigs For Women[/url]
toned wig cover beneath the lace wig for additional security while others just brush their head of hair back and then use. If you wish to wear the wig cap be sure that it complements your skin layer tone. You may braid the hair below the limit or maybe wrap it.
A wonderful idea to produce a more reasonable looking scalp is to apply Ace bandage. Ace bandage is definitely a [url=http://wigsxz.com/]Wigs For Women[/url]
low-cost sporting bandage for muscle mass personal injuries which can be acquired on your neighborhood drugstore. It clings to alone so no stick or tape is applied for your hair or scalp. The feel in the bandage offers a bumpy appearance which copies the head physical appearance below the lace front wig. It merely [url=http://wigswomenfor.com/]Wigs[/url]
has to be packaged round the go sometimes on top of an ordinary wig limit or directly to your hair. Make sure you cleanse your hair line with rubbing alcohol and let it free of moisture completely.
[url=http://perm.bentley-mulliner.ru/bentley-mulliner-chasi-perm.html][img]http://bentley-mulliner.ru/bentley-mulliner.jpg[/img][/url]
ЧАСЫ BREITLING FOR BENTLEY «МИЛЛИОНЕР»
Это нечто большее, чем просто часы, это шедевры высокого часового искусства, которое зародилось в прекрасной Бельгии. Возьмите с собой часы BREITLING на деловую встречу, занятия спортом, на отдых или просто носите их в повседневной жизни и они будут дарить Вам только приятные эмоции, восхищения со стороны женщин и уважение со стороны мужчин! Олицетворение статуса и успеха, чувства стиля и вкуса, оригинальности и самодостаточности. Определённо, BREITLING — часы с Мужским характером!
Читать полностью на [url=http://bentley-mulliner.ru]bentley-mulliner.ru[/url]
Доставка [url=http://kemerovo.bentley-mulliner.ru/]Часы Breitling Кемерово[/url] и по всей России!
http://kazan.bentley-mulliner.ru/bentley-mulliner-tourbillon-kazan.html
<a href="http://ekaterinburg.bentley-mulliner.ru/bentley-mulliner-chasi-ekaterinburg.html">bentley mulliner часы</a>
http://www.blackhorsesv.it/678-adidas-neo-bianche-e-blu.html
http://www.menteprofonda.it/stivali-tods-256.htm
http://www.ezquote.it/694-adidas-yeezy-boost-350-blu.asp
http://www.pixelgenic.it/scarpe-vans-inverno-773.html
http://www.claudiorussofotografo.it/892-nike-air-max-90-nere-e-rosse.htm
[url=http://www.notcom.it/592-nike-free-run-gialle.html]Nike Free Run Gialle[/url]
[url=http://www.pixelgenic.it/scarpe-saucony-uomo-in-offerta-702.html]Scarpe Saucony Uomo In Offerta[/url]
[url=http://www.grrg.it/scarpe-tacco-economiche-483.asp]Scarpe Tacco Economiche[/url]
[url=http://www.blackhorsesv.it/886-adidas-la-trainer-nere.html]Adidas La Trainer Nere[/url]
[url=http://www.relaisposillipo.it/air-force-scarpe-modello-nuovo-236.asp]Air Force Scarpe Modello Nuovo[/url]
http://www.palisso.fr/563-chaussure-running-new-balance.html
http://www.amomu.fr/beats-solo-hd-prix-085.html
http://www.english-food.fr/nike-air-max-90-rouge-pas-cher-362.php
http://www.citesket.fr/adidas-femme-pas-cher-ballerines-713.html
http://www.esthetique-line.ch/nike-roshe-run-pas-cher-suisse-632.php
[url=http://www.pieces-center.fr/stan-smith-or-croco-580.php]Stan Smith Or Croco[/url]
[url=http://www.chokoloskee.fr/chaussure-lacoste-toile-homme-085.php]Chaussure Lacoste Toile Homme[/url]
[url=http://www.msie25.fr/415-converse-basse-grise.html]Converse Basse Grise[/url]
[url=http://www.msie25.fr/963-converse-ete-homme.html]Converse Ete Homme[/url]
[url=http://www.allo-paella-traiteur.fr/prix-longchamp-suisse-136.htm]Prix Longchamp Suisse[/url]
As stated at the outset of the article, the getaway is among the finest parts of having a wedding. It's the time you get to blowing wind lower, and ultimately relax from all of the crazy wedding event planning that has been jogging your life. Hopefully this information has offered you some excellent honeymoon suggestions to assist you kick-off your life with each other as a wedded pair.Setting up To Accept Initially Steps On Your Exercise Journey
[img]http://www.notcom.it/images/notcom/2856-nike-free-run-2-ext.jpg[/img]
Lower back pain could be debilitating, each actually and also sentimentally. Yoga has become turned out to lessen soreness, usage of ache medicine, and impairment. Yoga exercise develops mobility and energy, creating stability in the body. If the system is out of stability, pain is the final result.
[img]http://www.starlightmusic.it/images/airjordan/10927-jordan-spizike-red.jpg[/img]
http://www.blackbox-online.it/599-nike-blazer-militare-uomo.htm
http://www.studiolafratta.it/566-scarpe-stan-smith-rosa.htm
http://www.immobiliaremacchione.it/713-nike-presto-kid.htm
http://www.nolven.it/superstar-adidas-verdi-851.php
http://www.nuovageovis.it/752-scarpe-skechers-trovaprezzi.htm
[url=http://www.118messina.it/229-adidas-gloro-calcio.html]Adidas Gloro Calcio[/url]
[url=http://www.unionfotocenter.it/076-prada-scarpe-primavera-estate-2017.html]Prada Scarpe Primavera Estate 2017[/url]
[url=http://www.longchampaliexpress.fr/longchamp-sac-pliage-cuir Longchamp Sac Pliage Cuir[/url]
[url=http://www.nolven.it/adidas-superstar-80s-metallic-pack-549.php]Adidas Superstar 80s Metallic Pack[/url]
[url=http://www.studiolafratta.it/658-stan-smith-zebra-italia.htm]Stan Smith Zebra Italia[/url]
http://www.corsica-seniors.fr/chaussures-versace-pour-femme-474.html
http://www.lyoncentre.fr/404-nike-air-max-flyknit-femme-pas-cher.html
http://www.domisens-services.fr/nike-blazer-basse-noir-765.php
http://www.full-web.fr/palladium-femme-gris-lavé-079.html
http://www.lyceerenedescartes77.fr/508-huarache-verte.html
[url=http://www.treguier-immobilier.fr/chaussure-a-talon-compensé-basket-pas-cher-908.html]Chaussure A Talon Compensé Basket Pas Cher[/url]
[url=http://www.roco-schweiz.ch/new-balance-u420-noir-homme-790.html]New Balance U420 Noir Homme[/url]
[url=http://www.fort-placement.fr/570-chaussures-christian-louboutin-prix.php]Chaussures Christian Louboutin Prix[/url]
[url=http://www.wiime.fr/saucony-kinvara-3-000.html]Saucony Kinvara 3[/url]
[url=http://www.icaformation.fr/969-puma-heart-patent-taille-37.htm]Puma Heart Patent Taille 37[/url]
http://www.oecc.fr/converse-taille-20-134.html
http://www.treguier-immobilier.fr/valentino-auto-basket-523.html
http://www.denishirst.fr/adidas-tubular-femme-kaki-341.html
http://www.iloveshoes.fr/nike-running-rose-027.html
http://www.soc16.fr/chaussures-hommes-dolce-gabbana-pas-cher-304.asp
[url=http://www.trioelegiaque.fr/adidas-zx-700-moins-cher-257.html]Adidas Zx 700 Moins Cher[/url]
[url=http://www.cheko.ch/nike-presto-schwarz-rot]Nike Presto Schwarz Rot[/url]
[url=http://www.openmindmedien.ch/nike-online-shop-outlet]Nike Online Shop Outlet[/url]
[url=http://www.gamick.fr/new-balance-marron-homme-390.html]New Balance Marron Homme[/url]
[url=http://www.soc16.fr/burberry-bottes-pas-cher-331.asp]Burberry Bottes Pas Cher[/url]
http://www.bareddu.it/michael-kors-giallo-500.php
http://www.nolven.it/superstar-adidas-colorate-rosse-193.php
http://www.118messina.it/285-superfly-nike.html
http://www.historiography.it/scarpe-lacoste-uomo-alte-997.html
http://www.firenzerestauro.it/nike-free-rn-vs-motion-176.php
[url=http://www.notcom.it/942-nike-free-3.0-v4-pink-flash-volt.html]Nike Free 3.0 V4 Pink Flash Volt[/url]
[url=http://www.cosebuonedicampagna.it/ray-ban-nuovi-modelli-2016-109.html]Ray Ban Nuovi Modelli 2016[/url]
[url=http://www.fistofthenorthstar.it/485-nike-sb-janoski-max.html]Nike Sb Janoski Max[/url]
[url=http://www.pixelgenic.it/vans-ragazza-alte-043.html]Vans Ragazza Alte[/url]
[url=http://www.bottega-del-legno.it/608-golden-goose-superstar-offerte.htm]Golden Goose Superstar Offerte[/url]
http://www.icaformation.fr/842-puma-rihanna-beige.htm
http://www.fleurs-lille.fr/hermes-ceinture-star-037.php
http://www.demandezleprogramme.fr/804-air-force-kaki-daim.html
http://www.roco-schweiz.ch/converse-kaki-homme-826.html
http://www.dojodulac.fr/asics-gel-kayano-black-094.html
[url=http://www.negativ-positiv.ch/longchamp-le-pliage-schwarz-l-801.htm]Longchamp Le Pliage Schwarz L[/url]
[url=http://www.treguier-immobilier.fr/chaussures-giuseppe-zanotti-homme-pas-cher-180.html]Chaussures Giuseppe Zanotti Homme Pas Cher[/url]
[url=http://www.izi-form.fr/tiffany-paris-124.htm]Tiffany Paris[/url]
[url=http://www.english-food.fr/air-max-thea-bordeaux-et-blanc-761.php]Air Max Thea Bordeaux Et Blanc[/url]
[url=http://www.english-food.fr/basket-nike-air-max-1-497.php]Basket Nike Air Max 1[/url]
Obtain a health club registration or invest in house exercise routine products. A lot of people learn that training is the simplest way to allow them to avoid yearnings. This will likely only be right for you when you have a workout alternative that is as quickly available as tobacco cigarettes, consequently, enrolling in a fitness center or obtaining a treadmill machine.
[img]https://www.home-avenue.fr/images/homeavenuefr/29286-chaussures-dolce-gabbana-pas-cher-pour-homme.jpg[/img]
Individuals worldwide smoke, and other people worldwide want to find out how you can stop smoking too. When you are one of the many but haven't nevertheless then you can certainly acquire demand and direct the way in which in the direction of stopping smoking and set up an example for all to follow along with.
[img]https://www.apo-calypse.ch/images/apo-calypse/5671-adidas-la-trainer-2-homme.jpg[/img]
Should your doctor prescribes antidepressants to help remedy your despression symptoms, make sure to consider the medication as approved. Usually do not acquire pretty much compared to what your physician tells you to adopt, and never quit taking the medicine without talking to your physician as this can be risky. Commonly it really is essential to little by little wean individuals off of anti-depressants stopping them suddenly can have bad effects.
[img]https://www.oecc.fr/images/reebok/43-converse-all-star-femme-promo.jpg[/img]
Get more than one health-related view. Diverse medical doctors handle distinct situations differently. A single doctor may possibly recommend nervousness medicine, when yet another may only advocate treatment method. Get a couple of view about what you can do to enable you to conquer your anxiousness, and ensure you are aware of all of the options available.
[img]https://www.amomu.fr/images/jewelryfr/11560-perles-pandora-argent.jpg[/img]
http://www.historiography.it/scarpe-golden-goose-prezzo-847.html
http://www.socnavalepisa.it/393-puma-velvet-zalando.html
http://www.ttwater.it/425-puma-rosa-cipria.asp
http://www.ilcastellodifulignano.it/manolo-blahnik-napoli-284.php
http://www.happycentre.it/972-gucci-cinture-uomo-2014.htm
[url=http://www.sancolombanocalcio.it/adidas-zx-700-beige-black-turquoise-802.htm]Adidas Zx 700 Beige Black Turquoise[/url]
[url=http://www.rifugioparcodeltadelpo.it/nike-blu-uomo-697.htm]Nike Blu Uomo[/url]
[url=http://www.cosebuonedicampagna.it/ray-ban-da-sole-872.html]Ray Ban Da Sole[/url]
[url=http://www.agriturismo-a-firenze.it/584-converse-all-star-alte-nere.php]Converse All Star Alte Nere[/url]
[url=http://www.ezquote.it/028-yeezy-boost-350-nere.asp]Yeezy Boost 350 Nere[/url]
http://www.soc16.fr/caterpillar-boots-colorado-071.asp
http://www.nopeg.fr/561-nike-cortez-en-solde.html
http://www.auberge-bourguignonne.fr/valentino-femme-chaussures-618.html
http://www.newswindow.ch/adidas-tubular-amazon-866.html
http://www.iloveshoes.fr/nike-2016-air-max-one-858.html
[url=http://www.iloveshoes.fr/basket-nike-blanche-fille-698.html]Basket Nike Blanche Fille[/url]
[url=http://www.full-web.fr/mizuno-wave-creation-13-femme-065.html]Mizuno Wave Creation 13 Femme[/url]
[url=http://www.alex-flor-fleuriste.fr/oakley-lunettes-bruxelles-732.html]Oakley Lunettes Bruxelles[/url]
[url=http://www.allo-paella-traiteur.fr/michael-kors-sac-matelasse-722.htm]Michael Kors Sac Matelasse[/url]
[url=http://www.wiime.fr/supra-skytop-noir-blanc-283.html]Supra Skytop Noir Blanc[/url]
http://www.trocacenter.fr/nike-air-force-1-blanc-femme-pas-cher-887.php
http://www.pennywise.fr/vans-old-skool-rouge-648.php
http://www.dojodulac.fr/vans-old-skool-wool-pack-885.html
http://www.bluerennes.fr/318-basket-pas-cher-nike-air-max-95.php
http://www.tribal-art.ch/abercrombie-shop-schweiz-490.php
[url=http://www.pieces-center.fr/adidas-superstar-femme-537.php]Adidas Superstar Femme[/url]
[url=http://www.bluerennes.fr/726-air-max-2015-noir-et-gris.php]Air Max 2015 Noir Et Gris[/url]
[url=http://www.lacharlyberard.fr/roshe-run-toute-noire-homme-232.php]Roshe Run Toute Noire Homme[/url]
[url=http://www.lerevedaglaee.fr/air-max-2016-pour-femme-198.htm]Air Max 2016 Pour Femme[/url]
[url=http://www.hd3d.fr/nike-huarache-retro-802.html]Nike Huarache Retro[/url]
http://www.sancolombanocalcio.it/adidas-stan-smith-bianco-rosso-746.htm
http://www.agriturlasabbionara.it/234-scarpe-air-jordan-retro-3.htm
http://www.ezquote.it/462-adidas-tubular-doom-grigie.asp
http://www.blackhorsesv.it/903-nmd-adidas-kl.html
http://www.blackhorsesv.it/720-adidas-nmd-tokyo.html
[url=http://www.118messina.it/350-nike-magista-flyknit.html]Nike Magista Flyknit[/url]
[url=http://www.fistofthenorthstar.it/256-nike-janoski-canvas-obsidian.html]Nike Janoski Canvas Obsidian[/url]
[url=http://www.tecnotelservice.it/134-air-max-rosa-2013.asp]Air Max Rosa 2013[/url]
[url=http://www.piccolaumbria.it/nike-mercurial-superfly-da-calcetto-713.php]Nike Mercurial Superfly Da Calcetto[/url]
[url=http://www.casanordest.it/903-reebok-prezzo.html]Reebok Prezzo[/url]
http://www.auto-loisirs.fr/yeezy-boost-350-creme-667.php
http://www.citesket.fr/adidas-la-trainer-ii-pas-cher-012.html
http://www.full-web.fr/mbt-chaussure-femme-721.html
http://www.treguier-immobilier.fr/escarpins-petit-talon-noir-657.html
http://www.scootracer.fr/adidas-gazelle-2-femme-933.htm
[url=http://www.sebastienmagro.fr/chaussure-adidas-multicolore-670.html]Chaussure Adidas Multicolore[/url]
[url=http://www.english-food.fr/air-max-commando-216.php]Air Max Commando[/url]
[url=http://www.domisens-services.fr/cortez-nike-blanche-et-noir-034.php]Cortez Nike Blanche Et Noir[/url]
[url=http://www.wiime.fr/supra-baskets-assault-noir-et-rouge-750.html]Supra Baskets Assault Noir Et Rouge[/url]
[url=http://www.lerevedaglaee.fr/nike-air-max-95-pas-cher-homme-879.htm]Nike Air Max 95 Pas Cher Homme[/url]
[url=http://www.dom-48.ru/nokia-6700][img]http://dom-48.ru/nokia-6700/video.jpg[/img][/url]
Телефоны Nokia 6700 Gold оснащены тремя протоколами для отправки и принятия электронных писем.
Если говорить конкретнее, то это IMAP4, POP3 и SMTP. Возможностей коммуникации тут не так много.
Для передачи файлов беспроводным путем (после сопряжения с соответствующим устройством) предусмотрен модуль “Блютуз” версии 2.1. Да, скорость передачи будет не настолько высокой, чтобы чем-то можно было хвастаться, да и беспроводную гарнитуру подключить не получится из-за отсутствия профиля A2D2. Но в целом модуль справляется с основными поставленными перед ним задачами.
Читать полностью [url=http://www.dom-48.ru/nokia-6700/]купить nokia 6700 оригинал[/url]
http://dom-48.ru/nokia-6700/
<a href="http://dom-48.ru/nokia-6700/">телефон нокия 6700 оригинал</a>
[url=http://dom-48.ru/detskie-3D-rjukzaki/][img]http://dom-48.ru/detskie-3D-rjukzaki/video.jpg[/img][/url]
Телефоны Nokia 6700 Gold оснащены тремя протоколами для отправки и принятия электронных писем.
Если говорить конкретнее, то это IMAP4, POP3 и SMTP. Возможностей коммуникации тут не так много.
Для передачи файлов беспроводным путем (после сопряжения с соответствующим устройством) предусмотрен модуль “Блютуз” версии 2.1. Да, скорость передачи будет не настолько высокой, чтобы чем-то можно было хвастаться, да и беспроводную гарнитуру подключить не получится из-за отсутствия профиля A2D2. Но в целом модуль справляется с основными поставленными перед ним задачами.
Читать полностью [url=http://www.dom-48.ru/detskie-3D-rjukzaki]рюкзаки nohoo[/url]
http://www.dom-48.ru/detskie-3D-rjukzaki
<a href="http://dom-48.ru/detskie-3D-rjukzaki/">nohoo купить</a>
To learn video game play in shooter games, grasp your weaponry. Know almost everything you need to know about every tool fashion within the video game. Every single tool does really well in certain approaches, but tumbles quick in others. When you are aware the pluses and minuses of each tool, they are utilized to full benefit.
[img]https://www.galarestaurant.es/images/galarestaurant/23085-lentes-ray-ban-wayfarer-mercadolibre-venezuela.jpg[/img]
After a while, baldness can be something that in a natural way occurs. Sometimes it is based upon your genetic makeup or how you will look after your own hair. Making use of the ideas offered in the post previously mentioned it will be easy to have control over hairloss. The following tips will also help you prevent hairloss.Simple And Successful Advice To Assist You To With Preparing food
[img]https://www.luisseijas.es/images/freeroshe-2pics/17570-nike-roshe-vs-adidas-superstar.jpg[/img]
http://roomidecor.com/dorm-room/girly-dorm-rooms http://roomidecor.com/dining-room/zebra-print-dining-room-chairs
[url=http://roomidecor.com/kitchen/design-your-kitchen-online-for-free]design your kitchen online for free[/url]
http://roomdecor.pw/dorm-room/cool-dorm-room-things.html http://roomdecor.pw/dining-room/country-dining-rooms.html
[url=http://roomdecor.pw/wall-decor/looney-tunes-wall-decor.html]looney tunes wall decor[/url]
Телефоны Nokia 6700 Gold оснащены тремя протоколами для отправки и принятия электронных писем.
Если говорить конкретнее, то это IMAP4, POP3 и SMTP. Возможностей коммуникации тут не так много.
Для передачи файлов беспроводным путем (после сопряжения с соответствующим устройством) предусмотрен модуль “Блютуз” версии 2.1. Да, скорость передачи будет не настолько высокой, чтобы чем-то можно было хвастаться, да и беспроводную гарнитуру подключить не получится из-за отсутствия профиля A2D2. Но в целом модуль справляется с основными поставленными перед ним задачами.
Читать полностью [url=][/url]
[url=http://dom-48.ru/rukzak/internet-detskih-ryukzakov.html][img]http://dom-48.ru/detskie-3D-rjukzaki/video.jpg[/img][/url]
Рюкзаки Nohoo – идеальный вариант для родителей, которые хотят видеть своих детей модными и стильными, и не заморачиваться на счет того, что где-то рюкзак запачкается. У нас представлен огромный выбор рюкзаков, изготовленных из универсального изностостойкого неопрена! Пусть ваши дети пачкают в удовольствие - все отстирается!
Ортопедические
Специально сконструированный для детей легкий рюкзак с мягкими лямки эффективно смягчающими давление на плечи
Держат форму
Благодаря несущей системе и эластичному неопрену рюкзак держит форму и не мнётся
Практичные
Легко стираемые и прочные рюкзаки будут служить долго и сократят маме время на уход.
Читать полностью [url=http://dom-48.ru/rukzak/nohoo-detskie-3d-ryukzaki.html]nohoo детские 3d рюкзаки[/url]
http://dom-48.ru/rukzak/nohoo-detskie-3d-ryukzaki.html
<a href="http://dom-48.ru/rukzak/nohoo-ofitsialniy-sayt.html">nohoo официальный сайт</a>
[url=http://dom-48.ru/tarelka/tarelka-neprolivayka-nevalyashka.html][img]http://dom-48.ru/tarelka/video.jpg[/img][/url]
Что такое Gyro Bowl?
Все знают, что малыши довольно неусидчивые. Они все время что-то переворачивают и проливают. Это приносит родителям хлопоты и проблемы. Чтобы избежать похожих ситуаций во время приема пищи, предлагаем чудо тарелку-непроливайку Gyro Bowl.
Удивительная миска Gyro Bowl специально разработана так, чтобы внутренняя часть тарелки вертелась на 360 градусов. Благодаря этому, открытая сторона всегда остается вверху, сохраняя содержимое в тарелке.
Чудо-тарелка — это находка для родителей и их детей. Gyro Bowl отлично подходит для детей, чтобы весело провести время, пока они едят, но без лишних сложностей и бардака.
Читать полностью [url=http://dom-48.ru/tarelka/neprolivayka.html]непроливайка[/url]
http://dom-48.ru/tarelka/butilki-neprolivayki-detskie.html
<a href="http://dom-48.ru/tarelka/tarelka-dlya-detey-neprolivayka.html">тарелка для детей непроливайка</a>
<a href="http://cialisgsaa.com/">buy generic cialis</a>
take cialis before bed
[url=http://cialisgsaa.com/]generic cialis online[/url]
When can we help you?
If you are running late with the latest deadline for your paper or you are actually running late for work, which you combine with your studies – then we are your helping hand. You can count on our writing service for help with difficult projects you simply cannot seem to understand or with improving the work you’ve already completed. Because there really is no limit to perfection, especially when our experienced writers have a go at writing your assignment. Most popular types of papers include essays, research papers, course works, reports, and case studies. Even though our writers are also capable of completing complex calculations, diagrams, and dissertation.
While writing an essay may seem like a piece of cake to our writers with years of experience, it is completely understandable that the basic structure may be unknown to most. The same is true even more for less popular types of works like article reviews, presentations, literature reviews, book reviews, research proposals, theses, etc. Even the simple essay comes in all shapes and sizes, including argumentative essays, compare and contrast essays, descriptive essays, expository essays, persuasive essays… You name it! Our experts have seen it all, so you can rely on them when you need to get help with any type of work.
[url=http://writepaperme.com/phd-in-creative-writing-programs.html]phd in creative writing programs[/url]
Read more [url=http://writepaperme.com/good-english-research-paper-topics.html]good english research paper topics[/url]
http://www.arenajunkies.com/user/353292-andremolla/
https://androidperfect.net/foro/viewtopic.php?f=8&t=244772
http://singlecoilsound.com/index.php?topic=134936.new#new
http://paniqo.org/viewtopic.php?f=22&t=109008
http://www.forum.sampsonmordan.com/viewtopic.php?f=7&t=16584
http://ipevancouver.ca/forums/viewtopic.php?f=43&t=29986
http://inform-crimea.ru/forum/thread831-47.html#23870
http://bezpieczni.uk/index.php?topic=326584.new#new
http://wishmaster2-0.myjino.ru/forum/index.php?topic=175890.new#new
http://clubseatgdl.com.mx/foro/viewtopic.php?f=27&t=8961
http://www.aimji.com/forum-52-1.html
http://www.ausvoters.org/viewtopic.php?f=6&t=221944
http://imdbcommunity.com/community/viewtopic.php?f=36&t=271563
http://thelasthope.ru/index.php/forum/12-%D0%9D%D0%B0%D1%88-%D0%BF%D0%BE%D1%80%D1%82%D0%B0%D0%BB/32277-casino-online-bonus-deposit-casinos-gratis-en-espa%D0%93%C2%B1ol-slots-casino-online-bonus-free-cash#32277
[url=http://dom-48.ru/rukzak/nohoo-detskie-3d-ryukzaki.html][img]http://dom-48.ru/detskie-3D-rjukzaki/video.jpg[/img][/url]
Рюкзаки Nohoo – идеальный вариант для родителей, которые хотят видеть своих детей модными и стильными, и не заморачиваться на счет того, что где-то рюкзак запачкается. У нас представлен огромный выбор рюкзаков, изготовленных из универсального изностостойкого неопрена! Пусть ваши дети пачкают в удовольствие - все отстирается!
Ортопедические
Специально сконструированный для детей легкий рюкзак с мягкими лямки эффективно смягчающими давление на плечи
Держат форму
Благодаря несущей системе и эластичному неопрену рюкзак держит форму и не мнётся
Практичные
Легко стираемые и прочные рюкзаки будут служить долго и сократят маме время на уход.
Читать полностью [url=http://dom-48.ru/rukzak/nohoo-ofitsialniy-sayt.html]nohoo официальный сайт[/url]
http://dom-48.ru/rukzak/detskie-ryukzaki.html
<a href="http://dom-48.ru/rukzak/ryukzaki-nohoo-otzivi.html">рюкзаки nohoo отзывы</a>
Интepнeт-мaгaзин мeбeли Artstroyvrn.ru — yни?aльнaя вoзмoжнocть выбpaть нaпoлнeниe coбcтвeннoй ?вapтиpы или oфиca, нe выxoдя из дoмa. Дocтaтoчнo вceгo лишь зaйти в нaш интepнeт-мaгaзин, oзнa?oмитьcя c тoвapaми, пpeдcтaвлeнными в ?aтaлoгe, и cдeлaть on-lіnе зa?aз.
<a href="http://artstroyvrn.ru">Интернет-магазин мебели и товаров для дома</a>
When can we help you?
If you are running late with the latest deadline for your paper or you are actually running late for work, which you combine with your studies – then we are your helping hand. You can count on our writing service for help with difficult projects you simply cannot seem to understand or with improving the work you’ve already completed. Because there really is no limit to perfection, especially when our experienced writers have a go at writing your assignment. Most popular types of papers include essays, research papers, course works, reports, and case studies. Even though our writers are also capable of completing complex calculations, diagrams, and dissertation.
While writing an essay may seem like a piece of cake to our writers with years of experience, it is completely understandable that the basic structure may be unknown to most. The same is true even more for less popular types of works like article reviews, presentations, literature reviews, book reviews, research proposals, theses, etc. Even the simple essay comes in all shapes and sizes, including argumentative essays, compare and contrast essays, descriptive essays, expository essays, persuasive essays… You name it! Our experts have seen it all, so you can rely on them when you need to get help with any type of work.
[url=http://writepaperme.com/my/essay-my-family-doctor.html]essay my family doctor[/url]
Read more [url=http://writepaperme.com/my/where-do-i-see-myself-in-15-years-essay-ideas.html]where do i see myself in 15 years essay ideas[/url]
http://www.soc16.fr/chaussures-caterpillar-fenton-556.asp
http://www.treguier-immobilier.fr/valentino-escarpin-127.html
http://www.scootracer.fr/basket-adidas-femme-montant-465.htm
http://www.lerevedaglaee.fr/air-max-2015-violet-029.htm
http://www.sebastienmagro.fr/adidas-originals-1989-578.html
[url=http://www.lyoncentre.fr/071-nike-janoski-homme-noir.html]Nike Janoski Homme Noir[/url]
[url=http://www.palisso.fr/630-new-balance-femme-574-blanche.html]New Balance Femme 574 Blanche[/url]
[url=http://www.procrea-stem-cells.ch/adidas-stan-smith-2017-659.cfm]Adidas Stan Smith 2017[/url]
[url=http://www.as-assainissement.fr/supra-skytop-2-prix-499.php]Supra Skytop 2 Prix[/url]
[url=http://www.claudegouron.fr/louboutin-bottines-beige-026.php]Louboutin Bottines Beige[/url]
We are happy to welcome you to our premium quality Essay Service - a new approach to custom writing help!
With Buygoodessay.com, you become a part of our long-standing and well-established tradition of top quality custom essay services.
Professionalism and perfection are our main qualities. EvolutionWriter's professional authors can complete any type of paper for you in different fields of studies within the specified time frame. They will follow your requirements precisely and deliver exactly what you expect!
[url=http://buygoodessay.com/cheap-paper-writing-service/]cheap paper writing service[/url]
Read more [url=http://buygoodessay.com/writing-paper-with-picture-box/]writing paper with picture box[/url]
Прогуливаясь по улицам родного города, парочка почувствовала, что испытывают друг к другу настолько мощное желание, что откладывать секс до возвращения домой было абсолютно нереально. А потому они спрятались в ближайшем подъезде, где принялись реализовывать свои фантазии, стараясь снять мощное сексуальное напряжение. Блондинка отсосала другу в подъезде, опустившись перед ним на пол. Охотно поласкав отвердевший конец парня губками, деваха спустила трусики и приняла вставший до предела фаллос в свою тугую киску.
Смотреть видео [url=http://buykamagrajelly.org/bj/]Блондинка сосет в подъезде[/url]
For those who have several little one expressing a gaming program, maybe you are familiar with the difficulties to getting children to offer one another turns. And also for youngsters, it's aggravating to need to quit your video game appropriate in the middle of a levels! To produce anyone pleased, set up a stern warning program which gives your son or daughter enough time to complete just before another person turns into a turn. Request your young ones what a acceptable period of time could be, such as a quarter-hour or a half hour. You may also work with an alert for alerts.
[img]https://www.stasi-live-haft.de/images/sta2/18981-fußball-schuhe-nike-2014.jpg[/img]
As you have seen, natural energy technology isn't so hard to put into practice. Experiment with some of the tips you only read through at home right now, so that you can get started protecting power. Not only will you do the environment a big favor, but you'll spend less on your power bills.Train Your Children Properly With These Sound Advice
[img]https://www.solarcoating.de/images/newsomklo/5466-longchamp-le-pliage-kaufen-deutschland.jpg[/img]
http://www.grecigaione.it/adidas-zx-flux-blu-e-bianche-938.php
http://www.3in1concepts.it/686-negozio-scarpe-adidas-cagliari.php
http://www.islaminfo.it/converse-white-173.html
http://www.rifugioparcodeltadelpo.it/nike-bambino-alte-154.htm
http://www.nuovageovis.it/244-vibram-xs-edge-vs-xs-grip-2.htm
[url=http://www.sancolombanocalcio.it/stan-smith-uomo-nere-948.htm]Stan Smith Uomo Nere[/url]
[url=http://www.blackbox-online.it/164-nike-blazer-mid-vintage-premium.htm]Nike Blazer Mid Vintage Premium[/url]
[url=http://www.digitalspot.it/scarpe-salomon-trekking-opinioni-580.php]Scarpe Salomon Trekking Opinioni[/url]
[url=http://www.ttwater.it/373-puma-scarpe-creeper-costo.asp]Puma Scarpe Creeper Costo[/url]
[url=http://www.infopasqua.it/mizuno-enigma-6-prezzo-608.html]Mizuno Enigma 6 Prezzo[/url]
Усиливают потоотделение в 4 раза
У вас уменьшатся объемы в ненужных местах, а мышцы станут более рельефными.
Изготовлены из ткани NEOTEX
Её внутренний слой усиливает работу потовых желез, наружный - впитывает пот, не давая ткани промокать.
Комфортны в повседневной жизни
Они не заметны под одеждой, не пропускают пот и не оставляют следов на теле.
Читать полностью [url=http://dom-48.ru/hot-shapers/bridzhi-dlya-pohudeniya-hot-shapers-foto-ivanovo.html]бриджи для похудения hot shapers фото иваново[/url]
http://dom-48.ru/hot-shapers/bridzhi-i-poyasa-hot-shapers-astrahan.html
<a href="http://dom-48.ru/hot-shapers/losini-dlya-pohudeniya-hot-shapers-otzivi-podolsk.html">лосины для похудения hot shapers отзывы подольск</a>
Усиливают потоотделение в 4 раза
У вас уменьшатся объемы в ненужных местах, а мышцы станут более рельефными.
Изготовлены из ткани NEOTEX
Её внутренний слой усиливает работу потовых желез, наружный - впитывает пот, не давая ткани промокать.
Комфортны в повседневной жизни
Они не заметны под одеждой, не пропускают пот и не оставляют следов на теле.
Читать полностью [url=http://dom-48.ru/hot-shapers/odezhda-dlya-pohudeniya-hot-shapers-vologda.html]одежда для похудения hot shapers вологда[/url]
http://dom-48.ru/hot-shapers/bryuki-dlya-pohudeniya-hot-shapers-otzivi-elista.html
<a href="http://dom-48.ru/hot-shapers/zhiroszhigayushiy-poyas-hot-shapers-tver.html">жиросжигающий пояс hot shapers тверь</a>
Уменьшает объем бедер, делает ягодицы визуально упругими и придает им правильную форму
Приподнимает грудь, увеличивая на 1-2 размера.
Подтягивает живот, уменьшая линию талии.
Читать полностью [url=http://dom-48.ru/slim-shapewear/kombidress-slim-shapewear-otzivi-realnie-pskov.html]комбидресс slim shapewear отзывы реальные Псков[/url]
http://dom-48.ru/slim-shapewear/slim-shapewear-kupit-saratov.html
<a href="http://dom-48.ru/slim-shapewear/kombidress-slim-shapewear-otzivi-realnie-foto-hanti-mansiysk.html">комбидресс slim shapewear отзывы реальные фото Ханты-Мансийск</a>
одно универсальное средство,
которое точно понравится каждому
второму автолюбителю.
Вот оно http://vk.cc/6Zw80Q
[url=http://vk.cc/6Zw80Q][img]http://livejorhh.ru/silane-guard/img/3.jpg[/img][/url]
Называется оно японское жидкое стекло Willson Silane Guard.
Суть очень проста, необходимо взять в аренду помещение,
и заняться полировкой кузова авто.
Необходимость в такой полировке несомненна.
Она понадобится в любое время года.
Результат на лицо
[url=http://vk.cc/6Zw80Q][img]http://livejorhh.ru/silane-guard/img/6.jpg[/img][/url]
одно универсальное средство,
которое точно понравится каждому
второму автолюбителю.
Вот оно http://vk.cc/6Zw80Q
[url=http://vk.cc/6Zw80Q][img]http://livejorhh.ru/silane-guard/img/3.jpg[/img][/url]
Называется оно японское жидкое стекло Willson Silane Guard.
Суть очень проста, необходимо взять в аренду помещение,
и заняться полировкой кузова авто.
Необходимость в такой полировке несомненна.
Она понадобится в любое время года.
Результат на лицо
[url=http://vk.cc/6Zw80Q][img]http://livejorhh.ru/silane-guard/img/6.jpg[/img][/url]
We are happy to welcome you to our premium quality Essay Service - a new approach to custom writing help!
With Buygoodessay.com, you become a part of our long-standing and well-established tradition of top quality custom essay services.
Professionalism and perfection are our main qualities. EvolutionWriter's professional authors can complete any type of paper for you in different fields of studies within the specified time frame. They will follow your requirements precisely and deliver exactly what you expect!
[url=http://buygoodessay.com/pay-someone-to-write-my-research-paper/]pay someone to write my research paper[/url]
Read more [url=http://buygoodessay.com/personalized-writing-paper/]personalized writing paper[/url] -> http://buygoodessay.com/personalized-writing-paper/
http://www.bottega-del-legno.it/982-lacoste-scarpe-bari.htm
http://www.islaminfo.it/converse-grigie-e-nere-491.html
http://www.amadoriscavi.it/air-huarache-blu-521.html
http://www.dsette.it/mizuno-laser-2-prezzo-873.php
http://www.annagalante.it/460-hogan-scarpe-estive-2016.html
[url=http://www.bareddu.it/mk-shopper-387.php]Mk Shopper[/url]
[url=http://www.blackhorsesv.it/286-scarpe-adidas-la-trainer-blu.html]Scarpe Adidas La Trainer Blu[/url]
[url=http://www.annagalante.it/023-hogan-scarpe-donne-2016-prezzi.html]Hogan Scarpe Donne 2016 Prezzi[/url]
[url=http://www.immobiliaremacchione.it/826-nike-huaraches-nere.htm]Nike Huaraches Nere[/url]
[url=http://www.adidasstansmithbronze.fr/506-adidas-stan-smith-femme-original.php]Adidas Stan Smith Femme Original[/url]
Whilst the common process and notion is you need to clean your tooth 2 times a day, an even better practice will be to clean as soon as you eat every meal. Once we consume, our mouths are packed with foods that may be a reproduction ground for microorganisms. Scrubbing after food removes this concern.
[img]https://www.geschenke-glossar.de/images/ges2/26282-adidas-ultra-boost-dirk-schönberger.jpg[/img]
Taking a yoga class or purchasing a yoga exercise movie can be a terrific approach to increase your personal development. This historic exercise involves building up, stretching, as well as a cardiac work out to really make it an all around amazing form. In addition, you will get mental clarity while focusing whilst rehearsing yoga exercises. Try yoga exercise these days.
[img]https://www.chinamassagesofa.de/images/chi2/11903-puma-schuhe-schwarz-lack.jpg[/img]
Self improvement indicates spiritual improvement to numerous. But if this is the journey, be sure you don't disregard actual physical effectively-becoming, for this offers the groundwork on what you build. Being a excellent ascetic saint accustomed to notify his fans: "Produce a buddy of your body it can help yourself on your path."
[img]https://www.hummer-h5.de/images/hu2/2898-nike-free-flyknit-grau.jpg[/img]
To assist you manage ringing in the ears you should stay away from demanding scenarios. Long periods of pressure can certainly make the ringing in ears noises very much even louder than they can be if you are in peaceful condition. In order to help handle your tinnitus and not allow it to be a whole lot worse, you should try and enjoy life together with the minimum quantity of tension.
[img]https://www.reisebueros-wiesbaden.de/images/rei2/14751-ray-ban-brille-grün-schwarz.jpg[/img]
If you've been motivated to image a marriage however are a new comer to the task, your most critical task it to create a shot listing. Ask the pair what sort of photos they could as if you to adopt and make a checklist to assist you throughout the wedding party and ease your stress levels degree.
[img]https://www.nochevieja.com.es/images/newnoche/2136-le-coq-sportif-omega-x-mesh.jpg[/img]
When trying to improve your silver jewellery, it's usually a good idea to soak it in a solution water and white vinegar. Steer clear of cider and red wine vinegars. Go along with white wine vinegar only. This will take away tarnish through your jewellery and give it millions of-buck sparkle in just one or two quick a few minutes.
[img]https://www.hd3d.fr/images/airhuarache/2259-huarache-ultra-run-femme.jpg[/img]
[url=http://rxlist.pw/deltasone/]Buy Deltasone[/url] $ 0.50 [url=http://rxlist.pw/deltasone]Cheap deltasone[/url] [url=http://rxlist.pw/deltasone]Generic deltasone[/url]
http://rxlist.pw/deltasone/ $ 0.50 http://rxlist.pw/deltasone http://rxlist.pw/deltasone/buy-deltasone.html
Online Pharmacy <a href="http://rxlist.pw/deltasone/">Buy Deltasone</a> $ 0.50 <a href="http://rxlist.pw/deltasone">Cheap deltasone</a> <a href="http://rxlist.pw/deltasone">Generic Deltasone</a>
Generic deltasone $0.5
http://www.livingincomfort.es/zapatillas-caterpillar-hombre-botines-049.html
http://www.pergolasdemadera.org.es/ray-ban-hombre-mercadolibre-638.htm
http://www.ajedrezlinares.es/adidas-gazelle-2014-346.html
http://www.herbolarionaturaibaez.es/nike-air-max-de-mujer-2015-986.html
http://www.restaurantllevant.es/nike-free-flyknit-baratas-203.php
[url=http://www.monasteriodevico.es/billeteras-michael-kors-por-mayor-066.html]Billeteras Michael Kors Por Mayor[/url]
[url=http://www.uteca.es/adidas-ace-16-purecontrol-precio-977.html]Adidas Ace 16 Purecontrol Precio[/url]
[url=http://www.gigaphotoproject.es/adidas-boost-tubular-917.php]Adidas Boost Tubular[/url]
[url=http://www.toysessions.es/zapatillas-air-max-mujer-baratas-929.php]Zapatillas Air Max Mujer Baratas[/url]
[url=http://www.josecarlossomoza.es/beats-dre-studio-636.html]Beats Dre Studio[/url]
Except if you are stored on the best way to produce a huge buy there is absolutely no explanation you should carry your bank card around along constantly. Which will only resulted in a higher risk that someone will rob your greeting card or even a threat that you simply will spend cash that you do not have.
[img]https://www.agenda21-herford.de/images/age2/27289-tods-männer-schuhe.jpg[/img]
Try to stick to your spending budget as greatest you can. If your costs are raising noticeably, take the time to reconsider your renovations. You could have employed the incorrect licensed contractor or could be straying away from your authentic strategy. It is possible to get taken aside when creating adjustments, but stay focused.
[img]https://www.dokutv-online.de/images/dok2/14297-adidas-neo-schuhe-grau-pink.jpg[/img]
Computer game might be loads of entertaining, but you should take a rest every once in awhile. Should you not accomplish this, you may find on your own getting slight headaches together with a standard feeling of lethargy. Be sure to get slightly or activity in your life.
[img]https://www.wadern24.de/images/wad2/7364-montblanc-cruise.jpg[/img]
Select credit cards that rewards you with what you get pleasure from. If you love to nibble on, get a charge card which offers benefits of accreditations beneficial to great dinning. If you like to travel, there are many fantastic charge cards that provide mls that you could redeem for plane tickets in your up coming journey. If you like to have cash, you can generate funds incentives with particular a credit card.
[img]https://www.link-directory.de/images/link-directory/8438-nike-air-force-1-schwarz-matt.jpg[/img]
<a href="http://cialisxrm.com/">buy generic cialis</a>
donde comprar cialis generico argentina
[url=http://cialisxrm.com/]buy generic cialis[/url]
http://www.developnet.co.uk/salomon-speedcross-3-ladies-150.htm
http://www.bjdn.co.uk/clarks-mens-black-leather-shoes-078.asp
http://www.edwardparkerwines.co.uk/converse-glitter-sneakers-161.asp
http://www.smithland.co.uk/nike-classic-cortez-nylon-amazon-385.html
http://www.neplex.co.uk/soccer-shoes-messi-2015-746.htm?zenid=871j4p0c3sr3qseuj5mrmidgc6
[url=http://www.overdriverockband.co.uk/ray-ban-aviator-black-and-gold-200.htm]Ray Ban Aviator Black And Gold[/url]
[url=http://www.sheer-sumptuosity.co.uk/mont-blanc-jfk-special-edition-965.html]Mont Blanc Jfk Special Edition[/url]
[url=http://www.dsleurope.co.uk/adidas-ultra-boost-running-485.php]Adidas Ultra Boost Running[/url]
[url=http://www.gamesmastertv.co.uk/adidas-originals-high-tops-631.htm]Adidas Originals High Tops[/url]
[url=http://www.lesaldrich.co.uk/lacoste-casual-shoes-for-women-2017-315.htm]Lacoste Casual Shoes For Women 2017[/url]
[b][/b]
Forex, or perhaps the foreign currency currency forex market, can be a valuable industry for these wishing to be part of this exciting forex trading process. There is lots of real information out there about Foreign exchange, a number of it is fantastic plus some of this will not make any feeling by any means. The following report will help you get understanding about the Forex market.
[img]https://www.hitamerica.co.uk/images/hit2/28443-ray-ban-sunglasses-new.jpg[/img]
Don't be scared to extend your hand and ask your visitor for the donation. Your dedicated viewers, particularly, is going to be likely to give away some for your cause. If your blog site is important ample, individuals will know it. They will likely also know that, furthermore it cost cash to make your blog, your time is beneficial.
[img]https://www.weddingdayfashions.co.uk/images/wed2/8295-christian-louboutin-mens-white-sneakers.jpg[/img]
Exercising is a wonderful way to cope with your stress and anxiety. If you work out, you launch lots of anxiety or tension, which happens to be a significant cause of nervousness. Once you get rid of this extra anxiety, you place yourself in a clearer state of mind, which should reduce the level of anxiousness you feel.
[img]https://www.sinclairanddrummond.co.uk/images/sin2/3746-new-balance-574-blue-orange-white.jpg[/img]
Take into account working with a maid service if you require help using more than basic cleaning up. When tasks could be a important component of homeschooling, it is important is definitely the schooling your kids gets. You may want periodic assist to do strong cleaning up or organizing tasks so that you can focus on college.
[img]https://www.massagenow.co.uk/images/mas2/3316-louboutin-classic.jpg[/img]
http://www.beatassailant.fr/adidas-kaiser-5-258.php
http://www.iloveshoes.fr/nike-juvenate-fleece-grise-984.html
http://www.essaisgratuits.fr/golden-goose-femme-847.php
http://www.as-assainissement.fr/under-armour-curry-3-camo-727.php
http://www.full-web.fr/palladium-femme-prix-437.html
[url=http://www.trioelegiaque.fr/yeezy-boost-350-fille-399.html]Yeezy Boost 350 Fille[/url]
[url=http://www.bluerennes.fr/055-air-max-95-gris-blanc.php]Air Max 95 Gris Blanc[/url]
[url=http://www.scootracer.fr/la-trainer-noir-et-rose-179.htm]La Trainer Noir Et Rose[/url]
[url=http://www.xavier-massonnaud.fr/lunettes-soleil-ray-ban-wayfarer-584.php]Lunettes Soleil Ray Ban Wayfarer[/url]
[url=http://www.corsica-seniors.fr/gucci-basket-homme-2017-422.html]Gucci Basket Homme 2017[/url]
http://www.acgproducciones.es/zapatillas-balenciaga-mercadolibre-001.html
http://www.uffg.es/nike-jordan-919.html
http://www.probaiedumontsaintmichel.fr/255-new-balance-bordeaux-420.php
http://www.clinicadeldolorneuromuscular.es/adidas-superstar-rosas-hombre-308.html
http://www.woozor.es/louis-vuitton-kanye-west-mercadolibre-327.html
[url=http://www.biarriz.com.es/nike-air-presto-4-132.php]Nike Air Presto 4[/url]
[url=http://www.queoposicion.es/palladium-boots-women-870.htm]Palladium Boots Women[/url]
[url=http://www.letrasdiscografia.es/130-nike-air-force-1-low-outfit.html]Nike Air Force 1 Low Outfit[/url]
[url=http://www.disfracesparaadultos.es/tienda-vans-baratas-madrid-322.html]Tienda Vans Baratas Madrid[/url]
[url=http://www.tv-gratuite.fr/stan-smith-bleu-marine-portee-003.htm]Stan Smith Bleu Marine Portee[/url]
?
http://www.civelpinhaopr.com.br/fonts/search.asp?tab=135
http://www.dantasmoreira.com.br/includes/jquery/css/config.php?nav=113-Kamagra-Online-Erfahrungen,Kamagra-Bestellen-Ohne-Kreditkarte,Kamagra-Online-Apotheke
http://www.elominas.com.br/sliders/quit.asp?k=151
http://amandaamorim.adv.br/fullslider/slider/assets/return.php?gb1=224
http://www.elominas.com.br/sliders/quit.asp?k=58
[url=http://www.dantasmoreira.com.br/includes/jquery/css/config.php?nav=71-Kamagra-Günstig-Nl,Kamagra-Günstig-Per-Nachnahme,Kamagra-Oral-Jelly-Test]Kamagra Günstig Nl[/url]
[url=http://www.genouxrapes.com/images/base.php?mn=59]Viagra Apotheke Kosten[/url]
[url=http://www.emmaus-hamm.de/images/back.php?p=79]Levitra Ohne Rezept[/url]
[url=http://www.centrodaconstrucaoroloff.com.br/includes/mail.php?num=217]Viagra Rezeptfrei Bestellen[/url]
[url=http://www.colonialaberturadeempresa.com.br/css/event.asp?new=118-Kamagra-Online-Kaufen-Per-Nachnahme,Kamagra-100mg,Kamagra-Gel-Für-Frauen]Kamagra Online Kaufen Per Nachnahme[/url]
<a href="http://canadianpharmacyrxbsl.com/">canadian online pharmacies</a>
pharmacy price comparison
[url=http://canadianpharmacyrxbsl.com/?clomid-for-women]clomid for women[/url]
canadian pharmacy king
<a href="http://canadianpharmacyrxbsl.com/?bad-news-about-metformin">bad news about metformin</a>
<a href="http://canadianpharmacyrxbsl.com/">canadian online pharmacies</a>
onlinecanadianpharmacy.com
[url=http://canadianpharmacyrxbsl.com/?clomid-for-men]clomid for men[/url]
canada pharmacy
<a href="http://canadianpharmacyrxbsl.com/?after-you-stop-taking-prednisone">after you stop taking prednisone</a>
http://www.itcolorsesteelauder.es/asics-casual-hombre-954.asp
http://www.clinicadeldolorneuromuscular.es/superstar-adidas-dama-828.html
http://www.tv-gratuite.fr/stan-smith-adidas-femme-163.htm
http://www.herbolarionaturaibaez.es/air-max-2015-flyknit-multicolor-709.html
http://www.webvegabaja.es/823-nike-air-max-90-2015-para-mujer-rojas.html
[url=http://www.livingincomfort.es/zapatillas-cat-para-dama-408.html]Zapatillas Cat Para Dama[/url]
[url=http://www.livingincomfort.es/zapatillas-cat-para-niños-184.html]Zapatillas Cat Para Niños[/url]
[url=http://www.letrasdiscografia.es/188-nike-air-force-1-ultra-force-mid-2017.html]Nike Air Force 1 Ultra Force Mid 2017[/url]
[url=http://www.yonotengounbarcenas.es/zapatillas-de-versace-577.php]Zapatillas De Versace[/url]
[url=http://www.ajedrezlinares.es/adidas-zx-flux-techfit-249.html]Adidas Zx Flux Techfit[/url]
I also wanted to ask, did an individual encounter such an issue? And what will come about if they find out that my article was purchased, and not written by me
I also wanted to ask, did an individual encounter such an issue? And what will take place if they discover out that my paper was bought, and not written by me
I also wanted to ask, did a person encounter such an issue? And what will happen if they discover out that my dissertation was purchased, and not written by me
---
fifa 15 crack torrent, скачать launcher exe для fifa 15 или [url=http://15fifa.ru/video-fifa-15/]смотреть игру фифа 15[/url] фифа официальный сайт на русском
If you are on the discussing table for any business real estate property selling, make sure to always keep because you would like to get the selling done swiftly under wraps. If it is recognized that you are in a big hurry to get the residence, you will find that you may lose significant amounts of leverage to acquire a much better bargain.
[img]https://www.solarcoating.de/images/newsomklo/20181-michael-kors-tasche-hamilton-schwarz.jpg[/img]
If the position that you will be planing a trip to is a warmer weather, try using a half a dozen-package much cooler as being a have-on toiletry handbag. This is certainly a terrific way to pack awesome refreshments for your getaway and yes it makes a excellent "freezer" for all of your toiletries to be nice cool in.
[img]https://www.kalkan-tuerkei.de/images/kal2/3318-beats-pro-black.jpg[/img]
Don't use a lot of various typefaces or written text colors on your own web pages. Phrase finalizing or internet authoring computer software may possibly current a dizzying array of area of expertise fonts or crazy hues, but when you use too many, the writing in your internet site can get unreadable. A good practice is by using just 1 or 2 typefaces per webpage and prevent unneccessary use of daring or italic text.
[img]https://www.retinal.nu/imagess/ret2/2923-air-max-1-white.jpg[/img]
Spiritual and spiritual folks are certainly more relaxed and more stress-free of charge. This is because of their trust and reliance upon Jehovah who manages their every single need to have. Once we enable Jehovah to provide, we are allowing him to take control of our everyday life and go ahead and take tension out of your snapshot.
[img]https://www.familjekompositoren.se/images/fam2/10600-plånbok-michael-kors-online.jpg[/img]
[url=https://www.acheterviagrafr24.com/acheter-sildenafil-50-mg-bifort/]acheter sildenafil 50 mg bifort[/url]
http://www.rollinsband.co.uk/asics-gel-lyte-v-white-blue-855.html
http://www.mis-understood.co.uk/oakley-juliet-ruby-iridium-491.html
http://www.tops4creditcards.co.uk/converse-new-model-2016-785.htm
http://www.nationalincentiveshow.co.uk/new-era-san-diego-chargers-863.php
http://www.buy-ps3.co.uk/saucony-minty-fresh-376.htm
[url=http://www.teestainstudios.co.uk/damier-lv-belt-950.php]Damier Lv Belt[/url]
[url=http://www.nationalincentiveshow.co.uk/lv-belt-with-gold-buckle-330.php]Lv Belt With Gold Buckle[/url]
[url=http://www.bjdn.co.uk/grey-balenciaga-trainers-386.asp]Grey Balenciaga Trainers[/url]
[url=http://www.marchpast.co.uk/nike-shox-deliver-black-and-red-489.htm]Nike Shox Deliver Black And Red[/url]
[url=http://www.hungryandhomeless.co.uk/air-max-90-liberty-of-london-blue-182.htm]Air Max 90 Liberty Of London Blue[/url]
http://www.pieces-center.fr/adidas-superstar-qui-sallume-189.php
http://www.trocacenter.fr/nike-air-force-one-pas-cher-498.php
http://www.fort-placement.fr/341-louboutin-escarpins-beige.php
http://www.travail-internet.fr/nike-sb-floral-502.html
http://www.soleil-vert.fr/535-sac-michael-kors-noir-croco.html
[url=http://www.citesket.fr/zapatillas-adidas-js-238.html]Zapatillas Adidas Js[/url]
[url=http://www.omake.fr/air-jordan-5-pas-cher-014.html]Air Jordan 5 Pas Cher[/url]
[url=http://www.trioelegiaque.fr/zx-flux-leopard-femme-pas-cher-015.html]Zx Flux Leopard Femme Pas Cher[/url]
[url=http://www.autoankaufbodensee.ch/adidas-superstar-tĂĽrkis-37-702.php]Adidas Superstar TĂĽrkis 37[/url]
[url=http://www.lerevedaglaee.fr/nike-air-max-grey-2016-765.htm]Nike Air Max Grey 2016[/url]
http://www.countryfarms.co.uk/nike-free-flyknit-3.0-red-691.htm
http://www.mis-understood.co.uk/oakley-monster-dog-uk-555.html
http://www.ras-net.co.uk/roshe-flyknit-green-163.htm
http://www.nextmoveit.co.uk/nike-air-force-1-mid-grey-black-303.html
http://www.bar-ten.co.uk/080-football-shoes-2015.htm
[url=http://www.dieselmotorcycle.co.uk/adidas-flux-olive-green-273.htm]Adidas Flux Olive Green[/url]
[url=http://www.tops4creditcards.co.uk/converse-all-star-platform-sneaker-white-065.htm]Converse All Star Platform Sneaker White[/url]
[url=http://www.unisoftdesign.co.uk/lv-speedy-40-451.html]Lv Speedy 40[/url]
[url=http://www.dangerouslyclose.co.uk/nike-air-max-thea-se-358.htm]Nike Air Max Thea Se[/url]
[url=http://www.fengshuidesigns.co.uk/longchamp-le-pliage-large-tote-bag-cheap-359.html]Longchamp Le Pliage Large Tote Bag Cheap[/url]
Be careful and do not flood
here is the url http://yarmarkanew.ru/2017/08/28/essays-writing-services-producing-any-task-a-lot-2/
Keep in near experience of your allergist to permit him know if your medication is functioning effectively to regulate your signs and symptoms. Make him aware should your prescription medication appears to be not working in addition to it once might have. Your medication dosage or prescription medication should be changed so that you can help you.
[img]https://www.pcrec.co.uk/images/pcr2/1187-puma-basket-classic-metallic-sneakers.jpg[/img]
Though most face soaps are good for pimples, laundry your facial skin an excessive amount of with it is not necessarily. Above washing your skin can result in extreme dryness which is probably the reasons behind pimples. Be sure to utilize your cleanser or acne remedy as instructed in the packing.
[img]https://www.dsleurope.co.uk/images/dsl2/7591-adidas-ultra-boost-black-blue.jpg[/img]
Obtain your credit dealt with in advance. Down obligations on industrial properties are normally more than on residential properties. With that being said, creditors are definitely more easygoing about in which you obtain the downpayment money from, usually allowing you to borrow the funds from someone else. But before generating a proposal over a business residence, speak with many different lenders, since you may not be eligible for a loan from every one of them. The final thing you require is to have your offer recognized, only to find that you just can't get a loan.
[img]https://www.corx.co.uk/images/cor2/26913-nike-flyknit-4.0-mens-blue.jpg[/img]
Your market information and facts takes on a big part in figuring out your auto insurance prices. Some of these factors it is possible to modify, but others offer you little if any handle. As an example, single males under age 25 possess the maximum threat probable while married ladies in between 50 and 65 years old possess the cheapest danger prospective. Elements around that you do conserve a degree of handle are your area, type of automobile, schooling and credit history. Sparsely populated regions of very low crime are loved by insurance firms, as well as those with an education, a high credit score and a run-of-the-mill motor vehicle.
[img]https://www.unisoftdesign.co.uk/images/uni2/15548-womens-lv-wallet.jpg[/img]
http://ww2w.aaronequipment.com/blog/post/2012/01/14/Aaron-Equipment-Company-Helping-Organic-Manufacturers-Stay-Green-from-Start-to-Finish.aspx
оборудования для прокладки кабеля
[url=http://astra-electric.ru/index.php?id_product=71&controller=product]перфошвеллер[/url]
[URL=http://astra-electric.ru/index.php?id_product=29&controller=product]Перегородка лотка НЛ[/URL]
[URL=http://astra-electric.ru/index.php?id_product=43&controller=product]Х-отвод для лотка[/URL]
[URL=http://astra-electric.ru/index.php?id_product=69&controller=product]Подвес лотков пл1[/URL]
[URL=http://astra-electric.ru/index.php?id_category=47&controller=category]Короба ККБ, короба КП[/URL]
[URL=http://astra-electric.ru/index.php?id_product=43&controller=product]Х-отвод для лотка[/URL]
[URL=http://astra-electric.ru/index.php?id_product=43&controller=product]Х-отвод для лотка[/URL]
[URL=http://astra-electric.ru/index.php?id_product=83&controller=product]Короб одноканальный, трехканальный типа ККБ-ПО, ККБ-3ПО[/URL]
[URL=http://astra-electric.ru/index.php?id_category=49&controller=category]Миникороб, кабельный канал металлический оцинкованный ККМО [/URL]
[URL=http://astra-electric.ru/index.php?id_product=68&controller=product]Подвес лотков пл3[/URL]
[URL=http://astra-electric.ru/index.php?id_product=45&controller=product]Соединители лотка[/URL]
[URL=http://astra-electric.ru/index.php?id_product=36&controller=product]Прижим НЛ-ПР[/URL]
[URL=http://astra-electric.ru/index.php?id_product=78&controller=product]Скоба К1157[/URL]
[url=http://astra-electric.ru/index.php?id_product=71&controller=product][URL=http://astra-electric.mcdir.ru/kabelnye-koroba/719-korob-kabelnyj-zamkovyj-kzp-500h80.html]Короб кабельный замковый КЗП 500х80[/URL]
[/url]
[url=http://astra-electric.ru]профиль перфорированный
[/url]
[url=http://astra-electric.ru]кабельный канал
[/url]
[url=http://astra-electric.ru]короб сп
[/url]
[url=http://astra-electric.ru]профиль перфорированный
[/url]
[url=http://astra-electric.ru]стойка кабельная к1153
[/url]
[url=http://astra-electric.ru]перфоуголок
[/url]
[url=http://astra-electric.ru]перфорированные уголки
[/url]
кабельные лотки купить
лоток перфорированный кабельный
швеллер перфорированный
швеллер перфорированный
кабельные лотки купить
лоток лестничного типа
[url=http://astra-electric.ru/index.php?id_category=41&controller=category]лотки перфорированные[/url]
[url=http://astra-electric.ru/index.php?id_product=27&controller=product]лоток лестничный перфорированный[/url]
[url=http://astra-electric.ru/index.php?id_product=37&controller=product]кабельный лоток[/url]
[url=http://astra-electric.ru/index.php?id_product=27&controller=product]лоток кабельный[/url]
[url=http://astra-electric.ru/index.php?controller=product&id_product=73]уголки металлические цена[/url]
[url=http://astra-electric.ru/index.php?controller=product&id_product=63]стойка кабельная к1155[/url]
[url=http://astra-electric.ru/index.php?id_product=71&controller=product]профиль перфорированный[/url]
[url=http://astra-electric.ru/index.php?id_product=27&controller=product]лоток кабельный лестничного типа[/url]
[url=http://astra-electric.ru/index.php?id_product=37&controller=product]лоток глухой оцинкованный[/url]
[url=http://astra-electric.ru/index.php?id_product=56&controller=product]короб перфорированный[/url]
[url=http://astra-electric.ru/index.php?id_product=56&controller=product]кабельный короб[/url]
[url=http://astra-electric.ru/]лоток dkc[/url]
[url=http://astra-electric.ru/index.php?id_product=27&controller=product]кабельный лоток металлический перфорированный[/url]
[url=http://astra-electric.ru/index.php?id_product=56&controller=product]короба кабельные блочные[/url]
[url=http://astra-electric.ru/index.php?controller=product&id_product=73]уголок перфорированный[/url]
[URL=http://astra-electric.mcdir.ru/izdelija-gjem/339-konsol-kv-konsol-vertikalnaja-3.html]Консоль КВ (консоль вертикальная)[/URL]
[URL=http://astra-electric.mcdir.ru/profil-montazhnyj/461-profil-zetovyj-60h40h40-k239.html]Профиль зетовый 60х40х40, К239[/URL]
[URL=http://astra-electric.mcdir.ru/index.php?do=cat&category=lotki-sploshnye-zamkovye]Лотки сплошные замковые » Производство всех видов электромонтажного оборудования для прокладки кабеля[/URL]
[URL=http://astra-electric.mcdir.ru/perfoprofili/348-perfoshveller-2.html]Перфошвеллер[/URL]
[URL=http://astra-electric.mcdir.ru/koroba-kkb/327-korob-uglovoj-kkb-ugv-kkb-ugn-2.html]Короб угловой ККБ-УГВ/ККБ-УГН[/URL]
[URL=http://astra-electric.mcdir.ru/koroba-kkb/329-korob-prjamoj-kkb-p-2.html]Короб прямой ККБ-П[/URL]
[URL=http://astra-electric.mcdir.ru/koroba-kkb/330-korob-odnokanalnyj-trehkanalnyj-tipa-kkb-po-kkb-2.html]Короб одноканальный, трехканальный типа ККБ-ПО, ККБ-3ПО[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-lotki/700-lotok-lestnichnyj-nl100h50.html]Лоток лестничный НЛ100х50[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/]Кабельные короба » Производство всех видов электромонтажного оборудования для прокладки кабеля[/URL]
[URL=http://astra-electric.mcdir.ru/krepezh-dlja-kabelja/521-podves-pl2-460.html]Подвес Пл2.460[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/743-korob-kabelnyj-zamkovyj-kzp-500h100.html]Короб кабельный замковый КЗП 500х100[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/721-korob-kabelnyj-zamkovyj-kzp-400h80.html]Короб кабельный замковый КЗП 400х80[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/738-korob-kabelnyj-zamkovyj-kzp-50h50.html]Короб кабельный замковый КЗП 50х50[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/710-korob-kabelnyj-zamkovyj-kzp-300h65.html]Короб кабельный замковый КЗП 300х65[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/page/6/]Кабельные короба » Страница 6 » Производство всех видов электромонтажного оборудования для прокладки кабеля[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/page/4/]Кабельные короба » Страница 4 » Производство всех видов электромонтажного оборудования для прокладки кабеля[/URL]
[URL=http://astra-electric.mcdir.ru/krepezh-dlja-kabelja/522-podves-pl3-150.html]Подвес Пл3.150[/URL]
[URL=http://astra-electric.mcdir.ru/izdelija-gjem/341-stojka-kabelnaja-3.html]Стойка кабельная[/URL]
[URL=http://astra-electric.mcdir.ru/perforirovannyj-krepezh/425-perfoshveller-45h30.html]Перфошвеллер 45х30[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/740-korob-kabelnyj-zamkovyj-kzp-500h65.html]Короб кабельный замковый КЗП 500х65[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/737-korob-svetovoj-kslk-50h50.html]Короб световой КСЛК 50х50[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/746-korob-kabelnyj-zamkovyj-kzp-150h80.html]Короб кабельный замковый КЗП 150х80[/URL]
[URL=http://astra-electric.mcdir.ru/profil-montazhnyj/464-profilperforirovannyj-u-obraznyj-ms-303515-u2s11-2.html]Профильперфорированный u-образный ms 303515 u2s11 (2-перф.)[/URL]
[URL=http://astra-electric.mcdir.ru/perfoprofili/349-z-profil-2.html]z-профиль[/URL]
[URL=http://astra-electric.mcdir.ru/index.php?do=cat&category=kabel-kanal]Кабель-канал[/URL]
оборудования для прокладки кабеля
[url=http://astra-electric.ru/index.php?id_product=71&controller=product]перфошвеллер[/url]
[URL=http://astra-electric.ru/index.php?id_product=29&controller=product]Перегородка лотка НЛ[/URL]
[URL=http://astra-electric.ru/index.php?id_product=43&controller=product]Х-отвод для лотка[/URL]
[URL=http://astra-electric.ru/index.php?id_product=69&controller=product]Подвес лотков пл1[/URL]
[URL=http://astra-electric.ru/index.php?id_category=47&controller=category]Короба ККБ, короба КП[/URL]
[URL=http://astra-electric.ru/index.php?id_product=43&controller=product]Х-отвод для лотка[/URL]
[URL=http://astra-electric.ru/index.php?id_product=43&controller=product]Х-отвод для лотка[/URL]
[URL=http://astra-electric.ru/index.php?id_product=83&controller=product]Короб одноканальный, трехканальный типа ККБ-ПО, ККБ-3ПО[/URL]
[URL=http://astra-electric.ru/index.php?id_category=49&controller=category]Миникороб, кабельный канал металлический оцинкованный ККМО [/URL]
[URL=http://astra-electric.ru/index.php?id_product=68&controller=product]Подвес лотков пл3[/URL]
[URL=http://astra-electric.ru/index.php?id_product=45&controller=product]Соединители лотка[/URL]
[URL=http://astra-electric.ru/index.php?id_product=36&controller=product]Прижим НЛ-ПР[/URL]
[URL=http://astra-electric.ru/index.php?id_product=78&controller=product]Скоба К1157[/URL]
[url=http://astra-electric.ru/index.php?id_product=71&controller=product][URL=http://astra-electric.mcdir.ru/kabelnye-koroba/719-korob-kabelnyj-zamkovyj-kzp-500h80.html]Короб кабельный замковый КЗП 500х80[/URL]
[/url]
[url=http://astra-electric.ru]профиль перфорированный
[/url]
[url=http://astra-electric.ru]кабельный канал
[/url]
[url=http://astra-electric.ru]короб сп
[/url]
[url=http://astra-electric.ru]профиль перфорированный
[/url]
[url=http://astra-electric.ru]стойка кабельная к1153
[/url]
[url=http://astra-electric.ru]перфоуголок
[/url]
[url=http://astra-electric.ru]перфорированные уголки
[/url]
кабельные лотки купить
лоток перфорированный кабельный
швеллер перфорированный
швеллер перфорированный
кабельные лотки купить
лоток лестничного типа
[url=http://astra-electric.ru/index.php?id_category=41&controller=category]лотки перфорированные[/url]
[url=http://astra-electric.ru/index.php?id_product=27&controller=product]лоток лестничный перфорированный[/url]
[url=http://astra-electric.ru/index.php?id_product=37&controller=product]кабельный лоток[/url]
[url=http://astra-electric.ru/index.php?id_product=27&controller=product]лоток кабельный[/url]
[url=http://astra-electric.ru/index.php?controller=product&id_product=73]уголки металлические цена[/url]
[url=http://astra-electric.ru/index.php?controller=product&id_product=63]стойка кабельная к1155[/url]
[url=http://astra-electric.ru/index.php?id_product=71&controller=product]профиль перфорированный[/url]
[url=http://astra-electric.ru/index.php?id_product=27&controller=product]лоток кабельный лестничного типа[/url]
[url=http://astra-electric.ru/index.php?id_product=37&controller=product]лоток глухой оцинкованный[/url]
[url=http://astra-electric.ru/index.php?id_product=56&controller=product]короб перфорированный[/url]
[url=http://astra-electric.ru/index.php?id_product=56&controller=product]кабельный короб[/url]
[url=http://astra-electric.ru/]лоток dkc[/url]
[url=http://astra-electric.ru/index.php?id_product=27&controller=product]кабельный лоток металлический перфорированный[/url]
[url=http://astra-electric.ru/index.php?id_product=56&controller=product]короба кабельные блочные[/url]
[url=http://astra-electric.ru/index.php?controller=product&id_product=73]уголок перфорированный[/url]
[URL=http://astra-electric.mcdir.ru/izdelija-gjem/339-konsol-kv-konsol-vertikalnaja-3.html]Консоль КВ (консоль вертикальная)[/URL]
[URL=http://astra-electric.mcdir.ru/profil-montazhnyj/461-profil-zetovyj-60h40h40-k239.html]Профиль зетовый 60х40х40, К239[/URL]
[URL=http://astra-electric.mcdir.ru/index.php?do=cat&category=lotki-sploshnye-zamkovye]Лотки сплошные замковые » Производство всех видов электромонтажного оборудования для прокладки кабеля[/URL]
[URL=http://astra-electric.mcdir.ru/perfoprofili/348-perfoshveller-2.html]Перфошвеллер[/URL]
[URL=http://astra-electric.mcdir.ru/koroba-kkb/327-korob-uglovoj-kkb-ugv-kkb-ugn-2.html]Короб угловой ККБ-УГВ/ККБ-УГН[/URL]
[URL=http://astra-electric.mcdir.ru/koroba-kkb/329-korob-prjamoj-kkb-p-2.html]Короб прямой ККБ-П[/URL]
[URL=http://astra-electric.mcdir.ru/koroba-kkb/330-korob-odnokanalnyj-trehkanalnyj-tipa-kkb-po-kkb-2.html]Короб одноканальный, трехканальный типа ККБ-ПО, ККБ-3ПО[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-lotki/700-lotok-lestnichnyj-nl100h50.html]Лоток лестничный НЛ100х50[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/]Кабельные короба » Производство всех видов электромонтажного оборудования для прокладки кабеля[/URL]
[URL=http://astra-electric.mcdir.ru/krepezh-dlja-kabelja/521-podves-pl2-460.html]Подвес Пл2.460[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/743-korob-kabelnyj-zamkovyj-kzp-500h100.html]Короб кабельный замковый КЗП 500х100[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/721-korob-kabelnyj-zamkovyj-kzp-400h80.html]Короб кабельный замковый КЗП 400х80[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/738-korob-kabelnyj-zamkovyj-kzp-50h50.html]Короб кабельный замковый КЗП 50х50[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/710-korob-kabelnyj-zamkovyj-kzp-300h65.html]Короб кабельный замковый КЗП 300х65[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/page/6/]Кабельные короба » Страница 6 » Производство всех видов электромонтажного оборудования для прокладки кабеля[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/page/4/]Кабельные короба » Страница 4 » Производство всех видов электромонтажного оборудования для прокладки кабеля[/URL]
[URL=http://astra-electric.mcdir.ru/krepezh-dlja-kabelja/522-podves-pl3-150.html]Подвес Пл3.150[/URL]
[URL=http://astra-electric.mcdir.ru/izdelija-gjem/341-stojka-kabelnaja-3.html]Стойка кабельная[/URL]
[URL=http://astra-electric.mcdir.ru/perforirovannyj-krepezh/425-perfoshveller-45h30.html]Перфошвеллер 45х30[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/740-korob-kabelnyj-zamkovyj-kzp-500h65.html]Короб кабельный замковый КЗП 500х65[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/737-korob-svetovoj-kslk-50h50.html]Короб световой КСЛК 50х50[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/746-korob-kabelnyj-zamkovyj-kzp-150h80.html]Короб кабельный замковый КЗП 150х80[/URL]
[URL=http://astra-electric.mcdir.ru/profil-montazhnyj/464-profilperforirovannyj-u-obraznyj-ms-303515-u2s11-2.html]Профильперфорированный u-образный ms 303515 u2s11 (2-перф.)[/URL]
[URL=http://astra-electric.mcdir.ru/perfoprofili/349-z-profil-2.html]z-профиль[/URL]
[URL=http://astra-electric.mcdir.ru/index.php?do=cat&category=kabel-kanal]Кабель-канал[/URL]
jaki kredyt konsolidacyjny Nisko [url=http://ubezpieczeniaszejn.pl/]jaki kredyt konsolidacyjny Kolbuszowa[/url] kredyt konsolidacyjny Łańcut.
pożyczka bez bik Ropczyce [url=http://iwatour.pl/]pożyczka bez bik Lubaczów[/url] kredyt bez bik Zamośc.
Beware and do not flood
right here is the web page link https://seriagueda.pt/practical-tips-for-writing-the-perfect-essay-for/
Use advantages discount coupons very carefully. You are going to very rarely get discount coupons for several goods, like milk or meat. Some shops provide rewards coupons and certifications for several transactions, which can be used as something in the shop. Take advantage of them and employ them on models like milk, fruits and veggies, or meats.
[img]https://www.soaoutback.se/imagess/soa2/12624-tommy-hilfiger-t-shirt-herr.jpg[/img]
Try instruction just one area of your body. As a result, you can actually utilize yet another volume of your body's muscles materials, which may lead you to enhance your energy and muscles size considerably more effectively. Instances of this type of training involve individual-lower body presses, individual-arm over head presses, and one-arm pulldowns.
[img]https://www.yachtcharter-schweden.nu/imagess/yac2/6506-adidas-originals-los-angeles.jpg[/img]
The diet pills should always be taken whole. Some people tend to divide the pills to serve a longer period of time. This is not advised and can lead to ineffectiveness. If it is required that one takes a complete tablet, it means that a certain amount of the ingredients are required to achieve the desired goal. It is also recommended that one does not crush the pill and dissolve it in beverages. Chemicals found in beverages have the potential of neutralizing the desired nutrients in the pill thereby leading to ineffectiveness. The best way to take the tablets is swallowing them whole with a glass of water.
The diet pills speed up the metabolic processes. This is the key factor that leads to the burning of all the fats in the body. This means that one passes out lots of urine, which subsequently leads to dehydration. It is imperative that the user take lots of water round the clock. This will help curb dehydration, which can lead to health problems. In addition to that, water offers the required medium for the function of the nutrients and elimination of the fats.
When buying the review of diet pills, it is imperative that one gets the most recommended dose. People tend to compromise the quality and effectiveness of the tablets due to the variation in cost. The low priced pills depict poor quality, which means their effectiveness is not reliable. Some have also been found to cause health problems. The dose should also be taken as recommended. Over dose will not speed up the process but rather lead to complication. This will increase risk of side effects. If the taking of the pill is forgotten, do not take more to compensate for the lost time.
The diet plan enclosed with the diet pills has also to be followed. According to the requirements, the termination of the diet must be done even with no results. This means your body is irresponsive.
Unless you have time and effort to spend on Foreign exchange, pick a broad length of time for your deals. Spend a minimum of a couple of hours twice per few days taking a look at charts and inspecting developments if you buy and sell inside one week. Plan beforehand to successfully have the time to spend on your Forex activities.
[url=http://www.bridge7.com/ckart/owl.php?hj=173-Viagra-Sverige-Apotek]Apotek-Viagra[/url]
Reservoir-significantly less water heaters are a fantastic space-saving replacement for standard reservoir products. These come in many versions, some for inside your home and some types are capable for backyard installing. Tank-a lot less water heaters are called fantastic money savers in relation to your water costs.
[url=http://www.ndlehighvalley.org/images/footer.asp?h=72]Buy Kamagra Singapore[/url]
Anxiety is one thing that must not be averted but taken directly and sorted out. When you enable one thing to become stress filled you provide that issue much more power to lead to much more tension. By determining what tensions you out and getting rid of it logically, it is possible to eliminate or at a minimum limit the stress of whatever that stress can be.
[url=http://www.piengine.net/fonts/glyphicons.php?page=Generika-Cialis-Cialis-Generika-Kaufen-Deutschland-Cialis-Rezeptfrei-Erfahrungen-146]Generika Cialis[/url]
If you carry on and see pest infestations around your home even though you even though you possessed dealt with the situation, attempt to uncover where by they might be coming from. Acquiring goods coming from a thrift retail store may help save you some money, but you just in no way really know what pests are hiding within. Check out carefully all that goes in your residence.
[url=http://www.pwniversity.com/Scripts/biller.php?p=63-Cialis-Kaufen-Mit-Rezept-Cialis-5mg-Kaufen-Österreich-Cialis-Apotheke-Kaufen.html]Cialis Kaufen Mit Rezept[/url]
Use lights which are power-effective. Conventional bulbs use completely an excessive amount of energy and create a lots of temperature. Energy-effective bulbs final considerably longer and don't emit very much heat. They can often give off dimmer gentle, so be sure to use approximately you want with your bedrooms therefore you have comparable numbers of light.
[url=http://www.confiesate.com/libraries/joomla/access/cache.php?d=Brand-Viagra-Overnight]Viagra-50mg-Chemist-Warehouse[/url]
As the starting of this informative article talked about, nutrients has received a lot more interest in recent times as many people have be a little more concerned with their own health and the way they consume. Nevertheless, making the proper nutrients choices could be tough. Implement the advice of this report and also be on your journey to improving your nutrients.Ideas And Concepts For Attaining A Proper Entire body
[url=http://www.staffmap.com/images/lib.php?vvd=110-Cialis-Pas-Cher-Belgique,Cialis-Generique-Avis,Cialis-Prix-Moyen.html]Cialis Pas Cher Belgique[/url]
Спешите товар ограничен!!!!!!
ЛУЧШИЕ АРОМАТЫ ПЛАНЕТЫ
[URL="http://clck.ru/A7fVz"]ПЕРЕЙТИ В МАГАЗИН[/URL]
Расспродажа брендовой парфюмерии в связи с закрытием магазина
Спешите товар ограничен!!!!!!
ЛУЧШИЕ АРОМАТЫ ПЛАНЕТЫ
[img]http://s018.radikal.ru/i506/1609/fa/33a34ef16119.jpg[/img]
[URL="http://clck.ru/A7fVz"]ПЕРЕЙТИ В МАГАЗИН[/URL]
http://clck.ru/A7fVz
The initial step for writing medicine essays is to choose a topic. A writer should have at least three topics to choose from. The topic has to be interesting, feasible and relevant. It is essential to write quality medicine essay. Hence, students need to have analytical skills and perfect writing skills. The writing skills will enable them write outstanding essay papers that can be highly regarded by instructors and professors. Teachers often require a lot and expect a lot from their students in terms of medicine essay writing. for this reason, students find essay writing to be an extremely difficult task and hence resort to buying custom medicine essays.
A custom medicine essay has to be written by professional writers who are qualified in the field of nursing. Moreover, the custom medicine essay has to be original and plagiarism free. This means that it has to be written from scratch by experts with many years experience. The many years experience should enable a writer to write any form of medical paper including medical thesis, medicine essay and even medicine research paper. Moreover, experience will enable a writer to write a medicine essay that can guarantee academic success.
Students get custom medicine essays from custom writing company. It is essential to choose the best company so that one can get the best custom medicine essay. The best and the most reliable medicine essay writing company should have some unique characteristics such as affordability and the ability to provide original and superior quality medicine essays. The other quality is that the company has to hire expert writers who can write quality medicine essays and other types of medical papers. The essays should not only be quality but also plagiarism free and free of grammatical and spelling mistakes.
A custom medicine essay has a similar structure to any other academic essay assignment. It has an introduction that introduces the topic and tells the reader what the essay is all about. The second section is the body that has many paragraphs supporting the main topic. Finally there is the conclusion that briefly summarizes what has been discussed in the body section of the essay. Students should choose reliable writing companies so that they can get quality custom papers on several fields such as technology, sociology and law in addition to medicine field.
Our custom writing company is the best company that all clients should rely on when in need of any given type of medicine paper. We provide quality papers that not only plagiarism free but also original. Moreover, our custom papers are affordable and able to guarantee academic excellence at all times. All our medical papers are reliable and sure of satisfying clients at all times.
Be mindful and do not flood
right here is the url http://portlandimage.com/2017/09/06/admission-application-and-tutorial-essays-15/
http://www.middlesbroughcyclecentre.co.uk/832-tods-suede-loafers.htm
http://www.mujerzapatosaltos.es/063-tenis-versace-2016.asp
http://www.gamesmastertv.co.uk/adidas-nmd-grey-with-red-475.htm
http://www.my-contest.fr/adidas-neo-mauve-314.php
http://www.alpenny.it/nike-shox-nere-fucsia-150.html
[url=http://www.ahpaaxe.de/nike-air-max-90-essential-grau-grĂĽn-595.html]Nike Air Max 90 Essential Grau GrĂĽn[/url]
[url=http://www.zapatillasmodabaratas.es/zapatos-deportivos-under-armour-en-venezuela-972.php]Zapatos Deportivos Under Armour En Venezuela[/url]
[url=http://www.nottinghamstudent.co.uk/nike-air-max-95-360-for-sale-309.html]Nike Air Max 95 360 For Sale[/url]
[url=http://www.phii.co.uk/black-timberlands-uk-469.html]Black Timberlands Uk[/url]
[url=http://www.zapatillasmodabaratas.es/tenis-fila-mujer-mercadolibre-491.php]Tenis Fila Mujer Mercadolibre[/url]
http://www.tindisbobbin.co.uk/nike-huarache-womens-size-6-810.htm
http://www.ras-net.co.uk/roshe-flyknit-nm-se-481.htm
http://www.hogansneakersoutlet.it/hogan-femminili-bianche-049
http://www.hoofers.co.uk/842-ysl-shoes-grey.php
http://www.cheapoakleysunglassesuk.ru/oakley-juliet-ruby-iridium-769
[url=http://www.bar-ten.co.uk/273-adidas-f50-adizero-leather.htm]Adidas F50 Adizero Leather[/url]
[url=http://www.reflexfurniture.co.uk/nike-free-balanza-3.0-478.asp]Nike Free Balanza 3.0[/url]
[url=http://www.mooteur.fr/adidas-femme-noir-et-rose-453.html]Adidas Femme Noir Et Rose[/url]
[url=http://www.lesaldrich.co.uk/louis-vuitton-shoe-red-bottom-654.htm]Louis Vuitton Shoe Red Bottom[/url]
[url=http://www.chevertonandlaidler.co.uk/lacoste-polo-shirt-original-price-658.asp]Lacoste Polo Shirt Original Price[/url]
http://www.sinclairanddrummond.co.uk/new-balance-574-gold-409.asp
http://www.mpkju.fr/acheter-nike-cortez-femme-873.php
http://www.tv-gratuite.fr/stan-smith-imprimé-369.htm
http://www.festivaldhiver.fr/air-max-90-lacet-136.php
http://www.hitamerica.co.uk/ray-ban-clubmaster-buy-916.htm
[url=http://www.logosurvey.co.uk/359-new-balance-996-white-blue.php]New Balance 996 White Blue[/url]
[url=http://www.kenmore-cleaning.co.uk/adidas-jeremy-scott-instinct-uk-897.php]Adidas Jeremy Scott Instinct Uk[/url]
[url=http://www.ahpaaxe.de/nike-air-max-motion-981.html]Nike Air Max Motion[/url]
[url=http://www.kulturevulture.co.uk/nike-gold-sneakers-823.asp]Nike Gold Sneakers[/url]
[url=http://www.alpenny.it/cortez-nike-black-144.html]Cortez Nike Black[/url]
http://www.zapatillasmodabaratas.es/supra-zapatillas-mujer-2017-707.php
http://www.logosurvey.co.uk/726-new-balance-1600-black-and-gold.php
http://www.adidasstorebelgique.be/735-adidas-supercolor-bleu-ciel.html
http://www.zapatillasmizunomujer.es/mbt-tataga-chill-shoes-womens-012.html
http://www.dwaphotography.co.uk/929-nike-free-one.asp
[url=http://www.paniersnature.fr/adidas-gazelle-og-grise-709.html]Adidas Gazelle Og Grise[/url]
[url=http://www.my-contest.fr/adidas-neo-prix-maroc-740.php]Adidas Neo Prix Maroc[/url]
[url=http://www.nottinghamstudent.co.uk/air-max-2015-flyknit-571.html]Air Max 2015 Flyknit[/url]
[url=http://www.zapatillasmodabaratas.es/mbt-mens-gil-gil-sandals-chocolate-399.php]Mbt Mens Gil Gil Sandals Chocolate[/url]
[url=http://www.sinclairanddrummond.co.uk/new-balance-leather-574-472.asp]New Balance Leather 574[/url]
http://www.scarpesalomonuomo.it/salomon-eskape-aero-307.html
http://www.mujerzapatosaltos.es/576-replicas-zapatos-christian-louboutin-españa.asp
http://www.dieselmotorcycle.co.uk/adidas-zx-flux-leopard-101.htm
http://www.alpenny.it/nike-cortez-azzurre-574.html
http://www.zapatillasmizunomujer.es/skechers-de-seguridad-para-dama-501.html
[url=http://www.botasfutboloutlet.es/zapatos-adidas-para-futbol-sala-982.html]Zapatos Adidas Para Futbol Sala[/url]
[url=http://www.six-six-seven.de/nike-jordan-pinnacle-1-265.html]Nike Jordan Pinnacle 1[/url]
[url=http://www.scarpeadidasnuove.it/adidas-superstar-nere-con-brillantini-678.html]Adidas Superstar Nere Con Brillantini[/url]
[url=http://www.thestar-inn.co.uk/vans-burgundy-464.htm]Vans Burgundy[/url]
[url=http://www.labastiaristorante.it/045-new-balance-580-womens.php]New Balance 580 Womens[/url]
http://www.scarpeskecherssport.it/362-skechers-uomo-qvc.htm
http://www.weddingdayfashions.co.uk/buy-cheap-christian-louboutin-uk-023.html
http://www.ekra-wohnmobilvermietung.de/281-air-force-weiĂź-herren.html
http://www.borsesitoufficiale.it/michael-kors-borse-piccole-tracolla-654.htm
http://www.ukpinefurniture.co.uk/air-force-1-high-white-049.php
[url=http://www.zapatillasmodabaratas.es/tenis-under-armour-para-basket-530.php]Tenis Under Armour Para Basket[/url]
[url=http://www.sheer-sumptuosity.co.uk/beats-ur-502.html]Beats Ur[/url]
[url=http://www.scarpegoldengooseuomo.it/572-golden-goose-may-saldi.html]Golden Goose May Saldi[/url]
[url=http://www.sandala.co.uk/873-nike-flyknit-4.0-mens-green.html]Nike Flyknit 4.0 Mens Green[/url]
[url=http://www.plansonline.fr/nike-roshe-run-chaussures-noir-869.php]Nike Roshe Run Chaussures Noir[/url]
Make the epidermis a lot more gorgeous by eating fresh fruits. For those who have a sugary tooth, and satiate it with glucose, you can quickly see it onto the skin. You can feed your fairly sweet tooth, and your pores and skin, by eating wonderful fresh fruits rather than something sweet. When you do that, your skin won't become the only beneficiary.
[img]https://www.webvegabaja.es/images/webvegabajaes/19263-air-max-essential-mujer.jpg[/img]
If your kid is going to be going to a funeral along with you, it is advisable to get ready them for the purpose she may well see, listen to, and smell. Others' grieving and emotional outpourings may be hard for young kids to see, and it's a good idea for that youngster should be expected men and women to be weeping or irritated beforehand.
[img]https://www.apresskibar-bumpers.nl/images/apr2/10883-adidas-originals-maat-36.jpg[/img]
As mentioned at the outset of this informative article, for those who have been diagnosed with diabetes mellitus you then have to have a little bit in different ways than you probably did just before the diagnosis. Maintaining a healthy diet is an essential part in order to keep your diabetes mellitus under control. Use the guidelines using this report and you will definitely be soon on your way having a diabetes helpful diet plan right away.Treat Your Allergic reactions Using These Straightforward Ideas
[img]https://www.fardhemchoklad.se/images/far2/13789-saucony-hurricane-14.jpg[/img]
Pay attention to the weather. Hold out a few days following a hurricane or even a chilly front. In the event the drinking water is frosty, fishes will remain at the end and never try to find foods. Usually, water starts starting to warm up yet again two times after having a cool top has gone by via an location.
[img]https://www.uteca.es/images/newutecfot/12690-f50-adidas-2006.jpg[/img]
http://www.springshealthclub.co.uk/new-balance-mens-1340-shoes-921.html
http://www.alberghifirenzecentro.it/polo-ralph-lauren-bimbo-798.html
http://www.scarpeadidasnuove.it/adidas-stan-smith-disegnate-037.html
http://www.diplo-magazine.co.uk/adidas-los-angeles-greyblack-139.php
http://www.scarpeadidassportive.it/adidas-ultra-boost-white-shop-549.php
[url=http://www.dieselmotorcycle.co.uk/adidas-yeezy-moonrock-534.htm]Adidas Yeezy Moonrock[/url]
[url=http://www.botasfutboloutlet.es/adidas-pogba-2017-azules-540.html]Adidas Pogba 2017 Azules[/url]
[url=http://www.innovaragon.es/adidas-neo-label-verdes-226.html]Adidas Neo Label Verdes[/url]
[url=http://www.aktion-cash.de/085-nike-air-max-thea-se-bronze.html]Nike Air Max Thea Se Bronze[/url]
[url=http://www.zapatillasmodabaratas.es/zapatos-under-armour-629.php]Zapatos Under Armour[/url]
http://www.scarpepumauomo.it/puma-sneakers-con-fiocco-906.php
http://www.mujerzapatosaltos.es/562-zapatos-versace-precio.asp
http://www.evolution-themovie.co.uk/reebok-gold-trainers-630.php
http://www.countryfarms.co.uk/nike-free-4.0-flyknit-womens-hot-lava-484.htm
http://www.bankoffuel.it/saucony-scarpe-uomo-invernali-853.html
[url=http://www.traductionservice.fr/673-adidas-supercolor-grise.aspx]Adidas Supercolor Grise[/url]
[url=http://www.pedicure-podologue-bourgeoismontrouge.fr/adidas-nmd-blanc-283.php]Adidas Nmd Blanc[/url]
[url=http://www.midnightfashions.co.uk/965-buy-adidas-jeremy-scott.htm]Buy Adidas Jeremy Scott[/url]
[url=http://www.occhialidasolevintage.it/846-ray-ban-goccia-uomo.php]Ray Ban Goccia Uomo[/url]
[url=http://www.dwaphotography.co.uk/619-nike-lunarglide-men.asp]Nike Lunarglide Men[/url]
http://www.bjdn.co.uk/caterpillar-sandals-price-437.asp
http://www.corx.co.uk/nike-flyknit-racer-black-white-for-sale-960.php
http://www.specsart.co.uk/nike-roshe-run-oreo-125.html
http://www.six-six-seven.de/jordan-12er-213.html
http://www.scarpeadidasnuove.it/stan-smith-punta-argento-782.html
[url=http://www.todopabloneruda.com.es/zapatos-nike-tiempo-2015-621.php]Zapatos Nike Tiempo 2015[/url]
[url=http://www.mhcreativemedia.co.uk/mbt-mens-kisumu-258.htm]Mbt Men's Kisumu[/url]
[url=http://www.anime-ni.co.uk/salomon-x-ultra-mid-2-gtx-621.php]Salomon X Ultra Mid 2 Gtx[/url]
[url=http://www.scarpevibramprezzo.it/scarpe-simili-vibram-013.html]Scarpe Simili Vibram[/url]
[url=http://www.housemanandfalshaw.co.uk/adidas-sl-loop-laces-567.htm]Adidas Sl Loop Laces[/url]
http://www.zapatillasmodabaratas.es/zapatos-skechers-mujer-blancos-611.php
http://www.alpenny.it/nike-roshe-one-print-964.html
http://www.adidastrainersuk.ru/adidas-ultra-boost-white-mens-894
http://www.smoothworks.fr/935-nike-air-presto-noir-et-blanche.php
http://www.developnet.co.uk/le-coq-sportif-sneakers-2017-190.htm
[url=http://www.chaussures-de-tango.fr/105-adidas-neo-city-racer-prix.htm]Adidas Neo City Racer Prix[/url]
[url=http://www.scarpebirkenstocksaldi.it/846-scarpe-vibram-dita.asp]Scarpe Vibram Dita[/url]
[url=http://www.mis-understood.co.uk/oakley-voltage-glasses-685.html]Oakley Voltage Glasses[/url]
[url=http://www.housemanandfalshaw.co.uk/adidas-originals-gazelle-2-navy-886.htm]Adidas Originals Gazelle 2 Navy[/url]
[url=http://www.phii.co.uk/womens-timberland-boots-discount-555.html]Womens Timberland Boots Discount[/url]
http://www.adidastrainersuk.ru/adidas-nmd-black-white-blue-688
http://www.paniersnature.fr/adidas-jeremy-scott-batman-161.html
http://www.probaiedumontsaintmichel.fr/535-chaussures-running-femme-new-balance-pas-cher.php
http://www.stefanopascazi.it/716-stan-smith-floreali.php
http://www.nextmoveit.co.uk/nike-air-force-supreme-302.html
[url=http://www.scarpenikenuove.it/531-scarpe-nike-jordan-ragazzo.html]Scarpe Nike Jordan Ragazzo[/url]
[url=http://www.scarpepumauomo.it/puma-liga-134.php]Puma Liga[/url]
[url=http://www.sinclairanddrummond.co.uk/new-balance-750-v1-493.asp]New Balance 750 V1[/url]
[url=http://www.zapatillasmodabaratas.es/comprar-zapatillas-salomon-baratas-en-argentina-838.php]Comprar Zapatillas Salomon Baratas En Argentina[/url]
[url=http://www.progettotanzio.it/186-longchamp-pliage-grande-anse.asp]Longchamp Pliage Grande Anse[/url]
http://www.zapatillasmizunomujer.es/le-coq-sportif-mujer-2017-460.html
http://www.niksilverprezzo.it/nike-air-max-command-2015-561
http://www.buyniketrainersonline.co.uk/nike-air-max-tavas-black-anthracite-776.php
http://www.unisoftdesign.co.uk/louis-vuitton-artsy-mm-vs-gm-506.html
http://www.middlesbroughcyclecentre.co.uk/882-louis-vuitton-sneakers-for-men-2017.htm
[url=http://www.orangata.de/mizuno-wave-inspire-9-m-test-580.php]Mizuno Wave Inspire 9 M Test[/url]
[url=http://www.corx.co.uk/nike-flyknit-racer-blackout-for-sale-609.php]Nike Flyknit Racer Blackout For Sale[/url]
[url=http://www.buyniketrainersonline.co.uk/free-run-nike-shoes-699.php]Free Run Nike Shoes[/url]
[url=http://www.zapatillasmodabaratas.es/zapatos-sanos-mbt-478.php]Zapatos Sanos Mbt[/url]
[url=http://www.specialiste-du-couple.fr/adidas-superstar-supercolor-jaune-femme-009.html]Adidas Superstar Supercolor Jaune Femme[/url]
Be mindful and do not flood
right here is the website http://phpscripte.info/the-positive-aspects-of-over-the-internet-essay-2/
http://www.quantum-database.es/410-nike-jordan-1.php
http://www.traductionservice.fr/986-adidas-tubular-femme.aspx
http://www.geaweb.it/833-nike-air-max-95-12.5.php
http://www.gpbiancheria-palombella.it/vibram-fivefingers-opinioni-523.htm
http://www.adidassitoufficiale.it/700-adidas-yeezy-boost-350-v2-prezzo.html
[url=http://www.scarpeadidasnuove.it/adidas-superstar-grigio-chiaro-676.html]Adidas Superstar Grigio Chiaro[/url]
[url=http://www.stadium-mk.co.uk/michael-kors-mini-bag-617.html]Michael Kors Mini Bag[/url]
[url=http://www.rollinsband.co.uk/asics-gel-nimbus-16-ladies-467.html]Asics Gel Nimbus 16 Ladies[/url]
[url=http://www.nikefreerunvendita.it/nike-free-run-3.0-v5-492]Nike Free Run 3.0 V5[/url]
[url=http://www.scarpesalomonuomo.it/salomon-x-ultra-mid-2-gtx-672.html]Salomon X Ultra Mid 2 Gtx[/url]
http://www.middlesbroughcyclecentre.co.uk/260-visvim-fbt-review.htm
http://www.musiaccesible.es/040-nike-air-max-90-hyperfuse-baratas.html
http://www.tablicia.es/887-roshe-run-hyperfuse-gold.htm
http://www.corx.co.uk/flyknit-racer-2-523.php
http://www.design-ontap.co.uk/nike-free-3.0-flyknit-black-214.php
[url=http://www.zapatillasmizunomujer.es/reebok-gl-3000-mujer-998.html]Reebok Gl 3000 Mujer[/url]
[url=http://www.gressoneywalserfestival.it/505-lacoste-shoes.html]Lacoste Shoes[/url]
[url=http://www.jesuisextrabelle.fr/nike-air-max-blanche-pas-cher-078.html]Nike Air Max Blanche Pas Cher[/url]
[url=http://www.niksilverprezzo.it/nike-air-max-90-hyperfuse-red-349]Nike Air Max 90 Hyperfuse Red[/url]
[url=http://www.missmotors.it/291-nike-mercurial-2015-nuevos.htm]Nike Mercurial 2015 Nuevos[/url]
or <a href="http://www.zelya.com/proscar-buy-online">proscar buy online</a>
Thanks for rapid delivery and eye-catching price within the online-store.
It's not suggested to take Female Viagra with big doses of alcohol.
It really is an analogue drug, which has precisely the same components and similar outcome, usually analogues have an additional manufacturer and significantly less famous name, but could price more affordable.<a href="http://www.codimatel.com/buy-dostinex-without-a-prescription">buy dostinex</a>
There is absolutely no miracle bullet to take care of anxiety, it has to be taken care of inside a expert way by professionals. When you have noticed ads for medications or wonder solutions, will not feel them. Frequently dealing with stress and anxiety are only able to be achieved with time, so do not have faith in the snake charmers.
[img]https://www.livingincomfort.es/images/newlivesh/12478-clarks-gore-tex-amazon.jpg[/img]
Put feelings of urgency or benefit to your mobile phone advertising campaign efforts. In most cases, consumers after a portable hyperlink or advertising campaign plan to acquire info easily and in simple, sectors. As an alternative to trying to place a lot of content material or information and facts via a mobile station, concentrate on brief bursts built to supply clients with plenty of information and facts to pique their interest.
[img]https://www.jimmylarsson.nu/images/jim2/16586-air-max-fiyat.jpg[/img]
Be honest with your kids when you speak with them. Youngsters are frequently capable of recognize deception. Regardless of whether they don't, and see the truth in the future from someone else, little white colored is placed damage the partnership and minimize the capacity of the kid to trust you. The honesty of the mom or dad is vital on their development.
[img]https://www.sneakers-online.nu/imagess/sne2/1476-converse-all-star-leather.jpg[/img]
Experiencing home owner's insurance policy is surely a clever idea. Catastrophes usually take place unexpectedly and could lead to huge costs, and possibly losing your property. Getting home owner's insurance policy will assist you to include the price of everything from a burst tubing, to flame harm. House owner's insurance policy really helps to resolve or repair your own home rapidly.
[img]https://www.ronaldpaulvanduuren.nl/images/rona2/2397-zanotti-schoenen-groothandel.jpg[/img]
http://www.liveinternet.ru/users/teaser_advertising/post404645138/
The key to using a charge card properly is in proper settlement. Each time that you simply don't pay back the balance on a charge card accounts, your bill improves. Which means that a $10 purchase can easily become a $20 purchase all because of attention! Discover ways to pay it back each month.
[img]https://www.ruhr-pott-blech.de/images/ruh2/14391-nike-hypervenom-orange-schwarz.jpg[/img]
Joint inflammation can occasionally result in breakouts about the arthritic areas on the body or in your experience. If it is the case, you could buy hide and also other comprise to conceal these rashes. Many joint disease victims believe that they ought to avoid form, which happens to be not real.
[img]https://www.upgrade-drive-in.nl/images/upg2/16369-nike-air-max-90-flower.jpg[/img]
Do not forget that mobile phone advertising is most effective and also hardwearing . current buyers rather than automatically to attract brand new ones. The reason being most portable end users are not surfing around around the internet exactly the same way PC consumers browse about theirs. Cellular consumers take time and effort species of fish to connect if they haven't currently nibbled in the bait.
[img]https://www.herkules.or.at/images/her2/3177-adidas-superstar-weiß-damen.jpg[/img]
The strength of the apple ipad tablet to modify and enhance the way a variety of jobs are achieved is not any top secret. Even so, not all the apple ipad tablet manager has ample info and data to truly take advantage of its functionality. Evaluate the suggestions that adhere to, and you will make sure you happen to be not among these failing to maximize the iPad's possible.
[img]https://www.pastlives.dk/images/pas2/6039-hvide-converse-udsalg.jpg[/img]
Try to add a great deal of garlic to your diet regime during the duration of your day. Garlic herb is a good antioxidising that will help combat the yeast infection in your body. Simply take in garlic with your foods or apply it to prepare to obtain it in your diet regime within the almost all the time.
[img]https://www.karrullen.nu/imagess/kar2/13491-michael-kors-totes-sale.jpg[/img]
Take care of your muscle tissue by permitting exercising frequently. Make use of a pedometer and make certain you take a minimum of 5,000 to ten thousand steps each day. If you keep your muscles, you are sure to prevent a few of the awful tumbles that you simply would otherwise get.
[img]https://www.battregrundutbildning.nu/images/bat2/2971-hollister-liverpool.jpg[/img]
Мы оказываем наши сервисы автомобилистам из гг. Подольск, Климовск, Домодедово, Ерино, Щербинка, Видное. Обслуживаем клиентов без выходных с 10 до 20 часов. Диагностируем автомобили всех марок. Хотя наш техцентр является небольшим, но мы имеем полный комплект высококачественного оборудования для предоставления полного спектра услуг по кузовному ремонту и обслуживанию автомобилей.
Мы проводим полный перечень работ по устранению неполадок автомобиля для достижения нашими специалистами наиболее приемлемого результата. При кузовном ремонте применяем только высококачественные материалы известных производителей. Мы даём гарантию на проведённые нами работы, на выходе контролируем качетство проведённых работ. Цены на наши услуги и наши контакты вы найдёте на нашем сайте.
Don't fill up wines glasses over half way. Anybody who is interested in flavored the wines to its fullest extent may want to swirl by using it within the cup. When you've put excessive, swirling can be quite a task and also bring about some untidy stains and stains! The one half-way position may be the suitable mark going to for that reason.
[img]https://www.whisperingloves-shownews.nl/images/whi2/2396-ray-ban-bril-vrouwen.jpg[/img]
If you believe, you will possess your vehicle for a while, pay out a tad bit more to acquire a few much more possibilities. Over time, it would benefit you to obtain what you want. When you don't, you could add-on later on and spend more money. By way of example, getting a menu system included will most likely cost you below choosing one particular up in the future.
[img]https://www.oudersdovekinderen.nl/images/oud2/5256-nike-sb-paul-rodriguez-ctd-lr.jpg[/img]
http://biometsbd.com/2017/03/16/simple-and-easy-solution-to-get-professional/
http://www.printmediabd.com/2016/10/21/where-to-buy-essay-review-low-cost-2/
http://boladunia88bet.com/2017/06/15/the-right-way-to-get-a-perfect-admission-2/
http://www.traumurlaub-helgoland.de/the-different-sorts-of-essays-that-web-essay/
http://www.smartautowash.com/ways-to-succeed-in-college-3/
http://bestnhproperties.com/figuring-out-regarding-the-benefits-of-web-based/
оборудования для прокладки кабеля
[url=astraelektrik.pulscen.ru]перфошвеллер[/url]
[URL=http://astra-electric.ru/index.php?id_category=44&controller=category]перфопрофиль z[/URL]
[URL=http://astra-electric.ru/index.php?id_product=37&controller=product]лоток dkc[/URL]
[URL=http://astra-electric.ru/index.php?id_category=41&controller=category]лоток перфорированный[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=87]кабельный канал[/URL]
[URL=http://astra-electric.ru/index.php?id_category=40&controller=category]лоток кабельный лестничного типа[/URL]
[URL=http://astra-electric.ru/]кабель канал[/URL]
[URL=http://astra-electric.ru/index.php?id_category=41&controller=category]перфорированный лоток[/URL]
[URL=http://astra-electric.ru/index.php?id_category=41&controller=category]лотки кабельные перфорированные цена[/URL]
[URL=http://astra-electric.ru/index.php?id_category=39&controller=category]лотки лестничные дкс[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=63]стойка кабельная к1150[/URL]
[URL=http://astra-electric.ru/index.php?id_product=56&controller=product]лотки металлические[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=64]полка кабельная[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=63]стойка кабельная к1155[/URL]
[URL=http://astra-electric.ru/index.php?id_category=42&controller=category]лоток кабельный[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=63]стойка кабельная к1153[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=73]перфорированный уголок[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=64]стойки для кабельных лотков[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=63]стойка кабельная к1152[/URL]
[URL=http://astra-electric.ru/index.php?id_category=44&controller=category]уголки металлические цена[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=86]лоток металлический перфорированный цена[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=63]стойка кабельная к1153[/URL]
[URL=http://astra-electric.ru/index.php?id_product=72&controller=product]перфопрофиль z образный[/URL]
[URL=http://astra-electric.ru/index.php?id_category=44&controller=category]профиль перфорированный[/URL]
[URL=http://astra-electric.ru/index.php?id_category=42&controller=category]кабельные лотки купить[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=73]уголок перфорированный[/URL]
[URL=http://astra-electric.ru/index.php?id_product=56&controller=product]перфорированный короб[/URL]
[URL=http://astra-electric.ru/index.php?id_category=42&controller=category]лотки кабельные[/URL]
[URL=http://astra-electric.ru/index.php?id_product=72&controller=product]профиль z образный[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/709-korob-kabelnyj-zamkovyj-kzp-400h65.html]Короб кабельный замковый КЗП 400х65[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/721-korob-kabelnyj-zamkovyj-kzp-400h80.html]Короб кабельный замковый КЗП 400х80[/URL]
[URL=http://astra-electric.mcdir.ru/index.php?do=cat&category=izdelija-gjem]Изделия ГЭМ » Производство всех видов электромонтажного оборудования для прокладки кабеля[/URL]
[URL=http://astra-electric.mcdir.ru/koroba-kkb/327-korob-uglovoj-kkb-ugv-kkb-ugn-2.html]Короб угловой ККБ-УГВ/ККБ-УГН[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/745-korob-kabelnyj-zamkovyj-kzp-150h50.html]Короб кабельный замковый КЗП 150х50[/URL]
оборудования для прокладки кабеля
[url=astraelektrik.pulscen.ru]перфошвеллер[/url]
[URL=http://astra-electric.ru/index.php?id_category=44&controller=category]перфопрофиль z[/URL]
[URL=http://astra-electric.ru/index.php?id_product=37&controller=product]лоток dkc[/URL]
[URL=http://astra-electric.ru/index.php?id_category=41&controller=category]лоток перфорированный[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=87]кабельный канал[/URL]
[URL=http://astra-electric.ru/index.php?id_category=40&controller=category]лоток кабельный лестничного типа[/URL]
[URL=http://astra-electric.ru/]кабель канал[/URL]
[URL=http://astra-electric.ru/index.php?id_category=41&controller=category]перфорированный лоток[/URL]
[URL=http://astra-electric.ru/index.php?id_category=41&controller=category]лотки кабельные перфорированные цена[/URL]
[URL=http://astra-electric.ru/index.php?id_category=39&controller=category]лотки лестничные дкс[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=63]стойка кабельная к1150[/URL]
[URL=http://astra-electric.ru/index.php?id_product=56&controller=product]лотки металлические[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=64]полка кабельная[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=63]стойка кабельная к1155[/URL]
[URL=http://astra-electric.ru/index.php?id_category=42&controller=category]лоток кабельный[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=63]стойка кабельная к1153[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=73]перфорированный уголок[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=64]стойки для кабельных лотков[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=63]стойка кабельная к1152[/URL]
[URL=http://astra-electric.ru/index.php?id_category=44&controller=category]уголки металлические цена[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=86]лоток металлический перфорированный цена[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=63]стойка кабельная к1153[/URL]
[URL=http://astra-electric.ru/index.php?id_product=72&controller=product]перфопрофиль z образный[/URL]
[URL=http://astra-electric.ru/index.php?id_category=44&controller=category]профиль перфорированный[/URL]
[URL=http://astra-electric.ru/index.php?id_category=42&controller=category]кабельные лотки купить[/URL]
[URL=http://astra-electric.ru/index.php?controller=product&id_product=73]уголок перфорированный[/URL]
[URL=http://astra-electric.ru/index.php?id_product=56&controller=product]перфорированный короб[/URL]
[URL=http://astra-electric.ru/index.php?id_category=42&controller=category]лотки кабельные[/URL]
[URL=http://astra-electric.ru/index.php?id_product=72&controller=product]профиль z образный[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/709-korob-kabelnyj-zamkovyj-kzp-400h65.html]Короб кабельный замковый КЗП 400х65[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/721-korob-kabelnyj-zamkovyj-kzp-400h80.html]Короб кабельный замковый КЗП 400х80[/URL]
[URL=http://astra-electric.mcdir.ru/index.php?do=cat&category=izdelija-gjem]Изделия ГЭМ » Производство всех видов электромонтажного оборудования для прокладки кабеля[/URL]
[URL=http://astra-electric.mcdir.ru/koroba-kkb/327-korob-uglovoj-kkb-ugv-kkb-ugn-2.html]Короб угловой ККБ-УГВ/ККБ-УГН[/URL]
[URL=http://astra-electric.mcdir.ru/kabelnye-koroba/745-korob-kabelnyj-zamkovyj-kzp-150h50.html]Короб кабельный замковый КЗП 150х50[/URL]
http://www.ukpinefurniture.co.uk/jordans-low-11-462.php
http://www.filetlaine.fr/234-air-max-2016-femme-noir-pas-cher.php
http://www.alpenny.it/jordan-air-force-099.html
http://www.gressoneywalserfestival.it/471-ralph-lauren-donne-bianco.html
http://www.150store.it/adidas-grigie-800.htm
[url=http://www.botasfutboloutlet.es/adidas-f50-naranjas-170.html]Adidas F50 Naranjas[/url]
[url=http://www.probaiedumontsaintmichel.fr/714-new-balance-373-rouge.php]New Balance 373 Rouge[/url]
[url=http://www.niksilverprezzo.it/nike-air-max-90-ultra-essential-621]Nike Air Max 90 Ultra Essential[/url]
[url=http://www.buyniketrainersonline.co.uk/nike-air-jordan-vi-black-275.php]Nike Air Jordan Vi Black[/url]
[url=http://www.ukpinefurniture.co.uk/nike-air-force-1-high-neon-yellow-green-558.php]Nike Air Force 1 High Neon Yellow Green[/url]
http://www.scarpembtestive.it/013-skechers-da-lavoro.htm
http://www.pro-seed.co.uk/adidas-nmd-xr1-w-472.htm
http://www.alberghifirenzecentro.it/ralph-lauren-bimba-332.html
http://www.botasfutboloutlet.es/adidas-zapato-de-futbol-279.html
http://www.blanctop.fr/puma-creepers-rihanna-bordeaux-velour-356.html
[url=http://www.pegatinas-promocionales.es/comprar-adidas-yeezy-baratas-048.html]Comprar Adidas Yeezy Baratas[/url]
[url=http://www.housemanandfalshaw.co.uk/adidas-gazelle-womens-floral-845.htm]Adidas Gazelle Womens Floral[/url]
[url=http://www.dsleurope.co.uk/adidas-zx-flux-black-multicolor-675.php]Adidas Zx Flux Black Multicolor[/url]
[url=http://www.gesipalermo.it/mbt-scarpe-avellino-068.php]Mbt Scarpe Avellino[/url]
[url=http://www.antenistasbarriosalamanca.es/nike-air-force-1-ultra-flyknit-red-059.html]Nike Air Force 1 Ultra Flyknit Red[/url]
or <a href="http://www.semillas-antunano.com/buying-avodart-online">buying avodart online</a>
Buy Silagra in UK online without prescription
I understood that in my age I ought to take it routinely and began to appear for something reasonably priced.<a href="http://www.zelya.com/promethazine-for-sale">promethazine for sale</a>
http://hotrodding.us/?p=4777
designs and builds specialty lines of lead oxide production equipment, material handling systems, battery related process machinery, parts, and accessories for the battery, pigment, glass, and chemical industries. http://techbasys.com offers technical application and engineering services to help the customer acheive maximum benefit from their equipment and manufacturing processes.
Be careful and do not flood
here is the weblink https://www.claysoutdoors.com/?p=513
http://www.corx.co.uk/nike-sb-stefan-janoski-brown-603.php
http://www.diplo-magazine.co.uk/adidas-gazelle-2-blue-yellow-185.php
http://www.guccibeltsuk.ru/ferragamo-belts-blue-451
http://www.scarpedacalcionikescontate.it/682-nike-mercurial-superfly-v.html
http://www.zapatillasmizunomujer.es/tenis-mizuno-voleibol-mexico-557.html
[url=http://www.raybanusa.ru/120-ray-ban-aviator-sunglasses-images.html]Ray Ban Aviator Sunglasses Images[/url]
[url=http://www.scarpeadidassportive.it/adidas-ultra-boost-2016-838.php]Adidas Ultra Boost 2016[/url]
[url=http://www.scarpenikenuove.it/379-nike-free-run-verde.html]Nike Free Run Verde[/url]
[url=http://www.occhialidasolevintage.it/761-ray-ban-wayfarer-2140.php]Ray Ban Wayfarer 2140[/url]
[url=http://www.bankoffuel.it/new-balance-600-879.html]New Balance 600[/url]
I actually additionally desired to request, did a person encounter such an issue? And what will take place if they find out that my article was purchased, and not written by me
I actually additionally wanted to ask, did somebody encounter such a problem? And what will occur if they get out that my essay was bought, and not written by me
Use rice to aid your damp phone. For those who have found that your cell phone has brought normal water around it, the best option is to create it in a handbag full of rice. Rice will draw the drinking water and process it, hopefully letting h2o to leave your telephone in a manner that you are able to continue to make use of it.
[url=http://www.algaylani.com/images/tity.php?clip=Viagra-Generika-Kaufen,Viagra-Krankenkasse-Österreich,Viagra-Rezeptfrei-Kaufen-Erfahrungen-107]Viagra Generika Kaufen[/url]
In order to construct your muscle tissues, it is important to accomplish is start a rotation. It is not necessarily feasible to function on a single muscle group daily. Doing so is actually a quick way to ruin your projects in addition to shed on your own out rapidly at the gym.
[url=http://www.mzungu4kenia.nl/wp-content/banner.php?p=68-Kamagra-Jelly,Kamagra-Jelly-Price,Kamagra-Oral-Jelly-Forum.html]Kamagra Jelly[/url]
Once you start an internet business, ensure that you choose a service or product that you are truly enthusiastic about. Most likely while in the first few years of business, you are likely to be paying significant amounts of time operating. When you purchase a product or service that excites you, it will be simpler to stick to it regardless of how very much work it will take.
[url=http://www.pptl-bd.com/images/back.php?PID=121-Viagra-Kamagra-Online,Kamagra-Sverige-Online,Köpa-Kamagra-I-Sverige.html]Viagra Kamagra Online[/url]
Try to reduce the quantity of environmental contaminants and toxins, such as dust particles, pollens, animal locks, molds and fungus, and foods particles. Keeping your home nice and clean can easily make a significant difference for your symptoms of asthma signs and symptoms. Getting an aura filtration system or purifier, and even washing out the filtration system within your Air conditioning process will also help.
[img]https://www.cafe-manhattan.dk/images/caf2/5299-ralph-lauren-kjole.jpg[/img]
It is crucial to never consider your worries out on these close to you if you have depression. Frequently, folks are so dissatisfied they bring other folks around them downward at the same time furthermore they treat them. As an alternative, let your family know how significantly you appreicate their assistance.
[img]https://www.aarhus-abk.dk/images/aar2/13142-vans-sko-butik.jpg[/img]
http://www.conversepascherparis.fr/240-converse-basse-blanche-femme-38.html
http://www.reflexfurniture.co.uk/nike-free-5.0-mens-black-red-668.asp
http://www.zapatillasmodabaratas.es/zapatos-mbt-segunda-mano-461.php
http://www.okakene.es/asics-speed-clay-3-990.html
http://www.rollinsband.co.uk/asics-gel-lyte-v-rose-gold-off-white-414.html
[url=http://www.pro-seed.co.uk/adidas-nmd-trainers-464.htm]Adidas Nmd Trainers[/url]
[url=http://www.specialiste-du-couple.fr/tubular-nova-adidas-131.html]Tubular Nova Adidas[/url]
[url=http://www.engineering-truck.es/358-zapatos-nike-de-damas-originales.html]Zapatos Nike De Damas Originales[/url]
[url=http://www.scarpeadidassportive.it/adidas-zx-flux-adv-asym-pk-582.php]Adidas Zx Flux Adv Asym Pk[/url]
[url=http://www.zapatillasmizunomujer.es/zapatillas-reebok-aliexpress-566.html]Zapatillas Reebok Aliexpress[/url]
It is vital that you retain your home and work environment clean for those who have asthma attack. Airborne dirt and dust and viruses can aggravate your asthma attack symptoms and stop fresh air to your lungs. Because dirt builds up quickly, our recommendation is that you dust your furnishings and appliances one or more times a week.
[url=http://www.srabiometricsurvey.com/images/move.php?p=80-Viagra-Frauen,Viagra-Ohne-Rezept-Kaufen-Auf-Rechnung,Viagra-Rezeptfrei-Apotheke.html]Viagra Frauen[/url]
So that you can stop smoking cigarettes, discover something else you can hold with your fingers and put in your mouth. Several cigarette smokers battle to cease since they provide an desire to possess a cigarette inside their hands and jaws. Instead of a cig, you can hold on to a straw.
[url=http://www.reddunestourism.com/images/banner/black.php?id=165-Prezzo-Cialis-10-Mg,Cialis-5-Mg-Controindicazioni,Cialis-Costo.html]Prezzo Cialis 10 Mg[/url]
A surprisingly large amount of people prevent receiving regular screenings to check on for malignancy, which happens to be a great way to fight the illness and are available aside healthy. This is because cancer is easier to get, ruin, or eliminate after it is in the very first stages. Through existence it would only grow and be more serious.
[url=http://www.mallku.org.pe/image/backup.asp?o=sitemap?o=203-Viagra-Romana]Viagra-Costo-In-Italia[/url]
Beware and do not flood
here is the web page link https://toutpourvous.ch/essays-and-its-altering-elements-of-importance-4/
If you are contemplating possessing some plastic surgery, you must understand that you will find a probability that there might be some skin damage. Not only will there be skin damage, however the after-negative effects of the surgical procedure could be very unpleasant. With any surgical treatment, regardless of how small you believe it is, it can be continue to surgical procedures and your body are experiencing some soon after-results.
[img]https://www.retinal.nu/imagess/ret2/8862-air-yeezy-2-solar-red.jpg[/img]
Acquiring a short-term personal loan might be just the issue you should allow you to by means of a tough time. These personal loans might be a fantastic assist, but only if you have every piece of information you require. Start using these tips to help you get choices about acquiring a cash advance, and you could survive through these tough times quicker.Tips For Living Much better With Anxiety Symptoms
[img]https://www.retinal.nu/imagess/ret2/11798-nike-lunarglide-6-flash-cena.jpg[/img]
I also wanted to ask, did someone encounter such an issue? And what will come about if they get out that my article was bought, and not written by me
I also wanted to ask, did a person encounter such an issue? And what will come about if they get out that my article was purchased, and not written by me
designs and builds specialty lines of lead oxide production equipment, material handling systems, battery related process machinery, parts, and accessories for the battery, pigment, glass, and chemical industries. http://techbasys.com offers technical application and engineering services to help the customer acheive maximum benefit from their equipment and manufacturing processes.
Be careful and do not flood
here is the website http://leicestershiredentist.co.uk/buy-essays-online-is-so-effortless/
http://leadershipessay53.blog2learn.com/8400848/the-transformation-of-on-the-net-composing-products
[url=http://www.dailystrength.org/people/4717767/journal/14062295]Acupuntura Para Adelgazar[/url]
[url=https://www.kiwibox.com/mccrayscvp733/blog/entry/135230915/adelgazar-en-un-mes/]Acupuntura Para Bajar De Peso[/url]
[url=https://www.kiwibox.com/madlyloser321/blog/entry/135230917/adelgazar-piernas/]Adelgar[/url]
[url=http://thereal-truthaboutsixpackabs.blogspot.com/2016/01/remedios-para-adelgazar.html]Adelgazar 10 Kilos[/url]
[url=http://www.blogigo.com/mcgeefyarbwuhap/Adelgazar-Rapido-En-Una-Semana/6/]Adelgazar 5 Kilos[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434152&profile_id=65536007&profile_name=fearlessowner424&user_id=65536007&username=fearlessowner424]Adelgazar Barriga[/url]
[url=http://www.dailystrength.org/people/4737493/journal/14062311]Adelgazar Comiendo[/url]
[url=http://www.blogigo.com/hester7guthrie13/Adelgazar-5-Kilos/7/]Adelgazar En Un Mes[/url]
[url=http://www.dailystrength.org]Adelgazar En Una Semana[/url]
[url=http://coherentscrutin19.jimdo.com/2016/02/02/adelgazar-comiendo/]Adelgazar Piernas[/url]
[url=https://app.box.com/s/9d3449niv5k5ibe2gmc3zhnd787eutiq]Adelgazar Rapido[/url]
[url=https://www.kiwibox.com/trickyinfo869/blog/entry/135230971/adelgazar-en-una-semana/]Adelgazar Rapido En Una Semana[/url]
[url=http://www.dailystrength.org]Adelgazar Sin Dieta[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434178&profile_id=65535862&profile_name=orangeguidebook85&user_id=65535862&username=orangeguidebook85]Alcachofa Para Adelgazar[/url]
[url=https://message.diigo.com/message/adelgazar-en-una-semana-4159067]Alcachofa Para Bajar De Peso[/url]
[url=https://app.box.com/s/x37d5f1tfw7tcqpeyjc1d8scpcnh84qa]Alimentos Para Adelgazar[/url]
[url=https://www.kiwibox.com/loganhjiwj698/blog/entry/135230989/adelgazar-piernas/]Alimentos Para Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434187&profile_id=65543689&profile_name=warycan899&user_id=65543689&username=warycan899]Alimentos Para Perder Barriga[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434192&profile_id=65798867&profile_name=absorbingformul98&user_id=65798867&username=absorbingformul98]Alimentos Que Adelgazan[/url]
[url=http://ejaculationtrainerxv.blogspot.com/2016/02/adelgazar-rapido.html]Alpiste Para Adelgazar[/url]
[url=https://message.diigo.com/message/adelgazar-rapido-en-una-semana-4159072]Anfetaminas Para Adelgazar[/url]
[url=https://app.box.com/s/7t8lxjrc5lt770yotkrc8c6ldyr41pdp]Auriculoterapia Para Adelgazar[/url]
[url=http://quackverse2860.snack.ws/adelgar.html]Avena Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434207&profile_id=65809165&profile_name=simmonsothvtnntjx&user_id=65809165&username=simmonsothvtnntjx]Baja De Peso[/url]
[url=https://app.box.com/s/uvwfr80k1eymb64js82953rkqamvxp6p]Bajar De Peso[/url]
[url=http://harrisonupnbzoxmak.snack.ws/adelgazar-5-kilos.html]Bajar De Peso Rapido[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434211&profile_id=65543626&profile_name=lucia0bartlett1&user_id=65543626&username=lucia0bartlett1]Bajar De Peso Urgente[/url]
[url=https://message.diigo.com/message/adelgazar-sin-dieta-4159080]Bajar La Barriga[/url]
[url=http://meghan5lowe4.jimdo.com/2016/02/02/adelgar/]Bajar Peso[/url]
[url=http://www.blogigo.com/greedyutensil752/Acupuntura-Para-Bajar-De-Peso/17/]Bajar Rapido De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434227&profile_id=65556664&profile_name=lilliemay7&user_id=65556664&username=lilliemay7]Batidos Adelgazantes[/url]
[url=http://www.blogigo.com/tacitutopia1993/Acupuntura-Para-Bajar-De-Peso/22/]Batidos De Proteinas Para Adelgazar[/url]
[url=http://wolfrrtmslfiga.snack.ws/adelgazar-10-kilos.html]Batidos Para Adelgazar[/url]
[url=http://thereal-truthaboutsixpackabs.blogspot.com/2016/02/adelgazar-rapido.html]Batidos Para Bajar De Peso[/url]
[url=http://themusclemaximizerreviewx.blogspot.com/2016/02/adelgazar-sin-dieta.html]Batidos Para Perder Peso[/url]
[url=https://app.box.com/s/d4by80uavvv7re864yog1hvs7esv6dp9]Bebidas Para Adelgazar[/url]
[url=http://technologyndgadgets.blogspot.com/2016/02/adelgazar-10-kilos.html]Bebidas Para Bajar De Peso[/url]
[url=http://glamorousrash6020.jimdo.com/2016/02/02/adelgazar-piernas/]Caminar Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434254&profile_id=65795595&profile_name=rowlandiryaxveisj&user_id=65795595&username=rowlandiryaxveisj]Cenas Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434255&profile_id=65543353&profile_name=nathan0barnett4&user_id=65543353&username=nathan0barnett4]Comida Para Adelgazar[/url]
[url=http://mabel3english34.snack.ws/adelgazar-piernas.html]Comida Para Bajar De Peso[/url]
[url=http://www.dailystrength.org/people/4718089/journal/14062379]Comidas Para Adelgazar[/url]
[url=http://www.dailystrength.org/people/4737969/journal/14062381]Comidas Para Bajar De Peso[/url]
[url=http://www.blogigo.com/gonzalesernihghkkx/Acupuntura-Para-Bajar-De-Peso/20/]Como Adelgasar[/url]
[url=http://www.blogigo.com/knoxnqdiypfhbs/Adelgazar-Piernas/19/]Cómo Adelgazar[/url]
[url=http://www.blogigo.com/louis2crawford62/Adelgazar-En-Un-Mes/19/]Como Adelgazar En Una Semana[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434284&profile_id=65535543&profile_name=brad6campos4&user_id=65535543&username=brad6campos4]Como Adelgazar La Panza[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434287&profile_id=65795595&profile_name=rowlandiryaxveisj&user_id=65795595&username=rowlandiryaxveisj]Como Adelgazar Las Piernas[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434288&profile_id=65798804&profile_name=jacquelyn3kemp04&user_id=65798804&username=jacquelyn3kemp04]Como Bajar De Peso Con Avena[/url]
[url=https://app.box.com/s/gosuwes0hvesgiglgl0tskarcndh79ln]Como Bajar De Peso En 3 Dias[/url]
[url=http://www.blogigo.com/bette0mays04/Adelgazar-Comiendo/20/]Como Bajar De Peso En Poco Tiempo[/url]
[url=https://www.kiwibox.com/dale9justi440/blog/entry/135231233/adelgazar-5-kilos/]Como Bajar De Peso En Un Dia[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434304&profile_id=65543603&profile_name=dillonbjxdpotuhf&user_id=65543603&username=dillonbjxdpotuhf]Como Bajar De Peso En Un Mes[/url]
[url=https://message.diigo.com/message/adelgazar-en-un-mes-4159103]Como Bajar De Peso Rápido[/url]
[url=https://www.kiwibox.com/rhoda2rose430/blog/entry/135231247/adelgazar-10-kilos/]Como Bajar De Peso En Una Semana[/url]
[url=http://howtomakeyourhairgrowfasternow.blogspot.com/2016/02/adelgazar-10-kilos.html]Como Bajar De Peso En Una Semana 10 Kilos[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434309&profile_id=65798949&profile_name=cherie5maldonado7&user_id=65798949&username=cherie5maldonado7]Como Bajar De Peso En Una Semana Sin Dieta[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434312&profile_id=65543735&profile_name=loganhjiwjbzsds&user_id=65543735&username=loganhjiwjbzsds]Como Bajar De Peso Rapido[/url]
[url=http://uttermostvisito16.snack.ws/acupuntura-para-adelgazar.html]Como Bajar De Peso Sin Dejar De Comer[/url]
[url=http://douglasnbtlbkgduw.jimdo.com/2016/02/02/acupuntura-para-bajar-de-peso/]Dietas Para Bajar De Peso Rapidamente[/url]
[url=http://fadedjailer490.snack.ws/acupuntura-para-bajar-de-peso.html]Como Bajar De Peso Rapido Y Efectivo[/url]
[url=http://gapingmaniac1558.jimdo.com/2016/02/02/adelgazar-rapido/]Como Bajar De Peso Rapido Y Facil[/url]
[url=http://www.dailystrength.org/people/4723911/journal/14062417]Como Bajar De Peso Sin Hacer Dieta[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434334&profile_id=65556802&profile_name=gilesrmwqyfyxah&user_id=65556802&username=gilesrmwqyfyxah]Como Bajar La Panza[/url]
[url=https://app.box.com/s/u238wo62jy5dubxdmqccn5bjpgge9o0k]Como Bajar Rapido De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434342&profile_id=65798776&profile_name=yellowphantom5763&user_id=65798776&username=yellowphantom5763]Como Baje 6 Libras En 3 Dias[/url]
[url=http://www.blogigo.com/fannyfowler77/Adelgazar-Rapido-En-Una-Semana/20/]Como Bajo De Peso[/url]
[url=http://longfreeway8613.snack.ws/adelgazar-comiendo.html]Como Bajo De Peso Rapido[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434350&profile_id=65798927&profile_name=trisha7ferguson92&user_id=65798927&username=trisha7ferguson92]Como Hacer Dieta[/url]
[url=https://app.box.com/s/l8si3j2r3marrkhsq562q64zlnrer6un]Como Hacer Para Adelgazar[/url]
[url=http://www.blogigo.com/materialisticme7/Acupuntura-Para-Bajar-De-Peso/17/]Como Hacer Una Dieta[/url]
[url=https://www.kiwibox.com/normanlpbi038/blog/entry/135231307/adelgazar-piernas/]Como Perder Barriga Rapido[/url]
[url=https://www.kiwibox.com/rachelle4m899/blog/entry/135231313/adelgar/]Como Perder Peso Com Saude[/url]
[url=http://www.dailystrength.org/people/4724419/journal/14062433]Como Perder Peso Em Uma Semana[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434375&profile_id=65795437&profile_name=healthycolleagu59&user_id=65795437&username=healthycolleagu59]Como Perder Peso En 3 Dias[/url]
[url=http://moaningnosh8810.jimdo.com/2016/02/02/adelgazar-piernas/]Como Perder Peso En Una Semana[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434388&profile_id=65809024&profile_name=roomylibrary1122&user_id=65809024&username=roomylibrary1122]Como Puedo Adelgazar[/url]
[url=http://plantasmedicinalesparaadelgazar.blogspot.com/2016/02/adelgazar-sin-dieta.html]Como Puedo Bajar De Peso[/url]
[url=http://akinademedia.blogspot.com/2016/02/adelgar.html]Como Subir De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434401&profile_id=65556828&profile_name=martin8frederick2&user_id=65556828&username=martin8frederick2]Como Vajar De Peso[/url]
[url=http://peacefulparish899.snack.ws/adelgazar-5-kilos.html]Consejos Para Adelgazar[/url]
[url=http://summer6mosley3.snack.ws/adelgazar-rapido.html]Consejos Para Bajar De Peso[/url]
[url=https://message.diigo.com/message/acupuntura-para-bajar-de-peso-4159173]De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434513&profile_id=65556781&profile_name=woozypenitentia44&user_id=65556781&username=woozypenitentia44]Dieta[/url]
[url=http://vigorousempathy43.snack.ws/adelgazar-rapido-en-una-semana.html]Dieta Adelgazar[/url]
[url=http://watsonanolflbhxg.snack.ws/adelgazar-en-un-mes.html]Dieta Dukan[/url]
[url=http://www.blogigo.com/scott6pace65/Adelgazar-Rapido/19/]Dieta Equilibrada Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434536&profile_id=65543302&profile_name=burkeujdloqjfwn&user_id=65543302&username=burkeujdloqjfwn]Dieta Mediterranea Para Adelgazar[/url]
[url=http://woodennun1206.jimdo.com/2016/02/02/acupuntura-para-bajar-de-peso/]Dieta Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434538&profile_id=65556899&profile_name=utopiancore1820&user_id=65556899&username=utopiancore1820]Dieta Para Adelgazar 10 Kilos[/url]
[url=http://www.blogigo.com/imperfectcabin964/Acupuntura-Para-Bajar-De-Peso/16/]Dieta Para Adelgazar 5 Kilos[/url]
[url=http://spiritualhypocr2.jimdo.com/2016/02/02/acupuntura-para-adelgazar/]Dieta Para Adelgazar Barriga[/url]
[url=https://www.kiwibox.com/needlesssc150/blog/entry/135231629/adelgazar-5-kilos/]Dieta Para Adelgazar Rapido[/url]
[url=https://message.diigo.com/message/adelgazar-piernas-4159178]Dieta Para Bajar Barriga[/url]
[url=http://premiumwordpressthemev.blogspot.com/2016/02/adelgazar-piernas.html]Dieta Para Bajar La Barriga[/url]
[url=http://sbiancamentodenticostox.blogspot.com/2016/02/adelgazar-en-un-mes.html]Dieta Para Bajar La Panza[/url]
[url=http://eugene6conrad09.jimdo.com/2016/02/02/adelgazar-10-kilos/]Dieta Para Perder Peso[/url]
[url=http://www.blogigo.com/tranquilhomicid47/Adelgazar-Rapido-En-Una-Semana/15/]Dieta Para Perder Peso Rapido[/url]
[url=https://app.box.com/s/c6hxd6og8ddxurl2nwuomgcw0uik422y]Dieta Perder Peso[/url]
[url=http://www.blogigo.com/rowlandiryaxveisj/Adelgazar-Comiendo/14/]Dieta Perder Peso Rapido[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434577&profile_id=65798942&profile_name=rogerspmgdlitudi&user_id=65798942&username=rogerspmgdlitudi]Dieta Proteica[/url]
[url=https://message.diigo.com/message/adelgazar-barriga-4159183]Dieta Proteica Para Adelgazar[/url]
[url=http://george0keller1.snack.ws/acupuntura-para-bajar-de-peso.html]Dieta Rapida[/url]
[url=http://livelydogma4668.snack.ws/adelgazar-10-kilos.html]Dieta Saludable Para Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434584&profile_id=65535493&profile_name=waggishleash2150&user_id=65535493&username=waggishleash2150]Dietas[/url]
[url=http://www.blogigo.com/woozypenitentia15/Adelgazar-5-Kilos/21/]Dietas De Adelgazamiento[/url]
[url=http://www.blogigo.com/alfred2david8/Adelgazar-En-Un-Mes/20/]Dietas De Proteinas[/url]
[url=http://rebecca9frank7.snack.ws/adelgazar-comiendo.html]Dietas Disociadas[/url]
[url=http://www.blogigo.com/vinsonoapekjwtba/Adelgazar-En-Un-Mes/28/]Dietas Efectivas[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434591&profile_id=65540390&profile_name=wilda2gutierrez12&user_id=65540390&username=wilda2gutierrez12]Dietas Faciles[/url]
[url=http://www.dailystrength.org/people/4724175/journal/14062557]Dietas Hipocaloricas[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434604&profile_id=65795576&profile_name=vinsonoapekjwtba&user_id=65795576&username=vinsonoapekjwtba]Dietas Milagrosas[/url]
[url=http://www.blogigo.com/nathan3barnett1/Adelgazar-Rapido/17/]Dietas Para Adelgazar[/url]
[url=https://app.box.com/s/sb3mh8pa55x03uq1ino3s1cx2xbc2xc0]Dietas Para Adelgazar 10 Kilos[/url]
[url=https://www.kiwibox.com/comobajard398/blog/entry/135231713/acupuntura-para-bajar-de-peso/]Dietas Para Adelgazar Rapido[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434614&profile_id=65809062&profile_name=dampstudent104&user_id=65809062&username=dampstudent104]Dietas Para Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434615&profile_id=65543206&profile_name=jessica4aguilar26&user_id=65543206&username=jessica4aguilar26]Dietas Para Perder Peso[/url]
[url=https://app.box.com/s/06lgiyp1t0jae405cjssncwk2idqjwtc]Dietas Para Perder Peso Rapido[/url]
[url=http://glibslogan1331.snack.ws/adelgazar-5-kilos.html]Dietas Proteicas[/url]
[url=http://www.dailystrength.org/people/4717951/journal/14062571]Ejercicios Para Perder Peso[/url]
[url=https://www.kiwibox.com/ludicrouss995/blog/entry/135231721/adelgazar-rapido/]Ensaladas Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434622&profile_id=65798854&profile_name=filthyadage5513&user_id=65798854&username=filthyadage5513]Ensaladas Para Bajar De Peso[/url]
[url=https://www.kiwibox.com/didacticva792/blog/entry/135231731/adelgazar-en-una-semana/]Jugos Para Perder Peso[/url]
[url=http://www.blogigo.com/brayqtwxyuwkmu/Adelgar/5/]La Mejor Dieta Para Adelgazar[/url]
[url=http://www.dailystrength.org/people/4721929/journal/14062583]La Mejor Dieta Para Bajar De Peso[/url]
[url=https://app.box.com/s/g8d6p5u77su65xwoofh14q9kql3oj549]Para Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434643&profile_id=65795422&profile_name=cageyface442&user_id=65795422&username=cageyface442]Para Bajar De Peso Rapido[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434646&profile_id=65798776&profile_name=yellowphantom5763&user_id=65798776&username=yellowphantom5763]Parches Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434653&profile_id=65798765&profile_name=muriel8schultz5&user_id=65798765&username=muriel8schultz5]Parches Para Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434655&profile_id=65798817&profile_name=knappiyfoazktfh&user_id=65798817&username=knappiyfoazktfh]Pastas Para Adelgazar[/url]
[url=http://fitzgeraldxxzafvubtk.jimdo.com/2016/02/02/adelgazar-barriga/]Pastilla Para Adelgazar[/url]
[url=https://app.box.com/s/y5oefa96mapgr57owdoflijc722rlcmp]Pastilla Para Bajar De Peso[/url]
[url=http://www.blogigo.com/maliciousportal7/Adelgazar-Barriga/8/]Pastillas Adelgazantes[/url]
[url=http://www.blogigo.com/succinctbevy1895/Adelgazar-10-Kilos/13/]Pastillas Chinas Para Adelgazar[/url]
[url=http://www.dailystrength.org/people/4724393/journal/14062609]Pastillas Naturales Para Adelgazar[/url]
[url=http://overtknack6386.snack.ws/adelgazar-sin-dieta.html]Pastillas Para Adelgazar[/url]
[url=http://www.dailystrength.org/people/4718217/journal/14062617]Pastillas Para Adelgazar Naturales[/url]
[url=http://beverly1justice53.snack.ws/acupuntura-para-bajar-de-peso.html]Pastillas Para Adelgazar Rapido[/url]
[url=http://breezybonfire170.snack.ws/adelgazar-en-una-semana.html]Pastillas Para Bajar De Peso[/url]
[url=http://www.dailystrength.org/people/4737755/journal/14062627]Pastillas Para Perder Peso[/url]
[url=http://www.blogigo.com/aboundingpedigr76/Adelgazar-Piernas/11/]Perder 10 Kilos[/url]
[url=http://variousconceit266.jimdo.com/2016/02/02/adelgazar-en-un-mes/]Perder Barriga[/url]
[url=http://utterzeal7998.jimdo.com/2016/02/02/adelgazar-en-una-semana/]Perder Barriga Rapido[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434702&profile_id=65809091&profile_name=evildormitory334&user_id=65809091&username=evildormitory334]Perder Grasa[/url]
[url=http://isabella2stevens65.snack.ws/adelgar.html]Perder Peso[/url]
[url=http://vacuousgroup6394.weebly.com/blog/adelgazar-en-una-semana]Perder Peso Corriendo[/url]
[url=https://message.diigo.com/message/adelgazar-en-una-semana-4159212]Perder Peso En Una Semana[/url]
[url=http://www.blogigo.com/toughupshot1609/Adelgazar-Barriga/20/]Perder Peso Rapido[/url]
[url=http://loganxmrophfeau.jimdo.com/2016/02/02/adelgazar-rapido-en-una-semana/]Perder Vientre Rápido[/url]
[url=http://www.blogigo.com/cody4sargent42/Adelgazar-Rapido-En-Una-Semana/20/]Plantas Medicinales Para Adelgazar[/url]
[url=http://www.dailystrength.org/people/4724379/journal/14062657]Plantas Para Adelgazar[/url]
[url=http://woodardtsdjfeyrfu.snack.ws/adelgar.html]Plantas Para Bajar De Peso[/url]
[url=http://www.blogigo.com/castillowvxvzyvdug/Acupuntura-Para-Bajar-De-Peso/19/]Productos Naturales Para Adelgazar[/url]
[url=http://www.dailystrength.org/people/4723869/journal/14062661]Productos Para Adelgazar[/url]
[url=http://www.blogigo.com/martinfrederick72/Adelgazar-Rapido/19/]Productos Para Bajar De Peso[/url]
[url=https://www.kiwibox.com/breezybonf739/blog/entry/135231871/adelgazar-en-un-mes/]Que Es Bueno Para Adelgazar[/url]
[url=https://www.kiwibox.com/boorishser433/blog/entry/135231875/adelgazar-en-una-semana/]Que Puedo Tomar Para Adelgazar[/url]
[url=http://www.blogigo.com/energeticcap9314/Adelgazar-En-Un-Mes/17/]Quema Grasas[/url]
[url=http://jeff7rasmussen9.snack.ws/acupuntura-para-bajar-de-peso.html]Quemagrasas[/url]
[url=http://smellyshoe741.snack.ws/adelgazar-sin-dieta.html]Quiero Adelgazar[/url]
[url=http://robertiknudson530.blogspot.com/2016/02/adelgazar-rapido-en-una-semana.html]Quiero Adelgazar Rapido[/url]
[url=http://jillrolling.blogspot.com/2016/02/adelgazar-piernas.html]Quiero Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434756&profile_id=65543542&profile_name=accidentaldunge45&user_id=65543542&username=accidentaldunge45]Quiero Bajar De Peso Rapido[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434761&profile_id=65798822&profile_name=actuallyyears1226&user_id=65798822&username=actuallyyears1226]Receta Para Adelgazar[/url]
[url=http://gruesomecity151.jimdo.com/2016/02/02/adelgazar-en-una-semana/]Receta Para Bajar De Peso[/url]
[url=https://app.box.com/s/agimxkym1o1dse7gedg2n4cwebumeh42]Recetas Caseras Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434772&profile_id=65795585&profile_name=culturedapex6137&user_id=65795585&username=culturedapex6137]Recetas De Dieta[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434774&profile_id=65795617&profile_name=aboundingpedigr16&user_id=65795617&username=aboundingpedigr16]Recetas De Dietas[/url]
[url=http://ochoauqqcxwxktz.snack.ws/adelgazar-rapido.html]Recetas Para Adelgazar[/url]
[url=http://www.dailystrength.org/people/4718361/journal/14062687]Recetas Para Adelgazar Rapido[/url]
[url=http://joniwashington24.snack.ws/adelgazar-piernas.html]Recetas Para Bajar De Peso[/url]
[url=http://www.dailystrength.org/people/4737655/journal/14062691]Recetas Para Dietas[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434781&profile_id=65798913&profile_name=noiselessquibbl67&user_id=65798913&username=noiselessquibbl67]Remedios Caseros Para Adelgazar[/url]
[url=http://comobajardepesoenunasemana10kilos1.blogspot.com/2016/02/adelgazar-5-kilos.html]Remedios Para Adelgazar[/url]
[url=http://www.blogigo.com/pertedepoids67/Acupuntura-Para-Bajar-De-Peso/20/]Remedios Para Bajar De Peso[/url]
[url=http://www.blogigo.com/endurableevent187/Acupuntura-Para-Bajar-De-Peso/20/]Sabila Para Adelgazar[/url]
[url=https://message.diigo.com/message/acupuntura-para-bajar-de-peso-4159241]Secretos Para Adelgazar[/url]
[url=https://app.box.com/s/gwvs0yfgg8t0f06mgq5ler368i50t3dd]Secretos Para Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4434804&profile_id=65799056&profile_name=makeshiftdiseas34&user_id=65799056&username=makeshiftdiseas34]Suplementos Para Bajar De Peso[/url]
[url=http://youthfulheritag62.jimdo.com/2016/02/02/adelgazar-en-un-mes/]Te Rojo Para Adelgazar[/url]
[url=http://tightfistedfabl20.snack.ws/adelgazar-barriga.html]Te Verde Para Adelgazar[/url]
[url=https://app.box.com/s/adajioyifzl7ctmog7ez5ywvwx31araa]Tips Para Adelgazar[/url]
[url=http://comoperderpesoemumasemana90.snack.ws/adelgazar-barriga.html]Tips Para Bajar De Peso[/url]
[url=https://www.kiwibox.com/credibleda174/blog/entry/135232095/adelgazar-10-kilos/]Tratamiento Para Adelgazar[/url]
[url=https://app.box.com/s/z6cngqtt1b4moilb5hxyze84z8c2kc6b]Tratamiento Para Bajar De Peso[/url]
[url=http://www.blogigo.com/tenuouszero838/Adelgazar-5-Kilos/7/]Tratamientos Para Adelgazar[/url]
[url=http://www.dailystrength.org/people/4737831/journal/14061763]Trucos Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433282&profile_id=65795585&profile_name=culturedapex6137&user_id=65795585&username=culturedapex6137]Trucos Para Adelgazar Rapido[/url]
[url=http://carmelajordan9.snack.ws/acupuntura-para-adelgazar.html]Trucos Para Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433287&profile_id=65543523&profile_name=delgadozazgnmincx&user_id=65543523&username=delgadozazgnmincx]Una Dieta Para Bajar De Peso[/url]
[url=http://exoticseer2581.snack.ws/adelgazar-comiendo.html]Verduras Para Bajar De Peso[/url]
[url=http://coleqmmbqjxlyf.jimdo.com/2016/02/02/adelgazar-en-un-mes/]Dietas Para Bajar De Peso Rapido[/url]
[url=http://www.blogigo.com/chunkynip537/Acupuntura-Para-Adelgazar/19/]Dietas Para Hombres[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433295&profile_id=65535462&profile_name=jeff5mcbride2&user_id=65535462&username=jeff5mcbride2]Dietas Rapidas[/url]
[url=http://www.blogigo.com/mushytreasury1284/Acupuntura-Para-Bajar-De-Peso/21/]Dietas Saludables[/url]
[url=http://www.blogigo.com/mushytreasury1284/Adelgazar-Piernas/22/]Dietas Sanas[/url]
[url=http://discreetnip410.jimdo.com/2016/02/02/adelgazar-en-una-semana/]Dietas Sanas Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433316&profile_id=65543335&profile_name=energeticcap9362&user_id=65543335&username=energeticcap9362]Ejercicio Para Adelgazar[/url]
[url=http://www.blogigo.com/anne2webster6/Adelgazar-Rapido/16/]Ejercicios Para Bajar De Peso[/url]
[url=http://clammydevil60.jimdo.com/2016/02/02/adelgazar-barriga/]Fajas Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433347&profile_id=65543444&profile_name=karin8chaney3&user_id=65543444&username=karin8chaney3]Fajas Para Bajar De Peso[/url]
[url=http://www.blogigo.com/ambitiousappend09/Adelgar/20/]Frutas Para Adelgazar[/url]
[url=http://www.dailystrength.org/people/4723695/journal/14061791]Frutas Para Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433360&profile_id=65803382&profile_name=lovingregion9675&user_id=65803382&username=lovingregion9675]Hierbas Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433362&profile_id=65798795&profile_name=pastoraljunk3645&user_id=65798795&username=pastoraljunk3645]Hierbas Para Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433380&profile_id=65795540&profile_name=mccarthyiucpwppnka&user_id=65795540&username=mccarthyiucpwppnka]Hipnosis Para Adelgazar[/url]
[url=http://www.dailystrength.org/people/4717723/journal/14061801]Hipnosis Para Bajar De Peso[/url]
[url=http://karin4giles56.jimdo.com/2016/02/02/adelgazar-rapido/]Homeopatia Para Adelgazar[/url]
[url=http://www.dailystrength.org/people/4718261/journal/14061805]Imanes Para Bajar De Peso[/url]
[url=http://watsonlvponmhnev.snack.ws/adelgazar-en-una-semana.html]Infusiones Para Adelgazar[/url]
[url=http://wisekeystone1868.snack.ws/adelgazar-en-un-mes.html]Inyecciones Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433424&profile_id=65556947&profile_name=glennkrkylkjmhy&user_id=65556947&username=glennkrkylkjmhy]Inyecciones Para Bajar De Peso[/url]
[url=https://www.kiwibox.com/versedtyco698/blog/entry/135229913/adelgazar-en-una-semana/]Jugos Para Adelgazar[/url]
[url=http://www.blogigo.com/axiomaticcadre953/Adelgazar-Barriga/19/]Jugos Para Bajar De Peso[/url]
[url=https://www.kiwibox.com/pertedepoi516/blog/entry/135229925/acupuntura-para-adelgazar/]Las Mejores Pastillas Para Adelgazar[/url]
[url=https://message.diigo.com/message/adelgazar-10-kilos-4158805]Laxantes Para Adelgazar[/url]
[url=https://message.diigo.com/message/adelgazar-en-un-mes-4158808]Licuados Para Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433444&profile_id=65556724&profile_name=knoxnqdiypfhbs&user_id=65556724&username=knoxnqdiypfhbs]Linaza Para Adelgazar[/url]
[url=http://olusolaalonge.blogspot.com/2016/02/adelgazar-rapido.html]Linaza Para Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433449&profile_id=65795513&profile_name=maliciousportal51&user_id=65795513&username=maliciousportal51]Malteadas Para Bajar De Peso[/url]
[url=https://www.kiwibox.com/longjwcagm786/blog/entry/135229939/acupuntura-para-bajar-de-peso/]Masajes Para Adelgazar[/url]
[url=http://buchananvgklmybkev.jimdo.com/2016/02/02/adelgazar-5-kilos/]Medicamento Para Bajar De Peso[/url]
[url=http://alan4gay91.snack.ws/adelgazar-rapido-en-una-semana.html]Medicamentos Para Adelgazar[/url]
[url=http://tranquilstudent3.jimdo.com/2016/02/02/adelgazar-sin-dieta/]Medicamentos Para Bajar De Peso[/url]
[url=http://www.dailystrength.org/people/4724397/journal/14061841]Medicina Natural Para Adelgazar[/url]
[url=https://message.diigo.com/message/adelgazar-piernas-4158818]Menu Para Adelgazar[/url]
[url=http://fatpersonnel9969.jimdo.com/2016/02/02/acupuntura-para-bajar-de-peso/]Menu Para Bajar De Peso[/url]
[url=http://www.dailystrength.org/people/4737695/journal/14061845]Menus Para Adelgazar[/url]
[url=https://app.box.com/s/sbncg6wibw5s5xt83ldipphixuvc7q33]Metformina Para Adelgazar[/url]
[url=https://app.box.com/s/w4meip55d29t0ua7erdmjrziic6fwdcn]Metodos Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433481&profile_id=65543717&profile_name=quackverse2839&user_id=65543717&username=quackverse2839]Metodos Para Bajar De Peso[/url]
[url=http://lovelydormitory42.snack.ws/adelgazar-en-una-semana.html]Naturhouse[/url]
[url=http://aaron4craig7.snack.ws/acupuntura-para-bajar-de-peso.html]Necesito Adelgazar[/url]
[url=http://knowledgeablelo36.snack.ws/acupuntura-para-adelgazar.html]Necesito Bajar De Peso Urgente[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433488&profile_id=65795500&profile_name=overjoyedhealth78&user_id=65795500&username=overjoyedhealth78]No Consigo Adelgazar[/url]
[url=http://www.dailystrength.org/people/4718393/journal/14061859]Nutricionista[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433493&profile_id=65795375&profile_name=thorntonmjxgqvkscd&user_id=65795375&username=thorntonmjxgqvkscd]Para Adelgazar[/url]
[url=http://wideplaza7625.jimdo.com/2016/02/02/adelgazar-rapido-en-una-semana/]Para Adelgazar Rapido[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433511&profile_id=65798962&profile_name=jeffrey2chapman86&user_id=65798962&username=jeffrey2chapman86]Acupuntura Para Adelgazar[/url]
[url=https://app.box.com/s/lajq4tst5ga5h34bqzmpethqidmhei7a]Acupuntura Para Bajar De Peso[/url]
[url=https://www.kiwibox.com/expensived430/blog/entry/135230015/adelgazar-en-un-mes/]Adelgar[/url]
[url=http://www.dailystrength.org/people/4737799/journal/14061885]Adelgazar 10 Kilos[/url]
[url=http://www.blogigo.com/mari1garza6/Adelgazar-En-Un-Mes/7/]Adelgazar 5 Kilos[/url]
[url=https://www.kiwibox.com/irene2burc322/blog/entry/135230027/acupuntura-para-adelgazar/]Adelgazar Barriga[/url]
[url=http://www.blogigo.com/vaughanvtzdawotec/Adelgazar-Rapido-En-Una-Semana/17/]Adelgazar Comiendo[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433528&profile_id=65535952&profile_name=eugene8hammond86&user_id=65535952&username=eugene8hammond86]Adelgazar En Un Mes[/url]
[url=https://message.diigo.com/message/adelgazar-en-una-semana-4158850]Adelgazar En Una Semana[/url]
[url=http://www.dailystrength.org/people/4718185/journal/14061905]Adelgazar Piernas[/url]
[url=http://dustin0hull38.jimdo.com/2016/02/02/adelgar/]Adelgazar Rapido[/url]
[url=https://app.box.com/s/1eszbuyn8fqo4mqnxomjdr87jkajmuu7]Adelgazar Rapido En Una Semana[/url]
[url=https://app.box.com/s/0fkw2cafiw13ffpjoeuhrmq7w8ccsk9n]Adelgazar Sin Dieta[/url]
[url=http://www.blogigo.com/torpidobstructi25/Adelgazar-En-Un-Mes/16/]Alcachofa Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433548&profile_id=65543580&profile_name=evasivehypocrit70&user_id=65543580&username=evasivehypocrit70]Alcachofa Para Bajar De Peso[/url]
[url=http://karla9kramer4.jimdo.com/2016/02/02/adelgazar-5-kilos/]Alimentos Para Adelgazar[/url]
[url=http://hendersonssofevjaiz.jimdo.com/2016/02/02/adelgazar-en-un-mes/]Alimentos Para Bajar De Peso[/url]
[url=http://www.blogigo.com/mysteriousimbec54/Adelgazar-10-Kilos/16/]Alimentos Para Perder Barriga[/url]
[url=https://www.kiwibox.com/youngckgoc536/blog/entry/135230077/adelgazar-rapido-en-una-semana/]Alimentos Que Adelgazan[/url]
[url=http://www.blogigo.com/murkyundercurre77/Acupuntura-Para-Adelgazar/7/]Alpiste Para Adelgazar[/url]
[url=http://www.blogigo.com/overjoyedpropos66/Adelgazar-Sin-Dieta/23/]Anfetaminas Para Adelgazar[/url]
[url=https://app.box.com/s/fi5opa88wjschize103dbxx6ooze2yt9]Auriculoterapia Para Adelgazar[/url]
[url=http://www.dailystrength.org/people/4724327/journal/14061937]Avena Para Adelgazar[/url]
[url=http://woodenprison4321.snack.ws/adelgazar-rapido-en-una-semana.html]Baja De Peso[/url]
[url=https://app.box.com/s/albse47mka8z87cwtc74p21z4ad1mzzw]Bajar De Peso[/url]
[url=http://www.blogigo.com/forgetfulbeach718/Adelgazar-Sin-Dieta/23/]Bajar De Peso Rapido[/url]
[url=https://app.box.com/s/kg4rojjbikycntepu7vfi77jxal2op0c]Bajar De Peso Urgente[/url]
[url=http://klicktopia.blogspot.com/2016/02/adelgazar-rapido-en-una-semana.html]Bajar La Barriga[/url]
[url=https://www.kiwibox.com/brawnyexam617/blog/entry/135230115/adelgazar-en-una-semana/]Bajar Peso[/url]
[url=http://harmoniousinvas60.jimdo.com/2016/02/02/acupuntura-para-adelgazar/]Bajar Rapido De Peso[/url]
[url=http://salinasamzkxaporb.jimdo.com/2016/02/02/adelgazar-rapido-en-una-semana/]Batidos Adelgazantes[/url]
[url=http://www.blogigo.com/utopiancore1816/Adelgazar-Rapido-En-Una-Semana/17/]Batidos De Proteinas Para Adelgazar[/url]
[url=http://francis8molina1.snack.ws/adelgazar-rapido-en-una-semana.html]Batidos Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433615&profile_id=65795558&profile_name=futuristicgun4628&user_id=65795558&username=futuristicgun4628]Batidos Para Bajar De Peso[/url]
[url=http://katherine3walters79.snack.ws/adelgazar-sin-dieta.html]Batidos Para Perder Peso[/url]
[url=http://www.blogigo.com/johnstonzbxpryjtgb/Adelgazar-Comiendo/18/]Bebidas Para Adelgazar[/url]
[url=http://kaputgem1873.snack.ws/adelgazar-en-una-semana.html]Bebidas Para Bajar De Peso[/url]
[url=http://tonsilstonesv.blogspot.com/2016/02/adelgazar-rapido-en-una-semana.html]Caminar Para Adelgazar[/url]
[url=https://www.kiwibox.com/allegedown557/blog/entry/135230167/adelgazar-piernas/]Cenas Para Adelgazar[/url]
[url=http://www.dailystrength.org/people/4717697/journal/14061967]Comida Para Adelgazar[/url]
[url=http://mccoytqynxbdkqn.snack.ws/adelgazar-10-kilos.html]Comida Para Bajar De Peso[/url]
[url=http://howtoloseweightfastwithoutexercisez.blogspot.com/2016/02/adelgar.html]Comidas Para Adelgazar[/url]
[url=https://app.box.com/s/bq8067z9eaao3tfuw2i6uob42802ezma]Comidas Para Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433641&profile_id=65535505&profile_name=lewisfrvemftkqf&user_id=65535505&username=lewisfrvemftkqf]Como Adelgasar[/url]
[url=http://www.blogigo.com/boonenumvjzkzqr/Adelgazar-Sin-Dieta/8/]Cómo Adelgazar[/url]
[url=http://www.blogigo.com/changeableshutt02/Adelgazar-Rapido-En-Una-Semana/19/]Como Adelgazar En Una Semana[/url]
[url=http://momydem732.blogspot.com/2015/03/why-you-should-date-woman-who-loves_97.html]Como Adelgazar La Panza[/url]
[url=http://madlyloser144.jimdo.com/2016/02/02/adelgazar-5-kilos/]Como Adelgazar Las Piernas[/url]
[url=http://reginald4orr75.snack.ws/adelgazar-sin-dieta.html]Como Bajar De Peso Con Avena[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433672&profile_id=65798895&profile_name=pleasantcanopy99&user_id=65798895&username=pleasantcanopy99]Como Bajar De Peso En 3 Dias[/url]
[url=http://www.blogigo.com/noiselessoutsid55/Adelgazar-Barriga/17/]Como Bajar De Peso En Poco Tiempo[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433677&profile_id=65543594&profile_name=robbie0bryant47&user_id=65543594&username=robbie0bryant47]Como Bajar De Peso En Un Dia[/url]
[url=https://www.kiwibox.com/longbabe97890/blog/entry/135230239/acupuntura-para-bajar-de-peso/]Como Bajar De Peso En Un Mes[/url]
[url=http://mcleanbubpjmhbdn.jimdo.com/2016/02/02/adelgazar-rapido-en-una-semana/]Como Bajar De Peso Rápido[/url]
[url=https://app.box.com/s/6h0rrkyrvhasxilyqr4a24j8n001iokg]Como Bajar De Peso En Una Semana[/url]
[url=http://possessivestem798.jimdo.com/2016/02/02/adelgar/]Como Bajar De Peso En Una Semana 10 Kilos[/url]
[url=http://www.blogigo.com/deirdre8beard6/Acupuntura-Para-Adelgazar/20/]Como Bajar De Peso En Una Semana Sin Dieta[/url]
[url=http://perdredupoidsfacilement67.snack.ws/adelgazar-en-un-mes.html]Como Bajar De Peso Rapido[/url]
[url=http://johnbgabriel313.blogspot.com/2016/02/adelgar.html]Como Bajar De Peso Sin Dejar De Comer[/url]
[url=http://lauriewatts1.jimdo.com/2016/02/02/adelgazar-barriga/]Dietas Para Bajar De Peso Rapidamente[/url]
[url=http://www.blogigo.com/boylemqxugtrvqd/Adelgazar-En-Un-Mes/14/]Como Bajar De Peso Rapido Y Efectivo[/url]
[url=http://unsuitablefacsi1.jimdo.com/2016/02/02/adelgar/]Como Bajar De Peso Rapido Y Facil[/url]
[url=http://unevenattorney710.jimdo.com/2016/02/02/adelgar/]Como Bajar De Peso Sin Hacer Dieta[/url]
[url=http://jonathan0battle6.jimdo.com/2016/02/02/adelgazar-sin-dieta/]Como Bajar La Panza[/url]
[url=http://steeleyhckitkmdk.snack.ws/adelgazar-en-un-mes.html]Como Bajar Rapido De Peso[/url]
[url=http://www.dailystrength.org]Como Baje 6 Libras En 3 Dias[/url]
[url=https://www.kiwibox.com/tearfulwan841/blog/entry/135230315/adelgazar-piernas/]Como Bajo De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433730&profile_id=65543507&profile_name=overratedvacanc90&user_id=65543507&username=overratedvacanc90]Como Bajo De Peso Rapido[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433732&profile_id=65798765&profile_name=muriel8schultz5&user_id=65798765&username=muriel8schultz5]Como Hacer Dieta[/url]
[url=http://www.blogigo.com/francis3fulton1/Adelgazar-5-Kilos/20/]Como Hacer Para Adelgazar[/url]
[url=http://squarepoet529.jimdo.com/2016/02/02/adelgazar-sin-dieta/]Como Hacer Una Dieta[/url]
[url=http://angelica3bailey0.snack.ws/adelgazar-piernas.html]Como Perder Barriga Rapido[/url]
[url=https://message.diigo.com/message/acupuntura-para-adelgazar-4158953]Como Perder Peso Com Saude[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433756&profile_id=65535891&profile_name=callie4vasquez&user_id=65535891&username=callie4vasquez]Como Perder Peso Em Uma Semana[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433760&profile_id=65543240&profile_name=cervantescfziditkff&user_id=65543240&username=cervantescfziditkff]Como Perder Peso En 3 Dias[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433769&profile_id=65536023&profile_name=evelyn5holman42&user_id=65536023&username=evelyn5holman42]Como Perder Peso En Una Semana[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433771&profile_id=65543763&profile_name=invincibleale3023&user_id=65543763&username=invincibleale3023]Como Puedo Adelgazar[/url]
[url=http://www.blogigo.com/callie1vasquez39/Adelgar/18/]Como Puedo Bajar De Peso[/url]
[url=http://www.blogigo.com/eddiereese66/Acupuntura-Para-Adelgazar/16/]Como Subir De Peso[/url]
[url=http://mirahairoilv.blogspot.com/2016/02/acupuntura-para-adelgazar.html]Como Vajar De Peso[/url]
[url=https://www.kiwibox.com/lindseyctd754/blog/entry/135230365/adelgazar-5-kilos/]Consejos Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433787&profile_id=65543379&profile_name=heavycyberspace56&user_id=65543379&username=heavycyberspace56]Consejos Para Bajar De Peso[/url]
[url=http://davidcrich526.blogspot.com/2016/02/adelgazar-5-kilos.html]De Peso[/url]
[url=http://www.blogigo.com/adorablecelebri26/Adelgazar-Rapido/18/]Dieta[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433797&profile_id=65543676&profile_name=overtfatherland08&user_id=65543676&username=overtfatherland08]Dieta Adelgazar[/url]
[url=http://lara9jacobs.weebly.com/blog/adelgazar-rapido]Dieta Dukan[/url]
[url=http://equablevolition7.snack.ws/adelgazar-comiendo.html]Dieta Equilibrada Para Adelgazar[/url]
[url=http://www.dailystrength.org/people/4717735/journal/14062075]Dieta Mediterranea Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433809&profile_id=65798836&profile_name=testedupset2946&user_id=65798836&username=testedupset2946]Dieta Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433812&profile_id=65535848&profile_name=forgetfulbeach783&user_id=65535848&username=forgetfulbeach783]Dieta Para Adelgazar 10 Kilos[/url]
[url=http://abandonedmirth618.jimdo.com/2016/02/02/acupuntura-para-adelgazar/]Dieta Para Adelgazar 5 Kilos[/url]
[url=https://www.kiwibox.com/enthusiast138/blog/entry/135230397/acupuntura-para-adelgazar/]Dieta Para Adelgazar Barriga[/url]
[url=http://www.blogigo.com/wheelerdlkqsckhbe/Adelgazar-Barriga/17/]Dieta Para Adelgazar Rapido[/url]
[url=http://www.dailystrength.org/people/4717749/journal/14062085]Dieta Para Bajar Barriga[/url]
[url=http://hester7guthrie14.jimdo.com/2016/02/02/adelgazar-sin-dieta/]Dieta Para Bajar La Barriga[/url]
[url=http://hallundaffzxvh.jimdo.com/2016/02/02/acupuntura-para-bajar-de-peso/]Dieta Para Bajar La Panza[/url]
[url=http://www.dailystrength.org/people/4718435/journal/14062091]Dieta Para Perder Peso[/url]
[url=http://www.dailystrength.org/people/4737623/journal/14062093]Dieta Para Perder Peso Rapido[/url]
[url=http://bringthefreshv.blogspot.com/2016/02/acupuntura-para-bajar-de-peso.html]Dieta Perder Peso[/url]
[url=http://proudloser6592.jimdo.com/2016/02/02/adelgazar-rapido/]Dieta Perder Peso Rapido[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433831&profile_id=65798876&profile_name=frymapqtemaaa&user_id=65798876&username=frymapqtemaaa]Dieta Proteica[/url]
[url=http://www.blogigo.com/determinedverdi32/Adelgazar-5-Kilos/15/]Dieta Proteica Para Adelgazar[/url]
[url=http://www.blogigo.com/bennettjdnvidqkrp/Adelgazar-Comiendo/19/]Dieta Rapida[/url]
[url=http://www.dailystrength.org/people/4718321/journal/14062105]Dieta Saludable Para Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433836&profile_id=65795576&profile_name=vinsonoapekjwtba&user_id=65795576&username=vinsonoapekjwtba]Dietas[/url]
[url=https://message.diigo.com/message/adelgazar-5-kilos-4158978]Dietas De Adelgazamiento[/url]
[url=https://www.kiwibox.com/spiffywand591/blog/entry/135230429/adelgazar-en-una-semana/]Dietas De Proteinas[/url]
[url=https://www.kiwibox.com/assortedpr840/blog/entry/135230435/adelgazar-comiendo/]Dietas Disociadas[/url]
[url=http://www.blogigo.com/debonairverse451/Adelgazar-Sin-Dieta/19/]Dietas Efectivas[/url]
[url=https://www.kiwibox.com/russofkqri974/blog/entry/135230445/adelgazar-rapido/]Dietas Faciles[/url]
[url=http://amparo3meyers9.snack.ws/adelgazar-comiendo.html]Dietas Hipocaloricas[/url]
[url=http://www.dailystrength.org/people/4717543/journal/14062125]Dietas Milagrosas[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433854&profile_id=65543460&profile_name=chillyhealth790&user_id=65543460&username=chillyhealth790]Dietas Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433861&profile_id=65556963&profile_name=smallbxcrhlxutg&user_id=65556963&username=smallbxcrhlxutg]Dietas Para Adelgazar 10 Kilos[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433862&profile_id=65798981&profile_name=swelteringpaddl63&user_id=65798981&username=swelteringpaddl63]Dietas Para Adelgazar Rapido[/url]
[url=https://app.box.com/s/ymca7anjvanfyggjc6ndhtifm81gbg6b]Dietas Para Bajar De Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433870&profile_id=65535874&profile_name=benjaminmhmtlcsktq&user_id=65535874&username=benjaminmhmtlcsktq]Dietas Para Perder Peso[/url]
[url=https://www.kiwibox.com/duranfwuwl372/blog/entry/135230495/adelgazar-piernas/]Dietas Para Perder Peso Rapido[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433877&profile_id=65543749&profile_name=robbie1contreras33&user_id=65543749&username=robbie1contreras33]Dietas Proteicas[/url]
[url=http://delores2cannon8.snack.ws/adelgazar-5-kilos.html]Ejercicios Para Perder Peso[/url]
[url=http://waterydome5895.snack.ws/adelgazar-rapido.html]Ensaladas Para Adelgazar[/url]
[url=https://app.box.com/s/x77xrkv2dqc84iywb3vkfn0k8pgn1o01]Ensaladas Para Bajar De Peso[/url]
[url=http://eatstopeatv.blogspot.com/2016/02/adelgazar-rapido.html]Jugos Para Perder Peso[/url]
[url=http://charity5nicholson86.snack.ws/adelgazar-rapido-en-una-semana.html]La Mejor Dieta Para Adelgazar[/url]
[url=http://oyeolabola.blogspot.com/2016/02/adelgazar-5-kilos.html]La Mejor Dieta Para Bajar De Peso[/url]
[url=http://www.blogigo.com/healthycolleagu35/Adelgazar-Rapido/8/]Para Bajar De Peso[/url]
[url=http://www.blogigo.com/haltinghijacker08/Adelgar/17/]Para Bajar De Peso Rapido[/url]
[url=http://www.blogigo.com/vinsonoapekjwtba/Adelgazar-En-Una-Semana/27/]Parches Para Adelgazar[/url]
[url=http://beachnvlgwuhphc.snack.ws/acupuntura-para-bajar-de-peso.html]Parches Para Bajar De Peso[/url]
[url=http://obscenesavior7283.snack.ws/adelgazar-sin-dieta.html]Pastas Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433905&profile_id=65556768&profile_name=castillowvxvzyvdug&user_id=65556768&username=castillowvxvzyvdug]Pastilla Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433910&profile_id=65535478&profile_name=axiomaticcadre965&user_id=65535478&username=axiomaticcadre965]Pastilla Para Bajar De Peso[/url]
[url=https://message.diigo.com/message/adelgar-4159000]Pastillas Adelgazantes[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433918&profile_id=65543224&profile_name=rhoda9rose&user_id=65543224&username=rhoda9rose]Pastillas Chinas Para Adelgazar[/url]
[url=http://www.blogigo.com/fuentesmfplcfdudp/Adelgazar-Comiendo/16/]Pastillas Naturales Para Adelgazar[/url]
[url=http://tommy2haney7.jimdo.com/2016/02/02/adelgazar-sin-dieta/]Pastillas Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433921&profile_id=65809133&profile_name=mari6garza1&user_id=65809133&username=mari6garza1]Pastillas Para Adelgazar Naturales[/url]
[url=http://navarrocjavmmrnya.jimdo.com/2016/02/02/adelgazar-en-un-mes/]Pastillas Para Adelgazar Rapido[/url]
[url=https://www.kiwibox.com/pruittdwym934/blog/entry/135230563/adelgazar-sin-dieta/]Pastillas Para Bajar De Peso[/url]
[url=http://www.blogigo.com/colelfixrfkopb/Adelgazar-10-Kilos/18/]Pastillas Para Perder Peso[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433926&profile_id=65535824&profile_name=jeff0cantrell46&user_id=65535824&username=jeff0cantrell46]Perder 10 Kilos[/url]
[url=http://www.blogigo.com/feignedneophyte72/Acupuntura-Para-Adelgazar/19/]Perder Barriga[/url]
[url=https://www.kiwibox.com/nullbreeze562/blog/entry/135230597/adelgazar-5-kilos/]Perder Barriga Rapido[/url]
[url=http://instinctiveearn53.snack.ws/adelgazar-en-un-mes.html]Perder Grasa[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433941&profile_id=65798841&profile_name=marian0mendez03&user_id=65798841&username=marian0mendez03]Perder Peso[/url]
[url=https://app.box.com/s/u1fp9cs19eve1ija9my2nqtiia5co0ks]Perder Peso Corriendo[/url]
[url=http://aquaticleader4962.jimdo.com/2016/02/02/adelgazar-en-un-mes/]Perder Peso En Una Semana[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433949&profile_id=65535520&profile_name=vaughanvtzdawotec&user_id=65535520&username=vaughanvtzdawotec]Perder Peso Rapido[/url]
[url=https://www.kiwibox.com/shallowape854/blog/entry/135230635/adelgazar-en-una-semana/]Perder Vientre Rápido[/url]
[url=https://app.box.com/s/ip86d2p4pt84x7ddl6hk24vsr134p7xf]Plantas Medicinales Para Adelgazar[/url]
[url=https://www.kiwibox.com/perdredupo644/blog/entry/135230655/adelgazar-rapido-en-una-semana/]Plantas Para Adelgazar[/url]
[url=http://www.blogigo.com/eagertechnique883/Adelgazar-Rapido/15/]Plantas Para Bajar De Peso[/url]
[url=http://www.blogigo.com/blackresidence230/Acupuntura-Para-Adelgazar/21/]Productos Naturales Para Adelgazar[/url]
[url=http://www.blackplanet.com/your_page/blog/view_posting.html?pid=4433970&profile_id=65535982&profile_name=delacruzntfrizrwyy&user_id=65535982&username=delacruzntfrizrwyy]Productos Para Adelgazar[/url]
https://neilbaintonphotography.com/post/167270956762/most-beneficial-professional-writing-service
I also wanted to ask, did an individual encounter such a problem? And what will come about if they obtain out that my article was purchased, and not written by me
Watch out and do not flood
here is the website http://mydailyorders.com/you-will-not-find-a-lot-more-talented-experts-than/
I apologize if I create off-topic
But I just recently had to seek out a detailed write-up about the best way to create essays for the university.
I just discovered a great article. Possibly an individual else will need this material.
http://mgd.dlg360.com/have-troubles-then-buy-college-essay-papers-4/
By the way, though I was looking for this short article, I learned that some people acquire house functions, compositions, documents and articles. I don't know how secure it's and what high quality could be obtained inside the end. Who faced this predicament, write, you create or obtain? Were you caught by professor for this?
I am sorry if I write off-topic
But I lately had to discover a detailed article about tips on how to write essays for that university.
I just located a fantastic short article. Maybe an individual else will will need this facts.
http://financialfocuscounseling.com/perfect-judgement-for-all-of-your-writing/
Incidentally, when I was on the lookout for this article, I learned that plenty of people obtain property works, compositions, documents and articles. I usually do not know how secure it's and what good quality will be obtained within the finish. Who faced this issue, write, you write or get? Had been you caught by your coach for this?
https://i-foulcollectorpost-blr.tumblr.com/post/167269587328/over-the-internet-writing-expert-services-a
Как вы считаете, положительные отзывы о вас
в интернете увеличивают ваши продажи?
Мы знаем, что ваши клиенты интересуются тем, что пишут о вас в интернете.
У нас есть замечательное решение для вас - написание и размещение положительных
упоминаний о вас в интернете.
По ссылке вы можете заказать отзывы с хорошей скидкой
Заманчиво?
http://clck.ru/C4mKx
http://samcastrophotography.com.au/capture-professional-essays-with-our-service-10/
http://digitalgenoma.com/high-quality-papers-for-students-2/
http://mercanrehabilitasyon.com/?p=10718
http://puremgmtgroup.com/a-literary-analysis-essay-web-based/
http://fashion-uniforms.com/exactly-where-to-buy-a-powerpoint-presentation/
https://followmint.com/post/167118340232/identify-excellent-custom-essays-writing-service
Beware and do not flood
here is the web page link:
http://retour-nail.com/2017/11/14/why-does-to-pay-for-an-excellently-written-essay/
No chance unravel and explore state of health, types health, and also other components of the healthy strong organism, if thoroughly not go into the next concept. Thus, the health of a person, to date, is called standard and durable psychosomatic state of the individual.
[url=http://aboutdiseases.50r.in/difference-between-type-i-and-type-ii-diabetes]difference between type1 and type 2 diabetes[/url]
The diet pills should always be taken whole. Some people tend to divide the pills to serve a longer period of time. This is not advised and can lead to ineffectiveness. If it is required that one takes a complete tablet, it means that a certain amount of the ingredients are required to achieve the desired goal. It is also recommended that one does not crush the pill and dissolve it in beverages. Chemicals found in beverages have the potential of neutralizing the desired nutrients in the pill thereby leading to ineffectiveness. The best way to take the tablets is swallowing them whole with a glass of water.
[url=https://www.cialissansordonnancefr24.com/le-meilleur-cialis/]https://www.cialissansordonnancefr24.com/le-meilleur-cialis/[/url]
Watch out and do not flood
right here is the link: https://clientsfromvideo.com/high-quality-papers-for-students/
Be mindful and do not flood
right here is the weblink: http://detailplusiowa.com/2016/07/20/inexpensive-tutorial-papers-crafting/
Beware and do not flood
right here is the weblink: http://www.zghnews.com/2017/03/high-quality-papers-writing-service-for-you/
http://www.carrent-kl.com/you-might-not-find-significantly-more-talented.html
???
I also wished to ask, did someone encounter such an issue?
The human foot is a biological masterpiece. Its strong, flexible, and functional design enables it to do its job well and without complaint—if you take care of it and don't take it for granted.
healthThe foot can be compared to a finely tuned race car, or a space shuttle, vehicles whose function dictates their design and structure. And like them, the human foot is complex, containing within its relatively small size 26 bones (the two feet contain a quarter of all the bones in the body), 33 joints, and a network of more than 100 tendons, muscles, and ligaments, to say nothing of blood vessels and nerves.
[url=https://www.cialissansordonnancefr24.com/achat-cialis-professional/]https://www.cialissansordonnancefr24.com/achat-cialis-professional/[/url]
I've been struggling with college a lot lately and was seeking for a resolution.
Located the website http://frontline-services.com.au/2017/05/15/buy-essays-online-is-so-painless/https://sakone.vn/the-differing-types-of-essays-that-internet-based/https://drawmax.org/?p=853
But I'm not certain if it's ok to utilize it or not, looks kinda fishy.
What do you consider?
http://www.blackplanet.com/your_page/blog/view_posting.html?pid=8654804&profile_id=106298330&profile_name=descriptivewriting87&user_id=106298330&username=descriptivewriting87
http://toymate.com.au/have-issues-then-buy-college-essay-papers/
http://www.e-techmanagement.com/straightforward-way-for-you-to-get-professional/
http://www.insantama.web.id/where-to-write-custom-essays-perfectly/
Watch out and do not flood
here is the website: http://www.logrind.com/we-know-how-to-prepare-article-critique-writing/
http://flag.inspectorpages.com/order-an-essay/why-need-to-you-buy-an-essay
Watch out and do not flood
here is the website: http://www.socialmediapros.guru/high-quality-critical-essay-help-online-59/
http://lagerversammlung.de/where-to-buy-an-excellently-written-essay-online-15/
https://outdooreye.net/uncomplicated-way-to-get-experienced-essay/
???
I also wished to ask, did someone encounter such an issue?
Be careful and do not flood
here is the website link: http://hongsheng.com.sg/articles-essay-services-finest-top-quality-for/
http://wcfamlaw.com/page
http://all4webs.com/scholarshipessay1/eitfnxuypl475.htm
https://www.zotero.org/groups/1950566/essaydefinition65380
http://helpwithessays98.diowebhost.com/5163708/great-choice-for-all-of-your-writing-requirements
https://www.spinchat.com/hp/bestcollegeessays6/blog/id/736050
Wonderful postings. With thanks.
http://mythyroidnow.com/write-my-college-essay-we-hear-it-every-single-day-17/
http://www.howtoaquaponics.info/custom-essays-for-sale/why-does-to-pay-for-an-excellently-written-essay-98.html
https://umrohbmwsemarang.com/experienced-essay-can-help-you-to-succeed-in-the/
http://businessdesmoines.com/2016/04/27/exactly-where-to-buy-essay-online-cheap-4/
http://screechingmoonmoon.tumblr.com/
http://keith-rogers.co.uk/
http://www.musicianhand.com/why-do-you-will-need-to-buy-an-essay-online-11/
http://ministeriocoronasdelrey.com/try-to-buy-essays-online-and-you-wont-quit-3/
http://zshuk.com/blog/2016/09/28/how-one-can-write-an-outstanding-admission-essay/
http://anaisosmont.com/?p=2214
http://www.traumurlaub-helgoland.de/preferred-writing-service-for-students-2/
https://notgonnagetfamous.com/post/168010169316/customized-papers-writing-services
http://gogreatbouquetstudent.tumblr.com/
To avoid erectile dysfunction, man should lead healthy way of life, have no bad habits, spend time for sport, eat healthy food etc.
Today this medicine is so popular that it can be available practically in every drugstore, but price there is usually overstated and as men often have no time for visiting drugstores, they buy Viagra online and in such a way they save money and time.<a href="http://www.semillas-antunano.com/buying-avodart-online">buying avodart online</a>
or <a href="http://www.zelya.com/buy-ventolin-online">buy ventolin online</a>
[url=http://temresults2018.com/]bbcode[/url]
<a href="http://temresults2018.com/">html</a>
http://temresults2018.com/ simple
<a href=http://prixcialisgenerique.net/>achat cialis</a> cialis pas cher
<a href=http://comprar-cialis-sinreceta.net/>cialis generico</a> precio cailis
<a href=http://acquistare-cialis-italia.net/>comprare cialis</a> costo cialis
<a href=http://commandercialisgenerique.net/>cialis generique</a> vente cialis
<a href=http://acquistarecialisitalia.net/>cialis acquisto</a> cialis
<a href=http://comprar-cialis-generico.net/>comprar cialis </a> venta cialis online
http://prixcialisgenerique.net/ vente cialis
http://comprar-cialis-sinreceta.net/ precio cialis
http://acquistare-cialis-italia.net/ prezzo cialis
http://commandercialisgenerique.net/ achat cialis
http://comprar-cialis-generico.net/ comprar cialis
http://acquistarecialisitalia.net/ cialis generico
<a href="http://kamagradxt.com/">kamagra store gutschein</a>
buy kamagra 100mg oral jelly uk
[url=http://kamagradxt.com/]kamagra oral jelly amazon nederland co[/url]
kamagra oral jelly amazon nederland tx
http://kamagradxt.com/
kamagra oral jelly kaufen berlin
[url=http://kamagradxt.com/]buy kamagra 100 mg oral jelly[/url]
apteka kamagra opinie forum
<a href="http://kamagradxt.com/">kamagra soft chewable tablets 100 mg</a>
kamagra jelly side effects
http://kamagradxt.com/
kamagra oral jelly india manufacturer
[url=http://temresults2018.com/]bbcode[/url]
<a href="http://temresults2018.com/">html</a>
http://temresults2018.com/ simple
[url=http://totalworldstore.com/shop/go.php?sid=1&search=Tizanidine] [u][b]>>> Want to buy with Discount? CLICK HERE! <<<[/b][/u] [/url]
GO to PHARMACY >>> http://trustedmeds.store/shop/go.php?sid=1
Canada Online Pharmacy Tizanidine c.o.d. no rx \\ http://ccmrs.org/index.php/kunena/3-releases-and-updates/400563-cheap-generic-vigora-how-to-use-side-effects-information-vigora-free-delivery-on-sale#400541
Cheapest Prices in Canada for Tizanidine tablet without script // http://www.applewindforum.com/cheap-prices-Parlodelovernight-delivery-w-899091-1-1.html
Order in GB / UK Cheap Generic Tizanidine no prescription next day delivery / http://www.tornadobattery.com/index.php/forum/welcome-mat/7767-brand-or-generic-ponstel-delivery-no-prescription-ponstel-how-to-use-side-effects-information
Order in UK cheapest Tizanidine overseas with no prescriptions = http://www.smartwealth.at/index.php/forum/welcome-mat/201864-cheap-price-of-lukol-no-prescription-needed-lukol-no-script-needed#201662
Discount Prices in GB / UK for Tizanidine no dr approval cash on delivery @ http://dayzforum.net/index.php?app=forums&module=post§ion=post&do=new_post&f=53
Purchase in Australia Cheapest Tizanidine pay cod without prescription \ http://www.ffna-network.com/Webboard/showthread.php?tid=259804
Order in Australia Online Cheap Tizanidine with no prescription * http://crossfaernet.tk/forum/3-3265-1#49421
Order in GB / UK Cheap Online Tizanidine fast shipping no prescription << http://www.job-board.ru/add_articlesjob.html
Order in GB / UK Cheap Online Tizanidine cash on delivery ??? http://www.norrvikenstradgardssallskap.se/index.php/kunena/welcome-mat/359161-discount-price-malegra-dxt-no-prescription-no-fees-malegra-dxt-c-o-d-saturday-delivery#359297
Buy in Canada Tizanidine overnight without dr approval ??? http://linen.campuslaundry.org/index.php/forum/welcome-mat/11376-buy-at-low-price-methocarbamol-pharmacy-without-prescription-methocarbamol-delivery-no-prescription
How Can I Buy Tizanidine without script pharmacy << http://bunte-haare.com/showthread.php?tid=26763&pid=35029#pid35029
Cheap Price Tizanidine with credit card no prescription << http://km.doh.go.th/doh/phpBB3/viewtopic.php?f=3&t=18595
Where Can I Order in Canada Tizanidine without a prescription # http://howtobecanadian.com/forum/immigration-forum/82350-low-cost-aciclovir-pharmacy-without-a-prescription-aciclovir-no-prescription-no-fees.html
Where Can I Purchase in USA Tizanidine c.o.d. no rx // http://www.xn----gtbl0aes.xn--p1ai/forum/15-160-15#1241
Purchase in Canada cheapest Tizanidine overnight delivery without a rx @ http://cursosmariale.com/index.php/component/kunena/2-welcome-mat/986339-low-price-for-quality-professional-pack-20-no-prescription-fast-delivery-professional-pack-20-overnight-without-dr-approval?Itemid=0#986339
Order in United States cheapest Tizanidine shipped by cash on delivery * http://www.tendobygg.se/index.php/forum/welcome-mat/44976-buy-online-augmentin-c-o-d-no-script-augmentin-cheap-c-o-d-no-rx#60281
Discount Prices in GB / UK for Tizanidine next day no prescription needed = http://www.veropukahome.com.tr/page11.php?post=3&messagePage=168
Fast Delivery in USA Tizanidine no dr approval cash on delivery * http://bappeda.acehutara.go.id/index.php/forum/welcome-mat/708773-purchase-fosamax-c-o-d-overnight-no-rx-fosamax-with-no-prescriptions#708683
Where Can I Purchase in GB / UK Tizanidine without prescription ! http://www.globalcare-logistics.com/index.php/en/forum/welcome-mat/197422-order-cheap-online-singulair-free-prescription-drug-singulair-fast-shipping-no-prescription#198608
Ordering in Australia Online Tizanidine pharmacy without prescription @ http://www.tonybrooksarchitects.net/index.php/forum/welcome-mat/26171-generic-drugs-cardarone-with-no-prescription-cardarone-with-no-prescriptions#52842
Low Prices Generic Tizanidine no prescription quick delivery ! http://orshagorodmoy.info/forum/22-391-6#51164
Ordering in USA Online Tizanidine cheap c.o.d. no rx * http://pugprof.ru/%D0%B3%D0%BE%D1%81%D1%82%D0%B5%D0%B2%D0%B0%D1%8F-%D0%BA%D0%BD%D0%B8%D0%B3%D0%B0/
Purchase in Canada At Lowest Price Tizanidine overnight without a prescription \ http://ccmrs.org/index.php/kunena/3-releases-and-updates/400433-how-much-bicalutamide-c-o-d-no-rx-bicalutamide-next-day-delivery#400411
Discount Prices Tizanidine without prescription overnight @ http://monteurzimmer-springe.de/index.php/forum/welcome-mat/180662-purchase-online-furacin-without-dr-prescription-furacin-without-a-prescription-shipped-overnight#180660
Order in USA Tizanidine cheap c.o.d. no rx \\ http://www.novabutikotel.com/index.php/forum/welcome-mat/153027-quality-generic-zyban-same-day-delivery-no-prescription-zyban-overnight-delivery-no-rx#152206
How To Purchase Tizanidine no prescription quick delivery @ http://sibregionservice.ru/index.php/kunena/3-razdel-predlozhenij/19140-fast-shipping-soft-pack-40-c-o-d-without-prescription-soft-pack-40-cash-on-delivery-overnight#19802
How To Order in USA Tizanidine no prescription ??? http://www.trainingtrust.org/forum/welcome-mat/24550-buying-at-lowest-price-imipramine-non-prescription-needed-imipramine-cheap-c-o-d-no-rx#24549
Buy Online Amoxicillin / Clavulanate with no rx ??? http://sibregionservice.ru/index.php/kunena/3-razdel-predlozhenij/19104-pharmacies-that-sell-ed-advanced-pack-no-script-required-ed-advanced-pack-without-a-rx-overnight#19766
Ordering in Canada Tizanidine with credit card no prescription / http://www.nakupnidivadlo.cz/index.php/forum/3-pripominky/36381-lr?start=312#94524
Quality Generic Olmesartan no script required @ http://dist.by/forum/razdel-predlozhenij/2071-mp4-audio-konverter/
Where Can I Order in GB / UK Tizanidine for sale online \ http://www.widowsandwidowers.co.uk/forum/welcome-mat/15045-quiqly-delivery-nifedipine-c-o-d-no-prescription-nifedipine-pharmacy-without-prescription
How To Order in Canada Tizanidine overnight without prescription > http://barcovaldeorras.grupotecopy.es/index.php/en/component/kunena/2-bienvenido-mat/244000-buy-at-low-price-lamivudinenext-day-delivery-lamivudine-pharmacy-without-a-prescription#244000
Order in United States cheapest Tizanidine in no prescription // http://smoothiestrong.com/index.php/forum/welcome-mat/5962-buying-aciphex-in-internet-next-day-delivery-aciphex-no-prior-script-overnight#5966
Purchase in Canada At Low Price Tizanidine without doctor prescription @ http://www.strengthcrew.com/forums/viewthread/336887/
Ordering in USA Online Tizanidine shipped with no prescription @ http://www.architekt-rottgardt.de/index.php/forum
Buy in USA Cheap Online Tizanidine no prescription overnight ??? http://www.alobateriasceara.com.br/forum/welcome-mat/112205-generic-drugs-leflunomide-no-script-needed-leflunomide-online#112208
Wholesale Cheapest Tizanidine pharmacy no prescription = http://www.unhcr.ml/index.php/forum/welcome-mat/22521-how-to-purchase-lincomycin-no-prescription-lincomycin-overnight-without-prescription
Purchase in USA At Lowest Price Tizanidine no script required >> http://debarrastattu.com/index.php/forum/welcome-mat/154-pharmacies-that-sell-elimite-buying-elimite-cash-on-delivery.html?start=840#8331
Buy in GB / UK Cheapest Tizanidine - how to use,side effects,information \\ http://www.allicin.us/forum/welcome-mat/481867-cheap-price-of-probenecid-with-no-prescription-probenecid-no-prescription-fast-delivery#484312
Purchase Cheap Online in USA Tizanidine with no prescriptions << http://www.orcasys.co/index.php/forum/general-questions/378530-purchase-at-low-cost-theo-24-cr-shipped-by-cash-on-delivery-theo-24-cr-with-no-rx#378667
How To Purchase in GB / UK Tizanidine c.o.d overnight no rx - http://ccmrs.org/index.php/kunena/3-releases-and-updates/400419-online-cefixime-no-prescription-cefixime-without-a-rx-overnight#400397
Buy Cheap Tizanidine no prescription c.o.d. > http://www.codinesolutions.com/index.php/forum/welcome-mat/53373-low-cost-viagra-no-prescription-needed-viagra-pharmacy-without-a-prescription#254917
Order in Australia At Low Price Tizanidine without a rx overnight - http://www.brevettoonline.com/en/forum/benvenuto/13452-fast-shipping-felodipine-without-script-felodipine-cash-on-delivery-online-prescriptions.html
Order in USA Cheapest Tizanidine c.o.d. no script ! http://www.stepanovice.eu/ostatni-informace/kniha-navstev/
Buy in UK cheapest Tizanidine from a pharmacy without a prescription \\ http://undergroundarcade.net/newreply.php?tid=78846&replyto=113215
Buy in USA Viagra Jelly without rx * http://bbs.infinixmobility.com/forum.php?mod=viewthread&tid=339625&extra=
Ordering in Australia Tizanidine no prescription c.o.d. = http://crosstrek.org/index.php/forum/welcome-mat/61302-buy-online-cipro-next-day-delivery-cipro-fast-shipping-no-prescription
Buying in USA Generic Tizanidine c.o.d overnight no rx )) http://drsantiagomoreno.com/index.php/forum/welcome-mat/166104-best-place-to-buy-mestinon-in-internet-drugs-overnight-mestinon-for-sale-online#166108
Ordering Online Tizanidine cheap c.o.d. no rx ! http://www.all-leasing.ru/forums/messages/forum17/topic63919/message66799/?sessid=48b04ef99261d640b8909373d585fc5c&TOPIC_SUBSCRIBE=Y&FORUM_SUBSCRIBE=Y&result=new
[url=http://trustedmeds.store/shop/go.php?sid=5&search=ED Trial Pack] [u][b]>>> Want to buy with Discount? CLICK HERE! <<<[/b][/u] [/url]
GO to PHARMACY >>> https://tr.im/unitedpharmacies
Where To Order in Canada ED Trial Pack cash on delivery overnight ! http://shaivitetemple.org/Forum/topic/ordering-online-abanaovernight-no-prescription-abana-next-day-no-prescription/
Buying in Australia ED Trial Pack next day delivery no rx \ http://www.intmarketing.org/en/kunena-3/hosgeldin/3140-fda-approved-fincar-discount-price-fincar-next-day-no-prescription.html?start=384#56285
Best Prices ED Trial Pack online consulation with no prescription / http://www.yahont.ru/index.php/forum/razdel-predlozhenij/76264-cheap-generic-differin-next-day-delivery-differin-c-o-d-no-prescription#96826
Purchase in USA ED Trial Pack overnight without prescription # http://www.haciendaspaloverde.com/en/component/kunena/2-welcome-mat/36923-how-to-purchase-tadalia-online-consulation-with-no-prescription-tadalia-with-credit-card-no-prescription#36923
Discount Prices in Australia for ED Trial Pack cheap c.o.d. no rx ??? http://lodzeh.de/kunena/muzika/240-backen-mit-christina-android-iphone-epub-mobi-und-pdf-format?start=340#15815
Pharmacies in Australia That Sell ED Trial Pack no prescription # http://test.shegoday.com/index.php?topic=6553.new#new
Fast Delivery in USA ED Trial Pack pharmacy without a prescription << http://www.architekt-rottgardt.de/index.php/forum
Wholesale Cheapest ED Trial Pack overnight no prescription required > http://prodagainfo.ru/product/sredstvo-ekover-dlja-posudy-grejpfrut/reviews/page803/?msg=8j0w#add-review
Purchase in Australia Cheapest ED Trial Pack from a pharmacy without a prescription )) http://hotel-trade.com/index.php?topic=174350.new#new
Where Can I Order ED Trial Pack no script required )) http://www.samsung-galaxy-ace.cz/
Order in GB / UK Online Cheap ED Trial Pack online consulation with no prescription @ http://www.trainingtrust.org/forum/welcome-mat/24852-order-cheap-online-thioridazine-no-prior-prescription-thioridazine-no-prescription#24851
Purchase in Canada At Lowest Price ED Trial Pack without dr prescription ??? http://zhsi-servis.ru/forum/6-10-82#21756
Australian Licensed Pharmacy ED Trial Pack - how to use,side effects,information * http://www.onlygames.pl/artykul-jak_zalozyc_konto_na_playstation_store_-_poradnik-1084.html
Buy in Canada Cheapest ED Trial Pack overnight delivery without a rx ??? http://www.bangsaitakuapa.go.th/forum/callrole/11699-fast-shipping-levitra-pack-90-overnight-no-prescription-required-levitra-pack-90-shipped-by-cash-on-delivery
Where Can I Buy in USA ED Trial Pack overnight delivery without a rx << http://evaundphilippheiraten.at/page/Gaestebuch
Pharmacies in Canada That Sell ED Trial Pack pharmacy no prescription / http://www.holomemory.ru/guestbook/
Ordering in Australia Online ED Trial Pack cheap c.o.d. no rx / http://unhcr.ml/index.php/forum/welcome-mat/23506-cheap-online-pharmacy-ceclor-cd-in-no-prescription-ceclor-cd-next-day-delivery-no-rx
Pharmacies in Canada That Sell ED Trial Pack no prior script overnight ! http://www.yahont.ru/index.php/forum/razdel-predlozhenij/75489-fast-shipping-cefdinir-no-prescription-c-o-d-cefdinir-no-prior-script-overnight#96051
Cheapest Prices in USA for ED Trial Pack non prescription \\ http://www.n5130.cz/
How Can I Buy ED Trial Pack with no rx \\ http://sibregionservice.ru/index.php/kunena/3-razdel-predlozhenij/19805-where-can-i-buy-norfloxacin-same-day-delivery-no-prescription-norfloxacin-overnight-delivery-no-r-x#20467
Cheap Price ED Trial Pack no prescription overnight << http://www.jindriskajirakova.cz/diskuze/strana:4/
Best Prices in Australia for ED Trial Pack no prescription quick delivery ! http://ortobotik.ru/otzyvy/?jn417c491b=3116
Buy ED Trial Pack next day no prescription needed )) http://unhcr.ml/index.php/forum/welcome-mat/23364-where-to-get-septilin-no-prescription-needed-septilin-no-script-needed
Buy in USA ED Trial Pack overnight no prescription << http://turkmodifiye.club/newreply.php?tid=101975
Where Can I Order in GB / UK ED Trial Pack overnight no prescription required / http://www.job-board.ru/add_articlesjob1795310.html?ac=6df575c3ca24a55eb398bfb22502c8c2
Cheap Prices ED Trial Pack pay cod without prescription ! http://energetic-news.ru/forum/topic114538/1/
Australia Online Pharmacy ED Trial Pack without script pharmacy // http://www.dinfor.ru/?news=904
Pharmacies in Canada That Sell Metoclopramide prescriptions online // http://amourlife.co.zw/forums/topic/buy-cheap-sildenafil-citrateno-rx-fast-worldwide-shipping-sildenafil-citrate-cash-on-delivery-online-prescriptions/
USA Licensed Pharmacy ED Trial Pack c.o.d overnight no rx / http://lodzeh.de/kunena/opcenita-rasprava-o-filmu/14784-buy-online-cheapest-bimatoprost-cheap-c-o-d-no-rx-bimatoprost-with-overnight-delivery
Buy in Canada Discount Levitra with Dapoxetine next day no prescription > http://effizienzen.de/index.php/forum/welcome-mat/137948-order-cheap-generic-effexor-xr-pharmacy-without-prescription-effexor-xr-no-rx-fast-worldwide-shipping#137569
Fast Shipping ED Trial Pack c.o.d. without rx * http://3comltd.com/index.php/component/kunena/2-welcome-mat/273373-best-place-to-buy-toprol-without-rx-toprol-c-o-d-without-prescription?Itemid=0#273373
Purchase Cheap Online in Australia ED Trial Pack pharmacy without a prescription / http://www.meddar.ru/guest/?showpage=84
Buy Discount ED Trial Pack with no prescriptions ??? http://barcovaldeorras.grupotecopy.es/index.php/en/component/kunena/2-bienvenido-mat/244355-lowest-price-urispascod-overnight-no-rx-urispas-without-a-prescription-shipped-overnight#244355
Buy in USA ED Trial Pack online = http://www.overwatchllc.com/index.php/forum/welcome-mat/34909-pharmacies-that-sell-glucophage-no-script-next-day-delivery-glucophage-cash-on-delivery-online-prescriptions#34639
Buy in Canada Cheap Online ED Trial Pack c.o.d. no rx > https://forum.cofe.ru/newreply.php?do=newreply&p=14018701www.pleasurepoison.biz/forums/showthread.php?p=14233368%20
Purchase in Canada ED Trial Pack online ??? http://www.louisraaijmakers.nl/forum/welcome-mat/79368-buying-cheapest-generic-sinemet-prescriptions-online-sinemet-pharmacy-without-a-prescription#79345
Buying Generic ED Trial Pack pharmacy without a prescription / http://chanalafrica.com/index.php/forum/welcome-mat/27702-online-actigall-fast-shipping-no-prescription-actigall-tablet-without-script#27701
Purchase Cheap Online in USA ED Trial Pack with credit card no prescription << http://myqualitytea.com/index.php/forum/welcome-mat/44409-cheap-prices-chloramphenicol-with-no-rx-chloramphenicol-pay-cod-without-prescription#44536
Buying in Australia At Lowest Price ED Trial Pack pay cod without prescription / http://garmonia.tom.ru/repl/
Purchase Cheapest ED Trial Pack delivered overnight no rx \\ http://www.overwatchllc.com/index.php/forum/welcome-mat/34879-purchase-cheapest-avanafil-with-dapoxetine-overnight-without-prescription-avanafil-with-dapoxetine-c-o-d-no-prescription#34609
I Want to order ED Trial Pack - how to use,side effects,information << http://quedensgaard.dk/index.php/forum/welcome-mat/313315-order-online-at-low-cost-microzide-with-no-rx-microzide-shipped-with-no-prescription
Purchase in Australia At Low Price ED Trial Pack without a prescription shipped overnight ! http://craftedmiracle.co.uk/index.php/forum/welcome-mat/18990-what-is-the-generic-of-synthroid-without-prescription-synthroid-from-a-pharmacy-without-a-prescription
Buy in Canada Cheapest ED Trial Pack without script = http://www.design-stu.nichost.ru/index.php/forum/welcome-mat/342138-buy-online-dostinex-no-prescription-next-day-delivery-dostinex-c-o-d-no-rx#342171
Wholesale Cheapest ED Trial Pack next day no prescription needed ??? http://www.videsprojekti.lv/vnews/22941.html
Best Place To Buy ED Trial Pack no prescription no fees / http://www.novabutikotel.com/index.php/forum/welcome-mat/182616-buy-at-low-cost-exelon-pay-cod-no-prescription-exelon-from-u-s-pharmacy-no-prescription#181552
Buy in Canada Cheapest Permethrin cash on delivery online prescriptions << http://fullpotentialdev.com/index.php/forum/welcome-mat/153938-order-cheap-prinivil-c-o-d-without-rx-prinivil-free-delivery-on-sale
I Want to order in USA ED Trial Pack no prescription needed / http://proficio.ru/forum/2-welcome-mat/4699-where-to-get-professional-pack-20-without-rx-professional-pack-20-no-script-required#4699
Discount Prices in GB / UK for ED Trial Pack in without prescription > http://www.almuslimon.net/article_view.php?id=21252&ref=sidebar
Buy in Canada ED Trial Pack pay cod without prescription > http://twood-team.de/index.php/forum/welcome-mat/213961-buy-at-low-cost-xeloda-non-prescription-xeloda-free-delivery-on-sale#212129
[url=http://totalworldstore.com/shop/go.php?sid=1&search=Imodium] [u][b]>>> Want to buy with Discount? CLICK HERE! <<<[/b][/u] [/url]
GO to PHARMACY >>> https://tinyurl.com/y9xxn3b9
Purchase Imodium without script @ http://www.aetaipas.pt/index.php/component/kunena/bem-vindo-companheiro/106818-lowest-price-of-menosan-next-day-delivery-no-rx-menosan-in-no-prescription#106778
Order in USA Cheap Generic Imodium shipped overnight without a prescription ??? http://www.yahont.ru/index.php/forum/razdel-predlozhenij/76027-purchase-fluconazole-shipped-by-cash-on-delivery-fluconazole-overnight-no-prescription-required#96589
Low Prices Generic Imodium no script needed \ http://3comltd.com/index.php/component/kunena/2-welcome-mat/271730-low-prices-glyburide-with-credit-card-no-prescription-glyburide-with-no-prescriptions?Itemid=0#271730
Buy Cheap in USA Imodium next day delivery no rx ! http://labobiondar.com/index.php/forum/welcome-mat/16386-what-is-the-generic-of-plan-b-with-credit-card-no-prescription-plan-b-in-without-prescription
Buy in Australia cheapest Imodium overnight delivery without a rx - http://unhcr.ml/index.php/forum/welcome-mat/23469-purchase-vigrx-plus-next-day-delivery-vigrx-plus-without-a-prescription
Order in USA Cheap Generic Imodium prescriptions online // http://crzy8.com/forum/index.php/topic,209280.new.html#new
Cheap Price Imodium without a prescription >> http://1stclasscare.org/forum/welcome-mat/27071-how-can-i-buy-dapsone-pharmacy-without-a-prescription-dapsone-without-script-pharmacy#27065
Buy in Australia Imodium shipped overnight without a prescription @ http://www.e-market.com.co/index.php/forum/welcome-mat/46264-buying-sparfloxacin-overnight-delivery-without-a-rx-sparfloxacin-non-prescription-needed#46268
Purchase At Low Cost in Canada Imodium next day delivery \\ http://apexschools.net/index.php/forum/welcome-mat/460542-low-prices-effexor-without-a-prescription-effexor-shipped-by-cash-on-delivery#460546
Order in Australia At Low Price Imodium tablet without script - http://linza62.ru/product/1-day-acuvue-moist/reviews/
How Can I Buy in GB / UK Imodium c.o.d. without rx \ http://www.radiostudio92.it/2015/kunena/benvenuto/topic/create
Buy in Australia At Low Price Imodium pharmacy without a prescription ??? http://www.geocontrol.cl/index.php/forum/welcome-mat/67529-wholesale-cheapest-clonidine-c-o-d-without-prescription-clonidine-overnight-without-dr-approval#67530
Purchase Cheap Online Imodium no prior prescription - http://www.growthegamecentral.com/board/index.php?app=forums&module=post§ion=post&do=new_post&f=14
Low Cost Imodium shipped by cash on delivery ! http://footbeauty.ru/blog/kak-bystro-snyat-ustalost-massazh-nog./
Order in Australia cheapest Imodium with credit card no prescription = http://demo.7910.org/forum/showthread.php?tid=8/newreply.php?tid=28042
Purchase in Canada Online Imodium no prescription overnight ??? http://www.infomures.ro/administratie/15942-seful-sri-romania-se-confrunta-cu-amenintari-din-ce-in-ce-mai-complexe-si-atipice.html
How To Purchase Imodium no prescription needed * http://kuliahsutrisno.com/diskusi/viewtopic.php?f=2&t=171083
Order Low Price Imodium without a rx overnight = http://drawings.wpblog.jp/forums/topic/low-prices-ranitidineovernight-no-prescription-ranitidine-in-without-prescription/
Buying in Canada Imodium overnight without a prescription / http://www.cs-cccp.ru/forum/54-2274-10#111797
Pharmacies in Australia That Sell Imodium saturday delivery = http://www.traum-strand.net/gaestebuch/
Buy in Canada cheapest Imodium c.o.d. no prescription @ http://www.jcent.ru/guestbook/
Buy in GB / UK Discount Imodium no prescription fast delivery / http://skinandtonicltd.com/index.php/forum/welcome-mat/24069-purchase-cheapest-himplasia-no-script-needed-c-o-d-overnight-himplasia-shipped-overnight-without-a-prescription#24069
I Want to order in GB / UK Imodium c.o.d. saturday delivery \\ http://cursosmariale.com/index.php/component/kunena/2-welcome-mat/1004018-order-herbal-extra-power-without-a-prescription-herbal-extra-power-next-day-no-prescription?Itemid=0#1004018
Buying in GB / UK Generic Imodium in without prescription - http://www.applewindforum.com/buy-at-low-cost-Indapamideonline-Indapam-948325-1-1.html
Buy in Canada cheapest Imodium shipped with no prescription > http://myqualitytea.com/index.php/forum/welcome-mat/44473-buy-at-low-price-astelin-without-rx-next-day-delivery-astelin-no-rx-required#44600
Best Prices in Canada for Imodium from u.s. pharmacy no prescription / http://www.trainingtrust.org/forum/welcome-mat/24883-brand-or-generic-sildenafil-with-dapoxetine-free-delivery-on-sale-sildenafil-with-dapoxetine-no-prescription-needed#24882
Discount Price Imodium without rx,next day delivery ! http://www.sman2metro.sch.id/bukutamu.html
Order in Australia Cheap Online Levitra Pack-60 without a prescription ??? http://www.youtubeindia.in/index.php/topic,388535.new.html#new
I Want to order Imodium no prescription fast delivery * http://www.lifespringministries.org/index.php/forum/welcome-mat/18981-mail-order-acarbose-overnight-delivery-no-rx-acarbose-without-prescription
Online Pharmacy ED Soft Medium Pack without prescription overnight // http://amnch.org/forum/welcome-mat/30717-buy-at-low-cost-vigora-pay-cod-without-prescription-vigora-no-prescription
Best Prices in Canada for Imodium in without prescription << http://www.ly-bbw.com/forum.php?mod=viewthread&tid=396238&extra=
Purchase At Lowest Price Imodium without dr prescription )) http://barcovaldeorras.grupotecopy.es/index.php/en/component/kunena/2-bienvenido-mat/244336-cheap-prices-grisactinno-prescription-cod-grisactin-overseas-with-no-prescriptions#244336
Buy Online in USA Imodium no script needed c.o.d. overnight \ http://kursyjezykoweonline.pl/forum/welcome-mat/124125-cheapest-price-to-order-keftab-tablet-without-script-keftab-cash-on-delivery#217310
Where To Get in USA Imodium pay cod no prescription >> http://www.dubaitranslation.com/index.php/forum/welcome-mat/340457-quality-generic-sinemet-pharmacy-without-a-prescription-sinemet-pay-cod-no-prescription#340440
Purchase in USA At Low Price Imodium overnight delivery no r x >> http://www.haciendaspaloverde.com/en/component/kunena/2-welcome-mat/36903-order-cheap-alendronate-no-script-next-day-delivery-alendronate-pharmacy-without-prescription#36903
Purchase At Low Cost in Canada Imodium no prescription overnight - http://forum.lustfordarkness.ru/viewtopic.php?pid=446933#p446933
Buy in USA Imodium without rx,next day delivery // http://mail.beyondpancakes.com/forum/welcome-mat/25990-order-at-low-price-actos-no-prescription-fast-delivery-actos-overnight-delivery-no-r-x#25692
Where To Buy in USA Imodium pharmacy no prescription \\ http://www.teamelec.ch/fr/forum/welcome-mat/55213-lowest-price-of-isoptin-no-prescription-needed-isoptin-with-overnight-delivery#55213
Ordering in USA Online Imodium delivered overnight no rx ??? http://www.videsprojekti.lv/vnews/22941.html
Buy in Canada At Low Price Imodium free prescription drug \\ http://wx.jydsdh.com/bbs/t-1259168-1-1.html
How Much Imodium with overnight delivery )) http://priesterenterprises.com/index.php/forum/welcome-mat/160770-what-is-the-generic-of-amiodarone-c-o-d-without-prescription-amiodarone-no-prescription#160759
Where To Order in Australia Imodium no script required ! http://harmonikaportal.de/showthread.php?tid=132437&pid=225594#pid225594
Buying in USA Imodium pay cod no prescription )) http://amnch.org/forum/welcome-mat/30655-indian-generic-luvox-overnight-no-prescription-luvox-overseas-with-no-prescriptions
Cost Of Imodium no script next day delivery // http://lakeshoreliftind.com/forums/topic/purchase-at-lowest-price-naprosynovernight-without-a-prescription-naprosyn-prescriptions-online/
Purchase in Australia Cheapest Imodium c.o.d. no prescription << http://www.e7nokia.cz/tapety-360x640-strana2
Online Pharmacy Lamivudine / Zidovudine no prescription required << http://doylesllc.com/index.php/forum/welcome-mat/199304-discount-prices-vitria-c-o-d-no-prescription-vitria-without-a-rx-overnight#199219
Purchase in Australia Cheapest Imodium overnight without a prescription ??? http://www.allegra.it/index.php/forum/welcome-mat/68462-online-pharmacy-phenazopyridine-no-prior-prescription-phenazopyridine-overnight-without-dr-approval
I Want to order in USA Imodium overseas with no prescriptions \\ http://www.mbugitv.co.ke/index.php/forum/welcome-mat/37628-fast-shipping-levlen-with-no-prescription-levlen-no-prescription-fedex-ups#37290
Lowest Price Of Imodium in internet drugs overnight \\ http://www.jindriskajirakova.cz/diskuze/strana:4/
[url=http://trustedmeds.store/shop/go.php?sid=5&search=Trecator-SC] [u][b]>>> Want to buy with Discount? CLICK HERE! <<<[/b][/u] [/url]
GO to PHARMACY >>> https://tr.im/americanpills
Buy in Canada Discount Trecator-SC cash on delivery > http://www.averagegeek.me/index.php/forum/welcome-maw/429481-how-to-buy-cardizem-c-o-d-saturday-delivery-cardizem-no-prescription-quick-delivery#429483
Canadian Licensed Pharmacy Trecator-SC without a prescription shipped overnight / http://www.mbugitv.co.ke/index.php/forum/welcome-mat/37711-cheap-online-pharmacy-levlen-overnight-delivery-no-rx-levlen-no-dr-approval-cash-on-delivery#37373
Discount Prices Trecator-SC in no prescription * http://shaivitetemple.org/Forum/topic/buy-discount-bromocriptinewithout-prescription-bromocriptine-no-prescription/
Buy in USA Trecator-SC c.o.d. without rx )) http://www.uzfiles.com/file_details.php?read=7178
Discount Price Trecator-SC without script pharmacy \ http://www.primariaprajeni.ro/forum/viewtopic.php?pid=783976#p783976
Order Trecator-SC online consulation with no prescription \ http://monteurzimmer-springe.de/index.php/forum/welcome-mat/184839-best-prices-sporanox-no-script-required-sporanox-without-a-rx-overnight#184839
Best Place To Buy Trecator-SC no script required @ http://www.dreierheinerhof.de/?page_id=350
Price Of Trecator-SC shipped with no prescription = http://moraviadogschool.cz/guestbook
Buy in USA Cheapest Trecator-SC without script # http://queenscontrivance.com/index.php/forum/welcome-mat/1555-buy-at-low-cost-clonidine-c-o-d-without-prescription-clonidine-online#158167
Lowest Prices Trecator-SC next day delivery )) http://www.trainingtrust.org/forum/welcome-mat/25106-buy-cardarone-overnight-without-dr-approval-cardarone-online#25105
Buy At Low Price Trecator-SC without prescription overnight / http://www.toneeldegoorn.nl/gastenboek/
Discount Prices in Canada for Trecator-SC pharmacy without prescription << http://lily-galant.ru/informacionnyy-razdel/sumki-pekof/
USA Online Pharmacy Trecator-SC no prescription required << http://amnch.org/forum/welcome-mat/31151-buy-safety-acyclovir-cream-5-without-script-acyclovir-cream-5-no-script-required-express-delivery
Buy in USA Trecator-SC with no rx @ http://thaihitz.xyz/index.php?topic=33649.new#new
Ordering Trecator-SC shipped overnight without a prescription > http://support.dagopert.at/index.php/forum/welcome/324850-purchase-cheapest-imipramine-overnight-no-prescription-imipramine-without-a-prescription#324891
Best Prices in Australia for Trecator-SC with overnight delivery )) http://terror-rs.com/community/index.php?showtopic=
Buy Trecator-SC pay cod no prescription )) http://sade.forumcrea.com/post.php?tid=33653
Quiqly Delivery Trecator-SC c.o.d. saturday delivery > http://crittendenfireky.com/page5.php?topic=38&category=2
Canada Online Pharmacy Trecator-SC no prescription fedex / ups - http://www.appleclubcity.com/cheapest-price-to-order-Eldeprylovernight-684497-1-1.html
Cost Of Trecator-SC shipped overnight without a prescription > http://www.coffee-car.ru/blog/jura-ena-9-micro-otzyvy-vladeltsev#comment_52667
Order in GB / UK At Low Price Trecator-SC pay cod without prescription << http://mail.beyondpancakes.com/forum/welcome-mat/26057-purchase-at-low-cost-methocarbamol-no-prescription-methocarbamol-no-script-needed#25759
Best Prices Trecator-SC in internet,next day delivery - http://www.all-leasing.ru/forums/topic/add/forum17/
Buy in Australia Trecator-SC no dr approval cash on delivery ??? http://3comltd.com/index.php/component/kunena/2-welcome-mat/273995-buy-cheap-online-serevent-without-a-prescription-shipped-overnight-serevent-no-prescription-quick-delivery?Itemid=0#273995
Buy Trecator-SC no script needed c.o.d. overnight * http://moraviadogschool.cz/guestbook
Ordering At Lowest Price Trecator-SC without rx,next day delivery >> http://www.lightingapps.de/index.php/forum/artnet-viewer/110537-buy-cheapest-melatonin-no-prescription-next-day-delivery-melatonin-pay-cod-without-prescription
Low Cost Trecator-SC shipped overnight without a prescription # http://www.schooleduc.ru/%D0%B3%D0%BE%D1%81%D1%82%D0%B5%D0%B2%D0%B0%D1%8F-%D0%BA%D0%BD%D0%B8%D0%B3%D0%B0.html
Buy in UK cheapest Trecator-SC c.o.d. without prescription \ http://www.domosrub.ru/forum
Order in Australia cheapest Kamagra Oral Jelly Vol-2 no dr approval cash on delivery ??? http://howtobecanadian.com/forum/immigration-forum/83385-purchase-at-low-cost-combivir-no-prior-prescription-combivir-without-prescription-overnight.html
Order in USA At Low Price Trecator-SC in internet,next day delivery * http://understudy.offstagejobs.com/index.php?topic=320212.new#new
Purchase in USA Zidovudine with overnight delivery = http://www.beespn.com/index.php?topic=207552.new#new
Ordering Trecator-SC c.o.d overnight no rx ??? http://crzy8.com/forum/index.php/topic,210057.new.html#new
Online in USA Trecator-SC no prescription next day delivery << http://shuum.ru/articles/728
How To Order in Australia Trecator-SC no prescription fedex / ups ! http://www.nsbbms.in/index.php/en/forum/welcome-mat/97111-fast-delivery-chlorambucil-shipped-overnight-without-a-prescription-chlorambucil-pay-cod-without-prescription
Low Prices Generic Trecator-SC c.o.d. no rx > http://www.widowsandwidowers.co.uk/forum/welcome-mat/35622-purchase-online-kamagra-oral-jelly-vol-2-pharmacy-without-a-prescription-kamagra-oral-jelly-vol-2-overnight-delivery-without-a-rx
Ordering in GB / UK Trecator-SC free prescription drug @ http://se-union.com/thread-1373779-1-1.html
How Much in USA Trecator-SC non prescription needed << http://bebetortore.com/content/05community/01_01.php?proc_type=view&b_num=7
Buy Cheapest Trecator-SC with no rx > http://www.dietasarok.hu/index.php/component/kunena/otletlada/157320-purchase-cheapest-ditropan-pay-cod-no-prescription-ditropan-without-prescription#159047
Buying in GB / UK At Lowest Price Trecator-SC - how to use,side effects,information )) http://cs.medixa.org/nemoci/vulvitis-a-kolpitis/
Buy in Canada Cheap Online Trecator-SC without prescription ??? http://codechoco.gov.co/portalwp/index.php/forums/topic/verahora-jumanji-bienvenidos-a-la-jungla-2017-pelicula-completa-en-espanol-lat/
Order in Australia Online Cheap Trecator-SC no prescription // http://www.commoncause.org/take-action/connect/connect-with-your-community/community/more-transparency.html
How Can I Buy in GB / UK Trecator-SC no prescriptions needed \\ http://sibregionservice.ru/index.php/kunena/3-razdel-predlozhenij/19919-buy-cheap-online-adapalene-without-a-rx-overnight-adapalene-fast-shipping-no-prescription#20581
Order in Canada Cheap Online Trecator-SC in no prescription // http://www.e7nokia.cz/tapety-360x640-strana2
Cheap Generic Trecator-SC overnight delivery no r x \ http://keepcalmandcruise.com/forum/phpBB3/viewtopic.php?f=8&t=154879
Cheapest Trecator-SC pharmacy without a prescription = http://www.allshoreplumbing.com/index.php/forum/welcome-mat/30696-buy-at-low-cost-spironolactone-next-day-delivery-spironolactone-no-prescription-needed
Best Prices Trecator-SC from a pharmacy without a prescription * http://www.e-market.com.co/index.php
How Much in Australia Simvastatin no prescription fedex / ups @ http://androids.lv/infnews/24420.html
Purchase At Low Cost in Canada Trecator-SC with no rx > http://forum.skoliose-therapie.ch/viewtopic.php?f=1&t=142256
Australia Online Pharmacy Trecator-SC pharmacy without a prescription // http://www.seelenharmonie.com/index.php/forum/welcome-mat/1-welcome-to-kunena?start=2880#13590
Buying in Australia At Lowest Price Trecator-SC without prescription * http://strizhki.ru/forum/ob-yavleniya/68898-i-want-to-buy-diclofenac-no-prescription-fedex-ups-diclofenac-fast-shipping-no-prescription#87044
[url=http://kamagradyn.com/]buy kamagra online[/url]
kamagra 100mg tablets side effects
<a href="http://kamagradyn.com/">buy kamagra 100 mg oral jelly</a>
side effects of kamagra oral jelly
http://kamagradyn.com/
kamagra bestellen rotterdam
Телефон: +79200396703
kamagra oral jelly kaufen amazon
kamagra oral jelly amazon
kamagra 100mg oral jelly suppliers india
<a href="http://viagrapipls.com/">buy viagra</a>
viagra commercial woman brunette
[url=http://viagrapipls.com/]buy viagra[/url]
viagra professional review
<a href="http://viagrapipls.com/">buy generic viagra</a>
kamagra 100mg generic viagra for sale
[url=http://viagrapipls.com/]buy generic viagra[/url]
female viagra pill fda approved
[url=http://bit.ly/2sm8VzW][IMG]http://i105.fastpic.ru/big/2018/0530/e0/b993bd8ae3365b94d98f1b69efdf87e0.jpg[/IMG][/url]
[url=http://bit.ly/2sm8VzW][b]Смотреть фильм Мир Юрского периода 2[/b][/url]
[url=http://bit.ly/2sm8VzW][b][color=red]Смотреть фильм Мир Юрского периода 2[/color][/b][/url]
[url=http://bit.ly/2sm8VzW][b][color=green]Смотреть фильм Мир Юрского периода 2[/color][/b][/url]
О сюжете фильма Мир Юрского периода - Этот мир древних созданий был сделан специально для.
Фильм Мир Юрского периода 2 2018 расскажет зрителям невероятную историю об Ежегодно в этот парк приезжают миллионы туристов со всего мира, чтобыМИР ЮРСКОГО ПЕРИОДА 2 Трейлер 2 (Universal Pictures) HD. Info.
Про фильм: Простым людям неведомо, что происходит в высоких эшелонах власти. Триллер Зеро 3 2017 смотреть онлайн бесплатно в хорошем качестве. Видео неУбить за 68 2017Мир Юрского периода 2 (2018).
Смотрите онлайн фильмы хорошего качества в приятной домашней обстановке и в удобное для вас время.Маугли. Трейлер (дублированный)Мир Юрского периода 2.Онлайн-кинотеатрэто самая большая коллекция отечественных и зарубежных фильмов в рунете.2018 ООО
14 hours ago - 7 sec МИР ЮРСКОГО ПЕРИОДА 2в кино с 7 июня. 564. Universal Pictures РоссияОпубликовано 28 мая 2018, 13
Когда выйдет худ . фильм " " Мир Юрского периода 4", премьера в России? вопрос закрыт. кудрявцев владимир семенович 102K 4 года назадрф, фильм, юрский период. категория: досуг и развлечения. в избранное. 2 ответа:.
Таблица-график выпуска 3D фильмов в российский прокат с указанием хронометража и количества копий.МИР ЮРСКОГО ПЕРИОДА 2Jurassic World: Fallen Kingdom (Atmos, Auro, D-Box, Aurox, 4DX (превью МЕГ: МОНСТР ГЛУБИНЫThe Meg, экшн, триллер, Каро Премьер, -27 декабря 2018.
Jannie Vex replied the topic: патриотический фильм Охота на воров - волгодонскволков смотреть онлайн бесплатно в хорошем качестве hd охоту на фильм Охота наПарк Юрского периода 2: Затерянный мир.
Фильм Мир Юрского периода (2015)Оригинальное название: Jurassic World. Фильм 2015 года Съёмочная группа фильма "Мир Юрского периода":
Афиша; Фильмы; Рейтинги; Журнал; Онлайн. Войти Тысячи людей спешат увидеть Мир Юрского периода, но безопасное наТрейлер 2 (дублированный), 02:28Первый фильм из серии, продюсером которого не стала КэтлинЛента расскажет зрителю о событиях, произошедших спустя 22 года с
(86133) 5-46-82 расписание сеансов. (86133) 3-20-08 бронирование билетов План залов. БОЛЬШОЙ ЗАЛ: МАЛЫЙМир Юрского периода 2 3D (12+)
Фильм Мир Юрского периода Jurassic World (2015) вы можете скачать бесплатно через торрент наАвтор: Таня Комендант(Беляева) 2 августа 2015 08:57. 0. Фильм шикоз просто !!! Спецывафекты динозавры все просто зашкаливает эмоцыями. Ответить.Автор: Кристина Индейкина(Карасева) 31 июля 2015 08:27. 0.
Просмотров: 268832. Дата добавления: , 00:44. После трагических событий в развлекательном Мир Юрского периода 2 парк аттракционов закрыли. Но через несколько лет бизнесмены вновь решили эксплуатировать эту золотую жилу для привлечения туристов. Те давние воспоминания улеглись.
20:48, 10. olegkrykov4297. Трейлер получился классным, чувствуется что создатели очень кропотливо прорабатывали каждую сцену. Сюжетная основа у ленты "Мир Юрского периода 2" конечно не оригинальная.
В нашем кинозале можно смотреть фильм Парк Юрского периода 2: Затерянный мир (1997) онлайн бесплатно! Самая главная особенность просмотра в том, что данное кино в хорошем качестве! (голосов: 11). 6-02-2015, 12:04. Категория: Боевики, Фантастика, Триллеры, Приключенческие, HD, 720p. Прошло четыре года с того времени, когда произошли события, описанные в первом фильме. Динозавры остались живы и оказались на острове, являющемся полигоном для испытаний, предоставлены сами себе. Но появляются те, кто в целях наживы, пытается перевезти чудовищ на Большую землю. Для этой цели на остров снаряжается группа наемников.
Чем удивят создатели фильма Мир юрского периода 2, который в 2018 году появится на экранах? Поклонники знаменитой саги о доисторических ящерах с нетерпением ожидают выхода пятой части, станет ли она успешным продолжением проекта? Автор идеи и сюжетная линия киноэпопеи А пока предлагаем посмотреть короткий тизер-трейлер фантастического фильма 2018 года Мир юрского периода 2. Похожие публикации: Первому игроку приготовитьсяфильм 2018 года. Фильм Собибор (2018). Фильм Железное небо: Ковчег (2018).
Определенно вы искали Мир Юрского периода 2 (2018). Что бы по смотреть онлайн в High Definition-1080 и 720p качестве! Будем очень рады любому вашему отзыву о просмотренном фильме. На острове Исла-Нублар, где не так давно располагался парк развлечений с динозаврами, правит бал дикая природа. Но без людей все далеко не так спокойно, как могло бы показаться Полный фильм Мир Юрского периода 2 (2018) смотреть онлайн можно со всех доступных мобильных устройств, андроид с поддержкой HLS, планшет, айпад, айфон "ipadiphone" в хорошем качестве HD-1080. Мир Юрского периода 2 (2018) смотреть онлайн бесплатно на HD-1080.
Фильмы смотреть бесплатно в хорошем качестве на . Go Kino онлайнБоевикиМир Юрского периода 2. Мир Юрского периода 2 (2018) смотреть онлайн. Jurassic World: Fallen Kingdom. В результате трагических событий нестандартный парк развлечений с весьма необычными аттракционами и гигантскими животными из далекого прошлого, располагающийся на острове Исла-Нублар, прекращает свое существование Гокино фильм Мир Юрского периода 2 смотреть онлайн в hd 1080 качестве бесплатно Самые любимые(43).
Понравился фильм Мир Юрского периода 2 2018 в хорошем качестве, поделись им с друзьями бесплатно онлайн Выпуск 73. Просто космос! (2018).
Скачать торрент Мир Юрского периода 2 (2018). Подписаться на добавление торрентов. + Мир Юрского периода 2Jurassic World: Fallen Kingdom2018WEBRip 1080p Трейлер. Выложил: Vitas66684. 23 Апреля 2018, 09:54. 0.MB. 7. 2 0. Скачать. Качество: WEBRip Время: 00:02:43 Видео: AVC (H264), 1563 kbps, 1920x1080 Аудио дорожка 1: Русский, Дублированное, AAC, 126 kbps. Что-бы бесплатно и без регистрации скачать Мир Юрского периода 2 (2018) через торрент - воспользутейсь данной инструкцией. Не забываем говорить "Спасибо" - кнопка возле торрента, а так же делить ссылкой на Мир Юрс
Другие трейлеры к фильму: Международный трейлер фильма "Мир Юрского периода 2". 3. Дублированный трейлер 3 фильма "Мир Юрского периода 2". 21. Всего комментариев: 112 Пользователи портала "Новости кино" в сиквеле популярного боевика. Самые обсуждаемые материалы.
Скорее всего Вы ищите Мир Юрского периода 2 (2018) в хорошем качестве. Наш ресурс содержит большую базу онлайн фильмов, которые вы сможете смотреть онлайн абсолютно бесплатно в 720p, и конечно же в HD1080. Не забывайте делиться вашими впечатлениями о киноленте, ведь нам интересно, что вы думаете о ней. И имейте введу, что Мир Юрского периода 2 (2018) можно будет посмотреть на телефоне и планшете, использую любую ОСайфон, анйдройд. Мы очень рады, что вы выбрали именно нас: . Советуем посмотреть: Девушка по вызову 1-2 сезон. Новые сериалы. Улица 2 сезон 94, 95, 96 серия ТНТ.
Тэги:
Мир Юрского периода 2 2018 смотреть онлайн без регистрации
Мир Юрского периода 2 гугл
Мир Юрского периода 2 фильм
Мир Юрского периода 2 кино
смотреть фильм Мир Юрского периода 2 в hd качестве
Мир Юрского периода 2 смотреть
Хиты:
[url=https://theboldprint.com/smfelectricallyspeaking/index.php?topic=56772.new#new]Мир Юрского периода 2 фильм смотреть j x g[/url]
[url=http://patriotfreedomfighters.com/smf/index.php?topic=529503.new#new]Собибор 2018 смотреть онлайн в хорошем качестве p z e[/url]
[url=http://www.whgsoba.org/forums/topic/%d1%81%d0%b5%d0%ba%d1%81%d0%b0-%d0%bd%d0%b5-%d0%b1%d1%83%d0%b4%d0%b5%d1%82-%d0%be%d0%bd%d0%bb%d0%b0%d0%b9%d0%bd-2018-g-j-b/]Секса не будет!!! онлайн 2018 g j b[/url]
[url=http://medprocessing.com/forums/topic/%d0%b4%d1%8d%d0%b4%d0%bf%d1%83%d0%bb-2-%d0%ba%d0%b8%d0%bd%d0%be-%d0%be%d0%bd%d0%bb%d0%b0%d0%b9%d0%bd-c-v-p/]Дэдпул 2 кино онлайн c v p[/url]
[url=http://www.breakarts.info/forum/viewtopic.php?f=5&t=16860]фильмы 2018 Собибор i d e[/url]
[url=http://uanet.info/viewtopic.php?pid=5449#p5449]Хан Соло: Звёздные Войны. Истории кинопоиск s y y[/url]
.
[url=http://bit.ly/2sm8VzW][IMG]http://i104.fastpic.ru/big/2018/0530/76/5d203aa86a6c15e9a747f7a6b49a2c76.jpg[/IMG][/url]
[url=http://bit.ly/2sm8VzW][b]Смотреть фильм Мир Юрского периода 2[/b][/url]
[url=http://bit.ly/2sm8VzW][b][color=red]Смотреть фильм Мир Юрского периода 2[/color][/b][/url]
[url=http://bit.ly/2sm8VzW][b][color=green]Смотреть фильм Мир Юрского периода 2[/color][/b][/url]
4 Dec 2017 - 3 min Все трейлеры к фильму Мир Юрского периода 2 (2018) смотреть онлайнбесплатно.Тизер (английский язык) 0:00:18; Промо
фильмы про вампиров45. Ловите свежую подборку фильмов про вампиров на Вокруг ТВ.Ферстер. Продолжение фильма 2012 года Другой мир: Пробуждение, событиясемейный мультфильм Монстры на каникулах 2 (Hotel Transylvania 2) от За кадром Как снимают шоу Ледниковый период.
В 2015 году фильм Мир Юрского периодасобрал более 1,6 млрд. долларов иневероятный масштаб и зрелищностьэто всё Мир Юрского периода 2.МИР ЮРСКОГО ПЕРИОДА 2 официальный трейлер.
bсмотреть фильм Без границ без регистрации 8ecb Скачать торрент Без границ. Скриншоты. Похожие файлы (2). 76. 0.было бы куда круче, а так сказка Мир Юрского периодаJurassic World (2015) WEB-DLRip.
Смотреть фильм Мир Юрского периода 2 (2018) онлайн всмотреть фильм 2018 в хорошем качестве Мир Юрского периода 2 81 6 82.
Мир Юрского периода 2Подробнее о фильме13 июня среда. Киномакс-Мозаика Москва. ул. 7-ая Кожуховская, , ТЦ Мозаика,Онлайн-бар.
Все кино Южно-Сахалинска и Сахалина - Расписание сеансов, каталог фильмов и Семейный тур в Ю.Корею. Прими участие и выиграй главный приз!Пока Мстители и их союзники продолжают защищать мир от различных опасностейДэдпул 2. Deadpool 2. Рейтинг , 56 оценок 56. Единственный и
May 27, 2018 at 11:09 AM 55738на Айпадbrсмотреть фильм Мир Юрского периода 2 2018 онлайн mkv боб фильмbr Мир Юрского периода 2
(2018). Новости кино. Свежий трейлер Мира юрского периода 2 Свежий трейлер Мира юрского периода 2Пила 2 (2005) Скачать с торрент бесплатно20. 13 января 2018 22:2643. 14 мая 2014 01:57
2001, 2000, 1999, 1998, 1997, 1996, 1995, 1994, 1993, 1992, 1991, 1990, 1989, 1988, 1987, 1986, 1985Смотреть Парк Юрского периода 2: Затерянный мир онлайн в HD качестве 720p Смотреть Парк культуры и отдыха онлайн в HD качестве Фильмниколай 656454, оставлен 7 февраля 2018 18:33 .
Русский трейлер 2 фильма "Мир Юрского периода 2" 2018 Продолжение приключений в Мире Юрского периода — на Мстители 3: Война Бесконечности — Русский трейлер (2018) - Продолжительность: 2:54 i Videos 4 450 600 просмотров.
Почта Мой Мир Одноклассники Игры Знакомства Новости Поиск. Все проекты. Авто Бонус Гороскопы Дети Добро Здоровье Календарь Кино Леди Недвижимость Облако 06:38. Крымский мост построили за три года протяженностью 19км. В Каменске при Якимове пообещали построить мост, при Астахове сделали проектную документацию и все деньги просрали. Вопрос: сколько времени должно пройти, чтоб наша Администрация зажралась уже деньгами.
Мир Юрского периода 2 2018 смотреть полностью бесплатно. Важно: Перед просмотром обязательно обратите внимание на вкладки в плеере (360480HD 720p HD 1080p) - от этого будет зависить скорость загрузки видео и качество. Посетителям мы даём возможность смотреть фильм 2018 года Мир Юрского периода 2 онлайн на телефоне или планшете Андроид, Айпад, Айфон без регистрации mishaaaa66. 15 мая 2018 13:29. Однозначно фильм хорош, отснят очень даже качественно, нравится игра актеров и хорошо продуманный сюжет Мир Юрского периода довольно таки замечательный фильм, который радует игрой актеров и графикой, рекомендую. Ответить. Цитата. antonaaaa. 14 мая 2018 20:19.
Премьера русского трейлера фильма "Мир Юрского периода 2" 2018 состоится в пятницу 8 декабря 2017 года.Премьера: 7 июня 2018Оригинальное название: "Jurassic World: Fallen Kingdom"Жанр: фантастика, боевик
Фантастика, боевик, приключения. Режиссер: Стивен Спилберг. В ролях: Джефф Голдблюм, Джулианна Мур, Винс Вон и др. События этого фильма разворачиваются через четыре года после того, что произошло в Парке Юрского периода.
Мир Юрского периода 2 (2018) смотреть онлайн бесплатно. Люди, побывавшие в удивительном парке на острове полны впечатлений. Там проживают настоящие динозавры, которые господствовали на Земле в мезозойской э Криминал. (22). Военные. (2).
Первый русский трейлер фильма Мир Юрского периода 2: Падшее царство 2018 года Русские трейлеры к фильмам, МИР ЮРСКОГО ПЕРИОДА 2 официальный трейлер. 5 мес. назад. Исполнительные продюсеры: Стивен Спилберг2 премии Оскар, Спасти рядового Райана, Список Шиндлера Колин МИР ЮРСКОГО ПЕРИОДА 2 Трейлер 2 (Universal Pictures) HD. 3 мес. назад. Жанр: Эпический блокбастер В ролях: Крис Пратт, Брайс Даллас Ховард, . Вонг, Джеймс Кромуэлл, Джастис Смит, Мир Юрского периода 2 — Русский трейлер 2 (4К, 2018). 3 мес. назад. Второй русский трейлер фильма Мир Юрского периода 2: Падшее царство 201
Колд ФильмСегодня мы подготовили для вас обзор на фильм - Мир Юрского периода 2, который выйдет в прокат с 7 июня 2018 года. Спонсор -Сегодняшний обзор будет посвящен фильму о динозаврах, да-да, именно им 12.27 1335:30. Оно приходит ночью 2017 ОбзорТрейлер 3 на русском. Опубликовано 14 января 2017, 23:40. Сегодня мы подготовили для вас обзор на фильм - Мир Юрского периода 2, который выйдет в прокат с 7 июня 2018 года. Спонсор - . Сегодняшний обзор будет посвящен фильму о динозаврах, да-да, именно им. Называется он Мир Юрского периода 2, и это прямое продолжение фильма с таким же названием, только уже без цифры.
Гости. Онлайн всего: 17. Гостей: 17. Пользователей: 0. Мир Юрского периода 2Jurassic World: Fallen Kingdom (2018) MP4 торрент. 1. 2 Фильм Мир Юрского периода 2 - это продолжение знаменитой франшизы про парк развлечений, населенный искусственно созданными динозаврами. Цитата. Премьера (мир): 7 июня 2018 года Премьера (РФ): 7 июня 2018 года. Теги материала -. Похожие фильмы для андроид Качайте 2018 торрент андроид на телефон от бестселлеров до новинок кино.карта сайта.2018 Хостинг от u Coz- Торрент андроид портал кино - Погрузись в мир фильмов для телефона в месте с нами .
1.Скачать бесплатно без регистрации и установить торрент-клиент(Torrent, Bit Torrent, Azureus и др) на компьютер. 2.Скачать торрент Парк Юрского периода 2: Затерянный мир.торрент на загрузку. 4.Скачать фильм Парк Юрского периода 2: Затерянный мир бесплатно. Информация. Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации. Скачать фильмы через торрент.2014 Торрент Torrent.
Смотреть фильм Мир Юрского периода 2 2018 онлайн бесплатно в хорошем качестве. Смотреть. Трейлер Самый адекватный в этом фильме, Крис Прат (Прэт), остальные дебилы. 21:04,German Volynskyi. Картина "Мир Юрского периода 2" обладает множеством жанров, начиная от фантастики заканчивая боевиком и драмой. Очень важно, что бы режиссер смог досконально передать зрителю дух этих невероятных событий, что бы все сцены были на реалистичный манер. Лично я люблю когда создатели детально прорабатывают каждый момент.
Боевик, приключения, фантастика. Режиссер: Хуан Антонио Байона. В ролях: Брайс Даллас Ховард, Крис Пратт, Джефф Голдблюм и др. Фильм "Мир юрского периода 2: Падшее царство" (2018) рассказывает невероятную историю о последствиях создания динозавров в условиях современного мира. В парке юрского периода происходит сбой, и все динозавры выбегают наружу. От парка остаются одни лишь руины, а динозавры в поисках убежища и пропитания вторглись в цивилизованный мир. Они угрожают не только людям, создавших этих рептилий, но и людям, которые пытаются получить выгоду от такого хаоса. Парк принос
Первый русский трейлер фильма Мир Юрского периода 2: Падшее царство 2018 года. Русские трейлеры к фильмам, сериалам и играм! Интересные ролики о фильмах и их съёмках! Подпишись на канал Новости,промо,трейлеры,даты выходов фильмов и сериалов только у нас:. . Дата выхода в РФ - 7 июня 2018.Оригинальное название: Jurassic World: Fallen KingdomСтрана: Испания, СШАДистрибьютор: Universal Pictures РоссияРежиссер: Хуан Антонио БайонаЖанр: боевик, приключения, фантастика 1 день 21 час 20 минут. Замечено в трендах.в 14:45.
Все в ожиданииdleфильмы бесплатно. Мир Юрского периода 2 2018 смотреть онлайн бесплатно в хорошем качестве. Смотреть трейлер Мир Юрского периода 2 ЗДЕСЬ---. 1 156. Загрузка 89-я церемония вручения премии Оскар (2017) , 21:00 Комментариев: 0 Просмотры: 1 347. Смотреть фильмы и сериалы онлайн бесплатно на . Приветствуем дорогих посетителей нашего увлекательного сайта. Если вы у нас впервые, тогда желаем вам познакомиться с порталом поближе и вскоре стать нашими постоянными друзьями.
Смотреть Мир Юрского периода 2 (2018) в хорошем качестве. Трейлер. Увы, фильм еще не появился в сети! В кино с 7 июня 2018 А пока мы удивим Вас уже вышедшими фильмами Смотреть новинки фильмов онлайн. x. 0:00. 0:00. Р—РРССРРР. Нравится. Твитнуть.
Тэги:
Мир Юрского периода 2 скачать
фильм Мир Юрского периода 2 2018 смотреть онлайн hd
Мир Юрского периода 2 смотреть онлайн 2018
Мир Юрского периода 2 2018 смотреть онлайн фильм без регистрации
Мир Юрского периода 2 смотреть
Похожие фильмы:
[url=https://kalakuta.com.ng/index.php/topic,85585.new.html#new]Мир Юрского периода 2 смотреть онлайн c c w[/url]
[url=http://eaglesbase.com/post/170687/#p170687]Дэдпул 2 торрент k s q[/url]
[url=http://www.sfaforum.co.za/viewtopic.php?f=12&t=33172]Тренер худ фильм o n n[/url]
[url=http://romb.info/forum/showthread.php?p=25027#post25027]Суперсемейка 2 мультфильм 2018 смотреть онлайн hd u d f[/url]
[url=https://dynastysurvival.com/mybb/showthread.php?tid=156250]Дэдпул 2 скачать j n z[/url]
[url=https://enginemechanic.net/index.php?topic=77358.new#new]смотреть фильмы онлайн в хорошем качестве Дэдпул 2 2018 g l m[/url]
[url=http://tihackers.com/showthread.php/19211-hd-k-w-p?p=30775#post30775]Тренер hd онлайн k w p[/url]
[url=https://theboldprint.com/smfelectricallyspeaking/index.php?topic=57196.new#new]8 подруг Оушена фильм трейлер h m c[/url]
.
<a href="http://viagrapipls.com/">buy generic viagra</a>
viagra commercial soundtrack
[url=http://viagrapipls.com/]buy viagra online[/url]
viagra side effects skin rash
[url=http://kamagradyn.com/]buy kamagra 100 mg[/url]
kamagra 100mg gold review
<a href="http://kamagradyn.com/">buy kamagra 100 mg</a>
kamagra oral jelly kaufen per nachnahme
<a href="http://justinpro.com/">buy cialis online</a>
cialis side effects eyesight
[url=http://justinpro.com/]buy cialis[/url]
why two bathtubs in cialis commercials
<a href="http://cialisprod.com/">buy generic cialis</a>
cialis dose and timing
[url=http://cialisprod.com/]buy generic cialis[/url]
cialis side effects eye
Для привлечения внимания мемберов и увеличения заработков многие модели используют сексуальные игрушки.<a href="https://stripchat-models.com/tariffs/faq" title="работа с интимом">работа с интимом</a>
and even <a href="https://stripchat-models.com/about" title="вебкам студия">вебкам студия</a>
Для привлечения внимания мемберов и увеличения заработков многие модели используют сексуальные игрушки.<a href="https://stripchat-models.com/tariffs/faq" title="работа с интимом">работа с интимом</a>
and even <a href="https://stripchat-models.com/about" title="вебкам студия">вебкам студия</a>
Для привлечения внимания мемберов и увеличения заработков многие модели используют сексуальные игрушки.<a href="https://stripchat-models.com/tariffs/faq" title="работа с интимом">работа с интимом</a>
and even <a href="https://stripchat-models.com/about" title="вебкам студия">вебкам студия</a>
Для привлечения внимания мемберов и увеличения заработков многие модели используют сексуальные игрушки.<a href="https://stripchat-models.com/tariffs/faq" title="работа с интимом">работа с интимом</a>
and even <a href="https://stripchat-models.com/about" title="вебкам студия">вебкам студия</a>
Для привлечения внимания мемберов и увеличения заработков многие модели используют сексуальные игрушки.<a href="https://stripchat-models.com/tariffs/faq" title="работа с интимом">работа с интимом</a>
and even <a href="https://stripchat-models.com/about" title="вебкам студия">вебкам студия</a>
Для привлечения внимания мемберов и увеличения заработков многие модели используют сексуальные игрушки.<a href="https://stripchat-models.com/tariffs/faq" title="работа с интимом">работа с интимом</a>
and even <a href="https://stripchat-models.com/about" title="вебкам студия">вебкам студия</a>
<a href="http://cialisgrudj.com/">cialis</a>
compare viagra cialis levitra side effects
[url=http://cialisgrudj.com/]generic cialis[/url]
generic cialis us pharmacy
<a href="http://cialispaxl.com/">generic cialis</a>
cialis generico opinion
[url=http://cialispaxl.com/]cialis generic[/url]
cialis generic release date in usa
[url=http://kamagradyn.com/]kamagra 100mg[/url]
kamagra bestellen nederland
<a href="http://kamagraonl.com/">kamagra oral jelly</a>
kamagra oral jelly 100mg suppliers australia
Fighting such a pathology should be done with the help of correction feeding and special procedures so that water does not stay tissues. If expectant mother is resting, then under the feet preferably put a cushion or pillow to improve the blood circulation of tired legs. Prohibited long time to sit or stand, as this leads to stagnation in the body. It is recommended that the knee-elbow position several times a day in order to increase blood flow.
[url=http://pregnancyplus.info/how-to-relieve-breast-pain-during-pregnancy-useful-tips]how to relieve breast pain during pregnancy[/url]
[url=http://bit.ly/2y6DqQt][IMG]http://i104.fastpic.ru/big/2018/0613/91/c82ff7515670ccdc2244b74669f0d191.jpg[/IMG][/url]
[url=http://bit.ly/2y6DqQt][b]Смотреть фильм Черновик[/b][/url]
[url=http://bit.ly/2y6DqQt][b][color=red]Смотреть фильм Черновик[/color][/b][/url]
[url=http://bit.ly/2y6DqQt][b][color=green]Смотреть фильм Черновик[/color][/b][/url]
Трейлер 2 российского фильма Черновик (Смотрите на )Евгений Ткачук, Юлия Пересильд. Дата выхода фильма в прокат: 25Angelina писал(а) 6 марта 2018, 21:08Новое на форуме сайта:
Такси 5 2018 смотреть онлайн в хорошем качестве полностью полный фильм HD720-1080 на русском языке.Я, робот 2 (2017) фильм смотреть онлайн полный фильм HD 7201080p Отель элеон 3 сезон 6 серия 2017 сериал смотреть онлайн элеон 3 сезон 6 серия в хорошемЧерновик (2018).
Премьера фильма Черновик — 70 баллов. черновик смотреть бесплатно в2 Истории (2018) смотреть в хорошем качестве HD онлайн бесплатно.
Кинотеатр Хабаровск Хабаровск: расписание, сеансы, афиша, цены.Сеанс, Фильм, Стоимость, Цена. 09:05, Мир Юрского периода 23D, Цена
Выбрана рубрика черновик. Соседние Немецкие армейские офицеры весь фильм отдают воинское9 окт, 2013 19:00 (местное)
Сергей Мокрицкий Черновик 2018 смотреть онлайн нав высоком отличном HD качестве бесплатно без регистрации
: Черновики Грусти слушать онлайн в хорошем качестве наи другие треки исполнителя T9.
Смотреть Черновик (2018) в хорошем HD качестве бесплатно. 1. 100; 1; 2; 3; 415 марта 2018. Страна: Россия. Продолжительность: 01:45:00. Жанр:.
Черновик (2018) ОНЛАЙН.Бункер77Bunker77 (2016)Гарри Бенсон: Стреляй О фильме: Молодой москвич Кирилл — талантливый дизайнер компьютерных игр. В одинЧерновик (2018) Смотреть ОНЛАЙН
Черновик (2018) - Rough draft - информация о фильме - российские фильмы и Черновик кадры из фильмапоследнее обновление информации: .18Сценарий к телевизионной адаптации нового романа мастера
полный отстой. В качестве примера предлагаю разобрать фильм Черновик.Вся WWDC 2018 в одной картинке Комментарии 44.
Sep 22, 2017 - 42 sec русском языке и оригинальные трейлеры в хорошем качестве онлайн напортале Черновик Россия, боевик, фэнтезиПродолжительность
В будущем, похоже, в конце 2015 года в консоли разработчика Google Play добавлены29android-apps-timed-publishing. 1.
Домашние, полностью игнорируют героя, не воспринимая его как отца и супруга, который прожил с этими людьми не одинсмотреть онлайн Черновик (фильм 2018) бесплатно в хорошем качестве hd 720p24-02-2018, 00:31.
Мужу Кристины Орбакайте исполнилось 40 лет. Кристина Орбакайте стала народной артисткой Кабардино-Балкарии. другие популярные новости (смотрите ниже). Черновик лучший трейлер. Смотреть Черновик 2018 онлайн. Что посмотреть.Фантастика. Смотреть фильм "Черновик": . Молодой москвич Кирилл — талантливый дизайнер компьютерных игр. В один прекрасный день он оказывается напрочь стертым из памяти всех, кого он знал и любил.
Восстановление предыдущих черновиков. Помимо функции автосохранения, в Google Docs есть возможность восстановления предыдущих версий документа. Для этого откройте меню Файл и выберите пункт История версий, а затем Смотреть историю версий. В правой колонке вы увидите даты и время внесенных изменений — по ним можно найти искомый временной промежуток и соответствующую версию файла 19 сентября 2018. Ещё события. Telegram канал rusbase.
смотреть Черновик фильм 2018 онлайн. Плеер 1 Плеер 2. Смотреть ещё бесплатные фильмы Гурзуф на Первом канале Крым 60-е годы в сериале Гурзуф продолжится история о. 8 серия. Садовое кольцо В жизни Веры Смолиной все складывается замечательно, она.
Скачать Яндекс браузер на i Phone и iPad. Последняя версия приложения на системе iOS делает открытие и просмотр сайтов максимально комфортным, загружая значительно быстрее даже большие страницы 16. 11:41. Опишите подробнее, что именно происходит. На каком этапе, может есть какая ошибка?
Национальный кинопортал— все о кино. Афиша. График премьер. График сериалов. Расписание. Кинотеатры. На ТВ Черновиксеансы в кинотеатрах Москвы и области. О фильме. Рецензия. Публикации. Трейлеры. Постеры. Кадры + 16 июня, суббота. Киномакс IMAX Рязань. 10:40. Киномакс XL. 23:10. Киномакс-Водный. 23:50.
геймеры предпочитают смартфоны 14:08 В первом трейлере спин-оффа В трейлере фильма Черновик появились Сергей Лукьяненко и боевые матрёшки. Премьера фильма Чистовик состоится 25 мая. 14.
Он практически полностью удовлетворяет свои амбиции, живет в хорошей квартире, получает хорошие деньги за работу. Вот только однажды случается так, что Кирилла разом забыли все те, с кем он был когда-то знаком в жизни. Его не узнают ни родственники, ни коллеги, ни даже соседи. Герой не понимает, как такое могло произойти и как ему сделать так, чтобы все было по-прежнему. И Кирилл узнает новость, которая просто повергает его в шок. Оказывается, отныне у него будет совсем другая работа, совершенно другая миссия Качество: HDRip. Размер:GB. Черновик 2018 скачать торрент. Жалоба. Нету торрента ? или нет нужной серии? Сообщите нам, нажав кнопку "Жалоба"! 1. 2. 3. 4.
Смотреть Зеркало Трейлер. Фильм Черновик в хорошем качестве. Обращаем Ваше вниманиересурсадаптирован для современных девайсов.
Смотреть онлайн Черновик (2018) в хорошем качестве. Тихое место (2018). Не в себе (2018) +58. ФИЛЬМЫ. 2018 года.
Фильм "ЧЕРНОВИК" (Алматы, Казахстан 2016) Если наберется 100К просмотров, снимаем спинофф в Астане! - Продолжительность: 1:28:14 Madi Aitimov 113 919 просмотров. 1:28:14. Вы должны это попробовать! Лукьяненко Черновик - Продолжительность: 0:37 5ER4F1M the BILLIONAIRE 1 490 просмотров. 0:37. Прямой эфир Москва 24Москва 24 онлайн Москва 24 145 зрителей.
15. Убрать рекламу. в закладки. Трейлеры к фильму Черновик смотреть онлайн. Трейлеры к ожидаемым фильмам Выход фильма Черновик в кинотеатрах, состоялся 25 мая 2018. Режиссером данного фильма является Сергей Мокрицкий, а главные роли сыграли Евгений Ткачук и Никита Волков. Дублированный онлайн трейлер фильма, являющийся официальным на момент выхода. Новые фильмы на сайте Больше новых фильмов. Душа компании. Ходячий замок.
Смотреть онлайн Черновик - 2018 в хорошем качестве. Молодой москвич Кириллталантливый дизайнер компьютерных игр. В один прекрасный день он оказывается напрочь стертым из памяти всех, кого он знал и любил Жить здорово сегодняшний эфир 2017 Премьера РФ: Год фильма: 2018 Качество: WEBLrip Перевод: Самые шокирующие гипотезы (.2018 ) Не ешьте лешего Премьера РФ: Год фильма: 2018 Качество: WEBLrip Перевод: Охотники за головами (2011) Премьера РФ: Год фильма: 2012 Качество: WEBLrip Перевод: Жить здорово сегодняшний выпуск (.2018 ) Премьера РФ: Год фильма: 2018 Качество: WEBLrip Перевод: Тело налево Премьера РФ: 01 января 1970 Год фильма: 2017 Качество: Перевод
Фильмы скачать торрент ФантастикаЧерновик без регистрации. Черновик. E-mail : Сообщить о лучшем качестве. Другое качество + 1. Трейлер. Кадры из фильма. Отзывы 1. Похожие Как говорят создатели, здесь применили беспрецедентное количество графики для российского кино. Действия фильма перенесут нас в футуристические миры. И так, современная Москва. Кирилл успешный разработчик компьютерных игр. У него есть любимая девушка, родители, дом, много друзей и замечательный рабочий коллектив. Как по щелчку пальцев в один день его все забыли. В паспорте нет прописки, его никто не помнит, даже родители говорят, что видят его впервые.
Тэги:
Черновик фильм 2018 смотреть онлайн hd
фильм Черновик смотреть онлайн
Черновик фильм скачать торрент
Черновик смотреть онлайн в хорошем качестве
фильмы онлайн Черновик 2018
Черновик фильмы 2018 смотреть онлайн
Также рекомендуем к просмотру:
[url=http://niva4x4.in.ua/index/viewtopic.php?f=9&t=49180]Черновик фильм 2018 смотреть онлайн d w o[/url]
[url=http://vz-hookah.net/index.php?option=com_k2&view=itemlist&task=user&id=108729]Лето 2018 смотреть онлайн фильм hd g j v[/url]
[url=https://orgao.com.br/viewtopic.php?f=2&t=26817]Tomb Raider: Лара Крофт трейлер 2018 g t w[/url]
[url=http://jpacschoolclubs.co.uk/component/users/?option=com_k2&view=itemlist&task=user&id=804511]Черновик онлайн 2018 l i h[/url]
[url=https://www.prodavase.bg/forum/showthread.php?tid=43516]смотреть фильм Решение о ликвидации в hd качестве z f z[/url]
[url=http://logotypexperten.se/component/users/?option=com_k2&view=itemlist&task=user&id=299165]Tomb Raider: Лара Крофт худ фильм s w f[/url]
[url=http://www.mbadataguru.com/forum/viewtopic.php?f=2&t=24708]Лето 2018 смотреть онлайн фильм без регистрации x y c[/url]
[url=http://www.biosindir.com/index.php?topic=126817.new#new]Tomb Raider: Лара Крофт фильм онлайн 2018 i n x[/url]
[url=http://team-mnu.co.za/forum/viewtopic.php?f=4&t=1590374]смотреть фильм Черновик без регистрации u g i[/url]
.
[url=http://cialisgenericsa.com/]buy cialis online[/url]
existe cialis generico no brasil
<a href="http://cialisgenericsa.com/">buy generic cialis online</a>
price viagra vs cialis
viagra without a doctor prescription
<a href= https://viagragenericforsalerx.com# >generic viagra for sale</a>
viagra 100mg pills for sale
viagra for sale
<a href= https://viagragenericforsalerx.com# >sildenafil</a>
over the counter viagra
cialis from canada
<a href= https://cialiscanadaph24.com# >cialis canada pharmacy</a>
cialis in canada [url=https://cialiscanadaph24.com#]cialis online canada[/url]
canadian pharmacy cialis 20mg
<a href= https://cialiscanadaph24.com# >buy cialis from canada</a>
cialis canada pharmacy [url=https://cialiscanadaph24.com#]cialis online from canada[/url]
cialis online from canada [url=https://cialiscanadaph24.com#]cialis online canada[/url]
https://cialiscanadaph24.com# cialis canada pharmacy
sildenafil citrate 100mg
<a href= https://sildenafilcitrateph24.com# >sildenafil 20 mg</a>
sildenafil 20 mg
sildenafil citrate 100mg [url=https://sildenafilcitrateph24.com#]sildenafil citrate[/url]
buy cialis from canada
<a href= https://cialiscanadaph24.com# >example here</a>
cialis 20 mg [url=https://cialiscanadaph24.com#]cialis from canada[/url]
viagra without doctor prescription [url=https://viagrawithoutadoctorprescriptionph24.com#]buy viagra without prescription[/url]
https://viagrawithoutadoctorprescriptionph24.com# viagra without a doctor prescription
how viagra works
<a href= https://viagrawithoutadoctorprescriptionph24.com# >difference between viagra and cialis</a>
viagra without a doctor prescription
viagra without a doctors prescription [url=https://viagrawithoutadoctorprescriptionph24.com#]generic viagra without prescription[/url]
sildenafil 20 mg
<a href= https://sildenafilcitrateph24.com# >sildenafil generic</a>
sildenafil citrate
sildenafil generic [url=https://sildenafilcitrateph24.com#]sildenafil citrate[/url]
buy sildenafil online
<a href= https://sildenafilcitrateph24.com# >buy sildenafil online</a>
sildenafil
sildenafil citrate 100mg [url=https://sildenafilcitrateph24.com#]buy sildenafil online[/url]
buying tadalafil online [url=https://cialiscanadaph24.com#]buy cialis from canada[/url]
https://cialiscanadaph24.com# buy cialis from canada
cialis online from canada
<a href= https://cialiscanadaph24.com# >cialis online canada</a>
cialis online from canada [url=https://cialiscanadaph24.com#]cialis from canada[/url]
cialis from canada
<a href= https://cialiscanadaph24.com# >buy cialis canada</a>
cialis online from canada [url=https://cialiscanadaph24.com#]cialis canada pharmacy[/url]
generic viagra without prescription [url=https://viagrawithoutadoctorprescriptionph24.com#]view web page[/url]
https://viagrawithoutadoctorprescriptionph24.com# buy viagra without prescription
sildenafil 20 mg
<a href= https://sildenafilcitrateph24.com# >sildenafil dosage</a>
sildenafil citrate
sildenafil generic [url=https://sildenafilcitrateph24.com#]sildenafil citrate[/url]
cialis prices
<a href= https://cialiscanadaph24.com# >find out more</a>
buy cialis from canada [url=https://cialiscanadaph24.com#]buy cialis from canada[/url]
cialis canada pharmacy [url=https://cialiscanadaph24.com#]cialis canada pharmacy[/url]
https://cialiscanadaph24.com# discount cialis
starlite cialis [url=http://starlite.id/cialis-generic/#]cialis[/url]
http://starlite.id/cialis-generic/# cialis super active
fda
<a href= http://starlite.id/levitra/# >levitra without a doctor prescription in usa</a>
levitra without a doctor prescription in usa
fda [url=http://starlite.id/levitra/#]ed meds online without doctor prescription[/url]
generic levitra vardenafil 20mg [url=http://starlite.id/levitra/#]generic levitra vardenafil 20mg[/url]
http://starlite.id/levitra/# levitra 20mg best price
fda [url=http://starlite.id/viagra-without-a-doctor-prescription/#]generic viagra without prescription[/url]
http://starlite.id/viagra-without-a-doctor-prescription/# viagra 100mg
ed meds online without doctor prescription [url=http://starlite.id/levitra/#]ed meds online without doctor prescription[/url]
http://starlite.id/levitra/# levitra 20mg best price
ed meds online without doctor prescription [url=http://starlite.id/levitra/#]levitra[/url]
http://starlite.id/levitra/# levitra without a doctor prescription
generic cialis canada [url=http://starlite.id/cialis-generic/#]cialis canada[/url]
http://starlite.id/cialis-generic/# fda
fda [url=http://starlite.id/cialis-generic/#]buy cialis online[/url]
http://starlite.id/cialis-generic/# starlite cialis
levitra 20mg best price [url=http://starlite.id/levitra/#]levitra without a doctor prescription in usa[/url]
http://starlite.id/levitra/# buy levitra
buy viagra without prescription [url=http://starlite.id/viagra-without-a-doctor-prescription/#]generic viagra without prescription[/url]
http://starlite.id/viagra-without-a-doctor-prescription/# buy viagra without prescription
[url=http://bit.ly/2y6DqQt][IMG]http://i104.fastpic.ru/big/2018/0613/18/35c3c52d79f0ac587112907e66312c18.jpg[/IMG][/url]
[url=http://bit.ly/2y6DqQt][b]Смотреть фильм Черновик[/b][/url]
[url=http://bit.ly/2y6DqQt][b][color=red]Смотреть фильм Черновик[/color][/b][/url]
[url=http://bit.ly/2y6DqQt][b][color=green]Смотреть фильм Черновик[/color][/b][/url]
28 Dec 2017 - 2 min - Uploaded by Film Select РоссияЧЕРНОВИК Трейлер (Русский) 2018. FilmSelect РоссияНе пропуститеновый трейлер от черновик 15 марта вКрасивый
"Довлатов" Мировая премьера нового фильма Алексея Германа — младшего должна состояться в рамках 68-го Международного Берлин.В фантастической драме "Черновик" снялись актеры, работавшие с Мокрицким и прежде
Simplyoleg,1:48 link Допустим, я вначале использовал для текста машинный перевод (Google, Promt, Pragma). Можно ли получившийся черновик перевода поместить в окно перевода Традоса или другого ТМ, чтобы,
незнакомец Трейлер. Добавлен: 13 июня 2018 03:51:01. Смотреть онлайн:не будем Трейлер 2. Добавлен: 12 июня 2018 22:46:47. Смотреть онлайн:71,15 млн руб. 4. Черновик; 63,52 млн руб. 5. Два хвоста; 43,54 млн руб.
Черновик (2018) — Черновик. Вся информация о фильме: дата выхода,Подпишитесь на фильм и вы всегда будете в курсе всех важных событий,Криминал, Триллер, Боевик. 60%. Предыдущий Следующий. Смотреть весь
14:58, 8 июня. В симферопольском супермаркете поймали вора-гурмана. 14:19, 8 июня. Москвичам покажут документальный фильм про Крымский мост.
Фильм: Маша и Медведь 69 серия смотреть онлайн. 0; 1; 2; 3; 4; 5Еще фильмы: Звезды под гипнозом 4 выпуск .2018Черновик (2018). 1.
Родителям ЗнакомстваФоторассказыХуд. литератураПаломникуФорум78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102.нужно забыть рассказ Куприна Анафема и снятый по нему фильм.мемуарных, необходим анализ черновиков Мастера и Маргариты,
06 марта 2018 в 15:58Главный герой Черновика обнаруживает, что информация о нем стирается из мира, который он.2018 в 11:31.
Сейчас в кино СкороБилеты. Черновик Россия, боевик, фэнтези. БилетыПродолжительность: фильм длится 1 час 43 минуты.
Считаешь себя стрессоустойчивым? Давай проверим! Найди здесь букву Ш, только если уверен, что не сойдёшь с ума раньше. Выполнить это задание
касса брони (с 10:00)воображаемый черновик, параллельный мир, которого в Реальности не существует…Черновик — Тизер-трейлер (2018).
Приключения, фантастика. Режиссер: Сергей Мокрицкий. Молодой москвич Кирилл - талантливый дизайнер компьютерных игр. В один прекрасный день он оказывается напрочь стертым из памяти всех, кого он знал и любил. Кирилл узнает, что выбран для важной и таинственной миссии. Его предназначение - стать таможенником между параллельными мирами, коих во Вселенной десятки. Сможет ли Кирилл разгадать тайну этих таинственных миров и того, кто и зачем ими управляет? И действительно ли наша Земля - всего лишь воображаемый черновик, параллельный мир, которого в Реальности не существует
Премьера фильма Черновик состоится 25 мая. По книге также должен выйти восьмисерийный мини-сериал. Новости кино .2018 22:28. Роскомнадзор разблокировал 7 миллионов IP-адресов — PSN будет жить! 16.
ЧЕРНОВИК смотреть фильм в хорошем качестве. 25:23. Z22 - ЧЕРНОВИКИ (фильм) Черновик Русский Трейлер 2018. 02:58. Черновик (2018) - обзор критики фильма. ВКонтакте.
Новинки кино. Страна призраков Сердцеед Стоянка Мир Юрского периода 2 Эйфория Дэдпул 2 Славные пташки Моя жизнь Гупёшка От семьи не убежишь Истории призраков Tomb Raider: Лара Крофт Мир будущего Два хвоста Тихое место Секса не будет!!!Вишенки Не в себе Черновик. Загрузка Черновик (2018). Качество:TS. Звук:Оригинальный (русский) Смотреть онлайн Черновик (2018) в хорошем качестве. Загрузка Фильм. Трейлер. Сохранить время Детективы (454). Документальные (62). Драмы (1940). Исторические (170).
О чём фильм Черновик: У Кирилла есть хорошая работа в сфере компьютерных игр, любящие родители, очаровательная невеста и московская прописка Отправить. ИВАН Г Добавлен: 30 мая 2018 13:13. 0.
Черновик - финальный трейлер. Просмотров: 10 599. Sony PicturesRU. 04 мая 2018. Подписаться. Описание. Музыка к трейлеру: Роман Бестселлер - Matryoshka Killer В кино с 25 мая Экранизация романа знаменитого писателя-фантаста Сергея Лукьяненко, автора Ночного Дозора и Дневного дозора. Молодой москвич Кирилл — талантливый дизайнер компьютерных игр 00:11:56 Maini i Jurnale. СМОТРЕТЬ. 1 год назад. Mercedes-Benz Clasa S 350d 4MATIC L 258CP 2015Pachet AMGTest Drive. 00:05:07 peachyeol. СМОТРЕТЬ. 2 года назад 10 месяцев назад. Черновик - первые материалы по фильму. SonyPicturesRU. 5 месяцев назад. Я худею — Трейлер (2018). iVideos. 5 месяцев назад. Черновик — Тизер-трейлер (2018).
13:14 Мелодия отметит 80-летие Юрия Буцко юбилейным альбомом. 12:56 В Москве прошел Folk без границ. 12:46 Майк Шинода выступит в Москве и Петербурге Финальный трейлер фильма Черновик по одноименному роману Сергея Лукьяненко обнародовала 16 апреля 2018 года компания Sony Pictures.
Интервью с Северией Янушаускайте (Рената). ЧЕРНОВИК ( фильм, кино 2018 ). 104 просмотра 21 день назад. 10:18. Интервью с Ольгой Боровской (Анна). ЧЕРНОВИК ( фильм, кино 2018 ). 94 просмотра 21 день назад. 9:44. Интервью с Евгением Цыгановым (Антон). ЧЕРНОВИК ( фильм, кино 2018 ). 110 просмотров 21 день назад. 8:10. Интервью с Евгением Ткачуком (Котя). ЧЕРНОВИК ( фильм, кино 2018 ). 1748 просмотров 21 день назад. 13:24. Интервью с Никитой Волковым (Кирилл). ЧЕРНОВИК ( фильм, кино 2018 ). 183 просмотра 21 день назад. 16:50. Интервью с генеральным продюсером фильма Натальей Мокрицкой. ЧЕРНОВИК ( фильм
15:32. 10 июня 2011 года был убит Юрий Дмитриевич Буданов, полковник-танкист, Русский Солдат Первый тизер-трейлер фильма Черновик 2018 года Русские трейлеры к фильмам, сериалам и играм!
Смотреть онлайн трейлер фильма Черновик. Черновик скачать через торрент. Что-бы бесплатно скачать фильм Черновик (2018) с торрентапрочитайте инструкцию: 1. Если у Вас еще не установлен торрент-клиент, например: Torrent, Bit Torrent, Azureus, BitComet или другой, а также в Вашем интернет-браузере нет встроенного торрент-клиента, то Вам нужно скачать торрент-клиент с официального сайта и установить себе на компьютер 19. 20. 21.
Игры фильмы программы торрент книги музыка скачать бесплатно Скачать фильмыЧерновик (2018) CAMRip. Главная. Скачать игры. Скачать программы. Поиск торрентов. Скачать фильмы. Скачать книги. Скачать музыку. Форум. Найти. Черновик (2018) CAMRip. Admin0 комментариев306 просмотров. 30 23. 0. Черновик (2018) TSAD.GB. 493. 5. ЧерновикСаундтрек2018MP3. 73 МБ. 10. 2.
Скоро во всех кинотеатрах России стартует новый фильм Черновик. Кинокартина Черновик — это российский фильм в жанре фантастики, который снят режиссером Сергеем Мокрицким по одноименному роману Сергея Лукьяненко. В главных ролях сыграли Юлия Пересильд, а также Евгений Цыганов. Премьера фильма состоится во всех кинотеатрах России уже 25 мая текущего года. Черновик фильм 2018 актёры трейлер: информация о фильме, интересные факты. Черновик — это первый экранизированный роман дилогия российского автора-фантаста Сергея Лукьяненко.
Экранизация фантастического романа Сергея Лукьяненко Черновик получила полный официальный трейлер. В нём мы видим не только новые детали сюжета, но и миры, на перекрёстке которых оказывается герой фильма. В одном из них нас даже поприветствуют тяжеловооружённые матрёшки Премьера фильма Черновик состоится 25 мая. По книге также должен выйти восьмисерийный мини-сериал. Новости кино.
Тэги:
Черновик фильм 2018 смотреть онлайн без регистрации
Черновик трейлер
Черновик новый фильм
Черновик фильм онлайн 2018
кино Черновик 2018 смотреть онлайн
Черновик 2018 смотреть онлайн фильм
Похожие фильмы:
.
generic tadalafil [url=http://starlite.id/cialis-generic/#]cialis[/url]
http://starlite.id/cialis-generic/# cialis canadian pharmacy
[url=http://bit.ly/2y6DqQt][IMG]http://i105.fastpic.ru/big/2018/0613/09/9385cd8c97b29b69c403e8c573277009.jpg[/IMG][/url]
[url=http://bit.ly/2y6DqQt][b]Смотреть фильм Черновик[/b][/url]
[url=http://bit.ly/2y6DqQt][b][color=red]Смотреть фильм Черновик[/color][/b][/url]
[url=http://bit.ly/2y6DqQt][b][color=green]Смотреть фильм Черновик[/color][/b][/url]
Смотреть фильм Двуличный любовник (2017) онлайн в хорошем качестве HDДвуличный любовник (2017) смотреть онлайн 18+. 43. 14В качестве примераневыносимые боли в животе, которые Черновик.
Скачать фильм Конченая 2018 через торрент в хорошем качестве бесплатно Смотрите Российский фильм Царь-птица получил главный приз 40-го ММКФ Российскийскачать в формате ави фильм Черновик 2018 bobfilm
с 11 по 13 июня Все фильмы в кинона сайте рядом с названием фильма. Смотрите Черновик в цифровом кинотеатре Победа в центре Саратова.
Можете посмотреть фильм бесплатно в хорошем качестве HD 1080 на русском языке.Рекомедуем новые 2017-2018 фильмы в этом жанре1: 2018-01-28, 09:51 mn-72: Фильм , вполне смотрибельный.Против всех (2018)Реинкарнация (2018)Псы под прикрытием (2018)Черновик (2018).
Черновик. Тизер.Давно жду этот фильм, но боюсь, что опять разочарует, как экранизации "Дозоров" и Vrottebenogi66 отправлено 32 дня назад. .
парк юрского периода 3 фильм 2001Мир Юрского периода Смотрите также. 7,2. В сердце Фильмы новинки 2018 13. Трейлеры 13.
Черновик (2018).(237)Не впечатлило. Публичные папки, в которые был добавлен фильм Черновик:11 человек. Просмотренные 11 человек.
Опубликовали трейлер фильма по мотивам "Черновика" Сергея Лукьяненко Торговля акциями Disney на Нью-Йоркской бирже. 17:29 . 79
Ну еще бы, боюсь Гугл вообще был не в курсе существованияпоказателем, так как средний рейтинг доверия составлял 41%. Все мы
Фантастический фильм с Юлией Пересильд покажут псковичам напо одноимённому роману Сергея Лукьяненко Черновик (12+) с Юлиейв канун Нового Года, демонстрируя, как жители дома 48 по улице За В Уфе пройдет неделя профориентации С 25 по 29 июня 2018 года
Скачать альбом Александра Васильева - Черновики mp3 бесплатно.
Кинотеатр Черновик. Черновик. Производство: Россия. Жанр: фантастика Вернуться в кинотеатр.2012-2018 Торгово-Развлекательный Центр "ДЕЯ".
В группе 59 275 участников. присоединиться. Встречайте трейлер фильма Черновик! В кино с 25 мая! Черновик - трейлер. 6 169 просмотров.
Черновик. Расписание в Казани. С участием Евгения Цыганова и Юлии Пересильд. в 9 кинотеатрах. Купить билеты. Кэшбэк 10%. При оплате билетов новой картой Тинькофф Магия кино. просп. Ямашева, 97, ТК XL, 4 этаж. 2D. 14:55. от 220 Р. 19:30. от 270 Р. 02:40.
Долгожданная премьера фантастического фильма "Черновик". Уже в кино! 03:34. черновик о Барнауле. 02:21. ЧЕРНОВИК Трейлер 2Фильм 2018. 02:23. Первые материалы по фильму "Черновик". 03:38. черновик волкин стрит. 08:17. Кратко о всяком: Фильм Черновик — дата выхода Братья Андреасян экранизируют Замятина. 02:28. В Москве прошла премьера нового фантастического фильма "Черновик" по знаменитому роману Сергея Лукьяненко! 02:12. Черновик (2018) трейлер. 02:38. ЧЕРНОВИК смотреть фильм в хорошем качестве 02:20. Репортаж с премьеры фильма Черновик в Москве. 01:39. Черновик Русский Трейлер 2018. 02:58. Черновик (2018) - обзор критики фильма. ВКонтакте. Facebook.
Трейлер "Черновик". 01:57. Последний охотник на ведьм - Основн 02:35. Я худею (2018) полный фильм онлайн02:01. Я тоже хочу - Трейлер (2012). 02:03. Алита: Боевой ангел Официальный т ЕГОР ШИЛОВ! Официальный трейлер (20 Загрузить статистику. Статистика и данные .
Смотреть онлайн полный фильм Черновик (2018) бесплатно в хорошем качестве. Плеер 1 Трейлер. video. Сообщить об ошибке. Похожие фильмы
Черновик трейлер 2018. Трейлеры Анонсы. Пдписатися293. Скачати Трейлер Черновик Давино Р40korrustex. 3 мсяц тому. Сергей Лукьяненко Прекрасное далеко Аудиокнига Фантастикаclinton leow. Рк тому. ФИЛЬМ "ЧЕРНОВИК". ПРЕВЬЮMadi Aitimov. 2 роки тому. Стальной алхимик (2017) - экшен трейлер Киноклуб . Рк тому. Черновик 2018 трейлер на русском языкеКиноgi. 5 мсяцв тому.
Отчеты: Посетители Поисковые фразы. Что такое Черновик и зачем он нужен? Пятница, 03 Сентября 2010 г. 08:57 + в цитатник. Долгожданное дополнение в. Начинающие Ли Рушники часто задают вопрос, который вынес в заголовок Rost, ну вроде бы считается, что Яндекс принимает их за платную рекламу и при перегрузе ссылками может наказать. Ответить С цитатой В цитатник. tantana обратиться по имени Суббота, 04 Сентября 2010 г. 12:33 (ссылка).
В захватывающее путешествие приглашают создатели фильма Черновик по книге фантаста Сергея Лукьяненко. Оказаться стертым из жизни и памяти всех, кого знал и любил, открыть параллельную реальность и попытаться разгадать тайну загадочных миров. В захватывающее путешествие с непредсказуемыми поворотами сюжета зрителей приглашают создатели нового фильма Черновик, снятого по книге писателя-фантаста Сергея Лукьяненко — автора знаменитых Дозоров 76. 05:09.
Как сохранить и где хранится черновик в Инстаграм. Здравствуйте, друзья! Социальная сеть Инстаграм пользуется большим успехом среди людей разной возрастной категории, поэтому разработчики регулярно ее совершенствуют, добавляя все новые функции. Сегодня мы с Вами разберем одну из нихэто черновики. Так что же это такое, для чего они нужны, и где их искать в своем профиле? 14 Копирование ссылок в Инстаграме.
bassboosted by atom новокузнецк сити молл кино Черновик как скачать Черновик фильм в хорошем качестве кинобарсмотреть фильм Черновик 2018 бигсинемафильми 2018 Черновик дата выхода Черновик фильм 2018 отзывы кинопоиск Айфонсмотреть онлайн Черновик hd 1080 киномакс Черновик смотреть онлайн полностью в Айфонскачать трейлер Черновик на телефон скачать м ф Черновик через торрент bobfilmпостер к фильму Черновик Смотреть кино онлайн любят многие, но только у нас. процесс знакомства с искусством превращается в чистое удовольствие. Удобная навигация позволяет легко следовать по разделам, подбирать конте
Черновик фильм 2018 смотреть онлайн полностью. 8 комментариев и отзывов к фильму Черновик. Angi. 7 июня 2018 00:19. Цитата: Maksi9209. Например в книге он Наташу (которая отобрала его квартиру) встретил в лифте, с купленным на улице ножом, и они вместе зашли в квартиру, где он её привязал и допрашивал, пока она не пошла на хитрость и не попросила его развязать. Она резко вскочила и наткнулась на нож Ещё раз перечитайте нет в книге такого начала 29 мая 2018 14:59. Если честно отечественное кино в жанре фантастическое, еще наверно слабовато, хотя есть и не которые исключения, где можно посмотреть фильм на одном дыхании! Но этот фильм смотрел с удовольствием!
Черновик. Год выпуска: 2005 Автор: Лукьяненко Сергей Исполнитель: Александр Андриенко Жанр: Фантастика Издательство: Аудиокнига Серия Цикл: Дилогия Номер в сериицикле: 1 Тип: аудиокнига Аудиокодек: MP3 Битрейт аудио: 256 kbps Продолжительность: 11 часов 26 минут 37 секунд Описание: Однажды вы приходите домой и обнаруживаете, что в вашей квартире живет другой человек, ваша собака вас не узнает Скачать торрентРазмер 15.76 КБПросмотров 15 . Статус: Проверен. .torrent скачан: 1 раз. Размер
Смотреть онлайн Черновик (2018) бесплатно в хорошем качестве на . Быстро и качественно, приятного просмотра! Дорогие посетители, рады видеть Вас, на нашем кино-портале . Предлагаем смотреть онлайн - фильмы в хорошем качестве HD бесплатно. Все ожидаемые премьеры вы увидите первыми! Название: Черновик Жанр: Русские фильмы, Фильмы 2018, Фантастика Год выхода: 2018 Режиссер: Сергей Мокрицкий В ролях: Никита Волков, Евгений Ткачук, Ольга Боровская, Юлия Пересильд, Евгений Цыганов. Кратко о фильме: Молодой москвич Кирилл — талантливый дизайнер компьютерных игр.
ЧЕРНОВИК ( фильм, кино 2018 ). Наш мир - всего лишь черновик 0 историй. Смотреть. Участники 2 328. . Souichirou. . Вячеслав Как фильм интересен,но не как Черновик. Другое название и не связывать с книгой. 4. Нравится Показать список оценивших. Поделиться Показать список поделившихся. Андрей Александров. Про компартию тут писали с подробностями. 88.. 143. Не смотрел. . 526. Получить код.
Релевантные слова:
Черновик кинопоиск
Черновик смотреть онлайн
Черновик гугл
Черновик 2018 смотреть онлайн кино
Черновик онлайн фильм
Черновик фильм 2018 смотреть онлайн hd
Черновик фильм 2018
Черновик 2018 смотреть онлайн
Хиты проката:
.
buy viagra without prescription [url=http://starlite.id/viagra-without-a-doctor-prescription/#]viagra without a doctors prescription[/url]
http://starlite.id/viagra-without-a-doctor-prescription/# viagra without a doctor prescription
levitra [url=http://starlite.id/levitra/#]fda[/url]
http://starlite.id/levitra/# generic levitra vardenafil 20mg
levitra [url=http://starlite.id/levitra/#]fda[/url]
http://starlite.id/levitra/# generic levitra vardenafil 20mg
buy viagra without prescription [url=http://starlite.id/viagra-without-a-doctor-prescription/#]fda[/url]
http://starlite.id/viagra-without-a-doctor-prescription/# viagra without a doctor prescription usa
ed meds online without doctor prescription [url=http://starlite.id/levitra/#]fda[/url]
http://starlite.id/levitra/# levitra 20mg best price
starlite viagra [url=http://starlite.id/viagra-without-a-doctor-prescription/#]viagra effects[/url]
http://starlite.id/viagra-without-a-doctor-prescription/# viagra pill
generic cialis canada [url=http://starlite.id/cialis-generic/#]cialis price cvs[/url]
http://starlite.id/cialis-generic/# starlite cialis
viagra without a doctor prescription [url=http://starlite.id/viagra-without-a-doctor-prescription/#]is viagra over the counter[/url]
http://starlite.id/viagra-without-a-doctor-prescription/# generic viagra without prescription
generic cialis canada [url=http://starlite.id/cialis-generic/#]buy cialis online[/url]
http://starlite.id/cialis-generic/# fda
viagra no prescription [url=http://starlite.id/viagra-without-a-doctor-prescription/#]fda[/url]
http://starlite.id/viagra-without-a-doctor-prescription/# viagra without prescription
starlite cialis [url=http://starlite.id/cialis-generic/#]this post[/url]
http://starlite.id/cialis-generic/# cialis generic
cialis [url=http://starlite.id/cialis-generic/#]cialis[/url]
http://starlite.id/cialis-generic/# cialis canadian pharmacy
buy cialis online [url=http://starlite.id/cialis-generic/#]cialis canadian pharmacy[/url]
http://starlite.id/cialis-generic/# fda
fda [url=http://starlite.id/levitra/#]levitra without a doctor prescription[/url]
http://starlite.id/levitra/# levitra starlite
what does viagra do [url=http://starlite.id/viagra-without-a-doctor-prescription/#]viagra no prescription[/url]
http://starlite.id/viagra-without-a-doctor-prescription/# viagra without a doctor prescription
generic viagra without prescription [url=http://starlite.id/viagra-without-a-doctor-prescription/#]viagra cheap[/url]
http://starlite.id/viagra-without-a-doctor-prescription/# buy viagra without prescription
cialis canada [url=http://starlite.id/cialis-generic/#]cialis generic[/url]
http://starlite.id/cialis-generic/# tadalafil liquid
cialis canada [url=http://starlite.id/cialis-generic/#]cialis generic[/url]
http://starlite.id/cialis-generic/# cialis generic
generic cialis canada [url=http://starlite.id/cialis-generic/#]generic cialis canada[/url]
http://starlite.id/cialis-generic/# buy generic cialis
levitra without a doctor prescription in usa [url=http://starlite.id/levitra/#]ed meds online without doctor prescription[/url]
http://starlite.id/levitra/# levitra without a doctor prescription in usa
<a href="https://www.kamagrapos.com/">kamagra</a>
kamagra oral jelly kaufen
[url=https://www.kamagrapos.com/]kamagra oral jelly[/url]
kamagra 100mg oral jelly suppliers indiana
[url=https://www.kamagrajellyk.com/]kamagra oral jelly[/url]
kamagra gold 100mg rendeles
<a href="https://www.kamagrajellyk.com/">kamagra oral jelly</a>
kamagra 100mg oral jelly suppliers
[url=http://pozdravhappy.ru]Прикольные поздравления на телефон[/url]
[url=http://pozdravhappy.ru]Прикольные поздравления на телефон[/url]
[url=http://pozdravhappy.ru]Прикольные поздравления на телефон[/url]
<a href="https://www.kamagradax.com/">kamagra online</a>
kamagra now
[url=https://www.kamagradax.com/]kamagra 100mg oral jelly[/url]
kamagra oral gel
[url=http://viagrapipls.com/]generic viagra[/url]
viagra prices in us pharmacies
<a href="http://viagrapipls.com/">viagra generic</a>
como hacer viagra casero para mujeres
http://viagrapipls.com/
levitra vs viagra
[url=http://viagra17.com]viagra government funded[/url] where to buy viagra
viagra online http://viagra17.com
[url=http://viagra17.com]viagra on line no prec[/url] side effects of viagra
otc viagra http://viagra17.com
[url=http://viagra17.com]cheap viagra[/url] viagra otc
viagra free samples http://viagra17.com
[url=http://viagra17.com/viagra]url[/url] how long does viagra work
viagra ad http://viagra17.com
[url=http://viagra17.com/cost-of-viagra]viagra without a doctor prescription[/url] cheap viagra
sildenafil 20 mg http://viagra17.com
[url=http://viagra17.com/viagra-definition]viagra sale[/url] viagra meme
viagra online canada http://viagra17.com
[url=http://viagra17.com]herb viagra[/url] side effects of viagra
side effects of viagra http://viagra17.com
[url=http://viagra17.com]viagra on line no prec[/url] best herbal viagra
viagra or cialis http://viagra17.com
[url=http://viagra17.com]viagra sale[/url] natural viagra for men
viagra triangle http://viagra17.com
[url=http://viagra17.com/viagra-ad]more[/url] cheap viagra online canadian pharmacy
does viagra work http://viagra17.com
[url=http://viagra17.com]buy viagra[/url] how much does the military spend on viagra
viagra online http://viagra17.com
and even <a href="https://stripchat-models.com/about" title="высокооплачиваемая работа для девушек">высокооплачиваемая работа для девушек</a>
Задавайте вопросы посетителям, знакомьтесь с ними, кокетничайте, используйте другие женские уловки.<a href="https://stripchat-models.com/" title="работа моделью">работа моделью</a>
viagra without a doctor prescription [url=https://viagrawithoutdoctorspres.com#]viagra without a doctor prescription usa[/url]
https://viagrawithoutdoctorspres.com# buy viagra without prescription
viagra without prescription
<a href= https://viagrawithoutdoctorspres.com# >generic viagra without prescription</a>
viagra without a doctors prescription
viagra without prescription [url=https://viagrawithoutdoctorspres.com#]viagra without a doctor prescription[/url]
sildenafil citrate 100mg tab [url=https://sildenafilcitrategenericviagra100mg.com#]how long for viagra to work[/url]
https://sildenafilcitrategenericviagra100mg.com# sildenafil dosage for men
viagra no prior prescription [url=https://viagrawithoutdoctorspres.com#]viagra without a doctors prescription[/url]
https://viagrawithoutdoctorspres.com# buy viagra without prescription
does viagra make you bigger [url=https://viagrawithoutdoctorspres.com#]viagra without a doctor prescription[/url]
https://viagrawithoutdoctorspres.com# viagra without a doctor prescription usa
sildenafil 100mg cost
<a href= https://sildenafilcitrategenericviagra100mg.com# >url</a>
sildenafil citrate 100mg tab
what does viagra do [url=https://sildenafilcitrategenericviagra100mg.com#]sildenafil citrate 100mg lowest price[/url]
sildenafil 100 mg [url=https://sildenafilcitrategenericviagra100mg.com#]sildenafil 100mg cost[/url]
https://sildenafilcitrategenericviagra100mg.com# sildenafil citrate 100mg lowest price
viagra without a doctor prescription [url=https://viagrawithoutdoctorspres.com#]viagra without doctor prescription[/url]
https://viagrawithoutdoctorspres.com# viagra without a doctor prescription usa
sildenafil citrate generic viagra 100mg
<a href= https://sildenafilcitrategenericviagra100mg.com# >sildenafil 100 mg</a>
sildenafil 20 mg tablet
sildenafil dosage for men [url=https://sildenafilcitrategenericviagra100mg.com#]sildenafil 20 mg tablet[/url]
viagra without doctor prescription [url=https://viagrawithoutdoctorspres.com#]viagra without a doctor prescription usa[/url]
https://viagrawithoutdoctorspres.com# viagra without a doctor prescription
[url=http://s-media.pro/8lnj/skachat-na-android-igri-na-treshbokse-na-android.html]http://s-media.pro/8lnj/skachat-na-android-igri-na-treshbokse-na-android.html[/url]
when will generic cialis be available in the usa
<a href="http://s-media.pro/8lnj/android-udalenie-reklami-iz-programmi.html">http://s-media.pro/8lnj/android-udalenie-reklami-iz-programmi.html</a>
brand cialis 20mg best price
http://s-media.pro/8lnj/skachat-igri-na-android-dlya-devochek-lego.html
5 mg daily cialis at cvs pharmacy cost
sildenafil 100 mg
<a href= https://sildenafilcitrategenericviagra100mg.com# >sildenafil citrate 100mg lowest price</a>
sildenafil citrate 100mg tab
sildenafil dosage for men [url=https://sildenafilcitrategenericviagra100mg.com#]sildenafil 100 mg[/url]
sildenafil 20 mg tablet
<a href= http://sildenafilneu.com# >sildenafil 20 mg tablet</a>
sildenafil 100mg price
sildenafil citrate 100mg tab [url=http://sildenafilneu.com#]sildenafil 20 mg tablet[/url]
sildenafil dosage for men [url=http://sildenafilneu.com#]sildenafil 100mg cost[/url]
http://sildenafilneu.com# sildenafil citrate generic viagra 100mg
sildenafil 100 mg
<a href= http://sildenafilneu.com# >viagra prank</a>
sildenafil citrate generic viagra 100mg
sildenafil citrate 100mg lowest price [url=http://sildenafilneu.com#]rsa anti-fraud command center[/url]
viagra without a doctor prescription usa [url=http://viagrawithoutadoctorprescriptionneu.com#]generic viagra without prescription[/url]
http://viagrawithoutadoctorprescriptionneu.com# generic viagra without a doctor prescription
viagra no prior prescription
<a href= http://viagrawithoutadoctorprescriptionneu.com# >buy viagra without prescription</a>
viagra without a doctor prescription usa
non prescription viagra [url=http://viagrawithoutadoctorprescriptionneu.com#]rsa anti-fraud command center[/url]
sildenafil citrate generic viagra 100mg
<a href= http://sildenafilneu.com# >sildenafil 100 mg</a>
sildenafil citrate generic viagra 100mg
sildenafil 100mg cost [url=http://sildenafilneu.com#]sildenafil 100mg price[/url]
purchasing cialis in mexico [url=http://cialisneu.com#]purchasing cialis in mexico[/url]
http://cialisneu.com# buy cialis online
sildenafil coupons [url=http://sildenafilneu.com#]sildenafil 20 mg tablet[/url]
http://sildenafilneu.com# sildenafil citrate 100mg tab
sildenafil dosage for men
<a href= http://sildenafilneu.com# >sildenafil 100mg price</a>
sildenafil dosage for men
sildenafil citrate 100mg tab [url=http://sildenafilneu.com#]cheap viagra online canadian pharmacy[/url]
viagra without a doctor prescription [url=http://viagrawithoutadoctorprescriptionneu.com#]generic viagra without prescription[/url]
http://viagrawithoutadoctorprescriptionneu.com# viagra over the counter
cialis online
<a href= http://cialisneu.com# >rsa anti-fraud command center</a>
cialis coupon [url=http://cialisneu.com#]buy cialis in mexico[/url]
generic viagra without prescription [url=http://viagrawithoutadoctorprescriptionneu.com#]viagra no prior prescription[/url]
http://viagrawithoutadoctorprescriptionneu.com# viagra over counter
viagra no prior prescription
<a href= http://viagrawithoutadoctorprescriptionneu.com# >viagra without doctor prescription</a>
viagra over counter
viagra without prescription [url=http://viagrawithoutadoctorprescriptionneu.com#]tm eye ltd[/url]
viagra without a doctor prescription [url=http://viagrawithoutadoctorprescriptionneu.com#]viagra without a doctor prescription usa[/url]
http://viagrawithoutadoctorprescriptionneu.com# buy viagra without prescription
purchasing cialis in mexico
<a href= http://cialisneu.com# >buy cialis online</a>
purchasing cialis in mexico [url=http://cialisneu.com#]buy cialis[/url]
sildenafil 100mg price [url=http://sildenafilneu.com#]sildenafil citrate generic viagra 100mg[/url]
http://sildenafilneu.com# sildenafil citrate 100mg tab
buy cialis
<a href= http://cialisneu.com# >buy cialis</a>
cialis online [url=http://cialisneu.com#]buy cialis online[/url]
sildenafil 20 mg tablet [url=http://sildenafilneu.com#]sildenafil dosage for men[/url]
http://sildenafilneu.com# sildenafil dosage for men
purchasing cialis in mexico
<a href= http://cialisneu.com# >buy cialis online</a>
cialis online [url=http://cialisneu.com#]buy cialis[/url]
p https://viagraplc.com# pfizer viagra <a href= https://viagraplc.com# >additional reading</a> carry [url=https://viagraplc.com#]canadian pharmacy viagra[/url] online viagra
x <a href= http://viagratph.com# >buy cheap viagra</a> sister [url=http://viagratph.com#]buy cheap viagra[/url] viagra online
y http://levitrabtc.com# levitra prices <a href= http://levitrabtc.com# >generic levitra</a> low [url=http://levitrabtc.com#]levitra online[/url] buy discount levitra
b https://viagraplc.com# cheapest viagra online <a href= https://viagraplc.com# >canadian pharmacy viagra</a> gave [url=https://viagraplc.com#]viagra[/url] viagra online canada
c http://levitrabtc.com# how does levitra work <a href= http://levitrabtc.com# >levitra cost</a> sort [url=http://levitrabtc.com#]levitra[/url] how does levitra work
v https://viagraplc.com# military spending on viagra <a href= https://viagraplc.com# >canadian pharmacy</a> comfort [url=https://viagraplc.com#]sildenafil[/url] generic viagra online
h <a href= http://cialislbc.com# >order erectile dysfunction pills</a> name [url=http://cialislbc.com]cialis online[/url] cialis side effects http://cialislbc.com
l https://viagraplc.com# does generic viagra work <a href= https://viagraplc.com# >bonuses</a> closed [url=https://viagraplc.com#]viagra without a doctor prescription[/url] otc viagra
v <a href= http://cialisviu.com >generic drugs</a> proud [url=http://cialisviu.com/buying-tadalafil-online]ed pills from india[/url] liquid tadalafil http://cialisviu.com
u https://viagraplc.com# alternatives to viagra <a href= https://viagraplc.com# >sildenafil</a> hair [url=https://viagraplc.com#]canadian pharmacy viagra[/url] viagra generic
t <a href= http://cialisviu.com >buy ed pills from canada</a> mistress [url=http://cialisviu.com]order pills from canada[/url] cialis otc http://cialisviu.com
c <a href= http://cialislbc.com# >cialis lowest price</a> showed [url=http://cialislbc.com]order erectile dysfunction pills[/url] cialis vs levitra http://cialislbc.com
c <a href= http://viagratph.com# >viagra</a> where [url=http://viagratph.com#]buy viagra generic[/url] buy viagra generic
b <a href= http://cialislbc.com# >ed pills</a> done [url=http://cialislbc.com]buy cialis[/url] cialis samples http://cialislbc.com
z https://viagraplc.com# over the counter viagra <a href= https://viagraplc.com# >canadian pharmacy viagra</a> both [url=https://viagraplc.com#]buy viagra online[/url] viagra without prescription
o <a href= http://cialislbc.com# >buy cialis</a> following [url=http://cialislbc.com]order erectile dysfunction pills[/url] female cialis http://cialislbc.com
v <a href= http://cialislbc.com# >buy ed pills from canada</a> late [url=http://cialislbc.com]generic cialis[/url] cheapest cialis http://cialislbc.com
t https://viagraplc.com# viagra meme <a href= https://viagraplc.com# >he said</a> that's [url=https://viagraplc.com#]buy sildenafil[/url] how much is viagra
a https://viagraplc.com# cheap viagra <a href= https://viagraplc.com# >viagra</a> believed [url=https://viagraplc.com#]sildenafil[/url] viagra walmart
k <a href= http://cialisviu.com/when-does-cialis-go-generic >cialis coupon</a> far [url=http://cialisviu.com]order pills from canada[/url] how long for cialis to work http://cialisviu.com
y https://viagraplc.com# women taking viagra <a href= https://viagraplc.com# >generic viagra without a doctor prescription</a> than [url=https://viagraplc.com#]sildenafil[/url] viagra samples free by mail
q http://levitrabtc.com# viagra vs cialis vs levitra <a href= http://levitrabtc.com# >levitra medication</a> brother [url=http://levitrabtc.com#]buy levitra[/url] levitra for women
c http://levitrabtc.com# cost of levitra <a href= http://levitrabtc.com# >levitra cost</a> desire [url=http://levitrabtc.com#]levitra[/url] best place to buy levitra online
h <a href= http://viagratph.com# >generic viagra</a> house [url=http://viagratph.com#]viagra online[/url] generic viagra
v <a href= http://cialislbc.com# >useful site</a> go [url=http://cialislbc.com]cialis online[/url] generic cialis reviews http://cialislbc.com
l <a href= http://cialisviu.com/cialis-generic-name >cheap erectile dysfunction pills online</a> help [url=http://cialisviu.com]generic cialis[/url] tadalafil dosage http://cialisviu.com
e https://viagraplc.com# buy generic viagra online <a href= https://viagraplc.com# >stendra vs viagra</a> far [url=https://viagraplc.com#]viagra[/url] viagra definition
q <a href= http://cialislbc.com# >cialis from india</a> years [url=http://cialislbc.com]generic cialis[/url] cialis online canada http://cialislbc.com
i http://levitrabtc.com# levitra dosage 40 mg <a href= http://levitrabtc.com# >levitra</a> waiting [url=http://levitrabtc.com#]generic levitra[/url] how much does levitra cost
k <a href= http://viagratph.com# >buy viagra generic</a> means [url=http://viagratph.com#]cheap viagra[/url] viagra
p <a href= http://viagratph.com# >buy viagra generic</a> glass [url=http://viagratph.com#]cheap viagra[/url] cheap viagra
b http://levitrabtc.com# what is levitra used for <a href= http://levitrabtc.com# >lavitra</a> girls [url=http://levitrabtc.com#]buy levitra[/url] levitra vs viagra vs cialis
q <a href= http://cialislbc.com# >ed pills from india</a> honest [url=http://cialislbc.com]cialis online[/url] cialis 20mg http://cialislbc.com
y <a href= http://cialisviu.com >cialis online</a> live [url=http://cialisviu.com]generic ed drugs from india[/url] cialis daily http://cialisviu.com
b http://levitrabtc.com# cheapest generic levitra <a href= http://levitrabtc.com# >levitra</a> talk [url=http://levitrabtc.com#]generic levitra[/url] levitra online pharmacy
e <a href= http://cialislbc.com# >buy cialis</a> bring [url=http://cialislbc.com]ed pills[/url] cialis cheap http://cialislbc.com
n http://levitrabtc.com# levitra without a doctor prescription <a href= http://levitrabtc.com# >buy levitra</a> silence [url=http://levitrabtc.com#]levitra online[/url] canadian pharmacy levitra
i <a href= http://cialisviu.com/cialis-manufacturer-coupon >generic ed drugs from india</a> ready [url=http://cialisviu.com]ed pills[/url] cialis pill http://cialisviu.com
l https://viagraplc.com# viagra sample <a href= https://viagraplc.com# >canadian pharmacy viagra</a> pray [url=https://viagraplc.com#]great site[/url] do you need a prescription for viagra
o <a href= http://cialislbc.com# >erectile dysfunction pills</a> added [url=http://cialislbc.com]cheap erectile dysfunction pills online[/url] cialis patent expiration date http://cialislbc.com
b <a href= http://cialislbc.com# >ed pills</a> whose [url=http://cialislbc.com]order erectile dysfunction pills[/url] cialis for women http://cialislbc.com
c <a href= http://cialisviu.com >cialis coupon</a> changed [url=http://cialisviu.com/when-will-cialis-go-generic]cheap erectile dysfunction pills online[/url] cialis 30 day free trial http://cialisviu.com
q http://levitrabtc.com# cheapest generic levitra <a href= http://levitrabtc.com# >levitra cost</a> shame [url=http://levitrabtc.com#]buy viagra[/url] levitra price
b <a href= http://cialislbc.com# >order pills from canada</a> placed [url=http://cialislbc.com]cialis coupons 2018[/url] buy tadalafil http://cialislbc.com
h <a href= http://cialislbc.com# >cheap erectile dysfunction pills online</a> somebody [url=http://cialislbc.com]ed pills[/url] cialis without prescription http://cialislbc.com
m <a href= http://cialisviu.com >buy cialis online</a> nearly [url=http://cialisviu.com]discount coupons[/url] generic cialis canada http://cialisviu.com
v <a href= http://cialislbc.com# >generic cialis</a> out [url=http://cialislbc.com]buy cialis[/url] cialis free sample http://cialislbc.com
l http://levitrabtc.com# levitra online pharmacy <a href= http://levitrabtc.com# >buy levitra</a> stand [url=http://levitrabtc.com#]levitra[/url] viagra cialis or levitra
n http://levitrabtc.com# levitra 10mg <a href= http://levitrabtc.com# >levitra</a> real [url=http://levitrabtc.com#]buy levitra[/url] levitra cost walmart
s <a href= http://cialislbc.com# >generic ed drugs from india</a> months [url=http://cialislbc.com]cialis lowest price[/url] canadian cialis http://cialislbc.com
a <a href= http://cialislbc.com# >buy ed pills from canada</a> rich [url=http://cialislbc.com]cheap erectile dysfunction pills online[/url] cialis half life http://cialislbc.com
l http://levitrabtc.com# levitra reviews <a href= http://levitrabtc.com# >buy levitra</a> circumstances [url=http://levitrabtc.com#]levitra vs viagra[/url] how does levitra work
j <a href= http://viagratph.com# >generic viagra</a> anxious [url=http://viagratph.com#]buy viagra generic[/url] viagra online
q http://levitrabtc.com# levitra price <a href= http://levitrabtc.com# >generic levitra</a> himself [url=http://levitrabtc.com#]levitra generic name[/url] generic levitra
e <a href= http://cialislbc.com# >erectile dysfunction pills</a> indeed [url=http://cialislbc.com]cialis online[/url] cialis prescription http://cialislbc.com
j <a href= http://viagratph.com# >buy viagra</a> sea [url=http://viagratph.com#]buy viagra generic[/url] viagra online
m <a href= http://cialislbc.com# >buy ed pills from canada</a> done [url=http://cialislbc.com]cialis coupons 2018[/url] buy cialis online http://cialislbc.com
o http://levitrabtc.com# levitra generic names <a href= http://levitrabtc.com# >buy levitra</a> wonder [url=http://levitrabtc.com#]levitra[/url] viagara cialis levitra
k https://viagraplc.com# sildenafil citrate 100mg <a href= https://viagraplc.com# >view web page</a> home [url=https://viagraplc.com#]viagra[/url] viagra free sample
l <a href= http://viagratph.com# >buy cheap viagra</a> position [url=http://viagratph.com#]cheap viagra[/url] generic viagra
a <a href= http://cialislbc.com# >cheap erectile dysfunction pills online</a> rest [url=http://cialislbc.com]buy cialis online[/url] cialis 20 mg price http://cialislbc.com
w https://viagraplc.com# sildenafil <a href= https://viagraplc.com# >generic viagra india</a> according [url=https://viagraplc.com#]sildenafil[/url] free viagra
d https://viagraplc.com# why is viagra so expensive <a href= https://viagraplc.com# >viagra</a> three [url=https://viagraplc.com#]viagra falls[/url] viagra definition
t <a href= http://cialislbc.com# >erectile dysfunction pills</a> glass [url=http://cialislbc.com]order erectile dysfunction pills[/url] does cialis lowers blood pressure http://cialislbc.com
x <a href= http://viagratph.com# >buy viagra generic</a> companion [url=http://viagratph.com#]generic viagra[/url] viagra
k https://viagraplc.com# canadian pharmacy viagra <a href= https://viagraplc.com# >buy viagra online</a> in [url=https://viagraplc.com#]viagra without a doctor prescription[/url] where can i buy viagra
w <a href= http://cialislbc.com# >cialis online</a> laughing [url=http://cialislbc.com]discount coupons[/url] when will generic cialis be available http://cialislbc.com
u <a href= http://viagratph.com# >generic viagra</a> distance [url=http://viagratph.com#]buy cheap viagra[/url] generic viagra
d https://viagraplc.com# is there a generic for viagra <a href= https://viagraplc.com# >generic viagra</a> difference [url=https://viagraplc.com#]Website[/url] sildenafil price
u <a href= http://cialisviu.com >generic ed drugs from india</a> seen [url=http://cialisviu.com]cialis coupon[/url] viagra or cialis http://cialisviu.com
s http://levitrabtc.com# levitra 20mg <a href= http://levitrabtc.com# >levitra</a> honest [url=http://levitrabtc.com#]generic levitra[/url] levitra cost
v <a href= http://viagratph.com# >buy viagra generic</a> joy [url=http://viagratph.com#]buy viagra[/url] generic viagra
q <a href= http://cialislbc.com# >ed pills</a> least [url=http://cialislbc.com]order pills from canada[/url] over the counter cialis http://cialislbc.com
m https://viagraplc.com# reload herbal viagra <a href= https://viagraplc.com# >sildenafil</a> stand [url=https://viagraplc.com#]buy sildenafil[/url] how does viagra work
o <a href= http://cialislbc.com# >cialis</a> fall [url=http://cialislbc.com]generic ed drugs from india[/url] cialis free trial http://cialislbc.com
c <a href= http://viagratph.com# >viagra online</a> took [url=http://viagratph.com#]generic viagra[/url] generic viagra
g http://levitrabtc.com# viagara cialis levitra <a href= http://levitrabtc.com# >levitra cost</a> place [url=http://levitrabtc.com#]generic levitra[/url] levitra cost per pill
j <a href= http://viagratph.com# >buy viagra</a> less [url=http://viagratph.com#]generic viagra[/url] buy viagra
a <a href= http://cialislbc.com# >cialis lowest price</a> before [url=http://cialislbc.com]order pills from canada[/url] cialis reviews http://cialislbc.com
f <a href= http://viagratph.com# >viagra online</a> around [url=http://viagratph.com#]viagra[/url] cheap viagra
t <a href= http://cialisviu.com/cialis-dosage >buy cialis</a> case [url=http://cialisviu.com]cialis coupon[/url] cialis no prescription http://cialisviu.com
c https://viagraplc.com# sildenafil citrate online <a href= https://viagraplc.com# >canadian pharmacy viagra</a> know [url=https://viagraplc.com#]viagra cheap[/url] stendra vs viagra
a http://levitrabtc.com# buy levitra now <a href= http://levitrabtc.com# >levitra online</a> business [url=http://levitrabtc.com#]lavitra[/url] levitra discount
c <a href= http://cialisviu.com/does-cialis-make-you-last-longer >cialis</a> times [url=http://cialisviu.com]generic drugs[/url] does cialis lower blood pressure http://cialisviu.com
y <a href= http://viagratph.com# >viagra</a> places [url=http://viagratph.com#]buy viagra[/url] buy viagra
k <a href= http://cialislbc.com# >cheap erectile dysfunction pills online</a> but [url=http://cialislbc.com]ed pills[/url] how long does it take for cialis to work http://cialislbc.com
b <a href= http://cialislbc.com# >order erectile dysfunction pills</a> couldn't [url=http://cialislbc.com]cheap erectile dysfunction pills online[/url] goodrx cialis http://cialislbc.com
f http://levitrabtc.com# levitra pill <a href= http://levitrabtc.com# >levitra</a> lay [url=http://levitrabtc.com#]levitra[/url] how long does levitra last
u <a href= http://cialisviu.com >erectile dysfunction pills</a> bear [url=http://cialisviu.com/cialis-vs-viagra]ed pills from india[/url] buying cialis online usa http://cialisviu.com
e https://viagraplc.com# viagra dosage <a href= https://viagraplc.com# >viagra without a doctor prescription</a> often [url=https://viagraplc.com#]buy viagra online[/url] viagra porn
i <a href= http://viagratph.com# >cheap viagra</a> me [url=http://viagratph.com#]buy viagra[/url] buy viagra generic
j http://levitrabtc.com# levitra bayer <a href= http://levitrabtc.com# >buy viagra</a> act [url=http://levitrabtc.com#]lavitra[/url] how to make levitra more effective
g https://viagraplc.com# viagra walmart <a href= https://viagraplc.com# >sildenafil</a> months [url=https://viagraplc.com#]viagra coupons[/url] viagra vs cialis
z <a href= http://cialislbc.com# >cialis coupons 2018</a> got [url=http://cialislbc.com]cheap erectile dysfunction pills online[/url] otc cialis http://cialislbc.com
t https://viagraplc.com# viagra samples <a href= https://viagraplc.com# >viagra</a> six [url=https://viagraplc.com#]viagra online no prior prescription[/url] viagra 100mg price
q <a href= http://viagratph.com# >cheap viagra</a> can [url=http://viagratph.com#]generic viagra[/url] buy viagra
h <a href= http://cialisviu.com >order pills from canada</a> pounds [url=http://cialisviu.com/cialis-daily-use]order pills from canada[/url] cialis online canada http://cialisviu.com
d <a href= http://viagratph.com# >viagra online</a> small [url=http://viagratph.com#]buy cheap viagra[/url] viagra
m https://viagraplc.com# viagra price <a href= https://viagraplc.com# >generic viagra</a> started [url=https://viagraplc.com#]buy sildenafil[/url] viagra no prescription
s http://levitrabtc.com# free levitra <a href= http://levitrabtc.com# >levitra</a> sure [url=http://levitrabtc.com#]generic levitra[/url] how long does it take for levitra to work
w https://viagraplc.com# is viagra covered by insurance <a href= https://viagraplc.com# >buy viagra online</a> different [url=https://viagraplc.com#]viagra[/url] viagra generic name
z <a href= http://cialislbc.com# >ed pills from india</a> means [url=http://cialislbc.com]this hyperlink[/url] tadalafil best price http://cialislbc.com
h <a href= http://cialisviu.com >cialis overdose</a> afraid [url=http://cialisviu.com]cialis professional[/url] cialis generic http://cialisviu.com
r https://viagraplc.com# buy real viagra online <a href= https://viagraplc.com# >buy viagra online</a> whenever [url=https://viagraplc.com#]viagra coupons[/url] viagra coupon
p https://viagraplc.com# generic sildenafil <a href= https://viagraplc.com# >how long does viagra stay in your system</a> a [url=https://viagraplc.com#]viagra[/url] pfizer viagra
r http://levitrabtc.com# buy discount levitra <a href= http://levitrabtc.com# >levitra online</a> woman [url=http://levitrabtc.com#]buy viagra[/url] viagara cialis levitra
h https://viagraplc.com# viagra ingredients <a href= https://viagraplc.com# >sildenafil</a> took [url=https://viagraplc.com#]generic viagra[/url] price of viagra
e http://levitrabtc.com# levitra pills <a href= http://levitrabtc.com# >buy levitra</a> feeling [url=http://levitrabtc.com#]levitra online[/url] levitra cost per pill
q <a href= http://viagratph.com# >viagra</a> mean [url=http://viagratph.com#]generic viagra[/url] buy viagra generic
g http://levitrabtc.com# how much does levitra cost <a href= http://levitrabtc.com# >buy levitra</a> school [url=http://levitrabtc.com#]levitra[/url] side effects of levitra
n <a href= http://viagratph.com# >buy cheap viagra</a> well [url=http://viagratph.com#]buy viagra generic[/url] generic viagra
t <a href= http://cialislbc.com# >cheap erectile dysfunction pills online</a> low [url=http://cialislbc.com]cialis coupons 2018[/url] what is tadalafil http://cialislbc.com
<a href="https://www.kamagrapos.com/">kamagra oral jelly</a>
kamagra shop erfahrungsberichte
[url=https://www.kamagrapos.com/]kamagra[/url]
kamagra soft / chewable 100 mg
t https://viagraplc.com# over the counter viagra substitute <a href= https://viagraplc.com# >generic viagra</a> good [url=https://viagraplc.com#]buy sildenafil[/url] viagra online prescription free
a <a href= http://cialislbc.com# >ed pills</a> looked [url=http://cialislbc.com]buy cialis online[/url] cialis from india http://cialislbc.com
z <a href= http://cialislbc.com# >cialis</a> whom [url=http://cialislbc.com]cialis coupons 2018[/url] buying tadalafil online http://cialislbc.com
l <a href= http://cialisviu.com/cialis-daily >order pills from canada</a> heart [url=http://cialisviu.com/how-to-take-cialis]have a peek at these guys[/url] cialis for prostate http://cialisviu.com
r <a href= http://viagratph.com# >buy viagra generic</a> fast [url=http://viagratph.com#]cheap viagra[/url] generic viagra
w <a href= http://cialislbc.com# >order pills from canada</a> feet [url=http://cialislbc.com]generic cialis[/url] cialis for bph http://cialislbc.com
r <a href= http://viagratph.com# >generic viagra</a> since [url=http://viagratph.com#]buy viagra generic[/url] viagra online
y https://viagraplc.com# best place to buy generic viagra online <a href= https://viagraplc.com# >buy sildenafil</a> beauty [url=https://viagraplc.com#]generic viagra[/url] natural viagra for men
n https://viagraplc.com# viagra jokes <a href= https://viagraplc.com# >sildenafil</a> secret [url=https://viagraplc.com#]canadian pharmacy[/url] viagra before and after
q <a href= http://viagratph.com# >buy viagra generic</a> our [url=http://viagratph.com#]buy cheap viagra[/url] viagra online
k <a href= http://viagratph.com# >buy viagra generic</a> hands [url=http://viagratph.com#]cheap viagra[/url] generic viagra
u http://levitrabtc.com# levitra reviews <a href= http://levitrabtc.com# >levitra online</a> advantage [url=http://levitrabtc.com#]levitra cost[/url] levitra generic name
n <a href= http://cialisviu.com >cialis coupons 2018</a> took [url=http://cialisviu.com/female-cialis]cialis coupon[/url] cialis for sale online http://cialisviu.com
v https://viagraplc.com# best place to buy generic viagra online <a href= https://viagraplc.com# >as example</a> send [url=https://viagraplc.com#]viagra without a doctor prescription[/url] sildenafil 100mg
<a href="https://www.kamagrajellyk.com/">kamagra jelly</a>
kamagra oral jelly usa
[url=https://www.kamagrajellyk.com/]buy kamagra[/url]
buy kamagra uk review
n <a href= http://viagratph.com# >buy viagra</a> are [url=http://viagratph.com#]viagra online[/url] viagra
b <a href= http://cialislbc.com# >discount coupons</a> than [url=http://cialislbc.com]ed pills[/url] buying cialis online usa http://cialislbc.com
o <a href= http://cialislbc.com# >cialis coupon</a> although [url=http://cialislbc.com]buy cialis online[/url] tadalafil dosage http://cialislbc.com
q http://levitrabtc.com# how long does levitra last <a href= http://levitrabtc.com# >buy viagra</a> visit [url=http://levitrabtc.com#]levitra coupons[/url] levitra professional
e <a href= http://cialisviu.com >ed pills online</a> call [url=http://cialisviu.com]ed pills online[/url] cialis half life http://cialisviu.com
k http://levitrabtc.com# buy levitra now <a href= http://levitrabtc.com# >generic levitra</a> rain [url=http://levitrabtc.com#]levitra[/url] levitra prices
q http://levitrabtc.com# buy discount levitra <a href= http://levitrabtc.com# >generic levitra</a> those [url=http://levitrabtc.com#]generic levitra[/url] cost of levitra
z <a href= http://cialisviu.com >here i found it</a> oh [url=http://cialisviu.com]buy cialis[/url] buying tadalafil http://cialisviu.com
[url=http://21sol.ru/assets/protokol-otkaza-ot-zaklyucheniya-kontrakta-po-44-fz-obrazets-skachat.html]http://21sol.ru/assets/protokol-otkaza-ot-zaklyucheniya-kontrakta-po-44-fz-obrazets-skachat.html[/url]
cialis generic best price
<a href="http://21sol.ru/assets/skachat-kontrolnie-zadaniya-po-angliyskomu-yaziku-5-klass-kuzovlev.html">http://21sol.ru/assets/skachat-kontrolnie-zadaniya-po-angliyskomu-yaziku-5-klass-kuzovlev.html</a>
price of viagra and cialis in indian rupees
http://21sol.ru/assets/skachat-amd-catalyst-dlya-windows-7-64-bit-poslednyaya-versiya.html
cost of viagra and cialis
[url=http://21sol.ru/assets/skachat-programmu-konvertirovanie-na-android.html]http://21sol.ru/assets/skachat-programmu-konvertirovanie-na-android.html[/url]
cialis professional
<a href="http://21sol.ru/assets/luchshiy-launcher-na-android-planshet.html">http://21sol.ru/assets/luchshiy-launcher-na-android-planshet.html</a>
cialis prices at walmart pharmacy
http://21sol.ru/assets/asphalt-8-mnogo-deneg-android.html
comprar cialis generico en chile
h https://viagraplc.com# cheap viagra 100mg <a href= https://viagraplc.com# >buy viagra online</a> seven [url=https://viagraplc.com#]canadian pharmacy viagra[/url] generic viagra india
v http://levitrabtc.com# canadian pharmacy levitra <a href= http://levitrabtc.com# >levitra coupons</a> however [url=http://levitrabtc.com#]buy levitra[/url] generic levitra online pharmacy
f https://viagraplc.com# how to use viagra <a href= https://viagraplc.com# >viagra ad</a> difference [url=https://viagraplc.com#]buy viagra online[/url] female viagra
z <a href= http://viagratph.com# >cheap viagra</a> dear [url=http://viagratph.com#]viagra[/url] buy cheap viagra
c https://viagraplc.com# how much does the military spend on viagra <a href= https://viagraplc.com# >viagra</a> hand [url=https://viagraplc.com#]canadian pharmacy viagra[/url] canadian pharmacy viagra
j <a href= http://cialislbc.com# >generic ed drugs from india</a> breath [url=http://cialislbc.com]generic drugs[/url] cialis generic http://cialislbc.com
k <a href= http://viagratph.com# >viagra online</a> light [url=http://viagratph.com#]buy viagra[/url] cheap viagra
i https://viagraplc.com# viagra for the brain <a href= https://viagraplc.com# >sildenafil</a> surprised [url=https://viagraplc.com#]viagra[/url] viagra
l http://levitrabtc.com# levitra generique <a href= http://levitrabtc.com# >levitra</a> placed [url=http://levitrabtc.com#]generic levitra[/url] generic levitra online pharmacy
n <a href= http://viagratph.com# >buy cheap viagra</a> following [url=http://viagratph.com#]cheap viagra[/url] buy viagra
u <a href= http://cialisviu.com/cialis-commercial >cialis online</a> seeing [url=http://cialisviu.com]ed pills[/url] cialis bathtub http://cialisviu.com
i http://levitrabtc.com# levitra manufacturer coupon <a href= http://levitrabtc.com# >generic levitra</a> several [url=http://levitrabtc.com#]generic levitra[/url] free levitra
r <a href= http://cialisviu.com >cialis lowest price</a> answered [url=http://cialisviu.com]generic drugs[/url] free cialis sample pack http://cialisviu.com
g http://levitrabtc.com# levitra 20mg <a href= http://levitrabtc.com# >buy levitra</a> gone [url=http://levitrabtc.com#]levitra online[/url] generic levitra
[url=http://news.ria-new.ru/assets/skachat-programmi-dlya-android-221.html]http://news.ria-new.ru/assets/skachat-programmi-dlya-android-221.html[/url]
<a href="http://news.ria-new.ru/assets/krasovskiy-ai-osnovi-proektirovaniya-svarochnih-tsehov-skachat.html">http://news.ria-new.ru/assets/krasovskiy-ai-osnovi-proektirovaniya-svarochnih-tsehov-skachat.html</a>
http://news.ria-new.ru/assets/what-does-crack-looks-like.html
[url=http://news.ria-new.ru/assets/igri-na-android-skachat-maincraft.html]http://news.ria-new.ru/assets/igri-na-android-skachat-maincraft.html[/url]
<a href="http://news.ria-new.ru/assets/virtual-dj-pro-with-crack.html">http://news.ria-new.ru/assets/virtual-dj-pro-with-crack.html</a>
http://news.ria-new.ru/assets/skachat-muzikalniy-pleer-dlya-android-21.html
o https://viagraplc.com# watermelon viagra <a href= https://viagraplc.com# >buy sildenafil</a> advantage [url=https://viagraplc.com#]canadian pharmacy[/url] is viagra covered by insurance
j <a href= http://cialisviu.com >erectile dysfunction pills</a> earth [url=http://cialisviu.com]buy ed pills from canada[/url] cialis over the counter 2017 http://cialisviu.com
x <a href= http://viagratph.com# >buy viagra generic</a> weather [url=http://viagratph.com#]buy viagra[/url] buy cheap viagra
v http://levitrabtc.com# levitra <a href= http://levitrabtc.com# >levitra coupons</a> exactly [url=http://levitrabtc.com#]levitra online[/url] buy generic levitra online
[url=http://alamo-a.ru/assets/postanovlenie-pravitelstva-604-ot-23072009-skachat.html]http://alamo-a.ru/assets/postanovlenie-pravitelstva-604-ot-23072009-skachat.html[/url]
lloyds pharmacy cialis price
<a href="http://alamo-a.ru/assets/skachat-na-android-igru-ohotniki-na-drakonov.html">http://alamo-a.ru/assets/skachat-na-android-igru-ohotniki-na-drakonov.html</a>
viagra cialis pharmacy
http://alamo-a.ru/assets/skachat-staruyu-versiyu-agenta-mayl-ru-dlya-android.html
comprar cialis generico en chile
p https://viagraplc.com# viagra for women <a href= https://viagraplc.com# >generic viagra</a> likely [url=https://viagraplc.com#]buy sildenafil[/url] viagra meme
j http://levitrabtc.com# levitra discount <a href= http://levitrabtc.com# >levitra online</a> back [url=http://levitrabtc.com#]lavitra[/url] how much does levitra cost
x <a href= http://cialisviu.com >cheap erectile dysfunction pills online</a> used [url=http://cialisviu.com]cheap erectile dysfunction pills online[/url] cialis from india http://cialisviu.com
u <a href= http://viagratph.com# >generic viagra</a> tea [url=http://viagratph.com#]buy cheap viagra[/url] generic viagra
w <a href= http://viagratph.com# >buy viagra generic</a> beauty [url=http://viagratph.com#]viagra online[/url] buy cheap viagra
f https://viagraplc.com# viagra natural <a href= https://viagraplc.com# >generic viagra</a> bright [url=https://viagraplc.com#]generic viagra[/url] is there a generic for viagra
[url=http://air-engineering.ru/ads/skachat-mod-dlya-skayrim-lanterns-of-skyrim-all-in-one.html]скачать мод для скайрим lanterns of skyrim all in one[/url]
do cialis side effects go away
<a href="http://air-engineering.ru/ads/novaya-versiya-fonbet-dlya-android.html">новая версия фонбет для андроид</a>
cialis and viagra side effects
http://air-engineering.ru/ads/pesn-lda-i-plameni-igra-prestolov-kniga-1-skachat-fb2.html
viagra cialis comparison
z <a href= http://cialisviu.com/cialis-for-sale-online >buy cialis online</a> saw [url=http://cialisviu.com]ed pills online[/url] over the counter cialis http://cialisviu.com
c <a href= http://viagratph.com# >generic viagra</a> difficulty [url=http://viagratph.com#]buy viagra generic[/url] cheap viagra
h <a href= http://cialislbc.com# >cialis</a> hill [url=http://cialislbc.com]buy cialis online[/url] how long does it take for cialis to work http://cialislbc.com
o http://levitrabtc.com# levitra bayer <a href= http://levitrabtc.com# >levitra cost</a> send [url=http://levitrabtc.com#]levitra price[/url] buy discount levitra
research paper topics
essay proofreader
maths revision gcse
tips on resume
uk essay writers
[url=http://tarturotary.ee/ev100-kingituselt-langes-saladuseloor/#comment-53]custom essay writing service[/url]
letter writing services
spanish gcse
igcse mathematics syllabus
how do i write a cover letter
resume preparation
[url=http://heliocentrisacademia.com/2017/10/23/center-of-scientific-research-in-algeria/#comment-43]writemypapers[/url]
how can i make cv
cv layout
cheap custom written papers
thesis for a research paper
analytical essay
[url=http://www.blanco-nino.com/mex-in-the-city-sunday-times/#comment-1435]write my paper for me[/url]
world peace essay
custom dissertation writing service
writing cvs
cv outline
essay checker
[url=https://www.4ward4x4.com/defender-rundrohr-seilwindenstossstange/#comment-715]custom essay writing[/url]
gcse english syllabus
a2 english language coursework
writing a cover letter for a cv
custom research paper writing service
igcse fees
[url=https://lovelandcappys.com/cappys-now-in-15-pack-cans-of-foundersbrewing-alldayipa/#comment-6307]write to them[/url]
how do i write a good resume
custom writing journals
create curriculum vitae
writing a covering letter for a cv
frankenstein essay
Все фильмы, сериалы и мультики в одной программе - просмотр и скачивание. Бесплатно и без рекламы.
Быстрый поиск по всему рунету. Обновления фильмов точно в день выхода в кинотеатрах.
Сегодня добавленно: [b]"Мег: Монстр глубины" "Кристофер Робин" "Судная ночь. Начало"[/b]
Скачать Kino-Torrent версии PRO можно здесь: [url=http://kino-top.tk][b]KinoTorrentSetup[/b][/url]
Communism essay writing Primary education essay writing A college debate essay writing Advantages of recycling essay writing Strikes and lock-outs essay writing Write about the biggest risk you have taken essay writing Common sense essay writing English - the world language essay writing What is the best advice you have ever received essay writing The problem of industrialism essay writing Stamp-collecting as a hobby essay writing Are actors and professional athletes paid way too much essay writing advantages of a university career essay writing Middle class unemployment essay writing A midnight adventure essay writing https://academic365.site/ best dissertation writing service freelancing websites igcse past questions cv resume creating curriculum vitae
A prize-giving ceremony essay writing The problem of food essay writing Life in college hostel essay writing Science and modern warfare essay writing What is the one gadget that you could not live without Explain essay writing Make hay while the sun shines essay writing Patriotism love of the country essay writing The green revolution essay writing The science of engineering essay writing The sorrows and joys of life essay writing The problem of national integration essay writing Describe your favorite literary character and what makes that character your favorite essay writing The cinema its uses and abuses essay writing General election essay writing School life and college life essay writing https://academic365.site/ dissertation proposal writing a essay paper custom essay writing custom write me an essay
http://fms.misionsucre.gob.ve/foro/viewtopic.php?f=2&t=329214
http://www.yubazhen.net/forum.php?mod=viewthread&tid=2986662&extra=
http://www.108bbs.com/forum.php?mod=viewthread&tid=102719&extra=
http://www.spotfirebrasil.com.br/forum/viewtopic.php?f=5&t=523555
http://space2010.ru/forum/viewtopic.php?f=5&t=68670
http://www.dianjingcn.com/forum.php?mod=viewthread&tid=179164&extra=
http://spiga.altervista.org/showthread.php?tid=42416
http://mcfen.orzweb.net/viewthread.php?tid=21878&extra=
http://www.avrmaker.com/forum.php?mod=viewthread&tid=1624561&extra=
http://www.ugeltacna.gob.pe/foro/index.php?topic=813983.new#new
http://www.hnzqmy.com/thread-73048-1-1.html
http://www.sceltic.at/forum/viewtopic.php?f=6&t=649933
https://blockchaindigitalvoting.com/index.php?topic=26315.new#new
http://discuss.blogvertex.com/showthread.php?tid=293605
http://edu.newrui.cn/forum.php?mod=viewthread&tid=4855387&extra=
http://go.alphabody-lippstadt.de/forum/showthread.php?tid=546219
http://asianpodcasters.com/index.php?topic=64149.new#new
http://py.aglyun.com/forum.php?mod=viewthread&tid=16397&extra=
http://xjyljsgc.com/forum.php?mod=viewthread&tid=39399&extra=
http://www.volareitalianogroup.it/forums/viewtopic.php?f=10&t=34361
http://creatio-ex-nihilo.us/forum/viewtopic.php?f=52&t=144189
http://qpjyfw.net/forum.php?mod=viewthread&tid=53164&extra=
http://forum.3gunnation.uk/viewtopic.php?f=30&t=416917
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217462
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217489
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217492
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217494
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217506
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217531
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217534
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217549
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217555
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217581
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217587
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217592
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217619
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217623
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217636
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=217658
Life is earnest life is real essay writing Describe your favorite literary character and what makes that character your favorite essay writing Life in college hostel essay writing Self-reliance essay writing The library and its uses essay writing [url=https://academic365.site/]movie review writing service[/url]
A college theatrical essay writing Obedience essay writing All things both great and small essay writing Lives of great men all remind us we can make our lives sublime essay writing All that glitters is not gold essay writing Technical education essay writing The one-act play essay writing Patriotism love of the country essay writing The value of discipline essay writing co-operative farming essay writing Life in the village essay writing The happiest day in my life essay writing Fast food nation essay writing How to judge a good novel essay writing Common sense essay writing https://academic365.site/ custom papers gcse textile coursework english igcse phd by coursework recycling essay
http://cerver.serva4ok.su/forum/viewtopic.php?f=3&t=162488
http://ptvsportsbisskey.mobi/viewtopic.php?f=3&t=41055
http://www.fdgbt.com/forum.php?mod=viewthread&tid=4435&extra=
http://www.023aw.com/forum.php?mod=viewthread&tid=24949&extra=
http://www.artritisreumatoide.info/forum/showthread.php?1923-%C2%AB-%C2%BB-17&p=2729#post2729
http://www.newstoyou.bid/index.php?topic=33338.new#new
http://www.pascalsgroenewereld.nl/forum/index.php?topic=117908.new#new
http://forum.rasschitai.ru/post/315161/#p315161
http://aod.the-reincarnation.org/darkfortress/viewtopic.php?f=72&t=48699
http://b3community.world/viewtopic.php?f=6&t=81929
http://wyznawcyslonca.ws/forum/viewtopic.php?pid=4616#p4616
http://www.m84website.nhely.hu/index.php?topic=50005.new#new
http://zqyx8.com/forum.php?mod=viewthread&tid=26685&extra=
http://offensive.ndo.pl/viewtopic.php?f=9&t=8150
http://www.7itn.com/vb/showthread.php?p=5519#post5519
http://www.nevarki.net/viewtopic.php?f=2&t=571080
http://www.ce5w.com/thread-8719862-1-1.html
http://www.gxcyr.com/forum.php?mod=viewthread&tid=6973&extra=
http://akoleso.com.ua/forum/viewtopic.php?pid=34045#p34045
http://bobbalife.altervista.org/showthread.php?tid=106693
http://www.ceyee.com/forum/forum.php?mod=viewthread&tid=569898&extra=
http://traderpips.com/forum/forum.php?mod=viewthread&tid=198753&extra=
http://monster4x4pryluky.in.ua/index.php?topic=310781.new#new
http://vne.bid/f/viewtopic.php?f=73&t=3696
http://lubanlm.com/forum.php?mod=viewthread&tid=17754&extra=
http://www.palacjuchowo.bornesulinowo.pl/www/forum/viewtopic.php?f=5&t=151579
https://team-crackers.org/forum/index.php?/topic/1106-%D0%B4%D0%BE%D0%BC%D0%B0%D1%88%D0%BD%D0%B8%D0%B9%D0%B0%D1%80%D0%B5%D1%81%D1%82%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB1%D1%81%D0%B5%D1%80%D0%B8%D1%8F/
http://forum.moippo.mk.ua/viewtopic.php?f=73&t=627735
http://tryk.tk/forum.php?mod=viewthread&tid=11812&extra=
http://itradepro.ru/forum/showthread.php?4306-%D0%92%C2%AB%D0%A0%E2%80%9D%D0%A0%D1%95%D0%A0%D1%98%D0%A0%C2%B0%D0%A1%E2%82%AC%D0%A0%D0%85%D0%A0%D1%91%D0%A0%E2%84%96-%D0%A0%C2%B0%D0%A1%D0%82%D0%A0%C2%B5%D0%A1%D0%83%D0%A1%E2%80%9A%D0%92%C2%BB-11-%D0%A0%D0%8E%D0%A0%E2%80%A2%D0%A0%C2%A0%D0%A0%C2%98%D0%A0%D0%87&p=5129#post5129
http://meidi.mroc.cn/forum.php?mod=viewthread&tid=1195516
http://www.freeforumzone.com/discussione.aspx?idd=11533308
http://www.zgcfyzz.com/forum.php?mod=viewthread&tid=198285&extra=
http://www.aimji.com/thread-130374-1-1.html
http://baskentankaragaming.com/index.php?topic=14890.new#new
http://forum.aquariophilieduquebec.org/viewtopic.php?f=8&t=34120
http://yinxingyuan.com.cn/viewthread.php?tid=11487&extra=
http://awmy.top/forum.php?mod=viewthread&tid=5029&pid=109843&page=9551&extra=#pid109843
http://forums2.wow-petopia.com/viewtopic.php?f=15&t=50937
http://community.subjectivetruthpictures.com/community/index.php?topic=5925.new#new
http://ooo-unipharm.ru/forum/index.php?topic=143527.new#new
http://khazovnh.bget.ru/index.php/component/k2/itemlist/user/887663
http://khazovnh.bget.ru/index.php/component/k2/itemlist/user/888537
http://khazovnh.bget.ru/index.php/component/k2/itemlist/user/890446
http://khazovnh.bget.ru/index.php/component/k2/itemlist/user/892003
http://khazovnh.bget.ru/index.php/component/k2/itemlist/user/892034
http://kora-crimea.ru/component/k2/itemlist/user/11936.html
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356140
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356141
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356142
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356144
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356151
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356155
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356157
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356161
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356176
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356182
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356184
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356185
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356189
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356194
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356195
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=356198
zdoe cxwu
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=705725
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=705730
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=705757
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=705765
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=705773
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=705775
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=705788
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=705790
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=705794
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=705820
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=705825
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=705833
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=705841
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=705880
shsn jubr
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87056
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87073
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87076
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87079
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87091
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87176
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87178
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87198
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87200
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87205
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87214
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87298
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87326
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87328
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87330
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87333
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87425
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87435
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87441
http://emrabq8.com/?option=com_k2&view=itemlist&task=user&id=87458
wbvp jlcd
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18440
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18445
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18446
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18450
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18454
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18460
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18463
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18464
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18473
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18474
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18481
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18482
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18488
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18489
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18491
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18492
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18493
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18495
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=18502
eqhm owce
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396541
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396548
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396553
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396561
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396570
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396599
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396604
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396613
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396619
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396622
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396653
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396656
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396665
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396672
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396676
http://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955396705
qtch wklc
--------
[url=https://superdachnik.com.ua/doglyad-za-rozsadoyu-pomidoriv-pislya-visadki-v-grunt/]догляд за розсадою помідорів[/url] | https://superdachnik.com.ua
--------
[url=https://superdachnik.com.ua/obrobka-sady-navesni-na-varti-maibytnogo-vrojau/]обробка саду[/url] | https://superdachnik.com.ua
https://apteka-stoletnik.ru/forum/index.php/topic,137190.new.html#new
http://samaznayu.ru/forum/viewtopic.php?f=3&t=76788
http://www.hydraulicallyboundmixtures.info/forum/viewtopic.php?f=3&t=361553&sid=0a33a252e69b090ceedb5257d762d97e
http://foro.bitagora.dx.am/showthread.php?tid=755
http://xn----8sbaagjotxjofhb7amji5d7h.xn--p1ai/forum/index.php?topic=17255.new#new
http://www.hydraulicallyboundmixtures.info/forum/viewtopic.php?f=3&t=361190&sid=d3e7a373ae09dbf7eb4238f7f34cac25
http://playhearthstone.ru/forum/viewtopic.php?f=7&t=103109
http://www.redingrpg.com/index.php?topic=469568.new#new
http://eletazutakon.hu/index.php?topic=5798.new#new
http://test.mir-saitov.info/forum/viewtopic.php?f=10&t=177592
http://rup33.ru/forum/viewtopic.php?f=1&t=27945
http://inkomtehnika.com/index.php/component/k2/itemlist/user/1534309
http://xe365.info/forum/viewtopic.php?pid=223256#p223256
http://accf.asia/forum/viewtopic.php?f=2&t=280348
http://seafoxowners.com/viewtopic.php?f=4&t=366272
http://www.sasistanbul.net/vb/showthread.php?p=275630#post275630
https://boe-conanexile.000webhostapp.com/showthread.php?tid=29024
http://rdstyl.info/forum/viewtopic.php?pid=255727#p255727
http://sintraemsdes.org.co/fo_ro/viewthread.php?tid=496194#pid501732
http://coalition.30mc.free-speicher.de/viewtopic.php?f=13&t=29441
http://optcement.kiev.ua/forum/showthread.php?p=74903#post74903
http://www.pitchnparty.com/showthread.php?tid=30536
http://kultura38.ru/forum/viewtopic.php?f=2&t=100689&sid=2586d38977e90c77f621dd73cf19e1fb
http://humbit.com/forums/viewtopic.php?f=1&t=58624
http://m.protestv.com/viewtopic.php?pid=96587#p96587
http://access-print.ru/forum/messages/forum1/topic266/message11861/?result=reply#message11861
http://www.thakhae.go.th/webboard/showthread.php?tid=34779
http://surgeofsouls.com/mybb/index.php?topic=1143369.new#new
http://classifiedsadsnow.online/viewtopic.php?pid=977142#p977142
http://webboard.banmaicamping.com/index.php?topic=200999.new#new
http://forum.nocnajazdabrodnica.pl/viewtopic.php?f=16&t=140461
http://www.thong-en.go.th/webboard/index.php?topic=28168.new#new
http://inkomtehnika.com/index.php/component/k2/itemlist/user/1534309
http://forum.goods4crypto.me/viewtopic.php?f=2&t=71210
http://intelligentonlinetools.com/research/viewtopic.php?f=7&t=24246
http://zarabotok-bystro.ru/viewtopic.php?f=3&t=213606
http://test.mir-saitov.info/forum/viewtopic.php?f=10&t=181560
http://siamovie.xyz/index.php?topic=275271.new#new
http://vne.bid/f/viewtopic.php?f=73&t=38677
https://www.summerdreams.group/showthread.php?tid=21426
http://multiverserp.com/forum/showthread.php?tid=39336
http://kultura38.ru/forum/viewtopic.php?f=2&t=101081&sid=c66549de23e9b8799b3a89354a833a0d
http://xn--80aaaondebbc3au4bnpo4d7h.xn--p1ai/forum/viewtopic.php?pid=84858#p84858
http://www.tosinsilverdam.com/forum/index.php?topic=1236128.new#new
http://bifc.org/phpbb/viewtopic.php?f=4&t=48856
http://omni-casino.org/forum/viewtopic.php?pid=5556#p5556
http://reseller.ediskdrive.com/index.php?topic=185164.new#new
http://poliklinika5.ru/forum/viewtopic.php?f=2&t=113383
http://rocknrollaccess.rocks/mb/showthread.php?tid=75887
http://dvadmin.ru/forum/index.php?topic=39601.new#new
http://www.f-i-t.xyz/viewtopic.php?f=2&t=279871
http://gsk.ez-network.ru/topic.php?forum=1&topic=173366
http://mainecoon-portal.ru/forum/index.php?topic=94385.new#new
http://forums.scumbrasil.com.br/index.php?topic=1379563.new#new
http://cryptomania.live/forum/index.php?topic=2067327.new#new
http://www.ssomep.com/viewtopic.php?f=6&t=71773&sid=ae1a53c0f2304cdbd2e1b29cd1ab5c0f
http://forum.as-lubava.ru/viewtopic.php?f=3&t=39068
http://www.wardanceclan.com/forum/index.php?topic=390058.new#new
Respect the author!
By the way interesting reviews also found here ...[url=https://technology4you.website/category/smartphone-reviews/]Smartphone Reviews[/url]
http://www.halalbekhandim.com/showthread.php?tid=6012
http://tomsulayman.com/forum/index.php?topic=79851.new#new
http://forum.mutitans.com/showthread.php?31780-5-6-5&p=40314#post40314
http://bmwlife.pl/forum/showthread.php?tid=34615
http://www.filmdiscuss.com/forum/index.php?topic=56874.new#new
http://85.25.193.62/forum/lc/showthread.php?tid=219298
https://www.imz.asia/showthread.php?31310-5&p=31442#post31442
http://www.bakardluai.bid/index.php?topic=28808.new#new
http://sgchinchillas.com/viewtopic.php?f=11&t=805901
http://cryptamining.com/viewtopic.php?f=4&t=94890
http://bankstalk.org/index.php?topic=719182.new#new
http://xn-----6kcacallcra3ckghvi6ciq2fsg8a.xn--p1ai/forum/index.php?topic=20683.new#new
https://assurancefrance.fr/viewtopic.php?f=53&t=382266
http://www.stchamvtt.fr/phpBB306/viewtopic.php?f=23&t=61477
http://forum.zvety-bashkirii.ru/index.php?topic=133181.new#new
http://anna-abreu.net/index.php?topic=494020.new#new
http://kultura38.ru/forum/viewtopic.php?f=2&t=106072&sid=681a127f0c69d21a477a4e258a79475c
http://www.eentke.com/forum/viewtopic.php?f=7&t=161330
http://www.palacjuchowo.bornesulinowo.pl/www/forum/viewtopic.php?f=5&t=246877
http://bizpotok.ru/forum/index.php?topic=150544.new#new
http://vb.so7bet7ob.com/showthread.php?p=181640#post181640
http://nmg.tdulko.pl/index.php?topic=46040.new#new
http://offensive.ndo.pl/viewtopic.php?f=9&t=69821
http://torrent.oss-ab.net/viewtopic.php?p=66629#66629
http://rust.dayz-rp.com/index.php?topic=317392.new#new
http://forum.funtasysport.com/viewtopic.php?f=2&t=74801
http://poliklinika5.ru/forum/viewtopic.php?f=2&t=114963
http://descargawarez.net/index.php?topic=1646.new#new
http://www.m84website.nhely.hu/index.php?topic=105547.new#new
http://cerver.serva4ok.su/forum/viewtopic.php?f=3&t=225913
http://forum.as-lubava.ru/viewtopic.php?f=3&t=41785
http://samaznayu.ru/forum/viewtopic.php?f=3&t=78779
http://reseller.ediskdrive.com/index.php?topic=188631.new#new
http://cristiancg.com/index.php?topic=50079.new#new
http://midas.jutiviwat.com/index.php?topic=58382.new#new
http://xn--80aeadlansei6abcbc5ak.xn--p1ai/forum/viewtopic.php?f=15&t=250905
http://ultimaiberia.es/foro/viewtopic.php?f=2&t=23024
http://spiga.altervista.org/showthread.php?tid=68056
http://school-ideas.com/showthread.php?tid=87251
http://www.antikcep.com/index.php?topic=38993.new#new
http://www.xblade-tech.com/ztw-forum/showthread.php?210091-5-2018&p=245573#post245573
http://minimail.eu/index.php?topic=104342.new#new
http://forum.aereya2.ro/viewtopic.php?f=16&t=47795
https://portfoliothought.com/forums/showthread.php?tid=107456
http://podarki-vtaganroge.ru/forum/viewtopic.php?f=3&t=147957
http://sgchinchillas.com/viewtopic.php?f=11&t=806628
http://missya.ru/index.php?showtopic=1044030
http://kitaballah.info/forum/showthread.php?tid=407555
http://www.deensidewheelers.com/component/kunena/2-welcome-mat/660971#660971
http://luxury-stone.com/communication/php/viewtopic.php?p=116151#116151
http://psdz-samp.pl/showthread.php?tid=44427
http://2atalk.org/viewtopic.php?f=21&t=1241831
http://poliklinika5.ru/forum/viewtopic.php?f=2&t=116752
http://forum.aslava.ru/viewtopic.php?f=3&t=148565
http://nauc.info/forums/viewtopic.php?f=3&t=9620510
http://ignivi.com/forum/viewtopic.php?f=14&t=379740
http://wtrawie.pl/index.php?topic=224890.new#new
http://forum.mutitans.com/showthread.php?31175-5-6-7-5-31&p=39573#post39573
http://decentralizedindia.org/index.php?topic=465656.new#new
http://cs-kurnik.eu/showthread.php?tid=598440
http://cerver.serva4ok.su/forum/viewtopic.php?f=3&t=226138
http://bbs.cyberc.tech/viewtopic.php?f=36&t=18718
http://www.hometalkentertainment.com/showthread.php/25020-5-5?p=30196#post30196
http://pharkhuntan.com/board/viewtopic.php?f=3&t=44594
http://www.homekoland.xyz/viewtopic.php?f=6&t=32808
http://petplanetguide.com/viewtopic.php?f=9&t=66370
http://www.thepedagogue.net/Forum/showthread.php?tid=34479
http://www.best2product.bid/index.php?topic=33662.new#new
http://bmwlife.pl/forum/showthread.php?tid=35328
http://www.artritisreumatoide.info/forum/showthread.php?14372-5-1-10&p=16696#post16696
http://forums.wedigitalconsult.com/index.php?topic=49676.new#new
http://www.daraboard.bid/index.php?topic=36788.new#new
http://d7.sitiq.com/node/674
http://d7.sitiq.com/node/677
http://d7.sitiq.com/node/678
http://d7.sitiq.com/node/680
http://d7.sitiq.com/node/682
http://d7.sitiq.com/node/683
http://d7.sitiq.com/node/684
http://www.3rd-specialoperations.site/forums/showthread.php?tid=16759
http://vonwolkenstein.ano-host.co.in/vb4-neu/showthread.php?42409-5-1-10&p=89607#post89607
http://www.entp.ru/forum/viewtopic.php?f=4&t=31363
http://webboard.banmaicamping.com/index.php?topic=206020.new#new
http://arkofsafetyonline.com/MyBB/showthread.php?tid=341624
http://sunglowsound.com/phpbb/viewtopic.php?f=1&t=97244
https://hwtphonemarket.com/index.php?topic=279693.new#new
http://cryptomania.live/forum/index.php?topic=2081580.new#new
http://www.epsihijatar.net/forum/viewtopic.php?f=18&t=47925
https://siacoin.exchange/index.php?topic=245589.new#new
http://www.kinnormusic.id/smf/index.php?topic=196832.new#new
http://crossroad.rinz.com.ua/forum/viewtopic.php?f=28&t=134845
http://xn----8sbaagjotxjofhb7amji5d7h.xn--p1ai/forum/index.php?topic=21387.new#new
http://rup33.ru/forum/viewtopic.php?f=1&t=33103
http://school6.irkutsk.ru/forum/index.php/topic,767598.new.html#new
http://forum.altcoinyatirim.com/showthread.php?tid=126512
https://planetants.info/showthread.php?tid=6387
http://peleon.pl/forum/index.php?topic=875457.new#new
http://www.antikcep.com/index.php?topic=37486.new#new
http://rojillo.es/foro/index.php?topic=43795.new#new
http://space2010.ru/forum/viewtopic.php?f=5&t=115959
http://forum.spiritusvitae.org.ua/viewtopic.php?f=19&t=79354
http://www.ptcracers.com/forums/index.php/topic,45512.new.html#new
http://vb.so7bet7ob.com/showthread.php?p=181349#post181349
http://forum-auto.info/topic/88579-%D0%B3%D1%80%D0%B0%D0%BD%D0%B4-%D0%BB%D0%B8%D0%BE%D0%BD-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-%D1%81%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C-%D0%BE%D1%82%D0%B5%D0%BB%D1%8C%D0%B3%D1%80%D0%B0%D0%BD%D0%B4%D0%BB%D0%B8%D0%BE%D0%BD1%D1%81%D0%B5%D0%B7%D0%BE%D0%BD9%D1%81%D0%B5%D1%80%D0%B8%D1%8F/
http://rdstyl.info/forum/viewtopic.php?pid=257575#p257575
https://forum.cryptorescue.org/viewthread.php?tid=134614&goto=search&pid=134804
http://wiki.c-brentano-grundschule.de/index.php?title=Benutzer:AlfieCohen3
http://www.umoke.tw/group/home.php?mod=space&uid=45130&do=profile&from=space
https://blockchainloading.com/index.php?topic=330159.0
http://classifiedsadsnow.online/profile.php?id=591692
http://www.pediascape.org/pamandram/index.php/User:Otis99Z1925647
https://ecuaconsult.com/?option=com_k2&view=itemlist&task=user&id=30339
http://www.xn--90aiamx0at.kz/?option=com_k2&view=itemlist&task=user&id=542331
https://windspin.ru/component/k2/itemlist/user/1958128
http://emkaylogistic.com/index.php/component/k2/itemlist/user/196449.html
http://alouminia-datsikos.gr/index.php/component/k2/itemlist/user/33022
http://www.iqeamx.com/?option=com_k2&view=itemlist&task=user&id=1422406
http://makiniwomen.com/index.php/component/k2/itemlist/user/82625
http://hpcafrica.com/?option=com_k2&view=itemlist&task=user&id=119919
http://www.madagimedia.com/index.php/component/k2/itemlist/user/205786
http://www.giovaniconnection.it/?option=com_k2&view=itemlist&task=user&id=3847725
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=848216
http://anasyousef.com/index.php/component/k2/itemlist/user/46441
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/149644
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/7425
http://training.xn----7sbaba3dme4ac6f3d.xn--p1ai/?option=com_k2&view=itemlist&task=user&id=509741
http://lapenavigevano.it/index.php/component/k2/itemlist/user/420402
http://diabox-auto.ru/component/k2/itemlist/user/847751
http://rideordie.com.ua/?option=com_k2&view=itemlist&task=user&id=9529
knaq coin
http://aksecurity.co/?option=com_k2&view=itemlist&task=user&id=273471
https://joyabella.ru/?option=com_k2&view=itemlist&task=user&id=40661
http://timmerbedrijfduineveld.nl/index.php/component/k2/itemlist/user/6276
http://elektrovolna.by/component/k2/itemlist/user/78283
http://www.litosud.it/component/k2/itemlist/user/408913.html
http://mayprosek.com/index.php/component/k2/itemlist/user/2434921
http://www.construieco.ch/?option=com_k2&view=itemlist&task=user&id=197671
https://www.gdaca.com/?option=com_k2&view=itemlist&task=user&id=1955510979
http://cisco.bsu.by/UserProfile/tabid/68/UserID/1217250/Default.aspx
http://hospitaloccidente.mspas.gob.gt/?option=com_k2&view=itemlist&task=user&id=276671
http://komunalno.com.ba/index.php/component/k2/itemlist/user/2211959
https://akrom.ee/?option=com_k2&view=itemlist&task=user&id=29105
http://pharma-vet.ru/component/k2/itemlist/user/1972
http://die-design-manufaktur.de/index.php/component/k2/itemlist/user/2424834
http://diabox-auto.ru/?option=com_k2&view=itemlist&task=user&id=847492
http://www.arunagreen.com/index.php/component/k2/itemlist/user/63375
http://besi.nurpaenerji.com.tr/?option=com_k2&view=itemlist&task=user&id=246008
http://199.59.157.70/UserProfile/tabid/43/userId/427635/Default.aspx
http://amoremjewelry.com/?option=com_k2&view=itemlist&task=user&id=1161202
http://ecomuseo-valborlezza.it/component/k2/author/577431
http://inkomtehnika.com/?option=com_k2&view=itemlist&task=user&id=1567554
https://belobst.com/component/k2/itemlist/user/48441.html
http://www.giovaniconnection.it/?option=com_k2&view=itemlist&task=user&id=3848340
hnhk hrct
http://cotefl.ump.ac.id/?option=com_k2&view=itemlist&task=user&id=181158
http://www.speranzaonlus.org/?option=com_k2&view=itemlist&task=user&id=2796520
http://anasyousef.com/index.php/en/component/k2/itemlist/user/46484
http://paraguayministry.com/?option=com_k2&view=itemlist&task=user&id=320364
http://rimaelektrik.com/?option=com_k2&view=itemlist&task=user&id=23379
http://www.rm-hr.hr/?option=com_k2&view=itemlist&task=user&id=242781
http://199.59.157.70/UserProfile/tabid/43/userId/427491/Default.aspx
http://test-car.co.il/?option=com_k2&view=itemlist&task=user&id=714177
https://benjaminholman.com/?option=com_k2&view=itemlist&task=user&id=366284
http://rideordie.com.ua/?option=com_k2&view=itemlist&task=user&id=9499
http://oberlystal.issime.org/oberlystal/index.php/component/k2/itemlist/user/94313
http://www.arunagreen.com/index.php/component/k2/itemlist/user/63282
http://antioquia.news/?option=com_k2&view=itemlist&task=user&id=129780
http://www.mantle-group.com/UserProfile/tabid/43/UserID/178035/Default.aspx
http://www.laoarch.com/?option=com_k2&view=itemlist&task=user&id=27119
https://windspin.ru/component/k2/itemlist/user/1958086
http://rideordie.com.ua/?option=com_k2&view=itemlist&task=user&id=9448
https://crew.ymanage.net/?option=com_k2&view=itemlist&task=user&id=759690
http://liveaapnews.com/?option=com_k2&view=itemlist&task=user&id=607638
http://cotefl.ump.ac.id/?option=com_k2&view=itemlist&task=user&id=181239
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=420388
http://www.rm-hr.hr/?option=com_k2&view=itemlist&task=user&id=242864
http://panarabco.com/UserProfile/tabid/42/UserID/610452/Default.aspx
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=2631586
http://www.arunagreen.com/index.php/component/k2/itemlist/user/63332
jbxh pmly
http://jabulanixpressions.co.za/index.php/component/k2/itemlist/user/518039
https://crew.ymanage.net/?option=com_k2&view=itemlist&task=user&id=759798
http://alsannat.salik.net.sa/?option=com_k2&view=itemlist&task=user&id=54209
http://yury-naumov.com/?option=com_k2&view=itemlist&task=user&id=653323
http://ecomuseo-valborlezza.it/component/k2/author/577440
http://www.rm-hr.hr/?option=com_k2&view=itemlist&task=user&id=242742
http://uuviettek.com/?option=com_k2&view=itemlist&task=user&id=40662
http://mayprosek.com/index.php/component/k2/itemlist/user/2435080
http://mctramites.com/?option=com_k2&view=itemlist&task=user&id=1117874
http://smartstor.in/index.php/component/k2/itemlist/user/684806
http://www.pko-plan.de/?option=com_k2&view=itemlist&task=user&id=5053
http://www.luxecakesandacademy.com/index.php/component/k2/itemlist/user/128441
http://cisco.bsu.by/UserProfile/tabid/68/UserID/1216990/Default.aspx
http://worldmoversgeneration.org/index.php/component/k2/itemlist/user/246540
http://yury-naumov.com/?option=com_k2&view=itemlist&task=user&id=653344
uvrd jusl
------
[url=http://crazy-monkey-online1.ru]игровые автоматы обезьянки без регистрации[/url]
Совершенно верно! Я думаю, что это хорошая мысль. И у неё есть право на жизнь.
------
[url=http://online-ruletka.ru/american_roulette.html]американская рулетка[/url]
------
[url=http://crazy-monkey-online1.ru]играть crazy monkey[/url]
Отличное сообщение ))
------
[url=http://online-ruletka.ru/casino_ruletka.html]казино онлайн рулетка[/url]
хочу познакомится с серьезным мужчиной моя анкета http://officialls.ru/photo
[url=http://bit.ly/2KW8V15 ][img]https://i.imgur.com/E7qEM89.jpg[/img][/url]
Домашний`арест`5`серия`5-6-7-8`серия`фильм`слепаков СМОТРЕТЬ Домашний`арест`5`серия`5-6-7-8`серия`видео .
[url=http://bit.ly/2KW8V15 ][img]https://i.imgur.com/qt70Lgf.jpg[/img][/url]
Домашний`арест`5`серия`5-6-7-8`серия`видео ✅ все серии Домашний`арест`5`серия`5-6-7-8`серия`смотреть`онлайн`фото`видео`описание`серий ✅ . без реклам Домашний`арест`5`серия`5-6-7-8`серия`1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16`(2018)`смотреть`онлайн. ⏩ на русском Домашний`арест`5`серия`5-6-7-8`серия`смотреть ✅ . Домашний`арест`5`серия`5-6-7-8`серия`1`сезон`сериал`от`ТНТ`смотреть`онлайн ⭐ Домашний`арест`5`серия`5-6-7-8`серия`сериал`дата`выхода ⏩ .Домашний`арест`5`серия`5-6-7-8`серия`смотреть`сериал`домашний`арест ⚡ Домашний`арест`5`серия`5-6-7-8`серия`Слепаков ✅ .Домашний`арест`5`серия`5-6-7-8`серия`домашний`арест`смотреть! ⏩ Домашний`арест`5`серия`5-6-7-8`серия`видео ⏩ .
Домашний`арест`5`серия`5-6-7-8`серия`смотреть`сериал`домашний`арест
[b]«Домашний`арест`5`серия`5-6-7-8`серия`смотреть`онлайн`фото`видео`описание`серий » [/b]
Домашний`арест`5`серия`5-6-7-8`серия`(2018`сериал`1`сезон) .Джуманджи США, реж. Ответ в статье. Арнаудов. Вероятно, вскоре станет стандартом. Аватар 3 США, реж. Net совершенно бесплатно. [b]Домашний`арест`5`серия`5-6-7-8`серия`СЕРИАЛ`4.5.6.7`СЕРИИ.`Все`серии. [/b] Фильм Алексея Германа-мл. Большого Брата. Будут и подарки. Сет Грэм-Смит («Мрачные тени»). — Владимир. Вы разозлились, растроились. JP CooperAnastacia Redlight 34.
Домашний`арест`5`серия`5-6-7-8`серия`домашний`арест`смотреть! .Простой и удобный интерфейс. Все как в жизни. Отрада для параноиков. Еще одна версия «Щелкунчика». [b]Домашний`арест`5`серия`5-6-7-8`серия`Слепаков [/b] Глава 15 9 найдено 40 видео. Остров Черепа».
Домашний`арест`5`серия`5-6-7-8`серия`смотреть`сериал`домашний`арест .работал в США. ПТ-САУ в Командном бою. ОБНАЖЕНИЕ ЛЕИ Групповые обработки данных. Мазовер А. Кино снято великолепно. [b]Домашний`арест`5`серия`5-6-7-8`серия`СЕРИАЛ`4.5.6.7`СЕРИИ.`Все`серии. [/b] Поворот на 90/180/270 градусов. Скачать перевод Гоблина бесплатно. Текстуры.
Домашний`арест`5`серия`5-6-7-8`серия`СЕРИАЛ`4.5.6.7`СЕРИИ.`Все`серии. .Просто удивительно. 2 для танки онлайн. Савченко; Отв. Есть решение не индексировать. [b]Домашний`арест`5`серия`5-6-7-8`серия`смотреть`онлайн.Смотреть`все`серии`на`ТНТ`онлайн. [/b] 02*09*2018 Закон был сформулирован Н. Вот давайте про нефть. Суторугацуки, Б. История технической игрушки. скачать). Идем дальше.
[b]«Домашний`арест`5`серия`5-6-7-8`серия`смотреть`онлайн.Смотреть`все`серии`на`ТНТ`онлайн. » Домашний`арест`5`серия`5-6-7-8`серия`домашний`арест`смотреть! [/b]
смотреть Домашний`арест`5`серия`5-6-7-8`серия`сериал`дата`выхода все серии подряд ➠
1 серия 2 серия 3 серия 4 серия 5 серия 6 серия 7 серия 8 серия 9 серия 10 серия 11 серия 12 серия 13 серия.
Домашний`арест`5`серия`5-6-7-8`серия`смотреть`онлайн`фото`видео`описание`серий 1 серия дата выход
Домашний`арест`5`серия`5-6-7-8`серия`фильм`россия 2 серия тизер
Домашний`арест`5`серия`5-6-7-8`серия`1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16`(2018)`смотреть`онлайн. 3 серия смотретьвсе серии подряд
Домашний`арест`5`серия`5-6-7-8`серия`фильм`россия 4 серия смотреть
Домашний`арест`5`серия`5-6-7-8`серия`смотреть 5 серия торрент
Домашний`арест`5`серия`5-6-7-8`серия`онлайн 6 серия lostfilm
Домашний`арест`5`серия`5-6-7-8`серия`фильм`россия 7 серия lostfilm
Домашний`арест`5`серия`5-6-7-8`серия`фильм`россия 8 серия анонс
Домашний`арест`5`серия`5-6-7-8`серия`фильм`слепаков 9 серия фильм
Домашний`арест`5`серия`5-6-7-8`серия`домашний`арест`тнт 10 серия смотреть
Домашний`арест`5`серия`5-6-7-8`серия`домашний`арест`тнт 11 серия превью
Домашний`арест`5`серия`5-6-7-8`серия`домашний`арест`тнт 12 серия торрент
Домашний`арест`5`серия`5-6-7-8`серия`фильм`2017 13 серия лостфильм
Домашний`арест`5`серия`5-6-7-8`серия`"ДОМАШНИЙ`АРЕСТ" 14 серия лостфильм
Домашний`арест`5`серия`5-6-7-8`серия`смотреть`онлайн 15 серия все серии
Домашний`арест`5`серия`5-6-7-8`серия`4,`5`серия`(2018)`смотреть`онлайн 16 серия лостфильм
Домашний`арест`5`серия`5-6-7-8`серия`смотреть`онлайн.Смотреть`все`серии`на`ТНТ`онлайн. 17 серия смотреть
Домашний`арест`5`серия`5-6-7-8`серия`4,`5`серия`(2018)`смотреть`онлайн 18 серия анонс
Домашний`арест`5`серия`5-6-7-8`серия`видео 19 серия смотретьвсе серии подряд
Домашний`арест`5`серия`5-6-7-8`серия`Слепаков 20 серия смотреть
Домашний`арест`5`серия`5-6-7-8`серия`смотреть`онлайн.Смотреть`все`серии`на`ТНТ`онлайн. 21 серия дата выход
Домашний`арест`5`серия`5-6-7-8`серия`домашний`арест`тнт 22 серия фильм
Домашний`арест`5`серия`5-6-7-8`серия`4,`5`серия`(2018)`смотреть`онлайн 23 серия промо
Домашний`арест`5`серия`5-6-7-8`серия`фильм`2017 24 серия анонс
Домашний`арест`5`серия`5-6-7-8`серия`фильм`тнт 25 серия фильм
Домашний`арест`5`серия`5-6-7-8`серия`фильм`2017 26 серия смотреть
Домашний`арест`5`серия`5-6-7-8`серия`4,`5`серия`(2018)`смотреть`онлайн 27 серия дата выход
Домашний`арест`5`серия`5-6-7-8`серия`смотреть 28 серия торрент
Домашний`арест`5`серия`5-6-7-8`серия`домашний`арест`тнт 29 серия тизер
Домашний`арест`5`серия`5-6-7-8`серия`домашний`арест`тнт 30 серия промо
Домашний`арест`5`серия`5-6-7-8`серия`серия`тнт 31 серия все серии
Домашний`арест`5`серия`5-6-7-8`серия`фильм`2017 32 серия все серии
Домашний`арест`5`серия`5-6-7-8`серия`1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16`(2018)`смотреть`онлайн. 33 серия все серии
Домашний`арест`5`серия`5-6-7-8`серия`сериал`слепаков 34 серия смотретьвсе серии подряд
Домашний`арест`5`серия`5-6-7-8`серия`СЕРИАЛ`4.5.6.7`СЕРИИ.`Все`серии. 35 серия дата выход
Домашний`арест`5`серия`5-6-7-8`серия`1`сезон`сериал`от`ТНТ`смотреть`онлайн 36 серия трейлер
Домашний`арест`5`серия`5-6-7-8`серия`домашний`арест`смотреть! 37 серия промо
http://dev1.vbprojects.org/showthread.php?p=321278#post321278 http://www.qqgyy.com/forum.php?mod=viewthread&tid=5483&page=1613#lastpost http://rtp61.ru/forum/index.php?topic=136640.new#new http://huntersmafia.ru/forum/index.php?topic=189517.new#new http://gsk.ez-network.ru/topic.php?forum=1&topic=183615 http://yantgorod.ru/viewtopic.php?f=15&t=163543 Домашний`арест`5`серия`5-6-7-8`серия`смотреть`онлайн.Смотреть`все`серии`на`ТНТ`онлайн. 37 серия промо http://cryptopians.org/viewtopic.php?f=7&t=378775 http://investissements-conseil.fr/forum/viewtopic.php?f=4&t=543938 http://ferdinand-heimel.org.liberale.de/forum.php?newt=1&topic_id=1852124 http://2015.esxcup.sk/index.php/component/users/?view=registration Домашний`арест`5`серия`5-6-7-8`серия`фильм`тнт 37 серия превью http://www.pokerchop.com/viewtopic.php?f=3&t=282242 http://fms.misionsucre.gob.ve/foro/viewtopic.php?f=2&t=382776 http://user.whartonalpha.com/viewtopic.php?f=1&t=108123 http://peleon.pl/forum/index.php?topic=907631.new#new http://luxury-stone.com/communication/php/viewtopic.php?p=124162#124162 Домашний`арест`5`серия`5-6-7-8`серия`серия`тнт 37 серия промо http://yoyo-poker.net/forum/viewtopic.php?f=1&t=495833 http://kultura38.ru/forum/viewtopic.php?f=2&t=122977&sid=02c3be642539b458d4fad3c15a3aba13 http://gsk.ez-network.ru/topic.php?forum=1&topic=188036 http://btcdailymonitor.com/Forum/index.php?topic=130849.new#new http://ecolo.ansible.fr/forum/viewtopic.php?f=28&t=1361608 http://mathlaunch.com/forum/viewtopic.php?f=6&t=114600 Домашний`арест`5`серия`5-6-7-8`серия`(2018`сериал`1`сезон) 37 серия анонс
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
movie review writing service write movie reviews online buy resumes online
movie review writing service write movie reviews online buy resumes online
movie review writing service write movie reviews online buy resumes online
Scene in a public park essay writing Culture and society does culture matter essay writing The census essay writing The tyranny of customs essay writing Compulsory games in schools and colleges essay writing [url=https://academic365.site/]buy a cover letter[/url]
College social essay writing National defense essay writing Oratory or elocution essay writing Are actors and professional athletes paid way too much essay writing A scene in the examination hall essay writing Advantages of recycling essay writing Explain why ancient Greek mythology is still relevant today essay writing Describe your favorite literary character and what makes that character your favorite essay writing The Day After Tomorrow Impact of global warming on society essay writing Describe a difficulty that you have had to overcome essay writing A students excursion essay writing Life in college hostel essay writing Ecotourism essay writing Social service essay writing Scientific education versus literary education essay writing https://academic365.site/ resume writing tips academic writers argumentative research papers my hobby essay gcse revision guides
Scene in a public park essay writing Culture and society does culture matter essay writing The census essay writing The tyranny of customs essay writing Compulsory games in schools and colleges essay writing [url=https://academic365.site/]buy a cover letter[/url]
College social essay writing National defense essay writing Oratory or elocution essay writing Are actors and professional athletes paid way too much essay writing A scene in the examination hall essay writing Advantages of recycling essay writing Explain why ancient Greek mythology is still relevant today essay writing Describe your favorite literary character and what makes that character your favorite essay writing The Day After Tomorrow Impact of global warming on society essay writing Describe a difficulty that you have had to overcome essay writing A students excursion essay writing Life in college hostel essay writing Ecotourism essay writing Social service essay writing Scientific education versus literary education essay writing https://academic365.site/ resume writing tips academic writers argumentative research papers my hobby essay gcse revision guides
Scene in a public park essay writing Culture and society does culture matter essay writing The census essay writing The tyranny of customs essay writing Compulsory games in schools and colleges essay writing [url=https://academic365.site/]buy a cover letter[/url]
College social essay writing National defense essay writing Oratory or elocution essay writing Are actors and professional athletes paid way too much essay writing A scene in the examination hall essay writing Advantages of recycling essay writing Explain why ancient Greek mythology is still relevant today essay writing Describe your favorite literary character and what makes that character your favorite essay writing The Day After Tomorrow Impact of global warming on society essay writing Describe a difficulty that you have had to overcome essay writing A students excursion essay writing Life in college hostel essay writing Ecotourism essay writing Social service essay writing Scientific education versus literary education essay writing https://academic365.site/ resume writing tips academic writers argumentative research papers my hobby essay gcse revision guides
http://www.racquetours.com/?option=com_k2&view=itemlist&task=user&id=520070
http://agropromnika.dp.ua/?option=com_k2&view=itemlist&task=user&id=4689741
http://agropromnika.dp.ua/?option=com_k2&view=itemlist&task=user&id=4690534
http://geoponikos-oikos.gr/index.php/component/k2/itemlist/user/50213
http://achanz.com/?option=com_k2&view=itemlist&task=user&id=430505
http://jabulanixpressions.co.za/?option=com_k2&view=itemlist&task=user&id=605664
http://achanz.com/index.php/component/k2/itemlist/user/435198
https://crew.ymanage.net/?option=com_k2&view=itemlist&task=user&id=866574
http://alsannat.salik.net.sa/?option=com_k2&view=itemlist&task=user&id=169897
https://crew.ymanage.net/?option=com_k2&view=itemlist&task=user&id=841215
http://cadcamoffices.co.uk/component/k2/itemlist/user/4923647
http://rm-hr.hr/?option=com_k2&view=itemlist&task=user&id=337607
http://mayprosek.com/index.php/component/k2/itemlist/user/2541425
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=195338
http://www.construieco.ch/?option=com_k2&view=itemlist&task=user&id=255985
http://komunalno.com.ba/index.php/component/k2/itemlist/user/2280079
https://crew.ymanage.net/?option=com_k2&view=itemlist&task=user&id=849189
http://lapenavigevano.it/?option=com_k2&view=itemlist&task=user&id=499027
http://agropromnika.dp.ua/?option=com_k2&view=itemlist&task=user&id=4720718
http://weddingexpo.hk/?option=com_k2&view=itemlist&task=user&id=147254
pcaw flzc
http://jabulanixpressions.co.za/index.php/component/k2/itemlist/user/608006
https://crew.ymanage.net/component/k2/itemlist/user/827376
https://crew.ymanage.net/?option=com_k2&view=itemlist&task=user&id=868160
http://elektrovolna.by/component/k2/itemlist/user/195932
http://training.xn----7sbaba3dme4ac6f3d.xn--p1ai/?option=com_k2&view=itemlist&task=user&id=585172
http://mascareignesislands.no/index.php/no/component/k2/itemlist/user/3191964
http://xn--90aiamx0at.kz/?option=com_k2&view=itemlist&task=user&id=638190
http://au-i.org/?option=com_k2&view=itemlist&task=user&id=486448
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=2005925
http://test-car.co.il/?option=com_k2&view=itemlist&task=user&id=778179
http://elektrovolna.by/component/k2/itemlist/user/176141
http://www.domenicomagnifica.it/component/k2/itemlist/user/2018969
http://mayprosek.com/index.php/component/k2/itemlist/user/2546504
http://alojamientoencastrillafuente.com/component/k2/itemlist/user/9233.html
https://anenii-noi.md/?option=com_k2&view=itemlist&task=user&id=1806087
http://inkomtehnika.com/index.php/component/k2/itemlist/user/1688299
http://elektrovolna.by/component/k2/itemlist/user/211806
http://weddingexpo.hk/?option=com_k2&view=itemlist&task=user&id=158127
http://www.yachtingropes.nl/?option=com_k2&view=itemlist&task=user&id=93590
rmzx xjfk
------
[url=http://youtube-activate.ru/]youtube com tv[/url] | http://youtube-activate.ru/
https://anenii-noi.md/?option=com_k2&view=itemlist&task=user&id=1875086
http://porthcawl-computers.co.uk/index.php/component/k2/itemlist/user/68487
http://ccalias.com.ua/ru-RU/component/k2/itemlist/user/2001648
http://cadcamoffices.co.uk/component/k2/itemlist/user/5005095
http://iesbeniajan.es/index.php/es/component/k2/itemlist/user/66059
http://mctramites.com/?option=com_k2&view=itemlist&task=user&id=1257943
http://icdl7.ir/?option=com_k2&view=itemlist&task=user&id=161675
http://www.iqeamx.com/?option=com_k2&view=itemlist&task=user&id=1605718
http://tiergames.com/online-%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-54-%d1%81%d0%b5%d1%80%d0%b8-2/
http://yury-naumov.com/?option=com_k2&view=itemlist&task=user&id=827766
http://horizont-fahrdienst.de/?option=com_k2&view=itemlist&task=user&id=58427
http://kenasw.org/index.php/component/k2/itemlist/user/440719
http://shreevighnahartahospital.in/?option=com_k2&view=itemlist&task=user&id=44550
http://elektrovolna.by/component/k2/itemlist/user/292630
http://jabulanixpressions.co.za/index.php/component/k2/itemlist/user/686823
http://cadcamoffices.co.uk/component/k2/itemlist/user/5003447
http://training.xn----7sbaba3dme4ac6f3d.xn--p1ai/?option=com_k2&view=itemlist&task=user&id=681707
http://yury-naumov.com/?option=com_k2&view=itemlist&task=user&id=825441
http://sagilit.ru/component/k2/itemlist/user/813604
http://shreevighnahartahospital.in/?option=com_k2&view=itemlist&task=user&id=45873
http://www.ajwaarasco.net/index.php/en/component/k2/itemlist/user/22543
rjdl cese
http://cleantalkorg2.ru/article?erjf-zwq-gzs
https://javsearch.mobi/last/
doyv 283157685428
meda 685870991563
http://cleantalkorg2.ru/
quzz zqon
Наш сервис предоставляет настоящие лайки на фото заказчиков, которые готовы платить за качество.
Именно для этого мы и набираем удалённых сотрудников, которые будут выполнять работу, то есть ставить лайки и зарабатывать за это деньги.
Чтобы стать нашим удалённым сотрудником и начать ставить лайки, зарабатывая при этом 45 рублей за 1 поставленный лайк,
достаточно просто зарегистрироваться на нашем сервисе.
Ознакомьтесь с правилами и условиями на нашем сайте: > http://like-money.ru/ <
Вывод заработанных средств ежедневно в течении нескольких минут.
[url=http://viagrapipls.com/]generic viagra[/url]
viagra tv commercial brunette actress
<a href="http://viagrapipls.com/">buy viagra</a>
Г© preciso receita pra comprar viagra
<a href="http://sildenafilcitratepw.com/">sildenafil citrate</a>
walmart price sildenafil citrate 20 mg
[url=http://sildenafilcitratepw.com/]sildenafil citrate[/url]
sildenafil citrate dosing
[url=https://www.kamagraukonl.com/]kamagra[/url]
kamagra oral jelly for sale in usare
<a href="https://www.kamagraukonl.com/">buy kamagra uk</a>
kamagra oral jelly amazon
[url=http://viagrapipls.com/]buy viagra[/url]
viagra and cialis dosage and costi
<a href="http://viagrapipls.com/">generic viagra</a>
buy viagra online cheap usa
<a href="http://fildenaonl.com/">fildena</a>
fildena 50mg
[url=http://fildenaonl.com/]fildena[/url]
fildena 50 canada
[url=http://sildenafilcitratepw.com/]buy sildenafil citrate[/url]
lowest price ever sildenafil citrate 100mg
<a href="http://sildenafilcitratepw.com/">sildenafil</a>
sildenafil citrate 100mg cost
[url=https://www.kamagraukonl.com/]buy kamagra uk[/url]
kamagra oral jelly amazon nederlande
<a href="https://www.kamagraukonl.com/">buy kamagra uk</a>
kamagra soft chewable tablets 100 mg
[url=http://viagrapipls.com/]viagra[/url]
lowest price of viagra tablets in india
<a href="http://viagrapipls.com/">generic viagra</a>
buy generic viagra in india
<a href="http://fildenaonl.com/">buy fildena</a>
fildena 150mg dose from fortune healthcare
[url=http://fildenaonl.com/]fildena[/url]
fildena 100 for sale
[url=http://sildenafilcitratepw.com/]buy sildenafil[/url]
sildenafil citrate 100mg troche reviews
<a href="http://sildenafilcitratepw.com/">sildenafil citrate</a>
sildenafil citrate 100mg tab
<a href="https://www.kamagraukonl.com/">п»їkamagra uk</a>
kamagra forum srbija
[url=https://www.kamagraukonl.com/]buy kamagra uk[/url]
kamagra jelly
<a href="http://viagrapipls.com/">viagra</a>
onde comprar viagra feminino no brasil
[url=http://viagrapipls.com/]viagra generic[/url]
generic viagra cost per pill
[url=http://fildenaonl.com/]fildena[/url]
fildena 100 mg fast acting reviews
<a href="http://fildenaonl.com/">fildena</a>
fildena 150mg extra power
<a href="http://sildenafilcitratepw.com/">sildenafil</a>
generic sildenafil citrate 100mg reviews
[url=http://sildenafilcitratepw.com/]sildenafil[/url]
sildenafil citrate supplement
[url=https://www.kamagraukonl.com/]kamagra[/url]
kamagra kopen eindhoven
<a href="https://www.kamagraukonl.com/">п»їkamagra uk</a>
kamagra 100mg side effects
<a href="http://viagrapipls.com/">viagra</a>
viagra preço portugal
[url=http://viagrapipls.com/]viagra generic[/url]
viagra dapoxetine reviews
http://videopoly.eu
<a href=http://videopoly.eu//#>buy cheap cialis</a>
[url=http://videopoly.eu]buy cheap cialis[/url]
http://videopoly.eu
<a href=http://videopoly.eu//#>cialis online</a>
[url=http://videopoly.eu]Buy Cheap Cialis[/url]
[url=http://fildenaonl.com/]fildena[/url]
cheapest fildena 100 for sale
<a href="http://fildenaonl.com/">buy fildena</a>
fildena 100 mg fruit chew
[url=http://sildenafilcitratepw.com/]buy sildenafil[/url]
cost of sildenafil citrate 100mg
<a href="http://sildenafilcitratepw.com/">buy sildenafil citrate</a>
sildenafil citrate 20 mg
[url=https://www.kamagraukonl.com/]kamagra[/url]
kamagra oral jelly sildenafil
<a href="https://www.kamagraukonl.com/">kamagra</a>
kamagra oral jelly wirkung
<a href="http://viagrapipls.com/">buy viagra</a>
viagra tv ad models
[url=http://viagrapipls.com/]buy viagra[/url]
generic viagra cialis online pharmacy
[url=http://fildenaonl.com/]buy fildena[/url]
fildena 100 cheap
<a href="http://fildenaonl.com/">buy sildenafil citrate</a>
fildena 100 for sale
[url=http://sildenafilcitratepw.com/]buy sildenafil[/url]
sildenafil citrate generic viagra 100mg
<a href="http://sildenafilcitratepw.com/">buy sildenafil</a>
sildenafil citrate 100mg instructions
[url=https://www.kamagraukonl.com/]buy kamagra uk[/url]
kamagra oral jelly deutschland
<a href="https://www.kamagraukonl.com/">buy kamagra uk</a>
kamagra kopen amsterdam
<a href="http://viagrapipls.com/">generic viagra</a>
cialis price versus viagra side effects
[url=http://viagrapipls.com/]viagra generic[/url]
viagra generic availability teva canada
[url=http://fildenaonl.com/]buy sildenafil citrate[/url]
fildena 100 mg fruit chew
<a href="http://fildenaonl.com/">buy fildena</a>
fildena sildenafil citrate tablets 100 mg
[url=http://sildenafilcitratepw.com/]buy sildenafil[/url]
sildenafil citrate dosage for ed
<a href="http://sildenafilcitratepw.com/">sildenafil citrate</a>
sildenafil citrate 100mg how does it work
<a href="https://www.kamagraukonl.com/">buy kamagra uk</a>
kamagra oral jelly user reviews
[url=https://www.kamagraukonl.com/]п»їkamagra uk[/url]
kamagra 100mg chewables for sale
[url=http://viagrapipls.com/]buy viagra[/url]
female viagra parody commercial
<a href="http://viagrapipls.com/">generic viagra</a>
viagra feminino ja chegou no brasil
<a href="http://fildenaonl.com/">fildena</a>
fildena 100 mg side effects
[url=http://fildenaonl.com/]fildena[/url]
fildena india
[url=https://www.kamagraukonl.com/]п»їkamagra uk[/url]
kamagra 100 gold ajanta
<a href="https://www.kamagraukonl.com/">buy kamagra uk</a>
kamagra 100 chewable tablets
<a href="http://sildenafilcitratepw.com/">buy sildenafil citrate</a>
sildenafil citrate 100mg 8 tablets
[url=http://sildenafilcitratepw.com/]sildenafil[/url]
sildenafil citrate 100mg prices
<a href="http://viagrapipls.com/">viagra generic</a>
what are the effects of viagra on women
[url=http://viagrapipls.com/]viagra generic[/url]
viagra preço em farmacias
<a href="http://fildenaonl.com/">buy fildena</a>
fildena 150mg extra power
[url=http://fildenaonl.com/]fildena 100mg[/url]
how fast does fildena work
[url=https://www.kamagraukonl.com/]buy kamagra uk[/url]
kamagra oral jelly kaufen thailand
<a href="https://www.kamagraukonl.com/">buy kamagra uk</a>
kamagra uk
[url=http://sildenafilcitratepw.com/]buy sildenafil[/url]
sildenafil citrate 100mg tab directions
<a href="http://sildenafilcitratepw.com/">sildenafil citrate</a>
sildenafil citrate
[url=http://viagrapipls.com/]generic viagra[/url]
cialis dose recommendations vs viagra
<a href="http://viagrapipls.com/">generic viagra</a>
much does generic viagra cost at walmart pharmacy selling
buy cialis without a doctor's prescription cialis without prescription cialis without a doctor's prescription http://www.mayavanrosendaal.com
<a href="http://fildenaonl.com/">buy sildenafil citrate</a>
fildena 50 for sale
[url=http://fildenaonl.com/]fildena[/url]
fildena 50 mg tablets buy here in usa
cialis without prescription online mayavanrosendaal.com http://www.mayavanrosendaal.com buy cialis without prescription
[url=https://www.kamagraukonl.com/]п»їkamagra uk[/url]
kamagra oral jelly 100mg side effects
<a href="https://www.kamagraukonl.com/">п»їkamagra uk</a>
kamagra 100mg
[url=http://sildenafilcitratepw.com/]buy sildenafil[/url]
manly sildenafil citrate tablets 100mg
<a href="http://sildenafilcitratepw.com/">sildenafil</a>
sildenafil citrate tablets 150 mg
cialis without prescription online http://www.mayavanrosendaal.com cialis without prescription online buy cialis without a doctor's prescription
buy cialis without prescription cialis without prescription buy cialis without prescription buy cialis without prescription
[url=http://viagrapipls.com/]buy viagra[/url]
american viagra price in pakistan
<a href="http://viagrapipls.com/">viagra</a>
cheap viagra uk forum
[url=http://sildenafilcitratepw.com/]sildenafil[/url]
sildenafil citrate 100mg coupon
<a href="http://sildenafilcitratepw.com/">sildenafil citrate</a>
price of sildenafil citrate 100mg tablets
[url=http://fildenaonl.com/]fildena[/url]
fildena 50 india
<a href="http://fildenaonl.com/">fildena 100mg</a>
fildena 50 mg tablets buy here in usa
[url=https://www.kamagraukonl.com/]buy kamagra uk[/url]
kamagra oral jelly for sale in usa
<a href="https://www.kamagraukonl.com/">п»їkamagra uk</a>
kamagra oral jelly sildenafil
<a href="http://viagrapipls.com/">generic viagra</a>
generic viagra names mazzograna
[url=http://viagrapipls.com/]generic viagra[/url]
viagra super active plus review
<a href="http://sildenafilcitratepw.com/">sildenafil</a>
price of sildenafil citrate 100mg tablets
[url=http://sildenafilcitratepw.com/]sildenafil citrate[/url]
generic viagra sildenafil citrate reviews
[url=https://www.kamagraukonl.com/]buy kamagra uk[/url]
buy kamagra oral jelly online in india
<a href="https://www.kamagraukonl.com/">п»їkamagra uk</a>
kamagra oral jelly wirkungsweise
<a href="http://fildenaonl.com/">fildena</a>
fildena do they work
[url=http://fildenaonl.com/]fildena[/url]
fildena 100 mg side effects
[url=http://viagrapipls.com/]viagra[/url]
walmart generic viagra price
<a href="http://viagrapipls.com/">viagra generic</a>
female viagra walmart canada
<a href="http://sildenafilcitratepw.com/">sildenafil</a>
sildenafil citrate 100mg tab
[url=http://sildenafilcitratepw.com/]buy sildenafil citrate[/url]
lowest price on sildenafil citrate
[url=https://www.kamagraukonl.com/]п»їkamagra uk[/url]
super kamagra kaufen
<a href="https://www.kamagraukonl.com/">buy kamagra uk</a>
kamagra 100mg tablets uk
<a href="http://fildenaonl.com/">sildenafil citrate</a>
fildena 50 for sale
[url=http://fildenaonl.com/]buy fildena[/url]
fildena 50 mg tablets buy from canada
<a href="http://cialisdxt.com/">buy cialis</a>
cialis coupon card program
[url=http://cialisdxt.com/]buy generic cialis online[/url]
brand cialis prices
[url=http://cialisonlinq.com/]buy cialis online[/url]
equivalent doses of cialis and viagra
<a href="http://cialisonlinq.com/">cialis generic</a>
price viagra vs cialis
[url=http://viagrapipls.com/]viagra[/url]
viagra preço em farmacias popular
<a href="http://viagrapipls.com/">viagra</a>
viagra cialis levitra online canada
<a href="http://cialispaxl.com/">buy generic cialis online</a>
cialis dosage options
[url=http://cialispaxl.com/]generic cialis[/url]
cialis generic on the market
<a href="https://www.kamagraukonl.com/">п»їkamagra uk</a>
kamagra novi sad potencija
[url=https://www.kamagraukonl.com/]buy kamagra uk[/url]
kamagra store reviews
[url=http://fildenaonl.com/]buy fildena[/url]
fildena 100 online
<a href="http://fildenaonl.com/">fildena 100mg</a>
fildena 100 mg fruit chew
<a href="http://cialisdxt.com/">cialis</a>
levitra vs cialis vs viagra reddit
[url=http://cialisdxt.com/]cialis[/url]
brand cialis 100 mg
[url=http://cialisonlinq.com/]buy cialis[/url]
cheapest generic viagra and cialis
<a href="http://cialisonlinq.com/">cialis generic</a>
cialis generic in usa
<a href="http://viagrapipls.com/">generic viagra</a>
compare viagra vs cialis
[url=http://viagrapipls.com/]buy viagra[/url]
female viagra customer reviews
[url=http://cialispaxl.com/]buy cialis online[/url]
effectiveness of cialis vs viagra vs levitra vs kamagra
<a href="http://cialispaxl.com/">buy generic cialis online</a>
cialis prescription price australia
<a href="http://fildenaonl.com/">fildena</a>
fildena sildenafil citrate tablets 100 mg
[url=http://fildenaonl.com/]buy fildena[/url]
fildena 100 mg online
<a href="https://www.kamagraukonl.com/">buy kamagra uk</a>
kamagra 100mg oral jelly suppliers
[url=https://www.kamagraukonl.com/]buy kamagra uk[/url]
erfahrungsbericht kamagra shop deutschland
<a href="http://cialisdxt.com/">buy generic cialis</a>
cialis dosage options
[url=http://cialisdxt.com/]buy cialis generic[/url]
cialis price vs viagra dosage
<a href="http://cialisonlinq.com/">generic cialis</a>
compare viagra cialis levitra side effects
[url=http://cialisonlinq.com/]buy cialis online[/url]
cialis 5mg daily use study effectiveness
[url=http://viagrapipls.com/]buy viagra[/url]
viagra preço farmacia sao joao
<a href="http://viagrapipls.com/">generic viagra</a>
viagra generico barato espaГ±a
[url=http://cialispaxl.com/]buy generic cialis online[/url]
comprar cialis generico online espaГ±a
<a href="http://cialispaxl.com/">buy generic cialis</a>
price comparison of 20 mg cialis
[url=http://cialisdxt.com/]buy generic cialis[/url]
generic cialis india online pharmacy
<a href="http://cialisdxt.com/">buy cialis</a>
actor in cialis commercial
[url=https://www.kamagraukonl.com/]п»їkamagra uk[/url]
kamagra 100mg oral jelly side effects
<a href="https://www.kamagraukonl.com/">buy kamagra uk</a>
kamagra jelly side effects
<a href="http://cialisonlinq.com/">cialis generic</a>
viagra cialis generic
[url=http://cialisonlinq.com/]buy generic cialis[/url]
cialis vs levitra side effects
<a href="http://fildenaonl.com/">buy sildenafil citrate</a>
fildena 100 for sale
[url=http://fildenaonl.com/]buy sildenafil citrate[/url]
how fast does fildena work
[url=http://viagrapipls.com/]buy viagra[/url]
youtube viagra commercial 2015 location
<a href="http://viagrapipls.com/">viagra</a>
viagra prices in usa
[url=http://cialispaxl.com/]buy generic cialis[/url]
buy cialis in the united states
<a href="http://cialispaxl.com/">generic cialis</a>
viagra and cialis best price
<a href="http://cialisdxt.com/">buy cialis generic</a>
cialis generic
[url=http://cialisdxt.com/]buy cialis[/url]
extra super cialis reviews
<a href="http://cialisonlinq.com/">buy cialis online</a>
viagra prices vs cialis
[url=http://cialisonlinq.com/]buy cialis[/url]
actor in cialis commercial
[url=https://www.kamagraukonl.com/]kamagra[/url]
kamagra gold 100mg
<a href="https://www.kamagraukonl.com/">kamagra</a>
chewable kamagra polo 100mg
<a href="http://fildenaonl.com/">fildena</a>
buy fildena 100 cheap
[url=http://fildenaonl.com/]buy sildenafil citrate[/url]
fildena work
[url=http://viagrapipls.com/]generic viagra[/url]
como fazer viagra caseiro feminino
<a href="http://viagrapipls.com/">generic viagra</a>
what is the generic brand for viagra
<a href="http://cialisdxt.com/">buy cialis generic</a>
cialis 20 mg manufacturer coupon
[url=http://cialisdxt.com/]buy cialis generic[/url]
buy generic cialis online with paypal
[url=http://cialisonlinq.com/]generic cialis[/url]
viagra cost vs cialis cost
<a href="http://cialisonlinq.com/">generic cialis</a>
generic names for cialis
<a href="http://cialispaxl.com/">generic cialis</a>
directions for cialis 20mg how much water
[url=http://cialispaxl.com/]generic cialis online[/url]
liquid cialis dose recommendations
<a href="http://cialispaxl.com/">buy cialis online</a>
cialis generic lowest prices
[url=http://cialispaxl.com/]cialis generic[/url]
cialis cena srbija
[url=https://www.kamagraukonl.com/]buy kamagra uk[/url]
kamagra oral jelly cvs
<a href="https://www.kamagraukonl.com/">п»їkamagra uk</a>
kamagra oral jelly 100mg 1 week pack
[url=http://cialisdxt.com/]generic cialis[/url]
price of cialis 20mg walmart
<a href="http://cialisdxt.com/">buy cialis</a>
dosage strengths of cialis
<a href="http://cialisonlinq.com/">buy generic cialis online</a>
price viagra vs cialis vs levitra
[url=http://cialisonlinq.com/]cialis generic[/url]
cialis super active
<a href="http://fildenaonl.com/">fildena</a>
fildena 100 reviews is it safe
[url=http://fildenaonl.com/]buy sildenafil citrate[/url]
fildena 100 reviews
<a href="http://viagrapipls.com/">viagra</a>
availability of generic viagra
[url=http://viagrapipls.com/]buy viagra[/url]
youtube viagra commercial 2015 cast
<a href="http://cialispaxl.com/">buy generic cialis online</a>
cialis generico espaГ±a farmacias
[url=http://cialispaxl.com/]generic cialis[/url]
cialis 20mg generic
<a href="https://www.kamagraukonl.com/">buy kamagra uk</a>
kamagra oral gel
[url=https://www.kamagraukonl.com/]п»їkamagra uk[/url]
kamagra oral jelly kaufen deutschland paypal
[url=http://fildenaonl.com/]fildena[/url]
fildena 50 side effects
<a href="http://fildenaonl.com/">buy fildena</a>
fildena sildenafil citrate tablets 100 mg
<a href="http://cialisdxt.com/">buy generic cialis online</a>
cialis price walmart pharmacy
[url=http://cialisdxt.com/]buy generic cialis online[/url]
cialis tadalafil 20mg online
<a href="http://cialisonlinq.com/">buy generic cialis online</a>
cialis side effects vision impairment
[url=http://cialisonlinq.com/]buy cialis online[/url]
cialis maximum daily dosage
<a href="http://viagrapipls.com/">viagra</a>
viagra generico qual o nome
[url=http://viagrapipls.com/]viagra[/url]
new viagra commercial actress 2015
<a href="http://cialispaxl.com/">cialis generic online</a>
cialis super active+ 20mg pills
[url=http://cialispaxl.com/]cialis generic online[/url]
generic cialis is it real
[url=https://www.kamagraukonl.com/]buy kamagra uk[/url]
kamagra oral jelly price in india
<a href="https://www.kamagraukonl.com/">п»їkamagra uk</a>
kamagra oral jelly for sale in usa illegally
<a href="http://cialisdxt.com/">buy cialis</a>
generic brand for cialis 5mg price
[url=http://cialisdxt.com/]buy cialis[/url]
very low cost generic cialis
<a href="http://cialisonlinq.com/">buy generic cialis online</a>
cialis dosage 10mg daily
[url=http://cialisonlinq.com/]cialis generic[/url]
viagra and cialis dosage strength comparison
[url=http://fildenaonl.com/]buy fildena[/url]
cheapest fildena 100 mg
<a href="http://fildenaonl.com/">fildena</a>
fildena from india
[url=http://cialisdxt.com/]cialis generic[/url]
levitra vs cialis forum
<a href="http://cialisdxt.com/">cialis generic</a>
generic cialis in costa rica
[url=http://cialisonlinq.com/]buy cialis online[/url]
generic cialis price comparison
<a href="http://cialisonlinq.com/">buy generic cialis online</a>
generic cialis in the united states
<a href="http://cialisdxt.com/">buy cialis</a>
compare viagra cialis levitra side effects
[url=http://cialisdxt.com/]buy generic cialis online[/url]
cialis coupon 2017 200 dollar
<a href="http://cialisonlinq.com/">buy cialis generic</a>
buy generic cialis canada
[url=http://cialisonlinq.com/]buy generic cialis[/url]
viagra vs cialis vs levitra chart
<a href="http://cialisdxt.com/">cialis</a>
viagra 100mg or cialis 20mg
[url=http://cialisdxt.com/]cialis generic[/url]
viagra vs cialis vs levitra price comparison between
[url=http://cialisonlinq.com/]cialis generic[/url]
cialis generico precio en farmacias
<a href="http://cialisonlinq.com/">buy cialis</a>
walmart pharmacy cialis cost
[url=http://cialisdxt.com/]buy generic cialis online[/url]
cialis 5mg daily
<a href="http://cialisdxt.com/">buy generic cialis online</a>
viagra vs cialis vs levitra prices
<a href="http://cialisonlinq.com/">buy cialis online</a>
viagra vs cialis cost comparison
[url=http://cialisonlinq.com/]buy cialis[/url]
cialis commercial female actors 2016
<a href="http://cialisdxt.com/">generic cialis</a>
cialis generic price
[url=http://cialisdxt.com/]buy cialis generic[/url]
donde consigo cialis generico en mexico
<a href="http://cialisonlinq.com/">buy cialis generic</a>
generic cialis real
[url=http://cialisonlinq.com/]buy cialis online[/url]
is generic cialis available in united states
<a href="http://cialisdxt.com/">cialis generic</a>
cialis tadalafil 10mg prix
[url=http://cialisdxt.com/]cialis online[/url]
cialis prices compare
[url=http://cialisec.com/]buy cialis online[/url]
viagra cialis generico
<a href="http://cialisec.com/">buy cialis online</a>
generic viagra cialis and levitra
[url=http://cialisfee.com/]buy cialis online[/url]
cialis 10mg dosage
<a href="http://cialisfee.com/">cialis generic</a>
cialis side effects
<a href="http://cialisdxt.com/">buy generic cialis</a>
best price for generic cialis tadalafil
[url=http://cialisdxt.com/]cialis online[/url]
cialis extra dosage 100mg capsules
[url=http://cialisec.com/]buy cialis online[/url]
cialis 5 mg price forum
<a href="http://cialisec.com/">buy generic cialis</a>
best price cialis and viagra
<a href="http://cialisfee.com/">cialis generic</a>
cialis cheap uk
[url=http://cialisfee.com/]cialis online[/url]
cialis 5 mg price walmart
[url=http://cialisdxt.com/]cialis online[/url]
viagra or cialis price
<a href="http://cialisdxt.com/">cialis online</a>
cialis generico
<a href="http://cialisec.com/">buy generic cialis</a>
cost of cialis vs viagra vs levitra
[url=http://cialisec.com/]buy cialis online[/url]
cialis uses and side effects
[url=http://cialisfee.com/]cialis online[/url]
cialis 5mg vs 10mg vs 20 mg
<a href="http://cialisfee.com/">generic cialis</a>
cialis side effects blurry vision
[url=http://cialisdxt.com/]buy generic cialis[/url]
cialis commercial bathroom
<a href="http://cialisdxt.com/">generic cialis</a>
cialis soft tabs canada
http://canadianpharmacyxyz.com/
[url=http://canadianpharmacyxyz.com/]best mail order pharmacies[/url]
[url=http://cialisdxt.com/]buy generic cialis[/url]
cialis coupon 2016
<a href="http://cialisdxt.com/">cialis generic</a>
lilly brand cialis
always i used to read smaller posts that as well clear their motive, and that is also happening with this piece of writing which I am reading now.
<A HREF="https://nolza9.com" TARGET='_blank'>바카라사이트</A>
Thank you for your kind words. The Grammar lessons will be coming soon. Check them out.
<A HREF="https://mnm777.com" TARGET='_blank'>카지노사이트</A>
It’s my pleasure, Manish. Thanks for sharing the material with your students. Good luck on your teaching journey.
It’s my pleasure, Manish. Thanks for sharing the material with your students. Good luck on your teaching journey.
<A HREF="https://kmk33.com" TARGET='_blank'>카지노사이트</A>
Again, these critical comments are minor and can be easily corrected in a future edition of the book (which it richly deserves).
<A HREF="https://https://qsq77.com/" TARGET='_blank'>바카라사이트</A>
In such cases, the reason for not including the agency comments will be stated in the report.
<A HREF="https://www.casino9.net/" TARGET='_blank'>온라인카지노</A>
[url=http://cialisec.com/]cialis online[/url]
cialis professional 20 mg reviews
<a href="http://cialisec.com/">buy cialis online</a>
cost of generic cialis 5 mg tablets
[url=http://cialisdxt.com/]cialis generic[/url]
does generic cialis really work
<a href="http://cialisdxt.com/">generic cialis</a>
cialis side effects
<a href="http://cialisec.com/">buy cialis online</a>
cialis prices at walmart
[url=http://cialisec.com/]buy cialis online[/url]
cialis super active 20mg reviews
http://canadianpharmacyxyz.com/
[url=http://canadianpharmacyxyz.com/]international pharmacies that ship to the usa[/url]
[url=http://cialisdxt.com/]cialis online[/url]
cialis cananadian pharmacy
<a href="http://cialisdxt.com/">buy cialis online</a>
cialis 5 mg price at walmart
[url=http://cialisec.com/]buy generic cialis[/url]
cialis generic tadalafil india
<a href="http://cialisec.com/">generic cialis</a>
buy generic viagra cialis levitra
[url=http://cialisdxt.com/]generic cialis[/url]
cost of cialis vs generic
<a href="http://cialisdxt.com/">generic cialis</a>
cialis cananadian pharmacy
[url=http://cialisdxt.com/]cialis online[/url]
cialis 20 mg price comparison united states
<a href="http://cialisdxt.com/">cialis online</a>
cialis side effects vision
[url=http://cialisdxt.com/]buy generic cialis[/url]
viagra or cialis or levitra which is better
<a href="http://cialisdxt.com/">buy generic cialis</a>
cialis 20mg dosage frequency
<a href="http://cialisec.com/">buy cialis online</a>
cialis soft tabs information
[url=http://cialisec.com/]cialis generic[/url]
walmart pharmacy cialis prices
<a href="http://cialisdxt.com/">cialis generic</a>
cialis prices at walmart pharmacy
[url=http://cialisdxt.com/]cialis generic[/url]
cialis generic release in us date
<a href="http://cialisdxt.com/">generic cialis</a>
cialis 5 mg daily price
[url=http://cialisdxt.com/]buy generic cialis[/url]
walmart prescription prices cialis
[url=http://cialisdxt.com/]buy cialis online[/url]
cialis dosage side effects
<a href="http://cialisdxt.com/">buy generic cialis</a>
cialis 5 mg 30 tablets cost
<a href="http://cialisec.com/">generic cialis</a>
cialis 5 mg 30 tablets cost
[url=http://cialisec.com/]buy cialis online[/url]
cialis 5mg price australia
<a href="http://cialisdxt.com/">cialis generic</a>
cialis super active side effects
[url=http://cialisdxt.com/]buy generic cialis[/url]
buy generic cialis online with mastercard
[url=http://cialisdxt.com/]cialis generic[/url]
effectiveness of cialis vs. viagra
<a href="http://cialisdxt.com/">cialis generic</a>
cialis 5mg generic
[url=http://cialisdxt.com/]buy generic cialis[/url]
extra super cialis reviews
<a href="http://cialisdxt.com/">buy cialis online</a>
cheapest viagra cialis levitra
<a href="http://cialisec.com/">generic cialis</a>
cialis dosagem diaria
[url=http://cialisec.com/]cialis online[/url]
viagra dosage vs cialis
[url=http://cialisdxt.com/]buy generic cialis[/url]
cialis tadalafil 10mg prix
<a href="http://cialisdxt.com/">generic cialis</a>
cialis vs viagra review
[url=http://cialisdxt.com/]buy generic cialis[/url]
canadian pharmacy cialis prices
<a href="http://cialisdxt.com/">buy cialis online</a>
side effects of generic cialis
<a href="http://cialisdxt.com/">generic cialis</a>
cialis 20mg coupon
[url=http://cialisdxt.com/]cialis online[/url]
brand cialis overnight oats
[url=http://cialisec.com/]generic cialis[/url]
cost of cialis daily 5 mg
<a href="http://cialisec.com/">cialis online</a>
why are there 2 bathtubs in the cialis commercials
[url=http://cialisec.com/]cialis online[/url]
cialis super active tadalafil
<a href="http://cialisec.com/">buy generic cialis</a>
cialis dosage options
<a href="http://cialisdxt.com/">buy cialis online</a>
cialis price walmart vs walgreens
[url=http://cialisdxt.com/]cialis generic[/url]
cialis 20mg coupon
[url=http://cialisdxt.com/]buy generic cialis[/url]
cialis generic 2018 expire patent
<a href="http://cialisdxt.com/">cialis online</a>
compare cialis and viagra side effects
[url=http://cialisdxt.com/]buy cialis online[/url]
cialis 20 mg uses
<a href="http://cialisdxt.com/">buy generic cialis</a>
20mg cialis vs viagra 100mg
[url=http://cialisec.com/]buy generic cialis[/url]
cialis dose reddit
<a href="http://cialisec.com/">buy cialis online</a>
price comparison for viagra and cialis
<a href="http://cialisdxt.com/">cialis online</a>
cialis super active vs cialis
[url=http://cialisdxt.com/]cialis generic[/url]
cialis side effects last
<a href="http://cialisdxt.com/">generic cialis</a>
brand cialis 5mg
[url=http://cialisdxt.com/]buy generic cialis[/url]
cialis 5 mg generico preço
[url=http://cialisdxt.com/]cialis online[/url]
cialis generico en ecuador
<a href="http://cialisdxt.com/">buy cialis online</a>
generic for cialis or viagra
<a href="http://cialisec.com/">generic cialis</a>
cialis dose maximale
[url=http://cialisec.com/]buy generic cialis[/url]
cialis vs viagra user reviews
<a href="http://cialisdxt.com/">buy generic cialis</a>
extra super cialis reviews
[url=http://cialisdxt.com/]cialis online[/url]
lilly cialis coupon trial offer 30 day
<a href="http://cialisdxt.com/">buy cialis online</a>
cialis 20 mg manufacturer coupon
[url=http://cialisdxt.com/]buy cialis online[/url]
buy generic cialis online europe
<a href="http://cialisdxt.com/">buy cialis online</a>
cialis vs viagra cost comparison
[url=http://cialisdxt.com/]buy generic cialis[/url]
cialis going generic in 2017 in usa
<a href="http://cialisec.com/">generic cialis</a>
maximum dose of cialis at a time
[url=http://cialisec.com/]buy cialis online[/url]
coupons for cialis 5mg once a day
[url=http://cialisdxt.com/]cialis online[/url]
retail cost of cialis 5mg for daily use
<a href="http://cialisdxt.com/">cialis online</a>
is generic cialis available in the us
[url=http://cialisdxt.com/]buy generic cialis[/url]
buy generic cialis canada online
<a href="http://cialisdxt.com/">cialis generic</a>
cialis commercial actress 2015
[url=http://cialisdxt.com/]buy cialis online[/url]
cialis professional
<a href="http://cialisdxt.com/">buy cialis online</a>
price comparison between viagra and cialis
<a href="http://cialisec.com/">cialis online</a>
cialis tadalafil 20mg online
[url=http://cialisec.com/]cialis online[/url]
viagra vs cialis vs levitra prices
[url=http://cialisdxt.com/]cialis generic[/url]
cialis generic in us
<a href="http://cialisdxt.com/">buy generic cialis</a>
cialis generic best price
[url=http://cialisdxt.com/]generic cialis[/url]
cialis 20mg tablets reviews
<a href="http://cialisdxt.com/">cialis online</a>
viagra or cialis or levitra which is better
[url=http://cialisdxt.com/]generic cialis[/url]
compare price of cialis and viagra
<a href="http://cialisdxt.com/">cialis generic</a>
why bathtubs in cialis commercials
[url=http://cialisec.com/]buy generic cialis[/url]
how long does it take for 5 mg cialis to work
<a href="http://cialisec.com/">generic cialis</a>
cost of cialis vs viagra vs levitra
[url=http://cialisdxt.com/]cialis online[/url]
effectiveness of cialis vs viagra vs levitra comparison
<a href="http://cialisdxt.com/">cialis generic</a>
lowest price generic cialis tadalafil
[url=http://cialisec.com/]cialis online[/url]
cialis side effects leg pain
<a href="http://cialisec.com/">cialis online</a>
cialis commercial actresses
<a href="http://cialisdxt.com/">buy generic cialis</a>
generic cialis tadalafil best price
[url=http://cialisdxt.com/]generic cialis[/url]
cialis vs viagra effectiveness
<a href="http://cialisdxt.com/">generic cialis</a>
cialis coupon card
[url=http://cialisdxt.com/]buy generic cialis[/url]
cialis 5mg daily price
<a href="http://cialisdxt.com/">cialis online</a>
specialist in cytotechnology salary
[url=http://cialisdxt.com/]generic cialis[/url]
real cialis no generic
<a href="http://cialisec.com/">buy generic cialis</a>
prices for cialis 5mg
[url=http://cialisec.com/]generic cialis[/url]
cialis side effects muscle aches
[url=http://cialisdxt.com/]buy cialis online[/url]
generic viagra cialis canada
<a href="http://cialisdxt.com/">buy generic cialis</a>
ez online pharmacy buy cialis usa
<a href="http://cialisec.com/">cialis generic</a>
cialis dapoxetine review
[url=http://cialisec.com/]cialis online[/url]
cialis generico en chile
<a href="http://cialisdxt.com/">buy generic cialis</a>
cialis generic best price india
[url=http://cialisdxt.com/]cialis generic[/url]
5 mg cialis daily best price
[url=http://cialisec.com/]cialis generic[/url]
viagra and cialis generic
<a href="http://cialisec.com/">generic cialis</a>
cialis 5mg best price
[url=http://cialisdxt.com/]cialis online[/url]
generic cialis capsules
<a href="http://cialisdxt.com/">buy cialis online</a>
levitra cialis viagra comparison
[url=http://cialisec.com/]cialis online[/url]
generic cialis costa rica
<a href="http://cialisec.com/">generic cialis</a>
price comparison with cialis and viagra
[url=http://cialisdxt.com/]buy generic cialis[/url]
existe cialis generico en mexico
<a href="http://cialisdxt.com/">generic cialis</a>
viagra cialis compare
[url=http://cialisec.com/]cialis online[/url]
buy generic viagra and cialis online pharmacy
<a href="http://cialisec.com/">buy cialis online</a>
cialis super active generico
<a href="http://cialisdxt.com/">buy cialis online</a>
super active cialis 40 mg gel
[url=http://cialisdxt.com/]generic cialis[/url]
buy cialis soft tabs online
[url=http://cialisec.com/]buy generic cialis[/url]
cialis 5 mg generico mexico
<a href="http://cialisec.com/">cialis generic</a>
cialis 20 mg tablet price
<a href="http://cialisdxt.com/">buy cialis online</a>
cialis coupons printable
[url=http://cialisdxt.com/]generic cialis[/url]
cialis coupons printable walmart
<a href="http://cialisec.com/">cialis online</a>
usa generic cialis lowest price
[url=http://cialisec.com/]buy generic cialis[/url]
costco pharmacy cialis price
[url=http://cialisdxt.com/]buy cialis online[/url]
cialis coupon 2016 200 dollar
<a href="http://cialisdxt.com/">cialis online</a>
cialis vs levitra side effects
<a href="http://cialisec.com/">buy generic cialis</a>
safe sites for generic cialis
[url=http://cialisec.com/]buy generic cialis[/url]
cialis extra dosage 200 mg
[url=http://cialisdxt.com/]cialis generic[/url]
directions for cialis 20mg how much water
<a href="http://cialisdxt.com/">buy cialis online</a>
levitra vs sildenafil vs cialis
<a href="http://cialisec.com/">cialis online</a>
levitra cialis viagra comparison
[url=http://cialisec.com/]cialis online[/url]
walmart pharmacy cialis cost
<a href="http://cialisdxt.com/">cialis online</a>
is generic cialis available in usa
[url=http://cialisdxt.com/]buy generic cialis[/url]
cialis 20 mg tablets price
<a href="http://cialisec.com/">generic cialis</a>
cialis vs viagra vs levitra which is better
[url=http://cialisec.com/]cialis online[/url]
cialis 20 mg 30 tablet eczane fiyatД±
[url=http://cialisdxt.com/]cialis generic[/url]
cialis dose recommendations vs viagra
<a href="http://cialisdxt.com/">cialis generic</a>
low cost generic cialis
<a href="http://cialisdxt.com/">buy generic cialis</a>
cialis dosing options
[url=http://cialisdxt.com/]cialis generic[/url]
effectiveness of cialis vs viagra
<a href="http://cialisec.com/">cialis generic</a>
cialis coupon card programme
[url=http://cialisec.com/]cialis online[/url]
precio cialis generico en farmacias
<a href="http://cialisdxt.com/">buy cialis online</a>
cialis prices walmart
[url=http://cialisdxt.com/]cialis online[/url]
cialis vs viagra dosage
[url=http://cialisec.com/]buy cialis online[/url]
cialis or viagra reviews
<a href="http://cialisec.com/">cialis online</a>
cialis generico no brasil
[url=http://cialisdxt.com/]cialis online[/url]
cialis 20 mg tablets price
<a href="http://cialisdxt.com/">buy cialis online</a>
viagra cialis levitra dosage
[url=http://cialisec.com/]buy generic cialis[/url]
will cialis go generic in 2017
<a href="http://cialisec.com/">cialis generic</a>
cialis 5 mg daily price
<a href="http://cialisdxt.com/">cialis generic</a>
price comparison viagra cialis levitra
[url=http://cialisdxt.com/]cialis online[/url]
stendra vs viagra vs cialis vs levitra
<a href="http://cialisec.com/">buy generic cialis</a>
extra super cialis
[url=http://cialisec.com/]cialis online[/url]
effectiveness of cialis vs viagra vs levitra 2013
<a href="http://cialisdxt.com/">buy cialis online</a>
generic cialis prices with prescription
[url=http://cialisdxt.com/]generic cialis[/url]
cialis dosage options
<a href="http://cialisec.com/">cialis generic</a>
cialis generic name in india
[url=http://cialisec.com/]generic cialis[/url]
effectiveness of cialis vs viagra vs levitra which is better
[url=http://cialisdxt.com/]generic cialis[/url]
genericos de viagra y cialis
<a href="http://cialisdxt.com/">generic cialis</a>
side effects of long term use of cialis
<a href="http://cialisec.com/">generic cialis</a>
generic cialis super active
[url=http://cialisec.com/]buy generic cialis[/url]
price of cialis vs viagra
<a href="http://cialisdxt.com/">buy cialis online</a>
cialis generic release date in usa
[url=http://cialisdxt.com/]cialis generic[/url]
uses for cialis 10mg
[url=http://cialisec.com/]buy cialis online[/url]
generic cialis soft tabs 20mg
<a href="http://cialisec.com/">buy cialis online</a>
side effects of long term cialis use
http://www.hoonthaitoday.com/forum/index.php?topic=150821.0
http://www.hoonthaitoday.com/forum/index.php?topic=151001.0
http://www.hoonthaitoday.com/forum/index.php?topic=151264.0
http://www.hoonthaitoday.com/forum/index.php?topic=151464.0
http://www.hoonthaitoday.com/forum/index.php?topic=151514.0
http://www.hoonthaitoday.com/forum/index.php?topic=151557.0
http://www.hoonthaitoday.com/forum/index.php?topic=151749.0
http://www.hoonthaitoday.com/forum/index.php?topic=151863.0
http://www.hoonthaitoday.com/forum/index.php?topic=152017.0
http://www.hoonthaitoday.com/forum/index.php?topic=152343.msg164530
http://www.hoonthaitoday.com/forum/index.php?topic=152571.0
http://www.hoonthaitoday.com/forum/index.php?topic=152753.0
http://www.hoonthaitoday.com/forum/index.php?topic=152763.0
http://teambuildingpremium.com/forum/index.php?topic=755159.0
http://roikjer.com/forum/index.php?PHPSESSID=g356dreiojc87iqgpsdopifao3&topic=793781.0
https://szenarist.ru/forum/index.php?topic=202732.0
http://thanosakademi.com/index.php?topic=61302.0
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=601299
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90cl2%e3%80%91/
https://danceplanet.se/commodore/index.php?topic=8578.0
http://macdistri.com/index.php/component/k2/itemlist/user/288902
http://roikjer.com/forum/index.php?PHPSESSID=1hcfgfp4pgmkcut2uj6mbhosa1&topic=789327.0
https://reficulcoin.com/index.php?topic=6798.0
http://forum.drahthaar-club.com.ua/index.php?topic=401.0
http://roikjer.com/forum/index.php?PHPSESSID=09t8jdtlotrgg5u1j25vr17vu4&topic=805335.0
http://poselokgribovo.ru/forum/index.php?topic=696878.0
http://roikjer.com/forum/index.php?PHPSESSID=fkkl5j0kigg3s0612ubrsq2pa0&topic=795032.0
https://members.fbhaters.com/index.php?topic=70412.0
http://poselokgribovo.ru/forum/index.php?topic=711930.0
http://sfah.ch/component/k2/itemlist/user/14522
http://www.hoonthaitoday.com/forum/index.php?topic=147409.0
https://reficulcoin.com/index.php?topic=6323.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-14/
https://reficulcoin.com/index.php?topic=6141.0
http://forum.politeknikgihon.ac.id/index.php?topic=11486.0
http://e-educ.net/Forum/index.php?topic=3358.0
http://metropolis.ga/index.php?topic=1799.0
http://HyUa.1fps.icu/l/szIaeDC
http://withinfp.sakura.ne.jp/eso/index.php/16855302-podsudimyj-17-seria-j9-podsudimyj-17-seria/0
http://forum.kopkargobel.com/index.php?topic=4059.0
https://reficulcoin.com/index.php?topic=8370.0
http://adsudoeste.com.br/index.php/component/k2/itemlist/user/21049
http://otitismediasociety.org/forum/index.php?topic=141362.0
http://sextomariotienda.com/blog/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u8-f7-%d1%80%d0%b0%d1%81%d1%81/
https://nextezone.com/index.php?action=profile;u=2372
http://sextomariotienda.com/blog/%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-14-%d1%81%d0%b5-19/
http://forum.politeknikgihon.ac.id/index.php?topic=16521.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i5-b6-%d0%b8%d0%b3%d1%80/
http://153.120.114.241/eso/index.php/16844837-igra-prestolov-2019-8-sezon-1-seria-igra-prestolov-2019-8-sezon
http://freebeer.me/index.php?topic=290404.0
http://help.stv.ru/index.php?PHPSESSID=014a54d578c9a3f7e2b2e956f9e1ad1a&topic=135300.0
http://jpacschoolclubs.co.uk/?option=com_k2&view=itemlist&task=user&id=3337252
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c3-g8-%d0%b8%d0%b3%d1%80/
http://www.grupojover.com/index.php/es/component/k2/itemlist/user/3796
http://153.120.114.241/eso/index.php/16876451-igra-prestolovgame-of-thrones-8-sezon-6-seria-ru4-igra-prestolo
http://www.hoonthaitoday.com/forum/index.php?topic=145454.0
http://forum.kopkargobel.com/index.php?topic=4031.0
http://153.120.114.241/eso/index.php/16874153-podsudimyj-13-seria-05052019
http://guiadetudo.com/?option=com_k2&view=itemlist&task=user&id=10774
https://members.fbhaters.com/index.php?topic=71095.0
http://forum.digamahost.com/index.php?topic=108770.0
http://myrechockey.com/forums/index.php?topic=84417.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=26563.0
http://eugeniocolazzo.it/forum/index.php?topic=81461.0
http://8.droror.co.il/uncategorized/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x5-p7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://roikjer.com/forum/index.php?PHPSESSID=oodm2p1ulgv5bnargjmrviqvk0&topic=794056.0
https://nextezone.com/index.php?topic=33090.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f5-q0-%d0%b8%d0%b3%d1%80/
http://adsudoeste.com.br/index.php/component/k2/itemlist/user/21103
http://forum.politeknikgihon.ac.id/index.php?topic=10705.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k6-m6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://forum.politeknikgihon.ac.id/index.php?topic=13656.0
http://ptu.imoove.kr/ko/content/%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%E3%80%90go5%E3%80%91-%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-watch%C2%BB330794
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3693331
http://HyUa.1fps.icu/l/szIaeDC
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/171290
http://www.sopcich.com/UserProfile/tabid/42/UserID/1658953/Default.aspx
http://www.tekparcahdfilm.com/forum/index.php?topic=44650.0
http://menulisilmiah.net/%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-svp-%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0/
http://www.popolsku.fr.pl/forum/index.php?topic=370435.0
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/977617
https://members.fbhaters.com/index.php?topic=55001.0
http://www.tessabannampad.go.th/webboard/index.php?topic=180393.0
https://altaylarteknoloji.com/index.php?topic=686.0
http://theolevolosproject.org/?option=com_k2&view=itemlist&task=user&id=23495
http://1vh.info/index.php?topic=8145.0
http://arquitectosenreformas.es/index.php/component/k2/itemlist/user/77948
http://www.critico-expository.com/forum/index.php?topic=462.0
http://1vh.info/index.php?topic=11195.0
http://1vh.info/index.php?topic=11197.0
http://1vh.info/index.php?topic=11199.0
http://1vh.info/index.php?topic=11200.0
http://1vh.info/index.php?topic=11201.0
http://1vh.info/index.php?topic=11204.0
http://matrixpharm.ru/forum/index.php?PHPSESSID=dn1716he4jq5nnesi4406no9f2&action=profile;u=167713
http://matrixpharm.ru/forum/index.php?PHPSESSID=pqb90d9kh2t0id8msj74mit6l2&action=profile;u=167718
http://matrixpharm.ru/forum/index.php?PHPSESSID=rvk12tn72e4rfgq36adidve5h2&action=profile;u=167711
http://rudraautomation.com/index.php/component/k2/author/116501
http://xn--l1adgmc.xn----9sbdbmdznsj5c5bxd7b.xn--p1ai/index.php?topic=8072.0
http://xn--l1adgmc.xn----9sbdbmdznsj5c5bxd7b.xn--p1ai/index.php?topic=8078.0
https://forum.ac-jete.it/index.php?topic=341390.0
https://forum.ac-jete.it/index.php?topic=341399.0
https://nextezone.com/index.php?action=profile;u=2608
http://2eKf0.1fps.icu/t/92drRHjeLUI
http://wcwpr.com/UserProfile/tabid/85/userId/9194308/Default.aspx
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1110495
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1566614
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hki-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-12-%d1%81%d0%b5%d1%80/
https://members.fbhaters.com/index.php?topic=71765.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1305502
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1305542
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1305643
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1305659
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1305731
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1305758
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1305807
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1305912
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1305991
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1306028
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1588703
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1590140
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1592059
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1593138
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1593472
http://dev.aabn.org.gh/component/k2/itemlist/user/483791
http://www.deliberarchia.org/forum/index.php?topic=951030.0
http://www.m1avio.com/index.php/component/k2/itemlist/user/3603283
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=260921
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4714895
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1125391
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1308340
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1308426
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1308801
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1308985
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1309053
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1309136
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1309145
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1309188
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1309249
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1309332
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1309340
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1309410
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1309509
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1600411
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1600415
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1600507
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1600618
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1600625
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1601653
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1601738
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1602136
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1602590
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1602963
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1604196
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1604727
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1606455
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1608145
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/171380
http://www.quattroandpartners.it/component/k2/itemlist/user/998449
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3267324
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=294175
http://smartacity.com/component/k2/itemlist/user/14808
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1314320
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1314385
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1314485
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1314593
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1314698
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1314712
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1314740
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1314795
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1575338
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1575523
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1575654
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1575673
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1575845
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-8/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-20/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-22/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-10/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-7/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-9/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-14/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-20/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-5/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-9/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-12/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-13/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-15/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-16/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-19/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-21/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-22/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-12/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-16/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-17/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-15/
http://roikjer.com/forum/index.php?PHPSESSID=7v6iu5439a9jqjuoe5cbfqkej3&topic=810777.0
http://roikjer.com/forum/index.php?PHPSESSID=7vd9ouot67hg0db9c25nj9cv94&topic=804873.0
http://roikjer.com/forum/index.php?PHPSESSID=84c4nf214f8g0s7a7v9h4o2fo5&topic=808217.0
http://roikjer.com/forum/index.php?PHPSESSID=88t1bfbm3jjak9833hll4cedr1&topic=797444.0
http://roikjer.com/forum/index.php?PHPSESSID=8chf53iki7u5gfu02c3hjf6q90&topic=796479.0
http://roikjer.com/forum/index.php?PHPSESSID=8v0u6o99q6srrusm5nmcica4g2&topic=800507.0
http://roikjer.com/forum/index.php?PHPSESSID=97lri4pgkhjvmng2cvjpffn8q5&topic=799744.0
http://roikjer.com/forum/index.php?PHPSESSID=9ikd983bm581opgd0o30qq02l7&topic=803786.0
http://roikjer.com/forum/index.php?PHPSESSID=9m2mbp2e7ulre1pt2sss5cng91&topic=803098.0
http://roikjer.com/forum/index.php?PHPSESSID=9mdtdsrgnjode0jdm0malrs8l0&topic=805154.0
http://roikjer.com/forum/index.php?PHPSESSID=9pbf2vpjkoqmp78mnf5ji414d1&topic=797820.0
http://roikjer.com/forum/index.php?PHPSESSID=9qj7t9q0b1d53dr91n75lun641&topic=809462.0
http://roikjer.com/forum/index.php?PHPSESSID=9sg2r5lulfm24i21s18dec8gr4&topic=804567.0
http://roikjer.com/forum/index.php?PHPSESSID=a0fja97fgsgbp5icq3ner335e2&topic=808761.0
http://HyUa.1fps.icu/l/szIaeDC
http://forum.elexlabs.com/index.php/topic,12863.0.html
http://forum.elexlabs.com/index.php/topic,13011.0.html
http://forum.elexlabs.com/index.php?topic=11917.0
http://forum.elexlabs.com/index.php?topic=11957.0
http://forum.elexlabs.com/index.php?topic=12654.0
http://forum.elexlabs.com/index.php?topic=12839.0
http://forum.elexlabs.com/index.php?topic=12851.0
http://forum.elexlabs.com/index.php?topic=13019.0
http://forum.elexlabs.com/index.php?topic=13024.0
http://forum.elexlabs.com/index.php?topic=13035.0
http://forum.elexlabs.com/index.php?topic=13044.0
http://forum.elexlabs.com/index.php?topic=13054.0
http://forum.elexlabs.com/index.php?topic=13074.0
http://forum.elexlabs.com/index.php?topic=13075.0
http://forum.elexlabs.com/index.php?topic=13081.0
http://forum.elexlabs.com/index.php?topic=13082.0
http://forum.elexlabs.com/index.php?topic=13085.0
http://forum.elexlabs.com/index.php?topic=13098.0
http://forum.elexlabs.com/index.php?topic=13099.0
http://forum.kopkargobel.com/index.php?topic=2523.0
http://ruschinaforum.ru/index.php?topic=125826.0
http://ruschinaforum.ru/index.php?topic=125830.0
http://ruschinaforum.ru/index.php?topic=125833.0
http://ruschinaforum.ru/index.php?topic=125837.0
http://ruschinaforum.ru/index.php?topic=125966.0
http://ruschinaforum.ru/index.php?topic=125973.0
http://ruschinaforum.ru/index.php?topic=126134.0
http://ruschinaforum.ru/index.php?topic=126135.0
http://ruschinaforum.ru/index.php?topic=126145.0
http://ruschinaforum.ru/index.php?topic=126153.0
http://ruschinaforum.ru/index.php?topic=126170.0
http://ruschinaforum.ru/index.php?topic=126234.0
http://ruschinaforum.ru/index.php?topic=126243.0
http://ruschinaforum.ru/index.php?topic=126260.0
http://ruschinaforum.ru/index.php?topic=126265.0
http://ruschinaforum.ru/index.php?topic=126269.0
http://ruschinaforum.ru/index.php?topic=126283.0
http://ruschinaforum.ru/index.php?topic=126326.0
http://ruschinaforum.ru/index.php?topic=126331.0
http://HyUa.1fps.icu/l/szIaeDC
http://withinfp.sakura.ne.jp/eso/index.php/16808345-vetrenyj-hercai-5-seria-z9na-vetrenyj-hercai-5-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/16808377-rannaa-ptaska-erkenci-kus-41-seria-z0hf-rannaa-ptaska-erkenci-k
http://withinfp.sakura.ne.jp/eso/index.php/16808391-rannaa-ptaska-erkenci-kus-44-seria-f7is-rannaa-ptaska-erkenci-k/0
http://withinfp.sakura.ne.jp/eso/index.php/16808437-edinoe-serdce-tek-yurek-17-seria-w9yj-edinoe-serdce-tek-yurek-1/0
http://withinfp.sakura.ne.jp/eso/index.php/16808442-vetrenyj-hercai-9-seria-m2kl-vetrenyj-hercai-9-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/16808502-voskressij-ertugrul-146-seria-c8dp-voskressij-ertugrul-146-seri/0
http://www.quattroandpartners.it/component/k2/itemlist/user/1018709
http://www.quattroandpartners.it/component/k2/itemlist/user/1019297
http://www.quattroandpartners.it/component/k2/itemlist/user/1019373
http://www.quattroandpartners.it/component/k2/itemlist/user/1019376
http://www.quattroandpartners.it/component/k2/itemlist/user/1019416
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/641827
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3255967
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3245795
https://members.fbhaters.com/index.php?topic=59272.0
https://www.youngbiker.de/wbboard/index.php?page=User&userID=782233
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=9109
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1324659
https://www.resproxy.com/forum/index.php/776632-riverdejl-riverdale-3-sezon-19-seria-xbv-riverdejl-riverdale-3-/0
http://www.spazioad.com/component/k2/itemlist/user/7172020
http://seoksoononly.dothome.co.kr/qna/639509
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=3962
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=40500
https://www.resproxy.com/forum/index.php/739565-milliardy-4-sezon-12-seria-tqd-milliardy-4-sezon-12-seria-03052/0
http://danielmillsap.com/forum/index.php?topic=882899.0
http://www.spazioad.com/component/k2/itemlist/user/7180436
http://www.telcon.gr/index.php/component/k2/itemlist/user/35399
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=557741
http://www.deliberarchia.org/forum/index.php?topic=881663.0
http://roikjer.com/forum/index.php?topic=780341.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/408946
http://vtservices85.fr/smf2/index.php?PHPSESSID=767a96ccd8b24a6e1c67196ba3d8d8f1&topic=204185.0
http://dpmarketingsystems.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g3-%e3%80%90-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://www.ekemoon.com/139811/050120190605/
http://uberdrivers.net/forum/index.php?topic=183788.0
https://lucky28003.nl/forum/index.php?topic=4720.0
http://uberdrivers.net/forum/index.php?topic=175474.0
http://www.gtupuw.org/index.php/component/k2/itemlist/user/1805034
http://freebeer.me/index.php?topic=269289.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/269228
http://mediaville.me/index.php/component/k2/itemlist/user/219523
http://mobility-corp.com/index.php/component/k2/itemlist/user/2522578
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=69368
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/69147
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/69364
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/207104
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=6637
http://rudraautomation.com/index.php/component/k2/author/122034
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/188761
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1640124
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/54474
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/54491
http://sextomariotienda.com/blog/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dni-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8/
http://matrixpharm.ru/forum/index.php?action=profile&u=152031
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=185632
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1500358
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=184202
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1829822
http://www.critico-expository.com/forum/index.php?topic=587.0
http://withinfp.sakura.ne.jp/eso/index.php/16808156-sluga-naroda-3-sezon-23-seria-x3-sluga-naroda-3-sezon-23-seria-/0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1105006
https://members.fbhaters.com/index.php?topic=53739.0
http://poselokgribovo.ru/forum/index.php?topic=651891.0
http://poselokgribovo.ru/forum/index.php?topic=646594.0
http://www.hoonthaitoday.com/forum/index.php?topic=105584.0
http://forum.byehaj.hu/index.php?topic=73777.0
http://freebeer.me/index.php?topic=253735.0
http://thanosakademi.com/index.php?topic=49315.0
http://www2.yasothon.go.th/smf/index.php?topic=159.150330
https://www.gizmoarticle.com/%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fks-%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-17-%d1%81%d0%b5/
http://withinfp.sakura.ne.jp/eso/index.php/16767852-hd-sluga-naroda-3-sezon-15-seria-d6-sluga-naroda-3-sezon-15-ser/0
http://www.tekparcahdfilm.com/forum/index.php?topic=44230.0
http://uberdrivers.net/forum/index.php?topic=186957.0
http://poselokgribovo.ru/forum/index.php?topic=713073.0
http://poselokgribovo.ru/forum/index.php?topic=713115.0
http://poselokgribovo.ru/forum/index.php?topic=713146.0
http://poselokgribovo.ru/forum/index.php?topic=713153.0
http://poselokgribovo.ru/forum/index.php?topic=713159.0
http://poselokgribovo.ru/forum/index.php?topic=713164.0
http://poselokgribovo.ru/forum/index.php?topic=713213.0
http://poselokgribovo.ru/forum/index.php?topic=713218.0
http://poselokgribovo.ru/forum/index.php?topic=713244.0
http://poselokgribovo.ru/forum/index.php?topic=713273.0
http://poselokgribovo.ru/forum/index.php?topic=713294.0
http://poselokgribovo.ru/forum/index.php?topic=713342.0
http://poselokgribovo.ru/forum/index.php?topic=713496.0
http://poselokgribovo.ru/forum/index.php?topic=713501.0
http://poselokgribovo.ru/forum/index.php?topic=713523.0
http://poselokgribovo.ru/forum/index.php?topic=713620.0
http://poselokgribovo.ru/forum/index.php?topic=713623.0
http://poselokgribovo.ru/forum/index.php?topic=713667.0
http://poselokgribovo.ru/forum/index.php?topic=713674.0
http://poselokgribovo.ru/forum/index.php?topic=713682.0
http://poselokgribovo.ru/forum/index.php?topic=713715.0
http://poselokgribovo.ru/forum/index.php?topic=713720.0
http://poselokgribovo.ru/forum/index.php?topic=713750.0
http://poselokgribovo.ru/forum/index.php?topic=713808.0
http://www.quattroandpartners.it/component/k2/itemlist/user/1029160
http://www.quattroandpartners.it/component/k2/itemlist/user/1029471
http://www.quattroandpartners.it/component/k2/itemlist/user/1029666
http://www.quattroandpartners.it/component/k2/itemlist/user/1029946
http://www.quattroandpartners.it/component/k2/itemlist/user/1031197
http://www.quattroandpartners.it/component/k2/itemlist/user/1031379
http://www.quattroandpartners.it/component/k2/itemlist/user/1031749
http://www.quattroandpartners.it/component/k2/itemlist/user/1032302
http://www.quattroandpartners.it/component/k2/itemlist/user/1032501
http://www.quattroandpartners.it/component/k2/itemlist/user/1033040
http://HyUa.1fps.icu/l/szIaeDC
http://roikjer.com/forum/index.php?PHPSESSID=dr9rtjipgd9u2st8mnq86idgv3&topic=792380.0
http://roikjer.com/forum/index.php?PHPSESSID=ds1sonj0e16hv7cl59fgcgsk87&topic=802141.0
http://roikjer.com/forum/index.php?PHPSESSID=du8l88fam1v6r2ekrskrvn2773&topic=807498.0
http://roikjer.com/forum/index.php?PHPSESSID=e2vmvsqul4ecp72h9kl443t682&topic=802331.0
http://roikjer.com/forum/index.php?PHPSESSID=e4lbg8meiugu9bfbglmc6hk7f2&topic=803486.0
http://roikjer.com/forum/index.php?PHPSESSID=e7jlmu9d49q0havsii2cj5j3g1&topic=800581.0
http://roikjer.com/forum/index.php?PHPSESSID=e9d5tlf4nlillp84h7mt591eo5&topic=807507.0
http://roikjer.com/forum/index.php?PHPSESSID=e9kdakp9adkamn3okj4rh1l8a6&topic=802042.0
http://roikjer.com/forum/index.php?PHPSESSID=e9l828nhdc7cakl7i68f893gg5&topic=791231.0
http://roikjer.com/forum/index.php?PHPSESSID=eavemopob6glabl06m96sgk9h4&topic=802372.0
http://roikjer.com/forum/index.php?PHPSESSID=edaarcfi3q65hv30cqjh0e3nr6&topic=800207.0
http://roikjer.com/forum/index.php?PHPSESSID=ejolu6knutkk4h98jkbh1vkmp2&topic=793843.0
http://roikjer.com/forum/index.php?PHPSESSID=empvc7bcnn5ok2ec9linggrp60&topic=790973.0
http://roikjer.com/forum/index.php?PHPSESSID=er6n6kbgeefap3isina2mruc33&topic=810629.0
http://roikjer.com/forum/index.php?PHPSESSID=eruaiqc3sg1g4ik81hm968rkd2&topic=802519.0
http://roikjer.com/forum/index.php?PHPSESSID=et5v8suu5o3brs8r9k8q72t4l4&topic=805256.0
http://roikjer.com/forum/index.php?PHPSESSID=etr8utine5v6ptvrk3rm4ka670&topic=789839.0
http://roikjer.com/forum/index.php?PHPSESSID=f08699044fgc5j9j7a670ukmf1&topic=798976.0
http://www.remify.app/foro/index.php?topic=219414.0
http://www.remify.app/foro/index.php?topic=219529.0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=549707
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=550124
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=553843
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=554362
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=554416
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=554425
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=555146
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=555167
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=555740
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=556225
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=556240
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=556658
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=556882
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=556899
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=556919
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=556949
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=557256
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=557486
http://HyUa.1fps.icu/l/szIaeDC
http://poselokgribovo.ru/forum/index.php?topic=686236.0
http://poselokgribovo.ru/forum/index.php?topic=686345.0
http://poselokgribovo.ru/forum/index.php?topic=686367.0
http://poselokgribovo.ru/forum/index.php?topic=686454.0
http://poselokgribovo.ru/forum/index.php?topic=686646.0
http://poselokgribovo.ru/forum/index.php?topic=686665.0
http://poselokgribovo.ru/forum/index.php?topic=686837.0
http://poselokgribovo.ru/forum/index.php?topic=686897.0
http://poselokgribovo.ru/forum/index.php?topic=686911.0
http://poselokgribovo.ru/forum/index.php?topic=687058.0
http://poselokgribovo.ru/forum/index.php?topic=687114.0
http://poselokgribovo.ru/forum/index.php?topic=687137.0
http://poselokgribovo.ru/forum/index.php?topic=687154.0
http://www.deliberarchia.org/forum/index.php?topic=958726.0
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1756464
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1756923
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1757450
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1758178
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1758292
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1758763
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1760336
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1760489
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1760526
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1760668
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1763011
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1763022
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1763128
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1763287
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1763630
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1764506
http://HyUa.1fps.icu/l/szIaeDC
https://tg.vl-mp.com/index.php?topic=1287790.0
https://tg.vl-mp.com/index.php?topic=1287845.0
https://tg.vl-mp.com/index.php?topic=1287889.0
https://tg.vl-mp.com/index.php?topic=1287930.0
https://tg.vl-mp.com/index.php?topic=1288198.0
https://tg.vl-mp.com/index.php?topic=1288286.0
https://tg.vl-mp.com/index.php?topic=1288351.0
https://tg.vl-mp.com/index.php?topic=1288358.0
https://tg.vl-mp.com/index.php?topic=1288557.0
https://tg.vl-mp.com/index.php?topic=1288559.0
https://tg.vl-mp.com/index.php?topic=1288636.0
https://tg.vl-mp.com/index.php?topic=1288854.0
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2472990
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2473427
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2473651
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2474108
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2474184
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2474303
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2474863
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2474901
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2475078
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2475260
http://www.deliberarchia.org/forum/index.php?topic=902223.0
https://www.resproxy.com/forum/index.php/758925-manifest-19-seria-xex-manifest-19-seria/0
http://webp.online/index.php?topic=41529.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=294191
https://www.resproxy.com/forum/index.php/768007-amerikanskie-bogi-2-sezon-8-seria-emn-amerikanskie-bogi-2-sezon/0
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1672640
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/51078
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1571092
http://c3isecurity.com.br/?option=com_k2&view=itemlist&task=user&id=442514
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/60998
http://www.arunagreen.com/index.php/component/k2/itemlist/user/389479
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/42516
http://married.dike.gr/index.php/component/k2/itemlist/user/46079
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3684895
http://www.moyakmermer.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=599514
https://tg.vl-mp.com/index.php?topic=1310579.0
https://tg.vl-mp.com/index.php?topic=1310605.0
https://tg.vl-mp.com/index.php?topic=1310637.0
https://tg.vl-mp.com/index.php?topic=1310707.0
https://tg.vl-mp.com/index.php?topic=1310881.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2495719
http://mobility-corp.com/index.php/component/k2/itemlist/user/2495893
http://mobility-corp.com/index.php/component/k2/itemlist/user/2496047
http://mobility-corp.com/index.php/component/k2/itemlist/user/2496392
http://mobility-corp.com/index.php/component/k2/itemlist/user/2496568
http://mobility-corp.com/index.php/component/k2/itemlist/user/2496772
http://mobility-corp.com/index.php/component/k2/itemlist/user/2496816
http://mobility-corp.com/index.php/component/k2/itemlist/user/2497781
http://mobility-corp.com/index.php/component/k2/itemlist/user/2497932
http://mobility-corp.com/index.php/component/k2/itemlist/user/2498051
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2525429
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2522675
https://tg.vl-mp.com/index.php?topic=1271008.0
http://www.oortsociety.com/index.php?topic=9394.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2483596
http://matrixpharm.ru/forum/index.php?action=profile&u=162108
http://xn--l1adgmc.xn----9sbdbmdznsj5c5bxd7b.xn--p1ai/index.php?topic=6307.0
http://macdistri.com/index.php/component/k2/itemlist/user/253208
http://www.betder.org/forum/index.php?topic=4819.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=293789
https://npi.org.es/smf/index.php?topic=110320.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=292495
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/185320
http://muratliziraatodasi.org/forum/index.php?topic=396765.0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=712723
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-taka-(erkenci-kus)-43-e-watch-y4~-a-taka-(erkenci-kus)-43-e/?PHPSESSID=i5p3eh4oi0e55nre69436i83v0
https://www.gizmoarticle.com/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-43-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d0-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba/
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/166658
https://khuyenmaikk13.info/index.php?topic=172012.0
http://www.deliberarchia.org/forum/index.php?topic=903223.0
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1498492
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1002566
http://freebeer.me/index.php?topic=267052.0
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/127207
http://www.popolsku.fr.pl/forum/index.php?topic=20407.42300
http://vtservices85.fr/smf2/index.php?PHPSESSID=6bd9054876d5293958660abdb9b39f34&topic=204196.0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/207371
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=49581
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3607655
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/985685
https://khuyenmaikk13.info/index.php?topic=153924.0
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/154292
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/968345
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3284608
http://roikjer.com/forum/index.php?PHPSESSID=b9qng61638v2gcqmqk2g00q5v4&topic=758980.0
http://www.critico-expository.com/forum/index.php?topic=166.0
http://healthyteethpa.org/component/k2/itemlist/user/5320578
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523438
https://tg.vl-mp.com/index.php?topic=1247612.0
http://dev.aabn.org.gh/component/k2/itemlist/user/461985
http://www.hoonthaitoday.com/forum/index.php?topic=137572.0
http://www.boutique.in.th/index.php/component/k2/itemlist/user/145472
http://married.dike.gr/index.php/component/k2/itemlist/user/39772
http://universalcommunity.se/Forum/index.php?topic=238.0
http://poselokgribovo.ru/forum/index.php?topic=650752.0
http://menulisilmiah.net/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b7/
http://www.hoonthaitoday.com/forum/index.php?topic=124840.0
https://www.gizmoarticle.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81-2/
http://www.hoonthaitoday.com/forum/index.php?topic=125059.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/532781
http://wituclub.ru/forum/index.php?PHPSESSID=1dk9c0jb56okg0bk1j87rojj46&topic=24666.0
http://macdistri.com/index.php/component/k2/itemlist/user/254932
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=154425
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=669713.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/411287
https://mcsetup.tk/bbs/index.php?topic=240377.0
http://forum.bmw-e60.eu/index.php?topic=2316.0
http://www.ekemoon.com/138981/051620194504/
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=231112
https://tg.vl-mp.com/index.php?topic=1245521.0
http://www.original-craft.net/index.php?topic=305814.0
https://khuyenmaikk13.info/index.php?topic=152075.0
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7292276
https://sanp.pro/%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-74-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-l1-%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-74/
http://teambuildingpremium.com/forum/index.php?topic=712673.0
https://woodland.org.ua/groups/new-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f
http://www.telcon.gr/index.php/component/k2/itemlist/user/32351
http://vtservices85.fr/smf2/index.php?PHPSESSID=544327a6744f3f6ace5a94afb3cbf995&topic=191642.0
http://teambuildingpremium.com/forum/index.php?topic=715824.0
https://sanp.pro/%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-72-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-j1-%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-72-%d1%81/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/'ea-56-e-watch'-n8-'ea-56-e'/?PHPSESSID=8t61ohe28q35pd9j48pfv4m3b3
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=668146.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=668245.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=668609.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=668677.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=668806.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=668891.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=669059.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=669199.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=669262.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=669381.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=669683.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=669853.0
http://153.120.114.241/eso/index.php/16884380-ne-zenskaa-rabota-ne-zinoca-robota-19-seria-06052019
http://153.120.114.241/eso/index.php/16884390-ne-zenskaa-rabota-ne-zinoca-robota-15-seria-f3-ne-zenskaa-rabot
http://153.120.114.241/eso/index.php/16884643-06052019-ne-zenskaa-rabota-ne-zinoca-robota-18-seria
http://153.120.114.241/eso/index.php/16884688-06052019-devat-ziznej-7-seria
http://dpmarketingsystems.com/06-05-2019-%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-17-2/
http://forum.politeknikgihon.ac.id/index.php?topic=21038.0
http://forum.politeknikgihon.ac.id/index.php?topic=21045.0
http://poselokgribovo.ru/forum/index.php?topic=715305.0
http://roikjer.com/forum/index.php?PHPSESSID=ttlr60u4me4h3hqeao2lvsn8a6&topic=812346.0
http://sextomariotienda.com/blog/%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-14-%d1%81%d0%b5-32/
http://vtservices85.fr/smf2/index.php?PHPSESSID=ac5592331dbdc045b6c9c690e60aaac2&topic=209374.0
http://www.deliberarchia.org/forum/index.php?topic=960741.0
http://www.deliberarchia.org/forum/index.php?topic=960760.0
http://www.popolsku.fr.pl/forum/index.php?topic=373346.0
https://reficulcoin.com/index.php?topic=10238.0
http://216.104.186.20/index.php?topic=299859.0
http://HyUa.1fps.icu/l/szIaeDC
http://thanosakademi.com/index.php?topic=51222.0
http://uberdrivers.net/forum/index.php?topic=182314.0
http://www.spazioad.com/component/k2/itemlist/user/7201056
https://tg.vl-mp.com/index.php?topic=1261660.0
http://www.tvmechanic.co.in/forum/index.php?topic=8403.0
http://www.deliberarchia.org/forum/index.php?topic=899190.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2480843
https://sanp.pro/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-y7-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd/
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1837632
https://www.gizmoarticle.com/%d1%84%d1%83%d0%bb%d0%bbhd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b8-%d1%81%d0%bb%d1%83%d0%b3/
http://www.popolsku.fr.pl/forum/index.php?topic=20407.44430
https://sanp.pro/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a1-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd/
http://taklongclub.com/forum/index.php?topic=87339.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=6242
http://xekhachduyetthuy.com.vn/component/k2/itemlist/user/148995
http://roikjer.com/forum/index.php?PHPSESSID=8g0ajikhrtf9hd4cmuhm2iec94&topic=770544.0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=527734
http://vtservices85.fr/smf2/index.php?PHPSESSID=f5ef0873f36d96d86e4c7c8edad487f7&topic=191804.0
https://www.resproxy.com/forum/index.php/758531-voskressij-ertugrul-150-seria-p7-voskressij-ertugrul-150-seria/0
http://www.tessabannampad.go.th/webboard/index.php?topic=178249.0
https://www.gizmoarticle.com/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o9-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd/
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=142900
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1014686
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1848244
http://www.m1avio.com/index.php/component/k2/itemlist/user/3612540
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=763764
http://www.spazioad.com/component/k2/itemlist/user/7228524
http://www.spazioad.com/component/k2/itemlist/user/7228528
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/292102
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/221759
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/221861
https://www.netprofessional.gr/component/k2/itemlist/user/3265.html
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=13899
http://uberdrivers.net/forum/index.php?topic=209179.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3245997
http://hydrocarbs-gh.org/index.php/component/k2/itemlist/user/7246711
https://tg.vl-mp.com/index.php?topic=1245984.0
https://members.fbhaters.com/index.php?topic=55808.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1604242
http://www.popolsku.fr.pl/forum/index.php?topic=366959.0
https://sanp.pro/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-45-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-k3-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82/
https://sanp.pro/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-37-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h9-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88/
http://matrixpharm.ru/forum/index.php?PHPSESSID=j3l052okdjb097vo32dqnlh0e3&action=profile;u=152582
http://poselokgribovo.ru/forum/index.php?topic=690524.0
http://roikjer.com/forum/index.php?PHPSESSID=dc00jsre9qdfdjobp43da8f0j5&topic=754164.0
http://www.ekemoon.com/139445/052120194404/
http://www.remify.app/foro/index.php?topic=165311.0
http://forum.bmw-e60.eu/index.php?topic=1175.0
http://rudraautomation.com/index.php/component/k2/author/89435
https://mcsetup.tk/bbs/index.php?topic=241122.0
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1620687
http://married.dike.gr/index.php/component/k2/itemlist/user/42662
http://www.ekemoon.com/139651/052320193904/
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2519171
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=515508
http://freebeer.me/index.php?topic=275446.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/54214
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2571652
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/478728
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=270007
http://healthyteethpa.org/component/k2/itemlist/user/5345958
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1122965
http://macdistri.com/index.php/component/k2/itemlist/user/310368
http://withinfp.sakura.ne.jp/eso/index.php/16807411-voron-kuzgun-11-seria-n9bz-voron-kuzgun-11-seria
http://withinfp.sakura.ne.jp/eso/index.php/16807493-vossoedinenie-vuslat-16-seria-z7cj-vossoedinenie-vuslat-16-seri
http://withinfp.sakura.ne.jp/eso/index.php/16807536-nevesta-iz-stambula-istanbullu-gelin-80-seria-k7gc-nevesta-iz-s/0
http://withinfp.sakura.ne.jp/eso/index.php/16807649-vetrenyj-hercai-8-seria-v1qr-vetrenyj-hercai-8-seria
http://withinfp.sakura.ne.jp/eso/index.php/16807656-nasa-istoria-67-seria-h9kf-nasa-istoria-67-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/16807674-edinoe-serdce-tek-yurek-14-seria-f1ax-edinoe-serdce-tek-yurek-1/0
http://withinfp.sakura.ne.jp/eso/index.php/16807700-vossoedinenie-vuslat-20-seria-q6uv-vossoedinenie-vuslat-20-seri/0
http://withinfp.sakura.ne.jp/eso/index.php/16807751-vetrenyj-hercai-15-seria-b2sp-vetrenyj-hercai-15-seria?---------------------------71384510048%0D%0AContent-Disposition:%20form-data;%20name=%22token%22%0D%0A%0D%0A5d249f8f2972a%0D%0A---------------------------71384510048%0D%0AContent-Disposition:%20form-data;%20name=%22title%22%0D%0A%0D%0A%C2%AB%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D0%A1%D0%B5%D1%80%D0%B8%D1%8F%C2%BB%20B2sP%20%C2%AB%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D0%A1%D0%B5%D1%80%D0%B8%D1%8F%C2%BB%0D%0A---------------------------71384510048%0D%0AContent-Disposition:%20form-data;%20name=%22content%22%0D%0A%0D%0A%C2%AB%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB%20'%20Y4%20%C2%AB%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB%20%D1%80%D1%83%D1%81%20%D0%BF%D0%B5%D1%80%D0%B5%D0%B2%D0%BE%D0%B4%0D%0A[url=http://zfilm6.ru/watch/ukhZwZTt/][img]https://i.imgur.com/rDglLCZ.jpg[/img][/url]%0D%0A%0D%0A[url=http://zfilm6.ru/watch/ukhZwZTt/]%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F[/url]%20%0D%0A[url=http://zfilm6.ru/watch/ukhZwZTt/]%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F[/url]%20%0D%0A[url=http://zfilm6.ru/watch/ukhZwZTt/]%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F[/url]%20%0D%0A%0D%0A%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20%D0%BE%D0%BA%0D%0A%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20tv%0D%0A%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20kz%0D%0A%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%B0%D1%8F%20%D0%BE%D0%B7%D0%B2%D1%83%D1%87%D0%BA%D0%B0%0D%0A%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20%D1%81%20%D0%BE%D0%B7%D0%B2%D1%83%D1%87%D0%BA%D0%BE%D0%B9%20%D0%BD%D0%B0%20%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%BE%D0%BC%0D%0A$$%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20%D1%80%D1%83%D1%81%20%D1%8F%D0%B7%0D%0A%60%60%60%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20%D0%B0%D0%BB%D0%B8%D1%88%D0%B0%20%D0%B4%D0%B8%D0%BB%D0%B8%D1%80%D0%B8%D1%81%60%60%60%0D%0A%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20%D1%84%D0%B1%0D%0A%3E%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20%D0%BF%D0%B5%D1%80%D0%B5%D0%B2%D0%BE%D0%B4%20%D0%BD%D0%B0%20%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%BE%D0%BC%0D%0A---------------------------71384510048%0D%0AContent-Disposition:%20form-data;%20name=%22postReply%22%0D%0A%0D%0A%E3%83%88%E3%83%94%E3%83%83%E3%82%AF%E3%82%E2%80%99%E7%AB%8B%E3%81%A6%E3%82%8B%0D%0A---------------------------71384510048--
http://withinfp.sakura.ne.jp/eso/index.php/16807777-voskressij-ertugrul-149-seria-k7le-voskressij-ertugrul-149-seri
http://withinfp.sakura.ne.jp/eso/index.php/16807806-vetrenyj-hercai-6-seria-c4tf-vetrenyj-hercai-6-seria
http://withinfp.sakura.ne.jp/eso/index.php/16807885-vetrenyj-hercai-19-seria-w8rw-vetrenyj-hercai-19-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/16771037-rannaa-ptaska-erkenci-kus-45-seria-l9ws-rannaa-ptaska-erkenci-k
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=272580
https://tg.vl-mp.com/index.php?topic=1283535.0
https://lucky28003.nl/forum/index.php?topic=4714.0
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1126915
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3552197
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3374525
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/169109
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1301902
http://danielmillsap.com/forum/index.php?topic=879556.0
http://withinfp.sakura.ne.jp/eso/index.php/16807536-nevesta-iz-stambula-istanbullu-gelin-80-seria-k7gc-nevesta-iz-s/0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ucr-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://dessa.com.br/component/k2/itemlist/user/296196
http://dscardip.com/board/index.php?page=User&userID=655238
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/185550
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3274311
http://webp.online/index.php?topic=45417.msg74195
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=48882
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=238559
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hfb-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4667347
https://tg.vl-mp.com/index.php?topic=1262128.0
http://withinfp.sakura.ne.jp/eso/index.php/16848973-edinoe-serdce-tek-yurek-20-seria-j6br-edinoe-serdce-tek-yurek-2/0
http://withinfp.sakura.ne.jp/eso/index.php/16849008-vetrenyj-hercai-6-seria-w9tv-vetrenyj-hercai-6-seria
http://withinfp.sakura.ne.jp/eso/index.php/16849077-ne-otpuskaj-mou-ruku-elimi-birakma-35-seria-q2eq-ne-otpuskaj-mo
http://withinfp.sakura.ne.jp/eso/index.php/16849159-edinoe-serdce-tek-yurek-13-seria-d3dl-edinoe-serdce-tek-yurek-1
http://withinfp.sakura.ne.jp/eso/index.php/16849241-rannaa-ptaska-erkenci-kus-44-seria-y0yz-rannaa-ptaska-erkenci-k
http://withinfp.sakura.ne.jp/eso/index.php/16849356-vossoedinenie-vuslat-18-seria-l5yc-vossoedinenie-vuslat-18-seri/0
https://www.resproxy.com/forum/index.php/760856-rasskaz-sluzanki-3-sezon-2-seria-nzj-rasskaz-sluzanki-3-sezon-2/0
http://smartacity.com/component/k2/itemlist/user/7661
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1079701
http://withinfp.sakura.ne.jp/eso/index.php/16845008-vossoedinenie-vuslat-17-seria-v7lk-vossoedinenie-vuslat-17-seri/0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=526685
http://danielmillsap.com/forum/index.php?topic=946294.0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=523499
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1815937
http://danielmillsap.com/forum/index.php?topic=887987.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/436896
http://married.dike.gr/index.php/component/k2/itemlist/user/34182
http://seoksoononly.dothome.co.kr/qna/646920
http://153.120.114.241/eso/index.php/16865844-milliardy-4-sezon-7-seria-ysr-milliardy-4-sezon-7-seria
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hu2-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14/
http://rudraautomation.com/index.php/component/k2/author/111524
http://macdistri.com/index.php/component/k2/itemlist/user/303090
http://married.dike.gr/index.php/component/k2/itemlist/user/37223
http://www.spazioad.com/component/k2/itemlist/user/7211554
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2467961
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=889594
https://danceplanet.se/commodore/index.php?topic=10478.0
https://danceplanet.se/commodore/index.php?topic=10507.0
https://danceplanet.se/commodore/index.php?topic=10539.0
https://danceplanet.se/commodore/index.php?topic=10542.0
https://danceplanet.se/commodore/index.php?topic=10561.0
https://danceplanet.se/commodore/index.php?topic=10574.0
https://danceplanet.se/commodore/index.php?topic=10596.0
https://danceplanet.se/commodore/index.php?topic=10630.0
https://danceplanet.se/commodore/index.php?topic=10648.0
https://danceplanet.se/commodore/index.php?topic=10661.0
https://danceplanet.se/commodore/index.php?topic=10668.0
https://danceplanet.se/commodore/index.php?topic=10675.0
https://danceplanet.se/commodore/index.php?topic=10703.0
https://danceplanet.se/commodore/index.php?topic=10711.0
https://danceplanet.se/commodore/index.php?topic=10714.0
https://danceplanet.se/commodore/index.php?topic=10754.0
https://danceplanet.se/commodore/index.php?topic=10792.0
https://danceplanet.se/commodore/index.php?topic=10795.0
https://danceplanet.se/commodore/index.php?topic=10800.0
http://poselokgribovo.ru/forum/index.php?topic=719539.0
http://poselokgribovo.ru/forum/index.php?topic=719545.0
http://poselokgribovo.ru/forum/index.php?topic=719549.0
http://poselokgribovo.ru/forum/index.php?topic=719555.0
http://storykingdom.forumside.com/index.php?topic=4054.0
http://storykingdom.forumside.com/index.php?topic=4917.0
http://thanosakademi.com/index.php?topic=65835.0
http://thanosakademi.com/index.php?topic=65839.0
http://www.critico-expository.com/forum/index.php?topic=3447.0
http://www.critico-expository.com/forum/index.php?topic=3450.0
http://www.deliberarchia.org/forum/index.php?topic=965865.0
http://www.deliberarchia.org/forum/index.php?topic=965876.0
http://HyUa.1fps.icu/l/szIaeDC
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-52/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-56/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-57/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-58/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-62/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-64/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-65/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-67/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-17/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/om-16-e-06-05-2019-418748/?PHPSESSID=r1gs4h4q680unb7o660flucrm0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/om-17-e-a4-om-17-e/?PHPSESSID=bl30bvoj39igfcfqe3llja5sq0
http://otitismediasociety.org/forum/index.php?topic=145914.0
http://roikjer.com/forum/index.php?PHPSESSID=93nbatgqj73g8vhgss3mhoqo65&topic=816836.0
http://www.deliberarchia.org/forum/index.php?topic=966350.0
http://www.tessabannampad.go.th/webboard/index.php?topic=191145.0
https://reficulcoin.com/index.php?topic=11853.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=27728.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=27730.0
http://roikjer.com/forum/index.php?PHPSESSID=anmapd5bak50pnlqsnbec8gjk1&topic=816865.0
http://roikjer.com/forum/index.php?PHPSESSID=u2ku1d03ec17bdvtuka5f2j5q4&topic=816843.0
https://members.fbhaters.com/index.php?topic=76551.0
http://216.104.186.20/index.php?topic=303075.0
http://cccpvideo.forumside.com/index.php?topic=581.0
http://danielmillsap.com/forum/index.php?topic=961059.0
http://euromouleusinage.com/index.php/component/k2/itemlist/user/110928
http://forum.drahthaar-club.com.ua/index.php?topic=687.0
http://golyboe.ru/forum/index.php?topic=25014.0
http://HyUa.1fps.icu/l/szIaeDC
http://mahdi.ehosseini.com/index.php/component/k2/itemlist/user/16704
http://theolevolosproject.org/?option=com_k2&view=itemlist&task=user&id=24187
http://poselokgribovo.ru/forum/index.php?topic=665512.0
http://danielmillsap.com/forum/index.php?topic=908328.0
http://www.original-craft.net/index.php?topic=295030.0
http://uberdrivers.net/forum/index.php?topic=204232.0
http://forum.byehaj.hu/index.php?topic=70801.0
http://www.tessabannampad.go.th/webboard/index.php?topic=174968.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=3fc0bb9d49011447d76aed8c92a461c6&topic=193482.0
https://khuyenmaikk13.info/index.php?topic=158085.0
http://dpmarketingsystems.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wkf-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-aoa-3-eo-4-e-online'-uyh'-a-aoa-3-eo-4-e-29-04-2019/?PHPSESSID=b2l0a7m3e24ta3lnnatvgcui03
http://teambuildingpremium.com/forum/index.php?topic=726601.0
https://sanp.pro/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-79-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j6-%d0%bd%d0%b5%d0%b2%d0%b5/
http://healthyteethpa.org/component/k2/itemlist/user/5267296
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/184352
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2519746
http://www.arunagreen.com/index.php/component/k2/itemlist/user/367918
http://dohairbiz.com/en/?option=com_k2&view=itemlist&task=user&id=2685770
http://www.ekemoon.com/141795/051520190105/
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1510664
http://israengineering.com/index.php/component/k2/itemlist/user/1079803
http://www.m1avio.com/index.php/component/k2/itemlist/user/3576989
http://matrixpharm.ru/forum/index.php?PHPSESSID=l69aqnj62k8o0qrgfc3dtqr4v0&action=profile;u=148667
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=266471
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=762857
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=762896
http://www.spazioad.com/component/k2/itemlist/user/7226081
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=42845
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=42853
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3574658
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=221125
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/221119
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/221134
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/221141
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/221153
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3301744
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3301749
https://www.netprofessional.gr/component/k2/itemlist/user/3149.html
http://forum.byehaj.hu/index.php?topic=70178.0
https://forum.ac-jete.it/index.php?topic=328512.0
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=76640
http://mvisage.sk/index.php/component/k2/itemlist/user/116962
http://poselokgribovo.ru/forum/index.php?topic=683020.0
http://macdistri.com/index.php/component/k2/itemlist/user/259612
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=25849.0
http://windowshopgoa.com/component/k2/itemlist/user/186297
http://dpmarketingsystems.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o8-%d1%81%d0%bb/
http://proxima.co.rw/index.php/component/k2/itemlist/user/550960
http://www.hoonthaitoday.com/forum/index.php?topic=128366.0
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1814251
http://www2.yasothon.go.th/smf/index.php?topic=159.msg174187
http://www.original-craft.net/index.php?topic=297893.0
http://www.edelweis.com/UserProfile/tabid/42/UserID/1612503/Default.aspx
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=513712
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w9-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://forum.byehaj.hu/index.php?topic=73635.0
http://dpmarketingsystems.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-niq-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
https://tg.vl-mp.com/index.php?topic=1265234.0
http://www.hoonthaitoday.com/forum/index.php?topic=133624.0
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/620313
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=762923
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=762942
http://www.spazioad.com/component/k2/itemlist/user/7226129
http://www.spazioad.com/component/k2/itemlist/user/7226134
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=42866
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=42868
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=42871
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/291238
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/221170
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/131722
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=671809.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/464829
http://dpmarketingsystems.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81-34/
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1104739
https://sanp.pro/%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gza-%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0/
http://www.original-craft.net/index.php?topic=294418.0
http://danielmillsap.com/forum/index.php?topic=912123.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/178225
http://www.ekemoon.com/141362/051220191805/
http://www.deliberarchia.org/forum/index.php?topic=906974.0
http://www.original-craft.net/index.php?topic=301880.0
http://www.remify.app/foro/index.php?topic=173158.0
http://dev.aabn.org.gh/component/k2/itemlist/user/484235
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/465682
http://roikjer.com/forum/index.php?PHPSESSID=4gk2hqi8teoichav024kjfftv4&topic=772259.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-l8-%d0%b8%d0%b3%d1%80%d0%b0/
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5524
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5527
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5530
http://proxima.co.rw/index.php/component/k2/itemlist/user/569633
http://proxima.co.rw/index.php/component/k2/itemlist/user/569635
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=116409
http://rudraautomation.com/index.php/component/k2/author/117703
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/187391
http://sfah.ch/de/component/k2/itemlist/user/14974
http://smartacity.com/component/k2/itemlist/user/18602
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1637111
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1637113
http://mobility-corp.com/index.php/component/k2/itemlist/user/2472785
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/176067
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7307664
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1127919
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2387857
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/41195
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/50506
http://sos.victoryaltar.org/tiki-index.php?page=UserPageraymonreinermpxwvrd
http://www.oortsociety.com/index.php?topic=8940.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1612116
http://withinfp.sakura.ne.jp/eso/index.php/16794800-zensina-58-seria-m0gs-zensina-58-seria/0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/208287
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/210156
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/210231
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/210488
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/213153
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/214852
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/215322
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/215672
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/215873
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/216275
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/217404
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/218208
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/220166
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=602089
http://withinfp.sakura.ne.jp/eso/index.php/16770692-vetrenyj-hercai-23-seria-f7yh-vetrenyj-hercai-23-seria/0
http://www.quattroandpartners.it/component/k2/itemlist/user/1025446
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1613635
http://dessa.com.br/component/k2/itemlist/user/299089
https://www.resproxy.com/forum/index.php/768425-rasskaz-sluzanki-3-sezon-1-seria-kvi-rasskaz-sluzanki-3-sezon-1/0
http://metropolis.ga/index.php?topic=790.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-goj-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/50244
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1510644
http://married.dike.gr/index.php/component/k2/itemlist/user/34577
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1315275
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4714951
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/169427
http://153.120.114.241/eso/index.php/16874823-lubov-smert-i-roboty-love-death-and-robots-4-seria-rmf-lubov-sm
http://www.telcon.gr/index.php/component/k2/itemlist/user/40420
http://seoksoononly.dothome.co.kr/qna/604886
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2486804
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/151113
http://proxima.co.rw/index.php/component/k2/itemlist/user/543620
http://rudraautomation.com/index.php/component/k2/author/108935
http://forumworldbestmt2.altervista.org/index.php?page=User&userID=119336
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=10524
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=37701
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1611106
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1840856
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3249542
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3249589
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3249590
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3249603
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3249612
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3539727
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1091441
http://healthyteethpa.org/component/k2/itemlist/user/5291863
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2520788
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1108979
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1834392
http://www.spazioad.com/component/k2/itemlist/user/7176098
http://www.spazioad.com/component/k2/itemlist/user/7214936
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1860243
http://travelsolution.info/index.php/component/k2/itemlist/user/713738
http://healthyteethpa.org/component/k2/itemlist/user/5297227
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1849427
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=77196
https://tg.vl-mp.com/index.php?topic=1267302.0
http://macdistri.com/index.php/component/k2/itemlist/user/261867
https://www.resproxy.com/forum/index.php/736310-igra-prestolov-8-sezon-1-seria-sgp-igra-prestolov-8-sezon-1-ser/0
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=14250
http://macdistri.com/index.php/component/k2/itemlist/user/258641
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=8980
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=9010
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=9026
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=9030
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=9044
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=9055
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=9089
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=9104
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=9106
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=9109
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=9114
http://withinfp.sakura.ne.jp/eso/index.php/16874955-rannaa-ptaska-erkenci-kus-40-seria-r6an-rannaa-ptaska-erkenci-k/0
https://members.fbhaters.com/index.php?topic=62279.0
http://withinfp.sakura.ne.jp/eso/index.php/16874122-edinoe-serdce-tek-yurek-10-seria-x0do-edinoe-serdce-tek-yurek-1/0
https://www.resproxy.com/forum/index.php/750537-sverh-estestvennoe-14-sezon-21-seria-shn-sverh-estestvennoe-14-/0
http://153.120.114.241/eso/index.php/16872439-lubov-smert-i-roboty-love-death-and-robots-18-seria-cga-lubov-s
http://www.arunagreen.com/index.php/component/k2/itemlist/user/385912
https://tg.vl-mp.com/index.php?topic=1255252.0
https://www.resproxy.com/forum/index.php/736992-rasskaz-sluzanki-3-sezon-5-seria-qwz-rasskaz-sluzanki-3-sezon-5
http://erhu.eu/viewtopic.php?t=233723
http://mobility-corp.com/index.php/component/k2/itemlist/user/2470275
https://lucky28003.nl/forum/index.php?topic=9660.0
https://lucky28003.nl/forum/index.php?topic=9668.0
https://lucky28003.nl/forum/index.php?topic=9811.0
https://mcsetup.tk/bbs/index.php?topic=243505.0
https://members.fbhaters.com/index.php?topic=72914.0
https://members.fbhaters.com/index.php?topic=73923.0
https://nextezone.com/index.php?action=profile;u=2261
https://nextezone.com/index.php?action=profile;u=2301
https://nextezone.com/index.php?action=profile;u=2315
https://nextezone.com/index.php?action=profile;u=2484
https://nextezone.com/index.php?topic=33017.0
https://nextezone.com/index.php?topic=33288.0
http://otitismediasociety.org/forum/index.php?topic=143023.0
https://reficulcoin.com/index.php?topic=6023.0
http://storykingdom.forumside.com/index.php?topic=4235.0
http://www.proandpro.it/index.php/component/k2/itemlist/user/4529274
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/184054
http://menulisilmiah.net/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y8-x2-%d1%80%d0%b0%d1%81%d1%81/
http://www.tessabannampad.go.th/webboard/index.php?topic=187405.0
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/998274
http://dpmarketingsystems.com/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://forum.kopkargobel.com/index.php?topic=3016.0
http://HyUa.1fps.icu/l/szIaeDC
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-18/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-19/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-20/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-8/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-9/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-6/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-7/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-16/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-17/
http://forum.stollen24.com/index.php?topic=3594.0
https://hackersuniversity.net/index.php?topic=6932.0
http://eugeniocolazzo.it/forum/index.php?topic=85482.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d2-q0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://freebeer.me/index.php?topic=284198.0
http://otitismediasociety.org/forum/index.php?topic=143798.0
http://forum.digamahost.com/index.php?topic=108413.0
http://thanosakademi.com/index.php?topic=60739.0
http://roikjer.com/forum/index.php?PHPSESSID=iiesfkf77j4hpsovtniet5trd7&topic=791527.0
http://www.critico-expository.com/forum/index.php?topic=1534.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j4-t5-%d0%b8%d0%b3%d1%80/
https://www.shaiyax.com/index.php?topic=326186.0
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-o5-g4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
https://reficulcoin.com/index.php?topic=7467.0
http://dpmarketingsystems.com/%d0%b3%d1%80%d0%b0%d0%bd%d0%b4-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2019-2/
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b0-s1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://freebeer.me/index.php?topic=289539.0
http://socialfbwidgets.com/component/k2/itemlist/user/12681.html
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a6-r3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://216.104.186.20/index.php?topic=298630.0
http://www.remify.app/foro/index.php?topic=214724.0
http://help.stv.ru/index.php?PHPSESSID=6c0169bea7045ef767a95230c7bf6982&topic=138229.0
http://forum.elexlabs.com/index.php?topic=12090.0
http://HyUa.1fps.icu/l/szIaeDC
http://forum.bmw-e60.eu/index.php?topic=1903.0
http://forum.bmw-e60.eu/index.php?topic=1915.0
http://forum.bmw-e60.eu/index.php?topic=1937.0
http://forum.bmw-e60.eu/index.php?topic=1956.0
http://forum.bmw-e60.eu/index.php?topic=2000.0
http://forum.bmw-e60.eu/index.php?topic=2002.0
http://forum.bmw-e60.eu/index.php?topic=2024.0
http://forum.bmw-e60.eu/index.php?topic=2101.0
http://forum.bmw-e60.eu/index.php?topic=2137.0
http://forum.bmw-e60.eu/index.php?topic=2177.0
http://forum.bmw-e60.eu/index.php?topic=2180.0
http://forum.bmw-e60.eu/index.php?topic=2248.0
http://forum.bmw-e60.eu/index.php?topic=2266.0
http://forum.bmw-e60.eu/index.php?topic=2268.0
http://roikjer.com/forum/index.php?PHPSESSID=ur9pbdgj9qb2fd4febm8htdgv5&topic=798843.0
http://sextomariotienda.com/blog/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2019-3/
http://poselokgribovo.ru/forum/index.php?topic=710785.0
https://npi.org.es/smf/index.php?topic=109973.0
http://www.popolsku.fr.pl/forum/index.php?topic=371960.0
http://metropolis.ga/index.php?topic=2493.0
http://sextomariotienda.com/blog/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u4-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://forum.digamahost.com/index.php?topic=107674.0
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f4-k4-%d0%b8%d0%b3%d1%80%d0%b0/
http://withinfp.sakura.ne.jp/eso/index.php/16869603-igra-prestolov-8-sezon-5-seria-rj0-igra-prestolov-8-sezon-5-ser/0
http://mir3sea.com/forum/index.php?topic=390.0
http://istakam.com/forum/index.php?topic=9115.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-22/
http://muonlineint.com/forum/index.php?topic=486.0
http://roikjer.com/forum/index.php?PHPSESSID=adui1q4ec48j0669kn4qt2rkq7&topic=809733.0
http://golyboe.ru/forum/index.php?topic=24858.0
http://withinfp.sakura.ne.jp/eso/index.php/16837266-ertugrul-150-seria-bk6-ertugrul-150-seria
http://teambuildingpremium.com/forum/index.php?topic=765245.0
https://www.thedezlab.com/lab/community/index.php?topic=127.0
http://ru-realty.com/forum/index.php?topic=449564.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90ac4%e3%80%91/
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/465438
http://HyUa.1fps.icu/l/szIaeDC
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=41002
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=499042
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/436484
https://www.resproxy.com/forum/index.php/774207-rasskaz-sluzanki-3-sezon-2-seria-spa-rasskaz-sluzanki-3-sezon-2/0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=268183
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3275010
http://webp.online/index.php?topic=40313.0
http://www.m1avio.com/index.php/component/k2/itemlist/user/3568406
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1980623
http://withinfp.sakura.ne.jp/eso/index.php/16852850-vetrenyj-hercai-20-seria-n1zf-vetrenyj-hercai-20-seria/0
http://danielmillsap.com/forum/index.php?topic=874857.0
http://smartacity.com/component/k2/itemlist/user/9860
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=265483
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=265504
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=265658
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=265674
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=265807
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=265814
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=265898
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=266014
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=266024
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=266054
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=266126
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=266326
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=266339
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=891077
http://webp.online/index.php?topic=44165.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/436551
http://withinfp.sakura.ne.jp/eso/index.php/16864051-nasa-istoria-71-seria-y4of-nasa-istoria-71-seria
http://healthyteethpa.org/component/k2/itemlist/user/5300639
http://israengineering.com/index.php/component/k2/itemlist/user/1086459
http://www.oortsociety.com/index.php?topic=8956.0
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2468715
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=63153
http://macdistri.com/index.php/component/k2/itemlist/user/286625
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kh3-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://tg.vl-mp.com/index.php?topic=1260661.0
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3687764
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=40159
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/174144
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2488084
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=8962
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-orm-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=2045
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/48539
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1317737
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4670762
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/269083
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3270658
https://www.youngbiker.de/wbboard/index.php?page=User&userID=784214
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1739367
http://153.120.114.241/eso/index.php/16860421-sverh-estestvennoe-14-sezon-21-seria-nxg-sverh-estestvennoe-14-
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=264966
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=264976
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=264988
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=265035
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=265076
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=265179
https://sto54.ru/index.php/component/k2/itemlist/user/3251122
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39873
https://tg.vl-mp.com/index.php?topic=1302047.0
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/59996
http://travelsolution.info/?option=com_k2&view=itemlist&task=user&id=697851
http://www.m1avio.com/index.php/component/k2/itemlist/user/3596421
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/51888
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=496266
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312106
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=304668
http://married.dike.gr/index.php/component/k2/itemlist/user/43931
http://married.dike.gr/index.php/component/k2/itemlist/user/44016
http://married.dike.gr/index.php/component/k2/itemlist/user/44055
http://married.dike.gr/index.php/component/k2/itemlist/user/44074
http://married.dike.gr/index.php/component/k2/itemlist/user/44277
http://married.dike.gr/index.php/component/k2/itemlist/user/44291
http://macdistri.com/index.php/component/k2/itemlist/user/264849
http://macdistri.com/index.php/component/k2/itemlist/user/264858
http://macdistri.com/index.php/component/k2/itemlist/user/264954
http://macdistri.com/index.php/component/k2/itemlist/user/265041
http://macdistri.com/index.php/component/k2/itemlist/user/265087
http://macdistri.com/index.php/component/k2/itemlist/user/265105
http://macdistri.com/index.php/component/k2/itemlist/user/265221
http://macdistri.com/index.php/component/k2/itemlist/user/265308
http://macdistri.com/index.php/component/k2/itemlist/user/265480
http://macdistri.com/index.php/component/k2/itemlist/user/265571
http://macdistri.com/index.php/component/k2/itemlist/user/265610
http://153.120.114.241/eso/index.php/16873410-igra-prestolov-game-of-thrones-8-sezon-7-seria-pj7-igra-prestol
http://153.120.114.241/eso/index.php/16873702-igra-prestolovgame-of-thrones-8-sezon-6-seria-yw0-igra-prestolo
http://153.120.114.241/eso/index.php/16873802-igra-prestolov-2019-8-sezon-5-seria-wd0-igra-prestolov-2019-8-s
http://153.120.114.241/eso/index.php/16873927-igra-prestolov-game-of-thrones-8-sezon-5-seria-mb8-igra-prestol
http://153.120.114.241/eso/index.php/16873964-igra-prestolovgame-of-thrones-8-sezon-6-seria-ve9-igra-prestolo
http://153.120.114.241/eso/index.php/16874066-igra-prestolov-2019-8-sezon-3-seria-be0-igra-prestolov-2019-8-s
http://153.120.114.241/eso/index.php/16874179-igra-prestolov-got-8-sezon-6-seria-yb9-igra-prestolov-got-8-sez
http://153.120.114.241/eso/index.php/16874326-igra-prestolov-got-8-sezon-3-seria-vp0-igra-prestolov-got-8-sez
http://153.120.114.241/eso/index.php/16874363-igra-prestolov-2019-8-sezon-5-seria-rj0-igra-prestolov-2019-8-s
http://153.120.114.241/eso/index.php/16874389-igra-prestolov-8-sezon-3-seria-yp3-igra-prestolov-8-sezon-3-ser
http://153.120.114.241/eso/index.php/16874432-igra-prestolovgame-of-thrones-8-sezon-7-seria-od3-igra-prestolo
http://153.120.114.241/eso/index.php/16874519-igra-prestolov-got-8-sezon-7-seria-zg6-igra-prestolov-got-8-sez
http://153.120.114.241/eso/index.php/16874713-igra-prestolovgame-of-thrones-8-sezon-3-seria-wt3-igra-prestolo
http://153.120.114.241/eso/index.php/16874730-igra-prestolovgame-of-thrones-8-sezon-7-seria-em9-igra-prestolo
http://153.120.114.241/eso/index.php/16874820-igra-prestolov-8-sezon-6-seria-ll3-igra-prestolov-8-sezon-6-ser
http://153.120.114.241/eso/index.php/16875730-igra-prestolov-got-8-sezon-5-seria-ep6-igra-prestolov-got-8-sez
http://153.120.114.241/eso/index.php/16875753-igra-prestolovgame-of-thrones-8-sezon-6-seria-zd0-igra-prestolo
http://153.120.114.241/eso/index.php/16876303-igra-prestolov-got-8-sezon-4-seria-xd0-igra-prestolov-got-8-sez
http://153.120.114.241/eso/index.php/16876412-igra-prestolovgame-of-thrones-8-sezon-7-seria-aw2-igra-prestolo
http://153.120.114.241/eso/index.php/16876581-igra-prestolov-2019-8-sezon-7-seria-cj5-igra-prestolov-2019-8-s
http://153.120.114.241/eso/index.php/16876641-igra-prestolov-8-sezon-7-seria-hh1-igra-prestolov-8-sezon-7-ser
http://153.120.114.241/eso/index.php/16876688-igra-prestolov-game-of-thrones-8-sezon-6-seria-nl0-igra-prestol
http://forum.elexlabs.com/index.php/topic,12917.0.html
http://healthyteethpa.org/component/k2/itemlist/user/5321531
http://bobr.site/index.php?topic=84521.0
http://www.vivelabmanizales.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j5-d3-%d1%80%d0%b0%d1%81%d1%81/
http://withinfp.sakura.ne.jp/eso/index.php/16855993-igra-prestolov-8-sezon-7-seria-kx5-igra-prestolov-8-sezon-7-ser/0
http://metropolis.ga/index.php?topic=1495.0
http://multikopterforum.hu/index.php?topic=6561.0
http://forum.politeknikgihon.ac.id/index.php?topic=17589.0
https://npi.org.es/smf/index.php?topic=110740.0
http://forum.santrope-rp.ru/index.php?topic=2428.0
http://1vh.info/index.php?topic=10231.0
https://khuyenmaikk13.info/index.php?topic=174423.0
http://withinfp.sakura.ne.jp/eso/index.php/16864445-ertugrul-145-seria-no4-ertugrul-145-seria
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3704275
https://reficulcoin.com/index.php?topic=4969.0
http://www.deliberarchia.org/forum/index.php?topic=946250.0
http://help.stv.ru/index.php?PHPSESSID=95653152cc37a385196e8709ee57a0d5&topic=135285.0
https://forum.ac-jete.it/index.php?topic=335877.0
http://multikopterforum.hu/index.php?topic=6639.0
http://sextomariotienda.com/blog/%d1%8d%d1%84%d0%b8%d1%80-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r5-%d1%81%d0%bb%d1%83%d0%b3/
http://otitismediasociety.org/forum/index.php?topic=144798.0
http://forum.politeknikgihon.ac.id/index.php?topic=14787.0
http://HyUa.1fps.icu/l/szIaeDC
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2514093
https://members.fbhaters.com/index.php?topic=60144.0
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7255029
http://dpmarketingsystems.com/smotret-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
https://members.fbhaters.com/index.php?topic=64933.0
http://ruschinaforum.ru/index.php?topic=121316.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/aa-to-67-e-k0~-'aa-to-67-e-watch'/?PHPSESSID=r952uqm25306iij7qcuve1ilm5
http://sextomariotienda.com/blog/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lhe-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://seoksoononly.dothome.co.kr/qna/616778
https://khuyenmaikk13.info/index.php?topic=167057.0
http://wb.hvekorat.com/index.php?topic=40124.0
http://poselokgribovo.ru/forum/index.php?topic=651100.0
https://khuyenmaikk13.info/index.php?topic=152001.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-z2-c3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
https://tg.vl-mp.com/index.php?topic=1316450.0
http://fbpharm.net/index.php/component/k2/itemlist/user/13181
https://nextezone.com/index.php?action=profile;u=2199
http://roikjer.com/forum/index.php?PHPSESSID=fissvl4uvqpqm1ht3j0dsekan3&topic=794608.0
http://withinfp.sakura.ne.jp/eso/index.php/16866077-holostak-9-sezon-10-vypusk-skacat-torent-hoholostak-9-sezon-10-/0
http://www.deliberarchia.org/forum/index.php?topic=923982.0
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2545197
http://www.oortsociety.com/index.php?topic=7541.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1099457
http://forum.politeknikgihon.ac.id/index.php?topic=18410.0
http://www.theparrotcentre.com/forum/index.php?topic=443562.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=657002.0
http://sextomariotienda.com/blog/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h7-%e3%80%90-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3678337
http://www.crnmedia.es/component/k2/itemlist/user/83192
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1846957
https://tg.vl-mp.com/index.php?topic=1321669.0
http://healthyteethpa.org/component/k2/itemlist/user/5311776
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/50854
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/641806
http://www2.yasothon.go.th/smf/index.php?topic=159.msg178891
http://www.deliberarchia.org/forum/index.php?topic=913878.0
http://sextomariotienda.com/blog/%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-67-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yao-%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-67/
https://www.2ayes.com/13326/vuslat-16-rri-vuslat-16
http://forum.byehaj.hu/index.php?topic=71509.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=249654
http://dev.aabn.org.gh/component/k2/itemlist/user/462073
http://153.120.114.241/eso/index.php/16825679-efir-sluga-naroda-3-sezon-19-seria-o2-sluga-naroda-3-sezon-19-s
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=560925
http://condolencias.servisa.es/9-06-05-2019-i9-9
http://guiadetudo.com/index.php/component/k2/itemlist/user/10700
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=274846
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3561560
http://www.vogtland.com.pl/index.php/component/k2/itemlist/user/10673
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1632350
http://otitismediasociety.org/forum/index.php?topic=142645.0
http://www.theparrotcentre.com/forum/index.php?topic=441593.0
http://withinfp.sakura.ne.jp/eso/index.php/16841291-devat-ziznej-8-seria-04052019
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2563828
https://khuyenmaikk13.info/index.php?topic=171875.0
https://nextezone.com/index.php?topic=28658.0
http://1vh.info/index.php?topic=3799.0
https://members.fbhaters.com/index.php?topic=63120.0
http://www.deliberarchia.org/forum/index.php?topic=947107.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/542025
http://webp.online/index.php?topic=44215.0
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1126245
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-md4-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://roikjer.com/forum/index.php?PHPSESSID=k53u85vfj591tal7p7g1io8h07&topic=778600.0
http://www.deliberarchia.org/forum/index.php?topic=953175.0
http://www.deliberarchia.org/forum/index.php?topic=953179.0
http://www.deliberarchia.org/forum/index.php?topic=953195.0
http://www.deliberarchia.org/forum/index.php?topic=953199.0
http://www.deliberarchia.org/forum/index.php?topic=953223.0
http://www.deliberarchia.org/forum/index.php?topic=953228.0
http://www.deliberarchia.org/forum/index.php?topic=953235.0
http://www.deliberarchia.org/forum/index.php?topic=953237.0
http://www.deliberarchia.org/forum/index.php?topic=953271.0
http://www.deliberarchia.org/forum/index.php?topic=953279.0
http://www.deliberarchia.org/forum/index.php?topic=953282.0
http://www.deliberarchia.org/forum/index.php?topic=953323.0
http://www.deliberarchia.org/forum/index.php?topic=953330.0
http://www.deliberarchia.org/forum/index.php?topic=953339.0
http://mediaville.me/index.php/component/k2/itemlist/user/195609
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=549359
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=37126
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/271442
https://www.youngbiker.de/wbboard/index.php?page=User&userID=781483
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=18942
https://tg.vl-mp.com/index.php?topic=1282702.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=261211
http://macdistri.com/index.php/component/k2/itemlist/user/261013
http://repofirmware.altervista.org/index.php?topic=99383.0
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ah9-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1083677
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1613616
http://proxima.co.rw/index.php/component/k2/itemlist/user/539558
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3270779
http://danielmillsap.com/forum/index.php?topic=944721.0
http://www.remify.app/foro/index.php?topic=173998.0
https://tg.vl-mp.com/index.php?topic=1256605.0
http://www.deliberarchia.org/forum/index.php?topic=883442.0
https://khuyenmaikk13.info/index.php?topic=177920.0
http://www.vivelabmanizales.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-5-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-29-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-l5-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-5/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/ma-4-eo-9-e-pq4p-ma-4-eo-9-e/?PHPSESSID=u9qjgl352863uvm57qolbi68b6
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=188753
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=285209
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42435
http://married.dike.gr/index.php/component/k2/itemlist/user/46547
http://xekhachduyetthuy.com.vn/component/k2/itemlist/user/162637
http://e-educ.net/Forum/index.php?topic=3840.0
http://macdistri.com/index.php/component/k2/itemlist/user/303796
http://danielmillsap.com/forum/index.php?topic=944659.0
http://dpmarketingsystems.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d6-%d1%81/
http://forum.politeknikgihon.ac.id/index.php?topic=19730.0
http://metropolis.ga/index.php?topic=2607.0
http://roikjer.com/forum/index.php?topic=807151.0
https://khuyenmaikk13.info/index.php?topic=172355.0
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/50029
http://www.deliberarchia.org/forum/index.php?topic=954917.0
http://alphacentauri2.info/index.php?topic=21059.msg119751
http://danielmillsap.com/forum/index.php?topic=877977.0
https://reficulcoin.com/index.php?topic=5476.0
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3710120
https://sanp.pro/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-04-05-2019-%e3%80%90pu%e3%80%91-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5/
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1130649
http://forum.politeknikgihon.ac.id/index.php?topic=7344.0
https://www.resproxy.com/forum/index.php/737717-nasledie-11-seria-rvg-nasledie-11-seria/0
http://minostech.co.kr/news/3384739
http://www2.yasothon.go.th/smf/index.php?topic=159.151020
http://www.sakitoandrichifantasy.gr/?option=com_k2&view=itemlist&task=user&id=143552
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=284860
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=773740
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yp0q-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://www.deliberarchia.org/forum/index.php?topic=942390.0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=545575
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=252983
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/184191
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=281914
https://www.gizmoarticle.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tvd-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8/
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/237267
http://thefreebitcoin.com/index.php?topic=27651.0
http://danielmillsap.com/forum/index.php?topic=951322.0
http://help.stv.ru/index.php?topic=135366.0
https://sanp.pro/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w9-06-05-2019-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://roikjer.com/forum/index.php?PHPSESSID=gqabr0p9kvc0ah9cls1muvocj6&topic=781883.0
https://npi.org.es/smf/index.php?topic=110870.0
http://withinfp.sakura.ne.jp/eso/index.php/16836051-tolarobot-9-seria-04052019/0
http://www.deliberarchia.org/forum/index.php?topic=924380.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2532158
https://khuyenmaikk13.info/index.php?topic=177817.0
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=11964
http://roikjer.com/forum/index.php?PHPSESSID=19qriosii3nnmefn7vg1gjii34&topic=808758.0
http://danielmillsap.com/forum/index.php?topic=869773.0
http://batubersurat.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=37827
http://www.deliberarchia.org/forum/index.php?topic=932235.0
http://poselokgribovo.ru/forum/index.php?topic=678060.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/'aa-to-69-e-watch'-z2'-aa-to-69-e-watch/?PHPSESSID=965e7in31hr9q4kg1m55vs9tl4
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1833014
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d0%b4%d0%b0%d1%82%d0%b0-8-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%82%d0%be%d0%bb%d1%8f-%d1%80-3/
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/11124
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=546548
http://vtservices85.fr/smf2/index.php?PHPSESSID=3d7a41c78f3e425e3fd342b32d142a6f&topic=207130.0
http://www.tessabannampad.go.th/webboard/index.php?topic=174993.0
http://dev.aabn.org.gh/component/k2/itemlist/user/485661
http://dpmarketingsystems.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sjw-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://sextomariotienda.com/blog/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81-2/
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/635712
http://www.deliberarchia.org/forum/index.php?topic=928040.0
https://forums.letstalkbeats.com/index.php?topic=52518.0
http://roikjer.com/forum/index.php?PHPSESSID=3cdl9jnahi3vl13b19jhmmlg67&topic=791969.0
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=14300
https://www.resproxy.com/forum/index.php/773054-vetrenyj-tureckij-serial-8-seria-aat3-vetrenyj-tureckij-serial-/0
http://withinfp.sakura.ne.jp/eso/index.php/16851632-04052019-tolarobot-1-seria/0
http://1vh.info/index.php?topic=9938.0
http://www.oortsociety.com/index.php?topic=6664.0
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=1231
http://fbpharm.net/index.php/component/k2/itemlist/user/9651
http://proxima.co.rw/index.php/component/k2/itemlist/user/544711
http://www.popolsku.fr.pl/forum/index.php?topic=367131.0
http://sextomariotienda.com/blog/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-04-05-2019-%e3%80%90lc%e3%80%91-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82/
https://tg.vl-mp.com/index.php?topic=1321163.0
http://taklongclub.com/forum/index.php?topic=86824.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1301931
http://uberdrivers.net/forum/index.php?topic=218160.0
https://tg.vl-mp.com/index.php?topic=1270924.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/375300
https://tg.vl-mp.com/index.php?topic=1297930.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3249448
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1110203
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/171502
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/150998
http://www.deliberarchia.org/forum/index.php?topic=936272.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523596
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1130585
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=29425
http://www.moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=594897
https://tg.vl-mp.com/index.php?topic=1283537.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=262833
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1336173
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1309465
http://www.m1avio.com/index.php/component/k2/itemlist/user/3603014
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=40137
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=37083
http://web.cas.identrics.net/phpBB3/viewtopic.php?t=118275
http://withinfp.sakura.ne.jp/eso/index.php/16840996-rannaa-ptaska-erkenci-kus-39-seria-w1xh-rannaa-ptaska-erkenci-k/0
http://withinfp.sakura.ne.jp/eso/index.php/16772632-milliardy-4-sezon-11-seria-fhm-milliardy-4-sezon-11-seria-01052/0
https://tg.vl-mp.com/index.php?topic=1292786.0
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/236988
http://healthyteethpa.org/component/k2/itemlist/user/5280786
http://healthyteethpa.org/component/k2/itemlist/user/5294771
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/237332
https://www.youngbiker.de/wbboard/index.php?page=User&userID=785268
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1843408
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=892731
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/441632
http://www.deliberarchia.org/forum/index.php?topic=953425.0
http://www.deliberarchia.org/forum/index.php?topic=953431.0
http://www.deliberarchia.org/forum/index.php?topic=953435.0
http://www.deliberarchia.org/forum/index.php?topic=953455.0
http://www.deliberarchia.org/forum/index.php?topic=953485.0
http://www.deliberarchia.org/forum/index.php?topic=953488.0
http://www.deliberarchia.org/forum/index.php?topic=953491.0
http://www.deliberarchia.org/forum/index.php?topic=953503.0
http://www.deliberarchia.org/forum/index.php?topic=953519.0
http://www.deliberarchia.org/forum/index.php?topic=953523.0
http://www.deliberarchia.org/forum/index.php?topic=953526.0
http://www.deliberarchia.org/forum/index.php?topic=953555.0
http://www.deliberarchia.org/forum/index.php?topic=953576.0
http://www.deliberarchia.org/forum/index.php?topic=953594.0
http://www.deliberarchia.org/forum/index.php?topic=894200.0
http://webp.online/index.php?topic=40652.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2540833
http://www.spazioad.com/component/k2/itemlist/user/7167106
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/55019
https://tg.vl-mp.com/index.php?topic=1310073.0
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=160855
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1630484
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1630513
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1630523
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1630648
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1630655
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1630691
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1630755
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1630784
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1630815
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1630824
[b]Что такое свобода слова? [/b]
Как следует понимать свободу слова и какие подводные камни таит в себе это социальное явление?
Свобода мысли и слова – это право каждого человека без страха
выражать свою позицию в том или ином вопросе.
Высказывать беспрепятственно свое мнение, излагать свое видение – это естественная
базовая потребность человека в самовыражении и признании.
Если бы человек не выражал свободно свои мысли,
не было бы такого огромного накопленного опыта человечества в
познании явлений и новых открытий.
[img]http://kak-bog.ru/sites/default/files/article_images/inessa/04/30/2018_-_2108/all/svoboda_slova.jpg[/img]
[b]Право на свободу слова[/b]
Право на свободу мысли и слова – естественное природное право самовыражения,
отражающее сам факт существования личности.
Убрать это право и личность становится обезличенной – «серая» масса,
знакомое всем выражения, когда «ты никто, и звать тебя никак, и слово сказать тебе нельзя».
В истории существовали времена, когда за выражение своего мнения грозила казнь, но даже под страхом смерти люди выпускали листовки,
памфлеты, собирались в подполье и принимали решения куда и как двигаться дальше в условиях несвободы.
Закон о свободе слова регламентирован в разных странах:
[u] «Конституция РФ» – статья 29;[/u]
[u] «Всеобщая декларация прав человека» – 19 статья;[/u]
[u] «Европейская конвенция о защите прав человека и основных свобод» – статья 10.[/u]
[b]Свобода слова – зло или благо? [/b]
Принцип свободы слова несет в себе как позитивные функции, так и темные стороны.
[u]Свобода слова «за» и «против»: [/u]
?человек уникален, его мысли, мировоззрение могут быть полезны для развития
?общества и открытия новых явлений, парадигм;
?озвучивание правды помогает людям сплачиваться вместе в трудные времена,
и возможность давать объективную оценку по тому или иному вопросу рассмотрев его с разных сторон;
?свобода слова в обществе – показатель развитой правовой системы.
[u]Негативные аспекты свободы слова: [/u]
?манипуляция сознанием людей;
?заведомое искажение истины и фактов, преувеличение, чем умело пользуются массовые СМИ;
в результате лжи, «промывания мозгов», нравственные устои общества, ценности, рушатся.
=========================================================
[b]Есть ресурсы которым не всё равно![/b]
[b] Только честные и самые свежие новости.[/b][u] #Stels_News_CREDIT_CARDS [/u] http://kartadlyavas.ru
[b] Самая быстрое и чёткая информация в сети. Без кюпюр[/b][u] #Fly_NEWS [/u] http://halvainrussia.ru
Всё молчат, а мы не станем!
[youtube]aMijt7xB_es[/youtube]
https://forum.ac-jete.it/index.php?topic=313037.0
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1822224
http://teambuildingpremium.com/forum/index.php?topic=743926.0
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1563236
http://macdistri.com/index.php/component/k2/itemlist/user/264938
http://yuptalk.ru/other_food_household_cosmetics_etc/-t12670.0.html
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1541771
http://www.theparrotcentre.com/forum/index.php?topic=444104.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=667159.0
http://mediaville.me/index.php/component/k2/itemlist/user/196386
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lc7p-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://yuptalk.ru/other_food_household_cosmetics_etc/-t12602.0.html
http://roikjer.com/forum/index.php?PHPSESSID=v5c0jlinli5v5mobuk1labap74&topic=786514.0
http://poselokgribovo.ru/forum/index.php?topic=666644.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3289250
http://sextomariotienda.com/blog/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e3-04-05-2019-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be/
https://khuyenmaikk13.info/index.php?topic=174055.0
https://members.fbhaters.com/index.php?topic=71473.0
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile;u=30986
http://thermoplast.envolgroupe.com/component/k2/itemlist/user/66390
http://www.deliberarchia.org/forum/index.php?topic=933561.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1110017
http://www.x2145-productions.technology/index.php?title=%C2%AB%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C_%D0%9B%D0%B5%D0%B2_2019_%C2%BB_06-05-2019_%22%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C_%D0%9B%D0%B5%D0%B2_2019_%22_%C2%AB%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C_%D0%9B%D0%B5%D0%B2_2019_%C2%BB&---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpAntispam%22%0D%0A%0D%0A%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpSection%22%0D%0A%0D%0A%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpStarttime%22%0D%0A%0D%0A20190506053633%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpEdittime%22%0D%0A%0D%0A20190506053633%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpScrolltop%22%0D%0A%0D%0A%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpAutoSummary%22%0D%0A%0D%0Ad41d8cd98f00b204e9800998ecf8427e%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22oldid%22%0D%0A%0D%0A0%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22format%22%0D%0A%0D%0Atext/x-wiki%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22model%22%0D%0A%0D%0Awikitext%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpTextbox1%22%0D%0A%0D%0Aonline%3E%20%C2%AB%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%C2%BB%20%20Zzu,%20%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E[http://hdseriionline.ru/%20hdseriionline.ru]%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20vk%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20kinovolya%3Cbr%3E%22%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20kinosled%22%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20%D1%84%D0%B8%D0%BB%D0%BC%D0%BE%D0%BD%D0%BB%D0%B8%D0%BD%D0%B5%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20%D0%BA%D0%B8%D0%BD%D0%BE%D0%B3%D0%B1%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20kinobriz%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20%D0%BA%D0%B8%D0%BD%D0%BE%D0%BA%D0%BB%D0%B0%D0%B4%D0%BE%D0%B2%D0%BA%D0%B0%3Cbr%3E..%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20kinokrad..%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20%D0%B7%D0%B9%D0%BA%D1%81%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20kinobar%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20filmix%3Cbr%3E%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20hdfilms%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20%D0%BA%D0%B8%D0%BD%D0%BE50%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20kinobriz%3C%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpSummary%22%0D%0A%0D%0A%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpSave%22%0D%0A%0D%0ASeite%20speichern%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpEditToken%22%0D%0A%0D%0Ac391a4ece0d0ac63d0a212bc1e744714+::%0D%0A---------------------------4292996597--%0D%0A&---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpAntispam%22%0D%0A%0D%0A%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpSection%22%0D%0A%0D%0A%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpStarttime%22%0D%0A%0D%0A20190506053633%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpEdittime%22%0D%0A%0D%0A20190506053633%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpScrolltop%22%0D%0A%0D%0A%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpAutoSummary%22%0D%0A%0D%0Ad41d8cd98f00b204e9800998ecf8427e%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22oldid%22%0D%0A%0D%0A0%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22format%22%0D%0A%0D%0Atext/x-wiki%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22model%22%0D%0A%0D%0Awikitext%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpTextbox1%22%0D%0A%0D%0Aonline%3E%20%C2%AB%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%C2%BB%20%20Zzu,%20%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E[http://hdseriionline.ru/%20hdseriionline.ru]%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20vk%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20kinovolya%3Cbr%3E%22%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20kinosled%22%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20%D1%84%D0%B8%D0%BB%D0%BC%D0%BE%D0%BD%D0%BB%D0%B8%D0%BD%D0%B5%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20%D0%BA%D0%B8%D0%BD%D0%BE%D0%B3%D0%B1%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20kinobriz%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20%D0%BA%D0%B8%D0%BD%D0%BE%D0%BA%D0%BB%D0%B0%D0%B4%D0%BE%D0%B2%D0%BA%D0%B0%3Cbr%3E..%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20kinokrad..%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20%D0%B7%D0%B9%D0%BA%D1%81%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20kinobar%3Cbr%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20filmix%3Cbr%3E%3E%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20hdfilms%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20%D0%BA%D0%B8%D0%BD%D0%BE50%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C%20%D0%9B%D0%B5%D0%B2%20(2019)%20kinobriz%3C%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpSummary%22%0D%0A%0D%0A%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpSave%22%0D%0A%0D%0ASeite%20speichern%0D%0A---------------------------4292996597%0D%0AContent-Disposition:%20form-data;%20name=%22wpEditToken%22%0D%0A%0D%0Ac391a4ece0d0ac63d0a212bc1e744714+::%0D%0A---------------------------4292996597--
https://khuyenmaikk13.info/index.php?topic=176657.0
http://www.hoonthaitoday.com/forum/index.php?topic=117597.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/380132
http://www.deliberarchia.org/forum/index.php?topic=950078.0
https://tg.vl-mp.com/index.php?topic=1297363.0
http://webp.online/index.php?topic=45647.0
http://metropolis.ga/index.php?topic=52.0
https://www.resproxy.com/forum/index.php/767245-mertvoe-ozero-9-seria-smotret-mertvoe-ozero-9-seria-05052019
http://www.deliberarchia.org/forum/index.php?topic=901346.0
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=110839
http://codeerror.in/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90xi7%e3%80%91-%d0%b8%d0%b3/
http://vervetama.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81-4/
http://www.deliberarchia.org/forum/index.php?topic=956129.0
http://roikjer.com/forum/index.php?topic=795538.0
http://associationsila.org/component/k2/itemlist/user/275365
http://roikjer.com/forum/index.php?PHPSESSID=3qt36d5dk9ghbr69qojn3s8q37&topic=793890.0
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/606733
http://myrechockey.com/forums/index.php?topic=80863.0
http://febrescordero.gob.ec/index.php/component/k2/itemlist/user/73374
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/286610
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/185888
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1092135
http://healthyteethpa.org/component/k2/itemlist/user/5293298
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/968096
http://withinfp.sakura.ne.jp/eso/index.php/16770095-vossoedinenie-vuslat-20-seria-x7-vossoedinenie-vuslat-20-seria-/0
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=145895
http://www.tessabannampad.go.th/webboard/index.php?topic=178233.0
https://lucky28003.nl/forum/index.php?topic=4432.0
https://npi.org.es/smf/index.php?topic=108283.0
http://ru-realty.com/forum/index.php?PHPSESSID=gtqa0oh8gveushnmjprjkh82c4&topic=443063.0
http://forum.politeknikgihon.ac.id/index.php?topic=9981.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w8-r3-%d0%b8%d0%b3%d1%80%d0%b0/
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t1-x7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://sanp.pro/05-05-2019-%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=275942
http://www.deliberarchia.org/forum/index.php?topic=948294.0
http://www.deliberarchia.org/forum/index.php?topic=939292.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-2019-8-eo-1-e-a-etoo-2019-8-eo-1-e-q3r3/?PHPSESSID=j9afer75o3c577h7dkq11tf6n6
http://guiadetudo.com/index.php/component/k2/itemlist/user/10921
http://www.oortsociety.com/index.php?topic=7005.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=255478
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/135456
http://smartacity.com/component/k2/itemlist/user/15904
http://seoksoononly.dothome.co.kr/qna/597643
https://tg.vl-mp.com/index.php?topic=1287383.0
http://soc-human.kz/index.php/component/k2/itemlist/user/1610991
http://mvisage.sk/index.php/component/k2/itemlist/user/116799
http://taklongclub.com/forum/index.php?topic=86417.0
http://seoksoononly.dothome.co.kr/qna/612652
http://teambuildingpremium.com/forum/index.php?topic=769502.0
http://153.120.114.241/eso/index.php/16871489-zvonar-18-seria-smotret-zvonar-18-seria-05052019
http://www.tessabannampad.go.th/webboard/index.php?topic=174837.0
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1671200
https://sanp.pro/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-showtime/
http://www.ekemoon.com/142191/051620194105/
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1098774
http://healthyteethpa.org/component/k2/itemlist/user/5318679
http://www.deliberarchia.org/forum/index.php?topic=897484.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172070
http://danielmillsap.com/forum/index.php?topic=947526.0
http://arunagreen.com/index.php/component/k2/itemlist/user/422708
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42379
http://salescoach.ro/content/%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-2019-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-7-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%E3%80%90hx5%E3%80%91-%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-2019-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-7-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://forum.kopkargobel.com/index.php?topic=2992.0
http://www.theparrotcentre.com/forum/index.php?topic=452763.0
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=38295
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1623652
http://multikopterforum.hu/index.php?topic=4588.0
http://help.stv.ru/index.php?PHPSESSID=6e1fb33917d3069043bffe7234135467&topic=136865.0
https://nextezone.com/index.php?topic=34029.0
https://members.fbhaters.com/index.php?topic=73396.0
http://istakam.com/forum/index.php?topic=9266.0
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x3-06-05-2019-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
https://tg.vl-mp.com/index.php?topic=1259235.0
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291373
http://www.deliberarchia.org/forum/index.php?topic=923501.0
http://www.lustralesdevallehermoso.com/index.php/component/k2/itemlist/user/47926
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1573063
http://married.dike.gr/index.php/component/k2/itemlist/user/38720
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=22490
http://www.nomaher.com/forum/index.php?topic=10247.0
https://khuyenmaikk13.info/index.php?topic=165630.0
http://danielmillsap.com/forum/index.php?topic=869884.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=ece390bacce17e53b23700c7f2ab8ab3&topic=193322.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=3c09601bcc1690b7e3da8533f3fb7c16&topic=198298.0
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3684226
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1331661
https://khuyenmaikk13.info/index.php?topic=175133.0
http://smartacity.com/component/k2/itemlist/user/11160
http://jesusandmarypatna.com/index.php/component/k2/itemlist/user/3344549
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vor-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.theparrotcentre.com/forum/index.php?topic=454738.0
http://www.theparrotcentre.com/forum/index.php?topic=447313.0
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=493815
https://nextezone.com/index.php?topic=32825.0
http://153.120.114.241/eso/index.php/16843950-igra-prestolovgame-of-thrones-8-sezon-2-seria-igra-prestolovgam
http://dev.aabn.org.gh/component/k2/itemlist/user/516314
http://www.rocktheboat.cc/members/audryblackburn/
http://www.m1avio.com/index.php/component/k2/itemlist/user/3598772
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1766226
http://1vh.info/index.php?topic=3496.0
https://www.amazingworldtop.com/entretenimiento/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b4%d0%be%d1%82%d0%be%d0%bb%d0%b5-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82/
http://erhu.eu/viewtopic.php?t=247177
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=62399
http://www.oortsociety.com/index.php?topic=6768.0
http://multikopterforum.hu/index.php?topic=2626.0
https://members.fbhaters.com/index.php?topic=67670.0
http://www.original-craft.net/index.php?topic=308961.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/52209
http://teambuildingpremium.com/forum/index.php?topic=767461.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1095992
http://poselokgribovo.ru/forum/index.php?topic=697303.0
http://roikjer.com/forum/index.php?PHPSESSID=9p01gpq6ujqd99drn7ppsc1qo6&topic=775230.0
http://jesusandmarypatna.com/index.php/component/k2/itemlist/user/3352073
https://www.gizmoarticle.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fi5b-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1562280
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1820517
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81-3/
https://members.fbhaters.com/index.php?topic=69835.0
https://woodland.org.ua/members/franziskalyell/
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3274156
http://jesusandmarypatna.com/index.php/component/k2/itemlist/user/3360722
http://www.theparrotcentre.com/forum/index.php?topic=452839.0
https://luckychancerescue.com/%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5%d0%b4%d0%be-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w7-06-05-2019-%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be/
http://otitismediasociety.org/forum/index.php?topic=142370.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=38046
https://forums.letstalkbeats.com/index.php?topic=60031.0
http://mjbosch.com/component/k2/itemlist/user/81591
http://vervetama.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z0-05-05-2019-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90lz6%e3%80%91-%d0%b8%d0%b3/
http://poselokgribovo.ru/forum/index.php?topic=699905.0
http://www.spazioad.com/index.php/component/k2/itemlist/user/7197802
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/46597
http://erhu.eu/viewtopic.php?f=7&t=242993
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/137738
https://reficulcoin.com/index.php?topic=1913.0
http://molweb.ru/groups/hd-tolya-robot-5-seriya-t5-tolya-robot-5-seriya/
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/45463
https://forum.ac-jete.it/index.php?topic=326234.0
http://www.original-craft.net/index.php?topic=309105.0
https://www.resproxy.com/forum/index.php/773959-sluga-naroda-3-sezon-10-seria-live-sluga-naroda-3-sezon-10-seri/0
http://poselokgribovo.ru/forum/index.php?topic=647637.0
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d0%b4%d0%b0%d1%82%d0%b0-%d0%b2%d1%8b%d1%85%d0%be%d0%b4%d0%b0-6-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/41680
http://dcasociados.eu/component/k2/itemlist/user/84520
http://salescoach.ro/content/%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-got-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%E3%80%90tc9%E3%80%91-%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-got-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://withinfp.sakura.ne.jp/eso/index.php/16860982-voron-kuzgun-17-seria-jbzj-voron-kuzgun-17-seria/0
http://poselokgribovo.ru/forum/index.php?topic=713750.0
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/554147
https://nextezone.com/index.php?topic=32273.0
http://www.teedinubon.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n7-05/
https://tg.vl-mp.com/index.php?topic=1308549.0
http://1vh.info/index.php?topic=6055.0
http://siirtorganik.com/index.php/component/k2/itemlist/user/748059
http://www.theparrotcentre.com/forum/index.php?topic=450401.0
http://www.atab.com.sa/?option=com_k2&view=itemlist&task=user&id=1546016
http://sextomariotienda.com/blog/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-5-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90qd1%e3%80%91-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-5-%d1%81/
http://www.oortsociety.com/index.php?topic=7036.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1106214
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=253984
http://forum.politeknikgihon.ac.id/index.php?topic=16771.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/174518
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1755275
http://www.studioaparo.it/?option=com_k2&view=itemlist&task=user&id=532026
http://vtservices85.fr/smf2/index.php?PHPSESSID=dbf7bc1fcc00ffeed4cfaa19691e5efe&topic=193431.0
http://153.120.114.241/eso/index.php/16880768-sosedi-2-sezon-13-seria-hd-sosedi-2-sezon-13-seria-06052019
https://www.gizmoarticle.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z4-%d1%81/
http://menulisilmiah.net/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-wcd-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/129637
http://eugeniocolazzo.it/forum/index.php?topic=73547.0
http://www.tekparcahdfilm.com/forum/index.php?topic=43851.0
http://www.hoonthaitoday.com/forum/index.php?topic=114522.0
http://www.quattroandpartners.it/component/k2/itemlist/user/1037570
http://www.remify.app/foro/index.php?topic=213212.0
http://matrixpharm.ru/forum/index.php?PHPSESSID=fkct5isbbne6frrs7nvr54u781&action=profile;u=162585
http://flashboot.ru/forum/index.php?topic=94351.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1113783
http://forum.kopkargobel.com/index.php?topic=3834.0
http://muratliziraatodasi.org/forum/index.php?topic=404079.0
http://rudraautomation.com/index.php/component/k2/author/109032
http://dohairbiz.com/en/component/k2/itemlist/user/2708269.html
http://roikjer.com/forum/index.php?PHPSESSID=j9o1704ii9124l456d7pjlm952&topic=799254.0
https://sanp.pro/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%80%d1%83%d1%81%d1%81-4/
http://multikopterforum.hu/index.php?topic=7929.0
https://nextezone.com/index.php?topic=31764.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=280422
http://menulisilmiah.net/%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-24-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-no0-%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-24-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.resproxy.com/forum/index.php/751894-uristy-17-seria-04052019-fj-uristy-17-seria/0
http://www.crnmedia.es/component/k2/itemlist/user/83770
http://healthyteethpa.org/component/k2/itemlist/user/5311544
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/474205
http://teambuildingpremium.com/forum/index.php?topic=724220.0
http://forum.politeknikgihon.ac.id/index.php?topic=11679.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/429590
https://hackersuniversity.net/index.php?topic=5717.0
http://dpmarketingsystems.com/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i5-%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5/
http://forum.politeknikgihon.ac.id/index.php?topic=13973.0
http://forum.politeknikgihon.ac.id/index.php?topic=9601.0
http://salescoach.ro/content/%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-95-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-%E2%80%99sqq%C2%BB-%C2%AB%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-95-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-05-05-2019
http://ruschinaforum.ru/index.php?topic=123262.0
http://www.quattroandpartners.it/component/k2/itemlist/user/982048
https://forums.letstalkbeats.com/index.php?topic=57695.0
https://www.resproxy.com/forum/index.php/725329-tola-robot-afisa-8-1-seria-tola-robot-afisa-8-1-seria/0
http://forum.kopkargobel.com/index.php?topic=2920.0
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1836370
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=670433.0
http://www.teedinubon.com/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d1%83%d0%b1%d1%82%d0%b8%d1%82%d1%80%d1%8b-ral5-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b/
http://www.theparrotcentre.com/forum/index.php?topic=444705.0
https://sanp.pro/%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5%d0%b4%d0%be-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y8-05-05-2019-%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be/
https://tg.vl-mp.com/index.php?topic=1304169.0
http://web2interactive.com/index.php/component/k2/itemlist/user/3566274
http://necinsurance.co.zw/component/k2/itemlist/user/18889.html
http://help.stv.ru/index.php?PHPSESSID=a11ed98b0ba366cf078a89fe495741b3&topic=136208.0
https://nextezone.com/index.php?topic=32402.0
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7277642
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/621655
http://sos.victoryaltar.org/tiki-index.php?page=UserPageroseannerubeozy
http://forum.kopkargobel.com/index.php?topic=2275.0
http://macdistri.com/index.php/component/k2/itemlist/user/261988
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1523414
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=24783
http://teambuildingpremium.com/forum/index.php?topic=743875.0
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=168191
http://thefreebitcoin.com/index.php?topic=33722.0
http://dev.aabn.org.gh/component/k2/itemlist/user/465985
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=185572
https://sanp.pro/%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-70-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-j9-%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-70/
http://sextomariotienda.com/blog/%d1%8d%d1%84%d0%b8%d1%80-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://roikjer.com/forum/index.php?PHPSESSID=7b4509nhj43fhpb9la7s4518k6&topic=800165.0
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=18522
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1812417
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/150583
http://freebeer.me/index.php?topic=286925.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/280344
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=494854
http://help.stv.ru/index.php?PHPSESSID=fd706b682c3f6e8ba7fce2e5533ca3d8&topic=137833.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3298104
http://danielmillsap.com/forum/index.php?topic=947212.0
http://codeerror.in/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u7-x4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://npi.org.es/smf/index.php?topic=110991.0
http://uberdrivers.net/forum/index.php?topic=203307.0
http://www.m1avio.com/index.php/component/k2/itemlist/user/3587403
http://married.dike.gr/index.php/component/k2/itemlist/user/44044
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2567633
http://www.oortsociety.com/index.php?topic=6546.0
http://macdistri.com/index.php/component/k2/itemlist/user/268967
http://teambuildingpremium.com/forum/index.php?topic=746604.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/473944
http://poselokgribovo.ru/forum/index.php?topic=685175.0
http://www.hoonthaitoday.com/forum/index.php?topic=120709.0
http://forum.byehaj.hu/index.php?topic=73122.0
http://www.m1avio.com/?option=com_k2&view=itemlist&task=user&id=3567738
http://withinfp.sakura.ne.jp/eso/index.php/16769586-milliardy-4-sezon-12-seria-hsh-milliardy-4-sezon-12-seria-01052
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/6748
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/51568
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2535542
http://danielmillsap.com/forum/index.php?topic=873840.0
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1802617
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-%d0%be%d0%bd%d0%bb%d0%b0%d0%b9%d0%bd-8-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82/
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1534434
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/167081
https://members.fbhaters.com/index.php?topic=66169.0
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=4197
http://dpmarketingsystems.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-gtn-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1086636
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=194431
http://153.120.114.241/eso/index.php/16852949-igra-prestolovgame-of-thrones-8-sezon-2-seria-igra-prestolovgam
http://macdistri.com/index.php/component/k2/itemlist/user/288681
http://www.deliberarchia.org/forum/index.php?topic=951033.0
https://nextezone.com/index.php?topic=34189.0
https://nextezone.com/index.php?topic=33917.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/184119
http://www.deliberarchia.org/forum/index.php?topic=938736.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-27/
http://withinfp.sakura.ne.jp/eso/index.php/16785125-zensina-58-seria-l5pc-zensina-58-seria/0
http://rudraautomation.com/index.php/component/k2/author/110942
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/586539
http://danielmillsap.com/forum/index.php?topic=933602.0
http://danielmillsap.com/forum/index.php?topic=893056.0
http://www.deliberarchia.org/forum/index.php?topic=947456.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-axk-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-12-%d1%81%d0%b5%d1%80/
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7310019
http://danielmillsap.com/forum/index.php?topic=932269.0
http://matrixpharm.ru/forum/index.php?PHPSESSID=anjkuoqqcrnor2lf0753mtkar6&action=profile;u=157244
http://sextomariotienda.com/blog/%d0%b3%d1%80%d0%b0%d0%bd%d0%b4-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-04-05-2019-%e3%80%90wd%e3%80%91-%d0%b3%d1%80%d0%b0%d0%bd%d0%b4-2-%d1%81%d0%b5%d0%b7%d0%be/
http://www.telcon.gr/index.php/component/k2/itemlist/user/35230
http://webp.online/index.php?topic=38345.0
http://153.120.114.241/eso/index.php/16827963-igra-prestolov-8-sezon-1-seria-quv-igra-prestolov-8-sezon-1-ser
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1608239
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=236670
http://married.dike.gr/index.php/component/k2/itemlist/user/34428
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3266055
http://www.deliberarchia.org/forum/index.php?topic=951460.0
http://married.dike.gr/index.php/component/k2/itemlist/user/36663
https://members.fbhaters.com/index.php?topic=63390.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2524981
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=268537
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/599967
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=40122
http://withinfp.sakura.ne.jp/eso/index.php/16836929-edinoe-serdce-tek-yurek-16-seria-x1io-edinoe-serdce-tek-yurek-1
http://dcasociados.eu/component/k2/itemlist/user/85599
http://153.120.114.241/eso/index.php/16786524-milliardy-4-sezon-6-seria-aqz-milliardy-4-sezon-6-seria
http://travelsolution.info/index.php/component/k2/itemlist/user/700423
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/464303
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=276296
http://mediaville.me/index.php/component/k2/itemlist/user/195350
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=300885
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81-20/
https://www.resproxy.com/forum/index.php/764675-milliardy-4-sezon-11-seria-yay-milliardy-4-sezon-11-seria-05052/0
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2566457
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7189840
http://arunagreen.com/index.php/component/k2/itemlist/user/430193
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1672190
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=605998
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=606081
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=606244
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=606389
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=606552
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=606639
http://mvisage.sk/?option=com_k2&view=itemlist&task=user&id=116492
http://batubersurat.com/index.php/component/k2/itemlist/user/41269
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1128430
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7291517
http://webp.online/index.php?topic=40475.0
http://married.dike.gr/index.php/component/k2/itemlist/user/34056
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3265929
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/45020
http://ts.bloodhand.de/forum/viewtopic.php?f=36&t=196354
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/560020
http://healthyteethpa.org/component/k2/itemlist/user/5278590
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kpz-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/55073
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2536128
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/155245
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=13965
http://withinfp.sakura.ne.jp/eso/index.php/16803276-nasa-istoria-65-seria-m5bb-nasa-istoria-65-seria
http://healthyteethpa.org/component/k2/itemlist/user/5296140
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=282535
http://www.deliberarchia.org/forum/index.php?topic=926119.0
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1605621
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=237140
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=250235
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1128033
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=16377
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=16389
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=16412
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=16418
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=16520
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=16577
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=16611
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=16626
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=16670
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=16677
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/247339
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4664759
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1315445
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2392483
http://dscardip.com/board/index.php?page=User&userID=654508
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mz6-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13/
https://tg.vl-mp.com/index.php?topic=1273476.0
https://tg.vl-mp.com/index.php?topic=1258679.0
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26159265/Default.aspx
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qx3-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14/
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1551455
https://tg.vl-mp.com/index.php?topic=1277989.0
http://withinfp.sakura.ne.jp/eso/index.php/16825039-voron-kuzgun-9-seria-x8nh-voron-kuzgun-9-seria
http://www.deliberarchia.org/forum/index.php?topic=944681.0
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1763929
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1764244
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1764368
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1764508
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1764527
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1764696
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1764788
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1766006
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=265105
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(e-ioa-oota-21-e)-e-ioa-oota-21-e-oot-oa/?PHPSESSID=ub8skin29c2913effkhdlh7li2
http://poselokgribovo.ru/forum/index.php?topic=655457.0
http://danielmillsap.com/forum/index.php?topic=881084.0
http://withinfp.sakura.ne.jp/eso/index.php/16838979-ertugrul-5-sezon-29-seria-c0-ertugrul-5-sezon-29-seria/0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3525906
https://hackersuniversity.net/index.php?topic=7075.0
http://teambuildingpremium.com/forum/index.php?topic=709904.0
http://www2.yasothon.go.th/smf/index.php?topic=159.150600
http://mobility-corp.com/index.php/component/k2/itemlist/user/2479589
http://www.deliberarchia.org/forum/index.php?topic=933655.0
http://matrixpharm.ru/forum/index.php?PHPSESSID=ggskgqajcuc45k0fl216j3vsj7&action=profile;u=160014
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=559738
http://forum.politeknikgihon.ac.id/index.php?topic=15323.0
http://forum.kopkargobel.com/index.php?topic=3041.0
http://www.alase.net/index.php/component/k2/itemlist/user/11304
http://153.120.114.241/eso/index.php/16874115-igra-prestolovgame-of-thrones-8-sezon-6-seria-lu5-igra-prestolo
https://khuyenmaikk13.info/index.php?topic=177133.0
http://withinfp.sakura.ne.jp/eso/index.php/16876833-po-zakonam-voennogo-vremeni-3-sezon-4-seria-06052019-d4-po-zako
http://8.droror.co.il/uncategorized/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c4-q1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://marjorieaperry.com/?option=com_k2&view=itemlist&task=user&id=479694
http://sextomariotienda.com/blog/%d0%b4%d0%b5%d1%82%d0%b8-%d1%81%d0%b5%d1%81%d1%82%d0%b5%d1%80-kardes-cocuklari-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bf%d0%b5%d1%80%d0%b5%d0%b2%d0%be%d0%b4-%d0%bd%d0%b0-%d1%80%d1%83-3/
http://uberdrivers.net/forum/index.php?topic=210787.0
https://www.resproxy.com/forum/index.php/757054-nasledie-17-seria-ydq-nasledie-17-seria/0
https://www.amazingworldtop.com/entretenimiento/%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-q6-%e3%80%90-%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f%e3%80%91/
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=265310
http://www.theparrotcentre.com/forum/index.php?topic=438231.0
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81-29/
https://tg.vl-mp.com/index.php?topic=1313876.0
http://sextomariotienda.com/blog/video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u2-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=648725.0
https://khuyenmaikk13.info/index.php?topic=172792.0
http://www.deliberarchia.org/forum/index.php?topic=884675.0
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=266636
http://www.deliberarchia.org/forum/index.php?topic=935304.0
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=496505
http://podwodnyswiat.eu/forum/index.php?topic=140.0
http://withinfp.sakura.ne.jp/eso/index.php/16853823-ertugrul-146-seria-kq6-ertugrul-146-seria/0
https://sanp.pro/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-g5i1-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-watch/
http://withinfp.sakura.ne.jp/eso/index.php/16869878-smotret-holostak-9-sezon-13-vypusk/0
http://forum.digamahost.com/index.php?topic=107138.0
http://otitismediasociety.org/forum/index.php?topic=142977.0
http://batubersurat.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=42486
http://patagroupofcompanies.com/component/k2/itemlist/user/195632
http://community.viajar.tur.br/index.php?p=/profile/tgflaura67
https://verdadesbiblicas.org.ec/index.php/component/k2/itemlist/user/3702732
http://forum.byehaj.hu/index.php?topic=76381.0
https://tg.vl-mp.com/index.php?topic=1258659.0
http://necinsurance.co.zw/component/k2/itemlist/user/18376.html
http://ru-realty.com/forum/index.php?PHPSESSID=vbpnl23ts8309q9pe7v2rf50n3&topic=451264.0
http://1vh.info/index.php?topic=8569.0
http://dev.aabn.org.gh/component/k2/itemlist/user/487666
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=296319
http://www.deliberarchia.org/forum/index.php?topic=890956.0
https://sanp.pro/%d0%b4%d0%b5%d1%82%d0%b8-%d1%81%d0%b5%d1%81%d1%82%d0%b5%d1%80-kardes-cocuklari-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bf%d0%b5%d1%80%d0%b5%d0%b2%d0%be%d0%b4-%d0%b8-%d1%81%d1%83%d0%b1/
http://www.deliberarchia.org/forum/index.php?topic=943187.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1077891
http://withinfp.sakura.ne.jp/eso/index.php/16778537-riverdejl-riverdale-3-sezon-24-seria-wyf-riverdejl-riverdale-3-/0
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/43939
http://travelsolution.info/?option=com_k2&view=itemlist&task=user&id=703997
http://danielmillsap.com/forum/index.php?topic=905862.0
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2538530
http://mediaville.me/index.php/component/k2/itemlist/user/209416
http://www.deliberarchia.org/forum/index.php?topic=957354.0
http://webp.online/index.php?topic=46007.30
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1827548
http://menulisilmiah.net/%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qx7-%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pf4-%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81-36/
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81-34/
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kp1-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ds5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wj6-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17/
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hz3-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9/
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mp0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-cr0-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://menulisilmiah.net/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-td7-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://menulisilmiah.net/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-fz8-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/172862
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=242878
http://withinfp.sakura.ne.jp/eso/index.php/16779366-cernoe-zerkalo-5-sezon-5-seria-arn-cernoe-zerkalo-5-sezon-5-ser/0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1108775
https://www.resproxy.com/forum/index.php/771543-milliardy-4-sezon-13-seria-zau-milliardy-4-sezon-13-seria/0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/279451
http://www.m1avio.com/index.php/component/k2/itemlist/user/3570289
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/273456
https://www.youngbiker.de/wbboard/index.php?page=User&userID=785810
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/521055
http://www.deliberarchia.org/forum/index.php?topic=897651.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/55903
http://mediaville.me/index.php/component/k2/itemlist/user/208551
http://www.deliberarchia.org/forum/index.php?topic=962343.0
http://www.deliberarchia.org/forum/index.php?topic=962354.0
http://www.deliberarchia.org/forum/index.php?topic=962364.0
http://www.deliberarchia.org/forum/index.php?topic=962377.0
https://lucky28003.nl/forum/index.php?topic=10350.0
http://myrechockey.com/forums/index.php?topic=86506.0
http://myrechockey.com/forums/index.php?topic=86508.0
http://webp.online/index.php?topic=46395.15
http://www.deliberarchia.org/forum/index.php?topic=962390.0
http://www.deliberarchia.org/forum/index.php?topic=962428.0
http://www.deliberarchia.org/forum/index.php?topic=962432.0
http://macdistri.com/index.php/component/k2/itemlist/user/283119
http://macdistri.com/index.php/component/k2/itemlist/user/283271
http://macdistri.com/index.php/component/k2/itemlist/user/283322
http://macdistri.com/index.php/component/k2/itemlist/user/283443
http://macdistri.com/index.php/component/k2/itemlist/user/283476
http://macdistri.com/index.php/component/k2/itemlist/user/283516
http://macdistri.com/index.php/component/k2/itemlist/user/283571
http://macdistri.com/index.php/component/k2/itemlist/user/283978
http://macdistri.com/index.php/component/k2/itemlist/user/284037
http://macdistri.com/index.php/component/k2/itemlist/user/284098
http://macdistri.com/index.php/component/k2/itemlist/user/284126
http://macdistri.com/index.php/component/k2/itemlist/user/284207
http://macdistri.com/index.php/component/k2/itemlist/user/284337
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42952
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42970
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43052
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43059
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43063
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43065
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43079
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43112
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43133
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43142
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43150
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43154
http://www.ekemoon.com/141149/051020194805/
https://www.resproxy.com/forum/index.php/731371-uristy-20-seria-uristy-20-seria-02052019/0
http://mediaville.me/index.php/component/k2/itemlist/user/201124
https://tg.vl-mp.com/index.php?topic=1249014.0
http://teambuildingpremium.com/forum/index.php?topic=744483.0
https://www.c-alice.org/forum/index.php?topic=67573.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1597417
http://seoksoononly.dothome.co.kr/qna/729539
http://myrechockey.com/forums/index.php?topic=80751.0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=562835
http://menulisilmiah.net/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-zbo-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://jpacschoolclubs.co.uk/?option=com_k2&view=itemlist&task=user&id=3337810
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/181067
http://www.remify.app/foro/index.php?topic=217564.0
http://koushatarabar.com/index.php/component/k2/itemlist/user/1313610
http://taklongclub.com/forum/index.php?topic=92749.0
http://guiadetudo.com/index.php/component/k2/itemlist/user/10594
http://www.teedinubon.com/%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5%d0%b4%d0%be-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m1-05-05-2019-%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be/
http://www.deliberarchia.org/forum/index.php?topic=953276.0
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j4-f4-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/48530
http://forums.abs-cbn.com/welcome-back-kapamilya%21/e-eka-aota-(e-ioa-oota)-18-e-05-05-2019/?PHPSESSID=i2g5qposqp2a2fjrk0scg3u6f4
http://withinfp.sakura.ne.jp/eso/index.php/16841179-igra-prestolov-8-sezon-5-seria-igra-prestolov-8-sezon-5-seria-r/0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=560652
http://mobility-corp.com/index.php/component/k2/itemlist/user/2478178
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/174812
http://sextomariotienda.com/blog/%d0%bd%d0%b5-%d0%be%d1%82%d0%bf%d1%83%d1%81%d0%ba%d0%b0%d0%b9-%d0%bc%d0%be%d1%8e-%d1%80%d1%83%d0%ba%d1%83-elimi-birakma-39-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%80%d1%83%d1%81-%d0%bf%d0%b5-2/
http://forum.politeknikgihon.ac.id/index.php?topic=7716.0
http://www.theparrotcentre.com/forum/index.php?topic=445567.0
http://travelsolution.info/index.php/component/k2/itemlist/user/697666
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3528561
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2517302
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3558856
https://www.c-alice.org/forum/index.php?topic=65886.0
http://matrixpharm.ru/forum/index.php?PHPSESSID=ure2lailuqoo48kqmgg02vale4&action=profile;u=149284
http://forum.byehaj.hu/index.php?topic=73047.0
http://www.original-craft.net/index.php?topic=300570.0
http://sextomariotienda.com/blog/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hcj-%d0%b2%d0%be%d1%81/
https://goagiletour.ca/node/1/sessions/%C2%AB%D0%B2%D0%BE%D1%81%D0%BA%D1%80%D0%B5%D1%81%D1%88%D0%B8%D0%B9-%D1%8D%D1%80%D1%82%D1%83%D0%B3%D1%80%D1%83%D0%BB-150-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%E2%80%98nfh-%C2%AB%D0%B2%D0%BE%D1%81%D0%BA%D1%80%D0%B5%D1%81%D1%88%D0%B8%D0%B9-%D1%8D%D1%80%D1%82%D1%83%D0%B3%D1%80%D1%83%D0%BB-150-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nc0d-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2524962
https://tg.vl-mp.com/index.php?topic=1294461.0
https://www.2ayes.com/11804/hercai-7-imm-hercai-7
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=287252
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=23999.0
http://www.deliberarchia.org/forum/index.php?topic=917973.0
http://danielmillsap.com/forum/index.php?topic=944118.0
http://153.120.114.241/eso/index.php/16857699-vetrenyj-8-seria-ozvucka-mta3-vetrenyj-8-seria-ozvucka
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=35489
http://www.deliberarchia.org/forum/index.php?topic=944326.0
http://forum.digamahost.com/index.php?topic=107111.0
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=185451
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2555279
http://www.hoonthaitoday.com/forum/index.php?topic=127876.0
http://sextomariotienda.com/blog/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-h9g5-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-watc/
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=677826.0
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42823
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=110334
http://multikopterforum.hu/index.php?topic=7199.0
http://forum.politeknikgihon.ac.id/index.php?topic=6769.0
https://www.resproxy.com/forum/index.php/736764-rasskaz-sluzanki-3-sezon-1-seria-cak-rasskaz-sluzanki-3-sezon-1/0
http://webp.online/index.php?topic=38055.0
http://minostech.co.kr/news/3381850
http://forum.bmw-e60.eu/index.php?topic=3493.0
<a href="http://cialisdxt.com/">buy generic cialis</a>
cialis price vs viagra which is better
[url=http://cialisdxt.com/]buy generic cialis[/url]
40 mg cialis dosage strengths
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2489781
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/231822
http://marjorieaperry.com/?option=com_k2&view=itemlist&task=user&id=475331
http://www.jobref.de/node/2124850
http://www.ekemoon.com/138675/051120191504/
http://theolevolosproject.org/index.php/component/k2/itemlist/user/23245
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-%d1%81%d0%b0%d1%83%d0%bd%d0%b4%d1%82%d1%80%d0%b5%d0%ba%d0%b8-1-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%82%d0%be%d0%bb%d1%8f-%d1%80/
http://mir3sea.com/forum/index.php?topic=301.0
http://roikjer.com/forum/index.php?topic=796095.0
https://nextezone.com/index.php?topic=30809.0
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3710122
http://www2.yasothon.go.th/smf/index.php?topic=159.154965
http://www.tessabannampad.go.th/webboard/index.php?topic=190003.0
http://muonlineint.com/forum/index.php?topic=1396.0
http://thanosakademi.com/index.php?topic=62810.0
http://webp.online/index.php?topic=45500.0
http://eugeniocolazzo.it/forum/index.php?topic=88796.0
http://danielmillsap.com/forum/index.php?topic=939875.0
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43198
http://www.deliberarchia.org/forum/index.php?topic=931475.0
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=17281
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/4011
http://associationsila.org/component/k2/itemlist/user/258568
http://www.original-craft.net/index.php?topic=305320.0
https://www.resproxy.com/forum/index.php/738307-milliardy-4-sezon-11-seria-buh-milliardy-4-sezon-11-seria-03052/0
http://webp.online/index.php?topic=38900.0
http://withinfp.sakura.ne.jp/eso/index.php/16804550-vossoedinenie-vuslat-16-seria-o6kz-vossoedinenie-vuslat-16-seri
http://teambuildingpremium.com/forum/index.php?topic=755327.0
http://necinsurance.co.zw/component/k2/itemlist/user/17874.html
https://ne-kuru.ru/index.php?topic=212002.0
http://www.deliberarchia.org/forum/index.php?topic=928541.0
http://www.deliberarchia.org/forum/index.php?topic=957738.0
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/983442
http://forum.politeknikgihon.ac.id/index.php?topic=16484.0
https://theprodigy.info/forum/index.php?topic=28410.0
http://forum.politeknikgihon.ac.id/index.php?topic=12767.0
http://withinfp.sakura.ne.jp/eso/index.php/16805278-uristy-16-seria-o1vk-uristy-16-seria/0
http://seoksoononly.dothome.co.kr/qna/712285
http://otitismediasociety.org/forum/index.php?topic=143970.0
http://1vh.info/index.php?topic=9916.0
https://www.resproxy.com/forum/index.php/738789-sotna-the-100-6-sezon-10-seria-aobv-sotna-the-100-6-sezon-10-se/0
http://help.stv.ru/index.php?PHPSESSID=2f88595fb73d3575a4999f9fdbfc0a75&topic=138132.0
http://thermoplast.envolgroupe.com/component/k2/author/65219
http://dpmarketingsystems.com/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://sextomariotienda.com/blog/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mqo5-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82/
http://www.m1avio.com/index.php/component/k2/itemlist/user/3598640
http://www.hoonthaitoday.com/forum/index.php?topic=134312.0
http://withinfp.sakura.ne.jp/eso/index.php/16794245-milliardy-4-sezon-10-seria-oxo-milliardy-4-sezon-10-seria/0
http://seoksoononly.dothome.co.kr/qna/591367
http://macdistri.com/index.php/component/k2/itemlist/user/302184
http://roikjer.com/forum/index.php?PHPSESSID=ajb5rktspbdlt8ncn4ffge8v32&topic=809126.0
https://www.resproxy.com/forum/index.php/778959-smotret-tolarobot-8-seria-v8-tolarobot-8-seria/0
http://travelsolution.info/?option=com_k2&view=itemlist&task=user&id=716297
http://www.hoonthaitoday.com/forum/index.php?topic=139630.0
https://www.resproxy.com/forum/index.php/769628-vetrenyj-hercai-17-seria-p5dj-vetrenyj-hercai-17-seria/0
http://1vh.info/index.php?topic=7169.0
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-a3-%e3%80%90-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.deliberarchia.org/forum/index.php?topic=948960.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39048
http://dscardip.com/board/index.php?page=User&userID=655510
http://www.deliberarchia.org/forum/index.php?topic=925373.0
https://tg.vl-mp.com/index.php?topic=1286186.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/445394
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/246097
http://www.x2145-productions.technology/index.php?title=%C2%AB%D0%9C%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%C2%BB_06-05-2019_%D0%9C%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4_%C2%AB%D0%9C%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%C2%BB
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2521279
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26107866/Default.aspx
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/150456
http://www.m1avio.com/index.php/component/k2/itemlist/user/3606235
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=172265
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312435
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312447
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312602
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312704
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312914
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4711863
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4711870
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4711923
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4711946
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4711976
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4712009
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4712129
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4712144
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4712197
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4712304
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4712350
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4712404
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4712460
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4712498
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1661633
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-%d0%bf%d1%80%d0%b5%d0%bc%d1%8c%d0%b5%d1%80%d0%b0-3-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1-3/
https://members.fbhaters.com/index.php?topic=63989.0
http://web2interactive.com/index.php/component/k2/itemlist/user/3517706
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=49648
http://www.m1avio.com/index.php/component/k2/itemlist/user/3565035
http://www.remify.app/foro/index.php?topic=186809.0
http://sextomariotienda.com/blog/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gfk-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://eugeniocolazzo.it/forum/index.php?topic=81816.0
http://www.nomaher.com/forum/index.php?topic=10831.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1092082
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/197494
http://teambuildingpremium.com/forum/index.php?topic=735604.0
https://tg.vl-mp.com/index.php?topic=1318282.0
http://poselokgribovo.ru/forum/index.php?topic=712536.0
http://macdistri.com/index.php/component/k2/itemlist/user/303347
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=201851
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/151314
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90lf6%e3%80%91-%d0%b8%d0%b3/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-55/
http://macdistri.com/index.php/component/k2/itemlist/user/299705
https://nextezone.com/index.php?topic=31591.0
http://1vh.info/index.php?topic=10607.0
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/143257
http://soc-human.kz/index.php/component/k2/itemlist/user/1619880
http://www.dap.com.py/index.php/component/k2/itemlist/user/779189
https://tg.vl-mp.com/index.php?topic=1312162.0
http://sextomariotienda.com/blog/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%be%d0%bd%d0%bb%d0%b0%d0%b9%d0%bd-%e3%80%90lq8%e3%80%91-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146/
http://proxima.co.rw/index.php/component/k2/itemlist/user/550494
https://www.resproxy.com/forum/index.php/770644-tola-robot-2-seria-watch-c7-tola-robot-2-seria-tola-robot-2-ser/0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1311385
https://khuyenmaikk13.info/index.php?topic=177028.0
http://www.tvmechanic.co.in/forum/index.php?topic=7792.0
http://matrixpharm.ru/forum/index.php?PHPSESSID=c2g4itp3oo2uqp543lgjri5m97&action=profile;u=163843
http://www.critico-expository.com/forum/index.php?topic=462.0
http://forum.stollen24.com/index.php?topic=1734.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=4a7e79dc1b036d96536856855faef6b0&topic=197800.0
http://www.theparrotcentre.com/forum/index.php?topic=433429.0
https://tg.vl-mp.com/index.php?topic=1300702.0
http://seoksoononly.dothome.co.kr/qna/621464
https://tg.vl-mp.com/index.php?topic=1269319.0
https://tg.vl-mp.com/index.php?topic=1279091.0
https://danceplanet.se/commodore/index.php?topic=8277.0
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=2148
http://roikjer.com/forum/index.php?topic=789246.0
http://forum.digamahost.com/index.php?topic=108139.0
http://roikjer.com/forum/index.php?PHPSESSID=ce5m395rj5dtb780njd2aod8o3&topic=793117.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=ad33e840b089d2178dddd04e3c08b59b&topic=208061.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1115870
http://www.popolsku.fr.pl/forum/index.php?topic=370016.0
http://withinfp.sakura.ne.jp/eso/index.php/16863758-ertugrul-149-seria-nz8-ertugrul-149-seria/0
https://forums.letstalkbeats.com/index.php?topic=62443.0
http://web.cas.identrics.net/phpBB3/viewtopic.php?f=14&t=117799
http://www.theparrotcentre.com/forum/index.php?topic=447448.0
https://members.fbhaters.com/index.php?topic=60699.0
http://danielmillsap.com/forum/index.php?topic=868484.0
http://mediaville.me/index.php/component/k2/itemlist/user/190240
https://www.youngbiker.de/wbboard/index.php?page=User&userID=785271
https://reficulcoin.com/index.php?topic=2086.0
http://poselokgribovo.ru/forum/index.php?topic=692658.0
http://uberdrivers.net/forum/index.php?topic=201571.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=290658
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/55691
http://matrixpharm.ru/forum/index.php?PHPSESSID=qhdkcinrg9tvt4u1j10pqio017&action=profile;u=159236
http://roikjer.com/forum/index.php?PHPSESSID=t7scvjglo2amp59034c8peubr7&topic=775170.0
http://www.deliberarchia.org/forum/index.php?topic=942540.0
http://www.deliberarchia.org/forum/index.php?topic=911587.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2475361
http://myrechockey.com/forums/index.php?topic=84340.0
http://forum.digamahost.com/index.php?topic=108862.0
http://metropolis.ga/index.php?topic=1659.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-3/
http://dpmarketingsystems.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d6-p3-%d1%80%d0%b0%d1%81%d1%81/
http://miklja.net/forum/index.php?topic=26086.0
https://tg.vl-mp.com/index.php?topic=1297916.0
http://1vh.info/index.php?topic=2655.0
http://ptu.imoove.kr/ko/content/%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-b1-%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F330672
http://healthyteethpa.org/component/k2/itemlist/user/5282852
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=780010
http://multikopterforum.hu/index.php?topic=7989.0
http://www.m1avio.com/index.php/component/k2/itemlist/user/3583813
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1631538
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12520
http://uberdrivers.net/forum/index.php?topic=206515.0
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1127738
http://taklongclub.com/forum/index.php?topic=80086.0
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1822455
http://taklongclub.com/forum/index.php?topic=71370.0
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=92315
http://teambuildingpremium.com/forum/index.php?topic=766391.0
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lostfilm-j5-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/167121
http://www.atab.com.sa/index.php/en/?option=com_k2&view=itemlist&task=user&id=1532995
http://withinfp.sakura.ne.jp/eso/index.php/16875733-igra-prestolov-game-of-thrones-8-sezon-4-seria-bs7-igra-prestol/0
http://myrechockey.com/forums/index.php?topic=84384.0
http://rudraautomation.com/index.php/component/k2/author/108303
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=200250
http://community.viajar.tur.br/index.php?p=/profile/dulciemcgr
https://sanp.pro/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p4-%d1%81%d0%bb/
http://batubersurat.com/index.php/component/k2/itemlist/user/42819
https://www.resproxy.com/forum/index.php/762623-vetrenyj-8-seria-russkaa-ozvucka-smotret-jtb1-vetrenyj-8-seria-/0
https://sanp.pro/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2019-2/
http://www.deliberarchia.org/forum/index.php?topic=956370.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12020
http://trunk.www.volkalize.com/members/kevinkobayashi/
http://freebeer.me/index.php?topic=298315.0
http://thanosakademi.com/index.php?topic=62334.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-b8-w0-%d0%b8%d0%b3%d1%80/
http://smartacity.com/component/k2/itemlist/user/15904
http://seoksoononly.dothome.co.kr/qna/597643
https://tg.vl-mp.com/index.php?topic=1287383.0
http://soc-human.kz/index.php/component/k2/itemlist/user/1610991
http://mvisage.sk/index.php/component/k2/itemlist/user/116799
http://taklongclub.com/forum/index.php?topic=86417.0
http://seoksoononly.dothome.co.kr/qna/612652
http://teambuildingpremium.com/forum/index.php?topic=769502.0
http://engeena.com/?option=com_k2&view=itemlist&task=user&id=7311
http://www.thenixnoob.com/viewtopic.php?t=636344
https://www.resproxy.com/forum/index.php/763336-uristy-8-seria-04052019-oo-uristy-8-seria
https://tg.vl-mp.com/index.php?topic=1291711.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/404175
http://teambuildingpremium.com/forum/index.php?topic=761937.0
http://xn--22cmah2caecpucll2cycdoj4d0knajrq3e5pbj9w0c.americanwolfthailand.com/DJPetjah/index.php?topic=1479953.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s4-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://www.resproxy.com/forum/index.php/730329-sosedi-2-sezon-11-seria-smotret-sosedi-2-sezon-11-seria-0205201/0
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/11101
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=276049
http://poselokgribovo.ru/forum/index.php?topic=700240.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=299905
http://k2.akademitelkom.ac.id/index.php/component/k2/itemlist/user/288255
http://www.quattroandpartners.it/component/k2/itemlist/user/1037898
https://khuyenmaikk13.info/index.php?topic=173305.0
http://www.babvallejo.com/index.php/component/k2/itemlist/user/604809
http://metropolis.ga/index.php?topic=2094.0
http://married.dike.gr/index.php/component/k2/itemlist/user/44556
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=607748
http://roikjer.com/forum/index.php?topic=778484.0
http://1vh.info/index.php?topic=10328.0
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1128369
http://www.arunagreen.com/index.php/component/k2/itemlist/user/405832
https://forums.letstalkbeats.com/index.php?topic=61219.0
http://adsudoeste.com.br/?option=com_k2&view=itemlist&task=user&id=20469
http://withinfp.sakura.ne.jp/eso/index.php/16802183-sluga-naroda-3-sezon-19-seria-smotret-sluga-naroda-3-sezon-19-s/0
http://teambuildingpremium.com/forum/index.php?topic=713167.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(om-15-e)-om-15-e-m/?PHPSESSID=m6j2l539mvjjdhkm9vajhc9o61
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3376228
http://poselokgribovo.ru/forum/index.php?topic=653038.0
http://www.telcon.gr/index.php/component/k2/itemlist/user/40832
http://thefreebitcoin.com/index.php?topic=34209.0
http://www.tekparcahdfilm.com/forum/index.php?topic=43635.0
http://soc-human.kz/index.php/component/k2/itemlist/user/1622351
http://www.m1avio.com/index.php/component/k2/itemlist/user/3541304
http://freebeer.me/index.php?topic=246781.0
http://multikopterforum.hu/index.php?topic=9382.0
http://danielmillsap.com/forum/index.php?topic=920169.0
https://members.fbhaters.com/index.php/topic,70593.0.html
http://freebeer.me/index.php?topic=294044.0
http://universaldrive-s.cba.pl/index.php?PHPSESSID=abeb1a35c862efcd4a3c786dfc23df1f&topic=18762.0
http://sextomariotienda.com/blog/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t0-04/
http://metropolis.ga/index.php?topic=2725.0
http://community.viajar.tur.br/index.php?p=/profile/stellabrew
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3374269
http://danielmillsap.com/forum/index.php?topic=932202.0
http://www.theparrotcentre.com/forum/index.php?topic=439715.0
http://bobr.site/index.php?topic=80192.0
http://poselokgribovo.ru/forum/index.php?topic=707245.0
https://sanp.pro/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-10-05-2019-i6a1-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://webp.online/index.php?topic=41155.0
http://www.thenixnoob.com/viewtopic.php?t=629067
http://travelsolution.info/index.php/component/k2/itemlist/user/705085
http://www.theparrotcentre.com/forum/index.php?topic=430612.0
http://e-educ.net/Forum/index.php?topic=1975.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=254340
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2524932
http://thermoplast.envolgroupe.com/component/k2/author/67164
http://mobility-corp.com/index.php/component/k2/itemlist/user/2479668
http://travelsolution.info/?option=com_k2&view=itemlist&task=user&id=706393
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1082046
https://tg.vl-mp.com/index.php?topic=1302419.0
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=163360
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=163431
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=163573
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=163760
http://xekhachduyetthuy.com.vn/component/k2/itemlist/user/157412
http://xekhachduyetthuy.com.vn/component/k2/itemlist/user/157751
http://xekhachduyetthuy.com.vn/component/k2/itemlist/user/157989
http://xekhachduyetthuy.com.vn/component/k2/itemlist/user/158142
http://xekhachduyetthuy.com.vn/component/k2/itemlist/user/158786
http://xekhachduyetthuy.com.vn/component/k2/itemlist/user/159293
http://xekhachduyetthuy.com.vn/component/k2/itemlist/user/159471
http://xekhachduyetthuy.com.vn/component/k2/itemlist/user/159502
http://withinfp.sakura.ne.jp/eso/index.php/16795639-igra-prestolov-8-sezon-3-seria-qrp-igra-prestolov-8-sezon-3-ser/0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=268853
http://www.sopcich.com/UserProfile/tabid/42/UserID/1713591/Default.aspx
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/55820
http://withinfp.sakura.ne.jp/eso/index.php/16803214-suzet-seriala-tola-robot-8-seria-qj-suzet-seriala-tola-robot-8-/0
http://webp.online/index.php?topic=44784.0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/188215
http://macdistri.com/index.php/component/k2/itemlist/user/259852
http://www.spazioad.com/component/k2/itemlist/user/7172677
http://www.spazioad.com/component/k2/itemlist/user/7169177
https://www.resproxy.com/forum/index.php/721281-hdvideo-igra-prestolov-8-sezon-5-seria-amedia-q2-igra-prestolov/0
http://www.theparrotcentre.com/forum/index.php?topic=432983.0
http://webp.online/index.php?topic=44934.0
http://molweb.ru/groups/rannyaya-ptashka-erkenci-kus-38-seriya-djl-rannyaya-ptashka-erkenci-kus-38-seriya/
http://www.nomaher.com/forum/index.php?topic=10310.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2567809
https://tg.vl-mp.com/index.php?topic=1282185.0
http://macdistri.com/index.php/component/k2/itemlist/user/260587
http://www.elpinatarense.com/?option=com_k2&view=itemlist&task=user&id=155097
https://www.resproxy.com/forum/index.php/755315-lucifer-lucifer-4-sezon-1-seria-rbno-lucifer-lucifer-4-sezon-1-/0
https://khuyenmaikk13.info/index.php?topic=171850.0
http://poselokgribovo.ru/forum/index.php?topic=690121.0
https://tg.vl-mp.com/index.php?topic=1320418.0
http://help.stv.ru/index.php?PHPSESSID=695b9ff17cebc9ca3c035d00cb48d1f2&topic=138235.0
http://sextomariotienda.com/blog/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y2-04-05-2019-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be/
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=673519.0
http://freebeer.me/index.php?topic=289124.0
http://otitismediasociety.org/forum/index.php?topic=144526.0
http://rockndata.net/UserProfile/tabid/61/userId/18159963/Default.aspx
http://metropolis.ga/index.php?topic=2320.0
https://danceplanet.se/commodore/index.php?topic=9236.0
http://koushatarabar.com/index.php/component/k2/itemlist/user/1314284
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-38/
http://www.oortsociety.com/index.php?topic=11126.0
http://seoksoononly.dothome.co.kr/qna/677038
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1296445
http://k2.akademitelkom.ac.id/component/k2/itemlist/user/289851
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/46617
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=294039
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1763601
http://matinbank.ir/component/k2/itemlist/user/4459859.html
https://tg.vl-mp.com/index.php?topic=1335746.0
https://tg.vl-mp.com/index.php?topic=1335752.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ret-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fns-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pdy-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qjw-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tmi-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yhu-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-czu-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-10-%d1%81%d0%b5%d1%80/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ugg-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-10-%d1%81%d0%b5%d1%80/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-osb-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-edu-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-15-%d1%81%d0%b5%d1%80/
http://healthyteethpa.org/component/k2/itemlist/user/5276350
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1081946
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=298054
http://webp.online/index.php?topic=43128.msg71056
https://tg.vl-mp.com/index.php?topic=1260156.0
http://withinfp.sakura.ne.jp/eso/index.php/16821860-edinoe-serdce-tek-yurek-16-seria-i4mk-edinoe-serdce-tek-yurek-1/0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=294076
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4663835
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=521000
http://withinfp.sakura.ne.jp/eso/index.php/16855139-vetrenyj-hercai-12-seria-f3fn-vetrenyj-hercai-12-seria/0
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1745200
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=239098
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1816364
http://www.aroshan.com/component/k2/itemlist/user/928237
http://travelsolution.info/?option=com_k2&view=itemlist&task=user&id=702150
http://www.m1avio.com/index.php/component/k2/itemlist/user/3603277
http://www.m1avio.com/index.php/component/k2/itemlist/user/3603283
http://www.m1avio.com/index.php/component/k2/itemlist/user/3603421
http://www.m1avio.com/index.php/component/k2/itemlist/user/3603490
http://www.m1avio.com/index.php/component/k2/itemlist/user/3603697
http://www.m1avio.com/index.php/component/k2/itemlist/user/3604036
http://www.m1avio.com/index.php/component/k2/itemlist/user/3604076
https://tg.vl-mp.com/index.php?topic=1336916.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-odf-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-15-%d1%81%d0%b5%d1%80/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fyb-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://www.deliberarchia.org/forum/index.php?topic=971773.0
http://macdistri.com/index.php/component/k2/itemlist/user/264797
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1106177
https://tg.vl-mp.com/index.php?topic=1282525.0
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1125173
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3547886
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4693873
http://soc-human.kz/index.php/component/k2/itemlist/user/1612179
http://proxima.co.rw/index.php/component/k2/itemlist/user/549926
http://mediaville.me/index.php/component/k2/itemlist/user/209168
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=95493
https://www.resproxy.com/forum/index.php/736233-cernoe-zerkalo-5-sezon-2-seria-tty-cernoe-zerkalo-5-sezon-2-ser/0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3298119
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=491681
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2562862
http://www.spazioad.com/component/k2/itemlist/user/7218180
http://www.spazioad.com/component/k2/itemlist/user/7218239
http://www.spazioad.com/component/k2/itemlist/user/7218682
http://www.spazioad.com/component/k2/itemlist/user/7219544
http://www.spazioad.com/component/k2/itemlist/user/7221101
http://www.spazioad.com/component/k2/itemlist/user/7221295
http://www.spazioad.com/index.php/component/k2/itemlist/user/7214299
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39030
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39037
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39071
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39076
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39114
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39117
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nbf-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.deliberarchia.org/forum/index.php?topic=972414.0
http://danielmillsap.com/forum/index.php?topic=968333.0
http://webp.online/index.php?topic=48427.0
https://tg.vl-mp.com/index.php?topic=1337599.0
https://www.resproxy.com/forum/index.php/794851-voron-kuzgun-11-seria-s7vi-voron-kuzgun-11-seria/0
http://www.deliberarchia.org/forum/index.php?topic=972422.0
http://menulisilmiah.net/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m5bl-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.resproxy.com/forum/index.php/794987-edinoe-serdce-tek-yurek-15-seria-x2ou-edinoe-serdce-tek-yurek-1/0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1078429
http://soc-human.kz/index.php/component/k2/itemlist/user/1604655
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=173968
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523265
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=10528
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/183979
https://tg.vl-mp.com/index.php?topic=1282430.0
http://withinfp.sakura.ne.jp/eso/index.php/16793719-voskressij-ertugrul-144-seria-m0ud-voskressij-ertugrul-144-seri/0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2541429
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1573482
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2566144
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=256958
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/287368
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/287408
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/287440
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/287465
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/287475
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/287481
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/287498
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/287508
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/287524
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/287553
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/287632
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/287730
http://forum.politeknikgihon.ac.id/index.php?topic=10811.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=27641
http://dpmarketingsystems.com/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u3-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://danielmillsap.com/forum/index.php?topic=943739.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=634987.0
http://seoksoononly.dothome.co.kr/qna/724030
https://reficulcoin.com/index.php?topic=7010.0
http://repofirmware.altervista.org/index.php?topic=90297.0
https://sanp.pro/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g1-02-05-2019-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80/
http://withinfp.sakura.ne.jp/eso/index.php/16880312-hdvideo-uristy-21-seria-t0-uristy-21-seria
http://153.120.114.241/eso/index.php/16838637-igra-prestolov-2019-8-sezon-5-seria-igra-prestolov-2019-8-sezon
http://metropolis.ga/index.php?topic=2795.0
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42188
http://highlanderonline.cmshelplive.net/%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-69-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kzwn-%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-69/
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=305324
http://www.critico-expository.com/forum/index.php?topic=1880.0
https://tg.vl-mp.com/index.php?topic=1265201.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/551712
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1828392
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=80179
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1516427
https://tg.vl-mp.com/index.php?topic=1295365.0
http://danielmillsap.com/forum/index.php?topic=947991.0
http://danielmillsap.com/forum/index.php?topic=948010.0
http://danielmillsap.com/forum/index.php?topic=948137.0
http://danielmillsap.com/forum/index.php?topic=948240.0
http://danielmillsap.com/forum/index.php?topic=948309.0
http://dessa.com.br/index.php/component/k2/itemlist/user/296041
http://dessa.com.br/index.php/component/k2/itemlist/user/296405
http://dessa.com.br/index.php/component/k2/itemlist/user/296870
http://dessa.com.br/index.php/component/k2/itemlist/user/297195
http://dessa.com.br/index.php/component/k2/itemlist/user/297498
http://dessa.com.br/index.php/component/k2/itemlist/user/298614
http://dessa.com.br/index.php/component/k2/itemlist/user/298799
http://dessa.com.br/index.php/component/k2/itemlist/user/300757
http://dessa.com.br/index.php/component/k2/itemlist/user/301074
http://dessa.com.br/index.php/component/k2/itemlist/user/301977
http://dessa.com.br/index.php/component/k2/itemlist/user/302548
https://tg.vl-mp.com/index.php?topic=1302311.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2520330
https://tg.vl-mp.com/index.php?topic=1280224.0
http://mediaville.me/?option=com_k2&view=itemlist&task=user&id=190594
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1575481
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/50127
http://withinfp.sakura.ne.jp/eso/index.php/16802895-edinoe-serdce-tek-yurek-16-seria-c0ue-edinoe-serdce-tek-yurek-1
http://seoksoononly.dothome.co.kr/qna/594541
http://www.arunagreen.com/index.php/component/k2/itemlist/user/406567
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=296958
http://www.sakitoandrichifantasy.gr/?option=com_k2&view=itemlist&task=user&id=139225
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=890887
http://mediaville.me/index.php/component/k2/itemlist/user/208052
http://withinfp.sakura.ne.jp/eso/index.php/16773836-rannaa-ptaska-erkenci-kus-37-seria-l8hk-rannaa-ptaska-erkenci-k
http://withinfp.sakura.ne.jp/eso/index.php/16773852-edinoe-serdce-tek-yurek-14-seria-w0ik-edinoe-serdce-tek-yurek-1/0
http://withinfp.sakura.ne.jp/eso/index.php/16773869-voron-kuzgun-14-seria-k8cb-voron-kuzgun-14-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/16773959-vetrenyj-hercai-25-seria-h9ug-vetrenyj-hercai-25-seria/0
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/241509
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/241611
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/241765
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/241933
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/242368
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/242412
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/242476
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/242495
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/242504
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/242574
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/242649
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/242721
http://webp.online/index.php?topic=39120.0
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=537763
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/560070
http://danielmillsap.com/forum/index.php?topic=881784.0
http://dessa.com.br/component/k2/itemlist/user/294540
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1127914
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1025202
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2547433
https://www.youngbiker.de/wbboard/index.php?page=User&userID=784291
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=296274
http://www.m1avio.com/index.php/component/k2/itemlist/user/3580985
http://jesusandmarypatna.com/index.php/component/k2/itemlist/user/3374261
http://healthyteethpa.org/component/k2/itemlist/user/5275932
http://www.deliberarchia.org/forum/index.php?topic=937071.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172082
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172108
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172109
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172120
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172138
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172142
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172168
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172176
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172189
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172195
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172216
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172253
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1102469
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1102508
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1102522
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1102541
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1102728
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1102899
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1102956
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1103052
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1103085
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3554969
http://www.deliberarchia.org/forum/index.php?topic=911903.0
http://macdistri.com/index.php/component/k2/itemlist/user/255038
http://dohairbiz.com/en/component/k2/itemlist/user/2693478.html
https://sanp.pro/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80-7/
https://theprodigy.info/forum/index.php?topic=28042.0
https://lucky28003.nl/forum/index.php?topic=5588.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=adf2f8a6e18cfa3b819f7ef125e2f4c9&topic=197788.0
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3664685
http://www.deliberarchia.org/forum/index.php?topic=943493.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/63249
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/271420
https://www.resproxy.com/forum/index.php/746636-hdvideo-sosedi-2-sezon-14-seria-q2-sosedi-2-sezon-14-seria
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=25877.0
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1837986
http://teambuildingpremium.com/forum/index.php?topic=758719.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cv1-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://forum.ac-jete.it/index.php?topic=332254.0
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=998774
http://community.viajar.tur.br/index.php?p=/profile/amosheath
http://www.spazioad.com/component/k2/itemlist/user/7200471
http://sextomariotienda.com/blog/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90pc5%e3%80%91-%d1%81/
http://www.oortsociety.com/index.php?topic=8649.0
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/193024
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=266166
http://danielmillsap.com/forum/index.php?topic=898123.0
http://miklja.net/forum/index.php?topic=24314.0
http://poselokgribovo.ru/forum/index.php?topic=675580.0
http://forum.politeknikgihon.ac.id/index.php?topic=9839.0
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/627113
https://www.resproxy.com/forum/index.php/731634-posmotret-fil-m-tola-robot-5-seria-ta-posmotret-fil-m-tola-robo/0
http://web.cas.identrics.net/phpBB3/viewtopic.php?t=117984
http://mediaville.me/index.php/component/k2/itemlist/user/202279
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/200768
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1675604
http://proxima.co.rw/index.php/component/k2/itemlist/user/544789
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=42579
http://menulisilmiah.net/%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ua2-%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://travelsolution.info/index.php/component/k2/itemlist/user/707395
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/471494
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=41018
http://www.arunagreen.com/index.php/component/k2/itemlist/user/404087
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1748631
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39569
http://computerscience.egerton.ac.ke/index.php/component/k2/itemlist/user/1980902
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/153968
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3536026
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3280654
http://withinfp.sakura.ne.jp/eso/index.php/16780951-milliardy-4-sezon-10-seria-ney-milliardy-4-sezon-10-seria-01052/0
http://macdistri.com/?option=com_k2&view=itemlist&task=user&id=258137
https://www.resproxy.com/forum/index.php/765756-cernoe-zerkalo-5-sezon-4-seria-lrh-cernoe-zerkalo-5-sezon-4-ser/0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=291281
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/153085
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1551075
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1585101
http://fbpharm.net/index.php/component/k2/itemlist/user/16345
http://dessa.com.br/index.php/component/k2/itemlist/user/298587
http://www.lustralesdevallehermoso.com/?option=com_k2&view=itemlist&task=user&id=47843
http://seoksoononly.dothome.co.kr/qna/612748
https://members.fbhaters.com/index.php?topic=60424.0
https://tg.vl-mp.com/index.php?topic=1293997.0
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7257293
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1303608
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yuo-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://withinfp.sakura.ne.jp/eso/index.php/16813949-vossoedinenie-vuslat-13-seria-o6lm-vossoedinenie-vuslat-13-seri/0
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3680371
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3559250
http://www.afikgan.co.il/index.php/component/k2/itemlist/user/25769
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/153468
http://poselokgribovo.ru/forum/index.php?topic=698727.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1074455
http://eugeniocolazzo.it/forum/index.php?topic=67751.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=232864
http://roikjer.com/forum/index.php?PHPSESSID=mjn5ll8ha2l5h224qaia06nvk5&topic=772181.0
http://forum.politeknikgihon.ac.id/index.php?topic=14233.0
http://roikjer.com/forum/index.php?PHPSESSID=9bnpjd6fjsfqtsgtms45l48al2&topic=780839.0
http://smartacity.com/component/k2/itemlist/user/16026
http://www.grupojover.com/component/k2/itemlist/user/3562
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4676450
http://forum.kopkargobel.com/index.php?topic=2700.0
http://community.viajar.tur.br/index.php?p=/discussion/56874/sluga-naroda-3-sezon-16-seriya-v8ib-sluga-naroda-3-sezon-16-seriya/p1%3Fnew=1
http://cccpvideo.forumside.com/index.php?topic=37.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-46/
https://tg.vl-mp.com/index.php?topic=1309593.0
http://www2.yasothon.go.th/smf/index.php?topic=159.155580
http://forum.politeknikgihon.ac.id/index.php?topic=7492.0
https://members.fbhaters.com/index.php?topic=72928.0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/217196
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3559186
http://teambuildingpremium.com/forum/index.php?topic=745957.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=656032.0
https://www.resproxy.com/forum/index.php/766253-sosedi-2-sezon-17-seria-hdvideo-sosedi-2-sezon-17-seria-0505201/0
http://poselokgribovo.ru/forum/index.php?topic=656986.0
https://sanp.pro/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j5-%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5/
http://roikjer.com/forum/index.php?topic=758404.0
http://roikjer.com/forum/index.php?PHPSESSID=tl2d8fkmsjot0avj270dosqm82&topic=774257.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1106189
http://8.droror.co.il/uncategorized/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-9-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%82%d0%be%d0%bb%d1%8f/
http://roikjer.com/forum/index.php?PHPSESSID=69mvmre7tjs5t1gauodh9r49s3&topic=770883.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=287156
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=244338
http://roikjer.com/forum/index.php?PHPSESSID=nhm4bhsa5i00akt59intbfhf95&topic=787033.0
http://sextomariotienda.com/blog/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wez-%d0%b2%d0%be%d1%81%d0%ba/
http://www.autospa.lv/index.php/component/k2/itemlist/user/8158
http://rudraautomation.com/index.php/component/k2/author/102003
https://reficulcoin.com/index.php?topic=8807.0
http://www.tessabannampad.go.th/webboard/index.php?topic=185699.0
http://freebeer.me/index.php?topic=288768.0
http://myrechockey.com/forums/index.php?topic=82498.0
https://sanp.pro/%d0%b0%d0%b3%d0%b5%d0%bd%d1%82%d1%8b-%d1%89%d0%b8%d1%82-6-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90sies%e3%80%91-%d0%b0%d0%b3%d0%b5%d0%bd%d1%82%d1%8b/
https://reficulcoin.com/index.php?topic=9661.0
https://tg.vl-mp.com/index.php?topic=1305539.0
http://www.spazioad.com/component/k2/itemlist/user/7169568
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/596986
http://153.120.114.241/eso/index.php/16858496-lubov-smert-i-roboty-love-death-and-robots-10-seria-sev-lubov-s
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1552843
http://www.theparrotcentre.com/forum/index.php?topic=443956.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=283930
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1077539
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/461283
http://www.deliberarchia.org/forum/index.php?topic=975710.0
http://www.tessabannampad.go.th/webboard/index.php?topic=192897.0
https://lucky28003.nl/forum/index.php?topic=11293.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bzm-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-10-%d1%81%d0%b5%d1%80/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xxg-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80/
http://dessa.com.br/component/k2/itemlist/user/291846
http://dessa.com.br/component/k2/itemlist/user/292355
http://dessa.com.br/component/k2/itemlist/user/292411
http://dessa.com.br/component/k2/itemlist/user/292698
http://dessa.com.br/component/k2/itemlist/user/292726
http://dessa.com.br/component/k2/itemlist/user/292756
http://dessa.com.br/component/k2/itemlist/user/292814
http://dessa.com.br/component/k2/itemlist/user/292994
http://dessa.com.br/component/k2/itemlist/user/293078
http://dessa.com.br/component/k2/itemlist/user/293087
http://dessa.com.br/component/k2/itemlist/user/293091
http://www.moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=626378
http://www.moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=628124
http://www.moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=628153
http://www.moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=628277
http://www.moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=635304
http://www.moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=635547
http://www.moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=635981
http://www.moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=636095
http://www.moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=641636
http://www.deliberarchia.org/forum/index.php?topic=901569.0
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=289657
http://israengineering.com/index.php/component/k2/itemlist/user/1114665
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3539938
http://proxima.co.rw/index.php/component/k2/itemlist/user/544081
http://www.telcon.gr/index.php/component/k2/itemlist/user/30028
http://www.telcon.gr/index.php/component/k2/itemlist/user/30060
http://www.telcon.gr/index.php/component/k2/itemlist/user/30134
http://www.telcon.gr/index.php/component/k2/itemlist/user/30135
http://www.telcon.gr/index.php/component/k2/itemlist/user/30160
http://www.telcon.gr/index.php/component/k2/itemlist/user/30302
http://www.telcon.gr/index.php/component/k2/itemlist/user/30353
http://www.telcon.gr/index.php/component/k2/itemlist/user/30436
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1556323
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1556324
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1556325
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=783151
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=783160
http://www.x2145-productions.technology/index.php?title=Benutzer:GiaWoodriff5985
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7317230
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=118334
http://rudraautomation.com/index.php/component/k2/author/118373
http://smartacity.com/component/k2/itemlist/user/18832
http://thermoplast.envolgroupe.com/component/k2/author/70887
http://www.m1avio.com/index.php/component/k2/itemlist/user/3611297
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/654439
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/654502
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/638673
http://travelsolution.info/index.php/component/k2/itemlist/user/703060
http://mobility-corp.com/index.php/component/k2/itemlist/user/2497781
https://www.resproxy.com/forum/index.php/731365-milliardy-4-sezon-5-seria-hjw-milliardy-4-sezon-5-seria
http://www.deliberarchia.org/forum/index.php?topic=909769.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4686571
http://rudraautomation.com/index.php/component/k2/author/103439
https://verdadesbiblicas.org.ec/index.php/component/k2/itemlist/user/3694583
http://married.dike.gr/index.php/component/k2/itemlist/user/35468
http://www.gtupuw.org/index.php/component/k2/itemlist/user/1818137
http://153.120.114.241/eso/index.php/16877232-lubov-smert-i-roboty-love-death-and-robots-3-seria-cfk-lubov-sm
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1538920
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=40737
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=40959
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=41432
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=42176
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=42208
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=42214
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=42258
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=42261
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=43242
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=43611
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3575575
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=81956
http://rudraautomation.com/index.php/component/k2/author/118297
http://rudraautomation.com/index.php/component/k2/author/118309
http://smartacity.com/component/k2/itemlist/user/18607
http://smartacity.com/component/k2/itemlist/user/18798
http://thermoplast.envolgroupe.com/component/k2/author/70869
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1673656
http://www.oortsociety.com/index.php?topic=9307.0
http://www.elpinatarense.es/?option=com_k2&view=itemlist&task=user&id=154634
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1850790
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1612608
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1820701
https://tg.vl-mp.com/index.php?topic=1305596.0
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3673739
http://proandpro.it/?option=com_k2&view=itemlist&task=user&id=4531871
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/150261
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=276433
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=276552
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=276618
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=276812
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=277159
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=277195
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=277616
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=277764
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=277888
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=278160
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=278358
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=278659
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=278732
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=278826
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=279131
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=44023
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/477823
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1848009
http://macdistri.com/index.php/component/k2/itemlist/user/309767
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5879
http://proandpro.it/?option=com_k2&view=itemlist&task=user&id=4539784
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/53621
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1556652
[url=http://cialisec.com/]cialis online[/url]
generic cialis lowest prices
<a href="http://cialisec.com/">cialis online</a>
buy cialis and viagra online
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3697570
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=65030
http://withinfp.sakura.ne.jp/eso/index.php/16826111-edinoe-serdce-tek-yurek-8-seria-d0wv-edinoe-serdce-tek-yurek-8-/0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3255604
https://tg.vl-mp.com/index.php?topic=1322113.0
https://tg.vl-mp.com/index.php?topic=1310652.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/558044
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=274112
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1843094
http://mediaville.me/index.php/component/k2/itemlist/user/203315
http://macdistri.com/index.php/component/k2/itemlist/user/263998
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/287481
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1109377
http://www.quattroandpartners.it/component/k2/itemlist/user/1023368
http://erhu.eu/viewtopic.php?t=232076
http://seoksoononly.dothome.co.kr/qna/599338
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=245925
http://withinfp.sakura.ne.jp/eso/index.php/16781936-milliardy-4-sezon-13-seria-bua-milliardy-4-sezon-13-seria/0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=30765
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1125589
http://erhu.eu/viewtopic.php?t=233461
http://www.deliberarchia.org/forum/index.php?topic=926821.0
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26172763/Default.aspx
http://macdistri.com/index.php/component/k2/itemlist/user/258945
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=369263
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/55289
https://tg.vl-mp.com/index.php?topic=1288834.0
http://boutique.in.th/?option=com_k2&view=itemlist&task=user&id=146205
http://danielmillsap.com/forum/index.php?topic=883328.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1304253
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39524
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4688354
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wj2-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
https://www.youngbiker.de/wbboard/index.php?page=User&userID=782012
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1612715
http://macdistri.com/index.php/component/k2/itemlist/user/260992
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1835200
http://dpmarketingsystems.com/hd1080-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r4-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2513272
https://wwwelibga.000webhostapp.com/%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-60-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-w2-%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-60-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch/romeo625383540/86010/
https://forums.letstalkbeats.com/index.php?topic=56870.0
http://teambuildingpremium.com/forum/index.php?topic=731734.0
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=153686
http://dpmarketingsystems.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ghs-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://mobility-corp.com/index.php/component/k2/itemlist/user/2510691
http://www.teedinubon.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%be%d0%b9-%d0%b0%d1%80%d1%82%d0%b8%d1%81%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o1vi-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%be%d0%b9-%d0%b0%d1%80%d1%82/
http://gtupuw.org/index.php/component/k2/itemlist/user/1842039
http://8.droror.co.il/uncategorized/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-%d1%83%d0%ba%d1%80%d0%b0%d0%b8%d0%bd%d0%b0-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-i6e2-%d1%85%d0%be%d0%bb%d0%be/
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/637630
http://forum.byehaj.hu/index.php?topic=74283.0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=535343
http://withinfp.sakura.ne.jp/eso/index.php/16812293-voskressij-ertugrul-149-seria-o3pi-voskressij-ertugrul-149-seri
http://sextomariotienda.com/blog/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u1-%e3%80%90-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f%e3%80%91-%d1%8e%d1%80%d0%b8%d1%81/
https://mcsetup.tk/bbs/index.php?topic=240501.0
http://poselokgribovo.ru/forum/index.php?topic=685116.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=34003
http://married.dike.gr/index.php/component/k2/itemlist/user/47266
https://www.gizmoarticle.com/new-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://www.ekemoon.com/140153/050420190405/
http://teambuildingpremium.com/forum/index.php?topic=753069.0
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=282907
http://forums.abs-cbn.com/welcome-back-kapamilya%21/ma-4-eo-12-e-sv4t-ma-4-eo-12-e/
https://khuyenmaikk13.info/index.php?topic=168283.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=37406
https://celekt.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l6-%e3%80%90-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://thanosakademi.com/index.php?topic=61268.0
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1123267
https://www.shaiyax.com/index.php?topic=326551.0
http://freebeer.me/index.php?topic=291104.0
http://wituclub.ru/forum/index.php?PHPSESSID=fa835jaau29sspr50brobcrv40&topic=25182.0
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=15367
http://multikopterforum.hu/index.php?topic=6070.0
http://codeerror.in/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://withinfp.sakura.ne.jp/eso/index.php/16872287-smotret-milliardy-4-sezon-10-seria-k7-milliardy-4-sezon-10-seri/0
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile;u=30572
https://sanp.pro/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%b0-%d1%80%d1%83%d1%81%d1%81%d0%ba%d0%be%d0%bc-%d1%8f%d0%b7%d1%8b%d0%ba%d0%b5-%d0%be%d0%bd%d0%bb%d0%b0-4/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gvx-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://1vh.info/index.php?topic=9255.0
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1551398
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=32901
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2529033
http://poselokgribovo.ru/forum/index.php?topic=688854.0
https://lucky28003.nl/forum/index.php?topic=4218.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2558154
http://uberdrivers.net/forum/index.php?topic=182600.0
http://roikjer.com/forum/index.php?PHPSESSID=biqarusgk12guqb432vt3b9or3&topic=801581.0
http://www.deliberarchia.org/forum/index.php?topic=932125.0
http://universalcommunity.se/Forum/index.php?topic=375.0
http://associationsila.org/index.php/component/k2/itemlist/user/278275
https://www.netprofessional.gr/?option=com_k2&view=itemlist&task=user&id=3024
http://danielmillsap.com/forum/index.php?topic=938613.0
http://muonlineint.com/forum/index.php?topic=668.0
http://mir3sea.com/forum/index.php?topic=25.0
https://tg.vl-mp.com/index.php?topic=1302616.0
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/198330
https://www.resproxy.com/forum/index.php/759885-milliardy-4-sezon-5-seria-wfxj-milliardy-4-sezon-5-seria/0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/184142
https://www.shaiyax.com/index.php?topic=327893.0
http://withinfp.sakura.ne.jp/eso/index.php/16862497-v-efire-taemnici-85-seria-q9-taemnici-85-seria
https://l2thalassic.org/Forum/index.php?topic=772.0
http://www.vivelabmanizales.com/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dyqz-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://roikjer.com/forum/index.php?PHPSESSID=f918raahak4h25je8jikqniiq1&topic=790332.0
https://khuyenmaikk13.info/index.php?topic=176787.0
http://jpacschoolclubs.co.uk/?option=com_k2&view=itemlist&task=user&id=3343263
http://proxima.co.rw/index.php/component/k2/itemlist/user/558869
http://xekhachduyetthuy.com.vn/component/k2/itemlist/user/160348
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/171959
http://help.stv.ru/index.php?PHPSESSID=805f3d96fa4c11e646750b4f81555bfd&topic=133928.0
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81-7/
http://dev.aabn.org.gh/component/k2/itemlist/user/492720
http://www.thenixnoob.com/viewtopic.php?t=631488
http://danielmillsap.com/forum/index.php?topic=946944.0
http://danielmillsap.com/forum/index.php?topic=946969.0
http://danielmillsap.com/forum/index.php?topic=947062.0
http://danielmillsap.com/forum/index.php?topic=947180.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/387258
http://www.arunagreen.com/index.php/component/k2/itemlist/user/387337
http://www.arunagreen.com/index.php/component/k2/itemlist/user/387504
http://www.arunagreen.com/index.php/component/k2/itemlist/user/387701
http://www.arunagreen.com/index.php/component/k2/itemlist/user/387708
http://www.arunagreen.com/index.php/component/k2/itemlist/user/387756
http://www.arunagreen.com/index.php/component/k2/itemlist/user/387763
http://www.arunagreen.com/index.php/component/k2/itemlist/user/387801
http://www.arunagreen.com/index.php/component/k2/itemlist/user/387945
http://www.arunagreen.com/index.php/component/k2/itemlist/user/387952
http://www.arunagreen.com/index.php/component/k2/itemlist/user/388285
http://www.arunagreen.com/index.php/component/k2/itemlist/user/388385
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=498361
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=498387
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=498559
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=498621
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=498911
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=498998
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=499042
http://77.93.38.205/index.php/component/k2/itemlist/user/492111
http://77.93.38.205/index.php/component/k2/itemlist/user/492124
http://77.93.38.205/index.php/component/k2/itemlist/user/493690
http://77.93.38.205/index.php/component/k2/itemlist/user/494091
http://77.93.38.205/index.php/component/k2/itemlist/user/494448
http://www.tessabannampad.go.th/webboard/index.php?topic=175669.0
http://dev.aabn.org.gh/component/k2/itemlist/user/467536
http://www2.yasothon.go.th/smf/index.php?topic=159.msg176734
http://www.remify.app/foro/index.php?topic=171537.0
https://www.resproxy.com/forum/index.php/769710-tola-robot-9-seria-tola-robot-9-seria-05052019
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=25646
http://www.deliberarchia.org/forum/index.php?topic=944778.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=622625.0
http://matrixpharm.ru/forum/index.php?PHPSESSID=vpn4n7ouib911abu91ik9l5su5&action=profile;u=150093
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/612708
http://bobr.site/index.php?topic=81304.0
http://www.deliberarchia.org/forum/index.php?topic=943986.0
http://associationsila.org/component/k2/itemlist/user/282419
https://members.fbhaters.com/index.php?topic=71930.0
http://community.viajar.tur.br/index.php?p=/profile/olivebeave
http://ru-realty.com/forum/index.php?PHPSESSID=mvlneuk4cqcncpiau56n3libk5&topic=456369.0
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1003848
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/184604
https://www.resproxy.com/forum/index.php/769843-tola-robot-8-seria-05052019-ar-tola-robot-8-seria/0
http://roikjer.com/forum/index.php?topic=781702.0
http://bobr.site/index.php?topic=88023.0
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=557854
http://poselokgribovo.ru/forum/index.php?topic=701135.0
http://dessa.com.br/component/k2/itemlist/user/295947
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-akk-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1848453
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=159868
http://danielmillsap.com/forum/index.php?topic=938700.0
http://www.gtupuw.org/index.php/component/k2/itemlist/user/1820781
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1126417
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1109078
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/435617
http://withinfp.sakura.ne.jp/eso/index.php/16773481-ne-otpuskaj-mou-ruku-elimi-birakma-40-seria-n0ng-ne-otpuskaj-mo/0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/170030
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81-34/
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cl3-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ys4-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nu6-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-kv3-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sx0-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ww5-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ag6-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ti5-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=79416
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=289535
http://rudraautomation.com/index.php/component/k2/author/118655
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1637605
http://thermoplast.envolgroupe.com/component/k2/author/71012
http://wcwpr.com/UserProfile/tabid/85/userId/9315597/Default.aspx
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/470658
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/470711
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/470790
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/470804
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/470904
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=758617
http://erhu.eu/viewtopic.php?f=7&t=232582
http://macdistri.com/index.php/component/k2/itemlist/user/284207
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=30786
http://mvisage.sk/index.php/component/k2/itemlist/user/116338
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2528146
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2528334
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2528376
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2528389
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2528401
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2528421
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2528468
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2528521
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2528617
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2528621
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2528649
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2528677
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2528738
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291004
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291041
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291045
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291085
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291109
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291161
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291181
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291204
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291229
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291260
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291299
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291373
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291428
http://withinfp.sakura.ne.jp/eso/index.php/16784293-voron-kuzgun-11-seria-p0zq-voron-kuzgun-11-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/16784356-edinoe-serdce-tek-yurek-16-seria-b3ty-edinoe-serdce-tek-yurek-1/0
http://withinfp.sakura.ne.jp/eso/index.php/16784408-edinoe-serdce-tek-yurek-17-seria-z7xe-edinoe-serdce-tek-yurek-1/0
http://withinfp.sakura.ne.jp/eso/index.php/16784478-edinoe-serdce-tek-yurek-15-seria-i5mn-edinoe-serdce-tek-yurek-1
http://withinfp.sakura.ne.jp/eso/index.php/16784502-rannaa-ptaska-erkenci-kus-44-seria-q5sd-rannaa-ptaska-erkenci-k/0
http://withinfp.sakura.ne.jp/eso/index.php/16784542-ne-otpuskaj-mou-ruku-elimi-birakma-42-seria-t6hf-ne-otpuskaj-mo
http://withinfp.sakura.ne.jp/eso/index.php/16784732-nasa-istoria-74-seria-g2co-nasa-istoria-74-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/16784777-ne-otpuskaj-mou-ruku-elimi-birakma-36-seria-j5ax-ne-otpuskaj-mo/0
http://withinfp.sakura.ne.jp/eso/index.php/16784793-ne-otpuskaj-mou-ruku-elimi-birakma-40-seria-r0gu-ne-otpuskaj-mo/0
http://withinfp.sakura.ne.jp/eso/index.php/16784839-voron-kuzgun-12-seria-w2bw-voron-kuzgun-12-seria
http://withinfp.sakura.ne.jp/eso/index.php/16784911-voskressij-ertugrul-144-seria-i7ri-voskressij-ertugrul-144-seri/0
http://withinfp.sakura.ne.jp/eso/index.php/16784940-zensina-60-seria-p2uc-zensina-60-seria/0
http://healthyteethpa.org/component/k2/itemlist/user/5306102
http://healthyteethpa.org/component/k2/itemlist/user/5306130
http://healthyteethpa.org/component/k2/itemlist/user/5306282
http://healthyteethpa.org/component/k2/itemlist/user/5306300
http://healthyteethpa.org/component/k2/itemlist/user/5306348
http://healthyteethpa.org/component/k2/itemlist/user/5306430
http://healthyteethpa.org/component/k2/itemlist/user/5306452
http://healthyteethpa.org/component/k2/itemlist/user/5306587
http://healthyteethpa.org/component/k2/itemlist/user/5306603
http://healthyteethpa.org/component/k2/itemlist/user/5306634
http://healthyteethpa.org/component/k2/itemlist/user/5306670
http://healthyteethpa.org/component/k2/itemlist/user/5306737
http://healthyteethpa.org/component/k2/itemlist/user/5306742
http://healthyteethpa.org/component/k2/itemlist/user/5306779
http://healthyteethpa.org/component/k2/itemlist/user/5306847
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1542509
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1106827
https://tg.vl-mp.com/index.php?topic=1277353.0
https://www.resproxy.com/forum/index.php/740460-sverh-estestvennoe-14-sezon-18-seria-mvv-sverh-estestvennoe-14-/0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/444096
http://www.oortsociety.com/index.php?topic=10425.0
http://withinfp.sakura.ne.jp/eso/index.php/16807734-edinoe-serdce-tek-yurek-9-seria-t4pi-edinoe-serdce-tek-yurek-9-
http://www.moyakmermer.com/index.php/component/k2/itemlist/user/627888
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1110135
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=262184
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3247757
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=290690
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=290702
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=290798
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=290822
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=290837
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=290853
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=290868
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=290983
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=290997
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=291120
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=291173
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=291177
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=291213
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=291241
http://mvisage.sk/index.php/component/k2/itemlist/user/116687
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81-28/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1340331
http://danielmillsap.com/forum/index.php?topic=878308.0
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=604865
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/263935
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=261939
http://married.dike.gr/index.php/component/k2/itemlist/user/35069
http://www.deliberarchia.org/forum/index.php?topic=912351.0
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2512856
http://smartacity.com/component/k2/itemlist/user/9537
http://ts.bloodhand.de/forum/viewtopic.php?t=196570
https://tg.vl-mp.com/index.php?topic=1279513.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1108783
https://www.resproxy.com/forum/index.php/783430-vetrenyj-hercai-25-seria-x1vn-vetrenyj-hercai-25-seria/0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mel-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://myrechockey.com/forums/index.php?topic=86488.0
http://myrechockey.com/forums/index.php?topic=86492.0
http://myrechockey.com/forums/index.php?topic=86498.0
http://www.deliberarchia.org/forum/index.php?topic=962312.0
http://www.deliberarchia.org/forum/index.php?topic=962321.0
http://www.deliberarchia.org/forum/index.php?topic=962330.0
http://menulisilmiah.net/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w0ax-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80/
https://members.fbhaters.com/index.php?topic=75692.0
https://members.fbhaters.com/index.php?topic=75699.0
https://tg.vl-mp.com/index.php?topic=1327441.0
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38039
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38056
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38057
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38073
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38074
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38082
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38087
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38088
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38093
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38098
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38111
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38120
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38134
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38140
http://healthyteethpa.org/component/k2/itemlist/user/5292181
http://healthyteethpa.org/component/k2/itemlist/user/5292188
http://healthyteethpa.org/component/k2/itemlist/user/5292215
http://healthyteethpa.org/component/k2/itemlist/user/5292263
http://healthyteethpa.org/component/k2/itemlist/user/5292389
http://healthyteethpa.org/component/k2/itemlist/user/5292480
http://healthyteethpa.org/component/k2/itemlist/user/5292624
http://healthyteethpa.org/component/k2/itemlist/user/5293123
http://healthyteethpa.org/component/k2/itemlist/user/5293298
http://healthyteethpa.org/component/k2/itemlist/user/5293396
http://healthyteethpa.org/component/k2/itemlist/user/5293457
http://healthyteethpa.org/component/k2/itemlist/user/5293565
http://healthyteethpa.org/component/k2/itemlist/user/5293658
http://healthyteethpa.org/component/k2/itemlist/user/5293737
http://menulisilmiah.net/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-43-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x1bu-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0/
http://withinfp.sakura.ne.jp/eso/index.php/16887707-vossoedinenie-vuslat-17-seria-f2au-vossoedinenie-vuslat-17-seri/0
https://members.fbhaters.com/index.php?topic=75766.0
https://www.resproxy.com/forum/index.php/783927-ne-otpuskaj-mou-ruku-elimi-birakma-42-seria-v1re-ne-otpuskaj-mo/0
https://www.resproxy.com/forum/index.php/783941-voskressij-ertugrul-143-seria-s5bu-voskressij-ertugrul-143-seri
https://www.resproxy.com/forum/index.php/783954-nasa-istoria-73-seria-f1cc-nasa-istoria-73-seria/0
https://www.resproxy.com/forum/index.php/783958-vossoedinenie-vuslat-14-seria-r4lk-vossoedinenie-vuslat-14-seri/0
https://www.resproxy.com/forum/index.php/783960-ne-otpuskaj-mou-ruku-elimi-birakma-37-seria-h4fl-ne-otpuskaj-mo
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39661
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39679
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39681
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39691
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39692
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39696
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39699
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39737
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39785
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39789
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39792
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39836
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39873
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39893
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39902
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19398
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19403
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19408
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19421
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19423
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19449
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19457
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19463
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19467
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19488
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19495
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19523
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39928
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3683023
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2530021
http://danielmillsap.com/forum/index.php?topic=881530.0
http://withinfp.sakura.ne.jp/eso/index.php/16786116-milliardy-4-sezon-11-seria-ohj-milliardy-4-sezon-11-seria-02052/0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1608207
http://batubersurat.com/index.php/component/k2/itemlist/user/39124
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=781495
http://associationsila.org/component/k2/itemlist/user/258548
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/601582
http://withinfp.sakura.ne.jp/eso/index.php/16822641-ne-otpuskaj-mou-ruku-elimi-birakma-37-seria-t4fe-ne-otpuskaj-mo
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=39002
http://healthyteethpa.org/component/k2/itemlist/user/5309299
https://tg.vl-mp.com/index.php?topic=1282418.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/448105
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3712530
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=267070
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=285509
http://menulisilmiah.net/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l2oj-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=891933
http://associationsila.org/component/k2/itemlist/user/272527
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7192840
https://www.resproxy.com/forum/index.php/779004-nasledie-13-seria-imn-nasledie-13-seria/0
https://tg.vl-mp.com/index.php?topic=1263933.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/375973
http://macdistri.com/index.php/component/k2/itemlist/user/258294
http://fbpharm.net/index.php/component/k2/itemlist/user/14229
http://proxima.co.rw/index.php/component/k2/itemlist/user/544424
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1835335
http://macdistri.com/index.php/component/k2/itemlist/user/260706
https://grajalesabogados.com.mx/?option=com_k2&view=itemlist&task=user&id=60309
http://www.spazioad.com/component/k2/itemlist/user/7181915
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=263929
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/40016
http://withinfp.sakura.ne.jp/eso/index.php/16781661-vetrenyj-hercai-25-seria-n4im-vetrenyj-hercai-25-seria
http://www.m1avio.com/index.php/component/k2/itemlist/user/3557136
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/50255
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2472990
http://smartacity.com/component/k2/itemlist/user/17640
http://withinfp.sakura.ne.jp/eso/index.php/16769592-milliardy-4-sezon-12-seria-efi-milliardy-4-sezon-12-seria-01052/0
https://members.fbhaters.com/index.php?topic=66725.0
http://www.tessabannampad.go.th/webboard/index.php?topic=189159.0
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/154194
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/257469
http://withinfp.sakura.ne.jp/eso/index.php/16872513-nasa-istoria-73-seria-s2dq-nasa-istoria-73-seria/0
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/646851
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/39794
https://tg.vl-mp.com/index.php?topic=1293221.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1573696
http://febrescordero.gob.ec/index.php/component/k2/itemlist/user/73032
http://www.meikai.com.ar/foro/index.php?topic=49028.0
https://tg.vl-mp.com/index.php?topic=1311426.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=298183
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12638
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7269113
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=276450
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=544224
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19304
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1849791
http://arquitectosenreformas.es/component/k2/itemlist/user/76901
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/277681
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=338538
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qa0-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13/
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tb5-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13/
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ve4-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13/
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vz0-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13/
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xs3-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13/
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xt7-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13/
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ys9-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13/
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zg5-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13/
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dn4-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14/
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gw3-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14/
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hu2-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14/
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ih8-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14/
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1083578
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1083625
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1083651
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1083759
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1083828
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1083847
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-flc-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tqg-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hrg-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qmc-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://www.deliberarchia.org/forum/index.php?topic=978021.0
http://www.deliberarchia.org/forum/index.php?topic=978050.0
http://www.tessabannampad.go.th/webboard/index.php?topic=193219.0
https://lucky28003.nl/forum/index.php?topic=11530.0
http://danielmillsap.com/forum/index.php?topic=976575.0
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1017689
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1018248
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1019234
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1019816
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1019938
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1023241
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1026918
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1030705
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4668080
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4665732
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1831152
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=892664
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7262521
http://thermoplast.envolgroupe.com/component/k2/author/67460
http://www.deliberarchia.org/forum/index.php?topic=910405.0
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1131524
https://tg.vl-mp.com/index.php?topic=1255297.0
http://metropolis.ga/index.php?topic=2834.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173308
http://proxima.co.rw/index.php/component/k2/itemlist/user/546165
http://batubersurat.com/index.php/component/k2/itemlist/user/40332
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=606391
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/46193
http://withinfp.sakura.ne.jp/eso/index.php/16880184-zensina-56-seria-o0lz-zensina-56-seria
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/155556
http://webp.online/index.php?topic=43930.0
http://menulisilmiah.net/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b5-%d0%b7%d0%b5%d1%80%d0%ba%d0%b0%d0%bb%d0%be-5-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dvq-%d1%87%d0%b5%d1%80%d0%bd/
https://tg.vl-mp.com/index.php?topic=1262418.0
http://rudraautomation.com/index.php/component/k2/author/114951
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/249771
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3248461
http://afinandoemociones.com.ar/index.php/component/k2/itemlist/user/388278
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1827548
http://www.crowdfundingchile.cl/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wm6-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.resproxy.com/forum/index.php/798842-sverh-estestvennoe-14-sezon-19-seria-ohi-sverh-estestvennoe-14-/0
https://www.resproxy.com/forum/index.php/798889-sverh-estestvennoe-14-sezon-20-seria-dlc-sverh-estestvennoe-14-/0
https://www.resproxy.com/forum/index.php/798898-riverdejl-riverdale-3-sezon-19-seria-wan-riverdejl-riverdale-3-/0
http://dscardip.com/board/index.php?page=User&userID=660525
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2580097
http://rudraautomation.com/index.php/component/k2/author/113564
http://rudraautomation.com/index.php/component/k2/author/113940
http://rudraautomation.com/index.php/component/k2/author/114047
http://rudraautomation.com/index.php/component/k2/author/114115
http://rudraautomation.com/index.php/component/k2/author/114171
http://rudraautomation.com/index.php/component/k2/author/114176
http://rudraautomation.com/index.php/component/k2/author/114304
http://rudraautomation.com/index.php/component/k2/author/114320
http://rudraautomation.com/index.php/component/k2/author/114325
http://rudraautomation.com/index.php/component/k2/author/114363
http://rudraautomation.com/index.php/component/k2/author/114513
http://rudraautomation.com/index.php/component/k2/author/114589
http://mediaville.me/index.php/component/k2/itemlist/user/210906
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/649874
https://tg.vl-mp.com/index.php?topic=1274135.0
http://withinfp.sakura.ne.jp/eso/index.php/16799704-pro-cto-fil-m-tola-robot-7-seria-wl-pro-cto-fil-m-tola-robot-7-/0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2556899
http://macdistri.com/component/k2/itemlist/user/301696
http://www.arunagreen.com/index.php/component/k2/itemlist/user/388923
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/185484
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/150351
http://withinfp.sakura.ne.jp/eso/index.php/16880797-voskressij-ertugrul-143-seria-q2iv-voskressij-ertugrul-143-seri/0
http://menulisilmiah.net/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-79-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u8px-%d0%bd%d0%b5%d0%b2/
https://lucky28003.nl/forum/index.php?topic=4672.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3255532
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1542849
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/147669
http://dev.aabn.org.gh/?option=com_k2&view=itemlist&task=user&id=490498
https://tg.vl-mp.com/index.php?topic=1284332.0
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=1480
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/992589
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1509031
http://myrechockey.com/forums/index.php?topic=82939.0
https://tg.vl-mp.com/index.php?topic=1265591.0
http://menulisilmiah.net/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lwt-%d0%b8%d0%b3%d1%80%d0%b0/
http://hydrocarbs-gh.org/index.php/component/k2/itemlist/user/7294349
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81-16/
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-irx-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1860218
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1126897
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/471854
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/49437
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=241171
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3543947
http://gtupuw.org/index.php/component/k2/itemlist/user/1811046
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1300825
http://computerscience.egerton.ac.ke/index.php/component/k2/itemlist/user/1983848
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1113732
https://www.resproxy.com/forum/index.php/734438-milliardy-4-sezon-12-seria-mpq-milliardy-4-sezon-12-seria-03052/0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1077938
http://withinfp.sakura.ne.jp/eso/index.php/16779821-ne-otpuskaj-mou-ruku-elimi-birakma-38-seria-x1dv-ne-otpuskaj-mo
http://www.deliberarchia.org/forum/index.php?topic=923008.0
http://withinfp.sakura.ne.jp/eso/index.php/16779301-cernoe-zerkalo-5-sezon-3-seria-aej-cernoe-zerkalo-5-sezon-3-ser
http://withinfp.sakura.ne.jp/eso/index.php/16878230-voskressij-ertugrul-144-seria-x1al-voskressij-ertugrul-144-seri
https://www.resproxy.com/forum/index.php/736762-milliardy-4-sezon-8-seria-jzl-milliardy-4-sezon-8-seria/0
https://www.youngbiker.de/wbboard/index.php?page=User&userID=784712
http://myrechockey.com/forums/index.php?topic=83067.0
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3543347
http://withinfp.sakura.ne.jp/eso/index.php/16774106-voron-kuzgun-17-seria-t1rg-voron-kuzgun-17-seria
http://withinfp.sakura.ne.jp/eso/index.php/16774126-edinoe-serdce-tek-yurek-13-seria-q0hv-edinoe-serdce-tek-yurek-1/0
http://withinfp.sakura.ne.jp/eso/index.php/16774153-ne-otpuskaj-mou-ruku-elimi-birakma-35-seria-c1yl-ne-otpuskaj-mo
http://withinfp.sakura.ne.jp/eso/index.php/16774283-vetrenyj-hercai-20-seria-e2sy-vetrenyj-hercai-20-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/16774558-edinoe-serdce-tek-yurek-13-seria-x1rh-edinoe-serdce-tek-yurek-1
http://withinfp.sakura.ne.jp/eso/index.php/16774620-edinoe-serdce-tek-yurek-19-seria-w8by-edinoe-serdce-tek-yurek-1/0
http://withinfp.sakura.ne.jp/eso/index.php/16774631-nasa-istoria-64-seria-l9tl-nasa-istoria-64-seria
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=336788
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=337498
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=337705
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=338538
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=338697
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=338969
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=338992
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=339523
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=339645
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=339966
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=341651
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=343417
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=344070
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=344870
http://healthyteethpa.org/component/k2/itemlist/user/5320201
http://www.m1avio.com/index.php/component/k2/itemlist/user/3594797
http://mvisage.sk/index.php/component/k2/itemlist/user/116307
https://www.resproxy.com/forum/index.php/729862-tola-robot-8-seria-utub-fi-tola-robot-8-seria-utub/0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=36754
http://www.arunagreen.com/index.php/component/k2/itemlist/user/373501
http://healthyteethpa.org/component/k2/itemlist/user/5306896
http://www.gtupuw.org/index.php/component/k2/itemlist/user/1832195
http://proxima.co.rw/index.php/component/k2/itemlist/user/544006
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/529456
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1308238
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1505303
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81-12/
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2538830
https://tg.vl-mp.com/index.php?topic=1292903.0
http://dohairbiz.com/?option=com_k2&view=itemlist&task=user&id=2689858
http://proxima.co.rw/index.php/component/k2/itemlist/user/544668
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1684635
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/174190
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1098603
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1827536
https://tg.vl-mp.com/index.php?topic=1269791.0
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=280550
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1133301
https://www.resproxy.com/forum/index.php/734385-riverdejl-riverdale-3-sezon-18-seria-fki-riverdejl-riverdale-3-/0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4692472
http://dev.aabn.org.gh/component/k2/itemlist/user/485546
http://www.spazioad.com/component/k2/itemlist/user/7171481
http://www.m1avio.com/index.php/component/k2/itemlist/user/3605427
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/134671
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/134705
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/135011
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/135102
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/135154
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/175087
http://menulisilmiah.net/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-dt4-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=298845
http://www.deliberarchia.org/forum/index.php?topic=930293.0
http://married.dike.gr/index.php/component/k2/itemlist/user/34539
https://tg.vl-mp.com/index.php?topic=1263668.0
http://macdistri.com/index.php/component/k2/itemlist/user/263831
https://members.fbhaters.com/index.php?topic=62075.0
https://tg.vl-mp.com/index.php?topic=1305956.0
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=162472
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3536224
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=10638
http://macdistri.com/index.php/component/k2/itemlist/user/260696
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/45001
https://tg.vl-mp.com/index.php?topic=1274687.0
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/143164
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/143196
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/143227
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/143258
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/143312
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/143396
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/143562
http://seoksoononly.dothome.co.kr/qna/609982
https://tg.vl-mp.com/index.php?topic=1268618.0
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1552658
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/173150
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=892722
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/271292
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3555676
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=163162
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/45169
http://married.dike.gr/index.php/component/k2/itemlist/user/37735
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=40526
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=79467
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=289996
http://withinfp.sakura.ne.jp/eso/index.php/16889133-igra-prestolov-8-sezon-3-seria-wma-igra-prestolov-8-sezon-3-ser
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4725582
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1556784
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1346733
http://www.spazioad.com/component/k2/itemlist/user/7228358
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=43556
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3302763
https://tg.vl-mp.com/index.php?topic=1328549.0
https://www.resproxy.com/forum/index.php/784950-igra-prestolov-8-sezon-7-seria-skb-igra-prestolov-8-sezon-7-ser/0
https://www.resproxy.com/forum/index.php/784969-milliardy-4-sezon-13-seria-qec-milliardy-4-sezon-13-seria/0
https://www.resproxy.com/forum/index.php/784977-manifest-19-seria-thj-manifest-19-seria/0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=13862
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=296087
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=33081
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3528456
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=80783
http://withinfp.sakura.ne.jp/eso/index.php/16781447-lubov-smert-i-roboty-love-death-and-robots-8-seria-svb-lubov-sm/0
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yuz-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
https://www.youngbiker.de/wbboard/index.php?page=User&userID=783588
https://www.resproxy.com/forum/index.php/764428-riverdejl-riverdale-3-sezon-22-seria-tol-riverdejl-riverdale-3-/0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1107691
https://www.resproxy.com/forum/index.php/765978-milliardy-4-sezon-9-seria-uun-milliardy-4-sezon-9-seria-0505201/0
http://withinfp.sakura.ne.jp/eso/index.php/16770481-igra-prestolov-8-sezon-5-seria-caq-igra-prestolov-8-sezon-5-ser/0
http://www.deliberarchia.org/forum/index.php?topic=917355.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=300317
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1296361
http://mediaville.me/index.php/component/k2/itemlist/user/206810
http://withinfp.sakura.ne.jp/eso/index.php/16780826-milliardy-4-sezon-9-seria-xka-milliardy-4-sezon-9-seria/0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/169996
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1862355
http://fbpharm.net/index.php/component/k2/itemlist/user/9613
http://rotary-laeliana.org/component/k2/itemlist/user/51621
http://dcasociados.eu/component/k2/itemlist/user/85031
http://www.m1avio.com/index.php/component/k2/itemlist/user/3558697
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172491
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2522828
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2522839
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2522925
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523003
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523034
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523058
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523093
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523127
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523195
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523213
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523219
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523280
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523293
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1305991
http://mediaville.me/index.php/component/k2/itemlist/user/202360
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1079650
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1675778
http://withinfp.sakura.ne.jp/eso/index.php/16784250-lubov-smert-i-roboty-love-death-and-robots-17-seria-hrl-lubov-s/0
http://danielmillsap.com/forum/index.php?topic=915583.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1296526
http://withinfp.sakura.ne.jp/eso/index.php/16860426-voskressij-ertugrul-146-seria-l2un-voskressij-ertugrul-146-seri/0
http://www.deliberarchia.org/forum/index.php?topic=907306.0
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=895048
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=536138
https://www.youngbiker.de/wbboard/index.php?page=User&userID=784294
https://tg.vl-mp.com/index.php?topic=1292608.0
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26096159/Default.aspx
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3683720
http://www.deliberarchia.org/forum/index.php?topic=901569.0
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=289657
http://israengineering.com/index.php/component/k2/itemlist/user/1114665
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3539938
http://proxima.co.rw/index.php/component/k2/itemlist/user/544081
http://www.spazioad.com/component/k2/itemlist/user/7198684
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1131339
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1090353
http://married.dike.gr/index.php/component/k2/itemlist/user/34585
https://www.youngbiker.de/wbboard/index.php?page=User&userID=782332
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1669539
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/1097
https://www.resproxy.com/forum/index.php/731101-tola-robot-9-seria-smotret-trejler-br-tola-robot-9-seria-smotre
https://members.fbhaters.com/index.php?topic=63728.0
http://arquitectosenreformas.es/index.php/component/k2/itemlist/user/77502
http://fbpharm.net/index.php/component/k2/itemlist/user/15742
https://members.fbhaters.com/index.php?topic=59567.0
http://thermoplast.envolgroupe.com/component/k2/author/68024
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/989702
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1125361
http://erhu.eu/viewtopic.php?t=229369
http://www.oortsociety.com/index.php?topic=7763.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3271762
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1676849
http://withinfp.sakura.ne.jp/eso/index.php/16794318-voron-kuzgun-19-seria-q2dz-voron-kuzgun-19-seria/0
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=80071
https://www.youngbiker.de/wbboard/index.php?page=User&userID=781196
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1573948
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3526867
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=95566
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1674782
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/201232
https://tg.vl-mp.com/index.php?topic=1309381.0
http://www.arunagreen.com/?option=com_k2&view=itemlist&task=user&id=393819
http://www.deliberarchia.org/forum/index.php?topic=955767.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2509418
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/42647
http://macdistri.com/component/k2/itemlist/user/303650
http://rudraautomation.com/index.php/component/k2/itemlist/user/109075
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rqt-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.m1avio.com/index.php/component/k2/itemlist/user/3552094
http://erhu.eu/viewtopic.php?f=7&t=229623
http://israengineering.com/index.php/component/k2/itemlist/user/1083946
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=296261
https://tg.vl-mp.com/index.php?topic=1281913.0
http://macdistri.com/index.php/component/k2/itemlist/user/302996
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2521415
[url=http://cialisdxt.com/]cialis online[/url]
cialis 20 mg directions for use
<a href="http://cialisdxt.com/">cialis generic</a>
cialis side effects stomach
https://tg.vl-mp.com/index.php?topic=1324117.0
https://tg.vl-mp.com/index.php?topic=1324129.0
https://tg.vl-mp.com/index.php?topic=1324138.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gnl-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gwy-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ecn-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ffk-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nhw-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mls-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-15-%d1%81%d0%b5%d1%80/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yyw-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-9-%d1%81%d0%b5%d1%80%d0%b8/
http://metropolis.ga/index.php?topic=2982.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3270788
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3270839
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3270931
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3270955
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3271001
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3271070
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3271124
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3271189
https://members.fbhaters.com/index.php?topic=69733.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4711389
http://danielmillsap.com/forum/index.php?topic=866792.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1578892
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=1223
http://www.deliberarchia.org/forum/index.php?topic=935028.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3270173
https://www.resproxy.com/forum/index.php/723099-tola-robot-4-seria-data-vyhoda-wk-tola-robot-4-seria-data-vyhod/0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/186473
http://matinbank.ir/component/k2/itemlist/user/4482780.html
http://danielmillsap.com/forum/index.php?topic=946181.0
https://tg.vl-mp.com/index.php?topic=1284508.0
https://www.youngbiker.de/wbboard/index.php?page=User&userID=782240
http://www.tessabannampad.go.th/webboard/index.php?topic=190263.0
http://www.tessabannampad.go.th/webboard/index.php?topic=190267.0
https://lucky28003.nl/forum/index.php?topic=9994.0
http://danielmillsap.com/forum/index.php?topic=952675.0
http://metropolis.ga/index.php?topic=3085.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3289200
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3289228
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3290262
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3290573
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3290739
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3291437
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1112929
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=41053
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3681045
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=291381
http://danielmillsap.com/forum/index.php?topic=944749.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3561264
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=48869
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-br8-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8/
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=606837
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1129470
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=299163
http://webp.online/index.php?topic=45843.0
http://www.deliberarchia.org/forum/index.php?topic=959157.0
http://www.deliberarchia.org/forum/index.php?topic=959167.0
http://www.deliberarchia.org/forum/index.php?topic=959176.0
http://www.deliberarchia.org/forum/index.php?topic=959189.0
http://www.deliberarchia.org/forum/index.php?topic=959197.0
http://www.tessabannampad.go.th/webboard/index.php?topic=190329.0
http://www.tessabannampad.go.th/webboard/index.php?topic=190364.0
http://www.tessabannampad.go.th/webboard/index.php?topic=190368.0
http://www.tessabannampad.go.th/webboard/index.php?topic=190383.0
http://www.tessabannampad.go.th/webboard/index.php?topic=190389.0
http://www.tessabannampad.go.th/webboard/index.php?topic=190391.0
http://danielmillsap.com/forum/index.php?topic=952960.0
http://danielmillsap.com/forum/index.php?topic=952985.0
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3681738
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3681744
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3681780
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3681793
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3681985
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3682077
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3682368
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3682424
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3682564
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3682582
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3683016
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3683350
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3683398
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3683570
http://www.m1avio.com/index.php/component/k2/itemlist/user/3559190
http://www.atab.com.sa/index.php/en/?option=com_k2&view=itemlist&task=user&id=1507330
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4713084
http://healthyteethpa.org/component/k2/itemlist/user/5322656
http://www.deliberarchia.org/forum/index.php?topic=955411.0
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=42506
https://www.resproxy.com/forum/index.php/737500-milliardy-4-sezon-6-seria-clt-milliardy-4-sezon-6-seria-0305201/0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1096478
http://smartacity.com/component/k2/itemlist/user/14170
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=239027
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4691450
https://tg.vl-mp.com/index.php?topic=1293915.0
http://married.dike.gr/index.php/component/k2/itemlist/user/39023
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/170527
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=163847
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1004763
https://www.resproxy.com/forum/index.php/771354-riverdejl-riverdale-3-sezon-20-seria-gij-riverdejl-riverdale-3-/0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=277167
http://macdistri.com/index.php/component/k2/itemlist/user/258090
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3277800
http://fbpharm.net/index.php/component/k2/itemlist/user/14863
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/60229
http://webp.online/index.php?topic=41728.0
http://febrescordero.gob.ec/index.php/component/k2/itemlist/user/72268
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/60106
http://boutique.in.th/?option=com_k2&view=itemlist&task=user&id=146267
http://withinfp.sakura.ne.jp/eso/index.php/16787351-nasa-istoria-71-seria-h3qv-nasa-istoria-71-seria/0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12266
http://www.m1avio.com/index.php/component/k2/itemlist/user/3601500
http://www.m1avio.com/index.php/component/k2/itemlist/user/3602268
http://www.m1avio.com/index.php/component/k2/itemlist/user/3602435
http://www.m1avio.com/index.php/component/k2/itemlist/user/3602481
http://www.m1avio.com/index.php/component/k2/itemlist/user/3602540
http://www.m1avio.com/index.php/component/k2/itemlist/user/3602555
http://www.m1avio.com/index.php/component/k2/itemlist/user/3602562
http://www.m1avio.com/index.php/component/k2/itemlist/user/3602572
http://www.m1avio.com/index.php/component/k2/itemlist/user/3602640
http://www.m1avio.com/index.php/component/k2/itemlist/user/3602653
http://www.m1avio.com/index.php/component/k2/itemlist/user/3602751
http://www.m1avio.com/index.php/component/k2/itemlist/user/3602827
http://www.m1avio.com/index.php/component/k2/itemlist/user/3602843
http://danielmillsap.com/forum/index.php?topic=896225.0
http://danielmillsap.com/forum/index.php?topic=896250.0
http://danielmillsap.com/forum/index.php?topic=896315.0
http://danielmillsap.com/forum/index.php?topic=896449.0
http://danielmillsap.com/forum/index.php?topic=896708.0
http://danielmillsap.com/forum/index.php?topic=896822.0
http://danielmillsap.com/forum/index.php?topic=896862.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1314082
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1830555
http://metropolis.ga/index.php?topic=2147.0
http://www.thenixnoob.com/viewtopic.php?t=638481
http://danielmillsap.com/forum/index.php?topic=901530.0
https://tg.vl-mp.com/index.php?topic=1287961.0
http://danielmillsap.com/forum/index.php?topic=888051.0
http://withinfp.sakura.ne.jp/eso/index.php/16783495-voron-kuzgun-18-seria-z7kb-voron-kuzgun-18-seria/0
http://www.deliberarchia.org/forum/index.php?topic=903498.0
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2529811
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1313859
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/51203
http://smartacity.com/component/k2/itemlist/user/13633
http://batubersurat.com/index.php/component/k2/itemlist/user/36538
http://www.x2145-productions.technology/index.php?title=%C2%AB%D0%9C%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%C2%BB_07-05-2019_%D0%9C%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4_%C2%AB%D0%9C%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%C2%BB
http://www.x2145-productions.technology/index.php?title=%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB_06-05-2019_%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB_%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB
http://www.x2145-productions.technology/index.php?title=%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB_06-05-2019_%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB_Watch%C2%BB_%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB
http://www.x2145-productions.technology/index.php?title=%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB_06-05-2019_%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB_%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB
http://www.x2145-productions.technology/index.php?title=%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB_06-05-2019_%E2%80%9E%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB_Online%22_%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB
http://www.x2145-productions.technology/index.php?title=%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB_07-05-2019_%22%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%22_%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB
http://www.deliberarchia.org/forum/index.php?topic=927204.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4666973
http://dev.aabn.org.gh/component/k2/itemlist/user/494522
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=549391
http://www.moyakmermer.com/index.php/component/k2/itemlist/user/641563
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/247339
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4664759
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1315445
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2392483
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7183875
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7184414
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7185264
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7185768
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7186801
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7187974
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7188664
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7190090
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7191443
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7192840
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=4523
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=4539
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=4544
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=4569
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=4571
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=4578
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=4583
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=159461
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/60024
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1576992
https://tg.vl-mp.com/index.php?topic=1264602.0
https://www.resproxy.com/forum/index.php/733167-igra-prestolov-8-sezon-8-seria-cqr-igra-prestolov-8-sezon-8-ser/0
https://alvarogarciatorero.com/index.php/component/k2/itemlist/user/46838
https://members.fbhaters.com/index.php?topic=65240.0
http://mvisage.sk/index.php/component/k2/itemlist/user/116527
https://outreach.wikimedia.org/wiki/%C3%82%C2%AB%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%90%C2%B5%C3%90%C2%BB%C3%90%C2%BE%C3%91%E2%80%9A%C3%90%C2%B0%C3%91%E2%80%A1%C3%90%C2%BA%C3%90%C2%B8%C3%82%C2%BB_05-05-2019_%C3%82%C2%AB%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%90%C2%B5%C3%90%C2%BB%C3%90%C2%BE%C3%91%E2%80%9A%C3%90%C2%B0%C3%91%E2%80%A1%C3%90%C2%BA%C3%90%C2%B8%C3%82%C2%BB_%C3%82%C2%AB%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%90%C2%B5%C3%90%C2%BB%C3%90%C2%BE%C3%91%E2%80%9A%C3%90%C2%B0%C3%91%E2%80%A1%C3%90%C2%BA%C3%90%C2%B8%C3%82%C2%BB
http://danielmillsap.com/forum/index.php?topic=905935.0
http://webp.online/index.php?topic=39930.15
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81-24/
https://tg.vl-mp.com/index.php?topic=1285843.0
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4826718
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523648
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523671
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523681
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523717
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523737
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523746
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523770
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523807
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523826
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523856
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523858
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523874
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523885
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=301006
https://tg.vl-mp.com/index.php?topic=1300641.0
http://israengineering.com/index.php/component/k2/itemlist/user/1088199
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1575082
http://dev.aabn.org.gh/component/k2/itemlist/user/516271
http://smartacity.com/index.php/component/k2/itemlist/user/8226
https://tg.vl-mp.com/index.php?topic=1277443.0
http://www.quattroandpartners.it/component/k2/itemlist/user/995696
http://withinfp.sakura.ne.jp/eso/index.php/16883742-vossoedinenie-vuslat-16-seria-l5qy-vossoedinenie-vuslat-16-seri/0
https://tg.vl-mp.com/index.php?topic=1325344.0
https://tg.vl-mp.com/index.php?topic=1325365.0
https://www.resproxy.com/forum/index.php/780949-voron-kuzgun-20-seria-y4zj-voron-kuzgun-20-seria/0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ecy-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dif-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1505246
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/469682
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1077945
http://danielmillsap.com/forum/index.php?topic=944049.0
http://hydrocarbs-gh.org/index.php/component/k2/itemlist/user/7279515
http://rudraautomation.com/index.php/component/k2/author/108421
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=31993
http://mediaville.me/index.php/component/k2/itemlist/user/201996
http://mediaville.me/index.php/component/k2/itemlist/user/202095
http://mediaville.me/index.php/component/k2/itemlist/user/202149
http://mediaville.me/index.php/component/k2/itemlist/user/202157
http://mediaville.me/index.php/component/k2/itemlist/user/202215
http://mediaville.me/index.php/component/k2/itemlist/user/202309
http://mediaville.me/index.php/component/k2/itemlist/user/202408
http://mediaville.me/index.php/component/k2/itemlist/user/202432
http://mediaville.me/index.php/component/k2/itemlist/user/202477
http://mediaville.me/index.php/component/k2/itemlist/user/202521
http://mediaville.me/index.php/component/k2/itemlist/user/202535
http://mediaville.me/index.php/component/k2/itemlist/user/202543
http://mediaville.me/index.php/component/k2/itemlist/user/202576
http://www.tessabannampad.go.th/webboard/index.php?topic=190745.0
http://www.tessabannampad.go.th/webboard/index.php?topic=190753.0
http://www.tessabannampad.go.th/webboard/index.php?topic=190759.0
https://lucky28003.nl/forum/index.php?topic=10120.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c0tu-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-17-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k6yt-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-19-%d1%81%d0%b5%d1%80%d0%b8/
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=36332
https://www.resproxy.com/forum/index.php/766510-milliardy-4-sezon-8-seria-nes-milliardy-4-sezon-8-seria-0505201/0
http://withinfp.sakura.ne.jp/eso/index.php/16870303-vossoedinenie-vuslat-19-seria-u8hn-vossoedinenie-vuslat-19-seri/0
https://tg.vl-mp.com/index.php?topic=1270602.0
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=264932
http://metropolis.ga/index.php?topic=1230.0
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1543603
http://withinfp.sakura.ne.jp/eso/index.php/16778585-igra-prestolov-8-sezon-6-seria-exk-igra-prestolov-8-sezon-6-ser
http://fbpharm.net/index.php/component/k2/itemlist/user/9374
http://withinfp.sakura.ne.jp/eso/index.php/16822337-vetrenyj-hercai-21-seria-u1gx-vetrenyj-hercai-21-seria/0
http://www.deliberarchia.org/forum/index.php?topic=953235.0
https://tg.vl-mp.com/index.php?topic=1273214.0
http://mediaville.me/index.php/component/k2/itemlist/user/205127
http://mediaville.me/index.php/component/k2/itemlist/user/205245
http://mediaville.me/index.php/component/k2/itemlist/user/205308
http://mediaville.me/index.php/component/k2/itemlist/user/205320
http://mediaville.me/index.php/component/k2/itemlist/user/205391
http://mediaville.me/index.php/component/k2/itemlist/user/205418
http://mediaville.me/index.php/component/k2/itemlist/user/205468
http://web2interactive.com/index.php/component/k2/itemlist/user/3541648
http://metropolis.ga/index.php?topic=690.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/396763
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1752932
http://danielmillsap.com/forum/index.php?topic=870401.0
http://dev.aabn.org.gh/component/k2/itemlist/user/477250
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4690578
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4690612
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4690935
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4691606
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4691733
http://seoksoononly.dothome.co.kr/?document_srl=656619
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=561340
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/43563
http://dcasociados.eu/component/k2/itemlist/user/84916
http://dev.aabn.org.gh/component/k2/itemlist/user/494664
http://dev.aabn.org.gh/component/k2/itemlist/user/480121
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3711228
http://withinfp.sakura.ne.jp/eso/index.php/16784839-voron-kuzgun-12-seria-w2bw-voron-kuzgun-12-seria
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1109971
https://www.resproxy.com/forum/index.php/755993-milliardy-4-sezon-10-seria-pye-milliardy-4-sezon-10-seria-05052/0
http://webp.online/index.php?topic=43812.msg71975
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1125201
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1108027
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1604287
http://www.deliberarchia.org/forum/index.php?topic=893422.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1109209
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/190233
http://web.cas.identrics.net/phpBB3/viewtopic.php?f=5&t=117493
http://withinfp.sakura.ne.jp/eso/index.php/16785856-nasa-istoria-69-seria-s5ed-nasa-istoria-69-seria/0
http://seoksoononly.dothome.co.kr/qna/596154
http://withinfp.sakura.ne.jp/eso/index.php/16839940-vetrenyj-hercai-19-seria-r1fm-vetrenyj-hercai-19-seria
http://www.arunagreen.com/index.php/component/k2/itemlist/user/393962
http://www.arunagreen.com/index.php/component/k2/itemlist/user/394224
http://www.arunagreen.com/index.php/component/k2/itemlist/user/394398
http://www.arunagreen.com/index.php/component/k2/itemlist/user/394471
http://www.arunagreen.com/index.php/component/k2/itemlist/user/394668
http://www.arunagreen.com/index.php/component/k2/itemlist/user/394751
http://www.arunagreen.com/index.php/component/k2/itemlist/user/394806
http://www.arunagreen.com/index.php/component/k2/itemlist/user/394854
http://www.arunagreen.com/index.php/component/k2/itemlist/user/394953
http://www.arunagreen.com/index.php/component/k2/itemlist/user/395166
http://www.arunagreen.com/index.php/component/k2/itemlist/user/395258
http://www.arunagreen.com/index.php/component/k2/itemlist/user/395324
http://www.arunagreen.com/index.php/component/k2/itemlist/user/395358
http://healthyteethpa.org/component/k2/itemlist/user/5283960
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1082139
http://esperanzazubieta.com/component/k2/itemlist/user/95133
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1606582
http://www.quattroandpartners.it/component/k2/itemlist/user/1040050
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38464
http://www.thenixnoob.com/viewtopic.php?t=632698
http://danielmillsap.com/forum/index.php?topic=881245.0
http://www.deliberarchia.org/forum/index.php?topic=937345.0
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43252
http://proxima.co.rw/index.php/component/k2/itemlist/user/565013
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3281665
http://macdistri.com/index.php/component/k2/itemlist/user/261081
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=555142
http://married.dike.gr/index.php/component/k2/itemlist/user/39890
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ja3-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://153.120.114.241/eso/index.php/16867721-nasledie-12-seria-dcx-nasledie-12-seria
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3541534
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=2288
http://travelsolution.info/?option=com_k2&view=itemlist&task=user&id=699010
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4707752
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4711130
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4719656
http://www.aroshan.com/?option=com_k2&view=itemlist&task=user&id=927181
http://www.aroshan.com/component/k2/itemlist/user/927054
http://withinfp.sakura.ne.jp/eso/index.php/16773875-milliardy-4-sezon-12-seria-sjx-milliardy-4-sezon-12-seria-01052/0
http://www.web2interactive.com/index.php/component/k2/itemlist/user/3538234
http://proxima.co.rw/index.php/component/k2/itemlist/user/543802
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=10709
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4666611
http://proxima.co.rw/index.php/component/k2/itemlist/user/544670
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iis-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ilt-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jdp-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jep-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jgi-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jsh-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ksq-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lae-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lba-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lks-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lrm-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://smartacity.com/component/k2/itemlist/user/8098
http://danielmillsap.com/forum/index.php?topic=870055.0
http://www.quattroandpartners.it/component/k2/itemlist/user/1002147
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3682630
http://grupotir.com/component/k2/itemlist/user/42209
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1106655
http://married.dike.gr/index.php/component/k2/itemlist/user/41862
http://www.spazioad.com/component/k2/itemlist/user/7220151
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=294123
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=496335
http://dessa.com.br/component/k2/itemlist/user/294513
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=895032
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172627
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1107404
http://seoksoononly.dothome.co.kr/qna/625965
http://macdistri.com/index.php/component/k2/itemlist/user/266055
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/267974
https://www.youngbiker.de/wbboard/index.php?page=User&userID=781177
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1516397
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1117577
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1119416
http://israengineering.com/index.php/component/k2/itemlist/user/1079121
http://israengineering.com/index.php/component/k2/itemlist/user/1079494
http://israengineering.com/index.php/component/k2/itemlist/user/1079497
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/264147
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/264161
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/264302
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/264436
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/264450
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/264808
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/264883
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/265050
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/265067
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/265243
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/265336
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/265567
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/265703
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/265810
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/132129
http://zsmr.com.ua/index.php/component/k2/itemlist/user/492590
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=298399
http://webp.online/index.php?topic=44453.0
https://www.youngbiker.de/wbboard/index.php?page=User&userID=785247
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4664111
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=10499
http://soc-human.kz/index.php/component/k2/itemlist/user/1632840
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1828256
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=14893
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/174186
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3694348
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3695210
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3696321
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3697092
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3697843
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3701982
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/274060
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/274141
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/274170
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/274213
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/274240
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/274256
http://www.deliberarchia.org/forum/index.php?topic=968437.0
http://www.deliberarchia.org/forum/index.php?topic=968447.0
http://danielmillsap.com/forum/index.php?topic=963394.0
https://members.fbhaters.com/index.php?topic=77057.0
https://tg.vl-mp.com/index.php?topic=1333477.0
https://tg.vl-mp.com/index.php?topic=1333482.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ndg-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-12-%d1%81%d0%b5%d1%80/
http://www.tessabannampad.go.th/webboard/index.php?topic=191642.0
https://members.fbhaters.com/index.php?topic=77072.0
http://www.deliberarchia.org/forum/index.php?topic=968458.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173079
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173114
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173133
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173156
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173178
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173195
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173203
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173220
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173229
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173265
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173276
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173308
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/172862
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=242878
http://withinfp.sakura.ne.jp/eso/index.php/16779366-cernoe-zerkalo-5-sezon-5-seria-arn-cernoe-zerkalo-5-sezon-5-ser/0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1108775
https://www.resproxy.com/forum/index.php/771543-milliardy-4-sezon-13-seria-zau-milliardy-4-sezon-13-seria/0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/279451
http://www.m1avio.com/index.php/component/k2/itemlist/user/3570289
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/273456
https://www.youngbiker.de/wbboard/index.php?page=User&userID=785810
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/521055
http://www.deliberarchia.org/forum/index.php?topic=897651.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/55903
http://mediaville.me/index.php/component/k2/itemlist/user/208551
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1078881
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fse-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.deliberarchia.org/forum/index.php?topic=968636.0
http://www.deliberarchia.org/forum/index.php?topic=968687.0
http://www.tessabannampad.go.th/webboard/index.php?topic=191712.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173794
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173796
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173812
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173815
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173817
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173821
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173829
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173839
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173856
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173865
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173875
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173894
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173918
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173936
http://www.sopcich.com/UserProfile/tabid/42/UserID/1665986/Default.aspx
http://www.oortsociety.com/index.php?topic=8649.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=258600
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=891439
http://dcasociados.eu/component/k2/itemlist/user/86591
https://www.youngbiker.de/wbboard/index.php?page=User&userID=783524
https://tg.vl-mp.com/index.php?topic=1265609.0
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1828964
https://www.resproxy.com/forum/index.php/737279-amerikanskie-bogi-2-sezon-6-seria-wdy-amerikanskie-bogi-2-sezon/0
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3536620
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=34226
http://www.arunagreen.com/index.php/component/k2/itemlist/user/373755
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=39605
http://xekhachduyetthuy.com.vn/component/k2/itemlist/user/160802
http://healthyteethpa.org/component/k2/itemlist/user/5276001
http://danielmillsap.com/forum/index.php?topic=867207.0
http://maderadepaulownia.com/?option=com_k2&view=itemlist&task=user&id=83835
https://www.resproxy.com/forum/index.php/777397-riverdejl-riverdale-3-sezon-20-seria-cih-riverdejl-riverdale-3-/0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3536365
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lz0-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20/
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rh9-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.resproxy.com/forum/index.php/799655-rasskaz-sluzanki-3-sezon-2-seria-jpd-rasskaz-sluzanki-3-sezon-2/0
https://www.resproxy.com/forum/index.php/799732-rasskaz-sluzanki-3-sezon-2-seria-hyq-rasskaz-sluzanki-3-sezon-2/0
https://www.resproxy.com/forum/index.php/799740-riverdejl-riverdale-3-sezon-23-seria-xwi-riverdejl-riverdale-3-/0
https://www.resproxy.com/forum/index.php/799749-milliardy-4-sezon-4-seria-zio-milliardy-4-sezon-4-seria/0
https://www.resproxy.com/forum/index.php/799764-cernoe-zerkalo-5-sezon-4-seria-jio-cernoe-zerkalo-5-sezon-4-ser/0
https://www.resproxy.com/forum/index.php/799770-sverh-estestvennoe-14-sezon-20-seria-hhk-sverh-estestvennoe-14-
https://www.resproxy.com/forum/index.php/799810-nasledie-12-seria-rog-nasledie-12-seria
http://healthyteethpa.org/component/k2/itemlist/user/5332697
http://healthyteethpa.org/component/k2/itemlist/user/5332811
http://healthyteethpa.org/component/k2/itemlist/user/5332891
http://healthyteethpa.org/component/k2/itemlist/user/5332912
http://healthyteethpa.org/component/k2/itemlist/user/5332951
http://healthyteethpa.org/component/k2/itemlist/user/5333025
http://healthyteethpa.org/component/k2/itemlist/user/5333044
http://healthyteethpa.org/component/k2/itemlist/user/5333310
http://healthyteethpa.org/component/k2/itemlist/user/5333322
http://healthyteethpa.org/component/k2/itemlist/user/5333351
http://healthyteethpa.org/component/k2/itemlist/user/5333386
http://healthyteethpa.org/component/k2/itemlist/user/5333392
http://www.m1avio.com/index.php/component/k2/itemlist/user/3561203
https://www.resproxy.com/forum/index.php/751168-cernoe-zerkalo-5-sezon-2-seria-zmf-cernoe-zerkalo-5-sezon-2-ser
http://grupotir.com/component/k2/itemlist/user/42166
http://proxima.co.rw/index.php/component/k2/itemlist/user/544198
https://www.youngbiker.de/wbboard/index.php?page=User&userID=781740
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2491258
http://www.quattroandpartners.it/component/k2/itemlist/user/995046
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/444688
http://www.m1avio.com/?option=com_k2&view=itemlist&task=user&id=3583672
http://www.x2145-productions.technology/index.php?title=%C2%AB%D0%9C%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%C2%BB_06-05-2019_%22%D0%9C%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4_Watch%22_%C2%AB%D0%9C%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%C2%BB
http://www.sopcich.com/UserProfile/tabid/42/UserID/1780661/Default.aspx
http://www.deliberarchia.org/forum/index.php?topic=934366.0
https://www.resproxy.com/forum/index.php/799825-rasskaz-sluzanki-3-sezon-3-seria-str-rasskaz-sluzanki-3-sezon-3/0
https://www.resproxy.com/forum/index.php/799885-riverdejl-riverdale-3-sezon-21-seria-edf-riverdejl-riverdale-3-/0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=296087
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1827548
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-of7-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.crowdfundingchile.cl/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kp6-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
https://tg.vl-mp.com/index.php?topic=1343227.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=296087
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=318670
http://www.dap.com.py/index.php/component/k2/itemlist/user/789307
https://www.resproxy.com/forum/index.php/799907-cernoe-zerkalo-5-sezon-5-seria-ild-cernoe-zerkalo-5-sezon-5-ser/0
https://www.resproxy.com/forum/index.php/799930-milliardy-4-sezon-5-seria-ega-milliardy-4-sezon-5-seria/0
http://healthyteethpa.org/component/k2/itemlist/user/5333433
http://healthyteethpa.org/component/k2/itemlist/user/5333444
http://healthyteethpa.org/component/k2/itemlist/user/5333478
http://healthyteethpa.org/component/k2/itemlist/user/5333528
http://healthyteethpa.org/component/k2/itemlist/user/5333537
http://healthyteethpa.org/component/k2/itemlist/user/5333571
http://healthyteethpa.org/component/k2/itemlist/user/5333655
http://healthyteethpa.org/component/k2/itemlist/user/5333744
http://healthyteethpa.org/component/k2/itemlist/user/5333799
http://healthyteethpa.org/component/k2/itemlist/user/5333859
http://healthyteethpa.org/component/k2/itemlist/user/5334001
http://healthyteethpa.org/component/k2/itemlist/user/5334078
http://healthyteethpa.org/component/k2/itemlist/user/5334090
http://healthyteethpa.org/component/k2/itemlist/user/5334103
https://tg.vl-mp.com/index.php?topic=1288424.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/454731
http://withinfp.sakura.ne.jp/eso/index.php/16821828-nasa-istoria-66-seria-i7tp-nasa-istoria-66-seria/0
http://dev.aabn.org.gh/component/k2/itemlist/user/518818
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=186042
http://danielmillsap.com/forum/index.php?topic=881851.0
http://www.deliberarchia.org/forum/index.php?topic=949525.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yva-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=243162
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uq1-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-vu8-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ik3-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qk7-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rj6-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sto54.ru/index.php/component/k2/itemlist/user/3315885
http://www.sopcich.com/UserProfile/tabid/42/UserID/1822833/Default.aspx
https://www.resproxy.com/forum/index.php/801319-riverdejl-riverdale-3-sezon-23-seria-pqs-riverdejl-riverdale-3-/0
https://www.resproxy.com/forum/index.php/801404-milliardy-4-sezon-10-seria-fbg-milliardy-4-sezon-10-seria
https://www.resproxy.com/forum/index.php/801427-manifest-19-seria-dwd-manifest-19-seria
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=292595
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=292635
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=292644
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=292695
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=292718
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=292749
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=292751
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=292757
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=292781
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=292788
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=292821
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=292844
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=292875
[url=http://cialisec.com/]buy generic cialis[/url]
cialis commercial bathtub 2016
<a href="http://cialisec.com/">buy cialis online</a>
viagra and cialis price comparison
http://www.deliberarchia.org/forum/index.php?topic=971215.0
http://www.deliberarchia.org/forum/index.php?topic=971267.0
http://www.deliberarchia.org/forum/index.php?topic=971274.0
http://www.deliberarchia.org/forum/index.php?topic=971279.0
http://www.deliberarchia.org/forum/index.php?topic=971286.0
http://www.deliberarchia.org/forum/index.php?topic=971296.0
http://www.deliberarchia.org/forum/index.php?topic=971305.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/435001
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/435091
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/435137
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/435185
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/435305
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/435341
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/435351
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/435356
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/435538
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/435591
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/435597
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/436082
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/436122
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/436210
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/436461
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1328573
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/173839
http://batubersurat.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=37482
http://proxima.co.rw/index.php/component/k2/itemlist/user/537005
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3252993
http://seoksoononly.dothome.co.kr/qna/622980
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3246857
http://www.deliberarchia.org/forum/index.php?topic=974682.0
http://www.deliberarchia.org/forum/index.php?topic=974693.0
http://www.deliberarchia.org/forum/index.php?topic=974701.0
http://www.deliberarchia.org/forum/index.php?topic=974706.0
http://www.deliberarchia.org/forum/index.php?topic=974716.0
http://www.deliberarchia.org/forum/index.php?topic=974722.0
http://www.deliberarchia.org/forum/index.php?topic=974728.0
http://www.deliberarchia.org/forum/index.php?topic=974732.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/446367
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/446374
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/446488
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/446570
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/446583
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/446626
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/446633
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/446677
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/446697
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/446730
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/446790
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/446821
https://tg.vl-mp.com/index.php?topic=1287549.0
http://153.120.114.241/eso/index.php/16864054-rasskaz-sluzanki-3-sezon-1-seria-xgp-rasskaz-sluzanki-3-sezon-1
http://dessa.com.br/component/k2/itemlist/user/297076
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1533411
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=291665
http://www.deliberarchia.org/forum/index.php?topic=983447.0
http://www.deliberarchia.org/forum/index.php?topic=983454.0
http://www.deliberarchia.org/forum/index.php?topic=983458.0
http://www.deliberarchia.org/forum/index.php?topic=983468.0
http://www.deliberarchia.org/forum/index.php?topic=983486.0
http://www.deliberarchia.org/forum/index.php?topic=983495.0
http://www.deliberarchia.org/forum/index.php?topic=983506.0
http://www.deliberarchia.org/forum/index.php?topic=983516.0
http://www.deliberarchia.org/forum/index.php?topic=983522.0
http://www.deliberarchia.org/forum/index.php?topic=983530.0
http://www.deliberarchia.org/forum/index.php?topic=983539.0
http://www.deliberarchia.org/forum/index.php?topic=983583.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=299042
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=299043
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=299046
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=299163
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=299196
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=299219
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=299235
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=66194
http://www.deliberarchia.org/forum/index.php?topic=954251.0
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=64166
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=47163
https://www.resproxy.com/forum/index.php/757316-sverh-estestvennoe-14-sezon-16-seria-lqh-sverh-estestvennoe-14-/0
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lz7-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://153.120.114.241/eso/index.php/16860325-amerikanskie-bogi-2-sezon-9-seria-gee-amerikanskie-bogi-2-sezon
http://www.thenixnoob.com/viewtopic.php?t=639464
https://members.fbhaters.com/index.php?topic=62085.0
http://minostech.co.kr/news/3352443
http://minostech.co.kr/news/3352563
http://minostech.co.kr/news/3352638
http://minostech.co.kr/news/3354003
http://minostech.co.kr/news/3356322
http://minostech.co.kr/news/3366565
http://minostech.co.kr/news/3374876
http://mobility-corp.com/index.php/component/k2/itemlist/user/2480191
http://mobility-corp.com/index.php/component/k2/itemlist/user/2480280
http://mobility-corp.com/index.php/component/k2/itemlist/user/2480412
http://mobility-corp.com/index.php/component/k2/itemlist/user/2480455
http://mobility-corp.com/index.php/component/k2/itemlist/user/2480488
http://mobility-corp.com/index.php/component/k2/itemlist/user/2480513
http://mobility-corp.com/index.php/component/k2/itemlist/user/2480600
http://mobility-corp.com/index.php/component/k2/itemlist/user/2480621
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7339583
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=790129
http://fbpharm.net/index.php/component/k2/itemlist/user/22802
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3395320
http://www.x2145-productions.technology/index.php?title=Benutzer:NormaWhitehouse
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1067903
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3732286
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1860057
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=44864
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=45361
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=45794
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=45913
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=48638
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=61682
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=62511
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/44294
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/44452
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/44464
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/44576
http://mobility-corp.com/index.php/component/k2/itemlist/user/2483860
http://mobility-corp.com/index.php/component/k2/itemlist/user/2483921
http://mobility-corp.com/index.php/component/k2/itemlist/user/2483984
http://mobility-corp.com/index.php/component/k2/itemlist/user/2484000
http://mobility-corp.com/index.php/component/k2/itemlist/user/2484018
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3732611
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7340151
http://www.quattroandpartners.it/component/k2/itemlist/user/1068294
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7340165
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=790284
http://www.x2145-productions.technology/index.php?title=%C3%82%C2%AB%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%91%E2%82%AC%C3%90%C2%B5%C3%90%C2%BC%C3%91_%C3%90%C5%93%C3%90%C2%BE%C3%90%C2%BD%C3%91%C3%91%E2%80%9A%C3%91%E2%82%AC%C3%90%C2%BE%C3%90%C2%B2%C3%82%C2%BB_08-05-2019_%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%91%E2%82%AC%C3%90%C2%B5%C3%90%C2%BC%C3%91_%C3%90%C5%93%C3%90%C2%BE%C3%90%C2%BD%C3%91%C3%91%E2%80%9A%C3%91%E2%82%AC%C3%90%C2%BE%C3%90%C2%B2_%C3%82%C2%AB%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%91%E2%82%AC%C3%90%C2%B5%C3%90%C2%BC%C3%91_%C3%90%C5%93%C3%90%C2%BE%C3%90%C2%BD%C3%91%C3%91%E2%80%9A%C3%91%E2%82%AC%C3%90%C2%BE%C3%90%C2%B2%C3%82%C2%BB
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=301575
http://sos.victoryaltar.org/tiki-index.php?page=UserPagealtagogginsjmpu
http://withinfp.sakura.ne.jp/eso/index.php/16776005-vossoedinenie-vuslat-20-seria-i4lw-vossoedinenie-vuslat-20-seri/0
http://withinfp.sakura.ne.jp/eso/index.php/16776043-zensina-58-seria-k5oy-zensina-58-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/16776097-voron-kuzgun-18-seria-q5rg-voron-kuzgun-18-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/16776162-ne-otpuskaj-mou-ruku-elimi-birakma-37-seria-z3hr-ne-otpuskaj-mo/0
http://withinfp.sakura.ne.jp/eso/index.php/16776213-vossoedinenie-vuslat-17-seria-e8el-vossoedinenie-vuslat-17-seri/0
http://withinfp.sakura.ne.jp/eso/index.php/16776296-vossoedinenie-vuslat-16-seria-h0ue-vossoedinenie-vuslat-16-seri/0
http://withinfp.sakura.ne.jp/eso/index.php/16776341-vetrenyj-hercai-12-seria-j6pg-vetrenyj-hercai-12-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/16776345-rannaa-ptaska-erkenci-kus-41-seria-j3wx-rannaa-ptaska-erkenci-k/0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/48879
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/48884
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/48949
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/48962
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/48968
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/48975
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/48992
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/49051
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=793275
http://www.quattroandpartners.it/component/k2/itemlist/user/1073125
http://www.quattroandpartners.it/component/k2/itemlist/user/1073176
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/61492
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1781871
http://koushatarabar.com/index.php/component/k2/itemlist/user/1341758
http://www.dap.com.py/index.php/component/k2/itemlist/user/793240
http://www.quattroandpartners.it/component/k2/itemlist/user/1073191
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=538042
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=79954
http://mobility-corp.com/index.php/component/k2/itemlist/user/2493745
http://hydrocarbs-gh.org/index.php/component/k2/itemlist/user/7291413
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=30443
http://associationsila.org/component/k2/itemlist/user/268330
http://withinfp.sakura.ne.jp/eso/index.php/16768201-manifest-18-seria-vop-manifest-18-seria/0
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ut4-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1743051
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=893573
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1551644
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=574464
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3311014
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1827548
http://dev.aabn.org.gh/component/k2/itemlist/user/536777
http://webp.online/index.php?topic=48593.0
http://webp.online/index.php?topic=48603.0
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26235142/Default.aspx
http://www.m1avio.com/index.php/component/k2/itemlist/user/3622295
http://boutique.in.th/?option=com_k2&view=itemlist&task=user&id=147942
http://boutique.in.th/?option=com_k2&view=itemlist&task=user&id=147945
http://boutique.in.th/?option=com_k2&view=itemlist&task=user&id=147947
http://boutique.in.th/?option=com_k2&view=itemlist&task=user&id=147984
http://boutique.in.th/?option=com_k2&view=itemlist&task=user&id=147991
https://tg.vl-mp.com/index.php?topic=1350304.0
https://tg.vl-mp.com/index.php?topic=1350330.0
http://metropolis.ga/index.php?topic=5437.0
http://metropolis.ga/index.php?topic=5438.0
http://www.deliberarchia.org/forum/index.php?topic=983336.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/451723
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/451773
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/452091
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/452268
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/452322
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=524162
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=4788
https://www.resproxy.com/forum/index.php/745030-amerikanskie-bogi-2-sezon-7-seria-tyr-amerikanskie-bogi-2-sezon
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3525730
http://webp.online/index.php?topic=37203.0
http://webp.online/index.php?topic=40567.0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=530183
http://married.dike.gr/index.php/component/k2/itemlist/user/47135
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/53290
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1127500
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=238676
http://dev.aabn.org.gh/component/k2/itemlist/user/485523
http://menulisilmiah.net/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-upc-%d0%b8%d0%b3%d1%80%d0%b0/
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1106220
http://rotary-laeliana.org/component/k2/itemlist/user/51456
http://rotary-laeliana.org/component/k2/itemlist/user/51464
http://rotary-laeliana.org/component/k2/itemlist/user/51466
http://rotary-laeliana.org/component/k2/itemlist/user/51469
http://rotary-laeliana.org/component/k2/itemlist/user/51471
http://rotary-laeliana.org/component/k2/itemlist/user/51474
http://rotary-laeliana.org/component/k2/itemlist/user/51481
http://rotary-laeliana.org/component/k2/itemlist/user/51491
http://rotary-laeliana.org/component/k2/itemlist/user/51504
http://rotary-laeliana.org/component/k2/itemlist/user/51507
http://rotary-laeliana.org/component/k2/itemlist/user/51525
http://rotary-laeliana.org/component/k2/itemlist/user/51529
http://rotary-laeliana.org/component/k2/itemlist/user/51543
http://rotary-laeliana.org/component/k2/itemlist/user/51582
http://rotary-laeliana.org/component/k2/itemlist/user/51585
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312106
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312129
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312189
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312216
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312220
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312224
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312267
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312274
http://webp.online/index.php?topic=51048.0
http://withinfp.sakura.ne.jp/eso/index.php/16935528-edinoe-serdce-tek-yurek-12-seria-r8zu-edinoe-serdce-tek-yurek-1/0
https://www.resproxy.com/forum/index.php/807437-vetrenyj-hercai-21-seria-t5lx-vetrenyj-hercai-21-seria/0
https://www.resproxy.com/forum/index.php/807479-vossoedinenie-vuslat-18-seria-z9mg-vossoedinenie-vuslat-18-seri/0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-spx-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.deliberarchia.org/forum/index.php?topic=987284.0
http://webp.online/index.php?topic=51043.0
http://webp.online/index.php?topic=51055.0
http://withinfp.sakura.ne.jp/eso/index.php/16935706-vetrenyj-hercai-25-seria-g0yg-vetrenyj-hercai-25-seria/0
https://tg.vl-mp.com/index.php?topic=1355116.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kdx-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://metropolis.ga/index.php?topic=5855.0
http://metropolis.ga/index.php?topic=5856.0
http://metropolis.ga/index.php?topic=5859.0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/220166
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/222311
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/222860
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/223087
https://alquilervideobeam.com.co/?option=com_k2&view=itemlist&task=user&id=54595
https://alquilervideobeam.com.co/?option=com_k2&view=itemlist&task=user&id=54667
https://alquilervideobeam.com.co/?option=com_k2&view=itemlist&task=user&id=54724
https://alquilervideobeam.com.co/?option=com_k2&view=itemlist&task=user&id=54794
https://alquilervideobeam.com.co/?option=com_k2&view=itemlist&task=user&id=54892
https://alquilervideobeam.com.co/?option=com_k2&view=itemlist&task=user&id=54940
https://alquilervideobeam.com.co/?option=com_k2&view=itemlist&task=user&id=54970
https://alquilervideobeam.com.co/?option=com_k2&view=itemlist&task=user&id=54981
https://alquilervideobeam.com.co/?option=com_k2&view=itemlist&task=user&id=55153
http://www.spazioad.com/index.php/component/k2/itemlist/user/7185894
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=77695
https://www.resproxy.com/forum/index.php/766627-milliardy-4-sezon-6-seria-pfx-milliardy-4-sezon-6-seria-0505201/0
http://www.elpinatarense.com/?option=com_k2&view=itemlist&task=user&id=155455
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=271552
http://mobility-corp.com/index.php/component/k2/itemlist/user/2513875
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1594929
http://erhu.eu/viewtopic.php?f=9&t=232455&view=print
http://israengineering.com/index.php/component/k2/itemlist/user/1078043
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/283290
http://www.deliberarchia.org/forum/index.php?topic=938061.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2501807
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1131454
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/60965
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/60986
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/60997
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/61015
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/61649
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3245715
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3245731
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3245763
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3245847
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=160777
http://myrechockey.com/forums/index.php?topic=85150.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2524150
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3266407
http://dev.aabn.org.gh/component/k2/itemlist/user/482819
http://married.dike.gr/index.php/component/k2/itemlist/user/34081
http://webp.online/index.php?topic=42306.0
https://www.resproxy.com/forum/index.php/737992-milliardy-4-sezon-5-seria-wkk-milliardy-4-sezon-5-seria-0305201/0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3299834
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=42251
http://menulisilmiah.net/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-ue0-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=77758
https://tg.vl-mp.com/index.php?topic=1296302.0
http://macdistri.com/index.php/component/k2/itemlist/user/280473
http://danielmillsap.com/forum/index.php?topic=935040.0
http://danielmillsap.com/forum/index.php?topic=935082.0
http://danielmillsap.com/forum/index.php?topic=935121.0
http://danielmillsap.com/forum/index.php?topic=935286.0
http://danielmillsap.com/forum/index.php?topic=935374.0
http://danielmillsap.com/forum/index.php?topic=935399.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/44147
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=47410
http://withinfp.sakura.ne.jp/eso/index.php/16871162-ne-otpuskaj-mou-ruku-elimi-birakma-38-seria-g4tw-ne-otpuskaj-mo
https://lucky28003.nl/forum/index.php?topic=6629.0
http://married.dike.gr/index.php/component/k2/itemlist/user/34224
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1544050
http://www.m1avio.com/index.php/component/k2/itemlist/user/3587609
http://www.m1avio.com/index.php/component/k2/itemlist/user/3590737
http://www.m1avio.com/index.php/component/k2/itemlist/user/3590793
http://www.m1avio.com/index.php/component/k2/itemlist/user/3590974
http://www.m1avio.com/index.php/component/k2/itemlist/user/3591001
http://www.m1avio.com/index.php/component/k2/itemlist/user/3591120
http://www.m1avio.com/index.php/component/k2/itemlist/user/3591541
http://www.m1avio.com/index.php/component/k2/itemlist/user/3591585
http://www.m1avio.com/index.php/component/k2/itemlist/user/3591676
http://metropolis.ga/index.php?topic=2937.0
https://tg.vl-mp.com/index.php?topic=1306959.0
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1525858
http://www.arunagreen.com/index.php/component/k2/itemlist/user/397869
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1109613
http://proxima.co.rw/index.php/component/k2/itemlist/user/544267
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1675876
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1675901
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1675939
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1675956
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1676005
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1676077
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1676083
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1676144
https://tg.vl-mp.com/index.php?topic=1264232.0
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1526569
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1119202
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26051488/Default.aspx
http://dev.aabn.org.gh/index.php/component/k2/itemlist/user/484160
http://travelsolution.info/?option=com_k2&view=itemlist&task=user&id=710576
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/130903
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=290553
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4676416
http://macdistri.com/index.php/component/k2/itemlist/user/285640
https://members.fbhaters.com/index.php?topic=66091.0
http://withinfp.sakura.ne.jp/eso/index.php/16784732-nasa-istoria-74-seria-g2co-nasa-istoria-74-seria/0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-olw-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/53428
https://www.resproxy.com/forum/index.php/745882-cernoe-zerkalo-5-sezon-3-seria-scn-cernoe-zerkalo-5-sezon-3-ser/0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1107574
http://healthyteethpa.org/component/k2/itemlist/user/5283169
https://tg.vl-mp.com/index.php?topic=1301389.0
http://withinfp.sakura.ne.jp/eso/index.php/16775098-sverh-estestvennoe-14-sezon-20-seria-jts-sverh-estestvennoe-14-/0
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1983998
http://menulisilmiah.net/%d0%b3%d1%80%d0%b0%d0%bd%d0%b4-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ch3-%d0%b3%d1%80%d0%b0%d0%bd%d0%b4-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81/
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2553437
https://tg.vl-mp.com/index.php?topic=1269098.0
http://seoksoononly.dothome.co.kr/qna/620656
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1553935
https://www.youngbiker.de/wbboard/index.php?page=User&userID=781233
http://married.dike.gr/index.php/component/k2/itemlist/user/37542
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1570465
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1699132
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1699319
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1699742
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1700172
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1700278
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1700427
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1700569
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1700903
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1701016
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1701278
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1701397
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1701421
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1701797
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1701935
https://tg.vl-mp.com/index.php?topic=1315838.0
http://macdistri.com/index.php/component/k2/itemlist/user/279776
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xl5-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://153.120.114.241/eso/index.php/16866957-milliardy-4-sezon-8-seria-ytq-milliardy-4-sezon-8-seria
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/247491
http://153.120.114.241/eso/index.php/16878050-lubov-smert-i-roboty-love-death-and-robots-8-seria-xqa-lubov-sm
https://www.resproxy.com/forum/index.php/750553-rannaa-ptaska-erkenci-kus-41-seria-h1pl-rannaa-ptaska-erkenci-k/0
http://www.deliberarchia.org/forum/index.php?topic=906581.0
http://withinfp.sakura.ne.jp/eso/index.php/16780529-milliardy-4-sezon-11-seria-wog-milliardy-4-sezon-11-seria/0
http://danielmillsap.com/forum/index.php?topic=950577.0
http://withinfp.sakura.ne.jp/eso/index.php/16824339-edinoe-serdce-tek-yurek-8-seria-w4sf-edinoe-serdce-tek-yurek-8-
http://withinfp.sakura.ne.jp/eso/index.php/16893409-voskressij-ertugrul-148-seria-x5ej-voskressij-ertugrul-148-seri
https://members.fbhaters.com/index.php?topic=76299.0
https://tg.vl-mp.com/index.php?topic=1330360.0
https://tg.vl-mp.com/index.php?topic=1330384.0
https://tg.vl-mp.com/index.php?topic=1330389.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pyj-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/175466
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/175476
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/175534
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/175535
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/175566
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/469672
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/469682
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/469734
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/469757
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/469765
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/469840
http://healthyteethpa.org/component/k2/itemlist/user/5303065
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1677692
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3314207
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1127469
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1130985
http://mobility-corp.com/index.php/component/k2/itemlist/user/2485131
https://mcsetup.tk/bbs/index.php?topic=226438.0
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=15240
http://married.dike.gr/index.php/component/k2/itemlist/user/47202
http://seoksoononly.dothome.co.kr/qna/440884
https://instaldec.com/?option=com_k2&view=itemlist&task=user&id=606982
http://danielmillsap.com/forum/index.php?topic=795189.0
http://www.phan-aen.go.th/forum/index.php?topic=606668.0
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1014644
https://www.resproxy.com/forum/index.php/794101-igra-prestolov-8-sezon-7-seria-zym-igra-prestolov-8-sezon-7-ser/0
http://www.phan-aen.go.th/forum/index.php?topic=612155.0
https://tg.vl-mp.com/index.php?topic=1264611.0
http://www.deliberarchia.org/forum/index.php?topic=929335.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pil-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.phan-aen.go.th/forum/index.php?topic=609359.0
http://macdistri.com/index.php/component/k2/itemlist/user/222433
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=235632
http://danielmillsap.com/forum/index.php?topic=819223.0
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1127727
http://metropolis.ga/index.php?topic=2968.0
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/200806
http://tradebest.org/board_MdUI61/1560079
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1003637
http://www.deliberarchia.org/forum/index.php?topic=899454.0
http://danielmillsap.com/forum/index.php?topic=843514.0
http://seoksoononly.dothome.co.kr/qna/412409
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1776197
http://avengerro.top/forum/index.php?topic=10686.0
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/999572
http://danielmillsap.com/forum/index.php?topic=811060.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/510861
https://www.resproxy.com/forum/index.php/755554-sverh-estestvennoe-14-sezon-16-seria-ysd-sverh-estestvennoe-14-/0
https://mcsetup.tk/bbs/index.php?topic=234619.0
http://www.telcon.gr/index.php/component/k2/itemlist/user/48566
https://tg.vl-mp.com/index.php?topic=1279890.0
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/458081
http://danielmillsap.com/forum/index.php?topic=833028.0
http://withinfp.sakura.ne.jp/eso/index.php/16774981-milliardy-4-sezon-10-seria-yqf-milliardy-4-sezon-10-seria/0
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=37600
http://married.dike.gr/index.php/component/k2/itemlist/user/35404
http://fbpharm.net/index.php/component/k2/itemlist/user/14843
https://www.blog.1mg.healthcare/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-aiu-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4
https://tg.vl-mp.com/index.php?topic=1302017.0
http://proandpro.it/?option=com_k2&view=itemlist&task=user&id=4428126
http://seoksoononly.dothome.co.kr/qna/444388
https://www.blog.quora.healthcare/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f9ln-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80
http://danielmillsap.com/forum/index.php?topic=901599.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lge-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://teambuildingpremium.com/forum/index.php?topic=689612.0
http://macdistri.com/index.php/component/k2/itemlist/user/203739
http://danielmillsap.com/forum/index.php?topic=817984.0
https://www.resproxy.com/forum/index.php/791489-milliardy-4-sezon-9-seria-sjz-milliardy-4-sezon-9-seria/0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/247383
http://travelsolution.info/index.php/component/k2/itemlist/user/706652
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=675017
http://dcasociados.eu/component/k2/itemlist/user/85330
http://153.120.114.241/eso/index.php/16881142-manifest-19-seria-ytd-manifest-19-seria
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1106408
http://teambuildingpremium.com/forum/index.php?topic=651759.0
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=893242
http://www.deliberarchia.org/forum/index.php?topic=981077.0
http://puppystoreatdoral.com/?option=com_k2&view=itemlist&task=user&id=280213
http://www.popolsku.fr.pl/forum/index.php?topic=347030.0
http://web2interactive.com/index.php/component/k2/itemlist/user/3567072
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81-34/
https://www.blog.quora.healthcare/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jib-%d1%80%d0%b0
https://members.fbhaters.com/index.php/topic,62401.0.html
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1095890
https://www.youngbiker.de/wbboard/index.php?page=User&userID=785810
http://danielmillsap.com/forum/index.php?topic=810630.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/321768
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=243732
http://married.dike.gr/index.php/component/k2/itemlist/user/37712
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wd1-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://members.fbhaters.com/index.php?topic=63429.0
http://www.glasshouseproject.com.ng/index.php/component/k2/itemlist/user/33190
http://sam-sanat.ir/?option=com_k2&view=itemlist&task=user&id=136715
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3195922
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/20548
http://metropolis.ga/index.php?topic=20.0
https://forum.ac-jete.it/index.php?topic=287731.0
http://macdistri.com/index.php/component/k2/itemlist/user/258945
https://mcsetup.tk/bbs/index.php?topic=233645.0
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=48421
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=891534
http://www.deliberarchia.org/forum/index.php?topic=786934.0
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xl1-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1116611
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=244451
https://www.resproxy.com/forum/index.php/761033-igra-prestolov-8-sezon-5-seria-nru-igra-prestolov-8-sezon-5-ser/0
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=400607
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/394819
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=43651
http://withinfp.sakura.ne.jp/eso/index.php/16774625-milliardy-4-sezon-13-seria-nsj-milliardy-4-sezon-13-seria/0
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ta4-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3194447
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1224601
http://danielmillsap.com/forum/index.php?topic=802907.0
http://danielmillsap.com/forum/index.php?topic=805873.0
https://www.blog.quora.healthcare/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bdd-%d1%80%d0%b0
http://married.dike.gr/index.php/component/k2/itemlist/user/44512
http://www.deliberarchia.org/forum/index.php?topic=788742.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1327290
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81-43/
http://macdistri.com/index.php/component/k2/itemlist/user/224267
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1129596
http://forum.thaibetrank.com/index.php?topic=1089806.0
http://mahdi.ehosseini.com/index.php/component/k2/itemlist/user/21351
http://macdistri.com/index.php/component/k2/itemlist/user/223143
http://danielmillsap.com/forum/index.php?topic=869756.0
http://teambuildingpremium.com/forum/index.php?topic=689291.0
http://withinfp.sakura.ne.jp/eso/index.php/16887021-nasa-istoria-72-seria-v8rl-nasa-istoria-72-seria/0
http://danielmillsap.com/forum/index.php?topic=799696.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2414988
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1832133
http://teambuildingpremium.com/forum/index.php?topic=622730.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=40803
http://avengerro.top/forum/index.php?topic=16997.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=267794
http://www.glasshouseproject.com.ng/index.php/component/k2/itemlist/user/37862
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-myp-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.popolsku.fr.pl/forum/index.php?topic=342203.0
http://avengerro.top/forum/index.php?topic=19688.0
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1564620
https://prosocyr.com/?option=com_k2&view=itemlist&task=user&id=603802
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/141681
http://danielmillsap.com/forum/index.php?topic=818891.0
http://webp.online/index.php?topic=40308.msg67460
http://muratliziraatodasi.org/forum/index.php?topic=335900.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1107464
http://metropolis.ga/index.php?topic=5807.0
http://teambuildingpremium.com/forum/index.php?topic=691985.0
http://macdistri.com/index.php/component/k2/itemlist/user/273877
http://poselokgribovo.ru/forum/index.php?topic=623255.0
http://withinfp.sakura.ne.jp/eso/index.php/16858718-nasa-istoria-74-seria-o8bh-nasa-istoria-74-seria
http://mobility-corp.com/index.php/component/k2/itemlist/user/2387799
https://prosocyr.com/index.php/component/k2/itemlist/user/572884
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1469528
http://danielmillsap.com/forum/index.php?topic=903088.0
http://teambuildingpremium.com/forum/index.php?topic=641997.0
http://menulisilmiah.net/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-qz9-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://teambuildingpremium.com/forum/index.php?topic=655294.0
http://ts.bloodhand.de/forum/viewtopic.php?t=253679
http://webp.online/index.php?topic=51264.msg85378
https://lucky28003.nl/forum/index.php?topic=12890.0
https://members.fbhaters.com/index.php?topic=82400.0
https://members.fbhaters.com/index.php?topic=82412.0
https://members.fbhaters.com/index.php?topic=82429.0
https://members.fbhaters.com/index.php?topic=82439.0
https://tg.vl-mp.com/index.php?topic=1357775.0
https://tg.vl-mp.com/index.php?topic=1357787.0
http://ayerawaddymyanmar.com/%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB_09-05-2019_%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB_%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB
http://ayerawaddymyanmar.com/%C2%AB%D0%A7%D0%B5%D0%BB%D0%BE%D0%B2%D0%B5%D0%BA-%D0%BF%D0%B0%D1%83%D0%BA_%D0%92%D0%B4%D0%B0%D0%BB%D0%B8_%D0%9E%D1%82_%D0%94%D0%BE%D0%BC%D0%B0_2019_%C2%BB_09-05-2019_%E2%80%9E%D0%A7%D0%B5%D0%BB%D0%BE%D0%B2%D0%B5%D0%BA-%D0%BF%D0%B0%D1%83%D0%BA_%D0%92%D0%B4%D0%B0%D0%BB%D0%B8_%D0%9E%D1%82_%D0%94%D0%BE%D0%BC%D0%B0_2019_Online%22_%C2%AB%D0%A7%D0%B5%D0%BB%D0%BE%D0%B2%D0%B5%D0%BA-%D0%BF%D0%B0%D1%83%D0%BA_%D0%92%D0%B4%D0%B0%D0%BB%D0%B8_%D0%9E%D1%82_%D0%94%D0%BE%D0%BC%D0%B0_2019_%C2%BB
http://boppern.de/index.php?title=%C2%AB%D0%9F%D0%BB%D0%BE%D1%85%D0%B8%D0%B5_%D0%9F%D0%B0%D1%80%D0%BD%D0%B8_3_2020_%C2%BB_09-05-2019_%22%D0%9F%D0%BB%D0%BE%D1%85%D0%B8%D0%B5_%D0%9F%D0%B0%D1%80%D0%BD%D0%B8_3_2020_%22_%C2%AB%D0%9F%D0%BB%D0%BE%D1%85%D0%B8%D0%B5_%D0%9F%D0%B0%D1%80%D0%BD%D0%B8_3_2020_%C2%BB
http://www.popolsku.fr.pl/forum/index.php?topic=355066.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2537892
http://danielmillsap.com/forum/index.php?topic=887407.0
http://macdistri.com/?option=com_k2&view=itemlist&task=user&id=258941
http://withinfp.sakura.ne.jp/eso/index.php/16782564-igra-prestolov-8-sezon-3-seria-nwx-igra-prestolov-8-sezon-3-ser
http://married.dike.gr/index.php/component/k2/itemlist/user/38611
http://macdistri.com/index.php/component/k2/itemlist/user/241014
http://batubersurat.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=36616
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1092953
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3566878
http://www.deliberarchia.org/forum/index.php?topic=773307.0
http://danielmillsap.com/forum/index.php?topic=895947.0
https://www.shaiyax.com/index.php?topic=285161.0
http://teambuildingpremium.com/forum/index.php?topic=616150.0
http://www.jadepedia.com/%C2%AB%D0%9F%D0%BE%D1%81%D0%BB%D0%B5%D0%B4%D1%81%D1%82%D0%B2%D0%B8%D1%8F%C2%BB_09-05-2019_%22%D0%9F%D0%BE%D1%81%D0%BB%D0%B5%D0%B4%D1%81%D1%82%D0%B2%D0%B8%D1%8F%22_%C2%AB%D0%9F%D0%BE%D1%81%D0%BB%D0%B5%D0%B4%D1%81%D1%82%D0%B2%D0%B8%D1%8F%C2%BB
http://www.jadepedia.com/User:AmberFroude5303
http://www.trcyberpatriot.com/index.php/User:GennieLevesque
http://www.xggu.net/wiki/%C2%AB%D0%9C%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%C2%BB_09-05-2019_%C2%AB%D0%9C%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4_Watch%C2%BB_%C2%AB%D0%9C%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%C2%BB
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2589822
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1641500
http://www.dap.com.py/index.php/component/k2/itemlist/user/794627
http://danielmillsap.com/forum/index.php?topic=871046.0
http://batubersurat.com/index.php/component/k2/itemlist/user/39070
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1078564
http://metropolis.ga/index.php?topic=2935.0
http://grupotir.com/component/k2/itemlist/user/42302
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jhy-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://153.120.114.241/eso/index.php/16881366-milliardy-4-sezon-12-seria-lff-milliardy-4-sezon-12-seria
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-isg-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.youngbiker.de/wbboard/index.php?page=User&userID=776530
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-aoa-3-eo-4-e-xxa-aoa-3-eo-4-e/
http://www.sakitoandrichifantasy.gr/?option=com_k2&view=itemlist&task=user&id=139225
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/51034
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1127742
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=11989
http://metropolis.ga/index.php?topic=826.0
http://www.arunagreen.com/?option=com_k2&view=itemlist&task=user&id=287762
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zk6-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://danielmillsap.com/forum/index.php?topic=834519.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1525653
http://forum.thaibetrank.com/index.php?topic=1091331.0
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=507217
https://www.blog.quora.healthcare/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b5-%d0%b7%d0%b5%d1%80%d0%ba%d0%b0%d0%bb%d0%be-5-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wvf-%d1%87%d0%b5%d1%80%d0%bd
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/368892
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/14954
http://proxima.co.rw/index.php/component/k2/itemlist/user/537739
https://tg.vl-mp.com/index.php?topic=1292730.0
http://www.deliberarchia.org/forum/index.php?topic=953491.0
http://www.aroshan.com/component/k2/itemlist/user/888789
http://www.popolsku.fr.pl/forum/index.php?topic=343670.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=34890
https://mcsetup.tk/bbs/index.php?topic=232252.0
http://91.250.77.10/wbb3/index.php?page=User&userID=403660
http://www.popolsku.fr.pl/forum/index.php?topic=341672.0
http://seoksoononly.dothome.co.kr/qna/463602
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/394338
http://www.deliberarchia.org/forum/index.php?topic=985857.0
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7308312
https://www.resproxy.com/forum/index.php/757639-riverdejl-riverdale-3-sezon-24-seria-ynh-riverdejl-riverdale-3-/0
http://matinbank.ir/component/k2/itemlist/user/4458200.html
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172253
http://withinfp.sakura.ne.jp/eso/index.php/16779528-milliardy-4-sezon-8-seria-mxp-milliardy-4-sezon-8-seria-0105201
http://withinfp.sakura.ne.jp/eso/index.php/16767740-nasledie-12-seria-wbr-nasledie-12-seria/0
http://c3isecurity.com.br/?option=com_k2&view=itemlist&task=user&id=455302
http://danielmillsap.com/forum/index.php?topic=869729.0
https://tg.vl-mp.com/index.php?topic=1348550.0
http://www.x2145-productions.technology/index.php?title=%C2%AB%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F_%D0%98%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA_4_2019_%C2%BB_09-05-2019_%22%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F_%D0%98%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA_4_2019_%22_%C2%AB%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F_%D0%98%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA_4_2019_%C2%BB&---------------------------70971276284%0D%0AContent-Disposition:%20form-data;%20name=%22wpAntispam%22%0D%0A%0D%0A%0D%0A---------------------------70971276284%0D%0AContent-Disposition:%20form-data;%20name=%22wpSection%22%0D%0A%0D%0A%0D%0A---------------------------70971276284%0D%0AContent-Disposition:%20form-data;%20name=%22wpStarttime%22%0D%0A%0D%0A20190509053552%0D%0A---------------------------70971276284%0D%0AContent-Disposition:%20form-data;%20name=%22wpEdittime%22%0D%0A%0D%0A20190509053552%0D%0A---------------------------70971276284%0D%0AContent-Disposition:%20form-data;%20name=%22wpScrolltop%22%0D%0A%0D%0A%0D%0A---------------------------70971276284%0D%0AContent-Disposition:%20form-data;%20name=%22wpAutoSummary%22%0D%0A%0D%0Ad41d8cd98f00b204e9800998ecf8427e%0D%0A---------------------------70971276284%0D%0AContent-Disposition:%20form-data;%20name=%22oldid%22%0D%0A%0D%0A0%0D%0A---------------------------70971276284%0D%0AContent-Disposition:%20form-data;%20name=%22format%22%0D%0A%0D%0Atext/x-wiki%0D%0A---------------------------70971276284%0D%0AContent-Disposition:%20form-data;%20name=%22model%22%0D%0A%0D%0Awikitext%0D%0A---------------------------70971276284%0D%0AContent-Disposition:%20form-data;%20name=%22wpTextbox1%22%0D%0A%0D%0Anew%20%C2%AB%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%C2%BB%20%20oNm:%20%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E[http://hdseriionline.ru/%20hdseriionline.ru]%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E~~%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20%D1%84%D0%B8%D0%BB%D0%BC%D1%81%D0%B5%D0%B3%D0%BE%D0%B4%D0%BD%D1%8F%60~%3Cbr%3E%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20filmonline%3Cbr%3E%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20kinobos%3Cbr%3E..%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20amovies..%3Cbr%3E%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20kinogo%3Cbr%3E%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20cinema%3Cbr%3E..%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20tvpixy..%3Cbr%3E%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20ereko%3Cbr%3E%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20%D0%BA%D0%B8%D0%BD%D0%BE%D0%B1%D0%B0%D1%80%3Cbr%3E..%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20kinoluvr..%3Cbr%3E%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20%D0%BE%D1%84%D0%BA%D1%81%3Cbr%3E%22%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20ofilme%22%3Cbr%3E%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20%D0%BC%D1%83%D0%B2%D0%B8%D0%BA%D1%81%3Cbr%3E%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20filmoserial%3Cbr%3E%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20hd1080%3Cbr%3E~~%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20hdkinoklub%60~%3Cbr%3E%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20%D0%BA%D0%B8%D0%BD%D0%BE%D0%BA%D0%BE%D0%BD%D0%B3%D0%BE%3Cbr%3E~~%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20russkoekino%60~%3Cbr%3E%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20%D0%BE%D0%BD%D0%BB%D0%B8%D0%BD%D0%B5%D1%84%D0%B8%D0%BB%D0%BC%D1%81%3Cbr%3E%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20vkinotv%3Cbr%3E~~%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20kovids%60~%3Cbr%3E%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D0%B8%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA%204%20(2019)%20%D0%BA%D0%B8%D0%BD%D0%BE%D0%B2%D0%BE%D0%BD%D0%BB%D0%B8%D0%BD%D0%B5%0D%0A---------------------------70971276284%0D%0AContent-Disposition:%20form-data;%20name=%22wpSummary%22%0D%0A%0D%0A%0D%0A---------------------------70971276284%0D%0AContent-Disposition:%20form-data;%20name=%22wpSave%22%0D%0A%0D%0ASeite%20speichern%0D%0A---------------------------70971276284%0D%0AContent-Disposition:%20form-data;%20name=%22wpEditToken%22%0D%0A%0D%0A058285626d1c6b0c020680649f15911b+::%0D%0A---------------------------70971276284--
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/109721
http://teambuildingpremium.com/forum/index.php?topic=693635.0
http://teambuildingpremium.com/forum/index.php?topic=663921.0
http://www.deliberarchia.org/forum/index.php?topic=952167.0
http://www.phan-aen.go.th/forum/index.php?topic=608669.0
http://withinfp.sakura.ne.jp/eso/index.php/16788074-voskressij-ertugrul-147-seria-f7gs-voskressij-ertugrul-147-seri/0
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2498167
http://boutique.in.th/?option=com_k2&view=itemlist&task=user&id=146205
http://webp.online/index.php?topic=41401.msg68957
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-egk-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://matinbank.ir/component/k2/itemlist/user/4459372
http://batubersurat.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=38761
https://www.resproxy.com/forum/index.php/767175-milliardy-4-sezon-13-seria-ees-milliardy-4-sezon-13-seria/0
http://travelsolution.info/?option=com_k2&view=itemlist&task=user&id=697675
http://dev.aabn.org.gh/component/k2/itemlist/user/487210
http://dcasociados.eu/component/k2/itemlist/user/81289
http://married.dike.gr/index.php/component/k2/itemlist/user/40183
https://khuyenmaikk13.info/index.php?topic=179263.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/469528
http://poselokgribovo.ru/forum/index.php?topic=717782.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1334266
http://www.vivelabmanizales.com/hd-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l9-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81/
http://proxima.co.rw/index.php/component/k2/itemlist/user/565567
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26228381/Default.aspx
http://www.vivelabmanizales.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-08-05-2019-j3-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://www.ekemoon.com/142695/051820193705/
https://khuyenmaikk13.info/index.php?topic=184047.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2572678
http://teambuildingpremium.com/forum/index.php?topic=780668.0
http://seoksoononly.dothome.co.kr/qna/712349
http://www.camaracoyhaique.cl/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zu5b-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://dcasociados.eu/?option=com_k2&view=itemlist&task=user&id=87618
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3708183
http://fbpharm.net/index.php/component/k2/itemlist/user/14806
http://smartacity.com/component/k2/itemlist/user/18443
http://seoksoononly.dothome.co.kr/qna/756149
http://www.ekemoon.com/154537/052120194707/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/68029
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1861669
http://forum.politeknikgihon.ac.id/index.php?topic=23688.0
http://www.die-design-manufaktur.de/?option=com_k2&view=itemlist&task=user&id=5179581
http://www.vivelabmanizales.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-da3z-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2563859
http://www.remify.app/foro/index.php?topic=239523.0
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=300287
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1842440
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1544668
http://healthyteethpa.org/component/k2/itemlist/user/5331477
http://rudraautomation.com/index.php/component/k2/author/134574
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2564034
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/189025
http://forum.digamahost.com/index.php?topic=109429.0
http://153.120.114.241/eso/index.php/16878547-edinoe-serdce-tek-yurek-9-seria-iucy-edinoe-serdce-tek-yurek-9-
https://khuyenmaikk13.info/index.php?topic=180675.0
http://webp.online/index.php?topic=50757.0
http://married.dike.gr/index.php/component/k2/itemlist/user/49125
http://www.telcon.gr/index.php/component/k2/itemlist/user/42405
http://withinfp.sakura.ne.jp/eso/index.php/16902535-tola-robot-4-seria-k5-tola-robot-4-seria
http://www.ekemoon.com/148453/052320190706/
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/479328
http://salescoach.ro/content/%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-20-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-ahyo-%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-20-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12548
http://ahudseafood.com/index.php/component/k2/itemlist/user/8246
http://islamiccall.info/?option=com_k2&view=itemlist&task=user&id=857123
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=199349
http://menulisilmiah.net/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b6-%d1%82%d0%be%d0%bb/
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=762660
http://www.ekemoon.com/148125/052220193606/
http://salescoach.ro/content/%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-xede-%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2563355
http://www.die-design-manufaktur.de/index.php/component/k2/itemlist/user/5174713
http://www.vivelabmanizales.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81-8/
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/647801
http://discussadeal.com/forum/index.php?topic=2111.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1109986
http://danielmillsap.com/forum/index.php?topic=818025.0
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3659324
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/187428
http://danielmillsap.com/forum/index.php?topic=832842.0
http://www.phan-aen.go.th/forum/index.php?topic=612261.0
http://webp.online/index.php?topic=46359.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=14282
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=42338
http://danielmillsap.com/forum/index.php?topic=807942.0
http://danielmillsap.com/forum/index.php?topic=809374.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-omg-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2130986
https://www.blog.quora.healthcare/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d6ju-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-12-%d1%81%d0%b5%d1%80%d0%b8
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/21707
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3254293
http://danielmillsap.com/forum/index.php?topic=802179.0
http://pptforum.dothome.co.kr/board_APMk06/652202
http://dcasociados.eu/component/k2/itemlist/user/87305
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=6300
http://www.deliberarchia.org/forum/index.php?topic=984482.0
http://www.deliberarchia.org/forum/index.php?topic=955476.0
http://seoksoononly.dothome.co.kr/qna/431299
http://www.meikai.com.ar/foro/index.php?topic=49028.0
http://married.dike.gr/index.php/component/k2/itemlist/user/25587
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-djo-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://danielmillsap.com/forum/index.php?topic=877848.0
https://tg.vl-mp.com/index.php?topic=1264349.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1107324
http://danielmillsap.com/forum/index.php?topic=868839.0
https://www.shaiyax.com/index.php?topic=298150.0
http://macdistri.com/component/k2/itemlist/user/302380
http://danielmillsap.com/forum/index.php?topic=833127.0
http://www.deliberarchia.org/forum/index.php?topic=923139.0
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=409145
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1546162
http://proxima.co.rw/index.php/component/k2/itemlist/user/542387
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=407390
http://forums.abs-cbn.com/welcome-back-kapamilya%21/ootk-9-eo-11-k-iaootk-9-eo-11-k/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/263568
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1094508
http://www.deliberarchia.org/forum/index.php?topic=914138.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/373579
http://batubersurat.com/index.php/component/k2/itemlist/user/38151
http://married.dike.gr/index.php/component/k2/itemlist/user/47346
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1106474
https://tg.vl-mp.com/index.php?topic=1273310.0
http://www.deliberarchia.org/forum/index.php?topic=976245.0
http://www.spazioad.com/component/k2/itemlist/user/7163976
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3590144
http://comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=104086
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=895234
http://danielmillsap.com/forum/index.php?topic=981919.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/246194
http://webp.online/index.php?topic=46798.0
http://www.tessabannampad.go.th/webboard/index.php?topic=189546.0
https://www.resproxy.com/forum/index.php/796020-nasledie-15-seria-ixa-nasledie-15-seria
http://danielmillsap.com/forum/index.php?topic=826783.0
http://married.dike.gr/index.php/component/k2/itemlist/user/22000
https://lucky28003.nl/forum/index.php?topic=10802.0
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1470642
https://npi.org.es/smf/index.php?topic=102916.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3534083
http://healthyteethpa.org/component/k2/itemlist/user/5286125
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/270639
https://members.fbhaters.com/index.php?topic=66063.0
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/249186
http://seoksoononly.dothome.co.kr/qna/465167
https://prosocyr.com/?option=com_k2&view=itemlist&task=user&id=572584
http://www.ekemoon.com/142569/051720195805/
http://www.vivelabmanizales.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81-21/
https://l2thalassic.org/Forum/index.php?topic=1758.0
http://www.deliberarchia.org/forum/index.php?topic=964105.0
http://dev.aabn.org.gh/component/k2/itemlist/user/526613
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=50706
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39191
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2404227
http://marjorieaperry.com/?option=com_k2&view=itemlist&task=user&id=482732
http://necinsurance.co.zw/component/k2/itemlist/user/19575.html
http://vsalda.edinros66.ru/component/k2/itemlist/user/44144
http://withinfp.sakura.ne.jp/eso/index.php/16859318-holostak-9-sezon-10-vypusk-6-cast-vbholostak-9-sezon-10-vypusk-/0
http://married.dike.gr/index.php/component/k2/itemlist/user/52387
http://rudraautomation.com/index.php/component/k2/author/133067
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=286614
http://mvisage.sk/index.php/component/k2/itemlist/user/118033
http://www.ekemoon.com/144985/051420193106/
https://l2thalassic.org/Forum/index.php?topic=2291.0
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=104753
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/207203
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=200629
http://withinfp.sakura.ne.jp/eso/index.php/16865299-holostak-9-sezon-10-vypusk-mail-qfholostak-9-sezon-10-vypusk-ma/0
http://community.viajar.tur.br/index.php?p=/discussion/57339/voskresshiy-ertugrul-149-seriya-chfi-voskresshiy-ertugrul-149-seriya
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=301775
http://poselokgribovo.ru/forum/index.php?topic=734826.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1134718
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=65123
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1550954
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=136751
http://menulisilmiah.net/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t3-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82/
http://menulisilmiah.net/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jg3%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3624220
http://thermoplast.envolgroupe.com/component/k2/author/75004
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2572875
http://www.aloeverasas.it/index.php/component/k2/itemlist/user/18750
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=603793
http://teambuildingpremium.com/forum/index.php?topic=780199.0
http://community.viajar.tur.br/index.php?p=/profile/franceboha
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=14314
http://withinfp.sakura.ne.jp/eso/index.php/16862010-uristy-11-seria-hdvideo-uristy-11-seria/0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=561096
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4711804
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2586187
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1875519
http://arunagreen.com/index.php/component/k2/itemlist/user/459784
http://theolevolosproject.org/index.php/component/k2/itemlist/user/24841
http://poselokgribovo.ru/forum/index.php?topic=715302.0
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2019-t6-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/214031
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=1004546
https://members.fbhaters.com/index.php?topic=74939.0
http://ovotecegg.com/component/k2/itemlist/user/117345
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1006511
http://www.spazioad.com/component/k2/itemlist/user/7241346
https://lucky28003.nl/forum/index.php?topic=10169.0
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1572752
http://arunagreen.com/index.php/component/k2/itemlist/user/461217
http://thermoplast.envolgroupe.com/component/k2/author/71537
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2388214
http://israengineering.com/index.php/component/k2/itemlist/user/1114641
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/69896
http://poselokgribovo.ru/forum/index.php?topic=729578.0
http://necinsurance.co.zw/component/k2/itemlist/user/19489.html
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=50143
http://associationsila.org/index.php/component/k2/itemlist/user/296394
http://www2.yasothon.go.th/smf/index.php?topic=159.157785
http://dev.aabn.org.gh/?option=com_k2&view=itemlist&task=user&id=517687
http://withinfp.sakura.ne.jp/eso/index.php/16885120-smotret-tola-robot-9-seria-l7-tola-robot-9-seria/0
http://www.afikgan.co.il/index.php/component/k2/itemlist/user/26014
http://webp.online/index.php?topic=50190.15
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4715517
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/69406
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/49770
http://rudraautomation.com/index.php/component/k2/author/128103
https://l2thalassic.org/Forum/index.php?topic=1793.0
http://menulisilmiah.net/hd-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81/
https://forums.letstalkbeats.com/index.php?topic=66906.0
[url=http://cialisdxt.com/]cialis generic[/url]
walgreens pharmacy cialis price
<a href="http://cialisdxt.com/">buy cialis online</a>
cialis brand name 10 mg
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/74613
http://seoksoononly.dothome.co.kr/qna/750830
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=23969
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3585329
http://www.vivelabmanizales.com/%d0%bd%d0%b5-%d0%be%d1%82%d0%bf%d1%83%d1%81%d0%ba%d0%b0%d0%b9-%d0%bc%d0%be%d1%8e-%d1%80%d1%83%d0%ba%d1%83-elimi-birakma-42-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qnti-%d0%bd%d0%b5-%d0%be/
http://socialfbwidgets.com/component/k2/itemlist/user/13637.html
http://dcasociados.eu/component/k2/itemlist/user/87297
http://matinbank.ir/component/k2/itemlist/user/4488104.html
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7308956
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2520370
http://rudraautomation.com/index.php/component/k2/author/102484
http://ptu.imoove.kr/ko/content/%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-hd-video-%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB331610
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=51824
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42319
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1647571
http://zsmr.com.ua/index.php/component/k2/itemlist/user/491889
http://community.viajar.tur.br/index.php?p=/discussion/57646/voskresshiy-ertugrul-148-seriya-cxqz-voskresshiy-ertugrul-148-seriya
http://dev.aabn.org.gh/component/k2/itemlist/user/513011
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1558009
http://thermoplast.envolgroupe.com/component/k2/author/66120
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/204613
http://ovotecegg.com/component/k2/itemlist/user/117801
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1116051
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=45850
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1008259
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/63606
http://rudraautomation.com/index.php/component/k2/author/129941
http://rudraautomation.com/index.php/component/k2/author/119040
http://healthyteethpa.org/?option=com_k2&view=itemlist&task=user&id=5328878
http://mediaville.me/index.php/component/k2/itemlist/user/206671
http://www.critico-expository.com/forum/index.php?topic=2947.0
http://www.m1avio.com/?option=com_k2&view=itemlist&task=user&id=3611220
http://www.ekemoon.com/143503/050020193906/
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1543893
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12893
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1566983
http://www.ekemoon.com/147527/052120193906/
http://forum.digamahost.com/index.php?topic=111108.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2564127
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1009169
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4824865
http://www.vivelabmanizales.com/live-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=42645
http://ovotecegg.com/index.php/component/k2/itemlist/user/116157
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=4707
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1855129
https://forums.letstalkbeats.com/index.php?topic=67934.0
http://dev.aabn.org.gh/component/k2/itemlist/user/534446
http://forum.politeknikgihon.ac.id/index.php?topic=25217.0
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2513623
http://miquirofisico.com/index.php/component/k2/itemlist/user/3805
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=754938
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/228743
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=45044
http://www.die-design-manufaktur.de/?option=com_k2&view=itemlist&task=user&id=5175568
http://www.phan-aen.go.th/forum/index.php?topic=628169.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1633357
https://tg.vl-mp.com/index.php?topic=1351758.0
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1861730
http://withinfp.sakura.ne.jp/eso/index.php/16863190-smotret-tajny-taemnici-99-seria-l4-tajny-taemnici-99-seria/0
http://macdistri.com/index.php/component/k2/itemlist/user/302462
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=292651
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=203548
http://153.120.114.241/eso/index.php/16865549-holostak-9-sezon-10-vypusk-smotret-onlajn-1-cast-zoholostak-9-s
http://condolencias.servisa.es/21-05-05-2019-k8-21
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=287164
http://poselokgribovo.ru/forum/index.php?topic=732761.0
http://mediaville.me/index.php/component/k2/itemlist/user/226327
https://tg.vl-mp.com/index.php?topic=1296025.0
http://teambuildingpremium.com/forum/index.php?topic=632631.0
http://teambuildingpremium.com/forum/index.php?topic=655535.0
http://www.phan-aen.go.th/forum/index.php?topic=606709.0
https://tg.vl-mp.com/index.php?topic=1290224.0
http://flyinghonda.de/wbb/index.php?page=User&userID=808120
http://withinfp.sakura.ne.jp/eso/index.php/16785545-igra-prestolov-8-sezon-1-seria-zrr-igra-prestolov-8-sezon-1-ser
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=239360
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3293723
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1129702
http://www.deliberarchia.org/forum/index.php?topic=984391.0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/194349
http://www.deliberarchia.org/forum/index.php?topic=802289.0
http://seoksoononly.dothome.co.kr/qna/424404
http://poselokgribovo.ru/forum/index.php?topic=715965.0
https://tg.vl-mp.com/index.php?topic=1325109.0
http://condolencias.servisa.es/3-6-05-05-2019-q5-3-6
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-3/
http://married.dike.gr/index.php/component/k2/itemlist/user/51362
http://webp.online/index.php?topic=48596.0
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3624302
http://withinfp.sakura.ne.jp/eso/index.php/16876616-efir-po-zakonam-voennogo-vremeni-3-sezon-4-seria-l2-po-zakonam-/0
http://www.spazioad.com/component/k2/itemlist/user/7230992
https://forums.letstalkbeats.com/index.php?topic=65774.0
http://www.ekemoon.com/158279/050920195708/
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=117796
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3734563
http://www.vivelabmanizales.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://koushatarabar.com/index.php/component/k2/itemlist/user/1314277
http://www.ekemoon.com/149245/050020193807/
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1766465
http://dcasociados.eu/component/k2/itemlist/user/86491
http://dev.aabn.org.gh/component/k2/itemlist/user/525792
http://smartacity.com/component/k2/itemlist/user/18304
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1995673
http://condolencias.servisa.es/19-06-05-2019-u7-19
http://community.viajar.tur.br/index.php?p=/profile/gtzstanton
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=210458
http://forum.digamahost.com/index.php?topic=109947.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=284255
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5-16/
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5387
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=49869
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1761585
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=210405
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=211640
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=303737
http://forum.politeknikgihon.ac.id/index.php?topic=24253.0
http://israengineering.com/index.php/component/k2/itemlist/user/1114081
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3747847
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=66506
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1862066
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D1%82%D0%BE%D1%80%D1%80%D0%B5%D0%BD%D1%82%D0%BE%D0%BC%C2%BB-lj%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D1%82%D0%BE%D1%80%D1%80%D0%B5%D0%BD%D1%82%D0%BE%D0%BC%C2%BB90-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1874719
http://arunagreen.com/index.php/component/k2/itemlist/user/420429
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/562022
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=77417
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/487207
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1858901
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=273454
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=287230
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/475841
https://khuyenmaikk13.info/index.php?topic=182792.0
http://gtupuw.org/index.php/component/k2/itemlist/user/1855706
http://healthyteethpa.org/component/k2/itemlist/user/5329047
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4846891
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1761832
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/50090
http://www.comfortcenter.es/index.php/component/k2/itemlist/user/104442
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1562203
http://seoksoononly.dothome.co.kr/?document_srl=799796
http://svgrossburgwedel.de/component/k2/itemlist/user/5366
http://thermoplast.envolgroupe.com/component/k2/author/80147
https://l2thalassic.org/Forum/index.php?topic=2130.0
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7194471
http://danielmillsap.com/forum/index.php?topic=987236.0
https://tg.vl-mp.com/index.php?topic=1265935.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ncs-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ucr-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://danielmillsap.com/forum/index.php?topic=836841.0
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=281001
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=306126
http://metropolis.ga/index.php?topic=5307.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wzy-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/192543
http://danielmillsap.com/forum/index.php?topic=888907.0
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=157633
http://danielmillsap.com/forum/index.php?topic=825783.0
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1741688
http://danielmillsap.com/forum/index.php?topic=840112.0
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=375069
http://withinfp.sakura.ne.jp/eso/index.php/16779031-zensina-58-seria-z9mv-zensina-58-seria/0
https://www.resproxy.com/forum/index.php/779354-zensina-58-seria-t2ay-zensina-58-seria/0
http://danielmillsap.com/forum/index.php?topic=890971.0
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=379769
http://withinfp.sakura.ne.jp/eso/index.php/16790832-milliardy-4-sezon-12-seria-cdr-milliardy-4-sezon-12-seria-02052/0
http://healthyteethpa.org/component/k2/itemlist/user/5299404
http://tradebest.org/board_MdUI61/1567097
http://www2.yasothon.go.th/smf/index.php?topic=159.127230
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3245847
http://www.elpinatarense.com/?option=com_k2&view=itemlist&task=user&id=155423
http://minostech.co.kr/news/3341764
https://www.youngbiker.de/wbboard/index.php?page=User&userID=781204
http://www.deliberarchia.org/forum/index.php?topic=973952.0
http://www.deliberarchia.org/forum/index.php?topic=949465.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/508670
https://www.shaiyax.com/index.php?topic=309877.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=265674
http://teambuildingpremium.com/forum/index.php?topic=664511.0
http://metropolis.ga/index.php?topic=3783.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/395306
http://forum.thaibetrank.com/index.php?topic=1072108.0
http://macdistri.com/index.php/component/k2/itemlist/user/210613
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=203289
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=259045
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1790517
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3342516
http://danielmillsap.com/forum/index.php?topic=828972.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=236542
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1671291
http://danielmillsap.com/forum/index.php?topic=815406.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=180619
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1332451
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sk0-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22/
http://withinfp.sakura.ne.jp/eso/index.php/16844280-nasa-istoria-70-seria-c6wr-nasa-istoria-70-seria/0
http://arquitectosenreformas.es/component/k2/itemlist/user/79477
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=763996
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3569561
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=20614
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=268207
http://withinfp.sakura.ne.jp/eso/index.php/16922056-uristy-12-seria-smotret-uristy-12-seria/0
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1620806
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1551566
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=14781
http://arunagreen.com/index.php/component/k2/itemlist/user/423477
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1360955
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=314314
http://www.die-design-manufaktur.de/?option=com_k2&view=itemlist&task=user&id=5183439
http://dev.aabn.org.gh/component/k2/itemlist/user/539148
http://www.quattroandpartners.it/component/k2/itemlist/user/1042918
http://menulisilmiah.net/%d1%8d%d1%84%d0%b8%d1%80-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e6-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be/
http://seoksoononly.dothome.co.kr/?document_srl=787980
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=568947
http://forum.digamahost.com/index.php?topic=109346.0
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%C2%BB-td%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%C2%BB53-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA
http://dev.aabn.org.gh/?option=com_k2&view=itemlist&task=user&id=538142
http://webp.online/index.php?topic=45158.0
http://lasvur.ru/component/k2/itemlist/user/36386
http://seoksoononly.dothome.co.kr/qna/773543
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5238
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2422933
http://poselokgribovo.ru/forum/index.php?topic=717536.0
http://www.ekemoon.com/143589/050120191606/
http://bitpark.co.kr/board_IzjM66/3737013
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=282412
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rv7%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4827091
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12529
http://153.120.114.241/eso/index.php/16877270-edinoe-serdce-tek-yurek-10-seria-bteq-edinoe-serdce-tek-yurek-1
http://withinfp.sakura.ne.jp/eso/index.php/16884010-uristy-17-seria-smotret-uristy-17-seria/0
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2388436
https://l2thalassic.org/Forum/index.php?topic=1666.0
http://www.camaracoyhaique.cl/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-rb8%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5/
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1127375
http://seoksoononly.dothome.co.kr/qna/785230
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=81671
http://www.m1avio.com/index.php/component/k2/itemlist/user/3603732
http://www.vivelabmanizales.com/hd-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q6-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26174860/Default.aspx
https://l2thalassic.org/Forum/index.php?topic=622.0
http://seoksoononly.dothome.co.kr/qna/790595
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3302151
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1743810
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4855197
http://poselokgribovo.ru/forum/index.php?topic=735318.0
http://www.vivelabmanizales.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2019-m7-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1339173
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=16969
http://menulisilmiah.net/hd-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k7-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-97-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gs0%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-97-%d1%81%d0%b5%d1%80%d0%b8%d1%8f07-05-2019/
http://www.phan-aen.go.th/forum/index.php?topic=626813.0
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1850261
https://l2thalassic.org/Forum/index.php?topic=1418.0
http://moyakmermer.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=641679
https://members.fbhaters.com/index.php?topic=75106.0
http://www.ekemoon.com/155863/050120195708/
http://www.vivelabmanizales.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%82%d0%b5%d0%bb%d0%b5%d0%bf%d0%be%d1%80%d1%82%d0%b0%d0%bb-fx/
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2579452
http://www.camaracoyhaique.cl/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lz1%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f07-05/
http://webp.online/index.php?topic=50282.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/488454
http://web2interactive.com/index.php/component/k2/itemlist/user/3569200
http://rudraautomation.com/index.php/component/k2/author/120289
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/292527
http://xplorefitness.com/blog/%D1%8D%D1%84%D0%B8%D1%80-%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-t5-%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1556212
http://www.vivelabmanizales.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g9-%d1%82%d0%be%d0%bb/
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1106471
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-clk-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.popolsku.fr.pl/forum/index.php?topic=340833.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=584581.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=261501
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1299200
https://tg.vl-mp.com/index.php?topic=1284675.0
http://www.m1avio.com/index.php/component/k2/itemlist/user/3569551
https://mcsetup.tk/bbs/index.php?topic=225585.0
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=255617
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=786390
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=293922
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=411035
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1361336
https://mcsetup.tk/bbs/index.php?topic=222506.0
https://instaldec.com/?option=com_k2&view=itemlist&task=user&id=601888
http://withinfp.sakura.ne.jp/eso/index.php/16860257-vetrenyj-hercai-18-seria-a7bo-vetrenyj-hercai-18-seria/0
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=36247
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1305102
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2546080
http://pptforum.dothome.co.kr/board_APMk06/864019
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=250349
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=407515
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-apb-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1980732
http://teambuildingpremium.com/forum/index.php?topic=602155.0
https://www.blog.quora.healthcare/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ngj-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b
http://withinfp.sakura.ne.jp/eso/index.php/16790052-amerikanskie-bogi-2-sezon-8-seria-qek-amerikanskie-bogi-2-sezon/0
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1790919
http://danielmillsap.com/forum/index.php?topic=839527.0
http://teambuildingpremium.com/forum/index.php?topic=639190.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3477282
https://mcsetup.tk/bbs/index.php?topic=225602.0
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5835
http://www.spazioad.com/component/k2/itemlist/user/7097792
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-aoa-3-eo-9-e-tna-aoa-3-eo-9-e/msg494025/
http://mobility-corp.com/index.php/component/k2/itemlist/user/2417369
http://withinfp.sakura.ne.jp/eso/index.php/16776225-lubov-smert-i-roboty-love-death-and-robots-12-seria-gwk-lubov-s/0
http://www.deliberarchia.org/forum/index.php?topic=946062.0
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=4618
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3480779
http://teambuildingpremium.com/forum/index.php?topic=648680.0
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26108663/Default.aspx
http://webp.online/index.php?topic=45492.0
http://www.popolsku.fr.pl/forum/index.php?topic=342051.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/387264
http://withinfp.sakura.ne.jp/eso/index.php/16772091-sverh-estestvennoe-14-sezon-21-seria-djd-sverh-estestvennoe-14-/0
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=188469
http://married.dike.gr/index.php/component/k2/itemlist/user/26373
http://healthyteethpa.org/?option=com_k2&view=itemlist&task=user&id=5292258
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/914398
http://metropolis.ga/index.php?topic=3085.0
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-oa3-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22/
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1773698
http://mobility-corp.com/index.php/component/k2/itemlist/user/2475578
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/639590
http://mediaville.me/index.php/component/k2/itemlist/user/195103
http://www.deliberarchia.org/forum/index.php?topic=767511.0
https://tg.vl-mp.com/index.php?topic=1261219.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1108777
http://danielmillsap.com/forum/index.php?topic=798756.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wvf-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80/
http://teambuildingpremium.com/forum/index.php?topic=626525.0
http://www.m1avio.com/?option=com_k2&view=itemlist&task=user&id=3571921
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1674582
http://macdistri.com/component/k2/itemlist/user/259186
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1455875
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3246104
http://withinfp.sakura.ne.jp/eso/index.php/16837782-voskressij-ertugrul-146-seria-l3wa-voskressij-ertugrul-146-seri/0
http://webp.online/index.php?topic=48719.0
http://hydrocarbs-gh.org/index.php/component/k2/itemlist/user/7273485
https://www.youngbiker.de/wbboard/index.php?page=User&userID=781188
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1128152
http://healthyteethpa.org/component/k2/itemlist/user/5190040
http://danielmillsap.com/forum/index.php?topic=834165.0
http://molweb.ru/groups/xolostyak-za-10-05-19-smotret-10-vypusk-ppxolostyak-za-10-05-19-smotret-10-vypusk18-xolostyak-za-10-05-19-smotret-10-vypusk/
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=782549
http://rudraautomation.com/index.php/component/k2/author/143150
http://svgrossburgwedel.de/component/k2/itemlist/user/5326
http://www.vivelabmanizales.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-07-05-2019-t8-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
https://szenarist.ru/forum/index.php?topic=205370.0
http://rockndata.net/UserProfile/tabid/61/userId/18234530/Default.aspx
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=10556
http://seoksoononly.dothome.co.kr/qna/795896
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D0%BD%D0%BE%D0%B2%D0%BE%D1%81%D1%82%D0%B5%D0%B9%C2%BB-vx%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D0%BD%D0%BE%D0%B2%D0%BE%D1%81%D1%82%D0%B5%D0%B9%C2%BB20-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=501787
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=501427
http://www.ekemoon.com/143041/052020195505/
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26245791/Default.aspx
http://www.spazioad.com/component/k2/itemlist/user/7235823
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=50575
http://bitpark.co.kr/board_IzjM66/3775989
https://l2thalassic.org/Forum/index.php?topic=859.0
http://seoksoononly.dothome.co.kr/qna/797269
http://www.crnmedia.es/?option=com_k2&view=itemlist&task=user&id=84587
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2567096
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=80250
http://www.comfortcenter.es/index.php/component/k2/itemlist/user/104405
http://poselokgribovo.ru/forum/index.php?topic=715301.0
http://www.ekemoon.com/142425/051720192505/
http://www.crnmedia.es/component/k2/itemlist/user/84467
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/558089
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4713180
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=1038619
http://withinfp.sakura.ne.jp/eso/index.php/16864810-smotret-tajny-taemnici-83-seria-v2-tajny-taemnici-83-seria
http://www.camaracoyhaique.cl/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rd1%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f07-05-2019/
http://matinbank.ir/component/k2/itemlist/user/4487443.html
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=189105
http://mobility-corp.com/index.php/component/k2/itemlist/user/2510808
http://153.120.114.241/eso/index.php/16866601-vossoedinenie-vuslat-20-seria-xeoy-vossoedinenie-vuslat-20-seri
http://marjorieaperry.com/?option=com_k2&view=itemlist&task=user&id=481583
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/219978
http://islamiccall.info/?option=com_k2&view=itemlist&task=user&id=857390
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3576919
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2531909
http://storykingdom.forumside.com/index.php?topic=4770.0
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D1%82%D0%BE%D0%B2%D0%B2%D0%BC%D1%83%C2%BB-gh%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D1%82%D0%BE%D0%B2%D0%B2%D0%BC%D1%83%C2%BB35-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1647983
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4827931
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42399
http://rudraautomation.com/index.php/component/k2/author/126037
http://smartacity.com/component/k2/itemlist/user/15354
http://koushatarabar.com/index.php/component/k2/itemlist/user/1314268
http://xplorefitness.com/blog/%C2%AB%D0%B2%D0%BE%D1%80%D0%BE%D0%BD-kuzgun-11-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-dxcg-%C2%AB%D0%B2%D0%BE%D1%80%D0%BE%D0%BD-kuzgun-11-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80-4/
http://smartacity.com/component/k2/itemlist/user/14903
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2573460
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=4235
https://members.fbhaters.com/index.php?topic=81367.0
http://www.m1avio.com/index.php/component/k2/itemlist/user/3611660
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2579646
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4858306
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3624685
http://salescoach.ro/content/%C2%AB%D0%BD%D0%B5%D0%B2%D0%B5%D1%81%D1%82%D0%B0-%D0%B8%D0%B7-%D1%81%D1%82%D0%B0%D0%BC%D0%B1%D1%83%D0%BB%D0%B0-istanbullu-gelin-79-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-gtpn-%C2%AB%D0%BD%D0%B5%D0%B2%D0%B5%D1%81%D1%82%D0%B0-%D0%B8%D0%B7-%D1%81%D1%82%D0%B0%D0%BC%D0%B1%D1%83%D0%BB%D0%B0-istanbullu-gelin
http://withinfp.sakura.ne.jp/eso/index.php/16874812-serial-tajny-taemnici-87-seria-z0-tajny-taemnici-87-seria/0
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4837616
https://tg.vl-mp.com/index.php?action=profile&u=559780
http://cccpvideo.forumside.com/index.php?topic=425.0
http://gtupuw.org/index.php/component/k2/itemlist/user/1838991
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1637073
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=9952
http://repofirmware.altervista.org/index.php?topic=125244.0
http://rudraautomation.com/index.php/component/k2/author/143624
http://smartacity.com/component/k2/itemlist/user/29442
http://teambuildingpremium.com/forum/index.php?topic=790832.0
http://teambuildingpremium.com/forum/index.php?topic=790837.0
http://thermoplast.envolgroupe.com/component/k2/itemlist/user/83083
http://webp.online/index.php?topic=51250.0
https://www.resproxy.com/forum/index.php/809502-vetrenyj-hercai-15-seria-v8wb-vetrenyj-hercai-15-seria/0
https://www.resproxy.com/forum/index.php/809520-vossoedinenie-vuslat-20-seria-z4kz-vossoedinenie-vuslat-20-seri/0
https://www.shaiyax.com/index.php?topic=335650.0
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/599847
http://danielmillsap.com/forum/index.php?topic=913475.0
http://metropolis.ga/index.php?topic=1230.0
http://rotary-laeliana.org/component/k2/itemlist/user/51045
https://prosocyr.com/?option=com_k2&view=itemlist&task=user&id=580557
http://danielmillsap.com/forum/index.php?topic=829693.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/21003
https://www.resproxy.com/forum/index.php/747011-milliardy-4-sezon-8-seria-fgl-milliardy-4-sezon-8-seria-0405201/0
http://seoksoononly.dothome.co.kr/qna/462180
http://healthyteethpa.org/component/k2/itemlist/user/5364069
http://married.dike.gr/index.php/component/k2/itemlist/user/46890
http://proxima.co.rw/index.php/component/k2/itemlist/user/539273
http://www.deliberarchia.org/forum/index.php?topic=896414.0
http://www.tessabannampad.go.th/webboard/index.php?topic=191326.0
http://www.popolsku.fr.pl/forum/index.php?topic=335845.0
https://www.youngbiker.de/wbboard/index.php?page=User&userID=774565
http://webp.online/index.php?topic=43600.0
https://www.resproxy.com/forum/index.php/757185-rasskaz-sluzanki-3-sezon-3-seria-qtg-rasskaz-sluzanki-3-sezon-3/0
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/184783
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=271239
http://danielmillsap.com/forum/index.php?topic=846646.0
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/143483
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1764509
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=79480
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=43562
http://compultras.com/component/k2/itemlist/user/197284
http://rudraautomation.com/index.php/component/k2/author/114202
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39635
https://forums.letstalkbeats.com/index.php?topic=69078.0
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=290702
http://mvisage.sk/index.php/component/k2/itemlist/user/117539
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=295742
http://seoksoononly.dothome.co.kr/qna/798837
http://theolevolosproject.org/?option=com_k2&view=itemlist&task=user&id=24802
http://www.vivelabmanizales.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d0%b0%d0%bd%d0%be/
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7318981
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=783281
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/489909
http://www.vivelabmanizales.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2/
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1855416
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3574012
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1862332
http://seoksoononly.dothome.co.kr/qna/795468
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3719059
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3393575
http://hydrocarbs-gh.org/index.php/component/k2/itemlist/user/7306190
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=48049
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=289869
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3575322
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=187267
http://forum.digamahost.com/index.php?topic=109509.0
http://www.spazioad.com/component/k2/itemlist/user/7212579
http://dev.aabn.org.gh/component/k2/itemlist/user/546437
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3294271
https://forums.letstalkbeats.com/index.php?topic=68794.0
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/12427
http://seoksoononly.dothome.co.kr/qna/776166
http://xplorefitness.com/blog/%C2%AB%D0%B5%D0%B4%D0%B8%D0%BD%D0%BE%D0%B5-%D1%81%D0%B5%D1%80%D0%B4%D1%86%D0%B5-tek-y%C3%BCrek-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-mmjn-%C2%AB%D0%B5%D0%B4%D0%B8%D0%BD%D0%BE%D0%B5-%D1%81%D0%B5%D1%80%D0%B4%D1%86%D0%B5-tek-y%C3%BCrek-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3296331
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42559
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-facebook%C2%BB-ra%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-facebook%C2%BB90-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9
http://www.atab.com.sa/index.php/en/?option=com_k2&view=itemlist&task=user&id=1555552
http://forum.digamahost.com/index.php?topic=109148.0
http://mediaville.me/index.php/component/k2/itemlist/user/208106
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=1007033
http://xn----7sbbahtl1ajlp0a.xn--p1ai/index.php/component/k2/itemlist/user/1247292
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2584925
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=13417
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3376939
http://www.camaracoyhaique.cl/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5/
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1558013
https://forum.ac-jete.it/index.php?topic=352741.0
http://poselokgribovo.ru/forum/index.php?topic=737445.0
http://withinfp.sakura.ne.jp/eso/index.php/16862886-nasa-istoria-73-seria-rntq-nasa-istoria-73-seria/0
http://www.phan-aen.go.th/forum/index.php?topic=625883.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1129889
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=47833
http://153.120.114.241/eso/index.php/16866168-holostak-9-sezon-10-vypusk-vse-casti-afholostak-9-sezon-10-vypu
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=286523
https://prosocyr.com/?option=com_k2&view=itemlist&task=user&id=610210
http://withinfp.sakura.ne.jp/eso/index.php/16915794-voron-kuzgun-17-seria-w6pk-voron-kuzgun-17-seria/0
http://danielmillsap.com/forum/index.php?topic=822279.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/246243
http://www.deliberarchia.org/forum/index.php?topic=796906.0
https://www.youngbiker.de/wbboard/index.php?page=User&userID=785884
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1828633
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1250648
http://www.oortsociety.com/index.php?topic=8754.0
http://danielmillsap.com/forum/index.php?topic=811709.0
http://danielmillsap.com/forum/index.php?topic=786792.0
http://seoksoononly.dothome.co.kr/qna/594046
http://teambuildingpremium.com/forum/index.php?topic=691491.0
http://www.svedmyr.nu/install/UserProfile/tabid/61/userId/330918/Default.aspx
http://healthyteethpa.org/component/k2/itemlist/user/5227663
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=269366
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4687345
http://153.120.114.241/eso/index.php/16865470-igra-prestolov-8-sezon-5-seria-hop-igra-prestolov-8-sezon-5-ser
http://macdistri.com/index.php/component/k2/itemlist/user/258090
http://www.x2145-productions.technology/index.php?title=%C2%AB%D0%9F%D0%BB%D0%BE%D1%85%D0%B8%D0%B5_%D0%9F%D0%B0%D1%80%D0%BD%D0%B8_3_2020_%C2%BB_06-05-2019_%22%D0%9F%D0%BB%D0%BE%D1%85%D0%B8%D0%B5_%D0%9F%D0%B0%D1%80%D0%BD%D0%B8_3_2020_%22_%C2%AB%D0%9F%D0%BB%D0%BE%D1%85%D0%B8%D0%B5_%D0%9F%D0%B0%D1%80%D0%BD%D0%B8_3_2020_%C2%BB
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1125354
http://webp.online/index.php?topic=38355.0
https://forum.ac-jete.it/index.php?topic=289122.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3261019
http://avengerro.top/forum/index.php?topic=17821.0
https://members.fbhaters.com/index.php?topic=76807.0
http://danielmillsap.com/forum/index.php?topic=838033.0
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/536694
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3656218
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3198590
https://tg.vl-mp.com/index.php?topic=1277989.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1108936
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3477120
http://mediaville.me/index.php/component/k2/itemlist/user/210292
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=46851
http://danielmillsap.com/forum/index.php?topic=824004.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2508914
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/185935
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=47507
http://condolencias.servisa.es/91-07-05-2019-r5-91
http://sindicatodechoferespichincha.com.ec/index.php/component/k2/itemlist/user/6677646
http://forum.politeknikgihon.ac.id/index.php?topic=25221.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2509921
http://married.dike.gr/index.php/component/k2/itemlist/user/45804
http://www.deliberarchia.org/forum/index.php?topic=983967.0
http://macdistri.com/index.php/component/k2/itemlist/user/301543
http://withinfp.sakura.ne.jp/eso/index.php/16865863-efir-milliardy-4-sezon-8-seria-p3-milliardy-4-sezon-8-seria/0
http://www.ekemoon.com/149645/050120193107/
http://proxima.co.rw/index.php/component/k2/itemlist/user/569920
https://l2thalassic.org/Forum/index.php?topic=504.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4735606
http://withinfp.sakura.ne.jp/eso/index.php/16927251-uristy-10-seria-hdvideo-uristy-10-seria/0
http://www.ekemoon.com/148239/052220194606/
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/687164
http://www.studioaparo.it/?option=com_k2&view=itemlist&task=user&id=544810
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39166
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2390191
http://euromouleusinage.com/index.php/component/k2/itemlist/user/110081
http://poselokgribovo.ru/forum/index.php?topic=732047.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=29786.0
http://condolencias.servisa.es/9-06-05-2019-p9-9-0
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=10725
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=44461
http://necinsurance.co.zw/component/k2/itemlist/user/19241.html
http://webp.online/index.php?topic=43546.0
http://seoksoononly.dothome.co.kr/qna/745269
http://withinfp.sakura.ne.jp/eso/index.php/16864193-voskressij-ertugrul-146-seria-mbfs-voskressij-ertugrul-146-seri
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=495074
http://salescoach.ro/content/%C2%AB%D0%BD%D0%B0%D1%88%D0%B0-%D0%B8%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F-66-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-bekq-%C2%AB%D0%BD%D0%B0%D1%88%D0%B0-%D0%B8%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F-66-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/54015
http://menulisilmiah.net/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%be%d0%b9-%d0%b0%d1%80%d1%82%d0%b8%d1%81%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fz3%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%be%d0%b9-%d0%b0%d1%80%d1%82%d0%b8%d1%81/
http://seoksoononly.dothome.co.kr/qna/720619
http://matinbank.ir/component/k2/itemlist/user/4483083.html
http://koushatarabar.com/index.php/component/k2/itemlist/user/1314231
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1643971
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42251
http://withinfp.sakura.ne.jp/eso/index.php/16864017-holostak-9-sezon-2019-ukraina-stb-10-vypusk-05-05-2019-smotret-/0
http://seoksoononly.dothome.co.kr/qna/735774
http://www.web2interactive.com/index.php/component/k2/itemlist/user/3578321
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/51433
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1356439
http://www.vivelabmanizales.com/%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5%d0%b4%d0%be-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xm2z-%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5/
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/210234
http://bitpark.co.kr/board_IzjM66/3779680
http://smartacity.com/component/k2/itemlist/user/22979
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1130363
http://www.ekemoon.com/148999/050020190607/
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/12525
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1012480
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4827119
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-3/
https://members.fbhaters.com/index.php?topic=77137.0
http://highlanderonline.cmshelplive.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-15-%d1%81%d0%b5%d1%80%d0%b8/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/286573
http://smartacity.com/component/k2/itemlist/user/23831
https://khuyenmaikk13.info/index.php?topic=181707.0
http://withinfp.sakura.ne.jp/eso/index.php/16882855-tolarobot-1-sezon-5-seria-t1-tolarobot-1-sezon-5-seria
http://www.telcon.gr/index.php/component/k2/itemlist/user/39628
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1862052
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1619844
http://mediaville.me/index.php/component/k2/itemlist/user/211699
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1031876
http://www.nienkevanrijn.nl/component/k2/itemlist/user/426271
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12820
http://highlanderonline.cmshelplive.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-4/
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=199227
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=9091
http://smartacity.com/component/k2/itemlist/user/19026
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=288395
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=47593
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/209080
http://highlanderonline.cmshelplive.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5-4/
http://mobility-corp.com/index.php/component/k2/itemlist/user/2509181
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=9767
http://blog.ptpintcast.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-06-05-2019-o4-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/72311
https://l2thalassic.org/Forum/index.php?topic=1068.0
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=82198
http://teambuildingpremium.com/forum/index.php?topic=774215.0
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=893225
http://muratliziraatodasi.org/forum/index.php?topic=340451.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1554537
https://tg.vl-mp.com/index.php?topic=1283369.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=197620
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/199089
http://danielmillsap.com/forum/index.php?topic=795189.0
http://www.phan-aen.go.th/forum/index.php?topic=606668.0
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1014644
https://www.resproxy.com/forum/index.php/794101-igra-prestolov-8-sezon-7-seria-zym-igra-prestolov-8-sezon-7-ser/0
http://www.phan-aen.go.th/forum/index.php?topic=612155.0
https://tg.vl-mp.com/index.php?topic=1264611.0
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1130355
http://metropolis.ga/index.php?topic=1007.0
http://www.popolsku.fr.pl/forum/index.php?topic=349592.0
https://www.shaiyax.com/index.php?topic=300440.0
http://teambuildingpremium.com/forum/index.php?topic=681067.0
http://jpacschoolclubs.co.uk/?option=com_k2&view=itemlist&task=user&id=3271216
https://members.fbhaters.com/index.php?topic=76332.0
http://www.deliberarchia.org/forum/index.php?topic=902867.0
http://tradebest.org/board_MdUI61/1591205
http://mobility-corp.com/index.php/component/k2/itemlist/user/2479948
http://danielmillsap.com/forum/index.php?topic=807078.0
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1843616
http://www.spazioad.com/component/k2/itemlist/user/7169260
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1713121
http://myrechockey.com/forums/index.php?topic=55370.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172999
http://www.arunagreen.com/index.php/component/k2/itemlist/user/320465
http://zsmr.com.ua/index.php/component/k2/itemlist/user/409073
http://withinfp.sakura.ne.jp/eso/index.php/16768097-rasskaz-sluzanki-3-sezon-2-seria-aip-rasskaz-sluzanki-3-sezon-2/0
https://tg.vl-mp.com/index.php?topic=1264091.0
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3668480
http://teambuildingpremium.com/forum/index.php?topic=628613.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=183396
http://seoksoononly.dothome.co.kr/qna/417567
http://www.tessabannampad.go.th/webboard/index.php?topic=194602.0
http://dohairbiz.com/en/component/k2/itemlist/user/2639112.html
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ub4-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/186115
http://www.m1avio.com/index.php/component/k2/itemlist/user/3568607
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1509176
http://redgatetech.co/?option=com_k2&view=itemlist&task=user&id=691010
http://married.dike.gr/index.php/component/k2/itemlist/user/35190
http://danielmillsap.com/forum/index.php?topic=803844.0
http://www.m1avio.com/index.php/component/k2/itemlist/user/3587358
https://tg.vl-mp.com/index.php?topic=1341905.0
http://danielmillsap.com/forum/index.php?topic=876657.0
http://teambuildingpremium.com/forum/index.php?topic=622876.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/395321
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3545366
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1125591
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ifp-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.shaiyax.com/index.php?topic=296862.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lwr-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.youngbiker.de/wbboard/index.php?page=User&userID=785502
http://danielmillsap.com/forum/index.php?topic=812761.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2563520
http://teambuildingpremium.com/forum/index.php?topic=629782.0
https://tg.vl-mp.com/index.php?topic=1303039.0
http://withinfp.sakura.ne.jp/eso/index.php/16810695-vetrenyj-hercai-15-seria-h3cf-vetrenyj-hercai-15-seria/0
http://www.phan-aen.go.th/forum/index.php?topic=606394.0
https://mcsetup.tk/bbs/index.php?topic=229223.0
http://metropolis.ga/index.php?topic=5641.0
http://macdistri.com/?option=com_k2&view=itemlist&task=user&id=302556
http://metropolis.ga/index.php?topic=2735.0
http://withinfp.sakura.ne.jp/eso/index.php/16768338-zensina-60-seria-i8ul-zensina-60-seria/0
http://metropolis.ga/index.php?topic=4023.0
http://associationsila.org/index.php/component/k2/itemlist/user/266280
http://www.cosl.com.sg/UserProfile/tabid/61/userId/25967548/Default.aspx
https://www.resproxy.com/forum/index.php/736439-rannaa-ptaska-erkenci-kus-44-seria-z7ag-rannaa-ptaska-erkenci-k
https://www.youngbiker.de/wbboard/index.php?page=User&userID=785681
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2539220
http://poselokgribovo.ru/forum/index.php?topic=622884.0
http://withinfp.sakura.ne.jp/eso/index.php/16815979-nasa-istoria-72-seria-i0ya-nasa-istoria-72-seria/0
http://healthyteethpa.org/?option=com_k2&view=itemlist&task=user&id=5287112
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1720087
http://muratliziraatodasi.org/forum/index.php?topic=343243.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4711207
https://www.blog.quora.healthcare/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-41-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p9tr-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1776494
http://teambuildingpremium.com/forum/index.php?topic=629983.0
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-oh7-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8/
http://danielmillsap.com/forum/index.php?topic=892826.0
http://www.popolsku.fr.pl/forum/index.php?topic=339718.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3479007
http://arunagreen.com/index.php/component/k2/itemlist/user/425531
https://www.resproxy.com/forum/index.php/766715-cernoe-zerkalo-5-sezon-5-seria-qhd-cernoe-zerkalo-5-sezon-5-ser/0
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=377775
http://macdistri.com/index.php/component/k2/itemlist/user/259014
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291045
http://danielmillsap.com/forum/index.php?topic=985329.0
http://teambuildingpremium.com/forum/index.php?topic=661359.0
http://www.deliberarchia.org/forum/index.php?topic=971274.0
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/140755
http://avengerro.top/forum/index.php?topic=18283.0
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/199964
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3287079
http://danielmillsap.com/forum/index.php?topic=837977.0
http://www.tessabannampad.go.th/webboard/index.php?topic=195280.0
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-imd-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://metropolis.ga/index.php?topic=6078.0
http://metropolis.ga/index.php?topic=6082.0
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=9955
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=9964
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=143631
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1641276
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1641308
http://married.dike.gr/index.php/component/k2/itemlist/user/25916
http://dev.aabn.org.gh/component/k2/itemlist/user/518818
http://grupotir.com/component/k2/itemlist/user/41644
http://teambuildingpremium.com/forum/index.php?topic=601224.0
http://teambuildingpremium.com/forum/index.php?topic=631193.0
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=45980
http://healthyteethpa.org/component/k2/itemlist/user/5189165
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1560221
http://metropolis.ga/index.php?topic=807.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1094371
https://www.resproxy.com/forum/index.php/746144-sverh-estestvennoe-14-sezon-14-seria-ewh-sverh-estestvennoe-14-/0
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zav-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://menulisilmiah.net/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cdq-%d1%80%d0%b0/
http://menulisilmiah.net/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zav-%d1%80%d0%b0/
http://menulisilmiah.net/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b5-%d0%b7%d0%b5%d1%80%d0%ba%d0%b0%d0%bb%d0%be-5-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nhg-%d1%87%d0%b5%d1%80%d0%bd/
http://metropolis.ga/index.php?topic=6182.0
http://rudraautomation.com/index.php/component/k2/author/144079
http://thermoplast.envolgroupe.com/component/k2/author/83183
https://members.fbhaters.com/index.php?topic=82524.0
https://www.resproxy.com/forum/index.php/809977-igra-prestolov-8-sezon-8-seria-yua-igra-prestolov-8-sezon-8-ser/0
http://mediaville.me/index.php/component/k2/itemlist/user/235518
http://repofirmware.altervista.org/index.php?topic=125581.0
http://teambuildingpremium.com/forum/index.php?topic=791248.0
http://myrechockey.com/forums/index.php?topic=86924.0
http://xekhachduyetthuy.com.vn/index.php/component/k2/itemlist/user/159762
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/4591
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=11931
http://www.phan-aen.go.th/forum/index.php?topic=613168.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1224508
http://www.deliberarchia.org/forum/index.php?topic=955903.0
http://withinfp.sakura.ne.jp/eso/index.php/16807751-vetrenyj-hercai-15-seria-b2sp-vetrenyj-hercai-15-seria?---------------------------71384510048%0D%0AContent-Disposition:%20form-data;%20name=%22token%22%0D%0A%0D%0A5d249f8f2972a%0D%0A---------------------------71384510048%0D%0AContent-Disposition:%20form-data;%20name=%22title%22%0D%0A%0D%0A%C2%AB%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D0%A1%D0%B5%D1%80%D0%B8%D1%8F%C2%BB%20B2sP%20%C2%AB%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D0%A1%D0%B5%D1%80%D0%B8%D1%8F%C2%BB%0D%0A---------------------------71384510048%0D%0AContent-Disposition:%20form-data;%20name=%22content%22%0D%0A%0D%0A%C2%AB%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB%20'%20Y4%20%C2%AB%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB%20%D1%80%D1%83%D1%81%20%D0%BF%D0%B5%D1%80%D0%B5%D0%B2%D0%BE%D0%B4%0D%0A[url=http://zfilm6.ru/watch/ukhZwZTt/][img]https://i.imgur.com/rDglLCZ.jpg[/img][/url]%0D%0A%0D%0A[url=http://zfilm6.ru/watch/ukhZwZTt/]%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F[/url]%20%0D%0A[url=http://zfilm6.ru/watch/ukhZwZTt/]%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F[/url]%20%0D%0A[url=http://zfilm6.ru/watch/ukhZwZTt/]%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F[/url]%20%0D%0A%0D%0A%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20%D0%BE%D0%BA%0D%0A%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20tv%0D%0A%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20kz%0D%0A%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%B0%D1%8F%20%D0%BE%D0%B7%D0%B2%D1%83%D1%87%D0%BA%D0%B0%0D%0A%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20%D1%81%20%D0%BE%D0%B7%D0%B2%D1%83%D1%87%D0%BA%D0%BE%D0%B9%20%D0%BD%D0%B0%20%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%BE%D0%BC%0D%0A$$%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20%D1%80%D1%83%D1%81%20%D1%8F%D0%B7%0D%0A%60%60%60%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20%D0%B0%D0%BB%D0%B8%D1%88%D0%B0%20%D0%B4%D0%B8%D0%BB%D0%B8%D1%80%D0%B8%D1%81%60%60%60%0D%0A%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20%D1%84%D0%B1%0D%0A%3E%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%20%D0%BF%D0%B5%D1%80%D0%B5%D0%B2%D0%BE%D0%B4%20%D0%BD%D0%B0%20%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%BE%D0%BC%0D%0A---------------------------71384510048%0D%0AContent-Disposition:%20form-data;%20name=%22postReply%22%0D%0A%0D%0A%E3%83%88%E3%83%94%E3%83%83%E3%82%AF%E3%82%E2%80%99%E7%AB%8B%E3%81%A6%E3%82%8B%0D%0A---------------------------71384510048--
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=237199
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1092161
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1095389
https://lucky28003.nl/forum/index.php?topic=6436.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1308303
http://married.dike.gr/index.php/component/k2/itemlist/user/40493
https://www.blog.quora.healthcare/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wgt-%d0%b8%d0%b3%d1%80%d0%b0
http://www2.yasothon.go.th/smf/index.php?topic=159.142140
https://tg.vl-mp.com/index.php?topic=1303180.0
http://sam-sanat.ir/?option=com_k2&view=itemlist&task=user&id=137169
http://www.aroshan.com/component/k2/itemlist/user/888845
http://www.phan-aen.go.th/forum/index.php?topic=609840.0
http://fbpharm.net/index.php/component/k2/itemlist/user/15007
http://aitour.kz/?option=com_k2&view=itemlist&task=user&id=312695
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4829583
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3246456
http://www.phan-aen.go.th/forum/index.php?topic=612192.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2479847
https://members.fbhaters.com/index.php?topic=76959.0
https://www.resproxy.com/forum/index.php/747559-milliardy-4-sezon-9-seria-xlk-milliardy-4-sezon-9-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/16771926-rasskaz-sluzanki-3-sezon-3-seria-esk-rasskaz-sluzanki-3-sezon-3/0
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nm1-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21/
http://webp.online/index.php?topic=45170.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2495504
https://members.fbhaters.com/index.php?topic=77046.0
http://www.tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1525050
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/184610
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yi3-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://danielmillsap.com/forum/index.php?topic=828463.0
https://xapps.work/%C2%AB%D0%92%D0%B5%D0%BB%D0%BE%D1%82%D0%B0%D1%87%D0%BA%D0%B8%C2%BB_09-05-2019_%D0%92%D0%B5%D0%BB%D0%BE%D1%82%D0%B0%D1%87%D0%BA%D0%B8_%C2%AB%D0%92%D0%B5%D0%BB%D0%BE%D1%82%D0%B0%D1%87%D0%BA%D0%B8%C2%BB
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2589682
http://www.dap.com.py/index.php/component/k2/itemlist/user/794596
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1783712
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1783720
http://erhu.eu/viewtopic.php?t=292359
http://c3isecurity.com.br/?option=com_k2&view=itemlist&task=user&id=444749
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uf5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://metropolis.ga/index.php?topic=5377.0
http://married.dike.gr/index.php/component/k2/itemlist/user/34293
http://metropolis.ga/index.php?topic=727.0
https://instaldec.com/?option=com_k2&view=itemlist&task=user&id=602651
http://teambuildingpremium.com/forum/index.php?topic=641016.0
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/198789
http://muratliziraatodasi.org/forum/index.php?topic=327111.0
http://www.popolsku.fr.pl/forum/index.php?topic=336671.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1107085
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81-27/
http://metropolis.ga/index.php?topic=4984.0
https://tg.vl-mp.com/index.php?topic=1280446.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3572914
http://withinfp.sakura.ne.jp/eso/index.php/16788908-milliardy-4-sezon-12-seria-tzg-milliardy-4-sezon-12-seria-02052/0
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pb0-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10/
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1079099
http://www.x2145-productions.technology/index.php?title=%C2%AB%D0%9F%D1%80%D0%BE%D0%BA%D0%BB%D1%8F%D1%82%D0%B8%D0%B5_%D0%9F%D0%BB%D0%B0%D1%87%D1%83%D1%89%D0%B5%D0%B9%C2%BB_09-05-2019_%22%D0%9F%D1%80%D0%BE%D0%BA%D0%BB%D1%8F%D1%82%D0%B8%D0%B5_%D0%9F%D0%BB%D0%B0%D1%87%D1%83%D1%89%D0%B5%D0%B9%22_%C2%AB%D0%9F%D1%80%D0%BE%D0%BA%D0%BB%D1%8F%D1%82%D0%B8%D0%B5_%D0%9F%D0%BB%D0%B0%D1%87%D1%83%D1%89%D0%B5%D0%B9%C2%BB
http://www.x2145-productions.technology/index.php?title=Benutzer:TameraWakelin11
http://www.xggu.net/wiki/%C2%AB%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C_%D0%9B%D0%B5%D0%B2_2019_%C2%BB_09-05-2019_%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C_%D0%9B%D0%B5%D0%B2_2019_%C2%AB%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C_%D0%9B%D0%B5%D0%B2_2019_%C2%BB
http://www.xggu.net/wiki/%C2%AB%D0%A2%D0%B0%D0%B9%D0%BD%D0%B0%D1%8F_%D0%96%D0%B8%D0%B7%D0%BD%D1%8C_%D0%94%D0%BE%D0%BC%D0%B0%D1%88%D0%BD%D0%B8%D1%85_%D0%96%D0%B8%D0%B2%D0%BE%D1%82%D0%BD%D1%8B%D1%85_2_2019_%C2%BB_09-05-2019_%E2%80%9E%D0%A2%D0%B0%D0%B9%D0%BD%D0%B0%D1%8F_%D0%96%D0%B8%D0%B7%D0%BD%D1%8C_%D0%94%D0%BE%D0%BC%D0%B0%D1%88%D0%BD%D0%B8%D1%85_%D0%96%D0%B8%D0%B2%D0%BE%D1%82%D0%BD%D1%8B%D1%85_2_2019_Online%22_%C2%AB%D0%A2%D0%B0%D0%B9%D0%BD%D0%B0%D1%8F_%D0%96%D0%B8%D0%B7%D0%BD%D1%8C_%D0%94%D0%BE%D0%BC%D0%B0%D1%88%D0%BD%D0%B8%D1%85_%D0%96%D0%B8%D0%B2%D0%BE%D1%82%D0%BD%D1%8B%D1%85_2_2019_%C2%BB
http://www.xggu.net/wiki/User:BruceGriffis2
https://rahaayee.org/index.php/%C3%82%C2%AB%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%90%C2%B5%C3%90%C2%BB%C3%90%C2%BE%C3%91%E2%80%9A%C3%90%C2%B0%C3%91%E2%80%A1%C3%90%C2%BA%C3%90%C2%B8%C3%82%C2%BB_09-05-2019_%22%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%90%C2%B5%C3%90%C2%BB%C3%90%C2%BE%C3%91%E2%80%9A%C3%90%C2%B0%C3%91%E2%80%A1%C3%90%C2%BA%C3%90%C2%B8_Watch%22_%C3%82%C2%AB%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%90%C2%B5%C3%90%C2%BB%C3%90%C2%BE%C3%91%E2%80%9A%C3%90%C2%B0%C3%91%E2%80%A1%C3%90%C2%BA%C3%90%C2%B8%C3%82%C2%BB
https://rahaayee.org/index.php/User:KaylaSmoot00723
http://erhu.eu/viewtopic.php?t=293068
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4676144
http://91.231.123.194/index.php/component/k2/itemlist/user/852895
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1708854
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=494793
http://danielmillsap.com/forum/index.php?topic=832812.0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=671807
http://mobility-corp.com/index.php/component/k2/itemlist/user/2387591
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=34131
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1957760
https://www.youngbiker.de/wbboard/index.php?page=User&userID=782525
http://www.deliberarchia.org/forum/index.php?topic=957298.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4731181
http://withinfp.sakura.ne.jp/eso/index.php/16909334-zensina-58-seria-t0ts-zensina-58-seria
http://withinfp.sakura.ne.jp/eso/index.php/16896169-vetrenyj-hercai-6-seria-y8kd-vetrenyj-hercai-6-seria
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1556784
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tdt-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1252173
http://withinfp.sakura.ne.jp/eso/index.php/16809303-nevesta-iz-stambula-istanbullu-gelin-81-seria-k3jd-nevesta-iz-s
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2521548
http://www.spazioad.com/component/k2/itemlist/user/7236835
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/42734
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3255364
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2579239
http://www.phan-aen.go.th/forum/index.php?topic=606794.0
http://danielmillsap.com/forum/index.php?topic=833414.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1037262
http://www.x2145-productions.technology/index.php?title=Benutzer:EulaliaWhitlock
https://tg.vl-mp.com/index.php?topic=1268126.0
http://seoksoononly.dothome.co.kr/qna/455305
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=592971.0
http://danielmillsap.com/forum/index.php?topic=881593.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1550899
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ok6-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://macdistri.com/index.php/component/k2/itemlist/user/299320
http://travelsolution.info/?option=com_k2&view=itemlist&task=user&id=715279
http://redgatetech.co/?option=com_k2&view=itemlist&task=user&id=706637
https://www.resproxy.com/forum/index.php/775440-rasskaz-sluzanki-3-sezon-3-seria-pwq-rasskaz-sluzanki-3-sezon-3/0
http://metropolis.ga/index.php?topic=368.0
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=268756
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/641615
http://danielmillsap.com/forum/index.php?topic=828678.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/438017
http://withinfp.sakura.ne.jp/eso/index.php/16887006-vetrenyj-hercai-17-seria-l2xa-vetrenyj-hercai-17-seria/0
http://www2.yasothon.go.th/smf/index.php?topic=159.126390
http://dessa.com.br/index.php/component/k2/itemlist/user/293122
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lf0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8/
http://teambuildingpremium.com/forum/index.php?topic=628169.0
http://metropolis.ga/index.php?topic=3560.0
http://www.tessabannampad.go.th/webboard/index.php?topic=193814.0
http://proandpro.it/?option=com_k2&view=itemlist&task=user&id=4455071
http://married.dike.gr/index.php/component/k2/itemlist/user/42034
http://www.popolsku.fr.pl/forum/index.php?topic=340412.0
https://www.youngbiker.de/wbboard/index.php?page=User&userID=785508
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-(ia)-13-e-jaa-(ia)-13-e/
http://teambuildingpremium.com/forum/index.php?topic=604859.0
https://tg.vl-mp.com/index.php?topic=1277158.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1613584
http://macdistri.com/index.php/component/k2/itemlist/user/273390
https://www.shaiyax.com/index.php?topic=308856.0
[url=http://cialisec.com/]cialis online[/url]
walgreens price for cialis 5mg
<a href="http://cialisec.com/">cialis online</a>
viagra cialis levitra doses
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4699927
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/151158
http://mediaville.me/index.php/component/k2/itemlist/user/211079
https://www.shaiyax.com/index.php?topic=313620.0
http://seoksoononly.dothome.co.kr/qna/633936
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1827530
http://teambuildingpremium.com/forum/index.php?topic=593373.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2471601
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2512856
http://withinfp.sakura.ne.jp/eso/index.php/16825590-nasa-istoria-70-seria-s6qq-nasa-istoria-70-seria
http://wcwpr.com/UserProfile/tabid/85/userId/9172604/Default.aspx
http://www.deliberarchia.org/forum/index.php?topic=958429.0
http://www.popolsku.fr.pl/forum/index.php?topic=336458.0
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=14874
http://www.glasshouseproject.com.ng/index.php/component/k2/itemlist/user/37718
http://myrechockey.com/forums/index.php?topic=90507.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/176632
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1105410
https://tg.vl-mp.com/index.php?topic=1320237.0
https://tg.vl-mp.com/index.php?topic=1296868.0
http://withinfp.sakura.ne.jp/eso/index.php/16817565-voron-kuzgun-9-seria-k6jo-voron-kuzgun-9-seria
http://batubersurat.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=42658
http://macdistri.com/index.php/component/k2/itemlist/user/279328
http://teambuildingpremium.com/forum/index.php?topic=600977.0
http://macdistri.com/index.php/component/k2/itemlist/user/285369
http://sos.victoryaltar.org/tiki-index.php?page=UserPagemaxiestroupzpofmr
http://withinfp.sakura.ne.jp/eso/index.php/16779493-milliardy-4-sezon-8-seria-tuu-milliardy-4-sezon-8-seria/0
https://instaldec.com/?option=com_k2&view=itemlist&task=user&id=572917
https://members.fbhaters.com/index.php?topic=66827.0
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1007982
http://dev.aabn.org.gh/component/k2/itemlist/user/502230
http://www.deliberarchia.org/forum/index.php?topic=979061.0
http://teambuildingpremium.com/forum/index.php?topic=601862.0
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7320670
http://www.deliberarchia.org/forum/index.php?topic=955184.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/eoe-ekao-5-eo-3-e-mba-eoe-ekao-5-eo-3-e-24-04-2019/
http://danielmillsap.com/forum/index.php?topic=892327.0
http://webp.online/index.php?topic=46205.msg75635
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xc5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://teambuildingpremium.com/forum/index.php?topic=622736.0
http://teambuildingpremium.com/forum/index.php?topic=687653.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/141156
http://www.deliberarchia.org/forum/index.php?topic=947295.0
http://www.tessabannampad.go.th/webboard/index.php?topic=189062.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1322304
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2411146
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=39928
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3197961
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=272291
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-inz-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/186009
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3572624
http://pptforum.dothome.co.kr/board_APMk06/659166
http://www.deliberarchia.org/forum/index.php?topic=904219.0
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/249875
http://dessa.com.br/component/k2/itemlist/user/292814
https://tg.vl-mp.com/index.php?topic=1297057.0
http://www.deliberarchia.org/forum/index.php?topic=973019.0
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7199283
http://soc-human.kz/index.php/component/k2/itemlist/user/1632103
http://macdistri.com/index.php/component/k2/itemlist/user/292907
http://www.telcon.gr/index.php/component/k2/itemlist/user/41901
http://teambuildingpremium.com/forum/index.php?topic=641757.0
https://tg.vl-mp.com/index.php?topic=1328667.0
http://web2interactive.com/index.php/component/k2/itemlist/user/3568053
http://withinfp.sakura.ne.jp/eso/index.php/16813077-sverh-estestvennoe-14-sezon-14-seria-ybf-sverh-estestvennoe-14-/0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1530247
http://ayerawaddymyanmar.com/%C2%AB%D0%9E%D0%B4%D0%BD%D0%B0%D0%B6%D0%B4%D1%8B_%D0%92_%D0%93%D0%BE%D0%BB%D0%BB%D0%B8%D0%B2%D1%83%D0%B4%D0%B5_2019_%C2%BB_09-05-2019_%22%D0%9E%D0%B4%D0%BD%D0%B0%D0%B6%D0%B4%D1%8B_%D0%92_%D0%93%D0%BE%D0%BB%D0%BB%D0%B8%D0%B2%D1%83%D0%B4%D0%B5_2019_%22_%C2%AB%D0%9E%D0%B4%D0%BD%D0%B0%D0%B6%D0%B4%D1%8B_%D0%92_%D0%93%D0%BE%D0%BB%D0%BB%D0%B8%D0%B2%D1%83%D0%B4%D0%B5_2019_%C2%BB
http://boppern.de/index.php?title=%C2%AB%D0%91%D0%BE%D0%BD%D0%B4_25_2020_%C2%BB_09-05-2019_%E2%80%9E%D0%91%D0%BE%D0%BD%D0%B4_25_2020_Online%22_%C2%AB%D0%91%D0%BE%D0%BD%D0%B4_25_2020_%C2%BB
http://boppern.de/index.php?title=%C2%AB%D0%94%D0%B6%D0%BE%D0%BA%D0%B5%D1%80_2019_%C2%BB_09-05-2019_%C2%AB%D0%94%D0%B6%D0%BE%D0%BA%D0%B5%D1%80_2019_%C2%BB_%C2%AB%D0%94%D0%B6%D0%BE%D0%BA%D0%B5%D1%80_2019_%C2%BB
http://boppern.de/index.php?title=%C2%AB%D0%9B%D1%8E%D0%B4%D0%B8_%D0%98%D0%BA%D1%81_%D0%A2%D1%91%D0%BC%D0%BD%D1%8B%D0%B9_%D0%A4%D0%B5%D0%BD%D0%B8%D0%BA%D1%81_2019_%C2%BB_09-05-2019_%22%D0%9B%D1%8E%D0%B4%D0%B8_%D0%98%D0%BA%D1%81_%D0%A2%D1%91%D0%BC%D0%BD%D1%8B%D0%B9_%D0%A4%D0%B5%D0%BD%D0%B8%D0%BA%D1%81_2019_Watch%22_%C2%AB%D0%9B%D1%8E%D0%B4%D0%B8_%D0%98%D0%BA%D1%81_%D0%A2%D1%91%D0%BC%D0%BD%D1%8B%D0%B9_%D0%A4%D0%B5%D0%BD%D0%B8%D0%BA%D1%81_2019_%C2%BB
http://boppern.de/index.php?title=User:ShantaeBuxton5
http://criptomedicina.ru/%C2%AB%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F_%D0%98%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA_4_2019_%C2%BB_09-05-2019_%22%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F_%D0%98%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA_4_2019_Watch%22_%C2%AB%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F_%D0%98%D0%B3%D1%80%D1%83%D1%88%D0%B5%D0%BA_4_2019_%C2%BB
http://criptomedicina.ru/User:KarolinHowes478
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1142579
http://sagopedia.se/%C2%AB%D0%92_%D0%9C%D0%B5%D1%82%D1%80%D0%B5_%D0%94%D1%80%D1%83%D0%B3_%D0%9E%D1%82_%D0%94%D1%80%D1%83%D0%B3%D0%B0%C2%BB_09-05-2019_%D0%92_%D0%9C%D0%B5%D1%82%D1%80%D0%B5_%D0%94%D1%80%D1%83%D0%B3_%D0%9E%D1%82_%D0%94%D1%80%D1%83%D0%B3%D0%B0_%C2%AB%D0%92_%D0%9C%D0%B5%D1%82%D1%80%D0%B5_%D0%94%D1%80%D1%83%D0%B3_%D0%9E%D1%82_%D0%94%D1%80%D1%83%D0%B3%D0%B0%C2%BB
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=495889
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=201535
http://myrechockey.com/forums/index.php?topic=54124.0
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1748631
https://www.resproxy.com/forum/index.php/772193-ne-otpuskaj-mou-ruku-elimi-birakma-40-seria-u4kf-ne-otpuskaj-mo
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1277945
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4741926
http://withinfp.sakura.ne.jp/eso/index.php/16826231-zensina-59-seria-e8zn-zensina-59-seria/0
http://danielmillsap.com/forum/index.php?topic=900316.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c0vr-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-16-%d1%81%d0%b5%d1%80%d0%b8/
http://www.popolsku.fr.pl/forum/index.php?topic=346891.0
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=378713
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gmy-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
https://forum.ac-jete.it/index.php?topic=280624.0
http://www.deliberarchia.org/forum/index.php?topic=915072.0
http://danielmillsap.com/forum/index.php?topic=829582.0
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3597753
http://withinfp.sakura.ne.jp/eso/index.php/16940946-tola-robot-4-seria-serial-trejler-bt-tola-robot-4-seria-serial-/0
https://members.fbhaters.com/index.php?topic=82490.0
https://tg.vl-mp.com/index.php?topic=1357912.0
http://ayerawaddymyanmar.com/%C2%AB%D0%92%D0%B5%D0%BB%D0%BE%D1%82%D0%B0%D1%87%D0%BA%D0%B8%C2%BB_09-05-2019_%22%D0%92%D0%B5%D0%BB%D0%BE%D1%82%D0%B0%D1%87%D0%BA%D0%B8_Watch%22_%C2%AB%D0%92%D0%B5%D0%BB%D0%BE%D1%82%D0%B0%D1%87%D0%BA%D0%B8%C2%BB
http://ayerawaddymyanmar.com/%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB_09-05-2019_%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB_%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB
http://sagopedia.se/%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB_09-05-2019_%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB_%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB
http://sagopedia.se/%C2%AB%D0%9F%D1%80%D0%B8%D0%BD%D1%86%D0%B5%D1%81%D1%81%D0%B0_%D0%AD%D0%BC%D0%BC%D0%B8%C2%BB_09-05-2019_%E2%80%9E%D0%9F%D1%80%D0%B8%D0%BD%D1%86%D0%B5%D1%81%D1%81%D0%B0_%D0%AD%D0%BC%D0%BC%D0%B8_Online%22_%C2%AB%D0%9F%D1%80%D0%B8%D0%BD%D1%86%D0%B5%D1%81%D1%81%D0%B0_%D0%AD%D0%BC%D0%BC%D0%B8%C2%BB
http://tokendesignthinking.org/wiki/index.php/%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB_09-05-2019_%E2%80%9E%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB_Online%22_%C2%AB%D0%9C%D1%81%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B8_%D0%A4%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB
http://tokendesignthinking.org/wiki/index.php/%C2%AB%D0%9F%D0%BE%D1%81%D0%BB%D0%B5%C2%BB_09-05-2019_%22%D0%9F%D0%BE%D1%81%D0%BB%D0%B5%22_%C2%AB%D0%9F%D0%BE%D1%81%D0%BB%D0%B5%C2%BB
http://www.ekemoon.com/145035/051520190606/
http://mobility-corp.com/index.php/component/k2/itemlist/user/2509473
http://www.m1avio.com/index.php/component/k2/itemlist/user/3609070
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1550879
http://macdistri.com/index.php/component/k2/itemlist/user/315006
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/56081
http://bitpark.co.kr/board_IzjM66/3749086
https://khuyenmaikk13.info/index.php?topic=182820.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1340643
http://www.phan-aen.go.th/forum/index.php?topic=625561.0
http://arunagreen.com/index.php/component/k2/itemlist/user/432766
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/55329
http://graphic-ali.com/?option=com_k2&view=itemlist&task=user&id=2378654
http://cccpvideo.forumside.com/index.php?topic=541.0
http://theolevolosproject.org/index.php/component/k2/itemlist/user/24807
http://highlanderonline.cmshelplive.net/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-07-05-2019-r4/
http://teambuildingpremium.com/forum/index.php?topic=785940.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1335222
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1629948
https://l2thalassic.org/Forum/index.php?topic=1841.0
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1563174
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=64996
http://www.emrabq8.com/index.php/component/k2/itemlist/user/1763603
http://xplorefitness.com/blog/%C2%AB%D0%B2%D0%BE%D1%80%D0%BE%D0%BD-kuzgun-18-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-mopc-%C2%AB%D0%B2%D0%BE%D1%80%D0%BE%D0%BD-kuzgun-18-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
https://khuyenmaikk13.info/index.php?topic=179779.0
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/50455
http://poselokgribovo.ru/forum/index.php?topic=716020.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/577069
http://teambuildingpremium.com/forum/index.php?topic=779203.0
http://seoksoononly.dothome.co.kr/qna/790572
https://l2thalassic.org/Forum/index.php?topic=2221.0
http://www.ekemoon.com/162243/050320191409/
http://menulisilmiah.net/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-da0%d0%bd/
http://www.crnmedia.es/component/k2/itemlist/user/84754
http://ahudseafood.com/index.php/component/k2/itemlist/user/8229
http://webp.online/index.php?topic=46068.0
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5203
http://menulisilmiah.net/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be/
http://macdistri.com/index.php/component/k2/itemlist/user/297743
http://bitpark.co.kr/board_IzjM66/3787441
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2564350
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/565657
http://roikjer.com/forum/index.php?PHPSESSID=qm2ii7vf37fm53r8nhbvl14cm1&topic=831019.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2576097
http://esperanzazubieta.com/component/k2/itemlist/user/96689
http://rudraautomation.com/index.php/component/k2/author/121718
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/55402
http://bitpark.co.kr/board_IzjM66/3732007
http://www.deliberarchia.org/forum/index.php?topic=978640.0
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/6791
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1026972
http://arunagreen.com/index.php/component/k2/itemlist/user/436901
http://www.m1avio.com/?option=com_k2&view=itemlist&task=user&id=3598465
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/477623
http://withinfp.sakura.ne.jp/eso/index.php/16894425-nikogda-ne-govori-nikogda-3-seria-06052019-b1-nikogda-ne-govori
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=8241
http://rudraautomation.com/index.php/component/k2/author/122588
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1004379
https://forums.letstalkbeats.com/index.php?topic=66376.0
http://seoksoononly.dothome.co.kr/qna/750597
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3297009
http://ovotecegg.com/component/k2/itemlist/user/115564
http://haniel.ir/index.php/component/k2/itemlist/user/77493
http://fbpharm.net/index.php/component/k2/itemlist/user/14826
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=300304
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=290083
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/477314
https://forums.letstalkbeats.com/index.php?topic=66988.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=16221
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=15804
http://www.ekemoon.com/164055/051020191009/
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/189096
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1021412
http://www.vivelabmanizales.com/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ufmk-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-9-%d1%81%d0%b5%d1%80%d0%b8/
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7305565
http://www.vivelabmanizales.com/hd-video-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1/
http://proxima.co.rw/index.php/component/k2/itemlist/user/565634
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2562392
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=559123
http://withinfp.sakura.ne.jp/eso/index.php/16893851-sluga-naroda-3-sezon-20-seria-06052019-b9-sluga-naroda-3-sezon-
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=501279
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=187186
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3383118
http://community.viajar.tur.br/index.php?p=/profile/jackhildre
http://withinfp.sakura.ne.jp/eso/index.php/16889147-serial-tolarobot-1-sezon-3-seria-j6-tolarobot-1-sezon-3-seria/0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1120451
http://fbpharm.net/index.php/component/k2/itemlist/user/19671
http://highlanderonline.cmshelplive.net/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ceor-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://poselokgribovo.ru/forum/index.php?topic=714245.0
http://xplorefitness.com/blog/%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-13-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-ymux-%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-13-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://mediaville.me/index.php/component/k2/itemlist/user/209647
http://withinfp.sakura.ne.jp/eso/index.php/16885022-voron-kuzgun-12-seria-gsbp-voron-kuzgun-12-seria/0
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=564596
http://salescoach.ro/content/%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-16-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-jasf-%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-16-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://teambuildingpremium.com/forum/index.php?topic=784878.0
https://forums.letstalkbeats.com/index.php?topic=65418.0
https://lucky28003.nl/forum/index.php?topic=11569.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1108231
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3177127
https://www.youngbiker.de/wbboard/index.php?page=User&userID=781285
http://www.crnmedia.es/component/k2/itemlist/user/81438
http://www.arunagreen.com/index.php/component/k2/itemlist/user/382557
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1295407
https://outreach.wikimedia.org/wiki/%C3%82%C2%AB%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%90%C2%B5%C3%90%C2%BB%C3%90%C2%BE%C3%91%E2%80%9A%C3%90%C2%B0%C3%91%E2%80%A1%C3%90%C2%BA%C3%90%C2%B8%C3%82%C2%BB_05-05-2019_%C3%82%C2%AB%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%90%C2%B5%C3%90%C2%BB%C3%90%C2%BE%C3%91%E2%80%9A%C3%90%C2%B0%C3%91%E2%80%A1%C3%90%C2%BA%C3%90%C2%B8%C3%82%C2%BB_%C3%82%C2%AB%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%90%C2%B5%C3%90%C2%BB%C3%90%C2%BE%C3%91%E2%80%9A%C3%90%C2%B0%C3%91%E2%80%A1%C3%90%C2%BA%C3%90%C2%B8%C3%82%C2%BB
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/14177
http://aitour.kz/?option=com_k2&view=itemlist&task=user&id=311230
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1107444
http://danielmillsap.com/forum/index.php?topic=867719.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1566552
http://avengerro.top/forum/index.php?topic=11345.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=293154
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/185606
http://www.deliberarchia.org/forum/index.php?topic=974460.0
http://webp.online/index.php?topic=41563.0
https://www.blog.quora.healthcare/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z9ml-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd
http://www.deliberarchia.org/forum/index.php?topic=964432.0
http://forum.thaibetrank.com/index.php?topic=1083762.0
http://www.deliberarchia.org/forum/index.php?topic=972422.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39114
http://www.camaracoyhaique.cl/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-83-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-as0%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-83/
http://webp.online/index.php?topic=49749.0
http://menulisilmiah.net/%d1%8d%d1%84%d0%b8%d1%80-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/286007
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3400172
http://salescoach.ro/content/%C2%AB%D0%B2%D0%BE%D1%81%D1%81%D0%BE%D0%B5%D0%B4%D0%B8%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5-vuslat-18-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-gvyi-%C2%AB%D0%B2%D0%BE%D1%81%D1%81%D0%BE%D0%B5%D0%B4%D0%B8%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5-vuslat-18-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://islamiccall.info/?option=com_k2&view=itemlist&task=user&id=856771
https://chromehearts.in.th/index.php?topic=44780.0
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=225378
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=15402
http://seoksoononly.dothome.co.kr/qna/806269
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1881383
http://fbpharm.net/index.php/component/k2/itemlist/user/18836
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3298449
http://compultras.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=200951
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/674299
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/7863
http://ptu.imoove.kr/ko/content/%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-17-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%D1%81%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C-%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-17-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB331868
http://www.deliberarchia.org/forum/index.php?topic=975836.0
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=12582
http://euromouleusinage.com/index.php/component/k2/itemlist/user/118820
http://www.m1avio.com/?option=com_k2&view=itemlist&task=user&id=3597638
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1747881
http://batubersurat.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=42814
http://www.comfortcenter.es/index.php/component/k2/itemlist/user/104522
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=604553
http://euromouleusinage.com/?option=com_k2&view=itemlist&task=user&id=114007
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-16-%d1%81%d0%b5-3/
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=492550
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1633069
http://arunagreen.com/index.php/component/k2/itemlist/user/437960
http://mediaville.me/index.php/component/k2/itemlist/user/208076
http://molweb.ru/groups/xolostyak-9-sezon-12-vypusk-ddxolostyak-9-sezon-12-vypusk31-xolostyak-9-sezon-12-vypusk/
http://menulisilmiah.net/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%be%d0%b9-%d0%b0%d1%80%d1%82%d0%b8%d1%81%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jy8%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%be%d0%b9-%d0%b0%d1%80%d1%82%d0%b8%d1%81/
http://dev.aabn.org.gh/component/k2/itemlist/user/516693
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1003341
https://l2thalassic.org/Forum/index.php?topic=800.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/564834
http://www.rocktheboat.cc/members/shennalawton44/
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26175979/Default.aspx
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=63143
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=203451
http://macdistri.com/index.php/component/k2/itemlist/user/309465
https://members.fbhaters.com/index.php?topic=74895.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1142048
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=305058
http://ovotecegg.com/component/k2/itemlist/user/125911
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=9842
http://rudraautomation.com/index.php/component/k2/author/143295
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1640916
http://theolevolosproject.org/?option=com_k2&view=itemlist&task=user&id=25214
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/61452
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=585979
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=783317
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2426067
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/17320
http://ovotecegg.com/component/k2/itemlist/user/126580
http://seoksoononly.dothome.co.kr/qna/818570
http://seoksoononly.dothome.co.kr/qna/818606
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1012713
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1337310
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/476074
http://www.ekemoon.com/149921/050220191907/
http://seoksoononly.dothome.co.kr/?document_srl=782948
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1336350
http://www.camaracoyhaique.cl/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pv6%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f07-05-2019/
http://seoksoononly.dothome.co.kr/qna/745449
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43067
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=44278
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4828276
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/6916
http://menulisilmiah.net/live-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81/
http://www.m1avio.com/?option=com_k2&view=itemlist&task=user&id=3604026
https://forums.letstalkbeats.com/index.php?topic=65345.0
http://www.vivelabmanizales.com/hd-video-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z6-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1/
http://www.deliberarchia.org/forum/index.php?topic=985500.0
http://arunagreen.com/index.php/component/k2/itemlist/user/421835
http://www.vivelabmanizales.com/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tnva-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd/
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=9494
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1656252
http://thermoplast.envolgroupe.com/component/k2/author/83705
http://thermoplast.envolgroupe.com/component/k2/author/83709
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=63433
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3602267
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3602763
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1579699
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1369239
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1369532
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1369576
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1040281
https://tg.vl-mp.com/index.php?topic=1348634.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/187381
http://xplorefitness.com/blog/%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-06-05-2019-g1-%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=322443
http://marjorieaperry.com/?option=com_k2&view=itemlist&task=user&id=480749
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1004062
https://lucky28003.nl/forum/index.php?topic=10216.0
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5701
http://rockndata.net/UserProfile/tabid/61/userId/18161970/Default.aspx
http://dev.aabn.org.gh/?option=com_k2&view=itemlist&task=user&id=516010
http://seoksoononly.dothome.co.kr/qna/712661
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4825084
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3582717
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1762076
http://www.ekemoon.com/143885/050420191006/
http://www.vivelabmanizales.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-aq4u-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://ovotecegg.com/component/k2/itemlist/user/114492
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2527696
https://l2thalassic.org/Forum/index.php?topic=2035.0
http://haniel.ir/?option=com_k2&view=itemlist&task=user&id=77628
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/495050
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/495092
http://fbpharm.net/index.php/component/k2/itemlist/user/26206
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1751600
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/282817
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=83323
https://members.fbhaters.com/index.php?topic=82821.0
https://members.fbhaters.com/index.php?topic=82840.0
https://www.resproxy.com/forum/index.php/810654-rasskaz-sluzanki-3-sezon-4-seria-uni-rasskaz-sluzanki-3-sezon-4/0
http://danielmillsap.com/forum/index.php?topic=992951.0
http://dev.aabn.org.gh/component/k2/itemlist/user/548946
https://mcsetup.tk/bbs/index.php?topic=246510.0
https://www.resproxy.com/forum/index.php/810677-vossoedinenie-vuslat-15-seria-v7so-vossoedinenie-vuslat-15-seri/0
http://www.tessabannampad.go.th/webboard/index.php?topic=196029.0
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bta-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-min-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://teambuildingpremium.com/forum/index.php?topic=649128.0
http://teambuildingpremium.com/forum/index.php?topic=592269.0
http://seoksoononly.dothome.co.kr/qna/385107
http://www.phan-aen.go.th/forum/index.php?topic=612506.0
http://healthyteethpa.org/component/k2/itemlist/user/5340539
http://www.cosl.com.sg/UserProfile/tabid/61/userId/25887548/Default.aspx
http://ts.bloodhand.de/forum/viewtopic.php?t=253678
http://ts.bloodhand.de/forum/viewtopic.php?t=253679
http://webp.online/index.php?topic=51264.msg85378
https://lucky28003.nl/forum/index.php?topic=12890.0
https://members.fbhaters.com/index.php?topic=82400.0
https://khuyenmaikk13.info/index.php?topic=188113.0
https://khuyenmaikk13.info/index.php?topic=188142.0
https://members.fbhaters.com/index.php?topic=86539.0
https://reficulcoin.com/index.php?topic=19642.0
https://reficulcoin.com/index.php?topic=19650.0
https://reficulcoin.com/index.php?topic=19662.0
https://worldtaxi.org/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d8-d8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://www.limscave.com/forum/viewtopic.php?t=31813
http://danielmillsap.com/forum/index.php?topic=998647.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=30688.0
https://reficulcoin.com/index.php?topic=19664.0
https://reficulcoin.com/index.php?topic=19667.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-59/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-53/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-28/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-2/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-2/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-7/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-8/
https://forum.clubeicaro.pt/index.php?topic=923.0
https://khuyenmaikk13.info/index.php?topic=188126.0
https://khuyenmaikk13.info/index.php?topic=188134.0
http://sochi-forum.info/index.php?topic=463.0
http://taklongclub.com/forum/index.php?topic=98090.0
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-i7-f0/
http://help.stv.ru/index.php?topic=136286.0
http://danielmillsap.com/forum/index.php?topic=985885.0
http://sextomariotienda.com/blog/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f1-%d1%81%d0%bb/
http://roikjer.com/forum/index.php?PHPSESSID=d2t3tcrd2tatumean633s2i8b7&topic=830406.0
http://muonlineint.com/forum/index.php?topic=853.0
http://muonlineint.com/forum/index.php?topic=1601.0
http://www.deliberarchia.org/forum/index.php?topic=975239.0
http://otitismediasociety.org/forum/index.php?topic=143368.0
https://reficulcoin.com/index.php?topic=15068.0
http://153.120.114.241/eso/index.php/16881437-igra-prestolovgame-of-thrones-8-sezon-4-seria-zj7-igra-prestolo
http://www.deliberarchia.org/forum/index.php?topic=958610.0
http://HyUa.1fps.icu/l/szIaeDC
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=10659
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=14620
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=589052
http://www.rocktheboat.cc/groups/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%83%d0%ba%d1%80%d0%b0%d0%b8%d0%bd%d0%b0-%d1%81%d0%bc%d0%be%d1%82-337209448/
http://www.rocktheboat.cc/groups/9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-9-qx9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d1%85%d0%be%d0%bb%d0%be/
http://haniel.ir/index.php/component/k2/itemlist/user/86373
http://seoksoononly.dothome.co.kr/qna/804356
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=44855
https://szenarist.ru/forum/index.php?topic=204956.0
http://www.autospa.lv/index.php/lv/component/k2/itemlist/user/9293
http://mobility-corp.com/index.php/component/k2/itemlist/user/2529698
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/291078
http://www.deliberarchia.org/forum/index.php?topic=975116.0
https://lucky28003.nl/forum/index.php?topic=11502.0
http://withinfp.sakura.ne.jp/eso/index.php/16899561-hdvideo-tolarobot-1-sezon-1-seria-l0-tolarobot-1-sezon-1-seria
http://smartacity.com/component/k2/itemlist/user/14748
http://macdistri.com/?option=com_k2&view=itemlist&task=user&id=297793
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1363685
http://c3isecurity.com.br/?option=com_k2&view=itemlist&task=user&id=475703
http://teambuildingpremium.com/forum/index.php?topic=788204.0
http://kurnaz.1to.us/index.php?topic=1.msg902
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4726505
https://lucky28003.nl/forum/index.php?topic=11483.0
http://seoksoononly.dothome.co.kr/?document_srl=778981
http://proandpro.it/?option=com_k2&view=itemlist&task=user&id=4533054
http://www.vivelabmanizales.com/%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-90-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-06-05-2019-r5-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-90-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.ekemoon.com/168083/050020192110/
http://www.rocktheboat.cc/groups/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%83%d0%ba%d1%80%d0%b0%d0%b8%d0%bd%d0%b0-%d1%81%d0%bc%d0%be%d1%82-1794626173/
http://www.theocraticamerica.org/forum/index.php?topic=28765.0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/238234
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=10838
http://webp.online/index.php?topic=51597.0
http://www.theocraticamerica.org/forum/index.php?topic=28780.0
http://webp.online/index.php?topic=51615.0
http://www.critico-expository.com/forum/index.php?topic=7176.0
http://www.quattroandpartners.it/component/k2/itemlist/user/1079141
http://married.dike.gr/index.php/component/k2/itemlist/user/45396
http://www.vivelabmanizales.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s9-%d1%82%d0%be%d0%bb%d1%8f/
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=23091
http://www.ekemoon.com/143699/050220192606/
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-live-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-4/
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-11-%d1%81%d0%b5%d1%80%d0%b8-3/
http://www.lustralesdevallehermoso.com/?option=com_k2&view=itemlist&task=user&id=48230
http://menulisilmiah.net/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-92-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-et4%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-92/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/291084
http://community.viajar.tur.br/index.php?p=/discussion/57498/rannyaya-ptashka-erkenci-kus-37-seriya-oykb-rannyaya-ptashka-erkenci-kus-37-seriya/p1%3Fnew=1
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1013632
http://k2.akademitelkom.ac.id/component/k2/itemlist/user/288180
https://l2thalassic.org/Forum/index.php?topic=2282.0
http://www.quattroandpartners.it/component/k2/itemlist/user/1063612
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3711420
http://seoksoononly.dothome.co.kr/?document_srl=718286
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/187975
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=237422
http://mvisage.sk/index.php/component/k2/itemlist/user/118241
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/10620
http://www.critico-expository.com/forum/index.php?topic=6889.0
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bn0%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f09-05/
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1891008
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1869653
http://proxima.co.rw/index.php/component/k2/itemlist/user/589438
http://webp.online/index.php?topic=51485.0
http://www.ekemoon.com/166772/052120191509/
http://www.rocktheboat.cc/groups/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-10-05-19-ju%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://8.droror.co.il/uncategorized/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kc1%d0%bd/
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/208583
http://www.ekemoon.com/158113/050920191708/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/292469
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=19137
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5-17/
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=16916
http://www.deliberarchia.org/forum/index.php?topic=968508.0
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=607854
http://bitpark.co.kr/board_IzjM66/3734226
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2562528
http://seoksoononly.dothome.co.kr/qna/733940
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=27627
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=14089
https://l2thalassic.org/Forum/index.php?topic=1015.0
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1007119
http://www.camaracoyhaique.cl/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xa2%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f05-05/
http://condolencias.servisa.es/3-6-05-05-2019-z4-3-6
http://euromouleusinage.com/index.php/component/k2/itemlist/user/106497
http://www.vivelabmanizales.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s8-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5/
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7307600
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=304818
https://lucky28003.nl/forum/index.php?topic=12069.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/436437
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/439013
https://prosocyr.com/?option=com_k2&view=itemlist&task=user&id=608364
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1773713
http://www.deliberarchia.org/forum/index.php?topic=891303.0
http://danielmillsap.com/forum/index.php?topic=978470.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1090907
http://153.120.114.241/eso/index.php/16880303-igra-prestolov-8-sezon-7-seria-ofr-igra-prestolov-8-sezon-7-ser
http://danielmillsap.com/forum/index.php?topic=822654.0
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=376117
https://www.resproxy.com/forum/index.php/755008-milliardy-4-sezon-5-seria-ppq-milliardy-4-sezon-5-seria-0405201/0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1123949
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=32636
https://tg.vl-mp.com/index.php?topic=1257108.0
http://thermoplast.envolgroupe.com/component/k2/author/66925
http://danielmillsap.com/forum/index.php?topic=810245.0
https://www.youngbiker.de/wbboard/index.php?page=User&userID=783248
http://avengerro.top/forum/index.php?topic=18373.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=35739
http://www.glasshouseproject.com.ng/index.php/component/k2/itemlist/user/33223
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1005567
http://www.tessabannampad.go.th/webboard/index.php?topic=188481.0
http://www.deliberarchia.org/forum/index.php?topic=910908.0
http://www.popolsku.fr.pl/forum/index.php?topic=340739.0
http://danielmillsap.com/forum/index.php?topic=948025.0
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7200652
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3452314
http://forum.thaibetrank.com/index.php?topic=1089518.0
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1126936
http://webp.online/index.php?topic=47198.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1108667
http://avengerro.top/forum/index.php?topic=9674.0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=757812
http://www.deliberarchia.org/forum/index.php?topic=986505.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bbf-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80/
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1793331
http://muratliziraatodasi.org/forum/index.php?topic=344078.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2467601
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1676363
http://www.arunagreen.com/index.php/component/k2/itemlist/user/375236
http://www.telcon.gr/index.php/component/k2/itemlist/user/36954
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/445748
http://forums.abs-cbn.com/welcome-back-kapamilya%21/ma-4-eo-9-e-fxg-ma-4-eo-9-e-25-04-2019/?PHPSESSID=51phb278ulkbtj2u2ff5tleic3
http://withinfp.sakura.ne.jp/eso/index.php/16802559-vetrenyj-hercai-10-seria-q5ar-vetrenyj-hercai-10-seria/0
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/251805
http://www.popolsku.fr.pl/forum/index.php?topic=347017.0
http://danielmillsap.com/forum/index.php?topic=831112.0
https://tg.vl-mp.com/index.php?topic=1289551.0
http://menulisilmiah.net/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sgw-%d0%b8%d0%b3%d1%80%d0%b0/
http://married.dike.gr/index.php/component/k2/itemlist/user/41453
http://healthyteethpa.org/component/k2/itemlist/user/5311043
http://153.120.114.241/eso/index.php/16876265-sverh-estestvennoe-14-sezon-19-seria-vzz-sverh-estestvennoe-14-
http://danielmillsap.com/forum/index.php?topic=846662.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1037735
http://seoksoononly.dothome.co.kr/qna/426928
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qo9-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8/
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bfi-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/62835
http://www.deliberarchia.org/forum/index.php?topic=770412.0
http://macdistri.com/index.php/component/k2/itemlist/user/275089
http://teambuildingpremium.com/forum/index.php?topic=593484.0
http://teambuildingpremium.com/forum/index.php?topic=629816.0
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1542711
http://healthyteethpa.org/component/k2/itemlist/user/5240246
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=895011
https://members.fbhaters.com/index.php?topic=65309.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1114067
http://smartacity.com/component/k2/itemlist/user/13093
http://married.dike.gr/index.php/component/k2/itemlist/user/40635
https://instaldec.com/?option=com_k2&view=itemlist&task=user&id=608794
https://www.youngbiker.de/wbboard/index.php?page=User&userID=783068
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=284114
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3285966
http://www.deliberarchia.org/forum/index.php?topic=901207.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2521393
http://danielmillsap.com/forum/index.php?topic=827406.0
http://healthyteethpa.org/component/k2/itemlist/user/5281204
http://www.arunagreen.com/index.php/component/k2/itemlist/user/379329
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dly-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=76879
http://travelsolution.info/index.php/component/k2/itemlist/user/707395
https://www.resproxy.com/forum/index.php/758833-milliardy-4-sezon-11-seria-vyt-milliardy-4-sezon-11-seria-05052
http://www.deliberarchia.org/forum/index.php?topic=781368.0
http://www.spazioad.com/component/k2/itemlist/user/7108677
http://www.deliberarchia.org/forum/index.php?topic=804597.0
https://www.shaiyax.com/index.php?topic=299514.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1108635
http://www.crnmedia.es/component/k2/itemlist/user/83254
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/246957
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3193321
http://153.120.114.241/eso/index.php/16873013-igra-prestolov-8-sezon-2-seria-grn-igra-prestolov-8-sezon-2-ser
https://www.shaiyax.com/index.php?topic=300303.0
http://withinfp.sakura.ne.jp/eso/index.php/16776720-riverdejl-riverdale-3-sezon-23-seria-yqe-riverdejl-riverdale-3-
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=34843
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/365713
http://danielmillsap.com/forum/index.php?topic=834102.0
http://danielmillsap.com/forum/index.php?topic=786281.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3454962
http://dcasociados.eu/component/k2/itemlist/user/82289
http://www.moyakmermer.com/index.php/component/k2/itemlist/user/524870
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3251607
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=592169.0
http://teambuildingpremium.com/forum/index.php?topic=593448.0
http://robocit.com/index.php/component/k2/itemlist/user/447540
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1555632
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=236692
http://seoksoononly.dothome.co.kr/qna/395556
http://thermoplast.envolgroupe.com/component/k2/author/73181
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1130144
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=889299
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/50800
https://www.resproxy.com/forum/index.php/744472-milliardy-4-sezon-7-seria-xcz-milliardy-4-sezon-7-seria-0405201/0
http://withinfp.sakura.ne.jp/eso/index.php/16840148-rannaa-ptaska-erkenci-kus-45-seria-u0vt-rannaa-ptaska-erkenci-k/0
http://myrechockey.com/forums/index.php?topic=55222.0
http://avengerro.top/forum/index.php?topic=19067.0
https://tg.vl-mp.com/index.php?topic=1263278.0
https://tg.vl-mp.com/index.php?topic=1288619.0
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1522443
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81-14/
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=36510
http://myrechockey.com/forums/index.php?topic=55250.0
http://www.deliberarchia.org/forum/index.php?topic=971554.0
http://webp.online/index.php?topic=40942.0
http://mediaville.me/index.php/component/k2/itemlist/user/210566
http://healthyteethpa.org/component/k2/itemlist/user/5279814
http://mobility-corp.com/index.php/component/k2/itemlist/user/2416854
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1130100
http://seoksoononly.dothome.co.kr/qna/457334
http://withinfp.sakura.ne.jp/eso/index.php/16865648-voskressij-ertugrul-143-seria-s9cq-voskressij-ertugrul-143-seri/0
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81-43/
http://www.tessabannampad.go.th/webboard/index.php?topic=193822.0
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xg6-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1310373
http://www.deliberarchia.org/forum/index.php?topic=775664.0
https://tg.vl-mp.com/index.php?topic=1324617.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pmj-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1557995
http://www.tessabannampad.go.th/webboard/index.php?topic=191664.0
http://www.popolsku.fr.pl/forum/index.php?topic=332135.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=33068
http://macdistri.com/index.php/component/k2/itemlist/user/310773
http://www.deliberarchia.org/forum/index.php?topic=973261.0
http://married.dike.gr/index.php/component/k2/itemlist/user/46179
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rq6%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5/
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/184687
https://lucky28003.nl/forum/index.php?topic=11676.0
http://www.ekemoon.com/141747/051420194605/
http://highlanderonline.cmshelplive.net/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2/
http://macdistri.com/index.php/component/k2/itemlist/user/311776
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=17497
http://www.camaracoyhaique.cl/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81-4/
http://euromouleusinage.com/index.php/component/k2/itemlist/user/113498
http://matrixpharm.ru/forum/index.php?PHPSESSID=s6sp2cjg5an4i72dd9ik4ddbk2&action=profile;u=173803
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1560311
http://menulisilmiah.net/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l3-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9/
http://forum.politeknikgihon.ac.id/index.php?topic=24790.0
http://withinfp.sakura.ne.jp/eso/index.php/16889575-efir-tola-robot-1-seria-r4-tola-robot-1-seria
http://dev.aabn.org.gh/component/k2/itemlist/user/516244
http://www.afikgan.co.il/index.php/component/k2/itemlist/user/26360
http://bitpark.co.kr/?document_srl=3763018
http://poselokgribovo.ru/forum/index.php?topic=734482.0
http://condolencias.servisa.es/3-10-06-05-2019-y4-3-10
http://www.vivelabmanizales.com/hd-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81/
https://tg.vl-mp.com/index.php?topic=1338071.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=291029
http://arunagreen.com/index.php/component/k2/itemlist/user/432255
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/14187
http://forum.byehaj.hu/index.php?topic=81704.0
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=500671
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-17-%d1%81%d0%b5-6/
http://dcasociados.eu/component/k2/itemlist/user/87252
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4743670
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/50061
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/766032
http://patagroupofcompanies.com/component/k2/itemlist/user/202935
http://associationsila.org/component/k2/itemlist/user/283794
http://thermoplast.envolgroupe.com/component/k2/author/82248
http://seoksoononly.dothome.co.kr/qna/758068
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/8548
http://dohairbiz.com/en/component/k2/itemlist/user/2710048.html
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1860282
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3569498
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/471060
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-xiaomi%C2%BB-lz%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-xiaomi%C2%BB11-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD
http://fbpharm.net/index.php/component/k2/itemlist/user/24664
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/297390
http://seoksoononly.dothome.co.kr/qna/772021
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4837285
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=299763
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=29302.0
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1557138
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=496032
http://seoksoononly.dothome.co.kr/qna/735726
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/66944
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4827137
http://poselokgribovo.ru/forum/index.php?topic=736170.0
http://menulisilmiah.net/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-88-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xz4%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-88-%d1%81%d0%b5%d1%80%d0%b8%d1%8f07-05-2019/
http://www.vivelabmanizales.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a5-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5/
http://febrescordero.gob.ec/?option=com_k2&view=itemlist&task=user&id=81135
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=779473
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/6931
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=78923
http://www.nienkevanrijn.nl/component/k2/itemlist/user/426259
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=65961
http://proandpro.it/index.php/component/k2/itemlist/user/4538280
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3374513
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4826109
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/292687
http://bitpark.co.kr/?document_srl=3770696
http://poselokgribovo.ru/forum/index.php?topic=730052.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=28708.0
http://www.vivelabmanizales.com/hd-video-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z3-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1/
http://moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=674253
http://poselokgribovo.ru/forum/index.php?topic=720417.0
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/198489
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/70596
http://poselokgribovo.ru/forum/index.php?topic=736727.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=682284.0
http://www.vivelabmanizales.com/%d1%81%d0%be%d0%b4%d0%b5%d1%80%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2019-f0-%d1%81%d0%be%d0%b4%d0%b5%d1%80%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-9-%d1%81/
http://maderadepaulownia.com/component/k2/itemlist/user/84077
http://arunagreen.com/?option=com_k2&view=itemlist&task=user&id=420996
http://molweb.ru/groups/xolostyak-9-sezon-10-vypusk-bosch-arxolostyak-9-sezon-10-vypusk-bosch22-xolostyak-9-sezon-10-vypusk-bosch/
http://www.m1avio.com/index.php/component/k2/itemlist/user/3622341
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7313575
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=268971
http://www.phan-aen.go.th/forum/index.php?topic=626743.0
http://batubersurat.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=44741
http://www.vivelabmanizales.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d0%ba%d1%80%d0%b8%d0%b4-ey%d1%85%d0%be%d0%bb%d0%be%d1%81/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-8-eo-2-e-hbn-a-etoo-8-eo-2-e-25-04-2019/
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3683686
http://married.dike.gr/index.php/component/k2/itemlist/user/25625
http://www.deliberarchia.org/forum/index.php?topic=953282.0
http://withinfp.sakura.ne.jp/eso/index.php/16772116-voron-kuzgun-13-seria-t3qt-voron-kuzgun-13-seria/0
http://www.popolsku.fr.pl/forum/index.php?topic=348686.0
https://mcsetup.tk/bbs/index.php?topic=224509.0
https://www.blog.quora.healthcare/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j1ha-%d0%b2%d0%be%d1%81%d0%ba%d1%80
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rg4-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16/
http://www.x2145-productions.technology/index.php?title=%C2%AB%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C_%D0%9B%D0%B5%D0%B2_2019_%C2%BB_09-05-2019_%C2%AB%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C_%D0%9B%D0%B5%D0%B2_2019_%C2%BB_%C2%AB%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C_%D0%9B%D0%B5%D0%B2_2019_%C2%BB
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/176113
http://metropolis.ga/index.php?topic=3646.0
http://danielmillsap.com/forum/index.php?topic=877444.0
https://tg.vl-mp.com/index.php?topic=1265591.0
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=894265
http://minostech.co.kr/news/3350638
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/935260
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/247329
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/145890
http://sam-sanat.ir/?option=com_k2&view=itemlist&task=user&id=140885
http://mobility-corp.com/index.php/component/k2/itemlist/user/2508411
http://healthyteethpa.org/component/k2/itemlist/user/5301105
http://pptforum.dothome.co.kr/board_APMk06/622920
http://www.arunagreen.com/index.php/component/k2/itemlist/user/376885
http://www.emrabq8.com/index.php/component/k2/itemlist/user/1741034
http://teambuildingpremium.com/forum/index.php?topic=648996.0
http://danielmillsap.com/forum/index.php?topic=793094.0
http://associationsila.org/component/k2/itemlist/user/261282
http://macdistri.com/index.php/component/k2/itemlist/user/222912
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gcc-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://www.phan-aen.go.th/forum/index.php?topic=610569.0
https://members.fbhaters.com/index.php?topic=71452.0
https://www.shaiyax.com/index.php?topic=284847.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3263997
http://thermoplast.envolgroupe.com/component/k2/author/65798
https://www.youngbiker.de/wbboard/index.php?page=User&userID=782363
https://tg.vl-mp.com/index.php?topic=1302919.0
http://withinfp.sakura.ne.jp/eso/index.php/16767298-rasskaz-sluzanki-3-sezon-4-seria-dsy-rasskaz-sluzanki-3-sezon-4/0
http://www.spazioad.com/component/k2/itemlist/user/7164846
https://tg.vl-mp.com/index.php?topic=1322726.0
https://tg.vl-mp.com/index.php?topic=1336905.0
http://webp.online/index.php?topic=48343.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/ootk-9-eo-12-k-kcootk-9-eo-12-k/?PHPSESSID=abr5a4cn75u251tlbv82c7dc61
http://boutique.in.th/?option=com_k2&view=itemlist&task=user&id=143321
http://mobility-corp.com/index.php/component/k2/itemlist/user/2495192
http://sam-sanat.ir/?option=com_k2&view=itemlist&task=user&id=137030
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1468809
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7172714
http://seoksoononly.dothome.co.kr/qna/425328
http://pptforum.dothome.co.kr/board_APMk06/647464
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1525496
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/242106
http://seoksoononly.dothome.co.kr/qna/453423
http://danielmillsap.com/forum/index.php?topic=839735.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1310025
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ls9-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8/
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/140991
http://danielmillsap.com/forum/index.php?topic=798380.0
https://www.blog.quora.healthcare/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a7pq-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=410186
http://seoksoononly.dothome.co.kr/qna/414961
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=157925
https://ne-kuru.ru/index.php?topic=202972.0
https://tg.vl-mp.com/index.php?topic=1347543.0
http://matinbank.ir/component/k2/itemlist/user/4459590.html
http://pptforum.dothome.co.kr/board_APMk06/826776
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pa8-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15/
http://muratliziraatodasi.org/forum/index.php?topic=344687.0
https://tg.vl-mp.com/index.php?topic=1257781.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/186001
http://arunagreen.com/index.php/component/k2/itemlist/user/425455
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=582709.0
http://withinfp.sakura.ne.jp/eso/index.php/16776021-voron-kuzgun-19-seria-e7at-voron-kuzgun-19-seria
http://married.dike.gr/index.php/component/k2/itemlist/user/36562
http://www.deliberarchia.org/forum/index.php?topic=769914.0
http://healthyteethpa.org/component/k2/itemlist/user/5279070
http://seoksoononly.dothome.co.kr/qna/427025
http://www.deliberarchia.org/forum/index.php?topic=961839.0
http://153.120.114.241/eso/index.php/16852169-milliardy-4-sezon-10-seria-fuw-milliardy-4-sezon-10-seria
https://www.youngbiker.de/wbboard/index.php?page=User&userID=781414
http://rudraautomation.com/index.php/component/k2/author/104839
http://www.atab.com.sa/index.php/en/?option=com_k2&view=itemlist&task=user&id=1560790
http://boutique.in.th/?option=com_k2&view=itemlist&task=user&id=143348
http://healthyteethpa.org/component/k2/itemlist/user/5298654
http://153.120.114.241/eso/index.php/16871647-lubov-smert-i-roboty-love-death-and-robots-13-seria-krp-lubov-s
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=381632
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/119408
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1674782
http://webp.online/index.php?topic=50534.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=271835
http://www.arunagreen.com/index.php/component/k2/itemlist/user/395818
https://www.wikisexguide.com/wiki/%C2%AB%D0%9F%D0%BE%D1%81%D0%BB%D0%B5%C2%BB_06-05-2019_%D0%9F%D0%BE%D1%81%D0%BB%D0%B5_%C2%AB%D0%9F%D0%BE%D1%81%D0%BB%D0%B5%C2%BB?wpName=DelorasHower954&wpPassword=453EQhRbuF&wploginattempt=Log+in&wpEditToken=%2B%5C&title=Special:UserLogin&authAction=login&force=&wpLoginToken=f3916ffef00bf9d8a819e37c9700c0165ccfbf15%2B%5C&wpName=DelorasHower954&wpPassword=453EQhRbuF&wploginattempt=Log+in&wpEditToken=%2B%5C&title=Special:UserLogin&authAction=login&force=&wpLoginToken=f3916ffef00bf9d8a819e37c9700c0165ccfbf15%2B%5C
http://www.quattroandpartners.it/component/k2/itemlist/user/1038234
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/455983
http://www.popolsku.fr.pl/forum/index.php?topic=343758.0
https://ne-kuru.ru/index.php?topic=204054.0
http://minostech.co.kr/news/3354003
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fvx-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-12-%d1%81%d0%b5%d1%80/
http://www.m1avio.com/?option=com_k2&view=itemlist&task=user&id=3585989
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1687074
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1576097
http://www.popolsku.fr.pl/forum/index.php?topic=340897.0
http://www.cosl.com.sg/UserProfile/tabid/61/userId/25885328/Default.aspx
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12194
http://www.oortsociety.com/index.php?topic=9879.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3193541
http://www.glasshouseproject.com.ng/index.php/component/k2/itemlist/user/38844
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1092698
https://tg.vl-mp.com/index.php?topic=1321748.0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=536058
http://metropolis.ga/index.php?topic=5814.0
http://danielmillsap.com/forum/index.php?topic=828797.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/440027
http://danielmillsap.com/forum/index.php?topic=823395.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/141803
http://danielmillsap.com/forum/index.php?topic=795365.0
http://teambuildingpremium.com/forum/index.php?topic=632142.0
http://healthyteethpa.org/component/k2/itemlist/user/5307297
https://tg.vl-mp.com/index.php?topic=1326228.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/172589
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=277616
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1610166
http://macdistri.com/index.php/component/k2/itemlist/user/224080
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1700736
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/255695
http://grupotir.com/component/k2/itemlist/user/41645
https://tg.vl-mp.com/index.php?topic=1328233.0
http://macdistri.com/index.php/component/k2/itemlist/user/218709
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1735808
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1592627
http://www.spazioad.com/component/k2/itemlist/user/7104785
http://danielmillsap.com/forum/index.php?topic=867784.0
http://danielmillsap.com/forum/index.php?topic=872318.0
https://www.youngbiker.de/wbboard/index.php?page=User&userID=783843
http://danielmillsap.com/forum/index.php?topic=801472.0
http://healthyteethpa.org/component/k2/itemlist/user/5346505
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2401863
http://macdistri.com/index.php/component/k2/itemlist/user/223659
https://members.fbhaters.com/index.php?topic=74826.0
http://malbeot.iptime.org:10009/xe/board/3831968
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26094731/Default.aspx
https://tg.vl-mp.com/index.php?topic=1327635.0
http://seoksoononly.dothome.co.kr/qna/441858
http://danielmillsap.com/forum/index.php?topic=882997.0
http://avengerro.top/forum/index.php?topic=16919.0
http://www.deliberarchia.org/forum/index.php?topic=768853.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/271235
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1454493
http://healthyteethpa.org/component/k2/itemlist/user/5331017
http://pptforum.dothome.co.kr/board_APMk06/619307
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=245804
http://www.deliberarchia.org/forum/index.php?topic=976863.0
http://danielmillsap.com/forum/index.php?topic=791552.0
http://www.elpinatarense.com/?option=com_k2&view=itemlist&task=user&id=151455
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/40598
http://teambuildingpremium.com/forum/index.php?topic=652733.0
http://teambuildingpremium.com/forum/index.php?topic=592768.0
http://www.deliberarchia.org/forum/index.php?topic=985422.0
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ty7-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://withinfp.sakura.ne.jp/eso/index.php/16769363-cernoe-zerkalo-5-sezon-2-seria-uqk-cernoe-zerkalo-5-sezon-2-ser/0
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2391517
http://teambuildingpremium.com/forum/index.php?topic=659417.0
http://www.deliberarchia.org/forum/index.php?topic=983420.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1327534
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/135632
http://muratliziraatodasi.org/forum/index.php?topic=335656.0
http://danielmillsap.com/forum/index.php?topic=825197.0
http://www.crowdfundingchile.cl/%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ca7-%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://danielmillsap.com/forum/index.php?topic=827714.0
http://seoksoononly.dothome.co.kr/qna/421945
https://www.resproxy.com/forum/index.php/738708-rasskaz-sluzanki-3-sezon-4-seria-fok-rasskaz-sluzanki-3-sezon-4/0
http://withinfp.sakura.ne.jp/eso/index.php/16840417-voskressij-ertugrul-145-seria-w3pe-voskressij-ertugrul-145-seri/0
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/529288
https://www.blog.quora.healthcare/%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-56-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s4bx-%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-56-%d1%81%d0%b5%d1%80%d0%b8%d1%8f
http://www.popolsku.fr.pl/forum/index.php?topic=336096.0
http://withinfp.sakura.ne.jp/eso/index.php/16781668-milliardy-4-sezon-10-seria-hve-milliardy-4-sezon-10-seria-01052/0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3297934
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/475565
http://forums.abs-cbn.com/welcome-back-kapamilya%21/et-e-7-e-zget-e-7-e/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1248265
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1608960
http://153.120.114.241/eso/index.php/16871478-cernoe-zerkalo-5-sezon-2-seria-ebr-cernoe-zerkalo-5-sezon-2-ser
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1091801
http://robocit.com/?option=com_k2&view=itemlist&task=user&id=447259
http://forum.thaibetrank.com/index.php?topic=1068356.0
http://withinfp.sakura.ne.jp/eso/index.php/16899779-vossoedinenie-vuslat-19-seria-d4au-vossoedinenie-vuslat-19-seri
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-eun-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://webp.online/index.php?topic=42202.0
http://www.deliberarchia.org/forum/index.php?topic=973545.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4606253
https://lucky28003.nl/forum/index.php?topic=9388.0
http://seoksoononly.dothome.co.kr/qna/652180
http://flyinghonda.de/wbb/index.php?page=User&userID=808150
http://www.deliberarchia.org/forum/index.php?topic=934258.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jnn-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.sopcich.com/UserProfile/tabid/42/UserID/1670780/Default.aspx
http://teambuildingpremium.com/forum/index.php?topic=646714.0
http://teambuildingpremium.com/forum/index.php?topic=607804.0
http://www.pcosmetic.ir/?option=com_k2&view=itemlist&task=user&id=10002
https://mcsetup.tk/bbs/index.php?topic=228549.0
http://pptforum.dothome.co.kr/board_APMk06/660240
http://metropolis.ga/index.php?topic=5422.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/om-7-e-jaom-7-e/?PHPSESSID=uahbvblgnq5mm5klqfa2m58l37
http://macdistri.com/index.php/component/k2/itemlist/user/302017
http://rudraautomation.com/index.php/component/k2/author/102574
http://boutique.in.th/?option=com_k2&view=itemlist&task=user&id=143390
http://withinfp.sakura.ne.jp/eso/index.php/16900909-voron-kuzgun-15-seria-s6jq-voron-kuzgun-15-seria/0
http://avengerro.top/forum/index.php?topic=18980.0
http://israengineering.com/index.php/component/k2/itemlist/user/1086593
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=685550
http://www.arunagreen.com/index.php/component/k2/itemlist/user/395258
http://webp.online/index.php?topic=45948.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/et-e-17-e-etet-e-17-e/?PHPSESSID=8slcl5i39pv4keki0hvbig1o71
https://members.fbhaters.com/index.php?topic=76948.0
https://www.youngbiker.de/wbboard/index.php?page=User&userID=782539
http://www.x2145-productions.technology/index.php?title=%C3%82%C2%AB%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%91%E2%82%AC%C3%90%C2%B5%C3%90%C2%BC%C3%91_%C3%90%C5%93%C3%90%C2%BE%C3%90%C2%BD%C3%91%C3%91%E2%80%9A%C3%91%E2%82%AC%C3%90%C2%BE%C3%90%C2%B2%C3%82%C2%BB_06-05-2019_%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%91%E2%82%AC%C3%90%C2%B5%C3%90%C2%BC%C3%91_%C3%90%C5%93%C3%90%C2%BE%C3%90%C2%BD%C3%91%C3%91%E2%80%9A%C3%91%E2%82%AC%C3%90%C2%BE%C3%90%C2%B2_%C3%82%C2%AB%C3%90%C3%A2%E2%82%AC%E2%84%A2%C3%91%E2%82%AC%C3%90%C2%B5%C3%90%C2%BC%C3%91_%C3%90%C5%93%C3%90%C2%BE%C3%90%C2%BD%C3%91%C3%91%E2%80%9A%C3%91%E2%82%AC%C3%90%C2%BE%C3%90%C2%B2%C3%82%C2%BB
http://www.m1avio.com/?option=com_k2&view=itemlist&task=user&id=3598545
http://teambuildingpremium.com/forum/index.php?topic=669545.0
http://www.tessabannampad.go.th/webboard/index.php?topic=188308.0
http://webp.online/index.php?topic=41371.0
http://poselokgribovo.ru/forum/index.php?topic=613005.0
http://danielmillsap.com/forum/index.php?topic=916034.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vot-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-14-%d1%81%d0%b5%d1%80/
http://danielmillsap.com/forum/index.php?topic=918679.0
https://www.resproxy.com/forum/index.php/807768-nasa-istoria-67-seria-c6fz-nasa-istoria-67-seria/0
http://tradebest.org/board_MdUI61/1581061
https://www.blog.quora.healthcare/%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-67-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l1np-%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-67
http://www.web2interactive.com/index.php/component/k2/itemlist/user/3583672
http://teambuildingpremium.com/forum/index.php?topic=615478.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/et-e-16-e-flet-e-16-e/?PHPSESSID=8a90sok0hcs1n6041dijn5s473
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=476416
http://www.deliberarchia.org/forum/index.php?topic=985867.0
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4733756
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1357676
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=483067
https://tg.vl-mp.com/index.php?topic=1304660.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/57788
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/140001
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2523275
http://associationsila.org/component/k2/itemlist/user/285853
http://www.glasshouseproject.com.ng/index.php/component/k2/itemlist/user/44984
http://dessa.com.br/index.php/component/k2/itemlist/user/306022
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/13863
http://metropolis.ga/index.php?topic=5164.0
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=290776
http://married.dike.gr/index.php/component/k2/itemlist/user/34875
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=410742
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43150
http://mediaville.me/index.php/component/k2/itemlist/user/216320
http://danielmillsap.com/forum/index.php?topic=816753.0
https://tg.vl-mp.com/index.php?topic=1314180.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/451630
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=873484
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1296559
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-8-eo-5-e-aye-a-etoo-8-eo-5-e-23-04-2019/
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1523967
http://seoksoononly.dothome.co.kr/qna/643680
http://forum.thaibetrank.com/index.php?topic=1094069.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39853
https://tg.vl-mp.com/index.php?topic=1325690.0
http://www.deliberarchia.org/forum/index.php?topic=968896.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=40951
http://danielmillsap.com/forum/index.php?topic=873785.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4732978
http://withinfp.sakura.ne.jp/eso/index.php/16815400-vossoedinenie-vuslat-16-seria-a8rn-vossoedinenie-vuslat-16-seri/0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2523737
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-doj-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-9-%d1%81%d0%b5%d1%80%d0%b8/
https://mcsetup.tk/bbs/index.php?topic=231579.0
http://www.deliberarchia.org/forum/index.php?topic=931852.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/263343
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1667080
http://mobility-corp.com/index.php/component/k2/itemlist/user/2506008
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39729
http://fbpharm.net/index.php/component/k2/itemlist/user/15350
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1348784
http://withinfp.sakura.ne.jp/eso/index.php/16803410-vetrenyj-hercai-12-seria-b2vf-vetrenyj-hercai-12-seria/0
http://dscardip.com/board/index.php?page=User&userID=648328
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3196912
http://tradebest.org/board_MdUI61/1591391
https://tg.vl-mp.com/index.php?topic=1314651.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/63565
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1108585
http://www.popolsku.fr.pl/forum/index.php?topic=328741.0
http://teambuildingpremium.com/forum/index.php?topic=607103.0
http://withinfp.sakura.ne.jp/eso/index.php/16826332-vetrenyj-hercai-24-seria-w3ao-vetrenyj-hercai-24-seria/0
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1606956
http://webp.online/index.php?topic=38203.15
http://153.120.114.241/eso/index.php/16876362-lubov-smert-i-roboty-love-death-and-robots-10-seria-ger-lubov-s
http://c3isecurity.com.br/component/k2/itemlist/user/437332
http://www.deliberarchia.org/forum/index.php?topic=790427.0
https://mcsetup.tk/bbs/index.php?topic=229231.0
http://www.phan-aen.go.th/forum/index.php?topic=611996.0
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3316970
http://77.93.38.205/index.php/component/k2/itemlist/user/381495
http://www.m1avio.com/index.php/component/k2/itemlist/user/3603101
http://dessa.com.br/index.php/component/k2/itemlist/user/300757
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/470575
http://www.phan-aen.go.th/forum/index.php?topic=609446.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1574033
http://metropolis.ga/index.php?topic=5234.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/511097
http://danielmillsap.com/forum/index.php?topic=872785.0
http://proandpro.it/index.php/component/k2/itemlist/user/4449059
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ed0-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12/
http://thermoplast.envolgroupe.com/component/k2/author/79196
http://teambuildingpremium.com/forum/index.php?topic=635430.0
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=262877
http://danielmillsap.com/forum/index.php?topic=804566.0
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1129550
http://www.sopcich.com/UserProfile/tabid/42/UserID/1776320/Default.aspx
http://minostech.co.kr/news/3373414
https://mcsetup.tk/bbs/index.php?topic=226232.0
http://married.dike.gr/index.php/component/k2/itemlist/user/39448
http://www.deliberarchia.org/forum/index.php?topic=804749.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=283768
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=24669
http://avengerro.top/forum/index.php?topic=17012.0
http://www.pcosmetic.ir/?option=com_k2&view=itemlist&task=user&id=10025
http://teambuildingpremium.com/forum/index.php?topic=608556.0
http://menulisilmiah.net/%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-59-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k3lw-%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-59-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.phan-aen.go.th/forum/index.php?topic=609258.0
https://www.resproxy.com/forum/index.php/756237-igra-prestolov-8-sezon-8-seria-avb-igra-prestolov-8-sezon-8-ser/0
http://dessa.com.br/component/k2/itemlist/user/302027
http://www.web2interactive.com/index.php/component/k2/itemlist/user/3471045
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=16100
https://tg.vl-mp.com/index.php?topic=1308140.0
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ne6-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8/
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/41672
http://danielmillsap.com/forum/index.php?topic=823222.0
http://danielmillsap.com/forum/index.php?topic=786144.0
http://www.deliberarchia.org/forum/index.php?topic=765761.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=291311
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1508732
https://tg.vl-mp.com/index.php?topic=1283210.0
http://teambuildingpremium.com/forum/index.php?topic=611957.0
http://c3isecurity.com.br/?option=com_k2&view=itemlist&task=user&id=387436
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1092956
http://muratliziraatodasi.org/forum/index.php?topic=344166.0
[url=http://cialisdxt.com/]buy generic cialis[/url]
cialis 20 mg 30'lu tablet
<a href="http://cialisdxt.com/">cialis online</a>
effectiveness of cialis vs viagra vs levitra comparison table
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/131731
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1127924
http://malbeot.iptime.org:10009/xe/board/3850300
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=592911.0
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3694848
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3312296
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=890885
https://www.blog.quora.healthcare/%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-67-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d8mt-%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-67
https://www.resproxy.com/forum/index.php/744741-milliardy-4-sezon-10-seria-hre-milliardy-4-sezon-10-seria-04052/0
http://muratliziraatodasi.org/forum/index.php?topic=345466.0
https://www.youngbiker.de/wbboard/index.php?page=User&userID=782529
https://tg.vl-mp.com/index.php?topic=1309284.0
https://www.blog.quora.healthcare/%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-58-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g2yw-%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-58-%d1%81%d0%b5%d1%80%d0%b8%d1%8f
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1091811
http://www2.yasothon.go.th/smf/index.php?topic=159.142590
https://www.resproxy.com/forum/index.php/764843-rasskaz-sluzanki-3-sezon-4-seria-wcv-rasskaz-sluzanki-3-sezon-4/0
http://www.deliberarchia.org/forum/index.php?topic=973472.0
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=266481
http://www.deliberarchia.org/forum/index.php?topic=773282.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3175680
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/699560
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ap8-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://muratliziraatodasi.org/forum/index.php?topic=329327.0
http://teambuildingpremium.com/forum/index.php?topic=620622.0
http://soc-human.kz/index.php/component/k2/itemlist/user/1549331
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1633140
http://macdistri.com/index.php/component/k2/itemlist/user/203961
https://mcsetup.tk/bbs/index.php?topic=226079.0
https://instaldec.com/?option=com_k2&view=itemlist&task=user&id=599380
http://danielmillsap.com/forum/index.php?topic=809584.0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=756566
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1771179
http://www.arunagreen.com/index.php/component/k2/itemlist/user/376948
https://tg.vl-mp.com/index.php?topic=1304798.0
http://seoksoononly.dothome.co.kr/qna/431414
http://avengerro.top/forum/index.php?topic=14793.0
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1955304
http://www.deliberarchia.org/forum/index.php?topic=943820.0
http://www.deliberarchia.org/forum/index.php?topic=919808.0
http://withinfp.sakura.ne.jp/eso/index.php/16844908-vetrenyj-hercai-8-seria-u2ma-vetrenyj-hercai-8-seria
http://metropolis.ga/index.php?topic=1728.0
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81-52/
http://forum.thaibetrank.com/index.php?topic=1079735.0
http://jpacschoolclubs.co.uk/?option=com_k2&view=itemlist&task=user&id=3267674
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2519738
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tkp-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://danielmillsap.com/forum/index.php?topic=808475.0
http://www.tessabannampad.go.th/webboard/index.php?topic=194608.0
https://tg.vl-mp.com/index.php?topic=1342940.0
https://www.shaiyax.com/index.php?topic=313727.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1605898
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7279965
https://members.fbhaters.com/index.php?topic=66691.0
http://zsmr.com.ua/index.php/component/k2/itemlist/user/491999
https://www.blog.quora.healthcare/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qev-%d0%b8%d0%b3%d1%80%d0%b0
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38673
http://danielmillsap.com/forum/index.php?topic=805319.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=591120.0
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7201615
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/266347
http://www.arunagreen.com/index.php/component/k2/itemlist/user/375973
http://teambuildingpremium.com/forum/index.php?topic=687494.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/511315
http://healthyteethpa.org/component/k2/itemlist/user/5319757
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=890888
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-grd-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://153.120.114.241/eso/index.php/16875899-sverh-estestvennoe-14-sezon-15-seria-rbk-sverh-estestvennoe-14-
http://afinandoemociones.com.ar/index.php/component/k2/itemlist/user/385659
http://danielmillsap.com/forum/index.php?topic=806950.0
http://menulisilmiah.net/%d0%bc%d0%b5%d1%80%d1%82%d0%b2%d0%be%d0%b5-%d0%be%d0%b7%d0%b5%d1%80%d0%be-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-px6-%d0%bc%d0%b5%d1%80%d1%82%d0%b2%d0%be%d0%b5-%d0%be%d0%b7%d0%b5%d1%80/
https://tg.vl-mp.com/index.php?topic=1342000.0
http://macdistri.com/index.php/component/k2/itemlist/user/222492
http://withinfp.sakura.ne.jp/eso/index.php/16802119-voskressij-ertugrul-146-seria-x6qz-voskressij-ertugrul-146-seri/0
http://seoksoononly.dothome.co.kr/qna/360302
http://pptforum.dothome.co.kr/board_APMk06/635471
http://seoksoononly.dothome.co.kr/qna/375371
http://www.deliberarchia.org/forum/index.php?topic=979442.0
https://www.youngbiker.de/wbboard/index.php?page=User&userID=781298
http://withinfp.sakura.ne.jp/eso/index.php/16767457-milliardy-4-sezon-7-seria-zeo-milliardy-4-sezon-7-seria-0105201/0
http://k2.akademitelkom.ac.id/component/k2/itemlist/user/293053
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1091064
http://www.deliberarchia.org/forum/index.php?topic=794354.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1250999
http://webp.online/index.php?topic=46453.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2562207
http://discussadeal.com/forum/index.php?topic=4251.0
http://mvisage.sk/index.php/component/k2/itemlist/user/114582
http://www.spazioad.com/component/k2/itemlist/user/7215545
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/460205
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=410103
http://danielmillsap.com/forum/index.php?topic=952154.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/287368
http://danielmillsap.com/forum/index.php?topic=845233.0
http://seoksoononly.dothome.co.kr/qna/421423
http://seoksoononly.dothome.co.kr/qna/400370
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3269022
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1126763
http://healthyteethpa.org/component/k2/itemlist/user/5276597
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=408398
https://www.resproxy.com/forum/index.php/743068-sverh-estestvennoe-14-sezon-17-seria-nsl-sverh-estestvennoe-14-/0
http://discussadeal.com/forum/index.php?topic=3299.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=223638
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2165338
https://www.blog.quora.healthcare/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t6ra-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80
http://forums.abs-cbn.com/welcome-back-kapamilya%21/e-eka-aota-11-e-cke-eka-aota-11-e/?PHPSESSID=dii3bkfciu2sf5j68pguintrh5
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1572688
http://www.deliberarchia.org/forum/index.php?topic=900245.0
http://www.tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1523669
http://jpacschoolclubs.co.uk/component/k2/itemlist/user/3256518
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=688286
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=10216
https://instaldec.com/?option=com_k2&view=itemlist&task=user&id=602241
http://withinfp.sakura.ne.jp/eso/index.php/16857367-zensina-59-seria-a1ae-zensina-59-seria
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1251976
http://muratliziraatodasi.org/forum/index.php?topic=345982.0
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/13674
https://sto54.ru/index.php/component/k2/itemlist/user/3178668
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39147
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1518028
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1108248
https://tg.vl-mp.com/index.php?topic=1297228.0
http://poselokgribovo.ru/forum/index.php?topic=620805.0
http://www.deliberarchia.org/forum/index.php?topic=903128.0
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=893388
https://mcsetup.tk/bbs/index.php?topic=232204.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=33933
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=667622
http://withinfp.sakura.ne.jp/eso/index.php/16925658-vetrenyj-hercai-5-seria-y9pd-vetrenyj-hercai-5-seria/0
http://www.oortsociety.com/index.php?topic=7782.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3257120
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=889402
http://teambuildingpremium.com/forum/index.php?topic=594721.0
http://www.popolsku.fr.pl/forum/index.php?topic=338805.0
http://danielmillsap.com/forum/index.php?topic=830327.0
http://metropolis.ga/index.php?topic=3215.0
http://teambuildingpremium.com/forum/index.php?topic=657425.0
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/583537
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=33928
http://danielmillsap.com/forum/index.php?topic=975951.0
http://www.deliberarchia.org/forum/index.php?topic=980771.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1631264
http://webp.online/index.php?topic=48871.0
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3374098
http://danielmillsap.com/forum/index.php?topic=801059.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1037010
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=296726
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=77333
http://www.deliberarchia.org/forum/index.php?topic=974538.0
http://soc-human.kz/index.php/component/k2/itemlist/user/1603497
http://fbpharm.net/index.php/component/k2/itemlist/user/16370
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=268790
https://www.resproxy.com/forum/index.php/753646-rasskaz-sluzanki-3-sezon-5-seria-ruq-rasskaz-sluzanki-3-sezon-5/0
http://webp.online/index.php?topic=43313.0
http://pptforum.dothome.co.kr/board_APMk06/618568
http://www.phan-aen.go.th/forum/index.php?topic=610327.0
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=890460
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12749
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/21221
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3251664
http://healthyteethpa.org/component/k2/itemlist/user/5320612
https://www.blog.quora.healthcare/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-45-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j3il-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0
http://mediaville.me/index.php/component/k2/itemlist/user/192626
http://poselokgribovo.ru/forum/index.php?topic=619771.0
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=246021
http://myrechockey.com/forums/index.php?topic=54480.0
http://zsmr.com.ua/index.php/component/k2/itemlist/user/379958
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3257151
http://danielmillsap.com/forum/index.php?topic=973662.0
http://macdistri.com/index.php/component/k2/itemlist/user/299877
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yzg-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80/
http://pptforum.dothome.co.kr/board_APMk06/659248
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1566083
http://www.x2145-productions.technology/index.php?title=%C2%AB%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C_%D0%9B%D0%B5%D0%B2_2019_%C2%BB_07-05-2019_%C2%AB%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C_%D0%9B%D0%B5%D0%B2_2019_%C2%BB_%C2%AB%D0%9A%D0%BE%D1%80%D0%BE%D0%BB%D1%8C_%D0%9B%D0%B5%D0%B2_2019_%C2%BB
http://fbpharm.net/index.php/component/k2/itemlist/user/13371
http://dcasociados.eu/component/k2/itemlist/user/81305
https://www.youngbiker.de/wbboard/index.php?page=User&userID=784343
http://hotelnomadpalace.com/index.php/component/k2/itemlist/user/19978
http://healthyteethpa.org/component/k2/itemlist/user/5280372
http://dscardip.com/board/index.php?page=User&userID=655185
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=242559
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=248264
http://danielmillsap.com/forum/index.php?topic=804698.0
http://www.popolsku.fr.pl/forum/index.php?topic=335884.0
http://batubersurat.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=37979
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/286983
http://danielmillsap.com/forum/index.php?topic=910603.0
https://www.blog.quora.healthcare/%d0%bd%d0%b5-%d0%be%d1%82%d0%bf%d1%83%d1%81%d0%ba%d0%b0%d0%b9-%d0%bc%d0%be%d1%8e-%d1%80%d1%83%d0%ba%d1%83-elimi-birakma-36-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k6wa-%d0%bd%d0%b5-%d0%be
http://menulisilmiah.net/%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hs9-%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/246893
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1116035
https://members.fbhaters.com/index.php?topic=62975.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=588574.0
http://153.120.114.241/eso/index.php/16876735-lubov-smert-i-roboty-love-death-and-robots-16-seria-wvl-lubov-s
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3677269
http://seoksoononly.dothome.co.kr/qna/457202
http://seoksoononly.dothome.co.kr/qna/421970
http://withinfp.sakura.ne.jp/eso/index.php/16789179-nasledie-14-seria-jtv-nasledie-14-seria
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3476940
https://www.blog.quora.healthcare/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r1ln-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80
http://www.tessabannampad.go.th/webboard/index.php?topic=190510.0
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=169957
http://teambuildingpremium.com/forum/index.php?topic=638976.0
http://www.popolsku.fr.pl/forum/index.php?topic=347154.0
http://teambuildingpremium.com/forum/index.php?topic=681241.0
http://withinfp.sakura.ne.jp/eso/index.php/16855464-vetrenyj-hercai-14-seria-j4ya-vetrenyj-hercai-14-seria
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1113622
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=285936
http://sdsn.rsu.edu.ng/?option=com_k2&view=itemlist&task=user&id=2126920
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1127841
http://myrechockey.com/forums/index.php?topic=85147.0
http://www.tessabannampad.go.th/webboard/index.php?topic=188341.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=586866.0
http://metropolis.ga/index.php?topic=18.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1297405
http://proxima.co.rw/index.php/component/k2/itemlist/user/548752
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=269116
http://healthyteethpa.org/component/k2/itemlist/user/5227617
http://www.m1avio.com/index.php/component/k2/itemlist/user/3493406
https://www.youngbiker.de/wbboard/index.php?page=User&userID=775244
http://danielmillsap.com/forum/index.php?topic=867055.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1223637
http://teambuildingpremium.com/forum/index.php?topic=625693.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1581505
http://pptforum.dothome.co.kr/board_APMk06/684619
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3199139
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1107295
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3250760
https://lucky28003.nl/forum/index.php?topic=7061.0
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2526183
http://www.deliberarchia.org/forum/index.php?topic=789833.0
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=874567
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1308126
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3479239
http://www.arunagreen.com/index.php/component/k2/itemlist/user/322208
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=13684
http://www.popolsku.fr.pl/forum/index.php?topic=329933.0
http://webp.online/index.php?topic=46116.0
http://danielmillsap.com/forum/index.php?topic=891569.0
http://seoksoononly.dothome.co.kr/qna/413712
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=48784
http://www.popolsku.fr.pl/forum/index.php?topic=345102.0
https://mcsetup.tk/bbs/index.php?topic=224012.0
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=46988
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-8-eo-5-e-qul-a-etoo-8-eo-5-e-24-04-2019/?PHPSESSID=j938prf7taf1eork2kv4uls2v4
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=41830
https://www.shaiyax.com/index.php?topic=312640.0
http://withinfp.sakura.ne.jp/eso/index.php/16786473-igra-prestolov-8-sezon-3-seria-jfu-igra-prestolov-8-sezon-3-ser/0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=688286
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=10216
https://instaldec.com/?option=com_k2&view=itemlist&task=user&id=602241
http://withinfp.sakura.ne.jp/eso/index.php/16857367-zensina-59-seria-a1ae-zensina-59-seria
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1251976
https://www.resproxy.com/forum/index.php/780155-ne-otpuskaj-mou-ruku-elimi-birakma-40-seria-i0tu-ne-otpuskaj-mo/0
http://healthyteethpa.org/component/k2/itemlist/user/5191165
http://mediaville.me/index.php/component/k2/itemlist/user/209233
https://tg.vl-mp.com/index.php?topic=1345477.0
http://danielmillsap.com/forum/index.php?topic=845256.0
https://www.youngbiker.de/wbboard/index.php?page=User&userID=785184
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81-36/
http://www.deliberarchia.org/forum/index.php?topic=971889.0
http://teambuildingpremium.com/forum/index.php?topic=592261.0
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=21154
http://travelsolution.info/?option=com_k2&view=itemlist&task=user&id=709309
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/370040
https://www.blog.quora.healthcare/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90nu%e3%80%91%d1%81%d0%bb%d1%83%d0%b3%d0%b0
http://withinfp.sakura.ne.jp/eso/index.php/16935357-vetrenyj-hercai-11-seria-a7yv-vetrenyj-hercai-11-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/16877994-voron-kuzgun-15-seria-h3go-voron-kuzgun-15-seria
https://www.resproxy.com/forum/index.php/774485-igra-prestolov-8-sezon-8-seria-krk-igra-prestolov-8-sezon-8-ser/0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/175290
http://healthyteethpa.org/component/k2/itemlist/user/5220395
http://jesusandmarypatna.com/index.php/component/k2/itemlist/user/3310977
https://www.resproxy.com/forum/index.php/734431-igra-prestolov-8-sezon-6-seria-eth-igra-prestolov-8-sezon-6-ser/0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/387637
https://www.shaiyax.com/index.php?topic=310872.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/509947
http://seoksoononly.dothome.co.kr/qna/423976
https://mcsetup.tk/bbs/index.php?topic=227069.0
https://tg.vl-mp.com/index.php?topic=1314752.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/374209
http://macdistri.com/index.php/component/k2/itemlist/user/279103
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=873761
https://www.blog.quora.healthcare/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ode-%d0%b8%d0%b3%d1%80%d0%b0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/373496
http://danielmillsap.com/forum/index.php?topic=879659.0
http://healthyteethpa.org/component/k2/itemlist/user/5318021
https://tg.vl-mp.com/index.php?topic=1271893.0
http://www.phan-aen.go.th/forum/index.php?topic=613283.0
http://www.deliberarchia.org/forum/index.php?topic=931220.0
http://minostech.co.kr/news/3347607
http://withinfp.sakura.ne.jp/eso/index.php/16777957-rannaa-ptaska-erkenci-kus-45-seria-b4zz-rannaa-ptaska-erkenci-k
http://www.deliberarchia.org/forum/index.php?topic=891381.0
https://tg.vl-mp.com/index.php?topic=1254495.0
http://travelsolution.info/?option=com_k2&view=itemlist&task=user&id=706252
http://pptforum.dothome.co.kr/board_APMk06/668813
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=593763.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1243842
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=34483
http://webp.online/index.php?topic=39976.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/aka-ak-3-eo-1-e-pxr-aka-ak-3-eo-1-e-25-04-2019/?PHPSESSID=vqol6koee7f84m5tm00998fhd4
http://withinfp.sakura.ne.jp/eso/index.php/16779035-manifest-18-seria-cxh-manifest-18-seria/0
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3666543
https://tg.vl-mp.com/index.php?topic=1305196.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4720778
https://forum.ac-jete.it/index.php?topic=291427.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1339026
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/177196
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3680020
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3476751
http://soc-human.kz/index.php/component/k2/itemlist/user/1605772
http://thermoplast.envolgroupe.com/component/k2/author/67553
http://webp.online/index.php?topic=39367.15
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=238177
https://mcsetup.tk/bbs/index.php?topic=226983.0
http://afinandoemociones.com.ar/index.php/component/k2/itemlist/user/385911
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3198116
http://withinfp.sakura.ne.jp/eso/index.php/16771783-riverdejl-riverdale-3-sezon-20-seria-dus-riverdejl-riverdale-3-/0
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1713271
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=584530.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/49727
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3474653
http://webp.online/index.php?topic=42363.0
http://seoksoononly.dothome.co.kr/qna/372661
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/203968
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/487586
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/242319
http://seoksoononly.dothome.co.kr/qna/426679
http://www.deliberarchia.org/forum/index.php?topic=761831.0
http://www.deliberarchia.org/forum/index.php?topic=979041.0
https://www.blog.quora.healthcare/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l9za-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26209525/Default.aspx
http://www.deliberarchia.org/forum/index.php?topic=981132.0
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=410534
http://withinfp.sakura.ne.jp/eso/index.php/16910995-vetrenyj-hercai-9-seria-r4qn-vetrenyj-hercai-9-seria
http://danielmillsap.com/forum/index.php?topic=835199.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3454957
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7266181
http://menulisilmiah.net/%d0%b3%d1%80%d0%b0%d0%bd%d0%b4-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cm2-%d0%b3%d1%80%d0%b0%d0%bd%d0%b4-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81/
http://metropolis.ga/index.php?topic=1211.0
http://www.cispace.com/?option=com_k2&view=itemlist&task=user&id=305482
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=669861
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4737208
http://danielmillsap.com/forum/index.php?topic=787365.0
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1566797
http://myrechockey.com/forums/index.php?topic=85292.0
http://teambuildingpremium.com/forum/index.php?topic=635863.0
http://teambuildingpremium.com/forum/index.php?topic=657294.0
https://tg.vl-mp.com/index.php?topic=1278315.0
http://teambuildingpremium.com/forum/index.php?topic=621535.0
http://withinfp.sakura.ne.jp/eso/index.php/16777777-rasskaz-sluzanki-3-sezon-3-seria-lqj-rasskaz-sluzanki-3-sezon-3/0
http://soc-human.kz/index.php/component/k2/itemlist/user/1551899
http://www.deliberarchia.org/forum/index.php?topic=761531.0
http://myrechockey.com/forums/index.php?topic=84657.0
http://www.deliberarchia.org/forum/index.php?topic=968447.0
http://travelsolution.info/?option=com_k2&view=itemlist&task=user&id=713042
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/931172
https://www.resproxy.com/forum/index.php/771334-nasa-istoria-64-seria-v8lt-nasa-istoria-64-seria/0
http://forum.thaibetrank.com/index.php?topic=1087576.0
https://tg.vl-mp.com/index.php?topic=1279929.0
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1572488
http://thermoplast.envolgroupe.com/component/k2/author/69913
http://www.popolsku.fr.pl/forum/index.php?topic=349232.0
https://www.resproxy.com/forum/index.php/779239-sverh-estestvennoe-14-sezon-18-seria-hgi-sverh-estestvennoe-14-/0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1524058
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1712018
http://teambuildingpremium.com/forum/index.php?topic=688588.0
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kb2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8/
https://www.resproxy.com/forum/index.php/766961-cernoe-zerkalo-5-sezon-4-seria-rmd-cernoe-zerkalo-5-sezon-4-ser/0
http://flyinghonda.de/wbb/index.php?page=User&userID=807571
http://www.tessabannampad.go.th/webboard/index.php?topic=193504.0
https://tg.vl-mp.com/index.php?topic=1258951.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4700284
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/437136
https://www.liliantrading.com/index.php/component/k2/itemlist/user/119205
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=284836
http://danielmillsap.com/forum/index.php?topic=825007.0
https://tg.vl-mp.com/index.php?topic=1273853.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=255236
https://mcsetup.tk/bbs/index.php?topic=221963.0
http://sam-sanat.ir/?option=com_k2&view=itemlist&task=user&id=134853
https://tg.vl-mp.com/index.php?topic=1331725.0
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1957285
http://153.120.114.241/eso/index.php/16865844-milliardy-4-sezon-7-seria-ysr-milliardy-4-sezon-7-seria
http://www.deliberarchia.org/forum/index.php?topic=980775.0
https://www.youngbiker.de/wbboard/index.php?page=User&userID=774421
http://muratliziraatodasi.org/forum/index.php?topic=336618.0
http://aitour.kz/index.php/component/k2/itemlist/user/310688
http://teambuildingpremium.com/forum/index.php?topic=616715.0
http://zsmr.com.ua/index.php/component/k2/itemlist/user/401139
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2487448
http://danielmillsap.com/forum/index.php?topic=798835.0
https://www.resproxy.com/forum/index.php/764840-milliardy-4-sezon-11-seria-qrx-milliardy-4-sezon-11-seria-05052/0
http://www.popolsku.fr.pl/forum/index.php?topic=343878.0
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=38074
http://robocit.com/index.php/component/k2/itemlist/user/448830
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=409293
http://danielmillsap.com/forum/index.php?topic=933530.0
http://metropolis.ga/index.php?topic=1268.0
https://www.resproxy.com/forum/index.php/772771-sverh-estestvennoe-14-sezon-18-seria-lfi-sverh-estestvennoe-14-/0
https://tg.vl-mp.com/index.php?topic=1321143.0
http://myrechockey.com/forums/index.php?topic=53935.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1297995
https://tg.vl-mp.com/index.php?topic=1255318.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-aoa-3-eo-14-e-ria-aoa-3-eo-14-e/?PHPSESSID=pgmkb8lhk9aronr8o4u3rgej40
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3453681
https://www.resproxy.com/forum/index.php/783960-ne-otpuskaj-mou-ruku-elimi-birakma-37-seria-h4fl-ne-otpuskaj-mo
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1610203
https://tg.vl-mp.com/index.php?topic=1323856.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/375376
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=459290
http://www.popolsku.fr.pl/forum/index.php?topic=353000.0
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1471729
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1850324
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=44310
http://metropolis.ga/index.php?topic=5801.0
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3302172
http://macdistri.com/index.php/component/k2/itemlist/user/269573
http://www.deliberarchia.org/forum/index.php?topic=894014.0
http://withinfp.sakura.ne.jp/eso/index.php/16783906-edinoe-serdce-tek-yurek-15-seria-x0if-edinoe-serdce-tek-yurek-1
http://withinfp.sakura.ne.jp/eso/index.php/16838350-rannaa-ptaska-erkenci-kus-37-seria-l1zh-rannaa-ptaska-erkenci-k/0
http://danielmillsap.com/forum/index.php?topic=827181.0
http://danielmillsap.com/forum/index.php?topic=802995.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/439334
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81-47/
https://tg.vl-mp.com/index.php?topic=1280663.0
https://tg.vl-mp.com/index.php?topic=1258876.0
https://members.fbhaters.com/index.php?topic=77072.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2417488
http://seoksoononly.dothome.co.kr/qna/459958
http://withinfp.sakura.ne.jp/eso/index.php/16902476-vetrenyj-hercai-14-seria-s0ld-vetrenyj-hercai-14-seria
http://teambuildingpremium.com/forum/index.php?topic=592843.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/169268
http://married.dike.gr/index.php/component/k2/itemlist/user/37439
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7217728
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iev-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.blog.quora.healthcare/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b5-%d0%b7%d0%b5%d1%80%d0%ba%d0%b0%d0%bb%d0%be-5-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-eqa-%d1%87%d0%b5%d1%80%d0%bd
https://www.blog.quora.healthcare/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i1lu-%d0%b2%d0%be%d1%81%d0%ba%d1%80
http://withinfp.sakura.ne.jp/eso/index.php/16877192-nasa-istoria-66-seria-a2ws-nasa-istoria-66-seria/0
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=424928
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1125094
http://macdistri.com/index.php/component/k2/itemlist/user/222938
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1555000
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/162511
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1699463
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=408440
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=271717
http://danielmillsap.com/forum/index.php?topic=836635.0
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81-20/
http://muratliziraatodasi.org/forum/index.php?topic=326346.0
http://febrescordero.gob.ec/?option=com_k2&view=itemlist&task=user&id=84704
http://soc-human.kz/index.php/component/k2/itemlist/user/1604402
http://www.deliberarchia.org/forum/index.php?topic=780589.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xon-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-15-%d1%81%d0%b5%d1%80/
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1109086
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=34783
http://poselokgribovo.ru/forum/index.php?topic=610485.0
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/537997
http://malbeot.iptime.org:10009/xe/board/3841928
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1129568
http://soc-human.kz/index.php/component/k2/itemlist/user/1549527
https://ne-kuru.ru/index.php?topic=202450.0
https://forum.ac-jete.it/index.php?topic=279075.0
http://menulisilmiah.net/%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-25-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sr2-%d0%b7%d0%b2%d0%be%d0%bd%d0%b0%d1%80%d1%8c-25-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.glasshouseproject.com.ng/index.php/component/k2/itemlist/user/38073
https://prosocyr.com/?option=com_k2&view=itemlist&task=user&id=609973
http://teambuildingpremium.com/forum/index.php?topic=611677.0
http://macdistri.com/index.php/component/k2/itemlist/user/275062
http://danielmillsap.com/forum/index.php?topic=936287.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1543038
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/93824
https://www.youngbiker.de/wbboard/index.php?page=User&userID=781131
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81-32/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1296876
<a href="http://cialisec.com/">cialis online</a>
cialis generico preço ultrafarma
[url=http://cialisec.com/]buy cialis online[/url]
cialis coupon 2016 200 dollars
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/21390
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/158555
http://mvisage.sk/?option=com_k2&view=itemlist&task=user&id=114739
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26049944/Default.aspx
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3195537
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=37901
http://withinfp.sakura.ne.jp/eso/index.php/16871094-vetrenyj-hercai-7-seria-y1ly-vetrenyj-hercai-7-seria/0
http://www.tessabannampad.go.th/webboard/index.php?topic=193236.0
http://batubersurat.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=39401
http://www.phan-aen.go.th/forum/index.php?topic=607134.0
https://www.resproxy.com/forum/index.php/783385-vossoedinenie-vuslat-13-seria-v6ki-vossoedinenie-vuslat-13-seri/0
https://tg.vl-mp.com/index.php?topic=1303465.0
https://tg.vl-mp.com/index.php?topic=1265184.0
http://macdistri.com/index.php/component/k2/itemlist/user/259669
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1095645
http://forums.abs-cbn.com/welcome-back-kapamilya%21/ma-4-eo-9-e-aus-ma-4-eo-9-e-24-04-2019/?PHPSESSID=387tp47h9dtnph1c8h3b0pn942
http://webp.online/index.php?topic=51032.0
http://www.crnmedia.es/component/k2/itemlist/user/80986
http://teambuildingpremium.com/forum/index.php?topic=628859.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3197768
http://www.glasshouseproject.com.ng/index.php/component/k2/itemlist/user/38948
http://withinfp.sakura.ne.jp/eso/index.php/16916312-ne-otpuskaj-mou-ruku-elimi-birakma-37-seria-i3nf-ne-otpuskaj-mo/0
http://healthyteethpa.org/component/k2/itemlist/user/5327199
http://seoksoononly.dothome.co.kr/qna/365292
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=66103
http://www.phan-aen.go.th/forum/index.php?topic=606980.0
http://web47.luke.servertools24.de/gw2/wbb/upload/index.php?page=User&userID=894489
http://healthyteethpa.org/component/k2/itemlist/user/5335707
http://www.popolsku.fr.pl/forum/index.php?topic=339066.0
http://withinfp.sakura.ne.jp/eso/index.php/16795173-riverdejl-riverdale-3-sezon-18-seria-lja-riverdejl-riverdale-3-
http://teambuildingpremium.com/forum/index.php?topic=660432.0
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=37104
http://robocit.com/index.php/component/k2/itemlist/user/448437
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1771901
http://www.oortsociety.com/index.php?topic=10881.0
http://danielmillsap.com/forum/index.php?topic=811057.0
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4728861
http://batubersurat.com/index.php/component/k2/itemlist/user/40204
http://macdistri.com/index.php/component/k2/itemlist/user/258323
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ww7-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8/
http://www.tessabannampad.go.th/webboard/index.php?topic=191293.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1098934
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/40806
http://healthyteethpa.org/component/k2/itemlist/user/5221041
http://forums.abs-cbn.com/welcome-back-kapamilya%21/e-ioa-oota-10-e-ixe-ioa-oota-10-e/?PHPSESSID=38ohaqk62ufp5a11nj3p5q5h71
http://www.spazioad.com/component/k2/itemlist/user/7228484
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=296308
http://danielmillsap.com/forum/index.php?topic=832032.0
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/44292
https://www.resproxy.com/forum/index.php/771095-rasskaz-sluzanki-3-sezon-2-seria-hkl-rasskaz-sluzanki-3-sezon-2
http://danielmillsap.com/forum/index.php?topic=877649.0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=543540
http://metropolis.ga/index.php?topic=998.0
http://withinfp.sakura.ne.jp/eso/index.php/16776341-vetrenyj-hercai-12-seria-j6pg-vetrenyj-hercai-12-seria/0
http://malbeot.iptime.org:10009/xe/board/3851776
http://seoksoononly.dothome.co.kr/qna/464504
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1580014
http://teambuildingpremium.com/forum/index.php?topic=628210.0
http://seoksoononly.dothome.co.kr/qna/475798
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=34967
http://thanosakademi.com/index.php?topic=60297.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-8-eo-3-e-cz9-a-etoo-8-eo-3-e-watch/?PHPSESSID=ieleqqml48qpm6l1ugtbj4iv54
http://www.popolsku.fr.pl/forum/index.php?topic=371137.0
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90sn4%e3%80%91-%d0%b8%d0%b3/
http://poselokgribovo.ru/forum/index.php?topic=704469.0
http://bankmitraniaga.co.id/index.php/component/k2/itemlist/user/4113283
http://myrechockey.com/forums/index.php?topic=88884.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=29507.0
http://teambuildingpremium.com/forum/index.php?topic=765615.0
http://www.deliberarchia.org/forum/index.php?topic=951834.0
http://otitismediasociety.org/forum/index.php?topic=148162.0
http://forum.elexlabs.com/index.php?topic=13381.0
http://thanosakademi.com/index.php?topic=66943.0
http://e-educ.net/Forum/index.php?topic=6326.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1334000
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90ks2%e3%80%91-%d0%b8%d0%b3%d1%80/
http://withinfp.sakura.ne.jp/eso/index.php/16838352-ertugrul-148-seria-oq4-ertugrul-148-seria/0
http://e-educ.net/Forum/index.php?topic=5585.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ra6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://mobility-corp.com/index.php/component/k2/itemlist/user/2508191
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=11303
http://thanosakademi.com/index.php?topic=65916.0
http://myrechockey.com/forums/index.php?topic=89689.0
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-h0-y6-%d1%80%d0%b0%d1%81/
https://reficulcoin.com/index.php?topic=15174.0
http://roikjer.com/forum/index.php?PHPSESSID=neifq604na2vsa3pcrlht3c6t5&topic=810787.0
http://seoksoononly.dothome.co.kr/qna/710537
http://www.hoonthaitoday.com/forum/index.php?topic=145699.0
http://miklja.net/forum/index.php?topic=27466.0
http://forum.digamahost.com/index.php?topic=108502.0
http://islamiccall.info/?option=com_k2&view=itemlist&task=user&id=855049
http://forum.elexlabs.com/index.php?topic=14997.0
http://istakam.com/forum/index.php?topic=8702.0
http://www.moyakmermer.com/index.php/en/component/k2/itemlist/user/627545
http://storykingdom.forumside.com/index.php?topic=4725.0
https://reficulcoin.com/index.php?topic=8010.0
http://forum.elexlabs.com/index.php?topic=13085.0
http://roikjer.com/forum/index.php?topic=813865.0
http://dpmarketingsystems.com/%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-16-%d1%81%d0%b5-67/
https://khuyenmaikk13.info/index.php?topic=181046.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.theparrotcentre.com/forum/index.php?topic=479288.0
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-h4-u2-%d0%b8%d0%b3%d1%80/
http://hydrocarbs-gh.org/index.php/component/k2/itemlist/user/7305019
http://roikjer.com/forum/index.php?PHPSESSID=asohbvt8i42ngcmfokmsqniar4&topic=812398.0
http://www.deliberarchia.org/forum/index.php?topic=956735.0
http://uberdrivers.net/forum/index.php?topic=223370.0
http://bobr.site/index.php?topic=82109.0
http://miklja.net/forum/index.php?topic=26739.0
http://www.hoonthaitoday.com/forum/index.php?topic=168064.0
https://adsensebih.com/index.php?topic=10704.0
http://taklongclub.com/forum/index.php?topic=85227.0
http://storykingdom.forumside.com/index.php?topic=4000.0
http://multikopterforum.hu/index.php?topic=6835.0
http://golyboe.ru/forum/index.php?topic=24877.0
http://wituclub.ru/forum/index.php?PHPSESSID=u7aa2kfn6s36ip8640i3tva0e2&topic=25890.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoogame-of-thrones-8-eo-4-e-do6-a-etoogame-of-thrones-8-eo-4-e/?PHPSESSID=fb3icecq0raahthhlbq33lobp4
http://blog.ptpintcast.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t9-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8/
http://poselokgribovo.ru/forum/index.php?topic=705363.0
http://otitismediasociety.org/forum/index.php?topic=148457.0
http://menulisilmiah.net/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-y7-k5-%d1%80%d0%b0/
https://reficulcoin.com/index.php?topic=12949.0
http://www.deliberarchia.org/forum/index.php?topic=947218.0
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90kx9%e3%80%91-%d0%b8%d0%b3/
https://nextezone.com/index.php?topic=34299.0
http://sextomariotienda.com/blog/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yq9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://HyUa.1fps.icu/l/szIaeDC
http://danielmillsap.com/forum/index.php?topic=964291.0
http://freebeer.me/index.php?topic=308741.0
http://multikopterforum.hu/index.php?topic=10710.0
http://miklja.net/forum/index.php?topic=26069.0
http://poselokgribovo.ru/forum/index.php?topic=709520.0
http://poselokgribovo.ru/forum/index.php?topic=689263.0
http://sextomariotienda.com/blog/05-05-2019-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=60844
http://menulisilmiah.net/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h6-u1-%d1%80%d0%b0%d1%81%d1%81/
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3294843
http://www.deliberarchia.org/forum/index.php?topic=937768.0
https://www.thedezlab.com/lab/community/index.php?topic=234.0
http://otitismediasociety.org/forum/index.php?topic=147314.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-w2-s9/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-10/
http://forum.byehaj.hu/index.php?topic=74915.0
http://otitismediasociety.org/forum/index.php?topic=147913.0
http://sextomariotienda.com/blog/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-io2-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://danielmillsap.com/forum/index.php?topic=955009.0
http://multikopterforum.hu/index.php?topic=12891.0
http://bobr.site/index.php?topic=91097.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vk2-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://HyUa.1fps.icu/l/szIaeDC
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1110679
http://poselokgribovo.ru/forum/index.php?topic=618406.0
http://www.deliberarchia.org/forum/index.php?topic=927083.0
http://danielmillsap.com/forum/index.php?topic=815575.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/oa-17-e-vwoa-17-e/?PHPSESSID=jh0lq7pgcj9iff6ama61trjin5
http://proandpro.it/?option=com_k2&view=itemlist&task=user&id=4448647
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=243949
http://withinfp.sakura.ne.jp/eso/index.php/16788351-cernoe-zerkalo-5-sezon-5-seria-qjx-cernoe-zerkalo-5-sezon-5-ser
http://www.arunagreen.com/?option=com_k2&view=itemlist&task=user&id=402839
http://discussadeal.com/forum/index.php?topic=3254.0
http://teambuildingpremium.com/forum/index.php?topic=613081.0
http://www.popolsku.fr.pl/forum/index.php?topic=351346.0
http://withinfp.sakura.ne.jp/eso/index.php/16795014-lubov-smert-i-roboty-love-death-and-robots-18-seria-myc-lubov-s
http://www.spazioad.com/component/k2/itemlist/user/7166860
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xmr-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://seoksoononly.dothome.co.kr/qna/462361
http://www.deliberarchia.org/forum/index.php?topic=808348.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2520303
https://www.resproxy.com/forum/index.php/752110-milliardy-4-sezon-6-seria-xwm-milliardy-4-sezon-6-seria-0405201/0
http://danielmillsap.com/forum/index.php?topic=871205.0
https://tg.vl-mp.com/index.php?topic=1259537.0
http://www.deliberarchia.org/forum/index.php?topic=918651.0
http://avengerro.top/forum/index.php?topic=17621.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1571718
http://jpacschoolclubs.co.uk/component/k2/itemlist/user/3269199
http://www2.yasothon.go.th/smf/index.php?topic=159.142155
http://www.popolsku.fr.pl/forum/index.php?topic=337759.0
https://tg.vl-mp.com/index.php?topic=1274831.0
http://dessa.com.br/component/k2/itemlist/user/291535
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81-48/
http://seoksoononly.dothome.co.kr/qna/472183
http://healthyteethpa.org/?option=com_k2&view=itemlist&task=user&id=5190481
http://webp.online/index.php?topic=48267.0
http://www.deliberarchia.org/forum/index.php?topic=920674.0
http://sam-sanat.ir/?option=com_k2&view=itemlist&task=user&id=146311
http://flyinghonda.de/wbb/index.php?page=User&userID=807474
http://www.glasshouseproject.com.ng/?option=com_k2&view=itemlist&task=user&id=37986
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=597518.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2582111
http://pptforum.dothome.co.kr/board_APMk06/619463
http://boutique.in.th/?option=com_k2&view=itemlist&task=user&id=146452
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/171502
http://menulisilmiah.net/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f4kc-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd/
http://seoksoononly.dothome.co.kr/qna/465460
http://danielmillsap.com/forum/index.php?topic=846070.0
http://danielmillsap.com/forum/index.php?topic=889800.0
http://www.x2145-productions.technology/index.php?title=Benutzer:GregElem266654
http://www.m1avio.com/index.php/component/k2/itemlist/user/3605427
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1524919
http://muratliziraatodasi.org/forum/index.php?topic=344508.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=299555
https://members.fbhaters.com/index.php?topic=65990.0
http://danielmillsap.com/forum/index.php?topic=796807.0
https://tg.vl-mp.com/index.php?topic=1290213.0
http://danielmillsap.com/forum/index.php?topic=842115.0
http://www.deliberarchia.org/forum/index.php?topic=761397.0
http://www.deliberarchia.org/forum/index.php?topic=977058.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3256087
https://members.fbhaters.com/index.php?topic=76266.0
http://www.deliberarchia.org/forum/index.php?topic=779114.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2520160
http://wcwpr.com/UserProfile/tabid/85/userId/9169449/Default.aspx
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4712144
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4695366
http://avengerro.top/forum/index.php?topic=17208.0
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1110400
http://webp.online/index.php?topic=47130.msg77159
http://teambuildingpremium.com/forum/index.php?topic=686716.0
http://menulisilmiah.net/%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ur3-%d1%81%d0%be%d1%81%d0%b5%d0%b4%d0%b8-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2/
http://dev.aabn.org.gh/component/k2/itemlist/user/495639
http://withinfp.sakura.ne.jp/eso/index.php/16796059-vetrenyj-hercai-15-seria-a7ry-vetrenyj-hercai-15-seria/0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=303389
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2569977
http://withinfp.sakura.ne.jp/eso/index.php/16789988-igra-prestolov-8-sezon-6-seria-kfd-igra-prestolov-8-sezon-6-ser/0
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=17171
http://danielmillsap.com/forum/index.php?topic=791383.0
http://macdistri.com/index.php/component/k2/itemlist/user/204575
http://robocit.com/index.php/component/k2/itemlist/user/449052
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7258298
https://tg.vl-mp.com/index.php?topic=1298721.0
http://teambuildingpremium.com/forum/index.php?topic=648239.0
https://tg.vl-mp.com/index.php?topic=1293480.0
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uox-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80/
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2128797
https://www.resproxy.com/forum/index.php/807768-nasa-istoria-67-seria-c6fz-nasa-istoria-67-seria/0
http://seoksoononly.dothome.co.kr/qna/457202
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1635402
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1225323
https://www.resproxy.com/forum/index.php/783368-rannaa-ptaska-erkenci-kus-44-seria-f7hi-rannaa-ptaska-erkenci-k
http://www.phan-aen.go.th/forum/index.php?topic=607886.0
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ks1-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://metropolis.ga/index.php?topic=4517.0
http://danielmillsap.com/forum/index.php?topic=795931.0
http://macdistri.com/index.php/component/k2/itemlist/user/220513
https://www.resproxy.com/forum/index.php/739410-milliardy-4-sezon-10-seria-qnq-milliardy-4-sezon-10-seria-03052/0
http://teambuildingpremium.com/forum/index.php?topic=627843.0
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3314450
http://www.deliberarchia.org/forum/index.php?topic=801371.0
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=48310
http://smartacity.com/component/k2/itemlist/user/11812
http://muratliziraatodasi.org/forum/index.php?topic=345611.0
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/55594
http://mobility-corp.com/index.php/component/k2/itemlist/user/2490651
http://danielmillsap.com/forum/index.php?topic=808063.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/44610
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cg5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://discussadeal.com/forum/index.php?topic=2600.0
https://instaldec.com/?option=com_k2&view=itemlist&task=user&id=574288
http://danielmillsap.com/forum/index.php?topic=974706.0
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=493080
http://forum.thaibetrank.com/index.php?topic=1088495.0
http://withinfp.sakura.ne.jp/eso/index.php/16771609-riverdejl-riverdale-3-sezon-21-seria-qjn-riverdejl-riverdale-3-/0
http://www.deliberarchia.org/forum/index.php?topic=800119.0
http://macdistri.com/index.php/component/k2/itemlist/user/232557
http://webp.online/index.php?topic=47676.0
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=381983
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/366889
http://teambuildingpremium.com/forum/index.php?topic=656075.0
http://seoksoononly.dothome.co.kr/qna/459257
http://proandpro.it/index.php/component/k2/itemlist/user/4449516
http://macdistri.com/?option=com_k2&view=itemlist&task=user&id=277711
http://www.deliberarchia.org/forum/index.php?topic=960223.0
https://www.blog.1mg.healthcare/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nnf-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4
http://healthyteethpa.org/component/k2/itemlist/user/5276608
https://meta.wikimedia.org/wiki/User:AnnisMacomber
https://www.resproxy.com/forum/index.php/780979-sverh-estestvennoe-14-sezon-20-seria-kbb-sverh-estestvennoe-14-
http://avengerro.top/forum/index.php?topic=10322.0
https://www.resproxy.com/forum/index.php/736411-nasledie-16-seria-yer-nasledie-16-seria/0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1310666
http://k2.akademitelkom.ac.id/index.php/component/k2/itemlist/user/246418
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3479747
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1093845
https://www.resproxy.com/forum/index.php/757012-rasskaz-sluzanki-3-sezon-3-seria-hrv-rasskaz-sluzanki-3-sezon-3/0
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2301084
http://jesusandmarypatna.com/index.php/component/k2/itemlist/user/3314424
https://prosocyr.com/?option=com_k2&view=itemlist&task=user&id=603851
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1604005
http://sam-sanat.ir/?option=com_k2&view=itemlist&task=user&id=135571
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/147158
https://www.youngbiker.de/wbboard/index.php?page=User&userID=776692
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=593250.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/ma-4-eo-12-e-rri-ma-4-eo-12-e-25-04-2019/?PHPSESSID=np8hqj9q9grlpsvpqn68hjurs6
https://www.youngbiker.de/wbboard/index.php?page=User&userID=784527
http://www.arunagreen.com/index.php/component/k2/itemlist/user/396393
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1127650
http://wcwpr.com/UserProfile/tabid/85/userId/9297868/Default.aspx
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=3946
http://withinfp.sakura.ne.jp/eso/index.php/16886446-voron-kuzgun-10-seria-u0hi-voron-kuzgun-10-seria/0
http://www.sc-chateau-malleprat.com/?option=com_k2&view=itemlist&task=user&id=24993
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=492860
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26067725/Default.aspx
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1957315
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=407789
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2390378
http://associationsila.org/component/k2/itemlist/user/266108
https://sto54.ru/index.php/component/k2/itemlist/user/3294418
http://withinfp.sakura.ne.jp/eso/index.php/16794182-igra-prestolov-8-sezon-2-seria-pjm-igra-prestolov-8-sezon-2-ser/0
https://tg.vl-mp.com/index.php?topic=1329999.0
http://danielmillsap.com/forum/index.php?topic=872359.0
http://www.nsc-radio.eu/ngs/index.php?page=User&userID=1108130
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=595137.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1312567
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-po1-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://teambuildingpremium.com/forum/index.php?topic=654972.0
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/993608
http://wcwpr.com/UserProfile/tabid/85/userId/9167381/Default.aspx
https://www.blog.quora.healthcare/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90lm%e3%80%91%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1836148
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4727676
http://www.deliberarchia.org/forum/index.php?topic=911182.0
http://danielmillsap.com/forum/index.php?topic=804036.0
http://153.120.114.241/eso/index.php/16879403-lubov-smert-i-roboty-love-death-and-robots-4-seria-ifl-lubov-sm
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=147472
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=160175
http://withinfp.sakura.ne.jp/eso/index.php/16775058-nasledie-11-seria-jxz-nasledie-11-seria/0
https://members.fbhaters.com/index.php?topic=66672.0
http://boutique.in.th/?option=com_k2&view=itemlist&task=user&id=143276
http://seoksoononly.dothome.co.kr/qna/471733
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1110648
http://menulisilmiah.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xod-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o7-m5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w2-u7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-c2-i9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z1-p2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://uberdrivers.net/forum/index.php?topic=246036.0
http://uberdrivers.net/forum/index.php?topic=246090.0
http://uberdrivers.net/forum/index.php?topic=246103.0
http://uberdrivers.net/forum/index.php?topic=246117.0
http://uberdrivers.net/forum/index.php?topic=246166.0
http://uberdrivers.net/forum/index.php?topic=246174.0
http://uberdrivers.net/forum/index.php?topic=246182.0
http://www.critico-expository.com/forum/index.php?topic=6924.0
https://reficulcoin.com/index.php?topic=5303.0
http://istakam.com/forum/index.php?topic=10382.0
http://www.deliberarchia.org/forum/index.php?topic=955649.0
http://freebeer.me/index.php?topic=299736.0
http://153.120.114.241/eso/index.php/16840111-igra-prestolovgame-of-thrones-8-sezon-3-seria-cp3-igra-prestolo
http://www.deliberarchia.org/forum/index.php?topic=945297.0
http://dpmarketingsystems.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nj0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://roikjer.com/forum/index.php?PHPSESSID=in4lfhcuv5thbto1p5i76n22s6&topic=808105.0
http://www.critico-expository.com/forum/index.php?topic=4850.0
http://forum.elexlabs.com/index.php?topic=12834.0
http://sextomariotienda.com/blog/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://danielmillsap.com/forum/index.php?topic=939605.0
http://sextomariotienda.com/blog/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n6-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5/
http://forum.santrope-rp.ru/index.php?topic=2106.0
http://multikopterforum.hu/index.php?topic=10944.0
http://poselokgribovo.ru/forum/index.php?topic=711287.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-54/
http://HyUa.1fps.icu/l/szIaeDC
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e4-i2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k6-s1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p8-t8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s9-t3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a6-h0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g4-b7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-g1-a0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y0-z6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q0-r3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e5-w8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w8-f5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o9-w8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-m4-j7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.theparrotcentre.com/forum/index.php?topic=485047.0
http://www.theparrotcentre.com/forum/index.php?topic=485082.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=8c859251dd354ef2e61b04a904ea1723&topic=976.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=ca6625c8b631914db46861f9d8a2ccf1&topic=975.0
http://xn--l1adgmc.xn----9sbdbmdznsj5c5bxd7b.xn--p1ai/index.php?topic=10642.0
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a9-w7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v3-o8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l4-c8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m9-e1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://forum.politeknikgihon.ac.id/index.php?topic=13883.0
http://menulisilmiah.net/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90dx8%e3%80%91/
http://danielmillsap.com/forum/index.php?topic=938835.0
http://www.ekemoon.com/155355/050020192608/
http://poselokgribovo.ru/forum/index.php?topic=695426.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=26058.0
http://withinfp.sakura.ne.jp/eso/index.php/16868637-igra-prestolov-got-8-sezon-7-seria-igra-prestolov-got-8-sezon-7/0
http://forum.digamahost.com/index.php?topic=108127.0
http://dohairbiz.com/en/component/k2/itemlist/user/2702619.html
http://sextomariotienda.com/blog/%d1%8d%d1%84%d0%b8%d1%80-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x2-%d1%81%d0%bb%d1%83%d0%b3/
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=679886.0
http://sextomariotienda.com/blog/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n5-%d1%81%d0%bb%d1%83/
https://lucky28003.nl/forum/index.php?topic=12548.0
http://www.tekparcahdfilm.com/forum/index.php?topic=46111.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3558953
http://metropolis.ga/index.php?topic=5426.0
http://otitismediasociety.org/forum/index.php?topic=143657.0
http://golyboe.ru/forum/index.php?topic=24625.0
https://reficulcoin.com/index.php?topic=11573.0
http://withinfp.sakura.ne.jp/eso/index.php/16862402-igra-prestolov-8-sezon-1-seria-igra-prestolov-8-sezon-1-seria-a/0
http://HyUa.1fps.icu/l/szIaeDC
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c2-e7-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-k6-r2/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b5-v3-%d0%b8%d0%b3%d1%80/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-x8-j7/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-m3-h7-%d0%b8/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s8-j2-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://worldtaxi.org/2019/05/09/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-x2-k0/
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b9-e1-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b9-y5-%d0%b8%d0%b3%d1%80%d0%b0/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tj2-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://danielmillsap.com/forum/index.php?topic=995682.0
http://uberdrivers.net/forum/index.php?topic=246210.0
http://www.hoonthaitoday.com/forum/index.php?topic=204220.0
http://www.popolsku.fr.pl/forum/index.php?topic=376867.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=683446.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=683447.0
https://forum.shaiyaslayer.tk/index.php?topic=100683.0
https://members.fbhaters.com/index.php?topic=84623.0
https://nextezone.com/index.php?action=profile&u=4002
https://nextezone.com/index.php?action=profile;u=4031
http://122.154.49.125/Forum/index.php?topic=131.0
http://www.theparrotcentre.com/forum/index.php?topic=457785.0
http://8.droror.co.il/uncategorized/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90sd3%e3%80%91/
http://forum.politeknikgihon.ac.id/index.php?topic=16463.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-(game-of-thrones)-8-eo-3-e-fi2-a-etoo-(game-of-thrones)-8-eo-3/?PHPSESSID=j76ls5im1dnsuthgferv7afvn4
http://www.remify.app/foro/index.php?topic=209993.0
http://poselokgribovo.ru/forum/index.php?topic=709452.0
http://wb.hvekorat.com/index.php?topic=40202.0
http://otitismediasociety.org/forum/index.php?topic=142260.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-j6-j3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.deliberarchia.org/forum/index.php?topic=940008.0
http://poselokgribovo.ru/forum/index.php?topic=694315.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.theocraticamerica.org/forum/index.php?topic=28935.0
http://www.theparrotcentre.com/forum/index.php?topic=487351.0
http://www.theparrotcentre.com/forum/index.php?topic=487354.0
http://www.theparrotcentre.com/forum/index.php?topic=487379.0
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-e4-o2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h9-t4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k2-i6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q9-c0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h6-l4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y9-a4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-e0-x4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-o1-m0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h9-u1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z8-r8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-v7-y9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r9-m5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fd4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://forum.kopkargobel.com/index.php?topic=2967.0
http://teambuildingpremium.com/forum/index.php?topic=779156.0
http://www.critico-expository.com/forum/index.php?topic=4910.0
https://sanp.pro/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g9-y3-%d1%80%d0%b0%d1%81%d1%81/
http://istakam.com/forum/index.php?topic=9591.0
http://www.deliberarchia.org/forum/index.php?topic=975569.0
http://uberdrivers.net/forum/index.php?topic=210097.0
http://forum.politeknikgihon.ac.id/index.php?topic=18024.0
http://freebeer.me/index.php?topic=290278.0
http://www.popolsku.fr.pl/forum/index.php?topic=372065.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=50ef5e85585a4940b0bc0a20ec6f262b&topic=203210.0
http://1vh.info/index.php?topic=5885.0
http://ru-realty.com/forum/index.php?PHPSESSID=n8eo1j3vgq6auaitt5fatvraf0&topic=445592.0
https://reficulcoin.com/index.php?topic=12742.0
https://adsensebih.com/index.php?topic=10081.0
http://www.deliberarchia.org/forum/index.php?topic=955004.0
http://sextomariotienda.com/blog/%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-17-%d1%81%d0%b5-24/
http://HyUa.1fps.icu/l/szIaeDC
http://roikjer.com/forum/index.php?topic=803184.0
http://otitismediasociety.org/forum/index.php?topic=145975.0
http://repofirmware.altervista.org/index.php?topic=91109.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k4-n6-%d0%b8%d0%b3%d1%80%d0%b0/
http://www.deliberarchia.org/forum/index.php?topic=945538.0
http://dpmarketingsystems.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d6-%d1%81/
http://codeerror.in/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-2/
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/193259
http://metropolis.ga/index.php?topic=1902.0
http://myrechockey.com/forums/index.php?topic=86540.0
http://otitismediasociety.org/forum/index.php?type=rss;action=.xml
http://1vh.info/index.php?topic=11506.0
https://members.fbhaters.com/index.php?topic=70991.0
https://szenarist.ru/forum/index.php?topic=203387.0
http://ru-realty.com/forum/index.php?topic=460815.0
http://www.ekemoon.com/149399/050020195907/
http://myrechockey.com/forums/index.php?topic=83794.0
http://poselokgribovo.ru/forum/index.php?topic=700435.0
http://forum.drahthaar-club.com.ua/index.php?topic=1364.0
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4825464
http://www.theparrotcentre.com/forum/index.php?topic=473617.0
https://reficulcoin.com/index.php?topic=5742.0
http://www.deliberarchia.org/forum/index.php?topic=940215.0
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n5-z6-%d1%80%d0%b0%d1%81%d1%81/
http://HyUa.1fps.icu/l/szIaeDC
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k9-j7-%d0%b8/
http://roikjer.com/forum/index.php?PHPSESSID=2s0aliqg1gkgetiqid3ocmbem6&topic=799366.0
http://www.obal-shop.sk/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-s3-s0-%d1%80%d0%b0%d1%81/
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1838279
https://sanp.pro/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i3-%d1%81%d0%bb/
https://adsensebih.com/index.php?topic=8267.0
http://sochi-forum.info/index.php?topic=495.0
http://danielmillsap.com/forum/index.php?topic=984924.0
http://www.critico-expository.com/forum/index.php?topic=4452.0
http://www.ekemoon.com/163897/050920193109/
http://www.popolsku.fr.pl/forum/index.php?topic=372184.0
http://e-educ.net/Forum/index.php?topic=3595.0
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-u0-p0-%d0%b8%d0%b3/
http://roikjer.com/forum/index.php?PHPSESSID=asj1692jogp4vuco2cockm5kc6&topic=807798.0
http://otitismediasociety.org/forum/index.php?topic=144266.0
http://roikjer.com/forum/index.php?PHPSESSID=hqdp2bdf8lb5h6lkfcdnp4t7u2&topic=791282.0
http://roikjer.com/forum/index.php?PHPSESSID=pnp76i0rooglsb1nab764qm9m5&topic=809531.0
http://www.hoonthaitoday.com/forum/index.php?topic=167675.0
https://reficulcoin.com/index.php?topic=9870.0
http://www.vivelabmanizales.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n6-q2-%d1%80%d0%b0%d1%81%d1%81/
http://bobr.site/index.php?topic=92525.0
https://reficulcoin.com/index.php?topic=9835.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u7-d8-%d0%b8%d0%b3%d1%80/
http://multikopterforum.hu/index.php?topic=12203.0
http://storykingdom.forumside.com/index.php?topic=5413.0
http://HyUa.1fps.icu/l/szIaeDC
http://freebeer.me/index.php?topic=309732.0
http://forum.byehaj.hu/index.php?topic=79543.0
https://nextezone.com/index.php?action=profile&u=2879
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(a-etoo-2019-8-eo-6-e)-a-etoo-2019-8-eo-6-e-n1z8/?PHPSESSID=l2pkkl38nh6p1guof19tndceq5
https://forums.letstalkbeats.com/index.php?topic=62516.0
http://otitismediasociety.org/forum/index.php?topic=146300.0
http://help.stv.ru/index.php?PHPSESSID=efcae418f0817967338080819cb6080c&topic=139177.0
https://reficulcoin.com/index.php?topic=14915.0
http://poselokgribovo.ru/forum/index.php?topic=705892.0
http://www.theparrotcentre.com/forum/index.php?topic=463835.0
http://153.120.114.241/eso/index.php/16849602-igra-prestolovgame-of-thrones-8-sezon-5-seria-ys0-igra-prestolo
http://poselokgribovo.ru/forum/index.php?topic=697316.0
https://forums.letstalkbeats.com/index.php?topic=69308.0
http://poselokgribovo.ru/forum/index.php?topic=736451.0
http://metropolis.ga/index.php?topic=2465.0
https://sanp.pro/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p4-y2-%d1%80%d0%b0%d1%81%d1%81/
http://danielmillsap.com/forum/index.php?topic=932154.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-h1-l5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
https://danceplanet.se/commodore/index.php?topic=10821.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-27/
http://153.120.114.241/eso/index.php/16853668-igra-prestolov-8-sezon-5-seria-igra-prestolov-8-sezon-5-seria-g
http://thanosakademi.com/index.php?topic=62139.0
https://danceplanet.se/commodore/index.php?topic=14147.0
http://forum.politeknikgihon.ac.id/index.php?topic=22637.0
http://www.tessabannampad.go.th/webboard/index.php?topic=190731.0
http://ptu.imoove.kr/ko/content/%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-4-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%E3%80%90to2%E3%80%91-%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-4-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-watch%C2%BB330234
http://freebeer.me/index.php?topic=283943.0
http://www.deliberarchia.org/forum/index.php?topic=946734.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=28132.0
http://www.deliberarchia.org/forum/index.php?topic=940915.0
https://reficulcoin.com/index.php?topic=12578.0
http://www.deliberarchia.org/forum/index.php?topic=945992.0
https://khuyenmaikk13.info/index.php?topic=176449.0
https://reficulcoin.com/index.php?topic=14496.0
http://miklja.net/forum/index.php?topic=26988.0
http://thanosakademi.com/index.php?topic=60838.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e2-p6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://HyUa.1fps.icu/l/szIaeDC
http://guiadetudo.com/index.php/component/k2/itemlist/user/10744
http://forum.elexlabs.com/index.php/topic,12970.0.html
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=24527.0
http://svgrossburgwedel.de/component/k2/itemlist/user/5023
http://danielmillsap.com/forum/index.php?topic=953327.0
http://myrechockey.com/forums/index.php?topic=88336.0
http://www.tessabannampad.go.th/webboard/index.php?topic=192437.0
http://www.theparrotcentre.com/forum/index.php?topic=478082.0
http://ptu.imoove.kr/ko/content/%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2game-thrones-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%E3%80%90su4%E3%80%91-%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2game-thrones-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-6-0
http://poselokgribovo.ru/forum/index.php?topic=706260.0
http://vtservices85.fr/smf2/index.php?topic=203931.0
http://uberdrivers.net/forum/index.php?topic=228332.0
http://storykingdom.forumside.com/index.php/topic,4249.0.html
http://e-educ.net/Forum/index.php?topic=3026.0
https://khuyenmaikk13.info/index.php?topic=174444.0
http://eugeniocolazzo.it/forum/index.php?topic=87786.0
https://danceplanet.se/commodore/index.php?topic=9682.0
http://sextomariotienda.com/blog/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mc6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.popolsku.fr.pl/forum/index.php?topic=20407.44700
http://forum.politeknikgihon.ac.id/index.php?topic=18587.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1327027
https://khuyenmaikk13.info/index.php?topic=180923.0
http://dpmarketingsystems.com/06-05-2019-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://myrechockey.com/forums/index.php?topic=90335.0
http://bobr.site/index.php?topic=82453.0
http://roikjer.com/forum/index.php?PHPSESSID=fnqavqa4488bi272pjv1bmbd13&topic=827246.0
http://forum.stollen24.com/index.php?topic=2815.0
http://forum.kopkargobel.com/index.php?topic=3377.0
http://www.deliberarchia.org/forum/index.php?topic=949031.0
http://metropolis.ga/index.php?topic=3088.0
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ow2-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.remify.app/foro/index.php?topic=210936.0
http://www.tessabannampad.go.th/webboard/index.php?topic=188423.0
http://e-educ.net/Forum/index.php?topic=3080.0
http://myrechockey.com/forums/index.php?topic=82338.0
http://www.theparrotcentre.com/forum/index.php?topic=457153.0
http://HyUa.1fps.icu/l/szIaeDC
https://reficulcoin.com/index.php?topic=19574.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z9-m3-%d0%b8%d0%b3%d1%80/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-u7-x3-%d0%b8%d0%b3%d1%80%d0%b0/
https://worldtaxi.org/2019/05/09/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h0-o4-%d0%b8%d0%b3%d1%80%d0%b0/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z6-r8-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-l7-e4-%d0%b8%d0%b3%d1%80/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p8-s5-%d0%b8%d0%b3%d1%80%d0%b0/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-i4-k6-%d0%b8/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-q3-l5-%d0%b8%d0%b3/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s0-a1-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://forum.clubeicaro.pt/index.php?topic=920.0
https://khuyenmaikk13.info/index.php?topic=188040.0
http://danielmillsap.com/forum/index.php?topic=998467.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=6eba59d35ed67b0d499c8b721be2d794&topic=215886.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=b62141c12c295704d3eaeede7529ff29&topic=215891.0
http://www.critico-expository.com/forum/index.php?topic=7725.0
http://www.critico-expository.com/forum/index.php?topic=7768.0
http://myrechockey.com/forums/index.php?topic=89556.0
https://members.fbhaters.com/index.php?topic=78712.0
http://cccpvideo.forumside.com/index.php?topic=282.0
http://photogrotto.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90ln7%e3%80%91/
https://npi.org.es/smf/index.php?topic=110980.0
http://danielmillsap.com/forum/index.php?topic=935428.0
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1761591
http://www.deliberarchia.org/forum/index.php?topic=941030.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-d7-q5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=677168.0
http://roikjer.com/forum/index.php?PHPSESSID=qfncpi59uk05bsf5eprqim0fm1&topic=830992.0
http://www.tessabannampad.go.th/webboard/index.php?topic=183996.0
http://dpmarketingsystems.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2019-2/
http://HyUa.1fps.icu/l/szIaeDC
https://hackersuniversity.net/index.php?topic=9757.0
https://hackersuniversity.net/index.php?topic=9758.0
https://khuyenmaikk13.info/index.php?topic=188159.0
https://khuyenmaikk13.info/index.php?topic=188175.0
https://members.fbhaters.com/index.php?topic=86566.0
https://reficulcoin.com/index.php?topic=19675.0
https://www.limscave.com/forum/viewtopic.php?f=6&t=31815
https://www.limscave.com/forum/viewtopic.php?t=31814
http://forum.kopkargobel.com/index.php?topic=6386.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(a-etoo-(got)-8-eo-2-e)-a-etoo-(got)-8-eo-2-e-k2b3/?PHPSESSID=5fqt8jo1mpfvrdg6hedem77ou4
http://www.hoonthaitoday.com/forum/index.php?topic=207872.0
http://www.hoonthaitoday.com/forum/index.php?topic=207908.0
https://reficulcoin.com/index.php?topic=19655.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-59/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-36/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-10/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0/
https://forum.clubeicaro.pt/index.php?topic=924.0
https://forum.clubeicaro.pt/index.php?topic=925.0
https://members.fbhaters.com/index.php?topic=86554.0
https://nextezone.com/index.php?topic=31392.0
http://freebeer.me/index.php?topic=308384.0
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h3-z4-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://roikjer.com/forum/index.php?PHPSESSID=sbg4jrvu13esbicpc3mdfa39t7&topic=813927.0
https://tg.vl-mp.com/index.php?topic=1299626.0
http://dpmarketingsystems.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-c2-n5-%d1%80/
http://danielmillsap.com/forum/index.php?topic=981040.0
https://luckychancerescue.com/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w4-%d1%81%d0%bb%d1%83/
http://uberdrivers.net/forum/index.php?topic=233315.0
http://freebeer.me/index.php?topic=301269.0
https://danceplanet.se/commodore/index.php?topic=14666.0
https://adsensebih.com/index.php?topic=9049.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=676402.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=675638.0
https://members.fbhaters.com/index.php?topic=79657.0
http://myrechockey.com/forums/index.php?topic=81367.0
http://muonlineint.com/forum/index.php?topic=369.0
http://e-educ.net/Forum/index.php?topic=3946.0
http://forum.elexlabs.com/index.php?topic=13357.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=24876.0
http://forum.politeknikgihon.ac.id/index.php?topic=16430.0
http://HyUa.1fps.icu/l/szIaeDC
http://metropolis.ga/index.php?topic=6639.0
http://metropolis.ga/index.php?topic=6640.0
http://metropolis.ga/index.php?topic=6641.0
http://metropolis.ga/index.php?topic=6642.0
http://metropolis.ga/index.php?topic=6643.0
http://partemp.com/en/groups/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f2-a2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c3-d8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f4-f8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f6-d5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n2-o9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o2-q7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
https://polyframetrade.co.uk/%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-3-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-e2-p3-%D1%80%D0%B0%D1%81%D1%81/
http://blog.ptpintcast.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i9-c4-%d0%b8%d0%b3%d1%80%d0%b0/
http://podwodnyswiat.eu/forum/index.php?topic=89.0
http://dpmarketingsystems.com/%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i3-%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-13-%d1%81%d0%b5%d1%80/
http://withinfp.sakura.ne.jp/eso/index.php/16840205-igra-prestolovgame-of-thrones-8-sezon-5-seria-igra-prestolovgam/0
http://dpmarketingsystems.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u1-h9-%d1%80%d0%b0%d1%81%d1%81/
https://members.fbhaters.com/index.php/topic,70107.0.html
http://forum.kopkargobel.com/index.php?topic=5131.0
http://metropolis.ga/index.php?topic=3676.0
http://bobr.site/index.php?topic=94709.0
http://uberdrivers.net/forum/index.php?topic=231731.0
http://teambuildingpremium.com/forum/index.php?topic=758706.0
https://khuyenmaikk13.info/index.php?topic=174428.0
http://forum.politeknikgihon.ac.id/index.php?topic=16768.0
http://myrechockey.com/forums/index.php?topic=84617.0
http://flashboot.ru/forum/index.php?topic=94421.0
http://forum.politeknikgihon.ac.id/index.php?topic=20489.0
http://HyUa.1fps.icu/l/szIaeDC
http://roikjer.com/forum/index.php?topic=828575.0
http://8.droror.co.il/uncategorized/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d0-n6-%d1%80%d0%b0%d1%81%d1%81/
http://153.120.114.241/eso/index.php/16861006-igra-prestolovgame-of-thrones-8-sezon-4-seria-igra-prestolovgam
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=27510.0
http://www.deliberarchia.org/forum/index.php?topic=950817.0
http://multikopterforum.hu/index.php?topic=10440.0
http://help.stv.ru/index.php?PHPSESSID=766af7b84bf24b84071771d82abe4be7&topic=138039.0
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1985706
http://www.critico-expository.com/forum/index.php?topic=3906.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=274277
http://vtservices85.fr/smf2/index.php?PHPSESSID=c3b67b1bc18a5196380d3104092c84bf&topic=205452.0
http://golyboe.ru/forum/index.php?topic=24951.0
http://myrechockey.com/forums/index.php?topic=82391.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2554499
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-a7-o7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://help.stv.ru/index.php?PHPSESSID=f4da1e05e4afac9b51bfafeb0a1faed9&topic=138505.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=1f2ae41a12914d5584dc797c8dc86962&topic=212248.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90av4%e3%80%91/
https://reficulcoin.com/index.php?topic=7989.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-8-eo-5-e-a-etoo-8-eo-5-e-v6z4/
http://multikopterforum.hu/index.php?topic=5492.0
http://www.deliberarchia.org/forum/index.php?topic=933408.0
http://HyUa.1fps.icu/l/szIaeDC
http://dpmarketingsystems.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w8-x9-%d1%80%d0%b0%d1%81%d1%81/
http://www.remify.app/foro/index.php?topic=214146.0
http://bobr.site/index.php?topic=81784.0
http://kurnaz.1to.us/index.php?topic=1.540
http://www.tessabannampad.go.th/webboard/index.php?topic=192344.0
http://forum.elexlabs.com/index.php/topic,14854.0.html
http://wituclub.ru/forum/index.php?PHPSESSID=jgulrtq6q1e7453emtd7ahlm21&topic=25264.0
http://teambuildingpremium.com/forum/index.php?topic=753970.0
http://freebeer.me/index.php?topic=300598.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-d5-f5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291371
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t9-l7-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://153.120.114.241/eso/index.php/16883971-06052019-podsudimyj-10-seria
http://vtservices85.fr/smf2/index.php?topic=205302.0
http://xplorefitness.com/blog/%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-got-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-4-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%E3%80%90vs9%E3%80%91-%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-got-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-4-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
https://www.gizmoarticle.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qu8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.tekparcahdfilm.com/forum/index.php?topic=46284.0
http://www.deliberarchia.org/forum/index.php?topic=943047.0
http://dpmarketingsystems.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d2-z1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://thanosakademi.com/index.php?topic=66207.0
http://1vh.info/index.php?topic=10444.0
http://ru-realty.com/forum/index.php?PHPSESSID=s6de25egq1nacaqovs3is02td5&topic=470321.0
http://forum.kopkargobel.com/index.php?topic=5240.0
https://www.c-alice.org/forum/index.php?topic=72966.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q3-s4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://help.stv.ru/index.php?topic=136822.0
http://poselokgribovo.ru/forum/index.php?topic=734974.0
http://sextomariotienda.com/blog/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-eq9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://forum.digamahost.com/index.php?topic=108853.0
http://forum.politeknikgihon.ac.id/index.php?topic=23597.0
https://khuyenmaikk13.info/index.php?topic=175859.0
http://HyUa.1fps.icu/l/szIaeDC
https://members.fbhaters.com/index.php?topic=81376.0
https://www.amazingworldtop.com/entretenimiento/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q7-l8-%d1%80%d0%b0%d1%81%d1%81/
http://teambuildingpremium.com/forum/index.php?topic=763043.0
http://otitismediasociety.org/forum/index.php?topic=146503.0
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7206020
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-8/
http://forum.stollen24.com/index.php?topic=3098.0
https://nextezone.com/index.php?topic=32566.0
http://danielmillsap.com/forum/index.php?topic=948869.0
https://chromehearts.in.th/index.php?topic=43337.0
http://danielmillsap.com/forum/index.php?topic=928062.0
http://dpmarketingsystems.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-e3-p3-%d1%80/
http://www.hoonthaitoday.com/forum/index.php?topic=135481.0
http://roikjer.com/forum/index.php?PHPSESSID=fjngq336k64hbn2kb0k9cd96v4&topic=806677.0
https://reficulcoin.com/index.php?topic=4645.0
https://forum.ac-jete.it/index.php?topic=330008.0
http://www.tessabannampad.go.th/webboard/index.php?topic=185600.0
http://ru-realty.com/forum/index.php?PHPSESSID=c6lugmmifdpn5v1165qdjmqng1&topic=449469.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=6d6a4a88c47eeec2f07056e3964efd87&topic=209098.0
http://e-educ.net/Forum/index.php?topic=5193.0
http://www.theocraticamerica.org/forum/index.php?topic=26732.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m2-w7-%d0%b8%d0%b3%d1%80/
http://dpmarketingsystems.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t3-y4-%d1%80%d0%b0%d1%81%d1%81/
https://reficulcoin.com/index.php?topic=15026.0
http://HyUa.1fps.icu/l/szIaeDC
[url=http://cialisdxt.com/]cialis online[/url]
cialis super active generic trust pharmacy
<a href="http://cialisdxt.com/">buy cialis online</a>
cialis super active dosage
[url=http://cialisec.com/]generic cialis[/url]
cialis dosage chart
<a href="http://cialisec.com/">cialis online</a>
canadian pharmacy cialis prices
http://otitismediasociety.org/forum/index.php?topic=142572.0
http://dpmarketingsystems.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d0-%d1%81/
http://marjorieaperry.com/?option=com_k2&view=itemlist&task=user&id=479227
http://216.104.186.20/index.php?topic=296109.0
http://sextomariotienda.com/blog/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-op0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://codeerror.in/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90no6%e3%80%91/
http://mir3sea.com/forum/index.php?topic=708.0
http://withinfp.sakura.ne.jp/eso/index.php/16862995-grand-2-sezon-23-seria-05052019/0
http://www.moyakmermer.com/index.php/component/k2/itemlist/user/637039
http://myrechockey.com/forums/index.php?topic=83192.0
http://istakam.com/forum/index.php?topic=9515.0
http://roikjer.com/forum/index.php?PHPSESSID=jcnsd4ci34qh7gvt8iql835oq7&topic=794986.0
http://forum.kopkargobel.com/index.php?topic=4134.0
http://xplorefitness.com/blog/%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-2019-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-7-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%E3%80%90xa0%E3%80%91-%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-2019-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-7-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://sextomariotienda.com/blog/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-er7-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://multikopterforum.hu/index.php?topic=5398.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ns6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.deliberarchia.org/forum/index.php?topic=958043.0
http://forum.bmw-e60.eu/index.php?topic=2420.0
https://reficulcoin.com/index.php?topic=4965.0
http://HyUa.1fps.icu/l/szIaeDC
https://danceplanet.se/commodore/index.php?topic=14640.0
http://www.tessabannampad.go.th/webboard/index.php?topic=188982.0
http://myrechockey.com/forums/index.php?topic=81374.0
http://freebeer.me/index.php?topic=286636.0
http://dpmarketingsystems.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o1-%d1%81/
http://mir3sea.com/forum/index.php?topic=1529.0
https://danceplanet.se/commodore/index.php?topic=11181.0
http://poselokgribovo.ru/forum/index.php?topic=712008.0
http://metropolis.ga/index.php?topic=1603.0
http://help.stv.ru/index.php?topic=137061.0
http://metropolis.ga/index.php?topic=2516.0
http://www.critico-expository.com/forum/index.php?topic=5929.0
http://www.deliberarchia.org/forum/index.php?topic=952842.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=8bff36d08612229dace83080c8728f9a&topic=211107.0
http://istakam.com/forum/index.php?topic=8787.0
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-t4-e3-%d1%80/
https://platforma-nonstop.ro/forum/index.php?topic=258976.0
http://multikopterforum.hu/index.php?topic=10049.0
https://members.fbhaters.com/index.php?topic=79117.0
http://otitismediasociety.org/forum/index.php?topic=146106.0
http://roikjer.com/forum/index.php?PHPSESSID=uj0l5ql9sdcsfiufepj4kn9510&topic=809183.0
http://www.hoonthaitoday.com/forum/index.php?topic=154307.0
http://freebeer.me/index.php?topic=312679.0
http://uberdrivers.net/forum/index.php?topic=218882.0
http://forum.politeknikgihon.ac.id/index.php?topic=17904.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=672651.0
http://www.deliberarchia.org/forum/index.php?topic=955797.0
http://eugeniocolazzo.it/forum/index.php?topic=84739.0
http://forum.elexlabs.com/index.php?topic=12545.0
http://www.deliberarchia.org/forum/index.php?topic=936736.0
http://www.remify.app/foro/index.php?topic=207752.0
http://1vh.info/index.php?topic=6512.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.deliberarchia.org/forum/index.php?topic=1001065.0
http://www.nomaher.com/forum/index.php?topic=13788.0
http://www.ofqj.org/hebergementquebec/4-13-b7-m5-4-13-4-13
http://www.ofqj.org/hebergementquebec/4-8-online-y9-r2-4-8-4-8
http://www.theparrotcentre.com/forum/index.php?topic=492436.0
https://altaylarteknoloji.com/index.php?topic=2389.0
https://cybergsm.es/index.php?topic=9095.0
https://hackersuniversity.net/index.php?topic=10324.0
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-x9-r6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://sextomariotienda.com/blog/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-x7-g9-%d1%80/
http://ptu.imoove.kr/ko/content/%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-2019-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-7-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%E3%80%90ce8%E3%80%91-%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-2019-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-7-%D1%81%D0%B5%D1%80%D0%B8%D1%8F330433
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/150206
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1985516
http://www.ekemoon.com/155011/052320192507/
https://reficulcoin.com/index.php?topic=10301.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=24486.0
http://forum.byehaj.hu/index.php?topic=75301.0
http://teambuildingpremium.com/forum/index.php?topic=753956.0
http://healthyteethpa.org/component/k2/itemlist/user/5320265
http://www.theocraticamerica.org/forum/index.php?topic=25468.0
http://guiadetudo.com/index.php/component/k2/itemlist/user/10808
http://www.deliberarchia.org/forum/index.php?topic=985134.0
http://taklongclub.com/forum/index.php?topic=92735.0
http://dpmarketingsystems.com/07-05-2019-%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://otitismediasociety.org/forum/index.php?topic=148663.0
http://forum.stollen24.com/index.php/topic,3202.0.html
http://poselokgribovo.ru/forum/index.php?topic=690885.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/09-05-2019-to-oot-7-e/msg558959/
http://teambuildingpremium.com/forum/index.php?topic=759460.0
http://HyUa.1fps.icu/l/szIaeDC
http://roikjer.com/forum/index.php?PHPSESSID=5ju28v5r62samp5n3rol382kr5&topic=843760.0
http://www.deliberarchia.org/forum/index.php?topic=1000716.0
https://members.fbhaters.com/index.php?topic=88640.0
https://members.fbhaters.com/index.php?topic=88655.0
https://nextezone.com/index.php?topic=42336.0
https://reficulcoin.com/index.php?topic=21463.0
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k4-l3-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-v8-b5-%d0%b8%d0%b3/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e6-s4-%d0%b8%d0%b3%d1%80/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-i2-k9-%d0%b8%d0%b3/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n8-p2-%d0%b8%d0%b3%d1%80/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j5-l8-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x9-q5-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-x4-o5-%d0%b8%d0%b3/
https://forum.clubeicaro.pt/index.php?topic=1013.0
https://forum.clubeicaro.pt/index.php?topic=1014.0
https://forum.clubeicaro.pt/index.php?topic=1015.0
https://forum.clubeicaro.pt/index.php?topic=1016.0
https://khuyenmaikk13.info/index.php?topic=190393.0
http://forum.elexlabs.com/index.php/topic,18078.0.html
http://forum.elexlabs.com/index.php?topic=18076.0
https://nextezone.com/index.php?topic=33933.0
http://forum.digamahost.com/index.php?topic=107129.0
http://soc-human.kz/index.php/component/k2/itemlist/user/1623605
http://menulisilmiah.net/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c2-i3-%d1%80%d0%b0%d1%81%d1%81/
http://forum.elexlabs.com/index.php?topic=15850.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=677183.0
http://www.theparrotcentre.com/forum/index.php?topic=446959.0
https://danceplanet.se/commodore/index.php?topic=8712.0
http://www.remify.app/foro/index.php?topic=207333.0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=757376
http://sextomariotienda.com/blog/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t3-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-q8-w4-%d0%b8%d0%b3%d1%80/
http://danielmillsap.com/forum/index.php?topic=986319.0
http://roikjer.com/forum/index.php?PHPSESSID=vt07gvbmb45b99dpep1vfi80f0&topic=804215.0
http://sextomariotienda.com/blog/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://miklja.net/forum/index.php?topic=26241.0
http://freebeer.me/index.php?topic=291314.0
http://muonlineint.com/forum/index.php?topic=1024.0
http://myrechockey.com/forums/index.php?topic=86131.0
https://forum.clubeicaro.pt/index.php?topic=785.0
http://153.120.114.241/eso/index.php/16852297-igra-prestolov-8-sezon-4-seria-mp3-igra-prestolov-8-sezon-4-ser
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=25116.0
http://www.hoonthaitoday.com/forum/index.php?topic=185506.0
http://HyUa.1fps.icu/l/szIaeDC
<a href="http://cialisdxt.com/">buy cialis online</a>
generic cialis at walmart pharmacy usa
[url=http://cialisdxt.com/]cialis generic[/url]
cialis dosage 40 mg
<a href="http://cialisec.com/">generic cialis</a>
20 mg dose of cialis
[url=http://cialisec.com/]cialis online[/url]
best deal on generic cialis
http://myrechockey.com/forums/index.php?topic=85890.0
http://otitismediasociety.org/forum/index.php?topic=148065.0
http://storykingdom.forumside.com/index.php?topic=5296.0
https://hackersuniversity.net/index.php?topic=6344.0
http://sextomariotienda.com/blog/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q5-%d1%81%d0%bb/
http://153.120.114.241/eso/index.php/16844336-04052019-ne-zenskaa-rabota-ne-zinoca-robota-17-seria
https://adsensebih.com/index.php?topic=8666.0
https://cybergsm.es/index.php?topic=8252.0
https://reficulcoin.com/index.php?topic=6152.0
http://multikopterforum.hu/index.php?topic=7849.0
http://www.theparrotcentre.com/forum/index.php?topic=478076.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/181436
https://danceplanet.se/commodore/index.php?topic=12962.0
http://freebeer.me/index.php?topic=302675.0
http://dpmarketingsystems.com/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j0-%d1%81%d0%bb%d1%83/
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f0-x3-%d1%80%d0%b0%d1%81%d1%81/
http://sextomariotienda.com/blog/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fz0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.remify.app/foro/index.php?topic=215353.0
http://www.deliberarchia.org/forum/index.php?topic=946013.0
http://storykingdom.forumside.com/index.php?topic=5435.0
http://dpmarketingsystems.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q7-%d1%81%d0%bb%d1%83%d0%b3/
http://www.deliberarchia.org/forum/index.php?topic=946604.0
http://www.hoonthaitoday.com/forum/index.php?topic=129020.0
https://khuyenmaikk13.info/index.php?topic=181681.0
http://www.deliberarchia.org/forum/index.php?topic=974009.0
http://sextomariotienda.com/blog/04-05-2019-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://withinfp.sakura.ne.jp/eso/index.php/16875908-igra-prestolovgame-of-thrones-8-sezon-3-seria-mg6-igra-prestolo/0
http://www.theparrotcentre.com/forum/index.php?topic=455637.0
http://www.autospa.lv/index.php/lv/component/k2/itemlist/user/8999
https://reficulcoin.com/index.php?topic=7730.0
http://c3isecurity.com.br/component/k2/itemlist/user/464017
https://reficulcoin.com/index.php?topic=13497.0
http://forum.stollen24.com/index.php?topic=2963.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yr6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.popolsku.fr.pl/forum/index.php?topic=374343.0
http://help.stv.ru/index.php?PHPSESSID=912feac5ab88e2611ea143c856b0885f&topic=136257.0
http://codeerror.in/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90sx5%e3%80%91/
http://www.remify.app/foro/index.php?topic=216193.0
http://mir3sea.com/forum/index.php?topic=472.0
http://bobr.site/index.php?topic=94509.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tz4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://mir3sea.com/forum/index.php?topic=1009.0
http://HyUa.1fps.icu/l/szIaeDC
http://multikopterforum.hu/index.php?topic=11092.0
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1011348
http://www.tessabannampad.go.th/webboard/index.php?topic=191313.0
http://otitismediasociety.org/forum/index.php?topic=142975.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-k7-b4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://salescoach.ro/content/%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%E3%80%90rx4%E3%80%91-%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://photogrotto.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90fb3%e3%80%91-%d0%b8%d0%b3/
http://teambuildingpremium.com/forum/index.php?topic=783411.0
https://sanp.pro/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l9-x9-%d1%80%d0%b0%d1%81%d1%81/
http://www.critico-expository.com/forum/index.php?topic=1735.0
http://1vh.info/index.php?topic=6341.0
http://www.tessabannampad.go.th/webboard/index.php?topic=193586.0
http://e-educ.net/Forum/index.php?topic=4882.0
http://www.tessabannampad.go.th/webboard/index.php?topic=188534.0
http://withinfp.sakura.ne.jp/eso/index.php/16860997-ertugrul-145-seria-gs7-ertugrul-145-seria/0
http://theolevolosproject.org/index.php/component/k2/itemlist/user/23631
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/210385
http://help.stv.ru/index.php?PHPSESSID=6c0169bea7045ef767a95230c7bf6982&topic=138229.0
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1838982
http://teambuildingpremium.com/forum/index.php?topic=766327.0
http://poselokgribovo.ru/forum/index.php?topic=721298.0
http://multikopterforum.hu/index.php?topic=7085.0
https://sanp.pro/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-l6-d7-%d1%80/
https://danceplanet.se/commodore/index.php?topic=8596.0
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s2-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s5-k2-%d1%80%d0%b0%d1%81%d1%81/
https://doe.go.th/prd/forum_nongkhai/1520048-147-ru8-147
http://roikjer.com/forum/index.php?topic=808528.0
http://sextomariotienda.com/blog/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a8-%d1%81%d0%bb/
https://hackersuniversity.net/index.php/topic,6156.0.html
http://dpmarketingsystems.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kp3-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://forum.politeknikgihon.ac.id/index.php?topic=14353.0
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1831890
http://immobilia.gr/index.php/de/component/k2/itemlist/user/15970
http://forum.stollen24.com/index.php?topic=2619.0
http://withinfp.sakura.ne.jp/eso/index.php/16867220-igra-prestolov-got-8-sezon-2-seria-igra-prestolov-got-8-sezon-2/0
http://fbpharm.net/index.php/component/k2/itemlist/user/18280
http://danielmillsap.com/forum/index.php?topic=983609.0
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=47974
http://adsudoeste.com.br/index.php/component/k2/itemlist/user/20911
http://menulisilmiah.net/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i9-p4-%d1%80%d0%b0/
http://ru-realty.com/forum/index.php?topic=463903.0
http://HyUa.1fps.icu/l/szIaeDC
http://forum.byehaj.hu/index.php?topic=76953.0
http://wituclub.ru/forum/index.php?PHPSESSID=tejb19f4d41krkge0n30fpons5&topic=25594.0
https://www.amazingworldtop.com/entretenimiento/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u5-q0-%d1%80%d0%b0%d1%81%d1%81/
http://cccpvideo.forumside.com/index.php?topic=566.0
http://ru-realty.com/forum/index.php?PHPSESSID=qhbmbftnfsu9t9jklhu1a395t5&topic=459727.0
http://ru-realty.com/forum/index.php?PHPSESSID=i8bl5d2abg8te20e85a714td27&topic=461482.0
http://freebeer.me/index.php?topic=303000.0
https://reficulcoin.com/index.php?topic=10512.0
http://poselokgribovo.ru/forum/index.php?topic=717134.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/184257
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=682045.0
http://multikopterforum.hu/index.php?topic=8954.0
https://forums.letstalkbeats.com/index.php?topic=69773.0
http://codeerror.in/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90oc7%e3%80%91/
http://www.deliberarchia.org/forum/index.php?topic=953636.0
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-18/
http://forum.politeknikgihon.ac.id/index.php?topic=13220.0
https://danceplanet.se/commodore/index.php?topic=12845.0
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w9-b0-%d1%80%d0%b0%d1%81%d1%81/
http://dpmarketingsystems.com/%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-16-%d1%81%d0%b5-66/
http://otitismediasociety.org/forum/index.php?topic=147218.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=300899
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o7-e5-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://necinsurance.co.zw/component/k2/itemlist/user/18754.html
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/996889
http://poselokgribovo.ru/forum/index.php?topic=720714.0
http://help.stv.ru/index.php?PHPSESSID=ae460114a240295e660f4bbb9b070a31&topic=137751.0
http://dpmarketingsystems.com/06-05-2019-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://roikjer.com/forum/index.php?PHPSESSID=29mub8bvvismvqkg10hb6plbs1&topic=790389.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90lf6%e3%80%91-%d0%b8%d0%b3/
http://www.ekemoon.com/153981/051920192807/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90fr1%e3%80%91/
http://seoksoononly.dothome.co.kr/qna/736802
http://dpmarketingsystems.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i0-c8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
https://cybergsm.es/index.php?topic=8070.0
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=43609
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-n6-o1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://danielmillsap.com/forum/index.php?topic=980400.0
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-7/
http://otitismediasociety.org/forum/index.php?topic=147389.0
https://sanp.pro/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y2-e6-%d1%80%d0%b0/
http://HyUa.1fps.icu/l/szIaeDC
http://216.104.186.20/index.php?topic=302473.0
https://hackersuniversity.net/index.php?topic=7500.0
http://www.hoonthaitoday.com/forum/index.php?topic=180065.0
http://www.deliberarchia.org/forum/index.php?topic=940752.0
http://withinfp.sakura.ne.jp/eso/index.php/16867452-igra-prestolovgame-of-thrones-8-sezon-6-seria-igra-prestolovgam/0
http://withinfp.sakura.ne.jp/eso/index.php/16857269-igra-prestolov-got-8-sezon-7-seria-igra-prestolov-got-8-sezon-7
http://blog.ptpintcast.com/04-05-2019-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.theocraticamerica.org/forum/index.php?topic=24565.0
http://www.tessabannampad.go.th/webboard/index.php?topic=183681.0
https://danceplanet.se/commodore/index.php?topic=8711.0
http://216.104.186.20/index.php?topic=307223.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=25124.0
http://istakam.com/forum/index.php?topic=8883.0
http://forum.politeknikgihon.ac.id/index.php?topic=25751.0
http://www.tessabannampad.go.th/webboard/index.php?topic=187429.0
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p8-d9-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://reficulcoin.com/index.php?topic=4614.0
https://forum.clubeicaro.pt/index.php?topic=720.0
http://eugeniocolazzo.it/forum/index.php?topic=88311.0
http://sextomariotienda.com/blog/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.ekemoon.com/150633/050520193107/
http://roikjer.com/forum/index.php?PHPSESSID=dbiml6a0oe2m3m7af0mkmosva3&topic=830343.0
http://multikopterforum.hu/index.php?topic=14492.0
http://storykingdom.forumside.com/index.php/topic,3867.0.html
https://khuyenmaikk13.info/index.php?topic=177090.0
http://poselokgribovo.ru/forum/index.php?topic=740256.0
http://myrechockey.com/forums/index.php?topic=85365.0
https://npi.org.es/smf/index.php?topic=110516.0
http://www.critico-expository.com/forum/index.php?topic=5109.0
http://poselokgribovo.ru/forum/index.php?topic=739896.0
http://roikjer.com/forum/index.php?PHPSESSID=ud7ngkcakb4tjskpc7j589bsp1&topic=811883.0
http://forum.politeknikgihon.ac.id/index.php?topic=19138.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4705969
https://reficulcoin.com/index.php?topic=8933.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vk5-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
https://luckychancerescue.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h3-d4-%d1%80%d0%b0%d1%81%d1%81/
http://www.hoonthaitoday.com/forum/index.php?topic=134573.0
http://golyboe.ru/forum/index.php?topic=25383.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3290316
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90fk2%e3%80%91-%d0%b8%d0%b3/
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/491366
http://istakam.com/forum/index.php?topic=9740.0
https://nextezone.com/index.php?topic=33979.0
http://muratliziraatodasi.org/forum/index.php?topic=152910.2010
http://poselokgribovo.ru/forum/index.php?topic=698620.0
http://HyUa.1fps.icu/l/szIaeDC
http://blog.ptpintcast.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-z6-o1-%d0%b8/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1328237
http://www.tessabannampad.go.th/webboard/index.php?topic=189271.0
http://storykingdom.forumside.com/index.php?topic=4160.0
http://www.tessabannampad.go.th/webboard/index.php?topic=186015.0
http://roikjer.com/forum/index.php?topic=806300.0
http://flashboot.ru/forum/index.php?topic=94144.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/et-e-15-e-07-05-2019-419916/?PHPSESSID=n70vi1af67ht8o8psvi5dhd166
http://dpmarketingsystems.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cs9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8/
http://www.deliberarchia.org/forum/index.php?topic=962189.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-q5-s7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://photogrotto.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90ys2%e3%80%91/
https://reficulcoin.com/index.php?topic=14619.0
http://www.hoonthaitoday.com/forum/index.php?topic=184212.0
http://multikopterforum.hu/index.php?topic=11556.0
http://www.hoonthaitoday.com/forum/index.php?topic=160270.0
https://polyframetrade.co.uk/%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-4-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-watch-f3-r2-%D1%80/
http://uberdrivers.net/forum/index.php?topic=219339.0
http://withinfp.sakura.ne.jp/eso/index.php/16858651-05052019-podsudimyj-8-seria/0
http://danielmillsap.com/forum/index.php?topic=927079.0
https://worldtaxi.org/2019/05/09/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-6/
https://members.fbhaters.com/index.php?topic=71418.0
http://poselokgribovo.ru/forum/index.php?topic=688640.0
http://www.popolsku.fr.pl/forum/index.php?topic=20407.49290
https://worldtaxi.org/2019/05/08/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-4/
http://vtservices85.fr/smf2/index.php?PHPSESSID=2337ceeb8900c983a127bfc7e38054c1&topic=212756.0
http://www.ekemoon.com/156615/050420195208/
http://thanosakademi.com/index.php?topic=61135.0
http://teambuildingpremium.com/forum/index.php?topic=760050.0
http://www.theparrotcentre.com/forum/index.php?topic=474635.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/60859
http://vtservices85.fr/smf2/index.php?PHPSESSID=9c2faf4d331bb8b4f760d5d814b1f215&topic=204948.0
http://HyUa.1fps.icu/l/szIaeDC
http://forum.drahthaar-club.com.ua/index.php?topic=1397.0
http://forum.elexlabs.com/index.php?topic=16532.0
http://forum.elexlabs.com/index.php?topic=16536.0
http://forum.elexlabs.com/index.php?topic=16538.0
http://forum.politeknikgihon.ac.id/index.php?topic=29038.0
http://forum.politeknikgihon.ac.id/index.php?topic=29041.0
http://forum.politeknikgihon.ac.id/index.php?topic=29047.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=30344.0
http://myrechockey.com/forums/index.php?topic=91490.0
http://partemp.com/en/groups/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f3-x3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://forums.letstalkbeats.com/index.php?topic=61288.0
http://myrechockey.com/forums/index.php?topic=81906.0
http://bobr.site/index.php?topic=87557.0
http://matrixpharm.ru/forum/index.php?PHPSESSID=m1jkrm0b7s17v6vn7d9tp3pgd6&action=profile;u=164155
http://www.deliberarchia.org/forum/index.php?topic=934411.0
http://www.deliberarchia.org/forum/index.php?topic=981192.0
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-e3-f6-%d1%80/
http://teambuildingpremium.com/forum/index.php?topic=760466.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=1f340e1004f6a1dd5fbaaffcf619cfa6&topic=203965.0
http://mir3sea.com/forum/index.php?topic=69.0
https://www.shaiyax.com/index.php?topic=326781.0
https://www.c-alice.org/forum/index.php?topic=73175.0
http://vtservices85.fr/smf2/index.php?topic=204183.0
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3367254
http://ru-realty.com/forum/index.php?PHPSESSID=l02rc3l3mbr1dd8t4dqfceo686&topic=455767.0
http://e-educ.net/Forum/index.php?topic=4285.0
http://1vh.info/index.php?topic=5721.0
https://forum.shaiyaslayer.tk/index.php?topic=89848.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2556195
http://withinfp.sakura.ne.jp/eso/index.php/16860613-ertugrul-148-seria-qz3-ertugrul-148-seria/0
https://members.fbhaters.com/index.php?topic=78275.0
http://HyUa.1fps.icu/l/szIaeDC
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=683440.0
https://forum.shaiyaslayer.tk/index.php?topic=100680.0
https://khuyenmaikk13.info/index.php?topic=186300.0
http://danielmillsap.com/forum/index.php?topic=995649.0
http://danielmillsap.com/forum/index.php?topic=995666.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=30381.0
https://reficulcoin.com/index.php?topic=17843.0
https://reficulcoin.com/index.php?topic=17850.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-31/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z3-x6-%d0%b8%d0%b3%d1%80/
https://danceplanet.se/commodore/index.php?topic=13301.0
https://lucky28003.nl/forum/index.php?topic=11999.0
http://roikjer.com/forum/index.php?PHPSESSID=vdhkvri0n0s3165n9av8a5n1f5&topic=813002.0
https://sanp.pro/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a5-f8-%d1%80%d0%b0%d1%81%d1%81/
https://reficulcoin.com/index.php?topic=8305.0
http://flashboot.ru/forum/index.php?topic=94167.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/06-05-2019-om-17-e-418647/
http://fbpharm.net/index.php/component/k2/itemlist/user/15413
http://eugeniocolazzo.it/forum/index.php?topic=100549.0
http://poselokgribovo.ru/forum/index.php?topic=687753.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3558077
http://otitismediasociety.org/forum/index.php?topic=144594.0
http://e-educ.net/Forum/index.php?topic=3239.0
http://roikjer.com/forum/index.php?PHPSESSID=1enn8as679p9ag8g51kpte2641&topic=828348.0
http://www.grupojover.com/index.php/es/component/k2/itemlist/user/3497
http://vervetama.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r8-d8-%d1%80%d0%b0%d1%81%d1%81/
http://forum.digamahost.com/index.php?topic=107184.0
https://polyframetrade.co.uk/%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-1-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-watch-w2-r9-%D1%80%D0%B0/
http://ru-realty.com/forum/index.php?PHPSESSID=g4ohbt0p8i88b6bc9iqnigbf24&topic=460335.0
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://forum.politeknikgihon.ac.id/index.php?topic=12713.0
http://poselokgribovo.ru/forum/index.php?topic=719802.0
http://poselokgribovo.ru/forum/index.php?topic=721245.0
http://menulisilmiah.net/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c1-w3-%d1%80%d0%b0%d1%81%d1%81/
http://HyUa.1fps.icu/l/szIaeDC
https://khuyenmaikk13.info/index.php?topic=186330.0
https://members.fbhaters.com/index.php/topic,84627.0.html
https://members.fbhaters.com/index.php?topic=84619.0
https://members.fbhaters.com/index.php?topic=84633.0
https://nextezone.com/index.php?topic=40131.0
https://npi.org.es/smf/index.php?topic=113565.0
https://npi.org.es/smf/index.php?topic=113566.0
https://reficulcoin.com/index.php?topic=17860.0
https://reficulcoin.com/index.php?topic=17874.0
https://worldtaxi.org/2019/05/09/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o8-h6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://worldtaxi.org/2019/05/09/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p6-p7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://worldtaxi.org/2019/05/09/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z8-o7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://worldtaxi.org/2019/05/09/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j2-z3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://forum.clubeicaro.pt/index.php?topic=878.0
http://www.critico-expository.com/forum/index.php?topic=6943.0
http://www.hoonthaitoday.com/forum/index.php?topic=204218.0
https://reficulcoin.com/index.php?topic=17887.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-25/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-32/
https://worldtaxi.org/2019/05/09/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-2/
http://otitismediasociety.org/forum/index.php?topic=149351.0
http://otitismediasociety.org/forum/index.php?topic=149352.0
https://www.c-alice.org/forum/index.php?topic=74680.0
http://multikopterforum.hu/index.php?topic=13708.0
http://sextomariotienda.com/blog/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e4-c0-%d1%80%d0%b0%d1%81%d1%81/
https://reficulcoin.com/index.php?topic=4456.0
http://otitismediasociety.org/forum/index.php?topic=146550.0
https://danceplanet.se/commodore/index.php?topic=14387.0
http://miklja.net/forum/index.php?topic=25173.0
http://withinfp.sakura.ne.jp/eso/index.php/16836768-ertugrul-146-seria-py4-ertugrul-146-seria
https://reficulcoin.com/index.php?topic=12005.0
http://macdistri.com/index.php/component/k2/itemlist/user/289717
http://otitismediasociety.org/forum/index.php?topic=144133.0
http://www.deliberarchia.org/forum/index.php?topic=950432.0
https://nextezone.com/index.php?topic=34238.0
https://nextezone.com/index.php?action=profile;u=1985
http://www.critico-expository.com/forum/index.php?topic=4368.0
http://1vh.info/index.php?topic=7328.0
http://HyUa.1fps.icu/l/szIaeDC
http://salescoach.ro/content/%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-game-thrones-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-4-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%E3%80%90da6%E3%80%91-%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-game-thrones-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-4
http://myrechockey.com/forums/index.php?topic=84854.0
http://216.104.186.20/index.php?topic=293489.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r9-b4-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
https://reficulcoin.com/index.php?topic=12481.0
http://guiadetudo.com/index.php/component/k2/itemlist/user/10741
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=679267.0
http://www.critico-expository.com/forum/index.php?topic=3166.0
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-4/
http://vtservices85.fr/smf2/index.php?PHPSESSID=0d933b876206277489922f323f8b78e9&topic=207269.0
http://withinfp.sakura.ne.jp/eso/index.php/16859137-igra-prestolov-2019-8-sezon-2-seria-igra-prestolov-2019-8-sezon
http://freebeer.me/index.php?topic=313064.0
http://www.popolsku.fr.pl/forum/index.php?topic=371062.0
https://www.amazingworldtop.com/entretenimiento/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-g2-e7-%d1%80/
http://danielmillsap.com/forum/index.php?topic=932815.0
http://www.deliberarchia.org/forum/index.php?topic=938426.0
http://withinfp.sakura.ne.jp/eso/index.php/16854643-ertugrul-148-seria-ot0-ertugrul-148-seria/0
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90ck0%e3%80%91-%d0%b8%d0%b3/
http://storykingdom.forumside.com/index.php?topic=4059.0
https://reficulcoin.com/index.php?topic=12547.0
http://www.grupojover.com/index.php/es/component/k2/itemlist/user/3750
http://HyUa.1fps.icu/l/szIaeDC
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u8-m1-%d0%b8%d0%b3%d1%80/
http://153.120.114.241/eso/index.php/16853446-igra-prestolovgame-of-thrones-8-sezon-4-seria-igra-prestolovgam
http://danielmillsap.com/forum/index.php?topic=918909.0
https://adsensebih.com/index.php?topic=8776.0
http://www.ekemoon.com/156693/050520190508/
http://roikjer.com/forum/index.php?PHPSESSID=l4erv0ttsl79a1a80f306hu5d0&topic=824020.0
http://myrechockey.com/forums/index.php?topic=88789.0
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-f9-u6-%d1%80%d0%b0%d1%81-2/
http://www.tekparcahdfilm.com/forum/index.php?topic=46802.0
http://ru-realty.com/forum/index.php?PHPSESSID=ekvhu1asms9oakpeujltdbg5o3&topic=455435.0
http://otitismediasociety.org/forum/index.php?topic=144141.0
http://sextomariotienda.com/blog/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d7-%d1%81/
https://www.amazingworldtop.com/entretenimiento/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-m7-n4-%d1%80/
http://webp.online/index.php?topic=47275.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=24410.0
http://sextomariotienda.com/blog/04-05-2019-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://danielmillsap.com/forum/index.php?topic=956445.0
https://khuyenmaikk13.info/index.php?topic=179676.0
http://forum.digamahost.com/index.php?topic=107600.0
https://nextezone.com/index.php?action=profile;u=2412
https://www.shaiyax.com/index.php?topic=333956.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=25440.0
http://www.m1avio.com/index.php/component/k2/itemlist/user/3587393
https://members.fbhaters.com/index.php?topic=69316.0
http://travelsolution.info/index.php/component/k2/itemlist/user/713347
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o5-a5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://reficulcoin.com/index.php?topic=10704.0
https://members.fbhaters.com/index.php?topic=72993.0
http://www.tessabannampad.go.th/webboard/index.php?topic=190408.0
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=110837
http://www.deliberarchia.org/forum/index.php?topic=983241.0
https://nextezone.com/index.php?topic=33847.0
http://forum.politeknikgihon.ac.id/index.php?topic=20829.0
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-g3-e5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
https://reficulcoin.com/index.php?topic=12628.0
http://ru-realty.com/forum/index.php?PHPSESSID=t5ki0d4tutb99dfo40oqev3qa7&topic=472241.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b4-n9-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://1vh.info/index.php?topic=13501.0
http://HyUa.1fps.icu/l/szIaeDC
<a href="http://cialisdxt.com/">buy cialis online</a>
viagra cialis canadian pharmacy
[url=http://cialisdxt.com/]generic cialis[/url]
buy generic cialis canada online
http://roikjer.com/forum/index.php?topic=820202.0
http://www.deliberarchia.org/forum/index.php?topic=957476.0
http://poselokgribovo.ru/forum/index.php?topic=707468.0
http://danielmillsap.com/forum/index.php?topic=926587.0
http://www.critico-expository.com/forum/index.php?topic=4414.0
http://kurnaz.1to.us/index.php?topic=1.msg1146
http://153.120.114.241/eso/index.php/16850209-igra-prestolov-game-of-thrones-8-sezon-5-seria-igra-prestolov-g
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90xu0%e3%80%91/
http://e-educ.net/Forum/index.php?topic=6735.0
http://www.deliberarchia.org/forum/index.php?topic=987907.0
http://danielmillsap.com/forum/index.php?topic=979040.0
http://withinfp.sakura.ne.jp/eso/index.php/16845723-ertugrul-146-seria-hb5-ertugrul-146-seria/0
https://worldtaxi.org/2019/05/08/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a2-i9-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://otitismediasociety.org/forum/index.php?topic=142261.0
http://metropolis.ga/index.php?topic=2714.0
http://thanosakademi.com/index.php?topic=59518.0
http://153.120.114.241/eso/index.php/16857233-igra-prestolov-8-sezon-4-seria-cn6-igra-prestolov-8-sezon-4-ser
http://forum.politeknikgihon.ac.id/index.php?topic=12391.0
http://www.theparrotcentre.com/forum/index.php?topic=470969.0
http://menulisilmiah.net/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90rv6%e3%80%91-%d0%b8%d0%b3%d1%80/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90tk4%e3%80%91-%d0%b8%d0%b3/
https://reficulcoin.com/index.php?topic=4234.0
https://sto54.ru/index.php/component/k2/itemlist/user/3287718
http://mir3sea.com/forum/index.php?topic=354.0
https://www.c-alice.org/forum/index.php?topic=72962.0
http://forum.stollen24.com/index.php?topic=2887.0
http://HyUa.1fps.icu/l/szIaeDC
http://istakam.com/forum/index.php?topic=8816.0
http://thanosakademi.com/index.php?topic=62448.0
http://danielmillsap.com/forum/index.php?topic=943488.0
http://withinfp.sakura.ne.jp/eso/index.php/16866215-ertugrul-146-seria-jl3-ertugrul-146-seria/0
http://www.ekemoon.com/144629/051120191306/
https://khuyenmaikk13.info/index.php?topic=180053.0
http://freebeer.me/index.php?topic=306871.0
http://istakam.com/forum/index.php?topic=9811.0
http://wb.hvekorat.com/index.php?topic=40878.0
http://forum.byehaj.hu/index.php?topic=76924.0
http://www.tessabannampad.go.th/webboard/index.php?topic=192795.0
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v4-j1-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=162033
https://lucky28003.nl/forum/index.php?topic=7419.0
http://matrixpharm.ru/forum/index.php?PHPSESSID=huhd4smc3q8vm1p3mtcvamoq33&action=profile;u=161437
http://forum.digamahost.com/index.php?topic=108337.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=1b9590dea0f101915fce4f15d89b39a3&topic=207442.0
http://roikjer.com/forum/index.php?PHPSESSID=l9g6b04a06lemcj5tk2i0052n2&topic=811945.0
http://forum.politeknikgihon.ac.id/index.php?topic=21128.0
http://www.tessabannampad.go.th/webboard/index.php?topic=188768.0
http://svgrossburgwedel.de/component/k2/itemlist/user/5415
http://menulisilmiah.net/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u1-a0-%d1%80%d0%b0%d1%81%d1%81/
http://withinfp.sakura.ne.jp/eso/index.php/16867230-05052019-podsudimyj-17-seria/0
http://myrechockey.com/forums/index.php?topic=85703.0
http://miklja.net/forum/index.php?topic=25692.0
http://matrixpharm.ru/forum/index.php?PHPSESSID=b0435fqlf4kvf4kqlr7psfelp1&action=profile;u=159901
https://www.amazingworldtop.com/entretenimiento/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x1-o1-%d1%80%d0%b0%d1%81%d1%81/
http://vtservices85.fr/smf2/index.php?PHPSESSID=85bfbf628532c1f6a989b84cb1638462&topic=204750.0
http://www.popolsku.fr.pl/forum/index.php?topic=20407.54495
http://freebeer.me/index.php?topic=290226.0
http://e-educ.net/Forum/index.php?topic=3361.0
http://taklongclub.com/forum/index.php?topic=83524.0
http://danielmillsap.com/forum/index.php?topic=921080.0
https://chromehearts.in.th/index.php/topic,43487.0.html
http://www.hoonthaitoday.com/forum/index.php?topic=126699.0
http://subforumna.x10.mx/mad/index.php?topic=219263.0
http://ru-realty.com/forum/index.php?PHPSESSID=2r3cnmblcsh5l0vcjugu244k13&topic=469353.0
https://l2thalassic.org/Forum/index.php?topic=1844.0
http://www.remify.app/foro/index.php?topic=237390.0
http://multikopterforum.hu/index.php?topic=11468.0
http://healthyteethpa.org/?option=com_k2&view=itemlist&task=user&id=5320560
http://www.tekparcahdfilm.com/forum/index.php?topic=46092.0
http://HyUa.1fps.icu/l/szIaeDC
http://vtservices85.fr/smf2/index.php?PHPSESSID=42fda4ee6104f6e9a3bc5d0e42942ef4&topic=204576.0
https://nextezone.com/index.php?topic=37533.0
https://nextezone.com/index.php?topic=37828.0
http://www.theocraticamerica.org/forum/index.php?topic=26324.0
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i3-e5-%d1%80%d0%b0%d1%81/
http://vtservices85.fr/smf2/index.php?PHPSESSID=d45c46a0d2aa3610b23108810f1ea93a&topic=205015.0
http://uberdrivers.net/forum/index.php?topic=239268.0
http://muonlineint.com/forum/index.php?topic=656.0
https://hackersuniversity.net/index.php?topic=6423.0
http://forum.bmw-e60.eu/index.php?topic=2114.0
http://highlanderonline.cmshelplive.net/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nl8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8/
http://codeerror.in/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-2/
https://adsensebih.com/index.php?topic=7667.0
http://teambuildingpremium.com/forum/index.php?topic=762536.0
http://8.droror.co.il/uncategorized/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t0-l9-%d1%80%d0%b0%d1%81%d1%81/
http://sextomariotienda.com/blog/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w7-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80-2/
http://www.hoonthaitoday.com/forum/index.php?topic=160300.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(a-etoo-(got)-8-eo-2-e)-a-etoo-(got)-8-eo-2-e-h7y7/
http://forum.bmw-e60.eu/index.php?topic=3868.0
http://mir3sea.com/forum/index.php?topic=150.0
http://taklongclub.com/forum/index.php?topic=85814.0
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-d9-q0-%d1%80/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-21/
http://danielmillsap.com/forum/index.php?topic=962059.0
http://golyboe.ru/forum/index.php?topic=25350.0
https://khuyenmaikk13.info/index.php?topic=183498.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=679289.0
http://dpmarketingsystems.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vz5-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://uberdrivers.net/forum/index.php?topic=226279.0
http://withinfp.sakura.ne.jp/eso/index.php/16859954-igra-prestolov-got-8-sezon-2-seria-igra-prestolov-got-8-sezon-2/0
http://poselokgribovo.ru/forum/index.php?topic=713674.0
http://1vh.info/index.php?topic=8245.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-v5-w8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://sextomariotienda.com/blog/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w9/
http://www.hoonthaitoday.com/forum/index.php?topic=146202.0
https://khuyenmaikk13.info/index.php?topic=174405.0
http://taklongclub.com/forum/index.php?topic=102147.0
http://help.stv.ru/index.php?topic=139095.0
http://www.critico-expository.com/forum/index.php?topic=3737.0
http://www.remify.app/foro/index.php?topic=207723.0
http://www.deliberarchia.org/forum/index.php?topic=958768.0
http://HyUa.1fps.icu/l/szIaeDC
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e5-z6-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f9-f3-%d0%b8%d0%b3%d1%80/
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z8-w4-%d0%b8%d0%b3%d1%80/
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g5-l8-%d0%b8%d0%b3%d1%80/
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ot3-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-va3-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pt8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-se9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ri0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://danielmillsap.com/forum/index.php?topic=1012268.0
http://forum.byehaj.hu/index.php?topic=86940.0
http://forum.elexlabs.com/index.php?topic=20790.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ps3-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://vtservices85.fr/smf2/index.php?PHPSESSID=64564d6d4caf59c57c7fcd22c9c98ce6&topic=221575.0
http://www.hoonthaitoday.com/forum/index.php?topic=228749.0
http://www.tessabannampad.go.th/webboard/index.php?topic=201492.0
http://www.tessabannampad.go.th/webboard/index.php?topic=201496.0
http://www.tessabannampad.go.th/webboard/index.php?topic=201504.0
http://forum.elexlabs.com/index.php?topic=20794.0
http://www.hoonthaitoday.com/forum/index.php?topic=228716.0
http://www.tessabannampad.go.th/webboard/index.php?topic=201502.0
http://www.tessabannampad.go.th/webboard/index.php?topic=201514.0
https://reficulcoin.com/index.php?topic=26389.0
http://otitismediasociety.org/forum/index.php?topic=143012.0
http://www.hoonthaitoday.com/forum/index.php?topic=162012.0
http://necinsurance.co.zw/?option=com_k2&view=itemlist&task=user&id=18635
http://poselokgribovo.ru/forum/index.php?topic=690656.0
https://www.shaiyax.com/index.php?topic=327461.0
http://www.tessabannampad.go.th/webboard/index.php?topic=187521.0
http://danielmillsap.com/forum/index.php?topic=951382.0
http://www.tessabannampad.go.th/webboard/index.php?topic=192611.0
http://matrixpharm.ru/forum/index.php?PHPSESSID=t48ck7u8ia33ua9jrabo5e32n6&action=profile;u=163572
http://withinfp.sakura.ne.jp/eso/index.php/16858940-igra-prestolov-2019-8-sezon-6-seria-igra-prestolov-2019-8-sezon
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/464530
https://khuyenmaikk13.info/index.php?topic=180309.0
http://necinsurance.co.zw/component/k2/itemlist/user/18686.html
http://HyUa.1fps.icu/l/szIaeDC
http://roikjer.com/forum/index.php?PHPSESSID=8ral280hujk6hv0uioalcdmst5&topic=854467.0
https://nextezone.com/index.php?topic=44392.0
https://reficulcoin.com/index.php?topic=26492.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-k2-k9-%d0%b8%d0%b3/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w8-y5-%d0%b8%d0%b3%d1%80/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r8-a0-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-oa6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mz0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yj5-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bz4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://danielmillsap.com/forum/index.php?topic=1012472.0
http://eugeniocolazzo.it/forum/index.php?topic=117665.0
http://eugeniocolazzo.it/forum/index.php?topic=117667.0
http://flashboot.ru/forum/index.php?topic=94284.0
https://members.fbhaters.com/index.php?topic=74571.0
http://multikopterforum.hu/index.php?topic=14805.0
http://upperlevelonevideogametruck.com/index.php/component/k2/itemlist/user/316946
http://danielmillsap.com/forum/index.php?topic=938705.0
http://www.tessabannampad.go.th/webboard/index.php?topic=192047.0
http://www.theparrotcentre.com/forum/index.php?topic=477455.0
https://members.fbhaters.com/index.php?topic=81821.0
http://www.deliberarchia.org/forum/index.php?topic=934936.0
http://www.tessabannampad.go.th/webboard/index.php?topic=193115.0
http://www.hoonthaitoday.com/forum/index.php?topic=132708.0
https://reficulcoin.com/index.php?topic=5152.0
http://golyboe.ru/forum/index.php?topic=25310.0
http://www.ekemoon.com/156939/050520194308/
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1105258
http://freebeer.me/index.php?topic=302112.0
https://sanp.pro/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u1-e6-%d1%80%d0%b0%d1%81%d1%81/
http://poselokgribovo.ru/forum/index.php?topic=726862.0
http://poselokgribovo.ru/forum/index.php?topic=711327.0
https://sanp.pro/%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e6-%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-12-%d1%81%d0%b5%d1%80/
http://miklja.net/forum/index.php?topic=28073.0
http://HyUa.1fps.icu/l/szIaeDC
http://forum.elexlabs.com/index.php?topic=20988.0
http://www.popolsku.fr.pl/forum/index.php?topic=381490.0
http://www.tessabannampad.go.th/webboard/index.php?topic=201838.0
http://forum.elexlabs.com/index.php/topic,20982.0.html
http://forum.elexlabs.com/index.php?topic=20992.0
http://forum.elexlabs.com/index.php?topic=20998.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/'a-etoo-2019-8-eo-5-e'-a-etoo-2019-8-eo-5-e-v0c8/
http://www.tessabannampad.go.th/webboard/index.php?topic=201849.0
http://otitismediasociety.org/forum/index.php?topic=152798.0
http://otitismediasociety.org/forum/index.php?topic=152915.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k4-x1-%d0%b8%d0%b3/
https://members.fbhaters.com/index.php?topic=81452.0
http://forum.santrope-rp.ru/index.php?topic=2523.0
http://www.tessabannampad.go.th/webboard/index.php?topic=193990.0
http://www.popolsku.fr.pl/forum/index.php?topic=20407.43665
https://members.fbhaters.com/index.php?topic=74854.0
http://otitismediasociety.org/forum/index.php?topic=146394.0
https://adsensebih.com/index.php?topic=10922.0
http://photogrotto.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90cr3%e3%80%91-%d0%b8%d0%b3%d1%80/
http://forum.bmw-e60.eu/index.php?topic=4285.0
http://help.stv.ru/index.php?PHPSESSID=64024d5e33cda8bb05665dbe098afd38&topic=138686.0
http://eugeniocolazzo.it/forum/index.php?topic=88387.0
https://forums.letstalkbeats.com/index.php?topic=60810.0
http://sextomariotienda.com/blog/%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-16-%d1%81%d0%b5-26/
http://www.ekemoon.com/156581/050420194808/
http://eugeniocolazzo.it/forum/index.php?topic=82343.0
http://HyUa.1fps.icu/l/szIaeDC
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-32/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n0-i6-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://eugeniocolazzo.it/forum/index.php?topic=118347.0
http://forum.elexlabs.com/index.php?topic=21117.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zr9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8/
http://www.popolsku.fr.pl/forum/index.php?topic=381630.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/'a-etoo-2019-8-eo-2-e'-a-etoo-2019-8-eo-2-e-a1i4/?PHPSESSID=s7tv9sgnn5t25m5ki3i883cbf1
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-2019-8-eo-3-e-a-etoo-2019-8-eo-3-e-c1g2/?PHPSESSID=cha7h1dit8095513b9b0dt1vo6
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile&u=34734
https://reficulcoin.com/index.php?topic=27014.0
http://roikjer.com/forum/index.php?PHPSESSID=96sjm89svu1beu39605ltll5q3&topic=855367.0
http://www.deliberarchia.org/forum/index.php?topic=1010463.0
https://nextezone.com/index.php?topic=44569.0
https://reficulcoin.com/index.php?topic=27031.0
http://forum.elexlabs.com/index.php?topic=21129.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=687648.0
http://danielmillsap.com/forum/index.php?topic=1013764.0
http://forum.elexlabs.com/index.php/topic,21125.0.html
http://www.deliberarchia.org/forum/index.php?topic=947813.0
http://storykingdom.forumside.com/index.php?topic=5652.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90vm8%e3%80%91/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-13/
http://teambuildingpremium.com/forum/index.php?topic=789109.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4700433
http://216.104.186.20/index.php?topic=300819.0
http://highlanderonline.cmshelplive.net/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0/
http://otitismediasociety.org/forum/index.php?topic=144938.0
http://danielmillsap.com/forum/index.php?topic=990577.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.critico-expository.com/forum/index.php?topic=4552.0
http://blog.ptpintcast.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r8-j8-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://216.104.186.20/index.php?topic=304268.0
http://forum.byehaj.hu/index.php?topic=81231.0
http://1vh.info/index.php?topic=7777.0
https://members.fbhaters.com/index.php?topic=72594.0
http://forum.elexlabs.com/index.php?topic=13386.0
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1855071
http://withinfp.sakura.ne.jp/eso/index.php/16854945-05052019-podsudimyj-9-seria/0
http://vervetama.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-q6-u8-%d1%80/
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=673978.0
http://sextomariotienda.com/blog/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-an7-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.hoonthaitoday.com/forum/index.php?topic=174585.0
http://otitismediasociety.org/forum/index.php?topic=143070.0
https://prelease.club/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://help.stv.ru/index.php?PHPSESSID=2f52d83399e5a24d512991a9b8ea9014&topic=140486.0
http://otitismediasociety.org/forum/index.php?topic=152738.0
https://prelease.club/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://help.stv.ru/index.php?PHPSESSID=68ede273a8f62e1252aa3a79f678c0e6&topic=140489.0
http://help.stv.ru/index.php?PHPSESSID=f5fb383c72f8de6dabe6c4ff54afe85f&topic=140490.0
http://otitismediasociety.org/forum/index.php?topic=152747.0
http://otitismediasociety.org/forum/index.php?topic=152750.0
http://otitismediasociety.org/forum/index.php?topic=152762.0
http://help.stv.ru/index.php?PHPSESSID=1b34460785d9acddb41b959330256ce5&topic=140493.0
http://help.stv.ru/index.php?PHPSESSID=3a7f77005bb8fd6a2cce8b6f33ba4499&topic=140492.0
http://otitismediasociety.org/forum/index.php?topic=152766.0
http://roikjer.com/forum/index.php?topic=854439.0
https://danceplanet.se/commodore/index.php?topic=24774.0
http://help.stv.ru/index.php?PHPSESSID=0b72dcc86ad29d7066deaef2cef1106b&topic=140494.0
http://myrechockey.com/forums/index.php?topic=95103.0
http://otitismediasociety.org/forum/index.php?topic=152771.0
http://otitismediasociety.org/forum/index.php?topic=152773.0
http://otitismediasociety.org/forum/index.php?topic=152777.0
https://danceplanet.se/commodore/index.php?topic=24782.0
http://myrechockey.com/forums/index.php?topic=95109.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.ekemoon.com/154457/052120193207/
http://153.120.114.241/eso/index.php/16855725-igra-prestolov-2019-8-sezon-5-seria-xx7-igra-prestolov-2019-8-s
http://www.remify.app/foro/index.php?topic=225913.0
http://mir3sea.com/forum/index.php?topic=34.0
http://help.stv.ru/index.php?PHPSESSID=695b9ff17cebc9ca3c035d00cb48d1f2&topic=138235.0
https://polyframetrade.co.uk/%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-1-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-watch-k4-y5-%D1%80%D0%B0/
http://otitismediasociety.org/forum/index.php?topic=142947.0
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1854471
http://sextomariotienda.com/blog/05-05-2019-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-3/
http://roikjer.com/forum/index.php?PHPSESSID=i2skm334cjqihtobudnon64td0&topic=818351.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90rm7%e3%80%91-%d0%b8%d0%b3%d1%80/
http://teambuildingpremium.com/forum/index.php?topic=764440.0
http://forum.politeknikgihon.ac.id/index.php?topic=13873.0
http://www.tessabannampad.go.th/webboard/index.php?topic=194343.0
https://lucky28003.nl/forum/index.php?topic=7262.0
http://www.tessabannampad.go.th/webboard/index.php?topic=188555.0
http://forum.politeknikgihon.ac.id/index.php?topic=19944.0
http://roikjer.com/forum/index.php?PHPSESSID=ctdd6rbrl5eak5sohf9klcr6c1&topic=791415.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=26798.0
http://otitismediasociety.org/forum/index.php?topic=153708.0
https://prelease.club/%d1%8d%d1%84%d0%b8%d1%80-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h8-%d1%81%d0%bb%d1%83%d0%b3/
http://help.stv.ru/index.php?PHPSESSID=127abe453f2d04d84aecedb7a98506fe&topic=140612.0
http://help.stv.ru/index.php?PHPSESSID=50619e0fd69f13b57237f4fbf570e3d0&topic=140614.0
http://myrechockey.com/forums/index.php?topic=95617.0
https://danceplanet.se/commodore/index.php?topic=25871.0
https://danceplanet.se/commodore/index.php?topic=25874.0
https://prelease.club/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x6-%d1%81%d0%bb/
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h0/
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r9-%d1%81/
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p7-%d1%81%d0%bb/
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b0-%d1%81/
http://myrechockey.com/forums/index.php?topic=95613.0
http://myrechockey.com/forums/index.php?topic=95621.0
http://otitismediasociety.org/forum/index.php?topic=153740.0
http://otitismediasociety.org/forum/index.php?topic=153746.0
http://roikjer.com/forum/index.php?PHPSESSID=qm3rf9fh102nnl8hgiakgnhnp6&topic=857401.0
https://prelease.club/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b5-%d1%81%d0%bb%d1%83/
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m1/
http://help.stv.ru/index.php?PHPSESSID=7ecca89d3c1f161d7c2c44c70326bd33&topic=140616.0
http://help.stv.ru/index.php?topic=140618.0
http://myrechockey.com/forums/index.php?topic=95634.0
https://prelease.club/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y3-%d1%81%d0%bb/
http://HyUa.1fps.icu/l/szIaeDC
http://photogrotto.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90ot0%e3%80%91/
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t1-r8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://miklja.net/forum/index.php?topic=27031.0
http://help.stv.ru/index.php?PHPSESSID=bfa64a3e3b9b026e7b9fb5941b5ece71&topic=138620.0
http://withinfp.sakura.ne.jp/eso/index.php/16836383-ertugrul-147-seria-eu3-ertugrul-147-seria/0
http://www.deliberarchia.org/forum/index.php?topic=964547.0
http://myrechockey.com/forums/index.php?topic=83675.0
http://www.theocraticamerica.org/forum/index.php?topic=26563.0
https://www.amazingworldtop.com/entretenimiento/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d6-m2-%d1%80%d0%b0%d1%81%d1%81/
https://sanp.pro/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o2-n6-%d1%80%d0%b0%d1%81%d1%81/
https://sanp.pro/04-05-2019-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://forum.stollen24.com/index.php?topic=3480.0
http://www.deliberarchia.org/forum/index.php?topic=954234.0
http://danielmillsap.com/forum/index.php?topic=946256.0
https://prelease.club/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i5-%d1%81%d0%bb/
https://prelease.club/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u2-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
https://prelease.club/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i4-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
https://prelease.club/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://myrechockey.com/forums/index.php?topic=95586.0
http://otitismediasociety.org/forum/index.php?topic=153654.0
https://prelease.club/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://roikjer.com/forum/index.php?PHPSESSID=6mtrbccdivadjdljqrdagkh1p5&topic=857170.0
http://roikjer.com/forum/index.php?PHPSESSID=g7v04ni431vls9iqr9jov1sv03&topic=857188.0
https://prelease.club/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m8-%d1%81/
http://help.stv.ru/index.php?PHPSESSID=9107cfc8dd7342626dd73a3fa4127468&topic=140608.0
http://HyUa.1fps.icu/l/szIaeDC
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-3/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-3/
https://reficulcoin.com/index.php?topic=28007.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-9/
http://otitismediasociety.org/forum/index.php?topic=153667.0
http://roikjer.com/forum/index.php?PHPSESSID=kfav0d75t7idq156q7o1qnecv5&topic=857179.0
http://roikjer.com/forum/index.php?topic=857167.0
http://www.deliberarchia.org/forum/index.php?topic=1012256.0
http://forum.elexlabs.com/index.php?topic=21662.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vh8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.hoonthaitoday.com/forum/index.php?topic=233096.0
http://www.hoonthaitoday.com/forum/index.php?topic=233124.0
http://www.deliberarchia.org/forum/index.php?topic=1012307.0
http://www.theocraticamerica.org/forum/index.php?topic=25256.0
http://roikjer.com/forum/index.php?PHPSESSID=7tfudkje87mm662kj8omas9hn4&topic=795441.0
http://www.deliberarchia.org/forum/index.php?topic=949621.0
http://roikjer.com/forum/index.php?topic=803927.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90hr7%e3%80%91/
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-6/
http://withinfp.sakura.ne.jp/eso/index.php/16858247-igra-prestolovgame-of-thrones-8-sezon-3-seria-igra-prestolovgam
https://reficulcoin.com/index.php?topic=12245.0
http://poselokgribovo.ru/forum/index.php?topic=718349.0
http://teambuildingpremium.com/forum/index.php?topic=756058.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=26647.0
https://reficulcoin.com/index.php?topic=7614.0
http://HyUa.1fps.icu/l/szIaeDC
http://roikjer.com/forum/index.php?PHPSESSID=vcjtoi8j9qsgen1egv08nva3k2&topic=860590.0
http://roikjer.com/forum/index.php?topic=860614.0
https://reficulcoin.com/index.php?topic=29847.0
https://reficulcoin.com/index.php?topic=29855.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s1-w4-%d0%b8%d0%b3%d1%80/
http://forum.elexlabs.com/index.php?topic=22410.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=32143.0
http://danielmillsap.com/forum/index.php?topic=1021276.0
http://eugeniocolazzo.it/forum/index.php?topic=122204.0
http://forum.elexlabs.com/index.php/topic,22413.0.html
http://forum.elexlabs.com/index.php?topic=22411.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=32140.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uq5-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://uberdrivers.net/forum/index.php?topic=258210.0
http://www.popolsku.fr.pl/forum/index.php?topic=383442.0
http://www.remify.app/foro/index.php?topic=272813.0
http://www.tessabannampad.go.th/webboard/index.php?topic=202380.0
http://istakam.com/forum/index.php?topic=15319.0
http://otitismediasociety.org/forum/index.php?topic=155011.0
http://www.deliberarchia.org/forum/index.php?topic=1015964.0
http://freebeer.me/index.php?topic=284551.0
http://ru-realty.com/forum/index.php?PHPSESSID=dcsgonjnjtsot2071trmlnrfl4&topic=468686.0
http://multikopterforum.hu/index.php?topic=6014.0
http://blog.ptpintcast.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d0-w4-%d0%b8%d0%b3%d1%80/
http://poselokgribovo.ru/forum/index.php?topic=697085.0
https://szenarist.ru/forum/index.php?topic=203477.0
http://www.hoonthaitoday.com/forum/index.php?topic=143271.0
http://roikjer.com/forum/index.php?topic=791058.0
http://153.120.114.241/eso/index.php/16840178-04052019-podsudimyj-16-seria
http://myrechockey.com/forums/index.php?topic=81402.0
http://roikjer.com/forum/index.php?topic=832842.0
http://forum.politeknikgihon.ac.id/index.php?topic=12067.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mk8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://poselokgribovo.ru/forum/index.php?topic=699965.0
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile;u=29659
https://khuyenmaikk13.info/index.php?topic=174007.0
http://poselokgribovo.ru/forum/index.php?topic=688200.0
http://metropolis.ga/index.php?topic=2798.0
http://HyUa.1fps.icu/l/szIaeDC
<a href="http://cialisec.com/">generic cialis</a>
lowest price generic cialis tadalafil
[url=http://cialisec.com/]cialis online[/url]
cialis coupon 2017 200.00
[url=http://mir-stoleshki.moscow/forum/user/16451/]http://mir-stoleshki.moscow/forum/user/16451/[/url]
[url=https://ivanovosvadba.ru/communication/forum/user/10711/]https://ivanovosvadba.ru/communication/forum/user/10711/[/url]
[url=http://www.rybak-rybaka.ru/forum/user/117453/]http://www.rybak-rybaka.ru/forum/user/117453/[/url]
[url=http://asdmc.ru/about/forum/user/4257/]http://asdmc.ru/about/forum/user/4257/[/url]
[url=http://www.pa-i.ru/forum/index.php?PAGE_NAME=profile_view&UID=4847]http://www.pa-i.ru/forum/index.php?PAGE_NAME=profile_view&UID=4847[/url]
Проверяй свои кошельки так как
[url=http://www.webviki.ru/farming-mods.com]http://www.webviki.ru/farming-mods.com[/url]
[url=http://israclub.ru/communication/forum/?PAGE_NAME=profile_view&UID=11283]http://israclub.ru/communication/forum/?PAGE_NAME=profile_view&UID=11283[/url]
[url=http://autorolla.ru/forum/?PAGE_NAME=profile_view&UID=1556]http://autorolla.ru/forum/?PAGE_NAME=profile_view&UID=1556[/url]
[url=https://up74.ru/forum/user/7346/]https://up74.ru/forum/user/7346/[/url]
[url=http://dmedi.ru/about/forum/user/1558/]http://dmedi.ru/about/forum/user/1558/[/url]
У нас тут бывали и такие ребята
[url=http://visitusadba.ru/forum/user/300/]http://visitusadba.ru/forum/user/300/[/url]
[url=https://www.karateist.ru/forum/user/3681/]https://www.karateist.ru/forum/user/3681/[/url]
[url=https://pravitelstvorb.ru/forum/user/6479/]https://pravitelstvorb.ru/forum/user/6479/[/url]
[url=https://www.ufapro.pw/forum/index.php?topic=44.0]https://www.ufapro.pw/forum/index.php?topic=44.0[/url]
[url=http://1-kordai.mektebi.kz/orys-tl-zhne-debiet-b/218-tehnika-chteniya.html]http://1-kordai.mektebi.kz/orys-tl-zhne-debiet-b/218-tehnika-chteniya.html[/url]
Тут тоже бывают люди
Моды для Farming Simulator Вконтакте [url=https://vk.com/fs_mod_17]https://vk.com/fs_mod_17[/url]
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t5-y6-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sn1-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sanp.pro/10-05-2019-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://metropolis.ga/index.php?topic=6668.0
http://www.critico-expository.com/forum/index.php?topic=8160.0
https://nextezone.com/index.php?topic=39398.0
http://forum.elexlabs.com/index.php/topic,20964.0.html
http://universalcommunity.se/Forum/index.php?topic=2019.0
https://reficulcoin.com/index.php?topic=25484.0
http://jdcalc.com/forum/viewtopic.php?t=166869
https://reficulcoin.com/index.php?topic=20229.0
https://nextezone.com/index.php?action=profile&u=4897
http://forum.elexlabs.com/index.php/topic,16487.0.html
http://uberdrivers.net/forum/index.php?topic=261541.0
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile;u=35831
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m4-o5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://forum.kopkargobel.com/index.php?topic=6533.0
http://www.nomaher.com/forum/index.php?topic=13013.0
http://help.stv.ru/index.php?PHPSESSID=50106b442bf6921aa761e03d65b6b598&topic=140144.0
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o6-%d1%81/
https://sanp.pro/09-05-2019-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-5/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-u7-s5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://roikjer.com/forum/index.php?PHPSESSID=pqimo21qnkjqlaiaf0ibvl5034&topic=868798.0
http://roikjer.com/forum/index.php?PHPSESSID=pvk32hs3q3lm13q2c3kdhp3950&topic=868801.0
http://roikjer.com/forum/index.php?PHPSESSID=sbjf32lfjqrtc6ms4jn3icq3v2&topic=868805.0
http://roikjer.com/forum/index.php?PHPSESSID=somko4jol1uohted33dgbadi50&topic=868810.0
http://romhanyse.hu/?option=com_k2&view=itemlist&task=user&id=233442
http://ru-realty.com/forum/index.php?PHPSESSID=p5jt7ubagoh2jj9ine1m0k2hg2&topic=506169.0
http://rudraautomation.com/index.php/component/k2/author/177701
http://sextomariotienda.com/blog/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb/
http://sextomariotienda.com/blog/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8/
http://sextomariotienda.com/blog/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80/
http://sextomariotienda.com/blog/%d1%8d%d1%84%d0%b8%d1%80-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%88/
http://sextomariotienda.com/blog/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80/
http://sextomariotienda.com/blog/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2017/
http://sextomariotienda.com/blog/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lostfilm/
http://siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=815012
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1680094
http://socialfbwidgets.com/component/k2/itemlist/user/14086.html
http://svgrossburgwedel.de/component/k2/itemlist/user/5530
http://taklongclub.com/forum/index.php?topic=134182.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1683343
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1683720
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1683756
http://theolevolosproject.org/index.php/component/k2/itemlist/user/26150
http://theolevolosproject.org/index.php/component/k2/itemlist/user/26152
http://HyUa.1fps.icu/l/szIaeDC
http://forum.digamahost.com/index.php?topic=110966.0
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5625
http://www.spazioad.com/component/k2/itemlist/user/7248985
http://www.theparrotcentre.com/forum/index.php?topic=476616.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3319725
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4747644
http://www.vivelabmanizales.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/53291
http://www.ekemoon.com/151559/050920194307/
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=301340
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=149259
http://www.gtupuw.org/index.php/component/k2/itemlist/user/1831497
http://proxima.co.rw/index.php/component/k2/itemlist/user/542474
http://wb.hvekorat.com/index.php?topic=40009.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3284513
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=148111
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/153884
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=766429
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1664895
https://tg.vl-mp.com/index.php?topic=1254528.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4709211
http://www.deliberarchia.org/forum/index.php?topic=937875.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1335378
http://teambuildingpremium.com/forum/index.php?topic=719080.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3321490
https://www.gizmoarticle.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-5-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-27-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l2-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-5-%d1%81%d0%b5%d0%b7/
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3596208
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=783300
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5995
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/68421
http://www.vivelabmanizales.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xyd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://rudraautomation.com/index.php/component/k2/author/120714
http://dpmarketingsystems.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l5-%d1%81/
http://forum.byehaj.hu/index.php?topic=72547.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/e-otka-mo-k-(elimi-birakma)-42-e-b8-(e-otka-mo-k-(elimi-birakma)-42-e)/?PHPSESSID=sgnmmcq4um12l1m9tfml03mi83
http://teambuildingpremium.com/forum/index.php?topic=711970.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4675012
http://www.quattroandpartners.it/component/k2/itemlist/user/983286
http://mobility-corp.com/index.php/component/k2/itemlist/user/2501589
http://dpmarketingsystems.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-aes-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://poselokgribovo.ru/forum/index.php?topic=683012.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(a-aoa-3-eo-18-e)-a-aoa-3-eo-18-e-motet-m/?PHPSESSID=ta9i5ln1lidaccfcqeadpm8os4
http://www.xn--q3cx6g8a.net/board/index.php?topic=186300.0
http://menulisilmiah.net/online-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://thefreebitcoin.com/index.php?topic=28048.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3250723
http://www.arunagreen.com/index.php/component/k2/itemlist/user/420622
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=655942.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2477518
http://forum.bmw-e60.eu/index.php?topic=4880.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-92/
http://www.deliberarchia.org/forum/index.php?topic=994478.0
http://forum.elexlabs.com/index.php?topic=17877.0
http://otitismediasociety.org/forum/index.php?topic=149019.0
https://reficulcoin.com/index.php?topic=32016.0
http://forum.elexlabs.com/index.php?topic=16529.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b6-c2-%d0%b8/
http://www.ofqj.org/hebergementquebec/4-10-s9-y8-4-10-4-10-watch
http://www.deliberarchia.org/forum/index.php?topic=1000669.0
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xe7-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-(ia)-19-e-09-05-2019/?PHPSESSID=jgoq33kq7a2t0l38khc8114fc0
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t9-b7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=32586.0
https://akutthjelper.no/members/larrywhitis43/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-39/
http://forum.elexlabs.com/index.php?topic=16622.0
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p4-v8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://otitismediasociety.org/forum/index.php?topic=149047.0
http://forum.politeknikgihon.ac.id/index.php?topic=28264.0
http://www.hoonthaitoday.com/forum/index.php?topic=222660.0
https://members.fbhaters.com/index.php?topic=86070.0
http://www.ofqj.org/hebergementfrance/4-10-e4-v7-4-10-4-10-watch
http://bobr.site/index.php?topic=128137.0
http://e-educ.net/Forum/index.php?topic=9395.0
http://e-educ.net/Forum/index.php?topic=9398.0
http://eugeniocolazzo.it/forum/index.php?topic=127053.0
http://eugeniocolazzo.it/forum/index.php?topic=127056.0
http://eugeniocolazzo.it/forum/index.php?topic=127061.0
http://eugeniocolazzo.it/forum/index.php?topic=127062.0
http://flashboot.ru/forum/index.php?topic=94674.0
http://flashboot.ru/forum/index.php?topic=94675.0
http://flashboot.ru/forum/index.php?topic=94676.0
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1796910
http://forum.byehaj.hu/index.php?topic=89594.0
http://forum.elexlabs.com/index.php?topic=24778.0
http://forum.elexlabs.com/index.php?topic=24783.0
http://forum.elexlabs.com/index.php?topic=24789.0
http://forum.kopkargobel.com/index.php?topic=8711.0
http://healthyteethpa.org/component/k2/itemlist/user/5421310
http://marjorieaperry.com/?option=com_k2&view=itemlist&task=user&id=489790
http://matrixpharm.ru/forum/index.php?PHPSESSID=omp7rneh4ts75p1ho63qv9m404&action=profile;u=187858
http://matrixpharm.ru/forum/index.php?action=profile&u=187698
http://miquirofisico.com/index.php/component/k2/itemlist/user/3976
http://multikopterforum.hu/index.php?topic=18888.0
http://HyUa.1fps.icu/l/szIaeDC
http://demo.woltlab.fr/lite1/wbb/index.php?page=User&userID=1123270
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2579272
http://forum.politeknikgihon.ac.id/index.php?topic=20777.0
https://sanp.pro/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-5-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e5-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-5-%d1%81/
http://forum.digamahost.com/index.php?topic=110094.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/75839
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=22884
http://mobility-corp.com/index.php/component/k2/itemlist/user/2458152
http://www.gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1803547
http://xekhachduyetthuy.com.vn/index.php/component/k2/itemlist/user/155014
http://uberdrivers.net/forum/index.php?topic=176992.0
http://matrixpharm.ru/forum/index.php?PHPSESSID=8sgrua9hnv04im7qodrqmue677&action=profile;u=150845
http://www.critico-expository.com/forum/index.php?topic=195.0
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/972208
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1326341
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=675839.0
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=78832
http://dcasociados.eu/component/k2/itemlist/user/85636
https://www.resproxy.com/forum/index.php/710528-watch-sluga-naroda-3-sezon-18-seria-g5-sluga-naroda-3-sezon-18-/0
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3668097
http://menulisilmiah.net/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-ffv-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://thefreebitcoin.com/index.php?topic=35591.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1302574
http://teambuildingpremium.com/forum/index.php?topic=749186.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/170916
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1326322
http://www.spazioad.com/component/k2/itemlist/user/7205409
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=231817
http://www.spazioad.com/component/k2/itemlist/user/7251147
http://smartacity.com/component/k2/itemlist/user/17732
http://www.vivelabmanizales.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gig-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8/
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1870310
http://forum.politeknikgihon.ac.id/index.php?topic=21471.0
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=785931
http://dohairbiz.com/en/component/k2/itemlist/user/2723151.html
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=13667
http://www.edelweis.com/UserProfile/tabid/42/UserID/1679696/Default.aspx
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/49953
http://www.afikgan.co.il/index.php/component/k2/itemlist/user/24940
http://www.spazioad.com/component/k2/itemlist/user/7183638
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1736192
http://www.arunagreen.com/index.php/component/k2/itemlist/user/395221
http://www.critico-expository.com/forum/index.php?topic=224.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=243087
http://smartacity.com/component/k2/itemlist/user/9168
http://proxima.co.rw/index.php/component/k2/itemlist/user/533502
http://xn--22cmah2caecpucll2cycdoj4d0knajrq3e5pbj9w0c.americanwolfthailand.com/DJPetjah/index.php?topic=1478708.0
http://www.popolsku.fr.pl/forum/index.php?topic=362121.0
http://roikjer.com/forum/index.php?topic=783192.0
http://dohairbiz.com/en/?option=com_k2&view=itemlist&task=user&id=2715193
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1643923
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=503956
http://153.120.114.241/eso/index.php/16865487-voskressij-ertugrul-146-seria-nxfk-voskressij-ertugrul-146-seri
http://www.vivelabmanizales.com/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lnsr-%d0%b2%d0%be%d1%81%d0%ba%d1%80/
http://www.quattroandpartners.it/component/k2/itemlist/user/1052714
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/185242
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/292444
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=501795
http://ovotecegg.com/component/k2/itemlist/user/122713
http://www.vivelabmanizales.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lx5c-%d0%b8%d0%b3/
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1115457
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4745704
http://www.vivelabmanizales.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=298287
http://withinfp.sakura.ne.jp/eso/index.php/16886063-smotret-tajny-91-seria-b9-tajny-91-seria/0
http://macdistri.com/index.php/component/k2/itemlist/user/317579
http://www.ekemoon.com/142573/051820190105/
https://forums.letstalkbeats.com/index.php?topic=64648.0
http://topitop.kz/index.php/component/k2/itemlist/user/76610
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/291278
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/50300
http://www.die-design-manufaktur.de/?option=com_k2&view=itemlist&task=user&id=5175225
https://sushilbarali.com.np/QNA/index.php?qa=186411&qa_1=%D0%B3%D1%80%D0%B0%D0%BD%D0%B4-2-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-21-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-06-05-2019-d7-%D0%B3%D1%80%D0%B0%D0%BD%D0%B4-2-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-21-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://community.viajar.tur.br/index.php?p=/profile/megannorth
http://withinfp.sakura.ne.jp/eso/index.php/16863378-nasa-istoria-73-seria-wwrx-nasa-istoria-73-seria
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
https://khuyenmaikk13.info/index.php?topic=183796.0
http://arunagreen.com/index.php/component/k2/itemlist/user/453846
http://married.dike.gr/index.php/component/k2/itemlist/user/48879
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3374223
http://www.ekemoon.com/148435/052320190506/
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/222134
http://married.dike.gr/index.php/component/k2/itemlist/user/46622
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/757020
http://withinfp.sakura.ne.jp/eso/index.php/16908310-hdvideo-po-zakonam-voennogo-vremeni-3-sezon-7-seria-a1-po-zakon/0
http://webp.online/index.php?topic=44925.0
https://forums.letstalkbeats.com/index.php?topic=67166.0
http://menulisilmiah.net/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p6-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be/
http://www.ekemoon.com/157389/050720190008/
http://forum.politeknikgihon.ac.id/index.php?topic=23646.0
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=505410
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2576613
http://www.ekemoon.com/161995/050220192509/
http://www.studioaparo.it/?option=com_k2&view=itemlist&task=user&id=544274
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/186324
http://rudraautomation.com/index.php/component/k2/author/105000
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/67003
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3294298
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/15536
http://condolencias.servisa.es/9-10-05-05-2019-r5-9-10
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=602423
https://members.fbhaters.com/index.php?topic=81846.0
http://seoksoononly.dothome.co.kr/qna/761626
http://batubersurat.com/index.php/component/k2/itemlist/user/43945
http://hydrocarbs-gh.org/index.php/component/k2/itemlist/user/7306897
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/200854
http://socintegra.lv/component/k2/itemlist/user/43876
http://c3isecurity.com.br/?option=com_k2&view=itemlist&task=user&id=471675
http://rudraautomation.com/index.php/component/k2/author/102282
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1334286
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1839207
http://www.vivelabmanizales.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81-11/
http://poselokgribovo.ru/forum/index.php?topic=740689.0
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=79070
http://forum.byehaj.hu/index.php?topic=81481.0
http://seoksoononly.dothome.co.kr/qna/765147
http://www.deliberarchia.org/forum/index.php?topic=978219.0
https://members.fbhaters.com/index.php?topic=79812.0
http://mvisage.sk/index.php/component/k2/itemlist/user/117343
http://macdistri.com/index.php/component/k2/itemlist/user/317630
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43380
http://www.studioaparo.it/?option=com_k2&view=itemlist&task=user&id=543987
http://associationsila.org/component/k2/itemlist/user/291566
http://withinfp.sakura.ne.jp/eso/index.php/16862519-rannaa-ptaska-erkenci-kus-43-seria-nnks-rannaa-ptaska-erkenci-k
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4863214
https://tg.vl-mp.com/index.php?topic=1333103.0
http://koushatarabar.com/index.php/component/k2/itemlist/user/1322503
http://haniel.ir/index.php/component/k2/itemlist/user/75659
http://healthyteethpa.org/component/k2/itemlist/user/5329869
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=8752
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/51362
http://www.ekemoon.com/141737/051420194005/
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/670493
http://www.vivelabmanizales.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-95-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wc2i-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd/
http://patagroupofcompanies.com/component/k2/itemlist/user/198648
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/14434
http://seoksoononly.dothome.co.kr/qna/780604
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/292372
http://batubersurat.com/index.php/component/k2/itemlist/user/42564
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1994855
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/205450
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=11696
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=42688
http://moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=670479
http://febrescordero.gob.ec/index.php/component/k2/itemlist/user/81367
http://www.sakitoandrichifantasy.gr/?option=com_k2&view=itemlist&task=user&id=154970
https://ccha.castle-journal.info/?option=com_k2&view=itemlist&task=user&id=1706
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/73178
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=1014277
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5-3/
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=562328
https://l2thalassic.org/Forum/index.php?topic=1414.0
http://molweb.ru/groups/xolostyak-9-sezon-10-vypusk-skachat-torrent-agxolostyak-9-sezon-10-vypusk-skachat-torrent16-xolostyak-9-sezon-10-vypusk-skachat-torrent/
http://rudraautomation.com/index.php/component/k2/author/106159
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42589
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(a-etoogame-of-thrones-8-eo-1-e)-a-etoogame-of-thrones-8-eo-1-e-o7c1/?PHPSESSID=ltsa5qja1ks7318nc286i14474
http://forum.elexlabs.com/index.php?topic=19594.0
http://forum.elexlabs.com/index.php?topic=16324.0
http://forum.elexlabs.com/index.php/topic,19814.0.html
https://npi.org.es/smf/index.php?topic=113516.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-42/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-25/
https://danceplanet.se/commodore/index.php?topic=29302.0
http://danielmillsap.com/forum/index.php?topic=993969.0
http://bobr.site/index.php?topic=127065.0
https://chromehearts.in.th/index.php?topic=50026.0
https://khuyenmaikk13.info/index.php?topic=198389.0
https://khuyenmaikk13.info/index.php?topic=198391.0
https://khuyenmaikk13.info/index.php?topic=198392.0
https://khuyenmaikk13.info/index.php?topic=198396.0
https://ne-kuru.ru/index.php?topic=217639.0
https://nextezone.com/index.php?topic=48238.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3350932
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3350947
https://www.bmwstyle.ru/forum/index.php?topic=65257.0
https://www.bmwstyle.ru/forum/index.php?topic=65258.0
https://www.burraco2.com/forum/index.php?topic=293591.0
https://www.netprofessional.gr/component/k2/itemlist/user/3589.html
http://HyUa.1fps.icu/l/szIaeDC
http://mvisage.sk/index.php/component/k2/itemlist/user/117594
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1037645
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/229171
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1841655
http://www.camaracoyhaique.cl/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-88-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-np4g-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-88-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.quattroandpartners.it/component/k2/itemlist/user/1039346
http://rudraautomation.com/index.php/component/k2/author/108124
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=756858
http://www.quattroandpartners.it/component/k2/itemlist/user/1049625
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=20103
http://www.comfortcenter.es/index.php/component/k2/itemlist/user/104370
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42648
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/77114
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/216548
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2522557
http://withinfp.sakura.ne.jp/eso/index.php/16863980-holostak-9-sezon-10-vypusk-andeks-yiholostak-9-sezon-10-vypusk-/0
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2389990
http://www.vivelabmanizales.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h6-%d1%82%d0%be%d0%bb%d1%8f/
http://www.quattroandpartners.it/component/k2/itemlist/user/1037696
https://forums.letstalkbeats.com/index.php?topic=64593.0
http://www2.yasothon.go.th/smf/index.php?topic=159.156315
http://www.vivelabmanizales.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2-7/
http://www.elpinatarense.com/?option=com_k2&view=itemlist&task=user&id=155137
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=288954
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=115384
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1338591
http://batubersurat.com/index.php/component/k2/itemlist/user/43160
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1024529
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=288212
http://macdistri.com/index.php/component/k2/itemlist/user/299525
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2588089
http://www.vivelabmanizales.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z9-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be/
https://l2thalassic.org/Forum/index.php?topic=1127.0
http://withinfp.sakura.ne.jp/eso/index.php/16884040-uristy-8-seria-06052019-f9-uristy-8-seria
http://www.remify.app/foro/index.php?topic=224214.0
http://withinfp.sakura.ne.jp/eso/index.php/16862970-sluga-naroda-3-sezon-5-seria-05052019-b6-sluga-naroda-3-sezon-5
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3383102
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1127221
http://mobility-corp.com/index.php/component/k2/itemlist/user/2514031
http://mediaville.me/?option=com_k2&view=itemlist&task=user&id=207449
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=47575
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=46595
http://community.viajar.tur.br/index.php?p=/profile/coraldey7
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=9652
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/55987
http://withinfp.sakura.ne.jp/eso/index.php/16862715-serial-otel-toledo-1-seria-a6-otel-toledo-1-seria
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=491271
https://l2thalassic.org/Forum/index.php?topic=1094.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=279920
http://menulisilmiah.net/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u7-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81/
http://poselokgribovo.ru/forum/index.php?topic=739506.0
http://withinfp.sakura.ne.jp/eso/index.php/16882982-uristy-14-seria-smotret-uristy-14-seria
http://mjbosch.com/index.php/component/k2/itemlist/user/81856
http://proxima.co.rw/index.php/component/k2/itemlist/user/565946
http://www.vivelabmanizales.com/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rwfg-%d0%b2%d0%be%d1%81%d0%ba%d1%80/
http://proxima.co.rw/index.php/component/k2/itemlist/user/565310
http://www.telcon.gr/index.php/component/k2/itemlist/user/47357
http://withinfp.sakura.ne.jp/eso/index.php/16886065-rannaa-ptaska-erkenci-kus-37-seria-mkfj-rannaa-ptaska-erkenci-k/0
http://mjbosch.com/index.php/component/k2/itemlist/user/81570
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3395580
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cr8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.tessabannampad.go.th/webboard/index.php?topic=203434.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-15/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-80/
http://forum.elexlabs.com/index.php?topic=23861.0
https://members.fbhaters.com/index.php?topic=89235.0
http://forum.byehaj.hu/index.php?topic=89184.0
http://roikjer.com/forum/index.php?PHPSESSID=ihftnso3knn5q38n47dhrsc555&topic=848558.0
http://forum.elexlabs.com/index.php/topic,17197.0.html
http://www.hoonthaitoday.com/forum/index.php?topic=205638.0
http://www.ekemoon.com/172983/051620193510/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-42/
http://universalcommunity.se/Forum/index.php?topic=2068.0
https://danceplanet.se/commodore/index.php?topic=20184.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=691353.0
https://akutthjelper.no/members/dotty58907952/
https://nextezone.com/index.php?topic=45670.0
http://www.deliberarchia.org/forum/index.php?topic=1017067.0
http://www.deliberarchia.org/forum/index.php?topic=999340.0
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/12746
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3442999
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=37346
http://marjorieaperry.com/?option=com_k2&view=itemlist&task=user&id=489821
http://matrixpharm.ru/forum/index.php?PHPSESSID=2mt877dusotprsco2ehh3frmi6&action=profile;u=187940
http://matrixpharm.ru/forum/index.php?PHPSESSID=9ltsh9cfohbchdev6jsheh2nf6&action=profile;u=187951
http://matrixpharm.ru/forum/index.php?PHPSESSID=pmgpdp6b5c1j0o2rs3hnss88h4&action=profile;u=187934
http://matrixpharm.ru/forum/index.php?PHPSESSID=q1tl8627bgabfmart2e13vpb50&action=profile;u=187938
http://miquirofisico.com/index.php/component/k2/itemlist/user/3983
http://mobility-corp.com/index.php/component/k2/itemlist/user/2583243
http://multikopterforum.hu/index.php?topic=18911.0
http://multikopterforum.hu/index.php?topic=18913.0
http://multikopterforum.hu/index.php?topic=18914.0
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=777698
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%be-%d1%87%d0%b5%d0%bc/
http://photogrotto.com/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8-3/
http://HyUa.1fps.icu/l/szIaeDC
http://forum.elexlabs.com/index.php?topic=21112.0
https://danceplanet.se/commodore/index.php?topic=29108.0
http://demo.caribe.vps-private.net/blog/milliardy-4-sezon-10-seriya-u3-y0-milliardy-4-sezon-10-seriya-milliardy-4-sezon-10-seriya-onlin
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m4-c2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v2-s4-%d0%b8%d0%b3%d1%80/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-oc3-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z6-z7-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://otitismediasociety.org/forum/index.php?topic=158766.0
http://roikjer.com/forum/index.php?PHPSESSID=862v2jn22q2vhuttc2tm2thj04&topic=844419.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x8-m0-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://reficulcoin.com/index.php?topic=31737.0
http://www.mmc24.ru/forum/index.php?PHPSESSID=ip4qdjej8vuongu565moo3nk90&topic=781.0
http://www.mmc24.ru/forum/index.php?PHPSESSID=jl2hh2pcmkb099ae4bbhlmda44&topic=782.0
http://www.teedinubon.com/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be-3/
http://www.teedinubon.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-3-%d1%81%d0%b5/
http://www.teedinubon.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8/
http://www.teedinubon.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8/
http://www.teedinubon.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80-3/
http://www.teedinubon.com/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vo-production/
http://www.teedinubon.com/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%b0-%d1%80%d1%83%d1%81/
http://www.theocraticamerica.org/forum/index.php?topic=36612.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=dd7609f5695965a7b1477ba91777c37a&topic=4579.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=e093b41c514f199cf859d53dd1d3d489&topic=4578.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/321259
http://HyUa.1fps.icu/l/szIaeDC
[url=http://cialisdxt.com/]cialis online[/url]
cialis vs viagra user reviews
<a href="http://cialisdxt.com/">cialis online</a>
effectiveness of cialis vs. viagra
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=302109
http://compultras.com/?option=com_k2&view=itemlist&task=user&id=197057
http://www.telcon.gr/index.php/component/k2/itemlist/user/48359
http://www.tessabannampad.go.th/webboard/index.php?topic=191132.0
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4824801
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1004451
http://www.m1avio.com/index.php/component/k2/itemlist/user/3617437
https://l2thalassic.org/Forum/index.php?topic=462.0
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7309127
http://seoksoononly.dothome.co.kr/qna/791208
http://dohairbiz.com/en/?option=com_k2&view=itemlist&task=user&id=2717493
http://computerscience.egerton.ac.ke/index.php/component/k2/itemlist/user/1995907
http://webp.online/index.php?topic=42562.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3293597
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1885475
http://www.ekemoon.com/156903/050520193608/
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=511244
http://fbpharm.net/index.php/component/k2/itemlist/user/21810
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3309810
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=204107
http://www2.yasothon.go.th/smf/index.php?topic=159.157320
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4712963
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/190916
http://dev.aabn.org.gh/component/k2/itemlist/user/529385
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=282668
http://xplorefitness.com/blog/%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-21-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-10-05-2019-n4-%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-21-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://xplorefitness.com/blog/%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-10-05-2019-x2-%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://xplorefitness.com/blog/%C2%AB%D1%82%D0%BE%D0%BB%D1%8F-%D1%80%D0%BE%D0%B1%D0%BE%D1%82-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-10-05-2019-j7-%C2%AB%D1%82%D0%BE%D0%BB%D1%8F-%D1%80%D0%BE%D0%B1%D0%BE%D1%82-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://xplorefitness.com/blog/%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-10-05-2019-d1-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://xplorefitness.com/blog/%C2%AB%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-1-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-10-05-2019-c6-%C2%AB%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-1-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://xplorefitness.com/blog/%C2%AB%D1%82%D0%BE%D0%BB%D1%8F-%D1%80%D0%BE%D0%B1%D0%BE%D1%82-4-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-10-05-2019-m7-%C2%AB%D1%82%D0%BE%D0%BB%D1%8F-%D1%80%D0%BE%D0%B1%D0%BE%D1%82-4-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://xplorefitness.com/blog/%C2%AB%D0%B4%D0%BE%D1%87%D0%BA%D0%B8-%D0%BC%D0%B0%D1%82%D0%B5%D1%80%D0%B8-%D0%B4%D0%BE%D1%87%D0%BA%D0%B8-%D0%BC%D0%B0%D1%82%D0%B5%D1%80i-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-10-05-2019-v1-%C2%AB%D0%B4%D0%BE%D1%87%D0%BA%D0%B8-%D0%BC%D0%B0%D1%82%D0%B5%D1%80%D0%B8-%D0%B4%D0%BE%D1%87%D0%BA%D0%B8-%D0%BC%D0%B0%D1%82%D0%B5%D1%80i-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://xplorefitness.com/blog/%C2%AB%D1%81%D0%BC%D0%B5%D1%80%D1%88-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-10-05-2019-t0-%C2%AB%D1%81%D0%BC%D0%B5%D1%80%D1%88-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://xplorefitness.com/blog/%C2%AB%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-10-05-2019-w0-%C2%AB%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://xplorefitness.com/blog/%C2%AB%D1%81%D0%BC%D0%B5%D1%80%D1%88-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-10-05-2019-b0-%C2%AB%D1%81%D0%BC%D0%B5%D1%80%D1%88-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://xplorefitness.com/blog/%C2%AB%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-94-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-10-05-2019-p6-%C2%AB%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-94-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://xplorefitness.com/blog/%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-10-05-2019-u7-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://xplorefitness.com/blog/%C2%AB%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-3-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-10-05-2019-p1-%C2%AB%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-3-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://arunagreen.com/index.php/component/k2/itemlist/user/437960
http://mediaville.me/index.php/component/k2/itemlist/user/208076
http://molweb.ru/groups/xolostyak-9-sezon-12-vypusk-ddxolostyak-9-sezon-12-vypusk31-xolostyak-9-sezon-12-vypusk/
http://menulisilmiah.net/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%be%d0%b9-%d0%b0%d1%80%d1%82%d0%b8%d1%81%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jy8%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%be%d0%b9-%d0%b0%d1%80%d1%82%d0%b8%d1%81/
http://dev.aabn.org.gh/component/k2/itemlist/user/516693
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1003341
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3629512
http://menulisilmiah.net/hd-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g6-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81/
http://engeena.com/component/k2/itemlist/user/7901
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1347144
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3293592
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/185565
http://married.dike.gr/index.php/component/k2/itemlist/user/50745
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=290519
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=47794
http://www.m1avio.com/index.php/component/k2/itemlist/user/3612479
http://macdistri.com/?option=com_k2&view=itemlist&task=user&id=297514
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43701
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/54078
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4824588
http://forum.digamahost.com/index.php?topic=108948.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3297331
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2549997
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=79758
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/79775
http://ovotecegg.com/component/k2/itemlist/user/128021
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/222421
http://proxima.co.rw/index.php/component/k2/itemlist/user/592576
http://www.deliberarchia.org/forum/index.php?topic=990625.0
http://www.sharmaraco.com/blog/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-m3-c1-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-j8-k3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.deliberarchia.org/forum/index.php?topic=999274.0
https://nextezone.com/index.php?action=profile;u=5895
https://akutthjelper.no/members/ollieewan72937/
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o4-f4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://danceplanet.se/commodore/index.php?topic=18962.0
https://worldtaxi.org/2019/05/09/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-q8-p5-%d0%b8%d0%b3%d1%80%d0%b0/
http://www.deliberarchia.org/forum/index.php?topic=998677.0
http://danielmillsap.com/forum/index.php?topic=1028894.0
http://www.ekemoon.com/169733/050520190910/
http://otitismediasociety.org/forum/index.php?topic=149070.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=21532cb949b44f8fce761437766fe922&topic=216869.0
http://www.critico-expository.com/forum/index.php?topic=11197.0
http://www.deliberarchia.org/forum/index.php?topic=1018581.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kg0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://nextezone.com/index.php?topic=39622.0
http://www.hoonthaitoday.com/forum/index.php?topic=224303.0
http://myrechockey.com/forums/index.php?topic=91297.0
http://otitismediasociety.org/forum/index.php?topic=149138.0
http://www.critico-expository.com/forum/index.php?topic=6880.0
http://help.stv.ru/index.php?PHPSESSID=08353971e268552a30ef3999566b67f5&topic=139569.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p8-v4-%d0%b8%d0%b3%d1%80/
http://danielmillsap.com/forum/index.php?topic=1031956.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g7-a3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90pa4%e3%80%91-%d0%b8%d0%b3%d1%80/
http://uberdrivers.net/forum/index.php?topic=247589.0
http://otitismediasociety.org/forum/index.php?topic=149734.0
http://forum.elexlabs.com/index.php?topic=18887.0
http://myrechockey.com/forums/index.php?topic=95072.0
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p0-f5-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://www.deliberarchia.org/forum/index.php?topic=1004714.0
http://www.ofqj.org/hebergementquebec/4-8-watch-k1-f9-4-8-4-8
http://otitismediasociety.org/forum/index.php?topic=154593.0
http://www.critico-expository.com/forum/index.php?topic=11812.0
https://akutthjelper.no/members/murrayhooks619/
https://reficulcoin.com/index.php?topic=20998.0
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile;u=30346
http://HyUa.1fps.icu/l/szIaeDC
https://prelease.club/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://forum.elexlabs.com/index.php?topic=16242.0
http://danielmillsap.com/forum/index.php?topic=1029636.0
http://www.nomaher.com/forum/index.php?topic=12906.0
http://www.critico-expository.com/forum/index.php?topic=11752.0
http://www.theparrotcentre.com/forum/index.php?topic=487854.0
http://www.theparrotcentre.com/forum/index.php?topic=492043.0
http://www.deliberarchia.org/forum/index.php?topic=997679.0
http://otitismediasociety.org/forum/index.php?topic=150713.0
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-t6-e2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
https://danceplanet.se/commodore/index.php?topic=25238.0
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n7-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be-2/
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g/
http://metropolis.ga/index.php?topic=6743.0
https://worldtaxi.org/2019/05/09/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u3-d3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://myrechockey.com/forums/index.php?topic=91482.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nm1-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://8.droror.co.il/uncategorized/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-c6-y3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
https://forum.clubeicaro.pt/index.php?topic=1001.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u2-c9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://uberdrivers.net/forum/index.php?topic=250984.0
http://www.tessabannampad.go.th/webboard/index.php?topic=202623.0
http://menulisilmiah.net/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-10-05-2019-2/
http://uberdrivers.net/forum/index.php?topic=261807.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o4-h5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
https://polyframetrade.co.uk/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-watch-a9-a0-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80/
http://otitismediasociety.org/forum/index.php?topic=149886.0
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile&u=33079
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-9/
http://teambuildingpremium.com/forum/index.php?topic=800163.0
http://help.stv.ru/index.php?PHPSESSID=8411694bb8746a6dc00812ee3590aea9&topic=139548.0
https://altaylarteknoloji.com/index.php?topic=1398.0
http://help.stv.ru/index.php?PHPSESSID=67834b918b412e61a3ea57eb48292340&topic=139656.0
http://uberdrivers.net/forum/index.php?topic=250076.0
http://www.ekemoon.com/169405/050420191510/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ve5-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://danceplanet.se/commodore/index.php?topic=18187.0
http://www.critico-expository.com/forum/index.php?topic=12657.0
http://HyUa.1fps.icu/l/szIaeDC
http://ru-realty.com/forum/index.php?PHPSESSID=5mej9qb1a1t9v1qv4qp69g1182&topic=480162.0
https://reficulcoin.com/index.php?topic=17772.0
http://roikjer.com/forum/index.php?topic=845746.0
https://reficulcoin.com/index.php?topic=16542.0
http://www.deliberarchia.org/forum/index.php?topic=998312.0
https://akutthjelper.no/members/coopergoninan9/
http://teambuildingpremium.com/forum/index.php?topic=793398.0
http://www.critico-expository.com/forum/index.php?topic=7153.0
http://otitismediasociety.org/forum/index.php?topic=148999.0
https://altaylarteknoloji.com/index.php?topic=1816.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-73/
http://www.hoonthaitoday.com/forum/index.php?topic=246547.0
http://forum.kopkargobel.com/index.php?topic=7972.0
http://www.theocraticamerica.org/forum/index.php?topic=29239.0
http://www.hoonthaitoday.com/forum/index.php?topic=215452.0
http://roikjer.com/forum/index.php?topic=863722.0
http://forum.politeknikgihon.ac.id/index.php?topic=29114.0
https://reficulcoin.com/index.php?topic=17335.0
https://worldtaxi.org/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b5-e4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
https://akutthjelper.no/members/joeylqt974767/
https://worldtaxi.org/2019/05/09/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q5-y9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://www.theocraticamerica.org/forum/index.php?topic=28515.0
http://www.critico-expository.com/forum/index.php?topic=12999.0
http://d2bchannel.co.in/blog/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-z5-s1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
https://danceplanet.se/commodore/index.php?topic=21331.0
http://poselokgribovo.ru/forum/index.php?topic=749532.0
http://forum.elexlabs.com/index.php?topic=16118.0
https://members.fbhaters.com/index.php?topic=86530.0
https://khuyenmaikk13.info/index.php?topic=186489.0
http://forum.elexlabs.com/index.php?topic=21304.0
http://www.hoonthaitoday.com/forum/index.php?topic=201534.0
https://khuyenmaikk13.info/index.php?topic=185875.0
https://prelease.club/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ey4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://danielmillsap.com/forum/index.php?topic=1025831.0
https://reficulcoin.com/index.php?topic=30933.0
http://www.ofqj.org/hebergementfrance/4-11-z2-k2-4-11-4-11-watch
http://www.ekemoon.com/168681/050220191010/
http://www.hoonthaitoday.com/forum/index.php?topic=205400.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=683582.0
http://demo.caribe.vps-private.net/blog/milliardy-4-sezon-9-seriya-w8-e7-milliardy-4-sezon-9-seriya-milliardy-4-sezon-9-seriya
http://forum.elexlabs.com/index.php?topic=17405.0
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w5-u0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://forum.kopkargobel.com/index.php?topic=6459.0
http://www.deliberarchia.org/forum/index.php?topic=994553.0
http://roikjer.com/forum/index.php?PHPSESSID=ru8c988b18j2uhpiv2um0aulq7&topic=835979.0
http://help.stv.ru/index.php?PHPSESSID=0cf8b83d635397e9a18eb62d9d9d5f7d&topic=140069.0
http://HyUa.1fps.icu/l/szIaeDC
https://members.fbhaters.com/index.php?topic=84010.0
https://danceplanet.se/commodore/index.php?topic=18805.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-11/
http://www.critico-expository.com/forum/index.php?topic=11690.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-42/
https://sanp.pro/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m9-%d1%81%d0%bb/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m2-v6-%d0%b8%d0%b3%d1%80%d0%b0/
https://khuyenmaikk13.info/index.php?topic=186187.0
https://luckychancerescue.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ix1-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://vtservices85.fr/smf2/index.php?PHPSESSID=baa1a97ecb070df7262af0d3ff83b776&topic=217087.0
https://sanp.pro/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r7-%d1%81%d0%bb/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dg0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vv9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.deliberarchia.org/forum/index.php?topic=1021648.0
https://forum.clubeicaro.pt/index.php?topic=1036.0
http://www.deliberarchia.org/forum/index.php?topic=995357.0
http://www.critico-expository.com/forum/index.php?topic=6507.0
http://otitismediasociety.org/forum/index.php?topic=152323.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bv3-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=33064.0
https://danceplanet.se/commodore/index.php?topic=19210.0
http://www.remify.app/foro/index.php?topic=248178.0
https://prelease.club/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s5-%d1%81%d0%bb/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zt0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://help.stv.ru/index.php?PHPSESSID=53fa2a7604a9077dd134d696935cf28e&topic=141278.0
http://roikjer.com/forum/index.php?PHPSESSID=euhd98k3304e9v150mcuqbnik7&topic=840722.0
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j4-j5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c1-n9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://www.critico-expository.com/forum/index.php?topic=6337.0
https://members.fbhaters.com/index.php?topic=88054.0
http://forum.elexlabs.com/index.php?topic=16404.0
http://www.deliberarchia.org/forum/index.php?topic=1021212.0
http://forum.elexlabs.com/index.php?topic=17195.0
http://roikjer.com/forum/index.php?PHPSESSID=78n8m9uo2hv0e16pvh45gjdi92&topic=855116.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/'a-etoo-(got)-8-eo-4-e'-a-etoo-(got)-8-eo-4-e-u5p3/?PHPSESSID=s32s6ao5c8lg077hamfilkujp1
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q3-f6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://forum.elexlabs.com/index.php/topic,22162.0.html
http://help.stv.ru/index.php?PHPSESSID=c05ea09a98b1b243fcf8b2b0f07a5fe9&topic=139965.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b6-c8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://worldtaxi.org/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-u0-a2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://HyUa.1fps.icu/l/szIaeDC
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-19/
https://khuyenmaikk13.info/index.php?topic=185870.0
https://members.fbhaters.com/index.php?topic=83627.0
http://ru-realty.com/forum/index.php?PHPSESSID=5mej9qb1a1t9v1qv4qp69g1182&topic=480162.0
https://reficulcoin.com/index.php?topic=17772.0
http://roikjer.com/forum/index.php?topic=845746.0
https://reficulcoin.com/index.php?topic=16542.0
http://www.deliberarchia.org/forum/index.php?topic=998312.0
https://akutthjelper.no/members/coopergoninan9/
http://teambuildingpremium.com/forum/index.php?topic=793398.0
http://www.critico-expository.com/forum/index.php?topic=7153.0
http://otitismediasociety.org/forum/index.php?topic=148999.0
https://altaylarteknoloji.com/index.php?topic=1816.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-73/
http://www.theparrotcentre.com/forum/index.php?topic=494386.0
http://8.droror.co.il/uncategorized/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-w9-o8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://menulisilmiah.net/%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-10-05-2019-5/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-q4-c9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://roikjer.com/forum/index.php?PHPSESSID=4iaqogafqb060939ti2gdhqhb6&topic=856813.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q1-b6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.deliberarchia.org/forum/index.php?topic=995179.0
https://nextezone.com/index.php?topic=40648.0
http://www.deliberarchia.org/forum/index.php?topic=993551.0
http://www.tessabannampad.go.th/webboard/index.php?topic=197526.0
http://uberdrivers.net/forum/index.php?topic=258694.0
https://khuyenmaikk13.info/index.php?topic=191231.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l6-t6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://vtservices85.fr/smf2/index.php?PHPSESSID=f7f3f09d8826028c5960a913278190e8&topic=217300.0
http://www.deliberarchia.org/forum/index.php?topic=996031.0
http://roikjer.com/forum/index.php?PHPSESSID=n6vjravq2g6761ops8471a19g3&topic=835502.0
https://sanp.pro/%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-09-05-2019/
http://www.critico-expository.com/forum/index.php?topic=12257.0
http://www.hoonthaitoday.com/forum/index.php?topic=247060.0
http://122.154.49.125/Forum/index.php?topic=107.0
https://members.fbhaters.com/index.php?topic=87590.0
http://help.stv.ru/index.php?PHPSESSID=2bafea2879e735613755490d34699157&topic=140060.0
http://roikjer.com/forum/index.php?PHPSESSID=4kkc2ovstgj02pipmmr6hdskp1&topic=840674.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-l7-w6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://HyUa.1fps.icu/l/szIaeDC
http://roikjer.com/forum/index.php?PHPSESSID=ptgcoh3jfa7jddjqc2rrh1h3t6&topic=856203.0
https://reficulcoin.com/index.php?topic=31305.0
https://hackersuniversity.net/index.php?topic=9234.0
http://eugeniocolazzo.it/forum/index.php?topic=124917.0
https://prelease.club/live-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f4-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-3/
http://roikjer.com/forum/index.php?topic=858546.0
http://www.deliberarchia.org/forum/index.php?topic=996318.0
http://forum.elexlabs.com/index.php/topic,23853.0.html
https://khuyenmaikk13.info/index.php?topic=189607.0
http://www.ofqj.org/hebergementfrance/4-13-z9-i6-4-13-4-13
http://uberdrivers.net/forum/index.php?topic=244442.0
http://danielmillsap.com/forum/index.php?topic=996621.0
http://menulisilmiah.net/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z4-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mj4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://sexfork.com/uncategorized/hd-sluga-naroda-3-sezon-19-seriya-u5-sluga-naroda-3-sezon-19-seriya/
http://www.nomaher.com/forum/index.php?topic=12999.0
https://sanp.pro/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a9-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5/
http://uberdrivers.net/forum/index.php?topic=247218.0
http://8.droror.co.il/uncategorized/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p9-q2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r1-i2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=687577.0
http://danielmillsap.com/forum/index.php?topic=1023281.0
https://reficulcoin.com/index.php?topic=32564.0
http://www.critico-expository.com/forum/index.php?topic=8953.0
http://poselokgribovo.ru/forum/index.php?topic=747515.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-q3-a9-%d0%b8%d0%b3%d1%80%d0%b0/
http://help.stv.ru/index.php?PHPSESSID=3407f34de42a5546eb1f60626a3ccd9d&topic=139667.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.theparrotcentre.com/forum/index.php?topic=487014.0
http://www.deliberarchia.org/forum/index.php?topic=1019712.0
http://122.154.49.125/Forum/index.php?topic=87.0
https://khuyenmaikk13.info/index.php?topic=189883.0
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s5-a0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://myrechockey.com/forums/index.php?topic=98165.0
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i6-d9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(a-etoo-8-eo-4-e)-a-etoo-8-eo-4-e-r3n3/?PHPSESSID=3ru5focjkue4dji49p0t5h9647
http://www.critico-expository.com/forum/index.php?topic=12231.0
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-10-05-2019-7/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-eu8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q9-u9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://danielmillsap.com/forum/index.php?topic=1032633.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/09-05-2019-to-oot-6-e-422780/?PHPSESSID=ree16ji6ta0i7e5fdivrmk51t3
http://ru-realty.com/forum/index.php?topic=491624.0
https://sanp.pro/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b6-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5/
http://forum.kopkargobel.com/index.php?topic=7137.0
http://www.nomaher.com/forum/index.php?topic=13272.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/'a-etoo-2019-8-eo-5-e'-a-etoo-2019-8-eo-5-e-i3z5/?PHPSESSID=t4cdtfmuqtm1rlj6ifnghsekn5
http://www.deliberarchia.org/forum/index.php?topic=993142.0
http://www.deliberarchia.org/forum/index.php?topic=1012392.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=683545.0
http://roikjer.com/forum/index.php?PHPSESSID=grf2tdk4jrgmj4qc3b1f8g6190&topic=861050.0
http://otitismediasociety.org/forum/index.php?topic=150703.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gf4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://jdcalc.com/forum/viewtopic.php?f=2&t=170118
https://danceplanet.se/commodore/index.php?topic=21212.0
https://khuyenmaikk13.info/index.php?topic=186477.0
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-g3-x5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
https://nextezone.com/index.php?topic=39376.0
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x6-n4-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://forum.politeknikgihon.ac.id/index.php?topic=31999.0
http://HyUa.1fps.icu/l/szIaeDC
http://forum.elexlabs.com/index.php?topic=16622.0
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p4-v8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://otitismediasociety.org/forum/index.php?topic=149047.0
http://forum.politeknikgihon.ac.id/index.php?topic=28264.0
http://www.hoonthaitoday.com/forum/index.php?topic=222660.0
https://members.fbhaters.com/index.php?topic=86070.0
http://www.ofqj.org/hebergementfrance/4-10-e4-v7-4-10-4-10-watch
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(a-etoogame-of-thrones-8-eo-7-e)-a-etoogame-of-thrones-8-eo-7-e-g3p6/?PHPSESSID=l3qlolln2uk24u9prp1hn6ut86
https://reficulcoin.com/index.php?topic=34055.0
http://roikjer.com/forum/index.php?PHPSESSID=q7b8d1guj5d1ltj7utect2ldb4&topic=837782.0
http://www.deliberarchia.org/forum/index.php?topic=992228.0
http://roikjer.com/forum/index.php?PHPSESSID=9av930463d6k7tqrtt3h5fnjv2&topic=838178.0
http://help.stv.ru/index.php?PHPSESSID=ed7a4782eab265f04099b50bfa08b461&topic=139809.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nr8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8/
http://help.stv.ru/index.php?PHPSESSID=01f537f919b34396604f2fa2afe1163d&topic=141329.0
http://www.nomaher.com/forum/index.php?topic=12370.0
https://worldtaxi.org/2019/05/09/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s6-f9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://sanp.pro/%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-09-05-2019-2/
http://www.ofqj.org/hebergementquebec/4-13-f3-o7-4-13-4-13-online
http://www.theparrotcentre.com/forum/index.php?topic=483709.0
http://www.deliberarchia.org/forum/index.php?topic=995827.0
http://www.teedinubon.com/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-eng/
http://www.theocraticamerica.org/forum/index.php?topic=36701.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=693018.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=693022.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=693027.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=693031.0
https://chromehearts.in.th/index.php?topic=50092.0
https://chromehearts.in.th/index.php?topic=50093.0
https://chromehearts.in.th/index.php?topic=50095.0
https://cybergsm.es/index.php?topic=12453.0
https://cybergsm.es/index.php?topic=12454.0
https://hackersuniversity.net/index.php?topic=13073.0
https://khuyenmaikk13.info/index.php?topic=198659.0
https://khuyenmaikk13.info/index.php?topic=198662.0
https://khuyenmaikk13.info/index.php?topic=198664.0
https://nextezone.com/index.php?topic=48399.0
https://prelease.club/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%84%d0%b8%d0%bb%d1%8c%d0%bc-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3/
https://prelease.club/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d1%81%d0%b5%d1%80%d0%b8%d0%b0/
https://prelease.club/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8/
https://prelease.club/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bb%d0%be%d1%81%d1%82%d1%84%d0%b8/
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80/
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5/
https://prelease.club/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d0%b4%d0%b0%d1%82%d0%b0/
https://sanp.pro/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8/
http://HyUa.1fps.icu/l/szIaeDC
http://danielmillsap.com/forum/index.php?topic=1032593.0
http://otitismediasociety.org/forum/index.php?topic=157936.0
http://forum.elexlabs.com/index.php/topic,16345.0.html
http://ru-realty.com/forum/index.php?PHPSESSID=mhhri2pdd5t9k4denfioj6shq0&topic=501623.0
http://roikjer.com/forum/index.php?PHPSESSID=6b4measau78faa19v179lpkvf5&topic=850686.0
http://uberdrivers.net/forum/index.php?topic=245583.0
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-n9-q2-%d0%b8/
http://d2bchannel.co.in/blog/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p7-y7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l5-s7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fy4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://nextezone.com/index.php?topic=39695.0
http://www.nomaher.com/forum/index.php?topic=12696.0
http://universalcommunity.se/Forum/index.php?topic=1269.0
https://akutthjelper.no/members/adriennehuber4/
https://nextezone.com/index.php?topic=42374.0
http://teambuildingpremium.com/forum/index.php?topic=812248.0
http://www.theparrotcentre.com/forum/index.php?topic=485695.0
http://eugeniocolazzo.it/forum/index.php?topic=105888.0
http://roikjer.com/forum/index.php?PHPSESSID=uf9r6oqa4eocgahops990qbv35&topic=850166.0
https://www.limscave.com/forum/viewtopic.php?t=31684
https://nextezone.com/index.php?topic=39234.0
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w7-z0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://altaylarteknoloji.com/index.php?topic=1990.0
https://members.fbhaters.com/index.php?topic=86563.0
http://8.droror.co.il/uncategorized/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-b5-i7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.hoonthaitoday.com/forum/index.php?topic=243577.0
http://teambuildingpremium.com/forum/index.php?topic=816744.0
https://reficulcoin.com/index.php?topic=19284.0
http://otitismediasociety.org/forum/index.php?topic=153545.0
http://otitismediasociety.org/forum/index.php?topic=149529.0
http://menulisilmiah.net/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x6-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5/
http://HyUa.1fps.icu/l/szIaeDC
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-54/
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g0-c3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://members.fbhaters.com/index.php?topic=87599.0
http://eugeniocolazzo.it/forum/index.php?topic=106849.0
https://altaylarteknoloji.com/index.php?topic=1871.0
http://www.hoonthaitoday.com/forum/index.php?topic=211225.0
http://poselokgribovo.ru/forum/index.php?topic=750215.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g9-l1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.theocraticamerica.org/forum/index.php?topic=28308.0
https://reficulcoin.com/index.php?topic=31577.0
http://otitismediasociety.org/forum/index.php?topic=150385.0
http://forum.elexlabs.com/index.php?topic=16400.0
http://help.stv.ru/index.php?PHPSESSID=9107cfc8dd7342626dd73a3fa4127468&topic=140608.0
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o0-d6-%d0%b8%d0%b3%d1%80%d0%b0/
https://khuyenmaikk13.info/index.php?topic=187707.0
http://www.tessabannampad.go.th/webboard/index.php?topic=197121.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-f9-n1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.critico-expository.com/forum/index.php?topic=8069.0
https://hackersuniversity.net/index.php?topic=10099.0
https://reficulcoin.com/index.php?topic=27887.0
http://www.critico-expository.com/forum/index.php?topic=7762.0
http://www.tessabannampad.go.th/webboard/index.php?topic=202811.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=31784.0
http://www.critico-expository.com/forum/index.php?topic=6448.0
http://menulisilmiah.net/%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-10-05-2019-3/
http://teambuildingpremium.com/forum/index.php?topic=801690.0
http://roikjer.com/forum/index.php?topic=840879.0
https://khuyenmaikk13.info/index.php?topic=186015.0
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c3-s2-%d0%b8%d0%b3%d1%80/
http://vtservices85.fr/smf2/index.php?PHPSESSID=0a8dd39c683c974a7493c70c60219cbf&topic=229870.0
https://nextezone.com/index.php?topic=42488.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r8-o7-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
https://members.fbhaters.com/index.php?topic=83258.0
http://danielmillsap.com/forum/index.php?topic=1033664.0
http://HyUa.1fps.icu/l/szIaeDC
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v9-x3-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v0-b0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mi4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sanp.pro/09-05-2019-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://www.nomaher.com/forum/index.php?topic=12984.0
http://www.ofqj.org/hebergementquebec/4-13-watch-k3-x9-4-13-4-13-online
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-14/
http://teambuildingpremium.com/forum/index.php?topic=793833.0
https://danceplanet.se/commodore/index.php?topic=20730.0
https://danceplanet.se/commodore/index.php?topic=24790.0
https://sanp.pro/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://ru-realty.com/forum/index.php?PHPSESSID=37a78mrj8kh6ubphdt47cdr097&topic=486409.0
http://www.deliberarchia.org/forum/index.php?topic=1001919.0
http://www.critico-expository.com/forum/index.php?topic=13264.0
http://www.deliberarchia.org/forum/index.php?topic=1018911.0
https://reficulcoin.com/index.php?topic=33012.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lx4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8/
http://roikjer.com/forum/index.php?topic=837121.0
http://forum.drahthaar-club.com.ua/index.php?topic=1460.0
https://hackersuniversity.net/index.php?topic=10124.0
https://akutthjelper.no/members/hesterz5733904/
http://www.tessabannampad.go.th/webboard/index.php?topic=197765.0
https://members.fbhaters.com/index.php?topic=85487.0
https://prelease.club/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b7-%d1%81%d0%bb/
http://roikjer.com/forum/index.php?PHPSESSID=madjgk35hf5us9b0msrm4v82c2&topic=840300.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t4-u5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=30418.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p5-m8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://khuyenmaikk13.info/index.php?topic=186604.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=687364.0
https://members.fbhaters.com/index.php?topic=84422.0
http://roikjer.com/forum/index.php?PHPSESSID=660r5ea12thlss68lphglkb1r7&topic=850795.0
http://d2bchannel.co.in/blog/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-u9-s6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://help.stv.ru/index.php?PHPSESSID=f8277706d4fb5f4024db59ad92e969bc&topic=139455.0
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p0-i1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://forum.elexlabs.com/index.php?topic=17912.0
http://teambuildingpremium.com/forum/index.php?topic=794308.0
http://HyUa.1fps.icu/l/szIaeDC
http://forum.elexlabs.com/index.php?topic=19575.0
http://forum.kopkargobel.com/index.php?topic=6822.0
https://khuyenmaikk13.info/index.php?topic=188150.0
http://www.critico-expository.com/forum/index.php?topic=11792.0
http://vtservices85.fr/smf2/index.php?topic=225046.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bm8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dj0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://vtservices85.fr/smf2/index.php?PHPSESSID=5f7bbbd0a763dc15c2c2f5738dd7f921&topic=229279.0
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j6-v1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.tessabannampad.go.th/webboard/index.php?topic=204105.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-za4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://forum.shaiyaslayer.tk/index.php?topic=101004.0
http://forum.elexlabs.com/index.php?topic=19194.0
http://www.hoonthaitoday.com/forum/index.php?topic=207299.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-13/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a1-z1-%d0%b8%d0%b3%d1%80/
http://www.hoonthaitoday.com/forum/index.php?topic=202265.0
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile;u=33938
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l8-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://members.fbhaters.com/index.php?topic=87873.0
http://forum.elexlabs.com/index.php?topic=18349.0
http://122.154.49.125/Forum/index.php?topic=150.0
https://prelease.club/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i6-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://forum.elexlabs.com/index.php?topic=18456.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-14/
http://forum.byehaj.hu/index.php?topic=85941.0
http://roikjer.com/forum/index.php?topic=854964.0
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o7-p7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c0-m3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://ru-realty.com/forum/index.php?PHPSESSID=uf1iqj823v81dlmm9ql46s7vp5&topic=481462.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=31006.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yb8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://ru-realty.com/forum/index.php?PHPSESSID=ivqjjo3lfcrnva3pu9u4h13qh4&topic=480315.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e9-l6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://forum.elexlabs.com/index.php?topic=22610.0
http://myrechockey.com/forums/index.php?topic=93957.0
http://www.tessabannampad.go.th/webboard/index.php?topic=197062.0
http://HyUa.1fps.icu/l/szIaeDC
http://help.stv.ru/index.php?PHPSESSID=5e0f2a4f35aa79a87baa0a541997bae8&topic=140619.0
http://www.hoonthaitoday.com/forum/index.php?topic=229816.0
http://metropolis.ga/index.php?topic=6805.0
http://www.critico-expository.com/forum/index.php?topic=12674.0
http://roikjer.com/forum/index.php?topic=842893.0
https://reficulcoin.com/index.php?topic=32408.0
http://forum.elexlabs.com/index.php?topic=22569.0
http://forum.kopkargobel.com/index.php?topic=6488.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=cbb8114503a68a3e009ae126abac2050&topic=761.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=d43d254a0f4ee9f929bb04c3a0631ea9&topic=226665.0
http://www.ofqj.org/hebergementfrance/4-13-watch-e2-r1-4-13-4-13
http://www.popolsku.fr.pl/forum/index.php?topic=377226.0
http://www.hoonthaitoday.com/forum/index.php?topic=243682.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h1-u6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://forum.elexlabs.com/index.php?topic=17829.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uq0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://members.fbhaters.com/index.php?topic=88526.0
http://uberdrivers.net/forum/index.php?topic=258651.0
https://members.fbhaters.com/index.php?topic=86878.0
http://www.tessabannampad.go.th/webboard/index.php?topic=203846.0
http://myrechockey.com/forums/index.php?topic=91697.0
http://otitismediasociety.org/forum/index.php?topic=149260.0
https://reficulcoin.com/index.php?topic=21008.0
https://nextezone.com/index.php?topic=45608.0
https://reficulcoin.com/index.php?topic=17217.0
http://poselokgribovo.ru/forum/index.php?topic=743723.0
https://prelease.club/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
https://reficulcoin.com/index.php?topic=31444.0
https://reficulcoin.com/index.php?topic=16878.0
http://otitismediasociety.org/forum/index.php?topic=149912.0
http://otitismediasociety.org/forum/index.php?topic=149659.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-69/
http://demo.caribe.vps-private.net/blog/milliardy-4-sezon-12-seriya-online-t3-a3-milliardy-4-sezon-12-seriya-milliardy-4-sezon-12-seriy
http://www.critico-expository.com/forum/index.php?topic=7068.0
http://www.tekparcahdfilm.com/forum/index.php?topic=47323.0
http://teambuildingpremium.com/forum/index.php?topic=795217.0
http://www.theparrotcentre.com/forum/index.php?topic=484027.0
http://HyUa.1fps.icu/l/szIaeDC
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ca7-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.hoonthaitoday.com/forum/index.php?topic=240313.0
https://reficulcoin.com/index.php?topic=23542.0
https://reficulcoin.com/index.php?topic=20777.0
http://www.ofqj.org/hebergementfrance/4-9-online-c4-m8-4-9-4-9
https://reficulcoin.com/index.php?topic=33157.0
http://myrechockey.com/forums/index.php?topic=92984.0
http://www.deliberarchia.org/forum/index.php?topic=999822.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k2-n2-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i4-x5-%d0%b8%d0%b3%d1%80/
http://otitismediasociety.org/forum/index.php?topic=152372.0
https://prelease.club/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y6-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wf1-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.deliberarchia.org/forum/index.php?topic=999570.0
http://www.nomaher.com/forum/index.php?topic=13079.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l0-z9-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://reficulcoin.com/index.php?topic=21594.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lw6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://teambuildingpremium.com/forum/index.php?topic=793690.0
http://www.tessabannampad.go.th/webboard/index.php?topic=203620.0
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-l9-p8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://vervetama.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k3-n1-%d0%b8%d0%b3%d1%80/
http://myrechockey.com/forums/index.php?topic=97996.0
https://reficulcoin.com/index.php?topic=17696.0
https://prelease.club/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i3-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.sharmaraco.com/blog/%E2%80%9E%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-online-s1-m1-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%E2%80%9E%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://roikjer.com/forum/index.php?PHPSESSID=mr8vbj09h03qvmm76576bt2gn5&topic=842347.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uk4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://eugeniocolazzo.it/forum/index.php?topic=118347.0
http://sexfork.com/uncategorized/ertugrul-147-seriya-es3-ertugrul-147-seriya/
http://help.stv.ru/index.php?PHPSESSID=17d628205d09f4f54614ff3fd4c6a655&topic=139946.0
http://www.ofqj.org/hebergementfrance/4-13-d0-x5-4-13-4-13-watch
http://HyUa.1fps.icu/l/szIaeDC
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d9-l5-%d0%b8%d0%b3%d1%80/
http://www.tessabannampad.go.th/webboard/index.php?topic=197488.0
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-q0-u3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
https://members.fbhaters.com/index.php?topic=83252.0
http://www.deliberarchia.org/forum/index.php?topic=1021868.0
http://roikjer.com/forum/index.php?PHPSESSID=r4grj95p51bu85viuij3i6o3v1&topic=841822.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=a3071cdf871fc3b4c98533b93517d09b&topic=225060.0
http://roikjer.com/forum/index.php?PHPSESSID=7q7cpi6ok5rgd08kmj57o3eqf0&topic=847760.0
http://roikjer.com/forum/index.php?topic=864759.0
http://forum.bmw-e60.eu/index.php?topic=6063.0
https://www.limscave.com/forum/viewtopic.php?t=31788
http://forum.elexlabs.com/index.php?topic=21742.0
https://nextezone.com/index.php?topic=41019.0
https://khuyenmaikk13.info/index.php?topic=185306.0
https://akutthjelper.no/members/ebonyfrizzell4/
http://help.stv.ru/index.php?PHPSESSID=e1981f39e8e38c5bcbad052f143620b6&topic=139629.0
http://help.stv.ru/index.php?PHPSESSID=28bcfa5dbc41b76b20fad87ec1fa0034&topic=140436.0
http://otitismediasociety.org/forum/index.php?topic=155344.0
http://www.deliberarchia.org/forum/index.php?topic=993355.0
http://forum.elexlabs.com/index.php?topic=23017.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q4-u6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://www.limscave.com/forum/viewtopic.php?f=6&t=31777&view=print
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n7-i2-%d0%b8%d0%b3%d1%80/
http://uberdrivers.net/forum/index.php?topic=245571.0
https://akutthjelper.no/members/petedanis19956/
http://myrechockey.com/forums/index.php?topic=92246.0
http://www.hoonthaitoday.com/forum/index.php?topic=218749.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=686112.0
http://forum.elexlabs.com/index.php?topic=22091.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=32618.0
https://reficulcoin.com/index.php?topic=31237.0
http://www.newb.northstarchiangrai.com/index.php?PHPSESSID=kttfc8p92mqsl37c3oe1121fq4&topic=23957.0
http://roikjer.com/forum/index.php?topic=838055.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g6-x8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://npi.org.es/smf/index.php?topic=113618.0
http://otitismediasociety.org/forum/index.php?topic=149520.0
http://vervetama.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qj6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x9-y0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://HyUa.1fps.icu/l/szIaeDC
http://ptu.imoove.kr/ko/content/%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-18-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB-%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-18-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB331929
http://socialfbwidgets.com/component/k2/itemlist/user/13447.html
http://israengineering.com/index.php/component/k2/itemlist/user/1113993
http://menulisilmiah.net/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l2-%d1%82%d0%be%d0%bb/
http://euromouleusinage.com/index.php/component/k2/itemlist/user/118818
http://seoksoononly.dothome.co.kr/qna/731827
https://tg.vl-mp.com/index.php?topic=1327561.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1337746
https://szenarist.ru/forum/index.php?topic=205943.0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/221645
https://tg.vl-mp.com/index.php?topic=1352635.0
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1020574
http://macdistri.com/index.php/component/k2/itemlist/user/301265
http://withinfp.sakura.ne.jp/eso/index.php/16882147-novinka-sluga-naroda-3-sezon-7-seria/0
http://laspoltrina.it/?option=com_k2&view=itemlist&task=user&id=1382496
http://www.ekemoon.com/143513/050020194406/
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19719
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/296816
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=318044
http://married.dike.gr/index.php/component/k2/itemlist/user/57464
http://mediaville.me/index.php/component/k2/itemlist/user/252125
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=83049
http://moyakmermer.com/index.php/component/k2/itemlist/user/712215
http://153.120.114.241/eso/index.php/16862198-vossoedinenie-vuslat-17-seria-frgl-vossoedinenie-vuslat-17-seri
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=282938
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2571518
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=120253
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4744277
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=303354
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/285512
http://153.120.114.241/eso/index.php/16880350-voron-kuzgun-15-seria-fclx-voron-kuzgun-15-seria
http://mediaville.me/?option=com_k2&view=itemlist&task=user&id=210839
http://withinfp.sakura.ne.jp/eso/index.php/16884827-taemnici-97-seria-06052019-m6-taemnici-97-seria
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=17193
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=22211
http://www.ekemoon.com/146725/051920194606/
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1121165
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43875
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/298715
http://webp.online/index.php?topic=46854.30
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=804415
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=804422
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=58609
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/315496
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/315609
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/249023
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3340878
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3340903
http://www.autospa.lv/?option=com_k2&view=itemlist&task=user&id=9277
http://married.dike.gr/index.php/component/k2/itemlist/user/46348
http://lavaggio.com.vn/index.php/component/k2/itemlist/user/3727695
https://forums.letstalkbeats.com/index.php?topic=66863.0
http://www.vivelabmanizales.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-08-05-2019-z9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://kurnaz.1to.us/index.php?topic=1.975
http://dohairbiz.com/en/component/k2/itemlist/user/2716277.html
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2391264
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/185910
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1556001
http://menulisilmiah.net/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-99-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tr5%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-99/
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=123048
http://danielmillsap.com/forum/index.php?topic=986886.0
http://bitpark.co.kr/board_IzjM66/3741625
http://www.vivelabmanizales.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-06-05-2019-v4-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=47781
http://ovotecegg.com/component/k2/itemlist/user/121523
http://bitpark.co.kr/board_IzjM66/3731921
http://islamiccall.info/index.php/component/k2/itemlist/user/856951
http://seoksoononly.dothome.co.kr/qna/723365
http://mobility-corp.com/index.php/component/k2/itemlist/user/2511974
http://thermoplast.envolgroupe.com/component/k2/author/94042
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1582008
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1582203
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1390972
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1391315
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1391344
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1391348
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4890168
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4890210
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/606115
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=58551
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/249074
http://ovotecegg.com/component/k2/itemlist/user/120509
https://sanp.pro/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-42-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xtna-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0/
http://roikjer.com/forum/index.php?PHPSESSID=k70aq7q047j37brh000fhmrps5&topic=827399.0
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1547211
http://mediaville.me/index.php/component/k2/itemlist/user/218818
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=763161
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=269303
http://topitop.kz/component/k2/itemlist/user/76411
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=69073
http://menulisilmiah.net/live-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://rudraautomation.com/index.php/component/k2/author/130686
http://xplorefitness.com/blog/%C2%AB%D0%B2%D0%BE%D1%81%D1%81%D0%BE%D0%B5%D0%B4%D0%B8%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5-vuslat-19-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-ifew-%C2%AB%D0%B2%D0%BE%D1%81%D1%81%D0%BE%D0%B5%D0%B4%D0%B8%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5-vuslat-19-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1545761
http://poselokgribovo.ru/forum/index.php?topic=717498.0
http://www.ekemoon.com/141887/051520192605/
http://married.dike.gr/index.php/component/k2/itemlist/user/50336
http://guiadetudo.com/index.php/component/k2/itemlist/user/11074
http://www2.yasothon.go.th/smf/index.php?topic=159.msg182165
http://marjorieaperry.com/?option=com_k2&view=itemlist&task=user&id=482099
http://fbpharm.net/index.php/component/k2/itemlist/user/32793
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1778282
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=297200
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/297158
http://haniel.ir/index.php/component/k2/itemlist/user/94630
http://hotelnomadpalace.com/es/?option=com_k2&view=itemlist&task=user&id=20641
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1165179
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=318497
http://lavaggio.com.vn/index.php/component/k2/itemlist/user/3774328
http://mediaville.me/index.php/component/k2/itemlist/user/252529
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=232476
http://forum.kopkargobel.com/index.php?topic=8250.0
http://www.popolsku.fr.pl/forum/index.php?topic=381363.0
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jp0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://teambuildingpremium.com/forum/index.php?topic=806566.0
http://forum.byehaj.hu/index.php?topic=88829.0
https://reficulcoin.com/index.php?topic=28927.0
http://www.hoonthaitoday.com/forum/index.php?topic=213271.0
http://menulisilmiah.net/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-09-05-2019-2/
http://otitismediasociety.org/forum/index.php?topic=150470.0
http://menulisilmiah.net/09-05-2019-%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-13-2/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-2/
http://uberdrivers.net/forum/index.php?topic=250589.0
http://poselokgribovo.ru/forum/index.php?topic=747873.0
https://fasttrack.education/groups/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g2-y0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://roikjer.com/forum/index.php?topic=843601.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a2-l3-%d0%b8%d0%b3%d1%80%d0%b0/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://nextezone.com/index.php?topic=45829.0
http://forum.elexlabs.com/index.php?topic=17328.0
http://forum.elexlabs.com/index.php/topic,20076.0.html
https://worldtaxi.org/2019/05/09/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s8-x0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.deliberarchia.org/forum/index.php?topic=1017552.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b7-d3-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rz8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/e-eka-aota-(e-ioa-oota)-21-e-(-b6-e-eka-aota-(e-ioa-oota)-21-e/?PHPSESSID=mle7pcos2bvg3jf4s5hseogiq3
http://www.hoonthaitoday.com/forum/index.php?topic=239365.0
https://members.fbhaters.com/index.php?topic=89340.0
http://www.deliberarchia.org/forum/index.php?topic=990877.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g4-r2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
https://members.fbhaters.com/index.php?topic=83018.0
http://otitismediasociety.org/forum/index.php?topic=155689.0
http://forum.elexlabs.com/index.php?topic=16081.0
https://reficulcoin.com/index.php?topic=17549.0
http://forum.politeknikgihon.ac.id/index.php?topic=33659.0
http://www.ofqj.org/hebergementfrance/4-10-b7-d5-4-10-4-10
http://www.critico-expository.com/forum/index.php?topic=8477.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.deliberarchia.org/forum/index.php?topic=1000215.0
https://reficulcoin.com/index.php?topic=20827.0
http://forum.elexlabs.com/index.php?topic=18536.0
https://members.fbhaters.com/index.php?topic=87319.0
http://ru-realty.com/forum/index.php?PHPSESSID=mskqr2143hjcalhqnpe7oso204&topic=478233.0
http://www.hoonthaitoday.com/forum/index.php?topic=208481.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-u3-j0-%d0%b8%d0%b3/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-61/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-go3-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://forum.digamahost.com/index.php?topic=111783.0
http://www.ofqj.org/hebergementfrance/4-8-k1-k0-4-8-4-8-watch
http://otitismediasociety.org/forum/index.php?topic=157552.0
http://www.deliberarchia.org/forum/index.php?topic=1005235.0
https://khuyenmaikk13.info/index.php?topic=188771.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(a-etoo-(got)-8-eo-2-e)-a-etoo-(got)-8-eo-2-e-m7y5/?PHPSESSID=ngi7ugqb7b7d7qg766v56eusn2
http://otitismediasociety.org/forum/index.php?topic=149754.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-x4-f0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://danielmillsap.com/forum/index.php?topic=1025771.0
https://sanp.pro/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o9-%d1%81/
https://danceplanet.se/commodore/index.php?topic=28772.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/'a-etoo-8-eo-6-e'-a-etoo-8-eo-6-e-k0t4/?PHPSESSID=ipuqg1h5avog6jbnsmm0rdu813
https://www.gizmoarticle.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g6-z2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://roikjer.com/forum/index.php?PHPSESSID=16f5k2lvqedm0a63hb3p5qh5l4&topic=836607.0
http://www.nomaher.com/forum/index.php?topic=12262.0
http://ru-realty.com/forum/index.php?PHPSESSID=362gul9sas302929oci6uc8hc3&topic=478988.0
https://nextezone.com/index.php?topic=46126.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kg4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.critico-expository.com/forum/index.php?topic=11634.0
https://worldtaxi.org/2019/05/09/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-s0-u7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
https://danceplanet.se/commodore/index.php?topic=28213.0
https://prelease.club/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j5-%d1%81%d0%bb/
https://members.fbhaters.com/index.php?topic=85114.0
http://www.ekemoon.com/165871/051920190009/
http://otitismediasociety.org/forum/index.php?topic=152956.0
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k1-g3-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile;u=34731
http://HyUa.1fps.icu/l/szIaeDC
http://k-cea.org/board_Hnyj62/4667
http://kfuav.kr/qna/5456
http://kfuav.kr/qna/5466
http://kfuav.kr/qna/5470
http://lahch.co.kr/index.php?mid=board_jHAP41&document_srl=6826
http://lahch.co.kr/index.php?mid=board_jHAP41&document_srl=6831
http://masarapphil.com/board_tmXx76/14993
http://masarapphil.com/board_tmXx76/15005
http://masarapphil.com/board_tmXx76/15025
http://masarapphil.com/board_tmXx76/15036
https://hackersuniversity.net/index.php?topic=9375.0
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-h4-t5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://demo.caribe.vps-private.net/blog/milliardy-4-sezon-10-seriya-b2-x1-milliardy-4-sezon-10-seriya-milliardy-4-sezon-10-seriya
http://danielmillsap.com/forum/index.php?topic=995929.0
http://danielmillsap.com/forum/index.php?topic=1026737.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=31323.0
http://dpmarketingsystems.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n1-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be-2/
http://roikjer.com/forum/index.php?PHPSESSID=6daebiknjhb4bfe9l6juubq7s7&topic=847781.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c3-f2-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://www.hoonthaitoday.com/forum/index.php?topic=210460.0
https://reficulcoin.com/index.php?topic=30744.0
https://nextezone.com/index.php?topic=40539.0
http://forum.elexlabs.com/index.php/topic,20808.0.html
http://roikjer.com/forum/index.php?PHPSESSID=fjm8qihfu0loelqfnp99at1nd7&topic=848050.0
http://www.tessabannampad.go.th/webboard/index.php?topic=198215.0
http://ru-realty.com/forum/index.php?PHPSESSID=858lr9l98u1p112i3estlbhrr1&topic=479095.0
http://www.remify.app/foro/index.php?topic=245130.0
http://www.theparrotcentre.com/forum/index.php?topic=485319.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-oz1-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sanp.pro/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w4-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://universalcommunity.se/Forum/index.php?topic=1261.0
http://forum.politeknikgihon.ac.id/index.php?topic=28487.0
http://www.nomaher.com/forum/index.php?topic=12992.0
https://nextezone.com/index.php?action=profile;u=6598
http://HyUa.1fps.icu/l/szIaeDC
http://indiefilm.kr/xe/board/5655
http://indiefilm.kr/xe/board/5664
http://indiefilm.kr/xe/board/5679
http://indiefilm.kr/xe/board/5693
http://isch.kr/board_PowH60/1627
http://isch.kr/board_PowH60/1638
http://isch.kr/board_PowH60/1643
http://isch.kr/board_PowH60/1647
http://jnk-ent.jp/index.php?mid=gallery&document_srl=4219
http://jnk-ent.jp/index.php?mid=gallery&document_srl=4228
http://jnk-ent.jp/index.php?mid=gallery&document_srl=4233
http://k-cea.org/board_Hnyj62/4631
http://www.popolsku.fr.pl/forum/index.php?topic=377848.0
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u4-j8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://otitismediasociety.org/forum/index.php?topic=155174.0
http://www.ekemoon.com/171017/050920190210/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(a-etoo-2019-8-eo-2-e)-a-etoo-2019-8-eo-2-e-s1d9/?PHPSESSID=p6ld366mh1ealca2o9q60v2144
http://danielmillsap.com/forum/index.php?topic=1030527.0
http://eugeniocolazzo.it/forum/index.php?topic=112991.0
http://demo.caribe.vps-private.net/blog/milliardy-4-sezon-10-seriya-watch-n3-g8-milliardy-4-sezon-10-seriya-milliardy-4-sezon-10-seriya
http://help.stv.ru/index.php?topic=139689.0
http://poselokgribovo.ru/forum/index.php?topic=743924.0
http://www.critico-expository.com/forum/index.php?topic=8689.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j8-v6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://prelease.club/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m2-%d1%81%d0%bb%d1%83/
http://sexfork.com/uncategorized/ertugrul-145-seriya-nv4-ertugrul-145-seriya/
http://HyUa.1fps.icu/l/szIaeDC
http://roikjer.com/forum/index.php?PHPSESSID=e7dvaupagv7khiv1i9ij6qb9e6&topic=838420.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/'a-etoo-2019-8-eo-1-e'-a-etoo-2019-8-eo-1-e-j6v5/?PHPSESSID=cik63vjoeldqrn8vh1111tp537
http://help.stv.ru/index.php?PHPSESSID=4888a3c1b2f56d0d23f5ad31a8067328&topic=139682.0
https://npi.org.es/smf/index.php?topic=113428.0
http://www.hoonthaitoday.com/forum/index.php?topic=201656.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s6-v9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g0-z7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://vtservices85.fr/smf2/index.php?PHPSESSID=e6b46c76748fc23c165b3b6f91f46e63&topic=217167.0
http://eugeniocolazzo.it/forum/index.php?topic=106058.0
https://danceplanet.se/commodore/index.php?topic=20093.0
https://danceplanet.se/commodore/index.php?topic=19990.0
http://demo.caribe.vps-private.net/blog/milliardy-4-sezon-9-seriya-s4-l3-milliardy-4-sezon-9-seriya-milliardy-4-sezon-9-seriya-online
https://polyframetrade.co.uk/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w5-a2-%d1%80%d0%b0/
http://metropolis.ga/index.php?topic=6671.0
https://members.fbhaters.com/index.php/topic,84529.0.html
http://myrechockey.com/forums/index.php?topic=91791.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-an7-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.tessabannampad.go.th/webboard/index.php?topic=197359.0
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d6-%d1%81%d0%bb/
http://www.deliberarchia.org/forum/index.php?topic=1017408.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f7-d1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://otitismediasociety.org/forum/index.php?topic=158909.0
http://partemp.com/en/groups/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f7-r6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://help.stv.ru/index.php?PHPSESSID=e810e644d2304474716bb2325227c151&topic=140058.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p3-u0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://adsensebih.com/index.php?topic=11237.0
https://sanp.pro/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r1-%d1%81/
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f5-a7-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://roikjer.com/forum/index.php?PHPSESSID=o6cisilcerd5ekp0f75lshj323&topic=864866.0
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g5-r2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.tessabannampad.go.th/webboard/index.php?topic=198517.0
http://tripviet.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p8-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://xn--l1adgmc.xn----9sbdbmdznsj5c5bxd7b.xn--p1ai/index.php?topic=10959.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-b3-t8-%d0%b8%d0%b3%d1%80/
http://www.deliberarchia.org/forum/index.php?topic=1012804.0
https://reficulcoin.com/index.php?topic=23580.0
https://reficulcoin.com/index.php?topic=26686.0
http://menulisilmiah.net/%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-17-%d1%81%d0%b5-19/
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t9-m1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://eugeniocolazzo.it/forum/index.php?topic=105938.0
https://khuyenmaikk13.info/index.php?topic=189274.0
http://roikjer.com/forum/index.php?PHPSESSID=jb42sk98o1n0cbg7l6ts9776v3&topic=836732.0
http://roikjer.com/forum/index.php?PHPSESSID=9mlsou0iqivl4c63216slulk13&topic=839674.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-up9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://HyUa.1fps.icu/l/szIaeDC
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u1-w6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-98/
http://www.theparrotcentre.com/forum/index.php?topic=484404.0
http://roikjer.com/forum/index.php?PHPSESSID=khram0ged5lcp1hf8bvk4b9bo6&topic=842461.0
http://demo.caribe.vps-private.net/blog/milliardy-4-sezon-13-seriya-e4-p0-milliardy-4-sezon-13-seriya-milliardy-4-sezon-13-seriya
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-m8-g0-%d0%b8%d0%b3/
http://www.tessabannampad.go.th/webboard/index.php?topic=203923.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-c8-x7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
https://reficulcoin.com/index.php?topic=16887.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-j0-d4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.ofqj.org/hebergementquebec/4-13-b6-o0-4-13-4-13
http://8.droror.co.il/uncategorized/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l3-y3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://prelease.club/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://forum.elexlabs.com/index.php/topic,19438.0.html
http://taklongclub.com/forum/index.php?topic=115798.0
http://danielmillsap.com/forum/index.php?topic=994355.0
http://www.theparrotcentre.com/forum/index.php?topic=490853.0
http://istakam.com/forum/index.php?topic=14650.0
https://worldtaxi.org/2019/05/09/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e6-y6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://prelease.club/live-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z7-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://forum.elexlabs.com/index.php?topic=23172.0
https://nextezone.com/index.php?action=profile;u=4688
http://forum.politeknikgihon.ac.id/index.php?topic=30774.0
https://nextezone.com/index.php?topic=41629.0
http://otitismediasociety.org/forum/index.php?topic=157304.0
http://www.theparrotcentre.com/forum/index.php?topic=492886.0
https://members.fbhaters.com/index.php?topic=88682.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1551735
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4837348
http://necinsurance.co.zw/component/k2/itemlist/user/19602.html
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=79569
http://webp.online/index.php?action=profile;u=161055
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=501135
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1014900
https://l2thalassic.org/Forum/index.php?topic=1778.0
http://healthyteethpa.org/component/k2/itemlist/user/5333273
https://members.fbhaters.com/index.php?topic=80726.0
http://matinbank.ir/component/k2/itemlist/user/4482766.html
http://koushatarabar.com/index.php/component/k2/itemlist/user/1314382
http://www.vogtland.com.pl/index.php/component/k2/itemlist/user/10408
http://www.ekemoon.com/145439/051720190306/
https://l2thalassic.org/Forum/index.php?topic=1827.0
http://smartacity.com/component/k2/itemlist/user/15482
http://www.camaracoyhaique.cl/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w4-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1/
http://cccpvideo.forumside.com/index.php?topic=808.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2562082
http://www.ekemoon.com/149917/050220191807/
http://kurnaz.1to.us/index.php?topic=1.750
http://thermoplast.envolgroupe.com/component/k2/author/70370
http://arunagreen.com/index.php/component/k2/itemlist/user/437791
http://febrescordero.gob.ec/index.php/component/k2/itemlist/user/79370
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=83341
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/726676
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/242106
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/16178
http://proxima.co.rw/index.php/component/k2/itemlist/user/619155
http://rudraautomation.com/index.php/component/k2/author/183583
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1686774
http://fbpharm.net/index.php/component/k2/itemlist/user/15514
http://rudraautomation.com/index.php/component/k2/author/120460
http://kurnaz.1to.us/index.php?topic=1.510
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1619510
http://teambuildingpremium.com/forum/index.php?topic=786509.0
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=303327
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1630527
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/64268
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3629114
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/185101
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1837691
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=203045
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/473014
http://seoksoononly.dothome.co.kr/?document_srl=754860
http://haniel.ir/index.php/component/k2/itemlist/user/74082
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1631718
http://thermoplast.envolgroupe.com/component/k2/author/81780
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=187513
http://c3isecurity.com.br/?option=com_k2&view=itemlist&task=user&id=470325
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=62530
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=109551
http://zsmr.com.ua/index.php/component/k2/itemlist/user/554579
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/17481
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=327092
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/208005
http://smartacity.com/index.php/component/k2/itemlist/user/43909
http://thermoplast.envolgroupe.com/component/k2/author/102255
http://w9builders.co.uk/index.php/component/k2/itemlist/user/71758
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=6627
http://www.arunagreen.com/index.php/component/k2/itemlist/user/505284
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=686081.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h0-w7-%d0%b8%d0%b3%d1%80%d0%b0/
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=4cf26111cc199bfd448bc29895e00fb6&topic=808.0
http://roikjer.com/forum/index.php?PHPSESSID=qaat4cks4gl3unk16ncm515se4&topic=841858.0
http://forum.elexlabs.com/index.php?topic=20390.0
http://www.critico-expository.com/forum/index.php?topic=6847.0
https://khuyenmaikk13.info/index.php?topic=188686.0
https://reficulcoin.com/index.php?topic=23993.0
https://hackersuniversity.net/index.php/topic,9513.0.html
http://poselokgribovo.ru/forum/index.php?topic=746208.0
http://www.deliberarchia.org/forum/index.php?topic=995224.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t6-a0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-39/
https://reficulcoin.com/index.php?topic=19820.0
http://myrechockey.com/forums/index.php?topic=96988.0
http://metropolis.ga/index.php?topic=6492.0
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile;u=33852
http://metropolis.ga/index.php?topic=6270.0
https://danceplanet.se/commodore/index.php?topic=29421.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-7/
http://forum.elexlabs.com/index.php/topic,22286.0.html
http://myrechockey.com/forums/index.php?topic=93905.0
http://www.ofqj.org/hebergementfrance/4-10-j1-x8-4-10-4-10
http://forum.kopkargobel.com/index.php?topic=8399.0
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s9-z6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.critico-expository.com/forum/index.php?topic=11459.0
http://d2bchannel.co.in/blog/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-v7-z9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://d2bchannel.co.in/blog/2019/05/09/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-q2-h3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://otitismediasociety.org/forum/index.php?topic=149803.0
https://members.fbhaters.com/index.php?topic=84638.0
http://roikjer.com/forum/index.php?PHPSESSID=ibpsr8tvims499uqquhmfoiju3&topic=840434.0
http://www.theparrotcentre.com/forum/index.php?topic=492079.0
http://forum.politeknikgihon.ac.id/index.php?topic=27685.0
http://www.hoonthaitoday.com/forum/index.php?topic=207982.0
https://prelease.club/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r1-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://teambuildingpremium.com/forum/index.php?topic=793001.0
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r4-y8-%d0%b8%d0%b3%d1%80/
http://vtservices85.fr/smf2/index.php?PHPSESSID=f10e8b49ebe2a15aedf2ec4eb06b32df&topic=220557.0
http://ru-realty.com/forum/index.php?PHPSESSID=3iehtouemcb7cga7i9ga7qvl54&topic=485682.0
http://poselokgribovo.ru/forum/index.php?topic=746014.0
https://nextezone.com/index.php?topic=45907.0
https://polyframetrade.co.uk/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-watch-d0-u8-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B/
http://roikjer.com/forum/index.php?PHPSESSID=p98lt5gkk92qapc1gdp2a95480&topic=842835.0
http://forum.politeknikgihon.ac.id/index.php?topic=29673.0
https://khuyenmaikk13.info/index.php?topic=188498.0
http://HyUa.1fps.icu/l/szIaeDC
http://roikjer.com/forum/index.php?PHPSESSID=ove22ukprphqrpud9j3sc6ib97&topic=842196.0
http://forum.elexlabs.com/index.php?topic=18063.0
http://poselokgribovo.ru/forum/index.php?topic=752748.0
http://eugeniocolazzo.it/forum/index.php?topic=106482.0
https://reficulcoin.com/index.php?topic=23839.0
http://otitismediasociety.org/forum/index.php?topic=155330.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bt3-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yx8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8/
https://danceplanet.se/commodore/index.php?topic=20677.0
https://sanp.pro/%d1%8d%d1%84%d0%b8%d1%80-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l4-%d1%81%d0%bb%d1%83%d0%b3/
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i4-m4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.popolsku.fr.pl/forum/index.php?topic=384333.0
http://www.ekemoon.com/170797/050820191810/
http://help.stv.ru/index.php?topic=140325.0
http://www.hoonthaitoday.com/forum/index.php?topic=214246.0
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://ru-realty.com/forum/index.php?topic=490388.0
https://reficulcoin.com/index.php?topic=30325.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=24d1bd0c10c7e184e77f180623616d9c&topic=215716.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-68/
https://members.fbhaters.com/index.php?topic=87356.0
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x2-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://sanp.pro/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c8-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://danielmillsap.com/forum/index.php?topic=998864.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-2019-8-eo-4-e-a-etoo-2019-8-eo-4-e-r4i0/
http://www.ofqj.org/hebergementfrance/4-10-w9-x8-4-10-4-10-online
http://menulisilmiah.net/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t1-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5/
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g9-n0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-71/
http://uberdrivers.net/forum/index.php?topic=263804.0
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t9-r7-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://poselokgribovo.ru/forum/index.php?topic=745484.0
http://otitismediasociety.org/forum/index.php?topic=159182.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-v7-i6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://myrechockey.com/forums/index.php?topic=91916.0
http://forum.elexlabs.com/index.php?topic=16099.0
http://www.deliberarchia.org/forum/index.php?topic=997450.0
http://www.deliberarchia.org/forum/index.php?topic=1005612.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.critico-expository.com/forum/index.php?topic=11926.0
http://danielmillsap.com/forum/index.php?topic=1024226.0
http://www.hoonthaitoday.com/forum/index.php?topic=214673.0
http://otitismediasociety.org/forum/index.php?topic=149616.0
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-i3-v6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://www.hoonthaitoday.com/forum/index.php?topic=213050.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-15/
http://www.remify.app/foro/index.php?topic=278245.0
http://ru-realty.com/forum/index.php?PHPSESSID=u61koef0vvn3n1b3bps7s4ppq5&topic=496857.0
http://bobr.site/index.php?topic=106507.0
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g6-b4-%d0%b8%d0%b3%d1%80/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-r0-s3-%d0%b8%d0%b3%d1%80/
http://www.tessabannampad.go.th/webboard/index.php?topic=197824.0
https://nextezone.com/index.php?action=profile;u=4403
http://otitismediasociety.org/forum/index.php?topic=152798.0
https://reficulcoin.com/index.php?topic=31858.0
http://www.tessabannampad.go.th/webboard/index.php?topic=201908.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cf3-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8/
http://www.deliberarchia.org/forum/index.php?topic=994209.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-37/
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://bobr.site/index.php?topic=117794.0
https://forum.clubeicaro.pt/index.php?topic=931.0
http://www.remify.app/foro/index.php?topic=273147.0
http://forum.elexlabs.com/index.php?topic=17039.0
https://nextezone.com/index.php?topic=40935.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w5-c7-%d0%b8%d0%b3%d1%80/
http://forum.elexlabs.com/index.php/topic,22444.0.html
https://sanp.pro/%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-10-05-2019/
http://www.deliberarchia.org/forum/index.php?topic=993216.0
http://HyUa.1fps.icu/l/szIaeDC
https://reficulcoin.com/index.php?topic=27733.0
https://reficulcoin.com/index.php?topic=29847.0
https://members.fbhaters.com/index.php?topic=86469.0
http://www.deliberarchia.org/forum/index.php?topic=1015536.0
http://www.theparrotcentre.com/forum/index.php?topic=491805.0
http://multikopterforum.hu/index.php?topic=18512.0
http://www.popolsku.fr.pl/forum/index.php?topic=376442.0
https://danceplanet.se/commodore/index.php?topic=30188.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f6-o0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://akutthjelper.no/members/jukkandi697490/
https://members.fbhaters.com/index.php/topic,86265.0.html
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=87c2d15997daa9fc626b53d3c28f13ad&topic=929.0
https://members.fbhaters.com/index.php?topic=84247.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f9-h5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-if1-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.tekparcahdfilm.com/forum/index.php?topic=46973.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kv2-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.remify.app/foro/index.php?topic=252667.0
http://forum.elexlabs.com/index.php?topic=16066.0
http://roikjer.com/forum/index.php?PHPSESSID=vn1ijdh52oj2p5vgg3vcg3kng3&topic=841639.0
https://reficulcoin.com/index.php?topic=21316.0
http://www.tekparcahdfilm.com/forum/index.php?topic=47386.0
http://forum.byehaj.hu/index.php?topic=88925.0
http://www.ofqj.org/hebergementfrance/4-13-online-a7-s9-4-13-4-13
http://vtservices85.fr/smf2/index.php?topic=218281.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-9/
https://khuyenmaikk13.info/index.php?topic=189125.0
https://sanp.pro/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://forum.byehaj.hu/index.php?topic=84724.0
https://khuyenmaikk13.info/index.php?topic=186562.0
https://www.gizmoarticle.com/%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-13-%d1%81%d0%b5-20/
http://forum.elexlabs.com/index.php?topic=17564.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-11/
http://www.deliberarchia.org/forum/index.php?topic=993517.0
http://roikjer.com/forum/index.php?PHPSESSID=mcq7dp1itsof7re8c9d8j9o095&topic=841140.0
http://otitismediasociety.org/forum/index.php?topic=149085.0
https://danceplanet.se/commodore/index.php?topic=19903.0
http://otitismediasociety.org/forum/index.php?topic=149424.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.theparrotcentre.com/forum/index.php?topic=490425.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-31/
http://www.ofqj.org/hebergementquebec/4-10-w8-a8-4-10-4-10
https://polyframetrade.co.uk/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-13-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-f4-r8-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4/
https://members.fbhaters.com/index.php?topic=89716.0
http://sexfork.com/uncategorized/ertugrul-147-seriya-pf5-ertugrul-147-seriya/
https://worldtaxi.org/2019/05/09/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c6-e8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-56/
http://otitismediasociety.org/forum/index.php?topic=149974.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-33/
http://www.hoonthaitoday.com/forum/index.php?topic=204218.0
http://www.tessabannampad.go.th/webboard/index.php?topic=199469.0
http://www.tessabannampad.go.th/webboard/index.php?topic=201331.0
http://forum.elexlabs.com/index.php?topic=22527.0
http://myrechockey.com/forums/index.php?topic=92651.0
http://www.ofqj.org/hebergementfrance/4-12-u4-k4-4-12-4-12
http://www.remify.app/foro/index.php?topic=275277.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-42/
http://roikjer.com/forum/index.php?topic=855437.0
http://www.nomaher.com/forum/index.php?topic=13131.0
http://otitismediasociety.org/forum/index.php?topic=149295.0
https://npi.org.es/smf/index.php?topic=113889.0
http://forum.kopkargobel.com/index.php?topic=7957.0
http://help.stv.ru/index.php?PHPSESSID=ab81a214ca2ab3303dd690ab1dec3fb2&topic=139927.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=688277.0
http://forum.elexlabs.com/index.php?topic=16528.0
http://forum.elexlabs.com/index.php?topic=23038.0
https://akutthjelper.no/members/margartmcgraw0/
https://members.fbhaters.com/index.php?topic=87007.0
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t0-%d1%81/
http://menulisilmiah.net/09-05-2019-%d0%b4%d1%80%d1%83%d0%b3%d0%b0%d1%8f-i%d0%bd%d1%88%d0%b0-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://poselokgribovo.ru/forum/index.php?topic=751743.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p9-r8-%d0%b8%d0%b3%d1%80/
https://nextezone.com/index.php?action=profile&u=3618
http://HyUa.1fps.icu/l/szIaeDC
http://jdcalc.com/forum/viewtopic.php?t=169096
http://www.tessabannampad.go.th/webboard/index.php?topic=197901.0
https://polyframetrade.co.uk/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d2-y7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile&u=33081
https://npi.org.es/smf/index.php?topic=114076.0
http://roikjer.com/forum/index.php?PHPSESSID=965n3js34920j1ag47uie9gai5&topic=851248.0
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-b1-d0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://uberdrivers.net/forum/index.php?topic=262536.0
http://www.ofqj.org/hebergementquebec/4-8-d9-p3-4-8-4-8
https://nextezone.com/index.php?action=profile;u=5530
https://members.fbhaters.com/index.php?topic=83766.0
http://www.deliberarchia.org/forum/index.php?topic=1008411.0
https://khuyenmaikk13.info/index.php?topic=188861.0
http://danielmillsap.com/forum/index.php?topic=1032703.0
https://prelease.club/%d1%8d%d1%84%d0%b8%d1%80-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z8-%d1%81%d0%bb%d1%83%d0%b3/
https://sanp.pro/%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-09-05-2019-3/
https://danceplanet.se/commodore/index.php?topic=19238.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=31879.0
http://forum.kopkargobel.com/index.php?topic=6202.0
https://sanp.pro/live-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r0-o3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://otitismediasociety.org/forum/index.php?topic=150027.0
http://menulisilmiah.net/10-05-2019-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-7/
https://hackersuniversity.net/index.php?topic=9493.0
https://polyframetrade.co.uk/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-g4-p4-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4/
http://otitismediasociety.org/forum/index.php?topic=158291.0
http://teambuildingpremium.com/forum/index.php?topic=802341.0
https://members.fbhaters.com/index.php/topic,87833.0.html
http://danielmillsap.com/forum/index.php?topic=1025081.0
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l9-r0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://HyUa.1fps.icu/l/szIaeDC
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g6-z5-%d0%b8%d0%b3%d1%80/
http://myrechockey.com/forums/index.php?topic=91813.0
http://www.theparrotcentre.com/forum/index.php?topic=487354.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s5-v5-%d0%b8%d0%b3%d1%80/
http://otitismediasociety.org/forum/index.php?topic=150398.0
http://dpmarketingsystems.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o0-%d1%81/
http://roikjer.com/forum/index.php?PHPSESSID=8cml9g4sd6q4ogseops46md9m3&topic=853291.0
https://members.fbhaters.com/index.php?topic=87852.0
http://roikjer.com/forum/index.php?PHPSESSID=b47ot7sn0h9qd4dae5d9sfc807&topic=862731.0
http://taklongclub.com/forum/index.php?topic=110141.0
http://help.stv.ru/index.php?PHPSESSID=223b4a4fc80166c6a57611aa08e9fdb5&topic=140405.0
http://forum.elexlabs.com/index.php?topic=18942.0
https://reficulcoin.com/index.php?topic=33107.0
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t9-d3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://forum.politeknikgihon.ac.id/index.php?topic=29170.0
http://www.deliberarchia.org/forum/index.php?topic=1015444.0
http://forum.elexlabs.com/index.php?topic=17213.0
https://prelease.club/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c6-g5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.hoonthaitoday.com/forum/index.php?topic=212246.0
http://forum.elexlabs.com/index.php?topic=17997.0
http://www.deliberarchia.org/forum/index.php?topic=1019719.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-28/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-102/
http://www.theparrotcentre.com/forum/index.php?topic=492780.0
http://forum.byehaj.hu/index.php?topic=88918.0
https://sanp.pro/%d0%b3%d1%80%d0%b0%d0%bd%d0%b4-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o2-%d0%b3%d1%80%d0%b0%d0%bd%d0%b4-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81/
http://poselokgribovo.ru/forum/index.php?topic=743169.0
http://otitismediasociety.org/forum/index.php?topic=149326.0
http://menulisilmiah.net/09-05-2019-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-4/
https://forum.clubeicaro.pt/index.php?topic=868.0
https://prelease.club/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b3-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jn5-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://metropolis.ga/index.php?topic=6503.0
http://forum.elexlabs.com/index.php?topic=18510.0
http://www.deliberarchia.org/forum/index.php?topic=1000022.0
http://www.critico-expository.com/forum/index.php?topic=12362.0
http://uberdrivers.net/forum/index.php?topic=260964.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.ekemoon.com/144265/050720194606/
http://vsalda.edinros66.ru/component/k2/itemlist/user/44135
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1543896
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=762604
http://www.phan-aen.go.th/forum/index.php?topic=628283.0
http://soc-human.kz/index.php/component/k2/itemlist/user/1630325
https://forums.letstalkbeats.com/index.php?topic=67738.0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=768764
http://www.ekemoon.com/144931/051420190606/
http://www.deliberarchia.org/forum/index.php?topic=976898.0
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2566169
http://mobility-corp.com/index.php/component/k2/itemlist/user/2510218
http://gtupuw.org/index.php/component/k2/itemlist/user/1837642
http://www.vivelabmanizales.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tb8i/
http://www.dap.com.py/index.php/component/k2/itemlist/user/789387
http://www.vivelabmanizales.com/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gwww-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-5-%d1%81%d0%b5%d1%80%d0%b8/
http://webp.online/index.php?topic=46552.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3321778
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3567525
http://www.die-design-manufaktur.de/?option=com_k2&view=itemlist&task=user&id=5183528
https://tg.vl-mp.com/index.php?topic=1349736.0
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=4706
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=560867
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1148162
http://married.dike.gr/index.php/component/k2/itemlist/user/55019
http://mobility-corp.com/index.php/component/k2/itemlist/user/2550025
http://mobility-corp.com/index.php/component/k2/itemlist/user/2550043
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/79757
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=128029
http://ovotecegg.com/component/k2/itemlist/user/127941
http://proxima.co.rw/index.php/component/k2/itemlist/user/592584
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=149921
http://rudraautomation.com/index.php/component/k2/author/149875
http://mediaville.me/index.php/component/k2/itemlist/user/210495
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3597433
http://hydrocarbs-gh.org/index.php/component/k2/itemlist/user/7335719
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=294199
http://www.vivelabmanizales.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v5-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/68140
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3321782
http://www.phan-aen.go.th/forum/index.php?topic=627539.0
http://koushatarabar.com/index.php/component/k2/itemlist/user/1328106
http://ptu.imoove.kr/ko/content/%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-17-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB-%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-17-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB332435
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4760432
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1045879
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=789184
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=55781
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/307996
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/308066
https://members.fbhaters.com/index.php/topic,75089.0.html
http://salescoach.ro/content/%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-19-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-rtke-%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-19-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://soc-human.kz/index.php/component/k2/itemlist/user/1637212
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1338841
http://forum.politeknikgihon.ac.id/index.php?topic=22217.0
https://tg.vl-mp.com/index.php?topic=1331817.0
http://menulisilmiah.net/hd-video-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p1-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=569426
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qw8%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5/
http://www.camaracoyhaique.cl/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-87-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zp5s-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-87-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3373594
http://www.camaracoyhaique.cl/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-im8%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/216530
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=295333
http://arunagreen.com/index.php/component/k2/itemlist/user/435719
http://153.120.114.241/eso/index.php/16865386-holostak-9-sezon-10-vypusk-aqholostak-9-sezon-10-vypusk48-holos
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1336171
http://poselokgribovo.ru/forum/index.php?topic=718336.0
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=14274
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=25642
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-%D1%83%D0%BA%D1%80%D0%B0%D0%B8%D0%BD%D0%B0-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D1%81%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C-%D0%BE%D0%BD%D0%BB%D0%B0%D0%B9%D0%BD%C2%BB-aq%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-%D1%83%D0%BA%D1%80%D0%B0%D0%B8%D0%BD%D0%B0-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/294401
http://withinfp.sakura.ne.jp/eso/index.php/16870787-voron-kuzgun-12-seria-yiem-voron-kuzgun-12-seria/0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=562851
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=296546
http://www.camaracoyhaique.cl/%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5%d0%b4%d0%be-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rl1q-%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5/
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-10-05-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA%C2%BB-va%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-10-05-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA%C2%BB37-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-10-05-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA
http://www.elpinatarense.es/index.php/component/k2/itemlist/user/155273
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1664326
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1654451
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3599988
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1571155
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1571229
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1374079
http://www.m1avio.com/index.php/component/k2/itemlist/user/3644448
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4877574
http://www.pcosmetic.ir/?option=com_k2&view=itemlist&task=user&id=10795
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=597048
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=789251
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2433428
http://www.web2interactive.com/index.php/component/k2/itemlist/user/3607185
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/240243
http://batubersurat.com/index.php/component/k2/itemlist/user/45968
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19686
http://smartacity.com/component/k2/itemlist/user/22851
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=295426
http://www.die-design-manufaktur.de/index.php/component/k2/itemlist/user/5179564
http://www.ekemoon.com/161073/052220194908/
http://rudraautomation.com/index.php/component/k2/author/142343
http://rudraautomation.com/index.php/component/k2/author/142270
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26228252/Default.aspx
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1643715
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=607975
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=17988
http://teambuildingpremium.com/forum/index.php?topic=774007.0
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1570277
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3635150
http://macdistri.com/index.php/component/k2/itemlist/user/298477
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=82145
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=502536
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4739959
http://mobility-corp.com/index.php/component/k2/itemlist/user/2510087
http://danielmillsap.com/forum/index.php?topic=966549.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2575237
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=769409
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=494537
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=8333
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/286625
http://arunagreen.com/?option=com_k2&view=itemlist&task=user&id=425812
http://153.120.114.241/eso/index.php/16861492-voskressij-ertugrul-144-seria-vshk-voskressij-ertugrul-144-seri
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=284278
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4839616
http://macdistri.com/index.php/component/k2/itemlist/user/301555
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=790924
http://macdistri.com/index.php/component/k2/itemlist/user/315690
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/12300
http://www.spazioad.com/component/k2/itemlist/user/7250172
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7330254
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/198857
http://ovotecegg.com/component/k2/itemlist/user/115027
http://koushatarabar.com/index.php/component/k2/itemlist/user/1316595
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=497922
http://www.phan-aen.go.th/forum/index.php?topic=626577.0
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=303893
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1633032
http://www.afikgan.co.il/index.php/component/k2/itemlist/user/26335
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1116525
http://www.remify.app/foro/index.php?topic=240691.0
http://c3isecurity.com.br/?option=com_k2&view=itemlist&task=user&id=492896
https://l2thalassic.org/Forum/index.php?topic=1546.0
http://thermoplast.envolgroupe.com/component/k2/author/71690
http://fbpharm.net/index.php/component/k2/itemlist/user/15746
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=82582
http://mobility-corp.com/index.php/component/k2/itemlist/user/2518990
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5748
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/757986
http://patagroupofcompanies.com/component/k2/itemlist/user/198472
http://www.ekemoon.com/148345/052220195606/
http://poselokgribovo.ru/forum/index.php?topic=733245.0
http://www.vivelabmanizales.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2019-j7-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80/
http://mvisage.sk/index.php/component/k2/itemlist/user/118307
http://www.ekemoon.com/169033/050320191510/
http://www.ekemoon.com/169043/050320191610/
http://www.ekemoon.com/169123/050320192910/
http://www.ekemoon.com/169253/050320195110/
https://alquilervideobeam.com.co/?option=com_k2&view=itemlist&task=user&id=57074
http://bitpark.co.kr/board_IzjM66/3817035
http://bitpark.co.kr/board_IzjM66/3817086
http://bitpark.co.kr/board_IzjM66/3817162
http://bitpark.co.kr/board_IzjM66/3817261
http://bitpark.co.kr/board_IzjM66/3817310
http://teambuildingpremium.com/forum/index.php?topic=797530.0
http://teambuildingpremium.com/forum/index.php?topic=797540.0
http://www.deliberarchia.org/forum/index.php?topic=997008.0
http://associationsila.org/component/k2/itemlist/user/308247
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=48467
http://c3isecurity.com.br/?option=com_k2&view=itemlist&task=user&id=497608
http://dev.aabn.org.gh/component/k2/itemlist/user/553242
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1893588
http://fbpharm.net/index.php/component/k2/itemlist/user/26868
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1871978
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=284921
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1147930
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1147940
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=65738
http://www.quattroandpartners.it/component/k2/itemlist/user/1070805
http://fbpharm.net/index.php/component/k2/itemlist/user/20864
http://www.ekemoon.com/146807/051920195506/
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1555844
http://mobility-corp.com/index.php/component/k2/itemlist/user/2541901
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=269768
http://danielmillsap.com/forum/index.php?topic=997611.0
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=195927
http://teambuildingpremium.com/forum/index.php?topic=796497.0
http://www.deliberarchia.org/forum/index.php?topic=995682.0
http://xplorefitness.com/blog/%C2%AB%D1%80%D0%B0%D0%BD%D0%BD%D1%8F%D1%8F-%D0%BF%D1%82%D0%B0%D1%88%D0%BA%D0%B0-erkenci-kus-42-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-pqjp-%C2%AB%D1%80%D0%B0%D0%BD%D0%BD%D1%8F%D1%8F-%D0%BF%D1%82%D0%B0%D1%88%D0%BA%D0%B0-erkenci-kus-42-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
https://sanp.pro/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-144-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gflu-%d0%b2%d0%be%d1%81%d0%ba%d1%80/
http://www.ekemoon.com/168407/050120192610/
http://rudraautomation.com/index.php/component/k2/author/148731
http://rudraautomation.com/index.php/component/k2/author/148781
http://sindicatodechoferespichincha.com.ec/?option=com_k2&view=itemlist&task=user&id=6700183
http://smartacity.com/component/k2/itemlist/user/31396
http://smartacity.com/component/k2/itemlist/user/31761
http://smartacity.com/component/k2/itemlist/user/31783
http://smartacity.com/component/k2/itemlist/user/31798
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1642838
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1646073
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1646118
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1643492
http://thermoplast.envolgroupe.com/component/k2/author/85928
http://thermoplast.envolgroupe.com/component/k2/author/85950
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/64666
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/64673
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=52209
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=561287
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1354426
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3564691
http://8.droror.co.il/uncategorized/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5-4/
http://fbpharm.net/index.php/component/k2/itemlist/user/14925
http://arunagreen.com/index.php/component/k2/itemlist/user/460072
http://macdistri.com/index.php/component/k2/itemlist/user/298185
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=97287
http://www.ekemoon.com/170847/050820192910/
http://www.deliberarchia.org/forum/index.php?topic=999568.0
http://withinfp.sakura.ne.jp/eso/index.php/16958132-hdvideo-smers-8-seria-j5-smers-8-seria/0
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7264645
http://xplorefitness.com/blog/%D0%BD%D0%BE%D0%B2%D0%B8%D0%BD%D0%BA%D0%B0-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-99-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-y6-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-99-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/57105
http://teambuildingpremium.com/forum/index.php?topic=799427.0
http://teambuildingpremium.com/forum/index.php?topic=799436.0
http://teambuildingpremium.com/forum/index.php?topic=799449.0
http://arquitectosenreformas.es/index.php/component/k2/itemlist/user/80671
http://arunagreen.com/index.php/component/k2/itemlist/user/468944
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=48597
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/498183
http://dev.aabn.org.gh/component/k2/itemlist/user/553973
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=26971
http://fbpharm.net/index.php/component/k2/itemlist/user/26989
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=285346
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/285324
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3755684
http://married.dike.gr/index.php/component/k2/itemlist/user/55001
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2549889
http://mobility-corp.com/index.php/component/k2/itemlist/user/2549899
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/696117
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/79732
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-53/
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=30423.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-31/
https://forum.ac-jete.it/index.php?topic=356519.0
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i0-w6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-16/
http://www.ekemoon.com/168559/050120194910/
http://menulisilmiah.net/10-05-2019-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://menulisilmiah.net/%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j3-%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-7-%d1%81%d0%b5%d1%80/
http://forum.elexlabs.com/index.php?topic=16819.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n1-z2-%d0%b8%d0%b3%d1%80%d0%b0/
http://www.hoonthaitoday.com/forum/index.php?topic=206875.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=683244.0
https://reficulcoin.com/index.php?topic=20849.0
https://danceplanet.se/commodore/index.php?topic=20090.0
https://nextezone.com/index.php?action=profile;u=4441
https://members.fbhaters.com/index.php?topic=84650.0
http://universalcommunity.se/Forum/index.php?topic=1264.0
https://reficulcoin.com/index.php?topic=31658.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wm0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8/
https://reficulcoin.com/index.php?topic=23314.0
http://poselokgribovo.ru/forum/index.php?topic=751004.0
http://roikjer.com/forum/index.php?PHPSESSID=mg11qkac48h5hvrglkue3pitm7&topic=836832.0
http://menulisilmiah.net/09-05-2019-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-3/
http://poselokgribovo.ru/forum/index.php?topic=747848.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=30454.0
http://forum.elexlabs.com/index.php?topic=22392.0
http://menulisilmiah.net/%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-20-%d1%81%d0%b5-25/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-29/
https://hackersuniversity.net/index.php?topic=9616.0
https://khuyenmaikk13.info/index.php?topic=191410.0
http://HyUa.1fps.icu/l/szIaeDC
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=282140
http://www.ekemoon.com/154499/052120194207/
http://mediaville.me/?option=com_k2&view=itemlist&task=user&id=231425
http://xplorefitness.com/blog/%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-15-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-gabv-%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-15-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://poselokgribovo.ru/forum/index.php?topic=732631.0
http://www.ekemoon.com/145079/051520193306/
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=13401
http://condolencias.servisa.es/3-2-06-05-2019-h0-3-2
http://thermoplast.envolgroupe.com/component/k2/author/67330
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3303260
http://www.deliberarchia.org/forum/index.php?topic=969030.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=13147
http://ru-realty.com/forum/index.php?PHPSESSID=8hj37p81krkcqrpfavlsbk1gt6&topic=474165.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1610727
http://danielmillsap.com/forum/index.php?topic=974764.0
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=500300
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=11780
http://forum.digamahost.com/index.php?topic=109614.0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=817894
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=62418
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=62421
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=62490
http://www.telcon.gr/index.php/component/k2/itemlist/user/62409
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=554050
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=554314
http://corumotoanahtar.com/component/k2/itemlist/user/1564.html
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=327105
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=327107
http://mvisage.sk/index.php/component/k2/itemlist/user/117699
http://proxima.co.rw/index.php/component/k2/itemlist/user/565419
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=765644
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3584451
http://www.deliberarchia.org/forum/index.php?topic=980000.0
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=14360
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/205274
http://teambuildingpremium.com/forum/index.php?topic=780992.0
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=61652
http://married.dike.gr/index.php/component/k2/itemlist/user/48162
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-6/
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=206024
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=288090
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=501982
http://www.ekemoon.com/163681/050820193509/
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1347332
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1687218
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=71958
http://wigalseguros.com.br/component/users/?task=user&view=itemlist&id=6692
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/3955
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4906519
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=818712
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=109607
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=555032
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/57737
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=1279
http://healthyteethpa.org/component/k2/itemlist/user/5331360
http://mediaville.me/index.php/component/k2/itemlist/user/210763
http://macdistri.com/index.php/component/k2/itemlist/user/298662
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=45807
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2513183
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2562202
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4828067
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42281
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/209618
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2566522
http://euromouleusinage.com/index.php/component/k2/itemlist/user/110371
http://www.ekemoon.com/146653/051920193706/
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/475972
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=607735
http://fbpharm.net/index.php/component/k2/itemlist/user/13409
http://fbpharm.net/index.php/component/k2/itemlist/user/22106
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1838071
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1120215
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1888855
http://gtupuw.org/index.php/component/k2/itemlist/user/1888636
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=299528
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=20695
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=322036
http://married.dike.gr/index.php/component/k2/itemlist/user/58063
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2574048
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/715566
http://ovotecegg.com/component/k2/itemlist/user/135754
http://ovotecegg.com/component/k2/itemlist/user/135927
http://ovotecegg.com/component/k2/itemlist/user/135934
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/234279
http://rudraautomation.com/index.php/component/k2/author/170011
http://dev.aabn.org.gh/component/k2/itemlist/user/524342
http://compultras.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=206112
http://153.120.114.241/eso/index.php/16868516-nasa-istoria-70-seria-beoh-nasa-istoria-70-seria
http://bitpark.co.kr/board_IzjM66/3729554
http://mediaville.me/index.php/component/k2/itemlist/user/209301
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=47615
http://www.quattroandpartners.it/component/k2/itemlist/user/1072588
https://l2thalassic.org/Forum/index.php?topic=2222.0
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=50945
http://seoksoononly.dothome.co.kr/qna/713789
http://macdistri.com/index.php/component/k2/itemlist/user/308685
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=575837
http://poselokgribovo.ru/forum/index.php?topic=714398.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/571957
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42516
http://www.vivelabmanizales.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2019-b9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1021014
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=2018285
http://computerscience.egerton.ac.ke/index.php/component/k2/itemlist/user/2018306
http://dev.aabn.org.gh/component/k2/itemlist/user/572519
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1889381
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1889438
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=300171
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1168136
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=323039
http://married.dike.gr/index.php/component/k2/itemlist/user/58194
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/715890
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=89741
http://dev.aabn.org.gh/component/k2/itemlist/user/514146
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/68832
http://www.deliberarchia.org/forum/index.php?topic=978918.0
http://withinfp.sakura.ne.jp/eso/index.php/16866002-tajny-taemnici-90-seria-05052019-b5-tajny-taemnici-90-seria
http://ovotecegg.com/component/k2/itemlist/user/115668
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/63895
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=82418
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t5-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81/
http://marjorieaperry.com/?option=com_k2&view=itemlist&task=user&id=480669
http://xplorefitness.com/blog/%C2%AB%D0%BD%D0%B5-%D0%BE%D1%82%D0%BF%D1%83%D1%81%D0%BA%D0%B0%D0%B9-%D0%BC%D0%BE%D1%8E-%D1%80%D1%83%D0%BA%D1%83-elimi-birakma-40-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-avgj-%C2%AB%D0%BD%D0%B5-%D0%BE%D1%82%D0%BF%D1%83%D1%81%D0%BA%D0%B0%D0%B9-%D0%BC%D0%BE%D1%8E-%D1%80%D1%83%D0%BA%D1%83-elimi-birakma-40-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://community.viajar.tur.br/index.php?p=/profile/fletaarmyt
http://married.dike.gr/index.php/component/k2/itemlist/user/50220
http://www.vivelabmanizales.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-06-05-2019-p3-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://seoksoononly.dothome.co.kr/qna/745399
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1848275
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/216849
http://www.vivelabmanizales.com/hd-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i1-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://macdistri.com/index.php/component/k2/itemlist/user/311488
http://married.dike.gr/index.php/component/k2/itemlist/user/57085
http://mediaville.me/index.php/component/k2/itemlist/user/250118
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=86358
http://ovotecegg.com/component/k2/itemlist/user/133052
http://smartacity.com/component/k2/itemlist/user/37231
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3623014
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1796382
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=603287
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-06-05-2019-p1-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://webp.online/index.php?action=profile;u=165937
http://salescoach.ro/content/%C2%AB%D0%B2%D0%BE%D1%81%D0%BA%D1%80%D0%B5%D1%81%D1%88%D0%B8%D0%B9-%D1%8D%D1%80%D1%82%D1%83%D0%B3%D1%80%D1%83%D0%BB-148-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-fort-%C2%AB%D0%B2%D0%BE%D1%81%D0%BA%D1%80%D0%B5%D1%81%D1%88%D0%B8%D0%B9-%D1%8D%D1%80%D1%82%D1%83%D0%B3%D1%80%D1%83%D0%BB-148-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://rudraautomation.com/index.php/component/k2/author/108768
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7218749
http://bitpark.co.kr/board_IzjM66/3782934
http://withinfp.sakura.ne.jp/eso/index.php/16872506-live-po-zakonam-voennogo-vremeni-3-sezon-1-seria-r0-po-zakonam-/0
http://smartacity.com/component/k2/itemlist/user/14546
http://www.ekemoon.com/147959/052220192206/
http://www.camaracoyhaique.cl/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fm0%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=40193
http://withinfp.sakura.ne.jp/eso/index.php/16893428-nikogda-ne-govori-nikogda-9-seria-06052019-j3-nikogda-ne-govori
http://withinfp.sakura.ne.jp/eso/index.php/16884848-vetrenyj-hercai-19-seria-ugyv-vetrenyj-hercai-19-seria/0
http://www.ekemoon.com/146107/051820193006/
http://associationsila.org/index.php/component/k2/itemlist/user/290451
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=199955
http://engeena.com/?option=com_k2&view=itemlist&task=user&id=8024
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/475593
http://withinfp.sakura.ne.jp/eso/index.php/16890680-tolarobot-1-sezon-1-seria-r7-tolarobot-1-sezon-1-seria/0
http://seoksoononly.dothome.co.kr/?document_srl=761636
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1741562
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/247055
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3336030
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3336413
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=19215
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=19217
http://xplorefitness.com/blog/%C2%AB%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-92-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-11-05-2019-e1-%C2%AB%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-92-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://arunagreen.com/index.php/component/k2/itemlist/user/482530
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=50856
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/507433
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/507720
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=2013843
http://dev.aabn.org.gh/component/k2/itemlist/user/565228
http://engeena.com/component/k2/itemlist/user/7906
https://l2thalassic.org/Forum/index.php?topic=1720.0
http://www.ekemoon.com/146159/051820193806/
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=1005458
http://condolencias.servisa.es/3-05-05-2019-y4-3
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4825017
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3576852
http://withinfp.sakura.ne.jp/eso/index.php/16860584-smotret-holostak-9-sezon-13-vypusk-h7-holostak-9-sezon-13-vypus/0
https://members.fbhaters.com/index.php/topic,75089.0.html
http://salescoach.ro/content/%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-19-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-rtke-%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-19-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://soc-human.kz/index.php/component/k2/itemlist/user/1637212
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1338841
http://forum.politeknikgihon.ac.id/index.php?topic=22217.0
http://salescoach.ro/content/%C2%AB%D0%B2%D0%BE%D1%81%D0%BA%D1%80%D0%B5%D1%81%D1%88%D0%B8%D0%B9-%D1%8D%D1%80%D1%82%D1%83%D0%B3%D1%80%D1%83%D0%BB-147-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-pzwv-%C2%AB%D0%B2%D0%BE%D1%81%D0%BA%D1%80%D0%B5%D1%81%D1%88%D0%B8%D0%B9-%D1%8D%D1%80%D1%82%D1%83%D0%B3%D1%80%D1%83%D0%BB-147-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1335997
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=81882
http://topitop.kz/component/k2/itemlist/user/76438
http://socialfbwidgets.com/component/k2/itemlist/user/13591.html
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=304619
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/72436
http://israengineering.com/index.php/component/k2/itemlist/user/1123304
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/480155
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=36528
http://teambuildingpremium.com/forum/index.php?topic=783271.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1369306
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1369341
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4865675
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=785082
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=52588
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=52592
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/304829
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3324327
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=17696
http://seoksoononly.dothome.co.kr/qna/819723
http://seoksoononly.dothome.co.kr/qna/819812
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2590948
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2590959
http://metropolis.ga/index.php?topic=6703.0
http://www.critico-expository.com/forum/index.php?topic=8987.0
http://forum.elexlabs.com/index.php/topic,19409.0.html
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l6-r3-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://forum.byehaj.hu/index.php?topic=84694.0
http://otitismediasociety.org/forum/index.php?topic=149271.0
http://www.nomaher.com/forum/index.php?topic=13139.0
http://ru-realty.com/forum/index.php?PHPSESSID=gbg9cea20g8qf9t1d4a0tc8l57&topic=501753.0
http://universalcommunity.se/Forum/index.php?topic=1282.0
http://roikjer.com/forum/index.php?PHPSESSID=eg14daj9bspkunreg5ru7bhff5&topic=839001.0
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f8-o7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile;u=30946
http://sexfork.com/uncategorized/igra-prestolov-game-of-thrones-8-sezon-5-seriya-igra-prestolov-game-of-thrones-8-sezon-5-seriya-q9x5/
https://members.fbhaters.com/index.php?topic=88070.0
https://danceplanet.se/commodore/index.php?topic=29949.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-3/
http://forum.elexlabs.com/index.php/topic,22184.0.html
https://worldtaxi.org/2019/05/09/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-8/
http://www.nomaher.com/forum/index.php?topic=12665.0
http://forum.elexlabs.com/index.php?topic=20940.0
http://www.ofqj.org/hebergementquebec/4-13-watch-f5-u4-4-13-4-13
http://www.hoonthaitoday.com/forum/index.php?topic=219472.0
https://danceplanet.se/commodore/index.php?topic=18982.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80-22/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sj2-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sanp.pro/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m1-%d1%81-2/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mb3-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-36/
http://HyUa.1fps.icu/l/szIaeDC
http://www.remify.app/foro/index.php?topic=251847.0
https://members.fbhaters.com/index.php?topic=86203.0
http://forum.elexlabs.com/index.php/topic,18548.0.html
http://www.theparrotcentre.com/forum/index.php?topic=482164.0
https://forum.clubeicaro.pt/index.php?topic=842.0
http://forum.elexlabs.com/index.php?topic=16668.0
http://www.hoonthaitoday.com/forum/index.php?topic=244252.0
https://prelease.club/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c7-%d1%81%d0%bb/
http://www.deliberarchia.org/forum/index.php?topic=1000589.0
https://members.fbhaters.com/index.php?topic=88482.0
http://universalcommunity.se/Forum/index.php?topic=1962.0
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k7-v5-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://www.popolsku.fr.pl/forum/index.php?topic=382021.0
http://8.droror.co.il/uncategorized/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-s6-f6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://forum.bmw-e60.eu/index.php?topic=5812.0
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-h9-z3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://help.stv.ru/index.php?PHPSESSID=c1ba1ba098abfb7f3adcd96f6e435a8a&topic=140756.0
http://www.critico-expository.com/forum/index.php?topic=8517.0
http://www.deliberarchia.org/forum/index.php?topic=997814.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-54/
http://ru-realty.com/forum/index.php?topic=482142.0
http://roikjer.com/forum/index.php?PHPSESSID=r0u5qunssbbid31dqo1l6sij17&topic=851275.0
http://danielmillsap.com/forum/index.php?topic=1030585.0
http://forum.byehaj.hu/index.php?topic=88458.0
https://woodland.org.ua/groups/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-b1-e3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.hoonthaitoday.com/forum/index.php?topic=241004.0
http://www.ofqj.org/hebergementquebec/4-10-online-k7-s5-4-10-4-10
https://reficulcoin.com/index.php?topic=30138.0
http://forum.elexlabs.com/index.php?topic=19280.0
https://worldtaxi.org/2019/05/09/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r9-f8-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://www.deliberarchia.org/forum/index.php?topic=1023669.0
http://www.deliberarchia.org/forum/index.php?topic=1019426.0
http://roikjer.com/forum/index.php?topic=846025.0
http://otitismediasociety.org/forum/index.php?topic=149679.0
http://help.stv.ru/index.php?PHPSESSID=5352364d7bfb38667b47341ea98893ea&topic=140701.0
http://roikjer.com/forum/index.php?PHPSESSID=e2sb0cnv77nebdmq5d1hcgu2r2&topic=844043.0
http://www.tessabannampad.go.th/webboard/index.php?topic=203286.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.nomaher.com/forum/index.php?topic=12652.0
https://nextezone.com/index.php?topic=39467.0
http://myrechockey.com/forums/index.php?topic=98148.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r2-e3-%d0%b8%d0%b3%d1%80%d0%b0/
http://roikjer.com/forum/index.php?PHPSESSID=1utqr309refn0cfj94c0rho9q7&topic=853231.0
https://khuyenmaikk13.info/index.php?topic=186079.0
http://roikjer.com/forum/index.php?PHPSESSID=a9om0j2ne9fabdqud578dr4lv4&topic=844734.0
http://www.critico-expository.com/forum/index.php?topic=10971.0
http://forum.elexlabs.com/index.php?topic=18434.0
http://www.deliberarchia.org/forum/index.php?topic=1008151.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xs5-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j3-m6-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-12/
https://khuyenmaikk13.info/index.php?topic=188994.0
http://forum.elexlabs.com/index.php?topic=22571.0
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile;u=34047
https://nextezone.com/index.php?action=profile;u=5794
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-36/
https://nextezone.com/index.php?action=profile;u=3806
https://nextezone.com/index.php?action=profile;u=6445
http://eugeniocolazzo.it/forum/index.php?topic=108860.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-11/
https://reficulcoin.com/index.php?topic=30135.0
https://akutthjelper.no/members/deanseabolt61/
http://uberdrivers.net/forum/index.php?topic=250784.0
http://otitismediasociety.org/forum/index.php?topic=149638.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-26/
https://sanp.pro/live-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://HyUa.1fps.icu/l/szIaeDC
http://www.remify.app/foro/index.php?topic=245599.0
http://otitismediasociety.org/forum/index.php?topic=149468.0
http://ru-realty.com/forum/index.php?PHPSESSID=2eee3bggbp4jdbk5s4v4akle80&topic=499128.0
http://www.tessabannampad.go.th/webboard/index.php?topic=200238.0
https://danceplanet.se/commodore/index.php?topic=19677.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=5e3b8ad52dbb74bc36052dbe9bf836c3&topic=224743.0
http://otitismediasociety.org/forum/index.php?topic=157149.0
http://www.hoonthaitoday.com/forum/index.php?topic=212318.0
http://www.theparrotcentre.com/forum/index.php?topic=489009.0
http://teambuildingpremium.com/forum/index.php?topic=816458.0
http://uberdrivers.net/forum/index.php?topic=248621.0
http://danielmillsap.com/forum/index.php?topic=1000579.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=684221.0
http://www.ekemoon.com/165891/051920190209/
http://www.theparrotcentre.com/forum/index.php?topic=489917.0
http://forum.kopkargobel.com/index.php?topic=8417.0
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile;u=33923
http://www.nomaher.com/forum/index.php?topic=13223.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-44/
https://sanp.pro/09-05-2019-%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://forum.politeknikgihon.ac.id/index.php?topic=30886.0
http://otitismediasociety.org/forum/index.php?topic=155114.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i2-p4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://roikjer.com/forum/index.php?PHPSESSID=l00sha82f352npno2rm6uts111&topic=856494.0
https://members.fbhaters.com/index.php?topic=87082.0
http://8.droror.co.il/uncategorized/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-v1-s4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://poselokgribovo.ru/forum/index.php?topic=750861.0
http://roikjer.com/forum/index.php?PHPSESSID=gt81ibpsf76qf7uajalemp1d10&topic=844516.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mb8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yo6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://ru-realty.com/forum/index.php?PHPSESSID=cv6vckaegd518jdi2na9pakvt4&topic=500587.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k2-j5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://istakam.com/forum/index.php?topic=11808.0
http://partemp.com/en/groups/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i7-p6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=685881.0
http://myrechockey.com/forums/index.php?topic=92377.0
http://forum.elexlabs.com/index.php?topic=21142.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=84907ce0227478ef1674c3f0836ab571&topic=216324.0
http://forum.politeknikgihon.ac.id/index.php?topic=29256.0
http://forum.kopkargobel.com/index.php?topic=7055.0
http://www.deliberarchia.org/forum/index.php?topic=1017500.0
http://www.theparrotcentre.com/forum/index.php?topic=492318.0
http://help.stv.ru/index.php?PHPSESSID=207fe9b99f29f1ce79b6dcbea4eae03f&topic=140441.0
http://otitismediasociety.org/forum/index.php?topic=156920.0
http://roikjer.com/forum/index.php?PHPSESSID=ft7fstpof48m4nunupd6280mh0&topic=839248.0
http://HyUa.1fps.icu/l/szIaeDC
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1643851
http://www.ekemoon.com/166814/052120192009/
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lh7%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://vehibook.com/members/stormyloera79/
http://webp.online/index.php?topic=51508.msg86130
http://www.critico-expository.com/forum/index.php?topic=6965.0
http://www.quattroandpartners.it/component/k2/itemlist/user/1077732
https://forums.letstalkbeats.com/index.php?topic=69835.0
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/206060
https://members.fbhaters.com/index.php?topic=79676.0
http://www.ekemoon.com/161167/052320191408/
http://thermoplast.envolgroupe.com/component/k2/author/65219
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=500294
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4826259
http://www.rocktheboat.cc/groups/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-windows-pi%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=291113
http://arunagreen.com/index.php/component/k2/itemlist/user/488305
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=2016715
http://fbpharm.net/index.php/component/k2/itemlist/user/33034
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1887542
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/297791
http://www.ekemoon.com/167637/052320191809/
http://www.ekemoon.com/167673/052320192209/
http://www.ekemoon.com/167691/052320192309/
http://www.ekemoon.com/167711/052320192509/
http://www.ekemoon.com/167737/052320192809/
http://www.ekemoon.com/167751/052320193009/
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1004222
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1627395
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/66821
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=492834
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-06-05-2019-h4-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://matrixpharm.ru/forum/index.php?PHPSESSID=gialk6am52c79io5e7ae2qms31&action=profile;u=167686
http://www.vivelabmanizales.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2019-v4-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/12334
http://euromouleusinage.com/?option=com_k2&view=itemlist&task=user&id=115655
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7232281
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=766190
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=297868
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=319832
http://mediaville.me/index.php/component/k2/itemlist/user/253298
http://mediaville.me/index.php/component/k2/itemlist/user/253301
http://mobility-corp.com/index.php/component/k2/itemlist/user/2571707
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/88359
http://ovotecegg.com/component/k2/itemlist/user/134881
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/233025
http://rudraautomation.com/index.php/component/k2/author/167941
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1672752
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1667355
http://thermoplast.envolgroupe.com/component/k2/author/94555
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1392655
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=1062946
http://8.droror.co.il/uncategorized/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dl5%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f08-05-2019/
http://vehibook.com/members/miaaskew822417/
http://webp.online/index.php?topic=51663.0
http://www.critico-expository.com/forum/index.php?topic=7631.0
http://www.critico-expository.com/forum/index.php?topic=7641.0
http://www.ekemoon.com/168687/050220191110/
http://www.ekemoon.com/168908/050220195410/
http://www.theocraticamerica.org/forum/index.php?topic=29032.0
http://webp.online/index.php?topic=51665.0
http://www.ekemoon.com/168941/050320190010/
http://mediaville.me/?option=com_k2&view=itemlist&task=user&id=208815
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1014439
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/488564
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=779549
https://l2thalassic.org/Forum/index.php?topic=669.0
http://minostech.co.kr/?document_srl=3399598
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=316160
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/316112
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/249633
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/249815
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3341792
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=19593
http://xplorefitness.com/blog/%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-14-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-12-05-2019-z1-%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-14-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2612329
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=81434
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/14182
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3297498
http://www.ekemoon.com/155339/050020192308/
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1006659
http://dev.aabn.org.gh/component/k2/itemlist/user/538571
https://khuyenmaikk13.info/index.php?topic=178604.0
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1556103
http://seoksoononly.dothome.co.kr/qna/757233
http://sindicatodechoferespichincha.com.ec/index.php/component/k2/itemlist/user/6691248
http://highlanderonline.cmshelplive.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=8060
http://fbpharm.net/index.php/component/k2/itemlist/user/13242
http://www.die-design-manufaktur.de/?option=com_k2&view=itemlist&task=user&id=5175901
http://salescoach.ro/content/%C2%AB%D0%B2%D0%BE%D1%81%D0%BA%D1%80%D0%B5%D1%81%D1%88%D0%B8%D0%B9-%D1%8D%D1%80%D1%82%D1%83%D0%B3%D1%80%D1%83%D0%BB-148-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-rxsz-%C2%AB%D0%B2%D0%BE%D1%81%D0%BA%D1%80%D0%B5%D1%81%D1%88%D0%B8%D0%B9-%D1%8D%D1%80%D1%82%D1%83%D0%B3%D1%80%D1%83%D0%BB-148-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/198583
http://haniel.ir/index.php/component/k2/itemlist/user/73372
https://szenarist.ru/forum/index.php?topic=205862.0
http://bitpark.co.kr/board_IzjM66/3734805
http://esperanzazubieta.com/component/k2/itemlist/user/95901
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=185692
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1334465
http://poselokgribovo.ru/forum/index.php?topic=714234.0
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3623953
http://dev.aabn.org.gh/component/k2/itemlist/user/517353
http://www.quattroandpartners.it/component/k2/itemlist/user/1039370
http://withinfp.sakura.ne.jp/eso/index.php/16871493-soderzanki-9-seria-05052019-q2-soderzanki-9-seria
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1344272
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/476353
http://svgrossburgwedel.de/component/k2/itemlist/user/5313
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=65957
http://salescoach.ro/content/%C2%AB%D0%B2%D0%BE%D1%81%D0%BA%D1%80%D0%B5%D1%81%D1%88%D0%B8%D0%B9-%D1%8D%D1%80%D1%82%D1%83%D0%B3%D1%80%D1%83%D0%BB-148-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-nwfi-%C2%AB%D0%B2%D0%BE%D1%81%D0%BA%D1%80%D0%B5%D1%81%D1%88%D0%B8%D0%B9-%D1%8D%D1%80%D1%82%D1%83%D0%B3%D1%80%D1%83%D0%BB-148-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/185055
http://8.droror.co.il/uncategorized/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o4-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-5/
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/55851
http://rockndata.net/UserProfile/tabid/61/userId/18165791/Default.aspx
http://married.dike.gr/index.php/component/k2/itemlist/user/45750
http://community.viajar.tur.br/index.php?p=/discussion/57684/edinoe-serdce-tek-yuerek-17-seriya-vcrm-edinoe-serdce-tek-yuerek-17-seriya
http://fbpharm.net/index.php/component/k2/itemlist/user/25272
http://www.spazioad.com/component/k2/itemlist/user/7215097
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/561359
http://www.pcosmetic.ir/index.php/component/k2/itemlist/user/10569
http://married.dike.gr/index.php/component/k2/itemlist/user/49921
https://alvarogarciatorero.com/component/k2/itemlist/user/47512
http://forum.politeknikgihon.ac.id/index.php?topic=24444.0
http://withinfp.sakura.ne.jp/eso/index.php/16864406-holostak-9-sezon-10-vypusk-utub-vvholostak-9-sezon-10-vypusk-ut
http://www2.yasothon.go.th/smf/index.php?topic=159.msg181241
http://macdistri.com/index.php/component/k2/itemlist/user/302472
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3318130
http://www.afikgan.co.il/index.php/component/k2/itemlist/user/26434
http://thermoplast.envolgroupe.com/component/k2/author/82547
http://hotelnomadpalace.com/es/?option=com_k2&view=itemlist&task=user&id=19564
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/303756
http://withinfp.sakura.ne.jp/eso/index.php/16901445-mertvoe-ozero-9-seria-j4-mertvoe-ozero-9-seria/0
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=290753
http://www.ekemoon.com/145671/051720193406/
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=316922
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1114277
http://webp.online/index.php?topic=45176.0
http://withinfp.sakura.ne.jp/eso/index.php/16882390-uristy-20-seria-06052019-w8-uristy-20-seria
http://www.ekemoon.com/145851/051720195606/
http://www.critico-expository.com/forum/index.php?topic=2972.0
https://l2thalassic.org/Forum/index.php?topic=1378.0
http://salescoach.ro/content/%C2%AB%D0%B2%D0%BE%D1%80%D0%BE%D0%BD-kuzgun-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-rjto-%C2%AB%D0%B2%D0%BE%D1%80%D0%BE%D0%BD-kuzgun-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=203527
http://www.ekemoon.com/146841/052020190006/
http://community.viajar.tur.br/index.php?p=/profile/karma55m67
http://fbpharm.net/index.php/component/k2/itemlist/user/17172
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1841892
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=1003192
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=272476
http://withinfp.sakura.ne.jp/eso/index.php/16879937-sluga-naroda-3-sezon-4-seria-06052019-g5-sluga-naroda-3-sezon-4
http://smartacity.com/component/k2/itemlist/user/18024
http://forum.politeknikgihon.ac.id/index.php?topic=22722.0
http://ovotecegg.com/component/k2/itemlist/user/121546
http://arunagreen.com/index.php/component/k2/itemlist/user/452817
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1014579
http://mobility-corp.com/index.php/component/k2/itemlist/user/2521967
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=761972
http://menulisilmiah.net/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lj3%d0%bd/
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/189313
http://dohairbiz.com/en/component/k2/itemlist/user/2717258.html
http://www.ekemoon.com/145019/051420195606/
http://thermoplast.envolgroupe.com/component/k2/author/82616
http://haniel.ir/index.php/component/k2/itemlist/user/74093
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=755359
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=289060
http://thermoplast.envolgroupe.com/component/k2/author/68182
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=45877
http://seoksoononly.dothome.co.kr/?document_srl=745216
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/55883
http://c3isecurity.com.br/?option=com_k2&view=itemlist&task=user&id=486296
http://c3isecurity.com.br/?option=com_k2&view=itemlist&task=user&id=492819
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/188182
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1550779
http://153.120.114.241/eso/index.php/16865836-ne-otpuskaj-mou-ruku-elimi-birakma-41-seria-pbiv-ne-otpuskaj-mo
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=8556
http://masarapphil.com/board_ghIT87/13147
http://mglpcm.org/board_ETkS12/542
http://mglpcm.org/board_ETkS12/546
http://nnkumw.org/xe/?document_srl=2226
http://nnkumw.org/xe/?document_srl=2235
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=1820
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=1824
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=1828
http://shinhwaair2017.cafe24.com/issue/49884
http://shinhwaair2017.cafe24.com/issue/49908
http://shinhwaair2017.cafe24.com/issue/49969
http://smartengbiz.com/s1/5287
http://smartengbiz.com/s1/5296
http://smartengbiz.com/s1/5321
http://twks.dothome.co.kr/qna/1350
http://vintage.codns.com/Board/8875
http://vintage.codns.com/Board/8880
http://vintage.codns.com/Board/8884
http://vn7.vn/qna/41248
http://warmfund.net/p/?document_srl=42021
http://warmfund.net/p/index.php?mid=financing&document_srl=42045
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=36446
http://www.deliberarchia.org/forum/index.php?topic=1030067.0
https://nextezone.com/index.php?topic=41969.0
http://vtservices85.fr/smf2/index.php?topic=232024.0
http://www.critico-expository.com/forum/index.php?topic=11507.0
http://www.hoonthaitoday.com/forum/index.php?topic=213835.0
https://forum.shaiyaslayer.tk/index.php?topic=115401.0
http://www.hoonthaitoday.com/forum/index.php?topic=232614.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-33/
http://www.ofqj.org/hebergementfrance/4-10-watch-l6-w9-4-10-4-10
https://reficulcoin.com/index.php?topic=33380.0
https://reficulcoin.com/index.php?topic=33398.0
http://roikjer.com/forum/index.php?PHPSESSID=9fv2lupqr3nuoprdru7k6kbh43&topic=843268.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.golden-nail.co.kr/press/1928
http://www.hicleaning.kr/?document_srl=13549
http://www.hicleaning.kr/?document_srl=13574
http://www.hicleaning.kr/board_wash/13558
http://www.hicleaning.kr/board_wash/13584
http://www.hsaura.com/license/6417
http://www.hsaura.com/noty/6382
http://www.hsaura.com/noty/6397
http://www.hsaura.com/noty/6426
http://www.jesusonly.life/calendar/5501
http://www.jesusonly.life/calendar/5561
http://www.jesusonly.life/calendar/5587
http://www.jesusonly.life/calendar/5592
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=12623
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=12692
http://www.leekeonsu-csi.com/index.php?mid=community1&document_srl=459677
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=459836
http://www.leekeonsu-csi.com/index.php?mid=gallery3&document_srl=459774
http://www.lozic.co.kr/gallery/5199
http://www.sp1.football/index.php?mid=faq&document_srl=5191
http://www.sp1.football/index.php?mid=tr_video&document_srl=5202
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s1-s5-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://dpmarketingsystems.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g8-%d1%81%d0%bb%d1%83%d0%b3/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m6-s4-%d0%b8%d0%b3%d1%80/
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-f3-g3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
https://reficulcoin.com/index.php?topic=21381.0
https://worldtaxi.org/2019/05/09/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-s8-x2-%d0%b8/
http://www.ofqj.org/hebergementquebec/4-10-z4-d6-4-10-4-10-online
http://eugeniocolazzo.it/forum/index.php?topic=106653.0
https://nextezone.com/index.php?action=profile;u=4806
http://ru-realty.com/forum/index.php?PHPSESSID=h4t3gk4lk0kbcesva2q5j4ih84&topic=500540.0
http://forum.elexlabs.com/index.php?topic=17374.0
http://uberdrivers.net/forum/index.php?topic=262765.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-41/
http://danielmillsap.com/forum/index.php?topic=1029393.0
http://forum.elexlabs.com/index.php?topic=17379.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/om-11-e-09-05-2019-422006/
https://sanp.pro/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b6-%d1%81/
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-r3-x9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
https://reficulcoin.com/index.php?topic=31808.0
http://roikjer.com/forum/index.php?PHPSESSID=sjt8jgqb67qf8j11v1oar8kpb3&topic=841211.0
http://help.stv.ru/index.php?PHPSESSID=114a6f4d513b22365161a7ec20ae6af8&topic=141246.0
http://HyUa.1fps.icu/l/szIaeDC
http://xn--ok1bpqi43ahtb.net/board_EkDG82/7552
http://yoriyorifood.com/xxxx/spacial/7444
https://dolcoin.net/free_talk/3286
https://dolcoin.net/free_talk/3295
https://dolcoin.net/free_talk/3305
https://esel.gist.ac.kr/esel2/board_hmgj23/5950
https://nextezone.com/index.php?topic=49816.0
https://reficulcoin.com/index.php?topic=37999.0
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=6676
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=30835
http://atemshow.com/?document_srl=3728
http://atemshow.com/atemfair_domestic/3718
http://bath-family.com/?document_srl=5413
http://bethanychurch.kr/board_vpkl62/2707
http://cafe.dokseosil.co.kr/community/31906
http://cafe.dokseosil.co.kr/community/32148
http://cafe.dokseosil.co.kr/community/32231
http://carrierworld.co.kr/?document_srl=3307
http://gallerychoi.com/Exhibition/15937
http://www.deliberarchia.org/forum/index.php?topic=1031239.0
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/3950
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/619294
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=819633
http://www.theocraticamerica.org/forum/index.php?topic=37938.0
http://www.theocraticamerica.org/forum/index.php?topic=37944.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=695105.0
http://xn--22cmah2caecpucll2cycdoj4d0knajrq3e5pbj9w0c.americanwolfthailand.com/DJPetjah/index.php?topic=1504154.0
https://adsensebih.com/index.php?topic=17090.0
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/16146
https://hackersuniversity.net/index.php?topic=13779.0
https://khuyenmaikk13.info/index.php?topic=199875.0
http://HyUa.1fps.icu/l/szIaeDC
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/492824
http://thermoplast.envolgroupe.com/component/k2/author/66309
http://svgrossburgwedel.de/component/k2/itemlist/user/5296
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1840740
http://batubersurat.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=42884
http://haniel.ir/index.php/component/k2/itemlist/user/73559
http://socialfbwidgets.com/component/k2/itemlist/user/13489.html
http://xplorefitness.com/blog/%D1%8D%D1%84%D0%B8%D1%80-%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-97-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-y4-%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-97-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://www.vivelabmanizales.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wa1z/
http://www.vivelabmanizales.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ol8y-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ex8b-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://grajalesabogados.com.mx/?option=com_k2&view=itemlist&task=user&id=62112
http://febrescordero.gob.ec/index.php/component/k2/itemlist/user/86182
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=20362
http://withinfp.sakura.ne.jp/eso/index.php/16945050-live-smers-4-seria-s8-smers-4-seria/0
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=105438
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4885835
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=801397
http://www.spazioad.com/component/k2/itemlist/user/7282096
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=57490
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12619
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/199305
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=28031.0
http://mediaville.me/index.php/component/k2/itemlist/user/206663
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=51748
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/199697
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1772491
http://sextomariotienda.com/blog/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8/
http://afinandoemociones.com.ar/?option=com_k2&view=itemlist&task=user&id=387714
http://withinfp.sakura.ne.jp/eso/index.php/16864526-hdvideo-po-zakonam-voennogo-vremeni-3-sezon-1-seria-o7-po-zakon/0
http://lavaggio.com.vn/index.php/component/k2/itemlist/user/3732103
http://forum.digamahost.com/index.php?topic=112189.0
http://teambuildingpremium.com/forum/index.php?topic=795229.0
http://www.deliberarchia.org/forum/index.php?topic=994167.0
http://euromouleusinage.com/?option=com_k2&view=itemlist&task=user&id=121608
http://laspoltrina.it/component/k2/itemlist/user/1400806
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=22686
http://www.crnmedia.es/component/k2/itemlist/user/84967
http://8.droror.co.il/uncategorized/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dw5u/
http://haniel.ir/?option=com_k2&view=itemlist&task=user&id=85762
http://haniel.ir/index.php/component/k2/itemlist/user/85769
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3750759
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3750777
http://mahdi.ehosseini.com/index.php/component/k2/itemlist/user/28230
http://www.vivelabmanizales.com/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w2-%d1%82%d0%be%d0%bb%d1%8f/
http://islamiccall.info/index.php/component/k2/itemlist/user/857169
http://c3isecurity.com.br/?option=com_k2&view=itemlist&task=user&id=483274
http://married.dike.gr/index.php/component/k2/itemlist/user/51891
http://dev.aabn.org.gh/component/k2/itemlist/user/513839
http://www.emrabq8.com/index.php/component/k2/itemlist/user/1785731
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=204484
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=204494
http://bitpark.co.kr/?document_srl=3805122
http://bitpark.co.kr/board_IzjM66/3804954
http://bitpark.co.kr/board_IzjM66/3805038
http://bitpark.co.kr/board_IzjM66/3805062
http://bitpark.co.kr/board_IzjM66/3805091
http://forum.digamahost.com/index.php?topic=112119.0
http://marjorieaperry.com/?option=com_k2&view=itemlist&task=user&id=484307
http://teambuildingpremium.com/forum/index.php?topic=794860.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3324357
http://seoksoononly.dothome.co.kr/qna/819632
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/304781
http://xplorefitness.com/blog/%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2/game-thrones-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-7-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-09-05-2019-h0-%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2/game-thrones-8
http://highlanderonline.cmshelplive.net/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-09-05-2019-f9-%d0%b8%d0%b3%d1%80/
http://highlanderonline.cmshelplive.net/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-08-05-2-4/
http://seoksoononly.dothome.co.kr/qna/819933
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2590879
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/494298
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=2004847
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=27728
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=27732
http://2872870.com/est/2400
http://2872870.com/est/2404
http://2872870.com/est/2408
http://9mantv.com/index.php?mid=board_IIbv50&document_srl=11904
http://9mantv.com/index.php?mid=board_LaTg55&document_srl=11891
http://9mantv.com/index.php?mid=board_LaTg55&document_srl=11895
http://9mantv.com/index.php?mid=board_LaTg55&document_srl=11899
http://9mantv.com/index.php?mid=board_LaTg55&document_srl=11910
http://9mantv.com/index.php?mid=board_LaTg55&document_srl=11914
http://ariji.kr/sub07/770632
http://azone.synology.me/xe/?document_srl=1664
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=1681
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=1691
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=1696
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=1701
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=1706
http://www.critico-expository.com/forum/index.php?topic=7870.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hq1-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://forum.elexlabs.com/index.php?topic=16607.0
http://www.critico-expository.com/forum/index.php?topic=8891.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p5-p1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://myrechockey.com/forums/index.php?topic=96169.0
http://www.critico-expository.com/forum/index.php?topic=7279.0
https://khuyenmaikk13.info/index.php?topic=191044.0
http://www.deliberarchia.org/forum/index.php?topic=1005217.0
http://www.tessabannampad.go.th/webboard/index.php?topic=200424.0
http://roikjer.com/forum/index.php?PHPSESSID=bm9bbhk84kkrd549ddfvqe4r07&topic=848919.0
https://danceplanet.se/commodore/index.php?topic=21170.0
https://prelease.club/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g2-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://forum.byehaj.hu/index.php?topic=86575.0
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-o9-a1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://bobr.site/index.php?topic=125920.0
http://www.theparrotcentre.com/forum/index.php?topic=485822.0
http://www.sharmaraco.com/blog/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-g0-r2-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://eugeniocolazzo.it/forum/index.php?topic=124565.0
http://www.tessabannampad.go.th/webboard/index.php?topic=200916.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gl0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://vtservices85.fr/smf2/index.php?PHPSESSID=9aae0ba561625cd57e7ca9b3935d6621&topic=221247.0
http://www.popolsku.fr.pl/forum/index.php?topic=386914.0
http://HyUa.1fps.icu/l/szIaeDC
http://twks.dothome.co.kr/qna/958
http://twks.dothome.co.kr/qna/965
http://twks.dothome.co.kr/qna/973
http://worldtkdwomen.com/Gallery/3030
http://worldtkdwomen.com/Gallery/3036
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=4504
http://www.gforgirl.com/xe/poster/2737
http://www.golden-nail.co.kr/press/1761
http://www.hicleaning.kr/board_wash/10812
http://www.hsaura.com/?document_srl=4042
http://www.jesusonly.life/calendar/3777
http://www.leekeonsu-csi.com/?document_srl=457086
http://www.leekeonsu-csi.com/index.php?mid=gallery3&document_srl=457048
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=456994
http://www.lozic.co.kr/gallery/4008
http://www.sp1.football/index.php?mid=faq&document_srl=3183
http://www.studyxray.com/?document_srl=2614
http://www.taeshinmedia.com/?document_srl=3261387
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3261316
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3261321
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3261359
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3261369
http://forum.elexlabs.com/index.php?topic=22803.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h1-n3-%d0%b8%d0%b3%d1%80/
https://nextezone.com/index.php?topic=41854.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/et-e-10-e-10-05-2019/?PHPSESSID=ohdv2ks1ndm849nlbe85ndooo0
http://forum.kopkargobel.com/index.php?topic=7623.0
http://www.popolsku.fr.pl/forum/index.php?topic=383946.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-6/
http://www.tessabannampad.go.th/webboard/index.php?topic=204608.0
http://www.deliberarchia.org/forum/index.php?topic=1009832.0
https://prelease.club/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-3/
http://bobr.site/index.php?topic=107259.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-19/
http://teambuildingpremium.com/forum/index.php?topic=792797.0
http://menulisilmiah.net/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-10-05-2019-5/
http://www.hoonthaitoday.com/forum/index.php?topic=240126.0
http://otitismediasociety.org/forum/index.php?topic=150676.0
https://altaylarteknoloji.com/index.php?topic=1617.0
http://menulisilmiah.net/10-05-2019-%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://www.critico-expository.com/forum/index.php?topic=12905.0
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ro9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://HyUa.1fps.icu/l/szIaeDC
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=1734
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=2138
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=1417
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=840
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=845
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=863
http://shinilspring.com/board_qsfb01/11150
http://smartengbiz.com/s1/3305
http://smartengbiz.com/s1/3342
http://stockpan.net/?document_srl=1268
http://stockpan.net/board_HNpV06/1280
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-c0-o2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
https://members.fbhaters.com/index.php?topic=83888.0
http://forum.elexlabs.com/index.php?topic=16372.0
https://nextezone.com/index.php?topic=47511.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gq2-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://reficulcoin.com/index.php?topic=31703.0
http://roikjer.com/forum/index.php?topic=848435.0
http://uberdrivers.net/forum/index.php?topic=258455.0
https://danceplanet.se/commodore/index.php?topic=19362.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=32827.0
http://www.deliberarchia.org/forum/index.php?topic=994665.0
https://nextezone.com/index.php?topic=40928.0
http://www.remify.app/foro/index.php?topic=262109.0
https://members.fbhaters.com/index.php?topic=86554.0
http://www.nomaher.com/forum/index.php?topic=13213.0
https://danceplanet.se/commodore/index.php?topic=30772.0
http://forum.3d-printer.top/index.php?topic=370.0
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-p5-q6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
https://members.fbhaters.com/index.php?topic=85494.0
http://www.nomaher.com/forum/index.php?topic=12565.0
https://members.fbhaters.com/index.php?topic=84921.0
https://danceplanet.se/commodore/index.php?topic=29606.0
http://HyUa.1fps.icu/l/szIaeDC
https://worldtaxi.org/2019/05/09/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-z5-g1-%d0%b8%d0%b3%d1%80/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-49/
https://sanp.pro/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://forum.byehaj.hu/index.php?topic=86232.0
https://reficulcoin.com/index.php?topic=25111.0
http://menulisilmiah.net/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-09-05-2019/
http://teambuildingpremium.com/forum/index.php?topic=818541.0
https://www.limscave.com/forum/viewtopic.php?f=6&t=31663&view=print
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s2-o2-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://khuyenmaikk13.info/index.php?topic=186390.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j8-g2-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://reficulcoin.com/index.php?topic=18688.0
https://reficulcoin.com/index.php?topic=17185.0
http://otitismediasociety.org/forum/index.php?topic=150143.0
http://www.critico-expository.com/forum/index.php?topic=11025.0
http://danielmillsap.com/forum/index.php?topic=1001233.0
http://www.popolsku.fr.pl/forum/index.php?topic=381490.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=e5e2a8d7b7973212f45f4388ec14ea26&topic=223321.0
http://d2bchannel.co.in/blog/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c4-i6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://ru-realty.com/forum/index.php?PHPSESSID=6lsgklhj7l0h4l0pou9q5fsol4&topic=481849.0
https://nextezone.com/index.php?topic=43448.0
http://www.deliberarchia.org/forum/index.php?topic=996887.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ug6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.tessabannampad.go.th/webboard/index.php?topic=199278.0
http://daesestudy.co.kr/ipsi_docu/3118
http://daesestudy.co.kr/ipsi_docu/3157
http://e-educ.net/Forum/index.php?topic=10113.0
http://e-educ.net/Forum/index.php?topic=10115.0
http://eugeniocolazzo.it/forum/index.php?topic=130541.0
http://forum.elexlabs.com/index.php?topic=27282.0
http://forum.elexlabs.com/index.php?topic=27285.0
http://myrechockey.com/forums/index.php?topic=101301.0
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bb%d0%be%d1%81%d1%82%d1%84%d0%b8/
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=3879
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=3890
http://HyUa.1fps.icu/l/szIaeDC
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1609879
http://www.sollazzorefrigerazione.it/?option=com_k2&view=itemlist&task=user&id=2405519
https://tg.vl-mp.com/index.php?topic=1355808.0
http://seoksoononly.dothome.co.kr/qna/793194
http://www.ekemoon.com/142969/052020191405/
http://roikjer.com/forum/index.php?PHPSESSID=eq9aoq5547hnmkeb12j1lfre61&topic=811422.0
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3376038
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7307699
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1334838
https://members.fbhaters.com/index.php?topic=75287.0
http://forum.politeknikgihon.ac.id/index.php?topic=23785.0
http://teambuildingpremium.com/forum/index.php?topic=780367.0
http://xplorefitness.com/blog/%C2%AB%D0%BE%D1%82%D0%B5%D0%BB%D1%8C-%C2%AB%D1%82%D0%BE%D0%BB%D0%B5%D0%B4%D0%BE%C2%BB-2-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-08-05-2019-n8-%C2%AB%D0%BE%D1%82%D0%B5%D0%BB%D1%8C-%C2%AB%D1%82%D0%BE%D0%BB%D0%B5%D0%B4%D0%BE%C2%BB-2-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=297031
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1761832
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/50090
http://www.comfortcenter.es/index.php/component/k2/itemlist/user/104442
http://poselokgribovo.ru/forum/index.php?topic=722736.0
http://withinfp.sakura.ne.jp/eso/index.php/16884091-nasa-istoria-70-seria-filr-nasa-istoria-70-seria/0
http://dev.aabn.org.gh/?option=com_k2&view=itemlist&task=user&id=530473
https://khuyenmaikk13.info/index.php?topic=182569.0
http://ovotecegg.com/component/k2/itemlist/user/134625
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=13890
http://robocit.com/index.php/component/k2/itemlist/user/449580
http://rudraautomation.com/index.php/component/k2/author/167501
http://rudraautomation.com/index.php/component/k2/author/167533
http://soc-human.kz/index.php/component/k2/itemlist/user/1672390
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1666967
http://thermoplast.envolgroupe.com/component/k2/author/94330
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1391787
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1392073
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4890865
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=805096
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=58871
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/62740
http://seoksoononly.dothome.co.kr/qna/749564
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43980
http://rudraautomation.com/index.php/component/k2/author/137950
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wa0%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://www.die-design-manufaktur.de/?option=com_k2&view=itemlist&task=user&id=5174727
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-7/
http://islamiccall.info/index.php/component/k2/itemlist/user/857609
http://thermoplast.envolgroupe.com/component/k2/author/77494
http://www.ekemoon.com/145799/051720194906/
http://www.ekemoon.com/146791/051920195306/
http://menulisilmiah.net/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-100-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wa9%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-1/
http://mobility-corp.com/index.php/component/k2/itemlist/user/2509306
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3321533
http://moyakmermer.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=660722
http://zsmr.com.ua/index.php/component/k2/itemlist/user/491885
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=296035
http://associationsila.org/component/k2/itemlist/user/283234
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=83063
http://mobility-corp.com/index.php/component/k2/itemlist/user/2571531
http://moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=712940
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/88206
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1672436
http://thermoplast.envolgroupe.com/component/k2/author/94338
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1582703
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1582705
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1392047
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1062616
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4890887
http://www.hoonthaitoday.com/forum/index.php?topic=250208.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=7439d7ec6f1a5c1a2d770b1570328b26&topic=214615.0
http://teambuildingpremium.com/forum/index.php?topic=796677.0
http://d2bchannel.co.in/blog/2019/05/09/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q0-h1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=32315.0
https://reficulcoin.com/index.php?topic=31940.0
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rt1-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vw9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://otitismediasociety.org/forum/index.php?topic=157794.0
http://www.theparrotcentre.com/forum/index.php?topic=484036.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-61/
https://www.limscave.com/forum/viewtopic.php?f=6&t=31917&view=print
http://vtservices85.fr/smf2/index.php?topic=220224.0
http://roikjer.com/forum/index.php?PHPSESSID=bpju7m9h4m5kht9ts227odqhd1&topic=856250.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uo9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://forum.elexlabs.com/index.php?topic=17089.0
http://forum.byehaj.hu/index.php?topic=86581.0
http://myrechockey.com/forums/index.php?topic=91951.0
http://www.tessabannampad.go.th/webboard/index.php?topic=199251.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=32001.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ew2-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8/
http://www.ekemoon.com/167513/052320190309/
https://forum.clubeicaro.pt/index.php?topic=940.0
http://roikjer.com/forum/index.php?topic=848733.0
http://www.remify.app/foro/index.php?topic=246582.0
http://www.deliberarchia.org/forum/index.php?topic=995273.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rb6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kt3-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.gizmoarticle.com/09-05-2019-%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://otitismediasociety.org/forum/index.php?topic=156430.0
https://akutthjelper.no/members/wesleygertrude/
http://www.critico-expository.com/forum/index.php?topic=7470.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=314662faebf082c75eb58f5d0537d993&topic=218449.0
http://uberdrivers.net/forum/index.php?topic=247683.0
http://dpmarketingsystems.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://HyUa.1fps.icu/l/szIaeDC
http://www.hoonthaitoday.com/forum/index.php?topic=233907.0
http://help.stv.ru/index.php?PHPSESSID=ebee7fbc088c16a864bf6d4ac8ab5355&topic=139981.0
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-10-05-2019/
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v5-%d1%81/
http://forum.byehaj.hu/index.php?topic=88462.0
http://uberdrivers.net/forum/index.php?topic=248464.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=74ed1579fc450367f4f2c12fa805c184&topic=215689.0
http://www.hoonthaitoday.com/forum/index.php?topic=244437.0
http://metropolis.ga/index.php?topic=6365.0
http://forum.elexlabs.com/index.php?topic=17450.0
http://dpmarketingsystems.com/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q1-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
https://sanp.pro/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t3-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://forum.elexlabs.com/index.php?topic=22738.0
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-k5-h0-%d0%b8%d0%b3%d1%80%d0%b0/
http://www.ofqj.org/hebergementquebec/4-11-b0-l9-4-11-4-11-online
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vv9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://reficulcoin.com/index.php?topic=23554.0
http://www.critico-expository.com/forum/index.php?topic=7184.0
https://reficulcoin.com/index.php?topic=17669.0
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-8/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a4-f2-%d0%b8%d0%b3%d1%80%d0%b0/
http://otitismediasociety.org/forum/index.php?topic=149315.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-33/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qe0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://danceplanet.se/commodore/index.php?topic=19459.0
http://HyUa.1fps.icu/l/szIaeDC
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-c6-r4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.ofqj.org/hebergementquebec/4-12-b1-e6-4-12-4-12
http://myrechockey.com/forums/index.php?topic=91256.0
http://www.ofqj.org/hebergementfrance/4-8-online-o2-z0-4-8-4-8
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b9-t6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://npi.org.es/smf/index.php?topic=113508.0
http://partemp.com/en/groups/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u3-w8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d9-c5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-em6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8/
http://jdcalc.com/forum/viewtopic.php?t=172308
http://poselokgribovo.ru/forum/index.php?topic=749337.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ds4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.deliberarchia.org/forum/index.php?topic=1000879.0
http://www.tekparcahdfilm.com/forum/index.php?topic=47560.0
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m3-p7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z5-n7-%d0%b8/
http://www.theocraticamerica.org/forum/index.php?topic=28296.0
http://www.critico-expository.com/forum/index.php?topic=9364.0
https://nextezone.com/index.php?action=profile;u=6056
http://d2bchannel.co.in/blog/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y7-p6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.deliberarchia.org/forum/index.php?topic=1005676.0
https://reficulcoin.com/index.php?topic=26492.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ks8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://vtservices85.fr/smf2/index.php?PHPSESSID=b5a244cd2e7fb0c956f8da3ec51ae17c&topic=218741.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1336655
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1006893
http://webp.online/index.php?topic=43920.msg72153
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=299115
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5-2/
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2563775
http://proxima.co.rw/index.php/component/k2/itemlist/user/575950
http://macdistri.com/index.php/component/k2/itemlist/user/297988
http://smartacity.com/component/k2/itemlist/user/18894
http://8.droror.co.il/uncategorized/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w4-%d1%82%d0%be%d0%bb%d1%8f/
http://thermoplast.envolgroupe.com/component/k2/author/76070
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=40084
http://cafe.dokseosil.co.kr/community/25380
http://cwon.kr/xe/board_bnSr36/2057
http://cwon.kr/xe/board_bnSr36/2067
http://cwon.kr/xe/board_bnSr36/2072
http://forum.digamahost.com/index.php?topic=121348.0
http://teambuildingpremium.com/forum/index.php?topic=824626.0
http://www.deliberarchia.org/forum/index.php?topic=1031275.0
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3374480
http://arunagreen.com/index.php/component/k2/itemlist/user/438153
http://arunagreen.com/index.php/component/k2/itemlist/user/426574
http://condolencias.servisa.es/11-06-05-2019-x9-11
http://www.ekemoon.com/156251/050320193208/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/286429
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=82289
http://danielmillsap.com/forum/index.php?topic=955931.0
http://highlanderonline.cmshelplive.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5-6/
http://macdistri.com/index.php/component/k2/itemlist/user/310027
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=203027
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=773132
http://www.ekemoon.com/144581/051020193806/
http://seoksoononly.dothome.co.kr/?document_srl=734530
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4837075
http://xplorefitness.com/blog/live-%D1%81%D0%BC%D0%B5%D1%80%D1%88-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-u9-%D1%81%D0%BC%D0%B5%D1%80%D1%88-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/257776
https://cfcestradareal.com.br/?option=com_k2&view=itemlist&task=user&id=18129
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3355839
https://turimex.mx.solemti.net/index.php/component/k2/itemlist/user/1455
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/524695
http://compultras.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=217886
http://corumotoanahtar.com/component/k2/itemlist/user/1739.html
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=39357
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r9-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81/
http://community.viajar.tur.br/index.php?p=/profile/berthacory
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1549649
http://www.ekemoon.com/162449/050320195709/
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=316661
http://menulisilmiah.net/hd-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b6-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/67331
http://mjbosch.com/component/k2/itemlist/user/81942
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=53140
http://forum.digamahost.com/index.php?topic=121554.0
http://teambuildingpremium.com/forum/index.php?topic=825720.0
http://teambuildingpremium.com/forum/index.php?topic=825726.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/525725
http://www.digitalbul.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-90-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ik7a-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-90-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.digitalbul.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ie3q-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.ekemoon.com/189289/051720195314/
http://bitpark.co.kr/board_IzjM66/3917354
http://bitpark.co.kr/board_IzjM66/3917428
http://withinfp.sakura.ne.jp/eso/index.php/16882259-smotret-tolarobot-1-sezon-9-seria-x3-tolarobot-1-sezon-9-seria/0
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=6016
http://smartacity.com/component/k2/itemlist/user/18053
https://l2thalassic.org/Forum/index.php?topic=1273.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4711317
http://ye-dream.com/qa/2566
http://ye-dream.com/qa/2576
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=1002
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=994
http://yoriyorifood.com/xxxx/?document_srl=3084
http://yoriyorifood.com/xxxx/spacial/3089
https://dolcoin.net/free_talk/1742
https://esel.gist.ac.kr/esel2/board_hmgj23/4401
https://esel.gist.ac.kr/esel2/board_hmgj23/4406
https://nextezone.com/index.php?topic=48748.0
https://hackersuniversity.net/index.php?topic=14178.0
https://www.thedezlab.com/lab/community/index.php?topic=2310.0
http://forum.elexlabs.com/index.php/topic,26880.0.html
http://forum.elexlabs.com/index.php/topic,26882.0.html
http://forum.elexlabs.com/index.php?topic=26886.0
http://forum.kopkargobel.com/index.php?topic=9321.0
http://matrixpharm.ru/forum/index.php?PHPSESSID=d0lsccu2521gjln45tuceo1sk7&action=profile;u=190645
http://myrechockey.com/forums/index.php?topic=101016.0
http://poselokgribovo.ru/forum/index.php?topic=783502.0
http://poselokgribovo.ru/forum/index.php?topic=783508.0
http://poselokgribovo.ru/forum/index.php?topic=783516.0
http://www.deliberarchia.org/forum/index.php?topic=1033796.0
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=1563
http://xn----3x5er9r48j7wemud0a387h.com/news/1557
http://xn--22cmah2caecpucll2cycdoj4d0knajrq3e5pbj9w0c.americanwolfthailand.com/DJPetjah/index.php?topic=1505049.0
http://xn--22cmah2caecpucll2cycdoj4d0knajrq3e5pbj9w0c.americanwolfthailand.com/DJPetjah/index.php?topic=1505052.0
https://chromehearts.in.th/index.php?topic=50796.0
https://chromehearts.in.th/index.php?topic=50797.0
https://khuyenmaikk13.info/index.php?topic=200797.0
https://khuyenmaikk13.info/index.php?topic=200803.0
http://1vh.info/index.php?topic=27132.0
http://HyUa.1fps.icu/l/szIaeDC
http://gxpfactory.net/index.php?mid=Guide&document_srl=422
http://gxpfactory.net/index.php?mid=Guide&document_srl=451
http://hyeonjun.co.kr/?document_srl=1092
http://hyeonjun.co.kr/menu3/1077
http://hyeonjun.co.kr/menu3/1082
http://hyeonjun.co.kr/menu3/1097
http://isch.kr/board_PowH60/744
http://isch.kr/board_PowH60/765
http://isch.kr/board_PowH60/781
http://isch.kr/board_PowH60/787
http://isch.kr/board_PowH60/791
http://isch.kr/board_PowH60/801
http://jnk-ent.jp/index.php?mid=gallery&document_srl=2316
http://jnk-ent.jp/index.php?mid=gallery&document_srl=2331
http://k-cea.org/?document_srl=2669
http://k-cea.org/board_Hnyj62/2594
http://k-cea.org/board_Hnyj62/2691
http://k-cea.org/board_Hnyj62/2706
http://kfuav.kr/qna/3805
http://eugeniocolazzo.it/forum/index.php?topic=130841.0
http://flashboot.ru/forum/index.php?topic=94950.0
http://flashboot.ru/forum/index.php?topic=94951.0
http://flashboot.ru/forum/index.php?topic=94952.0
http://forum.elexlabs.com/index.php?topic=27455.0
http://photogrotto.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-720/
http://poselokgribovo.ru/forum/index.php?topic=785159.0
http://roikjer.com/forum/index.php?PHPSESSID=jk38t4qek9nimlv5463ou9j8l6&topic=874650.0
http://sextomariotienda.com/blog/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://sextomariotienda.com/blog/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80/
http://www.deliberarchia.org/forum/index.php?topic=1035557.0
http://www.deliberarchia.org/forum/index.php?topic=1035586.0
http://www.teedinubon.com/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-04/
http://www.theocraticamerica.org/forum/index.php?topic=39039.0
http://www.theocraticamerica.org/forum/index.php?topic=39049.0
https://nextezone.com/index.php?action=profile;u=7284
https://prelease.club/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-day-after-day/
https://theprodigy.info/forum/index.php/topic,29121.0.html
https://www.gizmoarticle.com/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5/
https://www.shaiyax.com/index.php?topic=345402.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=766322
http://www.dezhiran.com/en/component/k2/itemlist/user/16294
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1630843
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=118096
http://www.vivelabmanizales.com/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-39-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ncuj-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0/
http://seoksoononly.dothome.co.kr/qna/722549
http://www.deliberarchia.org/forum/index.php?topic=984792.0
http://www.vivelabmanizales.com/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a6-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4/
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1117456
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1613340
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1344746
http://www.ekemoon.com/161515/050020193809/
http://batubersurat.com/index.php/component/k2/itemlist/user/44287
http://cwon.kr/xe/board_bnSr36/2247
http://cwon.kr/xe/board_bnSr36/2258
http://emjun.com/index.php?mid=hangtotal&document_srl=5562
http://www.urbantutorial.com/index.php/component/k2/itemlist/user/109877
http://zanoza.h1n.ru/2019/05/14/%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-59-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lvsb-%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-59-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/16421
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3356119
http://dohairbiz.com/en/component/k2/itemlist/user/2718070.html
http://www.ekemoon.com/142139/051620192905/
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=223423
http://www.elpinatarense.es/index.php/component/k2/itemlist/user/156235
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1542621
http://macdistri.com/index.php/component/k2/itemlist/user/297722
http://webp.online/index.php?topic=49618.0
http://fbpharm.net/index.php/component/k2/itemlist/user/15603
http://teambuildingpremium.com/forum/index.php?topic=788018.0
http://www.ekemoon.com/148458/052320190706/
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4711320
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=44484
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=492337
http://roikjer.com/forum/index.php?PHPSESSID=2dv33qgeevhua7dhvfpl4hga85&topic=817638.0
http://8.droror.co.il/uncategorized/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rd2w/
http://teambuildingpremium.com/forum/index.php?topic=770205.0
http://www.ekemoon.com/158125/050920191908/
http://cwon.kr/xe/board_bnSr36/2432
http://emjun.com/index.php?mid=hangtotal&document_srl=5735
http://emjun.com/index.php?mid=hangtotal&document_srl=5740
http://emjun.com/index.php?mid=hangtotal&document_srl=5745
http://forum.digamahost.com/index.php?topic=121475.0
http://forum.digamahost.com/index.php?topic=121477.0
http://forum.digamahost.com/index.php?topic=121478.0
http://www.deliberarchia.org/forum/index.php?topic=1032147.0
https://sanp.pro/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xark-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://euromouleusinage.com/index.php/component/k2/itemlist/user/138872
http://euromouleusinage.com/index.php/component/k2/itemlist/user/139004
http://proxima.co.rw/index.php/component/k2/itemlist/user/620708
http://mjbosch.com/component/k2/itemlist/user/81536
http://islamiccall.info/?option=com_k2&view=itemlist&task=user&id=856507
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43005
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/481097
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=279851
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=605357
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/483632
http://www.ekemoon.com/162459/050320195909/
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=503131
http://myrechockey.com/forums/index.php?topic=89952.0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/235139
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4734311
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=501244
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1566429
https://l2thalassic.org/Forum/index.php?topic=1190.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1629965
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=10785
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1621237
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/19116
http://bitpark.co.kr/board_IzjM66/3917976
http://emjun.com/index.php?mid=hangtotal&document_srl=6147
http://emjun.com/index.php?mid=hangtotal&document_srl=6152
http://compultras.com/component/k2/itemlist/user/218173
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/729343
http://www.arunagreen.com/index.php/component/k2/itemlist/user/508577
http://www.vivelabmanizales.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hm3x/
http://www.vivelabmanizales.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-my0o/
http://www.vivelabmanizales.com/%d1%81%d0%be%d0%b4%d0%b5%d1%80%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zd9o-%d1%81%d0%be%d0%b4%d0%b5%d1%80%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-9-%d1%81%d0%b5%d1%80/
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/258383
http://seoksoononly.dothome.co.kr/qna/737119
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2511784
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1654528
http://www.deliberarchia.org/forum/index.php?topic=986008.0
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=607841
http://www.ekemoon.com/146985/052020191906/
http://www.ekemoon.com/142831/051920191305/
http://seoksoononly.dothome.co.kr/?document_srl=777038
http://myrechockey.com/forums/index.php?topic=90292.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1334599
http://www2.yasothon.go.th/smf/index.php?topic=159.157200
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1731637
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=187858
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=779265
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/484940
http://arunagreen.com/index.php/component/k2/itemlist/user/432168
http://www.nienkevanrijn.nl/component/k2/itemlist/user/426328
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=283503
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3293845
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4841775
http://teambuildingpremium.com/forum/index.php?topic=784860.0
http://dev.aabn.org.gh/?option=com_k2&view=itemlist&task=user&id=516534
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/68398
http://cafe.dokseosil.co.kr/community/35460
http://corumotoanahtar.com/component/k2/itemlist/user/2017
http://teambuildingpremium.com/forum/index.php?topic=827358.0
https://khuyenmaikk13.info/index.php?topic=201172.0
https://khuyenmaikk13.info/index.php?topic=201173.0
https://prelease.club/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-drgw-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://prelease.club/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mrsq-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80/
https://prelease.club/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qjra-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80/
https://prelease.club/%d0%bd%d0%b5-%d0%be%d1%82%d0%bf%d1%83%d1%81%d0%ba%d0%b0%d0%b9-%d0%bc%d0%be%d1%8e-%d1%80%d1%83%d0%ba%d1%83-elimi-birakma-42-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pkvu-%d0%bd%d0%b5-%d0%be/
http://www.digitalbul.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-de6s/
http://www.ekemoon.com/191183/050220190615/
https://prelease.club/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-du9c/
https://prelease.club/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ge5l-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://cafe.dokseosil.co.kr/?document_srl=35507
http://cafe.dokseosil.co.kr/community/35500
http://mobility-corp.com/index.php/component/k2/itemlist/user/2585341
http://mobility-corp.com/index.php/component/k2/itemlist/user/2585407
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/725552
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/725717
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/94568
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/94618
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=16033
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/207673
http://teambuildingpremium.com/forum/index.php?topic=784722.0
http://withinfp.sakura.ne.jp/eso/index.php/16877255-sluga-naroda-3-sezon-17-seria-06052019-s7-sluga-naroda-3-sezon-
http://153.120.114.241/eso/index.php/16862634-holostak-10-vypusk-9-smotret-onlajn-bmholostak-10-vypusk-9-smot
https://tg.vl-mp.com/index.php?topic=1354760.0
http://seoksoononly.dothome.co.kr/qna/757229
http://www.elpinatarense.com/?option=com_k2&view=itemlist&task=user&id=155715
http://forum.digamahost.com/index.php?topic=122039.0
http://forum.digamahost.com/index.php?topic=122043.0
http://indiefilm.kr/xe/board/14605
http://indiefilm.kr/xe/board/14615
http://indiefilm.kr/xe/board/14625
http://jjimdak.callbank.kr/?document_srl=724230
http://teambuildingpremium.com/forum/index.php?topic=828286.0
http://teambuildingpremium.com/forum/index.php?topic=828290.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/625266
http://www.camaracoyhaique.cl/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xu4i-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://www.digitalbul.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81-4/
http://www.vivelabmanizales.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81-50/
http://zanoza.h1n.ru/2019/05/15/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-99-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-eu7g-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd/
http://corumotoanahtar.com/component/k2/itemlist/user/1485.html
http://fbpharm.net/index.php/component/k2/itemlist/user/38484
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7383430
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1179422
http://married.dike.gr/index.php/component/k2/itemlist/user/59941
http://mediaville.me/index.php/component/k2/itemlist/user/261668
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/726246
http://ovotecegg.com/component/k2/itemlist/user/141726
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=16102
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=502304
https://khuyenmaikk13.info/index.php?topic=183715.0
http://forum.byehaj.hu/index.php?topic=81535.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/483474
http://mobility-corp.com/index.php/component/k2/itemlist/user/2521117
https://khuyenmaikk13.info/index.php?topic=183807.0
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3398495
http://sextomariotienda.com/blog/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ogip-%d0%b2%d0%be%d1%81%d0%ba%d1%80/
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1019652
http://www.vivelabmanizales.com/%d0%bd%d0%b5-%d0%be%d1%82%d0%bf%d1%83%d1%81%d0%ba%d0%b0%d0%b9-%d0%bc%d0%be%d1%8e-%d1%80%d1%83%d0%ba%d1%83-elimi-birakma-41-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-etsn-%d0%bd%d0%b5-%d0%be/
http://www.spazioad.com/component/k2/itemlist/user/7242820
http://fbpharm.net/index.php/component/k2/itemlist/user/24736
https://forums.letstalkbeats.com/index.php?topic=68602.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3588407
http://xplorefitness.com/blog/%C2%AB%D0%BE%D1%82%D0%B5%D0%BB%D1%8C-%C2%AB%D1%82%D0%BE%D0%BB%D0%B5%D0%B4%D0%BE%C2%BB-1-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-08-05-2019-i4-%C2%AB%D0%BE%D1%82%D0%B5%D0%BB%D1%8C-%C2%AB%D1%82%D0%BE%D0%BB%D0%B5%D0%B4%D0%BE%C2%BB-1-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://smartacity.com/component/k2/itemlist/user/15494
http://forum.digamahost.com/index.php?topic=110019.0
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3582801
http://www.rocktheboat.cc/groups/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-80%d1%85-ih%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=681543.0
http://webp.online/index.php?topic=46594.15
http://proxima.co.rw/index.php/component/k2/itemlist/user/570413
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-2019-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA%C2%BB-vh%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-2019-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA%C2%BB03-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-2019-9
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3300764
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2588147
http://febrescordero.gob.ec/index.php/component/k2/itemlist/user/79020
http://proxima.co.rw/index.php/component/k2/itemlist/user/570635
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1657061
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1657084
http://thermoplast.envolgroupe.com/component/k2/author/83923
http://thermoplast.envolgroupe.com/component/k2/author/83952
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/63676
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/63691
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/63765
http://web2interactive.com/index.php/component/k2/itemlist/user/3603370
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1568871
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1568807
http://forum.byehaj.hu/index.php?topic=78234.0
http://poselokgribovo.ru/forum/index.php?topic=717730.0
http://webp.online/index.php?topic=46214.msg75685
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1356710
http://www.babvallejo.com/index.php/component/k2/itemlist/user/608090
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1762433
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1727698
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19700
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=316770
http://www.atab.com.sa/?option=com_k2&view=itemlist&task=user&id=1544708
http://withinfp.sakura.ne.jp/eso/index.php/16885559-serial-sluga-naroda-3-sezon-15-seria-k2-sluga-naroda-3-sezon-15/0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1638466
http://community.viajar.tur.br/index.php?p=/profile/kyqchristy
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=607561
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=289916
http://www.vivelabmanizales.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82/
http://married.dike.gr/index.php/component/k2/itemlist/user/47777
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4863428
http://mobility-corp.com/index.php/component/k2/itemlist/user/2547173
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/693600
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/78737
http://ovotecegg.com/component/k2/itemlist/user/127279
http://ovotecegg.com/component/k2/itemlist/user/127290
http://proxima.co.rw/index.php/component/k2/itemlist/user/589651
http://proxima.co.rw/index.php/component/k2/itemlist/user/589950
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3638511
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1657791
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1644085
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1644331
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1644351
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=5694
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=5698
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=5720
http://xn--ok1bpqi43ahtb.net/board_eASW07/15265
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=8568
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=8573
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/22573
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/22580
https://mencoin.net/talk_fm/4259
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=124327
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=124378
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=37776
http://bethanychurch.kr/board_vpkl62/3932
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=5199
http://foxy-tv.com/index.php?mid=board_lgTk68&document_srl=14046
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=22116
https://nextezone.com/index.php?topic=46788.0
https://reficulcoin.com/index.php?topic=31767.0
http://www.deliberarchia.org/forum/index.php?topic=1018366.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wc0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-108/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/et-e-7-e-10-05-2019/?PHPSESSID=5uu1imss8fdgdcql4hgmqj2do6
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z4-j3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://teambuildingpremium.com/forum/index.php?topic=804098.0
https://khuyenmaikk13.info/index.php?topic=190284.0
http://forum.kopkargobel.com/index.php?topic=6240.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=c3406e9cbf862da87ec61b7adc1a1f41&topic=216859.0
https://nextezone.com/index.php?action=profile;u=5079
http://vtservices85.fr/smf2/index.php?topic=215400.0
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r4-l2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://forum.elexlabs.com/index.php?topic=22228.0
http://danielmillsap.com/forum/index.php?topic=1031833.0
http://HyUa.1fps.icu/l/szIaeDC
http://xn--ok1bpqi43ahtb.net/?document_srl=22896
http://5starcoffee.co.kr/board_EBXY17/671
http://arte.dgau.ac.kr/?document_srl=694
http://atemshow.com/atemfair_domestic/9487
http://beautypouch.net/index.php?mid=board_09&document_srl=1063
http://daltso.com/index.php?mid=board_cUYy21&document_srl=193
http://indiefilm.kr/xe/?document_srl=29381
http://laokorea.com/orange_menu1/1196
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=56802
http://toeden.co.kr/Product_new/566
http://www.leekeonsu-csi.com/?document_srl=478496
https://betshin.com/Story/278
https://khuyenmaikk13.info/index.php?topic=202693.0
http://forum.elexlabs.com/index.php?topic=20858.0
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d0-%d1%81/
https://sanp.pro/%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u6-%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-11-%d1%81%d0%b5%d1%80/
http://www.tessabannampad.go.th/webboard/index.php?topic=204950.0
https://prelease.club/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/'a-etoo-(got)-8-eo-1-e'-a-etoo-(got)-8-eo-1-e-w2b8/?PHPSESSID=jf9mbcn13b0dpgh8nravs830n7
https://nextezone.com/index.php?action=profile&u=6064
http://forum.elexlabs.com/index.php/topic,16376.0.html
https://polyframetrade.co.uk/%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-3-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-o2-k3-%D1%80%D0%B0%D1%81%D1%81/
https://reficulcoin.com/index.php?topic=30817.0
https://reficulcoin.com/index.php?topic=18231.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qc9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-m2-q9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.deliberarchia.org/forum/index.php?topic=993061.0
https://sanp.pro/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-09-05-2019/
http://www.theparrotcentre.com/forum/index.php?topic=488881.0
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-7/
http://HyUa.1fps.icu/l/szIaeDC
http://worldtkdwomen.com/Gallery/2696
http://worldtkdwomen.com/Gallery/2707
http://www.betospot.com/index.php?mid=board_mIEg96&document_srl=1711
http://www.betospot.com/index.php?mid=board_wFHn31&document_srl=1570
http://www.betospot.com/index.php?mid=board_wFHn31&document_srl=1656
http://www.betospot.com/index.php?mid=board_wFHn31&document_srl=1676
http://www.betospot.com/index.php?mid=board_wFHn31&document_srl=1682
http://www.betospot.com/index.php?mid=board_wFHn31&document_srl=1692
http://www.betospot.com/index.php?mid=board_wFHn31&document_srl=1701
http://www.betospot.com/index.php?mid=board_wFHn31&document_srl=1722
http://www.datascientist.co.kr/?document_srl=32253
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=32218
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=32222
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=32227
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=32237
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=32243
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=32248
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=32258
http://www.deliberarchia.org/forum/index.php?topic=1027847.0
http://www.deliberarchia.org/forum/index.php?topic=1027861.0
http://moavalve.co.kr/faq/4411
http://poselokgribovo.ru/forum/index.php?topic=783114.0
http://poselokgribovo.ru/forum/index.php?topic=783123.0
http://roikjer.com/forum/index.php?PHPSESSID=u210j00s04933qdbfek08bs2f3&topic=873262.0
http://ru-realty.com/forum/index.php?PHPSESSID=kocj15mo64s758eu6v0n70gq67&topic=509943.0
http://sexfork.com/uncategorized/hd-video-rasskaz-sluzhanki-3-sezon-13-seriya-smotret-v-horoshem-kachestve/
http://sexfork.com/uncategorized/hd-video-rasskaz-sluzhanki-3-sezon-3-seriya-torrent/
http://sexfork.com/uncategorized/rasskaz-sluzhanki-3-sezon-9-seriya-hd/
http://twitchdevs.com/c/other/((hd))-rasskaz-sluzhanki-3-sezon-7-seriya-eh/
http://vervetama.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80-3/
http://www.deliberarchia.org/forum/index.php?topic=1033458.0
http://HyUa.1fps.icu/l/szIaeDC
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/473480
http://yoriyorifood.com/xxxx/spacial/2782
https://esel.gist.ac.kr/esel2/board_hmgj23/4138
https://nextezone.com/index.php?topic=48612.0
https://nextezone.com/index.php?topic=48615.0
https://nextezone.com/index.php?topic=48616.0
https://pacock.com/rec/3162
https://pacock.com/rec/3172
https://pacock.com/rec/3181
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-i8-v5-%d0%b8%d0%b3%d1%80%d0%b0/
http://2872870.com/est/2299
https://saltriverbg.com/2019/05/14/%d1%8d%d1%84%d0%b8%d1%80-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb/
https://woodland.org.ua/groups/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lostfilm/
https://www.thedezlab.com/lab/community/index.php?topic=2306.0
http://1vh.info/index.php?topic=27095.0
http://1vh.info/index.php?topic=27096.0
http://e-educ.net/Forum/index.php?topic=9966.0
http://eugeniocolazzo.it/forum/index.php?topic=129952.0
http://flashboot.ru/forum/index.php?topic=94845.0
http://forum.bmw-e60.eu/index.php?topic=7963.0
http://forum.byehaj.hu/index.php?topic=90132.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(hd-video)-m-aka-ak-3-eo-3-e/?PHPSESSID=7596rjcd0ba7dkmj73umb37mh3
http://gallerychoi.com/Exhibition/13228
http://gxpfactory.net/index.php?mid=Guide&document_srl=1647
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2763877
http://myrechockey.com/forums/index.php?topic=100958.0
http://roikjer.com/forum/index.php?PHPSESSID=1savbf24eh7a70o8go4jmvfd87&topic=873395.0
http://ru-realty.com/forum/index.php?PHPSESSID=tgkli7nbd04eld7m3011592r95&topic=510043.0
http://ru-realty.com/forum/index.php?PHPSESSID=tme37e32ndcs0afq1tsqnt7ac6&topic=510035.0
http://twitchdevs.com/c/other/()-rasskaz-sluzhanki-3-sezon-10-seriya-vo-production/
http://twitchdevs.com/c/other/(hd-video)-rasskaz-sluzhanki-3-sezon-1-seriya-anons/
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=696326.0
http://HyUa.1fps.icu/l/szIaeDC
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=899
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=902
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=751
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=756
http://ariji.kr/?document_srl=770141
http://ariji.kr/?document_srl=770145
http://ariji.kr/?document_srl=770154
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=1154
http://bath-family.com/?document_srl=1178
http://bath-family.com/photo_zone/1168
http://bath-family.com/photo_zone/1173
http://foxy-tv.com/index.php?mid=board_arik22&document_srl=1812
http://shinhwaair2017.cafe24.com/issue/43660
http://shinhwaair2017.cafe24.com/issue/43685
http://shinhwaair2017.cafe24.com/issue/43695
http://shinhwaair2017.cafe24.com/issue/43745
http://sounddrizzle.com/index.php?mid=boarda&document_srl=4521
https://www.gizmoarticle.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b5/
https://www.gizmoarticle.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-3/
http://e-educ.net/Forum/index.php?topic=10022.0
http://eugeniocolazzo.it/forum/index.php?topic=130220.0
http://forum.bmw-e60.eu/index.php?topic=7983.0
http://forum.bmw-e60.eu/index.php?topic=7984.0
http://forum.byehaj.hu/index.php?topic=90153.0
http://forum.elexlabs.com/index.php?topic=27041.0
http://forum.elexlabs.com/index.php?topic=27042.0
http://forum.elexlabs.com/index.php?topic=27045.0
http://forum.kopkargobel.com/index.php?topic=9358.0
http://myrechockey.com/forums/index.php?topic=101103.0
http://photogrotto.com/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8-6/
http://photogrotto.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d0%b4%d0%b0%d1%82%d0%b0-%d0%b2%d1%8b%d1%85%d0%be%d0%b4%d0%b0-9/
http://poselokgribovo.ru/forum/index.php?topic=783870.0
http://poselokgribovo.ru/forum/index.php?topic=783874.0
http://poselokgribovo.ru/forum/index.php?topic=783883.0
http://roikjer.com/forum/index.php?topic=873764.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/209323
http://sexfork.com/en/uncategorized/hd-video-rasskaz-sluzhanki-3-sezon-serial-data-vyihoda-2/
http://sexfork.com/uncategorized/hd-rasskaz-sluzhanki-3-sezon-7-seriya-2017/
http://sexfork.com/uncategorized/hd-video-rasskaz-sluzhanki-3-sezon-3-seriya-na-russkom-yazyike-smotret-onlayn/
http://sexfork.com/uncategorized/smotret-rasskaz-sluzhanki-serial-3-sezon-data-vyihoda-3/
http://sextomariotienda.com/blog/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://sextomariotienda.com/blog/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8/
http://HyUa.1fps.icu/l/szIaeDC
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=2887
http://www.gforgirl.com/xe/poster/1609
http://www.hicleaning.kr/board_wash/9680
http://www.hicleaning.kr/board_wash/9693
http://www.jshwanghoan.com/?document_srl=11612
http://www.jshwanghoan.com/index.php?document_srl=11442&mid=qna
http://www.jshwanghoan.com/index.php?mid=historical_figures&document_srl=11553
http://www.jshwanghoan.com/index.php?mid=historical_figures&document_srl=11592
http://www.jshwanghoan.com/index.php?mid=historical_figures&document_srl=11597
http://www.jshwanghoan.com/index.php?mid=historical_figures&document_srl=11643
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=11582
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=11639
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=455637
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=455818
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=455886
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=455850
http://www.lozic.co.kr/?document_srl=3600
http://www.lozic.co.kr/gallery/3553
http://www.lozic.co.kr/gallery/3595
http://www.naeri-love.com/?document_srl=4977
http://www.naeri-love.com/reservation/4953
http://www.naeri-love.com/reservation/4968
http://www.naeri-love.com/reservation/4992
http://www.naeri-love.com/reservation/5045
http://www.teedinubon.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-shachiburi/
http://www.theocraticamerica.org/forum/index.php?topic=38533.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=696510.0
https://nextezone.com/index.php?action=profile;u=7221
https://prelease.club/hd-video-%d1%84%d0%b8%d0%bb%d1%8c%d0%bc-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://theprodigy.info/forum/index.php?topic=29049.0
https://theprodigy.info/forum/index.php?topic=29050.0
https://theprodigy.info/forum/index.php?topic=29051.0
http://cwon.kr/xe/?document_srl=3115
http://flashboot.ru/forum/index.php?topic=94869.0
http://forum.bmw-e60.eu/index.php?topic=7977.0
http://forum.bmw-e60.eu/index.php?topic=7978.0
http://forum.elexlabs.com/index.php/topic,26973.0.html
http://forum.elexlabs.com/index.php?topic=26976.0
http://forum.kopkargobel.com/index.php?topic=9336.0
http://forum.kopkargobel.com/index.php?topic=9339.0
http://poselokgribovo.ru/forum/index.php?topic=783710.0
http://poselokgribovo.ru/forum/index.php?topic=783718.0
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=3086
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=3092
http://taklongclub.com/forum/index.php?topic=137797.0
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3263248
http://HyUa.1fps.icu/l/szIaeDC
http://www.studyxray.com/Sangdam/23772
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3266577
http://xn----3x5er9r48j7wemud0a387h.com/news/3814
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/480806
http://xn--ok1bpqi43ahtb.net/board_EkDG82/18445
http://ye-dream.com/?document_srl=15430
http://yoriyorifood.com/xxxx/spacial/17252
https://esel.gist.ac.kr/esel2/board_hmgj23/10331
http://emjun.com/index.php?mid=hangtotal&document_srl=17096
http://haeple.com/?document_srl=21818
http://haeple.com/index.php?mid=etc&document_srl=21813
http://hyeonjun.co.kr/menu3/10470
http://hyeonjun.co.kr/menu3/10480
http://indiefilm.kr/xe/board/24881
http://isch.kr/board_PowH60/7000
http://isch.kr/board_PowH60/7006
http://jjikduk.net/DATA/18069
http://jjikduk.net/DATA/18108
http://jjikduk.net/DATA/18113
http://k-cea.org/board_Hnyj62/15422
http://k-cea.org/board_Hnyj62/15433
http://lahch.co.kr/index.php?mid=board_jHAP41&document_srl=9884
http://lucky.kidspann.net/?document_srl=7156
http://lucky.kidspann.net/index.php?mid=qna&document_srl=7151
http://roikjer.com/forum/index.php?PHPSESSID=ck3hvlv9ii8qq35730on9jvuv0&topic=877027.0
http://uberdrivers.net/forum/index.php?topic=275970.0
http://uberdrivers.net/forum/index.php?topic=275972.0
http://universalcommunity.se/Forum/index.php?topic=9511.0
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%b0-%d1%80%d1%83%d1%81%d1%81/
http://yoriyorifood.com/xxxx/?document_srl=14037
http://yoriyorifood.com/xxxx/?document_srl=14055
http://yoriyorifood.com/xxxx/spacial/14088
https://saltriverbg.com/2019/05/15/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d1%81%d0%b5%d1%80%d0%b8%d0%b0/
https://sanp.pro/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b5%d1%85/
https://www.shaiyax.com/index.php?topic=346438.0
http://HyUa.1fps.icu/l/szIaeDC
http://ye-dream.com/qa/17974
http://ye-dream.com/qa/17984
http://shinilspring.com/?document_srl=25893
http://shinilspring.com/board_qsfb01/25886
http://skylinecam.co.kr/photo/23969
http://skylinecam.co.kr/photo/23985
http://smartengbiz.com/gallery/37155
http://smartengbiz.com/gallery/37184
http://smartengbiz.com/s1/37087
http://www.golden-nail.co.kr/press/14734
http://www.jesusonly.life/calendar/41454
http://www.jesusonly.life/calendar/41511
http://www.lozic.co.kr/gallery/22785
http://www.urimwelfare.or.kr/board_mfOh88/5003
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=8881
http://xn--ok1bpqi43ahtb.net/?document_srl=22083
http://xn--ok1bpqi43ahtb.net/board_eASW07/22110
http://xn--ok1bpqi43ahtb.net/board_eASW07/22137
http://xn--ok1bpqi43ahtb.net/board_eASW07/22146
http://bethanychurch.kr/board_vpkl62/4314
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=5748
http://cwon.kr/xe/board_bnSr36/9385
http://daesestudy.co.kr/ipsi_docu/8390
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1815717
http://gallerychoi.com/Exhibition/23560
http://gallerychoi.com/Exhibition/23565
http://gallerychoi.com/Exhibition/23575
http://gallerychoi.com/Exhibition/23588
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2766890
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2766905
http://HyUa.1fps.icu/l/szIaeDC
http://skylinecam.co.kr/photo/22482
http://skylinecam.co.kr/photo/22541
http://skylinecam.co.kr/photo/22602
http://skylinecam.co.kr/photo/22664
http://smartengbiz.com/gallery/35319
http://smartengbiz.com/gallery/35353
http://smartengbiz.com/gallery/35383
http://smartengbiz.com/gallery/35455
http://smartengbiz.com/s1/35244
http://smartengbiz.com/s1/35419
http://smartengbiz.com/s1/35434
http://smartengbiz.com/s1/35463
http://smartengbiz.com/s1/35488
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=3315
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=39725
http://www.jesusonly.life/calendar/39834
http://www.sp1.football/index.php?mid=faq&document_srl=34745
http://www.svteck.co.kr/customer_gratitude/16801
http://www.teedinubon.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d0%b4%d0%b0%d1%82-3/
http://www.teedinubon.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d1%81%d0%b5%d1%80-3/
http://www.teedinubon.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80-13/
http://www.teedinubon.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5-8/
http://www.teedinubon.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80-18/
http://www.teedinubon.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80-16/
http://www.teedinubon.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d0%b4%d0%b0%d1%82%d0%b0-%d0%b2%d1%8b-3/
http://www.teedinubon.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb/
http://www.teedinubon.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.teedinubon.com/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80-2/
http://www.teedinubon.com/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-youtube-2/
http://www.teedinubon.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d0%b4%d0%b0%d1%82%d0%b0/
http://www.teedinubon.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-8-03-2016/
http://HyUa.1fps.icu/l/szIaeDC
[url=http://eurocap54.ru/communication/forum/user/10926/]http://eurocap54.ru/communication/forum/user/10926/[/url]
[url=http://kupit-zemlu.ru/forum/user/30700/]http://kupit-zemlu.ru/forum/user/30700/[/url]
[url=https://www.pravpost.ru/forum/index.php?PAGE_NAME=profile_view&UID=13311]https://www.pravpost.ru/forum/index.php?PAGE_NAME=profile_view&UID=13311[/url]
[url=http://best4.ru/support/forum/index.php?PAGE_NAME=profile_view&UID=71998]http://best4.ru/support/forum/index.php?PAGE_NAME=profile_view&UID=71998[/url]
[url=http://socgorod74.ru/forum/?PAGE_NAME=profile_view&UID=69772]http://socgorod74.ru/forum/?PAGE_NAME=profile_view&UID=69772[/url]
Проверяй свои кошельки так как
[url=http://p-v.by/forum/user/10075/]http://p-v.by/forum/user/10075/[/url]
[url=http://israclub.ru/communication/forum/?PAGE_NAME=profile_view&UID=11304]http://israclub.ru/communication/forum/?PAGE_NAME=profile_view&UID=11304[/url]
[url=http://it-citynt.ru/forum/user/26932/]http://it-citynt.ru/forum/user/26932/[/url]
[url=http://www.astrabios.ru/forum/?PAGE_NAME=profile_view&UID=40048]http://www.astrabios.ru/forum/?PAGE_NAME=profile_view&UID=40048[/url]
[url=http://dom.mtt.ru/individuals/abonents/forum/?PAGE_NAME=profile_view&UID=6987]http://dom.mtt.ru/individuals/abonents/forum/?PAGE_NAME=profile_view&UID=6987[/url]
У нас тут бывали и такие ребята
[url=http://nrk.in.ua/novini-ukrayini/2050-postanova-pro-zabezpechennya-zhitlom-vnutrshno-peremschenih-osb-yak-zahischali-nezalezhnst-suverentet-ta-teritoralnu-clsnst-ukrayini.html]http://nrk.in.ua/novini-ukrayini/2050-postanova-pro-zabezpechennya-zhitlom-vnutrshno-peremschenih-osb-yak-zahischali-nezalezhnst-suverentet-ta-teritoralnu-clsnst-ukrayini.html[/url]
[url=http://moemnenie.club/member.php?u=4550]http://moemnenie.club/member.php?u=4550[/url]
[url=http://esebolatov-aksu.mektebi.kz/oushylar-zhetstkter/44-oushylar-zhetstkter.html]http://esebolatov-aksu.mektebi.kz/oushylar-zhetstkter/44-oushylar-zhetstkter.html[/url]
[url=https://fs-mods.com/publ/drugie_mody/skachat_farming_simulator_2017/15-1-0-1]https://fs-mods.com/publ/drugie_mody/skachat_farming_simulator_2017/15-1-0-1[/url]
[url=http://mafiozzi.ru/index.php?newsid=865]http://mafiozzi.ru/index.php?newsid=865[/url]
Тут тоже бывают люди
Моды для Farming Simulator Вконтакте [url=https://vk.com/fs_mod_17]https://vk.com/fs_mod_17[/url]
http://otitismediasociety.org/forum/index.php?topic=149579.0
http://teambuildingpremium.com/forum/index.php?topic=795289.0
https://hackersuniversity.net/index.php/topic,9117.0.html
http://menulisilmiah.net/%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-14-%d1%81%d0%b5-23/
http://www.ofqj.org/hebergementquebec/4-13-watch-k0-b0-4-13-4-13
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-12/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sd4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://help.stv.ru/index.php?topic=139810.0
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t2/
http://www.nomaher.com/forum/index.php?topic=13441.0
http://multikopterforum.hu/index.php?topic=18573.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gk8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://reficulcoin.com/index.php?topic=28818.0
http://ru-realty.com/forum/index.php?PHPSESSID=fvu09s0lfms0i6lbq2qvr595j6&topic=482691.0
http://www.deliberarchia.org/forum/index.php?topic=1001274.0
https://members.fbhaters.com/index.php?topic=83567.0
https://reficulcoin.com/index.php?topic=33630.0
http://www.ofqj.org/hebergementfrance/4-10-a2-s3-4-10-4-10-online
https://members.fbhaters.com/index.php?topic=85291.0
https://prelease.club/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i9-w6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://forum.elexlabs.com/index.php?topic=16877.0
http://imfl.sci.pfu.edu.ru/forum/index.php?action=profile;u=35811
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ij2-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f6-n6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://altaylarteknoloji.com/index.php?topic=1305.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-8-eo-1-e'-a-etoo-8-eo-1-e-q9w0/?PHPSESSID=v25bhl0ncbf4o7vdka46qlju20
http://forum.elexlabs.com/index.php?topic=16686.0
http://www.sharmaraco.com/blog/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-13-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-l5-a3-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-13-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-13-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://danielmillsap.com/forum/index.php?topic=1029522.0
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q1-i8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://teambuildingpremium.com/forum/index.php?topic=792337.0
http://forum.politeknikgihon.ac.id/index.php?topic=30227.0
http://metropolis.ga/index.php?topic=6552.0
http://www.ofqj.org/hebergementfrance/4-10-watch-v4-e0-4-10-4-10-watch
http://tripviet.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-d6-q2-%d0%b8%d0%b3/
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l3-%d1%81%d0%bb/
http://d2bchannel.co.in/blog/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r2-o7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://forum.byehaj.hu/index.php?topic=89249.0
http://forum.elexlabs.com/index.php?topic=22203.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=685256.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bi6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://forum.elexlabs.com/index.php?topic=22509.0
http://HyUa.1fps.icu/l/szIaeDC
https://members.fbhaters.com/index.php?topic=86398.0
http://forum.elexlabs.com/index.php?topic=16292.0
http://otitismediasociety.org/forum/index.php?topic=149798.0
http://sexfork.com/uncategorized/igra-prestolov-2019-8-sezon-6-seriya-igra-prestolov-2019-8-sezon-6-seriya-j9k2/
http://otitismediasociety.org/forum/index.php?topic=150905.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-g6-u6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.deliberarchia.org/forum/index.php?topic=1005658.0
http://www.deliberarchia.org/forum/index.php?topic=995642.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bx9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-10/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-37/
https://reficulcoin.com/index.php?topic=19632.0
https://nextezone.com/index.php?action=profile;u=5018
http://www.ofqj.org/hebergementquebec/4-8-watch-l6-g2-4-8-4-8-watch
https://members.fbhaters.com/index.php?topic=85894.0
http://eugeniocolazzo.it/forum/index.php?topic=123158.0
http://danielmillsap.com/forum/index.php?topic=995177.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-(got)-8-eo-5-e'-a-etoo-(got)-8-eo-5-e-u0x7/?PHPSESSID=jclh98o283ir1valen3q5smps5
http://forum.elexlabs.com/index.php?topic=16316.0
http://roikjer.com/forum/index.php?PHPSESSID=7drqukeilfo4tp3o7vie7afmo3&topic=860594.0
https://nextezone.com/index.php?topic=43500.0
http://www.theocraticamerica.org/forum/index.php?topic=28600.0
https://reficulcoin.com/index.php?topic=23404.0
http://uberdrivers.net/forum/index.php?topic=245750.0
http://help.stv.ru/index.php?PHPSESSID=724fd158f765af00553902f7446ea8dc&topic=140460.0
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-a6-l9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
https://danceplanet.se/commodore/index.php?topic=30225.0
http://www.critico-expository.com/forum/index.php?topic=8536.0
http://dpmarketingsystems.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p8-%d1%81/
http://forum.kopkargobel.com/index.php?topic=7988.0
https://worldtaxi.org/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g7-z8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
https://sanp.pro/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r3-%d1%81/
https://prelease.club/live-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://teambuildingpremium.com/forum/index.php?topic=807049.0
http://www.hoonthaitoday.com/forum/index.php?topic=250275.0
http://www.deliberarchia.org/forum/index.php?topic=1018806.0
http://HyUa.1fps.icu/l/szIaeDC
http://otitismediasociety.org/forum/index.php?topic=157192.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gi0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8/
http://www.popolsku.fr.pl/forum/index.php?topic=381916.0
https://reficulcoin.com/index.php?topic=17897.0
http://forum.elexlabs.com/index.php?topic=18760.0
http://www.deliberarchia.org/forum/index.php?topic=1017330.0
https://forum.shaiyaslayer.tk/index.php?topic=117248.0
http://poselokgribovo.ru/forum/index.php?topic=750121.0
https://members.fbhaters.com/index.php?topic=88280.0
http://www.deliberarchia.org/forum/index.php?topic=1010777.0
https://reficulcoin.com/index.php?topic=27148.0
http://multikopterforum.hu/index.php?topic=16222.0
http://otitismediasociety.org/forum/index.php?topic=150053.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iw6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://hackersuniversity.net/index.php?topic=10117.0
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p1-e4-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://worldtaxi.org/2019/05/09/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q4-u5-%d0%b8%d0%b3%d1%80%d0%b0/
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r7-k9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.sharmaraco.com/blog/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-l1-i2-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-watch
https://nextezone.com/index.php?topic=41109.0
https://hackersuniversity.net/index.php?topic=9616.0
https://khuyenmaikk13.info/index.php?topic=191410.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o0-z8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://roikjer.com/forum/index.php?PHPSESSID=7ednkpke9ag6v9t5r97so7igt3&topic=842649.0
https://prelease.club/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.sharmaraco.com/blog/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-f6-n4-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://danielmillsap.com/forum/index.php?topic=1030379.0
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-s0-b0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-s2-w7-%d0%b8%d0%b3%d1%80/
http://poselokgribovo.ru/forum/index.php?topic=745258.0
http://otitismediasociety.org/forum/index.php?topic=150075.0
http://forum.politeknikgihon.ac.id/index.php?topic=31236.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u7-f9-%d0%b8%d0%b3%d1%80/
http://HyUa.1fps.icu/l/szIaeDC
http://metropolis.ga/index.php?topic=6323.0
http://forum.politeknikgihon.ac.id/index.php?topic=31889.0
http://roikjer.com/forum/index.php?PHPSESSID=0j67dmbei8snvtgljo0fbb7ur6&topic=837769.0
http://help.stv.ru/index.php?topic=139533.0
https://prelease.club/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r7-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u3-a0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tx5-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-8-eo-5-e'-a-etoo-8-eo-5-e-i4o2/?PHPSESSID=s2j04f55cbqnvttqu2cp1k2d27
http://danielmillsap.com/forum/index.php?topic=1011823.0
http://danielmillsap.com/forum/index.php?topic=1030517.0
http://ru-realty.com/forum/index.php?PHPSESSID=k2v8v60psksp9vfb39u7i1lel6&topic=479681.0
http://forum.elexlabs.com/index.php?topic=17823.0
http://www.deliberarchia.org/forum/index.php?topic=1015637.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=ca8893ec9d07358bb4759cd8b609720f&topic=231051.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-69/
http://www.tessabannampad.go.th/webboard/index.php?topic=200636.0
http://otitismediasociety.org/forum/index.php?topic=158114.0
http://forum.elexlabs.com/index.php?topic=16283.0
http://teambuildingpremium.com/forum/index.php?topic=793712.0
http://www.critico-expository.com/forum/index.php?topic=8347.0
https://nextezone.com/index.php?topic=45854.0
http://danielmillsap.com/forum/index.php?topic=1006846.0
http://forum.byehaj.hu/index.php?topic=84626.0
http://teambuildingpremium.com/forum/index.php?topic=803663.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g7-s1-%d0%b8/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zd0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-w7-g9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(a-etoo-2019-8-eo-7-e)-a-etoo-2019-8-eo-7-e-m1a2/?PHPSESSID=nf80vg9ej6tamsnk3di3a3d7d4
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cf4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://akutthjelper.no/members/chuntrudeau953/
http://uberdrivers.net/forum/index.php?topic=244154.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=9cd5bbc109e2250d3b7a900d6bc2d6b4&topic=229587.0
http://HyUa.1fps.icu/l/szIaeDC
http://indiefilm.kr/xe/board/2690
http://indiefilm.kr/xe/board/2700
http://indiefilm.kr/xe/board/2705
http://indiefilm.kr/xe/board/2709
http://indiefilm.kr/xe/board/2738
http://indiefilm.kr/xe/board/2742
http://isch.kr/?document_srl=596
http://isch.kr/board_PowH60/592
http://isch.kr/board_PowH60/601
http://jjikduk.net/DATA/2951
http://jjikduk.net/DATA/2959
http://jjikduk.net/DATA/2966
http://jjikduk.net/DATA/2979
http://jnk-ent.jp/index.php?mid=gallery&document_srl=1864
http://jnk-ent.jp/index.php?mid=gallery&document_srl=1883
http://jstech.kr/index.php?mid=board_lqyj42&document_srl=2415
http://jstech.kr/index.php?mid=board_lqyj42&document_srl=2420
http://k-cea.org/board_Hnyj62/1912
http://teambuildingpremium.com/forum/index.php?topic=811937.0
http://uberdrivers.net/forum/index.php?topic=248743.0
https://khuyenmaikk13.info/index.php?topic=187957.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-4/
https://khuyenmaikk13.info/index.php?topic=189643.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/to-oot-7-e-a4-to-oot-7-e/?PHPSESSID=uoanrebbk7sq6anegcprson3g7
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-y7-w8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bp1-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://reficulcoin.com/index.php?topic=25091.0
http://roikjer.com/forum/index.php?PHPSESSID=svulp8rq8ms5e54b94i376tij4&topic=838764.0
https://nextezone.com/index.php?topic=45761.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=690781.0
http://www.deliberarchia.org/forum/index.php?topic=999791.0
http://roikjer.com/forum/index.php?PHPSESSID=g7oot2k113bboflsnppika65o0&topic=867271.0
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h1-e5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://roikjer.com/forum/index.php?topic=864091.0
http://HyUa.1fps.icu/l/szIaeDC
http://xn--2e0bk61btjo.com/notice/1847
http://xn--2e0bk61btjo.com/notice/1851
http://xn--ok1bpqi43ahtb.net/?document_srl=3148
http://xn--ok1bpqi43ahtb.net/board_EkDG82/3128
http://xn--ok1bpqi43ahtb.net/board_EkDG82/3133
http://ye-dream.com/qa/2608
http://ye-dream.com/qa/2612
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=1250
http://yoriyorifood.com/xxxx/spacial/3311
http://yoriyorifood.com/xxxx/spacial/3321
http://yoriyorifood.com/xxxx/spacial/3326
http://yoriyorifood.com/xxxx/spacial/3331
https://dolcoin.net/free_talk/1774
https://mencoin.net/talk_fm/1718
https://reficulcoin.com/index.php?topic=35879.0
https://reficulcoin.com/index.php?topic=35888.0
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=1565
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=1570
http://0433.net/budongsan/2383
http://1600-1590.com/?document_srl=28013
http://1600-1590.com/index.php?document_srl=27972&mid=board_ihsE13
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=28006
http://2872870.com/?document_srl=2638
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j7-l1-%d0%b8%d0%b3%d1%80/
http://www.remify.app/foro/index.php?topic=278454.0
http://xn--l1adgmc.xn----9sbdbmdznsj5c5bxd7b.xn--p1ai/index.php?topic=10502.0
https://www.shaiyax.com/index.php?topic=335840.0
http://www.ofqj.org/hebergementfrance/4-12-r8-o1-4-12-4-12-online
https://www.runcity.org/forum/index.php?action=profile;u=75023
http://www.deliberarchia.org/forum/index.php?topic=999237.0
http://forum.elexlabs.com/index.php?topic=20074.0
http://www.tessabannampad.go.th/webboard/index.php?topic=204173.0
http://www.nomaher.com/forum/index.php?topic=13102.0
http://poselokgribovo.ru/forum/index.php?topic=750832.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-13/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dr7-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://HyUa.1fps.icu/l/szIaeDC
http://bethanychurch.kr/board_vpkl62/1137
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=962
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=966
http://cafe.dokseosil.co.kr/community/21032
http://cafe.dokseosil.co.kr/community/21041
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=1062
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=1090
http://cwon.kr/xe/board_bnSr36/1202
http://cwon.kr/xe/board_bnSr36/1208
http://cwon.kr/xe/board_bnSr36/1212
http://emjun.com/?document_srl=4414
http://emjun.com/index.php?mid=hangtotal&document_srl=4401
http://emjun.com/index.php?mid=hangtotal&document_srl=4410
http://emjun.com/index.php?mid=hangtotal&document_srl=4418
http://foxy-tv.com/index.php?mid=board_arik22&document_srl=2353
http://foxy-tv.com/index.php?mid=board_xNxV93&document_srl=2366
http://gallerychoi.com/Exhibition/9593
http://gallerychoi.com/Exhibition/9607
http://gallerychoi.com/Exhibition/9613
http://gallerychoi.com/Exhibition/9617
http://goldenpowerball2.com/index.php?mid=board_Bnby34&document_srl=4396
http://goldenpowerball2.com/index.php?mid=board_Bnby34&document_srl=4416
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=4367
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=4409
http://help.stv.ru/index.php?topic=140262.0
http://roikjer.com/forum/index.php?PHPSESSID=bvqrod8kjt9rioetmlrfdsm7r1&topic=835148.0
http://forum.byehaj.hu/index.php?topic=86569.0
http://poselokgribovo.ru/forum/index.php?topic=747302.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uu6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://reficulcoin.com/index.php?topic=31282.0
https://members.fbhaters.com/index.php?topic=88134.0
https://khuyenmaikk13.info/index.php?topic=190869.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s8-j2-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://vtservices85.fr/smf2/index.php?topic=230110.0
http://www.theparrotcentre.com/forum/index.php?topic=484078.0
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e2-z6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://reficulcoin.com/index.php?topic=32793.0
http://teambuildingpremium.com/forum/index.php?topic=800326.0
https://worldtaxi.org/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-e1-e7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://HyUa.1fps.icu/l/szIaeDC
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=491217
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1346154
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7311121
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=15800
http://bitpark.co.kr/?document_srl=3754439
http://seoksoononly.dothome.co.kr/qna/729851
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=493188
http://sfah.ch/de/component/k2/itemlist/user/14896
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2562883
http://ptu.imoove.kr/ko/content/%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-19-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%D0%B2-%D1%8D%D1%84%D0%B8%D1%80%D0%B5-%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-19-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB332253
http://smartacity.com/component/k2/itemlist/user/15228
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=39673
http://vtservices85.fr/smf2/index.php?PHPSESSID=bbfafc8d3c6ed79f851153e72e6c1699&topic=213034.0
http://xplorefitness.com/blog/%C2%AB%D0%BF%D0%BE-%D0%B7%D0%B0%D0%BA%D0%BE%D0%BD%D0%B0%D0%BC-%D0%B2%D0%BE%D0%B5%D0%BD%D0%BD%D0%BE%D0%B3%D0%BE-%D0%B2%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-09-05-2019-o0-%C2%AB%D0%BF%D0%BE-%D0%B7%D0%B0%D0%BA%D0%BE%D0%BD%D0%B0%D0%BC-%D0%B2%D0%BE%D0%B5%D0%BD%D0%BD%D0%BE%D0%B3%D0%BE-%D0%B2%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%B8-3
http://www.studioaparo.it/?option=com_k2&view=itemlist&task=user&id=545693
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/184444
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3629423
http://condolencias.servisa.es/6-05-05-2019-n4-6
http://healthyteethpa.org/index.php/component/k2/itemlist/user/5328642
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=304084
http://dev.aabn.org.gh/?option=com_k2&view=itemlist&task=user&id=514096
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i8-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://mediaville.me/index.php/component/k2/itemlist/user/210418
http://seoksoononly.dothome.co.kr/qna/794232
http://mediaville.me/index.php/component/k2/itemlist/user/225063
http://arunagreen.com/index.php/component/k2/itemlist/user/426568
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1562487
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3296404
https://l2thalassic.org/Forum/index.php?topic=1506.0
http://poselokgribovo.ru/forum/index.php?topic=728249.0
http://euromouleusinage.com/?option=com_k2&view=itemlist&task=user&id=105238
http://www.ekemoon.com/149439/050120190407/
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1018462
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=78946
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/270292
http://fbpharm.net/index.php/component/k2/itemlist/user/17954
http://poselokgribovo.ru/forum/index.php?topic=735751.0
http://moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=642873
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291803
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/12284
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/53951
http://engeena.com/component/k2/itemlist/user/7978
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4730945
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=283671
http://fbpharm.net/index.php/component/k2/itemlist/user/17733
https://szenarist.ru/forum/index.php?topic=205783.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/507540
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=2013946
http://dev.aabn.org.gh/component/k2/itemlist/user/565013
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1882924
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2566390
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/707661
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/708036
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/85863
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=132487
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/229878
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/230156
http://www.phan-aen.go.th/forum/index.php?topic=625815.0
http://www.ekemoon.com/143605/050120192506/
https://khuyenmaikk13.info/index.php?topic=178546.0
http://batubersurat.com/index.php/component/k2/itemlist/user/43609
https://forums.letstalkbeats.com/index.php?topic=67049.0
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3595830
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1631060
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=15879
https://sto54.ru/index.php/component/k2/itemlist/user/3294736
http://macdistri.com/index.php/component/k2/itemlist/user/297365
http://danielmillsap.com/forum/index.php?topic=996036.0
http://forum.digamahost.com/index.php?topic=112147.0
http://forum.digamahost.com/index.php?topic=112152.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/195458
http://sextomariotienda.com/blog/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-24-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-smil-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-24-%d1%81%d0%b5%d1%80%d0%b8/
http://teambuildingpremium.com/forum/index.php?topic=795090.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1670211
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1663316
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1580140
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1580144
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1580221
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1580302
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1580314
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4886533
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4887132
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=57853
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=57866
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=51120
http://joocafe.com/board_HWSm10/63139
http://koais.com/data/6151
http://kyj1225.godohosting.com/board_mebR72/4535
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=10094
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=10109
http://skangseo.org/xe/board_Atnj46/20236
http://skangseo.org/xe/board_Atnj46/20260
http://woodpark.kr/?document_srl=2840
http://www.studyxray.com/?document_srl=49062
http://shinilspring.com/board_qsfb01/35021
http://shinilspring.com/board_qsfb01/35223
http://shinilspring.com/board_qsfb01/35229
http://shinilspring.com/board_qsfb01/35278
http://skangseo.org/xe/board_Atnj46/16236
http://twitchdevs.com/c/other/((hd))-rasskaz-sluzhanki-3-sezon-3-seriya-gde/
http://vervetama.com/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-4/
http://vervetama.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%b0-%d1%80%d1%83%d1%81%d1%81/
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=76274
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=76387
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=76421
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=76540
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=76648
http://www.deliberarchia.org/forum/index.php?topic=1043743.0
http://www.deliberarchia.org/forum/index.php?topic=1043777.0
http://HyUa.1fps.icu/l/szIaeDC
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=3537
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=6362
http://0433.net/junggo/3612
http://1600-1590.com/?document_srl=30716
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=30706
http://2872870.com/?document_srl=3360
http://ariji.kr/?document_srl=773865
http://bath-family.com/photo_zone/5032
http://bethanychurch.kr/board_vpkl62/2660
http://cafe.dokseosil.co.kr/community/31444
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=3097
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=3101
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=3110
http://gallerychoi.com/Exhibition/15366
http://goldenpowerball2.com/index.php?mid=board_Bnby34&document_srl=11787
http://haenamyun.taeshinmedia.com/index.php?document_srl=2763948&mid=notice
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2763933
http://haeple.com/index.php?mid=etc&document_srl=10046
http://hyeonjun.co.kr/menu3/4165
http://isch.kr/board_PowH60/3786
http://isch.kr/board_PowH60/3795
http://jjikduk.net/DATA/9105
http://jnk-ent.jp/index.php?mid=gallery&document_srl=7868
http://jnk-ent.jp/index.php?mid=gallery&document_srl=7892
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=15982
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=16013
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=16025
http://roikjer.com/forum/index.php?PHPSESSID=etovur37fldrit43r6himjdlf6&topic=878626.0
http://roikjer.com/forum/index.php?topic=878658.0
http://sextomariotienda.com/blog/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-4/
http://sextomariotienda.com/blog/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80-8/
http://sunele.co.kr/board_ReBD97/31739
http://uberdrivers.net/forum/index.php?topic=278223.0
http://uberdrivers.net/forum/index.php?topic=278231.0
http://vtservices85.fr/smf2/index.php?topic=244123.0
http://www.deliberarchia.org/forum/index.php?topic=1042201.0
http://www.deliberarchia.org/forum/index.php?topic=1042209.0
http://HyUa.1fps.icu/l/szIaeDC
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=2715
http://shinhwaair2017.cafe24.com/issue/64695
http://shinhwaair2017.cafe24.com/issue/64809
http://vn7.vn/?document_srl=48732
http://vn7.vn/qna/48475
http://vn7.vn/qna/48639
http://www.deliberarchia.org/forum/index.php?topic=1033747.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=15270
http://www.gforgirl.com/xe/poster/10147
http://www.hicleaning.kr/?document_srl=18042
http://www.hsaura.com/noty/14778
http://www.lozic.co.kr/gallery/9336
http://www.ds712.net/guest/?document_srl=43391
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=43441
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=43468
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=43516
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=43550
http://www.ekemoon.com/195047/052120194615/
http://www.ekemoon.com/195055/052120194715/
http://www.ekemoon.com/195073/052120195415/
http://www.ekemoon.com/195083/052120195715/
http://www.ekemoon.com/195127/052220191115/
http://HyUa.1fps.icu/l/szIaeDC
http://bitpark.co.kr/?document_srl=3737690
https://forums.letstalkbeats.com/index.php?topic=65862.0
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1561604
http://fbpharm.net/index.php/component/k2/itemlist/user/23348
https://www.gizmoarticle.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-14-%d1%81%d0%b5%d1%80%d0%b8/
http://batubersurat.com/index.php/component/k2/itemlist/user/45641
http://www.hsaura.com/noty/66112
http://www.hsaura.com/noty/66145
http://xplorefitness.com/blog/%C2%AB%D0%BD%D0%B5-%D0%BE%D1%82%D0%BF%D1%83%D1%81%D0%BA%D0%B0%D0%B9-%D0%BC%D0%BE%D1%8E-%D1%80%D1%83%D0%BA%D1%83-elimi-birakma-35-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-qzkx-%C2%AB%D0%BD%D0%B5-%D0%BE%D1%82%D0%BF%D1%83%D1%81%D0%BA%D0%B0%D0%B9-%D0%BC%D0%BE%D1%8E-%D1%80%D1%83%D0%BA%D1%83-elimi-birakma-35-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://zanoza.h1n.ru/2019/05/16/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-37-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mdar-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0/
http://zanoza.h1n.ru/2019/05/16/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-39-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-azyq-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0/
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=761452
http://www.ds712.net/guest/index.php?document_srl=76984&mid=guest07
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=76941
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=76966
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=77103
http://israengineering.com/index.php/component/k2/itemlist/user/1165229
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=57533
http://mediaville.me/index.php/component/k2/itemlist/user/252316
http://mediaville.me/index.php/component/k2/itemlist/user/252569
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=83057
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2571094
https://sanp.pro/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q6-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://sanp.pro/%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-10-05-2019/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vj3-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sanp.pro/09-05-2019-%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-20/
https://reficulcoin.com/index.php?topic=31850.0
http://www.ofqj.org/hebergementquebec/4-8-i0-r0-4-8-4-8
http://otitismediasociety.org/forum/index.php?topic=158329.0
http://www.theocraticamerica.org/forum/index.php?topic=28869.0
https://npi.org.es/smf/index.php?topic=113894.0
http://www.tekparcahdfilm.com/forum/index.php?topic=47039.0
https://reficulcoin.com/index.php?topic=32847.0
http://uberdrivers.net/forum/index.php?topic=263707.0
https://members.fbhaters.com/index.php?topic=86397.0
https://sanp.pro/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n7/
http://www.tessabannampad.go.th/webboard/index.php?topic=205156.0
http://uberdrivers.net/forum/index.php?topic=260749.0
http://forum.elexlabs.com/index.php/topic,21970.0.html
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ze4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://otitismediasociety.org/forum/index.php?topic=150731.0
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y8-o7-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://www.teedinubon.com/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ivi/
http://ye-dream.com/qa/11671
http://ye-dream.com/qa/11696
http://ye-dream.com/qa/11710
http://yoriyorifood.com/xxxx/?document_srl=13699
http://yoriyorifood.com/xxxx/spacial/13667
http://yoriyorifood.com/xxxx/spacial/13688
http://yoriyorifood.com/xxxx/spacial/13715
http://yoriyorifood.com/xxxx/spacial/5922
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80-9/
https://www.thedezlab.com/lab/community/index.php?topic=2729.0
https://www.thedezlab.com/lab/community/index.php?topic=2730.0
https://www.thedezlab.com/lab/community/index.php?topic=2732.0
https://www.thedezlab.com/lab/community/index.php?topic=2734.0
http://ariji.kr/index.php?mid=sub07&document_srl=776657&order_type=asc&sort_index=title
http://asiagroup.co.kr/index.php?mid=board_5&document_srl=127840
http://asiagroup.co.kr/index.php?mid=board_5&document_srl=127850
http://asiagroup.co.kr/index.php?mid=board_5&document_srl=127866
http://atemshow.com/atemfair_domestic/5382
http://atemshow.com/atemfair_domestic/5399
http://bankmitraniaga.co.id/?option=com_k2&view=itemlist&task=user&id=4213632
http://bethanychurch.kr/board_vpkl62/3738
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=4945
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=4950
http://cwon.kr/xe/board_bnSr36/4632
http://HyUa.1fps.icu/l/szIaeDC
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s2-%d1%81/
http://vtservices85.fr/smf2/index.php?PHPSESSID=48e67a1de779f0d0894a833894f902a7&topic=215779.0
https://reficulcoin.com/index.php?topic=23562.0
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-z2-r6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://dpmarketingsystems.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h1-y1-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://www.sharmaraco.com/blog/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-x4-k3-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://help.stv.ru/index.php?topic=139702.0
http://www.hoonthaitoday.com/forum/index.php?topic=205798.0
http://sexfork.com/uncategorized/ertugrul-148-seriya-cl1-ertugrul-148-seriya/
http://ru-realty.com/forum/index.php?PHPSESSID=4pacgg8ld0l9vo5qspjj9lt4c7&topic=478933.0
http://www.ofqj.org/hebergementfrance/4-12-z3-n1-4-12-4-12
http://www.critico-expository.com/forum/index.php?topic=7338.0
http://d2bchannel.co.in/blog/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q1-f5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-9/
https://www.limscave.com/forum/viewtopic.php?f=6&t=31932
https://lucky28003.nl/forum/index.php?topic=13080.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-3/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ac6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=29436
http://2872870.com/est/3697
http://2872870.com/est/3702
http://2872870.com/est/3707
http://cwon.kr/xe/board_bnSr36/2764
http://cwon.kr/xe/board_bnSr36/4612
http://cwon.kr/xe/index.php?mid=board_bnSr36&document_srl=2641&sort_index=readed_count&order_type=desc
http://eugeniocolazzo.it/forum/index.php?topic=132422.0
http://flashboot.ru/forum/index.php?topic=95112.0
http://forum.byehaj.hu/index.php?topic=90411.0
http://forum.elexlabs.com/index.php/topic,28317.0.html
http://poselokgribovo.ru/forum/index.php?topic=788393.0
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=9109
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1417612
http://www.deliberarchia.org/forum/index.php?topic=1039191.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=29516
http://www.teedinubon.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d0%b4%d0%b0%d1%82%d0%b0-4/
http://www.teedinubon.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bb%d0%be%d1%81%d1%82%d1%84-2/
http://www.teedinubon.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-youtube-3/
http://www.teedinubon.com/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vo-production/
http://www.theocraticamerica.org/forum/index.php?topic=40213.0
http://www.theocraticamerica.org/forum/index.php?topic=40223.0
http://HyUa.1fps.icu/l/szIaeDC
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-48/
http://menulisilmiah.net/09-05-2019-%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://www.critico-expository.com/forum/index.php?topic=12224.0
https://www.limscave.com/forum/viewtopic.php?t=31949
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-r6-o0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://forum.byehaj.hu/index.php?topic=87965.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=b6d0d1ad5917ab6f01b2387394baed00&topic=1275.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-s4-n8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
https://khuyenmaikk13.info/index.php?topic=190936.0
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r4-z4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://reficulcoin.com/index.php?topic=30098.0
http://partemp.com/en/groups/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t3-l2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80-4/
https://saltriverbg.com/2019/05/16/%d1%8d%d1%84%d0%b8%d1%80-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%ba/
https://www.gizmoarticle.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-3-%d1%81%d0%b5%d0%b7/
http://8.droror.co.il/uncategorized/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80-6/
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=30010
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=30020
http://bath-family.com/?document_srl=15013
http://bath-family.com/photo_zone/14802
http://bath-family.com/photo_zone/14933
http://bath-family.com/photo_zone/14997
http://bethanychurch.kr/board_vpkl62/5523
http://eugeniocolazzo.it/forum/index.php?topic=134785.0
http://f-tube.info/board/65378
http://flashboot.ru/forum/index.php?topic=95256.0
http://forum.elexlabs.com/index.php/topic,31042.0.html
http://forum.elexlabs.com/index.php?topic=31078.0
http://foxy-tv.com/?document_srl=19808
http://hyeonjun.co.kr/menu3/22073
http://indiefilm.kr/xe/board/41324
http://myrechockey.com/forums/index.php?topic=103501.0
http://myrechockey.com/forums/index.php?topic=103504.0
http://poselokgribovo.ru/forum/index.php?topic=793500.0
http://poselokgribovo.ru/forum/index.php?topic=793529.0
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=21433
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=21469
http://HyUa.1fps.icu/l/szIaeDC
https://khuyenmaikk13.info/index.php?topic=189222.0
https://sanp.pro/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u0-%d1%81%d0%bb/
http://roikjer.com/forum/index.php?PHPSESSID=jd98dajdvp67h4s94m9p6k1eq7&topic=842862.0
http://forum.elexlabs.com/index.php?topic=21206.0
https://reficulcoin.com/index.php?topic=19745.0
http://danielmillsap.com/forum/index.php?topic=1023445.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mz0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.deliberarchia.org/forum/index.php?topic=999388.0
http://www.ofqj.org/hebergementquebec/4-13-watch-h4-e9-4-13-4-13-watch
https://reficulcoin.com/index.php?topic=32789.0
http://www.tessabannampad.go.th/webboard/index.php?topic=202380.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w6-f1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://reficulcoin.com/index.php?topic=25665.0
http://myrechockey.com/forums/index.php?topic=91140.0
http://forum.elexlabs.com/index.php/topic,16305.0.html
http://forum.elexlabs.com/index.php?topic=17326.0
http://forum.digamahost.com/index.php?topic=112010.0
http://www.theocraticamerica.org/forum/index.php?topic=28474.0
http://roikjer.com/forum/index.php?PHPSESSID=lsbaefkrs96cg8m8n8cqkkj750&topic=837698.0
https://reficulcoin.com/index.php?topic=28216.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-35/
http://www.theparrotcentre.com/forum/index.php?topic=487247.0
http://ru-realty.com/forum/index.php?PHPSESSID=1em1r5kmt3pl91kg40ta76b3h5&topic=491570.0
http://forum.elexlabs.com/index.php?topic=21542.0
http://www.hoonthaitoday.com/forum/index.php?topic=247854.0
http://www.ofqj.org/hebergementfrance/4-8-watch-b7-v3-4-8-4-8
http://HyUa.1fps.icu/l/szIaeDC
https://forum.clubeicaro.pt/index.php?topic=920.0
https://hackersuniversity.net/index.php?topic=10049.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l5-i2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://teambuildingpremium.com/forum/index.php?topic=816486.0
http://www.deliberarchia.org/forum/index.php?topic=991846.0
http://poselokgribovo.ru/forum/index.php?topic=744396.0
http://forum.elexlabs.com/index.php/topic,17756.0.html
http://otitismediasociety.org/forum/index.php?topic=153054.0
http://forum.elexlabs.com/index.php?topic=21908.0
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90nh0%e3%80%91/
http://teambuildingpremium.com/forum/index.php?topic=796661.0
https://members.fbhaters.com/index.php?topic=88110.0
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n8-r1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.deliberarchia.org/forum/index.php?topic=1018706.0
http://help.stv.ru/index.php?PHPSESSID=a9724c1405ed9555424184bc267f7e5f&topic=140837.0
https://danceplanet.se/commodore/index.php?topic=18250.0
http://www.ofqj.org/hebergementfrance/4-12-r3-f8-4-12-4-12
https://members.fbhaters.com/index.php?topic=87907.0
http://forum.elexlabs.com/index.php?topic=16889.0
http://sexfork.com/en/uncategorized/hd-sluga-naroda-3-sezon-16-seriya-v1-sluga-naroda-3-sezon-16-seriya/
https://nextezone.com/index.php?topic=39759.0
http://sexfork.com/uncategorized/igra-prestolov-game-of-thrones-8-sezon-6-seriya-igra-prestolov-game-of-thrones-8-sezon-6-seriya-j0h3/
http://poselokgribovo.ru/forum/index.php?topic=743637.0
https://www.limscave.com/forum/viewtopic.php?t=31743
https://www.gizmoarticle.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-c1-e8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a6-g0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://vtservices85.fr/smf2/index.php?PHPSESSID=97b24baf7ed0a19e343fbf83f8254f02&topic=214592.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pq4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.deliberarchia.org/forum/index.php?topic=995227.0
http://HyUa.1fps.icu/l/szIaeDC
http://danielmillsap.com/forum/index.php?topic=1014428.0
http://www.nomaher.com/forum/index.php?topic=13501.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/10-05-2019-to-oot-7-e/?PHPSESSID=6g13ts3ea1r0jcslglpjrgfof6
http://www.deliberarchia.org/forum/index.php?topic=1015797.0
http://roikjer.com/forum/index.php?PHPSESSID=jhsjfjilh5vo3k0ufgn4f5ggj3&topic=854433.0
https://nextezone.com/index.php?action=profile;u=5362
http://roikjer.com/forum/index.php?topic=862112.0
http://forum.elexlabs.com/index.php?topic=17512.0
http://otitismediasociety.org/forum/index.php?topic=151557.0
http://8.droror.co.il/uncategorized/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u2-d3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iy4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://vtservices85.fr/smf2/index.php?PHPSESSID=ac65e42937ccee40e996d495fbd2b666&topic=215727.0
http://help.stv.ru/index.php?PHPSESSID=b4c1cbd8cf81687823c1ec1f8822edc4&topic=140099.0
https://reficulcoin.com/index.php?topic=24461.0
http://forum.elexlabs.com/index.php?topic=16246.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/'a-etoo-2019-8-eo-3-e'-a-etoo-2019-8-eo-3-e-h9i2/?PHPSESSID=urj15dbhakgv980s139g1v7ki3
http://www.hoonthaitoday.com/forum/index.php?topic=210637.0
http://www.deliberarchia.org/forum/index.php?topic=1000798.0
https://khuyenmaikk13.info/index.php?topic=190567.0
http://roikjer.com/forum/index.php?PHPSESSID=lq69polblb27blndoepsvou9g5&topic=845279.0
http://poselokgribovo.ru/forum/index.php?topic=751459.0
http://www.ofqj.org/hebergementfrance/4-9-c5-e2-4-9-4-9-online
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k2-t9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.theocraticamerica.org/forum/index.php?topic=36537.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=335aaa142aa000c124a560917fc77eab&topic=4559.0
http://www.xn--12cn5c7acf2ewbbx6xe.com/forum/index.php?PHPSESSID=b97710190004273777cba3e35e335167&topic=2032.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/321135
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=692740.0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/255686
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=551698
http://zsmr.com.ua/index.php/component/k2/itemlist/user/551680
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/15896
https://chromehearts.in.th/index.php?topic=50029.0
https://chromehearts.in.th/index.php?topic=50030.0
https://cybergsm.es/index.php?topic=12376.0
https://forum.ironlogic.ru/index.php?topic=1300.0
https://khuyenmaikk13.info/index.php?topic=198403.0
https://khuyenmaikk13.info/index.php?topic=198404.0
https://khuyenmaikk13.info/index.php?topic=198406.0
https://khuyenmaikk13.info/index.php?topic=198409.0
https://khuyenmaikk13.info/index.php?topic=198410.0
https://khuyenmaikk13.info/index.php?topic=198411.0
https://khuyenmaikk13.info/index.php?topic=198413.0
https://nextezone.com/index.php?action=profile;u=6903
https://nextezone.com/index.php?topic=48246.0
https://nextezone.com/index.php?topic=48260.0
https://nextezone.com/index.php?topic=48262.0
http://HyUa.1fps.icu/l/szIaeDC
http://necinsurance.co.zw/component/k2/itemlist/user/19278.html
http://www.phan-aen.go.th/forum/index.php?topic=628585.0
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=211522
http://www.elpinatarense.es/?option=com_k2&view=itemlist&task=user&id=154881
http://married.dike.gr/index.php/component/k2/itemlist/user/51781
http://seoksoononly.dothome.co.kr/qna/740478
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/17528
https://turimex.mx.solemti.net/index.php/component/k2/itemlist/user/1243
http://forum.digamahost.com/index.php?topic=120874.0
http://teambuildingpremium.com/forum/index.php?topic=823675.0
http://xplorefitness.com/blog/%C2%AB%D0%B2%D0%BE%D1%80%D0%BE%D0%BD-kuzgun-18-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-qrav-%C2%AB%D0%B2%D0%BE%D1%80%D0%BE%D0%BD-kuzgun-18-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
https://sanp.pro/%d0%bd%d0%b5-%d0%be%d1%82%d0%bf%d1%83%d1%81%d0%ba%d0%b0%d0%b9-%d0%bc%d0%be%d1%8e-%d1%80%d1%83%d0%ba%d1%83-elimi-birakma-37-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jmez-%d0%bd%d0%b5-%d0%be/
http://moyakmermer.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=726397
http://wigalseguros.com.br/index.php/component/k2/itemlist/user/6646
http://www.ekemoon.com/187257/050820192514/
http://www.ekemoon.com/187266/050820192714/
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2474105
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/17426
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2626327
http://dohairbiz.com/en/component/k2/itemlist/user/2705405.html
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8d%d1%84%d0%b8%d1%80-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://proxima.co.rw/index.php/component/k2/itemlist/user/573011
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/483058
https://l2thalassic.org/Forum/index.php?topic=606.0
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4848373
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2541913
http://mediaville.me/index.php/component/k2/itemlist/user/231451
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1556224
http://8.droror.co.il/uncategorized/%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-83-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ho2%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-83-%d1%81%d0%b5%d1%80%d0%b8%d1%8f08-05-2019/
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=17920
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/470773
http://withinfp.sakura.ne.jp/eso/index.php/16882075-edinoe-serdce-tek-yurek-15-seria-hpvd-edinoe-serdce-tek-yurek-1
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/71747
http://withinfp.sakura.ne.jp/eso/index.php/16863266-po-zakonam-voennogo-vremeni-3-sezon-3-seria-05052019-s8-po-zako
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/211303
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3600223
https://l2thalassic.org/Forum/index.php?topic=1329.0
http://seoksoononly.dothome.co.kr/qna/720169
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1006221
http://xplorefitness.com/blog/%C2%AB%D0%B5%D0%B4%D0%B8%D0%BD%D0%BE%D0%B5-%D1%81%D0%B5%D1%80%D0%B4%D1%86%D0%B5-tek-y%C3%BCrek-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-rusj-%C2%AB%D0%B5%D0%B4%D0%B8%D0%BD%D0%BE%D0%B5-%D1%81%D0%B5%D1%80%D0%B4%D1%86%D0%B5-tek-y%C3%BCrek-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
https://sanp.pro/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bgsa-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-22-%d1%81%d0%b5%d1%80%d0%b8/
https://sanp.pro/%d0%bd%d0%b5-%d0%be%d1%82%d0%bf%d1%83%d1%81%d0%ba%d0%b0%d0%b9-%d0%bc%d0%be%d1%8e-%d1%80%d1%83%d0%ba%d1%83-elimi-birakma-35-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-olsv-%d0%bd%d0%b5-%d0%be/
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2627497
http://healthyteethpa.org/component/k2/itemlist/user/5427175
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=16310
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=72148
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=6759
https://l2thalassic.org/Forum/index.php?topic=1191.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2576658
http://webp.online/index.php?topic=49783.0
http://bitpark.co.kr/board_IzjM66/3778384
http://smartacity.com/component/k2/itemlist/user/19928
http://seoksoononly.dothome.co.kr/qna/799238
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1640017
http://matrixpharm.ru/forum/index.php?PHPSESSID=jvr9urkrg6bl90fvv4c93true6&action=profile;u=173421
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4726498
http://rudraautomation.com/index.php/component/k2/author/103011
http://ovotecegg.com/component/k2/itemlist/user/118375
http://mediaville.me/index.php/component/k2/itemlist/user/225128
http://withinfp.sakura.ne.jp/eso/index.php/16895564-uristy-16-seria-efir-uristy-16-seria/0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1338615
http://poselokgribovo.ru/forum/index.php?topic=734338.0
http://www2.yasothon.go.th/smf/index.php?topic=159.157200
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1731637
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=187858
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=779265
http://xplorefitness.com/blog/%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB-%D1%82%D0%BE%D0%BB%D1%8F-%D1%80%D0%BE%D0%B1%D0%BE%D1%82-4-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-t2-%D1%82%D0%BE%D0%BB%D1%8F-%D1%80%D0%BE%D0%B1%D0%BE%D1%82-4-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/257328
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/17730
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=1283
http://c3isecurity.com.br/component/k2/itemlist/user/523821
http://fbpharm.net/index.php/component/k2/itemlist/user/38854
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/208125
http://wigalseguros.com.br/index.php/component/k2/itemlist/user/6697
http://www.arunagreen.com/index.php/component/k2/itemlist/user/505413
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=818823
http://zanoza.h1n.ru/2019/05/14/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xf8b-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ut0%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f06-05-2019/
http://153.120.114.241/eso/index.php/16860160-holostak-9-sezon-10-vypusk-torrent-uyholostak-9-sezon-10-vypusk
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1630306
http://married.dike.gr/index.php/component/k2/itemlist/user/49435
https://khuyenmaikk13.info/index.php?topic=183803.0
http://smartacity.com/component/k2/itemlist/user/22434
http://forum.politeknikgihon.ac.id/index.php?topic=24266.0
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=12455
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3708324
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2574500
http://teambuildingpremium.com/forum/index.php?topic=771840.0
http://seoksoononly.dothome.co.kr/qna/747971
https://khuyenmaikk13.info/index.php?topic=183732.0
http://thermoplast.envolgroupe.com/component/k2/author/65512
http://vtservices85.fr/smf2/index.php?PHPSESSID=89f3388aa836a52b4e22e38da558a3a9&topic=213032.0
http://ye-dream.com/qa/2474
http://yeonsen.com/?document_srl=848
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=853
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=862
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=867
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=875
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=884
https://dolcoin.net/?document_srl=1624
https://dolcoin.net/free_talk/1585
https://dolcoin.net/free_talk/1590
https://dolcoin.net/free_talk/1594
https://dolcoin.net/free_talk/1598
https://dolcoin.net/free_talk/1604
https://dolcoin.net/free_talk/1608
https://dolcoin.net/free_talk/1614
https://dolcoin.net/free_talk/1638
https://akutthjelper.no/members/devinwaldrop25/
https://members.fbhaters.com/index.php?topic=84959.0
http://www.deliberarchia.org/forum/index.php?topic=994125.0
http://www.hoonthaitoday.com/forum/index.php?topic=211525.0
https://nextezone.com/index.php?topic=42493.0
http://www.hoonthaitoday.com/forum/index.php?topic=206869.0
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j9-%d1%81/
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x9-q5-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://www.hoonthaitoday.com/forum/index.php?topic=242804.0
https://hackersuniversity.net/index.php?topic=9093.0
http://vtservices85.fr/smf2/index.php?topic=216737.0
https://www.limscave.com/forum/viewtopic.php?t=31912
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c8-b9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.sharmaraco.com/blog/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-i0-g7-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n3-m5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://nextezone.com/index.php?topic=40343.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3261426
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3261430
http://www.xn--xy1b45gp4h0qgb9g.com/?document_srl=2941
http://www.xn--xy1b45gp4h0qgb9g.com/?document_srl=2946
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=918
http://xn----3x5er9r48j7wemud0a387h.com/news/914
http://xn----3x5er9r48j7wemud0a387h.com/news/923
http://xn----3x5er9r48j7wemud0a387h.com/news/932
http://xn----3x5er9r48j7wemud0a387h.com/news/936
http://xn----3x5er9r48j7wemud0a387h.com/news/939
http://xn--2e0bk61btjo.com/notice/1694
https://khuyenmaikk13.info/index.php?topic=185450.0
https://prelease.club/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k3-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-2019-8-eo-2-e'-a-etoo-2019-8-eo-2-e-a9j5/?PHPSESSID=mtg78b1s6p4t5ml4tn9t638381
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l4-i0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://roikjer.com/forum/index.php?PHPSESSID=lrde2vjn7fecd4nl10rl6ncc47&topic=858420.0
http://eugeniocolazzo.it/forum/index.php?topic=125537.0
http://www.theocraticamerica.org/forum/index.php?topic=28763.0
http://danielmillsap.com/forum/index.php?topic=1032535.0
http://forum.elexlabs.com/index.php?topic=21946.0
https://members.fbhaters.com/index.php?topic=86789.0
http://d2bchannel.co.in/blog/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a0-p7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://roikjer.com/forum/index.php?PHPSESSID=bc3qeja9p4bhdcganlmn717uf3&topic=835392.0
http://forum.elexlabs.com/index.php?topic=22694.0
https://danceplanet.se/commodore/index.php?topic=18259.0
https://reficulcoin.com/index.php?topic=24364.0
http://roikjer.com/forum/index.php?PHPSESSID=tiie7tovh72t9f0hj7isb04nr4&topic=843936.0
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-f5-w6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://www.popolsku.fr.pl/forum/index.php?topic=376888.0
https://worldtaxi.org/2019/05/09/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-y6-i3-%d0%b8%d0%b3/
http://roikjer.com/forum/index.php?topic=851462.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gp4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://demo.caribe.vps-private.net/blog/milliardy-4-sezon-11-seriya-online-n0-k8-milliardy-4-sezon-11-seriya-milliardy-4-sezon-11-seriy
http://otitismediasociety.org/forum/index.php?topic=150291.0
http://www.critico-expository.com/forum/index.php?topic=7640.0
http://HyUa.1fps.icu/l/szIaeDC
http://viamania.net/index.php?mid=board_raYV15&document_srl=4708
http://wgamez.net/index.php?mid=board_KGzu43&document_srl=1664
http://wipln.com/?document_srl=26628
http://wipln.com/?document_srl=26643
http://wipln.com/?document_srl=26653
http://woodpark.kr/project/3685
http://www.coating.or.kr/atemfair_data/919
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=88199
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=88296
http://www.hicleaning.kr/?document_srl=51317
http://www.hyunjindc.com/qna/8679
http://www.theparrotcentre.com/forum/index.php?topic=485319.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-oz1-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sanp.pro/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w4-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://universalcommunity.se/Forum/index.php?topic=1261.0
http://forum.politeknikgihon.ac.id/index.php?topic=28487.0
http://www.nomaher.com/forum/index.php?topic=12992.0
https://nextezone.com/index.php?action=profile;u=6598
http://forum.kopkargobel.com/index.php?topic=6631.0
http://otitismediasociety.org/forum/index.php?topic=158520.0
https://forum.clubeicaro.pt/index.php?topic=934.0
http://HyUa.1fps.icu/l/szIaeDC
http://oneandonly1127.com/guest/2498
http://phmusic.dothome.co.kr/index.php?mid=PowerHouseMusic&document_srl=1878
http://praisesound.co.kr/sub04_01/3921
http://praisesound.co.kr/sub04_01/3931
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=66065
http://sd-xi.co.kr/?document_srl=6876
http://skangseo.org/xe/board_Atnj46/26980
http://sunele.co.kr/board_ReBD97/38300
http://themasters.pro/file_01/20412
http://toeden.co.kr/Product_new/8934
http://dpmarketingsystems.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n1-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be-2/
http://roikjer.com/forum/index.php?PHPSESSID=6daebiknjhb4bfe9l6juubq7s7&topic=847781.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c3-f2-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://www.hoonthaitoday.com/forum/index.php?topic=210460.0
https://reficulcoin.com/index.php?topic=30744.0
https://nextezone.com/index.php?topic=40539.0
http://forum.elexlabs.com/index.php/topic,20808.0.html
http://roikjer.com/forum/index.php?PHPSESSID=fjm8qihfu0loelqfnp99at1nd7&topic=848050.0
http://www.tessabannampad.go.th/webboard/index.php?topic=198215.0
http://ru-realty.com/forum/index.php?PHPSESSID=858lr9l98u1p112i3estlbhrr1&topic=479095.0
http://www.remify.app/foro/index.php?topic=245130.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.deliberarchia.org/forum/index.php?topic=1050178.0
http://www.deliberarchia.org/forum/index.php?topic=1050183.0
http://www.gforgirl.com/xe/poster/72252
http://www.hicleaning.kr/board_wash/51908
http://www.jshwanghoan.com/index.php?mid=historical_figures&document_srl=42284
http://www.sp1.football/index.php?mid=tr_video&document_srl=101381
http://www.studyxray.com/Sangdam/69786
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=29770
http://yoriyorifood.com/xxxx/spacial/46337
https://esel.gist.ac.kr/esel2/?document_srl=31248
http://danielmillsap.com/forum/index.php?topic=1021276.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-im9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-30/
http://forum.elexlabs.com/index.php/topic,18252.0.html
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-z4-q5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
https://prelease.club/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b5-%d1%81%d0%bb%d1%83/
http://www.deliberarchia.org/forum/index.php?topic=1022081.0
http://www.verenas-unterwasserwelt.de/forum/index.php?topic=1020.0
http://otitismediasociety.org/forum/index.php?topic=150068.0
http://istakam.com/forum/index.php?topic=10627.0
http://www.hoonthaitoday.com/forum/index.php?topic=206799.0
http://www.remify.app/foro/index.php?topic=272059.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-33/
http://forum.byehaj.hu/index.php?topic=85853.0
http://www.tessabannampad.go.th/webboard/index.php?topic=202108.0
http://uberdrivers.net/forum/index.php?topic=261312.0
http://forum.politeknikgihon.ac.id/index.php?topic=28793.0
http://8.droror.co.il/uncategorized/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p3-a0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://nextezone.com/index.php?topic=40522.0
http://www.popolsku.fr.pl/forum/index.php?topic=383001.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=683251.0
http://HyUa.1fps.icu/l/szIaeDC
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=681792.0
http://k2.akademitelkom.ac.id/component/k2/itemlist/user/288447
http://dev.aabn.org.gh/component/k2/itemlist/user/515566
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=1005422
http://hiyou.com.vn/index.php/component/k2/itemlist/user/1311659
http://mediaville.me/index.php/component/k2/itemlist/user/215378
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2392189
http://webp.online/index.php?topic=43773.15
http://mediaville.me/index.php/component/k2/itemlist/user/208149
http://corumotoanahtar.com/component/k2/itemlist/user/1524
http://euromouleusinage.com/index.php/component/k2/itemlist/user/137940
http://fbpharm.net/index.php/component/k2/itemlist/user/38606
http://jiquilisco.org/index.php/component/k2/itemlist/user/4306
http://ovotecegg.com/component/k2/itemlist/user/141819
http://www.arunagreen.com/index.php/component/k2/itemlist/user/504971
http://xplorefitness.com/blog/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-h2-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3353474
http://xplorefitness.com/blog/%C2%AB%D0%BD%D0%B5-%D0%BE%D1%82%D0%BF%D1%83%D1%81%D0%BA%D0%B0%D0%B9-%D0%BC%D0%BE%D1%8E-%D1%80%D1%83%D0%BA%D1%83-elimi-birakma-37-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-irzs-%C2%AB%D0%BD%D0%B5-%D0%BE%D1%82%D0%BF%D1%83%D1%81%D0%BA%D0%B0%D0%B9-%D0%BC%D0%BE%D1%8E-%D1%80%D1%83%D0%BA%D1%83-elimi-birakma-37-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=63384
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/258344
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=556581
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=82022
http://dcasociados.eu/?option=com_k2&view=itemlist&task=user&id=88917
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=326867
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1922781
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1804737
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=308995
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=20967
http://jiquilisco.org/index.php/component/k2/itemlist/user/4982
http://jiquilisco.org/index.php/component/k2/itemlist/user/4984
http://laspoltrina.it/component/k2/itemlist/user/1426924
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=33358
http://www.jesusonly.life/calendar/33748
http://www.josephmaul.org/menu41/34017
http://www.josephmaul.org/menu41/34082
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=18650
http://www.lozic.co.kr/gallery/18308
http://www.lozic.co.kr/gallery/18381
http://www.lozic.co.kr/gallery/18390
http://www.lozic.co.kr/gallery/18419
http://www.urimwelfare.or.kr/board_mfOh88/4373
http://www.urimwelfare.or.kr/board_mfOh88/4379
http://www.urimwelfare.or.kr/board_mfOh88/4383
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=8702
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=124626
https://www.thedezlab.com/lab/community/index.php?topic=2805.0
http://davichville.com/notice/board/26020
http://gxpfactory.net/index.php?mid=Guide&document_srl=2839
http://jjikduk.net/DATA/17016
http://www.studyxray.com/Sangdam/21314
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=8783
https://nextezone.com/index.php?topic=51098.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-s0-g5-%d0%b8%d0%b3%d1%80/
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=15894
http://emjun.com/index.php?mid=hangtotal&document_srl=14425
http://forum.byehaj.hu/index.php?topic=87585.0
https://sanp.pro/%d0%b4%d1%80%d1%83%d0%b3%d0%b0%d1%8f-i%d0%bd%d1%88%d0%b0-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-09-05-2019/
http://forum.elexlabs.com/index.php?topic=16402.0
http://www.theocraticamerica.org/forum/index.php/topic,29440.0.html
http://www.deliberarchia.org/forum/index.php?topic=996148.0
http://www.remify.app/foro/index.php?topic=277804.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=31224.0
http://www.deliberarchia.org/forum/index.php?topic=991855.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=d5192766c054b544c82db7a394776d4b&topic=1044.0
http://forum.drahthaar-club.com.ua/index.php?topic=1459.0
http://otitismediasociety.org/forum/index.php?topic=149805.0
http://roikjer.com/forum/index.php?PHPSESSID=4ajuh2shmb3g5321h9qtgupc27&topic=839636.0
https://danceplanet.se/commodore/index.php?topic=21817.0
http://forum.elexlabs.com/index.php/topic,16367.0.html
http://www.deliberarchia.org/forum/index.php?topic=997934.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-90/
http://www.tessabannampad.go.th/webboard/index.php?topic=198365.0
http://HyUa.1fps.icu/l/szIaeDC
http://menulisilmiah.net/%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-13-%d1%81%d0%b5-15/
http://help.stv.ru/index.php?PHPSESSID=5cdc2e013bc131c5d0cde2c934cd6089&topic=140455.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z4-j1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x2-u0-%d0%b8%d0%b3%d1%80%d0%b0/
http://dailypatriot.net/phpbb/viewtopic.php?t=410601
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-63/
https://members.fbhaters.com/index.php/topic,83186.0.html
http://forum.elexlabs.com/index.php/topic,16510.0.html
https://nextezone.com/index.php?action=profile&u=6773
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-4/
http://www.ofqj.org/hebergementfrance/4-9-q5-b7-4-9-4-9
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s7-s0-%d0%b8%d0%b3%d1%80/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o8-o0-%d0%b8%d0%b3/
http://help.stv.ru/index.php?PHPSESSID=0a9a87fe65a610cf4a8a31041bd212e4&topic=140163.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x3-y9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e6-p1-%d0%b8%d0%b3%d1%80%d0%b0/
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r2-r0-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://vtservices85.fr/smf2/index.php?PHPSESSID=3929fbc3d7fdc017ed770f73527e93cf&topic=227042.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=460be0243d272681183b44d4d8c9582c&topic=226761.0
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-v5-m8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b7-m1-%d0%b8%d0%b3%d1%80%d0%b0/
http://help.stv.ru/index.php?PHPSESSID=048ff0644ad3bf62d2623bef49f6aa8c&topic=139676.0
http://www.tessabannampad.go.th/webboard/index.php?topic=203981.0
http://www.tessabannampad.go.th/webboard/index.php?topic=201963.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-25/
http://www.hoonthaitoday.com/forum/index.php?topic=205896.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b0-l7-%d0%b8%d0%b3%d1%80/
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s2-b5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-31/
https://polyframetrade.co.uk/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-x9-z6-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81/
http://myrechockey.com/forums/index.php?topic=92545.0
http://www.theocraticamerica.org/forum/index.php?topic=29309.0
http://myrechockey.com/forums/index.php?topic=97929.0
http://forum.elexlabs.com/index.php?topic=19632.0
http://sextomariotienda.com/blog/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o1-s7-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-11/
http://HyUa.1fps.icu/l/szIaeDC
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u2-c9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://uberdrivers.net/forum/index.php?topic=250984.0
http://www.tessabannampad.go.th/webboard/index.php?topic=202623.0
http://menulisilmiah.net/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-10-05-2019-2/
http://uberdrivers.net/forum/index.php?topic=261807.0
http://www.ofqj.org/hebergementquebec/4-11-f7-v4-4-11-4-11
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-2019-8-eo-6-e-a-etoo-2019-8-eo-6-e-y2t3/?PHPSESSID=tc8pb6k1dohn53m7bmat0vblq6
http://www.critico-expository.com/forum/index.php?topic=9758.0
http://www.tessabannampad.go.th/webboard/index.php?topic=202749.0
https://polyframetrade.co.uk/%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-3-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-h7-j2-%D1%80%D0%B0%D1%81%D1%81/
http://www.hoonthaitoday.com/forum/index.php?topic=237641.0
http://poselokgribovo.ru/forum/index.php?topic=746102.0
http://www.nomaher.com/forum/index.php?topic=12175.0
http://roikjer.com/forum/index.php?PHPSESSID=cl1e3nehra7fc1233co4imj0q0&topic=835623.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r1-m3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-p3-i2-%d0%b8/
http://www.tessabannampad.go.th/webboard/index.php?topic=200580.0
http://dpmarketingsystems.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g0-%d1%81%d0%bb%d1%83%d0%b3/
http://forum.elexlabs.com/index.php?topic=17494.0
https://reficulcoin.com/index.php?topic=21263.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gt7-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://reficulcoin.com/index.php?topic=20945.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=31480.0
https://danceplanet.se/commodore/index.php?topic=28880.0
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z9-y1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://forum.elexlabs.com/index.php?topic=17762.0
http://bobr.site/index.php?topic=115000.0
https://reficulcoin.com/index.php?topic=32567.0
http://www.remify.app/foro/index.php?topic=249100.0
https://nextezone.com/index.php?action=profile;u=4636
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-36/
https://prelease.club/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u3-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://www.ofqj.org/hebergementquebec/4-9-m2-s4-4-9-4-9
http://taklongclub.com/forum/index.php?topic=113103.0
http://partemp.com/en/groups/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p7-k5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://www.critico-expository.com/forum/index.php?topic=7738.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s3-c6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://HyUa.1fps.icu/l/szIaeDC
http://www.deliberarchia.org/forum/index.php?topic=1044878.0
http://www.gforgirl.com/xe/poster/43029
http://uberdrivers.net/forum/index.php?topic=280598.0
http://www.remify.app/foro/index.php?topic=301375.0
http://www.remify.app/foro/index.php?topic=301387.0
http://forum.kopkargobel.com/index.php?topic=10545.0
http://uberdrivers.net/forum/index.php?topic=280608.0
http://www.remify.app/foro/index.php?topic=301391.0
http://www.remify.app/foro/index.php?topic=301409.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=701511.0
http://0433.net/junggo/13387
http://122.154.49.125/Forum/index.php?topic=90.0
http://www.hoonthaitoday.com/forum/index.php?topic=247913.0
https://reficulcoin.com/index.php?topic=19236.0
http://demo.caribe.vps-private.net/blog/milliardy-4-sezon-9-seriya-b8-m3-milliardy-4-sezon-9-seriya-milliardy-4-sezon-9-seriya
https://hackersuniversity.net/index.php?topic=9989.0
https://sanp.pro/09-05-2019-%d0%bd%d0%b5-%d0%b6%d0%b5%d0%bd%d1%81%d0%ba%d0%b0%d1%8f-%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%bd%d0%b5-%d0%b6i%d0%bd%d0%be%d1%87%d0%b0-%d1%80%d0%be%d0%b1%d0%be%d1%82%d0%b0-20-4/
http://poselokgribovo.ru/forum/index.php?topic=749486.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=688523.0
http://forum.elexlabs.com/index.php?topic=22385.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ed9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://HyUa.1fps.icu/l/szIaeDC
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=568556
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1742565
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=491115
http://withinfp.sakura.ne.jp/eso/index.php/16903271-hdvideo-tola-robot-3-seria-g9-tola-robot-3-seria
http://highlanderonline.cmshelplive.net/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dpbb-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://mjbosch.com/component/k2/itemlist/user/82549
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1640236
http://myrechockey.com/forums/index.php?topic=90185.0
http://withinfp.sakura.ne.jp/eso/index.php/16903318-smotret-tolarobot-1-sezon-4-seria-b5-tolarobot-1-sezon-4-seria
http://withinfp.sakura.ne.jp/eso/index.php/16861542-holostak-9-sezon-10-vypusk-andeks-unholostak-9-sezon-10-vypusk-/0
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/55854
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26241471/Default.aspx
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1858969
http://ye-dream.com/qa/27093
http://ye-dream.com/qa/27108
http://ye-dream.com/qa/27137
http://ye-dream.com/qa/27157
http://corumotoanahtar.com/component/k2/itemlist/user/2952
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=332400
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=332569
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1931309
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1819808
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1911067
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1911094
https://members.fbhaters.com/index.php?topic=80346.0
http://mediaville.me/index.php/component/k2/itemlist/user/215719
http://poselokgribovo.ru/forum/index.php?topic=735191.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1619672
https://forum.mu-hardcore.com.ve/index.php?topic=50.0
http://www.deliberarchia.org/forum/index.php?topic=998821.0
http://xplorefitness.com/blog/%C2%AB%D0%B6%D0%B5%D0%BD%D1%89%D0%B8%D0%BD%D0%B0-60-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-jebm-%C2%AB%D0%B6%D0%B5%D0%BD%D1%89%D0%B8%D0%BD%D0%B0-60-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
https://sanp.pro/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kdhr-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd/
http://koushatarabar.com/index.php/component/k2/itemlist/user/1349672
http://8.droror.co.il/uncategorized/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nl7u-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://corumotoanahtar.com/component/k2/itemlist/user/3526.html
http://corumotoanahtar.com/index.php/component/k2/itemlist/user/3523
http://corumotoanahtar.com/index.php/component/k2/itemlist/user/3524
http://dohairbiz.com/index.php/component/k2/itemlist/user/2754990
http://fbpharm.net/index.php/component/k2/itemlist/user/45789
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1828915
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1915066
http://jiquilisco.org/index.php/component/k2/itemlist/user/7229
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3815272
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3815279
http://mobility-corp.com/index.php/component/k2/itemlist/user/2604908
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/103579
http://forum.byehaj.hu/index.php?topic=91128.0
http://uberdrivers.net/forum/index.php?topic=280553.0
http://www.popolsku.fr.pl/forum/index.php?topic=20407.69090
http://forum.kopkargobel.com/index.php?topic=10536.0
http://forum.kopkargobel.com/index.php?topic=10540.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=7a48ef35e24b988fdb0688e5ffb07614&topic=245752.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=b056fe26af4816811fd2952e55b9da29&topic=245770.0
http://2872870.com/?document_srl=4849
http://2872870.com/est/4826
http://2872870.com/est/4844
http://2872870.com/est/4857
http://goldenpowerball2.com/?document_srl=32525
http://goldenpowerball2.com/?document_srl=32554
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=13289
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/323220
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=696021.0
http://xn--22cmah2caecpucll2cycdoj4d0knajrq3e5pbj9w0c.americanwolfthailand.com/DJPetjah/index.php?topic=1504798.0
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/476331
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/476341
https://chromehearts.in.th/index.php/topic,50695.0.html
https://khuyenmaikk13.info/index.php?topic=200493.0
https://khuyenmaikk13.info/index.php?topic=200495.0
https://khuyenmaikk13.info/index.php?topic=200498.0
https://khuyenmaikk13.info/index.php?topic=200499.0
https://www.shaiyax.com/index.php?topic=344720.0
https://www.synterra.co/?option=com_k2&view=itemlist&task=user&id=582
https://www.thedezlab.com/lab/community/index.php?topic=2286.0
http://1vh.info/index.php?topic=26986.0
http://cwon.kr/xe/?document_srl=2803
http://HyUa.1fps.icu/l/szIaeDC
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-by6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hy0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://8.droror.co.il/uncategorized/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hz1-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://www.hoonthaitoday.com/forum/index.php?topic=277718.0
http://www.hoonthaitoday.com/forum/index.php?topic=277773.0
http://forum.kopkargobel.com/index.php?topic=10642.0
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=34423
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=34446
http://oceangray.i234.me/?document_srl=9010
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=9001
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=9026
http://shinilspring.com/board_qsfb01/43991
http://skylinecam.co.kr/photo/40828
http://skylinecam.co.kr/photo/40866
http://skylinecam.co.kr/photo/40940
http://skylinecam.co.kr/photo/40975
http://skylinecam.co.kr/photo/41027
http://skylinecam.co.kr/photo/41051
http://toeden.co.kr/Product_new/3104
http://toeden.co.kr/Product_new/3115
http://toeden.co.kr/Product_new/3125
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bb%d0%be%d1%81%d1%82%d1%84%d0%b8-2/
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5-2/
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%88%d0%b0%d0%b4%d0%b8%d0%bd%d1%81/
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ivi/
http://photogrotto.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5-3/
http://photogrotto.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%83/
http://photogrotto.com/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%b0-%d1%80%d1%83%d1%81/
http://photogrotto.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80-2/
http://photogrotto.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8e%d1%82%d1%83%d0%b1/
http://poselokgribovo.ru/forum/index.php?topic=784408.0
http://poselokgribovo.ru/forum/index.php?topic=784411.0
http://poselokgribovo.ru/forum/index.php?topic=784416.0
http://poselokgribovo.ru/forum/index.php?topic=784428.0
http://roikjer.com/forum/index.php?topic=874136.0
http://ru-realty.com/forum/index.php?PHPSESSID=mqciv8epj4gp7lfqcil1mo5kj6&topic=510733.0
http://sexfork.com/uncategorized/smotret-rasskaz-sluzhanki-3-sezon-3-seriya-data-vyihoda/
http://HyUa.1fps.icu/l/szIaeDC
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3393899
http://highlanderonline.cmshelplive.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-live-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://bitpark.co.kr/board_IzjM66/3728408
http://bitpark.co.kr/board_IzjM66/3778024
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/292290
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=209431
http://fbpharm.net/index.php/component/k2/itemlist/user/13211
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2511131
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/185143
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=285629
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1566827
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/481479
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4732342
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=284471
http://www.ekemoon.com/144547/051020191706/
http://arunagreen.com/index.php/component/k2/itemlist/user/421795
http://withinfp.sakura.ne.jp/eso/index.php/16888303-serial-tola-robot-3-seria-t5-tola-robot-3-seria/0
http://married.dike.gr/index.php/component/k2/itemlist/user/48083
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42782
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=775183
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d5-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81/
http://storykingdom.forumside.com/index.php?topic=4819.0
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://www.camaracoyhaique.cl/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-2-%d1%87%d0%b0%d1%81%d1%82%d1%8c-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5-2/
http://soc-human.kz/index.php/component/k2/itemlist/user/1630828
http://married.dike.gr/index.php/component/k2/itemlist/user/49688
http://seoksoononly.dothome.co.kr/qna/730723
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kc3%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f05-05-2019/
https://lucky28003.nl/forum/index.php?topic=12495.0
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=26877
http://ovotecegg.com/component/k2/itemlist/user/118729
http://thermoplast.envolgroupe.com/component/k2/author/82831
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/277072
https://www.gizmoarticle.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sc8x/
https://www.gizmoarticle.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5/
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=291630
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=40524
http://bitpark.co.kr/?document_srl=3753122
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1337142
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/211486
http://withinfp.sakura.ne.jp/eso/index.php/16885177-serial-tolarobot-1-sezon-1-seria-h9-tolarobot-1-sezon-1-seria/0
http://proandpro.it/index.php/component/k2/itemlist/user/4527625
http://mobility-corp.com/index.php/component/k2/itemlist/user/2537459
http://www.ekemoon.com/161539/050020194209/
https://l2thalassic.org/Forum/index.php?topic=2112.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3565886
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/472187
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1636246
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1007310
https://szenarist.ru/forum/index.php?topic=205307.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2562039
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/56655
http://www.elpinatarense.com/?option=com_k2&view=itemlist&task=user&id=155295
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=12380
http://seoksoononly.dothome.co.kr/qna/757363
http://poselokgribovo.ru/forum/index.php?topic=718653.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/188420
http://smartacity.com/component/k2/itemlist/user/13316
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2580435
http://euromouleusinage.com/index.php/component/k2/itemlist/user/117652
http://xplorefitness.com/blog/%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-101-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-a7-%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-101-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1358816
http://k2.akademitelkom.ac.id/component/k2/itemlist/user/288098
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/660723
http://bitpark.co.kr/board_IzjM66/3735291
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=563058
http://ru-realty.com/forum/index.php?topic=472485.0
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=503132
http://k2.akademitelkom.ac.id/component/k2/itemlist/user/288280
http://xplorefitness.com/blog/%C2%AB%D1%80%D0%B0%D0%BD%D0%BD%D1%8F%D1%8F-%D0%BF%D1%82%D0%B0%D1%88%D0%BA%D0%B0-erkenci-kus-45-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-oimt-%C2%AB%D1%80%D0%B0%D0%BD%D0%BD%D1%8F%D1%8F-%D0%BF%D1%82%D0%B0%D1%88%D0%BA%D0%B0-erkenci-kus-45-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/297133
http://proandpro.it/index.php/component/k2/itemlist/user/4541084
http://bitpark.co.kr/board_IzjM66/3774580
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=774908
https://l2thalassic.org/Forum/index.php?topic=2250.0
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-6-%D1%87%D0%B0%D1%81%D1%82%D1%8C-%D1%81%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C-%D0%BE%D0%BD%D0%BB%D0%B0%D0%B9%D0%BD%C2%BB-hp%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-6-%D1%87%D0%B0%D1%81%D1%82%D1%8C
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4855197
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=558739
http://www.vivelabmanizales.com/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hylt-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80/
http://www.deliberarchia.org/forum/index.php?topic=960447.0
http://storykingdom.forumside.com/index.php?topic=4530.0
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1727440
https://sto54.ru/index.php/component/k2/itemlist/user/3294171
http://www.die-design-manufaktur.de/?option=com_k2&view=itemlist&task=user&id=5175689
https://members.fbhaters.com/index.php?topic=81719.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/292032
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5-5/
http://www.vivelabmanizales.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pa4n-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4709556
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/7862
http://forum.byehaj.hu/index.php?topic=81734.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3564731
http://www.dezhiran.com/en/component/k2/itemlist/user/14669
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/51938
http://mediaville.me/index.php/component/k2/itemlist/user/208537
http://macdistri.com/index.php/component/k2/itemlist/user/316011
http://www.phan-aen.go.th/forum/index.php?topic=625601.0
http://soc-human.kz/index.php/component/k2/itemlist/user/1630323
https://khuyenmaikk13.info/index.php?topic=179462.0
http://withinfp.sakura.ne.jp/eso/index.php/16905453-po-zakonam-voennogo-vremeni-3-sezon-4-seria-07052019-w6-po-zako
http://forum.politeknikgihon.ac.id/index.php?topic=25022.0
http://dcasociados.eu/?option=com_k2&view=itemlist&task=user&id=87111
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=40013
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/205111
http://healthyteethpa.org/component/k2/itemlist/user/5335008
http://condolencias.servisa.es/3-10-05-05-2019-f6-3-10
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=502514
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rm3-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-31/
http://roikjer.com/forum/index.php?PHPSESSID=drshuaije8mbqus8iqeemfiml3&topic=835342.0
http://www.critico-expository.com/forum/index.php?topic=8835.0
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90wu7%e3%80%91/
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k0-e4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81-39/
http://myrechockey.com/forums/index.php?topic=95900.0
http://www.theocraticamerica.org/forum/index.php?topic=28743.0
http://forum.elexlabs.com/index.php?topic=16285.0
http://www.ekemoon.com/169793/050520191910/
https://hackersuniversity.net/index.php?topic=9149.0
http://forum.elexlabs.com/index.php/topic,17813.0.html
http://help.stv.ru/index.php?PHPSESSID=6be9eef67acc1288cc25ea1e6e05b01a&topic=140834.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(a-etoogame-of-thrones-8-eo-7-e)-a-etoogame-of-thrones-8-eo-7-e-z1m5/?PHPSESSID=t2s2lau5do4nqv2d3bkep2djv1
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e8-z1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://khuyenmaikk13.info/index.php?topic=184966.0
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-r3-e8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://www.nomaher.com/forum/index.php?topic=13363.0
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-aa4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.hoonthaitoday.com/forum/index.php?topic=241575.0
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=120351
https://www.thedezlab.com/lab/community/index.php/topic,2382.0.html
https://www.thedezlab.com/lab/community/index.php?topic=2386.0
http://0433.net/budongsan/3885
http://eugeniocolazzo.it/forum/index.php?topic=130606.0
http://eugeniocolazzo.it/forum/index.php?topic=130609.0
http://flashboot.ru/forum/index.php?topic=94925.0
http://forum.bmw-e60.eu/index.php?topic=8013.0
http://poselokgribovo.ru/forum/index.php?topic=784610.0
http://poselokgribovo.ru/forum/index.php?topic=784616.0
http://poselokgribovo.ru/forum/index.php?topic=784622.0
http://poselokgribovo.ru/forum/index.php?topic=784641.0
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=4180
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=4230
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=4246
http://uberdrivers.net/forum/index.php?topic=272445.0
http://uberdrivers.net/forum/index.php?topic=272461.0
http://uberdrivers.net/forum/index.php?topic=272469.0
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1623872
http://www.deliberarchia.org/forum/index.php?topic=1035074.0
http://www.deliberarchia.org/forum/index.php?topic=1035077.0
http://www.deliberarchia.org/forum/index.php?topic=1035089.0
http://www.ds712.net/guest/?document_srl=18871
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=18843
http://HyUa.1fps.icu/l/szIaeDC
http://myrechockey.com/forums/index.php?topic=97400.0
http://www.ofqj.org/hebergementfrance/4-13-n4-e9-4-13-4-13
http://www.deliberarchia.org/forum/index.php?topic=1016699.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-t3-w4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
https://reficulcoin.com/index.php?topic=31781.0
http://otitismediasociety.org/forum/index.php?topic=157818.0
http://forum.elexlabs.com/index.php?topic=20992.0
http://www.popolsku.fr.pl/forum/index.php?topic=381516.0
http://www.tessabannampad.go.th/webboard/index.php?topic=199936.0
http://www.popolsku.fr.pl/forum/index.php?topic=20407.55890
http://www.theocraticamerica.org/forum/index.php?topic=29673.0
https://worldtaxi.org/2019/05/10/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y6-t0-%d0%b8%d0%b3%d1%80/
https://members.fbhaters.com/index.php/topic,88758.0.html
http://forum.kopkargobel.com/index.php?topic=6942.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o9-x1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://demo.caribe.vps-private.net/blog/milliardy-4-sezon-12-seriya-v0-i6-milliardy-4-sezon-12-seriya-milliardy-4-sezon-12-seriya
http://wituclub.ru/forum/index.php?topic=26082.0
https://prelease.club/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s2-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://uberdrivers.net/forum/index.php?topic=272314.0
http://vervetama.com/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8-4/
http://vervetama.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80-8/
http://vervetama.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ivi/
http://vervetama.com/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-8-03-2016/
http://www.deliberarchia.org/forum/index.php?topic=1034901.0
http://www.teedinubon.com/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://www.teedinubon.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80-4/
http://www.teedinubon.com/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%be-%d1%87%d0%b5%d0%bc/
http://www.teedinubon.com/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb/
http://www.theocraticamerica.org/forum/index.php?topic=38786.0
http://www.theocraticamerica.org/forum/index.php?topic=38788.0
http://www.urimwelfare.or.kr/board_mfOh88/4178
http://www.verenas-unterwasserwelt.de/forum/index.php?topic=4942.0
http://www.xn--xy1b45gp4h0qgb9g.com/sub_09_05/5614
http://xn----3x5er9r48j7wemud0a387h.com/news/1741
https://cybergsm.es/index.php?topic=13507.0
https://hackersuniversity.net/index.php?topic=14368.0
https://khuyenmaikk13.info/index.php?topic=201082.0
https://prelease.club/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8/
https://saltriverbg.com/2019/05/14/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8-2/
https://saltriverbg.com/2019/05/14/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd/
https://theprodigy.info/forum/index.php?topic=29081.0
https://theprodigy.info/forum/index.php?topic=29084.0
http://HyUa.1fps.icu/l/szIaeDC
[url=http://www.tpk-aksai.ru/forum.php/?PAGE_NAME=profile_view&UID=6844]http://www.tpk-aksai.ru/forum.php/?PAGE_NAME=profile_view&UID=6844[/url]
[url=https://i2hard.ru/forum/user/2684/]https://i2hard.ru/forum/user/2684/[/url]
[url=http://telesam5.ru/forum/user/880252/]http://telesam5.ru/forum/user/880252/[/url]
[url=https://klever-store.ru/forum/user/619/]https://klever-store.ru/forum/user/619/[/url]
[url=http://u37399.netangels.ru/about/forum/user/21989/]http://u37399.netangels.ru/about/forum/user/21989/[/url]
Проверяй свои кошельки так как
[url=https://dreldd.ru/forum/user/58472/]https://dreldd.ru/forum/user/58472/[/url]
[url=http://www.kprfnsk.ru/forum/index.php/user/81447/]http://www.kprfnsk.ru/forum/index.php/user/81447/[/url]
[url=http://xn--f1apaaqe.xn--p1ai/forum.php/?PAGE_NAME=profile_view&UID=18278]http://xn--f1apaaqe.xn--p1ai/forum.php/?PAGE_NAME=profile_view&UID=18278[/url]
[url=https://bataysk-gorod.ru/forum/user/18993/]https://bataysk-gorod.ru/forum/user/18993/[/url]
[url=http://dgs.rarus.ru/forum/?PAGE_NAME=profile_view&UID=4652]http://dgs.rarus.ru/forum/?PAGE_NAME=profile_view&UID=4652[/url]
У нас тут бывали и такие ребята
[url=http://www.client-fk.ru/forum/index.php?action=recent]http://www.client-fk.ru/forum/index.php?action=recent[/url]
[url=http://newsbizlife.ru/u-nas-mozhno-skachat-modyi-dlya-igryi-farming-simulator-2015-besplatno-po-pryamyim-ssyilkam]http://newsbizlife.ru/u-nas-mozhno-skachat-modyi-dlya-igryi-farming-simulator-2015-besplatno-po-pryamyim-ssyilkam[/url]
[url=http://xn--80aff1axlh.xn--p1ai/75-vpervye-pryamye-vylety-iz-kazani-na-kurorty-chernogo-morya.html]http://xn--80aff1axlh.xn--p1ai/75-vpervye-pryamye-vylety-iz-kazani-na-kurorty-chernogo-morya.html[/url]
[url=http://ruscigars.ru/forum/?PAGE_NAME=profile_view&UID=4676]http://ruscigars.ru/forum/?PAGE_NAME=profile_view&UID=4676[/url]
[url=http://baisembetuly-raiymbek.mektebi.kz/merekelk-s-sharalar/page,1,4,12-amorshyly.html]http://baisembetuly-raiymbek.mektebi.kz/merekelk-s-sharalar/page,1,4,12-amorshyly.html[/url]
Тут тоже бывают люди
Моды для Farming Simulator Вконтакте [url=https://vk.com/fs_mod_17]https://vk.com/fs_mod_17[/url]
http://www.datascientist.co.kr/index.php?mid=projects&document_srl=84170
http://www.haetsaldun-clinic.co.kr/Question/1978
http://www.haetsaldun-clinic.co.kr/Question/1984
http://www.haetsaldun-clinic.co.kr/Question/1990
http://www.hyunjindc.com/qna/3848
http://www.siheunglove.com/chulip/8497
http://www.studyxray.com/Sangdam/46307
http://www.svteck.co.kr/customer_gratitude/20000
http://www.sweetparis41.com/xe/board/261
http://www.vamoscontigo.org/Noticia/3291
http://www.yepia.com/board_ZCPG83/3843
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=5802
http://xn----c28e37pz5cp1g6wbrlo8pyxc812d.com/news/2236
http://xn--2e0b53df5ag1c804aphl.net/nuguna/3460
http://xn--2e0bk61btjo.com/notice/4349
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/?document_srl=2585
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=2590
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/487820
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/487839
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=688674.0
https://reficulcoin.com/index.php?topic=17058.0
http://www.ofqj.org/hebergementquebec/4-12-u2-e2-4-12-4-12-watch
http://forum.byehaj.hu/index.php?topic=88192.0
https://khuyenmaikk13.info/index.php?topic=186141.0
http://ru-realty.com/forum/index.php?PHPSESSID=bcf5ckk0763n4ngnfi64i7aqi4&topic=483327.0
https://danceplanet.se/commodore/index.php?topic=19045.0
http://www.theparrotcentre.com/forum/index.php?topic=488620.0
https://sanp.pro/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gt/
http://roikjer.com/forum/index.php?PHPSESSID=g1kn0ihf6uc51onq5lmc2dmil4&topic=847812.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/to-oot-6-e-~-i6-to-oot-6-e/
http://uberdrivers.net/forum/index.php?topic=263759.0
http://forum.elexlabs.com/index.php?topic=17051.0
http://HyUa.1fps.icu/l/szIaeDC
http://worldtkdwomen.com/Gallery/7802
http://worldtkdwomen.com/Gallery/7818
http://worldtkdwomen.com/Gallery/7824
http://worldtkdwomen.com/Gallery/7830
http://www.datascientist.co.kr/index.php?mid=projects&document_srl=84344
http://www.datascientist.co.kr/index.php?mid=projects&document_srl=84382
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=67839
http://www.haetsaldun-clinic.co.kr/Question/2014
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=30170
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=1497
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/488142
https://reelgosu.com/board_peJN24/272045
https://reelgosu.com/board_peJN24/272049
https://ttmt.net/crypto_lab_2F/403488
https://www.chirorg.com/?document_srl=6588
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=63718
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=63741
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=63751
http://indiefilm.kr/xe/board/47925
http://iymc.or.kr/freeboard/86117
http://research.kiu.ac.kr/?document_srl=26179
http://shinilspring.com/board_qsfb01/45764
http://shinilspring.com/board_qsfb01/45804
https://members.fbhaters.com/index.php?topic=83468.0
http://www.theparrotcentre.com/forum/index.php?topic=485082.0
http://www.remify.app/foro/index.php?topic=246614.0
http://roikjer.com/forum/index.php?PHPSESSID=5l5b5s2gj19cau4t8np1nidka2&topic=843101.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s4-u2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(a-etoo-(got)-8-eo-1-e)-a-etoo-(got)-8-eo-1-e-f2o9/msg561272/
http://www.critico-expository.com/forum/index.php?topic=8494.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qx7-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jm5-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-10-05-2019/
https://worldtaxi.org/2019/05/09/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-s3-j9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://HyUa.1fps.icu/l/szIaeDC
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/gumdanapt/18958
http://xn--ok1bpqi43ahtb.net/board_EkDG82/45149
http://yooseok.com/?document_srl=317203
http://yooseok.com/board_BkvT46/317198
https://esel.gist.ac.kr/esel2/board_hmgj23/20806
https://khuyenmaikk13.info/index.php?topic=203770.0
https://nple.com/xe/pds/4357
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90ki7%e3%80%91-%d0%b8%d0%b3/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90rq1%e3%80%91/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90rn1%e3%80%91/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90cy9%e3%80%91/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90lj7%e3%80%91-%d0%b8%d0%b3/
https://saltriverbg.com/2019/05/16/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90bl9%e3%80%91/
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=63271
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=63322
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=63348
http://emjun.com/index.php?mid=hangtotal&document_srl=38423
http://emjun.com/index.php?mid=hangtotal&document_srl=38511
http://sexfork.com/en/uncategorized/ertugrul-145-seriya-nm8-ertugrul-145-seriya/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qx8-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-36/
http://otitismediasociety.org/forum/index.php?topic=156633.0
http://demo.caribe.vps-private.net/blog/milliardy-4-sezon-10-seriya-l7-h4-milliardy-4-sezon-10-seriya-milliardy-4-sezon-10-seriya
http://www.newb.northstarchiangrai.com/index.php?PHPSESSID=9vh4jlephv4jgahf3gfd6v21a7&topic=23713.0
http://8.droror.co.il/uncategorized/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p1-s7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=688553.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h2-x0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qb0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://HyUa.1fps.icu/l/szIaeDC
http://www.ekemoon.com/148415/052320190306/
http://matinbank.ir/?option=com_k2&view=itemlist&task=user&id=4483022
http://rudraautomation.com/index.php/component/k2/author/107391
https://forums.letstalkbeats.com/index.php?topic=67336.0
http://highlanderonline.cmshelplive.net/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iimd-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd/
http://emjun.com/index.php?mid=hangtotal&document_srl=30367
http://emjun.com/index.php?mid=hangtotal&document_srl=30382
http://emjun.com/index.php?mid=hangtotal&document_srl=30461
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1691255
http://teambuildingpremium.com/forum/index.php?topic=832898.0
http://teambuildingpremium.com/forum/index.php?topic=832906.0
http://vn7.vn/?document_srl=82364
http://w9builders.co.uk/index.php/component/k2/itemlist/user/75912
http://www.arunagreen.com/?option=com_k2&view=itemlist&task=user&id=522315
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=819887
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/820192
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=63078
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=63080
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/322857
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/257922
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=556133
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/18565
http://xplorefitness.com/blog/%C2%AB%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-93-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-14-05-2019-q8-%C2%AB%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-93-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2628842
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2628942
http://arunagreen.com/index.php/component/k2/itemlist/user/507743
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/525030
http://corumotoanahtar.com/component/k2/itemlist/user/1771
http://153.120.114.241/eso/index.php/16880606-voron-kuzgun-12-seria-uxce-voron-kuzgun-12-seria
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7308668
http://www.m1avio.com/index.php/component/k2/itemlist/user/3600698
http://highlanderonline.cmshelplive.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8d%d1%84%d0%b8%d1%80-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-4/
http://dev.aabn.org.gh/component/k2/itemlist/user/540340
https://khuyenmaikk13.info/index.php?topic=180612.0
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=495833
http://ovotecegg.com/component/k2/itemlist/user/115614
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3307046
http://www.ds712.net/guest/index.php?document_srl=60864&mid=guest07
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=60828
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=60920
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=60935
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=60970
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/322882
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=556770
http://corumotoanahtar.com/component/k2/itemlist/user/1780.html
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=326676
http://dev.aabn.org.gh/component/k2/itemlist/user/584285
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1181967
http://jiquilisco.org/index.php/component/k2/itemlist/user/4854
http://jiquilisco.org/index.php/component/k2/itemlist/user/4856
http://jiquilisco.org/index.php/component/k2/itemlist/user/4908
http://forum.politeknikgihon.ac.id/index.php?topic=30557.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jj2-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://forum.elexlabs.com/index.php?topic=21834.0
http://myrechockey.com/forums/index.php?topic=94966.0
https://reficulcoin.com/index.php?topic=22314.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-c2-l6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90cs3%e3%80%91-%d0%b8%d0%b3/
https://sanp.pro/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
https://nextezone.com/index.php?topic=42324.0
http://www.critico-expository.com/forum/index.php?topic=6326.0
http://otitismediasociety.org/forum/index.php?topic=150124.0
http://forum.elexlabs.com/index.php?topic=22399.0
http://menulisilmiah.net/%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-09-05-2019/
http://danielmillsap.com/forum/index.php?topic=1015450.0
http://www.critico-expository.com/forum/index.php?topic=7616.0
https://woodland.org.ua/groups/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q4-r3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://otitismediasociety.org/forum/index.php?topic=151758.0
http://www.theparrotcentre.com/forum/index.php?topic=487561.0
http://danielmillsap.com/forum/index.php?topic=1013764.0
http://forum.elexlabs.com/index.php?topic=18466.0
https://worldtaxi.org/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-i1-p3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://bobr.site/index.php?topic=123974.0
http://roikjer.com/forum/index.php?topic=838179.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q0-v7-%d0%b8%d0%b3%d1%80%d0%b0/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uo6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://otitismediasociety.org/forum/index.php?topic=149012.0
https://polyframetrade.co.uk/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-l0-g8-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4/
http://HyUa.1fps.icu/l/szIaeDC
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-h9-u4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-i8-g2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
https://reficulcoin.com/index.php?topic=18150.0
http://uberdrivers.net/forum/index.php?topic=262097.0
https://reficulcoin.com/index.php?topic=17017.0
http://myrechockey.com/forums/index.php?topic=92153.0
http://forum.elexlabs.com/index.php?topic=17332.0
https://prelease.club/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://roikjer.com/forum/index.php?PHPSESSID=b2d86552u9i3r2mja64fp9g061&topic=841786.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-n2-g4-%d0%b8%d0%b3%d1%80%d0%b0/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fr4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-er7-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://reficulcoin.com/index.php?topic=21082.0
http://myrechockey.com/forums/index.php?topic=91982.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-10/
https://reficulcoin.com/index.php?topic=22173.0
http://otitismediasociety.org/forum/index.php?topic=156543.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=59e84f526679c021c1c5f79eae4628a8&topic=215770.0
https://khuyenmaikk13.info/index.php?topic=187602.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=683127.0
https://hackersuniversity.net/index.php/topic,10125.0.html
http://forum.politeknikgihon.ac.id/index.php?topic=29778.0
http://menulisilmiah.net/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-10-05-2019-3/
http://partemp.com/en/groups/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v8-o7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://otitismediasociety.org/forum/index.php?topic=150152.0
https://reficulcoin.com/index.php?topic=18830.0
http://menulisilmiah.net/09-05-2019-%d0%bf%d0%be%d0%b4%d1%81%d1%83%d0%b4%d0%b8%d0%bc%d1%8b%d0%b9-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-3/
http://www.deliberarchia.org/forum/index.php?topic=1020671.0
http://forum.elexlabs.com/index.php?topic=22049.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.tessabannampad.go.th/webboard/index.php?topic=201922.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ek1-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://prelease.club/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://danielmillsap.com/forum/index.php?topic=1028914.0
http://forum.elexlabs.com/index.php?topic=17888.0
http://help.stv.ru/index.php?PHPSESSID=fe6b8e0cbef6bfe69986a5812a7e5cb8&topic=140524.0
https://prelease.club/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
https://nextezone.com/index.php?topic=46664.0
https://nextezone.com/index.php?action=profile;u=4392
http://www.tessabannampad.go.th/webboard/index.php?topic=196474.0
http://www.hoonthaitoday.com/forum/index.php?topic=223392.0
http://teambuildingpremium.com/forum/index.php?topic=816545.0
https://luckychancerescue.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-z9-w2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
https://prelease.club/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gu0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://nextezone.com/index.php?topic=39715.0
https://reficulcoin.com/index.php?topic=21379.0
https://reficulcoin.com/index.php?topic=22871.0
http://roikjer.com/forum/index.php?topic=840883.0
https://members.fbhaters.com/index.php?topic=84164.0
http://www.remify.app/foro/index.php?topic=276184.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/to-oot-5-e-(-r1-to-oot-5-e/
http://www.sharmaraco.com/blog/%E2%80%9E%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-13-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-online-a3-z7-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-13-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-13
https://nextezone.com/index.php?action=profile;u=4195
https://prelease.club/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x7-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
http://myrechockey.com/forums/index.php?topic=91478.0
https://danceplanet.se/commodore/index.php?topic=17742.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z2-p9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
https://prelease.club/hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t1-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
https://khuyenmaikk13.info/index.php?topic=190674.0
http://poselokgribovo.ru/forum/index.php?topic=749499.0
http://forum.bmw-e60.eu/index.php?topic=6050.0
http://otitismediasociety.org/forum/index.php?topic=149099.0
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-h0-b9-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://forum.elexlabs.com/index.php?topic=18004.0
http://danielmillsap.com/forum/index.php?topic=1016449.0
https://reficulcoin.com/index.php?topic=20464.0
http://www.deliberarchia.org/forum/index.php?topic=1009352.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=d3c5dbb17682c21d331e7774d6394824&topic=218856.0
http://forum.elexlabs.com/index.php?topic=21722.0
https://members.fbhaters.com/index.php/topic,84379.0.html
http://roikjer.com/forum/index.php?PHPSESSID=29qgjh01u27t8k8t9ec830d977&topic=863298.0
http://help.stv.ru/index.php?PHPSESSID=372e10fd77c79516c7ce86369c21124e&topic=140416.0
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ru7-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8/
http://HyUa.1fps.icu/l/szIaeDC
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=31240.0
http://uberdrivers.net/forum/index.php?topic=248556.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=4ef9bf8234e439e6776ab7c069fc6495&topic=218533.0
http://www.hoonthaitoday.com/forum/index.php?topic=225680.0
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o0-u7-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://forum.elexlabs.com/index.php?topic=21278.0
https://nextezone.com/index.php?action=profile;u=5556
https://prelease.club/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y6-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-49/
http://www.deliberarchia.org/forum/index.php?topic=999307.0
https://members.fbhaters.com/index.php?topic=88733.0
https://reficulcoin.com/index.php?topic=17162.0
https://reficulcoin.com/index.php?topic=19929.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=4af0433532787cc2d8cc0c59b2b14c4d&topic=222172.0
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r7-f9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.deliberarchia.org/forum/index.php?topic=990855.0
https://members.fbhaters.com/index.php?topic=83469.0
http://teambuildingpremium.com/forum/index.php?topic=795389.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-59/
http://help.stv.ru/index.php?PHPSESSID=e4a7a97dd962eb425c91c07772f2937f&topic=140183.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-6/
http://www.tessabannampad.go.th/webboard/index.php?topic=199200.0
http://forum.politeknikgihon.ac.id/index.php?topic=29892.0
http://www.critico-expository.com/forum/index.php?topic=8029.0
http://vervetama.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p2-p8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xv7-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y8-h9-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://www.deliberarchia.org/forum/index.php?topic=997880.0
http://roikjer.com/forum/index.php?PHPSESSID=bmpdvcpntqblqta0o76nj224q7&topic=858065.0
http://photogrotto.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-p4-x9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://d2bchannel.co.in/blog/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e3-r8-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=31673.0
http://uberdrivers.net/forum/index.php?topic=246182.0
http://HyUa.1fps.icu/l/szIaeDC
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/49901
https://szenarist.ru/forum/index.php?topic=205954.0
http://www.ekemoon.com/151231/050820190707/
http://153.120.114.241/eso/index.php/16862682-voron-kuzgun-14-seria-iggu-voron-kuzgun-14-seria
http://www.ekemoon.com/148339/052220195606/
http://skylinecam.co.kr/photo/56520
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=77492
http://www.jesusonly.life/calendar/74874
http://www.jesusonly.life/calendar/74920
http://www.josephmaul.org/menu41/61307
http://www.josephmaul.org/menu41/61500
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=474455
http://www.sp1.football/index.php?mid=faq&document_srl=90977
http://www.sp1.football/index.php?mid=faq&document_srl=91026
http://xn--ok1bpqi43ahtb.net/board_eASW07/62188
https://prelease.club/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dhdy-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://prelease.club/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ykcr-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://prelease.club/%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-56-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xmaf-%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-56-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.tedyun.com/xe/?document_srl=154724
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/58351
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4846276
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=602460
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/581240
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3303157
http://bitpark.co.kr/board_IzjM66/3783931
http://153.120.114.241/eso/index.php/16880056-edinoe-serdce-tek-yurek-20-seria-ydnc-edinoe-serdce-tek-yurek-2
http://cccpvideo.forumside.com/index.php?topic=280.0
http://mediaville.me/index.php/component/k2/itemlist/user/219971
http://smartacity.com/component/k2/itemlist/user/24157
http://hotelnomadpalace.com/component/k2/itemlist/user/19946
http://ovotecegg.com/component/k2/itemlist/user/117931
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/50940
http://ptu.imoove.kr/ko/content/%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-live-%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB332024
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2583180
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=285662
http://soc-human.kz/index.php/component/k2/itemlist/user/1644411
http://fbpharm.net/index.php/component/k2/itemlist/user/16782
http://www.ekemoon.com/146529/051920191906/
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12894
http://molweb.ru/groups/xolostyak-9-sezon-10-vypuskukraina-icxolostyak-9-sezon-10-vypuskukraina07-xolostyak-9-sezon-10-vypuskukraina/
http://withinfp.sakura.ne.jp/eso/index.php/16884235-voron-kuzgun-17-seria-fsqn-voron-kuzgun-17-seria/0
http://macdistri.com/index.php/component/k2/itemlist/user/310000
http://married.dike.gr/index.php/component/k2/itemlist/user/46849
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3307538
http://www.supergondolas.com.br/index.php/component/k2/itemlist/user/203584
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/203411
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4849856
http://www.quattroandpartners.it/component/k2/itemlist/user/1037570
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1995908
http://withinfp.sakura.ne.jp/eso/index.php/16872156-holostak-9-sezon-12-vypusk-05052019-q4-holostak-9-sezon-12-vypu
http://highlanderonline.cmshelplive.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5-7/
http://healthyteethpa.org/component/k2/itemlist/user/5331262
http://www.vivelabmanizales.com/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e7-%d1%82%d0%be%d0%bb%d1%8f-%d1%80/
http://www.deliberarchia.org/forum/index.php?topic=962213.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2562944
https://khuyenmaikk13.info/index.php?topic=183772.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=285847
http://mobility-corp.com/index.php/component/k2/itemlist/user/2520811
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/221638
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=40217
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1338222
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=96095
http://mediaville.me/index.php/component/k2/itemlist/user/220079
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1542744
http://healthyteethpa.org/component/k2/itemlist/user/5331043
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2571772
http://www.deliberarchia.org/forum/index.php?topic=966534.0
http://withinfp.sakura.ne.jp/eso/index.php/16871724-voron-kuzgun-13-seria-vfjl-voron-kuzgun-13-seria/0
http://8.droror.co.il/uncategorized/%d1%81%d0%be%d0%b4%d0%b5%d1%80%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-li4z-%d1%81%d0%be%d0%b4%d0%b5%d1%80%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-9-%d1%81%d0%b5%d1%80/
http://smartacity.com/component/k2/itemlist/user/23997
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1861592
http://8.droror.co.il/uncategorized/%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-58-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wagm-%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-58-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/483767
http://dev.aabn.org.gh/component/k2/itemlist/user/546038
http://salescoach.ro/content/%C2%AB%D0%B3%D0%B4%D0%B5-%D0%BF%D0%BE%D1%81%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-%D1%83%D0%BA%D1%80%D0%B0%D0%B8%D0%BD%D0%B0%C2%BB-rh%C2%AB%D0%B3%D0%B4%D0%B5-%D0%BF%D0%BE%D1%81%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-%D1%83%D0%BA%D1%80%D0%B0%D0%B8%D0%BD%D0%B0%C2%BB17-%D0%B3%D0%B4%D0%B5
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42325
http://roikjer.com/forum/index.php?PHPSESSID=q4o1j8brdtsvdm90vdbme568n2&topic=829293.0
https://www.regalepadova.it/index.php/component/k2/itemlist/user/6872
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/303331
http://www.ekemoon.com/145275/051620193006/
https://khuyenmaikk13.info/index.php?topic=183618.0
https://mcsetup.tk/bbs/index.php?topic=243663.0
http://8.droror.co.il/uncategorized/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dh7%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=500533
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1123134
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3297047
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3723678
http://dev.aabn.org.gh/component/k2/itemlist/user/538665
http://www.spazioad.com/component/k2/itemlist/user/7215322
http://poselokgribovo.ru/forum/index.php?topic=735700.0
http://thermoplast.envolgroupe.com/component/k2/author/71105
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/199748
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=791544
https://l2thalassic.org/Forum/index.php?topic=618.0
http://mediaville.me/index.php/component/k2/itemlist/user/207196
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1545013
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/200818
http://153.120.114.241/eso/index.php/16861618-voron-kuzgun-10-seria-wbgv-voron-kuzgun-10-seria
http://www.vivelabmanizales.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81-14/
http://guiadetudo.com/index.php/component/k2/itemlist/user/11163
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3294137
http://smartacity.com/component/k2/itemlist/user/14097
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=495702
http://ptu.imoove.kr/ko/content/%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-15-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB-%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-15-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB331780
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4851190
http://dohairbiz.com/en/component/k2/itemlist/user/2710501.html
http://www.deliberarchia.org/forum/index.php?topic=972279.0
http://rudraautomation.com/index.php/component/k2/author/102563
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/472353
http://rudraautomation.com/index.php/component/k2/author/118397
http://healthyteethpa.org/component/k2/itemlist/user/5329643
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1861102
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1114408
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3731865
http://www.ekemoon.com/146251/051820195006/
http://arunagreen.com/?option=com_k2&view=itemlist&task=user&id=422612
http://community.viajar.tur.br/index.php?p=/profile/zacbelling
http://www.autospa.lv/index.php/lv/component/k2/itemlist/user/9291
http://withinfp.sakura.ne.jp/eso/index.php/16886737-otel-toledo-4-seria-06052019-g2-otel-toledo-4-seria
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43071
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-21-%d1%81%d0%b5%d1%80%d0%b8/
http://seoksoononly.dothome.co.kr/qna/752808
http://xplorefitness.com/blog/%D0%BD%D0%BE%D0%B2%D0%B8%D0%BD%D0%BA%D0%B0-%D0%BD%D0%B8%D0%BA%D0%BE%D0%B3%D0%B4%D0%B0-%D0%BD%D0%B5-%D0%B3%D0%BE%D0%B2%D0%BE%D1%80%D0%B8-%C2%AB%D0%BD%D0%B8%D0%BA%D0%BE%D0%B3%D0%B4%D0%B0%C2%BB-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-q5-%D0%BD%D0%B8%D0%BA%D0%BE%D0%B3%D0%B4%D0%B0-%D0%BD%D0%B5-%D0%B3%D0%BE%D0%B2%D0%BE%D1%80%D0%B8-%C2%AB%D0%BD%D0%B8%D0%BA%D0%BE%D0%B3%D0%B4%D0%B0%C2%BB-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://arunagreen.com/index.php/component/k2/itemlist/user/424497
http://teambuildingpremium.com/forum/index.php?topic=774394.0
http://jiquilisco.org/index.php/component/k2/itemlist/user/6370
http://jiquilisco.org/index.php/component/k2/itemlist/user/6460
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/101471
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/101540
http://w9builders.co.uk/index.php/component/k2/itemlist/user/75716
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1598683
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1423686
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=831174
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=831214
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3364653
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=2591
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/187902
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=500284
http://www.ekemoon.com/144619/051120190806/
http://withinfp.sakura.ne.jp/eso/index.php/16861229-hdvideo-taemnici-81-seria/0
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3629785
http://haniel.ir/index.php/component/k2/itemlist/user/74679
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1334373
http://married.dike.gr/index.php/component/k2/itemlist/user/51927
http://www.camaracoyhaique.cl/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b4-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://hotelnomadpalace.com/index.php/component/k2/itemlist/user/19954
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1126829
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=504293
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/480503
http://proxima.co.rw/index.php/component/k2/itemlist/user/565280
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=15314
http://mediaville.me/index.php/component/k2/itemlist/user/207514
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=136058
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=27418
http://corumotoanahtar.com/component/k2/itemlist/user/2840
http://fbpharm.net/index.php/component/k2/itemlist/user/43624
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1819504
http://mobility-corp.com/index.php/component/k2/itemlist/user/2599872
http://proxima.co.rw/index.php/component/k2/itemlist/user/630587
http://www.arunagreen.com/?option=com_k2&view=itemlist&task=user&id=521867
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1423227
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=830869
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=111426
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=111735
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=43662
http://skylinecam.co.kr/photo/32314
http://www.ekemoon.com/196143/050220193216/
http://trunk.www.volkalize.com/members/dustyheist4836/
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=22439
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1785118
http://www.quattroandpartners.it/component/k2/itemlist/user/1076522
http://menulisilmiah.net/%d0%b4%d0%be%d1%87%d0%ba%d0%b8-%d0%bc%d0%b0%d1%82%d0%b5%d1%80%d0%b8-%d0%b4%d0%be%d1%87%d0%ba%d0%b8-%d0%bc%d0%b0%d1%82%d0%b5%d1%80i-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-no2%d0%b4%d0%be%d1%87/
http://menulisilmiah.net/%d0%bc%d0%b5%d1%80%d1%82%d0%b2%d0%be%d0%b5-%d0%be%d0%b7%d0%b5%d1%80%d0%be-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dg4%d0%bc%d0%b5%d1%80%d1%82%d0%b2%d0%be%d0%b5-%d0%be%d0%b7%d0%b5%d1%80%d0%be-9-%d1%81/
http://menulisilmiah.net/%d0%bc%d0%b5%d1%80%d1%82%d0%b2%d0%be%d0%b5-%d0%be%d0%b7%d0%b5%d1%80%d0%be-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yd4%d0%bc%d0%b5%d1%80%d1%82%d0%b2%d0%be%d0%b5-%d0%be%d0%b7%d0%b5%d1%80%d0%be-9-%d1%81/
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gr8%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ih7%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nh4%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wm5%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3294195
http://dev.aabn.org.gh/component/k2/itemlist/user/513594
http://macdistri.com/index.php/component/k2/itemlist/user/314788
http://poselokgribovo.ru/forum/index.php?topic=739828.0
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=187012
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=51803
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1015300
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/473413
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1346711
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=251509
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/251558
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1705976
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1705982
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1599706
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1006341
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=116458
http://teambuildingpremium.com/forum/index.php?topic=771954.0
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291031
http://www.crnmedia.es/component/k2/itemlist/user/84755
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3702628
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-17-%d1%81%d0%b5-4/
http://smartacity.com/component/k2/itemlist/user/18075
http://thermoplast.envolgroupe.com/component/k2/author/66998
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=109412
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/256641
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/256744
https://cfcestradareal.com.br/?option=com_k2&view=itemlist&task=user&id=17127
http://bath-family.com/?document_srl=1491
http://bath-family.com/photo_zone/1496
http://bebopindia.com/notcie/1654
http://emjun.com/index.php?mid=hangtotal&document_srl=4466
http://www.deliberarchia.org/forum/index.php?topic=1028932.0
http://www.deliberarchia.org/forum/index.php?topic=1028936.0
http://soc-human.kz/index.php/component/k2/itemlist/user/1681590
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=817054
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-quattroporte%C2%BB-ml%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-quattroporte%C2%BB68
http://www.vivelabmanizales.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-z8-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be/
https://l2thalassic.org/Forum/index.php?topic=1119.0
http://8.droror.co.il/uncategorized/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-20-%d1%81%d0%b5/
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/769462
http://xplorefitness.com/blog/live-%D0%BF%D0%BE-%D0%B7%D0%B0%D0%BA%D0%BE%D0%BD%D0%B0%D0%BC-%D0%B2%D0%BE%D0%B5%D0%BD%D0%BD%D0%BE%D0%B3%D0%BE-%D0%B2%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-4-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-k8-%D0%BF%D0%BE-%D0%B7%D0%B0%D0%BA%D0%BE%D0%BD%D0%B0%D0%BC-%D0%B2%D0%BE%D0%B5%D0%BD%D0%BD%D0%BE%D0%B3%D0%BE-%D0%B2%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-4-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://www.ekemoon.com/146229/051820194806/
http://sindicatodechoferespichincha.com.ec/index.php/component/k2/itemlist/user/6682411
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=494640
http://poselokgribovo.ru/forum/index.php?topic=715285.0
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1995132
https://sanp.pro/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rodj-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd/
http://menulisilmiah.net/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ix4%d0%bd/
http://condolencias.servisa.es/1-06-05-2019-i2-1
http://mobility-corp.com/index.php/component/k2/itemlist/user/2520393
http://www.datascientist.co.kr/?document_srl=86775
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1580779
http://www.deliberarchia.org/forum/index.php?topic=1028534.0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=618220
http://danielmillsap.com/forum/index.php?topic=1027873.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1383153
http://thermoplast.envolgroupe.com/component/k2/author/104689
http://moavalve.co.kr/faq/8951
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=62530
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=288668
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1547494
http://www.camaracoyhaique.cl/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-93-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kg3%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-93-%d1%81%d0%b5%d1%80%d0%b8%d1%8f07-05-2019/
http://mobility-corp.com/index.php/component/k2/itemlist/user/2511062
http://smartacity.com/component/k2/itemlist/user/15985
http://poselokgribovo.ru/forum/index.php?topic=734750.0
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/52088
http://rockndata.net/UserProfile/tabid/61/userId/18181531/Default.aspx
http://poselokgribovo.ru/forum/index.php?topic=733277.0
http://xplorefitness.com/blog/%C2%AB%D0%B5%D0%B4%D0%B8%D0%BD%D0%BE%D0%B5-%D1%81%D0%B5%D1%80%D0%B4%D1%86%D0%B5-tek-y%C3%BCrek-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-qjvu-%C2%AB%D0%B5%D0%B4%D0%B8%D0%BD%D0%BE%D0%B5-%D1%81%D0%B5%D1%80%D0%B4%D1%86%D0%B5-tek-y%C3%BCrek-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://www.quattroandpartners.it/component/k2/itemlist/user/1097566
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=58142
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/314988
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/248115
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/248127
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/19352
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2609885
http://arunagreen.com/?option=com_k2&view=itemlist&task=user&id=484897
http://arunagreen.com/index.php/component/k2/itemlist/user/484885
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/509757
http://dohairbiz.com/?option=com_k2&view=itemlist&task=user&id=2731127
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/17965
http://www.jesusonly.life/calendar/43157
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=555523
http://dev.aabn.org.gh/component/k2/itemlist/user/566013
http://withinfp.sakura.ne.jp/eso/index.php/16864580-po-zakonam-voennogo-vremeni-3-sezon-4-seria-05052019-x9-po-zako
https://l2thalassic.org/Forum/index.php?topic=1640.0
http://withinfp.sakura.ne.jp/eso/index.php/16860809-vetrenyj-hercai-10-seria-npdg-vetrenyj-hercai-10-seria
http://webp.online/index.php?topic=50691.0
http://myrechockey.com/forums/index.php?topic=90194.0
http://poselokgribovo.ru/forum/index.php?topic=728561.0
http://gtupuw.org/index.php/component/k2/itemlist/user/1845877
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1554007
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=601814
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/57390
https://alvarogarciatorero.com/component/k2/itemlist/user/48717
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3340381
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=19339
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2609785
http://arunagreen.com/index.php/component/k2/itemlist/user/485021
http://arunagreen.com/index.php/component/k2/itemlist/user/485026
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=51303
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/509637
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=2015101
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=2015118
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1907080
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=39740
http://roikjer.com/forum/index.php?PHPSESSID=bh8n3nooiv2orqqre58h3e4hb2&topic=853918.0
http://www.jesusonly.life/calendar/72375
http://www.deliberarchia.org/forum/index.php?topic=1023170.0
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1912622
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=699887.0
http://dev.aabn.org.gh/component/k2/itemlist/user/597798
http://forum.digamahost.com/index.php?topic=121959.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=44846
https://szenarist.ru/forum/index.php?topic=206148.0
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=19901
http://mobility-corp.com/index.php/component/k2/itemlist/user/2534626
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1367308
http://www.m1avio.com/?option=com_k2&view=itemlist&task=user&id=3615476
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1038437
https://l2thalassic.org/Forum/index.php?topic=588.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=288458
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=79123
http://www.ekemoon.com/143349/052320192005/
http://forum.digamahost.com/index.php?topic=110011.0
http://dev.aabn.org.gh/component/k2/itemlist/user/517294
http://associationsila.org/index.php/component/k2/itemlist/user/297653
http://153.120.114.241/eso/index.php/16875026-vetrenyj-hercai-16-seria-fjaf-vetrenyj-hercai-16-seria
http://dev.aabn.org.gh/component/k2/itemlist/user/567630
http://dev.aabn.org.gh/component/k2/itemlist/user/567669
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1907395
http://fbpharm.net/index.php/component/k2/itemlist/user/32124
http://fbpharm.net/index.php/component/k2/itemlist/user/32213
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1776435
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=295859
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1164064
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=316629
https://khuyenmaikk13.info/index.php?topic=185973.0
http://www.critico-expository.com/forum/index.php?topic=11790.0
https://khuyenmaikk13.info/index.php?topic=186966.0
http://otitismediasociety.org/forum/index.php?topic=152241.0
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-online-h2-r1-%d0%b8/
http://menulisilmiah.net/%d0%b4%d0%b5%d0%b2%d1%8f%d1%82%d1%8c-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b5%d0%b9-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-09-05-2019-7/
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-8-eo-7-e-a-etoo-8-eo-7-e-a1h3/?PHPSESSID=me3ejoq9s4rgl1j6bl0cd59v34
http://roikjer.com/forum/index.php?PHPSESSID=hu0knruhv5dbd0ki1tcjea1fo4&topic=864440.0
https://prelease.club/hd-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80/
https://nextezone.com/index.php?topic=39849.0
https://reficulcoin.com/index.php?topic=19376.0
https://nextezone.com/index.php?topic=40543.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=acd31dab21ba89bbe5b692c6197d6c27&topic=223018.0
http://www.deliberarchia.org/forum/index.php?topic=1019769.0
http://help.stv.ru/index.php?PHPSESSID=f7ca5cbdbf45ef2e0ef016cfc07b1d62&topic=140250.0
http://uberdrivers.net/forum/index.php?topic=262432.0
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k6-%d1%81/
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t9-%d1%81/
https://reficulcoin.com/index.php?topic=20130.0
http://danielmillsap.com/forum/index.php?topic=995355.0
https://members.fbhaters.com/index.php?topic=89217.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j2-j5-%d0%b8%d0%b3%d1%80/
http://eugeniocolazzo.it/forum/index.php?topic=124505.0
http://www.studyxray.com/?document_srl=88521
http://www.studyxray.com/Sangdam/88554
http://www.taeshinmedia.com/index.php?document_srl=3286312&mid=genealogy_faq
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3286378
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=707045.0
http://xn--ok1bpqi43ahtb.net/board_eASW07/84608
http://xn--ok1bpqi43ahtb.net/board_eASW07/84634
http://xn--ok1bpqi43ahtb.net/board_eASW07/84679
http://xn--ok1bpqi43ahtb.net/board_eASW07/84707
http://xn--ok1bpqi43ahtb.net/board_eASW07/84725
http://xn--ok1bpqi43ahtb.net/board_eASW07/84757
http://2872870.com/est/9746
http://2872870.com/est/9754
http://eugeniocolazzo.it/forum/index.php?topic=138766.0
http://HyUa.1fps.icu/l/szIaeDC
http://themasters.pro/file_01/12656
http://themasters.pro/file_01/12741
http://www.artangel.co.kr/?document_srl=6058
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=6041
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=6054
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=6062
http://www.hsaura.com/noty/65827
http://www.hsaura.com/noty/65855
http://www.hsaura.com/noty/65870
http://www.hsaura.com/noty/65889
http://www.hsaura.com/noty/65928
http://www.jesusonly.life/?document_srl=66809
http://www.jesusonly.life/?document_srl=66862
http://www.jesusonly.life/calendar/66680
http://www.jesusonly.life/calendar/66782
http://www.jesusonly.life/calendar/66843
http://www.jesusonly.life/calendar/66847
http://www.jesusonly.life/calendar/66888
http://www.jesusonly.life/calendar/66903
http://zanoza.h1n.ru/2019/05/16/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m3-n9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
https://mencoin.net/talk_fm/20615
https://mencoin.net/talk_fm/20653
https://saltriverbg.com/2019/05/16/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j4-y9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://saltriverbg.com/2019/05/16/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y2-q4-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://bath-family.com/photo_zone/14933
http://bath-family.com/photo_zone/14997
http://bethanychurch.kr/board_vpkl62/5523
http://eugeniocolazzo.it/forum/index.php?topic=134785.0
http://f-tube.info/board/65378
http://flashboot.ru/forum/index.php?topic=95256.0
http://forum.elexlabs.com/index.php/topic,31042.0.html
http://forum.elexlabs.com/index.php?topic=31078.0
http://foxy-tv.com/?document_srl=19808
http://hyeonjun.co.kr/menu3/22073
http://indiefilm.kr/xe/board/41324
http://myrechockey.com/forums/index.php?topic=103501.0
http://myrechockey.com/forums/index.php?topic=103504.0
http://poselokgribovo.ru/forum/index.php?topic=793500.0
http://poselokgribovo.ru/forum/index.php?topic=793529.0
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=21433
http://HyUa.1fps.icu/l/szIaeDC
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=2788
http://www.gforgirl.com/xe/?document_srl=1604
http://www.golden-nail.co.kr/?document_srl=1448
http://www.hicleaning.kr/board_wash/9516
http://www.hicleaning.kr/board_wash/9521
http://www.hicleaning.kr/board_wash/9535
http://www.hicleaning.kr/board_wash/9540
http://www.hsaura.com/license/2895
http://www.hsaura.com/license/2909
http://www.hsaura.com/license/2913
http://www.hsaura.com/license/2942
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zi1-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://xn--l1adgmc.xn----9sbdbmdznsj5c5bxd7b.xn--p1ai/index.php?topic=10895.0
http://roikjer.com/forum/index.php?PHPSESSID=0o2u3toca3fh4vk24br47q59u0&topic=855231.0
https://www.limscave.com/forum/viewtopic.php?f=6&t=31700&view=print
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s6-y7-%d0%b8%d0%b3%d1%80/
http://forum.elexlabs.com/index.php?topic=22489.0
http://forum.byehaj.hu/index.php?topic=88990.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=94f4674b11c2f78c6affa13aa98d8561&topic=733.0
https://hackersuniversity.net/index.php?topic=9353.0
https://nextezone.com/index.php?topic=40370.0
https://www.limscave.com/forum/viewtopic.php?f=6&t=31800&view=print
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=e6c64cb1c07e02873dad7d519996048e&topic=1049.0
https://worldtaxi.org/2019/05/10/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-o0-u1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
https://khuyenmaikk13.info/index.php?topic=186437.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.betospot.com/index.php?mid=board_wFHn31&document_srl=2244
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=32857
http://www.deliberarchia.org/forum/index.php?topic=1028235.0
http://www.deliberarchia.org/forum/index.php?topic=1028238.0
http://www.deliberarchia.org/forum/index.php?topic=1028242.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=3144
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=3154
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=3183
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=3197
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=3231
http://www.generalwalker.org/board_Zyyd91/989
http://www.gforgirl.com/xe/?document_srl=1803
http://www.gforgirl.com/xe/?document_srl=1822
http://www.gforgirl.com/xe/poster/1807
http://www.gforgirl.com/xe/poster/1811
http://www.golden-nail.co.kr/press/1617
http://www.golden-nail.co.kr/press/1621
https://reficulcoin.com/index.php?topic=18340.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-f1-a8-%d0%b8%d0%b3%d1%80/
http://www.critico-expository.com/forum/index.php?topic=8802.0
https://forum.shaiyaslayer.tk/index.php?topic=117240.0
http://www.theocraticamerica.org/forum/index.php?topic=28668.0
https://worldtaxi.org/2019/05/09/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e5-p9-%d0%b8%d0%b3%d1%80/
http://www.ekemoon.com/173253/051720191310/
http://myrechockey.com/forums/index.php?topic=94855.0
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xl4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-146-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://photogrotto.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ez4-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-147-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://roikjer.com/forum/index.php?PHPSESSID=d49jebr9vk8q50niblmghqn3j4&topic=847771.0
https://reficulcoin.com/index.php?topic=17843.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5-12/
http://forum.politeknikgihon.ac.id/index.php?topic=31054.0
http://www.tessabannampad.go.th/webboard/index.php?topic=204012.0
http://forum.politeknikgihon.ac.id/index.php?topic=31063.0
https://polyframetrade.co.uk/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-watch-q0-q1-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4/
http://roikjer.com/forum/index.php?PHPSESSID=qdcs1gmngela28llg4hq49cga6&topic=862105.0
http://ru-realty.com/forum/index.php?PHPSESSID=laeu0ri2del9o1g798noc7l664&topic=478348.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=21f24fd6ca666adfe11bcb6c19d2a4bf&topic=227197.0
http://www.sharmaraco.com/blog/%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-m8-o1-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://forum.elexlabs.com/index.php?topic=22442.0
http://roikjer.com/forum/index.php?PHPSESSID=dnqnmq481vlib6dr2odibpkct6&topic=849178.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-8-eo-2-e-a-etoo-8-eo-2-e-m9t7/?PHPSESSID=bm8iassbuausjkpicku6pe0uc1
http://forum.kopkargobel.com/index.php?topic=7163.0
http://HyUa.1fps.icu/l/szIaeDC
http://xn----3x5er9r48j7wemud0a387h.com/news/611
http://xn--2e0bk61btjo.com/notice/1402
http://xn--2e0bk61btjo.com/notice/1408
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/473655
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/473669
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/473679
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=697
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=701
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=705
http://xn--ok1bpqi43ahtb.net/board_EkDG82/2502
http://xn--ok1bpqi43ahtb.net/board_EkDG82/2506
http://xn--ok1bpqi43ahtb.net/board_EkDG82/2530
http://xn--ok1bpqi43ahtb.net/board_YXVi77/2519
http://xn--ok1bpqi43ahtb.net/board_eASW07/2510
http://xn--ok1bpqi43ahtb.net/board_eASW07/2525
http://ye-dream.com/qa/2231
http://ye-dream.com/qa/2235
http://ye-dream.com/qa/2239
http://ye-dream.com/qa/2243
http://ye-dream.com/qa/2247
https://members.fbhaters.com/index.php?topic=87373.0
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-f4-u0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://forum.elexlabs.com/index.php?topic=18371.0
http://metropolis.ga/index.php?topic=6930.0
http://www.teedinubon.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-k4-u2-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
https://nextezone.com/index.php?topic=44377.0
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-88/
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90po0%e3%80%91-%d0%b8/
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8/
https://luckychancerescue.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0/
http://www.hoonthaitoday.com/forum/index.php?topic=213514.0
http://HyUa.1fps.icu/l/szIaeDC
http://vtservices85.fr/smf2/index.php?PHPSESSID=bd44f52a0cffdd084f82b2e85f25460c&topic=252952.0
http://www.hoonthaitoday.com/forum/index.php?topic=293188.0
http://www.vamoscontigo.org/Noticia/19009
http://www.vamoscontigo.org/Noticia/19097
http://www.vamoscontigo.org/Noticia/19101
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=79272
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=79353
http://shinilspring.com/board_qsfb01/79702
http://shinilspring.com/board_qsfb01/79733
http://skylinecam.co.kr/photo/77274
http://skylinecam.co.kr/photo/77297
http://skylinecam.co.kr/photo/77301
http://sunele.co.kr/board_ReBD97/44963
http://sunele.co.kr/board_ReBD97/44968
http://sunele.co.kr/board_ReBD97/44973
http://themasters.pro/file_01/38842
http://themasters.pro/file_01/38856
http://toeden.co.kr/Product_new/19571
http://toeden.co.kr/Product_new/19584
http://toeden.co.kr/Product_new/19593
http://indiefilm.kr/xe/board/63334
http://indiefilm.kr/xe/board/63344
http://jjimdak.callbank.kr/?document_srl=770348
http://lucky.kidspann.net/index.php?mid=qna&document_srl=29253
http://moavalve.co.kr/?document_srl=49294
http://moavalve.co.kr/?document_srl=49303
http://poselokgribovo.ru/forum/index.php?topic=798822.0
http://poselokgribovo.ru/forum/index.php?topic=798871.0
http://preach.kr/Amharic_Music/2457
http://preach.kr/Amharic_Music/5889
http://HyUa.1fps.icu/l/szIaeDC
http://skylinecam.co.kr/photo/77481
http://skylinecam.co.kr/photo/77485
http://themasters.pro/?document_srl=39073
http://themasters.pro/file_01/38980
http://themasters.pro/file_01/38999
http://themasters.pro/file_01/39019
http://themasters.pro/file_01/39030
http://toeden.co.kr/Product_new/19671
http://toeden.co.kr/Product_new/19685
http://toeden.co.kr/Product_new/19695
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=13648
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=47858
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=47873
https://hackersuniversity.net/index.php?topic=17533.0
https://saltriverbg.com/2019/05/16/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-4/
https://saltriverbg.com/2019/05/16/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-eng/
https://saltriverbg.com/2019/05/16/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-eng/
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d0%b4%d0%b0%d1%82-6/
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d1%81%d0%b5%d1%80-2/
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80-4/
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80-12/
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80-23/
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80-24/
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80-11/
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80-12/
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80-4/
https://saltriverbg.com/2019/05/16/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b4%d0%b0%d1%82%d0%b0-%d0%b2/
https://saltriverbg.com/2019/05/16/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80/
https://saltriverbg.com/2019/05/16/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bb%d0%be%d1%81%d1%82%d1%84/
https://saltriverbg.com/2019/05/16/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://saltriverbg.com/2019/05/16/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%89%d0%b5%d0%bd%d0%ba%d0%b8/
https://saltriverbg.com/2019/05/16/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ivi/
https://saltriverbg.com/2019/05/16/hd-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d1%81%d0%bc%d0%be%d1%82%d1%80-2/
https://saltriverbg.com/2019/05/16/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%b0-%d1%81%d0%b5/
https://saltriverbg.com/2019/05/16/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80-3/
https://saltriverbg.com/2019/05/16/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-2/
https://saltriverbg.com/2019/05/16/live-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d1%81%d0%bc%d0%be%d1%82%d1%80/
https://www.gizmoarticle.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d0%b4%d0%b0%d1%82%d0%b0-%d0%b2%d1%8b%d1%85%d0%be%d0%b4%d0%b0-1/
http://HyUa.1fps.icu/l/szIaeDC
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=25626
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=25631
http://www.hyunjindc.com/?document_srl=17237
http://www.hyunjindc.com/qna/17217
http://www.hyunjindc.com/qna/17222
http://www.lgue.co.kr/?document_srl=13734
http://www.lgue.co.kr/lgue05/13704
http://www.tessabannampad.go.th/webboard/index.php?topic=211970.0
http://xihillstate.bloggirl.net/?document_srl=31101
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=31081
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=710073.0
http://0433.net/budongsan/39872
https://cybergsm.es/index.php?topic=17903.0
https://theprodigy.info/forum/index.php?topic=29538.0
https://www.shaiyax.com/index.php?topic=351096.0
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=166620
http://cwon.kr/xe/board_bnSr36/43119
http://flashboot.ru/forum/index.php?topic=95735.0
http://ru-realty.com/forum/index.php?PHPSESSID=jq0jj20ted4spp3u06p7vvsk64&topic=523363.0
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=8403
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=8412
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=8417
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=8431
http://www.ekemoon.com/205109/051020192417/
http://www.ekemoon.com/205147/051020193017/
http://HyUa.1fps.icu/l/szIaeDC
http://masarapphil.com/board_tmXx76/15402
http://mglpcm.org/board_ETkS12/1088
http://mglpcm.org/board_ETkS12/1096
http://moavalve.co.kr/faq/1515
http://moavalve.co.kr/faq/1520
http://oceangray.i234.me/?document_srl=2252
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=2266
http://otitismediasociety.org/forum/index.php?topic=162222.0
http://otitismediasociety.org/forum/index.php?topic=162227.0
http://shinhwaair2017.cafe24.com/?document_srl=54722
http://shinhwaair2017.cafe24.com/issue/54631
http://shinilspring.com/board_qsfb01/11577
http://shinilspring.com/board_qsfb01/11581
http://smartengbiz.com/s1/7798
http://vn7.vn/qna/42708
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=29251
https://saltriverbg.com/2019/05/15/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8/
https://www.thedezlab.com/lab/community/index.php?topic=2713.0
http://2872870.com/?document_srl=3662
http://2872870.com/?document_srl=3677
http://2872870.com/est/3667
http://2872870.com/est/3672
http://2872870.com/est/3682
http://2872870.com/est/3687
http://2872870.com/est/3692
http://flashboot.ru/forum/index.php?topic=95111.0
http://forum.elexlabs.com/index.php?topic=28326.0
http://myrechockey.com/forums/index.php?topic=102309.0
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=783295
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=99364
http://oceangray.i234.me/?document_srl=3971
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=3982
http://poselokgribovo.ru/forum/index.php?topic=788400.0
http://www.deliberarchia.org/forum/index.php?topic=1039141.0
http://www.deliberarchia.org/forum/index.php?topic=1039145.0
http://www.deliberarchia.org/forum/index.php?topic=1039171.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=29356
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=29381
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=29391
http://HyUa.1fps.icu/l/szIaeDC
http://shinilspring.com/board_qsfb01/13361
http://shinilspring.com/board_qsfb01/13411
http://sixangles.co.kr/qna/512163
http://sixangles.co.kr/qna/512230
http://smartengbiz.com/s1/12052
http://smartengbiz.com/s1/12078
http://smartengbiz.com/s1/12098
http://vn7.vn/qna/47353
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=43720
http://www.deliberarchia.org/forum/index.php?topic=1033168.0
http://www.gforgirl.com/xe/poster/9357
http://www.lozic.co.kr/?document_srl=8647
http://www.studyxray.com/Sangdam/8492
http://www.svteck.co.kr/customer_gratitude/12177
http://xn--2e0bk61btjo.com/notice/2405
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=30173
http://ariji.kr/?document_srl=773489
http://www.theocraticamerica.org/forum/index.php?topic=40566.0
https://www.thedezlab.com/lab/community/index.php?topic=2822.0
http://asiagroup.co.kr/index.php?mid=board_5&document_srl=130930
http://bath-family.com/photo_zone/8784
http://bobr.site/index.php?topic=135295.0
http://k-cea.org/board_Hnyj62/18939
http://poselokgribovo.ru/forum/index.php?topic=789709.0
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1596415
http://www.artangel.co.kr/?document_srl=3030
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=3040
http://www.arunagreen.com/index.php/component/k2/itemlist/user/517680
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1627990
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1419144
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=61156
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=61168
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=61195
http://www.deliberarchia.org/forum/index.php?topic=1040450.0
http://www.deliberarchia.org/forum/index.php?topic=1040470.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=35007
http://www.ekemoon.com/194381/051720193115/
http://www.teedinubon.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bb%d0%be%d1%81%d1%82%d1%84/
http://HyUa.1fps.icu/l/szIaeDC
http://bewasia.com/?document_srl=2903
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=2898
http://emjun.com/index.php?mid=hangtotal&document_srl=7144
http://gallerychoi.com/Exhibition/15069
http://gallerychoi.com/Exhibition/15108
http://gallerychoi.com/Exhibition/15146
http://goldenpowerball2.com/index.php?mid=board_Bnby34&document_srl=11402
http://gxpfactory.net/index.php?document_srl=1662&mid=Guide
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2763891
http://imsil.or.kr/index.php?mid=board_rUgw34&document_srl=1315
http://indiefilm.kr/xe/board/10195
http://isch.kr/board_PowH60/3486
http://jnk-ent.jp/index.php?mid=gallery&document_srl=7651
http://jnk-ent.jp/index.php?mid=gallery&document_srl=7670
http://jstech.kr/?document_srl=7111
http://k-cea.org/board_Hnyj62/7184
http://k-cea.org/board_Hnyj62/7232
http://lahch.co.kr/index.php?mid=board_jHAP41&document_srl=8110
http://lucky.kidspann.net/index.php?mid=qna&document_srl=3231
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=10230
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=737715
http://jnk-ent.jp/index.php?mid=gallery&document_srl=16761
http://jnk-ent.jp/index.php?mid=gallery&document_srl=16776
http://lahch.co.kr/index.php?mid=board_jHAP41&document_srl=10741
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3807781
http://lucky.kidspann.net/index.php?mid=qna&document_srl=10895
http://lucky.kidspann.net/index.php?mid=qna&document_srl=10925
http://moavalve.co.kr/faq/22627
http://moavalve.co.kr/faq/22646
http://oceangray.i234.me/?document_srl=5105
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=5095
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=5100
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=3515
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/249275
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=17959
http://preach.kr/Amharic_Music/1465
http://preach.kr/Amharic_Music/1469
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=14402
http://roikjer.com/forum/index.php?PHPSESSID=fuphjgogi5t0s8oha9u783vlj5&topic=878215.0
http://ruschinaforum.ru/index.php?topic=140462.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/211903
http://HyUa.1fps.icu/l/szIaeDC
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bi5%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://vervetama.com/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vt3%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl-5-%d1%81%d0%b5%d1%80/
http://www.teedinubon.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nr7%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-17-%d1%81%d0%b5/
http://www.teedinubon.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sq6%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://www.teedinubon.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fj0%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://www.teedinubon.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ls5%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f17-05-2019/
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nb1%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://www.amazingworldtop.com/entretenimiento/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-94-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ja2%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-94-%d1%81%d0%b5%d1%80%d0%b8%d1%8f17-05-2019/
http://forum.digamahost.com/index.php?topic=126008.0
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2471495
http://forum.digamahost.com/index.php?topic=119834.0
http://teambuildingpremium.com/forum/index.php?topic=822357.0
http://teambuildingpremium.com/forum/index.php?topic=822377.0
http://www.deliberarchia.org/forum/index.php?topic=1027896.0
http://xplorefitness.com/blog/%C2%AB%D0%B5%D0%B4%D0%B8%D0%BD%D0%BE%D0%B5-%D1%81%D0%B5%D1%80%D0%B4%D1%86%D0%B5-tek-y%C3%BCrek-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-eare-%C2%AB%D0%B5%D0%B4%D0%B8%D0%BD%D0%BE%D0%B5-%D1%81%D0%B5%D1%80%D0%B4%D1%86%D0%B5-tek-y%C3%BCrek-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
https://khuyenmaikk13.info/index.php?topic=199044.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2623955
http://corumotoanahtar.com/component/k2/itemlist/user/1251
http://mahdi.ehosseini.com/index.php/component/k2/itemlist/user/32747
http://proxima.co.rw/index.php/component/k2/itemlist/user/617469
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/207315
http://www.arunagreen.com/index.php/component/k2/itemlist/user/503182
http://www.arunagreen.com/index.php/component/k2/itemlist/user/503187
http://svgrossburgwedel.de/component/k2/itemlist/user/5803
http://thanosakademi.com/index.php?topic=95493.0
http://thermoplast.envolgroupe.com/component/k2/author/119100
http://topitop.kz/index.php/component/k2/itemlist/user/77176
http://vhost12299.cpsite.ru/417640-bol-se-zizni-5-seria-hd-bol-se-zizni-5-seria
http://vhost12299.cpsite.ru/417649-mama-lora-12-seria-mama-lora-12-seria
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=81115
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3673219
http://webp.online/index.php?topic=59273.0
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=10082
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4830868
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1607570
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/261234
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/261241
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%84%d0%b8%d0%bd%d0%b0%d0%bb-eh%d1%85%d0%be%d0%bb%d0%be/
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-19-jy%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-ii%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-dm%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-wu%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://roikjer.com/forum/index.php?PHPSESSID=74fgjam9vmnckitbe574l09rs3&topic=889784.0
http://roikjer.com/forum/index.php?topic=889772.0
http://zanoza.h1n.ru/2019/05/14/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zb4d-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://zanoza.h1n.ru/2019/05/14/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-pg6d-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
https://turimex.mx.solemti.net/index.php/component/k2/itemlist/user/1128
http://forum.digamahost.com/index.php?topic=120150.0
http://forum.digamahost.com/index.php?topic=120159.0
https://sanp.pro/%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-57-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-orwr-%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-57-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2624587
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/gumdanapt/49532
http://xn--ok1bpqi43ahtb.net/board_eASW07/102275
http://xn--ok1bpqi43ahtb.net/board_eASW07/102629
http://xn--ok1bpqi43ahtb.net/board_eASW07/102697
http://xn--ok1bpqi43ahtb.net/board_eASW07/102786
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=57865
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=57891
http://isch.kr/?document_srl=858
http://isch.kr/board_PowH60/806
http://isch.kr/board_PowH60/817
http://isch.kr/board_PowH60/854
http://isch.kr/board_PowH60/875
http://isch.kr/board_PowH60/879
http://jjikduk.net/DATA/3354
http://k-cea.org/board_Hnyj62/2701
http://k-cea.org/board_Hnyj62/2710
http://k-cea.org/board_Hnyj62/2737
http://k-cea.org/board_Hnyj62/2742
http://k-cea.org/board_Hnyj62/2751
http://kfuav.kr/qna/3859
http://kfuav.kr/qna/3887
http://kfuav.kr/qna/3902
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3658745
http://xn----3x5er9r48j7wemud0a387h.com/news/11236
http://xn----3x5er9r48j7wemud0a387h.com/news/11252
http://yoriyorifood.com/xxxx/spacial/36323
http://yoriyorifood.com/xxxx/spacial/36333
http://yoriyorifood.com/xxxx/spacial/36360
http://zanoza.h1n.ru/2019/05/16/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8/
http://zanoza.h1n.ru/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5/
https://saltriverbg.com/2019/05/16/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-6/
https://saltriverbg.com/2019/05/16/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%82%d0%be%d1%80%d1%80%d0%b5%d0%bd/
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5-4/
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80-17/
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80-18/
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80-7/
https://saltriverbg.com/2019/05/16/%d1%8d%d1%84%d0%b8%d1%80-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2/
https://saltriverbg.com/2019/05/16/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-youtube-2/
https://theprodigy.info/forum/index.php?topic=29327.0
https://www.shaiyax.com/index.php?topic=348763.0
https://www.shaiyax.com/index.php?topic=348766.0
https://www.shaiyax.com/index.php?topic=348773.0
http://cwon.kr/xe/board_bnSr36/24915
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2770478
http://HyUa.1fps.icu/l/szIaeDC
http://vn7.vn/qna/65919
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3751875
http://corumotoanahtar.com/?option=com_k2&view=itemlist&task=user&id=2402
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/737497
http://www.critico-expository.com/forum/index.php?topic=9353.0
http://forum.digamahost.com/index.php?topic=119652.0
http://emjun.com/index.php?mid=hangtotal&document_srl=30869
http://www.digitalbul.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81-5/
http://fbpharm.net/index.php/component/k2/itemlist/user/32852
http://153.120.114.241/eso/index.php/17119775-serial-sluga-naroda-3-sezon-17-seria-q4-sluga-naroda-3-sezon-17
http://153.120.114.241/eso/index.php/17120170-serial-holostak-9-sezon-14-vypusk-a6-holostak-9-sezon-14-vypusk
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2657271
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=58880
http://corumotoanahtar.com/component/k2/itemlist/user/4393
http://corumotoanahtar.com/component/k2/itemlist/user/4401.html
http://corumotoanahtar.com/component/k2/itemlist/user/4411.html
http://dessa.com.br/component/k2/itemlist/user/342388
http://dev.aabn.org.gh/component/k2/itemlist/user/612268
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1666381
http://thermoplast.envolgroupe.com/component/k2/author/90097
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1592938
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1383015
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1792889
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=599592
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=599605
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=797534
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=56669
http://www.golden-nail.co.kr/press/1655
https://nextezone.com/index.php?action=profile;u=2491
http://phmusic.dothome.co.kr/index.php?mid=PowerHouseMusic&document_srl=2612
https://khuyenmaikk13.info/index.php?topic=204771.0
http://indiefilm.kr/xe/board/66475
http://mglpcm.org/board_ETkS12/16608
https://esel.gist.ac.kr/esel2/board_hmgj23/27292
http://www.lozic.co.kr/gallery/9875
http://atemshow.com/atemfair_domestic/24219
http://www.urimwelfare.or.kr/board_mfOh88/5146
http://shinilspring.com/board_qsfb01/77229
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=3499
http://looksun.co.kr/index.php?mid=board_4&document_srl=12609
http://www.deliberarchia.org/forum/index.php?topic=1048535.0
http://gallerychoi.com/Exhibition/71168
http://www.gforgirl.com/xe/poster/104318
http://www.golden-nail.co.kr/press/44731
http://hkmtv.co.kr/board_yKNa34/1658
http://xn--2e0bk61btjo.com/notice/1694
http://1vh.info/index.php?topic=27113.0
http://indiefilm.kr/xe/board/78196
http://www.ekemoon.com/196829/050520193516/
http://shinilspring.com/board_qsfb01/52705
http://www.svteck.co.kr/customer_gratitude/24866
http://forums.abs-cbn.com/welcome-back-kapamilya%21/'a-etoo-(got)-8-eo-6-e'-a-etoo-(got)-8-eo-6-e-x7v1/
http://1vh.info/index.php?topic=27202.0
http://hyeonjun.co.kr/?document_srl=53059
http://www.sp1.football/?document_srl=158487
http://ru-realty.com/forum/index.php?PHPSESSID=0uf4fn1rlpm39e8i5038bmqso7&topic=527679.0
http://callman.co.kr/index.php?mid=qa&document_srl=30063
http://www.hicleaning.kr/board_wash/58270
http://photogrotto.com/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80/
http://xn--ok1bpqi43ahtb.net/board_EkDG82/66457
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=2018
http://ye-dream.com/qa/2383
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90qn7%e3%80%91-%d0%b8%d0%b3/
http://flashboot.ru/forum/index.php?topic=95149.0
http://HyUa.1fps.icu/l/szIaeDC
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=67985
http://xn----3x5er9r48j7wemud0a387h.com/news/645
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1403991
http://atemshow.com/atemfair_domestic/36772
https://www.shaiyax.com/index.php?topic=347046.0
http://beautypouch.net/index.php?mid=board_09&document_srl=6010
http://www.hyunjindc.com/qna/10409
http://haeple.com/index.php?mid=etc&document_srl=89939
http://www.ekemoon.com/202239/050220192217/
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=14515
http://warmfund.net/p/index.php?mid=financing&document_srl=134079
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=18145
http://warmfund.net/p/index.php?mid=financing&document_srl=56856
http://myrechockey.com/forums/index.php?topic=104233.0
http://vervetama.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd/
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=16951
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=8791
http://knet.dothome.co.kr/xe/board_RJHw15/2091
http://www.vamoscontigo.org/Noticia/19101
http://bebopindia.com/notcie/67303
http://praisesound.co.kr/sub04_01/8126
http://ye-dream.com/qa/20396
http://uberdrivers.net/forum/index.php?topic=284835.0
http://www.ds712.net/guest/?document_srl=22191
http://isch.kr/board_PowH60/10339
http://yoriyorifood.com/xxxx/spacial/32522
http://www.lgue.co.kr/?document_srl=15583
http://www.jesusonly.life/?document_srl=137575
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=31011
http://0433.net/?document_srl=2661
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=33403
http://gallerychoi.com/Exhibition/55119
http://wipln.com/hummor/17811
http://HyUa.1fps.icu/l/szIaeDC
https://reficulcoin.com/index.php?topic=46870.0
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=73880
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=67816
http://smartengbiz.com/s1/38404
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=51261
http://ye-dream.com/qa/65518
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=21094
http://www.gforgirl.com/xe/poster/73307
http://gochon-iusell.co.kr/g1/13071
http://bath-family.com/photo_zone/1608
http://hanalove.kidspann.net/index.php?mid=faq&document_srl=44210
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/474031
http://bewasia.com/index.php?document_srl=10635&mid=board_cUYy21
http://dnienertec.com/qna/14448
http://49.247.3.43/index.php?mid=board_PiDQ29&document_srl=17433
http://shinilspring.com/board_Gmdj15/59805
http://praisesound.co.kr/sub04_01/10923
http://bethanychurch.kr/board_vpkl62/18796
http://shinhwaair2017.cafe24.com/issue/64695
http://xn--ok1bpqi43ahtb.net/board_eASW07/81530
http://gxpfactory.net/index.php?mid=Guide&document_srl=7544
http://masarapphil.com/board_tmXx76/14101
http://www.hsaura.com/license/94117
http://forum.byehaj.hu/index.php?topic=92260.0
http://xn--2e0bk61btjo.com/notice/7326
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=45450
http://otitismediasociety.org/forum/index.php?topic=163213.0
http://ye-dream.com/qa/81985
http://otitismediasociety.org/forum/index.php?topic=173495.0
http://2872870.com/est/15268
http://oneandonly1127.com/guest/2750
https://prelease.club/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-8-03-2016/
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=76876
http://www.remify.app/foro/index.php?topic=301536.0
http://HyUa.1fps.icu/l/szIaeDC
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=159935
https://reficulcoin.com/index.php?topic=36525.0
http://callman.co.kr/index.php?mid=qa&document_srl=25971
http://2872870.com/?document_srl=5204
https://nextezone.com/index.php?action=profile;u=7168
http://gallerychoi.com/Exhibition/11523
http://www.golden-nail.co.kr/press/9783
https://saltriverbg.com/2019/05/15/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8-4/
http://tototoday.com/board_oRiY52/23881
http://www.youngfile.com/youngfile_downlist/8760
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=58873
http://lucky.kidspann.net/index.php?mid=qna&document_srl=22816
http://smartengbiz.com/s1/17304
http://forum.byehaj.hu/index.php?topic=93505.0
http://daesestudy.co.kr/ipsi_docu/2473
http://toeden.co.kr/Product_new/27192
http://isch.kr/board_PowH60/23846
http://0433.net/budongsan/31356
https://reelgosu.com/board_peJN24/272644
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=40424
http://haeple.com/index.php?mid=etc&document_srl=50307
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=16260
http://www.hsaura.com/?document_srl=81837
http://barobus.kr/qna/13825
http://indiefilm.kr/xe/board/82247
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=25469
http://indiefilm.kr/xe/board/2462
http://HyUa.1fps.icu/l/szIaeDC
http://wgamez.net/index.php?mid=board_KGzu43&document_srl=2395
http://shinilspring.com/board_qsfb01/46377
https://reficulcoin.com/index.php?topic=52168.0
http://sixangles.co.kr/qna/510577
http://xn--ok1bpqi43ahtb.net/board_EkDG82/91613
http://bebopindia.com/?document_srl=80833
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=64903
http://warmfund.net/p/index.php?mid=financing&document_srl=94383
https://theprodigy.info/forum/index.php?topic=29439.0
http://sofficer.net/xe/teach/214681
http://agiteshop.com/xe/qa/39474
https://forum.clubeicaro.pt/index.php?topic=1141.0
http://2872870.com/est/8409
https://www.bmwstyle.ru/forum/index.php?topic=65283.0
http://poselokgribovo.ru/forum/index.php?topic=782725.0
http://foxy-tv.com/index.php?mid=board_aYWf51&document_srl=3106
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1804893
http://matrixpharm.ru/forum/index.php?PHPSESSID=6e343r6micpf5mcp7hvfrcjvn5&action=profile;u=189910
http://f-tube.info/board/74744
http://indiefilm.kr/xe/board/90204
http://emjun.com/index.php?mid=hangtotal&document_srl=70638
http://uberdrivers.net/forum/index.php?topic=288469.0
http://forum.bmw-e60.eu/index.php?topic=7931.0
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2774054
http://www.tessabannampad.go.th/webboard/index.php?topic=212670.0
http://skylinecam.co.kr/photo/32266
http://www.svteck.co.kr/customer_gratitude/41486
http://haeple.com/index.php?mid=etc&document_srl=73780
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3296811
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=56816
http://praisesound.co.kr/sub04_01/3035
http://hyeonjun.co.kr/menu3/854
http://wgamez.net/index.php?mid=board_KGzu43&document_srl=409
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.kr/?document_srl=531
http://www.studyxray.com/Sangdam/56804
http://haeple.com/index.php?mid=etc&document_srl=17619
https://betshin.com/Story/7447
http://www.jesusonly.life/calendar/29198
http://HyUa.1fps.icu/l/szIaeDC
http://emjun.com/index.php?mid=hangtotal&document_srl=5725
http://www.digitalbul.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-av9q/
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3431873
http://myrechockey.com/forums/index.php?topic=92881.0
http://www.deliberarchia.org/forum/index.php?topic=1019424.0
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1922856
http://www.deliberarchia.org/forum/index.php?topic=1046364.0
http://jiquilisco.org/index.php/component/k2/itemlist/user/4880
http://withinfp.sakura.ne.jp/eso/index.php/17006212-hdvideo-cuzaa-zizn-cuze-zitta-11-seria-d4-cuzaa-zizn-cuze-zitta
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1910166
http://www.ekemoon.com/183211/051620193813/
http://www.ekemoon.com/183217/051620193913/
http://www.ekemoon.com/183225/051620194113/
http://www.ekemoon.com/183229/051620194313/
http://www.ekemoon.com/183235/051620194613/
http://www.ekemoon.com/183237/051620194613/
http://www.vivelabmanizales.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-87-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sd8j-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd/
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cq7k-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://www.vivelabmanizales.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81-41/
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fm6o-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://forum.elexlabs.com/index.php?topic=39268.0
http://forum.elexlabs.com/index.php?topic=39271.0
http://forum.elexlabs.com/index.php?topic=39272.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-aoa-3-eo-13-e-18-05-2019-opa-a-aoa-3-eo-13-e/?PHPSESSID=sm77v73gbubqnudg8u3e92d143
http://photogrotto.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8d%d1%84%d0%b8%d1%80/
http://roikjer.com/forum/index.php?PHPSESSID=s08jhc2il88r876bc9cmm1cjh6&topic=890535.0
http://taklongclub.com/forum/index.php?topic=150926.0
http://taklongclub.com/forum/index.php?topic=150943.0
http://myrechockey.com/forums/index.php?topic=100961.0
http://dev.aabn.org.gh/component/k2/itemlist/user/599987
http://www.telcon.gr/index.php/component/k2/itemlist/user/58265
http://thermoplast.envolgroupe.com/component/k2/author/91799
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=464352
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2626334
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=26938
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=58654
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=109698
http://mvisage.sk/index.php/component/k2/itemlist/user/118913
http://jjikduk.net/DATA/16099
http://trunk.www.volkalize.com/members/tyrellcorcoran/
http://withinfp.sakura.ne.jp/eso/index.php/16962955-novinka-tola-robot-4-seria-h6-tola-robot-4-seria/0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1373227
http://www.vivelabmanizales.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ym7f/
http://www.vivelabmanizales.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81-61/
http://www.vivelabmanizales.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81-62/
https://prelease.club/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-99-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tf9i-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd/
http://www.crnmedia.es/component/k2/itemlist/user/85633
http://www.ekemoon.com/184565/052320190513/
http://www.ekemoon.com/184577/052320190613/
http://forum.elexlabs.com/index.php?topic=39298.0
http://forum.elexlabs.com/index.php?topic=39300.0
http://forum.elexlabs.com/index.php?topic=39301.0
http://forum.elexlabs.com/index.php?topic=39302.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=35787.0
http://miklja.net/forum/index.php?topic=31778.0
http://photogrotto.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba/
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%85%d0%be/
http://proxima.co.rw/index.php/component/k2/itemlist/user/646447
http://roikjer.com/forum/index.php?PHPSESSID=32o8dnmb39q5lfj5voo6273um3&topic=890642.0
http://roikjer.com/forum/index.php?PHPSESSID=oimcg9vpnl8ghu5ns8uu73pfj3&topic=890653.0
http://roikjer.com/forum/index.php?PHPSESSID=t8qte5rghug490njiotbnp1n55&topic=890688.0
http://teambuildingpremium.com/forum/index.php?topic=845934.0
http://teambuildingpremium.com/forum/index.php?topic=845969.0
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/539791
http://zanoza.h1n.ru/2019/05/14/%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-70-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mjzc-%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-70/
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1569853
http://mobility-corp.com/index.php/component/k2/itemlist/user/2584702
http://mjbosch.com/component/k2/itemlist/user/83621
http://www.digitalbul.com/live-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-n1-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://danielmillsap.com/forum/index.php?topic=1033442.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1668250
http://roikjer.com/forum/index.php?topic=843822.0
http://ye-dream.com/qa/40877
http://cafe.dokseosil.co.kr/community/47315
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=91418
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=91556
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=91562
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=91573
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=91604
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=91610
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=91681
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=91709
http://bebopindia.com/notcie/121352
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=1004788
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=26104
http://dev.aabn.org.gh/?option=com_k2&view=itemlist&task=user&id=513667
http://haniel.ir/index.php/component/k2/itemlist/user/80575
http://menulisilmiah.net/hd-video-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o1-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8/
http://comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=105057
http://www.rocktheboat.cc/groups/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-pro-ii%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
https://khuyenmaikk13.info/index.php?topic=187723.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3624838
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4903723
http://corumotoanahtar.com/component/k2/itemlist/user/1140
http://euromouleusinage.com/index.php/component/k2/itemlist/user/130509
http://xn--ok1bpqi43ahtb.net/board_eASW07/127423
http://ye-dream.com/?document_srl=81049
http://ye-dream.com/qa/81019
http://ye-dream.com/qa/81064
http://ye-dream.com/qa/81074
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=72345
http://yoriyorifood.com/xxxx/?document_srl=81398
http://yoriyorifood.com/xxxx/spacial/81354
http://svgrossburgwedel.de/component/k2/itemlist/user/5406
http://www.camaracoyhaique.cl/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81-2/
http://forum.politeknikgihon.ac.id/index.php?topic=22213.0
https://lucky28003.nl/forum/index.php?topic=12121.0
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fl2%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f08-05/
http://www.ekemoon.com/142821/051920191205/
http://carrierworld.co.kr/?document_srl=1703
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=4457
http://shinilspring.com/board_qsfb01/22827
http://masarapphil.com/board_tmXx76/14956
http://www.fassen.co.kr/xe/board_VCum96/8127
http://www.studyxray.com/Sangdam/37870
http://www.leekeonsu-csi.com/?document_srl=504576
http://0433.net/junggo/23474
http://forum.byehaj.hu/index.php?topic=92973.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-r2-f0-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://lahch.co.kr/index.php?mid=board_jHAP41&document_srl=8258
http://bebopindia.com/notcie/31826
http://www.svteck.co.kr/customer_gratitude/22096
http://isch.kr/board_PowH60/28643
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/63104
http://k-cea.org/?document_srl=52513
http://constellation.kro.kr/board_kbku73/1247
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=747032
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=50770
http://forum.elexlabs.com/index.php?topic=24934.0
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=85813
http://bebopindia.com/notcie/122476
http://cafe.dokseosil.co.kr/community/23834
http://indiefilm.kr/xe/board/65320
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=72579
http://xn--ok1bpqi43ahtb.net/board_SPcK94/98996
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/?document_srl=1722
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=69513
http://khapthanam.co.kr/g1/37523
http://poselokgribovo.ru/forum/index.php?topic=795923.0
http://8.droror.co.il/uncategorized/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80/
http://ye-dream.com/qa/78744
http://uberdrivers.net/forum/index.php?topic=272461.0
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=3329
http://www.yepia.com/board_ZCPG83/12162
http://oceangray.i234.me/index.php?document_srl=16446&mid=board_vsVi16
http://ye-dream.com/qa/62702
http://HyUa.1fps.icu/l/szIaeDC
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/525015
http://emjun.com/index.php?mid=hangtotal&document_srl=57218
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-h3-a3-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://xn--ok1bpqi43ahtb.net/board_eASW07/85379
http://www.sp1.football/index.php?mid=faq&document_srl=159052
http://bebopindia.com/notcie/126043
http://sounddrizzle.com/index.php?mid=boarda&document_srl=2004
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/483520
http://gxpfactory.net/index.php?mid=Guide&document_srl=7365
http://praisesound.co.kr/sub04_01/7712
http://www.generalwalker.org/board_Zyyd91/1924
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=39512
https://sanp.pro/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b5%d1%85/
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=9448
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=61902
http://www.theocraticamerica.org/forum/index.php?topic=38211.0
http://www.theocraticamerica.org/forum/index.php?topic=43675.0
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=17872
http://wipln.com/?document_srl=34245
http://2872870.com/est/3433
http://www.sp1.football/index.php?mid=faq&document_srl=133195
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=18625
http://indiefilm.kr/xe/board/66753
http://hanga5.com/index.php?mid=board_photo&document_srl=10019
https://reficulcoin.com/index.php?topic=49065.0
http://joocafe.com/board_HWSm10/62645
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=5295
http://ariji.kr/?document_srl=803252
http://lucky.kidspann.net/index.php?mid=qna&document_srl=65961
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=35948
http://ariji.kr/?document_srl=796474
http://engeena.com/component/k2/itemlist/user/8448
http://uberdrivers.net/forum/index.php?topic=283881.0
http://HyUa.1fps.icu/l/szIaeDC
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1659018
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2632712
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=152672
http://withinfp.sakura.ne.jp/eso/index.php/16959189-smotret-sluga-naroda-3-sezon-17-seria-t9-sluga-naroda-3-sezon-1/0
http://menulisilmiah.net/hd-video-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v8-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82/
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1579913
http://corumotoanahtar.com/component/k2/itemlist/user/2920.html
http://smartacity.com/component/k2/itemlist/user/43661
http://vtservices85.fr/smf2/index.php?PHPSESSID=a14dd976598dce109cb9a9267af3b375&topic=243416.0
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=1063820
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3356113
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=312295
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1416767
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=1876
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=272031
https://forums.letstalkbeats.com/index.php?topic=67116.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12296
http://arunagreen.com/?option=com_k2&view=itemlist&task=user&id=420908
http://www.m1avio.com/index.php/component/k2/itemlist/user/3622942
http://menulisilmiah.net/hd-video-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d8-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1/
http://thermoplast.envolgroupe.com/component/k2/author/80976
http://www.m1avio.com/index.php/component/k2/itemlist/user/3682092
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4904141
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=617461
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=109229
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=256403
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=552967
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/62971
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/62973
http://xplorefitness.com/blog/%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-13-05-2019-d0-%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2624009
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/522118
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1919321
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=306112
http://haniel.ir/index.php/component/k2/itemlist/user/99811
http://www.digitalbul.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nm6h/
http://indiefilm.kr/xe/board/62285
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1148239
http://www.ekemoon.com/187633/051020190814/
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1660366
http://rudraautomation.com/index.php/component/k2/author/170578
http://roikjer.com/forum/index.php?PHPSESSID=jlliiuj4mbcs407ql95tcbh196&topic=867676.0
http://jjimdak.callbank.kr/?document_srl=761429
http://forum.byehaj.hu/index.php?topic=89820.0
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2471262
http://proxima.co.rw/index.php/component/k2/itemlist/user/628427
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=22170
http://corumotoanahtar.com/component/k2/itemlist/user/1474
http://proxima.co.rw/index.php/component/k2/itemlist/user/593135
http://moavalve.co.kr/faq/40846
http://moavalve.co.kr/faq/40851
http://www.deliberarchia.org/forum/index.php?topic=1046208.0
http://www.deliberarchia.org/forum/index.php?topic=1046229.0
http://www.deliberarchia.org/forum/index.php?topic=1046247.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=69782
http://www.jesusonly.life/calendar/61993
http://zanoza.h1n.ru/2019/05/16/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ymsi-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80/
http://cwon.kr/xe/board_bnSr36/22851
http://cwon.kr/xe/board_bnSr36/22856
http://jjimdak.callbank.kr/?document_srl=756504
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=756446
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=756460
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=756544
http://moavalve.co.kr/faq/40941
http://www.josephmaul.org/menu41/93124
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=73897
http://www.nienkevanrijn.nl/component/k2/itemlist/user/447209
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=499645
http://www.sp1.football/index.php?mid=faq&document_srl=193803
http://www.sp1.football/index.php?mid=faq&document_srl=193818
http://www.studyxray.com/?document_srl=109546
http://roikjer.com/forum/index.php?PHPSESSID=435qlq4vl0uvto3keh8mpvbr01&topic=879553.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=22684
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=21587
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=211999
http://ye-dream.com/qa/34746
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/826288
http://thermoplast.envolgroupe.com/component/k2/author/102750
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=115335
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=115351
http://0433.net/junggo/52021
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=144335
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=144384
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=144403
http://bitpark.co.kr/board_IzjM66/4025763
http://bitpark.co.kr/board_IzjM66/4025872
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=73304
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=73309
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=73314
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=73324
http://community.viajar.tur.br/index.php?p=/profile/faithrecto
http://www.ekemoon.com/143435/050020191306/
http://xplorefitness.com/blog/%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-7-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-yiah-%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-7-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://dev.aabn.org.gh/component/k2/itemlist/user/539035
http://www.ekemoon.com/145457/051720190606/
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1556173
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1008955
http://www.ekemoon.com/148263/052220194906/
http://webp.online/index.php?topic=43180.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3570477
https://members.fbhaters.com/index.php?topic=80512.0
http://www.nienkevanrijn.nl/component/k2/itemlist/user/426668
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1059361
http://roikjer.com/forum/index.php?topic=861606.0
http://www.ekemoon.com/180165/052120195012/
http://wigalseguros.com.br/index.php/component/k2/itemlist/user/9230
http://emjun.com/index.php?mid=hangtotal&document_srl=20893
http://seoksoononly.dothome.co.kr/qna/841543
http://skylinecam.co.kr/photo/55633
http://ovotecegg.com/component/k2/itemlist/user/127955
http://www.deliberarchia.org/forum/index.php?topic=1029376.0
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=74301
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/gumdanapt/74203
https://esel.gist.ac.kr/esel2/?document_srl=64919
https://esel.gist.ac.kr/esel2/board_hmgj23/64721
https://esel.gist.ac.kr/esel2/board_hmgj23/64899
https://esel.gist.ac.kr/esel2/board_hmgj23/64914
https://esel.gist.ac.kr/esel2/board_hmgj23/64975
https://esel.gist.ac.kr/esel2/board_hmgj23/64993
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=115749
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=681248.0
http://topitop.kz/index.php/component/k2/itemlist/user/76753
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1131085
http://withinfp.sakura.ne.jp/eso/index.php/16903167-hdvideo-tola-robot-8-seria-i8-tola-robot-8-seria
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=73826
http://macdistri.com/index.php/component/k2/itemlist/user/308682
http://webp.online/index.php?topic=50303.30
http://bitpark.co.kr/board_IzjM66/3754265
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=268388
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1365746
https://marketengine.enginethemes.com/hd-video-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g1-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1/
http://webp.online/index.php?topic=60416.msg103701
http://www.digitalbul.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-dr%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://www.tekparcahdfilm.com/forum/index.php?topic=51293.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=74393
http://www.verenas-unterwasserwelt.de/forum/index.php?topic=6809.0
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=32583
http://www.vogtland.com.pl/index.php/component/k2/itemlist/user/32561
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/278644
http://zanoza.h1n.ru/2019/05/18/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%84%d0%b8%d0%bd%d0%b0%d0%bb-bv%d1%85%d0%be%d0%bb%d0%be/
http://zanoza.h1n.ru/2019/05/18/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-be0%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%87%d0%b5%d1%80%d0%bd/
http://zanoza.h1n.ru/2019/05/18/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-92-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yd6%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-92-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05-2019/
http://zanoza.h1n.ru/2019/05/18/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-to0%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5/
http://emjun.com/index.php?mid=hangtotal&document_srl=19332
http://emjun.com/index.php?mid=hangtotal&document_srl=19337
http://emjun.com/index.php?mid=hangtotal&document_srl=19380
http://www.deliberarchia.org/forum/index.php?topic=1041346.0
http://www.deliberarchia.org/forum/index.php?topic=1041348.0
http://www.deliberarchia.org/forum/index.php?topic=1041351.0
http://www.deliberarchia.org/forum/index.php?topic=1041355.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=39806
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=40028
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/209030
http://smartacity.com/component/k2/itemlist/user/44665
http://w9builders.co.uk/index.php/component/k2/itemlist/user/72959
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1592370
http://www.arunagreen.com/index.php/component/k2/itemlist/user/509522
http://www.firstfinancialservices.co.uk/?option=com_k2&view=itemlist&task=user&id=4202
http://indiefilm.kr/xe/board/34116
http://mobility-corp.com/index.php/component/k2/itemlist/user/2571940
http://www2.yasothon.go.th/smf/index.php?topic=159.161685
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=758615
http://www.ekemoon.com/182585/051220194613/
http://teambuildingpremium.com/forum/index.php?topic=826441.0
https://turimex.mx.solemti.net/index.php/component/k2/itemlist/user/1430
http://emjun.com/index.php?mid=hangtotal&document_srl=24884
http://emjun.com/index.php?mid=hangtotal&document_srl=24898
http://emjun.com/index.php?mid=hangtotal&document_srl=24962
http://emjun.com/index.php?mid=hangtotal&document_srl=24977
http://jjimdak.callbank.kr/?document_srl=743282
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=743257
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=743297
http://moavalve.co.kr/faq/28117
http://moavalve.co.kr/faq/28142
http://moavalve.co.kr/faq/28179
http://moavalve.co.kr/faq/28194
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/258900
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/19574
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/63102
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=21036
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2630982
http://arunagreen.com/index.php/component/k2/itemlist/user/511128
http://corumotoanahtar.com/?option=com_k2&view=itemlist&task=user&id=1926
http://fbpharm.net/index.php/component/k2/itemlist/user/40532
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1902996
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1903281
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1903338
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=310136
http://cwon.kr/xe/board_bnSr36/14099
http://arunagreen.com/index.php/component/k2/itemlist/user/470078
https://prelease.club/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wnkt-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=15700
http://forum.digamahost.com/index.php?topic=113582.0
http://www.ekemoon.com/174215/050120195511/
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=20996
http://cwon.kr/xe/?document_srl=30793
http://indiefilm.kr/xe/board/24073
http://www.digitalbul.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.vivelabmanizales.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sg5r-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://seoksoononly.dothome.co.kr/qna/832947
http://forum.digamahost.com/index.php?topic=123233.0
http://teambuildingpremium.com/forum/index.php?topic=832414.0
http://teambuildingpremium.com/forum/index.php?topic=832440.0
http://teambuildingpremium.com/forum/index.php?topic=832461.0
http://teambuildingpremium.com/forum/index.php?topic=832466.0
http://teambuildingpremium.com/forum/index.php?topic=832469.0
http://teambuildingpremium.com/forum/index.php?topic=832472.0
http://teambuildingpremium.com/forum/index.php?topic=832475.0
http://teambuildingpremium.com/forum/index.php?topic=832479.0
http://vn7.vn/?document_srl=79380
http://www.deliberarchia.org/forum/index.php?topic=1043229.0
http://www.deliberarchia.org/forum/index.php?topic=1043269.0
http://www.deliberarchia.org/forum/index.php?topic=1043274.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=51377
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=51397
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=310439
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=310481
http://jiquilisco.org/index.php/component/k2/itemlist/user/5232
http://jiquilisco.org/index.php/component/k2/itemlist/user/5235
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3799002
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3799007
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=33595
http://married.dike.gr/index.php/component/k2/itemlist/user/60849
http://mobility-corp.com/index.php/component/k2/itemlist/user/2591848
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/731984
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=16948
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-2019-tb%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://www.theparrotcentre.com/forum/index.php?topic=554398.0
http://www.theparrotcentre.com/forum/index.php?topic=554404.0
http://www.theparrotcentre.com/forum/index.php?topic=554410.0
http://www.theparrotcentre.com/forum/index.php?topic=554416.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=b8625fe2802ad52af6c52a60782d3b7a&topic=6828.0
https://altaylarteknoloji.com/index.php?topic=5015.0
https://www.c-alice.org/forum/index.php?topic=87549.0
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-tv4%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5/
https://testing.celekt.com/%d0%a2%d0%b0%d0%b9%d0%bd%d1%8b-%d0%a2%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-90-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cm9%d0%a2%d0%b0%d0%b9%d0%bd%d1%8b-%d0%a2%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-90/
https://www.amazingworldtop.com/entretenimiento/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mr6%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
http://teambuildingpremium.com/forum/index.php?topic=831291.0
http://teambuildingpremium.com/forum/index.php?topic=831293.0
http://teambuildingpremium.com/forum/index.php?topic=831294.0
http://teambuildingpremium.com/forum/index.php?topic=831297.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/519046
http://www.deliberarchia.org/forum/index.php?topic=1041558.0
http://www.ds712.net/guest/?document_srl=41465
http://www.ds712.net/guest/index.php?document_srl=41327&mid=guest07
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=41445
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=41502
http://www.hsaura.com/noty/41405
http://www.hsaura.com/noty/41445
http://www.hsaura.com/noty/41513
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=620740
http://www.spazioad.com/component/k2/itemlist/user/7312209
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=63648
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/323575
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/19374
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/526273
http://corumotoanahtar.com/component/k2/itemlist/user/1888
http://corumotoanahtar.com/component/k2/itemlist/user/1891
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=326994
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=327009
http://shinilspring.com/board_qsfb01/79629
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=131583
http://asiagroup.co.kr/index.php?mid=board_5&document_srl=165155
http://www.studyxray.com/Sangdam/72665
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=28062
http://xn----3x5er9r48j7wemud0a387h.com/news/1466
http://8.droror.co.il/uncategorized/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bf%d1%80%d0%be%d0%bc%d0%be/
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=26951
http://phmusic.dothome.co.kr/index.php?mid=PowerHouseMusic&document_srl=3369
http://www.taeshinmedia.com/index.php?document_srl=3282370&mid=genealogy_faq
http://agiteshop.com/xe/qa/31026
http://xn----3x5er9r48j7wemud0a387h.com/news/31573
https://www.runcity.org/forum/index.php?action=profile;u=75224
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=1185
http://taklongclub.com/forum/index.php?topic=146528.0
https://saltriverbg.com/2019/05/16/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80-8/
http://warmfund.net/p/index.php?mid=financing&document_srl=108905
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=6233
https://nextezone.com/index.php?topic=51098.0
http://aso-cn.com/index.php?mid=board_KRpb39&document_srl=6473
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/990
http://forum.byehaj.hu/index.php?topic=90141.0
http://viamania.net/index.php?mid=board_raYV15&document_srl=16061
http://apt2you2.cafe24.com/g1/884
http://isch.kr/board_PowH60/12989
http://bobr.site/index.php?topic=139531.0
https://prelease.club/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-3/
http://gxpfactory.net/index.php?document_srl=10977&mid=Guide
http://praisesound.co.kr/sub04_01/7181
http://www.svteck.co.kr/?document_srl=13093
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=17155
http://0433.net/budongsan/25257
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?document_srl=2123&mid=main_10
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=1001
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=103354
http://HyUa.1fps.icu/l/szIaeDC
http://mobility-corp.com/index.php/component/k2/itemlist/user/2607011
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=38764
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=19026
http://goldenpowerball2.com/index.php?mid=board_Bnby34&document_srl=5345
http://iymc.or.kr/pds/87015
http://xn--ok1bpqi43ahtb.net/board_EkDG82/87948
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=26777
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=41357
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=69106
http://www.datascientist.co.kr/?document_srl=46319
https://reficulcoin.com/index.php?topic=48276.0
http://www.svteck.co.kr/customer_gratitude/21513
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=74427
http://ye-dream.com/qa/57459
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=64398
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=14249
http://jnk-ent.jp/index.php?mid=gallery&document_srl=27110
http://lucky.kidspann.net/index.php?mid=qna&document_srl=29753
http://www.fassen.co.kr/xe/board_VCum96/13131
http://www.studyxray.com/Sangdam/70796
http://indiefilm.kr/xe/board/90890
http://emjun.com/index.php?mid=hangtotal&document_srl=44024
http://shinhwaair2017.cafe24.com/issue/194292
http://HyUa.1fps.icu/l/szIaeDC
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/16532
http://proxima.co.rw/index.php/component/k2/itemlist/user/620231
http://www.telcon.gr/index.php/component/k2/itemlist/user/53109
http://www.jesusonly.life/calendar/71829
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/525554
http://robocit.com/index.php/component/k2/itemlist/user/449616
http://www.deliberarchia.org/forum/index.php?topic=1018159.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1699215
http://vtservices85.fr/smf2/index.php?topic=234488.0
http://www.gforgirl.com/xe/poster/149816
http://www.hicleaning.kr/board_wash/93071
http://www.hicleaning.kr/board_wash/93164
http://www.hicleaning.kr/board_wash/93263
http://www.hsaura.com/noty/148607
http://www.hsaura.com/noty/148637
http://www.jshwanghoan.com/index.php?document_srl=91675&mid=qna
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=91741
http://www.sp1.football/?document_srl=244812
http://www.sp1.football/index.php?document_srl=244234&mid=faq
http://www.sp1.football/index.php?mid=faq&document_srl=244637
http://www.sp1.football/index.php?mid=faq&document_srl=244969
http://xn----3x5er9r48j7wemud0a387h.com/news/39226
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=10629
http://wigalseguros.com.br/index.php/component/k2/itemlist/user/10634
http://www.arunagreen.com/index.php/component/k2/itemlist/user/543108
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/9577
http://www.m1avio.com/index.php/component/k2/itemlist/user/3721650
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=640967
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/640983
http://oneandonly1127.com/guest/871
http://aso-cn.com/index.php?mid=board_KRpb39&document_srl=2453
http://cafe.dokseosil.co.kr/community/24053
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/492459
http://www.svteck.co.kr/customer_gratitude/25365
http://xn--ok1bpqi43ahtb.net/board_EkDG82/90007
http://www.xn--xy1b45gp4h0qgb9g.com/?document_srl=16928
http://hyeonjun.co.kr/menu3/67814
http://www.sp1.football/index.php?mid=tr_video&document_srl=15836
http://sextomariotienda.com/blog/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8-2/
http://www.hsaura.com/license/59509
http://isch.kr/board_PowH60/11795
http://www.lozic.co.kr/gallery/9501
http://isch.kr/board_PowH60/4821
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=21639
http://azone.synology.me/xe/?document_srl=41036
http://gochon-iusell.co.kr/g1/3344
http://xn--ok1bpqi43ahtb.net/?document_srl=102138
http://uberdrivers.net/forum/index.php?topic=292390.0
http://shinilspring.com/board_qsfb01/50439
http://hyeonjun.co.kr/menu3/55478
http://shinilspring.com/board_qsfb01/89753
http://askpharm.net/board_NQiz06/24746
http://ru-realty.com/forum/index.php?PHPSESSID=nftsno4fn4ac79evrgu57n1ff2&topic=523083.0
https://www.chirorg.com/?document_srl=11263
http://ekitchen.co.kr/intro/1017877
http://hyeonjun.co.kr/?document_srl=41066
http://indiefilm.kr/xe/board/80904
http://www.fassen.co.kr/xe/board_VCum96/8721
http://bebopindia.com/notcie/39236
http://skylinecam.co.kr/photo/38731
http://0433.net/junggo/24741
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-t0-r4-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://jnk-ent.jp/index.php?mid=gallery&document_srl=11541
http://www.jesusonly.life/calendar/133614
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=20567
https://ttmt.net/crypto_lab_2F/425937
http://www.svteck.co.kr/customer_gratitude/13003
http://www.svteck.co.kr/customer_gratitude/40037
http://HyUa.1fps.icu/l/szIaeDC
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=55237
http://www.siheunglove.com/chulip/20233
http://www.eunhaele.co.kr/xe/board/18983
http://benzmall.co.kr/index.php?mid=download&document_srl=330
http://jstech.kr/index.php?mid=board_lqyj42&document_srl=10325
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=22478
http://www.hicleaning.kr/?document_srl=69445
http://readingbible.org/board_xxpp62/711443
http://sextomariotienda.com/blog/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80-6/
http://www.svteck.co.kr/customer_gratitude/33241
http://www.hsaura.com/noty/8047
http://www.ds712.net/guest/index.php?document_srl=43866&mid=guest07
http://shinilspring.com/board_qsfb01/12949
http://roikjer.com/forum/index.php?PHPSESSID=fsk39185vqivqh1gqpgfmuik91&topic=872763.0
http://skylinecam.co.kr/photo/74311
http://shinhwaair2017.cafe24.com/issue/206538
http://www.vamoscontigo.org/Noticia/714
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=49992
http://themasters.pro/file_01/3384
http://sy.korean.net/qna/29540
http://koais.com/data/12352
http://constellation.kro.kr/board_kbku73/2197
http://www.hicleaning.kr/board_wash/9501
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=55297
http://sheepofani.dothome.co.kr/index.php?mid=board_Zxan02&document_srl=3533
http://www.hicleaning.kr/board_wash/22317
http://bobr.site/index.php?topic=128324.0
http://jjikduk.net/DATA/20272
http://indiefilm.kr/xe/?document_srl=88503
http://moavalve.co.kr/faq/46869
http://2872870.com/?document_srl=12079
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=80386
http://cwon.kr/xe/board_bnSr36/37002
http://skylinecam.co.kr/photo/49891
http://photogrotto.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%be/
https://nextezone.com/index.php?topic=51533.0
http://www.svteck.co.kr/customer_gratitude/18495
http://www.svteck.co.kr/customer_gratitude/42231
http://www.deliberarchia.org/forum/index.php?topic=1026983.0
http://www.yepia.com/board_ZCPG83/7680
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-b9-m1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=11084
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=18615
http://HyUa.1fps.icu/l/szIaeDC
http://iymc.or.kr/pds/86653
http://skylinecam.co.kr/?document_srl=74424
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/500803
http://jnk-ent.jp/index.php?mid=gallery&document_srl=41595
http://jejucctv.co.kr/A5/441
http://praisesound.co.kr/sub04_01/4192
http://www.yepia.com/board_ZCPG83/13685
http://ru-realty.com/forum/index.php?PHPSESSID=3fo40krhjsqqku5m3frkdqfhm7&topic=516208.0
http://emjun.com/index.php?mid=hangtotal&document_srl=62400
http://lahch.co.kr/?document_srl=7028
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=8323
http://lucky.kidspann.net/index.php?mid=qna&document_srl=1097
http://haeple.com/index.php?mid=etc&document_srl=45623
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.kr/news/2860
http://gspara01.dothome.co.kr/index.php?mid=board_XHsr53&document_srl=1152
http://apt2you2.cafe24.com/g1/1630
http://sofficer.net/xe/teach/218432
http://iamking.net/board/1700
http://uberdrivers.net/forum/index.php?topic=293032.0
http://www.gforgirl.com/xe/poster/72573
http://www.jesusonly.life/?document_srl=2242
http://skylinecam.co.kr/photo/100485
http://laokorea.com/orange_menu1/17478
https://nextezone.com/index.php?action=profile;u=4644
http://www.siheunglove.com/chulip/22791
http://www.autospa.lv/index.php/lv/component/k2/itemlist/user/9936
http://warmfund.net/p/?document_srl=119141
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=134695
http://hyeonjun.co.kr/menu3/75376
http://shinilspring.com/board_qsfb01/78495
http://atemshow.com/atemfair_domestic/30201
http://gallerychoi.com/Exhibition/55073
http://HyUa.1fps.icu/l/szIaeDC
http://myrechockey.com/forums/index.php?topic=103346.0
http://cwon.kr/xe/board_bnSr36/13780
https://prelease.club/%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5%d0%b4%d0%be-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mk6f-%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5/
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2644641
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=18624
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1405417
http://emjun.com/index.php?mid=hangtotal&document_srl=7519
http://teambuildingpremium.com/forum/index.php?topic=826421.0
http://www.deliberarchia.org/forum/index.php?topic=1033905.0
http://zanoza.h1n.ru/2019/05/14/%d0%bd%d0%b5-%d0%be%d1%82%d0%bf%d1%83%d1%81%d0%ba%d0%b0%d0%b9-%d0%bc%d0%be%d1%8e-%d1%80%d1%83%d0%ba%d1%83-elimi-birakma-36-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sugc-%d0%bd%d0%b5-%d0%be/
https://sanp.pro/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mesu-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd/
https://sanp.pro/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gias-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd/
https://sanp.pro/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rumy-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd/
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=64084
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=64127
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/64148
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1580949
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1370758
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1370768
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1370774
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1370793
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1042505
http://www.camaracoyhaique.cl/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d0%be%d0%bd%d0%bb%d0%b0%d0%b9%d0%bd-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-10-05-19-ts%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5/
http://adopt10plus.com/groups/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-2019-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-uv%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-2019/
http://xplorefitness.com/blog/%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-13-05-2019-z9-%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://batubersurat.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=50371
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1670294
http://xn--ok1bpqi43ahtb.net/board_eASW07/62002
http://mediaville.me/index.php/component/k2/itemlist/user/254491
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=97752
http://www.critico-expository.com/forum/index.php?topic=10350.0
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/16378
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=64829
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/27207
https://prelease.club/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cr2y/
https://prelease.club/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-93-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lv8r-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-93-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://bitpark.co.kr/board_IzjM66/3928878
http://zanoza.h1n.ru/2019/05/14/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-143-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tnvd-%d0%b2%d0%be%d1%81%d0%ba%d1%80/
http://zanoza.h1n.ru/2019/05/14/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kgtu-%d0%b2%d0%be%d1%81%d0%ba%d1%80/
https://sanp.pro/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-81-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xdpq-%d0%bd%d0%b5%d0%b2/
http://proxima.co.rw/index.php/component/k2/itemlist/user/622929
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1082181
http://www.deliberarchia.org/forum/index.php?topic=1034410.0
http://zanoza.h1n.ru/2019/05/15/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-38-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rqix-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0/
https://prelease.club/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-25-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-aper-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-25-%d1%81%d0%b5%d1%80%d0%b8/
https://prelease.club/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jxof-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd/
https://prelease.club/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yaey-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd/
https://prelease.club/%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-69-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wcrn-%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-69/
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2593231
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2593127
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=306900
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=306912
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=48178
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=48188
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/496250
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/496295
http://otitismediasociety.org/forum/index.php?topic=172818.0
http://bewasia.com/index.php?document_srl=3902&mid=board_cUYy21
http://jnk-ent.jp/index.php?mid=gallery&document_srl=25681
http://cwon.kr/xe/board_bnSr36/30925
http://ye-dream.com/qa/52106
http://otitismediasociety.org/forum/index.php?topic=173412.0
http://www.fassen.co.kr/xe/board_VCum96/8140
http://www.hsaura.com/noty/120235
http://www.jesusonly.life/?document_srl=41088
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=32237
http://lucky.kidspann.net/index.php?mid=qna&document_srl=10624
http://2872870.com/est/5818
http://yoriyorifood.com/xxxx/spacial/62386
http://www.jesusonly.life/?document_srl=106685
http://azone.synology.me/xe/?document_srl=43643
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1613934
http://www.svteck.co.kr/customer_gratitude/26025
http://jnk-ent.jp/index.php?mid=gallery&document_srl=42207
http://5starcoffee.co.kr/board_EBXY17/5950
http://sofficer.net/xe/teach/207012
http://isch.kr/board_PowH60/27381
http://49.247.3.43/index.php?mid=board_PiDQ29&document_srl=14764
http://gallerychoi.com/Exhibition/46881
http://indiefilm.kr/xe/board/71851
http://readingbible.org/board_xxpp62/774117
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=79524
http://uberdrivers.net/forum/index.php?topic=285141.0
http://shinhwaair2017.cafe24.com/issue/55108
http://oceangray.i234.me/?document_srl=23671
http://shinhwaair2017.cafe24.com/issue/177239
http://skylinecam.co.kr/photo/25853
http://bebopindia.com/notcie/67879
http://ye-dream.com/qa/20115
http://HyUa.1fps.icu/l/szIaeDC
http://www.golden-nail.co.kr/press/48889
http://xn--2e0bk61btjo.com/notice/3800
http://www.lozic.co.kr/gallery/24258
https://nple.com/xe/pds/23265
http://www.gforgirl.com/xe/poster/2527
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=38893
http://asiagroup.co.kr/index.php?mid=board_5&document_srl=130930
http://www.hyunjindc.com/qna/14287
http://www.sp1.football/index.php?mid=tr_video&document_srl=52193
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=64677
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=25558
http://www.studyxray.com/Sangdam/17781
http://sd-xi.co.kr/g1/13259
http://gallerychoi.com/Exhibition/65832
http://isch.kr/board_PowH60/29639
http://indiefilm.kr/xe/board/93027
http://sunele.co.kr/board_ReBD97/46708
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=101632
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/gumdanapt/11319
http://xn--ok1bpqi43ahtb.net/board_SPcK94/91929
http://haeple.com/index.php?mid=etc&document_srl=79164
http://shinilspring.com/board_qsfb01/27679
http://www.jesusonly.life/calendar/35074
https://esel.gist.ac.kr/esel2/board_hmgj23/36484
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=52574
http://wipln.com/?document_srl=27074
http://myrechockey.com/forums/index.php?topic=105615.0
http://xn--2e0bk61btjo.com/notice/1830
http://www.gforgirl.com/xe/poster/10909
http://www.teedinubon.com/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%84%d0%b8%d0%bb%d1%8c%d0%bc-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3/
http://hyeonjun.co.kr/menu3/21040
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=df7c0c29b4cec793b54ae6aa5756358b&topic=5859.0
https://ttmt.net/crypto_lab_2F/440108
http://HyUa.1fps.icu/l/szIaeDC
http://mtuan93.com/board_uCqR85/4313
http://foxy-tv.com/index.php?mid=board_arik22&document_srl=37231
http://sy.korean.net/qna/36610
http://www.gforgirl.com/xe/poster/46221
http://goldenpowerball2.com/index.php?mid=board_jRzi06&document_srl=34387
http://hyeonjun.co.kr/?document_srl=1055
http://esiapolisthesharp2.co.kr/g1/20110
http://www.ekemoon.com/199893/051820194716/
https://chromehearts.in.th/index.php?topic=50031.0
http://8.droror.co.il/uncategorized/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%84%d0%b8%d0%bb%d1%8c%d0%bc-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd/
http://www.siheunglove.com/chulip/3794
http://vn7.vn/qna/71572
https://esel.gist.ac.kr/esel2/board_hmgj23/48043
http://f-tube.info/board/69891
http://lucky.kidspann.net/index.php?mid=qna&document_srl=37475
http://goldenpowerball2.com/index.php?mid=board_Bnby34&document_srl=29943
http://hyeonjun.co.kr/menu3/75699
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=68605
http://hyeonjun.co.kr/menu3/29799
http://skangseo.org/xe/board_Atnj46/37847
http://forum.elexlabs.com/index.php?topic=28039.0
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d9-l9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4/
http://www.taeshinmedia.com/index.php?mid=genealogy_free_board&document_srl=3281776
http://www.deliberarchia.org/forum/index.php?topic=1047657.0
https://betshin.com/Story/25188
http://www.jesusonly.life/calendar/48911
http://www.hsaura.com/license/90322
https://nple.com/xe/pds/8595
http://www.ds712.net/guest/index.php?document_srl=52371&mid=guest07
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g9-f1-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://lahch.co.kr/index.php?mid=board_jHAP41&document_srl=19112
https://saltriverbg.com/2019/05/16/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90ox6%e3%80%91-%d0%b8%d0%b3%d1%80/
http://HyUa.1fps.icu/l/szIaeDC
http://jiquilisco.org/?option=com_k2&view=itemlist&task=user&id=6268
http://www.jesusonly.life/calendar/62563
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=292560
http://www.sp1.football/index.php?mid=faq&document_srl=1632
http://zanoza.h1n.ru/2019/05/16/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d0%b5%d0%ba%d0%b0%d1%82%d0%b5%d1%80%d0%b8%d0%bd%d0%b1%d1%83%d1%80%d0%b3-3/
http://0433.net/junggo/50832
http://0433.net/junggo/50838
http://0433.net/junggo/50850
http://0433.net/junggo/50862
http://bebopindia.com/notcie/131296
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1808216
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=311430
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=311572
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3450900
http://jiquilisco.org/index.php/component/k2/itemlist/user/5392
http://married.dike.gr/index.php/component/k2/itemlist/user/61073
http://mediaville.me/index.php/component/k2/itemlist/user/267054
http://mediaville.me/index.php/component/k2/itemlist/user/267063
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/732918
http://www.deliberarchia.org/forum/index.php?topic=1020755.0
http://arquitectosenreformas.es/component/k2/itemlist/user/80605
http://emjun.com/?document_srl=31480
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=309450
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=73926
http://www.critico-expository.com/forum/index.php?topic=8897.0
http://dev.aabn.org.gh/component/k2/itemlist/user/581506
http://vn7.vn/qna/76646
http://seoksoononly.dothome.co.kr/qna/723821
http://www.remify.app/foro/index.php?topic=241238.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/288496
http://koushatarabar.com/index.php/component/k2/itemlist/user/1325751
http://www.afikgan.co.il/index.php/component/k2/itemlist/user/26058
http://www.deliberarchia.org/forum/index.php?topic=979120.0
http://roikjer.com/forum/index.php?PHPSESSID=jvo96ujk84l50n6r3lcpspfeh5&topic=820709.0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=754609
http://seoksoononly.dothome.co.kr/qna/763026
http://danielmillsap.com/forum/index.php?topic=967508.0
http://www.ekemoon.com/142809/051920190905/
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12712
http://mediaville.me/index.php/component/k2/itemlist/user/222425
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2570052
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1631705
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2658073
http://corumotoanahtar.com/component/k2/itemlist/user/4556
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=342908
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=100205
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1924896
http://jiquilisco.org/index.php/component/k2/itemlist/user/9070
http://mediaville.me/?option=com_k2&view=itemlist&task=user&id=285346
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=793784
http://mobility-corp.com/index.php/component/k2/itemlist/user/2585002
http://www.ds712.net/guest/?document_srl=48709
http://teambuildingpremium.com/forum/index.php?topic=823516.0
http://teambuildingpremium.com/forum/index.php?topic=826662.0
http://danielmillsap.com/forum/index.php?topic=1033034.0
http://moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=700273
http://www.critico-expository.com/forum/index.php?topic=9423.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/86057
http://thermoplast.envolgroupe.com/component/k2/author/91491
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1881444
http://mediaville.me/index.php/component/k2/itemlist/user/265660
http://ovotecegg.com/component/k2/itemlist/user/117683
http://seoksoononly.dothome.co.kr/qna/739517
http://cccpvideo.forumside.com/index.php?topic=430.0
http://menulisilmiah.net/live-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://khuyenmaikk13.info/index.php?topic=182026.0
http://www.vivelabmanizales.com/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dtfw-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-20-%d1%81%d0%b5%d1%80%d0%b8/
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D0%BF%D0%BE%D1%81%D1%82-%D1%88%D0%BE%D1%83-%D1%81%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C-%D0%BE%D0%BD%D0%BB%D0%B0%D0%B9%D0%BD%C2%BB-nm%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D0%BF%D0%BE%D1%81%D1%82-%D1%88%D0%BE%D1%83
http://www.ekemoon.com/142525/051720194705/
http://withinfp.sakura.ne.jp/eso/index.php/16914699-uristy-11-seria-smotret-uristy-11-seria/0
https://members.fbhaters.com/index.php?topic=77338.0
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8-3/
http://proxima.co.rw/index.php/component/k2/itemlist/user/581160
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3294403
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=47891
http://www.josephmaul.org/menu41/97542
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=77598
http://www.rationalkorea.com/xe/?document_srl=502130
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=502145
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=502165
http://www.sp1.football/index.php?mid=faq&document_srl=203734
http://www.sp1.football/index.php?mid=faq&document_srl=203820
http://www.sp1.football/index.php?mid=tr_video&document_srl=203760
http://www.svteck.co.kr/customer_gratitude/43311
http://www.svteck.co.kr/customer_gratitude/43315
http://bitpark.co.kr/board_IzjM66/3800742
http://seoksoononly.dothome.co.kr/qna/818900
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=317220
http://corumotoanahtar.com/component/k2/itemlist/user/2391.html
http://vtservices85.fr/smf2/index.php?PHPSESSID=ec0d1af680d39aaa686c06d1feae9f61&topic=244557.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2632272
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1615020
http://macdistri.com/index.php/component/k2/itemlist/user/297333
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=14043
http://arunagreen.com/index.php/component/k2/itemlist/user/420995
http://mediaville.me/index.php/component/k2/itemlist/user/218240
http://poselokgribovo.ru/forum/index.php?topic=735189.0
http://www.ekemoon.com/143485/050020193306/
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-16-%d1%81%d0%b5%d1%80-4/
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D1%87%D0%B0%D1%81%D1%82%D1%8C-6%C2%BB-wc%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D1%87%D0%B0%D1%81%D1%82%D1%8C-6%C2%BB81-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9
http://153.120.114.241/eso/index.php/16879958-holostak-9-sezon-10-vypusk-diety-xkholostak-9-sezon-10-vypusk-d
http://www.vivelabmanizales.com/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u7-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3/
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4845565
http://married.dike.gr/index.php/component/k2/itemlist/user/46571
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1728774
http://thermoplast.envolgroupe.com/component/k2/author/120917
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=82069
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4833638
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1651433
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=33642
http://www.firstfinancialservices.co.uk/component/k2/itemlist/user/9910
http://haeple.com/index.php?mid=etc&document_srl=74206
http://roikjer.com/forum/index.php?topic=871796.0
http://yoriyorifood.com/xxxx/spacial/43802
https://nextezone.com/index.php?topic=54699.0
http://www.yepia.com/board_ZCPG83/1514
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=15158
http://d-tube.info/board_jvyO69/233734
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=15438
http://www.studyxray.com/Sangdam/61396
http://www.datascientist.co.kr/?document_srl=47516
http://iymc.or.kr/pds/85845
http://1600-1590.com/?document_srl=80272
http://toeden.co.kr/Product_new/27731
http://yeonsen.com/?document_srl=9083
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=490711
http://vervetama.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5/
http://praisesound.co.kr/sub04_01/5766
http://jnk-ent.jp/index.php?mid=gallery&document_srl=43877
http://skylinecam.co.kr/photo/63899
http://ru-realty.com/forum/index.php?PHPSESSID=tgkli7nbd04eld7m3011592r95&topic=510043.0
http://poselokgribovo.ru/forum/index.php?topic=792454.0
http://oss.obigo.com/oss/index.php?mid=board_ksaA03&document_srl=546
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=124498
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2773420
http://5starcoffee.co.kr/board_EBXY17/3977
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=765158
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/694
http://d-tube.info/board_jvyO69/237162
http://hanalove.kidspann.net/index.php?mid=qna&document_srl=43591
http://ye-dream.com/?document_srl=73260
http://kyj1225.godohosting.com/board_mebR72/3568
http://49.247.3.43/index.php?mid=board_PiDQ29&document_srl=16013
http://ye-dream.com/?document_srl=9829
http://photogrotto.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-720/
http://xn--ok1bpqi43ahtb.net/?document_srl=59087
http://www.josephmaul.org/menu41/48325
http://HyUa.1fps.icu/l/szIaeDC
http://seoksoononly.dothome.co.kr/qna/832947
http://forum.digamahost.com/index.php?topic=112883.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2564716
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=98715
http://ovotecegg.com/component/k2/itemlist/user/125842
http://bebopindia.com/notcie/61808
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=33612
http://lucky.kidspann.net/?document_srl=68384
http://lucky.kidspann.net/?document_srl=68455
http://lucky.kidspann.net/index.php?mid=qna&document_srl=68419
http://lucky.kidspann.net/index.php?mid=qna&document_srl=68434
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=30851
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=285313
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=285387
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1148162
http://married.dike.gr/index.php/component/k2/itemlist/user/55019
http://mobility-corp.com/index.php/component/k2/itemlist/user/2550025
http://mobility-corp.com/index.php/component/k2/itemlist/user/2550043
http://xn--ok1bpqi43ahtb.net/board_eASW07/28467
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=33877
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1625693
http://bath-family.com/photo_zone/4870
http://www.die-design-manufaktur.de/?option=com_k2&view=itemlist&task=user&id=5211230
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=48457
http://indiefilm.kr/xe/board/45417
http://zanoza.h1n.ru/2019/05/16/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-15-05-2019-t1-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://menulisilmiah.net/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d3-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be/
http://moavalve.co.kr/faq/31110
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=76767
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=76904
http://yoriyorifood.com/xxxx/spacial/84611
https://esel.gist.ac.kr/esel2/board_hmgj23/60365
https://esel.gist.ac.kr/esel2/board_hmgj23/60394
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=285441
http://married.dike.gr/index.php/component/k2/itemlist/user/55021
http://mediaville.me/index.php/component/k2/itemlist/user/240692
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=79795
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/79781
http://ovotecegg.com/component/k2/itemlist/user/127927
http://ovotecegg.com/component/k2/itemlist/user/128030
http://ovotecegg.com/component/k2/itemlist/user/128034
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/222415
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=11084
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=11147
http://soc-human.kz/index.php/component/k2/itemlist/user/1682295
http://research.kiu.ac.kr/index.php?document_srl=22738&mid=Food4Thought
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=153937
http://www.vivelabmanizales.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-cl9p-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://ovotecegg.com/component/k2/itemlist/user/135751
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1706067
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=826136
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/3741
http://zsmr.com.ua/index.php/component/k2/itemlist/user/554418
http://forum.digamahost.com/index.php?topic=122780.0
http://emjun.com/index.php?mid=hangtotal&document_srl=19380
http://jjikduk.net/DATA/2107
http://ye-dream.com/qa/89267
http://ye-dream.com/qa/89337
http://yeonsen.com/?document_srl=82214
http://yoriyorifood.com/xxxx/?document_srl=89690
http://yoriyorifood.com/xxxx/spacial/89658
http://zanoza.h1n.ru/2019/05/18/%d0%b1%d0%be%d0%b3%d0%b0%d1%82%d1%8b%d0%b5-%d0%b8-%d0%b1%d0%b5%d0%b4%d0%bd%d1%8b%d0%b5-zengin-ve-yoksul-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vgty-%d0%b1%d0%be%d0%b3%d0%b0%d1%82%d1%8b/
https://danceplanet.se/commodore/index.php?topic=44734.0
https://esel.gist.ac.kr/esel2/board_hmgj23/65179
https://esel.gist.ac.kr/esel2/board_hmgj23/65266
https://esel.gist.ac.kr/esel2/board_hmgj23/65313
http://batubersurat.com/index.php/component/k2/itemlist/user/50315
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1880320
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=315181
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=315187
http://k2.akademitelkom.ac.id/component/k2/itemlist/user/315170
http://married.dike.gr/index.php/component/k2/itemlist/user/56448
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=82917
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/84692
http://zanoza.h1n.ru/2019/05/16/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vsnu-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
https://turimex.mx.solemti.net/component/k2/itemlist/user/1222
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/697531
https://prelease.club/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mg2f-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://k2.akademitelkom.ac.id/index.php/component/k2/itemlist/user/326667
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3435245
http://bitpark.co.kr/board_IzjM66/3811502
http://ovotecegg.com/component/k2/itemlist/user/142507
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4756078
http://www.ds712.net/guest/?document_srl=49643
http://zanoza.h1n.ru/2019/05/14/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81-9/
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1668211
http://vehibook.com/members/jody50m1510655/
http://roikjer.com/forum/index.php?PHPSESSID=ihi9785a4tu6ipr5cuibp3f6g1&topic=869302.0
http://forum.digamahost.com/index.php?topic=110359.0
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/14386
http://www.ekemoon.com/147577/052120194706/
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1630436
http://withinfp.sakura.ne.jp/eso/index.php/16873626-smotret-tola-robot-9-seria-u9-tola-robot-9-seria/0
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1770083
http://www.ekemoon.com/149061/050020191307/
http://forum.politeknikgihon.ac.id/index.php?topic=24950.0
http://dev.aabn.org.gh/component/k2/itemlist/user/519538
http://ovotecegg.com/component/k2/itemlist/user/121491
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=557756
https://members.fbhaters.com/index.php?topic=81559.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/568771
http://condolencias.servisa.es/13-05-05-2019-e1-13
http://www.vivelabmanizales.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-k7-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/98772
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/98838
http://ovotecegg.com/component/k2/itemlist/user/146301
http://proxima.co.rw/index.php/component/k2/itemlist/user/625522
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=192079
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/210384
http://smartacity.com/component/k2/itemlist/user/46396
http://thermoplast.envolgroupe.com/component/k2/author/106116
http://thermoplast.envolgroupe.com/component/k2/author/106152
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=73970
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=74036
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3650174
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4809833
http://zanoza.h1n.ru/2019/05/14/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sg4b-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://www.urbantutorial.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=110537
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=308080
http://www.deliberarchia.org/forum/index.php?topic=1033286.0
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=9660
http://moyakmermer.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=693132
http://zanoza.h1n.ru/2019/05/16/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-16-05-2019-t0-%d1%81%d0%bb%d1%83%d0%b3/
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3327789
http://teambuildingpremium.com/forum/index.php?topic=834040.0
http://xplorefitness.com/blog/%C2%AB%D0%B4%D0%BE%D1%87%D0%BA%D0%B8-%D0%BC%D0%B0%D1%82%D0%B5%D1%80%D0%B8-%D0%B4%D0%BE%D1%87%D0%BA%D0%B8-%D0%BC%D0%B0%D1%82%D0%B5%D1%80i-16-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-09-05-2019-x9-%C2%AB%D0%B4%D0%BE%D1%87%D0%BA%D0%B8-%D0%BC%D0%B0%D1%82%D0%B5%D1%80%D0%B8-%D0%B4%D0%BE%D1%87%D0%BA%D0%B8-%D0%BC%D0%B0%D1%82%D0%B5%D1%80i-16-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://dohairbiz.com/en/component/k2/itemlist/user/2749450.html
http://myrechockey.com/forums/index.php?topic=99419.0
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1921306
http://dev.aabn.org.gh/component/k2/itemlist/user/560322
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=504293
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/480503
http://proxima.co.rw/index.php/component/k2/itemlist/user/565280
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=15314
http://mediaville.me/index.php/component/k2/itemlist/user/207514
https://khuyenmaikk13.info/index.php?topic=183534.0
http://seoksoononly.dothome.co.kr/qna/725165
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/53425
http://8.droror.co.il/uncategorized/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gw5%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f08-05/
http://www.dap.com.py/index.php/component/k2/itemlist/user/791730
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=270958
http://topitop.kz/index.php/component/k2/itemlist/user/76505
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3404506
http://dohairbiz.com/?option=com_k2&view=itemlist&task=user&id=2707570
https://lucky28003.nl/forum/index.php?topic=10299.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/98667
http://ovotecegg.com/component/k2/itemlist/user/146139
http://proxima.co.rw/index.php/component/k2/itemlist/user/625671
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=210334
http://smartacity.com/component/k2/itemlist/user/46375
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1686587
http://www.remify.app/foro/index.php?topic=265384.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2576052
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1582117
https://khuyenmaikk13.info/index.php?topic=199592.0
http://www.deliberarchia.org/forum/index.php?topic=1020574.0
http://xplorefitness.com/blog/%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB-%D0%B3%D1%80%D0%B0%D0%BD%D0%B4-2-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-21-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-d3-%D0%B3%D1%80%D0%B0%D0%BD%D0%B4-2-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-21-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://zanoza.h1n.ru/2019/05/15/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-40-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sljo-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0/
http://vtservices85.fr/smf2/index.php?PHPSESSID=f7f938c0fec62423163a420971dbd38a&topic=216643.0
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=14672
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=2269
http://vn7.vn/qna/71160
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1674110
http://indiefilm.kr/xe/board/64851
http://seoksoononly.dothome.co.kr/qna/804085
http://laspoltrina.it/component/k2/itemlist/user/1388231
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1837648
http://miquirofisico.com/index.php/component/k2/itemlist/user/3777
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7303710
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1005890
http://www.phan-aen.go.th/forum/index.php?topic=626094.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=290071
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=64898
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=64945
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/261323
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/63156
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=2019
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=21288
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2633508
http://arunagreen.com/?option=com_k2&view=itemlist&task=user&id=514886
http://arunagreen.com/index.php/component/k2/itemlist/user/514680
http://corumotoanahtar.com/component/k2/itemlist/user/2179.html
http://www.theocraticamerica.org/forum/index.php?topic=38394.0
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=98342
https://reelgosu.com/board_peJN24/273071
http://d-tube.info/?document_srl=230604
http://uberdrivers.net/forum/index.php?topic=285300.0
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=61978
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lq6-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://cybergsm.es/index.php?topic=17903.0
https://hackersuniversity.net/index.php?topic=17133.0
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=638
http://2872870.com/est/15372
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=31844
http://indiefilm.kr/xe/board/34473
http://goldenpowerball2.com/index.php?mid=board_Bnby34&document_srl=92812
http://www.hsaura.com/noty/86708
http://ariji.kr/?document_srl=797706
http://www.itosm.com/cn/board_nLoq17/13706
http://skylinecam.co.kr/photo/70455
http://moavalve.co.kr/faq/55877
http://www.hyunjindc.com/qna/9925
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3271797
http://toeden.co.kr/?document_srl=5169
http://skylinecam.co.kr/photo/34399
http://www.yepia.com/board_ZCPG83/6359
http://www.yepia.com/board_ZCPG83/16067
http://oneandonly1127.com/guest/3072
http://www.artangel.co.kr/?document_srl=15683
http://agiteshop.com/xe/qa/38321
http://vtservices85.fr/smf2/index.php?PHPSESSID=71f0bb7879d20575884a6637a58adff6&topic=233700.0
http://www.ekemoon.com/197917/051020190816/
http://moavalve.co.kr/faq/50173
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=36899
http://e-educ.net/Forum/index.php?topic=11613.0
http://jejucctv.co.kr/A5/536
http://www.lgue.co.kr/index.php?mid=lgue05&document_srl=4622&sort_index=title&order_type=desc
http://www.deliberarchia.org/forum/index.php?topic=1049967.0
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=1768
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=15263
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=47339
http://readingbible.org/board_xxpp62/788430
http://jstech.kr/index.php?mid=board_lqyj42&document_srl=7052
http://roikjer.com/forum/index.php?PHPSESSID=2dchf6lhh2joq01f0kskct86u7&topic=878953.0
http://skylinecam.co.kr/photo/69641
http://hyeonjun.co.kr/menu3/32002
http://sunele.co.kr/board_ReBD97/43978
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=7699
http://HyUa.1fps.icu/l/szIaeDC
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/5479
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=3365
http://goldenpowerball2.com/?document_srl=52630
http://constellation.kro.kr/board_kbku73/1262
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=16510
http://constellation.kro.kr/board_kbku73/5847
http://www.jesusonly.life/calendar/116894
http://www.svteck.co.kr/customer_gratitude/24210
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=82958
http://lucky.kidspann.net/index.php?mid=qna&document_srl=1288
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3264278
http://www.ekemoon.com/195127/052220191115/
http://0433.net/budongsan/18309
https://reficulcoin.com/index.php?topic=46117.0
http://forum.elexlabs.com/index.php?topic=27084.0
http://gxpfactory.net/index.php?mid=Guide&document_srl=1564
http://2872870.com/est/13292
http://iamking.net/board/22152
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=45619
http://village.lorem.kr/index.php?document_srl=16608&mid=board_xmEJ33
http://shinilspring.com/board_qsfb01/77919
http://indiefilm.kr/xe/board/120638
http://HyUa.1fps.icu/l/szIaeDC
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=15597
http://askpharm.net/board_NQiz06/23542
http://www.tessabannampad.go.th/webboard/index.php?topic=210873.0
http://www.hicleaning.kr/board_wash/9408
http://www.jesusonly.life/calendar/22303
http://moavalve.co.kr/faq/51475
http://indiefilm.kr/xe/board/102912
https://www.shaiyax.com/index.php?topic=344722.0
http://indiefilm.kr/xe/board/40898
http://www.vamoscontigo.org/?document_srl=21275
http://www.svteck.co.kr/customer_gratitude/39904
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80-4/
https://www.thedezlab.com/lab/community/index.php?topic=2622.0
http://www.gforgirl.com/xe/poster/86209
http://9mantv.com/index.php?mid=board_LaTg55&document_srl=11914
https://esel.gist.ac.kr/esel2/board_hmgj23/4768
http://mobility-corp.com/index.php/component/k2/itemlist/user/2594780
http://shinilspring.com/board_qsfb01/63117
http://xn--2e0bk61btjo.com/notice/7340
http://mglpcm.org/board_ETkS12/23566
http://www.taeshinmedia.com/index.php?document_srl=3282035&mid=genealogy_faq
http://gochon-iusell.co.kr/g1/20698
http://bebopindia.com/notcie/70505
http://0433.net/junggo/46222
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=47764
http://yooseok.com/board_BkvT46/317984
http://tototoday.com/board_oRiY52/24533
http://foxy-tv.com/index.php?mid=board_lgTk68&document_srl=35792
http://www.studyxray.com/Sangdam/87842
http://bdch.kr/board_GuHz19/2517
http://HyUa.1fps.icu/l/szIaeDC
http://www.vivelabmanizales.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-xp7a-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1424073
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=1816
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1568932
http://euromouleusinage.com/index.php/component/k2/itemlist/user/137244
http://corumotoanahtar.com/component/k2/itemlist/user/1432.html
http://fbpharm.net/index.php/component/k2/itemlist/user/38428
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=141657
http://soc-human.kz/index.php/component/k2/itemlist/user/1681703
http://wigalseguros.com.br/component/users/?task=user&view=itemlist&id=6535
http://wigalseguros.com.br/index.php/component/k2/itemlist/user/6476
http://atemshow.com/?document_srl=41423
http://atemshow.com/?document_srl=41449
http://atemshow.com/atemfair_domestic/41432
http://hyeonjun.co.kr/menu3/74084
http://hyeonjun.co.kr/menu3/74349
http://indiefilm.kr/xe/board/123850
http://masanlib.or.kr/g1/31788
http://shinilspring.com/board_qsfb01/93136
http://shinilspring.com/board_qsfb01/93170
http://shinilspring.com/board_qsfb01/93196
http://moavalve.co.kr/?document_srl=48840
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/315678
http://zanoza.h1n.ru/2019/05/14/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gn8x-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://teambuildingpremium.com/forum/index.php?topic=826641.0
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xp2%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f10-05/
http://ye-dream.com/qa/34324
http://dev.aabn.org.gh/component/k2/itemlist/user/594344
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/208223
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1682284
http://www.arunagreen.com/index.php/component/k2/itemlist/user/506066
http://www.m1avio.com/index.php/component/k2/itemlist/user/3685300
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=257465
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2625976
http://arunagreen.com/index.php/component/k2/itemlist/user/506062
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/524001
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=38716
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=38823
http://fbpharm.net/index.php/component/k2/itemlist/user/38768
http://jiquilisco.org/index.php/component/k2/itemlist/user/4552
http://proxima.co.rw/index.php/component/k2/itemlist/user/619364
http://robocit.com/index.php/component/k2/itemlist/user/449616
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=6731
http://shinilspring.com/board_qsfb01/94220
http://shinilspring.com/board_qsfb01/94255
http://skylinecam.co.kr/photo/95479
http://skylinecam.co.kr/photo/95489
http://skylinecam.co.kr/photo/95533
http://skylinecam.co.kr/photo/95548
http://skylinecam.co.kr/photo/95571
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=145301
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=145385
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=145414
http://www.gforgirl.com/xe/?document_srl=130247
http://www.gforgirl.com/xe/poster/130221
http://www.gforgirl.com/xe/poster/130291
http://www.gforgirl.com/xe/poster/130317
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=226284
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=308786
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=71690
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=211510
http://batubersurat.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=49761
http://moavalve.co.kr/faq/31032
http://www.vivelabmanizales.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fi0f-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/20459
http://www.deliberarchia.org/forum/index.php?topic=1006226.0
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=72225
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1147325
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/90024
http://ye-dream.com/qa/80342
http://ye-dream.com/qa/80352
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=71202
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=71222
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=71227
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=71251
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=71285
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=71290
http://yoriyorifood.com/xxxx/spacial/80514
http://yoriyorifood.com/xxxx/spacial/80530
http://community.viajar.tur.br/index.php?p=/discussion/57470/ne-otpuskay-moyu-ruku-elimi-birakma-40-seriya-kxrn-ne-otpuskay-moyu-ruku-elimi-birakma-40-seriya
http://www.vivelabmanizales.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2019-h2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80/
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1557655
http://healthyteethpa.org/component/k2/itemlist/user/5337012
http://www2.yasothon.go.th/smf/index.php?topic=159.156315
http://www.vivelabmanizales.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-05-05-2-7/
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/239875
http://www.ds712.net/guest/?document_srl=84949
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3340537
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1686362
http://xplorefitness.com/blog/hd-video-%D1%81%D0%BC%D0%B5%D1%80%D1%88-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-j8-%D1%81%D0%BC%D0%B5%D1%80%D1%88-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/229753
http://forum.digamahost.com/index.php?topic=123173.0
http://fbpharm.net/index.php/component/k2/itemlist/user/37972
http://married.dike.gr/index.php/component/k2/itemlist/user/56371
https://sto54.ru/index.php/component/k2/itemlist/user/3360925
http://ye-dream.com/qa/33627
http://vtservices85.fr/smf2/index.php?PHPSESSID=4bff5b00c6b067c1e1591382ff11e70d&topic=242634.0
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=30393
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=30416
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=30433
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=30438
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=30468
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=76235
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=76278
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=76318
http://skylinecam.co.kr/photo/103644
http://skylinecam.co.kr/photo/103772
http://skylinecam.co.kr/photo/103787
http://skylinecam.co.kr/photo/103800
http://skylinecam.co.kr/photo/103805
http://withinfp.sakura.ne.jp/eso/index.php/17139224-edinoe-serdce-tek-yurek-19-seria-cmqs-edinoe-serdce-tek-yurek-1/0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=155474
http://mediaville.me/index.php/component/k2/itemlist/user/206714
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2400240
http://community.viajar.tur.br/index.php?p=/profile/kzdantje1
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3585832
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3710836
http://c3isecurity.com.br/component/k2/itemlist/user/469226
http://thermoplast.envolgroupe.com/component/k2/author/70291
http://matinbank.ir/component/k2/itemlist/user/4487358.html
http://ovotecegg.com/component/k2/itemlist/user/121647
http://xplorefitness.com/blog/%C2%AB%D0%B2%D0%BE%D1%80%D0%BE%D0%BD-kuzgun-18-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-mopc-%C2%AB%D0%B2%D0%BE%D1%80%D0%BE%D0%BD-kuzgun-18-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=73670
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=12210
http://wigalseguros.com.br/component/users/?task=user&view=itemlist&id=8634
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3358692
http://www.telcon.gr/index.php/component/k2/itemlist/user/62684
http://vn7.vn/qna/49751
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=200116
http://associationsila.org/component/k2/itemlist/user/286697
http://thermoplast.envolgroupe.com/component/k2/author/82729
http://www.ekemoon.com/148343/052220195606/
http://proxima.co.rw/index.php/component/k2/itemlist/user/574998
http://sindicatodechoferespichincha.com.ec/index.php/component/k2/itemlist/user/6692029
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1854858
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=6059
http://batubersurat.com/index.php/component/k2/itemlist/user/48169
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/496267
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1891372
http://dohairbiz.com/?option=com_k2&view=itemlist&task=user&id=2726639
http://dohairbiz.com/en/component/k2/itemlist/user/2726470.html
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=97184
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1753556
http://gtupuw.org/index.php/component/k2/itemlist/user/1870043
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=283807
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=283821
http://haniel.ir/index.php/component/k2/itemlist/user/86499
http://zsmr.com.ua/index.php/component/k2/itemlist/user/552588
http://ovotecegg.com/component/k2/itemlist/user/130453
http://dev.aabn.org.gh/component/k2/itemlist/user/569321
http://forum.byehaj.hu/index.php?topic=87241.0
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1926305
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/14997
http://www.jesusonly.life/calendar/46950
http://www.digitalbul.com/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-l8-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1/
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=59511
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=289799
http://cafe.dokseosil.co.kr/community/36122
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1097824
http://mobility-corp.com/index.php/component/k2/itemlist/user/2595327
http://www.hsaura.com/noty/35311
http://153.120.114.241/eso/index.php/16861062-holostak-9-sezon-10-vypusk-torrentom-pqholostak-9-sezon-10-vypu
http://withinfp.sakura.ne.jp/eso/index.php/16895183-smotret-tola-robot-9-seria-n2-tola-robot-9-seria/0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=294352
http://www.elpinatarense.es/?option=com_k2&view=itemlist&task=user&id=156253
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=288779
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=40656
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=292228
https://l2thalassic.org/Forum/index.php?topic=1237.0
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=14707
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/496607
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/496669
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/496671
http://dcasociados.eu/component/k2/itemlist/user/87835
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1754270
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=284066
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=284077
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=284096
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1146494
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1146508
http://roikjer.com/forum/index.php?PHPSESSID=j4e7kf5qr259gmm76kjrpie3l7&topic=865861.0
http://moavalve.co.kr/faq/14017
http://jiquilisco.org/index.php/component/k2/itemlist/user/6570
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=20519
http://valleycapital.co.ke/?option=com_k2&view=itemlist&task=user&id=63939
http://married.dike.gr/index.php/component/k2/itemlist/user/56739
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=53435
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=460234
http://emjun.com/index.php?mid=hangtotal&document_srl=6366
http://teambuildingpremium.com/forum/index.php?topic=825853.0
http://www.atab.com.sa/index.php/en/?option=com_k2&view=itemlist&task=user&id=1621326
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1080528
http://www.ekemoon.com/189503/051820194614/
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-al7s-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://bitpark.co.kr/board_IzjM66/3919328
http://bitpark.co.kr/board_IzjM66/3919394
http://jiquilisco.org/index.php/component/k2/itemlist/user/5900
http://married.dike.gr/index.php/component/k2/itemlist/user/61918
http://married.dike.gr/index.php/component/k2/itemlist/user/61931
http://mediaville.me/index.php/component/k2/itemlist/user/270098
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/248797
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/17806
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/211489
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=22991
http://corumotoanahtar.com/index.php/component/k2/itemlist/user/1358
http://ovotecegg.com/component/k2/itemlist/user/132505
http://www.theocraticamerica.org/forum/index.php?topic=37265.0
https://prelease.club/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jp9j/
http://cafe.dokseosil.co.kr/community/42718
http://mobility-corp.com/index.php/component/k2/itemlist/user/2592312
http://dohairbiz.com/en/component/k2/itemlist/user/2735033.html
http://www.hsaura.com/noty/66015
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1410530
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1687218
http://euromouleusinage.com/index.php/component/k2/itemlist/user/139310
http://thermoplast.envolgroupe.com/component/k2/author/102125
https://sanp.pro/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tgvr-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80/
http://www.m1avio.com/?option=com_k2&view=itemlist&task=user&id=3687936
https://cfcestradareal.com.br/?option=com_k2&view=itemlist&task=user&id=19074
http://bitpark.co.kr/board_IzjM66/3917251
http://vn7.vn/qna/46129
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3361679
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=21579
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/532331
http://dev.aabn.org.gh/component/k2/itemlist/user/592692
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1778014
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1908219
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1189486
http://jiquilisco.org/index.php/component/k2/itemlist/user/5912
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=61875
http://married.dike.gr/index.php/component/k2/itemlist/user/61891
http://mediaville.me/index.php/component/k2/itemlist/user/269747
http://ovotecegg.com/component/k2/itemlist/user/147930
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/17774
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/17836
http://rudraautomation.com/index.php/component/k2/author/193885
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=13193
http://www.ekemoon.com/203955/050620193517/
http://blog.ptpintcast.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d5-m5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://xn----3x5er9r48j7wemud0a387h.com/news/2052
http://moavalve.co.kr/faq/53261
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/493655
http://hanalove.kidspann.net/index.php?mid=qna&document_srl=43977
http://poselokgribovo.ru/forum/index.php?topic=798745.0
https://nextezone.com/index.php?topic=51809.0
http://xn--2e0bk61btjo.com/notice/4109
http://sofficer.net/xe/teach/220314
http://sunele.co.kr/board_ReBD97/52051
http://sy.korean.net/qna/69571
http://sy.korean.net/qna/69592
http://sy.korean.net/qna/69722
http://sy.korean.net/qna/69775
http://sy.korean.net/qna/69779
http://sy.korean.net/qna/69789
http://sy.korean.net/qna/69834
http://sy.korean.net/qna/69847
http://sy.korean.net/qna/69858
http://sy.korean.net/qna/69873
http://sy.korean.net/qna/69878
http://HyUa.1fps.icu/l/szIaeDC
http://www.haetsaldun-clinic.co.kr/?document_srl=3441
http://www.haetsaldun-clinic.co.kr/Question/3429
http://www.itosm.com/cn/?document_srl=17165
http://www.kosamuitour.net/mn05_02t/972896
http://www.kosamuitour.net/mn05_02t/973029
http://www.patrasin.kr/?document_srl=4275817
http://www.patrasin.kr/index.php?mid=questions&document_srl=4275791
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=4416
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=4422
http://www.studyxray.com/Sangdam/116086
http://www.theparrotcentre.com/forum/index.php?topic=554480.0
http://www.theparrotcentre.com/forum/index.php?topic=554496.0
http://www.hsaura.com/license/52546
https://theprodigy.info/forum/index.php?topic=29162.0
http://azone.synology.me/xe/index.php?document_srl=7343&mid=board_SDnQ73
http://indiefilm.kr/xe/board/94005
http://jnk-ent.jp/index.php?document_srl=44920&mid=gallery
http://gochon-iusell.co.kr/g1/11747
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=10784
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=925
http://www.hsaura.com/?document_srl=82849
http://tototoday.com/board_oRiY52/28022
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=8720
http://emjun.com/?document_srl=90439
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=44020
https://2002.shyoon.com/?document_srl=26928
http://www.hoonthaitoday.com/forum/index.php?topic=282999.0
http://xn--ok1bpqi43ahtb.net/board_eASW07/49204
http://ariji.kr/sub0602/802717
http://indiefilm.kr/xe/board/91849
http://www.studyxray.com/Sangdam/65200
http://photogrotto.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80-4/
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/16069
http://emjun.com/index.php?mid=hangtotal&document_srl=68458
http://haeple.com/index.php?mid=etc&document_srl=4167
http://HyUa.1fps.icu/l/szIaeDC
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/9288
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.kr/news/12220
http://xn--2e0b53df5ag1c804aphl.net/nuguna/21052
http://xn--2e0bk61btjo.com/notice/9029
http://xn--2e0bk61btjo.com/notice/9034
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=19100
http://xn--9m1b83j39hz6exwonmf.com/?document_srl=521948
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/521967
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=75437
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/5053
http://yoriyorifood.com/xxxx/?document_srl=90052
https://esel.gist.ac.kr/esel2/board_hmgj23/65798
https://nple.com/xe/pds/34598
http://shinilspring.com/board_qsfb01/27308
http://vervetama.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%e3%80%90ec8%e3%80%91-%d0%b8%d0%b3/
http://www.lgue.co.kr/?document_srl=17123
http://hk-metal.co.kr/hkweb/QnA/12014
http://www.golden-nail.co.kr/press/48884
http://www.gforgirl.com/xe/poster/135094
http://www.gforgirl.com/xe/poster/83646
http://masanlib.or.kr/g1/31559
http://www.jshwanghoan.com/index.php?mid=historical_figures&document_srl=82735
http://www.hsaura.com/license/96960
http://jnk-ent.jp/index.php?mid=gallery&document_srl=32005
http://sofficer.net/xe/teach/215788
http://smartengbiz.com/s1/3232
http://shinilspring.com/board_qsfb01/72655
http://0433.net/budongsan/41371
http://goldenpowerball2.com/index.php?document_srl=70449&mid=board_Bnby34
http://HyUa.1fps.icu/l/szIaeDC
http://xn----3x5er9r48j7wemud0a387h.com/news/39739
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/10122
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/10155
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/10175
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/10196
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/10232
http://xn--2e0b53df5ag1c804aphl.net/nuguna/20918
http://xn--2e0bk61btjo.com/notice/9009
http://xn--2e0bk61btjo.com/notice/9018
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/5043
http://yoriyorifood.com/xxxx/spacial/89566
http://yoriyorifood.com/xxxx/spacial/89812
http://yourhelp.co.kr/?document_srl=2420
http://yourhelp.co.kr/index.php?document_srl=2342&mid=board_2
http://yourhelp.co.kr/index.php?document_srl=2376&mid=board_2
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=2451
http://zanoza.h1n.ru/2019/05/18/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-zlve-%d0%b8%d0%b3%d1%80%d0%b0/
http://yoriyorifood.com/xxxx/spacial/45914
http://www.jesusonly.life/calendar/54864
http://hk-metal.co.kr/hkweb/QnA/6475
http://forums.abs-cbn.com/welcome-back-kapamilya%21/oka-aka-ak-3-eo-5-e-uakino/?PHPSESSID=5oqqpso4cmba9qauppdpamho07
http://haeple.com/index.php?mid=etc&document_srl=79913
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3261321
http://xn--2e0bk61btjo.com/notice/6901
http://ariji.kr/sub0602/801010
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=70592
http://shinhwaair2017.cafe24.com/issue/177576
http://sounddrizzle.com/index.php?mid=boarda&document_srl=4376
http://skylinecam.co.kr/photo/61039
http://iamking.net/board/3441
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=49909
https://www.thedezlab.com/lab/community/index.php?topic=2019.0
http://otitismediasociety.org/forum/index.php?topic=175522.0
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf-23/
http://shinilspring.com/board_qsfb01/66947
http://barobus.kr/qna/472
http://www.sp1.football/index.php?mid=faq&document_srl=161454
http://otitismediasociety.org/forum/index.php?topic=171713.0
http://skylinecam.co.kr/photo/84892
http://HyUa.1fps.icu/l/szIaeDC
http://www.vamoscontigo.org/Noticia/30175
http://www.yepia.com/board_ZCPG83/18259
http://xihillstate.bloggirl.net/?document_srl=51472
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/7437
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/?document_srl=1427
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.kr/news/12166
http://xn--2e0b53df5ag1c804aphl.net/nuguna/21014
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=19017
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/521717
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/521752
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=75073
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/5034
http://xn--ok1bpqi43ahtb.net/board_EkDG82/146292
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3262506
http://www.yepia.com/board_ZCPG83/8284
https://www.chirorg.com/video/6778
https://nextezone.com/index.php?topic=51889.0
http://www.golden-nail.co.kr/press/1766
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-k7-h5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/3822
http://vintage.codns.com/Board/9196
http://ye-dream.com/qa/71728
http://moavalve.co.kr/faq/1465
http://www.svteck.co.kr/customer_gratitude/46010
http://skangseo.org/xe/board_Atnj46/19910
http://ye-dream.com/qa/28391
http://atemshow.com/?document_srl=33306
http://5starcoffee.co.kr/board_EBXY17/3023
http://HyUa.1fps.icu/l/szIaeDC
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/610
http://sextomariotienda.com/blog/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-s5-c9-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
https://2002.shyoon.com/board_2002/6197
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=2481
http://www.svteck.co.kr/?document_srl=24661
https://hackersuniversity.net/index.php?topic=16392.0
http://haeple.com/index.php?mid=etc&document_srl=86711
http://0433.net/junggo/5173
http://emjun.com/index.php?mid=hangtotal&document_srl=79258
http://haeple.com/index.php?mid=etc&document_srl=77360
http://forum.elexlabs.com/index.php?topic=29379.0
https://adsensebih.com/index.php?topic=24386.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=706782.0
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-day-after-day/
http://atemshow.com/?document_srl=24821
http://indiefilm.kr/xe/board/53193
http://www.studyxray.com/Sangdam/18875
http://themasters.pro/file_01/48272
http://www.hicleaning.kr/board_wash/82666
http://shinilspring.com/board_qsfb01/76917
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=737465
https://forum.ac-jete.it/index.php?topic=389002.0
http://shinhwaair2017.cafe24.com/issue/182877
http://forum.elexlabs.com/index.php?topic=26673.0
http://ye-dream.com/qa/46804
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=4778
http://emjun.com/index.php?mid=hangtotal&document_srl=64759
http://shinilspring.com/board_qsfb01/87732
http://moavalve.co.kr/faq/59486
http://www.svteck.co.kr/customer_gratitude/31425
http://www.gforgirl.com/xe/poster/26332
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=837135
http://indiefilm.kr/xe/board/77117
http://HyUa.1fps.icu/l/szIaeDC
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=59797
http://universalcommunity.se/Forum/index.php?topic=6955.0
http://haeple.com/index.php?mid=etc&document_srl=6067
https://sanp.pro/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-8-03-2016/
http://hkmtv.co.kr/board_yKNa34/1627
http://www.hicleaning.kr/?document_srl=41345
http://lucky.kidspann.net/index.php?mid=qna&document_srl=6580
http://pkgersang.dothome.co.kr/board_jiKY24/3624
http://yoriyorifood.com/xxxx/spacial/35438
http://k-cea.org/board_Hnyj62/51171
http://shinilspring.com/board_qsfb01/32636
http://jjikduk.net/DATA/43875
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=40365
https://nple.com/xe/pds/11241
https://www.chirorg.com/?document_srl=12526
http://jnk-ent.jp/index.php?document_srl=43964&mid=gallery
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=55163
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1073541
http://www.gforgirl.com/xe/?document_srl=118041
http://skylinecam.co.kr/photo/64425
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2766749
http://www.gforgirl.com/xe/poster/21649
http://xn--ok1bpqi43ahtb.net/board_EkDG82/125222
http://gochon-iusell.co.kr/g1/3355
http://theolevolosproject.org/?option=com_k2&view=itemlist&task=user&id=26184
http://2872870.com/est/7474
http://constellation.kro.kr/board_kbku73/1681
http://0433.net/budongsan/38504
https://sanp.pro/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w7-x5-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4/
http://www.lozic.co.kr/gallery/27072
http://HyUa.1fps.icu/l/szIaeDC
http://withinfp.sakura.ne.jp/eso/index.php/17006724-smotret-dockimateri-dockimateri-12-seria-t9-dockimateri-dockima
http://www.remify.app/foro/index.php?topic=294174.0
http://www.quattroandpartners.it/component/k2/itemlist/user/1099517
http://mobility-corp.com/index.php/component/k2/itemlist/user/2587682
http://withinfp.sakura.ne.jp/eso/index.php/17035902-serial-cuzaa-zizn-cuze-zitta-7-seria-o0-cuzaa-zizn-cuze-zitta-7/0
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=53193
http://www.urbantutorial.com/index.php/component/k2/itemlist/user/109462
http://withinfp.sakura.ne.jp/eso/index.php/16947859-hd-tola-robot-8-seria-z2-tola-robot-8-seria/0
http://febrescordero.gob.ec/?option=com_k2&view=itemlist&task=user&id=86097
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=19540
http://bitpark.co.kr/board_IzjM66/3799778
http://vtservices85.fr/smf2/index.php?PHPSESSID=f31ea429a1d4c57b529d820b33174e1f&topic=222087.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1380506
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=28451
http://teambuildingpremium.com/forum/index.php?topic=800740.0
http://www.deliberarchia.org/forum/index.php?topic=1001141.0
http://www.deliberarchia.org/forum/index.php?topic=1001159.0
http://withinfp.sakura.ne.jp/eso/index.php/16961764-hdvideo-milliardy-4-sezon-9-seria-v1-milliardy-4-sezon-9-seria/0
http://xplorefitness.com/blog/hd-video-%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-4-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-d6-%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-4-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://teambuildingpremium.com/forum/index.php?topic=800762.0
http://teambuildingpremium.com/forum/index.php?topic=800764.0
http://www.deliberarchia.org/forum/index.php?topic=1001195.0
http://xplorefitness.com/blog/%C2%AB%D0%B2%D0%BE%D1%80%D0%BE%D0%BD-kuzgun-15-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-zwki-%C2%AB%D0%B2%D0%BE%D1%80%D0%BE%D0%BD-kuzgun-15-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://withinfp.sakura.ne.jp/eso/index.php/16961967-novinka-soderzanki-9-seria-n5-soderzanki-9-seria/0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1447659
http://www.crnmedia.es/component/k2/itemlist/user/87364
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=33259
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/280192
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=4845
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/25219
http://indiefilm.kr/xe/board/143453
http://indiefilm.kr/xe/board/143538
http://indiefilm.kr/xe/board/143568
http://indiefilm.kr/xe/board/143607
http://seoksoononly.dothome.co.kr/qna/836978
http://cwon.kr/xe/board_bnSr36/6005
http://www.hsaura.com/noty/62892
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=54681
http://soc-human.kz/index.php/component/k2/itemlist/user/1682846
http://www.deliberarchia.org/forum/index.php?topic=1035158.0
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1892637
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/256930
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1394864
http://bitpark.co.kr/board_IzjM66/3809772
http://jjikduk.net/DATA/20733
http://corumotoanahtar.com/component/k2/itemlist/user/1394.html
http://hyeonjun.co.kr/menu3/68949
http://hyeonjun.co.kr/menu3/68964
http://indiefilm.kr/xe/board/117753
http://indiefilm.kr/xe/board/117808
http://indiefilm.kr/xe/board/117875
http://indiefilm.kr/xe/board/117880
http://indiefilm.kr/xe/board/117899
http://lucky.kidspann.net/index.php?mid=qna&document_srl=57560
http://lucky.kidspann.net/index.php?mid=qna&document_srl=57582
http://thermoplast.envolgroupe.com/component/k2/author/65507
https://l2thalassic.org/Forum/index.php?topic=850.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=279364
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=8346
http://www.ekemoon.com/147815/052220191106/
http://dohairbiz.com/index.php/component/k2/itemlist/user/2711168
http://community.viajar.tur.br/index.php?p=/discussion/57349/edinoe-serdce-tek-yuerek-20-seriya-syfe-edinoe-serdce-tek-yuerek-20-seriya/p1%3Fnew=1
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1555887
http://rudraautomation.com/index.php/component/k2/author/102405
http://rudraautomation.com/index.php/component/k2/author/187454
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=329495
http://moavalve.co.kr/faq/10647
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1602341
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/18106
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1164202
http://www.josephmaul.org/menu41/34186
http://israengineering.com/index.php/component/k2/itemlist/user/1179559
http://www.theocraticamerica.org/forum/index.php/topic,41683.0.html
http://vtservices85.fr/smf2/index.php?PHPSESSID=9467c15a71728cae7298d3c11a8888dc&topic=229386.0
http://zanoza.h1n.ru/2019/05/15/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%8d%d0%ba%d1%81%d1%82%d1%80%d0%b0%d1%81%d0%b5%d0%bd%d1%81%d0%be%d0%b2-3/
http://compultras.com/index.php/component/k2/itemlist/user/212387
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=64901
http://dev.aabn.org.gh/component/k2/itemlist/user/611940
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1942247
http://fbpharm.net/index.php/component/k2/itemlist/user/49971
http://guiadetudo.com/?option=com_k2&view=itemlist&task=user&id=12286
http://guiadetudo.com/index.php/component/k2/itemlist/user/12282
http://immobilia.gr/index.php/de/component/k2/itemlist/user/16478
http://lasvur.ru/component/k2/itemlist/user/38373
http://mobility-corp.com/index.php/component/k2/itemlist/user/2616522
http://mobility-corp.com/index.php/component/k2/itemlist/user/2616800
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=218531
http://rudraautomation.com/index.php/component/k2/author/218553
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/220724
http://sdsn.rsu.edu.ng/?option=com_k2&view=itemlist&task=user&id=2323913
http://vhost12299.cpsite.ru/428692-hd-cuzaa-zizn-cuze-zitta-4-seria-e1-cuzaa-zizn-cuze-zitta-4-ser
http://vhost12299.cpsite.ru/429111-hdvideo-dockimateri-dockimateri-18-seria-x7-dockimateri-dockima
http://xplorefitness.com/blog/%C2%AB%D0%BF%D0%BE-%D0%B7%D0%B0%D0%BA%D0%BE%D0%BD%D0%B0%D0%BC-%D0%B2%D0%BE%D0%B5%D0%BD%D0%BD%D0%BE%D0%B3%D0%BE-%D0%B2%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-06-05-2019-x7-%C2%AB%D0%BF%D0%BE-%D0%B7%D0%B0%D0%BA%D0%BE%D0%BD%D0%B0%D0%BC-%D0%B2%D0%BE%D0%B5%D0%BD%D0%BD%D0%BE%D0%B3%D0%BE-%D0%B2%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%B8-3
http://www.die-design-manufaktur.de/?option=com_k2&view=itemlist&task=user&id=5190431
http://www.ekemoon.com/142985/052020192605/
http://guiadetudo.com/index.php/component/k2/itemlist/user/11232
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2388662
http://xplorefitness.com/blog/%C2%AB%D0%BD%D0%B0%D1%88%D0%B0-%D0%B8%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F-70-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-wocu-%C2%AB%D0%BD%D0%B0%D1%88%D0%B0-%D0%B8%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F-70-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=497669
http://forum.digamahost.com/index.php?topic=111171.0
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1045702
http://www.theocraticamerica.org/forum/index.php?topic=29983.0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/261810
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4884203
http://bitpark.co.kr/board_IzjM66/3816475
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=13112
http://cwon.kr/xe/board_bnSr36/24642
http://zanoza.h1n.ru/2019/05/14/9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-9-ol9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-%d1%85%d0%be%d0%bb%d0%be/
http://seoksoononly.dothome.co.kr/qna/746808
http://menulisilmiah.net/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x4-%d1%82%d0%be%d0%bb/
https://members.fbhaters.com/index.php?topic=79916.0
https://members.fbhaters.com/index.php?topic=75885.0
http://www.ekemoon.com/160273/051920192808/
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/188103
http://ovotecegg.com/component/k2/itemlist/user/140885
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/240664
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/240914
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/14831
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/15867
http://rudraautomation.com/index.php/component/k2/author/179885
http://rudraautomation.com/index.php/component/k2/author/179939
http://rudraautomation.com/index.php/component/k2/author/180061
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/507154
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=62315
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1154585
http://ovotecegg.com/component/k2/itemlist/user/149999
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=628910
http://www.digitalbul.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-u1-%d1%82%d0%be/
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/250897
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/232801
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/187927
http://condolencias.servisa.es/3-15-06-05-2019-d6-3-15
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=601806
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=296801
http://www.ekemoon.com/142473/051720193605/
http://bitpark.co.kr/board_IzjM66/3775578
http://fbpharm.net/index.php/component/k2/itemlist/user/15428
http://macdistri.com/index.php/component/k2/itemlist/user/307381
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=44259
http://forum.politeknikgihon.ac.id/index.php?topic=24839.0
https://l2thalassic.org/Forum/index.php?topic=1712.0
http://www.vivelabmanizales.com/live-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-q5-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81/
http://www.vivelabmanizales.com/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g3-%d1%82%d0%be%d0%bb%d1%8f/
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/522514
http://corumotoanahtar.com/component/k2/itemlist/user/1319.html
http://dev.aabn.org.gh/component/k2/itemlist/user/580772
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1919648
http://fbpharm.net/index.php/component/k2/itemlist/user/38128
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=306163
http://jiquilisco.org/index.php/component/k2/itemlist/user/4107
http://mobility-corp.com/index.php/component/k2/itemlist/user/2585002
http://mvisage.sk/index.php/component/k2/itemlist/user/118770
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=141270
http://ovotecegg.com/component/k2/itemlist/user/141273
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=241035
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=15969
http://highlanderonline.cmshelplive.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jcwy-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-11-%d1%81%d0%b5%d1%80%d0%b8/
http://corumotoanahtar.com/component/k2/itemlist/user/1275.html
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=22199
http://married.dike.gr/index.php/component/k2/itemlist/user/62237
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/712831
http://www.deliberarchia.org/forum/index.php?topic=1026650.0
http://mediaville.me/index.php/component/k2/itemlist/user/251761
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3636909
http://www.deliberarchia.org/forum/index.php?topic=1024427.0
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=79593
https://l2thalassic.org/Forum/index.php?topic=2319.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1644137
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ll9%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.vivelabmanizales.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-aw8i-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://k2.akademitelkom.ac.id/index.php/component/k2/itemlist/user/299160
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-3/
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=4350
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1631303
http://www.deliberarchia.org/forum/index.php?topic=980479.0
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=6538
http://www.arunagreen.com/?option=com_k2&view=itemlist&task=user&id=504279
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1407049
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4905456
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=109469
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/322058
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=20571
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/523156
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/523255
http://corumotoanahtar.com/?option=com_k2&view=itemlist&task=user&id=1469
http://dev.aabn.org.gh/component/k2/itemlist/user/581596
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1920238
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1920196
http://euromouleusinage.com/index.php/component/k2/itemlist/user/137939
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=306931
http://bebopindia.com/notcie/22760
http://ye-dream.com/qa/31805
http://askpharm.net/board_NQiz06/9614
http://lucky.kidspann.net/index.php?mid=qna&document_srl=928
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3265178
http://mglpcm.org/board_ETkS12/19047
https://www.shaiyax.com/index.php?topic=351353.0
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=71799
https://www.shaiyax.com/index.php?topic=343043.0
http://sounddrizzle.com/index.php?mid=boarda&document_srl=3127
http://ru-realty.com/forum/index.php?PHPSESSID=khp1e3ertitmn2chlqhco8dc63&topic=520216.0
http://wipln.com/?document_srl=40358
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=3150
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=34844.0
http://shinilspring.com/board_qsfb01/10922
http://isch.kr/board_PowH60/15214
http://hyeonjun.co.kr/menu3/46995
http://yoriyorifood.com/xxxx/spacial/43050
http://haenamyun.taeshinmedia.com/?document_srl=2777047
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=68705
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=86025
http://edu-playground.net/boardgame/6010
http://www.hsaura.com/noty/104635
http://shinilspring.com/board_qsfb01/38791
http://k-cea.org/board_Hnyj62/45181
http://www.siheunglove.com/chulip/20204
http://www.studyxray.com/Sangdam/90202
http://praisesound.co.kr/sub04_01/3099
http://constellation.kro.kr/board_kbku73/386
http://HyUa.1fps.icu/l/szIaeDC
http://apt2you2.cafe24.com/g1/1362
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=821936
http://tototoday.com/board_oRiY52/24496
http://skylinecam.co.kr/photo/89517
http://bethelpray.com/counsel/2582
https://reelgosu.com/board_peJN24/272885
http://otitismediasociety.org/forum/index.php?topic=175617.0
http://www.phan-aen.go.th/forum/index.php?topic=636209.0
http://www.golden-nail.co.kr/press/55208
http://hyeonjun.co.kr/menu3/1275
http://vtservices85.fr/smf2/index.php?PHPSESSID=8158932cd35ffd961678a20db5e5265e&topic=254909.0
http://xn----3x5er9r48j7wemud0a387h.com/news/511
http://xn--ok1bpqi43ahtb.net/board_eASW07/25828
http://arnikabolt.ro/component/k2/itemlist/user/111652
http://forums.abs-cbn.com/welcome-back-kapamilya%21/(())-m-aka-ak-3-eo-3-e/?PHPSESSID=8pksc1h9vvbkloibh7sr48ifp0
http://e-educ.net/Forum/index.php?topic=10005.0
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=56327
http://www.ds712.net/guest/?document_srl=97339
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=15310
http://xn--ok1bpqi43ahtb.net/board_eASW07/119840
http://www.teedinubon.com/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8-3/
http://zanoza.h1n.ru/2019/05/17/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rf5-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.popolsku.fr.pl/forum/index.php?topic=399402.0
http://esiapolisthesharp2.co.kr/g1/12464
http://sunele.co.kr/board_ReBD97/46030
http://emjun.com/index.php?mid=hangtotal&document_srl=68485
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=25897
http://www.sp1.football/index.php?mid=tr_video&document_srl=216901
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=58023
http://iymc.or.kr/?document_srl=87662
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=10000
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=52878
http://vervetama.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%82/
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=714687
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0-11/
http://sixangles.co.kr/qna/556271
https://nple.com/xe/pds/10286
http://forum.bmw-e60.eu/index.php?topic=8133.0
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=27253
http://emjun.com/index.php?mid=hangtotal&document_srl=88821
https://forum.clubeicaro.pt/index.php?topic=1346.0
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=67171
http://otitismediasociety.org/forum/index.php?topic=171431.0
http://xn----3x5er9r48j7wemud0a387h.com/news/18264
http://jnk-ent.jp/index.php?mid=gallery&document_srl=31360
http://HyUa.1fps.icu/l/szIaeDC
http://www.jesusonly.life/calendar/131858
http://pkgersang.dothome.co.kr/board_jiKY24/3485
http://praisesound.co.kr/sub04_01/10854
http://mtuan93.com/board_uCqR85/4609
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=67734
https://khuyenmaikk13.info/index.php?topic=200430.0
http://www.lgue.co.kr/index.php?mid=lgue05&document_srl=559&sort_index=title&order_type=desc
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=191562
http://hyeonjun.co.kr/menu3/21481
http://8.droror.co.il/uncategorized/%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8-2/
http://jjikduk.net/DATA/3263
http://constellation.kro.kr/board_kbku73/5248
http://uberdrivers.net/forum/index.php?topic=281727.0
http://gallerychoi.com/Exhibition/87278
http://gallerychoi.com/Exhibition/87292
http://gallerychoi.com/Exhibition/87331
http://gallerychoi.com/Exhibition/87346
http://gallerychoi.com/Exhibition/87366
http://gallerychoi.com/Exhibition/87386
http://gallerychoi.com/Exhibition/87396
http://gallerychoi.com/Exhibition/87406
http://photogrotto.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%ba%d0%be%d0%b3%d0%b4%d0%b0/
http://pkgersang.dothome.co.kr/board_jiKY24/7077
http://sunele.co.kr/board_ReBD97/54296
http://HyUa.1fps.icu/l/szIaeDC
http://2872870.com/est/9698
http://e-educ.net/Forum/index.php?topic=9851.0
http://viamania.net/index.php?mid=board_raYV15&document_srl=13975
http://dohairbiz.com/en/component/k2/itemlist/user/2746080.html
http://www.golden-nail.co.kr/press/6556
http://blog.ptpintcast.com/%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-al0-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-149-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.svteck.co.kr/customer_gratitude/40919
http://gallerychoi.com/Exhibition/57420
http://www.jesusonly.life/?document_srl=70122
http://isch.kr/board_PowH60/29089
http://warmfund.net/p/index.php?mid=financing&document_srl=54724
http://www.sp1.football/index.php?mid=tr_video&document_srl=2163
http://tk-laser.co.kr/index.php?mid=board_QsEu43&document_srl=46641
http://tk-laser.co.kr/index.php?mid=board_QsEu43&document_srl=46646
http://tk-laser.co.kr/index.php?mid=board_QsEu43&document_srl=46662
http://toeden.co.kr/Product_new/39857
http://toeden.co.kr/Product_new/39867
http://toeden.co.kr/Product_new/39882
http://vervetama.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%b0-%d1%80%d1%83%d1%81%d1%81/
http://vervetama.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80-7/
http://wipln.com/?document_srl=56315
http://wipln.com/?document_srl=56325
http://wipln.com/?document_srl=56330
http://wipln.com/?document_srl=56340
http://www.cnsmaker.net/xe/?document_srl=75107
http://www.cnsmaker.net/xe/?document_srl=75115
http://www.cnsmaker.net/xe/?document_srl=75120
http://www.cnsmaker.net/xe/?document_srl=75129
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=183598
http://www.fassen.co.kr/xe/board_VCum96/20721
http://www.flixian.com/main/?document_srl=39913
http://www.flixian.com/main/?document_srl=39975
http://www.flixian.com/main/QnA/39881
http://www.flixian.com/main/QnA/39960
http://www.golden-nail.co.kr/press/110727
http://HyUa.1fps.icu/l/szIaeDC
http://haniel.ir/index.php/component/k2/itemlist/user/99950
http://corumotoanahtar.com/?option=com_k2&view=itemlist&task=user&id=3126
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=14715
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1591077
http://www.jesusonly.life/calendar/61220
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=313188
http://www.deliberarchia.org/forum/index.php?topic=1028133.0
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=2513
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=100294
http://seoksoononly.dothome.co.kr/qna/709599
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=80170
http://haniel.ir/index.php/component/k2/itemlist/user/84607
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=787730
http://withinfp.sakura.ne.jp/eso/index.php/16860910-uristy-11-seria-hd-uristy-11-seria
http://webp.online/index.php?topic=49870.75
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1348111
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=297096
http://webp.online/index.php?topic=46307.15
https://ccha.castle-journal.info/index.php/component/k2/itemlist/user/1690
http://www.vivelabmanizales.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81-11/
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2563235
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/184684
http://withinfp.sakura.ne.jp/eso/index.php/16869932-sluga-naroda-3-sezon-21-seria-05052019-f1-sluga-naroda-3-sezon-
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v3-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1/
http://www.babvallejo.com/index.php/component/k2/itemlist/user/607734
http://www.deliberarchia.org/forum/index.php?topic=978246.0
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7322877
http://thermoplast.envolgroupe.com/index.php/component/k2/itemlist/user/74657
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/200492
http://forum.byehaj.hu/index.php?topic=78457.0
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-17-%d1%81%d0%b5%d1%80-2/
http://mediaville.me/?option=com_k2&view=itemlist&task=user&id=226667
http://xplorefitness.com/blog/%C2%AB%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-90-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-06-05-2019-r6-%C2%AB%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-90-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://smartacity.com/component/k2/itemlist/user/18438
http://www.deliberarchia.org/forum/index.php?topic=1034410.0
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/4038
http://grupotir.com/component/k2/itemlist/user/42494
http://rudraautomation.com/index.php/component/k2/author/161398
http://married.dike.gr/index.php/component/k2/itemlist/user/62279
http://teambuildingpremium.com/forum/index.php?topic=796906.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=81213
http://www.deliberarchia.org/forum/index.php?topic=1025358.0
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=13506
http://jesusandmarypatna.com/index.php/component/k2/itemlist/user/3391419
http://www.camaracoyhaique.cl/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pu1o-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://mediaville.me/index.php/component/k2/itemlist/user/207665
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1115865
http://seoksoononly.dothome.co.kr/qna/736850
http://fbpharm.net/index.php/component/k2/itemlist/user/20456
http://highlanderonline.cmshelplive.net/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-87-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-07-05-2019-d6-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-87-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://153.120.114.241/eso/index.php/16861397-stb-holostak-9-sezon-10-vypusk-oestb-holostak-9-sezon-10-vypusk
http://condolencias.servisa.es/3-11-06-05-2019-o5-3-11
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/200060
https://forums.letstalkbeats.com/index.php?topic=65946.0
http://macdistri.com/index.php/component/k2/itemlist/user/308634
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/185079
http://www.quattroandpartners.it/component/k2/itemlist/user/1063519
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=299179
http://forum.digamahost.com/index.php?topic=109057.0
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=48083
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1113869
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1543719
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3598467
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=45317
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5113
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1552753
http://www.vivelabmanizales.com/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g5-%d1%82%d0%be%d0%bb%d1%8f-%d1%80/
http://thermoplast.envolgroupe.com/component/k2/author/75635
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7320633
http://sextomariotienda.com/blog/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://dev.aabn.org.gh/component/k2/itemlist/user/610571
http://forum.drahthaar-club.com.ua/index.php?topic=3180.0
http://forum.elexlabs.com/index.php?topic=37813.0
http://forum.kopkargobel.com/index.php?topic=11585.0
http://healthyteethpa.org/component/k2/itemlist/user/5461580
http://laspoltrina.it/component/k2/itemlist/user/1446183
http://mir3sea.com/forum/index.php?topic=3400.0
http://mir3sea.com/forum/index.php?topic=3401.0
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2615111
http://otitismediasociety.org/forum/index.php?topic=174413.0
http://forum.digamahost.com/index.php?topic=113192.0
http://teambuildingpremium.com/forum/index.php?topic=800041.0
http://www.deliberarchia.org/forum/index.php?topic=1000297.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/197236
http://www.deliberarchia.org/forum/index.php?topic=1000290.0
http://xplorefitness.com/blog/%C2%AB%D0%BD%D0%B5-%D0%BE%D1%82%D0%BF%D1%83%D1%81%D0%BA%D0%B0%D0%B9-%D0%BC%D0%BE%D1%8E-%D1%80%D1%83%D0%BA%D1%83-elimi-birakma-35-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-keam-%C2%AB%D0%BD%D0%B5-%D0%BE%D1%82%D0%BF%D1%83%D1%81%D0%BA%D0%B0%D0%B9-%D0%BC%D0%BE%D1%8E-%D1%80%D1%83%D0%BA%D1%83-elimi-birakma-35-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=80725
http://xplorefitness.com/blog/%D1%81%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C-%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-95-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-w0-%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-95-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/62327
http://forum.digamahost.com/index.php?topic=113215.0
http://teambuildingpremium.com/forum/index.php?topic=800107.0
http://teambuildingpremium.com/forum/index.php?topic=800112.0
http://teambuildingpremium.com/forum/index.php?topic=800116.0
http://www.deliberarchia.org/forum/index.php?topic=1000393.0
http://xplorefitness.com/blog/%C2%AB%D0%BD%D0%B0%D1%88%D0%B0-%D0%B8%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F-68-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-wlus-%C2%AB%D0%BD%D0%B0%D1%88%D0%B0-%D0%B8%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F-68-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://mediaville.me/index.php/component/k2/itemlist/user/249504
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2566529
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/229999
http://proxima.co.rw/index.php/component/k2/itemlist/user/602812
http://soc-human.kz/index.php/component/k2/itemlist/user/1669320
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1386698
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1058108
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=800951
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=801252
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/314024
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/314159
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/314165
https://alvarogarciatorero.com/index.php/component/k2/itemlist/user/48677
http://8.droror.co.il/uncategorized/%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-88-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xv6%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-88-%d1%81%d0%b5%d1%80%d0%b8%d1%8f17-05-2019/
http://photogrotto.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wg8%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-7-%d1%81%d0%b5%d1%80/
http://vervetama.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hf0%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
http://vervetama.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iy9%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.teedinubon.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cl3%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-6-%d1%81%d0%b5%d1%80/
http://zanoza.h1n.ru/2019/05/18/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-of0%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-va5%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-16-%d1%81%d0%b5/
https://testing.celekt.com/%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gg4%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f17-05-2019/
https://testing.celekt.com/%d0%a1%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d0%a7%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-to5%d0%a1%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c/
http://8.droror.co.il/uncategorized/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ww9%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-4-%d1%81%d0%b5%d1%80/
http://www.m1avio.com/index.php/component/k2/itemlist/user/3646597
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=48474
http://forum.digamahost.com/index.php?topic=113232.0
http://dcasociados.eu/?option=com_k2&view=itemlist&task=user&id=87936
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=204729
http://teambuildingpremium.com/forum/index.php?topic=800263.0
http://www.ekemoon.com/171475/051020195010/
http://dcasociados.eu/component/k2/itemlist/user/87937
http://withinfp.sakura.ne.jp/eso/index.php/16960411-efir-sluga-naroda-3-sezon-5-seria-j6-sluga-naroda-3-sezon-5-ser/0
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3747266
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/85939
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/230209
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=13112
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=13113
http://proxima.co.rw/index.php/component/k2/itemlist/user/602564
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=162328
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1669351
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1661596
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1661619
http://thermoplast.envolgroupe.com/component/k2/author/92141
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1386827
http://www.yepia.com/board_ZCPG83/6938
http://arte.dgau.ac.kr/board_qna/2037
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=734340
http://forum.kopkargobel.com/index.php?topic=9101.0
https://theprodigy.info/forum/index.php?topic=29184.0
http://otitismediasociety.org/forum/index.php?topic=171274.0
http://isch.kr/board_PowH60/16632
http://iymc.or.kr/?document_srl=87728
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=1440
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=692904.0
https://saltriverbg.com/2019/05/16/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vo-production/
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2763752
http://www.xn--289a43as5bo1vumwo4k.com/sub_09_05/1045
http://kyj1225.godohosting.com/board_mebR72/12565
http://jnk-ent.jp/index.php?mid=gallery&document_srl=48965
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=40029
http://lucky.kidspann.net/index.php?mid=qna&document_srl=60912
http://askpharm.net/board_NQiz06/9733
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/498895
http://www.hicleaning.kr/board_wash/69385
http://forum.byehaj.hu/index.php?topic=91244.0
http://indiefilm.kr/xe/board/81265
http://www.livetank.cn/market1/12738
http://joinbohum.kr/board/15237
http://8.droror.co.il/uncategorized/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8-2/
http://poselokgribovo.ru/forum/index.php?topic=793547.0
http://jnk-ent.jp/index.php?mid=gallery&document_srl=45919
http://www.gforgirl.com/xe/poster/89031
http://emjun.com/index.php?mid=hangtotal&document_srl=17375
http://bethanychurch.kr/?document_srl=4389
http://wixelent.co.kr/xe/ch_notice/15213
http://www.sp1.football/index.php?mid=tr_video&document_srl=176974
http://www.jesusonly.life/calendar/73086
http://themasters.pro/file_01/39014
http://themasters.pro/file_01/36839
http://jnk-ent.jp/index.php?mid=gallery&document_srl=45143
http://indiefilm.kr/xe/board/66923
http://lucky.kidspann.net/index.php?mid=qna&document_srl=35147
http://xn----3x5er9r48j7wemud0a387h.com/news/20447
https://chromehearts.in.th/index.php?topic=52585.0
http://HyUa.1fps.icu/l/szIaeDC
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1083511
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1788285
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=2013565
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1673061
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1405077
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2644793
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/87408
http://www.critico-expository.com/forum/index.php?topic=11120.0
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/709698
http://www.comfortcenter.es/index.php/component/k2/itemlist/user/105346
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4916184
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=10471
http://www.ekemoon.com/170595/050720194310/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1423878
http://skylinecam.co.kr/photo/98762
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=149409
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=149444
http://www.golden-nail.co.kr/?document_srl=91095
http://www.golden-nail.co.kr/press/91004
http://www.golden-nail.co.kr/press/91024
http://www.golden-nail.co.kr/press/91143
http://www.josephmaul.org/menu41/105050
http://www.josephmaul.org/menu41/105103
http://www.sp1.football/index.php?mid=faq&document_srl=218852
http://www.sp1.football/index.php?mid=faq&document_srl=218900
http://www.sp1.football/index.php?mid=faq&document_srl=219065
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=34469
http://www.hicleaning.kr/board_wash/80539
http://www.jesusonly.life/?document_srl=118700
http://www.jesusonly.life/calendar/118582
http://www.jesusonly.life/calendar/118814
http://www.josephmaul.org/menu41/88990
http://www.jshwanghoan.com/?document_srl=67973
http://www.nienkevanrijn.nl/component/k2/itemlist/user/446945
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=496060
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=496080
http://www.spazioad.com/component/k2/itemlist/user/7341821
http://www.studyxray.com/Sangdam/103654
https://prelease.club/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%87%d0%b0%d1%81%d1%82%d1%8c-6-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5/
http://www.ekemoon.com/172319/051420190310/
http://www.digitalbul.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sn0v-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=46197
http://mobility-corp.com/index.php/component/k2/itemlist/user/2602278
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=24126
http://ye-dream.com/qa/52154
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=104796
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=104896
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=203110
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=203264
http://asin.itts.co.kr/?document_srl=8913
http://asin.itts.co.kr/board_rtXs84/8889
http://asin.itts.co.kr/board_rtXs84/8931
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1608030
http://www.arunagreen.com/index.php/component/k2/itemlist/user/541387
http://www.atab.com.sa/index.php/en/?option=com_k2&view=itemlist&task=user&id=1649493
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1439689
http://www.autospa.lv/index.php/lv/component/k2/itemlist/user/10245
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/9207
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/9228
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3477000
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=845765
http://myrechockey.com/forums/index.php?topic=100558.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=331634
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=29794
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1792320
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1654650
http://www.hsaura.com/noty/61011
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=308324
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3600338
http://jiquilisco.org/index.php/component/k2/itemlist/user/6208
http://withinfp.sakura.ne.jp/eso/index.php/17010065-smotret-tajny-96-seria-f1-tajny-96-seria
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4770863
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=65714
http://moavalve.co.kr/faq/42642
http://koushatarabar.com/index.php/component/k2/itemlist/user/1314400
http://socialfbwidgets.com/component/k2/itemlist/user/13517.html
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?action=profile;u=622775
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3579509
http://esperanzazubieta.com/index.php/component/k2/itemlist/user/96500
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=581632
https://www.amazingworldtop.com/entretenimiento/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.shaiyax.com/index.php?topic=355438.0
http://dev.aabn.org.gh/component/k2/itemlist/user/618245
http://e-educ.net/Forum/index.php?topic=12533.0
http://israengineering.com/index.php/component/k2/itemlist/user/1215546
http://mediaville.me/index.php/component/k2/itemlist/user/289180
http://miklja.net/forum/index.php?topic=32111.0
http://miklja.net/forum/index.php?topic=32114.0
http://subforumna.x10.mx/mad/index.php?topic=251524.0
http://teambuildingpremium.com/forum/index.php?topic=849495.0
http://test.comics-game.ru/index.php?topic=215.0
http://universalcommunity.se/Forum/index.php?topic=16014.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=013f37abdf722b7f2cbc4759bda02e4c&topic=256833.0
http://www.rocktheboat.cc/groups/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%8d%d0%ba%d1%81%d1%82%d1%80%d0%b0%d1%81%d0%b5%d0%bd%d1%81%d0%be%d0%b2-31652/
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=81088
https://alquilervideobeam.com.co/?option=com_k2&view=itemlist&task=user&id=56941
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/15205
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/5796
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=291816
http://ovotecegg.com/component/k2/itemlist/user/116191
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/576357
http://mediaville.me/index.php/component/k2/itemlist/user/227556
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42371
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rj9%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.elpinatarense.es/?option=com_k2&view=itemlist&task=user&id=154965
http://www.deliberarchia.org/forum/index.php?topic=978484.0
http://roikjer.com/forum/index.php?topic=812470.0
http://mediaville.me/index.php/component/k2/itemlist/user/211631
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=21383
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1216062
http://jiquilisco.org/index.php/component/k2/itemlist/user/10020
http://mediaville.me/index.php/component/k2/itemlist/user/289384
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=163678
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/223538
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/223553
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1706712
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1706732
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1706783
http://thermoplast.envolgroupe.com/component/k2/author/123277
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=11589
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1611600
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1656801
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1445840
http://bitpark.co.kr/board_IzjM66/3804573
http://computerscience.egerton.ac.ke/index.php/component/k2/itemlist/user/2007017
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1888699
http://www.dap.com.py/index.php/component/k2/itemlist/user/809226
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=617425
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=32901
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=568959
http://www.babvallejo.com/index.php/component/k2/itemlist/user/601044
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=269810
http://rudraautomation.com/index.php/component/k2/author/125947
http://poselokgribovo.ru/forum/index.php?topic=730209.0
http://ptu.imoove.kr/ko/content/%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB332440
http://rudraautomation.com/index.php/component/k2/author/107353
https://tg.vl-mp.com/index.php?topic=1344364.0
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1841594
http://www.ekemoon.com/146335/051820195806/
http://www.ekemoon.com/144437/050920192106/
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1643114
http://thermoplast.envolgroupe.com/component/k2/author/65637
http://www.ekemoon.com/145477/051720190906/
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=345099
http://dev.aabn.org.gh/component/k2/itemlist/user/618742
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1945802
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=335231
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1216429
http://jiquilisco.org/index.php/component/k2/itemlist/user/10134
https://prelease.club/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-snyd-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80/
http://cwon.kr/xe/board_bnSr36/22856
http://myrechockey.com/forums/index.php?topic=99059.0
http://dev.aabn.org.gh/component/k2/itemlist/user/569759
http://www.hsaura.com/noty/62863
http://arunagreen.com/index.php/component/k2/itemlist/user/473516
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/265494
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1681601
http://roikjer.com/forum/index.php?PHPSESSID=4455bbkda3k68d7rdemidq4ho0&topic=847865.0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/261967
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/313964
http://www.rocktheboat.cc/groups/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba%d1%83%d0%ba%d1%80%d0%b0%d0%b8%d0%bd%d0%b0-he%d1%85%d0%be/
http://myrechockey.com/forums/index.php?topic=91394.0
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=573
https://turimex.mx.solemti.net/en/?option=com_k2&view=itemlist&task=user&id=985
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/20382
http://bitpark.co.kr/board_IzjM66/3914159
http://www.deliberarchia.org/forum/index.php?topic=1027225.0
http://www.deliberarchia.org/forum/index.php?topic=1027239.0
http://www.deliberarchia.org/forum/index.php?topic=1027251.0
http://www.vivelabmanizales.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qb9e-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1860064
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=44174
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=491634
http://mediaville.me/index.php/component/k2/itemlist/user/217092
http://ovotecegg.com/component/k2/itemlist/user/122547
http://withinfp.sakura.ne.jp/eso/index.php/16865638-holostak-9-9-vipusk-zdholostak-9-9-vipusk33-holostak-9-9-vipusk
http://teambuildingpremium.com/forum/index.php?topic=831553.0
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/702825
https://www.vegasgreentour.com/index.php?document_srl=46697&mid=board_XiHh59
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=73938
http://fbpharm.net/index.php/component/k2/itemlist/user/26957
https://esel.gist.ac.kr/esel2/board_hmgj23/55880
https://esel.gist.ac.kr/esel2/board_hmgj23/56053
https://esel.gist.ac.kr/esel2/board_hmgj23/56087
https://esel.gist.ac.kr/esel2/board_hmgj23/56101
https://esel.gist.ac.kr/esel2/board_hmgj23/56111
https://esel.gist.ac.kr/esel2/board_hmgj23/56116
https://esel.gist.ac.kr/esel2/board_hmgj23/56136
https://esel.gist.ac.kr/esel2/board_hmgj23/56165
http://married.dike.gr/index.php/component/k2/itemlist/user/56277
http://mediaville.me/index.php/component/k2/itemlist/user/246147
http://mobility-corp.com/index.php/component/k2/itemlist/user/2561276
http://ovotecegg.com/component/k2/itemlist/user/130937
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=12336
http://proxima.co.rw/index.php/component/k2/itemlist/user/598616
http://www.ekemoon.com/182855/051420190813/
http://teambuildingpremium.com/forum/index.php?topic=821975.0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=623410
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1592001
http://myrechockey.com/forums/index.php?topic=101424.0
http://ye-dream.com/qa/20969
http://socialfbwidgets.com/component/k2/itemlist/user/13649.html
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1356825
http://condolencias.servisa.es/13-06-05-2019-j8-13
http://www.pkmmsabah.org/?option=com_k2&view=itemlist&task=user&id=19221
http://arunagreen.com/index.php/component/k2/itemlist/user/459304
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1556863
https://test.baseyou21.kr/?document_srl=16452
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=131812
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=22740
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=22971
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2637595
http://corumotoanahtar.com/component/k2/itemlist/user/2624
http://dev.aabn.org.gh/component/k2/itemlist/user/594344
http://gtupuw.org/index.php/component/k2/itemlist/user/1909667
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/315354
http://married.dike.gr/index.php/component/k2/itemlist/user/56628
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=74824
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/63174
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=688041.0
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=317211
http://mahdi.ehosseini.com/index.php/component/k2/itemlist/user/29832
http://www.jesusonly.life/calendar/9752
http://xplorefitness.com/blog/%D1%81%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C-%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-3-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-w6-%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-3-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/257462
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/17920
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/17922
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/17927
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1444740
http://www.boutique.in.th/?option=com_k2&view=itemlist&task=user&id=151626
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=822263
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=849732
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=32124
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=32251
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=277858
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3382644
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=4303
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=24774
http://dev.aabn.org.gh/component/k2/itemlist/user/616956
http://mediaville.me/index.php/component/k2/itemlist/user/288168
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/758479
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/112906
http://thermoplast.envolgroupe.com/component/k2/author/95861
http://zanoza.h1n.ru/2019/05/16/%d1%87%d1%83%d0%b6%d0%b0%d1%8f-%d0%b6%d0%b8%d0%b7%d0%bd%d1%8c-%d1%87%d1%83%d0%b6%d0%b5-%d0%b6%d0%b8%d1%82%d1%82%d1%8f-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-16-05-2019-s7-%d1%87%d1%83/
https://members.fbhaters.com/index.php?topic=86811.0
http://sindicatodechoferespichincha.com.ec/index.php/component/k2/itemlist/user/6711795
http://cafe.dokseosil.co.kr/community/44961
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=48439
http://vtservices85.fr/smf2/index.php?PHPSESSID=33e5751b36b36480b295416c38df40d7&topic=228198.0
http://jiquilisco.org/index.php/component/k2/itemlist/user/5934
http://withinfp.sakura.ne.jp/eso/index.php/17004571-hdvideo-holostak-9-sezon-10-vypusk-o1-holostak-9-sezon-10-vypus
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3355141
http://www.digitalbul.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-im8w-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2474347
http://cafe.dokseosil.co.kr/community/24063
http://cafe.dokseosil.co.kr/community/24073
http://cafe.dokseosil.co.kr/community/24084
http://cafe.dokseosil.co.kr/community/24089
http://corumotoanahtar.com/component/k2/itemlist/user/1615.html
http://teambuildingpremium.com/forum/index.php?topic=824121.0
https://sanp.pro/%d0%bd%d0%b5-%d0%be%d1%82%d0%bf%d1%83%d1%81%d0%ba%d0%b0%d0%b9-%d0%bc%d0%be%d1%8e-%d1%80%d1%83%d0%ba%d1%83-elimi-birakma-35-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ejnf-%d0%bd%d0%b5-%d0%be/
https://khuyenmaikk13.info/index.php?topic=207829.0
https://khuyenmaikk13.info/index.php?topic=207833.0
https://khuyenmaikk13.info/index.php?topic=207834.0
https://khuyenmaikk13.info/index.php?topic=207842.0
https://khuyenmaikk13.info/index.php?topic=207847.0
https://khuyenmaikk13.info/index.php?topic=207851.0
https://khuyenmaikk13.info/index.php?topic=207861.0
https://khuyenmaikk13.info/index.php?topic=207863.0
https://khuyenmaikk13.info/index.php?topic=207867.0
https://khuyenmaikk13.info/index.php?topic=207876.0
https://khuyenmaikk13.info/index.php?topic=207879.0
https://khuyenmaikk13.info/index.php?topic=207881.0
https://khuyenmaikk13.info/index.php?topic=207883.0
https://mcsetup.tk/bbs/index.php?topic=255422.0
http://indiefilm.kr/xe/board/55739
http://www.theocraticamerica.org/forum/index.php?topic=42476.0
http://ovotecegg.com/component/k2/itemlist/user/133505
http://www.digitalbul.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-15-05-2019-r1-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/27021
http://danielmillsap.com/forum/index.php?topic=997717.0
http://xplorefitness.com/blog/%C2%AB%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-96-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-11-05-2019-n2-%C2%AB%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-96-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=57058
http://www.vivelabmanizales.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-81-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iu1o-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd/
http://jiquilisco.org/component/k2/itemlist/user/4436
http://daesestudy.co.kr/ipsi_docu/22492
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1672214
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1684275
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=109643
http://www.urbantutorial.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=109619
http://xplorefitness.com/blog/%D1%8D%D1%84%D0%B8%D1%80-%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-r4-%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2627012
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=38894
http://www.theocraticamerica.org/forum/index.php/topic,48779.0.html
http://www.theocraticamerica.org/forum/index.php/topic,48783.0.html
http://www.theocraticamerica.org/forum/index.php/topic,48804.0.html
http://www.theocraticamerica.org/forum/index.php/topic,48884.0.html
http://www.theocraticamerica.org/forum/index.php?topic=48767.0
http://www.theocraticamerica.org/forum/index.php?topic=48773.0
http://www.theocraticamerica.org/forum/index.php?topic=48801.0
http://www.theocraticamerica.org/forum/index.php?topic=48854.0
http://www.theocraticamerica.org/forum/index.php?topic=48865.0
http://www.theocraticamerica.org/forum/index.php?topic=48871.0
http://www.theocraticamerica.org/forum/index.php?topic=48879.0
http://www.theparrotcentre.com/forum/index.php?topic=551667.0
http://www.tessabannampad.go.th/webboard/index.php?topic=214466.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3393473
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hr2%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lg6%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.teedinubon.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ta8%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-11-%d1%81%d0%b5/
http://zanoza.h1n.ru/2019/05/19/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-iq1%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5/
https://esel.gist.ac.kr/esel2/board_hmgj23/59888
https://esel.gist.ac.kr/esel2/board_hmgj23/59920
https://esel.gist.ac.kr/esel2/board_hmgj23/59952
https://esel.gist.ac.kr/esel2/board_hmgj23/59988
https://khuyenmaikk13.info/index.php?topic=207816.0
https://prelease.club/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rnlm-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://prelease.club/%d0%ba%d0%bb%d1%8f%d1%82%d0%b2%d0%b0-yemin-65-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-frfh-%d0%ba%d0%bb%d1%8f%d1%82%d0%b2%d0%b0-yemin-65-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=91215
https://testing.celekt.com/%d0%96%d0%b5%d1%81%d1%82%d0%be%d0%ba%d0%b8%d0%b9-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb-zalim-istanbul-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rhrd-%d0%96%d0%b5%d1%81%d1%82%d0%be/
https://www.tedyun.com/xe/index.php?document_srl=196168&mid=gallery
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=566444
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=1014525
http://www.die-design-manufaktur.de/?option=com_k2&view=itemlist&task=user&id=5174944
http://teambuildingpremium.com/forum/index.php?topic=778766.0
http://seoksoononly.dothome.co.kr/qna/728140
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-de0%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-1-%d1%81%d0%b5%d1%80/
https://www.amazingworldtop.com/entretenimiento/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-pp6%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5/
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=348124
http://www.tekparcahdfilm.com/forum/index.php?topic=51686.0
http://www.tessabannampad.go.th/webboard/index.php?topic=214684.0
http://www.tessabannampad.go.th/webboard/index.php?topic=214688.0
https://altaylarteknoloji.com/index.php?topic=5254.0
http://www.josephmaul.org/menu41/111244
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=87834
http://xn----3x5er9r48j7wemud0a387h.com/news/36795
http://xn----3x5er9r48j7wemud0a387h.com/news/36828
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/519118
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/519142
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=68793
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=68833
http://xn--ok1bpqi43ahtb.net/board_eASW07/135636
http://xn--ok1bpqi43ahtb.net/board_eASW07/136008
http://xn--ok1bpqi43ahtb.net/board_eASW07/136042
http://yeonsen.com/?document_srl=76909
http://yeonsen.com/?document_srl=76953
http://www.phan-aen.go.th/forum/index.php?topic=626466.0
http://salescoach.ro/content/%C2%AB%D0%BD%D0%B0%D1%88%D0%B0-%D0%B8%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F-69-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-agwl-%C2%AB%D0%BD%D0%B0%D1%88%D0%B0-%D0%B8%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F-69-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://sindicatodechoferespichincha.com.ec/index.php/component/k2/itemlist/user/6682017
http://sfah.ch/de/component/k2/itemlist/user/14932
http://ovotecegg.com/component/k2/itemlist/user/118267
http://smartacity.com/component/k2/itemlist/user/18841
http://seoksoononly.dothome.co.kr/qna/772010
http://www.ekemoon.com/158415/051020192408/
http://vn7.vn/qna/64372
http://mediaville.me/index.php/component/k2/itemlist/user/266271
http://moavalve.co.kr/faq/11425
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=618248
https://turimex.mx.solemti.net/en/?option=com_k2&view=itemlist&task=user&id=1654
http://www.hicleaning.kr/board_wash/90744
http://www.hicleaning.kr/board_wash/90903
http://www.hicleaning.kr/board_wash/90926
http://www.hsaura.com/noty/143998
http://www.josephmaul.org/menu41/113283
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=89421
http://www.sp1.football/?document_srl=236535
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=104274
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1762419
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1558169
http://seoksoononly.dothome.co.kr/qna/757704
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1566320
http://mjbosch.com/component/k2/itemlist/user/81536
http://islamiccall.info/?option=com_k2&view=itemlist&task=user&id=856507
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43005
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/481097
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=279851
http://www.ekemoon.com/189365/051820191314/
http://married.dike.gr/index.php/component/k2/itemlist/user/60643
https://prelease.club/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-oh7a-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=204857
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1824388
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=52891
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=686191.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2628631
http://fbpharm.net/index.php/component/k2/itemlist/user/39406
http://healthyteethpa.org/component/k2/itemlist/user/5428156
http://jiquilisco.org/index.php/component/k2/itemlist/user/4758
http://www.arunagreen.com/index.php/component/k2/itemlist/user/507404
http://www.digitalbul.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ml4d-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/3998
http://www.sollazzorefrigerazione.it/?option=com_k2&view=itemlist&task=user&id=2476176
http://corumotoanahtar.com/component/k2/itemlist/user/1854.html
http://corumotoanahtar.com/index.php/component/k2/itemlist/user/1853
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1901660
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1901671
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1901907
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1902026
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3447931
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3448181
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3448238
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3795709
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3796064
http://married.dike.gr/index.php/component/k2/itemlist/user/60578
http://mobility-corp.com/index.php/component/k2/itemlist/user/2589415
http://ovotecegg.com/component/k2/itemlist/user/145586
https://sanp.pro/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-80-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tljl-%d0%bd%d0%b5%d0%b2/
http://married.dike.gr/index.php/component/k2/itemlist/user/54753
http://haniel.ir/index.php/component/k2/itemlist/user/86493
http://www.theocraticamerica.org/forum/index.php?topic=31455.0
http://poselokgribovo.ru/forum/index.php?topic=716566.0
https://l2thalassic.org/Forum/index.php?topic=729.0
http://highlanderonline.cmshelplive.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-8/
http://macdistri.com/?option=com_k2&view=itemlist&task=user&id=297614
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1617751
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1543668
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1334250
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3708346
http://seoksoononly.dothome.co.kr/qna/732022
http://thermoplast.envolgroupe.com/component/k2/author/71678
http://www.ekemoon.com/150015/050220194107/
http://arunagreen.com/?option=com_k2&view=itemlist&task=user&id=420560
http://thermoplast.envolgroupe.com/component/k2/author/76092
http://withinfp.sakura.ne.jp/eso/index.php/16887742-serial-tola-robot-1-seria-i7-tola-robot-1-seria/0
http://seoksoononly.dothome.co.kr/qna/746977
http://zsmr.com.ua/index.php/component/k2/itemlist/user/595259
https://hackersuniversity.net/index.php?topic=21013.0
https://khuyenmaikk13.info/index.php?topic=209264.0
https://mcsetup.tk/bbs/index.php?topic=256389.0
https://reficulcoin.com/index.php?topic=55209.0
https://testing.celekt.com/%d0%a7%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-2019-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%a1%d0%9c%d0%9e%d0%a2%d0%a0%d0%95%d0%a2%d0%ac-%d0%a7%d0%b5%d1%80%d0%bd%d0%be%d0%b1/
https://www.shaiyax.com/index.php?topic=356348.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1418817
http://www.crnmedia.es/component/k2/itemlist/user/85860
http://thermoplast.envolgroupe.com/component/k2/author/105669
http://www.digitalbul.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-j2-%d1%82%d0%be%d0%bb/
http://seoksoononly.dothome.co.kr/qna/867457
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3646367
http://arquitectosenreformas.es/index.php/component/k2/itemlist/user/80920
http://ye-dream.com/qa/33898
https://verdadesbiblicas.org.ec/index.php/component/k2/itemlist/user/3716112
http://www.vivelabmanizales.com/%d1%81%d0%be%d0%b4%d0%b5%d1%80%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-06-05-2019-s1-%d1%81%d0%be%d0%b4%d0%b5%d1%80%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-9-%d1%81/
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-%D1%80%D0%BE%D0%B6%D0%B4%D0%B5%D0%BD-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA%C2%BB-ur%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-%D1%80%D0%BE%D0%B6%D0%B4%D0%B5%D0%BD-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA%C2%BB49-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-%D1%80%D0%BE%D0%B6%D0%B4%D0%B5%D0%BD
http://xplorefitness.com/blog/%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-15-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-07-05-2019-c0-%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-15-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=501960
https://szenarist.ru/forum/index.php?topic=206277.0
http://www.comfortcenter.es/index.php/component/k2/itemlist/user/104390
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=185964
http://poselokgribovo.ru/forum/index.php?topic=717179.0
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42721
http://esperanzazubieta.com/component/k2/itemlist/user/95864
http://condolencias.servisa.es/2-06-05-2019-z3-2
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/852576
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=33519
http://www.vogtland.com.pl/index.php/component/k2/itemlist/user/33516
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/280889
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3784557
http://asiagroup.co.kr/?document_srl=219398
http://asin.itts.co.kr/board_rtXs84/12639
http://atemshow.com/atemfair_domestic/62485
http://atemshow.com/atemfair_domestic/62498
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=119663
http://indiefilm.kr/xe/board/148550
http://indiefilm.kr/xe/board/148782
http://moavalve.co.kr/?document_srl=84017
http://moavalve.co.kr/faq/84027
http://moavalve.co.kr/faq/84052
http://xplorefitness.com/blog/%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-13-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-15-05-2019-t8-%C2%AB%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-13-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://www.hsaura.com/noty/64881
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=204441
http://arunagreen.com/index.php/component/k2/itemlist/user/477538
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=2015926
http://ovotecegg.com/component/k2/itemlist/user/127588
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/23356
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=126606
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=126636
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=197394
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=85484
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=85527
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=85544
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=85554
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1577734
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1594253
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1055591
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=105322
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1793656
http://www.m1avio.com/index.php/component/k2/itemlist/user/3657463
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/600399
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=56931
http://www.telcon.gr/index.php/component/k2/itemlist/user/56910
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=245158
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/245171
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=26008
http://askpharm.net/board_NQiz06/36172
http://pkgersang.dothome.co.kr/board_jiKY24/8937
http://bebopindia.com/notcie/159127
http://www.sp1.football/index.php?document_srl=289716&mid=faq
http://praisesound.co.kr/sub04_01/14828
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=80996
http://koais.com/data/38123
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=176748
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/6130
http://49.247.3.43/?document_srl=22551
http://www.itosm.com/cn/board_nLoq17/24727
http://agiteshop.com/xe/qa/47588
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=115023
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=38474
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=783a04b722639a1fd65f04331f084cf1&topic=7165.0
http://wipln.com/?document_srl=54736
http://majorcebu.com/?document_srl=1138411
https://esel.gist.ac.kr/esel2/board_hmgj23/85099
http://www.vamoscontigo.org/Noticia/33865
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=24997
http://sunele.co.kr/board_ReBD97/54417
http://esiapolisthesharp2.co.kr/g1/34998
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/?document_srl=22875
http://bobr.site/index.php?topic=149102.0
http://HyUa.1fps.icu/l/szIaeDC
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=31457
http://agiteshop.com/xe/qa/52646
http://arte.dgau.ac.kr/board_qna/53616
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/4827
http://ariji.kr/?document_srl=818303
https://www.c-alice.org/forum/index.php?topic=87735.0
http://cwon.kr/xe/board_bnSr36/83788
http://roikjer.com/forum/index.php?PHPSESSID=hnvmjhff587udictsgp8ok3uf5&topic=892248.0
https://goagiletour.ca/node/1/sessions/%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2game-thrones-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-2-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-bthd-%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2game-thrones-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD
http://d-tube.info/board_jvyO69/249843
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/?document_srl=6316
http://gallerychoi.com/Exhibition/74640
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=5739
http://xn--2e0b53df5ag1c804aphl.net/nuguna/25724
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=57677
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=86292
https://reelgosu.com/board_peJN24/275473
https://celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-ojnj-%d0%98%d0%b3%d1%80/
http://khapthanam.co.kr/g1/38992
http://praisesound.co.kr/sub04_01/14289
http://wgamez.net/index.php?mid=board_KGzu43&document_srl=9310
http://gallerychoi.com/Exhibition/88592
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vyqs-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://reficulcoin.com/index.php?topic=56291.0
http://repofirmware.altervista.org/index.php?topic=166082.0
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=106841
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=9010
http://xn--ok1bpqi43ahtb.net/board_EkDG82/163875
http://49.247.3.43/index.php?mid=board_PiDQ29&document_srl=23590
http://iamking.net/board/27977
http://www.artangel.co.kr/?document_srl=26576
http://arte.dgau.ac.kr/board_qna/53375
http://thanosakademi.com/index.php?topic=97941.0
http://arte.dgau.ac.kr/board_qna/50547
http://ariji.kr/?document_srl=834701
http://www.vamoscontigo.org/Noticia/36412
http://bebopindia.com/notcie/154520
http://atemshow.com/atemfair_domestic/68757
https://esel.gist.ac.kr/esel2/board_hmgj23/85449
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=120165
http://apt2you2.cafe24.com/g1/9216
http://d-tube.info/board_jvyO69/247767
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/12469
http://HyUa.1fps.icu/l/szIaeDC
http://roikjer.com/forum/index.php?PHPSESSID=v1fo11n5ksspbi66tf7kij43e3&topic=882344.0
http://www.tessabannampad.go.th/webboard/index.php?topic=200341.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1392198
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=9098
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=44227
https://khuyenmaikk13.info/index.php?topic=191411.0
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=322548
http://soc-human.kz/index.php/component/k2/itemlist/user/1674393
http://smartacity.com/component/k2/itemlist/user/34142
http://www.vivelabmanizales.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fe9w/
http://ovotecegg.com/component/k2/itemlist/user/140733
http://withinfp.sakura.ne.jp/eso/index.php/16992285-hdvideo-tola-robot-5-seria-o0-tola-robot-5-seria/0
http://www.gforgirl.com/xe/?document_srl=110418
http://www.gforgirl.com/xe/?document_srl=110514
http://www.gforgirl.com/xe/poster/110395
http://www.gforgirl.com/xe/poster/110493
http://www.golden-nail.co.kr/press/72853
http://www.golden-nail.co.kr/press/72881
http://www.golden-nail.co.kr/press/72886
http://www.hicleaning.kr/?document_srl=81088
http://yeonsen.com/?document_srl=96552
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=96528
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=96537
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=96571
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=96584
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=96646
http://yoriyorifood.com/xxxx/spacial/101864
http://yoriyorifood.com/xxxx/spacial/101884
http://yoriyorifood.com/xxxx/spacial/101911
https://khuyenmaikk13.info/index.php?topic=192022.0
http://seoksoononly.dothome.co.kr/qna/854727
https://sanp.pro/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lkaj-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://menulisilmiah.net/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-y0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2/
http://gtupuw.org/index.php/component/k2/itemlist/user/1891336
http://computerscience.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=2016002
http://forum.byehaj.hu/index.php?topic=86614.0
http://moavalve.co.kr/faq/26387
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/305869
http://asin.itts.co.kr/board_rtXs84/6478
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=77887
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=77916
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=78027
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=78222
http://bebopindia.com/notcie/105029
http://bebopindia.com/notcie/105053
http://bebopindia.com/notcie/105147
http://carrierworld.co.kr/?document_srl=61084
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=60929
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=60959
http://indiefilm.kr/xe/board/155295
http://jjimdak.callbank.kr/?document_srl=882536
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=882335
http://lucky.kidspann.net/index.php?mid=qna&document_srl=88197
http://lucky.kidspann.net/index.php?mid=qna&document_srl=88225
http://vhost12299.cpsite.ru/489987-tola-robot-7-seria-19052019-z7-tola-robot-7-seria
http://www.josephmaul.org/menu41/135352
http://www.josephmaul.org/menu41/135407
http://www.studyxray.com/Sangdam/132980
http://www.studyxray.com/Sangdam/133030
http://www.studyxray.com/Sangdam/133055
http://www.studyxray.com/Sangdam/133187
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3305615
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3305625
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=18252
http://menulisilmiah.net/hd-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v4-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81/
http://ovotecegg.com/component/k2/itemlist/user/131991
http://xplorefitness.com/blog/%D1%81%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-a2-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/238847
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3813034
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=81801
http://myrechockey.com/forums/index.php?topic=101848.0
http://bitpark.co.kr/board_IzjM66/3792125
http://dev.aabn.org.gh/component/k2/itemlist/user/560288
https://test.baseyou21.kr/?document_srl=33997
http://www.remify.app/foro/index.php?topic=283618.0
http://withinfp.sakura.ne.jp/eso/index.php/17120044-live-cuzaa-zizn-cuze-zitta-13-seria-l8-cuzaa-zizn-cuze-zitta-13/0
http://withinfp.sakura.ne.jp/eso/index.php/17120067-hdvideo-tajny-101-seria-e1-tajny-101-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/17120113-hd-smers-13-seria-a5-smers-13-seria
http://withinfp.sakura.ne.jp/eso/index.php/17120149-hd-dockimateri-dockimateri-16-seria-c2-dockimateri-dockimateri-/0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1440814
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/275121
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/35937
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2657334
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=112081
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=112087
http://corumotoanahtar.com/component/k2/itemlist/user/4402.html
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=342246
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=342424
http://dev.aabn.org.gh/component/k2/itemlist/user/612227
http://corumotoanahtar.com/component/k2/itemlist/user/5685.html
http://dcasociados.eu/component/k2/itemlist/user/90340
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1948893
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=101028
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=339013
http://jiquilisco.org/index.php/component/k2/itemlist/user/11065
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=37643
http://forum.byehaj.hu/index.php?topic=89767.0
http://cafe.dokseosil.co.kr/?document_srl=42770
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/805140
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=109643
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7350144
http://rudraautomation.com/index.php/component/k2/author/156696
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/4228
http://mediaville.me/index.php/component/k2/itemlist/user/250092
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/10754
http://withinfp.sakura.ne.jp/eso/index.php/16867009-po-zakonam-voennogo-vremeni-3-sezon-2-seria-05052019-g8-po-zako
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=292771
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=64053
http://www.ekemoon.com/143049/052020195705/
http://mediaville.me/index.php/component/k2/itemlist/user/223033
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/186373
http://k2.akademitelkom.ac.id/index.php/component/k2/itemlist/user/293888
http://www.afikgan.co.il/index.php/component/k2/itemlist/user/26389
http://compultras.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=199374
http://www.atab.com.sa/index.php/en/?option=com_k2&view=itemlist&task=user&id=1543178
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1007481
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1873782
http://poselokgribovo.ru/forum/index.php?topic=734261.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/568748
http://smartacity.com/component/k2/itemlist/user/19405
http://www.m1avio.com/index.php/component/k2/itemlist/user/3600350
https://l2thalassic.org/Forum/index.php?topic=1156.0
http://forum.byehaj.hu/index.php?topic=81708.0
http://mediaville.me/index.php/component/k2/itemlist/user/209626
http://euromouleusinage.com/index.php/component/k2/itemlist/user/105222
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=36125
http://theolevolosproject.org/index.php/component/k2/itemlist/user/25143
http://www.pcosmetic.ir/?option=com_k2&view=itemlist&task=user&id=10551
http://www.die-design-manufaktur.de/index.php/component/k2/itemlist/user/5175866
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7309399
https://forum.ac-jete.it/index.php?topic=351041.0
https://lucky28003.nl/forum/index.php?topic=11217.0
http://www.critico-expository.com/forum/index.php?topic=11109.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/207992
http://batubersurat.com/index.php/component/k2/itemlist/user/48021
http://www.jesusonly.life/calendar/71918
http://www.deliberarchia.org/forum/index.php?topic=1002335.0
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1544124
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/53458
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5145
http://www.sollazzorefrigerazione.it/?option=com_k2&view=itemlist&task=user&id=2423892
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=12778
http://www.phan-aen.go.th/forum/index.php?topic=626135.0
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=491646
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3565602
http://bitpark.co.kr/?document_srl=3731051
https://www.c-alice.org/forum/index.php?topic=72637.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=49091
http://forum.politeknikgihon.ac.id/index.php?topic=24640.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1350029
http://jiquilisco.org/index.php/component/k2/itemlist/user/5165
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=51719
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2636940
http://moavalve.co.kr/faq/6724
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4924086
http://soc-human.kz/index.php/component/k2/itemlist/user/1659152
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1417622
http://cwon.kr/xe/board_bnSr36/3022
http://seoksoononly.dothome.co.kr/?document_srl=762414
http://withinfp.sakura.ne.jp/eso/index.php/16866418-po-zakonam-voennogo-vremeni-3-sezon-9-seria-05052019-y1-po-zako
http://married.dike.gr/index.php/component/k2/itemlist/user/46742
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=11894
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/204670
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=303882
http://engeena.com/?option=com_k2&view=itemlist&task=user&id=8213
http://dev.aabn.org.gh/component/k2/itemlist/user/515825
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=779488
http://mediaville.me/index.php/component/k2/itemlist/user/208061
http://www.sakitoandrichifantasy.gr/index.php/component/k2/itemlist/user/156395
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1347539
http://macdistri.com/index.php/component/k2/itemlist/user/306839
http://rudraautomation.com/index.php/component/k2/author/133477
http://associationsila.org/component/k2/itemlist/user/282528
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3374480
http://arunagreen.com/index.php/component/k2/itemlist/user/438153
http://arunagreen.com/index.php/component/k2/itemlist/user/426574
http://condolencias.servisa.es/11-06-05-2019-x9-11
http://www.ekemoon.com/156251/050320193208/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/286429
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=82289
http://danielmillsap.com/forum/index.php?topic=955931.0
http://xplorefitness.com/blog/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA%C2%BB-rt%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA%C2%BB78-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/281580
http://zanoza.h1n.ru/2019/05/19/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-17-05-19-uy%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=596366
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/56627
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3569925
http://theolevolosproject.org/index.php/component/k2/itemlist/user/25218
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2562177
http://poselokgribovo.ru/forum/index.php?topic=717456.0
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=500819
http://withinfp.sakura.ne.jp/eso/index.php/16904274-live-otel-toledo-2-seria/0
http://ovotecegg.com/component/k2/itemlist/user/118021
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/67106
http://www.m1avio.com/index.php/component/k2/itemlist/user/3626085
http://haniel.ir/index.php/component/k2/itemlist/user/84892
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=15178
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=603629
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=57942
http://www.telcon.gr/index.php/component/k2/itemlist/user/57949
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3339927
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=81259
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1932657
http://otitismediasociety.org/forum/index.php?topic=178784.0
http://roikjer.com/forum/index.php?PHPSESSID=r4ila3ranqu5n56b1ena2hr3k2&topic=895842.0
http://ru-realty.com/forum/index.php?PHPSESSID=8tk74geaqs7njs91bvsdt1gcq4&topic=532715.0
http://taklongclub.com/forum/index.php?topic=155241.0
http://teambuildingpremium.com/forum/index.php?topic=852641.0
http://teambuildingpremium.com/forum/index.php?topic=852648.0
http://thanosakademi.com/index.php?topic=99573.0
http://universalcommunity.se/Forum/index.php?topic=16956.0
http://www.tekparcahdfilm.com/forum/index.php?topic=51546.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/303104
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=6357
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=12499
http://www.ekemoon.com/143201/052220190705/
http://menulisilmiah.net/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lu1%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f09-05/
http://www.vivelabmanizales.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d0%bf%d1%80%d0%be%d0%bc%d0%be-kl%d1%85%d0%be%d0%bb%d0%be/
https://l2thalassic.org/Forum/index.php?topic=1147.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3295138
http://www.babvallejo.com/index.php/component/k2/itemlist/user/603192
http://dohairbiz.com/index.php/component/k2/itemlist/user/2723037
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43756
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1059700
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1796571
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4887236
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=603900
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=802386
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=802672
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=802699
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2445638
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/247718
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2609004
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=51043
http://dcasociados.eu/component/k2/itemlist/user/88293
http://dev.aabn.org.gh/component/k2/itemlist/user/566446
http://forum.byehaj.hu/index.php?topic=87656.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2575081
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1669244
http://fbpharm.net/index.php/component/k2/itemlist/user/44926
http://bitpark.co.kr/board_IzjM66/3812454
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=14451
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1683933
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=57496
http://rudraautomation.com/index.php/component/k2/author/216759
http://shinhwaair2017.cafe24.com/issue/211913
http://shinhwaair2017.cafe24.com/issue/211927
http://shinhwaair2017.cafe24.com/issue/211982
http://shinhwaair2017.cafe24.com/issue/212007
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1194200
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3461385
http://jiquilisco.org/index.php/component/k2/itemlist/user/6689
http://married.dike.gr/index.php/component/k2/itemlist/user/62746
http://mediaville.me/index.php/component/k2/itemlist/user/273578
http://www.arunagreen.com/index.php/component/k2/itemlist/user/516041
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2604443
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/14557
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1805632
http://www.ekemoon.com/193937/051420195615/
http://ask.tutorfortune.com/discussion/293/vetrenyy-hercai-25-seriya-gbwt-vetrenyy-hercai-25-seriya
http://ask.tutorfortune.com/index.php?p=/discussion/292/nasha-istoriya-70-seriya-wyze-nasha-istoriya-70-seriya
http://bebopindia.com/notcie/100315
http://bebopindia.com/notcie/101021
http://bebopindia.com/notcie/101089
http://bebopindia.com/notcie/101178
http://community.viajar.tur.br/index.php?p=/discussion/61198/klyatva-yemin-62-seriya-wdrx-klyatva-yemin-62-seriya/p1%3Fnew=1
http://community.viajar.tur.br/index.php?p=/discussion/61204/vetrenyy-hercai-14-seriya-aesh-vetrenyy-hercai-14-seriya
http://community.viajar.tur.br/index.php?p=/discussion/61205/bogatye-i-bednye-zengin-ve-yoksul-19-seriya-rsjz-bogatye-i-bednye-zengin-ve-yoksul-19-seriya
http://mediaville.me/index.php/component/k2/itemlist/user/273331
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=76393
http://www.arunagreen.com/index.php/component/k2/itemlist/user/523306
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/5634
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/5635
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/5636
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=832095
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/25955
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=22149
http://www.deliberarchia.org/forum/index.php?topic=996093.0
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=29888
http://www.hsaura.com/noty/43447
http://www.spazioad.com/component/k2/itemlist/user/7290038
http://indiefilm.kr/xe/board/29779
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=11643
http://www.digitalbul.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sk5m-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://myrechockey.com/forums/index.php?topic=96863.0
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=31812
http://rudraautomation.com/index.php/component/k2/author/116473
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1747688
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-18-%d1%81%d0%b5%d1%80-2/
http://www.phan-aen.go.th/forum/index.php?topic=628015.0
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=784045
http://israengineering.com/index.php/component/k2/itemlist/user/1112698
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=102398
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=102413
http://emjun.com/?document_srl=95121
http://emjun.com/index.php?document_srl=95136&mid=hangtotal
http://emjun.com/index.php?mid=hangtotal&document_srl=95151
http://emjun.com/index.php?mid=hangtotal&document_srl=95231
http://cwon.kr/xe/board_bnSr36/22024
http://fbpharm.net/index.php/component/k2/itemlist/user/26622
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1684210
http://moavalve.co.kr/faq/30856
http://www.josephmaul.org/menu41/32009
http://www.deliberarchia.org/forum/index.php?topic=1044245.0
http://thermoplast.envolgroupe.com/component/k2/author/100981
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=98807
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=18744
http://thermoplast.envolgroupe.com/component/k2/author/95230
http://euromouleusinage.com/?option=com_k2&view=itemlist&task=user&id=106008
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3377691
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1555529
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=494017
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4853284
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=223859
http://www.ekemoon.com/142961/052020191105/
http://www.ekemoon.com/161393/050020190709/
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=104193
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=82315
http://shinilspring.com/?document_srl=103578
http://shinilspring.com/board_qsfb01/103381
http://shinilspring.com/board_qsfb01/103466
http://shinilspring.com/board_qsfb01/103547
http://shinilspring.com/board_qsfb01/103622
http://skylinecam.co.kr/?document_srl=112701
http://skylinecam.co.kr/photo/112511
http://skylinecam.co.kr/photo/112686
http://skylinecam.co.kr/photo/107830
http://yooseok.com/board_BkvT46/334945
http://gallerychoi.com/Exhibition/76415
http://www.ekemoon.com/215213/050620194819/
http://www.svteck.co.kr/customer_gratitude/58651
http://mobility-corp.com/index.php/component/k2/itemlist/user/2626566
http://www.hicleaning.kr/board_wash/101555
https://betshin.com/Story/48503
http://www.svteck.co.kr/customer_gratitude/65170
http://www.hsaura.com/noty/164203
http://xn--ok1bpqi43ahtb.net/board_EkDG82/139895
http://www.teedinubon.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-8-03-2016/
https://nple.com/xe/pds/41058
http://8.droror.co.il/uncategorized/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lostfilm/
http://www.jshwanghoan.com/index.php?mid=historical_figures&document_srl=108732
http://2872870.com/est/17763
http://callman.co.kr/index.php?mid=qa&document_srl=49246
http://esiapolisthesharp2.co.kr/g1/34772
http://wipln.com/?document_srl=54668
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=45602
https://testing.celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-got-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ziqt-%d0%98%d0%b3%d1%80%d0%b0-%d0%bf/
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=69143
http://vervetama.com/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5/
http://callman.co.kr/index.php?mid=qa&document_srl=60688
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/10643
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?document_srl=2653&mid=main_08
http://woodpark.kr/project/8246
http://bebopindia.com/?document_srl=129292
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=76823
http://www.flixian.com/main/QnA/41894
http://projectcva.dothome.co.kr/?document_srl=589
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=102687
http://atemshow.com/atemfair_domestic/71233
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/9866
http://agiteshop.com/xe/qa/50651
http://pkgersang.dothome.co.kr/board_jiKY24/6500
http://daltso.com/index.php?mid=board_cUYy21&document_srl=22352
http://www.sp1.football/index.php?mid=tr_video&document_srl=279421
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/13406
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=98202
http://HyUa.1fps.icu/l/szIaeDC
https://celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dznm-%d0%98%d0%b3%d1%80%d0%b0-%d0%bf/
http://praisesound.co.kr/sub04_01/14447
https://www.gizmoarticle.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%88/
http://tototoday.com/board_oRiY52/29572
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=8552
http://constellation.kro.kr/board_kbku73/9343
http://xn----3x5er9r48j7wemud0a387h.com/news/46239
http://apt2you2.cafe24.com/g1/3806
http://www.vamoscontigo.org/Noticia/32030
http://atemshow.com/atemfair_domestic/69420
http://callman.co.kr/index.php?mid=qa&document_srl=41546
http://bebopindia.com/notcie/150475
http://oneandonly1127.com/guest/14808
http://www.youngfile.com/youngfile_downlist/19459
http://skylinecam.co.kr/photo/132226
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-(got)-8-eo-6-e-yiai-a-etoo-(got)-8-eo-6-e/?PHPSESSID=rih8m5nef7u3ran0dm040up3c1
http://www.hsaura.com/noty/168279
http://holysweat.dothome.co.kr/data/1879
http://www.patrasin.kr/?document_srl=4281554
http://2872870.com/est/18746
http://ptu.imoove.kr/ko/content/%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-got-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-2-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-pmow-%C2%AB%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-got-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-2-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB337272
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=93700
http://arte.dgau.ac.kr/board_qna/45216
http://apt2you2.cafe24.com/?document_srl=6745
http://apt2you2.cafe24.com/?document_srl=6897
http://apt2you2.cafe24.com/?document_srl=6981
http://apt2you2.cafe24.com/?document_srl=7073
http://apt2you2.cafe24.com/?document_srl=7222
http://apt2you2.cafe24.com/?document_srl=7816
http://apt2you2.cafe24.com/?document_srl=8162
http://apt2you2.cafe24.com/?document_srl=8764
http://apt2you2.cafe24.com/?document_srl=9157
http://apt2you2.cafe24.com/g1/10202
http://apt2you2.cafe24.com/g1/3801
http://apt2you2.cafe24.com/g1/3806
http://apt2you2.cafe24.com/g1/3812
http://HyUa.1fps.icu/l/szIaeDC
http://www.critico-expository.com/forum/index.php?topic=7423.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=309187
http://teambuildingpremium.com/forum/index.php?topic=831933.0
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/62384
https://turimex.mx.solemti.net/en/?option=com_k2&view=itemlist&task=user&id=1131
http://corumotoanahtar.com/component/k2/itemlist/user/2472.html
http://www.vivelabmanizales.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-nz2i-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=14287
http://soc-human.kz/index.php/component/k2/itemlist/user/1669080
http://skylinecam.co.kr/photo/55541
http://withinfp.sakura.ne.jp/eso/index.php/16976923-live-grand-2-sezon-21-seria-s1-grand-2-sezon-21-seria/0
http://hotelnomadpalace.com/es/?option=com_k2&view=itemlist&task=user&id=20641
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=63562
http://www.jesusonly.life/calendar/157850
http://www.jesusonly.life/calendar/157882
http://www.jshwanghoan.com/?document_srl=97402
http://www.jshwanghoan.com/?document_srl=97491
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=97463
http://www.original-craft.net/index.php?topic=337122.0
http://www.original-craft.net/index.php?topic=337127.0
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=513099
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=513109
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=513124
http://www.studyxray.com/Sangdam/120452
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3302253
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/233051
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=13987
http://proxima.co.rw/index.php/component/k2/itemlist/user/607137
http://rudraautomation.com/index.php/component/k2/author/168176
http://rudraautomation.com/index.php/component/k2/author/168212
http://soc-human.kz/index.php/component/k2/itemlist/user/1672948
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1582656
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1602813
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1392642
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1392955
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=105637
http://www.ekemoon.com/167065/052120195309/
http://ovotecegg.com/component/k2/itemlist/user/142281
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=75657
http://zanoza.h1n.ru/2019/05/14/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ip5n-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://www.digitalbul.com/%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5%d0%b4%d0%be-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zh0o-%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5/
https://sto54.ru/index.php/component/k2/itemlist/user/3342661
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/744710
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1369425
http://myrechockey.com/forums/index.php?topic=102979.0
http://withinfp.sakura.ne.jp/eso/index.php/16963710-novinka-cuzaa-zizn-cuze-zitta-9-seria-z7-cuzaa-zizn-cuze-zitta-/0
https://prelease.club/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-osig-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-14-%d1%81%d0%b5%d1%80%d0%b8/
https://prelease.club/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gilm-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-22-%d1%81%d0%b5%d1%80%d0%b8/
https://prelease.club/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xedg-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-22-%d1%81%d0%b5%d1%80%d0%b8/
https://prelease.club/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-25-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kjvg-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-25-%d1%81%d0%b5%d1%80%d0%b8/
https://prelease.club/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-148-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pcuj-%d0%b2%d0%be%d1%81%d0%ba%d1%80/
https://prelease.club/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%80%d1%83%d1%81%d1%81%d0%ba%d0%b0%d1%8f-%d0%be%d0%b7%d0%b2%d1%83-22/
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1887854
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1166430
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=320220
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=320222
http://married.dike.gr/index.php/component/k2/itemlist/user/57677
http://ovotecegg.com/component/k2/itemlist/user/134889
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=14021
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/7643
http://xn----3x5er9r48j7wemud0a387h.com/news/48174
http://www.sp1.football/index.php?mid=faq&document_srl=231483
http://xn--2e0bk61btjo.com/notice/8757
http://askpharm.net/board_NQiz06/28681
http://photogrotto.com/live-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%be%d0%bd%d0%bb%d0%b0%d0%b9%d0%bd/
http://arte.dgau.ac.kr/board_qna/50478
http://edu-playground.net/boardgame/8464
http://tiretech.co.kr/index.php?mid=qna&document_srl=35858
https://2002.shyoon.com/board_2002/46618
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/7246
http://daltso.com/index.php?mid=board_cUYy21&document_srl=21131
http://daltso.com/index.php?mid=board_cUYy21&document_srl=20787
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=77227
http://photogrotto.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80-10/
http://vervetama.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80-9/
http://photogrotto.com/%d1%8d%d1%84%d0%b8%d1%80-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5/
https://2002.shyoon.com/?document_srl=34770
http://beautypouch.net/index.php?mid=board_09&document_srl=15114
http://mediaville.me/index.php/component/k2/itemlist/user/295515
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2633642
http://neosky.net/xe/space_station/7943
http://neosky.net/xe/space_station/7956
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=89192
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=89203
http://sofficer.net/xe/teach/225124
http://tiretech.co.kr/index.php?document_srl=49120&mid=qna
http://tiretech.co.kr/index.php?mid=qna&document_srl=49207
http://tiretech.co.kr/index.php?mid=qna&document_srl=49227
http://HyUa.1fps.icu/l/szIaeDC
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1682531
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/27199
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3340371
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3429147
http://indiefilm.kr/xe/board/3020
http://gtupuw.org/index.php/component/k2/itemlist/user/1905022
http://www.josephmaul.org/menu41/29441
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/245508
http://roikjer.com/forum/index.php?PHPSESSID=ibmh1ql2elshqh47qgl68ifkj0&topic=848955.0
http://www.hsaura.com/noty/68197
http://ovotecegg.com/index.php/component/k2/itemlist/user/114810
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=68008
http://8.droror.co.il/uncategorized/%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-91-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tq4f-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-91-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://macdistri.com/?option=com_k2&view=itemlist&task=user&id=304830
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/211334
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1353569
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7305992
http://www.rationalkorea.com/xe/?document_srl=495048
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=495135
http://www.sp1.football/?document_srl=177009
http://www.sp1.football/index.php?mid=faq&document_srl=176949
http://www.svteck.co.kr/customer_gratitude/36497
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3291971
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3292011
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=48634
https://sanp.pro/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qlvm-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=1082204
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=142560
http://teambuildingpremium.com/forum/index.php?topic=830813.0
http://danielmillsap.com/forum/index.php?topic=1032259.0
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1897753
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1426480
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=51542
http://haniel.ir/index.php/component/k2/itemlist/user/95757
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=19597
http://fbpharm.net/index.php/component/k2/itemlist/user/20036
http://proxima.co.rw/index.php/component/k2/itemlist/user/575455
http://forum.byehaj.hu/index.php?topic=82298.0
http://www.elpinatarense.com/?option=com_k2&view=itemlist&task=user&id=154587
http://8.droror.co.il/uncategorized/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bl2%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f08-05/
http://seoksoononly.dothome.co.kr/?document_srl=738089
http://withinfp.sakura.ne.jp/eso/index.php/16882562-vetrenyj-hercai-5-seria-afgu-vetrenyj-hercai-5-seria/0
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=203229
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=316858
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/211321
http://subforumna.x10.mx/mad/index.php?topic=248573.0
http://teambuildingpremium.com/forum/index.php?topic=842988.0
http://universalcommunity.se/Forum/index.php?topic=14227.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/540217
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1649161
http://www.digitalbul.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-%d0%b8%d0%b3%d1%80%d0%b0/
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2511767
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=8702
http://www.vivelabmanizales.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81-60/
https://members.fbhaters.com/index.php?topic=89133.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1674690
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=8543
http://smartacity.com/component/k2/itemlist/user/31122
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/103048
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1425670
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=805517
https://khuyenmaikk13.info/index.php?topic=200826.0
http://xplorefitness.com/blog/%C2%AB%D0%B5%D0%B4%D0%B8%D0%BD%D0%BE%D0%B5-%D1%81%D0%B5%D1%80%D0%B4%D1%86%D0%B5-tek-y%C3%BCrek-20-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-wphh-%C2%AB%D0%B5%D0%B4%D0%B8%D0%BD%D0%BE%D0%B5-%D1%81%D0%B5%D1%80%D0%B4%D1%86%D0%B5-tek-y%C3%BCrek-20-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://jjikduk.net/?document_srl=36967
http://www.deliberarchia.org/forum/index.php?topic=1042728.0
http://www.deliberarchia.org/forum/index.php?topic=1042741.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=48032
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=48042
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=48086
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=48111
http://www.sp1.football/index.php?mid=faq&document_srl=44034
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/483751
http://zanoza.h1n.ru/2019/05/16/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-unli-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://zanoza.h1n.ru/2019/05/16/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nsps-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd/
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=74319
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=74425
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/278647
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=24959
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/24957
http://0433.net/junggo/52380
http://0433.net/junggo/52396
https://turimex.mx.solemti.net/en/?option=com_k2&view=itemlist&task=user&id=1012
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=166396
http://myrechockey.com/forums/index.php?topic=98000.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=82701
http://moavalve.co.kr/?document_srl=28758
http://moavalve.co.kr/faq/28575
http://moavalve.co.kr/faq/28672
http://moavalve.co.kr/faq/28681
http://moavalve.co.kr/faq/28700
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3385298
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3385342
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=4615
http://0433.net/?document_srl=52450
http://0433.net/?document_srl=52456
http://0433.net/junggo/52363
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=145570
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=145970
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=146051
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=145540
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4886446
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=58287
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1579228
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1373914
https://khuyenmaikk13.info/index.php?topic=191748.0
http://smartacity.com/component/k2/itemlist/user/47073
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=1299
http://jjikduk.net/?document_srl=12484
http://zanoza.h1n.ru/2019/05/16/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81-32/
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=514055
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=514118
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=514172
http://www.studyxray.com/Sangdam/122334
http://www.studyxray.com/Sangdam/122476
http://www.taeshinmedia.com/?document_srl=3302566
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3302591
http://xn----3x5er9r48j7wemud0a387h.com/news/42902
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/525669
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=81557
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=81585
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=81595
http://www.digitalbul.com/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-86-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22/
http://www.digitalbul.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-u7-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80/
http://www.digitalbul.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-l3-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5/
http://www.hicleaning.kr/board_wash/139924
http://www.josephmaul.org/menu41/168905
http://www.spazioad.com/component/k2/itemlist/user/7362897
http://www.studyxray.com/?document_srl=167745
http://www.studyxray.com/Sangdam/167699
https://prelease.club/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gvch-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-19-%d1%81%d0%b5%d1%80%d0%b8/
https://prelease.club/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81-4/
http://dohairbiz.com/en/component/k2/itemlist/user/2736003.html
http://gtupuw.org/index.php/component/k2/itemlist/user/1911151
http://www.jesusonly.life/calendar/161188
http://www.jesusonly.life/calendar/161209
http://www.josephmaul.org/menu41/124791
http://www.josephmaul.org/menu41/124852
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=100651
http://www.rationalkorea.com/xe/?document_srl=514945
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=514905
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=764484
http://arunagreen.com/?option=com_k2&view=itemlist&task=user&id=442738
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3575882
http://www.ekemoon.com/149131/050020192407/
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/200720
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=47645
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/216821
http://www.autospa.lv/index.php/lv/component/k2/itemlist/user/9298
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/290471
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=617067
http://danielmillsap.com/forum/index.php?topic=1002678.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1413948
http://www.theocraticamerica.org/forum/index.php?topic=29242.0
http://fbpharm.net/index.php/component/k2/itemlist/user/40263
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/708934
https://khuyenmaikk13.info/index.php?topic=191138.0
http://www.jesusonly.life/calendar/159748
http://www.jesusonly.life/calendar/159879
http://www.josephmaul.org/menu41/123529
http://www.josephmaul.org/menu41/123845
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=99846
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=99889
http://www.rationalkorea.com/xe/index.php?document_srl=514212&mid=pqna3
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=514252
http://www.hicleaning.kr/board_wash/140511
http://www.hicleaning.kr/board_wash/140716
http://www.hicleaning.kr/board_wash/140998
http://www.hicleaning.kr/board_wash/141034
http://www.hicleaning.kr/board_wash/141112
http://www.studyxray.com/Sangdam/168435
http://www.studyxray.com/Sangdam/168613
http://www.studyxray.com/Sangdam/168650
http://www.studyxray.com/Sangdam/168996
http://www.vivelabmanizales.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ck7l-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3446577
http://www.hsaura.com/noty/45411
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1681572
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/6139
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=83383
http://www.deliberarchia.org/forum/index.php?topic=1039092.0
https://esel.gist.ac.kr/esel2/board_hmgj23/72919
https://esel.gist.ac.kr/esel2/board_hmgj23/72948
https://khuyenmaikk13.info/index.php?topic=209107.0
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=207704
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=207719
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=207729
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=207739
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=207764
https://www.vegasgreentour.com/?document_srl=131284
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-20-%d1%81%d0%b5%d1%80%d0%b8/
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=201128
http://www.ekemoon.com/142201/051620194305/
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=28696.0
http://xplorefitness.com/blog/%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-16-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-ftex-%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-16-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://macdistri.com/index.php/component/k2/itemlist/user/299002
https://www.gizmoarticle.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-95-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-di2x-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-95-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=184986
http://mobility-corp.com/index.php/component/k2/itemlist/user/2518378
http://seoksoononly.dothome.co.kr/qna/738603
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1568975
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/57092
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1589780
http://emjun.com/index.php?mid=hangtotal&document_srl=20339
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/285550
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1559065
http://www.telcon.gr/index.php/component/k2/itemlist/user/51366
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4860078
http://seoksoononly.dothome.co.kr/qna/790872
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-11-%d1%81%d0%b5%d1%80%d0%b8-2/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/300014
http://matrixpharm.ru/forum/index.php?PHPSESSID=tedp79d1o3jc5gckjtmmsq1r15&action=profile;u=167827
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=273781
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/210002
http://www.vivelabmanizales.com/%d0%bd%d0%b5-%d0%be%d1%82%d0%bf%d1%83%d1%81%d0%ba%d0%b0%d0%b9-%d0%bc%d0%be%d1%8e-%d1%80%d1%83%d0%ba%d1%83-elimi-birakma-38-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qyut-%d0%bd%d0%b5-%d0%be/
http://afinandoemociones.com.ar/index.php/component/k2/itemlist/user/387970
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1727100
https://members.fbhaters.com/index.php?topic=75411.0
http://fbpharm.net/index.php/component/k2/itemlist/user/25377
http://fbpharm.net/index.php/component/k2/itemlist/user/25946
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1749253
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1749281
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1866238
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=280525
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=280669
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=280672
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3405128
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=305035
http://zanoza.h1n.ru/2019/05/16/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-41-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xjhn-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0/
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=446174
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=69996
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=210862
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1380268
http://robocit.com/index.php/component/k2/itemlist/user/449584
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/207165
http://cwon.kr/xe/board_bnSr36/8296
http://afinandoemociones.com.ar/index.php/component/k2/itemlist/user/388436
http://dev.aabn.org.gh/component/k2/itemlist/user/539121
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/8378
http://web2interactive.com/index.php/component/k2/itemlist/user/3587486
http://married.dike.gr/index.php/component/k2/itemlist/user/52130
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2577800
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1040375
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1040393
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4865746
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=52604
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/304822
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/56936
http://www.youngfile.com/?document_srl=15614
http://ye-dream.com/qa/85774
http://www.studyxray.com/Sangdam/132458
http://xn--9m1b83j39hz6exwonmf.com/?document_srl=538269
http://gallerychoi.com/Exhibition/75524
http://www.jshwanghoan.com/index.php?mid=historical_figures&document_srl=109632
http://oceangray.i234.me/?document_srl=60693
https://adsensebih.com/index.php?topic=25883.0
http://apt2you2.cafe24.com/g1/6032
https://nple.com/xe/pds/32783
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=1224
http://www.josephmaul.org/menu41/111817
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/7230
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=184558
http://majorcebu.com/board_OhfH50/1122427
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=64210
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/10264
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9366
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9371
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9376
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9382
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9405
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9411
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9428
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9434
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9481
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9486
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9492
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9610
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9621
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9633
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/9692
http://HyUa.1fps.icu/l/szIaeDC
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=19303
http://petromacorisanos.com.radiosenda1680.org/index.php/component/k2/itemlist/user/17965
http://www.jesusonly.life/calendar/43157
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=555523
http://dev.aabn.org.gh/component/k2/itemlist/user/566013
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=319081
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=76454
http://esperanzazubieta.com/component/k2/itemlist/user/97570
http://emjun.com/?document_srl=50208
http://adopt10plus.com/groups/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%81%d0%ba%d0%b0%d1%87%d0%b0%d1%82%d1%8c-%d1%82%d0%be%d1%80%d1%80/
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/514797
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/236850
http://skylinecam.co.kr/photo/51787
http://skylinecam.co.kr/photo/51802
http://www.hsaura.com/noty/67664
http://www.hsaura.com/noty/67708
http://zanoza.h1n.ru/2019/05/16/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-siwv-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://zanoza.h1n.ru/2019/05/16/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-czeo-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80/
http://zanoza.h1n.ru/2019/05/16/%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-69-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dpro-%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-69/
https://prelease.club/%d0%bd%d0%b5-%d0%be%d1%82%d0%bf%d1%83%d1%81%d0%ba%d0%b0%d0%b9-%d0%bc%d0%be%d1%8e-%d1%80%d1%83%d0%ba%d1%83-elimi-birakma-39-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uoph-%d0%bd%d0%b5-%d0%be/
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/4043
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4908225
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=63145
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=556525
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=1557
http://www.deliberarchia.org/forum/index.php?topic=1022708.0
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gr8%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=765652
http://zanoza.h1n.ru/2019/05/15/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yq1%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=327181
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1592186
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=71816
http://cwon.kr/xe/board_bnSr36/26697
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=762313
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=762323
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=762387
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=762407
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/619716
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=820117
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/820128
http://www.spazioad.com/component/k2/itemlist/user/7309350
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=63114
http://www.telcon.gr/index.php/component/k2/itemlist/user/63119
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/18580
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=1544
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/20822
http://c3isecurity.com.br/?option=com_k2&view=itemlist&task=user&id=505570
http://www.ekemoon.com/198725/051320191516/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/328627
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1064704
http://married.dike.gr/index.php/component/k2/itemlist/user/60376
http://www.hsaura.com/noty/71030
http://www.hsaura.com/noty/71117
http://www.hsaura.com/noty/71127
http://www.hsaura.com/noty/71176
http://www.hsaura.com/noty/71191
http://www.jesusonly.life/calendar/72226
http://www.jesusonly.life/calendar/72234
http://www.jesusonly.life/calendar/72306
http://xplorefitness.com/blog/%C2%AB%D0%B6%D0%B5%D0%BD%D1%89%D0%B8%D0%BD%D0%B0-60-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-tasb-%C2%AB%D0%B6%D0%B5%D0%BD%D1%89%D0%B8%D0%BD%D0%B0-60-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://zanoza.h1n.ru/2019/05/16/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-diml-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80/
http://zanoza.h1n.ru/2019/05/16/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-37-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jaei-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0/
https://prelease.club/%d0%bd%d0%b5-%d0%be%d1%82%d0%bf%d1%83%d1%81%d0%ba%d0%b0%d0%b9-%d0%bc%d0%be%d1%8e-%d1%80%d1%83%d0%ba%d1%83-elimi-birakma-38-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xwfg-%d0%bd%d0%b5-%d0%be/
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=39718
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=39734
http://smartacity.com/component/k2/itemlist/user/44432
http://thermoplast.envolgroupe.com/component/k2/author/103145
http://wigalseguros.com.br/component/users/?task=user&view=itemlist&id=6909
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1620805
http://www.atab.com.sa/index.php/en/?option=com_k2&view=itemlist&task=user&id=1620655
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1620677
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1410131
http://www.pcosmetic.ir/?option=com_k2&view=itemlist&task=user&id=10938
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=63278
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=109980
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=556923
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=20922
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/525393
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/525404
http://www.teedinubon.com/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8cchernobyl-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-av6%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8cchernobyl-3-%d1%81%d0%b5%d1%80%d0%b8/
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-or9%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-8-%d1%81%d0%b5%d1%80/
https://testing.celekt.com/%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nb1%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://www.amazingworldtop.com/entretenimiento/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mi2%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=83204
http://netsconsults.com/index.php/component/k2/itemlist/user/799674
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/269180
https://altaylarteknoloji.com/index.php?topic=5321.0
http://www.teedinubon.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-91-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zj1%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-91/
http://www.teedinubon.com/%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-100-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ii1%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-100-%d1%81%d0%b5%d1%80%d0%b8%d1%8f19-05-2019/
http://0433.net/?document_srl=55622
http://0433.net/junggo/55591
http://0433.net/junggo/55601
http://0433.net/junggo/55612
http://0433.net/junggo/55617
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=215433
http://asin.itts.co.kr/board_rtXs84/11852
http://community.viajar.tur.br/index.php?p=/profile/freddiebow
http://daesestudy.co.kr/ipsi_docu/51114
http://jjikduk.net/DATA/71741
http://jjikduk.net/DATA/71747
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=58098
http://xn--ok1bpqi43ahtb.net/board_EkDG82/116974
http://xn--ok1bpqi43ahtb.net/board_EkDG82/117052
http://xn--ok1bpqi43ahtb.net/board_EkDG82/117068
http://xn--ok1bpqi43ahtb.net/board_EkDG82/117079
http://xn--ok1bpqi43ahtb.net/board_EkDG82/117090
http://yeonsen.com/?document_srl=65792
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=65836
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=65869
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=65884
http://yoriyorifood.com/xxxx/spacial/76004
http://yoriyorifood.com/xxxx/spacial/76025
https://www.vegasgreentour.com/?document_srl=90560
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=90510
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=90515
http://xplorefitness.com/blog/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-24-05-2019%C2%BB-np%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-24-05-2019%C2%BB85-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-24-05-2019
http://zanoza.h1n.ru/2019/05/20/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-17-05-19-gz%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://zanoza.h1n.ru/2019/05/20/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-bi%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=601653
https://altaylarteknoloji.com/index.php?topic=5380.0
http://photogrotto.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sb6%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-15-%d1%81%d0%b5/
http://zanoza.h1n.ru/2019/05/20/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vh7%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-13-%d1%81%d0%b5/
http://zanoza.h1n.ru/2019/05/20/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nd8%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-7-%d1%81%d0%b5%d1%80/
http://zanoza.h1n.ru/2019/05/20/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vy3%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
http://zanoza.h1n.ru/2019/05/20/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vs7%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f19-05/
https://sanp.pro/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nw9%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-15-%d1%81%d0%b5/
http://www.ekemoon.com/144563/051020192806/
http://mvisage.sk/?option=com_k2&view=itemlist&task=user&id=117916
http://www.vivelabmanizales.com/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vhwh-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80/
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/185505
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2588535
http://condolencias.servisa.es/7-06-05-2019-o4-7
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=290950
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=58718
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=66460
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=66473
http://yoriyorifood.com/xxxx/spacial/76500
https://www.vegasgreentour.com/?document_srl=91544
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2657948
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=342627
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tk7z-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/99297
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/194926
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1394167
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/528400
http://mobility-corp.com/index.php/component/k2/itemlist/user/2547046
http://teambuildingpremium.com/forum/index.php?topic=831628.0
http://www.deliberarchia.org/forum/index.php?topic=1042017.0
http://www.deliberarchia.org/forum/index.php?topic=1042027.0
http://www.deliberarchia.org/forum/index.php?topic=1042041.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=43573
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=43587
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=43606
http://www.hsaura.com/noty/43738
http://www.hsaura.com/noty/43766
https://forum.ac-jete.it/index.php?topic=342819.0
http://fbpharm.net/index.php/component/k2/itemlist/user/17278
http://www.vivelabmanizales.com/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-g4-%d1%82%d0%be%d0%bb%d1%8f/
http://vtservices85.fr/smf2/index.php?PHPSESSID=7e7e8f3bb299078daf4f4cdb447a806e&action=profile;u=189509
http://thermoplast.envolgroupe.com/component/k2/author/66166
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1003270
https://khuyenmaikk13.info/index.php?topic=183707.0
http://www.ekemoon.com/179835/051520195212/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1385492
http://soc-human.kz/index.php/component/k2/itemlist/user/1664713
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3660553
http://www.theocraticamerica.org/forum/index.php?topic=29830.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3342712
http://www.datascientist.co.kr/index.php?mid=blog&document_srl=89018
http://smartacity.com/component/k2/itemlist/user/48045
http://www.ekemoon.com/181547/050720192913/
http://mvisage.sk/index.php/component/k2/itemlist/user/118520
http://teambuildingpremium.com/forum/index.php?topic=831480.0
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=73271
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=15993
http://www.hsaura.com/noty/42624
http://www.hsaura.com/noty/42669
http://www.hsaura.com/noty/42674
http://www.hsaura.com/noty/42716
http://www.jesusonly.life/?document_srl=42215
http://www.jesusonly.life/calendar/42205
http://zanoza.h1n.ru/2019/05/15/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-145-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-axjj-%d0%b2%d0%be%d1%81%d0%ba%d1%80/
http://cwon.kr/xe/board_bnSr36/10202
http://emjun.com/?document_srl=21162
http://emjun.com/index.php?mid=hangtotal&document_srl=21104
http://emjun.com/index.php?mid=hangtotal&document_srl=21127
http://emjun.com/index.php?mid=hangtotal&document_srl=21147
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=317289
http://www.phan-aen.go.th/forum/index.php?topic=628335.0
http://www.babvallejo.com/?option=com_k2&view=itemlist&task=user&id=607389
http://withinfp.sakura.ne.jp/eso/index.php/16888640-tajny-92-seria-06052019-o2-tajny-92-seria
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1357388
http://batubersurat.com/index.php/component/k2/itemlist/user/42872
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/205826
http://www.josephmaul.org/?document_srl=118578
http://sd-xi.co.kr/g1/20749
http://www.golden-nail.co.kr/press/117518
http://bethelpray.com/counsel/9504
http://www.teedinubon.com/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-3/
http://www.yepia.com/board_ZCPG83/17479
http://www.jshwanghoan.com/?document_srl=108037
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=106434
http://callman.co.kr/index.php?mid=qa&document_srl=68231
http://xn--2e0b53df5ag1c804aphl.net/nuguna/23091
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=47841
http://2872870.com/est/19796
https://www.c-alice.org/forum/index.php?topic=88117.0
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=8430
http://askpharm.net/board_NQiz06/32881
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qttg-%d0%b8%d0%b3%d1%80%d0%b0/
http://atemshow.com/atemfair_domestic/52886
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=55814
http://readingbible.org/board_xxpp62/855420
http://barobus.kr/?document_srl=23728
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/gumdanapt/81328
http://iamking.net/board/28602
https://sanp.pro/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xz9p/
https://sanp.pro/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nf5b/
https://sanp.pro/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lc4d/
https://sanp.pro/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sd3y/
https://sanp.pro/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bg8p/
https://sanp.pro/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ng2k/
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=130485
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=130502
https://ttmt.net/crypto_lab_2F/486467
https://ttmt.net/crypto_lab_2F/486664
https://ttmt.net/crypto_lab_2F/486991
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=193618
http://beautypouch.net/?document_srl=21683
http://beautypouch.net/index.php?mid=board_09&document_srl=21688
http://cwon.kr/xe/board_bnSr36/111555
http://cwon.kr/xe/board_bnSr36/111639
http://gxpfactory.net/index.php?mid=Guide&document_srl=24537
http://praisesound.co.kr/sub04_01/18850
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=235677
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=235803
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=235837
http://HyUa.1fps.icu/l/szIaeDC
http://ye-dream.com/qa/102693
http://xn--2e0bk61btjo.com/notice/9757
http://neosky.net/xe/space_station/2336
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/9779
http://atemshow.com/atemfair_domestic/54346
http://arte.dgau.ac.kr/board_qna/40398
http://www.tekparcahdfilm.com/forum/index.php?topic=51450.0
http://bebopindia.com/notcie/135081
http://arte.dgau.ac.kr/board_qna/53883
http://kyj1225.godohosting.com/board_mebR72/15876
http://iamking.net/?document_srl=42947
http://iamking.net/board/42932
http://jjimdak.callbank.kr/?document_srl=916959
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=916997
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=917016
http://joinbohum.kr/board/61817
http://laokorea.com/orange_menu1/45404
http://looksun.co.kr/?document_srl=33774
http://looksun.co.kr/index.php?mid=board_4&document_srl=33796
http://looksun.co.kr/index.php?mid=board_4&document_srl=33832
http://lucky.kidspann.net/index.php?mid=qna&document_srl=115210
http://lucky.kidspann.net/index.php?mid=qna&document_srl=115238
http://skylinecam.co.kr/photo/162262
http://tiretech.co.kr/index.php?mid=qna&document_srl=52728
http://tiretech.co.kr/index.php?mid=qna&document_srl=52748
http://toeden.co.kr/Product_new/46925
http://HyUa.1fps.icu/l/szIaeDC
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=757929
http://ovotecegg.com/component/k2/itemlist/user/132058
http://www.spazioad.com/component/k2/itemlist/user/7264272
http://fbpharm.net/index.php/component/k2/itemlist/user/38099
http://thermoplast.envolgroupe.com/component/k2/author/102684
http://cwon.kr/xe/board_bnSr36/19279
http://www.digitalbul.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bl7l/
http://menulisilmiah.net/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-x1-%d1%82%d0%be%d0%bb%d1%8f/
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=117976
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=118085
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=118115
http://0433.net/junggo/52704
http://1600-1590.com/?document_srl=146599
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1371538
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1371544
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1043362
http://www.comfortcenter.es/index.php/component/k2/itemlist/user/104990
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1786504
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=14685
http://danielmillsap.com/forum/index.php?topic=999706.0
http://www.jesusonly.life/calendar/48381
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=42964
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/317612
http://teambuildingpremium.com/forum/index.php?topic=832450.0
http://webp.online/index.php?topic=52061.0
http://dohairbiz.com/en/component/k2/itemlist/user/2725477.html
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2559926
http://shinilspring.com/board_qsfb01/105905
http://skylinecam.co.kr/?document_srl=115878
http://www.arunagreen.com/index.php/component/k2/itemlist/user/547788
http://www.critico-expository.com/forum/index.php?topic=14266.0
http://www.digitalbul.com/%d0%b1%d0%be%d0%b3%d0%b0%d1%82%d1%8b%d0%b5-%d0%b8-%d0%b1%d0%b5%d0%b4%d0%bd%d1%8b%d0%b5-zengin-ve-yoksul-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ppex-%d0%b1%d0%be%d0%b3%d0%b0%d1%82%d1%8b/
http://www.hsaura.com/noty/152274
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1643860
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1570323
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1372143
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=590575
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=787997
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=788019
http://www.jesusonly.life/calendar/47596
http://hotelnomadpalace.com/component/k2/itemlist/user/20640
http://www.ekemoon.com/167275/052220192009/
http://batubersurat.com/index.php/component/k2/itemlist/user/47662
http://myrechockey.com/forums/index.php?topic=92744.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=18584
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=60205
http://zanoza.h1n.ru/2019/05/16/%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-58-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-misf-%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-58-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://forum.byehaj.hu/index.php?topic=85032.0
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/3946
http://dcasociados.eu/component/k2/itemlist/user/89263
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=7498
http://proxima.co.rw/index.php/component/k2/itemlist/user/603390
http://www.hsaura.com/noty/122039
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=73902
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=73916
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=73967
http://www.original-craft.net/index.php?topic=335173.0
http://www.studyxray.com/Sangdam/109609
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3294799
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3294813
http://jiquilisco.org/index.php/component/k2/itemlist/user/10125
http://mediaville.me/?option=com_k2&view=itemlist&task=user&id=289550
http://mediaville.me/index.php/component/k2/itemlist/user/289535
http://mediaville.me/index.php/component/k2/itemlist/user/289546
http://mobility-corp.com/index.php/component/k2/itemlist/user/2623209
http://mobility-corp.com/index.php/component/k2/itemlist/user/2623224
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/759718
http://fbpharm.net/index.php/component/k2/itemlist/user/25377
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=554745
https://www.shaiyax.com/index.php?topic=336905.0
http://www.digitalbul.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qb0v-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-2/
http://wigalseguros.com.br/component/users/?task=user&view=itemlist&id=7166
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=588133
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=330565
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4758940
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kj5k-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://rudraautomation.com/index.php/component/k2/author/218230
http://rudraautomation.com/index.php/component/k2/author/218468
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/220756
http://sdsn.rsu.edu.ng/?option=com_k2&view=itemlist&task=user&id=2324049
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1703207
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1703213
http://svgrossburgwedel.de/component/k2/itemlist/user/5938
http://theolevolosproject.org/index.php/component/k2/itemlist/user/27003
http://thermoplast.envolgroupe.com/component/k2/author/120447
http://thermoplast.envolgroupe.com/component/k2/author/120454
http://vtservices85.fr/smf2/index.php?PHPSESSID=3c903bedec2ca5dbf4c6056718748e58&action=profile;u=226026
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3675408
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=10498
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=10548
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1929691
http://jiquilisco.org/index.php/component/k2/itemlist/user/10183
http://jiquilisco.org/index.php/component/k2/itemlist/user/10189
http://mediaville.me/index.php/component/k2/itemlist/user/289754
http://mediaville.me/index.php/component/k2/itemlist/user/289777
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2623884
http://netsconsults.com/index.php/component/k2/itemlist/user/796095
http://rudraautomation.com/index.php/component/k2/author/223628
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/223617
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/223777
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/223794
http://smartacity.com/component/k2/itemlist/user/55359
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1707194
http://soc-human.kz/index.php/component/k2/itemlist/user/1707127
http://cafe.dokseosil.co.kr/community/36175
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3644356
http://rudraautomation.com/index.php/component/k2/author/170205
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=557725
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1876894
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=284808
http://koushatarabar.com/index.php/component/k2/itemlist/user/1325502
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1609318
http://forum.digamahost.com/index.php?topic=110932.0
http://thermoplast.envolgroupe.com/component/k2/author/68333
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=591137
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=788618
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=53707
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=53709
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/307396
http://www.ekemoon.com/168875/050220194710/
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=5317
http://www.vivelabmanizales.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81-47/
http://www.ekemoon.com/175513/050520195411/
http://mobility-corp.com/index.php/component/k2/itemlist/user/2569239
http://www.remify.app/foro/index.php?topic=277551.0
http://www.ekemoon.com/189525/051820195014/
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1041010
http://www.ekemoon.com/142989/052020192705/
http://dohairbiz.com/en/component/k2/itemlist/user/2706242.html
http://www.camaracoyhaique.cl/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-84-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ps4g-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-84-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/53335
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=42331
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1334887
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/188552
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=493641
http://forum.politeknikgihon.ac.id/index.php?topic=23973.0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/216427
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1646160
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1646346
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/64868
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/64882
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1570876
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1583547
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1045296
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4869926
http://www.telcon.gr/index.php/component/k2/itemlist/user/53893
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/239934
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/57081
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3327647
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=18213
http://xplorefitness.com/blog/%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-09-05-2019-t4-%C2%AB%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2594841
http://indiefilm.kr/xe/?document_srl=31188
http://jiquilisco.org/index.php/component/k2/itemlist/user/6111
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1815868
http://mobility-corp.com/index.php/component/k2/itemlist/user/2575047
http://menulisilmiah.net/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.spazioad.com/component/k2/itemlist/user/7274682
http://indiefilm.kr/xe/board/16466
http://forum.digamahost.com/index.php?topic=112147.0
http://indiefilm.kr/xe/board/58213
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=283105
http://www.web2interactive.com/index.php/component/k2/itemlist/user/3578963
http://www.dezhiran.com/en/component/k2/itemlist/user/16091
http://menulisilmiah.net/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mg2%d0%bd/
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1551212
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=12674
http://teambuildingpremium.com/forum/index.php?topic=774307.0
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43942
http://mediaville.me/index.php/component/k2/itemlist/user/234041
http://arunagreen.com/index.php/component/k2/itemlist/user/423588
http://forum.digamahost.com/index.php?topic=110099.0
http://xplorefitness.com/blog/%D1%81%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C-%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-c8-%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1640006
http://engeena.com/component/k2/itemlist/user/7963
http://www.spazioad.com/component/k2/itemlist/user/7247030
http://storykingdom.forumside.com/index.php?topic=4811.0
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=82780
http://mobility-corp.com/index.php/component/k2/itemlist/user/2548499
http://mobility-corp.com/index.php/component/k2/itemlist/user/2549190
http://ovotecegg.com/component/k2/itemlist/user/127670
http://ovotecegg.com/component/k2/itemlist/user/127695
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/221529
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/221987
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=10956
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=10958
http://rudraautomation.com/index.php/component/k2/author/148731
http://rudraautomation.com/index.php/component/k2/author/148781
http://sindicatodechoferespichincha.com.ec/?option=com_k2&view=itemlist&task=user&id=6700183
http://smartacity.com/component/k2/itemlist/user/31396
http://smartacity.com/component/k2/itemlist/user/31761
http://smartacity.com/component/k2/itemlist/user/31783
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=105119
http://p9912.cafe24.com/board_LVgu51/1043
http://sejong-thesharpyemizi.co.kr/m1/1434
http://www.ds712.net/guest/?document_srl=157429
https://sanp.pro/hd-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%82%d0%be%d1%80%d1%80%d0%b5/
http://daltso.com/index.php?mid=board_cUYy21&document_srl=27911
http://herdental.co.kr/index.php?mid=online&document_srl=27964
http://laokorea.com/orange_menu1/32463
https://betshin.com/Story/43609
http://forum.santrope-rp.ru/index.php?topic=8306.0
http://looksun.co.kr/index.php?mid=board_4&document_srl=20138
http://atemshow.com/atemfair_domestic/46931
http://apt2you2.cafe24.com/g1/6634
https://betshin.com/Story/52344
http://www.sp1.football/index.php?mid=faq&document_srl=228058
http://bewasia.com/?document_srl=24311
http://tiretech.co.kr/index.php?mid=notice&document_srl=42606
http://www.hicleaning.kr/board_wash/107580
http://49.247.3.43/index.php?mid=board_PiDQ29&document_srl=21351
https://test.baseyou21.kr/?document_srl=146087
https://test.baseyou21.kr/?document_srl=146178
https://test.baseyou21.kr/?document_srl=146394
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=145815
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=146082
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=146163
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=146209
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=146235
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=146353
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=146384
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=146424
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=146433
https://ttmt.net/?document_srl=507005
https://ttmt.net/?document_srl=507038
https://ttmt.net/crypto_lab_2F/506325
https://ttmt.net/crypto_lab_2F/506489
http://HyUa.1fps.icu/l/szIaeDC
http://callman.co.kr/?document_srl=51655
http://agiteshop.com/xe/qa/51836
http://wipln.com/?document_srl=58496
https://testing.celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-srwt-%d0%98/
http://iamking.net/board/33933
http://agiteshop.com/xe/qa/45462
http://49.247.3.43/index.php?mid=board_PiDQ29&document_srl=21060
http://pkgersang.dothome.co.kr/?document_srl=6902
http://zanoza.h1n.ru/2019/05/19/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-qelb-%d0%b8%d0%b3%d1%80%d0%b0/
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=1806
http://beautypouch.net/index.php?mid=board_09&document_srl=16394
http://metropolis.ga/index.php?topic=12860.0
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=18229
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=29794
https://ttmt.net/crypto_lab_2F/507391
https://zakdu.com/?document_srl=3807
http://8.droror.co.il/uncategorized/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80-14/
http://8.droror.co.il/uncategorized/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%b0-%d1%80%d1%83%d1%81/
http://bitpark.co.kr/board_IzjM66/4094609
http://bitpark.co.kr/board_IzjM66/4094809
http://carand.co.kr/d2/5963
http://d-tube.info/board_jvyO69/270496
http://d-tube.info/board_jvyO69/270571
http://d-tube.info/board_jvyO69/270595
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=31680
http://renew.joum.kr/index.php?document_srl=99127&mid=Portfolio_bbs
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=99132
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=99138
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=99161
http://teambuildingpremium.com/forum/index.php?topic=862959.0
http://teambuildingpremium.com/forum/index.php?topic=862969.0
http://www.hicleaning.kr/board_wash/152614
http://www.hicleaning.kr/board_wash/152718
http://www.livetank.cn/market1/66263
http://www.livetank.cn/market1/66298
http://www.livetank.cn/market1/66403
http://www.livetank.cn/market1/66470
http://www.verenas-unterwasserwelt.de/forum/index.php?topic=8126.0
http://HyUa.1fps.icu/l/szIaeDC
http://toeden.co.kr/Product_new/41478
http://sunele.co.kr/board_ReBD97/50137
http://www.lgue.co.kr/?document_srl=20483
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/10181
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/?document_srl=11924
http://teambuildingpremium.com/forum/index.php?topic=850030.0
http://www.flixian.com/main/QnA/42571
https://esel.gist.ac.kr/esel2/board_hmgj23/61755
http://ariji.kr/sub07/826546
http://bobr.site/index.php?topic=147803.0
http://oneandonly1127.com/guest/11762
http://www.youngfile.com/youngfile_downlist/18926
http://zanoza.h1n.ru/2019/05/18/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-aqrw-%d0%b8%d0%b3%d1%80/
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=120469
http://xn--2e0b53df5ag1c804aphl.net/nuguna/20342
http://metropolis.ga/index.php?topic=13331.0
http://apt2you2.cafe24.com/g1/5190
http://hyundeok.iptime.org/zbxe/index.php?mid=family&document_srl=45048
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=166584
http://www.josephmaul.org/menu41/183707
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=43053
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=43062
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=43071
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=43084
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=43099
http://www.livetank.cn/?document_srl=65256
http://www.livetank.cn/?document_srl=65322
http://www.livetank.cn/?document_srl=65808
http://www.livetank.cn/market1/64947
http://www.livetank.cn/market1/65160
http://www.livetank.cn/market1/65190
http://www.livetank.cn/market1/65294
http://www.livetank.cn/market1/65360
http://www.livetank.cn/market1/65498
http://www.livetank.cn/market1/65566
http://www.livetank.cn/market1/65581
http://www.livetank.cn/market1/65639
http://www.livetank.cn/market1/65648
http://www.livetank.cn/market1/65673
http://www.livetank.cn/market1/65840
http://HyUa.1fps.icu/l/szIaeDC
http://ye-dream.com/qa/45701
http://thermoplast.envolgroupe.com/component/k2/author/103980
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2635356
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1579004
http://www.ekemoon.com/190679/050020191215/
http://zanoza.h1n.ru/2019/05/15/%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-100-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vl6s-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-100-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://prelease.club/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rh3t-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
https://prelease.club/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-95-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-id7o-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-95-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://bitpark.co.kr/board_IzjM66/3932171
http://teambuildingpremium.com/forum/index.php?topic=827010.0
http://zanoza.h1n.ru/2019/05/15/%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5%d0%b4%d0%be-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hp5g-%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5/
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-2019-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ya3f-%d0%b8%d0%b3%d1%80%d0%b0/
http://bitpark.co.kr/board_IzjM66/3932372
http://forum.digamahost.com/index.php?topic=121763.0
http://jiquilisco.org/?option=com_k2&view=itemlist&task=user&id=5221
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1623708
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1083032
http://rudraautomation.com/index.php/component/k2/author/102576
http://menulisilmiah.net/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-live-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://rudraautomation.com/index.php/component/k2/author/122048
http://seoksoononly.dothome.co.kr/qna/796854
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1006669
http://8.droror.co.il/uncategorized/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5-4/
http://www.aloeverasas.it/index.php/component/k2/itemlist/user/18616
http://www.babvallejo.com/index.php/component/k2/itemlist/user/608105
https://forums.letstalkbeats.com/index.php?topic=66169.0
http://engeena.com/component/k2/itemlist/user/8245
http://www.nienkevanrijn.nl/component/k2/itemlist/user/426662
https://tg.vl-mp.com/index.php?topic=1350920.0
http://engeena.com/component/k2/itemlist/user/8227
http://laokorea.com/orange_menu1/36754
http://www.vamoscontigo.org/Noticia/30897
http://khapthanam.co.kr/g1/39232
http://vhost12299.cpsite.ru/459394-smotret-rasskaz-sluzanki-3-sezon-3-seria
http://esiapolisthesharp2.co.kr/?document_srl=31672
https://testing.celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hsvu-%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80/
http://apt2you2.cafe24.com/g1/6113
http://www.youngfile.com/?document_srl=23647
http://www.itosm.com/cn/board_nLoq17/18630
https://www.chirorg.com/?document_srl=32663
http://juroweb.com/xe/juroweb_board/18300
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/?document_srl=10539
http://ariji.kr/sub07/830318
http://apt2you2.cafe24.com/g1/4614
http://blog.ptpintcast.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2017/
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=25722
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=37007
http://tototoday.com/board_oRiY52/35137
http://mglpcm.org/board_ETkS12/28944
http://agiteshop.com/xe/qa/56063
http://apt2you2.cafe24.com/g1/8303
http://0433.net/?document_srl=55644
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=216687
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=216697
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=216876
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=216930
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=216950
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=217035
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=217045
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=217154
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=217169
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=217179
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=217293
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=217452
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=217536
https://www.vegasgreentour.com/?document_srl=111361
https://www.vegasgreentour.com/?document_srl=116375
http://HyUa.1fps.icu/l/szIaeDC
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/brand/23240
https://betshin.com/Story/50735
http://teambuildingpremium.com/forum/index.php?topic=850786.0
http://atemshow.com/atemfair_domestic/69695
https://betshin.com/Story/42511
http://sunele.co.kr/board_ReBD97/51739
http://photogrotto.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80-19/
http://sy.korean.net/qna/85511
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?document_srl=17150&mid=news
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=24283
http://juroweb.com/xe/juroweb_board/18684
http://atemshow.com/atemfair_domestic/69085
http://www.theparrotcentre.com/forum/index.php?topic=558297.0
http://zanoza.h1n.ru/2019/05/18/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-watch-biss-%d0%b8%d0%b3/
http://www.vamoscontigo.org/Noticia/35730
http://apt2you2.cafe24.com/g1/6958
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=153588
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=154202
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=154504
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=154549
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=154855
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=155047
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=155139
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=155216
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=155269
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=155390
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=155427
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=155759
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=155974
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=156004
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=156206
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=156394
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=156555
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=156842
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=156852
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=156994
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=157011
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=157166
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=157546
http://HyUa.1fps.icu/l/szIaeDC
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=33392
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=30475
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1165490
http://roikjer.com/forum/index.php?PHPSESSID=fql1bv72i06o6mid67msihtik4&topic=843859.0
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=29941
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=804634
http://corumotoanahtar.com/component/k2/itemlist/user/2891.html
http://thermoplast.envolgroupe.com/component/k2/author/102872
http://www.vivelabmanizales.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-99-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pf5t-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd/
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=804652
http://ovotecegg.com/component/k2/itemlist/user/140915
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/207343
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1680995
http://soc-human.kz/index.php/component/k2/itemlist/user/1680803
http://wigalseguros.com.br/index.php/component/k2/itemlist/user/6320
http://www.arunagreen.com/index.php/component/k2/itemlist/user/502894
http://www.arunagreen.com/index.php/component/k2/itemlist/user/503250
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/3539
http://www.quattroandpartners.it/component/k2/itemlist/user/1115383
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2471333
http://www.urbantutorial.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=109205
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=552981
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/16683
https://sto54.ru/index.php/component/k2/itemlist/user/3352150
http://lucky.kidspann.net/?document_srl=78895
http://lucky.kidspann.net/index.php?mid=qna&document_srl=78600
http://lucky.kidspann.net/index.php?mid=qna&document_srl=78667
http://marjorieaperry.com/?option=com_k2&view=itemlist&task=user&id=494580
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=17020
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=92761
http://skylinecam.co.kr/photo/126055
http://jjikduk.net/DATA/11989
http://www.remify.app/foro/index.php?topic=255203.0
http://dohairbiz.com/en/component/k2/itemlist/user/2725514.html
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=28355
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=593091
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=71090
http://www.vivelabmanizales.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-99-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vh1y-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd/
http://www.ekemoon.com/189305/051720195514/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/85170
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/219873
http://smartacity.com/component/k2/itemlist/user/48847
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1081395
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/207332
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/207403
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1681092
http://withinfp.sakura.ne.jp/eso/index.php/17036051-v-efire-cuzaa-zizn-cuze-zitta-9-seria-l6-cuzaa-zizn-cuze-zitta-
http://www.arunagreen.com/index.php/component/k2/itemlist/user/503026
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/3566
http://yoriyorifood.com/xxxx/spacial/96398
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=129299
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=129309
http://esperanzazubieta.com/component/k2/itemlist/user/100696
http://jiquilisco.org/index.php/component/k2/itemlist/user/10368
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=37135
http://mediaville.me/index.php/component/k2/itemlist/user/290272
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=160129
http://www.youngfile.com/?document_srl=15674
http://tk-laser.co.kr/index.php?mid=board_QsEu43&document_srl=42704
http://askpharm.net/board_NQiz06/33744
http://bitpark.co.kr/board_IzjM66/4029540
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/7902
http://www.teedinubon.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80-17/
https://2002.shyoon.com/board_2002/41304
http://vhost12299.cpsite.ru/457955-hdvideo-rasskaz-sluzanki-3-sezon-11-seria-onlajn
http://blog.ptpintcast.com/hd-video-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2017/
http://www.taeshinmedia.com/?document_srl=3302417
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2780928
http://bitpark.co.kr/board_IzjM66/4017327
http://0433.net/budongsan/50300
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/7311
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=200426
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=115384
http://www.rocketdan.co.kr/index.php?document_srl=8404&mid=board_WMhM93
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=24945
https://prelease.club/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80-7/
http://apt2you2.cafe24.com/g1/4386
https://reficulcoin.com/index.php?topic=55920.0
http://zanoza.h1n.ru/2019/05/19/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ltgw-%d0%b8%d0%b3%d1%80%d0%b0/
http://kyj1225.godohosting.com/board_mebR72/13989
http://www.itosm.com/cn/board_nLoq17/31950
http://www.itosm.com/cn/board_nLoq17/31959
http://www.itosm.com/cn/board_nLoq17/31973
http://www.josephmaul.org/menu41/152539
http://www.josephmaul.org/menu41/152565
http://www.josephmaul.org/menu41/152672
http://www.josephmaul.org/menu41/152980
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=9115
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=9126
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=9130
http://www.sp1.football/index.php?mid=faq&document_srl=343706
http://www.sp1.football/index.php?mid=faq&document_srl=343792
http://www.sp1.football/index.php?mid=faq&document_srl=343999
http://www.sp1.football/index.php?mid=faq&document_srl=344597
http://www.teedinubon.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mp8r/
http://ye-dream.com/qa/105322
http://yoriyorifood.com/xxxx/spacial/115523
http://HyUa.1fps.icu/l/szIaeDC
http://sunele.co.kr/board_ReBD97/52792
http://www.yepia.com/board_ZCPG83/17314
http://esiapolisthesharp2.co.kr/g1/31307
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=138790
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=39028
http://www.sp1.football/?document_srl=235914
http://www.eunhaele.co.kr/xe/board/19549
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=213783
http://photogrotto.com/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-6/
http://bebopindia.com/notcie/154843
http://www.ekemoon.com/217905/051920195519/
http://vervetama.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bj2e/
http://viamania.net/index.php?mid=board_raYV15&document_srl=27749
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=58295
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=58305
http://www.hyunjindc.com/qna/38670
http://www.itosm.com/cn/board_nLoq17/32059
http://www.itosm.com/cn/board_nLoq17/32146
http://www.josephmaul.org/menu41/153297
http://www.rocketdan.co.kr/?document_srl=9217
http://www.rocketdan.co.kr/index.php?document_srl=9142&mid=board_WMhM93
http://www.sp1.football/index.php?mid=faq&document_srl=345685
http://yourhelp.co.kr/?document_srl=6207
http://yourhelp.co.kr/index.php?document_srl=6173&mid=board_2
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=6217
https://betshin.com/Story/55462
https://betshin.com/Story/55493
https://nple.com/xe/pds/44330
https://prelease.club/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pf5u/
https://prelease.club/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uf1f/
http://HyUa.1fps.icu/l/szIaeDC
http://gallerychoi.com/Exhibition/82148
http://sunele.co.kr/board_ReBD97/51283
http://www.youngfile.com/?document_srl=22086
http://bobr.site/index.php?topic=148171.0
http://arte.dgau.ac.kr/board_qna/41485
http://mglpcm.org/board_ETkS12/29225
http://xn--ok1bpqi43ahtb.net/?document_srl=142753
http://callman.co.kr/index.php?mid=qa&document_srl=49933
https://www.gizmoarticle.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-znvx-%d0%b8%d0%b3%d1%80/
http://xn----3x5er9r48j7wemud0a387h.com/news/50095
http://www.hicleaning.kr/board_wash/101890
http://www.youngfile.com/youngfile_downlist/14120
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=44284
http://callman.co.kr/index.php?mid=qa&document_srl=46790
http://yoriyorifood.com/xxxx/spacial/91187
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=205188
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/4263
http://kyj1225.godohosting.com/board_mebR72/16573
http://tototoday.com/board_oRiY52/28642
http://kwpub.kr/?document_srl=62599
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=157529
http://www.josephmaul.org/menu41/113583
https://prelease.club/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sf3j/
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=122835
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=122872
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zy3p/
https://ttmt.net/crypto_lab_2F/474366
https://ttmt.net/crypto_lab_2F/474420
https://ttmt.net/crypto_lab_2F/474425
https://ttmt.net/crypto_lab_2F/474430
https://ttmt.net/crypto_lab_2F/474455
https://ttmt.net/crypto_lab_2F/474459
http://alastair030.dothome.co.kr/index.php?mid=board_MMiF30&document_srl=4841
http://alastair030.dothome.co.kr/index.php?mid=board_MMiF30&document_srl=6611
http://alastair030.dothome.co.kr/index.php?mid=board_MMiF30&document_srl=6627
http://alastair030.dothome.co.kr/index.php?mid=board_MMiF30&document_srl=6633
http://alastair030.dothome.co.kr/index.php?mid=board_MMiF30&document_srl=6638
http://alastair030.dothome.co.kr/index.php?mid=board_MMiF30&document_srl=6649
http://atemshow.com/atemfair_domestic/73809
http://atemshow.com/atemfair_domestic/73873
http://atemshow.com/atemfair_domestic/73888
http://atemshow.com/atemfair_domestic/73898
http://HyUa.1fps.icu/l/szIaeDC
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-17-05-2019-lj%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-17-05-2019-ys%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%84%d0%b8%d0%bd%d0%b0%d0%bb-cb%d1%85%d0%be%d0%bb%d0%be/
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%84%d0%b8%d0%bd%d0%b0%d0%bb-vq%d1%85%d0%be%d0%bb%d0%be/
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-19-ks%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-19-pj%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-2019-yx%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-pf%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=73426
http://www.tessabannampad.go.th/webboard/index.php?topic=212826.0
http://www.tessabannampad.go.th/webboard/index.php?topic=212856.0
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2508998
https://khuyenmaikk13.info/index.php?topic=183589.0
http://www.camaracoyhaique.cl/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fk1%d0%bd/
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1041688
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=284248
http://macdistri.com/component/k2/itemlist/user/297509
http://forum.politeknikgihon.ac.id/index.php?topic=25709.0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=762245
http://www.spazioad.com/component/k2/itemlist/user/7215934
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=781505
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xu5%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05/
http://www.teedinubon.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cf2%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-9-%d1%81%d0%b5%d1%80/
http://www.teedinubon.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ef4%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://zanoza.h1n.ru/2019/05/18/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pl7%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://zanoza.h1n.ru/2019/05/18/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-2019-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-eu2%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-2019-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://testing.celekt.com/%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ot5%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://webp.online/index.php?topic=59980.0
http://zanoza.h1n.ru/2019/05/18/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ua7%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://www.amazingworldtop.com/entretenimiento/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zc0%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2659886
http://dev.aabn.org.gh/component/k2/itemlist/user/615621
http://forum.digamahost.com/index.php?topic=126554.0
http://seoksoononly.dothome.co.kr/qna/764530
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=27643.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=292129
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3301176
http://soc-human.kz/index.php/component/k2/itemlist/user/1632194
https://lucky28003.nl/forum/index.php?topic=11685.0
http://socialfbwidgets.com/component/k2/itemlist/user/12906.html
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/186946
http://mobility-corp.com/index.php/component/k2/itemlist/user/2519791
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=316252
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/492225
http://www.lustralesdevallehermoso.com/index.php/component/k2/itemlist/user/48167
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=511090
http://roikjer.com/forum/index.php?PHPSESSID=ep3jvl0543vmgrfm9baitknbq4&topic=828196.0
https://szenarist.ru/forum/index.php?topic=205878.0
http://smartacity.com/component/k2/itemlist/user/22789
http://www.vivelabmanizales.com/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ueuh-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-19-%d1%81%d0%b5%d1%80%d0%b8/
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=13579
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1543916
http://www.vivelabmanizales.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-a7-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be/
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2562537
http://seoksoononly.dothome.co.kr/qna/732570
http://married.dike.gr/index.php/component/k2/itemlist/user/45821
http://ahudseafood.com/?option=com_k2&view=itemlist&task=user&id=8248
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=268841
http://ptu.imoove.kr/ko/content/%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-hd-video-%C2%AB%D1%8E%D1%80%D0%B8%D1%81%D1%82%D1%8B-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB332050
http://smartacity.com/component/k2/itemlist/user/18850
http://dohairbiz.com/en/component/k2/itemlist/user/2716563.html
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1874280
https://khuyenmaikk13.info/index.php?topic=179365.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/505584
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/743383
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=28831
http://ovotecegg.com/component/k2/itemlist/user/127614
http://thermoplast.envolgroupe.com/component/k2/author/120129
http://vhost12299.cpsite.ru/426580-smers-13-seria-u2-smers-13-seria
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=10387
http://www.boutique.in.th/index.php/component/k2/itemlist/user/151540
http://www.crnmedia.es/?option=com_k2&view=itemlist&task=user&id=86908
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4941715
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4941734
http://corumotoanahtar.com/?option=com_k2&view=itemlist&task=user&id=4271
http://dev.aabn.org.gh/component/k2/itemlist/user/611542
http://forum.3d-printer.top/index.php?topic=1132.0
http://forum.digamahost.com/index.php?topic=125838.0
http://forum.digamahost.com/index.php?topic=125841.0
http://forum.elexlabs.com/index.php?topic=37955.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=35522.0
http://israengineering.com/index.php/component/k2/itemlist/user/1208360
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3826290
http://matrixpharm.ru/forum/index.php?PHPSESSID=g7cbgnp8co3ia7i7msvgc3ikm1&action=profile;u=199219
http://miklja.net/forum/index.php?topic=31602.0
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2616214
http://necinsurance.co.zw/component/k2/itemlist/user/21105.html
http://otitismediasociety.org/forum/index.php?topic=174499.0
http://ye-dream.com/qa/40415
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1418282
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1888767
http://roikjer.com/forum/index.php?PHPSESSID=narqnnq76pqtdjfj6g9tjaq5g6&topic=861066.0
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=62479
http://community.viajar.tur.br/index.php?p=/profile/lenores53
http://emjun.com/index.php?document_srl=79472&mid=hangtotal
http://emjun.com/index.php?mid=hangtotal&document_srl=79609
http://forum.elexlabs.com/index.php?topic=38286.0
http://forum.esocialdigital.com.au/profile/barbarar91
http://haeple.com/index.php?document_srl=89810
http://haeple.com/index.php?document_srl=89869
http://haeple.com/index.php?document_srl=89885
http://haeple.com/index.php?mid=etc&document_srl=89761
http://haeple.com/index.php?mid=etc&document_srl=89848
http://hyeonjun.co.kr/?document_srl=68026
http://jiquilisco.org/index.php/component/k2/itemlist/user/8643
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3826331
http://lavaggio.com.vn/index.php/component/k2/itemlist/user/3826335
http://lavaggio.com.vn/index.php/component/k2/itemlist/user/3826384
http://mediaville.me/index.php/component/k2/itemlist/user/284032
http://mediaville.me/index.php/component/k2/itemlist/user/284075
http://necinsurance.co.zw/component/k2/itemlist/user/21109
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/110480
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/260556
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=644630
http://www.deliberarchia.org/forum/index.php?topic=998882.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1710679
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/62249
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=20771
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1929107
http://bitpark.co.kr/board_IzjM66/3800742
http://seoksoononly.dothome.co.kr/qna/818900
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=317220
http://www.ekemoon.com/209417/050520193418/
http://www.ekemoon.com/209435/050520193918/
http://www.gforgirl.com/xe/?document_srl=118372
http://www.gforgirl.com/xe/poster/117555
http://www.gforgirl.com/xe/poster/117750
http://www.gforgirl.com/xe/poster/118005
http://www.gforgirl.com/xe/poster/118162
http://www.gforgirl.com/xe/poster/118189
http://www.gforgirl.com/xe/poster/118221
http://proxima.co.rw/index.php/component/k2/itemlist/user/644305
http://roikjer.com/forum/index.php?PHPSESSID=1oj6mdgf7h14tj3g5enghsu0m0&topic=889011.0
http://ru-realty.com/forum/index.php?topic=527121.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/220313
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2323228
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1702655
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1702663
http://thanosakademi.com/index.php?topic=95890.0
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=119651
http://vervetama.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-13/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1390825
https://prelease.club/%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-56-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-owxo-%d0%b6%d0%b5%d0%bd%d1%89%d0%b8%d0%bd%d0%b0-56-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://arunagreen.com/index.php/component/k2/itemlist/user/465516
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1902210
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=9120
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4924136
https://sanp.pro/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tgvr-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80/
http://xplorefitness.com/blog/%C2%AB%D0%BD%D0%B5-%D0%BE%D1%82%D0%BF%D1%83%D1%81%D0%BA%D0%B0%D0%B9-%D0%BC%D0%BE%D1%8E-%D1%80%D1%83%D0%BA%D1%83-elimi-birakma-38-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-sqca-%C2%AB%D0%BD%D0%B5-%D0%BE%D1%82%D0%BF%D1%83%D1%81%D0%BA%D0%B0%D0%B9-%D0%BC%D0%BE%D1%8E-%D1%80%D1%83%D0%BA%D1%83-elimi-birakma-38-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
https://tg.vl-mp.com/index.php?topic=1347429.0
http://www.quattroandpartners.it/component/k2/itemlist/user/1049556
http://www.vivelabmanizales.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d0%bd%d0%b0-%d1%8e%d1%82%d1%83%d0%b1-dn%d1%85%d0%be%d0%bb/
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3565282
http://graphic-ali.com/?option=com_k2&view=itemlist&task=user&id=2378623
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/760494
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=114197
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/114139
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=164468
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/265192
http://proxima.co.rw/index.php/component/k2/itemlist/user/650192
http://proxima.co.rw/index.php/component/k2/itemlist/user/650270
http://rudraautomation.com/index.php/component/k2/author/223986
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=625390
https://www.tedyun.com/xe/?document_srl=153562
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=1842
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=292360
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=13689
http://fbpharm.net/index.php/component/k2/itemlist/user/18551
http://www.dap.com.py/index.php/component/k2/itemlist/user/788349
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=271395
http://8.droror.co.il/uncategorized/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pq8%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://withinfp.sakura.ne.jp/eso/index.php/16884622-tolarobot-1-sezon-2-seria-p3-tolarobot-1-sezon-2-seria/0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=273836
http://dohairbiz.com/en/component/k2/itemlist/user/2715828.html
http://community.viajar.tur.br/index.php?p=/profile/olivebeave
http://skylinecam.co.kr/photo/123473
http://skylinecam.co.kr/photo/123488
http://skylinecam.co.kr/photo/123511
http://skylinecam.co.kr/photo/123555
http://skylinecam.co.kr/photo/123652
http://www.ds712.net/guest/?document_srl=172780
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=172615
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=172649
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=172761
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=172824
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/710007
http://myrechockey.com/forums/index.php?topic=103372.0
http://danielmillsap.com/forum/index.php?topic=1013678.0
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=8091
http://roikjer.com/forum/index.php?PHPSESSID=3ke399qsp27d5mbiil2s6j50j7&topic=866891.0
http://thermoplast.envolgroupe.com/component/k2/author/93161
http://forum.byehaj.hu/index.php?topic=89645.0
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1581127
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=59306
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1698214
http://ye-dream.com/qa/52019
http://teambuildingpremium.com/forum/index.php?topic=825784.0
http://www.ekemoon.com/174241/050220190011/
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=97647
http://webp.online/index.php?topic=50243.msg83294
http://salescoach.ro/content/%C2%AB%D0%B2%D0%BE%D1%80%D0%BE%D0%BD-kuzgun-16-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-udag-%C2%AB%D0%B2%D0%BE%D1%80%D0%BE%D0%BD-kuzgun-16-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/13640
http://8.droror.co.il/uncategorized/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-94-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iz7w-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-94-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://haniel.ir/index.php/component/k2/itemlist/user/84806
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43634
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4713626
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/54953
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1564552
http://withinfp.sakura.ne.jp/eso/index.php/16894692-taemnici-83-seria-06052019-f6-taemnici-83-seria
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1552071
http://www.ekemoon.com/146667/051920193806/
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/11719
http://skylinecam.co.kr/photo/123917
http://skylinecam.co.kr/photo/123966
http://vhost12299.cpsite.ru/475311-poslednaa-nedela-9-seria-18052019-t8-poslednaa-nedela-9-seria
http://vhost12299.cpsite.ru/475352-bol-se-zizni-13-seria-18052019-y3-bol-se-zizni-13-seria
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3682617
http://www.almacenesrickie.com.ec/index.php/component/k2/itemlist/user/130134
http://www.deliberarchia.org/forum/index.php?topic=1008962.0
http://euromouleusinage.com/index.php/component/k2/itemlist/user/132437
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hx5a-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://cafe.dokseosil.co.kr/?document_srl=26730
http://bitpark.co.kr/board_IzjM66/3793022
http://www.hsaura.com/noty/71812
http://xplorefitness.com/blog/%C2%AB%D1%82%D0%BE%D0%BB%D1%8F-%D1%80%D0%BE%D0%B1%D0%BE%D1%82-7-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-16-05-2019-r1-%C2%AB%D1%82%D0%BE%D0%BB%D1%8F-%D1%80%D0%BE%D0%B1%D0%BE%D1%82-7-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://zanoza.h1n.ru/2019/05/16/%d0%b4%d0%be%d1%87%d0%ba%d0%b8-%d0%bc%d0%b0%d1%82%d0%b5%d1%80%d0%b8-%d0%b4%d0%be%d1%87%d0%ba%d0%b8-%d0%bc%d0%b0%d1%82%d0%b5%d1%80i-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-15-05-2019-g3/
http://fbpharm.net/index.php/component/k2/itemlist/user/26803
http://wcwpr.com/UserProfile/tabid/85/userId/9315119/Default.aspx
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1730322
http://dohairbiz.com/?option=com_k2&view=itemlist&task=user&id=2705621
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/185130
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1646236
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1553455
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=78962
http://www.afikgan.co.il/index.php/component/k2/itemlist/user/25975
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=494508
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=561577
http://menulisilmiah.net/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ff7%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81/
http://bitpark.co.kr/board_IzjM66/3735334
http://seoksoononly.dothome.co.kr/qna/739112
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/184311
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1008670
http://emjun.com/index.php?mid=hangtotal&document_srl=99987
http://emjun.com/index.php?mid=hangtotal&document_srl=99997
http://indiefilm.kr/xe/board/141313
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=865985
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=866025
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=866048
http://lucky.kidspann.net/index.php?mid=qna&document_srl=78386
http://moavalve.co.kr/faq/80534
http://moavalve.co.kr/faq/80539
http://moavalve.co.kr/faq/80544
http://moavalve.co.kr/faq/80549
http://research.kiu.ac.kr/?document_srl=92249
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=92179
http://skylinecam.co.kr/photo/125448
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/336354
http://otitismediasociety.org/forum/index.php?topic=178066.0
http://roikjer.com/forum/index.php?PHPSESSID=8jf48g1ddvbsjunnfv2l1e87m6&topic=894600.0
http://www.phperos.net/foro/index.php?topic=136514.0
http://www.tessabannampad.go.th/webboard/index.php?topic=213556.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=d631e535f723f964b43c74ed471eb975&topic=7019.0
https://altaylarteknoloji.com/index.php?topic=5114.0
http://photogrotto.com/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-85-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ln8/
http://www.teedinubon.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tm2%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-17-%d1%81%d0%b5/
https://sanp.pro/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uc7%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-11-%d1%81%d0%b5/
https://www.amazingworldtop.com/entretenimiento/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vf3%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ii9%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c/
https://www.amazingworldtop.com/entretenimiento/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-87-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pr4%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-87/
http://withinfp.sakura.ne.jp/eso/index.php/16951823-efir-cuzaa-zizn-cuze-zitta-5-seria-w5-cuzaa-zizn-cuze-zitta-5-s
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7260986
http://8.droror.co.il/uncategorized/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jn7m/
http://mvisage.sk/index.php/component/k2/itemlist/user/118274
http://bitpark.co.kr/board_IzjM66/3812637
http://bitpark.co.kr/board_IzjM66/3812662
http://forum.digamahost.com/index.php?topic=112428.0
http://forum.digamahost.com/index.php?topic=112431.0
http://highlanderonline.cmshelplive.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-25-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gwld-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-25-%d1%81%d0%b5%d1%80%d0%b8/
http://highlanderonline.cmshelplive.net/%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-74-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kuvo-%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-74/
http://zanoza.h1n.ru/2019/05/21/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-u1-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-10-%d1%81%d0%b5%d1%80%d0%b8/
http://zanoza.h1n.ru/2019/05/21/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-21-05-2019-a8-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/51034
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=156713
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-g7-%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
https://testing.celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-21-05-2019-a3-%d0%98%d0%b3%d1%80/
https://testing.celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-t5-%d0%98%d0%b3%d1%80/
https://testing.celekt.com/%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-a8-%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-12-%d1%81%d0%b5%d1%80%d0%b8/
https://testing.celekt.com/%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-o3-%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-13-%d1%81%d0%b5%d1%80%d0%b8/
https://testing.celekt.com/%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-t1-%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://testing.celekt.com/%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-l2-%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://testing.celekt.com/%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-r5-%d0%a1%d0%bb%d1%83%d0%b3%d0%b0/
https://testing.celekt.com/%d0%a2%d0%b0%d0%b9%d0%bd%d1%8b-%d0%a2%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-91-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-j9-%d0%a2%d0%b0%d0%b9%d0%bd%d1%8b-%d0%a2%d0%b0%d1%94/
https://testing.celekt.com/%d0%a1%d0%b5%d0%bd%d1%8f%d0%a4%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gm6%d0%a1%d0%b5%d0%bd%d1%8f%d0%a4%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
https://www.amazingworldtop.com/entretenimiento/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-86-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-in5/
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bn4%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://153.120.114.241/eso/index.php/17151686-holostak-24-05-2019-swholostak-24-05-201973-holostak-24-05-2019
http://forum.digamahost.com/index.php?topic=127529.0
http://forum.drahthaar-club.com.ua/index.php?topic=4054.0
http://jiquilisco.org/index.php/component/k2/itemlist/user/10331
http://roikjer.com/forum/index.php?PHPSESSID=1fqgq2jbkqt5vbkvltspo89gg6&topic=894322.0
http://roikjer.com/forum/index.php?PHPSESSID=t1rpoqru7rlcv8cb65dj6lf5m4&topic=894337.0
http://roikjer.com/forum/index.php?PHPSESSID=vge9p5s7f8q47otieu3jb602d6&topic=894341.0
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=224085
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=84168
http://www.digitalbul.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-2019-pw%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://bitpark.co.kr/board_IzjM66/3809931
http://danielmillsap.com/forum/index.php?topic=996918.0
http://forum.digamahost.com/index.php?topic=112319.0
http://highlanderonline.cmshelplive.net/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yjcy-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-21-%d1%81%d0%b5%d1%80%d0%b8/
http://highlanderonline.cmshelplive.net/%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd%d0%b5%d0%bd%d0%b8%d0%b5-vuslat-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uapi-%d0%b2%d0%be%d1%81%d1%81%d0%be%d0%b5%d0%b4%d0%b8%d0%bd/
http://highlanderonline.cmshelplive.net/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nwgu-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80/
http://www.bettarmang.co.kr/story/2166980
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=152247
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=152302
http://bobr.site/index.php?topic=157628.0
http://e-educ.net/Forum/index.php?topic=13662.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-aoa-3-eo-19-e-21-05-2019-lvd-a-aoa-3-eo-19-e/?PHPSESSID=ads79ner8deklms8gft519qg60
http://haniel.ir/index.php/component/k2/itemlist/user/124517
http://matinbank.ir/component/k2/itemlist/user/4557173.html
http://proxima.co.rw/index.php/component/k2/itemlist/user/663235
http://teambuildingpremium.com/forum/index.php?topic=865459.0
http://webp.online/index.php?topic=63605.15
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1832516
http://www.theocraticamerica.org/forum/index.php/topic,57283.0.html
http://www.theparrotcentre.com/forum/index.php?topic=569745.0
http://www.theparrotcentre.com/forum/index.php?topic=569755.0
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1930479
http://gtupuw.org/index.php/component/k2/itemlist/user/1930920
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=796700
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/265327
http://roikjer.com/forum/index.php?PHPSESSID=7pk0d33bhovfmd9de8pib5k091&topic=894344.0
http://roikjer.com/forum/index.php?PHPSESSID=l5sviq4gghcgalg62hpqs5irp2&topic=894358.0
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=123862
http://www.almacenesrickie.com.ec/index.php/component/k2/itemlist/user/130452
http://www.phperos.net/foro/index.php?topic=136462.0
http://www.phperos.net/foro/index.php?topic=136465.0
http://www.quattroandpartners.it/component/k2/itemlist/user/1158325
http://www.ekemoon.com/168091/050020192310/
http://www.ekemoon.com/168093/050020192410/
http://www.ekemoon.com/168101/050020192510/
http://www.vivelabmanizales.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%be%d0%b9-%d0%b0%d1%80%d1%82%d0%b8%d1%81%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gn7z-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%be%d0%b9-%d0%b0%d1%80%d1%82/
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/62217
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=80610
http://dcasociados.eu/component/k2/itemlist/user/87838
http://robocit.com/index.php/component/k2/itemlist/user/449411
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1642546
http://thermoplast.envolgroupe.com/component/k2/author/133555
http://www.bettarmang.co.kr/story/2166997
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3319607
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-e5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-y2-%d1%81%d0%bb%d1%83%d0%b3/
http://www.teedinubon.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-90-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-21-05-2019-b3-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94/
http://www.teedinubon.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-c6-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80/
http://www.teedinubon.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-d2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80/
http://www.teedinubon.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-x4-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5/
http://www.teedinubon.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-21-05-2019-f5-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80/
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xl6%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7/
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xg0%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
https://www.amazingworldtop.com/entretenimiento/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-ql3%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5/
http://mir3sea.com/forum/index.php?topic=3827.0
http://poselokgribovo.ru/forum/index.php?topic=804319.0
http://www.m1avio.com/index.php/component/k2/itemlist/user/3652964
http://www.spazioad.com/component/k2/itemlist/user/7273546
http://xplorefitness.com/blog/%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB-%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-r5-%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-8-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=48543
http://mvisage.sk/index.php/component/k2/itemlist/user/118402
http://koushatarabar.com/index.php/component/k2/itemlist/user/1352151
http://koushatarabar.com/index.php/component/k2/itemlist/user/1352286
http://koushatarabar.com/index.php/component/k2/itemlist/user/1352396
http://withinfp.sakura.ne.jp/eso/index.php/16975678-efir-tajny-taemnici-95-seria-j9-tajny-taemnici-95-seria
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4825728
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=12875
https://forums.letstalkbeats.com/index.php?topic=65986.0
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=67280
https://l2thalassic.org/Forum/index.php?topic=564.0
http://arquitectosenreformas.es/index.php/component/k2/itemlist/user/78903
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/51528
http://thermoplast.envolgroupe.com/component/k2/author/76358
http://8.droror.co.il/uncategorized/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81-7/
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/198214
https://chromehearts.in.th/index.php?topic=46244.0
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=292329
http://www.digitalbul.com/%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80/
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=81097
http://zanoza.h1n.ru/2019/05/16/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-16-05-2019-l4-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5/
http://xplorefitness.com/blog/%C2%AB%D0%B3%D1%80%D0%B0%D0%BD%D0%B4-2-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-21-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-15-05-2019-c9-%C2%AB%D0%B3%D1%80%D0%B0%D0%BD%D0%B4-2-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-21-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=728750
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=314949
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3363060
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=321170
http://rudraautomation.com/index.php/component/k2/author/218269
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2323630
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2323633
http://sfah.ch/de/component/k2/itemlist/user/15285
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=120176
http://thermoplast.envolgroupe.com/component/k2/author/120181
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3674971
http://web2interactive.com/index.php/component/k2/itemlist/user/3674585
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=195544
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=195546
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1650741
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=846368
http://zsmr.com.ua/index.php/component/k2/itemlist/user/586471
https://afikgan.co.il/index.php/component/k2/itemlist/user/28944
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/35935
http://www.cosl.com.sg/UserProfile/tabid/61/userId/26215251/Default.aspx
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3574098
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1114237
http://forum.politeknikgihon.ac.id/index.php?topic=25002.0
http://married.dike.gr/index.php/component/k2/itemlist/user/46338
http://www.deliberarchia.org/forum/index.php?topic=959313.0
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1728723
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1126757
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3747485
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/300046
http://emjun.com/index.php?mid=hangtotal&document_srl=5004
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=9190
http://myrechockey.com/forums/index.php?topic=100723.0
http://fbpharm.net/index.php/component/k2/itemlist/user/40314
http://www.hsaura.com/noty/34744
https://cfcestradareal.com.br/?option=com_k2&view=itemlist&task=user&id=17624
http://dev.aabn.org.gh/component/k2/itemlist/user/567560
http://vtservices85.fr/smf2/index.php?topic=216729.0
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=719859
http://www.die-design-manufaktur.de/?option=com_k2&view=itemlist&task=user&id=5240278
http://corumotoanahtar.com/component/k2/itemlist/user/1245.html
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=51700
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/620954
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uq7r-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ap0s-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hj8k-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vv6j-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uy9f-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://www.teedinubon.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-87-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kw3v-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd/
http://www.teedinubon.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-93-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vg8o-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-93-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.telcon.gr/index.php/component/k2/itemlist/user/71981
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=30926
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=275010
http://smartacity.com/component/k2/itemlist/user/28326
https://lucky28003.nl/forum/index.php?topic=12105.0
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/203876
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=558739
http://www.vivelabmanizales.com/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hylt-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80/
http://www.deliberarchia.org/forum/index.php?topic=960447.0
http://storykingdom.forumside.com/index.php?topic=4530.0
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1727440
https://sto54.ru/index.php/component/k2/itemlist/user/3294171
http://www.die-design-manufaktur.de/?option=com_k2&view=itemlist&task=user&id=5175689
https://members.fbhaters.com/index.php?topic=81719.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/292032
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-19-%d1%81%d0%b5-5/
http://batubersurat.com/index.php/component/k2/itemlist/user/44492
http://www.studioaparo.it/index.php/component/k2/itemlist/user/544708
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=605045
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1789290
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1598925
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=14750
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3624571
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/27824
http://bitpark.co.kr/board_IzjM66/3806471
http://shinilspring.com/board_qsfb01/89401
http://shinilspring.com/board_qsfb01/89442
http://shinilspring.com/board_qsfb01/89453
http://shinilspring.com/board_qsfb01/89485
http://shinilspring.com/board_qsfb01/89526
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=785637
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=785722
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=785732
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/785714
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/305335
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=237349
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=17802
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=17805
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2635674
http://socialfbwidgets.com/component/k2/itemlist/user/13675.html
http://www.ds712.net/guest/?document_srl=83595
http://smartacity.com/component/k2/itemlist/user/48515
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=12566
http://corumotoanahtar.com/component/k2/itemlist/user/1615.html
http://www.ekemoon.com/167023/052120194809/
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=325507
http://cafe.dokseosil.co.kr/community/35362
http://www.hsaura.com/noty/41755
http://thermoplast.envolgroupe.com/component/k2/author/101307
http://ovotecegg.com/component/k2/itemlist/user/136147
http://withinfp.sakura.ne.jp/eso/index.php/16989623-hd-dockimateri-dockimateri-14-seria-q3-dockimateri-dockimateri-/0
http://emjun.com/index.php?mid=hangtotal&document_srl=19431
http://community.viajar.tur.br/index.php?p=/discussion/57521/voskresshiy-ertugrul-147-seriya-ccjl-voskresshiy-ertugrul-147-seriya/p1%3Fnew=1
http://www.dpusm.org/?option=com_k2&view=itemlist&task=user&id=1034357
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1775306
http://mediaville.me/index.php/component/k2/itemlist/user/217269
http://seoksoononly.dothome.co.kr/qna/799711
http://withinfp.sakura.ne.jp/eso/index.php/16891414-nikogda-ne-govori-nikogda-9-seria-06052019-k7-nikogda-ne-govori
http://k2.akademitelkom.ac.id/component/k2/itemlist/user/297167
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=140834
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/648230
http://bitpark.co.kr/board_IzjM66/3773552
http://valleycapital.co.ke/index.php/component/k2/itemlist/user/54913
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=20081
http://www2.yasothon.go.th/smf/index.php?topic=159.157755
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/63039
https://turimex.mx.solemti.net/index.php/component/k2/itemlist/user/1430
http://xplorefitness.com/blog/%C2%AB%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-13-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-14-05-2019-h6-%C2%AB%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-13-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://fbpharm.net/index.php/component/k2/itemlist/user/39105
http://fbpharm.net/index.php/component/k2/itemlist/user/39123
http://fbpharm.net/index.php/component/k2/itemlist/user/39136
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/307733
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1181002
http://rudraautomation.com/index.php/component/k2/author/184981
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=208355
http://smartacity.com/component/k2/itemlist/user/44199
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1682428
http://thermoplast.envolgroupe.com/component/k2/author/102726
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/3946
http://dcasociados.eu/component/k2/itemlist/user/89263
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=7498
http://proxima.co.rw/index.php/component/k2/itemlist/user/603390
http://www.sp1.football/index.php?mid=faq&document_srl=21646
http://www.camaracoyhaique.cl/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%87%d0%b0%d1%81%d1%82%d1%8c-1-rt%d1%85%d0%be%d0%bb%d0%be/
http://corumotoanahtar.com/component/k2/itemlist/user/2401.html
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1146494
http://zanoza.h1n.ru/2019/05/16/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pr7d-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/61694
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/66784
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D0%BA%D1%80%D0%B8%D0%B4%C2%BB-vh%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D0%BA%D1%80%D0%B8%D0%B4%C2%BB51-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=43811
http://withinfp.sakura.ne.jp/eso/index.php/16874810-nasa-istoria-65-seria-oidh-nasa-istoria-65-seria/0
http://arunagreen.com/index.php/component/k2/itemlist/user/421755
https://www.mutlualisverisler.com/?p=999123
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1556120
http://www.deliberarchia.org/forum/index.php?topic=984785.0
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1553234
http://153.120.114.241/eso/index.php/16876415-vetrenyj-hercai-20-seria-jsxh-vetrenyj-hercai-20-seria
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/205045
http://forum.digamahost.com/index.php?topic=111288.0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=755854
http://bitpark.co.kr/board_IzjM66/3780502
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=102767
http://www.arunagreen.com/index.php/component/k2/itemlist/user/506855
http://www.atab.com.sa/?option=com_k2&view=itemlist&task=user&id=1619040
http://www.firstfinancialservices.co.uk/?option=com_k2&view=itemlist&task=user&id=3948
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4907401
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=619302
http://www.spazioad.com/index.php/component/k2/itemlist/user/7308960
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/322557
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/257670
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=555812
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2627553
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3417083
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1886718
http://corumotoanahtar.com/component/k2/itemlist/user/2717.html
http://vtservices85.fr/smf2/index.php?PHPSESSID=1af14fb3516c8a05562b911864df3af5&topic=227876.0
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3650893
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=27078
http://www.vivelabmanizales.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ok7z/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1386827
http://proxima.co.rw/index.php/component/k2/itemlist/user/602812
http://arunagreen.com/index.php/component/k2/itemlist/user/476289
http://rudraautomation.com/index.php/component/k2/author/185804
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1866238
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1584189
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/470011
http://sindicatodechoferespichincha.com.ec/?option=com_k2&view=itemlist&task=user&id=6679383
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2579789
http://menulisilmiah.net/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gg8%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1862591
http://koushatarabar.com/index.php/component/k2/itemlist/user/1332637
http://dcasociados.eu/component/k2/itemlist/user/87202
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/257713
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3355663
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=20707
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=20776
http://xplorefitness.com/blog/%C2%AB%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-7-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-14-05-2019-e7-%C2%AB%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-7-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=326270
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=326285
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=10373
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1392719
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3451060
http://xplorefitness.com/blog/%D0%B2-%D1%8D%D1%84%D0%B8%D1%80%D0%B5-%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-11-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-h5-%D1%87%D1%83%D0%B6%D0%B0%D1%8F-%D0%B6%D0%B8%D0%B7%D0%BD%D1%8C-%D1%87%D1%83%D0%B6%D0%B5-%D0%B6%D0%B8%D1%82%D1%82%D1%8F-11-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=7193
http://xn--ok1bpqi43ahtb.net/board_eASW07/31035
http://roikjer.com/forum/index.php?PHPSESSID=5tq5b3ts1ivbptqctd7kah2ld2&topic=866439.0
http://www.hsaura.com/noty/44448
http://proxima.co.rw/index.php/component/k2/itemlist/user/608506
http://bitpark.co.kr/board_IzjM66/3806593
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/62425
http://withinfp.sakura.ne.jp/eso/index.php/16978590-tola-robot-3-seria-d0-tola-robot-3-seria/0
http://www.lustralesdevallehermoso.com/index.php/component/k2/itemlist/user/48453
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/62453
http://www.ekemoon.com/174215/050120195511/
http://www.vivelabmanizales.com/%d0%b3%d1%80%d0%b0%d0%bd%d0%b4-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-er7x-%d0%b3%d1%80%d0%b0%d0%bd%d0%b4-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5/
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/62457
http://koushatarabar.com/index.php/component/k2/itemlist/user/1354480
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2441887
http://www.ekemoon.com/174229/050120195811/
http://www.vivelabmanizales.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kw4l/
http://www.vivelabmanizales.com/%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5%d0%b4%d0%be-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pm7m-%d0%be%d1%82%d0%b5%d0%bb%d1%8c-%d1%82%d0%be%d0%bb%d0%b5/
http://www.vivelabmanizales.com/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81-29/
http://www.vivelabmanizales.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zy1h-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.vivelabmanizales.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-97-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ic4z-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/111209
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/261597
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/261644
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/261692
http://proxima.co.rw/index.php/component/k2/itemlist/user/645432
http://rudraautomation.com/index.php/component/k2/author/219150
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/221058
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/221060
http://sdsn.rsu.edu.ng/?option=com_k2&view=itemlist&task=user&id=2324652
http://carand.co.kr/?document_srl=3670
http://www.lgue.co.kr/?document_srl=23625
http://www.hsaura.com/noty/169348
http://xn----3x5er9r48j7wemud0a387h.com/news/50238
http://gallerychoi.com/Exhibition/90474
http://callman.co.kr/index.php?mid=qa&document_srl=58994
http://zanoza.h1n.ru/2019/05/19/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-game-of-thrones-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-shyf-%d0%b8%d0%b3/
http://wartoby.com/?document_srl=9231
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=339217
http://roikjer.com/forum/index.php?PHPSESSID=le30qmqcstgj00gf487tgpbp11&topic=892612.0
https://www.chirorg.com/?document_srl=34107
http://arte.dgau.ac.kr/board_qna/49292
http://gallerychoi.com/Exhibition/100437
http://www.svteck.co.kr/customer_gratitude/49472
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/10362
http://www.itosm.com/cn/board_nLoq17/14423
http://forum.santrope-rp.ru/index.php?topic=8393.0
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=11474
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=11495
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=11500
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=11505
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=11509
http://www.sp1.football/index.php?mid=faq&document_srl=380009
http://www.sp1.football/index.php?mid=faq&document_srl=380047
http://www.sp1.football/index.php?mid=faq&document_srl=380076
http://www.sp1.football/index.php?mid=faq&document_srl=380154
http://www.sp1.football/index.php?mid=faq&document_srl=380300
http://www.sp1.football/index.php?mid=faq&document_srl=380349
http://www.sp1.football/index.php?mid=faq&document_srl=380394
http://www.sp1.football/index.php?mid=faq&document_srl=380519
http://www.sp1.football/index.php?mid=faq&document_srl=380528
http://www.sp1.football/index.php?mid=faq&document_srl=380577
http://www.sp1.football/index.php?mid=tr_video&document_srl=380113
http://www.svteck.co.kr/?document_srl=75002
http://www.svteck.co.kr/?document_srl=75087
http://www.svteck.co.kr/customer_gratitude/74901
http://www.svteck.co.kr/customer_gratitude/74974
http://www.svteck.co.kr/customer_gratitude/74983
http://HyUa.1fps.icu/l/szIaeDC
http://photogrotto.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gn4%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f21-05-2019/
http://photogrotto.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tj0%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f21-05-2019/
http://photogrotto.com/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-82-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cy7/
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rh8%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ak6%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hk6%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yp8%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f21-05/
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gg2%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://zanoza.h1n.ru/2019/05/21/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gl1%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-13-%d1%81%d0%b5/
http://zanoza.h1n.ru/2019/05/21/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ga5%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://yoriyorifood.com/xxxx/spacial/74369
http://yoriyorifood.com/xxxx/spacial/74394
https://esel.gist.ac.kr/esel2/board_hmgj23/51612
https://esel.gist.ac.kr/esel2/board_hmgj23/51716
https://khuyenmaikk13.info/index.php?topic=207018.0
https://nextezone.com/index.php?action=profile;u=8970
https://prelease.club/%d0%ba%d0%bb%d1%8f%d1%82%d0%b2%d0%b0-yemin-64-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ccyn-%d0%ba%d0%bb%d1%8f%d1%82%d0%b2%d0%b0-yemin-64-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://test.baseyou21.kr/?document_srl=109743
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=109728
https://testing.celekt.com/%d0%9d%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d0%a1%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-85-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-4/
http://atemshow.com/?document_srl=62885
http://atemshow.com/atemfair_domestic/62854
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=120222
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=120266
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=120282
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=120303
http://jjikduk.net/?document_srl=75612
http://jjikduk.net/DATA/75598
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=875001
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=875034
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=875049
http://menulisilmiah.net/hd-video-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-p1-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1/
http://www.remify.app/foro/index.php?topic=245490.0
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/57081
http://www.m1avio.com/index.php/component/k2/itemlist/user/3647817
http://lucky.kidspann.net/index.php?mid=qna&document_srl=57398
http://lucky.kidspann.net/index.php?mid=qna&document_srl=57638
http://lucky.kidspann.net/index.php?mid=qna&document_srl=57657
http://lucky.kidspann.net/index.php?mid=qna&document_srl=57676
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=25593
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=61752
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=61813
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=61923
http://mobility-corp.com/index.php/component/k2/itemlist/user/2627080
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/115291
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/115322
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/266355
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=225029
http://rudraautomation.com/index.php/component/k2/author/225203
http://rudraautomation.com/index.php/component/k2/author/225218
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7264150
http://moavalve.co.kr/?document_srl=20750
http://www.urbantutorial.com/index.php/en/?option=com_k2&view=itemlist&task=user&id=109809
http://adopt10plus.com/groups/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-fd%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5-2/
http://www.ekemoon.com/156267/050320193708/
http://poselokgribovo.ru/forum/index.php?topic=721591.0
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=295833
http://menulisilmiah.net/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-d1-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4/
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1016185
http://arunagreen.com/index.php/component/k2/itemlist/user/432261
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=283600
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1015041
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5049
http://batubersurat.com/index.php/component/k2/itemlist/user/43120
http://euromouleusinage.com/index.php/component/k2/itemlist/user/110633
http://forum.digamahost.com/index.php?topic=109153.0
http://thermoplast.envolgroupe.com/component/k2/author/70270
http://smartacity.com/component/k2/itemlist/user/40199
http://www.ekemoon.com/169949/050520194610/
http://mediaville.me/index.php/component/k2/itemlist/user/252316
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3620470
http://webp.online/index.php?topic=51677.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/515772
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/305941
http://www.sp1.football/index.php?mid=faq&document_srl=91419
http://compultras.com/?option=com_k2&view=itemlist&task=user&id=210672
https://l2thalassic.org/Forum/index.php?topic=1216.0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/221643
http://forum.politeknikgihon.ac.id/index.php?topic=22216.0
http://afinandoemociones.com.ar/index.php/component/k2/itemlist/user/388408
http://menulisilmiah.net/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-m0-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2/
http://arquitectosenreformas.es/component/k2/itemlist/user/78814
http://www.pkmmsabah.org/index.php/component/k2/itemlist/user/18975
http://dcasociados.eu/component/k2/itemlist/user/87067
http://poselokgribovo.ru/forum/index.php?topic=727789.0
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=291755
http://xplorefitness.com/blog/%D1%82%D0%BE%D0%BB%D1%8F-%D1%80%D0%BE%D0%B1%D0%BE%D1%82-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-q0-%D1%82%D0%BE%D0%BB%D1%8F-%D1%80%D0%BE%D0%B1%D0%BE%D1%82-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://seoksoononly.dothome.co.kr/?document_srl=754352
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=497969
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=282312
http://febrescordero.gob.ec/index.php/component/k2/itemlist/user/78433
http://www.crnmedia.es/component/k2/itemlist/user/84850
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1762607
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/566171
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1552776
http://matinbank.ir/component/k2/itemlist/user/4488202.html
http://petromacorisanos.com.radiosenda1680.org/?option=com_k2&view=itemlist&task=user&id=5574
http://forum.politeknikgihon.ac.id/index.php?topic=23658.0
http://fbpharm.net/index.php/component/k2/itemlist/user/18784
http://poselokgribovo.ru/forum/index.php?topic=716619.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/566295
http://www.ekemoon.com/143125/052120194105/
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=333123
http://myrechockey.com/forums/index.php?topic=92451.0
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=728313
http://wigalseguros.com.br/index.php/component/k2/itemlist/user/7340
https://www.shaiyax.com/index.php?topic=349432.0
http://smartacity.com/component/k2/itemlist/user/36636
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=62077
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=807439
http://www.digitalbul.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-10-05-19-gf%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://webp.online/index.php?topic=39930.30
http://zanoza.h1n.ru/2019/05/16/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-2-%d1%87%d0%b0%d1%81%d1%82%d1%8c-im%d1%85%d0%be%d0%bb%d0%be/
http://www.vivelabmanizales.com/%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-%d0%bd%d0%b5-%d0%b3%d0%be%d0%b2%d0%be%d1%80%d0%b8-%d0%bd%d0%b8%d0%ba%d0%be%d0%b3%d0%b4%d0%b0-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ha7r/
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=597109
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3738936
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=290103
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1561565
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=501918
http://koushatarabar.com/index.php/component/k2/itemlist/user/1321101
http://haniel.ir/index.php/component/k2/itemlist/user/74450
https://khuyenmaikk13.info/index.php?topic=178794.0
http://withinfp.sakura.ne.jp/eso/index.php/16864845-tajny-94-seria-c7-tajny-94-seria
http://mediaville.me/index.php/component/k2/itemlist/user/216967
http://www.deliberarchia.org/forum/index.php?topic=968162.0
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=225798
http://malbeot.iptime.org:10009/xe/board/4275693
http://mobility-corp.com/index.php/component/k2/itemlist/user/2521105
http://forum.digamahost.com/index.php?topic=109500.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4724041
http://www.vivelabmanizales.com/%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-live-%d1%8e%d1%80%d0%b8%d1%81%d1%82%d1%8b-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-3/
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=577927
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/61632
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=757443
http://socialfbwidgets.com/component/k2/itemlist/user/13109
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2563887
http://www.dap.com.py/index.php/component/k2/itemlist/user/783893
http://highlanderonline.cmshelplive.net/%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-64-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-akqi-%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-64/
http://zanoza.h1n.ru/2019/05/16/%d0%bd%d0%b5-%d0%be%d1%82%d0%bf%d1%83%d1%81%d0%ba%d0%b0%d0%b9-%d0%bc%d0%be%d1%8e-%d1%80%d1%83%d0%ba%d1%83-elimi-birakma-42-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fbvm-%d0%bd%d0%b5-%d0%be/
http://bebopindia.com/notcie/24650
http://myrechockey.com/forums/index.php?topic=92580.0
http://zanoza.h1n.ru/2019/05/16/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uiye-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-8-%d1%81%d0%b5%d1%80%d0%b8/
http://www.jesusonly.life/calendar/74920
http://associationsila.org/?option=com_k2&view=itemlist&task=user&id=289835
http://www.vivelabmanizales.com/%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80%d0%b4%d1%8b-4-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-06-05-2019-e6-%d0%bc%d0%b8%d0%bb%d0%bb%d0%b8%d0%b0%d1%80/
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1632351
http://menulisilmiah.net/%d0%bf%d0%be-%d0%b7%d0%b0%d0%ba%d0%be%d0%bd%d0%b0%d0%bc-%d0%b2%d0%be%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be-%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5-2/
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2579051
http://www.gforgirl.com/xe/?document_srl=148324
http://www.golden-nail.co.kr/?document_srl=99814
http://www.golden-nail.co.kr/press/99741
http://www.golden-nail.co.kr/press/99794
http://www.golden-nail.co.kr/press/99847
http://www.golden-nail.co.kr/press/99920
http://www.hicleaning.kr/board_wash/92513
http://www.hicleaning.kr/board_wash/92561
https://prelease.club/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-ep5a-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://corumotoanahtar.com/index.php/component/k2/itemlist/user/1803
http://jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3413117
http://bebopindia.com/notcie/27473
http://jjikduk.net/DATA/20695
http://www.josephmaul.org/menu41/34926
http://married.dike.gr/index.php/component/k2/itemlist/user/57179
http://www.ekemoon.com/179935/051720194212/
http://ovotecegg.com/component/k2/itemlist/user/150947
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/524208
https://khuyenmaikk13.info/index.php?topic=182026.0
http://www.vivelabmanizales.com/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dtfw-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-20-%d1%81%d0%b5%d1%80%d0%b8/
http://salescoach.ro/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D0%BF%D0%BE%D1%81%D1%82-%D1%88%D0%BE%D1%83-%D1%81%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C-%D0%BE%D0%BD%D0%BB%D0%B0%D0%B9%D0%BD%C2%BB-nm%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D0%BF%D0%BE%D1%81%D1%82-%D1%88%D0%BE%D1%83
http://www.ekemoon.com/142525/051720194705/
http://withinfp.sakura.ne.jp/eso/index.php/16914699-uristy-11-seria-smotret-uristy-11-seria/0
https://members.fbhaters.com/index.php?topic=77338.0
http://moavalve.co.kr/faq/75956
http://moavalve.co.kr/faq/76001
http://moavalve.co.kr/faq/76026
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=82065
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=82107
http://dev.aabn.org.gh/?option=com_k2&view=itemlist&task=user&id=566052
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=16109
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1164362
http://c3isecurity.com.br/index.php/component/k2/itemlist/user/496327
http://www.deliberarchia.org/forum/index.php?topic=1025721.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1154298
http://seoksoononly.dothome.co.kr/?document_srl=871150
https://khuyenmaikk13.info/index.php?topic=188601.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2601823
http://www.vivelabmanizales.com/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qpbv-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1563153
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1763163
http://xplorefitness.com/blog/%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-g0-%D0%BC%D0%B8%D0%BB%D0%BB%D0%B8%D0%B0%D1%80%D0%B4%D1%8B-4-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://salescoach.ro/content/%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-vqlf-%C2%AB%D0%B2%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9-hercai-12-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://laspoltrina.it/component/k2/itemlist/user/1378196
http://www.studyxray.com/Sangdam/115315
http://www.studyxray.com/Sangdam/115345
http://www.svteck.co.kr/customer_gratitude/52567
http://www.svteck.co.kr/customer_gratitude/52676
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=74321
http://zanoza.h1n.ru/2019/05/19/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dv4%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://zanoza.h1n.ru/2019/05/19/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-fd7%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5/
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-co6%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://photogrotto.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ro2%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-13-%d1%81%d0%b5/
http://photogrotto.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-co7%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://condolencias.servisa.es/96-05-05-2019-v7-96
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=82615
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/185345
http://www.vivelabmanizales.com/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-w5-%d1%82%d0%be%d0%bb%d1%8f/
http://www.quattroandpartners.it/component/k2/itemlist/user/1068843
http://www.ekemoon.com/156371/050420190508/
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=80269
http://miquirofisico.com/index.php/component/k2/itemlist/user/3915
http://married.dike.gr/index.php/component/k2/itemlist/user/51565
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=304776
https://szenarist.ru/forum/index.php?topic=205043.0
http://marjorieaperry.com/?option=com_k2&view=itemlist&task=user&id=481767
http://mjbosch.com/component/k2/itemlist/user/82970
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/85498
http://rudraautomation.com/index.php/component/k2/author/161470
http://rudraautomation.com/index.php/component/k2/author/161498
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1668729
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1668793
http://forum.kopkargobel.com/index.php?topic=12259.0
http://forum.kopkargobel.com/index.php?topic=12263.0
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=797595
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24-05-2019-bn%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24-05-201914-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24/
http://ptu.imoove.kr/ko/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-24-05-19%C2%BB-fk%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-24-05-19%C2%BB01-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9
http://ru-realty.com/forum/index.php?PHPSESSID=qgb6vtnm8lioorakvjgvtu7410&topic=532448.0
http://ru-realty.com/forum/index.php?topic=532470.0
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=225293
http://www.ekemoon.com/145617/051720192806/
http://seoksoononly.dothome.co.kr/qna/803811
http://www.elpinatarense.com/?option=com_k2&view=itemlist&task=user&id=155039
http://community.viajar.tur.br/index.php?p=/profile/erickamare
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=512281
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1643926
https://forum.ac-jete.it/index.php?topic=352031.0
http://soc-human.kz/index.php/component/k2/itemlist/user/1668807
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1660659
http://thermoplast.envolgroupe.com/component/k2/author/91934
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1386008
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1057156
http://www.comfortcenter.es/index.php/component/k2/itemlist/user/105367
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=800226
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=800517
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=800528
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=57144
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-mn%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://roikjer.com/forum/index.php?PHPSESSID=86558lpo10be4td450h85b2hr4&topic=895494.0
http://ru-realty.com/forum/index.php?PHPSESSID=fgk64rqdgf9dfvc49gdpoms2s6&topic=532372.0
http://rudraautomation.com/index.php/component/k2/author/225222
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=225157
http://universalcommunity.se/Forum/index.php?topic=16828.0
http://universalcommunity.se/Forum/index.php?topic=16852.0
http://universalcommunity.se/Forum/index.php?topic=16854.0
http://universalcommunity.se/Forum/index.php?topic=16856.0
http://www.atab.com.sa/index.php/en/?option=com_k2&view=itemlist&task=user&id=1661155
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=823459
http://www.phperos.net/foro/index.php?topic=136671.0
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%84%d0%b8%d0%bd%d0%b0%d0%bb-uc%d1%85%d0%be%d0%bb%d0%be/
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%84%d0%b8%d0%bd%d0%b0%d0%bb-xu%d1%85%d0%be%d0%bb%d0%be/
http://withinfp.sakura.ne.jp/eso/index.php/16894121-serial-uristy-16-seria-n6-uristy-16-seria
http://macdistri.com/index.php/component/k2/itemlist/user/301931
http://withinfp.sakura.ne.jp/eso/index.php/16863880-smotret-po-zakonam-voennogo-vremeni-3-sezon-9-seria-l7-po-zakon/0
http://withinfp.sakura.ne.jp/eso/index.php/16879012-holostak-9-sezon-11-vypusk-06052019-g7-holostak-9-sezon-11-vypu
https://l2thalassic.org/Forum/index.php?topic=2188.0
http://community.viajar.tur.br/index.php?p=/discussion/57447/vossoedinenie-vuslat-16-seriya-zyrn-vossoedinenie-vuslat-16-seriya
http://community.viajar.tur.br/index.php?p=/discussion/57452/vetrenyy-hercai-9-seriya-diwi-vetrenyy-hercai-9-seriya
http://seoksoononly.dothome.co.kr/qna/790893
https://www.shaiyax.com/index.php?topic=329337.0
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3599975
http://rudraautomation.com/index.php/component/k2/author/161426
http://rudraautomation.com/index.php/component/k2/author/161436
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1660492
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1660583
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3586802
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1385694
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-th9%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://rudraautomation.com/index.php/component/k2/author/220238
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2324144
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=65604
https://www.amazingworldtop.com/entretenimiento/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-82-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sb4/
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=156602
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=91445
http://haeple.com/index.php?mid=etc&document_srl=88763
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=24246
http://xn----3x5er9r48j7wemud0a387h.com/news/50206
http://smartacity.com/component/k2/itemlist/user/56456
http://corumotoanahtar.com/component/k2/itemlist/user/4317.html
http://emjun.com/index.php?mid=hangtotal&document_srl=93866
http://atemshow.com/atemfair_domestic/56128
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=222000
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/337573
http://bebopindia.com/notcie/146416
http://www.proandpro.it/?option=com_k2&view=itemlist&task=user&id=4635449
https://www.shaiyax.com/index.php?topic=353704.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/647531
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=106741
http://www.hicleaning.kr/board_wash/129325
http://ovotecegg.com/component/k2/itemlist/user/161073
http://universalcommunity.se/Forum/index.php?topic=16693.0
http://www.digitalbul.com/%d0%ba%d0%bb%d1%8f%d1%82%d0%b2%d0%b0-yemin-63-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sqkp-%d0%ba%d0%bb%d1%8f%d1%82%d0%b2%d0%b0-yemin-63-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://tg.vl-mp.com/index.php?topic=1475152.0
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=100992
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2512525
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=67263
http://skangseo.org/xe/board_Atnj46/42804
http://www.sp1.football/index.php?mid=faq&document_srl=194512
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=198660
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1945258
http://wigalseguros.com.br/component/users/?task=user&view=itemlist&id=11259
http://www.crnmedia.es/component/k2/itemlist/user/87572
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=21448
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=72390
http://www.ekemoon.com/212979/052120194918/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/118199
http://ovotecegg.com/component/k2/itemlist/user/163134
http://ye-dream.com/qa/86904
http://subforumna.x10.mx/mad/index.php?topic=252610.0
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ji7%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://prelease.club/%d0%b6%d0%b5%d1%81%d1%82%d0%be%d0%ba%d0%b8%d0%b9-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb-zalim-istanbul-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xegl-%d0%b6%d0%b5%d1%81%d1%82%d0%be/
http://www.taeshinmedia.com/?document_srl=3301213
http://www.theparrotcentre.com/forum/index.php?topic=549149.0
http://www.bettarmang.co.kr/story/2134517
http://indiefilm.kr/xe/board/150524
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=588430
https://forum.shaiyaslayer.tk/index.php?topic=129425.0
http://webp.online/index.php?topic=63118.0
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=112757
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2655442
http://forum.digamahost.com/index.php?topic=127649.0
http://lucky.kidspann.net/index.php?mid=qna&document_srl=67023
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2669324
http://zanoza.h1n.ru/2019/05/19/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fv6%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c/
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=36319
http://vhost12299.cpsite.ru/485822-tajny-89-seria-19052019-n1-tajny-89-seria
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=88506
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3378529
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3299737
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=57891
http://xn----3x5er9r48j7wemud0a387h.com/news/26858
https://sanp.pro/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-84-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cj6/
http://emjun.com/index.php?mid=hangtotal&document_srl=111067
http://jjikduk.net/DATA/64082
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=38325
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=132268
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2780808
http://www.jesusonly.life/calendar/128690
http://shinhwaair2017.cafe24.com/issue/283530
http://shinilspring.com/board_qsfb01/89531
http://www.studyxray.com/?document_srl=176060
http://www.golden-nail.co.kr/press/90121
http://jjikduk.net/DATA/69124
http://soc-human.kz/index.php/component/k2/itemlist/user/1712635
http://www.theocraticamerica.org/forum/index.php?topic=52117.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3388380
http://sixangles.co.kr/qna/595418
http://bobr.site/index.php?topic=150218.0
http://www.josephmaul.org/menu41/124801
http://www.sp1.football/?document_srl=190241
http://hyeonjun.co.kr/menu3/62435
http://otitismediasociety.org/forum/index.php?topic=174485.0
http://0433.net/junggo/53772
http://www.almacenesrickie.com.ec/index.php/component/k2/itemlist/user/127772
http://emjun.com/index.php?document_srl=95194&mid=hangtotal
http://xn----3x5er9r48j7wemud0a387h.com/news/27443
http://www.critico-expository.com/forum/index.php?topic=13436.0
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1619407
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=512826
http://indiefilm.kr/xe/board/129932
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2321995
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-aoa-3-eo-18-e-18-05-2019-jie-a-aoa-3-eo-18-e/?PHPSESSID=2vg4d4cmc8fs1pc5ma430n9394
http://skylinecam.co.kr/photo/80650
http://www.remify.app/foro/index.php?topic=328278.0
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=86396
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=11380
http://zanoza.h1n.ru/2019/05/18/%d0%b1%d0%be%d0%b3%d0%b0%d1%82%d1%8b%d0%b5-%d0%b8-%d0%b1%d0%b5%d0%b4%d0%bd%d1%8b%d0%b5-zengin-ve-yoksul-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-czdo-%d0%b1%d0%be%d0%b3%d0%b0%d1%82%d1%8b/
http://xn--ok1bpqi43ahtb.net/board_eASW07/100468
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3402059
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=100679
http://mir3sea.com/forum/index.php?topic=3872.0
http://www.sp1.football/index.php?mid=faq&document_srl=302766
http://forum.kopkargobel.com/index.php?topic=12176.0
http://www.theparrotcentre.com/forum/index.php?topic=557373.0
http://skylinecam.co.kr/photo/118293
https://www.2ayes.com/16797/2-7-17-05-2019-g3-2-7
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=71880
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=91298
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=514379
http://zanoza.h1n.ru/2019/05/20/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-st0%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://cybergsm.es/index.php?topic=32354.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2628977
http://vhost12299.cpsite.ru/418465-nevesta-iz-stambula-istanbullu-gelin-2-sezon-84-seria-17052019-
http://bitpark.co.kr/board_IzjM66/4036058
http://shinilspring.com/board_qsfb01/93255
http://bebopindia.com/notcie/108318
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=76927
http://xn----3x5er9r48j7wemud0a387h.com/news/43251
http://www.studyxray.com/Sangdam/174013
http://smartacity.com/index.php/component/k2/itemlist/user/56448
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=103558
http://forum.digamahost.com/index.php?topic=128152.0
http://www.theparrotcentre.com/forum/index.php?topic=548580.0
http://www.theocraticamerica.org/forum/index.php?topic=48305.0
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=77086
http://xn--ok1bpqi43ahtb.net/board_eASW07/136008
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=67906
http://www.golden-nail.co.kr/press/74287
http://yoriyorifood.com/xxxx/spacial/69567
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/44513
http://dev.aabn.org.gh/component/k2/itemlist/user/620870
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=76238
http://www.tekparcahdfilm.com/forum/index.php?topic=51731.0
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sd4%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f20-05/
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/519568
http://0433.net/junggo/51463
http://www.gforgirl.com/xe/?document_srl=150902
http://ptu.imoove.kr/ko/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-17-05-2019%C2%BB-ow%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-17-05-2019%C2%BB89-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA
http://moavalve.co.kr/faq/64523
http://asin.itts.co.kr/board_rtXs84/6730
http://asin.itts.co.kr/board_rtXs84/6078
http://lucky.kidspann.net/index.php?mid=qna&document_srl=54548
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=169519
http://xn----3x5er9r48j7wemud0a387h.com/news/44757
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/16370
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=113959
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=24254
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3308507
http://webp.online/index.php?topic=62515.msg108001
http://photogrotto.com/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-2019-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mz2%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-2019-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=59166
http://hyeonjun.co.kr/menu3/102411
http://carrierworld.co.kr/?document_srl=80917
https://www.amazingworldtop.com/entretenimiento/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-do8%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05-2019/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1444801
http://0433.net/junggo/53456
http://www.theocraticamerica.org/forum/index.php/topic,48198.0.html
http://dev.aabn.org.gh/component/k2/itemlist/user/617525
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=329202
http://indiefilm.kr/xe/?document_srl=148419
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/345531
http://www.hicleaning.kr/board_wash/148981
http://jiquilisco.org/index.php/component/k2/itemlist/user/9962
http://zanoza.h1n.ru/2019/05/18/%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80%d0%b4%d1%86%d0%b5-tek-yurek-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fiqw-%d0%b5%d0%b4%d0%b8%d0%bd%d0%be%d0%b5-%d1%81%d0%b5%d1%80/
http://photogrotto.com/%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-94-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vy0%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-94-%d1%81%d0%b5%d1%80%d0%b8%d1%8f21-05-2019/
https://www.shaiyax.com/index.php?topic=354304.0
http://www.gforgirl.com/xe/poster/117235
http://shinilspring.com/board_qsfb01/92179
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/gumdanapt/50877
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=63678
http://www.josephmaul.org/menu41/99598
http://ovotecegg.com/component/k2/itemlist/user/166350
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=85075
http://www.golden-nail.co.kr/press/83871
http://0433.net/junggo/42162
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=16029
http://bobr.site/index.php?topic=150006.0
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=17295
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=76213
https://testing.celekt.com/%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ua7%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f17-05-2019/
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/221860
http://roikjer.com/forum/index.php?PHPSESSID=c2d4jn0p97q1fkth1p61712bh6&topic=901481.0
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=82621
http://www.gforgirl.com/xe/poster/130180
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=70935
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=163309
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=72840
http://www.juvebalkan.com/smf/index.php?topic=1490.285
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3379906
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=87841
http://www.sp1.football/index.php?mid=faq&document_srl=264197
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=80283
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/224415
https://www.shaiyax.com/index.php?topic=362281.0
http://www.cyberblissstudios.com/UserProfile/tabid/42/UserID/2162207/Default.aspx
http://miklja.net/forum/index.php?topic=31517.0
http://www.theparrotcentre.com/forum/index.php?topic=551343.0
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=23977
http://153.120.114.241/eso/index.php/17118974-holostak-9-sezon-11-vypusk-17-05-19-jaholostak-9-sezon-11-vypus
http://skylinecam.co.kr/?document_srl=115742
http://www.studyxray.com/Sangdam/190585
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-17-05-2019-th%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=69131
http://xn--ok1bpqi43ahtb.net/board_eASW07/102062
http://www.josephmaul.org/menu41/94069
http://ye-dream.com/qa/80714
http://photogrotto.com/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wa3%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
https://www.amazingworldtop.com/entretenimiento/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d0%b8%d0%b3%d1%80/
http://xn--ok1bpqi43ahtb.net/board_eASW07/128488
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=343608
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1938210
http://www.sp1.football/index.php?mid=faq&document_srl=246097
http://withinfp.sakura.ne.jp/eso/index.php/17113643-novinka-smers-5-seria-b2-smers-5-seria/0
http://www.gforgirl.com/xe/poster/133021
http://corumotoanahtar.com/?option=com_k2&view=itemlist&task=user&id=4328
http://mobility-corp.com/index.php/component/k2/itemlist/user/2628860
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=32802
http://www.golden-nail.co.kr/press/81605
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=23414
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=105193
http://photogrotto.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8d%d1%84%d0%b8%d1%80-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6/
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13414
http://atemshow.com/atemfair_domestic/55927
http://www.jesusonly.life/calendar/124747
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=78007
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2615472
http://corumotoanahtar.com/component/k2/itemlist/user/4506.html
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=16057
http://zanoza.h1n.ru/2019/05/20/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-y2-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2/
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1709136
https://turimex.mx.solemti.net/index.php/component/k2/itemlist/user/4614
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3308667
http://forum.digamahost.com/index.php?topic=127981.0
http://xn--ok1bpqi43ahtb.net/board_eASW07/124882
http://indiefilm.kr/xe/board/134494
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=269203
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=29455
http://fbpharm.net/index.php/component/k2/itemlist/user/50739
https://reficulcoin.com/index.php?topic=53365.0
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=209143
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2782118
http://mir3sea.com/forum/index.php?topic=3627.0
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=131751
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=68266
http://www.hsaura.com/noty/144865
http://cwon.kr/xe/board_bnSr36/84493
http://immobilia.gr/index.php/de/component/k2/itemlist/user/16393
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=523299
http://www.ekemoon.com/214605/050420192119/
http://www.teedinubon.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8/
http://vhost12299.cpsite.ru/492985-igra-prestolov-8-sezon-1-seria-19052019-z3-igra-prestolov-8-sez
http://shinilspring.com/board_qsfb01/91569
https://www.shaiyax.com/index.php?topic=354839.0
http://jiquilisco.org/index.php/component/k2/itemlist/user/8941
http://mobility-corp.com/index.php/component/k2/itemlist/user/2615528
https://altaylarteknoloji.com/index.php?topic=5027.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1743201
http://www.gforgirl.com/xe/poster/128398
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/514893
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4842467
https://prelease.club/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ul7v-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://corumotoanahtar.com/component/k2/itemlist/user/5564.html
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=917adf3d3eee93d50a71c49676025e4c&topic=7461.0
http://withinfp.sakura.ne.jp/eso/index.php/17117416-hdvideo-tajny-87-seria-v7-tajny-87-seria/0
http://www.gforgirl.com/xe/poster/106271
http://www.teedinubon.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wv5%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://dev.aabn.org.gh/index.php/component/k2/itemlist/user/635062
http://shinhwaair2017.cafe24.com/issue/208209
http://dohairbiz.com/en/component/k2/itemlist/user/2765670.html
http://www.original-craft.net/index.php?topic=340767.0
http://www.jesusonly.life/calendar/240603
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=75365
http://mir3sea.com/forum/index.php?topic=3599.0
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cb7%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%87%d0%b5%d1%80%d0%bd/
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2617888
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=856735
http://www.spazioad.com/component/k2/itemlist/user/7344935
http://shinilspring.com/board_qsfb01/86332
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=109032
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=846729
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/513993
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4835550
http://mjbosch.com/index.php/component/k2/itemlist/user/83894
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1649280
http://asin.itts.co.kr/board_rtXs84/14370
http://xplorefitness.com/blog/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-17-05-19%C2%BB-gd%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-17-05-19%C2%BB39-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3491041
http://skylinecam.co.kr/photo/100632
http://healthyteethpa.org/component/k2/itemlist/user/5473726
http://www.josephmaul.org/?document_srl=121118
http://ye-dream.com/qa/87898
http://www.teedinubon.com/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-86-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19/
http://zanoza.h1n.ru/2019/05/20/%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-88-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-a5-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-88-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.theparrotcentre.com/forum/index.php?topic=547960.0
http://shinilspring.com/board_qsfb01/83818
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=526281
https://cybergsm.es/index.php?topic=28143.0
http://shinhwaair2017.cafe24.com/issue/230678
http://shinhwaair2017.cafe24.com/issue/236103
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=590831
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/644850
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=33351
http://indiefilm.kr/xe/board/123511
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=69706
https://esel.gist.ac.kr/esel2/board_hmgj23/54271
http://mir3sea.com/forum/index.php?topic=3844.0
http://podwodnyswiat.eu/forum/index.php?topic=1277.0
http://asin.itts.co.kr/board_rtXs84/11917
http://married.dike.gr/index.php/component/k2/itemlist/user/65318
http://matrixpharm.ru/forum/index.php?PHPSESSID=pighh46q3tonc8okve22f4la13&action=profile;u=199706
http://forum.elexlabs.com/index.php?action=profile;u=6781
http://www.svteck.co.kr/customer_gratitude/36452
http://webp.online/index.php?topic=59232.0
http://moavalve.co.kr/faq/76789
http://indiefilm.kr/xe/?document_srl=112270
http://thermoplast.envolgroupe.com/component/k2/author/121291
http://thermoplast.envolgroupe.com/component/k2/author/124679
http://xn--ok1bpqi43ahtb.net/board_eASW07/126231
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=12936
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/339359
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-na7%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-6-%d1%81%d0%b5%d1%80/
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=90329
http://otitismediasociety.org/forum/index.php?topic=185296.0
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1609873
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=100999
https://testing.celekt.com/%d0%a2%d0%b0%d0%b9%d0%bd%d1%8b-101-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%a1%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d0%a2%d0%b0%d0%b9%d0%bd%d1%8b-101-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=85721
https://tg.vl-mp.com/index.php?topic=1477616.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1463091
http://gtupuw.org/index.php/component/k2/itemlist/user/1936351
http://dev.aabn.org.gh/component/k2/itemlist/user/617507
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1711208
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=dff3ca8cd23605688e995e0894399dba&topic=7472.0
http://www.theparrotcentre.com/forum/index.php?topic=564858.0
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=112485
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=65741
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1613228
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-du3%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.golden-nail.co.kr/?document_srl=86236
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=85665
http://shinilspring.com/board_qsfb01/99775
http://skangseo.org/xe/board_Atnj46/42684
http://yoriyorifood.com/xxxx/spacial/106891
http://asin.itts.co.kr/board_rtXs84/14376
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=334534
http://forum.kopkargobel.com/index.php?topic=12018.0
http://www.sp1.football/index.php?document_srl=186648&mid=faq
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/gumdanapt/58745
http://smartacity.com/component/k2/itemlist/user/55295
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1942573
http://jiquilisco.org/?option=com_k2&view=itemlist&task=user&id=10534
http://zanoza.h1n.ru/2019/05/20/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wd1%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/24118
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4841974
https://sanp.pro/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kt8k-%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f/
http://www.teedinubon.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-a1-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80/
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=111946
http://web2interactive.com/index.php/component/k2/itemlist/user/3690519
http://zanoza.h1n.ru/2019/05/20/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ne7%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1152784
http://asin.itts.co.kr/board_rtXs84/10363
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=80015
https://khuyenmaikk13.info/index.php?topic=208623.0
http://xn----3x5er9r48j7wemud0a387h.com/news/50429
http://www.sp1.football/index.php?mid=faq&document_srl=182197
http://mjbosch.com/component/k2/itemlist/user/84089
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1923483
http://www.critico-expository.com/forum/index.php?topic=13449.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3388091
http://universalcommunity.se/Forum/index.php?topic=20305.0
http://shinilspring.com/board_qsfb01/108318
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=66323
http://fbpharm.net/index.php/component/k2/itemlist/user/66014
http://fbpharm.net/index.php/component/k2/itemlist/user/66018
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1950738
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=21574
http://jiquilisco.org/index.php/component/k2/itemlist/user/14312
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=40083
http://married.dike.gr/index.php/component/k2/itemlist/user/70653
http://married.dike.gr/index.php/component/k2/itemlist/user/70655
https://khuyenmaikk13.info/index.php?topic=207961.0
http://socialfbwidgets.com/component/k2/itemlist/user/15157.html
https://mcsetup.tk/bbs/index.php?topic=257391.0
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-18-05-2019-g1-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80/
http://www.almacenesrickie.com.ec/index.php/component/k2/itemlist/user/129847
http://bobr.site/index.php?topic=150754.0
http://vehibook.com/members/mabelrcp09588/
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=e5d37fa8e912a2d04f673ad8fad0de01&topic=6928.0
http://xn--ok1bpqi43ahtb.net/board_eASW07/122221
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=871506
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=150918
http://subforumna.x10.mx/mad/index.php?topic=255470.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1439461
http://xn----3x5er9r48j7wemud0a387h.com/news/35831
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=140733
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=60771
https://testing.celekt.com/%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ha9%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f17-05/
http://www.jesusonly.life/calendar/128496
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/266746
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=185702
http://www.hsaura.com/noty/115822
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=86363
https://ne-kuru.ru/index.php?topic=222827.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=74471
http://www.tekparcahdfilm.com/forum/index.php?topic=51605.0
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=7394
http://www.sollazzorefrigerazione.it/?option=com_k2&view=itemlist&task=user&id=2523466
http://mir3sea.com/forum/index.php?topic=3560.0
http://engeena.com/component/k2/itemlist/user/8861
http://yoriyorifood.com/xxxx/spacial/93848
http://taklongclub.com/forum/index.php?topic=152410.0
http://indiefilm.kr/xe/board/150539
http://corumotoanahtar.com/component/k2/itemlist/user/4197.html
http://www.jesusonly.life/calendar/148563
https://reficulcoin.com/index.php?topic=54344.0
http://www.gforgirl.com/xe/poster/127984
http://www.theparrotcentre.com/forum/index.php?topic=551943.0
http://www.golden-nail.co.kr/press/98988
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3685347
http://xn----3x5er9r48j7wemud0a387h.com/news/35878
http://roikjer.com/forum/index.php?PHPSESSID=i8iuelihah71fk5qln8hr5fgb3&topic=890243.0
http://www.svteck.co.kr/customer_gratitude/51531
http://marjorieaperry.com/?option=com_k2&view=itemlist&task=user&id=497759
http://soc-human.kz/index.php/component/k2/itemlist/user/1703901
http://www.gforgirl.com/xe/poster/130262
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=879452
http://dev.aabn.org.gh/?option=com_k2&view=itemlist&task=user&id=624731
http://vhost12299.cpsite.ru/427561-smotret-soderzanki-9-seria-r8-soderzanki-9-seria
http://zsmr.com.ua/index.php/component/k2/itemlist/user/588135
http://skylinecam.co.kr/photo/119073
http://miklja.net/forum/index.php?topic=31967.0
http://subforumna.x10.mx/mad/index.php?topic=251164.0
http://www.remify.app/foro/index.php?topic=319901.0
https://esel.gist.ac.kr/esel2/board_hmgj23/55212
http://dev.aabn.org.gh/component/k2/itemlist/user/611127
http://indiefilm.kr/xe/board/153360
http://roikjer.com/forum/index.php?PHPSESSID=01g54ttv1tsai2u7buicpps5q3&topic=904260.0
https://forum.ac-jete.it/index.php?topic=396905.0
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qh3%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
http://corumotoanahtar.com/component/k2/itemlist/user/4079.html
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/281561
http://forums.abs-cbn.com/welcome-back-kapamilya%21/oe-ee-1-e-19-05-2019-vcu-oe-ee-1-e/?PHPSESSID=2pf5fdrg0r2p7riuufgcgkemj4
https://ne-kuru.ru/index.php?topic=221559.0
http://indiefilm.kr/xe/board/156195
http://subforumna.x10.mx/mad/index.php?topic=248892.0
http://jjikduk.net/DATA/59282
http://photogrotto.com/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nl4%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
http://ye-dream.com/qa/82557
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=512896
http://mediaville.me/index.php/component/k2/itemlist/user/287538
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2618555
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=78077
http://vhost12299.cpsite.ru/463083-sluga-naroda-3-sezon-21-seria-18052019-p3-sluga-naroda-3-sezon-
http://yoriyorifood.com/xxxx/spacial/125823
http://carrierworld.co.kr/?document_srl=58466
http://www.theocraticamerica.org/forum/index.php?topic=53628.0
https://hackersuniversity.net/index.php?topic=19573.0
http://zanoza.h1n.ru/2019/05/18/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%84%d0%b8%d0%bd%d0%b0%d0%bb-tp%d1%85%d0%be%d0%bb%d0%be/
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=102517
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=24750
http://asin.itts.co.kr/board_rtXs84/6130
http://wigalseguros.com.br/index.php/component/k2/itemlist/user/10851
http://ptu.imoove.kr/ko/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D1%84%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB-bd%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D1%84%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB74-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD
http://poselokgribovo.ru/forum/index.php?topic=806429.0
http://svgrossburgwedel.de/component/k2/itemlist/user/5892
http://www.digitalbul.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-17-05-2019-q5-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80/
https://www.amazingworldtop.com/entretenimiento/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ah6%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://moavalve.co.kr/faq/79524
https://www.shaiyax.com/index.php?topic=365255.0
http://shinhwaair2017.cafe24.com/issue/247292
http://webp.online/index.php?topic=63340.0
http://roikjer.com/forum/index.php?PHPSESSID=7rmsbvchsqkamfaoques6537b0&topic=893610.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/647945
http://www.josephmaul.org/menu41/98621
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/41148
http://photogrotto.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-92-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tv0%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-92-%d1%81%d0%b5%d1%80%d0%b8%d1%8f21-05-2019/
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1941809
http://cwon.kr/xe/board_bnSr36/110011
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/338251
http://corumotoanahtar.com/component/k2/itemlist/user/5738.html
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=175430
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=92505
http://0433.net/junggo/48073
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=103366
http://www.crnmedia.es/?option=com_k2&view=itemlist&task=user&id=86868
http://married.dike.gr/index.php/component/k2/itemlist/user/66490
http://dev.aabn.org.gh/component/k2/itemlist/user/615248
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=642279
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4939510
https://npi.org.es/smf/index.php?topic=119601.0
http://carrierworld.co.kr/?document_srl=71649
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=58945
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=511194
http://guiadetudo.com/?option=com_k2&view=itemlist&task=user&id=12173
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=11787
http://www.cyberblissstudios.com/UserProfile/tabid/42/UserID/2158116/Default.aspx
http://0433.net/junggo/38103
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/510206
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1737747
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=193562
http://www.tessabannampad.go.th/webboard/index.php?topic=214661.0
http://forum.drahthaar-club.com.ua/index.php?topic=5014.0
http://www.digitalbul.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-17-05-2019-h0-%d0%b8%d0%b3%d1%80/
http://rudraautomation.com/index.php/component/k2/author/225549
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=96556
http://masanlib.or.kr/g1/37879
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/222295
http://proxima.co.rw/index.php/component/k2/itemlist/user/657262
http://zanoza.h1n.ru/2019/05/18/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd/
http://shinhwaair2017.cafe24.com/issue/236913
http://maka-222.com/?document_srl=35369
http://www.jesusonly.life/calendar/121000
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8d%d1%84%d0%b8%d1%80-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6/
http://otitismediasociety.org/forum/index.php?topic=174876.0
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=220376
http://teambuildingpremium.com/forum/index.php?topic=861575.0
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3296260
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=86662
http://vhost12299.cpsite.ru/424944-poslednaa-nedela-4-seria-live-poslednaa-nedela-4-seria
http://emjun.com/index.php?mid=hangtotal&document_srl=116372
http://www.phperos.net/foro/index.php?topic=136083.0
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=73195
https://www.tedyun.com/xe/index.php?document_srl=201429&mid=gallery
http://emjun.com/index.php?mid=hangtotal&document_srl=95151
http://daesestudy.co.kr/ipsi_docu/77152
http://shinilspring.com/board_qsfb01/107047
http://emjun.com/index.php?mid=hangtotal&document_srl=86447
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2660700
http://www.jesusonly.life/calendar/160977
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=38582
http://www.digitalbul.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24-05-2019-nx%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24-05-201930-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24/
http://forum.bmw-e60.eu/index.php?topic=8736.0
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-19-qg%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://www.hsaura.com/noty/142497
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=849313
http://mahdi.ehosseini.com/index.php/component/k2/itemlist/user/37837
http://lucky.kidspann.net/?document_srl=75718
http://shinilspring.com/board_qsfb01/102394
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=114632
http://skylinecam.co.kr/?document_srl=96486
http://www.hicleaning.kr/board_wash/153255
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=82640
http://emjun.com/index.php?mid=hangtotal&document_srl=87970
http://www.vogtland.com.pl/index.php/component/k2/itemlist/user/33984
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=35645
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=74928
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2672142
http://emjun.com/?document_srl=86742
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-18-05-2019-s8-%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
http://www.original-craft.net/index.php?topic=341706.0
http://dohairbiz.com/en/component/k2/itemlist/user/2775579.html
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=102584
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=102588
http://fbpharm.net/index.php/component/k2/itemlist/user/66020
http://fbpharm.net/index.php/component/k2/itemlist/user/66057
http://fbpharm.net/index.php/component/k2/itemlist/user/66068
http://fbpharm.net/index.php/component/k2/itemlist/user/66091
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1893452
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1893453
http://grupotir.com/component/k2/itemlist/user/42596
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=352767
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=352770
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=352791
http://web2interactive.com/index.php/component/k2/itemlist/user/3713358
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=107503
http://www.crnmedia.es/component/k2/itemlist/user/88404
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1835442
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/20337
http://www.meuforum.net/index.php?action=profile&u=13877
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=71968
http://www.svteck.co.kr/customer_gratitude/43757
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3378986
http://ru-realty.com/forum/index.php?PHPSESSID=127qsrd7uuo1oipsic5k5k6a35&topic=533961.0
http://www.jesusonly.life/calendar/241042
http://skylinecam.co.kr/photo/79713
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=76624
http://masanlib.or.kr/g1/24947
http://0433.net/junggo/65660
http://0433.net/junggo/65671
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=290572
http://jjikduk.net/DATA/113928
http://jjikduk.net/DATA/113987
http://jjikduk.net/DATA/114009
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1688363
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1467455
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=16617
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=871735
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=871834
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=83459
http://www.telcon.gr/index.php/component/k2/itemlist/user/83467
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/297290
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3415272
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3415282
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3415303
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=8245
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=8253
http://esperanzazubieta.com/component/k2/itemlist/user/102677
http://www.theocraticamerica.org/forum/index.php?topic=48139.0
http://www.teedinubon.com/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-85-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20/
http://www.rationalkorea.com/xe/?document_srl=528463
https://sanp.pro/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sv4%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-8-%d1%81%d0%b5%d1%80/
http://thermoplast.envolgroupe.com/component/k2/author/125113
http://xn--ok1bpqi43ahtb.net/board_eASW07/130411
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3387859
http://www.theparrotcentre.com/forum/index.php?topic=554149.0
http://www.sp1.football/index.php?mid=faq&document_srl=199113
http://www.theocraticamerica.org/forum/index.php/topic,57198.0.html
https://forum.ac-jete.it/index.php?topic=403165.0
http://miklja.net/forum/index.php?topic=31525.0
https://testing.celekt.com/%d0%9d%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d0%a1%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-86-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.remify.app/foro/index.php?topic=320155.0
http://153.120.114.241/eso/index.php/17112997-hd-sluga-naroda-3-sezon-8-seria-q3-sluga-naroda-3-sezon-8-seria
http://www.verenas-unterwasserwelt.de/forum/index.php?topic=7684.0
http://hyeonjun.co.kr/menu3/67475
http://photogrotto.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-97-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-um3%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-97-%d1%81%d0%b5%d1%80%d0%b8%d1%8f20-05-2019/
http://lucky.kidspann.net/index.php?mid=qna&document_srl=66798
http://asin.itts.co.kr/?document_srl=6049
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=50945
http://hyeonjun.co.kr/menu3/71113
http://forum.kopkargobel.com/index.php?topic=11665.0
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/9572
http://corumotoanahtar.com/component/k2/itemlist/user/4707.html
https://prelease.club/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-17-05-19-pn%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=72675
http://moavalve.co.kr/faq/64243
http://rudraautomation.com/index.php/component/k2/author/224524
http://indiefilm.kr/xe/board/147353
http://taklongclub.com/forum/index.php?topic=152836.0
http://www.digitalbul.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-90-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-s1-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-90-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=104713
http://www.vapewatchforum.com/profile/tangelaapm
http://www.gforgirl.com/xe/poster/130365
http://indiefilm.kr/xe/board/147891
http://research.kiu.ac.kr/?document_srl=72647
https://www.2ayes.com/16800/6-17-05-2019-h6-6
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1609654
http://www.hsaura.com/noty/112600
http://www.rationalkorea.com/xe/index.php?document_srl=525293&mid=pqna3
http://www.studyxray.com/Sangdam/150487
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4839272
http://web2interactive.com/index.php/component/k2/itemlist/user/3674182
http://www.studyxray.com/?document_srl=139695
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=69363
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5/
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=113178
https://www.shaiyax.com/index.php?topic=363388.0
https://khuyenmaikk13.info/index.php?topic=207249.0
http://corumotoanahtar.com/component/k2/itemlist/user/4923
http://asin.itts.co.kr/board_rtXs84/7387
http://maka-222.com/index.php?document_srl=24895&mid=board_hcFa40
https://hackersuniversity.net/index.php?topic=19760.0
http://forum.digamahost.com/index.php?topic=126098.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/110597
http://zanoza.h1n.ru/2019/05/20/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-o6-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2/
http://test.comics-game.ru/index.php?topic=124.0
http://www.josephmaul.org/menu41/141033
http://webp.online/index.php?topic=63601.0
http://www.taeshinmedia.com/index.php?document_srl=3308303&mid=genealogy_faq
http://xn--ok1bpqi43ahtb.net/board_eASW07/102440
http://sfah.ch/de/component/k2/itemlist/user/15215
http://www.hsaura.com/noty/144601
http://www.jshwanghoan.com/?document_srl=83489
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3773636
http://forum.drahthaar-club.com.ua/index.php?action=profile;u=2944
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1945572
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=79686
http://atemshow.com/?document_srl=34575
http://otitismediasociety.org/forum/index.php?topic=175573.0
http://0433.net/junggo/44218
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=852243
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=185387
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=342048
http://www.sp1.football/index.php?mid=faq&document_srl=176693
http://shinilspring.com/board_qsfb01/86775
http://www.critico-expository.com/forum/index.php?topic=14035.0
http://www.jesusonly.life/calendar/132395
http://ptu.imoove.kr/ko/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA%C2%BB-tz%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA%C2%BB66-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12
http://www.digitalbul.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qy6h-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=12265
http://vhost12299.cpsite.ru/441143-tola-robot-2-seria-18052019-f4-tola-robot-2-seria
http://indiefilm.kr/xe/board/148264
http://xn--ok1bpqi43ahtb.net/board_eASW07/146578
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=156661
http://otitismediasociety.org/forum/index.php?topic=174895.0
http://0433.net/junggo/41502
http://moavalve.co.kr/?document_srl=87505
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=125972
http://indiefilm.kr/xe/board/107027
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vf7%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://npi.org.es/smf/index.php?topic=119272.0
http://www.hicleaning.kr/board_wash/100964
http://www.teedinubon.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dl5n-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://arnikabolt.ro/component/k2/itemlist/user/111936
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/763000
http://www.jesusonly.life/calendar/137641
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=349544
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=35416
http://www.taeshinmedia.com/index.php?document_srl=3297344&mid=genealogy_faq
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3388620
http://thermoplast.envolgroupe.com/component/k2/itemlist/user/119335
http://forum.elexlabs.com/index.php?topic=45811.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=152152
http://0433.net/junggo/55585
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/18094
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1933663
http://www.digitalbul.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80/
http://hyeonjun.co.kr/menu3/63917
https://adsensebih.com/index.php?topic=26205.0
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-17-05-19-wr%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://www.josephmaul.org/menu41/96359
http://indiefilm.kr/xe/board/110991
https://www.amazingworldtop.com/entretenimiento/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ao3%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-12-%d1%81%d0%b5/
http://indiefilm.kr/xe/board/125238
http://www.arunagreen.com/index.php/component/k2/itemlist/user/555320
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3686485
http://jjikduk.net/DATA/76302
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1607515
https://altaylarteknoloji.com/index.php?topic=4928.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3397305
http://1600-1590.com/?document_srl=117382
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=82718
http://healthyteethpa.org/component/k2/itemlist/user/5490311
http://xn----3x5er9r48j7wemud0a387h.com/news/50662
http://www.svteck.co.kr/customer_gratitude/94553
http://e-educ.net/Forum/index.php?topic=12064.0
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=55459
http://forum.elexlabs.com/index.php?topic=37460.0
http://www.teedinubon.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gg7%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-3-%d1%81%d0%b5%d1%80/
http://corumotoanahtar.com/?option=com_k2&view=itemlist&task=user&id=4593
http://forum.elexlabs.com/index.php?topic=37327.0
http://vhost12299.cpsite.ru/422480-mama-lora-6-seria-17052019-u4-mama-lora-6-seria
https://www.shaiyax.com/index.php?topic=353098.0
http://dessa.com.br/component/k2/itemlist/user/343103
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=122705
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/516415
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=267160
http://forum.digamahost.com/index.php?topic=126618.0
http://bebopindia.com/notcie/99439
http://www.jshwanghoan.com/?document_srl=99664
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1449279
https://www.c-alice.org/forum/index.php?topic=89187.0
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=91656
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=30416
http://ru-realty.com/forum/index.php?PHPSESSID=9el3o4u53utguedribus07ust4&topic=529735.0
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pk9%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2325136
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=92767
http://xn----3x5er9r48j7wemud0a387h.com/news/41591
http://yoriyorifood.com/xxxx/?document_srl=97155
http://thanosakademi.com/index.php?topic=101908.0
https://prelease.club/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-yk%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/338429
http://www.phperos.net/foro/index.php?topic=136724.0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=845061
http://lucky.kidspann.net/index.php?document_srl=60527&mid=qna
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=199254
http://www.jesusonly.life/calendar/147597
http://lucky.kidspann.net/index.php?mid=qna&document_srl=61012
https://www.amazingworldtop.com/entretenimiento/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ij9%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-14-%d1%81%d0%b5/
http://yoriyorifood.com/xxxx/spacial/91347
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ap6%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.studyxray.com/Sangdam/167864
https://npi.org.es/smf/index.php?topic=119638.0
http://0433.net/junggo/55804
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=74216
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=118650
https://testing.celekt.com/%d0%a1%d0%b5%d0%bd%d1%8f%d0%a4%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mk3%d0%a1%d0%b5%d0%bd%d1%8f%d0%a4%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
http://indiefilm.kr/xe/board/120297
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-21-05-2019-b9-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2/
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/278717
https://testing.celekt.com/%d0%a2%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-90-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iq0%d0%a2%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-90-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05-2019/
http://oss.obigo.com/oss/?document_srl=18539
http://www.original-craft.net/index.php?topic=342864.0
http://daesestudy.co.kr/ipsi_docu/49604
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=94492
http://carrierworld.co.kr/?document_srl=73385
https://www.amazingworldtop.com/entretenimiento/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lq6%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-11-%d1%81%d0%b5/
http://www.tessabannampad.go.th/webboard/index.php?topic=214002.0
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=62344
https://esel.gist.ac.kr/esel2/board_hmgj23/63300
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3293234
http://www.studyxray.com/Sangdam/114076
http://otitismediasociety.org/forum/index.php?topic=184216.0
http://hyeonjun.co.kr/menu3/77657
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=166758
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4844695
http://mediaville.me/index.php/component/k2/itemlist/user/287661
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/gumdanapt/53070
http://cwon.kr/xe/board_bnSr36/109052
http://engeena.com/index.php/component/k2/itemlist/user/8818
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=128598
http://indiefilm.kr/xe/board/123914
https://reficulcoin.com/index.php?topic=50573.0
https://testing.celekt.com/%d0%a7%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-by8l-%d0%a7%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl-5-%d1%81%d0%b5/
http://www.arunagreen.com/index.php/component/k2/itemlist/user/546501
http://www.theocraticamerica.org/forum/index.php/topic,48513.0.html
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1105822
http://indiefilm.kr/xe/board/139794
http://bobr.site/index.php?topic=150369.0
http://poselokgribovo.ru/forum/index.php?topic=804474.0
http://sixangles.co.kr/?document_srl=597386
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2671157
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1732178
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1706220
http://ru-realty.com/forum/index.php?PHPSESSID=mllrpir3i3a1d9h06uc5qccfn4&topic=532747.0
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=495033
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2322251
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=137117
http://universalcommunity.se/Forum/index.php?topic=16132.0
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=341249
http://www.phperos.net/foro/index.php?topic=136578.0
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=81714
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=129666
http://www.sp1.football/index.php?mid=faq&document_srl=178851
http://www.tessabannampad.go.th/webboard/index.php?topic=213880.0
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ic7%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.theparrotcentre.com/forum/index.php?topic=555592.0
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=81286
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=74253
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=194468
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=528268
http://0433.net/junggo/54238
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=343525
https://testing.celekt.com/%d0%9f%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wv7%d0%9f%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
http://www.josephmaul.org/menu41/103863
http://corumotoanahtar.com/component/k2/itemlist/user/5019.html
http://jjikduk.net/DATA/57479
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=195858
http://www.original-craft.net/index.php?topic=336771.0
http://research.kiu.ac.kr/?document_srl=87486
http://forum.drahthaar-club.com.ua/index.php?topic=3213.0
http://ye-dream.com/qa/87569
https://cybergsm.es/index.php?topic=31816.0
http://www.jesusonly.life/calendar/152910
http://moavalve.co.kr/faq/67564
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=101493
https://altaylarteknoloji.com/index.php?topic=5119.0
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1827372
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/522360
http://www.spazioad.com/component/k2/itemlist/user/7346839
http://withinfp.sakura.ne.jp/eso/index.php/17150573-vetrenyj-hercai-19-seria-yrzs-vetrenyj-hercai-19-seria
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=35690
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=142753
http://bebopindia.com/?document_srl=165942
http://www.lustralesdevallehermoso.com/index.php/component/k2/itemlist/user/48568
http://masanlib.or.kr/g1/33249
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=73314
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=122696
http://www.almacenesrickie.com.ec/index.php/component/k2/itemlist/user/127724
http://www.taeshinmedia.com/index.php?document_srl=3302781&mid=genealogy_faq
https://testing.celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-og5%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://otitismediasociety.org/forum/index.php?topic=184022.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=f686a6cba29ce232451c591c3269fa8a&topic=7643.0
http://zanoza.h1n.ru/2019/05/19/%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0%d1%88%d0%ba%d0%b0-erkenci-kus-42-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-psnk-%d1%80%d0%b0%d0%bd%d0%bd%d1%8f%d1%8f-%d0%bf%d1%82%d0%b0/
http://otitismediasociety.org/forum/index.php?topic=175461.0
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=83011
http://www.hicleaning.kr/board_wash/98181
http://lucky.kidspann.net/index.php?mid=qna&document_srl=62500
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=124507
http://forum.drahthaar-club.com.ua/index.php?topic=3229.0
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=32463
http://vhost12299.cpsite.ru/531083-tola-robot-1-seria-live-tola-robot-1-seria
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d1%85%d0%be/
http://forum.elexlabs.com/index.php/topic,39255.0.html
http://www.josephmaul.org/menu41/125507
http://www.svteck.co.kr/customer_gratitude/37597
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=346510
http://www.theocraticamerica.org/forum/index.php?topic=49288.0
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=83205
http://masanlib.or.kr/g1/41021
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=523712
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2625791
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=600757
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1219432
http://www.josephmaul.org/menu41/98369
https://afikgan.co.il/index.php/component/k2/itemlist/user/28848
http://lucky.kidspann.net/index.php?document_srl=77191&mid=qna
http://k-cea.org/board_Hnyj62/89376
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=218531
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=268011
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=122559
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wg3%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-3-%d1%81%d0%b5%d1%80/
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=43630
http://rudraautomation.com/index.php/component/k2/author/228837
http://indiefilm.kr/xe/board/110823
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=341340
https://sanp.pro/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-et6%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f21-05-2019/
https://adsensebih.com/index.php?topic=24575.0
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=170234
http://yoriyorifood.com/xxxx/spacial/160132
http://yoriyorifood.com/xxxx/spacial/160172
https://esel.gist.ac.kr/esel2/board_hmgj23/133002
https://esel.gist.ac.kr/esel2/board_hmgj23/133012
https://esel.gist.ac.kr/esel2/board_hmgj23/133017
https://esel.gist.ac.kr/esel2/board_hmgj23/133087
http://thermoplast.envolgroupe.com/component/k2/author/123122
http://forum.digamahost.com/index.php?topic=126370.0
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=34459
http://fbpharm.net/index.php/component/k2/itemlist/user/49694
http://forum.elexlabs.com/index.php?topic=44239.0
http://hyeonjun.co.kr/menu3/94260
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-mn%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
https://testing.celekt.com/%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hj8s-%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://indiefilm.kr/xe/board/114500
http://xn--ok1bpqi43ahtb.net/board_eASW07/105412
http://zanoza.h1n.ru/2019/05/20/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-l9-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
https://khuyenmaikk13.info/index.php?topic=209250.0
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=181733
http://www.digitalbul.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%84%d0%b8%d0%bd%d0%b0%d0%bb-dk%d1%85%d0%be%d0%bb%d0%be/
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=54402
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=58356
https://sanp.pro/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zc5%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=523063
http://0433.net/junggo/48249
http://www.josephmaul.org/menu41/217696
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=183399
http://www.original-craft.net/index.php?topic=345087.0
http://www.rationalkorea.com/xe/?document_srl=583884
http://www.rationalkorea.com/xe/?document_srl=583903
http://proxima.co.rw/index.php/component/k2/itemlist/user/651498
http://teambuildingpremium.com/forum/index.php?topic=860185.0
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=80231
https://reficulcoin.com/index.php?topic=52312.0
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=10105
http://sixangles.co.kr/qna/639982
https://prelease.club/%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-70-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kwml-%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-70/
https://testing.celekt.com/%d0%a7%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-2019-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hb3%d0%a7%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-2019-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.jesusonly.life/calendar/135589
http://indiefilm.kr/xe/board/117880
http://www.studyxray.com/Sangdam/146739
http://www.josephmaul.org/menu41/140887
http://www.golden-nail.co.kr/press/103511
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2779011
http://www.hicleaning.kr/board_wash/108239
http://withinfp.sakura.ne.jp/eso/index.php/17120702-serial-cuzaa-zizn-cuze-zitta-4-seria-x7-cuzaa-zizn-cuze-zitta-4
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1688000
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1467221
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1467228
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1467241
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1126490
http://www.crnmedia.es/component/k2/itemlist/user/88403
http://www.firstfinancialservices.co.uk/?option=com_k2&view=itemlist&task=user&id=20522
http://www.firstfinancialservices.co.uk/component/k2/itemlist/user/20510
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/20519
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3512210
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1446612
http://www.studyxray.com/Sangdam/122807
https://sanp.pro/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-to1%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f19-05-2019/
http://www.quattroandpartners.it/component/k2/itemlist/user/1156121
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4830936
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=92813
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3308755
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=181768
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=0d01b6c5bf8181ecf993f4b80545e41c&topic=7063.0
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=507096
https://adsensebih.com/index.php?topic=28071.0
https://www.2ayes.com/16809/8-6-17-05-2019-k1-8-6
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xx9%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f19-05/
http://www.hsaura.com/noty/119892
http://zanoza.h1n.ru/2019/05/21/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-av5%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://mobility-corp.com/index.php/component/k2/itemlist/user/2618073
http://www.digitalbul.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-17-05-2019-p4-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
https://sanp.pro/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-92-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-be2%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-92/
http://www.theocraticamerica.org/forum/index.php?topic=53487.0
https://tg.vl-mp.com/index.php?topic=1474810.0
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=66500
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/515288
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=74950
http://www.ds712.net/guest/?document_srl=127943
http://www.studyxray.com/Sangdam/113091
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=84343
http://www.jesusonly.life/?document_srl=120984
http://0433.net/junggo/50810
https://esel.gist.ac.kr/esel2/board_hmgj23/56476
http://www.hsaura.com/?document_srl=117606
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=855228
http://bobr.site/index.php?topic=151739.0
http://zanoza.h1n.ru/2019/05/20/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-97-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ve8%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-97/
http://soc-human.kz/index.php/component/k2/itemlist/user/1706413
http://photogrotto.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pj7d-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://cwon.kr/xe/board_bnSr36/82044
http://indiefilm.kr/xe/board/124285
http://esperanzazubieta.com/component/k2/itemlist/user/100767
http://www.josephmaul.org/menu41/131319
http://haeple.com/index.php?mid=etc&document_srl=86054
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3683862
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=92050
https://www.vegasgreentour.com/index.php?document_srl=82571&mid=board_XiHh59
http://forum.elexlabs.com/index.php?topic=41834.0
http://zanoza.h1n.ru/2019/05/20/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zz5%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=137101
http://jiquilisco.org/index.php/component/k2/itemlist/user/8632
https://cybergsm.es/index.php?topic=26763.0
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=82247
http://thermoplast.envolgroupe.com/component/k2/author/118904
http://yoriyorifood.com/xxxx/spacial/102883
http://xplorefitness.com/blog/%C2%AB%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-94-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%D0%B2-%D1%8D%D1%84%D0%B8%D1%80%D0%B5-%C2%AB%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-94-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=94859
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=341647
http://shinilspring.com/board_qsfb01/92749
http://lucky.kidspann.net/?document_srl=86872
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=7340
http://xn--ok1bpqi43ahtb.net/board_eASW07/134630
http://www.sp1.football/index.php?mid=faq&document_srl=193226
http://www.theparrotcentre.com/forum/index.php?topic=550544.0
http://azone.synology.me/xe/?document_srl=96508
http://www.original-craft.net/index.php?topic=335610.0
http://www.original-craft.net/index.php?topic=337169.0
http://e-educ.net/Forum/index.php?topic=12794.0
https://sanp.pro/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-89-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sv9%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-89/
http://asiagroup.co.kr/index.php?document_srl=201749&mid=board_11
http://www.gforgirl.com/xe/poster/118251
http://israengineering.com/index.php/component/k2/itemlist/user/1217874
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=231761
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=88656
http://otitismediasociety.org/forum/index.php?topic=174737.0
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=79228
http://vhost12299.cpsite.ru/498067-taemnici-89-seria-19052019-q9-taemnici-89-seria
http://shinilspring.com/board_qsfb01/101428
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=80584
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=23090
https://altaylarteknoloji.com/index.php?topic=5200.0
http://xn--ok1bpqi43ahtb.net/board_eASW07/120314
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=74132
http://teambuildingpremium.com/forum/index.php?topic=845688.0
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=77141
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/gumdanapt/77591
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=112872
http://www.gforgirl.com/xe/poster/114069
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=73788
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=85706
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1944038
http://zanoza.h1n.ru/2019/05/18/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d0%b1%d0%be%d0%bb%d1%8c%d1%88/
http://indiefilm.kr/xe/board/134647
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=70233
http://corumotoanahtar.com/component/k2/itemlist/user/4358.html
http://zanoza.h1n.ru/2019/05/22/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dh8%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://zanoza.h1n.ru/2019/05/22/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wp0%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://zanoza.h1n.ru/2019/05/22/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-96-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iz0%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-96/
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-so4%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mg8%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=67600
http://fbpharm.net/index.php/component/k2/itemlist/user/67299
http://fbpharm.net/index.php/component/k2/itemlist/user/67498
http://fbpharm.net/index.php/component/k2/itemlist/user/67632
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=70894
http://mediaville.me/index.php/component/k2/itemlist/user/307287
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/127474
http://proxima.co.rw/index.php/component/k2/itemlist/user/668908
http://rudraautomation.com/index.php/component/k2/author/250088
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2352224
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1725770
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1725792
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1762504
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1762515
http://carrierworld.co.kr/?document_srl=72045
http://hyeonjun.co.kr/?document_srl=155002
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4843724
http://zanoza.h1n.ru/2019/05/19/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-rk0%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5/
http://mobility-corp.com/index.php/component/k2/itemlist/user/2614818
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=68995
http://www.jesusonly.life/calendar/130374
http://vhost12299.cpsite.ru/420010-live-sluga-naroda-3-sezon-17-seria-i0-sluga-naroda-3-sezon-17-s
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=81451
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=87932
http://zanoza.h1n.ru/2019/05/20/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%8d%d1%84%d0%b8%d1%80-%d1%85%d0%be%d0%bb%d0%be/
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-zm%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
https://www.amazingworldtop.com/entretenimiento/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pb8%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05-2019/
http://masanlib.or.kr/g1/23661
http://emjun.com/index.php?mid=hangtotal&document_srl=104014
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=83039
http://indiefilm.kr/xe/board/157760
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=71041
http://0433.net/?document_srl=40612
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-2019-ng%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://asiagroup.co.kr/?document_srl=192717
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=220981
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=497679
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=52465
http://vtservices85.fr/smf2/index.php?topic=257957.0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=853469
http://www.critico-expository.com/forum/index.php?topic=14050.0
http://sixangles.co.kr/qna/639272
http://shinilspring.com/board_qsfb01/93398
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ik4%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.hsaura.com/noty/115286
http://www.hicleaning.kr/?document_srl=116905
http://zanoza.h1n.ru/2019/05/20/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-b5-%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4/
http://bebopindia.com/notcie/109061
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1922764
https://forum.ac-jete.it/index.php?topic=396983.0
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=108276
https://www.tedyun.com/xe/?document_srl=199859
http://poselokgribovo.ru/forum/index.php?topic=804219.0
https://cybergsm.es/index.php?topic=28081.0
https://tg.vl-mp.com/index.php?topic=1474489.0
http://www.golden-nail.co.kr/press/100931
http://www.golden-nail.co.kr/press/70525
http://forum.kopkargobel.com/index.php?topic=11828.0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=644969
http://ye-dream.com/?document_srl=90235
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/16292
http://ye-dream.com/qa/92310
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/526031
http://ye-dream.com/qa/80446
http://lucky.kidspann.net/index.php?mid=qna&document_srl=75713
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=81362
http://bitpark.co.kr/board_IzjM66/4010631
http://www.boutique.in.th/?option=com_k2&view=itemlist&task=user&id=151575
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=851331
http://shinilspring.com/board_qsfb01/98468
https://www.amazingworldtop.com/entretenimiento/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-99-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ov3%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-99/
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=84726
http://photogrotto.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-96-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-re8h-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-96-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sanp.pro/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-hq8%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5/
http://soc-human.kz/index.php/component/k2/itemlist/user/1712806
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=13249
http://shinilspring.com/board_qsfb01/90150
http://vhost12299.cpsite.ru/551996-smotret-tajny-99-seria-w6-tajny-99-seria
http://vhost12299.cpsite.ru/552033-novinka-smers-5-seria-j7-smers-5-seria
http://vhost12299.cpsite.ru/552041-smotret-dockimateri-dockimateri-16-seria-f0-dockimateri-dockima
http://vhost12299.cpsite.ru/552065-hdvideo-smers-8-seria-o3-smers-8-seria
http://vhost12299.cpsite.ru/552077-efir-grand-2-sezon-21-seria-e5-grand-2-sezon-21-seria
http://vhost12299.cpsite.ru/552088-cuzaa-zizn-cuze-zitta-2-seria-r9-cuzaa-zizn-cuze-zitta-2-seria
http://vhost12299.cpsite.ru/552102-efir-sluga-naroda-3-sezon-15-seria-x0-sluga-naroda-3-sezon-15-s
http://vhost12299.cpsite.ru/552119-efir-dockimateri-dockimateri-15-seria
http://vhost12299.cpsite.ru/552193-live-dockimateri-dockimateri-16-seria-d7-dockimateri-dockimater
http://vhost12299.cpsite.ru/552217-live-cuzaa-zizn-cuze-zitta-13-seria-p8-cuzaa-zizn-cuze-zitta-13
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3715944
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=17216
https://sanp.pro/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nm3%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f17-05-2019/
http://www.jesusonly.life/calendar/120075
http://mediaville.me/?option=com_k2&view=itemlist&task=user&id=289550
http://www.theparrotcentre.com/forum/index.php?topic=548512.0
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/38994
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=192418
http://mir3sea.com/forum/index.php?topic=3558.0
http://xplorefitness.com/blog/%C2%AB%D0%B1%D0%BE%D0%BB%D1%8C%D1%88%D0%B5-%D0%B6%D0%B8%D0%B7%D0%BD%D0%B8-14-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-%C2%AB%D0%B1%D0%BE%D0%BB%D1%8C%D1%88%D0%B5-%D0%B6%D0%B8%D0%B7%D0%BD%D0%B8-14-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=206342
http://www.josephmaul.org/?document_srl=90325
http://vhost12299.cpsite.ru/489094-senafeda-2-sezon-13-seria-19052019-m2-senafeda-2-sezon-13-seria
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/109748
http://www.teedinubon.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xi3%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05/
http://www.teedinubon.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-le0%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=71775
http://www.proandpro.it/?option=com_k2&view=itemlist&task=user&id=4627244
http://rudraautomation.com/index.php/component/k2/author/218066
http://forum.digamahost.com/index.php?topic=126189.0
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=85789
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=82751
http://xn--ok1bpqi43ahtb.net/board_eASW07/128649
http://yoriyorifood.com/xxxx/spacial/167506
http://yoriyorifood.com/xxxx/spacial/167522
https://esel.gist.ac.kr/esel2/board_hmgj23/145497
https://esel.gist.ac.kr/esel2/board_hmgj23/145558
https://esel.gist.ac.kr/esel2/board_hmgj23/145568
https://esel.gist.ac.kr/esel2/board_hmgj23/145612
https://esel.gist.ac.kr/esel2/board_hmgj23/145649
https://esel.gist.ac.kr/esel2/board_hmgj23/145667
https://www.amazingworldtop.com/entretenimiento/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-oy3%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
http://daesestudy.co.kr/ipsi_docu/47178
http://web2interactive.com/index.php/component/k2/itemlist/user/3684654
http://shinilspring.com/board_qsfb01/100785
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/276356
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=113444
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=96921
https://testing.celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-x0-%d0%98%d0%b3%d1%80/
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-rj%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://www.jesusonly.life/calendar/124314
http://emjun.com/?document_srl=79272
http://dev.aabn.org.gh/component/k2/itemlist/user/618716
http://vhost12299.cpsite.ru/480469-sluga-naroda-3-sezon-18-seria-18052019-f5-sluga-naroda-3-sezon-
http://www.digitalbul.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-2019-jy%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://indiefilm.kr/xe/board/146591
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-aw5%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://www.amazingworldtop.com/entretenimiento/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-93-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ad1%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-93/
http://universalcommunity.se/Forum/index.php?topic=17392.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1224256
http://0433.net/junggo/69116
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=300824
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=184932
http://community.viajar.tur.br/index.php?p=/profile/MirtaWorga
http://community.viajar.tur.br/index.php?p=/profile/huldaamado
http://lucky.kidspann.net/index.php?document_srl=173649&mid=qna
http://lucky.kidspann.net/index.php?mid=qna&document_srl=173919
http://lucky.kidspann.net/index.php?mid=qna&document_srl=173944
http://www.hicleaning.kr/board_wash/176324
http://www.hicleaning.kr/board_wash/176365
http://www.jshwanghoan.com/?document_srl=191555
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=191565
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=591917
http://www2.yasothon.go.th/smf/index.php?topic=159.166080
http://svgrossburgwedel.de/component/k2/itemlist/user/5934
http://rudraautomation.com/index.php/component/k2/author/225113
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1106155
http://mediaville.me/index.php/component/k2/itemlist/user/291097
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2327195
http://atemshow.com/atemfair_domestic/42478
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1744247
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=71698
http://www.svteck.co.kr/customer_gratitude/36535
http://e-educ.net/Forum/index.php?topic=13201.0
http://dev.aabn.org.gh/component/k2/itemlist/user/612596
http://thermoplast.envolgroupe.com/component/k2/author/125483
http://www.dap.com.py/index.php/component/k2/itemlist/user/825653
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=73109
http://forum.elexlabs.com/index.php?topic=38103.0
http://www.teedinubon.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-i3-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://necinsurance.co.zw/component/k2/itemlist/user/21141.html
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=83287
http://zanoza.h1n.ru/2019/05/20/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82-2/
http://atemshow.com/atemfair_domestic/59940
https://testing.celekt.com/%d0%9f%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bd3%d0%9f%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
http://forum.digamahost.com/index.php?topic=129255.0
http://www.sp1.football/index.php?mid=faq&document_srl=197991
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=17226
https://esel.gist.ac.kr/esel2/board_hmgj23/69914
https://www.shaiyax.com/index.php?topic=352954.0
http://atemshow.com/atemfair_domestic/40378
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=138975
http://ovotecegg.com/component/k2/itemlist/user/161135
http://emjun.com/?document_srl=97450
https://prelease.club/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-id%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://www.teedinubon.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-94-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-eg7%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-94-%d1%81%d0%b5%d1%80%d0%b8%d1%8f17-05-2019/
http://rudraautomation.com/index.php/component/k2/author/232355
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=83477
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=100038
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=146919
http://vehibook.com/members/helenemarvin62/
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=83843
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=341302
http://smartacity.com/component/k2/itemlist/user/52898
http://carrierworld.co.kr/?document_srl=73408
http://www.almacenesrickie.com.ec/index.php/component/k2/itemlist/user/127709
http://www.gforgirl.com/xe/poster/125511
http://thermoplast.envolgroupe.com/component/k2/author/127539
http://bitpark.co.kr/board_IzjM66/4031715
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rm5%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-8-%d1%81%d0%b5%d1%80/
http://emjun.com/index.php?mid=hangtotal&document_srl=96924
https://afikgan.co.il/index.php/component/k2/itemlist/user/28868
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3398894
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=100086
http://www.sp1.football/index.php?mid=faq&document_srl=408209
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=861032
http://indiefilm.kr/xe/?document_srl=112459
http://skylinecam.co.kr/photo/78278
http://www.tessabannampad.go.th/webboard/index.php?topic=213614.0
http://www.sp1.football/index.php?mid=faq&document_srl=179658
http://www.sp1.football/index.php?mid=faq&document_srl=231519
https://cybergsm.es/index.php?topic=26185.0
http://www.theocraticamerica.org/forum/index.php?topic=47664.0
http://shinilspring.com/board_qsfb01/95944
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-md0%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-7-%d1%81%d0%b5%d1%80/
https://testing.celekt.com/%d0%a2%d0%b0%d0%b9%d0%bd%d1%8b-%d0%a2%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-92-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zw2m-%d0%a2%d0%b0%d0%b9%d0%bd%d1%8b-%d0%a2%d0%b0%d1%94%d0%bc%d0%bd/
http://www.digitalbul.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-5-%d1%81/
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ls0%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3301491
https://reficulcoin.com/index.php?topic=52756.0
http://bebopindia.com/notcie/98457
http://www.jesusonly.life/calendar/136961
http://dev.aabn.org.gh/component/k2/itemlist/user/618277
http://ovotecegg.com/component/k2/itemlist/user/164329
http://dev.aabn.org.gh/component/k2/itemlist/user/618263
http://www.josephmaul.org/menu41/95601
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=200274
http://atemshow.com/atemfair_domestic/62119
http://xn--ok1bpqi43ahtb.net/board_EkDG82/116796
http://asin.itts.co.kr/board_rtXs84/14167
http://roikjer.com/forum/index.php?PHPSESSID=k26c5hhtfb6gph9q6fbp6f9eh6&topic=902203.0
http://yoriyorifood.com/xxxx/spacial/94085
http://vhost12299.cpsite.ru/530477-senafeda-2-sezon-8-seria-smotret-senafeda-2-sezon-8-seria
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-u2-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=17907
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=524231
http://emjun.com/index.php?mid=hangtotal&document_srl=76828
http://www.boutique.in.th/?option=com_k2&view=itemlist&task=user&id=151531
http://0433.net/junggo/37769
http://www.hsaura.com/noty/148607
https://testing.celekt.com/%d0%a2%d0%b0%d0%b9%d0%bd%d1%8b-%d0%a2%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-91-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-za9%d0%a2%d0%b0%d0%b9%d0%bd%d1%8b-%d0%a2%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-91/
http://www.svteck.co.kr/customer_gratitude/62284
http://0433.net/junggo/71124
http://0433.net/junggo/71130
http://0433.net/junggo/71136
http://153.120.114.241/eso/index.php/17378351-zestokij-stambul-zalim-istanbul-13-seria-eeqg-zestokij-stambul-
http://asiagroup.co.kr/index.php?document_srl=307619&mid=board_11
http://bitpark.co.kr/board_IzjM66/4118049
http://community.viajar.tur.br/index.php?p=/discussion/62346/vetrenyy-hercai-22-seriya-ctyh-vetrenyy-hercai-22-seriya
http://community.viajar.tur.br/index.php?p=/discussion/62348/rannyaya-ptashka-erkenci-kus-42-seriya-pkbr-rannyaya-ptashka-erkenci-kus-42-seriya/p1%3Fnew=1
http://community.viajar.tur.br/index.php?p=/discussion/62349/klyatva-yemin-58-seriya-bcnx-klyatva-yemin-58-seriya/p1%3Fnew=1
http://jjikduk.net/DATA/120599
http://jjikduk.net/DATA/120615
http://jjikduk.net/DATA/120669
http://jjikduk.net/DATA/120710
http://lucky.kidspann.net/index.php?mid=qna&document_srl=181159
http://lucky.kidspann.net/index.php?mid=qna&document_srl=181184
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=872709
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/872674
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/352495
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=8394
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2699324
http://arquitectosenreformas.es/index.php/component/k2/itemlist/user/83635
http://dcasociados.eu/component/k2/itemlist/user/91324
http://dev.aabn.org.gh/component/k2/itemlist/user/640878
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1962601
http://gtupuw.org/index.php/component/k2/itemlist/user/1951999
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=890808
http://thermoplast.envolgroupe.com/component/k2/author/120550
http://www.svteck.co.kr/customer_gratitude/66363
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qy1%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://forum.bmw-e60.eu/index.php?topic=8409.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1737704
http://carrierworld.co.kr/?document_srl=82781
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=83641
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=68037
http://proxima.co.rw/index.php/component/k2/itemlist/user/644278
http://skangseo.org/xe/board_Atnj46/42721
http://www.tessabannampad.go.th/webboard/index.php?topic=215210.0
http://roikjer.com/forum/index.php?PHPSESSID=s67t1t1m6rvrdm0l92hs43uc83&topic=903810.0
http://www.theocraticamerica.org/forum/index.php/topic,50337.0.html
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/345705
http://dohairbiz.com/en/component/k2/itemlist/user/2766718.html
http://universalcommunity.se/Forum/index.php?topic=16418.0
http://www.theparrotcentre.com/forum/index.php?topic=549874.0
http://www.sp1.football/?document_srl=192681
https://hackersuniversity.net/index.php?topic=22057.0
http://0433.net/junggo/52525
http://sfah.ch/de/component/k2/itemlist/user/15265
http://masanlib.or.kr/?document_srl=27710
http://sixangles.co.kr/?document_srl=613300
http://moavalve.co.kr/faq/77387
https://reficulcoin.com/index.php?topic=53263.0
http://zanoza.h1n.ru/2019/05/20/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-x5-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4/
http://www.jesusonly.life/calendar/148232
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=846341
http://www.sp1.football/index.php?mid=faq&document_srl=258059
http://moavalve.co.kr/faq/81476
http://dessa.com.br/component/k2/itemlist/user/349308
http://xn--ok1bpqi43ahtb.net/board_eASW07/101342
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=110088
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/gumdanapt/78366
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=64012
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/224584
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=193974
http://research.kiu.ac.kr/?document_srl=101976
http://thermoplast.envolgroupe.com/component/k2/author/123726
https://altaylarteknoloji.com/index.php?topic=5602.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/643856
http://yoriyorifood.com/xxxx/spacial/102888
http://bebopindia.com/notcie/121433
https://www.amazingworldtop.com/entretenimiento/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hs8%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1957852
https://turimex.mx.solemti.net/index.php/component/k2/itemlist/user/5060
http://xn----3x5er9r48j7wemud0a387h.com/news/33677
http://0433.net/junggo/43332
http://rudraautomation.com/index.php/component/k2/author/223881
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=86382
http://www.rationalkorea.com/xe/index.php?document_srl=511860&mid=pqna3
https://testing.celekt.com/%d0%a2%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-89-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yf3%d0%a2%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-89-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05-2019/
http://indiefilm.kr/xe/board/130448
http://www.boutique.in.th/?option=com_k2&view=itemlist&task=user&id=151583
http://skylinecam.co.kr/photo/126359
http://www.josephmaul.org/menu41/106065
http://zanoza.h1n.ru/2019/05/19/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-94-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fa8%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-94/
http://hyeonjun.co.kr/menu3/76338
http://teambuildingpremium.com/forum/index.php?topic=864173.0
http://www.hsaura.com/noty/116228
http://sixangles.co.kr/qna/636189
http://emjun.com/index.php?mid=hangtotal&document_srl=97993
https://testing.celekt.com/%d0%a5%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-19-qd%d0%a5%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://www.sp1.football/index.php?mid=faq&document_srl=182671
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=80852
http://www.digitalbul.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-91-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-91-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=646799
http://yoriyorifood.com/xxxx/spacial/110005
https://altaylarteknoloji.com/index.php?topic=5368.0
http://emjun.com/index.php?mid=hangtotal&document_srl=89498
https://testing.celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%9d%d0%9e%d0%92%d0%98%d0%9d%d0%9a/
http://proxima.co.rw/index.php/component/k2/itemlist/user/644881
http://www.teedinubon.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tk8%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-2-%d1%81%d0%b5%d1%80/
http://www.theocraticamerica.org/forum/index.php?topic=53310.0
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=88776
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=13437
http://www.hicleaning.kr/board_wash/138565
http://atemshow.com/atemfair_domestic/64469
https://www.vegasgreentour.com/?document_srl=129901
http://rudraautomation.com/index.php/component/k2/author/225222
http://indiefilm.kr/xe/board/120202
http://zanoza.h1n.ru/2019/05/19/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ja5%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
https://khuyenmaikk13.info/index.php?topic=207723.0
http://jiquilisco.org/index.php/component/k2/itemlist/user/9025
http://www.gforgirl.com/xe/poster/137822
https://prelease.club/%d0%b2%d0%be%d1%81%d0%ba%d1%80%d0%b5%d1%81%d1%88%d0%b8%d0%b9-%d1%8d%d1%80%d1%82%d1%83%d0%b3%d1%80%d1%83%d0%bb-150-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gklq-%d0%b2%d0%be%d1%81%d0%ba%d1%80/
http://www.gforgirl.com/xe/poster/138259
http://zanoza.h1n.ru/2019/05/21/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lz3%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://teambuildingpremium.com/forum/index.php?topic=843762.0
http://esperanzazubieta.com/index.php/component/k2/itemlist/user/100919
http://skylinecam.co.kr/photo/110614
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3314815
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=94765
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/58271
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=20139
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/338781
http://www2.yasothon.go.th/smf/index.php?topic=159.166320
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=86558
http://fbpharm.net/index.php/component/k2/itemlist/user/52749
http://withinfp.sakura.ne.jp/eso/index.php/17141561-bogatye-i-bednye-zengin-ve-yoksul-9-seria-madg-bogatye-i-bednye/0
http://mir3sea.com/forum/index.php?topic=3583.0
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=89425
http://www.svteck.co.kr/customer_gratitude/37174
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=12657
http://www.jshwanghoan.com/?document_srl=76031
http://bebopindia.com/notcie/114927
http://indiefilm.kr/xe/board/116841
https://cybergsm.es/index.php?topic=35223.0
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=117826
https://mcsetup.tk/bbs/index.php?topic=254786.0
http://skylinecam.co.kr/photo/89636
https://cybergsm.es/index.php?topic=32288.0
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=98917
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/gumdanapt/85819
http://ye-dream.com/qa/77660
http://bebopindia.com/notcie/107789
http://skylinecam.co.kr/photo/95430
http://www.original-craft.net/index.php?topic=334788.0
http://maka-222.com/?document_srl=25084
http://lucky.kidspann.net/?document_srl=59493
http://www.arunagreen.com/index.php/component/k2/itemlist/user/545566
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/264222
http://www.sp1.football/index.php?mid=faq&document_srl=217783
http://www.teedinubon.com/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-i7-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/339154
http://www.original-craft.net/index.php?topic=334543.0
http://www.teedinubon.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nb3%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f20-05/
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2624279
http://emjun.com/index.php?mid=hangtotal&document_srl=77116
http://emjun.com/index.php?mid=hangtotal&document_srl=74513
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=97035
http://daesestudy.co.kr/ipsi_docu/76613
http://research.kiu.ac.kr/index.php?document_srl=60763&mid=Food4Thought
http://moavalve.co.kr/faq/63131
http://www.critico-expository.com/forum/index.php?topic=14923.0
http://www.golden-nail.co.kr/press/70498
http://skylinecam.co.kr/?document_srl=98501
http://www.digitalbul.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d0%b1%d0%be%d0%bb%d1%8c%d1%88/
http://skylinecam.co.kr/photo/80619
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=107102
http://atemshow.com/atemfair_domestic/59728
http://www.gforgirl.com/xe/poster/116179
http://www.golden-nail.co.kr/press/103735
http://153.120.114.241/eso/index.php/17127994-holostak-9-sezon-11-vypusk-17-05-2019-epholostak-9-sezon-11-vyp
http://adsudoeste.com.br/index.php/component/k2/itemlist/user/22140
http://thermoplast.envolgroupe.com/component/k2/author/122353
http://photogrotto.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vf1%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-10-%d1%81%d0%b5/
http://teambuildingpremium.com/forum/index.php?topic=862426.0
http://jjikduk.net/DATA/92425
http://www.teedinubon.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ls5%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f17-05-2019/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/343028
https://www.tedyun.com/xe/?document_srl=193314
http://emjun.com/index.php?mid=hangtotal&document_srl=111077
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2327471
http://www.critico-expository.com/forum/index.php?topic=14728.0
http://forum.drahthaar-club.com.ua/index.php?topic=3248.0
https://testing.celekt.com/%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-b6-%d0%a1%d0%bb%d1%83%d0%b3%d0%b0/
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1672665
http://yoriyorifood.com/xxxx/spacial/101884
http://www.proandpro.it/?option=com_k2&view=itemlist&task=user&id=4643957
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/10339
http://shinilspring.com/board_qsfb01/109318
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3379488
http://lucky.kidspann.net/index.php?mid=qna&document_srl=80860
http://www.sp1.football/index.php?mid=faq&document_srl=184220
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1825507
http://hyeonjun.co.kr/menu3/71785
https://testing.celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cd3%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=49448
http://thanosakademi.com/index.php?topic=96281.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2657755
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/227067
http://jiquilisco.org/index.php/component/k2/itemlist/user/11351
https://esel.gist.ac.kr/esel2/board_hmgj23/52852
http://www.golden-nail.co.kr/press/102247
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=79268
http://asiagroup.co.kr/index.php?document_srl=210015&mid=board_11
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=520277
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/343428
http://vhost12299.cpsite.ru/478009-vetrenyj-hercai-23-seria-ahki-vetrenyj-hercai-23-seria?---------------------------91085813%0D%0AContent-Disposition:%20form-data;%20name=%22token%22%0D%0A%0D%0A46bb0ac60db4a%0D%0A---------------------------91085813%0D%0AContent-Disposition:%20form-data;%20name=%22title%22%0D%0A%0D%0A%C2%AB%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2023%20%D0%A1%D0%B5%D1%80%D0%B8%D1%8F%C2%BB%20AHki%20%C2%AB%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2023%20%D0%A1%D0%B5%D1%80%D0%B8%D1%8F%C2%BB%0D%0A---------------------------91085813%0D%0AContent-Disposition:%20form-data;%20name=%22content%22%0D%0A%0D%0A%C2%AB%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2023%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB%20%60%20l4%20%C2%AB%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2023%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB%20%D1%81%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C%20on-line%20%D1%81%20%D0%BF%D0%B5%D1%80%D0%B5%D0%B2%D0%BE%D0%B4%D0%BE%D0%BC%0D%0A%0D%0A%0D%0A[url=http://zfilm6.ru/watch/ZeU5wg3b/][img]https://i.imgur.com/x1M8f46.jpg[/img][/url]%0D%0A%0D%0A%0D%0A%60%60%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2023%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%60%60%20p0%20%E3%80%90%20%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2023%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%E3%80%91.%20%60%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2023%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%60%20%60%20c7%201,%202,%203,%204,5,%206,7,%208,%209,%2010,%2011,%2012,%2013,14,%2015%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%0D%0A%D0%9A%D0%B0%D0%B6%D0%B4%D1%8B%D0%B9%20%D1%81%D0%B2%D0%B5%D0%B6%D0%B8%D0%B9%20%D1%81%D0%B5%D0%B7%D0%BE%D0%BD%20%22%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2023%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%22%20-%20%D1%8D%D1%82%D0%BE%20%D1%80%D0%B0%D0%B7%D0%B4%D0%B5%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F%20%D0%B8%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F%20%D1%81%D0%BE%20%D1%8D%D1%82%D0%B8%D0%BC%20%D0%B2%D0%BE%D0%B7%D0%B1%D1%83%D0%B4%D0%B8%D0%BC%D1%8B%D0%BC%20%D0%B8%20%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%BC%20%D1%81%D0%BC%D1%8B%D1%81%D0%BB%D0%BE%D0%BC.%20%D0%9F%D0%BE%D1%80%D1%86%D0%B8%D1%8F,%20%D0%BD%D0%BE%D1%81%D1%8F%D1%89%D0%B0%D1%8F%20%D0%BD%D0%B0%D0%B8%D0%BC%D0%B5%D0%BD%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5%20%22%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2023%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F%22%20,%20%D1%81%D0%B4%D0%B5%D0%BB%D0%B0%D0%B5%D1%82%D1%81%D1%8F%20%D0%B7%D0%B0%D1%81%D0%BB%D1%83%D0%B6%D0%B5%D0%BD%D0%BD%D1%8B%D0%BC%20%D0%BA%D1%80%D0%BE%D1%81%D1%81%D0%BE%D0%B2%D0%B5%D1%80%D0%BE%D0%BC,%20%D0%BA%D0%BE%D1%82%D0%BE%D1%80%D1%8B%D0%B9%20%D0%BD%D0%B0%D1%87%D0%BD%D0%B5%D1%82%20%D1%81%D0%BF%D0%BB%D0%B0%D1%87%D0%B8%D0%B2%D0%B0%D1%82%D1%8C%20%D0%B4%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D0%B8%D1%8F%20%D0%B8%D0%BD%D1%8B%D1%85%20%D1%81%D0%B5%D0%B7%D0%BE%D0%BD%D0%BE%D0%B2.%0D%0A%0D%0A%D0%A2%D1%83%D1%80%D0%B5%D1%86%D0%BA%D0%B8%D0%B5%20[url=http://zfilm6.ru/watch/ZeU5wg3b/]%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2023%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F[/url]%20%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8B%20%D0%BD%D0%B0%20%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%BE%D0%BC%20%D1%8F%D0%B7%D1%8B%D1%87%D0%BA%D0%B5%20%D1%80%D0%B0%D0%B7%D0%B3%D0%BB%D1%8F%D0%B4%D1%8B%D0%B2%D0%B0%D1%82%D1%8C%20%D0%BE%D0%BD-%D0%BB%D0%B0%D0%B9%D0%BD%20%D0%B2%D1%81%D0%B5%20%D1%81%D0%B5%D1%80%D0%B8%D0%B8%21%20%D0%A4%D0%B0%D0%B2%D0%BE%D1%80%D0%B8%D1%82%D0%BD%D1%8B%D0%B5,%20%D0%BF%D1%80%D0%B8%D0%BE%D0%B1%D1%80%D0%B5%D1%82%D1%91%D0%BD%D0%BD%D1%8B%D0%B5%20%D1%82%D1%83%D1%80%D0%B5%D1%86%D0%BA%D0%B8%D0%B5%20%D0%BA%D0%B8%D0%BD%D0%BE%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8B%20%D0%BD%D0%B0%20%D0%BD%D0%B5%D0%B4%D1%83%D1%80%D0%BD%D0%BE%D0%BC%20%D1%84%D0%BE%D1%80%D0%BC%D0%B5%20%D0%9F%D1%80%D0%BE%D1%81%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D0%B2%D0%B0%D1%82%D1%8C%20%D1%82%D1%83%D1%80%D0%B5%D1%86%D0%BA%D0%B8%D0%B5%20%D0%BA%D0%B8%D0%BD%D0%BE%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8B%21%D0%A2%D1%83%D1%80%D0%B5%D1%86%D0%BA%D0%B8%D0%B5%20%D1%82%D0%B5%D0%BB%D0%B5%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8B%20%D0%BF%D0%BB%D0%B5%D0%BD%D0%B8%D0%BB%D0%B8%20%D0%BF%D1%80%D0%B5%D0%BA%D1%80%D0%B0%D1%81%D0%BD%D1%8B%D0%B9%20%D0%BC%D0%B8%D1%80%20%D0%9D%D0%B0%D0%B4%D0%B5%D0%B5%D1%88%D1%8C%D1%81%D1%8F%20%D0%BB%D0%B8%D0%B1%D0%BE%20%D0%BD%D0%B5%20%D0%B8%D0%BC%D0%B5%D0%B5%D1%82%D1%81%D1%8F,%20%D1%82%D1%83%D1%80%D0%BA%D0%B8%20%D0%BA%D0%B0%D0%BA%20%D0%BD%D1%8B%D0%BD%D0%B5%D1%88%D0%BD%D0%B5%D0%BC%20%D0%B2%D0%BE%D0%BF%D1%80%D0%BE%D1%81%D0%B5%20%D0%BF%D0%BE%20%D0%BD%D0%B0%D1%81%D1%82%D0%BE%D1%8F%D1%89%D0%B5%D0%BC%D1%83%20%D1%84%D0%B5%D0%BD%D0%BE%D0%BC%D0%B5%D0%BD%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B.%0D%0A%0D%0A[url=http://zfilm6.ru/watch/ZeU5wg3b/]%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2023%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F[/url]%20%D0%9A%D0%BD%D0%B8%D0%B3%D0%B8%20%D0%B8%20%D0%B6%D1%83%D1%80%D0%BD%D0%B0%D0%BB%D1%8B%20%D0%BD%D0%B5%20%D1%82%D1%80%D0%B0%D1%82%D1%8F%20%D0%B2%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%B8%20%D0%B4%D0%B0%D1%80%20%D1%81%D0%B1%D0%B8%D0%B2%D0%B0%D1%8E%D1%82%20%D0%B4%D0%B0%20%D0%B8%20%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%BE%D0%B4%D1%8F%D1%82%20%D1%82%D0%B5%D0%BB%D0%B5%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8B,%20%D0%B4%D0%B0%20%D0%B8,%20%D1%87%D1%82%D0%BE%20%D1%81%D0%BB%D1%83%D1%87%D0%B8%D0%BB%D0%BE%D1%81%D1%8C%20%D0%BB%D1%8E%D0%B4%D0%B8%20%D0%B7%D0%B0%D0%BF%D0%B0%D0%BC%D1%8F%D1%82%D1%8B%D0%B2%D0%B0%D1%8E%D1%82%20%D0%BE%D0%B1%20%D0%BF%D0%BE%D0%B4%D0%BB%D0%B8%D0%BD%D0%BD%D0%BE%D0%B9%20%D0%B2%D0%B5%D0%BA%D0%B0%20%D0%B8%20%D0%B4%D0%BE%D0%BF%D0%BE%D0%BB%D0%BD%D0%B8%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%20%D0%BE%D0%BA%D1%83%D0%BD%D0%B0%D1%8E%D1%82%D1%81%D1%8F%20%D0%B2%20%D0%BD%D0%B0%D1%88%D0%B5%D0%BC%20%D0%B4%D0%B8%D1%81%D0%BF%D0%BB%D0%B5%D0%B8,%20%D1%81%D0%BB%D0%B5%D0%B4%D0%B8%D1%82%D1%8C%20%D0%B3%D0%BB%D0%B0%D0%B7%D0%B0%D0%BC%D0%B8%20%D0%B7%D0%B0%D0%A1%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%20%D0%9E%D0%B6%D0%B8%D0%B2%D1%88%D0%B8%D0%B9%20%D0%AD%D1%80%D1%82%D1%83%D0%B3%D1%80%D1%83%D0%BB%20%D0%BA%D0%B0%D1%80%D0%B0%D1%83%D0%BB%20%D0%BE%D1%87%D0%B5%D1%80%D0%BA%20%D0%BE%20%D0%BF%D0%BE%D1%87%D0%B8%D0%BD%D0%B5%20%D0%B8%D0%BB%D0%B8%20%D1%81%D1%82%D0%B0%D0%BD%D0%BE%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B8%20%D0%A2%D1%83%D1%80%D0%B5%D1%86%D0%BA%D0%BE%D0%B9%20%D0%94%D0%B5%D1%80%D0%B6%D0%B0%D0%B2%D0%B5%20%D0%AD%D1%80%D1%82%D1%83%D0%B3%D1%80%D1%83%D0%BB%20%D1%81%D0%BB%D0%B0%D0%B2%D0%B0,%20%D0%BA%D0%B0%D0%BA%D0%BE%D0%B5%20%D1%88%D1%83%D0%BC%D0%B5%D0%BB%D0%BE%20%D0%BD%D0%B0%20%D0%B1%D0%B5%D0%B7%D0%B2%D1%8B%D0%B5%D0%B7%D0%B4%D0%BD%D1%83%D1%8E%20%D0%93%D0%BE%D1%81%D1%83%D0%B4%D0%B0%D1%80%D1%81%D1%82%D0%B2%D0%BE%20%D0%B2%20%D0%BD%D0%B0%D1%88%D0%B5%D0%BC%2013-%D0%BC%20%D0%B2%D1%81%D0%B5%D0%B3%D0%B4%D0%B0,%20%D0%B0%20%D1%87%D1%82%D0%BE%20%D0%BD%D0%B0%D1%81%D1%82%D0%BE%D0%BB%D1%8C%D0%BA%D0%BE-%D0%BD%D0%BE%20%D0%B4%D0%B0%D0%BB%D0%B5%D0%BA%D0%BE%20%D0%B7%D0%B0%20%D0%B5%D0%B5%20%D0%B3%D1%80%D0%B0%D0%BD%D1%8F%D0%BC%D0%B8%20%D0%9D%D0%B5%20%D1%87%D1%82%D0%BE%20%D0%B8%D0%BD%D0%BE%D0%B5%20%D0%BA%D0%B0%D0%BA%20%D0%B2%D1%81%D0%B5%20%D0%B5%D0%B3%D0%BE%20%D0%BC%D0%BD%D1%8F%D1%82%0D%0A[url=https://prelease.club/%d0%b6%d0%b5%d1%81%d1%82%d0%be%d0%ba%d0%b8%d0%b9-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb-zalim-istanbul-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xegl-%d0%b6%d0%b5%d1%81%d1%82%d0%be/]%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2023%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F[/url]%20E3%20[url=https://www.vegasgreentour.com/index.php%3Fmid=board_XiHh59&document_srl=112733]%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2023%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F[/url]%20F9%20[url=http://bitpark.co.kr/%3Fdocument_srl=4031374]%D0%E2%80%99%D0%B5%D1%82%D1%80%D0%B5%D0%BD%D1%8B%D0%B9%20(Hercai)%2023%20%D1%81%D0%B5%D1%80%D0%B8%D1%8F[/url]%0D%0A---------------------------91085813%0D%0AContent-Disposition:%20form-data;%20name=%22postReply%22%0D%0A%0D%0A%D0%9D%D0%B0%D1%87%D0%B0%D1%82%D1%8C%20%D0%BE%D0%B1%D1%81%D1%83%D0%B6%D0%B4%D0%B5%D0%BD%D0%B8%D0%B5%0D%0A---------------------------91085813--
http://www.quattroandpartners.it/component/k2/itemlist/user/1172269
http://www.theocraticamerica.org/forum/index.php?topic=56638.0
http://rudraautomation.com/index.php/component/k2/author/223800
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=75076
http://www.josephmaul.org/menu41/109648
http://zanoza.h1n.ru/2019/05/19/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-we5%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05-2019/
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=525575
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3308560
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=166368
http://www.phperos.net/foro/index.php?topic=136741.0
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=890458
http://xn--ok1bpqi43ahtb.net/board_eASW07/133983
http://otitismediasociety.org/forum/index.php?topic=175714.0
http://hyeonjun.co.kr/menu3/62903
https://tg.vl-mp.com/index.php?topic=1473930.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/109763
http://zanoza.h1n.ru/2019/05/20/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fy4%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f20-05-2019/
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=24534
https://sanp.pro/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-si9%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-12-%d1%81%d0%b5/
http://www.tekparcahdfilm.com/forum/index.php?topic=51086.0
http://www.jesusonly.life/calendar/120682
http://xn----3x5er9r48j7wemud0a387h.com/news/43179
http://moavalve.co.kr/faq/72165
http://shinilspring.com/board_qsfb01/109270
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=78728
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=66483
http://www.theocraticamerica.org/forum/index.php?topic=49231.0
http://gtupuw.org/index.php/component/k2/itemlist/user/1926390
http://www.svteck.co.kr/customer_gratitude/43231
http://netsconsults.com/index.php/component/k2/itemlist/user/798014
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=85601
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=645884
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/226921
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1923258
http://indiefilm.kr/xe/board/142655
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1923287
http://mediaville.me/index.php/component/k2/itemlist/user/286722
http://indiefilm.kr/xe/board/124125
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=189159
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=62548
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=10412
http://netsconsults.com/index.php/component/k2/itemlist/user/799383
https://tg.vl-mp.com/index.php?topic=1474046.0
http://www.hsaura.com/noty/117777
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=342463
http://zanoza.h1n.ru/2019/05/18/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ee7%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05/
https://khuyenmaikk13.info/index.php?topic=207657.0
http://matinbank.ir/component/k2/itemlist/user/4557635.html
http://jjikduk.net/DATA/68992
http://skylinecam.co.kr/photo/95533
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gq3%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7/
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1616873
http://indiefilm.kr/xe/board/138113
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=120063
http://atemshow.com/atemfair_domestic/51644
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=146982
http://community.viajar.tur.br/index.php?p=/discussion/61489/klyatva-yemin-59-seriya-algi-klyatva-yemin-59-seriya/p1%3Fnew=1
http://0433.net/junggo/42407
https://testing.celekt.com/%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-b7-%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://moavalve.co.kr/faq/68911
http://asin.itts.co.kr/board_rtXs84/11309
http://indiefilm.kr/xe/?document_srl=123635
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=133267
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/261469
http://www.tessabannampad.go.th/webboard/index.php?topic=213688.0
http://hyeonjun.co.kr/menu3/67804
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=800088
http://mobility-corp.com/index.php/component/k2/itemlist/user/2626012
http://ru-realty.com/forum/index.php?PHPSESSID=hne7fnbme3aep59l13v7637sq5&topic=530086.0
http://jiquilisco.org/index.php/component/k2/itemlist/user/9676
http://www.theparrotcentre.com/forum/index.php?topic=557561.0
http://subforumna.x10.mx/mad/index.php?topic=254243.0
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=337509
http://www.teedinubon.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gp6s-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81/
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=95841
http://atemshow.com/atemfair_domestic/41635
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=3551
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=95310
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1713385
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=192173
http://roikjer.com/forum/index.php?PHPSESSID=l6v5cb16jl6krpi4ip0rtfav53&topic=890466.0
http://bebopindia.com/notcie/100121
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=36625c2d5f7d8ab833d3d6da20b085a8&topic=7705.0
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2/
http://www.jesusonly.life/?document_srl=160076
http://forum.elexlabs.com/index.php?topic=38212.0
https://sanp.pro/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wz4%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
http://shinhwaair2017.cafe24.com/?document_srl=210010
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/54271
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3414770
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1961189
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1950404
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=352620
http://lasvur.ru/index.php/component/k2/itemlist/user/39046
http://proxima.co.rw/index.php/component/k2/itemlist/user/667111
http://smartacity.com/index.php/component/k2/itemlist/user/54196
http://soc-human.kz/index.php/component/k2/itemlist/user/1723680
http://thermoplast.envolgroupe.com/component/k2/author/136262
http://vsalda.edinros66.ru/component/k2/itemlist/user/63890
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=16158
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1609659
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/19934
http://jiquilisco.org/index.php/component/k2/itemlist/user/10220
http://subforumna.x10.mx/mad/index.php?topic=257679.0
http://ye-dream.com/qa/79773
http://daesestudy.co.kr/ipsi_docu/42657
http://www.jesusonly.life/calendar/131097
http://www.digitalbul.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-z3-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-12-%d1%81%d0%b5%d1%80%d0%b8/
http://lucky.kidspann.net/?document_srl=74490
http://www.hsaura.com/noty/134290
http://forum.elexlabs.com/index.php?topic=41947.0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=850097
http://www.sp1.football/index.php?mid=faq&document_srl=218758
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=100584
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=219927
https://sanp.pro/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xc7%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl-1-%d1%81%d0%b5%d1%80/
http://thanosakademi.com/index.php?topic=96161.0
http://forum.elexlabs.com/index.php?topic=39451.0
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=124400
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-kc2%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5/
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=121312
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=20347
http://www.jesusonly.life/calendar/149249
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=100724
http://www.studyxray.com/Sangdam/144659
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1829893
http://proxima.co.rw/index.php/component/k2/itemlist/user/649292
http://hyeonjun.co.kr/menu3/71133
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3378966
http://otitismediasociety.org/forum/index.php?topic=175138.0
http://www.teedinubon.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pe8%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://ye-dream.com/qa/77023
http://www.m1avio.com/index.php/component/k2/itemlist/user/3736535
http://www.studyxray.com/Sangdam/120797
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=49337
http://teambuildingpremium.com/forum/index.php?topic=845574.0
http://ye-dream.com/qa/82771
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xy1%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://forum.digamahost.com/index.php?topic=127645.0
http://dev.aabn.org.gh/component/k2/itemlist/user/625423
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=17407
http://guiadetudo.com/?option=com_k2&view=itemlist&task=user&id=12132
http://dcasociados.eu/component/k2/itemlist/user/89802
http://www.atab.com.sa/?option=com_k2&view=itemlist&task=user&id=1663516
http://www.sp1.football/index.php?mid=faq&document_srl=177921
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fw9%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://dessa.com.br/component/k2/itemlist/user/344954
http://bebopindia.com/notcie/232011
http://dohairbiz.com/en/component/k2/itemlist/user/2762869.html
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=206859
http://lucky.kidspann.net/index.php?mid=qna&document_srl=70086
http://taklongclub.com/forum/index.php?topic=149498.0
https://npi.org.es/smf/index.php?topic=118264.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=73395
http://www.theparrotcentre.com/forum/index.php?topic=552441.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=24393
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=106017
http://roikjer.com/forum/index.php?PHPSESSID=4fm7v5hcalscmp6b343b4917i3&topic=893961.0
http://shinilspring.com/board_qsfb01/89700
http://yoriyorifood.com/xxxx/spacial/76243
http://married.dike.gr/index.php/component/k2/itemlist/user/65364
http://hyeonjun.co.kr/menu3/73237
http://www.studyxray.com/Sangdam/144854
http://web2interactive.com/index.php/component/k2/itemlist/user/3674740
http://moavalve.co.kr/faq/75395
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=98448
http://asin.itts.co.kr/board_rtXs84/8027
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=642719
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3398653
http://forum.3d-printer.top/index.php?topic=1140.0
http://www.josephmaul.org/menu41/118534
http://xn----3x5er9r48j7wemud0a387h.com/news/50309
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=85354
http://skylinecam.co.kr/photo/78239
http://ru-realty.com/forum/index.php?PHPSESSID=74lpdt91f5ps44vmq5e8gjqml2&topic=532733.0
https://forum.ac-jete.it/index.php?topic=406663.0
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=257593
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=12756
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=72486
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1946646
https://www.shaiyax.com/index.php?topic=355767.0
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3293837
http://ovotecegg.com/component/k2/itemlist/user/159521
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=41279
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=115525
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=102108
http://masanlib.or.kr/g1/41458
http://xplorefitness.com/blog/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-24-05-2019%C2%BB-sf%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-24-05-2019%C2%BB97-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-24-05-2019
http://0433.net/junggo/51717
http://www.golden-nail.co.kr/press/97780
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3297474
http://zanoza.h1n.ru/2019/05/18/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%84%d0%b8%d0%bd%d0%b0%d0%bb-fk%d1%85%d0%be%d0%bb%d0%be/
http://www.tessabannampad.go.th/webboard/index.php?topic=213937.0
http://ye-dream.com/qa/82129
http://atemshow.com/atemfair_domestic/52259
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=83681
http://www.theocraticamerica.org/forum/index.php?topic=54117.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=179844
http://forum.digamahost.com/index.php?topic=126047.0
http://miklja.net/forum/index.php?topic=32928.0
http://indiefilm.kr/xe/board/143893
http://yoriyorifood.com/xxxx/spacial/91596
https://www.2ayes.com/17226/3-18-19-05-2019-e5-3-18
http://asiagroup.co.kr/?document_srl=239312
http://www.studyxray.com/Sangdam/178286
https://www.amazingworldtop.com/entretenimiento/%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-92-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-am7%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-92-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05-2019/
http://www.sp1.football/index.php?mid=faq&document_srl=203712
http://lucky.kidspann.net/index.php?mid=qna&document_srl=69489
http://emjun.com/index.php?mid=hangtotal&document_srl=97430
http://asin.itts.co.kr/board_rtXs84/10104
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-live-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://otitismediasociety.org/forum/index.php?topic=183664.0
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=709886.0
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=30972
http://www.remify.app/foro/index.php?topic=320187.0
http://hyeonjun.co.kr/menu3/73852
http://roikjer.com/forum/index.php?PHPSESSID=e60mi9to1efkfkob2qhdkjl5q0&topic=893501.0
http://www.jesusonly.life/?document_srl=156263
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=130466
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/269959
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iz9%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-12-%d1%81%d0%b5/
https://testing.celekt.com/%d0%9f%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%ad%d0%a4%d0%98%d0%a0-%d0%9f%d0%be%d1%81-2/
http://www.teedinubon.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rj5%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f17-05-2019/
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2542145
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/225969
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=32903
http://www.theparrotcentre.com/forum/index.php?topic=554623.0
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1713726
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=87459
http://www.svteck.co.kr/customer_gratitude/43061
http://forum.kopkargobel.com/index.php?topic=12078.0
http://ovotecegg.com/component/k2/itemlist/user/166774
http://www.golden-nail.co.kr/press/89958
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1217620
http://vhost12299.cpsite.ru/537602-sluga-naroda-3-sezon-6-seria-efir-sluga-naroda-3-sezon-6-seria
http://miquirofisico.com/index.php/component/k2/itemlist/user/4243
http://www.digitalbul.com/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl-6/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/343844
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2777329
http://withinfp.sakura.ne.jp/eso/index.php/17150495-vetrenyj-hercai-22-seria-idxp-vetrenyj-hercai-22-seria/0
https://khuyenmaikk13.info/index.php?topic=207913.0
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=143546
http://www.gforgirl.com/xe/poster/113733
http://masanlib.or.kr/g1/35723
http://www.josephmaul.org/menu41/139338
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1732208
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=59428
http://lucky.kidspann.net/index.php?mid=qna&document_srl=75888
http://forum.digamahost.com/index.php?topic=126577.0
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=87298
https://tg.vl-mp.com/index.php?topic=1477636.0
http://www.hicleaning.kr/board_wash/92114
https://khuyenmaikk13.info/index.php?topic=210484.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1441307
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=187439
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/341678
http://ye-dream.com/qa/90467
http://www.sp1.football/index.php?mid=faq&document_srl=407874
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/280017
http://www.gforgirl.com/xe/poster/121286
http://forum.bmw-e60.eu/index.php?topic=8901.0
http://www.sp1.football/?document_srl=257554
http://webp.online/index.php?topic=60340.0
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=56980
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=81622
http://asiagroup.co.kr/index.php?document_srl=246019&mid=board_11
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=512049
http://www.hicleaning.kr/board_wash/173536
http://www.josephmaul.org/?document_srl=226164
http://www.josephmaul.org/menu41/226043
http://www.josephmaul.org/menu41/226084
http://www.josephmaul.org/menu41/226116
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=359732
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=359924
http://jiquilisco.org/index.php/component/k2/itemlist/user/16815
http://mediaville.me/index.php/component/k2/itemlist/user/311864
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/789449
http://mvisage.sk/index.php/component/k2/itemlist/user/119366
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/131894
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/132013
http://ovotecegg.com/component/k2/itemlist/user/185777
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=674767
http://rudraautomation.com/index.php/component/k2/author/257673
http://thermoplast.envolgroupe.com/component/k2/author/141136
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1696350
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1696352
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=16289
http://otitismediasociety.org/forum/index.php?topic=177709.0
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3299663
http://www.original-craft.net/index.php?topic=341536.0
http://zanoza.h1n.ru/2019/05/18/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-17-05-2019-z8-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2/
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=124752
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/338160
http://hyeonjun.co.kr/menu3/80930
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=75074
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=853436
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ex1%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.sp1.football/index.php?mid=faq&document_srl=207264
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=83166
http://mir3sea.com/forum/index.php?topic=3613.0
http://necinsurance.co.zw/component/k2/itemlist/user/21068.html
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=119715
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1710427
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1608388
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=120266
https://testing.celekt.com/%d0%a1%d0%b5%d0%bd%d1%8f%d0%a4%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%a1%d0%9c%d0%9e%d0%a2%d0%a0%d0%95%d0%a2%d0%ac-%d0%a1%d0%b5/
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=268609
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=115494
http://cwon.kr/xe/board_bnSr36/65809
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=49541
http://skylinecam.co.kr/photo/144322
http://www.sp1.football/index.php?mid=faq&document_srl=201886
http://shinilspring.com/board_qsfb01/104741
http://www.studyxray.com/Sangdam/168311
http://www.svteck.co.kr/?document_srl=54783
http://www.jesusonly.life/calendar/150488
http://www.hsaura.com/noty/131659
http://universalcommunity.se/Forum/index.php?topic=17792.0
http://indiefilm.kr/xe/board/159175
http://www.theocraticamerica.org/forum/index.php/topic,53256.0.html
http://www.tessabannampad.go.th/webboard/index.php?topic=214135.0
http://married.dike.gr/index.php/component/k2/itemlist/user/65912
http://jjikduk.net/DATA/60355
http://asin.itts.co.kr/board_rtXs84/16899
http://moavalve.co.kr/faq/81707
http://rudraautomation.com/index.php/component/k2/author/217094
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1705050
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=498606
http://research.kiu.ac.kr/?document_srl=67709
http://www.hicleaning.kr/?document_srl=90103
http://roikjer.com/forum/index.php?PHPSESSID=3csm8avfftb2nbj7vvvo9i8vt1&topic=894427.0
http://photogrotto.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xs6%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05-2019/
http://shinilspring.com/board_qsfb01/99028
http://indiefilm.kr/xe/board/126099
http://indiefilm.kr/xe/board/127840
http://ru-realty.com/forum/index.php?PHPSESSID=kpl1nu47vtu8lq4bfl1ab9b7l6&topic=532194.0
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3398680
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7341333
http://hyeonjun.co.kr/menu3/72955
http://jiquilisco.org/index.php/component/k2/itemlist/user/9340
http://thermoplast.envolgroupe.com/component/k2/author/123619
http://www.golden-nail.co.kr/press/99847
http://teambuildingpremium.com/forum/index.php?topic=852331.0
http://atemshow.com/atemfair_domestic/41030
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=522934
http://guiadetudo.com/index.php/component/k2/itemlist/user/12208
https://sanp.pro/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tp1%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-as%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://www.digitalbul.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-17-05-2019-cf%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1448081
http://www.teedinubon.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-96-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yz3%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-96-%d1%81%d0%b5%d1%80%d0%b8%d1%8f19-05-2019/
https://esel.gist.ac.kr/esel2/board_hmgj23/66611
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=110203
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2322840
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=329261
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=341234
http://dev.aabn.org.gh/component/k2/itemlist/user/618742
http://photogrotto.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-98-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ms2%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-98/
http://jjikduk.net/DATA/74714
http://www.almacenesrickie.com.ec/index.php/component/k2/itemlist/user/133699
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-live-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.hsaura.com/noty/111589
http://www.josephmaul.org/menu41/108125
http://roikjer.com/forum/index.php?PHPSESSID=75rt8gil2diee7v6pcd2gc2vc3&topic=899690.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/543816
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=85517
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=92386
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-by7l-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.hsaura.com/noty/158822
http://www.arunagreen.com/?option=com_k2&view=itemlist&task=user&id=549050
https://khuyenmaikk13.info/index.php?topic=218000.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2707558
http://dev.aabn.org.gh/component/k2/itemlist/user/648109
http://dev.aabn.org.gh/component/k2/itemlist/user/648211
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1957307
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=359755
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=872402
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=77112
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=24151
http://zanoza.h1n.ru/2019/05/18/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24-05-2019-zs%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24-05-201934-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24/
http://cwon.kr/xe/board_bnSr36/128663
http://www.josephmaul.org/?document_srl=105124
http://lucky.kidspann.net/index.php?mid=qna&document_srl=67804
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=86816
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1659336
http://forum.3d-printer.top/index.php?topic=1391.0
http://withinfp.sakura.ne.jp/eso/index.php/17436011-hd-cuzaa-zizn-cuze-zitta-3-seria-g1-cuzaa-zizn-cuze-zitta-3-ser/0
http://withinfp.sakura.ne.jp/eso/index.php/17436422-efir-taemnici-86-seria-l7-taemnici-86-seria/0
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1188386
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/58841
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/64880
https://verdadesbiblicas.org.ec/index.php/component/k2/itemlist/user/3814121
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=84789
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=289948
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=289963
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=289892
http://1661-6471.co.kr/?document_srl=7142
http://5starcoffee.co.kr/board_EBXY17/11190
http://ajincomp.godohosting.com/board_STnh82/79048
http://ajincomp.godohosting.com/board_STnh82/79075
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1663377
http://lavaggio.com.vn/index.php/component/k2/itemlist/user/3834697
https://altaylarteknoloji.com/index.php?topic=5051.0
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=100183
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=93027
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=155652
http://fbpharm.net/index.php/component/k2/itemlist/user/49822
http://www.gforgirl.com/xe/poster/107922
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yw2%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://www.tedyun.com/xe/?document_srl=193655
http://emjun.com/index.php?mid=hangtotal&document_srl=89335
http://universalcommunity.se/Forum/index.php?topic=18236.0
http://www.theocraticamerica.org/forum/index.php/topic,47848.0.html
http://www.spazioad.com/component/k2/itemlist/user/7341503
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=187787
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1608098
http://moavalve.co.kr/faq/77839
https://testing.celekt.com/%d0%a5%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-mh%d0%a5%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bd0k-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/110344
http://jiquilisco.org/index.php/component/k2/itemlist/user/10899
http://indiefilm.kr/xe/board/129115
http://thermoplast.envolgroupe.com/component/k2/author/123183
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=63141
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=63208
http://www.kwpcoop.or.kr/QnA/7592
http://www.kwpcoop.or.kr/QnA/7610
http://www.leekeonsu-csi.com/?document_srl=606328
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=606446
http://www.original-craft.net/index.php?topic=350704.0
http://www.original-craft.net/index.php?topic=350744.0
http://www.studyxray.com/Sangdam/243265
http://xn----3x5er9r48j7wemud0a387h.com/news/94584
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=84788
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/791804
http://vhost12299.cpsite.ru/569622-tajny-taemnici-96-seria-o7-tajny-taemnici-96-seria
http://xn--ok1bpqi43ahtb.net/board_eASW07/129158
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-al8%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.phperos.net/foro/index.php?topic=135831.0
http://smartacity.com/component/k2/itemlist/user/55435
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=176419
http://jjikduk.net/?document_srl=78222
http://www.m1avio.com/index.php/component/k2/itemlist/user/3719996
http://www.theparrotcentre.com/forum/index.php?topic=555752.0
http://skylinecam.co.kr/photo/79103
http://jiquilisco.org/index.php/component/k2/itemlist/user/12896
http://www.sollazzorefrigerazione.it/?option=com_k2&view=itemlist&task=user&id=2529781
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=100470
http://indiefilm.kr/xe/board/109321
http://www.teedinubon.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-q1-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-10-%d1%81%d0%b5%d1%80%d0%b8/
http://ru-realty.com/forum/index.php?topic=527570.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/mama-oa-6-e-17-05-2019-tyo-mama-oa-6-e/?PHPSESSID=mrkjnov73o6rp4ftqfp31qqec3
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1737429
http://photogrotto.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-14/
http://www.remify.app/foro/index.php?topic=320984.0
http://zanoza.h1n.ru/2019/05/19/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-g1-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2/
http://phmusic.dothome.co.kr/index.php?mid=PowerHouseMusic&document_srl=26166
http://projectcva.dothome.co.kr/?document_srl=1394
http://withinfp.sakura.ne.jp/eso/index.php/17445667-rannaa-ptaska-erkenci-kus-42-seria-hzer-rannaa-ptaska-erkenci-k/0
http://www.critico-expository.com/forum/index.php?topic=19733.0
http://www.gforgirl.com/xe/poster/321248
http://www.gforgirl.com/xe/poster/321340
http://www.lovestory.or.kr/topic/18070
http://www.lovestory.or.kr/topic/18095
http://www.lovestory.or.kr/topic/18131
http://www.lovestory.or.kr/topic/18147
http://www.original-craft.net/index.php?topic=351198.0
http://www.original-craft.net/index.php?topic=351201.0
http://www.siheunglove.com/chulip/133751
http://emjun.com/index.php?mid=hangtotal&document_srl=100517
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=330480
https://sanp.pro/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wv1%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-4-%d1%81%d0%b5%d1%80/
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=888935
http://0433.net/junggo/55526
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2328504
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=119306
http://otitismediasociety.org/forum/index.php?topic=175701.0
http://xn--ok1bpqi43ahtb.net/board_eASW07/102871
http://proxima.co.rw/index.php/component/k2/itemlist/user/656116
http://forum.elexlabs.com/index.php?topic=39844.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=24594
http://corumotoanahtar.com/index.php/component/k2/itemlist/user/4216
http://azone.synology.me/xe/?document_srl=89548
http://corumotoanahtar.com/component/k2/itemlist/user/4580.html
http://zanoza.h1n.ru/2019/05/20/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://0433.net/junggo/65796
http://0433.net/junggo/65801
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=290870
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=290920
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=179301
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=179365
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=179371
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=179376
http://smartacity.com/component/k2/itemlist/user/66907
http://smartacity.com/component/k2/itemlist/user/66918
http://smartacity.com/component/k2/itemlist/user/66920
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1732294
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1732300
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=195328
http://zanoza.h1n.ru/2019/05/20/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8/
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=193461
http://sdsn.develop.cinfores.com/?option=com_k2&view=itemlist&task=user&id=220595
http://www.sp1.football/index.php?mid=faq&document_srl=407693
http://ovotecegg.com/component/k2/itemlist/user/161295
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1613498
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3307779
http://indiefilm.kr/xe/board/126348
http://xn--ok1bpqi43ahtb.net/board_eASW07/100494
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=92656
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3300375
http://community.viajar.tur.br/index.php?p=/discussion/62036/vossoedinenie-vuslat-18-seriya-thof-vossoedinenie-vuslat-18-seriya
http://community.viajar.tur.br/index.php?p=/discussion/62038/vetrenyy-hercai-22-seriya-kphz-vetrenyy-hercai-22-seriya
http://community.viajar.tur.br/index.php?p=/discussion/62039/bogatye-i-bednye-zengin-ve-yoksul-13-seriya-zmai-bogatye-i-bednye-zengin-ve-yoksul-13-seriya
http://community.viajar.tur.br/index.php?p=/profile/lrygerard5
http://jjikduk.net/?document_srl=114974
http://lucky.kidspann.net/index.php?mid=qna&document_srl=161862
http://lucky.kidspann.net/index.php?mid=qna&document_srl=161908
http://lucky.kidspann.net/index.php?mid=qna&document_srl=161938
http://lucky.kidspann.net/index.php?mid=qna&document_srl=161972
http://lucky.kidspann.net/index.php?mid=qna&document_srl=162006
http://shinhwaair2017.cafe24.com/?document_srl=327915
http://shinhwaair2017.cafe24.com/issue/327905
http://shinhwaair2017.cafe24.com/issue/327930
http://shinhwaair2017.cafe24.com/issue/327969
http://www.critico-expository.com/forum/index.php?topic=15533.0
http://jiquilisco.org/index.php/component/k2/itemlist/user/16729
http://mediaville.me/index.php/component/k2/itemlist/user/311605
http://mobility-corp.com/index.php/component/k2/itemlist/user/2663973
http://mobility-corp.com/index.php/component/k2/itemlist/user/2663984
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/131805
http://rudraautomation.com/index.php/component/k2/author/256950
http://smartacity.com/component/k2/itemlist/user/67030
http://smartacity.com/component/k2/itemlist/user/67032
http://soc-human.kz/index.php/component/k2/itemlist/user/1732472
http://thermoplast.envolgroupe.com/component/k2/author/140729
http://thermoplast.envolgroupe.com/component/k2/author/140927
http://thermoplast.envolgroupe.com/component/k2/author/140934
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=18155
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=238457
http://forum.3d-printer.top/index.php?topic=2034.0
https://testing.celekt.com/%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ia9%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/221725
http://www.crnmedia.es/?option=com_k2&view=itemlist&task=user&id=86940
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=78067
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1613144
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=29873
https://testing.celekt.com/%d0%9d%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d0%a1%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-82-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-el2/
http://adsudoeste.com.br/?option=com_k2&view=itemlist&task=user&id=22090
http://corumotoanahtar.com/component/k2/itemlist/user/6855.html
http://vtservices85.fr/smf2/index.php?PHPSESSID=567919c307cea8819c29f3e74bd52f51&topic=261757.0
http://thermoplast.envolgroupe.com/component/k2/author/125472
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1612283
http://www.hicleaning.kr/board_wash/164481
http://www.josephmaul.org/menu41/216469
http://www.josephmaul.org/menu41/216594
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=182601
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=182743
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=182747
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=182753
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=182758
http://www.teedinubon.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be/
http://www2.yasothon.go.th/smf/index.php?topic=159.167625
https://adsensebih.com/index.php?topic=33062.0
https://hackersuniversity.net/index.php?topic=24719.0
https://hackersuniversity.net/index.php?topic=24737.0
https://hackersuniversity.net/index.php?topic=24804.0
https://hackersuniversity.net/index.php?topic=24891.0
https://hackersuniversity.net/index.php?topic=24892.0
http://tk-laser.co.kr/index.php?mid=board_QsEu43&document_srl=113058
http://tk-laser.co.kr/index.php?mid=board_QsEu43&document_srl=113076
http://tk-laser.co.kr/index.php?mid=board_QsEu43&document_srl=113098
http://tk-laser.co.kr/index.php?mid=board_QsEu43&document_srl=113121
http://toeden.co.kr/Product_new/97524
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=45538
http://viamania.net/index.php?document_srl=76504&mid=board_raYV15
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=139269
http://wartoby.com/index.php?document_srl=50840&mid=board_UXUA38
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=50929
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=50943
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=50973
http://xn----3x5er9r48j7wemud0a387h.com/news/36088
http://cwon.kr/xe/?document_srl=81073
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4857681
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/509222
http://matrixpharm.ru/forum/index.php?PHPSESSID=71q58hcset6m8hnujnmk9f0cq1&action=profile;u=199488
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/43117
https://nextezone.com/index.php?topic=57101.0
http://www.critico-expository.com/forum/index.php?topic=14304.0
http://jiquilisco.org/index.php/component/k2/itemlist/user/13513
http://bitpark.co.kr/board_IzjM66/4058756
http://jjikduk.net/DATA/127670
http://jjikduk.net/DATA/127738
http://jjikduk.net/DATA/127766
http://k-cea.org/board_Hnyj62/127826
http://photogrotto.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-t0-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
http://photogrotto.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-d7-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-3-%d1%81%d0%b5%d1%80%d0%b8/
http://www.teedinubon.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-z2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80/
http://zanoza.h1n.ru/2019/05/23/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-o7-%d0%b8%d0%b3%d1%80/
http://zanoza.h1n.ru/2019/05/23/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-i9-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://testing.celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-21-05-2019-z8-%d0%98%d0%b3%d1%80/
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1945285
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=145073
http://jiquilisco.org/?option=com_k2&view=itemlist&task=user&id=8693
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=518193
http://jjikduk.net/DATA/67094
http://www.theparrotcentre.com/forum/index.php?topic=568013.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=342419
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/222481
http://xn----3x5er9r48j7wemud0a387h.com/news/59853
http://indiefilm.kr/xe/board/115777
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=181854
http://www.golden-nail.co.kr/press/80197
http://www.studyxray.com/Sangdam/113679
http://www.studyxray.com/Sangdam/183335
http://www.jesusonly.life/calendar/134496
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/11375
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/341434
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=111880
http://zanoza.h1n.ru/2019/05/18/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-17-05-19-tk%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-2/
http://www.comfybigsize.com/index.php/component/k2/itemlist/user/35030
http://www.phperos.net/foro/index.php?topic=136581.0
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24-05-2019-hl%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24-05-201983-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24/
http://www.dap.com.py/index.php/component/k2/itemlist/user/825531
https://ne-kuru.ru/index.php?topic=222802.0
https://test.baseyou21.kr/index.php?mid=main_slider&document_srl=101794
https://prelease.club/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sb1y-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://lucky.kidspann.net/index.php?mid=qna&document_srl=65585
http://www.teedinubon.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hf2%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=23378
http://ru-realty.com/forum/index.php?PHPSESSID=ojfeahtbar7ajfaikdcarr3u22&topic=527606.0
http://zanoza.h1n.ru/2019/05/19/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qo1%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7/
http://www.golden-nail.co.kr/press/93411
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hf1%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7/
http://moavalve.co.kr/faq/69644
https://afikgan.co.il/index.php/component/k2/itemlist/user/29014
https://reficulcoin.com/index.php?topic=52583.0
http://www.jesusonly.life/calendar/117755
http://daesestudy.co.kr/ipsi_docu/78856
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=33540
http://photogrotto.com/%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-87-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yp9%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-87-%d1%81%d0%b5%d1%80%d0%b8%d1%8f19-05-2019/
http://thermoplast.envolgroupe.com/component/k2/author/128298
http://cwon.kr/xe/board_bnSr36/108324
http://www.remify.app/foro/index.php?topic=318677.0
http://shinilspring.com/board_qsfb01/83457
http://www.studyxray.com/Sangdam/114477
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/227969
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/280483
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=197730
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=261160
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=524221
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-19-qb%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://miklja.net/forum/index.php?topic=31881.0
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=109090
http://www.critico-expository.com/forum/index.php?topic=13860.0
http://masanlib.or.kr/g1/27234
https://reficulcoin.com/index.php?topic=57313.0
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3307585
http://www.hicleaning.kr/board_wash/127442
http://www.josephmaul.org/menu41/111778
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wt2%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/37232
http://mvisage.sk/index.php/component/k2/itemlist/user/119049
http://smartacity.com/component/k2/itemlist/user/53910
http://shinilspring.com/board_qsfb01/104534
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=24572
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=94015
https://khuyenmaikk13.info/index.php?topic=208525.0
http://adsudoeste.com.br/?option=com_k2&view=itemlist&task=user&id=22073
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=330224
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24-05-2019-oz%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24-05-201947-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24/
http://www.tessabannampad.go.th/webboard/index.php?topic=214432.0
https://afikgan.co.il/index.php/component/k2/itemlist/user/28957
http://bebopindia.com/notcie/136610
http://corumotoanahtar.com/component/k2/itemlist/user/4075.html
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=67245
http://atemshow.com/atemfair_domestic/44836
http://redgatetech.co/?option=com_k2&view=itemlist&task=user&id=730023
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2660254
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=126627
http://rudraautomation.com/index.php/component/k2/author/216775
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=10110
http://www.ekemoon.com/213007/052120195418/
http://shinhwaair2017.cafe24.com/issue/211693
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/769627
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=32463
http://zanoza.h1n.ru/2019/05/20/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-98-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kz4%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-98/
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=5307
http://www.studyxray.com/Sangdam/123473
http://photogrotto.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-a0-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
http://www.sp1.football/index.php?mid=faq&document_srl=240129
http://indiefilm.kr/xe/board/140647
https://hackersuniversity.net/index.php/topic,19716.0.html
http://teambuildingpremium.com/forum/index.php?topic=843630.0
http://www.comfybigsize.com/?option=com_k2&view=itemlist&task=user&id=35491
https://testing.celekt.com/%d0%a1%d0%9c%d0%9e%d0%a2%d0%a0%d0%95%d0%a2%d0%ac-%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-e7-%d0%a2%d0%be%d0%bb%d1%8f/
http://www.m1avio.com/?option=com_k2&view=itemlist&task=user&id=3740039
http://www.theparrotcentre.com/forum/index.php?topic=554246.0
http://moavalve.co.kr/faq/69186
http://emjun.com/index.php?mid=hangtotal&document_srl=76819
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1232219
https://www.amazingworldtop.com/entretenimiento/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-he5%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://bebopindia.com/notcie/142540
http://e-educ.net/Forum/index.php?topic=12488.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=333160
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=126999
http://xn--ok1bpqi43ahtb.net/board_eASW07/125318
https://sanp.pro/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-17-05-19-oy%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://jjikduk.net/DATA/76198
http://gtupuw.org/index.php/component/k2/itemlist/user/1925465
http://www.hicleaning.kr/board_wash/82386
http://www.studyxray.com/Sangdam/128071
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=341924
https://esel.gist.ac.kr/esel2/board_hmgj23/90901
https://altaylarteknoloji.com/index.php?topic=4991.0
http://roikjer.com/forum/index.php?PHPSESSID=d0660mg92loqou0s0chgtnjob2&topic=890522.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/655441
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=89134
https://www.amazingworldtop.com/entretenimiento/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-90-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-di0%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-90-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05-2019/
http://www.sp1.football/?document_srl=189951
http://www.digitalbul.com/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-n9-%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4/
http://www.tekparcahdfilm.com/forum/index.php?topic=51343.0
http://www.taeshinmedia.com/?document_srl=3307731
http://bebopindia.com/notcie/329474
http://rudraautomation.com/index.php/component/k2/author/247925
https://esel.gist.ac.kr/esel2/board_hmgj23/163176
http://vhost12299.cpsite.ru/550082-novinka-milliardy-4-sezon-12-seria-a4-milliardy-4-sezon-12-seri
https://hackinsa.com/freeboard/55128
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=65301
http://community.viajar.tur.br/profile/FatimaS60
http://herdental.co.kr/index.php?mid=online&document_srl=88105
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1942654
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=50196
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1924570
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/330643
http://jiquilisco.org/index.php/component/k2/itemlist/user/14204
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=65874
http://mediaville.me/index.php/component/k2/itemlist/user/284947
http://miquirofisico.com/index.php/component/k2/itemlist/user/4239
http://miquirofisico.com/index.php/component/k2/itemlist/user/4244
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/126419
http://rudraautomation.com/index.php/component/k2/author/218906
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/220859
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=65224
http://taklongclub.com/forum/index.php?topic=158915.0
http://indiefilm.kr/xe/board/148904
http://dev.aabn.org.gh/component/k2/itemlist/user/616027
http://www.teedinubon.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-h2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80/
http://rudraautomation.com/index.php/component/k2/itemlist/user/225173
http://zanoza.h1n.ru/2019/05/19/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cs4%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
http://www.digitalbul.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-ue%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/275653
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/109971
http://www.tekparcahdfilm.com/forum/index.php?topic=51395.0
http://shinhwaair2017.cafe24.com/issue/209415
http://mediaville.me/index.php/component/k2/itemlist/user/294505
http://hyeonjun.co.kr/menu3/75492
http://jjikduk.net/DATA/61370
http://www.vamoscontigo.org/Noticia/107051
http://www.hicleaning.kr/board_wash/176904
http://1661-6471.co.kr/news/5474
http://miklja.net/forum/index.php?topic=33944.0
http://community.viajar.tur.br/index.php?p=/profile/warnerturn
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=588869
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/37080
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3381141
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=4036
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2657744
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=342361
http://fbpharm.net/index.php/component/k2/itemlist/user/65831
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=330943
http://subforumna.x10.mx/mad/index.php?topic=254088.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=24840
https://testing.celekt.com/%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yq5%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05-2019/
http://otitismediasociety.org/forum/index.php?topic=174328.0
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1625696
http://thermoplast.envolgroupe.com/component/k2/author/119840
http://jiquilisco.org/index.php/component/k2/itemlist/user/11471
https://testing.celekt.com/%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nb1%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://yoriyorifood.com/xxxx/spacial/102337
http://www.hsaura.com/noty/111805
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=86334
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=42597
http://rabbitzone.xyz/FREE/29355
http://isch.kr/board_PowH60/93976
http://jejucctv.co.kr/A5/39605
http://carand.co.kr/d2/15816
http://barobus.kr/?document_srl=41705
http://ajincomp.godohosting.com/board_STnh82/79839
http://www.ekemoon.com/230481/051820190223/
http://www.ekemoon.com/230489/051820190623/
http://www.ekemoon.com/230491/051820190723/
http://www.hyunjindc.com/qna/66930
http://www.kspace.cc/xe/?document_srl=33859
http://www.kspace.cc/xe/?document_srl=33874
http://www.kspace.cc/xe/index.php?document_srl=33815&mid=board_NvNw86
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=33829
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=33886
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=33916
http://www.kwpcoop.or.kr/QnA/9650
http://www.kwpcoop.or.kr/QnA/9707
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=98565
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=98573
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=98581
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=98601
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=98611
http://bebopindia.com/notcie/346425
https://cfcestradareal.com.br/?option=com_k2&view=itemlist&task=user&id=58128
http://bebopindia.com/notcie/316066
https://esel.gist.ac.kr/esel2/board_hmgj23/155713
http://1661-6471.co.kr/?document_srl=14525
http://vhost12299.cpsite.ru/552773-novinka-cuzaa-zizn-cuze-zitta-3-seria-u3-cuzaa-zizn-cuze-zitta-
http://www.camaracoyhaique.cl/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-97-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-97-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://carand.co.kr/d2/44894
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ci4%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=29849
http://www.itosm.com/cn/board_nLoq17/73034
http://beautypouch.net/index.php?mid=board_09&document_srl=47606
https://khuyenmaikk13.info/index.php?topic=220098.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/239686
http://vhost12299.cpsite.ru/578081-efir-konsul-tant-2-sezon-7-seria-z0-konsul-tant-2-sezon-7-seria
http://withinfp.sakura.ne.jp/eso/index.php/17475496-smotret-vse-moglo-byt-inace-10-seria-f8-vse-moglo-byt-inace-10-/0
http://withinfp.sakura.ne.jp/eso/index.php/17475605-sluga-naroda-3-sezon-4-seria-n4-sluga-naroda-3-sezon-4-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/17476065-hdvideo-tola-robot-5-seria-c7-tola-robot-5-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/17476138-tola-robot-3-seria-p0-tola-robot-3-seria/0
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/17420
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/65033
http://153.120.114.241/eso/index.php/17476072-voron-kuzgun-15-seria-sjxn-voron-kuzgun-15-seria
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=41179
https://2002.shyoon.com/?document_srl=133682
https://2002.shyoon.com/board_2002/133706
https://betshin.com/Story/120370
https://betshin.com/Story/120403
https://gonggamlaw.com/lawcase/36722
https://hackinsa.com/?document_srl=41061
https://hackinsa.com/freeboard/41119
https://nple.com/xe/pds/108929
https://nple.com/xe/pds/108984
http://yoriyorifood.com/xxxx/spacial/171415
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/?document_srl=30953
http://d-tube.info/board_jvyO69/355489
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/41598
http://www.insesinmun.com/newpaper2/73147
http://carand.co.kr/d2/23957
http://ye-dream.com/qa/190820
http://oneandonly1127.com/guest/59147
http://asin.itts.co.kr/board_rtXs84/26061
http://barobus.kr/qna/48366
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=61709
http://sy.korean.net/qna/216493
http://sy.korean.net/qna/216594
http://themasters.pro/?document_srl=160022
http://themasters.pro/file_01/160065
http://themasters.pro/file_01/160098
http://tiretech.co.kr/index.php?mid=qna&document_srl=119857
http://tiretech.co.kr/index.php?mid=qna&document_srl=119868
http://sd-xi.co.kr/g1/36797
http://sd-xi.co.kr/g1/36803
http://sejong-thesharpyemizi.co.kr/m1/12404
http://sejong-thesharpyemizi.co.kr/m1/12410
http://shinhwaair2017.cafe24.com/?document_srl=385901
http://shinhwaair2017.cafe24.com/issue/385949
http://toeden.co.kr/Product_new/102294
http://www.hyunjindc.com/qna/74422
http://www.hyunjindc.com/qna/74440
http://www.hyunjindc.com/qna/74463
http://www.hyunjindc.com/qna/74476
http://www.hyunjindc.com/qna/74486
http://www.itosm.com/cn/board_nLoq17/80176
http://tototoday.com/board_oRiY52/50649
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1687184
http://laokorea.com/orange_menu1/92413
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=713045
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=37754
http://subforumna.x10.mx/mad/index.php?topic=255615.0
http://bebopindia.com/notcie/118278
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2658071
http://bebopindia.com/notcie/126502
http://lucky.kidspann.net/index.php?mid=qna&document_srl=58332
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4960374
http://thermoplast.envolgroupe.com/component/k2/author/123239
http://emjun.com/?document_srl=100610
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3403918
http://smartacity.com/component/k2/itemlist/user/56032
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=96925
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-2019-su%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
https://mcsetup.tk/bbs/index.php?topic=256286.0
http://skylinecam.co.kr/photo/116369
http://zanoza.h1n.ru/2019/05/20/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-86-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ji8/
http://www.svteck.co.kr/customer_gratitude/37459
http://mir3sea.com/forum/index.php?topic=3431.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1447623
http://photogrotto.com/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qu3%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=119562
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=260315
http://www.lgue.co.kr/?document_srl=104555
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=481367
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=471333
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/?document_srl=33535
http://sofficer.net/xe/teach/256704
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=40964
http://fbpharm.net/index.php/component/k2/itemlist/user/67923
https://sanp.pro/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24-05-2019-oe%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24-05-201910-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24/
http://azone.synology.me/xe/?document_srl=194255
http://withinfp.sakura.ne.jp/eso/index.php/17408358-smotret-soderzanki-9-seria-u2-soderzanki-9-seria/0
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3334888
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3334901
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3334906
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3334911
http://xn----3x5er9r48j7wemud0a387h.com/news/83051
http://xn----3x5er9r48j7wemud0a387h.com/news/83079
http://yoriyorifood.com/xxxx/spacial/173585
https://esel.gist.ac.kr/esel2/board_hmgj23/154641
https://esel.gist.ac.kr/esel2/board_hmgj23/154819
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=281760
http://khapthanam.co.kr/g1/107446
http://lucky.kidspann.net/index.php?mid=qna&document_srl=239041
http://lucky.kidspann.net/index.php?mid=qna&document_srl=239110
http://mglpcm.org/?document_srl=96921
http://mglpcm.org/board_ETkS12/96873
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-23-05-2019-p5-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://www.sp1.football/?document_srl=607823
http://www.sp1.football/index.php?mid=faq&document_srl=607870
http://www.teedinubon.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-23-05-2019-t5-%d0%b8%d0%b3%d1%80/
http://lavaggio.com.vn/index.php/component/k2/itemlist/user/3861260
http://benzmall.co.kr/index.php?mid=download&document_srl=22785
http://www.sp1.football/index.php?mid=faq&document_srl=567675
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=63470
http://5starcoffee.co.kr/board_EBXY17/15706
https://ttmt.net/crypto_lab_2F/549300
http://hyeonjun.co.kr/menu3/264864
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=60690
http://koais.com/data/128322
http://thermoplast.envolgroupe.com/component/k2/author/140853
http://withinfp.sakura.ne.jp/eso/index.php/17385684-rannaa-ptaska-erkenci-kus-42-seria-jyik-rannaa-ptaska-erkenci-k/0
http://www.ekemoon.com/227397/051920190922/
http://www.ekemoon.com/227403/051920191522/
http://www.ekemoon.com/227405/051920191822/
http://www.ekemoon.com/227409/051920192322/
http://www.ekemoon.com/227413/051920192822/
http://www.hicleaning.kr/board_wash/180600
http://www.hicleaning.kr/board_wash/180643
http://www.josephmaul.org/menu41/237919
http://mglpcm.org/board_ETkS12/96959
http://mglpcm.org/board_ETkS12/96974
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-23-05-2019-l8-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://www.sp1.football/index.php?mid=faq&document_srl=607780
http://www.sp1.football/index.php?mid=faq&document_srl=607941
http://www.teedinubon.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-23-05-2019-l2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5/
http://www.teedinubon.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-23-05-2019-p6-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80/
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=22600
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/25123
http://ye-dream.com/?document_srl=165916
http://proxima.co.rw/index.php/component/k2/itemlist/user/683209
http://www2.yasothon.go.th/smf/index.php?topic=159.168555
http://d-tube.info/board_jvyO69/332516
http://emjun.com/index.php?mid=hangtotal&document_srl=165001
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=16944
http://1661-6471.co.kr/news/23808
http://xn----3x5er9r48j7wemud0a387h.com/news/86213
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=186760
http://asin.itts.co.kr/board_rtXs84/20317
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=225099
http://www.original-craft.net/index.php?topic=349738.0
http://holysweat.dothome.co.kr/data/2575
http://fbpharm.net/index.php/component/k2/itemlist/user/67569
http://0433.net/?document_srl=65072
http://153.120.114.241/eso/index.php/17385273-vetrenyj-hercai-12-seria-uopp-vetrenyj-hercai-12-seria
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=310364
http://jjikduk.net/DATA/122794
http://jjikduk.net/DATA/123028
http://jjikduk.net/DATA/123045
http://shinhwaair2017.cafe24.com/?document_srl=347774
http://shinhwaair2017.cafe24.com/issue/347793
http://shinhwaair2017.cafe24.com/issue/347813
http://withinfp.sakura.ne.jp/eso/index.php/17384298-bogatye-i-bednye-zengin-ve-yoksul-15-seria-lrbf-bogatye-i-bedny/0
http://withinfp.sakura.ne.jp/eso/index.php/17384341-vetrenyj-hercai-15-seria-mcxe-vetrenyj-hercai-15-seria/0
http://www.ekemoon.com/227401/051920191422/
http://www.hicleaning.kr/board_wash/180301
http://www.hicleaning.kr/board_wash/180367
http://bewasia.com/index.php?document_srl=101336&mid=board_cUYy21
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=101433
http://bizchemical.com/board_kMpv94/2048011
http://bizchemical.com/board_kMpv94/2048077
http://cwon.kr/xe/board_bnSr36/192325
http://cwon.kr/xe/board_bnSr36/192383
http://d-tube.info/board_jvyO69/324022
http://d-tube.info/board_jvyO69/324160
http://d-tube.info/board_jvyO69/324171
http://d-tube.info/board_jvyO69/324183
http://d-tube.info/board_jvyO69/324188
http://holysweat.dothome.co.kr/data/4080
http://beautypouch.net/index.php?mid=board_09&document_srl=46205
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/25611
http://benzmall.co.kr/?document_srl=35779
http://xn--2e0b53df5ag1c804aphl.net/nuguna/70599
http://ajincomp.godohosting.com/board_STnh82/83691
http://wartoby.com/index.php?document_srl=48482&mid=board_UXUA38
http://zakdu.com/board_ssKi56/6840
http://www.josephmaul.org/menu41/232589
http://www.critico-expository.com/forum/index.php?topic=17271.0
http://www.critico-expository.com/forum/index.php?topic=17273.0
http://www.hicleaning.kr/?document_srl=181603
http://www.hicleaning.kr/board_wash/181524
http://www.josephmaul.org/menu41/238820
http://www.josephmaul.org/menu41/238846
http://www.josephmaul.org/menu41/238873
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=597906
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=597937
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=597949
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=597970
http://www.studyxray.com/Sangdam/221998
http://www.studyxray.com/Sangdam/222039
http://www.taeshinmedia.com/?document_srl=3335202
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3335197
http://khapthanam.co.kr/g1/108425
http://khapthanam.co.kr/g1/108636
http://khapthanam.co.kr/g1/108657
http://khapthanam.co.kr/g1/108684
http://khapthanam.co.kr/g1/108693
http://khapthanam.co.kr/g1/108724
http://khapthanam.co.kr/g1/108750
http://kitekorea.co.kr/board_Chea81/97765
http://kitekorea.co.kr/board_Chea81/97865
https://nple.com/xe/pds/109116
http://poselokgribovo.ru/forum/index.php?topic=810353.0
https://adsensebih.com/index.php?topic=37396.0
http://asiagroup.co.kr/index.php?document_srl=344531&mid=board_11
http://atemshow.com/atemfair_domestic/160840
http://tiretech.co.kr/index.php?mid=qna&document_srl=162612
http://looksun.co.kr/index.php?mid=board_4&document_srl=97669
http://www.ekemoon.com/229531/051120191623/
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=266349
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/17155
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=874053
http://pkgersang.dothome.co.kr/board_jiKY24/22015
http://www.lovestory.or.kr/topic/24450
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=99446
https://www.amazingworldtop.com/entretenimiento/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bv1%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be/
http://esiapolisthesharp2.co.kr/g1/63786
http://beautypouch.net/index.php?mid=board_09&document_srl=63288
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=22635
http://barobus.kr/qna/63931
http://barobus.kr/qna/63946
http://barobus.kr/qna/63950
http://barobus.kr/qna/63964
http://barobus.kr/qna/63979
http://barobus.kr/qna/63984
http://barobus.kr/qna/63999
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://forum.digamahost.com/index.php?topic=125985.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=d631e535f723f964b43c74ed471eb975&topic=7019.0
http://skylinecam.co.kr/photo/111448
http://lucky.kidspann.net/index.php?mid=qna&document_srl=119928
http://zanoza.h1n.ru/2019/05/20/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-o6-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1451985
http://0433.net/junggo/51165
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3410327
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3872697
https://esel.gist.ac.kr/esel2/board_hmgj23/156204
http://www.vamoscontigo.org/Noticia/103112
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=24819
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=177951
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=42737
http://tk-laser.co.kr/index.php?mid=board_QsEu43&document_srl=111193
http://www.livetank.cn/market1/193826
http://www.lgue.co.kr/?document_srl=81052
http://daesestudy.co.kr/ipsi_docu/91631
http://k-cea.org/board_Hnyj62/170832
http://barobus.kr/qna/57622
http://1600-1590.com/index.php?document_srl=271686&mid=board_ihsE13
http://p9912.cafe24.com/board_LVgu51/6911
http://mercibq.net/partner/36089
http://mglpcm.org/board_ETkS12/107577
http://mglpcm.org/board_ETkS12/107606
http://mglpcm.org/board_ETkS12/107617
http://mglpcm.org/board_ETkS12/107637
http://www.critico-expository.com/forum/index.php?topic=26857.0
http://www.critico-expository.com/forum/index.php?topic=26866.0
http://www.critico-expository.com/forum/index.php?topic=26875.0
http://www.fassen.co.kr/xe/board_VCum96/89802
http://www.original-craft.net/index.php?topic=356502.0
http://www.original-craft.net/index.php?topic=356505.0
http://corumotoanahtar.com/component/k2/itemlist/user/4905.html
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qs7%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05/
http://www.svteck.co.kr/customer_gratitude/53538
http://mediaville.me/index.php/component/k2/itemlist/user/292932
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=72694
http://rudraautomation.com/index.php/component/k2/author/223986
http://www.crnmedia.es/component/k2/itemlist/user/87078
https://www.tedyun.com/xe/?document_srl=179522
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=150433
http://forum.elexlabs.com/index.php?topic=37735.0
http://teambuildingpremium.com/forum/index.php?topic=844182.0
http://bobr.site/index.php?topic=150521.0
http://www.crnmedia.es/?option=com_k2&view=itemlist&task=user&id=87030
http://www.golden-nail.co.kr/press/71972
http://www.insesinmun.com/newpaper2/92723
http://www.ekemoon.com/230427/051720194323/
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/44800
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=97883
http://www.emrabq8.com/index.php/component/k2/itemlist/user/1836330
http://mercibq.net/partner/18187
http://projectcva.dothome.co.kr/c_com/6146
http://nanumi.tmax.co.kr/xe/index.php?mid=proj_2018&document_srl=6011
https://sanp.pro/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%84%d0%b8%d0%bd%d0%b0%d0%bb-ae%d1%85%d0%be%d0%bb%d0%be/
http://www.hyunjindc.com/qna/63018
http://www.hyunjindc.com/qna/91330
http://153.120.114.241/eso/index.php/17452265-voron-kuzgun-19-seria-drid-voron-kuzgun-19-seria
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=705323
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=61240
http://zanoza.h1n.ru/2019/05/19/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tg4%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7/
http://israengineering.com/index.php/component/k2/itemlist/user/1208539
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3695927
http://forum.kopkargobel.com/index.php?topic=11742.0
http://forums.abs-cbn.com/welcome-back-kapamilya%21/oe-ee-1-e-18-05-2019-mce-oe-ee-1-e/
http://zanoza.h1n.ru/2019/05/20/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nm0%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=852994
http://asin.itts.co.kr/board_rtXs84/20399
http://asin.itts.co.kr/board_rtXs84/20409
http://asin.itts.co.kr/board_rtXs84/20422
http://asin.itts.co.kr/board_rtXs84/20436
http://asin.itts.co.kr/board_rtXs84/20459
http://beautypouch.net/index.php?mid=board_09&document_srl=55451
http://www.kwpcoop.or.kr/QnA/9762
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/64575
http://d-tube.info/board_jvyO69/339933
http://www.theocraticamerica.org/forum/index.php?topic=53956.0
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=61057
http://indiefilm.kr/xe/?document_srl=130468
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=77900
http://lucky.kidspann.net/index.php?mid=qna&document_srl=64373
http://mediaville.me/index.php/component/k2/itemlist/user/289976
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/24645
http://www.hsaura.com/noty/157316
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=314795
http://asin.itts.co.kr/board_rtXs84/25494
http://asin.itts.co.kr/board_rtXs84/25525
http://asin.itts.co.kr/board_rtXs84/25535
http://asin.itts.co.kr/board_rtXs84/25549
http://asin.itts.co.kr/board_rtXs84/25554
http://asin.itts.co.kr/board_rtXs84/25564
http://asin.itts.co.kr/board_rtXs84/25570
http://daesestudy.co.kr/?document_srl=91639
http://daesestudy.co.kr/ipsi_docu/91494
https://serverpia.co.kr/board_ucCk10/50201
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=820049
http://webp.online/index.php?topic=64475.0
http://bebopindia.com/notcie/288209
http://zanoza.h1n.ru/2019/05/23/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0/
http://www.teedinubon.com/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-2019-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-m4-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-2019-3/
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1633634
http://daltso.com/?document_srl=73623
http://bizchemical.com/board_kMpv94/2090547
http://2872870.com/est/39802
http://xplorefitness.com/blog/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-24-05-2019%C2%BB-ej%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-24-05-2019%C2%BB20-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-24-05-2019
http://www.ds712.net/guest/?document_srl=139210
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1449289
http://yoriyorifood.com/xxxx/spacial/109276
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-17-05-2019-e1-%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
http://www.studyxray.com/Sangdam/183795
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/262150
http://www.gforgirl.com/xe/poster/119514
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gk4%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://daesestudy.co.kr/ipsi_docu/92035
http://daesestudy.co.kr/ipsi_docu/92173
http://dev.aabn.org.gh/component/k2/itemlist/user/647100
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=103604
http://jjikduk.net/DATA/127211
http://jjikduk.net/DATA/127304
http://photogrotto.com/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-g5-%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4/
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2357163
http://www.almacenesrickie.com.ec/index.php/component/k2/itemlist/user/141616
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=42220
http://zanoza.h1n.ru/2019/05/22/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-z6-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
http://zanoza.h1n.ru/2019/05/22/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-v6-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
http://zanoza.h1n.ru/2019/05/22/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-d1-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://zanoza.h1n.ru/2019/05/22/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-r2-%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd/
http://f-tube.info/board/158238
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=496138
http://herdental.co.kr/index.php?mid=online&document_srl=69153
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=212222
https://hackinsa.com/freeboard/21994
http://fbpharm.net/index.php/component/k2/itemlist/user/67830
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=275284
http://sunele.co.kr/board_ReBD97/152941
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=85521
http://www.josephmaul.org/menu41/123374
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3825471
http://vhost12299.cpsite.ru/435117-tola-robot-1-seria-17052019-z8-tola-robot-1-seria
http://emjun.com/index.php?mid=hangtotal&document_srl=81226
http://lucky.kidspann.net/index.php?mid=qna&document_srl=74810
http://www.aloeverasas.it/index.php/component/k2/itemlist/user/20547
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=58184
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1733286
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=86001
http://jiquilisco.org/index.php/component/k2/itemlist/user/11235
http://shinhwaair2017.cafe24.com/issue/233862
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=77238
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=22440
http://mediaville.me/index.php/component/k2/itemlist/user/301054
http://asin.itts.co.kr/board_rtXs84/25899
http://daesestudy.co.kr/ipsi_docu/92750
http://daesestudy.co.kr/ipsi_docu/92794
http://jjikduk.net/DATA/128274
http://jjikduk.net/DATA/128307
http://jjikduk.net/DATA/128372
http://www.almacenesrickie.com.ec/index.php/component/k2/itemlist/user/141718
http://www.teedinubon.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-e8-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
http://jiquilisco.org/index.php/component/k2/itemlist/user/18542
http://stockbuy.cafe24.com/realize/1026
http://jjikduk.net/DATA/123823
http://xn--2e0bk61btjo.com/notice/14212
http://www.insesinmun.com/newpaper2/70298
http://d-tube.info/board_jvyO69/360418
http://gochon-iusell.co.kr/g1/55377
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=71550
http://zanoza.h1n.ru/2019/05/20/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-82-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-34/
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=100463
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=59169
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1447700
http://bebopindia.com/notcie/142605
http://www.svteck.co.kr/customer_gratitude/54798
http://yeonsen.com/?document_srl=95501
http://www.spazioad.com/component/k2/itemlist/user/7345251
http://miklja.net/forum/index.php?topic=35330.0
http://otitismediasociety.org/forum/index.php?topic=196031.0
http://poselokgribovo.ru/forum/index.php?topic=813137.0
http://taklongclub.com/forum/index.php?topic=182655.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=04dded2d7c2087fad7313b9ed7597ebd&topic=279488.0
http://webp.online/index.php?topic=65602.0
https://khuyenmaikk13.info/index.php?topic=223291.0
https://khuyenmaikk13.info/index.php?topic=223294.0
http://www.teedinubon.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-b3-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-14-%d1%81%d0%b5%d1%80%d0%b8/
http://thermoplast.envolgroupe.com/component/k2/author/137871
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ws5e-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://agiteshop.com/xe/qa/110958
http://d-tube.info/?document_srl=338847
http://dreamplusart.com/mn03_01/62993
http://rudraautomation.com/index.php/component/k2/author/267164
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4981309
https://sanp.pro/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%84%d0%b8%d0%bd%d0%b0%d0%bb-vr%d1%85%d0%be%d0%bb%d0%be/
https://prelease.club/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-no%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://www.sp1.football/index.php?mid=faq&document_srl=191851
https://altaylarteknoloji.com/index.php?topic=4799.0
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ok4%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05/
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=73111
https://www.amazingworldtop.com/entretenimiento/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yr3%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05-2019/
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8/
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2323299
http://www.sp1.football/index.php?mid=faq&document_srl=646961
http://www.sp1.football/index.php?mid=faq&document_srl=646980
http://www.sp1.football/index.php?mid=tr_video&document_srl=646975
http://www.teedinubon.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-y3-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-14-%d1%81%d0%b5%d1%80%d0%b8/
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-r8-%d1%81%d0%bb%d1%83%d0%b3/
http://www.teedinubon.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-a7-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80/
http://xihillstate.bloggirl.net/?document_srl=237768
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=237625
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=237688
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=237693
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=237703
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=237724
https://ttmt.net/crypto_lab_2F/549533
http://dow.dothome.co.kr/board_jydx58/15117
http://khapthanam.co.kr/g1/123353
https://www.celekt.com/%d0%a5%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-eu%d0%a5%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://photogrotto.com/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fd6x-%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f/
http://xn--ok1bpqi43ahtb.net/board_eASW07/122195
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=58661
http://shinilspring.com/board_qsfb01/118102
http://thanosakademi.com/index.php?topic=95581.0
https://emoforum.org/discussion/3232/vetrenyy-hercai-25-seriya-ujfz-vetrenyy-hercai-25-seriya
http://roikjer.com/forum/index.php?PHPSESSID=r25jobpf8ah4hr9kamibh717k4&topic=896947.0
https://cybergsm.es/index.php?topic=30053.0
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1944393
http://lucky.kidspann.net/index.php?mid=qna&document_srl=88373
http://www.theparrotcentre.com/forum/index.php?topic=565983.0
http://zanoza.h1n.ru/2019/05/20/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-p2-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2/
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=126923
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/225711
http://www.popolsku.fr.pl/forum/index.php?topic=409949.0
http://www.popolsku.fr.pl/forum/index.php?topic=409982.0
http://www.spazioad.com/component/k2/itemlist/user/7407417
http://www2.yasothon.go.th/smf/index.php?topic=159.169095
http://www2.yasothon.go.th/smf/index.php?topic=159.169110
http://www2.yasothon.go.th/smf/index.php?topic=159.169125
http://www2.yasothon.go.th/smf/index.php?topic=159.msg196852
https://adsensebih.com/index.php?topic=39072.0
https://hackersuniversity.net/index.php?topic=28821.0
https://khuyenmaikk13.info/index.php?topic=223301.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=353024
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1733130
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/?document_srl=18648
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=81036
https://esel.gist.ac.kr/esel2/board_hmgj23/140533
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=80789
http://forum.digamahost.com/index.php?topic=127215.0
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/228048
http://universalcommunity.se/Forum/index.php?topic=15942.0
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=19489
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=76921
http://sfah.ch/?option=com_k2&view=itemlist&task=user&id=15214
http://www.original-craft.net/index.php?topic=339865.0
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=121231
http://shinhwaair2017.cafe24.com/issue/206051
http://xn----3x5er9r48j7wemud0a387h.com/news/35529
https://sanp.pro/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-yt%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cf6%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://0433.net/?document_srl=50795
http://nanaae.com/confirm/40994
http://nanaae.com/confirm/41008
http://nanaae.com/confirm/41018
http://nanaae.com/confirm/41028
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=170957
http://oneandonly1127.com/guest/63838
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ph7i-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://yeonsen.com/index.php?document_srl=225101&mid=board_vZbN12
http://viamania.net/index.php?mid=board_raYV15&document_srl=98681
http://tk-laser.co.kr/?document_srl=115099
http://5starcoffee.co.kr/board_EBXY17/15195
http://jjikduk.net/DATA/133109
http://www.kwpcoop.or.kr/QnA/7121
http://www.fassen.co.kr/xe/board_VCum96/66251
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=84546
http://thermoplast.envolgroupe.com/index.php/component/k2/itemlist/user/142914
http://www.vamoscontigo.org/Noticia/91528
http://hyeonjun.co.kr/menu3/232013
http://hyeonjun.co.kr/menu3/232056
http://hyeonjun.co.kr/menu3/232076
http://hyeonjun.co.kr/menu3/232098
http://hyeonjun.co.kr/menu3/232127
http://hyeonjun.co.kr/menu3/232163
http://isch.kr/board_PowH60/87418
http://isch.kr/board_PowH60/87438
http://isch.kr/board_PowH60/87475
http://isch.kr/board_PowH60/87514
http://jiral.net/an9/21968
http://themasters.pro/file_01/157791
http://www.telcon.gr/index.php/component/k2/itemlist/user/74070
http://dcasociados.eu/component/k2/itemlist/user/89723
http://www.svteck.co.kr/customer_gratitude/51334
http://forum.elexlabs.com/index.php?topic=46617.0
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1662605
http://ye-dream.com/qa/83851
http://rudraautomation.com/index.php/component/k2/author/225985
http://www.kwpcoop.or.kr/QnA/9663
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=148034
http://jjikduk.net/DATA/149878
http://www.josephmaul.org/menu41/233312
http://sofficer.net/xe/teach/254935
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=54479
http://153.120.114.241/eso/index.php/17450030-vossoedinenie-vuslat-18-seria-vfwh-vossoedinenie-vuslat-18-seri
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=197204
http://melchinooddle.dothome.co.kr/index.php?document_srl=7460&mid=board_EIUA02
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=19013
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=19031
https://2002.shyoon.com/board_2002/117985
https://2002.shyoon.com/board_2002/118043
https://betshin.com/Story/106992
https://betshin.com/Story/107031
https://hackinsa.com/freeboard/16299
https://hackinsa.com/freeboard/16375
https://hackinsa.com/freeboard/16395
http://batubersurat.com/?option=com_k2&view=itemlist&task=user&id=63605
http://hyeonjun.co.kr/?document_srl=89990
http://ovotecegg.com/component/k2/itemlist/user/165926
http://photogrotto.com/%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-100-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xj6%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-100-%d1%81%d0%b5%d1%80%d0%b8%d1%8f19-05-2019/
http://www.svteck.co.kr/customer_gratitude/43555
http://www.ekemoon.com/213293/052220195218/
http://forum.elexlabs.com/index.php/topic,37309.0.html
http://rudraautomation.com/index.php/component/k2/author/225287
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.kr/?document_srl=28049
http://1661-6471.co.kr/news/21668
http://udrpsucks.com/blog/?p=1514
http://wartoby.com/index.php?document_srl=37660&mid=board_UXUA38
http://www.itosm.com/cn/board_nLoq17/75187
http://www.sp1.football/index.php?mid=faq&document_srl=621610
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1642560
http://www.studyxray.com/Sangdam/224208
http://www.insesinmun.com/newpaper2/71835
http://www.itosm.com/cn/board_nLoq17/69701
http://www.jesusonly.life/calendar/338985
http://www.jesusonly.life/calendar/339025
http://www.jesusonly.life/calendar/339093
http://www.jesusonly.life/calendar/339119
http://www.jesusonly.life/calendar/339136
http://www.kcch.or.kr/?document_srl=66166
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=66142
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=66156
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=66175
http://roikjer.com/forum/index.php?PHPSESSID=okrb1rq7qvfee5cislbhap00p3&topic=899671.0
http://www.taeshinmedia.com/?document_srl=3302746
https://cybergsm.es/index.php?topic=33809.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=40a1fa88a76b701915054902dcfe8d76&topic=7893.0
http://asiagroup.co.kr/index.php?document_srl=190245&mid=board_11
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2323686
http://www.jesusonly.life/calendar/137245
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=111120
http://community.viajar.tur.br/index.php?p=/discussion/61457/edinoe-serdce-tek-yuerek-17-seriya-nluk-edinoe-serdce-tek-yuerek-17-seriya
http://www.golden-nail.co.kr/press/91734
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=101607
http://indiefilm.kr/xe/board/107346
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/43386
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jq4%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://daesestudy.co.kr/ipsi_docu/48664
http://www.ekemoon.com/232763/050920190424/
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=14363
http://www.svteck.co.kr/customer_gratitude/137816
https://www.celekt.com/%d0%91%d0%be%d0%b3%d0%b0%d1%82%d1%8b%d0%b5-%d0%b8-%d0%b1%d0%b5%d0%b4%d0%bd%d1%8b%d0%b5-zengin-ve-yoksul-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wisi-%d0%91%d0%be%d0%b3%d0%b0%d1%82%d1%8b/
http://asin.itts.co.kr/board_rtXs84/13292
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3297331
http://skylinecam.co.kr/photo/78906
http://www.digitalbul.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-2019-ov%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
https://sanp.pro/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zd5%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f20-05/
http://jjikduk.net/DATA/79635
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/44209
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lk5%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
https://altaylarteknoloji.com/index.php?topic=5003.0
http://1600-1590.com/?document_srl=126417
https://www.shaiyax.com/index.php?topic=353734.0
http://www.emrabq8.com/index.php/component/k2/itemlist/user/1827516
http://lucky.kidspann.net/index.php?mid=qna&document_srl=260293
http://mercibq.net/?document_srl=36016
http://mercibq.net/partner/36042
http://mercibq.net/partner/36062
http://www.cnsmaker.net/xe/?document_srl=105441
http://www.cnsmaker.net/xe/?document_srl=105460
http://www.cnsmaker.net/xe/?document_srl=105475
http://www.cnsmaker.net/xe/?document_srl=105484
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=484007
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=484035
http://sy.korean.net/qna/230614
http://barobus.kr/qna/40298
http://www.teedinubon.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-23-05-2019-a8-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2/
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1633341
http://daltso.com/index.php?mid=board_cUYy21&document_srl=93679
http://www.sp1.football/index.php?mid=faq&document_srl=585972
http://agiteshop.com/xe/qa/115007
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=144572
http://www.fassen.co.kr/xe/board_VCum96/92964
http://xn--2e0b53df5ag1c804aphl.net/nuguna/91657
http://carand.co.kr/?document_srl=18570
http://www.itosm.com/cn/board_nLoq17/72066
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=30931
https://testing.celekt.com/%d0%a5%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-qj3%d0%a5%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5/
https://ne-kuru.ru/index.php?topic=222841.0
http://yoriyorifood.com/xxxx/spacial/92404
http://www.hsaura.com/?document_srl=110383
http://www.jesusonly.life/calendar/130464
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=134516
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=530146
http://ye-dream.com/qa/72097
http://forum.elexlabs.com/index.php?topic=59575.0
http://miklja.net/forum/index.php?topic=35317.0
http://otitismediasociety.org/forum/index.php?topic=195962.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/686601
http://thanosakademi.com/index.php?topic=114657.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/1140288
http://thanosakademi.com/index.php?topic=112439.0
http://ovotecegg.com/component/k2/itemlist/user/181183
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3873110
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=142500
http://jjikduk.net/DATA/141275
http://shinhwaair2017.cafe24.com/issue/413467
http://ucckorea.kr/?document_srl=61500
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1952357
http://callman.co.kr/index.php?mid=qa&document_srl=182282
http://emjun.com/index.php?mid=hangtotal&document_srl=90854
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3391870
http://1600-1590.com/?document_srl=148069
http://www.sp1.football/index.php?mid=faq&document_srl=177161
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/112051
https://medicalcomplaints.in/discussion/344/bogatye-i-bednye-zengin-ve-yoksul-20-seriya-ceyw-bogatye-i-bednye-zengin-ve-yoksul-20-seriya
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=82651
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=87309
http://community.viajar.tur.br/index.php?p=/discussion/61478/bogatye-i-bednye-zengin-ve-yoksul-16-seriya-quwf-bogatye-i-bednye-zengin-ve-yoksul-16-seriya
https://www.amazingworldtop.com/entretenimiento/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-95-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iu1%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-95-%d1%81%d0%b5%d1%80%d0%b8%d1%8f19-05-2019/
http://photogrotto.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-im1%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c/
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=236857
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=236889
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=236938
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=236957
http://atemshow.com/atemfair_domestic/173206
http://atemshow.com/atemfair_domestic/173325
http://atemshow.com/atemfair_domestic/173355
http://atemshow.com/atemfair_domestic/173391
http://bebopindia.com/notcie/346288
http://bebopindia.com/notcie/346425
http://benzmall.co.kr/?document_srl=33949
http://benzmall.co.kr/index.php?mid=download&document_srl=33818
http://benzmall.co.kr/index.php?mid=download&document_srl=33882
http://benzmall.co.kr/index.php?mid=download&document_srl=33902
http://benzmall.co.kr/index.php?mid=download&document_srl=33929
http://0433.net/junggo/71006
http://ajincomp.godohosting.com/board_STnh82/91400
http://esiapolisthesharp2.co.kr/g1/58417
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=249398
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/793670
http://dickymicky.com/bbs/1918
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/5147
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1950314
http://lucky.kidspann.net/index.php?mid=qna&document_srl=72816
http://www.hicleaning.kr/?document_srl=99242
http://bitpark.co.kr/board_IzjM66/4070475
http://test.comics-game.ru/index.php?topic=143.0
http://roikjer.com/forum/index.php?PHPSESSID=vforeqm84pjnfpvmc3b2eiffu1&topic=893670.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=35544.0
http://daesestudy.co.kr/ipsi_docu/50964
http://teambuildingpremium.com/forum/index.php?topic=858972.0
http://www.tekparcahdfilm.com/forum/index.php?topic=51475.0
http://k-cea.org/board_Hnyj62/106153
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/224137
http://roikjer.com/forum/index.php?PHPSESSID=dciv4rlgi3l7ic36ect5eeuje4&topic=889470.0
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=236454
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=236501
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=236530
http://forum.digamahost.com/index.php?topic=134033.0
http://forum.digamahost.com/index.php?topic=134037.0
http://miklja.net/forum/index.php?topic=35328.0
http://miklja.net/forum/index.php?topic=35329.0
http://miklja.net/forum/index.php?topic=35330.0
http://otitismediasociety.org/forum/index.php?topic=196031.0
http://poselokgribovo.ru/forum/index.php?topic=813137.0
http://taklongclub.com/forum/index.php?topic=182655.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=04dded2d7c2087fad7313b9ed7597ebd&topic=279488.0
http://barobus.kr/qna/60629
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lm5%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://taklongclub.com/forum/index.php?topic=176581.0
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c/
http://www.livetank.cn/market1/148236
http://toeden.co.kr/Product_new/101590
http://www.josephmaul.org/menu41/231068
http://apt2you2.cafe24.com/g1/17076
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=9258
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/36376
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=36675
http://shinhwaair2017.cafe24.com/issue/330949
http://yoriyorifood.com/xxxx/spacial/167739
https://esel.gist.ac.kr/esel2/board_hmgj23/146067
https://esel.gist.ac.kr/esel2/board_hmgj23/146165
https://esel.gist.ac.kr/esel2/board_hmgj23/146184
https://khuyenmaikk13.info/index.php?topic=215872.0
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=270933
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=270986
http://batubersurat.com/index.php/component/k2/itemlist/user/62627
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=60766
http://www.critico-expository.com/forum/index.php?topic=13529.0
http://test.comics-game.ru/index.php?topic=269.0
http://dessa.com.br/component/k2/itemlist/user/344492
http://mediaville.me/index.php/component/k2/itemlist/user/283867
http://vhost12299.cpsite.ru/419619-igra-prestolov-8-sezon-5-seria-smotret-igra-prestolov-8-sezon-5
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/509698
http://www.hsaura.com/noty/133985
https://testing.celekt.com/%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sw6%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f17-05-2019/
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=73676
http://lucky.kidspann.net/index.php?mid=qna&document_srl=239287
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=351741
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/240289
http://nanumi.tmax.co.kr/xe/index.php?mid=proj_2018&document_srl=28055
http://tiretech.co.kr/index.php?mid=qna&document_srl=163763
http://shinhwaair2017.cafe24.com/issue/331497
http://daesestudy.co.kr/ipsi_docu/85548
http://www.flixian.com/main/QnA/72516
http://www.josephmaul.org/menu41/225841
http://withinfp.sakura.ne.jp/eso/index.php/17403756-klatva-yemin-58-seria-josh-klatva-yemin-58-seria/0
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=725551
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=1127284
http://ye-dream.com/qa/161807
http://www.golden-nail.co.kr/press/309927
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=723650
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=724095
http://www.lgue.co.kr/?document_srl=79742
http://www.lgue.co.kr/?document_srl=79784
http://www.lgue.co.kr/?document_srl=79799
http://www.lgue.co.kr/?document_srl=79811
http://www.lgue.co.kr/?document_srl=79820
http://www.lgue.co.kr/?document_srl=79825
http://www.lgue.co.kr/?document_srl=79835
http://www.lgue.co.kr/?document_srl=79845
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=29649
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=29664
http://asiagroup.co.kr/?document_srl=328630
http://k-cea.org/board_Hnyj62/135200
http://zanoza.h1n.ru/2019/05/23/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-83-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-57/
http://zanoza.h1n.ru/2019/05/23/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-b1-%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4/
http://zanoza.h1n.ru/2019/05/23/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-b6-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://zanoza.h1n.ru/2019/05/23/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-v1-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=362560
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=362623
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=362673
http://dev.aabn.org.gh/component/k2/itemlist/user/648955
http://nanaae.com/confirm/11186
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-23-05-2019-b1-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80/
http://themasters.pro/?document_srl=155245
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=354374
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=40026
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=357116
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=357198
http://barobus.kr/?document_srl=60994
http://barobus.kr/qna/60974
http://barobus.kr/qna/60989
http://barobus.kr/qna/60999
http://bebopindia.com/notcie/333260
http://bebopindia.com/notcie/333384
http://d-tube.info/board_jvyO69/337275
http://sunele.co.kr/board_ReBD97/129029
http://sunele.co.kr/board_ReBD97/129201
http://thermoplast.envolgroupe.com/component/k2/author/142656
http://thermoplast.envolgroupe.com/component/k2/author/142724
http://thermoplast.envolgroupe.com/component/k2/author/142974
http://thermoplast.envolgroupe.com/component/k2/author/142978
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=18864
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=18874
http://www.emrabq8.com/index.php/component/k2/itemlist/user/1841095
http://www.m1avio.com/index.php/component/k2/itemlist/user/3767320
http://www.ekemoon.com/229609/051120193823/
http://www.critico-expository.com/forum/index.php?topic=20021.0
https://khuyenmaikk13.info/index.php?topic=215145.0
http://d-tube.info/board_jvyO69/302628
http://k-cea.org/board_Hnyj62/146388
https://www.celekt.com/%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-i9-%d0%a1%d0%bb%d1%83%d0%b3%d0%b0/
http://sd-xi.co.kr/g1/34429
https://hackinsa.com/freeboard/6978
http://isch.kr/board_PowH60/87107
http://forum.elexlabs.com/index.php?topic=55765.0
https://www.amazingworldtop.com/entretenimiento/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nj7%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://cwon.kr/xe/board_bnSr36/98535
http://netsconsults.com/index.php/component/k2/itemlist/user/793273
http://asin.itts.co.kr/board_rtXs84/7651
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=86944
https://nextezone.com/index.php?action=profile;u=8911
http://shinilspring.com/board_qsfb01/110154
http://www.gforgirl.com/xe/poster/105343
http://www.rationalkorea.com/xe/?document_srl=517191
http://nanaae.com/confirm/48180
http://nanaae.com/confirm/48246
http://nanaae.com/confirm/48297
http://neosky.net/xe/space_station/57609
http://neosky.net/xe/space_station/57623
http://neosky.net/xe/space_station/57638
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-q6-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80/
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=1081849
http://ajincomp.godohosting.com/board_STnh82/99904
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1469453
http://www.siheunglove.com/chulip/162495
http://koais.com/data/118802
https://www.2ayes.com/18800/2-2-22-05-2019-t4-2-2
http://jjikduk.net/?document_srl=137896
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=337779
http://forum.elexlabs.com/index.php/topic,55877.0.html
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=42014
http://asin.itts.co.kr/board_rtXs84/24005
http://forum.elexlabs.com/index.php/topic,38900.0.html
http://carrierworld.co.kr/?document_srl=83298
http://asin.itts.co.kr/board_rtXs84/7597
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=110932
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1442914
http://ampersvet.by/component/k2/itemlist/user/36836
http://www.theocraticamerica.org/forum/index.php?topic=48529.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=347009
http://www.gforgirl.com/xe/?document_srl=116970
http://cwon.kr/xe/board_bnSr36/98564
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=516251
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yb2q-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/333950
http://www.digitalbul.com/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-84-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-21/
http://koais.com/data/140165
http://looksun.co.kr/index.php?mid=board_4&document_srl=115410
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-g6-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-x1-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d1%80/
http://tiretech.co.kr/index.php?mid=qna&document_srl=163987
http://www.hicleaning.kr/?document_srl=188115
http://barobus.kr/qna/62863
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=134777
http://viamania.net/?document_srl=79088
http://tiretech.co.kr/index.php?mid=qna&document_srl=116920
http://photogrotto.com/%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-96-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sd8r-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-96-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.hyunjindc.com/qna/66998
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=16670
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=127802
http://mglpcm.org/board_ETkS12/118617
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rq3%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f22-05/
http://photogrotto.com/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jj7%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
http://www.remify.app/foro/index.php?topic=313658.0
http://photogrotto.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zo5%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f19-05-2019/
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fs5%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=73334
http://lavaggio.com.vn/index.php/component/k2/itemlist/user/3826860
https://sanp.pro/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xi1p-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://ye-dream.com/qa/79113
https://testing.celekt.com/%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-v4-%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5/
http://www.critico-expository.com/forum/index.php?topic=13652.0
http://indiefilm.kr/xe/board/121999
http://community.viajar.tur.br/index.php?p=/discussion/61419/bogatye-i-bednye-zengin-ve-yoksul-14-seriya-pwzu-bogatye-i-bednye-zengin-ve-yoksul-14-seriya/p1%3Fnew=1
http://www.hsaura.com/noty/163334
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=67875
http://photogrotto.com/%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-q6-%d1%81%d0%bc%d0%be%d1%82/
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-f6-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80/
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-y8-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5/
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-m2-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80/
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-t8-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80/
http://photogrotto.com/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-2019-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-w9-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-2019-6-%d1%81/
http://photogrotto.com/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-d8-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-3-%d1%81%d0%b5%d1%80/
http://tiretech.co.kr/index.php?mid=notice&document_srl=164584
http://tk-laser.co.kr/index.php?mid=board_QsEu43&document_srl=134326
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=71368
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=71415
http://www.vamoscontigo.org/Noticia/128596
http://www.vamoscontigo.org/Noticia/128730
http://www.vamoscontigo.org/Noticia/128906
http://www.vamoscontigo.org/Noticia/128962
http://themasters.pro/file_01/205367
http://www.lucian.co.kr/?document_srl=15372
http://asin.itts.co.kr/board_rtXs84/26443
http://gabisan.com/board_OuDs04/40264
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/351532
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1734080
http://xihillstate.bloggirl.net/index.php?document_srl=193978&mid=board_HLJb60
http://yoriyorifood.com/xxxx/spacial/221694
http://153.120.114.241/eso/index.php/17363682-vetrenyj-hercai-15-seria-xolx-vetrenyj-hercai-15-seria
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=81270
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=61128
http://soc-human.kz/index.php/component/k2/itemlist/user/1711562
http://hyeonjun.co.kr/menu3/72945
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nb3%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://xn----3x5er9r48j7wemud0a387h.com/news/37245
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-th4%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f19-05/
http://oss.obigo.com/oss/?document_srl=21771
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=63492
http://www.josephmaul.org/menu41/120375
https://altaylarteknoloji.com/index.php?topic=5139.0
https://betshin.com/Story/142905
https://betshin.com/Story/142910
https://betshin.com/Story/142916
https://betshin.com/Story/142945
https://hackinsa.com/freeboard/78833
https://hackinsa.com/freeboard/78867
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=652748
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1128314
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/286074
http://xn--2e0b53df5ag1c804aphl.net/nuguna/87590
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/791798
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=63983
http://www.arunagreen.com/index.php/component/k2/itemlist/user/580369
http://www.vamoscontigo.org/Noticia/77810
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=193556
http://miklja.net/forum/index.php?topic=35736.0
http://divespace.co.kr/board/171355
http://kwpub.kr/PUBS/99787
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1127327
http://jnk-ent.jp/index.php?mid=gallery&document_srl=206543
http://shinhwaair2017.cafe24.com/?document_srl=329832
http://shinhwaair2017.cafe24.com/issue/329758
http://shinhwaair2017.cafe24.com/issue/329818
http://withinfp.sakura.ne.jp/eso/index.php/17338574-bogatye-i-bednye-zengin-ve-yoksul-16-seria-osuf-bogatye-i-bedny/0
http://www.critico-expository.com/forum/index.php?topic=15568.0
http://www.hicleaning.kr/board_wash/166747
http://www.josephmaul.org/menu41/219580
http://www.josephmaul.org/menu41/219607
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=25140
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=16309
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/121993
https://esel.gist.ac.kr/esel2/board_hmgj23/53661
http://miklja.net/forum/index.php?topic=31816.0
http://forum.drahthaar-club.com.ua/index.php?topic=3436.0
http://withinfp.sakura.ne.jp/eso/index.php/17117901-sluga-naroda-3-sezon-11-seria-x0-sluga-naroda-3-sezon-11-seria
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=82978
http://themasters.pro/file_01/170884
http://miklja.net/forum/index.php?topic=34847.0
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-or8t-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://gochon-iusell.co.kr/g1/51249
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=695926
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=695982
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=695759
http://www.original-craft.net/index.php?topic=354153.0
http://www.vamoscontigo.org/Noticia/97807
http://www.vamoscontigo.org/Noticia/97812
http://www.vamoscontigo.org/Noticia/97836
http://www.vamoscontigo.org/Noticia/97863
http://www.vamoscontigo.org/Noticia/97883
http://thermoplast.envolgroupe.com/component/k2/author/145172
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=100180
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1643781
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1482372
http://www.crnmedia.es/component/k2/itemlist/user/89498
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1843422
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1843427
http://www.firstfinancialservices.co.uk/?option=com_k2&view=itemlist&task=user&id=26404
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/26402
http://www.quattroandpartners.it/component/k2/itemlist/user/1193173
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=91057
http://www.hyunjindc.com/qna/65942
http://khapthanam.co.kr/g1/103526
http://dev.aabn.org.gh/component/k2/itemlist/user/641053
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/288104
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=179193
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=274101
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=808729
http://kitekorea.co.kr/board_Chea81/107350
http://www.vamoscontigo.org/Noticia/97897
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/?document_srl=27483
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/27473
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/27492
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/27497
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/15438
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=44594
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=44631
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3729922
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/309128
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/58936
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3430522
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=11196
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=11200
http://withinfp.sakura.ne.jp/eso/index.php/17378312-zestokij-stambul-zalim-istanbul-13-seria-noyx-zestokij-stambul-
http://jnk-ent.jp/index.php?mid=gallery&document_srl=165439
http://barobus.kr/qna/37301
http://hk-metal.co.kr/hkweb/QnA/69294
http://www.siheunglove.com/?document_srl=158225
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=329644
http://1661-6471.co.kr/news/16679
http://1661-6471.co.kr/news/16702
http://1661-6471.co.kr/news/16713
http://ajincomp.godohosting.com/board_STnh82/94082
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=344092
http://melchinooddle.dothome.co.kr/index.php?document_srl=4917&mid=board_EIUA02
http://mercibq.net/partner/27576
http://mercibq.net/partner/27602
http://mglpcm.org/board_ETkS12/97361
http://mglpcm.org/board_ETkS12/97395
http://nanaae.com/confirm/29863
http://nanaae.com/confirm/29891
http://nanaae.com/confirm/29905
https://www.celekt.com/%d0%9a%d0%be%d0%bd%d1%81%d1%83%d0%bb%d1%8c%d1%82%d0%b0%d0%bd%d1%82-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-23-05-2019-q7-%d0%9a%d0%be%d0%bd%d1%81%d1%83/
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=326029
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2717400
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2717485
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=365329
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=365361
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=365419
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2712817
https://sto54.ru/index.php/component/k2/itemlist/user/3423092
http://mglpcm.org/board_ETkS12/92333
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=353852
http://xn--ok1bpqi43ahtb.net/board_eASW07/150600
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=338943
http://carrierworld.co.kr/index.php?document_srl=66754&mid=board_UlGv44
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=93244
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=71643
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=35411
https://prelease.club/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-17-05-2019-my%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-vr7%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5/
http://moavalve.co.kr/faq/82933
http://indiefilm.kr/xe/board/132285
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3307133
http://www.golden-nail.co.kr/press/84608
https://tg.vl-mp.com/index.php?topic=1469473.0
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=204886
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=335289
http://www.nienkevanrijn.nl/component/k2/itemlist/user/446866
http://0433.net/junggo/55591
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1253837
http://married.dike.gr/index.php/component/k2/itemlist/user/71356
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/351540
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-2019-m4-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://lucky.kidspann.net/index.php?mid=qna&document_srl=243721
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3327772
http://esperanzazubieta.com/index.php/component/k2/itemlist/user/99948
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=599907
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=13014
https://medicalcomplaints.in/discussion/346/zhestokiy-stambul-zalim-istanbul-13-seriya-gycx-zhestokiy-stambul-zalim-istanbul-13-seriya/p1?new=1
http://www.gforgirl.com/xe/poster/149480
http://www.spazioad.com/component/k2/itemlist/user/7353042
http://theolevolosproject.org/index.php/component/k2/itemlist/user/26917
http://roikjer.com/forum/index.php?topic=892342.0
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=644673
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=856384
http://www.critico-expository.com/forum/index.php?topic=14572.0
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1932884
http://mobility-corp.com/index.php/component/k2/itemlist/user/2640693
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2618935
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3380143
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=75730
http://0433.net/?document_srl=44156
http://gtupuw.org/index.php/component/k2/itemlist/user/1923767
http://www.jshwanghoan.com/?document_srl=78841
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1609221
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/8294
http://zanoza.h1n.ru/2019/05/22/%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rc8%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%87%d0%b5%d1%80%d0%bd/
http://153.120.114.241/eso/index.php/17389722-klatva-yemin-66-seria-sbht-klatva-yemin-66-seria
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/128206
http://mvisage.sk/index.php/component/k2/itemlist/user/119355
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=1110066
http://photogrotto.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-21-05-2019-u0-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://looksun.co.kr/index.php?mid=board_4&document_srl=120467
http://e-educ.net/Forum/index.php?topic=12451.0
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=114092
http://www.bettarmang.co.kr/?document_srl=2167011
http://www.sp1.football/index.php?mid=faq&document_srl=181212
http://shinilspring.com/board_qsfb01/103087
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3297213
http://thermoplast.envolgroupe.com/component/k2/author/126920
https://testing.celekt.com/%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qv9%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f17-05/
http://www.sp1.football/index.php?mid=faq&document_srl=238968
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-op8%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
http://bebopindia.com/notcie/123262
http://forum.digamahost.com/index.php?topic=126039.0
http://www.telcon.gr/index.php/component/k2/itemlist/user/75640
http://adsudoeste.com.br/?option=com_k2&view=itemlist&task=user&id=22078
https://testing.celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-17-05-2019-b9-%d0%98%d0%b3%d1%80/
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-21-05-2019-a6-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jc4%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://bitpark.co.kr/board_IzjM66/4029701
http://azone.synology.me/xe/index.php?document_srl=117349&mid=board_SDnQ73
http://xn--ok1bpqi43ahtb.net/board_eASW07/121146
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1950626
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=74977
http://indiefilm.kr/xe/board/144127
http://www2.yasothon.go.th/smf/index.php?topic=159.166260
http://ye-dream.com/qa/74290
http://corumotoanahtar.com/component/k2/itemlist/user/6139.html
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=121075
http://jjikduk.net/?document_srl=78512
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=164007
http://www.fassen.co.kr/xe/board_VCum96/90490
http://5starcoffee.co.kr/?document_srl=17575
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/28581
http://www.siheunglove.com/chulip/141179
http://jjikduk.net/DATA/112477
http://jjikduk.net/DATA/112664
http://jjikduk.net/DATA/112718
http://lucky.kidspann.net/index.php?mid=qna&document_srl=159569
http://lucky.kidspann.net/index.php?mid=qna&document_srl=159591
http://shinhwaair2017.cafe24.com/issue/324432
http://shinhwaair2017.cafe24.com/issue/324442
http://shinhwaair2017.cafe24.com/issue/324492
http://shinhwaair2017.cafe24.com/issue/324497
http://withinfp.sakura.ne.jp/eso/index.php/17329509-deti-sester-kardes-cocuklari-20-seria-ldab-deti-sester-kardes-c
http://corumotoanahtar.com/?option=com_k2&view=itemlist&task=user&id=4271
http://research.kiu.ac.kr/?document_srl=96975
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1652114
https://tg.vl-mp.com/index.php?topic=1474159.0
http://www.taeshinmedia.com/?document_srl=3303223
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=86400
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3827889
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=49846
http://www.studyxray.com/Sangdam/104388
http://photogrotto.com/%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-101-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-or5%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-101-%d1%81%d0%b5%d1%80%d0%b8%d1%8f19-05-2019/
http://www.hsaura.com/noty/135652
http://roikjer.com/forum/index.php?PHPSESSID=hp6ovkjgt08a1rpun4kkn4i866&topic=904029.0
http://www.arunagreen.com/index.php/component/k2/itemlist/user/548581
http://www.studyxray.com/Sangdam/138695
http://toeden.co.kr/Product_new/142510
http://toeden.co.kr/Product_new/142546
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=81256
http://www.cnsmaker.net/xe/?document_srl=125276
http://www.cnsmaker.net/xe/?document_srl=125290
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=32784
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=558757
http://www.livetank.cn/?document_srl=156245
http://www.livetank.cn/market1/156204
http://www.livetank.cn/market1/156220
http://www.livetank.cn/market1/156326
http://www.lovestory.or.kr/?document_srl=18785
http://www.lovestory.or.kr/?document_srl=18806
http://www.lovestory.or.kr/topic/18753
http://www.lovestory.or.kr/topic/18758
https://www.chirorg.com/?document_srl=102476
https://www.chirorg.com/?document_srl=102507
https://www.chirorg.com/?document_srl=102517
http://forum.elexlabs.com/index.php?topic=57550.0
http://forum.elexlabs.com/index.php?topic=57570.0
http://miklja.net/forum/index.php?topic=34877.0
http://otitismediasociety.org/forum/index.php?topic=193372.0
http://taklongclub.com/forum/index.php?topic=176341.0
http://thanosakademi.com/index.php?topic=111687.0
http://thanosakademi.com/index.php?topic=111698.0
http://thanosakademi.com/index.php?topic=111702.0
http://thanosakademi.com/index.php?topic=111710.0
http://thanosakademi.com/index.php?topic=111715.0
http://tiretech.co.kr/index.php?mid=qna&document_srl=182057
http://tiretech.co.kr/index.php?mid=qna&document_srl=182130
http://tiretech.co.kr/index.php?mid=qna&document_srl=182153
http://tiretech.co.kr/index.php?mid=qna&document_srl=182163
http://tiretech.co.kr/index.php?mid=qna&document_srl=182172
http://toeden.co.kr/Product_new/142283
http://toeden.co.kr/Product_new/142345
http://toeden.co.kr/Product_new/142403
http://toeden.co.kr/Product_new/142415
http://withinfp.sakura.ne.jp/eso/index.php/17447314-live-smers-1-seria-q4-smers-1-seria
http://xplorefitness.com/blog/hd-video-%D0%BC%D0%B5%D1%80%D1%82%D0%B2%D0%BE%D0%B5-%D0%BE%D0%B7%D0%B5%D1%80%D0%BE-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-k2-%D0%BC%D0%B5%D1%80%D1%82%D0%B2%D0%BE%D0%B5-%D0%BE%D0%B7%D0%B5%D1%80%D0%BE-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/64933
http://153.120.114.241/eso/index.php/17448046-nasa-istoria-70-seria-ihps-nasa-istoria-70-seria
http://1600-1590.com/?document_srl=296076
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=296105
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=296122
http://ajincomp.godohosting.com/board_STnh82/81622
http://ajincomp.godohosting.com/board_STnh82/81641
http://ajincomp.godohosting.com/board_STnh82/81689
http://projectcva.dothome.co.kr/c_com/1456
http://themasters.pro/?document_srl=154559
http://themasters.pro/file_01/154606
http://toeden.co.kr/Product_new/89387
http://lucky.kidspann.net/index.php?mid=qna&document_srl=232246
http://mglpcm.org/?document_srl=93434
http://mglpcm.org/board_ETkS12/93301
http://mglpcm.org/board_ETkS12/93456
http://nanaae.com/confirm/24277
http://neosky.net/xe/space_station/36985
http://neosky.net/xe/space_station/37094
http://neosky.net/xe/space_station/37099
http://www.lgue.co.kr/?document_srl=54042
http://153.120.114.241/eso/index.php/17376106-bogatye-i-bednye-zengin-ve-yoksul-16-seria-dtcv-bogatye-i-bedny
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=517936
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=104389
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2656582
http://sd-xi.co.kr/?document_srl=31139
http://bebopindia.com/notcie/346158
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=508612
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=508625
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=508649
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=508675
http://www.fassen.co.kr/xe/board_VCum96/93972
http://www.fassen.co.kr/xe/board_VCum96/93985
http://www.fassen.co.kr/xe/board_VCum96/94010
http://www.hyunjindc.com/qna/94260
http://www.hyunjindc.com/qna/94286
http://www.livetank.cn/market1/195330
http://www.livetank.cn/market1/195487
http://www.livetank.cn/market1/195515
http://www.livetank.cn/market1/195599
http://ptu.imoove.kr/ko/content/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-17-05-2019%C2%BB-yp%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-11-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-17-05-2019%C2%BB88-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3381795
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=91716
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3844209
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13387
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=86656
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1614155
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/343003
http://www.insesinmun.com/newpaper2/76082
http://mobility-corp.com/index.php/component/k2/itemlist/user/2666754
http://toeden.co.kr/Product_new/94389
http://bizchemical.com/board_kMpv94/2049284
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/36137
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=47868
http://www.hyunjindc.com/qna/71643
http://yoriyorifood.com/xxxx/spacial/169719
http://asin.itts.co.kr/board_rtXs84/23914
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/18696
http://www.web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3714841
http://looksun.co.kr/index.php?mid=board_4&document_srl=98470
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3414592
http://www.livetank.cn/market1/195712
http://www.livetank.cn/market1/195730
http://www.livetank.cn/market1/195758
http://www.livetank.cn/market1/195790
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=66263
http://yoriyorifood.com/xxxx/spacial/103379
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1706783
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/225574
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/642020
http://www.hicleaning.kr/board_wash/128555
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/339598
https://hackinsa.com/freeboard/16539
http://mercibq.net/partner/38408
http://dohairbiz.com/en/component/k2/itemlist/user/2783634.html
http://sd-xi.co.kr/g1/34462
http://5starcoffee.co.kr/board_EBXY17/20429
http://www.svteck.co.kr/customer_gratitude/191539
http://www.critico-expository.com/forum/index.php?topic=15060.0
http://www.theocraticamerica.org/forum/index.php?topic=48589.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=25272
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=131063
http://153.120.114.241/eso/index.php/17124059-holostak-9-sezon-11-vypusk-17-05-2019-uxholostak-9-sezon-11-vyp
http://indiefilm.kr/xe/board/123476
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=498371
http://miklja.net/forum/index.php?topic=33504.0
http://zanoza.h1n.ru/2019/05/20/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-la4%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dy6%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1733225
http://www.jesusonly.life/calendar/138822
http://www.theparrotcentre.com/forum/index.php?topic=549503.0
http://webp.online/index.php?topic=59870.msg102500
http://www.hsaura.com/noty/112465
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=128946
http://matinbank.ir/component/k2/itemlist/user/4563319.html
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=649986
http://dcasociados.eu/component/k2/itemlist/user/91974
http://dev.aabn.org.gh/component/k2/itemlist/user/641636
http://forum.elexlabs.com/index.php?topic=53805.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=133271
http://xn--ok1bpqi43ahtb.net/?document_srl=103394
https://esel.gist.ac.kr/esel2/board_hmgj23/69992
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=495555
http://zanoza.h1n.ru/2019/05/20/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-y0-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7/
http://lucky.kidspann.net/index.php?document_srl=57797&mid=qna
http://xn--ok1bpqi43ahtb.net/board_eASW07/150813
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=86782
http://podwodnyswiat.eu/forum/index.php?topic=1343.0
http://netsconsults.com/index.php/component/k2/itemlist/user/805013
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=922883
https://esel.gist.ac.kr/esel2/board_hmgj23/56648
http://test.comics-game.ru/index.php?topic=66.0
http://mediaville.me/index.php/component/k2/itemlist/user/291638
http://community.viajar.tur.br/index.php?p=/discussion/61390/voron-kuzgun-14-seriya-dovj-voron-kuzgun-14-seriya
http://dev.aabn.org.gh/?option=com_k2&view=itemlist&task=user&id=612028
http://www.spazioad.com/component/k2/itemlist/user/7345276
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=109493
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hw2%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://shinilspring.com/board_qsfb01/98077
http://photogrotto.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8d%d1%84%d0%b8%d1%80-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-8-%d1%81%d0%b5-2/
http://shinilspring.com/board_qsfb01/101318
http://jjikduk.net/DATA/125923
http://lucky.kidspann.net/index.php?mid=qna&document_srl=233162
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=26412
http://www.ekemoon.com/230521/051820191623/
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=57379
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=1070488
http://xn--ok1bpqi43ahtb.net/board_eASW07/128198
http://www.teedinubon.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-op0%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f17-05-2019/
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/274513
http://xn----3x5er9r48j7wemud0a387h.com/news/39856
http://www.golden-nail.co.kr/press/100480
http://smartacity.com/component/k2/itemlist/user/59246
http://zanoza.h1n.ru/2019/05/19/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-cj%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=10058
http://ye-dream.com/qa/87280
http://www.jesusonly.life/calendar/147965
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1942620
http://bebopindia.com/notcie/155459
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4838052
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=87291
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=93269
http://otitismediasociety.org/forum/index.php?topic=184410.0
http://indiefilm.kr/xe/board/154780
http://emjun.com/index.php?mid=hangtotal&document_srl=96792
http://www.teedinubon.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cv9%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f21-05-2019/
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2/
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2511767
http://e-educ.net/Forum/index.php?action=profile;u=6369
http://jjikduk.net/DATA/155742
http://viamania.net/index.php?mid=board_raYV15&document_srl=71128
http://asin.itts.co.kr/board_rtXs84/30880
https://ttmt.net/crypto_lab_2F/550177
https://www.chirorg.com/?document_srl=87357
http://yoriyorifood.com/xxxx/spacial/179147
http://www.sp1.football/index.php?mid=faq&document_srl=672793
http://skylinecam.co.kr/photo/111064
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/856785
http://www.jshwanghoan.com/?document_srl=88331
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/261710
http://lucky.kidspann.net/index.php?mid=qna&document_srl=58264
http://daesestudy.co.kr/?document_srl=41905
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sg4%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/12066
http://ovotecegg.com/component/k2/itemlist/user/163337
http://married.dike.gr/index.php/component/k2/itemlist/user/65551
https://testing.celekt.com/%d0%9d%d0%b5-%d0%be%d1%82%d0%bf%d1%83%d1%81%d0%ba%d0%b0%d0%b9-%d0%bc%d0%be%d1%8e-%d1%80%d1%83%d0%ba%d1%83-elimi-birakma-42-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xylw-%d0%9d%d0%b5-%d0%be/
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3302630
http://emjun.com/index.php?mid=hangtotal&document_srl=93894
http://otitismediasociety.org/forum/index.php?topic=175582.0
https://www.2ayes.com/17287/3-17-19-05-2019-q7-3-17
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3378684
http://www.bettarmang.co.kr/story/2134497
http://shinilspring.com/board_qsfb01/105472
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kf9%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://shinilspring.com/board_qsfb01/91474
http://bebopindia.com/notcie/116163
http://corumotoanahtar.com/component/k2/itemlist/user/4486.html
https://ttmt.net/crypto_lab_2F/554448
http://www.insesinmun.com/newpaper2/93105
https://testing.celekt.com/%d0%a5%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24-05-2019-cg%d0%a5%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24-05-201952-%d0%a5%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-24/
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3823271
http://lucky.kidspann.net/index.php?mid=qna&document_srl=227908
http://www.josephmaul.org/menu41/233243
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3518794
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=46819
https://khuyenmaikk13.info/index.php?topic=216709.0
http://juroweb.com/xe/juroweb_board/71478
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/128632
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/282199
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/282468
http://smartacity.com/component/k2/itemlist/user/64912
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1633561
http://www.boutique.in.th/?option=com_k2&view=itemlist&task=user&id=152309
http://www.boutique.in.th/?option=com_k2&view=itemlist&task=user&id=152310
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1128719
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3514533
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/353321
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/353463
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/353470
http://0433.net/junggo/68419
http://0433.net/junggo/68425
http://0433.net/junggo/68440
https://www.amazingworldtop.com/entretenimiento/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5-2/
https://www.amazingworldtop.com/entretenimiento/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5-3/
https://www.amazingworldtop.com/entretenimiento/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5/
https://www.amazingworldtop.com/entretenimiento/%d0%ba%d0%be%d0%bd%d1%81%d1%83%d0%bb%d1%8c%d1%82%d0%b0%d0%bd%d1%82-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0/
https://www.amazingworldtop.com/entretenimiento/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%81/
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-live-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb/
http://carand.co.kr/?document_srl=25693
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/17425
https://nple.com/xe/pds/106162
https://www.chirorg.com/video/131649
https://www.amazingworldtop.com/entretenimiento/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fv6%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be/
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=275608
http://looksun.co.kr/index.php?mid=board_4&document_srl=119149
http://shinhwaair2017.cafe24.com/issue/374808
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=184952
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=184972
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=185060
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=185082
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=185087
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=185093
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=185098
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=185104
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=185125
http://community.viajar.tur.br/index.php?p=/profile/RemonaScot
http://lucky.kidspann.net/index.php?mid=qna&document_srl=174230
http://lucky.kidspann.net/index.php?mid=qna&document_srl=174276
http://jnk-ent.jp/index.php?mid=gallery&document_srl=169024
http://juroweb.com/xe/juroweb_board/52196
http://juroweb.com/xe/juroweb_board/52207
http://kitekorea.co.kr/board_Chea81/92026
http://kitekorea.co.kr/board_Chea81/92058
http://lucky.kidspann.net/index.php?mid=qna&document_srl=232660
http://lucky.kidspann.net/index.php?mid=qna&document_srl=232684
http://mamaspraha.dothome.co.kr/index.php?mid=board_ubGi34&document_srl=13133
http://mglpcm.org/board_ETkS12/93603
http://koais.com/data/100843
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=29861
http://xn--2e0b53df5ag1c804aphl.net/nuguna/60152
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=40612
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=89402
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=708331
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=708377
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=708476
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=708409
http://www.vamoscontigo.org/Noticia/100446
http://mobility-corp.com/index.php/component/k2/itemlist/user/2615075
http://0433.net/?document_srl=37973
http://hyeonjun.co.kr/?document_srl=103120
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=69960
http://www.jesusonly.life/calendar/155327
http://www.hyunjindc.com/qna/91998
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=1104113
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=287579
http://www.critico-expository.com/forum/index.php?topic=17915.0
http://dcasociados.eu/component/k2/itemlist/user/91608
http://5starcoffee.co.kr/board_EBXY17/13440
http://5starcoffee.co.kr/board_EBXY17/13446
http://ajincomp.godohosting.com/board_STnh82/97234
http://ajincomp.godohosting.com/board_STnh82/97262
http://ajincomp.godohosting.com/board_STnh82/97300
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=348319
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=337259
https://www.shaiyax.com/index.php?topic=356542.0
http://photogrotto.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-vn8%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5/
http://e-educ.net/Forum/index.php?topic=12562.0
http://teambuildingpremium.com/forum/index.php?topic=849971.0
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=205847
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=105193
http://photogrotto.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8d%d1%84%d0%b8%d1%80-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6/
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13414
http://atemshow.com/atemfair_domestic/55927
http://withinfp.sakura.ne.jp/eso/index.php/17384223-sluga-naroda-3-sezon-21-seria-x2-sluga-naroda-3-sezon-21-seria
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=200111
http://www.itosm.com/cn/board_nLoq17/68790
http://5starcoffee.co.kr/board_EBXY17/15763
http://d-tube.info/board_jvyO69/362058
http://yoriyorifood.com/xxxx/spacial/159683
http://divespace.co.kr/board/147671
http://barobus.kr/qna/37443
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/18083
http://sheepofani.dothome.co.kr/index.php?mid=shibalggeog&document_srl=8902
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=17768
https://esel.gist.ac.kr/esel2/?document_srl=250660
https://sanp.pro/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-bl%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
http://proxima.co.rw/index.php/component/k2/itemlist/user/658173
http://matinbank.ir/component/k2/itemlist/user/4557258.html
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=129224
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=74647
https://testing.celekt.com/%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%a1%d0%9c%d0%9e%d0%a2%d0%a0%d0%95%d0%a2%d0%ac-%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be/
http://www.critico-expository.com/forum/index.php?topic=13911.0
https://testing.celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-z6-%d0%98%d0%b3%d1%80/
http://www.tekparcahdfilm.com/forum/index.php?topic=51395.0
http://shinhwaair2017.cafe24.com/issue/209415
http://mediaville.me/index.php/component/k2/itemlist/user/294505
http://hyeonjun.co.kr/menu3/75492
http://jjikduk.net/DATA/61370
http://www.josephmaul.org/menu41/134479
http://hyeonjun.co.kr/menu3/69310
http://vhost12299.cpsite.ru/432825-bol-se-zizni-3-seria-17052019-p6-bol-se-zizni-3-seria
http://teambuildingpremium.com/forum/index.php?topic=843443.0
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=19740
http://test.comics-game.ru/index.php?topic=204.0
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=31243
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1619371
http://jiquilisco.org/index.php/component/k2/itemlist/user/11248
http://xn--9m1b83j39hz6exwonmf.com/?document_srl=521649
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/788447
http://xn----3x5er9r48j7wemud0a387h.com/news/78633
http://www.hyunjindc.com/qna/65956
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=137394
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=359834
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-o4-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80/
http://shinhwaair2017.cafe24.com/issue/388266
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2803453
http://callman.co.kr/index.php?mid=qa&document_srl=159085
http://taklongclub.com/forum/index.php?topic=166320.0
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=820830
http://juroweb.com/xe/juroweb_board/58416
http://divespace.co.kr/board/171715
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/511953
http://smartacity.com/component/k2/itemlist/user/52572
http://forum.elexlabs.com/index.php?topic=39674.0
http://thermoplast.envolgroupe.com/component/k2/author/121954
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1608030
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=499716
http://mir3sea.com/forum/index.php?topic=3473.0
http://www.digitalbul.com/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%87%d0%b5%d1%80/
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=83676
https://esel.gist.ac.kr/esel2/board_hmgj23/50566
https://testing.celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iv9%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/114899
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=130231
http://married.dike.gr/index.php/component/k2/itemlist/user/67736
http://universalcommunity.se/Forum/index.php?topic=16930.0
http://www.almacenesrickie.com.ec/index.php/component/k2/itemlist/user/133290
https://testing.celekt.com/%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yn0%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=869517
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=36218.0
http://www.josephmaul.org/menu41/91985
http://indiefilm.kr/xe/board/118997
http://xn--ok1bpqi43ahtb.net/board_eASW07/102791
http://lucky.kidspann.net/?document_srl=67784
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1925513
http://withinfp.sakura.ne.jp/eso/index.php/17338556-dockimateri-dockimateri-13-seria-z3-dockimateri-dockimateri-13-
http://tototoday.com/board_oRiY52/50898
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/356878
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=136660
http://5starcoffee.co.kr/board_EBXY17/21057
http://www.critico-expository.com/forum/index.php?topic=19454.0
http://www.teedinubon.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-p5-%d0%b2%d1%81%d1%91-%d0%bc/
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=369768
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=62700
http://bizchemical.com/board_kMpv94/2080236
http://www.jesusonly.life/calendar/378874
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/10176
http://yoriyorifood.com/xxxx/spacial/102989
http://www.digitalbul.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-e2-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1945236
http://forum.digamahost.com/index.php?topic=128938.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2627645
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=77342
http://www.gforgirl.com/xe/poster/149570
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=884131
http://lucky.kidspann.net/index.php?mid=qna&document_srl=78172
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=201731
http://zanoza.h1n.ru/2019/05/20/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ga4%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://dev.aabn.org.gh/component/k2/itemlist/user/619722
http://www.almacenesrickie.com.ec/index.php/component/k2/itemlist/user/131099
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2660161
http://esperanzazubieta.com/component/k2/itemlist/user/100145
http://www.original-craft.net/index.php?topic=335401.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=147322
http://www.digitalbul.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-21-05-2019-o5-%d1%81%d0%bb%d1%83%d0%b3/
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1708660
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=89666
http://www.theocraticamerica.org/forum/index.php?topic=54423.0
http://www.sp1.football/index.php?mid=faq&document_srl=185880
https://esel.gist.ac.kr/esel2/board_hmgj23/90959
http://shinilspring.com/board_qsfb01/105223
http://www.m1avio.com/index.php/component/k2/itemlist/user/3796322
http://www.telcon.gr/index.php/component/k2/itemlist/user/98639
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=127239
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/370498
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=652220
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3449893
https://www.regalepadova.it/index.php/component/k2/itemlist/user/8195
http://ariji.kr/?document_srl=974778
http://bebopindia.com/?document_srl=389918
http://bebopindia.com/notcie/390059
http://benzmall.co.kr/index.php?mid=download&document_srl=47990
http://benzmall.co.kr/index.php?mid=download&document_srl=48043
http://skylinecam.co.kr/photo/87863
https://testing.celekt.com/%d0%94%d0%b5%d1%82%d0%b8-%d1%81%d0%b5%d1%81%d1%82%d0%b5%d1%80-kardes-cocuklari-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ydxz-%d0%94%d0%b5%d1%82%d0%b8-%d1%81%d0%b5%d1%81%d1%82%d0%b5%d1%80/
http://hyeonjun.co.kr/menu3/103163
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=102162
http://www.sp1.football/index.php?mid=faq&document_srl=262542
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3305568
http://k-cea.org/board_Hnyj62/152003
http://k-cea.org/board_Hnyj62/152189
http://k-cea.org/board_Hnyj62/152225
http://k-cea.org/board_Hnyj62/152352
http://matinbank.ir/?option=com_k2&view=itemlist&task=user&id=4577950
http://xn--2e0b53df5ag1c804aphl.net/nuguna/107651
http://xn--2e0b53df5ag1c804aphl.net/nuguna/107661
http://xn--2e0b53df5ag1c804aphl.net/nuguna/107673
http://xn--2e0b53df5ag1c804aphl.net/nuguna/107701
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=72116
https://esel.gist.ac.kr/esel2/board_hmgj23/274021
https://mcsetup.tk/bbs/index.php?topic=261829.0
https://mcsetup.tk/bbs/index.php?topic=261830.0
https://nple.com/xe/pds/156750
https://nple.com/xe/pds/156776
http://zanoza.h1n.ru/2019/05/19/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b2-%d1%8d%d1%84%d0%b8%d1%80%d0%b5-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-1/
http://skylinecam.co.kr/?document_srl=96603
http://shinhwaair2017.cafe24.com/issue/222660
http://0433.net/junggo/37872
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=61878
http://www.almacenesrickie.com.ec/index.php/component/k2/itemlist/user/130667
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1676004
http://corumotoanahtar.com/component/k2/itemlist/user/4315.html
http://zanoza.h1n.ru/2019/05/19/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d0%b8%d0%b3%d1%80%d0%b0/
http://www.hicleaning.kr/?document_srl=124048
http://www.teedinubon.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-il2%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
http://www.tekparcahdfilm.com/forum/index.php?topic=51352.0
http://zanoza.h1n.ru/2019/05/19/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-18-05-2019-b9-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://fbpharm.net/index.php/component/k2/itemlist/user/53526
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=201333
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=201420
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/20306
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/20322
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=21187
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=21207
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=37747
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=37929
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=37945
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=37971
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=127811
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3809046
http://vhost12299.cpsite.ru/551207-sluga-naroda-3-sezon-14-seria-n4-sluga-naroda-3-sezon-14-seria
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/15360
http://callman.co.kr/?document_srl=167855
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3861602
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/42870
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=20326
http://theolevolosproject.org/index.php/component/k2/itemlist/user/27332
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=198391
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=233389
http://153.120.114.241/eso/index.php/17465503-zestokij-stambul-zalim-istanbul-13-seria-slhf-zestokij-stambul-
http://153.120.114.241/eso/index.php/17465569-vetrenyj-hercai-12-seria-wqre-vetrenyj-hercai-12-seria
http://1600-1590.com/index.php?document_srl=303254&mid=board_ihsE13
http://1600-1590.com/index.php?document_srl=303276&mid=board_ihsE13
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=303420
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=303526
http://hyeonjun.co.kr/menu3/64676
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=85513
http://0433.net/junggo/53286
http://www.jshwanghoan.com/?document_srl=93894
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=74002
http://sixangles.co.kr/?document_srl=619801
http://www.hicleaning.kr/?document_srl=105768
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=123907
http://www.svteck.co.kr/customer_gratitude/71413
http://skylinecam.co.kr/?document_srl=127215
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1705163
https://prelease.club/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-17-05-19-yc%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
https://www.amazingworldtop.com/entretenimiento/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kc7%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://sanp.pro/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vt7%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl-6-%d1%81%d0%b5%d1%80%d0%b8/
http://rabbitzone.xyz/FREE/39443
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=131970
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=90579
http://1661-6471.co.kr/news/15860
http://sunele.co.kr/board_ReBD97/124791
http://2872870.com/est/44543
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=19051
http://sy.korean.net/qna/254766
http://herdental.co.kr/index.php?mid=online&document_srl=82217
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fx5o-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://kyj1225.godohosting.com/board_mebR72/45101
http://www.hicleaning.kr/board_wash/180499
http://knet.dothome.co.kr/xe/board_RJHw15/13301
http://knet.dothome.co.kr/xe/board_RJHw15/13306
http://knet.dothome.co.kr/xe/board_RJHw15/13312
http://knet.dothome.co.kr/xe/board_RJHw15/13318
http://koais.com/data/150581
http://koais.com/data/150611
http://koais.com/data/150664
http://koais.com/data/150692
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1725044
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1725401
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1762050
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1761977
http://thermoplast.envolgroupe.com/component/k2/author/137567
http://web2interactive.com/index.php/component/k2/itemlist/user/3714031
http://wigalseguros.com.br/index.php/component/k2/itemlist/user/16527
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4862245
http://www.arunagreen.com/index.php/component/k2/itemlist/user/580348
http://www.dap.com.py/index.php/component/k2/itemlist/user/829905
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1835932
http://asiagroup.co.kr/?document_srl=327527
http://jnk-ent.jp/index.php?mid=gallery&document_srl=153054
http://daesestudy.co.kr/ipsi_docu/113915
http://kwpub.kr/PUBS/85515
http://emjun.com/index.php?mid=hangtotal&document_srl=253417
http://emjun.com/index.php?mid=hangtotal&document_srl=253431
http://emjun.com/index.php?mid=hangtotal&document_srl=253459
http://emjun.com/index.php?mid=hangtotal&document_srl=253494
http://emjun.com/index.php?mid=hangtotal&document_srl=253505
http://www.arunagreen.com/index.php/component/k2/itemlist/user/580436
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1688814
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1688912
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1468000
http://www.firstfinancialservices.co.uk/?option=com_k2&view=itemlist&task=user&id=20874
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3512988
http://www.lustralesdevallehermoso.com/index.php/component/k2/itemlist/user/48608
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=16675
http://www.spazioad.com/component/k2/itemlist/user/7377070
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/352400
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/352410
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=297799
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=8281
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=41872
http://netsconsults.com/index.php/component/k2/itemlist/user/811866
https://www.celekt.com/%d0%a5%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-2019-bu%d0%a5%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://photogrotto.com/%d0%ba%d0%be%d0%bd%d1%81%d1%83%d0%bb%d1%8c%d1%82%d0%b0%d0%bd%d1%82-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tv8y-%d0%ba%d0%be%d0%bd%d1%81%d1%83%d0%bb%d1%8c/
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xo1%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f24-05/
http://www.spazioad.com/component/k2/itemlist/user/7378525
http://mercibq.net/partner/49681
http://bebopindia.com/notcie/360253
https://sanp.pro/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-19-se%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://www.vamoscontigo.org/Noticia/98695
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=34175
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=220664
https://khuyenmaikk13.info/index.php?topic=207457.0
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=87147
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=83368
http://www.digitalbul.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-24-05-19-dm%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba/
http://skylinecam.co.kr/?document_srl=90646
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/353109
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/298862
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/64493
https://turimex.mx.solemti.net/index.php/component/k2/itemlist/user/8682
http://dcasociados.eu/?option=com_k2&view=itemlist&task=user&id=91427
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=358816
http://dev.aabn.org.gh/component/k2/itemlist/user/641884
http://dev.aabn.org.gh/component/k2/itemlist/user/641894
http://www.studyxray.com/Sangdam/206871
http://www.vogtland.com.pl/index.php/component/k2/itemlist/user/42405
http://dreamplusart.com/mn03_01/89984
http://www.sp1.football/index.php?mid=faq&document_srl=623937
http://www.vamoscontigo.org/Noticia/105360
http://1644-4404.com/index.php?document_srl=167980&mid=board_VFri46
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=678055
http://www.sp1.football/index.php?mid=faq&document_srl=655674
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=44585
http://barobus.kr/qna/44215
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/20054
http://asin.itts.co.kr/board_rtXs84/20785
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=875130
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1256544
http://e-educ.net/Forum/index.php?topic=12057.0
http://www.remify.app/foro/index.php?topic=337298.0
http://zanoza.h1n.ru/2019/05/19/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-18-05-2019-i7-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80/
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=204097
https://esel.gist.ac.kr/esel2/board_hmgj23/63114
http://skylinecam.co.kr/photo/116747
http://xplorefitness.com/blog/%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D1%84%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB-qi%C2%AB%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12-%D0%B2%D1%8B%D0%BF%D1%83%D1%81%D0%BA-%D1%84%D0%B8%D0%BD%D0%B0%D0%BB%C2%BB63-%D1%85%D0%BE%D0%BB%D0%BE%D1%81%D1%82%D1%8F%D0%BA-9-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-12
http://moavalve.co.kr/faq/78648
http://shinilspring.com/?document_srl=95013
http://www.gforgirl.com/xe/poster/150114
http://0433.net/junggo/41652
http://153.120.114.241/eso/index.php/17117298-novinka-milliardy-4-sezon-11-seria-p2-milliardy-4-sezon-11-seri
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1612592
http://daesestudy.co.kr/?document_srl=42318
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=155908
http://juroweb.com/xe/juroweb_board/56161
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4869292
http://themasters.pro/file_01/183037
http://gochon-iusell.co.kr/g1/56540
https://gonggamlaw.com/lawcase/20996
http://barobus.kr/qna/60639
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=513810
http://nanaae.com/confirm/43589
http://beautypouch.net/index.php?mid=board_09&document_srl=52094
http://toeden.co.kr/Product_new/95687
https://nple.com/xe/pds/119509
http://thermoplast.envolgroupe.com/component/k2/author/138238
http://sixangles.co.kr/?document_srl=591195
http://www.jesusonly.life/calendar/133056
http://www.sp1.football/index.php?mid=faq&document_srl=182831
http://redgatetech.co/?option=com_k2&view=itemlist&task=user&id=733047
http://0433.net/?document_srl=47561
https://reficulcoin.com/index.php?topic=53382.0
http://teambuildingpremium.com/forum/index.php?topic=853512.0
https://cybergsm.es/index.php?topic=33719.0
https://prelease.club/hd-video-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-o9-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-1/
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cx4%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
http://www.critico-expository.com/forum/index.php?topic=13445.0
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1731281
http://www.gforgirl.com/xe/poster/137396
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1112904
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4844052
https://esel.gist.ac.kr/esel2/board_hmgj23/67735
http://proxima.co.rw/index.php/component/k2/itemlist/user/657935
http://asin.itts.co.kr/board_rtXs84/8860
https://www.chirorg.com/?document_srl=126435
http://photogrotto.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-os4%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-1-%d1%81%d0%b5%d1%80/
http://sd-xi.co.kr/g1/33465
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/19951
http://jejucctv.co.kr/A5/46472
http://lucky.kidspann.net/index.php?mid=qna&document_srl=232731
http://carand.co.kr/d2/14715
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/357931
https://sanp.pro/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gw1i-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81/
https://sanp.pro/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jh0c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://arquitectosenreformas.es/component/k2/itemlist/user/84095
http://mahdi.ehosseini.com/index.php/component/k2/itemlist/user/41426
http://vhost12299.cpsite.ru/571216-serial-cuzaa-zizn-cuze-zitta-12-seria-f5-cuzaa-zizn-cuze-zitta-
http://withinfp.sakura.ne.jp/eso/index.php/17443516-smotret-soderzanki-9-seria-w1-soderzanki-9-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/17443683-smotret-tajny-98-seria-s7-tajny-98-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/17443790-hdvideo-sluga-naroda-3-sezon-19-seria-l5-sluga-naroda-3-sezon-1/0
http://withinfp.sakura.ne.jp/eso/index.php/17444145-serial-cuzaa-zizn-cuze-zitta-8-seria-a2-cuzaa-zizn-cuze-zitta-8/0
https://alquilervideobeam.com.co/?option=com_k2&view=itemlist&task=user&id=58862
http://0433.net/junggo/77648
http://withinfp.sakura.ne.jp/eso/index.php/17443679-klatva-yemin-66-seria-gxgc-klatva-yemin-66-seria
http://soc-human.kz/index.php/component/k2/itemlist/user/1708218
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1738222
http://mediaville.me/?option=com_k2&view=itemlist&task=user&id=290048
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=193061
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=711403.0
http://bebopindia.com/notcie/132338
http://rudraautomation.com/index.php/component/k2/author/224704
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=585654
http://zanoza.h1n.ru/2019/05/19/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-je3%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
http://www.digitalbul.com/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-92-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d1%82%d0%b0%d0%b9%d0%bd/
http://community.viajar.tur.br/index.php?p=/profile/irvinsheeh
http://www.josephmaul.org/menu41/97480
http://jiquilisco.org/index.php/component/k2/itemlist/user/10220
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.kr/news/27995
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=18738
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=323200
https://gonggamlaw.com/lawcase/52434
http://www.m1avio.com/index.php/component/k2/itemlist/user/3762127
http://kyj1225.godohosting.com/?document_srl=42110
http://www.ekemoon.com/229669/051120195223/
http://www.ekemoon.com/229673/051120195323/
http://www.ekemoon.com/229683/051120195623/
http://www.ekemoon.com/229687/051120195723/
http://www.lovestory.or.kr/?document_srl=17863
http://www.lovestory.or.kr/topic/17874
http://www.lovestory.or.kr/topic/17879
http://www.sp1.football/index.php?mid=faq&document_srl=564510
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=97181
http://xn----3x5er9r48j7wemud0a387h.com/news/97080
https://hackinsa.com/?document_srl=10902
https://hackinsa.com/?document_srl=10971
https://hackinsa.com/freeboard/10869
https://hackinsa.com/freeboard/10940
https://hackinsa.com/freeboard/11003
http://www.josephmaul.org/menu41/105851
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-17-05-2019-s6-%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=65438
http://moavalve.co.kr/faq/83479
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/260006
https://cybergsm.es/index.php?topic=26409.0
http://rudraautomation.com/index.php/component/k2/author/228233
http://bebopindia.com/?document_srl=105152
http://www.tessabannampad.go.th/webboard/index.php?topic=213810.0
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=131924
http://married.dike.gr/index.php/component/k2/itemlist/user/71214
http://www.m1avio.com/index.php/component/k2/itemlist/user/3766294
http://www.lgue.co.kr/?document_srl=72939
http://www.teedinubon.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zx8%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f23-05-2019/
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=104754
http://www.kwpcoop.or.kr/QnA/10649
http://vhost12299.cpsite.ru/571345-hdvideo-tajny-85-seria-b2-tajny-85-seria
http://vhost12299.cpsite.ru/571353-hdvideo-sluga-naroda-3-sezon-21-seria-a5-sluga-naroda-3-sezon-2
http://vhost12299.cpsite.ru/571491-hdvideo-tajny-taemnici-101-seria-e9-tajny-taemnici-101-seria
http://vhost12299.cpsite.ru/571546-smotret-sluga-naroda-3-sezon-7-seria-k7-sluga-naroda-3-sezon-7-
http://withinfp.sakura.ne.jp/eso/index.php/17444760-sluga-naroda-3-sezon-23-seria-m4-sluga-naroda-3-sezon-23-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/17445008-holostak-9-sezon-10-vypusk-f7-holostak-9-sezon-10-vypusk
http://withinfp.sakura.ne.jp/eso/index.php/17445205-smotret-milliardy-4-sezon-11-seria-i0-milliardy-4-sezon-11-seri/0
http://withinfp.sakura.ne.jp/eso/index.php/17445299-smotret-sluga-naroda-3-sezon-23-seria-j2-sluga-naroda-3-sezon-2/0
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1841699
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2565527
http://xplorefitness.com/blog/%D0%BD%D0%BE%D0%B2%D0%B8%D0%BD%D0%BA%D0%B0-%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-23-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-n7-%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-23-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://bebopindia.com/notcie/117509
http://forum.elexlabs.com/index.php?topic=44864.0
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=125496
http://test.comics-game.ru/index.php?topic=235.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/336578
http://thanosakademi.com/index.php?topic=99380.0
https://khuyenmaikk13.info/index.php?topic=208058.0
http://asin.itts.co.kr/board_rtXs84/15103
http://www.studyxray.com/Sangdam/152846
http://www.theparrotcentre.com/forum/index.php?topic=549256.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=36586.0
http://hanga5.com/index.php?mid=board_photo&document_srl=65655
http://woodpark.kr/project/30166
http://divespace.co.kr/board/171095
https://adsensebih.com/index.php?topic=34277.0
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1970224
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=124089
http://bebopindia.com/notcie/282900
https://khuyenmaikk13.info/index.php?topic=219335.0
https://khuyenmaikk13.info/index.php?topic=219339.0
https://nple.com/xe/pds/89527
https://nple.com/xe/pds/89778
https://nple.com/xe/pds/89803
https://serverpia.co.kr/board_ucCk10/46158
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=310588
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=84827
http://vhost12299.cpsite.ru/571909-novinka-igra-prestolov-2019-8-sezon-7-seria-q1-igra-prestolov-2
http://vhost12299.cpsite.ru/571976-serial-milliardy-4-sezon-10-seria-v0-milliardy-4-sezon-10-seria
http://withinfp.sakura.ne.jp/eso/index.php/17446389-hdvideo-tola-robot-5-seria-m8-tola-robot-5-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/17446696-serial-smers-7-seria-g0-smers-7-seria/0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=139969
http://tekagrafica.com.br/index.php/component/k2/itemlist/user/1745547
http://www.jesusonly.life/calendar/135296
http://xn----ctbtiediism0a6h.xn--p1ai/index.php?topic=724484.0
http://www.studyxray.com/Sangdam/160781
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=343165
http://emjun.com/index.php?mid=hangtotal&document_srl=110936
http://tekagrafica.com.br/?option=com_k2&view=itemlist&task=user&id=1735813
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=88863
http://f-tube.info/board/132457
http://asin.itts.co.kr/board_rtXs84/27165
http://ajincomp.godohosting.com/board_STnh82/88436
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=24763
http://carand.co.kr/d2/24319
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=96397
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2324439
http://ptu.imoove.kr/ko/content/%C2%AB%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-96-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-19-05-2019-m6-%C2%AB%D1%82%D0%B0%D0%B9%D0%BD%D1%8B-%D1%82%D0%B0%D1%94%D0%BC%D0%BD%D0%B8%D1%86i-96-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB337860
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1613122
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2322419
http://hyeonjun.co.kr/?document_srl=63572
http://emjun.com/index.php?mid=hangtotal&document_srl=86848
http://shinhwaair2017.cafe24.com/issue/234647
http://corumotoanahtar.com/component/k2/itemlist/user/5010.html
http://hyeonjun.co.kr/menu3/63013
http://dreamplusart.com/mn03_01/91881
http://dreamplusart.com/mn03_01/91956
http://dreamplusart.com/mn03_01/91970
http://juroweb.com/xe/juroweb_board/64221
http://juroweb.com/xe/juroweb_board/64242
http://juroweb.com/xe/juroweb_board/64252
http://juroweb.com/xe/juroweb_board/64257
http://juroweb.com/xe/juroweb_board/64262
http://juroweb.com/xe/juroweb_board/64268
http://www.lovestory.or.kr/topic/23641
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3334218
http://mglpcm.org/board_ETkS12/93547
http://www.ekemoon.com/225671/050220195022/
http://callman.co.kr/index.php?mid=qa&document_srl=154324
http://taklongclub.com/forum/index.php?topic=166568.0
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105327
http://soc-human.kz/index.php/component/k2/itemlist/user/1733652
http://dohairbiz.com/en/component/k2/itemlist/user/2783615.html
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1468747
http://bebopindia.com/notcie/364666
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=14920
http://themasters.pro/file_01/213124
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=275278
http://subforumna.x10.mx/mad/index.php?topic=256887.0
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3844965
http://lucky.kidspann.net/index.php?mid=qna&document_srl=55573
http://emjun.com/index.php?mid=hangtotal&document_srl=88870
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=37495.0
http://www.teedinubon.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-v4-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
http://hyeonjun.co.kr/menu3/67755
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jn1%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-5-%d1%81%d0%b5%d1%80/
http://shinilspring.com/?document_srl=88124
http://corumotoanahtar.com/component/k2/itemlist/user/4520
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=87738
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=62887
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1446777
http://www.sp1.football/index.php?mid=faq&document_srl=359611
http://benzmall.co.kr/index.php?mid=download&document_srl=31431
http://daesestudy.co.kr/?document_srl=108749
http://daesestudy.co.kr/ipsi_docu/108709
http://juroweb.com/xe/juroweb_board/64709
http://juroweb.com/xe/juroweb_board/64725
http://juroweb.com/xe/juroweb_board/64731
http://juroweb.com/xe/juroweb_board/64742
http://juroweb.com/xe/juroweb_board/64769
http://khapthanam.co.kr/g1/117597
http://kitekorea.co.kr/board_Chea81/105422
http://kitekorea.co.kr/board_Chea81/105463
http://kitekorea.co.kr/board_Chea81/105482
http://themasters.pro/file_01/207425
http://rudraautomation.com/index.php/component/k2/author/266162
http://vhost12299.cpsite.ru/557929-novinka-sluga-naroda-3-sezon-8-seria-k4-sluga-naroda-3-sezon-8-
https://www.celekt.com/%d0%9a%d0%bb%d1%8f%d1%82%d0%b2%d0%b0-yemin-67-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jalx-%d0%9a%d0%bb%d1%8f%d1%82%d0%b2%d0%b0-yemin-67-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://toeden.co.kr/Product_new/88157
https://www.celekt.com/%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qy1%d0%98%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://koais.com/data/142714
http://dcasociados.eu/component/k2/itemlist/user/91988
https://sanp.pro/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-wp%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81/
https://tg.vl-mp.com/index.php?topic=1472981.0
http://soc-human.kz/index.php/component/k2/itemlist/user/1702687
https://testing.celekt.com/%d0%a1%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-17-05-2019-v2-%d0%a1%d0%bb%d1%83%d0%b3%d0%b0/
http://vtservices85.fr/smf2/index.php?PHPSESSID=00151c6b95c1273c15c8f83237df186a&topic=253478.0
http://asiagroup.co.kr/?document_srl=212547
http://forum.bmw-e60.eu/index.php?topic=9101.0
http://israengineering.com/index.php/component/k2/itemlist/user/1239402
http://asin.itts.co.kr/board_rtXs84/12210
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=882749
http://www.critico-expository.com/forum/index.php?topic=13503.0
http://thanosakademi.com/index.php?topic=114459.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=0ce0aec5d84f444a04c6526e97bd36f2&topic=279119.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=b5e915cbb116ea79e315a42eb0d6bbda&topic=279114.0
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4887976
https://khuyenmaikk13.info/index.php?topic=223023.0
http://atemshow.com/atemfair_domestic/170352
http://atemshow.com/atemfair_domestic/170362
http://atemshow.com/atemfair_domestic/170396
http://atemshow.com/atemfair_domestic/170401
http://atemshow.com/atemfair_domestic/170426
http://bebopindia.com/notcie/341649
http://bebopindia.com/notcie/341718
http://herdental.co.kr/index.php?mid=online&document_srl=106771
http://webp.online/index.php?topic=64472.0
http://askpharm.net/board_NQiz06/131635
https://www.vegasgreentour.com/?document_srl=277745
http://rabbitzone.xyz/FREE/39300
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-22-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-21-05-2019-n7-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://benzmall.co.kr/index.php?mid=download&document_srl=19290
https://nple.com/xe/pds/87323
http://gochon-iusell.co.kr/g1/50848
http://carand.co.kr/d2/18792
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1476665
http://kitekorea.co.kr/board_Chea81/95293
http://zanoza.h1n.ru/2019/05/23/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-22-05-2019-z0-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://shinhwaair2017.cafe24.com/issue/230678
http://shinhwaair2017.cafe24.com/issue/236103
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=590831
http://www.renovaleplanejados.com.br/index.php/component/k2/itemlist/user/644850
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=33351
http://indiefilm.kr/xe/board/123511
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=69706
https://esel.gist.ac.kr/esel2/board_hmgj23/54271
http://mir3sea.com/forum/index.php?topic=3844.0
http://podwodnyswiat.eu/forum/index.php?topic=1277.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=332343
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=589078
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=158715
http://zanoza.h1n.ru/2019/05/20/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-17-05-2019-do%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f/
http://153.120.114.241/eso/index.php/17197326-holostak-24-05-2019-gdholostak-24-05-201944-holostak-24-05-2019
http://www.hsaura.com/noty/113028
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=601430
http://juroweb.com/xe/juroweb_board/50756
http://readingbible.org/board_xxpp62/1078458
http://shinhwaair2017.cafe24.com/issue/385801
http://www.livetank.cn/market1/179871
https://betshin.com/Story/96762
http://zanoza.h1n.ru/2019/05/21/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gi8%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=167378
http://w9builders.co.uk/index.php/component/k2/itemlist/user/84154
http://ovotecegg.com/component/k2/itemlist/user/163941
http://haniel.ir/index.php/component/k2/itemlist/user/116658
http://thanosakademi.com/index.php?topic=97494.0
http://withinfp.sakura.ne.jp/eso/index.php/17112398-novinka-tajny-taemnici-86-seria-f5-tajny-taemnici-86-seria/0
https://altaylarteknoloji.com/index.php?topic=5187.0
http://atemshow.com/atemfair_domestic/36501
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ht0%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-8-%d1%81%d0%b5%d1%80/
http://www.tekparcahdfilm.com/forum/index.php?topic=51608.0
http://www.hicleaning.kr/board_wash/124526
http://www.sp1.football/index.php?mid=faq&document_srl=176938
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=222704
http://mobility-corp.com/index.php/component/k2/itemlist/user/2623448
http://shinilspring.com/board_qsfb01/110432
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/113575
http://www.svteck.co.kr/customer_gratitude/44948
http://www.jesusonly.life/calendar/130408
http://zanoza.h1n.ru/2019/05/23/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-8/
http://mediaville.me/index.php/component/k2/itemlist/user/314599
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=1088904
http://beautypouch.net/index.php?mid=board_09&document_srl=47284
http://benzmall.co.kr/index.php?mid=download&document_srl=32558
http://sunele.co.kr/board_ReBD97/108165
http://soc-human.kz/index.php/component/k2/itemlist/user/1724798
http://sheepofani.dothome.co.kr/index.php?mid=shibalggeog&document_srl=5029
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1472735
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1472742
http://www.sollazzorefrigerazione.it/?option=com_k2&view=itemlist&task=user&id=2558254
http://153.120.114.241/eso/index.php/17397103-zestokij-stambul-zalim-istanbul-15-seria-dmaw-zestokij-stambul-
http://asiagroup.co.kr/?document_srl=314629
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=314668
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=314711
http://www.critico-expository.com/forum/index.php?topic=17545.0
http://www.ekemoon.com/227631/052220190222/
http://www.ekemoon.com/227639/052220190822/
http://www.hicleaning.kr/board_wash/184499
https://www.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-s9-%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
https://www.celekt.com/%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-21-05-2019-z8-%d0%9c%d0%b0%d0%bc%d0%b0-%d0%9b%d0%be%d1%80%d0%b0-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=313559
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=313610
http://asin.itts.co.kr/board_rtXs84/25314
http://jjikduk.net/DATA/125442
http://jjikduk.net/DATA/125465
http://k-cea.org/board_Hnyj62/126417
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=313653
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=313709
http://asin.itts.co.kr/board_rtXs84/25297
http://erhu.eu/viewtopic.php?t=398007
http://erhu.eu/viewtopic.php?t=398016
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=18165
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2827637
http://knet.dothome.co.kr/xe/board_RJHw15/15753
http://myrechockey.com/forums/index.php?topic=117975.0
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/51584
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/69060
http://xn--2e0bk61btjo.com/notice/23534
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=78873
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=109539
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=299223
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=511705
http://www.hyunjindc.com/qna/95582
http://www.hyunjindc.com/qna/95628
http://www.hyunjindc.com/qna/95671
http://www.hyunjindc.com/qna/95700
http://www.livetank.cn/market1/197424
http://www.livetank.cn/market1/197451
http://www.livetank.cn/market1/197485
http://www.livetank.cn/market1/197516
http://nanaae.com/confirm/47980
http://nanaae.com/confirm/47993
http://nanumi.tmax.co.kr/xe/index.php?mid=proj_2018&document_srl=35712
http://nanumi.tmax.co.kr/xe/index.php?mid=proj_2018&document_srl=35717
http://nanumi.tmax.co.kr/xe/index.php?mid=proj_2018&document_srl=35760
http://neosky.net/xe/?document_srl=57427
http://neosky.net/xe/space_station/57362
http://neosky.net/xe/space_station/57411
http://neosky.net/xe/space_station/57439
http://neosky.net/xe/space_station/57444
http://neosky.net/xe/space_station/57462
http://neosky.net/xe/space_station/57471
http://neosky.net/xe/space_station/57476
http://erhu.eu/viewtopic.php?t=398182
http://forum.bmw-e60.eu/index.php?topic=10938.0
http://forum.bmw-e60.eu/index.php?topic=10940.0
http://gallerychoi.com/Exhibition/364073
http://gochon-iusell.co.kr/g1/88178
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=142589
http://herdental.co.kr/index.php?mid=online&document_srl=130474
http://hyeonjun.co.kr/menu3/315098
http://vhost12299.cpsite.ru/598508-v-efire-sluga-naroda-3-sezon-8-seria-x2-sluga-naroda-3-sezon-8-
http://vhost12299.cpsite.ru/598529-novinka-mama-lora-16-seria-o7-mama-lora-16-seria
http://vhost12299.cpsite.ru/598536-smotret-vse-moglo-byt-inace-16-seria-o0-vse-moglo-byt-inace-16-
http://vhost12299.cpsite.ru/598542-smotret-senafeda-2-sezon-9-seria-f4-senafeda-2-sezon-9-seria
http://withinfp.sakura.ne.jp/eso/index.php/17515800-hdvideo-sluga-naroda-3-sezon-9-seria-h9-sluga-naroda-3-sezon-9-/0
http://withinfp.sakura.ne.jp/eso/index.php/17515828-sluga-naroda-3-sezon-7-seria-x6-sluga-naroda-3-sezon-7-seria/0
http://withinfp.sakura.ne.jp/eso/index.php/17515856-efir-igra-prestolov-8-sezon-7-seria-b5-igra-prestolov-8-sezon-7/0
http://withinfp.sakura.ne.jp/eso/index.php/17515858-hd-cernobyl-2019-1-seria-t8-cernobyl-2019-1-seria/0
http://xplorefitness.com/blog/%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-g6-%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://bebopindia.com/notcie/361180
http://bebopindia.com/notcie/361305
http://cwon.kr/xe/board_bnSr36/214465
http://divespace.co.kr/board/167000
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=90526
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=90536
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=90579
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=90594
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=90614
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=1100264
http://www.livetank.cn/market1/160387
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=305269
http://laokorea.com/orange_menu1/104143
http://www.haetsaldun-clinic.co.kr/Question/11571
http://asiagroup.co.kr/?document_srl=306798
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=306622
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=306674
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=189084
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=189148
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=189182
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=189212
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=189223
http://community.viajar.tur.br/index.php?p=/discussion/62333/vetrenyy-hercai-10-seriya-jboz-vetrenyy-hercai-10-seriya
http://community.viajar.tur.br/index.php?p=/discussion/62334/vetrenyy-hercai-14-seriya-ivad-vetrenyy-hercai-14-seriya/p1%3Fnew=1
http://community.viajar.tur.br/index.php?p=/discussion/62336/deti-sester-kardes-cocuklari-18-seriya-cmyq-deti-sester-kardes-cocuklari-18-seriya
http://community.viajar.tur.br/index.php?p=/discussion/62342/klyatva-yemin-59-seriya-wvpe-klyatva-yemin-59-seriya
http://community.viajar.tur.br/index.php?p=/profile/vivienconn
http://lucky.kidspann.net/index.php?mid=qna&document_srl=180201
https://khuyenmaikk13.info/index.php?topic=219868.0
http://barobus.kr/qna/43184
http://barobus.kr/qna/43217
http://barobus.kr/qna/43232
http://daesestudy.co.kr/ipsi_docu/98011
http://jjikduk.net/DATA/135439
http://jjikduk.net/DATA/135508
http://melchinooddle.dothome.co.kr/index.php?document_srl=7871&mid=board_EIUA02
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=83283
https://2002.shyoon.com/board_2002/143742
http://carand.co.kr/d2/43975
http://1661-6471.co.kr/news/28513
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=9712
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2807350
http://ajincomp.godohosting.com/board_STnh82/104796
http://yoriyorifood.com/xxxx/spacial/176927
https://testing.celekt.com/%d0%a7%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-up0q-%d0%a7%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-chernobyl-5-%d1%81%d0%b5/
http://benzmall.co.kr/index.php?mid=download&document_srl=40672
http://photogrotto.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-23-05-2019-g9-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-17-%d1%81%d0%b5%d1%80%d0%b8/
http://yoriyorifood.com/xxxx/spacial/171305
http://yoriyorifood.com/xxxx/spacial/171310
https://esel.gist.ac.kr/esel2/board_hmgj23/151814
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=277869
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=277894
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=277944
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=360462
http://dev.aabn.org.gh/component/k2/itemlist/user/644889
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=21669
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7451468
http://mvisage.sk/?option=com_k2&view=itemlist&task=user&id=119312
http://withinfp.sakura.ne.jp/eso/index.php/17374645-hd-sluga-naroda-3-sezon-7-seria-o5-sluga-naroda-3-sezon-7-seria
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/794075
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/135491
http://ovotecegg.com/component/k2/itemlist/user/188823
http://ovotecegg.com/component/k2/itemlist/user/188828
http://ovotecegg.com/component/k2/itemlist/user/188850
http://soc-human.kz/index.php/component/k2/itemlist/user/1735576
http://thermoplast.envolgroupe.com/component/k2/author/144492
http://thermoplast.envolgroupe.com/component/k2/author/144526
http://thermoplast.envolgroupe.com/component/k2/itemlist/user/144494
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=99335
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=19598
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=19599
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/18746
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/31281
http://www.livetank.cn/?document_srl=193363
http://www.studyxray.com/Sangdam/221259
http://proxima.co.rw/index.php/component/k2/itemlist/user/672777
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=226131
http://thermoplast.envolgroupe.com/component/k2/author/141797
http://5starcoffee.co.kr/board_EBXY17/12981
http://themasters.pro/file_01/188461
http://www.hicleaning.kr/board_wash/168162
http://jnk-ent.jp/index.php?mid=gallery&document_srl=162218
http://www.kwpcoop.or.kr/QnA/7808
http://www.original-craft.net/index.php?topic=355736.0
http://nanaae.com/confirm/12674
http://www.lgue.co.kr/?document_srl=88237
http://www.original-craft.net/index.php?topic=356431.0
http://www.original-craft.net/index.php?topic=356436.0
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=57282
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=57372
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/33384
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/43933
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=35011
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=35025
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/858839
http://www.phperos.net/foro/index.php?topic=137326.0
http://webp.online/index.php?topic=60910.0
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1951068
http://photogrotto.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-7/
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/35153
http://www.renovaleplanejados.com.br/?option=com_k2&view=itemlist&task=user&id=644976
http://www.teedinubon.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gs2%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-2-%d1%81%d0%b5%d1%80/
http://www.rationalkorea.com/xe/?document_srl=628813
http://studiokoon.net/board_tzri25/603
http://www.haetsaldun-clinic.co.kr/Question/16243
http://jjikduk.net/DATA/148443
http://153.120.114.241/eso/index.php/17113787-hdvideo-sluga-naroda-3-sezon-15-seria-z8-sluga-naroda-3-sezon-1
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=853196
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=94813
http://www.svteck.co.kr/customer_gratitude/73174
http://www.josephmaul.org/menu41/123026
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=87678
http://emjun.com/index.php?mid=hangtotal&document_srl=108277
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=81102
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=348329
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=84585
http://ariji.kr/?document_srl=852388
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3499473
http://www.remify.app/foro/index.php?topic=320158.0
http://zanoza.h1n.ru/2019/05/19/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-18-05-2019-m9-%d0%b8%d0%b3%d1%80/
http://ahudseafood.com/?option=com_k2&view=itemlist&task=user&id=9342
http://zanoza.h1n.ru/2019/05/19/%d0%ba%d0%bb%d1%8f%d1%82%d0%b2%d0%b0-yemin-61-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rxvm-%d0%ba%d0%bb%d1%8f%d1%82%d0%b2%d0%b0-yemin-61-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=101421
http://zanoza.h1n.ru/2019/05/19/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sr1%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be/
http://vhost12299.cpsite.ru/417464-poslednaa-nedela-3-seria-17052019-e7-poslednaa-nedela-3-seria
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=53816
http://agiteshop.com/xe/qa/121419
http://esiapolisthesharp2.co.kr/g1/69555
http://esiapolisthesharp2.co.kr/g1/61437
http://dev.aabn.org.gh/component/k2/itemlist/user/621505
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=345024
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=145301
http://shinilspring.com/board_qsfb01/98632
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=119781
http://photogrotto.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vi2%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
http://vhost12299.cpsite.ru/424121-serial-milliardy-4-sezon-9-seria-s3-milliardy-4-sezon-9-seria
https://altaylarteknoloji.com/index.php?topic=4811.0
http://dcasociados.eu/component/k2/itemlist/user/90067
https://testing.celekt.com/%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nv6%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f17-05/
http://sixangles.co.kr/qna/644082
http://theolevolosproject.org/?option=com_k2&view=itemlist&task=user&id=26906
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/58375
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=217775
http://xn--ok1bpqi43ahtb.net/board_eASW07/117899
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-d8-%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=168690
http://shinilspring.com/board_qsfb01/95727
http://www.jesusonly.life/calendar/126230
http://yoriyorifood.com/xxxx/spacial/96109
http://daesestudy.co.kr/ipsi_docu/93419
https://sanp.pro/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gw1w-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=166528
http://gallerychoi.com/Exhibition/307200
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=240158
http://ajincomp.godohosting.com/board_STnh82/88813
http://khapthanam.co.kr/g1/104862
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=116361
http://www.arunagreen.com/?option=com_k2&view=itemlist&task=user&id=558284
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=d8513780890fa33873d3df4c017652f5&topic=7214.0
http://jiquilisco.org/index.php/component/k2/itemlist/user/11505
http://vhost12299.cpsite.ru/418643-sluga-naroda-3-sezon-9-seria-17052019-k6-sluga-naroda-3-sezon-9
http://www.jesusonly.life/calendar/240019
http://zanoza.h1n.ru/2019/05/20/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sc7%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-17-05-2019-l5-%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
https://mcsetup.tk/bbs/index.php?topic=257645.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/110921
http://www.proandpro.it/?option=com_k2&view=itemlist&task=user&id=4627246
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=131929
http://www.hicleaning.kr/?document_srl=94766
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=24432
http://research.kiu.ac.kr/?document_srl=62966
https://www.amazingworldtop.com/entretenimiento/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pu9%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1447481
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=112256
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1944494
http://forum.3d-printer.top/index.php?topic=1104.0
http://hyeonjun.co.kr/?document_srl=94003
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/75170
http://xn--2e0b53df5ag1c804aphl.net/nuguna/106514
http://xn--2e0b53df5ag1c804aphl.net/nuguna/106562
http://xn--2e0b53df5ag1c804aphl.net/nuguna/106717
http://xn--2e0b53df5ag1c804aphl.net/nuguna/106738
http://xn--2e0b53df5ag1c804aphl.net/nuguna/106793
http://xn--2e0b53df5ag1c804aphl.net/nuguna/106842
http://yoriyorifood.com/xxxx/spacial/171415
http://yoriyorifood.com/xxxx/spacial/171420
http://yoriyorifood.com/xxxx/spacial/171425
https://esel.gist.ac.kr/esel2/board_hmgj23/152049
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=278106
http://gallerychoi.com/?document_srl=271349
http://gallerychoi.com/Exhibition/271039
http://gallerychoi.com/Exhibition/271104
http://gallerychoi.com/Exhibition/271209
http://gallerychoi.com/Exhibition/271223
http://gallerychoi.com/Exhibition/271248
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=10593
http://haenamyun.taeshinmedia.com/index.php?document_srl=2813105&mid=notice
http://0433.net/junggo/115791
http://0433.net/junggo/115816
http://0433.net/junggo/116088
http://1644-4404.com/?document_srl=232844
http://1644-4404.com/?document_srl=233027
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=232893
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=232975
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=232987
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=233010
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=233016
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=233021
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=199192
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=597703
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=597730
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=597740
http://www.studyxray.com/Sangdam/221562
http://www.studyxray.com/Sangdam/221639
http://www.taeshinmedia.com/?document_srl=3335094
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3335084
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3335089
http://xn----3x5er9r48j7wemud0a387h.com/news/83373
http://yoriyorifood.com/xxxx/spacial/173954
http://yoriyorifood.com/xxxx/spacial/173975
http://yoriyorifood.com/xxxx/spacial/174015
https://esel.gist.ac.kr/esel2/board_hmgj23/155406
https://esel.gist.ac.kr/esel2/board_hmgj23/155416
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=232635
http://xn--hu1bs8ufrd6ucyz0aooa.kr/?document_srl=29424
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=29414
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=29449
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=29463
http://www.leekeonsu-csi.com/?document_srl=924871
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=924336
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=925240
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kfqf-%d1%80%d0%b0%d1%81/
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ognw-%d1%80%d0%b0%d1%81/
http://www.theocraticamerica.org/forum/index.php?topic=69846.0
http://www.theocraticamerica.org/forum/index.php?topic=69849.0
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/?document_srl=100856
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/?document_srl=101150
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=100252
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=100667
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=100699
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=100736
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=100991
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=597970
http://www.studyxray.com/Sangdam/221998
http://www.studyxray.com/Sangdam/222039
http://www.taeshinmedia.com/?document_srl=3335202
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3335197
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3335212
http://xn----3x5er9r48j7wemud0a387h.com/news/83514
http://yoriyorifood.com/xxxx/spacial/174352
https://esel.gist.ac.kr/esel2/?document_srl=155767
https://esel.gist.ac.kr/esel2/board_hmgj23/155735
https://esel.gist.ac.kr/esel2/board_hmgj23/155822
https://khuyenmaikk13.info/index.php?topic=217136.0
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=282976
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=83836
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=21691
http://juroweb.com/xe/juroweb_board/64775
http://kitekorea.co.kr/board_Chea81/105526
http://kitekorea.co.kr/board_Chea81/105577
http://kitekorea.co.kr/board_Chea81/105630
http://looksun.co.kr/index.php?mid=board_4&document_srl=105452
http://looksun.co.kr/index.php?mid=board_4&document_srl=105462
http://looksun.co.kr/index.php?mid=board_4&document_srl=105498
http://sofficer.net/xe/teach/248337
http://rabbitzone.xyz/FREE/53964
http://asiagroup.co.kr/index.php?document_srl=337995&mid=board_11
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/297893
https://khuyenmaikk13.info/index.php?topic=216576.0
http://asin.itts.co.kr/board_rtXs84/23210
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=193051
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/285708
http://divespace.co.kr/board/152743
http://bebopindia.com/notcie/130180
http://yeonsen.com/index.php?document_srl=68563&mid=board_vZbN12
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3293744
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=102894
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=111888
http://indiefilm.kr/xe/board/156606
http://lucky.kidspann.net/?document_srl=80241
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=13823
http://www.golden-nail.co.kr/press/94374
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=61606
http://www.ds712.net/guest/?document_srl=176296
http://www.jesusonly.life/calendar/129262
http://photogrotto.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hi3%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-14-%d1%81%d0%b5/
https://emoforum.org/discussion/3236/bogatye-i-bednye-zengin-ve-yoksul-7-seriya-usab-bogatye-i-bednye-zengin-ve-yoksul-7-seriya
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=94202
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=94244
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3713415
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1631230
http://www.arredoufficiomarca.com/index.php/component/k2/itemlist/user/1631231
http://www.arunagreen.com/?option=com_k2&view=itemlist&task=user&id=578990
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1467208
http://www.crnmedia.es/component/k2/itemlist/user/88413
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.kr/news/36563
http://holysweat.dothome.co.kr/data/2925
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=872240
http://www.ekemoon.com/232543/050720194924/
http://nanumi.tmax.co.kr/xe/index.php?mid=proj_2018&document_srl=7225
http://dow.dothome.co.kr/board_jydx58/24396
http://hanga5.com/index.php?mid=board_photo&document_srl=58590
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-23-05-2019-m1-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://azone.synology.me/xe/index.php?document_srl=186932&mid=board_SDnQ73
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3334851
http://www.phperos.net/foro/index.php?topic=136020.0
http://lucky.kidspann.net/index.php?mid=qna&document_srl=72566
http://zanoza.h1n.ru/2019/05/19/%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-70-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rzsh-%d0%bd%d0%b0%d1%88%d0%b0-%d0%b8%d1%81%d1%82%d0%be%d1%80%d0%b8%d1%8f-70/
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=111755
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=237270
http://asin.itts.co.kr/board_rtXs84/7900
http://www.siheunglove.com/chulip/149850
http://www.sp1.football/index.php?mid=faq&document_srl=603476
http://www.sp1.football/index.php?mid=faq&document_srl=603533
http://www.svteck.co.kr/?document_srl=149202
http://www.svteck.co.kr/customer_gratitude/149013
http://www.svteck.co.kr/customer_gratitude/149158
http://www.svteck.co.kr/customer_gratitude/149173
http://www.svteck.co.kr/customer_gratitude/149257
http://www.ekemoon.com/228815/050620190323/
http://projectcva.dothome.co.kr/c_com/2613
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=887789
http://kyj1225.godohosting.com/board_mebR72/54192
https://2002.shyoon.com/board_2002/146069
http://www.insesinmun.com/newpaper2/74997
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=164416
http://f-tube.info/board/124609
http://www.studyxray.com/Sangdam/213659
http://photogrotto.com/%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-95-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-aa4%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-95-%d1%81%d0%b5%d1%80%d0%b8%d1%8f22-05-2019/
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/29941
https://hackinsa.com/freeboard/10940
http://photogrotto.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xi8%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-3-%d1%81%d0%b5%d1%80/
http://hyeonjun.co.kr/menu3/62557
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=70893
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2777393
http://yoriyorifood.com/xxxx/spacial/111407
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/13111
http://www.theparrotcentre.com/forum/index.php?topic=557988.0
https://tg.vl-mp.com/index.php?topic=1472554.0
http://lucky.kidspann.net/index.php?mid=qna&document_srl=71322
http://www.svteck.co.kr/customer_gratitude/54513
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=21454
http://daesestudy.co.kr/ipsi_docu/76279
http://lucky.kidspann.net/index.php?mid=qna&document_srl=119789
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=88477
http://otitismediasociety.org/forum/index.php?topic=185239.0
http://atemshow.com/atemfair_domestic/158141
http://atemshow.com/atemfair_domestic/158193
http://beautypouch.net/?document_srl=62862
http://beautypouch.net/index.php?mid=board_09&document_srl=62837
http://benzmall.co.kr/index.php?mid=download&document_srl=23593
http://benzmall.co.kr/index.php?mid=download&document_srl=23654
http://jnk-ent.jp/index.php?mid=gallery&document_srl=177416
http://jnk-ent.jp/index.php?mid=gallery&document_srl=177621
http://jnk-ent.jp/index.php?mid=gallery&document_srl=177687
http://jnk-ent.jp/index.php?mid=gallery&document_srl=177767
http://k-cea.org/board_Hnyj62/156534
http://khapthanam.co.kr/g1/105830
http://khapthanam.co.kr/g1/105852
http://emjun.com/index.php?mid=hangtotal&document_srl=214307
http://lucky.kidspann.net/index.php?mid=qna&document_srl=179946
http://sofficer.net/xe/teach/253375
http://asiagroup.co.kr/index.php?document_srl=355913&mid=board_11
http://daltso.com/index.php?mid=board_cUYy21&document_srl=73290
http://www.siheunglove.com/chulip/167043
http://gallerychoi.com/Exhibition/291982
http://d-tube.info/board_jvyO69/310914
http://jnk-ent.jp/index.php?mid=gallery&document_srl=192053
http://daltso.com/index.php?mid=board_cUYy21&document_srl=72572
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/37932
http://vhost12299.cpsite.ru/547009-serial-dockimateri-dockimateri-15-seria-a9-dockimateri-dockimat
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=135661
http://www.siheunglove.com/?document_srl=132835
http://www.siheunglove.com/?document_srl=132877
http://www.siheunglove.com/chulip/132893
http://www.siheunglove.com/chulip/132908
http://www.sp1.football/index.php?mid=tr_video&document_srl=564066
http://www.sp1.football/index.php?mid=tr_video&document_srl=564082
http://www.sp1.football/index.php?mid=tr_video&document_srl=564110
http://www.vamoscontigo.org/Noticia/78750
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=174253
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=174264
http://xn----3x5er9r48j7wemud0a387h.com/news/96707
http://xn----3x5er9r48j7wemud0a387h.com/news/96757
http://skylinecam.co.kr/photo/121658
http://bebopindia.com/notcie/198798
http://forum.kopkargobel.com/index.php?topic=12194.0
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/40990
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-20-05-2019-d9-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://cwon.kr/xe/board_bnSr36/67577
http://jjikduk.net/DATA/125384
http://fbpharm.net/?option=com_k2&view=itemlist&task=user&id=72490
https://2002.shyoon.com/board_2002/123157
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-v8-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4/
https://sanp.pro/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fx3m-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sanp.pro/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-fe0c-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=814065
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=4988732
http://www.spazioad.com/component/k2/itemlist/user/7390064
http://www.critico-expository.com/forum/index.php?topic=19624.0
http://www.lovestory.or.kr/topic/17814
http://www.lovestory.or.kr/topic/17819
http://www.original-craft.net/index.php?topic=351117.0
http://www.siheunglove.com/chulip/132951
http://www.sp1.football/index.php?mid=faq&document_srl=564246
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=525427
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=263425
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=330301
http://www.sp1.football/index.php?mid=faq&document_srl=206398
http://www.jesusonly.life/calendar/133151
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=157794
http://webp.online/index.php?topic=62231.msg107520
http://zanoza.h1n.ru/2019/05/20/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-99-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-x2-%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-99-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=341736
https://sanp.pro/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kd7i-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-6-%d1%81/
http://dickymicky.com/bbs/1644
http://www.ekemoon.com/227857/050020193523/
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2709839
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=381252
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/36112
http://ajincomp.godohosting.com/board_STnh82/106150
http://www.golden-nail.co.kr/press/287640
http://shinhwaair2017.cafe24.com/issue/378444
http://www.critico-expository.com/forum/index.php?topic=26993.0
http://www.lgue.co.kr/?document_srl=80576
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/282931
http://otitismediasociety.org/forum/index.php?topic=189178.0
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.kr/news/29115
http://www.original-craft.net/index.php?topic=351198.0
http://www.original-craft.net/index.php?topic=351201.0
http://www.siheunglove.com/chulip/133751
http://www.sp1.football/?document_srl=565824
http://www.sp1.football/index.php?mid=faq&document_srl=565877
http://www.vamoscontigo.org/Noticia/79516
http://www.vamoscontigo.org/Noticia/79568
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=175728
https://hackinsa.com/?document_srl=11366
http://israengineering.com/index.php/component/k2/itemlist/user/1237231
https://testing.celekt.com/%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-18-05-2019-d1-%d0%91%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/519455
http://moavalve.co.kr/faq/77725
http://forums.abs-cbn.com/welcome-back-kapamilya%21/ootk-9-eo-10-k-20-05-2019-nke-ootk-9-eo-10-k/?PHPSESSID=ld1702902hng9u65krh4fae1g7
http://gtupuw.org/index.php/component/k2/itemlist/user/1925377
http://dev.aabn.org.gh/component/k2/itemlist/user/628939
https://prelease.club/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rg6o-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-4-%d1%81/
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1923897
http://www.golden-nail.co.kr/press/81064
https://sanp.pro/%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-94-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zh5%d1%82%d0%b0%d0%b9%d0%bd%d1%8b-%d1%82%d0%b0%d1%94%d0%bc%d0%bd%d0%b8%d1%86i-94/
http://subforumna.x10.mx/mad/index.php?topic=252032.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=35880.0
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=77283
http://rudraautomation.com/index.php/component/k2/author/266958
http://fbpharm.net/index.php/component/k2/itemlist/user/66235
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=186975
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/25985
http://www.ekemoon.com/236743/050720195625/
http://www.teedinubon.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-su7c-%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.teedinubon.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-le8v-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81/
http://www.teedinubon.com/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-fr8b-%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9/
https://www.celekt.com/%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-eb4d-%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://vhost12299.cpsite.ru/599605-sluga-naroda-3-sezon-10-seria-a5-sluga-naroda-3-sezon-10-seria
http://vhost12299.cpsite.ru/599616-live-senafeda-2-sezon-9-seria-c3-senafeda-2-sezon-9-seria
http://vhost12299.cpsite.ru/599641-smotret-sluga-naroda-3-sezon-17-seria-p7-sluga-naroda-3-sezon-1
http://xplorefitness.com/blog/%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-20-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-z1-%D1%81%D0%BB%D1%83%D0%B3%D0%B0-%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%B0-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-20-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://5starcoffee.co.kr/?document_srl=21021
http://5starcoffee.co.kr/board_EBXY17/21013
http://5starcoffee.co.kr/board_EBXY17/21045
http://5starcoffee.co.kr/board_EBXY17/21057
http://5starcoffee.co.kr/board_EBXY17/21066
http://mediaville.me/index.php/component/k2/itemlist/user/307402
http://mvisage.sk/index.php/component/k2/itemlist/user/119249
http://ovotecegg.com/component/k2/itemlist/user/181442
http://rotary-laeliana.org/component/k2/itemlist/user/51892
http://rudraautomation.com/index.php/component/k2/author/249869
http://rudraautomation.com/index.php/component/k2/author/250172
http://rudraautomation.com/index.php/component/k2/author/250308
http://rudraautomation.com/index.php/component/k2/author/250309
http://rudraautomation.com/index.php/component/k2/itemlist/user/250301
https://adsensebih.com/index.php?topic=36541.0
https://serverpia.co.kr/board_ucCk10/47826
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kq3p-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://www.itosm.com/cn/board_nLoq17/76946
http://gabisan.com/board_OuDs04/12937
http://mercibq.net/partner/36341
http://atemshow.com/atemfair_domestic/169801
http://yoriyorifood.com/xxxx/spacial/167822
http://zanoza.h1n.ru/2019/05/22/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-22-05-2019-o0-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd/
http://rudraautomation.com/index.php/component/k2/itemlist/user/266096
http://jjikduk.net/DATA/130628
http://esiapolisthesharp2.co.kr/g1/62070
http://vhost12299.cpsite.ru/599216-novinka-igra-prestolov-8-sezon-7-seria-k5-igra-prestolov-8-sezo
http://vhost12299.cpsite.ru/599219-hdvideo-senafeda-2-sezon-13-seria-i1-senafeda-2-sezon-13-seria
http://vhost12299.cpsite.ru/599229-sluga-naroda-3-sezon-18-seria-i4-sluga-naroda-3-sezon-18-seria
http://vhost12299.cpsite.ru/599260-tola-robot-5-seria-q8-tola-robot-5-seria
http://vhost12299.cpsite.ru/599276-smotret-igra-prestolov-8-sezon-1-seria-m6-igra-prestolov-8-sezo
http://vhost12299.cpsite.ru/599278-hd-sluga-naroda-3-sezon-15-seria-v0-sluga-naroda-3-sezon-15-ser
http://vhost12299.cpsite.ru/599282-hdvideo-tola-robot-1-seria-u8-tola-robot-1-seria
http://vhost12299.cpsite.ru/599358-smotret-tola-robot-6-seria-u2-tola-robot-6-seria
http://withinfp.sakura.ne.jp/eso/index.php/17516874-sluga-naroda-3-sezon-9-seria-k6-sluga-naroda-3-sezon-9-seria/0
http://xplorefitness.com/blog/%D1%81%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C-%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-3-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-w3-%D0%B8%D0%B3%D1%80%D0%B0-%D0%BF%D1%80%D0%B5%D1%81%D1%82%D0%BE%D0%BB%D0%BE%D0%B2-8-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-3-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://5starcoffee.co.kr/board_EBXY17/20728
http://5starcoffee.co.kr/board_EBXY17/20735
http://bebopindia.com/notcie/364983
http://themasters.pro/?document_srl=206739
http://themasters.pro/file_01/206546
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1468166
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1468289
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1468312
http://www.crnmedia.es/component/k2/itemlist/user/88537
http://www.crnmedia.es/component/k2/itemlist/user/88542
http://www.crnmedia.es/component/k2/itemlist/user/88543
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/21159
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/21191
http://www.m1avio.com/index.php/component/k2/itemlist/user/3755382
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/16715
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1179617
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=872437
http://rudraautomation.com/index.php/component/k2/author/250294
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=124576
http://bebopindia.com/notcie/355967
http://ajincomp.godohosting.com/board_STnh82/93323
http://barobus.kr/qna/46486
http://sy.korean.net/qna/210861
http://jnk-ent.jp/?document_srl=224482
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1724620
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/43624
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/?document_srl=27074
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/51110
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/51125
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/51146
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=873884
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=41072
http://www.vogtland.com.pl/index.php/component/k2/itemlist/user/41068
http://www.zoraholidays.net/?option=com_k2&view=itemlist&task=user&id=353023
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/353012
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/298726
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/64485
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=8641
http://esperanzazubieta.com/component/k2/itemlist/user/102952
http://healthyteethpa.org/component/k2/itemlist/user/5546265
http://mahdi.ehosseini.com/index.php/component/k2/itemlist/user/44127
http://married.dike.gr/index.php/component/k2/itemlist/user/77995
http://miquirofisico.com/index.php/component/k2/itemlist/user/4457
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=206859
http://lucky.kidspann.net/index.php?mid=qna&document_srl=70086
http://taklongclub.com/forum/index.php?topic=149498.0
https://npi.org.es/smf/index.php?topic=118264.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=73395
http://www.theparrotcentre.com/forum/index.php?topic=552441.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=24393
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=106017
http://roikjer.com/forum/index.php?PHPSESSID=4fm7v5hcalscmp6b343b4917i3&topic=893961.0
https://afikgan.co.il/?option=com_k2&view=itemlist&task=user&id=28865
http://zanoza.h1n.ru/2019/05/21/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pb9%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5/
https://testing.celekt.com/%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xt4%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f18-05/
http://smartacity.com/component/k2/itemlist/user/52752
http://nanaae.com/confirm/37656
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-l4-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2/
http://www.teedinubon.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-y5-%d0%b8%d0%b3%d1%80/
http://www.teedinubon.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-c8-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4/
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/25595
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/25600
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/?document_srl=20000
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/19983
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/20018
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/42354
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/42391
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/42410
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/42428
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/62638
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=302457
https://reficulcoin.com/index.php?topic=83641.0
https://saltriverbg.com/2019/05/25/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zjcm-%d1%80%d0%b0%d1%81/
https://www.2ayes.com/19478/3-4-dloo-3-4-showtime
https://www.chirorg.com/?document_srl=147602
https://www.chirorg.com/?document_srl=147638
https://www.chirorg.com/?document_srl=147647
https://www.hohoyoga.com/testboard/3972446
https://www.limscave.com/forum/viewtopic.php?t=54974
https://www.limscave.com/forum/viewtopic.php?t=54976
https://www.runcity.org/forum/index.php?action=profile;u=77582
https://www.shaiyax.com/index.php?topic=397809.0
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=415432
http://www.tekparcahdfilm.com/forum/index.php?topic=51311.0
https://www.tedyun.com/xe/index.php?mid=gallery&document_srl=191289
http://ovotecegg.com/component/k2/itemlist/user/169071
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=158639
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=514890
http://skylinecam.co.kr/photo/82187
http://8.droror.co.il/uncategorized/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ww9%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-4-%d1%81%d0%b5%d1%80/
http://azone.synology.me/xe/?document_srl=82229
http://bobr.site/index.php?topic=149839.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=333795
http://mediaville.me/index.php/component/k2/itemlist/user/284418
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=88850
http://ru-realty.com/forum/index.php?topic=533319.0
http://asin.itts.co.kr/board_rtXs84/11951
http://thanosakademi.com/index.php?topic=97479.0
http://daesestudy.co.kr/?document_srl=107557
http://kitekorea.co.kr/board_Chea81/103758
http://kitekorea.co.kr/board_Chea81/103792
http://looksun.co.kr/index.php?mid=board_4&document_srl=104373
http://lucky.kidspann.net/?document_srl=254897
http://lucky.kidspann.net/index.php?mid=qna&document_srl=254917
http://mercibq.net/partner/33542
http://www.itosm.com/cn/board_nLoq17/135724
http://www.itosm.com/cn/board_nLoq17/135729
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=318093
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=318116
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=318229
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=318253
http://www.kcch.or.kr/?document_srl=92106
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=92101
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=91107
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=91120
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=91179
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=91189
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=341680
http://universalcommunity.se/Forum/index.php?topic=18565.0
http://xn--9m1b83j39hz6exwonmf.com/board_IYPe43/521844
http://www.hsaura.com/noty/117765
http://bitpark.co.kr/board_IzjM66/4025264
https://esel.gist.ac.kr/esel2/board_hmgj23/55197
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=24267
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=64044
http://smartacity.com/component/k2/itemlist/user/57991
http://forums.abs-cbn.com/welcome-back-kapamilya%21/a-etoo-8-eo-1-e-19-05-2019-llj-a-etoo-8-eo-1-e/?PHPSESSID=i4f7uh3upnf4n123j5ii85g204
http://photogrotto.com/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ww1%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f21-05-2019/
http://rabbitzone.xyz/FREE/41715
http://rfc11th13th.dothome.co.kr/Board5/13132
http://rfc11th13th.dothome.co.kr/Board5/13142
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3739870
http://www.teedinubon.com/%d0%ba%d0%be%d0%bd%d1%81%d1%83%d0%bb%d1%8c%d1%82%d0%b0%d0%bd%d1%82-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-d5-%d0%ba%d0%be%d0%bd%d1%81%d1%83/
http://www.telcon.gr/index.php/component/k2/itemlist/user/94709
http://www.vamoscontigo.org/Noticia/110607
http://www.vamoscontigo.org/Noticia/110690
http://www.vamoscontigo.org/Noticia/110695
http://www.vamoscontigo.org/Noticia/110724
http://www.vamoscontigo.org/Noticia/110766
http://gochon-iusell.co.kr/g1/77108
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=123231
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=123245
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=345650
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=345772
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=345795
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=345822
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=345832
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=345844
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=345871
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2827637
http://masanlib.or.kr/g1/32651
http://www.golden-nail.co.kr/press/91214
http://www.sp1.football/index.php?mid=faq&document_srl=202684
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/283285
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/9255
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=50883
http://www.svteck.co.kr/customer_gratitude/44038
http://lucky.kidspann.net/index.php?mid=qna&document_srl=67383
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3829549
http://atemshow.com/atemfair_domestic/170446
http://atemshow.com/atemfair_domestic/170558
http://bebopindia.com/notcie/341776
http://bebopindia.com/notcie/341931
http://bebopindia.com/notcie/341973
http://benzmall.co.kr/?document_srl=31943
http://benzmall.co.kr/index.php?mid=download&document_srl=31967
http://callman.co.kr/?document_srl=200138
http://callman.co.kr/index.php?document_srl=200025&mid=qa
http://callman.co.kr/index.php?mid=qa&document_srl=200066
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3718225
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1894651
http://callman.co.kr/index.php?mid=qa&document_srl=175844
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=520994
http://www.lgue.co.kr/?document_srl=104612
http://0433.net/junggo/66259
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=203617
https://serverpia.co.kr/board_ucCk10/46880
http://www.sp1.football/index.php?mid=faq&document_srl=588518
http://tk-laser.co.kr/index.php?mid=board_QsEu43&document_srl=109278
http://hanga5.com/index.php?mid=board_photo&document_srl=68270
http://www.original-craft.net/index.php?topic=352668.0
http://isch.kr/?document_srl=130195
http://proxima.co.rw/index.php/component/k2/itemlist/user/683184
http://mediaville.me/index.php/component/k2/itemlist/user/309598
http://mobility-corp.com/index.php/component/k2/itemlist/user/2658787
http://mobility-corp.com/index.php/component/k2/itemlist/user/2660259
http://mobility-corp.com/index.php/component/k2/itemlist/user/2660971
http://mvisage.sk/index.php/component/k2/itemlist/user/119308
http://netsconsults.com/index.php/component/k2/itemlist/user/810224
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/129887
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=282356
http://photogrotto.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-es9b-%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-14/
http://photogrotto.com/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-85-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-28/
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fa1a-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-im5f-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://dev.aabn.org.gh/?option=com_k2&view=itemlist&task=user&id=616761
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/336387
http://www.theparrotcentre.com/forum/index.php?topic=556353.0
http://shinilspring.com/board_qsfb01/102980
http://zanoza.h1n.ru/2019/05/19/%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ydif-%d0%b2%d0%be%d1%80%d0%be%d0%bd-kuzgun-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://indiefilm.kr/xe/board/123531
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=85050
http://daesestudy.co.kr/ipsi_docu/88736
http://www.generalwalker.org/board_Zyyd91/2756
http://xn----3x5er9r48j7wemud0a387h.com/news/76861
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=658113
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/18168
http://xn----3x5er9r48j7wemud0a387h.com/news/82408
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=186893
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=186913
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=186927
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=186946
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=186980
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=186986
http://yoriyorifood.com/xxxx/spacial/172062
http://yoriyorifood.com/xxxx/spacial/172092
http://yoriyorifood.com/xxxx/spacial/172112
http://yoriyorifood.com/xxxx/spacial/172145
https://esel.gist.ac.kr/esel2/?document_srl=152799
https://esel.gist.ac.kr/esel2/board_hmgj23/152775
https://esel.gist.ac.kr/esel2/board_hmgj23/152814
http://www.hsaura.com/?document_srl=145648
https://prelease.club/%d0%ba%d0%bb%d1%8f%d1%82%d0%b2%d0%b0-yemin-62-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ftal-%d0%ba%d0%bb%d1%8f%d1%82%d0%b2%d0%b0-yemin-62-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.digitalbul.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-19-05-2019-q3-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2/
http://vhost12299.cpsite.ru/477850-senafeda-2-sezon-9-seria-18052019-z5-senafeda-2-sezon-9-seria
https://www.amazingworldtop.com/entretenimiento/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-en2%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
http://photogrotto.com/%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd%d0%b5%d0%b4%d0%b5%d0%bb%d1%8f-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gq8%d0%bf%d0%be%d1%81%d0%bb%d0%b5%d0%b4%d0%bd%d1%8f%d1%8f-%d0%bd/
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=530130
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/40486
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=23107
http://www.teedinubon.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-24-05-2019-n8-%d0%b2%d1%81%d1%91-%d0%bc/
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/55337
http://www.vamoscontigo.org/Noticia/105629
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=223055
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/?document_srl=18336
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/18310
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/18315
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/18362
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/18368
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/?document_srl=39719
http://yoriyorifood.com/xxxx/spacial/221642
http://www2.yasothon.go.th/smf/index.php?topic=159.167340
http://zanoza.h1n.ru/2019/05/22/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%b8%d0%b3%d1%80%d0%b0/
http://zanoza.h1n.ru/2019/05/22/%d0%bd%d0%b5%d0%b2%d0%b5%d1%81%d1%82%d0%b0-%d0%b8%d0%b7-%d1%81%d1%82%d0%b0%d0%bc%d0%b1%d1%83%d0%bb%d0%b0-istanbullu-gelin-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-82-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-44/
http://zanoza.h1n.ru/2019/05/22/%d1%85%d0%be%d0%bb%d0%be%d1%81%d1%82%d1%8f%d0%ba-9-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d0%b2%d1%8b%d0%bf%d1%83%d1%81%d0%ba-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d1%85-3/
https://adsensebih.com/index.php?topic=31964.0
https://hackersuniversity.net/index.php/topic,24071.0.html
https://hackersuniversity.net/index.php?topic=24074.0
https://khuyenmaikk13.info/index.php?topic=215645.0
https://khuyenmaikk13.info/index.php?topic=215656.0
https://khuyenmaikk13.info/index.php?topic=215683.0
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3809173
http://smartacity.com/component/k2/itemlist/user/64630
http://webp.online/index.php?topic=64320.15
https://khuyenmaikk13.info/index.php?topic=215694.0
http://hanga5.com/index.php?mid=board_photo&document_srl=63511
http://www.arunagreen.com/index.php/component/k2/itemlist/user/580540
http://www.lgue.co.kr/lgue05/66016
https://khuyenmaikk13.info/index.php?topic=222395.0
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=13118
http://photogrotto.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qy7v-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://www.hyunjindc.com/qna/89289
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=114678
http://divespace.co.kr/board/153280
https://gonggamlaw.com/lawcase/20622
http://otitismediasociety.org/forum/index.php?topic=195798.0
http://d-tube.info/board_jvyO69/334971
http://otitismediasociety.org/forum/index.php?topic=187531.0
http://haeple.com/index.php?mid=etc&document_srl=83171
https://altaylarteknoloji.com/index.php?topic=5328.0
https://sto54.ru/index.php/component/k2/itemlist/user/3391723
http://matrixpharm.ru/forum/index.php?PHPSESSID=pnfbnstb3kmeov89n41cqioar0&action=profile;u=199078
http://xn----3x5er9r48j7wemud0a387h.com/news/39528
http://podwodnyswiat.eu/forum/index.php?topic=1269.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=342051
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=65976
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/273159
http://kitekorea.co.kr/board_Chea81/105295
http://kitekorea.co.kr/board_Chea81/105333
http://kitekorea.co.kr/board_Chea81/105391
http://mglpcm.org/board_ETkS12/105847
http://projectcva.dothome.co.kr/c_com/6092
http://projectcva.dothome.co.kr/c_com/6097
http://projectcva.dothome.co.kr/c_com/6102
http://projectcva.dothome.co.kr/c_com/6121
http://www.itosm.com/cn/board_nLoq17/105096
http://neosky.net/xe/space_station/35710
http://d-tube.info/board_jvyO69/361997
http://callman.co.kr/?document_srl=199753
http://ajincomp.godohosting.com/board_STnh82/87314
https://sanp.pro/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pt3w-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=136997
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=352682
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=50743
http://zanoza.h1n.ru/2019/05/23/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-23-05-2019-r2-%d1%81%d0%bb%d1%83%d0%b3/
http://xn--2e0b53df5ag1c804aphl.net/nuguna/98439
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/11293
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=647243
http://shinhwaair2017.cafe24.com/issue/326625
http://skylinecam.co.kr/photo/112368
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1929407
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=82385
http://forum.elexlabs.com/index.php?topic=37668.0
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/768754
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=93633
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3675181
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=79217
http://forum.elexlabs.com/index.php?topic=59347.0
http://forum.elexlabs.com/index.php?topic=59351.0
http://forum.elexlabs.com/index.php?topic=59353.0
http://poselokgribovo.ru/forum/index.php?topic=812650.0
http://thanosakademi.com/index.php?topic=114376.0
http://webp.online/index.php?topic=65559.0
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1847317
http://atemshow.com/?document_srl=169661
http://atemshow.com/atemfair_domestic/169639
http://www.camaracoyhaique.cl/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b5-%d0%b6%d0%b8%d0%b7%d0%bd%d0%b8-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d0%b1%d0%be%d0%bb%d1%8c/
http://153.120.114.241/eso/index.php/17366610-bogatye-i-bednye-zengin-ve-yoksul-18-seria-mvwo-bogatye-i-bedny
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1259223
http://www.golden-nail.co.kr/press/322482
http://mercibq.net/partner/29903
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/358482
http://0433.net/junggo/65200
http://www.hicleaning.kr/board_wash/181116
http://asiagroup.co.kr/index.php?mid=board_11&document_srl=369551
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=97534
http://jjikduk.net/DATA/56972
http://www.hsaura.com/noty/116061
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1607855
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=77914
http://yoriyorifood.com/xxxx/spacial/68870
http://www.gforgirl.com/xe/poster/149246
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=479322
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=479370
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=479426
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=479528
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=479581
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=479595
http://www.golden-nail.co.kr/press/321061
http://www.golden-nail.co.kr/press/321080
http://www.golden-nail.co.kr/press/321118
http://bewasia.com/index.php?document_srl=135018&mid=board_cUYy21
http://asin.itts.co.kr/board_rtXs84/25677
http://zakdu.com/board_ssKi56/8325
http://beautypouch.net/index.php?mid=board_09&document_srl=97941
https://sanp.pro/%d0%ba%d0%be%d0%bd%d1%81%d1%83%d0%bb%d1%8c%d1%82%d0%b0%d0%bd%d1%82-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-et9w-%d0%ba%d0%be%d0%bd%d1%81%d1%83%d0%bb%d1%8c/
http://viamania.net/index.php?mid=board_raYV15&document_srl=73464
http://www.spazioad.com/component/k2/itemlist/user/7378512
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=184872
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1963209
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=620316
http://tototoday.com/board_oRiY52/50644
http://dcasociados.eu/component/k2/itemlist/user/91397
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1696052
http://withinfp.sakura.ne.jp/eso/index.php/17332325-smotret-smers-4-seria
http://withinfp.sakura.ne.jp/eso/index.php/17332468-hd-sluga-naroda-3-sezon-22-seria-p1-sluga-naroda-3-sezon-22-ser/0
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1631029
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1441415
http://www.civilservantsacco.co.zm/?option=com_k2&view=itemlist&task=user&id=1126365
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=228150
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=619108
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3414891
http://0433.net/?document_srl=65714
http://0433.net/junggo/65628
http://0433.net/junggo/65650
http://bebopindia.com/notcie/103965
http://thanosakademi.com/index.php?topic=101587.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=0199607c4cffc1b0a5c9a47bbdd807c0&topic=6592.0
http://www.arredoufficiomarca.com/?option=com_k2&view=itemlist&task=user&id=1619376
http://www.arunagreen.com/?option=com_k2&view=itemlist&task=user&id=546735
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=84099
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=341128
http://ovotecegg.com/component/k2/itemlist/user/164312
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=85002
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=95761
http://sdsn.rsu.edu.ng/index.php/component/k2/itemlist/user/2322238
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=72144
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1654619
http://www.digitalbul.com/%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-25-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tyfc-%d0%b2%d0%b5%d1%82%d1%80%d0%b5%d0%bd%d1%8b%d0%b9-hercai-25-%d1%81%d0%b5%d1%80%d0%b8/
http://kitekorea.co.kr/board_Chea81/93018
http://www.hyunjindc.com/qna/95739
http://dreamplusart.com/mn03_01/70081
http://nanumi.tmax.co.kr/xe/index.php?mid=proj_2018&document_srl=9486
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3723387
https://hackinsa.com/freeboard/14262
http://www.studyxray.com/Sangdam/206664
http://www.studyxray.com/Sangdam/206721
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3326604
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3326680
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3326685
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3326690
http://xn----3x5er9r48j7wemud0a387h.com/news/75421
http://xn----3x5er9r48j7wemud0a387h.com/news/75437
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=169590
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=169639
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=169684
http://yoriyorifood.com/xxxx/spacial/159705
https://www.amazingworldtop.com/entretenimiento/%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-oz6%d0%bc%d0%b0%d0%bc%d0%b0-%d0%bb%d0%be%d1%80%d0%b0-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f20-05-2019/
http://jjikduk.net/DATA/73711
http://shinilspring.com/board_qsfb01/83914
http://fbpharm.net/index.php/component/k2/itemlist/user/51802
http://shinilspring.com/board_qsfb01/91192
http://matrixpharm.ru/forum/index.php?action=profile&u=199516
http://healthyteethpa.org/component/k2/itemlist/user/5469677
http://thermoplast.envolgroupe.com/component/k2/author/119605
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=73629
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=345495
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=78090
http://2872870.com/est/49932
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yf8%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7/
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=365536
http://bizchemical.com/board_kMpv94/2088420
http://esiapolisthesharp2.co.kr/g1/56367
http://vhost12299.cpsite.ru/554222-smotret-smers-2-seria-a5-smers-2-seria
http://zanoza.h1n.ru/2019/05/23/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-23-05-2019-i0-%d1%81%d0%bb%d1%83%d0%b3%d0%b0/
http://callman.co.kr/?document_srl=174256
http://jnk-ent.jp/index.php?mid=gallery&document_srl=136248
http://www.ekemoon.com/228115/050220190223/
http://viamania.net/index.php?mid=board_raYV15&document_srl=76557
http://herdental.co.kr/index.php?mid=online&document_srl=82336
http://themasters.pro/file_01/178015
http://bebopindia.com/notcie/287268
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/?document_srl=28088
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/28077
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/28083
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/52248
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/52253
http://www.teedinubon.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-live-%d0%b2%d1%81%d1%91-%d0%bc%d0%be/
http://www.teedinubon.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-2/
http://www.teedinubon.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-2/
http://www2.yasothon.go.th/smf/index.php?topic=159.168930
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=50179
https://khuyenmaikk13.info/index.php?topic=222706.0
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3828318
http://atemshow.com/atemfair_domestic/167608
http://atemshow.com/atemfair_domestic/167757
http://www.vamoscontigo.org/Noticia/135904
http://www.vamoscontigo.org/Noticia/135910
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=9d466359754f8e21dd79210cab8fadbb&topic=10272.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=adeedde6bd9c40484af4d39e5935a640&topic=10273.0
http://photogrotto.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dj3d-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://photogrotto.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-oc3c-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cd2s-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81/
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xr7s-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://www.ekemoon.com/237643/051220195725/
http://www.teedinubon.com/%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf%d1%80%d0%b5%d1%81%d1%82%d0%be%d0%bb%d0%be%d0%b2-8-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-my6i-%d0%b8%d0%b3%d1%80%d0%b0-%d0%bf/
https://www.celekt.com/%d0%9a%d0%be%d0%bd%d1%81%d1%83%d0%bb%d1%8c%d1%82%d0%b0%d0%bd%d1%82-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yk1s-%d0%9a%d0%be%d0%bd%d1%81%d1%83%d0%bb%d1%8c/
http://vhost12299.cpsite.ru/601869-smotret-tola-robot-7-seria-k2-tola-robot-7-seria
http://kitekorea.co.kr/board_Chea81/105463
http://kitekorea.co.kr/board_Chea81/105482
http://looksun.co.kr/index.php?mid=board_4&document_srl=105388
http://looksun.co.kr/index.php?mid=board_4&document_srl=105392
http://looksun.co.kr/index.php?mid=board_4&document_srl=105421
http://mglpcm.org/board_ETkS12/105932
http://looksun.co.kr/index.php?mid=board_4&document_srl=122849
http://lucky.kidspann.net/index.php?mid=qna&document_srl=288866
http://lucky.kidspann.net/index.php?mid=qna&document_srl=288879
http://lucky.kidspann.net/index.php?mid=qna&document_srl=288925
http://www.kwpcoop.or.kr/QnA/18426
http://www.lgue.co.kr/?document_srl=109921
http://www.livetank.cn/market1/213213
http://www.livetank.cn/market1/213241
http://www.livetank.cn/market1/213246
http://www.lovestory.or.kr/topic/34987
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=661832
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1276288
http://proxima.co.rw/index.php/component/k2/itemlist/user/686596
http://smartacity.com/component/k2/itemlist/user/74294
http://vtservices85.fr/smf2/index.php?PHPSESSID=3ead26ca9efb482b732bb82090800ebe&topic=279122.0
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=838012
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3536020
http://www.quattroandpartners.it/component/k2/itemlist/user/1203363
http://www2.yasothon.go.th/smf/index.php?topic=159.169020
https://adsensebih.com/index.php?topic=38789.0
https://khuyenmaikk13.info/index.php?topic=223035.0
https://khuyenmaikk13.info/index.php?topic=223039.0
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3829549
http://atemshow.com/atemfair_domestic/170446
http://healthyteethpa.org/component/k2/itemlist/user/5545208
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=98905
http://miquirofisico.com/index.php/component/k2/itemlist/user/4571
http://mglpcm.org/?document_srl=172536
http://mglpcm.org/board_ETkS12/127812
http://withinfp.sakura.ne.jp/eso/index.php/17577322-rasskaz-sluzanki-3-sezon-7-seria-sewz-rasskaz-sluzanki-3-sezon-/0
http://sy.korean.net/qna/390107
http://archeaudio.com/xe/board_AOYj82/11322
http://phmusic.dothome.co.kr/index.php?mid=PowerHouseMusic&document_srl=46704
http://blog.ptpintcast.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pszx-%d1%80%d0%b0%d1%81/
http://knet.dothome.co.kr/xe/board_RJHw15/17691
http://xn--2e0b53df5ag1c804aphl.net/nuguna/103403
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=274470
http://smartacity.com/component/k2/itemlist/user/78852
http://x-crew.center/guest/4844984
http://sfah.ch/de/component/k2/itemlist/user/15515
http://www.cnsmaker.net/xe/?document_srl=124969
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=20575
http://www.svteck.co.kr/customer_gratitude/224018
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=155296
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=101299
http://callman.co.kr/index.php?mid=qa&document_srl=222665
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=69863
https://adsensebih.com/index.php?topic=48552.0
http://www.ekemoon.com/240783/051120192126/
http://mercibq.net/partner/101085
http://beautypouch.net/index.php?mid=board_09&document_srl=102216
http://design-381.com/xe/qna/4892
http://rabbitzone.xyz/FREE/60593
http://jdcalc.com/forum/viewtopic.php?t=278062
http://sd-xi.co.kr/g1/83072
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=129759
http://ilsannabgol.kr/board_brJk31/1370704
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=188851
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/49544
http://archeaudio.com/xe/board_AOYj82/11007
http://ko.myds.me/board_story/247107
http://0433.net/?document_srl=114032
https://www.celekt.com/%d0%a0%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qhdk-%d0%a0%d0%b0%d1%81/
http://www.quattroandpartners.it/component/k2/itemlist/user/1211565
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=7bed248615e813d7e779219a97fa42c7&topic=10619.0
http://www.hmotors.co.kr/inquiry/23919
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=106293
http://gochon-iusell.co.kr/g1/76638
http://e-educ.net/Forum/index.php?topic=16564.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=546930
http://k-cea.org/board_Hnyj62/199242
http://kwpub.kr/PUBS/136979
http://isch.kr/board_PowH60/154066
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=140407
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=378173
http://www.leekeonsu-csi.com/index.php?document_srl=908086&mid=community7
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/75568
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39676
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=91795
http://test.comics-game.ru/index.php?topic=461.0
http://kwpub.kr/PUBS/159611
http://sofficer.net/xe/teach/287729
http://sd-xi.co.kr/g1/59487
http://www.svteck.co.kr/customer_gratitude/219660
http://erdfsa.iptime.org/xe/index.php?mid=board&document_srl=12628
http://www.haetsaldun-clinic.co.kr/Question/42888
http://myrechockey.com/forums/index.php?topic=118470.0
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/89188
http://masanlib.or.kr/g1/97068
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=13575
http://fbpharm.net/index.php/component/k2/itemlist/user/85638
http://callman.co.kr/index.php?mid=qa&document_srl=283250
http://apt2you2.cafe24.com/g1/36013
http://viamania.net/index.php?mid=board_raYV15&document_srl=164965
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=23260
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=371501
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=903162
http://rudraautomation.com/index.php/component/k2/author/292018
http://mercibq.net/partner/55914
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=111037
http://askpharm.net/board_NQiz06/157318
http://kwpub.kr/PUBS/172691
http://daltso.com/index.php?mid=board_cUYy21&document_srl=178954
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/55905
http://daesestudy.co.kr/ipsi_docu/119818
http://ko.myds.me/board_story/249337
http://sejong-thesharpyemizi.co.kr/m1/27008
http://dev.aabn.org.gh/component/k2/itemlist/user/682988
http://taklongclub.com/forum/index.php?topic=202032.0
http://8.droror.co.il/uncategorized/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kxdb-%d1%80%d0%b0%d1%81/
http://sejong-thesharpyemizi.co.kr/m1/27998
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=89218
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1499737
https://forums.lfstats.com/viewtopic.php?t=319633
http://myrechockey.com/forums/index.php?topic=118621.0
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=378781
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=381032
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=381215
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=385238
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=386737
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=387922
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=391194
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=392527
http://forum.bmw-e60.eu/index.php?topic=11382.0
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=313054
http://jdcalc.com/forum/viewtopic.php?t=290689
http://hyeonjun.co.kr/menu3/290010
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2745270
http://mercibq.net/partner/75405
http://www.ekemoon.com/240867/051120195126/
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=378354
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/147280
https://forums.lfstats.com/viewtopic.php?t=319706
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=199784
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=56087
http://forum.bmw-e60.eu/index.php?topic=11155.0
http://d-tube.info/board_jvyO69/371576
http://midorijapaneserestaurant.ca/menu/News/24499
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=a1c1c3755a573bb8bd76ac3522e3021e&topic=11321.0
https://forum.clubeicaro.pt/index.php?topic=2181.0
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=826026
http://www.theocraticamerica.org/forum/index.php?topic=70120.0
http://hyeonjun.co.kr/menu3/374307
http://www.svteck.co.kr/customer_gratitude/237274
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/37562
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=22097
http://toeden.co.kr/Product_new/168083
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=92085
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=92101
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=92239
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=92621
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=92635
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=92677
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=92705
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=92710
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=92715
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=92735
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=92742
http://neosky.net/xe/?document_srl=69026
http://ye-dream.com/qa/235712
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1284166
https://www.hwbms.com/web/qna/11902
http://herdental.co.kr/index.php?mid=online&document_srl=115758
https://www.shaiyax.com/index.php?topic=408218.0
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/34117
http://yoriyorifood.com/xxxx/spacial/271375
http://myrechockey.com/forums/index.php?topic=118282.0
http://153.120.114.241/eso/index.php/17529225-rasskaz-sluzanki-3-sezon-8-seria-zwof-rasskaz-sluzanki-3-sezon-
https://www.c-alice.org/forum/index.php?topic=98279.0
http://forum.bmw-e60.eu/index.php?topic=11751.0
http://dreamplusart.com/mn03_01/171031
http://myrechockey.com/forums/index.php?topic=119242.0
https://timecker.com/anonymous/188770
http://dcasociados.eu/index.php/component/k2/itemlist/user/93493
http://thermoplast.envolgroupe.com/component/k2/author/157309
http://yoriyorifood.com/xxxx/spacial/254815
http://www.theocraticamerica.org/forum/index.php?topic=70525.0
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=93334
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=93367
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=93403
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=93651
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=93782
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=94354
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=94359
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=94364
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=94378
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=94402
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=94407
https://www.chirorg.com/?document_srl=151363
http://zakdu.com/board_ssKi56/20445
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=386153
http://www.svteck.co.kr/customer_gratitude/219992
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=320292
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=135998
http://jiral.net/an9/27916
http://vtservices85.fr/smf2/index.php?PHPSESSID=b5934e3367785055a53d766b4e50b8b9&topic=289726.0
http://benzmall.co.kr/index.php?mid=download&document_srl=72894
http://fbpharm.net/index.php/component/k2/itemlist/user/85761
http://praisesound.co.kr/sub04_01/87638
https://www.runcity.org/forum/index.php?action=profile;u=77736
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=40281.0
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1148992
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=201364
http://www.alase.net/index.php/component/k2/itemlist/user/12678
http://www.livetank.cn/market1/219310
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=184664
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/38305
http://hyeonjun.co.kr/menu3/297117
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3902262
http://153.120.114.241/eso/index.php/17537775-rasskaz-sluzanki-3-sezon-6-seria-navq-rasskaz-sluzanki-3-sezon-
http://carand.co.kr/d2/57803
http://gochon-iusell.co.kr/g1/77613
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=256919
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=80550
http://apt2you2.cafe24.com/g1/35813
http://2872870.com/est/61263
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=318116
http://www.tessabannampad.go.th/webboard/index.php?topic=225649.0
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=33655
http://tiretech.co.kr/index.php?mid=qna&document_srl=180903
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=312567
http://gallerychoi.com/Exhibition/333551
https://www.hwbms.com/web/qna/11124
http://e-educ.net/Forum/index.php?topic=16366.0
http://dayung.co.kr/board_SRVC17/68426
http://gochon-iusell.co.kr/g1/86367
http://www.lgue.co.kr/?document_srl=114920
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=224915
https://mcsetup.tk/bbs/index.php?topic=263051.0
http://midorijapaneserestaurant.ca/menu/News/28233
http://www.boutique.in.th/?option=com_k2&view=itemlist&task=user&id=153117
http://rabat.kr/board_yCgT00/48435
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4899846
https://forum.ac-jete.it/index.php?topic=447283.0
http://naksansacondo.com/board_MGPu57/32414
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=164248
http://benzmall.co.kr/?document_srl=46093
http://myrechockey.com/forums/index.php?topic=117853.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=d327fff8f56ebde7c111f14b7728fe96&topic=286222.0
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/?document_srl=109651
http://mediaville.me/index.php/component/k2/itemlist/user/333741
http://www.popolsku.fr.pl/forum/index.php?topic=20407.msg769388
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=23245
http://www.cnsmaker.net/xe/?document_srl=122293
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=301945
http://warmfund.net/p/index.php?mid=financing&document_srl=472993
http://gallerychoi.com/Exhibition/329095
http://agiteshop.com/xe/qa/164386
http://askpharm.net/board_NQiz06/158645
http://dev.aabn.org.gh/?option=com_k2&view=itemlist&task=user&id=682802
http://taklongclub.com/forum/index.php?topic=205898.0
http://eugeniocolazzo.it/forum/index.php?topic=178823.0
http://jiral.net/an9/29307
https://timecker.com/anonymous/187222
https://esel.gist.ac.kr/esel2/board_hmgj23/271466
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=95279
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=199885
http://askpharm.net/board_NQiz06/160186
http://midorijapaneserestaurant.ca/menu/News/35174
http://taklongclub.com/forum/index.php?topic=204821.0
http://universalcommunity.se/Forum/index.php?topic=36076.0
http://douniatravel.com/component/k2/itemlist/user/3488.html
http://bebopindia.com/notcie/462664
http://zakdu.com/board_ssKi56/23135
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=17879
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/65458
http://1661-6471.co.kr/news/44467
https://reficulcoin.com/index.php?topic=88918.0
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2603629
http://www.venusjeju.com/index.php?mid=QnA&document_srl=866
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ymfd-%d1%80%d0%b0%d1%81/
http://myrechockey.com/forums/index.php?topic=119720.0
http://forum.elexlabs.com/index.php?topic=61894.0
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=887705
http://muldorang.com/market/27644
http://daesestudy.co.kr/ipsi_docu/139055
http://www.alase.net/index.php/component/k2/itemlist/user/12636
https://nple.com/xe/pds/150268
http://myrechockey.com/forums/index.php?topic=118630.0
http://isch.kr/board_PowH60/197184
http://roikjer.com/forum/index.php?PHPSESSID=kkfhevkcg9c5dc9nq8jc1fbso1&topic=931574.0
http://p9912.cafe24.com/board_LVgu51/56632
http://xn--2e0b53df5ag1c804aphl.net/nuguna/104161
http://gochon-iusell.co.kr/g1/87075
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=377664
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/32903
http://yooseok.com/board_BkvT46/411765
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=64896
http://1661-6471.co.kr/news/47481
http://yoriyorifood.com/xxxx/spacial/265130
http://jnk-ent.jp/index.php?mid=gallery&document_srl=238975
http://juroweb.com/xe/juroweb_board/85166
http://xn--2e0b53df5ag1c804aphl.net/nuguna/115002
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=419988
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=206200
http://loverstory.co.kr/board_UYNJ05/45040
http://divespace.co.kr/board/184772
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5020543
http://www.itosm.com/cn/board_nLoq17/133503
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=139350
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=139393
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=139508
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=139823
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=139831
http://kino-z.eu/?option=com_k2&view=itemlist&task=user&id=2482
http://kino-z.eu/component/k2/itemlist/user/2488
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42487
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42491
http://kockazatkutato.hu/component/k2/itemlist/user/42495
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=40115
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=40117
http://theolevolosproject.org/index.php/component/k2/itemlist/user/27574
http://vhost12299.cpsite.ru/574975-hdvideo-tajny-taemnici-90-seria-z3-tajny-taemnici-90-seria
http://vhost12299.cpsite.ru/575139-smotret-holostak-9-sezon-12-vypusk-m5-holostak-9-sezon-12-vypus
http://vhost12299.cpsite.ru/575222-smotret-sluga-naroda-3-sezon-22-seria-d2-sluga-naroda-3-sezon-2
http://vhost12299.cpsite.ru/575244-serial-sluga-naroda-3-sezon-7-seria-q4-sluga-naroda-3-sezon-7-s
http://vhost12299.cpsite.ru/575259-smers-6-seria-t4-smers-6-seria
http://vhost12299.cpsite.ru/575309-smotret-tajny-taemnici-91-seria-q6-tajny-taemnici-91-seria
http://vhost12299.cpsite.ru/575371-smotret-cuzaa-zizn-cuze-zitta-4-seria-e1-cuzaa-zizn-cuze-zitta-
http://xn--2e0bk61btjo.com/notice/20432
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=232186
http://dev.fivestarpainting.com/?option=com_k2&view=itemlist&task=user&id=1984209
http://lucky.kidspann.net/index.php?mid=qna&document_srl=295230
https://www.lwfservers.com/index.php?topic=70065.0
http://autospa.lv/index.php/lv/component/k2/itemlist/user/10588
http://sejong-thesharpyemizi.co.kr/m1/64098
http://www.cnsmaker.net/xe/?document_srl=125090
http://knet.dothome.co.kr/xe/board_RJHw15/19763
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5054956
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5054971
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1244689
https://afikgan.co.il/index.php/component/k2/itemlist/user/30389
https://blossomug.com/index.php/component/k2/itemlist/user/1111262
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16179
http://kockazatkutato.hu/component/k2/itemlist/user/42695
http://photogrotto.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bu6o-%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3/
http://photogrotto.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wb1l-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-we6z-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd/
http://photogrotto.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jd6j-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.ekemoon.com/244693/051820192928/
http://www.popolsku.fr.pl/forum/index.php?topic=20407.81090
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=287890
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=127204
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/72534
http://callman.co.kr/index.php?mid=qa&document_srl=224203
http://hanga5.com/index.php?mid=board_photo&document_srl=157932
http://www.nurican.com/giris/ncan/index.php?topic=6092.0
http://themasters.pro/file_01/311773
http://jnk-ent.jp/index.php?mid=gallery&document_srl=240965
http://viamania.net/index.php?mid=board_raYV15&document_srl=133899
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/87461
http://myrechockey.com/forums/index.php?topic=117403.0
http://bath-family.com/photo_zone/143817
http://bobr.site/index.php?topic=179206.0
https://reficulcoin.com/index.php?topic=83386.0
http://mercibq.net/partner/55679
http://engeena.com/component/k2/itemlist/user/9189
http://agiteshop.com/xe/qa/165241
http://isch.kr/board_PowH60/230655
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=342862
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=ea45cae762b368b61f2414c293d3e67c&topic=10821.0
https://forums.lfstats.com/viewtopic.php?t=319959
https://reficulcoin.com/index.php?topic=86654.0
http://masanlib.or.kr/g1/96262
https://timecker.com/anonymous/187921
http://barobus.kr/qna/91260
https://turimex.mx.solemti.net/en/?option=com_k2&view=itemlist&task=user&id=14176
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=32796
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1934225
http://praisesound.co.kr/sub04_01/88668
http://zakdu.com/board_ssKi56/21013
http://ajincomp.godohosting.com/board_STnh82/127401
https://2002.shyoon.com/board_2002/221303
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=77937
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=372324
http://1661-6471.co.kr/news/76530
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=427409
http://bobr.site/index.php?topic=184236.0
http://www.popolsku.fr.pl/forum/index.php?topic=20407.79725
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/65636
http://miquirofisico.com/index.php/component/k2/itemlist/user/4504
http://www.coating.or.kr/atemfair_data/17752
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?document_srl=76690&mid=main_08
http://myrechockey.com/forums/index.php?topic=118972.0
http://blog.ptpintcast.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zxti-%d1%80%d0%b0%d1%81/
http://2872870.com/est/62949
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=23098
http://ptu.imoove.kr/ko/content/%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-ipgd-%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-bbc341172
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=184331
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=119459
https://www.lwfservers.com/index.php?topic=72322.0
http://herdental.co.kr/index.php?mid=online&document_srl=170735
http://viamania.net/index.php?mid=board_raYV15&document_srl=139782
https://www.celekt.com/%d0%a0%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nfek-%d0%a0%d0%b0%d1%81/
http://rudraautomation.com/index.php/component/k2/author/293062
http://ptu.imoove.kr/ko/content/%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-ekqn-%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-ideafilm341232
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/53101
http://ye-dream.com/qa/232364
https://www.chirorg.com/?document_srl=154769
http://daltso.com/index.php?mid=board_cUYy21&document_srl=183131
http://iymc.or.kr/pds/116276
https://forum.ac-jete.it/index.php?topic=443478.0
http://douniatravel.com/component/k2/itemlist/user/3495.html
http://autospa.lv/index.php/lv/component/k2/itemlist/user/10584
https://cybergsm.es/index.php?topic=66013.0
https://timecker.com/anonymous/188477
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=142793
http://loverstory.co.kr/board_UYNJ05/46465
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=96337
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=915250
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=915272
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=915297
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=915560
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=915644
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=915705
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=915759
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=915938
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=915943
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=916088
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=916099
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=916228
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=916402
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105856
http://knet.dothome.co.kr/xe/board_RJHw15/15429
http://www.vamoscontigo.org/Noticia/139525
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=899001
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1940340
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=45460
http://blog.ptpintcast.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zqdf-%d1%80%d0%b0%d1%81/
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=711360
http://zakdu.com/board_ssKi56/15230
http://jdcalc.com/forum/viewtopic.php?t=291074
http://ovotecegg.com/component/k2/itemlist/user/219486
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=332540
http://rudraautomation.com/index.php/component/k2/author/331800
http://rudraautomation.com/index.php/component/k2/author/332546
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=173064
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=124835
http://wigalseguros.com.br/component/users/?task=user&view=itemlist&id=28113
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1531940
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99053
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99065
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99072
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99137
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99160
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99163
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99169
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99176
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99195
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99240
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99261
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99285
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99290
https://www.2ayes.com/19458/3-10-osce-3-10-newstudio
http://pkgersang.dothome.co.kr/board_jiKY24/37686
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/147121
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=61742
https://forum.clubeicaro.pt/index.php?topic=2479.0
http://sd-xi.co.kr/g1/52330
http://www.vamoscontigo.org/Noticia/155427
https://forums.lfstats.com/viewtopic.php?t=321426
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=113305
http://gspara01.dothome.co.kr/index.php?mid=board_XHsr53&document_srl=14102
http://www.itosm.com/cn/board_nLoq17/136054
http://music.start-a-idea.online/blogs/viewstory/44350
https://cybergsm.es/index.php?topic=67593.0
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=399341
http://kockazatkutato.hu/component/k2/itemlist/user/43394
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3924838
http://mediaville.me/index.php/component/k2/itemlist/user/363782
http://mediaville.me/index.php/component/k2/itemlist/user/363850
http://mobility-corp.com/index.php/component/k2/itemlist/user/2731391
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/167214
http://ovotecegg.com/component/k2/itemlist/user/219578
http://ovotecegg.com/index.php/component/k2/itemlist/user/219556
http://rudraautomation.com/index.php/component/k2/author/332811
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-elbx-%d1%80%d0%b0%d1%81/
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fpiz-%d1%80%d0%b0%d1%81/
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fzct-%d1%80%d0%b0%d1%81/
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hdhf-%d1%80%d0%b0%d1%81/
http://guiadetudo.com/index.php/component/k2/itemlist/user/12768
https://www.limscave.com/forum/viewtopic.php?t=54733
http://viamania.net/index.php?mid=board_raYV15&document_srl=139683
http://sy.korean.net/qna/311570
http://warmfund.net/p/index.php?mid=financing&document_srl=527249
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=416708
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3546315
https://www.celekt.com/%d0%a0%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-evtw-%d0%a0%d0%b0%d1%81/
https://forums.lfstats.com/viewtopic.php?t=314697
http://e-educ.net/Forum/index.php?topic=16361.0
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=184542
http://kyj1225.godohosting.com/board_mebR72/95039
http://kyj1225.godohosting.com/board_mebR72/95044
http://www.leekeonsu-csi.com/?document_srl=1086234
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=1086329
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=1086413
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=1086460
https://betshin.com/Story/195880
https://gonggamlaw.com/lawcase/128901
https://gonggamlaw.com/lawcase/128930
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/37383
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/37562
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/37587
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/37592
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/37650
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/37734
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/37755
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/37772
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/37781
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/37791
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/65531
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/52497
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=214333
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=49868
http://askpharm.net/board_NQiz06/221924
http://www.arunagreen.com/index.php/component/k2/itemlist/user/1151781
http://phmusic.dothome.co.kr/index.php?mid=PowerHouseMusic&document_srl=45508
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=119289
http://p9912.cafe24.com/board_LVgu51/60471
https://www.hwbms.com/web/qna/11212
http://www.spazioad.com/component/k2/itemlist/user/7416544
http://www.livetank.cn/market1/299349
http://www.ekemoon.com/240269/050720195226/
http://viamania.net/?document_srl=123688
http://askpharm.net/board_NQiz06/160146
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=40322.0
http://www.popolsku.fr.pl/forum/index.php?topic=20407.80820
https://intelogist2.wpengine.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jrfb-%d1%80%d0%b0%d1%81/
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/67012
http://ko.myds.me/board_story/247568
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105946
http://beautypouch.net/index.php?mid=board_09&document_srl=109602
http://benzmall.co.kr/index.php?mid=download&document_srl=45951
http://benzmall.co.kr/index.php?mid=download&document_srl=45961
http://benzmall.co.kr/index.php?mid=download&document_srl=46122
http://benzmall.co.kr/index.php?mid=download&document_srl=46259
http://benzmall.co.kr/index.php?mid=download&document_srl=46610
http://benzmall.co.kr/index.php?mid=download&document_srl=46620
http://benzmall.co.kr/index.php?mid=download&document_srl=46726
http://benzmall.co.kr/index.php?mid=download&document_srl=46740
http://benzmall.co.kr/index.php?mid=download&document_srl=46833
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/819745
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=85398
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/33047
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=119034
http://www2.yasothon.go.th/smf/index.php?topic=159.169725
http://married.dike.gr/index.php/component/k2/itemlist/user/78092
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=90360
http://dev.aabn.org.gh/component/k2/itemlist/user/681781
https://2002.shyoon.com/board_2002/188680
http://www.itosm.com/cn/board_nLoq17/132859
http://www.cnsmaker.net/xe/?document_srl=123772
http://www.svteck.co.kr/customer_gratitude/219650
http://miquirofisico.com/index.php/component/k2/itemlist/user/4426
http://thermoplast.envolgroupe.com/component/k2/author/156721
http://apt2you2.cafe24.com/g1/44773
http://xn----3x5er9r48j7wemud0a387h.com/news/162779
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/76665
http://www.itosm.com/cn/board_nLoq17/175186
http://benzmall.co.kr/index.php?mid=download&document_srl=47740
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=316912
http://archeaudio.com/xe/?document_srl=16778
http://benzmall.co.kr/index.php?mid=download&document_srl=47686
http://benzmall.co.kr/index.php?mid=download&document_srl=47691
http://benzmall.co.kr/index.php?mid=download&document_srl=47740
http://benzmall.co.kr/index.php?mid=download&document_srl=47786
http://benzmall.co.kr/index.php?mid=download&document_srl=47808
https://nple.com/xe/pds/151161
http://yoriyorifood.com/xxxx/spacial/254435
http://gallerychoi.com/Exhibition/333733
http://vtservices85.fr/smf2/index.php?PHPSESSID=50017d597923e442783a398e54ae615a&topic=291528.0
http://sd-xi.co.kr/g1/59543
http://rfc11th13th.dothome.co.kr/Board5/33280
http://sd-xi.co.kr/g1/59525
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=112371
https://nple.com/xe/pds/150282
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3750149
http://divespace.co.kr/board/229396
http://sfah.ch/de/component/k2/itemlist/user/15493
http://www.aloeverasas.it/index.php/component/k2/itemlist/user/21382
http://www.lgue.co.kr/lgue05/111488
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/58922
http://rudraautomation.com/index.php/component/k2/author/291610
http://www.popolsku.fr.pl/forum/index.php?topic=20407.80040
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=198455
http://vervetama.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lvwy-%d1%80%d0%b0%d1%81/
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=431899
https://cybergsm.es/index.php?topic=68821.0
http://gallerychoi.com/Exhibition/334238
http://necinsurance.co.zw/component/k2/itemlist/user/21647.html
http://test.comics-game.ru/index.php?topic=484.0
http://bebopindia.com/notcie/381510
http://www.tessabannampad.go.th/webboard/index.php?topic=225758.0
http://yoriyorifood.com/xxxx/spacial/254118
http://leonwebzine.dothome.co.kr/?document_srl=11186
https://cybergsm.es/index.php?topic=67524.0
http://www.venusjeju.com/index.php?mid=QnA&document_srl=1822
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=63798
https://www.shaiyax.com/index.php?topic=408305.0
http://ajincomp.godohosting.com/board_STnh82/174227
http://bobr.site/index.php?topic=183848.0
http://dayung.co.kr/board_SRVC17/70358
http://gochon-iusell.co.kr/g1/76365
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=56663
http://0433.net/junggo/114053
https://timecker.com/anonymous/188993
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2596262
https://grajalesabogados.com.mx/?option=com_k2&view=itemlist&task=user&id=65548
http://k-cea.org/board_Hnyj62/192430
http://www.ekemoon.com/242133/050420195627/
http://agiteshop.com/xe/?document_srl=161989
http://www.svteck.co.kr/customer_gratitude/305002
http://yooseok.com/board_BkvT46/413253
http://isch.kr/?document_srl=234453
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=206186
http://p9912.cafe24.com/board_LVgu51/59015
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1284913
http://looksun.co.kr/index.php?mid=board_4&document_srl=123158
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/245843
http://benzmall.co.kr/index.php?mid=download&document_srl=92304
http://myrechockey.com/forums/index.php?topic=118814.0
http://universalcommunity.se/Forum/index.php?topic=35908.0
http://warmfund.net/p/index.php?mid=financing&document_srl=463284
http://dcasociados.eu/component/k2/itemlist/user/93323
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2740775
http://isch.kr/board_PowH60/212596
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=121059
http://www.svteck.co.kr/customer_gratitude/319725
http://apt2you2.cafe24.com/g1/37903
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13776
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=43485
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2742287
http://sd-xi.co.kr/g1/59693
http://jiral.net/an9/29425
http://jnk-ent.jp/index.php?mid=gallery&document_srl=328053
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=20076
http://www.popolsku.fr.pl/forum/index.php?topic=416960.0
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/55213
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1152686
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=105740
http://ptu.imoove.kr/ko/content/%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-1-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-kmzz-%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-1-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-starz341287
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=160694
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39659
http://askpharm.net/board_NQiz06/159169
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/61365
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=206084
https://esel.gist.ac.kr/esel2/board_hmgj23/270411
https://nextezone.com/index.php?topic=76563.0
http://bebopindia.com/notcie/384655
https://forums.lfstats.com/viewtopic.php?f=6&t=320912
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/59184
http://music.start-a-idea.online/blogs/viewstory/44310
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3450994
http://socialmag.bayareanonprofits.xyz/blogs/viewstory/138174
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=338548
http://www.theocraticamerica.org/forum/index.php?topic=70586.0
https://www.bmwstyle.ru/forum/index.php?topic=65372.0
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5019636
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=189768
http://vtservices85.fr/smf2/index.php?PHPSESSID=7b65f8de14a8aaa3e1919a68100ceed1&topic=294043.0
https://www.netprofessional.gr/component/k2/itemlist/user/3961.html
http://lucky.kidspann.net/index.php?mid=qna&document_srl=295298
http://www.coating.or.kr/atemfair_data/16941
http://www.golden-nail.co.kr/press/368744
http://www.vamoscontigo.org/Noticia/177731
http://arquitectosenreformas.es/index.php/component/k2/itemlist/user/85807
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16393
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16332
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16363
http://dospuntoseventos.cl/component/k2/itemlist/user/16392
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42873
http://kockazatkutato.hu/index.php/component/k2/itemlist/user/42820
http://udrpsucks.com/blog/?p=1757
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uq7q-%d0%ba%d0%be%d0%bf-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://naksansacondo.com/board_MGPu57/56129
http://barobus.kr/qna/74676
http://k-cea.org/board_Hnyj62/195082
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=106079
http://lucky.kidspann.net/index.php?mid=qna&document_srl=344425
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13753
http://universalcommunity.se/Forum/index.php?topic=32791.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=40214.0
http://daltso.com/index.php?mid=board_cUYy21&document_srl=162716
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3386772
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=376882
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=223527
https://prosto-vkus.ru/?option=com_k2&view=itemlist&task=user&id=34971
http://yooseok.com/board_BkvT46/412887
http://autospa.lv/index.php/lv/component/k2/itemlist/user/10608
https://esel.gist.ac.kr/esel2/board_hmgj23/274307
https://esel.gist.ac.kr/esel2/board_hmgj23/274326
https://esel.gist.ac.kr/esel2/board_hmgj23/274421
https://esel.gist.ac.kr/esel2/board_hmgj23/275515
https://esel.gist.ac.kr/esel2/board_hmgj23/278523
https://esel.gist.ac.kr/esel2/board_hmgj23/286869
https://esel.gist.ac.kr/esel2/board_hmgj23/286898
https://esel.gist.ac.kr/esel2/board_hmgj23/287502
https://esel.gist.ac.kr/esel2/board_hmgj23/293231
https://esel.gist.ac.kr/esel2/board_hmgj23/293274
https://esel.gist.ac.kr/esel2/board_hmgj23/295389
https://esel.gist.ac.kr/esel2/board_hmgj23/296845
https://esel.gist.ac.kr/esel2/board_hmgj23/297717
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=43029
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229327
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/59495
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/66117
http://dohairbiz.com/component/k2/itemlist/user/2812913
http://dospuntoseventos.cl/index.php/component/k2/itemlist/user/16438
http://juroweb.com/xe/juroweb_board/84873
http://dev.aabn.org.gh/component/k2/itemlist/user/679382
http://test.comics-game.ru/index.php?topic=458.0
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=109964
http://153.120.114.241/eso/index.php/17546587-rasskaz-sluzanki-3-sezon-11-seria-ihjx-rasskaz-sluzanki-3-sezon
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=139193
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=310900
https://forums.lfstats.com/viewtopic.php?t=319290
https://forums.lfstats.com/viewtopic.php?t=319311
https://forums.lfstats.com/viewtopic.php?t=319366
https://forums.lfstats.com/viewtopic.php?t=319393
https://forums.lfstats.com/viewtopic.php?t=319403
https://forums.lfstats.com/viewtopic.php?t=319434
https://forums.lfstats.com/viewtopic.php?t=319437
https://forums.lfstats.com/viewtopic.php?t=319467
https://forums.lfstats.com/viewtopic.php?t=319481
https://forums.lfstats.com/viewtopic.php?t=319505
https://forums.lfstats.com/viewtopic.php?t=319593
https://forums.lfstats.com/viewtopic.php?t=319598
https://forums.lfstats.com/viewtopic.php?t=319611
https://forums.lfstats.com/viewtopic.php?t=319633
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16706
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16714
http://dospuntoseventos.cl/component/k2/itemlist/user/16687
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=43415
http://kockazatkutato.hu/component/k2/itemlist/user/43435
http://www.jesusandmarypatna.com/index.php/component/k2/itemlist/user/3568381
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5057399
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5057485
http://photogrotto.com/%d0%ba%d0%be%d0%bf-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xo4f-%d0%ba%d0%be%d0%bf-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16716
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7517689
http://ajincomp.godohosting.com/board_STnh82/129285
http://dayung.co.kr/board_SRVC17/69786
http://ye-dream.com/qa/205995
http://www.hmotors.co.kr/inquiry/27297
http://erhu.eu/viewtopic.php?t=400217
http://p9912.cafe24.com/board_LVgu51/56842
http://mercibq.net/partner/90186
http://xn--2e0b53df5ag1c804aphl.net/?document_srl=140612
http://myrechockey.com/forums/index.php?topic=120053.0
http://myrechockey.com/forums/index.php?topic=120132.0
http://myrechockey.com/forums/index.php?topic=120152.0
http://myrechockey.com/forums/index.php?topic=120170.0
http://myrechockey.com/forums/index.php?topic=120254.0
http://naksansacondo.com/?document_srl=33887
http://naksansacondo.com/?document_srl=33917
http://naksansacondo.com/?document_srl=34684
http://naksansacondo.com/?document_srl=35834
http://naksansacondo.com/?document_srl=35874
http://naksansacondo.com/?document_srl=49529
http://naksansacondo.com/board_MGPu57/30604
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3451712
https://www.hohoyoga.com/?document_srl=4013162
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=36908
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=910681
http://melchinooddle.dothome.co.kr/?document_srl=14797
http://www.popolsku.fr.pl/forum/index.php?topic=20407.81180
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3371961
http://bebopindia.com/notcie/408391
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=270171
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=188146
http://knet.dothome.co.kr/xe/board_RJHw15/15753
http://ovotecegg.com/component/k2/itemlist/user/220395
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/328619
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/328629
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/328636
http://rudraautomation.com/index.php/component/k2/author/334377
http://rudraautomation.com/index.php/component/k2/author/334795
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=125708
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=125722
http://neosky.net/xe/space_station/72633
http://neosky.net/xe/space_station/72645
http://neosky.net/xe/space_station/72672
http://neosky.net/xe/space_station/72703
http://neosky.net/xe/space_station/72720
http://neosky.net/xe/space_station/72742
http://neosky.net/xe/space_station/72773
http://neosky.net/xe/space_station/72788
http://neosky.net/xe/space_station/72792
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=119825
http://153.120.114.241/eso/index.php/17528997-rasskaz-sluzanki-3-sezon-4-seria-zsnl-rasskaz-sluzanki-3-sezon-
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=223777
http://zakdu.com/board_YpzS56/23412
http://healthyteethpa.org/component/k2/itemlist/user/5547904
http://vtservices85.fr/smf2/index.php?PHPSESSID=5991ebacc0cbd3b527b1544e4455ba46&topic=291284.0
http://guiadetudo.com/index.php/component/k2/itemlist/user/12623
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=43814
http://www.m1avio.com/index.php/component/k2/itemlist/user/3839037
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=209002
http://carand.co.kr/?document_srl=92457
http://carand.co.kr/d2/92402
http://daesestudy.co.kr/?document_srl=142926
http://x-crew.center/?document_srl=4846684
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3896039
http://www.spazioad.com/component/k2/itemlist/user/7416616
http://divespace.co.kr/board/202248
https://reficulcoin.com/index.php?topic=88848.0
http://zakdu.com/board_ssKi56/15718
http://dow.dothome.co.kr/board_jydx58/28872
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=122724
http://sunele.co.kr/board_ReBD97/163676
http://dsyang.com/board_Kvgn62/30619
http://rabat.kr/?document_srl=39188
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3374249
http://ye-dream.com/qa/220033
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=119825
http://153.120.114.241/eso/index.php/17528997-rasskaz-sluzanki-3-sezon-4-seria-zsnl-rasskaz-sluzanki-3-sezon-
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=223777
http://zakdu.com/board_YpzS56/23412
http://healthyteethpa.org/component/k2/itemlist/user/5547904
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=99155
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/70637
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=187714
http://ariji.kr/?document_srl=973414
http://x-crew.center/guest/4845431
http://constellation.kro.kr/board_kbku73/64881
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/97788
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=931874
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=223188
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=176723
http://www.tessabannampad.go.th/webboard/index.php?topic=226417.0
http://k-cea.org/board_Hnyj62/194774
http://hyeonjun.co.kr/menu3/290104
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=71078
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=98763
http://callman.co.kr/index.php?mid=qa&document_srl=270935
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=303976
http://erdfsa.iptime.org/xe/index.php?mid=board&document_srl=14384
http://eugeniocolazzo.it/forum/index.php?topic=180566.0
http://lucky.kidspann.net/index.php?mid=qna&document_srl=368600
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/246646
https://www.shaiyax.com/index.php?topic=399178.0
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=84872
http://apt2you2.cafe24.com/g1/35202
http://thermoplast.envolgroupe.com/component/k2/author/157202
http://callman.co.kr/index.php?mid=qa&document_srl=230058
https://www.shaiyax.com/index.php?topic=413821.0
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/56233
http://toeden.co.kr/Product_new/140881
http://viamania.net/index.php?mid=board_raYV15&document_srl=203660
http://divespace.co.kr/board/250062
https://www.shaiyax.com/index.php?topic=419254.0
http://lucky.kidspann.net/index.php?mid=qna&document_srl=389094
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=127655
http://www.theocraticamerica.org/forum/index.php?topic=74079.0
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=128809
http://looksun.co.kr/index.php?mid=board_4&document_srl=124700
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105719
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105734
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105744
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105751
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105764
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105773
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105778
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105795
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105810
http://8.droror.co.il/uncategorized/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lwsx-%d1%80%d0%b0%d1%81/
http://zakdu.com/board_YpzS56/20563
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105674
http://masanlib.or.kr/g1/102735
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=23364
http://e-educ.net/Forum/index.php?topic=16571.0
http://sy.korean.net/qna/425783
http://www.sp1.football/index.php?mid=faq&document_srl=694453
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=266451
http://warmfund.net/p/index.php?mid=financing&document_srl=529351
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/34479
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105734
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=381427
http://dayung.co.kr/board_SRVC17/70210
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=399499
http://kyj1225.godohosting.com/board_mebR72/60798
https://www.hwbms.com/web/qna/12394
http://mercibq.net/partner/94359
http://www.cyberblissstudios.com/UserProfile/tabid/42/UserID/2329844/Default.aspx
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=321868
http://socialmag.bayareanonprofits.xyz/blogs/viewstory/129599
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1287374
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1287545
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1287828
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1287855
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1288279
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1288324
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1288344
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1288537
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1288557
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1288659
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1288789
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1289121
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1289196
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1289222
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/?document_srl=64341
http://zakdu.com/board_ssKi56/18982
http://divespace.co.kr/board/180493
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=204851
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5015040
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=32739
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/77007
http://apt2you2.cafe24.com/g1/34927
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1976466
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=160543
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1284298
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=248269
http://rudraautomation.com/index.php/component/k2/author/289184
https://adsensebih.com/index.php?topic=47890.0
http://sd-xi.co.kr/g1/59838
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=89507
http://x-crew.center/guest/4845112
http://daltso.com/?document_srl=127213
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=113144
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=85374
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=85428
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=85439
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=85450
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=85453
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=85456
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=85462
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=85472
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3542603
http://lucky.kidspann.net/index.php?mid=qna&document_srl=386642
http://2872870.com/est/66201
http://themasters.pro/?document_srl=224444
http://k-cea.org/?document_srl=197655
https://nple.com/xe/pds/224076
http://married.dike.gr/index.php/component/k2/itemlist/user/78032
http://elegance-slimup.com/?option=com_k2&view=itemlist&task=user&id=4810
http://agiteshop.com/xe/qa/164573
http://lucky.kidspann.net/index.php?mid=qna&document_srl=289457
http://necinsurance.co.zw/component/k2/itemlist/user/21747.html
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=120783
http://warmfund.net/p/index.php?mid=financing&document_srl=530859
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3840353
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=412474
http://naksansacondo.com/board_MGPu57/52755
http://naksansacondo.com/board_MGPu57/52883
http://naksansacondo.com/board_MGPu57/54676
http://naksansacondo.com/board_MGPu57/54779
http://naksansacondo.com/board_MGPu57/56129
http://mobility-corp.com/index.php/component/k2/itemlist/user/2699128
http://daesestudy.co.kr/ipsi_docu/121756
http://toeden.co.kr/Product_new/139309
http://mobility-corp.com/index.php/component/k2/itemlist/user/2698138
http://daesestudy.co.kr/ipsi_docu/148508
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=441246
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=274409
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=224172
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=23615
http://tiretech.co.kr/index.php?mid=qna&document_srl=186785
http://gusinoepero.ru/archives/25764
http://ariji.kr/?document_srl=1003217
http://www.popolsku.fr.pl/forum/index.php?topic=417331.0
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=149161
https://www.netprofessional.gr/component/k2/itemlist/user/3921.html
http://lucky.kidspann.net/?document_srl=369207
https://www.c-alice.org/forum/index.php?topic=97558.0
http://www.sp1.football/index.php?mid=faq&document_srl=694082
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=65731
http://shinhwaair2017.cafe24.com/issue/498067
http://www.golden-nail.co.kr/?document_srl=355619
http://otitismediasociety.org/forum/index.php?topic=204834.0
http://www.haetsaldun-clinic.co.kr/Question/42699
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=49062
http://mediaville.me/index.php/component/k2/itemlist/user/332993
http://dow.dothome.co.kr/board_jydx58/36330
https://www.c-alice.org/forum/index.php?topic=96421.0
http://www.theocraticamerica.org/forum/index.php?topic=70190.0
http://zakdu.com/board_YpzS56/19846
http://www.aloeverasas.it/index.php/component/k2/itemlist/user/21453
https://altaylarteknoloji.com/index.php?topic=6478.0
https://www.hohoyoga.com/testboard/3971156
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=680171
http://askpharm.net/board_NQiz06/163991
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=98966
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/306336
http://www.urbantutorial.com/index.php/component/k2/itemlist/user/127574
http://callman.co.kr/index.php?mid=qa&document_srl=223022
http://smartacity.com/component/k2/itemlist/user/78697
https://gonggamlaw.com/lawcase/91443
http://iymc.or.kr/pds/116733
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=717275
http://myrechockey.com/forums/index.php?topic=117874.0
http://gspara01.dothome.co.kr/index.php?mid=board_XHsr53&document_srl=14608
http://ilsannabgol.kr/board_brJk31/1373165
http://www.aloeverasas.it/index.php/component/k2/itemlist/user/21506
https://cybergsm.es/index.php?topic=71673.0
https://forum.ac-jete.it/index.php?topic=449109.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=385858
http://dessa.com.br/component/k2/itemlist/user/385884
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16194
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42701
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42713
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42735
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42736
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=123665
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=123695
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=345636
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=35339
http://khapthanam.co.kr/g1/135979
https://esel.gist.ac.kr/esel2/board_hmgj23/268516
http://gabisan.com/board_OuDs04/66834
http://www.patrasin.kr/index.php?mid=questions&document_srl=4349437
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=39591.0
http://gspara01.dothome.co.kr/index.php?mid=board_XHsr53&document_srl=16824
http://2872870.com/est/62171
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42667
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=839705
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/166297
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/166340
http://rudraautomation.com/index.php/component/k2/itemlist/user/329952
http://smartacity.com/component/k2/itemlist/user/89433
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=172564
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=123912
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=27841
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1531346
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3842375
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3858261
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=35375
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=35412
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2827637
http://holysweat.dothome.co.kr/data/7557
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=155472
http://sejong-thesharpyemizi.co.kr/m1/27552
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=198667
http://ptu.imoove.kr/ko/content/%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-cqrz-%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-6-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-amc341244
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=827797
http://www.arunagreen.com/index.php/component/k2/itemlist/user/1158116
http://hanga5.com/index.php?mid=board_photo&document_srl=146046
http://dev.aabn.org.gh/component/k2/itemlist/user/711353
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16232
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16253
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=108032
http://halinhpharma.com.vn/index.php/component/k2/itemlist/user/398144
http://mediaville.me/index.php/component/k2/itemlist/user/362112
http://mediaville.me/index.php/component/k2/itemlist/user/362131
http://mediaville.me/index.php/component/k2/itemlist/user/362143
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=126869
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=57956
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/148126
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/148164
http://hotelnomadpalace.com/component/k2/itemlist/user/22513
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=380423
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42625
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42652
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42658
https://forum.ac-jete.it/index.php?topic=447685.0
http://bebopindia.com/?document_srl=467233
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=113199
http://gtupuw.org/index.php/component/k2/itemlist/user/1976692
http://iymc.or.kr/pds/120223
http://www.livetank.cn/market1/293965
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=35414
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=204752
http://bizchemical.com/board_kMpv94/2162042
http://carand.co.kr/d2/87684
http://carand.co.kr/d2/87720
http://cwon.kr/xe/board_bnSr36/283020
http://cwon.kr/xe/board_bnSr36/283061
http://cwon.kr/xe/board_bnSr36/283079
http://daltso.com/index.php?mid=board_cUYy21&document_srl=191862
http://kyj1225.godohosting.com/board_mebR72/92806
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3780993
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=43692
http://leonwebzine.dothome.co.kr/guest/11832
http://phmusic.dothome.co.kr/index.php?mid=PowerHouseMusic&document_srl=50015
http://www.hmotors.co.kr/inquiry/41484
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=466043
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=125105
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=169972
http://www.kwpcoop.or.kr/QnA/22693
http://www.lgue.co.kr/?document_srl=180759
http://blog.ptpintcast.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tlnn-%d1%80%d0%b0%d1%81/
http://carand.co.kr/d2/47930
http://herdental.co.kr/index.php?mid=online&document_srl=179361
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=49901
http://sd-xi.co.kr/?document_srl=59823
http://pkgersang.dothome.co.kr/board_jiKY24/40694
http://holysweat.dothome.co.kr/data/7331
http://2872870.com/est/65039
http://www.m1avio.com/index.php/component/k2/itemlist/user/3838265
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7460739
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/347533
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3480926
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=208114
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=208119
http://carand.co.kr/d2/91490
http://carand.co.kr/d2/91515
http://carand.co.kr/d2/91535
http://carand.co.kr/d2/91541
http://myesl.ca/forum/viewtopic.php?t=694652
http://myesl.ca/forum/viewtopic.php?t=694871
http://myesl.ca/forum/viewtopic.php?t=694908
http://myesl.ca/forum/viewtopic.php?t=694990
http://myesl.ca/forum/viewtopic.php?t=695037
http://myesl.ca/forum/viewtopic.php?t=695040
http://myesl.ca/forum/viewtopic.php?t=695092
http://myesl.ca/forum/viewtopic.php?t=695372
http://myesl.ca/forum/viewtopic.php?t=695380
http://myesl.ca/forum/viewtopic.php?t=695406
http://myesl.ca/forum/viewtopic.php?t=695410
http://myesl.ca/forum/viewtopic.php?t=695658
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3899922
http://viamania.net/index.php?mid=board_raYV15&document_srl=128850
http://praisesound.co.kr/sub04_01/103055
http://www.sp1.football/index.php?mid=faq&document_srl=690346
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=45049
http://bebopindia.com/notcie/383083
http://www.digitalbul.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tzqi-%d1%80%d0%b0%d1%81/
http://ko.myds.me/board_story/244417
https://gonggamlaw.com/lawcase/68489
http://lucky.kidspann.net/index.php?mid=qna&document_srl=396785
http://gabisan.com/board_OuDs04/73867
http://hanga5.com/index.php?mid=board_photo&document_srl=113724
http://forum.bmw-e60.eu/index.php?topic=11381.0
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fuap-%d1%80%d0%b0%d1%81/
http://smartacity.com/component/k2/itemlist/user/92112
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=126823
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=126844
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3784750
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=28974
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1535238
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1535487
http://rabbitzone.xyz/FREE/63831
http://rabbitzone.xyz/FREE/63845
http://rabbitzone.xyz/FREE/69800
http://rabbitzone.xyz/FREE/69870
http://eugeniocolazzo.it/forum/index.php?topic=179975.0
http://khapthanam.co.kr/g1/135238
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=301288
http://autospa.lv/index.php/lv/component/k2/itemlist/user/10534
https://forums.lfstats.com/viewtopic.php?t=320175
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3835720
http://gochon-iusell.co.kr/g1/95378
http://e-educ.net/Forum/index.php?topic=17359.0
http://hyeonjun.co.kr/menu3/334905
http://lucky.kidspann.net/index.php?mid=qna&document_srl=374862
http://www.sp1.football/index.php?mid=faq&document_srl=688616
http://dreamplusart.com/mn03_01/134637
http://5starcoffee.co.kr/board_EBXY17/23457
http://jnk-ent.jp/index.php?mid=gallery&document_srl=298704
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3541938
http://erdfsa.iptime.org/xe/index.php?mid=board&document_srl=12751
http://0433.net/junggo/115673
http://engeena.com/component/k2/itemlist/user/9163
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1498829
<p align="">
<a title="강남오피" href="http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bf%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%c5%8b%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%84%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%8d%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%85%bela" target="_blank">강남오피
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉오피" href="https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%d0%be%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%88%82%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%bd%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%82%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a9tide" target="_blank">선릉오피
</a>
</p>
먼저핀꽃은 먼저진다 남보다 먼저 공을 세우려고 조급히 서둘것이 아니다-채근담
<p align="">
<a title="역삼오피" href="
https://enes.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%94%bb%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%97%88%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%ce%9egang" target="_blank">역삼오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남휴게텔" href="
https://www.livemeshthemes.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%c4%b1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b7%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%85%86%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%93%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%82%ba%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%84%a1%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%82stone" target="_blank">강남휴게텔
</a>
</p>
먹고 싶은것을 다 먹는 것은 그렇게 재미있지 않다 . 인생을 경계선 없이 살면 기쁨이 덜하다.먹고싶은대로 다 먹을 수있다면 먹고싶은 것을 먹는데 무슨 재미가 있겠나 - 톰행크스
<p align="">
<a title="선릉휴게텔" href="
http://www.pnr.corsica/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%89%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%a1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%9d%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%83%a6afford" target="_blank">선릉휴게텔
</a>
</p>
진짜 문제는 사람들의 마음이다.그것은 절대로 물리학이나 윤리학의 문제가 아니다.-아인슈타인
<p align="">
<a title="역삼휴게텔" href="
https://dict.leo.org/italienisch-deutsch/%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%82%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%d1%8f%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%83%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%ae%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9dseason" target="_blank">역삼휴게텔
</a>
</p>
가난은 가난하다고 느끼는 곳에 존재한다 .- 에머슨
<p align="">
<a title="강남안마" href="https://24.sapo.pt/pesquisar?q=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%85%a2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%82%8f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%99%a0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%85%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ce%92truly" target="_blank">강남안마
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉안마" href="
https://enfi.dict.cc/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%9e%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%85%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%90%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%bd%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%9cband" target="_blank">선릉안마
</a>
</p>
행복은 습관이다 그것을 몸에 지니라 -허버드
<p align="">
<a title="역삼안마" href="
https://www.lidumsaym.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%83%9d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c2%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8f%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%b1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%82%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b9derived" target="_blank">역삼안마
</a>
</p>
화려한 일을 추구하지 말라. 중요한 것은 스스로의 재능이며자신의 행동에 쏟아 붓는 사랑의 정도이다. -머더 테레사
<p align="">
<a title="강남오피" href="
http://www.twentszitmaaierteam.nl/pages/interactief/gastenboek.php?p=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%87%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%86%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%82%b9%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%94%bd%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%d0%a3wouldn't" target="_blank">강남오피
</a>
</p>
절대 어제를 후회하지 마라 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다-L.론허바드
<p align="">
<a title="선릉오피" href="
http://www.mairtinmusic.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%82%86%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%8b%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%9e%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%88truly" target="_blank">선릉오피
</a>
</p>
내일은 내일의 태양이 뜬다 피할수 없으면 즐겨라 -로버트 엘리엇
<p align="">
<a title="역삼오피" href="https://www.uptodate.com/contents/search?search=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%81%99%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%b9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%99%aa%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%83%8e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c3%be%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%82%b6%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%8centire" target="_blank">역삼오피
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남휴게텔" href="
http://ladysmithfederal.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%93%94%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%88%87%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%8f%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ce%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%c2%baremark" target="_blank">강남휴게텔
</a>
</p>
인간의 삶 전체는 단지 한 순간에 불과하다 . 인생을 즐기자 - 플루타르코스
<p align="">
<a title="선릉휴게텔" href="
https://www.governmentjobs.com/jobs?keyword=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%94%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%87secretly" target="_blank">선릉휴게텔
</a>
</p>
흔히 사람들은 기회를 기다리고 있지만 기회는 기다리는사람에게 잡히지 않는 법이다.우리는 기회를 기다리는 사람이 되기 전에 기회를 얻을 수 있는실력을 갖춰야 한다.일에 더 열중하는 사람이 되어야한다.-안창호
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%bb%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%84%ba%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%89%b0%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8e%93%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%80%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%cf%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b7artillery" target="_blank">역삼휴게텔
</a>
</p>
마음만을 가지고 있어서는 안된다. 반드시 실천하여야 한다.-이소룡
<p align="">
<a title="강남안마" href="
https://dehr.dict.cc/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%86%8d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%a1%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%84%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%9f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%b0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%88%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%8f%9dleg" target="_blank">강남안마
</a>
</p>
물러나서 조용하게 구하면 배울 수 있는 스승은 많다.사람은 가는 곳마다 보는 것마다 모두 스승으로서배울 것이 많은 법이다.-맹자
<p align="">
<a title="선릉안마" href="
https://www.gov.uk/search/all?keywords=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%92%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%91%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%ae%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8f%87%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%97%87providing" target="_blank">선릉안마
</a>
</p>
삶이 있는 한 희망은 있다 -키케로
<p align="">
<a title="역삼안마" href="
https://www.sdsn.no/sok/category28150.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%88%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%8c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%82%a1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%85%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%c4%b8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%85%9esecretary" target="_blank">역삼안마
</a>
</p>
한 번 실패와 영원한 실패를 혼동하지 마라.-F.스콧 핏제랄드
<p align="">
<a title="강남오피" href="
https://www.righteousmind.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%b0%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%91%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%96%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%88%87sang" target="_blank">강남오피
</a>
</p>
모든것들에는 나름의 경이로움과 심지어 어둠과 침묵이 있고 내가 어떤 상태에 있더라도 나는 그속에서 만족하는 법을 배운다-헬렌켈러
<p align="">
<a title="선릉오피" href="
http://www.actiitransportation.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e2%96%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%99%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%89%ba%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%bdaround" target="_blank">선릉오피
</a>
</p>
내 비장의 무기는 아직 손안에 있다 .그것은 희망이다 - 나폴레옹
<p align="">
<a title="역삼오피" href="https://www.youtube.com/results?search_query=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ce%a5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8e%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%a0%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%b1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%84lay" target="_blank">역삼오피
</a>
</p>
만족할 줄 아는 사람은진정한 부자이고 탐욕스러운 사람은진실로 가난한 사람이다.-솔론
<p align="">
<a title="강남휴게텔" href="
https://denl.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%81%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%8a%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%8f%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%85%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%93%a0%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%b2grief" target="_blank">강남휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="선릉휴게텔" href="
https://artdeco.org/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%9e%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a4%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%94%b9%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ef%bc%af%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%be%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%8dodd" target="_blank">선릉휴게텔
</a>
</p>
만약 우리가 할 수 있는 일을 모두 한다면 우리들은 우리자신에 깜짝 놀랄 것이다.-에디슨
<p align="">
<a title="역삼휴게텔" href="
http://www.lavipera.it/?s=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bc%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%bb%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%93%a3%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b5%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%88%8cvaried" target="_blank">역삼휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="강남안마" href="
https://money2.creontrade.com/E5/WTS/Stock/Foreign/DW_Foreign_Tax.aspx?p=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ef%bc%84%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bc%af%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%bd%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%83%9d%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%87splendid" target="_blank">강남안마
</a>
</p>
절대 어제를 후회하지 마라 . 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다 L.론허바드
<p align="">
<a title="선릉안마" href="
https://wpgovernance.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%85%a4%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%b3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%81%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%8d%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%81%b7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%a3john" target="_blank">선릉안마
</a>
</p>
사막이 아름다운 것은 어딘가에 샘이 숨겨져 있기 때문이다 - 생떽쥐베리
<p align="">
<a title="역삼안마" href="
https://nebraska.aiga.org/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%96%92%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%86%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%88%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%95%80%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ef%bd%87goes" target="_blank">역삼안마
</a>
</p>
</div>
<div style='width: 1px; height: 1px; overflow: hidden'><div align='center'>
<img name='target_resize_image[]' onclick='image_window(this)' style='cursor:pointer;' alt="" class="view_photo up" src="http://file.osen.co.kr/article/2019/05/01/201905011854774508_5cc96e7d1d3c2.jpg" >
그라운드 뷰는 차의 앞쪽 아랫부분
<div style="position:absolute; left:-9999px; top:-9999px;" class="sound_only">
피할수 없으면 즐겨라 - 로버트 엘리엇
<p align="">
<a title="강남오피" href="
http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%83%b1%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a4%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%a7%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%aa%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%a4forward" target="_blank">강남오피
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="선릉오피" href="
http://www.ambrosiocinema.it/page/5/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%83%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%a8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%b8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%bf%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ef%bc%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%96%bc%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%86spring" target="_blank">선릉오피
</a>
</p>
아래에 비교하면 남음이 있다.-명심보감
<p align="">
<a title="역삼오피" href="
https://www.openrice.com/zh/hongkong/restaurants?what=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%99%a5%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a0both" target="_blank">역삼오피
</a>
</p>
실패는 잊어라 그러나 그것이 준 교훈은절대 잊으면 안된다-하버트 개서
<p align="">
<a title="강남휴게텔" href="
https://desk.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%88%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%88%99%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%85%b4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%82%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%81boat" target="_blank">강남휴게텔
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉휴게텔" href="http://www.blueskyspaworks.com/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%c2%bc%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%91%ad%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%95%89%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%bb%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%92%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%ef%bc%84damage" target="_blank">선릉휴게텔
</a>
</p>
절대 포기하지 말라. 당신이 되고 싶은 무언가가 있다면그에 대해 자부심을 가져라. 당신 자신에게 기회를 주어라. 스스로가 형편없다고 생각하지 말라.그래봐야 아무 것도 얻을 것이 없다. 목표를 높이 세워라.인생은 그렇게 살아야 한다.-마이크 맥라렌
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%80%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%92%b2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%92%a4%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bf%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%8e%97sworn" target="_blank">역삼휴게텔
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="강남안마" href="
https://www.wfs-dreieich.de/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%d0%93%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%97%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%88%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%a3%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%a4%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%84blame" target="_blank">강남안마
</a>
</p>
계단을 밟아야 계단 위에 올라설수 있다 -터키속담
<p align="">
<a title="선릉안마" href="
http://ypsistudio.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%82%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c4%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ef%bc%b0%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bf%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%cf%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%91%a4contain" target="_blank">선릉안마
</a>
</p>
지금이야 말로 일할때다. 지금이야말로 싸울때다. 지금이야말로 나를 더 훌륭한 사람으로 만들때다오늘 그것을 못하면 내일 그것을 할수있는가- 토마스 아켐피스
<p align="">
<a title="역삼안마" href="
https://www.matematikk.org/trinn8-10/sok/index.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%81%af%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bc%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%98%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%b3%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%b4understand" target="_blank">역삼안마
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남오피" href="
https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%86%90%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%85%b5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ef%bc%a8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c5%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8f%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%80bred" target="_blank">강남오피
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="선릉오피" href="
https://www.pexels.com/ko-kr/search/%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ef%bd%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%b9%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%83%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%8f%9cshelter" target="_blank">선릉오피
</a>
</p>
단순하게 살라. 쓸데없는 절차와 일 때문에 얼마나 복잡한 삶을 살아가는가?-이드리스 샤흐
<p align="">
<a title="역삼오피" href="
https://ciscentraltexas.org/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%ae%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b2%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8f%87%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%8a%83%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%97%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%92philadelphia" target="_blank">역삼오피
</a>
</p>
직접 눈으로 본 일도 오히려 참인지 아닌지염려스러운데 더구나 등뒤에서 남이 말하는것이야 어찌 이것을 깊이 믿을 수 있으랴?-명심보감-
<p align="">
<a title="강남휴게텔" href="
http://www.kuenselonline.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ce%a8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%9c%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%86%96%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%b2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bd%90%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%87quickly" target="_blank">강남휴게텔
</a>
</p>
내가 헛되이 보낸 오늘은 어제 죽어간 이들이그토록 바라던 하루이다 단 하루면 인간적인 모든 것을 멸망시킬수도 다시 소생시킬수도 있다-소포클레스
<p align="">
<a title="선릉휴게텔" href="https://www.sony.com/electronics/support/results?query=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%86%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%81%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ce%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%bd%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bc%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9bboat" target="_blank">선릉휴게텔
</a>
</p>
돈이란 바닷물과도 같다. 그것은 마시면 마실수록 목이 말라진다.-쇼펜하우어
<p align="">
<a title="역삼휴게텔" href="
https://jobs.rbc.com/ca/en/search-results?keywords=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%8c%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%d0%9e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%82%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%a6%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%c5%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%82joke" target="_blank">역삼휴게텔
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남안마" href="
http://www.makinamekawa.com/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%91%a9%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%d0%96%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bc%a2%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%92dreaming" target="_blank">강남안마
</a>
</p>
진정으로 웃으려면 고통을 참아야하며 나아가 고통을 즐길 줄 알아야 해 -찰리 채플린
<p align="">
<a title="선릉안마" href="
https://www.reddit.com/search?q=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%ac%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%9b%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%92%a5%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%a7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%99%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%a7grant" target="_blank">선릉안마
</a>
</p>
한번의 실패와 영원한 실패를 혼동하지 마라 -F.스콧 핏제랄드
<p align="">
<a title="역삼안마" href="
https://desk.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%95%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%9e%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ce%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%b5%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%85%b9%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%d1%89%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%93goal" target="_blank">역삼안마
</a>
</p>
행복은 결코 많고 큰데만 있는 것이 아니다 작은 것을 가지고도 고마워 하고 만족할 줄 안다면그는 행복한 사람이다여백과 공간의 아름다움은 단순함과 간소함에 있다법정스님 - 홀로사는 즐거움 에서
<p align="">
<a title="강남오피" href="
http://www.alberguerioaragon.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%bd%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%a6%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%87%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%80%b3%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%85%a5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%93%98%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%81seem" target="_blank">강남오피
</a>
</p>
길을 잃는 다는 것은 곧 길을 알게 된다는 것이다. - 동아프리카속담
<p align="">
<a title="선릉오피" href="
https://www.isistassinari.gov.it/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%8e%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%ce%b7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%89%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ce%95%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%95%88awhile" target="_blank">선릉오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="역삼오피" href="
http://isb.az/ru/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%89%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%d1%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%93%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%8cindependent" target="_blank">역삼오피
</a>
</p>
자신을 내보여라. 그러면 재능이 드러날 것이다.- 발타사르 그라시안
<p align="">
<a title="강남휴게텔" href="
http://biz.heraldcorp.com/view.php?ud=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%b2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bd%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%ef%bc%95%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%89%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%bbmarks" target="_blank">강남휴게텔
</a>
</p>
화가 날 때는 100까지 세라. 최악일 때는 욕설을 퍼부어라. -마크 트웨인
<p align="">
<a title="선릉휴게텔" href="
https://www.americanas.com.br/busca?conteudo=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ef%bc%b0%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%84%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%9a%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%81%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%8e%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%a8portrait" target="_blank">선릉휴게텔
</a>
</p>
1퍼센트의 가능성 그것이 나의 길이다-나폴레옹
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%83%99%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8f%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%83%95%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%d0%af%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b9personal" target="_blank">역삼휴게텔
</a>
</p>
최고에 도달하려면 최저에서 시작하라.-P.시루스
<p align="">
<a title="강남안마" href="
http://jozankei.jp/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%92%9f%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%81%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%c3%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%88%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%84%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%96%a6%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b6parted" target="_blank">강남안마
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉안마" href="
http://www.somoseducacao.com.br/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%98%85%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%be%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%9a%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%a1%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%a5greatly" target="_blank">선릉안마
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="역삼안마" href="
https://riftio.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%8e%80%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bd%99%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%99%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%8a%83%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%9d%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%a6%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%84%b9had" target="_blank">역삼안마 ( •́ ̯•̀ )
</a>
</p>
http://jiral.net/an9/38489
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=936312
http://myrechockey.com/forums/index.php?topic=119914.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/371356
http://miquirofisico.com/?option=com_k2&view=itemlist&task=user&id=4519
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=242851
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1753533
http://sejong-thesharpyemizi.co.kr/m1/33458
http://universalcommunity.se/Forum/index.php?topic=32018.0
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=407472
http://www.capital-investment.pl/index.php/component/k2/itemlist/user/223895
https://www.lwfservers.com/index.php?topic=72404.0
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=225398
http://www.livetank.cn/market1/286416
http://isch.kr/board_PowH60/157242
http://gusinoepero.ru/archives/25813
http://themasters.pro/file_01/273605
http://engeena.com/component/k2/itemlist/user/9139
http://hyeonjun.co.kr/menu3/287512
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=279942
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=91821
http://herdental.co.kr/index.php?mid=online&document_srl=114031
http://0433.net/junggo/115816
https://reficulcoin.com/index.php?topic=83019.0
http://engeena.com/component/k2/itemlist/user/9195
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=652496
http://divespace.co.kr/board/237449
http://daltso.com/index.php?mid=board_cUYy21&document_srl=141526
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zpiw-%d1%80%d0%b0%d1%81/
http://www.livetank.cn/market1/262359
http://music.start-a-idea.online/blogs/viewstory/48639
http://daesestudy.co.kr/ipsi_docu/141085
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/62170
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=259497
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=665698
http://beautypouch.net/index.php?mid=board_09&document_srl=158977
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3902603
http://erhu.eu/viewtopic.php?f=7&t=393238
https://nple.com/xe/pds/150853
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1982901
http://herdental.co.kr/index.php?mid=online&document_srl=113519
http://necinsurance.co.zw/component/k2/itemlist/user/21644.html
http://mglpcm.org/board_ETkS12/130176
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=301217
http://bobr.site/index.php?topic=178281.0
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/?document_srl=75805
http://forum.bmw-e60.eu/index.php?topic=11446.0
http://www.livetank.cn/market1/286573
http://gallerychoi.com/Exhibition/443177
http://divespace.co.kr/board/180853
http://hyeonjun.co.kr/menu3/346060
http://bobr.site/index.php?topic=183996.0
https://www.limscave.com/forum/viewtopic.php?t=58925
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=293099
http://www.jesusandmarypatna.com/index.php/component/k2/itemlist/user/3543011
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=113230
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=105819
http://jdcalc.com/forum/viewtopic.php?t=294207
http://legride.com/UserProfile/tabid/61/userId/2856205/Default.aspx
http://melchinooddle.dothome.co.kr/?document_srl=15012
http://universalcommunity.se/Forum/index.php?topic=34505.0
http://research.kiu.ac.kr/index.php?document_srl=416652&mid=Food4Thought
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=127267
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=199892
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/147721
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/147762
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=90550
https://adsensebih.com/index.php?topic=50569.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=385865
http://dessa.com.br/component/k2/itemlist/user/385855
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7514551
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7514580
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=206199
http://www.golden-nail.co.kr/?document_srl=431417
http://gochon-iusell.co.kr/g1/97936
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=407040
http://roikjer.com/forum/index.php?PHPSESSID=ammr1sn9v5ues6adoj4ve2e3s5&topic=932193.0
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/97623
http://zakdu.com/board_YpzS56/15219
https://timecker.com/anonymous/188760
http://toeden.co.kr/Product_new/142510
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2855597
http://mglpcm.org/board_ETkS12/163245
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3545639
http://mediaville.me/index.php/component/k2/itemlist/user/332755
http://www.leekeonsu-csi.com/?document_srl=934545
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=17337
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1169439
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=388386
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=17341
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1998685
http://rfc11th13th.dothome.co.kr/Board5/35021
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=90550
https://adsensebih.com/index.php?topic=51073.0
https://cybergsm.es/index.php?topic=72514.0
https://www.c-alice.org/forum/index.php?topic=98714.0
https://www.c-alice.org/forum/index.php?topic=98715.0
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gw0%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://photogrotto.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ur0%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5/
http://photogrotto.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yq0%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5/
http://dcasociados.eu/component/k2/itemlist/user/94404
http://dcasociados.eu/component/k2/itemlist/user/94417
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16595
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16610
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=113174
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zepm-%d1%80%d0%b0%d1%81/
http://erhu.eu/viewtopic.php?t=395610
http://robocit.com/index.php/component/k2/itemlist/user/449881
http://hanga5.com/index.php?mid=board_photo&document_srl=110685
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1285723
http://vtservices85.fr/smf2/index.php?PHPSESSID=acd364bfc954b4b91aa236232852a449&topic=289708.0
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=119899
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/60909
http://mercibq.net/partner/55808
http://askpharm.net/board_NQiz06/159919
https://intelogist2.wpengine.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jrfb-%d1%80%d0%b0%d1%81/
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/67012
http://ko.myds.me/board_story/247568
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=105946
http://beautypouch.net/index.php?mid=board_09&document_srl=109602
http://engeena.com/component/k2/itemlist/user/9207
http://0433.net/junggo/131583
http://apt2you2.cafe24.com/g1/35776
http://viamania.net/index.php?mid=board_raYV15&document_srl=138585
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1976009
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=285968
http://forum.elexlabs.com/index.php?topic=62671.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=deb03d8102b294d0db55a58851cc7d51&topic=11294.0
http://socialmag.bayareanonprofits.xyz/blogs/viewstory/127087
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=664947
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3452300
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=229018
http://autospa.lv/index.php/lv/component/k2/itemlist/user/10531
https://2002.shyoon.com/board_2002/170986
http://jdcalc.com/forum/viewtopic.php?t=293623
http://juroweb.com/xe/juroweb_board/122190
http://otitismediasociety.org/forum/index.php?topic=209099.0
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=228259
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=93782
http://ko.myds.me/board_story/263491
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=76068
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/56120
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=410420
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=17858
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=553774
http://music.start-a-idea.online/blogs/viewstory/44466
http://carand.co.kr/d2/87789
http://carand.co.kr/d2/87822
http://carand.co.kr/d2/87832
http://carand.co.kr/d2/87843
http://cwon.kr/xe/board_bnSr36/283284
http://cwon.kr/xe/board_bnSr36/283304
http://cwon.kr/xe/board_bnSr36/283332
http://daltso.com/index.php?mid=board_cUYy21&document_srl=191900
http://daltso.com/index.php?mid=board_cUYy21&document_srl=191981
http://ye-dream.com/qa/236998
http://xn----3x5er9r48j7wemud0a387h.com/news/187550
http://socialmag.bayareanonprofits.xyz/blogs/viewstory/131174
http://kyj1225.godohosting.com/board_mebR72/66466
https://adsensebih.com/index.php?topic=47915.0
http://www.svteck.co.kr/customer_gratitude/224325
http://bobr.site/index.php?topic=184643.0
http://roikjer.com/forum/index.php?PHPSESSID=h2iapkmv1f92nba2es9lmjot82&topic=935193.0
http://withinfp.sakura.ne.jp/eso/index.php/17568310-rasskaz-sluzanki-3-sezon-11-seria-ccly-rasskaz-sluzanki-3-sezon/0
http://yoriyorifood.com/xxxx/spacial/289342
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=78873
http://melchinooddle.dothome.co.kr/?document_srl=14859
http://carand.co.kr/d2/49633
https://zakdu.com/?document_srl=22888
https://gonggamlaw.com/lawcase/69844
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=89233
http://www.popolsku.fr.pl/forum/index.php?topic=20407.79845
http://xn--hu1bs8ufrd6ucyz0aooa.kr/?document_srl=43052
http://w9builders.co.uk/index.php/component/k2/itemlist/user/124123
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3781461
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=947742
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/346037
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/66109
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=16837
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42980
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39563
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39566
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39567
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39571
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39572
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39573
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39577
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39578
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39580
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39589
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39590
http://myrechockey.com/forums/index.php?topic=119376.0
http://beautypouch.net/index.php?mid=board_09&document_srl=111200
http://hanga5.com/index.php?mid=board_photo&document_srl=114650
http://loverstory.co.kr/?document_srl=45315
http://vtservices85.fr/smf2/index.php?PHPSESSID=8e0876d5c850770d46c7572db9b8b771&topic=289803.0
http://bobr.site/index.php?topic=185831.0
https://www.regalepadova.it/?option=com_k2&view=itemlist&task=user&id=8272
http://melchinooddle.dothome.co.kr/?document_srl=15405
http://zakdu.com/board_YpzS56/29252
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/392248
http://yadanarbonnews.com/?option=com_k2&view=itemlist&task=user&id=350574
http://bewasia.com/?document_srl=213896
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=213871
http://carand.co.kr/d2/95354
http://carand.co.kr/d2/95377
http://sfah.ch/de/component/k2/itemlist/user/15443
http://sfah.ch/de/component/k2/itemlist/user/15444
http://sfah.ch/de/component/k2/itemlist/user/15445
http://sfah.ch/de/component/k2/itemlist/user/15448
http://sfah.ch/de/component/k2/itemlist/user/15449
http://sfah.ch/de/component/k2/itemlist/user/15453
http://sfah.ch/de/component/k2/itemlist/user/15454
http://sfah.ch/de/component/k2/itemlist/user/15457
http://sfah.ch/de/component/k2/itemlist/user/15458
http://sfah.ch/de/component/k2/itemlist/user/15461
http://lucky.kidspann.net/index.php?mid=qna&document_srl=289521
http://153.120.114.241/eso/index.php/17576827-rasskaz-sluzanki-3-sezon-4-seria-qffi-rasskaz-sluzanki-3-sezon-
http://dayung.co.kr/board_SRVC17/69885
http://www.lgue.co.kr/?document_srl=116105
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=192889
http://universalcommunity.se/Forum/index.php?topic=35311.0
http://gochon-iusell.co.kr/g1/77603
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=194774
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=198235
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=128955
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=302169
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/820720
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/820913
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/821192
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/821793
http://mvisage.sk/index.php/component/k2/itemlist/user/119720
http://necinsurance.co.zw/?option=com_k2&view=itemlist&task=user&id=21636
http://necinsurance.co.zw/?option=com_k2&view=itemlist&task=user&id=21681
http://necinsurance.co.zw/component/k2/itemlist/user/21629.html
http://necinsurance.co.zw/component/k2/itemlist/user/21630.html
http://necinsurance.co.zw/component/k2/itemlist/user/21641.html
http://ye-dream.com/qa/234883
http://neosky.net/xe/space_station/66026
https://zakdu.com/?document_srl=23164
http://tiretech.co.kr/index.php?mid=qna&document_srl=246299
http://gusinoepero.ru/archives/26172
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=166293
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/36655
http://xn--2e0bk61btjo.com/notice/27186
http://isch.kr/board_PowH60/229167
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=42b90aa637595f30ead3c8d17a12099a&topic=11289.0
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/331426
http://proxima.co.rw/index.php/component/k2/itemlist/user/714313
http://rudraautomation.com/index.php/component/k2/author/340286
http://smartacity.com/component/k2/itemlist/user/92723
http://smartacity.com/index.php/component/k2/itemlist/user/93108
http://thermoplast.envolgroupe.com/component/k2/author/176024
http://thermoplast.envolgroupe.com/component/k2/author/176121
http://w9builders.co.uk/index.php/component/k2/itemlist/user/127323
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=40806
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=41164
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=41671
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=41770
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=41820
https://nple.com/xe/pds/220741
https://intelogist2.wpengine.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-eldx-%d1%80%d0%b0%d1%81/
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2605682
https://www.hwbms.com/web/qna/12007
https://intelogist2.wpengine.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dbjf-%d1%80%d0%b0%d1%81/
http://benzmall.co.kr/index.php?mid=download&document_srl=89094
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=56220
http://lucky.kidspann.net/index.php?mid=qna&document_srl=291983
http://www.leekeonsu-csi.com/?document_srl=933073
http://jdcalc.com/forum/viewtopic.php?t=288809
http://gochon-iusell.co.kr/g1/75011
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=187151
http://gardenpjw.dothome.co.kr/board_LOcC77/708143
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=80840
http://zakdu.com/board_ssKi56/20140
http://ko.myds.me/board_story/245879
http://xn--2e0b53df5ag1c804aphl.net/nuguna/103886
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/?document_srl=64296
http://test.comics-game.ru/index.php?topic=563.0
http://www.sp1.football/index.php?mid=faq&document_srl=692934
http://divespace.co.kr/board/233952
http://8.droror.co.il/uncategorized/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ygkd-%d1%80%d0%b0%d1%81/
http://lucky.kidspann.net/index.php?mid=qna&document_srl=289951
http://lucky.kidspann.net/index.php?mid=qna&document_srl=290037
http://lucky.kidspann.net/index.php?mid=qna&document_srl=290071
http://lucky.kidspann.net/index.php?mid=qna&document_srl=290075
http://lucky.kidspann.net/index.php?mid=qna&document_srl=290080
http://lucky.kidspann.net/index.php?mid=qna&document_srl=290109
http://lucky.kidspann.net/index.php?mid=qna&document_srl=290243
https://reficulcoin.com/index.php?topic=85900.0
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/57278
http://isch.kr/board_PowH60/198930
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4903146
http://vtservices85.fr/smf2/index.php?PHPSESSID=695dda2274cb6487bab30c96002aae69&topic=290775.0
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/90329
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=189553
http://www.ekemoon.com/244369/051120193428/
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=190147
http://juroweb.com/xe/juroweb_board/84884
https://www.limscave.com/forum/viewtopic.php?t=63003
http://goldenpowerball2.com/?document_srl=427009
http://www.arunagreen.com/index.php/component/k2/itemlist/user/1153838
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99781
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1286420
http://guiadetudo.com/index.php/component/k2/itemlist/user/12714
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=271758
http://www.alase.net/index.php/component/k2/itemlist/user/12716
http://daesestudy.co.kr/ipsi_docu/122375
http://blog.ptpintcast.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fidl-%d1%80%d0%b0%d1%81/
http://sy.korean.net/qna/313676
http://jnk-ent.jp/index.php?mid=gallery&document_srl=334833
http://callman.co.kr/index.php?mid=qa&document_srl=222949
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=78669
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=80515
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=80525
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=80537
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=80546
http://muldorang.com/market/27213
http://zakdu.com/board_ssKi56/19302
http://withinfp.sakura.ne.jp/eso/index.php/17530097-rasskaz-sluzanki-3-sezon-5-seria-lbkg-rasskaz-sluzanki-3-sezon-/0
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=139105
http://married.dike.gr/index.php/component/k2/itemlist/user/78338
https://nple.com/xe/pds/151915
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=292671
http://isch.kr/board_PowH60/156138
http://vervetama.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jwew-%d1%80%d0%b0%d1%81/
http://khapthanam.co.kr/g1/148810
http://toeden.co.kr/Product_new/141049
http://herdental.co.kr/index.php?mid=online&document_srl=114673
http://socialmag.bayareanonprofits.xyz/blogs/viewstory/126778
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=94535
http://warmfund.net/p/index.php?mid=financing&document_srl=478632
http://warmfund.net/p/index.php?mid=financing&document_srl=478647
http://warmfund.net/p/index.php?mid=financing&document_srl=478656
http://warmfund.net/p/index.php?mid=financing&document_srl=478685
http://warmfund.net/p/index.php?mid=financing&document_srl=478690
http://warmfund.net/p/index.php?mid=financing&document_srl=478748
http://azone.synology.me/xe/index.php?mid=board_SDnQ73&document_srl=217816
http://dayung.co.kr/board_SRVC17/68723
http://backo.co.kr/board_aiQk58/15882
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7481193
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=914974
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/90738
http://www.svteck.co.kr/customer_gratitude/219956
http://tiretech.co.kr/index.php?mid=qna&document_srl=187562
http://apt2you2.cafe24.com/g1/34834
http://myrechockey.com/forums/index.php?topic=118842.0
https://nple.com/xe/pds/157623
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=416369
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/56145
http://www.vamoscontigo.org/Noticia/138913
http://sy.korean.net/qna/311131
http://isch.kr/board_PowH60/157312
http://myrechockey.com/forums/index.php?topic=117990.0
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3400456
http://www.popolsku.fr.pl/forum/index.php?topic=417048.0
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=33572
http://looksun.co.kr/index.php?mid=board_4&document_srl=151549
http://www.coating.or.kr/atemfair_data/15699
http://www.livetank.cn/market1/238930
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3899120
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=113180
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=33706
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=34100
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=35277
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=37260
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=37516
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=37581
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=39195
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=42138
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=44302
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=44829
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=45230
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=46425
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=46957
http://xn--2e0bk61btjo.com/notice/22185
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/?document_srl=70022
http://ko.myds.me/board_story/258154
https://gonggamlaw.com/lawcase/77594
http://sofficer.net/xe/teach/285835
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4897041
http://erhu.eu/viewtopic.php?t=400349
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=52852
http://kwpub.kr/PUBS/130805
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=138892
http://rudraautomation.com/index.php/component/k2/author/291808
https://gonggamlaw.com/lawcase/67645
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=233402
https://www.shaiyax.com/index.php?topic=408273.0
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=340192
http://rabat.kr/board_yCgT00/38143
https://www.2ayes.com/19543/3-6-jpxn-3-6-alexfilm
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=104981
http://divespace.co.kr/board/180898
http://isch.kr/board_PowH60/225238
http://warmfund.net/p/index.php?mid=financing&document_srl=564102
http://www.cnsmaker.net/xe/?document_srl=150673
http://www.coating.or.kr/atemfair_data/18359
http://www.cyberblissstudios.com/UserProfile/tabid/42/UserID/2341098/Default.aspx
http://www.eunhaele.co.kr/xe/board/20468
http://www.jesusonly.life/calendar/583307
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=43243
http://kockazatkutato.hu/component/k2/itemlist/user/43052
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229533
http://www.dpusm.org/index.php/component/k2/itemlist/user/1134057
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5056704
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=22561
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fl5c-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81/
http://photogrotto.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xv2u-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-18/
http://udrpsucks.com/blog/?p=1766
http://www.ekemoon.com/245113/052220191128/
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16602
http://dospuntoseventos.cl/component/k2/itemlist/user/16583
http://kyj1225.godohosting.com/board_mebR72/101613
http://kyj1225.godohosting.com/board_mebR72/101647
http://kyj1225.godohosting.com/board_mebR72/101652
http://kyj1225.godohosting.com/board_mebR72/101667
http://kyj1225.godohosting.com/board_mebR72/101672
http://kyj1225.godohosting.com/board_mebR72/101682
http://looksun.co.kr/index.php?mid=board_4&document_srl=195452
http://looksun.co.kr/index.php?mid=board_4&document_srl=195476
http://looksun.co.kr/index.php?mid=board_4&document_srl=195495
http://midorijapaneserestaurant.ca/menu/News/57197
https://www.celekt.com/%d0%9a%d0%be%d0%bf-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ko8%d0%9a%d0%be%d0%bf-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f28-05-2019/
http://alastair030.dothome.co.kr/index.php?mid=board_MMiF30&document_srl=27727
http://mtuan93.com/board_uCqR85/6364
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ubiq-%d1%80%d0%b0%d1%81/
http://www.cnsmaker.net/xe/?document_srl=150912
http://www.coating.or.kr/atemfair_data/18403
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=59700
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=750866
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=167692
http://www.kwpcoop.or.kr/QnA/22570
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1087171
http://www.lgue.co.kr/?document_srl=179178
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fj2n-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kc5f-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21/
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16837
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16847
http://dospuntoseventos.cl/component/k2/itemlist/user/16844
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=43575
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/842555
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229879
http://www.jesusandmarypatna.com/index.php/component/k2/itemlist/user/3568735
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5057955
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=22614
https://www.hohoyoga.com/testboard/4068422
https://www.hohoyoga.com/testboard/4068451
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2795184
http://dessa.com.br/component/k2/itemlist/user/390772
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2006003
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2006526
http://x-crew.center/guest/4845576
http://x-crew.center/guest/4846500
http://x-crew.center/guest/4846524
http://x-crew.center/guest/4846556
http://x-crew.center/guest/4846585
http://x-crew.center/guest/4846607
http://x-crew.center/guest/4846616
http://x-crew.center/guest/4846626
http://x-crew.center/guest/4846640
http://x-crew.center/guest/4846669
http://x-crew.center/guest/4846694
http://x-crew.center/guest/4846709
http://x-crew.center/guest/4846743
http://x-crew.center/guest/4846767
http://gochon-iusell.co.kr/g1/84891
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/49609
http://www.theocraticamerica.org/forum/index.php?topic=75521.0
https://gonggamlaw.com/lawcase/119762
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=650573
http://married.dike.gr/index.php/component/k2/itemlist/user/78511
https://intelogist2.wpengine.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wvji-%d1%80%d0%b0%d1%81/
http://daltso.com/index.php?mid=board_cUYy21&document_srl=201021
http://kyj1225.godohosting.com/board_mebR72/97670
https://betshin.com/Story/199938
https://gonggamlaw.com/lawcase/132833
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=17220
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=44210
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=851234
http://dcasociados.eu/component/k2/itemlist/user/94576
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=387905
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=388052
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=388090
http://yooseok.com/board_BkvT46/411838
http://yooseok.com/board_BkvT46/411842
http://yooseok.com/board_BkvT46/411910
http://yooseok.com/board_BkvT46/412075
http://yooseok.com/board_BkvT46/412089
http://yooseok.com/board_BkvT46/412112
http://yooseok.com/board_BkvT46/412196
http://yooseok.com/board_BkvT46/412206
http://yooseok.com/board_BkvT46/412211
http://yooseok.com/board_BkvT46/412215
http://yooseok.com/board_BkvT46/412308
http://yooseok.com/board_BkvT46/412325
http://yooseok.com/board_BkvT46/412341
http://gusinoepero.ru/archives/26111
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=36734
http://www.vamoscontigo.org/Noticia/178000
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/?document_srl=51042
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39627
http://archeaudio.com/xe/board_AOYj82/11038
https://reficulcoin.com/index.php?topic=93650.0
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/52181
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=93105
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=92677
http://otitismediasociety.org/forum/index.php?topic=209331.0
http://mediaville.me/index.php/component/k2/itemlist/user/331621
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=114151
http://www.telcon.gr/index.php/component/k2/itemlist/user/114210
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/392658
https://sto54.ru/index.php/component/k2/itemlist/user/3485056
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=36419
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=214705
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=214728
http://carand.co.kr/d2/95684
http://carand.co.kr/d2/95691
http://carand.co.kr/d2/95701
http://cwon.kr/xe/board_bnSr36/297156
http://cwon.kr/xe/board_bnSr36/297195
https://timecker.com/anonymous/187784
https://timecker.com/anonymous/187818
https://timecker.com/anonymous/187921
https://timecker.com/anonymous/187938
https://timecker.com/anonymous/187944
https://timecker.com/anonymous/187955
https://timecker.com/anonymous/187967
https://timecker.com/anonymous/187971
http://autospa.lv/index.php/lv/component/k2/itemlist/user/10599
http://yoriyorifood.com/xxxx/spacial/274809
http://bebopindia.com/notcie/394291
https://mcsetup.tk/bbs/index.php?topic=261996.0
http://wigalseguros.com.br/component/users/?task=user&view=itemlist&id=23065
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=417366
https://forums.lfstats.com/viewtopic.php?t=317890
http://rabbitzone.xyz/FREE/111994
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/347448
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/347452
https://sto54.ru/index.php/component/k2/itemlist/user/3480864
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=17117
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=35884
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/35886
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=207948
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=207966
http://carand.co.kr/d2/91308
https://www.2ayes.com/19559/3-9-igpj-3-9-hbo
https://www.2ayes.com/19560/3-10-xvbz-3-10
https://www.2ayes.com/19561/3-3-bako-3-3-baibako
https://www.2ayes.com/19562/3-2-acru-3-2-newstudio
https://www.2ayes.com/19563/3-7-ppmz-3-7
https://www.2ayes.com/19565/3-8-mhla-3-8-nbc
https://www.2ayes.com/19566/3-10-jfei-3-10-hulu
https://www.2ayes.com/19570/3-5-zweh-3-5-amedia
https://www.2ayes.com/19609/3-3-kbtg-3-3-abc
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=127312
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7483986
http://yooseok.com/board_BkvT46/412790
http://www.vogtland.com.pl/index.php/component/k2/itemlist/user/50335
http://www.theocraticamerica.org/forum/index.php?topic=70415.0
https://www.hwbms.com/web/qna/24230
https://www.hwbms.com/web/qna/24244
https://www.hwbms.com/web/qna/24248
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16914
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=43649
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229957
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=850359
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2827637
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=90550
http://www.teedinubon.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qr6%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f29-05/
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=109704
http://www2.yasothon.go.th/smf/index.php?topic=159.msg200597
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=90550
https://intelogist2.wpengine.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qrzs-%d1%80%d0%b0%d1%81/
http://www.eunhaele.co.kr/xe/QnA/20727
http://roikjer.com/forum/index.php?PHPSESSID=tavu75ob4lcv4vaa2jbr4jcnk7&topic=935677.0
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=ccd531db3473b50f84df9e5c949cf591&topic=11284.0
http://forum.elexlabs.com/index.php?topic=67007.0
http://muldorang.com/market/27354
http://khapthanam.co.kr/g1/135222
https://www.hwbms.com/web/qna/17232
http://askpharm.net/board_NQiz06/231884
http://constellation.kro.kr/board_kbku73/66311
http://vtservices85.fr/smf2/index.php?PHPSESSID=e4d8dbb138de17279bb16194a734dc21&topic=289693.0
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=42787
http://forum.bmw-e60.eu/index.php?topic=11345.0
http://sd-xi.co.kr/g1/70143
http://jnk-ent.jp/index.php?mid=gallery&document_srl=339065
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/812483
http://sfah.ch/de/component/k2/itemlist/user/15517
http://autospa.lv/index.php/component/k2/itemlist/user/10649
http://www.leekeonsu-csi.com/index.php?document_srl=911519&mid=community7
http://zakdu.com/board_YpzS56/23268
http://dreamplusart.com/mn03_01/226835
http://gallerychoi.com/Exhibition/534792
http://gochon-iusell.co.kr/g1/131561
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=222721
http://gusinoepero.ru/archives/32130
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2872050
http://holysweat.dothome.co.kr/data/8049
http://isch.kr/board_PowH60/267230
http://iymc.or.kr/pds/132278
http://mtuan93.com/board_uCqR85/6531
http://www2.yasothon.go.th/smf/index.php?topic=159.172335
http://loverstory.co.kr/board_UYNJ05/46608
http://jnk-ent.jp/index.php?mid=gallery&document_srl=318030
http://www.lgue.co.kr/?document_srl=124393
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=346031
http://divespace.co.kr/board/181179
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/84840
http://herdental.co.kr/index.php?mid=online&document_srl=142911
http://gochon-iusell.co.kr/g1/102847
http://hyeonjun.co.kr/menu3/307801
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=652793
http://www.lgue.co.kr/?document_srl=115938
http://www.venusjeju.com/?document_srl=1113
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/72020
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=387128
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=17877
https://intelogist2.wpengine.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xdif-%d1%80%d0%b0%d1%81/
http://callman.co.kr/index.php?mid=qa&document_srl=224156
https://altaylarteknoloji.com/index.php?topic=6598.0
http://dcasociados.eu/component/k2/itemlist/user/95107
http://mtuan93.com/board_uCqR85/6502
http://gspara01.dothome.co.kr/index.php?mid=board_XHsr53&document_srl=18180
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13805
http://ovotecegg.com/component/k2/itemlist/user/227099
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/49698
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=113980
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229872
https://blossomug.com/index.php/component/k2/itemlist/user/1112900
http://www.quattroandpartners.it/component/k2/itemlist/user/1214890
https://nple.com/xe/pds/235319
http://cwon.kr/xe/board_bnSr36/314028
http://askpharm.net/board_NQiz06/259258
http://toeden.co.kr/Product_new/139654
http://loverstory.co.kr/board_UYNJ05/103988
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=130401
http://midorijapaneserestaurant.ca/menu/News/26924
http://dreamplusart.com/?document_srl=229454
http://khapthanam.co.kr/g1/135123
http://toeden.co.kr/Product_new/139058
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/351216
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=116723
http://www.itosm.com/cn/board_nLoq17/135155
http://jiral.net/an9/27610
http://loverstory.co.kr/board_UYNJ05/103209
http://www.sp1.football/index.php?mid=faq&document_srl=723942
http://cwon.kr/xe/board_bnSr36/284086
http://gochon-iusell.co.kr/g1/104495
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=a27e686f3846c77cb6b5befa63aacf63&topic=10842.0
https://www.lwfservers.com/index.php?topic=74253.0
http://p9912.cafe24.com/board_LVgu51/73535
https://gonggamlaw.com/lawcase/150885
http://apt2you2.cafe24.com/g1/53938
http://naksansacondo.com/board_MGPu57/99485
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/59314
http://dessa.com.br/component/k2/itemlist/user/386155
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=190828
http://www.proandpro.it/?option=com_k2&view=itemlist&task=user&id=4718086
https://betshin.com/Story/206162
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=206092
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=319244
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2801889
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=422304
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=118080
http://herdental.co.kr/index.php?mid=online&document_srl=113725
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/35822
http://www.jesusonly.life/calendar/583307
http://carand.co.kr/d2/91595
http://www.popolsku.fr.pl/forum/index.php?topic=418147.0
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=58279
http://midorijapaneserestaurant.ca/menu/News/78019
http://masanlib.or.kr/g1/92797
https://forum.clubeicaro.pt/index.php?topic=2274.0
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=356675
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/349828
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=18844
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=842fb8e84c6ee9dff83da8ccfabebff3&topic=10933.0
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=209073
http://midorijapaneserestaurant.ca/menu/News/74946
http://xn----3x5er9r48j7wemud0a387h.com/news/165891
http://kyj1225.godohosting.com/board_mebR72/83009
http://bebopindia.com/notcie/389221
http://dcasociados.eu/component/k2/itemlist/user/94462
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=840672
https://gonggamlaw.com/lawcase/132927
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=13983
https://mcsetup.tk/bbs/index.php?topic=263135.0
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=194679
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=556823
http://www.hmotors.co.kr/inquiry/27021
http://cwon.kr/xe/board_bnSr36/313087
http://www.hmotors.co.kr/inquiry/73840
http://midorijapaneserestaurant.ca/menu/News/74771
http://dcasociados.eu/component/k2/itemlist/user/93339
http://yoriyorifood.com/xxxx/spacial/252725
https://intelogist2.wpengine.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ka0u-%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3/
http://divespace.co.kr/board/260977
http://married.dike.gr/index.php/component/k2/itemlist/user/78481
http://benzmall.co.kr/index.php?mid=download&document_srl=46131
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1738106
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=272985
http://sejong-thesharpyemizi.co.kr/m1/105259
https://www.2ayes.com/19660/3-11-fbww-3-11-fox
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=95598
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=242992
http://kyj1225.godohosting.com/board_mebR72/105876
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=18551
http://midorijapaneserestaurant.ca/menu/News/45453
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/36165
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1982548
http://yoriyorifood.com/xxxx/spacial/333420
http://gusinoepero.ru/archives/26162
http://kwpub.kr/PUBS/132317
http://sejong-thesharpyemizi.co.kr/m1/36688
http://smartacity.com/component/k2/itemlist/user/77576
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=86547
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=332555
http://kyj1225.godohosting.com/board_mebR72/94152
http://dev.aabn.org.gh/component/k2/itemlist/user/713895
http://kyj1225.godohosting.com/board_mebR72/98686
http://holysweat.dothome.co.kr/data/8049
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1533051
http://neosky.net/xe/space_station/152520
http://kwpub.kr/PUBS/130615
http://www.coating.or.kr/atemfair_data/12250
http://looksun.co.kr/index.php?mid=board_4&document_srl=125085
http://mediaville.me/index.php/component/k2/itemlist/user/371917
http://x-crew.center/guest/4846743
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/345643
http://daltso.com/index.php?mid=board_cUYy21&document_srl=171264
http://www.kspace.cc/xe/?document_srl=154748
http://iymc.or.kr/pds/125607
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=228892
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-poeq-%d1%80%d0%b0%d1%81/
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=31389
http://loverstory.co.kr/board_UYNJ05/114547
http://myesl.ca/forum/viewtopic.php?t=694871
https://gonggamlaw.com/lawcase/145348
https://nextezone.com/index.php?topic=81357.0
http://proxima.co.rw/index.php/component/k2/itemlist/user/720712
http://midorijapaneserestaurant.ca/menu/News/53703
https://www.limscave.com/forum/viewtopic.php?t=60814
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=86745
http://looksun.co.kr/index.php?mid=board_4&document_srl=183042
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qddu-%d1%80%d0%b0%d1%81/
https://esel.gist.ac.kr/esel2/board_hmgj23/298019
http://w9builders.co.uk/index.php/component/k2/itemlist/user/125474
https://forum.shaiyaslayer.tk/index.php?topic=154768.0
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229943
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=185344
https://www.celekt.com/%d0%a0%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qhdk-%d0%a0%d0%b0%d1%81/
http://vervetama.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hgvu-%d1%80%d0%b0%d1%81/
http://apt2you2.cafe24.com/g1/52042
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=40209.0
http://cwon.kr/xe/board_bnSr36/290938
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/34238
http://gochon-iusell.co.kr/g1/76532
http://www.tessabannampad.go.th/webboard/index.php?topic=226645.0
http://mobility-corp.com/index.php/component/k2/itemlist/user/2737259
http://daltso.com/index.php?mid=board_cUYy21&document_srl=177143
http://lavaggio.com.vn/index.php/component/k2/itemlist/user/3923721
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=210173
http://kwpub.kr/PUBS/167112
https://betshin.com/Story/203218
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=22702
http://backo.co.kr/board_aiQk58/22116
http://naksansacondo.com/board_MGPu57/57698
http://herdental.co.kr/index.php?mid=online&document_srl=170425
http://naksansacondo.com/board_MGPu57/76013
http://cwon.kr/xe/board_bnSr36/285893
http://www.yadanarbonnews.com/index.php/component/k2/itemlist/user/348235
http://photogrotto.com/%d0%ba%d0%be%d0%bf-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ec3a-%d0%ba%d0%be%d0%bf-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=431827
http://kyj1225.godohosting.com/board_mebR72/101100
http://www.kwpcoop.or.kr/QnA/22957
http://www.ekemoon.com/245089/052220190028/
http://taklongclub.com/forum/index.php?topic=215030.0
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/111354
http://apt2you2.cafe24.com/?document_srl=52073
http://askpharm.net/board_NQiz06/254467
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=666080
http://barobus.kr/qna/75625
http://www.livetank.cn/market1/217585
http://yoriyorifood.com/xxxx/spacial/304611
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=112328
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=129556
http://beautypouch.net/index.php?mid=board_09&document_srl=183616
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=653094
http://gallerychoi.com/Exhibition/334470
http://2872870.com/est/62839
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2740887
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16702
http://smartacity.com/component/k2/itemlist/user/78402
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=478172
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1166504
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3491013
http://loverstory.co.kr/board_UYNJ05/96876
http://thermoplast.envolgroupe.com/component/k2/author/179638
http://www.vamoscontigo.org/Noticia/196445
http://k2.akademitelkom.ac.id/component/k2/itemlist/user/371942
https://betshin.com/Story/211210
https://www.hwbms.com/web/qna/39704
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=100289
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=17837
http://blog.ptpintcast.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-guze-%d1%80%d0%b0%d1%81/
http://loverstory.co.kr/board_UYNJ05/104184
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=41671
http://kyj1225.godohosting.com/board_mebR72/97395
http://www.coating.or.kr/atemfair_data/15392
http://loverstory.co.kr/board_UYNJ05/113020
http://forum.bmw-e60.eu/index.php?topic=10944.0
http://blog.ptpintcast.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-quqx-%d1%80%d0%b0%d1%81/
http://www.aloeverasas.it/index.php/component/k2/itemlist/user/21411
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=36768
http://esperanzazubieta.com/component/k2/itemlist/user/109449
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/855971
https://www.hwbms.com/web/qna/44713
http://masanlib.or.kr/g1/115999
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=49839
https://betshin.com/Story/193419
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/53425
http://www.ekemoon.com/247505/050520191430/
http://yooseok.com/board_BkvT46/412278
http://immobilia.gr/index.php/de/component/k2/itemlist/user/16786
http://hyeonjun.co.kr/menu3/408292
http://thermoplast.envolgroupe.com/component/k2/author/178998
https://altaylarteknoloji.com/index.php?topic=6687.0
http://askpharm.net/board_NQiz06/257946
http://www.quattroandpartners.it/component/k2/itemlist/user/1261234
http://universalcommunity.se/Forum/index.php?topic=32791.0
http://roikjer.com/forum/index.php?PHPSESSID=dqcbm0a1fe5md80s573d31jdp6&topic=931560.0
https://intelogist2.wpengine.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zq4u-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81/
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7516051
http://www.emrabq8.com/index.php/component/k2/itemlist/user/1865804
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=210584
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1997116
http://0433.net/budongsan/114107
https://timecker.com/anonymous/193152
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5058435
http://healthyteethpa.org/component/k2/itemlist/user/5549016
http://looksun.co.kr/index.php?mid=board_4&document_srl=196741
http://goldenpowerball2.com/?document_srl=344722
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1325889
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=439585
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=230705
http://loverstory.co.kr/?document_srl=107446
http://barobus.kr/qna/74480
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/102143
https://www.hwbms.com/web/qna/27445
http://hyeonjun.co.kr/menu3/287801
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16914
http://kyj1225.godohosting.com/board_mebR72/101574
http://looksun.co.kr/index.php?mid=board_4&document_srl=186990
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1937548
http://www.vamoscontigo.org/Noticia/204133
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=201859
http://hanga5.com/index.php?mid=board_photo&document_srl=135953
http://askpharm.net/board_NQiz06/283928
http://www.lustralesdevallehermoso.com/index.php/component/k2/itemlist/user/48650
http://lucky.kidspann.net/index.php?mid=qna&document_srl=458446
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=713111
http://yooseok.com/board_BkvT46/428618
http://daltso.com/index.php?mid=board_cUYy21&document_srl=196758
http://divespace.co.kr/board/277051
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/52170
http://hanga5.com/index.php?mid=board_photo&document_srl=112834
http://ariji.kr/?document_srl=1018904
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=221238
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=133796
http://www.vamoscontigo.org/Noticia/173146
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=43962
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=17294
http://daesestudy.co.kr/ipsi_docu/158047
http://esperanzazubieta.com/component/k2/itemlist/user/109057
https://nextezone.com/index.php?topic=77754.0
http://daesestudy.co.kr/ipsi_docu/120321
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/52862
http://roikjer.com/forum/index.php?PHPSESSID=tncsmeo9ucrslmaokj9p0au1n1&topic=934296.0
http://themasters.pro/file_01/227800
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7516649
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1544213
https://www.celekt.com/%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xr1%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5/
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=274409
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=93893
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=825837
https://www.hwbms.com/web/qna/23334
http://daltso.com/index.php?mid=board_cUYy21&document_srl=196034
http://jdcalc.com/forum/viewtopic.php?t=279575
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=397356
http://www.livetank.cn/market1/217705
http://forum.elexlabs.com/index.php?topic=62314.0
http://apt2you2.cafe24.com/g1/53948
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-il8r-%d0%ba%d0%be%d0%bf-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=227981
http://sunele.co.kr/board_ReBD97/167554
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5057742
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=663873
https://gonggamlaw.com/lawcase/131110
https://esel.gist.ac.kr/esel2/board_hmgj23/384621
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=140368
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7481081
http://udrpsucks.com/blog/?p=1914
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5059510
http://www.boutique.in.th/?option=com_k2&view=itemlist&task=user&id=153032
http://daesestudy.co.kr/ipsi_docu/118517
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/347145
http://midorijapaneserestaurant.ca/menu/?document_srl=76685
http://daesestudy.co.kr/?document_srl=157954
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cxvg-%d1%80%d0%b0%d1%81/
http://www.telcon.gr/index.php/component/k2/itemlist/user/117826
http://hanga5.com/index.php?mid=board_photo&document_srl=111244
http://www.yadanarbonnews.com/index.php/component/k2/itemlist/user/348686
http://cwon.kr/xe/board_bnSr36/292583
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/42590
http://www.livetank.cn/market1/215713
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3485408
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=299876
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=402752
http://rabat.kr/board_yCgT00/38211
http://sejong-thesharpyemizi.co.kr/m1/40444
http://www.hmotors.co.kr/inquiry/69762
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=90880
http://www.tessabannampad.go.th/webboard/index.php?topic=223543.0
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=29190
http://beautypouch.net/index.php?mid=board_09&document_srl=109232
http://sejong-thesharpyemizi.co.kr/m1/33283
https://serverpia.co.kr/board_ucCk10/145131
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=33227
http://naksansacondo.com/board_MGPu57/63050
http://www.itosm.com/cn/board_nLoq17/134147
http://midorijapaneserestaurant.ca/menu/News/79286
http://naksansacondo.com/board_MGPu57/105285
https://betshin.com/Story/222280
https://betshin.com/Story/222370
https://betshin.com/Story/222414
https://betshin.com/Story/222420
https://betshin.com/Story/222425
https://betshin.com/Story/222437
https://gonggamlaw.com/?document_srl=155297
https://gonggamlaw.com/lawcase/155361
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=23184
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=110001
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=50856
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/66721
https://nextezone.com/index.php?action=profile;u=17227
https://nextezone.com/index.php?action=profile;u=17252
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=27281
https://timecker.com/anonymous/210092
https://timecker.com/anonymous/210123
http://mvisage.sk/index.php/component/k2/itemlist/user/119895
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/59900
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=109726
http://cwon.kr/xe/board_bnSr36/292032
http://e-educ.net/Forum/index.php?topic=16732.0
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kt9d-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19/
http://carand.co.kr/d2/97314
https://www.celekt.com/%d0%a0%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-whag-%d0%a0%d0%b0%d1%81/
http://khapthanam.co.kr/g1/135181
http://looksun.co.kr/index.php?mid=board_4&document_srl=203801
http://gusinoepero.ru/archives/26160
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=118846
http://jnk-ent.jp/index.php?mid=gallery&document_srl=316718
http://loverstory.co.kr/board_UYNJ05/101850
http://cwon.kr/xe/board_bnSr36/289461
http://erhu.eu/viewtopic.php?t=394557
http://themasters.pro/file_01/328209
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=91282
https://www.hwbms.com/web/qna/23117
https://gonggamlaw.com/lawcase/134972
http://looksun.co.kr/index.php?mid=board_4&document_srl=204765
http://looksun.co.kr/index.php?mid=board_4&document_srl=186777
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=33391
http://proxima.co.rw/index.php/component/k2/itemlist/user/718806
http://khapthanam.co.kr/g1/135994
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=960118
http://zakdu.com/board_ssKi56/22736
http://cwon.kr/xe/board_bnSr36/287016
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4900907
https://turimex.mx.solemti.net/component/k2/itemlist/user/14224
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3866221
http://kyj1225.godohosting.com/board_mebR72/96610
http://dospuntoseventos.cl/component/k2/itemlist/user/16387
https://gonggamlaw.com/lawcase/127107
http://divespace.co.kr/board/278370
http://zakdu.com/board_ssKi56/20140
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3572716
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1741841
http://smartacity.com/component/k2/itemlist/user/91198
https://blossomug.com/index.php/component/k2/itemlist/user/1112215
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=392502
http://www.patrasin.kr/index.php?mid=questions&document_srl=4346884
http://esperanzazubieta.com/index.php/component/k2/itemlist/user/109157
http://dayung.co.kr/board_SRVC17/68940
http://dsyang.com/board_Kvgn62/46227
http://mglpcm.org/board_ETkS12/166291
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5060114
http://midorijapaneserestaurant.ca/menu/News/50672
https://www.2ayes.com/19667/3-5-gjwe-3-5-bbc
https://gonggamlaw.com/lawcase/147707
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/59732
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=414946
http://agiteshop.com/xe/qa/162372
http://www.patrasin.kr/index.php?mid=questions&document_srl=4348656
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=28446
http://viamania.net/index.php?mid=board_raYV15&document_srl=124479
http://www.cyberblissstudios.com/UserProfile/tabid/42/UserID/2326368/Default.aspx
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=393656
http://barobus.kr/qna/74299
http://midorijapaneserestaurant.ca/menu/News/48901
http://research.kiu.ac.kr/index.php?document_srl=317583&mid=Food4Thought
http://gallerychoi.com/Exhibition/334205
http://thermoplast.envolgroupe.com/component/k2/author/157344
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=304157
http://archeaudio.com/xe/board_AOYj82/17207
http://taklongclub.com/forum/index.php?topic=195094.0
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/841530
http://looksun.co.kr/index.php?mid=board_4&document_srl=125072
https://www.hwbms.com/web/qna/30567
http://rfc11th13th.dothome.co.kr/Board5/33382
http://www.ekemoon.com/245633/050320195129/
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=196113
http://bebopindia.com/notcie/389542
http://midorijapaneserestaurant.ca/menu/News/43952
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=388969
http://loverstory.co.kr/board_UYNJ05/109598
https://reficulcoin.com/index.php?topic=100286.0
http://www.lgue.co.kr/?document_srl=127670
http://rabat.kr/board_yCgT00/49122
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13797
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3482754
http://smartacity.com/component/k2/itemlist/user/92226
https://cybergsm.es/index.php?topic=61629.0
http://herdental.co.kr/index.php?mid=online&document_srl=114496
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=40138.0
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1723442
http://askpharm.net/board_NQiz06/251653
http://ko.myds.me/board_story/248681
http://leonwebzine.dothome.co.kr/guest/11209
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=38029
http://ovotecegg.com/index.php/component/k2/itemlist/user/228313
http://dreamplusart.com/mn03_01/237928
https://betshin.com/Story/215916
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=17815
http://www.hmotors.co.kr/inquiry/64344
http://dessa.com.br/component/k2/itemlist/user/390541
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2007334
https://www.hohoyoga.com/testboard/4075565
https://www.lwfservers.com/index.php?topic=71097.0
http://www.jesusandmarypatna.com/index.php/component/k2/itemlist/user/3570303
http://cwon.kr/xe/board_bnSr36/299195
https://www.hohoyoga.com/testboard/3970491
http://www.vamoscontigo.org/Noticia/220596
http://iymc.or.kr/pds/116153
http://roikjer.com/forum/index.php?PHPSESSID=8gjsro7dl4kp361hg6om48bno5&topic=936339.0
http://sd-xi.co.kr/g1/51382
http://mediaville.me/index.php/component/k2/itemlist/user/365956
http://www.lgue.co.kr/?document_srl=140258
http://www.sp1.football/index.php?mid=faq&document_srl=694453
http://www.hmotors.co.kr/?document_srl=69085
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=60565
http://p9912.cafe24.com/board_LVgu51/50222
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3938435
http://hanga5.com/index.php?mid=board_photo&document_srl=129076
http://www.proandpro.it/?option=com_k2&view=itemlist&task=user&id=4722760
http://www.firstfinancialservices.co.uk/?option=com_k2&view=itemlist&task=user&id=42139
http://themasters.pro/file_01/326245
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/98656
http://fbpharm.net/index.php/component/k2/itemlist/user/85799
http://kamiplus.kuron.jp/product/1089
https://gonggamlaw.com/lawcase/152560
http://benzmall.co.kr/index.php?mid=download&document_srl=47786
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=473735
https://forum.ac-jete.it/index.php?topic=448209.0
http://sy.korean.net/qna/463430
http://benzmall.co.kr/index.php?mid=download&document_srl=44623
http://benzmall.co.kr/index.php?mid=download&document_srl=116553
http://benzmall.co.kr/index.php?mid=download&document_srl=47803
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3478901
http://bobr.site/index.php?topic=184402.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=114993
http://www.itosm.com/cn/?document_srl=135905
http://www.yadanarbonnews.com/index.php/component/k2/itemlist/user/354071
http://ovotecegg.com/component/k2/itemlist/user/225414
http://herdental.co.kr/index.php?mid=online&document_srl=154761
http://kyj1225.godohosting.com/board_mebR72/94802
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2801570
http://toeden.co.kr/Product_new/138629
http://mglpcm.org/board_ETkS12/131163
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/66566
http://mtuan93.com/board_uCqR85/6152
http://loverstory.co.kr/board_UYNJ05/112450
http://askpharm.net/board_NQiz06/281539
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=125432
http://www.popolsku.fr.pl/forum/index.php?topic=419867.0
https://gonggamlaw.com/lawcase/125649
http://www.cnsmaker.net/xe/board_AbYD20/124993
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vnav-%d1%80%d0%b0%d1%81/
http://naksansacondo.com/board_MGPu57/98509
http://bizchemical.com/board_kMpv94/2160177
http://looksun.co.kr/index.php?mid=board_4&document_srl=186048
http://askpharm.net/board_NQiz06/274207
https://www.limscave.com/forum/viewtopic.php?t=58756
http://mediaville.me/index.php/component/k2/itemlist/user/376238
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=216059
https://www.celekt.com/%d0%9a%d0%be%d0%bf-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bp3%d0%9a%d0%be%d0%bf-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f29-05-2019/
http://www.spazioad.com/component/k2/itemlist/user/7417677
http://carand.co.kr/d2/96360
https://betshin.com/Story/205610
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/78908
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1853312
http://dessa.com.br/component/k2/itemlist/user/391907
http://vervetama.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wgho-%d1%80%d0%b0%d1%81/
http://hyeonjun.co.kr/menu3/288862
http://midorijapaneserestaurant.ca/menu/News/73152
https://betshin.com/Story/208491
http://www.ekemoon.com/245041/052120193628/
http://immobilia.gr/index.php/component/k2/itemlist/user/16849
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jq5q-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20/
http://sd-xi.co.kr/g1/56085
http://melchinooddle.dothome.co.kr/?document_srl=14773
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=184288
http://kwpub.kr/PUBS/130700
https://www.hwbms.com/web/qna/32892
http://beautypouch.net/index.php?mid=board_09&document_srl=165391
https://www.hwbms.com/web/qna/12436
https://www.hohoyoga.com/testboard/4079499
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=31608
http://ajincomp.godohosting.com/board_STnh82/196073
http://holysweat.dothome.co.kr/data/7504
http://rabat.kr/board_yCgT00/82419
https://www.hwbms.com/web/qna/34297
http://www.venusjeju.com/index.php?mid=QnA&document_srl=2148
http://dreamplusart.com/mn03_01/211716
https://2002.shyoon.com/board_2002/221782
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=417546
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/119557
https://gonggamlaw.com/lawcase/134850
http://www.capital-investment.pl/index.php/component/k2/itemlist/user/229560
http://sy.korean.net/qna/454070
https://gonggamlaw.com/lawcase/68188
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/74156
http://daltso.com/index.php?mid=board_cUYy21&document_srl=202201
http://looksun.co.kr/index.php?mid=board_4&document_srl=189980
http://mobility-corp.com/index.php/component/k2/itemlist/user/2740271
https://blossomug.com/?option=com_k2&view=itemlist&task=user&id=1112465
http://zakdu.com/board_YpzS56/23352
http://iymc.or.kr/?document_srl=126061
http://naksansacondo.com/?document_srl=103033
http://ovotecegg.com/component/k2/itemlist/user/219924
http://isch.kr/board_PowH60/158061
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/141425
http://mglpcm.org/board_ETkS12/199910
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=395538
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=388129
http://divespace.co.kr/board/264873
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13707
http://cwon.kr/xe/board_bnSr36/307570
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=960736
https://2002.shyoon.com/board_2002/270278
http://www2.yasothon.go.th/smf/index.php?topic=159.msg199861
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=112398
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=666061
http://www.hmotors.co.kr/inquiry/27625
http://8.droror.co.il/uncategorized/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qlnn-%d1%80%d0%b0%d1%81/
http://www.ekemoon.com/245125/052220192128/
http://dev.aabn.org.gh/component/k2/itemlist/user/713759
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/158816
https://cybergsm.es/index.php?topic=72900.0
http://lavaggio.com.vn/index.php/component/k2/itemlist/user/3924846
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=43816
http://thermoplast.envolgroupe.com/component/k2/author/183519
http://khapthanam.co.kr/g1/160098
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=23130
http://www.patrasin.kr/index.php?mid=questions&document_srl=4349363
http://divespace.co.kr/board/295535
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3795698
http://www.popolsku.fr.pl/forum/index.php?topic=416509.0
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=29103
https://forum.ac-jete.it/index.php?topic=448924.0
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=49267
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=199906
http://lucky.kidspann.net/index.php?mid=qna&document_srl=463227
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=190691
http://cwon.kr/xe/board_bnSr36/291827
http://www.crnmedia.es/component/k2/itemlist/user/91748
http://jdcalc.com/forum/viewtopic.php?t=289909
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ak0v-%d0%ba%d0%be%d0%bf-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://esperanzazubieta.com/component/k2/itemlist/user/108469
http://photogrotto.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-am8o-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15/
http://ko.myds.me/board_story/280068
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1030942
http://dreamplusart.com/mn03_01/238158
http://rabat.kr/board_yCgT00/37420
http://loverstory.co.kr/board_UYNJ05/102968
http://www.hmotors.co.kr/inquiry/39092
http://daltso.com/index.php?mid=board_cUYy21&document_srl=192411
http://www.crnmedia.es/component/k2/itemlist/user/92039
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3504218
http://loverstory.co.kr/board_UYNJ05/111316
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-me7i-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2/
http://myrechockey.com/forums/index.php?topic=117847.0
http://neosky.net/xe/space_station/72672
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=479346
https://betshin.com/Story/216114
http://masanlib.or.kr/g1/98918
https://www.hwbms.com/web/qna/20641
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3549286
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=395281
http://daesestudy.co.kr/ipsi_docu/121258
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-orxb-%d1%80%d0%b0%d1%81/
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/351601
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=316366
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1868574
http://www.vamoscontigo.org/Noticia/136578
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=290156
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=64882
http://ariji.kr/?document_srl=970468
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-os3%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7/
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1215085
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=113209
http://dreamplusart.com/mn03_01/207037
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13796
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/122101
http://dreamplusart.com/mn03_01/172754
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=132918
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=13584
http://zakdu.com/board_YpzS56/25827
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=380981
http://dohairbiz.com/en/component/k2/itemlist/user/2813159.html
http://www.venusjeju.com/index.php?mid=QnA&document_srl=1009
http://test.comics-game.ru/index.php?topic=562.0
https://www.hohoyoga.com/testboard/4084607
http://www.quattroandpartners.it/component/k2/itemlist/user/1219781
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/52208
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229906
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4900645
http://carand.co.kr/d2/89790
https://www.celekt.com/%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gc9j-%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16/
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=315968
http://pekosmile.dothome.co.kr/index.php?mid=seoulitestudio&document_srl=438023
http://www.lgue.co.kr/?document_srl=114968
https://www.hwbms.com/web/qna/37840
http://carand.co.kr/d2/71517
http://daltso.com/index.php?mid=board_cUYy21&document_srl=127194
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=177748
http://daesestudy.co.kr/ipsi_docu/174487
http://ko.myds.me/board_story/261303
http://kwpub.kr/PUBS/131132
http://www.cnsmaker.net/xe/?document_srl=125003
http://www.atab.com.sa/index.php/component/k2/itemlist/user/1747223
http://p9912.cafe24.com/board_LVgu51/73613
http://mglpcm.org/board_ETkS12/211376
http://khapthanam.co.kr/g1/134143
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=301486
http://www.haetsaldun-clinic.co.kr/Question/43634
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=331621
http://www2.yasothon.go.th/smf/index.php?topic=159.172440
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=108987
http://vervetama.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ikyq-%d1%80%d0%b0%d1%81/
http://ko.myds.me/board_story/279984
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=359618
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=37038
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=44146
http://universalcommunity.se/Forum/index.php?topic=39567.0
http://callman.co.kr/?document_srl=221460
http://dessa.com.br/index.php/component/k2/itemlist/user/389728
http://www.atab.com.sa/index.php/en/?option=com_k2&view=itemlist&task=user&id=1733267
http://looksun.co.kr/index.php?mid=board_4&document_srl=198338
http://bobr.site/index.php?topic=176443.0
http://www.proandpro.it/?option=com_k2&view=itemlist&task=user&id=4726690
http://naksansacondo.com/board_MGPu57/67133
https://gonggamlaw.com/lawcase/146407
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=166823
http://ajincomp.godohosting.com/board_STnh82/129567
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1754573
https://betshin.com/Story/214519
http://midorijapaneserestaurant.ca/menu/News/58537
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=394292
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1770255
https://betshin.com/Story/213264
http://dow.dothome.co.kr/board_jydx58/36302
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=220271
http://photogrotto.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dt2d-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81/
http://village.lorem.kr/index.php?document_srl=290622&mid=board_xmEJ33
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/61642
http://sejong-thesharpyemizi.co.kr/m1/75038
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/52317
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=558247
http://constellation.kro.kr/board_kbku73/68618
http://sy.korean.net/qna/444621
http://kyj1225.godohosting.com/board_mebR72/94331
http://moyakmermer.com/?option=com_k2&view=itemlist&task=user&id=848207
http://autospa.lv/index.php/lv/component/k2/itemlist/user/10591
http://tiretech.co.kr/index.php?mid=qna&document_srl=186946
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3896082
http://zakdu.com/board_ssKi56/20058
http://gochon-iusell.co.kr/g1/131561
https://www.shaiyax.com/index.php?topic=420142.0
http://sejong-thesharpyemizi.co.kr/m1/63201
http://gallerychoi.com/Exhibition/334825
http://erhu.eu/viewtopic.php?f=7&t=396500
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=853642
http://looksun.co.kr/index.php?mid=board_4&document_srl=208935
http://looksun.co.kr/index.php?mid=board_4&document_srl=214336
http://www.tunes-interiors.com/UserProfile/tabid/81/userId/8785652/Default.aspx
http://ilsannabgol.kr/board_brJk31/1377710
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=210125
http://www.eunhaele.co.kr/xe/board/20875
https://forum.clubeicaro.pt/index.php?topic=2873.0
https://nextezone.com/index.php?topic=90202.0
https://www.c-alice.org/forum/index.php?topic=100593.0
https://www.regalepadova.it/index.php/component/k2/itemlist/user/8477
https://nextezone.com/index.php?action=profile;u=17283
http://dow.dothome.co.kr/board_jydx58/35298
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=31667
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=393330
http://midorijapaneserestaurant.ca/menu/News/63582
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/172208
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42626
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=229070
http://loverstory.co.kr/board_UYNJ05/84171
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/246527
http://daltso.com/index.php?mid=board_cUYy21&document_srl=191679
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2781194
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/61365
http://rabat.kr/board_yCgT00/81537
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=210811
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/245530
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=172927
http://hotelnomadpalace.com/component/k2/itemlist/user/22024
http://ko.myds.me/board_story/247705
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=116798
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=139823
http://www.vamoscontigo.org/Noticia/223552
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=433110
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=492509
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/148080
http://xn--2e0b53df5ag1c804aphl.net/nuguna/104102
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229880
http://rabat.kr/board_yCgT00/84348
http://themasters.pro/file_01/224872
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2007809
https://www.celekt.com/%d0%92%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-29-05-2019-y5-%d0%92%d1%81%d1%91-%d0%bc/
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=432989
https://2002.shyoon.com/board_2002/225644
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=349193
http://daltso.com/index.php?mid=board_cUYy21&document_srl=123829
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=398443
https://www.hwbms.com/web/qna/46174
https://www.hwbms.com/web/qna/46184
http://proxima.co.rw/index.php/component/k2/itemlist/user/722681
http://www.emrabq8.com/index.php/component/k2/itemlist/user/1876914
http://dcasociados.eu/component/k2/itemlist/user/95319
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/178471
http://muldorang.com/market/27076
https://2002.shyoon.com/board_2002/168373
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/49594
http://www.grupojover.com/index.php/es/component/k2/itemlist/user/4437
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1543402
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=394286
http://sfah.ch/de/component/k2/itemlist/user/15441
http://necinsurance.co.zw/component/k2/itemlist/user/21700.html
https://www.celekt.com/%d0%a0%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rree-%d0%a0%d0%b0%d1%81/
http://naksansacondo.com/board_MGPu57/95558
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=393292
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=124762
http://roikjer.com/forum/index.php?PHPSESSID=nmhvbo99lgusf0jsuok622b3t5&topic=934620.0
http://divespace.co.kr/board/268212
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=88644
http://dospuntoseventos.cl/component/k2/itemlist/user/17137
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=36473
https://gonggamlaw.com/lawcase/144448
https://saltriverbg.com/2019/05/28/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gaya-%d1%80%d0%b0%d1%81/
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/850678
https://www.hohoyoga.com/testboard/4058427
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=117048
http://thermoplast.envolgroupe.com/component/k2/author/182419
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=390627
http://gabisan.com/board_OuDs04/72619
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229944
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=211819
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=65214
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/63339
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1855642
http://rabbitzone.xyz/FREE/126751
http://proxima.co.rw/index.php/component/k2/itemlist/user/696850
http://jnk-ent.jp/index.php?mid=gallery&document_srl=238859
http://www.theocraticamerica.org/forum/index.php?topic=69267.0
http://midorijapaneserestaurant.ca/menu/News/57124
http://themasters.pro/file_01/316424
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5019081
http://rabat.kr/board_yCgT00/82747
http://bobr.site/index.php?topic=184023.0
http://jnk-ent.jp/index.php?mid=gallery&document_srl=241362
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2796420
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/50593
http://looksun.co.kr/index.php?mid=board_4&document_srl=173738
http://ovotecegg.com/component/k2/itemlist/user/224741
http://loverstory.co.kr/board_UYNJ05/113189
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5058497
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=123726
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3570090
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=116492
http://sd-xi.co.kr/g1/56141
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2785603
http://www.venusjeju.com/index.php?mid=QnA&document_srl=857
http://proxima.co.rw/index.php/component/k2/itemlist/user/713715
https://intelogist2.wpengine.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uj3%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7/
http://sfah.ch/de/component/k2/itemlist/user/15475
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/78844
http://roikjer.com/forum/index.php?PHPSESSID=5qqahajqnasg4nm56ot34e0760&topic=932327.0
http://www.capital-investment.pl/index.php/component/k2/itemlist/user/228958
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=65439
http://www.m1avio.com/index.php/component/k2/itemlist/user/3803206
http://loverstory.co.kr/board_UYNJ05/83496
http://www.svteck.co.kr/?document_srl=315520
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=138345
http://looksun.co.kr/index.php?mid=board_4&document_srl=187791
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42555
http://www.sp1.football/index.php?mid=faq&document_srl=844143
http://backo.co.kr/board_aiQk58/21899
http://ovotecegg.com/component/k2/itemlist/user/221363
http://daltso.com/index.php?mid=board_cUYy21&document_srl=197725
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3486235
https://www.hwbms.com/web/qna/21208
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=91313
http://www.cnsmaker.net/xe/?document_srl=122367
http://sd-xi.co.kr/g1/59843
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/41838
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=209173
http://1661-6471.co.kr/news/44530
http://windowshopgoa.com/component/k2/itemlist/user/199949
http://kockazatkutato.hu/index.php/component/k2/itemlist/user/42845
http://dreamplusart.com/mn03_01/213025
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=399983
http://constellation.kro.kr/board_kbku73/71039
http://rabat.kr/board_yCgT00/79784
http://web2interactive.com/index.php/component/k2/itemlist/user/3780333
http://ye-dream.com/qa/270530
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=390056
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1737881
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2872380
http://sy.korean.net/qna/315288
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=393297
http://www.crnmedia.es/component/k2/itemlist/user/91353
http://www.hmotors.co.kr/inquiry/48290
http://www.lgue.co.kr/?document_srl=116556
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=539829
http://apt2you2.cafe24.com/g1/34753
http://soc-human.kz/index.php/en/?option=com_k2&view=itemlist&task=user&id=1755070
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/390133
http://herdental.co.kr/index.php?mid=online&document_srl=146525
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2798652
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3797362
http://www.ekemoon.com/243789/050420190328/
http://www.boutique.in.th/?option=com_k2&view=itemlist&task=user&id=153028
http://dcasociados.eu/component/k2/itemlist/user/93127
http://socialmag.bayareanonprofits.xyz/blogs/viewstory/131016
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=45099
http://looksun.co.kr/index.php?mid=board_4&document_srl=122877
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/65024
https://gonggamlaw.com/lawcase/136515
http://sy.korean.net/qna/454744
http://dreamplusart.com/mn03_01/229479
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=283143
http://www.svteck.co.kr/customer_gratitude/282323
http://erdfsa.iptime.org/xe/index.php?mid=board&document_srl=31851
http://dev.aabn.org.gh/component/k2/itemlist/user/678375
http://2872870.com/est/64978
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229554
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=288867
http://gochon-iusell.co.kr/g1/77447
https://www.hwbms.com/web/qna/29020
http://otitismediasociety.org/forum/index.php?topic=205620.0
http://www.itosm.com/cn/board_nLoq17/134121
https://www.c-alice.org/forum/index.php?topic=97535.0
http://www.cnsmaker.net/xe/?document_srl=155776
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=101701
http://music.start-a-idea.online/blogs/viewstory/43378
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=529528
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3858026
http://otitismediasociety.org/forum/index.php?topic=209617.0
http://praisesound.co.kr/sub04_01/87048
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=58062
http://www.lgue.co.kr/?document_srl=180602
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yfwu-%d1%80%d0%b0%d1%81/
http://daltso.com/index.php?mid=board_cUYy21&document_srl=193815
http://mobility-corp.com/index.php/component/k2/itemlist/user/2698257
http://universalcommunity.se/Forum/index.php?topic=34589.0
https://forum.ac-jete.it/index.php?topic=445566.0
http://www.m1avio.com/index.php/component/k2/itemlist/user/3801440
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=140249
https://intelogist2.wpengine.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fr4t-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81/
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/370788
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=56075
https://www.celekt.com/%d0%a0%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fogf-%d0%a0%d0%b0%d1%81/
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=1081376
http://www.ekemoon.com/240487/050920191826/
http://www.vamoscontigo.org/Noticia/222007
https://gonggamlaw.com/lawcase/147662
http://cwon.kr/xe/board_bnSr36/293863
http://mediaville.me/index.php/component/k2/itemlist/user/366067
https://betshin.com/Story/203207
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tapp-%d1%80%d0%b0%d1%81/
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=329814
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/169922
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3877628
http://music.start-a-idea.online/blogs/viewstory/46200
http://www.ekemoon.com/244163/050920192428/
https://betshin.com/Story/195001
http://music.start-a-idea.online/blogs/viewstory/44257
http://lucky.kidspann.net/index.php?mid=qna&document_srl=292074
http://ajincomp.godohosting.com/board_STnh82/129299
http://www.hmotors.co.kr/?document_srl=69775
http://sunele.co.kr/board_ReBD97/216943
http://xn--2e0b53df5ag1c804aphl.net/nuguna/182417
http://tiretech.co.kr/index.php?mid=qna&document_srl=181949
https://intelogist2.wpengine.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-of9p-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://mobility-corp.com/index.php/component/k2/itemlist/user/2732805
http://herdental.co.kr/index.php?mid=online&document_srl=113123
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1310991
http://www.emrabq8.com/index.php/component/k2/itemlist/user/1867472
http://fbpharm.net/index.php/component/k2/itemlist/user/87434
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=139738
http://www.theocraticamerica.org/forum/index.php?topic=74012.0
http://rfc11th13th.dothome.co.kr/Board5/35112
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=302457
http://kockazatkutato.hu/component/k2/itemlist/user/42967
http://midorijapaneserestaurant.ca/menu/News/51281
http://proxima.co.rw/index.php/component/k2/itemlist/user/695239
https://forum.clubeicaro.pt/index.php?topic=2762.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/174600
http://muldorang.com/market/28419
http://kwpub.kr/PUBS/171604
http://kyj1225.godohosting.com/board_mebR72/98361
http://looksun.co.kr/index.php?mid=board_4&document_srl=202296
http://www.svteck.co.kr/customer_gratitude/248752
http://miquirofisico.com/index.php/component/k2/itemlist/user/4446
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=208555
http://www.hmotors.co.kr/inquiry/68089
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=852012
http://bebopindia.com/notcie/382250
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/44466
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-li7%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5/
http://mglpcm.org/board_ETkS12/127340
https://gonggamlaw.com/lawcase/133742
https://blossomug.com/index.php/component/k2/itemlist/user/1112885
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/43330
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=31867
https://www.hohoyoga.com/testboard/4065225
http://midorijapaneserestaurant.ca/menu/News/49073
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lc9g-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17/
http://rabat.kr/board_yCgT00/37802
http://gusinoepero.ru/archives/26176
http://benzmall.co.kr/index.php?mid=download&document_srl=92205
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=110563
http://www.livetank.cn/market1/216378
http://naksansacondo.com/board_MGPu57/32279
http://www.ekemoon.com/245105/052220191028/
https://adsensebih.com/index.php?topic=45655.0
https://bcit-tmgt.com/viewtopic.php?t=49183
https://adsensebih.com/index.php?topic=49910.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1533064
http://sammyungsa.com/board_dltP23/4052
http://hyeonjun.co.kr/menu3/369148
http://cwon.kr/xe/board_bnSr36/299510
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/167886
http://myrechockey.com/forums/index.php?topic=118447.0
http://khapthanam.co.kr/g1/155722
http://carand.co.kr/d2/88661
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13847
http://thermoplast.envolgroupe.com/component/k2/author/182423
http://www2.yasothon.go.th/smf/index.php?topic=159.169965
http://sejong-thesharpyemizi.co.kr/m1/50466
http://test.comics-game.ru/index.php?topic=549.0
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3545639
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=566872
http://mediaville.me/index.php/component/k2/itemlist/user/373194
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=b8671d7c9e0f773e3f20b1209b19df24&topic=11291.0
http://isch.kr/board_PowH60/205012
http://juroweb.com/xe/juroweb_board/82574
http://dreamplusart.com/mn03_01/212745
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=109291
http://apt2you2.cafe24.com/g1/53727
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=948559
http://masanlib.or.kr/g1/102122
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1548526
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=30649
http://jiral.net/an9/36672
http://www.lgue.co.kr/?document_srl=169203
http://www.jesusonly.life/calendar/445885
http://mercibq.net/?document_srl=55869
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3796473
http://www.hmotors.co.kr/inquiry/38266
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/114828
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=225408
http://bebopindia.com/notcie/381554
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=78020
http://jdcalc.com/forum/viewtopic.php?t=281046
http://kino-z.eu/component/k2/itemlist/user/2485
http://praisesound.co.kr/sub04_01/103562
http://praisesound.co.kr/sub04_01/87638
https://mcsetup.tk/bbs/index.php?topic=261780.0
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=124927
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=175360
http://sunele.co.kr/board_ReBD97/167214
http://www.lgue.co.kr/?document_srl=147640
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3938405
http://www2.yasothon.go.th/smf/index.php?topic=159.msg200102
https://forum.ac-jete.it/index.php?topic=437448.0
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=151798
https://www.celekt.com/%d0%92%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pl6j-%d0%92%d1%81%d1%91-%d0%bc%d0%be%d0%b3/
http://sd-xi.co.kr/g1/90566
http://www.leekeonsu-csi.com/?document_srl=1173669
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=81509
http://beautypouch.net/index.php?mid=board_09&document_srl=102103
https://nple.com/xe/pds/157221
http://kyj1225.godohosting.com/board_mebR72/99719
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3450090
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ypnu-%d1%80%d0%b0%d1%81/
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=827353
http://sfah.ch/de/component/k2/itemlist/user/15558
http://pkgersang.dothome.co.kr/board_jiKY24/35113
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=171138
http://kockazatkutato.hu/index.php/component/k2/itemlist/user/44734
https://adsensebih.com/index.php?topic=48596.0
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=589893
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=849966
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=194758
http://loverstory.co.kr/board_UYNJ05/47387
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=829609
http://looksun.co.kr/index.php?mid=board_4&document_srl=186855
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=33645
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=17378
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=274238
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/303645
http://guiadetudo.com/index.php/component/k2/itemlist/user/12712
http://lucky.kidspann.net/index.php?mid=qna&document_srl=338270
http://isch.kr/board_PowH60/154061
http://looksun.co.kr/index.php?mid=board_4&document_srl=124938
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1870938
http://www.dap.com.py/index.php/component/k2/itemlist/user/850512
http://www.lgue.co.kr/?document_srl=129239
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=233168
http://daltso.com/index.php?document_srl=229782&mid=board_cUYy21
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5016033
http://askpharm.net/board_NQiz06/250073
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=537609
http://www.arunagreen.com/index.php/component/k2/itemlist/user/1157372
http://kockazatkutato.hu/component/k2/itemlist/user/42495
http://www.hmotors.co.kr/inquiry/27454
https://gonggamlaw.com/lawcase/131490
http://music.start-a-idea.online/blogs/viewstory/48501
http://www.ekemoon.com/240987/051220195626/
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=212101
http://sd-xi.co.kr/g1/90947
http://yooseok.com/board_BkvT46/426867
https://intelogist2.wpengine.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xj3n-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
https://khuyenmaikk13.info/index.php?topic=226402.0
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=139199
http://gochon-iusell.co.kr/g1/127797
http://jdcalc.com/forum/viewtopic.php?t=291101
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=340822
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=199876
http://melchinooddle.dothome.co.kr/?document_srl=13276
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1530627
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1867053
http://archeaudio.com/xe/board_AOYj82/15242
http://xihillstate.bloggirl.net/index.php?document_srl=254341&mid=board_HLJb60
http://gabisan.com/board_OuDs04/73675
http://kyj1225.godohosting.com/board_mebR72/95808
http://ko.myds.me/board_story/248351
http://loverstory.co.kr/?document_srl=45315
http://ko.myds.me/board_story/312579
http://loverstory.co.kr/board_UYNJ05/107265
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=158986
http://engeena.com/component/k2/itemlist/user/9227
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=665008
http://rabbitzone.xyz/FREE/122411
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=172574
http://dcasociados.eu/component/k2/itemlist/user/93357
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1216637
http://mglpcm.org/board_ETkS12/204487
http://rudraautomation.com/index.php/component/k2/author/347677
https://www.hohoyoga.com/testboard/4050654
http://smartacity.com/component/k2/itemlist/user/97330
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=95166
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=537149
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3937913
http://bobr.site/index.php?topic=177235.0
http://daltso.com/index.php?mid=board_cUYy21&document_srl=126019
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=393755
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=119619
http://kyj1225.godohosting.com/board_mebR72/92542
http://carand.co.kr/d2/49259
http://gallerychoi.com/Exhibition/537808
http://kyj1225.godohosting.com/board_mebR72/97560
http://cwon.kr/xe/board_bnSr36/296497
http://www.itosm.com/cn/board_nLoq17/135206
http://withinfp.sakura.ne.jp/eso/index.php/17594347-rasskaz-sluzanki-3-sezon-11-seria-evsc-rasskaz-sluzanki-3-sezon
http://www2.yasothon.go.th/smf/index.php?topic=159.171945
http://dohairbiz.com/en/component/k2/itemlist/user/2814381.html
http://xn--2e0bk61btjo.com/notice/22716
http://sy.korean.net/qna/452009
https://gonggamlaw.com/lawcase/139878
http://e-educ.net/Forum/index.php?topic=16515.0
http://rudraautomation.com/index.php/component/k2/author/345966
http://xn--hu1bs8ufrd6ucyz0aooa.kr/?document_srl=43343
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1499882
http://hyeonjun.co.kr/menu3/384681
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hshx-%d1%80%d0%b0%d1%81/
http://www.capital-investment.pl/index.php/component/k2/itemlist/user/234232
http://hydrocarbs-gh.org/index.php/component/k2/itemlist/user/7488347
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/847529
http://jnk-ent.jp/index.php?mid=gallery&document_srl=299582
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2659294
http://hyeonjun.co.kr/menu3/368102
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=18437
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13840
http://8.droror.co.il/uncategorized/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gqov-%d1%80%d0%b0%d1%81/
http://married.dike.gr/?option=com_k2&view=itemlist&task=user&id=78234
http://ye-dream.com/qa/236321
http://xn--2e0bk61btjo.com/notice/23107
http://looksun.co.kr/index.php?mid=board_4&document_srl=185529
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/84058
http://rabat.kr/board_yCgT00/44901
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=30313
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=44210
http://thermoplast.envolgroupe.com/component/k2/author/182383
http://www.sp1.football/index.php?mid=faq&document_srl=827878
https://forums.lfstats.com/viewtopic.php?t=315054
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/75922
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=663229
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=14202
http://www.cyberblissstudios.com/UserProfile/tabid/42/UserID/2307717/Default.aspx
http://www.svteck.co.kr/customer_gratitude/330389
http://midorijapaneserestaurant.ca/menu/News/47386
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=559141
http://kyj1225.godohosting.com/board_mebR72/96800
http://loverstory.co.kr/board_UYNJ05/109536
http://midorijapaneserestaurant.ca/menu/News/62364
http://gochon-iusell.co.kr/g1/98429
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=335710
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16737
http://daltso.com/index.php?mid=board_cUYy21&document_srl=192917
http://lucky.kidspann.net/index.php?mid=qna&document_srl=394504
https://gonggamlaw.com/lawcase/148353
http://ilsannabgol.kr/board_brJk31/1369351
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=136224
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=850485
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=37945
http://mobility-corp.com/index.php/component/k2/itemlist/user/2733242
http://forum.bmw-e60.eu/index.php?topic=11150.0
http://www.patrasin.kr/index.php?mid=questions&document_srl=4357909
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=321198
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3877287
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=73848
http://cwon.kr/xe/board_bnSr36/299725
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=190042
http://looksun.co.kr/index.php?mid=board_4&document_srl=203672
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229987
http://www.digitalbul.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ohmq-%d1%80%d0%b0%d1%81/
http://matinbank.ir/component/k2/itemlist/user/4591786.html
http://ko.myds.me/board_story/279669
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=1070906
https://gonggamlaw.com/lawcase/141498
http://www.tessabannampad.go.th/webboard/index.php?topic=225658.0
https://www.celekt.com/%d0%92%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-29-05-2019-n1-%d0%92%d1%81%d1%91-%d0%bc/
http://rabbitzone.xyz/FREE/87936
http://design-381.com/xe/qna/5484
http://dreamplusart.com/mn03_01/237409
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=380072
https://saltriverbg.com/2019/05/29/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mjgo-%d1%80%d0%b0%d1%81/
http://sejong-thesharpyemizi.co.kr/m1/110062
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=110153
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=1084814
http://jnk-ent.jp/index.php?mid=gallery&document_srl=239560
http://gtupuw.org/index.php/component/k2/itemlist/user/1975849
http://dreamplusart.com/mn03_01/127763
http://juroweb.com/xe/juroweb_board/83202
http://sy.korean.net/qna/456146
http://loverstory.co.kr/board_UYNJ05/110796
http://yoriyorifood.com/xxxx/spacial/265655
http://esperanzazubieta.com/component/k2/itemlist/user/108192
http://www.quattroandpartners.it/component/k2/itemlist/user/1245018
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1855090
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=34958
http://sy.korean.net/qna/317677
http://ariji.kr/?document_srl=1010938
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2830123
http://apt2you2.cafe24.com/g1/37787
http://www.itosm.com/cn/board_nLoq17/133498
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13711
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=183310
http://mobility-corp.com/index.php/component/k2/itemlist/user/2741953
https://forum.ac-jete.it/index.php?topic=449213.0
http://blog.ptpintcast.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mtrf-%d1%80%d0%b0%d1%81/
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=1070384
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=391416
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=29362
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1532774
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nm0%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5/
http://beautypouch.net/index.php?mid=board_09&document_srl=101870
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/388287
http://thermoplast.envolgroupe.com/component/k2/author/181268
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=218756
http://guiadetudo.com/index.php/component/k2/itemlist/user/12616
http://www.popolsku.fr.pl/forum/index.php?topic=416805.0
http://hotelnomadpalace.com/index.php/component/k2/itemlist/user/22759
http://kyj1225.godohosting.com/board_mebR72/109943
http://www.coating.or.kr/atemfair_data/19279
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=954803
http://backo.co.kr/board_aiQk58/22246
http://1644-4404.com/index.php?document_srl=337363&mid=board_VFri46
http://myrechockey.com/forums/index.php?topic=118604.0
https://gonggamlaw.com/lawcase/144270
http://daltso.com/index.php?mid=board_cUYy21&document_srl=179027
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=173518
http://bobr.site/index.php?topic=179716.0
http://0433.net/budongsan/136616
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=28503
https://bcit-tmgt.com/viewtopic.php?t=53203
http://rabat.kr/board_yCgT00/70314
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=5b26ed4ebf439e50de707ab322e66a97&topic=11684.0
http://blog.ptpintcast.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cmud-%d1%80%d0%b0%d1%81/
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=313007
http://divespace.co.kr/board/276355
http://gochon-iusell.co.kr/g1/118141
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/852585
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/334032
http://www.hmotors.co.kr/inquiry/70775
http://neosky.net/xe/space_station/68761
http://myrechockey.com/forums/index.php?topic=118859.0
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hdhf-%d1%80%d0%b0%d1%81/
https://www.2ayes.com/19609/3-3-kbtg-3-3-abc
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=117025
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=48653
https://www.chirorg.com/?document_srl=145945
http://cwon.kr/xe/?document_srl=282760
http://mercibq.net/partner/97694
http://loverstory.co.kr/board_UYNJ05/95874
http://www.cnsmaker.net/xe/?document_srl=122045
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=730997
http://e-educ.net/Forum/index.php?topic=15905.0
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=85867
http://yooseok.com/board_BkvT46/412808
http://holysweat.dothome.co.kr/data/7796
http://rabbitzone.xyz/FREE/71981
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=108704
https://www.chirorg.com/?document_srl=154826
http://ko.myds.me/board_story/276006
http://rfc11th13th.dothome.co.kr/Board5/35066
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=226511
http://x-crew.center/guest/4845093
http://erdfsa.iptime.org/xe/index.php?mid=board&document_srl=12746
http://loverstory.co.kr/board_UYNJ05/95809
http://withinfp.sakura.ne.jp/eso/index.php/17526528-rasskaz-sluzanki-3-sezon-11-seria-ecei-rasskaz-sluzanki-3-sezon/0
https://www.regalepadova.it/index.php/component/k2/itemlist/user/8250
http://gabisan.com/board_OuDs04/69014
http://looksun.co.kr/index.php?mid=board_4&document_srl=188455
http://k-cea.org/board_Hnyj62/197882
http://www.itosm.com/cn/?document_srl=131905
http://vtservices85.fr/smf2/index.php?PHPSESSID=3061b910aa74df0642101e9e861304b7&topic=289301.0
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/149298
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=48365
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=139302
http://loverstory.co.kr/board_UYNJ05/96502
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ocay-%d1%80%d0%b0%d1%81/
http://jnk-ent.jp/index.php?mid=gallery&document_srl=241753
http://k-cea.org/board_Hnyj62/191851
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=431617
http://neosky.net/xe/space_station/138530
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=301570
http://photogrotto.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cn2c-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13/
http://ovotecegg.com/component/k2/itemlist/user/225505
http://midorijapaneserestaurant.ca/menu/News/29351
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/34061
http://www.theocraticamerica.org/forum/index.php?topic=69957.0
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=190719
http://carand.co.kr/d2/90832
http://carand.co.kr/d2/90323
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=889477
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=435921
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=40007.0
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dr8e-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20/
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=431635
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=29506
http://forum.elexlabs.com/index.php?topic=62160.0
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=29591
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=58283
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=36994
https://www.limscave.com/forum/viewtopic.php?t=57272
http://music.start-a-idea.online/blogs/viewstory/44218
http://k-cea.org/board_Hnyj62/191784
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=327404
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3478651
https://adsensebih.com/index.php?topic=48202.0
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1873077
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/60309
http://dreamplusart.com/mn03_01/213645
http://toeden.co.kr/Product_new/173300
http://myrechockey.com/forums/index.php?topic=118943.0
http://naksansacondo.com/board_MGPu57/33215
http://ovotecegg.com/component/k2/itemlist/user/223873
http://arquitectosenreformas.es/component/k2/itemlist/user/86065
http://www.kwpcoop.or.kr/QnA/19663
http://kyj1225.godohosting.com/board_mebR72/92860
http://www.golden-nail.co.kr/press/375356
http://withinfp.sakura.ne.jp/eso/index.php/17574927-rasskaz-sluzanki-3-sezon-5-seria-uzjo-rasskaz-sluzanki-3-sezon-/0
https://www.hwbms.com/web/qna/38865
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cx1v-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15/
http://carand.co.kr/d2/90201
https://gonggamlaw.com/lawcase/143316
http://thermoplast.envolgroupe.com/component/k2/author/182947
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=259159
http://rabbitzone.xyz/FREE/110047
http://callman.co.kr/index.php?mid=qa&document_srl=222921
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/34128
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=153860
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=849271
http://gspara01.dothome.co.kr/?document_srl=19783
http://lucky.kidspann.net/index.php?mid=qna&document_srl=411147
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=1185257
http://sunele.co.kr/board_ReBD97/213215
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=113233
http://beautypouch.net/index.php?mid=board_09&document_srl=118190
http://barobus.kr/qna/75584
http://callman.co.kr/index.php?mid=qa&document_srl=221499
http://bobr.site/index.php?topic=192348.0
https://adsensebih.com/index.php?topic=51675.0
http://warmfund.net/p/index.php?mid=financing&document_srl=474990
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=291275
https://www.chirorg.com/?document_srl=154891
http://xn----3x5er9r48j7wemud0a387h.com/news/164135
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1746987
http://herdental.co.kr/index.php?mid=online&document_srl=114474
http://vervetama.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-esoz-%d1%80%d0%b0%d1%81/
http://dohairbiz.com/en/?option=com_k2&view=itemlist&task=user&id=2813002
http://hotelnomadpalace.com/component/k2/itemlist/user/22778
http://beautypouch.net/index.php?mid=board_09&document_srl=109863
<p align="">
<a title="강남오피" href="http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bf%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%c5%8b%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%84%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%8d%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%85%bela" target="_blank">강남오피
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉오피" href="https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%d0%be%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%88%82%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%bd%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%82%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a9tide" target="_blank">선릉오피
</a>
</p>
먼저핀꽃은 먼저진다 남보다 먼저 공을 세우려고 조급히 서둘것이 아니다-채근담
<p align="">
<a title="역삼오피" href="
https://enes.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%94%bb%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%97%88%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%ce%9egang" target="_blank">역삼오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남휴게텔" href="
https://www.livemeshthemes.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%c4%b1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b7%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%85%86%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%93%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%82%ba%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%84%a1%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%82stone" target="_blank">강남휴게텔
</a>
</p>
먹고 싶은것을 다 먹는 것은 그렇게 재미있지 않다 . 인생을 경계선 없이 살면 기쁨이 덜하다.먹고싶은대로 다 먹을 수있다면 먹고싶은 것을 먹는데 무슨 재미가 있겠나 - 톰행크스
<p align="">
<a title="선릉휴게텔" href="
http://www.pnr.corsica/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%89%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%a1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%9d%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%83%a6afford" target="_blank">선릉휴게텔
</a>
</p>
진짜 문제는 사람들의 마음이다.그것은 절대로 물리학이나 윤리학의 문제가 아니다.-아인슈타인
<p align="">
<a title="역삼휴게텔" href="
https://dict.leo.org/italienisch-deutsch/%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%82%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%d1%8f%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%83%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%ae%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9dseason" target="_blank">역삼휴게텔
</a>
</p>
가난은 가난하다고 느끼는 곳에 존재한다 .- 에머슨
<p align="">
<a title="강남안마" href="https://24.sapo.pt/pesquisar?q=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%85%a2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%82%8f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%99%a0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%85%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ce%92truly" target="_blank">강남안마
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉안마" href="
https://enfi.dict.cc/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%9e%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%85%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%90%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%bd%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%9cband" target="_blank">선릉안마
</a>
</p>
행복은 습관이다 그것을 몸에 지니라 -허버드
<p align="">
<a title="역삼안마" href="
https://www.lidumsaym.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%83%9d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c2%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8f%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%b1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%82%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b9derived" target="_blank">역삼안마
</a>
</p>
화려한 일을 추구하지 말라. 중요한 것은 스스로의 재능이며자신의 행동에 쏟아 붓는 사랑의 정도이다. -머더 테레사
<p align="">
<a title="강남오피" href="
http://www.twentszitmaaierteam.nl/pages/interactief/gastenboek.php?p=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%87%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%86%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%82%b9%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%94%bd%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%d0%a3wouldn't" target="_blank">강남오피
</a>
</p>
절대 어제를 후회하지 마라 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다-L.론허바드
<p align="">
<a title="선릉오피" href="
http://www.mairtinmusic.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%82%86%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%8b%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%9e%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%88truly" target="_blank">선릉오피
</a>
</p>
내일은 내일의 태양이 뜬다 피할수 없으면 즐겨라 -로버트 엘리엇
<p align="">
<a title="역삼오피" href="https://www.uptodate.com/contents/search?search=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%81%99%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%b9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%99%aa%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%83%8e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c3%be%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%82%b6%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%8centire" target="_blank">역삼오피
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남휴게텔" href="
http://ladysmithfederal.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%93%94%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%88%87%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%8f%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ce%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%c2%baremark" target="_blank">강남휴게텔
</a>
</p>
인간의 삶 전체는 단지 한 순간에 불과하다 . 인생을 즐기자 - 플루타르코스
<p align="">
<a title="선릉휴게텔" href="
https://www.governmentjobs.com/jobs?keyword=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%94%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%87secretly" target="_blank">선릉휴게텔
</a>
</p>
흔히 사람들은 기회를 기다리고 있지만 기회는 기다리는사람에게 잡히지 않는 법이다.우리는 기회를 기다리는 사람이 되기 전에 기회를 얻을 수 있는실력을 갖춰야 한다.일에 더 열중하는 사람이 되어야한다.-안창호
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%bb%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%84%ba%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%89%b0%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8e%93%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%80%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%cf%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b7artillery" target="_blank">역삼휴게텔
</a>
</p>
마음만을 가지고 있어서는 안된다. 반드시 실천하여야 한다.-이소룡
<p align="">
<a title="강남안마" href="
https://dehr.dict.cc/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%86%8d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%a1%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%84%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%9f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%b0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%88%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%8f%9dleg" target="_blank">강남안마
</a>
</p>
물러나서 조용하게 구하면 배울 수 있는 스승은 많다.사람은 가는 곳마다 보는 것마다 모두 스승으로서배울 것이 많은 법이다.-맹자
<p align="">
<a title="선릉안마" href="
https://www.gov.uk/search/all?keywords=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%92%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%91%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%ae%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8f%87%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%97%87providing" target="_blank">선릉안마
</a>
</p>
삶이 있는 한 희망은 있다 -키케로
<p align="">
<a title="역삼안마" href="
https://www.sdsn.no/sok/category28150.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%88%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%8c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%82%a1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%85%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%c4%b8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%85%9esecretary" target="_blank">역삼안마
</a>
</p>
한 번 실패와 영원한 실패를 혼동하지 마라.-F.스콧 핏제랄드
<p align="">
<a title="강남오피" href="
https://www.righteousmind.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%b0%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%91%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%96%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%88%87sang" target="_blank">강남오피
</a>
</p>
모든것들에는 나름의 경이로움과 심지어 어둠과 침묵이 있고 내가 어떤 상태에 있더라도 나는 그속에서 만족하는 법을 배운다-헬렌켈러
<p align="">
<a title="선릉오피" href="
http://www.actiitransportation.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e2%96%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%99%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%89%ba%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%bdaround" target="_blank">선릉오피
</a>
</p>
내 비장의 무기는 아직 손안에 있다 .그것은 희망이다 - 나폴레옹
<p align="">
<a title="역삼오피" href="https://www.youtube.com/results?search_query=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ce%a5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8e%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%a0%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%b1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%84lay" target="_blank">역삼오피
</a>
</p>
만족할 줄 아는 사람은진정한 부자이고 탐욕스러운 사람은진실로 가난한 사람이다.-솔론
<p align="">
<a title="강남휴게텔" href="
https://denl.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%81%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%8a%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%8f%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%85%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%93%a0%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%b2grief" target="_blank">강남휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="선릉휴게텔" href="
https://artdeco.org/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%9e%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a4%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%94%b9%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ef%bc%af%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%be%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%8dodd" target="_blank">선릉휴게텔
</a>
</p>
만약 우리가 할 수 있는 일을 모두 한다면 우리들은 우리자신에 깜짝 놀랄 것이다.-에디슨
<p align="">
<a title="역삼휴게텔" href="
http://www.lavipera.it/?s=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bc%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%bb%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%93%a3%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b5%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%88%8cvaried" target="_blank">역삼휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="강남안마" href="
https://money2.creontrade.com/E5/WTS/Stock/Foreign/DW_Foreign_Tax.aspx?p=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ef%bc%84%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bc%af%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%bd%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%83%9d%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%87splendid" target="_blank">강남안마
</a>
</p>
절대 어제를 후회하지 마라 . 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다 L.론허바드
<p align="">
<a title="선릉안마" href="
https://wpgovernance.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%85%a4%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%b3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%81%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%8d%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%81%b7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%a3john" target="_blank">선릉안마
</a>
</p>
사막이 아름다운 것은 어딘가에 샘이 숨겨져 있기 때문이다 - 생떽쥐베리
<p align="">
<a title="역삼안마" href="
https://nebraska.aiga.org/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%96%92%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%86%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%88%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%95%80%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ef%bd%87goes" target="_blank">역삼안마
</a>
</p>
</div>
<div style='width: 1px; height: 1px; overflow: hidden'><div align='center'>
<img name='target_resize_image[]' onclick='image_window(this)' style='cursor:pointer;' alt="" class="view_photo up" src="http://file.osen.co.kr/article/2019/05/01/201905011854774508_5cc96e7d1d3c2.jpg" >
그라운드 뷰는 차의 앞쪽 아랫부분
<div style="position:absolute; left:-9999px; top:-9999px;" class="sound_only">
피할수 없으면 즐겨라 - 로버트 엘리엇
<p align="">
<a title="강남오피" href="
http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%83%b1%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a4%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%a7%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%aa%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%a4forward" target="_blank">강남오피
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="선릉오피" href="
http://www.ambrosiocinema.it/page/5/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%83%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%a8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%b8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%bf%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ef%bc%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%96%bc%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%86spring" target="_blank">선릉오피
</a>
</p>
아래에 비교하면 남음이 있다.-명심보감
<p align="">
<a title="역삼오피" href="
https://www.openrice.com/zh/hongkong/restaurants?what=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%99%a5%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a0both" target="_blank">역삼오피
</a>
</p>
실패는 잊어라 그러나 그것이 준 교훈은절대 잊으면 안된다-하버트 개서
<p align="">
<a title="강남휴게텔" href="
https://desk.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%88%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%88%99%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%85%b4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%82%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%81boat" target="_blank">강남휴게텔
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉휴게텔" href="http://www.blueskyspaworks.com/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%c2%bc%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%91%ad%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%95%89%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%bb%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%92%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%ef%bc%84damage" target="_blank">선릉휴게텔
</a>
</p>
절대 포기하지 말라. 당신이 되고 싶은 무언가가 있다면그에 대해 자부심을 가져라. 당신 자신에게 기회를 주어라. 스스로가 형편없다고 생각하지 말라.그래봐야 아무 것도 얻을 것이 없다. 목표를 높이 세워라.인생은 그렇게 살아야 한다.-마이크 맥라렌
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%80%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%92%b2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%92%a4%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bf%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%8e%97sworn" target="_blank">역삼휴게텔
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="강남안마" href="
https://www.wfs-dreieich.de/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%d0%93%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%97%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%88%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%a3%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%a4%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%84blame" target="_blank">강남안마
</a>
</p>
계단을 밟아야 계단 위에 올라설수 있다 -터키속담
<p align="">
<a title="선릉안마" href="
http://ypsistudio.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%82%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c4%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ef%bc%b0%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bf%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%cf%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%91%a4contain" target="_blank">선릉안마
</a>
</p>
지금이야 말로 일할때다. 지금이야말로 싸울때다. 지금이야말로 나를 더 훌륭한 사람으로 만들때다오늘 그것을 못하면 내일 그것을 할수있는가- 토마스 아켐피스
<p align="">
<a title="역삼안마" href="
https://www.matematikk.org/trinn8-10/sok/index.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%81%af%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bc%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%98%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%b3%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%b4understand" target="_blank">역삼안마
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남오피" href="
https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%86%90%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%85%b5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ef%bc%a8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c5%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8f%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%80bred" target="_blank">강남오피
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="선릉오피" href="
https://www.pexels.com/ko-kr/search/%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ef%bd%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%b9%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%83%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%8f%9cshelter" target="_blank">선릉오피
</a>
</p>
단순하게 살라. 쓸데없는 절차와 일 때문에 얼마나 복잡한 삶을 살아가는가?-이드리스 샤흐
<p align="">
<a title="역삼오피" href="
https://ciscentraltexas.org/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%ae%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b2%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8f%87%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%8a%83%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%97%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%92philadelphia" target="_blank">역삼오피
</a>
</p>
직접 눈으로 본 일도 오히려 참인지 아닌지염려스러운데 더구나 등뒤에서 남이 말하는것이야 어찌 이것을 깊이 믿을 수 있으랴?-명심보감-
<p align="">
<a title="강남휴게텔" href="
http://www.kuenselonline.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ce%a8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%9c%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%86%96%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%b2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bd%90%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%87quickly" target="_blank">강남휴게텔
</a>
</p>
내가 헛되이 보낸 오늘은 어제 죽어간 이들이그토록 바라던 하루이다 단 하루면 인간적인 모든 것을 멸망시킬수도 다시 소생시킬수도 있다-소포클레스
<p align="">
<a title="선릉휴게텔" href="https://www.sony.com/electronics/support/results?query=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%86%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%81%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ce%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%bd%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bc%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9bboat" target="_blank">선릉휴게텔
</a>
</p>
돈이란 바닷물과도 같다. 그것은 마시면 마실수록 목이 말라진다.-쇼펜하우어
<p align="">
<a title="역삼휴게텔" href="
https://jobs.rbc.com/ca/en/search-results?keywords=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%8c%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%d0%9e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%82%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%a6%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%c5%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%82joke" target="_blank">역삼휴게텔
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남안마" href="
http://www.makinamekawa.com/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%91%a9%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%d0%96%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bc%a2%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%92dreaming" target="_blank">강남안마
</a>
</p>
진정으로 웃으려면 고통을 참아야하며 나아가 고통을 즐길 줄 알아야 해 -찰리 채플린
<p align="">
<a title="선릉안마" href="
https://www.reddit.com/search?q=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%ac%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%9b%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%92%a5%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%a7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%99%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%a7grant" target="_blank">선릉안마
</a>
</p>
한번의 실패와 영원한 실패를 혼동하지 마라 -F.스콧 핏제랄드
<p align="">
<a title="역삼안마" href="
https://desk.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%95%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%9e%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ce%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%b5%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%85%b9%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%d1%89%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%93goal" target="_blank">역삼안마
</a>
</p>
행복은 결코 많고 큰데만 있는 것이 아니다 작은 것을 가지고도 고마워 하고 만족할 줄 안다면그는 행복한 사람이다여백과 공간의 아름다움은 단순함과 간소함에 있다법정스님 - 홀로사는 즐거움 에서
<p align="">
<a title="강남오피" href="
http://www.alberguerioaragon.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%bd%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%a6%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%87%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%80%b3%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%85%a5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%93%98%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%81seem" target="_blank">강남오피
</a>
</p>
길을 잃는 다는 것은 곧 길을 알게 된다는 것이다. - 동아프리카속담
<p align="">
<a title="선릉오피" href="
https://www.isistassinari.gov.it/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%8e%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%ce%b7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%89%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ce%95%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%95%88awhile" target="_blank">선릉오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="역삼오피" href="
http://isb.az/ru/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%89%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%d1%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%93%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%8cindependent" target="_blank">역삼오피
</a>
</p>
자신을 내보여라. 그러면 재능이 드러날 것이다.- 발타사르 그라시안
<p align="">
<a title="강남휴게텔" href="
http://biz.heraldcorp.com/view.php?ud=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%b2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bd%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%ef%bc%95%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%89%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%bbmarks" target="_blank">강남휴게텔
</a>
</p>
화가 날 때는 100까지 세라. 최악일 때는 욕설을 퍼부어라. -마크 트웨인
<p align="">
<a title="선릉휴게텔" href="
https://www.americanas.com.br/busca?conteudo=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ef%bc%b0%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%84%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%9a%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%81%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%8e%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%a8portrait" target="_blank">선릉휴게텔
</a>
</p>
1퍼센트의 가능성 그것이 나의 길이다-나폴레옹
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%83%99%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8f%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%83%95%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%d0%af%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b9personal" target="_blank">역삼휴게텔
</a>
</p>
최고에 도달하려면 최저에서 시작하라.-P.시루스
<p align="">
<a title="강남안마" href="
http://jozankei.jp/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%92%9f%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%81%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%c3%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%88%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%84%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%96%a6%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b6parted" target="_blank">강남안마
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉안마" href="
http://www.somoseducacao.com.br/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%98%85%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%be%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%9a%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%a1%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%a5greatly" target="_blank">선릉안마
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="역삼안마" href="
https://riftio.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%8e%80%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bd%99%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%99%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%8a%83%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%9d%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%a6%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%84%b9had" target="_blank">역삼안마 (ง •̀_•́)ง ddakbam.com
</a>
</p>
https://intelogist2.wpengine.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uyhv-%d1%80%d0%b0%d1%81/
https://www.2ayes.com/19713/3-11-cclr-3-11-hulu
http://alastair030.dothome.co.kr/?document_srl=21532
http://bobr.site/index.php?topic=184574.0
https://cybergsm.es/index.php?topic=62836.0
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=399162
http://divespace.co.kr/board/276512
https://betshin.com/Story/210305
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/55350
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=377914
http://muldorang.com/market/24866
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2799927
http://mobility-corp.com/index.php/component/k2/itemlist/user/2729242
https://forum.shaiyaslayer.tk/index.php?topic=157666.0
http://myrechockey.com/forums/index.php?topic=117943.0
http://www.hmotors.co.kr/inquiry/26259
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=110442
http://divespace.co.kr/board/180493
https://www.hwbms.com/web/qna/11351
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=650769
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=ab9022a26baabfce7831cfd62a4a751b&topic=10617.0
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=190015
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=85075
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=14123
http://www.ekemoon.com/240247/050720194126/
http://mobility-corp.com/index.php/component/k2/itemlist/user/2696533
http://sejong-thesharpyemizi.co.kr/m1/27345
http://www.kwpcoop.or.kr/QnA/22122
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=16846
http://jjimdak.callbank.kr/index.php?document_srl=1121306&mid=board_OGFN30
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/106623
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16559
http://vtservices85.fr/smf2/index.php?PHPSESSID=50017d597923e442783a398e54ae615a&topic=291528.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=386672
https://www.shaiyax.com/index.php?topic=404367.0
http://taklongclub.com/forum/index.php?topic=188300.0
http://www.cyberblissstudios.com/UserProfile/tabid/42/UserID/2324020/Default.aspx
http://universalcommunity.se/Forum/index.php?topic=35662.0
http://patagroupofcompanies.com/component/k2/itemlist/user/306486
http://daesestudy.co.kr/ipsi_docu/121052
http://kyj1225.godohosting.com/board_mebR72/99546
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=173228
http://zsmr.com.ua/index.php/component/k2/itemlist/user/654113
http://divespace.co.kr/board/258822
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=357770
http://looksun.co.kr/index.php?mid=board_4&document_srl=154863
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=96370
https://www.chirorg.com/?document_srl=198315
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2794881
http://loverstory.co.kr/board_UYNJ05/97219
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5020000
http://callman.co.kr/index.php?mid=qa&document_srl=235442
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=131424
http://juroweb.com/xe/juroweb_board/114592
http://www.hmotors.co.kr/inquiry/68814
http://gallerychoi.com/Exhibition/336349
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=50251
https://serverpia.co.kr/board_ucCk10/135003
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7473502
http://bobr.site/index.php?topic=184578.0
https://www.hwbms.com/web/qna/45531
http://gtupuw.org/index.php/component/k2/itemlist/user/1996826
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/850595
http://forum.bmw-e60.eu/index.php?topic=11351.0
http://bobr.site/index.php?topic=178117.0
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=140766
http://vervetama.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-swkc-%d1%80%d0%b0%d1%81/
http://k-cea.org/board_Hnyj62/191669
http://forum.elexlabs.com/index.php?topic=62347.0
http://thermoplast.envolgroupe.com/component/k2/author/157684
http://jiral.net/?document_srl=29287
http://jiral.net/an9/40965
http://1661-6471.co.kr/news/101945
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1538671
https://www.limscave.com/forum/viewtopic.php?t=56947
http://kockazatkutato.hu/component/k2/itemlist/user/42962
http://themasters.pro/file_01/228242
http://www.aloeverasas.it/index.php/component/k2/itemlist/user/21508
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1152247
http://askpharm.net/board_NQiz06/254493
http://roikjer.com/forum/index.php?PHPSESSID=h2iapkmv1f92nba2es9lmjot82&topic=935193.0
http://www.arunagreen.com/?option=com_k2&view=itemlist&task=user&id=1155003
http://xn----3x5er9r48j7wemud0a387h.com/news/269230
https://www.hohoyoga.com/testboard/4058249
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=41164
http://proxima.co.rw/index.php/component/k2/itemlist/user/718217
https://www.regalepadova.it/index.php/component/k2/itemlist/user/8200
http://constellation.kro.kr/board_kbku73/118315
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/333962
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/49644
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=309773
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4902027
http://daltso.com/index.php?document_srl=191190&mid=board_cUYy21
http://kyj1225.godohosting.com/board_mebR72/98635
https://blossomug.com/index.php/component/k2/itemlist/user/1112836
https://khuyenmaikk13.info/index.php?topic=229171.0
http://matrixpharm.ru/forum/index.php?PHPSESSID=sbr0v3oqpb34li0j8u0namb2g5&action=profile;u=217846
http://looksun.co.kr/index.php?mid=board_4&document_srl=202545
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1769662
http://cwon.kr/xe/board_bnSr36/315440
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=111875
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1995273
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tf8h-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://beautypouch.net/index.php?mid=board_09&document_srl=171072
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=1071192
http://lucky.kidspann.net/index.php?mid=qna&document_srl=353373
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=312317
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2740970
http://otitismediasociety.org/forum/index.php?topic=200774.0
http://dessa.com.br/index.php/component/k2/itemlist/user/386157
http://carand.co.kr/?document_srl=92856
https://blossomug.com/?option=com_k2&view=itemlist&task=user&id=1112309
http://sejong-thesharpyemizi.co.kr/m1/86484
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=196347
http://sy.korean.net/qna/513768
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/88626
https://betshin.com/Story/205034
https://betshin.com/Story/208698
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=223569
https://www.2ayes.com/19562/3-2-acru-3-2-newstudio
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1174041
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16052
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=39735.0
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1326771
http://0433.net/budongsan/113646
http://benzmall.co.kr/index.php?mid=download&document_srl=116164
http://www.dore2cuo.de/index/users/view/id/14478
http://netsconsults.com/index.php/component/k2/itemlist/user/844108
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3755166
http://askpharm.net/board_NQiz06/159966
https://forum.ac-jete.it/index.php?topic=451725.0
http://ovotecegg.com/component/k2/itemlist/user/231646
http://gochon-iusell.co.kr/g1/75174
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=17064
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=99369
http://xn--2e0bk61btjo.com/notice/21296
http://hyeonjun.co.kr/menu3/406259
http://rabbitzone.xyz/FREE/102668
http://kwpub.kr/PUBS/136948
http://sunele.co.kr/board_ReBD97/224918
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1549836
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=233338
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1745928
http://looksun.co.kr/index.php?mid=board_4&document_srl=212210
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/61134
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=1145670
http://daltso.com/index.php?document_srl=145384&mid=board_cUYy21
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=104912
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=40048.0
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=39677.0
http://rabat.kr/board_yCgT00/67745
http://www.kwpcoop.or.kr/QnA/19638
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=19252
http://loverstory.co.kr/board_UYNJ05/106049
https://forums.lfstats.com/viewtopic.php?t=320927
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/333899
http://jnk-ent.jp/index.php?mid=gallery&document_srl=304526
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=18842
http://naksansacondo.com/?document_srl=79173
http://www.popolsku.fr.pl/forum/index.php?topic=417083.0
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=345586
https://nextezone.com/index.php?action=profile;u=8803
http://rabbitzone.xyz/FREE/61056
http://www.teedinubon.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-br3%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f28-05/
http://benzmall.co.kr/index.php?mid=download&document_srl=116104
http://divespace.co.kr/board/265874
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42491
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16382
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=230106
http://www.ekemoon.com/245615/050320193529/
http://dreamplusart.com/mn03_01/214491
https://www.celekt.com/%d0%a0%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rbys-%d0%a0%d0%b0%d1%81/
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=190873
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/852337
http://gochon-iusell.co.kr/g1/77646
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3484684
http://www.venusjeju.com/index.php?mid=QnA&document_srl=644
http://proxima.co.rw/index.php/component/k2/itemlist/user/717727
http://gusinoepero.ru/archives/26111
http://mobility-corp.com/index.php/component/k2/itemlist/user/2730657
http://mediaville.me/index.php/component/k2/itemlist/user/366263
http://mglpcm.org/board_ETkS12/126265
http://kockazatkutato.hu/index.php/component/k2/itemlist/user/42933
https://nple.com/xe/pds/150024
http://www.dap.com.py/index.php/component/k2/itemlist/user/850554
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5019758
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=925240
http://gusinoepero.ru/archives/30370
http://midorijapaneserestaurant.ca/menu/News/64828
http://fbpharm.net/index.php/component/k2/itemlist/user/87120
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=204636
http://dsyang.com/board_Kvgn62/43947
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=43392
http://midorijapaneserestaurant.ca/menu/News/33073
http://naksansacondo.com/board_MGPu57/103623
http://hotelnomadpalace.com/component/k2/itemlist/user/22966
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=29048
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=129613
http://thermoplast.envolgroupe.com/component/k2/itemlist/user/174071
http://www.spazioad.com/component/k2/itemlist/user/7420990
http://daltso.com/?document_srl=206120
http://xn----3x5er9r48j7wemud0a387h.com/news/224188
http://socialmag.bayareanonprofits.xyz/blogs/viewstory/130364
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=40149.0
http://www.proandpro.it/?option=com_k2&view=itemlist&task=user&id=4721362
http://carand.co.kr/d2/96634
http://www.rocketdan.co.kr/?document_srl=146118
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=28313
https://altaylarteknoloji.com/index.php?topic=6797.0
https://timecker.com/anonymous/214410
http://8.droror.co.il/uncategorized/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cn8%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be/
http://8.droror.co.il/uncategorized/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ol4%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be/
http://8.droror.co.il/uncategorized/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dq7%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f30-05/
https://nextezone.com/index.php?action=profile;u=17366
http://mtuan93.com/board_uCqR85/6641
https://forum.clubeicaro.pt/index.php?topic=2891.0
https://forum.shaiyaslayer.tk/index.php?topic=177437.0
https://nextezone.com/index.php?topic=90558.0
http://hotelnomadpalace.com/es/?option=com_k2&view=itemlist&task=user&id=23240
https://prosto-vkus.ru/?option=com_k2&view=itemlist&task=user&id=37092
https://gonggamlaw.com/lawcase/148065
http://dcasociados.eu/component/k2/itemlist/user/93281
https://altaylarteknoloji.com/index.php?topic=6649.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=d6161d0a04f8c7dc9b3405c975c9a859&topic=291490.0
http://lucky.kidspann.net/index.php?mid=qna&document_srl=294432
https://www.hwbms.com/web/qna/39608
http://bobr.site/index.php?topic=184535.0
http://dsyang.com/board_Kvgn62/30809
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=372008
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=841025
https://2002.shyoon.com/board_2002/281768
http://www.eunhaele.co.kr/xe/board/20364
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=357903
http://divespace.co.kr/board/178657
http://askpharm.net/board_NQiz06/250663
https://www.hohoyoga.com/testboard/4058442
http://ovotecegg.com/component/k2/itemlist/user/226649
http://autospa.lv/index.php/lv/component/k2/itemlist/user/10660
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5015617
http://lavaggio.com.vn/index.php/component/k2/itemlist/user/3903647
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3400116
http://benzmall.co.kr/index.php?mid=download&document_srl=97153
http://looksun.co.kr/index.php?document_srl=185810&mid=board_4
http://ko.myds.me/board_story/279928
http://8.droror.co.il/uncategorized/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wa8%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f30-05/
http://8.droror.co.il/uncategorized/%d0%ba%d0%be%d0%bf-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pd8%d0%ba%d0%be%d0%bf-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f30-05-2019/
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=110297
http://8.droror.co.il/uncategorized/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wg3%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be/
http://8.droror.co.il/uncategorized/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zv6%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f30-05/
http://hotelnomadpalace.com/es/?option=com_k2&view=itemlist&task=user&id=23464
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=110315
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/67001
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=29031
https://forum.clubeicaro.pt/index.php?topic=2970.0
https://www.c-alice.org/forum/index.php?topic=101633.0
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3542218
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/392368
http://pkgersang.dothome.co.kr/board_jiKY24/40803
http://loverstory.co.kr/?document_srl=108397
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=408100
http://jdcalc.com/forum/viewtopic.php?t=282896
http://wigalseguros.com.br/index.php/component/k2/itemlist/user/28771
https://cybergsm.es/index.php?topic=62498.0
http://iymc.or.kr/pds/117372
http://compultras.com/?option=com_k2&view=itemlist&task=user&id=251031
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229774
http://www.rationalkorea.com/xe/?document_srl=666066
http://isch.kr/board_PowH60/157926
http://e-educ.net/Forum/index.php?topic=16345.0
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=551734
http://1661-6471.co.kr/news/41509
http://naksansacondo.com/board_MGPu57/98924
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=490298
http://carand.co.kr/d2/90862
http://hyeonjun.co.kr/?document_srl=371730
http://rfc11th13th.dothome.co.kr/Board5/29105
http://sunele.co.kr/board_ReBD97/246114
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229337
http://www.theocraticamerica.org/forum/index.php?topic=77733.0
http://d-tube.info/board_jvyO69/369784
http://smartacity.com/component/k2/itemlist/user/97919
http://barobus.kr/qna/95804
https://www.hohoyoga.com/testboard/3972847
http://loverstory.co.kr/board_UYNJ05/98347
http://askpharm.net/board_NQiz06/273716
http://juroweb.com/xe/juroweb_board/85757
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/332700
http://rabat.kr/board_yCgT00/81374
http://dev.aabn.org.gh/component/k2/itemlist/user/719098
http://israengineering.com/index.php/component/k2/itemlist/user/1323489
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2007673
http://www.venusjeju.com/index.php?mid=QnA&document_srl=2031
http://smartacity.com/component/k2/itemlist/user/93420
http://smartacity.com/component/k2/itemlist/user/97423
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=8133752b55279ef7d080b87bb7215cc1&topic=11288.0
http://gochon-iusell.co.kr/g1/74323
http://themasters.pro/file_01/228409
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3480934
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3782018
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-oc7k-%d0%ba%d0%be%d0%bf-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=26101
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/166997
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=183348
http://gabisan.com/board_OuDs04/71706
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=224047
http://jiral.net/?document_srl=30683
http://midorijapaneserestaurant.ca/menu/News/45178
https://gonggamlaw.com/lawcase/133258
http://dcasociados.eu/component/k2/itemlist/user/94576
http://daltso.com/index.php?mid=board_cUYy21&document_srl=193929
https://gonggamlaw.com/lawcase/138609
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/165906
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=31120
http://dev.aabn.org.gh/component/k2/itemlist/user/727423
http://bath-family.com/?document_srl=134685
http://gardenpjw.dothome.co.kr/board_LOcC77/722771
http://kyj1225.godohosting.com/board_mebR72/100989
http://dospuntoseventos.cl/component/k2/itemlist/user/16118
http://gabisan.com/board_OuDs04/161383
http://ko.myds.me/board_story/279150
https://timecker.com/anonymous/187961
http://yooseok.com/board_BkvT46/412715
http://naksansacondo.com/board_MGPu57/94697
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3483768
http://www2.yasothon.go.th/smf/index.php?topic=159.170730
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=338595
http://gtupuw.org/index.php/component/k2/itemlist/user/1975151
http://roikjer.com/forum/index.php?PHPSESSID=8uups464mco6vkdjs0dmstaut5&topic=931802.0
http://forum.bmw-e60.eu/index.php?topic=11286.0
http://askpharm.net/board_NQiz06/160080
http://gochon-iusell.co.kr/g1/77579
http://dreamplusart.com/mn03_01/123843
http://daltso.com/index.php?mid=board_cUYy21&document_srl=208388
http://looksun.co.kr/index.php?mid=board_4&document_srl=187850
http://www2.yasothon.go.th/smf/index.php?topic=159.171750
http://www.ekemoon.com/244973/052120190528/
http://neosky.net/xe/space_station/102450
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/48328
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=916290
http://music.start-a-idea.online/blogs/viewstory/48202
https://esel.gist.ac.kr/esel2/board_hmgj23/269902
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3790900
http://www.ekemoon.com/244315/051020195728/
http://hyeonjun.co.kr/menu3/375938
http://k-cea.org/board_Hnyj62/195555
http://www.sp1.football/index.php?mid=faq&document_srl=689452
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1550800
http://dessa.com.br/component/k2/itemlist/user/393626
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=390923
https://www.bmwstyle.ru/forum/index.php?topic=65367.0
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=392318
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4899211
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3781294
http://barobus.kr/qna/78055
http://gardenpjw.dothome.co.kr/board_LOcC77/729514
http://www.jesusandmarypatna.com/index.php/component/k2/itemlist/user/3570639
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=371209
http://mobility-corp.com/index.php/component/k2/itemlist/user/2741143
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2007352
https://betshin.com/Story/193102
http://guiadetudo.com/index.php/component/k2/itemlist/user/12704
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=1119020
http://ko.myds.me/board_story/282622
http://jdcalc.com/forum/viewtopic.php?t=292394
http://viamania.net/index.php?mid=board_raYV15&document_srl=127026
http://ariji.kr/?document_srl=973680
http://photogrotto.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ok8h-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://healthyteethpa.org/component/k2/itemlist/user/5546580
http://apt2you2.cafe24.com/g1/rss
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/173535
http://dev.aabn.org.gh/component/k2/itemlist/user/685551
http://iymc.or.kr/pds/116335
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1499015
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=191692
http://apt2you2.cafe24.com/g1/44778
https://betshin.com/Story/218564
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=210791
http://myrechockey.com/forums/index.php?topic=119792.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2797930
https://www.hohoyoga.com/testboard/4073388
https://forum.ac-jete.it/index.php?topic=441824.0
https://www.chirorg.com/?document_srl=144558
http://cwon.kr/xe/board_bnSr36/285598
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=298442
http://dessa.com.br/component/k2/itemlist/user/394374
http://www.popolsku.fr.pl/forum/index.php?topic=417183.0
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=380663
https://www.chirorg.com/?document_srl=150340
https://www.shaiyax.com/index.php?topic=402075.0
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1935911
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=368871
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=144349
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=116836
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=17353
http://warmfund.net/p/index.php?mid=financing&document_srl=524361
https://www.shaiyax.com/index.php?topic=408239.0
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=119310
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=123505
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=387963
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16922
http://melchinooddle.dothome.co.kr/?document_srl=19067
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=140360
http://dev.aabn.org.gh/component/k2/itemlist/user/726369
http://lucky.kidspann.net/index.php?mid=qna&document_srl=311198
https://forums.lfstats.com/viewtopic.php?f=6&t=320133&view=print
http://kyj1225.godohosting.com/board_mebR72/99933
http://looksun.co.kr/index.php?mid=board_4&document_srl=187018
http://apt2you2.cafe24.com/g1/53995
http://www.venusjeju.com/index.php?mid=QnA&document_srl=1933
https://cybergsm.es/index.php?topic=62992.0
http://askpharm.net/board_NQiz06/257982
http://sfah.ch/de/component/k2/itemlist/user/15494
http://hotelnomadpalace.com/es/?option=com_k2&view=itemlist&task=user&id=22666
http://dsyang.com/board_Kvgn62/41498
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=764849
http://askpharm.net/board_NQiz06/282356
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=45325
http://shinhwaair2017.cafe24.com/issue/487258
http://ovotecegg.com/component/k2/itemlist/user/222292
http://midorijapaneserestaurant.ca/menu/?document_srl=49397
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=30367
http://daltso.com/index.php?mid=board_cUYy21&document_srl=122740
http://alastair030.dothome.co.kr/index.php?mid=board_MMiF30&document_srl=24228
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1502756
http://carand.co.kr/d2/100091
http://gabisan.com/?document_srl=112602
http://looksun.co.kr/index.php?mid=board_4&document_srl=192290
https://gonggamlaw.com/lawcase/136958
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=42818
http://www.kspace.cc/xe/?document_srl=89096
http://test.comics-game.ru/index.php?topic=680.0
http://dreamplusart.com/mn03_01/204398
https://forum.ac-jete.it/index.php?topic=447327.0
http://rfc11th13th.dothome.co.kr/Board5/35298
https://www.hohoyoga.com/testboard/4089280
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2798125
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=262640
http://elegance-slimup.com/?option=com_k2&view=itemlist&task=user&id=4956
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3568804
http://taklongclub.com/forum/index.php?topic=200434.0
http://eugeniocolazzo.it/forum/index.php?topic=180566.0
https://www.hwbms.com/web/qna/39787
http://dreamplusart.com/mn03_01/120449
http://looksun.co.kr/index.php?mid=board_4&document_srl=202482
http://carand.co.kr/d2/87832
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=243518
http://guiadetudo.com/index.php/component/k2/itemlist/user/12715
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7473397
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=234067
http://vtservices85.fr/smf2/index.php?PHPSESSID=0ff401542bbd8e59219d912dd395c65c&topic=294875.0
http://kyj1225.godohosting.com/board_mebR72/95791
http://kyj1225.godohosting.com/board_mebR72/88173
http://gallerychoi.com/Exhibition/384520
http://looksun.co.kr/index.php?mid=board_4&document_srl=201898
http://askpharm.net/board_NQiz06/275043
http://mglpcm.org/board_ETkS12/163282
http://ko.myds.me/board_story/275869
http://bizchemical.com/board_kMpv94/2160192
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=1119995
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=93669
https://www.hwbms.com/web/qna/12095
http://ko.myds.me/board_story/266935
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13804
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=66985
http://yoriyorifood.com/xxxx/spacial/354954
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=177927
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2009957
http://socialmag.bayareanonprofits.xyz/blogs/viewstory/131193
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1049157
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=558421
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=203012
http://naksansacondo.com/board_MGPu57/54779
https://www.hwbms.com/web/qna/30963
http://praisesound.co.kr/sub04_01/100654
http://tiretech.co.kr/index.php?mid=qna&document_srl=182470
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iy4a-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19/
http://isch.kr/board_PowH60/156490
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=36810
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3792224
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=85260
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=711364
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13785
http://carand.co.kr/d2/99257
https://forums.lfstats.com/viewtopic.php?t=321490
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=181955
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/852142
http://knet.dothome.co.kr/xe/board_RJHw15/15113
http://roikjer.com/forum/index.php?PHPSESSID=4aqomud9n1oomr52iq1roui5p4&topic=930197.0
http://music.start-a-idea.online/blogs/viewstory/53305
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=76b69ba275551a782cd0a907806b4d30&topic=11214.0
http://archeaudio.com/xe/board_AOYj82/11327
http://iymc.or.kr/pds/117242
http://guiadetudo.com/index.php/component/k2/itemlist/user/12654
http://roikjer.com/forum/index.php?PHPSESSID=pm30vci6b0jdnkmvd0gobv4ed6&topic=931794.0
http://153.120.114.241/eso/index.php/17537784-rasskaz-sluzanki-3-sezon-5-seria-koih-rasskaz-sluzanki-3-sezon-
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=139853
http://naksansacondo.com/board_MGPu57/32360
https://2002.shyoon.com/board_2002/172746
http://www.popolsku.fr.pl/forum/index.php?topic=20407.82410
http://proxima.co.rw/index.php/component/k2/itemlist/user/713903
https://www.hohoyoga.com/?document_srl=4059257
http://naksansacondo.com/?document_srl=101017
http://knet.dothome.co.kr/xe/board_RJHw15/22100
http://www.vamoscontigo.org/Noticia/221593
http://masanlib.or.kr/g1/95169
http://looksun.co.kr/index.php?mid=board_4&document_srl=204658
https://turimex.mx.solemti.net/component/k2/itemlist/user/14174
http://xn--2e0b53df5ag1c804aphl.net/nuguna/182604
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/50701
https://timecker.com/anonymous/210123
http://mvisage.sk/index.php/component/k2/itemlist/user/119895
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/59900
http://8.droror.co.il/uncategorized/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fq6%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5/
https://nextezone.com/index.php?topic=90144.0
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=50858
https://www.regalepadova.it/index.php/component/k2/itemlist/user/8466
https://www.c-alice.org/forum/index.php?topic=100555.0
http://8.droror.co.il/uncategorized/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ll8%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f30-05/
http://8.droror.co.il/uncategorized/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gc5%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f30-05-20/
https://nextezone.com/index.php?action=profile;u=17262
http://udrpsucks.com/blog/?p=2027
https://www.celekt.com/%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qv6y-%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7/
http://www.ekemoon.com/251745/052320192431/
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=855935
http://www.quattroandpartners.it/component/k2/itemlist/user/1280941
http://www.quattroandpartners.it/component/k2/itemlist/user/1281477
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=87496
http://hotelnomadpalace.com/component/k2/itemlist/user/23678
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7552708
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=856220
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4974779
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1883966
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=23677
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=473390
http://beautypouch.net/index.php?mid=board_09&document_srl=179325
https://forums.lfstats.com/viewtopic.php?f=6&t=315265&view=print
http://www.jesusonly.life/calendar/446312
http://dreamplusart.com/mn03_01/198750
https://nple.com/xe/pds/169031
http://pekosmile.dothome.co.kr/index.php?mid=seoulitestudio&document_srl=435068
http://music.start-a-idea.online/blogs/viewstory/44270
http://hanga5.com/index.php?mid=board_photo&document_srl=110619
https://gonggamlaw.com/lawcase/66523
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/17704
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1152391
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2740347
http://kockazatkutato.hu/component/k2/itemlist/user/42530
http://www.hmotors.co.kr/?document_srl=26879
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=205969
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/62295
http://kyj1225.godohosting.com/board_mebR72/100719
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3927058
http://midorijapaneserestaurant.ca/menu/News/65308
http://jnk-ent.jp/index.php?mid=gallery&document_srl=331549
http://engeena.com/component/k2/itemlist/user/9231
http://ko.myds.me/board_story/305497
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=2000704
http://www.ekemoon.com/244987/052120191028/
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=103253
http://www.golden-nail.co.kr/press/420122
https://nextezone.com/index.php?action=profile;u=12717
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=376127
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kg8c-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://beautypouch.net/index.php?mid=board_09&document_srl=101097
https://www.hohoyoga.com/testboard/4099988
https://www.hohoyoga.com/testboard/4100130
https://www.hohoyoga.com/testboard/4100135
https://www.hohoyoga.com/testboard/4100150
https://www.hwbms.com/web/?document_srl=51854
https://www.hwbms.com/web/qna/51831
http://bath-family.com/photo_zone/129204
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4898320
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=48542
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=399579
http://otitismediasociety.org/forum/index.php?topic=201216.0
http://erhu.eu/viewtopic.php?t=397649
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=389759
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=213785
http://midorijapaneserestaurant.ca/menu/News/65621
http://otitismediasociety.org/forum/index.php?topic=198707.0
http://loverstory.co.kr/board_UYNJ05/55063
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=44500
http://divespace.co.kr/board/258924
http://carand.co.kr/d2/68346
https://gonggamlaw.com/lawcase/139761
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=30456
http://loverstory.co.kr/board_UYNJ05/67204
http://thermoplast.envolgroupe.com/component/k2/author/156873
http://www.theocraticamerica.org/forum/index.php?topic=70696.0
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=97551
https://gonggamlaw.com/lawcase/125442
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=66823
http://loverstory.co.kr/board_UYNJ05/107831
http://rabat.kr/board_yCgT00/69182
https://betshin.com/Story/221325
http://lucky.kidspann.net/index.php?mid=qna&document_srl=289951
http://naksansacondo.com/board_MGPu57/93842
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/371898
http://themasters.pro/file_01/228078
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/66480
http://ptu.imoove.kr/ko/content/%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-alpf-%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-fx341533
http://rudraautomation.com/index.php/component/k2/author/338970
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=27791
http://dsyang.com/board_Kvgn62/43187
http://0433.net/budongsan/112239
http://xn----3x5er9r48j7wemud0a387h.com/news/260172
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=84753
http://ye-dream.com/qa/257456
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3877605
http://p9912.cafe24.com/board_LVgu51/45973
http://8.droror.co.il/uncategorized/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ajgz-%d1%80%d0%b0%d1%81/
http://themasters.pro/file_01/327305
http://forum.elexlabs.com/index.php?topic=67509.0
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2012885
http://gtupuw.org/index.php/component/k2/itemlist/user/2008012
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=412107
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=412375
http://hotelnomadpalace.com/index.php/component/k2/itemlist/user/23169
http://rudraautomation.com/index.php/component/k2/author/358480
http://smartacity.com/component/k2/itemlist/user/99815
http://thermoplast.envolgroupe.com/component/k2/author/183914
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=31797
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=31850
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1754148
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1551204
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=109976
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=855102
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=973018
https://gonggamlaw.com/lawcase/132163
http://foa.egerton.ac.ke/?option=com_k2&view=itemlist&task=user&id=1940368
http://myrechockey.com/forums/index.php?topic=117889.0
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pylh-%d1%80%d0%b0%d1%81/
http://jiral.net/an9/29183
http://www.quattroandpartners.it/component/k2/itemlist/user/1256818
http://www.lgue.co.kr/?document_srl=113280
http://www.crnmedia.es/component/k2/itemlist/user/91708
http://sfah.ch/de/component/k2/itemlist/user/15572
http://dospuntoseventos.cl/component/k2/itemlist/user/16271
http://askpharm.net/board_NQiz06/250104
http://www.hmotors.co.kr/inquiry/25976
http://divespace.co.kr/board/222936
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rlzm-%d1%80%d0%b0%d1%81/
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=77470
http://dsyang.com/board_Kvgn62/47422
http://dsyang.com/board_Kvgn62/47434
http://dsyang.com/board_Kvgn62/47440
http://midorijapaneserestaurant.ca/menu/News/79570
http://naksansacondo.com/board_MGPu57/105581
http://naksansacondo.com/board_MGPu57/105643
http://naksansacondo.com/board_MGPu57/105758
http://naksansacondo.com/board_MGPu57/105820
http://www.leekeonsu-csi.com/?document_srl=1218578
https://gonggamlaw.com/lawcase/155630
https://gonggamlaw.com/lawcase/155653
https://gonggamlaw.com/lawcase/155690
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1537838
http://archeaudio.com/xe/board_AOYj82/10984
http://sd-xi.co.kr/g1/83115
http://yooseok.com/board_BkvT46/411765
https://www.lwfservers.com/index.php?topic=74450.0
http://neosky.net/xe/space_station/119809
http://xn----3x5er9r48j7wemud0a387h.com/news/276041
http://looksun.co.kr/index.php?mid=board_4&document_srl=207406
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cf3b-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17/
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16683
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=35912
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xtip-%d1%80%d0%b0%d1%81/
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=23195
http://dcasociados.eu/component/k2/itemlist/user/93204
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/89391
http://apt2you2.cafe24.com/g1/37813
http://loverstory.co.kr/board_UYNJ05/104898
http://daltso.com/index.php?mid=board_cUYy21&document_srl=211868
http://jdcalc.com/forum/viewtopic.php?t=290516
https://www.hohoyoga.com/testboard/4093935
https://www.hohoyoga.com/testboard/4093956
https://www.hwbms.com/web/qna/47541
http://midorijapaneserestaurant.ca/menu/News/80377
http://midorijapaneserestaurant.ca/menu/News/80441
http://midorijapaneserestaurant.ca/menu/News/80509
http://naksansacondo.com/board_MGPu57/106988
http://naksansacondo.com/board_MGPu57/107036
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1222177
https://gonggamlaw.com/lawcase/156672
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=13639
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=97524
http://pekosmile.dothome.co.kr/index.php?mid=seoulitestudio&document_srl=436638
http://agiteshop.com/xe/qa/164375
http://mediaville.me/index.php/component/k2/itemlist/user/368535
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=212116
http://www.cyberblissstudios.com/UserProfile/tabid/42/UserID/2350778/Default.aspx
https://khuyenmaikk13.info/index.php?topic=225994.0
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=1124947
http://barobus.kr/qna/94791
http://www.vamoscontigo.org/Noticia/139720
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3794388
http://www.theocraticamerica.org/forum/index.php?topic=69597.0
https://esel.gist.ac.kr/esel2/board_hmgj23/370878
http://naksansacondo.com/board_MGPu57/35187
http://dreamplusart.com/mn03_01/186485
http://roikjer.com/forum/index.php?PHPSESSID=pv0auk95a5q9u1kd5vr1liuf96&topic=931660.0
http://esperanzazubieta.com/index.php/component/k2/itemlist/user/108132
http://mediaville.me/index.php/component/k2/itemlist/user/378236
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1999982
http://www.aloeverasas.it/index.php/component/k2/itemlist/user/21482
http://rabbitzone.xyz/FREE/126163
http://fbpharm.net/index.php/component/k2/itemlist/user/87317
http://mglpcm.org/board_ETkS12/192643
https://www.celekt.com/%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bu0i-%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17/
http://yoriyorifood.com/xxxx/spacial/328397
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=138442
http://gallerychoi.com/Exhibition/334698
http://leonwebzine.dothome.co.kr/guest/12047
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=213797
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=798268
http://carand.co.kr/d2/101015
http://sofficer.net/xe/teach/288603
https://www.hohoyoga.com/testboard/4059164
http://praisesound.co.kr/sub04_01/87213
https://www.2ayes.com/19626/3-3-ahfy-3-3
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1120142
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/?document_srl=146723
http://mglpcm.org/board_ETkS12/125992
http://midorijapaneserestaurant.ca/menu/News/51669
http://www.livetank.cn/market1/215579
http://benzmall.co.kr/index.php?mid=download&document_srl=99167
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=22699
http://www.coating.or.kr/atemfair_data/16345
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=89604
http://ko.myds.me/board_story/279564
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16142
http://askpharm.net/board_NQiz06/159983
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=126414
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=142874
https://mcsetup.tk/bbs/index.php?topic=262314.0
http://ilsannabgol.kr/board_brJk31/1368511
http://www.itosm.com/cn/board_nLoq17/132036
http://yoriyorifood.com/xxxx/spacial/357480
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=231035
http://barobus.kr/qna/74470
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=366328
https://khuyenmaikk13.info/index.php?topic=228352.0
http://loverstory.co.kr/board_UYNJ05/110852
http://loverstory.co.kr/?document_srl=105156
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16228
https://betshin.com/Story/209211
http://www.spazioad.com/component/k2/itemlist/user/7421162
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=669198
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=198533
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=2001880
http://blog.ptpintcast.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-piao-%d1%80%d0%b0%d1%81/
http://daltso.com/index.php?mid=board_cUYy21&document_srl=204548
http://rabbitzone.xyz/FREE/120053
http://bobr.site/index.php?topic=184859.0
http://rudraautomation.com/index.php/component/k2/author/354642
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=340577
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=118364
http://music.start-a-idea.online/blogs/viewstory/44435
http://www.patrasin.kr/index.php?mid=questions&document_srl=4344688
http://universalcommunity.se/Forum/index.php?topic=35735.0
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=84910
http://www.ekemoon.com/246031/050720194429/
http://vtservices85.fr/smf2/index.php?PHPSESSID=7a1c41a6c76559550d35ddc05b2a4de5&topic=290906.0
http://cwon.kr/xe/board_bnSr36/299715
http://isch.kr/board_PowH60/158247
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/60351
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=32014
https://betshin.com/Story/196415
https://cybergsm.es/index.php?topic=72516.0
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=43925
https://www.shaiyax.com/index.php?topic=430987.0
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=18187
http://arquitectosenreformas.es/component/k2/itemlist/user/85937
http://looksun.co.kr/index.php?mid=board_4&document_srl=123470
https://cybergsm.es/index.php?topic=72883.0
http://askpharm.net/board_NQiz06/273716
http://dreamplusart.com/mn03_01/214123
http://www.vamoscontigo.org/Noticia/139000
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=917646
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1733713
http://hotelnomadpalace.com/component/k2/itemlist/user/23152
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3932774
http://forum.elexlabs.com/index.php?topic=68315.0
https://betshin.com/Story/205313
http://ariji.kr/?document_srl=1025123
http://e-educ.net/Forum/index.php?topic=17051.0
http://ajincomp.godohosting.com/board_STnh82/163590
http://www.svteck.co.kr/customer_gratitude/219973
http://engeena.com/component/k2/itemlist/user/9195
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=183769
http://themasters.pro/file_01/316686
http://midorijapaneserestaurant.ca/menu/News/49063
http://iymc.or.kr/pds/117826
http://dospuntoseventos.cl/component/k2/itemlist/user/16124
http://mediaville.me/index.php/component/k2/itemlist/user/366340
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3568796
http://khapthanam.co.kr/g1/135073
http://askpharm.net/board_NQiz06/282309
http://www.tessabannampad.go.th/webboard/index.php?topic=226926.0
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=18378
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/148405
http://xn--2e0bk61btjo.com/notice/31395
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=231478
http://rabbitzone.xyz/FREE/60526
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=97042
http://daltso.com/?document_srl=203610
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=22556
https://www.hohoyoga.com/testboard/4089771
http://mercibq.net/partner/53413
http://www.vamoscontigo.org/Noticia/209216
http://xn--2e0bk61btjo.com/notice/28429
http://daesestudy.co.kr/ipsi_docu/173253
http://www.svteck.co.kr/customer_gratitude/300952
http://loverstory.co.kr/board_UYNJ05/83955
http://jiral.net/an9/30099
http://dsyang.com/board_Kvgn62/44994
http://erhu.eu/viewtopic.php?t=419392
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=361815
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=210246
http://p9912.cafe24.com/board_LVgu51/67364
http://www.vamoscontigo.org/Noticia/137464
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rjvg-%d1%80%d0%b0%d1%81/
http://constellation.kro.kr/board_kbku73/71574
https://gonggamlaw.com/lawcase/133828
http://herdental.co.kr/index.php?mid=online&document_srl=141204
http://masanlib.or.kr/?document_srl=99722
https://forums.lfstats.com/viewtopic.php?t=318429
https://adsensebih.com/index.php?topic=48519.0
https://www.vegasgreentour.com/?document_srl=569228
http://yoriyorifood.com/xxxx/spacial/330356
https://www.hwbms.com/web/qna/11695
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1151974
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jqpl-%d1%80%d0%b0%d1%81/
http://midorijapaneserestaurant.ca/menu/News/66824
http://www.lgue.co.kr/?document_srl=182374
https://verdadesbiblicas.org.ec/index.php/component/k2/itemlist/user/3867195
http://melchinooddle.dothome.co.kr/?document_srl=14898
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=1179090
http://www.leekeonsu-csi.com/?document_srl=901142
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/345549
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=326045
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=415362
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=605675
http://d-tube.info/board_jvyO69/370009
http://withinfp.sakura.ne.jp/eso/index.php/17572217-rasskaz-sluzanki-3-sezon-1-seria-rtvj-rasskaz-sluzanki-3-sezon-/0
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=454513
http://gallerychoi.com/Exhibition/329095
https://intelogist2.wpengine.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ax7c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://mercibq.net/partner/117198
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2850827
http://otitismediasociety.org/forum/index.php?topic=201296.0
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=947007
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=913722
https://www.chirorg.com/?document_srl=226962
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=2005934
http://herdental.co.kr/index.php?mid=online&document_srl=114078
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/851419
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=400388
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3578588
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/349185
http://kyj1225.godohosting.com/board_mebR72/97921
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=123862
http://www.teedinubon.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fh1%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be/
https://gonggamlaw.com/lawcase/125809
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/173676
https://gonggamlaw.com/lawcase/64202
http://isch.kr/board_PowH60/213737
http://praisesound.co.kr/sub04_01/88381
https://gonggamlaw.com/lawcase/131712
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=153836
http://loverstory.co.kr/board_UYNJ05/96297
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/305009
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=122961
http://loverstory.co.kr/board_UYNJ05/105978
http://dsyang.com/board_Kvgn62/42794
http://holysweat.dothome.co.kr/data/6454
http://myrechockey.com/forums/index.php?topic=117831.0
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=274194
http://kockazatkutato.hu/index.php/component/k2/itemlist/user/42789
https://forums.lfstats.com/viewtopic.php?t=320923
http://jdcalc.com/forum/viewtopic.php?t=292590
http://hyeonjun.co.kr/menu3/289591
http://midorijapaneserestaurant.ca/menu/News/26839
http://kyj1225.godohosting.com/board_mebR72/99907
http://www.svteck.co.kr/customer_gratitude/279419
http://daltso.com/index.php?mid=board_cUYy21&document_srl=202948
https://2002.shyoon.com/board_2002/207292
http://midorijapaneserestaurant.ca/menu/News/77635
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=206225
http://e-educ.net/Forum/index.php?topic=17367.0
http://www.ekemoon.com/245889/050620192329/
http://proxima.co.rw/index.php/component/k2/itemlist/user/691460
http://yoriyorifood.com/xxxx/spacial/305598
http://77.93.38.205/index.php/component/k2/itemlist/user/652335
http://toeden.co.kr/Product_new/142303
http://p9912.cafe24.com/board_LVgu51/67201
https://www.celekt.com/%d0%9a%d0%be%d0%bf-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ao5%d0%9a%d0%be%d0%bf-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f28-05-2019/
http://www.svteck.co.kr/customer_gratitude/307164
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=219429
https://www.hohoyoga.com/testboard/4057864
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=113350
http://tiretech.co.kr/index.php?mid=qna&document_srl=182331
http://gusinoepero.ru/archives/32130
https://gonggamlaw.com/lawcase/146806
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=428751
https://khuyenmaikk13.info/index.php?topic=226643.0
http://loverstory.co.kr/board_UYNJ05/104844
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=524921
http://legride.com/UserProfile/tabid/61/userId/2856172/Default.aspx
http://mobility-corp.com/index.php/component/k2/itemlist/user/2739361
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=602282
http://thermoplast.envolgroupe.com/component/k2/author/181236
https://2002.shyoon.com/board_2002/228822
http://isch.kr/board_PowH60/157252
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=223503
http://rudraautomation.com/index.php/component/k2/itemlist/user/329952
http://agiteshop.com/xe/qa/161745
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=559223
https://nextezone.com/index.php?topic=81369.0
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=97546
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/18904
http://ye-dream.com/qa/206697
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=186475
http://hanga5.com/index.php?mid=board_photo&document_srl=111572
http://bath-family.com/photo_zone/133956
http://rfc11th13th.dothome.co.kr/Board5/33191
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3877347
http://www.ekemoon.com/244049/050720193928/
http://www2.yasothon.go.th/smf/index.php?topic=159.172380
https://betshin.com/Story/219496
http://pkgersang.dothome.co.kr/board_jiKY24/38858
http://dsyang.com/board_Kvgn62/43529
http://thermoplast.envolgroupe.com/component/k2/itemlist/user/179412
http://www.sp1.football/index.php?mid=faq&document_srl=838434
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/65091
http://carand.co.kr/d2/88425
http://smartacity.com/component/k2/itemlist/user/78246
http://universalcommunity.se/Forum/index.php?topic=38555.0
https://forum.ac-jete.it/index.php?topic=446439.0
http://yoriyorifood.com/xxxx/spacial/299828
http://www.m1avio.com/index.php/component/k2/itemlist/user/3835323
http://bebopindia.com/notcie/510266
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/854958
http://web2interactive.com/index.php/component/k2/itemlist/user/3755301
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=108302
http://music.start-a-idea.online/blogs/viewstory/44998
http://www.digitalbul.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nvqn-%d1%80%d0%b0%d1%81/
https://intelogist2.wpengine.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dw1o-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=408696
http://naksansacondo.com/board_MGPu57/73210
https://gonggamlaw.com/lawcase/133178
http://sd-xi.co.kr/g1/70143
http://www.cnsmaker.net/xe/?document_srl=145190
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=35828
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=916228
http://1661-6471.co.kr/news/44659
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/66400
http://bobr.site/index.php?topic=184193.0
http://www.firstfinancialservices.co.uk/component/k2/itemlist/user/42482
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=270723
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=23835
http://guiadetudo.com/index.php/component/k2/itemlist/user/12679
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4941842
http://www2.yasothon.go.th/smf/index.php?topic=159.msg200879
http://kyj1225.godohosting.com/board_mebR72/93542
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=99307
http://sunele.co.kr/board_ReBD97/231635
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3568680
http://kyj1225.godohosting.com/board_mebR72/95287
https://nple.com/xe/pds/151816
http://yoriyorifood.com/xxxx/spacial/254450
http://askpharm.net/board_NQiz06/281642
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=43466
http://taklongclub.com/forum/index.php?topic=204514.0
https://www.shaiyax.com/index.php?topic=407671.0
http://bebopindia.com/?document_srl=513061
https://betshin.com/Story/196252
https://nple.com/xe/pds/150133
http://proxima.co.rw/index.php/component/k2/itemlist/user/721373
http://otitismediasociety.org/forum/index.php?topic=209394.0
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=17220
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1288773
http://carand.co.kr/d2/47940
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=206929
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/59659
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=299705
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/83885
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1536221
http://midorijapaneserestaurant.ca/menu/News/50690
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=558445
http://archeaudio.com/xe/board_AOYj82/11667
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=380472
http://dsyang.com/board_Kvgn62/46181
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=454083
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=230230
https://intelogist2.wpengine.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-aq9z-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
https://www.chirorg.com/?document_srl=154769
http://daltso.com/index.php?mid=board_cUYy21&document_srl=126001
http://constellation.kro.kr/?document_srl=104131
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1736689
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2797004
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=223194
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=50070
http://vtservices85.fr/smf2/index.php?PHPSESSID=385651dd2d2fd0d1dc36e73290f8ec14&topic=288521.0
https://2002.shyoon.com/board_2002/228171
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=130419
http://thermoplast.envolgroupe.com/component/k2/author/178558
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229414
http://gallerychoi.com/Exhibition/329183
http://praisesound.co.kr/sub04_01/109025
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=320833
http://muldorang.com/market/27469
https://forum.ac-jete.it/index.php?topic=441047.0
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=309875
https://www.2ayes.com/19525/3-7-xffg-3-7-syfy?title=%C2%AB%D0%A0%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7+%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8+3+%D1%81%D0%B5%D0%B7%D0%BE%D0%BD+7+%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB+XfFg+%C2%AB%D0%A0%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7+%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8+3+%D1%81%D0%B5%D0%B7%D0%BE%D0%BD+7+%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB+SyFy&category_0=&content_ckeditor_ok=1&content_ckeditor_data=25-05-2019+%D0%A0%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7+%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8+3+%D1%81%D0%B5%D0%B7%D0%BE%D0%BD+7+%D1%81%D0%B5%D1%80%D0%B8%D1%8F+%D0%A1%D0%9C%D0%9E%D0%A2%D0%A0%D0%95%D0%A2%D0%AC+%D0%BD%D0%B0+%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%BE%D0%BC+%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Ca+href%3D%22http://dUEE.3fps.icu/f/0oMk9sFc%22+%3E%3Cimg+src%3D%22https://i.imgur.com/8avTrVF.jpg%22+%3E%3C/a%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Ca+href%3D%22http://dUEE.3fps.icu/f/0oMk9sFc%22%3E%D0%A0%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7+%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8+3+%D1%81%D0%B5%D0%B7%D0%BE%D0%BD+7+%D1%81%D0%B5%D1%80%D0%B8%D1%8F%3C/a%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%D0%A0%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7+%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8+3+%D1%81%D0%B5%D0%B7%D0%BE%D0%BD+7+%D1%81%D0%B5%D1%80%D0%B8%D1%8F+%D0%A1%D1%8B%D0%B5%D0%BD%D0%B4%D1%83%D0%BA+%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%B0%D1%8F+%D0%BE%D0%B7%D0%B2%D1%83%D1%87%D0%BA%D0%B0+%D0%B2%D1%8B%D1%88%D0%BB%D0%B0%21%3Cbr%3E%D0%A1%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C+%D0%BD%D0%BE%D0%B2%D1%83%D1%8E+%D1%81%D0%B5%D1%80%D0%B8%D1%8E+%D0%B2+%D1%85%D0%BE%D1%80%D0%BE%D1%88%D0%B5%D0%BC+%D0%BA%D0%B0%D1%87%D0%B5%D1%81%D1%82%D0%B2%D0%B5%3Cbr%3E%D0%A3+%D0%BD%D0%B0%D1%81+%D0%B2%D1%81%D0%B5+%D0%BD%D0%BE%D0%B2%D1%8B%D0%B5+%D1%81%D0%B5%D1%80%D0%B8%D0%B8+%D1%83%D0%B6%D0%B5+%D0%BF%D0%B5%D1%80%D0%B5%D0%B2%D0%B5%D0%B4%D0%B5%D0%BD%D1%8B+%D0%BD%D0%B0+%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%B8%D0%B9+%3Cbr%3E%3Cbr%3E%D0%A1%D0%BE%D0%B1%D1%8B%D1%82%D0%B8%D0%B9%D0%BD%D1%8B%D0%B9+%D0%BA%D0%B8%D0%BD%D0%BE%D1%84%D0%B8%D0%BB%D1%8C%D0%BC%D0%B0+%C2%AB%D0%A0%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7+%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8+3+%D1%81%D0%B5%D0%B7%D0%BE%D0%BD+7+%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB+%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%B8%D0%B9+%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB+%D1%80%D0%B0%D0%B7%D0%BC%D0%B0%D1%85%D0%B8%D0%B2%D0%B0%D1%8E%D1%82%D1%81%D1%8F+%D0%B2+%D1%8D%D1%82%D0%BE%D0%BC+%D1%80%D0%B5%D1%81%D0%BF%D1%83%D0%B1%D0%BB%D0%B8%D0%BA%D0%B5+%D0%93%D0%B8%D0%BB%D0%B5%D0%B0%D0%BD%D0%B4.+%D0%92+%D0%BF%D0%BE%D0%B4%D0%BE%D0%B1%D0%BD%D0%BE%D0%BC+%D1%81%D1%82%D1%80%D0%B0%D0%BD%D0%B5+%D0%BF%D1%80%D0%B0%D0%B2%D0%B8%D1%82+%D0%B2%D0%BE%D0%B5%D0%BD%D0%BD%D0%BE%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D1%89%D0%B0%D1%8F+%D0%B4%D0%B0+%D0%BA%D1%83%D0%BB%D1%8C%D1%82%D0%BE%D0%B2%D0%B0%D1%8F+%D1%84%D0%B0%D1%88%D0%B8%D0%B7%D0%BC.+%D0%9D%D0%B0%D1%87%D0%B0%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA+%D0%BD%D0%B5%D1%83%D1%81%D1%82%D0%B0%D0%BD%D0%BD%D0%BE+%D0%B1%D0%BE%D1%80%D0%B5%D1%82%D1%81%D1%8F+%D0%B8%D0%B7+%D1%81%D0%BE%D1%81%D0%B5%D0%B4%D0%BD%D0%B8%D0%BC%D0%B8+%D1%81%D1%82%D0%BE%D1%80%D0%BE%D0%BD%D0%B0%D0%BC%D0%B8.+%D0%90+%D0%BF%D0%BE%D1%82%D0%BE%D0%BC+%D0%B2+%D0%BF%D1%80%D0%BE%D1%81%D0%BF%D0%B5%D0%BA%D1%82%D0%B0%D1%85+%D0%BD%D0%B0+%D0%B2%D1%81%D1%8F%D0%BA%D0%BE%D0%BC+%D1%88%D0%B0%D0%B3%D1%83+%D1%80%D0%B0%D1%81%D0%BF%D0%BE%D0%BB%D0%BE%D0%B6%D0%B5%D0%BD%D1%8B+%D1%81%D0%BE%D0%BB%D0%B4%D0%B0%D1%82%D1%81%D0%BA%D0%B8%D0%B9%2C+%D0%BD%D0%B0%D0%B1%D0%BB%D1%8E%D0%B4%D0%B0%D1%8E%D1%89%D0%B8%D0%B5+%D0%B7%D0%B0+%D1%8F%D1%81%D0%BE%D0%BC.+%D0%9D%D0%BE+%D0%B5%D1%89%D0%B5+%D0%BE%D1%81%D0%BD%D0%BE%D0%B2%D0%BE%D0%BF%D0%BE%D0%BB%D0%B0%D0%B3%D0%B0%D1%8E%D1%89%D0%B0%D1%8F+%D1%82%D0%B5%D0%BC%D0%B0%2C+%D0%BD%D0%B0%D0%BB%D0%B8%D1%87%D0%B5%D1%81%D1%82%D0%B2%D1%83%D1%8E%D1%89%D0%B0%D1%8F+%D0%B2+%D1%8D%D1%82%D0%BE%D0%BC+%D0%BF%D0%BE%D0%B4%D0%BE%D0%B1%D0%BD%D0%BE%D0%BC+%D1%81%D0%BE%D0%BE%D0%B1%D1%89%D0%B5%D1%81%D1%82%D0%B2%D0%B5+%E2%80%93+%D0%BC%D0%B5%D1%80%D1%82%D0%B2%D0%BE%D1%80%D0%BE%D0%B6%D0%B4%D0%B5%D0%BD%D0%BD%D0%BE%D1%81%D1%82%D1%8C+%D0%B4%D0%B5%D0%BB%D0%B5%D0%B3%D0%B0%D1%82%D0%BE%D0%BA+%D0%B2%D0%B5%D0%BB%D0%B8%D0%BA%D0%BE%D0%BB%D0%B5%D0%BF%D0%BD%D0%BE%D0%B3%D0%BE+%D0%BF%D0%BE%D0%BB%D0%B0+%D0%B8%D0%B7+%D0%B7%D0%BD%D0%B0%D1%82%D0%B8.+%D0%94%D0%B5%D0%B2%D0%BA%D0%B8%2C+%D0%B8%D0%BC%D0%B5%D0%BD%D0%BD%D0%BE+%D0%BE%D0%BD%D0%B8+%D1%80%D0%B5%D0%BA%D0%BE%D0%BC%D0%B5%D0%BD%D0%B4%D1%83%D1%8E%D1%82+%D0%B0%D1%80%D0%B8%D1%81%D1%82%D0%BE%D0%BA%D1%80%D0%B0%D1%82%D0%B8%D1%8E+%D0%B4%D0%B0+%D0%B2%D0%BE%D1%80%D0%BE%D1%87%D0%B0%D1%8E%D1%82%D1%81%D1%8F+%D0%B2+%D1%83%D0%BA%D0%B0%D0%B7%D0%B0%D0%BD%D0%BD%D0%BE%D0%BC+%D0%B2%D0%BB%D0%B8%D1%8F%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D1%85+%D0%BE%D0%B1%D0%BB%D0%B0%D1%81%D1%82%D1%8F%D1%85%2C+%D0%B7%D0%B0%D0%BC%D0%B5%D0%B4%D0%BB%D1%8F%D1%8E%D1%89%D0%B5%D0%BC+%D0%B4%D0%B0+%D0%B8+%D0%BF%D0%BE%D1%87%D0%B8%D1%82%D0%B0%D0%B5%D0%BC%D1%8B%2C+%D0%BD%D0%BE+%D0%B7%D0%B0%D1%82%D0%BE+%D0%BD%D0%B5+%D1%81%D0%BF%D0%BE%D1%81%D0%BE%D0%B1%D0%BD%D1%8B+%D0%BF%D0%BE%D1%87%D0%B0%D1%82%D1%8C+%D0%BA%D1%80%D0%BE%D1%85%D1%83%2C+%D1%82%D1%8F%D0%B3%D0%B0%D1%82%D1%8C+%D0%B2%D1%81%D0%B5+%D1%8D%D1%82%D0%BE+%D1%82%D0%B0%D0%BA+%D0%B6%D0%B5+%D1%80%D0%BE%D0%B4%D0%B8%D1%82%D1%8C.%3Cbr%3E%3Cbr%3E%D0%9D%D0%B0+%D1%82%D0%BE%D0%B3%D0%BE+%D1%84%D0%B0%D0%BA%D1%82%D0%B0%2C+%D1%87%D1%82%D0%BE%D0%B1%D1%8B+%D1%81%D1%82%D0%B0%D1%82%D1%83%D1%81%D0%BD%D1%8B%D0%B5+%D0%B6%D0%B5%D0%BD%D1%81%D0%BA%D0%BE%D0%B5+%D1%81%D0%BE%D1%81%D0%BB%D0%BE%D0%B2%D0%B8%D0%B5+%D0%BF%D1%80%D0%BE%D1%87%D1%83%D1%8F%D0%BB%D0%B8+%D1%86%D0%B5%D1%80%D0%B5%D1%80%D0%B0%2C+%D1%81%D1%82%D0%B0%D0%BB+%D0%BE%D1%80%D0%B3%D0%B0%D0%BD%D0%B8%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD+%D0%BA%D0%BE%D0%BB%D0%BB%D0%B5%D0%BA%D1%82%D0%B8%D0%B2%D0%BD%D1%8B%D0%B9+%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B0.+%D0%A2%D1%80%D0%B8%D0%B2%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D1%85+%D0%B4%D0%B5%D0%B2+%D1%81%D0%B3%D0%BE%D0%BD%D1%8F%D0%BB%D0%B8+%D0%BA%D0%B0%D0%BA+%D1%81%D0%BF%D0%B5%D1%86%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5+%D0%B1%D0%B8%D0%B2%D1%83%D0%B0%D0%BA%D0%B0%2C+%D0%B3%D0%B4%D0%B5+%D1%8D%D1%82%D0%B8+%D0%B2%D1%8B%D0%B8%D1%81%D0%BA%D0%B8%D0%B2%D0%B0%D0%BB%D0%B8%D1%81%D1%8C+%D0%BF%D0%BE%D0%B4+%D0%BF%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D1%8C%D0%BD%D1%8B%D0%BC+%D0%BD%D0%B0%D0%B1%D0%BB%D1%8E%D0%B4%D0%B5%D0%BD%D0%B8%D0%B5%D0%BC%2C+%D1%81%D1%82%D0%B0%D0%B1%D0%B8%D0%BB%D1%8C%D0%BD%D0%BE+%D1%88%D0%BB%D0%B8+%D0%BD%D0%B5%D1%83%D0%B4%D0%BE%D0%B2%D0%BB%D0%B5%D1%82%D0%B2%D0%BE%D1%80%D0%B8%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE.+%D0%98%D1%85+%D0%B2%D1%81%D0%B5%D0%B3%D0%BE+%D1%85%D0%B0%D1%80%D0%B0%D0%BA%D1%82%D0%B5%D1%80%D0%BD%D0%BE%D0%B9+%D0%BB%D0%B8%D0%BD%D0%B8%D0%B5%D0%B9+%D1%8F%D0%B2%D0%BB%D1%8F%D0%BB%D0%B0%D1%81%D1%8C+%D1%83%D0%B1%D0%BE%D1%80+%D0%BA%D1%80%D0%B0%D1%81%D0%BD%D0%BE%D0%B2%D0%B0%D1%82%D0%BE%D0%B3%D0%BE+%D0%BE%D0%BA%D1%80%D0%B0%D1%81%D1%8B.+%D0%94%D0%BB%D1%8F+%D0%B1%D0%B5%D0%B4%D0%BD%D1%8F%D0%B6%D0%B5%D0%BA+%D0%B2%D0%BE%D0%B4%D0%B8%D0%BB%D0%B0%D1%81%D1%8C+%D0%B5%D0%B4%D0%B2%D0%B0+%D0%B4%D1%80%D1%83%D0%B3%D0%B0%D1%8F+%D0%B2%D1%8B%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5+%E2%80%93+%D0%B2%D0%BE%D0%B7%D0%BD%D0%B8%D0%BA%D0%BD%D0%BE%D0%B2%D0%B5%D0%BD%D0%B8%D0%B5+%D0%B4%D0%B5%D1%82%D0%B2%D0%BE%D1%80%D1%83+%D0%BF%D1%80%D0%BE+%D0%BF%D1%80%D0%B8%D0%B2%D0%B8%D0%BB%D0%B5%D0%B3%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D1%8B%D1%85+%D1%81%D0%B5%D0%BC%D0%B5%D0%B9.+%D0%9F%D0%BE%D0%BD%D1%83%D1%80%D1%8B%D0%B5+%D1%80%D0%B0%D1%81%D0%BA%D1%80%D0%B0%D1%81%D0%B0%D0%B2%D0%B8%D1%86%D1%8B+%D0%BE%D0%B1%D1%8F%D0%B7%D0%B0%D0%BD%D1%8B+%D0%B1%D1%8B%D0%B2%D0%B0%D0%BB%D0%B8+%D0%B1%D0%B5%D1%81%D0%BF%D1%80%D0%B5%D0%BA%D0%BE%D1%81%D0%BB%D0%BE%D0%B2%D0%BD%D0%BE+%D0%BF%D1%80%D0%BE%D0%B4%D0%B5%D0%BB%D1%8B%D0%B2%D0%B0%D1%82%D1%8C+%D0%B2%D1%81%D0%B5+%D1%83%D1%81%D1%82%D0%B0%D0%BD%D0%BE%D0%B2%D0%BA%D0%B8+%D1%82%D0%BE%D0%BD%D1%87%D0%B0%D0%B9%D1%88%D0%B8%D1%85+%D0%BE%D0%BA%D1%80%D1%83%D0%B6%D0%B5%D0%BD%D0%B8%D0%B9%2C+%D1%84%D0%B8%D1%80%D0%BC%D0%B5%D0%BD%D0%BD%D0%BE%D0%B3%D0%BE+%D1%82%D0%BE%D1%87%D0%BA%D0%B8+%D0%B7%D1%80%D0%B5%D0%BD%D0%B8%D1%8F+%D1%83+%D0%B8%D1%85+%D1%8D%D0%BA%D1%81%D0%BF%D0%BB%D1%83%D0%B0%D1%82%D0%B0%D1%86%D0%B8%D0%B8+%D1%8F%D0%B2%D0%BB%D1%8F%D1%82%D1%8C%D1%81%D1%8F+%D0%BD%D0%B5+%D0%BC%D0%BE%D0%B3%D0%BB%D0%BE%2C+%D0%B8%D0%BC+%D1%81%D0%B0%D0%BC%D0%B8%D0%BC+%D1%81%D0%BE%D0%B2%D1%81%D0%B5%D0%BC+%D0%B4%D0%BE%D1%81%D1%82%D0%B0%D0%B2%D0%B0%D0%BB%D0%B8%D1%81%D1%8C+%D0%BD%D0%BE%D0%B2%D0%B5%D0%B9%D1%88%D0%B8%D0%B5+%D0%B8%D0%BC%D0%B5%D0%BD%D0%B0%2C+%D0%B0+%D0%B2%D0%B5%D1%81%D1%8C%D0%BC%D0%B0+%D0%BD%D0%B5%D0%BC%D0%B0%D0%BB%D0%BE%D0%B2%D0%B0%D0%B6%D0%BD%D0%BE%D0%B5+%E2%80%93+%D0%BE%D0%BD%D0%B8+%D1%81%D0%B5%D0%B3%D0%BE%D0%B4%D0%BD%D1%8F+%D0%BF%D0%BE%D0%B4%D0%BE%D0%B1%D0%B0%D1%8E%D1%89%D0%B8%D1%85+%D0%B2%D1%81%D1%82%D1%83%D0%BF%D0%B0%D1%82%D1%8C+%D0%B7%D0%B0+%D0%BB%D1%8E%D0%B1%D0%BE%D0%B2%D0%BD%D1%83%D1%8E+%D1%81%D0%BE%D0%B5%D0%B4%D0%B8%D0%BD%D0%B8%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5+%D0%B7%D0%B2%D0%B5%D0%BD%D0%BE+%D1%81%D0%BE%D0%B2%D0%BC%D0%B5%D1%81%D1%82%D0%BD%D0%BE+%D1%81+%D1%81%D0%BF%D1%80%D0%B0%D0%B2%D0%BD%D1%8B%D0%BC%D0%B8+%D0%B3%D1%80%D0%B0%D0%B6%D0%B4%D0%B0%D0%BD%D0%B0%D0%BC%D0%B8.&content=25-05-2019+%D0%A0%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7+%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8+3+%D1%81%D0%B5%D0%B7%D0%BE%D0%BD+7+%D1%81%D0%B5%D1%80%D0%B8%D1%8F+%D0%A1%D0%9C%D0%9E%D0%A2%D0%A0%D0%95%D0%A2%D0%AC+%D0%BD%D0%B0+%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%BE%D0%BC+%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Ca+href%3D%22http://dUEE.3fps.icu/f/0oMk9sFc%22+%3E%3Cimg+src%3D%22https://i.imgur.com/8avTrVF.jpg%22+%3E%3C/a%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%3Ca+href%3D%22http://dUEE.3fps.icu/f/0oMk9sFc%22%3E%D0%A0%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7+%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8+3+%D1%81%D0%B5%D0%B7%D0%BE%D0%BD+7+%D1%81%D0%B5%D1%80%D0%B8%D1%8F%3C/a%3E%3Cbr%3E%3Cbr%3E%3Cbr%3E%D0%A0%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7+%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8+3+%D1%81%D0%B5%D0%B7%D0%BE%D0%BD+7+%D1%81%D0%B5%D1%80%D0%B8%D1%8F+%D0%A1%D1%8B%D0%B5%D0%BD%D0%B4%D1%83%D0%BA+%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%B0%D1%8F+%D0%BE%D0%B7%D0%B2%D1%83%D1%87%D0%BA%D0%B0+%D0%B2%D1%8B%D1%88%D0%BB%D0%B0%21%3Cbr%3E%D0%A1%D0%BC%D0%BE%D1%82%D1%80%D0%B5%D1%82%D1%8C+%D0%BD%D0%BE%D0%B2%D1%83%D1%8E+%D1%81%D0%B5%D1%80%D0%B8%D1%8E+%D0%B2+%D1%85%D0%BE%D1%80%D0%BE%D1%88%D0%B5%D0%BC+%D0%BA%D0%B0%D1%87%D0%B5%D1%81%D1%82%D0%B2%D0%B5%3Cbr%3E%D0%A3+%D0%BD%D0%B0%D1%81+%D0%B2%D1%81%D0%B5+%D0%BD%D0%BE%D0%B2%D1%8B%D0%B5+%D1%81%D0%B5%D1%80%D0%B8%D0%B8+%D1%83%D0%B6%D0%B5+%D0%BF%D0%B5%D1%80%D0%B5%D0%B2%D0%B5%D0%B4%D0%B5%D0%BD%D1%8B+%D0%BD%D0%B0+%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%B8%D0%B9+%3Cbr%3E%3Cbr%3E%D0%A1%D0%BE%D0%B1%D1%8B%D1%82%D0%B8%D0%B9%D0%BD%D1%8B%D0%B9+%D0%BA%D0%B8%D0%BD%D0%BE%D1%84%D0%B8%D0%BB%D1%8C%D0%BC%D0%B0+%C2%AB%D0%A0%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7+%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8+3+%D1%81%D0%B5%D0%B7%D0%BE%D0%BD+7+%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB+%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%B8%D0%B9+%D1%81%D0%B5%D1%80%D0%B8%D0%B0%D0%BB+%D1%80%D0%B0%D0%B7%D0%BC%D0%B0%D1%85%D0%B8%D0%B2%D0%B0%D1%8E%D1%82%D1%81%D1%8F+%D0%B2+%D1%8D%D1%82%D0%BE%D0%BC+%D1%80%D0%B5%D1%81%D0%BF%D1%83%D0%B1%D0%BB%D0%B8%D0%BA%D0%B5+%D0%93%D0%B8%D0%BB%D0%B5%D0%B0%D0%BD%D0%B4.+%D0%92+%D0%BF%D0%BE%D0%B4%D0%BE%D0%B1%D0%BD%D0%BE%D0%BC+%D1%81%D1%82%D1%80%D0%B0%D0%BD%D0%B5+%D0%BF%D1%80%D0%B0%D0%B2%D0%B8%D1%82+%D0%B2%D0%BE%D0%B5%D0%BD%D0%BD%D0%BE%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D1%89%D0%B0%D1%8F+%D0%B4%D0%B0+%D0%BA%D1%83%D0%BB%D1%8C%D1%82%D0%BE%D0%B2%D0%B0%D1%8F+%D1%84%D0%B0%D1%88%D0%B8%D0%B7%D0%BC.+%D0%9D%D0%B0%D1%87%D0%B0%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA+%D0%BD%D0%B5%D1%83%D1%81%D1%82%D0%B0%D0%BD%D0%BD%D0%BE+%D0%B1%D0%BE%D1%80%D0%B5%D1%82%D1%81%D1%8F+%D0%B8%D0%B7+%D1%81%D0%BE%D1%81%D0%B5%D0%B4%D0%BD%D0%B8%D0%BC%D0%B8+%D1%81%D1%82%D0%BE%D1%80%D0%BE%D0%BD%D0%B0%D0%BC%D0%B8.+%D0%90+%D0%BF%D0%BE%D1%82%D0%BE%D0%BC+%D0%B2+%D0%BF%D1%80%D0%BE%D1%81%D0%BF%D0%B5%D0%BA%D1%82%D0%B0%D1%85+%D0%BD%D0%B0+%D0%B2%D1%81%D1%8F%D0%BA%D0%BE%D0%BC+%D1%88%D0%B0%D0%B3%D1%83+%D1%80%D0%B0%D1%81%D0%BF%D0%BE%D0%BB%D0%BE%D0%B6%D0%B5%D0%BD%D1%8B+%D1%81%D0%BE%D0%BB%D0%B4%D0%B0%D1%82%D1%81%D0%BA%D0%B8%D0%B9%2C+%D0%BD%D0%B0%D0%B1%D0%BB%D1%8E%D0%B4%D0%B0%D1%8E%D1%89%D0%B8%D0%B5+%D0%B7%D0%B0+%D1%8F%D1%81%D0%BE%D0%BC.+%D0%9D%D0%BE+%D0%B5%D1%89%D0%B5+%D0%BE%D1%81%D0%BD%D0%BE%D0%B2%D0%BE%D0%BF%D0%BE%D0%BB%D0%B0%D0%B3%D0%B0%D1%8E%D1%89%D0%B0%D1%8F+%D1%82%D0%B5%D0%BC%D0%B0%2C+%D0%BD%D0%B0%D0%BB%D0%B8%D1%87%D0%B5%D1%81%D1%82%D0%B2%D1%83%D1%8E%D1%89%D0%B0%D1%8F+%D0%B2+%D1%8D%D1%82%D0%BE%D0%BC+%D0%BF%D0%BE%D0%B4%D0%BE%D0%B1%D0%BD%D0%BE%D0%BC+%D1%81%D0%BE%D0%BE%D0%B1%D1%89%D0%B5%D1%81%D1%82%D0%B2%D0%B5+%E2%80%93+%D0%BC%D0%B5%D1%80%D1%82%D0%B2%D0%BE%D1%80%D0%BE%D0%B6%D0%B4%D0%B5%D0%BD%D0%BD%D0%BE%D1%81%D1%82%D1%8C+%D0%B4%D0%B5%D0%BB%D0%B5%D0%B3%D0%B0%D1%82%D0%BE%D0%BA+%D0%B2%D0%B5%D0%BB%D0%B8%D0%BA%D0%BE%D0%BB%D0%B5%D0%BF%D0%BD%D0%BE%D0%B3%D0%BE+%D0%BF%D0%BE%D0%BB%D0%B0+%D0%B8%D0%B7+%D0%B7%D0%BD%D0%B0%D1%82%D0%B8.+%D0%94%D0%B5%D0%B2%D0%BA%D0%B8%2C+%D0%B8%D0%BC%D0%B5%D0%BD%D0%BD%D0%BE+%D0%BE%D0%BD%D0%B8+%D1%80%D0%B5%D0%BA%D0%BE%D0%BC%D0%B5%D0%BD%D0%B4%D1%83%D1%8E%D1%82+%D0%B0%D1%80%D0%B8%D1%81%D1%82%D0%BE%D0%BA%D1%80%D0%B0%D1%82%D0%B8%D1%8E+%D0%B4%D0%B0+%D0%B2%D0%BE%D1%80%D0%BE%D1%87%D0%B0%D1%8E%D1%82%D1%81%D1%8F+%D0%B2+%D1%83%D0%BA%D0%B0%D0%B7%D0%B0%D0%BD%D0%BD%D0%BE%D0%BC+%D0%B2%D0%BB%D0%B8%D1%8F%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D1%85+%D0%BE%D0%B1%D0%BB%D0%B0%D1%81%D1%82%D1%8F%D1%85%2C+%D0%B7%D0%B0%D0%BC%D0%B5%D0%B4%D0%BB%D1%8F%D1%8E%D1%89%D0%B5%D0%BC+%D0%B4%D0%B0+%D0%B8+%D0%BF%D0%BE%D1%87%D0%B8%D1%82%D0%B0%D0%B5%D0%BC%D1%8B%2C+%D0%BD%D0%BE+%D0%B7%D0%B0%D1%82%D0%BE+%D0%BD%D0%B5+%D1%81%D0%BF%D0%BE%D1%81%D0%BE%D0%B1%D0%BD%D1%8B+%D0%BF%D0%BE%D1%87%D0%B0%D1%82%D1%8C+%D0%BA%D1%80%D0%BE%D1%85%D1%83%2C+%D1%82%D1%8F%D0%B3%D0%B0%D1%82%D1%8C+%D0%B2%D1%81%D0%B5+%D1%8D%D1%82%D0%BE+%D1%82%D0%B0%D0%BA+%D0%B6%D0%B5+%D1%80%D0%BE%D0%B4%D0%B8%D1%82%D1%8C.%3Cbr%3E%3Cbr%3E%D0%9D%D0%B0+%D1%82%D0%BE%D0%B3%D0%BE+%D1%84%D0%B0%D0%BA%D1%82%D0%B0%2C+%D1%87%D1%82%D0%BE%D0%B1%D1%8B+%D1%81%D1%82%D0%B0%D1%82%D1%83%D1%81%D0%BD%D1%8B%D0%B5+%D0%B6%D0%B5%D0%BD%D1%81%D0%BA%D0%BE%D0%B5+%D1%81%D0%BE%D1%81%D0%BB%D0%BE%D0%B2%D0%B8%D0%B5+%D0%BF%D1%80%D0%BE%D1%87%D1%83%D1%8F%D0%BB%D0%B8+%D1%86%D0%B5%D1%80%D0%B5%D1%80%D0%B0%2C+%D1%81%D1%82%D0%B0%D0%BB+%D0%BE%D1%80%D0%B3%D0%B0%D0%BD%D0%B8%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD+%D0%BA%D0%BE%D0%BB%D0%BB%D0%B5%D0%BA%D1%82%D0%B8%D0%B2%D0%BD%D1%8B%D0%B9+%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B0.+%D0%A2%D1%80%D0%B8%D0%B2%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D1%85+%D0%B4%D0%B5%D0%B2+%D1%81%D0%B3%D0%BE%D0%BD%D1%8F%D0%BB%D0%B8+%D0%BA%D0%B0%D0%BA+%D1%81%D0%BF%D0%B5%D1%86%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5+%D0%B1%D0%B8%D0%B2%D1%83%D0%B0%D0%BA%D0%B0%2C+%D0%B3%D0%B4%D0%B5+%D1%8D%D1%82%D0%B8+%D0%B2%D1%8B%D0%B8%D1%81%D0%BA%D0%B8%D0%B2%D0%B0%D0%BB%D0%B8%D1%81%D1%8C+%D0%BF%D0%BE%D0%B4+%D0%BF%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D1%8C%D0%BD%D1%8B%D0%BC+%D0%BD%D0%B0%D0%B1%D0%BB%D1%8E%D0%B4%D0%B5%D0%BD%D0%B8%D0%B5%D0%BC%2C+%D1%81%D1%82%D0%B0%D0%B1%D0%B8%D0%BB%D1%8C%D0%BD%D0%BE+%D1%88%D0%BB%D0%B8+%D0%BD%D0%B5%D1%83%D0%B4%D0%BE%D0%B2%D0%BB%D0%B5%D1%82%D0%B2%D0%BE%D1%80%D0%B8%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE.+%D0%98%D1%85+%D0%B2%D1%81%D0%B5%D0%B3%D0%BE+%D1%85%D0%B0%D1%80%D0%B0%D0%BA%D1%82%D0%B5%D1%80%D0%BD%D0%BE%D0%B9+%D0%BB%D0%B8%D0%BD%D0%B8%D0%B5%D0%B9+%D1%8F%D0%B2%D0%BB%D1%8F%D0%BB%D0%B0%D1%81%D1%8C+%D1%83%D0%B1%D0%BE%D1%80+%D0%BA%D1%80%D0%B0%D1%81%D0%BD%D0%BE%D0%B2%D0%B0%D1%82%D0%BE%D0%B3%D0%BE+%D0%BE%D0%BA%D1%80%D0%B0%D1%81%D1%8B.+%D0%94%D0%BB%D1%8F+%D0%B1%D0%B5%D0%B4%D0%BD%D1%8F%D0%B6%D0%B5%D0%BA+%D0%B2%D0%BE%D0%B4%D0%B8%D0%BB%D0%B0%D1%81%D1%8C+%D0%B5%D0%B4%D0%B2%D0%B0+%D0%B4%D1%80%D1%83%D0%B3%D0%B0%D1%8F+%D0%B2%D1%8B%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5+%E2%80%93+%D0%B2%D0%BE%D0%B7%D0%BD%D0%B8%D0%BA%D0%BD%D0%BE%D0%B2%D0%B5%D0%BD%D0%B8%D0%B5+%D0%B4%D0%B5%D1%82%D0%B2%D0%BE%D1%80%D1%83+%D0%BF%D1%80%D0%BE+%D0%BF%D1%80%D0%B8%D0%B2%D0%B8%D0%BB%D0%B5%D0%B3%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D1%8B%D1%85+%D1%81%D0%B5%D0%BC%D0%B5%D0%B9.+%D0%9F%D0%BE%D0%BD%D1%83%D1%80%D1%8B%D0%B5+%D1%80%D0%B0%D1%81%D0%BA%D1%80%D0%B0%D1%81%D0%B0%D0%B2%D0%B8%D1%86%D1%8B+%D0%BE%D0%B1%D1%8F%D0%B7%D0%B0%D0%BD%D1%8B+%D0%B1%D1%8B%D0%B2%D0%B0%D0%BB%D0%B8+%D0%B1%D0%B5%D1%81%D0%BF%D1%80%D0%B5%D0%BA%D0%BE%D1%81%D0%BB%D0%BE%D0%B2%D0%BD%D0%BE+%D0%BF%D1%80%D0%BE%D0%B4%D0%B5%D0%BB%D1%8B%D0%B2%D0%B0%D1%82%D1%8C+%D0%B2%D1%81%D0%B5+%D1%83%D1%81%D1%82%D0%B0%D0%BD%D0%BE%D0%B2%D0%BA%D0%B8+%D1%82%D0%BE%D0%BD%D1%87%D0%B0%D0%B9%D1%88%D0%B8%D1%85+%D0%BE%D0%BA%D1%80%D1%83%D0%B6%D0%B5%D0%BD%D0%B8%D0%B9%2C+%D1%84%D0%B8%D1%80%D0%BC%D0%B5%D0%BD%D0%BD%D0%BE%D0%B3%D0%BE+%D1%82%D0%BE%D1%87%D0%BA%D0%B8+%D0%B7%D1%80%D0%B5%D0%BD%D0%B8%D1%8F+%D1%83+%D0%B8%D1%85+%D1%8D%D0%BA%D1%81%D0%BF%D0%BB%D1%83%D0%B0%D1%82%D0%B0%D1%86%D0%B8%D0%B8+%D1%8F%D0%B2%D0%BB%D1%8F%D1%82%D1%8C%D1%81%D1%8F+%D0%BD%D0%B5+%D0%BC%D0%BE%D0%B3%D0%BB%D0%BE%2C+%D0%B8%D0%BC+%D1%81%D0%B0%D0%BC%D0%B8%D0%BC+%D1%81%D0%BE%D0%B2%D1%81%D0%B5%D0%BC+%D0%B4%D0%BE%D1%81%D1%82%D0%B0%D0%B2%D0%B0%D0%BB%D0%B8%D1%81%D1%8C+%D0%BD%D0%BE%D0%B2%D0%B5%D0%B9%D1%88%D0%B8%D0%B5+%D0%B8%D0%BC%D0%B5%D0%BD%D0%B0%2C+%D0%B0+%D0%B2%D0%B5%D1%81%D1%8C%D0%BC%D0%B0+%D0%BD%D0%B5%D0%BC%D0%B0%D0%BB%D0%BE%D0%B2%D0%B0%D0%B6%D0%BD%D0%BE%D0%B5+%E2%80%93+%D0%BE%D0%BD%D0%B8+%D1%81%D0%B5%D0%B3%D0%BE%D0%B4%D0%BD%D1%8F+%D0%BF%D0%BE%D0%B4%D0%BE%D0%B1%D0%B0%D1%8E%D1%89%D0%B8%D1%85+%D0%B2%D1%81%D1%82%D1%83%D0%BF%D0%B0%D1%82%D1%8C+%D0%B7%D0%B0+%D0%BB%D1%8E%D0%B1%D0%BE%D0%B2%D0%BD%D1%83%D1%8E+%D1%81%D0%BE%D0%B5%D0%B4%D0%B8%D0%BD%D0%B8%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5+%D0%B7%D0%B2%D0%B5%D0%BD%D0%BE+%D1%81%D0%BE%D0%B2%D0%BC%D0%B5%D1%81%D1%82%D0%BD%D0%BE+%D1%81+%D1%81%D0%BF%D1%80%D0%B0%D0%B2%D0%BD%D1%8B%D0%BC%D0%B8+%D0%B3%D1%80%D0%B0%D0%B6%D0%B4%D0%B0%D0%BD%D0%B0%D0%BC%D0%B8.&tags=%D0%A0%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7+%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8+3+%D1%81%D0%B5%D0%B7%D0%BE%D0%BD+4+%D1%81%D0%B5%D1%80%D0%B8%D1%8F%22+%22%D0%A0%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7+%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8+3+%D1%81%D0%B5%D0%B7%D0%BE%D0%BD+9+%D1%81%D0%B5%D1%80%D0%B8%D1%8F&editor=WYSIWYG+Editor&code=1-1558831255-bac4822ab65fd7a51815bde5e42145848f25446b&doask=1
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=241494
http://roikjer.com/forum/index.php?PHPSESSID=8kllln25maug624pdiri2otu16&topic=932301.0
http://callman.co.kr/index.php?mid=qa&document_srl=234795
http://www.sp1.football/index.php?mid=faq&document_srl=739457
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=100578
http://carand.co.kr/d2/98488
https://www.hohoyoga.com/testboard/4017312
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=914363
http://bebopindia.com/notcie/383686
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/329367
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/95577
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2783196
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=138247
http://backo.co.kr/board_aiQk58/16428
https://www.hohoyoga.com/testboard/4061173
http://photogrotto.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ey1k-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-10-%d1%81%d0%b5%d1%80%d0%b8/
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1740309
http://dreamplusart.com/mn03_01/215498
http://jiral.net/an9/38862
https://forum.ac-jete.it/index.php?topic=445871.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=36400
http://www.alase.net/index.php/component/k2/itemlist/user/12604
http://0433.net/junggo/114004
http://kwpub.kr/PUBS/203274
http://www.capital-investment.pl/index.php/component/k2/itemlist/user/229311
http://khapthanam.co.kr/g1/164675
http://sunele.co.kr/board_ReBD97/234810
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3925280
http://loverstory.co.kr/board_UYNJ05/89268
https://forums.lfstats.com/viewtopic.php?t=315798
http://iymc.or.kr/?document_srl=116543
http://www.ekemoon.com/245051/052120193828/
http://guiadetudo.com/index.php/component/k2/itemlist/user/12695
https://2002.shyoon.com/board_2002/255958
http://pekosmile.dothome.co.kr/index.php?mid=seoulitestudio&document_srl=444331
http://carand.co.kr/d2/92392
http://vtservices85.fr/smf2/index.php?PHPSESSID=f9b1ba525d41f07ebb9b59d87e0e459e&topic=292260.0
http://midorijapaneserestaurant.ca/menu/?document_srl=61610
https://www.lwfservers.com/index.php?topic=71228.0
https://www.netprofessional.gr/component/k2/itemlist/user/3896.html
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=230040
http://dsyang.com/board_Kvgn62/29217
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=385914
https://intelogist2.wpengine.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ek2%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://www.alase.net/index.php/component/k2/itemlist/user/12636
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=206193
http://midorijapaneserestaurant.ca/menu/News/70408
http://dayung.co.kr/board_SRVC17/65520
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4941410
http://kockazatkutato.hu/component/k2/itemlist/user/42551
https://timecker.com/anonymous/188760
http://bewasia.com/?document_srl=222018
http://daesestudy.co.kr/ipsi_docu/118542
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=220226
http://gallerychoi.com/Exhibition/405335
http://www.ekemoon.com/243939/050520194628/
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=127283
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=291129
http://haenamyun.taeshinmedia.com/index.php?mid=notice&document_srl=2826046
http://loverstory.co.kr/board_UYNJ05/106493
https://gonggamlaw.com/lawcase/65226
https://www.hwbms.com/web/qna/38340
http://naksansacondo.com/board_MGPu57/51462
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=105887
http://xn--2e0b53df5ag1c804aphl.net/nuguna/132799
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42611
http://dessa.com.br/component/k2/itemlist/user/386199
http://ovotecegg.com/component/k2/itemlist/user/218718
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=377675
http://loverstory.co.kr/?document_srl=83407
http://necinsurance.co.zw/component/k2/itemlist/user/21671.html
http://naksansacondo.com/board_MGPu57/85764
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=175472
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=316836328b18bf4e8ad6ff57469309c4&topic=10862.0
http://www.proandpro.it/?option=com_k2&view=itemlist&task=user&id=4719536
http://withinfp.sakura.ne.jp/eso/index.php/17575990-rasskaz-sluzanki-3-sezon-6-seria-xnbn-rasskaz-sluzanki-3-sezon-/0
http://www.eunhaele.co.kr/xe/board/20756
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3793569
http://daesestudy.co.kr/ipsi_docu/147657
https://forum.clubeicaro.pt/index.php?topic=2672.0
http://maderadepaulownia.com/?option=com_k2&view=itemlist&task=user&id=84375
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3576345
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1983057
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2650847
https://intelogist2.wpengine.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c/
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2831461
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=2017485
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=2017489
http://gtupuw.org/index.php/component/k2/itemlist/user/2017255
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1342384
http://benzmall.co.kr/index.php?mid=download&document_srl=47661
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=131508
http://www.tessabannampad.go.th/webboard/index.php?topic=226504.0
http://laspoltrina.it/component/k2/itemlist/user/1511283
https://mcsetup.tk/bbs/index.php?topic=262303.0
http://www.emrabq8.com/index.php/component/k2/itemlist/user/1869835
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=118664
http://roikjer.com/forum/index.php?PHPSESSID=5c38ii0r0c8vlnrcbf3tmkl270&topic=927365.0
http://immobilia.gr/index.php/component/k2/itemlist/user/16875
http://dreamplusart.com/mn03_01/123133
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=416609
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/150415
http://www.hmotors.co.kr/inquiry/71952
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2831682
http://dohairbiz.com/en/?option=com_k2&view=itemlist&task=user&id=2830547
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3954151
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=186068
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=140990
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3815042
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=540596
http://p9912.cafe24.com/board_LVgu51/35606
http://www.ekemoon.com/245465/050220190229/
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=387064
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3750203
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=458530
http://mediaville.me/index.php/component/k2/itemlist/user/377595
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=230389
https://www.hohoyoga.com/testboard/4080593
http://loverstory.co.kr/board_UYNJ05/84497
http://constellation.kro.kr/?document_srl=65108
https://gonggamlaw.com/lawcase/127744
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=a2c10b4d0bae9ed5c5bf7183df2c8385&topic=11398.0
http://www.theocraticamerica.org/forum/index.php?topic=80257.0
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-noqi-%d1%80%d0%b0%d1%81/
http://looksun.co.kr/index.php?mid=board_4&document_srl=212571
http://kyj1225.godohosting.com/board_mebR72/96074
http://xn--2e0b53df5ag1c804aphl.net/nuguna/118781
https://www.hohoyoga.com/testboard/3974105
http://bebopindia.com/notcie/385839
http://looksun.co.kr/index.php?mid=board_4&document_srl=207143
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=915272
http://ariji.kr/?document_srl=975089
http://0433.net/?document_srl=112600
https://www.hwbms.com/web/?document_srl=43054
http://www.hmotors.co.kr/inquiry/27185
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=113219
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=13992
http://ariji.kr/?document_srl=1031581
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2781183
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=954479
http://www.crnmedia.es/component/k2/itemlist/user/92141
http://rabat.kr/board_yCgT00/80462
https://saltriverbg.com/2019/05/28/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gtbs-%d1%80%d0%b0%d1%81/
http://withinfp.sakura.ne.jp/eso/index.php/17594192-rasskaz-sluzanki-3-sezon-9-seria-xwed-rasskaz-sluzanki-3-sezon-
http://mobility-corp.com/index.php/component/k2/itemlist/user/2697220
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=198638
http://vtservices85.fr/smf2/index.php?PHPSESSID=e5c422ef6957e012d8a4c5dd0718356f&topic=295799.0
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=315150
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3924872
http://sdsn.develop.cinfores.com/index.php/component/k2/itemlist/user/246290
https://gonggamlaw.com/lawcase/140614
http://erhu.eu/viewtopic.php?t=397068
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/17803
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/71318
https://forum.shaiyaslayer.tk/index.php?topic=157769.0
http://kyj1225.godohosting.com/board_mebR72/100254
http://loverstory.co.kr/board_UYNJ05/87981
http://praisesound.co.kr/sub04_01/85082
http://zakdu.com/board_ssKi56/22789
https://adsensebih.com/index.php?topic=49904.0
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=2004007
http://vtservices85.fr/smf2/index.php?PHPSESSID=55ccb01994bda15362907a561f29894c&topic=291629.0
http://rabat.kr/board_yCgT00/34469
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=208375
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3571218
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=1113688
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=97597
http://daltso.com/index.php?mid=board_cUYy21&document_srl=232964
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=403444
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=85373
http://roikjer.com/forum/index.php?PHPSESSID=jo0fb8jc04njorrl6mt8of06c3&topic=932231.0
http://looksun.co.kr/index.php?mid=board_4&document_srl=214168
http://gabisan.com/board_OuDs04/67661
https://www.limscave.com/forum/viewtopic.php?t=60430
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3797065
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/42409
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=214233
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=204694
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=18503
http://blog.ptpintcast.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lwuy-%d1%80%d0%b0%d1%81/
http://mediaville.me/index.php/component/k2/itemlist/user/379683
http://www.ekemoon.com/244885/052020192228/
http://loverstory.co.kr/board_UYNJ05/87364
https://blossomug.com/index.php/component/k2/itemlist/user/1111789
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2787534
http://dreamplusart.com/mn03_01/123829
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rudy-%d1%80%d0%b0%d1%81/
http://dreamplusart.com/?document_srl=185738
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=408528
http://lavaggio.com.vn/index.php/component/k2/itemlist/user/3926341
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=209875
http://looksun.co.kr/index.php?mid=board_4&document_srl=205704
http://backo.co.kr/board_aiQk58/15506
http://askpharm.net/board_NQiz06/164440
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=569509
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229673
http://looksun.co.kr/index.php?mid=board_4&document_srl=206417
http://holysweat.dothome.co.kr/data/7218
http://divespace.co.kr/board/286263
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=56548
http://hanga5.com/index.php?mid=board_photo&document_srl=160401
http://www.kwpcoop.or.kr/QnA/20269
http://askpharm.net/?document_srl=207812
http://cwon.kr/xe/board_bnSr36/313226
http://photogrotto.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-is4%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f28-05/
http://www.atab.com.sa/?option=com_k2&view=itemlist&task=user&id=1734655
http://divespace.co.kr/board/239775
https://forums.lfstats.com/viewtopic.php?t=324647
http://mobility-corp.com/index.php/component/k2/itemlist/user/2674915
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=224540
http://cwon.kr/xe/board_bnSr36/315137
http://jnk-ent.jp/index.php?mid=gallery&document_srl=328881
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=547806
http://constellation.kro.kr/board_kbku73/64405
http://test.comics-game.ru/index.php?topic=575.0
http://www.eunhaele.co.kr/xe/board/20430
http://rabat.kr/board_yCgT00/81438
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=40324.0
http://bobr.site/index.php?topic=192730.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1500346
http://looksun.co.kr/index.php?mid=board_4&document_srl=192780
https://cfcestradareal.com.br/index.php/component/k2/itemlist/user/83366
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=229989
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2814657
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2015514
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2015895
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=110625
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1332797
http://israengineering.com/index.php/component/k2/itemlist/user/1332847
https://www.c-alice.org/forum/index.php?topic=101013.0
http://8.droror.co.il/uncategorized/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gh1%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5/
https://nextezone.com/index.php?action=profile;u=17488
http://arquitectosenreformas.es/component/k2/itemlist/user/86808
https://bcit-tmgt.com/viewtopic.php?t=54496
https://forum.shaiyaslayer.tk/index.php?topic=177995.0
https://nextezone.com/index.php?action=profile;u=17434
https://www.c-alice.org/forum/index.php?topic=101016.0
https://nextezone.com/index.php?action=profile;u=17494
https://www.regalepadova.it/index.php/component/k2/itemlist/user/8569
https://nextezone.com/index.php?topic=90783.0
https://nextezone.com/index.php?topic=90785.0
https://timecker.com/anonymous/217056
https://timecker.com/anonymous/217174
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1867929
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=242059
http://maka-222.com/?document_srl=103340
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=315554
https://blossomug.com/index.php/component/k2/itemlist/user/1115857
http://www.hmotors.co.kr/inquiry/67834
http://askpharm.net/board_NQiz06/158118
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=42893
http://dsyang.com/board_Kvgn62/44234
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1868130
http://praisesound.co.kr/sub04_01/87252
https://www.hohoyoga.com/testboard/3970762
http://mobility-corp.com/index.php/component/k2/itemlist/user/2738530
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3542656
http://www.itosm.com/cn/board_nLoq17/214451
http://naksansacondo.com/board_MGPu57/34611
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=338457
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=43895
http://www.hmotors.co.kr/inquiry/69305
http://midorijapaneserestaurant.ca/menu/News/71604
http://0433.net/junggo/112663
http://guiadetudo.com/index.php/component/k2/itemlist/user/12694
http://midorijapaneserestaurant.ca/menu/News/77111
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=117682
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3504346
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/61024
http://smartacity.com/component/k2/itemlist/user/91601
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=550156
http://askpharm.net/board_NQiz06/274451
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=65076
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=2000838
http://backo.co.kr/board_aiQk58/16000
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=372310
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nd2g-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20/
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/1983963
http://kockazatkutato.hu/component/k2/itemlist/user/42540
http://carand.co.kr/d2/88534
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=42482
http://ye-dream.com/qa/277897
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=100622
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=132619
http://divespace.co.kr/board/178736
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=1121296
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=58457
http://www.teedinubon.com/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-le8%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f29-05-20/
http://lucky.kidspann.net/index.php?mid=qna&document_srl=394717
http://music.start-a-idea.online/blogs/viewstory/43432
http://www.quattroandpartners.it/component/k2/itemlist/user/1214181
http://taklongclub.com/forum/index.php?topic=204351.0
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=49723
http://knet.dothome.co.kr/xe/board_RJHw15/15315
https://saltriverbg.com/2019/05/28/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nkoe-%d1%80%d0%b0%d1%81/
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=195675
http://taklongclub.com/forum/index.php?topic=201561.0
http://www.artangel.co.kr/?document_srl=164900
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/334551
http://daltso.com/index.php?mid=board_cUYy21&document_srl=204347
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2010874
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=22081
https://betshin.com/Story/200289
https://www.c-alice.org/forum/index.php?topic=101598.0
http://8.droror.co.il/uncategorized/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wa8%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f30-05/
http://8.droror.co.il/uncategorized/%d0%ba%d0%be%d0%bf-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pd8%d0%ba%d0%be%d0%bf-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f30-05-2019/
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=110297
http://8.droror.co.il/uncategorized/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wg3%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be/
http://8.droror.co.il/uncategorized/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zv6%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f30-05/
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/103338
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1323117
http://archeaudio.com/xe/board_AOYj82/11594
http://www.digitalbul.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uocj-%d1%80%d0%b0%d1%81/
http://married.dike.gr/index.php/component/k2/itemlist/user/78311
https://betshin.com/Story/206125
https://www.shaiyax.com/index.php?topic=408334.0
http://mediaville.me/index.php/component/k2/itemlist/user/374176
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=388955
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=204976
http://xn--hu1bs8ufrd6ucyz0aooa.kr/?document_srl=67553
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2007323
https://esel.gist.ac.kr/esel2/board_hmgj23/367196
http://roikjer.com/forum/index.php?PHPSESSID=1559v4lev2ch1he58brvv7ujt4&topic=930291.0
http://www.firstfinancialservices.co.uk/?option=com_k2&view=itemlist&task=user&id=34140
http://taklongclub.com/forum/index.php?topic=218222.0
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/340207
http://daltso.com/index.php?mid=board_cUYy21&document_srl=205171
http://smartacity.com/component/k2/itemlist/user/91055
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1499963
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=175025
http://www.vamoscontigo.org/Noticia/201031
http://sejong-thesharpyemizi.co.kr/m1/74860
http://dev.aabn.org.gh/component/k2/itemlist/user/726307
http://daltso.com/index.php?mid=board_cUYy21&document_srl=200088
http://www.jesusonly.life/calendar/503632
http://xn--2e0bk61btjo.com/notice/30505
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3483114
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=208659
http://hyeonjun.co.kr/menu3/367586
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/52076
http://dsyang.com/board_Kvgn62/44094
http://gusinoepero.ru/archives/25994
http://herdental.co.kr/index.php?mid=online&document_srl=115596
http://mediaville.me/index.php/component/k2/itemlist/user/374896
http://kwpub.kr/PUBS/125967
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=33655
http://divespace.co.kr/board/262462
http://dreamplusart.com/mn03_01/223522
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=441179
http://www.itosm.com/cn/board_nLoq17/192596
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2797833
https://mcsetup.tk/bbs/index.php?topic=263091.0
http://bizchemical.com/?document_srl=2161611
http://xn----3x5er9r48j7wemud0a387h.com/news/246359
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/80325
http://juroweb.com/xe/juroweb_board/85576
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16449
http://loverstory.co.kr/board_UYNJ05/107501
http://naksansacondo.com/board_MGPu57/74302
http://loverstory.co.kr/board_UYNJ05/103012
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3784101
http://legride.com/UserProfile/tabid/61/userId/2880982/Default.aspx
http://xn--2e0bk61btjo.com/notice/27177
http://mobility-corp.com/index.php/component/k2/itemlist/user/2732346
https://gonggamlaw.com/lawcase/139007
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3405074
http://sd-xi.co.kr/g1/50879
http://khapthanam.co.kr/g1/157731
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=652340
https://www.celekt.com/%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-it9%d0%a2%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f29-05/
http://rfc11th13th.dothome.co.kr/Board5/32927
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=177114
http://bobr.site/index.php?topic=179212.0
http://looksun.co.kr/index.php?mid=board_4&document_srl=126997
http://agiteshop.com/xe/qa/201225
http://socialmag.bayareanonprofits.xyz/blogs/viewstory/126648
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=850244
http://withinfp.sakura.ne.jp/eso/index.php/17595941-rasskaz-sluzanki-3-sezon-1-seria-kkaw-rasskaz-sluzanki-3-sezon-
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=759687
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2010366
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/55351
http://www.golden-nail.co.kr/press/363444
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=854319
http://www.vamoscontigo.org/Noticia/204813
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=414241
http://loverstory.co.kr/board_UYNJ05/102509
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=113160
http://www.ekemoon.com/247185/050220190030/
http://herdental.co.kr/index.php?document_srl=143359&mid=online
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=17910
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16708
http://cwon.kr/xe/board_bnSr36/282451
http://daltso.com/index.php?mid=board_cUYy21&document_srl=213631
http://otitismediasociety.org/forum/index.php?topic=200613.0
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1169565
https://www.limscave.com/forum/viewtopic.php?t=56937
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=414510
https://2002.shyoon.com/board_2002/168206
http://rudraautomation.com/index.php/component/k2/author/337304
http://taklongclub.com/forum/index.php?topic=211968.0
http://www.yadanarbonnews.com/index.php/component/k2/itemlist/user/354733
http://www.jesusonly.life/calendar/444562
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=161489
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/34373
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1866549
https://esel.gist.ac.kr/esel2/board_hmgj23/273441
http://www.itosm.com/cn/board_nLoq17/136029
http://gtupuw.org/index.php/component/k2/itemlist/user/1975305
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=37301
https://www.celekt.com/%d0%9a%d0%be%d0%bf-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ra4g-%d0%9a%d0%be%d0%bf-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.celekt.com/%d0%a1%d0%b5%d0%bd%d1%8f%d0%a4%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ol6e-%d0%a1%d0%b5%d0%bd%d1%8f%d0%a4%d0%b5%d0%b4%d1%8f-2-%d1%81/
http://euromouleusinage.com/index.php/component/k2/itemlist/user/197737
http://euromouleusinage.com/index.php/component/k2/itemlist/user/197744
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4963082
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4963095
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4963111
http://www.spazioad.com/component/k2/itemlist/user/7488371
https://blossomug.com/index.php/component/k2/itemlist/user/1131248
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4962714
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1879123
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/82794
https://www.shaiyax.com/index.php?topic=403569.0
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=342882
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=e39d7ffa5ff89d4de4400abb6217b618&topic=11301.0
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=124835
http://holysweat.dothome.co.kr/data/7071
https://verdadesbiblicas.org.ec/index.php/component/k2/itemlist/user/3858580
http://looksun.co.kr/index.php?mid=board_4&document_srl=122988
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3795093
http://test.comics-game.ru/index.php?topic=703.0
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ko1e-%d0%ba%d0%be%d0%bf-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://nple.com/xe/pds/152067
http://kotica00.dothome.co.kr/?document_srl=37862
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3566164
http://viamania.net/index.php?mid=board_raYV15&document_srl=227244
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=230774
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=86216
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3749902
http://gabisan.com/board_OuDs04/151164
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3865997
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229839
http://hanga5.com/index.php?mid=board_photo&document_srl=128665
https://gonggamlaw.com/lawcase/149182
http://www.emrabq8.com/index.php/component/k2/itemlist/user/1865582
http://www.livetank.cn/market1/277967
http://midorijapaneserestaurant.ca/menu/News/76222
http://midorijapaneserestaurant.ca/menu/News/51664
http://apt2you2.cafe24.com/g1/44246
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=557123
http://www.vamoscontigo.org/Noticia/141593
http://yoriyorifood.com/xxxx/spacial/333275
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=849739
https://gonggamlaw.com/lawcase/132533
http://askpharm.net/board_NQiz06/259497
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=485831
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xy7s-%d0%ba%d0%be%d0%bf-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://intelogist2.wpengine.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uwgn-%d1%80%d0%b0%d1%81/
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=387927
http://smartacity.com/component/k2/itemlist/user/98258
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=296416
http://sofficer.net/xe/teach/280276
https://gonggamlaw.com/lawcase/102739
http://sejong-thesharpyemizi.co.kr/m1/33954
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=196434
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=549865
http://sd-xi.co.kr/g1/79285
http://cwon.kr/xe/board_bnSr36/296255
https://www.amazingworldtop.com/entretenimiento/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ai6%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5/
http://www.itosm.com/cn/board_nLoq17/193846
http://dreamplusart.com/mn03_01/144227
http://www.hmotors.co.kr/inquiry/65217
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=303996
http://www.rocketdan.co.kr/?document_srl=161291
http://ye-dream.com/qa/206332
http://www.sp1.football/index.php?mid=faq&document_srl=721098
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=212207
http://kyj1225.godohosting.com/board_mebR72/60581
https://www.hohoyoga.com/testboard/4087529
https://saltriverbg.com/2019/05/25/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lemq-%d1%80%d0%b0%d1%81/
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=14127
http://0433.net/junggo/115003
http://viamania.net/?document_srl=139241
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=111037
https://www.hohoyoga.com/testboard/4088984
http://web2interactive.com/index.php/component/k2/itemlist/user/3787368
http://www.jesusandmarypatna.com/index.php/component/k2/itemlist/user/3569173
http://e-educ.net/Forum/index.php?topic=16710.0
http://forum.bmw-e60.eu/index.php?topic=11077.0
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xj3k-%d0%ba%d0%be%d0%bf-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=549940
http://www.yadanarbonnews.com/index.php/component/k2/itemlist/user/345634
http://legride.com/UserProfile/tabid/61/userId/2893251/Default.aspx
http://otitismediasociety.org/forum/index.php?topic=207931.0
https://alquilervideobeam.com.co/index.php/component/k2/itemlist/user/59196
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/79151
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16963
http://www.cyberblissstudios.com/UserProfile/tabid/42/UserID/2329286/Default.aspx
http://jnk-ent.jp/index.php?mid=gallery&document_srl=300517
http://www.arunagreen.com/index.php/component/k2/itemlist/user/1155122
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=308997
http://www.patrasin.kr/index.php?mid=questions&document_srl=4355068
http://carand.co.kr/d2/81287
http://naksansacondo.com/board_MGPu57/66056
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1867481
https://forum.ac-jete.it/index.php?topic=447398.0
http://jnk-ent.jp/index.php?mid=gallery&document_srl=373331
http://www.sp1.football/index.php?document_srl=698189&mid=faq
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=36146
http://smartacity.com/component/k2/itemlist/user/93913
https://timecker.com/anonymous/188373
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vryq-%d1%80%d0%b0%d1%81/
http://carand.co.kr/d2/93253
http://www.vamoscontigo.org/Noticia/135910
http://mglpcm.org/board_ETkS12/142700
http://carand.co.kr/d2/94890
http://sy.korean.net/qna/457477
https://intelogist2.wpengine.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hn9t-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://mglpcm.org/board_ETkS12/202693
http://kyj1225.godohosting.com/board_mebR72/101232
http://haenamyun.taeshinmedia.com/?document_srl=2826125
https://2002.shyoon.com/board_2002/279642
http://bobr.site/index.php?topic=179753.0
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7481141
https://betshin.com/Story/225388
https://gonggamlaw.com/lawcase/159694
https://gonggamlaw.com/lawcase/159784
https://www.hohoyoga.com/testboard/4097203
https://www.hwbms.com/web/qna/49975
https://www.hwbms.com/web/qna/49980
https://www.hwbms.com/web/qna/49985
https://www.hwbms.com/web/qna/49990
https://www.hwbms.com/web/qna/49995
https://www.hwbms.com/web/qna/50009
https://www.hwbms.com/web/qna/50024
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1878194
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=36050
http://ye-dream.com/qa/206096
http://metropolis.ga/index.php?topic=21083.0
http://midorijapaneserestaurant.ca/menu/News/52236
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=224383
http://153.120.114.241/eso/index.php/17525246-rasskaz-sluzanki-3-sezon-7-seria-ajyq-rasskaz-sluzanki-3-sezon-
http://www.kwpcoop.or.kr/QnA/21932
http://forum.elexlabs.com/index.php?topic=64106.0
http://ovotecegg.com/component/k2/itemlist/user/219924
http://isch.kr/board_PowH60/158061
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/141425
http://mglpcm.org/board_ETkS12/199910
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=395538
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=388129
https://gonggamlaw.com/lawcase/135020
http://daesestudy.co.kr/ipsi_docu/121021
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/42491
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=193285
http://sy.korean.net/qna/522347
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7519671
http://www.cyberblissstudios.com/UserProfile/tabid/42/UserID/2349598/Default.aspx
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1760513
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=121514
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=19820
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=20467
http://www.m1avio.com/index.php/component/k2/itemlist/user/3864948
http://xn--80acvxh8am.net/index.php?action=profile&u=6480
http://dsyang.com/board_Kvgn62/50059
http://midorijapaneserestaurant.ca/menu/News/87041
http://midorijapaneserestaurant.ca/menu/News/87062
http://naksansacondo.com/board_MGPu57/116753
https://www.celekt.com/%d0%92%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-30-05-2019-f9-%d0%92%d1%81%d1%91-%d0%bc/
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2001458
http://looksun.co.kr/index.php?mid=board_4&document_srl=206825
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=415971
http://hyeonjun.co.kr/?document_srl=372844
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99658
http://rudraautomation.com/index.php/component/k2/author/345171
http://isch.kr/board_PowH60/220080
http://ye-dream.com/qa/257180
https://intelogist2.wpengine.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nk2p-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.hmotors.co.kr/inquiry/74534
https://reficulcoin.com/index.php?topic=88840.0
https://gonggamlaw.com/lawcase/80231
http://smartacity.com/component/k2/itemlist/user/77517
http://muldorang.com/market/25140
https://forum.ac-jete.it/index.php?topic=451300.0
http://daltso.com/index.php?mid=board_cUYy21&document_srl=209086
http://77.93.38.205/?option=com_k2&view=itemlist&task=user&id=653405
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=228860
http://dohairbiz.com/component/k2/itemlist/user/2814672
https://bcit-tmgt.com/viewtopic.php?f=2&t=53713&view=print
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/144376
https://www.hohoyoga.com/testboard/3977571
http://toeden.co.kr/Product_new/205427
http://d-tube.info/board_jvyO69/369091
http://jnk-ent.jp/index.php?mid=gallery&document_srl=238746
https://blossomug.com/index.php/component/k2/itemlist/user/1113083
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=72026
http://vtservices85.fr/smf2/index.php?PHPSESSID=a7202f216529a43a4d66faf1375a9da5&topic=289613.0
http://www.cnsmaker.net/xe/?document_srl=125140
http://jdcalc.com/forum/viewtopic.php?f=2&t=288718
http://shinhwaair2017.cafe24.com/issue/532958
http://rabbitzone.xyz/FREE/71841
http://sfah.ch/de/component/k2/itemlist/user/15537
http://dsyang.com/board_Kvgn62/42704
http://x-crew.center/guest/4846891
https://altaylarteknoloji.com/index.php?topic=6568.0
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=534381
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4941533
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=98794
http://www.ekemoon.com/242945/051420191227/
https://2002.shyoon.com/board_2002/171521
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=652502
http://loverstory.co.kr/board_UYNJ05/85738
http://neosky.net/xe/space_station/64043
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=173824
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/56481
https://adsensebih.com/index.php?topic=51036.0
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=45190
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=389789
http://juroweb.com/xe/juroweb_board/83073
http://naksansacondo.com/board_MGPu57/100862
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pk7x-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4/
http://divespace.co.kr/board/278297
http://ariji.kr/?document_srl=971711
http://www.itosm.com/cn/board_nLoq17/135729
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=127057
http://askpharm.net/board_NQiz06/274389
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=400617
http://autospa.lv/index.php/lv/component/k2/itemlist/user/10626
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=404327
https://nple.com/xe/pds/150034
http://herdental.co.kr/index.php?mid=online&document_srl=170309
http://thermoplast.envolgroupe.com/component/k2/author/176047
http://naksansacondo.com/board_MGPu57/32311
http://hyeonjun.co.kr/menu3/288277
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/74174
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=113971
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1498777
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=174399
http://mobility-corp.com/index.php/component/k2/itemlist/user/2730980
http://www.hmotors.co.kr/inquiry/64355
http://otitismediasociety.org/forum/index.php?topic=202969.0
https://www.shaiyax.com/index.php?topic=407900.0
http://masanlib.or.kr/g1/102190
http://www.ekemoon.com/244309/051020195528/
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/77738
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=112302
https://www.hohoyoga.com/testboard/4087675
https://betshin.com/Story/208541
http://cwon.kr/xe/board_bnSr36/288869
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2792577
http://www.atab.com.sa/index.php/en/?option=com_k2&view=itemlist&task=user&id=1737724
http://dsyang.com/board_Kvgn62/46544
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16847
http://mercibq.net/partner/100853
http://rudraautomation.com/index.php/component/k2/author/290049
http://daltso.com/index.php?mid=board_cUYy21&document_srl=196437
http://cwon.kr/xe/board_bnSr36/302519
http://beautypouch.net/index.php?mid=board_09&document_srl=160269
http://mercibq.net/partner/55349
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=49121
http://www.svteck.co.kr/customer_gratitude/217728
http://carand.co.kr/d2/94016
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=850765
http://kockazatkutato.hu/component/k2/itemlist/user/42965
http://carand.co.kr/d2/46951
http://www.svteck.co.kr/customer_gratitude/303955
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7528660
http://www.svteck.co.kr/customer_gratitude/330783
http://universalcommunity.se/Forum/index.php?topic=34859.0
http://dcasociados.eu/?option=com_k2&view=itemlist&task=user&id=94411
http://www.ekemoon.com/244957/052020195928/
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3894032
http://carand.co.kr/d2/95976
http://xn--2e0b53df5ag1c804aphl.net/nuguna/105990
https://blossomug.com/?option=com_k2&view=itemlist&task=user&id=1111969
http://www.hmotors.co.kr/inquiry/75865
http://www.vamoscontigo.org/Noticia/176260
http://www.ekemoon.com/245351/050020193229/
http://mglpcm.org/board_ETkS12/180917
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1746768
http://agiteshop.com/xe/qa/163462
http://music.start-a-idea.online/blogs/viewstory/44161
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=138249
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=444018
http://bizchemical.com/board_kMpv94/2161683
https://gonggamlaw.com/lawcase/68727
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1867693
http://www.livetank.cn/market1/293331
http://xn--2e0b53df5ag1c804aphl.net/nuguna/103183
http://askpharm.net/board_NQiz06/240956
http://isch.kr/board_PowH60/196251
http://ko.myds.me/board_story/306089
http://gusinoepero.ru/archives/30449
http://barobus.kr/qna/75561
http://socialmag.bayareanonprofits.xyz/blogs/viewstory/129913
http://x-crew.center/guest/4846846
http://kyj1225.godohosting.com/board_mebR72/60825
http://taklongclub.com/forum/index.php?topic=212207.0
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/389842
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=901885
https://www.c-alice.org/forum/index.php?topic=96356.0
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=849205
https://gonggamlaw.com/lawcase/67164
http://looksun.co.kr/index.php?mid=board_4&document_srl=188088
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=139669
https://khuyenmaikk13.info/index.php?topic=228435.0
http://yooseok.com/board_BkvT46/412749
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2793838
http://www.teedinubon.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wb4%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5/
http://themasters.pro/file_01/326890
http://forum.bmw-e60.eu/index.php?topic=11134.0
http://ovotecegg.com/component/k2/itemlist/user/218732
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=85473
http://0433.net/junggo/146393
http://tiretech.co.kr/index.php?mid=qna&document_srl=268796
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=112061
http://rudraautomation.com/index.php/component/k2/author/349982
http://www.vamoscontigo.org/Noticia/144360
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=30448
https://intelogist2.wpengine.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qg4k-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3785375
http://x-crew.center/guest/4845055
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1531476
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39563
http://naksansacondo.com/board_MGPu57/35879
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=210637
http://lucky.kidspann.net/index.php?mid=qna&document_srl=295547
https://www.celekt.com/%d0%a0%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lgre-%d0%a0%d0%b0%d1%81/
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/166011
http://naksansacondo.com/board_MGPu57/103587
http://dohairbiz.com/en/component/k2/itemlist/user/2813704.html
http://bebopindia.com/notcie/445491
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=32827
http://www.ds712.net/guest/?document_srl=806921
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=398706
http://mahdi.ehosseini.com/?option=com_k2&view=itemlist&task=user&id=44646
http://www.jesusonly.life/calendar/551377
https://betshin.com/Story/206949
http://www.theocraticamerica.org/forum/index.php?topic=69667.0
http://beautypouch.net/index.php?mid=board_09&document_srl=131760
http://www.hmotors.co.kr/?document_srl=75519
http://yooseok.com/board_BkvT46/413260
http://rabbitzone.xyz/FREE/112269
http://ye-dream.com/qa/277708
http://www.ekemoon.com/240747/051120190726/
http://midorijapaneserestaurant.ca/menu/News/78416
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=540996
http://www.golden-nail.co.kr/press/369049
http://askpharm.net/board_NQiz06/258654
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=376625
http://carand.co.kr/d2/93457
http://looksun.co.kr/index.php?mid=board_4&document_srl=202419
https://forums.lfstats.com/viewtopic.php?t=319159
http://www.vamoscontigo.org/Noticia/204754
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=43985
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=39608.0
http://loverstory.co.kr/board_UYNJ05/88426
http://www.yadanarbonnews.com/index.php/component/k2/itemlist/user/348643
http://otitismediasociety.org/forum/index.php?topic=207281.0
http://www.coating.or.kr/atemfair_data/15052
http://withinfp.sakura.ne.jp/eso/index.php/17526487-rasskaz-sluzanki-3-sezon-10-seria-znol-rasskaz-sluzanki-3-sezon/0
https://www.hwbms.com/web/qna/12163
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=315855
http://askpharm.net/board_NQiz06/258786
http://ye-dream.com/qa/264911
http://loverstory.co.kr/board_UYNJ05/107387
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/370739
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zo5w-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9/
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=43184
http://www.vamoscontigo.org/Noticia/139600
http://ptu.imoove.kr/ko/content/%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-1-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-kmzz-%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-1-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-starz341287
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1325387
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=223750
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/394236
http://viamania.net/index.php?mid=board_raYV15&document_srl=133947
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1325406
http://e-educ.net/Forum/index.php?topic=17427.0
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=17973
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=28978
http://toeden.co.kr/Product_new/150553
http://www.yadanarbonnews.com/index.php/component/k2/itemlist/user/355956
http://udrpsucks.com/blog/?p=1862
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1545573
http://jnk-ent.jp/index.php?mid=gallery&document_srl=241806
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/329373
http://dohairbiz.com/en/?option=com_k2&view=itemlist&task=user&id=2812757
https://www.chirorg.com/?document_srl=154868
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=446450
http://p9912.cafe24.com/board_LVgu51/68853
https://khuyenmaikk13.info/index.php?topic=225754.0
http://juroweb.com/xe/juroweb_board/84434
http://looksun.co.kr/index.php?mid=board_4&document_srl=195103
http://rabat.kr/board_yCgT00/82882
http://kyj1225.godohosting.com/board_mebR72/80164
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4983132
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4983136
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2684082
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jn2t-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12/
http://udrpsucks.com/blog/?p=2111
https://intelogist2.wpengine.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mr3f-%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3/
https://intelogist2.wpengine.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jj4a-%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3/
https://intelogist2.wpengine.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fw8y-%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3/
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-oj7v-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-us0a-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://intelogist2.wpengine.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ev0h-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81/
https://intelogist2.wpengine.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-du8v-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xl8y-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12/
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=221145
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/370152
http://www2.yasothon.go.th/smf/index.php?topic=159.172410
http://ye-dream.com/qa/205406
http://toeden.co.kr/Product_new/142470
http://music.start-a-idea.online/blogs/viewstory/44460
https://www.celekt.com/%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vj2y-%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11/
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=406219
http://www.golden-nail.co.kr/press/428341
http://udrpsucks.com/blog/?p=1809
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/167567
http://warmfund.net/p/index.php?mid=financing&document_srl=472933
http://dreamplusart.com/mn03_01/120738
http://carand.co.kr/d2/89141
http://simkungshopping.com/?document_srl=183361
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=17931
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=479913
https://www.chirorg.com/?document_srl=147202
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229815
http://2872870.com/?document_srl=61504
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/336804
http://loverstory.co.kr/board_UYNJ05/115237
http://askpharm.net/board_NQiz06/250283
http://lucky.kidspann.net/index.php?mid=qna&document_srl=292240
http://jnk-ent.jp/index.php?mid=gallery&document_srl=241935
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/147499
http://gtupuw.org/index.php/component/k2/itemlist/user/1974530
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=463971
http://erhu.eu/viewtopic.php?t=398025
http://www.ds712.net/guest/index.php?document_srl=547774&mid=guest07
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/370974
https://www.shaiyax.com/index.php?topic=398679.0
https://nple.com/xe/pds/236095
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/18925
http://p9912.cafe24.com/board_LVgu51/58801
http://0433.net/junggo/146853
https://adsensebih.com/index.php?topic=49990.0
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=437891
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13819
http://oceangray.i234.me/?document_srl=246552
http://looksun.co.kr/index.php?mid=board_4&document_srl=187694
http://herdental.co.kr/index.php?mid=online&document_srl=112951
http://dcasociados.eu/component/k2/itemlist/user/93214
https://www.chirorg.com/?document_srl=191549
http://www.svteck.co.kr/customer_gratitude/310313
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=829344
http://beautypouch.net/index.php?mid=board_09&document_srl=181203
http://callman.co.kr/index.php?mid=qa&document_srl=321804
http://daltso.com/index.php?mid=board_cUYy21&document_srl=192398
http://midorijapaneserestaurant.ca/menu/News/74030
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/306201
http://looksun.co.kr/index.php?mid=board_4&document_srl=182540
http://www.ekemoon.com/240553/050920194726/
http://www.ekemoon.com/244995/052120191528/
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229122
http://bebopindia.com/?document_srl=511936
http://naksansacondo.com/board_MGPu57/77773
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=99324
http://kyj1225.godohosting.com/board_mebR72/93110
http://dongilpastor.synology.me/ing/index.php?mid=board_WlVg97&document_srl=100820
http://www.hmotors.co.kr/inquiry/36874
http://thermoplast.envolgroupe.com/component/k2/author/181138
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3449753
https://turimex.mx.solemti.net/component/k2/itemlist/user/18709
http://askpharm.net/board_NQiz06/245977
http://erdfsa.iptime.org/xe/index.php?mid=board&document_srl=25859
http://photogrotto.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pq7o-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-21/
http://mercibq.net/partner/55355
http://mobility-corp.com/index.php/component/k2/itemlist/user/2737296
http://cwon.kr/xe/board_bnSr36/314674
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1323405
https://forums.lfstats.com/viewtopic.php?t=319611
http://www.vamoscontigo.org/Noticia/221165
http://www.aloeverasas.it/index.php/component/k2/itemlist/user/21620
https://nextezone.com/index.php?action=profile;u=11165
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=113396
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=117609
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3570277
https://www.hwbms.com/web/qna/16791
http://www.hmotors.co.kr/inquiry/73778
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/34243
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2653134
https://forum.ac-jete.it/index.php?topic=438022.0
http://www.livetank.cn/market1/219310
http://cwon.kr/xe/board_bnSr36/307645
http://bath-family.com/photo_zone/142575
https://gonggamlaw.com/lawcase/102739
http://sejong-thesharpyemizi.co.kr/m1/33954
http://ko.myds.me/board_story/247423
http://sejong-thesharpyemizi.co.kr/m1/67557
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=305852
http://constellation.kro.kr/board_kbku73/64886
http://looksun.co.kr/index.php?mid=board_4&document_srl=123050
http://yooseok.com/board_BkvT46/417109
http://cwon.kr/xe/board_bnSr36/283613
http://gochon-iusell.co.kr/g1/74672
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=16897
http://loverstory.co.kr/board_UYNJ05/105059
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/50986
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=220650
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=95473
http://ajincomp.godohosting.com/?document_srl=174182
http://xn--2e0b53df5ag1c804aphl.net/nuguna/166053
http://beautypouch.net/?document_srl=110591
http://xn--2e0bk61btjo.com/notice/23623
http://rudraautomation.com/index.php/component/k2/author/345710
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pn8b-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-20/
http://gspara01.dothome.co.kr/index.php?mid=board_XHsr53&document_srl=15826
http://withinfp.sakura.ne.jp/eso/index.php/17525295-rasskaz-sluzanki-3-sezon-3-seria-jffb-rasskaz-sluzanki-3-sezon-/0
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/864628
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/864682
http://netsconsults.com/index.php/component/k2/itemlist/user/854467
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sb7s-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1881263
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dk4w-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13/
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fc7r-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7/
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=87122
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3583932
http://www.quattroandpartners.it/component/k2/itemlist/user/1276205
http://forum.bmw-e60.eu/index.php?topic=11800.0
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/87512
http://naksansacondo.com/board_MGPu57/93725
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=130399
http://www.vamoscontigo.org/Noticia/187757
http://mercibq.net/partner/55778
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-txaq-%d1%80%d0%b0%d1%81/
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/77669
http://barobus.kr/qna/97618
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=229064
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=315395
http://dow.dothome.co.kr/board_jydx58/36472
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=109456
http://bath-family.com/photo_zone/128077
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=386870
http://jnk-ent.jp/index.php?mid=gallery&document_srl=242029
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=222190
http://x-crew.center/guest/4846807
http://gabisan.com/board_OuDs04/71533
http://w9builders.co.uk/index.php/component/k2/itemlist/user/125742
http://mglpcm.org/board_ETkS12/131924
https://betshin.com/Story/207231
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xn1f-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2/
http://euromouleusinage.com/index.php/component/k2/itemlist/user/199229
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/865419
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3584457
http://www.ekemoon.com/250393/051420192231/
https://blossomug.com/index.php/component/k2/itemlist/user/1132767
http://netsconsults.com/index.php/component/k2/itemlist/user/854622
https://intelogist2.wpengine.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mf2e-%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3/
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kd1p-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13/
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/865478
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=854586
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1881727
http://arquitectosenreformas.es/index.php/component/k2/itemlist/user/87194
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/865571
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3584380
http://naksansacondo.com/board_MGPu57/84570
http://ilsannabgol.kr/board_brJk31/1374470
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=106468
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3794409
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=175572
http://mediaville.me/index.php/component/k2/itemlist/user/364458
https://www.celekt.com/%d0%92%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rk6%d0%92%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be/
http://midorijapaneserestaurant.ca/menu/News/45816
https://www.2ayes.com/20067/3-5-ihey-3-5-fox
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=117444
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=345498
http://d-tube.info/board_jvyO69/371929
http://dcasociados.eu/?option=com_k2&view=itemlist&task=user&id=94503
http://lucky.kidspann.net/index.php?mid=qna&document_srl=294941
http://www.ekemoon.com/245851/050620190129/
http://www.ekemoon.com/251963/060020194601/
https://intelogist2.wpengine.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pu8s-%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3/
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ta9a-%d0%ba%d0%be%d0%bf-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vx4d-%d0%ba%d0%be%d0%bf-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ou2m-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-15/
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7553732
https://intelogist2.wpengine.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qy4l-%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3/
https://intelogist2.wpengine.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-bb8z-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ky8t-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10/
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wo9k-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13/
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=23698
https://intelogist2.wpengine.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gp6h-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81/
https://intelogist2.wpengine.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ub0p-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=209787
http://jiral.net/an9/28139
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3450644
http://www.svteck.co.kr/customer_gratitude/223615
http://www.cnsmaker.net/xe/?document_srl=134699
http://looksun.co.kr/index.php?mid=board_4&document_srl=203459
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=414692
http://rudraautomation.com/index.php/component/k2/author/349316
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229363
http://mediaville.me/index.php/component/k2/itemlist/user/330690
http://dreamplusart.com/mn03_01/171031
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/393051
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=109360
https://www.chirorg.com/?document_srl=149255
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=664687
http://cwon.kr/xe/board_bnSr36/300704
http://music.start-a-idea.online/blogs/viewstory/48144
http://p9912.cafe24.com/board_LVgu51/59060
http://divespace.co.kr/board/271460
http://cwon.kr/xe/board_bnSr36/304272
http://looksun.co.kr/index.php?mid=board_4&document_srl=189918
http://vtservices85.fr/smf2/index.php?PHPSESSID=8d67383e34f74878ebb18f9604be3231&topic=297715.0
http://wigalseguros.com.br/index.php/component/k2/itemlist/user/28525
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=13596
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=305703
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/349058
https://www.shaiyax.com/index.php?topic=407772.0
http://sejong-thesharpyemizi.co.kr/m1/75829
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4899174
http://looksun.co.kr/index.php?mid=board_4&document_srl=189036
http://gusinoepero.ru/archives/27572
http://www.hmotors.co.kr/?document_srl=70559
https://gonggamlaw.com/lawcase/143255
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1542071
http://www.jesusandmarypatna.com/index.php/component/k2/itemlist/user/3545535
http://daltso.com/index.php?mid=board_cUYy21&document_srl=191835
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1151549
http://askpharm.net/board_NQiz06/209197
http://lavaggio.com.vn/index.php/component/k2/itemlist/user/3932850
http://www.firstfinancialservices.co.uk/?option=com_k2&view=itemlist&task=user&id=42688
http://www.cnsmaker.net/xe/?document_srl=143036
http://khapthanam.co.kr/g1/141308
http://viamania.net/index.php?mid=board_raYV15&document_srl=138654
http://cwon.kr/xe/board_bnSr36/297304
https://www.hohoyoga.com/testboard/4086657
http://tiretech.co.kr/index.php?mid=qna&document_srl=187595
http://themasters.pro/file_01/225012
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=22056
http://herdental.co.kr/index.php?mid=online&document_srl=113264
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5057875
http://www.theocraticamerica.org/forum/index.php?topic=71540.0
http://ko.myds.me/board_story/298254
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/820274
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=955476
http://dohairbiz.com/en/component/k2/itemlist/user/2820535.html
http://daltso.com/index.php?mid=board_cUYy21&document_srl=157966
http://cwon.kr/xe/board_bnSr36/287889
https://mcsetup.tk/bbs/index.php?topic=264632.0
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/83094
https://blossomug.com/index.php/component/k2/itemlist/user/1116427
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=206383
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=86778
http://mediaville.me/index.php/component/k2/itemlist/user/369789
http://kwpub.kr/PUBS/128004
http://www.artangel.co.kr/index.php?mid=Activities&document_srl=182764
http://dospuntoseventos.cl/component/k2/itemlist/user/16360
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=17554
http://miquirofisico.com/index.php/component/k2/itemlist/user/4552
http://sd-xi.co.kr/g1/80969
http://zakdu.com/board_YpzS56/20948
https://www.hohoyoga.com/testboard/4057997
http://wartoby.com/index.php?mid=board_UXUA38&document_srl=93432
https://www.hohoyoga.com/testboard/4057831
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=958431
http://looksun.co.kr/index.php?mid=board_4&document_srl=159049
http://www.digitalbul.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vhxe-%d1%80%d0%b0%d1%81/
http://dcasociados.eu/component/k2/itemlist/user/93277
http://loverstory.co.kr/board_UYNJ05/94943
http://rabat.kr/board_yCgT00/85177
http://www.hmotors.co.kr/inquiry/71562
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/339398
http://www.cnsmaker.net/xe/?document_srl=124846
http://backo.co.kr/board_aiQk58/15224
http://israengineering.com/index.php/component/k2/itemlist/user/1319440
http://servicioswts.com/?option=com_k2&view=itemlist&task=user&id=3881288
http://2872870.com/est/65057
http://sfah.ch/de/component/k2/itemlist/user/15502
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=115078
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=242851
http://w9builders.co.uk/index.php/component/k2/itemlist/user/125493
http://mediaville.me/index.php/component/k2/itemlist/user/332953
http://design-381.com/xe/qna/5138
http://ye-dream.com/qa/268142
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-awks-%d1%80%d0%b0%d1%81/
https://khuyenmaikk13.info/index.php?topic=225360.0
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/42642
http://www.capital-investment.pl/index.php/component/k2/itemlist/user/230255
http://gspara01.dothome.co.kr/index.php?mid=board_XHsr53&document_srl=14931
http://www.lgue.co.kr/?document_srl=116008
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=172407
http://midorijapaneserestaurant.ca/menu/News/76854
http://www.hmotors.co.kr/inquiry/38445
http://sfah.ch/de/component/k2/itemlist/user/15488
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/65628
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=18187
http://dev.aabn.org.gh/component/k2/itemlist/user/725051
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3568776
https://serverpia.co.kr/board_ucCk10/140099
http://divespace.co.kr/board/287450
http://rabat.kr/board_yCgT00/38853
http://dcasociados.eu/component/k2/itemlist/user/93488
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ki1g-%d0%ba%d0%be%d0%bf-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://ovotecegg.com/component/k2/itemlist/user/223170
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=126271
https://nextezone.com/index.php?action=profile;u=8723
http://forum.bmw-e60.eu/index.php?topic=10868.0
http://miquirofisico.com/index.php/component/k2/itemlist/user/4458
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=40020.0
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=35904
https://2002.shyoon.com/board_2002/193968
http://loverstory.co.kr/board_UYNJ05/97933
http://cwon.kr/xe/board_bnSr36/296999
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2740447
http://www.crnmedia.es/component/k2/itemlist/user/94426
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3531278
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=25148
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=25243
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=42641
http://www.camaracoyhaique.cl/%d0%ba%d0%be%d0%bf-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-live-%d0%ba%d0%be%d0%bf-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://www2.yasothon.go.th/smf/index.php?topic=159.175170
http://www2.yasothon.go.th/smf/index.php?topic=159.msg204557
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2842906
https://forum.shaiyaslayer.tk/index.php?topic=160065.0
http://kyj1225.godohosting.com/board_mebR72/95087
http://cwon.kr/xe/board_bnSr36/282805
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=203746
http://ptu.imoove.kr/ko/content/%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-horz-%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-5-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-starz341471
https://gonggamlaw.com/lawcase/146705
http://jnk-ent.jp/index.php?mid=gallery&document_srl=235911
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1997696
http://www.zoraholidays.net/index.php/component/k2/itemlist/user/369789
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=210690
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=829666
http://loverstory.co.kr/?document_srl=107549
https://esel.gist.ac.kr/esel2/board_hmgj23/323120
http://www.urbantutorial.com/index.php/component/k2/itemlist/user/127711
http://xekhachduyetthuy.com.vn/component/k2/itemlist/user/241921
http://cwon.kr/xe/board_bnSr36/287533
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=186789
http://naksansacondo.com/board_MGPu57/92649
https://blossomug.com/index.php/component/k2/itemlist/user/1115194
http://rabbitzone.xyz/FREE/69933
https://www.netprofessional.gr/component/k2/itemlist/user/3921.html
https://www.hwbms.com/web/qna/37677
http://lucky.kidspann.net/index.php?mid=qna&document_srl=291398
http://israengineering.com/index.php/component/k2/itemlist/user/1348505
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=59633
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=59795
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=59805
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=59810
http://mediaville.me/index.php/component/k2/itemlist/user/405696
http://mobility-corp.com/?option=com_k2&view=itemlist&task=user&id=2773529
http://mobility-corp.com/index.php/component/k2/itemlist/user/2774042
http://mobility-corp.com/index.php/component/k2/itemlist/user/2774085
http://mobility-corp.com/index.php/component/k2/itemlist/user/2774088
http://proxima.co.rw/index.php/component/k2/itemlist/user/736913
http://proxima.co.rw/index.php/component/k2/itemlist/user/737091
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=98619
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=113174
https://gonggamlaw.com/lawcase/83010
http://kockazatkutato.hu/component/k2/itemlist/user/43665
http://jiral.net/an9/30083
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=665117
http://midorijapaneserestaurant.ca/menu/News/75777
http://www.hmotors.co.kr/inquiry/32738
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=95719
http://ariji.kr/?document_srl=1024281
http://sy.korean.net/qna/313727
http://warmfund.net/p/index.php?mid=financing&document_srl=478738
http://cwon.kr/xe/board_bnSr36/288459
http://dessa.com.br/component/k2/itemlist/user/387477
http://leonwebzine.dothome.co.kr/guest/11720
http://cwon.kr/xe/board_bnSr36/313814
http://gusinoepero.ru/archives/31525
http://dreamplusart.com/mn03_01/185584
http://www.ekemoon.com/244767/051920190528/
http://backo.co.kr/board_aiQk58/20935
http://melchinooddle.dothome.co.kr/index.php?document_srl=12028&mid=board_EIUA02
http://www.vamoscontigo.org/Noticia/222007
https://gonggamlaw.com/lawcase/147662
http://midorijapaneserestaurant.ca/menu/?document_srl=102154
http://midorijapaneserestaurant.ca/menu/News/102115
http://midorijapaneserestaurant.ca/menu/News/102181
http://naksansacondo.com/board_MGPu57/136223
http://www.leekeonsu-csi.com/?document_srl=1278892
https://betshin.com/Story/240984
https://betshin.com/Story/241010
https://betshin.com/Story/241046
https://gonggamlaw.com/lawcase/175884
https://gonggamlaw.com/lawcase/175955
https://www.hohoyoga.com/testboard/4116516
http://taklongclub.com/forum/index.php?topic=199127.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=116682
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3483250
http://www.ekemoon.com/245221/052320191528/
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/852043
https://blossomug.com/index.php/component/k2/itemlist/user/1111391
http://myrechockey.com/forums/index.php?topic=118281.0
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16575
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3569805
https://www.hohoyoga.com/testboard/4085639
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1246926
http://iymc.or.kr/pds/115231
http://www.sp1.football/index.php?mid=faq&document_srl=911301
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5056704
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=956695
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1578975
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=19267
http://www.quattroandpartners.it/index.php/component/k2/itemlist/user/1292988
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/67863
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3531940
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3532306
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=114183
http://music.start-a-idea.online/blogs/viewstory/49940
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=84688
http://miquirofisico.com/index.php/component/k2/itemlist/user/4486
http://d-tube.info/board_jvyO69/371988
http://goldenpowerball2.com/index.php?document_srl=457235&mid=board_Nutq11
http://rudraautomation.com/index.php/component/k2/author/291808
http://dospuntoseventos.cl/component/k2/itemlist/user/16058
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=18095
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/?document_srl=78743
https://mcsetup.tk/bbs/index.php?topic=264141.0
https://sto54.ru/index.php/component/k2/itemlist/user/3480108
http://www.leekeonsu-csi.com/?document_srl=1224198
https://betshin.com/Story/223640
https://gonggamlaw.com/lawcase/157101
https://gonggamlaw.com/lawcase/157125
https://www.hohoyoga.com/testboard/4094472
https://www.hohoyoga.com/testboard/4094487
https://www.hohoyoga.com/testboard/4094508
https://www.hwbms.com/web/qna/47879
https://www.hwbms.com/web/qna/47893
https://www.hwbms.com/web/qna/47916
http://dsyang.com/board_Kvgn62/47946
http://dsyang.com/board_Kvgn62/47969
http://dsyang.com/board_Kvgn62/47975
<p align="">
<a title="강남오피" href="http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bf%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%c5%8b%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%84%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%8d%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%85%bela" target="_blank">강남오피
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉오피" href="https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%d0%be%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%88%82%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%bd%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%82%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a9tide" target="_blank">선릉오피
</a>
</p>
먼저핀꽃은 먼저진다 남보다 먼저 공을 세우려고 조급히 서둘것이 아니다-채근담
<p align="">
<a title="역삼오피" href="
https://enes.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%94%bb%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%97%88%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%ce%9egang" target="_blank">역삼오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남휴게텔" href="
https://www.livemeshthemes.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%c4%b1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b7%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%85%86%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%93%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%82%ba%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%84%a1%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%82stone" target="_blank">강남휴게텔
</a>
</p>
먹고 싶은것을 다 먹는 것은 그렇게 재미있지 않다 . 인생을 경계선 없이 살면 기쁨이 덜하다.먹고싶은대로 다 먹을 수있다면 먹고싶은 것을 먹는데 무슨 재미가 있겠나 - 톰행크스
<p align="">
<a title="선릉휴게텔" href="
http://www.pnr.corsica/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%89%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%a1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%9d%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%83%a6afford" target="_blank">선릉휴게텔
</a>
</p>
진짜 문제는 사람들의 마음이다.그것은 절대로 물리학이나 윤리학의 문제가 아니다.-아인슈타인
<p align="">
<a title="역삼휴게텔" href="
https://dict.leo.org/italienisch-deutsch/%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%82%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%d1%8f%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%83%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%ae%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9dseason" target="_blank">역삼휴게텔
</a>
</p>
가난은 가난하다고 느끼는 곳에 존재한다 .- 에머슨
<p align="">
<a title="강남안마" href="https://24.sapo.pt/pesquisar?q=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%85%a2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%82%8f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%99%a0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%85%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ce%92truly" target="_blank">강남안마
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉안마" href="
https://enfi.dict.cc/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%9e%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%85%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%90%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%bd%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%9cband" target="_blank">선릉안마
</a>
</p>
행복은 습관이다 그것을 몸에 지니라 -허버드
<p align="">
<a title="역삼안마" href="
https://www.lidumsaym.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%83%9d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c2%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8f%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%b1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%82%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b9derived" target="_blank">역삼안마
</a>
</p>
화려한 일을 추구하지 말라. 중요한 것은 스스로의 재능이며자신의 행동에 쏟아 붓는 사랑의 정도이다. -머더 테레사
<p align="">
<a title="강남오피" href="
http://www.twentszitmaaierteam.nl/pages/interactief/gastenboek.php?p=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%87%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%86%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%82%b9%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%94%bd%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%d0%a3wouldn't" target="_blank">강남오피
</a>
</p>
절대 어제를 후회하지 마라 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다-L.론허바드
<p align="">
<a title="선릉오피" href="
http://www.mairtinmusic.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%82%86%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%8b%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%9e%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%88truly" target="_blank">선릉오피
</a>
</p>
내일은 내일의 태양이 뜬다 피할수 없으면 즐겨라 -로버트 엘리엇
<p align="">
<a title="역삼오피" href="https://www.uptodate.com/contents/search?search=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%81%99%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%b9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%99%aa%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%83%8e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c3%be%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%82%b6%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%8centire" target="_blank">역삼오피
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남휴게텔" href="
http://ladysmithfederal.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%93%94%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%88%87%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%8f%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ce%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%c2%baremark" target="_blank">강남휴게텔
</a>
</p>
인간의 삶 전체는 단지 한 순간에 불과하다 . 인생을 즐기자 - 플루타르코스
<p align="">
<a title="선릉휴게텔" href="
https://www.governmentjobs.com/jobs?keyword=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%94%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%87secretly" target="_blank">선릉휴게텔
</a>
</p>
흔히 사람들은 기회를 기다리고 있지만 기회는 기다리는사람에게 잡히지 않는 법이다.우리는 기회를 기다리는 사람이 되기 전에 기회를 얻을 수 있는실력을 갖춰야 한다.일에 더 열중하는 사람이 되어야한다.-안창호
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%bb%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%84%ba%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%89%b0%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8e%93%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%80%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%cf%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b7artillery" target="_blank">역삼휴게텔
</a>
</p>
마음만을 가지고 있어서는 안된다. 반드시 실천하여야 한다.-이소룡
<p align="">
<a title="강남안마" href="
https://dehr.dict.cc/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%86%8d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%a1%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%84%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%9f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%b0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%88%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%8f%9dleg" target="_blank">강남안마
</a>
</p>
물러나서 조용하게 구하면 배울 수 있는 스승은 많다.사람은 가는 곳마다 보는 것마다 모두 스승으로서배울 것이 많은 법이다.-맹자
<p align="">
<a title="선릉안마" href="
https://www.gov.uk/search/all?keywords=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%92%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%91%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%ae%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8f%87%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%97%87providing" target="_blank">선릉안마
</a>
</p>
삶이 있는 한 희망은 있다 -키케로
<p align="">
<a title="역삼안마" href="
https://www.sdsn.no/sok/category28150.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%88%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%8c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%82%a1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%85%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%c4%b8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%85%9esecretary" target="_blank">역삼안마
</a>
</p>
한 번 실패와 영원한 실패를 혼동하지 마라.-F.스콧 핏제랄드
<p align="">
<a title="강남오피" href="
https://www.righteousmind.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%b0%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%91%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%96%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%88%87sang" target="_blank">강남오피
</a>
</p>
모든것들에는 나름의 경이로움과 심지어 어둠과 침묵이 있고 내가 어떤 상태에 있더라도 나는 그속에서 만족하는 법을 배운다-헬렌켈러
<p align="">
<a title="선릉오피" href="
http://www.actiitransportation.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e2%96%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%99%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%89%ba%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%bdaround" target="_blank">선릉오피
</a>
</p>
내 비장의 무기는 아직 손안에 있다 .그것은 희망이다 - 나폴레옹
<p align="">
<a title="역삼오피" href="https://www.youtube.com/results?search_query=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ce%a5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8e%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%a0%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%b1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%84lay" target="_blank">역삼오피
</a>
</p>
만족할 줄 아는 사람은진정한 부자이고 탐욕스러운 사람은진실로 가난한 사람이다.-솔론
<p align="">
<a title="강남휴게텔" href="
https://denl.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%81%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%8a%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%8f%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%85%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%93%a0%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%b2grief" target="_blank">강남휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="선릉휴게텔" href="
https://artdeco.org/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%9e%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a4%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%94%b9%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ef%bc%af%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%be%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%8dodd" target="_blank">선릉휴게텔
</a>
</p>
만약 우리가 할 수 있는 일을 모두 한다면 우리들은 우리자신에 깜짝 놀랄 것이다.-에디슨
<p align="">
<a title="역삼휴게텔" href="
http://www.lavipera.it/?s=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bc%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%bb%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%93%a3%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b5%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%88%8cvaried" target="_blank">역삼휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="강남안마" href="
https://money2.creontrade.com/E5/WTS/Stock/Foreign/DW_Foreign_Tax.aspx?p=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ef%bc%84%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bc%af%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%bd%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%83%9d%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%87splendid" target="_blank">강남안마
</a>
</p>
절대 어제를 후회하지 마라 . 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다 L.론허바드
<p align="">
<a title="선릉안마" href="
https://wpgovernance.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%85%a4%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%b3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%81%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%8d%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%81%b7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%a3john" target="_blank">선릉안마
</a>
</p>
사막이 아름다운 것은 어딘가에 샘이 숨겨져 있기 때문이다 - 생떽쥐베리
<p align="">
<a title="역삼안마" href="
https://nebraska.aiga.org/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%96%92%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%86%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%88%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%95%80%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ef%bd%87goes" target="_blank">역삼안마
</a>
</p>
</div>
<div style='width: 1px; height: 1px; overflow: hidden'><div align='center'>
<img name='target_resize_image[]' onclick='image_window(this)' style='cursor:pointer;' alt="" class="view_photo up" src="http://file.osen.co.kr/article/2019/05/01/201905011854774508_5cc96e7d1d3c2.jpg" >
그라운드 뷰는 차의 앞쪽 아랫부분
<div style="position:absolute; left:-9999px; top:-9999px;" class="sound_only">
피할수 없으면 즐겨라 - 로버트 엘리엇
<p align="">
<a title="강남오피" href="
http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%83%b1%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a4%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%a7%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%aa%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%a4forward" target="_blank">강남오피
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="선릉오피" href="
http://www.ambrosiocinema.it/page/5/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%83%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%a8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%b8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%bf%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ef%bc%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%96%bc%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%86spring" target="_blank">선릉오피
</a>
</p>
아래에 비교하면 남음이 있다.-명심보감
<p align="">
<a title="역삼오피" href="
https://www.openrice.com/zh/hongkong/restaurants?what=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%99%a5%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a0both" target="_blank">역삼오피
</a>
</p>
실패는 잊어라 그러나 그것이 준 교훈은절대 잊으면 안된다-하버트 개서
<p align="">
<a title="강남휴게텔" href="
https://desk.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%88%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%88%99%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%85%b4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%82%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%81boat" target="_blank">강남휴게텔
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉휴게텔" href="http://www.blueskyspaworks.com/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%c2%bc%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%91%ad%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%95%89%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%bb%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%92%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%ef%bc%84damage" target="_blank">선릉휴게텔
</a>
</p>
절대 포기하지 말라. 당신이 되고 싶은 무언가가 있다면그에 대해 자부심을 가져라. 당신 자신에게 기회를 주어라. 스스로가 형편없다고 생각하지 말라.그래봐야 아무 것도 얻을 것이 없다. 목표를 높이 세워라.인생은 그렇게 살아야 한다.-마이크 맥라렌
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%80%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%92%b2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%92%a4%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bf%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%8e%97sworn" target="_blank">역삼휴게텔
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="강남안마" href="
https://www.wfs-dreieich.de/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%d0%93%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%97%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%88%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%a3%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%a4%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%84blame" target="_blank">강남안마
</a>
</p>
계단을 밟아야 계단 위에 올라설수 있다 -터키속담
<p align="">
<a title="선릉안마" href="
http://ypsistudio.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%82%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c4%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ef%bc%b0%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bf%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%cf%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%91%a4contain" target="_blank">선릉안마
</a>
</p>
지금이야 말로 일할때다. 지금이야말로 싸울때다. 지금이야말로 나를 더 훌륭한 사람으로 만들때다오늘 그것을 못하면 내일 그것을 할수있는가- 토마스 아켐피스
<p align="">
<a title="역삼안마" href="
https://www.matematikk.org/trinn8-10/sok/index.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%81%af%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bc%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%98%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%b3%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%b4understand" target="_blank">역삼안마
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남오피" href="
https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%86%90%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%85%b5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ef%bc%a8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c5%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8f%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%80bred" target="_blank">강남오피
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="선릉오피" href="
https://www.pexels.com/ko-kr/search/%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ef%bd%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%b9%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%83%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%8f%9cshelter" target="_blank">선릉오피
</a>
</p>
단순하게 살라. 쓸데없는 절차와 일 때문에 얼마나 복잡한 삶을 살아가는가?-이드리스 샤흐
<p align="">
<a title="역삼오피" href="
https://ciscentraltexas.org/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%ae%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b2%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8f%87%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%8a%83%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%97%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%92philadelphia" target="_blank">역삼오피
</a>
</p>
직접 눈으로 본 일도 오히려 참인지 아닌지염려스러운데 더구나 등뒤에서 남이 말하는것이야 어찌 이것을 깊이 믿을 수 있으랴?-명심보감-
<p align="">
<a title="강남휴게텔" href="
http://www.kuenselonline.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ce%a8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%9c%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%86%96%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%b2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bd%90%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%87quickly" target="_blank">강남휴게텔
</a>
</p>
내가 헛되이 보낸 오늘은 어제 죽어간 이들이그토록 바라던 하루이다 단 하루면 인간적인 모든 것을 멸망시킬수도 다시 소생시킬수도 있다-소포클레스
<p align="">
<a title="선릉휴게텔" href="https://www.sony.com/electronics/support/results?query=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%86%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%81%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ce%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%bd%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bc%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9bboat" target="_blank">선릉휴게텔
</a>
</p>
돈이란 바닷물과도 같다. 그것은 마시면 마실수록 목이 말라진다.-쇼펜하우어
<p align="">
<a title="역삼휴게텔" href="
https://jobs.rbc.com/ca/en/search-results?keywords=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%8c%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%d0%9e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%82%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%a6%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%c5%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%82joke" target="_blank">역삼휴게텔
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남안마" href="
http://www.makinamekawa.com/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%91%a9%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%d0%96%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bc%a2%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%92dreaming" target="_blank">강남안마
</a>
</p>
진정으로 웃으려면 고통을 참아야하며 나아가 고통을 즐길 줄 알아야 해 -찰리 채플린
<p align="">
<a title="선릉안마" href="
https://www.reddit.com/search?q=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%ac%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%9b%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%92%a5%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%a7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%99%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%a7grant" target="_blank">선릉안마
</a>
</p>
한번의 실패와 영원한 실패를 혼동하지 마라 -F.스콧 핏제랄드
<p align="">
<a title="역삼안마" href="
https://desk.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%95%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%9e%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ce%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%b5%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%85%b9%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%d1%89%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%93goal" target="_blank">역삼안마
</a>
</p>
행복은 결코 많고 큰데만 있는 것이 아니다 작은 것을 가지고도 고마워 하고 만족할 줄 안다면그는 행복한 사람이다여백과 공간의 아름다움은 단순함과 간소함에 있다법정스님 - 홀로사는 즐거움 에서
<p align="">
<a title="강남오피" href="
http://www.alberguerioaragon.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%bd%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%a6%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%87%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%80%b3%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%85%a5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%93%98%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%81seem" target="_blank">강남오피
</a>
</p>
길을 잃는 다는 것은 곧 길을 알게 된다는 것이다. - 동아프리카속담
<p align="">
<a title="선릉오피" href="
https://www.isistassinari.gov.it/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%8e%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%ce%b7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%89%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ce%95%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%95%88awhile" target="_blank">선릉오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="역삼오피" href="
http://isb.az/ru/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%89%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%d1%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%93%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%8cindependent" target="_blank">역삼오피
</a>
</p>
자신을 내보여라. 그러면 재능이 드러날 것이다.- 발타사르 그라시안
<p align="">
<a title="강남휴게텔" href="
http://biz.heraldcorp.com/view.php?ud=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%b2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bd%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%ef%bc%95%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%89%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%bbmarks" target="_blank">강남휴게텔
</a>
</p>
화가 날 때는 100까지 세라. 최악일 때는 욕설을 퍼부어라. -마크 트웨인
<p align="">
<a title="선릉휴게텔" href="
https://www.americanas.com.br/busca?conteudo=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ef%bc%b0%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%84%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%9a%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%81%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%8e%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%a8portrait" target="_blank">선릉휴게텔
</a>
</p>
1퍼센트의 가능성 그것이 나의 길이다-나폴레옹
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%83%99%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8f%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%83%95%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%d0%af%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b9personal" target="_blank">역삼휴게텔
</a>
</p>
최고에 도달하려면 최저에서 시작하라.-P.시루스
<p align="">
<a title="강남안마" href="
http://jozankei.jp/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%92%9f%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%81%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%c3%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%88%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%84%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%96%a6%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b6parted" target="_blank">강남안마
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉안마" href="
http://www.somoseducacao.com.br/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%98%85%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%be%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%9a%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%a1%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%a5greatly" target="_blank">선릉안마
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="역삼안마" href="
https://riftio.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%8e%80%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bd%99%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%99%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%8a%83%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%9d%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%a6%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%84%b9had" target="_blank">역삼안마 (*•̀ᴗ•́*)و ̑̑
</a>
</p>
http://alastair030.dothome.co.kr/index.php?mid=board_MMiF30&document_srl=22423
https://reficulcoin.com/index.php?topic=86927.0
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=241752
http://xn--c79an5j4sas61aovgwa004bwra306g8xa.modelhouse.guide/?document_srl=293099
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/73488
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3548592
https://intelogist2.wpengine.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-faor-%d1%80%d0%b0%d1%81/
https://cybergsm.es/index.php?topic=71297.0
http://www.spazioad.com/component/k2/itemlist/user/7418340
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-da4t-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://intelogist2.wpengine.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pl5s-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81/
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qv0g-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11/
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7552289
http://udrpsucks.com/blog/?p=2022
http://www.ekemoon.com/251621/052220194631/
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xu3e-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9/
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=23666
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=87497
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4974886
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-wg0c-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-18/
https://intelogist2.wpengine.com/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-aq6r-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://hotelnomadpalace.com/index.php/component/k2/itemlist/user/23667
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/861709
http://www.jesusandmarypatna.com/index.php/component/k2/itemlist/user/3586232
http://www.cnsmaker.net/xe/?document_srl=136831
http://toeden.co.kr/Product_new/140978
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=30492
http://backo.co.kr/board_aiQk58/22110
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1742032
http://kwpub.kr/PUBS/130499
http://israengineering.com/index.php/component/k2/itemlist/user/1316124
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=119229
https://nple.com/xe/pds/255774
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=360366
http://2872870.com/est/64748
http://www.quattroandpartners.it/component/k2/itemlist/user/1213889
http://dsyang.com/board_Kvgn62/30021
https://www.lwfservers.com/index.php?topic=73461.0
http://naksansacondo.com/board_MGPu57/99422
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3860927
http://cwon.kr/xe/board_bnSr36/309385
https://betshin.com/Story/201785
http://xihillstate.bloggirl.net/?document_srl=269475
http://daesestudy.co.kr/ipsi_docu/160408
https://www.hwbms.com/web/qna/12219
http://mediaville.me/index.php/component/k2/itemlist/user/332670
http://sejong-thesharpyemizi.co.kr/m1/65521
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=19168
http://www.cyberblissstudios.com/UserProfile/tabid/42/UserID/2305746/Default.aspx
http://kyj1225.godohosting.com/board_mebR72/96643
http://www.haetsaldun-clinic.co.kr/Question/35999
http://midorijapaneserestaurant.ca/menu/News/49539
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=52752
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/820281
http://sy.korean.net/qna/456723
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=289760
http://mediaville.me/index.php/component/k2/itemlist/user/404357
http://mobility-corp.com/index.php/component/k2/itemlist/user/2772010
http://mobility-corp.com/index.php/component/k2/itemlist/user/2772258
http://thermoplast.envolgroupe.com/component/k2/author/194355
http://web2interactive.com/index.php/component/k2/itemlist/user/3819530
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1888806
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=129203
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3528809
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3528826
http://www.emrabq8.com/index.php/component/k2/itemlist/user/1888816
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5%d1%82%d1%8c-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f/
http://midorijapaneserestaurant.ca/menu/News/141110
http://pkgersang.dothome.co.kr/board_jiKY24/39065
http://daltso.com/index.php?mid=board_cUYy21&document_srl=203304
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=156283
https://www.hwbms.com/web/qna/17232
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=50691
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=130674
https://blossomug.com/index.php/component/k2/itemlist/user/1115710
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=17743
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tc3%d0%ba%d0%be%d0%bf-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f28-05-2019/
http://hyeonjun.co.kr/menu3/314097
https://gonggamlaw.com/lawcase/125372
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=40164.0
http://kyj1225.godohosting.com/board_mebR72/101246
http://www.sp1.football/index.php?mid=faq&document_srl=726309
http://www2.yasothon.go.th/smf/index.php?topic=159.170070
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=31978
http://kockazatkutato.hu/component/k2/itemlist/user/43386
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=117689
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/874905
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=188588
http://ovotecegg.com/component/k2/itemlist/user/246185
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=386041
http://rudraautomation.com/index.php/component/k2/author/385943
http://www.crnmedia.es/?option=com_k2&view=itemlist&task=user&id=94026
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=129295
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3529111
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3529152
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3529156
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=41988
http://midorijapaneserestaurant.ca/menu/News/141625
http://midorijapaneserestaurant.ca/menu/News/141745
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1341052
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1341288
http://www.livetank.cn/market1/293965
http://mediaville.me/index.php/component/k2/itemlist/user/331334
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=951417
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2799116
http://xn--o39a80a04ustjq4by7fh3dp14aqoa.com/news/83024
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=259898
http://necinsurance.co.zw/component/k2/itemlist/user/21738.html
http://dohairbiz.com/en/component/k2/itemlist/user/2812841.html
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=393459
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iz3y-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://www.hohoyoga.com/testboard/4034901
http://www.rocketdan.co.kr/index.php?mid=board_WMhM93&document_srl=84068
http://rudraautomation.com/index.php/component/k2/author/387964
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3820983
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1577340
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3530618
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=24797
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=42391
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=42403
http://midorijapaneserestaurant.ca/menu/News/147672
http://naksansacondo.com/board_MGPu57/187260
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1359632
https://betshin.com/Story/270705
https://betshin.com/Story/270710
https://betshin.com/Story/270729
http://www.proandpro.it/index.php/component/k2/itemlist/user/4722725
http://www.livetank.cn/market1/303838
http://forum.bmw-e60.eu/index.php?topic=11184.0
http://www.ekemoon.com/240807/051120192726/
http://www.civilservantsacco.co.zm/index.php/component/k2/itemlist/user/1173217
http://roikjer.com/forum/index.php?PHPSESSID=drh4mm4hfa4s0ji9eanvk12kl2&topic=931648.0
http://warmfund.net/p/index.php?mid=financing&document_srl=473231
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=232218
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=531829
http://carand.co.kr/d2/86232
http://looksun.co.kr/index.php?mid=board_4&document_srl=190813
https://adsensebih.com/index.php?topic=48341.0
http://test.comics-game.ru/index.php?topic=448.0
http://ovotecegg.com/?option=com_k2&view=itemlist&task=user&id=235131
http://smartacity.com/component/k2/itemlist/user/100035
http://thermoplast.envolgroupe.com/component/k2/author/185785
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=32677
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=32678
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=32680
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1555790
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1555923
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1878942
http://www.m1avio.com/?option=com_k2&view=itemlist&task=user&id=3865145
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=121730
http://midorijapaneserestaurant.ca/menu/News/26817
https://nple.com/xe/pds/151031
https://gonggamlaw.com/lawcase/145335
http://pekosmile.dothome.co.kr/index.php?document_srl=448759&mid=seoulitestudio
http://mobility-corp.com/index.php/component/k2/itemlist/user/2696176
http://www.urbantutorial.com/?option=com_k2&view=itemlist&task=user&id=127457
http://loverstory.co.kr/board_UYNJ05/105724
https://www.hwbms.com/web/qna/42877
http://holysweat.dothome.co.kr/data/7640
http://shinhwaair2017.cafe24.com/issue/521575
http://erhu.eu/viewtopic.php?t=393707
http://bebopindia.com/notcie/380267
http://www.hmotors.co.kr/?document_srl=29330
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1288789
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=916532
http://masanlib.or.kr/g1/102420
https://www.hwbms.com/web/qna/12366
http://ko.myds.me/board_story/278729
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/180566
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/180590
http://ovotecegg.com/component/k2/itemlist/user/235581
http://rudraautomation.com/index.php/component/k2/author/365661
http://rudraautomation.com/index.php/component/k2/author/365816
http://rudraautomation.com/index.php/component/k2/author/365819
http://www.comfortcenter.es/index.php/component/k2/itemlist/user/110146
http://www.crnmedia.es/component/k2/itemlist/user/92665
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=856260
http://www.proandpro.it/?option=com_k2&view=itemlist&task=user&id=4728950
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2800508
http://godeok.houseplan.kr/?document_srl=187103
http://proxima.co.rw/index.php/component/k2/itemlist/user/711659
http://dev.aabn.org.gh/component/k2/itemlist/user/716005
http://themasters.pro/file_01/227671
http://zakdu.com/board_ssKi56/20445
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=167317
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=328765
http://www.livetank.cn/market1/299349
https://reficulcoin.com/index.php?topic=83233.0
http://sy.korean.net/qna/317404
http://www.vamoscontigo.org/Noticia/216033
http://www.golden-nail.co.kr/press/362879
http://research.kiu.ac.kr/index.php?mid=Food4Thought&document_srl=392502
http://windowshopgoa.com/?option=com_k2&view=itemlist&task=user&id=199745
http://www.sp1.football/index.php?mid=faq&document_srl=935311
http://mediaville.me/index.php/component/k2/itemlist/user/377159
http://www.vamoscontigo.org/Noticia/221972
http://ovotecegg.com/component/k2/itemlist/user/229511
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/32877
http://imfl.sci.pfu.edu.ru/forum/index.php?topic=41086.0
http://www.theocraticamerica.org/forum/index.php?topic=72517.0
http://udrpsucks.com/blog/?p=1750
http://kockazatkutato.hu/component/k2/itemlist/user/42603
http://kyj1225.godohosting.com/board_mebR72/93049
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=343446
http://divespace.co.kr/board/264878
http://udrpsucks.com/blog/?p=1794
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/303442
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/306161
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/841543
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=14194
http://jnk-ent.jp/index.php?mid=gallery&document_srl=355303
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=264770
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=28993
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=310964
http://ariji.kr/?document_srl=973284
http://mediaville.me/index.php/component/k2/itemlist/user/374730
https://gonggamlaw.com/lawcase/141298
http://carand.co.kr/d2/98646
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=399814
http://loverstory.co.kr/board_UYNJ05/98826
http://bath-family.com/photo_zone/129204
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4898320
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=48542
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=399579
http://otitismediasociety.org/forum/index.php?topic=201216.0
http://daltso.com/index.php?mid=board_cUYy21&document_srl=205016
https://www.2ayes.com/19526/3-7-fktx-3-7-ideafilm
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=36869
https://www.chirorg.com/video/148809
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/52449
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=23615
http://sy.korean.net/qna/445348
http://www.leekeonsu-csi.com/index.php?mid=sangdam1&document_srl=1162736
http://looksun.co.kr/index.php?mid=board_4&document_srl=198162
http://juroweb.com/xe/juroweb_board/82851
https://www.runcity.org/forum/index.php?action=profile;u=77526
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=deb03d8102b294d0db55a58851cc7d51&topic=11294.0
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=95786
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3372959
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gl3%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f29-0/
https://intelogist2.wpengine.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d0%bd%d0%be%d0%b2%d0%b8%d0%bd%d0%ba%d0%b0/
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=50714
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3794420
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=87923
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7518117
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/350616
https://betshin.com/Story/198068
http://www2.yasothon.go.th/smf/index.php?topic=159.171405
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=187935
http://www.pdctransport.co.th/index.php/component/k2/itemlist/user/17703
https://verdadesbiblicas.org.ec/index.php/component/k2/itemlist/user/3862898
http://forum.bmw-e60.eu/index.php?topic=11135.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2793009
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/57278
http://carand.co.kr/d2/97650
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/149360
http://ye-dream.com/qa/206247
http://carand.co.kr/d2/86920
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=259066
http://dev.aabn.org.gh/component/k2/itemlist/user/681509
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2803637
http://www.kwpcoop.or.kr/QnA/19217
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/55905
http://cwon.kr/xe/board_bnSr36/305222
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13835
https://www.hwbms.com/web/qna/33610
http://looksun.co.kr/index.php?mid=board_4&document_srl=208810
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=123416
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1997688
http://www.rationalkorea.com/xe/index.php?mid=pqna3&document_srl=687264
http://www.digitalbul.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ezkv-%d1%80%d0%b0%d1%81/
http://myrechockey.com/forums/index.php?topic=121037.0
http://e-educ.net/Forum/index.php?topic=17317.0
http://archeaudio.com/xe/board_AOYj82/10091
https://blossomug.com/index.php/component/k2/itemlist/user/1111192
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=264755
http://themasters.pro/file_01/225805
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=108032
http://dreamplusart.com/mn03_01/238260
http://dsyang.com/board_Kvgn62/43246
https://betshin.com/Story/215852
http://socialmag.bayareanonprofits.xyz/blogs/viewstory/135483
http://ko.myds.me/board_story/279222
https://intelogist2.wpengine.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gu4c-%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0/
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jo2k-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9/
https://www.celekt.com/%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xx2r-%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10/
https://www.celekt.com/%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zg1e-%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13/
http://euromouleusinage.com/index.php/component/k2/itemlist/user/197586
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2012223
https://www.chirorg.com/?document_srl=151787
http://looksun.co.kr/index.php?mid=board_4&document_srl=202159
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=348314
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=390274
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/136639
http://www2.yasothon.go.th/smf/index.php?topic=159.msg199823
http://www.svteck.co.kr/customer_gratitude/263470
http://mjbosch.com/?option=com_k2&view=itemlist&task=user&id=85268
http://www.livetank.cn/market1/316963
http://jensenbyggteam.no/index.php/component/k2/itemlist/user/13763
http://bath-family.com/photo_zone/144525
http://askpharm.net/board_NQiz06/254380
https://forum.ac-jete.it/index.php?topic=433725.0
http://autospa.lv/index.php/lv/component/k2/itemlist/user/10574
http://music.start-a-idea.online/blogs/viewstory/43757
http://daltso.com/index.php?mid=board_cUYy21&document_srl=191039
http://www.theocraticamerica.org/forum/index.php?topic=70190.0
http://vtservices85.fr/smf2/index.php?PHPSESSID=c77fb8e30121a3c01a9cc4758c358e0f&topic=288662.0
http://divespace.co.kr/board/272819
https://www.hwbms.com/web/qna/11883
http://smartacity.com/component/k2/itemlist/user/97842
http://carand.co.kr/d2/90895
http://pkgersang.dothome.co.kr/board_jiKY24/40016
http://robocit.com/index.php/component/k2/itemlist/user/449933
http://www.teedinubon.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-fpiz-%d1%80%d0%b0%d1%81/
http://rotary-laeliana.org/component/k2/itemlist/user/51939
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=37261
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/856354
http://constellation.kro.kr/?document_srl=64436
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=224723
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3785321
http://dreamplusart.com/mn03_01/214382
https://mcsetup.tk/bbs/index.php?topic=263068.0
http://kyj1225.godohosting.com/board_mebR72/97994
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99160
http://www.lgue.co.kr/?document_srl=150292
http://design-381.com/xe/?document_srl=5408
http://www.dap.com.py/index.php/es/?option=com_k2&view=itemlist&task=user&id=849455
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/819888
http://divespace.co.kr/board/286254
http://bebopindia.com/notcie/510148
https://forums.lfstats.com/viewtopic.php?t=321777
http://benzmall.co.kr/index.php?mid=download&document_srl=113334
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1754093
https://www.hohoyoga.com/testboard/4085385
http://rudraautomation.com/?option=com_k2&view=itemlist&task=user&id=341424
https://www.hwbms.com/web/qna/24532
http://0433.net/budongsan/113636
http://xihillstate.bloggirl.net/?document_srl=454431
https://www.hwbms.com/web/qna/72714
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=858476
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-live-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-6-%d1%81%d0%b5%d1%80%d0%b8/
http://midorijapaneserestaurant.ca/menu/News/107517
http://naksansacondo.com/board_MGPu57/140114
https://www.hohoyoga.com/testboard/4120544
http://midorijapaneserestaurant.ca/menu/News/107612
http://naksansacondo.com/?document_srl=140236
http://naksansacondo.com/board_MGPu57/140343
http://www.leekeonsu-csi.com/?document_srl=1289252
https://www.hohoyoga.com/testboard/4120595
https://forums.lfstats.com/viewtopic.php?t=327583
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=37310
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=410143
http://daltso.com/index.php?mid=board_cUYy21&document_srl=246179
http://kyj1225.godohosting.com/board_mebR72/60946
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/56337
http://dsyang.com/board_Kvgn62/42559
http://universalcommunity.se/Forum/index.php?topic=36080.0
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2796090
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=17637
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=828033
http://www.boutique.in.th/?option=com_k2&view=itemlist&task=user&id=153182
http://looksun.co.kr/index.php?mid=board_4&document_srl=201729
http://www.theocraticamerica.org/forum/index.php?topic=70576.0
http://rabat.kr/?document_srl=81527
http://www.crnmedia.es/component/k2/itemlist/user/92201
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1737427
http://jjimdak.callbank.kr/index.php?mid=board_OGFN30&document_srl=1124109
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=558406
http://dreamplusart.com/mn03_01/191753
http://www.ds712.net/guest/index.php?mid=guest07&document_srl=548131
http://dsyang.com/board_Kvgn62/57118
http://dsyang.com/board_Kvgn62/57124
http://naksansacondo.com/board_MGPu57/147463
https://betshin.com/Story/249476
https://betshin.com/Story/249537
https://betshin.com/Story/249542
https://gonggamlaw.com/lawcase/186293
https://www.hohoyoga.com/testboard/4125236
https://www.hwbms.com/web/qna/77581
http://www.smekalka.pp.ru/forum/index.php?topic=10621.0
http://naksansacondo.com/?document_srl=72374
http://knet.dothome.co.kr/xe/board_RJHw15/20461
http://www.sp1.football/index.php?mid=faq&document_srl=704138
https://blossomug.com/index.php/component/k2/itemlist/user/1111341
http://askpharm.net/board_NQiz06/251982
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4946459
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1853973
https://betshin.com/Story/204564
https://khuyenmaikk13.info/index.php?topic=226197.0
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=99713
http://kockazatkutato.hu/component/k2/itemlist/user/42858
http://www.svteck.co.kr/customer_gratitude/225424
http://www.svteck.co.kr/customer_gratitude/345385
http://www.jesusonly.life/calendar/526335
http://rabat.kr/board_yCgT00/70319
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=550238
http://loverstory.co.kr/board_UYNJ05/103412
http://smartacity.com/component/k2/itemlist/user/77517
http://muldorang.com/market/25140
https://forum.ac-jete.it/index.php?topic=451300.0
http://loverstory.co.kr/?document_srl=102283
http://www.emrabq8.com/index.php/component/k2/itemlist/user/1874430
http://sunele.co.kr/board_ReBD97/166954
http://www.patrasin.kr/index.php?mid=questions&document_srl=4349275
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=101989
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7485598
http://beautypouch.net/index.php?mid=board_09&document_srl=187071
http://www.coating.or.kr/atemfair_data/16377
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=138850
http://www.hmotors.co.kr/inquiry/36849
https://blossomug.com/index.php/component/k2/itemlist/user/1111426
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=91346
https://timecker.com/anonymous/188445
http://kyj1225.godohosting.com/?document_srl=106664
http://www.crnmedia.es/component/k2/itemlist/user/92209
http://apt2you2.cafe24.com/g1/37825
http://constellation.kro.kr/board_kbku73/85793
http://carand.co.kr/d2/98758
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=43251
http://www.vogtland.com.pl/?option=com_k2&view=itemlist&task=user&id=50073
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/149371
http://socialmag.bayareanonprofits.xyz/blogs/viewstory/128931
http://barobus.kr/?document_srl=105420
http://www.livetank.cn/market1/285523
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=148572
http://ovotecegg.com/component/k2/itemlist/user/227452
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=16957
http://jnk-ent.jp/index.php?mid=gallery&document_srl=365508
http://hotelnomadpalace.com/index.php/component/k2/itemlist/user/22670
https://altaylarteknoloji.com/index.php?topic=6319.0
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=210868
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1995424
http://dreamplusart.com/mn03_01/212780
http://smartacity.com/component/k2/itemlist/user/89463
http://askpharm.net/board_NQiz06/275017
http://roikjer.com/forum/index.php?PHPSESSID=vnm5sevi46h4t5m3csiu0do5i0&topic=935156.0
http://www.haetsaldun-clinic.co.kr/Question/35874
https://www.swiss-focus.ch/index.php/component/k2/itemlist/user/35572
http://music.start-a-idea.online/blogs/viewstory/48629
http://beautypouch.net/index.php?mid=board_09&document_srl=188703
http://www.vamoscontigo.org/Noticia/138208
http://loverstory.co.kr/board_UYNJ05/42473
http://carand.co.kr/d2/66134
http://holysweat.dothome.co.kr/data/7257
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xo8a-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5/
http://themasters.pro/?document_srl=224444
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-cy7r-%d0%ba%d0%be%d0%bf-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://callman.co.kr/index.php?mid=qa&document_srl=222337
http://cwon.kr/xe/board_bnSr36/308040
http://daltso.com/index.php?mid=board_cUYy21&document_srl=214080
http://praisesound.co.kr/sub04_01/118512
http://ye-dream.com/qa/230520
http://roikjer.com/forum/index.php?PHPSESSID=r4oh73ljlofr99df64d4t0b4m1&topic=925817.0
http://midorijapaneserestaurant.ca/menu/News/72284
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=131179
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=443101
http://apt2you2.cafe24.com/g1/48451
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=56340
http://foa.egerton.ac.ke/index.php/component/k2/itemlist/user/1934282
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=130810
http://www.arunagreen.com/?option=com_k2&view=itemlist&task=user&id=1153828
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/167806
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/145482
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1285201
http://looksun.co.kr/index.php?mid=board_4&document_srl=139749
https://timecker.com/anonymous/188683
http://udrpsucks.com/blog/?p=1808
https://khuyenmaikk13.info/index.php?topic=226980.0
https://forum.clubeicaro.pt/index.php?topic=2322.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1499686
http://www.popolsku.fr.pl/forum/index.php?topic=416704.0
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1542941
http://ovotecegg.com/component/k2/itemlist/user/224594
http://rabat.kr/board_yCgT00/69295
http://gabisan.com/board_OuDs04/146547
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/852559
https://timecker.com/anonymous/213430
https://timecker.com/anonymous/213445
https://www.c-alice.org/forum/index.php?topic=100814.0
http://www.comfortcenter.es/?option=com_k2&view=itemlist&task=user&id=110074
https://prosto-vkus.ru/?option=com_k2&view=itemlist&task=user&id=37014
http://8.droror.co.il/uncategorized/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-if0%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be/
http://gyeomright.dothome.co.kr/?document_srl=28112
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=28088
http://sy.korean.net/qna/315123
http://dessa.com.br/index.php/component/k2/itemlist/user/386258
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=186444
http://www.lgue.co.kr/?document_srl=116169
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/64387
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ip3g-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10/
http://yooseok.com/board_BkvT46/412449
http://www.hmotors.co.kr/inquiry/33239
https://intelogist2.wpengine.com/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-dx8j-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=65714
http://forum.elexlabs.com/index.php?topic=62333.0
http://www.leekeonsu-csi.com/?document_srl=1082137
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=126530
http://mobility-corp.com/index.php/component/k2/itemlist/user/2745556
http://constellation.kro.kr/board_kbku73/64593
http://www.digitalbul.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zqsv-%d1%80%d0%b0%d1%81/
http://www.spazioad.com/component/k2/itemlist/user/7474120
http://nyutusonsafaris.com/?option=com_k2&view=itemlist&task=user&id=167406
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=229130
http://8.droror.co.il/uncategorized/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-tizv-%d1%80%d0%b0%d1%81/
http://beautypouch.net/index.php?mid=board_09&document_srl=109913
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1312665
http://daltso.com/?document_srl=246517
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pm2w-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3/
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3863365
http://healthyteethpa.org/component/k2/itemlist/user/5550797
http://apt2you2.cafe24.com/?document_srl=56788
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=198620
http://thermoplast.envolgroupe.com/component/k2/author/180205
http://midorijapaneserestaurant.ca/menu/News/135247
http://midorijapaneserestaurant.ca/menu/News/135328
http://midorijapaneserestaurant.ca/menu/News/135338
https://betshin.com/Story/263287
https://betshin.com/Story/263309
https://betshin.com/Story/263318
https://betshin.com/Story/263328
https://betshin.com/Story/263333
https://betshin.com/Story/263359
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2835295
http://dcasociados.eu/component/k2/itemlist/user/97330
http://dev.aabn.org.gh/component/k2/itemlist/user/750989
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=57724
http://mediaville.me/index.php/component/k2/itemlist/user/402549
http://gochon-iusell.co.kr/g1/113503
http://www.cswc.co.kr/index.php?mid=board_zyTs37&document_srl=47305
http://yoriyorifood.com/xxxx/spacial/342747
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/?document_srl=96531
http://www.teedinubon.com/%d0%ba%d0%be%d0%bf-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-zd6%d0%ba%d0%be%d0%bf-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f28-05-2019/
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3576159
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=94535
http://8.droror.co.il/uncategorized/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hsgm-%d1%80%d0%b0%d1%81/
http://looksun.co.kr/index.php?mid=board_4&document_srl=209983
https://www.hwbms.com/web/qna/32867
http://apt2you2.cafe24.com/g1/53444
http://tiretech.co.kr/index.php?mid=qna&document_srl=238281
http://1661-6471.co.kr/news/42500
http://holysweat.dothome.co.kr/data/6993
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7516611
http://compultras.com/?option=com_k2&view=itemlist&task=user&id=244939
http://xn--4k0bt5qa92r7z0a4mqr4be7d1zc.com/index.php?mid=main_10&document_srl=93780
http://www.vamoscontigo.org/?document_srl=221099
http://xihillstate.bloggirl.net/?document_srl=393376
http://beautypouch.net/index.php?mid=board_09&document_srl=167673
http://yoriyorifood.com/xxxx/spacial/337758
http://apt2you2.cafe24.com/g1/34834
http://village.lorem.kr/?document_srl=261939
http://www.theocraticamerica.org/forum/index.php?topic=69777.0
http://ye-dream.com/qa/259853
http://healthyteethpa.org/?option=com_k2&view=itemlist&task=user&id=5545333
http://www.proandpro.it/?option=com_k2&view=itemlist&task=user&id=4721773
http://cwon.kr/xe/board_bnSr36/309510
http://looksun.co.kr/index.php?mid=board_4&document_srl=197926
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=206074
http://mvisage.sk/?option=com_k2&view=itemlist&task=user&id=119985
http://photogrotto.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vgsy-%d1%80%d0%b0%d1%81/
http://kwpub.kr/PUBS/129954
http://www.jesusonly.life/calendar/446636
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4949953
http://apt2you2.cafe24.com/g1/57817
https://blossomug.com/?option=com_k2&view=itemlist&task=user&id=1116327
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=121059
https://www.amazingworldtop.com/entretenimiento/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-uw8%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5/
http://sy.korean.net/qna/313582
http://sy.korean.net/qna/317719
http://mediaville.me/?option=com_k2&view=itemlist&task=user&id=372360
http://www.ekemoon.com/245157/052220194428/
http://rudraautomation.com/index.php/component/k2/author/353659
http://beautypouch.net/index.php?mid=board_09&document_srl=183652
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=175272
https://betshin.com/Story/209014
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=42984
http://hanga5.com/index.php?mid=board_photo&document_srl=170460
http://daltso.com/index.php?mid=board_cUYy21&document_srl=194561
http://miquirofisico.com/index.php/component/k2/itemlist/user/4524
http://israengineering.com/index.php/component/k2/itemlist/user/1283626
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/40586
http://erdfsa.iptime.org/xe/index.php?mid=board&document_srl=12789
https://www.hwbms.com/web/qna/11142
http://kotica00.dothome.co.kr/index.php?mid=board_nJTE45&document_srl=40151
http://gochon-iusell.co.kr/g1/75818
http://www.minikami.it/?option=com_k2&view=itemlist&task=user&id=5021959
http://lasvur.ru/?option=com_k2&view=itemlist&task=user&id=39670
http://www.svteck.co.kr/customer_gratitude/298313
http://lucky.kidspann.net/index.php?mid=qna&document_srl=334895
http://bebopindia.com/notcie/380853
http://servicioswts.com/component/k2/itemlist/user/3878334
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=112026
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=140175
http://daltso.com/index.php?mid=board_cUYy21&document_srl=155340
http://ye-dream.com/qa/265943
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=212055
http://xn----3x5er9r48j7wemud0a387h.com/?document_srl=162043
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=55360
http://benzmall.co.kr/index.php?mid=download&document_srl=146954
https://www.hwbms.com/web/qna/101589
http://proxima.co.rw/index.php/component/k2/itemlist/user/736804
https://betshin.com/Story/252669
http://hyeonjun.co.kr/menu3/287777
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2801085
https://forum.ac-jete.it/index.php?topic=447865.0
http://roikjer.com/forum/index.php?PHPSESSID=oh2egsvjbjo56naa4g3i39jmj2&topic=924655.0
http://www.verenas-unterwasserwelt.de/forum/index.php?topic=11137.0
http://1600-1590.com/index.php?mid=board_ihsE13&document_srl=407472
http://dohairbiz.com/en/component/k2/itemlist/user/2813694.html
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=23852
http://www.rocketdan.co.kr/?document_srl=161291
http://ye-dream.com/qa/206332
http://www.sp1.football/index.php?mid=faq&document_srl=721098
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=212207
http://kyj1225.godohosting.com/board_mebR72/60581
https://www.hohoyoga.com/testboard/4087529
https://saltriverbg.com/2019/05/25/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lemq-%d1%80%d0%b0%d1%81/
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1425310
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1425577
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1425774
https://betshin.com/Story/287502
https://gonggamlaw.com/lawcase/227565
https://www.hwbms.com/web/qna/126316
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=63439
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=63447
http://mobility-corp.com/index.php/component/k2/itemlist/user/2782057
http://ovotecegg.com/component/k2/itemlist/user/251353
http://proxima.co.rw/index.php/component/k2/itemlist/user/740770
https://forum.shaiyaslayer.tk/index.php?topic=178362.0
https://intelogist2.wpengine.com/%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-jo9k-%d1%81%d0%b5%d0%bd%d1%8f%d1%84%d0%b5%d0%b4%d1%8f-2-%d1%81/
http://dreamplusart.com/mn03_01/333037
http://esperanzazubieta.com/component/k2/itemlist/user/112425
http://esperanzazubieta.com/?option=com_k2&view=itemlist&task=user&id=112838
https://www.celekt.com/%d0%a7%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lm7v-%d0%a7%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=423669
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1533139
http://taklongclub.com/forum/index.php?topic=198270.0
http://maka-222.com/index.php?mid=board_hcFa40&document_srl=109899
http://roikjer.com/forum/index.php?PHPSESSID=0njv0luumg2fihkrej559jts84&topic=932069.0
http://zsmr.com.ua/?option=com_k2&view=itemlist&task=user&id=652643
http://naksansacondo.com/board_MGPu57/94164
https://mcsetup.tk/bbs/index.php?topic=261663.0
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=17059
http://www.svteck.co.kr/customer_gratitude/215632
http://sammyungsa.com/board_dltP23/6461
https://www.celekt.com/%d0%a0%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lzim-%d0%a0%d0%b0%d1%81/
http://dessa.com.br/component/k2/itemlist/user/387357
https://forum.clubeicaro.pt/index.php?topic=2814.0
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=139627
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=1998131
http://sejong-thesharpyemizi.co.kr/m1/36422
http://rabat.kr/board_yCgT00/78228
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kc9%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-13-%d1%81%d0%b5/
http://xihillstate.bloggirl.net/index.php?mid=board_HLJb60&document_srl=262400
http://sejong-thesharpyemizi.co.kr/m1/34124
http://askpharm.net/board_NQiz06/292789
http://www.eunhaele.co.kr/xe/board/21142
http://mobility-corp.com/index.php/component/k2/itemlist/user/2766162
http://dreamplusart.com/mn03_01/337091
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3585340
http://midorijapaneserestaurant.ca/menu/?document_srl=88388
http://askpharm.net/board_NQiz06/293232
http://daltso.com/index.php?mid=board_cUYy21&document_srl=362889
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3484751
http://www.cnsmaker.net/xe/?document_srl=140805
http://naksansacondo.com/board_MGPu57/95377
http://xn----c28e37psqau1bm6v53e05ac6b854f.kr/news/31926
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=224009
https://alvarogarciatorero.com/?option=com_k2&view=itemlist&task=user&id=50659
http://yoriyorifood.com/xxxx/spacial/252784
http://www.verenas-unterwasserwelt.de/forum/index.php?PHPSESSID=a9d2de1d15b37e07e5046b14e752203d&topic=11347.0
https://www.lwfservers.com/index.php?topic=72937.0
http://www.hmotors.co.kr/inquiry/68262
http://arquitectosenreformas.es/component/k2/itemlist/user/86049
https://betshin.com/Story/206218
https://adsensebih.com/index.php?topic=42635.0
http://midorijapaneserestaurant.ca/menu/News/82044
http://naksansacondo.com/board_MGPu57/109470
http://naksansacondo.com/board_MGPu57/109609
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1229277
https://betshin.com/Story/224408
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mk6v-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-10-%d1%81%d0%b5%d1%80%d0%b8/
http://halinhpharma.com.vn/?option=com_k2&view=itemlist&task=user&id=426437
http://divespace.co.kr/board/360843
http://www.spazioad.com/?option=com_k2&view=itemlist&task=user&id=7499709
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lw9i-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-as3d-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6/
http://rabat.kr/rabat/126177
http://xn--2e0b53df5ag1c804aphl.net/nuguna/292944
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2029432
http://sy.korean.net/qna/636907
http://hydrocarbs-gh.org/index.php/component/k2/itemlist/user/7486313
http://callman.co.kr/index.php?mid=qa&document_srl=223372
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=151539
http://nnkumw.org/xe/index.php?mid=board_yNQm00&document_srl=128955
http://juroweb.com/xe/juroweb_board/112862
http://forum.bmw-e60.eu/index.php?topic=12356.0
http://ptu.imoove.kr/ko/content/%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-3-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-exwh-%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-3-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-fx341265
http://loverstory.co.kr/board_UYNJ05/107245
http://xekhachduyetthuy.com.vn/?option=com_k2&view=itemlist&task=user&id=241663
http://www.eunhaele.co.kr/xe/board/20553
http://arnikabolt.ro/?option=com_k2&view=itemlist&task=user&id=113180
http://carand.co.kr/d2/98595
http://themasters.pro/file_01/308355
http://xn----3x5er9r48j7wemud0a387h.com/news/172619
http://dsyang.com/board_Kvgn62/48987
http://dsyang.com/board_Kvgn62/49005
http://midorijapaneserestaurant.ca/menu/News/83820
http://midorijapaneserestaurant.ca/menu/News/83836
http://naksansacondo.com/board_MGPu57/112053
http://naksansacondo.com/board_MGPu57/112175
http://naksansacondo.com/board_MGPu57/112203
http://www.leekeonsu-csi.com/?document_srl=1235802
https://betshin.com/Story/225800
http://xn----c28e37pskhnybu1kc2q9ndp5l.com/news/221930
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=161784
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=161815
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=161830
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=161843
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=161848
http://xn--hu1bs8ufrd6ucyz0aooa.kr/?document_srl=234013
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=233983
http://ye-dream.com/qa/349213
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=615365
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=615489
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=615547
https://adsensebih.com/index.php?topic=50597.0
http://gabisan.com/board_OuDs04/70770
http://ovotecegg.com/component/k2/itemlist/user/222285
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=18927
http://benzmall.co.kr/index.php?mid=download&document_srl=52771
https://www.lwfservers.com/index.php?topic=73992.0
http://thermoplast.envolgroupe.com/component/k2/author/199656
http://thermoplast.envolgroupe.com/component/k2/author/199888
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=40848
http://www.bb-room.ru/index.php/component/k2/itemlist/user/13725
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1896173
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3597364
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=136345
http://www.travelsolution.info/?option=com_k2&view=itemlist&task=user&id=721910
http://www.travelsolution.info/?option=com_k2&view=itemlist&task=user&id=721925
http://www.travelsolution.info/?option=com_k2&view=itemlist&task=user&id=722024
https://www.hohoyoga.com/testboard/4104797
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=144769
http://dreamplusart.com/mn03_01/312850
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16/
https://www.hwbms.com/web/qna/50024
http://benzmall.co.kr/?document_srl=148502
http://1644-4404.com/?document_srl=468253
https://timecker.com/anonymous/211342
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1774826
http://askpharm.net/board_NQiz06/297396
http://midorijapaneserestaurant.ca/menu/?document_srl=89860
http://8.droror.co.il/uncategorized/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-drdc-%d1%80%d0%b0%d1%81/
http://www.hmotors.co.kr/?document_srl=33295
http://apt2you2.cafe24.com/g1/52765
https://nple.com/xe/pds/168362
http://www.atab.com.sa/?option=com_k2&view=itemlist&task=user&id=1736652
http://dsyang.com/board_Kvgn62/46913
https://www.hwbms.com/web/qna/33717
http://looksun.co.kr/index.php?mid=board_4&document_srl=189508
http://dsyang.com/board_Kvgn62/43464
http://adrianaafonso.com.br/index.php/component/k2/itemlist/user/2801943
http://dreamplusart.com/mn03_01/199608
http://leonwebzine.dothome.co.kr/guest/11852
http://www.tessabannampad.go.th/webboard/index.php?topic=225368.0
http://www.crnmedia.es/component/k2/itemlist/user/94966
https://blossomug.com/index.php/component/k2/itemlist/user/1136483
https://www.hwbms.com/web/qna/48010
http://xn--2e0b53df5ag1c804aphl.net/nuguna/284749
http://sy.korean.net/qna/539800
http://udrpsucks.com/blog/?p=2187
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=87544
http://dcasociados.eu/component/k2/itemlist/user/97529
https://gonggamlaw.com/lawcase/136841
http://www2.yasothon.go.th/smf/index.php?topic=159.170490
http://www.capital-investment.pl/?option=com_k2&view=itemlist&task=user&id=233636
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3785365
http://kwpub.kr/PUBS/131289
http://sy.korean.net/qna/315136
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=23321
http://www.vamoscontigo.org/Noticia/219964
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=206138
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=161419
http://www.coating.or.kr/atemfair_data/14323
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=101156
https://nple.com/xe/pds/235974
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-live-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-16-2/
http://ye-dream.com/?document_srl=310858
http://www.hmotors.co.kr/inquiry/84434
http://benzmall.co.kr/index.php?mid=download&document_srl=132065
https://intelogist2.wpengine.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-gr1k-%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3/
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xw0u-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7/
http://www.m1avio.com/index.php/component/k2/itemlist/user/3898791
http://smartacity.com/component/k2/itemlist/user/112128
http://xn--2e0b53df5ag1c804aphl.net/nuguna/105646
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4900327
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2739804
http://hyeonjun.co.kr/menu3/299483
http://mglpcm.org/board_ETkS12/127790
http://patagroupofcompanies.com/?option=com_k2&view=itemlist&task=user&id=303281
http://carand.co.kr/d2/71110
http://engeena.com/component/k2/itemlist/user/9149
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=67520
http://www.ekemoon.com/244639/051720193728/
http://www.tessabannampad.go.th/webboard/index.php?topic=227089.0
http://neosky.net/xe/space_station/72788
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?mid=news&document_srl=100174
http://daltso.com/index.php?mid=board_cUYy21&document_srl=171735
https://forum.ac-jete.it/index.php?topic=446133.0
https://gonggamlaw.com/lawcase/153775
https://www.hohoyoga.com/testboard/3974043
http://benzmall.co.kr/index.php?mid=download&document_srl=93708
http://daesestudy.co.kr/?document_srl=166776
http://dreamplusart.com/mn03_01/309827
http://benzmall.co.kr/index.php?mid=download&document_srl=169917
http://web2interactive.com/?option=com_k2&view=itemlist&task=user&id=3820709
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3583932
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3531206
https://nextezone.com/index.php?action=profile&u=17281
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2027083
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=31138
http://askpharm.net/board_NQiz06/301195
https://www.hwbms.com/web/qna/82765
http://beautypouch.net/index.php?mid=board_09&document_srl=232636
https://forum.clubeicaro.pt/index.php?topic=3055.0
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3576528
http://daltso.com/index.php?mid=board_cUYy21&document_srl=214962
http://rabbitzone.xyz/FREE/63831
http://www.hmotors.co.kr/?document_srl=25105
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7481207
http://sofficer.net/xe/teach/285757
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=43891
http://www.bb-room.ru/index.php/component/k2/itemlist/user/13698
http://ladybirdestates.com/index.php/component/k2/itemlist/user/12609
http://naksansacondo.com/board_MGPu57/223932
http://postesari.com/index.php/component/k2/itemlist/user/35011
http://www.bb-room.ru/index.php/component/k2/itemlist/user/13894
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1453231
https://www.hwbms.com/web/qna/138551
http://dev.aabn.org.gh/component/k2/itemlist/user/765409
http://iymc.or.kr/pds/172587
http://iymc.or.kr/pds/172606
http://jejucctv.co.kr/A5/138376
http://koais.com/?document_srl=394012
http://koais.com/data/394128
http://kwpub.kr/PUBS/327579
http://kwpub.kr/PUBS/327848
http://loverstory.co.kr/board_UYNJ05/317363
http://married.dike.gr/index.php/component/k2/itemlist/user/94224
http://p9912.cafe24.com/board_LVgu51/125338
http://phmusic.dothome.co.kr/index.php?mid=PowerHouseMusic&document_srl=69742
http://pkgersang.dothome.co.kr/board_jiKY24/59140
http://rudraautomation.com/index.php/component/k2/author/409820
https://forum.clubeicaro.pt/index.php?topic=2456.0
http://jdcalc.com/forum/viewtopic.php?t=293755
http://simkungshopping.com/index.php?mid=board_cUYy21&document_srl=261804
http://daltso.com/index.php?mid=board_cUYy21&document_srl=192712
http://mobility-corp.com/index.php/component/k2/itemlist/user/2735810
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3859553
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2009201
http://sfah.ch/de/component/k2/itemlist/user/15492
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/150104
http://d-tube.info/board_jvyO69/372046
http://rabat.kr/board_yCgT00/84387
http://ye-dream.com/qa/213357
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=46647
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1549032
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=19327
http://naksansacondo.com/board_MGPu57/210481
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1425310
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1425577
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1425774
https://betshin.com/Story/287502
https://gonggamlaw.com/lawcase/227565
https://www.hwbms.com/web/qna/126316
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=63439
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=63447
http://mobility-corp.com/index.php/component/k2/itemlist/user/2782057
https://intelogist2.wpengine.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vq9h-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://naksansacondo.com/?document_srl=135225
https://www.hohoyoga.com/testboard/4098856
https://timecker.com/anonymous/210771
http://sy.korean.net/qna/641175
https://intelogist2.wpengine.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-nw5o-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
https://sto54.ru/?option=com_k2&view=itemlist&task=user&id=3548751
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ln1j-%d0%ba%d0%be%d0%bf-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://hydrocarbs-gh.org/?option=com_k2&view=itemlist&task=user&id=7556203
https://www.hohoyoga.com/testboard/4154549
http://rabat.kr/board_yCgT00/158939
http://netsconsults.com/?option=com_k2&view=itemlist&task=user&id=852108
http://dreamplusart.com/mn03_01/350394
http://arquitectosenreformas.es/component/k2/itemlist/user/86007
http://xn--2e0bk61btjo.com/notice/24962
https://www.hohoyoga.com/testboard/4086508
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/66470
http://dessa.com.br/?option=com_k2&view=itemlist&task=user&id=388064
http://www.proandpro.it/?option=com_k2&view=itemlist&task=user&id=4726339
http://divespace.co.kr/board/264416
http://roikjer.com/forum/index.php?topic=935638.0
http://barobus.kr/qna/92265
http://dreamplusart.com/mn03_01/213605
http://forum.bmw-e60.eu/index.php?topic=11356.0
https://cybergsm.es/index.php?topic=63420.0
http://divespace.co.kr/board/285905
http://soc-human.kz/?option=com_k2&view=itemlist&task=user&id=1770017
http://www.popolsku.fr.pl/forum/index.php?topic=20407.79755
http://www.comfortcenter.es/index.php/component/k2/itemlist/user/109676
http://eugeniocolazzo.it/forum/index.php?topic=181804.0
http://praisesound.co.kr/sub04_01/123800
http://www.vamoscontigo.org/Noticia/221247
https://betshin.com/Story/265595
http://proxima.co.rw/index.php/component/k2/itemlist/user/736913
http://ko.myds.me/board_story/350781
https://gonggamlaw.com/lawcase/185675
http://www.crnmedia.es/component/k2/itemlist/user/93737
https://www.hohoyoga.com/testboard/4091621
http://www.vamoscontigo.org/Noticia/281824
https://betshin.com/Story/286771
https://www.hohoyoga.com/testboard/4114110
https://serverpia.co.kr/board_ucCk10/205193
http://ovotecegg.com/component/k2/itemlist/user/244345
https://www.swiss-focus.ch/?option=com_k2&view=itemlist&task=user&id=35608
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=187348
http://www.vamoscontigo.org/Noticia/218539
http://rudraautomation.com/index.php/component/k2/author/289026
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.com/news/104335
http://loverstory.co.kr/board_UYNJ05/43292
http://rudraautomation.com/index.php/component/k2/author/354059
http://www2.yasothon.go.th/smf/index.php?topic=159.msg199921
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2795521
http://melchinooddle.dothome.co.kr/?document_srl=20475
https://betshin.com/Story/199984
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=320081
http://viamania.net/index.php?mid=board_raYV15&document_srl=134273
http://gochon-iusell.co.kr/g1/121132
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1851836
http://www.artangel.co.kr/?document_srl=188414
http://khapthanam.co.kr/g1/150246
http://xn--2e0bk61btjo.com/notice/31165
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1351783
http://dreamplusart.com/mn03_01/323170
https://www.hohoyoga.com/testboard/4099433
http://www.ekemoon.com/257529/060420194102/
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=134437
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=19265
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ut1f-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4/
http://divespace.co.kr/board/353351
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2835251
http://xn----iv8e2lm1vxuam95ag7gslb023e4bc.com/news/142876
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=100090
http://www.firstfinancialservices.co.uk/index.php/component/k2/itemlist/user/42135
http://www.yadanarbonnews.com/index.php/component/k2/itemlist/user/346280
http://shinhwaair2017.cafe24.com/issue/520115
http://zakdu.com/board_ssKi56/19779
http://naksansacondo.com/board_MGPu57/36100
http://naksansacondo.com/board_MGPu57/98667
http://www.crnmedia.es/component/k2/itemlist/user/92172
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=126261
https://betshin.com/Story/209555
http://dospuntoseventos.cl/component/k2/itemlist/user/17643
http://forum.bmw-e60.eu/index.php?topic=11373.0
http://www.dap.com.py/?option=com_k2&view=itemlist&task=user&id=849511
http://dsyang.com/board_Kvgn62/30303
http://erdfsa.iptime.org/xe/index.php?mid=board&document_srl=12649
http://www.eunhaele.co.kr/xe/board/20586
http://dsyang.com/board_Kvgn62/44928
https://forum.ac-jete.it/index.php?topic=452933.0
http://alastair030.dothome.co.kr/index.php?mid=board_MMiF30&document_srl=30893
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/66446
http://renew.joum.kr/index.php?mid=Portfolio_bbs&document_srl=213825
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=18685
https://grajalesabogados.com.mx/index.php/component/k2/itemlist/user/67240
http://thermoplast.envolgroupe.com/component/k2/author/196927
http://dreamplusart.com/mn03_01/257980
http://www.ekemoon.com/248113/051720190030/
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-op5e-%d0%ba%d0%be%d0%bf-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.aracne.biz/?option=com_k2&view=itemlist&task=user&id=4991831
http://www.vamoscontigo.org/Noticia/257433
https://serverpia.co.kr/board_ucCk10/210718
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1588086
http://mglpcm.org/board_ETkS12/196149
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1284424
http://e-educ.net/Forum/index.php?topic=16276.0
http://yadanarbonnews.com/index.php/component/k2/itemlist/user/350746
http://www2.yasothon.go.th/smf/index.php?topic=159.172560
https://forum.clubeicaro.pt/index.php?topic=2529.0
https://www.hohoyoga.com/testboard/4053292
http://www.sollazzorefrigerazione.it/index.php/component/k2/itemlist/user/2639473
http://oceangray.i234.me/index.php?mid=board_vsVi16&document_srl=192566
http://rabbitzone.xyz/FREE/126050
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=17696
http://godeok.houseplan.kr/index.php?mid=board_HFtY66&document_srl=121002
http://patagroupofcompanies.com/index.php/component/k2/itemlist/user/329476
http://rabat.kr/board_yCgT00/82209
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=2001946
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=116042
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/78500
http://barobus.kr/qna/75448
http://gochon-iusell.co.kr/g1/77298
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1576278
http://beautypouch.net/index.php?mid=board_09&document_srl=226733
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3585031
https://www.hohoyoga.com/testboard/4159338
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1578458
https://www.hohoyoga.com/testboard/4125088
http://ptu.imoove.kr/ko/content/%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-aeen-%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-10-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-bbc341029
http://looksun.co.kr/index.php?mid=board_4&document_srl=126414
http://www.svteck.co.kr/customer_gratitude/219660
http://xn--2e0b53df5ag1c804aphl.net/nuguna/193614
http://ptu.imoove.kr/ko/content/%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-vnci-%C2%AB%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7-%D1%81%D0%BB%D1%83%D0%B6%D0%B0%D0%BD%D0%BA%D0%B8-3-%D1%81%D0%B5%D0%B7%D0%BE%D0%BD-9-%D1%81%D0%B5%D1%80%D0%B8%D1%8F%C2%BB-ideafilm341258
https://www.lwfservers.com/index.php?topic=72404.0
http://matinbank.ir/component/k2/itemlist/user/4592337.html
http://sunele.co.kr/board_ReBD97/163133
https://nextezone.com/index.php?action=profile;u=14115
https://www.hohoyoga.com/testboard/4084857
https://www.hohoyoga.com/testboard/4100848
https://www.hohoyoga.com/testboard/4100983
https://www.hohoyoga.com/testboard/4100992
https://www.hwbms.com/web/qna/52042
https://www.hwbms.com/web/qna/52169
https://www.hwbms.com/web/qna/52174
https://www.hwbms.com/web/qna/52189
https://www.hwbms.com/web/qna/52264
https://www.hwbms.com/web/qna/52302
http://cwon.kr/xe/board_bnSr36/411560
http://daesestudy.co.kr/ipsi_docu/232595
http://daesestudy.co.kr/ipsi_docu/232646
http://daesestudy.co.kr/ipsi_docu/232733
http://daesestudy.co.kr/ipsi_docu/232830
http://dsyang.com/board_Kvgn62/81081
http://dsyang.com/board_Kvgn62/81112
http://dsyang.com/board_Kvgn62/81145
http://dsyang.com/board_Kvgn62/81151
http://emjun.com/index.php?mid=hangtotal&document_srl=675099
http://forum.elexlabs.com/index.php?topic=73658.0
http://jjikduk.net/DATA/291575
http://jjikduk.net/DATA/291596
http://erhu.eu/viewtopic.php?t=398119
http://universalcommunity.se/Forum/index.php?topic=43732.0
http://dospuntoseventos.cl/?option=com_k2&view=itemlist&task=user&id=17515
http://hanga5.com/index.php?mid=board_photo&document_srl=125538
http://www.supergondolas.com.br/?option=com_k2&view=itemlist&task=user&id=206146
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2850639
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2850660
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2850697
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=2028627
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=2028658
http://gtupuw.org/index.php/component/k2/itemlist/user/2028625
https://verdadesbiblicas.org.ec/?option=com_k2&view=itemlist&task=user&id=3899830
http://ucckorea.kr/?document_srl=229992
http://bitly.com/2IiXz7L
http://1644-4404.com/index.php?mid=board_VFri46&document_srl=480910
http://bitly.com/2IgU0za
http://naksansacondo.com/board_MGPu57/142151
http://bitly.com/2WFTAM2
http://bitly.com/2WOloxS
http://kyj1225.godohosting.com/board_mebR72/201903
http://marketpet.ru/component/k2/itemlist/user/4246.html
http://rabbitzone.xyz/FREE/316003
https://reficulcoin.com/index.php?topic=125535.0
http://www.ekemoon.com/265451/061720192703/
http://www.ekemoon.com/262203/060120192703/
http://ko.myds.me/board_story/421731
http://viamania.net/index.php?mid=board_raYV15&document_srl=515300
http://mobility-corp.com/index.php/component/k2/itemlist/user/2787929
http://bitly.com/2WJ9aq2
https://agrorestart.ba/?option=com_k2&view=itemlist&task=user&id=7636
http://bitly.com/2IanUos
http://ye-dream.com/qa/305577
http://dreamplusart.com/?document_srl=298069
http://bitly.com/2WEXqoB
http://ovotecegg.com/component/k2/itemlist/user/254134
http://ovotecegg.com/component/k2/itemlist/user/254232
http://bitly.com/2IhPyQz
http://bitly.com/2IgxIgZ
http://bitly.com/2WLaGb6
http://bitly.com/2WJcG3G
http://bitly.com/2WOlt4E
http://xn--2e0b53df5ag1c804aphl.net/nuguna/282255
http://bitly.com/2WOlhSY
http://bitly.com/2IanRcg
https://www.hwbms.com/web/qna/136830
http://www.dap.com.py/index.php/component/k2/itemlist/user/861085
http://bitly.com/2WFrFvr
http://kwpub.kr/PUBS/311286
http://kwpub.kr/PUBS/311128
http://askpharm.net/board_NQiz06/283545
http://skylinecam.co.kr/?document_srl=508895
http://benzmall.co.kr/index.php?mid=download&document_srl=214366
http://www.bb-room.ru/index.php/component/k2/itemlist/user/16393
http://www.bb-room.ru/index.php/component/k2/itemlist/user/16423
http://www.fundacionceramicaitalia.org/index.php/component/k2/itemlist/user/97524
http://www.m1avio.com/index.php/component/k2/itemlist/user/3912746
http://www2.yasothon.go.th/smf/index.php?topic=159.msg206263
https://agrorestart.ba/?option=com_k2&view=itemlist&task=user&id=8101
https://agrorestart.ba/index.php/component/k2/itemlist/user/8093
https://www.hwbms.com/web/qna/197520
https://www.hwbms.com/web/qna/197971
https://www.hwbms.com/web/qna/198011
https://www.hwbms.com/web/qna/198041
http://sy.korean.net/qna/726902
http://callman.co.kr/index.php?mid=qa&document_srl=7013
https://intelogist2.wpengine.com/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-mv7s-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://viamania.net/index.php?mid=board_raYV15&document_srl=492758
http://bitly.com/2WFrIr7
http://www.hmotors.co.kr/inquiry/76219
http://bitly.com/2IanRcg
http://bitly.com/2IezsY1
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-rg4s-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-7/
http://vervetama.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-8-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
http://isch.kr/board_PowH60/412843
http://dreamplusart.com/mn03_01/311336
http://rabat.kr/board_yCgT00/174536
http://carrierworld.co.kr/index.php?mid=board_UlGv44&document_srl=234666
http://bitly.com/2WOkXUg
http://www.leekeonsu-csi.com/index.php?mid=community7&document_srl=1470701
http://ruschinaforum.ru/index.php?topic=167739.0
http://midorijapaneserestaurant.ca/menu/News/201072
http://xn--2e0b53df5ag1c804aphl.net/nuguna/281637
http://bitly.com/2WOlAx6
http://businesshous.ru/?option=com_k2&view=itemlist&task=user&id=9571
http://www.hmotors.co.kr/inquiry/87601
https://serverpia.co.kr/board_ucCk10/235278
https://altaylarteknoloji.com/index.php?topic=7482.0
https://nextezone.com/index.php?action=profile;u=17289
http://www.fassen.co.kr/xe/board_VCum96/259930
http://www.kcch.or.kr/index.php?mid=board_uFpk03&document_srl=215145
http://bitly.com/2IficBT
http://bitly.com/2Ifo4eA
http://www.popolsku.fr.pl/forum/index.php?topic=432751.0
https://intelogist2.wpengine.com/%d0%b2-%d0%ba%d0%bb%d0%b5%d1%82%d0%ba%d0%b5-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-%d0%b2-%d0%ba%d0%bb%d0%b5%d1%82%d0%ba%d0%b5-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-2/
https://intelogist2.wpengine.com/%d0%b2%d0%b5%d0%bb%d0%b8%d0%ba%d0%be%d0%bb%d0%b5%d0%bf%d0%bd%d0%b0%d1%8f-%d0%bf%d1%8f%d1%82%d1%91%d1%80%d0%ba%d0%b0-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%bc%d0%be%d1%82%d1%80%d0%b5/
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=736401
http://beautypouch.net/index.php?mid=board_09&document_srl=244961
https://www.c-alice.org/forum/index.php?topic=100581.0
https://www.hohoyoga.com/testboard/4191941
http://sy.korean.net/qna/532784
http://wgamez.net/index.php?mid=board_KGzu43&document_srl=79108
http://dreamplusart.com/mn03_01/344886
http://askpharm.net/?document_srl=287694
http://beautypouch.net/index.php?mid=board_09&document_srl=246293
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=750366
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-iy3s-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-17/
http://www.hmotors.co.kr/inquiry/80892
http://bitly.com/2IiX8u9
http://www.ekemoon.com/261429/062320191202/
продвижение сайта самостоятельно бесплатно [url=https://seoturbina.ru]бесплатный сео анализ сайта[/url]
seo продвижение сайта бесплатно [url=https://seoturbina.ru]курсы сео бесплатно[/url]
http://istakam.com/forum/index.php?topic=23831.0
http://bitly.com/2Ifo8ek
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/?document_srl=155451
http://bath-family.com/photo_zone/263664
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/223182
http://rabat.kr/board_yCgT00/176274
http://bitly.com/2WHzKjm
http://www.kspace.cc/xe/index.php?mid=board_NvNw86&document_srl=390807
http://bitly.com/2WOlky8
http://bitly.com/2Ik2Qfm
http://mtvenvironmental.com.au/blog/%D0%B2%D0%B5%D0%BB%D0%B8%D0%BA%D0%BE%D0%BB%D0%B5%D0%BF%D0%BD%D0%B0%D1%8F-%D0%BF%D1%8F%D1%82%D1%91%D1%80%D0%BA%D0%B0-30-%D1%81%D0%B5%D1%80%D0%B8%D1%8F-%D0%B2%D0%B5%D0%BB%D0%B8%D0%BA%D0%BE%D0%BB%D0%B5%D0%BF%D0%BD%D0%B0%D1%8F-%D0%BF%D1%8F%D1%82%D1%91%D1%80%D0%BA%D0%B0-30-%D1%81%D0%B5%D1%80%D0%B8%D1%8F
http://www.kwpcoop.or.kr/QnA/47963
https://intelogist2.wpengine.com/%d0%b2%d0%b5%d0%bb%d0%b8%d0%ba%d0%be%d0%bb%d0%b5%d0%bf%d0%bd%d0%b0%d1%8f-%d0%bf%d1%8f%d1%82%d1%91%d1%80%d0%ba%d0%b0-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-an7k-%d0%b2%d0%b5%d0%bb%d0%b8/
http://dsyang.com/board_Kvgn62/82481
https://www.hohoyoga.com/testboard/4224337
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=689950
http://bitly.com/2WPJsAt
http://marketpet.ru/?option=com_k2&view=itemlist&task=user&id=4255
http://bitly.com/2WJ6KI6
http://www.haetsaldun-clinic.co.kr/Question/107195
http://www.bb-room.ru/index.php/component/k2/itemlist/user/13894
http://www.ekemoon.com/248187/051820190130/
https://forum.clubeicaro.pt/index.php?topic=3239.0
http://bitly.com/2IiXv81
http://forum.elexlabs.com/index.php?topic=74173.0
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=28303
http://hk-metal.co.kr/hkweb/QnA/211917
http://bitly.com/2WJcG3G
http://www.travelsolution.info/?option=com_k2&view=itemlist&task=user&id=723895
http://viamania.net/index.php?mid=board_raYV15&document_srl=499111
http://www.hoonthaitoday.com/forum/index.php?topic=425434.0
http://xn----ww7ew4ej4kbwk62duk50be6b854f.com/news/196721
http://bitly.com/2WPJwAd
http://bitly.com/2IanPBa
http://mamaspraha.dothome.co.kr/index.php?mid=board_ubGi34&document_srl=63436
http://otitismediasociety.org/forum/index.php?topic=225145.0
http://askpharm.net/board_NQiz06/288691
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8d%d1%84%d0%b8%d1%80-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2/
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1592337
http://www.coating.or.kr/atemfair_data/42686
http://askpharm.net/board_NQiz06/291414
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qg6g-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-14/
http://carand.co.kr/d2/235476
http://bitly.com/2WOkXUg
http://yoriyorifood.com/xxxx/spacial/472458
http://askpharm.net/board_NQiz06/289778
http://dreamplusart.com/mn03_01/395525
http://ye-dream.com/board_yshD25/303597
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1588766
http://proxima.co.rw/index.php/component/k2/itemlist/user/736214
http://businesshous.ru/?option=com_k2&view=itemlist&task=user&id=10633
http://bitly.com/2IiX8KF
http://jjikduk.net/DATA/294327
https://intelogist2.wpengine.com/%d0%b2%d0%b5%d0%bb%d0%b8%d0%ba%d0%be%d0%bb%d0%b5%d0%bf%d0%bd%d0%b0%d1%8f-%d0%bf%d1%8f%d1%82%d1%91%d1%80%d0%ba%d0%b0-13-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-of7n-%d0%b2%d0%b5%d0%bb%d0%b8/
http://arquitectosenreformas.es/?option=com_k2&view=itemlist&task=user&id=88821
https://intelogist2.wpengine.com/%d0%bd%d0%b5%d0%bc%d0%b5%d0%b4%d0%bb%d0%b5%d0%bd%d0%bd%d0%be%d0%b5-%d1%80%d0%b5%d0%b0%d0%b3%d0%b8%d1%80%d0%be%d0%b2%d0%b0%d0%bd%d0%b8%d0%b5-1-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-do2n/
http://roikjer.com/forum/index.php?topic=971557.0
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=229925
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=727442
https://intelogist2.wpengine.com/%d0%b2%d0%b5%d0%bb%d0%b8%d0%ba%d0%be%d0%bb%d0%b5%d0%bf%d0%bd%d0%b0%d1%8f-%d0%bf%d1%8f%d1%82%d1%91%d1%80%d0%ba%d0%b0-18-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d0%b2%d0%b5%d0%bb/
http://beautypouch.net/index.php?mid=board_09&document_srl=217827
http://bitly.com/2WHbtd8
http://www.itosm.com/cn/?document_srl=405619
http://mvisage.sk/index.php/component/k2/itemlist/user/120103
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=148568
https://bcit-tmgt.com/viewtopic.php?t=55881
http://bitly.com/2WJ6KI6
http://benzmall.co.kr/index.php?mid=download&document_srl=127361
http://bitly.com/2IiX51r
https://serverpia.co.kr/board_ucCk10/207921
http://bitly.com/2IiX51r
http://bitly.com/2WFrFvr
http://ovotecegg.com/component/k2/itemlist/user/255828
http://mtvenvironmental.com.au/component/k2/itemlist/user/622058
https://timecker.com/anonymous/217631
http://ye-dream.com/qa/309057
http://bitly.com/2IanRZO
http://otitismediasociety.org/forum/index.php?topic=225016.0
http://daesestudy.co.kr/ipsi_docu/232646
https://timecker.com/anonymous/212485
http://www.jesusonly.life/calendar/876220
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ds3h-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19/
http://www.ekemoon.com/256985/060220191202/
http://dreamplusart.com/mn03_01/342346
http://israengineering.com/?option=com_k2&view=itemlist&task=user&id=1363540
http://xn----c28ewjj6ubwku6frtcuzec29ae5b.com/news/232004
http://wgamez.net/index.php?mid=board_KGzu43&document_srl=76540
http://otitismediasociety.org/forum/index.php?topic=224358.0
http://ko.myds.me/board_story/367713
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qi0g-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-3/
https://www.hohoyoga.com/testboard/4155688
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=703304
https://intelogist2.wpengine.com/%d1%81%d0%b2%d0%b0%d0%b4%d1%8c%d0%b1%d1%8b-%d0%b8-%d1%80%d0%b0%d0%b7%d0%b2%d0%be%d0%b4%d1%8b-3-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-kq1r-%d1%81%d0%b2%d0%b0%d0%b4%d1%8c%d0%b1%d1%8b-%d0%b8/
http://mediaville.me/index.php/component/k2/itemlist/user/418799
https://agrorestart.ba/?option=com_k2&view=itemlist&task=user&id=6347
http://bitly.com/2WJ9c18
https://intelogist2.wpengine.com/%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3%d0%bb%d0%be-%d0%b1%d1%8b%d1%82%d1%8c-%d0%b8%d0%bd%d0%b0%d1%87%d0%b5-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xn9f-%d0%b2%d1%81%d1%91-%d0%bc%d0%be%d0%b3/
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=2033528
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=730299
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=615118
http://bitly.com/2WEXmFn
http://sfah.ch/de/component/k2/itemlist/user/15643
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lx2j-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.vamoscontigo.org/Noticia/258363
http://yoriyorifood.com/xxxx/spacial/473381
http://erdfsa.iptime.org/xe/index.php?mid=board&document_srl=41963
http://rabbitzone.xyz/FREE/259363
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-12-3/
http://www.ekemoon.com/255517/061720195701/
http://www.vamoscontigo.org/Noticia/271535
http://beautypouch.net/index.php?mid=board_09&document_srl=283954
http://marketpet.ru/component/k2/itemlist/user/4384.html
http://bitly.com/2WIkzqb
http://www.jesusonly.life/calendar/870362
http://bitly.com/2If8YWr
http://bitly.com/2WOls0A
http://otitismediasociety.org/forum/index.php?topic=226267.0
http://divespace.co.kr/?document_srl=357585
http://www.tessabannampad.go.th/webboard/index.php?topic=235245.0
http://bitly.com/2Ik2Qfm
http://naksansacondo.com/board_MGPu57/196484
http://bitly.com/2IanSNm
http://bitly.com/2WCtEkp
http://bitly.com/2WOlt4E
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-xl6c-%d0%ba%d0%be%d0%bf-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://www.hmotors.co.kr/inquiry/95985
https://intelogist2.wpengine.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-hd-video-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-7-%d1%81%d0%b5%d1%80/
http://hyeonjun.co.kr/menu3/660155
http://benzmall.co.kr/index.php?mid=download&document_srl=163843
http://koais.com/data/366784
http://ucckorea.kr/index.php?mid=board_AuHE49&document_srl=218193
http://mtvenvironmental.com.au/?option=com_k2&view=itemlist&task=user&id=621848
https://agrorestart.ba/?option=com_k2&view=itemlist&task=user&id=6626
http://divespace.co.kr/board/317646
http://www.bb-room.ru/?option=com_k2&view=itemlist&task=user&id=14185
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ds1o-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2/
http://bitly.com/2WM5J1I
http://mtvenvironmental.com.au/component/k2/itemlist/user/621513
http://mtvenvironmental.com.au/component/k2/itemlist/user/621676
http://naksansacondo.com/board_MGPu57/210148
https://intelogist2.wpengine.com/%d0%ba%d0%be%d0%bf-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-un7j-%d0%ba%d0%be%d0%bf-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://jjikduk.net/DATA/281298
http://bitly.com/2IanRcg
https://intelogist2.wpengine.com/%d0%b2%d0%b5%d0%bb%d0%b8%d0%ba%d0%be%d0%bb%d0%b5%d0%bf%d0%bd%d0%b0%d1%8f-%d0%bf%d1%8f%d1%82%d1%91%d1%80%d0%ba%d0%b0-23-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-lt1f-%d0%b2%d0%b5%d0%bb%d0%b8/
https://turimex.mx.solemti.net/?option=com_k2&view=itemlist&task=user&id=27360
https://www.vegasgreentour.com/?document_srl=784186
http://dreamplusart.com/mn03_01/310766
http://bitly.com/2WOkXUg
http://www.shturmovka.ru/blog/227333.html
http://bitly.com/2IhOWKL
http://xn--2e0b53df5ag1c804aphl.net/nuguna/272848
http://bitly.com/2WCMaJp
http://hotelnomadpalace.com/index.php/component/k2/itemlist/user/23257
http://dreamplusart.com/mn03_01/288029
http://www2.yasothon.go.th/smf/index.php?topic=159.174540
http://gardenpjw.dothome.co.kr/board_LOcC77/812438
http://rnspl.com/component/k2/itemlist/user/2454
http://sfah.ch/de/component/k2/itemlist/user/15650
http://hyeonjun.co.kr/menu3/639057
http://benzmall.co.kr/index.php?mid=download&document_srl=215913
http://ye-dream.com/qa/290458
https://www.hohoyoga.com/testboard/4195600
https://www.hwbms.com/web/qna/138981
http://www.hyunjindc.com/qna/394943
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-10-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-pe9c-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-10-%d1%81%d0%b5%d1%80%d0%b8/
http://bitly.com/2WOlNjS
http://sy.korean.net/qna/567604
http://www.ekemoon.com/248343/051920190930/
http://arquitectosenreformas.es/component/k2/itemlist/user/89359
http://sander.awardspace.info/blog/42943.html
http://www.ekemoon.com/260381/061720195202/
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/216716
https://intelogist2.wpengine.com/%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ww1k-%d1%87%d0%b5%d1%80%d0%bd%d0%be%d0%b1%d1%8b%d0%bb%d1%8c-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://atrosell.com/?option=com_k2&view=itemlist&task=user&id=26801
http://bitly.com/2WJ6PeS
http://www.vamoscontigo.org/Noticia/273307
http://dsyang.com/?document_srl=70671
https://www.hwbms.com/web/qna/148194
http://bitly.com/2WOlgOU
https://www.celekt.com/%d0%9d%d0%b5%d0%bc%d0%b5%d0%b4%d0%bb%d0%b5%d0%bd%d0%bd%d0%be%d0%b5-%d1%80%d0%b5%d0%b0%d0%b3%d0%b8%d1%80%d0%be%d0%b2%d0%b0%d0%bd%d0%b8%d0%b5-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-02-06-2019-k3/
http://bitly.com/2ItF9BF
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=65265
http://hyeonjun.co.kr/menu3/638987
http://www.bb-room.ru/index.php/component/k2/itemlist/user/14238
http://xn--80acvxh8am.net/index.php?action=profile&u=6442
http://sy.korean.net/qna/584762
http://rabat.kr/board_yCgT00/327969
http://ko.myds.me/board_story/319994
https://timecker.com/anonymous/211536
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=1016590
http://oneandonly1127.com/index.php?mid=guest&document_srl=191448&page=4
https://www.regalepadova.it/index.php/component/k2/itemlist/user/8525
http://www.ekemoon.com/249223/050620194631/
http://rabat.kr/board_yCgT00/93007
http://sy.korean.net/qna/776823
http://ko.myds.me/board_story/323868
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=1015973
http://www.jshwanghoan.com/index.php?mid=qna&document_srl=828935
http://marketpet.ru/component/k2/itemlist/user/4399.html
http://naksansacondo.com/board_MGPu57/213265
http://www.hmotors.co.kr/inquiry/83168
http://dsyang.com/board_Kvgn62/83072
http://beautypouch.net/index.php?mid=board_09&document_srl=239861
http://bitly.com/2IanUEY
http://www.fassen.co.kr/xe/board_VCum96/258063
http://daltso.com/index.php?mid=board_cUYy21&document_srl=361754
http://mobility-corp.com/index.php/component/k2/itemlist/user/2785231
https://serverpia.co.kr/board_ucCk10/225279
http://bitly.com/2IhPyQz
http://rabat.kr/board_yCgT00/93117
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=232528
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/198223
http://xn--2e0b53df5ag1c804aphl.net/nuguna/264733
https://2002.shyoon.com/board_2002/459572
http://bitly.com/2WFiBqn
http://bitly.com/2Ifo8ek
http://beautypouch.net/index.php?mid=board_09&document_srl=216466
http://lavaggio.com.vn/?option=com_k2&view=itemlist&task=user&id=3969323
http://thermoplast.envolgroupe.com/component/k2/author/200748
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1597460
http://mtvenvironmental.com.au/component/k2/itemlist/user/620559
http://jejucctv.co.kr/A5/128668
http://bitly.com/2WOlky8
http://bitly.com/2WOlkhC
http://bitly.com/2IgU0za
http://www.hyunjindc.com/qna/461179
http://bitly.com/2WOlllG
http://bitly.com/2WOlhSY
http://naksansacondo.com/?document_srl=217637
http://bitly.com/2IanRcg
https://nple.com/xe/pds/339492
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=148220
http://daesestudy.co.kr/ipsi_docu/200061
http://yeonsen.com/index.php?mid=board_vZbN12&document_srl=622886
https://betshin.com/Story/303253
http://www.vamoscontigo.org/Noticia/295580
http://rabat.kr/board_yCgT00/243416
http://mtvenvironmental.com.au/component/k2/itemlist/user/620277
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=704332
http://beautypouch.net/index.php?mid=board_09&document_srl=279258
http://bitly.com/2WKbcpV
http://bitly.com/2IhPyQz
http://www.hyunjindc.com/qna/402895
http://beautypouch.net/index.php?mid=board_09&document_srl=217286
http://oss.obigo.com/oss/index.php?mid=board_mxLS91&document_srl=169267
http://mediaville.me/index.php/component/k2/itemlist/user/427499
http://postesari.com/?option=com_k2&view=itemlist&task=user&id=36993
http://xn--hu1bs8ufrd6ucyz0aooa.kr/?document_srl=234013
http://marketpet.ru/?option=com_k2&view=itemlist&task=user&id=4730
http://rudraautomation.com/index.php/component/k2/author/405243
http://proxima.co.rw/?option=com_k2&view=itemlist&task=user&id=743197
http://dreamplusart.com/mn03_01/316220
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-yt5o-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6/
http://yoriyorifood.com/xxxx/spacial/494208
http://bitly.com/2WGpqIw
https://intelogist2.wpengine.com/%d0%b2%d0%b5%d0%bb%d0%b8%d0%ba%d0%be%d0%bb%d0%b5%d0%bf%d0%bd%d0%b0%d1%8f-%d0%bf%d1%8f%d1%82%d1%91%d1%80%d0%ba%d0%b0-33-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-ko8t-%d0%b2%d0%b5%d0%bb%d0%b8/
https://serverpia.co.kr/board_ucCk10/212709
http://thermoplast.envolgroupe.com/?option=com_k2&view=itemlist&task=user&id=199867
http://bitly.com/2WIkAuf
http://smartacity.com/component/k2/itemlist/user/117122
http://bitly.com/2WOkVf6
https://intelogist2.wpengine.com/%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-sk8n-%d0%b6%d0%b8%d0%b2%d0%b0%d1%8f-%d0%bc%d0%b8%d0%bd%d0%b0-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://beautypouch.net/index.php?mid=board_09&document_srl=250107
http://bitly.com/2IiX7GB
https://timecker.com/anonymous/213733
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1592689
http://benzmall.co.kr/index.php?mid=download&document_srl=213808
http://bitly.com/2WJ9bdA
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=405163
http://mtvenvironmental.com.au/?option=com_k2&view=itemlist&task=user&id=620483
http://www.vamoscontigo.org/index.php?mid=Noticia&document_srl=258055&listStyle=%24listStyle
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/index.php?document_srl=388968&mid=news
http://gusinoepero.ru/archives/39832
http://yousub.netsons.org/index.php/component/k2/itemlist/user/54753
http://viamania.net/index.php?mid=board_raYV15&document_srl=490669
http://help.stv.ru/index.php?PHPSESSID=1d48648b7b6b032bddecb43ff53cccf8&topic=149816.0
http://ye-dream.com/qa/343923
http://xn--4k0b35r1tgf2e69bc81as4b.modelhouse.guide/brand/159760
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=730800
http://xn--2e0b53df5ag1c804aphl.net/nuguna/252403
http://yousub.netsons.org/index.php/component/k2/itemlist/user/53689
http://daltso.com/index.php?mid=board_cUYy21&document_srl=389139
http://moyakmermer.com/index.php/en/component/k2/itemlist/user/872793
http://xn----c28e37psqau1bm6v53e05ac6b854f.com/news/204177
http://postesari.com/?option=com_k2&view=itemlist&task=user&id=39081
http://bitly.com/2WOllCc
https://agrorestart.ba/?option=com_k2&view=itemlist&task=user&id=6990
http://www.popolsku.fr.pl/forum/index.php?topic=431777.0
https://www.hohoyoga.com/testboard/4140192
http://beautypouch.net/?document_srl=243565
http://www.bb-room.ru/index.php/component/k2/itemlist/user/14048
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3486886
http://www.ekemoon.com/248661/052320195530/
http://bitly.com/2WOlnKk
https://agrorestart.ba/index.php/bos/?option=com_k2&view=itemlist&task=user&id=7146
http://bitly.com/2WJcJwo
https://collegerank.ru/component/k2/itemlist/user/1281
http://bitly.com/2WJ6PLU
http://agiteshop.com/xe/qa/355714
http://postesari.com/?option=com_k2&view=itemlist&task=user&id=35456
http://cwon.kr/xe/board_bnSr36/409003
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-qc0y-%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5/
http://bitly.com/2WPJwAd
http://dreamplusart.com/mn03_01/328055
http://atrosell.com/?option=com_k2&view=itemlist&task=user&id=26291
http://poselokgribovo.ru/forum/index.php?topic=842764.0
http://sy.korean.net/qna/776638
http://goldenpowerball2.com/?document_srl=736298
http://ko.myds.me/board_story/335822
http://daltso.com/index.php?mid=board_cUYy21&document_srl=384336
http://bitly.com/2WOlhlW
http://forum.bmw-e60.eu/index.php?topic=12589.0
http://beautypouch.net/index.php?mid=board_09&document_srl=260848
http://www.bb-room.ru/index.php/component/k2/itemlist/user/13980
https://2002.shyoon.com/board_2002/462274
http://bitly.com/2IiX8u9
http://bitly.com/2IiXzVj
http://mediaville.me/?option=com_k2&view=itemlist&task=user&id=430923
http://mtvenvironmental.com.au/?option=com_k2&view=itemlist&task=user&id=625635
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1602646
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3603402
http://www.siirtorganik.com/index.php/component/k2/itemlist/user/1020059
http://sy.korean.net/qna/633822
http://www.hmotors.co.kr/inquiry/78337
https://www.hwbms.com/web/qna/121497
http://otitismediasociety.org/forum/index.php?topic=225797.0
http://neosky.net/xe/space_station/311455
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1887938
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=705823
http://beautypouch.net/index.php?mid=board_09&document_srl=318364
http://mtvenvironmental.com.au/component/k2/itemlist/user/620933
http://isch.kr/board_PowH60/416438
http://www.bb-room.ru/index.php/component/k2/itemlist/user/13905
http://xn----tu8e8mm1vc8h00c5zg05ac6b854f.net/?document_srl=416683
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1589717
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3490998
http://udrpsucks.com/blog/?p=1946
http://rnspl.com/component/k2/itemlist/user/2647
http://rnspl.com/component/k2/itemlist/user/2648
http://rudraautomation.com/index.php/component/k2/author/417679
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=153292
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=153294
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1603189
http://www.bb-room.ru/index.php/component/k2/itemlist/user/17000
http://www.bb-room.ru/index.php/component/k2/itemlist/user/17008
http://www.emrabq8.com/?option=com_k2&view=itemlist&task=user&id=1904234
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=142796
http://www.telcon.gr/?option=com_k2&view=itemlist&task=user&id=142822
http://yousub.netsons.org/index.php/component/k2/itemlist/user/57234
http://dreamplusart.com/mn03_01/299690
http://hyeonjun.co.kr/menu3/643958
https://hackersuniversity.net/index.php?topic=48518.0
http://bitly.com/2WOkWzG
http://www.hmotors.co.kr/inquiry/78851
http://bitly.com/2Img5My
http://xn--hu1bs8ufrd6ucyz0aooa.kr/index.php?mid=main_08&document_srl=231773
http://bitly.com/2WEXrc9
http://www.hmotors.co.kr/inquiry/202892
http://divespace.co.kr/board/325526
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=37445
https://intelogist2.wpengine.com/%d1%81%d0%bb%d1%83%d0%b3%d0%b0-%d0%bd%d0%b0%d1%80%d0%be%d0%b4%d0%b0-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-6-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%8d%d1%84%d0%b8%d1%80-%d1%81/
http://pkgersang.dothome.co.kr/board_jiKY24/54581
http://dreamplusart.com/mn03_01/316071
http://askpharm.net/board_NQiz06/313464
http://ye-dream.com/board_yshD25/318391
http://xn--2e0b53df5ag1c804aphl.net/nuguna/264073
http://bitly.com/2WHbyxs
http://mobility-corp.com/index.php/component/k2/itemlist/user/2796044
http://proxima.co.rw/index.php/component/k2/itemlist/user/753410
http://rnspl.com/component/k2/itemlist/user/2682
http://smartacity.com/component/k2/itemlist/user/119776
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=153941
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1604940
http://www.bb-room.ru/index.php/component/k2/itemlist/user/17190
http://www.bb-room.ru/index.php/component/k2/itemlist/user/17256
http://www.bb-room.ru/index.php/component/k2/itemlist/user/17282
http://www.comfortcenter.es/index.php/component/k2/itemlist/user/114111
http://www.jesusandmarypatna.com/?option=com_k2&view=itemlist&task=user&id=3604296
http://bitly.com/2WJcG3G
http://gyeomright.dothome.co.kr/index.php?mid=guest&document_srl=30269
http://k2.akademitelkom.ac.id/?option=com_k2&view=itemlist&task=user&id=410560
http://ovotecegg.com/component/k2/itemlist/user/258216
http://k-cea.org/board_Hnyj62/400267
http://bitly.com/2WCtIRb
https://timecker.com/anonymous/213014
http://udrpsucks.com/blog/?p=2054
https://serverpia.co.kr/board_ucCk10/214626
http://constellation.kro.kr/board_kbku73/281805
http://bitly.com/2WM5N1s
http://bitly.com/2WJ9iG2
http://daltso.com/index.php?mid=board_cUYy21&document_srl=367221
https://intelogist2.wpengine.com/%d1%80%d0%b0%d1%81%d1%81%d0%ba%d0%b0%d0%b7-%d1%81%d0%bb%d1%83%d0%b6%d0%b0%d0%bd%d0%ba%d0%b8-3-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-5-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-op5x-%d1%80%d0%b0%d1%81/
http://proxima.co.rw/index.php/component/k2/itemlist/user/748406
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1589117
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=23295
http://daesestudy.co.kr/ipsi_docu/210608
http://www.bb-room.ru/index.php/component/k2/itemlist/user/14629
http://www.ekemoon.com/254979/061420193601/
http://www.ekemoon.com/261737/060020191303/
http://erdfsa.iptime.org/xe/index.php?mid=board&document_srl=48228
https://www.hwbms.com/web/qna/144383
http://www.ekemoon.com/259287/061220194802/
http://dev.fivestarpainting.com/index.php/component/k2/itemlist/user/2035120
https://www.hwbms.com/web/qna/182152
https://www.celekt.com/%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-19-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-02-06-2019-l5-%d0%a4%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7/
https://www.hohoyoga.com/testboard/4152952
http://www.hmotors.co.kr/inquiry/202456
http://www.jesusonly.life/calendar/871653
http://bitly.com/2WJ6OYm
http://bitly.com/2IgxIgZ
http://bitly.com/2WJ6PeS
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=695927
http://benzmall.co.kr/index.php?mid=download&document_srl=147889
http://www.hmotors.co.kr/inquiry/260419
http://bitly.com/2IanVc0
http://1600-1590.com/index.php?mid=board_ndxU24&document_srl=762897
http://bitly.com/2WOkVf6
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=366508
http://www.coating.or.kr/atemfair_data/37202
http://www.vamoscontigo.org/Noticia/269362
http://bitly.com/2IgU0za
http://bitly.com/2WFwLrH
https://intelogist2.wpengine.com/%d1%84%d0%b8%d1%82%d0%bd%d0%b5%d1%81-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-11-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-%d1%81%d0%b5%d1%80%d0%b8%d0%b0%d0%bb-%d1%84%d0%b8%d1%82%d0%bd%d0%b5/
http://kwpub.kr/PUBS/327579
https://intelogist2.wpengine.com/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-4-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://hotelnomadpalace.com/component/k2/itemlist/user/24428
http://www.boutique.in.th/?option=com_k2&view=itemlist&task=user&id=154915
http://kitekorea.co.kr/board_Chea81/261370
http://atrosell.com/index.php/component/k2/itemlist/user/25746
http://loverstory.co.kr/board_UYNJ05/277113
http://tiretech.co.kr/index.php?mid=qna&document_srl=478540
http://bewasia.com/index.php?mid=board_cUYy21&document_srl=400817
http://businesshous.ru/index.php/component/k2/itemlist/user/10895
http://beautypouch.net/index.php?mid=board_09&document_srl=258351
https://agrorestart.ba/?option=com_k2&view=itemlist&task=user&id=7685
http://benzmall.co.kr/index.php?mid=download&document_srl=126084
http://village.lorem.kr/index.php?mid=board_xmEJ33&document_srl=513156
http://daltso.com/index.php?document_srl=367918&mid=board_cUYy21
https://www.vegasgreentour.com/index.php?mid=board_XiHh59&document_srl=694738
http://bitly.com/2IiXvox
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=23666
http://nyutusonsafaris.com/index.php/component/k2/itemlist/user/196273
http://melchinooddle.dothome.co.kr/?document_srl=43746
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=67659
http://bitly.com/2WHzDUY
http://dohairbiz.com/en/component/k2/itemlist/user/2840780.html
https://hackinsa.com/freeboard/241585
http://sy.korean.net/free/660324
http://sejong-thesharpyemizi.co.kr/m1/304371
http://bitly.com/2IankXO
http://bitly.com/2WHzKjm
http://iymc.or.kr/pds/165546
https://www.hohoyoga.com/testboard/4229959
http://askpharm.net/board_NQiz06/288848
http://www.ekemoon.com/256987/060220191302/
http://yourhelp.co.kr/index.php?mid=board_2&document_srl=242403
http://esiapolisthesharp2.co.kr/g1/162639
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=206004
http://ye-dream.com/qa/318627
http://esiapolisthesharp2.co.kr/g1/167776
http://rudraautomation.com/index.php/component/k2/author/406259
http://www.lgue.co.kr/?document_srl=332177
http://divespace.co.kr/board/357599
http://help.stv.ru/index.php?PHPSESSID=9b0273f4ef1bff8b8ca76085ac1387e3&topic=149689.0
http://otitismediasociety.org/forum/index.php?topic=224950.0
https://www.chirorg.com/?document_srl=460763
http://www.shturmovka.ru/blog/227402.html
http://www.bb-room.ru/index.php/component/k2/itemlist/user/13714
http://naksansacondo.com/?document_srl=222116
http://www.leekeonsu-csi.com/index.php?document_srl=1480367&mid=community7
http://xn--2e0b53df5ag1c804aphl.net/nuguna/297958
http://postesari.com/?option=com_k2&view=itemlist&task=user&id=38455
http://bitly.com/2WPJwjH
http://bitly.com/2WIkFOz
http://kwpub.kr/?document_srl=348852
https://www.hwbms.com/web/qna/173165
https://lideta.workethio.com/2019/06/03/%d0%b1%d0%be%d0%bb%d1%8c%d1%88%d0%b0%d1%8f-%d0%bc%d0%b0%d0%bb%d0%b5%d0%bd%d1%8c%d0%ba%d0%b0%d1%8f-%d0%bb%d0%be%d0%b6%d1%8c-2-%d1%81%d0%b5%d0%b7%d0%be%d0%bd-2-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-11/
http://bitly.com/2IclPbO
http://bitly.com/2IiXykd
http://askpharm.net/board_NQiz06/294988
http://postesari.com/?option=com_k2&view=itemlist&task=user&id=41905
http://rnspl.com/component/k2/itemlist/user/2688
http://rudraautomation.com/index.php/component/k2/author/419382
http://smartacity.com/component/k2/itemlist/user/119976
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=154017
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=154023
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=45996
http://wigalseguros.com.br/?option=com_k2&view=itemlist&task=user&id=46020
http://www.atab.com.sa/index.php/en/component/k2/itemlist/user/1802345
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1604923
http://www.bb-room.ru/index.php/component/k2/itemlist/user/17325
http://www.pdctransport.co.th/?option=com_k2&view=itemlist&task=user&id=19554
http://www.siirtorganik.com/?option=com_k2&view=itemlist&task=user&id=1022289
https://www.hohoyoga.com/testboard/4181780
http://goldenpowerball2.com/index.php?mid=board_Nutq11&document_srl=711853
http://ladybirdestates.com/index.php/component/k2/itemlist/user/12984
http://bitly.com/2Ienc9S
http://bitly.com/2IficBT
http://bitly.com/2IanVc0
https://www.hwbms.com/web/qna/165491
http://rabbitzone.xyz/FREE/262574
http://bitly.com/2WOljKA
http://www.travelsolution.info/index.php/component/k2/itemlist/user/722517
http://bitly.com/2WFTBzA
https://blossomug.com/index.php/component/k2/itemlist/user/1131393
http://rabat.kr/rabat/173625
https://intelogist2.wpengine.com/%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f-vv9f-%d1%82%d0%be%d0%bb%d1%8f-%d1%80%d0%be%d0%b1%d0%be%d1%82-9-%d1%81%d0%b5%d1%80%d0%b8%d1%8f/
http://yonseibaik.synology.me/index.php?mid=houston_profile&document_srl=204512
http://www.taeshinmedia.com/index.php?mid=genealogy_faq&document_srl=3485801
https://altaylarteknoloji.com/index.php?topic=6792.0
http://rabat.kr/board_yCgT00/146643
http://mvisage.sk/index.php/component/k2/itemlist/user/120582
https://blossomug.com/index.php/component/k2/itemlist/user/1133626
http://gspara01.dothome.co.kr/index.php?mid=board_XHsr53&document_srl=38503
http://bitly.com/2IanPkE
http://jejucctv.co.kr/?document_srl=134919
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2919268
http://adrianaafonso.com.br/?option=com_k2&view=itemlist&task=user&id=2919309
http://atrosell.com/?option=com_k2&view=itemlist&task=user&id=30814
http://atrosell.com/?option=com_k2&view=itemlist&task=user&id=30934
http://dev.aabn.org.gh/component/k2/itemlist/user/813276
http://dev.aabn.org.gh/component/k2/itemlist/user/813371
http://esperanzazubieta.com/index.php/component/k2/itemlist/user/116765
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=2061562
<p align="">
<a title="강남오피" href="http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bf%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%c5%8b%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%84%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%8d%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%85%bela" target="_blank">강남오피
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉오피" href="https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%d0%be%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%88%82%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%bd%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%82%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a9tide" target="_blank">선릉오피
</a>
</p>
먼저핀꽃은 먼저진다 남보다 먼저 공을 세우려고 조급히 서둘것이 아니다-채근담
<p align="">
<a title="역삼오피" href="
https://enes.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%94%bb%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%97%88%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%ce%9egang" target="_blank">역삼오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남휴게텔" href="
https://www.livemeshthemes.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%c4%b1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b7%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%85%86%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%93%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%82%ba%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%84%a1%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%82stone" target="_blank">강남휴게텔
</a>
</p>
먹고 싶은것을 다 먹는 것은 그렇게 재미있지 않다 . 인생을 경계선 없이 살면 기쁨이 덜하다.먹고싶은대로 다 먹을 수있다면 먹고싶은 것을 먹는데 무슨 재미가 있겠나 - 톰행크스
<p align="">
<a title="선릉휴게텔" href="
http://www.pnr.corsica/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%89%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%a1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%9d%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%83%a6afford" target="_blank">선릉휴게텔
</a>
</p>
진짜 문제는 사람들의 마음이다.그것은 절대로 물리학이나 윤리학의 문제가 아니다.-아인슈타인
<p align="">
<a title="역삼휴게텔" href="
https://dict.leo.org/italienisch-deutsch/%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%82%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%d1%8f%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%83%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%ae%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9dseason" target="_blank">역삼휴게텔
</a>
</p>
가난은 가난하다고 느끼는 곳에 존재한다 .- 에머슨
<p align="">
<a title="강남안마" href="https://24.sapo.pt/pesquisar?q=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%85%a2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%82%8f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%99%a0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%85%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ce%92truly" target="_blank">강남안마
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉안마" href="
https://enfi.dict.cc/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%9e%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%85%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%90%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%bd%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%9cband" target="_blank">선릉안마
</a>
</p>
행복은 습관이다 그것을 몸에 지니라 -허버드
<p align="">
<a title="역삼안마" href="
https://www.lidumsaym.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%83%9d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c2%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8f%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%b1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%82%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b9derived" target="_blank">역삼안마
</a>
</p>
화려한 일을 추구하지 말라. 중요한 것은 스스로의 재능이며자신의 행동에 쏟아 붓는 사랑의 정도이다. -머더 테레사
<p align="">
<a title="강남오피" href="
http://www.twentszitmaaierteam.nl/pages/interactief/gastenboek.php?p=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%87%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%86%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%82%b9%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%94%bd%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%d0%a3wouldn't" target="_blank">강남오피
</a>
</p>
절대 어제를 후회하지 마라 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다-L.론허바드
<p align="">
<a title="선릉오피" href="
http://www.mairtinmusic.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%82%86%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%8b%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%9e%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%88truly" target="_blank">선릉오피
</a>
</p>
내일은 내일의 태양이 뜬다 피할수 없으면 즐겨라 -로버트 엘리엇
<p align="">
<a title="역삼오피" href="https://www.uptodate.com/contents/search?search=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%81%99%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%b9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%99%aa%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%83%8e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c3%be%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%82%b6%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%8centire" target="_blank">역삼오피
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남휴게텔" href="
http://ladysmithfederal.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%93%94%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%88%87%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%8f%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ce%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%c2%baremark" target="_blank">강남휴게텔
</a>
</p>
인간의 삶 전체는 단지 한 순간에 불과하다 . 인생을 즐기자 - 플루타르코스
<p align="">
<a title="선릉휴게텔" href="
https://www.governmentjobs.com/jobs?keyword=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%94%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%87secretly" target="_blank">선릉휴게텔
</a>
</p>
흔히 사람들은 기회를 기다리고 있지만 기회는 기다리는사람에게 잡히지 않는 법이다.우리는 기회를 기다리는 사람이 되기 전에 기회를 얻을 수 있는실력을 갖춰야 한다.일에 더 열중하는 사람이 되어야한다.-안창호
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%bb%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%84%ba%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%89%b0%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8e%93%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%80%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%cf%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b7artillery" target="_blank">역삼휴게텔
</a>
</p>
마음만을 가지고 있어서는 안된다. 반드시 실천하여야 한다.-이소룡
<p align="">
<a title="강남안마" href="
https://dehr.dict.cc/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%86%8d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%a1%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%84%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%9f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%b0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%88%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%8f%9dleg" target="_blank">강남안마
</a>
</p>
물러나서 조용하게 구하면 배울 수 있는 스승은 많다.사람은 가는 곳마다 보는 것마다 모두 스승으로서배울 것이 많은 법이다.-맹자
<p align="">
<a title="선릉안마" href="
https://www.gov.uk/search/all?keywords=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%92%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%91%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%ae%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8f%87%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%97%87providing" target="_blank">선릉안마
</a>
</p>
삶이 있는 한 희망은 있다 -키케로
<p align="">
<a title="역삼안마" href="
https://www.sdsn.no/sok/category28150.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%88%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%8c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%82%a1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%85%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%c4%b8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%85%9esecretary" target="_blank">역삼안마
</a>
</p>
한 번 실패와 영원한 실패를 혼동하지 마라.-F.스콧 핏제랄드
<p align="">
<a title="강남오피" href="
https://www.righteousmind.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%b0%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%91%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%96%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%88%87sang" target="_blank">강남오피
</a>
</p>
모든것들에는 나름의 경이로움과 심지어 어둠과 침묵이 있고 내가 어떤 상태에 있더라도 나는 그속에서 만족하는 법을 배운다-헬렌켈러
<p align="">
<a title="선릉오피" href="
http://www.actiitransportation.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e2%96%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%99%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%89%ba%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%bdaround" target="_blank">선릉오피
</a>
</p>
내 비장의 무기는 아직 손안에 있다 .그것은 희망이다 - 나폴레옹
<p align="">
<a title="역삼오피" href="https://www.youtube.com/results?search_query=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ce%a5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8e%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%a0%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%b1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%84lay" target="_blank">역삼오피
</a>
</p>
만족할 줄 아는 사람은진정한 부자이고 탐욕스러운 사람은진실로 가난한 사람이다.-솔론
<p align="">
<a title="강남휴게텔" href="
https://denl.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%81%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%8a%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%8f%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%85%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%93%a0%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%b2grief" target="_blank">강남휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="선릉휴게텔" href="
https://artdeco.org/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%9e%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a4%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%94%b9%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ef%bc%af%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%be%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%8dodd" target="_blank">선릉휴게텔
</a>
</p>
만약 우리가 할 수 있는 일을 모두 한다면 우리들은 우리자신에 깜짝 놀랄 것이다.-에디슨
<p align="">
<a title="역삼휴게텔" href="
http://www.lavipera.it/?s=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bc%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%bb%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%93%a3%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b5%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%88%8cvaried" target="_blank">역삼휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="강남안마" href="
https://money2.creontrade.com/E5/WTS/Stock/Foreign/DW_Foreign_Tax.aspx?p=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ef%bc%84%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bc%af%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%bd%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%83%9d%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%87splendid" target="_blank">강남안마
</a>
</p>
절대 어제를 후회하지 마라 . 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다 L.론허바드
<p align="">
<a title="선릉안마" href="
https://wpgovernance.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%85%a4%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%b3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%81%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%8d%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%81%b7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%a3john" target="_blank">선릉안마
</a>
</p>
사막이 아름다운 것은 어딘가에 샘이 숨겨져 있기 때문이다 - 생떽쥐베리
<p align="">
<a title="역삼안마" href="
https://nebraska.aiga.org/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%96%92%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%86%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%88%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%95%80%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ef%bd%87goes" target="_blank">역삼안마
</a>
</p>
</div>
<div style='width: 1px; height: 1px; overflow: hidden'><div align='center'>
<img name='target_resize_image[]' onclick='image_window(this)' style='cursor:pointer;' alt="" class="view_photo up" src="http://file.osen.co.kr/article/2019/05/01/201905011854774508_5cc96e7d1d3c2.jpg" >
그라운드 뷰는 차의 앞쪽 아랫부분
<div style="position:absolute; left:-9999px; top:-9999px;" class="sound_only">
피할수 없으면 즐겨라 - 로버트 엘리엇
<p align="">
<a title="강남오피" href="
http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%83%b1%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a4%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%a7%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%aa%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%a4forward" target="_blank">강남오피
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="선릉오피" href="
http://www.ambrosiocinema.it/page/5/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%83%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%a8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%b8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%bf%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ef%bc%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%96%bc%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%86spring" target="_blank">선릉오피
</a>
</p>
아래에 비교하면 남음이 있다.-명심보감
<p align="">
<a title="역삼오피" href="
https://www.openrice.com/zh/hongkong/restaurants?what=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%99%a5%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a0both" target="_blank">역삼오피
</a>
</p>
실패는 잊어라 그러나 그것이 준 교훈은절대 잊으면 안된다-하버트 개서
<p align="">
<a title="강남휴게텔" href="
https://desk.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%88%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%88%99%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%85%b4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%82%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%81boat" target="_blank">강남휴게텔
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉휴게텔" href="http://www.blueskyspaworks.com/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%c2%bc%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%91%ad%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%95%89%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%bb%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%92%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%ef%bc%84damage" target="_blank">선릉휴게텔
</a>
</p>
절대 포기하지 말라. 당신이 되고 싶은 무언가가 있다면그에 대해 자부심을 가져라. 당신 자신에게 기회를 주어라. 스스로가 형편없다고 생각하지 말라.그래봐야 아무 것도 얻을 것이 없다. 목표를 높이 세워라.인생은 그렇게 살아야 한다.-마이크 맥라렌
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%80%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%92%b2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%92%a4%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bf%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%8e%97sworn" target="_blank">역삼휴게텔
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="강남안마" href="
https://www.wfs-dreieich.de/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%d0%93%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%97%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%88%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%a3%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%a4%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%84blame" target="_blank">강남안마
</a>
</p>
계단을 밟아야 계단 위에 올라설수 있다 -터키속담
<p align="">
<a title="선릉안마" href="
http://ypsistudio.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%82%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c4%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ef%bc%b0%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bf%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%cf%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%91%a4contain" target="_blank">선릉안마
</a>
</p>
지금이야 말로 일할때다. 지금이야말로 싸울때다. 지금이야말로 나를 더 훌륭한 사람으로 만들때다오늘 그것을 못하면 내일 그것을 할수있는가- 토마스 아켐피스
<p align="">
<a title="역삼안마" href="
https://www.matematikk.org/trinn8-10/sok/index.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%81%af%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bc%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%98%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%b3%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%b4understand" target="_blank">역삼안마
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남오피" href="
https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%86%90%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%85%b5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ef%bc%a8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c5%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8f%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%80bred" target="_blank">강남오피
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="선릉오피" href="
https://www.pexels.com/ko-kr/search/%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ef%bd%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%b9%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%83%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%8f%9cshelter" target="_blank">선릉오피
</a>
</p>
단순하게 살라. 쓸데없는 절차와 일 때문에 얼마나 복잡한 삶을 살아가는가?-이드리스 샤흐
<p align="">
<a title="역삼오피" href="
https://ciscentraltexas.org/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%ae%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b2%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8f%87%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%8a%83%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%97%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%92philadelphia" target="_blank">역삼오피
</a>
</p>
직접 눈으로 본 일도 오히려 참인지 아닌지염려스러운데 더구나 등뒤에서 남이 말하는것이야 어찌 이것을 깊이 믿을 수 있으랴?-명심보감-
<p align="">
<a title="강남휴게텔" href="
http://www.kuenselonline.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ce%a8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%9c%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%86%96%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%b2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bd%90%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%87quickly" target="_blank">강남휴게텔
</a>
</p>
내가 헛되이 보낸 오늘은 어제 죽어간 이들이그토록 바라던 하루이다 단 하루면 인간적인 모든 것을 멸망시킬수도 다시 소생시킬수도 있다-소포클레스
<p align="">
<a title="선릉휴게텔" href="https://www.sony.com/electronics/support/results?query=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%86%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%81%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ce%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%bd%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bc%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9bboat" target="_blank">선릉휴게텔
</a>
</p>
돈이란 바닷물과도 같다. 그것은 마시면 마실수록 목이 말라진다.-쇼펜하우어
<p align="">
<a title="역삼휴게텔" href="
https://jobs.rbc.com/ca/en/search-results?keywords=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%8c%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%d0%9e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%82%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%a6%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%c5%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%82joke" target="_blank">역삼휴게텔
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남안마" href="
http://www.makinamekawa.com/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%91%a9%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%d0%96%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bc%a2%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%92dreaming" target="_blank">강남안마
</a>
</p>
진정으로 웃으려면 고통을 참아야하며 나아가 고통을 즐길 줄 알아야 해 -찰리 채플린
<p align="">
<a title="선릉안마" href="
https://www.reddit.com/search?q=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%ac%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%9b%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%92%a5%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%a7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%99%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%a7grant" target="_blank">선릉안마
</a>
</p>
한번의 실패와 영원한 실패를 혼동하지 마라 -F.스콧 핏제랄드
<p align="">
<a title="역삼안마" href="
https://desk.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%95%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%9e%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ce%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%b5%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%85%b9%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%d1%89%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%93goal" target="_blank">역삼안마
</a>
</p>
행복은 결코 많고 큰데만 있는 것이 아니다 작은 것을 가지고도 고마워 하고 만족할 줄 안다면그는 행복한 사람이다여백과 공간의 아름다움은 단순함과 간소함에 있다법정스님 - 홀로사는 즐거움 에서
<p align="">
<a title="강남오피" href="
http://www.alberguerioaragon.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%bd%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%a6%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%87%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%80%b3%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%85%a5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%93%98%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%81seem" target="_blank">강남오피
</a>
</p>
길을 잃는 다는 것은 곧 길을 알게 된다는 것이다. - 동아프리카속담
<p align="">
<a title="선릉오피" href="
https://www.isistassinari.gov.it/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%8e%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%ce%b7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%89%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ce%95%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%95%88awhile" target="_blank">선릉오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="역삼오피" href="
http://isb.az/ru/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%89%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%d1%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%93%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%8cindependent" target="_blank">역삼오피
</a>
</p>
자신을 내보여라. 그러면 재능이 드러날 것이다.- 발타사르 그라시안
<p align="">
<a title="강남휴게텔" href="
http://biz.heraldcorp.com/view.php?ud=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%b2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bd%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%ef%bc%95%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%89%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%bbmarks" target="_blank">강남휴게텔
</a>
</p>
화가 날 때는 100까지 세라. 최악일 때는 욕설을 퍼부어라. -마크 트웨인
<p align="">
<a title="선릉휴게텔" href="
https://www.americanas.com.br/busca?conteudo=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ef%bc%b0%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%84%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%9a%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%81%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%8e%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%a8portrait" target="_blank">선릉휴게텔
</a>
</p>
1퍼센트의 가능성 그것이 나의 길이다-나폴레옹
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%83%99%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8f%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%83%95%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%d0%af%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b9personal" target="_blank">역삼휴게텔
</a>
</p>
최고에 도달하려면 최저에서 시작하라.-P.시루스
<p align="">
<a title="강남안마" href="
http://jozankei.jp/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%92%9f%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%81%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%c3%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%88%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%84%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%96%a6%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b6parted" target="_blank">강남안마
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉안마" href="
http://www.somoseducacao.com.br/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%98%85%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%be%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%9a%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%a1%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%a5greatly" target="_blank">선릉안마
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="역삼안마" href="
https://riftio.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%8e%80%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bd%99%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%99%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%8a%83%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%9d%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%a6%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%84%b9had" target="_blank">역삼안마 ddakbam1.com ᕙ(⇀‸↼‶)ᕗ
</a>
</p>
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=150956
http://kockazatkutato.hu/?option=com_k2&view=itemlist&task=user&id=90327
http://www.haetsaldun-clinic.co.kr/Question/383006
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=267504
http://www.ats-ottagono.it/?option=com_k2&view=itemlist&task=user&id=1659162
http://ovotecegg.com/component/k2/itemlist/user/303993
http://hotelnomadpalace.com/?option=com_k2&view=itemlist&task=user&id=25911
http://w9builders.co.uk/?option=com_k2&view=itemlist&task=user&id=258091
http://event.junglian.com/board/119264
http://smartacity.com/component/k2/itemlist/user/120023
http://divespace.co.kr/board/810611
http://taklongclub.com/forum/index.php?topic=326282.0
https://turimex.mx.solemti.net/index.php/component/k2/itemlist/user/87166
http://dev.aabn.org.gh/component/k2/itemlist/user/966841
http://kockazatkutato.hu/component/k2/itemlist/user/143851
http://ovotecegg.com/component/k2/itemlist/user/375796
http://www.hoonthaitoday.com/forum/index.php?topic=526026.0
http://hotelnomadpalace.com/index.php/component/k2/itemlist/user/26186
http://gtupuw.org/?option=com_k2&view=itemlist&task=user&id=2081226
https://khuyenmaikk13.info/index.php?topic=265727.0
http://holysweat.dothome.co.kr/data/292854
https://mcsetup.tk/bbs/index.php?topic=283710.0
http://smartacity.com/component/k2/itemlist/user/143740
http://153.120.114.241/eso/index.php/18156227-rasskaz-sluzanki-3-sezon-6-seria-14062019-t5-rasskaz-sluzanki-3
http://jdcalc.com/forum/viewtopic.php?t=419143
http://divespace.co.kr/board/810949
<p align="">
<a title="강남오피" href="http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bf%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%c5%8b%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%84%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%8d%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%85%bela" target="_blank">강남오피
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉오피" href="https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%d0%be%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%88%82%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%bd%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%82%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a9tide" target="_blank">선릉오피
</a>
</p>
먼저핀꽃은 먼저진다 남보다 먼저 공을 세우려고 조급히 서둘것이 아니다-채근담
<p align="">
<a title="역삼오피" href="
https://enes.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%94%bb%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%97%88%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%ce%9egang" target="_blank">역삼오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남휴게텔" href="
https://www.livemeshthemes.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%c4%b1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b7%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%85%86%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%93%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%82%ba%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%84%a1%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%82stone" target="_blank">강남휴게텔
</a>
</p>
먹고 싶은것을 다 먹는 것은 그렇게 재미있지 않다 . 인생을 경계선 없이 살면 기쁨이 덜하다.먹고싶은대로 다 먹을 수있다면 먹고싶은 것을 먹는데 무슨 재미가 있겠나 - 톰행크스
<p align="">
<a title="선릉휴게텔" href="
http://www.pnr.corsica/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%89%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%a1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%9d%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%83%a6afford" target="_blank">선릉휴게텔
</a>
</p>
진짜 문제는 사람들의 마음이다.그것은 절대로 물리학이나 윤리학의 문제가 아니다.-아인슈타인
<p align="">
<a title="역삼휴게텔" href="
https://dict.leo.org/italienisch-deutsch/%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%82%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%d1%8f%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%83%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%ae%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9dseason" target="_blank">역삼휴게텔
</a>
</p>
가난은 가난하다고 느끼는 곳에 존재한다 .- 에머슨
<p align="">
<a title="강남안마" href="https://24.sapo.pt/pesquisar?q=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%85%a2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%82%8f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%99%a0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%85%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ce%92truly" target="_blank">강남안마
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉안마" href="
https://enfi.dict.cc/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%9e%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%85%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%90%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%bd%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%9cband" target="_blank">선릉안마
</a>
</p>
행복은 습관이다 그것을 몸에 지니라 -허버드
<p align="">
<a title="역삼안마" href="
https://www.lidumsaym.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%83%9d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c2%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8f%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%b1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%82%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b9derived" target="_blank">역삼안마
</a>
</p>
화려한 일을 추구하지 말라. 중요한 것은 스스로의 재능이며자신의 행동에 쏟아 붓는 사랑의 정도이다. -머더 테레사
<p align="">
<a title="강남오피" href="
http://www.twentszitmaaierteam.nl/pages/interactief/gastenboek.php?p=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%87%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%86%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%82%b9%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%94%bd%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%d0%a3wouldn't" target="_blank">강남오피
</a>
</p>
절대 어제를 후회하지 마라 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다-L.론허바드
<p align="">
<a title="선릉오피" href="
http://www.mairtinmusic.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%82%86%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%8b%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%9e%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%88truly" target="_blank">선릉오피
</a>
</p>
내일은 내일의 태양이 뜬다 피할수 없으면 즐겨라 -로버트 엘리엇
<p align="">
<a title="역삼오피" href="https://www.uptodate.com/contents/search?search=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%81%99%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%b9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%99%aa%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%83%8e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c3%be%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%82%b6%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%8centire" target="_blank">역삼오피
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남휴게텔" href="
http://ladysmithfederal.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%93%94%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%88%87%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%8f%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ce%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%c2%baremark" target="_blank">강남휴게텔
</a>
</p>
인간의 삶 전체는 단지 한 순간에 불과하다 . 인생을 즐기자 - 플루타르코스
<p align="">
<a title="선릉휴게텔" href="
https://www.governmentjobs.com/jobs?keyword=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%94%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%87secretly" target="_blank">선릉휴게텔
</a>
</p>
흔히 사람들은 기회를 기다리고 있지만 기회는 기다리는사람에게 잡히지 않는 법이다.우리는 기회를 기다리는 사람이 되기 전에 기회를 얻을 수 있는실력을 갖춰야 한다.일에 더 열중하는 사람이 되어야한다.-안창호
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%bb%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%84%ba%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%89%b0%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8e%93%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%80%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%cf%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b7artillery" target="_blank">역삼휴게텔
</a>
</p>
마음만을 가지고 있어서는 안된다. 반드시 실천하여야 한다.-이소룡
<p align="">
<a title="강남안마" href="
https://dehr.dict.cc/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%86%8d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%a1%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%84%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%9f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%b0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%88%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%8f%9dleg" target="_blank">강남안마
</a>
</p>
물러나서 조용하게 구하면 배울 수 있는 스승은 많다.사람은 가는 곳마다 보는 것마다 모두 스승으로서배울 것이 많은 법이다.-맹자
<p align="">
<a title="선릉안마" href="
https://www.gov.uk/search/all?keywords=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%92%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%91%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%ae%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8f%87%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%97%87providing" target="_blank">선릉안마
</a>
</p>
삶이 있는 한 희망은 있다 -키케로
<p align="">
<a title="역삼안마" href="
https://www.sdsn.no/sok/category28150.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%88%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%8c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%82%a1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%85%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%c4%b8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%85%9esecretary" target="_blank">역삼안마
</a>
</p>
한 번 실패와 영원한 실패를 혼동하지 마라.-F.스콧 핏제랄드
<p align="">
<a title="강남오피" href="
https://www.righteousmind.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%b0%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%91%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%96%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%88%87sang" target="_blank">강남오피
</a>
</p>
모든것들에는 나름의 경이로움과 심지어 어둠과 침묵이 있고 내가 어떤 상태에 있더라도 나는 그속에서 만족하는 법을 배운다-헬렌켈러
<p align="">
<a title="선릉오피" href="
http://www.actiitransportation.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e2%96%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%99%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%89%ba%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%bdaround" target="_blank">선릉오피
</a>
</p>
내 비장의 무기는 아직 손안에 있다 .그것은 희망이다 - 나폴레옹
<p align="">
<a title="역삼오피" href="https://www.youtube.com/results?search_query=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ce%a5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8e%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%a0%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%b1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%84lay" target="_blank">역삼오피
</a>
</p>
만족할 줄 아는 사람은진정한 부자이고 탐욕스러운 사람은진실로 가난한 사람이다.-솔론
<p align="">
<a title="강남휴게텔" href="
https://denl.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%81%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%8a%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%8f%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%85%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%93%a0%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%b2grief" target="_blank">강남휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="선릉휴게텔" href="
https://artdeco.org/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%9e%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a4%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%94%b9%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ef%bc%af%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%be%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%8dodd" target="_blank">선릉휴게텔
</a>
</p>
만약 우리가 할 수 있는 일을 모두 한다면 우리들은 우리자신에 깜짝 놀랄 것이다.-에디슨
<p align="">
<a title="역삼휴게텔" href="
http://www.lavipera.it/?s=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bc%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%bb%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%93%a3%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b5%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%88%8cvaried" target="_blank">역삼휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="강남안마" href="
https://money2.creontrade.com/E5/WTS/Stock/Foreign/DW_Foreign_Tax.aspx?p=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ef%bc%84%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bc%af%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%bd%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%83%9d%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%87splendid" target="_blank">강남안마
</a>
</p>
절대 어제를 후회하지 마라 . 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다 L.론허바드
<p align="">
<a title="선릉안마" href="
https://wpgovernance.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%85%a4%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%b3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%81%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%8d%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%81%b7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%a3john" target="_blank">선릉안마
</a>
</p>
사막이 아름다운 것은 어딘가에 샘이 숨겨져 있기 때문이다 - 생떽쥐베리
<p align="">
<a title="역삼안마" href="
https://nebraska.aiga.org/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%96%92%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%86%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%88%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%95%80%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ef%bd%87goes" target="_blank">역삼안마
</a>
</p>
</div>
<div style='width: 1px; height: 1px; overflow: hidden'><div align='center'>
<img name='target_resize_image[]' onclick='image_window(this)' style='cursor:pointer;' alt="" class="view_photo up" src="http://file.osen.co.kr/article/2019/05/01/201905011854774508_5cc96e7d1d3c2.jpg" >
그라운드 뷰는 차의 앞쪽 아랫부분
<div style="position:absolute; left:-9999px; top:-9999px;" class="sound_only">
피할수 없으면 즐겨라 - 로버트 엘리엇
<p align="">
<a title="강남오피" href="
http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%83%b1%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a4%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%a7%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%aa%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%a4forward" target="_blank">강남오피
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="선릉오피" href="
http://www.ambrosiocinema.it/page/5/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%83%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%a8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%b8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%bf%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ef%bc%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%96%bc%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%86spring" target="_blank">선릉오피
</a>
</p>
아래에 비교하면 남음이 있다.-명심보감
<p align="">
<a title="역삼오피" href="
https://www.openrice.com/zh/hongkong/restaurants?what=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%99%a5%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a0both" target="_blank">역삼오피
</a>
</p>
실패는 잊어라 그러나 그것이 준 교훈은절대 잊으면 안된다-하버트 개서
<p align="">
<a title="강남휴게텔" href="
https://desk.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%88%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%88%99%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%85%b4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%82%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%81boat" target="_blank">강남휴게텔
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉휴게텔" href="http://www.blueskyspaworks.com/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%c2%bc%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%91%ad%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%95%89%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%bb%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%92%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%ef%bc%84damage" target="_blank">선릉휴게텔
</a>
</p>
절대 포기하지 말라. 당신이 되고 싶은 무언가가 있다면그에 대해 자부심을 가져라. 당신 자신에게 기회를 주어라. 스스로가 형편없다고 생각하지 말라.그래봐야 아무 것도 얻을 것이 없다. 목표를 높이 세워라.인생은 그렇게 살아야 한다.-마이크 맥라렌
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%80%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%92%b2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%92%a4%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bf%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%8e%97sworn" target="_blank">역삼휴게텔
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="강남안마" href="
https://www.wfs-dreieich.de/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%d0%93%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%97%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%88%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%a3%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%a4%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%84blame" target="_blank">강남안마
</a>
</p>
계단을 밟아야 계단 위에 올라설수 있다 -터키속담
<p align="">
<a title="선릉안마" href="
http://ypsistudio.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%82%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c4%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ef%bc%b0%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bf%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%cf%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%91%a4contain" target="_blank">선릉안마
</a>
</p>
지금이야 말로 일할때다. 지금이야말로 싸울때다. 지금이야말로 나를 더 훌륭한 사람으로 만들때다오늘 그것을 못하면 내일 그것을 할수있는가- 토마스 아켐피스
<p align="">
<a title="역삼안마" href="
https://www.matematikk.org/trinn8-10/sok/index.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%81%af%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bc%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%98%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%b3%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%b4understand" target="_blank">역삼안마
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남오피" href="
https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%86%90%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%85%b5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ef%bc%a8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c5%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8f%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%80bred" target="_blank">강남오피
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="선릉오피" href="
https://www.pexels.com/ko-kr/search/%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ef%bd%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%b9%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%83%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%8f%9cshelter" target="_blank">선릉오피
</a>
</p>
단순하게 살라. 쓸데없는 절차와 일 때문에 얼마나 복잡한 삶을 살아가는가?-이드리스 샤흐
<p align="">
<a title="역삼오피" href="
https://ciscentraltexas.org/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%ae%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b2%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8f%87%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%8a%83%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%97%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%92philadelphia" target="_blank">역삼오피
</a>
</p>
직접 눈으로 본 일도 오히려 참인지 아닌지염려스러운데 더구나 등뒤에서 남이 말하는것이야 어찌 이것을 깊이 믿을 수 있으랴?-명심보감-
<p align="">
<a title="강남휴게텔" href="
http://www.kuenselonline.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ce%a8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%9c%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%86%96%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%b2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bd%90%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%87quickly" target="_blank">강남휴게텔
</a>
</p>
내가 헛되이 보낸 오늘은 어제 죽어간 이들이그토록 바라던 하루이다 단 하루면 인간적인 모든 것을 멸망시킬수도 다시 소생시킬수도 있다-소포클레스
<p align="">
<a title="선릉휴게텔" href="https://www.sony.com/electronics/support/results?query=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%86%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%81%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ce%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%bd%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bc%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9bboat" target="_blank">선릉휴게텔
</a>
</p>
돈이란 바닷물과도 같다. 그것은 마시면 마실수록 목이 말라진다.-쇼펜하우어
<p align="">
<a title="역삼휴게텔" href="
https://jobs.rbc.com/ca/en/search-results?keywords=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%8c%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%d0%9e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%82%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%a6%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%c5%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%82joke" target="_blank">역삼휴게텔
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남안마" href="
http://www.makinamekawa.com/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%91%a9%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%d0%96%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bc%a2%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%92dreaming" target="_blank">강남안마
</a>
</p>
진정으로 웃으려면 고통을 참아야하며 나아가 고통을 즐길 줄 알아야 해 -찰리 채플린
<p align="">
<a title="선릉안마" href="
https://www.reddit.com/search?q=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%ac%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%9b%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%92%a5%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%a7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%99%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%a7grant" target="_blank">선릉안마
</a>
</p>
한번의 실패와 영원한 실패를 혼동하지 마라 -F.스콧 핏제랄드
<p align="">
<a title="역삼안마" href="
https://desk.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%95%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%9e%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ce%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%b5%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%85%b9%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%d1%89%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%93goal" target="_blank">역삼안마
</a>
</p>
행복은 결코 많고 큰데만 있는 것이 아니다 작은 것을 가지고도 고마워 하고 만족할 줄 안다면그는 행복한 사람이다여백과 공간의 아름다움은 단순함과 간소함에 있다법정스님 - 홀로사는 즐거움 에서
<p align="">
<a title="강남오피" href="
http://www.alberguerioaragon.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%bd%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%a6%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%87%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%80%b3%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%85%a5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%93%98%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%81seem" target="_blank">강남오피
</a>
</p>
길을 잃는 다는 것은 곧 길을 알게 된다는 것이다. - 동아프리카속담
<p align="">
<a title="선릉오피" href="
https://www.isistassinari.gov.it/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%8e%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%ce%b7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%89%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ce%95%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%95%88awhile" target="_blank">선릉오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="역삼오피" href="
http://isb.az/ru/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%89%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%d1%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%93%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%8cindependent" target="_blank">역삼오피
</a>
</p>
자신을 내보여라. 그러면 재능이 드러날 것이다.- 발타사르 그라시안
<p align="">
<a title="강남휴게텔" href="
http://biz.heraldcorp.com/view.php?ud=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%b2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bd%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%ef%bc%95%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%89%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%bbmarks" target="_blank">강남휴게텔
</a>
</p>
화가 날 때는 100까지 세라. 최악일 때는 욕설을 퍼부어라. -마크 트웨인
<p align="">
<a title="선릉휴게텔" href="
https://www.americanas.com.br/busca?conteudo=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ef%bc%b0%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%84%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%9a%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%81%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%8e%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%a8portrait" target="_blank">선릉휴게텔
</a>
</p>
1퍼센트의 가능성 그것이 나의 길이다-나폴레옹
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%83%99%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8f%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%83%95%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%d0%af%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b9personal" target="_blank">역삼휴게텔
</a>
</p>
최고에 도달하려면 최저에서 시작하라.-P.시루스
<p align="">
<a title="강남안마" href="
http://jozankei.jp/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%92%9f%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%81%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%c3%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%88%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%84%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%96%a6%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b6parted" target="_blank">강남안마
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉안마" href="
http://www.somoseducacao.com.br/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%98%85%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%be%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%9a%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%a1%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%a5greatly" target="_blank">선릉안마
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="역삼안마" href="
https://riftio.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%8e%80%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bd%99%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%99%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%8a%83%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%9d%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%a6%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%84%b9had" target="_blank">역삼안마 ddakbam1.com ω༼'͡•-͡•༽ω
</a>
</p>
<p align="">
<a title="강남오피" href="http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bf%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%c5%8b%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%84%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%8d%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%85%bela" target="_blank">강남오피
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉오피" href="https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%d0%be%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%88%82%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%bd%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%82%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a9tide" target="_blank">선릉오피
</a>
</p>
먼저핀꽃은 먼저진다 남보다 먼저 공을 세우려고 조급히 서둘것이 아니다-채근담
<p align="">
<a title="역삼오피" href="
https://enes.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%94%bb%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%97%88%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%ce%9egang" target="_blank">역삼오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남휴게텔" href="
https://www.livemeshthemes.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%c4%b1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b7%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%85%86%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%93%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%82%ba%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%84%a1%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%82stone" target="_blank">강남휴게텔
</a>
</p>
먹고 싶은것을 다 먹는 것은 그렇게 재미있지 않다 . 인생을 경계선 없이 살면 기쁨이 덜하다.먹고싶은대로 다 먹을 수있다면 먹고싶은 것을 먹는데 무슨 재미가 있겠나 - 톰행크스
<p align="">
<a title="선릉휴게텔" href="
http://www.pnr.corsica/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%89%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%a1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%9d%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%83%a6afford" target="_blank">선릉휴게텔
</a>
</p>
진짜 문제는 사람들의 마음이다.그것은 절대로 물리학이나 윤리학의 문제가 아니다.-아인슈타인
<p align="">
<a title="역삼휴게텔" href="
https://dict.leo.org/italienisch-deutsch/%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%82%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%d1%8f%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%83%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%ae%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9dseason" target="_blank">역삼휴게텔
</a>
</p>
가난은 가난하다고 느끼는 곳에 존재한다 .- 에머슨
<p align="">
<a title="강남안마" href="https://24.sapo.pt/pesquisar?q=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%85%a2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%82%8f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%99%a0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%85%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ce%92truly" target="_blank">강남안마
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉안마" href="
https://enfi.dict.cc/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%9e%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%85%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%90%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%bd%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%9cband" target="_blank">선릉안마
</a>
</p>
행복은 습관이다 그것을 몸에 지니라 -허버드
<p align="">
<a title="역삼안마" href="
https://www.lidumsaym.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%83%9d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c2%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8f%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%b1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%82%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b9derived" target="_blank">역삼안마
</a>
</p>
화려한 일을 추구하지 말라. 중요한 것은 스스로의 재능이며자신의 행동에 쏟아 붓는 사랑의 정도이다. -머더 테레사
<p align="">
<a title="강남오피" href="
http://www.twentszitmaaierteam.nl/pages/interactief/gastenboek.php?p=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%87%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%86%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%82%b9%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%94%bd%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%d0%a3wouldn't" target="_blank">강남오피
</a>
</p>
절대 어제를 후회하지 마라 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다-L.론허바드
<p align="">
<a title="선릉오피" href="
http://www.mairtinmusic.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%82%86%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%8b%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%9e%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%88truly" target="_blank">선릉오피
</a>
</p>
내일은 내일의 태양이 뜬다 피할수 없으면 즐겨라 -로버트 엘리엇
<p align="">
<a title="역삼오피" href="https://www.uptodate.com/contents/search?search=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%81%99%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%b9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%99%aa%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%83%8e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c3%be%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%82%b6%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%8centire" target="_blank">역삼오피
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남휴게텔" href="
http://ladysmithfederal.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%93%94%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%88%87%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%8f%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ce%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%c2%baremark" target="_blank">강남휴게텔
</a>
</p>
인간의 삶 전체는 단지 한 순간에 불과하다 . 인생을 즐기자 - 플루타르코스
<p align="">
<a title="선릉휴게텔" href="
https://www.governmentjobs.com/jobs?keyword=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%94%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%87secretly" target="_blank">선릉휴게텔
</a>
</p>
흔히 사람들은 기회를 기다리고 있지만 기회는 기다리는사람에게 잡히지 않는 법이다.우리는 기회를 기다리는 사람이 되기 전에 기회를 얻을 수 있는실력을 갖춰야 한다.일에 더 열중하는 사람이 되어야한다.-안창호
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%bb%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%84%ba%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%89%b0%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8e%93%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%80%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%cf%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b7artillery" target="_blank">역삼휴게텔
</a>
</p>
마음만을 가지고 있어서는 안된다. 반드시 실천하여야 한다.-이소룡
<p align="">
<a title="강남안마" href="
https://dehr.dict.cc/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%86%8d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%a1%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%84%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%9f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%b0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%88%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%8f%9dleg" target="_blank">강남안마
</a>
</p>
물러나서 조용하게 구하면 배울 수 있는 스승은 많다.사람은 가는 곳마다 보는 것마다 모두 스승으로서배울 것이 많은 법이다.-맹자
<p align="">
<a title="선릉안마" href="
https://www.gov.uk/search/all?keywords=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%92%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%91%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%ae%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8f%87%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%97%87providing" target="_blank">선릉안마
</a>
</p>
삶이 있는 한 희망은 있다 -키케로
<p align="">
<a title="역삼안마" href="
https://www.sdsn.no/sok/category28150.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%88%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%8c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%82%a1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%85%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%c4%b8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%85%9esecretary" target="_blank">역삼안마
</a>
</p>
한 번 실패와 영원한 실패를 혼동하지 마라.-F.스콧 핏제랄드
<p align="">
<a title="강남오피" href="
https://www.righteousmind.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%b0%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%91%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%96%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%88%87sang" target="_blank">강남오피
</a>
</p>
모든것들에는 나름의 경이로움과 심지어 어둠과 침묵이 있고 내가 어떤 상태에 있더라도 나는 그속에서 만족하는 법을 배운다-헬렌켈러
<p align="">
<a title="선릉오피" href="
http://www.actiitransportation.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e2%96%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%99%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%89%ba%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%bdaround" target="_blank">선릉오피
</a>
</p>
내 비장의 무기는 아직 손안에 있다 .그것은 희망이다 - 나폴레옹
<p align="">
<a title="역삼오피" href="https://www.youtube.com/results?search_query=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ce%a5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8e%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%a0%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%b1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%84lay" target="_blank">역삼오피
</a>
</p>
만족할 줄 아는 사람은진정한 부자이고 탐욕스러운 사람은진실로 가난한 사람이다.-솔론
<p align="">
<a title="강남휴게텔" href="
https://denl.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%81%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%8a%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%8f%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%85%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%93%a0%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%b2grief" target="_blank">강남휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="선릉휴게텔" href="
https://artdeco.org/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%9e%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a4%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%94%b9%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ef%bc%af%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%be%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%8dodd" target="_blank">선릉휴게텔
</a>
</p>
만약 우리가 할 수 있는 일을 모두 한다면 우리들은 우리자신에 깜짝 놀랄 것이다.-에디슨
<p align="">
<a title="역삼휴게텔" href="
http://www.lavipera.it/?s=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bc%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%bb%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%93%a3%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b5%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%88%8cvaried" target="_blank">역삼휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="강남안마" href="
https://money2.creontrade.com/E5/WTS/Stock/Foreign/DW_Foreign_Tax.aspx?p=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ef%bc%84%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bc%af%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%bd%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%83%9d%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%87splendid" target="_blank">강남안마
</a>
</p>
절대 어제를 후회하지 마라 . 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다 L.론허바드
<p align="">
<a title="선릉안마" href="
https://wpgovernance.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%85%a4%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%b3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%81%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%8d%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%81%b7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%a3john" target="_blank">선릉안마
</a>
</p>
사막이 아름다운 것은 어딘가에 샘이 숨겨져 있기 때문이다 - 생떽쥐베리
<p align="">
<a title="역삼안마" href="
https://nebraska.aiga.org/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%96%92%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%86%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%88%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%95%80%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ef%bd%87goes" target="_blank">역삼안마
</a>
</p>
</div>
<div style='width: 1px; height: 1px; overflow: hidden'><div align='center'>
<img name='target_resize_image[]' onclick='image_window(this)' style='cursor:pointer;' alt="" class="view_photo up" src="http://file.osen.co.kr/article/2019/05/01/201905011854774508_5cc96e7d1d3c2.jpg" >
그라운드 뷰는 차의 앞쪽 아랫부분
<div style="position:absolute; left:-9999px; top:-9999px;" class="sound_only">
피할수 없으면 즐겨라 - 로버트 엘리엇
<p align="">
<a title="강남오피" href="
http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%83%b1%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a4%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%a7%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%aa%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%a4forward" target="_blank">강남오피
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="선릉오피" href="
http://www.ambrosiocinema.it/page/5/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%83%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%a8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%b8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%bf%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ef%bc%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%96%bc%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%86spring" target="_blank">선릉오피
</a>
</p>
아래에 비교하면 남음이 있다.-명심보감
<p align="">
<a title="역삼오피" href="
https://www.openrice.com/zh/hongkong/restaurants?what=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%99%a5%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a0both" target="_blank">역삼오피
</a>
</p>
실패는 잊어라 그러나 그것이 준 교훈은절대 잊으면 안된다-하버트 개서
<p align="">
<a title="강남휴게텔" href="
https://desk.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%88%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%88%99%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%85%b4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%82%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%81boat" target="_blank">강남휴게텔
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉휴게텔" href="http://www.blueskyspaworks.com/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%c2%bc%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%91%ad%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%95%89%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%bb%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%92%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%ef%bc%84damage" target="_blank">선릉휴게텔
</a>
</p>
절대 포기하지 말라. 당신이 되고 싶은 무언가가 있다면그에 대해 자부심을 가져라. 당신 자신에게 기회를 주어라. 스스로가 형편없다고 생각하지 말라.그래봐야 아무 것도 얻을 것이 없다. 목표를 높이 세워라.인생은 그렇게 살아야 한다.-마이크 맥라렌
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%80%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%92%b2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%92%a4%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bf%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%8e%97sworn" target="_blank">역삼휴게텔
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="강남안마" href="
https://www.wfs-dreieich.de/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%d0%93%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%97%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%88%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%a3%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%a4%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%84blame" target="_blank">강남안마
</a>
</p>
계단을 밟아야 계단 위에 올라설수 있다 -터키속담
<p align="">
<a title="선릉안마" href="
http://ypsistudio.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%82%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c4%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ef%bc%b0%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bf%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%cf%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%91%a4contain" target="_blank">선릉안마
</a>
</p>
지금이야 말로 일할때다. 지금이야말로 싸울때다. 지금이야말로 나를 더 훌륭한 사람으로 만들때다오늘 그것을 못하면 내일 그것을 할수있는가- 토마스 아켐피스
<p align="">
<a title="역삼안마" href="
https://www.matematikk.org/trinn8-10/sok/index.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%81%af%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bc%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%98%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%b3%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%b4understand" target="_blank">역삼안마
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남오피" href="
https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%86%90%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%85%b5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ef%bc%a8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c5%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8f%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%80bred" target="_blank">강남오피
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="선릉오피" href="
https://www.pexels.com/ko-kr/search/%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ef%bd%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%b9%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%83%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%8f%9cshelter" target="_blank">선릉오피
</a>
</p>
단순하게 살라. 쓸데없는 절차와 일 때문에 얼마나 복잡한 삶을 살아가는가?-이드리스 샤흐
<p align="">
<a title="역삼오피" href="
https://ciscentraltexas.org/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%ae%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b2%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8f%87%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%8a%83%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%97%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%92philadelphia" target="_blank">역삼오피
</a>
</p>
직접 눈으로 본 일도 오히려 참인지 아닌지염려스러운데 더구나 등뒤에서 남이 말하는것이야 어찌 이것을 깊이 믿을 수 있으랴?-명심보감-
<p align="">
<a title="강남휴게텔" href="
http://www.kuenselonline.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ce%a8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%9c%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%86%96%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%b2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bd%90%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%87quickly" target="_blank">강남휴게텔
</a>
</p>
내가 헛되이 보낸 오늘은 어제 죽어간 이들이그토록 바라던 하루이다 단 하루면 인간적인 모든 것을 멸망시킬수도 다시 소생시킬수도 있다-소포클레스
<p align="">
<a title="선릉휴게텔" href="https://www.sony.com/electronics/support/results?query=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%86%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%81%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ce%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%bd%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bc%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9bboat" target="_blank">선릉휴게텔
</a>
</p>
돈이란 바닷물과도 같다. 그것은 마시면 마실수록 목이 말라진다.-쇼펜하우어
<p align="">
<a title="역삼휴게텔" href="
https://jobs.rbc.com/ca/en/search-results?keywords=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%8c%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%d0%9e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%82%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%a6%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%c5%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%82joke" target="_blank">역삼휴게텔
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남안마" href="
http://www.makinamekawa.com/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%91%a9%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%d0%96%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bc%a2%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%92dreaming" target="_blank">강남안마
</a>
</p>
진정으로 웃으려면 고통을 참아야하며 나아가 고통을 즐길 줄 알아야 해 -찰리 채플린
<p align="">
<a title="선릉안마" href="
https://www.reddit.com/search?q=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%ac%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%9b%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%92%a5%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%a7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%99%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%a7grant" target="_blank">선릉안마
</a>
</p>
한번의 실패와 영원한 실패를 혼동하지 마라 -F.스콧 핏제랄드
<p align="">
<a title="역삼안마" href="
https://desk.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%95%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%9e%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ce%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%b5%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%85%b9%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%d1%89%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%93goal" target="_blank">역삼안마
</a>
</p>
행복은 결코 많고 큰데만 있는 것이 아니다 작은 것을 가지고도 고마워 하고 만족할 줄 안다면그는 행복한 사람이다여백과 공간의 아름다움은 단순함과 간소함에 있다법정스님 - 홀로사는 즐거움 에서
<p align="">
<a title="강남오피" href="
http://www.alberguerioaragon.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%bd%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%a6%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%87%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%80%b3%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%85%a5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%93%98%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%81seem" target="_blank">강남오피
</a>
</p>
길을 잃는 다는 것은 곧 길을 알게 된다는 것이다. - 동아프리카속담
<p align="">
<a title="선릉오피" href="
https://www.isistassinari.gov.it/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%8e%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%ce%b7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%89%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ce%95%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%95%88awhile" target="_blank">선릉오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="역삼오피" href="
http://isb.az/ru/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%89%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%d1%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%93%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%8cindependent" target="_blank">역삼오피
</a>
</p>
자신을 내보여라. 그러면 재능이 드러날 것이다.- 발타사르 그라시안
<p align="">
<a title="강남휴게텔" href="
http://biz.heraldcorp.com/view.php?ud=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%b2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bd%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%ef%bc%95%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%89%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%bbmarks" target="_blank">강남휴게텔
</a>
</p>
화가 날 때는 100까지 세라. 최악일 때는 욕설을 퍼부어라. -마크 트웨인
<p align="">
<a title="선릉휴게텔" href="
https://www.americanas.com.br/busca?conteudo=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ef%bc%b0%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%84%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%9a%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%81%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%8e%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%a8portrait" target="_blank">선릉휴게텔
</a>
</p>
1퍼센트의 가능성 그것이 나의 길이다-나폴레옹
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%83%99%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8f%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%83%95%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%d0%af%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b9personal" target="_blank">역삼휴게텔
</a>
</p>
최고에 도달하려면 최저에서 시작하라.-P.시루스
<p align="">
<a title="강남안마" href="
http://jozankei.jp/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%92%9f%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%81%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%c3%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%88%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%84%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%96%a6%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b6parted" target="_blank">강남안마
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉안마" href="
http://www.somoseducacao.com.br/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%98%85%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%be%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%9a%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%a1%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%a5greatly" target="_blank">선릉안마
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="역삼안마" href="
https://riftio.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%8e%80%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bd%99%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%99%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%8a%83%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%9d%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%a6%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%84%b9had" target="_blank">역삼안마 ddakbam1.com ༼͡ຈ╭͜ʖ╮͡ຈ༽
</a>
</p>
https://mnm777.com
<A HREF="https://kmk33.com/firstcasino/" TARGET='_blank'>퍼스트카지노</A>
<A HREF="https://kmk33.com/firstcasino/" TARGET='_blank'>퍼스트카지노</A>
<A HREF="https://qsq77.com" TARGET='_blank'>카지노사이트</A>
<A HREF=" https://www.casino.net/" TARGET='_blank'>온라인카지노</A>
<A HREF=" https://twitter.com/yunju0925?lang=en" TARGET='_blank'>카지노사이트</A>
<p align="">
<a title="강남오피" href="http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bf%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%c5%8b%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%84%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%8d%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%85%bela" target="_blank">강남오피
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉오피" href="https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%d0%be%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%88%82%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%bd%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%82%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a9tide" target="_blank">선릉오피
</a>
</p>
먼저핀꽃은 먼저진다 남보다 먼저 공을 세우려고 조급히 서둘것이 아니다-채근담
<p align="">
<a title="역삼오피" href="
https://enes.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%94%bb%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%97%88%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%ce%9egang" target="_blank">역삼오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남휴게텔" href="
https://www.livemeshthemes.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%c4%b1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b7%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%85%86%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%93%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%82%ba%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%84%a1%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%82stone" target="_blank">강남휴게텔
</a>
</p>
먹고 싶은것을 다 먹는 것은 그렇게 재미있지 않다 . 인생을 경계선 없이 살면 기쁨이 덜하다.먹고싶은대로 다 먹을 수있다면 먹고싶은 것을 먹는데 무슨 재미가 있겠나 - 톰행크스
<p align="">
<a title="선릉휴게텔" href="
http://www.pnr.corsica/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%89%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%a1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%9d%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%83%a6afford" target="_blank">선릉휴게텔
</a>
</p>
진짜 문제는 사람들의 마음이다.그것은 절대로 물리학이나 윤리학의 문제가 아니다.-아인슈타인
<p align="">
<a title="역삼휴게텔" href="
https://dict.leo.org/italienisch-deutsch/%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%82%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%d1%8f%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%83%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%ae%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9dseason" target="_blank">역삼휴게텔
</a>
</p>
가난은 가난하다고 느끼는 곳에 존재한다 .- 에머슨
<p align="">
<a title="강남안마" href="https://24.sapo.pt/pesquisar?q=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%85%a2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%82%8f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%99%a0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%85%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ce%92truly" target="_blank">강남안마
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉안마" href="
https://enfi.dict.cc/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%9e%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%85%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%90%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%bd%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%9cband" target="_blank">선릉안마
</a>
</p>
행복은 습관이다 그것을 몸에 지니라 -허버드
<p align="">
<a title="역삼안마" href="
https://www.lidumsaym.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%83%9d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c2%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8f%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%b1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%82%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b9derived" target="_blank">역삼안마
</a>
</p>
화려한 일을 추구하지 말라. 중요한 것은 스스로의 재능이며자신의 행동에 쏟아 붓는 사랑의 정도이다. -머더 테레사
<p align="">
<a title="강남오피" href="
http://www.twentszitmaaierteam.nl/pages/interactief/gastenboek.php?p=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%87%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%86%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%82%b9%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%94%bd%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%d0%a3wouldn't" target="_blank">강남오피
</a>
</p>
절대 어제를 후회하지 마라 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다-L.론허바드
<p align="">
<a title="선릉오피" href="
http://www.mairtinmusic.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%82%86%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%8b%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%9e%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%88truly" target="_blank">선릉오피
</a>
</p>
내일은 내일의 태양이 뜬다 피할수 없으면 즐겨라 -로버트 엘리엇
<p align="">
<a title="역삼오피" href="https://www.uptodate.com/contents/search?search=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%81%99%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%b9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%99%aa%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%83%8e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c3%be%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%82%b6%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%8centire" target="_blank">역삼오피
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남휴게텔" href="
http://ladysmithfederal.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%93%94%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%88%87%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%8f%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ce%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%c2%baremark" target="_blank">강남휴게텔
</a>
</p>
인간의 삶 전체는 단지 한 순간에 불과하다 . 인생을 즐기자 - 플루타르코스
<p align="">
<a title="선릉휴게텔" href="
https://www.governmentjobs.com/jobs?keyword=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%94%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%87secretly" target="_blank">선릉휴게텔
</a>
</p>
흔히 사람들은 기회를 기다리고 있지만 기회는 기다리는사람에게 잡히지 않는 법이다.우리는 기회를 기다리는 사람이 되기 전에 기회를 얻을 수 있는실력을 갖춰야 한다.일에 더 열중하는 사람이 되어야한다.-안창호
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%bb%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%84%ba%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%89%b0%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8e%93%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%80%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%cf%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b7artillery" target="_blank">역삼휴게텔
</a>
</p>
마음만을 가지고 있어서는 안된다. 반드시 실천하여야 한다.-이소룡
<p align="">
<a title="강남안마" href="
https://dehr.dict.cc/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%86%8d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%a1%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%84%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%9f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%b0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%88%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%8f%9dleg" target="_blank">강남안마
</a>
</p>
물러나서 조용하게 구하면 배울 수 있는 스승은 많다.사람은 가는 곳마다 보는 것마다 모두 스승으로서배울 것이 많은 법이다.-맹자
<p align="">
<a title="선릉안마" href="
https://www.gov.uk/search/all?keywords=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%92%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%91%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%ae%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8f%87%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%97%87providing" target="_blank">선릉안마
</a>
</p>
삶이 있는 한 희망은 있다 -키케로
<p align="">
<a title="역삼안마" href="
https://www.sdsn.no/sok/category28150.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%88%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%8c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%82%a1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%85%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%c4%b8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%85%9esecretary" target="_blank">역삼안마
</a>
</p>
한 번 실패와 영원한 실패를 혼동하지 마라.-F.스콧 핏제랄드
<p align="">
<a title="강남오피" href="
https://www.righteousmind.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%b0%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%91%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%96%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%88%87sang" target="_blank">강남오피
</a>
</p>
모든것들에는 나름의 경이로움과 심지어 어둠과 침묵이 있고 내가 어떤 상태에 있더라도 나는 그속에서 만족하는 법을 배운다-헬렌켈러
<p align="">
<a title="선릉오피" href="
http://www.actiitransportation.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e2%96%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%99%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%89%ba%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%bdaround" target="_blank">선릉오피
</a>
</p>
내 비장의 무기는 아직 손안에 있다 .그것은 희망이다 - 나폴레옹
<p align="">
<a title="역삼오피" href="https://www.youtube.com/results?search_query=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ce%a5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8e%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%a0%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%b1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%84lay" target="_blank">역삼오피
</a>
</p>
만족할 줄 아는 사람은진정한 부자이고 탐욕스러운 사람은진실로 가난한 사람이다.-솔론
<p align="">
<a title="강남휴게텔" href="
https://denl.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%81%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%8a%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%8f%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%85%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%93%a0%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%b2grief" target="_blank">강남휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="선릉휴게텔" href="
https://artdeco.org/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%9e%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a4%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%94%b9%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ef%bc%af%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%be%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%8dodd" target="_blank">선릉휴게텔
</a>
</p>
만약 우리가 할 수 있는 일을 모두 한다면 우리들은 우리자신에 깜짝 놀랄 것이다.-에디슨
<p align="">
<a title="역삼휴게텔" href="
http://www.lavipera.it/?s=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bc%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%bb%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%93%a3%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b5%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%88%8cvaried" target="_blank">역삼휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="강남안마" href="
https://money2.creontrade.com/E5/WTS/Stock/Foreign/DW_Foreign_Tax.aspx?p=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ef%bc%84%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bc%af%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%bd%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%83%9d%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%87splendid" target="_blank">강남안마
</a>
</p>
절대 어제를 후회하지 마라 . 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다 L.론허바드
<p align="">
<a title="선릉안마" href="
https://wpgovernance.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%85%a4%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%b3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%81%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%8d%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%81%b7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%a3john" target="_blank">선릉안마
</a>
</p>
사막이 아름다운 것은 어딘가에 샘이 숨겨져 있기 때문이다 - 생떽쥐베리
<p align="">
<a title="역삼안마" href="
https://nebraska.aiga.org/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%96%92%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%86%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%88%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%95%80%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ef%bd%87goes" target="_blank">역삼안마
</a>
</p>
</div>
<div style='width: 1px; height: 1px; overflow: hidden'><div align='center'>
<img name='target_resize_image[]' onclick='image_window(this)' style='cursor:pointer;' alt="" class="view_photo up" src="http://file.osen.co.kr/article/2019/05/01/201905011854774508_5cc96e7d1d3c2.jpg" >
그라운드 뷰는 차의 앞쪽 아랫부분
<div style="position:absolute; left:-9999px; top:-9999px;" class="sound_only">
피할수 없으면 즐겨라 - 로버트 엘리엇
<p align="">
<a title="강남오피" href="
http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%83%b1%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a4%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%a7%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%aa%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%a4forward" target="_blank">강남오피
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="선릉오피" href="
http://www.ambrosiocinema.it/page/5/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%83%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%a8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%b8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%bf%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ef%bc%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%96%bc%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%86spring" target="_blank">선릉오피
</a>
</p>
아래에 비교하면 남음이 있다.-명심보감
<p align="">
<a title="역삼오피" href="
https://www.openrice.com/zh/hongkong/restaurants?what=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%99%a5%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a0both" target="_blank">역삼오피
</a>
</p>
실패는 잊어라 그러나 그것이 준 교훈은절대 잊으면 안된다-하버트 개서
<p align="">
<a title="강남휴게텔" href="
https://desk.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%88%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%88%99%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%85%b4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%82%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%81boat" target="_blank">강남휴게텔
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉휴게텔" href="http://www.blueskyspaworks.com/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%c2%bc%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%91%ad%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%95%89%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%bb%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%92%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%ef%bc%84damage" target="_blank">선릉휴게텔
</a>
</p>
절대 포기하지 말라. 당신이 되고 싶은 무언가가 있다면그에 대해 자부심을 가져라. 당신 자신에게 기회를 주어라. 스스로가 형편없다고 생각하지 말라.그래봐야 아무 것도 얻을 것이 없다. 목표를 높이 세워라.인생은 그렇게 살아야 한다.-마이크 맥라렌
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%80%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%92%b2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%92%a4%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bf%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%8e%97sworn" target="_blank">역삼휴게텔
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="강남안마" href="
https://www.wfs-dreieich.de/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%d0%93%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%97%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%88%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%a3%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%a4%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%84blame" target="_blank">강남안마
</a>
</p>
계단을 밟아야 계단 위에 올라설수 있다 -터키속담
<p align="">
<a title="선릉안마" href="
http://ypsistudio.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%82%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c4%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ef%bc%b0%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bf%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%cf%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%91%a4contain" target="_blank">선릉안마
</a>
</p>
지금이야 말로 일할때다. 지금이야말로 싸울때다. 지금이야말로 나를 더 훌륭한 사람으로 만들때다오늘 그것을 못하면 내일 그것을 할수있는가- 토마스 아켐피스
<p align="">
<a title="역삼안마" href="
https://www.matematikk.org/trinn8-10/sok/index.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%81%af%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bc%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%98%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%b3%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%b4understand" target="_blank">역삼안마
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남오피" href="
https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%86%90%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%85%b5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ef%bc%a8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c5%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8f%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%80bred" target="_blank">강남오피
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="선릉오피" href="
https://www.pexels.com/ko-kr/search/%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ef%bd%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%b9%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%83%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%8f%9cshelter" target="_blank">선릉오피
</a>
</p>
단순하게 살라. 쓸데없는 절차와 일 때문에 얼마나 복잡한 삶을 살아가는가?-이드리스 샤흐
<p align="">
<a title="역삼오피" href="
https://ciscentraltexas.org/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%ae%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b2%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8f%87%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%8a%83%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%97%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%92philadelphia" target="_blank">역삼오피
</a>
</p>
직접 눈으로 본 일도 오히려 참인지 아닌지염려스러운데 더구나 등뒤에서 남이 말하는것이야 어찌 이것을 깊이 믿을 수 있으랴?-명심보감-
<p align="">
<a title="강남휴게텔" href="
http://www.kuenselonline.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ce%a8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%9c%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%86%96%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%b2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bd%90%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%87quickly" target="_blank">강남휴게텔
</a>
</p>
내가 헛되이 보낸 오늘은 어제 죽어간 이들이그토록 바라던 하루이다 단 하루면 인간적인 모든 것을 멸망시킬수도 다시 소생시킬수도 있다-소포클레스
<p align="">
<a title="선릉휴게텔" href="https://www.sony.com/electronics/support/results?query=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%86%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%81%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ce%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%bd%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bc%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9bboat" target="_blank">선릉휴게텔
</a>
</p>
돈이란 바닷물과도 같다. 그것은 마시면 마실수록 목이 말라진다.-쇼펜하우어
<p align="">
<a title="역삼휴게텔" href="
https://jobs.rbc.com/ca/en/search-results?keywords=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%8c%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%d0%9e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%82%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%a6%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%c5%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%82joke" target="_blank">역삼휴게텔
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남안마" href="
http://www.makinamekawa.com/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%91%a9%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%d0%96%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bc%a2%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%92dreaming" target="_blank">강남안마
</a>
</p>
진정으로 웃으려면 고통을 참아야하며 나아가 고통을 즐길 줄 알아야 해 -찰리 채플린
<p align="">
<a title="선릉안마" href="
https://www.reddit.com/search?q=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%ac%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%9b%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%92%a5%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%a7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%99%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%a7grant" target="_blank">선릉안마
</a>
</p>
한번의 실패와 영원한 실패를 혼동하지 마라 -F.스콧 핏제랄드
<p align="">
<a title="역삼안마" href="
https://desk.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%95%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%9e%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ce%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%b5%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%85%b9%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%d1%89%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%93goal" target="_blank">역삼안마
</a>
</p>
행복은 결코 많고 큰데만 있는 것이 아니다 작은 것을 가지고도 고마워 하고 만족할 줄 안다면그는 행복한 사람이다여백과 공간의 아름다움은 단순함과 간소함에 있다법정스님 - 홀로사는 즐거움 에서
<p align="">
<a title="강남오피" href="
http://www.alberguerioaragon.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%bd%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%a6%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%87%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%80%b3%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%85%a5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%93%98%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%81seem" target="_blank">강남오피
</a>
</p>
길을 잃는 다는 것은 곧 길을 알게 된다는 것이다. - 동아프리카속담
<p align="">
<a title="선릉오피" href="
https://www.isistassinari.gov.it/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%8e%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%ce%b7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%89%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ce%95%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%95%88awhile" target="_blank">선릉오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="역삼오피" href="
http://isb.az/ru/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%89%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%d1%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%93%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%8cindependent" target="_blank">역삼오피
</a>
</p>
자신을 내보여라. 그러면 재능이 드러날 것이다.- 발타사르 그라시안
<p align="">
<a title="강남휴게텔" href="
http://biz.heraldcorp.com/view.php?ud=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%b2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bd%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%ef%bc%95%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%89%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%bbmarks" target="_blank">강남휴게텔
</a>
</p>
화가 날 때는 100까지 세라. 최악일 때는 욕설을 퍼부어라. -마크 트웨인
<p align="">
<a title="선릉휴게텔" href="
https://www.americanas.com.br/busca?conteudo=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ef%bc%b0%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%84%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%9a%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%81%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%8e%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%a8portrait" target="_blank">선릉휴게텔
</a>
</p>
1퍼센트의 가능성 그것이 나의 길이다-나폴레옹
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%83%99%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8f%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%83%95%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%d0%af%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b9personal" target="_blank">역삼휴게텔
</a>
</p>
최고에 도달하려면 최저에서 시작하라.-P.시루스
<p align="">
<a title="강남안마" href="
http://jozankei.jp/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%92%9f%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%81%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%c3%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%88%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%84%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%96%a6%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b6parted" target="_blank">강남안마
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉안마" href="
http://www.somoseducacao.com.br/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%98%85%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%be%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%9a%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%a1%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%a5greatly" target="_blank">선릉안마
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="역삼안마" href="
https://riftio.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%8e%80%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bd%99%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%99%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%8a%83%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%9d%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%a6%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%84%b9had" target="_blank">역삼안마 ddakbam1.com ლ(◉❥◉ ლ)
</a>
</p>
<p align="">
<a title="강남오피" href="http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bf%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%c5%8b%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%84%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%8d%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%85%bela" target="_blank">강남오피
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉오피" href="https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%d0%be%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%88%82%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%bd%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%82%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a9tide" target="_blank">선릉오피
</a>
</p>
먼저핀꽃은 먼저진다 남보다 먼저 공을 세우려고 조급히 서둘것이 아니다-채근담
<p align="">
<a title="역삼오피" href="
https://enes.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%94%bb%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%97%88%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%ce%9egang" target="_blank">역삼오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남휴게텔" href="
https://www.livemeshthemes.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%c4%b1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b7%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%85%86%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%93%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%82%ba%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%84%a1%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%82stone" target="_blank">강남휴게텔
</a>
</p>
먹고 싶은것을 다 먹는 것은 그렇게 재미있지 않다 . 인생을 경계선 없이 살면 기쁨이 덜하다.먹고싶은대로 다 먹을 수있다면 먹고싶은 것을 먹는데 무슨 재미가 있겠나 - 톰행크스
<p align="">
<a title="선릉휴게텔" href="
http://www.pnr.corsica/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%89%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%a1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%9d%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%83%a6afford" target="_blank">선릉휴게텔
</a>
</p>
진짜 문제는 사람들의 마음이다.그것은 절대로 물리학이나 윤리학의 문제가 아니다.-아인슈타인
<p align="">
<a title="역삼휴게텔" href="
https://dict.leo.org/italienisch-deutsch/%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%82%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%d1%8f%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%83%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%ae%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9dseason" target="_blank">역삼휴게텔
</a>
</p>
가난은 가난하다고 느끼는 곳에 존재한다 .- 에머슨
<p align="">
<a title="강남안마" href="https://24.sapo.pt/pesquisar?q=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%85%a2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%82%8f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%99%a0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%85%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ce%92truly" target="_blank">강남안마
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉안마" href="
https://enfi.dict.cc/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%9e%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%85%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%90%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%bd%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%9cband" target="_blank">선릉안마
</a>
</p>
행복은 습관이다 그것을 몸에 지니라 -허버드
<p align="">
<a title="역삼안마" href="
https://www.lidumsaym.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%83%9d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c2%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8f%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%b1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%82%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b9derived" target="_blank">역삼안마
</a>
</p>
화려한 일을 추구하지 말라. 중요한 것은 스스로의 재능이며자신의 행동에 쏟아 붓는 사랑의 정도이다. -머더 테레사
<p align="">
<a title="강남오피" href="
http://www.twentszitmaaierteam.nl/pages/interactief/gastenboek.php?p=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%87%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%86%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%82%b9%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%94%bd%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%d0%a3wouldn't" target="_blank">강남오피
</a>
</p>
절대 어제를 후회하지 마라 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다-L.론허바드
<p align="">
<a title="선릉오피" href="
http://www.mairtinmusic.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%82%86%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%8b%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%9e%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%88truly" target="_blank">선릉오피
</a>
</p>
내일은 내일의 태양이 뜬다 피할수 없으면 즐겨라 -로버트 엘리엇
<p align="">
<a title="역삼오피" href="https://www.uptodate.com/contents/search?search=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%81%99%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%b9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%99%aa%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%83%8e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c3%be%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%82%b6%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%8centire" target="_blank">역삼오피
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남휴게텔" href="
http://ladysmithfederal.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%93%94%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%88%87%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%8f%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ce%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%c2%baremark" target="_blank">강남휴게텔
</a>
</p>
인간의 삶 전체는 단지 한 순간에 불과하다 . 인생을 즐기자 - 플루타르코스
<p align="">
<a title="선릉휴게텔" href="
https://www.governmentjobs.com/jobs?keyword=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%94%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%87secretly" target="_blank">선릉휴게텔
</a>
</p>
흔히 사람들은 기회를 기다리고 있지만 기회는 기다리는사람에게 잡히지 않는 법이다.우리는 기회를 기다리는 사람이 되기 전에 기회를 얻을 수 있는실력을 갖춰야 한다.일에 더 열중하는 사람이 되어야한다.-안창호
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%bb%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%84%ba%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%89%b0%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8e%93%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%80%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%cf%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b7artillery" target="_blank">역삼휴게텔
</a>
</p>
마음만을 가지고 있어서는 안된다. 반드시 실천하여야 한다.-이소룡
<p align="">
<a title="강남안마" href="
https://dehr.dict.cc/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%86%8d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%a1%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%84%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%9f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%b0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%88%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%8f%9dleg" target="_blank">강남안마
</a>
</p>
물러나서 조용하게 구하면 배울 수 있는 스승은 많다.사람은 가는 곳마다 보는 것마다 모두 스승으로서배울 것이 많은 법이다.-맹자
<p align="">
<a title="선릉안마" href="
https://www.gov.uk/search/all?keywords=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%92%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%91%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%ae%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8f%87%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%97%87providing" target="_blank">선릉안마
</a>
</p>
삶이 있는 한 희망은 있다 -키케로
<p align="">
<a title="역삼안마" href="
https://www.sdsn.no/sok/category28150.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%88%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%8c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%82%a1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%85%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%c4%b8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%85%9esecretary" target="_blank">역삼안마
</a>
</p>
한 번 실패와 영원한 실패를 혼동하지 마라.-F.스콧 핏제랄드
<p align="">
<a title="강남오피" href="
https://www.righteousmind.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%b0%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%91%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%96%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%88%87sang" target="_blank">강남오피
</a>
</p>
모든것들에는 나름의 경이로움과 심지어 어둠과 침묵이 있고 내가 어떤 상태에 있더라도 나는 그속에서 만족하는 법을 배운다-헬렌켈러
<p align="">
<a title="선릉오피" href="
http://www.actiitransportation.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e2%96%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%99%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%89%ba%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%bdaround" target="_blank">선릉오피
</a>
</p>
내 비장의 무기는 아직 손안에 있다 .그것은 희망이다 - 나폴레옹
<p align="">
<a title="역삼오피" href="https://www.youtube.com/results?search_query=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ce%a5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8e%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%a0%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%b1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%84lay" target="_blank">역삼오피
</a>
</p>
만족할 줄 아는 사람은진정한 부자이고 탐욕스러운 사람은진실로 가난한 사람이다.-솔론
<p align="">
<a title="강남휴게텔" href="
https://denl.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%81%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%8a%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%8f%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%85%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%93%a0%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%b2grief" target="_blank">강남휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="선릉휴게텔" href="
https://artdeco.org/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%9e%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a4%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%94%b9%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ef%bc%af%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%be%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%8dodd" target="_blank">선릉휴게텔
</a>
</p>
만약 우리가 할 수 있는 일을 모두 한다면 우리들은 우리자신에 깜짝 놀랄 것이다.-에디슨
<p align="">
<a title="역삼휴게텔" href="
http://www.lavipera.it/?s=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bc%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%bb%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%93%a3%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b5%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%88%8cvaried" target="_blank">역삼휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="강남안마" href="
https://money2.creontrade.com/E5/WTS/Stock/Foreign/DW_Foreign_Tax.aspx?p=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ef%bc%84%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bc%af%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%bd%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%83%9d%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%87splendid" target="_blank">강남안마
</a>
</p>
절대 어제를 후회하지 마라 . 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다 L.론허바드
<p align="">
<a title="선릉안마" href="
https://wpgovernance.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%85%a4%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%b3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%81%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%8d%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%81%b7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%a3john" target="_blank">선릉안마
</a>
</p>
사막이 아름다운 것은 어딘가에 샘이 숨겨져 있기 때문이다 - 생떽쥐베리
<p align="">
<a title="역삼안마" href="
https://nebraska.aiga.org/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%96%92%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%86%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%88%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%95%80%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ef%bd%87goes" target="_blank">역삼안마
</a>
</p>
</div>
<div style='width: 1px; height: 1px; overflow: hidden'><div align='center'>
<img name='target_resize_image[]' onclick='image_window(this)' style='cursor:pointer;' alt="" class="view_photo up" src="http://file.osen.co.kr/article/2019/05/01/201905011854774508_5cc96e7d1d3c2.jpg" >
그라운드 뷰는 차의 앞쪽 아랫부분
<div style="position:absolute; left:-9999px; top:-9999px;" class="sound_only">
피할수 없으면 즐겨라 - 로버트 엘리엇
<p align="">
<a title="강남오피" href="
http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%83%b1%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a4%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%a7%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%aa%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%a4forward" target="_blank">강남오피
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="선릉오피" href="
http://www.ambrosiocinema.it/page/5/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%83%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%a8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%b8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%bf%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ef%bc%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%96%bc%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%86spring" target="_blank">선릉오피
</a>
</p>
아래에 비교하면 남음이 있다.-명심보감
<p align="">
<a title="역삼오피" href="
https://www.openrice.com/zh/hongkong/restaurants?what=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%99%a5%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a0both" target="_blank">역삼오피
</a>
</p>
실패는 잊어라 그러나 그것이 준 교훈은절대 잊으면 안된다-하버트 개서
<p align="">
<a title="강남휴게텔" href="
https://desk.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%88%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%88%99%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%85%b4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%82%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%81boat" target="_blank">강남휴게텔
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉휴게텔" href="http://www.blueskyspaworks.com/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%c2%bc%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%91%ad%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%95%89%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%bb%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%92%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%ef%bc%84damage" target="_blank">선릉휴게텔
</a>
</p>
절대 포기하지 말라. 당신이 되고 싶은 무언가가 있다면그에 대해 자부심을 가져라. 당신 자신에게 기회를 주어라. 스스로가 형편없다고 생각하지 말라.그래봐야 아무 것도 얻을 것이 없다. 목표를 높이 세워라.인생은 그렇게 살아야 한다.-마이크 맥라렌
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%80%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%92%b2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%92%a4%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bf%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%8e%97sworn" target="_blank">역삼휴게텔
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="강남안마" href="
https://www.wfs-dreieich.de/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%d0%93%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%97%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%88%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%a3%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%a4%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%84blame" target="_blank">강남안마
</a>
</p>
계단을 밟아야 계단 위에 올라설수 있다 -터키속담
<p align="">
<a title="선릉안마" href="
http://ypsistudio.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%82%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c4%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ef%bc%b0%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bf%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%cf%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%91%a4contain" target="_blank">선릉안마
</a>
</p>
지금이야 말로 일할때다. 지금이야말로 싸울때다. 지금이야말로 나를 더 훌륭한 사람으로 만들때다오늘 그것을 못하면 내일 그것을 할수있는가- 토마스 아켐피스
<p align="">
<a title="역삼안마" href="
https://www.matematikk.org/trinn8-10/sok/index.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%81%af%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bc%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%98%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%b3%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%b4understand" target="_blank">역삼안마
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남오피" href="
https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%86%90%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%85%b5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ef%bc%a8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c5%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8f%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%80bred" target="_blank">강남오피
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="선릉오피" href="
https://www.pexels.com/ko-kr/search/%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ef%bd%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%b9%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%83%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%8f%9cshelter" target="_blank">선릉오피
</a>
</p>
단순하게 살라. 쓸데없는 절차와 일 때문에 얼마나 복잡한 삶을 살아가는가?-이드리스 샤흐
<p align="">
<a title="역삼오피" href="
https://ciscentraltexas.org/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%ae%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b2%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8f%87%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%8a%83%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%97%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%92philadelphia" target="_blank">역삼오피
</a>
</p>
직접 눈으로 본 일도 오히려 참인지 아닌지염려스러운데 더구나 등뒤에서 남이 말하는것이야 어찌 이것을 깊이 믿을 수 있으랴?-명심보감-
<p align="">
<a title="강남휴게텔" href="
http://www.kuenselonline.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ce%a8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%9c%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%86%96%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%b2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bd%90%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%87quickly" target="_blank">강남휴게텔
</a>
</p>
내가 헛되이 보낸 오늘은 어제 죽어간 이들이그토록 바라던 하루이다 단 하루면 인간적인 모든 것을 멸망시킬수도 다시 소생시킬수도 있다-소포클레스
<p align="">
<a title="선릉휴게텔" href="https://www.sony.com/electronics/support/results?query=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%86%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%81%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ce%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%bd%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bc%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9bboat" target="_blank">선릉휴게텔
</a>
</p>
돈이란 바닷물과도 같다. 그것은 마시면 마실수록 목이 말라진다.-쇼펜하우어
<p align="">
<a title="역삼휴게텔" href="
https://jobs.rbc.com/ca/en/search-results?keywords=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%8c%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%d0%9e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%82%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%a6%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%c5%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%82joke" target="_blank">역삼휴게텔
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남안마" href="
http://www.makinamekawa.com/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%91%a9%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%d0%96%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bc%a2%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%92dreaming" target="_blank">강남안마
</a>
</p>
진정으로 웃으려면 고통을 참아야하며 나아가 고통을 즐길 줄 알아야 해 -찰리 채플린
<p align="">
<a title="선릉안마" href="
https://www.reddit.com/search?q=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%ac%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%9b%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%92%a5%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%a7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%99%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%a7grant" target="_blank">선릉안마
</a>
</p>
한번의 실패와 영원한 실패를 혼동하지 마라 -F.스콧 핏제랄드
<p align="">
<a title="역삼안마" href="
https://desk.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%95%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%9e%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ce%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%b5%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%85%b9%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%d1%89%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%93goal" target="_blank">역삼안마
</a>
</p>
행복은 결코 많고 큰데만 있는 것이 아니다 작은 것을 가지고도 고마워 하고 만족할 줄 안다면그는 행복한 사람이다여백과 공간의 아름다움은 단순함과 간소함에 있다법정스님 - 홀로사는 즐거움 에서
<p align="">
<a title="강남오피" href="
http://www.alberguerioaragon.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%bd%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%a6%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%87%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%80%b3%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%85%a5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%93%98%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%81seem" target="_blank">강남오피
</a>
</p>
길을 잃는 다는 것은 곧 길을 알게 된다는 것이다. - 동아프리카속담
<p align="">
<a title="선릉오피" href="
https://www.isistassinari.gov.it/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%8e%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%ce%b7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%89%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ce%95%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%95%88awhile" target="_blank">선릉오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="역삼오피" href="
http://isb.az/ru/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%89%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%d1%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%93%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%8cindependent" target="_blank">역삼오피
</a>
</p>
자신을 내보여라. 그러면 재능이 드러날 것이다.- 발타사르 그라시안
<p align="">
<a title="강남휴게텔" href="
http://biz.heraldcorp.com/view.php?ud=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%b2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bd%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%ef%bc%95%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%89%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%bbmarks" target="_blank">강남휴게텔
</a>
</p>
화가 날 때는 100까지 세라. 최악일 때는 욕설을 퍼부어라. -마크 트웨인
<p align="">
<a title="선릉휴게텔" href="
https://www.americanas.com.br/busca?conteudo=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ef%bc%b0%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%84%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%9a%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%81%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%8e%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%a8portrait" target="_blank">선릉휴게텔
</a>
</p>
1퍼센트의 가능성 그것이 나의 길이다-나폴레옹
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%83%99%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8f%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%83%95%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%d0%af%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b9personal" target="_blank">역삼휴게텔
</a>
</p>
최고에 도달하려면 최저에서 시작하라.-P.시루스
<p align="">
<a title="강남안마" href="
http://jozankei.jp/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%92%9f%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%81%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%c3%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%88%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%84%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%96%a6%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b6parted" target="_blank">강남안마
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉안마" href="
http://www.somoseducacao.com.br/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%98%85%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%be%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%9a%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%a1%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%a5greatly" target="_blank">선릉안마
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="역삼안마" href="
https://riftio.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%8e%80%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bd%99%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%99%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%8a%83%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%9d%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%a6%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%84%b9had" target="_blank">역삼안마
</a>
</p>
<p align="">
<a title="강남오피" href="http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bf%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%c5%8b%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%84%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%8d%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%85%bela" target="_blank">강남오피
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉오피" href="https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%d0%be%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%88%82%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%bd%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%82%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a9tide" target="_blank">선릉오피
</a>
</p>
먼저핀꽃은 먼저진다 남보다 먼저 공을 세우려고 조급히 서둘것이 아니다-채근담
<p align="">
<a title="역삼오피" href="
https://enes.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%94%bb%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%97%88%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%ce%9egang" target="_blank">역삼오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남휴게텔" href="
https://www.livemeshthemes.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%c4%b1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b7%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%85%86%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%93%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%82%ba%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%84%a1%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%82stone" target="_blank">강남휴게텔
</a>
</p>
먹고 싶은것을 다 먹는 것은 그렇게 재미있지 않다 . 인생을 경계선 없이 살면 기쁨이 덜하다.먹고싶은대로 다 먹을 수있다면 먹고싶은 것을 먹는데 무슨 재미가 있겠나 - 톰행크스
<p align="">
<a title="선릉휴게텔" href="
http://www.pnr.corsica/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%89%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%a1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%9d%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%83%a6afford" target="_blank">선릉휴게텔
</a>
</p>
진짜 문제는 사람들의 마음이다.그것은 절대로 물리학이나 윤리학의 문제가 아니다.-아인슈타인
<p align="">
<a title="역삼휴게텔" href="
https://dict.leo.org/italienisch-deutsch/%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%82%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%d1%8f%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%83%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%ae%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9dseason" target="_blank">역삼휴게텔
</a>
</p>
가난은 가난하다고 느끼는 곳에 존재한다 .- 에머슨
<p align="">
<a title="강남안마" href="https://24.sapo.pt/pesquisar?q=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%85%a2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%82%8f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%99%a0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%85%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ce%92truly" target="_blank">강남안마
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉안마" href="
https://enfi.dict.cc/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%9e%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%85%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%90%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%bd%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%9cband" target="_blank">선릉안마
</a>
</p>
행복은 습관이다 그것을 몸에 지니라 -허버드
<p align="">
<a title="역삼안마" href="
https://www.lidumsaym.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%83%9d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c2%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8f%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%b1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%82%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b9derived" target="_blank">역삼안마
</a>
</p>
화려한 일을 추구하지 말라. 중요한 것은 스스로의 재능이며자신의 행동에 쏟아 붓는 사랑의 정도이다. -머더 테레사
<p align="">
<a title="강남오피" href="
http://www.twentszitmaaierteam.nl/pages/interactief/gastenboek.php?p=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%87%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%86%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%82%b9%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%94%bd%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%d0%a3wouldn't" target="_blank">강남오피
</a>
</p>
절대 어제를 후회하지 마라 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다-L.론허바드
<p align="">
<a title="선릉오피" href="
http://www.mairtinmusic.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%82%86%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%8b%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%9e%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%88truly" target="_blank">선릉오피
</a>
</p>
내일은 내일의 태양이 뜬다 피할수 없으면 즐겨라 -로버트 엘리엇
<p align="">
<a title="역삼오피" href="https://www.uptodate.com/contents/search?search=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%81%99%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%b9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%99%aa%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%83%8e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c3%be%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%82%b6%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%8centire" target="_blank">역삼오피
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남휴게텔" href="
http://ladysmithfederal.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%93%94%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%88%87%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%8f%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ce%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%c2%baremark" target="_blank">강남휴게텔
</a>
</p>
인간의 삶 전체는 단지 한 순간에 불과하다 . 인생을 즐기자 - 플루타르코스
<p align="">
<a title="선릉휴게텔" href="
https://www.governmentjobs.com/jobs?keyword=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%94%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%87secretly" target="_blank">선릉휴게텔
</a>
</p>
흔히 사람들은 기회를 기다리고 있지만 기회는 기다리는사람에게 잡히지 않는 법이다.우리는 기회를 기다리는 사람이 되기 전에 기회를 얻을 수 있는실력을 갖춰야 한다.일에 더 열중하는 사람이 되어야한다.-안창호
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%bb%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%84%ba%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%89%b0%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8e%93%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%80%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%cf%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b7artillery" target="_blank">역삼휴게텔
</a>
</p>
마음만을 가지고 있어서는 안된다. 반드시 실천하여야 한다.-이소룡
<p align="">
<a title="강남안마" href="
https://dehr.dict.cc/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%86%8d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%a1%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%84%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%9f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%b0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%88%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%8f%9dleg" target="_blank">강남안마
</a>
</p>
물러나서 조용하게 구하면 배울 수 있는 스승은 많다.사람은 가는 곳마다 보는 것마다 모두 스승으로서배울 것이 많은 법이다.-맹자
<p align="">
<a title="선릉안마" href="
https://www.gov.uk/search/all?keywords=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%92%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%91%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%ae%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8f%87%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%97%87providing" target="_blank">선릉안마
</a>
</p>
삶이 있는 한 희망은 있다 -키케로
<p align="">
<a title="역삼안마" href="
https://www.sdsn.no/sok/category28150.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%88%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%8c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%82%a1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%85%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%c4%b8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%85%9esecretary" target="_blank">역삼안마
</a>
</p>
한 번 실패와 영원한 실패를 혼동하지 마라.-F.스콧 핏제랄드
<p align="">
<a title="강남오피" href="
https://www.righteousmind.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%b0%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%91%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%96%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%88%87sang" target="_blank">강남오피
</a>
</p>
모든것들에는 나름의 경이로움과 심지어 어둠과 침묵이 있고 내가 어떤 상태에 있더라도 나는 그속에서 만족하는 법을 배운다-헬렌켈러
<p align="">
<a title="선릉오피" href="
http://www.actiitransportation.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e2%96%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%99%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%89%ba%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%bdaround" target="_blank">선릉오피
</a>
</p>
내 비장의 무기는 아직 손안에 있다 .그것은 희망이다 - 나폴레옹
<p align="">
<a title="역삼오피" href="https://www.youtube.com/results?search_query=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ce%a5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8e%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%a0%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%b1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%84lay" target="_blank">역삼오피
</a>
</p>
만족할 줄 아는 사람은진정한 부자이고 탐욕스러운 사람은진실로 가난한 사람이다.-솔론
<p align="">
<a title="강남휴게텔" href="
https://denl.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%81%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%8a%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%8f%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%85%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%93%a0%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%b2grief" target="_blank">강남휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="선릉휴게텔" href="
https://artdeco.org/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%9e%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a4%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%94%b9%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ef%bc%af%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%be%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%8dodd" target="_blank">선릉휴게텔
</a>
</p>
만약 우리가 할 수 있는 일을 모두 한다면 우리들은 우리자신에 깜짝 놀랄 것이다.-에디슨
<p align="">
<a title="역삼휴게텔" href="
http://www.lavipera.it/?s=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bc%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%bb%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%93%a3%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b5%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%88%8cvaried" target="_blank">역삼휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="강남안마" href="
https://money2.creontrade.com/E5/WTS/Stock/Foreign/DW_Foreign_Tax.aspx?p=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ef%bc%84%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bc%af%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%bd%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%83%9d%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%87splendid" target="_blank">강남안마
</a>
</p>
절대 어제를 후회하지 마라 . 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다 L.론허바드
<p align="">
<a title="선릉안마" href="
https://wpgovernance.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%85%a4%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%b3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%81%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%8d%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%81%b7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%a3john" target="_blank">선릉안마
</a>
</p>
사막이 아름다운 것은 어딘가에 샘이 숨겨져 있기 때문이다 - 생떽쥐베리
<p align="">
<a title="역삼안마" href="
https://nebraska.aiga.org/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%96%92%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%86%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%88%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%95%80%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ef%bd%87goes" target="_blank">역삼안마
</a>
</p>
</div>
<div style='width: 1px; height: 1px; overflow: hidden'><div align='center'>
<img name='target_resize_image[]' onclick='image_window(this)' style='cursor:pointer;' alt="" class="view_photo up" src="http://file.osen.co.kr/article/2019/05/01/201905011854774508_5cc96e7d1d3c2.jpg" >
그라운드 뷰는 차의 앞쪽 아랫부분
<div style="position:absolute; left:-9999px; top:-9999px;" class="sound_only">
피할수 없으면 즐겨라 - 로버트 엘리엇
<p align="">
<a title="강남오피" href="
http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%83%b1%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a4%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%a7%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%aa%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%a4forward" target="_blank">강남오피
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="선릉오피" href="
http://www.ambrosiocinema.it/page/5/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%83%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%a8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%b8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%bf%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ef%bc%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%96%bc%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%86spring" target="_blank">선릉오피
</a>
</p>
아래에 비교하면 남음이 있다.-명심보감
<p align="">
<a title="역삼오피" href="
https://www.openrice.com/zh/hongkong/restaurants?what=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%99%a5%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a0both" target="_blank">역삼오피
</a>
</p>
실패는 잊어라 그러나 그것이 준 교훈은절대 잊으면 안된다-하버트 개서
<p align="">
<a title="강남휴게텔" href="
https://desk.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%88%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%88%99%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%85%b4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%82%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%81boat" target="_blank">강남휴게텔
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉휴게텔" href="http://www.blueskyspaworks.com/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%c2%bc%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%91%ad%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%95%89%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%bb%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%92%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%ef%bc%84damage" target="_blank">선릉휴게텔
</a>
</p>
절대 포기하지 말라. 당신이 되고 싶은 무언가가 있다면그에 대해 자부심을 가져라. 당신 자신에게 기회를 주어라. 스스로가 형편없다고 생각하지 말라.그래봐야 아무 것도 얻을 것이 없다. 목표를 높이 세워라.인생은 그렇게 살아야 한다.-마이크 맥라렌
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%80%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%92%b2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%92%a4%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bf%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%8e%97sworn" target="_blank">역삼휴게텔
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="강남안마" href="
https://www.wfs-dreieich.de/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%d0%93%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%97%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%88%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%a3%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%a4%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%84blame" target="_blank">강남안마
</a>
</p>
계단을 밟아야 계단 위에 올라설수 있다 -터키속담
<p align="">
<a title="선릉안마" href="
http://ypsistudio.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%82%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c4%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ef%bc%b0%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bf%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%cf%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%91%a4contain" target="_blank">선릉안마
</a>
</p>
지금이야 말로 일할때다. 지금이야말로 싸울때다. 지금이야말로 나를 더 훌륭한 사람으로 만들때다오늘 그것을 못하면 내일 그것을 할수있는가- 토마스 아켐피스
<p align="">
<a title="역삼안마" href="
https://www.matematikk.org/trinn8-10/sok/index.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%81%af%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bc%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%98%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%b3%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%b4understand" target="_blank">역삼안마
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남오피" href="
https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%86%90%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%85%b5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ef%bc%a8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c5%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8f%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%80bred" target="_blank">강남오피
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="선릉오피" href="
https://www.pexels.com/ko-kr/search/%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ef%bd%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%b9%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%83%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%8f%9cshelter" target="_blank">선릉오피
</a>
</p>
단순하게 살라. 쓸데없는 절차와 일 때문에 얼마나 복잡한 삶을 살아가는가?-이드리스 샤흐
<p align="">
<a title="역삼오피" href="
https://ciscentraltexas.org/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%ae%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b2%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8f%87%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%8a%83%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%97%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%92philadelphia" target="_blank">역삼오피
</a>
</p>
직접 눈으로 본 일도 오히려 참인지 아닌지염려스러운데 더구나 등뒤에서 남이 말하는것이야 어찌 이것을 깊이 믿을 수 있으랴?-명심보감-
<p align="">
<a title="강남휴게텔" href="
http://www.kuenselonline.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ce%a8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%9c%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%86%96%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%b2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bd%90%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%87quickly" target="_blank">강남휴게텔
</a>
</p>
내가 헛되이 보낸 오늘은 어제 죽어간 이들이그토록 바라던 하루이다 단 하루면 인간적인 모든 것을 멸망시킬수도 다시 소생시킬수도 있다-소포클레스
<p align="">
<a title="선릉휴게텔" href="https://www.sony.com/electronics/support/results?query=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%86%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%81%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ce%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%bd%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bc%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9bboat" target="_blank">선릉휴게텔
</a>
</p>
돈이란 바닷물과도 같다. 그것은 마시면 마실수록 목이 말라진다.-쇼펜하우어
<p align="">
<a title="역삼휴게텔" href="
https://jobs.rbc.com/ca/en/search-results?keywords=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%8c%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%d0%9e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%82%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%a6%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%c5%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%82joke" target="_blank">역삼휴게텔
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남안마" href="
http://www.makinamekawa.com/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%91%a9%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%d0%96%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bc%a2%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%92dreaming" target="_blank">강남안마
</a>
</p>
진정으로 웃으려면 고통을 참아야하며 나아가 고통을 즐길 줄 알아야 해 -찰리 채플린
<p align="">
<a title="선릉안마" href="
https://www.reddit.com/search?q=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%ac%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%9b%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%92%a5%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%a7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%99%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%a7grant" target="_blank">선릉안마
</a>
</p>
한번의 실패와 영원한 실패를 혼동하지 마라 -F.스콧 핏제랄드
<p align="">
<a title="역삼안마" href="
https://desk.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%95%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%9e%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ce%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%b5%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%85%b9%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%d1%89%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%93goal" target="_blank">역삼안마
</a>
</p>
행복은 결코 많고 큰데만 있는 것이 아니다 작은 것을 가지고도 고마워 하고 만족할 줄 안다면그는 행복한 사람이다여백과 공간의 아름다움은 단순함과 간소함에 있다법정스님 - 홀로사는 즐거움 에서
<p align="">
<a title="강남오피" href="
http://www.alberguerioaragon.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%bd%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%a6%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%87%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%80%b3%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%85%a5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%93%98%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%81seem" target="_blank">강남오피
</a>
</p>
길을 잃는 다는 것은 곧 길을 알게 된다는 것이다. - 동아프리카속담
<p align="">
<a title="선릉오피" href="
https://www.isistassinari.gov.it/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%8e%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%ce%b7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%89%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ce%95%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%95%88awhile" target="_blank">선릉오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="역삼오피" href="
http://isb.az/ru/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%89%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%d1%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%93%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%8cindependent" target="_blank">역삼오피
</a>
</p>
자신을 내보여라. 그러면 재능이 드러날 것이다.- 발타사르 그라시안
<p align="">
<a title="강남휴게텔" href="
http://biz.heraldcorp.com/view.php?ud=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%b2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bd%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%ef%bc%95%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%89%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%bbmarks" target="_blank">강남휴게텔
</a>
</p>
화가 날 때는 100까지 세라. 최악일 때는 욕설을 퍼부어라. -마크 트웨인
<p align="">
<a title="선릉휴게텔" href="
https://www.americanas.com.br/busca?conteudo=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ef%bc%b0%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%84%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%9a%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%81%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%8e%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%a8portrait" target="_blank">선릉휴게텔
</a>
</p>
1퍼센트의 가능성 그것이 나의 길이다-나폴레옹
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%83%99%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8f%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%83%95%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%d0%af%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b9personal" target="_blank">역삼휴게텔
</a>
</p>
최고에 도달하려면 최저에서 시작하라.-P.시루스
<p align="">
<a title="강남안마" href="
http://jozankei.jp/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%92%9f%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%81%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%c3%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%88%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%84%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%96%a6%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b6parted" target="_blank">강남안마
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉안마" href="
http://www.somoseducacao.com.br/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%98%85%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%be%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%9a%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%a1%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%a5greatly" target="_blank">선릉안마
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="역삼안마" href="
https://riftio.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%8e%80%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bd%99%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%99%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%8a%83%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%9d%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%a6%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%84%b9had" target="_blank">역삼안마 ddakbam1.com (∩`-´)⊃━☆゚.*・。゚
</a>
</p>
<p align="">
<a title="강남오피" href="http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bf%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%c5%8b%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%84%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%8d%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%85%bela" target="_blank">강남오피
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉오피" href="https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%d0%be%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%88%82%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%bd%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%82%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a9tide" target="_blank">선릉오피
</a>
</p>
먼저핀꽃은 먼저진다 남보다 먼저 공을 세우려고 조급히 서둘것이 아니다-채근담
<p align="">
<a title="역삼오피" href="
https://enes.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%94%bb%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%97%88%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%ce%9egang" target="_blank">역삼오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남휴게텔" href="
https://www.livemeshthemes.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%c4%b1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b7%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%85%86%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%93%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%82%ba%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%84%a1%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%82stone" target="_blank">강남휴게텔
</a>
</p>
먹고 싶은것을 다 먹는 것은 그렇게 재미있지 않다 . 인생을 경계선 없이 살면 기쁨이 덜하다.먹고싶은대로 다 먹을 수있다면 먹고싶은 것을 먹는데 무슨 재미가 있겠나 - 톰행크스
<p align="">
<a title="선릉휴게텔" href="
http://www.pnr.corsica/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%89%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%a1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%9d%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%83%a6afford" target="_blank">선릉휴게텔
</a>
</p>
진짜 문제는 사람들의 마음이다.그것은 절대로 물리학이나 윤리학의 문제가 아니다.-아인슈타인
<p align="">
<a title="역삼휴게텔" href="
https://dict.leo.org/italienisch-deutsch/%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%82%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%d1%8f%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%83%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%ae%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9dseason" target="_blank">역삼휴게텔
</a>
</p>
가난은 가난하다고 느끼는 곳에 존재한다 .- 에머슨
<p align="">
<a title="강남안마" href="https://24.sapo.pt/pesquisar?q=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%85%a2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%82%8f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%99%a0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%85%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ce%92truly" target="_blank">강남안마
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉안마" href="
https://enfi.dict.cc/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%9e%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%85%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%90%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%bd%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%9cband" target="_blank">선릉안마
</a>
</p>
행복은 습관이다 그것을 몸에 지니라 -허버드
<p align="">
<a title="역삼안마" href="
https://www.lidumsaym.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%83%9d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c2%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8f%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%b1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%82%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b9derived" target="_blank">역삼안마
</a>
</p>
화려한 일을 추구하지 말라. 중요한 것은 스스로의 재능이며자신의 행동에 쏟아 붓는 사랑의 정도이다. -머더 테레사
<p align="">
<a title="강남오피" href="
http://www.twentszitmaaierteam.nl/pages/interactief/gastenboek.php?p=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%87%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%86%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%82%b9%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%94%bd%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%d0%a3wouldn't" target="_blank">강남오피
</a>
</p>
절대 어제를 후회하지 마라 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다-L.론허바드
<p align="">
<a title="선릉오피" href="
http://www.mairtinmusic.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%82%86%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%8b%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%9e%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%88truly" target="_blank">선릉오피
</a>
</p>
내일은 내일의 태양이 뜬다 피할수 없으면 즐겨라 -로버트 엘리엇
<p align="">
<a title="역삼오피" href="https://www.uptodate.com/contents/search?search=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%81%99%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%b9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%99%aa%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%83%8e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c3%be%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%82%b6%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%8centire" target="_blank">역삼오피
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남휴게텔" href="
http://ladysmithfederal.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%93%94%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%88%87%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%8f%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ce%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%c2%baremark" target="_blank">강남휴게텔
</a>
</p>
인간의 삶 전체는 단지 한 순간에 불과하다 . 인생을 즐기자 - 플루타르코스
<p align="">
<a title="선릉휴게텔" href="
https://www.governmentjobs.com/jobs?keyword=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%94%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%87secretly" target="_blank">선릉휴게텔
</a>
</p>
흔히 사람들은 기회를 기다리고 있지만 기회는 기다리는사람에게 잡히지 않는 법이다.우리는 기회를 기다리는 사람이 되기 전에 기회를 얻을 수 있는실력을 갖춰야 한다.일에 더 열중하는 사람이 되어야한다.-안창호
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%bb%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%84%ba%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%89%b0%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8e%93%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%80%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%cf%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b7artillery" target="_blank">역삼휴게텔
</a>
</p>
마음만을 가지고 있어서는 안된다. 반드시 실천하여야 한다.-이소룡
<p align="">
<a title="강남안마" href="
https://dehr.dict.cc/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%86%8d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%a1%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%84%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%9f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%b0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%88%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%8f%9dleg" target="_blank">강남안마
</a>
</p>
물러나서 조용하게 구하면 배울 수 있는 스승은 많다.사람은 가는 곳마다 보는 것마다 모두 스승으로서배울 것이 많은 법이다.-맹자
<p align="">
<a title="선릉안마" href="
https://www.gov.uk/search/all?keywords=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%92%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%91%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%ae%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8f%87%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%97%87providing" target="_blank">선릉안마
</a>
</p>
삶이 있는 한 희망은 있다 -키케로
<p align="">
<a title="역삼안마" href="
https://www.sdsn.no/sok/category28150.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%88%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%8c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%82%a1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%85%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%c4%b8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%85%9esecretary" target="_blank">역삼안마
</a>
</p>
한 번 실패와 영원한 실패를 혼동하지 마라.-F.스콧 핏제랄드
<p align="">
<a title="강남오피" href="
https://www.righteousmind.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%b0%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%91%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%96%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%88%87sang" target="_blank">강남오피
</a>
</p>
모든것들에는 나름의 경이로움과 심지어 어둠과 침묵이 있고 내가 어떤 상태에 있더라도 나는 그속에서 만족하는 법을 배운다-헬렌켈러
<p align="">
<a title="선릉오피" href="
http://www.actiitransportation.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e2%96%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%99%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%89%ba%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%bdaround" target="_blank">선릉오피
</a>
</p>
내 비장의 무기는 아직 손안에 있다 .그것은 희망이다 - 나폴레옹
<p align="">
<a title="역삼오피" href="https://www.youtube.com/results?search_query=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ce%a5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8e%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%a0%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%b1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%84lay" target="_blank">역삼오피
</a>
</p>
만족할 줄 아는 사람은진정한 부자이고 탐욕스러운 사람은진실로 가난한 사람이다.-솔론
<p align="">
<a title="강남휴게텔" href="
https://denl.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%81%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%8a%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%8f%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%85%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%93%a0%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%b2grief" target="_blank">강남휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="선릉휴게텔" href="
https://artdeco.org/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%9e%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a4%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%94%b9%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ef%bc%af%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%be%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%8dodd" target="_blank">선릉휴게텔
</a>
</p>
만약 우리가 할 수 있는 일을 모두 한다면 우리들은 우리자신에 깜짝 놀랄 것이다.-에디슨
<p align="">
<a title="역삼휴게텔" href="
http://www.lavipera.it/?s=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bc%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%bb%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%93%a3%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b5%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%88%8cvaried" target="_blank">역삼휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="강남안마" href="
https://money2.creontrade.com/E5/WTS/Stock/Foreign/DW_Foreign_Tax.aspx?p=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ef%bc%84%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bc%af%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%bd%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%83%9d%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%87splendid" target="_blank">강남안마
</a>
</p>
절대 어제를 후회하지 마라 . 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다 L.론허바드
<p align="">
<a title="선릉안마" href="
https://wpgovernance.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%85%a4%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%b3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%81%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%8d%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%81%b7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%a3john" target="_blank">선릉안마
</a>
</p>
사막이 아름다운 것은 어딘가에 샘이 숨겨져 있기 때문이다 - 생떽쥐베리
<p align="">
<a title="역삼안마" href="
https://nebraska.aiga.org/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%96%92%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%86%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%88%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%95%80%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ef%bd%87goes" target="_blank">역삼안마
</a>
</p>
</div>
<div style='width: 1px; height: 1px; overflow: hidden'><div align='center'>
<img name='target_resize_image[]' onclick='image_window(this)' style='cursor:pointer;' alt="" class="view_photo up" src="http://file.osen.co.kr/article/2019/05/01/201905011854774508_5cc96e7d1d3c2.jpg" >
그라운드 뷰는 차의 앞쪽 아랫부분
<div style="position:absolute; left:-9999px; top:-9999px;" class="sound_only">
피할수 없으면 즐겨라 - 로버트 엘리엇
<p align="">
<a title="강남오피" href="
http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%83%b1%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a4%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%a7%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%aa%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%a4forward" target="_blank">강남오피
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="선릉오피" href="
http://www.ambrosiocinema.it/page/5/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%83%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%a8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%b8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%bf%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ef%bc%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%96%bc%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%86spring" target="_blank">선릉오피
</a>
</p>
아래에 비교하면 남음이 있다.-명심보감
<p align="">
<a title="역삼오피" href="
https://www.openrice.com/zh/hongkong/restaurants?what=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%99%a5%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a0both" target="_blank">역삼오피
</a>
</p>
실패는 잊어라 그러나 그것이 준 교훈은절대 잊으면 안된다-하버트 개서
<p align="">
<a title="강남휴게텔" href="
https://desk.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%88%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%88%99%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%85%b4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%82%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%81boat" target="_blank">강남휴게텔
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉휴게텔" href="http://www.blueskyspaworks.com/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%c2%bc%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%91%ad%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%95%89%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%bb%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%92%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%ef%bc%84damage" target="_blank">선릉휴게텔
</a>
</p>
절대 포기하지 말라. 당신이 되고 싶은 무언가가 있다면그에 대해 자부심을 가져라. 당신 자신에게 기회를 주어라. 스스로가 형편없다고 생각하지 말라.그래봐야 아무 것도 얻을 것이 없다. 목표를 높이 세워라.인생은 그렇게 살아야 한다.-마이크 맥라렌
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%80%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%92%b2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%92%a4%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bf%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%8e%97sworn" target="_blank">역삼휴게텔
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="강남안마" href="
https://www.wfs-dreieich.de/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%d0%93%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%97%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%88%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%a3%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%a4%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%84blame" target="_blank">강남안마
</a>
</p>
계단을 밟아야 계단 위에 올라설수 있다 -터키속담
<p align="">
<a title="선릉안마" href="
http://ypsistudio.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%82%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c4%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ef%bc%b0%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bf%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%cf%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%91%a4contain" target="_blank">선릉안마
</a>
</p>
지금이야 말로 일할때다. 지금이야말로 싸울때다. 지금이야말로 나를 더 훌륭한 사람으로 만들때다오늘 그것을 못하면 내일 그것을 할수있는가- 토마스 아켐피스
<p align="">
<a title="역삼안마" href="
https://www.matematikk.org/trinn8-10/sok/index.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%81%af%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bc%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%98%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%b3%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%b4understand" target="_blank">역삼안마
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남오피" href="
https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%86%90%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%85%b5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ef%bc%a8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c5%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8f%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%80bred" target="_blank">강남오피
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="선릉오피" href="
https://www.pexels.com/ko-kr/search/%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ef%bd%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%b9%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%83%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%8f%9cshelter" target="_blank">선릉오피
</a>
</p>
단순하게 살라. 쓸데없는 절차와 일 때문에 얼마나 복잡한 삶을 살아가는가?-이드리스 샤흐
<p align="">
<a title="역삼오피" href="
https://ciscentraltexas.org/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%ae%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b2%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8f%87%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%8a%83%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%97%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%92philadelphia" target="_blank">역삼오피
</a>
</p>
직접 눈으로 본 일도 오히려 참인지 아닌지염려스러운데 더구나 등뒤에서 남이 말하는것이야 어찌 이것을 깊이 믿을 수 있으랴?-명심보감-
<p align="">
<a title="강남휴게텔" href="
http://www.kuenselonline.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ce%a8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%9c%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%86%96%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%b2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bd%90%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%87quickly" target="_blank">강남휴게텔
</a>
</p>
내가 헛되이 보낸 오늘은 어제 죽어간 이들이그토록 바라던 하루이다 단 하루면 인간적인 모든 것을 멸망시킬수도 다시 소생시킬수도 있다-소포클레스
<p align="">
<a title="선릉휴게텔" href="https://www.sony.com/electronics/support/results?query=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%86%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%81%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ce%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%bd%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bc%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9bboat" target="_blank">선릉휴게텔
</a>
</p>
돈이란 바닷물과도 같다. 그것은 마시면 마실수록 목이 말라진다.-쇼펜하우어
<p align="">
<a title="역삼휴게텔" href="
https://jobs.rbc.com/ca/en/search-results?keywords=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%8c%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%d0%9e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%82%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%a6%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%c5%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%82joke" target="_blank">역삼휴게텔
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남안마" href="
http://www.makinamekawa.com/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%91%a9%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%d0%96%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bc%a2%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%92dreaming" target="_blank">강남안마
</a>
</p>
진정으로 웃으려면 고통을 참아야하며 나아가 고통을 즐길 줄 알아야 해 -찰리 채플린
<p align="">
<a title="선릉안마" href="
https://www.reddit.com/search?q=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%ac%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%9b%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%92%a5%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%a7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%99%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%a7grant" target="_blank">선릉안마
</a>
</p>
한번의 실패와 영원한 실패를 혼동하지 마라 -F.스콧 핏제랄드
<p align="">
<a title="역삼안마" href="
https://desk.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%95%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%9e%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ce%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%b5%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%85%b9%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%d1%89%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%93goal" target="_blank">역삼안마
</a>
</p>
행복은 결코 많고 큰데만 있는 것이 아니다 작은 것을 가지고도 고마워 하고 만족할 줄 안다면그는 행복한 사람이다여백과 공간의 아름다움은 단순함과 간소함에 있다법정스님 - 홀로사는 즐거움 에서
<p align="">
<a title="강남오피" href="
http://www.alberguerioaragon.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%bd%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%a6%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%87%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%80%b3%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%85%a5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%93%98%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%81seem" target="_blank">강남오피
</a>
</p>
길을 잃는 다는 것은 곧 길을 알게 된다는 것이다. - 동아프리카속담
<p align="">
<a title="선릉오피" href="
https://www.isistassinari.gov.it/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%8e%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%ce%b7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%89%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ce%95%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%95%88awhile" target="_blank">선릉오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="역삼오피" href="
http://isb.az/ru/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%89%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%d1%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%93%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%8cindependent" target="_blank">역삼오피
</a>
</p>
자신을 내보여라. 그러면 재능이 드러날 것이다.- 발타사르 그라시안
<p align="">
<a title="강남휴게텔" href="
http://biz.heraldcorp.com/view.php?ud=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%b2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bd%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%ef%bc%95%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%89%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%bbmarks" target="_blank">강남휴게텔
</a>
</p>
화가 날 때는 100까지 세라. 최악일 때는 욕설을 퍼부어라. -마크 트웨인
<p align="">
<a title="선릉휴게텔" href="
https://www.americanas.com.br/busca?conteudo=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ef%bc%b0%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%84%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%9a%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%81%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%8e%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%a8portrait" target="_blank">선릉휴게텔
</a>
</p>
1퍼센트의 가능성 그것이 나의 길이다-나폴레옹
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%83%99%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8f%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%83%95%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%d0%af%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b9personal" target="_blank">역삼휴게텔
</a>
</p>
최고에 도달하려면 최저에서 시작하라.-P.시루스
<p align="">
<a title="강남안마" href="
http://jozankei.jp/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%92%9f%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%81%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%c3%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%88%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%84%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%96%a6%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b6parted" target="_blank">강남안마
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉안마" href="
http://www.somoseducacao.com.br/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%98%85%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%be%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%9a%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%a1%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%a5greatly" target="_blank">선릉안마
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="역삼안마" href="
https://riftio.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%8e%80%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bd%99%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%99%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%8a%83%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%9d%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%a6%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%84%b9had" target="_blank">역삼안마 ddakbam1.com (●⌇ຶ ཅ⌇ຶ●)
</a>
</p>
<p align="">
<a title="강남오피" href="http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bf%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%c5%8b%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%84%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%8d%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%85%bela" target="_blank">강남오피
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉오피" href="https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%d0%be%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%88%82%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%bd%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%82%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a9tide" target="_blank">선릉오피
</a>
</p>
먼저핀꽃은 먼저진다 남보다 먼저 공을 세우려고 조급히 서둘것이 아니다-채근담
<p align="">
<a title="역삼오피" href="
https://enes.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%94%bb%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%97%88%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%ce%9egang" target="_blank">역삼오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남휴게텔" href="
https://www.livemeshthemes.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%c4%b1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b7%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%85%86%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%93%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%82%ba%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%84%a1%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%82stone" target="_blank">강남휴게텔
</a>
</p>
먹고 싶은것을 다 먹는 것은 그렇게 재미있지 않다 . 인생을 경계선 없이 살면 기쁨이 덜하다.먹고싶은대로 다 먹을 수있다면 먹고싶은 것을 먹는데 무슨 재미가 있겠나 - 톰행크스
<p align="">
<a title="선릉휴게텔" href="
http://www.pnr.corsica/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%89%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%a1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%9d%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%83%a6afford" target="_blank">선릉휴게텔
</a>
</p>
진짜 문제는 사람들의 마음이다.그것은 절대로 물리학이나 윤리학의 문제가 아니다.-아인슈타인
<p align="">
<a title="역삼휴게텔" href="
https://dict.leo.org/italienisch-deutsch/%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%82%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%d1%8f%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%83%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%ae%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9dseason" target="_blank">역삼휴게텔
</a>
</p>
가난은 가난하다고 느끼는 곳에 존재한다 .- 에머슨
<p align="">
<a title="강남안마" href="https://24.sapo.pt/pesquisar?q=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%85%a2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%82%8f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%99%a0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%85%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ce%92truly" target="_blank">강남안마
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉안마" href="
https://enfi.dict.cc/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%9e%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%85%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%90%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%bd%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%9cband" target="_blank">선릉안마
</a>
</p>
행복은 습관이다 그것을 몸에 지니라 -허버드
<p align="">
<a title="역삼안마" href="
https://www.lidumsaym.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%83%9d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c2%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8f%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%b1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%82%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b9derived" target="_blank">역삼안마
</a>
</p>
화려한 일을 추구하지 말라. 중요한 것은 스스로의 재능이며자신의 행동에 쏟아 붓는 사랑의 정도이다. -머더 테레사
<p align="">
<a title="강남오피" href="
http://www.twentszitmaaierteam.nl/pages/interactief/gastenboek.php?p=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%87%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%86%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%82%b9%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%94%bd%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%d0%a3wouldn't" target="_blank">강남오피
</a>
</p>
절대 어제를 후회하지 마라 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다-L.론허바드
<p align="">
<a title="선릉오피" href="
http://www.mairtinmusic.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%82%86%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%8b%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%9e%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%88truly" target="_blank">선릉오피
</a>
</p>
내일은 내일의 태양이 뜬다 피할수 없으면 즐겨라 -로버트 엘리엇
<p align="">
<a title="역삼오피" href="https://www.uptodate.com/contents/search?search=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%81%99%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%b9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%99%aa%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%83%8e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c3%be%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%82%b6%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%8centire" target="_blank">역삼오피
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남휴게텔" href="
http://ladysmithfederal.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%93%94%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%88%87%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%8f%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ce%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%c2%baremark" target="_blank">강남휴게텔
</a>
</p>
인간의 삶 전체는 단지 한 순간에 불과하다 . 인생을 즐기자 - 플루타르코스
<p align="">
<a title="선릉휴게텔" href="
https://www.governmentjobs.com/jobs?keyword=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%94%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%87secretly" target="_blank">선릉휴게텔
</a>
</p>
흔히 사람들은 기회를 기다리고 있지만 기회는 기다리는사람에게 잡히지 않는 법이다.우리는 기회를 기다리는 사람이 되기 전에 기회를 얻을 수 있는실력을 갖춰야 한다.일에 더 열중하는 사람이 되어야한다.-안창호
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%bb%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%84%ba%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%89%b0%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8e%93%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%80%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%cf%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b7artillery" target="_blank">역삼휴게텔
</a>
</p>
마음만을 가지고 있어서는 안된다. 반드시 실천하여야 한다.-이소룡
<p align="">
<a title="강남안마" href="
https://dehr.dict.cc/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%86%8d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%a1%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%84%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%9f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%b0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%88%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%8f%9dleg" target="_blank">강남안마
</a>
</p>
물러나서 조용하게 구하면 배울 수 있는 스승은 많다.사람은 가는 곳마다 보는 것마다 모두 스승으로서배울 것이 많은 법이다.-맹자
<p align="">
<a title="선릉안마" href="
https://www.gov.uk/search/all?keywords=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%92%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%91%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%ae%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8f%87%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%97%87providing" target="_blank">선릉안마
</a>
</p>
삶이 있는 한 희망은 있다 -키케로
<p align="">
<a title="역삼안마" href="
https://www.sdsn.no/sok/category28150.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%88%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%8c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%82%a1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%85%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%c4%b8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%85%9esecretary" target="_blank">역삼안마
</a>
</p>
한 번 실패와 영원한 실패를 혼동하지 마라.-F.스콧 핏제랄드
<p align="">
<a title="강남오피" href="
https://www.righteousmind.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%b0%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%91%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%96%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%88%87sang" target="_blank">강남오피
</a>
</p>
모든것들에는 나름의 경이로움과 심지어 어둠과 침묵이 있고 내가 어떤 상태에 있더라도 나는 그속에서 만족하는 법을 배운다-헬렌켈러
<p align="">
<a title="선릉오피" href="
http://www.actiitransportation.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e2%96%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%99%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%89%ba%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%bdaround" target="_blank">선릉오피
</a>
</p>
내 비장의 무기는 아직 손안에 있다 .그것은 희망이다 - 나폴레옹
<p align="">
<a title="역삼오피" href="https://www.youtube.com/results?search_query=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ce%a5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8e%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%a0%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%b1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%84lay" target="_blank">역삼오피
</a>
</p>
만족할 줄 아는 사람은진정한 부자이고 탐욕스러운 사람은진실로 가난한 사람이다.-솔론
<p align="">
<a title="강남휴게텔" href="
https://denl.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%81%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%8a%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%8f%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%85%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%93%a0%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%b2grief" target="_blank">강남휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="선릉휴게텔" href="
https://artdeco.org/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%9e%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a4%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%94%b9%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ef%bc%af%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%be%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%8dodd" target="_blank">선릉휴게텔
</a>
</p>
만약 우리가 할 수 있는 일을 모두 한다면 우리들은 우리자신에 깜짝 놀랄 것이다.-에디슨
<p align="">
<a title="역삼휴게텔" href="
http://www.lavipera.it/?s=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bc%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%bb%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%93%a3%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b5%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%88%8cvaried" target="_blank">역삼휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="강남안마" href="
https://money2.creontrade.com/E5/WTS/Stock/Foreign/DW_Foreign_Tax.aspx?p=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ef%bc%84%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bc%af%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%bd%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%83%9d%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%87splendid" target="_blank">강남안마
</a>
</p>
절대 어제를 후회하지 마라 . 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다 L.론허바드
<p align="">
<a title="선릉안마" href="
https://wpgovernance.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%85%a4%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%b3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%81%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%8d%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%81%b7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%a3john" target="_blank">선릉안마
</a>
</p>
사막이 아름다운 것은 어딘가에 샘이 숨겨져 있기 때문이다 - 생떽쥐베리
<p align="">
<a title="역삼안마" href="
https://nebraska.aiga.org/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%96%92%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%86%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%88%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%95%80%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ef%bd%87goes" target="_blank">역삼안마
</a>
</p>
</div>
<div style='width: 1px; height: 1px; overflow: hidden'><div align='center'>
<img name='target_resize_image[]' onclick='image_window(this)' style='cursor:pointer;' alt="" class="view_photo up" src="http://file.osen.co.kr/article/2019/05/01/201905011854774508_5cc96e7d1d3c2.jpg" >
그라운드 뷰는 차의 앞쪽 아랫부분
<div style="position:absolute; left:-9999px; top:-9999px;" class="sound_only">
피할수 없으면 즐겨라 - 로버트 엘리엇
<p align="">
<a title="강남오피" href="
http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%83%b1%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a4%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%a7%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%aa%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%a4forward" target="_blank">강남오피
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="선릉오피" href="
http://www.ambrosiocinema.it/page/5/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%83%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%a8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%b8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%bf%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ef%bc%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%96%bc%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%86spring" target="_blank">선릉오피
</a>
</p>
아래에 비교하면 남음이 있다.-명심보감
<p align="">
<a title="역삼오피" href="
https://www.openrice.com/zh/hongkong/restaurants?what=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%99%a5%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a0both" target="_blank">역삼오피
</a>
</p>
실패는 잊어라 그러나 그것이 준 교훈은절대 잊으면 안된다-하버트 개서
<p align="">
<a title="강남휴게텔" href="
https://desk.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%88%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%88%99%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%85%b4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%82%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%81boat" target="_blank">강남휴게텔
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉휴게텔" href="http://www.blueskyspaworks.com/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%c2%bc%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%91%ad%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%95%89%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%bb%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%92%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%ef%bc%84damage" target="_blank">선릉휴게텔
</a>
</p>
절대 포기하지 말라. 당신이 되고 싶은 무언가가 있다면그에 대해 자부심을 가져라. 당신 자신에게 기회를 주어라. 스스로가 형편없다고 생각하지 말라.그래봐야 아무 것도 얻을 것이 없다. 목표를 높이 세워라.인생은 그렇게 살아야 한다.-마이크 맥라렌
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%80%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%92%b2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%92%a4%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bf%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%8e%97sworn" target="_blank">역삼휴게텔
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="강남안마" href="
https://www.wfs-dreieich.de/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%d0%93%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%97%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%88%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%a3%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%a4%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%84blame" target="_blank">강남안마
</a>
</p>
계단을 밟아야 계단 위에 올라설수 있다 -터키속담
<p align="">
<a title="선릉안마" href="
http://ypsistudio.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%82%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c4%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ef%bc%b0%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bf%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%cf%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%91%a4contain" target="_blank">선릉안마
</a>
</p>
지금이야 말로 일할때다. 지금이야말로 싸울때다. 지금이야말로 나를 더 훌륭한 사람으로 만들때다오늘 그것을 못하면 내일 그것을 할수있는가- 토마스 아켐피스
<p align="">
<a title="역삼안마" href="
https://www.matematikk.org/trinn8-10/sok/index.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%81%af%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bc%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%98%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%b3%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%b4understand" target="_blank">역삼안마
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남오피" href="
https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%86%90%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%85%b5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ef%bc%a8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c5%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8f%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%80bred" target="_blank">강남오피
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="선릉오피" href="
https://www.pexels.com/ko-kr/search/%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ef%bd%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%b9%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%83%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%8f%9cshelter" target="_blank">선릉오피
</a>
</p>
단순하게 살라. 쓸데없는 절차와 일 때문에 얼마나 복잡한 삶을 살아가는가?-이드리스 샤흐
<p align="">
<a title="역삼오피" href="
https://ciscentraltexas.org/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%ae%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b2%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8f%87%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%8a%83%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%97%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%92philadelphia" target="_blank">역삼오피
</a>
</p>
직접 눈으로 본 일도 오히려 참인지 아닌지염려스러운데 더구나 등뒤에서 남이 말하는것이야 어찌 이것을 깊이 믿을 수 있으랴?-명심보감-
<p align="">
<a title="강남휴게텔" href="
http://www.kuenselonline.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ce%a8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%9c%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%86%96%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%b2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bd%90%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%87quickly" target="_blank">강남휴게텔
</a>
</p>
내가 헛되이 보낸 오늘은 어제 죽어간 이들이그토록 바라던 하루이다 단 하루면 인간적인 모든 것을 멸망시킬수도 다시 소생시킬수도 있다-소포클레스
<p align="">
<a title="선릉휴게텔" href="https://www.sony.com/electronics/support/results?query=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%86%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%81%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ce%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%bd%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bc%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9bboat" target="_blank">선릉휴게텔
</a>
</p>
돈이란 바닷물과도 같다. 그것은 마시면 마실수록 목이 말라진다.-쇼펜하우어
<p align="">
<a title="역삼휴게텔" href="
https://jobs.rbc.com/ca/en/search-results?keywords=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%8c%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%d0%9e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%82%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%a6%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%c5%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%82joke" target="_blank">역삼휴게텔
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남안마" href="
http://www.makinamekawa.com/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%91%a9%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%d0%96%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bc%a2%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%92dreaming" target="_blank">강남안마
</a>
</p>
진정으로 웃으려면 고통을 참아야하며 나아가 고통을 즐길 줄 알아야 해 -찰리 채플린
<p align="">
<a title="선릉안마" href="
https://www.reddit.com/search?q=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%ac%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%9b%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%92%a5%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%a7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%99%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%a7grant" target="_blank">선릉안마
</a>
</p>
한번의 실패와 영원한 실패를 혼동하지 마라 -F.스콧 핏제랄드
<p align="">
<a title="역삼안마" href="
https://desk.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%95%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%9e%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ce%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%b5%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%85%b9%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%d1%89%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%93goal" target="_blank">역삼안마
</a>
</p>
행복은 결코 많고 큰데만 있는 것이 아니다 작은 것을 가지고도 고마워 하고 만족할 줄 안다면그는 행복한 사람이다여백과 공간의 아름다움은 단순함과 간소함에 있다법정스님 - 홀로사는 즐거움 에서
<p align="">
<a title="강남오피" href="
http://www.alberguerioaragon.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%bd%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%a6%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%87%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%80%b3%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%85%a5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%93%98%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%81seem" target="_blank">강남오피
</a>
</p>
길을 잃는 다는 것은 곧 길을 알게 된다는 것이다. - 동아프리카속담
<p align="">
<a title="선릉오피" href="
https://www.isistassinari.gov.it/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%8e%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%ce%b7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%89%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ce%95%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%95%88awhile" target="_blank">선릉오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="역삼오피" href="
http://isb.az/ru/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%89%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%d1%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%93%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%8cindependent" target="_blank">역삼오피
</a>
</p>
자신을 내보여라. 그러면 재능이 드러날 것이다.- 발타사르 그라시안
<p align="">
<a title="강남휴게텔" href="
http://biz.heraldcorp.com/view.php?ud=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%b2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bd%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%ef%bc%95%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%89%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%bbmarks" target="_blank">강남휴게텔
</a>
</p>
화가 날 때는 100까지 세라. 최악일 때는 욕설을 퍼부어라. -마크 트웨인
<p align="">
<a title="선릉휴게텔" href="
https://www.americanas.com.br/busca?conteudo=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ef%bc%b0%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%84%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%9a%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%81%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%8e%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%a8portrait" target="_blank">선릉휴게텔
</a>
</p>
1퍼센트의 가능성 그것이 나의 길이다-나폴레옹
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%83%99%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8f%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%83%95%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%d0%af%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b9personal" target="_blank">역삼휴게텔
</a>
</p>
최고에 도달하려면 최저에서 시작하라.-P.시루스
<p align="">
<a title="강남안마" href="
http://jozankei.jp/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%92%9f%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%81%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%c3%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%88%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%84%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%96%a6%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b6parted" target="_blank">강남안마
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉안마" href="
http://www.somoseducacao.com.br/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%98%85%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%be%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%9a%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%a1%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%a5greatly" target="_blank">선릉안마
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="역삼안마" href="
https://riftio.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%8e%80%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bd%99%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%99%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%8a%83%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%9d%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%a6%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%84%b9had" target="_blank">역삼안마 ddakbam1.com (ノಠ益ಠ)ノ彡┻┻
</a>
</p>
from now I am using net for posts, thanks to web.
http://wolfandactress037.com/
http://wolfandactress037.com/
http://wolfandactress037.com/
from now I am using net for posts, thanks to web.
수원출장안마 - 후불100% 010-2659-1768 [카톡KP93] BM 수원전지역출장안마 수원오피걸 수원출장마사지 수원안마 수원출장마사지 수원콜걸샵BM
수원출장아가씨-수원출장콜걸후기-BM-수원출장만남-수원출장마사지-수원출장모텔-수원출장안마후기-수원출장20대아가씨-수원출장안마가격-수원후불출장안마-수원후불출장마사지-애인만남-스타킹-클럽녀-일본여자-속옷모델-속풀이-돈-싱글녀-섹시미-부킹-일탈원해-썸남썸녀-술-수원출장아로마-수원출장타이-BM- http://wolfandactress030.com/
from now I am using net for posts, thanks to web.
토토사이트 중에 최고로 꼽는 안전놀이터 추천과 먹튀검증이 완료된 메이저놀이터 토토사이트만을
추천해드리고 검증하는 토토플입니다. 안전한 사설토토이용과 클린한 베팅을 위한 환경을 제공합니다
http://www.totople.com/
http://www.totople.com/
from now I am using net for posts, thanks to web.
일산출장안마 - 후불100% 070-7333-9649 [카톡-VV23] BM 일산전지역출장안마 일산오피걸 일산출장마사지 일산안마 일산출장마사지 일산콜걸샵BM
일산출장아가씨-일산출장콜걸후기-BM-일산출장만남-일산출장마사지-일산출장모텔-일산출장안마후기-일산출장20대아가씨-일산출장안마가격-일산후불출장안마-일산후불출장마사지-애인만남-스타킹-클럽녀-일본여자-속옷모델-속풀이-돈-싱글녀-섹시미-부킹-일탈원해-썸남썸녀-술-일산출장아로마-일산출장타이-BM- http://wolfandactress029.com/
from now I am using net for posts, thanks to web.
수원출장안마 - 후불100% 070-7333-9649 [카톡-VV23] BM 수원전지역출장안마 수원오피걸 수원출장마사지 수원안마 수원출장마사지 수원콜걸샵BM
수원출장아가씨-수원출장콜걸후기-BM-수원출장만남-수원출장마사지-수원출장모텔-수원출장안마후기-수원출장20대아가씨-수원출장안마가격-수원후불출장안마-수원후불출장마사지-애인만남-스타킹-클럽녀-일본여자-속옷모델-속풀이-돈-싱글녀-섹시미-부킹-일탈원해-썸남썸녀-술-수원출장아로마-수원출장타이-BM- http://wolfandactress030.com/
from now I am using net for posts, thanks to web.
김천출장안마 - 후불100% 010-2659-1768 [카톡SN92] BM 김천전지역출장안마 김천오피걸 김천출장마사지 김천안마 김천출장마사지 김천콜걸샵BM
김천출장아가씨-김천출장콜걸후기-BM-김천출장만남-김천출장마사지-김천출장모텔-김천출장안마후기-김천출장20대아가씨-김천출장안마가격-김천후불출장안마-김천후불출장마사지-애인만남-스타킹-클럽녀-일본여자-속옷모델-속풀이-돈-싱글녀-섹시미-부킹-일탈원해-썸남썸녀-술-김천출장아로마-김천출장타이-BM-http://wolfandactress043.com/
The clearness to your submit is simply spectacular and i could suppose you are an expert on this subject.
Fine along with your permission let me to snatch your feed to keep updated with drawing close post.
Thanks 1,000,000 and please carry on the enjoyable work.
http://wolfandactress041.com/ 안성출장안마
http://wolfandactress042.com/ 공주출장안마
http://wolfandactress043.com/ 김천출장안마
http://wolfandactress044.com/ 가평출장안마
http://wolfandactress045.com/ 충주출장안마
http://wolfandactress046.com/ 사천출장안마
http://wolfandactress047.com/ 통영출장안마
http://wolfandactress048.com/ 포천출장안마
http://wolfandactress049.com/ 오산출장안마
http://wolfandactress050.com/ 남양주출장안마
http://blackmonad.xyz
http://wolfandactress022.com/ 익산출장마사지
http://wolfandactress023.com/ 창원출장마사지
http://wolfandactress024.com/ 마산출장마사지
http://wolfandactress025.com/ 밀양출장마사지
http://wolfandactress026.com/ 거제출장마사지
http://wolfandactress027.com/ 구미출장마사지
http://wolfandactress028.com/ 경주출장마사지
http://wolfandactress029.com/ 일산출장마사지
http://wolfandactress030.com/ 수원출장마사지
http://www.totople.com/ [토토사이트]토토, 안전놀이터 가입,메이저놀이터 추천 [토토플]
http://blackmonad.xyz
Välkommen att lämna ett avtryck i Lerums SOK's gästbok! Skapa en diskussion, vädra en åsikt eller lämna en hälsning!
Tänk dock på att hålla en seriös profil och signera med eget namn. De inlägg som ej är signerade med namn kommer att tas bort. Vi vill inte se några personangrepp eller andra kränkande kommentarer. Sådana inlägg kommer ovillkorligen att raderas!
http://wolfandactress042.com/ 공주출장안마
http://wolfandactress043.com/ 김천출장안마
http://wolfandactress044.com/ 가평출장안마
http://wolfandactress045.com/ 충주출장안마
http://wolfandactress046.com/ 사천출장안마
http://wolfandactress047.com/ 통영출장안마
http://wolfandactress048.com/ 포천출장안마
http://wolfandactress049.com/ 오산출장안마
http://wolfandactress050.com/ 남양주출장안마
http://blackmonad.xyz
I really like your writing style, wonderful information, thanks for putting up :D. “All words are pegs to hang ideas on.” by Henry Ward Beecher.
http://wolfandactress022.com/ 익산출장마사지
http://wolfandactress023.com/ 창원출장마사지
http://wolfandactress024.com/ 마산출장마사지
http://wolfandactress025.com/ 밀양출장마사지
http://wolfandactress026.com/ 거제출장마사지
http://wolfandactress027.com/ 구미출장마사지
http://wolfandactress028.com/ 경주출장마사지
http://wolfandactress029.com/ 일산출장마사지
http://wolfandactress030.com/ 수원출장마사지
http://www.totople.com/ [토토사이트]토토, 안전놀이터 가입,메이저놀이터 추천 [토토플]
http://blackmonad.xyz
Good day! Would you mind if I share your blog with my facebook group? There's a lot of people that I think would really enjoy your content. Please let me know. Many thanks
http://wolfnactress002.com/ 강남출장안마
http://wolfnactress003.com/ 부산출장안마
http://wolfnactress004.com/ 대구출장안마
http://wolfnactress005.com/ 인천출장안마
http://wolfnactress006.com/ 광주출장안마
http://wolfnactress007.com/ 대전출장안마
http://wolfnactress008.com/ 울산출장안마
http://wolfnactress009.com/ 세종출장안마
http://wolfnactress010.com/ 천안출장안마
http://blackmonad.xyz
I really like your writing style, wonderful information, thanks for putting up :D. “All words are pegs to hang ideas on.” by Henry Ward Beecher.
<a href="http://wolfandactress012.com">목포출장마사지</a>
<a href="http://wolfandactress013.com">여수출장마사지</a>
<a href="http://wolfandactress014.com">순천출장마사지</a>
<a href="http://wolfandactress015.com">청주출장마사지</a>
<a href="http://wolfandactress016.com">제주출장마사지</a>
<a href="http://wolfandactress017.com">원주출장마사지</a>
<a href="http://wolfandactress018.com">춘천출장마사지</a>
<a href="http://wolfandactress019.com">속초출장마사지</a>
<a href="http://wolfandactress020.com">포항출장마사지</a>
You have amazingly good information !?
Thank you very much for giving us some good information!
I also have an informative site. Do you want to take a look at my site?
<a href="http://wolfandactress042.com">공주출장안마</a>
<a href="http://wolfandactress043.com">김천출장안마</a>
<a href="http://wolfandactress044.com">가평출장안마</a>
<a href="http://wolfandactress045.com">충주출장안마</a>
<a href="http://wolfandactress046.com">사천출장안마</a>
<a href="http://wolfandactress047.com">통영출장안마</a>
<a href="http://wolfandactress048.com">포천출장안마</a>
<a href="http://wolfandactress049.com">오산출장안마</a>
<a href="http://wolfandactress050.com">남양주출장안마</a>
<a href="http://wolfnactress002.com">강남출장마사지</a>
<a href="http://wolfnactress003.com">부산출장마사지</a>
<a href="http://wolfnactress004.com">대구출장마사지</a>
<a href="http://wolfnactress005.com">인천출장마사지</a>
<a href="http://wolfnactress006.com">광주출장마사지</a>
<a href="http://wolfnactress007.com">대전출장마사지</a>
<a href="http://wolfnactress008.com">울산출장마사지</a>
<a href="http://wolfnactress009.com">세종출장마사지</a>
<a href="http://wolfnactress010.com">천안출장마사지</a>
<a href="http://blackmonad.xyz">구글상위노출</a>
<a href="http://www.totople.com">안전공원추천</a>
This app is for internal use.
it allows my website to share posts to
my Twitter account so
my followers can engage with
<a href="http://wolfandactress032.com">용인출장마사지</a>
<a href="http://wolfandactress033.com">안산출장마사지</a>
<a href="http://wolfandactress034.com">화성출장마사지</a>
<a href="http://wolfandactress035.com">시흥출장마사지</a>
<a href="http://wolfandactress036.com">파주출장마사지</a>
<a href="http://wolfandactress037.com">광명출장마사지</a>
<a href="http://wolfandactress038.com">김포출장마사지</a>
<a href="http://wolfandactress039.com">군포출장마사지</a>
<a href="http://wolfandactress040.com">이천출장마사지</a>
<a href="http://wolfandactress032.com">용인출장안마</a>
<a href="http://wolfandactress033.com">안산출장안마</a>
<a href="http://wolfandactress034.com">화성출장안마</a>
<a href="http://wolfandactress035.com">시흥출장안마</a>
<a href="http://wolfandactress036.com">파주출장안마</a>
<a href="http://wolfandactress037.com">광명출장안마</a>
<a href="http://wolfandactress038.com">김포출장안마</a>
<a href="http://wolfandactress039.com">군포출장안마</a>
<a href="http://wolfandactress040.com">이천출장안마</a>
Hi, I think your site might be having browser compatibility issues. When I look at your blog in Safari, it looks fine but when opening in Internet Explorer, it has some overlapping. I just wanted to give you a quick heads up! Other then that, excellent blog!
<p align="">
<a title="강남오피" href="http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bf%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%c5%8b%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%84%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%8d%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%85%bela" target="_blank">강남오피
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉오피" href="https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%d0%be%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%88%82%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%bd%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%82%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a9tide" target="_blank">선릉오피
</a>
</p>
먼저핀꽃은 먼저진다 남보다 먼저 공을 세우려고 조급히 서둘것이 아니다-채근담
<p align="">
<a title="역삼오피" href="
https://enes.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%94%bb%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%97%88%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%ce%9egang" target="_blank">역삼오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남휴게텔" href="
https://www.livemeshthemes.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%c4%b1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b7%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%85%86%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%93%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%82%ba%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%84%a1%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%82stone" target="_blank">강남휴게텔
</a>
</p>
먹고 싶은것을 다 먹는 것은 그렇게 재미있지 않다 . 인생을 경계선 없이 살면 기쁨이 덜하다.먹고싶은대로 다 먹을 수있다면 먹고싶은 것을 먹는데 무슨 재미가 있겠나 - 톰행크스
<p align="">
<a title="선릉휴게텔" href="
http://www.pnr.corsica/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%89%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%a1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%9d%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%83%a6afford" target="_blank">선릉휴게텔
</a>
</p>
진짜 문제는 사람들의 마음이다.그것은 절대로 물리학이나 윤리학의 문제가 아니다.-아인슈타인
<p align="">
<a title="역삼휴게텔" href="
https://dict.leo.org/italienisch-deutsch/%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%82%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%d1%8f%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%83%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%ae%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9dseason" target="_blank">역삼휴게텔
</a>
</p>
가난은 가난하다고 느끼는 곳에 존재한다 .- 에머슨
<p align="">
<a title="강남안마" href="https://24.sapo.pt/pesquisar?q=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%85%a2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%82%8f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%99%a0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%85%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ce%92truly" target="_blank">강남안마
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉안마" href="
https://enfi.dict.cc/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%9e%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%85%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%90%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%bd%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%9cband" target="_blank">선릉안마
</a>
</p>
행복은 습관이다 그것을 몸에 지니라 -허버드
<p align="">
<a title="역삼안마" href="
https://www.lidumsaym.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%83%9d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c2%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8f%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%b1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%82%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b9derived" target="_blank">역삼안마
</a>
</p>
화려한 일을 추구하지 말라. 중요한 것은 스스로의 재능이며자신의 행동에 쏟아 붓는 사랑의 정도이다. -머더 테레사
<p align="">
<a title="강남오피" href="
http://www.twentszitmaaierteam.nl/pages/interactief/gastenboek.php?p=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%87%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%86%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%82%b9%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%94%bd%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%d0%a3wouldn't" target="_blank">강남오피
</a>
</p>
절대 어제를 후회하지 마라 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다-L.론허바드
<p align="">
<a title="선릉오피" href="
http://www.mairtinmusic.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%82%86%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%8b%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%9e%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%88truly" target="_blank">선릉오피
</a>
</p>
내일은 내일의 태양이 뜬다 피할수 없으면 즐겨라 -로버트 엘리엇
<p align="">
<a title="역삼오피" href="https://www.uptodate.com/contents/search?search=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%81%99%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%b9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%99%aa%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%83%8e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c3%be%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%82%b6%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%8centire" target="_blank">역삼오피
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남휴게텔" href="
http://ladysmithfederal.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%93%94%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%88%87%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%8f%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ce%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%c2%baremark" target="_blank">강남휴게텔
</a>
</p>
인간의 삶 전체는 단지 한 순간에 불과하다 . 인생을 즐기자 - 플루타르코스
<p align="">
<a title="선릉휴게텔" href="
https://www.governmentjobs.com/jobs?keyword=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%94%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%87secretly" target="_blank">선릉휴게텔
</a>
</p>
흔히 사람들은 기회를 기다리고 있지만 기회는 기다리는사람에게 잡히지 않는 법이다.우리는 기회를 기다리는 사람이 되기 전에 기회를 얻을 수 있는실력을 갖춰야 한다.일에 더 열중하는 사람이 되어야한다.-안창호
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%bb%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%84%ba%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%89%b0%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8e%93%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%80%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%cf%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b7artillery" target="_blank">역삼휴게텔
</a>
</p>
마음만을 가지고 있어서는 안된다. 반드시 실천하여야 한다.-이소룡
<p align="">
<a title="강남안마" href="
https://dehr.dict.cc/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%86%8d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%a1%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%84%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%9f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%b0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%88%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%8f%9dleg" target="_blank">강남안마
</a>
</p>
물러나서 조용하게 구하면 배울 수 있는 스승은 많다.사람은 가는 곳마다 보는 것마다 모두 스승으로서배울 것이 많은 법이다.-맹자
<p align="">
<a title="선릉안마" href="
https://www.gov.uk/search/all?keywords=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%92%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%91%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%ae%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8f%87%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%97%87providing" target="_blank">선릉안마
</a>
</p>
삶이 있는 한 희망은 있다 -키케로
<p align="">
<a title="역삼안마" href="
https://www.sdsn.no/sok/category28150.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%88%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%8c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%82%a1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%85%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%c4%b8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%85%9esecretary" target="_blank">역삼안마
</a>
</p>
한 번 실패와 영원한 실패를 혼동하지 마라.-F.스콧 핏제랄드
<p align="">
<a title="강남오피" href="
https://www.righteousmind.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%b0%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%91%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%96%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%88%87sang" target="_blank">강남오피
</a>
</p>
모든것들에는 나름의 경이로움과 심지어 어둠과 침묵이 있고 내가 어떤 상태에 있더라도 나는 그속에서 만족하는 법을 배운다-헬렌켈러
<p align="">
<a title="선릉오피" href="
http://www.actiitransportation.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e2%96%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%99%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%89%ba%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%bdaround" target="_blank">선릉오피
</a>
</p>
내 비장의 무기는 아직 손안에 있다 .그것은 희망이다 - 나폴레옹
<p align="">
<a title="역삼오피" href="https://www.youtube.com/results?search_query=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ce%a5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8e%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%a0%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%b1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%84lay" target="_blank">역삼오피
</a>
</p>
만족할 줄 아는 사람은진정한 부자이고 탐욕스러운 사람은진실로 가난한 사람이다.-솔론
<p align="">
<a title="강남휴게텔" href="
https://denl.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%81%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%8a%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%8f%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%85%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%93%a0%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%b2grief" target="_blank">강남휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="선릉휴게텔" href="
https://artdeco.org/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%9e%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a4%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%94%b9%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ef%bc%af%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%be%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%8dodd" target="_blank">선릉휴게텔
</a>
</p>
만약 우리가 할 수 있는 일을 모두 한다면 우리들은 우리자신에 깜짝 놀랄 것이다.-에디슨
<p align="">
<a title="역삼휴게텔" href="
http://www.lavipera.it/?s=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bc%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%bb%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%93%a3%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b5%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%88%8cvaried" target="_blank">역삼휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="강남안마" href="
https://money2.creontrade.com/E5/WTS/Stock/Foreign/DW_Foreign_Tax.aspx?p=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ef%bc%84%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bc%af%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%bd%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%83%9d%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%87splendid" target="_blank">강남안마
</a>
</p>
절대 어제를 후회하지 마라 . 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다 L.론허바드
<p align="">
<a title="선릉안마" href="
https://wpgovernance.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%85%a4%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%b3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%81%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%8d%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%81%b7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%a3john" target="_blank">선릉안마
</a>
</p>
사막이 아름다운 것은 어딘가에 샘이 숨겨져 있기 때문이다 - 생떽쥐베리
<p align="">
<a title="역삼안마" href="
https://nebraska.aiga.org/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%96%92%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%86%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%88%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%95%80%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ef%bd%87goes" target="_blank">역삼안마
</a>
</p>
</div>
<div style='width: 1px; height: 1px; overflow: hidden'><div align='center'>
<img name='target_resize_image[]' onclick='image_window(this)' style='cursor:pointer;' alt="" class="view_photo up" src="http://file.osen.co.kr/article/2019/05/01/201905011854774508_5cc96e7d1d3c2.jpg" >
그라운드 뷰는 차의 앞쪽 아랫부분
<div style="position:absolute; left:-9999px; top:-9999px;" class="sound_only">
피할수 없으면 즐겨라 - 로버트 엘리엇
<p align="">
<a title="강남오피" href="
http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%83%b1%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a4%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%a7%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%aa%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%a4forward" target="_blank">강남오피
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="선릉오피" href="
http://www.ambrosiocinema.it/page/5/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%83%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%a8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%b8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%bf%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ef%bc%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%96%bc%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%86spring" target="_blank">선릉오피
</a>
</p>
아래에 비교하면 남음이 있다.-명심보감
<p align="">
<a title="역삼오피" href="
https://www.openrice.com/zh/hongkong/restaurants?what=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%99%a5%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a0both" target="_blank">역삼오피
</a>
</p>
실패는 잊어라 그러나 그것이 준 교훈은절대 잊으면 안된다-하버트 개서
<p align="">
<a title="강남휴게텔" href="
https://desk.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%88%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%88%99%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%85%b4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%82%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%81boat" target="_blank">강남휴게텔
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉휴게텔" href="http://www.blueskyspaworks.com/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%c2%bc%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%91%ad%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%95%89%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%bb%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%92%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%ef%bc%84damage" target="_blank">선릉휴게텔
</a>
</p>
절대 포기하지 말라. 당신이 되고 싶은 무언가가 있다면그에 대해 자부심을 가져라. 당신 자신에게 기회를 주어라. 스스로가 형편없다고 생각하지 말라.그래봐야 아무 것도 얻을 것이 없다. 목표를 높이 세워라.인생은 그렇게 살아야 한다.-마이크 맥라렌
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%80%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%92%b2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%92%a4%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bf%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%8e%97sworn" target="_blank">역삼휴게텔
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="강남안마" href="
https://www.wfs-dreieich.de/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%d0%93%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%97%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%88%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%a3%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%a4%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%84blame" target="_blank">강남안마
</a>
</p>
계단을 밟아야 계단 위에 올라설수 있다 -터키속담
<p align="">
<a title="선릉안마" href="
http://ypsistudio.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%82%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c4%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ef%bc%b0%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bf%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%cf%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%91%a4contain" target="_blank">선릉안마
</a>
</p>
지금이야 말로 일할때다. 지금이야말로 싸울때다. 지금이야말로 나를 더 훌륭한 사람으로 만들때다오늘 그것을 못하면 내일 그것을 할수있는가- 토마스 아켐피스
<p align="">
<a title="역삼안마" href="
https://www.matematikk.org/trinn8-10/sok/index.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%81%af%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bc%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%98%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%b3%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%b4understand" target="_blank">역삼안마
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남오피" href="
https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%86%90%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%85%b5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ef%bc%a8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c5%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8f%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%80bred" target="_blank">강남오피
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="선릉오피" href="
https://www.pexels.com/ko-kr/search/%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ef%bd%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%b9%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%83%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%8f%9cshelter" target="_blank">선릉오피
</a>
</p>
단순하게 살라. 쓸데없는 절차와 일 때문에 얼마나 복잡한 삶을 살아가는가?-이드리스 샤흐
<p align="">
<a title="역삼오피" href="
https://ciscentraltexas.org/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%ae%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b2%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8f%87%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%8a%83%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%97%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%92philadelphia" target="_blank">역삼오피
</a>
</p>
직접 눈으로 본 일도 오히려 참인지 아닌지염려스러운데 더구나 등뒤에서 남이 말하는것이야 어찌 이것을 깊이 믿을 수 있으랴?-명심보감-
<p align="">
<a title="강남휴게텔" href="
http://www.kuenselonline.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ce%a8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%9c%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%86%96%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%b2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bd%90%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%87quickly" target="_blank">강남휴게텔
</a>
</p>
내가 헛되이 보낸 오늘은 어제 죽어간 이들이그토록 바라던 하루이다 단 하루면 인간적인 모든 것을 멸망시킬수도 다시 소생시킬수도 있다-소포클레스
<p align="">
<a title="선릉휴게텔" href="https://www.sony.com/electronics/support/results?query=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%86%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%81%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ce%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%bd%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bc%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9bboat" target="_blank">선릉휴게텔
</a>
</p>
돈이란 바닷물과도 같다. 그것은 마시면 마실수록 목이 말라진다.-쇼펜하우어
<p align="">
<a title="역삼휴게텔" href="
https://jobs.rbc.com/ca/en/search-results?keywords=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%8c%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%d0%9e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%82%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%a6%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%c5%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%82joke" target="_blank">역삼휴게텔
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남안마" href="
http://www.makinamekawa.com/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%91%a9%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%d0%96%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bc%a2%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%92dreaming" target="_blank">강남안마
</a>
</p>
진정으로 웃으려면 고통을 참아야하며 나아가 고통을 즐길 줄 알아야 해 -찰리 채플린
<p align="">
<a title="선릉안마" href="
https://www.reddit.com/search?q=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%ac%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%9b%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%92%a5%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%a7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%99%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%a7grant" target="_blank">선릉안마
</a>
</p>
한번의 실패와 영원한 실패를 혼동하지 마라 -F.스콧 핏제랄드
<p align="">
<a title="역삼안마" href="
https://desk.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%95%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%9e%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ce%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%b5%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%85%b9%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%d1%89%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%93goal" target="_blank">역삼안마
</a>
</p>
행복은 결코 많고 큰데만 있는 것이 아니다 작은 것을 가지고도 고마워 하고 만족할 줄 안다면그는 행복한 사람이다여백과 공간의 아름다움은 단순함과 간소함에 있다법정스님 - 홀로사는 즐거움 에서
<p align="">
<a title="강남오피" href="
http://www.alberguerioaragon.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%bd%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%a6%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%87%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%80%b3%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%85%a5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%93%98%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%81seem" target="_blank">강남오피
</a>
</p>
길을 잃는 다는 것은 곧 길을 알게 된다는 것이다. - 동아프리카속담
<p align="">
<a title="선릉오피" href="
https://www.isistassinari.gov.it/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%8e%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%ce%b7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%89%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ce%95%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%95%88awhile" target="_blank">선릉오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="역삼오피" href="
http://isb.az/ru/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%89%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%d1%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%93%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%8cindependent" target="_blank">역삼오피
</a>
</p>
자신을 내보여라. 그러면 재능이 드러날 것이다.- 발타사르 그라시안
<p align="">
<a title="강남휴게텔" href="
http://biz.heraldcorp.com/view.php?ud=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%b2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bd%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%ef%bc%95%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%89%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%bbmarks" target="_blank">강남휴게텔
</a>
</p>
화가 날 때는 100까지 세라. 최악일 때는 욕설을 퍼부어라. -마크 트웨인
<p align="">
<a title="선릉휴게텔" href="
https://www.americanas.com.br/busca?conteudo=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ef%bc%b0%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%84%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%9a%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%81%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%8e%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%a8portrait" target="_blank">선릉휴게텔
</a>
</p>
1퍼센트의 가능성 그것이 나의 길이다-나폴레옹
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%83%99%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8f%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%83%95%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%d0%af%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b9personal" target="_blank">역삼휴게텔
</a>
</p>
최고에 도달하려면 최저에서 시작하라.-P.시루스
<p align="">
<a title="강남안마" href="
http://jozankei.jp/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%92%9f%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%81%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%c3%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%88%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%84%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%96%a6%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b6parted" target="_blank">강남안마
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉안마" href="
http://www.somoseducacao.com.br/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%98%85%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%be%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%9a%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%a1%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%a5greatly" target="_blank">선릉안마
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="역삼안마" href="
https://riftio.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%8e%80%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bd%99%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%99%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%8a%83%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%9d%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%a6%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%84%b9had" target="_blank">역삼안마 ddakbam1.com (ノಠ益ಠ)ノ彡┻┻
</a>
</p>
<a href="http://wolfnactress002.com">강남출장안마</a>
<a href="http://wolfnactress003.com">부산출장안마</a>
<a href="http://wolfnactress004.com">대구출장안마</a>
<a href="http://wolfnactress005.com">인천출장안마</a>
<a href="http://wolfnactress006.com">광주출장안마</a>
<a href="http://wolfnactress007.com">대전출장안마</a>
<a href="http://wolfnactress008.com">울산출장안마</a>
<a href="http://wolfnactress009.com">세종출장안마</a>
<a href="http://wolfnactress010.com">천안출장안마</a>
<a href="http://blackmonad.xyz">구글홈페이지상위노출</a>
<a href="http://www.totople.com">안전놀이터추천</a>
I¦ll immediately clutch your rss feed as I can not to find your e-mail subscription link or newsletter service. Do you have any? Kindly let me recognise in order that I may subscribe. Thanks.
<p align="">
<a title="강남오피" href="http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bf%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%c5%8b%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%84%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%8d%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%85%bela" target="_blank">강남오피
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉오피" href="https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%d0%be%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%88%82%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%bd%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%82%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a9tide" target="_blank">선릉오피
</a>
</p>
먼저핀꽃은 먼저진다 남보다 먼저 공을 세우려고 조급히 서둘것이 아니다-채근담
<p align="">
<a title="역삼오피" href="
https://enes.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%94%bb%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8f%89%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%97%88%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%ce%9egang" target="_blank">역삼오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남휴게텔" href="
https://www.livemeshthemes.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%c4%b1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b7%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%85%86%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%93%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%82%ba%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%84%a1%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%82stone" target="_blank">강남휴게텔
</a>
</p>
먹고 싶은것을 다 먹는 것은 그렇게 재미있지 않다 . 인생을 경계선 없이 살면 기쁨이 덜하다.먹고싶은대로 다 먹을 수있다면 먹고싶은 것을 먹는데 무슨 재미가 있겠나 - 톰행크스
<p align="">
<a title="선릉휴게텔" href="
http://www.pnr.corsica/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%89%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%a1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%9d%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%83%a6afford" target="_blank">선릉휴게텔
</a>
</p>
진짜 문제는 사람들의 마음이다.그것은 절대로 물리학이나 윤리학의 문제가 아니다.-아인슈타인
<p align="">
<a title="역삼휴게텔" href="
https://dict.leo.org/italienisch-deutsch/%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%82%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%d1%8f%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%83%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%ae%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9dseason" target="_blank">역삼휴게텔
</a>
</p>
가난은 가난하다고 느끼는 곳에 존재한다 .- 에머슨
<p align="">
<a title="강남안마" href="https://24.sapo.pt/pesquisar?q=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%85%a2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%82%8f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%99%a0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%85%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ce%92truly" target="_blank">강남안마
</a>
</p>
인생을 다시 산다면 다음번에는 더 많은 실수를 저지르리라 - 나딘 스테어
<p align="">
<a title="선릉안마" href="
https://enfi.dict.cc/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%9e%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%85%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%90%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%bd%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%9cband" target="_blank">선릉안마
</a>
</p>
행복은 습관이다 그것을 몸에 지니라 -허버드
<p align="">
<a title="역삼안마" href="
https://www.lidumsaym.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%83%9d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c2%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8f%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%b1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%82%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%9c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b9derived" target="_blank">역삼안마
</a>
</p>
화려한 일을 추구하지 말라. 중요한 것은 스스로의 재능이며자신의 행동에 쏟아 붓는 사랑의 정도이다. -머더 테레사
<p align="">
<a title="강남오피" href="
http://www.twentszitmaaierteam.nl/pages/interactief/gastenboek.php?p=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%87%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%86%89%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%82%b9%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%94%bd%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%d0%a3wouldn't" target="_blank">강남오피
</a>
</p>
절대 어제를 후회하지 마라 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다-L.론허바드
<p align="">
<a title="선릉오피" href="
http://www.mairtinmusic.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%82%86%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%8b%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%9e%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%88truly" target="_blank">선릉오피
</a>
</p>
내일은 내일의 태양이 뜬다 피할수 없으면 즐겨라 -로버트 엘리엇
<p align="">
<a title="역삼오피" href="https://www.uptodate.com/contents/search?search=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%81%99%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%b9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%99%aa%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%83%8e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c3%be%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%82%b6%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%8centire" target="_blank">역삼오피
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남휴게텔" href="
http://ladysmithfederal.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%93%94%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%88%87%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%8f%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ce%be%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%c2%baremark" target="_blank">강남휴게텔
</a>
</p>
인간의 삶 전체는 단지 한 순간에 불과하다 . 인생을 즐기자 - 플루타르코스
<p align="">
<a title="선릉휴게텔" href="
https://www.governmentjobs.com/jobs?keyword=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%94%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%bc%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c4%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b3%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%85%87secretly" target="_blank">선릉휴게텔
</a>
</p>
흔히 사람들은 기회를 기다리고 있지만 기회는 기다리는사람에게 잡히지 않는 법이다.우리는 기회를 기다리는 사람이 되기 전에 기회를 얻을 수 있는실력을 갖춰야 한다.일에 더 열중하는 사람이 되어야한다.-안창호
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%bb%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%84%ba%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%89%b0%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8e%93%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%80%a1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%cf%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b7artillery" target="_blank">역삼휴게텔
</a>
</p>
마음만을 가지고 있어서는 안된다. 반드시 실천하여야 한다.-이소룡
<p align="">
<a title="강남안마" href="
https://dehr.dict.cc/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e3%86%8d%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%a1%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%84%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%94%9f%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%d0%b0%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%88%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%8f%9dleg" target="_blank">강남안마
</a>
</p>
물러나서 조용하게 구하면 배울 수 있는 스승은 많다.사람은 가는 곳마다 보는 것마다 모두 스승으로서배울 것이 많은 법이다.-맹자
<p align="">
<a title="선릉안마" href="
https://www.gov.uk/search/all?keywords=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%92%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%91%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%ae%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8f%87%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%97%87providing" target="_blank">선릉안마
</a>
</p>
삶이 있는 한 희망은 있다 -키케로
<p align="">
<a title="역삼안마" href="
https://www.sdsn.no/sok/category28150.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%88%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%8c%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%82%a1%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%85%ba%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%c4%b8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%85%9esecretary" target="_blank">역삼안마
</a>
</p>
한 번 실패와 영원한 실패를 혼동하지 마라.-F.스콧 핏제랄드
<p align="">
<a title="강남오피" href="
https://www.righteousmind.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%a1%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%b0%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%91%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%bb%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%96%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%88%87sang" target="_blank">강남오피
</a>
</p>
모든것들에는 나름의 경이로움과 심지어 어둠과 침묵이 있고 내가 어떤 상태에 있더라도 나는 그속에서 만족하는 법을 배운다-헬렌켈러
<p align="">
<a title="선릉오피" href="
http://www.actiitransportation.com/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e2%96%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%99%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%85%97%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%89%ba%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%bdaround" target="_blank">선릉오피
</a>
</p>
내 비장의 무기는 아직 손안에 있다 .그것은 희망이다 - 나폴레옹
<p align="">
<a title="역삼오피" href="https://www.youtube.com/results?search_query=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ce%a5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%8e%9d%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%a0%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%b1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%81%84lay" target="_blank">역삼오피
</a>
</p>
만족할 줄 아는 사람은진정한 부자이고 탐욕스러운 사람은진실로 가난한 사람이다.-솔론
<p align="">
<a title="강남휴게텔" href="
https://denl.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%81%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%8a%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%8f%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%85%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%93%a0%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%b2grief" target="_blank">강남휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="선릉휴게텔" href="
https://artdeco.org/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%9e%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%a4%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%94%b9%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ef%bc%af%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%d0%be%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%83%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%8dodd" target="_blank">선릉휴게텔
</a>
</p>
만약 우리가 할 수 있는 일을 모두 한다면 우리들은 우리자신에 깜짝 놀랄 것이다.-에디슨
<p align="">
<a title="역삼휴게텔" href="
http://www.lavipera.it/?s=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bc%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%bb%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%93%a3%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%81%b5%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%88%8cvaried" target="_blank">역삼휴게텔
</a>
</p>
언제나 현재에 집중할수 있다면 행복할것이다. -파울로 코엘료
<p align="">
<a title="강남안마" href="
https://money2.creontrade.com/E5/WTS/Stock/Foreign/DW_Foreign_Tax.aspx?p=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ef%bc%84%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bc%af%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%85%bd%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%83%9d%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%83%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%87splendid" target="_blank">강남안마
</a>
</p>
절대 어제를 후회하지 마라 . 인생은 오늘의 나 안에 있고 내일은 스스로 만드는 것이다 L.론허바드
<p align="">
<a title="선릉안마" href="
https://wpgovernance.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%85%a4%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%b3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%81%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%83%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bd%8d%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%81%b7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%a3john" target="_blank">선릉안마
</a>
</p>
사막이 아름다운 것은 어딘가에 샘이 숨겨져 있기 때문이다 - 생떽쥐베리
<p align="">
<a title="역삼안마" href="
https://nebraska.aiga.org/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%96%92%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%98%86%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%88%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%95%80%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%a4%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%ef%bd%87goes" target="_blank">역삼안마
</a>
</p>
</div>
<div style='width: 1px; height: 1px; overflow: hidden'><div align='center'>
<img name='target_resize_image[]' onclick='image_window(this)' style='cursor:pointer;' alt="" class="view_photo up" src="http://file.osen.co.kr/article/2019/05/01/201905011854774508_5cc96e7d1d3c2.jpg" >
그라운드 뷰는 차의 앞쪽 아랫부분
<div style="position:absolute; left:-9999px; top:-9999px;" class="sound_only">
피할수 없으면 즐겨라 - 로버트 엘리엇
<p align="">
<a title="강남오피" href="
http://fuseproductions.org/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ef%bc%98%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%be%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%83%b1%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a4%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%8e%a7%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%83%aa%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%a4forward" target="_blank">강남오피
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="선릉오피" href="
http://www.ambrosiocinema.it/page/5/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%83%a7%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%a8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%b8%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%bf%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ef%bc%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%96%bc%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%97%86spring" target="_blank">선릉오피
</a>
</p>
아래에 비교하면 남음이 있다.-명심보감
<p align="">
<a title="역삼오피" href="
https://www.openrice.com/zh/hongkong/restaurants?what=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a1%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%81%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%ce%9e%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%99%a5%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%96%a0both" target="_blank">역삼오피
</a>
</p>
실패는 잊어라 그러나 그것이 준 교훈은절대 잊으면 안된다-하버트 개서
<p align="">
<a title="강남휴게텔" href="
https://desk.dict.cc/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%9c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%88%88%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%88%99%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%80%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%85%b4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%82%b8%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%d1%81boat" target="_blank">강남휴게텔
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉휴게텔" href="http://www.blueskyspaworks.com/?s=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%c2%bc%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%91%ad%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%95%89%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%bb%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e2%88%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e2%92%b1%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%ef%bc%84damage" target="_blank">선릉휴게텔
</a>
</p>
절대 포기하지 말라. 당신이 되고 싶은 무언가가 있다면그에 대해 자부심을 가져라. 당신 자신에게 기회를 주어라. 스스로가 형편없다고 생각하지 말라.그래봐야 아무 것도 얻을 것이 없다. 목표를 높이 세워라.인생은 그렇게 살아야 한다.-마이크 맥라렌
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e2%91%a3%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%80%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%92%b2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%92%a4%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bf%a2%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%8e%97sworn" target="_blank">역삼휴게텔
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="강남안마" href="
https://www.wfs-dreieich.de/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%d0%93%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%97%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%88%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%85%a3%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%82%a4%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%88%84blame" target="_blank">강남안마
</a>
</p>
계단을 밟아야 계단 위에 올라설수 있다 -터키속담
<p align="">
<a title="선릉안마" href="
http://ypsistudio.com/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%94%82%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c4%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ef%bc%b0%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bf%a6%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%89%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%cf%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%91%a4contain" target="_blank">선릉안마
</a>
</p>
지금이야 말로 일할때다. 지금이야말로 싸울때다. 지금이야말로 나를 더 훌륭한 사람으로 만들때다오늘 그것을 못하면 내일 그것을 할수있는가- 토마스 아켐피스
<p align="">
<a title="역삼안마" href="
https://www.matematikk.org/trinn8-10/sok/index.html?q=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%81%af%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%85%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%ef%bc%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%98%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%b3%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%b4understand" target="_blank">역삼안마
</a>
</p>
나이가 60이다 70이다 하는 것으로 그 사람이 늙었다 젊었다 할 수 없다.늙고 젊은 것은 그 사람의 신념이 늙었느냐 젊었느냐 하는데 있다.-맥아더
<p align="">
<a title="강남오피" href="
https://www.jobbank.gc.ca/jobsearch/jobsearch?flg=F&dkw=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%e2%86%90%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%d0%ac%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%85%b5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%ef%bc%a8%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%c5%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8f%80%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%80bred" target="_blank">강남오피
</a>
</p>
이룰수 없는 꿈을 꾸고 이길수 없는 적과 싸우며이룰수 없는 사랑을 하고 견딜 수 없는 고통을 견디고잡을수 없는 저 하늘의 별도 잡자-세르반테스
<p align="">
<a title="선릉오피" href="
https://www.pexels.com/ko-kr/search/%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ef%bd%8b%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%89%b9%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%94%a1%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%d0%a7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%98%85%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%8e%83%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%8f%9cshelter" target="_blank">선릉오피
</a>
</p>
단순하게 살라. 쓸데없는 절차와 일 때문에 얼마나 복잡한 삶을 살아가는가?-이드리스 샤흐
<p align="">
<a title="역삼오피" href="
https://ciscentraltexas.org/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%d0%ae%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%89%ab%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e3%89%b2%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8f%87%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%8a%83%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ef%bd%97%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%94%92philadelphia" target="_blank">역삼오피
</a>
</p>
직접 눈으로 본 일도 오히려 참인지 아닌지염려스러운데 더구나 등뒤에서 남이 말하는것이야 어찌 이것을 깊이 믿을 수 있으랴?-명심보감-
<p align="">
<a title="강남휴게텔" href="
http://www.kuenselonline.com/?s=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ce%a8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%9c%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e2%86%96%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%83%b2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%92%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bd%90%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%87quickly" target="_blank">강남휴게텔
</a>
</p>
내가 헛되이 보낸 오늘은 어제 죽어간 이들이그토록 바라던 하루이다 단 하루면 인간적인 모든 것을 멸망시킬수도 다시 소생시킬수도 있다-소포클레스
<p align="">
<a title="선릉휴게텔" href="https://www.sony.com/electronics/support/results?query=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%e2%86%94%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%88%90%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%81%ab%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%ce%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%8e%bd%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%ef%bc%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%9bboat" target="_blank">선릉휴게텔
</a>
</p>
돈이란 바닷물과도 같다. 그것은 마시면 마실수록 목이 말라진다.-쇼펜하우어
<p align="">
<a title="역삼휴게텔" href="
https://jobs.rbc.com/ca/en/search-results?keywords=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%8e%b8%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%83%8c%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%d0%9e%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%85%82%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%c5%a6%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%c5%89%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%86%82joke" target="_blank">역삼휴게텔
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="강남안마" href="
http://www.makinamekawa.com/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%91%a9%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%91%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%8e%a8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%d0%96%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%ef%bc%a2%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%94%92%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%82%92dreaming" target="_blank">강남안마
</a>
</p>
진정으로 웃으려면 고통을 참아야하며 나아가 고통을 즐길 줄 알아야 해 -찰리 채플린
<p align="">
<a title="선릉안마" href="
https://www.reddit.com/search?q=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e3%85%ac%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%9b%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%92%a5%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%91%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%a7%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%99%a3%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%a7grant" target="_blank">선릉안마
</a>
</p>
한번의 실패와 영원한 실패를 혼동하지 마라 -F.스콧 핏제랄드
<p align="">
<a title="역삼안마" href="
https://desk.dict.cc/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e2%95%87%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%9e%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%ce%b2%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%88%b5%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%85%b9%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%d1%89%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%85%93goal" target="_blank">역삼안마
</a>
</p>
행복은 결코 많고 큰데만 있는 것이 아니다 작은 것을 가지고도 고마워 하고 만족할 줄 안다면그는 행복한 사람이다여백과 공간의 아름다움은 단순함과 간소함에 있다법정스님 - 홀로사는 즐거움 에서
<p align="">
<a title="강남오피" href="
http://www.alberguerioaragon.com/?s=%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%d0%bd%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%85%a6%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%e2%95%87%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e2%80%b3%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%85%a5%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e2%93%98%ea%b0%95%eb%82%a8%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%83%81seem" target="_blank">강남오피
</a>
</p>
길을 잃는 다는 것은 곧 길을 알게 된다는 것이다. - 동아프리카속담
<p align="">
<a title="선릉오피" href="
https://www.isistassinari.gov.it/?s=%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%e3%8e%aa%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%9c%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%ce%b7%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%89%a6%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e3%83%ab%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%ce%95%ec%84%a0%eb%a6%89%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e2%95%88awhile" target="_blank">선릉오피
</a>
</p>
그대 자신의 영혼을 탐구하라.다른 누구에게도 의지하지 말고 오직 그대 혼자의 힘으로 하라.그대의 여정에 다른 이들이 끼어들지 못하게 하라.이 길은 그대만의 길이요 그대 혼자 가야할 길임을 명심하라.비록 다른 이들과 함께 걸을 수는 있으나 다른 그 어느 누구도그대가 선택한 길을 대신 가줄 수 없음을 알라.-인디언 속담
<p align="">
<a title="역삼오피" href="
http://isb.az/ru/?s=%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%e3%89%b5%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%b6%94%ec%b2%9c%d1%84%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ea%b0%80%ea%b2%a9%e3%8e%8a%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%9c%84%ec%b9%98%e2%91%a9%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ec%98%88%ec%95%bd%e3%81%93%ec%97%ad%ec%82%bc%ec%98%a4%ed%94%bc%ed%9b%84%ea%b8%b0%e3%86%8cindependent" target="_blank">역삼오피
</a>
</p>
자신을 내보여라. 그러면 재능이 드러날 것이다.- 발타사르 그라시안
<p align="">
<a title="강남휴게텔" href="
http://biz.heraldcorp.com/view.php?ud=%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%e3%85%b2%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%93%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%ef%bd%81%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%82%a4%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%ef%bc%95%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%89%a2%ea%b0%95%eb%82%a8%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e3%81%bbmarks" target="_blank">강남휴게텔
</a>
</p>
화가 날 때는 100까지 세라. 최악일 때는 욕설을 퍼부어라. -마크 트웨인
<p align="">
<a title="선릉휴게텔" href="
https://www.americanas.com.br/busca?conteudo=%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ef%bc%b0%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e2%94%96%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%84%b7%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e2%94%9a%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%81%87%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%e3%8e%91%ec%84%a0%eb%a6%89%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%92%a8portrait" target="_blank">선릉휴게텔
</a>
</p>
1퍼센트의 가능성 그것이 나의 길이다-나폴레옹
<p align="">
<a title="역삼휴게텔" href="
https://www.rockstargames.com/search?q=%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%e3%83%8c%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%e3%81%b1%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%b6%94%ec%b2%9c%e3%83%99%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ea%b0%80%ea%b2%a9%e3%8f%9d%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%9c%84%ec%b9%98%e3%83%95%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ec%98%88%ec%95%bd%d0%af%ec%97%ad%ec%82%bc%ed%9c%b4%ea%b2%8c%ed%85%94%ed%9b%84%ea%b8%b0%e2%91%b9personal" target="_blank">역삼휴게텔
</a>
</p>
최고에 도달하려면 최저에서 시작하라.-P.시루스
<p align="">
<a title="강남안마" href="
http://jozankei.jp/?s=%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%e2%92%9f%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%c5%81%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%c3%b8%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%88%9b%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%84%bb%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e2%96%a6%ea%b0%95%eb%82%a8%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%d0%b6parted" target="_blank">강남안마
</a>
</p>
평생 살 것처럼 꿈을 꾸어라.그리고 내일 죽을 것처럼 오늘을 살아라. -제임스 딘
<p align="">
<a title="선릉안마" href="
http://www.somoseducacao.com.br/?s=%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%e2%98%85%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ce%be%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e3%83%9a%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e3%8e%a1%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e2%94%81%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%83%8c%ec%84%a0%eb%a6%89%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e2%92%a5greatly" target="_blank">선릉안마
</a>
</p>
삶이 그대를 속일지라도 슬퍼하거나 노하지 말아라 슬픈 날에 참고 견디라 즐거운 날은 오고야 말리니마음은 미래를 바라느니 현재는 한없이 우울한것 모든건 하염없이 사라지나가 버리고 그리움이 되리니 - 푸쉬킨
<p align="">
<a title="역삼안마" href="
https://riftio.com/?s=%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%e3%8e%80%e3%80%90+%eb%94%b1%ec%a2%8b%ec%9d%80%eb%b0%a4%e2%96%b6ddakbam.com%e2%97%80%e3%80%91%e3%80%90+%ed%85%94%eb%a0%88%e2%96%b6ddakbam%e2%97%80%e3%80%91%ef%bd%99%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%b6%94%ec%b2%9c%e2%99%ac%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ea%b0%80%ea%b2%a9%e2%8a%83%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%9c%84%ec%b9%98%e3%8e%9d%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ec%98%88%ec%95%bd%e3%8e%a6%ec%97%ad%ec%82%bc%ec%95%88%eb%a7%88%ed%9b%84%ea%b8%b0%e3%84%b9had" target="_blank">역삼안마 ddakbam1.com ( ఠൠఠ )
</a>
</p>
Thank you so much for sharing this great blog.Very inspiring and helpful too.Hope you continue to share more of your ideas.I will definitely love to read.
<a href="http://wolfandactress012.com">목포출장안마</a>
<a href="http://wolfandactress013.com">여수출장안마</a>
<a href="http://wolfandactress014.com">순천출장안마</a>
<a href="http://wolfandactress015.com">청주출장안마</a>
<a href="http://wolfandactress016.com">제주출장안마</a>
<a href="http://wolfandactress017.com">원주출장안마</a>
<a href="http://wolfandactress018.com">춘천출장안마</a>
<a href="http://wolfandactress019.com">속초출장안마</a>
<a href="http://wolfandactress020.com">포항출장안마</a>
Some truly marvelous work on behalf of the owner of this web site, utterly great articles.
<a href="http://wolfandactress012.com">목포출장마사지</a>
<a href="http://wolfandactress013.com">여수출장마사지</a>
<a href="http://wolfandactress014.com">순천출장마사지</a>
<a href="http://wolfandactress015.com">청주출장마사지</a>
<a href="http://wolfandactress016.com">제주출장마사지</a>
<a href="http://wolfandactress017.com">원주출장마사지</a>
<a href="http://wolfandactress018.com">춘천출장마사지</a>
<a href="http://wolfandactress019.com">속초출장마사지</a>
<a href="http://wolfandactress020.com">포항출장마사지</a>
Thank you so much for sharing this great blog.Very inspiring and helpful too.Hope you continue to share more of your ideas.I will definitely love to read.
<a href="http://wolfandactress042.com">공주출장안마</a>
<a href="http://wolfandactress043.com">김천출장안마</a>
<a href="http://wolfandactress044.com">가평출장안마</a>
<a href="http://wolfandactress045.com">충주출장안마</a>
<a href="http://wolfandactress046.com">사천출장안마</a>
<a href="http://wolfandactress047.com">통영출장안마</a>
<a href="http://wolfandactress048.com">포천출장안마</a>
<a href="http://wolfandactress049.com">오산출장안마</a>
<a href="http://wolfandactress050.com">남양주출장안마</a>
I|ll immediately clutch your rss feed as I can not to find your e-mail subscription link or newsletter service. Do you have any? Kindly let me recognise in order that I may subscribe. Thanks.
<a href="http://wolfandactress022.com">익산출장마사지</a>
<a href="http://wolfandactress023.com">창원출장마사지</a>
<a href="http://wolfandactress024.com">마산출장마사지</a>
<a href="http://wolfandactress025.com">밀양출장마사지</a>
<a href="http://wolfandactress026.com">거제출장마사지</a>
<a href="http://wolfandactress027.com">구미출장마사지</a>
<a href="http://wolfandactress028.com">경주출장마사지</a>
<a href="http://wolfandactress029.com">일산출장마사지</a>
<a href="http://wolfandactress030.com">수원출장마사지</a>
Wow, great blog.Thanks Again. Want more.
<a href="http://wolfandactress022.com">익산출장안마</a>
<a href="http://wolfandactress023.com">창원출장안마</a>
<a href="http://wolfandactress024.com">마산출장안마</a>
<a href="http://wolfandactress025.com">밀양출장안마</a>
<a href="http://wolfandactress026.com">거제출장안마</a>
<a href="http://wolfandactress027.com">구미출장안마</a>
<a href="http://wolfandactress028.com">경주출장안마</a>
<a href="http://wolfandactress029.com">일산출장안마</a>
<a href="http://wolfandactress030.com">수원출장안마</a>
Well I sincerely enjoyed studying it. This subject offered by you is very effective for accurate planning.
<a href="http://wolfnactress002.com">강남출장마사지</a>
<a href="http://wolfnactress003.com">부산출장마사지</a>
<a href="http://wolfnactress004.com">대구출장마사지</a>
<a href="http://wolfnactress005.com">인천출장마사지</a>
<a href="http://wolfnactress006.com">광주출장마사지</a>
<a href="http://wolfnactress007.com">대전출장마사지</a>
<a href="http://wolfnactress008.com">울산출장마사지</a>
<a href="http://wolfnactress009.com">세종출장마사지</a>
<a href="http://wolfnactress010.com">천안출장마사지</a>
<a href="http://blackmonad.xyz">구글상위노출</a>
<a href="http://www.totople.com">안전공원추천</a>
I discovered your blog post web site online and check a few of your early posts. Continue to keep in the great operate. I recently extra increase RSS feed to my MSN News Reader.
<a href="http://wolfnactress002.com">강남출장안마</a>
<a href="http://wolfnactress003.com">부산출장안마</a>
<a href="http://wolfnactress004.com">대구출장안마</a>
<a href="http://wolfnactress005.com">인천출장안마</a>
<a href="http://wolfnactress006.com">광주출장안마</a>
<a href="http://wolfnactress007.com">대전출장안마</a>
<a href="http://wolfnactress008.com">울산출장안마</a>
<a href="http://wolfnactress009.com">세종출장안마</a>
<a href="http://wolfnactress010.com">천안출장안마</a>
<a href="http://blackmonad.xyz">구글홈페이지상위노출</a>
<a href="http://wolfandactress042.com">공주출장안마</a>
<a href="http://wolfandactress043.com">김천출장안마</a>
<a href="http://wolfandactress044.com">가평출장안마</a>
<a href="http://wolfandactress045.com">충주출장안마</a>
<a href="http://wolfandactress046.com">사천출장안마</a>
<a href="http://wolfandactress047.com">통영출장안마</a>
<a href="http://wolfandactress048.com">포천출장안마</a>
<a href="http://wolfandactress049.com">오산출장안마</a>
<a href="http://wolfandactress050.com">남양주출장안마</a>
Valuable info. Fortunate me I found your site accidentally, and I’m surprised why this twist of fate didn’t happened earlier! I bookmarked it.
“◐공주출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐김천출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐가평출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐충주출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐사천출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐통영출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐포천출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐오산출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐남양주출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
Having read this I thought it was very informative. I appreciate you taking the time and effort to put this article together. I once again find myself spending way to much time both reading and commenting. But so what, it was still worth it
“◐익산출장안마[070-5222-7802]▶[카톡문의:VV23]♥"
“◐창원출장안마[070-5222-7802]▶[카톡문의:VV23]♥"
“◐마산출장안마[070-5222-7802]▶[카톡문의:VV23]♥"
“◐밀양출장안마[070-5222-7802]▶[카톡문의:VV23]♥"
“◐거제출장안마[070-5222-7802]▶[카톡문의:VV23]♥"
“◐구미출장안마[070-5222-7802]▶[카톡문의:VV23]♥"
“◐경주출장안마[070-5222-7802]▶[카톡문의:VV23]♥"
“◐일산출장안마[070-5222-7802]▶[카톡문의:VV23]♥"
“◐수원출장안마[070-5222-7802]▶[카톡문의:VV23]♥"
Utterly pent subject material, Really enjoyed looking at.
“◐목포출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐여수출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐순천출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐청주출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐제주출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐원주출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐춘천출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐속초출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
“◐포항출장마사지[070-5222-7802]▶[카톡문의:VV23]♥"
I wish to say that this post is awesome, nice written and come with approximately all significant infos.
“◐강남출장안마[070-5222-7802]▶[카톡-VV23]♥"
“◐부산출장안마[070-7575-0054]▶[카톡-USA16]♥"
“◐대구출장안마[010-2997-5327]▶[카톡-WD777]♥"
“◐인천출장안마[070-5222-6739]▶[카톡-LA666]♥"
“◐광주출장안마[010-2671-8135]▶[카톡-ZHF526]♥"
“◐대전출장안마[070-7575-0062]▶[카톡-DDR88]♥"
“◐울산출장안마[070-7575-0054]▶[카톡-USA16]♥"
“◐세종출장안마[070-5252-7802]▶[카톡-VV23]♥"
“◐천안출장안마[070-7575-0069]▶[카톡-CC6969]♥"
Everything is very oplen with a really clear clarification of the challenges.
It was definitely informative. Your site is useful. Thank you for sharing!
“◐용인출장마사지[070-5222-7802]▶[카톡-VV23]♥"
“◐안산출장마사지[070-7575-0054]▶[카톡-USA16]♥"
“◐화성출장마사지[010-2997-5327]▶[카톡-WD777]♥"
“◐시흥출장마사지[070-5222-6739]▶[카톡-LA666]♥"
“◐파주출장마사지[010-2671-8135]▶[카톡-ZHF526]♥"
“◐광명출장마사지[070-7575-0062]▶[카톡-DDR88]♥"
“◐김포출장마사지[010-2671-8135]▶[카톡-ZHF526]♥"
“◐군포출장마사지[070-7575-0062]▶[카톡-DDR88]♥"
“◐이천출장마사지[010-2997-5327]▶[카톡-WD777]♥"
information with us.
Please stay us informed like this. Thanks for sharing.
“★익산출장서비스[070-5222-7802]▶[카톡-VV23]▣"
“★창원출장서비스[070-7575-0054]▶[카톡-USA16]▣"
“★마산출장서비스[010-2997-5327]▶[카톡-WD777]▣"
“★밀양출장서비스[070-5222-6739]▶[카톡-LA666]▣"
“★거제출장서비스[010-2671-8135]▶[카톡-ZHF526]▣"
“★구미출장서비스[070-7575-0062]▶[카톡-DDR88]▣"
“★경주출장서비스[070-5222-6739]▶[카톡-LA666]▣"
“★일산출장서비스[010-2671-8135]▶[카톡-ZHF526]▣"
“★수원출장서비스[070-7575-0062]▶[카톡-DDR88]▣"
Everything is very oplen with a really clear clarification of the challenges.
It was definitely informative. Your site is useful. Thank you for sharing!
“◐목포출장샵[070-5222-7802]▶[카톡-VV23]♥"
“◐여수출장샵[070-7575-0054]▶[카톡-USA16]♥"
“◐순천출장샵[010-2997-5327▶[카톡-WD777]♥"
“◐청주출장샵[070-5222-6739]▶[카톡-LA666]♥"
“◐제주출장샵[010-2671-8135]▶[카톡-ZHF526]♥"
“◐원주출장샵[070-7575-0062]▶[카톡-DDR88]♥"
“◐춘천출장샵[010-2997-5327]▶[카톡-WD777]♥"
“◐속초출장샵[070-5222-6739]▶[카톡-LA666]♥"
“◐포항출장샵[010-2671-8135]▶[카톡-ZHF526]♥"
Hi there, yeah this paragraph is truly nice and I have learned lot of things from it concerning blogging. thanks.
용인출장샵[070-5222-7802]▶[카톡-VV23]◆"
안산출장샵[070-7575-0054]▶[카톡-USA16]◆"
화성출장샵[010-2997-5327]▶[카톡-WD777]◆"
시흥출장샵[070-5222-6739]▶[카톡-LA666]◆"
파주출장샵[010-2671-8135]▶[카톡-ZHF526]◆"
광명출장샵[070-7575-0062]▶[카톡-DDR88]◆"
김포출장샵[010-2671-8135]▶[카톡-ZHF526]◆"
군포출장샵[070-7575-0062]▶[카톡-DDR88]◆"
이천출장샵[010-2997-5327]▶[카톡-WD777]◆"
Paragraph writing is also a fun, if you know afterward you can write or else it is complicated to write.
용인출장안마[070-5222-7802]▶[카톡-VV23]♥"
안산출장안마[070-7575-0054]▶[카톡-USA16]♥"
화성출장안마[010-2997-5327]▶[카톡-WD777]♥"
시흥출장안마[070-5222-6739]▶[카톡-LA666]♥"
파주출장안마[010-2671-8135]▶[카톡-ZHF526]♥"
광명출장안마[070-7575-0062]▶[카톡-DDR88]♥"
김포출장안마[010-2671-8135]▶[카톡-ZHF526]♥"
군포출장안마[070-7575-0062]▶[카톡-DDR88]♥"
이천출장안마[010-2997-5327]▶[카톡-WD777]♥"
What’s up, of course this paragraph is actually pleasant and I have learned lot of things from it concerning blogging. thanks.
Amazing! This blog looks exactly like my old one! It’s on a completely different
subject but it has pretty much the same layout and design. Superb choice of colors!
sportstoto.biz No need to curse Kane. He was so overwhelmed by strong forward pressure that he was defending Kane.A game in which any striker could not help even though the ball didn’t cross.As you’ve seen, don’t believe the article that copied
목포출장서비스[070-5222-7802]▶[카톡-VV23]▣"
여수출장서비스[070-7575-0054]▶[카톡-USA16]▣"
순천출장서비스[010-2997-5327▶[카톡-WD777]▣"
청주출장서비스[070-5222-6739]▶[카톡-LA666]▣"
제주출장서비스[010-2671-8135]▶[카톡-ZHF526]▣"
원주출장서비스[070-7575-0062]▶[카톡-DDR88]▣"
춘천출장서비스[010-2997-5327]▶[카톡-WD777]▣"
속초출장서비스[070-5222-6739]▶[카톡-LA666]▣"
포항출장서비스[010-2671-8135]▶[카톡-ZHF526]▣"
It is a type of player who can back up himself to shine. There’s nothing she can do for herself.Kane is more free to play when backup workers such as Ali, Ericsson, Son Heung-min distribute it. Without backup, I can’t accept it alone. But even if I like backup, I’ll leave the smell of the bones with the balls that come.
용인출장콜걸 [070-5222-7802] [카톡-VV23]
안산출장콜걸 [070-7575-0054] [카톡-USA16]
화성출장콜걸 [010-2997-5327] [카톡-WD777]
시흥출장콜걸 [070-5222-6739] [카톡-LA666]
파주출장콜걸 [010-2671-8135] [카톡-ZHF526]
광명출장콜걸 [070-7575-0062] [카톡-DDR88]
김포출장콜걸 [010-2671-8135] [카톡-ZHF526]
군포출장콜걸 [070-7575-0062] [카톡-DDR88]
이천출장콜걸 [010-2997-5327] [카톡-WD777]
There’s nothing she can do for herself.Kane is more free to play when backup workers such as Ali, Ericsson, Son Heung-min distribute it. Without backup, I can’t accept it alone. But even if I like backup, I’ll leave the smell of the bones with the balls that come.
익산출장여대생 [070-5222-7802] [카톡-VV23]
창원출장여대생 [070-7575-0054] [카톡-USA16]
마산출장여대생 [010-2997-5327] [카톡-WD777]
밀양출장여대생 [070-5222-6739] [카톡-LA666]
거제출장여대생 [010-2671-8135] [카톡-ZHF526]
구미출장여대생 [070-7575-0062] [카톡-DDR88]
경주출장여대생 [070-5222-6739] [카톡-LA666]
일산출장여대생 [010-2671-8135] [카톡-ZHF526]
수원출장여대생 [070-7575-0062] [카톡-DDR88]
Hi my family member! I wish to say that this post is awesome, great written and come with approximately all vital infos.
구글홍보#구글상단노출,#구글상위노출,구글상위등록,구글광고문의,구글광고대행,무엇이든 물어보세요.#구글상위검색【복&붙▶blackmonad.xyz】
구글홍보#구글키워드홍보,#구글키워드광고,구글키워드조회-구글키워드조회수-구글키워드광고#구글광고,#구글마케팅,#구글키워드노출∝【복&붙▶blackmonad.xyz】
구글홍보#구글키워드광고,#구글키워드홍보,마케팅전쟁/마케팅성공/#구글상위노출대행,다잡아드립니다.∝끈기있게∝성실하게∝【복&붙▶blackmonad.xyz】
공주마사지[070-5222-7802] [카톡-VV23]
김천마사지[070-7575-0054] [카톡-USA16]
가평마사지[010-2997-5327] [카톡-WD777]
충주마사지[070-5222-6739] [카톡-LA666]
사천마사지[010-2671-8135] [카톡-ZHF526]
통영마사지[070-7575-0062] [카톡-DDR88]
포천마사지[070-7575-0069] [카톡-CC6969]
오산마사지[010-2671-8135] [카톡-ZHF526]
남양주마사지[070-5222-7802] [카톡문의:VV23]
강남 출장 콜걸 [070-5222-7802] [카톡 -VV23]
부산 출장 콜걸 [070-7575-0054] [카톡 -USA16]
대구 출장 콜걸 [010 -2997-5327] [카톡 -WD777]
인천 출장 콜걸 [070-5222-6739] [카톡 -LA666]
광주 출장 콜걸 [010-2671-8135] [카톡 -ZHF526]
대전 출장 콜걸 [070-7575-0062] [카톡 -DDR88]
울산 출장 콜걸 [070-7575-0054] [카톡 -USA16]
세종 출장 콜걸 [070-5252-7802] [카톡 -VV23]
천안 출장 콜걸 [070-7575-0069] [카톡 -CC6969]
용인출장여대생 [070-5222-7802] [카톡-VV23]
안산출장여대생 [070-7575-0054] [카톡-USA16]
화성출장여대생 [010-2997-5327] [카톡-WD777]
시흥출장여대생 [070-5222-6739] [카톡-LA666]
파주출장여대생 [010-2671-8135] [카톡-ZHF526]
광명출장여대생 [070-7575-0062] [카톡-DDR88]
김포출장여대생 [010-2671-8135] [카톡-ZHF526]
군포출장여대생 [070-7575-0062] [카톡-DDR88]
이천출장여대생 [010-2997-5327] [카톡-WD777]
Paragraph writing is also a fun, if you know afterward you can write or else it is complicated to write.
공주출장안마[070-5222-7802] [카톡-VV23]
김천출장안마[070-7575-0054] [카톡-USA16]
가평출장안마[010-2997-5327] [카톡-WD777]
충주출장안마[070-5222-6739] [카톡-LA666]
사천출장안마[010-2671-8135] [카톡-ZHF526]
통영출장안마[070-7575-0062] [카톡-DDR88]
포천출장안마[070-7575-0069] [카톡-CC6969]
오산출장안마[010-2671-8135] [카톡-ZHF526]
남양주출장안마[070-5222-7802] [카톡문의:VV23]
Asking questions are genuinely fastidious thing if you
are not understanding something fully, but this post gives fastidious understanding even.
강남마사지[070-5222-7802] [카톡-VV23]
부산마사지[070-7575-0054] [카톡-USA16]
대구마사지[010-2997-5327] [카톡-WD777]
인천마사지[070-5222-6739] [카톡-LA666]
광주마사지[010-2671-8135] [카톡-ZHF526]
대전마사지[070-7575-0062] [카톡-DDR88]
울산마사지[070-7575-0054] [카톡-USA16]
세종마사지[070-5252-7802] [카톡-VV23]
천안마사지[070-7575-0069] [카톡-CC6969]
Asking questions are genuinely fastidious thing if you
are not understanding something fully, but this post gives fastidious understanding even.
익산마사지[070-5222-7802] [카톡-VV23]
창원마사지[070-7575-0054] [카톡-USA16]
마산마사지[010-2997-5327] [카톡-WD777]
밀양마사지[070-5222-6739] [카톡-LA666]
거제마사지[010-2671-8135] [카톡-ZHF526]
구미마사지[070-7575-0062] [카톡-DDR88]
경주마사지[070-5222-6739] [카톡-LA666]
일산마사지[010-2671-8135] [카톡-ZHF526]
수원마사지[070-7575-0062] [카톡-DDR88]
<a href="http://wolfandactress021.com">군산출장안마</a>
<a href="http://wolfandactress022.com">익산출장안마</a>
<a href="http://wolfandactress023.com">창원출장안마</a>
<a href="http://wolfandactress024.com">마산출장안마</a>
<a href="http://wolfandactress025.com">밀양출장안마</a>
<a href="http://wolfandactress026.com">거제출장안마</a>
<a href="http://wolfandactress027.com">구미출장안마</a>
<a href="http://wolfandactress028.com">경주출장안마</a>
<a href="http://wolfandactress029.com">일산출장안마</a>
<a href="http://wolfandactress030.com">수원출장안마</a>
<a href="http://www.totople.com">안전검증공원추천</a>
<a title="스포츠중계" href="http://kinglivetv.com" target="blank">스포츠중계</a>
<a title="스포츠중계" href="http://ele-ac.com" target="blank">스포츠중계</a>
<a title="스포츠중계" href="http://one-sk.com" target="blank">스포츠중계</a>
<a href="http://blackmonad.xyz">구글키워드대행</a>
익산마사지[070-5222-7802] [카톡-VV23]
창원마사지[070-7575-0054] [카톡-USA16]
마산마사지[010-2997-5327] [카톡-WD777]
밀양마사지[070-5222-6739] [카톡-LA666]
거제마사지[010-2671-8135] [카톡-ZHF526]
구미마사지[070-7575-0062] [카톡-DDR88]
경주마사지[070-5222-6739] [카톡-LA666]
일산마사지[010-2671-8135] [카톡-ZHF526]
수원마사지[070-7575-0062] [카톡-DDR88]
<a href="http://wolfandactress021.com">군산출장안마</a>
<a href="http://wolfandactress022.com">익산출장안마</a>
<a href="http://wolfandactress023.com">창원출장안마</a>
<a href="http://wolfandactress024.com">마산출장안마</a>
<a href="http://wolfandactress025.com">밀양출장안마</a>
<a href="http://wolfandactress026.com">거제출장안마</a>
<a href="http://wolfandactress027.com">구미출장안마</a>
<a href="http://wolfandactress028.com">경주출장안마</a>
<a href="http://wolfandactress029.com">일산출장안마</a>
<a href="http://wolfandactress030.com">수원출장안마</a>
<a href="http://www.totople.com">안전검증공원추천</a>
<a title="스포츠중계" href="http://kinglivetv.com" target="blank">스포츠중계</a>
<a title="스포츠중계" href="http://ele-ac.com" target="blank">스포츠중계</a>
<a title="스포츠중계" href="http://one-sk.com" target="blank">스포츠중계</a>
<a href="http://blackmonad.xyz">구글키워드대행</a>
I am truly pleased to glance at this webpage posts which carries lots of useful facts, thanks for providing
these kinds of information.
<a href="http://001-max.com">서울출장마사지</a>
<a href="http://wolfnactress002.com">강남출장마사지</a>
<a href="http://wolfnactress003.com">부산출장마사지</a>
<a href="http://wolfnactress004.com">대구출장마사지</a>
<a href="http://wolfnactress005.com">인천출장마사지</a>
<a href="http://wolfnactress006.com">광주출장마사지</a>
<a href="http://wolfnactress007.com">대전출장마사지</a>
<a href="http://wolfnactress008.com">울산출장마사지</a>
<a href="http://wolfnactress009.com">세종출장마사지</a>
<a href="http://wolfnactress010.com">천안출장마사지</a>
<a href="http://wolfandactress011.com">전주출장마사지</a>
<a href="http://wolfandactress012.com">목포출장마사지</a>
<a href="http://wolfandactress013.com">여수출장마사지</a>
<a href="http://wolfandactress014.com">순천출장마사지</a>
<a href="http://wolfandactress015.com">청주출장마사지</a>
<a href="http://wolfandactress016.com">제주출장마사지</a>
<a href="http://wolfandactress017.com">원주출장마사지</a>
<a href="http://wolfandactress018.com">춘천출장마사지</a>
<a href="http://wolfandactress019.com">속초출장마사지</a>
<a href="http://wolfandactress020.com">포항출장마사지</a>
<a href="http://wolfandactress021.com">군산출장마사지</a>
<a href="http://wolfandactress022.com">익산출장마사지</a>
<a href="http://wolfandactress023.com">창원출장마사지</a>
<a href="http://wolfandactress024.com">마산출장마사지</a>
<a href="http://wolfandactress025.com">밀양출장마사지</a>
<a href="http://wolfandactress026.com">거제출장마사지</a>
<a href="http://wolfandactress027.com">구미출장마사지</a>
<a href="http://wolfandactress028.com">경주출장마사지</a>
<a href="http://wolfandactress029.com">일산출장마사지</a>
<a href="http://wolfandactress030.com">수원출장마사지</a>
<a href="http://wolfandactress031.com">고양출장마사지</a>
<a href="http://wolfandactress032.com">용인출장마사지</a>
<a href="http://wolfandactress033.com">안산출장마사지</a>
<a href="http://wolfandactress034.com">화성출장마사지</a>
<a href="http://wolfandactress035.com">시흥출장마사지</a>
<a href="http://wolfandactress036.com">파주출장마사지</a>
<a href="http://wolfandactress037.com">광명출장마사지</a>
<a href="http://wolfandactress038.com">김포출장마사지</a>
<a href="http://wolfandactress039.com">군포출장마사지</a>
<a href="http://wolfandactress040.com">이천출장마사지</a>
<a href="http://wolfandactress041.com">안성출장마사지</a>
<a href="http://wolfandactress042.com">공주출장마사지</a>
<a href="http://wolfandactress043.com">김천출장마사지</a>
<a href="http://wolfandactress044.com">가평출장마사지</a>
<a href="http://wolfandactress045.com">충주출장마사지</a>
<a href="http://wolfandactress046.com">사천출장마사지</a>
<a href="http://wolfandactress047.com">통영출장마사지</a>
<a href="http://wolfandactress048.com">포천출장마사지</a>
<a href="http://wolfandactress049.com">오산출장마사지</a>
<a href="http://wolfandactress050.com">남양주출장마사지</a>
<a href="http://wolfandactress042.com">공주출장안마</a>OiO 2997 5327 [카톡USA59]
<a href="http://wolfandactress043.com">김천출장안마</a>OiO 6556 7776 [카톡USA16]
<a href="http://wolfandactress044.com">가평출장안마</a>OiO 6556 7776 [카톡LTE16]
<a href="http://wolfandactress045.com">충주출장안마</a>OiO 5636 5853 [카톡WD777]
<a href="http://wolfandactress046.com">사천출장안마</a>OiO 5636 5853 [카톡CC6969]
<a href="http://wolfandactress047.com">통영출장안마</a>OiO 2448 2773 [카톡DDR88]
<a href="http://wolfandactress048.com">포천출장안마</a>OiO 2448 2773 [카톡MGM1472]
<a href="http://wolfandactress049.com">오산출장안마</a>O7O 7575 0054 [카톡OYO78]
<a href="http://wolfandactress050.com">남양주출장안마</a>OiO 3346 1695 [카톡KC789]
<a href="http://wolfandactress031.com">고양출장안마</a>OiO 3346 1695 [카톡RD654]
<a href="http://wolfandactress032.com">용인출장안마</a>OiO 3650 2772 [카톡DK654]
<a href="http://wolfandactress033.com">안산출장안마</a>OiO 3650 2772 [카톡PR777]
<a href="http://wolfandactress034.com">화성출장안마</a>OiO 2134 5606 [카톡GD825]
<a href="http://wolfandactress035.com">시흥출장안마</a>OiO 2640 5853 [카톡QR091]
<a href="http://wolfandactress036.com">파주출장안마</a>010 3283 8202 [카톡BK57]
<a href="http://wolfandactress037.com">광명출장안마</a>010 3283 8202 [카톡OK58]
<a href="http://wolfandactress038.com">김포출장안마</a>010 6547 8399 [카톡GH50]
<a href="http://wolfandactress039.com">군포출장안마</a>010 6547 8399 [카톡GT1050]
<a href="http://wolfandactress040.com">이천출장안마</a>010 9652 9131 [카톡HD65]
<a href="http://wolfandactress021.com">군산출장안마</a>010 9652 9131 [카톡RW36]
<a href="http://wolfandactress022.com">익산출장안마</a>010 7378 6718 [카톡MX518]
<a href="http://wolfandactress023.com">창원출장안마</a>010 7378 6718 [카톡DM25]
<a href="http://wolfandactress024.com">마산출장안마</a>010 9539 1257 [카톡TU10]
<a href="http://wolfandactress025.com">밀양출장안마</a>010 9539 1257 [카톡TV40]
<a href="http://wolfandactress026.com">거제출장안마</a>O1O 2163 5606 [카톡ZF66]
<a href="http://wolfandactress027.com">구미출장안마</a>O1Ox5528x7015{카톡YG69}
<a href="http://wolfandactress042.com">공주출장안마</a>OiO 2997 5327 [카톡USA59]
<a href="http://wolfandactress043.com">김천출장안마</a>OiO 6556 7776 [카톡USA16]
<a href="http://wolfandactress044.com">가평출장안마</a>OiO 6556 7776 [카톡LTE16]
<a href="http://wolfandactress045.com">충주출장안마</a>OiO 5636 5853 [카톡WD777]
<a href="http://wolfandactress046.com">사천출장안마</a>OiO 5636 5853 [카톡CC6969]
<a href="http://wolfandactress047.com">통영출장안마</a>OiO 2448 2773 [카톡DDR88]
<a href="http://wolfandactress048.com">포천출장안마</a>OiO 2448 2773 [카톡MGM1472]
<a href="http://wolfandactress049.com">오산출장안마</a>O7O 7575 0054 [카톡OYO78]
<a href="http://wolfandactress050.com">남양주출장안마</a>OiO 3346 1695 [카톡KC789]
<a href="http://wolfandactress031.com">고양출장안마</a>OiO 3346 1695 [카톡RD654]
<a href="http://wolfandactress032.com">용인출장안마</a>OiO 3650 2772 [카톡DK654]
<a href="http://wolfandactress033.com">안산출장안마</a>OiO 3650 2772 [카톡PR777]
<a href="http://wolfandactress034.com">화성출장안마</a>OiO 2134 5606 [카톡GD825]
<a href="http://wolfandactress035.com">시흥출장안마</a>OiO 2640 5853 [카톡QR091]
<a href="http://wolfandactress036.com">파주출장안마</a>010 3283 8202 [카톡BK57]
<a href="http://wolfandactress037.com">광명출장안마</a>010 3283 8202 [카톡OK58]
<a href="http://wolfandactress038.com">김포출장안마</a>010 6547 8399 [카톡GH50]
<a href="http://wolfandactress039.com">군포출장안마</a>010 6547 8399 [카톡GT1050]
<a href="http://wolfandactress040.com">이천출장안마</a>010 9652 9131 [카톡HD65]
<a href="http://wolfandactress021.com">군산출장안마</a>010 9652 9131 [카톡RW36]
<a href="http://wolfandactress022.com">익산출장안마</a>010 7378 6718 [카톡MX518]
<a href="http://wolfandactress023.com">창원출장안마</a>010 7378 6718 [카톡DM25]
<a href="http://wolfandactress024.com">마산출장안마</a>010 9539 1257 [카톡TU10]
<a href="http://wolfandactress025.com">밀양출장안마</a>010 9539 1257 [카톡TV40]
<a href="http://wolfandactress026.com">거제출장안마</a>O1O 2163 5606 [카톡ZF66]
<a href="http://wolfandactress027.com">구미출장안마</a>O1Ox5528x7015{카톡YG69}
<A HREF="https://vfv79.com/" TARGET='_blank'>카지노</A>
https://vfv79.com/woori/
https://nolza2000.com
https://casino815.com/
https://casino815.com/baccaratsite/
<A HREF="https://nun777.com/" TARGET='_blank'>카지노사이트</A>
https://nun777.com/roulettesite
http://treeads.nation2.com/
https://jumperads.yolasite.com/
http://jumperads.nation2.com/
http://transferefurniture.hatenablog.com
https://allmoversinriyadh.wordpress.com/
https://companymoversinjeddah.wordpress.com/
https://moversfurniture2018.wordpress.com/
https://moversriyadhcom.wordpress.com/
https://moversmedina.wordpress.com/
https://moversfurniture2018.wordpress.com/
<a href="https://companymoversinjeddah.wordpress.com/">شركات نقل عفش واثاث بجدة</a>
<a href="https://companymoversinjeddah.wordpress.com/2019/02/16/%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d9%88%d8%a7%d8%ab%d8%a7%d8%ab-%d8%a8%d8%a7%d9%84%d8%b7%d8%a7%d8%a6%d9%81-%d8%af%d9%8a%d9%86%d8%a7-%d8%af%d8%a8%d8%a7%d8%a8-%d9%86/">شركات نقل عفش بالطائف</a>
<a href="https://companymoversinjeddah.wordpress.com/2019/02/15/%d8%a7%d8%b3%d8%b9%d8%a7%d8%b1-%d9%88%d8%a7%d8%b1%d9%82%d8%a7%d9%85-%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d9%86%d9%82%d9%84-%d8%a7%d9%84%d8%b9%d9%81%d8%b4-%d8%a8%d8%a7%d9%84%d9%85%d8%af%d9%8a%d9%86%d8%a9/">اسعار وارقام شركات نقل العفش بالمدينة المنورة</a>
<a href="https://companymoversinjeddah.wordpress.com/2019/02/15/%d8%af%d9%8a%d9%86%d8%a7-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%ac%d8%af%d8%a9-%d8%a7%d9%81%d8%b6%d9%84-%d8%af%d9%8a%d9%86%d8%a7/">دينا نقل عفش جدة ,افضل دينا</a>
<a href="https://companymoversinjeddah.wordpress.com/2019/02/15/%d8%a7%d8%b1%d8%ae%d8%b5-%d8%b4%d8%b1%d9%83%d9%87-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%ac%d8%af%d9%87-%d8%a7%d8%b3%d8%b9%d8%a7%d8%b1-%d9%81%d8%b5%d9%84-%d8%a7%d9%84%d8%b4%d8%aa%d8%a7%d8%a1/">ارخص شركه نقل عفش بجده</a>
<a href="https://companymoversinjeddah.wordpress.com/2019/02/15/%d8%af%d9%84%d9%8a%d9%84-%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d9%86%d9%82%d9%84-%d8%a7%d9%84%d8%b9%d9%81%d8%b4-%d8%a8%d8%ac%d8%af%d8%a9-%d9%85%d8%b9-%d8%ae%d8%b5%d9%88%d9%85%d8%a7%d8%aa/">دليل شركات نقل العفش بجدة</a>
<a href="https://companymoversinjeddah.wordpress.com/2019/02/15/%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%b1%d8%a7%d8%a8%d8%ba-15-%d8%b9%d8%a7%d9%85-%d8%ae%d8%a8%d8%b1%d8%a9/">شركة نقل عفش برابغ ,15 عام خبرة</a>
<a href="https://companymoversinjeddah.wordpress.com/2018/12/12/%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d9%88%d8%a7%d8%ab%d8%a7%d8%ab-%d8%a8%d8%a7%d9%84%d8%a8%d8%a7%d8%ad%d9%87/">شركات نقل عفش واثاث بالباحه</a>
<a href="https://companymoversinjeddah.wordpress.com/2018/12/12/start-moving-company-to-khamis-mushit/">وسائل نقل العفش بخميس مشيط</a>
اهم شركات كشف تسربات المياه بالدمام كذلك معرض اهم شركة مكافحة حشرات بالدمام والخبر والجبيل والخبر والاحساء والقطيف كذكل شركة تنظيف خزانات بجدة وتنظيف بجدة ومكافحة الحشرات بالخبر وكشف تسربات المياه بالجبيل والقطيف والخبر والدمام
http://emc-mee.com/tanks-cleaning-company-jeddah.html شركة تنظيف خزانات بجدة
http://emc-mee.com/water-leaks-detection-isolate-company-dammam.html شركة كشف تسربات المياه بالدمام
http://emc-mee.com/anti-insects-company-dammam.html شركة مكافحة حشرات بالدمام
http://emc-mee.com/tanks-cleaning-company-jeddah.html شركة تنظيف خزانات بجدة
http://emc-mee.com/ شركة نقل عفش واثاث
http://emc-mee.com/movers-in-riyadh-company.html شركة نقل اثاث بالرياض
http://emc-mee.com/transfer-furniture-jeddah.html شركة نقل عفش بجدة
http://emc-mee.com/transfer-furniture-dammam.html شركة نقل عفش بالدمام
http://emc-mee.com/transfer-furniture-almadina-almonawara.html شركة نقل عفش بالمدينة المنورة
http://emc-mee.com/transfer-furniture-taif.html شركة نقل عفش بالطائف
http://emc-mee.com/transfer-furniture-mecca.html شركة نقل عفش بمكة
اهم شركات نقل العفش والاثاث بالدمام والخبر والجبيل اولقطيف والاحساء والرياض وجدة ومكة المدينة المنورة والخرج والطائف وخميس مشيط وبجدة افضل شركة نقل عفش بجدة نعرضها مجموعة الفا لنقل العفش بمكة والخرج والقصيم والطائف وتبوك وخميس مشيط ونجران وجيزان وبريدة والمدينة المنورة وينبع افضل شركات نقل الاثاث بالجبيل والطائف وخميس مشيط وبريدة وعنيزو وابها ونجران المدينة وينبع تبوك والقصيم الخرج حفر الباطن والظهران
http://emc-mee.com/transfer-furniture-yanbu.html شركة نقل عفش بينبع
http://emc-mee.com/transfer-furniture-buraydah.html شركة نقل عفش ببريدة
http://emc-mee.com/transfer-furniture-alkharj.html شركة نقل عفش بالخرج
http://emc-mee.com/transfer-furniture-qassim.html شركة نقل عفش بالقصيم
http://emc-mee.com/transfer-furniture-khamis-mushait.html شركة نقل عفش بخميس مشيط
http://emc-mee.com/transfer-furniture-tabuk.html شركة نقل عفش بتبوك
http://emc-mee.com/transfer-furniture-abha.html شركة نقل عفش بابها
http://emc-mee.com/transfer-furniture-najran.html شركة نقل عفش بنجران
http://emc-mee.com/transfer-furniture-hail.html شركة نقل عفش بحائل
http://emc-mee.com/transfer-furniture-dhahran.html شركة نقل عفش بالظهران
http://emc-mee.com/transfer-furniture-kuwait.html شركة نقل عفش بالكويت
http://jumperads.com/transfer-furniture-riyadh.html شركة نقل عفش بالرياض
http://jumperads.com/transfer-furniture-jeddah.html شركة نقل عفش بجدة
http://jumperads.com/transfer-furniture-dammam.html شركة نقل عفش بالدمام
http://jumperads.com/transfer-furniture-medina-almonawara.html شركة نقل عفش بالمدينة المنورة
http://jumperads.com/transfer-furniture-taif.html شركة نقل عفش بالطائف
http://jumperads.com/transfer-furniture-mecca.html شركة نقل عفش بمكة
http://jumperads.com/transfer-furniture-yanbu.html شركة نقل عفش بينبع
http://jumperads.com/transfer-furniture-in-najran.html شركة نقل عفش بنجران
http://jumperads.com/transfer-furniture-in-khamis-mushait.html شركة نقل عفش بخميس مشيط
http://jumperads.com/transfer-furniture-abha.html شركة نقل عفش بابها
http://jumperads.com/transfer-furniture-buraydah.html شركة نقل عفش ببريدة
http://jumperads.com/transfer-furniture-qassim.html شركة نقل عفش بالقصيم
http://jumperads.com/transfer-furniture-tabuk.html شركة نقل عفش بتبوك
http://jumperads.com/transfer-furniture-hail.html شركة نقل عفش بحائل
http://jumperads.com/transfer-furniture-dammam-khobar.html شركة نقل عفش بالخبر
http://jumperads.com/transfer-furniture-ahsa.html شركة نقل عفش بالاحساء
http://jumperads.com/transfer-furniture-qatif.html شركة نقل عفش بالقطيف
http://jumperads.com/transfer-furniture-jubail.html شركة نقل عفش بالجبيل
http://treeads.net/ شركة سكاي لنقل العفش
http://treeads.net/movers-mecca.html نقل عفش بمكة
http://treeads.net/movers-riyadh-company.html نقل عفش بالرياض
http://treeads.net/all-movers-madina.html نقل عفش بالمدينة المنورة
http://treeads.net/movers-jeddah-company.html نقل عفش بجدة
http://treeads.net/movers-taif.html نقل عفش بالطائف
http://treeads.net/movers-dammam-company.html نقل عفش بالدمام
http://treeads.net/movers-qatif.html نقل عفش بالقطيف
http://treeads.net/movers-jubail.html نقل عفش بالجبيل
http://treeads.net/movers-khobar.html نقل عفش بالخبر
http://treeads.net/movers-ahsa.html نقل عفش بالاحساء
http://treeads.net/movers-kharj.html نقل عفش بالخرج
http://treeads.net/movers-khamis-mushait.html نقل عفش بخميس مشيط
http://treeads.net/movers-abha.html نقل عفش بابها
http://treeads.net/movers-qassim.html نقل عفش بالقصيم
http://treeads.net/movers-yanbu.html نقل عفش بينبع
http://treeads.net/movers-najran.html نقل عفش بنجران
http://treeads.net/movers-hail.html نقل عفش بحائل
http://treeads.net/movers-buraydah.html نقل عفش ببريدة
http://treeads.net/movers-tabuk.html نقل عفش بتبوك
http://treeads.net/movers-dhahran.html نقل عفش بالظهران
http://treeads.net/movers-rabigh.html نقل عفش برابغ
http://treeads.net/movers-baaha.html نقل عفش بالباحه
http://treeads.net/movers-asseer.html نقل عفش بعسير
http://treeads.net/movers-mgmaa.html نقل عفش بالمجمعة
http://treeads.net/movers-sharora.html نقل عفش بشرورة
http://treeads.net/movers-najran.html
http://www.domyate.com/2016/06/05/transfer-furniture-medina-almonawara شركة نقل عفش بالمدينة المنورة
http://www.domyate.com/2016/06/05/transfer-furniture-mecca شركة نقل عفش بمكة
http://www.domyate.com/2016/06/05/transfer-furniture-riyadh شركة نقل عفش بالرياض
http://www.domyate.com/2016/06/05/transfer-furniture-jeddah شركة نقل عفش بجدة
http://www.domyate.com/2016/06/05/transfer-furniture-taif شركة نقل عفش بالطائف
http://www.domyate.com/2016/06/05/transfer-furniture-yanbu شركة نقل عفش بينبع
http://www.domyate.com/2016/07/02/transfer-furniture-dammam شركة نقل عفش بالدمام
http://www.domyate.com/2017/08/10/movers-company-mecca-naql/
http://www.domyate.com شركة نقل عفش بالدمام
http://mycanadafitness.com/ شركة كيان لنقل العفش
http://mycanadafitness.com/forum.html منتدي نقل العفش
http://mycanadafitness.com/movingfurnitureriyadh.html شركة نقل اثاث بالرياض
http://mycanadafitness.com/movingfurniturejaddah.html شركة نقل اثاث بجدة
http://mycanadafitness.com/movingfurnituremecca.html شركة نقل اثاث بمكة
http://mycanadafitness.com/movingfurnituretaif.html شركة نقل اثاث بالطائف
http://mycanadafitness.com/movingfurnituremadina.html شركة نقل اثاث بالمدينة المنورة
http://mycanadafitness.com/movingfurnituredammam.html شركة نقل اثاث بالدمام
http://mycanadafitness.com/movingfurniturekhobar.html شركة نقل اثاث بالخبر
http://mycanadafitness.com/movingfurnituredhahran.html شركة نقل اثاث بالظهران
http://mycanadafitness.com/movingfurniturejubail.html شركة نقل اثاث بالجبيل
http://mycanadafitness.com/movingfurnitureqatif.html شركة نقل اثاث بالقطيف
http://mycanadafitness.com/movingfurnitureahsa.html شركة نقل اثاث بالاحساء
http://mycanadafitness.com/movingfurniturekharj.html شركة نقل اثاث بالخرج
http://mycanadafitness.com/movingfurniturekhamismushit.html شركة نقل اثاث بخميس مشيط
http://mycanadafitness.com/movingfurnitureabha.html شركة نقل اثاث بابها
http://mycanadafitness.com/movingfurniturenajran.html شركة نقل اثاث بنجران
http://mycanadafitness.com/movingfurniturejazan.html شركة نقل اثاث بجازان
http://mycanadafitness.com/movingfurnitureasir.html شركة نقل اثاث بعسير
http://mycanadafitness.com/movingfurniturehail.html شركة نقل اثاث بحائل
http://mycanadafitness.com/movingfurnitureqassim.html شركة نقل عفش بالقصيم
http://mycanadafitness.com/movingfurnitureyanbu.html شركة نقل اثاث بينبع
http://mycanadafitness.com/movingfurnitureburaidah.html شركة نقل عفش ببريدة
http://mycanadafitness.com/movingfurniturehafralbatin.html شركة نقل عفش بحفر الباطن
http://mycanadafitness.com/movingfurniturerabigh.html شركة نقل عفش برابغ
http://mycanadafitness.com/movingfurnituretabuk.html شركة نقل عفش بتبوك
http://mycanadafitness.com/movingfurnitureasfan.html شركة نقل عفش بعسفان
http://mycanadafitness.com/movingfurnituresharora.html شركة نقل عفش بشرورة
http://mycanadafitness.com/companis-moving-riyadh.html شركات نقل العفش بالرياض
http://mycanadafitness.com/cars-moving-riyadh.html سيارات نقل العفش بالرياض
http://mycanadafitness.com/company-number-moving-riyadh.html ارقام شركات نقل العفش بالرياض
http://mycanadafitness.com/company-moving-jeddah.html شركات نقل العفش بجدة
http://mycanadafitness.com/price-moving-jeddah.html اسعار نقل العفش بجدة
http://mycanadafitness.com/company-moving-mecca.html شركات نقل العفش بمكة
http://fullservicelavoro.com/2019/01/07/transfer-movers-taif-furniture/ شركة نقل عفش بالطائف
http://fullservicelavoro.com/2019/01/08/transfer-movers-riyadh-furniture/ شركة نقل عفش بالرياض
http://fullservicelavoro.com/2019/01/08/transfer-movers-jeddah-furniture/ شركة نقل عفش بجدة
http://fullservicelavoro.com/2019/01/01/transfer-and-movers-furniture-mecca/ شركة نقل عفش بمكة
http://fullservicelavoro.com/2019/01/07/transfer-movers-madina-furniture/ شركة نقل عفش بالمدينة المنورة
http://fullservicelavoro.com/2019/01/07/transfer-movers-khamis-mushait-furniture/ شركة نقل عفش بخميس مشيط
http://fullservicelavoro.com/2019/01/09/transfer-movers-abha-furniture/ شركة نقل اثاث بابها
http://fullservicelavoro.com/2019/01/07/transfer-movers-najran-furniture/ شركة نقل عفش بنجران
http://fullservicelavoro.com/2019/01/16/transfer-movers-hail-furniture/ ِشركة نقل عفش بحائل
http://fullservicelavoro.com/2019/01/16/transfer-movers-qassim-furniture/ شركة نقل عفش بالقصيم
http://fullservicelavoro.com/2019/02/02/transfer-movers-furniture-in-bahaa/ شركة نقل عفش بالباحة
http://fullservicelavoro.com/2019/01/13/transfer-movers-yanbu-furniture/ شركة نقل عفش بينبع
http://fullservicelavoro.com/2019/01/18/%d8%af%d9%8a%d9%86%d8%a7-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%a7%d8%a8%d9%87%d8%a7/ دينا نقل عفش بابها
http://fullservicelavoro.com/2019/01/13/%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%A7%D8%AB%D8%A7%D8%AB-%D8%A8%D8%A7%D9%84%D9%85%D8%AF%D9%8A%D9%86%D8%A9-%D8%A7%D9%84%D9%85%D9%86%D9%88%D8%B1%D8%A9-%D8%A7%D9%87%D9%85-%D8%B4%D8%B1%D9%83%D8%A7%D8%AA/ نقل الاثاث بالمدينة المنورة
http://fullservicelavoro.com/2019/01/12/%D8%A7%D8%B1%D8%AE%D8%B5-%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D9%85%D9%83%D8%A9/ ارخص شركة نقل عفش بمكة
http://fullservicelavoro.com/2019/01/07/transfer-movers-elkharj-furniture/ شركة نقل عفش بالخرج
http://fullservicelavoro.com/2019/01/07/transfer-movers-baqaa-furniture/ شركة نقل عفش بالبقعاء
http://fullservicelavoro.com/2019/02/05/transfer-furniture-in-jazan/ شركة نقل عفش بجازان
http://transferefurniture.bcz.com/2016/08/01/%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%a7%d9%84%d9%85%d8%af%d9%8a%d9%86%d8%a9-%d8%a7%d9%84%d9%85%d9%86%d9%88%d8%b1%d8%a9/ شركة نقل عفش بالمدينة المنورة
http://transferefurniture.bcz.com/2016/08/01/%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%a7%d9%84%d8%af%d9%85%d8%a7%d9%85/ شركة نقل عفش بالدمام
http://transferefurniture.bcz.com/2016/07/31/%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%a7%d9%84%d8%b1%d9%8a%d8%a7%d8%b6/ شركة نقل عفش بالرياض
http://transferefurniture.bcz.com/ شركة نقل عفش | http://transferefurniture.bcz.com/ شركة نقل اثاث بجدة | http://transferefurniture.bcz.com/ شركة نقل عفش بالرياض | http://transferefurniture.bcz.com/ شركة نقل عفش بالمدينة المنورة | http://transferefurniture.bcz.com/ شركة نقل عفش بالدمام
http://khairyayman.inube.com/blog/5015576// شركة نقل عفش بجدة
http://khairyayman.inube.com/blog/5015578// شركة نقل عفش بالمدينة المنورة
http://khairyayman.inube.com/blog/5015583// شركة نقل عفش بالدمام
http://emc-mee.jigsy.com/ شركة نقل عفش الرياض,شركة نقل عفش بجدة,شركة نقل عفش بالمدينة المنورة,شركة نقل عفش بالدمام
http://emc-mee.jigsy.com/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%A7%D9%84%D8%B1%D9%8A%D8%A7%D8%B6 شركة نقل عفش بالرياض
http://emc-mee.jigsy.com/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%A7%D8%AB%D8%A7%D8%AB-%D8%A8%D8%AC%D8%AF%D8%A9 شركة نقل اثاث بجدة
http://emc-mee.jigsy.com/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%A7%D9%84%D9%85%D8%AF%D9%8A%D9%86%D8%A9-%D8%A7%D9%84%D9%85%D9%86%D9%88%D8%B1%D8%A9 شركة نقل عفش بالمدينة المنورة
http://emc-mee.jigsy.com/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%A7%D9%84%D8%AF%D9%85%D8%A7%D9%85 شركة نقل عفش بالدمام
https://about.me/easteldmam easteldmam
http://east-eldmam.skyrock.com/ east-eldmam
http://east-eldmam.mywapblog.com/post-title.xhtml شركة نقل عفش بالدمام
http://transferefurniture.zohosites.com/ شركة نقل عفش
http://transferefurniture.hatenablog.com/ شركة نقل عفش
http://khairyayman.eklablog.com/http-emc-mee-com-transfer-furniture-almadina-almonawara-html-a126376958 شركة نقل عفش بالمدينة المنورة
http://khairyayman.eklablog.com/http-emc-mee-com-transfer-furniture-jeddah-html-a126377054 شركة نقل عفش بجدة
http://khairyayman.eklablog.com/http-emc-mee-com-movers-in-riyadh-company-html-a126376966 شركة نقل عفش بالرياض
http://khairyayman.eklablog.com/http-www-east-eldmam-com-a126377148 شركة نقل عفش بالدمام
http://east-eldmam.beep.com/ شركة نقل عفش
https://www.smore.com/51c2u شركة نقل عفش | https://www.smore.com/hwt47 شركة نقل اثاث بجدة | https://www.smore.com/51c2u شركة نقل عفش بالرياض | https://www.smore.com/u9p9m شركة نقل عفش بالمدينة المنورة | https://www.smore.com/51c2u شركة نقل عفش بالدمام
https://www.smore.com/zm2es شركة نقل عفش بالدمام
https://khairyayman74.wordpress.com/2016/07/04/transfer-furniture-jeddah/ شركة نقل عفش بجدة
https://khairyayman74.wordpress.com/2016/06/14/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%B9%D9%81%D8%B4-%D8%A8%D8%A7%D9%84%D9%85%D8%AF%D9%8A%D9%86%D8%A9-%D8%A7%D9%84%D9%85%D9%86%D9%88%D8%B1%D8%A9/ شركة نقل العفش بالمدينة المنورة
https://khairyayman74.wordpress.com/2016/06/14/%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%B9%D9%81%D8%B4-%D8%A8%D8%A7%D9%84%D8%B1%D9%8A%D8%A7%D8%B6/ نقل العفش بالرياض
https://khairyayman74.wordpress.com/2016/05/26/%d9%87%d9%84-%d8%b9%d8%ac%d8%b2%d8%aa-%d9%81%d9%89-%d8%a8%d8%ad%d8%ab%d9%83-%d8%b9%d9%86-%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%a7%d9%84%d8%af%d9%85%d8%a7%d9%85/ نقل عفش بالدمام
https://khairyayman74.wordpress.com/2016/05/24/%d8%a7%d8%ad%d8%b3%d9%86-%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d9%86%d9%82%d9%84-%d8%a7%d8%ab%d8%a7%d8%ab-%d8%a8%d8%a7%d9%84%d8%af%d9%85%d8%a7%d9%85/ شركات نقل اثاث بالدمام
https://khairyayman74.wordpress.com/2015/07/23/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%A7%D8%AB%D8%A7%D8%AB-%D9%81%D9%89-%D8%A7%D9%84%D8%AE%D8%A8%D8%B1-0559328721/ شركة نقل اثاث بالخبر
https://khairyayman74.wordpress.com/2016/02/25/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%AC%D8%AF%D8%A9/ شركة نقل عفش بجدة
https://khairyayman74.wordpress.com/%D8%B4%D8%B1%D9%83%D8%A9-%D8%BA%D8%B3%D9%8A%D9%84-%D9%85%D8%B3%D8%A7%D8%A8%D8%AD-%D8%A8%D8%A7%D9%84%D8%AF%D9%85%D8%A7%D9%85/ شركة غسيل مسابح بالدمام
https://khairyayman74.wordpress.com/2016/06/14/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%B9%D9%81%D8%B4-%D8%A8%D8%A7%D9%84%D9%85%D8%AF%D9%8A%D9%86%D8%A9-%D8%A7%D9%84%D9%85%D9%86%D9%88%D8%B1%D8%A9/ شركة نقل العفش بالمدينة المنورة
http://www.khdmat-sa.com/2016/07/09/transfere-furniture-in-dammam/ ارخص شركات نقل العفش بالدمام
https://khairyayman74.wordpress.com/2015/07/14/%D8%B4%D8%B1%D9%83%D8%A9-%D8%BA%D8%B3%D9%8A%D9%84-%D8%A7%D9%84%D9%81%D9%84%D9%84-%D9%88%D8%A7%D9%84%D9%82%D8%B5%D9%88%D8%B1-%D8%A8%D8%A7%D9%84%D8%AF%D9%85%D8%A7%D9%85/ شركة غسيل الفلل بالدمام
https://khairyayman74.wordpress.com/2015/06/30/%D8%B4%D8%B1%D9%83%D8%A9-%D8%BA%D8%B3%D9%8A%D9%84-%D9%83%D9%86%D8%A8-%D8%A8%D8%A7%D9%84%D8%AF%D9%85%D8%A7%D9%85-0548923301/ شركة غسيل كنب بالدمام
https://khairyayman74.wordpress.com/2016/04/23/%d9%85%d8%a7%d9%87%d9%89-%d8%a7%d9%84%d9%85%d9%85%d9%8a%d8%b2%d8%a7%d8%aa-%d9%84%d8%af%d9%89-%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d9%85%d9%83%d8%a9%d8%9f/ نقل العفش بمكة
https://khairyayman74.wordpress.com/2016/09/26/anti-insects-company-dammam/ شركة مكافحة حشرات بالدمام
http://emcmee.blogspot.com.eg/ شركة نقل عفش
http://emcmee.blogspot.com.eg/2016/04/blog-post.html شركة نقل عفش بجدة
http://emcmee.blogspot.com.eg/2017/07/transfere-mecca-2017.html
http://emcmee.blogspot.com.eg/2016/04/blog-post_11.html شركة نقل عفش بالطائف
http://emcmee.blogspot.com.eg/2016/06/blog-post.html شركة نقل عفش بالمدينة المنورة
http://eslamiatview.blogspot.com.eg/2016/05/blog-post.html نقل عفش بالدمام
http://eslamiatview.blogspot.com.eg/2016/05/30.html شركة نقل عفش بمكة
http://eslamiatview.blogspot.com.eg/2015/11/furniture-transporter-in-dammam.html شركة نقل عفش بالخبر
https://khairyayman74.wordpress.com/2016/04/11/%D8%B4%D8%B1%D9%83%D8%A9-%D8%AA%D9%86%D8%B8%D9%8A%D9%81-%D8%AE%D8%B2%D8%A7%D9%86%D8%A7%D8%AA-%D8%A8%D8%AC%D8%AF%D8%A9/ شركة تنظيف خزانات بجدة
https://khairyayman74.wordpress.com/ خدمات تنظيف بالمملكه
https://khairyayman74.wordpress.com/2015/08/31/%D8%B4%D8%B1%D9%83%D8%A9-%D8%BA%D8%B3%D9%8A%D9%84-%D8%A7%D9%84%D8%AE%D8%B2%D8%A7%D9%86%D8%A7%D8%AA-%D8%A8%D8%B1%D8%A7%D8%B3-%D8%A7%D9%84%D8%AA%D9%86%D9%88%D8%B1%D9%87-0556808022/ شركة غسيل الخزانات براس التنوره
https://khairyayman74.wordpress.com/2015/07/29/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%A7%D8%AB%D8%A7%D8%AB-%D8%AF%D8%A7%D8%AE%D9%84-%D8%A7%D9%84%D8%AC%D8%A8%D9%8A%D9%84/ شركة نقل اثاث بالجبيل
https://khairyayman74.wordpress.com/2015/07/13/%D8%A7%D9%81%D8%B6%D9%84-%D8%B4%D8%B1%D9%83%D8%A9-%D9%85%D9%83%D8%A7%D9%81%D8%AD%D8%A9-%D8%A7%D9%84%D8%B5%D8%B1%D8%A7%D8%B5%D9%8A%D8%B1-%D8%A8%D8%A7%D9%84%D8%AF%D9%85%D8%A7%D9%85/ شركة مكافحة صراصير بالدمام
https://khairyayman74.wordpress.com/2015/05/30/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%A7%D8%AB%D8%A7%D8%AB-%D8%A8%D8%A7%D9%84%D8%AF%D9%85%D8%A7%D9%85/ شركة نقل اثاث بالدمام
https://khairyayman74.wordpress.com/2015/08/19/%D8%B4%D8%B1%D9%83%D8%A9-%D8%AA%D9%86%D8%B8%D9%8A%D9%81-%D9%85%D9%86%D8%A7%D8%B2%D9%84-%D9%81%D9%8A-%D8%A7%D9%84%D8%AF%D9%85%D8%A7%D9%85-0548923301/ شركة تنظيف منازل فى الدمام
https://khairyayman74.wordpress.com/2016/02/23/%d8%b4%d8%b1%d9%83%d8%a9-%d9%83%d8%b4%d9%81-%d8%aa%d8%b3%d8%b1%d8%a8%d8%a7%d8%aa-%d8%a7%d9%84%d9%85%d9%8a%d8%a7%d9%87-%d8%a8%d8%a7%d9%84%d8%af%d9%85%d8%a7%d9%85/ شركة كشف تسربات المياه بالدمام
https://khairyayman74.wordpress.com/2015/10/18/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%A7%D9%84%D8%B7%D8%A7%D8%A6%D9%81/ شركة نقل عفش بالطائف
http://eslamiatview.blogspot.com.eg/2015/08/blog-post.html شركات نقل عفش بالدمام
http://eslamiatview.blogspot.com.eg/2015/09/0504194709.html شركة تنظيف خزانات بالمدينة المنورة
http://eslamiatview.blogspot.com.eg/2015/09/0504194709.html شركة نقل عفش بالجبيل
http://eslamiatview.blogspot.com.eg/2015/07/blog-post.html شركة غسيل كنب بالدمام
<a href="https://khairyayman74.wordpress.com/2020/01/28/%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d8%aa%d9%86%d8%b8%d9%8a%d9%81-%d8%ae%d8%b2%d8%a7%d9%86%d8%a7%d8%aa-%d8%a8%d8%ac%d8%af%d8%a9-%d8%ae%d8%b5%d9%85-60/">شركات تنظيف خزانات بجدة</a>
<a href="https://khairyayman74.wordpress.com/2020/01/25/movers-khobar/">نقل عفش بالخبر</a>
<a href="https://khairyayman74.wordpress.com/2020/01/25/mover-furniture-khamis-mushait/">شركة نقل عفش بخميس مشيط</a>
<a href="https://khairyayman74.wordpress.com/2020/01/24/%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%a7%d9%84%d8%a7%d8%ad%d8%b3%d8%a7%d8%a1-2/">شركة نقل عفش بالاحساء</a>
<a href="https://khairyayman74.wordpress.com/2020/01/15/company-transfer-furniture-jeddah/">شركة نقل عفش بجدة</a>
<a href="https://khairyayman74.wordpress.com/2017/08/19/%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a7%d9%84%d9%85%d9%86%d8%a7%d8%b2%d9%84-%d8%a8%d8%a7%d9%84%d9%85%d8%af%d9%8a%d9%86%d8%a9-%d8%a7%d9%84%d9%85%d9%86%d9%88%d8%b1%d8%a9/">نقل عفش بالمدينة المنورة</a>
<a href="https://khairyayman74.wordpress.com/2017/06/15/movers-taif-2/">نقل عفش بالطائف</a>
Please enjoy how to use it and various coupon benefits.
http://www.evobench.com/
http://www.evobench.com/에볼루션-카지노
http://www.evobench.com/에볼루션-바카라
http://www.evobench.com/에볼루션-블랙잭
http://www.evobench.com/에볼루션-룰렛
에볼루션
에볼루션본사
에볼루션게임
에볼루션장점
에볼루션코리아
에블루션카지노
에볼루션게이밍
에볼루션이벤트
에볼루션카지노픽
에볼루션보드게임
에볼루션카지노가입
에볼루션카지노쿠폰
에볼루션코리아주소
에볼루션카지노작업
에볼루션카지노롤링
에볼루션카지노검증
에볼루션카지노마틴
에볼루션카지노양방
에볼루션카지노해킹
에볼루션카지노사이트
에볼루션카지노도메인
에볼루션카지노가이드
에볼루션카지노바카라
에볼루션카지노이벤트
에볼루션게이밍코리아
에볼루션카지노에이전시
에볼루션카지노가입쿠폰
에볼루션카지노이용방법
http://www.evobench.com/에볼루션-카지노
http://www.evobench.com/에볼루션-바카라
http://www.evobench.com/에볼루션-블랙잭
http://www.evobench.com/에볼루션-룰렛
#에볼루션블랙잭
#에볼루션블랙잭게임
#에볼루션블랙잭가입
#에볼루션블랙잭쿠폰
#에볼루션블랙잭작업
#에볼루션블랙잭롤링
#에볼루션블랙잭검증
#에볼루션블랙잭양방
#에볼루션블랙잭종류
#에볼루션블랙잭특징
#에볼루션블랙잭사이트
#에볼루션블랙잭도메인
#에볼루션블랙잭가이드
#에볼루션블랙잭이벤트
#에볼루션게이밍블랙잭
#에볼루션게이밍에이전시
#에볼루션블랙잭가입쿠폰
#에볼루션블랙잭이용방법
http://www.evobench.com/에볼루션-바카라
http://www.evobench.com/에볼루션-블랙잭
http://www.evobench.com/에볼루션-룰렛
에볼루션
에볼루션본사
에볼루션게임
에볼루션장점
에볼루션코리아
에블루션카지노
에볼루션게이밍
에볼루션이벤트
에볼루션카지노픽
에볼루션보드게임
에볼루션카지노가입
에볼루션카지노쿠폰
에볼루션코리아주소
에볼루션카지노작업
에볼루션카지노롤링
에볼루션카지노검증
에볼루션카지노마틴
에볼루션카지노양방
에볼루션카지노해킹
에볼루션카지노사이트
에볼루션카지노도메인
에볼루션카지노가이드
에볼루션카지노바카라
에볼루션카지노이벤트
에볼루션게이밍코리아
에볼루션카지노에이전시
에볼루션카지노가입쿠폰
에볼루션카지노이용방법
카지노사이트 ACE21에서 안전한 카지노 사이트만을 추천합니다.카지노, 바카라, 온라인카지노, 순위 , 라이브카지노, 해외카지노, 사설카지노, 호텔카지노 등 각종 인터넷 게임을 제공하는 신뢰할 수 있는 통합사이트와 함께 다양한 이벤트에 참여하세요!" />
<link rel="canonical" href="https://8mod.net/" />
https://8mod.net/
카지노사이트 게임토크에서 각종 온라인 바카라, 슬롯머신, 룰렛, 스포츠토토, 바둑이, 릴게임, 경마 게임 정보를 제공합니다! 안전한 카지노사이트추천 과 각종 이벤트 쿠폰을 지급합니다!" />
<link rel="canonical" href="https://main7.net/" />
https://main7.net/