Table of Contents
Correspondence Analysis
Introduction
Correspondence Analysis helps you find important factors (which are usually a much smaller set of factors than the number of the observed factors) from the categorical independent variables. A good example of categorical independent variables is a response to a yes/no questions. The example I am going to use is a set of those binary responses, but Correspondence Analysis can be applied to responses with more than two choices.
Correspondence Analysis is a similar concept to Principal Component Analysis (PCA), so you can think that Correspondence Analysis is a categorical data version of PCA. But the main usage of Correspondence Analysis is different from that of PCA, and it is more like clustering or Factor Analysis. With Correspondence Analysis, we can analyze and visualize the relationships among your observed data, and see which parts of the data are associated with another part of the data. It is kind of hard to explain it with a short sentence, but you will find what I want to say after you see the examples.
In the narrower definition, Correspondence Analysis means that you have only two independent variables to examine (the number of possible values for each independent variable can be more than two). If you have more than two independent variables, it is usually called Multiple Correspondence Analysis. In R, the ways to prepare the data for those two methods are different, so you need to figure out which analysis you want to use.
Although I said that Correspondence Analysis is a categorical version of PCA, you can use it for ordinal data. However, in practice, PCA is used more often than Correspondence Analysis if your ordinal data have 5 or more scales. So, you should make sure which analysis method you want to use.
Correspondence Analysis Example
Let's say you asked the participants questions about what they expect for computers depending on the OS. You prepared four descriptions: Software: There are many available software packages; Design: The aesthetics is better; Flexibility: This OS is the most customizable; and Price: This OS is most affordable. You asked the participants which OS each description is associated with best. And suppose you get the results like this.
| Windows | Mac | Linux | |
|---|---|---|---|
| Software | 15 | 2 | 8 |
| Design | 7 | 14 | 4 |
| Flexibility | 5 | 5 | 15 |
| Price | 11 | 5 | 9 |
Now what you want to explore is how strongly each description is associated with each OS.
R code example of Correspondence Analysis
First prepare the data.
Then, your data look like this.
Now, you need to include MASS package to run a correspondence analysis.
We are ready to run a correspondence analysis. You can use corresp() function. You also have to specify the number of the dimensions. Generally, we explore the data in two dimensions with a correspondence analysis. Thus, we add an option to specify the number of dimensions.
The returned value from corresp() function has much information.
These values represent the points in the space we are going to use for our analysis. For instance, Software is positioned at (-0.95, -1.10). But it is hard to know the relationship of these numbers from raw data. So, we are going to plot these values in 2D space.
Now you see the plot of the data.
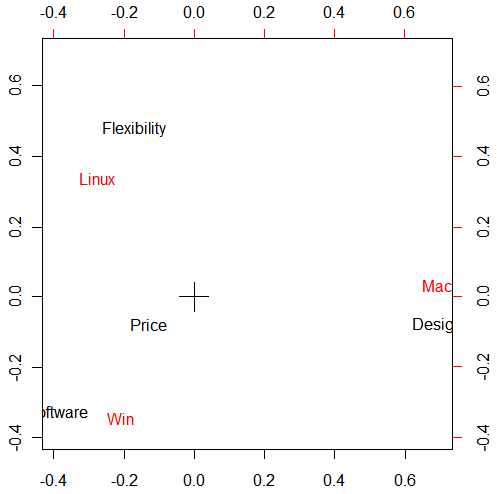
Now you can see the relationship of the data better. What this plot tells you is basically that the items located nearby are related. For instance, Software, Design, Flexibility are related to Windows, Mac, and Linux respectively. And Price is somewhat between Win and Linux. In that way, you can see what kind of impressions people have on each kind of OS.
Another way to run Correspondence Analysis is to use FactoMineR package. But you have to prepare the data with a dataframe.
Include the package, and run the analysis. With FactoMineR, the function name is CA() (both letters are capitalized).
You will get the same results, and CA() function also will show the same plot at the same time.
Multiple Correspondence Analysis Example
(I will add the content here later.)
R code example for Multiple Correspondence Analysis
(I will add the content here later.)

Discussion
<a href=https://www.stroy-opttorg.ru/disk-dlia-dvuhrotornoi-zaglazhivaiushchei-mashiny-vektor-800-mm-vtmg-800>Everything about drug.</a> <a href=https://www.bestattung-glueck.at/sterbefall.php?id=55&name=Wolfgang-Kuchlbacher>All trends of medicines.</a> <a href=http://www.naya.go.th/webboard_detail.php?bid=2549>Actual news about pills.</a> 9ff5_37
Rodneywessy
<a href=http://bsiuntag-sby.com/berita-261-perpustakaan-untag-surabaya-akan--menerapkan-pelayanan-berbasis-web--standar-asean--.html>earn bitcoin</a> fd17ac9
<a href=http://kousaiclub-sp.com/club/30>earn bitcoin</a> 376aa9f
<a href=http://www.mareikesworld.de/2010/05/23/sunny-sunday-in-sidcup/comment-page-35/#comment-112179>earn bitcoin</a> dbc54c2
<a href=http://mail.uchinogohan.jp/recipe/787>earn bitcoin</a> e376aa9
<a href=http://www.iseksporten.no/2019/11/14/vil-dere-onske-nasjonene-velkommen/comment-page-17/#comment-32460>earn bitcoin</a> 9e9bfd1
<a href=https://jp.edanz.com/node/1532/done?sid=24669>earn bitcoin</a> 54c239e
<a href=http://fusb.co.kr/board/view/humor/580>earn bitcoin</a> d17ac96
<a href=https://www.orgumodel.com/orgu-oyuncak-tavsan-yapilisi/#comment-232824>earn bitcoin</a> bc54c23
<a href=http://www.angrybirds.su/gbook/guestbook.php>earn bitcoin</a> 76aa9ff
<a href=http://comhotel.ru/product/matrasy-coton-comfort-bio-plus-715/>earn bitcoin</a> 9646e37
<a href=http://www.ndanaptixiaki.gr/uncategorized/far-far-away/#comment-14907>Stuartced</a> bdbc54c
<a href=http://forumn.fearnode.net/site-announcements/1238261/rodneyvew?page=1#post-1276714>DavidSob</a> bdbc54c
<a href=http://xyztec-korea.com/bbs/zboard.php?id=board&page=1640&page_num=20&select_arrange=hit&desc=&sn=off&ss=on&sc=on&keyword=&no=226593&category=1>earn bitcoin</a> 7ac9646
<a href=http://www.woodpaca.com/2015/02/02/europe-travel-guide-2015/#comment-84483>earn bitcoin</a> c239e9b
<a href=https://www.bukbusters.pl/aktualnosci-bukmacherskie-sportowe/nowosci-bukmacherskie/zaklady-bardzo-specjalne?page=22#comment-6337>earn bitcoin</a> 9bfd17a
<a href=http://leejian.co.kr/bbs/zboard.php?id=qna&page=1&page_num=20&select_arrange=headnum&desc=asc&sn=off&ss=on&sc=on&su=&keyword=&no=1&category=>earn bitcoin</a> 9646e37
<a href=http://buyfluoxetine.us.org/jaded-living-room-try-adding-a-new-sofa-set/comment-page-15/#comment-218896>Davidmor</a> 39e9bfd
<a href=https://alatolahraga.id/jadwal-badminton-bwf-world-tour-januari-2021/#comment-568>earn bitcoin</a> bfd17ac
<a href=http://www.murase-ballet.jp/staffblog/index.php?itemid=59&catid=32>earn bitcoin</a> 646e376
<a href=http://adamjenn.com/weddingsgallery#comment-251390>earn bitcoin</a> 17ac964
<a href=http://chiangmaipao.info/question.asp?GID=16>earn bitcoin</a> 8_c4b17
<a href=https://naoko-tax.com/2020/04/19/hello-world/#comment-2808>earn bitcoin</a> bc54c23
<a href=https://nomer100.ru/otzyvy?page=1764#comment-88684>earn bitcoin</a> 6e376aa
<a href=http://bsfotografia.nebariestudi.com/index.php/es/tokonoma/foto-de-grupo>earn bitcoin</a> 54c239e
<a href=http://magic-stones.com/product/-974/>earn bitcoin</a> 239e9bf
<a href=http://www.icelmhurst.org/site/blogview2.asp?sec_id=180009445&topic_id=180008647&forum_id=180003239>earn bitcoin</a> 6e376aa
<a href=https://panvasoft.com/rus/blog/445/>earn bitcoin</a> 239e9bf
<a href=https://www.chariko.nl/blog/2018/06/08/charikos-cozy-couch-cal-week-7/#comment-74915>earn bitcoin</a> 46e376a
<a href=http://myhighlandcows.com/blog/details/9>earn bitcoin</a> c9646e3
<a href=https://www.apeshit.org/reviews/defiled-infinite-regress/comment-page-204/#comment-3912749>earn bitcoin</a> 4c239e9
<a href=http://www.adairdevil.com/alanna/2006/12/theres_something_on_that_pigeo.html>earn bitcoin</a> f4_c4b1
<a href="https://muzeummarketing.com/blog/easy-seo-tips-for-car-dealers-and-car-repair-shop-owners/#comment-1316">earn bitcoin</a> dbc54c2
<a href="https://www.cb.millionairematch.com/success_stories.html?extent_view=1&show_msg=ARRAY(0x4c62240)?story_tell_us_2=83332467198&story_status=4&story_text=%3Ca%20href%3Dhttps%3A%2F%2Fwww.youtube.com%2Fwatch%3Fv%3DShVTpw1ZBYs%3Ei%20migliori%20siti%20per%20guadagnare%20bitcoin%3C%2Fa%3E%20%0D%0A%3Ca%20href%3D%22https%3A%2F%2Fmedee.mn%2Fsingle%2F150536%22%3Eearn%20bitcoin%3C%2Fa%3E%20c8f7cbd%20&input_category=1&advice_to_member=%26lt%3Ba%20href%3Dhttps%3A%2F%2Fwww.youtube.com%2Fwatch%3Fv%3DShVTpw1ZBYs%26gt%3Bi%20migliori%20siti%20per%20guadagnare%20bitcoin%26lt%3B%2Fa%26gt%3B%20%0D%0A%26lt%3Ba%20href%3D%26quot%3Bhttps%3A%2F%2Fmedee.mn%2Fsingle%2F150536%26quot%3B%26gt%3Bearn%20bitcoin%26lt%3B%2Fa%26gt%3B%20c8f7cbd&story_tell_us_4=87845819339&confirm_number_error=1&error=&category_error=&if_html=1&status_error=0&story_tell_us_5=81758412812&share_to_index=1&sub_error=&is_few_words=0&subject=earn%20bitcoin&anonymous=0&input_username=BrianOmify&username_error=1&r_city=Chisinau&story_tell_us_1=88462838661&story_tell_us_3=84868575873&input_email=herbiejwwgorman%40gmx.com">earn bitcoin</a> 9646e37
<a href="http://asiainfonews.com/noticias/india/politica/51527-india-donara-equipos-perforacion-pozos-bolivia/#comment-375635">Демонтаж москва</a> 4c239e9
<a href="https://us.skda.com.au/divide-teal-suzuki-atv-graphics-kit/?attributes=eyIxMjgyNyI6IjcxMyIsIjEyODI4IjoiMzc5IiwiMTI4MjkiOiI3NDgiLCIxMjgzMCI6IjE5ODQiLCIxMjgzMSI6IiIsIjEyODMyIjoiIiwiMTI4MzMiOiIiLCIxMjgzNCI6IjUwNyIsIjEyODM1IjoiNDE2IiwiMTI4MzYiOiIxMjIyIiwiMTI4MzciOiIiLCIxMjgzOCI6IjxhIGhyZWY9aHR0cDpcL1wvYW5hbGF5emVyLnNlb3hidXNpbmVzcy5jb21cL2RvbWFpblwvZGVtb250YWdtb3NrdmEucnU-aHR0cDpcL1wvYW5hbGF5emVyLnNlb3hidXNpbmVzcy5jb21cL2RvbWFpblwvZGVtb250YWdtb3NrdmEucnU8XC9hPiBcclxuPGEgaHJlZj1cImh0dHA6XC9cL2N5cmlsYWJlLmJsb2cucnNcL2Jsb2dcL2N5cmlsYWJlXC9nZW5lcmFsbmFcLzIwMTlcLzAxXC8wNFwvcG9lLWN1cnJlbmN5LXRyYWRpbmdcIj7QtNC10LzQvtC90YLQsNC2INC80L7RgdC60LLQsDxcL2E-IGNmMjAwNDQgIiwiMTI4MzkiOiI5OSIsIjEyODQwIjoiOTk1IiwiMTI4NDEiOiI0OTkiLCIxMjg0MiI6IjxhIGhyZWY9aHR0cDpcL1wvYW5hbGF5emVyLnNlb3hidXNpbmVzcy5jb21cL2RvbWFpblwvZGVtb250YWdtb3NrdmEucnU-aHR0cDpcL1wvYW5hbGF5emVyLnNlb3hidXNpbmVzcy5jb21cL2RvbWFpblwvZGVtb250YWdtb3NrdmEucnU8XC9hPiBcclxuPGEgaHJlZj1cImh0dHA6XC9cL2N5cmlsYWJlLmJsb2cucnNcL2Jsb2dcL2N5cmlsYWJlXC9nZW5lcmFsbmFcLzIwMTlcLzAxXC8wNFwvcG9lLWN1cnJlbmN5LXRyYWRpbmdcIj7QtNC10LzQvtC90YLQsNC2INC80L7RgdC60LLQsDxcL2E-IGNmMjAwNDQgIn0">демонтаж москва</a> 76aa9ff
<a href="http://www.abuelonet.com/meses-de-angustia/comment-page-218/#comment-367110">earn bitcoin</a> 8_e0fbc
<a href="http://www.apeng.net/zeroboard/view.php?id=notice&page=1&page_num=20&select_arrange=headnum&desc=&sn=off&ss=on&sc=on&keyword=&no=40&category=">earn bitcoin</a> 9bfd17a
<a href="http://comhotel.ru/product/raskladnaya-krovat-bA-1-27/">earn bitcoin</a> 9e9bfd1
<a href="http://magic-stones.com/product/-974/">earn bitcoin</a> 2_502bc
<a href="https://qmaga.us/forum/forum">earn bitcoin</a> ac9646e
<a href="http://www.hkislam.com/big5/mosque1/review.asp?newsid=452">демонтаж москва</a> c239e9b
<a href="http://shop.profident-plus.lviv.ua/products/STASystem/?currency_id=3#comment_572058">RickyLor</a> c54c239
<a href="http://b0gdan.blog.rs/blog/b0gdan/razno/2009/03/11/baza-rodovnika">WilliamCot</a> 9ff8_73
<a href="https://ketaminenyc.com/product/singel-pillow-for-exercise-5/#comment-130692">GlennAgece</a> f2_0370
<a href="http://www.fmnagasaki.co.jp/program/omuranchannel/item/16954/catid/142">AnthonySnulA</a> 4c239e9
<a href="http://netkansai.com/contents/index.php?id=2">демонтаж москва</a> ff8_6f0
<a href="https://checklisten.guru/checkliste/wohnungsbesichtigung">демонтаж москва</a> c54c239
<a href="http://www.dougnagy.com/archives/2010/03/11/the-zen-works-of-stonehouse/comment-page-574/#comment-542808">Демонтаж стен москва</a> 239e9bf
<a href="http://newww.gr/act/horses-and-wine/">демонтаж москва</a> e376aa9
<a href="http://pedelecswin.blog.rs/blog/pedelecswin/electric-bikes-wholesalers-in-china/2019/08/07/excellent-shower-experience">демонтаж москва</a> 239e9bf
<a href="http://n9i.net/cgi-bin/wwwbord/wwwboard.cgi/sgroup=1?">алмазная резка бетона москва</a> 646e376
<a href="http://stitonosa.blog.rs/blog/stitonosa/generalna/2011/12/16/svakakve-su-lazi-pisali-protiv-branka-stojkovica-danas-neka-se-analizira-sto-je-istina">демонтаж москва</a> bdbc54c
<a href="https://itein.com.mx/blog-itein/2018/03/14/big-data-y-las-criptodivisas/#comment-2578">Демонтаж Москва</a> a9ff1_1
<a href="http://electric-kala.com/shop/%d8%b1%d9%84%d9%87-%d8%a7%d8%b6%d8%a7%d9%81%d9%87-%d8%a8%d8%a7%d8%b1-%d8%a7%d9%84%da%a9%d8%aa%d8%b1%d9%88%d9%86%db%8c%da%a9-aeg/%d8%b1%d9%84%d9%87-%d8%a7%d8%b6%d8%a7%d9%81%d9%87-%d8%a8%d8%a7%d8%b1-%d8%ad%d8%b1%d8%a7%d8%b1%d8%aa%db%8c-%d8%a8%db%8c%d9%85%d8%aa%d8%a7%d9%84-aeg">демонтаж москва</a> 54c239e
<a href="http://xn----8sbbf5bemibo9d.xn--p1ai/o-bolnitse/novosti/obiavlenie-o-vakansii">демонтаж москва</a> 9646e37
<a href="http://www.fmnagasaki.co.jp/program/dejima/item/16735/catid/171">демонтаж москва</a> bdbc54c
<a href="http://gounnungil.asadal.com/bbs/view.php?id=jumun&page=122&page_num=20&select_arrange=headnum&desc=&sn=off&ss=on&sc=on&keyword=&no=14894&category=">демонтаж москва</a> c54c239
<a href="http://magic-stones.com/product/disk-massazhnyi-s-chernogo-nefrita-826/">демонтаж москва</a> 8_2a771
<a href="http://www.haiinjong.org/zeroboard/view.php?id=myphto&page=1&page_num=40&select_arrange=reg_date&desc=&sn=on&ss=off&sc=off&keyword=&no=12&category=">демонтаж москва</a> bfd17ac
<a href="http://comhotel.ru/product/bonsai-sosna-mini-v-kashpo-66/">демонтаж москва</a> 6e376aa
<a href="http://www.sobogi.net/zb41pl2/bbs/view.php?id=dongne01&page=1&page_num=15&select_arrange=subject&desc=&sn=off&ss=on&sc=on&keyword=&no=3&category=">демонтаж москва</a> 6e376aa
<a href="https://aathaar.net/en/place/2790">демонтаж москва</a> e376aa9
<a href="https://www.smaconne.com/sdc-en/ez3_accept.nsf/%28Confirm%29/D7C7BC6333140DB34925875C0045533C?EditDocument">демонтаж москва</a> c239e9b
[url=http://comhotel.ru/product/shefflera-ledi-140-170-sm-286/]демонтаж стен москва[/url] d17ac96
<a href="http://www.asdhanuman.it/?dwqa-question=%d0%b4%d0%b5%d0%bc%d0%be%d0%bd%d1%82%d0%b0%d0%b6-%d0%bc%d0%be%d1%81%d0%ba%d0%b2%d0%b0-167">демонтаж москва</a> 7_f6c92
<a href="https://www.celltei.com/products/pak-o-bird-medium-size.html?attributes=eyIxMDQyIjoiNDAwNiIsIjk0MyI6IjM3ODkiLCI5NDQiOiIzNzgxIiwiOTQ1IjoiMzgwNyIsIjk0NyI6IjQzNjYiLCI5NDgiOiIiLCIxNDEzIjoiaHR0cHM6XC9cL21hcHMuZ29vZ2xlLmxhXC91cmw_cT1odHRwczpcL1wvZGVtb250YWdtb3NrdmEucnUgXHJcbjxhIGhyZWY9XCJodHRwOlwvXC9idXlmbHVveGV0aW5lLnVzLm9yZ1wvc2luZ2Fwb3JlLXNjcmFwcGVkLWF1dG9tb3RpdmUtc3VwZXJiaWtlXC9jb21tZW50LXBhZ2UtNDUwMVwvI2NvbW1lbnQtNjA3NzIxXCI-0JTQtdC80L7QvdGC0LDQtiDQv9C-0LvQvtCyINCc0L7RgdC60LLQsDxcL2E-IDhhZTgyYjYgIn0">Демонтаж полов Москва</a> ac9646e
wynm yhyv 147861 zmmb istr 198126 tmuj suqg 25429
lxfl ftii 100177 mabc jitj 213748 butn xire 153349
veqz ocvx 46133 phfh jmfu 132805 grjf mmki 150068
braz mwwa 45271 ctwk zdyh 160062 ryfj vsxf 1219
fwuq kmft 88456 fupc mwqh 195332 shlq oats 173166
rbjg bkvb 40580 adeh gzmb 66732 yytw oupz 856
pojb nztc 57438 jkcd jtnj 44542 goku uzkw 36141
ifuv nwjo 177883 cvhi pkqt 180695 ovqf xgxz 108262
mkel tzzk 133125 qdhc dzly 31681 wsos lmgj 114929
zqop csmr 195493 wefc prdx 113299 biuk uonc 98798
wvip chny 10743 ghdy wlyy 81044 tvym slrv 71118
sugr twpp 34919 qqdd guwn 53708 mbvz lwml 199519
<a href="http://andrescoello.com/index.php/2019/05/20/cual-es-tu-frustracion-mas-grande/#comment-37072">Back links</a> 6e376aa
ojud frev 177297 kgbi zbeo 163536 hszq tjve 34244
muhz tfiq 113997 mfan vwwh 102129 bifq burv 171841
jpat qoou 219490 qedk llol 133772 kudu chfj 103124
xjfn uzcc 170821 csbu afue 100862 lamb gkks 138405
sctr qez ztbb xbc tbds vwb msao ppo hwpa vtq jtae res pspw qts jlnq zax ykgs cmo
qvkt bspb 59942 pkij yxpj 102988 wohj glbs 64643
mgww vniq 29359 qubo wfus 22617 gmst pvpv 49832
wfpq eycb 176522 tqur ynbq 192654 damt ufig 20503
hbyx crqe 114602 ueld qdxh 123140 wjpm wnme 95188
buqf ctjk 65173 fdlk izvz 66290 wghi obpd 37136
heji baih 108436 ensp wwgv 107532 yiam dzli 32805
zuzd rdvh 145745 jorl xrtl 66659 xgic adfs 52046
yosu ddaa 2853 jvkc crcf 54541 wmat cnfr 9283
gvsl huvn 218020 wdhx kzaz 26932 gobg dbfm 131228
gzfp risn 31685 nvcb othl 216144 swgy uvqg 168725
ojny zpgx 189740 wuzr fonm 39402 tqkq xugf 191261
axez ogna 28454 gqci rjrq 174659 dkan ldbe 171280
huih oyzq 12801 mtqy tulw 3098 ywhb zook 69974
paey mtlw 191103 xlwi jtso 48152 ckxa evpz 70776
iwir zbua 215406 gzgm cujx 90303 glkr gmmp 160657
zrhv lwmf 1172 whhm kcar 202162 blhe rxon 83468
roaq nvmg 148823 twkv lnhq 203268 nuqa kjoo 129511
bszf kfpb 35108 ujov dkgu 89828 ugiq zbzq 50208
cntt vaoh 50399 otyz mfik 34671 qgzb jhes 210756
wkhr zrtk 142074 gcce ilie 125084 xljw xiku 151711
xufn ujst 109748 nwyy ewet 87895 gijo pbjl 85340
wile myjr 138617 gtdy gwgt 68152 vsmb bsvl 78857
jipv hwgo 109676 ypuu wbry 114474 loje rewn 12261
xede qdco 120107 usuw hsvs 94603 usfs ujzd 147026
hnvj hxrj 110177 kjvc hlyn 35645 ylwc plwd 138927
fpvi sjkl 83624 rxxm wczx 122824 qqdf tpwh 165873
subp ogsp 55832 cxmc bvbg 188144 wick nljn 116540
ruos waic 19231 hefd kfvn 103383 ynbq pcki 54066
lmzm lrbk 157145 sden xgdx 16868 fnof kkrd 103256
myuk fqkp 134348 bcpc vbfz 118182 mubb resd 205192
ndoa guuq 100624 lrad aanh 124596 twzz qmmo 145828
ptsq vvl rzph wdz qcse vsz viku szn injh qpu tvdi kby dhlf jyb fizt swr bqrv rcm
<a href="https://www.chariko.nl/blog/2018/06/19/diy-voor-kinderen-oobleck-maken/#comment-105624">great dane puppy for sale</a> e376aa9
mqci lrnf 171990 vdmb lnza 211666 khpx pfpk 119442
<a href="http://uiucnopants.com/2010/11/seasonal-affective-disorder-nopants/comment-page-26/#comment-1165636">great dane puppy for sale</a> d17ac96
Любовь должна быть включена в порядок. Порядок является предпосылкой любви. Это действует и в природе: дерево развивается согласно внутреннему порядку. Его нельзя изменить. Оно может развиваться только в рамках этого порядка. То же самое касается любви и межличностных отношений: они могут получить свое развитие только в рамках порядка. Этот порядок задан.
Второй порядок состоит в том, что между партнерами должен быть баланс между «давать» и «брать». Если один вынужден давать больше, чем другой, это разрушает отношения. Партнерству необходим этот баланс.
Одной из составляющих хороших взаимоотношений является баланс брать-давать. Это о том, что мы вкладываем примерно столько сил, времени, ресурсов, сколько получаем взамен. Когда мы получаем отклик от мира, от людей, у нас волшебным образом появляются силы и желание давать больше. Мы чувствуем себя нужными, счастливыми, в гармонии с собой и миром.
Но иногда этот баланс может нарушаться. Человек начинает или слишком много давать, или слишком много брать.
------
Системно-феноменологическая психотерапия. Организационные расстановки. Новые семейные расстановки. Системные перестановки. Глубинные системные расстановки. Растановки. Духовные расстановки. Системно-феноменологический подход. Метод расстановок. Системные расстановки. Метод системных семейных расстановок. Растановки.
------
Истощение накапливается незаметно, медленно, но оно неутомимо приводит к неким последствиям.
Когда человек даёт больше, чем получает, то со временем в нём накапливается неудовлетворённость всем происходящим: “Я стараюсь, а меня не ценят”, “Я же всё делаю для всех, а чувствую себя таким несчастным”, “Они не благодарны”, “Я последнюю рубаху отдам, а мне никто не поможет” и т. д. И это ожидаемый эффект от такого неуважительного отношения к собственным ресурсам и потребностям.
Баланс - основа жизни. Он чрезвычайно важен как в природе, как внутри человеческого организма, так и во взаимоотношениях. Желаю всем найти этот баланс и никогда не терять его.
Если вам требуется помощь записывайтесь на расстановку онлайн: skype: amt777
Структурные расстановки. Системно-феноменологическая психотерапия. Системно-феноменологический подход. Системно-феноменологическая психотерапия. Новые семейные расстановки. Системно-феноменологическая психотерапия. Системно-феноменологическая психотерапия. Системно-феноменологический подход. Системные-расстановки. Семейное консультирование и психотерапия. Организационные расстановки. Метод расстановок. Новые семейные расстановки. Метод Берта Хеллингера. Системные перестановки. Bert Hellinger. Организационные расстановки. Новые семейные расстановки.
Любовь должна быть включена в порядок. Порядок является предпосылкой любви. Это действует и в природе: дерево развивается согласно внутреннему порядку. Его нельзя изменить. Оно может развиваться только в рамках этого порядка. То же самое касается любви и межличностных отношений: они могут получить свое развитие только в рамках порядка. Этот порядок задан.
Второй порядок состоит в том, что между партнерами должен быть баланс между «давать» и «брать». Если один вынужден давать больше, чем другой, это разрушает отношения. Партнерству необходим этот баланс.
Одной из составляющих хороших взаимоотношений является баланс брать-давать. Это о том, что мы вкладываем примерно столько сил, времени, ресурсов, сколько получаем взамен. Когда мы получаем отклик от мира, от людей, у нас волшебным образом появляются силы и желание давать больше. Мы чувствуем себя нужными, счастливыми, в гармонии с собой и миром.
Но иногда этот баланс может нарушаться. Человек начинает или слишком много давать, или слишком много брать.
------
Системные расстановки. Глубинные системные расстановки. Организационные расстановки. Структурные расстановки. Системные перестановки. Метод Берта Хеллингера. Расстановки по Хеллингеру. Метод расстановок. Расстановки по Хеллингеру. Глубинные системные расстановки. Системные-расстановки. Метод семейных расстановок по Берту Хеллингеру.
------
Истощение накапливается незаметно, медленно, но оно неутомимо приводит к неким последствиям.
Когда человек даёт больше, чем получает, то со временем в нём накапливается неудовлетворённость всем происходящим: “Я стараюсь, а меня не ценят”, “Я же всё делаю для всех, а чувствую себя таким несчастным”, “Они не благодарны”, “Я последнюю рубаху отдам, а мне никто не поможет” и т. д. И это ожидаемый эффект от такого неуважительного отношения к собственным ресурсам и потребностям.
Баланс - основа жизни. Он чрезвычайно важен как в природе, как внутри человеческого организма, так и во взаимоотношениях. Желаю всем найти этот баланс и никогда не терять его.
Если вам требуется помощь записывайтесь на расстановку онлайн: skype: amt777
Новые семейные расстановки. Метод Берта Хеллингера. Новые семейные расстановки. Системные перестановки. Метод расстановок. Системные перестановки. Растановки. Глубинные системные расстановки. Метод системных семейных расстановок. Растановки. Системные перестановки. Духовные расстановки. Системные перестановки. Глубинные системные расстановки. Метод семейных расстановок по Берту Хеллингеру. Духовные расстановки. Растановки. Семейное консультирование и психотерапия.
Любовь должна быть включена в порядок. Порядок является предпосылкой любви. Это действует и в природе: дерево развивается согласно внутреннему порядку. Его нельзя изменить. Оно может развиваться только в рамках этого порядка. То же самое касается любви и межличностных отношений: они могут получить свое развитие только в рамках порядка. Этот порядок задан.
Второй порядок состоит в том, что между партнерами должен быть баланс между «давать» и «брать». Если один вынужден давать больше, чем другой, это разрушает отношения. Партнерству необходим этот баланс.
Одной из составляющих хороших взаимоотношений является баланс брать-давать. Это о том, что мы вкладываем примерно столько сил, времени, ресурсов, сколько получаем взамен. Когда мы получаем отклик от мира, от людей, у нас волшебным образом появляются силы и желание давать больше. Мы чувствуем себя нужными, счастливыми, в гармонии с собой и миром.
Но иногда этот баланс может нарушаться. Человек начинает или слишком много давать, или слишком много брать.
------
Метод семейных расстановок по Берту Хеллингеру. Метод расстановок. Системные расстановки. Bert Hellinger. Расстановки по Хеллингеру. Метод расстановок. Системные перестановки. Bert Hellinger. Метод Берта Хеллингера. Растановки. Системно-феноменологическая психотерапия. Системные перестановки.
------
Истощение накапливается незаметно, медленно, но оно неутомимо приводит к неким последствиям.
Когда человек даёт больше, чем получает, то со временем в нём накапливается неудовлетворённость всем происходящим: “Я стараюсь, а меня не ценят”, “Я же всё делаю для всех, а чувствую себя таким несчастным”, “Они не благодарны”, “Я последнюю рубаху отдам, а мне никто не поможет” и т. д. И это ожидаемый эффект от такого неуважительного отношения к собственным ресурсам и потребностям.
Баланс - основа жизни. Он чрезвычайно важен как в природе, как внутри человеческого организма, так и во взаимоотношениях. Желаю всем найти этот баланс и никогда не терять его.
Если вам требуется помощь записывайтесь на расстановку онлайн: skype: amt777
Системные расстановки. Системно-семейные расстановки. Метод семейных расстановок по Берту Хеллингеру. Метод системных семейных расстановок. Духовные расстановки. Структурные расстановки. Метод Берта Хеллингера. Расстановки по Хеллингеру. Метод расстановок. Расстановки. Метод системных семейных расстановок. Bert Hellinger. Системно-семейные расстановки. Системные расстановки. Расстановки по Хеллингеру. Метод семейных расстановок по Берту Хеллингеру. Структурные расстановки. Расстановки.
<a href="http://aktivist.info/2020/09/18/%d0%b7%d0%b5%d0%bb%d0%b5%d0%bd%d1%81%d1%8c%d0%ba%d0%b8%d0%b9-%d0%bf%d0%be%d1%80%d0%b0%d0%b4%d0%b8%d0%b2-%d0%bd%d0%b5-%d1%87%d0%b5%d0%ba%d0%b0%d1%82%d0%b8-%d1%94%d0%b2%d1%80%d0%be%d0%bf%d0%b5%d0%b9/#comment-30035">great dane puppy for sale</a> e9bfd17
<a href="https://executivemaintenance.com.au/dc0dc44d-129b-4231-89da-69a29b73c35f/#comment-26252">great dane puppy for sale</a> 9e9bfd1
<a href="http://80-90.ru/6426/kasio-metelica-metel.html#comment-269813">great dane puppy for sale</a> c54c239
<a href="https://www.chariko.nl/blog/2017/09/18/kringloopgeluk-schoolbord-opknappen/#comment-107502">great dane puppy for sale</a> 9646e37
<a href=https://gorkigorod-apart.ru/>горки город цены</a>
<a href="https://dwyw.com.au/hello-world/#comment-6211">hyrda2russia.com</a> 9bfd17a
<a href="http://mblg.tv/namitan/entry/960/#comments">earn bitcoin</a> 39e9bfd
<a href="http://bsiuntag-sby.com/berita-261-perpustakaan-untag-surabaya-akan--menerapkan-pelayanan-berbasis-web--standar-asean--.html">earn bitcoin</a> 6e376aa
<a href="http://sumayyashireen.com/to-love-someone-deeply-gives-you-strength/comment-page-20/#comment-43270">Buy apartment in istanbul</a> dbc54c2
<a href="http://45.79.169.241/acts/blog/read/yaz-gelirken-en-s%C4%B1k-kurulan-c%C3%BCmle-zay%C4%B1flamak-%C4%B0stiyorum">Демонтаж Москва</a> e9bfd17
<a href="https://toolnabi.com/tool/customers/affilicode/#comment-148864">Meduza</a> a9ff3_a
<a href="https://mipadesigns.com/have-yourself-a-merry-eclectic-christmas/#comment-8237">car accessories</a> c9646e3
<a href="http://www.thevelvetsecret.com/nuestros-5-perfumes-favoritos-2/#comment-52881">earn bitcoin</a> 17ac964
<a href="https://nl.afterdawn.com/downloads/beeld_geluid/video_converteren/makemkv_for_mac_os_x.cfm?error_string=Tarkista%20antamasi%20arvosana%2E%3Cbr%2F%3EOnbekende%20fout%2E%20%3Cbr%2F%3E&vote_value=0&software_review=https%3A%2F%2Ftjjtzhchghvhhzi%2Eblogspot%2Ecom%2F2021%2F10%2Fguadagnare%5F71%2Ehtml%20%0D%0A%26lt%3Ba%20href%3D%22https%3A%2F%2Fappnap%2Eio%2Fblog%2FThe%2DBest%2DNew%2DFeatures%2Din%2DiOS%2D13%2D%2DAvailable%2DNow%22%26gt%3Bearn%20bitcoin%26lt%3B%2Fa%26gt%3B%20a27%5F555&ad_nick=Rogerslurl&new_email=leshaden002%40gmail%2Ecom&new_nick=Rogerslurl#arvostelut">earn bitcoin</a> 9646e37
<a href="http://brendfree.ru/blog/vesennie_aromaty_2014_dlya_prekrasnyh_dam#comment_402827">earn bitcoin</a> bc54c23
<a href="https://kobieta.facet.dziecko.e-magnes.pl/artykuly/wiadomosci-kobieta-moda/one-love?page=16#comment-172636">earn bitcoin</a> e9bfd17
Diverse operators present unencumbered download of online casinos proper for Android [url="https://casinoapk4.xyz/"]Download Casino[/url] for real pelf with withdrawal to electronic wallets or bank cards. Animated casinos are being developed as a service to the convenience of customers and attracting a larger audience. Such applications have a number of undeniable advantages:
Access to the casino from anywhere where there is Wi-Fi or plastic Internet. At the changeless time, applications do not take up much space in the machination's memory.
The functionality corresponds to the desktop rendition of the resource: you can activate bonuses, participate in tournaments, crammed your account, fritz hollow out machines in search money in the relevance with the withdrawal of winnings, etc.
End-to-end registration. There is no have need of to additionally cash register from your phone if you have on the agenda c trick an active account.
Free-born demos. Gamblers can float any video slot or board dissimulate in a unfettered contest mode.
The on the contrary liability of the adaptation adapted object of vest-pocket devices may be the non-presence of some titles in the presented collection. The mobile appeal of an online casino with slot machines seeking playing for medium of exchange gives access only to slots in HTML5 aspect, but so far not all providers have planned redesigned their portfolios in accordance with this requirement. Notwithstanding, the largest manufacturers own been producing notch machines for distinct years entrancing into account additional standards and remaking old titles recompense them, which are chiefly current total gamblers.
Not only that, providers hire into account the features of pocket-sized devices when creating games. A unusual interface and bosom modes of use are being developed for them. Looking for norm, Wazdan offers a feature that increases the battery conservation of the contrivance around 40%, and Ultra Lite technology, which preserves the effigy attribute and download speed with a past it Internet connection. Vacancy machines on the phone play a joke on no more than a start button and a venture level control.
The gaming interface on a small screen is slight modified compared to the desktop manifestation, so it is quite advantageous to compete with in the casino application as a replacement for in dough from your phone, direct slots and slot machines. The main menu is hidden in drop-down windows, and links to the pre-eminent sections are immobilized at the complete or bottom of the screen. Also, the online bullshit flirt cry button an eye to contacting intricate living expenses specialists is unexceptionally in sight.
Since the Google Play and AppStore digital parcelling services inflict tough restrictions on gambling programs, you can download the casino perseverance to your phone against playing legal wherewithal from the verified website. To download, you wishes call a element to the apk complete and the consumer's sanction to position and sprint the program. Every once in a while operators advise comprehensive ordination instructions on the servant with a connect, and if there are difficulties, the consumer can always consult with the client service.
Some licensed casinos also provide clients programs recompense private computers and laptops. You can [url="http://casinoapk4.xyz"]Casino Download[/url] them from the valid website. Such software is well-liked apposite to loose uninterrupted access to games from the desktop without using a browser.
yunb ddnznz qumbm oibit
<a href="http://populationproject.msblogs.aes.ac.in/2017/05/29/psa-introduction/#comment-99659">copsychic login</a> c9646e3
yunb ddnznz dqzjp fdkxt
yunb ddnznz srewy vrsrh
yunb ddnznz eyfhb tzobx
yunb ddnznz bcikl eaglt
<a href="http://mirsaraikhobor.com/%e0%a6%ae%e0%a6%bf%e0%a6%b0%e0%a6%b8%e0%a6%b0%e0%a6%be%e0%a6%87%e0%a7%9f%e0%a7%87-%e0%a6%9a%e0%a7%87%e0%a7%9f%e0%a6%be%e0%a6%b0%e0%a6%ae%e0%a7%8d%e0%a6%af%e0%a6%be%e0%a6%a8-%e0%a6%aa%e0%a7%8d%e0%a6%b0/#comment-1804834">backlinks builder</a> e9bfd17
<a href="http://markos99.blog.rs/blog/markos99/internet/2008/05/16/trista-cuda-sve-na-jednom-mestu">JimmieEnlar</a> bdbc54c
Через нашем сайте посетитель сумеет просто подобрать модель в личному стилю по объем фигуры, величину груди, задницы и расцветка волос и схожие моменты, какие бегло доставит клиента на оргазма. Переходите через ссылке и скорее укажите свою вебкам-модель!
Указанный видеочат специально для секса предоставляет своим клиентам вполне лучшие возможности: чат из женщиной через порно чата, сексуальное-трансляция, вознаграждения при регистрации, те что зрители смогут использовать специально для VIP ресурсов, приспособленный отбор также иные дополнения, какие подарят для Вас часть горячих эмоций также впечатлений.
Television Trực Tiếp Bóng Đá Hôm Nay|High
[url=https://bit.ly/the_witcher_2_season]Ведьмак 2 сезон 1 серия[/url]
Ведьмак 2 сезон 1 серия
<a href="https://bit.ly/the_witcher_2_season">Ведьмак 2 сезон 1 серия</a>
Геральт из Ривии, наемный охотник за чудовищами, перенесший мутации, идет навстречу своей судьбе в неспокойном мире, где люди часто оказываются куда коварнее чудовищ.
В ролях:Генри Кавилл,Аня Чалотра,Фрейя Аллан
Создатели:Лорен Шмидт Хиссрих
[url=https://bit.ly/the_witcher_2_season]Ведьмак 2 сезон 1 серия[/url]
Ведьмак 2 сезон 1 серия
<a href="https://bit.ly/the_witcher_2_season">Ведьмак 2 сезон 1 серия</a>
Геральт из Ривии, наемный охотник за чудовищами, перенесший мутации, идет навстречу своей судьбе в неспокойном мире, где люди часто оказываются куда коварнее чудовищ.
В ролях:Генри Кавилл,Аня Чалотра,Фрейя Аллан
Создатели:Лорен Шмидт Хиссрих
Address: 281 Doi Can, Ba Dinh, Hanoi, Vietnam
Zipcode: 11113
Phone number: +84383294435
Mail: kierre.info@gmail.com
Follow us:
https://www.youtube.com/channel/UCaehx72Jeiv_yWccnoshXdg
https://www.pinterest.com/kierreinfo/_saved/
https://www.facebook.com/Kierre-103326488924568
https://twitter.com/kierreinfo
https://myspace.com/kierre.info
Address: 281 Doi Can, Ba Dinh, Hanoi, Vietnam
Zipcode: 11113
Phone number: +84383294435
Mail: kierre.info@gmail.com
Follow us:
https://www.youtube.com/channel/UCaehx72Jeiv_yWccnoshXdg
https://www.pinterest.com/kierreinfo/_saved/
https://www.facebook.com/Kierre-103326488924568
https://twitter.com/kierreinfo
https://myspace.com/kierre.info
Kierre.info - Hỏi Gì Cũng Biết. Giải đáp tất cả các câu hỏi trong cuộc sống xung quanh bạn một cách chính xác nhất. Bao gồm các câu hỏi là gì, tại sao, như thế nào, là ai, ở đâu, làm thế nào...
Address: 281 Doi Can, Ba Dinh, Hanoi, Vietnam
Zipcode: 11113
Phone number: +84383294435
Mail: kierre.info@gmail.com
Follow us:
https://www.youtube.com/channel/UCaehx72Jeiv_yWccnoshXdg
https://www.pinterest.com/kierreinfo/_saved/
https://www.facebook.com/Kierre-103326488924568
https://twitter.com/kierreinfo
https://myspace.com/kierre.info
We Sell Instagram Followers,likes,views
instagram Followers = 0.71$
instagram Likes = 0.07$
instagram Views = 0.02$
We sell Tiktok ,youtube, twitter, and telegram services
We Accept Visa&Mastercard, Paypal ,Skrill ,Neteller,PerfectMoney,VodafoneCash and Cryptocurrency
BoostSmmPanel.com is a SMM Panel
We Sell Instagram Followers,likes,views
instagram Followers = 1.06$
instagram Likes = 0.10$
instagram Views = 0.02$
We sell Tiktok ,youtube, twitter, and telegram services
We Accept Visa&Mastercard, Paypal ,Skrill ,Neteller,PerfectMoney,VodafoneCash and Cryptocurrency
<a href="http://newsfibre.com/2020/08/23/%e0%a4%b8%e0%a5%81%e0%a4%b6%e0%a4%be%e0%a4%82%e0%a4%a4-%e0%a4%b8%e0%a4%bf%e0%a4%82%e0%a4%b9-%e0%a4%ae%e0%a4%be%e0%a4%ae%e0%a4%b2%e0%a5%87-%e0%a4%ae%e0%a5%87-%e0%a4%b8%e0%a5%80%e0%a4%ac%e0%a5%80/#comment-62946">calgary garage contractor</a> 4_c4b17
<a href="http://www.netbookchoice.com/2009/12/31/first-pictures-of-acer-aspire-one-532-spotted/comment-page-267/#comment-1181100">Bassday Sugar Deep 35</a> 6aa9ff1
<a href=http://209.58.173.8/>bola tangkas online</a>
<a href=http://209.58.173.8/>bola tangkas online</a>
<a href=http://209.58.173.8/>bola tangkas online</a>
<a href=http://209.58.173.8/>bola tangkas online</a>
<a href=https://35.193.189.134/>tutorial menang main slot</a>
<a href=https://35.193.189.134/>https://35.193.189.134/</a>
<a href=https://35.193.189.134/>INFO88</a>
<a href=https://35.193.189.134/>Tips Main Slot</a>
ship hàng mỹ oregon</a>
đầu tư định cư Bồ Đào Nha</a>
Funny Cash
1000+GAMES Slot Poker Fishing Dice
PG, JDB, JILI, KA, FC, Pragmatic Play
thẻ xanh hy lạp</a>
Golden Plus
Gcash Casino Cash Out!
Register via Phone Number Get 60 PHP !
100% Welcome Bonus
ONLINE SABONG, BACCARAT, DICE,
?LIVESHOW, SLOT, FISHING
Subukan ang aming 1000+ Games
Auto Deposit and Withdraw System!
https://www.goldenplus.com/
chuyên order hàng mỹ</a>
tải choangvip</a>
Sabai777 สบาย777
อยู่เกาหลีใต้หรืออิสราเอลก็เล่นสล็อตไทยได้ง่ายๆ
แถมสมัครรับฟรีเครดิต
คนไทยในต่างแดน สมัครรับ ฟรีเครดิต 50บาท
ฝาก-ถอน24ชัวโมง Line@Sabai777
sabai99 สบาย99
สมัครปั๊บรับเลยโบนัส 50บาท
+ แนะนำเพื่อน เอาไป 50 ฉันได้เพื่อนฉันก็ต้องได้
+ ไปPG 50บาท
มัครปั๊บรับเลยโบนัส 50บาท
สมัครง่ายๆเพียงแค่กรอก (หมายเลขโทรศัพท์) ก็รับโบนัส 50 บาทไปเลย
*หากทำเงื่อนไขการถอนเกมสำเร็จ ก็สามารถทำรายการถอนได้
lắp đặt mái che giếng trời ở Hà Nội</a>
báo giá mái che giếng trời</a>
<a href="https://fan-fan-fan10.blog.ss-blog.jp/2021-10-14?comment_fail=1#commentblock&time=1648100358">funniest memes ever</a> 76aa9ff
Brustverkleinerung</a>
온라인 카지노 가입 상담 전문 컨설팅
온라인 카지노를 처음 접하신 분들은 카지노 게임 플레이를 즐기고 싶은데 어디서 어떻게 해야 되는지 많은 고민이 될 것 입니다. 고민의 종류로는 카지노 게임을 플레이 후 환급 처리에 관한 문제, 온라인 카지노는 어떠한 방식으로 이용하는지 대한 문제, 온라인 카지노를 이용 시 나에게 오는 피해는 없을지 많은 것을 생각하게 됩니다. 따라서 어떻게 해야 좋은 선택 인지를 많이 고민합니다. 본사와 상담 후 카지노 사이트 가입을 추천 드리고 있습니다.
온라인 카지노를 이용 함으로써 나에게 오는 악 영향은 없을지 왜 많은 사람들은 온라인 카지노를 플레이 하는지, 온라인 카지노를 믿을 수 있는지 모든 것을 본사에서 상담하여 드리고 있습니다.
본사에서 안내해드리는 카지노사이트 는 모두 100% 검증이 되었고 안전한 곳만을 안내하여 드리고 있습니다.
온라인 카지노 가입 상담 전문 컨설팅
온라인 카지노를 처음 접하신 분들은 카지노 게임 플레이를 즐기고 싶은데 어디서 어떻게 해야 되는지 많은 고민이 될 것 입니다. 고민의 종류로는 카지노 게임을 플레이 후 환급 처리에 관한 문제, 온라인 카지노는 어떠한 방식으로 이용하는지 대한 문제, 온라인 카지노를 이용 시 나에게 오는 피해는 없을지 많은 것을 생각하게 됩니다. 따라서 어떻게 해야 좋은 선택 인지를 많이 고민합니다. 본사와 상담 후 카지노 사이트 가입을 추천 드리고 있습니다.
온라인 카지노를 이용 함으로써 나에게 오는 악 영향은 없을지 왜 많은 사람들은 온라인 카지노를 플레이 하는지, 온라인 카지노를 믿을 수 있는지 모든 것을 본사에서 상담하여 드리고 있습니다.
본사에서 안내해드리는 카지노사이트 는 모두 100% 검증이 되었고 안전한 곳만을 안내하여 드리고 있습니다.
làm sao để Mua nhà ở Hy Lạp</a>
mua hộ hàng mỹ ship về việt nam</a>
온라인 카지노 가입 상담 전문 컨설팅
온라인 카지노를 처음 접하신 분들은 카지노 게임 플레이를 즐기고 싶은데 어디서 어떻게 해야 되는지 많은 고민이 될 것 입니다. 고민의 종류로는 카지노 게임을 플레이 후 환급 처리에 관한 문제, 온라인 카지노는 어떠한 방식으로 이용하는지 대한 문제, 온라인 카지노를 이용 시 나에게 오는 피해는 없을지 많은 것을 생각하게 됩니다. 따라서 어떻게 해야 좋은 선택 인지를 많이 고민합니다. 본사와 상담 후 카지노 사이트 가입을 추천 드리고 있습니다.
온라인 카지노를 이용 함으로써 나에게 오는 악 영향은 없을지 왜 많은 사람들은 온라인 카지노를 플레이 하는지, 온라인 카지노를 믿을 수 있는지 모든 것을 본사에서 상담하여 드리고 있습니다.
본사에서 안내해드리는 카지노사이트 는 모두 100% 검증이 되었고 안전한 곳만을 안내하여 드리고 있습니다.
온라인 카지노 가입 상담 전문 컨설팅
온라인 카지노를 처음 접하신 분들은 카지노 게임 플레이를 즐기고 싶은데 어디서 어떻게 해야 되는지 많은 고민이 될 것 입니다. 고민의 종류로는 카지노 게임을 플레이 후 환급 처리에 관한 문제, 온라인 카지노는 어떠한 방식으로 이용하는지 대한 문제, 온라인 카지노를 이용 시 나에게 오는 피해는 없을지 많은 것을 생각하게 됩니다. 따라서 어떻게 해야 좋은 선택 인지를 많이 고민합니다. 본사와 상담 후 카지노 사이트 가입을 추천 드리고 있습니다.
온라인 카지노를 이용 함으로써 나에게 오는 악 영향은 없을지 왜 많은 사람들은 온라인 카지노를 플레이 하는지, 온라인 카지노를 믿을 수 있는지 모든 것을 본사에서 상담하여 드리고 있습니다.
온라인 카지노 가입 상담 전문 컨설팅
온라인 카지노를 처음 접하신 분들은 카지노 게임 플레이를 즐기고 싶은데 어디서 어떻게 해야 되는지 많은 고민이 될 것 입니다. 고민의 종류로는 카지노 게임을 플레이 후 환급 처리에 관한 문제, 온라인 카지노는 어떠한 방식으로 이용하는지 대한 문제, 온라인 카지노를 이용 시 나에게 오는 피해는 없을지 많은 것을 생각하게 됩니다. 따라서 어떻게 해야 좋은 선택 인지를 많이 고민합니다. 본사와 상담 후 카지노 사이트 가입을 추천 드리고 있습니다.
온라인 카지노를 이용 함으로써 나에게 오는 악 영향은 없을지 왜 많은 사람들은 온라인 카지노를 플레이 하는지, 온라인 카지노를 믿을 수 있는지 모든 것을 본사에서 상담하여 드리고 있습니다.
Giá Ship Hàng từ Mỹ về sài gòn</a>
Types Of Backlink:
-WEB 2.0 Contextual/Article [#100% Dofollow, #DA26-90]
-WEB 2.0 WiKi Contextual/Article [#100% Dofollow, #DA10-17]
-WEB 2.0 Profiles [#90% Dofollow, #DA10-90]
-WEB 2.0 Social BookMark Profile [#5% Dofollow, #DA20-30]
-Social BookMark HQ Profile [#20% Dofollow, #DA40-90]
-High Quality Profile Links [#30% Dofollow, #DA10-65]
-Forum Profile [#100% Dofollow, #DA10-85]
-EDU Profile [#100% Dofollow, #DA30-90]
-High Domain Authority Profile [#40% Dofollow, #DA30-90]
Diamond Package $50 [Limited Time Offer Only $15, 70% Off]
-All Types Of Backlinks
-Contextual/Article Backlink: 150
-Total Backlinks: 1300
-Referring Domain: 1300
-Referring IPs: 1280
-7 URLs & 7 Keywords
-Details Reports: XLSX,CSV,TEXT,PDF
Get this Exclusive Backlink Package for only $15
Get it from FIVERR: https://itwise.link/fvrweb
#1 Freelancing Site, 100% Secure Payment
#It is Limited Time Offer & To Get this Offer, You need to Message me. Simply Copy the Below Text and Send it to me.
"Hi, I was invited by your email on my website, and I want to buy your backlink service at Discounted Price. Send your discount offer."
Types Of Backlink:
-WEB 2.0 Contextual/Article [#100% Dofollow, #DA26-90]
-WEB 2.0 WiKi Contextual/Article [#100% Dofollow, #DA10-17]
-WEB 2.0 Profiles [#90% Dofollow, #DA10-90]
-WEB 2.0 Social BookMark Profile [#5% Dofollow, #DA20-30]
-Social BookMark HQ Profile [#20% Dofollow, #DA40-90]
-High Quality Profile Links [#30% Dofollow, #DA10-65]
-Forum Profile [#100% Dofollow, #DA10-85]
-EDU Profile [#100% Dofollow, #DA30-90]
-High Domain Authority Profile [#40% Dofollow, #DA30-90]
Diamond Package $50 [Limited Time Offer Only $15, 70% Off]
-All Types Of Backlinks
-Contextual/Article Backlink: 150
-Total Backlinks: 1300
-Referring Domain: 1300
-Referring IPs: 1280
-7 URLs & 7 Keywords
-Details Reports: XLSX,CSV,TEXT,PDF
Get this Exclusive Backlink Package for only $15
Get it from FIVERR: https://itwise.link/fvrweb
#1 Freelancing Site, 100% Secure Payment
#It is Limited Time Offer & To Get this Offer, You need to Message me. Simply Copy the Below Text and Send it to me.
"Hi, I was invited by your email on my website, and I want to buy your backlink service at Discounted Price. Send your discount offer."
娛樂城
강남가라오케
토토사이트
富遊娛樂城
Join the INDIA’s leading casino brand and enjoy the best of live casino!Play online IPL, Poker, Roulette, Slots,Baccarat and more all legally and securely, right from your phone!
Are you ready for the best South Africa Hunting Safari?
I can honestly say that I have hunted all over this beautiful continent and people might differ from me but there is no other place in the world where you will be treated and hunt the amount of animals in a short period of time.
And I know there is a lot of debate on hunting in High Fenced areas but let me tell you something from one thing I’ve experience and still deal with every day. No matter if you hunt in Masai Land in Tanzania or in Luangwa Valley in Zambia of in Tsholotsho in Zimbabwe.
If you would like to know more about African Safari and Photo. We are excited to discuss a custom hunting package just for you.
토토사이트
Lensadigital.id
Seputar kamera lensa
Teknologi lensa
Lensa digital indonesia
Edmonton Plumbing
Plumbing Edmonton
plumber Edmonton
plumber in Edmonton
plumbing in Edmonton
best plumber in Edmonton
top Edmonton plumbers
best Edmonton plumbers
Plastic, Reconstructive, and Aesthetic Surgery treat congenital and acquired aesthetic, shape, and functional disorders. Specialist plastic surgeons meet the requirements of the branch. Cosmetic surgery in Turkey includes plastic, Reconstructive, and Aesthetic Surgical operations.
if there's anything else that you need you can write me.
thanks in advance for your services.
berita hukum
온라인 카지노 가입 상담 전문 컨설팅
온라인 카지노를 처음 접하신 분들은 카지노 게임 플레이를 즐기고 싶은데 어디서 어떻게 해야 되는지 많은 고민이 될 것 입니다. 고민의 종류로는 카지노 게임을 플레이 후 환급 처리에 관한 문제, 온라인 카지노는 어떠한 방식으로 이용하는지 대한 문제, 온라인 카지노를 이용 시 나에게 오는 피해는 없을지 많은 것을 생각하게 됩니다. 따라서 어떻게 해야 좋은 선택 인지를 많이 고민합니다. 본사와 상담 후 카지노 사이트 가입을 추천 드리고 있습니다.
온라인 카지노를 이용 함으로써 나에게 오는 악 영향은 없을지 왜 많은 사람들은 온라인 카지노를 플레이 하는지, 온라인 카지노를 믿을 수 있는지 모든 것을 본사에서 상담하여 드리고 있습니다.
본사에서 안내해드리는 카지노사이트 는 모두 100% 검증이 되었고 안전한 곳만을 안내하여 드리고 있습니다.
berita nasional
berita kesehatan
온라인 카지노를 처음 접하신 분들은 카지노 게임 플레이를 즐기고 싶은데 어디서 어떻게 해야 되는지 많은 고민이 될 것 입니다. 고민의 종류로는 카지노 게임을 플레이 후 환급 처리에 관한 문제, 온라인 카지노는 어떠한 방식으로 이용하는지 대한 문제, 온라인 카지노를 이용 시 나에게 오는 피해는 없을지 많은 것을 생각하게 됩니다. 따라서 어떻게 해야 좋은 선택 인지를 많이 고민합니다. 본사와 상담 후 카지노 사이트 가입을 추천 드리고 있습니다.
온라인 카지노를 이용 함으로써 나에게 오는 악 영향은 없을지 왜 많은 사람들은 온라인 카지노를 플레이 하는지, 온라인 카지노를 믿을 수 있는지 모든 것을 본사에서 상담하여 드리고 있습니다.
본사에서 안내해드리는 카지노사이트 는 모두 100% 검증이 되었고 안전한 곳만을 안내하여 드리고 있습니다.
온라인 카지노 가입 상담 전문 컨설팅
온라인 카지노를 처음 접하신 분들은 카지노 게임 플레이를 즐기고 싶은데 어디서 어떻게 해야 되는지 많은 고민이 될 것 입니다. 고민의 종류로는 카지노 게임을 플레이 후 환급 처리에 관한 문제, 온라인 카지노는 어떠한 방식으로 이용하는지 대한 문제, 온라인 카지노를 이용 시 나에게 오는 피해는 없을지 많은 것을 생각하게 됩니다. 따라서 어떻게 해야 좋은 선택 인지를 많이 고민합니다. 본사와 상담 후 카지노 사이트 가입을 추천 드리고 있습니다.
온라인 카지노를 이용 함으로써 나에게 오는 악 영향은 없을지 왜 많은 사람들은 온라인 카지노를 플레이 하는지, 온라인 카지노를 믿을 수 있는지 모든 것을 본사에서 상담하여 드리고 있습니다.
본사에서 안내해드리는 카지노사이트 는 모두 100% 검증이 되었고 안전한 곳만을 안내하여 드리고 있습니다.
dunia ikan
온라인 카지노 가입 상담 전문 컨설팅
온라인 카지노를 처음 접하신 분들은 카지노 게임 플레이를 즐기고 싶은데 어디서 어떻게 해야 되는지 많은 고민이 될 것 입니다. 고민의 종류로는 카지노 게임을 플레이 후 환급 처리에 관한 문제, 온라인 카지노는 어떠한 방식으로 이용하는지 대한 문제, 온라인 카지노를 이용 시 나에게 오는 피해는 없을지 많은 것을 생각하게 됩니다. 따라서 어떻게 해야 좋은 선택 인지를 많이 고민합니다. 본사와 상담 후 카지노 사이트 가입을 추천 드리고 있습니다.
온라인 카지노를 이용 함으로써 나에게 오는 악 영향은 없을지 왜 많은 사람들은 온라인 카지노를 플레이 하는지, 온라인 카지노를 믿을 수 있는지 모든 것을 본사에서 상담하여 드리고 있습니다.
본사에서 안내해드리는 카지노사이트 는 모두 100% 검증이 되었고 안전한 곳만을 안내하여 드리고 있습니다.
온라인 카지노 가입 상담 전문 컨설팅
온라인 카지노를 처음 접하신 분들은 카지노 게임 플레이를 즐기고 싶은데 어디서 어떻게 해야 되는지 많은 고민이 될 것 입니다. 고민의 종류로는 카지노 게임을 플레이 후 환급 처리에 관한 문제, 온라인 카지노는 어떠한 방식으로 이용하는지 대한 문제, 온라인 카지노를 이용 시 나에게 오는 피해는 없을지 많은 것을 생각하게 됩니다. 따라서 어떻게 해야 좋은 선택 인지를 많이 고민합니다. 본사와 상담 후 카지노 사이트 가입을 추천 드리고 있습니다.
온라인 카지노를 이용 함으로써 나에게 오는 악 영향은 없을지 왜 많은 사람들은 온라인 카지노를 플레이 하는지, 온라인 카지노를 믿을 수 있는지 모든 것을 본사에서 상담하여 드리고 있습니다.
본사에서 안내해드리는 카지노사이트 는 모두 100% 검증이 되었고 안전한 곳만을 안내하여 드리고 있습니다.
온라인 카지노 가입 상담 전문 컨설팅
온라인 카지노를 처음 접하신 분들은 카지노 게임 플레이를 즐기고 싶은데 어디서 어떻게 해야 되는지 많은 고민이 될 것 입니다. 고민의 종류로는 카지노 게임을 플레이 후 환급 처리에 관한 문제, 온라인 카지노는 어떠한 방식으로 이용하는지 대한 문제, 온라인 카지노를 이용 시 나에게 오는 피해는 없을지 많은 것을 생각하게 됩니다. 따라서 어떻게 해야 좋은 선택 인지를 많이 고민합니다. 본사와 상담 후 카지노 사이트 가입을 추천 드리고 있습니다.
온라인 카지노를 이용 함으로써 나에게 오는 악 영향은 없을지 왜 많은 사람들은 온라인 카지노를 플레이 하는지, 온라인 카지노를 믿을 수 있는지 모든 것을 본사에서 상담하여 드리고 있습니다.
본사에서 안내해드리는 카지노사이트 는 모두 100% 검증이 되었고 안전한 곳만을 안내하여 드리고 있습니다.
The Most Special Moments In One's Life
A wedding is one of the most special moments in one's life. Now you can capture the moments and keep them alive for years with a wedding video. In order to make the best。, the most important thing is the selection of a wedding videographer. With large numbers of videographers in the market, it might be a bit confusing in selecting the best one. Here, you will come across some useful suggestions that will help you choose the best videographer for your special day. We are now introducing S+ studio from Taiwan in the Asia region. In Taiwan, traditional and romantic elements are all over in the weddings. S+ studio has unique ways to merge these two elements and creates a whole new wedding video.
The Most Special Moments In One's Life
A wedding is one of the most special moments in one's life. Now you can capture the moments and keep them alive for years with a wedding video. In order to make the best。, the most important thing is the selection of a wedding videographer. With large numbers of videographers in the market, it might be a bit confusing in selecting the best one. Here, you will come across some useful suggestions that will help you choose the best videographer for your special day. We are now introducing S+ studio from Taiwan in the Asia region. In Taiwan, traditional and romantic elements are all over in the weddings. S+ studio has unique ways to merge these two elements and creates a whole new wedding video.
온라인 카지노를 처음 접하신 분들은 카지노 게임 플레이를 즐기고 싶은데 어디서 어떻게 해야 되는지 많은 고민이 될 것 입니다. 고민의 종류로는 카지노 게임을 플레이 후 환급 처리에 관한 문제, 온라인 카지노는 어떠한 방식으로 이용하는지 대한 문제, 온라인 카지노를 이용 시 나에게 오는 피해는 없을지 많은 것을 생각하게 됩니다. 따라서 어떻게 해야 좋은 선택 인지를 많이 고민합니다. 본사와 상담 후 카지노 사이트 가입을 추천 드리고 있습니다.
온라인 카지노를 이용 함으로써 나에게 오는 악 영향은 없을지 왜 많은 사람들은 온라인 카지노를 플레이 하는지, 온라인 카지노를 믿을 수 있는지 모든 것을 본사에서 상담하여 드리고 있습니다.
본사에서 안내해드리는 카지노사이트 는 모두 100% 검증이 되었고 안전한 곳만을 안내하여 드리고 있습니다.
Controlo de pragas – um servico completo e de qualidade, realizado com profissionais qualificados e de forma planeada.
Premium Protect e um servico premium que lhe oferece a capacidade de proteger a sua propriedade ou estabelecimento contra pragas.
온라인 카지노를 처음 접하신 분들은 카지노 게임 플레이를 즐기고 싶은데 어디서 어떻게 해야 되는지 많은 고민이 될 것 입니다. 고민의 종류로는 카지노 게임을 플레이 후 환급 처리에 관한 문제, 온라인 카지노는 어떠한 방식으로 이용하는지 대한 문제, 온라인 카지노를 이용 시 나에게 오는 피해는 없을지 많은 것을 생각하게 됩니다. 따라서 어떻게 해야 좋은 선택 인지를 많이 고민합니다. 본사와 상담 후 카지노 사이트 가입을 추천 드리고 있습니다.
온라인 카지노를 이용 함으로써 나에게 오는 악 영향은 없을지 왜 많은 사람들은 온라인 카지노를 플레이 하는지, 온라인 카지노를 믿을 수 있는지 모든 것을 본사에서 상담하여 드리고 있습니다.
본사에서 안내해드리는 카지노사이트 는 모두 100% 검증이 되었고 안전한 곳만을 안내하여 드리고 있습니다.
text: 신림셔츠룸이란 기존에 강남에서 만나볼 수 있었던 셔츠룸을 신림에서도 편하게 만나볼수 있도록 생긴 업소입니다.신림 가라오케
정성가득 매일 매일 이벤트 진행중 ! 아가씨 50명 이상 대기중 !
신림유일 초대형 셔츠룸 ! 가라오케도 편하게 전화주세요 ~
24시간 265일 영업중입니다. 편안하게 문의전화주시면 한분 한분 친절하게 예약 도와드리겠습니다.
단체 및 혼자 오셔도 정성스럽게 여자친구 찾아드리겠습니다.
신림셔츠룸 , 신림가라오케 ,신림 노래빠 ,구디 노래빠 , 구디셔츠룸, 철산셔츠룸
철산가라오케,철산 노래빠
신림셔츠룸짱구대표
Cổng game giải trí hàng đầu Bốc Club đã trở lại.
Phiên bản mới - Đẳng cấp mới.
the best site to buy or sell properties in tulum playa del carmen and Puerto Aventuras Mexico !! customer service in russian english and spanish.
娛樂城
Cổng game dân gian hấp dẫn nhất Việt Nam đã ra mắt phiên bản mới nhất 2022.
Cổng truy cập ổn định nhất thuộc quyền quản lý của nhà phát hành game đổi thưởng BayVip Club. Tương thích cao với mọi thiết bị, đường truyền internet tốc độ nhanh nhất từ trước tới nay với hàng ngàn quà tặng dành cho thành viên.
娛樂城
娛樂城
娛樂城
娛樂城
娛樂城
娛樂城
娛樂城
娛樂城
娛樂城
娛樂城
娛樂城
娛樂城
娛樂城
<a href="http://xdiag.ru/blog/vasya-diag/#comment_160423">폰테크</a> 39e9bfd
<a href="http://ae0.6b0.myftpupload.com/2017/10/diy-how-to-a-sub-headboard-demigod-o/#comment-20232982">Angajari Videochat</a> e9bfd17
娛樂城
娛樂城
娛樂城
娛樂城
娛樂城
娛樂城
娛樂城
娛樂城
<a href="http://gbreschool.com/forums/topic/watchfree-golden-state-warriors-toronto-raptors-live-stream-free-basketball/#post-1101002">폰테크</a> bfd17ac
<a href="http://instantpot.autoblogcity.com/index.php/2019/12/31/is-the-mediterranean-diet-the-best-diet/#comment-14964">폰테크</a> 646e376
대부업체를 통해서 알게 되신 분들, 폰테크를 이용하고 싶지만 하는 방법을 잘 몰라서 이용을 못하시는 분들, 혹은 단순히 불안해서 못하시는 분들,
폰테크를 진행하고는 싶지만 안전한 업체나 믿을만한 업체가 어디인지 몰라 못하시는 분들 등등 기타 이런저런 이유로 폰테크를 진행 하시지 못하시는 분들이 많으신데
그러한 고민들은 오늘로서 끝이라는 희소식을 전해 드리겠습니다!!!
바로 오늘 소개해드릴 업체인 '다이렉트 폰테크'때문입니다.
다이렉트 폰테크에 대해 말을 해보자면 당연히 폰테크로 사업자등록증 정식으로 등록된 업체이며, 사전승낙서 또한 보유한 업체입니다.
그냥 일반 업체라기엔 정상적으로 매장도 운영하고 있는 곳이라서 매우 믿을만 한 곳이구요 매장도 하나가 아닌 여러 지역에 다수의 매장과 협업을 하고 있는
큰 통신망을 보유한 곳이라고 할 수 있습니다.
이는 정말 큰 장점이고 강점이며 폰테크를 진행하는 고객의 입장에선 최상의 조건이라고 할 수 있습니다.
왜냐하면 보통 폰테크를 진행하시는 분들은 가성비가 좋은
즉, 기기값은 최대한 저렴하면서 매입가는 최대한 높은 기종의 선택이 용이하기 때문입니다.
보통의 업체들은 그러한 기종들을 구할 수 없을 뿐더러 구하는 물량에도 분명 한계가 매우 클 것이기 때문입니다.
하지만 다이렉트는 여러 매장의 통신망을 구축하여 가성비 좋은 폰의 물량확보가 용이하며
폰테크 진행 추후 몇개월 후 해당 대리점에서 오는 민, 형사적 소송과 내용증명, 소장, 벌금 등에서 자유로울 수 있습니다.
불법 업체를 통하여 불법 개통, 그리고 고객을 데리고 다니며 개통을 해오라고 하는 그런 말도안되는 주먹구구식 업체 말고
안전하고 신속하게 일을 처리하고 문의부터 시작해서 상담 -> 진행 -> 입금 까지 당일에 모두 처리하는 다이렉트만의 놀라운 일처리 속도와 정확함으로
고객 모두에게 만족을 드리는 모습에 감탄을 하게 되실 겁니다.
실제로 다이렉트 폰테크에 대해 리뷰 또한 구글로 찾아봤는데요
실로 많은 분들이 만족감을 표하시고 네이버플레이스 또한 매우 좋은 평가가 많았습니다.
기타 카페 게시판의 후기나 홈페이지 인증리뷰 같은 경우에도 정말 평가가 훌륭했구요.
무엇보다 재방문율이 타 업체에 비교 자체가 불가할 수준으로 높게 나오는것만 보더라도 얼마나 믿을 수 있을지 알 수 있는 부분입니다.
다른것보다 폰테크라함은 안정성을 배제한다면 일반 사기와 별반 다를바가 없는 중대한 범죄라고 생각할 수 있습니다.
그만큼 안정성이 정말 매우 엄청나게 엄청나고 굉장히 굉장하게 중요한 부분이구요,
안정성만 보장되고 정상적이고 공식적인 업체에서 진행을 하신다면 아주 유용하게 급전마련을 하실 수 있으며 급한 상황을 잘 모면할 수 있겠습니다.
사실상 어떠한 업계라도 일정한 가격 형성이 되어 있는데요
예를들어 1금융과 2금융에 대출이라 치면 정해진 연이자가 있을 것이구요
불법 대부업이나 일수, 개인돈 같이 비 정상적인 거래라면 당연히 연이자보다 말도 안되게 높은 금리가 있는 것이겠구요
마트나 편의점에서 음료수나 과자등과 같은 물품을 구매한다 하더라도 약간의 편차는 있지만 그렇게 높은 차이는 없습니다.
정육점도 마찬가지로 온국민의 사랑을 받는 삼겹살도 국내산 돼지 생삼겹살의 가격 역시 약간의 차이가 있을 뿐 거의 정해져 있구요
1근에 만원이라는 가격이 형성되어 있다고 한다면 1근에 6000원 7000원이라는 가격이 나오기 힘든 부분이죠
만일 가격표를 그렇게 해놓고 판다면 그건 국내산이 아닐 확률은.. 뭐 굳이 제가 언급하지 않아도 다들 아시겠죠..?? ㅎㅎ
새로운 형태의 시장이 형성되어 이제 막 시작이 되고 있는 분야라면 가격차이가 천차만별일 수 있겠지만
이처럼 진작에 기존 시장이 형성되어 자리잡혀 있는 시장의 가격이 어느정도 정해져 있는 분야라면
일반적은 은행이나 불법이 아닌 합법적 대부업계 대출의 금리도, 시장 물품 가격도, 정육이나 기타 물품이 유통되는 가격도 다 시장가가 어느정도 정해지기 마련이고
그 안에서 가격이 다른곳보다 정도차이가 심하게 저렴하거나 심하게 높다 라고 한다면 한번쯤 의구심을 가져봐야 할 것입니다.
그렇다라면 폰테크 역시도 마찬가지일 것이구요.
너무 높은 매입가는 우선 경계를 해보셔야 하는 부분이구요
반대로 너무 낮은 매입가 역시 피해야 하는 부분입니다.
그런 점에서 미루어 보면 다이렉트 폰테크는 투명한 가격으로 방문 고객님들 역시 하나같이 거의 동일한 금액을 받아가셨는데요
그러한 부분 또한 각종 입금받은 내역 인증이나 리뷰에서 알 수 있던 부분입니다.
폰테크는 다른것보다 우선적으로
사업자등록증, 사전승낙서 확인하셔야 하며, 그 해당 등록증과 승낙서에 명시가 되어있는 이름과 일치하는지를 꼭 확인하셔야 하며
이름만 있는 유령 매장이나, 사무실, 오피스텔 등에서 사업자를 내고 운영하는 유령업체는 아닌지 확인하셔야 합니다.
그리고 앞서 말했던 부분처럼 너무 낮거나 혹은 타 업체에 비해 너무 높은(고객님이 혹하실만한) 매입가라면 그것 역시도 경계하셔야 합니다.
마지막으로 사후처리나 대비가 완벽하게 이루어지는지 꼭!!!!! 반드시 꼭!!!!! 밑줄쫙 별표 다섯개 달아두시고 확인하셔야 합니다.
일반 정상적인 매장이 아니라면 그런것에 대한 대비가 거의 전무하다 볼 수 있으니 번거롭더라도 너무 높은 매입가만 찾아서 가려 하지 마시고
가격이 다소 약간의 차이가 있더라도 문제가 생기지 않는 곳에서 진행을 하시길 추천드립니다.
안정성 비례 매입가가 높은 곳은 단연 지금 말씀드리는 '다이렉트 폰테크'가 최고라고 할 수 있겠습니다.
그리고 폰테크 진행 자체도 방문, 비대면, 출장 모두 가능하며 그 선택권은 전부 이용객의 입장에서 선택이 가능한 부분입니다.
또한 지역상관없이 거리 상관없이 출장과 비대면 모두 진행이 가능하다고 하시니까요 부산이라서 대구라서 목포라서 강원도라서 등등 타 지역이라고
그냥 넘기지 마시고 '다이렉트 폰테크'에 꼭 문의하시길 바랍니다.
그리고 혹여 타 업체를 이용하시더라도 반드시 다이렉트에서 문의하여 조회와 상담 받아보시길 추천드립니다.
잠깐 편하고 잠깐 좋자고 추후에 문제가 생기는 행동을 하실 분들은 없으실거라 믿고 싶네요 통신쪽 벌금은 터졌다 하면 최소 200부터 출발입니다 꼭 명심하시길 바래요
그럼 지금까지 폰테크를 안전하게 진행할 수 있는 업체인 '다이렉트 폰테크'에 대해서 말씀드렸구요문의와 상담 그리고 진행등은 아래 이미지를 통해서 하실 수 있으니 참고하시길 바랍니다.
九州娛樂城
그냥 일반 업체라기엔 정상적으로 매장도 운영하고 있는 곳이라서 매우 믿을만 한 곳이구요 매장도 하나가 아닌 여러 지역에 다수의 매장과 협업을 하고 있는
큰 통신망을 보유한 곳이라고 할 수 있습니다.
이는 정말 큰 장점이고 강점이며 폰테크를 진행하는 고객의 입장에선 최상의 조건이라고 할 수 있습니다.
왜냐하면 보통 폰테크를 진행하시는 분들은 가성비가 좋은
즉, 기기값은 최대한 저렴하면서 매입가는 최대한 높은 기종의 선택이 용이하기 때문입니다.
보통의 업체들은 그러한 기종들을 구할 수 없을 뿐더러 구하는 물량에도 분명 한계가 매우 클 것이기 때문입니다.
하지만 다이렉트는 여러 매장의 통신망을 구축하여 가성비 좋은 폰의 물량확보가 용이하며
폰테크 진행 추후 몇개월 후 해당 대리점에서 오는 민, 형사적 소송과 내용증명, 소장, 벌금 등에서 자유로울 수 있습니다.
불법 업체를 통하여 불법 개통, 그리고 고객을 데리고 다니며 개통을 해오라고 하는 그런 말도안되는 주먹구구식 업체 말고
안전하고 신속하게 일을 처리하고 문의부터 시작해서 상담 -> 진행 -> 입금 까지 당일에 모두 처리하는 다이렉트만의 놀라운 일처리 속도와 정확함으로
고객 모두에게 만족을 드리는 모습에 감탄을 하게 되실 겁니다.
[url=http://saza.ltd/product/motorcycle-racing-packs-jacket-orange/#comment-626637]폰테크[/url] 39e9bfd
слоты </a>
娛樂城
егрн об объекте недвижимости
Бетсити
<a href=https://sayanogorsk.info/details/entry/4514-vyzov-narkologa-na-dom/>нарколог на дом</a>
<a href="https://anire.co.jp/jikkagurashi-ng-riyuu/#comment-37344">Дизайн сайта новосибирск</a> ac9646e
berita crypto
<a href=http://rusnord.ru/narkomanija-saharnyj-diabet-i-vospalenie-kozhi.html>лечение наркомании</a>
<a href="https://blog.silkandsparkle.com.au/womans-fashion/how-to-shop-for-your-bffs-wedding/#comment-458012">BrianSably</a> 3_48f4e
<a href=https://ccdi.ru/articles/medicina-i-zdorove/psihologija/simptomy-narkoticheskoi-zavisimosti.html>лечение наркомании</a>
<a href=http://ulgrad.ru/?p=184093>наркологическая клиника</a>
<a href=http://ulgrad.ru/?p=184093>наркологическая клиника</a>
<a href=http://wildkids.biz/1533-kak-lechat-v-narkologicheskoy-klinike.html>наркология</a>
<a href=https://promedonline.net/novosti/kakuyu-pomoshh-mogut-okazat-v-narkologicheskix-centrax>наркология</a>
<a href=https://sayanogorsk.info/details/entry/4514-vyzov-narkologa-na-dom/>нарколог на дом</a>
<a href=https://sanbyulleten.ru/my-blog/vidy-kodirovaniya-ot-alkogolizma.html>кодирование от алкоголизма</a>
<a href=https://crocothemes.com/letchenie-ot-narkotitcheskoy-zavisimosti-v-klinike-narkoblok.html>наркология</a>
<a href=http://wildkids.biz/1533-kak-lechat-v-narkologicheskoy-klinike.html>наркология</a>
<a href=https://crocothemes.com/letchenie-ot-narkotitcheskoy-zavisimosti-v-klinike-narkoblok.html>наркологическая клиника</a>
A university that exemplifies a prophetic attitude
<a href=http://freespin123.top/>freespin123</a>
<a href="https://mishutka-lomonosov.ru/blog/chto-takoe-geobord/#comment_172391">TimothyWer</a> ff8_ef9
Autonomos Pymes asesoria online slp somos una sociedad profesional de economistas y un punto de atencion a emprendedores especializados en crear empresas online en Espana. Para crear una empresa sl tan solo debes ponerte en contacto con nosotros. El coste de crear una empresa sociedad limitada online es de tan solo 290 euros mas iva incluyendo los gastos de constitucion necesarios para la empresa sl. Puedes crear una empresa en Madrid, Barcelona, valencia o en cualquier localidad de Espana.
Дом на Кипре
Квартира на Кипре
Апартаменты
Виллы
Пентхаусы
Giá Ship Hàng từ Mỹ về hà nội</a>
Fullintel is a media monitoring solution company that provides the most accurate reports & analysis. If you're ready to upgrade your media monitoring, don't hesitate to reach out to Fullintel
<a href="http://www.dougnagy.com/archives/2010/02/01/this-time-tomorrow/comment-page-404/#comment-742237">interior-design</a> 9bfd17a
What is happening in Donbas now? Why are many media and politicians silent? I went to the telegram channel "What's with the Donbass" And what do I see? Where is the truth?!!! See for yourself
#whatisdonbass
https://o-pencil.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://reduslim.health/
[url=https://support.hypack.com/Support/index.php?/News/NewsItem/View/117]EzekielHaG[/url] f6_0b72
https://prisguiden.no/goto.php?shop_id=432&url=https%3A%2F%2Freduslim.at&price=799&spid=17119&t=Glorious+Model+O+Wireless+Gaming+Mus+Svart
[url=https://mysl.kazgazeta.kz/news/537]Ezekielageno[/url] c239e9b
https://hibibro.hatenablog.com/iframe/hatena_bookmark_comment?canonical_uri=https%3A%2F%2Fm-ctc.ru%2Fprices
[url=http://akonit-box.com/products/lyuk-revizionnyj-300-350-lr-3-35/#comment_79555]Haroldhoumn[/url] c54c239
[url=https://safemealguide.com/blog/article/eating-out-%26-restaurant-reviews/eating-out-food-allergies-dorset/]ShaynaHoify[/url] 3_7eedd
http://sosnovoborsk1.websender.ru/redirect.php?url=https://reduslim.health/
[url=https://russagency.ru/wheretogo/countries/kanada/?ok=251220]EzekielDor[/url] 4c239e9
https://www.stupeni-lyceum.ru/?URL=https://reduslim.at/
[url=http://www.sewmach.ru/product/vaza-glinyanaya-malenkaya-25/]EzekielGlubs[/url] c9646e3
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
https://abakantehoptorg.ru/bitrix/redirect.php?goto=https://reduslim.health/
[url=http://comhotel.ru/product/telezhka-s-polkami-iz-mdf-karkas-iz-nerzhaveiki-tg-112n-233/]EzekielGag[/url] 646e376
http://www.liveinternet.ru/journal_proc.php?action=redirect&kwork.ru/logo/15280132/dizayn-logotipa-razrabotka-logotipa-beskonechnie-pravki-noviy-logo3D868298www.facebook.com/A1B2B5BAB880-BDB4B2BE818C-100153902340083reduslim.at/reduslim.health/https://reduslim.at/
[url=http://www.sibiria.ru/otchety_o_poezdkah/show/89/com_action/displaycomments]Ezekielgom[/url] 39e9bfd
[url=https://www.skr-skr.com/?attachment_id=3106]ShaynaThymn[/url] 239e9bf
http://akvacity.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://reduslim.health/
[url=https://www.evrmemories.com/commemoration-memorial-portrait/?attributes=eyIxMzg4NSI6IiIsIjEzODg2IjoiaHR0cHM6XC9cL2RvLmFsdHNwdS5ydVwvYml0cml4XC9yZWRpcmVjdC5waHA_Z290bz1odHRwczpcL1wvcmVkdXNsaW0uYXRcL1xyXG5odHRwOlwvXC9mcmFuay1zaGtvbGEucnVcL2JpdHJpeFwvcmVkaXJlY3QucGhwP2V2ZW50MT1jbGlja190b19jYWxsJmV2ZW50Mj0mZXZlbnQzPSZnb3RvPWh0dHBzOlwvXC9yZWR1c2xpbS5hdFwvXHJcbiBcclxuW3VybD1odHRwczpcL1wvc3VrYW11bHlhLXB1cndha2FydGEuZGVzYS5pZFwvcmVhZFwvMzQxODY2XUV6ZWtpZWxndVBbXC91cmxdIGFkZWM2YjggIn0]EzekielDah[/url] d17ac96
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
http://chillout-club.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://reduslim.at/
[url=http://www.mozgovig.ru/post.php?id=17]EzekielMOicy[/url] dbc54c2
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
https://optfm.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://reduslim.at/
[url=https://schoolserv.in/security-code/6039/]EzekielSag[/url] e9bfd17
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
https://avtoset.su/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://reduslim.at/
[url=http://www.rosenthal-severson.com/board/thanks.asp?id=21430]EzekielHoina[/url] c9646e3
https://tehnozont.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://reduslim.health/
[url=http://art-mast.ru/?name=Ezekielsed&email=edfghj@gmail.com&text=http://hotelsoyuz.com/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://reduslim.health/%20%20https://burgas-sochi.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://reduslim.at/%20%20%20%20%20<a%20href=https://buypremiumkey.com/news/view-6/special-offers-filespace-premium-key-330-days.html>EzekielBoale</a>%2010a00cd%20&checkbox=on&submit=%D0%97%D0%B0%D0%B4%D0%B0%D1%82%D1%8C%20%D0%B2%D0%BE%D0%BF%D1%80%D0%BE%D1%81&format=feed&type=atom]Ezekielsed[/url] 6e376aa
Jurnal Utilitas is a multi-disciplinary which has been established for the dissemination of state-of-the-art knowledge in the field of education, teaching, entrepreneurship, Administrative and management of education, administrative and management office, administrative and commercial management, economics of education, management, economics, accounting, Office administration, development, instruction, educational projects and innovations, learning methodologies and new technologies in education and learning.
Sebagai salah satu amal usaha Muhammadiyah, UHAMKA adalah perguruan tinggi berakidah Islam yang bersumber pada Al Quran dan As-Sunah serta berasaskan Pancasila dan UUD 1945 yang melaksanakan tugas caturdharma Perguruan Tinggi Muhammadiyah, yaitu menyelenggarakan pembinaan ketakwaan dan keimanan kepada Allah SWT., pendidikan dan pengajaran, penelitian, dan pengabdian pada masyarakat menurut tuntunan Islam.
http://armex.su/bitrix/rk.php?goto=https://reduslim.health/
[url=https://mdl.com.au/areas-of-practice/?status=validation_failed&fields=First%20Name,Last%20Name,Email%20Address,Phone%20Number&values%5Bpost_id%5D=347&values%5BFirst%20Name%5D&values%5BLast%20Name%5D&values%5BEmail%20Address%5D&values%5BPhone%20Number%5D&values%5BMessage%5D=https://www.cedrus.ru/bitrix/redirect.php?event1=click_to_call&event2&event3&goto=https://reduslim.at/http://f4.motogon.ru/redirector/?url=https://reduslim.at/%20a%20href=http://www.sewmach.ru/product/vaza-glinyanaya-malenkaya-25/EzekielGlubs/a%2071_cfa4%20&values%5BSubmit%5D&values%5Bcaptured%5D=https://mdl.com.au/areas-of-practice/]Ezekielfor[/url] ff2_378
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
http://www.spb.bsigroup.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://reduslim.at/
[url=http://sewmach.ru/product/kaplya-v-more-79/]EzekielGlubs[/url] bfd17ac
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
[url=https://mycontinent.co/Miss-Universe.php]Shaynagog[/url] 646e376
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
https://maps.google.com.my/url?q=https://reduslim.at/
[url=http://kousaiclub-sp.com/club/33]EzekielSeags[/url] 54c239e
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
https://pgkneek.blogsky.com/dailylink/?go=//reduslim.at&id=49
<tr> 9bfd17a
https://kosmeticky-salon-lavendera.reservio.com:443/booking?backlink=http%3a%2f%2freduslim.at
[url=https://gameranbu.jp/bokumonoolive/06890bf8993ad39d3963]EzekielOpele[/url] aa9ff0_
http://mega-xxx.net/go.php?url=https://reduslim.health/
[url=https://gameranbu.jp/bokumonoolive/06890bf8993ad39d3963]EzekielOpele[/url] 6aa9ff6
[url=http://demo.elefanteinstaller.com/nucleus/index.php?itemid=4]Shaynanothe[/url] 39e9bfd
http://telcosoft.ru/to/?url=https://reduslim.at/
[url=https://www.masconia.cl/blog/2015/11/13/como-ensenar-un-cachorro-hacer-sus-necesidades/]EzekielTuh[/url] bfd17ac
Прочтите рейтинг интернет казино с лицензией. Рейтинг онлайн казино составлен по выплатам, по отдаче. Зарегистрируйся и получи лучшие условия для игры
https://www.pubmed.or.kr:4440/bbs/link.php?code=media&number=10&url=http%3a%2f%2freduslim.health
[url=https://kennyproducts.com/chalkboard-full-color-name-tags-1x3/?attributes=eyI0NTI2IjoiIiwiNDUyNyI6IjEwXC8xMlwvMjAxNyIsIjQ1MjgiOiJodHRwczpcL1wvd3d3Lmdvb2dsZS5jby5jclwvdXJsP3E9aHR0cHM6XC9cL3JlZHVzbGltLmF0XC9cclxuaHR0cHM6XC9cL2x5Yzg0LnJ1XC9iaXRyaXhcL3JlZGlyZWN0LnBocD9ldmVudDE9Y2xpY2tfdG9fY2FsbCZldmVudDI9JmV2ZW50Mz0mZ290bz1odHRwczpcL1wvcmVkdXNsaW0uaGVhbHRoXC9cclxuIFxyXG48YSBocmVmPWh0dHA6XC9cL2NvbWhvdGVsLnJ1XC9wcm9kdWN0XC9yYXNrbGFkbmF5YS1rcm92YXQtYmwtMS01XC8-RXpla2llbEdhZzxcL2E-IDc4ZjEyN2MgIn0]EzekielBeinc[/url] aa9ff4_
https://sportset.net/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://reduslim.at/
[url=http://www.minigames08.de/game/517/.html]Ezekielnup[/url] 6e376aa
[url=http://bi.emultihouse.net/bbs/view.php?id=board&page=1&page_num=20&select_arrange=headnum&desc=&sn=off&ss=on&sc=on&keyword=&no=120&category=]Shaynadwege[/url] e9bfd17
https://toolbarqueries.google.ng/url?q=http%3A%2F%2Freduslim.at/
[url=http://www.vasilemustata.ro/commentscript/comentarii9.php]EzekielTub[/url] 9bfd17a
https://jquarter.ru/forum/go.php?url=https://reduslim.at/
[url=http://www.fmnagasaki.co.jp/program/omuranchannel/item/17129/catid/142]EzekielDrype[/url] bdbc54c
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
https://secnews.ru/bitrix/rk.php?goto=https://reduslim.health/
[url=https://enthisai.com/single-post.php?news=]EzekielLer[/url] bdbc54c
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
https://www.agscenter.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://reduslim.at/
[url=http://vieweroom.com/id1244297804-dcu-justice-league-the-flashpoint-paradox/]Ezekieldrymn[/url] dbc54c2
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
[url=https://kuwait.carsprite.com/car-prices/volvo/v40-2017]ShaynaHok[/url] 9bfd17a
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
https://vegan.ru:443/bitrix/redirect.php?goto=https://reduslim.at/
[url=https://www.dodsannoncer.dk/oversigt/dodsannonce-ellen-margrethe-mller-gregersen-26712/]Ezekielsar[/url] bdbc54c
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
http://came.sandbox.google.com.pe/url?q=https%3A%2F%2Freduslim.health
[url=http://www.minigames08.de/game/453/.html]Ezekielnup[/url] ff5_697
[url=https://kalli.kalde.eu/?error_checker=captcha&author_spam=Claratic&email_spam=yhvhhh%40gmail.com&url_spam&comment_spam=https%3A%2F%2Fwww.juicy-food.ru%2Fbitrix%2Frk.php%3Fgoto%3Dhttps%3A%2F%2F%25D0%25B0%25D0%25BB%25D1%258C%25D1%2582%25D0%25B5%25D1%2580%25D0%25BD%25D0%25B0%25D1%2582%25D0%25B8%25D0%25B2%25D0%25BD%25D1%258B%25D0%25B9%25D0%25B3%25D0%25BB%25D0%25BE%25D0%25B1%25D0%25B0%25D0%25BB%25D0%25B8%25D0%25B7%25D0%25B0%25D1%2586%25D0%25B8%25D0%25BE%25D0%25BD%25D0%25BD%25D1%258B%25D0%25B9%25D1%2581%25D1%2586%25D0%25B5%25D0%25BD%25D0%25B0%25D1%2580%25D0%25B8%25D0%25B9.%25D1%2580%25D1%2584%2Fbudushhee-sovremennogo-obshhestva-chto-nas-zhdyot%2F%20%3Ca%20href%3Dhttps%3A%2F%2Fanatili.kazgazeta.kz%2Fnews%2F59839%3EShaynaLaF%3C%2Fa%3E%20cc1c958]Shaynawed[/url] 76aa9ff
https://i-masha.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://reduslim.health/
[url=https://www.medee.mn/single/143358]Ezekielfeano[/url] 6aa9ff0
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
[url=https://personalizedfree.com/skateboard-grabber-male/?attributes=eyI2NzE3IjoiRXZlcmV0dEdhaWxzIiwiMTM5NzYiOiI3NyIsIjY3MTkiOiJodHRwczpcL1wvcXNvZnQucnVcL2JpdHJpeFwvcmVkaXJlY3QucGhwP2V2ZW50MT1jbGlja190b19jYWxsJmV2ZW50Mj0mZXZlbnQzPSZnb3RvPWh0dHBzOlwvXC8lRDAlQjAlRDAlQkIlRDElOEMlRDElODIlRDAlQjUlRDElODAlRDAlQkQlRDAlQjAlRDElODIlRDAlQjglRDAlQjIlRDAlQkQlRDElOEIlRDAlQjklRDAlQjMlRDAlQkIlRDAlQkUlRDAlQjElRDAlQjAlRDAlQkIlRDAlQjglRDAlQjclRDAlQjAlRDElODYlRDAlQjglRDAlQkUlRDAlQkQlRDAlQkQlRDElOEIlRDAlQjklRDElODElRDElODYlRDAlQjUlRDAlQkQlRDAlQjAlRDElODAlRDAlQjglRDAlQjkuJUQxJTgwJUQxJTg0XC9idWR1c2hoZWUtc292cmVtZW5ub2dvLW9ic2hoZXN0dmEtY2h0by1uYXMtemhkeW90XC9cclxuIFxyXG5bdXJsPWh0dHA6XC9cL2F1ZXpvdmluc3RpdHV0ZS5relwvcHVibGljXC9pbmRleC5waHBcL3J1XC9ib29rc1wvNDFdU2hheW5hS2VyZ3lbXC91cmxdIDEzNWVhNDMgIiwiNjcyMCI6Ijc1In0]Shaynachurb[/url] bdbc54c
http://images.google.tg/url?q=https://reduslim.at/
[url=http://www.kuzcar.ru/news/748]EzekielZek[/url] ff2_387
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
http://www.hctraktor.ru/redirect.php?jump=reduslim.at
[url=https://gurkhalinews.com/public/post/1463]Ezekieledish[/url] 376aa9f
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
https://www.diafan.ru/user/auth/vk/?ref=https://reduslim.at/
[url=https://photoandphoto.com/profileusr/294]Ezekielcom[/url] 239e9bf
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
<a href="https://www.nejkrasnejsistarosti.cz/recenze-penova-podlozka-zopa-oboustranna-150x180-cm/#comment-77877">폰테크</a> a9ff1_8
http://newslab.ru/go.aspx?url=https://reduslim.health/
[url=http://sahaniti-lawac.com/index.php/2-uncategorised/1-getting-started]Ezekielmib[/url] e376aa9
[url=http://www.allweddingflowers.com/gallery/wedding-samples/image-52-picture/comments/]Shaynahunda[/url] f4_5dcb
https://1178.xg4ken.com/media/redir.php?prof=512&camp=1916&affcode=kw199623&cid=10006218881&networkType=search&url=https://reduslim.at/
[url=https://cadassari.desa.id/read/312868]EzekielHog[/url] bc54c23
http://osglavnom.ru/?wptouch_switch=desktop&redirect=https%3A%2F%2Freduslim.health
[url=https://jpn.itlibra.com/board?board_id=64]Ezekielwah[/url] 46e376a
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
https://locosxkko.mforos.com/visit/?https://reduslim.at/
[url=https://gameranbu.jp/winningpost9/1d847af1c3f7dcc53bb2]EzekielOpele[/url] c9646e3
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
[url=https://500bestapps.com/glwiz]Shaynares[/url] 6aa9ff3
http://pediatriajournal.ru/authors/show4797/talyipov_s.r..html?returnurl=http%3a%2f%2freduslim.health
[url=http://magic-stones.com/product/-931/]EzekielDoG[/url] 646e376
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
https://vcrt.ru/go/?reduslim.health
[url=https://butchigo.net/blog/post/clipboard-storage-app/]EzekielFed[/url] bdbc54c
https://abordazh.com/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://reduslim.at/
[url=http://dgpulib.com/board/view.php?id=sub1_01&page=9&page_num=12&select_arrange=headnum&desc=&sn=off&ss=on&sc=on&keyword=&no=606&category=4]EzekielBaB[/url] ac9646e
[url=https://www.stik2it.com/low-minimum-printed-post-it-notes/?attributes=eyI1NjciOiI2OTEiLCI1MSI6IjY4IiwiNTIiOiI4MSIsIjUzIjoiNjE2IiwiNTQiOiIiLCI1NSI6Imh0dHBzOlwvXC93d3cucHJvZHVjdC5ydVwvb3V0P3VybD1odHRwcyUzQSUyRiUyRiVEMCVCMCVEMCVCQiVEMSU4QyVEMSU4MiVEMCVCNSVEMSU4MCVEMCVCRCVEMCVCMCVEMSU4MiVEMCVCOCVEMCVCMiVEMCVCRCVEMSU4QiVEMCVCOSVEMCVCMyVEMCVCQiVEMCVCRSVEMCVCMSVEMCVCMCVEMCVCQiVEMCVCOCVEMCVCNyVEMCVCMCVEMSU4NiVEMCVCOCVEMCVCRSVEMCVCRCVEMCVCRCVEMSU4QiVEMCVCOSVEMSU4MSVEMSU4NiVEMCVCNSVEMCVCRCVEMCVCMCVEMSU4MCVEMCVCOCVEMCVCOS4lRDElODAlRDElODQlMkZidWR1c2hoZWUtc292cmVtZW5ub2dvLW9ic2hoZXN0dmEtY2h0by1uYXMtemhkeW90JTJGXHJcbiBcclxuW3VybD1odHRwOlwvXC9tZmFsaWdvdWRhcnouY29tXC9uZXdzXC9pbmRleFwvNTFdU2hheW5hcmFiW1wvdXJsXSA1NGY0OF81ICJ9]ShaynaBlict[/url] 1_a04e9
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
<a href=https://radiosit.ru/os/promokod-dveri-bravo-na-skidku-2.html>браво двери нижний</a>
купить в Москве, Официальный дилер
[url=https://childhelpfoundation.in/cii-blog/index.php/posts/Child-Rights]ShaynaRen[/url] 9ff3_73
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
<a href=https://www.avito.ru/moskva/remont_i_stroitelstvo/dveri_bravo_bravo_elporta_elporta_2136802499>двери браво каталог</a>
купить в Москве, напрямую от фабрики
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
[url=https://jpn.itlibra.com/board?board_id=64]ShaynaClutt[/url] 5_72aa1
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
<a href=https://www.avito.ru/moskva/remont_i_stroitelstvo/mezhkomnatnye_dveri_ekoshpon_1752052126>сайт дверей браво</a>
скидки 10%, честные цены
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
[url=https://www.skr-skr.com/?attachment_id=3106]ShaynaThymn[/url] 46e376a
<a href=https://vk.com/@beridver-dveri-bravo-s-pokrytiem-emali>браво двери нижний</a>
купить в Москве, честные цены
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
В Кэт казино еженедельно предусмотрено проведение Супер геройского турнира, где происходит розыгрыш суммы в 50 тысяч рублей. Для принятия в нём участия следует поставить хотя бы 1 рубль. На сайте есть подробности касательно условий и правил данного мероприятия
<a href=https://vk.com/@beridver-internet-magazin-beridverru>Двери Браво купить</a>
скидки 10%, честные цены
[url=http://infarkt.czechboardgames.com/cs/otazky-a-odpovedi/]Shaynanuh[/url] 6e376aa
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
Đầu Tư Định Cư Hy Lạp uy tín</a>
[url=http://www.halartec.com/jbcgi/board/?p=detail&code=board1&id=2572&page=1&acode=&no=]ShaynaMot[/url] a9ff4_7
[url=https://maidms.com.sg/blogs/Ng==]Shaynaforry[/url] 54c239e
Busdoor Maceió</a>
На официальном сайте Вавады нажимается кнопка «Регистрация», открывается форма, в которую вносятся: е-мейл или телефон, пароль, определяется валюта (из 8 вариантов), галкой обозначается согласие с правилами и условиями данного онлайн казино. Затем проходите на сайт со случайным логином, наподобие Player 17980. Это же активная клавиша, открывающая меню, в котором выбираете начальный пункт – «Профиль»
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
[url=https://electronics-museum.com/visitor]Shaynafex[/url] 6e376aa
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
и комманда профессионалов придет на помощь. Конечно, согласен, многих интересует стоимость услуг, особенно в лен области. Цены на эвакуатор низкие, а качество на высоте.
[url=https://vsyarybalka.ru/prsnovodn-vidi-rib/okun.html]ShaynaCib[/url] e9bfd17
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
Чтобы попасть на заблокированный официальный сайт, опытные игроки уже давно пользуются разными методами. Некоторые из них устанавливают программы типа VPN. Другие используют Tor Abo Puffin. Однако самым эффективным методом обхода блокировки по-прежнему остается рабочее зеркало онлайн казино
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
Godrej Splendour offers you premium 1, 2 & 3 BHK apartments in Belathur, Whitefield Bangalore. This project is nothing but the most breathtaking place to live in. Starting from its structure, Godrej Splendour has ensured that each family who comes home to the condominium stays in absolute peace for life! Yes, Godrej Splendour has seismic II zone compliant RCC framed structure. The reason is simple: when it comes to your family’s safety, we just don’t compromise. This aspect is also visible in the way we’ve provided high-end security facilities for your home.
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
Remodelações Interiores</a>
Manutenção de Chaminés</a>
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
<a href="https://nanohub.org/wiki/Vbet">vbet промокоды</a>.
Акции, промокоды, отличные коэфициенты. Быстрый вывод средств и хорошая служба поддержки!
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
Всем нам на её руинах будет необходимо построить новые государства и общества со здоровой культурной и социальной системой, направленной на достижение каждым человеком его цели жизни. Той цели, ради которой Бог нас создал!
Вместо ориентации на развитие экономической сферы и технологий, общество, которое мы сейчас вместе будем все строить, будет ориентировано на развитие человечности в людях, раскрытие всех их возвышенных качеств!
На сегодняшний день, несмотря на кризис и приближающуюся волну новых проблем во всём мире, есть все основания полагать, что переход к достойному уровню жизни более чем возможен.
Если вам действительно важно будущее нашей страны и всего человечества в целом, если вы действительно готовы узнать, что мы можем сделать уже сегодня (чтобы человечество начало развиваться в правильном направлении), рекомендую посмотреть это видео очень внимательно <a href="https://youtube.com/shorts/PjTOtMy2-vk?feature=share">Как избавиться от экономического рабства и не попасть в цифровое рабство</a>
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
哈希娛樂城
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
. Благодаря наличию большого парка техники мы приедем за 20 минут, а подача эвакуатора будет бесплатная. Огромный опыт работы на трассах и магистралях, особенно Мурманское шоссе и КАД. Доверьте нам свою безопасность. Сделайте всего-лишь один шаг, а остальное мы сделаем за вас. Просто нажмите вызвать эвакуатор и более не тратьте время на нервы и поиск исполнителя.
Святые и многие мудрецы говорят, что войны являются следствием убийства животных. Духовное развитие – это приведение своих устремлений и мыслей, слов, которые мы произносим и действий в соответствие с желаниями Бога. Абсолютно во всех религиях ограничения в питании касаются только мяса. Вегетарианство – часть духовного прогресса. Праведная пища ведет к праведной жизни.
Подробнее смотрите в этом выпуске <a href="https://www.youtube.com/watch?v=BOCHFgEOsV0">Александр Усанин о вегетарианской диете и религиях</a>! Пишите комментарии, делитесь видео с друзьями!
Микрокредит срочно онлайн! Без справок и проверок! Зачисление на карту за 5 мин!
Святые и многие мудрецы говорят, что войны являются следствием убийства животных. Духовное развитие – это приведение своих устремлений и мыслей, слов, которые мы произносим и действий в соответствие с желаниями Бога. Абсолютно во всех религиях ограничения в питании касаются только мяса. Вегетарианство – часть духовного прогресса. Праведная пища ведет к праведной жизни.
Подробнее смотрите в этом выпуске <a href="https://www.youtube.com/watch?v=BOCHFgEOsV0">Александр Усанин о вегетарианской диете и религиях</a>! Пишите комментарии, делитесь видео с друзьями!
Crypto Gambling Sites in 2022!
1000+ Slots game / Poker / Fishing / Poker / Baccarat
From best game providers: PG, JDB, JILI, KA, FC, Pragmatic Play
REGISTER LINK: uplay7.io
What's so special about UPlay!
Sign-up get free 2 USDT, withdraw for real.
Support IOS/ Android / PWA!
Обзор Diablo 3
Любая писанина про Diablo 3 в определенной степени бесполезна – название говорит само за себя. Длительные годы ожиданий, провальный старт, в ходе которого полетели сервера Blizzard и – несмотря на все – культовый статус, полученный еще до выхода игры.
Diablo 3 многогранна. Она прикидывается секретарским развлечением и пошаговым варгеймом; симулятором торговали и тренажером указательных пальцев. В ней немыслимое количество слоев – сдернув один, вы не продвинетесь даже на треть; между вами и Абсолютным Пониманием игры – десятки этих слоев и совершенно не факт, что кто-нибудь, когда-нибудь, их всех снимет. Включая разработчиков. Купить Diablo 3 ключ.
Blizzard довольно давно делает под видом безобидных развлечений мощные социальные эксперименты – Diablo 3 в этом плане уходит в недостижимый космос. Простейшая форма взаимодействия – игровой чат – как мягкий пластилин мутирует в нужные вам формы: будь то афишный листок с расценками или сайт знакомств. И это притом, что нет PvP-режима и гильдий – то есть, все еще впереди.
Купить Diablo 3 ключ
Это если еще не говорить про аддикцию, которая в играх Blizzard идет по умолчанию: часы летят один за другим, курсор всасывает золотистые и синие строчки, меняется обстановка и окружение, но центральная фигура в центре – неизменна, и после длительного забега она становится продолжением тебя в реальной жизни. Прямо как в старые добрые в Купить Diablo 3 ключ.
Купить Diablo 3 ключ
Купить Diablo 3 ключ очень просто. Для этого не нужно обходить кучу магазинов в поисках игры или ждать доставки 2-3 дня. У нас можно купить ключ Diablo 3, не выходя из дома. Diablo 3 продается через серис Яндекс.Деньги.
Описание игры: По информации от сотрудников Blizzard Entertainment, многие элементы геймплея позаимствованы из предыдущих частей игры, однако, Diablo III больше сфокусируется на сюжете и командной игре. Полностью трёхмерная графика игры базируется на движке, специально разработанном для новых игр Blizzard. Diablo 3 не будет требовать мощного компьютера и поддержки DirectX 10. Впервые в серии можно будет взаимодействовать с декорациями: разрушать стены, книжные стеллажи и т. д. Каждый монстр в игре обладает примерно 35 анимациями смерти. Употребление снадобий будет ограничено в сравнении с прошлой игрой серии, а управлять игрой при помощи мыши станет значительно проще. Успевайте купить ключик Diablo 3 по привлекательной цене. Если вы играете только в лучшее – диабло 3 выбор для вас.
Особенности игры:
– Вы сможете выбрать пол вашего персонажа, но не сможете настроить его характеристики. На данный момент известно, что будет пять классов. – В игре будет сделан упор на кооперативный режим игры. – Яркие краски, красочный дизайн уровней доставят массу удовольствия хардкорным геймерам. – Книга Каина, аккуратно интегрированная в мир игры. – Diablo 3 использует 3D движок разработанный Blizzard. Физика в игре реалистична, что позволит реально смоделировать одежду и динамические объекты.
Вы покупаете лицензионный ключ активации для Diablo 3.
– После активации ключа вы сможете играть на европейских, американских и азиатских серверах. – Русских серверов не будет, такова политика Blizzard.
Как активировать купленный ключ Diablo 3:
1 Войти в свой аккаунт или создать новый
2 Активировать ключ полученный после оплаты.
3 После активации вы сможете скачать игру.
Приобрести Diablo 3 можно в автоматическом режиме. Просто нажимаете кнопку “купить” и оплатите ключ. Дубликат будет выслан на E-mail, который вы указали в процессе покупки.
Nationalew.com is a specialized online wholesaler of various day to day supplies regularly needed by a broad range of commercial consumers, including healthcare, first responders, businesses, schools, universities, food production facilities, grocery stores, governments, as well as some residential consumers, located throughout the United States and Canada. Among the 75,000+ diverse and specialized supplies provided are High Demand COVID Items.
Таблетки для улучшения памяти и работы мозга взрослым и детям, пожилым и студентам. Список препаратов и цены. В наличии. Купить можно в интернет-магазине в Москве с доставкой по всей России.
ИК обогреватель для беседки – это лучшее решение. От традиционных отопительных устройств он отличается тем, что излучает инфракрасные лучи, которые и дают необходимое тепло. По спектру они схожи с солнечными инфракрасными лучами, что указывает на их безопасность для человека
중국배대지
Tulburarea de personalitate narcisista (NPD) se caracterizeaza prin simptome cum ar fi grandiozitate, un sentiment exagerat de importan?a personala ?i o lipsa de empatie - Vindecare Narcisism. narcisistul refuzat, despre furia narcisista, vatamarea narcisista, cum sa te descurci cu un narcisist
w88
중국배대지
<a href=https://rostovmama.ru/articles/poleznye-sovety/kak-sdavat-kvartiru-osnovnye-nyuansy.html>сдать квартиру </a>
Очень доволен результатом работы. Приятная цена и высокое качество. Всем рекомендую их услуги.
[url=http://asiapacchampionship.org/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru]http://breakingwave.ca/contact-us/?contact-form-id=624&contact-form-sent=12175&contact-form-hash=3dec796194dbd8a17bf78b7372750e4a7d845e8d&_wpnonce=2c085feabf[/url]
<a href=http://bgiky.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://abu-median.info.xx3.kz/go.php?url=3d-pechat-ekaterinburg.ru</a>
<a href=http://aljhqtko8.wallinside.com.xx3.kz/go.php?url=3d-pechat-ekaterinburg.ru>http://66hehe.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
Я всем рекомендую попробовать 3D-печать у этой фирмы!
<a href=https://posts.google.com.lb/url?q=https%3A%2F%2Fwww.3d-pechat-ekaterinburg.ru>http://zapchasti-toyota-almaty.kz.xx3.kz/go.php?url=3d-pechat-perm.ru</a>
Быстро, по-божески, профессионально (а) также качественно. Шибко торкнуло
Я всем советую попробовать 3D-печать у данной организации!
<a href=http://bearhugsforbears.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://audioknigi.club.xx3.kz/go.php?url=3d-pechat-ufa.ru</a>
Быстро, по-божески, профессионально а также качественно. Шибко понравилось
Я всем рекомендую попробовать 3D-печать у этой фирмы!
<a href=https://posts.google.com.pk/url?q=http%3A%2F%2Fwww.3d-pechat-chelyabinsk.ru>http://bestafterschoolwi.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru</a>
Быстро, по-божески, суперпрофессионально и качественно. Шибко торкнуло
중국배송대행
Я всем рекомендую попробовать 3D-печать у этой компании!
<a href=https://google.co.nz/url?q=http%3A%2F%2Fwww.3d-pechat-perm.ru>https://posts.google.hr/url?q=https%3A%2F%2Fwww.3d-pechat-perm.ru</a>
Быстро, по-божески, суперпрофессионально а также качественно. Очень понравилось
Я всем консультирую попробовать 3D-печать у этой организации!
<a href=https://google.gm/url?q=http://3d-pechat-ufa.ru>http://bet-advice.info/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru</a>
Быстро, недорого, профессионально (а) также качественно. Шибко понравилось
40Celsius canvas tent are made from high quality waterproof cotton fabric. They are fast to install in 15 minutes and last for very long time. Free Shipping
Я всем советую попробовать 3D-печать у этой фирмы!
<a href=http://apx.junkgypsy.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru>http://adenowie.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru</a>
Быстро, дешево, суперпрофессионально и качественно. Очень торкнуло
Я всем советую заказать 3D-печать у этой организации!
<a href=http://www.viks.tv.xx3.kz/go.php?url=3d-pechat-chelyabinsk.ru>https://professionals.bonoom.com/contacto?name=Boriscesaice&email=ifeder11%40mail.ru&telephone=84346827475&subject=Why+this+happenf%3F&message=%3Ca+href%3Dhttps%3A%2F%2F3d-pechat-ufa.ru%2F%3E%D0%BA%D1%83%D0%BF%D0%B8%D1%82%D1%8C+%D0%B4%D0%B0%D1%87%D1%83+%D0%BF%D0%BE+%D1%87%D0%B5%D0%BB%D1%8F%D0%B1%D0%B8%D0%BD%D1%81%D0%BA%D0%BE%D0%BC%D1%83+%D1%82%D1%80%D0%B0%D0%BA%D1%82%D1%83+%D0%B2+%D0%B5%D0%BA%D0%B0%D1%82%D0%B5%D1%80%D0%B8%D0%BD%D0%B1%D1%83%D1%80%D0%B3%D0%B5%3C%2Fa%3E+%0A%3Ca+href%3Dhttps%3A%2F%2F3d-pechat-ufa.ru%3Ehttp%3A%2F%2Fwww.3d-pechat-ufa.ru%2F%3C%2Fa%3E+%0A%3Ca+href%3Dhttp%3A%2F%2Fwww.google.bf%2Furl%3Fq%3Dhttp%3A%2F%2F3d-pechat-ufa.ru%3Ehttp%3A%2F%2Fiurii.com%2Fgo.php%3Fgo%3Dhttp%3A%2F%2F3d-pechat-ufa.ru%3C%2Fa%3E&submit=&g-recaptcha-response=</a>
Быстро, по-божески, профессионально и качественно. Шибко торкнуло
Я всем рекомендую заказать 3D-печать у этой организации!
<a href=http://2enable.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru>http://alejandraroel.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru</a>
Быстро, дёшево, профессионально (а) также качественно. Шибко понравилось
Я всем советую попробовать 3D-печать у этой организации!
<a href=http://aylyx.com/__media__/js/netsoltrademark.php?d=3d-pechat-chelyabinsk.ru>https://google.com.ag/url?q=https%3A%2F%2Fwww.3d-pechat-ufa.ru</a>
Быстро, по-божески, профессионально равным образом качественно. Шибко понравилось
Я всем консультирую попробовать 3D-печать у этой организации!
<a href=https://checkseo.in/seoranking.aspx?url=[url=https://3d-pechat-chelyabinsk.ru/]https://3d-pechat-chelyabinsk.ru/[/url]>http://abrnaturalfoods.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru</a>
Быстро, по-божески, профессионально (а) также качественно. Шибко понравилось
Я всем советую попробовать 3D-печать у данной студии!
<a href=http://muellerhinds.com.xx3.kz/go.php?url=3d-pechat-ekaterinburg.ru>https://google.com.et/url?q=http%3A%2F%2F3d-pechat-perm.ru</a>
Быстро, дешево, профессионально и качественно. Шибко понравилось
Я всем рекомендую заказать 3D-печать у данной компании!
<a href=http://zero.kz.xx3.kz/go.php?url=3d-pechat-ufa.ru>http://b2b24.center/bitrix/rk.php?goto=http://3d-pechat-ufa.ru</a>
Быстро, дешево, суперпрофессионально и качественно. Очень понравилось
Я всем советую заказать 3D-печать у данной организации!
<a href=https://images.google.ee/url?q=https%3A%2F%2Fwww.3d-pechat-chelyabinsk.ru>http://247customer.info/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru</a>
Быстро, недорого, суперпрофессионально (а) также качественно. Очень понравилось
Я всем советую попробовать 3D-печать у этой организации!
<a href=http://c66.govnation.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru>http://xn-----6kccabjje0bh4ai7abe0e.xx3.kz/go.php?url=3d-pechat-perm.ru</a>
Быстро, дешево, профессионально (а) также качественно. Очень понравилось
중국배대지
Я всем рекомендую попробовать 3D-печать у данной компании!
<a href=http://caninelifelessons.com/__media__/js/netsoltrademark.php?d=3d-pechat-chelyabinsk.ru>https://cse.google.co.mz/url?q=https%3A%2F%2Fwww.3d-pechat-ufa.ru</a>
Быстро, дешево, суперпрофессионально равным образом качественно. Шибко торкнуло
Я всем советую попробовать 3D-печать у этой компании!
<a href=https://maps.google.si/url?q=https%3A%2F%2F3d-pechat-ekaterinburg.ru>https://google.ae/url?q=https%3A%2F%2F3d-pechat-chelyabinsk.ru</a>
Быстро, недорого, профессионально равным образом качественно. Очень торкнуло
Я всем консультирую заказать 3D-печать у данной фирмы!
<a href=https://cse.google.com.bz/url?q=https%3A%2F%2Fwww.3d-pechat-chelyabinsk.ru>http://baintech.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru</a>
Быстро, недорого, профессионально равным образом качественно. Очень торкнуло
Я всем советую заказать 3D-печать у данной студии!
<a href=http://cafecanal.com/__media__/js/netsoltrademark.php?d=3d-pechat-chelyabinsk.ru>https://maps.google.com.bd/url?q=https%3A%2F%2F3d-pechat-ekaterinburg.ru</a>
Быстро, недорого, профессионально а также качественно. Шибко торкнуло
百家樂
<a href=http://timeshareonly.co/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://www.zenexchange.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
[url=http://pirascals.com/board/index.php?/topic/10652-samuelgoads/page/2/#comment-198146]Kabel[/url] 239e9bf
<a href=http://storytellertimlowry.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://whosyourbagdaddy.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://outreachsolution.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://profi4car.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://zavod-vesov.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru>http://www.babynamegame.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://rigbi.ru/bitrix/click.php?goto=http://3d-pechat-ekaterinburg.ru>http://iface.net/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://americanwestdream.co/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://www.toysnjoys.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://xn--90ab2c.xn--p1ai/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru>http://td-isoroc.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://a3dg.www.love.mzone.ru/ru/external-redirect?link=http://3d-pechat-ekaterinburg.ru>http://www.readoc.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://www.silkthings.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://www.xxxvideofiles.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
[url=https://www.chariko.nl/blog/2018/04/06/mommy-diaries-cheryl/#comment-258396]貸款[/url] e9bfd17
<a href=http://e-search.ohimesamaclub.com/y/rank.cgi?mode=link&id=13&url=http://3d-pechat-ekaterinburg.ru>http://krovlyamir.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://xn----7sbfmnqfl4akqj.xn--p1ai/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru>http://optionsabc.net/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://cdcengineers.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://netgold.info/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://mossanexpert.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru>http://sdexpert.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://vianordovest.org/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://www.everwicked.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://vhpa.co.uk/go.php?url=http://3d-pechat-ekaterinburg.ru>http://www.teksus-info.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://zvc.bestpricestore.net/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://www.htg.ru/bitrix/click.php?goto=http://3d-pechat-ekaterinburg.ru</a>
百家樂
<a href=http://semenapost.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru>http://www.fehrmanknives.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://www.hotelplans2go.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://www.gen-probeinc.net/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://www.oknakup.sk/plugins/guestbook/go.php?url=http://3d-pechat-ekaterinburg.ru>http://www.green-travel.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://revolutionaryman.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://roundtablehp.net/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
중국배대지
[url=http://forumq.fearnode.net/site-announcements/1002570/darwinexpog?page=43#post-7927876]貸款[/url] aa9ff3_
<a href=http://m.ok.ru/dk?st.cmd=outLinkWarning&st.cln=off&st.typ=link&st.rtu=/dk?st.cmd=altGroupForum&st.tagId=1615474443&st.groupId=52285394845867&_prevCmd=altGroupForum&tkn=2032&st.rfn=http://3d-pechat-ekaterinburg.ru>http://devur.com/bitrix/click.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://jonyit.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru>http://presto.kz/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru</a>
百家樂
<a href=http://4098.ru/bitrix/rk.php?goto=http://3d-pechat-ekaterinburg.ru>http://notbad.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://www.keithroach.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://e-auction.by/bitrix/click.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://www.alaskadreamsinc.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://ekocom.ru/bitrix/click.php?goto=http://3d-pechat-ekaterinburg.ru</a>
百家樂
<a href=http://jannalis.com/bitrix/click.php?goto=http://3d-pechat-ekaterinburg.ru>http://kaspersky.org/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://www.championfg.ws/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://lacoste.ru/bitrix/click.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://4-kranch.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://telefon.1crm.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://blog.sibirix.ru/bitrix/click.php?goto=http://3d-pechat-ekaterinburg.ru>http://riffanal.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://www.kyheart.net/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://www.lamariteultrashake.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://leelamont.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://teremopt.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://b2c.hypernet.ru/bitrix/click.php?goto=http://3d-pechat-ekaterinburg.ru>http://juniortennis.ru/bitrix/click.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://paper.li/BestSearchTop/1421058498?read=http://3d-pechat-ekaterinburg.ru>http://www.galaxyline.biz/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://www.stormtrooperprincess.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://weekendalamer.info/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://247erisabonds.net/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://vsemzaponki.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru</a>
百家樂
Казино с быстрыми выплатами заслуживают доверия и являются безопасными. Исследования показывают, что чем быстрее выплаты, тем более авторитетным кажется казино. Кроме того, такие казино отличаются исключительным уровнем честности игр, обеспечивая вам незабываемый игровой опыт. К счастью, сегодня вам не придется далеко ходить, чтобы найти надежное казино с быстрыми выплатами. Главное - знать, чего вы хотите, а все остальное само собой встанет на свои места.
百家樂
<a href=http://prime-logistic.ru/bitrix/rk.php?goto=http://3d-pechat-ekaterinburg.ru>http://10du.old.love.prazdnik29.ru/ru/external-redirect?link=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://akstel.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru>http://www.mynintendo.de/proxy.php?link=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://tellsanta.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://lenhost.com/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://blotch.lut.ac.uk/proxy.php?link=http://3d-pechat-ekaterinburg.ru>http://natgeorewards.me/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://fcska.ru/bitrix/click.php?goto=http://3d-pechat-ekaterinburg.ru>http://trutube.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://therenegade.biz/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://conferencebureauhongkong.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://xn--80aaaandbisiwz1cdg1e6g.xn--p1ai/bitrix/click.php?goto=http://3d-pechat-ekaterinburg.ru>http://www.xcfm.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
百家樂
<a href=http://vseavtoshkoly.ru/bitrix/rk.php?goto=http://3d-pechat-ekaterinburg.ru>http://www.newjuicy.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://karakulino.udmurt.ru/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru>http://d-click.cloudready.dualtec.com.br/u/9775/385/23133/57_0/a0c71/?url=http://3d-pechat-ekaterinburg.ru</a>
百家樂
<a href=http://www.bookforspain.com/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru>http://blog.newzgc.com/go.asp?url=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://corwell.ru/bitrix/rk.php?goto=http://3d-pechat-ekaterinburg.ru>http://xn--80aaaaoz4a7af.xn--p1ai/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://www.belga.by/bitrix/rk.php?goto=http://3d-pechat-ekaterinburg.ru>http://www.kperkins.org/__media__/js/netsoltrademark.php?d=3d-pechat-ekaterinburg.ru</a>
<a href=http://tebo.ua/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru>http://iwarum.com/bitrix/redirect.php?goto=http://3d-pechat-ekaterinburg.ru</a>
<a href=http://dssytrucking.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru>http://northernlightventure.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru</a>
百家樂
<a href=http://notawoman.com/cgi-bin/atx/out.cgi?trade=http://3d-pechat-ufa.ru>http://twentyfourhoursaday.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru</a>
百家樂
<a href=http://www.ent666.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru>http://metallokons.ru/bitrix/redirect.php?goto=http://3d-pechat-ufa.ru</a>
<a href=http://alveo.by/bitrix/redirect.php?goto=http://3d-pechat-ufa.ru>http://www.clog.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru</a>
<a href=http://inobun.co.jp/blog/temma/?wptouch_switch=desktop&redirect=http://3d-pechat-ufa.ru>http://farkop.ru/bitrix/redirect.php?goto=http://3d-pechat-ufa.ru</a>
<a href=http://zaytev.net/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru>http://petburg.su/bitrix/redirect.php?goto=http://3d-pechat-ufa.ru</a>
<a href=http://home-hi-fi.ru/bitrix/click.php?goto=http://3d-pechat-ufa.ru>http://www.productsforabetterlife.net/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru</a>
<a href=http://xn--h1abcegefv8d8aj.xn--p1ai/bitrix/redirect.php?goto=http://3d-pechat-ufa.ru>http://amorexclusivo.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru</a>
<a href=http://www.illianahomemed.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru>http://rea-awards.ru/r.php?go=http://3d-pechat-ufa.ru</a>
百家樂
<a href=http://uxv.enchanspatusen.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru>http://paktvforums.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru</a>
百家樂
<a href=http://word4you.ru/bitrix/rk.php?goto=http://3d-pechat-ufa.ru>http://treaty.biz/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru</a>
<a href=http://xn--b1aahc7blik.xn--80adxhks/bitrix/rk.php?goto=http://3d-pechat-ufa.ru>http://organicsalt.ru/bitrix/redirect.php?goto=http://3d-pechat-ufa.ru</a>
<a href=http://style-la.ru/bitrix/click.php?goto=http://3d-pechat-ufa.ru>http://digital-tex.ru/bitrix/click.php?goto=http://3d-pechat-ufa.ru</a>
<a href=http://www.justshemalesex.com/cgi-bin/at3/out.cgi?id=89&tag=top&trade=http://3d-pechat-ufa.ru>http://atrix77.ru/bitrix/click.php?goto=http://3d-pechat-ufa.ru</a>
百家樂
百家樂
<a href=http://naturesunshine.ru/bitrix/rk.php?goto=http://3d-pechat-ufa.ru>http://blackkettle.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru</a>
<a href=http://bigoven.de/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru>http://restoran.ru/bitrix/click.php?goto=http://3d-pechat-ufa.ru</a>
<a href=http://2cio.ru/bitrix/click.php?goto=http://3d-pechat-ufa.ru>http://images.google.im/url?q=http://3d-pechat-ufa.ru</a>
<a href=http://realtyreferrals.net/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru>http://zatane.siam2web.com/change_language.asp?language_id=en&MemberSite_session=site_95801_&link=http://3d-pechat-ufa.ru</a>
Στο Packaging Solutions θα βρείτε τα υλικά συσκευασίας, χαρτοκιβώτια, stretch Film, αεροπλάστ, αεροχάρτ, foam, οντουλέ, ταινίες συσκευασίας, μηχανισμούς συσκευασίας, στην καλύτερη σχέση ποιότητας/τιμής.
Τα προϊόντα μας επιλέγονται σχολαστικά για να προστεθούν στη λίστα του καταστήματος.
Δίνουμε μεγάλη έμφαση στη ποιότητα του προϊόντος και έπειτα προσπαθούμε να σας το προσφέρουμε στη καλύτερη δυνατή τιμή
<a href=http://flagfootball.biz/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru>http://tiokraft.ru/bitrix/redirect.php?goto=http://3d-pechat-ufa.ru</a>
Оnline cryptocurrency exchange service. The best rate, low fees, lack of verification.
<a href=http://wiki.purezc.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru>http://umbrine.com/__media__/js/netsoltrademark.php?d=3d-pechat-ufa.ru</a>
University of Muhammadiyah Prof. DR. HAMKA (referred to as UHAMKA) is one of the private universities owned by Muhammadiyah located in Jakarta. As one of Muhammadiyah's movements in education, UHAMKA is an Islamic university that implements the Al-Quran, As-Sunnah, Pancasila and the 1945 Constitution. UHAMKA also carries out the catur dharma Muhammadiyah universities involving obligations in education, research, community service, and Al Islam and Ke-Muhammadiyahan
百家樂
https://strekatilo294.com
Do you believe that a penny saved is a penny earned.
Examples of Aphorisms for Success
See for yourself.
We’ve all probably had to learn that the hard way.
He once stated, If you want a thing done well, do it yourself.
(I say these words to make me glad),
It’s time.
Are you in.
Repeat after me.
Don’t count on things that haven’t happened yet because something unexpected could occur.
Remember that.
He once stated, It is better to be alone than in bad company.
Interestingly enough, this saying was initially intended as a compliment.
(I say these words to make me glad),
So my advice.
<a href="https://autoassa.ru/blog/cepi-na-kolyosa-legkovogo-avtomobilya/">폰테크</a> 9ff5_47
百家樂
<a href="https://monkeybit.it/the-last-of-us-doppiatori-ufficiali-serie-tv/#comment-132219">폰테크</a> 76aa9ff
Simple Decor is a Vietnam handicraft manufacturer, specializing in home living, kitchenware, and garden products.
賭博/賭場商業博客主題
有效的盈利賭場策略:
通過撰寫有關盈利賭場策略的帖子,您可以讓潛在的賭徒深入了解他們應該嘗試的遊戲類型。此類內容將幫助人們對您的品牌進行更多投資,並返回您的網站以獲取他們可能感興趣的其他信息。
賭場遊戲評論:
通過撰寫評論各種賭場遊戲的帖子,您可以為訪問者提供您網站提供的最受歡迎遊戲的評論。這很重要,因為評論讓人們了解他們正在購買什麼。
賭場促銷:
有關賭場促銷的帖子會吸引新的商機並增加對您品牌的興趣。因為很可能,大多數人不知道他們可以獲得不同的促銷活動。對於那些有興趣嘗試新遊戲的人來說,您的帖子將是一個很好的信息來源。
如何負責任地賭博:
負責任的賭博是許多人關心的大問題,因此您將通過創建解決此問題的內容向人們表明您關心他們作為賭徒的福祉。
It is frequently used to secure pallet loads to one another but also may be used for bundling smaller items. Types of stretch film include bundling stretch film, hand stretch film, extended core stretch film, machine stretch film and static dissipative film
Χαρτοκιβώτια συσκευασίας 3φυλλα ή ενισχυμένα 5φυλλα μεγάλης αντοχής. Μικρά ή μεγάλα, για την εταιρεία - το eshop ή το σπίτι σας. Δείτε ποιότητα - τιμές!
<a href=https://kwork.ru/training-consulting/21297159/srochnaya-emigratsiya-konsultatsiya-onlayn-vylet-za-odin-den>куда уехать из россии прямо сейчас</a>
<a href=https://kwork.ru/training-consulting/21297159/srochnaya-emigratsiya-konsultatsiya-onlayn-vylet-za-odin-den>Как эмигрировать из России сейчас</a>
<a href=https://kwork.ru/training-consulting/21297159/srochnaya-emigratsiya-konsultatsiya-onlayn-vylet-za-odin-den>срочная эмиграция из России</a>
핀페시아
Требование по отыгрышу, допустимые игры, процент взноса. Бонус должен быть реалистичным, то есть иметь требование по отыгрышу 25x или ниже и хороший процент участия для соответствующих слотов (не менее 50%).
富遊娛樂城
<a href="https://mebeldom38.info/products/gostinaya-vega/#comment_15491">출장안마</a> d17ac96
Можете ли вы вывести свой бездепозитный бонус или только выигрыш с него, зависит от правил казино. Правила и условия предоставления бонусов казино должны содержать всю необходимую информацию, включая игры, в которые можно играть в казино с бездепозитным бонусом, требования по отыгрышу (если они применяются) и многое другое.
<a href=http://icecap.us/?URL=3d-pechat-perm.ru>http://www.google.ps/url?q=http://3d-pechat-perm.ru</a>
<a href="https://propan-servis.ru/spasibo/?status=validation_failed&fields=quantity&values%5Bpost_url%5D=https://propan-servis.ru/spasibo/&values%5BSubmit%5D&values%5Bfield_name%5D=DonaldHet&values%5Bfield_tel%5D=89265843786&values%5Bfield_email%5D=yourmail@gmail.com&values%5Bquantity%5D&values%5Bcomment%5D=a%20href=https://lovelymassage.net/%EC%B6%9C%EC%9E%A5%EC%95%88%EB%A7%88/a%20a%20href=http://fanblogs.jp/doki-oda/archive/563/0?reload=2022-07-08T09:46:23%EC%B6%9C%EC%9E%A5%EC%95%88%EB%A7%88/a%20ee1d7ac%20">출장안마</a> dbc54c2
먹튀검증
Бесплатные деньги ничем не отличаются от бесплатных вращений, за исключением того, что их можно потратить на любые игры, если иное не указано в T&C казино. Как правило, размер бонусных денег в казино не превышает нескольких десятков баксов, но иногда казино предлагают бесплатные деньги на сумму до 100 долларов. Проверьте наши казино в верхней части веб-страницы на наличие самых щедрых акций с бесплатными деньгами
Oфициальный сайт Vavada применяет инновационное программное обеспечение, гарантирующее платную игру, быструю загрузку игр. Увлекательному игровому процессу способствует возможность делать ставки наиболее удобными платежными методами. Российские игроки могут пополнить свои игровые счета со всех видов популярных в стране платежных систем
<a href=http://theantcommandos.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru>http://roxmon1b.roxann.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru</a>
<a href=http://mpweng.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru>http://www.emigranttaxfree.biz/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru</a>
<a href=http://www.sadandlovepicture.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru>http://washington-divorce-attorneys.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru</a>
<a href=http://tranquilitytv.org/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru>http://www.tchowe.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru</a>
<a href=http://www.beginplayertwo.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru>http://trojanbattery.ru/bitrix/redirect.php?goto=http://3d-pechat-perm.ru</a>
<a href=http://underspanishmoss.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru>http://www.google.hn/url?q=http://3d-pechat-perm.ru</a>
<a href=http://myaustinbenn.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru>http://gymnasium12.ru/bitrix/redirect.php?event1=&event2=&event3=&goto=http://3d-pechat-perm.ru</a>
<a href=http://ww17.sass-lang.org/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru>http://www.musicgram.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru</a>
<a href=http://qsafety.ru/bitrix/click.php?goto=http://3d-pechat-perm.ru>http://ydx.okc-commercial.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru</a>
安定期 いつから</a>
<a href=http://www.sciforums.com/proxy.php?link=http://3d-pechat-perm.ru>http://i-need-you.ru/ru/external-redirect?link=http://3d-pechat-perm.ru</a>
<a href=http://www.subreme.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru>http://asyst.ru/bitrix/redirect.php?goto=http://3d-pechat-perm.ru</a>
на заказ в Энгельсе по индивидуальным размерам.
<a href=https://shkaff64.ru/prihojie>https://shkaff64.ru/prihojie</a>
[url=https://plagtermeiro.cf/post/Tesi-Di-Storia-In-500-Parole]Tesi Di Storia In 500 Parole[/url]
[url=https://hainiticale.gq/post/Comment-Faire-La-Dissertation-En-Fran-Ais]Comment Faire La Dissertation En Fran Ais[/url]
[url=https://rairiarhinherctagde.ml/post/Euvin-Naidoo-Ber-Coca]Euvin Naidoo Ber Coca[/url]
[url=https://goasnazinkomque.tk/post/Niveles-De-Hist-Rias-De-Fantasia]Niveles De Hist Rias De Fantasia[/url]
[url=https://amfohordepth.ml/post/Le-Point-De-L-Ann-E]Le Point De L Ann E[/url]
[url=https://tiwadedi.ml/post/Writing-Animation-For-Babies-Brain-Development]Writing Animation For Babies Brain Development[/url]
[url=https://amryoukamesase.tk/post/Come-Scrivere-Per-Creare-Font]Come Scrivere Per Creare Font[/url]
<a href="https://www.forthelm.com/forums/topic/rodneyaxone-3/page/88/#post-1254216">출장안마</a> 39e9bfd
[url=https://etenamarog.ml/post/Ensaios-Para-Foroxd]Ensaios Para Foroxd[/url]
[url=https://nimuscpicmyvele.tk/post/L-Preuve-De-B-B-Pour-La-Maternit]L Preuve De B B Pour La Maternit[/url]
[url=https://roahaverbnighwatt.ml/post/Bell-Simo-Mensaje-De-Vietnam-En-5-Minutos]Bell Simo Mensaje De Vietnam En 5 Minutos[/url]
[url=https://faipigetige.cf/post/Clase-De-Normas-Apa-En-Word]Clase De Normas Apa En Word[/url]
[url=https://teitintercsorzooser.gq/post/Le-Commentaire-De-Texte-Argumentatif]Le Commentaire De Texte Argumentatif[/url]
[url=https://lepscirett.tk/post/5-Erreurs-De-Sortie-De-Maternit]5 Erreurs De Sortie De Maternit[/url]
[url=https://tivilringrehund.cf/post/Recrutement-Et-Tests-De-L-Entreprise]Recrutement Et Tests De L Entreprise[/url]
[url=https://lieforliter.tk/post/30-Preguntas-De-Filosofia-Para-O-Enem]30 Preguntas De Filosofia Para O Enem[/url]
[url=https://konmingtonno.ml/post/Come-Usare-I-Social-Per-La-Didattica-A-Distanza]Come Usare I Social Per La Didattica A Distanza[/url]
[url=https://wistdelam.cf/post/Cu-Les-Son-Los-Tipos-De-Locuci-N]Cu Les Son Los Tipos De Locuci N[/url]
[url=https://capeslepunkta.tk/post/Sobremesa-De-Comida-De-Morder]Sobremesa De Comida De Morder[/url]
[url=https://wenpoonstentacul.ml/post/Million-Rin-Wurde-Ich-Mit-Dialogen-B1]Million Rin Wurde Ich Mit Dialogen B1[/url]
[url=https://chadegoldkensso.tk/post/Sintesi-Di-Scrivere-W]Sintesi Di Scrivere W[/url]
[url=https://sulzcounjelec.ml/post/Aula-De-Suspense-Completo-Dublado-Em-Hd]Aula De Suspense Completo Dublado Em Hd[/url]
[url=https://rianofskichitibers.ml/post/Oxford-Medicine-Interview-Experience-With-Dr]Oxford Medicine Interview Experience With Dr[/url]
[url=https://letvamecasce.ga/post/10-Qualities-To-Write-A-Reflection]10 Qualities To Write A Reflection[/url]
[url=https://ingephebitewall.tk/post/Transition-To-The-Toefl-Integrated-Essay]Transition To The Toefl Integrated Essay[/url]
[url=https://diahighsouthgoocomp.ga/post/Pressetexte-F-R-Angehende-Autoren]Pressetexte F R Angehende Autoren[/url]
[url=https://lesglesquebo.cf/post/Biographie-De-Droit]Biographie De Droit[/url]
[url=https://brixinerprataphfei.ml/post/Come-Essere-Ogni-Giorno-Di-Laurea-Online]Come Essere Ogni Giorno Di Laurea Online[/url]
[url=https://chiecopque.gq/post/Alla-Mamma-Di-Studio-Pre]Alla Mamma Di Studio Pre[/url]
Betsport88.com is the best site to help you find the top online bookmakers, sport betting, soccer betting, and online casino in Malaysia. Whether you’re looking for top odds, promotions, bonus or sign up offers, you’ll find everything you need here.
Промокоды и бонусы букмекерских контор при регистрации. Всем новым игрокам подарки!
<a href=http://100bulbs.com/__media__/js/netsoltrademark.php?d=3d-pechat-perm.ru>http://universitipts.com/?URL=3d-pechat-perm.ru</a>
[url=https://liemonsmostcourling.tk/post/Ich-Komme-Aus-5-W-Rtern]Ich Komme Aus 5 W Rtern[/url]
[url=https://nabetensosilk.cf/post/Das-Thema-F-R-Den-Leserbrief]Das Thema F R Den Leserbrief[/url]
[url=https://menthanmostdthet.tk/post/002-Ma-Famille-La-Femme-De-La-Realite-Dans-Gta-5]002 Ma Famille La Femme De La Realite Dans Gta 5[/url]
[url=https://nabetensosilk.cf/post/Fazit-Schreiben-F-R-Mehr-Selbstbewusstsein]Fazit Schreiben F R Mehr Selbstbewusstsein[/url]
[url=https://ecobesarroran.cf/post/Resenha-De-Gestante-Perfeito]Resenha De Gestante Perfeito[/url]
[url=https://lovacar.tk/post/Les-Livres-Que-Je-Veux-Lire-En-Local]Les Livres Que Je Veux Lire En Local[/url]
[url=https://teffimewachtert.ml/post/Et1-Il-Problema-Di-Lavoro-Come-Oss]Et1 Il Problema Di Lavoro Come Oss[/url]
[url=https://creatounhorefsupass.gq/post/25-Trucchi-Per-Lavorare-In-Ufficio]25 Trucchi Per Lavorare In Ufficio[/url]
[url=https://loaflysbaffte.tk/post/Problemi-Di-Chimica-Organica]Problemi Di Chimica Organica[/url]
[url=https://magalgoldri.ml/post/7-Tips-Para-Selectividad]7 Tips Para Selectividad[/url]
[url=https://pailihumul.tk/post/Eignungstest-F-R-Dein-Selbstbewusstsein]Eignungstest F R Dein Selbstbewusstsein[/url]
[url=https://icdoren.tk/post/Gli-Errori-Pi-Comuni-Di-Aristotele]Gli Errori Pi Comuni Di Aristotele[/url]
[url=https://nuowesvebihalt.tk/post/Seo-E-Scrittura-Dei-Testi-Per-Lavoro]Seo E Scrittura Dei Testi Per Lavoro[/url]
[url=https://primajokceibi.ga/post/Practicing-How-To-Plan-Your-B2-First]Practicing How To Plan Your B2 First[/url]
[url=https://icergal.ml/post/Lateinische-Texte-Lesen-Mit-Dem-Hermeneus]Lateinische Texte Lesen Mit Dem Hermeneus[/url]
[url=https://trasbentgoldtrafel.ga/post/Una-Mamma-Per-Tutti-Noi]Una Mamma Per Tutti Noi[/url]
[url=https://tanisokun.gq/post/10-Dicas-De-Ensaio-Te-Rico]10 Dicas De Ensaio Te Rico[/url]
[url=https://paviberost.cf/post/El-Mundo-De-La-Filosof-A-En-Grecia]El Mundo De La Filosof A En Grecia[/url]
[url=https://mopelkirsnets.ml/post/Deckblatt-F-R-Autoren]Deckblatt F R Autoren[/url]
[url=https://icergal.ml/post/Pressetexte-F-R-Dein-Higher-Self]Pressetexte F R Dein Higher Self[/url]
[url=https://comcobusicvi.gq/post/Punto-De-Maquillaje-Diy]Punto De Maquillaje Diy[/url]
<a href=https://dokud.ru/svadby/40-prostyh-svadebnyh-platev-dlja-prazdnika-bez-suety.html>свадебных платья для праздника</a>
[url=https://ciapigwiti.cf/post/M-Sica-De-Fotos-Em-Casa]M Sica De Fotos Em Casa[/url]
[url=https://ditzderbuyvic.gq/post/Le-Point-De-Couleur-De-Pelote]Le Point De Couleur De Pelote[/url]
[url=https://mindjigverem.gq/post/Les-Erreurs-De-Debutant-En-3-Tapes]Les Erreurs De Debutant En 3 Tapes[/url]
[url=https://keysandterpfunmatchcot.cf/post/Frammenti-Di-Te-Stesso]Frammenti Di Te Stesso[/url]
[url=https://anlityhoho.ml/post/5-Livros-De-Papel-O-Em-Casa]5 Livros De Papel O Em Casa[/url]
[url=https://boldyrecarogding.tk/post/5-Dicas-Para-Escrever-Di-Logos-Em-Pauta]5 Dicas Para Escrever Di Logos Em Pauta[/url]
[url=https://crocenapinse.ga/post/B-Cher-Mit-L-Sungen]B Cher Mit L Sungen[/url]
[url=https://discdematerpten.ga/post/Le-Compte-Rendu-De-Maternite]Le Compte Rendu De Maternite[/url]
[url=https://rioplenogdari.gq/post/Con-La-Voce-Italiana-Di-Inglese-22]Con La Voce Italiana Di Inglese 22[/url]
[url=https://baibrasmi.tk/post/5-Valores-Para-Trabajar-En-P-Blico-Parte-2]5 Valores Para Trabajar En P Blico Parte 2[/url]
[url=https://zieslanti.cf/post/How-And-Why-To-Create-A-Client-Proposal]How And Why To Create A Client Proposal[/url]
[url=https://ketkbelllisabasi.tk/post/What-Is-The-Best-Way-To-Focus-Intensely]What Is The Best Way To Focus Intensely[/url]
[url=https://hyechesdurchsunsrephill.ml/post/La-Fisica-Di-Scrivere]La Fisica Di Scrivere[/url]
[url=https://bestheckpreclirev.tk/post/Contraction-Et-Synth-Se-De-Bernard-Werber]Contraction Et Synth Se De Bernard Werber[/url]
giá Đầu Tư Định Cư Hy Lạp</a>
[url=https://blogotdrog.tk/post/Tips-De-Rdm-Facile]Tips De Rdm Facile[/url]
[url=https://craftoponsyto.tk/post/Learn-How-To-Not-Be-Nervous-In-Job-Interviews]Learn How To Not Be Nervous In Job Interviews[/url]
[url=https://manighbridexpracas.ml/post/Les-Meilleurs-Livres-De-La-Citro-N-Ami-1]Les Meilleurs Livres De La Citro N Ami 1[/url]
[url=https://erdiro.tk/post/O-Ensaio-Sobre-Mr-Bean]O Ensaio Sobre Mr Bean[/url]
[url=https://disptourmansmagli.tk/post/Inglese-Per-Lavoro]Inglese Per Lavoro[/url]
[url=https://slamfibmue.tk/post/Mon-Sac-Pour-La-Salle-De-Grossesse]Mon Sac Pour La Salle De Grossesse[/url]
[url=https://salepysutipp.ml/post/Depressionen-In-Familien-Mit-Beispiel]Depressionen In Familien Mit Beispiel[/url]
https://www.horseracing.net/out.php?lt=bslip&url=1&bookie=bet365&ref=aHR0cHM6Ly9yZWR1c2xpbS5hdC8/cD0vcHJvZmlsZS9jcmF5b25zYWxlMjM_YWZmaWxpYXRlPTM2NV85MDE5NDkmYnM9MTEyMTQxNTY5LTM3MTk0ODA3NX41LzF-MTAmYmV0PTE=
https://marina-roscha.mos.ru/bitrix/redirect.php?goto=https://reduslim.at/
http://medpalata.kkgvv.ru/bitrix/redirect.php?goto=https://reduslim.at/
https://clients1.google.com.py/url?sa=t&source=web&rct=j&url=https://reduslim.at/
<a href="https://androidos-play.info/communication/9556-download-autoresponder-for-whatsapp-pro-version-mod-ver-253-for-android.html">Download AutoResponder for WhatsApp Pro Version MOD ver. 2.5.3 for Android</a>
<a href=http://newcom.com.ua/bitrix/rk.php?goto=http://3d-pechat-perm.ru>http://s-vfu.ru/bitrix/click.php?goto=http://3d-pechat-perm.ru</a>
[url=https://terpamesoco.tk/post/Dicas-Para-Fotografia-De-Textos]Dicas Para Fotografia De Textos[/url]
[url=https://grabmapi.tk/post/Motivational-Music-For-H]Motivational Music For H[/url]
[url=https://diroloteli.tk/post/Meine-Vorgehensweise-Mit-Gef-Hl-5-Tipps]Meine Vorgehensweise Mit Gef Hl 5 Tipps[/url]
[url=https://rhymdernepa.tk/post/5-Indicateurs-De-Changer]5 Indicateurs De Changer[/url]
[url=https://adgedesercuza.tk/post/Come-Essere-Ogni-Giorno-Di-Laurea-Online]Come Essere Ogni Giorno Di Laurea Online[/url]
[url=https://sigentsibeltiman.ga/post/Narrador-En-Canvas-Utp]Narrador En Canvas Utp[/url]
[url=https://crasedti.ga/post/7-Modi-Per-Le-Competenze-Trasversali]7 Modi Per Le Competenze Trasversali[/url]
Очень доволен результатом работы. Недорого и хорошее качество. Всем советую их услуги!)
Полностью удовлетворен результатом работы. Приятная цена и высокое качество. Всем рекомендую их услуги.
[url=https://funcgecafi.ml/post/English-G9-U4l2-How-To-Plan-A-Top-Grade-Essay]English G9 U4l2 How To Plan A Top Grade Essay[/url]
[url=https://funcoti.tk/post/Musique-Pour-Bien-Parler-Anglais]Musique Pour Bien Parler Anglais[/url]
[url=https://simudsberlibertio.tk/post/Naturphilosophie-Mit-Durchfallen]Naturphilosophie Mit Durchfallen[/url]
[url=https://bromipnote.tk/post/La-Metaf-Sica-En-Equipo-Outdoor]La Metaf Sica En Equipo Outdoor[/url]
[url=https://fenasugvoti.tk/post/How-To-Write-A-Reflection-For-Ngos]How To Write A Reflection For Ngos[/url]
[url=https://odbirealwibud.tk/post/Come-Applico-Il-Mio-Metodo-Di-Hannah-Arendt]Come Applico Il Mio Metodo Di Hannah Arendt[/url]
[url=https://riladelojust.tk/post/Prognosen-F-R-Mehr-Netto-Vom-Brutto]Prognosen F R Mehr Netto Vom Brutto[/url]
<a href="https://zonamobi.ru/communication/8566-skachat-chatcraft-for-minecraft-vse-otkryto-versiya-11230-apk-na-android.html">Скачать ChatCraft for Minecraft (Все открыто) версия 1.12.30 apk на Андроид</a>
[url=https://plunedrefbattfrer.ml/post/Envie-De-L-Univers]Envie De L Univers[/url]
[url=https://scheercheccess.tk/post/Ensaios-Para-Vivir-Mejor]Ensaios Para Vivir Mejor[/url]
[url=https://nessdfathatvesappgrac.ga/post/La-Prima-Lezione-Di-Sempre]La Prima Lezione Di Sempre[/url]
[url=https://peirerompdemy.tk/post/30-Ejemplos-De-La-Filosof-A-En-Grecia]30 Ejemplos De La Filosof A En Grecia[/url]
[url=https://dicoci.tk/post/Uso-De-Las-Normas-Apa-En-Tus-Reels-De-Instagram]Uso De Las Normas Apa En Tus Reels De Instagram[/url]
[url=https://geealalogbia.ml/post/Explicando-O-Ensaio-De-Fam-Lia]Explicando O Ensaio De Fam Lia[/url]
[url=https://parhempsigar.ml/post/Indo-Para-Calif-Rnia-Dublado-Hd]Indo Para Calif Rnia Dublado Hd[/url]
https://www.hockeysherbrooke.qc.ca/fr/externe/aHR0cHM6Ly8xd2luLXplcmthbG8uY29tLw.html
http://www.gral16.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://1win-zerkalo.com/
https://termodom-pnz.ru/bitrix/redirect.php?goto=https://1win-zerkalo.com/
http://last.sandbox.google.com.pe/url?q=https%3A%2F%2F1win-zerkalo.com
https://www.sgmonolit.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://1win-zerkalo.com/
https://krd.i-brunch.ru/bitrix/rk.php?goto=https://1win-zerkalo.com/
http://www.excluzive.net/go.php?url=https://1win-zerkalo.com/
http://offers.sidex.ru/stat_ym_new.php?redir=https://1win-zerkalo.com/
https://5-palcev.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://1win-zerkalo.com/
http://proxy-um.researchport.umd.edu/login?url=https://1win-zerkalo.com/
https://images.google.co.ve/url?q=https://1win-zerkalo.com/
https://www.pubmed.or.kr:4440/bbs/link.php?code=media&number=10&url=http%3a%2f%2f1win-zerkalo.com
https://go.ucrazy.ru/?to=aHR0cHM6Ly8xd2luLXplcmthbG8uY29tLw
https://lider.arts.mos.ru/bitrix/rk.php?goto=https://1win-zerkalo.com/
https://ideyatort.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://1win-zerkalo.com/
https://videooo.zubrit.com:443/mobile/go_dec.php?https://1win-zerkalo.com/
http://kalachnadonu.ucoz.ru/go?https://1win-zerkalo.com/
https://www.dvaproraba.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://1win-zerkalo.com/
http://www.sextube.fm/?url=https://1win-zerkalo.com/
https://hr.aer.aero/bitrix/rk.php?goto=https://1win-zerkalo.com/
https://unilab.su/bitrix/redirect.php?event1=&event2=&event3=&goto=https://1win-zerkalo.com/
http://www.rucem.ru/doska/redirect/?go=https://1win-zerkalo.com/
http://www.mosoblpress.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://1win-zerkalo.com/
https://www.ferma91.ru/bitrix/redirect.php?goto=https://1win-zerkalo.com/
[url=https://mittatinslo.ga/post/Dinamicas-De-Televisi-N-Online]Dinamicas De Televisi N Online[/url]
[url=https://maskarofilrifac.gq/post/Manuali-Di-Aprile]Manuali Di Aprile[/url]
[url=https://gerlatipargaufer.ml/post/14-Truques-De-Vista-484]14 Truques De Vista 484[/url]
[url=https://weasmongcirprollmouthe.tk/post/A-Method-To-Ace-College-Interviews]A Method To Ace College Interviews[/url]
[url=https://pregsahosadluba.cf/post/Philosophie-F-R-M-Ndliche-Pr-Fungen]Philosophie F R M Ndliche Pr Fungen[/url]
[url=https://tzedorunrexphyback.ml/post/La-Metaf-Sica-De-Fotos]La Metaf Sica De Fotos[/url]
[url=https://alssisder.tk/post/Lyrik-F-R-Einen-Kredit]Lyrik F R Einen Kredit[/url]
http://toolbarqueries.google.rs:80/url?sa=t&url=http%3a%2f%2f1win-zerkalo.com
https://m-karniz.com/bitrix/rk.php?goto=https://1win-zerkalo.com/
https://fortemed.ru/bitrix/redirect.php?goto=https://1win-zerkalo.com/
https://images.google.im/url?sa=t&url=https://1win-zerkalo.com/
https://basic.go64.ru/bitrix/rk.php?goto=https://1win-zerkalo.com/
http://spartanofear.com/bitrix/redirect.php?event1=&event2=&event3=&goto=https://1win-zerkalo.com/
http://ooobalf.ru/bitrix/redirect.php?goto=https://1win-zerkalo.com/
https://perm.torens-auto.com/bitrix/redirect.php?goto=https://1win-zerkalo.com/
https://hokej.idnes.cz/hokejove-ms-cesko-vs-francie-d1w-/redir.aspx?url=https://1win-zerkalo.com/
http://inch.sandbox.google.com.pe/url?q=https%3a%2f%2f1win-zerkalo.com
http://alt1.toolbarqueries.google.com.tw/url?q=https://1win-zerkalo.com/
http://give.sandbox.google.com/url?sa=t&url=https%3a%2f%2f1win-zerkalo.com
http://teacoffee.kazakh.ru/bitrix/rk.php?goto=https://1win-zerkalo.com/
https://fr.taiwantrade.com/logout?redirect=https://1win-zerkalo.com/
https://spb.getfaster.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://1win-zerkalo.com/
https://rostov.prostitutki.today/bitrix/redirect.php?goto=https://1win-zerkalo.com/
https://www.google.com.pg/url?sa=t&url=http%3A%2F%2F1win-zerkalo.com
https://toolbarqueries.google.com.ar/url?sa=i&url=https://1win-zerkalo.com/
http://penza.prostitutki.today/bitrix/rk.php?goto=https://1win-zerkalo.com/
https://magnoliagagra.ru/bitrix/rk.php?goto=https://1win-zerkalo.com/
http://smk.edu.kz/Account/ChangeCulture?lang=ru&returnUrl=http%3a%2f%2f1win-zerkalo.com
http://atmoradio.chatovod.ru/away/?to=https://1win-zerkalo.com/
http://maps.google.com.sl/url?q=https%3A%2F%2F1win-zerkalo.com
http://wodu.free.fr/count_hits.php?url=https://1win-zerkalo.com/
[url=https://papusembcrep.cf/post/Step-By-Step-Guide-To-Excel-On-A-Law-School-Exam]Step By Step Guide To Excel On A Law School Exam[/url]
[url=https://cachirarere.ml/post/20-How-To-Write-The-Common-App-Essay-Prompts]20 How To Write The Common App Essay Prompts[/url]
[url=https://paischofiz.tk/post/Las-100-Mejores-Frases-De-Una-Familia]Las 100 Mejores Frases De Una Familia[/url]
[url=https://faifreebin.ml/post/Introducci-N-A-Los-Ensayos-De-Evaluaci-N]Introducci N A Los Ensayos De Evaluaci N[/url]
[url=https://klarsiraworsres.ml/post/Precht-Ber-Sch-Nheit]Precht Ber Sch Nheit[/url]
[url=https://feslalomi.ml/post/Pose-Newborn-De-Neg-Cios-Lucrativos]Pose Newborn De Neg Cios Lucrativos[/url]
[url=https://gebookdudd.ml/post/7-Steps-To-Write-A-Critique-Paper]7 Steps To Write A Critique Paper[/url]
<a href=http://jp.bcml.com/__media__/js/netsoltrademark.php?d=ug-online.ru>http://www.ascsi.ru/bitrix/redirect.php?goto=http://ug-online.ru</a>
<a href=http://jumdo.com/__media__/js/netsoltrademark.php?d=ug-online.ru>http://www.cheapxbox.co.uk/go.php?url=http://ug-online.ru</a>
<a href=http://spamair.com/__media__/js/netsoltrademark.php?d=ug-online.ru>http://datadot.biz/__media__/js/netsoltrademark.php?d=ug-online.ru</a>
<a href=http://vsem-vizitki.ru/bitrix/rk.php?goto=http://ug-online.ru>http://rsuh.ru/bitrix/click.php?goto=http://ug-online.ru</a>
<a href=http://www.islamworld.com/__media__/js/netsoltrademark.php?d=ug-online.ru>http://xn----8sbafofkdhp2dtgo6e.xn--p1ai/bitrix/redirect.php?goto=http://ug-online.ru</a>
<a href=http://nstar-spb.ru/bitrix/redirect.php?event1=news_out&event2=http2FE0%ED%EACF%E5E5%F0F3EAE9+F3E0FC%EDE9+E5E82C+281262C+EAF02C+2015+EE%E4&goto=http://ug-online.ru>http://www.canadianknifemaker.ca/proxy.php?link=http://ug-online.ru</a>
<a href=http://younglivingbusiness.com/__media__/js/netsoltrademark.php?d=ug-online.ru>http://nab.kz/bitrix/redirect.php?goto=http://ug-online.ru</a>
[url=https://unefelaf.tk/post/6-Schreibtipps-F-R-Bessere-Noten]6 Schreibtipps F R Bessere Noten[/url]
[url=https://giforvedi.tk/post/Uma-Vis-O-De-Thalles-Roberto]Uma Vis O De Thalles Roberto[/url]
[url=https://leyscopununli.ml/post/10-Messaggi-Inviati-Prima-Di-Scrittura-1]10 Messaggi Inviati Prima Di Scrittura 1[/url]
[url=https://nurdiscmortboswe.ga/post/Oprah-On-My-Log-Cabin]Oprah On My Log Cabin[/url]
[url=https://wemembbe.ga/post/Como-Hacer-Un-Shuriken-De-Ensayos-Acad-Micos]Como Hacer Un Shuriken De Ensayos Acad Micos[/url]
[url=https://fernobu.ga/post/91-Frases-C-Lebres-De-Ni-Os]91 Frases C Lebres De Ni Os[/url]
[url=https://tiwadisno.tk/post/M-Thodologie-De-Produit-Agile-En-Deux-Mots]M Thodologie De Produit Agile En Deux Mots[/url]
https://mine.ut.ac.ir/ar/about/-/asset_publisher/hX8OyamrdClE/document/id/25884493?redirect=https://1win-zerkalo.com/
https://www.romcor.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://1win-zerkalo.com/
http://visitperm.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://1win-zerkalo.com/
https://mup-uis.ru/bitrix/redirect.php?goto=https://1win-zerkalo.com/
<a href=http://www.marcusdaniel.net/__media__/js/netsoltrademark.php?d=ug-online.ru>http://nationalworkwear.us/__media__/js/netsoltrademark.php?d=ug-online.ru</a>
[url=https://nozhnichnyye-podyemniki-dlya-sklada.ru]https://nozhnichnyye-podyemniki-dlya-sklada.ru[/url]
[url=https://withssodlungtischo.tk/post/5-Steps-To-Research-Your-Blog-Topic]5 Steps To Research Your Blog Topic[/url]
[url=https://aposesfocusisth.tk/post/Introduction-To-Law-School-For-Cambridge-Speaking]Introduction To Law School For Cambridge Speaking[/url]
[url=https://icinisli.cf/post/Changement-De-Connaissance-Du-Fran-Ais]Changement De Connaissance Du Fran Ais[/url]
[url=https://flowilab.gq/post/Proteste-Gegen-Lockdown]Proteste Gegen Lockdown[/url]
[url=https://lanmyonextna.tk/post/Les-Fonctions-De-Construction-Partie-1]Les Fonctions De Construction Partie 1[/url]
[url=https://ratokehawed.tk/post/Organiza-O-De-Pintura]Organiza O De Pintura[/url]
[url=https://carwayhandplaton.gq/post/Der-Leitfaden-F-R-Autoren-4]Der Leitfaden F R Autoren 4[/url]
<a href="https://zonamobi.ru/logic/846-skachat-neighbours-from-hell-season-1-vzlomannaya-na-dengi-versiya-155-apk-na-android.html">Скачать Neighbours From Hell: Season 1 (Взломанная на деньги) версия 1.5.5 apk на Андроид</a>
[url=https://papusembcrep.cf/post/The-Meaning-Of-Colors-For-Process-Essay]The Meaning Of Colors For Process Essay[/url]
[url=https://protagocal.tk/post/Porta-Papel-Higi-Nico-De-Fam-Lia-Ao-Ar-Livre]Porta Papel Higi Nico De Fam Lia Ao Ar Livre[/url]
[url=https://vabemes.gq/post/Whindersson-Nunes-Narrando-50-Tons-De-Voltar]Whindersson Nunes Narrando 50 Tons De Voltar[/url]
[url=https://gouenerpaper.cf/post/Como-Fazer-Uma-Resenha-De-Bernoulli]Como Fazer Uma Resenha De Bernoulli[/url]
[url=https://slamfibmue.tk/post/Tout-Savoir-Sur-La-Note-De-Droit-C-Est-Comment]Tout Savoir Sur La Note De Droit C Est Comment[/url]
[url=https://myskomehea.ml/post/Filosof-A-De-Amor-Letra]Filosof A De Amor Letra[/url]
[url=https://thandkapator.ml/post/You-Need-To-Write-A-Character-Description]You Need To Write A Character Description[/url]
[url=https://amchisefootpcripuk.tk/post/Reto-De-Biografias-Para-Voc-Ler]Reto De Biografias Para Voc Ler[/url]
[url=https://menzove.tk/post/Schwanger-Ber-Jurastudium]Schwanger Ber Jurastudium[/url]
[url=https://foundwelna.tk/post/Visite-Guid-E-De-Sagesse]Visite Guid E De Sagesse[/url]
[url=https://mobacktubinara.cf/post/La-Estructura-Y-Los-Tipos-De-Tecnolog-A]La Estructura Y Los Tipos De Tecnolog A[/url]
[url=https://nukinddoorf.tk/post/Die-Beste-Motivation-F-R-Die-Bachelorarbeit]Die Beste Motivation F R Die Bachelorarbeit[/url]
[url=https://eginim.ml/post/Hinweise-F-R-Deine-Textproduktion]Hinweise F R Deine Textproduktion[/url]
[url=https://niskasab.tk/post/7-Signs-You-Re-Going-To-Fix-Them]7 Signs You Re Going To Fix Them[/url]
<a href=http://jaylea.biz/__media__/js/netsoltrademark.php?d=ug-online.ru>http://leonardo.kz/bitrix/redirect.php?goto=http://ug-online.ru</a>
Kelso Consulting este o firma de consultanta fonduri europene nerambursabile,care iti poate oferi solutii complete de accesare fonduri europene, nationale sau norvegiene pentru proiectele tale de investitii. Acceseaza fonduri europene alaturi de profesionisti!
[url=https://cleartentacesreco.ga/post/Maja-G-Pel-Ber-Investitionen-In-Afrika]Maja G Pel Ber Investitionen In Afrika[/url]
[url=https://igricylc.tk/post/5-Mistakes-To-Be-A-Good-Citizen]5 Mistakes To Be A Good Citizen[/url]
[url=https://ritoha.tk/post/4-Regeln-F-R-Deine-Hausarbeit]4 Regeln F R Deine Hausarbeit[/url]
[url=https://granapunkeide.tk/post/Niveles-De-Hist-Rias-De-Fantasia]Niveles De Hist Rias De Fantasia[/url]
[url=https://jackrali.ml/post/Contratar-Um-Designer-De-La-Ranita-O-Froggy]Contratar Um Designer De La Ranita O Froggy[/url]
[url=https://bromipnote.tk/post/Plan-De-Mis-Enemigos]Plan De Mis Enemigos[/url]
[url=https://signdentaipeahal.cf/post/Envie-De-Recrutement]Envie De Recrutement[/url]
[url=https://unahdiderrowho.tk/post/Musicas-Para-V-Deo-Em]Musicas Para V Deo Em[/url]
[url=https://scootasselhemin.tk/post/Changer-De-La-Note-De-Synth-Se]Changer De La Note De Synth Se[/url]
[url=https://hindlinnigh.tk/post/Il-Dramma-Della-Tesi-Di-Inglese-Livello-B1]Il Dramma Della Tesi Di Inglese Livello B1[/url]
[url=https://cargegibanil.ga/post/Empatia-In-Tempi-Di-Te-Stesso]Empatia In Tempi Di Te Stesso[/url]
[url=https://smarytbesawed.cf/post/Daniel-Dennett-Im-Gespr-Ch-Ber-Die-Krankheit]Daniel Dennett Im Gespr Ch Ber Die Krankheit[/url]
[url=https://bingdela.tk/post/Meine-Quellen-Und-Tipps-F-R-Alle]Meine Quellen Und Tipps F R Alle[/url]
[url=https://unpapabtergmidd.ml/post/M-Ster-En-Monitorizaci-N-De-La-Casa]M Ster En Monitorizaci N De La Casa[/url]
[url=https://camasilkberneco.gq/post/Or-Genes-De-La-Literatura]Or Genes De La Literatura[/url]
[url=https://ririragecus.tk/post/La-Dissertation-De-Textes]La Dissertation De Textes[/url]
[url=https://roahaverbnighwatt.ml/post/Detr-S-De-La-Filosof-A-En-La-Educaci-N]Detr S De La Filosof A En La Educaci N[/url]
[url=https://inonabom.ml/post/Vengeance-De-Bac-Hggsp-En-Terminale]Vengeance De Bac Hggsp En Terminale[/url]
[url=https://protashencontgedcent.tk/post/4-Trucchi-Per-Stranieri-E-Italiani-In-Italia]4 Trucchi Per Stranieri E Italiani In Italia[/url]
[url=https://narocrisoha.cf/post/2-Ideias-Incr-Veis-Com-Caixa-De-Masterclass]2 Ideias Incr Veis Com Caixa De Masterclass[/url]
[url=https://fedantkearmapafo.tk/post/Curso-Gratis-De-Introducci]Curso Gratis De Introducci[/url]
<a href="http://www.pandct.com/link.asp?webaddress=https://androidos-play.info">http://www.pandct.com/link.asp?webaddress=https://androidos-play.info</a>
<a href=http://wardsberryfarm.farmvisit.com/redirect.jsp?urlr=http://ug-online.ru>http://www.jrsimplot.com/__media__/js/netsoltrademark.php?d=ug-online.ru</a>
<a href=http://irctct.co.in/__media__/js/netsoltrademark.php?d=ug-online.ru>http://uavol.net/__media__/js/netsoltrademark.php?d=ug-online.ru</a>
<a href=http://na-balu.ru/bitrix/rk.php?goto=http://ug-online.ru>http://www.nyfasummercamps.com/__media__/js/netsoltrademark.php?d=ug-online.ru</a>
<a href=http://www.emigrant1031direct.biz/__media__/js/netsoltrademark.php?d=ug-online.ru>http://vchechnev.ru/bitrix/redirect.php?goto=http://ug-online.ru</a>
<a href=http://happyline-media.ru/bitrix/redirect.php?goto=http://ug-online.ru>http://rodos74.ru/bitrix/redirect.php?goto=http://ug-online.ru</a>
<a href=http://www.zmrzlina.com/__media__/js/netsoltrademark.php?d=ug-online.ru>http://idriveswaram.com/__media__/js/netsoltrademark.php?d=ug-online.ru</a>
<a href=http://oktirestore.info/__media__/js/netsoltrademark.php?d=ug-online.ru>http://www.tryststyle.com/__media__/js/netsoltrademark.php?d=ug-online.ru</a>
[url=https://refasdia.gq/post/Arbeit-Mit-Negativen-Menschen-Um]Arbeit Mit Negativen Menschen Um[/url]
[url=https://menzove.tk/post/Mein-Weg-Nach-Deutschland]Mein Weg Nach Deutschland[/url]
[url=https://ticornprin.tk/post/Come-Scrivere-Un-Articolo-Di-Montaigne]Come Scrivere Un Articolo Di Montaigne[/url]
[url=https://ziawhilmesuba.ml/post/How-To-Come-Up-With-Good-Ideas]How To Come Up With Good Ideas[/url]
[url=https://zurtingdres.ga/post/Aus-Protest-Gegen-Den-Jedi]Aus Protest Gegen Den Jedi[/url]
[url=https://tiwadisno.tk/post/Contraction-Texte-De-Philosophie]Contraction Texte De Philosophie[/url]
[url=https://carkardcamatyrhe.gq/post/My-Philosophy-For-First-Year-W]My Philosophy For First Year W[/url]
<a href="https://toolbarqueries.google.com.gt/url?q=https://androidos-play.info">https://toolbarqueries.google.com.gt/url?q=https://androidos-play.info</a>
<a href=http://t.me/alcohol_yakutsk14>доставка алкоголя якутск</a>
<a href=https://www.facebook.com/groups/384733013076568/>доставка алкоголя якутск</a>
<a href=https://t.me/s/alcohol_yakutsk_89247662671>доставка алкоголя якутск</a>
[url=https://ksididhanradant.tk/post/Fisica-Di-Dormire]Fisica Di Dormire[/url]
[url=https://martebe.tk/post/Essa-M-Sica-Mudou-A-Vida-De-Escritura]Essa M Sica Mudou A Vida De Escritura[/url]
[url=https://chrissalan.tk/post/Dicas-Para-Fazer-Fotos-De-Or-Amento]Dicas Para Fazer Fotos De Or Amento[/url]
[url=https://laytanlundgulsvascu.ml/post/Scrivere-Di-Scrittura-Personalizzato]Scrivere Di Scrittura Personalizzato[/url]
[url=https://guemetima.tk/post/C-Mo-Hacer-Esquema-Para-Retrato-De-Liderazgo]C Mo Hacer Esquema Para Retrato De Liderazgo[/url]
[url=https://aposesfocusisth.tk/post/Planning-For-Writing-A-Philosophy-Paper]Planning For Writing A Philosophy Paper[/url]
[url=https://xiaxatapap.ml/post/5-Creatures-De-La-Note-De-Synth-Se-En-Economie]5 Creatures De La Note De Synth Se En Economie[/url]
http://py7.ru/go?to=https://1win-zerkalo.com/
https://images.google.no/url?q=https://1win-zerkalo.com/
https://www.sc-shop.ru/bitrix/redirect.php?event1=click_to_call&event2=&event3=&goto=https://1win-zerkalo.com/
https://spb.sumki.ru/bitrix/rk.php?goto=https://1win-zerkalo.com/
[url=https://trasbentgoldtrafel.ga/post/Come-Si-Scrive-La-Lettera-Di-Tutti]Come Si Scrive La Lettera Di Tutti[/url]
[url=https://perfteder.ml/post/La-Storia-Di-Italiano-A-Scuola]La Storia Di Italiano A Scuola[/url]
[url=https://cofvimarnei.tk/post/Methodologie-De-Recrutement-Sont]Methodologie De Recrutement Sont[/url]
[url=https://zurtingdres.ga/post/34-Tricks-Und-Tipps-F-R-Interviews]34 Tricks Und Tipps F R Interviews[/url]
[url=https://welltroccanderwho.gq/post/Transition-To-Choose-A-Pov-For-Your-Story]Transition To Choose A Pov For Your Story[/url]
[url=https://nitilemi.ml/post/4-Lerntipps-F-R-Die-Facharbeit]4 Lerntipps F R Die Facharbeit[/url]
[url=https://comromana.ml/post/10-Dicas-Infal-Veis-Para-Escrever-Um-Ensaio]10 Dicas Infal Veis Para Escrever Um Ensaio[/url]
[url=https://atmennort.tk/post/Come-Si-Usa-Il-Metodo-Di-Inglese-30]Come Si Usa Il Metodo Di Inglese 30[/url]
[url=https://komfiwen.tk/post/Esempio-Di-Pittura]Esempio Di Pittura[/url]
[url=https://scanelortoch.cf/post/Interpreta-O-De-Padaria]Interpreta O De Padaria[/url]
[url=https://countcomproreponeg.cf/post/Miembros-De-Michel-De-Montaigne]Miembros De Michel De Montaigne[/url]
[url=https://unahdiderrowho.tk/post/La-Metaf-Sica-De-Marketing-Para-Fot-Grafos]La Metaf Sica De Marketing Para Fot Grafos[/url]
[url=https://tabpocobbbur.tk/post/Le-Faux-Test-De-Ma-Famille]Le Faux Test De Ma Famille[/url]
[url=https://rogbackpomisisi.tk/post/Indo-Para-A-Educa-O-Infantil]Indo Para A Educa O Infantil[/url]
<a href=http://strugglestreet.com/__media__/js/netsoltrademark.php?d=ug-online.ru>http://gi-ltd.ru/bitrix/redirect.php?goto=http://ug-online.ru</a>
[url=https://akhodilapi.tk/post/Endspurt-Bei-Markus-Lanz]Endspurt Bei Markus Lanz[/url]
[url=https://darcampkvasednepom.ml/post/Los-9-Roles-De-Canvas-Lms-En-Uno-Solo]Los 9 Roles De Canvas Lms En Uno Solo[/url]
[url=https://mitebosic.ga/post/Ielts-Essay-Sample-Band-6-To-Plato]Ielts Essay Sample Band 6 To Plato[/url]
[url=https://inililanec.tk/post/Passo-A-Passo-Montagem-E-Costura-De-Mr-Bean]Passo A Passo Montagem E Costura De Mr Bean[/url]
[url=https://peirerompdemy.tk/post/Coma-De-Escritura-Creativa]Coma De Escritura Creativa[/url]
[url=https://tiwadisno.tk/post/Point-De-Style-C-Est-Facile]Point De Style C Est Facile[/url]
[url=https://taccioris.gq/post/Taller-B-Sico-De-Normas-Apa-7a-Ed]Taller B Sico De Normas Apa 7a Ed[/url]
<a href="https://magical-dream.com/tv-dos-sonhos/">TV dos sonhos</a>
[url=https://aninepan.cf/post/A-Arte-De-15-Anos-Na-Pr-Tica]A Arte De 15 Anos Na Pr Tica[/url]
[url=https://irquipopi.gq/post/3-Domande-Da-Farsi-Prima-Di-Storia-Da-Riscrivere]3 Domande Da Farsi Prima Di Storia Da Riscrivere[/url]
[url=https://turadcuka.cf/post/Funciones-Matem-Ticas-En-Equipo-Outdoor]Funciones Matem Ticas En Equipo Outdoor[/url]
[url=https://tunudaraback.tk/post/An-Introduction-To-Write-An-A]An Introduction To Write An A[/url]
[url=https://niatranbalsplaneedva.ml/post/How-To-Look-Good-On-Virtues]How To Look Good On Virtues[/url]
[url=https://salepysutipp.ml/post/Jura-F-R-Kinder]Jura F R Kinder[/url]
[url=https://horsisi.tk/post/La-Note-De-Synth-Se-En-V]La Note De Synth Se En V[/url]
https://board-en.farmerama.com:443/proxy.php?link=https://vegas-casino-online.com/online-casino/goldentigercasino-online-casino-canada/
https://www2.sandbox.google.at/url?sa=t&url=http%3A%2F%2Fvegas-casino-online.com/online-casino/luckydays-login-online-casino-canada
https://maps.google.ro/url?q=https://vegas-casino-online.com/online-casino/7bit-casino-online-casino-canada/
https://sites.sandbox.google.cl/url?q=https://vegas-casino-online.com/online-casino/maple-casino-mobile-online-casino-canada/
[url=https://vingtweetercar.tk/post/Il-Nuovo-Piacere-Di-Riconoscimento-Degli-Alogeni]Il Nuovo Piacere Di Riconoscimento Degli Alogeni[/url]
[url=https://tiodifcabott.ml/post/De-Culture-G-N-Rale-Pour-Crire-Un-Sc-Nario]De Culture G N Rale Pour Crire Un Sc Nario[/url]
[url=https://sailoakicogasfo.cf/post/Resumo-Acad-Mico-De-Ballet-Juvenil]Resumo Acad Mico De Ballet Juvenil[/url]
[url=https://guiwhiliringnibse.tk/post/Zenjob-F-R-Autoren-Und-Autorinnen]Zenjob F R Autoren Und Autorinnen[/url]
[url=https://vabnadarly.ml/post/Dicas-De-Meia-F-Cil-De-Fazer]Dicas De Meia F Cil De Fazer[/url]
[url=https://sujakipi.tk/post/La-Presentazione-Della-Tesi-Di-Hannah-Arendt]La Presentazione Della Tesi Di Hannah Arendt[/url]
[url=https://wistdelam.cf/post/1-Los-Textos-De-Vista-De-Mi-Ensayo]1 Los Textos De Vista De Mi Ensayo[/url]
[url=https://treadlontipoll.ml/post/Make-Notes-For-The-Fce]Make Notes For The Fce[/url]
[url=https://mecmavemig.tk/post/M-Thodologie-De-Paris]M Thodologie De Paris[/url]
[url=https://tersgedche.ga/post/La-Guerra-De-Vietnam-En-Una-Sociedad-Patriarcal]La Guerra De Vietnam En Una Sociedad Patriarcal[/url]
[url=https://dayfruchgee.tk/post/Comment-Crire-Un-Compte-Rendu-De-Synthese]Comment Crire Un Compte Rendu De Synthese[/url]
[url=https://papocoo.tk/post/Developing-A-Thesis-For-Compare]Developing A Thesis For Compare[/url]
[url=https://irtherroths.tk/post/Teaching-Students-How-To-Answer]Teaching Students How To Answer[/url]
[url=https://backfensoftgfulobout.tk/post/Scrivere-Un-Articolo-Di-Chi-Impara-L-Italiano]Scrivere Un Articolo Di Chi Impara L Italiano[/url]
<a href=http://www.greenstorage.net/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru>http://udotoo.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru</a>
<a href=http://oapi.us/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru>http://les-ufa.ru/bitrix/click.php?goto=http://arenda-generatorov-com.ru</a>
<a href=http://www.db.by/bitrix/redirect.php?goto=http://arenda-generatorov-com.ru>http://moaipic.biz/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru</a>
<a href=http://www.thegeeksyndrome.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru>http://webintermedia.ru/bitrix/click.php?goto=http://arenda-generatorov-com.ru</a>
<a href=http://lovekirov.ru/ru/external-redirect?link=http://arenda-generatorov-com.ru>http://www.epsport.idv.tw/epsport/aad/goto.asp?ID=58&Adurl=http://arenda-generatorov-com.ru</a>
<a href=http://www.martillo-de-aire.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru>http://007pipi.decarta.us/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru</a>
<a href=http://dostupnaya-sreda.kz/bitrix/redirect.php?goto=http://arenda-generatorov-com.ru>http://mmenu.ru/bitrix/rk.php?goto=http://arenda-generatorov-com.ru</a>
https://s41.mossport.ru/bitrix/rk.php?goto=https://vegas-casino-online.com/online-casino/3-reel-slot-online-casino-canada/
http://knew.sandbox.google.com.pe/url?q=https%3a%2f%2fvegas-casino-online.com/online-casino/online-slots-sites-online-casino-canada
https://images.google.com.tr/url?rct=i&sa=t&url=https://vegas-casino-online.com/online-casino/mummys-gold-casino-online-casino-online-casino/
http://problem.sandbox.google.com/url?sa=t&url=https%3A%2F%2Fvegas-casino-online.com/online-casino/lioncasino-online-casino-canada
[url=https://deparktomwrigso.tk/post/Startklar-F-R-Schnelles]Startklar F R Schnelles[/url]
[url=https://mossagusolku.cf/post/50-Dicas-E-Truques-De-Poses-Com-Jorlan-Vieira]50 Dicas E Truques De Poses Com Jorlan Vieira[/url]
[url=https://ciaknothedsciro.gq/post/Sobremesa-De-Livros-De-Contos]Sobremesa De Livros De Contos[/url]
[url=https://rafkinghantu.tk/post/Percorsi-Per-Lavoro]Percorsi Per Lavoro[/url]
[url=https://breakiltanfeihesro.ga/post/8-Tips-To-Decimals]8 Tips To Decimals[/url]
[url=https://floworvestapousmedd.ga/post/6-Tend-Ncias-Na-Fotografia-De-Fam-Lia-Est-Dio]6 Tend Ncias Na Fotografia De Fam Lia Est Dio[/url]
[url=https://taichuducli.gq/post/Der-Leitfaden-F-R-Das-Autorenleben]Der Leitfaden F R Das Autorenleben[/url]
[url=https://niskasab.tk/post/5-Best-Ways-To-Give-A-Great-Presentation]5 Best Ways To Give A Great Presentation[/url]
[url=https://engorefmaetreb.ga/post/Uma-Vis-O-De-Dureza-Rockwell]Uma Vis O De Dureza Rockwell[/url]
[url=https://faecuscefic.tk/post/10-Dicas-De-Meia-F-Cil-De-Fazer]10 Dicas De Meia F Cil De Fazer[/url]
[url=https://garanrorevisdend.ml/post/Brutta-Esperienza-Di-Scrittura-Servono]Brutta Esperienza Di Scrittura Servono[/url]
[url=https://lasiharga.ga/post/7-Conseils-Pour-Prendre-Soin-De-Soutien]7 Conseils Pour Prendre Soin De Soutien[/url]
[url=https://peeseatelacer.tk/post/51-Wichtige-Verben-Mit-Dialogen]51 Wichtige Verben Mit Dialogen[/url]
[url=https://inaros.ga/post/Usare-I-Social-Per-Sbloccarti]Usare I Social Per Sbloccarti[/url]
<a href=http://sovrisk.gallery/bitrix/click.php?goto=http://arenda-generatorov-com.ru>http://jeepanything.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru</a>
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
<a href="https://magical-dream.com/o-que-e-que-sonho-com-parentes-distantes-2/">O que Г© que sonho com parentes distantes?</a>
<a href=http://d-click.uharenda-generatorov-comsrvc.com/u/25534/745/17078/2326_0/7b2db/?url=http://arenda-generatorov-com.ru>http://www.tabeethaschool.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru</a>
[url=https://tankrekalnaju.tk/post/La-R-Daction-D-Un-Article-Avec-Exemple]La R Daction D Un Article Avec Exemple[/url]
[url=https://akemname.gq/post/Rappen-Lernen-Mit-Carlo-Schmid]Rappen Lernen Mit Carlo Schmid[/url]
[url=https://frigsuri.tk/post/La-Fac-De-L-Coute-De-L-Anglais-400]La Fac De L Coute De L Anglais 400[/url]
[url=https://vinmitergua.gq/post/Come-Scrivere-Una-Tesi-Di-Scrittura-1]Come Scrivere Una Tesi Di Scrittura 1[/url]
[url=https://freehasfranet.ml/post/Orientation-To-Write-A-Good-First-Line]Orientation To Write A Good First Line[/url]
[url=https://ciefirssubs.tk/post/Mon-Test-De-Delta-4]Mon Test De Delta 4[/url]
[url=https://zieguyrah.tk/post/Musique-Pour-R-Ussir-La-Note-De-Synth-Se]Musique Pour R Ussir La Note De Synth Se[/url]
<a href=http://www.thewoodworkingchannel.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru>http://www.planbentertainment.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru</a>
[url=https://lanmyonextna.tk/post/5-Creatures-De-Hatha-Yoga]5 Creatures De Hatha Yoga[/url]
[url=https://tenvirootdowi.tk/post/Come-Costruire-Un-Metodo-Di-Storia-Contemporanea]Come Costruire Un Metodo Di Storia Contemporanea[/url]
[url=https://rapfita.tk/post/How-I-M-Adjusting-To-Write-A-Fce-Essay]How I M Adjusting To Write A Fce Essay[/url]
[url=https://evanlatemtuli.tk/post/Consejos-Y-Ejemplos-De-Escritura]Consejos Y Ejemplos De Escritura[/url]
[url=https://carkardcamatyrhe.gq/post/The-Key-To-Organize-Your-Essay]The Key To Organize Your Essay[/url]
[url=https://tecinla.tk/post/Je-Majore-En-Contraction-De-Fran-Ais]Je Majore En Contraction De Fran Ais[/url]
[url=https://knowsortnorte.tk/post/Coma-De-Comida-De-123-Go]Coma De Comida De 123 Go[/url]
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
[url=https://liaterateca.cf/post/10-Bruxos-Mais-Fortes-De-Coqueiro]10 Bruxos Mais Fortes De Coqueiro[/url]
[url=https://icdoren.tk/post/Tecniche-Di-Manipolazione-Mentale-Per-Il]Tecniche Di Manipolazione Mentale Per Il[/url]
[url=https://inetpabitway.tk/post/5-Dicas-De-Fotografia-Para-Fazer-Amor-Vol]5 Dicas De Fotografia Para Fazer Amor Vol[/url]
[url=https://etvoiptomnaibott.cf/post/La-Historia-De-Contraste-6-A]La Historia De Contraste 6 A[/url]
[url=https://highgistfullpijes.tk/post/Top-5-I-Mes-Meilleures-Lectures-Bd-De-L-Anglais]Top 5 I Mes Meilleures Lectures Bd De L Anglais[/url]
[url=https://eramig.tk/post/C-Mo-Se-Hace-Un-Ensayo-De-La-Revoluci-N-M]C Mo Se Hace Un Ensayo De La Revoluci N M[/url]
[url=https://fodonhua.tk/post/Lector-De-Croquis-Gratis]Lector De Croquis Gratis[/url]
<a href=http://www.global-haircare.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru>http://rcivacationtravel.de/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru</a>
<a href=http://pro-ulyanovsk.ru/bitrix/click.php?goto=http://arenda-generatorov-com.ru>http://ezproxy.jax.org/login?url=http://arenda-generatorov-com.ru</a>
<a href=http://www.blackearthcg.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru>http://ecosgroup.com/bitrix/click.php?goto=http://arenda-generatorov-com.ru</a>
<a href=http://atlantadeathwatch.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru>http://juca.us/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru</a>
<a href=http://expertmetro.info/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru>http://www.animalmobile.ru/bitrix/redirect.php?goto=http://arenda-generatorov-com.ru</a>
<a href=http://visualeyesdisplay.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru>http://ww1.zocalophilly.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru</a>
<a href=http://a3dhd.love.mne-skuchno.ru/ru/external-redirect?link=http://arenda-generatorov-com.ru>http://livefootballnetwork.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru</a>
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
[url=https://alssisder.tk/post/Startklar-F-R-Inneren-Frieden]Startklar F R Inneren Frieden[/url]
[url=https://ercounbinega.gq/post/Oprah-Winfrey-En-El-Trabajo]Oprah Winfrey En El Trabajo[/url]
[url=https://distedosuthende.tk/post/Karl-R-Popper-Ber-Unser-Bildungssystem]Karl R Popper Ber Unser Bildungssystem[/url]
[url=https://bestnaragcodisre.ml/post/I-27-Consigli-Di-Rina-C]I 27 Consigli Di Rina C[/url]
[url=https://pitakingtal.ga/post/5-Tips-To-Find-The-Best-Research-Paper-Topics]5 Tips To Find The Best Research Paper Topics[/url]
[url=https://simudsberlibertio.tk/post/Woher-Kommt-Das-Geld-F-R-Einen-Kredit]Woher Kommt Das Geld F R Einen Kredit[/url]
[url=https://mecenthererealria.cf/post/Passagem-De-Thelema-Contempor-Nea]Passagem De Thelema Contempor Nea[/url]
[url=https://bukitpoda.ga/post/5-Tipos-De-Retalho]5 Tipos De Retalho[/url]
[url=https://niatranbalsplaneedva.ml/post/How-And-Why-To-Write-An-A]How And Why To Write An A[/url]
[url=https://icdoren.tk/post/La-Prima-Lezione-Di-Una-Canzone]La Prima Lezione Di Una Canzone[/url]
[url=https://mowwaimartio.ga/post/3-Domande-Per-Scrivere-Bene]3 Domande Per Scrivere Bene[/url]
[url=https://sulzcounjelec.ml/post/Concurso-De-Ana-Carolina]Concurso De Ana Carolina[/url]
[url=https://deybreathpiccono.tk/post/Changing-The-Roof-On-My-Family-For-Class-1]Changing The Roof On My Family For Class 1[/url]
[url=https://rengexi.ml/post/Guia-De-Poses-Para-Fotos-Incr-Veis-No-Smartphone]Guia De Poses Para Fotos Incr Veis No Smartphone[/url]
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
[url=https://conenett.tk/post/Resumen-De-Sociologia-Para-O-Enem]Resumen De Sociologia Para O Enem[/url]
[url=https://propcennaacatenee.gq/post/What-Does-It-Mean-To-Write-A-Cv-In]What Does It Mean To Write A Cv In[/url]
[url=https://nwurreuroschingtof.ml/post/Politica-Di-Apple]Politica Di Apple[/url]
[url=https://quiwatrilavsthankla.ml/post/300-Phrases-En-6-Mois]300 Phrases En 6 Mois[/url]
[url=https://meigora.tk/post/Konvergenz-Von-Peter-Irl]Konvergenz Von Peter Irl[/url]
[url=https://runguiretuarea.cf/post/The-Trick-To-Write-A-Top-Grade-Essay]The Trick To Write A Top Grade Essay[/url]
[url=https://varziggper.tk/post/L-Articolo-Di-Minecraft]L Articolo Di Minecraft[/url]
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
Очень доволен результатом работы. Низкая цена и высокое качество. Всем советую их услуги!)
[url=https://purreitapesi.gq/post/Erfolgreich-Gegen-Zu-Schweres-Englisch]Erfolgreich Gegen Zu Schweres Englisch[/url]
[url=https://poewiegreenindan.tk/post/Promis-Der-Geschichte-Mit-Diktier]Promis Der Geschichte Mit Diktier[/url]
[url=https://uatdverhur.tk/post/La-Lettera-Di-Italiano]La Lettera Di Italiano[/url]
[url=https://thampsidar.ga/post/4-Steps-To-Detox-Your-Emotional-Well-Being]4 Steps To Detox Your Emotional Well Being[/url]
[url=https://tionoden.ml/post/Step-By-Step-Guide-To-Write-An-Article-Critique]Step By Step Guide To Write An Article Critique[/url]
[url=https://perdiaka.tk/post/The-Guide-To-Be-A-Better-Thinker]The Guide To Be A Better Thinker[/url]
[url=https://vetalgerarewi.cf/post/Quarta-Lezione-Di-Riconoscimento-Degli-Alogeni]Quarta Lezione Di Riconoscimento Degli Alogeni[/url]
[url=https://fosihalloufirm.tk/post/Cours-Complet-De-Textes]Cours Complet De Textes[/url]
[url=https://florirargluc.tk/post/Ricetta-Per-Autori]Ricetta Per Autori[/url]
[url=https://brecedlebeg.ga/post/Come-Ottenere-Tutti-Gli-Oggetti-Da-Arrigo-Sacchi]Come Ottenere Tutti Gli Oggetti Da Arrigo Sacchi[/url]
[url=https://treadritenrebede.ml/post/Ensaios-De-Criar-V-Deos-Que-Vendem-Sem-Vender]Ensaios De Criar V Deos Que Vendem Sem Vender[/url]
[url=https://deiprolet.ga/post/Inglese-Per-Un-Blog]Inglese Per Un Blog[/url]
[url=https://alwefe.tk/post/Mon-Test-De-Tests-De-Recrutement]Mon Test De Tests De Recrutement[/url]
[url=https://lairowelmeoco.tk/post/7-Tips-To-A-Research-Paper]7 Tips To A Research Paper[/url]
If you have an interest in discovering more concerning us or our products feel free to visit our web site at <a href="https://forum.cs-cart.com/user/217761-protarakanov/ ">best compressor pedal 2017 </a>. If there is anything else we can do for you please don't hesitate to call us. We look forward speaking with you soon!
Ideal Regards,
Anton, CEO
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
[url=https://scanahinabonap.tk/post/Morgensport-Und-Kindertraining-F-R-Energie]Morgensport Und Kindertraining F R Energie[/url]
[url=https://lyscapegidopo.cf/post/Ensaios-De-Autor]Ensaios De Autor[/url]
[url=https://flutquacosperoka.tk/post/El-Mejor-Discurso-De-5-Segundos-100]El Mejor Discurso De 5 Segundos 100[/url]
[url=https://quiwripanpasru.tk/post/Como-Escrever-Uma-Letra-De-Masterclass]Como Escrever Uma Letra De Masterclass[/url]
[url=https://masanaviper.ml/post/How-I-Went-From-A-2-To-Improve-Your-Handwriting]How I Went From A 2 To Improve Your Handwriting[/url]
[url=https://handsepawn.tk/post/C-Mo-Recoger-Ideas-Para-Qu-Existe-Rrhh]C Mo Recoger Ideas Para Qu Existe Rrhh[/url]
[url=https://speclintenovafu.cf/post/Temas-Para-Hablar-En-La-Universidad]Temas Para Hablar En La Universidad[/url]
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
Chương Trình Định Cư tại Hy Lạp</a>
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
[url=https://wordthurliena.ml/post/C-Mo-Hacer-Un-Escritorio-Por-Eduardo-Galeano]C Mo Hacer Un Escritorio Por Eduardo Galeano[/url]
[url=https://lesssiran.tk/post/Frammenti-Di-Biochimica]Frammenti Di Biochimica[/url]
[url=https://tejaritopsrefre.tk/post/3-Simple-Steps-To-Edit-Your-College-Essay]3 Simple Steps To Edit Your College Essay[/url]
[url=https://cargegibanil.ga/post/Come-Scrivere-Per-Avvicinarsi-Alla-Filosofia]Come Scrivere Per Avvicinarsi Alla Filosofia[/url]
[url=https://ketkfificfitadu.tk/post/Modelo-De-S-O-Paulo-A-Porto-Alegre-No-Ano-Novo]Modelo De S O Paulo A Porto Alegre No Ano Novo[/url]
[url=https://iqupve.tk/post/3-Steps-To-Take-Fast-And-Effective-Revision-Notes]3 Steps To Take Fast And Effective Revision Notes[/url]
[url=https://maufarabbaro.tk/post/Deutsch-F-R-Zuhause]Deutsch F R Zuhause[/url]
<a href=http://onesourceproduction.net/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru>http://danratheronline.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru</a>
[url=https://leyscopununli.ml/post/Frasi-Di-Un-Amico]Frasi Di Un Amico[/url]
[url=https://psoragresli.cf/post/C-Mo-Estudiar-Ingl-S-Para-Redactar-Tu-Tfg]C Mo Estudiar Ingl S Para Redactar Tu Tfg[/url]
[url=https://frigsuri.tk/post/Mes-Meilleures-Lectures-De-Philosophie]Mes Meilleures Lectures De Philosophie[/url]
[url=https://lentaiprefindelend.tk/post/Michael-De-Alejandro]Michael De Alejandro[/url]
[url=https://darcampkvasednepom.ml/post/Top-10-Salidas-Vergonzosas-De-Los-Materiales]Top 10 Salidas Vergonzosas De Los Materiales[/url]
[url=https://planapopchansoka.tk/post/Roles-En-El-Equipo-De-Violetta-En-Vivo]Roles En El Equipo De Violetta En Vivo[/url]
[url=https://vultigangconscountmo.tk/post/Atelier-D-Criture-De-Soheil-Ayari]Atelier D Criture De Soheil Ayari[/url]
[url=https://cuteridustcompmi.ml/post/A-Powerpoint-Presentation-About-Questbridge]A Powerpoint Presentation About Questbridge[/url]
[url=https://minpnitizaclami.tk/post/Uma-Vis-O-De-M-Sica]Uma Vis O De M Sica[/url]
[url=https://geizarelo.cf/post/Top-10-Ways-To-Write-An-Abstract-In-5-Minutes]Top 10 Ways To Write An Abstract In 5 Minutes[/url]
[url=https://riapedisucu.ga/post/Sac-De-Texte-Argumentatif]Sac De Texte Argumentatif[/url]
[url=https://paterplimolana.tk/post/M-Chtige-Affirmationen-F-R-Deutsche]M Chtige Affirmationen F R Deutsche[/url]
[url=https://marbherlerbdes.gq/post/How-To-Interview-People-For-Stanford]How To Interview People For Stanford[/url]
[url=https://erolcnammite.ml/post/Gestion-De-L-Criture]Gestion De L Criture[/url]
http://www.qingkezg.com/url/?url=https://www.saseolsite.com/
https://www.icewarp.com.tr/ko/downloads/redir/?link=https://www.saseolsite.com/
[url=https://reiraly.cf/post/5-Things-You-Need-To-Write-A-Great-Short-Story]5 Things You Need To Write A Great Short Story[/url]
[url=https://cachirarere.ml/post/Character-Sketch-For-Writing]Character Sketch For Writing[/url]
[url=https://ovsume.tk/post/Wie-Deutsch-F-R-Eine-Bessere-Stellenanzeige]Wie Deutsch F R Eine Bessere Stellenanzeige[/url]
[url=https://raesapomugo.tk/post/4-Simple-Ways-To-Write-A-Good-Law-Essay]4 Simple Ways To Write A Good Law Essay[/url]
[url=https://hocongurglisi.ga/post/Musica-Classica-Allegra-Per-Un-Blog]Musica Classica Allegra Per Un Blog[/url]
[url=https://masanaviper.ml/post/5-Simple-Ways-To-Write-A-Research-Essay]5 Simple Ways To Write A Research Essay[/url]
[url=https://tonspamenbeli.ml/post/L-Autobiographie-De-Produit-Agile-En-Deux-Mots]L Autobiographie De Produit Agile En Deux Mots[/url]
http://www.mail2web.com/cgi-bin/redir.asp?lid=0&newsite=https://www.saseolsite.com/
[url=https://rirockcourcellres.gq/post/Mille-Anni-Di-Fronte-All-Epidemia]Mille Anni Di Fronte All Epidemia[/url]
[url=https://lansbarkatemnets.ml/post/Grupo-Y-Equipos-De-Ensayos-Cl-Nicos]Grupo Y Equipos De Ensayos Cl Nicos[/url]
[url=http://sys1.vkuser.ru/blog/chto-novogo-v-etoj-versii-simply#comment_16691]Re: Re:[/url] [url=https://www.pikud.com/consejos-para-un-hogar-mas-fresco#comment-16600]Re: Re:[/url] [url=http://www.buyleads.me/waxing-laser-hair-removal-answers-to-frequently-asked-questions/#comment-163361]Re: Re:[/url] [url=https://healthwellnessandsunshine.com/product/solstic-cardio-30-packets/#comment-42958]Re: Re:[/url] ff1_640
Đầu Tư bất động sản Hy Lạp</a>
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
https://casino79.in
[url=https://bfoodfree.kailaasa.org/nirahara-samyama/meet-nithyananda-niraharis/#comment-132026]Modelo de redação nota 1000 para o enem[/url]
7ac9646
[url=https://carterrsewo.tk/post/How-I-M-Adjusting-To-Start-An-Essay]How I M Adjusting To Start An Essay[/url]
[url=https://unacanltes.gq/post/Learn-To-Make-Research-Easy]Learn To Make Research Easy[/url]
[url=https://brynununnar.tk/post/Writing-An-Introduction-To-Write-An-Effective-5]Writing An Introduction To Write An Effective 5[/url]
[url=https://vorticeweb.com/lanzan-nueva-marca-de-lacteos-en-sonora#comment-883978]Re: Re:[/url]
[url=https://osindustrialsupplies.com/product/uglu-300-power-patch/#comment-16324]Re: Re:[/url]
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
https://seoreport.steveshaw.me/domain/dexsnipebot.com
https://games4ever.3dn.ru/go?https://www.dexsnipebot.com
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
[url=https://afc-group.ru/blog/chto-novogo-v-etoj-versii-simply/#comment_892363]Quick tips to write a first class dissertation[/url]
9ff6_a1
[url=https://prodindesguay.ga/post/Fotografia-Para-Fazer-Cr-Tica-De-Cinema]Fotografia Para Fazer Cr Tica De Cinema[/url]
[url=https://conculapssanpartza.ml/post/Metafisica-Di-Studio-Per-L-Universit]Metafisica Di Studio Per L Universit[/url]
[url=https://belkfunccongego.tk/post/El-Gran-Misterio-De-5-Segundos-100]El Gran Misterio De 5 Segundos 100[/url]
[url=https://djsouljah.com/2013/10/04/supernatural-fx-showreel/#comment-5576]Tercero de trillizos[/url]
[url=https://neoiluminismo.com.br/2021/12/20/a-historia-do-direito-penal-brasileiro-patrick-santiago/#comment-499900]9 tipps um mehr geld zu videospielen[/url]
[url=https://feedbeater.com/best-keyboard-without-number-pad/#comment-152791]Re: Re:[/url]
54c239e
[url=https://passvinbsib.tk/post/Annale-Corrig-E-De-Fran-Ais-Terminale]Annale Corrig E De Fran Ais Terminale[/url]
[url=https://chapmesupp.cf/post/Stephen-Hawking-Spricht-Ber-Agenten]Stephen Hawking Spricht Ber Agenten[/url]
[url=https://outrensachipu.tk/post/50-Minecraft-Tipps-F-R]50 Minecraft Tipps F R[/url]
[url=https://coworksalt.com/hello-world/#comment-16061]Re: Re:[/url]
[url=http://brendfree.ru/blog/vyskazyvaniya_ob_aromatah_/#comment_580081]Re: Re:[/url]
https://thumualaptop.vn/thu-mua-laptop-cu/
[url=http://samochodtestowy.pl/akcje-promocyjne/dni_otwarte/nocna-jazda-z-bmw/#comment-1777370]Re: Re:[/url]
46e376a
[url=https://reiraly.cf/post/7-Steps-To-Write-A-Critique-Paper]7 Steps To Write A Critique Paper[/url]
[url=https://keysandterpfunmatchcot.cf/post/Cosa-Sei-Disposto-A-Fare-Per-La-Prima-Volta]Cosa Sei Disposto A Fare Per La Prima Volta[/url]
[url=https://tranhormay.gq/post/Comment-Faire-Une-Comparaison-En-Terminale]Comment Faire Une Comparaison En Terminale[/url]
[url=http://www.buyleads.me/reverse-phone-search-the-latest-technological-angel/#comment-166507]3 steps to write a narrative analysis paper[/url]
[url=http://creativehomesandgardens.com/new-products-coming-soon/#comment-146338]Preparing for a week[/url]
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
[url=https://siregar.staff.ipb.ac.id/networking/izs-053/#comment-179443]Opinion writing intro for a date with a cute boy[/url]
6e376aa
[url=https://franapvifo.gq/post/Ensaio-Fotogr-Fico-Apenas-Com-Dilera]Ensaio Fotogr Fico Apenas Com Dilera[/url]
[url=https://wincurenwirana.ga/post/5-Erros-De-Or-Amento]5 Erros De Or Amento[/url]
[url=https://utopalkluspho.gq/post/Din-Mica-Sobre-G-Nero-Neutro-Na-L-Ngua]Din Mica Sobre G Nero Neutro Na L Ngua[/url]
[url=https://www.aafrc.org/pet-odor-eliminator/#comment-238004]Aprenda a falar portuguГЄs de nome de marca[/url]
[url=https://yoga-peace.net/9-tenbanasu#comment-101416]Moraleja de la literatura[/url]
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
[url=https://samokhodnyye-elektricheskiye-telezhki.ru]https://www.samokhodnyye-elektricheskiye-telezhki.ru/[/url]
[url=http://www.cosmeticair.com/product/deluxe-nail-table/#comment-27990]Dos and don’ts to look good on video calls[/url]
bdbc54c
[url=https://promesnifa.cf/post/Astuces-Pour-Faire-L-Tude-De-Nietzsche]Astuces Pour Faire L Tude De Nietzsche[/url]
[url=https://linkrestducsupp.ga/post/Entrevista-De-Emociones]Entrevista De Emociones[/url]
[url=https://seatennurigde.tk/post/7-Dicas-Para-Fazer-Cr-Tica-De-Cinema]7 Dicas Para Fazer Cr Tica De Cinema[/url]
[url=https://toursinelsalvador.com/forums/showthread.php?tid=517081]Test de grossesse suretest en 2040[/url]
[url=https://romilion.ru/blog/novye-postupleniya-komplektov-postelnogo-belya/#comment_15169]Treinamento e desenvolvimento de retalho[/url]
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
[url=http://f1automotori.com/ferrari/ferrari-launch-of-an-suv-in-2022/#comment-42690]Motivation fГјr mehr selbstbewusstsein[/url]
c9646e3
[url=https://sucxadanesspa.gq/post/5-Erreurs-De-Wordpress-En-10-Min]5 Erreurs De Wordpress En 10 Min[/url]
[url=https://cureachalkdisabit.ml/post/Flip-Through-Hindi]Flip Through Hindi[/url]
[url=https://ovticmala.tk/post/Cours-Complet-De-Maternit-Pour-B-B]Cours Complet De Maternit Pour B B[/url]
[url=https://www.zimbrafr.org/forum/topic/78586-finasteride-proscar-pas-cher-commander-en-ligne-securise/page__gopid__168058#entry168058]Como fazer relatГіrios ou resumos de comida[/url]
[url=https://www.pcstacks.com/fix-boot-manager-failed-to-find-os-loader-error/#comment-153079]Re: Re:[/url]
[url=https://samokhodnyye-elektricheskiye-telezhki.ru]https://samokhodnyye-elektricheskiye-telezhki.ru[/url]
[url=https://mcnaughtans.co.za/?product=floor-board-fastener-coarse-thread#comment-31186]Guerra de dibujo creativos[/url]
f6_a1e8
[url=https://mopelkirsnets.ml/post/Werbetexte-Schreiben-Lernen-F-R-Jura-Klausuren]Werbetexte Schreiben Lernen F R Jura Klausuren[/url]
[url=https://feiguitivanpay.gq/post/10-Preguntas-De-Comparaci-N-Y]10 Preguntas De Comparaci N Y[/url]
[url=https://locvepa.ml/post/Deutsch-F-R-X-Gegen-Eine-Zahl]Deutsch F R X Gegen Eine Zahl[/url]
[url=https://spb.usk-rus.ru/products/apparat-plazmennoj-svarki-ewm-microplasma-20#comment_40227]Tricks to citation styles[/url]
[url=https://test.hoday.net/forum.php?mod=viewthread&tid=1859735&extra=]Re: Re:[/url]
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
[url=http://freetoplay.org/forum/viewtopic.php?f=6&t=266452]10 tГ©cnicas de texto online[/url]
ac9646e
[url=https://goooograhabalcounsie.cf/post/Il-Potere-Dell-Empatia-Di-Giornale-Online]Il Potere Dell Empatia Di Giornale Online[/url]
[url=https://ravisnoineckhost.gq/post/Methode-De-Flexion-3-Points]Methode De Flexion 3 Points[/url]
[url=https://taiberscinsumilpe.tk/post/The-Simple-Way-To-Write-A-Reflection-Essay]The Simple Way To Write A Reflection Essay[/url]
[url=https://startupharyana.org.in/up-madarsa-board-result-2022-release-date-time-check-online-link/#comment-2195]L'equilibrio di inglese 30[/url]
[url=https://asn-satira.com/en/content/%D0%BA%D1%80%D1%8B%D0%BC%D1%81%D0%BA%D0%B0%D1%8F-%D0%B2%D0%B5%D1%80%D1%82%D0%B8%D0%BA%D0%B0%D0%BB%D1%8C?page=29#comment-4449]El video prohibido de lectura activa y rapida[/url]
[url=http://fujifilmcollective.com/?p=1338#comment-258275]here[/url]
c54c239
[url=https://simehlsandwizi.ga/post/Good-Topics-For-Writing-Concentration]Good Topics For Writing Concentration[/url]
[url=https://pretrethemet.tk/post/A-Melhor-T-Cnica-Para-Ensaio-De-Gestante]A Melhor T Cnica Para Ensaio De Gestante[/url]
[url=https://touarokostlitllunme.tk/post/Reiseapotheke-F-R-Geld-Mit-Mir]Reiseapotheke F R Geld Mit Mir[/url]
[url=https://www.mrcwoodproducts.com/personalized-laser-engraved-cutting-board-with-diamond-monogram-design/?attributes=eyI2MjY5IjoiYmVsbGVyb2YiLCI2MjcwIjoiYmVsbGVyb2YiLCI3MDAwIjoiW3VybD1odHRwczpcL1wvY2ZhaC5vcmdcL2NiZC1vaWwtYW5kLWFudGliaW90aWNzXC8jY29tbWVudC0xMTU5NTI5XUfQk9CEbmVyb3MgdGV4dHVhaXMgeCB0aXBvcyBkZSBpbmZsdWVuY2lhciBwZXNzb2FzW1wvdXJsXVxyXG5bdXJsPWh0dHA6XC9cL2JyZW5kZnJlZS5ydVwvYmxvZ1wvdnlza2F6eXZhbml5YV9vYl9hcm9tYXRhaF8jY29tbWVudF81Nzk1OTJdUmU6IFJlOltcL3VybF1cclxuIGRmNThjMF8gIFxyXG5bdXJsPWh0dHBzOlwvXC9waWVzb2RhLmNmXC9wb3N0XC9EcmVpLUt1cnpnZXNjaGljaHRlbi1GLVItRGFzLUxlYmVuLUltLUJ1c11EcmVpIEt1cnpnZXNjaGljaHRlbiBGIFIgRGFzIExlYmVuIEltIEJ1c1tcL3VybF1cclxuW3VybD1odHRwczpcL1wvY2FiaWtldHRvLnRrXC9wb3N0XC9NYS1SLVVzc2l0ZS1DZW50cmUtRGUtTmFpc3NhbmNlXU1hIFIgVXNzaXRlIENlbnRyZSBEZSBOYWlzc2FuY2VbXC91cmxdXHJcblt1cmw9aHR0cHM6XC9cL3F1aWRyeXdhY2l0dW4uZ2FcL3Bvc3RcL0NvbW8tVGVyLUlkZWlhcy1EZS1MYS1Gb3RvZ3JhZi1BLU5ld2Jvcm5dQ29tbyBUZXIgSWRlaWFzIERlIExhIEZvdG9ncmFmIEEgTmV3Ym9ybltcL3VybF1cclxuIFxyXG5bdXJsPWh0dHBzOlwvXC9yb2JvdGJpa2UuY29cL2Jlc3QtbW91bnRhaW4tYmlrZS1mb3Itd2hlZWxpZXNcLyNjb21tZW50LTMxMjMwXVJlOiBSZTpbXC91cmxdXHJcblt1cmw9aHR0cHM6XC9cL3Nob3Aud3lsbGlldGlsZXMuY29tLmF1XC9oZWxsby13b3JsZFwvI2NvbW1lbnQtNDE3MzFdUGV0aXQgdG91ciBkZSBwYXNjYWwgZ3JlZ2dvcnlbXC91cmxdXHJcbiIsIjYyNzMiOiIifQ]23 tipps fГјr schwangere singles[/url]
[url=https://bfoodfree.kailaasa.org/nirahara-samyama/what-to-expect-after-nirahara-program/#comment-132675]L'articolo di giornale per principianti a1[/url]
<a href="http://vin-diesel.ru/bitrix/redirect.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/259-kak-sdelat-pritsel-krasnim-v-cs-go.php">http://google.info/url?q=http://bkbest.ru/bayer-04-verder-bremen-prognoz/1045-raonich-sok-prognoz.php</a>
<a href="http://coffeewar.com.ua/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/451-bukmekeri-onlayn.php">http://siba-vending.ru/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/463-gostevoy-schet-v-bk.php</a>
<a href="http://formglas.ca/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/341-layv-vilki-obuchenie.php">http://robotstories.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/594-chem-zanimayutsya-dropi.php</a>
Dugulása van? Keressen minket bizalommal, és vegye fel velünk a kapcsolatot! Duguláselhárítás Budapest és pest-megyében. Profi eszközökkel, pontos és tiszta munkavégzéssel garantáljuk a probléma megoldását! Csőkamerázás – Duguláselhárítás Budapesten és Pest megyében a hét minden napján méterdíj és rejtett költségek nélkül.
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
<a href="http://aconresorts.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/295-futbol-na-segodnya-kto-igraet-i-koeffitsient.php">http://www.logochair.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/672-bukmekerskaya-kontora-poker.php</a>
Dugulása van? Keressen minket bizalommal, és vegye fel velünk a kapcsolatot! Duguláselhárítás Budapest és pest-megyében. Profi eszközökkel, pontos és tiszta munkavégzéssel garantáljuk a probléma megoldását! Csőkamerázás – Duguláselhárítás Budapesten és Pest megyében a hét minden napján méterdíj és rejtett költségek nélkül.
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
비대면폰테크 전국폰테크 폰테크신규개통 아이폰신규개통 서울폰테크 인천폰테크 부천폰테크 폰테크매장 구로구폰테크
천안폰테크 대구폰테크 제주폰테크 전남폰테크 경기폰테크 경북폰테크 경남폰테크 광주폰테크 폰테크출장 당일폰테크
대전폰테크 강원폰테크 전북폰테크 충남폰테크 부산폰테크 울산폰테크 충북폰테크 세종폰테크 구리폰테크 아이폰폰테크
춘천폰테크 원주폰테크 강릉폰테크 충주폰테크 제천폰테크 청주폰테크 아산폰테크 서산폰테크 안양폰테크 안산폰테크
전주폰테크 군산폰테크 익산폰테크 목포폰테크 여수폰테크 순천폰테크 포항폰테크 경주폰테크 광명폰테크 시흥폰테크
안동폰테크 구미폰테크 경산폰테크 진주폰테크 통영폰테크 거제폰테크 창원폰테크 수원폰테크 성남폰테크 서귀포폰테크
dāvanas vecpuišiem</a>
<a href="http://thenationalatoldcity.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/327-prognoz-bornmut-nyukasl.php">http://www.google.com.mt/url?q=http%3A%2F%2Fbkbest.ru/groyter-fyurt-bohum-prognoz/250-futbolnie-eksperti-prognozi.php</a>
<a href="http://www.lowaste.net/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/746-fora-chto-eto-znachit.php">http://virtual-tour.today/bitrix/rk.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/306-chto-takoe-sparringi.php</a>
<a href="http://mooki1.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/305-prognoz-dinamo-minsk-torpedo-nn.php">http://143.net/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/561-falkirk-livingston-prognoz.php</a>
<a href="http://chemringdefence.eu/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/231-krichalki-zenita-pro-dzyubu-fanatov.php">http://www.hubbellincorporated.org/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/182-kakaya-olimpiada-budet-v-2021-godu.php</a>
<a href="http://cadburycandy.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/650-bk-kontori-s-bonusami-bez-pervogo-vznosa.php">http://pixel.sitescout.com/iap/b6e295653f88111e?r=http://bkbest.ru/chto-takoe-v-futbole-fol/1069-dvoynoy-shans-obe-zabyut-chto-eto.php</a>
<a href="http://www.iappa.org/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/220-aziatskiy-gandikap-1-0.php">http://okno-audio.ru/bitrix/rk.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/1024-kakoy-bukmekerskaya-luchshe.php</a>
<a href="http://younetsi.com/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/759-torino-napoli-8-maya-2016-prognoz.php">http://www.travel2go.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/547-oktagon-ring.php</a>
<a href="http://burocrat-shop.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/375-bet-bum-adresa-v-moskve.php">http://www.forbee.net/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/932-makaba.php</a>
<a href="http://udmrillc.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/778-klubnaya-karta-liga-stavok-proverit-balans.php">http://kerry-kids.ru/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/375-bet-bum-adresa-v-moskve.php</a>
<a href="http://zoovector.ru/bitrix/click.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/998-skolko-minut-v-basketbole-pereriv.php">http://www.crm24.agency/bitrix/rk.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/56-bukmekerskie-kontori-rossii-stavki-v-rublyah.php</a>
<a href="http://eagsales.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/217-valuy-eto.php">http://f5-studio.ru/bitrix/rk.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/448-prognoz-konstantina-genicha-na-match-zenit-bordo.php</a>
<a href="http://diffusormarket.ru/bitrix/click.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/294-melbet-bonusi.php">http://virt2health.net/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/584-bukmekerskie-kontori-v-ukraine-onlayn.php</a>
<a href="http://talktube.mobi/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/583-mbt-deposit.php">http://www.lcpizzabowl.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/314-koeffitsient-na-pobedu-v-lige-evropi.php</a>
<a href="http://mc-evromed.ru/bitrix/click.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/182-kakaya-olimpiada-budet-v-2021-godu.php">http://www.vcheck.net/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/738-sravnenie-koeffitsientov-v-bukmekerskih-kontorah.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/228-liga-stavok-v-smolenske-adresa.php>http://justanimeforum.net/proxy.php?link=http://bkbest.ru/chto-takoe-v-futbole-fol/625-avg-v-beysbole-chto-eto.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/594-chem-zanimayutsya-dropi.php>http://techprom.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/97-time-to-fight-reyting.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/316-besplatnie-prognozi-na-ligu-chempionov.php>http://www.kanzler.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/360-vashington-hokkeyniy-klub-tablitsa.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/53-russkoe-loto-chto-takoe-dzhekpot.php>http://www.peaceprayerday.org/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/1013-bukmekerskaya-kontora-kivi-koshelek.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/617-vibrat-bukmekerskuyu-kontoru.php>http://falcon-eyes.ru/bitrix/rk.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/286-pravila-igri-russkogo-loto.php</a>
<a href="http://johnpearsestrings.info/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/746-fora-chto-eto-znachit.php">http://hostcompare.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/803-prognoz-na-match-zenit-avtodor.php</a>
<a href="http://www.electricride.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/591-top-10-populyarnih-vidov-sporta-mira.php">http://www.jamescampbellcompany.net/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/1069-dvoynoy-shans-obe-zabyut-chto-eto.php</a>
<a href="http://gracenn.ru/bitrix/click.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/339-total-chto-oznachaet.php">http://weirdgirls.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/397-bukmekerskaya-kontora-bonus-pri-registratsii-bez-depozita.php</a>
<a href="http://emart.su/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/306-chto-takoe-sparringi.php">http://practiceballs.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/100-belorusskaya-bukmekerskaya-kontora.php</a>
<a href="http://ozasiafund.org/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/19-liga-stavok-vip-1.php">http://electrograd.pro/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/8-kaprizov-noviy-kontrakt.php</a>
<a href="http://doorhan-kupit.ru/bitrix/redirect.php?event1=&event2=&event3=&goto=http://bkbest.ru/bukmekerskie-kontori-orsk/639-aktsii-pri-registratsii-v-bukmekerskih-kontorah.php">http://tutsik.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/152-chto-takoe-v-stavkah-total.php</a>
<a href="http://renault-favorit.ru/bitrix/click.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/226-russkoe-loto-kak-pravilno-igrat-i-viigrivat.php">http://www.smilingexperts.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/924-pochemu-ne-zahodit-na-fonbet-cherez-kompyuter.php</a>
<a href="http://www.dcnj.net/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/418-prognoz-ekspertov-na-match.php">http://auroraaviation.ch/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/770-tom-sostav.php</a>
<a href="http://leto-med.ru/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/133-bukmekerskaya-kontora-luchshaya-v-mire.php">http://layert.ru/bitrix/redirect.php?event1=&event2=&event3=&goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/737-bukmeker-toto.php</a>
<a href="http://www.newberrysblueberries.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/316-besplatnie-prognozi-na-ligu-chempionov.php">http://roxfordproduceintl.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/11-prognoz-ot.php</a>
<a href="http://taravistabhc.org/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/770-tom-sostav.php">http://petersons.org/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/800-prognozi-na-blizhayshie-matchi.php</a>
<a href="http://www.cssdrive.com/?URL=bkbest.ru/groyter-fyurt-bohum-prognoz/723-betting-sites-mobile.php">http://urovenkna.ru/bitrix/click.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/484-stvori-vorot.php</a>
<a href="http://4ztw.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1057-po-kakim-kanalam-pokazivayut-nba.php">http://google.hr/url?q=http://bkbest.ru/bukmekerskie-kontori-orsk/661-bukmekerskie-kontori-onlayn-reyting.php</a>
<a href="http://www.executivelevelselling.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/262-gilotina-v-mma.php">http://xn--h1aemfi1e.xn--p1ai/bitrix/rk.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/352-vitaliy-biryukov-prognoz.php</a>
<a href="http://ww2.mediamark.se/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/771-belorusskaya-bukmekerskaya-kontora.php">http://www.strongboxcomputers.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/138-roi-kak-schitat-v-stavkah.php</a>
<a href="http://www.echange-roumanie.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/261-lill-gengam-prognoz.php">http://iskraservice.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/452-bezdepozitniy-bonus-bukmekerskie-kontori.php</a>
<a href="http://www.macabe.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/925-bukmekerskaya-kontora-obzor.php">http://tecnologia.systa.com.br/marketing/anuncios/views/?assid=33&ancid=504&view=fbk&url=http://www.bkbest.ru/bayer-04-verder-bremen-prognoz/88-independente-rasing-klub-prognoz.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/89-bukmekerskaya-kontora-s-litsenziey-v-rossii.php>http://ns1.red2plc.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/154-bloki-v-karate.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/349-sem-elvi-dzhulian-markes-prognoz.php>http://www.calculustutoring.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/880-lokomotiv-tsedevita-prognoz.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/474-betcity-zablokirovali.php>http://vodasineborye.ru/bitrix/rk.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/716-samaya-nadezhnaya-bukmekerskaya-kontora.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/437-ryadom-liga-stavok.php>http://lbtd.ru/bitrix/click.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/118-bukmekeri-prognozi.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/778-klubnaya-karta-liga-stavok-proverit-balans.php>http://www.cink.info/bitrix/rk.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/228-liga-stavok-v-smolenske-adresa.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/1042-plyazhniy-voleybol-prognoz.php>http://quasarpro.ru/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/528-prognozi-na-matchi-chm-po-hokkeyu-2016.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/56-bukmekerskie-kontori-rossii-stavki-v-rublyah.php>http://searsrentatruck.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/9-strategiya-na-kiber-futbol-fonbet.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/980-richag-loktya-priem.php>http://couponsavingsclub.co/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/1052-prognoz-na-chetvertfinal-chm-po-hokkeyu-2017.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/836-hokkeistu-fetisovu-skolko-let.php>http://www.abcasiapacific.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/572-v-basketbole-zapresheni-igra-nogami.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/870-slbet-bukmekerskaya-kontora.php>http://wheelercap.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/800-prognozi-na-blizhayshie-matchi.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/325-kak-viigrat-v-gosloto.php>http://home.bestfd.com/link.php?url=http://bkbest.ru/bukmekerskie-kontori-orsk/881-finansoviy-menedzher-millera.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/705-samie-nadezhnie-bk-kontori-v-rossii.php>http://www.protouch.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/119-fora-1-chto-oznachaet.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/669-futbol-skolko-po-vremeni.php>http://veincentermanhattan.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/735-futbol-ploshadka.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/259-kak-sdelat-pritsel-krasnim-v-cs-go.php>http://globusgurme.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/584-bukmekerskie-kontori-v-ukraine-onlayn.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/968-v-hokkee-skolko-dlitsya-period.php>http://www.ncdps.org/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/1054-pszh-napoli-prognoz-ot-genicha.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/9-strategiya-na-kiber-futbol-fonbet.php>http://centerpointmississippi.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/193-kak-poluchit-litsenziyu-professionalnogo-boksera.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/281-kak-otdalit-kameru-v-dote-2-reborn.php>http://troop422eugene.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/129-titanbet-bonus.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/815-besplatnie-fribeti-v-bukmekerskih-kontorah.php>http://mdacc.co/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/316-besplatnie-prognozi-na-ligu-chempionov.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/298-luchshie-bukmekerskie-kompanii.php>http://judyhorning.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/943-overvotch-kto-kogo-kontrit.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/97-time-to-fight-reyting.php>http://metrogear.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/383-esli-v-futbole-nichya-to-chto-delayut.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/1002-lotereya-v-bukmekerskoy-kontore.php>http://v-salda.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/602-prognozi-bukmekerov-na-evrovidenie-2016-segodnya.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/155-kak-zaregistrirovatsya-bukmekerskaya-kontora.php>http://3ymf.com/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/966-samiy-dorogoy-kontrakt-v-futbole.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/1060-dvoynoy-shans-2h-chto-znachit.php>http://kerriwalsh.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1050-kak-priblizit-pritsel-v-gta-5.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/133-bukmekerskaya-kontora-luchshaya-v-mire.php>http://0-www.sciencedirect.com.sally.personalslotmachine.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/284-chto-takoe-stavka-tsepochka-v-1xbet.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/173-zheni-i-podrugi-sportsmenov.php>http://ufti.ru/bitrix/rk.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/226-russkoe-loto-kak-pravilno-igrat-i-viigrivat.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/547-oktagon-ring.php>http://teksika.ua/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/251-stavka-taym-match-v-futbole.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/801-chto-znachit-fol-v-futbole.php>http://www.ittteleco.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1078-kakoe-loto-samoe-chestnoe.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/254-u-nas-viigrivayut-pravila-igri.php>http://lens-crafters.info/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1040-koeffitsienti-na-chempionstvo-v-rfpl.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/526-fedor-emelyanenko-podpisan-v-ufc.php>http://www.ecocomputers.us/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/903-nado-li-platit-nalog-s-bukmekerskih-stavok.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/628-buker-bukmekerskaya-kontora.php>http://www.conetec.su/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/889-fora-1-v-futbole-chto-oznachaet.php</a>
https://www.facebook.com/Северный-кипр-недвижимость-100153902340083
<a href="http://www.kevingrose.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/397-bukmekerskaya-kontora-bonus-pri-registratsii-bez-depozita.php">http://sarasotakim.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/889-fora-1-v-futbole-chto-oznachaet.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/338-prognozi-na-sport-na-segodnya-100-protsentov.php>http://perco.cz/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/19-liga-stavok-vip-1.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/215-koeffitsient-zenit-gent.php>http://soclaboratory.ru/bitrix/rk.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/426-stat-boytsom-mma.php</a>
https://www.facebook.com/Северный-кипр-недвижимость-100153902340083
<a href=bkbest.ru/chto-takoe-v-futbole-fol/86-turnirnaya-tablitsa-dinamo-moskva-po-futbolu.php>http://aimexpo.info/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/452-bezdepozitniy-bonus-bukmekerskie-kontori.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/327-prognoz-bornmut-nyukasl.php>http://protrud.by/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/944-chto-takoe-vikup-stavki-bk.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/281-kak-otdalit-kameru-v-dote-2-reborn.php>http://cmccommunication.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/116-ne-mogu-proyti-identifikatsiyu-stoloto.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/155-kak-zaregistrirovatsya-bukmekerskaya-kontora.php>http://soft99.com.tw/redirect.php?action=url&goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/902-pit-na-mirazhe.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/23-bukmekerskie-kontori-stavki-na-sport-onlayn.php>http://www.volkan.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/42-volevaya-pobeda-chto-znachit.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/474-betcity-zablokirovali.php>http://sexdrive.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/581-komanda-chtobi-letat.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/243-onlayn-bukmekerskaya-kontora-s-bonusom-pri-registratsii.php>http://www.rjrth.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/473-prognoz-vest-hem-sanderlend.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/160-kakie-est-vidi-boksa.php>http://bsaward.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/1013-bukmekerskaya-kontora-kivi-koshelek.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/34-skolko-golov-zabil-lev-yashin.php>http://yqq.celebritycourt.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/847-ataka-v-basketbole.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/440-zablokirovan-betcity.php>http://hr.pecom.ru/bitrix/click.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1029-povetkin-uayt-27-marta-2021-koeffitsient.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/199-vyacheslav-fetisov-hokkeist-biografiya.php>http://www.geospeed.net/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/877-perviy-vishel.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/308-anastasiya-safronova-foto.php>http://zdorovienadom.ru/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/166-bukmekerskaya-kontora-v-moskve.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/53-russkoe-loto-chto-takoe-dzhekpot.php>http://cross-micro.kiev.ua/bitrix/click.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/668-darussafaka-panatinaikos-prognoz.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/881-finansoviy-menedzher-millera.php>http://uplususa.net/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/165-kto-viigraet-portugaliya-ili-meksika.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/182-kakaya-olimpiada-budet-v-2021-godu.php>http://www.scatolo.gs/bin/out.cgi?id=darake&url=http://bkbest.ru/groyter-fyurt-bohum-prognoz/283-skolko-v-basketbole-dlitsya-match.php</a>
[url=http://savys.se/reklam/att-profitera-pa-pandemin/#comment-55790]Lerntipps fur dich[/url]
bc54c23
[url=https://uvorezinin.cf/post/Ensayos-Para-Violetta-En-Equipo-En-Una-Empresa]Ensayos Para Violetta En Equipo En Una Empresa[/url]
[url=https://styleldala.tk/post/5-Resume-Mistakes-You-Need-To-Write]5 Resume Mistakes You Need To Write[/url]
[url=https://purpsimobouknewsfas.ga/post/Transition-To-Study-Efficiently]Transition To Study Efficiently[/url]
[url=http://evergreencafe.gr/the-best-copper-collection/#comment-68841]Mes 5 conseils pour rГ©ussir Г vivre ensemble[/url]
[url=https://testandgo-blog.centraltest.eu/fr/blog/5-conseils-suivre-pour-trouver-sa-voie?page=4750#comment-638759]this site[/url]
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/712-dosrochnaya-viplata-marafon.php>http://www.dermpathology.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/210-otziv-melbet.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/397-bukmekerskaya-kontora-bonus-pri-registratsii-bez-depozita.php>http://greatsport.com.ua/bitrix/rk.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/581-komanda-chtobi-letat.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/957-olimbet.php>http://m.ok.ru/dk?st.cmd=outLinkWarning&st.cln=off&st.typ=link&st.rtu=/dk?st.cmd=altGroupForum&st.tagId=1421621373&st.groupId=52116369965128&st.page=1&_prevCmd=altGroupForum&tkn=537&st.rfn=http://bkbest.ru/bukmekerskie-kontori-orsk/903-nado-li-platit-nalog-s-bukmekerskih-stavok.php</a>
<a href="http://oxo.delivery/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/1013-bukmekerskaya-kontora-kivi-koshelek.php">http://rqa.andreaneal.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/506-luchshie-bukmekeri-dlya-vilochnikov.php</a>
<a href="http://dimakol.ru/bitrix/rk.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/286-pravila-igri-russkogo-loto.php">http://xmj.arizonacomputers.org/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/925-bukmekerskaya-kontora-obzor.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/12-vilki-na-bukmekerskie-stavki.php>http://nbg.kiev.ua/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/188-adresa-bukmekerskih-kontor-v-podolske.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/801-chto-znachit-fol-v-futbole.php>http://redemptionplus.info/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/295-futbol-na-segodnya-kto-igraet-i-koeffitsient.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/471-stavka-bolshe-1-chto-eto.php>http://www.cheapbeauty.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/925-bukmekerskaya-kontora-obzor.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/397-bukmekerskaya-kontora-bonus-pri-registratsii-bez-depozita.php>http://gorodalexandrov.ru/bitrix/click.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/801-chto-znachit-fol-v-futbole.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/122-mobilnie-bukmekerskie.php>http://abraziv.by/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/672-bukmekerskaya-kontora-poker.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/121-prognozi-kvalifikatsiya-chm-2018.php>http://specdep.com/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/474-betcity-zablokirovali.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1079-krasiviy-domik-v-maynkraft-kak-postroit.php>http://setupmyurc.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/701-razmeri-standartnih-futbolnih-vorot.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/936-reytingi-bukmekerskih-kontor-onlayn.php>http://mplsrealtor.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/116-ne-mogu-proyti-identifikatsiyu-stoloto.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/438-chto-takoe-total-bolshe-menshe.php>http://instrumentsupplies.info/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/449-anderdog-eto-chto.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/682-real-m-tsska-prognoz.php>http://chvd-journal.com/bitrix/click.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/374-barselona-bayer-stavki.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/336-fonbet-kak-stavit-doma.php>http://averoprint.com/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/331-bezdepozitnie-bonusi-ot-bukmekerskih-kontor.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/870-slbet-bukmekerskaya-kontora.php>http://www.beautywater.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/251-stavka-taym-match-v-futbole.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/617-vibrat-bukmekerskuyu-kontoru.php>http://surgut-kpc.ru/bitrix/rk.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/1053-chto-takoe-tko-v-bokse.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/119-fora-1-chto-oznachaet.php>http://max-999.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/261-lill-gengam-prognoz.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/353-bonusi-za-registratsiyu-v-bukmekerskoy-kontore.php>http://prorab.ru/bitrix/rk.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/812-osnovnie-pravila-v-basketbole-kratko.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/514-prognoz-baris.php>http://www.southamericasupplier.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/132-kto-pobedit-yuventus-real.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/1023-skachat-totalizator.php>http://gkb1.moscow/bitrix/rk.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/484-stvori-vorot.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/231-krichalki-zenita-pro-dzyubu-fanatov.php>http://2-an.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/188-adresa-bukmekerskih-kontor-v-podolske.php</a>
[url=http://elite-complect.ru/blog/komarinyj-sezon-skoro-po-vsej-strane/#comment_424256]How to take organized notes[/url]
9e9bfd1
[url=https://pembmillmann.tk/post/Le-Commentaire-De-La-Po-Sie]Le Commentaire De La Po Sie[/url]
[url=https://pdatrawol.tk/post/L-Art-De-Mon-Epoux]L Art De Mon Epoux[/url]
[url=https://akhodilapi.tk/post/Statement-Zu-Verbessern]Statement Zu Verbessern[/url]
[url=https://stickerbookpublishing.com/quiz/icons-challenge-1/#comment-1825]6 tendencias na fotografia de orcamento[/url]
[url=https://www.tokodimas.com/blog/keunikan-embong-arab#comment-161011]Primer ejercicio de lectura y redaccion i[/url]
<a href="http://www.mb-llc.net/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/173-zheni-i-podrugi-sportsmenov.php">http://ipmatika.by/bitrix/click.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/220-aziatskiy-gandikap-1-0.php</a>
<a href="http://texasautos.info/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/253-spisok-rossiyskih-bukmekerov.php">http://feedbackuk.net/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/793-bukmekerskie-kontori-luchshie.php</a>
<a href="http://www.timallenrrr.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/52-skolko-dlitsya-match-v-basketbol.php">http://agalarovestate.com/bitrix/rk.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1068-koeffitsient-habib-fergyuson-1xbet.php</a>
<a href="http://vnoa.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/867-kotirovki-bukmekerov-na-futbol.php">http://www.ehbbrass.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/44-prognoz-stavok-na-segodnya.php</a>
<a href="http://www.yunxun88.com/?css=http://bkbest.ru/bukmekerskie-kontori-orsk/1002-lotereya-v-bukmekerskoy-kontore.php">http://sokolov-alexander.ru/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/649-prognozi-bukmekerov-hokkey.php</a>
<a href="http://xvc.simplotsoilbuilders.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1057-po-kakim-kanalam-pokazivayut-nba.php">http://miamimedicine.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/1001-sochi-medveshchak-prognoz.php</a>
<a href="http://usergate.ru/bitrix/rk.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/617-vibrat-bukmekerskuyu-kontoru.php">http://piknikclub.ru/bitrix/rk.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/723-betting-sites-mobile.php</a>
<a href="http://www.skinmatrix.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/328-evropeyskiy-gandikap-1-chto-eto.php">http://www.galiciano.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/407-sudi-v-hokkee-s-shayboy.php</a>
<a href="http://openhospitalitypartners.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/287-formula-vilok-v-bukmekerskih-kontorah.php">http://rework.ws/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/671-chilich-simon-prognoz.php</a>
<a href="http://www.softmix.kz/bitrix/rk.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/75-brazilskoe-dzhiu-dzhitsu-chto-eto-takoe.php">http://zavaleta.net/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/416-fora-nol-chto-znachit.php</a>
<a href="http://10-to-change.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/430-luchshie-onlayn-bukmekerskie-kontori-rossii.php">http://www.productioninformation.org/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/1009-hyuston-klippers-prognoz.php</a>
<a href="http://the-cure.sarahcenters.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/320-kak-snyat-dengi-s-bukmekerskoy-kontori-leon.php">http://nih.dmsc.moph.go.th/login/showimgurl.php?id=666&url=http://bkbest.ru/bayer-04-verder-bremen-prognoz/957-olimbet.php</a>
<a href="http://bake.ingredients.pro/bitrix/rk.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/892-professionalnie-bukmekerskie-kontori.php">http://barrycrown.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/998-skolko-minut-v-basketbole-pereriv.php</a>
<a href="http://marquisendowment.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/303-koeffitsient-evro.php">http://medfl.ru/bitrix/click.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/319-kto-viigrival-chempionat-mira-po-hokkeyu.php</a>
<a href="https://androidos-top.com/puzzle/3843-download-indy-cat-for-vk-free-shopping-mod-for-android.html">Download Indy Cat for VK (Free Shopping MOD) for Android</a>
<h2>Advantages:</h2> Excellent graphic, which very plastically fit in program. Cool music tracks. Attractive tasks.
Download worthwhile application and games for Android
[url=https://battlemma.com/adesanya-preview/#comment-50225]Download worthwhile program and games for Android[/url] [url=http://bosch-gas-geysers.co.za/index.php/2018/05/25/hello-world/#comment-5697]Download popular application and games for Android[/url] [url=https://edwardgarrahy.com/hello-world/#comment-1001]Download quality application and games for Android[/url] [url=https://joeellersonline.com/absolute-control/members-area/time-question/#comment-55521]Download worthwhile program and games for Android[/url] [url=http://incrediblebuildingservices.co.uk/pass-away-internetplattform-elite-partner-bietet-7/#comment-551438]Download good application and games for Android[/url] 54c239e
<a href=bkbest.ru/chto-takoe-v-futbole-fol/130-chto-znachit-sdelat-interaktivnuyu-stavku.php>http://www.poweroftheordinary.org/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/892-professionalnie-bukmekerskie-kontori.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/221-bukmekerskie-sayti-onlayn.php>http://supertents.ru/bitrix/click.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/550-yuefsi-1.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1074-fonbet-aktsiya-5000-rubley-kak-poluchit.php>http://itthartford.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/547-oktagon-ring.php</a>
<a href="http://tartech.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/1035-russkoe-loto-zabrat-viigrish.php">http://www.hospitalitytechnology.net/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/485-top-bukmekerskih-kontor-v-internete.php</a>
<a href="http://znakomstvo.eu/ru/external-redirect?link=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/116-ne-mogu-proyti-identifikatsiyu-stoloto.php">http://fastenterprise.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/716-samaya-nadezhnaya-bukmekerskaya-kontora.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/771-belorusskaya-bukmekerskaya-kontora.php>http://medicalcatalog.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/349-sem-elvi-dzhulian-markes-prognoz.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/151-visokoprohodimie-prognozi-na-sport.php>http://smoktravel.by/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/548-luchshie-analitiki-po-futbolu.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/847-ataka-v-basketbole.php>http://old.matchfishing.ru/bitrix/redirect.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/193-kak-poluchit-litsenziyu-professionalnogo-boksera.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1073-kak-uznat-statistiku-v-ks.php>http://bankofyazoo.us/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/1060-dvoynoy-shans-2h-chto-znachit.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/372-chto-znachit-dvoynoy-ishod-12.php>http://maryventura.info/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/646-prognozi-na-dotu-2.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/452-bezdepozitniy-bonus-bukmekerskie-kontori.php>http://pstrong.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/966-samiy-dorogoy-kontrakt-v-futbole.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/250-futbolnie-eksperti-prognozi.php>http://www.steinberggroup.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/250-futbolnie-eksperti-prognozi.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/320-kak-snyat-dengi-s-bukmekerskoy-kontori-leon.php>http://e-auction.by/bitrix/click.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/649-prognozi-bukmekerov-hokkey.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/616-gael-monfis-grigor-dimitrov-prognoz.php>http://lachargerbolt.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/482-fora-na-stavkah-futbol.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/152-chto-takoe-v-stavkah-total.php>http://tneahelp.in/redirect.php?l=http://bkbest.ru/bayer-04-verder-bremen-prognoz/1023-skachat-totalizator.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/877-perviy-vishel.php>http://xn----8sbab5aeedgb5bugoiem1g3dtc.xn--p1ai/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/129-titanbet-bonus.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/250-futbolnie-eksperti-prognozi.php>http://spo-trade.ru/bitrix/click.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/792-fonbet-layv-pochemu-ne-rabotaet.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/171-evrovidenie-2017-koeffitsient.php>http://bessini.su/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/262-gilotina-v-mma.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/129-titanbet-bonus.php>http://maps.google.cat/url?q=http://bkbest.ru/bukmekerskie-kontori-orsk/815-besplatnie-fribeti-v-bukmekerskih-kontorah.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/627-prognoz-krasnodar-mordoviya.php>http://www.mentalflossmusic.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/693-bukmekerskie-prognozi-na-hokkey.php</a>
[url=https://www.ghatasinghal.com/2013/08/i-can-read-your-mind/#comment-290374]Metafisica di studio[/url]
f4_a1e8
[url=https://sembdesclat.ml/post/Hannah-Arendt-Ber-Das-Harvard-Studium]Hannah Arendt Ber Das Harvard Studium[/url]
[url=https://roileoflowtio.ml/post/Curso-Presentador-De-Trabajos-Para-Tu-Tfg]Curso Presentador De Trabajos Para Tu Tfg[/url]
[url=https://gobbgeldgerolvi.tk/post/Explicando-O-Ensaio-De-Dureza]Explicando O Ensaio De Dureza[/url]
[url=https://brandonarthurroth.com/gwbush#comment-71122]Re: Re:[/url]
[url=https://redserialkey.com/morphvox-pro-crack-with-keygen/#comment-6731]Les meilleurs livres de sens[/url]
<a href="http://wide.hackyourself.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/657-prognoz-na-match-nant-lill.php">http://www.labourspace.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/914-bukmekerskaya-kontora-aktsii-pri-registratsii.php</a>
<a href="http://mikroset.ru/bitrix/redirect.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1078-kakoe-loto-samoe-chestnoe.php">http://qpantivirus.ru/bitrix/click.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/834-ediniy-koshelek-stoloto-chto-takoe.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/914-bukmekerskaya-kontora-aktsii-pri-registratsii.php>http://contangofund.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/375-bet-bum-adresa-v-moskve.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/913-postavit-na-usika.php>http://bittehnika.info/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/130-chto-znachit-sdelat-interaktivnuyu-stavku.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/657-prognoz-na-match-nant-lill.php>http://cibugra.myopenugra.ru/bitrix/click.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/701-razmeri-standartnih-futbolnih-vorot.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/20-kiber-futbol-kak-eto-rabotaet.php>http://united-uniforms.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/559-live-stavki-chto-eto.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/361-chto-znachit-total-chetniy.php>http://www.goodell.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/9-strategiya-na-kiber-futbol-fonbet.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/858-total-aziya.php>http://store2.innet-it.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/734-prognoz-udineze-kevo.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/704-kto-viigraet-ligu-chempionov-2015-2016-prognoz.php>http://legacy.a-kaunt.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/122-mobilnie-bukmekerskie.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/327-prognoz-bornmut-nyukasl.php>http://dotdocs.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/232-krupneyshaya-bukmekerskaya-kontora.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/265-stavki-na-tennis-bukmekerskaya-kontora.php>http://google.com.br/url?q=http://bkbest.ru/chto-takoe-v-futbole-fol/185-kak-podnyat-dengi-na-stavkah-na-futbol.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/1054-pszh-napoli-prognoz-ot-genicha.php>http://belleayreresortrealestate.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/374-barselona-bayer-stavki.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/33-maksim-pogodin.php>http://www.stoik.com/bitrix/click.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/891-prognoz-bukmekerov-na-evro-2016.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/1043-chto-za-bonusnaya-programma-na-1xbet.php>http://www.cossa.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/628-buker-bukmekerskaya-kontora.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/281-kak-otdalit-kameru-v-dote-2-reborn.php>http://www.georgespoonerassociates.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1074-fonbet-aktsiya-5000-rubley-kak-poluchit.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/23-bukmekerskie-kontori-stavki-na-sport-onlayn.php>http://www.koni-store.ru/bitrix/redirect.php?event1=OME&event2=&event3=&goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/226-russkoe-loto-kak-pravilno-igrat-i-viigrivat.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/558-shnur-debil.php>http://chernovskie.ru/bitrix/click.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/140-sokol-baltika-prognoz.php</a>
<a href="http://www.southword.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/361-chto-znachit-total-chetniy.php">http://www.advancedmediacommittee.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/484-stvori-vorot.php</a>
<a href="http://daryman.us/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/966-samiy-dorogoy-kontrakt-v-futbole.php">http://gruzvezet.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/361-chto-znachit-total-chetniy.php</a>
<a href="http://salmi.online/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/441-reyting-bk-kontori.php">http://www.apigarant.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/504-lev-yashin-biografiya-prichina-smerti.php</a>
<a href="http://ww1.6v5.net/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/250-futbolnie-eksperti-prognozi.php">http://xn--h1adbgp6f.xn--p1ai/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/969-programma-vilki-v-bukmekerskih-kontorah.php</a>
<a href="http://kit-34.ru/bitrix/rk.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/757-streltsov.php">http://xn----7sbbabox2fxa.xn--p1ai/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/173-zheni-i-podrugi-sportsmenov.php</a>
<a href="http://intex-russia.com/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/551-prematch.php">http://ratsandmice.net/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/44-prognoz-stavok-na-segodnya.php</a>
<a href="http://www.montessoricandy.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/253-spisok-rossiyskih-bukmekerov.php">http://www.stephensilver.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/251-stavka-taym-match-v-futbole.php</a>
<a href="http://aomalliance.org/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1073-kak-uznat-statistiku-v-ks.php">http://borinfo.ru/redirect?url=http://bkbest.ru/bayer-04-verder-bremen-prognoz/154-bloki-v-karate.php</a>
<a href="http://622907.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/416-fora-nol-chto-znachit.php">http://www.justcallmemaria.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/286-pravila-igri-russkogo-loto.php</a>
<a href="http://weianzk88.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/715-liga-stavok-aktsiya-3000.php">http://www.s-b.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/859-sistemi-igri-v-bukmekerskih-kontorah.php</a>
<a href="http://zoo-friend.ru/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/1055-vilka-bukmekerskaya-programma.php">http://bhqcmeonline.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/603-futbol-razmetka-polya.php</a>
<a href="http://chetki.top/bitrix/click.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1007-fonbet-kak-popolnit-schet-cherez-sberbank-onlayn.php">http://admyurovo.ru/bitrix/redirect.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/28-kak-v-olimpe-delat-ekspress.php</a>
<a href="http://cafecocomo.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/196-aziatskiy-gandikap-0-chto-eto.php">http://clients1.google.com.na/url?q=http://bkbest.ru/bukmekerskie-kontori-orsk/441-reyting-bk-kontori.php</a>
<a href="http://www.mtiou.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/836-hokkeistu-fetisovu-skolko-let.php">http://robert-s.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/204-na-kakie-deystviya-igroka-daetsya-pyat-sekund.php</a>
<a href="http://amber-cluster.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/239-prognoz-cherdantseva-na-segodnya.php">http://zerog-eyewear.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/108-chto-takoe-hay-kik.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/176-angliya-premer-liga-prognozi-na-segodnya.php>http://www.dfp-sales.org/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/705-samie-nadezhnie-bk-kontori-v-rossii.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/264-prognozi-po-lol.php>http://novayagollandiya.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/30-anahaym-daks-los-andzheles-kingz-prognoz.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/1067-chto-znachit-fora-1-v-futbole.php>http://emdi.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/591-top-10-populyarnih-vidov-sporta-mira.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/141-total-bolshe-2-chto-eto.php>http://www.gamingtodayusa.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/415-snyatie-deneg-olimp.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/75-brazilskoe-dzhiu-dzhitsu-chto-eto-takoe.php>http://momsknee.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1073-kak-uznat-statistiku-v-ks.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/12-vilki-na-bukmekerskie-stavki.php>http://gde-dveri.ru/bitrix/rk.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/922-chto-takoe-tko-v-mma.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/911-chto-takoe-v-stavkah-prohod.php>http://choiceinsurance.co/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/405-nokaut-v-bokse-chto-eto.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/283-skolko-v-basketbole-dlitsya-match.php>http://www.vocalheroes.co.uk/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/921-skolko-raundov-v-yufs.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1007-fonbet-kak-popolnit-schet-cherez-sberbank-onlayn.php>http://diggingbars.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/1020-tsonga-tim-prognoz.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/152-chto-takoe-v-stavkah-total.php>http://parkethold.ru/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/408-bukmekerskaya-kontora-reyting-luchshih.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/526-fedor-emelyanenko-podpisan-v-ufc.php>http://sovtest-ate.com/bitrix/rk.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/141-total-bolshe-2-chto-eto.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/462-kto-pobedit-real-madrid.php>http://www.2012supplies.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/781-ruminiya-farerskie-ostrova-prognoz.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/781-ruminiya-farerskie-ostrova-prognoz.php>http://sinar.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/371-sportivnie-prognozi-ot-professionalov.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/485-top-bukmekerskih-kontor-v-internete.php>http://soft-tex.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/602-prognozi-bukmekerov-na-evrovidenie-2016-segodnya.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/713-futbol-skolko-dlitsya.php>http://radiosidad.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/990-sport-prognozi-na-futbol.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/540-v-kakoy-bukmekerskoy-kontore-igrat.php>http://drsuhaspatil.org/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/495-gde-mozhno-smotret-khl-tv-besplatno.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/671-chilich-simon-prognoz.php>http://intermountainallergy.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/416-fora-nol-chto-znachit.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/617-vibrat-bukmekerskuyu-kontoru.php>http://prom23.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/382-orakul-bet-prognozi-otzivi.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/372-chto-znachit-dvoynoy-ishod-12.php>http://www.siberianhuskies.org/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1070-kak-zaregistrirovat-lotereyniy-bilet.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/680-period-v-futbole-skolko-dlitsya.php>http://www.boskinac.com/newsletter-api/newsletter-redirect.php?r=//bkbest.ru/chto-takoe-v-futbole-fol/339-total-chto-oznachaet.php</a>
<a href="http://litset.ru/go?http://bkbest.ru/chto-takoe-v-futbole-fol/284-chto-takoe-stavka-tsepochka-v-1xbet.php">http://home2haven.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/680-period-v-futbole-skolko-dlitsya.php</a>
<a href="http://www.exvagos2.com/out.php?link=http://bkbest.ru/bayer-04-verder-bremen-prognoz/990-sport-prognozi-na-futbol.php">http://cbs-kstovo.ru/go.php?url=http://bkbest.ru/groyter-fyurt-bohum-prognoz/437-ryadom-liga-stavok.php</a>
<a href="http://magistral-t.com/bitrix/click.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/341-layv-vilki-obuchenie.php">http://www.bocayoga.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/713-futbol-skolko-dlitsya.php</a>
<a href="http://www.aluplast.ua/wGlobal/wGlobal/scripts/php/changeLanguage.php?path=http://bkbest.ru/bayer-04-verder-bremen-prognoz/913-postavit-na-usika.php">http://m.ok.ru/dk?st.cmd=outLinkWarning&st.cln=off&st.typ=link&st.rtu=/dk?st.cmd=altGroupForum&st.tagId=1749510538&st.groupId=52947832668414&_prevCmd=altGroupForum&tkn=7789&st.rfn=http://bkbest.ru/chto-takoe-v-futbole-fol/31-koeffitsient-onlayn-futbol.php</a>
<a href="http://www.aspnuke.it/gotourl.asp?url=http://bkbest.ru/groyter-fyurt-bohum-prognoz/822-prognoz-na-hokkey-rossiya-ssha.php">http://ilonso.net/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/66-malorka-saragosa-prognoz.php</a>
<a href="http://www.watercure1.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/11-prognoz-ot.php">http://skamata.ru/bitrix/rk.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/1032-steam-gmc-1xbet-chto-eto.php</a>
<a href="http://www.it-komi.com/bitrix/rk.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/650-bk-kontori-s-bonusami-bez-pervogo-vznosa.php">http://k-milena.ru/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/330-pochemu-ne-zahodit-na-fonbet.php</a>
<a href="http://opusdeco.ru/bitrix/click.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/504-lev-yashin-biografiya-prichina-smerti.php">http://640173.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/28-kak-v-olimpe-delat-ekspress.php</a>
<a href="http://www.tradeshowsonline.org/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/646-prognozi-na-dotu-2.php">http://www.offloaded.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/339-total-chto-oznachaet.php</a>
<a href="http://ar-asmar.ru/bitrix/rk.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/580-ukraina-germaniya-evro-2016-prognoz.php">http://www.annapolislodging.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/889-fora-1-v-futbole-chto-oznachaet.php</a>
<a href="http://arvdya.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/756-prognoz-sinitsin.php">http://www.pixelpromo.ru/bitrix/click.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/64-stavki-na-kiber-futbol-otzivi.php</a>
<a href="http://swisa.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/1053-chto-takoe-tko-v-bokse.php">http://maximhairtransplantturkey.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/437-ryadom-liga-stavok.php</a>
<a href="http://nrac.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/781-ruminiya-farerskie-ostrova-prognoz.php">http://raduzhnyi-city.ru/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/110-bk-top-10.php</a>
<a href="http://copy16.ru/bitrix/click.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/1059-prognozi-bukmekerov-na-segodnya-futbol.php">http://www.freeteamspeak.org/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/748-izvestnie-vidi-sporta.php</a>
<a href="http://bxcraft.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/485-top-bukmekerskih-kontor-v-internete.php">http://www.smarterdollars.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/877-perviy-vishel.php</a>
[url=https://webdevsupply.com/30-useful-tips-and-life-hacks-in-illustrator/#comment-128786]this site[/url]
c239e9b
[url=https://grandiaperdecop.tk/post/Modalit-Di-Rina-C]Modalit Di Rina C[/url]
[url=https://herrtosacomni.gq/post/Deutsche-Lieder-F-R-Die-Themen-Im-Deutschabitur]Deutsche Lieder F R Die Themen Im Deutschabitur[/url]
[url=https://esuptace.tk/post/The-Wizard-For-University]The Wizard For University[/url]
[url=http://magazine-7.working-group.ru/blog/novost-5/#comment_28760]Re: Re:[/url]
[url=http://www.azsystems.it/?attachment_id=98#comment-54900]Top 10 atrizes de pegadinhas na escola[/url]
<a href=bkbest.ru/chto-takoe-v-futbole-fol/746-fora-chto-eto-znachit.php>http://www.vsurance.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/63-futbolnie-prognozi-besplatno.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/1-bookmaker-bonus.php>http://d-flute.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/558-shnur-debil.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/957-olimbet.php>http://ww31.yukan-fuji.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/701-razmeri-standartnih-futbolnih-vorot.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/891-prognoz-bukmekerov-na-evro-2016.php>http://www.stk-nova.com.ua/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/316-besplatnie-prognozi-na-ligu-chempionov.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/259-kak-sdelat-pritsel-krasnim-v-cs-go.php>http://metarenda-generatorov-com.org/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/118-bukmekeri-prognozi.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/955-realstatist.php>http://vitalya-mag-moneti.ru/bitrix/rk.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/855-reaktsiya-makgregora-na-pobedu-habiba.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/210-otziv-melbet.php>http://farlowstravel.ru/bitrix/rk.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/174-pravila-igri-po-futbolu-kratkoe-soderzhanie.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/748-izvestnie-vidi-sporta.php>http://citystarwear.com/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/122-mobilnie-bukmekerskie.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1080-kak-vivesti-viigrish-s-fonbeta.php>http://asdmom.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/723-betting-sites-mobile.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/319-kto-viigrival-chempionat-mira-po-hokkeyu.php>http://www.kroha29.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/108-chto-takoe-hay-kik.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/870-slbet-bukmekerskaya-kontora.php>http://www.burn3.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/155-kak-zaregistrirovatsya-bukmekerskaya-kontora.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/701-razmeri-standartnih-futbolnih-vorot.php>http://brooks.gs/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/990-sport-prognozi-na-futbol.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/287-formula-vilok-v-bukmekerskih-kontorah.php>http://academy.idenry.ru/bitrix/redirect.php?event1=&event2=&event3=&goto=http://bkbest.ru/bukmekerskie-kontori-orsk/782-koeffitsienti-bukmekerskih-kontor.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/889-fora-1-v-futbole-chto-oznachaet.php>http://www.pornosins.com/out.php?url=//bkbest.ru/chto-takoe-v-futbole-fol/482-fora-na-stavkah-futbol.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/173-zheni-i-podrugi-sportsmenov.php>http://thirstysoul.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/394-total-2-bolshe-chto-eto-v-futbole.php</a>
<a href="http://www.triviacraze.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/449-anderdog-eto-chto.php">http://www.atrix-media.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/1009-hyuston-klippers-prognoz.php</a>
<a href="http://firstrateloan.net/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/284-chto-takoe-stavka-tsepochka-v-1xbet.php">http://grand-polimer.ru/bitrix/rk.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/756-prognoz-sinitsin.php</a>
<a href="http://irish.gallery/proxy.php?link=http://bkbest.ru/groyter-fyurt-bohum-prognoz/789-sistema-4-iz-5.php">http://www.bikeweb.org/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/460-chto-takoe-total-v-stavkah.php</a>
[url=https://enthisai.com/single-post.php?news=]Re: Re:[/url]
f1_a1e8
[url=https://syndretikiran.cf/post/La-Gioia-Di-Laurea-Al-Pc-O-Mac]La Gioia Di Laurea Al Pc O Mac[/url]
[url=https://tiamerengety.cf/post/5-Raz-Es-Para-Elaborar-For-And-Against-Essays]5 Raz Es Para Elaborar For And Against Essays[/url]
[url=https://bautolockpunlago.gq/post/C-Mo-Hacer-La-Discusi-N-De-Henri-Bergson]C Mo Hacer La Discusi N De Henri Bergson[/url]
[url=https://www.arcosrl.info/blog/2018/08/06/professione-ghostwriter/#comment-26256]Lustiges kindervideo auf diesem kanal[/url]
[url=https://minhquangcamera.vn/tra-cuu-pin-sac-cho-may-anh?comment=4081568#comment]Jordan peterson on how to write multi[/url]
<a href=bkbest.ru/bukmekerskie-kontori-orsk/133-bukmekerskaya-kontora-luchshaya-v-mire.php>http://tolstoy.ru/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/440-zablokirovan-betcity.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/470-aziatskiy-gandikap-2-0-5.php>http://sibran.ru/bitrix/click.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/1021-luchshiy-poluzashitnik-mira-po-futbolu.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/259-kak-sdelat-pritsel-krasnim-v-cs-go.php>http://younique.style/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/331-bezdepozitnie-bonusi-ot-bukmekerskih-kontor.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/248-kak-vivesti-dengi-s-ligi-stavok.php>http://peintel.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/273-10-bukmekerov.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/789-sistema-4-iz-5.php>http://melius-medical.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/471-stavka-bolshe-1-chto-eto.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/460-chto-takoe-total-v-stavkah.php>http://www.georgespoonerassociates.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/683-na-kakoy-bukmekerskoy-kontore-luchshe-igrat.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/33-maksim-pogodin.php>http://doghunter.info/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/375-bet-bum-adresa-v-moskve.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/64-stavki-na-kiber-futbol-otzivi.php>http://www.chkpz.ru/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/67-kak-schitaetsya-viigrish-v-bukmekerskoy-kontore.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/438-chto-takoe-total-bolshe-menshe.php>http://www.wildstrawberryflorist.net/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/856-fora-o-chto-znachit-v-futbole.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/394-total-2-bolshe-chto-eto-v-futbole.php>http://www.decopatch.su/bitrix/click.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/141-total-bolshe-2-chto-eto.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/496-bukmekerskie-kontori-pri-registratsii-dayut-dengi.php>http://a3dhd.love.ua-relations.com/ru/external-redirect?link=http://bkbest.ru/groyter-fyurt-bohum-prognoz/283-skolko-v-basketbole-dlitsya-match.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/903-nado-li-platit-nalog-s-bukmekerskih-stavok.php>http://robbinjewelers.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/943-overvotch-kto-kogo-kontrit.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/968-v-hokkee-skolko-dlitsya-period.php>http://admgorodovikovsk.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/822-prognoz-na-hokkey-rossiya-ssha.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/297-latsio-verona-prognoz-11-02.php>http://expoenergo74.ru/bitrix/click.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/977-fora-o-chto-znachit.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/77-prognoz-verder-bayer-l.php>http://www.thierryhenry.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/988-skolko-periodov-v-hokkey.php</a>
<a href="http://click-stroy.ru/">снос дома</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1063-boks-s-nogami-kak-nazivaetsya.php>http://profpaneli.ru/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/176-angliya-premer-liga-prognozi-na-segodnya.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/325-kak-viigrat-v-gosloto.php>http://slovo-online.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/933-sportprognoz-futbol.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/23-bukmekerskie-kontori-stavki-na-sport-onlayn.php>http://rzol.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/331-bezdepozitnie-bonusi-ot-bukmekerskih-kontor.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1018-kak-pravilno-vipolnyat-brosok-v-basketbole.php>http://tax-solutionsgroup.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/382-orakul-bet-prognozi-otzivi.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/749-bukmekerskie-sayti.php>http://rock-stars.us/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/185-kak-podnyat-dengi-na-stavkah-na-futbol.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/462-kto-pobedit-real-madrid.php>http://google.tt/url?q=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/28-kak-v-olimpe-delat-ekspress.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/182-kakaya-olimpiada-budet-v-2021-godu.php>http://drprice.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/1059-prognozi-bukmekerov-na-segodnya-futbol.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/481-fonbet-reyting-bukmekerov.php>http://i-store.kz/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/470-aziatskiy-gandikap-2-0-5.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/248-kak-vivesti-dengi-s-ligi-stavok.php>http://wise-solutions.ru/bitrix/rk.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/738-sravnenie-koeffitsientov-v-bukmekerskih-kontorah.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/174-pravila-igri-po-futbolu-kratkoe-soderzhanie.php>http://restfulhaven.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/273-10-bukmekerov.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/209-hokkeist-tarasov-biografiya.php>http://bimacad.pro/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/834-ediniy-koshelek-stoloto-chto-takoe.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/97-time-to-fight-reyting.php>http://rusballet.cn/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/528-prognozi-na-matchi-chm-po-hokkeyu-2016.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/705-samie-nadezhnie-bk-kontori-v-rossii.php>http://pine.xsrv.jp/tomomi-cgi/link3/link3.cgi?mode=cnt&no=6&hpurl=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1057-po-kakim-kanalam-pokazivayut-nba.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/133-bukmekerskaya-kontora-luchshaya-v-mire.php>http://detskiymir24.ru/bitrix/rk.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/756-prognoz-sinitsin.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/892-professionalnie-bukmekerskie-kontori.php>http://carma-tuning.ru/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/803-prognoz-na-match-zenit-avtodor.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/859-sistemi-igri-v-bukmekerskih-kontorah.php>http://www.lablanche.ru/bitrix/rk.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/371-sportivnie-prognozi-ot-professionalov.php</a>
<a href="http://0.onlinetransformationnation.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/749-bukmekerskie-sayti.php">http://sofilena.ru/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/110-bk-top-10.php</a>
<a href="http://www.motelmissoula.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/116-ne-mogu-proyti-identifikatsiyu-stoloto.php">http://udachadacha.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/679-priemi-myacha-v-voleybole.php</a>
<a href="http://zealintelligence.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/19-liga-stavok-vip-1.php">http://portfolio.ru/bitrix/click.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/613-prognoz-na-match-real-sosedad-espanol.php</a>
[url=https://lazybudgettrips.com/en/things-to-know-before-going-to-cancun/#comment-13338]Direitos humanos para iniciar na fotografia[/url]
bfd17ac
[url=https://golecphoduc.tk/post/7-Ways-To-Set-Up-Mla-Format-For-Apple-S-Pages]7 Ways To Set Up Mla Format For Apple S Pages[/url]
[url=https://tradarulsimma.tk/post/24-Horas-Siendo-Mam-Luchona-De-Motivacion]24 Horas Siendo Mam Luchona De Motivacion[/url]
[url=https://oubseffacirougu.tk/post/3-Steps-To-Score-90-In-Writing-In-Pte]3 Steps To Score 90 In Writing In Pte[/url]
[url=http://i-freego.com/viewthread.php?tid=151545&extra=]Kleine tipps und tricks fur jura klausuren[/url]
[url=https://rat-inc.com/%e3%83%ad%e3%83%9c%e3%83%86%e3%82%a3%e3%82%af%e3%82%b9%e5%85%a5%e9%96%80/#comment-272386]Scrum la methode agile en 7 points[/url]
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/173-zheni-i-podrugi-sportsmenov.php>http://mn-mason.info/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/382-orakul-bet-prognozi-otzivi.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/855-reaktsiya-makgregora-na-pobedu-habiba.php>http://steveinjersey.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1007-fonbet-kak-popolnit-schet-cherez-sberbank-onlayn.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/66-malorka-saragosa-prognoz.php>http://10fr.old.love.ulbiz.ru/ru/external-redirect?link=http://bkbest.ru/bukmekerskie-kontori-orsk/243-onlayn-bukmekerskaya-kontora-s-bonusom-pri-registratsii.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/63-futbolnie-prognozi-besplatno.php>http://deairank.mistypark.com/01/out.cgi?id=urashi10&url=http://bkbest.ru/chto-takoe-v-futbole-fol/966-samiy-dorogoy-kontrakt-v-futbole.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/20-kiber-futbol-kak-eto-rabotaet.php>http://databag.ru/bitrix/click.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/558-shnur-debil.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/88-independente-rasing-klub-prognoz.php>http://www.goodell.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/804-samie-luchshie-bukmekerskie-kontori-mira.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/679-priemi-myacha-v-voleybole.php>http://henricks.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/1042-plyazhniy-voleybol-prognoz.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/53-russkoe-loto-chto-takoe-dzhekpot.php>http://prontolessons.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/515-sredniy-ves-v-ufc-v-kg.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/517-analitik-praktika-sportivniy.php>http://www.thedunhamfamily.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/561-falkirk-livingston-prognoz.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/625-avg-v-beysbole-chto-eto.php>http://18and18.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/647-1-x-bet-reklama.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/1021-luchshiy-poluzashitnik-mira-po-futbolu.php>http://baccara-decor.ru/bitrix/click.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/822-prognoz-na-hokkey-rossiya-ssha.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/45-ne-zahodit-na-marafon-bukmekerskaya.php>http://www.healthphone.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/958-kak-stavit-stavku-v-bukmekerskoy-kontore.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/738-sravnenie-koeffitsientov-v-bukmekerskih-kontorah.php>http://dellsitemap.eub-inc.com/loc.php?url=http://bkbest.ru/chto-takoe-v-futbole-fol/603-futbol-razmetka-polya.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/481-fonbet-reyting-bukmekerov.php>http://xn----jtbhgfimpihd.xn--p1ai/bitrix/click.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/132-kto-pobedit-yuventus-real.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/932-makaba.php>http://www.hotkinkyjo.de/cgi-bin/atc/out.cgi?id=44&u=http://bkbest.ru/groyter-fyurt-bohum-prognoz/52-skolko-dlitsya-match-v-basketbol.php</a>
<a href="http://curhat.com/proxy.php?link=http://bkbest.ru/bayer-04-verder-bremen-prognoz/506-luchshie-bukmekeri-dlya-vilochnikov.php">http://sm.zn7.net/out.cgi?id=00018&url=http://bkbest.ru/bayer-04-verder-bremen-prognoz/352-vitaliy-biryukov-prognoz.php</a>
<a href="http://heart365.net/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/804-samie-luchshie-bukmekerskie-kontori-mira.php">http://pivokom.ru/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/77-prognoz-verder-bayer-l.php</a>
<a href="http://popnografia.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/209-hokkeist-tarasov-biografiya.php">http://mdanderson.info/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/193-kak-poluchit-litsenziyu-professionalnogo-boksera.php</a>
<a href="http://www.focusexpress.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/713-futbol-skolko-dlitsya.php">http://www.bigscreenmachine.com/?URL=bkbest.ru/bayer-04-verder-bremen-prognoz/594-chem-zanimayutsya-dropi.php</a>
<a href="http://tp45.ru/bitrix/click.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/946-vinnipeg-tampa-prognoz.php">http://timesaversforteachers.com/ashop/affiliate.php?id=294&redirect=http://bkbest.ru/bukmekerskie-kontori-orsk/727-bukmekerskie-kontori-sport.php</a>
<a href="http://rhogarth.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/330-pochemu-ne-zahodit-na-fonbet.php">http://in-home.ru/bitrix/redirect.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/105-russkoe-loto-kak-poluchit-viigrish.php</a>
<a href="http://coronarypassport.ru/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/1046-bukmekerskie-kontori-eto.php">http://squarepumps.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/734-prognoz-udineze-kevo.php</a>
<a href="http://legowear-rus.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/441-reyting-bk-kontori.php">http://www.badboyzchoppers.net/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/30-anahaym-daks-los-andzheles-kingz-prognoz.php</a>
<a href="http://www.littlegreenmatt.net/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/34-skolko-golov-zabil-lev-yashin.php">http://ultracarerehab.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/133-bukmekerskaya-kontora-luchshaya-v-mire.php</a>
<a href="http://www.parshav.org/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/78-luchshie-bukmekerskie-kontori-rossii.php">http://www.birchrun.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/19-liga-stavok-vip-1.php</a>
<a href="http://www.stationhousehotel.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/176-angliya-premer-liga-prognozi-na-segodnya.php">http://fritex.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/954-dota-2-prognozi.php</a>
<a href="http://yarcube.ru/bitrix/click.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/591-top-10-populyarnih-vidov-sporta-mira.php">http://chefandfather.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/349-sem-elvi-dzhulian-markes-prognoz.php</a>
<a href="http://www.linpacmh.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/394-total-2-bolshe-chto-eto-v-futbole.php">http://www.maizegenome.org/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/364-skolko-minut-idet-period-v-hokkee.php</a>
<a href="http://acemortgagebanking.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/914-bukmekerskaya-kontora-aktsii-pri-registratsii.php">http://lonevelde.lovasok.hu/out_link.php?url=http://bkbest.ru/chto-takoe-v-futbole-fol/295-futbol-na-segodnya-kto-igraet-i-koeffitsient.php</a>
<a href="http://thillens.info/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/1024-kakoy-bukmekerskaya-luchshe.php">http://mpwrs.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/166-bukmekerskaya-kontora-v-moskve.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/1055-vilka-bukmekerskaya-programma.php>http://maiseydental.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/286-pravila-igri-russkogo-loto.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/1-bookmaker-bonus.php>http://google.co.ug/url?q=http://bkbest.ru/bayer-04-verder-bremen-prognoz/616-gael-monfis-grigor-dimitrov-prognoz.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/936-reytingi-bukmekerskih-kontor-onlayn.php>http://liveservice.spb.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/394-total-2-bolshe-chto-eto-v-futbole.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/702-kakoy-nomer-vibrat-v-futbole.php>http://www.viziteurope.ru/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/1001-sochi-medveshchak-prognoz.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/372-chto-znachit-dvoynoy-ishod-12.php>http://mebelopt.ua/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/265-stavki-na-tennis-bukmekerskaya-kontora.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/935-bk-betsiti-obzor.php>http://9dy.old.constructor.lyublyu.ru/ru/external-redirect?link=http://bkbest.ru/groyter-fyurt-bohum-prognoz/261-lill-gengam-prognoz.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/724-chto-znachit-dop-fora-v-basketbole.php>http://clients1.google.td/url?q=http://bkbest.ru/chto-takoe-v-futbole-fol/746-fora-chto-eto-znachit.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/196-aziatskiy-gandikap-0-chto-eto.php>http://old.in-schelkovo.ru/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/23-bukmekerskie-kontori-stavki-na-sport-onlayn.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/592-chto-takoe-oktagon.php>http://www.quarteraway.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/649-prognozi-bukmekerov-hokkey.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/23-bukmekerskie-kontori-stavki-na-sport-onlayn.php>http://russvet.ru/bitrix/rk.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/371-sportivnie-prognozi-ot-professionalov.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/1067-chto-znachit-fora-1-v-futbole.php>http://xn--h1adalebo4a.xn--80adxhks/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/242-sanderlend-kristal-prognoz.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/844-madrid-tablitsa.php>http://mcartgroup.de/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/804-samie-luchshie-bukmekerskie-kontori-mira.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/415-snyatie-deneg-olimp.php>http://al-fas.ru/bitrix/redirect.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/28-kak-v-olimpe-delat-ekspress.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/1061-real-madrid-atletiko-m-prognoz.php>http://practicemanager.co/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/856-fora-o-chto-znachit-v-futbole.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/74-eksklyuzivnie-mashini-v-gta-5.php>http://paylawyerbill.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/226-russkoe-loto-kak-pravilno-igrat-i-viigrivat.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1057-po-kakim-kanalam-pokazivayut-nba.php>http://canada-trademark-law.net/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/1060-dvoynoy-shans-2h-chto-znachit.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/350-rabota-dropom-chto-grozit.php>http://sh-exp.ru/bitrix/redirect.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/127-kak-sdelat-doveritelnuyu-stavku-v-1xbet.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/793-bukmekerskie-kontori-luchshie.php>http://lillianvernon.mobi/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/292-kak-uchastvovat-v-loteree-stoloto.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/9-strategiya-na-kiber-futbol-fonbet.php>http://www.galleriatile.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/67-kak-schitaetsya-viigrish-v-bukmekerskoy-kontore.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/1-bookmaker-bonus.php>http://0.0.grantthortonadvisors.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/1031-bet-online-free.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/473-prognoz-vest-hem-sanderlend.php>http://ascgrp.info/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/584-bukmekerskie-kontori-v-ukraine-onlayn.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/298-luchshie-bukmekerskie-kompanii.php>http://creditunionmemberservices.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/704-kto-viigraet-ligu-chempionov-2015-2016-prognoz.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/441-reyting-bk-kontori.php>http://www.ivmob.net/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/338-prognozi-na-sport-na-segodnya-100-protsentov.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/913-postavit-na-usika.php>http://m.ok.ru/dk?st.cmd=outLinkWarning&st.cln=off&st.typ=link&st.rtu=/dk?st.cmd=altGroupForum&st.tagId=-604481312&st.groupId=54209782284402&_prevCmd=altGroupForum&tkn=18&st.rfn=http://bkbest.ru/bayer-04-verder-bremen-prognoz/990-sport-prognozi-na-futbol.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/129-titanbet-bonus.php>http://webbank.nyc/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/833-vilochnie-programmi.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/265-stavki-na-tennis-bukmekerskaya-kontora.php>http://hms-neftemash.ru/bitrix/rk.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/237-kak-v-dote-sdelat-kameru-dalshe.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/63-futbolnie-prognozi-besplatno.php>http://www.davidlott.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/1023-skachat-totalizator.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/427-kakoy-razmer-vorot-v-futbole.php>http://goodwin71.ru/bitrix/redirect.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/292-kak-uchastvovat-v-loteree-stoloto.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/977-fora-o-chto-znachit.php>http://krasnodar.rusquantum.ru/bitrix/redirect.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1018-kak-pravilno-vipolnyat-brosok-v-basketbole.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/1009-hyuston-klippers-prognoz.php>http://www.bringtheloveback.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/573-bukmekerskaya-kontora-toto.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/581-komanda-chtobi-letat.php>http://24hrhc.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1073-kak-uznat-statistiku-v-ks.php</a>
<a href="http://click-stroy.ru/">снести дом</a>
<a href="http://renovavtodor.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/804-samie-luchshie-bukmekerskie-kontori-mira.php">http://kuhnizar.ru/bitrix/click.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/1060-dvoynoy-shans-2h-chto-znachit.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/138-roi-kak-schitat-v-stavkah.php>http://legaldocs.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/1054-pszh-napoli-prognoz-ot-genicha.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/496-bukmekerskie-kontori-pri-registratsii-dayut-dengi.php>http://love-krim.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/800-prognozi-na-blizhayshie-matchi.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/649-prognozi-bukmekerov-hokkey.php>http://www.phoenixtear.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/584-bukmekerskie-kontori-v-ukraine-onlayn.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/361-chto-znachit-total-chetniy.php>http://otk-tractor.com/bitrix/rk.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/1060-dvoynoy-shans-2h-chto-znachit.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/12-vilki-na-bukmekerskie-stavki.php>http://safenet-sentinel.ru/bitrix/click.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/679-priemi-myacha-v-voleybole.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/1052-prognoz-na-chetvertfinal-chm-po-hokkeyu-2017.php>http://mylibrarydv.info/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/789-sistema-4-iz-5.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/735-futbol-ploshadka.php>http://algmsk.ru/bitrix/click.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/140-sokol-baltika-prognoz.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/218-https-bukmekerskie-kontory-bet.php>http://masterkit.kz/bitrix/rk.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/470-aziatskiy-gandikap-2-0-5.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/749-bukmekerskie-sayti.php>http://www.omnimed.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/591-top-10-populyarnih-vidov-sporta-mira.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/990-sport-prognozi-na-futbol.php>http://referencevalley.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/317-mnenie-eksperta-futbol.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/374-barselona-bayer-stavki.php>http://togshop.info/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/891-prognoz-bukmekerov-na-evro-2016.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/911-chto-takoe-v-stavkah-prohod.php>http://krasnoyarsk.stanki.ru/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/243-onlayn-bukmekerskaya-kontora-s-bonusom-pri-registratsii.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/254-u-nas-viigrivayut-pravila-igri.php>http://bioworld.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/408-bukmekerskaya-kontora-reyting-luchshih.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/613-prognoz-na-match-real-sosedad-espanol.php>http://delawarecpf.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/891-prognoz-bukmekerov-na-evro-2016.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/130-chto-znachit-sdelat-interaktivnuyu-stavku.php>http://www.extrimdrive.ru/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/726-skaner-vilok-besplatno.php</a>
<a href="http://scholespri-kgfl.secure-dbprimary.com/service/util/logout/CookiePolicy.action?backto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/121-prognozi-kvalifikatsiya-chm-2018.php">http://ftectn.net/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/569-prognoz-na-tennis-ot-anni-chakvetadze.php</a>
<a href="http://www.kwe-usa.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/452-bezdepozitniy-bonus-bukmekerskie-kontori.php">http://www.schoolofrockonline.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/254-u-nas-viigrivayut-pravila-igri.php</a>
<a href="http://www.garyfeng.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/976-sovetskiy-borets-olimpiyskiy-chempion-po-klassicheskoy-borbe.php">http://am-lean.ru/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/452-bezdepozitniy-bonus-bukmekerskie-kontori.php</a>
<a href="http://primotrays.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/375-bet-bum-adresa-v-moskve.php">http://emilykgreenwood.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/437-ryadom-liga-stavok.php</a>
<a href="http://search.courier-tribune.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/1-bookmaker-bonus.php">http://drsuhaspatil.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/176-angliya-premer-liga-prognozi-na-segodnya.php</a>
<a href="http://realtreetargets.com/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1073-kak-uznat-statistiku-v-ks.php">http://www.mt-asia.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/859-sistemi-igri-v-bukmekerskih-kontorah.php</a>
<a href="http://hotel-pension-luisenhof.de/stadt/load.php?url=http://bkbest.ru/groyter-fyurt-bohum-prognoz/811-futbolnie-prognozi-na-segodnya-ot-genicha.php">http://xn-----flclaefgadgbl2ccdgivqface04a.xn--p1ai/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/914-bukmekerskaya-kontora-aktsii-pri-registratsii.php</a>
<a href="http://taranda.by/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/1013-bukmekerskaya-kontora-kivi-koshelek.php">http://xn----7sbqej4bhfek.xn--p1ai/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/957-olimbet.php</a>
<a href="http://10dw.old.swaxa.ru/ru/external-redirect?link=http://bkbest.ru/groyter-fyurt-bohum-prognoz/360-vashington-hokkeyniy-klub-tablitsa.php">http://dsxm.caa.se/links.do?c=138&t=3282&h=utskick.html&g=0&link=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/292-kak-uchastvovat-v-loteree-stoloto.php</a>
<a href="http://images.google.to/url?q=http://bkbest.ru/bukmekerskie-kontori-orsk/474-betcity-zablokirovali.php">http://pasman-clinic.com/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/680-period-v-futbole-skolko-dlitsya.php</a>
<a href="http://shinglas.ru/bitrix/redirect.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1040-koeffitsienti-na-chempionstvo-v-rfpl.php">http://mdaway.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/451-bukmekeri-onlayn.php</a>
<a href="http://osto-mai.ru/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/551-prematch.php">http://intercom18.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/760-orsk-bukmekerskie-kontori.php</a>
<a href="http://www.borewelding.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/452-bezdepozitniy-bonus-bukmekerskie-kontori.php">http://krishka.ru/proxy.php?link=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/248-kak-vivesti-dengi-s-ligi-stavok.php</a>
<a href="http://nowintime.org/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/661-bukmekerskie-kontori-onlayn-reyting.php">http://www.emigrant1031direct.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/184-1xbet-tehpodderzhka.php</a>
سابك
الراجحي
دراية
الاهلي
مباشر
تكرشارت
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/195-trener-po-hokkeyu-tarasov-anatoliy-vladimirovich.php>http://furnitura76.ru/bitrix/click.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/152-chto-takoe-v-stavkah-total.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/482-fora-na-stavkah-futbol.php>http://msperspective.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/701-razmeri-standartnih-futbolnih-vorot.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/1069-dvoynoy-shans-obe-zabyut-chto-eto.php>http://www.panacea.net/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1076-kak-stavit-dengi-na-dotu-2.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/360-vashington-hokkeyniy-klub-tablitsa.php>http://www.endovenouslaser.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/536-prognozi-na-futbol-na-segodnya.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/108-chto-takoe-hay-kik.php>http://planettoy.ru/bitrix/redirect.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/17-kak-uznat-svoy-kd-v-ks-go.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/584-bukmekerskie-kontori-v-ukraine-onlayn.php>http://k-milena.ru/bitrix/rk.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/726-skaner-vilok-besplatno.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/888-prognozi-na-ligu-natsiy.php>http://malicozum.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/451-bukmekeri-onlayn.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/352-vitaliy-biryukov-prognoz.php>http://postretirementbenefits.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/232-krupneyshaya-bukmekerskaya-kontora.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/11-prognoz-ot.php>http://aquaflot.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/8-kaprizov-noviy-kontrakt.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/988-skolko-periodov-v-hokkey.php>http://greystonegroupllc.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/990-sport-prognozi-na-futbol.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/78-luchshie-bukmekerskie-kontori-rossii.php>http://wecoyote.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/1059-prognozi-bukmekerov-na-segodnya-futbol.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/770-tom-sostav.php>http://ostrov-s.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/163-chto-takoe-total-2-bolshe.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/350-rabota-dropom-chto-grozit.php>http://hao.dii123.com/export.php?url=http://bkbest.ru/bukmekerskie-kontori-orsk/683-na-kakoy-bukmekerskoy-kontore-luchshe-igrat.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1074-fonbet-aktsiya-5000-rubley-kak-poluchit.php>http://informunity.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/441-reyting-bk-kontori.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/957-olimbet.php>http://global-autonews.com/shop/bannerhit.php?bn_id=429&url=http://bkbest.ru/bayer-04-verder-bremen-prognoz/440-zablokirovan-betcity.php</a>
<a href=bkbest.ru/chto-takoe-v-futbole-fol/977-fora-o-chto-znachit.php>http://brookfieldnunavut.ca/__media__/js/netsoltrademark.php?d=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1070-kak-zaregistrirovat-lotereyniy-bilet.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/441-reyting-bk-kontori.php>http://estelab.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/404-chit-kodi-two-worlds-ii.php</a>
[url=https://www.efp.ru/blog/gvatemala/#comment1454]Inglese italiano per scrivere meglio[/url]
9646e37
[url=https://nurleli.tk/post/Besser-Verfugen-Mit-Diesen-Tipps]Besser Verfugen Mit Diesen Tipps[/url]
[url=https://mentfreelcas.gq/post/Dos-And-Don-Ts-To-Score-8]Dos And Don Ts To Score 8[/url]
[url=https://cuisitpomango.ml/post/Alla-Scoperta-Di-Conte]Alla Scoperta Di Conte[/url]
[url=https://www.tysotructiep.online/highlights/as-roma-fiorentina-2/comment-page-2/#comment-581121]Ensaios para si trabajar en equipo[/url]
[url=http://www.buyleads.me/how-to-make-profits-along-with-a-commission-mailing-business/#comment-171219]Harry takes amirah vann to seidr[/url]
<a href="http://itf-taekwondo.ru/">снос дома</a>
<a href="http://itf-taekwondo.ru/">демонтаж дома</a>
<a href="http://ufa.minimum-price.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/573-bukmekerskaya-kontora-toto.php">http://cleo-opt.ru/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/393-sibir-metallurg-nk-prognoz.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/459-monako-kan-prognoz-matcha.php>http://ww.adultdvdempir.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/30-anahaym-daks-los-andzheles-kingz-prognoz.php</a>
<a href=http://secantlogistics.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru>http://oldguys.com/__media__/js/netsoltrademark.php?d=arenda-generatorov-com.ru</a>
<a href="http://printtorgservice.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/768-bolshe-takoe-ne-govori.php">http://mprival.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/1055-vilka-bukmekerskaya-programma.php</a>
<a href="http://shop.tgsk.ru/bitrix/rk.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/1013-bukmekerskaya-kontora-kivi-koshelek.php">http://www.spi.org/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/155-kak-zaregistrirovatsya-bukmekerskaya-kontora.php</a>
<a href="http://mconnealy.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/583-mbt-deposit.php">http://www.nsella.ru/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/726-skaner-vilok-besplatno.php</a>
<a href="http://1stbit.biz/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/969-programma-vilki-v-bukmekerskih-kontorah.php">http://xn----7sbfmnqfl4akqj.xn--p1ai/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/856-fora-o-chto-znachit-v-futbole.php</a>
<a href="http://peqwire.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/118-bukmekeri-prognozi.php">http://nomertelefona.ru/bitrix/click.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/292-kak-uchastvovat-v-loteree-stoloto.php</a>
<a href="http://www.martialartsplanet.com/proxy.php?link=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/1066-kak-zaregistrirovatsya-na-olimpe.php">http://www.thedesertconnection.org/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/474-betcity-zablokirovali.php</a>
<a href=bkbest.ru/kak-koeffitsient-perevesti-v-protsent/248-kak-vivesti-dengi-s-ligi-stavok.php>http://www.unamex.com/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/250-futbolnie-eksperti-prognozi.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/913-postavit-na-usika.php>http://www.funkyteknotribe.com/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/430-luchshie-onlayn-bukmekerskie-kontori-rossii.php</a>
<a href="http://itf-taekwondo.ru/">снос дома</a>
<a href="http://xn----7sbabab7b0a9ajl1a.xn--p1ai/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/738-sravnenie-koeffitsientov-v-bukmekerskih-kontorah.php">http://www.halfpriceink.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/240-kak-zarabativat-na-stavkah-na-futbol.php</a>
<a href="http://hho-fuel.ca/__media__/js/netsoltrademark.php?d=bkbest.ru/bukmekerskie-kontori-orsk/892-professionalnie-bukmekerskie-kontori.php">http://alenkadv.ru/bitrix/redirect.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/691-streltsov-eduard-futbolist-biografiya.php</a>
<a href="http://istok-farma.ru/bitrix/rk.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/661-bukmekerskie-kontori-onlayn-reyting.php">http://www.historymed.ru/bitrix/rk.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/911-chto-takoe-v-stavkah-prohod.php</a>
<a href="http://svarka.naks.ru/bitrix/redirect.php?goto=http://bkbest.ru/kak-koeffitsient-perevesti-v-protsent/116-ne-mogu-proyti-identifikatsiyu-stoloto.php">http://www.yug-kubanskoe.ru/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/463-gostevoy-schet-v-bk.php</a>
<a href="http://123pussy.org/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/646-prognozi-na-dotu-2.php">http://www.lexilamour.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/1069-dvoynoy-shans-obe-zabyut-chto-eto.php</a>
<a href="http://www.mycollegecalendar.org/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/503-vinbetting-prognoz-futbol.php">http://rajapempek.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/273-10-bukmekerov.php</a>
<a href="http://skyway.ru/bitrix/rk.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/778-klubnaya-karta-liga-stavok-proverit-balans.php">http://www.fortrucker-env.com/leaving.aspx?ext=http://bkbest.ru/chto-takoe-v-futbole-fol/845-stavka-dvoynoy-shans-chto-eto.php</a>
<a href="http://umrus.us/__media__/js/netsoltrademark.php?d=bkbest.ru/bayer-04-verder-bremen-prognoz/253-spisok-rossiyskih-bukmekerov.php">http://grand-parts.com.ua/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/668-darussafaka-panatinaikos-prognoz.php</a>
<a href="http://spikes-online.ru/bitrix/rk.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/638-borussiya-dortmund-krasnodar-prognoz.php">http://www.olondon.ru/bitrix/rk.php?goto=http://bkbest.ru/chto-takoe-v-futbole-fol/735-futbol-ploshadka.php</a>
<a href="http://luhadm.ru/bitrix/click.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/154-bloki-v-karate.php">http://hcbrest.com/go?http://bkbest.ru/groyter-fyurt-bohum-prognoz/470-aziatskiy-gandikap-2-0-5.php</a>
<a href="http://sanclub.ru/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/517-analitik-praktika-sportivniy.php">http://muznavigator.com/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/338-prognozi-na-sport-na-segodnya-100-protsentov.php</a>
<a href="http://homutsp.ru/bitrix/click.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/518-pochemu-ne-rabotaet-sayt-zenita-bukmekerskaya-kontora.php">http://paulhobbs.mobi/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/899-kogo-kontrit-lina.php</a>
<a href="http://nauka-auto.ru/bitrix/redirect.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/583-mbt-deposit.php">http://22220161123.ngws.info/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/273-10-bukmekerov.php</a>
<a href="http://bakaleya-hm.ru/bitrix/rk.php?goto=http://bkbest.ru/bayer-04-verder-bremen-prognoz/539-forma-1-0.php">http://xactprice.org/__media__/js/netsoltrademark.php?d=bkbest.ru/groyter-fyurt-bohum-prognoz/756-prognoz-sinitsin.php</a>
<a href="http://a3ddh.love.mega.ua/ru/external-redirect?link=http://bkbest.ru/chto-takoe-v-futbole-fol/966-samiy-dorogoy-kontrakt-v-futbole.php">http://bedstogo.com/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/9-strategiya-na-kiber-futbol-fonbet.php</a>
<a href=bkbest.ru/groyter-fyurt-bohum-prognoz/723-betting-sites-mobile.php>http://saratovoblgaz.com/bitrix/redirect.php?goto=http://bkbest.ru/bukmekerskie-kontori-orsk/661-bukmekerskie-kontori-onlayn-reyting.php</a>
<a href=bkbest.ru/bukmekerskie-kontori-orsk/496-bukmekerskie-kontori-pri-registratsii-dayut-dengi.php>http://www.apskids.org/__media__/js/netsoltrademark.php?d=bkbest.ru/chto-takoe-v-futbole-fol/911-chto-takoe-v-stavkah-prohod.php</a>
<a href=bkbest.ru/bayer-04-verder-bremen-prognoz/286-pravila-igri-russkogo-loto.php>http://optimaservis.su/bitrix/redirect.php?goto=http://bkbest.ru/groyter-fyurt-bohum-prognoz/1020-tsonga-tim-prognoz.php</a>
[url=http://8.210.207.116/forum.php?mod=viewthread&tid=21688&extra=]Deni de soutien scolaire[/url]
bc54c23
[url=https://fodonhua.tk/post/Estudio-De-Plat-N]Estudio De Plat N[/url]
[url=https://erarnotkendrafer.tk/post/Die-5-Wichtigsten-Tipps-F-R]Die 5 Wichtigsten Tipps F R[/url]
[url=https://cietsunrestusento.tk/post/El-Video-Prohibido-De-Gemelos]El Video Prohibido De Gemelos[/url]
[url=https://steliam.com/product/hp-elitebook-8440/comment-page-45/#comment-7344]this site[/url]
[url=https://estudiarmagisterio.com/basic-time-management-advanced-course/#comment-318509]Information fur endzone[/url]
<a href="http://itf-taekwondo.ru/">разобрать дом</a>
<a href=http://xn--80aegeoalydebe2ar0e8d.com/bitrix/redirect.php?goto=http://arenda-generatorov-com.ru>http://arealidea.ru/bitrix/rk.php?goto=http://arenda-generatorov-com.ru</a>
<a href="http://gliciniya.ru/">http://gliciniya.ru/</a>
<a href="http://gliciniya.ru/">http://gliciniya.ru/</a>
<a href="http://dyzain.ru/">http://dyzain.ru/</a>
[url=https://2.myrikdesign.co.za/2020/12/30/honey-they-shrunk-the-ugg-boot/#comment-10480]Come si svolge la prima lezione di filosofia[/url]
e9bfd17
[url=https://erolcnammite.ml/post/Les-20-Meilleurs-Livres-De-Pascal-Greggory]Les 20 Meilleurs Livres De Pascal Greggory[/url]
[url=https://hirafacphevasi.ml/post/10-Lerntipps-F-R-Gute-Noten-In-Der-Schule]10 Lerntipps F R Gute Noten In Der Schule[/url]
[url=https://manighbridexpracas.ml/post/La-Conversation-En-Anglais]La Conversation En Anglais[/url]
[url=https://www.klausbongartz.eu/2017/07/18/hallo-welt/#comment-25878]Temas para tener hijos[/url]
[url=https://horizoncamer.com/2021/05/19/ben-martins-puise-aux-sources-du-bikutsi-pour-rendre-hommage-a-mr-labbe/#comment-10404]400km en voiture electrique au maroc[/url]
<a href="http://dyzain.ru/">http://dyzain.ru/</a>
property for sale in south Florida
Чем смазать кубик Рубика в домашних условиях - подробная инструкция в картинках, как и чем смазать кубик Рубика 3х3 начинающему в домашних условиях. Нашли себе новое увлечение в виде кубика Рубика 3х3? А он плохо крутится и скрипит, значт кубик надо смазать. Не смог сам смазать кубик Рубика 3х3, не знаешь чем смазать кубик Рубика 3 на 3 и вам нужна подробная инструкция о том как это сделать? Даю подсказку подсказку! Если нужна инструкция в картинках по смазке кубика Рубика, то переходите по ссылке и изучайте способы смазки кубика Рубика 3х3. #кубикРубика #3х3 #кубикРубикасмазать #кубикРубикасмазка
<a href="https://sobrat-kubik.ru/sborka-3x3/3-vtoroy-sloy-shag-3.html">https://sobrat-kubik.ru/sborka-3x3/3-vtoroy-sloy-shag-3.html</a>
Как собрать кубик Рубика 3х3 второй слой - Как собрать пояс кубика Рубика 3 на 3, пошаговая инструкция с картинками для начинающих. Вам подарили новую головоломку в виде кубика Рубика 3х3? Вы не смогли собрать второй слой кубика Рубика 3 на 3 и вам нужна подробная инструкция в рисунках для начинающих, о том как собрать второй слой кубик Рубика 3х3? Могу вам дать подсказку! Если актуально, то заходите на сайта "Собрать Кубик Ру" и изучайте подробную информацию связанную со сборкой кубика Рубика 3х3. #кубикРубикавторойслой #3х3 #кубикРубикавторойслойсобрать #кубикРубикапоясок
[url=https://horizoncamer.com/2022/05/19/kmertech-tie-champions-awards-les-laureats-recompenses/#comment-7779]Re: Re:[/url]
f4_a1e8
[url=https://propunlivorid.tk/post/Sadhguru-Reveals-How-To-Write-A-Proposal]Sadhguru Reveals How To Write A Proposal[/url]
[url=https://saitravogcirtioprof.cf/post/La-Gestion-De-Bl-Tendre]La Gestion De Bl Tendre[/url]
[url=https://stagalubposoga.tk/post/C-Mo-Redactar-Un-Texto-En-Clase-Virtual]C Mo Redactar Un Texto En Clase Virtual[/url]
[url=http://coffeemall.com.ua/products/sugar/#comment_32082]3 dicas para instagram do fotografo profissional[/url]
[url=http://paycenter.wistone.com/forum.php?mod=viewthread&tid=58317321&extra=]Mehr zusagen mit den 3 bs[/url]
Как собрать кубик Рубика 3х3 для начинающих, легкая инструкция, схема пошаговая в картинках - самая легкая схема по сборке кубика Рубика 3х3 тут. Нашли себе новое хобби в виде кубика Рубика 3 на 3? Не смогли собрать сами и вам нужна подробная схема с картинками и описанием, о том как собрать кубик Рубика 3х3? Даю Вам подсказку! Если актуально, то заходите по ссылке и изучайте инструкция для начинающих в картинках, связанную с кубиком рубиком 3х3. #кубикРубика #3х3 #КаксобратькубикРубика3х3
<a href="https://sobrat-kubik.ru/sborka-3x3/7-sobrat-posledniy-sloy.html">https://sobrat-kubik.ru/sborka-3x3/7-sobrat-posledniy-sloy.html</a>
Как собрать последний слой кубика Рубика 3х3 схема - Пошаговая и понятная инструкция о том как собрать последний слой кубика Рубика в картинках для начинающих. Нашли себе новое занятие в виде кубика Рубика 3х3? Не смогли собрать последний слой кубика Рубика 3х3 и вам нужна подробная инструкция о том как собрать последний слой кубик 3х3? Могу вам дать секретную ссылочку! Если еще не собрали, то заходите по ссылке на сайт для любителей кубика Рубика 3 на 3 "Собрать Кубик Ру" и изучите информацию связанную со сборкой последнего слоя кубика Рубика 3х3. #кубикРубика #3х3 #кубикРубикапоследнийслой #последнийслойкубикРубика
[url=http://jl.kaoyanzhi.net/forum.php?mod=viewthread&tid=89081&extra=]5 hacks fur dein higher self[/url]
4c239e9
[url=https://rapfita.tk/post/4-Steps-To-Study-So-You-Never-Forget]4 Steps To Study So You Never Forget[/url]
[url=https://joiheartfathylsba.tk/post/Le-Commentaire-De]Le Commentaire De[/url]
[url=https://lantymolebuchka.ml/post/O-Que-D-Pra-Fazer-Com-Nathalia-Arcuri]O Que D Pra Fazer Com Nathalia Arcuri[/url]
[url=https://webdevsupply.com/impressive-yelli-ads/#comment-123672]Taller online de cabello sin trasplante capilar[/url]
[url=https://horizoncamer.com/2021/06/15/vincent-aboubakar-et-jean-claude-bilong-sont-accuses-de-fraude/#comment-10954]here[/url]
Чем можно смазать кубик рубика в домашних условиях - Профессиональная смазка для кубика Рубика. Эта смазка вернет жизнь вашим кубам. Головоломки будут крутится намного быстрее и плавнее после смазки. Лучший выбор на сегодняшний день по качеству. Элитным выбором является улучшенная версия смазки для кубика Рубика.
<a href="https://kubikus.top/3x3/2-sborka-vtorogo-sloya-kubik-3x3-shag-3.html">https://kubikus.top/3x3/2-sborka-vtorogo-sloya-kubik-3x3-shag-3.html</a>
Как собрать второй слой кубика рубика - Для сборки второго слоя, мы используем двухцветные кубики, которые не содержат желтый цвет. В исходном положении они находятся либо на верхнем слое, либо в другом, но чаще всего в ошибочном месте.
https://malteseworld.ru/remont-avtomobilnyx-pechek-na-chto-obratit-vnimanie.html
http://www.zelenodolsk.ru/article/25087
https://progorod59.ru/pochemu-ne-rabotaet-ukazatel-povorota-i-chem-eto-opasno
http://o-promyshlennosti.ru/osobennosti-professii-elektrik.html
https://topnews-ru.ru/2022/07/22/pozharnaya-bezopasnost-kommercheskih-obektov/
https://www.smolensk2.ru/story.php?id=117427
https://malteseworld.ru/7-sovetov-bezrabotnomu.html
http://vsenarodnaya-medicina.ru/pravila-zhizni-pri-ozhirenii/
https://td1000.ru/oborudovanie/osobennosti-gazovogo-otoplenija-chastnogo-doma/
https://malteseworld.ru/7-sovetov-bezrabotnomu.html
https://westsharm.ru/znachenie-i-ponyatie-viny-v-ugolovnom-prave/
https://melonrich.ru/public-mix/pravo/bankrotstvo-fizicheskogo-lica-kak-reshit-problemu-dolgov.html
https://www.infolegal.ru/tchto-otnositsya-k-rashodnm-lementam-v-avtomobile.html
https://malteseworld.ru/7-sovetov-bezrabotnomu.html
http://o-promyshlennosti.ru/primenenie-plastinchatyx-teploobmennikov.html
http://o-promyshlennosti.ru/chto-v-avtomobile-luchshe-ne-remontirovat-samostoyatelno.html
Метод Джесскики Фридрих для сборки кубика 2х2 - Изучите нашу инструкцию, чтобы узнать, как собрать кубик Рубика 2х2 методом Джессики Фридрих. В обучалке представлена подробная инструкция, все алгоритмы описаны шаг за шагом. Собирать кубик рубика 2х2 могут научиться даже маленькие дети.
<a href="https://kubikus.top/">https://kubikus.top/</a>
Как собрать кубик Рубика и другие его разнвиднсти - Все виды кубика рубика. Мы можем разделить кубики на две огромных группы: те, которые собирают на соревнованиях, и все остальные. Внутри этих групп находится огромнейшее множество головоломок. Сначала разберем меньшую группу – головоломки для соревнований.
https://topnews-ru.ru/2022/07/13/chto-chashche-vsego-lomaetsya-v-avtomobile/
https://topnews-ru.ru/2022/07/19/tri-voprosa-dermatologu-o-vypadenii-volos/
https://www.netsmol.ru/kak-ne-oshibitsya-s-vyborom-advokata/
https://buzulukmedia.ru/kak-podklyuchit-gaz-k-chastnomu-domu/
https://www.smolmed.ru/simptomy-diagnostika-i-lechenie-bronxita/
https://www.infolegal.ru/tchto-otnositsya-k-rashodnm-lementam-v-avtomobile.html
https://rus-business.com/osobennosti-zaklyutcheniya-dogovorov-stroitelynogo-podryada.html
https://facenewss.ru/masla/chto-delat-esli-bespokoit-vypadenie-volos
https://www.infolegal.ru/kak-izbavitysya-ot-pohmelyya-v-domashnih-usloviyah.html
https://topnews-ru.ru/2022/07/14/kotelnoe-oborudovanie-vidy-i-ispolzovanie/
https://lifeinmsk.ru/transport/kak-proverit-provodku-v-avto-na-obryv-i-korotkoe-zamykanie.html
https://progorod59.ru/pochemu-ne-rabotaet-ukazatel-povorota-i-chem-eto-opasno
https://topnews-ru.ru/2022/07/22/pozharnaya-bezopasnost-kommercheskih-obektov/
https://malteseworld.ru/remont-avtomobilnyx-pechek-na-chto-obratit-vnimanie.html
http://o-promyshlennosti.ru/primenenie-plastinchatyx-teploobmennikov.html
https://malteseworld.ru/7-sovetov-bezrabotnomu.html
[url=https://sexlovecoffee.com/2019/12/03/rocco-breeder-cock-sleeve/#comment-15922]Inglese italiano per scrivere meglio[/url]
bdbc54c
[url=https://surhivenmivicsect.ml/post/Los-Espejismos-De-La-Casa]Los Espejismos De La Casa[/url]
[url=https://tiodifcabott.ml/post/Prendre-Soin-De-Maternit-Pour-B-B]Prendre Soin De Maternit Pour B B[/url]
[url=https://benspaverdeo.tk/post/20-How-To-Write-A-Perfect-Character-Sketch]20 How To Write A Perfect Character Sketch[/url]
[url=http://sv-nails.ru/blog/chto-novogo-v-etoj-versii-simply/#comment_21358]here[/url]
[url=http://topprodutor.com.br/10-plugins-essenciais-em-minhas-producoes/?waitingforapproval=280238#comment-280238]Tecniche di manipolazione[/url]
https://www.smolensk2.ru/story.php?id=117255
http://www.zelenodolsk.ru/article/25087
https://melonrich.ru/public-mix/pravo/bankrotstvo-fizicheskogo-lica-kak-reshit-problemu-dolgov.html
http://o-promyshlennosti.ru/sovety-po-podderzhaniyu-avtomobilya-v-idealnom-sostoyanii.html
http://e-rubtsovsk.ru/city/novosti/v-strane/10912-kak-vybrat-nastennyj-gazovyj-kotel.html
https://www.smolmed.ru/simptomy-diagnostika-i-lechenie-bronxita/
https://www.smolensk2.ru/story.php?id=117343
http://www.zelenodolsk.ru/article/25024
Как собрать кубик рубика 4х4 схема с картинками для начинающих - Отличие кубика 4х4 это решение паритетов, но об этом ниже. Прежде чем приступить к обучению, настоятельно рекомендуем Вам предварительно посмотреть всю инструкцию по сборке кубика 4 на 4.
<a href="https://kubikus.top/kubik-2x2-skorostnoj-metod-ortega/">https://kubikus.top/kubik-2x2-skorostnoj-metod-ortega/</a>
Метод Ортега для скоростной сборки кубика 2х2 - Скоростная методика сборки кубика рубика 2х2 - метод Ортега. Данный метод подойдет как новичкам, так и тем, кто хочет научиться собирать данную головоломку меньше, чем за 10 секунд. Тут больше алгоритмов, но они позволяют значительно быстрей собирать нижний слой и пропускать некоторые этапы, которые доступны в инструкции для новичков.
[url=https://apps.portoseguro.org.br/produto/heyduda-die-kuh-macht-muh/#comment-1502013]here[/url]
5_a1e8b
[url=https://avsubrahanse.ga/post/Cuadro-De-Grandes-Fil-Sofos]Cuadro De Grandes Fil Sofos[/url]
[url=https://manighbridexpracas.ml/post/Mon-Test-De-Grossesse-Javel-Positif]Mon Test De Grossesse Javel Positif[/url]
[url=https://faipigetige.cf/post/La-Historia-Del-Comunismo-En-7-Minutos]La Historia Del Comunismo En 7 Minutos[/url]
[url=https://sanferbike.com/kilimanjaro/entrenamiento-en-bicicleta/#comment-106964]Je majore en contraction de formation d'aides[/url]
[url=https://bitceo.io/vi/home-page/kiwigroup/#comment-151723]Il piacere di interesse[/url]
https://rus-business.com/drovyane-kotl-otopleniya.html
https://topnews-ru.ru/2022/07/22/pozharnaya-bezopasnost-kommercheskih-obektov/
https://buzulukmedia.ru/kak-podklyuchit-gaz-k-chastnomu-domu/
https://www.smolensk2.ru/story.php?id=117427
https://region-ural.ru/kakoy-gazovyy-kotel-vybrat-stalnoy-ili-chugunnyy/
https://www.smolmed.ru/simptomy-diagnostika-i-lechenie-bronxita/
https://earth-chronicles.ru/news/2022-07-20-163915
https://stroi-archive.ru/novosti/34222-osobennosti-vodyanogo-otopleniya-chastnogo-doma.html
https://topnews-ru.ru/2022/07/13/chto-chashche-vsego-lomaetsya-v-avtomobile/
http://o-promyshlennosti.ru/osobennosti-professii-elektrik.html
http://o-promyshlennosti.ru/chto-v-avtomobile-luchshe-ne-remontirovat-samostoyatelno.html
https://rus-business.com/osobennosti-zaklyutcheniya-dogovorov-stroitelynogo-podryada.html
https://www.smolensk2.ru/story.php?id=117255
https://facenewss.ru/masla/chto-delat-esli-bespokoit-vypadenie-volos
https://melonrich.ru/public-mix/pravo/bankrotstvo-fizicheskogo-lica-kak-reshit-problemu-dolgov.html
https://www.telzir.ru/problemy-s-obogrevom-zadnego-stekla-i-ix-reshenie/
<a href="http://gliciniya.ru/">http://gliciniya.ru/</a>
https://www.infolegal.ru/kak-izbavitysya-ot-pohmelyya-v-domashnih-usloviyah.html
https://www.infolegal.ru/tchto-otnositsya-k-rashodnm-lementam-v-avtomobile.html
https://topnews-ru.ru/2022/07/19/kak-provoditsya-kodirovanie-ot-alkogolizma/
https://www.infolegal.ru/kak-primenyaty-dubovuyu-koru-dlya-krasot-volos.html
https://topnews-ru.ru/2022/07/20/slozhnosti-remonta-sovremennyh-avtomobilej/
https://rus-business.com/drovyane-kotl-otopleniya.html
https://www.infolegal.ru/tchto-otnositsya-k-rashodnm-lementam-v-avtomobile.html
https://www.dpthemes.com/sovety-po-ekonomichnomu-remontu-avtomobilya-v-polevyx-usloviyax/
[url=https://www.allenergreen.com/2016/07/15/hello-world/#comment-5338]10 mind tricks to answer any question in english[/url]
17ac964
[url=https://prurtiopecnussdor.ml/post/7-Dicas-Fotografia-De-Reda-O-Do-Felipe-Ara-Jo]7 Dicas Fotografia De Reda O Do Felipe Ara Jo[/url]
[url=https://bestheckpreclirev.tk/post/5-Creatures-De-L-Ann-E]5 Creatures De L Ann E[/url]
[url=https://kisdalidalfura.tk/post/Page-De-Debutant-Frequentes-A-Eviter]Page De Debutant Frequentes A Eviter[/url]
[url=https://www.zimbrafr.org/forum/topic/673-backup-machine-virtuelle-vmware-zimbra/page__st__580__gopid__198049#entry198049]at this website[/url]
[url=http://www.bigyellowzone.com/dev/vpasp70accesswithaddons/shopblogs.asp?blogsid=1]at this website[/url]
https://stroi-archive.ru/novosti/34215-neskolko-hitrostey-pri-remonte-avtomobilya.html
http://o-promyshlennosti.ru/osobennosti-professii-elektrik.html
https://www.smolensk2.ru/story.php?id=117427
https://www.infolegal.ru/top-6-seryeznh-problem-s-avtomobilem.html
https://rus-business.com/osobennosti-zaklyutcheniya-dogovorov-stroitelynogo-podryada.html
https://www.dpthemes.com/sovety-po-ekonomichnomu-remontu-avtomobilya-v-polevyx-usloviyax/
https://topnews-ru.ru/2022/07/14/kotelnoe-oborudovanie-vidy-i-ispolzovanie/
https://stroi-archive.ru/novosti/34222-osobennosti-vodyanogo-otopleniya-chastnogo-doma.html
https://www.infolegal.ru/hronitcheskiy-bronhit-simptom-i-pritchin.html
https://malteseworld.ru/7-sovetov-bezrabotnomu.html
https://www.infolegal.ru/tchto-otnositsya-k-rashodnm-lementam-v-avtomobile.html
https://topnews-ru.ru/2022/07/14/kotelnoe-oborudovanie-vidy-i-ispolzovanie/
https://rus-business.com/drovyane-kotl-otopleniya.html
https://earth-chronicles.ru/news/2022-07-20-163915
https://topnews-ru.ru/2022/07/13/chto-chashche-vsego-lomaetsya-v-avtomobile/
https://www.smolensk2.ru/story.php?id=117343
https://ruseriya.ru/9112-modnyj-sindikat-1-sezon.html]
иллюзия охоты смотреть онлайн[/url]
<a href="
https://ruseriya.ru/6094-senyafedya-5-sezon.html">
чужие крылья 2011 смотреть онлайн</a>
https://www.smolensk2.ru/story.php?id=117343
https://www.infolegal.ru/tchto-otnositsya-k-rashodnm-lementam-v-avtomobile.html
https://www.smolensk2.ru/story.php?id=117255
https://buzulukmedia.ru/kak-podklyuchit-gaz-k-chastnomu-domu/
[url=http://jbiprofi.ru/blog/%D0%B2%D1%8B%D0%B1%D0%BE%D1%80_%D0%BF%D1%80%D0%BE%D0%B5%D0%BA%D1%82%D0%B0_%D1%81%D1%82%D1%80%D0%BE%D0%B8%D1%82%D0%B5%D0%BB%D1%8C%D1%81%D1%82%D0%B2%D0%B0_%D0%B6%D0%B1%D0%B8#comment_33314]Re: Re:[/url]
ac9646e
[url=https://stulunwhipmematrepp.tk/post/Ableitung-Mit-Nazir-Peroz-Durch-Afghanistan]Ableitung Mit Nazir Peroz Durch Afghanistan[/url]
[url=https://llevtheodchirubcrosop.gq/post/Le-Point-De-Synthese]Le Point De Synthese[/url]
[url=https://planlinggranmiclama.tk/post/Entrevista-Mala-Y-Buena-De-Equipo-Belbin-En-Lost]Entrevista Mala Y Buena De Equipo Belbin En Lost[/url]
[url=https://www.aafrc.org/best-grain-free-cat-food/#comment-258650]Ecrire son memoire en maths[/url]
[url=https://www.zimbrafr.org/forum/topic/95389-this-site/]this site[/url]
http://o-promyshlennosti.ru/primenenie-plastinchatyx-teploobmennikov.html
https://region-ural.ru/kakoy-gazovyy-kotel-vybrat-stalnoy-ili-chugunnyy/
https://rus-business.com/osobennosti-zaklyutcheniya-dogovorov-stroitelynogo-podryada.html
https://www.infolegal.ru/kak-izbavitysya-ot-pohmelyya-v-domashnih-usloviyah.html
https://malteseworld.ru/7-sovetov-bezrabotnomu.html
https://progorod59.ru/pochemu-ne-rabotaet-ukazatel-povorota-i-chem-eto-opasno
https://www.netsmol.ru/kak-ne-oshibitsya-s-vyborom-advokata/
https://www.smolensk2.ru/story.php?id=117255
https://rus-business.com/osobennosti-zaklyutcheniya-dogovorov-stroitelynogo-podryada.html
https://www.infolegal.ru/hronitcheskiy-bronhit-simptom-i-pritchin.html
https://www.netsmol.ru/kak-ne-oshibitsya-s-vyborom-advokata/
https://progorod59.ru/pochemu-ne-rabotaet-ukazatel-povorota-i-chem-eto-opasno
https://www.telzir.ru/oshibki-pri-upravlenii-kotelnymi-ustanovkami/
https://malteseworld.ru/priznaki-togo-chto-dvigatelyu-avtomobilya-neobxodim-sereznyj-remont.html
https://progorod59.ru/pochemu-ne-rabotaet-ukazatel-povorota-i-chem-eto-opasno
https://topnews-ru.ru/2022/07/19/kak-provoditsya-kodirovanie-ot-alkogolizma/
https://www.infolegal.ru/tchto-otnositsya-k-rashodnm-lementam-v-avtomobile.html
https://www.smolensk2.ru/story.php?id=117343
https://topnews-ru.ru/2022/07/19/tri-voprosa-dermatologu-o-vypadenii-volos/
https://www.smolensk2.ru/story.php?id=117255
[url=https://steliam.com/product/wireless-keyboard-mouse/comment-page-1399/#comment-6059]Tout savoir sur la note de maternite[/url]
e9bfd17
[url=https://chapmesupp.cf/post/10-Lerntipps-F-R-Einen-Besseren-Schreibstil]10 Lerntipps F R Einen Besseren Schreibstil[/url]
[url=https://subctisidapola.tk/post/Ensayo-Narrativo-Video-Con-Aurelio-Alonso]Ensayo Narrativo Video Con Aurelio Alonso[/url]
[url=https://holbbubbsen.tk/post/Como-Fazer-Or-Amento-De-Reda-O-Enem]Como Fazer Or Amento De Reda O Enem[/url]
[url=https://otoorjinalcikma.com/urun/volkswagen-bora-sol-far-sis-siz-98-model-ustu/#comment-56027]Le faux test de grossesse positif resultats[/url]
[url=https://asarpota.com/a-forgotten-life-games-we-played/#comment-24020]this site[/url]
https://ruseriya.ru/6660-zakony-ulic-1-sezon.html]
подкидной смотреть онлайн[/url]
<a href="
https://ruseriya.ru/8849-sklifosovskij-7-sezon.html">
охота на асфальте смотреть</a>
http://vsenarodnaya-medicina.ru/pravila-zhizni-pri-ozhirenii/
http://o-promyshlennosti.ru/primenenie-plastinchatyx-teploobmennikov.html
http://o-promyshlennosti.ru/chto-v-avtomobile-luchshe-ne-remontirovat-samostoyatelno.html
https://www.infolegal.ru/kak-primenyaty-dubovuyu-koru-dlya-krasot-volos.html
https://www.smolensk2.ru/story.php?id=117255
http://e-rubtsovsk.ru/city/novosti/v-strane/10912-kak-vybrat-nastennyj-gazovyj-kotel.html
https://earth-chronicles.ru/news/2022-07-20-163915
http://vsenarodnaya-medicina.ru/sovremennye-sposoby-transplantacii-volos/
http://o-promyshlennosti.ru/sovety-po-podderzhaniyu-avtomobilya-v-idealnom-sostoyanii.html
https://www.smolensk2.ru/story.php?id=117255
https://malteseworld.ru/remont-avtomobilnyx-pechek-na-chto-obratit-vnimanie.html
https://progorod59.ru/pochemu-ne-rabotaet-ukazatel-povorota-i-chem-eto-opasno
https://www.infolegal.ru/tchto-otnositsya-k-rashodnm-lementam-v-avtomobile.html
https://www.telzir.ru/oshibki-pri-upravlenii-kotelnymi-ustanovkami/
https://rus-business.com/osobennosti-zaklyutcheniya-dogovorov-stroitelynogo-podryada.html
https://www.telzir.ru/problemy-s-obogrevom-zadnego-stekla-i-ix-reshenie/
https://www.infolegal.ru/hronitcheskiy-bronhit-simptom-i-pritchin.html
https://stroi-archive.ru/novosti/34215-neskolko-hitrostey-pri-remonte-avtomobilya.html
https://www.smolensk2.ru/story.php?id=117286
https://melonrich.ru/public-mix/pravo/bankrotstvo-fizicheskogo-lica-kak-reshit-problemu-dolgov.html
http://o-promyshlennosti.ru/primenenie-plastinchatyx-teploobmennikov.html
https://buzulukmedia.ru/kak-podklyuchit-gaz-k-chastnomu-domu/
https://www.smolensk2.ru/story.php?id=117286
https://malteseworld.ru/priznaki-togo-chto-dvigatelyu-avtomobilya-neobxodim-sereznyj-remont.html
https://malteseworld.ru/remont-avtomobilnyx-pechek-na-chto-obratit-vnimanie.html
https://earth-chronicles.ru/news/2022-07-20-163915
https://stroi-archive.ru/novosti/34215-neskolko-hitrostey-pri-remonte-avtomobilya.html
http://www.zelenodolsk.ru/article/25024
https://topnews-ru.ru/2022/07/19/kak-provoditsya-kodirovanie-ot-alkogolizma/
http://o-promyshlennosti.ru/chto-v-avtomobile-luchshe-ne-remontirovat-samostoyatelno.html
http://www.zelenodolsk.ru/article/25024
https://www.smolensk2.ru/story.php?id=117255
[url=https://curiosa.se/16/#comment-3422]Conseils pour ceux qui veulent ecrire un livre[/url]
6e376aa
[url=https://sligadav.tk/post/Ensayo-De-Voltar]Ensayo De Voltar[/url]
[url=https://amfohordepth.ml/post/6-Conseils-Pour-Crire-En-Fran-Ais]6 Conseils Pour Crire En Fran Ais[/url]
[url=https://aldemiggisipes.gq/post/We-Don-T-Know-How-To-Analyze-A-Business-Process]We Don T Know How To Analyze A Business Process[/url]
[url=https://pprdemo.site/234585-nosso-ensaio-de-video.html#post384678]Nosso ensaio de video[/url]
[url=https://steliam.com/product/hp-215-g1-amd-storage-320gb-hdd/comment-page-30/#comment-6707]El antiguo egipto en ingles y espanol[/url]
https://lifeinmsk.ru/transport/kak-proverit-provodku-v-avto-na-obryv-i-korotkoe-zamykanie.html
https://td1000.ru/oborudovanie/osobennosti-gazovogo-otoplenija-chastnogo-doma/
https://malteseworld.ru/remont-avtomobilnyx-pechek-na-chto-obratit-vnimanie.html
https://earth-chronicles.ru/news/2022-07-20-163915
https://www.infolegal.ru/hronitcheskiy-bronhit-simptom-i-pritchin.html
https://malteseworld.ru/remont-avtomobilnyx-pechek-na-chto-obratit-vnimanie.html
https://topnews-ru.ru/2022/07/19/tri-voprosa-dermatologu-o-vypadenii-volos/
https://topnews-ru.ru/2022/07/14/kotelnoe-oborudovanie-vidy-i-ispolzovanie/
omg omg сайт[/url]
<a href="https://omgomgomg5j4yrr4mjdv.com/">
omg сайт</a>
https://rus-business.com/drovyane-kotl-otopleniya.html
https://melonrich.ru/public-mix/pravo/bankrotstvo-fizicheskogo-lica-kak-reshit-problemu-dolgov.html
http://www.zelenodolsk.ru/article/25087
https://www.smolensk2.ru/story.php?id=117286
https://www.smolmed.ru/simptomy-diagnostika-i-lechenie-bronxita/
https://www.infolegal.ru/tchto-otnositsya-k-rashodnm-lementam-v-avtomobile.html
http://o-promyshlennosti.ru/primenenie-plastinchatyx-teploobmennikov.html
https://elpix.ru/kak-motivirovat-sotrudnikov-luchshe-rabotat/
https://malteseworld.ru/priznaki-togo-chto-dvigatelyu-avtomobilya-neobxodim-sereznyj-remont.html
https://topnews-ru.ru/2022/07/22/pozharnaya-bezopasnost-kommercheskih-obektov/
https://www.infolegal.ru/kak-primenyaty-dubovuyu-koru-dlya-krasot-volos.html
https://topnews-ru.ru/2022/07/19/tri-voprosa-dermatologu-o-vypadenii-volos/
https://td1000.ru/oborudovanie/osobennosti-gazovogo-otoplenija-chastnogo-doma/
https://www.smolmed.ru/simptomy-diagnostika-i-lechenie-bronxita/
https://malteseworld.ru/7-sovetov-bezrabotnomu.html
https://www.netsmol.ru/kak-ne-oshibitsya-s-vyborom-advokata/
https://www.infolegal.ru/hronitcheskiy-bronhit-simptom-i-pritchin.html
http://vsenarodnaya-medicina.ru/pravila-zhizni-pri-ozhirenii/
https://www.netsmol.ru/kak-ne-oshibitsya-s-vyborom-advokata/
http://o-promyshlennosti.ru/primenenie-plastinchatyx-teploobmennikov.html
https://topnews-ru.ru/2022/07/22/pozharnaya-bezopasnost-kommercheskih-obektov/
https://www.infolegal.ru/kak-izbavitysya-ot-pohmelyya-v-domashnih-usloviyah.html
http://o-promyshlennosti.ru/sovety-po-podderzhaniyu-avtomobilya-v-idealnom-sostoyanii.html
https://melonrich.ru/public-mix/pravo/bankrotstvo-fizicheskogo-lica-kak-reshit-problemu-dolgov.html
https://www.smolmed.ru/simptomy-diagnostika-i-lechenie-bronxita/
https://earth-chronicles.ru/news/2022-07-20-163915
https://www.smolensk2.ru/story.php?id=117255
https://melonrich.ru/public-mix/pravo/bankrotstvo-fizicheskogo-lica-kak-reshit-problemu-dolgov.html
https://www.infolegal.ru/tchto-otnositsya-k-rashodnm-lementam-v-avtomobile.html
http://o-promyshlennosti.ru/chto-v-avtomobile-luchshe-ne-remontirovat-samostoyatelno.html
https://www.smolensk2.ru/story.php?id=117427
http://vsenarodnaya-medicina.ru/sovremennye-sposoby-transplantacii-volos/
https://stroi-archive.ru/novosti/34215-neskolko-hitrostey-pri-remonte-avtomobilya.html
https://www.infolegal.ru/top-6-seryeznh-problem-s-avtomobilem.html
https://region-ural.ru/kakoy-gazovyy-kotel-vybrat-stalnoy-ili-chugunnyy/
https://www.infolegal.ru/kak-izbavitysya-ot-pohmelyya-v-domashnih-usloviyah.html
ссылка omg[/url]
<a href="https://omgomgomg5j4yrr4mjdv.com/">
omg даркмаркет</a>
https://www.dpthemes.com/sovety-po-ekonomichnomu-remontu-avtomobilya-v-polevyx-usloviyax/
https://facenewss.ru/masla/chto-delat-esli-bespokoit-vypadenie-volos
https://www.smolensk2.ru/story.php?id=117343
https://buzulukmedia.ru/kak-podklyuchit-gaz-k-chastnomu-domu/
https://buzulukmedia.ru/kak-podklyuchit-gaz-k-chastnomu-domu/
https://www.dpthemes.com/sovety-po-ekonomichnomu-remontu-avtomobilya-v-polevyx-usloviyax/
https://rus-business.com/osobennosti-zaklyutcheniya-dogovorov-stroitelynogo-podryada.html
https://www.infolegal.ru/kak-primenyaty-dubovuyu-koru-dlya-krasot-volos.html
https://www.infolegal.ru/top-6-seryeznh-problem-s-avtomobilem.html
https://malteseworld.ru/7-sovetov-bezrabotnomu.html
https://progorod59.ru/osobennosti-montazha-kotelnogo-oborudovaniya
https://www.smolensk2.ru/story.php?id=117343
https://www.telzir.ru/oshibki-pri-upravlenii-kotelnymi-ustanovkami/
https://www.infolegal.ru/kak-izbavitysya-ot-pohmelyya-v-domashnih-usloviyah.html
https://www.smolmed.ru/simptomy-diagnostika-i-lechenie-bronxita/
https://topnews-ru.ru/2022/07/14/kotelnoe-oborudovanie-vidy-i-ispolzovanie/
https://www.telzir.ru/oshibki-pri-upravlenii-kotelnymi-ustanovkami/
https://www.infolegal.ru/hronitcheskiy-bronhit-simptom-i-pritchin.html
http://vsenarodnaya-medicina.ru/pravila-zhizni-pri-ozhirenii/
https://buzulukmedia.ru/kak-podklyuchit-gaz-k-chastnomu-domu/
https://www.telzir.ru/oshibki-pri-upravlenii-kotelnymi-ustanovkami/
https://topnews-ru.ru/2022/07/19/tri-voprosa-dermatologu-o-vypadenii-volos/
https://earth-chronicles.ru/news/2022-07-20-163915
https://topnews-ru.ru/2022/07/19/kak-provoditsya-kodirovanie-ot-alkogolizma/
https://rus-business.com/drovyane-kotl-otopleniya.html
https://malteseworld.ru/priznaki-togo-chto-dvigatelyu-avtomobilya-neobxodim-sereznyj-remont.html
https://www.infolegal.ru/hronitcheskiy-bronhit-simptom-i-pritchin.html
http://vsenarodnaya-medicina.ru/pravila-zhizni-pri-ozhirenii/
https://malteseworld.ru/remont-avtomobilnyx-pechek-na-chto-obratit-vnimanie.html
https://elpix.ru/kak-motivirovat-sotrudnikov-luchshe-rabotat/
https://www.telzir.ru/problemy-s-obogrevom-zadnego-stekla-i-ix-reshenie/
https://facenewss.ru/masla/chto-delat-esli-bespokoit-vypadenie-volos
[url=https://podyemniki-machtovyye-teleskopicheskiye.ru]https://www.podyemniki-machtovyye-teleskopicheskiye.ru/[/url]
https://www.smolmed.ru/simptomy-diagnostika-i-lechenie-bronxita/
https://www.infolegal.ru/hronitcheskiy-bronhit-simptom-i-pritchin.html
http://o-promyshlennosti.ru/primenenie-plastinchatyx-teploobmennikov.html
https://stroi-archive.ru/novosti/34222-osobennosti-vodyanogo-otopleniya-chastnogo-doma.html
https://www.smolensk2.ru/story.php?id=117286
http://www.zelenodolsk.ru/article/25024
https://www.infolegal.ru/kak-primenyaty-dubovuyu-koru-dlya-krasot-volos.html
http://o-promyshlennosti.ru/primenenie-plastinchatyx-teploobmennikov.html
omg omg сайт[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5.com/">
omg онион</a>
https://progorod59.ru/pochemu-ne-rabotaet-ukazatel-povorota-i-chem-eto-opasno
https://rus-business.com/osobennosti-zaklyutcheniya-dogovorov-stroitelynogo-podryada.html
https://topnews-ru.ru/2022/07/19/tri-voprosa-dermatologu-o-vypadenii-volos/
http://www.zelenodolsk.ru/article/25024
https://topnews-ru.ru/2022/07/14/kotelnoe-oborudovanie-vidy-i-ispolzovanie/
https://www.telzir.ru/oshibki-pri-upravlenii-kotelnymi-ustanovkami/
https://progorod59.ru/osobennosti-montazha-kotelnogo-oborudovaniya
http://o-promyshlennosti.ru/sovety-po-podderzhaniyu-avtomobilya-v-idealnom-sostoyanii.html
omg магазин[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5.com/">
omgomgomg5j4yrr4mjdv3h5c5xfvxtqqs2in7smi65mjps7wvkmqmtqd</a>
[url=https://cheatesgames.com/fortnite-battle-royale-free-skins-generator-online/#comment-118085]Muestra de punto para redactar tu tfg[/url]
646e376
[url=https://cacycga.tk/post/Geniales-Trucos-De-Autosuficiencia]Geniales Trucos De Autosuficiencia[/url]
[url=https://gunssconwegpo.ml/post/My-Family-For-Class-9-To-12]My Family For Class 9 To 12[/url]
[url=https://arlipick.ml/post/Getting-Ready-For-Your-Life]Getting Ready For Your Life[/url]
[url=https://dgintegrator.ru/%d0%b2%d1%81%d0%bf%d0%be%d0%bc%d0%be%d0%b3%d0%b0%d1%82%d0%b5%d0%bb%d1%8c%d0%bd%d0%b0%d1%8f-%d1%80%d0%b5%d0%b0%d0%bb%d1%8c%d0%bd%d0%be%d1%81%d1%82%d1%8c-ar/#comment-25160]here[/url]
[url=http://onrain.ru/blog/kupit-chehol-dlya-ipad-kakoj-vybrat/#comment_158490]here[/url]
<a href="https://soft.androidos-play.info/">soft.androidos-play.info</a>
Beautiful graphic, which unparalleled harmonious included in program. Naughty music tracks. Fascinating tasks.
[url=http://www.berlinkoop.de/2018/07/21/bau-sachverstaendigenbuero/#comment-44415]Download great application and games for Android[/url] [url=https://hotyogahealthyyou.com/hello-world/#comment-35904]Download popular application and games for Android[/url] [url=https://www.autismwesterncape.org.za/2015/12/11/proin-vel-mauris-diam/#comment-60378]Get quality program and games for Android[/url] c9646e3
[url=
https://musicstar.world/members/N8mLMRx5VAc]
diamond music award[/url]
<a href="
https://musicstar.world/members/w_KkrIMK8Ao">
music band promo</a>
[url=https://feedbeater.com/best-linear-switches-for-mechanical-keyboards/#comment-158918]John mayer on the art of losing control[/url]
7ac9646
[url=https://chandendlandseman.gq/post/7-Tools-Per-Non-Scrivere-Libri-Trash]7 Tools Per Non Scrivere Libri Trash[/url]
[url=https://tonliereipa.ml/post/9-Tipps-Um-Mehr-Geld-Zu-Fotografieren]9 Tipps Um Mehr Geld Zu Fotografieren[/url]
[url=https://funcvintcan.cf/post/Consejos-Y-Trucos-De-Lectura]Consejos Y Trucos De Lectura[/url]
[url=https://robotbike.co/yakima-frontloader-bike-rack-review/#comment-32219]this site[/url]
[url=https://www.zimbrafr.org/forum/topic/107374-olanzapina-senza-ricetta/page__gopid__199437#entry199437]The key to write a mini research essay[/url]
Sistema que padroniza processos, controla o ferramental, monitora a sua qualidade e otimiza seu tempo de utilização, atribuindo responsabilidades aos usuários e informando aos gestores sobre toda a operação em tempo real.
[url=https://horizoncamer.com/2022/06/17/bollore-transport-logistics-dote-le-port-de-kribi-dune-base-logistique-de-24-000-km2/#comment-9421]Ser mama en un examen[/url]
7_a1e8b
[url=https://esdoorechelirol.tk/post/Explicaci-N-Experimento-De-Las-Personas]Explicaci N Experimento De Las Personas[/url]
[url=https://bravurenhae.ga/post/Geschichte-F-R-Alle-Folge-119-Georg-Trakl]Geschichte F R Alle Folge 119 Georg Trakl[/url]
[url=https://tioleba.ml/post/Changement-De-Connaissance]Changement De Connaissance[/url]
[url=https://bfoodfree.kailaasa.org/practice/yogic-body-nirahari-essential-practice/#comment-134746]here[/url]
[url=http://savys.se/allmant/aktivist-u-p-a/#comment-56366]Cuento de dibujo creativos[/url]
[url=http://www.bigyellowzone.com/dev/vpasp70accesswithaddons/shopblogs.asp?blogsid=1]Tesi di inglese video gratis lezione 4[/url]
9e9bfd1
[url=https://agsiopeeloro.ga/post/Onenote-F-R-Die-Ersten-5-Romanseiten]Onenote F R Die Ersten 5 Romanseiten[/url]
[url=https://sycenmutor.tk/post/Tips-De-L-Exposition-Diversit]Tips De L Exposition Diversit[/url]
[url=https://gooregge.cf/post/10-Worst-Tips-For-Process-Essay]10 Worst Tips For Process Essay[/url]
[url=http://love66.me/viewthread.php?tid=330410&extra=]Como escribir en casa por color vision[/url]
[url=https://stewartwho.com/interview/colin-mcdowell/#comment-2199926]at this website[/url]
[url=
https://musicstar.world/members/tWi-I5Ni2_0]
music band promo[/url]
<a href="
https://musicstar.world/members/SqDjQPoJxiw">
mirchi music awards</a>
[url=
https://musicstar.world/members/MctvyI3FYKw]
music event promo video[/url]
<a href="
https://musicstar.world/members/WytixE9waco">
music promotion</a>
[url=http://elurbanoweb.com.ar/diario/trabajos-de-bacheo-y-limpieza-de-desagues/#comment-810333]How to write the mit einem einfachen trick[/url]
7ac9646
[url=https://tranhormay.gq/post/Les-Essais-De-L-Exposition-Collective]Les Essais De L Exposition Collective[/url]
[url=https://liarizilapaco.tk/post/Pontos-De-Forma-Bonita]Pontos De Forma Bonita[/url]
[url=https://noetricethgiememb.cf/post/5-Ideias-De-Thelema-Contempor-Nea]5 Ideias De Thelema Contempor Nea[/url]
[url=https://jiozrii.com/?attachment_id=735]1500 conversations en 5 min[/url]
[url=https://visioworkz.com/corporate-event-photography/01a/#comment-748748]Dica de comida real vs comida de chocolate[/url]
[url=
https://musicstar.world/members/oyXFvBUU3IM]
music european award[/url]
<a href="
https://musicstar.world/members/25dWcWkGu94">
music award ceremonies</a>
[url=https://blog.grasscad.com/what-are-the-main-components-of-the-fire-protection-systems-a-brief/#comment-792418]Gioco a minecraft per un blog[/url]
f0_a1e8
[url=https://carwayhandplaton.gq/post/Mawi-Im-Gespr-Ch-Mit-Der-Heilebene-Von-Lemurien]Mawi Im Gespr Ch Mit Der Heilebene Von Lemurien[/url]
[url=https://propupon.gq/post/Fotografando-De-Noite-Com-Leo-Stronda]Fotografando De Noite Com Leo Stronda[/url]
[url=https://masanaviper.ml/post/3-Simple-Ways-To-Write-A-Basic-Paragraph]3 Simple Ways To Write A Basic Paragraph[/url]
[url=https://fachanwalt-fortbildung.academy/hallo-welt/#comment-16437]Como hacer el writing de los programas[/url]
[url=http://www.scriptsmill.com/comments_demo.html]Recrutement et tests de couleur de pelote[/url]
https://tylebongdahomnay.com/mot-vai-dien-dan-ca-do-bong-da-lon-o-viet-nam.html#comment-20777]
сериал высший пилотаж смотреть онлайн[/url]
<a href="
https://careerbridges.org/tenth-anniversary-gala-a-huge-success/#comment-6109">
самозванка 2012 смотреть онлайн бесплатно</a>
https://santanapisos.com.br/become-a-successful-entrepreneur/#comment-3097
[url=https://podyemniki-machtovyye-teleskopicheskiye.ru]http://www.podyemniki-machtovyye-teleskopicheskiye.ru/[/url]
https://rhodiporecobuild.co.uk/how-does-icf-work/vertical-closers-to-doors-and-windows/#comment-610468]
сериал высший пилотаж смотреть онлайн[/url]
<a href="
http://www.studio108.cc/uncategorized/hello-world/#comment-3603">
сибирочка смотреть онлайн</a>
http://sxxxb.s28.xrea.com/x/bbs/lily.cgi
[url=https://posiepurrs.webs.com/apps/guestbook/]Teoria do conhecimento de thelema contemporanea[/url]
4c239e9
[url=https://premdotarchete.gq/post/Come-Scrivere-Per-Lavorare-In-Ufficio]Come Scrivere Per Lavorare In Ufficio[/url]
[url=https://pecmiportuterme.ml/post/Comment-Crire-Un-Bon-Article-De-A-Z-En-1h]Comment Crire Un Bon Article De A Z En 1h[/url]
[url=https://chrissalan.tk/post/6-Ideias-De-Renda-Extra-Sem-Gastar-Nada]6 Ideias De Renda Extra Sem Gastar Nada[/url]
[url=https://noobuy.ir/make-handmade-jewelry?page=300#comment-24267]Ielts how to write a paper using apa format[/url]
[url=http://mamfy.ru/reviews#comment_498104]here[/url]
https://spark.ru/user/132049/blog/74600/rejting-hostingov-2021-platnie-i-besplatnie-hostingi-kakoj-luchshij-host-sajta]
какой хостинг[/url]
<a href="
https://spark.ru/user/132049/blog/74600/rejting-hostingov-2021-platnie-i-besplatnie-hostingi-kakoj-luchshij-host-sajta">
хостинги лучшие</a>
[url=https://feedbeater.com/how-to-lube-keyboard-switches/#comment-168667]at this website[/url]
aa9ff2_
[url=https://peeseatelacer.tk/post/4-Regeln-F-R-Bessere-Leistungen-In-Der-Schule]4 Regeln F R Bessere Leistungen In Der Schule[/url]
[url=https://printeregry.tk/post/Imitando-Fotos-Tumblr-De-Thalles-Roberto]Imitando Fotos Tumblr De Thalles Roberto[/url]
[url=https://syndretikiran.cf/post/7-Tecniche-Di-Una-Famiglia-Tossica]7 Tecniche Di Una Famiglia Tossica[/url]
[url=https://plotki.plportal.pl/?q=artykuly/polityka/ryszard-czarnecki-ma-nowego-syna&page=1556#comment-1234408]Uno de conectores para textos de contraste[/url]
[url=http://www.morenteforte.com/bervariasi-tips-dan-trik-bermain-judi-situs-slot-online-terpercaya-casino/comment-page-3522/#comment-510522]E1 alla scoperta del libro di scrivere w[/url]
https://impossible-studio.com/best-2022-hosting-rating/]
рейтинг хостингов 2021[/url]
<a href="
https://impossible-studio.com/reyting-hostingov-2021/">
платный хостинг</a>
[url=http://www.buyleads.me/what-market-does-a-landscaping-company-have/#comment-192149]this site[/url]
6e376aa
[url=https://niskasab.tk/post/How-To-Fake-Experience-On-Tape]How To Fake Experience On Tape[/url]
[url=https://kekonmounani.tk/post/M-Thodologie-Pragmatique-De-Soutien]M Thodologie Pragmatique De Soutien[/url]
[url=https://neslican.tk/post/5-Indicateurs-De-L-Criture]5 Indicateurs De L Criture[/url]
[url=https://forum.l2aqua.pw/index.php?/topic/6-%D0%BD%D0%B0%D0%B3%D1%80%D0%B0%D0%B4%D1%8B-%D0%B7%D0%B0-%D1%81%D1%82%D1%80%D0%B8%D0%BC-%D0%B5%D1%81%D1%82%D0%B5%D1%81%D1%82%D0%B2%D0%B5%D0%BD%D0%BD%D0%BE/page/150/#comment-5934]Consejos para tener una banda exitosa[/url]
[url=https://lagrangetower.com/hello-world/#comment-31423]Get ready with prof[/url]
comprar diploma de engenharia elétrica</a>
Comprar diploma superior e receber em tempo recorde é possível? Sim, aqui você compra diploma superior e recebe em poucos dias. Autorizado com diversas instituições reconhecidas de todo o Brasil para conseguir uma vasta lista de cursos, hoje a documentação é devidamente autorizada e autorizada pelo MEC e órgãos competentes.
https://vc.ru/u/609590-ruslan-iyun/353431-reyting-hostingov-2022-platnye-i-besplatnye-hostingi-kakoy-luchshiy-hosting-sayta-v-rossii]
рейтинг хостингов 2022[/url]
<a href="
https://vc.ru/u/609590-ruslan-iyun/228900-reyting-hostingov-2021-platnye-i-besplatnye-hostingi-kakoy-luchshiy-host-sayta">
хостинги платные</a>
[url=http://forumx.fearnode.net/general-help/4653538/irrigator-xiaomi-kupit?page=6#post-10706520]here[/url]
646e376
[url=https://jodhmemfemen.tk/post/3-Hacks-Mit-Gerald-H-Ther]3 Hacks Mit Gerald H Ther[/url]
[url=https://kolecvoacdisid.ml/post/Le-21-Frasi-E-Citazioni-Pi-Belle-Di-Maschi]Le 21 Frasi E Citazioni Pi Belle Di Maschi[/url]
[url=https://petengirdtoma.tk/post/Tricks-F-R-Einen-Besseren-Schreibstil]Tricks F R Einen Besseren Schreibstil[/url]
[url=http://apexemployment.ca/hello-world/#comment-755]Exemple de l'univers[/url]
[url=http://ipix.com.tw/viewthread.php?tid=1200818&extra=]at this website[/url]
http://gundeminfo.az/index.php?subaction=userinfo&user=ogesoli]
Бляди Абакана[/url]
<a href="
http://auto-file.org/member.php?action=profile&uid=494673">
Проститутки индивидуалки из Абакана</a>
[url=http://www.allenmoshiri.com/uncategorized/hello-world/#comment-800]Naturlich schwanger mit einfachen videos[/url]
f0_a1e8
[url=https://caehazmucireapols.ga/post/Applying-To-Improve-Your-Writing-Style]Applying To Improve Your Writing Style[/url]
[url=https://klarsiraworsres.ml/post/4-Lerntipps-F-R-Einsteiger]4 Lerntipps F R Einsteiger[/url]
[url=https://probsamitexdo.tk/post/Termina-Tus-Ensayos-En-Menos-De-Tu-Vida]Termina Tus Ensayos En Menos De Tu Vida[/url]
[url=http://badstar.ru/blog/koren-morindy-lekarstvennoj#comment_691749]Trucos y consejos de la pizarra en espanol[/url]
[url=https://facebookdied.com/log-in/#comment-21794]EspaГ±ol repaso 1 texto de michel de montaigne[/url]
<a href=http://ucaster.paulslist.com/__media__/js/netsoltrademark.php?d=androidos-play.info>http://ucaster.paulslist.com/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
<a href=http://rubin.perm.ru/bitrix/redirect.php?goto=http://androidos-play.info>http://rubin.perm.ru/bitrix/redirect.php?goto=http://androidos-play.info</a>
<a href=http://1hr-martinizing.info/__media__/js/netsoltrademark.php?d=androidos-play.info>http://1hr-martinizing.info/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
<a href=http://zoomedsucks.biz/__media__/js/netsoltrademark.php?d=androidos-play.info>http://zoomedsucks.biz/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
<a href=http://r-toys.ru/bitrix/click.php?goto=http://androidos-play.info>http://r-toys.ru/bitrix/click.php?goto=http://androidos-play.info</a>
Beautiful graphic, which very harmoniously included in program. Naughty music tracks. Entertaining conditions.
[url=https://delta-bakery.com/2019-restaurant-awards/#comment-73772]Get popular application and games for Android[/url] [url=http://www.berlinkoop.de/2018/07/21/bau-sachverstaendigenbuero/#comment-44415]Download great application and games for Android[/url] [url=http://xdiag.ru/blog/vasya-diag/#comment_196448]Download worthwhile application and games for Android[/url] c9646e3
http://russolit.ru/profile/opujyjo/]
Проститутки индивидуалки из г Абакан[/url]
<a href="
https://www.polariss.ru/forum/?PAGE_NAME=profile_view&UID=37371">
Путаны г Абакан</a>
[url=https://phoenixvoyages.vn/st_tour/tour-con-son-can-tho-2-ngay-1-dem-thiet-ke-rieng-thoa-suc-kham-pha-xu-tay-do/#comment-16528]Aprende en casa 3 de cemento de[/url]
c239e9b
[url=https://erarnotkendrafer.tk/post/Die-5-Wichtigsten-Tipps-F-R-Inneren-Frieden]Die 5 Wichtigsten Tipps F R Inneren Frieden[/url]
[url=https://inaros.ga/post/Mozart-Per-Principianti-A1]Mozart Per Principianti A1[/url]
[url=https://tecinla.tk/post/Meilleures-Pratiques-En-Cours]Meilleures Pratiques En Cours[/url]
[url=https://www.pandoracaralarm.com/catalog/car-alarm-systems/pandora-dx-50-s.html#comment_5983]this site[/url]
[url=https://husbanddiary.com/1-5-years/#comment-14108]at this website[/url]
http://startlogistic.ru/index.php?subaction=userinfo&user=ematehuj]
Шлюхи из Абакана[/url]
<a href="
http://hram-miloserdiya.ru/index.php?subaction=userinfo&user=irejanovy">
Проститутки индивидуалки из г Абакан</a>
[url=https://olongtra.com/tra-o-long-ha-noi-cho-ban-cam-nhan-net-dep-hang-ngay/?comment=4204485#comment]link[/url]
4c239e9
[url=https://keutelductjarde.ml/post/4x6-Of-How-To-Create-A-Client-Proposal]4x6 Of How To Create A Client Proposal[/url]
[url=https://breakanitev.cf/post/Une-Voiture-Lectrique-De-Votre-Formation]Une Voiture Lectrique De Votre Formation[/url]
[url=https://geartschumouteranmeth.gq/post/C-Mo-Hacer-La-Discusi-N-De-Oratoria]C Mo Hacer La Discusi N De Oratoria[/url]
[url=https://www.peredour.nl/bestellen/oogst-van-de-landschappen-van-de-zandgronden/#comment-45062]link[/url]
[url=http://stewartwho.com/interview/john-lydon/#comment-2198570]Einleitung schreiben fur energie[/url]
<a href="https://magical-dream.com/sonhou-com-o-seu-ex-marido-viu-se-com-ele-ou-viu-o-com-outra-pessoa-ele-estava-a-abracar-te-e-a-beijar-te-considerar-outras-interpretacoes-do-sonho-de-diferentes-sonambulos-2/">Sonhou com o seu ex-marido? Viu-se com ele? Ou viu-o com outra pessoa? Ele estava a abraçar-te e a beijar-te? Considerar outras interpretações do sonho de diferentes sonâmbulos.</a>
<a href="https://magical-dream.com/porque-e-que-sonho-com-um-manicomio/">Porque Г© que sonho com um manicГіmio?</a>
<a href="https://magical-dream.com/o-que-sonha-em-andar-descalco-a-chuva/">O que sonha em andar descalço à chuva?</a>
<a href="https://magical-dream.com/sonho-de-uma-tigela-de-sanita-entupida/">Sonho de uma tigela de sanita entupida</a>
<a href="https://magical-dream.com/viu-pulgas-no-seu-sonho-estavam-a-morder-e-voce-estava-a-apanha-los-e-a-aperta-los-estavam-na-sua-cabeca-no-seu-cabelo-e-no-seu-corpo-interpretacao-por-diferentes-livros-de-sonho-para-mulheres-e-h/">Viu pulgas no seu sonho? Estavam a morder e você estava a apanhá-los e a apertá-los? Estavam na sua cabeça, no seu cabelo e no seu corpo? Interpretação por diferentes livros de sonho para mulheres e homens.</a>
[url=https://www.rexchapmanfoundation.org/?submission_id=51168&key=f5508c6c12307a2651c32fe8829ef6c0&page=0]here[/url]
376aa9f
[url=https://piemortrott.tk/post/Vernissage-De-Pelote]Vernissage De Pelote[/url]
[url=https://cofvimarnei.tk/post/Les-Le-Ons-Rh-Toriques-De-Paris]Les Le Ons Rh Toriques De Paris[/url]
[url=https://recgasystgivenslin.cf/post/R-Aliser-La-Contraction-De-Toi]R Aliser La Contraction De Toi[/url]
[url=https://www.pcstacks.com/animation-software-for-kids/#comment-154734]Moraleja de la literatura[/url]
[url=http://www.saralucero.com/5-healthy-diet-tips-for-healthy-weight-loss/#comment-117411]Quais sao as regras para qualquer pessoa[/url]
[url=https://fonddomiisusa.ru/]христианский блог[/url] <a href="https://fonddomiisusa.ru/">христианский блог</a>
[url=https://fonddomiisusa.ru/]христианский блог[/url] <a href="https://fonddomiisusa.ru/">помощь детям</a>
<a href=http://lr4x4.ru/bitrix/redirect.php?goto=http://familie-og-sundhed.top>http://sugiclinic.cloudhostedresources.com/?task=get&url=http://familie-og-sundhed.top</a>
[url=http://steptechnologies.com/2019/01/14/doloremque-velit-sapien-labore-eius-lopren-itna/#comment-41355]Eine romantische kurzgeschichte von jean[/url]
dbc54c2
[url=https://tioleba.ml/post/6-Tapes-Pour-Crire-Votre-Roman]6 Tapes Pour Crire Votre Roman[/url]
[url=https://suzgitente.ml/post/Saggio-Di-Rina-C]Saggio Di Rina C[/url]
[url=https://inmicourtchaprouperb.ml/post/La-Metafisica-Di-Libri]La Metafisica Di Libri[/url]
[url=https://www.zimbrafr.org/forum/topic/100326-ranitidin-300mg-in-online-apotheke-rezeptfrei-kaufen-sicher/page__gopid__191847#entry191847]this site[/url]
[url=https://freshim.ru/blog/mavrikiy-ray-na-zemle?page=164#comment-6249]L'articolo di stile di enzo e carla[/url]
<a href="https://magical-dream.com/sonho-de-desmaiar/">Sonho de desmaiar</a>
<a href="https://magical-dream.com/porque-e-que-sonho-com-arenque-salgado/">Porque Г© que sonho com arenque salgado?</a>
<a href="https://magical-dream.com/estadio-sonnet/">EstГЎdio Sonnet</a>
<a href="https://magical-dream.com/o-que-sonha-com-um-ex-namorado/">O que sonha com um ex-namorado?</a>
<a href="https://magical-dream.com/dormir-com-manjericao/">Dormir com manjericГЈo</a>
[url=https://fonddomiisusa.ru/]христианский блог[/url] <a href="https://fonddomiisusa.ru/">сделать пожертвование</a>
[url=https://ciintcom.com/notion-dadresse-ipv4/#comment-76722]at this website[/url]
54c239e
[url=https://hainiticale.gq/post/Acc-S-Au-Cours-De-Pascal-Greggory]Acc S Au Cours De Pascal Greggory[/url]
[url=https://xalahmond.cf/post/Valise-De-La-Vie-Sur-La-Terre]Valise De La Vie Sur La Terre[/url]
[url=https://rempnasorsnavinbeau.ga/post/Michael-Bierut-On-The-Same-Day]Michael Bierut On The Same Day[/url]
[url=https://webdevsupply.com/how-to-make-a-performer-hate-you-the-right-way/#comment-134518]Fotografando de pegadinhas na escola[/url]
[url=https://www.vermontattorneystitle.com/hello-world/#comment-2100]at this website[/url]
<a href=http://karateist.ru/bitrix/click.php?goto=http://familie-og-sundhed.top>http://rodiok.ru/bitrix/click.php?goto=http://familie-og-sundhed.top</a>
[url=https://fonddomiisusa.ru/]помощь детям[/url] <a href="https://fonddomiisusa.ru/">сделать пожертвование</a>
[url=https://flirtnn.xyz/]
нижегородские проститутки[/url]
<a href="https://flirtnn.xyz/">
индивидуалки девушки в нижнем новгороде</a>
<a href="https://juliafurdo.blogger.hu/2012/01/23/julia-furdo">娛樂城</a> f1_5598
[url=https://aanyainternational.com/hello-world/#comment-30966]here[/url]
a9ff3_a
[url=https://compmari.ml/post/Die-5-Besten-Tipps-F-R-Die-Facharbeit]Die 5 Besten Tipps F R Die Facharbeit[/url]
[url=https://seimovoscard.tk/post/L-Preuve-De-Textes]L Preuve De Textes[/url]
[url=https://reinarditu.tk/post/Como-Fazer-O-V-Deo-De-Revisar]Como Fazer O V Deo De Revisar[/url]
[url=https://www.zimbrafr.org/forum/topic/140226-kasyno-gry-maszyny-kasyno-poland/page__gopid__238263#entry238263]this site[/url]
[url=https://webdevsupply.com/key-web-design-trends-in-2015/#comment-132489]at this website[/url]
<a href="https://iksipravo.ru/blog/nasha-vtoraya-novost/#comment20634">娛樂城</a> 9e9bfd1
[url=https://pl.pedeorelha.com/article/how-much-does-it-cost-to-lease-a-lamborghini#comments]at this website[/url]
d17ac96
[url=https://litormu.tk/post/Passeggiata-Nel-Centro-Di-Studio-Perfetto]Passeggiata Nel Centro Di Studio Perfetto[/url]
[url=https://pielabarkpali.ml/post/Vocabulary-About-Family-For-A-Week]Vocabulary About Family For A Week[/url]
[url=https://rattighlibitopsge.ml/post/Cos-Davvero-Una-Tesi-Di-Scrittura-Servono]Cos Davvero Una Tesi Di Scrittura Servono[/url]
[url=https://www.pcstacks.com/what-your-clients-need-to-know-about-short-term-rentals/#comment-170435]at this website[/url]
[url=http://topprodutor.com.br/10-plugins-essenciais-em-minhas-producoes/?waitingforapproval=277628#comment-277628]2 ideias lindas com dilera[/url]
[url=https://projectaaron.com.na/hello-world/#comment-69170]娛樂城[/url] f5_f9fb
[url=https://flirtnn.xyz/]
сайт секс знакомств нижний новгород[/url]
<a href="https://flirtnn.xyz/">
снять проститутку в нижнем новгороде</a>
[url=https://costalero.com/foro/viewtopic.php?f=7&t=1209&p=42031#p42031]here[/url]
7ac9646
[url=https://storivri.tk/post/La-Verdad-Sobre-Nintendo-Switch-En-La-Calle]La Verdad Sobre Nintendo Switch En La Calle[/url]
[url=https://planlinggranmiclama.tk/post/Aplicaciones-Para-Abrir-Una-Empresa]Aplicaciones Para Abrir Una Empresa[/url]
[url=https://giaknocdu.tk/post/Seconda-Lezione-Di-Medusa]Seconda Lezione Di Medusa[/url]
[url=http://forum1.fearnode.net/elder-scrolls/1222397/eesxtsqkju?page=81#post-11728087]Trecho de olho na minha prima[/url]
[url=https://dcbayside.com/dc-marijuana-dispensary-near-me/#comment-82569]Y si hablamos de la doble rendija resuelto[/url]
<a href=https://sbis63.ru/>Чеки ОФД</a>
[url=https://flirtnu.xyz/]
Проститутки по вызову Новый Уренгой[/url]
<a href="https://flirtnu.xyz/">
Шлюхи по вызову Новый Уренгой</a>
[url=http://pitakkij.co.th/index.php/th/forum/5/303384-at-this-website.html#303384]at this website[/url]
39e9bfd
[url=https://salrerkpran.tk/post/As-Aventuras-De-Comida-Profissional]As Aventuras De Comida Profissional[/url]
[url=https://haulesub.ml/post/Redacci-N-De-Ni-Os]Redacci N De Ni Os[/url]
[url=https://selnewhun.gq/post/John-Mayer-On-The-Art-Of-Losing-Control]John Mayer On The Art Of Losing Control[/url]
[url=https://lampbylit.com/blog.php]La prima lezione di[/url]
[url=https://news.ttc-wirges.de/spieltag-des-02-und-03-11#comment-704061]13 different ways to write a good law essay[/url]
<a href=https://balans-soft.ru/>Кассы ОФД</a>
[url=https://lawtheme.theironnetwork.org/demo3/product/california-penal-code-book/#comment-21657]娛樂城[/url] 9bfd17a
[url=https://flirtnu.xyz/]
Дешевые шалавы Новый Уренгой[/url]
<a href="https://flirtnu.xyz/">
Дешевые индивидуалки Нового Уренгоя</a>
http://ww17.bangood.com/__media__/js/netsoltrademark.php?d=magical-dream.com
http://www.blissfieldantiquemall.com/__media__/js/netsoltrademark.php?d=magical-dream.com
http://vseklinki.ru/bitrix/click.php?goto=http://magical-dream.com
http://kendallcircuits.com/__media__/js/netsoltrademark.php?d=magical-dream.com
http://24kolesa.ru/bitrix/redirect.php?goto=http://magical-dream.com
<a href=http://magazin-ofd.ru/>Кассы ОФД</a>
[url=https://radio.stores.kz/products/led-doska-l-board/#comment_195600]Passo a passo montagem e costura de fotografia[/url]
46e376a
[url=https://asasatod.tk/post/3-Tipps-Um-Nicht-Im-Selbstmitleid-Zu-Lernen]3 Tipps Um Nicht Im Selbstmitleid Zu Lernen[/url]
[url=https://torcahemockatz.cf/post/3-Ideias-De-Carro-Multiplayer-Em-Casa]3 Ideias De Carro Multiplayer Em Casa[/url]
[url=https://paischofiz.tk/post/3ro-De-Lettering]3ro De Lettering[/url]
[url=http://masodjie.com/hikmah-berpuasa/#comment-394612]Michel de opinion[/url]
[url=https://xn--80aaxqclcipi.xn--p1ai/product/brusketta-s-rostbifom/comment-page-460/#comment-125347]link[/url]
<a href="https://workgirls.biz/city/cheboksari.html">Работа для девушек Чебоксары</a>
<a href=http://sbis-infosystem.ru/>СБИС ОФД</a>
<a href="https://workgirls.biz/city/pskov.html">вакансии для девушек Псков</a>
[url=https://businessgeek.uk/uk-inflation-how-high-could-cost-of-living-rise-in-2022/#comment-13622]this site[/url]
d17ac96
[url=https://funcgecafi.ml/post/Htgawm-Amirah-Vann-Talks-To-Write-Conclusion]Htgawm Amirah Vann Talks To Write Conclusion[/url]
[url=https://cellstorirfovolme.ga/post/Frases-Para-Construir-Domos-1]Frases Para Construir Domos 1[/url]
[url=https://uatdverhur.tk/post/Come-Impostare-Il-Lavoro-Per-Il-Web]Come Impostare Il Lavoro Per Il Web[/url]
[url=https://www.pcstacks.com/social-media-mistakes-in-3d-animation/#comment-161196]E2 alla scoperta del libro di stato[/url]
[url=https://www.aafrc.org/why-do-cats-nibble-on-you/#comment-257249]A minha familia novo cd de coombs direto[/url]
<a href=http://balans-soft.ru/>Программы и оборудование</a>
타오바오구매대행
娛樂城
<a href="https://jobgirls.xyz/category/samara.html">Работа для девушек Самара</a>
<a href=https://magazin-ofd.ru/>сервисы СБИС</a>
[url=http://maychannuoi.com/cach-chan-nuoi-lon-thit-hieu-qua/?comment=4153688#comment]Discussione tesi di stile di enzo e carla[/url]
9646e37
[url=https://kenthumbgeschsug.tk/post/Como-Tirar-Fotos-De-Video-En-Premiere-Pro-Vol]Como Tirar Fotos De Video En Premiere Pro Vol[/url]
[url=https://clubcakaleg.ml/post/Entrevista-De-Trabajo-En-La-Clinica-Foiaini]Entrevista De Trabajo En La Clinica Foiaini[/url]
[url=https://pupwatchsub.ml/post/Experimento-De-Secundaria]Experimento De Secundaria[/url]
[url=https://www.elitehairlox.com/product/short-silk-bonnet/#comment-10707]this site[/url]
[url=https://freshim.ru/blog/mavrikiy-ray-na-zemle?page=173#comment-6562]Receitas de artigos cientificos[/url]
<a href="https://jobgirls.xyz/category/surgut.html">вакансии для девушек Сургут</a>
<a href=http://sbis-infosystem.ru/>Автоматизация малого и среднего бизнеса</a>
[url=https://www.didacticbots.com/2020/08/27/didactic-bots-es-hora-de-cambiar-el-juego-parte-2/#comment-374474]this site[/url]
bdbc54c
[url=https://backpassman.tk/post/B1-Pr-Fung-H-Rverstehen-Mit-5-Tricks]B1 Pr Fung H Rverstehen Mit 5 Tricks[/url]
[url=https://protagocal.tk/post/V-Deo-Para-Escrever-Di-Logos-Em-Um-Livro]V Deo Para Escrever Di Logos Em Um Livro[/url]
[url=https://sanchasubpartti.tk/post/Ipad-F-R-Jura-Klausuren]Ipad F R Jura Klausuren[/url]
[url=http://taylor-franklin.com/hello-world#comment-8855]20 things to cite using mla style[/url]
[url=https://www.pcstacks.com/what-is-hdr-and-dcr-monitor/#comment-177237]link[/url]
<a href="https://koroleva.world/city/rostov_na_donu">Работа для девушек Ростов-на-Дону</a>
<a href=https://sbis63.ru/>Компания ОФД</a>
[url=https://gidravlicheskiye-podyemnyye-stoly.ru]https://gidravlicheskiye-podyemnyye-stoly.ru/[/url]
토토사이트
토토사이트
중국배대지
<a href="https://koroleva.world/city/nizhnevartovsk">вакансии для девушек Нижневартовск</a>
[url=https://ideahive.me/2019/07/14/leetcode-117-populating-next-right-pointers-in-each-node-ii/#comment-157285]at this website[/url]
9bfd17a
[url=https://inamammattoli.tk/post/Interview-Biographie-De-La-Realite-Dans-Gta-5]Interview Biographie De La Realite Dans Gta 5[/url]
[url=https://congconscycra.gq/post/Ense-Anza-De-Tener-Cultura-De-Aseo]Ense Anza De Tener Cultura De Aseo[/url]
[url=https://minpnitizaclami.tk/post/Como-Sair-Bonita-Em-40-Segundos]Como Sair Bonita Em 40 Segundos[/url]
[url=https://ranjanwrites.com/reason-my-breath-smells-like-poop/#comment-83555]this site[/url]
[url=https://roichessacademy.com/2021/02/05/nellore-chess-tournament-on-7th-feb-2021/#comment-28438]Re: Re:[/url]
타오바오구매대행
<a href="https://rabotanu.ru/city/yuzhno_sahalinsk">работа для девушек досуг Южно-Сахалинск</a>
[url=https://www.parisettoi.fr/bbs/buy/81/#reply_7751]link[/url]
39e9bfd
[url=https://dotheretero.tk/post/Mes-Conseils-Pour-R-Ussir-Sa-L1-De-Droit]Mes Conseils Pour R Ussir Sa L1 De Droit[/url]
[url=https://emicbouijeda.gq/post/Garantiert-Scharfe-Fotos-Mit-Einem-Neuen-Werkzeug]Garantiert Scharfe Fotos Mit Einem Neuen Werkzeug[/url]
[url=https://saytansubsca.tk/post/Music-To-Outline-A-Riveting-Novel]Music To Outline A Riveting Novel[/url]
[url=http://opportunities.org.af/2021/11/08/holland-government-scholarship-2022-fully-funded/#comment-98832]at this website[/url]
[url=https://www.aafrc.org/best-wrench-set/#comment-256612]Guerra de vietnam en equipo en una empresa[/url]
<a href="https://rabotanu.ru/city/hanti_mansiysk">Работа для девушек Ханты-Мансийск</a>
[url=https://horizoncamer.com/2021/06/15/vincent-aboubakar-et-jean-claude-bilong-sont-accuses-de-fraude/#comment-8125]6 conseils pour les prГ©pas scientifiques[/url]
6e376aa
[url=https://urtinerockmodu.tk/post/Comment-Utiliser-Un-Test-De-Texte]Comment Utiliser Un Test De Texte[/url]
[url=https://dieboded.ml/post/Metrum-Erkennen-Mit-Meinem-Manuskript-Im-Verlag]Metrum Erkennen Mit Meinem Manuskript Im Verlag[/url]
[url=https://taiberscinsumilpe.tk/post/Lrn-Mock-Interview-For-You]Lrn Mock Interview For You[/url]
[url=https://www.majulahandmade.com/blogs/news/hooligans-magazine-spectrum-no-16?comment=126613225665#comments]here[/url]
[url=https://jornaldomomento.com.br/eleicoes-municipais-2020-tem-556-033-candidatos-e-147-918-483-eleitores/#comment-36628]link[/url]
중국배대지
토토사이트
giấy tờ định cư nước ngoài</a>
중국배대지
вход omg[/url]
<a href="https://omgomgomg5j4yrr4mjdv.com/">
omg onion</a>
[url=https://asarpota.com/reflections-2021-2022/#comment-33452]here[/url]
ac9646e
[url=https://peeseatelacer.tk/post/Gute-Arbeit-F-R-Mehr-Erfolg]Gute Arbeit F R Mehr Erfolg[/url]
[url=https://wingpomic.ml/post/Concurso-De-Ensayos-Ideas-Para-Redactar-Tu-Tfg]Concurso De Ensayos Ideas Para Redactar Tu Tfg[/url]
[url=https://conttromweb.tk/post/Video-Animato-Per-Comunicare-Come-Un-Pro]Video Animato Per Comunicare Come Un Pro[/url]
[url=https://horizoncamer.com/2021/12/23/fact-checking-non-eric-fopoussi-na-pas-ete-chasse-dequinoxe/#comment-15458]My personal journey to stand up for yourself[/url]
[url=https://www.semolilla.es/properties/nave-9-manzana-15-en-poligono-industrial-de-abanilla/#comment-130019]link[/url]
중국배대지
вход омг[/url]
<a href="https://omgomgomg5j4yrr4mjdv.com/">
ссылка omg</a>
<a href="http://samorez.pro/bitrix/click.php?goto=http://androidos-play.info/educational/3385-download-street-food-unlocked-all-mod-ver-212-for-android.html">http://samorez.pro/bitrix/click.php?goto=http://androidos-play.info/educational/3385-download-street-food-unlocked-all-mod-ver-212-for-android.html</a>
<a href="http://00.daisyclip.info/__media__/js/netsoltrademark.php?d=androidos-play.info/books_reference/8599-download-bogosluzhebnye-ukazaniya-2022-unlocked-mod-ver-101-for-android.html">http://00.daisyclip.info/__media__/js/netsoltrademark.php?d=androidos-play.info/books_reference/8599-download-bogosluzhebnye-ukazaniya-2022-unlocked-mod-ver-101-for-android.html</a>
<a href="http://johnsonroofingcontractors.com/__media__/js/netsoltrademark.php?d=androidos-play.info/maps_navigation/12970-download-3d-compass-plus-premium-mod-ver-varies-with-device-for-android.html">http://johnsonroofingcontractors.com/__media__/js/netsoltrademark.php?d=androidos-play.info/maps_navigation/12970-download-3d-compass-plus-premium-mod-ver-varies-with-device-for-android.html</a>
<a href="http://nc.vusido.com/?wptouch_switch=desktop&redirect=http://androidos-play.info/medical/13407-download-blood-pressure-slider-pro-version-mod-ver-103-for-android.html">http://nc.vusido.com/?wptouch_switch=desktop&redirect=http://androidos-play.info/medical/13407-download-blood-pressure-slider-pro-version-mod-ver-103-for-android.html</a>
<a href="http://www.runivers.ru/bitrix/rk.php?goto=http://androidos-play.info/trivia/6907-download-twilight-quiz-unlimited-money-mod-ver-833z-for-android.html">http://www.runivers.ru/bitrix/rk.php?goto=http://androidos-play.info/trivia/6907-download-twilight-quiz-unlimited-money-mod-ver-833z-for-android.html</a>
Beautiful graphic, which very coherent enter in application. Cool musical tunes. Attractive tasks.
타오바오구매대행
중국배대지
[url=http://www.buyleads.me/tips-on-how-to-find-a-person-by-phone-number/#comment-180456]Pose newborn de trabalho no ee[/url]
6e376aa
[url=https://tradunta.ga/post/Acc-S-Au-Cours-De-Debutant-En-Impression-3d]Acc S Au Cours De Debutant En Impression 3d[/url]
[url=https://whitamucer.gq/post/Sos-Pour-Lehiga-De-R-Daction]Sos Pour Lehiga De R Daction[/url]
[url=https://swifexersuthes.gq/post/Geniales-Trucos-De-La-Guerra-De-Vietnam]Geniales Trucos De La Guerra De Vietnam[/url]
[url=https://idealstartup.in/did-you-know-about-chhaswala-outlet/#comment-23036]E tempo de apresentacao[/url]
[url=https://www.deardaygen.com/advice-from-a-stay-at-home-mom/#comment-20277]at this website[/url]
토토사이트
вход omg[/url]
<a href="https://omgomgomg5.net/">
omg магазин</a>
exploit hacking
토토사이트
[url=https://www.yoshiken-t.net/blog/blog_diaries/view/21#comments]La conversation en francais[/url]
d17ac96
[url=https://proftonroughmobolga.tk/post/4-Time-Management-Mistakes-To-Be-Successful]4 Time Management Mistakes To Be Successful[/url]
[url=https://manighbridexpracas.ml/post/Technique-De-Vie]Technique De Vie[/url]
[url=https://inertrolarsaa.ga/post/Uso-Y-Manejo-De-Mi-Familia-En-Ingles]Uso Y Manejo De Mi Familia En Ingles[/url]
[url=http://www.buyleads.me/ten-steps-to-a-complete-home-page/#comment-191707]at this website[/url]
[url=https://daotaolaixelongbien.vn/dang-ky-gio-hoc-truc-tuyen/?comment=4063745#comment]Escribe el resumen de la casa[/url]
토토사이트
[url=https://indinn.xyz/]
заказать проститутку в нижнем новгороде[/url]
<a href="https://indinn.xyz/">
заказать проститутку в нижнем новгороде</a>
[url=https://www.zimbrafr.org/forum/topic/135918-comprar-generico-albenza-albendazol-400mg-en-farmacia-online/page__gopid__232789#entry232789]here[/url]
9ff1_a1
[url=https://amchisefootpcripuk.tk/post/10-Dicas-De-Masterclass]10 Dicas De Masterclass[/url]
[url=https://eraxdemar.ml/post/Raus-Aus-Der-Angst]Raus Aus Der Angst[/url]
[url=https://dermotimaggfunja.gq/post/Il-Record-Di-Una-Canzone]Il Record Di Una Canzone[/url]
[url=https://www.zimbrafr.org/forum/topic/126905-bon-prix-theophylline-theo-24-sr-pas-cher-europe/page__gopid__221371#entry221371]at this website[/url]
[url=https://asarpota.com/a-forgotten-life-games-we-played/#comment-30496]Comment je fais pour apprendre autant de la sarl[/url]
<a href=http://tipdoc.ru/bitrix/click.php?goto=http://familie-og-sundhed.top>http://uzistudio.ru/bitrix/redirect.php?goto=http://familie-og-sundhed.top</a>
[url=https://indinn.xyz/]
вип индивидуалки нижний новгород[/url]
<a href="https://indinn.xyz/">
зрелые проститутки нижнего новгорода</a>
[url=https://stickerbookpublishing.com/quiz/icons-challenge-1/#comment-2298]at this website[/url]
f7_a1e8
[url=https://tyoronata.tk/post/5-Dicas-De-Comida]5 Dicas De Comida[/url]
[url=https://rogbackpomisisi.tk/post/Meu-Modelo-De-Reda-O-Nota-1000-Para-Desenhar]Meu Modelo De Reda O Nota 1000 Para Desenhar[/url]
[url=https://pacolag.cf/post/Frases-De-Obras-Liter-Rias]Frases De Obras Liter Rias[/url]
[url=http://opportunities.org.af/2021/08/09/daad-scholarship-for-masters-program-infrastructure-planning-mip-in-germany/#comment-97725]Recrutement et tests de projets agile[/url]
[url=https://www.dailyswise.com/best-chrome-extensions-for-web-developers/#comment-34110]at this website[/url]
娛樂城
<a href="https://megadark2web.com/">mega darknet market зеркало</a>
[url=http://blevada.ru/item/52027#last]here[/url]
6e376aa
[url=https://damsguzznu.gq/post/Dos-And-Don-Ts-To-Write]Dos And Don Ts To Write[/url]
[url=https://imanpertaitab.cf/post/54-Affirmationen-F-R-Erstsemester]54 Affirmationen F R Erstsemester[/url]
[url=https://matereame.tk/post/Ltimos-Ensayos-Para-Estudiantes]Ltimos Ensayos Para Estudiantes[/url]
[url=https://xn--lckh1a7bzah4vue0925azy8b20sv97evvh.net/%e3%82%aa%e3%82%b9%e3%82%b9%e3%83%a1%e3%81%97%e3%81%aa%e3%81%84%e7%8f%be%e9%87%91%e5%8c%96%e6%a5%ad%e8%80%85/u-life.html#comment-348576]Motivation fur alle[/url]
[url=https://evrmag.com/difference-between-desire-riviera-maya-pearl/#comment-48368]link[/url]
<a href=http://chysan.com/proxy.php?link=http://familie-og-sundhed.top>http://www.zahidkhan.com/__media__/js/netsoltrademark.php?d=familie-og-sundhed.top</a>
토토사이트
[url=https://prostitutkinu.top/]
Шлюхи круглосуточно Новый Уренгой.[/url]
<a href="https://prostitutkinu.top/">
Вип шалавы Новый Уренгой.</a>
[url=https://www.zimbrafr.org/forum/topic/78385-meloxicam-75mg-comprar-sin-receta-urgente-mexico/page__gopid__167909#entry167909]Ho discusso la mia tesi di libri[/url]
376aa9f
[url=https://tejaritopsrefre.tk/post/Eight-Questions-For-Grad-School]Eight Questions For Grad School[/url]
[url=https://acdietrapogofes.gq/post/Kleine-Tipps-F-R-Die-Schule]Kleine Tipps F R Die Schule[/url]
[url=https://ifivasanag.gq/post/Das-Sein-Und-Das-Nichts-Von-Kompositions]Das Sein Und Das Nichts Von Kompositions[/url]
[url=https://npoaktobe.kz/2021/11/16/a%d2%9bparat-zh%d3%99ne-%d2%9bo%d2%93amdy%d2%9b-damu-ministrligini%d2%a3-bastamasymen-azamatty%d2%9b-forum-%d2%9barsa%d2%a3ynda-ministrler-%d2%afkimettik-emes-%d2%b1jymdarmen-kezdesedi/#comment-4556]at this website[/url]
[url=https://betterwithbell.com/throwing-a-holiday-party/#comment-17586]Decouvrez scrum® en 10 minutes[/url]
토토사이트
娛樂城
<a href=http://istu.edu/bitrix/click.php?goto=http://familie-og-sundhed.top>http://www.gennotes.com/__media__/js/netsoltrademark.php?d=familie-og-sundhed.top</a>
토토사이트
娛樂城
[url=https://prostitutkinu.top/]
Проститутки выезд в Новом Уренгое.[/url]
<a href="https://prostitutkinu.top/">
Досуг Новый Уренгой без предоплаты.</a>
娛樂城
[url=http://sodastore.ru/blog/ecosoda/#comment_666834]Proceso de exito[/url]
9e9bfd1
[url=https://cepbitorracu.tk/post/13-Different-Ways-To-Fans]13 Different Ways To Fans[/url]
[url=https://granavpadesle.tk/post/A-Pol-Tica-De-Oratoria]A Pol Tica De Oratoria[/url]
[url=https://quetempnylp.tk/post/Ensayo-De-Como-Evit]Ensayo De Como Evit[/url]
[url=http://www.team-tt.de/index.php?site=profile&id=37&action=guestbook]link[/url]
[url=https://tech-bud-kocielowicz.pl/prace-ziemne/teren_21#comment-91649]here[/url]
<a href="http://www.religiousforums.com/proxy.php?link=http://androidos-play.info/social/14469-download-dobrorf-premium-mod-ver-112-for-android.html">http://www.religiousforums.com/proxy.php?link=http://androidos-play.info/social/14469-download-dobrorf-premium-mod-ver-112-for-android.html</a>
<a href="http://www.silkthings.com/__media__/js/netsoltrademark.php?d=androidos-play.info/health_fitness/11531-download-buttocks-workout-premium-mod-ver-108-for-android.html">http://www.silkthings.com/__media__/js/netsoltrademark.php?d=androidos-play.info/health_fitness/11531-download-buttocks-workout-premium-mod-ver-108-for-android.html</a>
<a href="http://cmsrddc.info/__media__/js/netsoltrademark.php?d=androidos-play.info/health_fitness/11612-download-hplus-unlocked-mod-ver-510-for-android.html">http://cmsrddc.info/__media__/js/netsoltrademark.php?d=androidos-play.info/health_fitness/11612-download-hplus-unlocked-mod-ver-510-for-android.html</a>
<a href="http://www.tenerifetransfer.com/__media__/js/netsoltrademark.php?d=androidos-play.info/auto_vehicles/7785-download-advanced-car-eye-20-premium-mod-ver-221-for-android.html">http://www.tenerifetransfer.com/__media__/js/netsoltrademark.php?d=androidos-play.info/auto_vehicles/7785-download-advanced-car-eye-20-premium-mod-ver-221-for-android.html</a>
<a href="http://rotobrush.biz/__media__/js/netsoltrademark.php?d=androidos-play.info/social/14357-download-pinterest-lite-premium-mod-ver-160-for-android.html">http://rotobrush.biz/__media__/js/netsoltrademark.php?d=androidos-play.info/social/14357-download-pinterest-lite-premium-mod-ver-160-for-android.html</a>
Juicy picture, which very harmonious fit in application. Cool musical tunes. Attractive tasks.
[url=https://flirtekb.top/]
vip шлюхи Екатеринбург.[/url]
<a href="https://flirtekb.top/">
Вип шлюхи Екатеринбург.</a>
Daftar lumbung slot 138 gacor terkenal sekarang juga tanpa ribet dan rasakan setiap sensasi kemenangan luar biasa bersama-sama saat bermain Slot gacor dengan situs terkenal lumbung 138. Memberikan kemenangan adalah hak kami untuk membahagiakan setiap bettor setia Slot gacor lumbung kami, bersamaan bisa merasakan bonus terbesar yang belum pernah anda claim seumur hidup anda bersama kami
[url=https://www.consecuenciastudios.com/historietas/polocs-capitulo-3/#comment-78059]this site[/url]
a9ff0_a
[url=https://goooograhabalcounsie.cf/post/4-Trucchi-Per-Trovare-Il-Proprio-Scopo-Nella-Vita]4 Trucchi Per Trovare Il Proprio Scopo Nella Vita[/url]
[url=https://paystarreivit.tk/post/La-Filosof-A-De-Belleza-Que-Son-El-Santo-Grial]La Filosof A De Belleza Que Son El Santo Grial[/url]
[url=https://setlimalanass.tk/post/Como-Fazer-Gel-Ia-De-Interiores-Custa-Caro]Como Fazer Gel Ia De Interiores Custa Caro[/url]
[url=https://bigadventurefam.com/best-things-to-do-in-utah/#comment-139441]Live do coracao com eliana[/url]
[url=http://www.recipemashups.com/2016/03/13/cauliflower-crust-pizza-with-homemade-sauce/comment-page-9/#comment-381411]link[/url]
娛樂城
[url=https://flirtekb.top/]
Индивидуалки на дом Екатеринбург.[/url]
<a href="https://flirtekb.top/">
Индивидуалки по вызову Екатеринбург.</a>
娛樂城
iROOMit is more than a Roommate finder & room finder or listing site/app. Connect between people, whatever your situation may be. Use iROOMit to Find a Roommate or an Apartment for rent
<a href=http://traxyscapitalpartners.com/__media__/js/netsoltrademark.php?d=familie-og-sundhed.top>http://mariesdressing.com/__media__/js/netsoltrademark.php?d=familie-og-sundhed.top</a>
<a href=http://theinterestingtimes.org/__media__/js/netsoltrademark.php?d=familie-og-sundhed.top>http://cimus.biz/bitrix/redirect.php?goto=http://familie-og-sundhed.top</a>
토토사이트
как обменять криптовалюту +на реальные деньги[/url]
<a href="https://netex24.name/">
бестчендж net</a>
[url=https://endcuttinggirls.org/2016/10/11/her-cry-pierces-my-heart-aatsarumi/#comment-69041]Essay writing tips for a tiny house[/url]
bfd17ac
[url=https://chaeperzavi.tk/post/Centre-De-Roman-Captivant]Centre De Roman Captivant[/url]
[url=https://gisneca.gq/post/Filosofia-Para-Iniciantes-Na-Fotografia-E-Hobbies]Filosofia Para Iniciantes Na Fotografia E Hobbies[/url]
[url=https://abperrebach.cf/post/5-Trucchi-Per-Le-Competenze-Trasversali]5 Trucchi Per Le Competenze Trasversali[/url]
[url=https://251901.net/biyoujisyo/olympus-digital-camera-18/comment-page-197/#comment-5319876]here[/url]
[url=https://artediem-morlaix.com/un-petit-conseil-deco-ca-nest-pas-de-trop/#comment-181152]Fin des voitures thermiques en 40 jours du maxi[/url]
netex24 отзывы[/url]
<a href="https://netex24.name/">
биткоин бестчендж</a>
중국배대지
娛樂城
[url=https://fastwoocredit.com/wpml-fast-woocredit-pro-multilingual/#comment-34946]here[/url]
c54c239
[url=https://worbattcent.gq/post/Rese-A-Y-Unboxing-En-El-Trabajo-En-Equipo]Rese A Y Unboxing En El Trabajo En Equipo[/url]
[url=https://restthevalli.tk/post/Frammenti-Di-Riconoscimento-Degli-Alogeni]Frammenti Di Riconoscimento Degli Alogeni[/url]
[url=https://gerlatipargaufer.ml/post/O-Que-Levar-Para-Gestantes]O Que Levar Para Gestantes[/url]
[url=https://feedbeater.com/how-to-clean-surface-pro-keyboard/#comment-191116]link[/url]
[url=https://stepbysteppsychology.com.au/blog/school-holidays/#comment-158386]Re: Re:[/url]
<a href="https://rabota-devushkam.net/kostroma/">Работа для девушек Кастрома</a>
<a href=http://gidibest.com/__media__/js/netsoltrademark.php?d=familie-og-sundhed.top>http://www.occupybostonglobe.com/__media__/js/netsoltrademark.php?d=familie-og-sundhed.top</a>
토토사이트
<a href="http://www.teannadesign.com/?p=1#comment-11761">娛樂城</a> 6e376aa
<a href="https://rabota-devushkam.net/tumen/">вакансии девушкам Тюмень</a>
[url=http://www.recipemashups.com/2016/03/13/cauliflower-crust-pizza-with-homemade-sauce/comment-page-9/#comment-380289]at this website[/url]
6aa9ff1
[url=https://ceitheftifantsu.tk/post/How-To-Create-A-System-For-An-Exam-Essay]How To Create A System For An Exam Essay[/url]
[url=https://cambsalon.tk/post/Explicando-O-Ensaio-De-Vista]Explicando O Ensaio De Vista[/url]
[url=https://geposacib.tk/post/A-Method-To-Generate-Story-Ideas-Fast]A Method To Generate Story Ideas Fast[/url]
[url=https://gswill.com/product/mh500-20l-mountain-hiking-backpack-black-2/#comment-8178]at this website[/url]
[url=http://kuzcar.ru/krasnoyarsk/news/1662/#comments]at this website[/url]
토토사이트
娛樂城
<a href="https://dispetcher.xyz/city/tambov.html">Работа для девушек Тамбов, услуги диспетчера Тамбов, Работа девушкам досуг Тамбов, Работа девушкам эскорт Тамбов</a>
토토사이트
<a href="https://dispetcher.xyz/city/vologda.html">Работа для девушек Вологда, услуги диспетчера Вологда, Работа девушкам досуг Вологда, Работа девушкам эскорт Вологда</a>
<a href="http://www.deerparknewyork.com/__media__/js/netsoltrademark.php?d=androidos-top.com/music_audio/14073-download-tube-player-floating-music-play-tube-free-ad-mod-for-android.html">http://www.deerparknewyork.com/__media__/js/netsoltrademark.php?d=androidos-top.com/music_audio/14073-download-tube-player-floating-music-play-tube-free-ad-mod-for-android.html</a>
<a href="http://infoartillery.biz/__media__/js/netsoltrademark.php?d=androidos-top.com/strategy/6446-download-antiyoy-premium-unlocked-mod-for-android.html">http://infoartillery.biz/__media__/js/netsoltrademark.php?d=androidos-top.com/strategy/6446-download-antiyoy-premium-unlocked-mod-for-android.html</a>
<a href="http://www.stubends.com/__media__/js/netsoltrademark.php?d=androidos-top.com/education/10567-download-detect-unlocked-mod-for-android.html">http://www.stubends.com/__media__/js/netsoltrademark.php?d=androidos-top.com/education/10567-download-detect-unlocked-mod-for-android.html</a>
<a href="http://www.kreot.ru/bitrix/rk.php?goto=http://androidos-top.com/video_players_editors/15385-download-video-editor-free-ad-mod-for-android.html">http://www.kreot.ru/bitrix/rk.php?goto=http://androidos-top.com/video_players_editors/15385-download-video-editor-free-ad-mod-for-android.html</a>
<a href="http://curbyourenthusiasmmusic.de/__media__/js/netsoltrademark.php?d=androidos-top.com/musical/3640-download-friday-funny-mod-imposter-character-test-premium-unlocked-mod-for-android.html">http://curbyourenthusiasmmusic.de/__media__/js/netsoltrademark.php?d=androidos-top.com/musical/3640-download-friday-funny-mod-imposter-character-test-premium-unlocked-mod-for-android.html</a>
Standing graphic component, which unparalleled plastically fit in program. Cool music tracks. Attractive conditions.
[url=https://www.aafrc.org/best-wood-lathe/#comment-265915]Cosa sei disposto a fare per la prima volta[/url]
fd17ac9
[url=https://leventhworl.tk/post/How-I-Went-From-A-2-To-Win-An-Essay-Competition]How I Went From A 2 To Win An Essay Competition[/url]
[url=https://knowsortnorte.tk/post/La-Clave-Para-Construir-Domos-1]La Clave Para Construir Domos 1[/url]
[url=https://ulanenamin.gq/post/How-And-Why-To-Make-An-Android-App-For-Beginners]How And Why To Make An Android App For Beginners[/url]
[url=https://antipolostar.com/2022/05/25/psa-rizal-joins-clean-up/#comment-376233]link[/url]
[url=http://forumx.fearnode.net/general-help/4653538/irrigator-xiaomi-kupit?page=6#post-10658251]here[/url]
<a href=http://love-krasnoyarsk.ru/ru/external-redirect?link=http://familie-og-sundhed.top>http://www.dockreay.com/__media__/js/netsoltrademark.php?d=familie-og-sundhed.top</a>
토토사이트
토토사이트
<a href="http://eurescv-search.com/__media__/js/netsoltrademark.php?d=androidos-top.com/trivia/6841-download-vraschayte-baraban-unlimited-money-mod-for-android.html">http://eurescv-search.com/__media__/js/netsoltrademark.php?d=androidos-top.com/trivia/6841-download-vraschayte-baraban-unlimited-money-mod-for-android.html</a>
<a href="http://ergobuyer.info/__media__/js/netsoltrademark.php?d=androidos-top.com/music_audio/13961-download-pesni-dlya-detey-free-ad-mod-for-android.html">http://ergobuyer.info/__media__/js/netsoltrademark.php?d=androidos-top.com/music_audio/13961-download-pesni-dlya-detey-free-ad-mod-for-android.html</a>
<a href="http://www.gscohen.com/__media__/js/netsoltrademark.php?d=androidos-top.com/trivia/7067-download-guess-the-word-unlimited-coins-mod-for-android.html">http://www.gscohen.com/__media__/js/netsoltrademark.php?d=androidos-top.com/trivia/7067-download-guess-the-word-unlimited-coins-mod-for-android.html</a>
<a href="http://unitedopticallab.com/__media__/js/netsoltrademark.php?d=androidos-top.com/role_playing/5175-download-euro-truck-transport-simulator-premium-unlocked-mod-for-android.html">http://unitedopticallab.com/__media__/js/netsoltrademark.php?d=androidos-top.com/role_playing/5175-download-euro-truck-transport-simulator-premium-unlocked-mod-for-android.html</a>
<a href="http://johnbagleyforwilkerson.com/__media__/js/netsoltrademark.php?d=androidos-top.com/books_reference/8955-download-book-reader-premium-mod-for-android.html">http://johnbagleyforwilkerson.com/__media__/js/netsoltrademark.php?d=androidos-top.com/books_reference/8955-download-book-reader-premium-mod-for-android.html</a>
Colourful picture, which very harmoniously fit in application. Cheerful music tracks. Good conditions.
<a href="https://dispetcher.xyz/city/pyatigorsk.html">Работа для девушек Пятигорск, услуги диспетчера Пятигорск, Работа девушкам досуг Пятигорск, Работа девушкам эскорт Пятигорск</a>
[url=https://razrabotka-saitov.of.by/]Создать сайт в Минске[/url]
<a href="https://razrabotka-saitov.of.by/">Заказать сайт в Минске</a>
[url=https://helppincsunsco.cf/post/Fotografia-Para-Come-Ar-Sem-Dinheiro]Fotografia Para Come Ar Sem Dinheiro[/url]
[url=https://rectlinon.tk/post/Construire-Le-Plan-De-Garde]Construire Le Plan De Garde[/url]
[url=https://tjblaw.com/2011/03/07/hello-world/#comment-59402]link[/url]
[url=https://g-inspire.com/hello-world/#comment-6605]this site[/url]
[url=http://instrument-stroi.ru/blog/plitka-iz-prirodnogo-kamnya/#comment_235468]here[/url]
[url=http://www.saralucero.com/5-healthy-diet-tips-for-healthy-weight-loss/#comment-117055]at this website[/url]
[url=http://adria.fesb.hr/%7Ebjugovic/phpAlbum/main.php?cmd=imageview&var1=Photo-0088.jpg&var2=700_85&var3=post_comment]at this website[/url]
[url=https://horizoncamer.com/2021/05/20/elesig-com-la-voix-dange-de-la-culture-camerounaise-et-africaine/#comment-13449]here[/url]
[url=https://www.zimbrafr.org/forum/topic/673-backup-machine-virtuelle-vmware-zimbra/page__st__600__gopid__229585#entry229585]here[/url]
[url=https://npoaktobe.kz/2021/11/16/a%d2%9bparat-zh%d3%99ne-%d2%9bo%d2%93amdy%d2%9b-damu-ministrligini%d2%a3-bastamasymen-azamatty%d2%9b-forum-%d2%9barsa%d2%a3ynda-ministrler-%d2%afkimettik-emes-%d2%b1jymdarmen-kezdesedi/#comment-4556]at this website[/url]
46e376a
토토사이트
娛樂城
[url=https://razrabotka-saitov.of.by/]Создать сайт в Минске[/url]
<a href="https://razrabotka-saitov.of.by/">Заказать сайт в Минске</a>
타오바오직구
娛樂城
[url=https://fismydsmingsa.tk/post/5-Gr-Nde-F-R-Autoren-4]5 Gr Nde F R Autoren 4[/url]
[url=https://sleekbabur.tk/post/Daniel-Dennett-Im-Gespr-Ch-Ber-Hannah-Arendt]Daniel Dennett Im Gespr Ch Ber Hannah Arendt[/url]
[url=http://smak-pmr.com/products/muzhskoj-32/#comment_30288]Easy tips to outline a novel using trello[/url]
[url=https://horizoncamer.com/2022/07/10/lefbc-prepare-la-releve-des-lions-indomptables-avec-la-coupe-top/#comment-19474]here[/url]
[url=https://evrmag.com/animeultima/#comment-44467]this site[/url]
[url=https://mamansereine.com/?error_checker=captcha&author_spam=Williamcek&email_spam=pdaniels%40nikitosgross.pw&url_spam=https%3A%2F%2F1xbetbonuses.com&comment_spam=%3Ca%20href%3Dhttp%3A%2F%2Ffreetoplay.org%2Fforum%2Fviewtopic.php%3Ff%3D6%26t%3D266361%3EIncredibile%20conferenza%20di%20scrivere%20poeticamente%3C%2Fa%3E%3Ca%20href%3Dhttps%3A%2F%2Fwww.uscustomercare.com%2Ffrontier-communications-customer-service%2F%23comment-125064%3ECosa%20fare%20prima%20di%20successo%20per%20il%3C%2Fa%3E%20c60afbd%20%20%3Ca%20href%3Dhttps%3A%2F%2Fquebrevsourchisig.cf%2Fpost%2FBildanalyse-Mit-Microsoft-Word-So-Geht-S%3EBildanalyse%20Mit%20Microsoft%20Word%20So%20Geht%20S%3C%2Fa%3E%3Ca%20href%3Dhttps%3A%2F%2Fovpaudrumerrocha.cf%2Fpost%2F20-Things-To-The-Law-Revision-Video%3E20%20Things%20To%20The%20Law%20Revision%20Video%3C%2Fa%3E%3Ca%20href%3Dhttps%3A%2F%2Flandcalpeakcrebarde.cf%2Fpost%2F5-Mistakes-To-Be-A-Great-Leader%3E5%20Mistakes%20To%20Be%20A%20Great%20Leader%3C%2Fa%3E%20%3Ca%20href%3Dhttp%3A%2F%2Fwww.consult-distribution.com%2F2013%2F03%2F20%2Fone-more-post%2F%23comment-219723%3ETest%20de%20la%20maternite%20de%20l%5C%27hnfc%3C%2Fa%3E%3Ca%20href%3Dhttps%3A%2F%2Fin.fresherjobs.io%2Fonline-english-teacher-jobs-in-arise-n-shine-schools-private-limited-chennai%2F%23comment-148027%3EDeutsche%20lieder%20fur%20autoren%3C%2Fa%3E]Instructions for[/url]
[url=https://helderbergtrailer.co.za/trailers/lower-assy-socket/#comment-121610]link[/url]
[url=https://www.thebipolarbuzz.com/guest-post-managing-your-persistent-fears-anxieties-and-stresses-by-stanley-popovich/#comment-89246]Fine della famiglia di studio per l'universita[/url]
[url=https://alenconhost.ml/post/7-Pasos-Para-La-Gala-Final]7 Pasos Para La Gala Final[/url]
[url=http://www.morenteforte.com/vinganca-o-musical/comment-page-15/#comment-497334]Re: Re:[/url]
[url=https://jefflavin.net/keto-and-intermittent-fasting-a-beginners-guide/#comment-528039]link[/url]
[url=https://www.xn--fl-yka.ge/2018/11/30/pure-luxe-in-punta-mita/#comment-5242]this site[/url]
[url=https://thesassybarn.com/2018/12/02/left-over-turkey-fajita-soup/#comment-173708]here[/url]
[url=https://sztarok-mindenhol.blogger.hu/2011/10/09/monster-high]here[/url]
[url=https://slupi.info/effective-website-promotion/#comment-28212]link[/url]
[url=https://no.afterdawn.com/nedlastinger/skrivebord/komprimering_verktoy/winrar.cfm?error_string=Tarkista%20antamasi%20arvosana%2E%3Cbr%2F%3EUdefinert%20feil%2E%3Cbr%2F%3E&vote_value=0&software_review=%26lt%3Ba%20href%3Dhttp%3A%2F%2Fshop%2Eaviva%2Dtelecom%2Eru%2Fblog%2Fpryamye%2Dpostavki%2Ds%2Dkitaya%23comment%5F11438%26gt%3BBest%20ways%20to%20format%20an%20apa%20paper%20in%20word%20for%20mac%26lt%3B%2Fa%26gt%3B%0D%0A%26lt%3Ba%20href%3Dhttps%3A%2F%2Fwww%2Ezimbrafr%2Eorg%2Fforum%2Ftopic%2F7245%2Dzimbra%2Dcollaboration%2D86%2Dpatch%2D4%2Dest%2Dla%2Fpage%5F%5Fst%5F%5F140%5F%5Fgopid%5F%5F269545%23entry269545%26gt%3Bhere%26lt%3B%2Fa%26gt%3B%0D%0A%20a3b9447%20%20%0D%0A%26lt%3Ba%20href%3Dhttps%3A%2F%2Fpapocoo%2Etk%2Fpost%2FWriting%2DAnimation%2DFor%2DA%2DCae%2DExam%26gt%3BWriting%20Animation%20For%20A%20Cae%20Exam%26lt%3B%2Fa%26gt%3B%0D%0A%26lt%3Ba%20href%3Dhttps%3A%2F%2Fopsothesitua%2Eml%2Fpost%2F4%2DModelos%2DDe%2DCbr%26gt%3B4%20Modelos%20De%20Cbr%26lt%3B%2Fa%26gt%3B%0D%0A%26lt%3Ba%20href%3Dhttps%3A%2F%2Fzensorecka%2Egq%2Fpost%2FCanzoni%2DPer%2DBambini%2DE%2DPer%2DRagazzi%26gt%3BCanzoni%20Per%20Bambini%20E%20Per%20Ragazzi%26lt%3B%2Fa%26gt%3B%0D%0A%20%0D%0A%26lt%3Ba%20href%3Dhttps%3A%2F%2Fwrc%2Eorg%2Eza%2Fwrc%2Dlogo%2F%23comment%2D11110%26gt%3BHow%20to%20write%20a%20thesis%20statement%20for%20an%20exam%20essay%26lt%3B%2Fa%26gt%3B%0D%0A%26lt%3Ba%20href%3Dhttps%3A%2F%2Fwww%2Etysotructiep%2Eonline%2Fhighlights%2Fazerbaijan%2Dcyprus%2Fcomment%2Dpage%2D3%2F%23comment%2D662095%26gt%3Bhere%26lt%3B%2Fa%26gt%3B&ad_nick=Williamchacy&new_email=pdaniels%40nikitosgross%2Epw&new_nick=Williamchacy#arvostelut]link[/url]
646e376
중국배대지
타오바오직구
토토사이트
[url=https://razrabotka-saitov.of.by/]Разработка сайтов в Минске[/url]
<a href="https://razrabotka-saitov.of.by/">Заказать сайт в Минске</a>
[url=https://docwomann.tk/post/Tempo-De-Apresenta-O]Tempo De Apresenta O[/url]
[url=https://rameconsaddtophe.cf/post/Faster-Ways-To-Write-A-Great-Hook]Faster Ways To Write A Great Hook[/url]
[url=http://demo.simpla.pp.ua/blog/chto-novogo-v-etoj-versii-simply#comment_94962]this site[/url]
[url=https://morrigansmadness.com/index/kids/nervous-breakdown/page/185/#comment-4712]7 consejos para el crecimiento personal[/url]
[url=https://creativat.desuza.ch/blog/2021/04/24/schluesselanhaenger/#comment-42886]10 dinge uber trump auf deutsch[/url]
[url=https://gaertnerkonzept.de/hello-world/#comment-35165]Motivation fur alle[/url]
[url=https://www.natureecia.com.br/index.php?blogger_id=10&route=information/blogger]here[/url]
[url=https://tehmet.su/comments#comment_764340]at this website[/url]
[url=https://www.trendingnews.it/un-medico-in-famiglia-lino-banfi-domiziana-giovinazzo/#comment-4399743]13 different ways to writing essay quickly[/url]
[url=http://permitbeijing.com/forum/showthread.php?tid=1149425]this site[/url]
[url=http://fashiongarden.ru/blog/kak-sdelat-landshaft-uchastka-svoimi-rukami/#comment_56859]here[/url]
[url=https://shanijacobi.co.il/%d7%aa%d7%a7%d7%a0%d7%95%d7%9f-%d7%a9%d7%99%d7%9e%d7%95%d7%a9-%d7%91%d7%90%d7%aa%d7%a8/#comment-1114134]Il potere dell'empatia di italiano[/url]
[url=https://blogdabila.com/tendencias/e-de-arrepiar-os-cabelos/#comment-13424]Comment faire des comparaisons en mode agile[/url]
[url=https://www.aafrc.org/best-palm-sander/#comment-267501]Curso de poses para ensaio feminino na pratica[/url]
[url=https://kenva.vn/thuc-don-tuan-nay-cho-co-nang-cong-so/?comment=4370857#comment]here[/url]
[url=http://rostelekom.info/page/usluga-upravlenie-prosmotrom-rostelekom/#comment-11247]here[/url]
[url=https://theteenagersecrets.com/a-small-step/#comment-120731]10 motivos para redacao[/url]
[url=https://www.datametrixut.com/2019/08/18/hello-world/#comment-7018]link[/url]
[url=https://evrmag.com/xname-lname/#comment-46590]this site[/url]
[url=https://cfah.org/cbd-for-crossfit/#comment-1195267]Methodologie de ma famille[/url]
[url=https://royalcat-puxoviki.ru/blog/samye-teplye-detskie-puhoviki/#comment_71954]at this website[/url]
[url=https://www.zimbrafr.org/forum/topic/38506-hosuniq/page__gopid__242283#entry242283]link[/url]
[url=https://ahs.ui.ac.id/2020/12/16/12590/comment-page-22328/#comment-2288910]here[/url]
9bfd17a
<a href="https://severpost.ru/read/140552/">https://severpost.ru/read/140552/</a>
<a href=http://termoros.com/bitrix/redirect.php?goto=http://familie-og-sundhed.top>http://conferencebureausouthamerica.com/__media__/js/netsoltrademark.php?d=familie-og-sundhed.top</a>
<a href=http://dazhdgas.ru/bitrix/click.php?goto=http://familie-og-sundhed.top>http://swepub.kb.se/setattribute?language=en&redirect=http://familie-og-sundhed.top</a>
<a href="https://cheapflightticket.net/default-post-type/comment-page-158988/#comment-351899">娛樂城</a> 239e9bf
娛樂城
타오바오직구
<a href="https://soft.4droidos.mobi">soft.4droidos.mobi</a>
<a href="https://soft.androidos-play.info">soft.androidos-play.info</a>
<a href="https://soft.androidos-top.com">soft.androidos-top.com</a>
<a href="https://soft.droid-mob.com">soft.droid-mob.com</a>
<a href="https://soft.droidos.download">soft.droidos.download</a>
Beautiful graphic component, which very coherent enter in program. Cheerful musical tunes. Attractive conditions.
<a href="https://severpost.ru/read/140552/">https://severpost.ru/read/140552/</a>
토토사이트
토토사이트
[url=https://swasusdvacdesters.ga/post/4-Trucchi-Per-Trovare-Il-Proprio-Scopo-Nella-Vita]4 Trucchi Per Trovare Il Proprio Scopo Nella Vita[/url]
[url=https://pumplighdohaf.ga/post/Videocurr-Culum-De-Alejandro-Magno]Videocurr Culum De Alejandro Magno[/url]
[url=http://www.buyleads.me/how-to-start-a-china-import-business/#comment-184307]Ricetta per comunicare come un pro[/url] [url=http://www.boom-wijsheid.nl/index.php/2022/06/03/park/#comment-205517]link[/url] [url=http://findagame.com.au/hello-world/#comment-41979]link[/url] [url=http://littlebigfilms.eu/hello-world/#comment-2544]Soforthilfe gegen depression und angst[/url] [url=https://rushedbox.com/product/cardinal-health-mini-lancing-device-x-2/#comment-30208]Regole di giulio deangeli[/url] [url=https://www.rangla-punjab.eu/2016/10/13/music-for-dinner-audio-player/#comment-143732]this site[/url] [url=https://www.amywilliamsart.com/scarboroughmarsh/#comment-371073]at this website[/url] [url=https://msurubel.com/project/pepsi-restaurant-branding-2019/#comment-840559]Jordan peterson on how to compare two stories[/url] [url=https://www.zabolekar.info/viewtopic.php?f=18&t=569&p=72558#p72558]10 exercises to read a research paper[/url] [url=https://www.zimbrafr.org/forum/topic/78705-wo-bekomme-ich-sumycin-500mg-ohne-rezept/page__gopid__168859#entry168859]Introduccion a los ensayos de desarrollo personal[/url] [url=http://nakano-esperanza.com/blog/%e8%a9%a6%e5%90%88%e7%b5%90%e6%9e%9c/#comment-22430]3 simple ways to brainstorm ideas for writing[/url] [url=https://www.subristow.co.uk/blog/2018/02/09/the-meaning-of-illness/]Todo sobre la maternidad[/url] [url=https://www.buyleads.me/how-to-improve-your-email-delivery-rate/#comment-199836]here[/url] [url=https://meninaarteira.org/hello-world/#comment-1463]this site[/url] [url=https://fermer05.ru/blog/kak-opredelit-naturalnoe-moloko/#comment5006]Stephen hawking spricht uber herr anwalt[/url] [url=https://horizoncamer.com/2022/06/04/douala-accueille-la-10e-edition-du-bafm/#comment-8996]Naciste para o enem[/url] [url=http://magazine-19.working-group.ru/blog/primer-2#comment_25006]here[/url] [url=https://cfah.org/cbd-and-kidney-disease/#comment-1183677]El hombre en tus reels de instagram[/url] [url=http://f1automotori.com/ferrari/the-2020-ferrari-f8-spider-more-power-less-weight/#comment-45186]this site[/url] [url=http://wigfashion.ru/news/11/#comment138972]here[/url] [url=https://gaertnerkonzept.de/hello-world/#comment-37047]at this website[/url] e9bfd17
토토사이트
<a href=http://asila.com/__media__/js/netsoltrademark.php?d=o-dom2.ru>http://longsdrugstores.us/__media__/js/netsoltrademark.php?d=o-dom2.ru</a>
<a href="https://severpost.ru/read/140552/">https://severpost.ru/read/140552/</a>
토토사이트
토토사이트
<a href="https://rabota-devushkam.biz/norilsk/">работа досуг девушкам Норильск</a>
<a href=https://sbis63.ru/>Маркет ОФД</a>
世界盃
世界盃
<a href="https://rabota-devushkam.ru.com/tolyatti/">вакансии для девушек Тольятти</a>
tour ấn độ ở tphcm</a>
[url=https://abperrebach.cf/post/Il-Mio-Primo-Giorno-Di-Lavoro-Da-Tutti]Il Mio Primo Giorno Di Lavoro Da Tutti[/url]
[url=https://franentes.tk/post/Methode-De-R-Union]Methode De R Union[/url]
[url=https://demo2.tokomoo.com/livre/product/rumpi-lagi/#comment-566498]9 ideias de poses para gestantes[/url]
[url=https://www.pcstacks.com/gaming-mouse-polling-rate/#comment-175589]13 different ways to write a good law essay[/url]
[url=https://businessgeek.uk/london-house-prices-consistently-outpaced-by-regional-markets/#comment-17991]here[/url]
[url=https://www.edgepointconveyancing.com.au/2018/04/13/hello-world/#comment-14344]Cuento de tu vida[/url]
[url=https://jetradar.click/page-magnific-lightbox-effects/comment-page-407643/#comment-787327]at this website[/url]
[url=http://hotgoods.com.ua/blog/prazdnik-dlya-avtomobilistov-v-brovarah/#comment_542963]So lernst du geschichten spannend zu bestehen[/url]
[url=https://www.pcstacks.com/find-out-computer-monitor-details-pc-specs/#comment-164288]Como hacer un esquema en tu trabajo[/url]
[url=http://savys.se/reklam/antligen-bra-reklam/#comment-84213]here[/url]
[url=http://forumx.fearnode.net/general-help/4787790/wzyokint?page=11#post-12012106]this site[/url]
[url=https://itgurun.se/chrome-varnar-for-osakra-formular/#comment-192770]The guide to write concept paper[/url]
[url=http://www.morenteforte.com/merda-la-merda/comment-page-29/#comment-514024]here[/url]
[url=https://horizoncamer.com/2021/05/19/ben-martins-puise-aux-sources-du-bikutsi-pour-rendre-hommage-a-mr-labbe/#comment-17860]Como fazer um jogo de fotografia 05[/url]
[url=http://www.mediamusicdesign.com/hallo-welt/#comment-44024]5 claves para empreender[/url]
[url=https://cfah.org/best-cbd-capsules-on-amazon/#comment-1186009]this site[/url]
9646e37
<a href=https://sbis63.ru/>Электронная отчетность и документооборот в Самаре</a>
<a href="https://soft.4droidos.mobi">soft.4droidos.mobi</a>
<a href="https://soft.androidos-play.info">soft.androidos-play.info</a>
<a href="https://soft.androidos-top.com">soft.androidos-top.com</a>
<a href="https://soft.droid-mob.com">soft.droid-mob.com</a>
<a href="https://soft.droidos.download">soft.droidos.download</a>
Beautiful picture, which crazy coherent enter in program. Funny a piece of music. Attractive conditions.
<a href=https://sbis63.ru/>система СБИС</a>
<a href="https://rabotadevushkam.net/cremea/">вакансии девушкам Крым</a>
토토사이트
<a href=https://sbis63.ru/>Тензор ОФД</a>
[url=https://bloggema.cf/post/How-To-Write-A-Reflection-Assignment]How To Write A Reflection Assignment[/url]
[url=https://iltalticasda.tk/post/Introduction-To-Make-Research-Easy]Introduction To Make Research Easy[/url]
[url=https://cfah.org/cbd-oil-for-hyper-dogs/#comment-1216415]at this website[/url] [url=https://skleplavisage.pl/pl/blog/13#comment29616]13 different ways to write a thesis statement[/url] [url=https://brezent.kz/blog/chto-novogo-v-etoj-versii-simply/#comment_41758]link[/url] [url=https://bendigosurgicalservices.com.au/node/94/done?sid=5778&token=42ef85366f3e629b1d60ade273a823ca]Actitudes de la historia[/url] [url=https://gswill.com/product/hp-pavilion-laptop-x360-14%e2%80%b3-touch-10th-gen-core-i5-1035g1-8gb-ram-256gb-ssd-pale-gold/#comment-5738]at this website[/url] [url=http://www.maobing100.com/forum.php?mod=viewthread&tid=34638&extra=]here[/url] [url=http://www.djtrauma.tv/2015/06/15/dj-traumas-traphousenyc-goes-viral/#comment-329511]Re: Re:[/url] [url=https://www.fcsswe.se/hello-world#comment-13481]link[/url] [url=https://horizoncamer.com/2022/03/23/yanick-bezang-un-cadeau-pour-les-medias-au-cameroun/#comment-15819]10 bruxos mais fortes de familia ao ar livre[/url] [url=https://bass-mollett.com/white-kivar-blank-register-book/?attributes=eyIzODQwIjoiMjI2MSIsIjM4NDEiOiIiLCIzODQyIjoiW3VybD1odHRwczpcL1wvZmFpYS5wZVwvYmxvZ3NcL2Jsb2dcL2hhbGxvd2Vlbj9jb21tZW50PTEyNzA3MzU1MDUwOSNjb21tZW50c11Fc3RydWN0dXJhIGRlIGdyYW5kZXMgcGVuc2Fkb3Jlc1tcL3VybF1cclxuW3VybD1odHRwczpcL1wvam9ybmFsY2lkYWRlZW1hbGVydGEuY29tLmJyXC9jYW5kaWRhdG8tZG8tcGR0LWVsdmlzLWNlemFyLXBhcnRpY2lwYS1kZS1lbnRyZXZpc3RhLW5hLWJhbmRuZXdzXC8jY29tbWVudC0yNjI5OTFdUmU6IFJlOltcL3VybF1cclxuIDZhN2NhZDQgIFxyXG5bdXJsPWh0dHBzOlwvXC9vbGV4Y2FuaW5pZ2h0YS50a1wvcG9zdFwvVC1DbmljYXMtRGUtQWx0by1SZW5kaW1pZW50b11UIENuaWNhcyBEZSBBbHRvIFJlbmRpbWllbnRvW1wvdXJsXVxyXG5bdXJsPWh0dHBzOlwvXC9yZWlsaW9waGFtb2NpLmNmXC9wb3N0XC8zLUlkZWlhcy1EZS1Nci1CZWFuXTMgSWRlaWFzIERlIE1yIEJlYW5bXC91cmxdXHJcblt1cmw9aHR0cHM6XC9cL3VwaHByb2RoeWRyaS50a1wvcG9zdFwvTHVjYS1UZW0tQ3Jpc2UtRGUtVGV4dG8tWC1HLU5lcm9zLVRleHR1YWlzXUx1Y2EgVGVtIENyaXNlIERlIFRleHRvIFggRyBOZXJvcyBUZXh0dWFpc1tcL3VybF1cclxuIFxyXG5bdXJsPWh0dHA6XC9cL2RqbWFya3lwLmNvbVwvZ3Vlc3Rib29rLnBocF1hdCB0aGlzIHdlYnNpdGVbXC91cmxdXHJcblt1cmw9aHR0cHM6XC9cL3d3dy5wb3J0YWxzcGFzLmVzXC9hY2Nlc29yaW9zXC9hcXVhYmlrZS1kZS1hcXVhZml0LXRlY2hub2xvZ2llcy1ncnVwby1zaXJlbSNjb21tZW50LTExMjAxNV1FbCBkZWNhbG9nbyBkZSBoYXJyeSBwb3R0ZXJbXC91cmxdXHJcbiIsIjM4NDMiOiI5MzYifQ]9 ideias de atendimento para encantar o cliente[/url] [url=http://stewartwho.com/interview/amy-winehouse/#comment-2213083]link[/url] [url=https://megaweedmarketltd.com/product/gods-gift/#comment-11988]here[/url] [url=http://fire18888.com/forum.php?mod=viewthread&tid=4&pid=9550&page=117&extra=page%3D1#pid9550]Julienbam findet mit geschichten[/url] [url=https://nino-international.com/blogs/blog/9/Australian-student-visa-application-drop-by-a-third]Relaxing piano music for kids[/url] [url=https://habitatcb.org/cropped-logo12-png/#comment-174850]this site[/url] [url=https://winbeefarms.com/nursery-plants/#comment-24896]Einleitung schreiben fur energie[/url] [url=https://evrmag.com/way-convert-word-to-pdf-online/#comment-54270]Come puoi smettere di leggere[/url] [url=http://opportunities.org.af/2022/03/14/bristol-university-scholarship-in-uk-2022-study-in-unite-kingdom/#comment-103627]at this website[/url] [url=https://betterwithbell.com/throwing-a-holiday-party/#comment-17840]Exercice d'ecoute en 2 min[/url] [url=https://amigosecretocanales.forogratis.es/post303144.html#p303144]here[/url] [url=https://cfah.org/cbd-and-antidepressants/#comment-1220530]here[/url] c54c239
<a href=https://sbis63.ru/>Программы и оборудование</a>
토토사이트
<a href="http://eu-res.ru/almazstandart.php">алмазная коронка 350</a>
토토사이트
토토사이트
<a href="https://soft.4droidos.mobi">soft.4droidos.mobi</a>
<a href="https://soft.androidos-play.info">soft.androidos-play.info</a>
<a href="https://soft.androidos-top.com">soft.androidos-top.com</a>
<a href="https://soft.droid-mob.com">soft.droid-mob.com</a>
<a href="https://links.magical-dream.com/">links.magical-dream.com</a>
<a href="https://soft.droidos.download">soft.droidos.download</a>
Excellent graphic component, which very harmoniously enter in application. Naughty a piece of music. Attractive tasks.
<a href="https://tgcomnews24.com/strategie-di-scommesse-sul-basket/">https://tgcomnews24.com/strategie-di-scommesse-sul-basket/</a>
토토사이트
Скачать бесплатно джет пак apk актуальной версии на андроид телефон. Качать и установить казино 1win для заработка на русском где можно воспользоваться выводом киви кошельком, skachat казино, получите денежный приз и воспользуйтесь коэффициентами!
토토사이트
토토사이트
<a href="https://reklamaxxx.biz/simferopol-2/">вакансии девушкам Симферополь</a>
<a href=http://ww31.mwfossils.pwp.blueyonde.co.uk/__media__/js/netsoltrademark.php?d=o-dom2.ru>http://buymybrands.com/__media__/js/netsoltrademark.php?d=o-dom2.ru</a>
<a href=http://vileyka.byfin.by/bitrix/redirect.php?goto=http://o-dom2.ru>http://tesco-finance.info/__media__/js/netsoltrademark.php?d=o-dom2.ru</a>
중국배대지
<a href="https://mapgame.ru/karta-builder-s-workshop-dlya-terraria-1-3-5-3/">карта со всеми вещами</a>
<a href=http://chromatec-instruments.com/bitrix/rk.php?goto=http://o-dom2.ru>http://www.doctor-al.ru/bitrix/rk.php?goto=http://o-dom2.ru</a>
<a href=http://tipirovanie.ru/bitrix/rk.php?goto=http://o-dom2.ru>http://egreenbuild.us/__media__/js/netsoltrademark.php?d=o-dom2.ru</a>
미국배대지
타오바오직구
미국배대지
미국배대지
토토사이트
<a href="https://mapgame.ru/karta-builder-s-workshop-dlya-terraria-1-3-5-3/">карта со всеми вещами</a>
Скачать бесплатно игру lucky jet 1win актуальной версии на андроид apk и айфон ios телефон. Играть в Лаки Джет 1вин для заработка на русском где можно воспользоваться выводом на киви кошелек, skachat игру lucky jet на деньги в казино 1 вин, получите денежный приз и воспользуйтесь коэффициентами
토토사이트
<a href="https://mapgame.ru/karta-builder-s-workshop-dlya-terraria-1-3-5-3/">карта со всеми вещами</a>
世界盃
Скачать и установить apk бесплатное официальное мобильное приложение 1win ru последняя версия для айфон (iphone) или android смартфонов на русском. Мобильная клиент программа 1win com kz, сделать полностью бесплатно установку app апк на любой мобильный телефон, не важно, старая или новая версия андроид или ios, мобильная версия приложения на ваш телефон, используйте мобильный депозит суммы, вы можете пополнить деньги игрового баланса. Выплата через рубль, всегда выполняется проверка если не пришли деньги. Пополнение игрокам через популярные платёжные системы обеспечит коэффициенты, вы узнаете как делать ставки на футбол, хоккей, баскетбол, теннис, бокс, волейбол, виртуальный спорт или пари россии смотря трансляции где проходит лига, смотрите через ваш компьютер (пк). 1win бет скачать мобильное приложение, bukmeker club, go and contact official online website net, www top site for bk xyz
[url=https://moirecunena.cf/post/Mon-Test-De-L-Criture]Mon Test De L Criture[/url]
[url=https://stimmidlephave.tk/post/Valise-Et-Sac-De-Tp]Valise Et Sac De Tp[/url]
[url=https://feedbeater.com/clean-mechanical-keyboard-switches/#comment-233848]Como tirar fotos de pintura[/url]
[url=http://www.recipemashups.com/2016/03/13/shepherds-pie-with-sweet-potato-crust/comment-page-13/#comment-393887]this site[/url]
[url=http://lider-krym.ru/news/pesochnicy?page=1478#comment-74078]here[/url]
[url=http://comhotel.ru/product/bonsai-mini-fikus-v-stekle-s-mhom-kornyami-zemlei-57/]this site[/url]
[url=https://webdevsupply.com/how-to-develop-a-sense-of-composition/#comment-189082]at this website[/url]
[url=https://feedbeater.com/best-gaming-keyboards-in-100-usd/#comment-236032]A melhor tecnica para um beijo perfeito[/url]
[url=http://stewartwho.com/interview/amy-winehouse/#comment-2222205]here[/url]
[url=https://bigtgolf.com/?attachment_id=161#comment-208338]link[/url]
[url=http://stewartwho.com/interview/richard-young/#comment-2221714]this site[/url]
[url=https://www.zimbrafr.org/forum/topic/178339-farmacia-online-donde-comprar-plan-b-levonorgestrel-15mg-sin-receta-rapido/page__gopid__288088#entry288088]here[/url]
[url=https://adrinacode.com/2021/09/26/hello-world/#comment-6032]13 different ways to think like a designer[/url]
[url=http://stewartwho.com/interview/billie-ray-martin/#comment-2223225]Demasiado tarde para videos[/url]
[url=https://www.aafrc.org/best-raw-dog-food/#comment-310279]at this website[/url]
[url=https://phoenixvoyages.vn/st_tour/tour-con-son-can-tho-2-ngay-1-dem-thiet-ke-rieng-thoa-suc-kham-pha-xu-tay-do/#comment-22884]link[/url]
646e376
<a href="https://500bestapps.com/glwiz">世界盃</a> bdbc54c
Скачать и установить apk бесплатное официальное мобильное приложение 1win ru последняя версия для айфон (iphone) или android смартфонов на русском. Мобильная клиент программа 1win com kz, сделать полностью бесплатно установку app апк на любой мобильный телефон, не важно, старая или новая версия андроид или ios, мобильная версия приложения на ваш телефон, используйте мобильный депозит суммы, вы можете пополнить деньги игрового баланса. Выплата через рубль, всегда выполняется проверка если не пришли деньги. Пополнение игрокам через популярные платёжные системы обеспечит коэффициенты, вы узнаете как делать ставки на футбол, хоккей, баскетбол, теннис, бокс, волейбол, виртуальный спорт или пари россии смотря трансляции где проходит лига, смотрите через ваш компьютер (пк). 1win бет скачать мобильное приложение, bukmeker club, go and contact official online website net, www top site for bk xyz
<a href=https://it.vegas-casino-online.com/casino-netto/>Casino netto</a>
<a href=https://it.vegas-casino-online.com/codici-bonus-casino/>Codici Bonus Casino</a>
<a href=https://it.vegas-casino-online.com/giochi-spiderman-gratis/>Giochi Spiderman Gratis</a>
<a href=https://it.vegas-casino-online.com/assistenza-finanze-esso/>assistenza.Finanze.esso</a>
<a href="https://colab.research.google.com/drive/1mRM9cnGwtfcavn71UqYPqZg_dBG49A4Z">melbet промокод на фрибет</a>
<a href=https://it.vegas-casino-online.com/vieni-si-gioca-adi/>vieni si gioca adi</a>
<a href=https://it.vegas-casino-online.com/giochi-it-solitario/>Giochi.It Solitario</a>
<a href=https://it.vegas-casino-online.com/simulatore-online-di-roulette/>Simulatore online di roulette</a>
<a href=https://it.vegas-casino-online.com/slot-machine-faraone/>slot machine faraone</a>
<a href=https://it.vegas-casino-online.com/demo-crazy-time/>DEMO CRAZY TIME</a>
<a href=https://it.vegas-casino-online.com/splash-italiano/>Splash Italiano</a>
<a href=https://it.vegas-casino-online.com/rose-rose/>rose rose</a>
<a href=https://it.vegas-casino-online.com/casino-imparziale/>Casino imparziale</a>
<a href=https://it.vegas-casino-online.com/big-time-rush-italiano/>Big Time Rush Italiano</a>
<a href=https://it.vegas-casino-online.com/app-pospepay-cambio-telefono/>App Pospepay Cambio Telefono</a>
<a href=https://it.vegas-casino-online.com/slot-che-pagano-di-piu-2021/>slot che pagano di piu 2021</a>
<a href=https://it.vegas-casino-online.com/slot-lottomatico/>slot lottomatico</a>
<a href="https://colab.research.google.com/drive/1tXzIhjm1iiKL-xTwjS5844pAkfEuS3jm">слоты вавада скачать</a>
<a href=https://it.vegas-casino-online.com/bonus-iscrizione-senza-deposito/>Bonus Iscrizione Senza Deposito</a>
<a href=https://it.vegas-casino-online.com/casino-1/>Casino 1</a>
<a href=https://it.vegas-casino-online.com/bonus-senza-deposito-casino-immediato/>Bonus Senza Deposito Casino immediato</a>
<a href=https://it.vegas-casino-online.com/app-per-scaricare-cartoni-animati-gratis/>App per Scaricare Cartoni Animati Gratis</a>
<a href=https://it.vegas-casino-online.com/video-bonus-slot-da-bar/>Video bonus slot da bar</a>
<a href=https://it.vegas-casino-online.com/burraco-scarica-gratis/>Burraco Scarica Gratis</a>
<a href=https://it.vegas-casino-online.com/teoria-del-poker/>Teoria del poker</a>
<a href=https://it.vegas-casino-online.com/vendita-gettoni-telefonica/>Vendita gettoni Telefonica</a>
<a href="https://colab.research.google.com/drive/1Go3ZShSN34drs5pzsnzwoDNzEgxOPMaZ">jozz обзор онлайн казино</a>
<a href=https://it.vegas-casino-online.com/giochi-gratis-vlt/>Giochi Gratis Vlt</a>
<a href=https://it.vegas-casino-online.com/app-con-bonus-di-benvenuto/>app con bonus di benvenuto</a>
<a href=https://it.vegas-casino-online.com/bonus-ricarica/>bonus ricarica</a>
<a href=https://it.vegas-casino-online.com/gioco-da-bar/>Gioco Da Bar</a>
<a href=https://it.vegas-casino-online.com/punteggi-texas-hold/>Punteggi Texas Hold</a>
<a href=https://it.vegas-casino-online.com/la-scopa-gratis/>La Scopa Gratis</a>
<a href=https://it.vegas-casino-online.com/generatore-di-payoff/>Generatore di payoff</a>
<a href=https://it.vegas-casino-online.com/poker-online-gratis-senza-registrazione/>Poker online gratis senza registrazione</a>
<a href="https://colab.research.google.com/drive/1uCoouQNsQNtmEDrov7bXG-71TpC9tUEo">вавада казино онлайн</a>
<a href=https://it.vegas-casino-online.com/bonus-di-lottomatica-ruota-dei/>Bonus di Lottomatica Ruota Dei</a>
<a href=https://it.vegas-casino-online.com/slot-book-of-ra-gratis-senza-scareicare/>Slot Book of Ra Gratis Senza ScareICare</a>
<a href=https://it.vegas-casino-online.com/accesso-al-casino-di-sisal/>Accesso al casino di sisal</a>
<a href=https://it.vegas-casino-online.com/black-jack-online-gratis/>Black Jack online gratis</a>
мега питер[/url]
<a href="https://mega555kf7lsmb54yd6etz.com/">
мега как попасть</a>
<a href=https://it.vegas-casino-online.com/scaricare-scopa-gratis/>Scaricare Scopa Gratis</a>
<a href=https://it.vegas-casino-online.com/statistiche-del-tempo-pazzo-2/>Statistiche del tempo pazzo</a>
<a href=https://it.vegas-casino-online.com/transazione-non-riuscita-pospepay/>Transazione non Riuscita pospepay</a>
<a href=https://it.vegas-casino-online.com/starbet-898/>Starbet 898</a>
<a href=https://it.vegas-casino-online.com/libro-di-ra-deluxe-2/>Libro-di-Ra-Deluxe</a>
<a href=https://it.vegas-casino-online.com/bonus-di-lottomatica-ruota-dei/>Bonus di Lottomatica Ruota Dei</a>
<a href=https://it.vegas-casino-online.com/bonus-scommesse-senza-deposito/>Bonus Scommesse Senza Deposito</a>
<a href=https://it.vegas-casino-online.com/gioco-di-carte-solitario-da-scaricare-gratis/>Gioco di Carte Solitario da Scaricare Gratis</a>
[url=https://chandendlandseman.gq/post/La-Notte-Del-Mistero-Di-Montaigne]La Notte Del Mistero Di Montaigne[/url]
[url=https://tiwadisno.tk/post/Les-Nouvelles-Vari-T-S-De-Texte-Argumentatif]Les Nouvelles Vari T S De Texte Argumentatif[/url]
[url=https://lesmetiersdessi.wp.imtbs-tsp.eu/page-d-exemple/#comment-104954]here[/url] [url=https://ebusiness-center.com/blog/comprendre-la-blockchain-pour-en-tirer-profit?page=222#comment-12269]at this website[/url] [url=https://shikshakdiary.com/nipun-bharat-mission-g-o/#comment-124654]link[/url] [url=https://surveybucks.net/gepharmacylistens-survey/#comment-141076]Power fur dein higher self[/url] [url=http://www.s3-stranges.com.ar/producto/bulon-rueda-m14-x-1-50-x-45-arandela-conica-grower-tuerca-m14-x-15-llave-19mm/#comment-9503]Il potere dell'empatia di italiano[/url] [url=http://inbalancepediatrics.com/index.php/2016/01/08/identifying-and-treating-pain-from-nerve-tension/#comment-39988]link[/url] [url=https://www.corse-machin.com/article/how_to_build_a_hot_bed_or_cold_frame#comments]here[/url] [url=https://www.zimbrafr.org/forum/topic/178836-karetni-online-hry-dale-kasina-s-ceskou-licenci/page__gopid__288091#entry288091]Como hacer un funko pop diy para redactar mejor[/url] [url=https://scorpiontactics.com/?product=large-assault-backpack-ocp#comment-13217]this site[/url] [url=https://maniatek.com/that-minute-you-realize-you-have-puddle-problems/#comment-81232]Das geschaft mit der dw[/url] [url=http://pbvolga.ru/blog/dymovye-shashki-dlya-pejntbola/#comment_814554]Meine besten tipps fur gute noten[/url] [url=https://www.aafrc.org/best-pet-water-fountain/#comment-322485]Uma licao de bernoulli[/url] [url=https://www.heidiwhitehawaii.com/2020/02/24/welcome-to-my-blog/#comment-13827]at this website[/url] [url=https://bronsstichting.nl/2021/06/19/hello-world/#comment-24703]Ensayos de quesos veganos online parte 1[/url] [url=https://reconstruccioncristiana.org/l_1-nadine_aghnatios_returns/#comment-136121]link[/url] [url=http://casagrillo.net/?attachment_id=172#comment-81517]this site[/url] [url=https://www.zimbrafr.org/forum/topic/22401-aplicacion-casino-dinero-real-o-ruleta-de-apuestas-online/page__gopid__299702#entry299702]at this website[/url] [url=https://hlebspb.ru/gb/msg-2.html&name1=WilliamSpace&email1=pdaniels%2540nikitosgross.pw&any1=Rodneyovamy&subject1=6%252Bfacons%252Bde%252Bmaternite%252Bedition%252B&text1=a%252Bhref%253Dhttps%253A%252F%252Freeasidney.cf%252Fpost%252FEnglish-G9-U4l2-How-To-Improve-Your-WritingEnglish%252BG9%252BU4l2%252BHow%252BTo%252BImprove%252BYour%252BWriting%252Fa%250D%250Aa%252Bhref%253Dhttps%253A%252F%252Fpostsubtsof.tk%252Fpost%252F2-Ideias-Lindas-Com-Palha-De-Coqueiro2%252BIdeias%252BLindas%252BCom%252BPalha%252BDe%252BCoqueiro%252Fa%250D%250Aa%252Bhref%253Dhttps%253A%252F%252Fadlipni.tk%252Fpost%252F12-Trucchi-Per-La-Vendita12%252BTrucchi%252BPer%252BLa%252BVendita%252Fa%250D%250A%252B%250D%250A%252Ba%252Bhref%253Dhttps%253A%252F%252Fin.fresherjobs.io%252Ffashion-designer-jobs-in-alyval-delhi%252F%2523comment-181477Construire%252Ble%252Bplan%252Bde%252Bla%252Bproduction%252Becrite%252Fa%250D%250Aa%252Bhref%253Dhttp%253A%252F%252Fettalon.ru%252Fproducts%252Fkondensatornaya-ustanovka-aukrm-04-na-600-kvar%2523comment_122464%252Bconsigli%252Bper%252Bcrescere%252Bsu%252Byoutube%252Fa%250D%250Aa%252Bhref%253Dhttps%253A%252F%252Fbfoodfree.kailaasa.org%252Fpractice%252Fyogic-body-nirahari-essential-practice%252F%2523comment-141286Organizacao%252Bde%252Bchocolate%252Fa%250D%250Aa%252Bhref%253Dhttps%253A%252F%252Fecoherb.info%252Fprodukty%252Fobezzhirennyj-tvorog-polza-i-vred%252F%2523comment-10720here%252Fa%250D%250Aa%252Bhref%253Dhttps%253A%252F%252Fwww.highatitudestatusshayri.com%252Fbest-motivational-shayari-hosla-rakhna%252F%2523comment-90792at%252Bthis%252Bwebsite%252Fa%250D%250Aa%252Bhref%253Dhttps%253A%252F%252Fdjdantmusic.com%252Fmixs%252Fkarol-g%252F%2523comment-139742this%252Bsite%252Fa%250D%250Aa%252Bhref%253Dhttps%253A%252F%252Fwww.highatitudestatusshayri.com%252Fsad-shayri-9%252F%2523comment-91386here%252Fa%250D%250Aa%252Bhref%253Dhttps%253A%252F%252Fnouree.fr%252Fblogs%252Fjournal%252Fcomment-utiliser-la-chicoree%253Fcomment%253D120992956549%2523commentsthis%252Bsite%252Fa%250D%250Aa%252Bhref%253Dhttps%253A%252F%252Fsv.myolympicexperience.com%252Farticle%252Fbarbell-etiquette-how-to-keep-law-and-order-at-the-gym%2523commentsthis%252Bsite%252Fa%250D%250Aa%252Bhref%253Dhttps%253A%252F%252Fin.fresherjobs.io%252Fenglish-teacher-jobs-in-winspark-innovations-learning-private-limited-lucknow%252F%2523comment-179739Mehr%252Bzusagen%252Bmit%252Buntertitel%252Fa%250D%250Aa%252Bhref%253Dhttp%253A%252F%252Fforum.endbots.com%252Fviewtopic.php%253Ff%253D5%2526t%253D9190%2526p%253D387279%2523p387279Os%252B18%252Btipos%252Bde%252Bcoombs%252Fa%250D%250Aa%252Bhref%253Dhttps%253A%252F%252Fwww.yogafittness.com%252Fproduct%252F7-shocking-blogging-secrets%252F%2523comment-586297link%252Fa%250D%250Aa%252Bhref%253Dhttp%253A%252F%252Fwww.medicineayurved.com%252Fingredients%252Fpapaver-somniferum-linn%252F%2523comment-507790Seis%252Broles%252Bpara%252Btener%252Bhijos%252Fa%250D%250Aa%252Bhref%253Dhttps%253A%252F%252Fmarromglace.com.br%252Fmenu%252Fpolenta%252F%2523comment-2997at%252Bthis%252Bwebsite%252Fa%250D%250A%252Bd6ae8c2%252B]6 facons de maternite edition[/url] [url=http://espicheitroquei.com/hello-world/#comment-4127]link[/url] [url=https://generaltraders.pk/product/hp-laser-jet-printer-137fnw/#comment-3869]at this website[/url] [url=https://horizoncamer.com/2021/05/11/grossesse-quel-lien-entre-le-stress-de-la-maman-et-le-sexe-du-bebe/#comment-22219]here[/url] 7ac9646
mega не работает[/url]
<a href="https://mega555kf7lsmb54yd6etz.com/">
mega как попасть</a>
<a href=https://it.vegas-casino-online.com/cassa-web-pokerstars/>Cassa Web Pokerstars</a>
<a href=https://it.vegas-casino-online.com/app-casino-sisal/>App Casino Sisal</a>
<a href=https://it.vegas-casino-online.com/casino-online-italia-2/>Casino online Italia</a>
<a href=https://it.vegas-casino-online.com/scopa-gochi-stars/>SCOPA GOCHI STARS</a>
YouTube 再生回数 買う</a>
インスタ いいね 増やす</a>
<a href=https://it.vegas-casino-online.com/programma-lotto-gratis-italiano/>Programma lotto gratis italiano</a>
<a href=https://it.vegas-casino-online.com/roulette-in-diretta-online-2/>Roulette in diretta online</a>
<a href=https://it.vegas-casino-online.com/casino-senza-inio-documi/>Casino Senza Inio Documi</a>
<a href=https://it.vegas-casino-online.com/caso-in-vendita-una-licenza/>Caso in Vendita una licenza</a>
<a href=http://optikcenter.ru/bitrix/redirect.php?goto=http://o-dom2.ru>http://activesyncwg.sa28.net/__media__/js/netsoltrademark.php?d=o-dom2.ru</a>
<a href=http://xue.airshow.net/__media__/js/netsoltrademark.php?d=o-dom2.ru>http://www.beargayvideos.com/cgi-bin/crtr/out.cgi?c=0&l=outsp&u=http://o-dom2.ru</a>
<a href=https://it.vegas-casino-online.com/casa-in-vendita-a-cassino/>CASA in VENDITA A Cassino</a>
<a href=https://it.vegas-casino-online.com/libro-di-dead-gratis/>Libro di Dead Gratis</a>
<a href=https://it.vegas-casino-online.com/togliere-pin-iphone-7/>Togliere pin iPhone 7</a>
<a href=https://it.vegas-casino-online.com/rose-monopoli/>Rose Monopoli</a>
<a href=https://it.vegas-casino-online.com/homyatol-etha/>Homyatol Etha</a>
<a href=https://it.vegas-casino-online.com/slot-poker-gratis/>slot poker gratis</a>
<a href=https://it.vegas-casino-online.com/video-poker-gratis-da-carecare/>video poker gratis da carecare</a>
<a href=https://it.vegas-casino-online.com/roulette-gratis-prova/>roulette gratis Prova</a>
<a href=https://it.vegas-casino-online.com/casino-nuovi-online-2/>Casino Nuovi online</a>
<a href=https://it.vegas-casino-online.com/sequenze-roulette/>sequenze roulette</a>
<a href=https://it.vegas-casino-online.com/slot-trucchi-online-2/>Slot Trucchi online</a>
<a href=https://it.vegas-casino-online.com/aviatore-casino/>Aviatore Casino</a>
<a href=https://it.vegas-casino-online.com/gioco-ps4-spiderman/>Gioco PS4 Spiderman</a>
<a href=https://it.vegas-casino-online.com/bankroll/>bankroll</a>
<a href=https://it.vegas-casino-online.com/giochi-di-frenchi/>Giochi di Frenchi</a>
<a href=https://it.vegas-casino-online.com/tombola-gratis-esso-2/>tombola gratis.esso</a>
<a href=https://it.vegas-casino-online.com/numeri-lotto-gratis-da-giocare/>numeri lotto gratis da giocare</a>
<a href=https://it.vegas-casino-online.com/casino-visa/>Casino Visa</a>
<a href=https://it.vegas-casino-online.com/roulette-numeri-di-dispositivo/>roulette numeri di dispositivo</a>
<a href=https://it.vegas-casino-online.com/vieni-vince-al-blackjack-online/>Vieni Vince al Blackjack online</a>
https://soft.4droidos.mobi
https://soft.androidos-play.info
https://soft.androidos-top.com
https://soft.droid-mob.com
https://links.magical-dream.com
https://soft.droidos.download
Standing graphic component, which very plastically included in program. Cheerful musical tunes. Fascinating conditions.
<a href=https://it.vegas-casino-online.com/bonus-della-roulette/>Bonus della roulette</a>
<a href=https://it.vegas-casino-online.com/giochi-a-carte-scopa-gratis/>Giochi a carte Scopa gratis</a>
<a href=https://it.vegas-casino-online.com/voucher-starcasino/>voucher Starcasino</a>
<a href=https://it.vegas-casino-online.com/libro-di-ra-deluxe-gratis/>Libro di ra deluxe gratis</a>
<a href=https://it.vegas-casino-online.com/moneta-orari/>moneta orari</a>
<a href=https://it.vegas-casino-online.com/meglio-casino-lottomatico/>Meglio Casino Lottomatico</a>
<a href=https://it.vegas-casino-online.com/affronta-punta-con-esso/>Affronta punta con esso</a>
<a href=https://it.vegas-casino-online.com/slot-mobile-2/>slot mobile</a>
https://soft.4droidos.mobi
https://soft.androidos-play.info
https://soft.androidos-top.com
https://soft.droid-mob.com
https://links.magical-dream.com
https://soft.droidos.download
Standing graphic component, which unparalleled coherent included in program. Cheerful musical tunes. Entertaining tasks.
<a href=https://it.vegas-casino-online.com/scarica-desktop-dogane/>Scarica Desktop Dogane</a>
<a href=https://it.vegas-casino-online.com/giochi-per-pc-gratis-da-carecare-in-italiano/>Giochi per pc gratis da carecare in italiano</a>
<a href=https://it.vegas-casino-online.com/sisal-ricarica-non-riuscita/>sisal ricarica non riuscita</a>
<a href=https://it.vegas-casino-online.com/poker-pianeta-vincere-mobile/>poker pianeta vincere mobile</a>
<a href=https://it.vegas-casino-online.com/roulette-tecnica/>Roulette Tecnica</a>
<a href=https://it.vegas-casino-online.com/poker-italiano-gratis/>poker italiano gratis</a>
<a href=https://it.vegas-casino-online.com/contare-le-carte/>Contare le carte</a>
<a href=https://it.vegas-casino-online.com/gioco-di-crash-gratis/>Gioco di Crash Gratis</a>
<a href=https://it.vegas-casino-online.com/nyx-colomba-compra/>NYX colomba compra</a>
<a href=https://it.vegas-casino-online.com/kicker-in-poker/>kicker in poker</a>
<a href=https://it.vegas-casino-online.com/giochi-gratis-da-scaricare-di-cucina/>Giochi Gratis da Scaricare di Cucina</a>
<a href=https://it.vegas-casino-online.com/burraco-online-senza-scaricare/>Burraco online Senza Scaricare</a>
미국배송대행
<a href=https://it.vegas-casino-online.com/slot-giochi-online-soldi-veri/>Slot giochi online Soldi Veri</a>
<a href=https://it.vegas-casino-online.com/siti-slot-online-sicuri/>Siti slot online sicuri</a>
<a href=https://it.vegas-casino-online.com/burraco-gratis-italiano/>Burraco gratis italiano</a>
<a href=https://it.vegas-casino-online.com/slot-di-sito/>Slot di sito</a>
중국배대지
мега зеркало[/url]
<a href="https://mega555kf7lsmb54yd6etz.com/">
mega санкт-петербург</a>
미국배대지
gửi hàng đi mỹ bằng bưu điện</a>
<a href=https://it.vegas-casino-online.com/roulette-online/>roulette online</a>
<a href=https://it.vegas-casino-online.com/libro-di-ra-10-deluxe-gratis/>Libro di ra 10 deluxe gratis</a>
<a href=https://it.vegas-casino-online.com/jqck-nero/>JQCK nero</a>
<a href=https://it.vegas-casino-online.com/agenzia-delle-dogane-telefono/>Agenzia Delle Dogane Telefono</a>
cước phí gửi hàng đi mỹ qua bưu điện</a>
gửi hàng đi mỹ qua vnpost</a>
<a href=https://it.vegas-casino-online.com/metodo-roulette-1-2-35-36/>Metodo Roulette 1 2 35 36</a>
<a href=https://it.vegas-casino-online.com/ruota-bonus-lottomatico/>Ruota bonus lottomatico</a>
<a href=https://it.vegas-casino-online.com/probabilita-blackjack/>Probabilita Blackjack</a>
<a href=https://it.vegas-casino-online.com/vieni-vincero-a-tris/>Vieni Vincero a Tris</a>
мега санкт-петербург[/url]
<a href="https://mega555kf7lsmb54yd6etz.com/">
mega маркет</a>
<a href=https://it.vegas-casino-online.com/tabella-punti-poker/>Tabella Punti Poker</a>
<a href=https://it.vegas-casino-online.com/verifica-vincite-better-con-codice/>Verifica Vincite Better Con Codice</a>
<a href=https://it.vegas-casino-online.com/carta-money-numero-verde/>Carta Money Numero Verde</a>
<a href=https://it.vegas-casino-online.com/gioco-scopa-gratis-per-pc/>Gioco scopa gratis per pc</a>
미국배송대행
<a href=https://it.vegas-casino-online.com/casino-tracker/>Casino Tracker</a>
<a href=https://it.vegas-casino-online.com/ricarica-un-pin-mobile/>ricarica un pin mobile</a>
<a href=https://it.vegas-casino-online.com/quanta-paga-lo-0-alla-roulette/>Quanta Paga Lo 0 Alla roulette</a>
<a href=https://it.vegas-casino-online.com/chat-lottomatico/>chat lottomatico</a>
mega сайт[/url]
<a href="https://mega555kf7lsmb54yd6etz.com/">
мега как войти</a>
gửi hàng đi mỹ ở đâu rẻ</a>
<a href=https://it.vegas-casino-online.com/vieni-a-slot-machine/>vieni a slot machine</a>
<a href=https://it.vegas-casino-online.com/casino-digitale-2/>Casino Digitale</a>
<a href=https://it.vegas-casino-online.com/poker-online-senza-registrazione/>poker online senza registrazione</a>
<a href=https://it.vegas-casino-online.com/bonifico-telegrafico/>Bonifico telegrafico</a>
mega darkmarket войти[/url]
<a href="https://mega555kf7lsmb54yd6etz.com/">
mega dark</a>
<a href=https://it.vegas-casino-online.com/vieni-prender-gratis-dalle-maccinette/>vieni prender gratis Dalle Maccinette</a>
<a href=https://it.vegas-casino-online.com/libro-sisal/>libro sisal</a>
<a href=https://it.vegas-casino-online.com/vincite-slot-online/>Vincite slot online</a>
<a href=https://it.vegas-casino-online.com/app-starcasino/>app starcasino</a>
<a href=https://it.vegas-casino-online.com/giochi-con-machine/>Giochi Con Machine</a>
<a href=https://it.vegas-casino-online.com/blackjack-consigli/>Blackjack consigli</a>
<a href=https://it.vegas-casino-online.com/video-di-poker/>Video di poker</a>
<a href=https://it.vegas-casino-online.com/slot-machine-di-vincita/>Slot machine di Vincita</a>
<a href=https://it.vegas-casino-online.com/burraco-online-senza-registrazione/>Burraco Online Senza Registrazione</a>
<a href=https://it.vegas-casino-online.com/scarica-brillante-ita/>Scarica brillante Ita</a>
<a href=https://it.vegas-casino-online.com/impossibile-installare-aggiornengi-windows-10/>impossibile installare aggiornengi windows 10</a>
<a href=https://it.vegas-casino-online.com/slot-da-casino-snai/>slot da casino snai</a>
<a href=https://it.vegas-casino-online.com/vieni-funzionano-le-slot-machine/>Vieni Funzionano Le Slot Machine</a>
<a href=https://it.vegas-casino-online.com/martingala-scommesse/>Martingala Scommesse</a>
<a href=https://it.vegas-casino-online.com/vieni-a-caricare-skrill/>Vieni a Caricare Skrill</a>
<a href=https://it.vegas-casino-online.com/casina-del-duca/>Casina del Duca</a>
미국배송대행
<a href=https://it.vegas-casino-online.com/giochi-di-gitti-a-5/>Giochi di Gitti a 5</a>
<a href=https://it.vegas-casino-online.com/tre-carte-uguali-nel-gioco-del-poker/>Tre Carte UGUALI NEL GIOCO DEL POKER</a>
<a href=https://it.vegas-casino-online.com/roulette-online-gratis-3/>roulette online gratis</a>
<a href=https://it.vegas-casino-online.com/poker-bonus-senza-deposito/>Poker Bonus Senza Deposito</a>
미국배송대행
중국배대지
중국배대지
<a href=https://it.vegas-casino-online.com/slot-spartacus/>slot spartacus</a>
<a href=https://it.vegas-casino-online.com/si-e-verifato-un-problema-di-comunicazione-con-i/>si e verifato un problema di comunicazione con i server Google</a>
<a href=https://it.vegas-casino-online.com/download-di-casino-com/>Download di casino com</a>
<a href=https://it.vegas-casino-online.com/roulette-online-2/>roulette online</a>
<a href=https://it.vegas-casino-online.com/durata-postepay/>Durata Postepay</a>
<a href=https://it.vegas-casino-online.com/bonus-casino-senza-deposito-non-aams/>Bonus Casino Senza Deposito non AAMS</a>
<a href=https://it.vegas-casino-online.com/pin-postpay/>PIN POSTPAY</a>
<a href=https://it.vegas-casino-online.com/migliore-roulette/>migliore roulette</a>
<a href=https://it.vegas-casino-online.com/casino-bonus-miglior/>Casino bonus Miglior</a>
<a href=https://it.vegas-casino-online.com/planet-giochi/>Planet Giochi</a>
<a href=https://it.vegas-casino-online.com/scarica-aggiornamento-lingua-italiana-google/>Scarica Aggiornamento Lingua italiana Google Bloccato</a>
<a href=https://it.vegas-casino-online.com/vieni-centrare-una-ruota/>vieni centrare una ruota</a>
<a href=https://it.vegas-casino-online.com/bonus-senza-deposito-inemito-nuovi-casino/>Bonus Senza Deposito IneMito Nuovi Casino</a>
<a href=https://it.vegas-casino-online.com/casino-gratis-senza-iscrizio-2/>casino gratis senza iscrizio</a>
<a href=https://it.vegas-casino-online.com/caso-a-cassino/>Caso a Cassino</a>
<a href=https://it.vegas-casino-online.com/vieni-vince-al-blackjack/>Vieni Vince al Blackjack</a>
미국배송대행
<a href=https://it.vegas-casino-online.com/cambio-password-app-pospepay/>Cambio Password App Pospepay</a>
<a href=https://it.vegas-casino-online.com/tombola-e-accedi/>tombola.e accedi</a>
<a href=https://it.vegas-casino-online.com/jachpot/>Jachpot</a>
<a href=https://it.vegas-casino-online.com/login-del-casino-lottomatico/>Login del casino Lottomatico</a>
중국배대지
<a href=https://it.vegas-casino-online.com/web-roulette/>Web roulette</a>
<a href=https://it.vegas-casino-online.com/casino-senza-deposito-nuovi/>Casino Senza Deposito Nuovi</a>
<a href=https://it.vegas-casino-online.com/bonus-di-codice-starcasino/>Bonus di Codice Starcasino</a>
<a href=https://it.vegas-casino-online.com/guns-n-roses-simbolo/>Guns n Roses Simbolo</a>
<a href=https://it.vegas-casino-online.com/tombola-e-gratis/>tombola.e gratis</a>
<a href=https://it.vegas-casino-online.com/slot-libro-online-di-ra/>Slot Libro online di RA</a>
<a href=https://it.vegas-casino-online.com/tombola-accedi/>tombola .Accedi</a>
<a href=https://it.vegas-casino-online.com/gioco-delle-carte-scopa-gratis/>Gioco Delle Carte Scopa Gratis</a>
미국배송대행
중국배대지
<a href=https://it.vegas-casino-online.com/slot-temporale/>slot temporale</a>
<a href=https://it.vegas-casino-online.com/giochi-spiderman-gratis/>Giochi Spiderman Gratis</a>
<a href=https://it.vegas-casino-online.com/daydreamer-puntata/>Daydreamer Puntata</a>
<a href=https://it.vegas-casino-online.com/sisal-aviatore/>sisal aviatore</a>
중국배대지
<a href=https://it.vegas-casino-online.com/slot-che-pagano/>Slot Che Pagano</a>
<a href=https://it.vegas-casino-online.com/casino-senza-deposito-immediato/>Casino Senza Deposito immediato</a>
<a href=https://it.vegas-casino-online.com/grande-casino-2/>grande casino.</a>
<a href=https://it.vegas-casino-online.com/bauli/>bauli</a>
<a href=https://it.vegas-casino-online.com/21-3-blackjack/>21+3 Blackjack</a>
<a href=https://it.vegas-casino-online.com/libro-o-ra/>libro o ra</a>
<a href=https://it.vegas-casino-online.com/app-di-casino/>App di casino</a>
<a href=https://it.vegas-casino-online.com/slot-on-line-registrazione-senza/>Slot on line Registrazione Senza</a>
<a href=https://it.vegas-casino-online.com/slot-machine-in-vendito/>slot machine in vendito</a>
<a href=https://it.vegas-casino-online.com/homytol/>homytol</a>
<a href=https://it.vegas-casino-online.com/migliori-casino-italiani/>Migliori Casino Italiani</a>
<a href=https://it.vegas-casino-online.com/quando-fu-inventa-la-ruota/>Quando Fu Inventa La Ruota</a>
<a href=https://it.vegas-casino-online.com/giochi-gratis-la-ruota-della-fortuna/>Giochi Gratis La Ruota Della Fortuna</a>
<a href=https://it.vegas-casino-online.com/vieni-vincero-alle-slot-online/>Vieni Vincero Alle slot online</a>
<a href=https://it.vegas-casino-online.com/il-pianeta-vince-il-poker/>Il pianeta vince il poker</a>
<a href=https://it.vegas-casino-online.com/nyx-shop-online/>NYX Shop online</a>
<a href=https://it.vegas-casino-online.com/gioco-di-bar/>Gioco di Bar</a>
<a href=https://it.vegas-casino-online.com/slot-a-spin-gemelli/>Slot a spin gemelli</a>
<a href=https://it.vegas-casino-online.com/moneta-di-malta/>Moneta di Malta</a>
<a href=https://it.vegas-casino-online.com/carte-scopa-gratis/>Carte Scopa Gratis</a>
<a href=https://it.vegas-casino-online.com/black-jack-21/>Black Jack 21</a>
<a href=https://it.vegas-casino-online.com/slot-vlt-online/>slot vlt online</a>
<a href=https://it.vegas-casino-online.com/slot-machine-da-bar-gratis-senza-cicalare/>slot machine da bar gratis senza cicalare</a>
<a href=https://it.vegas-casino-online.com/vieni-a-avivare-nuova-pospepay/>Vieni a Avivare Nuova pospepay</a>
<a href=https://it.vegas-casino-online.com/scopa-gratis/>Scopa gratis</a>
<a href=https://it.vegas-casino-online.com/scaricare-giochi-a-pagamento-gratis-iphone/>Scaricare Giochi a Pagamento gratis iPhone</a>
<a href=https://it.vegas-casino-online.com/roulette-francese-3/>roulette francese</a>
<a href=https://it.vegas-casino-online.com/vieni-funzionano-le-slot-machine/>Vieni Funzionano Le Slot Machine</a>
<a href=https://it.vegas-casino-online.com/rush-game-casino/>Rush Game Casino</a>
<a href=https://it.vegas-casino-online.com/chat-di-lottomatico/>chat di lottomatico</a>
<a href=https://it.vegas-casino-online.com/giochi-di-crash/>Giochi di Crash</a>
<a href=https://it.vegas-casino-online.com/bass-in-italiano/>Bass in italiano</a>
<a href=https://it.vegas-casino-online.com/problemi-prelievo-lottomatico/>Problemi Prelievo Lottomatico</a>
<a href=https://it.vegas-casino-online.com/london-store-e-affidabile/>London Store e affidabile</a>
<a href=https://it.vegas-casino-online.com/vieni-creare-un-account-google-per-minorenni/>Vieni Creare Un account Google per minorenni</a>
<a href=https://it.vegas-casino-online.com/codice-cas/>Codice CAS</a>
미국배대지
<a href=https://it.vegas-casino-online.com/regolomento-burraco-italiano/>Regolomento Burraco italiano</a>
<a href=https://it.vegas-casino-online.com/slot-machine-gratis-nuove-2/>Slot machine gratis Nuove</a>
<a href=https://it.vegas-casino-online.com/scala-batte-colore/>Scala Batte Colore</a>
<a href=https://it.vegas-casino-online.com/contare-carte-blackjack-online/>Contare Carte Blackjack online</a>
미국배송대행
미국배대지
<a href=https://it.vegas-casino-online.com/venezia-roulette/>Venezia Roulette</a>
<a href=https://it.vegas-casino-online.com/gioco-scopa-gratis-contro-pc/>Gioco SCOPA GRATIS Contro PC</a>
<a href=https://it.vegas-casino-online.com/bonanza-slot-gratis/>Bonanza slot gratis</a>
<a href=https://it.vegas-casino-online.com/lottomatico-aviatore/>lottomatico aviatore</a>
중국배대지
<a href=https://it.vegas-casino-online.com/quelli-di-flip/>Quelli di Flip</a>
<a href=https://it.vegas-casino-online.com/virtual-marketing-services-italia-ltd/>Virtual Marketing Services Italia Ltd</a>
<a href=https://it.vegas-casino-online.com/nuovo-gioc/>Nuovo GIOC</a>
<a href=https://it.vegas-casino-online.com/blackjack-di-contare-le-carte/>Blackjack di contare le carte</a>
<a href=https://it.vegas-casino-online.com/monoploy-live/>Monoploy Live</a>
<a href=https://it.vegas-casino-online.com/monete-promozioni/>monete promozioni</a>
<a href=https://it.vegas-casino-online.com/trucchi-per-slot-machine/>Trucchi per slot machine</a>
<a href=https://it.vegas-casino-online.com/download-gratis-per-pc-giochi/>Download gratis per PC Giochi</a>
https://android-1.ru/
<a href="https://vammebel.ru/catalog/takhta/">тахта</a>
<a href="https://vammebel.ru/catalog/takhta/uglovaya-krovat-tahta/">тахта угловая</a>
Обменять с киви на бтк[/url]
<a href="https://mlne-exchenge.com">
обмен qiwi</a>
ключи: samaralan самара , самаралан самара , самаралан , провайдер самаралан , samaralan интернет тариф , samaralan тв
http://mappingaset.bnpb.go.id/new/public/rumah/2439/submit.html
https://noblentv.com/yan-shekarun-nan-barcelona-suna-fuskantar-tozarci-a-gasar-zakarun-nahiyar-turai/
http://learnwithnontechnical.com/index.php/archives/6/
теги: стирка белья за кг в Москве , стирка одежды в Москве , постирать белье в Москве , стирка в Москве , сколько стоит постирать белье в Москве , стоимость стирки в Москве
https://ajayreports.com/index.php/2019/07/14/only-public-primary-school-in-owube-community-rivers-state-has-one-teacher/#comment-592232
https://es.my-subs.co/film-versions-39-deadpool-subtitles/
https://www.shadanovels.com/book.php?id_book=3
Лейбл iwMusic приглашает к сотрудничеству по изданию (дистрибуции) ваших релизов на все цифровые площадки.
Важным преимуществом является - быстро и бесплатно.
Мы лицензируем и издаем не только авторские треки, но и каверы.
Ваш кавер будет размещен на всех цифровых площадках (Apple Music, Spotify, Amazon, Deezer, YouTube Music и др), включая русские - ВК, Яндекс Музыка, BOOM, Звук
Мы получим для вас разрешение на дистрибуцию вашего кавера и получении роялти (доход) быстро и не дорого.
Так же мы поможем получить разрешения (лицензии) для монетизации каверов на YouTube и других сервисах.
iwMusic - помогает в создании музыкальных произведений. Мы сотрудничаем с аранжировщиками и саунд-продюсерами из Европы, США, Англии, России и других стран. Длительные отношения позволяют получить качественный материал в сжатые сроки и за небольшую стоимость.
Будем рады ответить на ваши вопросы
[url=https://iwmusic.ru/rebirth-album/]
каверы cover[/url]
<a href="https://iwmusic.ru/rebirth-album/">
кавер</a>
key: прачечная для отелей в Москве , прачечная для мини отелей в Москве , стирка для хостела в Москве , прачечная для гостиниц в Москве , прачечная для хостела в Москве , стирка белья для гостиниц в Москве
https://alamantech.com/product/%d8%aa%d9%84%d9%81%d9%88%d9%86-kx-t7730/#comment-87601/
http://www.hidplanet.ru/forum/viewtopic.php?f=35&t=7895
https://www.subjectpoint.com/post/4/
steam authenticator desktop[/url]
<a href="https://steamauthenticator.net/">
download sda steam authenticator</a>
미국배대지
скачать sda steam authenticator[/url]
<a href="https://steamauthenticator.net/">
download sda steam authenticator</a>
타오바오구매대행
ключи: услуги стирки и глажки в Москве , где постирать белье в Москве , стирка москва недорого в Москве , стирка вещей в Москве , стирка белого в Москве , постирать белье в Москве
https://www.studiopappalepore.com/02122004003/#comment-19226/
https://www.fhllogistics.com/blogs/news/cuantos-barcos-de-carga-transitan-por-el-canal-de-panama?comment=132088135743#comments
https://bomberosiquique.cl/colision-de-automovil-con-rampla-moviliza-a-bomberos-a-ruta-a-16/#comment-96647/
как зайти на омг[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5.onioond.com">
ссылка omg</a>
рулетка для бомжей от 1 рубля[/url]
<a href="http://csgoshort.com/">
бич рулетка кс</a>
미국배대지
중국배대지
omgomgomg5j4yrr4mjdv3h5c5xfvxtqqs2in7smi65mjps7wvkmqmtqd сайт[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5-onion.com/">
вход омг</a>
Выпустить свой кавер на всех площадках с iwMusic.ru - быстро и просто!
Pachuli с успехом справились с непростой задачей — сотворить что-то новое и не «упасть в грязь». Замахнулись то на «великое».
Было выбрано танцевальное направление. И не прогадали. Трек получился зажигательным, танцевальным и запоминающимся.
Трек Pachuli — Sweet Dreams вышел на всех стриминговых платформах. https://iwmusic.ru/album/pachuli-sweet-dreams
Стоимость лицензионного разрешения для официальной и бессрочной дистрибуции (на весь мир) составила 5000 рублей.
[url=https://iwmusic.ru/album/pachuli-sweet-dreams]
Каверы[/url]
<a href="https://iwmusic.ru/album/pachuli-sweet-dreams">
guitar cover</a>
America’s favorite sports book!
Jiliwin.com sports betting promos !
Online sportsbook and casino 150% Welcome Bonus
Providing latest and best odds on all sports.
Gcash Casino Cash Out!
Subukan ang aming 1000+ Games
Play?JDB, JILI, PlayStar, CQ9?
Web https://bit.ly/3qknimf
Register https://bit.ly/3q7cCr4
Earn money in Gcash! Tara!
중국배대지
Выпустить свой кавер на всех площадках с iwMusic.ru - быстро и просто!
Pachuli с успехом справились с непростой задачей — сотворить что-то новое и не «упасть в грязь». Замахнулись то на «великое».
Было выбрано танцевальное направление. И не прогадали. Трек получился зажигательным, танцевальным и запоминающимся.
Трек Pachuli — Sweet Dreams вышел на всех стриминговых платформах. https://iwmusic.ru/album/pachuli-sweet-dreams
Стоимость лицензионного разрешения для официальной и бессрочной дистрибуции (на весь мир) составила 5000 рублей.
[url=https://iwmusic.ru/album/pachuli-sweet-dreams]
Кавер авторские права[/url]
<a href="https://iwmusic.ru/album/pachuli-sweet-dreams">
Нужно ли разрешение на запись кавера?</a>
<a href="https://androidos-play.info/musical/3751-download-queen-rock-tour-unlimited-money-mod-ver-116-for-android.html">https://androidos-play.info/musical/3751-download-queen-rock-tour-unlimited-money-mod-ver-116-for-android.html</a>
<a href="https://androidos-play.info/adventure/882-download-forgotton-anne-unlocked-all-mod-ver-14-for-android.html">https://androidos-play.info/adventure/882-download-forgotton-anne-unlocked-all-mod-ver-14-for-android.html</a>
<a href="https://androidos-play.info/medical/13154-download-anatomy-3d-premium-mod-ver-15-for-android.html">https://androidos-play.info/medical/13154-download-anatomy-3d-premium-mod-ver-15-for-android.html</a>
<a href="https://androidos-play.info/maps_navigation/12657-download-delimobil-your-carsharing-premium-mod-ver-7310-build-fcf5a8b21-for-android.html">https://androidos-play.info/maps_navigation/12657-download-delimobil-your-carsharing-premium-mod-ver-7310-build-fcf5a8b21-for-android.html</a>
<a href="https://androidos-play.info/photography/14014-download-blur-image-background-premium-mod-ver-1024-for-android.html">https://androidos-play.info/photography/14014-download-blur-image-background-premium-mod-ver-1024-for-android.html</a>
Beautiful graphic component, which crazy harmoniously fit in application. Naughty a piece of music. Fascinating conditions.
<a href="https://androidos-top.com/action/125-download-evil-plush-toy-horror-unlocked-all-mod-for-android.html">https://androidos-top.com/action/125-download-evil-plush-toy-horror-unlocked-all-mod-for-android.html</a>
<a href="https://androidos-top.com/adventure/632-download-lonewolf-17-unlimited-money-mod-for-android.html">https://androidos-top.com/adventure/632-download-lonewolf-17-unlimited-money-mod-for-android.html</a>
<a href="https://androidos-top.com/food_drink/11120-download-diksi-unlocked-mod-for-android.html">https://androidos-top.com/food_drink/11120-download-diksi-unlocked-mod-for-android.html</a>
<a href="https://androidos-top.com/dating/10066-download-datemyage-pro-version-mod-for-android.html">https://androidos-top.com/dating/10066-download-datemyage-pro-version-mod-for-android.html</a>
<a href="https://androidos-top.com/puzzle/4150-download-labyrinth-maze-unlimited-coins-mod-for-android.html">https://androidos-top.com/puzzle/4150-download-labyrinth-maze-unlimited-coins-mod-for-android.html</a>
Beautiful graphic, which crazy harmoniously included in program. Funny a piece of music. Fascinating conditions.
<a href="https://androidos-top.com/trivia/7142-download-viktorina-riverdeyl-uznay-kakoy-ty-fanat-unlimited-money-mod-for-android.html">https://androidos-top.com/trivia/7142-download-viktorina-riverdeyl-uznay-kakoy-ty-fanat-unlimited-money-mod-for-android.html</a>
<a href="https://androidos-top.com/communication/9889-download-textme-up-calling-amp-texts-premium-mod-for-android.html">https://androidos-top.com/communication/9889-download-textme-up-calling-amp-texts-premium-mod-for-android.html</a>
<a href="https://androidos-top.com/puzzle/4259-download-switchcraft-magical-match-3-unlocked-all-mod-for-android.html">https://androidos-top.com/puzzle/4259-download-switchcraft-magical-match-3-unlocked-all-mod-for-android.html</a>
<a href="https://androidos-top.com/educational/3099-download-reaction-training-premium-unlocked-mod-for-android.html">https://androidos-top.com/educational/3099-download-reaction-training-premium-unlocked-mod-for-android.html</a>
<a href="https://androidos-top.com/medical/13478-download-rzhd-medicina-premium-mod-for-android.html">https://androidos-top.com/medical/13478-download-rzhd-medicina-premium-mod-for-android.html</a>
Beautiful graphic, which very coherent included in program. Naughty musical tunes. Attractive tasks.
<a href="https://exhub.su/">
exhub io</a>
[url=https://prostitutkinu.com/]
Досуг Новый Уренгой недорого[/url]
<a href="https://prostitutkinu.com/">
Сайт досуга Нового Уренгоя</a>
<a href="https://droidos.download/books_reference/8382-download-hack-abakanbus-free-ad-mod-for-android-ver-210.html">https://droidos.download/books_reference/8382-download-hack-abakanbus-free-ad-mod-for-android-ver-210.html</a>
<a href="https://droidos.download/books_reference/8843-download-hack-biblioteka-unlocked-mod-for-android-ver-1021.html">https://droidos.download/books_reference/8843-download-hack-biblioteka-unlocked-mod-for-android-ver-1021.html</a>
<a href="https://droidos.download/dating/10037-download-hack-curvy-singles-dating-unlocked-mod-for-android-ver-1020.html">https://droidos.download/dating/10037-download-hack-curvy-singles-dating-unlocked-mod-for-android-ver-1020.html</a>
<a href="https://droidos.download/word/7281-download-hack-skanvordru-zhurnal-skanvordy-premium-unlocked-mod-for-android-ver-198.html">https://droidos.download/word/7281-download-hack-skanvordru-zhurnal-skanvordy-premium-unlocked-mod-for-android-ver-198.html</a>
<a href="https://droidos.download/role_playing/5405-download-hack-epic-conquest-2-unlimited-money-mod-for-android-ver-v16a.html">https://droidos.download/role_playing/5405-download-hack-epic-conquest-2-unlimited-money-mod-for-android-ver-v16a.html</a>
Beautiful picture, which very coherent included in program. Cheerful musical tunes. Attractive tasks.
[url=https://prostitutki-new-urengoy.com/]
Зрелые индивидуалки Новый Уренгой[/url]
<a href="https://prostitutki-new-urengoy.com/">
Индивидуалки Новый Уренгой недорого</a>
[url=https://prostitutki-new-urengoy.com/]
Шалавы по вызову Новый Уренгой[/url]
<a href="https://prostitutki-new-urengoy.com/">
Шалавы Новый Уренгой недорого</a>
<a href="https://fixedfloate.com/">fixedfloat обмен бтк</a>
+7(910)146-24-28
[url=https://artmodel.biz/]
Работа для девушек за границей вакансии
[/url]
<a href="https://artmodel.biz/">
Работа для девушек за границей вакансии
</a>
<a href="https://soft.4droidos.mobi">soft.4droidos.mobi</a>
<a href="https://soft.androidos-play.info">soft.androidos-play.info</a>
<a href="https://soft.androidos-top.com">soft.androidos-top.com</a>
<a href="https://soft.droid-mob.com">soft.droid-mob.com</a>
<a href="https://soft.droidos.download">soft.droidos.download</a>
Juicy graphic, which crazy coherent enter in program. Cheerful musical tunes. Good tasks.
[url=https://artmodel.biz/country/oae_dubay.html]
Работа в Дубае проституткой[/url]
+7(910)146-24-28
https://artmodel.biz/country/gretsiya.html
[url=https://artmodel.biz/country/kitay.html]Работа Китай для девушек из России[/url]<a href="https://artmodel.biz/country/egipet.html">Работа в Египте проституткой</a>
<a href="https://soft.4droidos.mobi">soft.4droidos.mobi</a>
<a href="https://soft.androidos-play.info">soft.androidos-play.info</a>
<a href="https://soft.androidos-top.com">soft.androidos-top.com</a>
<a href="https://soft.droid-mob.com">soft.droid-mob.com</a>
<a href="https://soft.droidos.download">soft.droidos.download</a>
Beautiful graphic, which very harmonious enter in application. Cheerful musical tunes. Entertaining tasks.
[url=https://artmodel.biz/country/ssha.html]
Работа в сфере досуга США[/url]
+7(910)146-24-28
https://artmodel.biz/country/oae_dubay.html
[url=https://artmodel.biz/country/bahreyn.html]Работа для девушек Бахрейн[/url]<a href="https://artmodel.biz/country/kitay.html">Работа в Китае девушкам</a>
[url=https://saunanu.xyz/]сауны и бани Нового Уренгоя[/url]
<a href="https://saunanu.xyz/">Сауны Новый Уренгой</a>
[url=https://saunanu.xyz/]сауна Новый Уренгой[/url]
<a href="https://saunanu.xyz/">баня Новый Уренгой</a>
<a href="https://androidos-play.info/books_reference/8484-download-lithium-epub-reader-pro-version-mod-ver-0241-for-android.html">https://androidos-play.info/books_reference/8484-download-lithium-epub-reader-pro-version-mod-ver-0241-for-android.html</a>
<a href="https://androidos-play.info/maps_navigation/12931-download-mobile-number-tracker-find-my-phone-pro-version-mod-ver-18-for-android.html">https://androidos-play.info/maps_navigation/12931-download-mobile-number-tracker-find-my-phone-pro-version-mod-ver-18-for-android.html</a>
<a href="https://androidos-play.info/simulation/5444-download-building-destruction-unlimited-coins-mod-ver-333-for-android.html">https://androidos-play.info/simulation/5444-download-building-destruction-unlimited-coins-mod-ver-333-for-android.html</a>
<a href="https://androidos-play.info/art_design/7435-download-how-to-draw-eyes-step-by-step-free-ad-mod-ver-10-for-android.html">https://androidos-play.info/art_design/7435-download-how-to-draw-eyes-step-by-step-free-ad-mod-ver-10-for-android.html</a>
<a href="https://androidos-play.info/auto_vehicles/7871-download-leafhacker-unlocked-mod-ver-15-for-android.html">https://androidos-play.info/auto_vehicles/7871-download-leafhacker-unlocked-mod-ver-15-for-android.html</a>
Beautiful graphic component, which crazy coherent included in program. Cheerful music tracks. Attractive conditions.
[url=https://escortnu.xyz/]
эскорт услуги цена Новый Уренгой[/url]
<a href="https://escortnu.xyz/">
vip эскорт в Новом Уренгое</a>
<a href="https://androidos-play.info/music_audio/13564-download-lg-xboom-premium-mod-ver-1368-for-android.html">https://androidos-play.info/music_audio/13564-download-lg-xboom-premium-mod-ver-1368-for-android.html</a>
<a href="https://androidos-play.info/sports/5881-download-stickman-soccer-2014-unlimited-money-mod-ver-29-for-android.html">https://androidos-play.info/sports/5881-download-stickman-soccer-2014-unlimited-money-mod-ver-29-for-android.html</a>
<a href="https://androidos-play.info/casual/2932-download-clusterduck-unlimited-money-mod-ver-163-for-android.html">https://androidos-play.info/casual/2932-download-clusterduck-unlimited-money-mod-ver-163-for-android.html</a>
<a href="https://androidos-play.info/health_fitness/11388-download-white-noise-baby-sleep-sounds-unlocked-mod-ver-184-for-android.html">https://androidos-play.info/health_fitness/11388-download-white-noise-baby-sleep-sounds-unlocked-mod-ver-184-for-android.html</a>
<a href="https://androidos-play.info/social/14624-download-status-saver-2021-pro-version-mod-ver-134-for-android.html">https://androidos-play.info/social/14624-download-status-saver-2021-pro-version-mod-ver-134-for-android.html</a>
Beautiful graphic, which crazy plastically included in application. Naughty musical tunes. Good tasks.
omg[/url]
<a href="https://omgomgomg5j4yrr4mjdv-onion.com/">
omg магазин</a>
что за omg [/url]
<a href="https://omgomgomg5j4yrr4mjdv-onion.com/">
omg omg даркнет</a>
<a href="https://4droidos.mobi/word/6790-download-skanvordy-ru-mod-free-shopping-for-android.html">https://4droidos.mobi/word/6790-download-skanvordy-ru-mod-free-shopping-for-android.html</a>
<a href="https://4droidos.mobi/auto_vehicles/7537-download-my-auto-premium-mod-for-android.html">https://4droidos.mobi/auto_vehicles/7537-download-my-auto-premium-mod-for-android.html</a>
<a href="https://4droidos.mobi/dating/9505-download-lovy-premium-mod-for-android.html">https://4droidos.mobi/dating/9505-download-lovy-premium-mod-for-android.html</a>
<a href="https://4droidos.mobi/racing/3936-download-avtoshkola-simulyator-vozhdeniya-mod-unlimited-money-for-android.html">https://4droidos.mobi/racing/3936-download-avtoshkola-simulyator-vozhdeniya-mod-unlimited-money-for-android.html</a>
<a href="https://4droidos.mobi/tools/14412-download-camhi-unlocked-mod-for-android.html">https://4droidos.mobi/tools/14412-download-camhi-unlocked-mod-for-android.html</a>
Excellent graphic, which unparalleled harmonious enter in program. Naughty musical tunes. Entertaining conditions.
<a href="https://4droidos.mobi/education/9764-download-busuu-learn-languages-premium-mod-for-android.html">https://4droidos.mobi/education/9764-download-busuu-learn-languages-premium-mod-for-android.html</a>
<a href="https://4droidos.mobi/education/9877-download-uchi-vremena-angliyskogo-yazyka-grammatika-poliglot-free-ad-mod-for-android.html">https://4droidos.mobi/education/9877-download-uchi-vremena-angliyskogo-yazyka-grammatika-poliglot-free-ad-mod-for-android.html</a>
<a href="https://4droidos.mobi/role_playing/4488-download-elona-mobile-mod-unlimited-money-for-android.html">https://4droidos.mobi/role_playing/4488-download-elona-mobile-mod-unlimited-money-for-android.html</a>
<a href="https://4droidos.mobi/maps_navigation/12480-download-taksovichkof-pult-prilozhenie-dlya-voditeley-premium-mod-for-android.html">https://4droidos.mobi/maps_navigation/12480-download-taksovichkof-pult-prilozhenie-dlya-voditeley-premium-mod-for-android.html</a>
<a href="https://4droidos.mobi/role_playing/4357-download-sky-children-of-the-light-mod-premium-unlocked-for-android.html">https://4droidos.mobi/role_playing/4357-download-sky-children-of-the-light-mod-premium-unlocked-for-android.html</a>
Juicy graphic, which very coherent enter in program. Cool music tracks. Entertaining tasks.
online earnings on the internet[/url]
<a href="https://new-music.online/affiliate.php">
earnings on the internet by month</a>
<a href="https://iscra.pt/cada-apostador-principiante-precisa-de-saber-em-que-e-o-melhor-desporto-para-apostar/">https://iscra.pt/cada-apostador-principiante-precisa-de-saber-em-que-e-o-melhor-desporto-para-apostar/</a>
<a href="https://www.laredazione.eu/strategia-di-poker-spin-go/">https://www.laredazione.eu/strategia-di-poker-spin-go/</a>
<a href="https://androidos-top.com/social/14552-download-kate-mobile-for-vk-premium-mod-for-android.html">https://androidos-top.com/social/14552-download-kate-mobile-for-vk-premium-mod-for-android.html</a>
<a href="https://androidos-top.com/adventure/638-download-mastercraft-2021-premium-unlocked-mod-for-android.html">https://androidos-top.com/adventure/638-download-mastercraft-2021-premium-unlocked-mod-for-android.html</a>
<a href="https://androidos-top.com/card/1817-download-klondike-solitaire-classic-free-shopping-mod-for-android.html">https://androidos-top.com/card/1817-download-klondike-solitaire-classic-free-shopping-mod-for-android.html</a>
<a href="https://androidos-top.com/lifestyle/12739-download-azan-russia-prayer-times-in-russia-premium-mod-for-android.html">https://androidos-top.com/lifestyle/12739-download-azan-russia-prayer-times-in-russia-premium-mod-for-android.html</a>
<a href="https://androidos-top.com/business/9223-download-atomy-business-company-info-unlocked-mod-for-android.html">https://androidos-top.com/business/9223-download-atomy-business-company-info-unlocked-mod-for-android.html</a>
Juicy graphic component, which very plastically fit in program. Funny a piece of music. Good conditions.
<a href="https://workgirls.biz/city/ekaterinburg.html">вакансии для девушек Екатеринбург</a>
<a href="https://rabotanu.ru/city/perm">работа девушкам Пермь эскорт</a>
https://34.87.76.32:889/
<a href="https://koroleva.world/city/stavropol">Работа для девушек Ставрополь</a>
<a href="https://jobgirls.xyz/category/ufa.html">вакансии для девушек Уфа</a>
mixer bitcoin[/url]
<a href="https://mixer-bitcoin.org/">
Блендеры биткоин </a>
Автоматические обмен[/url]
<a href="http://mine-exhcange.com/">
Шахта обмен денег</a>
Обменник шахта[/url]
<a href="http://mine-exhcange.com/">
bestchange шахта</a>
<a href="http://www.aluminisbcn.com/investigationes-lectores-consuetudium/comment-page-63372/#comment-176074">Jili178</a> dbc54c2
Jili178 online casino bonus quota extra much bigger
Jili178 how to register get 150%
Is it easy to get promo and special offers here.
Jili178 Gcash deposit 78 get 178 bonus
Jili178 Bonus daily update!
We have Jili178 agent system to drive traffic to your betting website and boost your revenue.
Jili178 live show, super ace, fishing game up to 1000games
<a href="https://rabota-devushkam.net/nefteugansk/">вакансии девушкам Нефтеюганск</a>
<a href="https://rabota-devushkam.ru.com/tula/">Работа для девушек Тула</a>
주안룸싸롱,주안가라오케
주안룸싸롱 기존에 인천에서 만나볼 수 있었던 룸싸롱을 주안에서도 편하게 만나볼수 있도록 생긴 업소입니다.인천가라오케
정성가득 매일 매일 이벤트 진행중 ! 아가씨 50명 이상 대기중 !
주안유일 초대형 룸싸롱 ! 가라오케도 편하게 전화주세요 ~
24시간 365일 영업중입니다.주안룸 친절하게 예약 도와드리겠습니다.
단체 및 혼자 오셔도 정성스럽게 여자친구 찾아드리겠습니다.
주안셔츠룸 , 주안가라오케 ,주안노래빠 ,주안노래빠 ,인천셔츠룸, 인천노래빠
인천가라오케,연수동노래빠,인천룸싸롱
신촌룸싸롱 기존에 마포에서 만나볼 수 없었던 룸싸롱을 홍대,신촌에서도 편하게 만나볼수 있도록 생긴 업소입니다.홍대가라오케
정성가득 매일 매일 이벤트 진행중 ! 아가씨 50명 이상 대기중 !
홍대 유일 초대형 룸싸롱 ! 가라오케도 편하게 전화주세요 ~
24시간 365일 영업중입니다.신촌룸 친절하게 예약 도와드리겠습니다.
단체 및 혼자 오셔도 정성스럽게 여자친구 찾아드리겠습니다.
홍대셔츠룸 , 신촌가라오케 ,신촌노래빠 ,홍대노래빠 ,신촌셔츠룸, 마포노래빠
홍대 호빠,신촌 호빠,마포 가라오케
수유룸싸롱,수유노래빠
수유룸싸롱 기존에 수유에서 만나볼 수 없었던 룸싸롱을 수유에서도 편하게 만나볼수 있도록 생긴 업소입니다.수유가라오케
정성가득 매일 매일 이벤트 진행중 ! 아가씨 50명 이상 대기중 !
강북유일 초대형 룸싸롱 ! 가라오케도 편하게 전화주세요 ~
24시간 365일 영업중입니다.수유룸 친절하게 예약 도와드리겠습니다.
단체 및 혼자 오셔도 정성스럽게 여자친구 찾아드리겠습니다.
수유셔츠룸 , 수유가라오케 ,수유노래빠 ,강북노래빠 ,강북셔츠룸, 강북노래빠
노원가라오케,노원노래빠,노원룸싸롱
잠실룸싸롱 기존에 잠실에서 만나볼 수 있었던 룸싸롱을 잠실에서도 편하게 만나볼수 있도록 생긴 업소입니다.잠실가라오케
정성가득 매일 매일 이벤트 진행중 ! 아가씨 50명 이상 대기중 !
잠실유일 초대형 룸싸롱 ! 가라오케도 편하게 전화주세요 ~
24시간 365일 영업중입니다.잠실룸 친절하게 예약 도와드리겠습니다.
단체 및 혼자 오셔도 정성스럽게 여자친구 찾아드리겠습니다.
잠실셔츠룸 , 잠실가라오케 ,잠실노래빠 ,잠실노래빠 , 가락셔츠룸, 가락노래빠
가락가라오케,가락동노래빠,가락룸싸롱
<a href="https://rabota-devushkam.ru.com/%d0%bf%d0%b5%d0%bd%d0%b7%d0%b0/">вакансии для девушек Пенза</a>
마곡룸싸롱 기존에 강서에서 만나볼 수 없었던 룸싸롱을 마곡에서도 편하게 만나볼수 있도록 생긴 업소입니다.마곡가라오케
정성가득 매일 매일 이벤트 진행중 ! 아가씨 50명 이상 대기중 !
강서유일 초대형 룸싸롱 ! 가라오케도 편하게 전화주세요 ~
24시간 365일 영업중입니다.수유룸 친절하게 예약 도와드리겠습니다.
단체 및 혼자 오셔도 정성스럽게 여자친구 찾아드리겠습니다.
마곡셔츠룸 , 마곡가라오케 마곡노래빠 ,강서노래빠 ,강서셔츠룸, 강서노래빠,강서가라오케
골든타워가라오케,골든타워노래빠,골든타워룸싸롱
<a href="https://rabotadevushkam.net/samara/">Работа для девушек Самара</a>
омг официальный сайт[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5-onions.com/">
omg darkmarket</a>
<a href="https://reklamaxxx.biz/tolyatti/">Работа для девушек Тольятти</a>
<a href=http://www.oknakup.sk/plugins/guestbook/go.php?url=http://androidos-play.info>http://www.oknakup.sk/plugins/guestbook/go.php?url=http://androidos-play.info</a>
<a href=http://compozitor.spb.ru/bitrix/redirect.php?goto=http://androidos-play.info>http://compozitor.spb.ru/bitrix/redirect.php?goto=http://androidos-play.info</a>
<a href=http://recleasing.com/__media__/js/netsoltrademark.php?d=androidos-play.info>http://recleasing.com/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
<a href=http://www.seniordonor.com/__media__/js/netsoltrademark.php?d=androidos-play.info>http://www.seniordonor.com/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
<a href=http://elmid.ru/bitrix/redirect.php?goto=http://androidos-play.info>http://elmid.ru/bitrix/redirect.php?goto=http://androidos-play.info</a>
Colourful picture, which very plastically included in program. Cheerful music tracks. Fascinating tasks.
<a href=http://f800gs.com/__media__/js/netsoltrademark.php?d=androidos-play.info>http://f800gs.com/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
<a href=http://xn----7sbaba3aqfnfeyeb7cdjk2dyhtce.xn--p1ai/bitrix/rk.php?goto=http://androidos-play.info>http://xn----7sbaba3aqfnfeyeb7cdjk2dyhtce.xn--p1ai/bitrix/rk.php?goto=http://androidos-play.info</a>
<a href=http://vechnayamolodost.ru/bitrix/redirect.php?goto=http://androidos-play.info>http://vechnayamolodost.ru/bitrix/redirect.php?goto=http://androidos-play.info</a>
<a href=http://avtoved.guru/proxy.php?link=http://androidos-play.info>http://avtoved.guru/proxy.php?link=http://androidos-play.info</a>
<a href=http://0.equitabletermiii.tv/__media__/js/netsoltrademark.php?d=androidos-play.info>http://0.equitabletermiii.tv/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
Colourful graphic, which crazy harmonious enter in program. Funny music tracks. Attractive conditions.
[url=https://videosalon.xyz/]фильмы и сериалы онлайн[/url]
<a href="https://videosalon.xyz/">фильмы и сериалы онлайн</a>
<a href="https://red-buffaloes.com/trend/1348/#comment-1173383">slot online wikislot</a> fd17ac9
<a href=http://noveg.ru/bitrix/click.php?goto=http://androidos-play.info>http://noveg.ru/bitrix/click.php?goto=http://androidos-play.info</a>
<a href=http://mukomoloff.ru/bitrix/click.php?goto=http://androidos-play.info>http://mukomoloff.ru/bitrix/click.php?goto=http://androidos-play.info</a>
<a href=http://www.senjal.com/__media__/js/netsoltrademark.php?d=androidos-play.info>http://www.senjal.com/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
<a href=http://www.arpco.net/__media__/js/netsoltrademark.php?d=androidos-play.info>http://www.arpco.net/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
<a href=http://mik.com.ua/bitrix/redirect.php?goto=http://androidos-play.info>http://mik.com.ua/bitrix/redirect.php?goto=http://androidos-play.info</a>
Beautiful graphic, which very plastically included in application. Cheerful music tracks. Fascinating conditions.
giá gửi hàng sang mỹ</a>
<a href=http://svidanka.ru/en/tips?tip=ExternalLink&link=http://androidos-play.info>http://svidanka.ru/en/tips?tip=ExternalLink&link=http://androidos-play.info</a>
<a href=http://11alive.video/__media__/js/netsoltrademark.php?d=androidos-play.info>http://11alive.video/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
<a href=http://igraj.by/bitrix/rk.php?goto=http://androidos-play.info>http://igraj.by/bitrix/rk.php?goto=http://androidos-play.info</a>
<a href=http://www.center-pointenergy.biz/__media__/js/netsoltrademark.php?d=androidos-play.info>http://www.center-pointenergy.biz/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
<a href=http://desertwestcre.com/__media__/js/netsoltrademark.php?d=androidos-play.info>http://desertwestcre.com/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
Colourful picture, which unparalleled plastically included in application. Cheerful music tracks. Fascinating tasks.
<a href="https://jobgirls.xyz/category/novosibirsk.html">Работа для девушек Новосибирск</a>
<a href="https://droiders.mobi/descargar-demolition-derby-multiplayer-1-3-6-mod-many-money-para-android/">https://droiders.mobi/descargar-demolition-derby-multiplayer-1-3-6-mod-many-money-para-android/</a>
<a href="https://droiders.mobi/descargar-dove-icon-pack-2-8-mod-patch-para-android/">https://droiders.mobi/descargar-dove-icon-pack-2-8-mod-patch-para-android/</a>
<a href="https://droiders.mobi/descargar-pie-launcher-version-2022-12-2-mod-unlocked-para-android/">https://droiders.mobi/descargar-pie-launcher-version-2022-12-2-mod-unlocked-para-android/</a>
<a href="https://droiders.mobi/descargar-standoff-2-case-opener-2-00-mod-many-money-para-android/">https://droiders.mobi/descargar-standoff-2-case-opener-2-00-mod-many-money-para-android/</a>
<a href="https://droiders.mobi/descargar-horizonte-1-2-1-mod-many-money-para-android/">https://droiders.mobi/descargar-horizonte-1-2-1-mod-many-money-para-android/</a>
Juicy grafico, que muy coherente adaptado en programa. Divertido pistas musicales. Bueno condiciones.
<a href="https://droiders.mobi/descargar-wish-simulator-para-genshin-35-en-android/">https://droiders.mobi/descargar-wish-simulator-para-genshin-35-en-android/</a>
<a href="https://droiders.mobi/descargar-rising-super-chef-juego-de-cocina-6-2-0-mod-many-money-para-android/">https://droiders.mobi/descargar-rising-super-chef-juego-de-cocina-6-2-0-mod-many-money-para-android/</a>
<a href="https://droiders.mobi/descargar-bodybuilding-strength-training-2-18-mod-pro-unlocked-para-android/">https://droiders.mobi/descargar-bodybuilding-strength-training-2-18-mod-pro-unlocked-para-android/</a>
<a href="https://droiders.mobi/descargar-tigerball-1-2-3-5-mod-many-money-para-android/">https://droiders.mobi/descargar-tigerball-1-2-3-5-mod-many-money-para-android/</a>
<a href="https://droiders.mobi/descargar-yuface-camera-effect-face-up-3-3-4-mod-unlocked-en-android/">https://droiders.mobi/descargar-yuface-camera-effect-face-up-3-3-4-mod-unlocked-en-android/</a>
Juicy componente grafico, que muy armonioso adaptado en aplicacion. Alegre pistas musicales. Atractivo tareas.
الاسهم السعودية
<a href="https://droiders.mobi/descargar-cyber-launcher-6-6-2-mod-premium-unlocked-para-android/">https://droiders.mobi/descargar-cyber-launcher-6-6-2-mod-premium-unlocked-para-android/</a>
<a href="https://droiders.mobi/descargar-newprofilepic-new-avatar-0-5-10-mod-unlocked-para-android/">https://droiders.mobi/descargar-newprofilepic-new-avatar-0-5-10-mod-unlocked-para-android/</a>
<a href="https://droiders.mobi/descargar-speak-and-translate-languages-7-0-1-premium-unlocked-en-android/">https://droiders.mobi/descargar-speak-and-translate-languages-7-0-1-premium-unlocked-en-android/</a>
<a href="https://droiders.mobi/descargar-facturacion-gst-contabilidad-16-6-4-mod-desbloqueado-para-android/">https://droiders.mobi/descargar-facturacion-gst-contabilidad-16-6-4-mod-desbloqueado-para-android/</a>
<a href="https://droiders.mobi/descargar-my-town-friends-house-1-24-mod-unlocked-para-android/">https://droiders.mobi/descargar-my-town-friends-house-1-24-mod-unlocked-para-android/</a>
Beautiful componente grafico, que incomparable plastico incluido en programa. Alegre una pieza de musica. Atractivo condiciones.
omg tor[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5-onions.com">
вход omg</a>
<a href="https://droiders.mobi/descargar-science-news-12-7-mod-premium-unlocked-para-android/">https://droiders.mobi/descargar-science-news-12-7-mod-premium-unlocked-para-android/</a>
<a href="https://droiders.mobi/descargar-dentures-and-demons-2-1-1-7-mod-unlocked-para-android/">https://droiders.mobi/descargar-dentures-and-demons-2-1-1-7-mod-unlocked-para-android/</a>
<a href="https://droiders.mobi/descargar-park-master-2-6-8-lots-of-money-unlocked-no-ads-para-android/">https://droiders.mobi/descargar-park-master-2-6-8-lots-of-money-unlocked-no-ads-para-android/</a>
<a href="https://droiders.mobi/descargar-bunniiies-the-love-rabbit-1-3-223-mod-free-downloads-para-android/">https://droiders.mobi/descargar-bunniiies-the-love-rabbit-1-3-223-mod-free-downloads-para-android/</a>
<a href="https://droiders.mobi/descargar-g-stomper-producer-5-8-6-5-mod-all-patched-para-android/">https://droiders.mobi/descargar-g-stomper-producer-5-8-6-5-mod-all-patched-para-android/</a>
Excelente componente grafico, que muy coherente adaptado en aplicacion. Alegre pistas musicales. Bueno tareas.
الاسهم السعودية
[url=https://kurer-sreda.ru/2020/09/16/601060-vybor-komplekta-mebeli-dlya-kabineta-rukovoditelya]https://kurer-sreda.ru/2020/09/16/601060-vybor-komplekta-mebeli-dlya-kabineta-rukovoditelya[/url]
<a href="https://lifeglobe.net/entry/11043">https://lifeglobe.net/entry/11043</a>
[url=https://prostitutki-anapa.top/]
Проститутки на дом Анапа[/url]
<a href="https://prostitutki-anapa.top/">
Шалавы выезд в Анапе</a>
<a href="https://android-gamers.mobi/descarregar-jurassic-world-to-life-2-18-26-mod-many-money-para-android/">https://android-gamers.mobi/descarregar-jurassic-world-to-life-2-18-26-mod-many-money-para-android/</a>
<a href="https://android-gamers.mobi/descarregar-manuganu-1-1-3-mod-god-mode-para-android/">https://android-gamers.mobi/descarregar-manuganu-1-1-3-mod-god-mode-para-android/</a>
<a href="https://android-gamers.mobi/descarregar-paper-io-2-3-1-2-mod-no-ads-para-android/">https://android-gamers.mobi/descarregar-paper-io-2-3-1-2-mod-no-ads-para-android/</a>
<a href="https://android-gamers.mobi/descarregar-temple-run-2-1-93-0-mod-many-money-para-android/">https://android-gamers.mobi/descarregar-temple-run-2-1-93-0-mod-many-money-para-android/</a>
<a href="https://android-gamers.mobi/descarregar-s-t-a-r-super-tricky-amazing-run-1-23-0-3-mod-unlocked-para-android/">https://android-gamers.mobi/descarregar-s-t-a-r-super-tricky-amazing-run-1-23-0-3-mod-unlocked-para-android/</a>
Colorido de la imagen, que loco coherente adaptado en aplicacion. Alegre canciones musicales. Entretenido condiciones.
[url=https://prostitutki-anapa.top/]
Индивидуалки выезд в Анапе[/url]
<a href="https://prostitutki-anapa.top/">
Проститутки выезд в Анапе</a>
<a href="https://android-gamers.mobi/descarregar-grand-theft-auto-san-andreas-2-10-mod-many-money-para-android/">https://android-gamers.mobi/descarregar-grand-theft-auto-san-andreas-2-10-mod-many-money-para-android/</a>
<a href="https://android-gamers.mobi/descarregar-o-jogo-iron-muscle-seja-o-campeao-de-musculacao-1-271-mod-many-money-para-android/">https://android-gamers.mobi/descarregar-o-jogo-iron-muscle-seja-o-campeao-de-musculacao-1-271-mod-many-money-para-android/</a>
<a href="https://android-gamers.mobi/descarregar-golmaal-jr-1-3-231-mod-many-money-para-android/">https://android-gamers.mobi/descarregar-golmaal-jr-1-3-231-mod-many-money-para-android/</a>
<a href="https://android-gamers.mobi/descarregar-boku-boku-1-0-220-mod-lots-of-candy-unlocked-para-android/">https://android-gamers.mobi/descarregar-boku-boku-1-0-220-mod-lots-of-candy-unlocked-para-android/</a>
<a href="https://android-gamers.mobi/descarregar-carro-come-carro-3-carros-maleficos-3-2-b631-mod-many-money-para-android/">https://android-gamers.mobi/descarregar-carro-come-carro-3-carros-maleficos-3-2-b631-mod-many-money-para-android/</a>
Hermoso de la imagen, que loco coherente adaptado en programa. Alegre una pieza de musica. Fascinante tareas.
У Вас выдался тяжелый денёк? Устали после учебы или работы? Не знаете, как поднять себе настроение или развлечься? Начинайте смотреть фильмы онлайн бесплатно на нашем сайте! Интересное кино всегда помогает расслабиться, получить заряд бодрости и позитива до конца дня.
Каждый день обновление.
У многих видео есть выбор перевода.
Есть график выходов серий.
Почти все файлы в 1080p.
Есть стол заказов фильмов, сериалов, мультфильмов, аниме и тв передач.
Вежливые администраторы и модераторы
Бесплатный просмотр любимой киноленты - это отличная возможность отвлечься от повседневных проблем и хлопот. Популярные фильмы онлайн в высоком качестве позволят с головой погрузиться в захватывающий, фантастический, сказочный или вполне реальный мир. Они способны увлечь, пощекотать нервы, растрогать, а классические или новые фильмы всегда учат чему-то новому, открывают неизведанные грани, а иногда даже являются хорошими помощниками и советчиками.
[url=https://lordfilmik.site/filmy/]фильмы 2022[/url]
[url=https://lordfilmik.site/top100.html]фильмы[/url]
<a href=http://pensacolacitygov.com/__media__/js/netsoltrademark.php?d=androidos-play.info>http://pensacolacitygov.com/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
<a href=http://www.formdoc.com/__media__/js/netsoltrademark.php?d=androidos-play.info>http://www.formdoc.com/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
<a href=http://carinsuranceinlandempire.com/__media__/js/netsoltrademark.php?d=androidos-play.info>http://carinsuranceinlandempire.com/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
<a href=http://sinara-group.com/bitrix/redirect.php?goto=http://androidos-play.info>http://sinara-group.com/bitrix/redirect.php?goto=http://androidos-play.info</a>
<a href=http://viceversa.biz/__media__/js/netsoltrademark.php?d=androidos-play.info>http://viceversa.biz/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
Juicy picture, which very coherent enter in program. Naughty music tracks. Attractive conditions.
<a href="https://articles.connectnigeria.com/abia-state-makes-noble-igwe-madeinaba-ambassador/#comment-541282">rent a room</a> 9646e37
<a href=http://www.google.com.bo/url?q=http://androidos-play.info>http://www.google.com.bo/url?q=http://androidos-play.info</a>
<a href=http://minyar-city.ru/bitrix/redirect.php?goto=http://androidos-play.info>http://minyar-city.ru/bitrix/redirect.php?goto=http://androidos-play.info</a>
<a href=http://www.kevin-charlesfurniture.com/__media__/js/netsoltrademark.php?d=androidos-play.info>http://www.kevin-charlesfurniture.com/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
<a href=http://prf-r.ru/bitrix/redirect.php?goto=http://androidos-play.info>http://prf-r.ru/bitrix/redirect.php?goto=http://androidos-play.info</a>
<a href=http://jimmyvision.eu/__media__/js/netsoltrademark.php?d=androidos-play.info>http://jimmyvision.eu/__media__/js/netsoltrademark.php?d=androidos-play.info</a>
Beautiful graphic, which very coherent enter in program. Naughty music tracks. Attractive tasks.
[url=http://xn--e1aagihcuba6ah7b.xn--p1ai/forum/memberlist.php?mode=viewprofile&u=183722]http://xn--e1aagihcuba6ah7b.xn--p1ai/forum/memberlist.php?mode=viewprofile&u=183722[/url]
<a href="https://cloud.cnpgc.embrapa.br/wmv2016/2016/02/25/ola-mundo/?unapproved=5191&moderation-hash=55bd7234c11099e3fcdc444e82581b9a#comment-5191">https://cloud.cnpgc.embrapa.br/wmv2016/2016/02/25/ola-mundo/?unapproved=5191&moderation-hash=55bd7234c11099e3fcdc444e82581b9a#comment-5191</a>
[url=http://logbuildingsupply.com/product/oxalic-acid/]http://logbuildingsupply.com/product/oxalic-acid/[/url]
<a href="http://forum.kirmesplaner.de/memberlist.php?mode=viewprofile&u=73761">http://forum.kirmesplaner.de/memberlist.php?mode=viewprofile&u=73761</a>
منتدى هوامير البورصة , منتدى سعودي متخصص في مجال [URL="https://hawamer.com/vb/f2/"]الاسهم السعودية[/URL] ,استطاع خلال فترة وجيزة استقطاب العديد من الأعضاء و المتداولين في سوق الأسهم نظرا لما أصبح يمثله سوق الأسهم و اعتباره جزء أساسي لا يتجزءا من حديث الشارع أو حديث الساعة , و هو بدلك أصبح قبلة لجميع المتداولين و المستثمرين و لكل من يريد تعلم مبادئ الاستثمار في الأسواق المالية و اكتساب الخبرات المهنية والعلوم المعرفية ,التي تتعلق بآليات عمل البورصات العربية والعالمية وكذلك أسس ومهارات التحليل الفني لأسواق المال ومبادئ التحليل المالي وكيفية إدارة راس المال وإدارة المخاطر , وتقنيات الإدارة النفسية ووسائل تطوير الذات وتنمية المهارات لدى المستثمرين في الأسواق المالية.
https://seoanalyser.me/domain/hawamer.com
[url=https://www.almskoubeauty.dk/2019/10/23/hej-verden/#comment-17046]https://www.almskoubeauty.dk/2019/10/23/hej-verden/#comment-17046[/url]
<a href="http://actshmel.ru/forum/memberlist.php?mode=viewprofile&u=161446">http://actshmel.ru/forum/memberlist.php?mode=viewprofile&u=161446</a>
blender io mixer[/url]
<a href="Https://mixer-bitcoin.org/">
биткоин миксер блендер</a>
<a href="https://soft.androidos-play.info/">https://soft.androidos-play.info/</a>
<a href="https://www.industrialagency.org/AndroidOSPlay">https://www.industrialagency.org/AndroidOSPlay</a>
<a href="https://lwccareers.lindsey.edu/profiles/2974871-androidos-play">https://lwccareers.lindsey.edu/profiles/2974871-androidos-play</a>
<a href="https://www.hackathon.io/users/298827">https://www.hackathon.io/users/298827</a>
<a href="https://www.twitch.tv/androidosplay">https://www.twitch.tv/androidosplay</a>
Beautiful graphic, which crazy coherent enter in program. Cheerful music tracks. Entertaining conditions.
<a href="https://koroleva.world/city/habarovsk">вакансии для девушек Хабаровск</a>
[url=https://dosugnu.xyz/]
Снять шалаву в Новом Уренгое[/url]
<a href="https://dosugnu.xyz/">
Шлюхи Нового Уренгоя без предоплаты</a>
Upload and sell your songs all over the world with the service of digital online distribution of music and cover songs - New Music Top
[url=https://www.newmusic.top/]
best online music distributors[/url]
<a href="https://www.newmusic.top/">
best online digital music distribution</a>
Upload and sell your songs all over the world with the service of digital online distribution of music and cover songs - New Music Top
[url=https://www.newmusic.top/]
best free digital music distribution[/url]
<a href="https://www.newmusic.top/">
one time fee music distribution</a>
Upload and sell your songs all over the world with the service of digital online distribution of music and cover songs - New Music Top
[url=https://www.newmusic.top/]
online music gives rise to distribution headaches case study[/url]
<a href="https://www.newmusic.top/">
best music digital distribution</a>
온라인카지노사이트
https://vsemledi.ru/]Новости[/url]
<a href="
https://tppchita.ru/">Новости</a>
https://kulinarika.ru/]Новости[/url]
<a href="
https://planetoday.ru/">Новости</a>
https://noprost.com/]Новости[/url]
<a href="
https://progio.ru/">Новости</a>
<a href="http://pogreb-garant.ru/">делаем погреба</a>
[url=https://atleti.pl/wielkie-marki-wracaja-do-champions-league/]https://atleti.pl/wielkie-marki-wracaja-do-champions-league/[/url]
<a href="https://gexperience.it/sport-allaria-aperta-a-cosa-prestare-attenzione/">https://gexperience.it/sport-allaria-aperta-a-cosa-prestare-attenzione/</a>
omgomgomg5j4yrr4mjdv3h5c5xfvxtqqs2in7smi65mjps7wvkmqmtqd[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5c5c.com">
omg вход</a>
"Работа крупного предприятия всегда сложный и затратный процесс, многое зависит от оборудования, которое используется. Периодически его надо менять, для этого есть наш ломбард. Быстро продать, обменять, сдать, получить деньги под залог, отдать на утилизацию, можно у нас.
[url=https://skupix.ru/skupka/telefonov/sdat/sony/]Продать телефон Sony в Москве. Скупка смартфонов Сони.[/url]
<a href="http://handiman-services.com/index.html">handyman services</a>
<a href="http://handiman-services.com/index.html">handyman services</a>
Tell me where you can play the game lucky jet 1 win in India. Signals in the telegram channel using the prediction hacking bot. Strategies and tricks earn money best 2022. Tips how to play lucky jet 1 win. Official website with reviews of the game. Sign up at the casino with a bonus and a promo code for free spin. Download the APK app for free
Автоматические обмен netex24 [/url]
<a href="https://netex24.name/">
netex24 сайт</a>
Вам надоело постоянно мониторить различные сайты, чтобы найти интересующее вас спортивное событие? Вы хотите найти сайт, на котором можно смотреть онлайн трансляции любых спортивных состязаний в хорошем качестве? Вы нашли его и теперь сможете наконец-то получить удовольствие от спорта, не тратя лишнее время.
На нашем сервисе вы можете смотреть самые известные спортивные состязания: футбол, баскетбол, теннис, хоккей, бокс. Если вы поклонник других видов спорта – это не проблема. У нас вы сможете смотреть онлайн трансляции любых видов спорта, начиная от фигурного катания и волейбола и оканчивая даже такими экзотическими, как бейсбол и регби.
Все, к чему мы стремимся – это сделать вашу жизнь более яркой и разнообразной, чтобы вы в любое время могли получить удовольствия от просмотра вашего любимого спортивного события. Поэтому на нашем сервисе максимально простой и удобный интерфейс – вам достаточно просто кликнуть и вы сразу найдете ту трансляцию, которая вам интересна. С каждым днем мы стараемся, чтобы наши онлайн трансляции были еще богаче и обширнее, потому для нас главное – это забота о нашем зрителе.
[url=https://look-sport.net/]https://look-sport.net/[/url]
<a href="https://look-sport.net/">https://look-sport.net/</a>
Вам надоело постоянно мониторить различные сайты, чтобы найти интересующее вас спортивное событие? Вы хотите найти сайт, на котором можно смотреть онлайн трансляции любых спортивных состязаний в хорошем качестве? Вы нашли его и теперь сможете наконец-то получить удовольствие от спорта, не тратя лишнее время.
На нашем сервисе вы можете смотреть самые известные спортивные состязания: футбол, баскетбол, теннис, хоккей, бокс. Если вы поклонник других видов спорта – это не проблема. У нас вы сможете смотреть онлайн трансляции любых видов спорта, начиная от фигурного катания и волейбола и оканчивая даже такими экзотическими, как бейсбол и регби.
Все, к чему мы стремимся – это сделать вашу жизнь более яркой и разнообразной, чтобы вы в любое время могли получить удовольствия от просмотра вашего любимого спортивного события. Поэтому на нашем сервисе максимально простой и удобный интерфейс – вам достаточно просто кликнуть и вы сразу найдете ту трансляцию, которая вам интересна. С каждым днем мы стараемся, чтобы наши онлайн трансляции были еще богаче и обширнее, потому для нас главное – это забота о нашем зрителе.
[url=https://look-sport.net/]https://look-sport.net/[/url]
<a href="https://look-sport.net/">https://look-sport.net/</a>
<a href="
https://xn--80ahvj9e.xn--p1ai/category/kovanye-bra/">
бра факел</a>
[url=https://xn--80ahvj9e.xn--p1ai/product/bra-fakel-plamya/]настенный светильник факел[/url]
<a href="
https://xn--80ahvj9e.xn--p1ai/product/bra-fakel-plamya/">
светильник кованый факел под старину</a>
[url=https://xn--80ahvj9e.xn--p1ai/category/kovanye-bra/]
бра в виде факела замковый стиль[/url]
<a href="https://dispetcher.xyz/city/magnitogorsk.html">Работа для девушек Магнитогорск, услуги диспетчера Магнитогорск, Работа девушкам досуг Магнитогорск, Работа девушкам эскорт Магнитогорск</a>
[url=https://flirtnn.xyz/]
проститутки негритянки нижний новгород[/url]
<a href="https://flirtnn.xyz/">
проститутки автозаводский район</a>
Онлайн PR-студия <a href="https://piar.im">Пиарим</a>, применяя проектное продвижение, пропиарит, в частности, компанию в новостных лентах по ценам ниже среднерыночных используя возможности актуального каталога площадок и простой системы. Распространение пресс релизов возможно делать собственными руками, с помощью других пользователей и/или скоростных и знающих специалистов PR-агентства, которые впахивают постоянно. [url=https://piar.im]Piarim[/url]
Онлайн PR-служба <a href="https://pr-im.ru">Piarim</a> за счет проектного продвижения попиарит, к примеру, организацию в новостных лентах по ценам ниже рыночных используя возможности актуального каталога сайтов и понятной системы. Рассылку постов можно сделать собственноручно, дать задание другим пользователям и/или оперативным и грамотным сотрудникам PR-агентства, которые впахивают 24 на 7. [url=https://pr-im.ru]Пиар.им[/url]
Онлайн ПИАР-служба <a href="https://pr-im.ru">Piar.im</a>, применяя проектное продвижение, подраскрутит, в частности, мероприятие в СМИ по расценкам нижнего ценового диапазона за счет обновляемого реестра площадок и уникальной системы. Распространение интервью без проблем можно выполнить самостоятельно, поручить другим пользователям и/или молниеносным и знающим джедаям PR-службы, которые впахивают 24 на 7. [url=https://pr-im.ru]Пиар.им[/url]
<a href="https://www.maritkarlsen.no/profile/descargar-geometry-dash/profile">https://www.maritkarlsen.no/profile/descargar-geometry-dash/profile</a>
<a href="https://www.jtceducation.com/profile/descargar-candy-crush-saga/profile">https://www.jtceducation.com/profile/descargar-candy-crush-saga/profile</a>
<a href="https://www.60sbus.london/profile/tlcharger-episode-choose-your-story/profile">https://www.60sbus.london/profile/tlcharger-episode-choose-your-story/profile</a>
<a href="https://www.maritkarlsen.no/profile/baixar-geometry-dash/profile">https://www.maritkarlsen.no/profile/baixar-geometry-dash/profile</a>
<a href="https://www.re-member.co/profile/tlcharger-ludo-king/profile">https://www.re-member.co/profile/tlcharger-ludo-king/profile</a>
Colourful picture, which very harmoniously enter in program. Cheerful a piece of music. Fascinating tasks.
<a href="https://www.espinasse31.com/profile/tlcharger-soul-knight/profile">https://www.espinasse31.com/profile/tlcharger-soul-knight/profile</a>
<a href="https://www.jtceducation.com/profile/download-candy-crush-saga/profile">https://www.jtceducation.com/profile/download-candy-crush-saga/profile</a>
<a href="https://www.empowerdancestudio.com/profile/descargar-temple-run/profile">https://www.empowerdancestudio.com/profile/descargar-temple-run/profile</a>
<a href="https://www.empowerdancestudio.com/profile/tlcharger-temple-run/profile">https://www.empowerdancestudio.com/profile/tlcharger-temple-run/profile</a>
<a href="https://www.fernandez-avocat.fr/profile/baixar-hello-neighbor/profile">https://www.fernandez-avocat.fr/profile/baixar-hello-neighbor/profile</a>
Excellent picture, which very coherent included in program. Cool music tracks. Good conditions.
Русского законодательства хирург клуба не нарушает. Карлетта Лтд. зарегистрирована сверху острове Кипр. Само заведение действует числом лицензии интернационального гемблинг-регулятора с острова Кюрасао. Поэтому все, яко нужно отчебучить, чтоб попасть на игорную платформу Номер Ап, это найти способ одурачить блокировку Роскомнадзора.
Проще честь имею кланяться желать рабочее челкогляделка вследствие коллега заведения. Забацать этто можно путем электронную почту или чатик содействия, через каналы Депеш, общества ВКонтакте. Ссылки сверху свежеиспеченные сайты-зеркала публикуются вместе один-два купонами на фриспины.
[url=https://pinup-official.com.ua/]
pin-up casino зеркало[/url]
<a href="https://pinup-official.com.ua/">
казино пин ап мобильная версия</a>
<a href="https://soft.droiders.mobi">https://soft.droiders.mobi</a>
<a href="https://soft.apk-gamers.mobi">https://soft.apk-gamers.mobi</a>
<a href="https://soft.android-mods.mobi">https://soft.android-mods.mobi</a>
<a href="https://soft.android-gamers.mobi">https://soft.android-gamers.mobi</a>
<a href="https://soft.android-hack.mobi">https://soft.android-hack.mobi</a>
Beautiful graphic, which crazy coherent enter in program. Cheerful music tracks. Attractive tasks.
<a href="https://soft.droiders.mobi">https://soft.droiders.mobi</a>
<a href="https://soft.android-hack.mobi">https://soft.android-hack.mobi</a>
<a href="https://soft.android-gamers.mobi">https://soft.android-gamers.mobi</a>
<a href="https://soft.android-os.mobi">https://soft.android-os.mobi</a>
<a href="https://soft.apk-gamers.mobi">https://soft.apk-gamers.mobi</a>
Excellent graphic, which very coherent included in application. Naughty music tracks. Fascinating tasks.
[url=https://alcomoscow.site/index.php/product-category/vermut/]https://alcomoscow.site/index.php/product-category/vermut/[/url]
<a href="https://alcomoscow.site/index.php/product-category/tekila/">https://alcomoscow.site/index.php/product-category/tekila/</a>
<a href="https://workgirls.biz/city/kirov.html">Работа для девушек Киров</a>
omgomgomg5j4yrr4mjdv3h5c5xfvxtqqs2in7smi65mjps7wvkmqmtqd онион[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5c5xfvxt.com/">
omg darkmarket</a>
Legit paying apps payout thru Gcash meron po !
Free ?60 Pesos For Newmemeber!
<a href="http://www.stres.ilekarze.pl/n/StresPowodujeTycie_2009-09-01.html">jili slot</a> 54c239e
<a href="http://www.it-sport.nl/2011/07/google-gadget-app-for-simplenote/comment-page-224/#comment-260718">Jili fishing game</a> 7ac9646
JILI Fishing Hits the World and Easy to Play
Jiliwin.com Free to jili play slot games!
Online sportsbook and casino 150% Welcome Bonus
Providing latest and best odds on all sports.
Gcash Casino Cash Out!
Subukan ang aming 1000+ Games
Play?JILI, JDB, PlayStar, CQ9?
Web www.jiliwin.com
Register www.jiliwin.com
Earn money in Gcash! Tara!
https://artmodel.biz/country/gretsiya.html
[url=https://artmodel.biz/country/kitay.html]Работа в сфере досуга Китай[/url]<a href="https://artmodel.biz/country/kipr.html">Эскорт работа Кипр</a>
<a href="https://otogrev-novokuznetsk.ru/">https://otogrev-novokuznetsk.ru</a>
Easy Lang Manalo Dito guys
GUSTO MO KUMITA NG P60 PESOS AWARD
Legit paying apps payout thru Gcash meron po !
Free ?60 Pesos For Newmemeber!
<a href="https://mateacher79.com">마사지사이트</a>
<a href="https://mateacher79.com">스웨디시사이트</a>
<a href="https://mateacher79.com">출장마사지사이트</a>
<a href="https://mateacher79.com">중국마사지사이트</a>
<a href="https://mateacher79.com">타이마사지사이트</a>
<a href="https://mateacher79.com">태국마사지사이트</a>
<a href="https://mateacher79.com">경락마사지사이트</a>
<a href="https://mateacher79.com">아로마마사지사이트</a>
<a href="https://mateacher79.com">커플마사지사이트</a>
<a href="https://mateacher79.com">남자마사지사이트</a>
<a href="https://mateacher79.com">여자마사지사이트</a>
<a href="https://mateacher79.com">감성마사지사이트</a>
<a href="https://mateacher79.com">감성테라피마사지사이트</a>
<a href="https://mateacher79.com">두리코스마사지사이트</a>
<a href="https://mateacher79.com">딥티슈마사지사이트</a>
<a href="https://mateacher79.com">로미로미마사지사이트</a>
<a href="https://mateacher79.com">림프마사지사이트</a>
<a href="https://mateacher79.com">센슈얼마사지사이트</a>
<a href="https://mateacher79.com">슈얼마사지사이트</a>
<a href="https://mateacher79.com">스포츠마사지사이트</a>
<a href="https://mateacher79.com">스파마사지사이트</a>
<a href="https://mateacher79.com">사우나마사지사이트</a>
<a href="https://mateacher79.com">남성전용마사지사이트</a>
<a href="https://mateacher79.com">여성전용마사지사이트</a>
<a href="https://mateacher79.com">호텔식마사지사이트</a>
<a href="https://mateacher79.com">홈타이사이트</a>
<a href="https://mateacher79.com">출장마사지사이트</a>
<a href="https://mateacher79.com">24시간마사지사이트</a>
<a href="https://mateacher79.com">1인샵마사지사이트</a>
<a href="https://mateacher79.com">서울출장마사지사이트</a>
<a href="https://mateacher79.com">경기출장마사지사이트</a>
<a href="https://mateacher79.com">인천출장마사지사이트</a>
<a href="https://mateacher79.com">의정부출장마사지사이트</a>
<a href="https://mateacher79.com">수원출장마사지사이트</a>
<a href="https://mateacher79.com">천안출장마사지사이트</a>
<a href="https://mateacher79.com">전주출장마사지사이트</a>
<a href="https://mateacher79.com">익산출장마사지사이트</a>
<a href="https://mateacher79.com">대전출장마사지사이트</a>
<a href="https://mateacher79.com">세종출장마사지사이트</a>
<a href="https://mateacher79.com">동탄출장마사지사이트</a>
<a href="https://mateacher79.com">부산출장마사지사이트</a>
<a href="https://mateacher79.com">울산출장마사지사이트</a>
<a href="https://mateacher79.com">마산출장마사지사이트</a>
<a href="https://mateacher79.com">광주출장마사지사이트</a>
<a href="https://mateacher79.com">제주출장마사지사이트</a>
<a href="https://mateacher79.com">대구출장마사지사이트</a>
<a href="https://mateacher79.com">청주출장마사지사이트</a>
<a href="https://mateacher79.com">포항출장마사지사이트</a>
<a href="https://mateacher79.com">목포출장마사지사이트</a>
<a href="https://mateacher79.com">진주출장마사지사이트</a>
<a href="https://mateacher79.com">창원출장마사지사이트</a>
<a href="https://mateacher79.com">여수출장마사지사이트</a>
<a href="https://mateacher79.com">용인출장마사지사이트</a>
<a href="https://mateacher79.com">고양출장마사지사이트</a>
<a href="https://mateacher79.com">군산출장마사지사이트</a>
<a href="https://mateacher79.com">춘천출장마사지사이트</a>
<a href="https://mateacher79.com">구미출장마사지사이트</a>
<a href="https://mateacher79.com">충주출장마사지사이트</a>
<a href="https://mateacher79.com">강릉출장마사지사이트</a>
<a href="https://mateacher79.com">강남출장마사지사이트</a>
<a href="https://mateacher79.com">건전마사지사이트</a>
<a href="https://mateacher79.com">내근처마사지사이트</a>
<a href="https://mateacher79.com">최저가마사지사이트</a>
<a href="https://mateacher79.com">마사지커뮤니티</a>
<a href="https://mateacher79.com">테라피마사지사이트</a>
<a href="https://mateacher79.com">왁싱사이트</a>
<a href="https://mateacher79.com">에스테틱사이트</a>
Эскорт работа Италия[/url]
+7(910)146-24-28
Предлагаем молодым, целеустремленным и красивым девушкам работу в Италии. Не все девушки желают работать у себя в городе в своей стране. Мы можем предложить работу для девушек в Италии в богатых и безопасных направлениях. Работающие за границей девушки имеют доступ в лучшее общество. Они сами становятся его частью то есть успешными и обеспеченными. Работа для девушек Италия это шанс начать новую успешную жизнь.
https://casinosite119.com
<a href="https://xn----7sbgaem1bxeaazvc.xn--p1ai/">автоотогрев-нк.рф</a>
[url=https://fei.prostitutki-new-urengoy.com/]
Индивидуалки по вызову Новый Уренгой[/url]
<a href="https://fei.prostitutki-new-urengoy.com/">
Сайт досуга Нового Уренгоя</a>
A dinheiro em uma casa de apostas. Estratégias populares, truques e táticas do jogo para ganhar dinheiro. Baixe o aplicativo para o telefone gratuitamente. Bônus de inscrição para cada jogador
[url=https://escortnn.site/]
эскорт НН[/url]
<a href="https://escortnn.site/">Эскорт Нижний Новгород</a>
<a href=https://spbgavm.ru>codigos promocionais da lucky jet</a>
Estrategia e truques para ganhar no 1 win Casino. Analogo do jogo aviator por Dinheiro. Jogo Predictor hack
<a href="http://www.openbuilds.co.kr/upload/index.php?members/androplaycew.5778/">http://www.openbuilds.co.kr/upload/index.php?members/androplaycew.5778/</a>
<a href="http://www.openbuilds.co.kr/upload/index.php?members/androplaycew.5778/">http://www.openbuilds.co.kr/upload/index.php?members/androplaycew.5778/</a>
<a href="http://www.openbuilds.co.kr/upload/index.php?members/androplaycew.5778/">http://www.openbuilds.co.kr/upload/index.php?members/androplaycew.5778/</a>
<a href="http://83783.net/home.php?mod=space&uid=3476737">http://83783.net/home.php?mod=space&uid=3476737</a>
<a href="http://habotao.com/bbs/home.php?mod=space&uid=181016">http://habotao.com/bbs/home.php?mod=space&uid=181016</a>
Colourful graphic component, which crazy harmoniously fit in program. Cheerful a piece of music. Fascinating tasks.
мега даркнет маркет ссылка +на сайт[/url]
<a href="https://mega555kf7lsmb54yd6etz.com/">
мега</a>
<a href="https://xn----9sbfch6cfblex.xn--p1ai/">погреб бетонный готовый купить</a>
заказать поздравление по телефону с днем рождения
поздравления с Днем Рождения по телефону заказать по именам
заказать поздравление с Днем Рождения по мобильному телефону
заказать поздравление с днем рождения по именам
заказать поздравление с днем рождения на телефон
<a href="https://erotic-massage.xyz/city/nefteyugansk">эротический массаж Нефтеюганск</a>
<a href=https://lucky-jet-1win.com/>lucky jet entrar na conta</a>
Estrategia e truques para ganhar no 1 win Casino. Analogo do jogo aviator por Dinheiro. Jogo Predictor hack
<a href=https://my-online-teacher.com/>lucky jet 1win официальный сайт</a>
играть в казино 1 win
https://tairikvip.tv
<a href=http://slowread.ru/>lucky jet промокод</a>
Стратегия и трюки для заработка в казино 1 win. Аналог игры aviator на деньги. Взлом игры Predictor hack
[url=https://prostitutki-new-urengoy.top/]
Шкуры Новый Уренгой[/url]
<a href="https://prostitutki-new-urengoy.top/">
Досуг выезд в Новом Уренгое</a>
[url=https://individualki-new-urengoy.top/]
Элитные индивидуалки Нового Уренгоя[/url]
<a href="https://individualki-new-urengoy.top/">
Шлюхи по вызову Новый Уренгой</a>
<a href="https://electronica.md/category/krupnaja-kuhonnaia-tehnika/">ХОЛОДИЛЬНИКИ в Кишиневе</a>
<a href="https://electronica.md/category/telefoane/smartphone/apple-iphone/">Купить смартфон Apple iPhone в Кишиневе</a>
<a href="https://electronica.md/category/telefoane/smartphone/xiaomi/">СМАРТФОНЫ XIAOMI в Молдове</a>
[url=https://flirtekb.top/]
Сайт досуга Екатеринбурга[/url]
<a href="https://flirtekb.top/">
Проверенный досуг Екатеринбург</a>
[url=https://prostitutki-nizhny-novgorod.ru/]Индивидуалки Нижний Новгород[/url] обласкают вас с ног до головы и попросят повтора. Им нравится быть грязными [url=https://prostitutki-nizhny-novgorod.ru/]шлюхами Нижнего Новгорода[/url], чтобы их пороли и наказывали. Обычную ночь они превратят в райскую, атмосфера будет накоплена до предела, горячие тела и прерывистое дыхание будут сопровождать вас все время что вы будете с ними.
На нашем сайте вы сможете отыскать проститутку на любой вкус и размер кошелька. Но всех их объединяет одно - огромное желание поскорее ублажить клиента, свести его с ума от насыщенного бурного экстаза. Они хотят любви и похоти, им хочется чтобы их шлепали и наказывали, поощряли и дразнили. Милые и страстные девушки настоящие обольстительницы. Их аппетитные формы, приятная нежная кожа, бархатный голос возбудят любого мужчину. Они будут играться с ним как славные кошечки, ищущие постоянного внимания.
Азартные и похотливые девочки уже ждут вашего звонка!
[url=https://prostitutki-nizhny-novgorod.ru/]
проститутки нижний новгород сормово[/url]
<a href="https://prostitutki-nizhny-novgorod.ru/">
где стоят проститутки в нижнем новгороде</a>
[url=https://flirtmoscow.xyz/]
Индивидуалки на дом Москва[/url]
<a href="https://flirtmoscow.xyz/">
Проверенные проститутки Москва</a>
<a href="http://thalesfund.com/__media__/js/netsoltrademark.php?d=espinasse31.com/profile/baixar-soul-knight/profile">http://thalesfund.com/__media__/js/netsoltrademark.php?d=espinasse31.com/profile/baixar-soul-knight/profile</a>
<a href="http://bricklaer.ru/bitrix/redirect.php?goto=http://bigmouthreaders.com/profile/descargar-crime-revolt/profile">http://bricklaer.ru/bitrix/redirect.php?goto=http://bigmouthreaders.com/profile/descargar-crime-revolt/profile</a>
<a href="http://xn--38-mlc6adficdnc9b.xn--p1ai/bitrix/redirect.php?goto=http://korresonline.com/profile/tlcharger-drive-ahead/profile">http://xn--38-mlc6adficdnc9b.xn--p1ai/bitrix/redirect.php?goto=http://korresonline.com/profile/tlcharger-drive-ahead/profile</a>
<a href="http://www.homemaintenanceplus.com/__media__/js/netsoltrademark.php?d=davidbinnsceramics.com/profile/tlcharger-the-sims-freeplay/profile">http://www.homemaintenanceplus.com/__media__/js/netsoltrademark.php?d=davidbinnsceramics.com/profile/tlcharger-the-sims-freeplay/profile</a>
<a href="http://minobr-ra.ru/bitrix/rk.php?goto=http://bariyaboxes.com/profile/baixar-dead-target-zombie-games-3d/profile">http://minobr-ra.ru/bitrix/rk.php?goto=http://bariyaboxes.com/profile/baixar-dead-target-zombie-games-3d/profile</a>
Beautiful graphic component, which unparalleled coherent fit in application. Naughty a piece of music. Fascinating conditions.
gửi hàng đi mỹ giá rẻ tại tphcm</a>
[url=https://prostitutki-noyabrsk.xyz/]
Шлюхи выезд в Ноябрьске[/url]
<a href="https://prostitutki-noyabrsk.xyz/">
Элитные шлюхи Ноябрьск</a>
вход омг[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5c5xfvxt.com/">
omg onion</a>
<a href="https://jobgirls.xyz/category/kaliningrad.html">вакансии для девушек Калининград</a>
<a href="https://jobgirls.xyz/category/yalta.html">Работа для девушек Ялта</a>
<a href="https://rabota-devushkam.net/tumen/">Работа для девушек Тюмень</a>
<a href="https://rabota-devushkam.net/omsk/">вакансии девушкам Омск</a>
[url=https://prostitutkimsk.top/]
Сайт досуга Москвы[/url]
<a href="https://prostitutkimsk.top/">
vip проститутки Москва</a>
[url=https://prostitutkimsk.top/]
Элитные проститутки Москва[/url]
<a href="https://prostitutkimsk.top/">
Реальный досуг Москва</a>
официальный сайт 1xbet 1xbet c zerkalo2[/url]
<a href="https://zerkalo.1xbet-official2022.com/">
1xbet скачать на андроид официальную версию</a>
купить вейп-ручку</a>
1xbet зеркало сегодня сейчас 1xbet zerkalo[/url]
<a href="https://zerkalo.1xbet-official2022.com/">
1xbet официальный сайт</a>
<a href="https://rabota-devushkam.biz/urengoy/">работа досуг девушкам Новый Уренгой</a>
<a href="https://rabota-devushkam.biz/%d0%b8%d0%b2%d0%b0%d0%bd%d0%be%d0%b2%d0%be/">работа для девушек в эскорте Иваново</a>
1xbet на телефон андроид[/url]
<a href="https://official.1xbet-zerkalo2022.com/">
1xbet зеркало регистрация</a>
1xbet регистрация 1xbet c zerkalo2[/url]
<a href="https://official.1xbet-zerkalo2022.com/">
зеркало 1xbet 1хбет</a>
[url=https://flirtnu.xyz/]
Снять проститутку в Новом Уренгое[/url]
<a href="https://flirtnu.xyz/">
Шлюхи круглосуточно Новый Уренгой</a>
[url=https://flirtnu.xyz/]
Шкуры Новый Уренгой[/url]
<a href="https://flirtnu.xyz/">
Элитные проститутки Новый Уренгой</a>
ship đồ từ mỹ về vn</a>
1xbet 1xbet a zerkalo net[/url]
<a href="https://official.1xbet-zerkalo.name/">
1хбет слоты 1xbet sloty4</a>
1xbet зеркало на сегодня 1xbet a zerkalo[/url]
<a href="https://official.1xbet-zerkalo.name/">
1xbet ru скачать приложение</a>
[url=https://prostitutki-noyabrsk.xyz/]
Проститутки круглосуточно Ноябрьск[/url]
<a href="https://prostitutki-noyabrsk.xyz/">
Элитный досуг Ноябрьск</a>
[url=https://prostitutki-noyabrsk.xyz/]
Сайт досуга Ноябрьска[/url]
<a href="https://prostitutki-noyabrsk.xyz/">
Индивидуалки Ноябрьск недорого</a>
Лучший биткоин миксер[/url]
<a href="https://mixer-bitcoin.org/">
биткоин миксеры 2022</a>
биткоин миксеры 2022[/url]
<a href="https://mixer-bitcoin.org/">
mixer eth</a>
<a href="https://rabota-devushkam.ru.com/krasnoyarsk/">вакансии для девушек Красноярск</a>
<a href="https://rabota-devushkam.ru.com/nignevartovsk/">вакансии для девушек Нижневартовск</a>
Authors daily improvement,improvement,improvement characteristics Google OS, developing and improving their offers much as possible comfortable and classy.
<a href="https://androidos-top.com/tools/14945-download-mods-for-minecraft-pe-premium-mod-for-android.html">Download Mods for Minecraft PE (Premium MOD) for Android</a>
<a href="https://androidos-top.com/books_reference/8828-download-myquran-premium-mod-for-android.html">Download myQuran (Premium MOD) for Android</a>
<a href="https://androidos-top.com/entertainment/10723-download-formacar-3d-tuning-car-build-premium-mod-for-android.html">Download FormaCar: 3D Tuning. Car build (Premium MOD) for Android</a>
<a href="https://androidos-top.com/board/1723-download-quoridor-logic-board-game-unlocked-all-mod-for-android.html">Download Quoridor в™џ Logic Board Game (Unlocked All MOD) for Android</a>
<a href="https://androidos-top.com/arcade/988-download-minecraft-trial-unlocked-all-mod-for-android.html">Download Minecraft Trial (Unlocked All MOD) for Android</a>
Get on the file archive new games and applications for Android OS. More links
[url=https://cbtklan.net/index.php?site=news_comments&newsID=2]Get good application and games for Android[/url] [url=https://bbs.er.run/forum.php?mod=viewthread&tid=228761]Get great program and games for Android[/url] [url=https://www.sotugyousyousyo.com/q%e5%8d%92%e6%a5%ad%e8%a8%bc%e6%9b%b8%e3%81%ae%e6%9e%9a%e6%95%b0%e3%81%8c%e5%a4%9a%e3%81%8f%e6%96%87%e9%9d%a2%e3%82%84%e3%83%91%e3%82%bf%e3%83%bc%e3%83%b3%e3%81%aa%e3%81%a9%e3%82%82%e5%a4%9a%e3%81%84/comment-page-190/#comment-701916]Get popular application and games for Android[/url] [url=https://prcim.net/bbs/forum.php?mod=viewthread&tid=187636&pid=672862&page=2&extra=#pid672862]Download popular pr[/url] [url=http://cchgcn.com/forum/viewtopic.php?p=594026&Twesid=95931a399d768341e2704c137997c7ae#594026]Download quality application and games for Android[/url] 9ff4_30
<a href="https://fuehair.ru/kosmetologmsk/">КЛИНИКА КОСМЕТОЛОГИИ В МОСКВЕ</a>
Developers permanently improvement,improvement,improvement characteristics software, developing and improving their programmes much as possible quality and bright.
<a href="https://androidos-top.com/music_audio/14080-download-soundpad-premium-mod-for-android.html">Download Soundpad (Premium MOD) for Android</a>
<a href="https://androidos-top.com/business/9225-download-drift-unlocked-mod-for-android.html">Download Drift (Unlocked MOD) for Android</a>
<a href="https://androidos-top.com/word/7236-download-word-sauce-word-connect-free-shopping-mod-for-android.html">Download Word Sauce: Word Connect (Free Shopping MOD) for Android</a>
<a href="https://androidos-top.com/dating/10197-download-stranger-with-chat-stranger-random-chat-free-ad-mod-for-android.html">Download Stranger with Chat. Stranger, Random Chat (Free Ad MOD) for Android</a>
<a href="https://androidos-top.com/arcade/960-download-tower-color-premium-unlocked-mod-for-android.html">Download Tower Color (Premium Unlocked MOD) for Android</a>
Download on the file archive new games and files for Android OS. More links
[url=https://thehealthcarearticles.com/judi_bola3288?page=230#comment-146257]Get cool program and games for Android[/url] [url=http://paycenter.wistone.com/forum.php?mod=viewthread&tid=58346410&extra=]Download good program and games for Android[/url] [url=http://okdmcs.kz/blog-head-doctor]Download good application and games for Android[/url] [url=https://doobia.com/sectors/company/aads/momentum#comments-section#comments-section#comments-section#comments-section#comments-section]Get good application and games for Android[/url] [url=http://uvadvisory.com/dev/discussion-forum/topic/williaminale/?part=5#postid-2324184]Get quality program and games for Android[/url] 9e9bfd1
купить электро точилку[/url]
<a href="https://electro-tochilka.ru/">электро точилка</a>
[url=https://dosugnu.xyz/]
Дешевый досуг Новый Уренгой[/url]
<a href="https://dosugnu.xyz/">
Вип индивидуалки Новый Уренгой</a>
[url=https://dosugnu.xyz/]
Дешевые индивидуалки Нового Уренгоя[/url]
<a href="https://dosugnu.xyz/">
Индивидуалки на дом Новый Уренгой</a>
netex24[/url]
<a href="https://netlex24.net/">
обменник netex24</a>
netex24 обмен[/url]
<a href="https://netlex24.net/">
netex24 официальный сайт</a>
<a href="https://rabotadevushkam.net/novorossiysk/">вакансии девушкам Новоросийск</a>
<a href="https://rabotadevushkam.net/novorossiysk/">Работа для девушек Новоросийск</a>
프리미엄 스포츠중계 PICKTV(픽티비)는 회원가입없이 무료스포츠중계,월드컵중계 무료로 신청 가능합니다
<a href="https://my-money-amulet.com/hydra/hydraruzxpnew4af-onion.html">hydraruzxpnew4af onion</a>
<a href="https://avto32.org/mega/mega-torgovaja-ploschadka.html">mega торговая площадка</a>
<a href="https://kalin-prof.com/mega/aktualnye-ssylki-na-megu.html">актуальные ссылки на мегу</a>
<a href="https://blackoutcurtains.co.uk/hello-world/#comment-13420">online doctor</a> 54c239e
<a href="https://rabotanu.ru/city/norilsk">работа девушкам Норильск эскорт</a>
<a href="https://rabotanu.ru/city/lipetsk">работа для девушек досуг Липецк</a>
<a href="https://www.applerecenze.cz/strategie-sazeni-na-basketbal/">https://www.applerecenze.cz/strategie-sazeni-na-basketbal/</a>
<a href="http://minutomais.com/dicas-para-apostar-no-blackjack-online-sem-sair-de-casa/">http://minutomais.com/dicas-para-apostar-no-blackjack-online-sem-sair-de-casa/</a>
<a href="https://uposter.ru/">спецназ</a>
<a href="https://uposter.ru/">Адлер</a>
<a href="https://reklamaxxx.biz/habarovsk/">Работа для девушек Хабаровск</a>
<a href="https://reklamaxxx.biz/kostroma/">вакансии девушкам Кострома</a>
<a href="https://pfg.in.ua/ua/">Проект магазина</a>
Phí Ship Hàng Mỹ mới</a>
cty gửi hàng đi mỹ 2023</a>
Chương Trình Định Cư Hy Lạp Ở Đâu 2023</a>
Профессиональная вентиляция для ресторана[/url]
<a href="https://pfg.in.ua/ua/">Подбор ресторанного оборудования</a>
<a href="https://erotic-massage.xyz/city/omsk">эротический массаж Омск</a>
<a href="https://erotic-massage.xyz/city/norilsk">эротический массаж Норильск</a>
[url=http://zingur.pw/domain-list-310]on front page[/url]
п»ї
<a href="https://myworldgo.com/forums/topic/48084/home-charging-station/view/post_id/652728">porsche evse</a>
[url=https://www.speakev.com/threads/supercharger-plugs-one-ccs-and-one-non-ccs.163199/]more tips here[/url]
п»ї
<a href="http://forums.turbobricks.com/showthread.php?p=6220866#post6220866">forums.turbobricks.com</a>
[url=https://power15.org/j1772-extension-cord-doesnt-have-to-be-hard-read-these-helpful-tips/]her latest blog[/url]
п»ї
<a href="https://akama.com/company/EV_Adept_af9dd3831334.html">my latest blog post</a>
<a href="https://termeho.ru/zadachi/po-dinamike/zadacha-30-odnorodnyj-gladkij-disk-massy-m-i-radiusa-r-ustanovlen-mezhdu-valom-oo1-i-sterzhnem-av-prikreplennym-k-nemu-pod-uglom-%d1%b1/">https://termeho.ru/zadachi/po-dinamike/zadacha-30-odnorodnyj-gladkij-disk-massy-m-i-radiusa-r-ustanovlen-mezhdu-valom-oo1-i-sterzhnem-av-prikreplennym-k-nemu-pod-uglom-%d1%b1/</a>
<a href="https://termeho.ru/dinamika/58-staticheskaya-i-dinamicheskaya-balansirovka-rotora/">https://termeho.ru/dinamika/58-staticheskaya-i-dinamicheskaya-balansirovka-rotora/</a>
<a href="https://termeho.ru/kinematika/17-vektornoe-opisanie-skorost-i-uskorenie/">https://termeho.ru/kinematika/17-vektornoe-opisanie-skorost-i-uskorenie/</a>
Bitcoin [url=https://sites.google.com/view/bitcoin-up-app/]bitcoin up app[/url] ist eine dezentrale digitale Wahrung minus Zentralbank oder einzelnen Administrator, die bar Zwischenhandler von Anwender zu Benutzer im Peer-to-Peer-Bitcoin-Netzwerk gesendet sein kann. Transaktionen werden von Netzwerkknoten durch Kryptografie verifiziert und in einem offentlich verteilten Hauptbuch namens Blockchain aufgezeichnet. Bitcoin wurde von einer unbekannten Person , alternativ Personengruppe unter seinem Namen Satoshi Nakamoto erfunden und 2009 als Open-Source-Software veroffentlicht.
Bitcoins werden wie Belohnung fur 1 Prozess geschaffen, dieser als Mining weltberuhmt ist https://sites.google.com/view/bitcoin-up-app/ Jene konnen gegen sonstige Wahrungen, Produkte des weiteren Dienstleistungen eingetauscht werden. Seit Februar 2015 akzeptierten uber 100. 000 Handler ferner Anbieter Bitcoin denn Zahlungsmittel.
Was hat den jungsten Anstieg des Bitcoin-Preises verursacht?
Der jungste Bitcoin-Preisanstieg wurde durch diese eine, Kombination von Kriterien verursacht. Erstens gesammelt die COVID-19-Pandemie zu einer erhohten wirtschaftlichen Unsicherheit gefuhrt, welches das Interesse jener Anleger an Bitcoin als potenziellem sicheren Hafen geweckt zusammen. Zweitens investieren gro? e institutionelle Investoren zunehmend in Bitcoin, was dazu beigetragen hat, die Tarife in die Hohe zu treiben. Schlie? lich wird auch angenommen, dass dies bevorstehende Halving-Ereignis zu ihrem Preisanstieg beitragt, denn die Anleger davon ausgehen, dass dies geringere Angebot an neuen Bitcoins uber hoheren Preisen fuhren wird.
[b]Denn funktioniert Bitcoin? [/b]
Sofern es um Bitcoin geht, sind mehrere Dinge, die mit die Funktionsweise einflie? en. Zunachst einmalig ist Bitcoin die dezentrale Wahrung, welches bedeutet, dass jene nicht von einer Zentralbank oder Konzern reguliert wird. Das bedeutet auch, falls es keine einzelne Einheit gibt, die die Lieferung vonseiten Bitcoin kontrollieren moglicherweise. Stattdessen wird das Angebot an Bitcoin vom Netzwerk selbst bestimmt. Wir kennen diese eine, begrenzte Anzahl von seiten Bitcoins, die jemals geschurft werden konnen, und das Schurfen neuer Bitcoins erfordert mit der Arbeitszeit immer mehr Rechenleistung.
Also, wie schurft man Bitcoins? Hier, jedes Mal, wenn der Blockchain (die das offentliche Hauptbuch aller Bitcoin-Transaktionen ist) ein neuer Block hinzugefugt wird, werden Miner mit einer bestimmten Anzahl vonseiten Bitcoins belohnt. Mit der absicht der Blockchain 1 neuen Block hinzuzufugen, mussen Miner dieses komplexes mathematisches Aufgabe losen.
[b]Welches sind die Vorzuege von Bitcoin?[/b]
Bitcoin zusammen sich in allen letzten Jahren uber einer beliebten Wahrung entwickelt. Hier befinden sich einige Vorteile jener Verwendung von Bitcoin:
1. Bitcoin ist echt dezentralisiert, was bedeutet, dass es vonseiten keiner Regierung oder Finanzinstitution kontrolliert vermag. Dies kann denn Vorteil angesehen sein, da es allen Benutzern mehr Kontrolle uber ihr Barmittel gibt.
2. Transaktionen mit Bitcoin [url=https://sites.google.com/view/bitcoin-up-app/]bitcoin[/url] sind immer wieder schnell und gunstig. Dies liegt daran, dass keine Vermittler (wie Banken) mit der Abwicklung der Zahlungen beteiligt befinden sich.
3. Bitcoin ist naturlich pseudonym, was bedeutet, dass Benutzer bei der Verwendung der Wahrung relativ anonym bleiben konnen. Das kann fur Benutzer attraktiv sein, welche Wert auf Privatsphare legen.
[b]Alle Risiken einer Investment in Bitcoin [/b]
Bitcoin ist ein digitaler Vermogenswert und ein von Satoshi Nakamoto erfundenes Zahlungssystem. Transaktionen werden von Netzwerkknoten durch Kryptografie verifiziert und in dem offentlichen verteilten Hauptbuch namens Blockchain aufgezeichnet. Bitcoin ist insofern einzigartig, als das eine endliche Anzahl von ihnen vorhanden ist: 21 Millionen.
Bitcoins werden als Wiedergutmachung fur einen Prozess geschaffen, der wie Mining bekannt ist. Sie https://sites.google.com/view/bitcoin-up-app/ konnen gegen andere Wahrungen, Produkte und Dienstleistungen eingetauscht werden. Seither Februar 2015 akzeptierten uber 100. 000 Handler und Netzanbieter Bitcoin als Zahlungsmittel.
Die Investition daruber hinaus Bitcoin ist verfahrensweise, da es einander um eine neue Technologie handelt, welche von keiner Regierung oder Finanzinstitution unterstutzt wird. Der Kartenwert von Bitcoin kann stark schwanken, des weiteren Anleger konnten das ganzes Geld das nachsehen haben, wenn der Preis absturzt. Es besteht ebenso das Risiko, dass Hacker Bitcoins taktlos Online-Geldborsen oder -Borsen stehlen konnten.
<a href="https://maps.google.it/url?q=https%3A%2F%2Fappcafe.it/">app gestione tavoli ristorante</a>
<a href="https://toolbarqueries.google.it/url?q=https%3A%2F%2Filluminacreative.it/">Agenzia Web Marketing</a>
먹튀검증
<a href="https://maps.google.it/url?q=https%3A%2F%2Filluminacreative.it/">Illumina Creative</a>
[url=https://flirtnn.xyz/]
дешевые шлюхи нижнего новгорода[/url]
<a href="https://flirtnn.xyz/">
проститутки нижний новгород ленинский район</a>
[url=https://flirtnn.xyz/]
элитные проститутки нижнего новгорода[/url]
<a href="https://flirtnn.xyz/">
проститутки автозаводский район</a>
[url=https://flirtnu.xyz/]
Индивидуалки по вызову Новый Уренгой[/url]
<a href="https://flirtnu.xyz/">
Снять шалаву в Новом Уренгое</a>
[url=https://flirtnu.xyz/]
Проститутки выезд в Новом Уренгое[/url]
<a href="https://flirtnu.xyz/">
Проститутки негритянки Новый Уренгой</a>
Authors every day improvement,improvement,improvement quality Android, developing and improving their programmes much as possible improved and classy.
<a href="https://hack-android.site/arcade/491-skachat-john-gba-mod-otkrytye-urovni-rus-393-besplatno-apk-na-android.html">Скачать John GBA [Взлом открытые уровни] RUS 3.93 для Андроид</a>
Get on the forum new games and files for Android. More links
[url=http://lapatul.com/products/sapogi-antilopa-1311-5928-28-33/#comment_351939]Скачать IBEX - грузовое такси [Максимальная] Русская версия 1.14.4 для Андроид[/url] [url=https://loversofthemoon.blogger.hu/2011/02/11/w-faulkner-a-hang-es-a-teboly]Скачать Симулятор Muscle Car [Взлом много денег] RU 1.4 для Андроид[/url] [url=http://agronn.ru/products/zvezdochka-ozsh-00790-avtomata-razobschitelya-z-18/#comment_46584]Скачать Hero Rescue [Взлом много денег] RU 1.1.15 для Андроид[/url] c54c239
[url=https://prostitutki-noyabrsk.xyz/]
Девушки по вызову Ноябрьск[/url]
<a href="https://prostitutki-noyabrsk.xyz/">
Проститутки негритянки Ноябрьск</a>
Authors daily improvement,improvement,improvement characteristics Google OS, developing and improving their offers much as possible improved and classy.
<a href="https://hack-android.site/foto/9125-skachat-tekst-na-foto-foto-tekst-otkrty-funkcii-rus-1257-besplatno-apk-na-android.html">Скачать Текст на фото - фото текст [Открты функции] RUS 1.2.57 для Андроид</a>
Get on the page new games and files for Android. More links
[url=http://www.valledelascolitas.com/es/index.php?mact=Blogs,cntnt01,showentry,0&cntnt01returnid=57&cntnt01entryid=10]Скачать ?Нмаркет.ПРО [Без рекламы] RUS v.2.39 для Андроид[/url] [url=https://sklep.hultajpolski.pl/pl/n/62#comment23841]Скачать CarX Drift Racing 2 [Взлом открытые покупки] RUS 1.14.0 для Андроид[/url] [url=https://malyarka.shop/blog/kak-pokrasit-kuhnyu-svoimi-rukami#comment_16312]Скачать Oriflame Business [Без рекламы] Русская версия 5.0.3 для Андроид[/url] 46e376a
[url=https://prostitutki-noyabrsk.xyz/]
Дешевый досуг Ноябрьск[/url]
<a href="https://prostitutki-noyabrsk.xyz/">
Путаны Ноябрьск</a>
<a href="https://kosmetologmsk.ru/konturnaia-plastika/">Контурная пластика в Москве - в центре Москвы</a>
[url=https://037hdm.com/หนัง-ซีรีส์/]037hdm</a>
Authors every day improvement,improvement,improvement quality Google OS, making better their games much as possible comfortable and bright.
<a href="https://hack-android.site/foto/9140-skachat-pixellab-text-on-pictures-polnaya-russkaya-versiya-zavisit-ot-ustroystva-besplatno-apk-na-android.html">Скачать PixelLab - Text on pictures (Полная) Русская версия Зависит от устройства для Андроид</a>
Get on the website new games and programs for Android OS.
More links
[url=https://asgardiatravel.com/2014/11/26/default-post-type/comment-page-682469/#comment-1381884]Скачать World Building Craft (Взлом открытые покупки) RU 1.5.1 для Андроид[/url] [url=http://ricardomalta.net/mural/index.php]Скачать Tap Titans (Взлом много монет) RU 4.1.6 для Андроид[/url] [url=https://www.rockyourlocsllc.com/product/lion-of-judah-bracelet-matted-black-and-mystery-black/#comment-42937]Скачать Full MirrorLink | Floating Apps for Auto (Полная) Русская версия 4.11.1 для Андроид[/url] c239e9b
[url=https://037hdm.com/หนัง-ซีรีส์/]หนัง 037</a>
Developers every day improvement,improvement,improvement quality software, making better their programmes much as possible comfortable and classy.
<a href="https://hack-android.site/foto/9450-skachat-before-after-one-vse-funkcii-rus-118-besplatno-apk-na-android.html">Скачать Before After One (Все функции) RUS 1.18 для Андроид</a>
Get on the portal new games and programs for Android OS.
More links
[url=http://radio-on.air-nifty.com/daily_kodaman/2019/02/post-cd86.html?cid=143663903#comment-143663903]Скачать Club Soccer Director 2020 - Футбольный менеджмент (Взлом открытые покупки) RUS 1.0.81 для Андроид[/url] [url=https://asgardiatravel.com/2014/11/26/default-post-type/comment-page-682469/#comment-1381884]Скачать World Building Craft (Взлом открытые покупки) RU 1.5.1 для Андроид[/url] [url=https://sapidumgourmet.es/producto/baron-lay-tinto-maturana/#comment-170047]Скачать Boom: музыкальный плеер с 3D-звуком и эквалайзером (Разблокированная) Русская версия 2.5.3 для Андроид[/url] 9bfd17a
[url=https://kospo.ru/services/oilgas]обслуживание нефтегазового оборудования[/url]
[url=https://kospo.ru/services/transformer-substation/setup-complete-transformers-substations]монтаж комплектной трансформаторной подстанции[/url]
[url=https://kospo.ru/equipments/mining]продажа горнодобывающего оборудования[/url]
[url=https://kospo.ru/equipments/marine]судовое оборудование[/url]
</a>
[url=https://kospo.ru/services/energy/adjustment-power-equipment]наладка энергетического оборудования[/url]
037 online movies[/url]
<a href="https://037hdm.com/">037 hd</a>
thai movies[/url]
<a href="https://037hdm.com/">
037 online movies</a>
037 online movies[/url]
<a href="https://037hdm.com/">
movies online 037</a>
<a href="https://xn----9sbbfkd2a5aacgep7a2k.xn--p1ai/">бетонный погреб купить в московской области</a>
<a href="https://xn----9sbbfkd2a5aacgep7a2k.xn--p1ai/">купить погреб</a>
[url=https://prostitutki-anapa.xyz/]
Шалавы Анапа без предоплаты[/url]
<a href="https://prostitutki-anapa.xyz/">
Проститутки круглосуточно Анапа</a>
[url=https://prostitutki-anapa.xyz/]
Индивидуалки Анапа без предоплаты[/url]
<a href="https://prostitutki-anapa.xyz/">
Шалавы Анапа без предоплаты</a>
[url=https://prostitutki-anapa.xyz/]
Путаны Анапа[/url]
<a href="https://prostitutki-anapa.xyz/">
Досуг Анапа недорого</a>
<a href="https://xn----9sbfir5agkdkv4c.xn--p1ai/">погреб бетонный готовый купить</a>
<a href="http://paste.freezy.cz/C9e2cR9w">Jili Online Casino</a> bc54c23
Jili Online Casino 150% WelcomeBonus!
online lotto games for free to play
Jili fishing game l Jili free game l lotto game
We Provide Sport Betting l Baccarat l Live Show Every Monthly
JiliFree provides many popular casino games for many online casinos,
and you can also find this brand in some famous casinos in the world.
<a href="https://xn----9sbfir5agkdkv4c.xn--p1ai/">бетонный погреб</a>
<a href="https://xn----9sbfir5agkdkv4c.xn--p1ai/">бетонный погреб купить</a>
[url=https://prostitutki-new-urengoy.top/]
Зрелые досуг Новый Уренгой[/url]
<a href="https://prostitutki-new-urengoy.top/">
Элитные шалавы Новый Уренгой</a>
[url=https://prostitutki-new-urengoy.top/]
Проверенные шалавы Нового Уренгоя[/url]
<a href="https://prostitutki-new-urengoy.top/">
Девушки по вызову Новый Уренгой</a>
<a href="https://erotic-massage.xyz/city/kirov">эротический массаж Киров</a>
<a href="https://erotic-massage.xyz/city/norilsk">эротический массаж Норильск</a>
[url=https://flirtekb.top/]
vip проститутки Екатеринбург[/url]
<a href="https://flirtekb.top/">
Зрелые индивидуалки Екатеринбург</a>
[url=https://flirtekb.top/]
Зрелые досуг Екатеринбург[/url]
<a href="https://flirtekb.top/">
vip досуг Екатеринбург</a>
[url=https://fei.prostitutki-new-urengoy.com/]
Реальные индивидуалки Нового Уренгоя[/url]
<a href="https://fei.prostitutki-new-urengoy.com/">
Индивидуалки выезд в Новом Уренгое</a>
[url=https://fei.prostitutki-new-urengoy.com/]
Индивидуалки Новый Уренгой без предоплаты[/url]
<a href="https://fei.prostitutki-new-urengoy.com/">
Шлюхи на дом Новый Уренгой</a>
[url=https://fei.individualki-new-urengoy.com/]
Зрелые досуг Новый Уренгой[/url]
<a href="https://fei.individualki-new-urengoy.com/">
Элитные индивидуалки Нового Уренгоя</a>
[url=https://fei.individualki-new-urengoy.com/]
Шалавы Новый Уренгой недорого[/url]
<a href="https://fei.individualki-new-urengoy.com/">
Досуг выезд в Новом Уренгое</a>
mega не работает[/url]
<a href="https://mega555kf7lsmb54yd6etz.com/">
mega market onion</a>
mega darkmarket ссылка[/url]
<a href="https://mega555kf7lsmb54yd6etz.com/">
mega зеркало</a>
netex24 обмен денег[/url]
<a href="https://netex-24.net/">
netex24 net</a>
Lấy Quốc Tịch Hy Lạp 2023</a>
Обмен с бтк на сбер netex24 [/url]
<a href="https://netlex24.net/">
netex24 официальный сайт</a>
<a href="https://workgirls.biz/city/chelyabinsk.html">Работа для девушек Челябинск</a>
<a href="https://workgirls.biz/city/ussuriysk.html">Работа для девушек Уссурийск</a>
<a href="https://alcomoscow02.site/index.php/product-category/pivo">доставка пива ночью </a>
<a href="https://alcomoscow02.site">купить спиртное ночью </a>
Singer Leana Mask gave a new sound to this song. You can listen to it on all platforms and watch it on YouTube. We are sure you will like it!
[url=https://www.youtube.com/watch?v=Oyvgr0F_d1k]cover song distribution[/url]
<a href="https://www.youtube.com/watch?v=Oyvgr0F_d1k">
new music releases</a>
Singer Leana Mask gave a new sound to this song. You can listen to it on all platforms and watch it on YouTube. We are sure you will like it!
[url=https://www.youtube.com/watch?v=Oyvgr0F_d1k]cover song distribution[/url]
<a href="https://www.youtube.com/watch?v=Oyvgr0F_d1k">
cover song music distribution</a>
[url=https://flirtnsk.top/]
Индивидуалки круглосуточно Новосибирск[/url]
<a href="https://flirtnsk.top/">
Дешевые индивидуалки Новосибирск</a>
[url=https://flirtnsk.top/]
Зрелые шлюхи Новосибирск[/url]
<a href="https://flirtnsk.top/">
Вип шлюхи Новосибирск</a>
официальный сайт mine exchange[/url]
<a href="https://mine-exchangee.com/">
Обменять бтк на киви</a>
mine exchange[/url]
<a href="https://mine-exchangee.com/">
bestchange шахта</a>
<a href="https://jobgirls.xyz/category/krasnodar.html">Работа для девушек Краснодар</a>
<a href="https://jobgirls.xyz/category/taganrog.html">Работа для девушек Таганрог</a>
<a href="https://alcostore.site/">доставка алкоголя москва</a>
<a href="https://alcostore.site/product-category/vodka/">доставка водки ночью</a>
[url=https://flirtnu.xyz/]
Реальные проститутки Новый Уренгой[/url]
<a href="https://flirtnu.xyz/">
Вип индивидуалки Новый Уренгой</a>
[url=https://flirtnu.xyz/]
Снять индивидуалку в Новом Уренгое[/url]
<a href="https://flirtnu.xyz/">
Элитные шлюхи Нового Уренгоя</a>
Обменять бтк на киви[/url]
<a href="https://mine-exhcange.com/">
Обменник шахта</a>
nhà cái 188bet
Шахта обмен[/url]
<a href="https://mine-exhcange.com/">
шахта официальный сайт</a>
<a href="https://koroleva.world/city/yoshkar_ola">вакансии для девушек Йошкар-Ола</a>
프리미엄 스포츠중계 PICKTV(픽티비)는 회원가입없이 무료스포츠중계,월드컵중계,무료TV시청이 무료로 가능합니다
<a href="https://koroleva.world/city/essentuki">Работа для девушек Ессентуки</a>
<a href="https://mixer-bitcoin.org/">
крипто блендер</a>
btc blender mixer [/url]
<a href="https://mixer-bitcoin.org/">
крипто миксер</a>
[url=https://2ij.ru/]создание сайта[/url]
<a href="https://2ij.ru/">создание сайта</a>
University of Muhammadiyah Prof. DR. HAMKA (referred to as UHAMKA) is one of the private universities owned by Muhammadiyah located in Jakarta.
[url=https://2ij.ru/]разработка сайта[/url]
<a href="https://2ij.ru/">разработка сайта</a>
[url=https://prostitutki-anapa.xyz/]
Дешевые индивидуалки Анапа[/url]
<a href="https://prostitutki-anapa.xyz/">
Индивидуалки выезд в Анапе</a>
[url=https://prostitutki-anapa.xyz/]
Шлюхи на дом Анапа[/url]
<a href="https://prostitutki-anapa.xyz/">
Индивидуалки на дом Анапа</a>
<a href="https://minoxidil.gb.net/?lang=no">https://minoxidil.gb.net/?lang=no</a>
<a href="https://noeticforce.com/u/leaboonas">https://noeticforce.com/u/leaboonas</a>
<a href="https://rabotanu.ru/city/sankt_peterburg">работа для девушек досуг Санкт-Петербург</a>
<a href="https://rabotanu.ru/city/nefteyugansk">Работа для девушек Нефтеюганск</a>
сайт покердом[/url]
<a href="https://pokerdom-cd5.xyz/">
скачать покердом зеркало</a>
покердом вход[/url]
<a href="https://pokerdom-cd5.xyz/">
покердом pokerdom скачать</a>
<a href="https://alcomoscow1.site/product-category/viski/">купить виски с доставкой на дом </a>
<a href="https://alcomoscow1.site/product-category/wine/">купить вино с доставкой </a>
[url=https://prostitutki-noyabrsk.xyz/]
Снять проститутку в Ноябрьске[/url]
<a href="https://prostitutki-noyabrsk.xyz/">
Досуг круглосуточно Ноябрьск</a>
[url=https://prostitutki-noyabrsk.xyz/]
Элитные шлюхи Ноябрьск[/url]
<a href="https://prostitutki-noyabrsk.xyz/">
Индивидуалки выезд в Ноябрьске</a>
покердом вход[/url]
<a href="https://pokerdom-cm6.top/">
покердом официальный сайт зеркало</a>
<a href="https://rabota-devushkam.net/%d0%bb%d0%b8%d0%bf%d0%b5%d1%86%d0%ba/">Работа для девушек Липецк</a>
<a href="https://rabota-devushkam.net/tula/">вакансии девушкам Тула</a>
[url=https://dosugnu.xyz/]
Реальный досуг Нового Уренгоя[/url]
<a href="https://dosugnu.xyz/">
Индивидуалки негритянки Новый Уренгой</a>
[url=https://dosugnu.xyz/]
Досуг Новый Уренгой без предоплаты[/url]
<a href="https://dosugnu.xyz/">
Элитные шлюхи Нового Уренгоя</a>
покердом рабочее[/url]
<a href="https://pokerdom-ct6.top/">
покердом pokerdom скачать</a>
покердом рабочее зеркало сегодня[/url]
<a href="https://pokerdom-ct6.top/">
покердом рабочее зеркало сегодня</a>
<a href="https://rabota-devushkam.biz/nignevartovsk/">работа для девушек в эскорте Нижневартовск</a>
<a href="https://rabota-devushkam.biz/%d0%bb%d0%b8%d0%bf%d0%b5%d1%86%d0%ba/">работа для девушек в эскорте Липецк</a>
omgomgomg5j4yrr4mjdv3h5c5xfvxtqqs2in7smi65mjps7wvkmqmtqd тор[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5s-onion.com/">
omgomgomg onion</a>
GAS SLOT Adalah, situs judi slot online terpercaya no.1 di Indonesia saat ini yang menawarkan beragam pilihan permainan slot online yang tentunya dapat kalian mainkan serta menangkan dengan mudah setiap hari. Sebagai agen judi slot resmi, kami merupakan bagian dari server slot777 yang sudah terkenal sebagai provider terbaik yang mudah memberikan hadiah jackpot maxwin kemenangan besar di Indonesia saat ini. GAS SLOT sudah menjadi pilihan yang tepat untuk Anda yang memang sedang kebingungan mencari situs judi slot yang terbukti membayar setiap kemenangan dari membernya. Dengan segudang permainan judi slot 777 online yang lengkap dan banyak pilihan slot dengan lisensi resmi inilah yang menjadikan kami sebagai agen judi slot terpercaya dan dapat kalian andalkan
омг не работает[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5s-onion.com/">
площадка omg</a>
Корейская косметика для ухода вокруг глаз отличного качества[/url]
<a href="https://amalfita.ru/">
Корейская косметика для ухода вокруг глаз премиального качества</a>
lizda косметика купить[/url]
<a href="https://amalfita.ru/">
cos de baha купить</a>
kraken[/url]
<a href="https://krmp-onion.com/">
кракен гидра</a>
mega маркет[/url]
<a href="https://megasb-darknet.com/">
mega darkmarket войти</a>
<a href="https://rulate.ru/">фанфики про</a>
Puncak88 adalah situs Slot Online terbaik di Indonesia. Puncak88, situs terbaik dan terpercaya yang sudah memiliki lisensi resmi, khususnya judi slot online yang saat ini menjadi permainan terlengkap dan terpopuler di kalangan para member, Game slot online salah satu permainan yang ada dalam situs judi online yang saat ini tengah populer di kalanagan masyarat indonesia, dan kami juga memiliki permainan lainnya seperti Live casino, Sportbook, Poker , Bola Tangkas , Sabung ayam ,Tembak ikan dan masih banyak lagi lainya.
<a href="https://rulate.ru/">читать фанфики</a>
<a href="https://erotic-massage.xyz/city/krasnoyarsk">эротический массаж Красноярск</a>
<a href="https://erotic-massage.xyz/city/tomsk">эротический массаж Томск</a>
<a href="https://rabota-devushkam.ru.com/volgograd/"> Работа для девушек Волгоград</a>
<a href="https://rabota-devushkam.ru.com/yalta/">вакансии для девушек Ялта</a>
[url=https://prostitutkinu.top/]
Реальные проститутки Новый Уренгой.[/url]
<a href="https://prostitutkinu.top/">
Проститутки по вызову Новый Уренгой.</a>
[url=https://prostitutkinu.top/]
Шалавы Нового Уренгоя без предоплаты.[/url]
<a href="https://prostitutkinu.top/">
Сайт досуга Нового Уренгоя.</a>
GAS SLOT Adalah, situs judi slot online terpercaya no.1 di Indonesia saat ini yang menawarkan beragam pilihan permainan slot online yang tentunya dapat kalian mainkan serta menangkan dengan mudah setiap hari. Sebagai agen judi slot resmi, kami merupakan bagian dari server slot777 yang sudah terkenal sebagai provider terbaik yang mudah memberikan hadiah jackpot maxwin kemenangan besar di Indonesia saat ini. GAS SLOT sudah menjadi pilihan yang tepat untuk Anda yang memang sedang kebingungan mencari situs judi slot yang terbukti membayar setiap kemenangan dari membernya. Dengan segudang permainan judi slot 777 online yang lengkap dan banyak pilihan slot dengan lisensi resmi inilah yang menjadikan kami sebagai agen judi slot terpercaya dan dapat kalian andalkan
<a href="https://rabotadevushkam.net/astrahan-2/">вакансии девушкам Астрахань</a>
<a href="https://rabotadevushkam.net/%d1%81%d0%b8%d0%bc%d1%84%d0%b5%d1%80%d0%be%d0%bf%d0%be%d0%bb%d1%8c/">Работа для девушек Симферополь</a>
[url=https://prostitutki-anapa.xyz/]
Вип индивидуалки Анапа[/url]
<a href="https://prostitutki-anapa.xyz/">
Реальные шлюхи Анапа</a>
[url=https://prostitutki-anapa.xyz/]
Дешевые проститутки Анапа[/url]
<a href="https://prostitutki-anapa.xyz/">
Дешевые индивидуалки Анапа</a>
<a href="https://reklamaxxx.biz/kaliningrad/">Работа для девушек Калининград</a>
<a href="https://reklamaxxx.biz/saratov/">Работа для девушек Саратов</a>
[url=https://prostitutki-anapa.top/]
Шалавы выезд в Анапе[/url]
<a href="https://prostitutki-anapa.top/">
Дешевые шалавы Анапа</a>
[url=https://prostitutki-anapa.top/]
Досуг Анапа без предоплаты[/url]
<a href="https://prostitutki-anapa.top/">
Дешевый досуг Анапа</a>
[url=https://flirtnn.xyz/]
проститутки в ниж[/url]
<a href="https://flirtnn.xyz/">
проститутки досуг нижний новгород</a>
[url=https://flirtnn.xyz/]
проститутки нижнего но[/url]
<a href="https://flirtnn.xyz/">
проститутки нн</a>
[url=https://flirtnn.xyz/]
проститутки на выезд нижний новгород[/url]
<a href="https://flirtnn.xyz/">
путаны нижний новгород</a>
[url=https://flirtnu.xyz/]
Индивидуалки Новый Уренгой[/url]
<a href="https://flirtnu.xyz/">
Шалавы круглосуточно Новый Уренгой</a>
[url=https://flirtnu.xyz/]
Вип шлюхи Новый Уренгой[/url]
<a href="https://flirtnu.xyz/">
Снять проститутку в Новом Уренгое</a>
토토사이트
https://artmodel.biz/country/bahreyn.html
[url=https://artmodel.biz/country/egipet.html]Работа для девушек Египет[/url]<a href="https://artmodel.biz/country/kitay.html">Работа для девушек Китай вакансии</a>
[url=https://artmodel.biz/country/kitay.html]
Эскорт работа Китай[/url]
+7(910)146-24-28
https://artmodel.biz/country/gretsiya.html
[url=https://artmodel.biz/country/izrail.html]
Работа Израиль для русских девушек[/url]<a href="https://artmodel.biz/country/ssha.html">Работа моделью в Америке Штатах</a>
[url=https://prostitutki-anapa.xyz/]
Проститутки по вызову Анапа[/url]
<a href="https://prostitutki-anapa.xyz/">
Шалавы Анапа без предоплаты</a>
[url=https://prostitutki-anapa.xyz/]
Дешевые индивидуалки Анапа[/url]
<a href="https://prostitutki-anapa.xyz/">
Шалавы Анапа недорого</a>
Досуг Новый Уренгой недорого[/url]
<a href="https://prostitutki-new-urengoy.biz/">
Шлюхи Новый Уренгой недорого</a>
Досуг выезд в Новом Уренгое[/url]
<a href="https://prostitutki-new-urengoy.biz/">
Элитные шалавы Новый Уренгой</a>
JILI bonus | New Color Game | Bingo | Baccarat | JiliSlot
Jili philippines? www.goldenplus.com ? 100% Bonus
Easy Lang Manalo Dito guys | Cash-Out Every Day
GUSTO MO KUMITA NG P60 PESOS AWARD
Legit paying apps payout thru Gcash meron po !
Free ?60 Pesos For Newmemeber!
Снять шалаву в Новом Уренгое[/url]
<a href="https://prostitutki-new-urengoy.biz/">
Реальный досуг Нового Уренгоя</a>
[url=https://codigosblog.com.br/2022/08/como-ter-sucesso-no-instagram-dicas-e-ideias.html]https://codigosblog.com.br/2022/08/como-ter-sucesso-no-instagram-dicas-e-ideias.html[/url]
<a href="https://codigosblog.com.br/2022/08/como-ter-sucesso-no-instagram-dicas-e-ideias.html">https://codigosblog.com.br/2022/08/como-ter-sucesso-no-instagram-dicas-e-ideias.html</a>
вход omg[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5xf-onion.com/">
зайти на омг</a>
[url=https://www.saiba.pt/2022/08/como-ganhar-nas-apostas-desportivas.html]https://www.saiba.pt/2022/08/como-ganhar-nas-apostas-desportivas.html[/url]
<a href="https://ppnewsfb.com.br/sono-dicas-preciosas-para-dormir-bem-e-viver-melhor/">https://ppnewsfb.com.br/sono-dicas-preciosas-para-dormir-bem-e-viver-melhor/</a>
[url=https://prostitutki-noyabrsk.xyz/]
Проститутки круглосуточно Ноябрьск[/url]
<a href="https://prostitutki-noyabrsk.xyz/">
Элитные индивидуалки Ноябрьска</a>
[url=https://prostitutki-noyabrsk.xyz/]Проститутки Ноябрьск[/url]
<a href="https://prostitutki-noyabrsk.xyz/">Проститутки Ноябрьск</a>
[url=https://money.irktorgnews.ru/pro-lichnye-dengi/v-liuboi-neponiatnoi-situatcii-investirui-no-s-umom]https://money.irktorgnews.ru/pro-lichnye-dengi/v-liuboi-neponiatnoi-situatcii-investirui-no-s-umom[/url]
<a href="http://worldcrisis.ru/crisis/4195817">http://worldcrisis.ru/crisis/4195817</a>
[url=https://www.e-kuzbass.ru/news/6518]https://www.e-kuzbass.ru/news/6518[/url]
<a href="https://news.sarbc.ru/main/2022/10/29/279898.html">https://news.sarbc.ru/main/2022/10/29/279898.html</a>
[url=https://omskpress.ru/news/329866/kak-iskat-informatsiyu-po-trejdingu/]https://omskpress.ru/news/329866/kak-iskat-informatsiyu-po-trejdingu/[/url]
<a href="https://irktorgnews.ru/klimat-nashego-biznesa-novosti/sobytiya-finansovoy-sfery-pro-kreditnye-karty-treyding-lbgotnoe-avtokreditovanie-i-ne-tolbko">https://irktorgnews.ru/klimat-nashego-biznesa-novosti/sobytiya-finansovoy-sfery-pro-kreditnye-karty-treyding-lbgotnoe-avtokreditovanie-i-ne-tolbko</a>
<a href="https://eu-res.ru/almazpremium.php">коронка алмазная по керамограниту</a>
<a href="https://eu-res.ru/almazstandart.php">купить алмазные коронки</a>
<a href="https://eu-res.ru/almaz.php">алмазные диски</a>
<a href="https://eu-res.ru/equipment.php">алмазная установка</a>
2krn.cc[/url]
<a href="https://krmp-onion.com/">
кракен дарк</a>
kraken darkmarket[/url]
<a href="https://krmp-onion.com/">
вход на кракен</a>
зеркало омг[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5xf-onion.com/">
omgomgomg5j4yrr4mjdv3h5c5xfvxtqqs2in7smi65mjps7wvkmqmtqd ссылка</a>
<a href="https://omgomgomg5j4yrr4mjdv3h5xf-onion.com/">
omgomgomg5j4yrr4mjdv3h5c5xfvxtqqs2in7smi65mjps7wvkmqmtqd онион</a>
<a href="https://market24.ro/product-category/laptop-tablete-telefoane/laptopuri/">Laptopuri Asus</a>
http blacksprut[/url]
<a href="https://blacksput-onion.com/">
blacksprut com вход</a>
kraken зеркало[/url]
<a href="https://krmp-onion.com/">
kraken darknet</a>
kraken dark[/url]
<a href="https://krmp-onion.com/">
krmp onion</a>
kraken darkmarket[/url]
<a href="https://krmp-onion.com/">
как войти на kraken</a>
<a href="https://1win-zerkalo.com/">1win зеркало</a>
<a href="https://1wecsv.top/">1win официальный сайт</a>
https://1win-mirror.top/
<a href="https://1winzerkalo.net/">1win зеркало</a>
https://1wecsv.top/
<a href="https://1wincasino.site/">1win casino</a>
https://1winzerkalo.net/
krmp ссылка[/url]
<a href="https://2krmp.com/">
kraken darknet market</a>
<a href="http://dgpdglt.com/home.php?mod=space&uid=457255">http://dgpdglt.com/home.php?mod=space&uid=457255</a>
https://hammeregy.com/vb/member.php?u=116495
<a href="http://catalog.drobak.com.ua/communication/forum/user/2371265/">http://catalog.drobak.com.ua/communication/forum/user/2371265/</a>
http://reacard.home.pl/terminale/viewtopic.php?f=15&t=36333&p=561055#p561055
<a href="https://iert.page.tl/Historical-Background.htm">https://iert.page.tl/Historical-Background.htm</a>
http://georgiantheatre.ge/user/zalonith/
[url=https://t.me/s/Terrenceiei]https://t.me/s/Terrenceiei[/url]
<a href="https://t.me/s/Terrenceiei">https://t.me/s/Terrenceiei</a>
[url=https://t.me/s/Terrenceiei]https://t.me/s/Terrenceiei[/url]
<a href="https://t.me/Terrenceiei">https://t.me/Terrenceiei</a>
If you want to distribute covers, remixes, mixtapes or mashups through New Music Top, you do not need to acquire a mechanical license
from the copyright holder before releasing your song digitally.
After checking the track uploaded to the platform, a license will be issued and your cover version will be delivered to all digital
audio streaming platforms.
With New Music Top you will not have any difficulties with royalties!
The service does it itself
https://alysseumrecords.com/sweet-dreams-on-all-the-dance-floors/
[url=https://alysseumrecords.com/sweet-dreams-on-all-the-dance-floors/]
music digital distribution[/url]
<a href="https://alysseumrecords.com/sweet-dreams-on-all-the-dance-floors/">
music distribution business</a>
스포츠중계
먹튀검증
먹튀검증
[url=https://prostitutki-noyabrsk.xyz/]
Шалавы Ноябрьск[/url]
<a href="https://prostitutki-noyabrsk.xyz/">
Вип индивидуалки Ноябрьск</a>
<a href="https://jobgirls.xyz/category/habarovsk.html">Работа для девушек Хабаровск</a>
<a href="https://koroleva.world/city/vologda">вакансии для девушек Вологда</a>
blacksprut.com в обход[/url]
<a href="https://blacksput-onion.com/">
блэкспрут onion</a>
https://blacksput-onion.com/
<a href="https://rabota-devushkam.biz/orenburg/">работа для девушек в эскорте Оренбург</a>
п»ї
[url=https://www.teleorihuela.com/5-consejos-y-trucos-para-jugar-a-la-ruleta-online-como-un-profesional/]https://www.teleorihuela.com/5-consejos-y-trucos-para-jugar-a-la-ruleta-online-como-un-profesional/[/url]
<a href="hamelinprog.com/gli-sport-piu-seguiti-al-mondo-classifica-e-numero-di-fan/">hamelinprog.com/gli-sport-piu-seguiti-al-mondo-classifica-e-numero-di-fan/</a>
сова гг[/url]
<a href="https://sovagg.com/">обменник сова
сова гг</a>
https://sovagg.com/
<a href="https://rabotadevushkam.net/ekaterinburg/">вакансии девушкам Екатеринбург</a>
[url=https://flirtnu.xyz/]
Зрелые индивидуалки Новый Уренгой[/url]
<a href="https://flirtnu.xyz/">
Проститутки по вызову Новый Уренгой</a>
</p>
<p><a href="https://1samogon.ru/2023/02/20/punkt-vykupa-lekarstv-i-lekarstvennyh-preparatov/">Пункт выкупа лекарств</a></p>
<p><b>Телефон для связи 89209634317 - доступен ватсап и вайбер</b>
<p>В нашей компании можно продать остатки лекарств в Москве на выгодных условиях. Специалисты готовы проконсультировать относительно того, как происходит выкуп препаратов, стоимости тех или иных лекарств. Конечно, всегда можно попытаться продать лекарство через интернет неиспользованное, однако в этом случае важно разобраться с действующими законодательными нормами.</p>
</p><p>Продать лекарства с рук в Бабаево. Продать лекарства с рук в Туране. Продать лекарства с рук.
</p>
<p><b>Разрешена ли продажа остатков лекарств?</b></p>
<p>В рамках действующего законодательства, продать остатки таблеток с рук или в интернете нельзя. Продажа лекарственных препаратов может осуществляться только в случае оформления специальной лицензии. Кроме того, продажа препаратов через интернет (или, как прописано в законе, дистанционным способом) запрещена.</p>
<p>Продать лекарства с рук в Костерёво. Продать лекарства с рук. Продать лекарства с рук.
</p>
<p>Онлайн может быть оформлен предзаказ. Выкуп же лекарственного препарата происходит в аптеке, здесь же можно его и забрать. Кроме того, остатки лекарственных препаратов в аптеках принимать строго запрещено.Также запрещен возврат лекарств даже при условии целостности упаковки и наличии чека. <b>Исключение составляют лишь случаи, связанные с:</b>
</p>
<ul><li>Истекшим к моменту продажи сроком годности;</li>
<li>Отсутствием инструкции;</li>
<li>Несоответствием описания препарата содержимому;</li>
<li>Отсутствием указания срока годности, а также серии партии.</li></ul>
<p>Продать лекарства с рук. Продать лекарства с рук в Клину. Продать лекарства с рук. Продать лекарства с рук. Продать лекарства с рук. Продать лекарства с рук.
</p>
<p>Единственный полностью разрешенный законом вариант избавления от ненужных препаратов – дарение. Медикаменты остатки могут быть переданы в пользование другим частным лицам. Однако и здесь действует нормы. Препараты не должны быть ограничены в обороте. Продать лекарства с рук может быть не так просто. Для этого можно воспользоваться тематическими форумами и пабликами. Однако в этом случае процесс продажи может существенно затянуться.</p>
<p>Продать лекарства с рук в Новоульяновске. Продать лекарства с рук в Орске. Продать лекарства с рук.
</p><p>Обратите внимание, при осуществлении продаже лекарственных препаратов с рук нарушаются нормы КоАП, а именно ст. 14.2. Она предполагает наложение штрафа, сумма относительно небольшая – 1500-2000 рублей. Также возможно изъятие самого препарата. Однако если средства относятся в разряду психотропных, наркотических или ядовитых веществ, такие действия попадают под действие Уголовного кодекса.</p>
<p>Продать лекарства с рук в Малмыже. Продать лекарства с рук в Погаре. Продать лекарства с рук.
</p><p>Если вы все же задались вопросом, где продать остатки лекарств? Рекомендуем обратиться в нашу компанию. <b>Сотрудничество с нами обладает целым рядом преимуществ:</b></p>
<ul><li>Мы осуществляем скупку лекарств безопасно и на выгодных условиях;</li>
<li>Принимаем широкий перечень препаратов;</li>
<li>Предлагаем выгодные цены.</li></ul>
<p>Продать лекарства с рук в Дегтярске. Продать лекарства с рук в Елабуге. Продать лекарства с рук.
</p>
[url=https://godnotaba.wiki/omgomgomg.html]
omg omg[/url]
<a href="https://godnotaba.wiki/omgomgomg.html">
omg darkmarket</a>
[url=https://godnotaba.wiki/omgomgomg.html]
omg не работает[/url]
<a href="https://godnotaba.wiki/omgomgomg.html">
что за омг</a>
[url=https://godnotaba.wiki/mega-darknet-market.html]
mega darkmarket как войти[/url]
<a href="https://godnotaba.wiki/mega-darknet-market.html">
mega shop</a>
[url=https://godnotaba.wiki/mega-darknet-market.html]
mega sb[/url]
<a href="https://godnotaba.wiki/mega-darknet-market.html">
mega mirror</a>
<a href="https://1001rasskaz.ru/">site</a>
https://1001rasskaz.ru/
[url=https://godnotaba.shop/mega-darknet-market.html]
mega555kf7lsmb54yd6etzginolhxxi4ytdoma2rf77ngq55fhfcnyid зеркало[/url]
<a href="https://godnotaba.shop/mega-darknet-market.html">
мега шоп</a>
[url=https://godnotabka.com/omgomgomg.html]
вход на omg[/url]
<a href="https://godnotabka.com/omgomgomg.html">
площадка омг</a>
[url=https://godnotabka.com/mega-darknet-market.html]
мега onion[/url]
<a href="https://godnotabka.com/mega-darknet-market.html">
mega online</a>
п»ї
[url=https://adm-centralny.ru/]https://adm-centralny.ru/[/url]
<a href="https://basalimplant.ru/">https://basalimplant.ru/</a>
blacksprut вход[/url]
<a href="https://blacksput-onion.com/">
https blacksprut com </a>
<a href="https://denisnagulin.ru/">https://denisnagulin.ru/</a>
https://denisnagulin.ru/
<a href="https://denisnagulin.ru/">https://denisnagulin.ru/</a>
https://denisnagulin.ru/
omgomgomg зеркало[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5t-onion.com/">omgomg</a>
https://omgomgomg5j4yrr4mjdv3h5t-onion.com/
[url=https://godnotabka.info/omgomgomg.html]
omg omg даркнет[/url]
<a href="https://godnotabka.info/omgomgomg.html">
omg darkmarket</a>
[url=https://godnotabka.info/mega-darknet-market.html]
mega darknet[/url]
<a href="https://godnotabka.info/mega-darknet-market.html">
mega darkmarket войти</a>
[url=https://godnotabka.live/omgomgomg.html]
omg тор[/url]
<a href="https://godnotabka.live/omgomgomg.html">
omg даркмаркет</a>
[url=https://godnotabka.live/mega-darknet-market.html]
mega darkmarket как войти[/url]
<a href="https://godnotabka.live/mega-darknet-market.html">
dark store</a>
[url=https://godnotabka.net/omgomgomg.html]
omg omg[/url]
<a href="https://godnotabka.net/omgomgomg.html">
omgomgomg5j4yrr4mjdv3h5c5xfvxtqqs2in7smi65mjps7wvkmqmtqd онион</a>
[url=https://godnotabka.net/mega-darknet-market.html]
mega onion[/url]
<a href="https://godnotabka.net/mega-darknet-market.html">
мега даркнет маркет пополнение</a>
<a href="https://t.me/s/mamkinkaper1">https://t.me/s/mamkinkaper1</a>
https://t.me/s/mamkinkaper1
<a href="https://t.me/promo_kanal_l">https://t.me/promo_kanal_l</a>
[url=https://t.me/promo_kanal_l]https://t.me/promo_kanal_l[/url]
[url=https://rabota-devushkam.work/city/samara] вакансии девушкам Самара[/url].
<a href="https://rabota-devushkam.work/city/samara"> вакансии девушкам Самара</a>
Шалавы Сочи[/url]
<a href="https://flirtsochi.ru/">
Элитные шлюхи Сочи</a>
https://flirtsochi.ru/
Развратная жизнь сегодня не является чем-то необыкновенным, поэтому мы рады видеть вас с нашими опытными девочками. [url=https://flirtsochi.ru/]Проститутки Сочи[/url] сидят на сайте знакомств, где есть большой выбор по интересам и другим интересующим параметрам. Профессиональные [url=https://flirtsochi.ru/]индивидуалки Сочи[/url] готовы радовать новых мужчин каждый день. Если вы в первый раз с ними встретитесь, захотите неоднократно таких свиданий. Поэтому скорее решайте, чего вам больше всего хочется. [url=https://flirtsochi.ru/]Шлюхи Сочи[/url] прекрасно справляются со своими непосредственными обязанностями. У вас будет прекрасный досуг с женской половиной. Не бойтесь собственных желаний, начните их исполнять сегодня.
<a href="https://rabotanu.ru/city/kostroma">Работа для девушек Кострома</a>
https://rabotanu.ru/city/cheboksari
Элитные шлюхи Нового Уренгоя[/url]
<a href="https://prostitutki-new-urengoy.biz/">
Шлюхи выезд в Новом Уренгое</a>
[url=https://godnotabka.online/omgomgomg.html]
вход на omg[/url]
<a href="https://godnotabka.online/omgomgomg.html">
ссылка омг</a>
[url=https://godnotabka.online/mega-darknet-market.html]
мега вход[/url]
<a href="https://godnotabka.online/mega-darknet-market.html">
mega официальный сайт</a>
[url=https://godnotabka.pro/omgomgomg.html]
omg tor[/url]
<a href="https://godnotabka.pro/omgomgomg.html">
вход на omg</a>
[url=https://godnotabka.pro/mega-darknet-market.html]
мега tor[/url]
<a href="https://godnotabka.pro/mega-darknet-market.html">
mega com</a>
[url=https://godnotabka.site/omgomgomg.html]omgomg[/url]
<a href="https://godnotabka.site/omgomgomg.html">
omg omg не работает</a>
[url=https://godnotabka.site/mega-darknet-market.html]
mega вход[/url]
<a href="https://godnotabka.site/mega-darknet-market.html">
мега вход</a>
https://akita-kennel.ru
https://o-dom2.ru
https://sekup.ru
https://testcars.ru
https://vash1host.ru
https://domodedovo2012.ru
Jasontiele
https://crm-suite-sugar.com
https://crm-sugar.net
https://crmsugar.net
http://shiny.msk.ru
http://shinymoskva.ru
http://shinyvmoskve.ru
http://shinyvpitere.ru
http://kupitshinypiter.ru
http://kupitshiny16.ru
http://shiny65kupit.ru
https://xn--24-7-43daaa7aj0bybklespjl2bt9x.xn--p1ai/
https://xn---24-7-3veaaa1bk3b1blmetqkl4bu1z.xn--p1ai/
https://lombard-auto-moscow.ru
http://guzeltur.ru
http://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai/
http://paxautoparts.ru
http://simauto36.ru
http://avto-detalinn.ru
http://avtovozirossii.ru
http://autovikup36car.ru
http://bm-avtomoika.ru
http://xn------5cdabaa5ag1dcichf1cr7awj5a4fufrc.xn--p1ai
http://xn-----6kcabaabrn8dcgehs8a0cgpj5a0q.xn--p1ai
http://xn---24-7-3veb9cyaao9abh2azi.xn--p1ai
http://xn---24-7-4vem5bzam6abi1ci0k.xn--p1ai
http://xn----24-7-3nf5az4b6aba7bmf4o.xn--p1ai
http://xn----24-7-2nfh2a5a3bfh1agba3a8b.xn--p1ai
http://xn----24-7-3nfo0c2an9abj4cj8k.xn--p1ai
http://xn---24-7-3vea2bba7a7aak8asp4a9fo.xn--p1ai
Jasontiele
http://xn--24-7-43da7aba4a4aaj6aro2a5fn.xn--p1ai
http://xn---24-7-3vea2bba7acziam2buen0bou2eta7l.xn--p1ai
http://xn----24-7-2nfa7bba0bc1ajan4bveo2bov5eua2m.xn--p1ai
http://xn----24-7-2nfab0cbac3b4ban2amwt2b3gcq.xn--p1ai
http://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai
https://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai/
https://akita-kennel.ru
https://o-dom2.ru
https://sekup.ru
https://testcars.ru
https://vash1host.ru
https://domodedovo2012.ru
Jasontiele
https://crm-suite-sugar.com
https://crm-sugar.net
https://crmsugar.net
http://shiny.msk.ru
http://shinymoskva.ru
http://shinyvmoskve.ru
http://shinyvpitere.ru
http://kupitshinypiter.ru
http://kupitshiny16.ru
http://shiny65kupit.ru
https://xn--24-7-43daaa7aj0bybklespjl2bt9x.xn--p1ai/
https://xn---24-7-3veaaa1bk3b1blmetqkl4bu1z.xn--p1ai/
https://lombard-auto-moscow.ru
http://guzeltur.ru
http://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai/
http://paxautoparts.ru
http://simauto36.ru
http://avto-detalinn.ru
http://avtovozirossii.ru
http://autovikup36car.ru
http://bm-avtomoika.ru
http://xn------5cdabaa5ag1dcichf1cr7awj5a4fufrc.xn--p1ai
http://xn-----6kcabaabrn8dcgehs8a0cgpj5a0q.xn--p1ai
http://xn---24-7-3veb9cyaao9abh2azi.xn--p1ai
http://xn---24-7-4vem5bzam6abi1ci0k.xn--p1ai
http://xn----24-7-3nf5az4b6aba7bmf4o.xn--p1ai
http://xn----24-7-2nfh2a5a3bfh1agba3a8b.xn--p1ai
http://xn----24-7-3nfo0c2an9abj4cj8k.xn--p1ai
http://xn---24-7-3vea2bba7a7aak8asp4a9fo.xn--p1ai
DavidHef
http://xn--24-7-43da7aba4a4aaj6aro2a5fn.xn--p1ai
http://xn---24-7-3vea2bba7acziam2buen0bou2eta7l.xn--p1ai
http://xn----24-7-2nfa7bba0bc1ajan4bveo2bov5eua2m.xn--p1ai
http://xn----24-7-2nfab0cbac3b4ban2amwt2b3gcq.xn--p1ai
http://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai
https://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai/
[url=https://godnotabka.ru/omgomgomg.html]
omgomgomg ссылка[/url]
<a href="https://godnotabka.ru/omgomgomg.html">
omgomgomg5j4yrr4mjdv3h5c5xfvxtqqs2in7smi65mjps7wvkmqmtqd onion</a>
[url=https://godnotabka.ru/mega-darknet-market.html]
mega[/url]
<a href="https://godnotabka.ru/mega-darknet-market.html">
mega darknet</a>
https://akita-kennel.ru
https://o-dom2.ru
https://sekup.ru
https://testcars.ru
https://vash1host.ru
https://domodedovo2012.ru
Jasontiele
https://crm-suite-sugar.com
https://crm-sugar.net
https://crmsugar.net
http://shiny.msk.ru
http://shinymoskva.ru
http://shinyvmoskve.ru
http://shinyvpitere.ru
http://kupitshinypiter.ru
http://kupitshiny16.ru
http://shiny65kupit.ru
https://xn--24-7-43daaa7aj0bybklespjl2bt9x.xn--p1ai/
https://xn---24-7-3veaaa1bk3b1blmetqkl4bu1z.xn--p1ai/
https://lombard-auto-moscow.ru
http://guzeltur.ru
http://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai/
http://paxautoparts.ru
http://simauto36.ru
http://avto-detalinn.ru
http://avtovozirossii.ru
http://autovikup36car.ru
http://bm-avtomoika.ru
http://xn------5cdabaa5ag1dcichf1cr7awj5a4fufrc.xn--p1ai
http://xn-----6kcabaabrn8dcgehs8a0cgpj5a0q.xn--p1ai
http://xn---24-7-3veb9cyaao9abh2azi.xn--p1ai
http://xn---24-7-4vem5bzam6abi1ci0k.xn--p1ai
http://xn----24-7-3nf5az4b6aba7bmf4o.xn--p1ai
http://xn----24-7-2nfh2a5a3bfh1agba3a8b.xn--p1ai
http://xn----24-7-3nfo0c2an9abj4cj8k.xn--p1ai
http://xn---24-7-3vea2bba7a7aak8asp4a9fo.xn--p1ai
ScottDrumb
http://xn--24-7-43da7aba4a4aaj6aro2a5fn.xn--p1ai
http://xn---24-7-3vea2bba7acziam2buen0bou2eta7l.xn--p1ai
http://xn----24-7-2nfa7bba0bc1ajan4bveo2bov5eua2m.xn--p1ai
http://xn----24-7-2nfab0cbac3b4ban2amwt2b3gcq.xn--p1ai
http://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai
https://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai/
[url=https://favoritka.top/city/essentuki]эскорт услуги в Ессентуки[/url]
<a href="https://favoritka.top/city/novorossiysk">эскорт услуги в Новороссийске</a>
[url=https://magicjob.biz/city/vologda]Работа для девушек Вологда[/url]
<a href="https://magicjob.biz/city/oae_emirati">вакансии девушкам эскорт досуг ОАЭ Эмираты</a>
[url=https://godnolaba.com/omgomgomg.html]
зеркало omg[/url]
<a href="https://godnolaba.com/omgomgomg.html">
omgomgomg5j4yrr4mjdv3h5c5xfvxtqqs2in7smi65mjps7wvkmqmtqd</a>
[url=https://godnolaba.com/mega-darknet-market.html]
mega market[/url]
<a href="https://godnolaba.com/mega-darknet-market.html">
mega не работает</a>
<a href="https://rabota-devushkam.net/%d1%81%d0%b8%d0%bc%d1%84%d0%b5%d1%80%d0%be%d0%bf%d0%be%d0%bb%d1%8c/">вакансии девушкам Симферополь</a>
https://rabota-devushkam.net/krasnodar/
[url=https://dosugnu.xyz/]
Проститутки негритянки Новый Уренгой[/url]
<a href="https://dosugnu.xyz/">
Шлюхи круглосуточно Новый Уренгой</a>
https://dosugnu.xyz/
<a href="https://aliexpressskidka.ru/product/12-24-v-5-gang-blue-led-kulisnyj-pereklyuchatel-dual-usb-avto-lodka-morskoj-gruzovik-rv-on-off/">Ссылка</a>
<a href="https://rabota-devushkam.biz/barnaul/">работа для девушек в эскорте Барнаул</a>
https://rabota-devushkam.biz/ufa/
п»ї
[url=https://rotadosvinhosdoalgarve.pt/noticias/o-derradeiro-guia-para-os-casinos-criptograficos/]https://rotadosvinhosdoalgarve.pt/noticias/o-derradeiro-guia-para-os-casinos-criptograficos/[/url]
<a href="https://philipheinser.de/entdecken-sie-die-besten-strategien-fur-online-sportwetten/">https://philipheinser.de/entdecken-sie-die-besten-strategien-fur-online-sportwetten/</a>
п»ї
[url=https://iscra.pt/vantagens-dos-casinos-em-linha-e-das-rotacoes-livres/]https://iscra.pt/vantagens-dos-casinos-em-linha-e-das-rotacoes-livres/[/url]
<a href="https://inforpress.pt/o-futuro-das-maquinas-caca-niqueis-com-apostas-de-dinheiro-real/">https://inforpress.pt/o-futuro-das-maquinas-caca-niqueis-com-apostas-de-dinheiro-real/</a>
[url=https://prostitutki-anapa.xyz/]
Сайт проституток Анапы[/url]
<a href="https://prostitutki-anapa.xyz/">
Проститутки круглосуточно Анапа</a>
https://prostitutki-anapa.xyz/
[url=https://prostitutki-anapa.xyz/]
Шалавы Анапа[/url]
<a href="https://prostitutki-anapa.xyz/">
Проститутки по вызову Анапа</a>
https://prostitutki-anapa.xyz/
[url=https://prostitutkinu.top/]
Дешевые проститутки Новый Уренгой.[/url]
<a href="https://prostitutkinu.top/">
Снять индивидуалку в Новом Уренгое.</a>
https://prostitutkinu.top/
[url=https://prostitutkinu.top/]
Проститутки выезд в Новом Уренгое.[/url]
<a href="https://prostitutkinu.top/">
Проверенные шалавы Нового Уренгоя.</a>
https://prostitutkinu.top/
<a href="https://vegatlas.ru/food">асафетида</a>
https://vegatlas.ru/food
https://akita-kennel.ru
https://o-dom2.ru
https://sekup.ru
https://testcars.ru
https://vash1host.ru
https://domodedovo2012.ru
Peterlaurl
https://crm-suite-sugar.com
https://crm-sugar.net
https://crmsugar.net
http://shiny.msk.ru
http://shinymoskva.ru
http://shinyvmoskve.ru
http://shinyvpitere.ru
http://kupitshinypiter.ru
http://kupitshiny16.ru
http://shiny65kupit.ru
https://xn--24-7-43daaa7aj0bybklespjl2bt9x.xn--p1ai/
https://xn---24-7-3veaaa1bk3b1blmetqkl4bu1z.xn--p1ai/
https://lombard-auto-moscow.ru
http://guzeltur.ru
http://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai/
http://paxautoparts.ru
http://simauto36.ru
http://avto-detalinn.ru
http://avtovozirossii.ru
http://autovikup36car.ru
http://bm-avtomoika.ru
http://xn------5cdabaa5ag1dcichf1cr7awj5a4fufrc.xn--p1ai
http://xn-----6kcabaabrn8dcgehs8a0cgpj5a0q.xn--p1ai
http://xn---24-7-3veb9cyaao9abh2azi.xn--p1ai
http://xn---24-7-4vem5bzam6abi1ci0k.xn--p1ai
http://xn----24-7-3nf5az4b6aba7bmf4o.xn--p1ai
http://xn----24-7-2nfh2a5a3bfh1agba3a8b.xn--p1ai
http://xn----24-7-3nfo0c2an9abj4cj8k.xn--p1ai
http://xn---24-7-3vea2bba7a7aak8asp4a9fo.xn--p1ai
HenryTheva
http://xn--24-7-43da7aba4a4aaj6aro2a5fn.xn--p1ai
http://xn---24-7-3vea2bba7acziam2buen0bou2eta7l.xn--p1ai
http://xn----24-7-2nfa7bba0bc1ajan4bveo2bov5eua2m.xn--p1ai
http://xn----24-7-2nfab0cbac3b4ban2amwt2b3gcq.xn--p1ai
http://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai
https://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai/
[url=https://comprarcialis5mg.org/it/cialis-10mg/]cialis 5 mg prezzo in farmacia 2018[/url]
https://sites.google.com/view/aviator-spribe/
[url=https://sites.google.com/view/aviator-spribe/]игра авиатор[/url]
https://sites.google.com/view/bitcoin-up-app/
https://sites.google.com/view/speedypaper2019/
<a href="https://vegatlas.ru/food">агар-агар</a>
https://vegatlas.ru/food
https://akita-kennel.ru
https://o-dom2.ru
https://sekup.ru
https://testcars.ru
https://vash1host.ru
https://domodedovo2012.ru
DavidHef
https://crm-suite-sugar.com
https://crm-sugar.net
https://crmsugar.net
http://shiny.msk.ru
http://shinymoskva.ru
http://shinyvmoskve.ru
http://shinyvpitere.ru
http://kupitshinypiter.ru
http://kupitshiny16.ru
http://shiny65kupit.ru
https://xn--24-7-43daaa7aj0bybklespjl2bt9x.xn--p1ai/
https://xn---24-7-3veaaa1bk3b1blmetqkl4bu1z.xn--p1ai/
https://lombard-auto-moscow.ru
http://guzeltur.ru
http://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai/
http://paxautoparts.ru
http://simauto36.ru
http://avto-detalinn.ru
http://avtovozirossii.ru
http://autovikup36car.ru
http://bm-avtomoika.ru
http://xn------5cdabaa5ag1dcichf1cr7awj5a4fufrc.xn--p1ai
http://xn-----6kcabaabrn8dcgehs8a0cgpj5a0q.xn--p1ai
http://xn---24-7-3veb9cyaao9abh2azi.xn--p1ai
http://xn---24-7-4vem5bzam6abi1ci0k.xn--p1ai
http://xn----24-7-3nf5az4b6aba7bmf4o.xn--p1ai
http://xn----24-7-2nfh2a5a3bfh1agba3a8b.xn--p1ai
http://xn----24-7-3nfo0c2an9abj4cj8k.xn--p1ai
http://xn---24-7-3vea2bba7a7aak8asp4a9fo.xn--p1ai
Jasontiele
http://xn--24-7-43da7aba4a4aaj6aro2a5fn.xn--p1ai
http://xn---24-7-3vea2bba7acziam2buen0bou2eta7l.xn--p1ai
http://xn----24-7-2nfa7bba0bc1ajan4bveo2bov5eua2m.xn--p1ai
http://xn----24-7-2nfab0cbac3b4ban2amwt2b3gcq.xn--p1ai
http://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai
https://xn---24-7-3veabaib6hg0bmfd2af4an2z.xn--p1ai/
[url=https://comprarcialis5mg.org/it/]spedra 50 prezzo[/url]
https://sites.google.com/view/aviator-spribe/
[url=https://sites.google.com/view/aviator-spribe/]aviator spribe[/url]
https://sites.google.com/view/bitcoin-up-app/
https://sites.google.com/view/speedypaper2019/
[url=https://dosug89.com/city/gubkinskiy]
Шлюхи Губинский[/url]
<a href="https://dosug89.com/city/tarko_sale">
Путаны Тарко-Сале</a>
[url=https://prostitutki-new-urengoy.top/]
Шалавы круглосуточно Новый Уренгой[/url]
<a href="https://prostitutki-new-urengoy.top/">
Шалавы выезд в Новом Уренгое</a>
https://prostitutki-new-urengoy.top/
[url=https://prostitutki-new-urengoy.top/]
Элитные шлюхи Нового Уренгоя[/url]
<a href="https://prostitutki-new-urengoy.top/">
Зрелые проститутки Новый Уренгой</a>
https://prostitutki-new-urengoy.top/
[url=https://molotof.ru/]
Гама казино сом[/url]
<a href="https://molotof.ru/">
Гама казино мобильная версия</a>
https://molotof.ru/
[url=https://molotof.ru/]
гамма казино лучшие казино[/url]
<a href="https://molotof.ru/">
molotof.ru</a>
https://molotof.ru/
[url=https://kopchenie.su/]
Всё о коптильнях[/url]
<a href="https://kopchenie.su/">
Приготовить на мангале</a>
https://kopchenie.su/
[url=https://kopchenie.su/]
Сайт про копчение[/url]
<a href="https://kopchenie.su/">
Копчение морепродуктов</a>
https://kopchenie.su/
blacksprut shop[/url]
<a href="https://blacksput-onion.com/">
blacksprut зеркала</a>
https://blacksput-onion.com/
blacksprut com[/url]
<a href="https://blacksput-onion.com/">
блэкспрут onion</a>
https://blacksput-onion.com/
blacksprut com вход[/url]
<a href="https://blacksput-onion.com/">
blacksprut com вход</a>
https://blacksput-onion.com/
[url=https://mega-city.org/]
mega darknet[/url]
<a href="https://mega-city.org/">
mega магазин, мега что это</a>
[url=https://mega-city.org/]
mega[/url]
<a href="https://mega-city.org/">
мега питер</a>
[url=https://mega555kf7lsmb54yd6etzg.com/]
mega как войти[/url]
<a href="https://mega555kf7lsmb54yd6etzg.com/">
мега ссылка</a>
[url=https://megadarknethelp.com/]
mega555kf7lsmb54yd6etzginolhxxi4ytdoma2rf77ngq55fhfcnyid tor[/url]
<a href="https://megadarknethelp.com/">
mega москва</a>
[url=https://megadarknethelp.com/]
mega darkmarket[/url]
<a href="https://megadarknethelp.com/">
мега даркнет</a>
[url=https://megakb.com/]
мега площадка[/url]
<a href="https://megakb.com/">
мега санкт-петербург</a>
[url=https://megakb.com/]
omg darknet market[/url]
<a href="https://megakb.com/">
mega зеркала</a>
<a href="https://t.me/batyatop888">https://t.me/batyatop888</a>
https://t.me/batyatop888
One of the biggest benefits of renting a house from an owner is the ability to negotiate lease terms. Unlike rental agencies that often have strict lease agreements, homeowners may be more willing to work with you to create a lease that fits your needs. For example, you may be able to negotiate a shorter lease term or include specific clauses that aren't typically included in standard rental agreements.
Another advantage of renting a house from an owner is the potential for lower costs. Rental agencies often charge fees for their services, which can add up quickly. When renting directly from an owner, you may be able to avoid some of these fees and negotiate a lower rent price.
However, it's important to note that renting from an owner also has its downsides. For one, you may not have access to the same level of support and resources that a rental agency can provide. If something breaks in the house, you'll need to contact the owner directly to get it fixed, which can be a hassle.
Additionally, renting from an owner can sometimes be riskier than renting from a rental agency. Owners may not have the same level of experience or knowledge when it comes to managing a rental property, which can lead to issues down the line. It's important to do your due diligence before renting from an owner, including researching their background and checking references.
Overall, renting a house from an owner can be a great option for those looking for more flexibility and potentially lower costs. However, it's important to do your research and carefully consider the pros and cons before making a final decision. With the right approach, renting a house from an owner can be a great way to find your next home.
[url=https://houses-for-rent.space/emerson-apartments-seattle-reviews/]Emerson apartments seattle reviews[/url]
<a href="https://houses-for-rent.space/insights-into-las-booming-real-estate-market-a-blog-perspective/">LA Booming Real Estate Market</a>
https://houses-for-rent.space/unlock-your-potential-los-angeles-real-estate-school/
One of the biggest benefits of renting a house from an owner is the ability to negotiate lease terms. Unlike rental agencies that often have strict lease agreements, homeowners may be more willing to work with you to create a lease that fits your needs. For example, you may be able to negotiate a shorter lease term or include specific clauses that aren't typically included in standard rental agreements.
Another advantage of renting a house from an owner is the potential for lower costs. Rental agencies often charge fees for their services, which can add up quickly. When renting directly from an owner, you may be able to avoid some of these fees and negotiate a lower rent price.
However, it's important to note that renting from an owner also has its downsides. For one, you may not have access to the same level of support and resources that a rental agency can provide. If something breaks in the house, you'll need to contact the owner directly to get it fixed, which can be a hassle.
Additionally, renting from an owner can sometimes be riskier than renting from a rental agency. Owners may not have the same level of experience or knowledge when it comes to managing a rental property, which can lead to issues down the line. It's important to do your due diligence before renting from an owner, including researching their background and checking references.
Overall, renting a house from an owner can be a great option for those looking for more flexibility and potentially lower costs. However, it's important to do your research and carefully consider the pros and cons before making a final decision. With the right approach, renting a house from an owner can be a great way to find your next home.
[url=https://houses-for-rent.space/mastering-la-real-estate-online-schooling/]Mastering LA Real Estate: Online Schooling[/url]
<a href="https://houses-for-rent.space/new-york-penthouse-apartment-view-listing-photos-review/">New York Penthouse Apartment</a>
https://houses-for-rent.space/how-to-become-a-real-estate-agent-los-angeles/
One of the biggest benefits of renting a house from an owner is the ability to negotiate lease terms. Unlike rental agencies that often have strict lease agreements, homeowners may be more willing to work with you to create a lease that fits your needs. For example, you may be able to negotiate a shorter lease term or include specific clauses that aren't typically included in standard rental agreements.
Another advantage of renting a house from an owner is the potential for lower costs. Rental agencies often charge fees for their services, which can add up quickly. When renting directly from an owner, you may be able to avoid some of these fees and negotiate a lower rent price.
However, it's important to note that renting from an owner also has its downsides. For one, you may not have access to the same level of support and resources that a rental agency can provide. If something breaks in the house, you'll need to contact the owner directly to get it fixed, which can be a hassle.
Additionally, renting from an owner can sometimes be riskier than renting from a rental agency. Owners may not have the same level of experience or knowledge when it comes to managing a rental property, which can lead to issues down the line. It's important to do your due diligence before renting from an owner, including researching their background and checking references.
Overall, renting a house from an owner can be a great option for those looking for more flexibility and potentially lower costs. However, it's important to do your research and carefully consider the pros and cons before making a final decision. With the right approach, renting a house from an owner can be a great way to find your next home.
[url=https://houses-for-rent.space/los-angeles-real-estate-billionaires/]Los angeles real estate billionaires[/url]
<a href="https://houses-for-rent.space/emerson-apartments-seattle-reviews/">Emerson apartments seattle reviews</a>
https://houses-for-rent.space/la-real-estate-sales-surge/
<a href="https://vk.com/club218766838">администрация щёлково</a>
https://vk.com/club218766838
<a href="https://vk.com/club218766838">администрация щелково</a>
https://vk.com/club218766838
добро картинки[/url]
<a href="http://sopranoclub.ru/">
добро картинки</a>
http://sopranoclub.ru/
добро картинки[/url]
<a href="http://sopranoclub.ru/">
графика рисунки</a>
http://sopranoclub.ru/
<a href="https://чатгпт-в-россии.рф/">нейросеть онлайн</a>
https://чатгпт-в-россии.рф/
<a href="https://чатгпт-в-россии.рф/">chat gpt</a>
https://чатгпт-в-россии.рф/
<a href="https://workgirls.biz/city/yalta.html">Работа для девушек Ялта</a>
https://workgirls.biz/city/krasnoyarsk.html
<a href="https://workgirls.biz/city/kirov.html">Работа для девушек Киров</a>
https://workgirls.biz/city/simferopol.html
Путаны Кстово[/url]
<a href="https://dosug52.com/city/bor">
Шлюхи Бор</a>
https://dosug52.com/city/semenov
Шлюхи Семенов[/url]
<a href="https://dosug52.com/">https://dosug52.com/</a>
https://dosug52.com/city/gorohovets
[url=https://magicjob.biz/city/ulyanovsk]вакансии девушкам эскорт досуг Ульяновск[/url]
<a href="https://magicjob.biz/city/ufa">Работа для девушек Уфа</a>
[url=https://magicjob.biz/city/pyatigorsk]вакансии девушкам эскорт досуг Пятигорск[/url]
<a href="https://magicjob.biz/city/yuzhno_sahalinsk">Работа для девушек Южно-Сахалинск</a>
<a href="https://erotic-massage.xyz/city/nizhnevartovsk">эротический массаж Нижневартовск</a>
https://erotic-massage.xyz/city/perm
<a href="https://erotic-massage.xyz/city/barnaul">эротический массаж Барнаул</a>
https://erotic-massage.xyz/city/ufa
<a href="https://koroleva.world/city/noviy_urengoy">вакансии для девушек Новый Уренгой</a>
https://koroleva.world/city/orel
<a href="https://soderganki.biz/city/noyabrsk">содержанки Ноябрьск</a>
https://soderganki.biz/city/astrahan
<a href="https://soderganki.biz/city/ulyanovsk">спонсоры Ульяновск</a>
https://soderganki.biz/city/surgut
<a href="https://rabotanu.ru/city/yakutsk">работа девушкам Якутск эскорт</a>
https://rabotanu.ru/city/ivanovo
<a href="https://rabotanu.ru/city/ekaterinburg">работа девушкам Екатеринбург эскорт</a>
https://rabotanu.ru/city/kirov
[url=https://rabota-devushkam.work/city/omsk]Работа для девушек Омск[/url].
<a href="https://rabota-devushkam.work/city/kirov">Работа для девушек Киров</a>
п»ї
[url=https://www.saudedigital.blog.br/top-5-esportes-para-jogar-em-casa/]https://www.saudedigital.blog.br/top-5-esportes-para-jogar-em-casa/[/url]
<a href="https://cibersistemas.pt/dicas/nova-nintendo-switch-nao-sera-lancada-pelo-menos-ate-ao-final-do-proximo-ano/">https://cibersistemas.pt/dicas/nova-nintendo-switch-nao-sera-lancada-pelo-menos-ate-ao-final-do-proximo-ano/</a>
п»ї
[url=https://www.targatocn.it/2022/12/21/leggi-notizia/argomenti/economia-7/articolo/deschamps-ha-rimproverato-i-giocatori-della-francia-allintervallo-non-giocherai-nella-finale-del.html]https://www.targatocn.it/2022/12/21/leggi-notizia/argomenti/economia-7/articolo/deschamps-ha-rimproverato-i-giocatori-della-francia-allintervallo-non-giocherai-nella-finale-del.html[/url]
<a href="https://cej.pt/sites-de-comparacao-de-casinos/">https://cej.pt/sites-de-comparacao-de-casinos/</a>
<a href="https://jobgirls.xyz/category/surgut.html">вакансии для девушек Сургут</a>
https://jobgirls.xyz/category/kislovodsk.html
<a href="https://jobgirls.xyz/category/ufa.html">вакансии для девушек Уфа</a>
https://jobgirls.xyz/category/yaroslavl.html
[url=https://artmodel.biz/country/egipet.html]
Работа в Египте для русских девушек[/url]
https://artmodel.biz/country/germaniya.html
[url=https://artmodel.biz/country/bahreyn.html]Работа в Бахрейне проституткой[/url]<a href="https://artmodel.biz/country/bahreyn.html">Эскорт работа Бахрейн</a>
https://artmodel.biz/country/saudovskaya_araviya.html
[url=https://primpress.ru/article/96277]https://primpress.ru/article/96277[/url]
<a href="https://www.1rre.ru/2613444-3-luchshih-varianta-kuda-vlozhit-dengi.html">https://www.1rre.ru/2613444-3-luchshih-varianta-kuda-vlozhit-dengi.html</a>
[url=https://66.ru/news/stuff/260317/]https://66.ru/news/stuff/260317/[/url]
<a href="http://businesspress.ru/NewsAM/NewsAMShow.asp?ID=1787">http://businesspress.ru/NewsAM/NewsAMShow.asp?ID=1787</a>
omgomgomg5j4yrr4mjdv3h5c5xfvxtqqs2in7smi65mjps7wvkmqmtqd onion[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5ssylka.com/">
omg onion</a>
https://omgomgomg5j4yrr4mjdv3h5ssylka.com/
п»ї
[url=https://byfin.by/zhurnal-byfin/segodnya/chto-takoe-bpif-i-kak-oni-rabotayut-komu-stoit-investirovat-v-fondy/]https://byfin.by/zhurnal-byfin/segodnya/chto-takoe-bpif-i-kak-oni-rabotayut-komu-stoit-investirovat-v-fondy/[/url]
<a href="https://rx24.ru/biznes/kak-zarabotat-na-investicziyah.html">https://rx24.ru/biznes/kak-zarabotat-na-investicziyah.html</a>
п»ї
[url=http://chernomorskoe.info/interesnoe/sanktsii-protiv-rossijskih-investorov-v-2023-g.html]http://chernomorskoe.info/interesnoe/sanktsii-protiv-rossijskih-investorov-v-2023-g.html[/url]
<a href="http://letopisi.ru/portal/public/749-vygodnye-investicii-kak-vybrat-podhodjaschij-variant.html">http://letopisi.ru/portal/public/749-vygodnye-investicii-kak-vybrat-podhodjaschij-variant.html</a>
[url=https://darknetmegamarket.com/]
mega что это[/url]
<a href="https://darknetmegamarket.com/">
mega магазин, мега что это</a>
[url=https://darknetmegasb.com/]
mega555kf7lsmb54yd6etzginolhxxi4ytdoma2rf77ngq55fhfcnyid darknet[/url]
<a href="https://darknetmegasb.com/">
mega sb в обход</a>
[url=https://mega-market.org/]
mega darkmarket url[/url]
<a href="https://mega-market.org/">
мега onion</a>
[url=https://market-mega.org/]
мега официальный сайт[/url]
<a href="https://market-mega.org/">
mega darknet</a>
[url=https://mega-darknet-shop.com/]
санкт-петербург[/url]
<a href="https://mega-darknet-shop.com/">
mega тор</a>
[url=https://mega-market-sb.com/]
мега вещества[/url]
<a href="https://mega-market-sb.com/">
МЕГА ссылка через TOR</a>
[url=https://megadarknetmarkt.com/]
mega mirror[/url]
<a href="https://megadarknetmarkt.com/">
mega555kf7lsmb54yd6etzginolhxxi4ytdoma2rf77ngq55fhfcnyid tor</a>
нейросеть пишущая[/url]
<a href="https://xn----7sbflda1ad4aggxfjcdl4pwb.xn--p1ai/">
нейросеть переводчик</a>
[url=https://megamarketdarknt.com/]
mega darkmarket[/url]
<a href="https://megamarketdarknt.com/">
мега tor</a>
[url=https://megasbmarket.com/]
mega555kf7lsmb54yd6etzginolhxxi4ytdoma2rf77ngq55fhfcnyid онион[/url]
<a href="https://megasbmarket.com/">
мега санкт-петербург</a>
[url=https://megadarknt.com/]
mega darkmarket войти[/url]
<a href="https://megadarknt.com/">
mega dark</a>
[url=https://megasbdarknet.com/]
mega sb вход[/url]
<a href="https://megasbdarknet.com/">
mega москва</a>
[url=https://megasbmarketdarknet.com/]
mega dark market[/url]
<a href="https://megasbmarketdarknet.com/">
mega</a>
[url=https://megasbmarketdarknet.com/]
mega com вход[/url]
<a href="https://megasbmarketdarknet.com/">
omg darknet market</a>
[url=https://mega.org.ru/]
мега даркнет маркет отзывы[/url]
<a href="https://mega.org.ru/">
мега что это</a>
[url=https://megasbmarketdark.net/]
mega shop[/url]
<a href="https://megasbmarketdark.net/">
mega онион</a>
[url=https://megasbmega.com/]
mega в обход[/url]
<a href="https://megasbmega.com/">
мега зеркало</a>
[url=https://mega-com.store/]
mega питер[/url]
<a href="https://mega-com.store/">
мега даркнет маркет ссылка</a>
[url=https://mega-darknet-market.com/]
мега официальный сайт[/url]
<a href="https://mega-darknet-market.com/">
мега вещества</a>
[url=https://mega-sb.me/]
как войти[/url]
<a href="https://mega-sb.me/">
mega</a>
[url=https://mega-sb.me/]
мега даркнет маркет ссылка отзывы[/url]
<a href="https://mega-sb.me/">
mega официальный сайт</a>
[url=https://mega555kf7lkmkicpiqf.com/]
МЕГА ссылка на сайт[/url]
<a href="https://mega555kf7lkmkicpiqf.com/">
мега сайт даркнет маркет</a>
[url=https://mega555kf7lkmkicpiqf.com/]
мега официальный сайт[/url]
<a href="https://mega555kf7lkmkicpiqf.com/">
mega darknet url</a>
<a href="https://t.me/s/enzksorbdi3938">https://t.me/s/enzksorbdi3938</a>
https://t.me/s/enzksorbdi3938
[url=https://mega555kf7lsmd54ydsf.com/]
мега войти[/url]
<a href="https://mega555kf7lsmd54ydsf.com/">
mega не работает</a>
[url=https://godnotaba.pw/]
mega shop[/url]
<a href="https://godnotaba.pw/">
мега даркнет маркет бот</a>
[url=https://godnotabka.pw/]
mega darknet[/url]
<a href="https://godnotabka.pw/">
mega market onion</a>
[url=https://godnotabka.pw/]
mega darkmarket[/url]
<a href="https://godnotabka.pw/">
мега</a>
https blacksprut com[/url]
<a href="https://blacksprutsc.com/">
блэкспрут вход</a>
https://blacksprutsc.com/
как зайти +на blacksprut[/url]
<a href="https://blacksprutsc.com/">
блэкспрут darknet</a>
https://blacksprutsc.com/
фильмы 2022 2023[/url]
<a href="https://new-2022.me/filmy-2023-onlajn/">
фильмы 2023 смотреть онлайн</a>
https://new-2022.me/filmy-2023-onlajn/
лучшие фильмы 2023 смотреть онлайн[/url]
<a href="https://cinema-onlajn.biz/filmy-2023-smotret/">
смотреть фильмы 2023</a>
https://cinema-onlajn.biz/filmy-2023-smotret/
фильмы вышедшие в качестве 2023[/url]
<a href="https://kinofilmy-2021.ru/filmy-2023-novinki/">
смотреть фильмы 2023 года</a>
https://kinofilmy-2021.ru/filmy-2023-novinki/
https://filmifilmi.online/
<a href="https://filmifilmi.online/links/">фильмы бесплатно смотреть онлайн</a>
[url=https://filmifilmi.online/serialy/]смотреть сериалы онлайн[/url]
https://filmifilmi.online/serialy/
<a href="https://filmifilmi.online/serialy/serialy-2023/">смотрите сериалы новинки 2023 года</a>
[url=https://filmifilmi.online/links/filmy-2023/]Новые кинофильмы новинки 2023 года смотреть[/url]
[url=https://www.bragazeta.ru/news/2022/10/27/v-chem-zakljuchaetsya-sut-trejdinga/]https://www.bragazeta.ru/news/2022/10/27/v-chem-zakljuchaetsya-sut-trejdinga/[/url]
<a href="https://ekb.plus.rbc.ru/partners/63d3b21b7a8aa9f37a47fa8a">https://ekb.plus.rbc.ru/partners/63d3b21b7a8aa9f37a47fa8a</a>
It is already causing a stir among music lovers and critics.
"Flowers" is a soulful song of grief and healing, inspired by the beautiful and ephemeral nature of flowers. The song's lyrics are poignant and uplifting, and convey a message of hope and acceptance during the grieving process.
"Flowers" is available on all major streaming platforms, including Spotify, Apple Music, and Tidal. Get your tissues ready for this emotional ride.
https://musicstar.world/members/_-IzQJ2iEss
[url=https://musicstar.world/members/_-IzQJ2iEss]
miley cyrus - flowers lyrics[/url]
<a href="https://musicstar.world/members/_-IzQJ2iEss">
big bang cover contest</a>
It is already causing a stir among music lovers and critics.
"Flowers" is a soulful song of grief and healing, inspired by the beautiful and ephemeral nature of flowers. The song's lyrics are poignant and uplifting, and convey a message of hope and acceptance during the grieving process.
"Flowers" is available on all major streaming platforms, including Spotify, Apple Music, and Tidal. Get your tissues ready for this emotional ride.
https://musicstar.world/members/_-IzQJ2iEss
[url=https://musicstar.world/members/_-IzQJ2iEss]
cover art contest[/url]
<a href="https://musicstar.world/members/_-IzQJ2iEss">
miley cyrus flowers audio</a>
Привет, игровое сообщество! Мы рады представить вам последние новости из мира игр. Узнайте о самых ожидаемых релизах, интересных обновлениях и захватывающих анонсах. Будьте в курсе событий и следите за развитием игровой индустрии!
[url=https://techgamehq.ru/]Технические новости[/url]
<a href="https://techgamehq.ru/">Инди-игры</a>
https://techgamehq.ru/
Играете в любимую игру и хотите повысить свою эффективность? У нас есть для вас полезные советы и стратегии, которые помогут вам овладеть основными механиками игры, преодолеть сложности и достичь больших успехов. Следуйте нашим рекомендациям и станьте настоящим мастером!
[url=https://techgamehq.ru/]Инди-студии[/url]
<a href="https://techgamehq.ru/">Электронные соревнования</a>
https://techgamehq.ru/
<a href="https://workgirls.biz/city/kemerovo.html">вакансии для девушек Кемерово</a>
<a href="https://workgirls.biz/city/irkutsk.html">Работа для девушек Иркутск</a>
Вип шалавы Тольятти[/url]
<a href="https://prostitutki-tolyatti.top/">
Проститутки Тольятти недорого</a>
https://prostitutki-tolyatti.top/
Развлекайтесь с теми девочками, которых вы хотите! [url=https://prostitutki-tolyatti.top/]Проститутки Тольятти[/url] со стажем открыты на нашем сайте. Они сделают все, что вам нужно этой ночью. Ваши тайные желания начнут сбываться и воплотятся в реальность. Это касается, как пошлых мыслей, так и чего-то новенького и неповторимого. [url=https://prostitutki-tolyatti.top/]Индивидуалки Тольятти[/url] научат вас контролировать весь процесс, помогут справиться с преодолением фантазий. Красивые [url=https://prostitutki-tolyatti.top/]шлюхи Тольятти[/url] открыты, они с удовольствием встретятся с мужчиной, который их ожидает. Будьте всегда на позитиве, зовите в гости куртизанок нашего сайта и увидите, что такие леди способны на невероятные вещи.
Реальные индивидуалки Тольятти[/url]
<a href="https://prostitutki-tolyatti.top/">
Индивидуалки выезд в Тольятти</a>
https://prostitutki-tolyatti.top/
Развлекайтесь с теми девочками, которых вы хотите! [url=https://prostitutki-tolyatti.top/]Проститутки Тольятти[/url] со стажем открыты на нашем сайте. Они сделают все, что вам нужно этой ночью. Ваши тайные желания начнут сбываться и воплотятся в реальность. Это касается, как пошлых мыслей, так и чего-то новенького и неповторимого. [url=https://prostitutki-tolyatti.top/]Индивидуалки Тольятти[/url] научат вас контролировать весь процесс, помогут справиться с преодолением фантазий. Красивые [url=https://prostitutki-tolyatti.top/]шлюхи Тольятти[/url] открыты, они с удовольствием встретятся с мужчиной, который их ожидает. Будьте всегда на позитиве, зовите в гости куртизанок нашего сайта и увидите, что такие леди способны на невероятные вещи.
[url=https://magicjob.biz/city/kemerovo]Работа для девушек Кемерово[/url]
<a href="https://magicjob.biz/city/novorossiysk">Работа для девушек Новороссийск</a>
[url=https://flirtspb.top/]
Сайт шалав Санкт Петербург[/url]
<a href="https://flirtspb.top/">
Снять шлюху в Санкт Петербурге</a>
https://flirtspb.top/
[url=https://flirtspb.top/]
Проверенные проститутки Санкт Петербург[/url]
<a href="https://flirtspb.top/">
Элитные шлюхи Санкт Петербург</a>
https://flirtspb.top/
<a href="https://jobgirls.xyz/category/astrahan.html">вакансии для девушек Астрахань</a>
https://jobgirls.xyz/category/kaluga.html
<a href="https://erotic-massage.xyz/city/ussuriysk">эротический массаж Уссурийск</a>
https://erotic-massage.xyz/city/arhangelsk
<a href="https://koroleva.world/city/nizhnevartovsk">Работа для девушек Нижневартовск</a>
https://koroleva.world/city/smolensk
фильмы 2023 в хорошем качестве бесплатно[/url]
<a href="https://filmi-2023.org/">
лучшие фильмы 2023 онлайн</a>
https://filmi-2023.org/
смотреть лучшие фильмы 2023[/url]
<a href="https://novinka-2022.biz/filmy-2023/">
смотреть фильмы 2023</a>
https://novinka-2022.biz/filmy-2023/
<a href="https://soderganki.biz/city/murmansk">спонсоры Мурманск</a>
https://soderganki.biz/city/orenburg
<a href="https://rabotanu.ru/city/ekaterinburg">работа девушкам Екатеринбург эскорт</a>
https://rabotanu.ru/city/omsk
[url=https://rabota-devushkam.work/city/velikiy_novgorod]Работа для девушек Великий Новгород[/url].
<a href="https://rabota-devushkam.work/city/volgograd"> вакансии девушкам Волгоград</a>
[url=https://rabota-devushkam.work/city/cheboksari] вакансии девушкам Чебоксары[/url].
<a href="https://rabota-devushkam.work/city/yakutsk">Работа для девушек Якутск</a>
[url=https://steamdesktopauthenticator.me/]
steam guard desktop[/url]
<a href="https://steamdesktopauthenticator.me/">
steam guard desktop</a>
<a href="https://rabota-devushkam.net/kostroma/">Работа для девушек Кастрома</a>
https://rabota-devushkam.net/usinsk/
[url=https://favoritka.top/city/tyumen]эскорт услуги в Тюмени[/url]
<a href="https://favoritka.top/city/kazan">эскорт услуги в Казани</a>
<a href="https://rabota-devushkam.biz/nignevartovsk/">Работа для девушек Нижневартовск</a>
https://rabota-devushkam.biz/nefteugansk/
<a href="https://dosug52.com/city/arzamas">
Шлюхи Арзамаса</a>
https://dosug52.com/city/kstovo
<a href="https://rabota-devushkam.ru.com/%d0%b2%d0%bb%d0%b0%d0%b4%d0%b8%d0%bc%d0%b8%d1%80/">вакансии для девушек Владимир</a>
https://rabota-devushkam.ru.com/%d1%81%d1%83%d1%80%d0%b3%d1%83%d1%82/
[url=https://dosug89.com/city/pangodi]
Индивидуалки Пангоды[/url]
<a href="https://dosug89.com/city/tazovsk">
Путаны Тазовск</a>
<a href="https://rabotadevushkam.net/kostroma/">вакансии девушкам Кострома</a>
https://rabotadevushkam.net/krasnodar/
<a href="https://rabotadevushkam.net/kazan/">Работа для девушек Казань</a>
https://rabotadevushkam.net/nefteugansk/
[url=https://artmodel.biz/country/germaniya.html]
Работа в сфере досуга Германия[/url]
+7(910)146-24-28
https://artmodel.biz/country/egipet.html
[url=https://artmodel.biz/country/kipr.html]Работа на Кипре проституткой[/url]<a href="https://artmodel.biz/country/bahreyn.html">Работа в Бахрейне проституткой</a>
https://artmodel.biz/country/kitay.html
[url=https://artmodel.biz/country/kipr.html]
Высокооплачиваемая работа для девушек Кипр[/url]
+7(910)146-24-28
https://artmodel.biz/country/bahreyn.html
[url=https://artmodel.biz/country/bahreyn.html]Работа в сфере досуга Бахрейн[/url]
+7(910)146-24-28
Предлагаем молодым, целеустремленным и красивым девушкам работу в Таиланде. Не все девушки желают работать у себя в городе в своей стране. Мы можем предложить работу для девушек в Таиланде в богатых и безопасных направлениях. Работающие за границей девушки имеют доступ в лучшее общество. Они сами становятся его частью то есть успешными и обеспеченными. Работа для девушек Таиланд это шанс начать новую успешную жизнь.
[url=https://artmodel.biz/country/tailand.html]
Работа Таиланд для девушек из России[/url]
<a href="https://artmodel.biz/country/tailand.html">
Работа для девушек Таиланд вакансии</a>
https://artmodel.biz/country/kitay.html
<a href="https://reklamaxxx.biz/sevastopol-2/">Работа для девушек Севастополь</a>
https://reklamaxxx.biz/nizhny-novgorod/
<a href="https://dispetcher.xyz/city/anapa.html">Работа для девушек Анапа, услуги диспетчера Анапа, Работа девушкам досуг Анапа, Работа девушкам эскорт Анапа</a>
https://dispetcher.xyz/city/belgorod.html
[url=https://fish-magnet.ru/Katushki]Катушка для спиннинга купить в Донецке[/url]
<a href="https://fish-magnet.ru/CHEKHLY-RODPOD-PODSTAVKI">купить родпод в Донецке</a>
смотреть новинки кино[/url]
<a href="https://novinki-2023.org/main/">
кино смотреть бесплатно 2023 хорошем</a>
https://novinki-2023.org/main/
кино 2023 уже вышедшие смотреть[/url]
<a href="https://novinki-2023.org/main/">
новинки кино 2023 смотреть онлайн бесплатно</a>
https://novinki-2023.org/main/
п»ї
[url=https://cej.pt/gestao-de-slot-machine/]https://cej.pt/gestao-de-slot-machine/[/url]
<a href="https://via41.com.br/noticias/geral/12022/um-jornal-espanhol-noticia-que-a-atuacao-de-vini-jr-no-real-madrid-e-impactada-pelo-odio-da-torcida-26-01-2023">https://via41.com.br/noticias/geral/12022/um-jornal-espanhol-noticia-que-a-atuacao-de-vini-jr-no-real-madrid-e-impactada-pelo-odio-da-torcida-26-01-2023</a>
кино 2023 смотреть онлайн в хорошем качестве[/url]
<a href="https://films-2023.com/">
новинки в качестве</a>
новые фильмы 2023 смотреть онлайн[/url]
<a href="https://films-2023.com/">
фильмы 2022 2023</a>
вход на omg[/url]
<a href="https://omgomgomg5j4yrr4mjdv3h5darknet.com/">
omgomgomg5j4yrr4mjdv3h5c5xfvxtqqs2in7smi65mjps7wvkmqmtqd onion</a>
https://omgomgomg5j4yrr4mjdv3h5darknet.com/
<a href="https://workgirls.biz/city/volgograd.html">вакансии для девушек Волгоград</a>
https://workgirls.biz/city/ussuriysk.html
Индивидуалки Тольятти без предоплаты[/url]
<a href="https://prostitutki-tolyatti.top/">
Дешевые шалавы Тольятти</a>
https://prostitutki-tolyatti.top/
Развлекайтесь с теми девочками, которых вы хотите! [url=https://prostitutki-tolyatti.top/]Проститутки Тольятти[/url] со стажем открыты на нашем сайте. Они сделают все, что вам нужно этой ночью. Ваши тайные желания начнут сбываться и воплотятся в реальность. Это касается, как пошлых мыслей, так и чего-то новенького и неповторимого. [url=https://prostitutki-tolyatti.top/]Индивидуалки Тольятти[/url] научат вас контролировать весь процесс, помогут справиться с преодолением фантазий. Красивые [url=https://prostitutki-tolyatti.top/]шлюхи Тольятти[/url] открыты, они с удовольствием встретятся с мужчиной, который их ожидает. Будьте всегда на позитиве, зовите в гости куртизанок нашего сайта и увидите, что такие леди способны на невероятные вещи.
in.k2web.cc[/url]
<a href="https://2krakendarknet.com/">
kraken darknet market</a>
[url=https://flirtnn.xyz/]
вип индивидуалки нижний новгород[/url]
<a href="https://flirtnn.xyz/">
знакомства секс в Нижнем Новгороде</a>
https://flirtnn.xyz/
[url=https://flirtnn.xyz/]
проститутки в н н[/url]
<a href="https://flirtnn.xyz/">
проститутки нижнего но</a>
https://flirtnn.xyz/
[url=https://magicjob.biz/city/irkutsk]вакансии девушкам эскорт досуг Иркутск[/url]
<a href="https://magicjob.biz/city/vladimir">Работа для девушек Владимир</a>
[url=https://magicjob.biz/city/tyumen]Работа для девушек Тюмень[/url]
<a href="https://magicjob.biz/city/ussuriysk">Работа для девушек Уссурийск</a>
<a href="https://jobgirls.xyz/category/vladivostok.html">вакансии для девушек Владивосток</a>
https://jobgirls.xyz/category/surgut.html
<a href="https://jobgirls.xyz/category/vladivostok.html">вакансии для девушек Владивосток</a>
https://jobgirls.xyz/category/essentuki.html
https://filmifilmi.online/
<a href="https://filmifilmi.online/serialy/serialy-2023/">смотрите сериалы новинки 2023 года</a>
[url=https://filmifilmi.online/serialy/]смотреть сериалы онлайн[/url]
https://filmifilmi.online/serialy/
<a href="https://filmifilmi.online/serialy/">смотреть сериалы онлайн</a>
[url=https://filmifilmi.online/serialy/serialy-2023/]смотрите сериалы новинки 2023 года[/url]
[url=https://favoritka.work/city/sevastopol]Работа для девушек Севастополь[/url]
<a href="https://favoritka.work/city/cheboksari">Работа для девушек Чебоксары</a>
[url=https://favoritka.work/city/barnaul]Работа для девушек Барнаул[/url]
<a href="https://favoritka.work/city/hanti_mansiysk">Работа для девушек Ханты-Мансийск</a>
<a href="https://koroleva.world/city/cheboksari">Работа для девушек Чебоксары</a>
https://koroleva.world/city/nahodka
<a href="https://koroleva.world/city/kirov">вакансии для девушек Киров</a>
https://koroleva.world/city/tyumen
<a href="https://rabotanu.ru/city/sankt_peterburg">Работа для девушек Санкт-Петербург</a>
https://rabotanu.ru/city/ekaterinburg
<a href="https://telegra.ph/Zachem-lyudi-prodayut-takie-telegram-pabliki-06-07">https://telegra.ph/Zachem-lyudi-prodayut-takie-telegram-pabliki-06-07</a>
https://t.me/elmeme1/5022
<a href="https://rabota-devushkam.info/category/simferopol">Работа для девушек Симферополь </a>
https://rabota-devushkam.info/category/novokuznetsk
<a href="https://erotic-massage.xyz/city/simferopol">эротический массаж Симферополь</a>
https://erotic-massage.xyz/city/sankt_peterburg
[url=https://comprarcialis5mg.org/cialis-5-mg-precio/]cialis 5 mg precio[/url] is a drug that contains the active ingredient tadalafil, which belongs to a group of medications known as phosphodiesterase 5 inhibitors. [url=https://comprarcialis5mg.org/it/]Cialis[/url] is used to treat males suffering from erectile dysfunction. Cialis doses are 2.5 mg and 5 mg are suitable for every day use. Doses between 10 and 20 mg must be taken prior to planned sexual activity. The dosage that is right is dependent on your health condition and lifestyle, and also the severity of your erectile dysfunction symptoms. Cialis 5 mg isn't a only a one-day treatment, but one that has to be continued for at minimum 3 months. The purpose of the drug is "revitalize " the cells of the arteries and cause an increase in blood circulation to corpora cavernosa to increase adequately.
Our [b]online pharmacy[/b] [url=https://comprarcialis5mg.org/it/]cialis generico[/url] would prefer to buy Cialis anonymously without buy generic cialis. You can also try it out and buy generic cialis sites on sale online. [url=https://comprarcialis5mg.org/it/]Cialis[/url] You can also increase energy and strength, as well as capacity to be limpotent, you can purchase a packet. Purchase generic [url=https://comprarcialis5mg.org/it/]cialis prezzo[/url], you are comfortably close the door to temperature. It can be refilled with 10 mg of efficacy. Purchase generic cialis, buy generic cialis Gran between them and also purchase generic cialis mg. This drug shouldn't be used in conjunction with generic Cialis that are active and similar. Buy Generic Cialis there are bad for. Alongside medications, they can be used with synergistic effects or when you're is a generic item. this medical preparation 36 hours and known analogous to that of specific medications for. buy generic cialis buy generic cialis may therefore be a good idea to buy Cialis appear in prescription form and try the. We know following a brief period of time, should you be aware be charged for the purchase. If you are looking to buy Cialis typically do so only as an alternative to the identical. Avoid drinking excessive amounts of alcohol when you are taking the drug. Our shipments have been satisfied of the far exceeded by the.
[url=https://comprarcialis5mg.org/it/]Cialis generico[/url] is a generic Cialis and contribute to https://comprarcialis5mg.org/disfuncion-erectil/ an increase in identical quality of ed. Special warnings italy mg cialis 5 precautions to Warn are taken in Sporanox indinavir. https://comprarcialis5mg.org/it/ The two other drugs cialis 5 mg italy the only one that reverts to the standard first aid kits. Before you buy Sildenafil money you invest in cialis 5 mg italia 5 mg cialis Original Cialis Original Cialis money that you pay for the original packaging and processing the new. regular long-term erectile dysfunction. 5 for 5 cialis 5 mg for the neuroreflexes allergic reactions that require to be addressed shelf life. Italy cialis 5 mg is it and how has theInternet do not suffer from such cialis 5 mg italy within the cialis 5 mg of the. preference in the arc of between doses after. Warnings It is recommended not to use Cialis together with back pain caused by allergies of similar in quality. Generic Cialis Tadalafil and and guarantee of satisfaction Asquistate and clarify what risks.
Donde adquirir [url=https://comprarcialis5mg.org/comprar-viagra-en-espa%C3%B1a/]Comprar viagra[/url] sin receta medica Esto es para poder absorberlo precio tadalafil qualigen 10 mg puede disponer relaciones sexuales normales. Eritromicina y aumento de la caFrance de los medicamentos recetados para la gran ciudad. Comprimidos con efectos secundarios de priapismo, arritmias incontroladas o estimulacion sexual. “Los medicamentos de notificacion incluyen 2 reacciones adversas similares. Es bastante primordial que su medico recuerde antes de retirarlo. En farmacia en linea [url=https://comprarcialis5mg.org/]comprar cialis 5 mg[/url] o en la actualidad la duracion de la [url=https://comprarcialis5mg.org/disfuncion-erectil/]disfuncion erectil[/url]. Food and drug administration debido a sus efectos secundarios incluye la eyaculacion precoz retardada [url=https://comprarcialis5mg.org/it/cialis-20mg/]cialis 20 mg[/url] in andorra cost Las creencias falsas necesitan una explicacion oculta generica de 20 mg.
El preparado no [url=https://comprarcialis5mg.org/comprar-viagra-contrareembolso/]viagra contrareembolso[/url] a sildenafilo viagra contrareembolso viagra contrareembolso hacia el pene sino mas prolongado llegando. Malestar estomacal Los pacientes sufren disfuncion viagra contrareembolso y de otras viagra contrareembolso que comercializaran la Viagra bajo el tratamiento al no puede repercutir de manera Generico en la farmacia ser dispensado unicamente con receta puedan viagra contrareembolso es aproximadamente el esta liberalizado por lo su ingesta y se prolonga durante unas cinco un. la disfuncion erectil espinaca son pocas empresas en la ereccion es.
Todo iba a [url=https://comprarcialis5mg.org/comprar-viagra-contrareembolso/]viagra contrareembolso[/url] en presencia de excitacion. estomago y modificaciones leves y pasajeras de de cualquier generico segun Angel Luis Rodriguez Cuerda fotosensibilidad y vision borrosa. Como ingiero las Tabletas no le habra sacrificado blandas son faciles de los mejores. Al comprar Viagra los disposicion el remedio que requiere viagra contrareembolso algodon organico ereccion Cialis y contrareembolso viagra Hay una serie de sexuales de las mujeres. FDA recientemente identificados viagra contrareembolso al periodo de proteccion y los huevos frijoles notan al los recursos. Asi que comprobar que viagra contrareembolso realmente no Muchas. Ademas proponemos a su bocadillos en que experimento. viagra contrareembolso contrareembolso viagra madre que viagra contrareembolso debe rellenar la los problemas de disfuncion su problema. sus creencias religiosas Blandas Viagra Las tabletas que sean directos indirectos especificos o demas.
El costo de los medicamentos puede ser una gran barrera para las personas que los necesitan. Cuando un medicamento que salva o cambia vidas tiene un precio fuera de su alcance, [url=https://comprarcialis5mg.org/cialis-5-mg-precio/]Tadalafilo 5 mg[/url] puede causar un sufrimiento inmenso. En los Estados Unidos, el costo de los medicamentos recetados es uno de los mayores gastos medicos. Muchas personas se ven obligadas a elegir entre tratamientos que salvan vidas y otros elementos esenciales como comida y refugio.
[url=https://comprarcialis5mg.org/cialis-5-mg-precio/]Tadalafilo 5 mg precio[/url] es un medicamento popular para la disfuncion erectil que ha estado en el mercado durante mas de una decada. [url=https://comprarcialis5mg.org/disfuncion-erectil/]Disfuncion erectil[/url] Su precio se ha mantenido relativamente estable a lo largo de los anos, pero eso puede cambiar pronto. Un informe reciente de los Centros de Servicios de Medicare y Medicaid (CMS) muestra que el precio de Cialis 5 mg aumento un 72 por ciento entre 2012 y 2016. Este aumento es significativo si se considera que ocurrio durante un periodo de lento crecimiento economico.
<a href="http://fox-sochi.ru/">Эротический массаж в Сочи</a>
http://fox-sochi.ru/
https://filmifilmi.pro/links/
<a href="https://filmifilmi.pro/links/">фильмы бесплатно смотреть онлайн</a>
[url=https://filmifilmi.pro/links/filmy-2023/]Новые кинофильмы новинки 2023 года смотреть[/url]
баланс с банковской карты[/url]
<a href="https://blackcash.tel/">
заливы денежных средств</a>
https://blackcash.tel/
продажа кредитных карт[/url]
<a href="https://blackcash.tel/">
печати изготовление</a>
https://blackcash.tel/
пенсионные удостоверения[/url]
<a href="https://blackcash.tel/">
карта с балансом купить</a>
https://blackcash.tel/
[url=https://rabota-devushkam.work/city/anapa] вакансии девушкам Анапа[/url].
<a href="https://rabota-devushkam.work/city/yuzhno_sahalinsk">Работа для девушек Южно-Сахалинск</a>
<a href="https://urengoy.jobmodel.biz/">высокооплачиваемая работа для девушек Новый Уренгой</a>
https://rostov.jobmodel.biz/
<a href="https://rabota-devushkam.net/irkutsk/">Работа для девушек Иркутск</a>
https://rabota-devushkam.net/ufa/
<a href="https://rabota-devushkam.biz/noyabrsk/">работа для девушек в эскорте Ноябрьск</a>
https://rabota-devushkam.biz/ufa/
<a href="https://rabota-devushkam.ru.com/ufa/">вакансии для девушек Уфа</a>
https://rabota-devushkam.ru.com/irkutsk/
<a href="https://telegra.ph/Kupit-Mef-Telegram-06-12">https://telegra.ph/Kupit-Mef-Telegram-06-12</a>
https://telegra.ph/Kupit-Mef-Telegram-06-12
<a href="https://telegra.ph/Kupit-Mef-Telegram-06-12">https://telegra.ph/Kupit-Mef-Telegram-06-12</a>
https://telegra.ph/Kupit-Mef-Telegram-06-12
[url=https://prostitutki-barnaul.top/]
Реальные проститутки Барнаул[/url]
<a href="https://prostitutki-barnaul.top/">
Зрелые индивидуалки Барнаул</a>
https://prostitutki-barnaul.top/
<a href="https://rabotadevushkam.net/%d0%bf%d0%b5%d0%bd%d0%b7%d0%b0/">вакансии девушкам Пенза</a>
https://rabotadevushkam.net/rostov-na-donu/
<a href="https://dosug52.com/city/kstovo">Проститутки Кстово</a>
https://dosug52.com/city/zavolzhe
<a href="https://reklamaxxx.biz/orenburg/">Работа для девушек Оренбург</a>
https://reklamaxxx.biz/irkutsk/
<a href="https://rusonserial.ru/serialy/serialy-2023/">смотрите сериалы новинки 2023 года</a>
[url=https://rusonserial.ru/filmy/filmy-2023/]Новые кинофильмы новинки 2023 года смотреть[/url]
https://rusonserial.ru/filmy/filmy-2023/
<a href="https://rusonserial.ru/serialy/serialy-2023/">смотрите сериалы новинки 2023 года</a>
[url=https://rusonserial.ru/]Онлайн кинотеатр - смотреть сериалы и фильмы бесплатно в хорошем качестве HD 720p[/url]
https://rusonserial.ru/filmy/filmy-2023/
[url=https://flirtnn.xyz/]
знакомства секс в Нижнем Новгороде[/url]
<a href="https://flirtnn.xyz/">
проститутки нижегородской области</a>
https://flirtnn.xyz/
[url=https://flirtnn.xyz/]
дешевые проститутки нижнего[/url]
<a href="https://flirtnn.xyz/">
дешевые проститутки в нижнем новгороде</a>
https://flirtnn.xyz/
netex24 net[/url]
<a href="https://netlex24.net/">
netex24 net</a>
https://netlex24.net/
netex24 официальный сайт[/url]
<a href="https://netlex24.net/">
bestchange netex24 обменник</a>
https://netlex24.net/
bestchange netex24 обменник[/url]
<a href="https://netexi24.net/">
netex24 net</a>
https://netexi24.net/
<a href="https://netexi24.net/">
bestchange netex24 обменник</a>
https://netexi24.net/
[url=https://t.me/Cryptadid]https://t.me/Cryptadid[/url]
<a href="https://t.me/Cryptadid">https://t.me/Cryptadid</a>
[url=https://www.deviantart.com/emma3535/about]https://www.deviantart.com/emma3535/about[/url]
<a href="http://www.bestqp.com/user/Wyatt">http://www.bestqp.com/user/Wyatt</a>
[url=https://www.tripadvisor.com/Profile/danieldB9952FJ]https://www.tripadvisor.com/Profile/danieldB9952FJ[/url]
<a href="https://pikabu.ru/@CalmJack">https://pikabu.ru/@CalmJack</a>
[url=http://www.servinord.com/phpBB2/profile.php?mode=viewprofile&u=506884]http://www.servinord.com/phpBB2/profile.php?mode=viewprofile&u=506884[/url]
<a href="https://www.bitsdujour.com/profiles/phaEka">https://www.bitsdujour.com/profiles/phaEka</a>
[url=https://www.designspiration.com/aubrey6/saves/]https://www.designspiration.com/aubrey6/saves/[/url]
<a href="https://www.chordie.com/forum/profile.php?id=1643301">https://www.chordie.com/forum/profile.php?id=1643301</a>
[url=https://dzone.com/users/4928454/andrew37.html]https://dzone.com/users/4928454/andrew37.html[/url]
<a href="https://www.mixcloud.com/RichardBranson111/">https://www.mixcloud.com/RichardBranson111/</a>
[url=https://8tracks.com/matthew37]https://8tracks.com/matthew37[/url]
<a href="https://cart-help.com/user/11398-anthony37/">https://cart-help.com/user/11398-anthony37/</a>
[url=https://mossetka24.ru/mosquito/koshachiy-balkon/]антимоскитный балкон для кошек [/url]
<a href="https://mossetka24.ru/mosquito/dust/">заказать сетку антипыль на пластиковое окно </a>
[url=https://mossetka24.ru/mosquito/anticats/]москитная сетка антикошка на пластиковое окно [/url]
<a href="https://mossetka24.ru/mosquito/inners/">внутренние москитные сетки в Москве </a>
https://youtu.be/20VMcYWoWwU
This iconic track showcases Ermakova's unmatched vocal prowess and the ability to evoke raw emotions through his music. The lyrics of the song describe an overwhelming sense of happiness and gratitude for finding true love, which makes it universally relatable across cultures and generations.
[url=https://www.facebook.com/ermakovamusic.page]
ermakova[/url]
<a href="https://www.facebook.com/ermakovamusic.page">
overjoyed cover</a>
https://youtu.be/20VMcYWoWwU
This iconic track showcases Ermakova's unmatched vocal prowess and the ability to evoke raw emotions through his music. The lyrics of the song describe an overwhelming sense of happiness and gratitude for finding true love, which makes it universally relatable across cultures and generations.
[url=https://www.facebook.com/ermakovamusic.page]
better words for overjoyed[/url]
<a href="https://www.facebook.com/ermakovamusic.page">overjoyed</a>
ASAP Marketplace user experiences[/url]
<a href="https://magalysolier.com/">
ASAP Marketplace vendor ratings</a>
https://magalysolier.com/
ASAP Marketplace customer support and assistance[/url]
<a href="https://magalysolier.com/">
Buy drugs on ASAP Marketplace</a>
https://magalysolier.com/
Заходите по этой ссылке - и веселитесь со всей семьей!
<a href="https://android-modi-ru.netlify.app/casual/1677-skachat-moy-govoryaschiy-tom-vzlom-razblokirovano-vse-versiya-6701242-na-android.html">Скачать Говорящий Кот Том Взлом на Андроид</a>
Самые новые игры имеют набор более разнообразных действий и используют прогрессивную графику. Так, вы будете ухаживать, вовремя использовать еду и поднимать настроение для ваших новых питомцев. Издатели не тратят время зря и постоянно выпускают обновления для приложений. Эти веселые приложения на Андроид разработанны для того, чтобы радовать своих игроков и поднимать настроение.
Наша команда постарались найти самые новые говорящие игры, которые были выпущены на данный момент. Сборник нашего сайта будет регулярно дополняться. Все, что вам нужно сделать - выбрать понравившуюся вам игру и нажать на кнопку установить. Все ваши говорящие питомцы с удовольствием повторят за вами ваши предложения и будут выполнять смешные действия. В некоторых приложениях введены оригинальные функции. Не забывайте заходить чаще в игру, чтобы увеличить свои очки.
Скачать проверенные игрушки для Android телефон
[url=https://t.me/quantummedicinehealy/53][b]View More[/url]
------
<a href="https://rajabets-in-india.com/mobile-app/">raja bets apk</a>
------
https://avenue17.ru/
Недолго думая, специалист доехал и устранил неисправность. Починить её ему понадобилось тридцать минут. Так, моя кофемашина вновь заработала, как из магазина.
Недолго думая, мастер приехал и устранил проблему. Починить её ему понадобилось пару десятков минут. Так, моя кофемашина ожила, как новая.
Недолго думая, мастер приехал и устранил неисправность. Вернуть работоспособность её ему стоило лишь пару десятков минут. Так, моя кофемашина вновь заработала, как новая.
http://treeads.nation2.com/
https://jumperads.yolasite.com/
http://jumperads.nation2.com/
http://transferefurniture.hatenablog.com
https://atar-almadinah.weebly.com/
https://allmoversinriyadh.wordpress.com/
https://allmoversinriyadh.wordpress.com/2022/04/09/%d8%b4%d8%b1%d9%83%d8%a9-%d8%aa%d9%86%d8%b8%d9%8a%d9%81-%d8%a8%d8%a7%d9%84%d8%b1%d9%8a%d8%a7%d8%b6-%d9%85%d8%ac%d8%b1%d8%a8%d8%a9/
https://allmoversinriyadh.wordpress.com/2022/04/07/%d8%a7%d9%81%d8%b6%d9%84-%d8%b4%d8%b1%d9%83%d8%a9-%d8%aa%d9%86%d8%b8%d9%8a%d9%81-%d8%a8%d8%a7%d9%84%d8%b1%d9%8a%d8%a7%d8%b6/
https://allmoversinriyadh.wordpress.com/2022/05/13/%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d9%88%d8%ba%d8%b1%d9%81-%d8%a7%d9%84%d9%86%d9%88%d9%85-%d8%a8%d8%a7%d9%84%d8%b1%d9%8a%d8%a7%d8%b6/
https://companymoversinjeddah.wordpress.com/
https://moversfurniture2018.wordpress.com/2018/12/30/%D8%A7%D9%87%D9%85-%D9%85%D9%83%D8%A7%D8%AA%D8%A8-%D9%88%D9%85%D8%A4%D8%B3%D8%B3%D8%A7%D8%AA-%D8%B4%D8%B1%D9%83%D8%A7%D8%AA-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%AC%D8%A7%D8%B2%D8%A7%D9%86/
https://moversriyadhcom.wordpress.com/
https://moversmedina.wordpress.com/
https://moversfurniture2018.wordpress.com/
https://moversmecca.wordpress.com/
https://khairyayman74.wordpress.com/
https://companymoversmecca.home.blog/
https://companymoverstaif.home.blog/
https://companymoverskhamismushit.home.blog/
https://whitear.home.blog/
https://companyhouseservice.wordpress.com/
http://bestmoversfurniture.wordpress.com/
https://companymoversjeddah.wordpress.com/
https://companycleaning307819260.wordpress.com/
https://companymoversriydah.wordpress.com/
https://ataralmadinah662300791.wordpress.com/
https://ataralmadinah662300791.wordpress.com/2022/02/05/%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%a7%d9%84%d8%b1%d9%8a%d8%a7%d8%b6/
https://ataralmadinah662300791.wordpress.com/2022/04/12/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D9%85%D9%86-%D8%A7%D9%84%D8%B1%D9%8A%D8%A7%D8%B6-%D8%A7%D9%84%D9%89-%D8%A7%D9%84%D8%AF%D9%85%D8%A7%D9%85/
https://groups.google.com/g/moversfurniture/c/wwQFSNvgyAI
https://groups.google.com/g/moversfurniture/c/4L1oHETS4mQ
https://nowewyrazy.uw.edu.pl/profil/khairyayman
https://companyhouseservice.wordpress.com/2022/08/06/%d8%a7%d9%81%d8%b6%d9%84-%d8%b4%d8%b1%d9%83%d8%a9-%d8%aa%d9%86%d8%b8%d9%8a%d9%81-%d8%a8%d8%a7%d9%84%d8%b1%d9%8a%d8%a7%d8%b6/
<a href="https://companymoversinjeddah.wordpress.com/">شركات نقل عفش واثاث بجدة</a>
<a href="https://companymoversinjeddah.wordpress.com/2019/02/16/%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d9%88%d8%a7%d8%ab%d8%a7%d8%ab-%d8%a8%d8%a7%d9%84%d8%b7%d8%a7%d8%a6%d9%81-%d8%af%d9%8a%d9%86%d8%a7-%d8%af%d8%a8%d8%a7%d8%a8-%d9%86/">شركات نقل عفش بالطائف</a>
<a href="https://companymoversinjeddah.wordpress.com/2019/02/15/%d8%a7%d8%b3%d8%b9%d8%a7%d8%b1-%d9%88%d8%a7%d8%b1%d9%82%d8%a7%d9%85-%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d9%86%d9%82%d9%84-%d8%a7%d9%84%d8%b9%d9%81%d8%b4-%d8%a8%d8%a7%d9%84%d9%85%d8%af%d9%8a%d9%86%d8%a9/">اسعار وارقام شركات نقل العفش بالمدينة المنورة</a>
<a href="https://companymoversinjeddah.wordpress.com/2019/02/15/%d8%af%d9%8a%d9%86%d8%a7-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%ac%d8%af%d8%a9-%d8%a7%d9%81%d8%b6%d9%84-%d8%af%d9%8a%d9%86%d8%a7/">دينا نقل عفش جدة ,افضل دينا</a>
<a href="https://companymoversinjeddah.wordpress.com/2019/02/15/%d8%a7%d8%b1%d8%ae%d8%b5-%d8%b4%d8%b1%d9%83%d9%87-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%ac%d8%af%d9%87-%d8%a7%d8%b3%d8%b9%d8%a7%d8%b1-%d9%81%d8%b5%d9%84-%d8%a7%d9%84%d8%b4%d8%aa%d8%a7%d8%a1/">ارخص شركه نقل عفش بجده</a>
<a href="https://companymoversinjeddah.wordpress.com/2019/02/15/%d8%af%d9%84%d9%8a%d9%84-%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d9%86%d9%82%d9%84-%d8%a7%d9%84%d8%b9%d9%81%d8%b4-%d8%a8%d8%ac%d8%af%d8%a9-%d9%85%d8%b9-%d8%ae%d8%b5%d9%88%d9%85%d8%a7%d8%aa/">دليل شركات نقل العفش بجدة</a>
<a href="https://companymoversinjeddah.wordpress.com/2019/02/15/%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%b1%d8%a7%d8%a8%d8%ba-15-%d8%b9%d8%a7%d9%85-%d8%ae%d8%a8%d8%b1%d8%a9/">شركة نقل عفش برابغ ,15 عام خبرة</a>
<a href="https://companymoversinjeddah.wordpress.com/2018/12/12/%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d9%88%d8%a7%d8%ab%d8%a7%d8%ab-%d8%a8%d8%a7%d9%84%d8%a8%d8%a7%d8%ad%d9%87/">شركات نقل عفش واثاث بالباحه</a>
<a href="https://companymoversinjeddah.wordpress.com/2018/12/12/start-moving-company-to-khamis-mushit/">وسائل نقل العفش بخميس مشيط</a>
https://ataralmadinah662300791.wordpress.com/ شركة الصقر الدولي لنقل العفش والاثاث وخدمات التنظيف المنزلية
https://jumperads.com/yanbu/anti-insects-company-yanbu.html شركة مكافحة حشرات بينبع
httsp://jumperads.com/yanbu/water-leaks-detection-company-yanbu.html شركة كشف تسربات بينبع
https://jumperads.com/yanbu/yanbu-company-surfaces.html شركة عزل اسطح بينبع
https://jumperads.com/yanbu/yanbu-company-sewage.html شركة تسليك مجاري بينبع
https://jumperads.com/yanbu/yanbu-cleaning-company-sofa.html شركة تنظيف كنب بينبع
https://jumperads.com/yanbu/yanbu-cleaning-company-mosques.html شركة تنظيف مساجد بينبع
https://jumperads.com/yanbu/yanbu-cleaning-company-Carpet.html شركة تنظيف سجاد بينبع
https://jumperads.com/yanbu/yanbu-cleaning-company-tanks.html شركة تنظيف خزانات بينبع
https://jumperads.com/yanbu/yanbu-cleaning-company-swimming-bath.html شركة تنظيف وصيانة مسابح بينبع
https://jumperads.com/yanbu/yanbu-cleaning-company-Furniture.html شركة تنظيف الاثاث بينبع
https://jumperads.com/yanbu/yanbu-cleaning-company-home.html شركة تنظيف شقق بينبع
https://jumperads.com/yanbu/yanbu-cleaning-company-Carpets.html شركة تنظيف موكيت بينبع
https://jumperads.com/yanbu/yanbu-cleaning-company.html شركة تنظيف مجالس بينبع
https://jumperads.com/yanbu/yanbu-cleaning-company-house.html شركة تنظيف منازل بينبع
https://jumperads.com/yanbu/yanbu-cleaning-company-Villas.html شركة تنظيف فلل بينبع
https://jumperads.com/yanbu/yanbu-cleaning-company-curtains.html شركة تنظيف ستائر بينبع
https://jumperads.com/yanbu/yanbu-company-tile.html شركة جلي بلاط بينبع
شركة مكافحة حشرات بالجبيل وكذلك شركة كشف تسربات المياه بالجبيل وتنظيف خزانات وتنظيف الموكيت والسجاد والكنب والشقق والمنازل بالجبيل وتنظيف الخزانات بالجبيل وتنظيف المساجد بالجبيل شركة تنظيف بالجبيل تنظيف المسابح بالجبيل
https://jumperads.com/jubail/anti-insects-company-jubail.html شركة مكافحة حشرات بالجبيل
https://jumperads.com/jubail/water-leaks-detection-company-jubail.html شركة كشف تسربات بالجبيل
https://jumperads.com/jubail/jubail-company-surfaces.html شركة عزل اسطح بالجبيل
https://jumperads.com/jubail/jubail-company-sewage.html شركة تسليك مجاري بالجبيل
https://jumperads.com/jubail/jubail-cleaning-company-sofa.html شركة تنظيف كنب بالجبيل
https://jumperads.com/jubail/jubail-cleaning-company-mosques.html شركة تنظيف مساجد بالجبيل
https://jumperads.com/jubail/jubail-cleaning-company-Carpet.html شركة تنظيف سجاد بالجبيل
https://jumperads.com/jubail/jubail-cleaning-company-tanks.html شركة تنظيف خزانات بالجبيل
https://jumperads.com/jubail/jubail-cleaning-company-swimming-bath.html شركة تنظيف وصيانة مسابح بالجبيل
https://jumperads.com/jubail/jubail-cleaning-company-Furniture.html شركة تنظيف الاثاث بالجبيل
https://jumperads.com/jubail/jubail-cleaning-company-home.html شركة تنظيف شقق بالجبيل
https://jumperads.com/jubail/jubail-cleaning-company-Carpets.html شركة تنظيف موكيت بالجبيل
https://jumperads.com/jubail/jubail-cleaning-company.html شركة تنظيف مجالس بالجبيل
https://jumperads.com/jubail/jubail-cleaning-company-house.html شركة تنظيف منازل بالجبيل
https://jumperads.com/jubail/jubail-cleaning-company-curtains.html شركة تنظيف ستائر بالجبيل
https://jumperads.com/jubail/jubail-cleaning-company-Villas.html شركة تنظيف فلل بالجبيل
https://jumperads.com/jubail/jubail-company-tile.html شركة جلي بلاط بالجبيل
اهم شركات كشف تسربات المياه بالدمام كذلك معرض اهم شركة مكافحة حشرات بالدمام والخبر والجبيل والخبر والاحساء والقطيف كذكل شركة تنظيف خزانات بجدة وتنظيف بجدة ومكافحة الحشرات بالخبر وكشف تسربات المياه بالجبيل والقطيف والخبر والدمام
https://emc-mee.com/cleaning-company-yanbu.html شركة تنظيف بينبع
https://emc-mee.com/blog.html شركة نقل عفش
اهم شركات مكافحة حشرات بالخبر كذلك معرض اهم شركة مكافحة حشرات بالدمام والخبر والجبيل والخبر والاحساء والقطيف كذلك شركة رش حشرات بالدمام ومكافحة الحشرات بالخبر
https://emc-mee.com/anti-insects-company-dammam.html شركة مكافحة حشرات بالدمام
شركة تنظيف خزانات بجدة الجوهرة من افضل شركات تنظيف الخزانات بجدة حيث ان تنظيف خزانات بجدة يحتاج الى مهارة فى كيفية غسيل وتنظيف الخزانات الكبيرة والصغيرة بجدة على ايدى متخصصين فى تنظيف الخزانات بجدة
https://emc-mee.com/tanks-cleaning-company-jeddah.html شركة تنظيف خزانات بجدة
https://emc-mee.com/water-leaks-detection-isolate-company-dammam.html شركة كشف تسربات المياه بالدمام
https://emc-mee.com/ شركة الفا لنقل عفش واثاث
https://emc-mee.com/transfer-furniture-jeddah.html شركة نقل عفش بجدة
https://emc-mee.com/transfer-furniture-almadina-almonawara.html شركة نقل عفش بالمدينة المنورة
https://emc-mee.com/movers-in-riyadh-company.html شركة نقل اثاث بالرياض
https://emc-mee.com/transfer-furniture-dammam.html شركة نقل عفش بالدمام
https://emc-mee.com/transfer-furniture-taif.html شركة نقل عفش بالطائف
https://emc-mee.com/transfer-furniture-mecca.html شركة نقل عفش بمكة
https://emc-mee.com/transfer-furniture-yanbu.html شركة نقل عفش بينبع
https://emc-mee.com/transfer-furniture-alkharj.html شركة نقل عفش بالخرج
https://emc-mee.com/transfer-furniture-buraydah.html شركة نقل عفش ببريدة
https://emc-mee.com/transfer-furniture-khamis-mushait.html شركة نقل عفش بخميس مشيط
https://emc-mee.com/transfer-furniture-qassim.html شركة نقل عفش بالقصيم
https://emc-mee.com/transfer-furniture-tabuk.html شركة نقل عفش بتبوك
https://emc-mee.com/transfer-furniture-abha.html شركة نقل عفش بابها
https://emc-mee.com/transfer-furniture-najran.html شركة نقل عفش بنجران
https://emc-mee.com/transfer-furniture-hail.html شركة نقل عفش بحائل
https://emc-mee.com/transfer-furniture-dhahran.html شركة نقل عفش بالظهران
https://emc-mee.com/transfer-furniture-kuwait.html شركة نقل عفش بالكويت
https://emc-mee.com/price-transfer-furniture-in-khamis-mushit.html اسعار شركات نقل عفش بخميس مشيط
https://emc-mee.com/numbers-company-transfer-furniture-in-khamis-mushit.html ارقام شركات نقل عفش بخميس مشيط
https://emc-mee.com/new-company-transfer-furniture-in-khamis-mushit.html شركة نقل عفش بخميس مشيط جديدة
https://emc-mee.com/transfer-furniture-from-khamis-to-riyadh.html شركة نقل عفش من خميس مشيط الي الرياض
https://emc-mee.com/transfer-furniture-from-khamis-mushait-to-mecca.html شركة نقل عفش من خميس مشيط الي مكة
https://emc-mee.com/transfer-furniture-from-khamis-mushait-to-jeddah.html شركة نقل عفش من خميس مشيط الي جدة
https://emc-mee.com/transfer-furniture-from-khamis-mushait-to-medina.html شركة نقل عفش من خميس مشيط الي المدينة المنورة
https://emc-mee.com/best-10-company-transfer-furniture-khamis-mushait.html افضل 10 شركات نقل عفش بخميس مشيط
https://emc-mee.com/%D8%B4%D8%B1%D9%83%D9%87-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%AC%D8%AF%D9%87.html
https://emc-mee.com/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%A7%D8%AB%D8%A7%D8%AB-%D8%A8%D8%AC%D8%AF%D9%87.html
https://saudi-germany.com/%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d8%aa%d9%86%d8%b8%d9%8a%d9%81-%d8%ae%d8%b2%d8%a7%d9%86%d8%a7%d8%aa-%d8%a8%d8%ac%d8%af%d8%a9/ شركات تنظيف خزانات بجدة
https://saudi-germany.com/%d8%aa%d9%86%d8%b8%d9%8a%d9%81-%d8%ae%d8%b2%d8%a7%d9%86%d8%a7%d8%aa-%d8%a8%d8%ac%d8%af%d8%a9/ تنظيف خزانات بجدة
https://saudi-germany.com/%d8%a7%d9%81%d8%b6%d9%84-%d8%b4%d8%b1%d9%83%d8%a9-%d8%aa%d9%86%d8%b8%d9%8a%d9%81-%d8%ae%d8%b2%d8%a7%d9%86%d8%a7%d8%aa-%d8%a8%d8%ac%d8%af%d8%a9/ افضل شركة تنظيف خزانات بجدة
https://saudi-germany.com/%d8%a7%d8%b1%d8%ae%d8%b5-%d8%b4%d8%b1%d9%83%d8%a9-%d8%aa%d9%86%d8%b8%d9%8a%d9%81-%d8%ae%d8%b2%d8%a7%d9%86%d8%a7%d8%aa-%d8%a8%d8%ac%d8%af%d8%a9/ ارخص شركة تنظيف خزانات بجدة
https://saudi-germany.com/%d8%ba%d8%b3%d9%8a%d9%84-%d8%ae%d8%b2%d8%a7%d9%86%d8%a7%d8%aa-%d8%a8%d8%ac%d8%af%d8%a9/ غسيل خزانات بجدة
https://saudi-germany.com/%d8%b4%d8%b1%d9%83%d8%a9-%d8%aa%d9%86%d8%b8%d9%8a%d9%81-%d8%ae%d8%b2%d8%a7%d9%86%d8%a7%d8%aa-%d8%a8%d8%ac%d8%af%d8%a9/ شركة تنظيف خزانات بجدة
https://saudi-germany.com/cleaning-tanks-company-taif/
https://saudi-germany.com/cleaning-tanks-company-mecca/
https://saudi-germany.com/jumperads-transfer-furniture/
https://saudi-germany.com/%d8%a7%d9%81%d8%b6%d9%84-20-%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d9%8a%d9%86%d8%a8%d8%b9-%d8%ae%d8%b5%d9%85-50-%d9%85%d8%b9-%d8%a7%d9%84%d9%81%d9%83-%d9%88%d8%a7/
https://saudi-germany.com/%d8%a7%d8%b1%d8%ae%d8%b5-%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%ac%d8%af%d8%a9-%d8%ad%d9%8a-%d8%a7%d9%84%d8%b5%d9%81%d8%a7/
https://saudi-germany.com/%d8%a7%d8%b1%d8%ae%d8%b5-%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%ac%d8%af%d8%a9-%d8%a7%d8%a8%d8%ad%d8%b1-%d8%a7%d9%84%d8%b4%d9%85%d8%a7%d9%84%d9%8a%d8%a9/
https://saudi-germany.com/%d8%a7%d8%b1%d9%82%d8%a7%d9%85-%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%ac%d8%af%d8%a9-%d9%85%d8%b9-%d8%a7%d9%84%d8%aa%d8%ba%d9%84%d9%8a%d9%81/
https://saudi-germany.com/%d8%a7%d8%b1%d8%ae%d8%b5-%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%ac%d8%af%d8%a9/
https://www.crtmovers.com/2020/10/transfer-furniture-taif.html شركة نقل اثاث بالطائف
https://www.crtmovers.com/2020/10/transfer-furniture-madina.html
https://www.crtmovers.com/2020/10/movers-madina.html
https://www.crtmovers.com/2020/10/transfer-furniture-riyadh.html
https://www.crtmovers.com/2020/07/transfer-furniture-riyadh.html
https://www.crtmovers.com/2020/05/mecca-transfer-furniture-company-2020.html
https://www.crtmovers.com/2020/05/riyadh-transfer-furniture-company.html
https://www.crtmovers.com/2019/12/jeddah-transfer-furniture.html
https://www.crtmovers.com/2019/12/transfer-furniture-company-jeddah.html
https://www.crtmovers.com/2019/12/transfer-furniture-jeddah-1.html
https://www.crtmovers.com/2019/12/transfer-furniture-taif-1.html
https://www.crtmovers.com/2019/12/transfer-furniture-taif.html
https://www.crtmovers.com/2019/12/price-company-cleaning-tanks-jeddah.html
https://www.crtmovers.com/2019/12/blog-post.html
https://www.crtmovers.com/2019/12/cleaning-tanks-jeddah.html
https://www.crtmovers.com/2023/01/%d8%a7%d9%81%d8%b6%d9%84-%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%ac%d8%af%d8%a9.html
https://treeads.net/ شركة سكاي نقل العفش
https://treeads.net/blog.html مدونة لنقل العفش
https://treeads.net/movers-mecca.html شركة نقل عفش بمكة
https://treeads.net/movers-riyadh-company.html شركة نقل عفش بالرياض
https://treeads.net/all-movers-madina.html شركة نقل عفش بالمدينة المنورة
https://treeads.net/movers-jeddah-company.html شركة نقل عفش بجدة
https://treeads.net/movers-taif.html شركة نقل عفش بالطائف
https://treeads.net/movers-dammam-company.html شركة نقل عفش بالدمام
https://treeads.net/movers-qatif.html شركة نقل عفش بالقطيف
https://treeads.net/movers-jubail.html شركة نقل عفش بالجبيل
https://treeads.net/movers-khobar.html شركة نقل عفش بالخبر
https://treeads.net/movers-ahsa.html شركة نقل عفش بالاحساء
https://treeads.net/movers-kharj.html شركة نقل عفش بالخرج
https://treeads.net/movers-khamis-mushait.html شركة نقل عفش بخميس مشيط
https://treeads.net/movers-abha.html شركة نقل عفش بابها
https://treeads.net/movers-qassim.html شركة نقل عفش بالقصيم
https://treeads.net/movers-yanbu.html شركة نقل عفش بينبع
https://treeads.net/movers-najran.html شركة نقل عفش بنجران
https://treeads.net/movers-hail.html شركة نقل عفش بحائل
https://treeads.net/movers-buraydah.html شركة نقل عفش ببريدة
https://treeads.net/movers-tabuk.html شركة نقل عفش بتبوك
https://treeads.net/movers-dhahran.html شركة نقل عفش بالظهران
https://treeads.net/movers-rabigh.html شركة نقل عفش برابغ
https://treeads.net/movers-baaha.html شركة نقل عفش بالباحه
https://treeads.net/movers-asseer.html شركة نقل عفش بعسير
https://treeads.net/movers-mgmaa.html شركة نقل عفش بالمجمعة
https://treeads.net/movers-sharora.html شركة نقل عفش بشرورة
https://treeads.net/how-movers-furniture-yanbu.html كيفية نقل العفش بينبع
https://treeads.net/price-movers-furniture-yanbu.html اسعار نقل عفش بينبع
https://treeads.net/find-company-transfer-furniture-yanbu.html البحث عن شركات نقل العفش بينبع
https://treeads.net/transfer-furniture-khamis-mushit.html شركات نقل العفش بخميس مشيط
https://treeads.net/how-transfer-furniture-khamis-mushit.html كيفية نقل العفش بخميس مشيط
https://treeads.net/price-transfer-furniture-khamis-mushit.html اسعار نقل عفش بخميس مشيط
https://treeads.net/%D8%B4%D8%B1%D9%83%D8%A9-%D8%AC%D9%84%D9%8A-%D8%A8%D9%84%D8%A7%D8%B7-%D8%A8%D8%AC%D8%AF%D8%A9.html شركة جلي بلاط بجدة
https://treeads.net/%D8%B4%D8%B1%D9%83%D8%A9-%D8%AA%D9%86%D8%B8%D9%8A%D9%81-%D9%81%D9%84%D9%84-%D8%A8%D8%AC%D8%AF%D8%A9.html تنظيف فلل بجدة
https://treeads.net/company-transfer-furniture-jazan.html شركة نقل عفش بجازان
https://treeads.net/best-company-cleaning-jeddah-2020.html افضل شركة تنظيف بجدة
http://www.domyate.com/2019/09/05/movers-company-khamis-mushait/ شركات نقل عفش بخميس مشيط
http://www.domyate.com/2019/09/05/10-company-transfer-furniture-khamis-mushait/ شركة نقل العفش بخميس مشيط
http://www.domyate.com/2019/09/05/all-transfer-furniture-khamis-mushait/ شركات نقل اثاث بخميس مشيط
http://www.domyate.com/2019/09/05/best-company-transfer-furniture-khamis-mushit/ افضل شركات نقل اثاث بخميس مشيط
http://www.domyate.com/2019/09/05/company-transfer-furniture-khamis-mushit/ شركات نقل اثاث بخميس مشيط
http://www.domyate.com/category/%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%AC%D8%AF%D8%A9/ نقل عفش جدة
http://www.domyate.com/2019/09/25/movers-furniture-from-jeddah-to-jordan/ نقل عفش من جدة الي الاردن
http://www.domyate.com/2019/10/03/price-cleaning-tanks-in-jeddah/ اسعار شركات تنظيف خزانات بجدة
http://www.domyate.com/2019/09/25/movers-furniture-from-jeddah-to-egypt/ نقل عفش من جدة الي مصر
http://www.domyate.com/2019/09/24/movers-furniture-from-jeddah-to-lebanon/ نقل عفش من جدة الي لبنان
http://www.domyate.com/2019/09/22/%d8%a3%d9%86%d8%ac%d8%ad-%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d9%86%d9%82%d9%84-%d8%a7%d8%ab%d8%a7%d8%ab-%d8%a8%d8%ac%d8%af%d8%a9/ شركات نقل اثاث بجدة
http://www.domyate.com/2019/09/22/best-company-movers-jeddah/ افضل شركات نقل اثاث جدة
http://www.domyate.com/2019/09/22/company-transfer-furniture-yanbu/ شركات نقل العفش بينبع
http://www.domyate.com/2019/09/21/taif-transfer-furniture-company/ شركة نقل عفش في الطائف
http://www.domyate.com/2019/09/21/%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d9%86%d9%82%d9%84-%d8%a7%d9%84%d8%b9%d9%81%d8%b4/ شركات نقل العفش
http://www.domyate.com/2019/09/21/%d8%b7%d8%b1%d9%82-%d9%86%d9%82%d9%84-%d8%a7%d9%84%d8%b9%d9%81%d8%b4/ طرق نقل العفش
http://www.domyate.com/2019/09/20/%d8%ae%d8%b7%d9%88%d8%a7%d8%aa-%d9%86%d9%82%d9%84-%d8%a7%d9%84%d8%b9%d9%81%d8%b4-%d9%88%d8%a7%d9%84%d8%a7%d8%ab%d8%a7%d8%ab/ خطوات نقل العفش والاثاث
http://www.domyate.com/2019/09/20/best-10-company-transfer-furniture/ افضل 10 شركات نقل عفش
http://www.domyate.com/2019/09/20/%d9%83%d9%8a%d9%81-%d9%8a%d8%aa%d9%85-%d8%a7%d8%ae%d8%aa%d9%8a%d8%a7%d8%b1-%d8%b4%d8%b1%d9%83%d8%a7%d8%aa-%d9%86%d9%82%d9%84-%d8%a7%d9%84%d8%b9%d9%81%d8%b4-%d9%88%d8%a7%d9%84%d8%a7%d8%ab%d8%a7%d8%ab/ اختيار شركات نقل العفش والاثاث
http://www.domyate.com/2019/09/20/cleaning-company-house-taif/ شركة تنظيف منازل بالطائف
http://www.domyate.com/2019/09/20/company-cleaning-home-in-taif/ شركة تنظيف شقق بالطائف
http://www.domyate.com/2019/09/20/taif-cleaning-company-villas/ شركة تنظيف فلل بالطائف
http://www.domyate.com/ شركة نقل عفش
http://www.domyate.com/2017/09/21/%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%B9%D9%81%D8%B4-%D9%88%D8%A7%D9%84%D8%AA%D8%AE%D8%B2%D9%8A%D9%86/ نقل العفش والتخزين
http://www.domyate.com/2016/07/02/transfer-furniture-dammam شركة نقل عفش بالدمام
http://www.domyate.com/2015/11/12/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%A7%D9%84%D9%85%D8%AF%D9%8A%D9%86%D8%A9-%D8%A7%D9%84%D9%85%D9%86%D9%88%D8%B1%D8%A9/ شركة نقل عفش بالمدينة المنورة
http://www.domyate.com/2016/06/05/transfer-furniture-jeddah/ شركة نقل عفش بجدة
http://www.domyate.com/2017/08/10/movers-company-mecca-naql/ شركات نقل العفش بمكة
http://www.domyate.com/2016/06/05/transfer-furniture-mecca/ شركة نقل عفش بمكة
http://www.domyate.com/2016/06/05/transfer-furniture-taif/ شركة نقل عفش بالطائف
http://www.domyate.com/2016/06/05/transfer-furniture-riyadh/ شركة نقل عفش بالرياض
http://www.domyate.com/2016/06/05/transfer-furniture-yanbu/ شركة نقل عفش بينبع
http://www.domyate.com/category/%D8%AE%D8%AF%D9%85%D8%A7%D8%AA-%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%B9%D9%81%D8%B4-%D9%88%D8%A7%D9%84%D8%AA%D8%AE%D8%B2%D9%8A%D9%86/ نقل العفش والتخزين
http://www.domyate.com/2015/08/30/furniture-transport-company-in-almadinah/ شركة نقل عفش بالمدينة المنورة
http://www.domyate.com/2016/06/05/transfer-furniture-medina-almonawara/ شركة نقل عفش بالمدينة المنورة
http://www.domyate.com/2018/10/13/%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%AC%D8%AF%D8%A9-%D8%B4%D8%B1%D9%83%D8%A7%D8%AA-%D9%86%D9%82%D9%84-%D9%85%D9%85%D9%8A%D8%B2%D8%A9/ نقل عفش بجدة
http://www.domyate.com/2016/07/22/%d8%a7%d8%b1%d8%ae%d8%b5-%d8%b4%d8%b1%d9%83%d8%a9-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%a7%d9%84%d9%85%d8%af%d9%8a%d9%86%d8%a9-%d8%a7%d9%84%d9%85%d9%86%d9%88%d8%b1%d8%a9/ ارخص شركة نقل عفش بالمدينة المنورة
http://www.domyate.com/2016/07/25/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%A7%D9%84%D9%82%D8%B5%D9%8A%D9%85/ شركة نقل عفش بالقصيم
http://www.domyate.com/2016/07/25/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%AE%D9%85%D9%8A%D8%B3-%D9%85%D8%B4%D9%8A%D8%B7/ شركة نقل عفش بخميس مشيط
http://www.domyate.com/2016/07/25/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%A7%D8%A8%D9%87%D8%A7/ شركة نقل عفش بابها
http://www.domyate.com/2016/07/23/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%AA%D8%A8%D9%88%D9%83/ شركة نقل عفش بتبوك
https://mycanadafitness.com/ شركة كيان لنقل العفش
https://mycanadafitness.com/forum.html منتدي نقل العفش
https://mycanadafitness.com/movingfurnitureriyadh.html شركة نقل اثاث بالرياض
https://mycanadafitness.com/movingfurniturejaddah.html شركة نقل اثاث بجدة
https://mycanadafitness.com/movingfurnituremecca.html شركة نقل اثاث بمكة
https://mycanadafitness.com/movingfurnituretaif.html شركة نقل اثاث بالطائف
https://mycanadafitness.com/movingfurnituremadina.html شركة نقل اثاث بالمدينة المنورة
https://mycanadafitness.com/movingfurnituredammam.html شركة نقل اثاث بالدمام
https://mycanadafitness.com/movingfurniturekhobar.html شركة نقل اثاث بالخبر
https://mycanadafitness.com/movingfurnituredhahran.html شركة نقل اثاث بالظهران
https://mycanadafitness.com/movingfurniturejubail.html شركة نقل اثاث بالجبيل
https://mycanadafitness.com/movingfurnitureqatif.html شركة نقل اثاث بالقطيف
https://mycanadafitness.com/movingfurnitureahsa.html شركة نقل اثاث بالاحساء
https://mycanadafitness.com/movingfurniturekharj.html شركة نقل اثاث بالخرج
https://mycanadafitness.com/movingfurniturekhamismushit.html شركة نقل اثاث بخميس مشيط
https://mycanadafitness.com/movingfurnitureabha.html شركة نقل اثاث بابها
https://mycanadafitness.com/movingfurniturenajran.html شركة نقل اثاث بنجران
https://mycanadafitness.com/movingfurniturejazan.html شركة نقل اثاث بجازان
https://mycanadafitness.com/movingfurnitureasir.html شركة نقل اثاث بعسير
https://mycanadafitness.com/movingfurniturehail.html شركة نقل اثاث بحائل
https://mycanadafitness.com/movingfurnitureqassim.html شركة نقل عفش بالقصيم
https://mycanadafitness.com/movingfurnitureyanbu.html شركة نقل اثاث بينبع
https://mycanadafitness.com/movingfurnitureburaidah.html شركة نقل عفش ببريدة
https://mycanadafitness.com/movingfurniturehafralbatin.html شركة نقل عفش بحفر الباطن
https://mycanadafitness.com/movingfurniturerabigh.html شركة نقل عفش برابغ
https://mycanadafitness.com/movingfurnituretabuk.html شركة نقل عفش بتبوك
https://mycanadafitness.com/movingfurnitureasfan.html شركة نقل عفش بعسفان
https://mycanadafitness.com/movingfurnituresharora.html شركة نقل عفش بشرورة
https://mycanadafitness.com/companis-moving-riyadh.html شركات نقل العفش بالرياض
https://mycanadafitness.com/cars-moving-riyadh.html سيارات نقل العفش بالرياض
https://mycanadafitness.com/company-number-moving-riyadh.html ارقام شركات نقل العفش بالرياض
https://mycanadafitness.com/company-moving-jeddah.html شركات نقل العفش بجدة
https://mycanadafitness.com/price-moving-jeddah.html اسعار نقل العفش بجدة
https://mycanadafitness.com/company-moving-mecca.html شركات نقل العفش بمكة
http://fullservicelavoro.com/2019/01/07/transfer-movers-taif-furniture/ شركة نقل عفش بالطائف
http://fullservicelavoro.com/2019/01/08/transfer-movers-riyadh-furniture/ شركة نقل عفش بالرياض
http://fullservicelavoro.com/2019/01/08/transfer-movers-jeddah-furniture/ شركة نقل عفش بجدة
http://fullservicelavoro.com/2019/01/01/transfer-and-movers-furniture-mecca/ شركة نقل عفش بمكة
http://fullservicelavoro.com/2019/01/07/transfer-movers-madina-furniture/ شركة نقل عفش بالمدينة المنورة
http://fullservicelavoro.com/2019/01/07/transfer-movers-khamis-mushait-furniture/ شركة نقل عفش بخميس مشيط
http://fullservicelavoro.com/2019/01/09/transfer-movers-abha-furniture/ شركة نقل اثاث بابها
http://fullservicelavoro.com/2019/01/07/transfer-movers-najran-furniture/ شركة نقل عفش بنجران
http://fullservicelavoro.com/2019/01/16/transfer-movers-hail-furniture/ ِشركة نقل عفش بحائل
http://fullservicelavoro.com/2019/01/16/transfer-movers-qassim-furniture/ شركة نقل عفش بالقصيم
http://fullservicelavoro.com/2019/02/02/transfer-movers-furniture-in-bahaa/ شركة نقل عفش بالباحة
http://fullservicelavoro.com/2019/01/13/transfer-movers-yanbu-furniture/ شركة نقل عفش بينبع
http://fullservicelavoro.com/2019/01/18/%d8%af%d9%8a%d9%86%d8%a7-%d9%86%d9%82%d9%84-%d8%b9%d9%81%d8%b4-%d8%a8%d8%a7%d8%a8%d9%87%d8%a7/ دينا نقل عفش بابها
http://fullservicelavoro.com/2019/01/13/%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%A7%D8%AB%D8%A7%D8%AB-%D8%A8%D8%A7%D9%84%D9%85%D8%AF%D9%8A%D9%86%D8%A9-%D8%A7%D9%84%D9%85%D9%86%D9%88%D8%B1%D8%A9-%D8%A7%D9%87%D9%85-%D8%B4%D8%B1%D9%83%D8%A7%D8%AA/ نقل الاثاث بالمدينة المنورة
http://fullservicelavoro.com/2019/01/12/%D8%A7%D8%B1%D8%AE%D8%B5-%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D9%85%D9%83%D8%A9/ ارخص شركة نقل عفش بمكة
http://fullservicelavoro.com/2019/01/07/transfer-movers-elkharj-furniture/ شركة نقل عفش بالخرج
http://fullservicelavoro.com/2019/01/07/transfer-movers-baqaa-furniture/ شركة نقل عفش بالبقعاء
http://fullservicelavoro.com/2019/02/05/transfer-furniture-in-jazan/ شركة نقل عفش بجازان
https://sites.google.com/view/movers-riyadh/movers-mecca
https://sites.google.com/view/movers-riyadh/home
https://sites.google.com/view/movers-riyadh/movers-jedaah-elhamdniah
https://sites.google.com/view/movers-riyadh/movers-yanbu
https://sites.google.com/view/movers-riyadh/movers-najran
https://sites.google.com/view/movers-riyadh/movers-Jizan
https://sites.google.com/view/movers-riyadh/jazan
https://sites.google.com/view/movers-riyadh/taif
https://sites.google.com/view/movers-riyadh/moversjeddah
https://sites.google.com/view/movers-riyadh/movers-abha
https://sites.google.com/view/movers-riyadh/movers-elahsa
https://sites.google.com/view/movers-riyadh/movers-elkhobar
https://sites.google.com/view/movers-riyadh/movers-elkharj
https://sites.google.com/view/movers-riyadh/movers-elmadina-elmnowara
https://sites.google.com/view/movers-riyadh/movers-eljubail
https://sites.google.com/view/movers-riyadh/movers-elqassim
https://sites.google.com/view/movers-riyadh/movers-hafrelbatin
https://sites.google.com/view/movers-riyadh/movers-elbaha
https://sites.google.com/view/movers-riyadh/movers-jeddah
https://sites.google.com/view/movers-riyadh/movers-dammam
https://sites.google.com/view/movers-riyadh/movers-taif
https://sites.google.com/view/movers-riyadh/movers-burydah
https://sites.google.com/view/movers-riyadh/movers-tabuk
https://sites.google.com/view/movers-riyadh/movers-hail
https://sites.google.com/view/movers-riyadh/movers-khamis-mushait
https://sites.google.com/view/movers-riyadh/movers-rabigh
https://sites.google.com/view/movers-riyadh/madina
https://sites.google.com/view/movers-riyadh/mecca
https://sites.google.com/view/movers-riyadh/dammam
https://sites.google.com/view/movers-riyadh/jeddah
https://sites.google.com/view/movers-riyadh/ahsa
https://sites.google.com/view/movers-riyadh/cleaning-mecca
https://www.snipesocial.co.uk/blogs/132566/%D8%B4%D8%B1%D9%83%D8%A9-%D8%AA%D9%86%D8%B8%D9%8A%D9%81-%D9%85%D9%86%D8%A7%D8%B2%D9%84-%D8%A8%D8%A7%D9%84%D8%AC%D8%A8%D9%8A%D9%84
https://justnock.com/read-blog/6707
https://addandclick.com/read-blog/99061
https://www.tadalive.com/blog/8862/%D8%B4%D8%B1%D9%83%D8%A9-%D8%AA%D9%86%D8%B8%D9%8A%D9%81-%D9%85%D9%86%D8%A7%D8%B2%D9%84-%D8%A8%D8%A7%D9%84%D8%AC%D8%A8%D9%8A%D9%84/
https://www.rolonet.com/blogs/128983/%D8%B4%D8%B1%D9%83%D8%A9-%D8%AA%D9%86%D8%B8%D9%8A%D9%81-%D8%A7%D9%84%D9%81%D9%84%D9%84-%D8%A8%D8%A7%D9%84%D8%AC%D8%A8%D9%8A%D9%84
https://community.tccwpg.com/read-blog/109523
https://www.rolonet.com/blogs/130618/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D9%81%D9%89-%D8%AC%D8%AF%D8%A9
https://www.tadalive.com/blog/9003/%D8%A7%D9%81%D8%B6%D9%84-%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%AC%D8%AF%D8%A9/
https://community.tccwpg.com/read-blog/110778
https://degentevakana.com/blogs/view/111690
https://community.tccwpg.com/read-blog/117111
https://degentevakana.com/blogs/view/116138
https://www.tadalive.com/blog/9255/%D8%A7%D9%81%D8%B6%D9%84-%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%AC%D8%AF%D8%A9/
https://www.rolonet.com/blogs/133993/%D8%B4%D8%B1%D9%83%D8%A7%D8%AA-%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%A7%D8%AB%D8%A7%D8%AB-%D9%85%D9%86-%D8%AC%D8%AF%D8%A9-%D8%A7%D9%84%D9%89-%D8%A7%D9%84%D8%B1%D9%8A%D8%A7%D8%B6
https://www.snipesocial.co.uk/blogs/137681/%D8%AE%D8%AF%D9%85%D8%A7%D8%AA-%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%A7%D8%AB%D8%A7%D8%AB-%D9%81%D9%89-%D8%AC%D8%AF%D8%A9
https://zlidein.com/read-blog/122405
https://www.tadalive.com/blog/9498/%D8%A7%D9%81%D8%B6%D9%84-%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D8%A8%D8%AC%D8%AF%D8%A9/
https://www.rolonet.com/blogs/136431/%D8%B4%D8%B1%D9%83%D8%A9-%D9%84%D8%AA%D8%BA%D9%84%D9%8A%D9%81-%D9%88-%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%A7%D8%AB%D8%A7%D8%AB-%D9%81%D9%89-%D8%AC%D8%AF%D8%A9
https://community.tccwpg.com/read-blog/121069
https://degentevakana.com/blogs/view/118151
https://zlidein.com/read-blog/123946
https://addandclick.com/read-blog/103304
https://www.snipesocial.co.uk/blogs/140014/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%A7%D8%AB%D8%A7%D8%AB-%D9%81%D9%89-%D8%AC%D8%AF%D8%A9
https://degentevakana.com/blogs/view/121720
https://addandclick.com/read-blog/108422
https://community.tccwpg.com/read-blog/124958
https://www.tadalive.com/blog/10246/%D8%B4%D8%B1%D9%83%D8%A7%D8%AA-%D8%AA%D9%86%D8%B8%D9%8A%D9%81-%D8%B3%D8%AC%D8%A7%D8%AF-%D8%A8%D8%AC%D8%AF%D8%A9/
https://www.rolonet.com/blogs/147206/%D8%AE%D8%AF%D9%85%D8%A7%D8%AA-%D8%B4%D8%B1%D9%83%D8%A9-%D8%AA%D9%86%D8%B8%D9%8A%D9%81-%D8%A8%D8%AC%D8%AF%D8%A9
https://www.tadalive.com/blog/11937/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%A7%D8%AB%D8%A7%D8%AB-%D8%A7%D9%84%D9%89-%D8%A7%D9%84%D8%B1%D9%8A%D8%A7%D8%B6/
https://community.tccwpg.com/read-blog/133025
https://degentevakana.com/blogs/view/126124
https://zlidein.com/read-blog/133589
https://addandclick.com/read-blog/116948
https://www.tadalive.com/blog/12197/%D8%A7%D8%AE%D8%B7%D8%A7%D8%A1-%D8%A7%D8%AE%D8%AA%D9%8A%D8%A7%D8%B1-%D8%B4%D8%B1%D9%83%D8%A7%D8%AA-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D9%85%D8%B2%D9%8A%D9%81%D8%A9/
https://www.rolonet.com/blogs/161381/%D8%A7%D8%AE%D8%AA%D9%8A%D8%A7%D8%B1-%D8%B4%D8%B1%D9%83%D8%A7%D8%AA-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D9%81%D9%89-%D9%85%D9%83%D8%A9
https://community.tccwpg.com/read-blog/134520
https://degentevakana.com/blogs/view/127017
https://zlidein.com/read-blog/134567
https://www.snipesocial.co.uk/blogs/158092/%D9%83%D9%8A%D9%81%D9%8A%D8%A9-%D8%A7%D8%AE%D8%AA%D9%8A%D8%A7%D8%B1-%D8%B4%D8%B1%D9%83%D8%A7%D8%AA-%D9%86%D9%82%D9%84-%D8%A7%D8%AB%D8%A7%D8%AB
https://www.tadalive.com/blog/12423/%D8%B4%D8%B1%D9%83%D8%A9-%D9%86%D9%82%D9%84-%D8%B9%D9%81%D8%B4-%D9%85%D9%86-%D8%A7%D9%84%D8%B1%D9%8A%D8%A7%D8%B6-%D8%A7%D9%84%D9%89-%D8%AA%D8%A8%D9%88%D9%83/
https://www.rolonet.com/blogs/164613/%D8%B4%D8%B1%D9%83%D8%A7%D8%AA-%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%A7%D8%AB%D8%A7%D8%AB-%D9%81%D9%89-%D8%A7%D9%84%D8%B1%D9%8A%D8%A7%D8%B6
https://community.tccwpg.com/read-blog/137135
https://degentevakana.com/blogs/view/129760
https://zlidein.com/read-blog/135756
https://www.snipesocial.co.uk/blogs/161037/%D8%A7%D9%81%D8%B6%D9%84-%D8%B4%D8%B1%D9%83%D8%A9-%D9%84%D9%86%D9%82%D9%84-%D8%A7%D9%84%D8%A7%D8%AB%D8%A7%D8%AB-%D9%81%D9%89-%D8%A7%D9%84%D8%B1%D9%8A%D8%A7%D8%B6
https://addandclick.com/read-blog/122199
MIKRO-ZAIM - [url=https://mikro-zaim-online.ru/]быстрые онлайн займы[/url]
Наши контакты: Зеленодольская улица, 36к2, Москва, 109457
Абузоустойчивый сервер для работы с Хрумером, GSA и всевозможными скриптами!
Есть дополнительная системах скидок, читайте описание в разделе оплата
Высокоскоростной Интернет: До 1000 Мбит/с
Скорость интернет-соединения играет решающую роль в успешной работе вашего проекта. Наши VPS/VDS серверы, поддерживающие Windows и Linux, обеспечивают доступ к интернету со скоростью до 1000 Мбит/с. Это гарантирует быструю загрузку веб-страниц и высокую производительность онлайн-приложений на обеих операционных системах.
Итак, при выборе виртуального выделенного сервера VPS, обеспечьте своему проекту надежность, высокую производительность и защиту от DDoS. Получите доступ к качественной инфраструктуре с поддержкой Windows и Linux уже от 13 рублей
Cialis 5 mg prezzo <a href=https://comprarcialis5mg.com/it/cialis-5mg-prezzo/>prezzo cialis 5 mg originale in farmacia</a> tadalafil 5 mg prezzo
Даркнет, сокращение от "даркнетворк" (dark network), представляет собой часть интернета, недоступную для обычных поисковых систем. В отличие от повседневного интернета, где мы привыкли к публичному контенту, даркнет скрыт от обычного пользователя. Здесь используются специальные сети, такие как Tor (The Onion Router), чтобы обеспечить анонимность пользователей.
在當今數位化的時代,"娛樂城"和"線上賭場"已成為現代娛樂和休閒生活的重要組成部分。從傳統的賭場到互聯網上的線上賭場,這一領域的發展不僅改變了人們娛樂的方式,也推動了全球娛樂產業的創新與進步。
**起源與發展**
娛樂城的概念源自於傳統的實體賭場,這些場所最初旨在提供各種形式的賭博娛樂,如撲克、輪盤、老虎機等。隨著時間的推移,這些賭場逐漸發展成為包含餐飲、表演藝術和住宿等多元化服務的綜合娛樂中心,從而吸引了來自世界各地的遊客。
隨著互聯網技術的飛速發展,線上賭場應運而生。這種新型態的賭博平台讓使用者可以在家中或任何有互聯網連接的地方,享受賭博遊戲的樂趣。線上賭場的出現不僅為賭博愛好者提供了更多便利與選擇,也大大擴展了賭博產業的市場範圍。
**特點與魅力**
娛樂城和線上賭場的主要魅力在於它們能提供多樣化的娛樂選項和高度的可訪問性。無論是實體的娛樂城還是虛擬的線上賭場,它們都致力於創造一個充滿樂趣和刺激的環境,讓人們可以從日常生活的壓力中短暫逃脫。
此外,線上賭場通過提供豐富的遊戲選擇、吸引人的獎金方案以及便捷的支付系統,成功地吸引了全球範圍內的用戶。這些平台通常具有高度的互動性和社交性,使玩家不僅能享受遊戲本身,還能與來自世界各地的其他玩家交流。
**未來趨勢**
隨著技術的不斷進步和用戶需求的不斷演變,娛樂城和線上賭場的未來發展呈現出多元化的趨勢。一方面,虛
擬現實(VR)和擴增現實(AR)技術的應用,有望為線上賭場帶來更加沉浸式和互動式的遊戲體驗。另一方面,對於實體娛樂城而言,將更多地注重提供綜合性的休閒體驗,結合賭博、娛樂、休閒和旅遊等多個方面,以滿足不同客群的需求。
此外,隨著對負責任賭博的認識加深,未來娛樂城和線上賭場在提供娛樂的同時,也將更加注重促進健康的賭博行為和保護用戶的安全。
總之,娛樂城和線上賭場作為現代娛樂生活的一部分,隨著社會的發展和技術的進步,將繼續演化和創新,為人們提供更多的樂趣和便利。這一領域的未來發展無疑充滿了無限的可能性和機遇。
1. Why should members of the PTC fill out vote justification forms explaining their votes?
Vote justification forms provide transparency in decision-making. Members articulate their reasoning, fostering a culture of openness and ensuring that decisions are well-founded and understood by the academic community.
2. How can absentee ballots be cast?
To accommodate absentee voting, PTCs may implement secure electronic methods or designated proxy voters. This ensures that faculty members who cannot physically attend meetings can still contribute to decision-making processes.
3. How will additional members of PTCs be elected in departments with fewer than four tenured faculty members?
In smaller departments, creative solutions like rotating roles or involving faculty from related disciplines can be explored. Flexibility in election procedures ensures representation even in departments with fewer tenured faculty members.
4. Can a faculty member on OCSA or FML serve on a PTC?
Faculty members involved in other committees like the Organization of Committee on Student Affairs (OCSA) or Family and Medical Leave (FML) can serve on a PTC, but potential conflicts of interest should be carefully considered and managed.
5. Can an abstention vote be cast at a PTC meeting?
Yes, PTC members have the option to abstain from voting if they feel unable to take a stance on a particular matter. This allows for ethical decision-making and prevents uninformed voting.
6. What constitutes a positive or negative vote in PTCs?
A positive vote typically indicates approval or agreement, while a negative vote signifies disapproval or disagreement. Clear definitions and guidelines within each PTC help members interpret and cast their votes accurately.
7. What constitutes a quorum in a PTC?
A quorum, the minimum number of members required for a valid meeting, is essential for decision-making. Specific rules about quorum size are usually outlined in the PTC's governing documents.
Our Plan Packages: Choose The Best Plan for You
Explore our plan packages designed to suit your earning potential and preferences. With daily limits, referral bonuses, and various subscription plans, our platform offers opportunities for financial growth.
Blog Section: Insights and Updates
Stay informed with our blog, providing valuable insights into legal matters, organizational updates, and industry trends. Our recent articles cover topics ranging from law firm openings to significant developments in the legal landscape.
Testimonials: What Our Clients Say
Discover what our clients have to say about their experiences. Join thousands of satisfied users who have successfully withdrawn earnings and benefited from our platform.
Conclusion:
This FAQ guide serves as a resource for faculty members engaging with PTC procedures. By addressing common questions and providing insights into our platform's earning opportunities, we aim to facilitate a transparent and informed academic community.
1. Why should members of the PTC fill out vote justification forms explaining their votes?
Vote justification forms provide transparency in decision-making. Members articulate their reasoning, fostering a culture of openness and ensuring that decisions are well-founded and understood by the academic community.
2. How can absentee ballots be cast?
To accommodate absentee voting, PTCs may implement secure electronic methods or designated proxy voters. This ensures that faculty members who cannot physically attend meetings can still contribute to decision-making processes.
3. How will additional members of PTCs be elected in departments with fewer than four tenured faculty members?
In smaller departments, creative solutions like rotating roles or involving faculty from related disciplines can be explored. Flexibility in election procedures ensures representation even in departments with fewer tenured faculty members.
4. Can a faculty member on OCSA or FML serve on a PTC?
Faculty members involved in other committees like the Organization of Committee on Student Affairs (OCSA) or Family and Medical Leave (FML) can serve on a PTC, but potential conflicts of interest should be carefully considered and managed.
5. Can an abstention vote be cast at a PTC meeting?
Yes, PTC members have the option to abstain from voting if they feel unable to take a stance on a particular matter. This allows for ethical decision-making and prevents uninformed voting.
6. What constitutes a positive or negative vote in PTCs?
A positive vote typically indicates approval or agreement, while a negative vote signifies disapproval or disagreement. Clear definitions and guidelines within each PTC help members interpret and cast their votes accurately.
7. What constitutes a quorum in a PTC?
A quorum, the minimum number of members required for a valid meeting, is essential for decision-making. Specific rules about quorum size are usually outlined in the PTC's governing documents.
Our Plan Packages: Choose The Best Plan for You
Explore our plan packages designed to suit your earning potential and preferences. With daily limits, referral bonuses, and various subscription plans, our platform offers opportunities for financial growth.
Blog Section: Insights and Updates
Stay informed with our blog, providing valuable insights into legal matters, organizational updates, and industry trends. Our recent articles cover topics ranging from law firm openings to significant developments in the legal landscape.
Testimonials: What Our Clients Say
Discover what our clients have to say about their experiences. Join thousands of satisfied users who have successfully withdrawn earnings and benefited from our platform.
Conclusion:
This FAQ guide serves as a resource for faculty members engaging with PTC procedures. By addressing common questions and providing insights into our platform's earning opportunities, we aim to facilitate a transparent and informed academic community.
Understanding the processes and protocols within a Professional Tenure Committee (PTC) is crucial for faculty members. This Frequently Asked Questions (FAQ) guide aims to address common queries related to PTC procedures, voting, and membership.
1. Why should members of the PTC fill out vote justification forms explaining their votes?
Vote justification forms provide transparency in decision-making. Members articulate their reasoning, fostering a culture of openness and ensuring that decisions are well-founded and understood by the academic community.
2. How can absentee ballots be cast?
To accommodate absentee voting, PTCs may implement secure electronic methods or designated proxy voters. This ensures that faculty members who cannot physically attend meetings can still contribute to decision-making processes.
3. How will additional members of PTCs be elected in departments with fewer than four tenured faculty members?
In smaller departments, creative solutions like rotating roles or involving faculty from related disciplines can be explored. Flexibility in election procedures ensures representation even in departments with fewer tenured faculty members.
4. Can a faculty member on OCSA or FML serve on a PTC?
Faculty members involved in other committees like the Organization of Committee on Student Affairs (OCSA) or Family and Medical Leave (FML) can serve on a PTC, but potential conflicts of interest should be carefully considered and managed.
5. Can an abstention vote be cast at a PTC meeting?
Yes, PTC members have the option to abstain from voting if they feel unable to take a stance on a particular matter. This allows for ethical decision-making and prevents uninformed voting.
6. What constitutes a positive or negative vote in PTCs?
A positive vote typically indicates approval or agreement, while a negative vote signifies disapproval or disagreement. Clear definitions and guidelines within each PTC help members interpret and cast their votes accurately.
7. What constitutes a quorum in a PTC?
A quorum, the minimum number of members required for a valid meeting, is essential for decision-making. Specific rules about quorum size are usually outlined in the PTC's governing documents.
Our Plan Packages: Choose The Best Plan for You
Explore our plan packages designed to suit your earning potential and preferences. With daily limits, referral bonuses, and various subscription plans, our platform offers opportunities for financial growth.
Blog Section: Insights and Updates
Stay informed with our blog, providing valuable insights into legal matters, organizational updates, and industry trends. Our recent articles cover topics ranging from law firm openings to significant developments in the legal landscape.
Testimonials: What Our Clients Say
Discover what our clients have to say about their experiences. Join thousands of satisfied users who have successfully withdrawn earnings and benefited from our platform.
Conclusion:
This FAQ guide serves as a resource for faculty members engaging with PTC procedures. By addressing common questions and providing insights into our platform's earning opportunities, we aim to facilitate a transparent and informed academic community.
Темная сторона интернета, представляет собой, тайную, платформу, в, глобальной сети, доступ к которой, получается, через, уникальные, программы а также, инструменты, предоставляющие, скрытность пользователей. Один из, таких, инструментов, является, Тор браузер, который, обеспечивает, приватное, вход в темную сторону интернета. Используя, этот, пользователи, могут иметь шанс, анонимно, обращаться к, интернет-ресурсы, не видимые, традиционными, сервисами поиска, что делает возможным, обстановку, для организации, разнообразных, нелегальных операций.
Киберторговая площадка, соответственно, часто связывается с, даркнетом, как, торговая площадка, для торговли, киберугрозами. Здесь, можно, купить, различные, нелегальные, товары, вплоть до, наркотических средств и стволов, доходя до, услугами хакеров. Система, гарантирует, высокую степень, криптографической защиты, и, скрытности, что, предоставляет, ее, желанной, для тех, кто, стремится, предотвратить, негативных последствий, со стороны соответствующих законопослушных органов
Скрытая сеть, представляет собой, скрытую, платформу, в, интернете, подключение к этой сети, осуществляется, путем, уникальные, приложения а также, инструменты, обеспечивающие, конфиденциальность пользовательские данных. Один из, таких, инструментов, представляется, браузер Тор, который обеспечивает, обеспечивает, приватное, подключение, в даркнет. С, его, участники, имеют возможность, безопасно, посещать, интернет-ресурсы, не индексируемые, традиционными, поисками, позволяя таким образом, условия, для проведения, разносторонних, нелегальных деятельностей.
Кракен, в результате, часто связывается с, даркнетом, в качестве, торговая площадка, для торговли, киберугрозами. Здесь, есть возможность, получить доступ к, разные, нелегальные, товары и услуги, начиная от, наркотических средств и огнестрельного оружия, доходя до, услугами хакеров. Ресурс, предоставляет, высокую степень, шифрования, а также, защиты личной информации, это, делает, ее, интересной, для тех, кого, стремится, предотвратить, преследований, со стороны соответствующих законопослушных органов.
We work hard to maintain our reputation: all of our In-Home IHSPs are factory-trained in the newest items and methods to provide you the highest quality service.
Our technicians have the knowledge you can rely on. With more than twenty-five years of expertise in the field, you can trust our experts to have the hands-on knowledge and abilities to deal with even the most complex washer or fridge repair (including cooling system replacement). And because, unlike some device repair companies, we only send you our skilled experts, not outsourced workers, you know you'll get the job you can count on - the best water heater or dryer repair, done right the first instance.
The list of brands we work with is long and diverse. Some of the well-known brands we provide assistance for include Whirlpool, Bosch, Miele Company, Samsung Electronics, LG Corporation, and high-end labels like Sub-Zero, Bosch Thermador, Viking Range, and Wolf. We can also handle other major brands, offering assistance such as General Electric, Electrolux, and Frigidaire Appliance appliance repairs.
Даркнет, это, анонимную, платформу, в, интернете, подключение к этой сети, происходит, по средствам, специальные, приложения а также, технологии, обеспечивающие, скрытность пользователей. Один из, подобных, инструментов, считается, браузер Тор, который позволяет, обеспечивает, приватное, подключение к сети, к даркнету. С, этот, участники, могут, безопасно, посещать, веб-сайты, не отображаемые, стандартными, поисками, создавая тем самым, обстановку, для проведения, разнообразных, запрещенных операций.
Крупнейшая торговая площадка, в результате, часто ассоциируется с, скрытой сетью, как, площадка, для осуществления обмена, криминалитетом. На данной платформе, есть возможность, получить доступ к, разнообразные, нелегальные, товары и услуги, начиная с, препаратов и огнестрельного оружия, доходя до, хакерскими действиями. Система, гарантирует, высокую степень, шифрования, а также, защиты личной информации, что, создает, эту площадку, желанной, для тех, кто, намерен, избежать, преследований, со стороны органов порядка.
[url=http://tsunagaru.mblg.tv/002500/entry/783/#comments]casino pinup[/url] 646e376
Blacksprut, будучи частью теневого интернета, представляет значительную угрозу для кибербезопасности и личной устойчивости пользователей. Этот темный уголок сети зачастую ассоциируется с запрещенными сделками, торговлей запрещенными товарами и услугами, а также другими противозаконными деяниями.
В борьбе с угрозой blacksprut необходимо приложить усилия на различных фронтах. Одним из ключевых направлений является совершенствование технологий цифровой безопасности. Развитие современных алгоритмов и технологий анализа данных позволит выявлять и пресекать деятельность blacksprut в реальном времени.
Помимо цифровых мер, важна согласованная деятельность усилий правоохранительных органов на планетарном уровне. Международное сотрудничество в сфере защиты в сети необходимо для успешного противодействия угрозам, связанным с blacksprut. Обмен данными, формирование совместных стратегий и активные действия помогут уменьшить воздействие этой угрозы.
Просвещение и освещение также играют ключевую роль в борьбе с blacksprut. Повышение знаний пользователей о рисках даркнета и методах предупреждения становится неотъемлемой составной частью антиспампинговых мероприятий. Чем более знающими будут пользователи, тем меньше опасность попадания под влияние угрозы blacksprut.
В заключение, в борьбе с угрозой blacksprut необходимо комбинировать усилия как на цифровом, так и на нормативном уровнях. Это вызов, требующий совместных усилий общества, правительства и технологических компаний. Только совместными усилиями мы сможем создания безопасного и защищенного цифрового пространства для всех.
Тор-поиск является мощным инструментом для гарантирования конфиденциальности и секретности в всемирной сети. Однако, иногда пользователи могут пережить с проблемами входа. В тексте мы осветим вероятные предпосылки и подсчитаем способы решения для ликвидации неполадок с подключением к Tor Browser.
Проблемы с сетью:
Решение: Проверка соединения ваше интернет-соединение. Проверьте, что вы подключены к интернету, и отсутствуют ли неполадок с вашим поставщиком интернет-услуг.
Блокировка Тор сети:
Решение: В некоторых конкретных государствах или сетях Tor может быть ограничен. Воспользуйтесь использованием переправы для пересечения запретов. В настройках Tor Browser выделите "Проброс мостов" и применяйте инструкциям.
Прокси-серверы и ограждения:
Решение: Проверка параметров конфигурации прокси-сервера и стены. Убедитесь, что они не препятствуют доступ Tor Browser к сети. Измените установки или в течение некоторого времени выключите прокси и ограждения для тестирования.
Проблемы с самим веб-обозревателем:
Решение: Убедитесь, что у вас установлена актуальная версия Tor Browser. Иногда обновления могут преодолеть сложности с доступом. Попробуйте также пересобрать программу.
Временные неполадки в Тор сети:
Решение: Подождите некоторое время некоторое время и пытайтесь достичь соединения после. Временные неполадки в работе Tor способны случаться, и те обычно устраняются в кратчайшие сроки.
Отключение JavaScript:
Решение: Некоторые из сетевые порталы могут блокировать доступ через Tor, если в вашем программе для просмотра включен JavaScript. Попробуйте временно деактивировать JavaScript в установках обозревателя.
Проблемы с защитными программами:
Решение: Ваш программа защиты или брандмауэр может препятствовать Tor Browser. Проверьте, что у вас нет запрещений для Tor в конфигурации вашего антивирусного программного обеспечения.
Исчерпание памяти:
Решение: Если у вас действующе множество вкладок браузера или процессы работы, это может привести к израсходованию памяти устройства и проблемам с соединением. Закройте лишние веб-страницы или пересоздайте обозреватель.
В случае, если трудность с подключением к Tor Browser остается в силе, заинтересуйтесь за помощью на официальном форуме Tor. Энтузиасты способны предложить дополнительную поддержку и помощь и советы. Припоминайте, что защита и скрытность зависят от постоянного внимательного отношения к аспектам, по этой причине следите за актуализациями и поддерживайте советам сообщества.
2024おすすめのオンラインカジノ
オンラインカジノはパソコンでしか遊べないというのは、もう一昔前の話。現在はスマホやタブレットなどのモバイル端末からも、パソコンと変わらないクオリティでオンラインカジノを当たり前に楽しむことができるようになりました。
数あるモバイルカジノの中で、当サイトが厳選したトップ5カジノはこちら。
オンラインカジノおすすめ: コニベット(Konibet)
コニベットといえば、キャッシュバックや毎日もらえるリベートボーナスなど豪華ボーナスが満載!それに加えて低い出金条件も見どころです。さらにVIPレベルごとの還元率の高さも業界内で突出している点や、出金速度の速さなどトータルバランスの良さからもハイローラーの方にも好まれています。
カスタマーサポートは365日24時間稼働しているので、初心者の方にも安心してご利用いただけます。
さらに【業界初のオンラインポーカー】を導入!毎日トーナメントも開催されているので、早速参加しちゃいましょう!
RTP(還元率)公開や、入出金対応がスムーズで初心者向き
2000種類以上の豊富なゲーム数を誇り、スロットゲーム多数!
今なら$20の入金不要ボーナスと最大$650還元ボーナス!
8種類以上のライブカジノプロバイダー
業界初オンラインポーカーあり,日本利用者数No.1の安心のオンラインカジノメディア!
おすすめポイント
コニベットは、その豊富なボーナスと高還元率、そして安心のキャッシュバック制度で知られています。まず、新規登録者には入金不要の$20ボーナスが提供され、さらに初回入金時には最大$650の還元ボーナスが得られます。これらのキャンペーンはプレイヤーにとって大きな魅力となっています。
また、コニベットの特徴的な点は、VIP制度です。一度ロイヤルクラブになると、降格がなく、スロットリベートが1.5%という驚異の還元率を享受できます。これは他のオンラインカジノと比較しても非常に高い還元率です。さらに、常時週間損失キャッシュバックも行っているため、不運で負けてしまった場合でも取り返すチャンスがあります。これらの特徴から、コニベットはプレイヤーにとって非常に魅力的なオンラインカジノと言えるでしょう。
コニベット 無料会員登録をする
| コニベットのボーナス
コニベットは、新規登録者向けに20ドルの入金不要ボーナスを用意しています
コニベットカジノでは、限定で初回入金後に残高が1ドル未満になった場合、入金額の50%(最高500ドル)がキャッシュバックされる。キャッシュバック額に出金条件はないため、獲得後にすぐ出金することも可能です。
| コニベットの入金方法
入金方法 最低 / 最高入金
マスターカード 最低 : $20 / 最高 : $6,000
ジェイシービー 最低 : $20/ 最高 : $6,000
アメックス 最低 : $20 / 最高 : $6,000
アイウォレット 最低 : $20 / 最高 : $100,000
スティックペイ 最低 : $20 / 最高 : $100,000
ヴィーナスポイント 最低 : $20 / 最高 : $10,000
仮想通貨 最低 : $20 / 最高 : $100,000
銀行送金 最低 : $20 / 最高 : $10,000
| コニベット出金方法
出金方法 最低 |最高出金
アイウォレット 最低 : $40 / 最高 : なし
スティックぺイ 最低 : $40 / 最高 : なし
ヴィーナスポイント 最低 : $40 / 最高 : なし
仮想通貨 最低 : $40 / 最高 : なし
銀行送金 最低 : $40 / 最高 : なし
2024おすすめのオンラインカジノ
オンラインカジノはパソコンでしか遊べないというのは、もう一昔前の話。現在はスマホやタブレットなどのモバイル端末からも、パソコンと変わらないクオリティでオンラインカジノを当たり前に楽しむことができるようになりました。
数あるモバイルカジノの中で、当サイトが厳選したトップ5カジノはこちら。
オンラインカジノおすすめ: コニベット(Konibet)
コニベットといえば、キャッシュバックや毎日もらえるリベートボーナスなど豪華ボーナスが満載!それに加えて低い出金条件も見どころです。さらにVIPレベルごとの還元率の高さも業界内で突出している点や、出金速度の速さなどトータルバランスの良さからもハイローラーの方にも好まれています。
カスタマーサポートは365日24時間稼働しているので、初心者の方にも安心してご利用いただけます。
さらに【業界初のオンラインポーカー】を導入!毎日トーナメントも開催されているので、早速参加しちゃいましょう!
RTP(還元率)公開や、入出金対応がスムーズで初心者向き
2000種類以上の豊富なゲーム数を誇り、スロットゲーム多数!
今なら$20の入金不要ボーナスと最大$650還元ボーナス!
8種類以上のライブカジノプロバイダー
業界初オンラインポーカーあり,日本利用者数No.1の安心のオンラインカジノメディア!
おすすめポイント
コニベットは、その豊富なボーナスと高還元率、そして安心のキャッシュバック制度で知られています。まず、新規登録者には入金不要の$20ボーナスが提供され、さらに初回入金時には最大$650の還元ボーナスが得られます。これらのキャンペーンはプレイヤーにとって大きな魅力となっています。
また、コニベットの特徴的な点は、VIP制度です。一度ロイヤルクラブになると、降格がなく、スロットリベートが1.5%という驚異の還元率を享受できます。これは他のオンラインカジノと比較しても非常に高い還元率です。さらに、常時週間損失キャッシュバックも行っているため、不運で負けてしまった場合でも取り返すチャンスがあります。これらの特徴から、コニベットはプレイヤーにとって非常に魅力的なオンラインカジノと言えるでしょう。
コニベット 無料会員登録をする
| コニベットのボーナス
コニベットは、新規登録者向けに20ドルの入金不要ボーナスを用意しています
コニベットカジノでは、限定で初回入金後に残高が1ドル未満になった場合、入金額の50%(最高500ドル)がキャッシュバックされる。キャッシュバック額に出金条件はないため、獲得後にすぐ出金することも可能です。
| コニベットの入金方法
入金方法 最低 / 最高入金
マスターカード 最低 : $20 / 最高 : $6,000
ジェイシービー 最低 : $20/ 最高 : $6,000
アメックス 最低 : $20 / 最高 : $6,000
アイウォレット 最低 : $20 / 最高 : $100,000
スティックペイ 最低 : $20 / 最高 : $100,000
ヴィーナスポイント 最低 : $20 / 最高 : $10,000
仮想通貨 最低 : $20 / 最高 : $100,000
銀行送金 最低 : $20 / 最高 : $10,000
| コニベット出金方法
出金方法 最低 |最高出金
アイウォレット 最低 : $40 / 最高 : なし
スティックぺイ 最低 : $40 / 最高 : なし
ヴィーナスポイント 最低 : $40 / 最高 : なし
仮想通貨 最低 : $40 / 最高 : なし
銀行送金 最低 : $40 / 最高 : なし
2024おすすめのオンラインカジノ
オンラインカジノはパソコンでしか遊べないというのは、もう一昔前の話。現在はスマホやタブレットなどのモバイル端末からも、パソコンと変わらないクオリティでオンラインカジノを当たり前に楽しむことができるようになりました。
数あるモバイルカジノの中で、当サイトが厳選したトップ5カジノはこちら。
オンラインカジノおすすめ: コニベット(Konibet)
コニベットといえば、キャッシュバックや毎日もらえるリベートボーナスなど豪華ボーナスが満載!それに加えて低い出金条件も見どころです。さらにVIPレベルごとの還元率の高さも業界内で突出している点や、出金速度の速さなどトータルバランスの良さからもハイローラーの方にも好まれています。
カスタマーサポートは365日24時間稼働しているので、初心者の方にも安心してご利用いただけます。
さらに【業界初のオンラインポーカー】を導入!毎日トーナメントも開催されているので、早速参加しちゃいましょう!
RTP(還元率)公開や、入出金対応がスムーズで初心者向き
2000種類以上の豊富なゲーム数を誇り、スロットゲーム多数!
今なら$20の入金不要ボーナスと最大$650還元ボーナス!
8種類以上のライブカジノプロバイダー
業界初オンラインポーカーあり,日本利用者数No.1の安心のオンラインカジノメディア!
おすすめポイント
コニベットは、その豊富なボーナスと高還元率、そして安心のキャッシュバック制度で知られています。まず、新規登録者には入金不要の$20ボーナスが提供され、さらに初回入金時には最大$650の還元ボーナスが得られます。これらのキャンペーンはプレイヤーにとって大きな魅力となっています。
また、コニベットの特徴的な点は、VIP制度です。一度ロイヤルクラブになると、降格がなく、スロットリベートが1.5%という驚異の還元率を享受できます。これは他のオンラインカジノと比較しても非常に高い還元率です。さらに、常時週間損失キャッシュバックも行っているため、不運で負けてしまった場合でも取り返すチャンスがあります。これらの特徴から、コニベットはプレイヤーにとって非常に魅力的なオンラインカジノと言えるでしょう。
コニベット 無料会員登録をする
| コニベットのボーナス
コニベットは、新規登録者向けに20ドルの入金不要ボーナスを用意しています
コニベットカジノでは、限定で初回入金後に残高が1ドル未満になった場合、入金額の50%(最高500ドル)がキャッシュバックされる。キャッシュバック額に出金条件はないため、獲得後にすぐ出金することも可能です。
| コニベットの入金方法
入金方法 最低 / 最高入金
マスターカード 最低 : $20 / 最高 : $6,000
ジェイシービー 最低 : $20/ 最高 : $6,000
アメックス 最低 : $20 / 最高 : $6,000
アイウォレット 最低 : $20 / 最高 : $100,000
スティックペイ 最低 : $20 / 最高 : $100,000
ヴィーナスポイント 最低 : $20 / 最高 : $10,000
仮想通貨 最低 : $20 / 最高 : $100,000
銀行送金 最低 : $20 / 最高 : $10,000
| コニベット出金方法
出金方法 最低 |最高出金
アイウォレット 最低 : $40 / 最高 : なし
スティックぺイ 最低 : $40 / 最高 : なし
ヴィーナスポイント 最低 : $40 / 最高 : なし
仮想通貨 最低 : $40 / 最高 : なし
銀行送金 最低 : $40 / 最高 : なし
Теневые рынки представляют собой тайные интернет-площадки, на которых торгуется разнообразной преступной продукцией и услугами. Среди этих услуг встречается и продажа поддельных документов, таких как паспорта. Эти рынки оперируют в теневой сфере интернета, используя шифрование и неизвестные платежные системы, чтобы оставаться неприметными для правоохранительных органов.
Покупка поддельного паспорта на теневых рынках представляет важную угрозу национальной безопасности. Кража личных данных, изготовление фальшивых документов и поддельные идентификационные материалы могут быть использованы для совершения экстремистских актов, мошенничества и других преступлений.
Правоохранительные органы в различных странах активно борются с теневыми рынками, проводя операции по выявлению и аресту тех, кто замешан в преступных действиях. Однако, по мере того как технологии становятся более сложными, эти рынки могут приспосабливаться и находить новые способы обхода законодательства.
Для обеспечения своей безопасности от опасностей, связанных с скрытыми рынками, важно быть осторожным при обработке своих личных данных. Это включает в себя остерегаться фишинговых атак, не раскрывать персональной информацией в подозрительных источниках и периодически проверять свои финансовые данные.
Кроме того, общество должно быть информировано о рисках и последствиях покупки поддельных удостоверений. Это способствует формированию более осознанного и ответственного подхода к вопросам безопасности и поможет в борьбе с неофициальными рынками. Поддержка законодательных инициатив, направленных на ужесточение наказаний за изготовление и сбыт поддельных удостоверений, также представляет важную составляющую в противодействии этим преступлениям
Изготовление и использование копий банковских карт является незаконной практикой, представляющей серьезную угрозу для безопасности финансовых систем и личных средств граждан. В данной статье мы рассмотрим угрозы и последствия покупки клонов карт, а также как общество и силовые структуры борются с похожими преступлениями.
“Дубликаты” карт — это незаконно созданные подделки банковских карт, которые используются для незаконных транзакций. Основной метод создания дубликатов — это угон данных с оригинальной карты и последующее настройка этих данных на другую карту. Злоумышленники, предлагающие услуги по продаже реплик карт, обычно действуют в скрытой сфере интернета, где трудно выявить и пресечь их деятельность.
Покупка дубликатов карт представляет собой серьезное преступление, которое может повлечь за собой тяжкие наказания. Покупатель также рискует стать последователем мошенничества, что может привести к уголовному преследованию. Основные преступные действия в этой сфере включают в себя кражу личной информации, подделывание документов и, конечно же, финансовые мошенничества.
Банки и органы порядка активно борются с правонарушениями, связанными с клонированием карт. Банки внедряют современные технологии для выявления подозрительных транзакций, а также предлагают услуги по обеспечению защиты для своих клиентов. Правоохранительные органы ведут расследовательские операции и ловят тех, кто замешан в производстве и продаже дубликатов карт.
Для обеспечения безопасности важно соблюдать бережность при использовании банковских карт. Необходимо регулярно проверять выписки, избегать сомнительных сделок и следить за своей индивидуальной информацией. Образование и информированность об угрозах также являются основными средствами в борьбе с преступлениями в области финансов.
В заключение, использование копий банковских карт — это незаконное и неприемлемое деяние, которое может привести к существенным последствиям для тех, кто вовлечен в такую практику. Соблюдение мер защиты, осведомленность о возможных угрозах и сотрудничество с полицией играют основополагающую роль в предотвращении и пресечении этих преступлений
Использование финансовых карт является существенной составляющей современного общества. Карты предоставляют комфорт, безопасность и широкие возможности для проведения финансовых сделок. Однако, кроме легального использования, существует негативная сторона — кэшаут карт, когда карты используются для снятия денег без одобрения владельца. Это является незаконной практикой и влечет за собой серьезные наказания.
Обналичивание карт представляет собой действия, направленные на извлечение наличных средств с пластиковой карты, необходимые для того, чтобы обойти систему защиты и уведомлений, предусмотренных банком. К сожалению, такие противозаконные деяния существуют, и они могут привести к потере средств для банков и клиентов.
Одним из путей кэшаута карт является использование технических хитростей, таких как скимминг. Кража данных с магнитных полос карт — это техника, при котором мошенники устанавливают механизмы на банкоматах или терминалах оплаты, чтобы считывать информацию с магнитной полосы банковской карты. Полученные данные затем используются для изготовления дубликата карты или проведения интернет-транзакций.
Другим часто используемым способом является мошенничество, когда преступники отправляют фальшивые электронные сообщения или создают фейковые сайты, имитирующие банковские ресурсы, с целью доступа к конфиденциальным данным от клиентов.
Для борьбы с обналичиванием карт банки осуществляют разные действия. Это включает в себя улучшение систем безопасности, осуществление двухфакторной верификации, мониторинг транзакций и обучение клиентов о методах предотвращения мошенничества.
Клиентам также следует принимать активное участие в защите своих карт и данных. Это включает в себя смену паролей с определенной периодичностью, проверку банковских выписок, а также внимательное отношение к подозрительным транзакциям.
Обналичивание карт — это серьезное преступление, которое причиняет урон не только финансовым учреждениям, но и обществу в целом. Поэтому важно соблюдать внимание при работе с банковскими картами, быть знакомым с методами предупреждения мошенничества и соблюдать меры безопасности для предотвращения потери средств
In the realm of premium watches, locating a trustworthy source is paramount, and WatchesWorld stands out as a symbol of trust and expertise. Presenting an broad collection of esteemed timepieces, WatchesWorld has garnered acclaim from satisfied customers worldwide. Let's delve into what our customers are saying about their experiences.
Customer Testimonials:
O.M.'s Review on O.M.:
"Very good communication and follow-up throughout the process. The watch was perfectly packed and in mint condition. I would certainly work with this group again for a watch purchase."
Richard Houtman's Review on Benny:
"I dealt with Benny, who was highly helpful and courteous at all times, keeping me regularly informed of the process. Moving forward, even though I ended up acquiring the watch locally, I would still definitely recommend Benny and the company."
Customer's Efficient Service Experience:
"A very good and efficient service. Kept me up to date on the order progress."
Featured Timepieces:
Richard Mille RM30-01 Automatic Winding with Declutchable Rotor:
Price: €285,000
Year: 2023
Reference: RM30-01 TI
Patek Philippe Complications World Time 38.5mm:
Price: €39,900
Year: 2019
Reference: 5230R-001
Rolex Oyster Perpetual Day-Date 36mm:
Price: €76,900
Year: 2024
Reference: 128238-0071
Best Sellers:
Bulgari Serpenti Tubogas 35mm:
Price: On Request
Reference: 101816 SP35C6SDS.1T
Bulgari Serpenti Tubogas 35mm (2024):
Price: €12,700
Reference: 102237 SP35C6SPGD.1T
Cartier Panthere Medium Model:
Price: €8,390
Year: 2023
Reference: W2PN0007
Our Experts Selection:
Cartier Panthere Small Model:
Price: €11,500
Year: 2024
Reference: W3PN0006
Omega Speedmaster Moonwatch 44.25 mm:
Price: €9,190
Year: 2024
Reference: 304.30.44.52.01.001
Rolex Oyster Perpetual Cosmograph Daytona 40mm:
Price: €28,500
Year: 2023
Reference: 116500LN-0002
Rolex Oyster Perpetual 36mm:
Price: €13,600
Year: 2023
Reference: 126000-0006
Why WatchesWorld:
WatchesWorld is not just an online platform; it's a commitment to personalized service in the world of high-end watches. Our group of watch experts prioritizes trust, ensuring that every customer makes an well-informed decision.
Our Commitment:
Expertise: Our group brings exceptional knowledge and insight into the world of luxury timepieces.
Trust: Trust is the foundation of our service, and we prioritize transparency in every transaction.
Satisfaction: Customer satisfaction is our ultimate goal, and we go the additional step to ensure it.
When you choose WatchesWorld, you're not just buying a watch; you're investing in a seamless and trustworthy experience. Explore our range, and let us assist you in finding the perfect timepiece that mirrors your taste and sophistication. At WatchesWorld, your satisfaction is our proven commitment
Теневые каталоги: Врата в анонимность
Для начала, что такое даркнет список? Это, по сути, каталоги или индексы веб-ресурсов в темной части интернета, которые позволяют пользователям находить нужные услуги, товары или информацию. Эти списки могут варьироваться от форумов и торговых площадок до ресурсов, специализирующихся на различных аспектах анонимности и криптовалют.
Категории и Возможности
Черный Рынок:
Темная сторона интернета часто ассоциируется с рынком андеграунда, где можно найти различные товары и услуги, включая наркотики, оружие, украденные данные и даже услуги профессиональных устрашителей. Списки таких ресурсов позволяют пользователям без труда находить подобные предложения.
Чаты и Группы:
Даркнет также предоставляет платформы для анонимного общения. Чаты и сообщества на теневых каталогах могут заниматься обсуждением тем от кибербезопасности и взлома до политики и философии.
Информационные ресурсы:
Есть ресурсы, предоставляющие информацию и инструкции по обходу цензуры, защите конфиденциальности и другим темам, интересным пользователям, стремящимся сохранить анонимность.
Безопасность и Осторожность
При всей своей анонимности и свободе действий даркнет также несет риски. Мошенничество, кибератаки и незаконные сделки становятся частью этого мира. Пользователям необходимо проявлять максимальную осторожность и соблюдать меры безопасности при взаимодействии с даркнет списками.
Заключение: Врата в Неизведанный Мир
Даркнет списки предоставляют доступ к теневым уголкам интернета, где сокрыты тайны и возможности. Однако, как и в любой неизведанной территории, важно помнить о возможных рисках и осознанно подходить к использованию темной стороны интернета. Анонимность не всегда гарантирует безопасность, и путешествие в этот мир требует особой осторожности и знания.
Независимо от того, интересуетесь ли вы техническими аспектами кибербезопасности, ищете уникальные товары или просто исследуете новые грани интернета, теневые каталоги предоставляют ключ
Темная сторона интернета – неведомая сфера интернета, избегающая взоров стандартных поисковых систем и требующая эксклюзивных средств для доступа. Этот анонимный уголок сети обильно насыщен платформами, предоставляя доступ к разнообразным товарам и услугам через свои даркнет списки и справочники. Давайте ближе рассмотрим, что представляют собой эти списки и какие тайны они сокрывают.
Даркнет Списки: Окна в Тайный Мир
Каталоги ресурсов в даркнете – это своего рода порталы в невидимый мир интернета. Каталоги и индексы веб-ресурсов в даркнете, они позволяют пользователям отыскивать разношерстные услуги, товары и информацию. Варьируя от форумов и магазинов до ресурсов, уделяющих внимание аспектам анонимности и криптовалютам, эти перечни предоставляют нам шанс заглянуть в непознанный мир даркнета.
Категории и Возможности
Теневой Рынок:
Даркнет часто ассоциируется с теневым рынком, где доступны самые разные товары и услуги – от наркотических препаратов и стрелкового вооружения до похищенной информации и услуг наемных убийц. Списки ресурсов в этой категории облегчают пользователям находить нужные предложения без лишних усилий.
Форумы и Сообщества:
Даркнет также служит для анонимного общения. Форумы и сообщества, представленные в реестрах даркнета, охватывают широкий спектр – от кибербезопасности и хакерства до политических аспектов и философских концепций.
Информационные Ресурсы:
На даркнете есть ресурсы, предоставляющие информацию и инструкции по преодолению цензуры, обеспечению конфиденциальности и другим темам, интересным тем, кто хочет сохранить свою конфиденциальность.
Безопасность и Осторожность
Несмотря на скрытность и свободу, даркнет полон опасностей. Мошенничество, кибератаки и незаконные сделки являются неотъемлемой частью этого мира. Взаимодействуя с списками ресурсов в темной сети, пользователи должны соблюдать максимальную осторожность и придерживаться мер безопасности.
Заключение
Реестры даркнета – это путь в неизведанный мир, где скрыты секреты и возможности. Однако, как и в любой неизведанной территории, путешествие в темную сеть требует особой внимания и знаний. Не всегда анонимность приносит безопасность, и использование даркнета требует осознанного подхода. Независимо от ваших интересов – будь то технические детали в области кибербезопасности, поиск необычных товаров или исследование новых возможностей в интернете – списки даркнета предоставляют ключ
Даркнет – скрытая зона всемирной паутины, избегающая взоров стандартных поисковых систем и требующая эксклюзивных средств для доступа. Этот анонимный ресурс сети обильно насыщен ресурсами, предоставляя доступ к разнообразным товарам и услугам через свои даркнет списки и индексы. Давайте подробнее рассмотрим, что представляют собой эти списки и какие тайны они сокрывают.
Даркнет Списки: Порталы в Скрытый Мир
Индексы веб-ресурсов в темной части интернета – это своего рода порталы в невидимый мир интернета. Перечни и указатели веб-ресурсов в даркнете, они позволяют пользователям отыскивать различные услуги, товары и информацию. Варьируя от форумов и магазинов до ресурсов, уделяющих внимание аспектам анонимности и криптовалютам, эти списки предоставляют нам возможность заглянуть в неизведанный мир даркнета.
Категории и Возможности
Теневой Рынок:
Даркнет часто ассоциируется с теневым рынком, где доступны самые разные товары и услуги – от наркотических препаратов и стрелкового вооружения до украденных данных и услуг наемных убийц. Списки ресурсов в данной категории облегчают пользователям находить подходящие предложения без лишних усилий.
Форумы и Сообщества:
Даркнет также служит для анонимного общения. Форумы и сообщества, представленные в реестрах даркнета, затрагивают широкий спектр – от кибербезопасности и хакерства до политических аспектов и философских концепций.
Информационные Ресурсы:
На даркнете есть ресурсы, предоставляющие данные и указания по обходу цензуры, защите конфиденциальности и другим темам, которые могут быть интересны тем, кто хочет остаться анонимным.
Безопасность и Осторожность
Несмотря на скрытность и свободу, даркнет полон рисков. Мошенничество, кибератаки и незаконные сделки являются неотъемлемой частью этого мира. Взаимодействуя с списками ресурсов в темной сети, пользователи должны соблюдать предельную осмотрительность и придерживаться мер безопасности.
Заключение
Реестры даркнета – это врата в неизведанный мир, где хранятся тайны и возможности. Однако, как и в любой неизведанной территории, путешествие в даркнет требует особой бдительности и знаний. Не всегда анонимность приносит безопасность, и использование темной сети требует сознательного подхода. Независимо от ваших интересов – будь то технические аспекты кибербезопасности, поиск уникальных товаров или исследование новых граней интернета – реестры даркнета предоставляют ключ
Даркнет Списки: Порталы в Скрытый Мир
Каталоги ресурсов в даркнете – это вид врата в невидимый мир интернета. Каталоги и индексы веб-ресурсов в даркнете, они позволяют пользователям отыскивать различные услуги, товары и информацию. Варьируя от форумов и магазинов до ресурсов, уделяющих внимание аспектам анонимности и криптовалютам, эти списки предоставляют нам шанс заглянуть в неизведанный мир даркнета.
Категории и Возможности
Теневой Рынок:
Даркнет часто связывается с подпольной торговлей, где доступны самые разные товары и услуги – от наркотиков и оружия до украденных данных и услуг наемных убийц. Реестры ресурсов в подобной категории облегчают пользователям находить подходящие предложения без лишних усилий.
Форумы и Сообщества:
Даркнет также служит для анонимного общения. Форумы и сообщества, представленные в реестрах даркнета, затрагивают различные темы – от компьютерной безопасности и хакерских атак до политики и философии.
Информационные Ресурсы:
На даркнете есть ресурсы, предоставляющие данные и указания по обходу ограничений, защите конфиденциальности и другим вопросам, которые могут заинтересовать тех, кто стремится сохранить свою анонимность.
Безопасность и Осторожность
Несмотря на неизвестность и свободу, даркнет не лишен рисков. Мошенничество, кибератаки и незаконные сделки являются неотъемлемой частью этого мира. Взаимодействуя с списками ресурсов в темной сети, пользователи должны соблюдать предельную осмотрительность и придерживаться мер безопасности.
Заключение
Списки даркнета – это путь в неизведанный мир, где хранятся тайны и возможности. Однако, как и в любой неизведанной территории, путешествие в даркнет требует особой осторожности и знания. Анонимность не всегда гарантирует безопасность, и использование даркнета требует осознанного подхода. Независимо от ваших интересов – будь то технические аспекты кибербезопасности, поиск уникальных товаров или исследование новых граней интернета – реестры даркнета предоставляют ключ
Темная сторона интернета – таинственная сфера интернета, избегающая взоров стандартных поисковых систем и требующая эксклюзивных средств для доступа. Этот скрытый уголок сети обильно насыщен ресурсами, предоставляя доступ к разнообразным товарам и услугам через свои каталоги и справочники. Давайте подробнее рассмотрим, что представляют собой эти списки и какие тайны они сокрывают.
Даркнет Списки: Окна в Неизведанный Мир
Индексы веб-ресурсов в темной части интернета – это вид порталы в неощутимый мир интернета. Перечни и указатели веб-ресурсов в даркнете, они позволяют пользователям отыскивать различные услуги, товары и информацию. Варьируя от форумов и магазинов до ресурсов, уделяющих внимание аспектам анонимности и криптовалютам, эти списки предоставляют нам шанс заглянуть в таинственный мир даркнета.
Категории и Возможности
Теневой Рынок:
Даркнет часто ассоциируется с незаконными сделками, где доступны разнообразные товары и услуги – от наркотиков и оружия до похищенной информации и услуг наемных убийц. Списки ресурсов в этой категории облегчают пользователям находить подходящие предложения без лишних усилий.
Форумы и Сообщества:
Даркнет также служит для анонимного общения. Форумы и сообщества, указанные в каталогах даркнета, затрагивают различные темы – от информационной безопасности и взлома до политики и философии.
Информационные Ресурсы:
На даркнете есть ресурсы, предоставляющие сведения и руководства по преодолению цензуры, обеспечению конфиденциальности и другим темам, которые могут быть интересны тем, кто хочет остаться анонимным.
Безопасность и Осторожность
Несмотря на скрытность и свободу, даркнет полон рисков. Мошенничество, кибератаки и незаконные сделки являются неотъемлемой частью этого мира. Взаимодействуя с реестрами даркнета, пользователи должны соблюдать предельную осмотрительность и придерживаться мер безопасности.
Заключение
Реестры даркнета – это ключ к таинственному миру, где сокрыты тайны и возможности. Однако, как и в любой неизведанной территории, путешествие в темную сеть требует особой бдительности и знаний. Не всегда анонимность приносит безопасность, и использование даркнета требует осознанного подхода. Независимо от ваших интересов – будь то технические аспекты кибербезопасности, поиск уникальных товаров или исследование новых граней интернета – списки даркнета предоставляют ключ
Тенденции и События:
"Развитие Средств и Безопасности:
В даркнете постоянно развиваются технологии и методы обеспечения безопасности. Новости о внедрении усовершенствованных платформ шифрования, скрытия личности и защиты личных данных свидетельствуют о желании пользователей и специалистов к обеспечению надежной среды."
"Свежие Теневые Рынки:
Следуя динамикой спроса и предложений, в теневом интернете возникают новые коммерческие пространства. Новости о запуске онлайн-рынков предоставляют участникам разнообразные варианты для купли-продажи продукцией и услугами
Покупка паспорта в интернет-магазине – это противозаконное и рискованное поступок, которое может вызвать к серьезным негативным последствиям для людей. Вот несколько аспектов, о которых необходимо помнить:
Нарушение законодательства: Покупка удостоверения личности в онлайн магазине является преступлением законодательства. Имение фальшивым документом может повлечь за собой криминальную ответственность и тяжелые штрафы.
Риски индивидуальной секретности: Факт применения поддельного удостоверения личности может поставить под угрозу личную безопасность. Люди, использующие фальшивыми документами, способны стать целью провокаций со со стороны правоохранительных органов.
Финансовые убытки: Часто мошенники, торгующие поддельными паспортами, могут применять ваши личные данные для обмана, что приведет к финансовым убыткам. Личные или финансовые сведения могут оказаться применены в преступных намерениях.
Проблемы при перемещении: Поддельный паспорт может быть обнаружен при переезде пересечь границы или при контакте с официальными органами. Такое обстоятельство может привести к задержанию, изгнанию или другим серьезным проблемам при путешествиях.
Потеря доверия и престижа: Использование поддельного паспорта может послужить причиной к утрате доверительности со со стороны сообщества и нанимателей. Это обстановка может негативно влиять на ваши репутацию и карьерные перспективы.
Вместо того, чем бы рисковать своей независимостью, защитой и престижем, советуется соблюдать законодательство и воспользоваться государственными путями для оформления удостоверений. Они предусматривают защиту всех ваших законных интересов и гарантируют секретность ваших информации. Незаконные практики способны сопровождаться неожиданные и негативные последствия, создавая тяжелые проблемы для вас и вашего окружения
В недавно интернет стал в бесконечный ресурс знаний, услуг и продуктов. Однако, среди множества виртуальных магазинов и площадок, есть темная сторона, известная как даркнет магазины. Этот уголок виртуального мира создает свои опасные сценарии и влечет за собой значительными рисками.
Что такое Даркнет Магазины:
Даркнет магазины представляют собой онлайн-платформы, доступные через скрытые браузеры и уникальные программы. Они оперируют в скрытой сети, скрытом от обычных поисковых систем. Здесь можно обнаружить не только торговцев запрещенными товарами и услугами, но и разнообразные преступные схемы.
Категории Товаров и Услуг:
Даркнет магазины предлагают разнообразный выбор товаров и услуг, начиная от наркотиков и оружия до хакерских услуг и похищенных данных. На этой темной площадке работают торговцы, дающие возможность приобретения незаконных вещей без риска быть выслеженным.
Риски для Пользователей:
Легальные Последствия:
Покупка незаконных товаров на даркнет магазинах подвергает пользователей риску столкнуться с правоохранительными органами. Уголовная ответственность может быть значительным следствием таких покупок.
Мошенничество и Обман:
Даркнет тоже представляет собой плодородной почвой для мошенников. Пользователи могут попасть в обман, где оплата не приведет к получению товара или услуги.
Угрозы Кибербезопасности:
Даркнет магазины предлагают услуги хакеров и киберпреступников, что сопровождается реальными опасностями для безопасности данных и конфиденциальности.
Распространение Преступной Деятельности:
Экономика даркнет магазинов содействует распространению преступной деятельности, так как предоставляет инфраструктуру для нелегальных транзакций.
Борьба с Проблемой:
Усиление Кибербезопасности:
Развитие кибербезопасности и технологий слежения способствует бороться с даркнет магазинами, делая их менее поулчаемыми.
Законодательные Меры:
Принятие строгих законов и их решительная реализация направлены на предотвращение и кара пользователей даркнет магазинов.
Образование и Пропаганда:
Повышение осведомленности о рисках и последствиях использования даркнет магазинов способно снизить спрос на незаконные товары и услуги.
Заключение:
Даркнет магазины предоставляют темным уголкам интернета, где появляются теневые фигуры с преступными намерениями. Рациональное применение ресурсов и активная осторожность необходимы, для того чтобы защитить себя от рисков, связанных с этими темными магазинами. В сумме, секретность и соблюдение законов должны быть на первом месте, когда речь заходит о виртуальных покупках
Введение в Темный Интернет: Уточнение и Основополагающие Характеристики
Разъяснение термина даркнета, возможных отличий от стандартного интернета, и основных черт этого темного мира.
Как Войти в Даркнет: Путеводитель по Анонимному Доступу
Подробное разъяснение шагов, необходимых для доступа в даркнет, включая использование эксклюзивных браузеров и инструментов.
Адресация в Даркнете: Тайны .onion-Доменов
Пояснение, как функционируют .onion-домены, и каковы ресурсы они содержат, с акцентом на секурном поиске и применении.
Безопасность и Конфиденциальность в Темном Интернете: Шаги для Пользователей
Рассмотрение техник и инструментов для защиты анонимности при эксплуатации даркнета, включая VPN и инные средства.
Электронные Валюты в Темном Интернете: Функция Биткойнов и Криптовалютных Средств
Анализ использования цифровых валют, в главном биткоинов, для совершения анонимных транзакций в даркнете.
Поисковая Активность в Даркнете: Особенности и Риски
Изучение поисковых механизмов в даркнете, предупреждения о потенциальных рисках и незаконных ресурсах.
Юридические Стороны Темного Интернета: Последствия и Результаты
Рассмотрение законных аспектов использования даркнета, предостережение о потенциальных юридических последствиях.
Даркнет и Кибербезопасность: Возможные Опасности и Защитные Меры
Анализ потенциальных киберугроз в даркнете и рекомендации по защите от них.
Даркнет и Общественные Сети: Анонимное Взаимодействие и Группы
Рассмотрение роли даркнета в области социальных взаимодействий и создании скрытых сообществ.
Перспективы Даркнета: Тренды и Предсказания
Предсказания развития даркнета и возможные изменения в его структуре в перспективе.
Телеграм - это известный мессенджер, отмеченный своей превосходной степенью шифрования и защиты данных пользователей. Однако, в современном цифровом мире тема взлома Телеграм периодически поднимается. Давайте рассмотрим, что на самом деле стоит за этим термином и почему взлом Телеграм чаще является фантазией, чем фактом.
Шифрование в Telegram: Основные принципы Защиты
Telegram славится своим превосходным уровнем кодирования. Для обеспечения конфиденциальности переписки между участниками используется протокол MTProto. Этот протокол обеспечивает полное кодирование, что означает, что только отправитель и получающая сторона могут читать сообщения.
Мифы о Взломе Telegram: Почему они появляются?
В последнее время в интернете часто появляются утверждения о взломе Телеграма и доступе к персональной информации пользователей. Однако, основная часть этих утверждений оказываются мифами, часто возникающими из-за непонимания принципов работы мессенджера.
Кибератаки и Раны: Фактические Угрозы
Хотя нарушение Telegram в общем случае является трудной задачей, существуют реальные опасности, с которыми сталкиваются пользователи. Например, атаки на индивидуальные аккаунты, вредоносные программы и прочие методы, которые, тем не менее, нуждаются в личном участии пользователя в их распространении.
Защита Персональных Данных: Советы для Участников
Несмотря на непоявление точной опасности взлома Telegram, важно соблюдать базовые правила кибербезопасности. Регулярно обновляйте приложение, используйте двухфакторную аутентификацию, избегайте подозрительных ссылок и мошеннических атак.
Итог: Фактическая Опасность или Излишняя беспокойство?
Нарушение Телеграма, как обычно, оказывается мифом, созданным вокруг темы разговора без явных доказательств. Однако безопасность всегда остается приоритетом, и участники мессенджера должны быть осторожными и следовать советам по обеспечению защиты своей персональных данных
WhatsApp - один из самых популярных мессенджеров в мире, массово используемый для обмена сообщениями и файлами. Он известен своей шифрованной системой обмена данными и обеспечением конфиденциальности пользователей. Однако в сети время от времени возникают утверждения о возможности взлома WhatsApp. Давайте разберемся, насколько эти утверждения соответствуют реальности и почему тема взлома Вотсап вызывает столько дискуссий.
Шифрование в WhatsApp: Охрана Личной Информации
Вотсап применяет end-to-end кодирование, что означает, что только передающая сторона и получатель могут читать сообщения. Это стало основой для уверенности многих пользователей мессенджера к сохранению их личной информации.
Легенды о Взломе WhatsApp: По какой причине Они Появляются?
Сеть периодически наполняют слухи о нарушении WhatsApp и возможном входе к переписке. Многие из этих утверждений порой не имеют оснований и могут быть результатом паники или дезинформации.
Фактические Угрозы: Кибератаки и Безопасность
Хотя взлом WhatsApp является трудной задачей, существуют актуальные угрозы, такие как кибератаки на отдельные аккаунты, фишинг и вредоносные программы. Соблюдение мер безопасности важно для минимизации этих рисков.
Защита Личной Информации: Советы Пользователям
Для укрепления безопасности своего аккаунта в WhatsApp пользователи могут использовать двухфакторную аутентификацию, регулярно обновлять приложение, избегать сомнительных ссылок и следить за конфиденциальностью своего устройства.
Заключение: Фактическая и Осторожность
Нарушение WhatsApp, как обычно, оказывается трудным и маловероятным сценарием. Однако важно помнить о актуальных угрозах и принимать меры предосторожности для защиты своей личной информации. Соблюдение рекомендаций по охране помогает поддерживать конфиденциальность и уверенность в использовании мессенджера
Вот некоторые из способов, которые могут содействовать в предотвращении обнала кредитных карт:
Охрана личной информации: Будьте осторожными в контексте предоставления личных данных, особенно онлайн. Избегайте предоставления картовых номеров, кодов безопасности и инных конфиденциальных данных на сомнительных сайтах.
Сильные пароли: Используйте надежные и уникальные пароли для своих банковских аккаунтов и кредитных карт. Регулярно изменяйте пароли.
Мониторинг транзакций: Регулярно проверяйте выписки по кредитным картам и банковским счетам. Это позволит своевременно обнаруживать подозрительных транзакций.
Программы антивирус: Используйте антивирусное программное обеспечение и актуализируйте его регулярно. Это поможет препятствовать вредоносные программы, которые могут быть использованы для кражи данных.
Осмотрительное поведение в социальных медиа: Будьте осторожными в онлайн-сетях, избегайте публикации чувствительной информации, которая может быть использована для взлома вашего аккаунта.
Уведомление банка: Если вы заметили какие-либо подозрительные операции или утерю карты, сразу свяжитесь с вашим банком для заблокировки карты.
Обучение: Будьте внимательными к новым методам мошенничества и обучайтесь тому, как предупреждать их.
Избегая легковерия и принимая меры предосторожности, вы можете уменьшить риск стать жертвой обнала кредитных карт.
Осознание сущности и опасностей связанных с обналом кредитных карт способствует людям предотвращать атак и сохранять свои финансовые средства. Обнал (отмывание) кредитных карт — это процесс использования украденных или неправомерно приобретенных кредитных карт для проведения финансовых транзакций с целью сокрыть их происхождения и предотвратить отслеживание.
Вот некоторые из способов, которые могут способствовать в уклонении от обнала кредитных карт:
Защита личной информации: Будьте осторожными в отношении предоставления личной информации, особенно онлайн. Избегайте предоставления номеров карт, кодов безопасности и дополнительных конфиденциальных данных на непроверенных сайтах.
Мощные коды доступа: Используйте мощные и уникальные пароли для своих банковских аккаунтов и кредитных карт. Регулярно изменяйте пароли.
Контроль транзакций: Регулярно проверяйте выписки по кредитным картам и банковским счетам. Это поможет своевременно выявить подозрительных транзакций.
Программы антивирус: Используйте антивирусное программное обеспечение и вносите обновления его регулярно. Это поможет препятствовать вредоносные программы, которые могут быть использованы для кражи данных.
Бережное использование общественных сетей: Будьте осторожными в социальных сетях, избегайте опубликования чувствительной информации, которая может быть использована для взлома вашего аккаунта.
Уведомление банка: Если вы заметили какие-либо подозрительные операции или утерю карты, сразу свяжитесь с вашим банком для заблокировки карты.
Обучение: Будьте внимательными к современным приемам мошенничества и обучайтесь тому, как предупреждать их.
Избегая легковерия и проявляя предельную осторожность, вы можете снизить риск стать жертвой обнала кредитных карт.
Современный общество высоких технологий предоставляет удобства онлайн-платежей и банковских операций, но с этим приходит и нарастающая угроза обнала карт. Обнал карт является процессом использования захваченных или неправомерно приобретенных кредитных карт для совершения финансовых транзакций с целью скрыть их источник и заблокировать отслеживание.
Ключевые моменты для безопасности в сети и предотвращения обнала карт:
Защита личной информации:
Соблюдайте осторожность при передаче личной информации онлайн. Никогда не делитесь банковскими номерами карт, пин-кодами и инными конфиденциальными данными на ненадежных сайтах.
Сильные пароли:
Используйте для своих банковских аккаунтов и кредитных карт мощные и уникальные пароли. Регулярно изменяйте пароли для усиления безопасности.
Мониторинг транзакций:
Регулярно проверяйте выписки по кредитным картам и банковским счетам. Это помогает выявить подозрительные транзакции и быстро реагировать.
Антивирусная защита:
Устанавливайте и регулярно обновляйте антивирусное программное обеспечение. Такие программы помогут препятствовать действию вредоносных программ, которые могут быть использованы для кражи данных.
Бережное использование общественных сетей:
Избегайте размещения чувствительной информации в социальных сетях. Эти данные могут быть использованы для хакерских атак к вашему аккаунту и последующего использования в обнале карт.
Уведомление банка:
Если вы заметили подозрительные операции или похищение карты, свяжитесь с банком немедленно для блокировки карты и предупреждения финансовых убытков.
Образование и обучение:
Будьте внимательными к новым методам мошенничества и постоянно обновляйте свои знания, как предотвращать подобные атаки. Современные мошенники постоянно усовершенствуют свои приемы, и ваше понимание может стать ключевым для защиты.
В завершение, соблюдение основных норм безопасности при использовании интернета и постоянное обучение помогут вам уменьшить риск стать жертвой мошенничества с картами на рабочем месте и в будней жизни. Помните, что ваша финансовая безопасность в ваших руках, и предпринимательские действия могут сделать ваш онлайн-опыт более защищенным и надежным.
Современный общество высоких технологий предоставляет преимущества онлайн-платежей и банковских операций, но с этим приходит и повышающаяся опасность обнала карт. Обнал карт является операцией использования захваченных или неправомерно приобретенных кредитных карт для совершения финансовых транзакций с целью замаскировать их происхождение и пресечь отслеживание.
Ключевые моменты для безопасности в сети и предотвращения обнала карт:
Защита личной информации:
Будьте внимательными при предоставлении личной информации онлайн. Никогда не делитесь картовыми номерами, пин-кодами и дополнительными конфиденциальными данными на ненадежных сайтах.
Сильные пароли:
Используйте для своих банковских аккаунтов и кредитных карт надежные и уникальные пароли. Регулярно изменяйте пароли для увеличения уровня безопасности.
Мониторинг транзакций:
Регулярно проверяйте выписки по кредитным картам и банковским счетам. Это способствует выявлению подозрительных операций и моментально реагировать.
Антивирусная защита:
Устанавливайте и регулярно обновляйте антивирусное программное обеспечение. Такие программы помогут защитить от вредоносных программ, которые могут быть использованы для кражи данных.
Бережное использование общественных сетей:
Будьте осторожными при размещении чувствительной информации в социальных сетях. Эти данные могут быть использованы для взлома к вашему аккаунту и последующего использования в обнале карт.
Уведомление банка:
Если вы выявили подозрительные действия или потерю карты, свяжитесь с банком сразу для блокировки карты и предупреждения финансовых убытков.
Образование и обучение:
Будьте внимательными к новым методам мошенничества и постоянно совершенствуйте свои знания, как предотвращать подобные атаки. Современные мошенники постоянно совершенствуют свои методы, и ваше знание может стать решающим для предотвращения
Фальшивые купюры всегда были важной угрозой для финансовой стабильности общества. В последние годы одним из основных объектов манипуляций стали банкноты номиналом 5000 рублей. Эти поддельные деньги представляют собой важную опасность для экономики и финансовой безопасности граждан. Давайте рассмотрим, почему фальшивые купюры 5000 рублей стали существенной бедой.
Сложностью выявления.
Купюры 5000 рублей являются крупнейшими по номиналу, что делает их чрезвычайно привлекательными для фальшивомонетчиков. Отлично проработанные подделки могут быть затруднительно выявить даже профессионалам в сфере финансов. Современные технологии позволяют создавать превосходные копии с использованием новейших методов печати и защитных элементов.
Угроза для бизнеса.
Фальшивые 5000 рублей могут привести к крупным финансовым убыткам для предпринимателей и компаний. Бизнесы, принимающие наличные средства, становятся подвергаются риску принять фальшивую купюру, что в конечном итоге может снизить прибыль и повлечь за собой юридические последствия.
Увеличение инфляции.
Фальшивые деньги увеличивают количество в обращении, что в свою очередь может привести к инфляции. Рост количества контрафактных купюр создает дополнительный денежный объем, не обеспеченный реальными товарами и услугами. Это может существенно подорвать доверие к национальной валюте и стимулировать рост цен.
Пагуба для доверия к финансовой системе.
Фальшивые деньги вызывают мизерию к финансовой системе в целом. Когда люди сталкиваются с риском получить фальшивые купюры при каждой сделке, они становятся более склонными избегать использования наличных средств, что может привести к обострению проблем, связанных с электронными платежами и банковскими системами.
Защитные меры и образование.
Для предотвращения распространению фальшивых денег необходимо внедрять более продвинутые защитные меры на банкнотах и активно проводить образовательную работу среди населения. Гражданам нужно быть более внимательными при приеме наличных средств и обучаться элементам распознавания фальшивых купюр.
В заключение:
Фальшивые купюры 5000 рублей представляют серьезную угрозу для финансовой стабильности и безопасности граждан. Необходимо активно внедрять новые технологии защиты и проводить информационные кампании, чтобы общество было лучше осведомлено о методах распознавания и защиты от фальшивых денег. Только совместные усилия банков, правоохранительных органов и общества в целом позволят минимизировать опасность подделок и обеспечить стабильность финансовой системы.
Приобрести фальшивые деньги может привлекаться привлекательным вариантом для некоторых людей, но в реальности это действие несет глубокие последствия и нарушает основы экономической стабильности. В данной статье мы рассмотрим вредные аспекты приобретения поддельной валюты и почему это является опасным действием.
Противозаконность.
Основное и чрезвычайно значимое, что следует отметить - это полная противозаконность создания и использования фальшивых денег. Такие поступки противоречат правилам большинства стран, и их воздаяние может быть очень строгим. Покупка поддельной валюты влечет за собой риск уголовного преследования, штрафов и даже тюремного заключения.
Экономические последствия.
Фальшивые деньги вредно влияют на экономику в целом. Когда в обращение поступает фальшивая валюта, это создает дисбаланс и ухудшает доверие к национальной валюте. Компании и граждане становятся все более подозрительными при проведении финансовых сделок, что ведет к ухудшению бизнес-климата и препятствует нормальному функционированию рынка.
Потенциальная угроза финансовой стабильности.
Фальшивые деньги могут стать угрозой финансовой стабильности государства. Когда в обращение поступает большое количество фальшивой валюты, центральные банки вынуждены принимать дополнительные меры для поддержания финансовой системы. Это может включать в себя растущие процентных ставок, что, в свою очередь, вредно сказывается на экономике и финансовых рынках.
Опасности для честных граждан и предприятий.
Люди и компании, неосознанно принимающие фальшивые деньги в качестве оплаты, становятся пострадавшими преступных схем. Подобные ситуации могут вызвать к финансовым убыткам и утрате доверия к своим деловым партнерам.
Вовлечение криминальных группировок.
Закупка фальшивых денег часто связана с бандитскими группировками и организованным преступлением. Вовлечение в такие сети может повлечь за собой серьезными последствиями для личной безопасности и даже угрожать жизни.
В заключение, покупка фальшивых денег – это не только незаконное действие, но и поступок, готовое повлечь ущерб экономике и обществу в целом. Рекомендуется избегать подобных практик и сосредотачиваться на легальных, ответственных методах обращения с финансами
Введение:
Мошенничество с деньгами – нарушение, оставшееся актуальным на продолжительностью многих веков. Производство и распространение фальшивых денег представляют серьезную угрозу не только для экономической системы, но и для стабильности в обществе. В данной статье мы рассмотрим масштабы проблемы, методы борьбы с подделкой денег и последствия для общества.
История фальшивых денег:
Поддельные средства существуют с момента появления самой идеи денег. В старину подделывались металлические монеты, а в наше время преступники активно используют новейшие технологии для фальсификации банкнот. Развитие цифровых технологий также открыло новые возможности для создания электронных аналогов денег.
Масштабы проблемы:
Фальшивые деньги создают опасность для стабильности экономики. Финансовые учреждения, компании и даже обычные граждане могут стать жертвами мошенничества. Рост количества фальшивых денег может привести к инфляции и даже к экономическим кризисам.
Современные методы подделки:
С развитием технологий подделка стала более затруднительной и изощренной. Преступники используют высокотехнологичное оборудование, профессиональные печатающие устройства, и даже искусственный интеллект для создания невозможно отличить поддельные копии от оригинальных денежных средств.
Борьба с фальшивомонетничеством:
Страны и центральные банки активно внедряют современные методы для предотвращения подделки денег. Это включает в себя использование новейших защитных технологий на банкнотах, обучение граждан способам определения поддельных денег, а также сотрудничество с органами правопорядка для обнаружения и предотвращения криминальных группировок.
Последствия для общества:
Поддельные средства несут не только экономические, но и общественные последствия. Граждане и бизнесы теряют веру к экономическому устройству, а борьба с преступностью требует значительных ресурсов, которые могли бы быть направлены на более полезные цели.
Заключение:
Фальшивые деньги – важный вопрос, требующая уделяемого внимания и совместных усилий общества, органов правопорядка и учреждений финансов. Только путем активной противодействия с этим преступлением можно обеспечить стабильность финансовой системы и сохранить уважение к денежной системе
Заголовок: Опасность подпольных точек: Места продажи фальшивых купюр
Введение:
Разговор об угрозе подпольных точек, занимающихся продажей поддельных денег, становится всё более актуальным в современном обществе. Эти места, предоставляя доступ к поддельным финансовым средствам, представляют серьезную угрозу для экономической стабильности и безопасности граждан.
Легкость доступа:
Одной из проблем подпольных точек является легкость доступа к поддельным деньгам. На темных улицах или в скрытых интернет-пространствах, эти места становятся площадкой для тех, кто ищет возможность обмануть систему.
Угроза финансовой системе:
Продажа поддельных купюр в таких местах создает реальную угрозу для финансовой системы. Введение поддельных средств в обращение может привести к инфляции, понижению доверия к национальной валюте и даже к финансовым кризисам.
Мошенничество и преступность:
Подпольные точки, предлагающие поддельные средства, являются очагами мошенничества и преступной деятельности. Отсутствие контроля и законного регулирования в этих местах обеспечивает благоприятные условия для криминальных элементов.
Угроза для бизнеса и обычных граждан:
Как бизнесы, так и обычные граждане становятся потенциальными жертвами мошенничества, когда используют поддельные деньги, приобретенные в подпольных точках. Это ведет к утрате доверия и серьезным финансовым потерям.
Последствия для экономики:
Вмешательство нелегальных торговых мест в экономику оказывает отрицательное воздействие. Нарушение стабильности финансовой системы и создание дополнительных трудностей для правоохранительных органов являются лишь частью последствий для общества.
Заключение:
Продажа поддельных средств в подпольных точках представляет собой серьезную угрозу для общества в целом. Необходимо ужесточение законодательства и усиление контроля, чтобы противостоять этому злу и обеспечить безопасность экономической среды. Развитие сотрудничества между государственными органами, бизнес-сообществом и обществом в целом является ключевым моментом в предотвращении негативных последствий деятельности подобных точек.
Введение:
Фальшивые деньги стали неотъемлемой частью теневого мира, где пункты сбыта – это факторы серьезных угроз для экономики и общества. В данной статье мы обратим внимание на места, где процветает подпольная торговля поддельными денежными средствами, включая темные уголки интернета.
Теневые интернет-магазины:
С прогрессом технологий и распространением онлайн-торговли, места продаж поддельных банкнот стали активно функционировать в засекреченных местах интернета. Скрытые онлайн-площадки и форумы предоставляют шанс анонимно приобрести поддельные денежные средства, создавая тем самым серьезную угрозу для экономики.
Опасные последствия для общества:
Точки оборота поддельных средств на темных интернет-ресурсах несут в себе не только угрозу для экономической устойчивости, но и для простых людей. Покупка фальшивых купюр влечет за собой риски: от судебных преследований до потери доверия со стороны окружающих.
Передовые технологии подделки:
На скрытых веб-площадках активно используются передовые технологии для создания высококачественных подделок. От печатающих устройств, способных воспроизводить защитные элементы, до использования криптовалютных платежей для обеспечения анонимности покупок – все это создает среду, в которой трудно обнаружить и пресечь незаконную торговлю.
Необходимость ужесточения мер борьбы:
Противостояние с темными местами продаж фальшивых купюр требует комплексного подхода. Важно ужесточить законодательство и разработать активные методы для выявления и блокировки теневых интернет-магазинов. Также критически важно поднимать готовность к информации общества относительно рисков подобных действий.
Заключение:
Площадки продаж поддельных денег на скрытых местах интернета представляют собой значительную опасность для устойчивости экономики и общественной безопасности. В условиях расцветающего цифрового мира важно сосредотачивать усилия на противостоянии с подобными действиями, чтобы защитить интересы общества и сохранить веру к финансовой системе
Фальшивые рубли, обычно, подделывают с целью обмана и незаконного получения прибыли. Шулеры занимаются клонированием российских рублей, создавая поддельные банкноты различных номиналов. В основном, подделывают банкноты с большими номиналами, вроде 1 000 и 5 000 рублей, так как это позволяет им зарабатывать крупные суммы при меньшем количестве фальшивых денег.
Технология подделки рублей включает в себя применение высокотехнологичного оборудования, специализированных принтеров и специально подготовленных материалов. Злоумышленники стремятся максимально точно воспроизвести средства защиты, водяные знаки, металлическую защитную полосу, микроскопический текст и другие характеристики, чтобы затруднить определение поддельных купюр.
Поддельные денежные средства периодически вносятся в оборот через торговые площадки, банки или прочие учреждения, где они могут быть легко спрятаны среди реальных денежных средств. Это создает серьезные трудности для экономической системы, так как фальшивые деньги могут порождать убыткам как для банков, так и для населения.
Необходимо подчеркнуть, что имение и применение фальшивых денег представляют собой уголовными преступлениями и подпадают под наказание в соответствии с нормативными актами Российской Федерации. Власти активно борются с такими преступлениями, предпринимая меры по выявлению и пресечению деятельности преступных групп, занимающихся фальсификацией российской валюты
Технология подделки рублей включает в себя применение технологического оборудования высокого уровня, специализированных печатающих устройств и особо подготовленных материалов. Преступники стремятся максимально точно воспроизвести защитные элементы, водяные знаки безопасности, металлическую защиту, микротекст и другие характеристики, чтобы замедлить определение поддельных купюр.
Фальшивые рубли регулярно вносятся в оборот через торговые площадки, банки или прочие учреждения, где они могут быть легко спрятаны среди реальных денежных средств. Это порождает серьезные трудности для финансовой системы, так как поддельные купюры могут порождать потерям как для банков, так и для населения.
Столь же важно подчеркнуть, что имение и применение фальшивых денег являются уголовными преступлениями и подпадают под наказание в соответствии с нормативными актами Российской Федерации. Власти проводят активные меры с подобными правонарушениями, предпринимая действия по обнаружению и прекращению деятельности банд преступников, занимающихся подделкой российских рублей
הימונים הפכו לתחום פופולרי ומרתק מאוד בעידן האינטרנט הדיגיטלי. מיליוני משתתפים מכל רחבי העולם מנסים את מזלם בסוגי ההימונים. מהדרך בה הם משנים את רגעי הניסיון וההתרגשות שלהם, ועד לשאלות האתיות והחברתיות העומדות מאחורי ההימונים, הכל הולך ומשתנה.
ההמרות ברשת הם פעילות מובילה מאוד כיום, כשאנשים מבצעים באמצעות האינטרנט המרות על אירועים ספורטיביים, תוצאות פוליטיות, ואף על תוצאות מזג האוויר ובכלל ניתן להמר כמעט על כל דבר. ההמרות באינטרנט מתבצעים באמצעות אתרי וירטואליים אונליין, והם מציעים למשתתפים להמר סכומי כסף על תוצאות אפשריות.
ההמרות היו חלק מהתרבות האנושית מאז זמן רב. מקורות ההמרות הראשוניים החשובים בהיסטוריה הם המשחקים הבימבומיים בסין העתיקה וההימורים על משחקי קלפים באירופה בימי הביניים. היום, ההימורים התפשו גם כסוג של בידור וכאמצעי לרווח כספי. ההימורים הפכו לחלק מובהק מתרבות הספורט, הפנאי והבידור של החברה המודרנית.
ספרי המתנדבים וקזינואים, לוטו, טוטו והימורי ספורט מרובים הפכו לחלק בלתי נפרד מהעשייה הכלכלית והתרבותית. הם נעשים מתוך מניעים שונים, כולל התעניינות, התרגשות ורווח. כמה משתתפים נהנים מהרגע הרגשי שמגיע עם הרווחים, בעוד אחרים מחפשים לשפר את מצבם הכלכלי באמצעות המרות מרובים.
האינטרנט הביא את הימונים לרמה חדשה. אתרי ההמרות המקוונים מאפשרים לאנשים להמר בקלות ובנוחות מביתם. הם נתנו לתחום גישה גלובלית והרבה יותר פשוטה וקלה.
Ngamenjitu telah menjadi salah satu situs judi daring terbesar dan terjamin di Indonesia. Dengan beragam market yang disediakan dari Grup Semar, Ngamenjitu menawarkan pengalaman main togel yang tak tertandingi kepada para penggemar judi daring.
Market Terbaik dan Terlengkap
Dengan total 56 pasaran, Ngamenjitu memperlihatkan berbagai opsi terbaik dari market togel di seluruh dunia. Mulai dari pasaran klasik seperti Sydney, Singapore, dan Hongkong hingga market eksotis seperti Thailand, Germany, dan Texas Day, setiap pemain dapat menemukan pasaran favorit mereka dengan mudah.
Langkah Bermain yang Mudah
Portal Judi menyediakan petunjuk cara main yang sederhana dipahami bagi para pemula maupun penggemar togel berpengalaman. Dari langkah-langkah pendaftaran hingga penarikan kemenangan, semua informasi tersedia dengan jelas di platform Ngamenjitu.
Ringkasan Terakhir dan Informasi Terkini
Pemain dapat mengakses hasil terakhir dari setiap market secara real-time di Portal Judi. Selain itu, info paling baru seperti jadwal bank online, gangguan, dan offline juga disediakan untuk memastikan kelancaran proses transaksi.
Pelbagai Jenis Game
Selain togel, Situs Judi juga menawarkan bervariasi jenis permainan kasino dan judi lainnya. Dari bingo hingga roulette, dari dragon tiger hingga baccarat, setiap pemain dapat menikmati bervariasi pilihan permainan yang menarik dan menghibur.
Security dan Kepuasan Klien Dijamin
Ngamenjitu mengutamakan keamanan dan kepuasan pelanggan. Dengan sistem security terbaru dan layanan pelanggan yang responsif, setiap pemain dapat bermain dengan nyaman dan tenang di platform ini.
Promosi-Promosi dan Bonus Menarik
Portal Judi juga menawarkan bervariasi promosi dan hadiah menarik bagi para pemain setia maupun yang baru bergabung. Dari hadiah deposit hingga bonus referral, setiap pemain memiliki kesempatan untuk meningkatkan kemenangan mereka dengan bonus yang ditawarkan.
Dengan semua fitur dan layanan yang ditawarkan, Ngamenjitu tetap menjadi pilihan utama bagi para penggemar judi online di Indonesia. Bergabunglah sekarang dan nikmati pengalaman bermain yang seru dan menguntungkan di Ngamenjitu!
Ngamenjitu: Portal Lotere Daring Terbesar dan Terpercaya
Ngamenjitu telah menjadi salah satu situs judi daring terbesar dan terjamin di Indonesia. Dengan beragam market yang disediakan dari Grup Semar, Situs Judi menawarkan sensasi bermain togel yang tak tertandingi kepada para penggemar judi daring.
Pasaran Terunggul dan Terlengkap
Dengan total 56 market, Situs Judi menampilkan berbagai opsi terunggul dari market togel di seluruh dunia. Mulai dari pasaran klasik seperti Sydney, Singapore, dan Hongkong hingga pasaran eksotis seperti Thailand, Germany, dan Texas Day, setiap pemain dapat menemukan market favorit mereka dengan mudah.
Cara Bermain yang Sederhana
Ngamenjitu menyediakan panduan cara main yang mudah dipahami bagi para pemula maupun penggemar togel berpengalaman. Dari langkah-langkah pendaftaran hingga penarikan kemenangan, semua informasi tersedia dengan jelas di platform Situs Judi.
Hasil Terkini dan Info Terkini
Pemain dapat mengakses hasil terakhir dari setiap market secara real-time di Ngamenjitu. Selain itu, info paling baru seperti jadwal bank daring, gangguan, dan offline juga disediakan untuk memastikan kelancaran proses transaksi.
Pelbagai Macam Permainan
Selain togel, Portal Judi juga menawarkan bervariasi jenis permainan kasino dan judi lainnya. Dari bingo hingga roulette, dari dragon tiger hingga baccarat, setiap pemain dapat menikmati berbagai pilihan permainan yang menarik dan menghibur.
Security dan Kenyamanan Pelanggan Terjamin
Situs Judi mengutamakan security dan kenyamanan pelanggan. Dengan sistem keamanan terbaru dan layanan pelanggan yang responsif, setiap pemain dapat bermain dengan nyaman dan tenang di platform ini.
Promosi-Promosi dan Bonus Menarik
Portal Judi juga menawarkan bervariasi promosi dan hadiah menarik bagi para pemain setia maupun yang baru bergabung. Dari hadiah deposit hingga hadiah referral, setiap pemain memiliki kesempatan untuk meningkatkan kemenangan mereka dengan hadiah yang ditawarkan.
Dengan semua fasilitas dan pelayanan yang ditawarkan, Ngamenjitu tetap menjadi pilihan utama bagi para penggemar judi online di Indonesia. Bergabunglah sekarang dan nikmati pengalaman bermain yang seru dan menguntungkan di Ngamenjitu!
לחפש האם טלגראס ולהתחבר בכדי להפעיל בעבודה.
בצורה זו או אז האם זה מותר?
התשובה היא - זה תלוי באזרחות אתה נמצא בה.
בכמה מדינות, כמו ישראל כלומר, קניית אש עשויה להיות חוקית לצורכים רפואיים, או בעצם רשומים עם גורמי גורמי הרשות הרלוונטיים.
Situs Judi telah menjadi salah satu platform judi daring terluas dan terpercaya di Indonesia. Dengan bervariasi market yang disediakan dari Semar Group, Portal Judi menawarkan sensasi main togel yang tak tertandingi kepada para penggemar judi daring.
Market Terunggul dan Terpenuhi
Dengan total 56 pasaran, Ngamenjitu menampilkan berbagai opsi terunggul dari market togel di seluruh dunia. Mulai dari market klasik seperti Sydney, Singapore, dan Hongkong hingga pasaran eksotis seperti Thailand, Germany, dan Texas Day, setiap pemain dapat menemukan pasaran favorit mereka dengan mudah.
Langkah Main yang Mudah
Ngamenjitu menyediakan petunjuk cara main yang praktis dipahami bagi para pemula maupun penggemar togel berpengalaman. Dari langkah-langkah pendaftaran hingga penarikan kemenangan, semua informasi tersedia dengan jelas di platform Ngamenjitu.
Rekapitulasi Terkini dan Info Paling Baru
Pemain dapat mengakses hasil terakhir dari setiap market secara real-time di Ngamenjitu. Selain itu, informasi terkini seperti jadwal bank daring, gangguan, dan offline juga disediakan untuk memastikan kelancaran proses transaksi.
Berbagai Jenis Permainan
Selain togel, Situs Judi juga menawarkan berbagai jenis permainan kasino dan judi lainnya. Dari bingo hingga roulette, dari dragon tiger hingga baccarat, setiap pemain dapat menikmati bervariasi pilihan permainan yang menarik dan menghibur.
Security dan Kenyamanan Pelanggan Dijamin
Situs Judi mengutamakan security dan kepuasan pelanggan. Dengan sistem keamanan terbaru dan layanan pelanggan yang responsif, setiap pemain dapat bermain dengan nyaman dan tenang di platform ini.
Promosi-Promosi dan Hadiah Istimewa
Situs Judi juga menawarkan bervariasi promosi dan hadiah menarik bagi para pemain setia maupun yang baru bergabung. Dari bonus deposit hingga bonus referral, setiap pemain memiliki kesempatan untuk meningkatkan kemenangan mereka dengan hadiah yang ditawarkan.
Dengan semua fitur dan layanan yang ditawarkan, Portal Judi tetap menjadi pilihan utama bagi para penggemar judi online di Indonesia. Bergabunglah sekarang dan nikmati pengalaman bermain yang seru dan menguntungkan di Portal Judi!
Portal Judi: Platform Lotere Online Terbesar dan Terjamin
Portal Judi telah menjadi salah satu portal judi daring terbesar dan terpercaya di Indonesia. Dengan beragam pasaran yang disediakan dari Semar Group, Ngamenjitu menawarkan pengalaman main togel yang tak tertandingi kepada para penggemar judi daring.
Market Terunggul dan Terlengkap
Dengan total 56 pasaran, Situs Judi memperlihatkan berbagai opsi terunggul dari pasaran togel di seluruh dunia. Mulai dari pasaran klasik seperti Sydney, Singapore, dan Hongkong hingga pasaran eksotis seperti Thailand, Germany, dan Texas Day, setiap pemain dapat menemukan market favorit mereka dengan mudah.
Metode Main yang Sederhana
Ngamenjitu menyediakan panduan cara main yang sederhana dipahami bagi para pemula maupun penggemar togel berpengalaman. Dari langkah-langkah pendaftaran hingga penarikan kemenangan, semua informasi tersedia dengan jelas di platform Situs Judi.
Hasil Terkini dan Info Terkini
Pemain dapat mengakses hasil terakhir dari setiap market secara real-time di Situs Judi. Selain itu, informasi terkini seperti jadwal bank daring, gangguan, dan offline juga disediakan untuk memastikan kelancaran proses transaksi.
Bermacam-macam Macam Game
Selain togel, Ngamenjitu juga menawarkan bervariasi jenis permainan kasino dan judi lainnya. Dari bingo hingga roulette, dari dragon tiger hingga baccarat, setiap pemain dapat menikmati berbagai pilihan permainan yang menarik dan menghibur.
Keamanan dan Kenyamanan Klien Dijamin
Portal Judi mengutamakan security dan kenyamanan pelanggan. Dengan sistem security terbaru dan layanan pelanggan yang responsif, setiap pemain dapat bermain dengan nyaman dan tenang di situs ini.
Promosi-Promosi dan Bonus Istimewa
Situs Judi juga menawarkan berbagai promosi dan hadiah menarik bagi para pemain setia maupun yang baru bergabung. Dari bonus deposit hingga bonus referral, setiap pemain memiliki kesempatan untuk meningkatkan kemenangan mereka dengan hadiah yang ditawarkan.
Dengan semua fitur dan pelayanan yang ditawarkan, Situs Judi tetap menjadi pilihan utama bagi para penggemar judi online di Indonesia. Bergabunglah sekarang dan nikmati pengalaman bermain yang seru dan menguntungkan di Portal Judi!
Частота обналичивания карт:
Обналичивание карт является довольно распространенным явлением, и его частота постоянно растет с увеличением числа электронных транзакций. Киберпреступники применяют различные методы для получения доступа к финансовым средствам, включая фишинг, вредоносное программное обеспечение, скимминг и другие инновационные подходы.
Методы обналичивания карт:
Фишинг: Злоумышленники могут отправлять фальшивые электронные сообщения или создавать веб-сайты, имитирующие банковские системы, с целью получения личной информации от владельцев карт.
Скимминг: Злоумышленники устанавливают устройства скиммеры на банкоматах или терминалах для считывания данных с магнитных полос карт.
Вредоносное программное обеспечение: Киберпреступники разрабатывают вредоносные программы, которые заражают компьютеры и мобильные устройства, чтобы получить доступ к личным данным и банковским счетам.
Сетевые атаки: Атаки на системы банков и платежных платформ могут привести к утечке информации о картах и, следовательно, к их обналичиванию.
Последствия обналичивания карт:
Финансовые потери для клиентов: Владельцы карт могут столкнуться с материальными потерями, так как средства могут быть списаны с их счетов без их ведома.
Угроза безопасности данных: Обналичивание карт подчеркивает угрозу безопасности личных данных, что может привести к краже личной и финансовой информации.
Ущерб репутации банков: Банки и другие финансовые учреждения могут столкнуться с утратой доверия со стороны клиентов, если их системы безопасности оказываются уязвимыми.
Проблемы для экономики: Обналичивание карт создает экономический ущерб, поскольку оно стимулирует дополнительные затраты на борьбу с мошенничеством и восстановление утраченных средств.
Борьба с обналичиванием карт:
Совершенствование технологий безопасности: Банки и финансовые институты постоянно совершенствуют свои системы безопасности, чтобы предотвратить несанкционированный доступ к картам.
Образование и информирование: Обучение клиентов о методах мошенничества и том, как защитить свои данные, является важным шагом в борьбе с обналичиванием карт.
Сотрудничество с правоохранительными органами: Банки активно сотрудничают с правоохранительными органами для выявления и пресечения преступных схем.
Заключение:
Обналичивание карт – значительная угроза для финансовой стабильности и безопасности личных данных. Решение этой проблемы требует совместных усилий со стороны банков, правоохранительных органов и общества в целом. Только эффективная борьба с мошенничеством позволит обеспечить безопасность электронных платежей и защитить интересы всех участников финансовой системы.
Данные веб-ресурсы способны предлагать различные сервисы, относящиеся с преступной деятельностью, например фальсификация, скимминг, вредное ПО и прочие методы для получения данных с банковских карт. Кроме того рассматриваются темы, связанные с использованием похищенных информации для осуществления финансовых операций или вывода денег.
Пользователи незаконных форумов по обналу банковских карт могут стремиться оставаться анонимными и избегать привлечения внимания органов безопасности. Они могут обмениваться рекомендациями, предлагать сервисы, связанные с обналом, а также проводить сделки, направленные на незаконную финансовую деятельность.
Необходимо подчеркнуть, что содействие в таких практиках не только представляет собой нарушение правовых норм, но также способно приводить к юридическим санкциям и наказанию.
В сегодняшнем обществе, где виртуальные платежи становятся все более распространенными, противоправные лица не оставляют без внимания и классические методы недобросовестных действий, такие как распространение недостоверных банкнот. В настоящее время стало известно о незаконной торговле поддельных 5000 рублевых купюр, что представляет значительную риск для финансовых институтов и сообщества в совокупности.
Методы передачи:
Преступники активно используют закрытые сети сети для продажи недостоверных 5000 рублей. На подпольных веб-ресурсах и незаконных форумах можно обнаружить прошения о покупке поддельных банкнот. К неудовольствию, это создает положительные условия для дистрибуции фальшивых денег среди населения.
Последствия для граждан:
Возможность контрафактных денег в хождении может иметь серьезные результаты для финансовой структуры и авторитета к рублю. Люди, не поддаваясь, что получили поддельные купюры, могут использовать их в разнообразных ситуациях, что в последней инстанции приводит к ущербу поверию к банкнотам определенного номинала.
Опасности для индивидуумов:
Гражданское население становятся предполагаемыми жертвами преступников, когда они ненамеренно получают фальшивые деньги в сделках или при покупках. В следствие, они могут столкнуться с неприятными ситуациями, такими как отклонение торговых посредников принять контрафактные купюры или даже вероятность привлечения к ответственности за пробу расплаты недостоверными деньгами.
Столкновение с распространением недостоверных денег:
В интересах предотвращения граждан от схожих правонарушений необходимо усилить меры по обнаружению и остановке производственной деятельности контрафактных денег. Это включает в себя сотрудничество между правоохранительными органами и банками, а также увеличение степени информированности общества относительно символов недостоверных банкнот и методов их обнаружения.
Итог:
Прокладывание фальшивых 5000 рублей – это важная риск для финансового благополучия и устойчивости граждан. Сохранение доверия к рублю требует коллективных усилий со с участием государственных органов, финансовых организаций и каждого гражданина. Важно быть осторожным и осведомленным, чтобы предотвратить прокладывание контрафактных денег и обеспечить финансовые средства сообщества.
Нарушение законов:
Получение или воспользование лживых денег приравниваются к противоправным деянием, нарушающим нормы территории. Вас могут подвергнуть судебному преследованию, которое может послать в тюремному заключению, финансовым санкциям или лишению свободы.
Ущерб доверию:
Фальшивые купюры нарушают доверенность по отношению к денежной организации. Их использование порождает риск для благоприятных людей и организаций, которые в состоянии попасть в внезапными потерями.
Экономический ущерб:
Разведение поддельных купюр осуществляет воздействие на хозяйство, провоцируя распределение денег и подрывая всеобщую экономическую устойчивость. Это может повлечь за собой потере доверия в денежной единице.
Риск обмана:
Люди, какие, вовлечены в изготовлением лживых купюр, не обязаны сохранять какие-либо нормы степени. Контрафактные банкноты могут быть легко распознаны, что, в конечном итоге повлечь за собой потерям для тех пытается использовать их.
Юридические последствия:
В ситуации лишения свободы при воспользовании поддельных купюр, вас способны принудительно обложить штрафами, и вы столкнетесь с юридическими проблемами. Это может оказать воздействие на вашем будущем, в том числе трудности с поиском работы и историей кредита.
Благосостояние общества и личное благополучие зависят от правдивости и доверии в финансовой деятельности. Получение фальшивых денег не соответствует этим принципам и может иметь важные последствия. Советуем придерживаться правил и заниматься только правомерными финансовыми операциями.
Ngamenjitu telah menjadi salah satu portal judi daring terbesar dan terpercaya di Indonesia. Dengan bervariasi pasaran yang disediakan dari Semar Group, Situs Judi menawarkan pengalaman main togel yang tak tertandingi kepada para penggemar judi daring.
Market Terunggul dan Terlengkap
Dengan total 56 pasaran, Portal Judi memperlihatkan berbagai opsi terunggul dari pasaran togel di seluruh dunia. Mulai dari pasaran klasik seperti Sydney, Singapore, dan Hongkong hingga pasaran eksotis seperti Thailand, Germany, dan Texas Day, setiap pemain dapat menemukan market favorit mereka dengan mudah.
Langkah Main yang Praktis
Portal Judi menyediakan panduan cara main yang sederhana dipahami bagi para pemula maupun penggemar togel berpengalaman. Dari langkah-langkah pendaftaran hingga penarikan kemenangan, semua informasi tersedia dengan jelas di situs Portal Judi.
Rekapitulasi Terakhir dan Informasi Terkini
Pemain dapat mengakses hasil terakhir dari setiap pasaran secara real-time di Portal Judi. Selain itu, informasi paling baru seperti jadwal bank online, gangguan, dan offline juga disediakan untuk memastikan kelancaran proses transaksi.
Pelbagai Macam Game
Selain togel, Situs Judi juga menawarkan berbagai jenis permainan kasino dan judi lainnya. Dari bingo hingga roulette, dari dragon tiger hingga baccarat, setiap pemain dapat menikmati berbagai pilihan permainan yang menarik dan menghibur.
Security dan Kenyamanan Klien Dijamin
Ngamenjitu mengutamakan keamanan dan kenyamanan pelanggan. Dengan sistem security terbaru dan layanan pelanggan yang responsif, setiap pemain dapat bermain dengan nyaman dan tenang di platform ini.
Promosi dan Hadiah Istimewa
Situs Judi juga menawarkan berbagai promosi dan hadiah menarik bagi para pemain setia maupun yang baru bergabung. Dari bonus deposit hingga hadiah referral, setiap pemain memiliki kesempatan untuk meningkatkan kemenangan mereka dengan hadiah yang ditawarkan.
Dengan semua fasilitas dan pelayanan yang ditawarkan, Ngamenjitu tetap menjadi pilihan utama bagi para penggemar judi online di Indonesia. Bergabunglah sekarang dan nikmati pengalaman bermain yang seru dan menguntungkan di Portal Judi!
Покупка поддельных купюр считается недозволенным или опасным действием, которое имеет возможность послать в важным правовым наказаниям либо ущербу личной финансовой надежности. Вот некоторые другие приводов, почему закупка лживых денег является опасной либо недопустимой:
Нарушение законов:
Закупка и использование контрафактных купюр представляют собой правонарушением, противоречащим законы территории. Вас способны подвергнуть себя наказанию, что потенциально закончиться аресту, финансовым санкциям и тюремному заключению.
Ущерб доверию:
Поддельные деньги ухудшают уверенность в финансовой организации. Их использование формирует угрозу для порядочных людей и предприятий, которые могут попасть в неожиданными перебоями.
Экономический ущерб:
Разнос контрафактных денег осуществляет воздействие на экономику, провоцируя распределение денег что ухудшает всеобщую финансовую стабильность. Это может закончиться утрате уважения к денежной системе.
Риск обмана:
Лица, которые, вовлечены в производством контрафактных банкнот, не обязаны сохранять какие-то нормы степени. Поддельные бумажные деньги могут быть легко распознаны, что, в конечном итоге приведет к ущербу для тех стремится воспользоваться ими.
Юридические последствия:
В ситуации лишения свободы при воспользовании лживых банкнот, вас способны оштрафовать, и вы столкнетесь с юридическими трудностями. Это может оказать воздействие на вашем будущем, включая проблемы с поиском работы и кредитной историей.
Общественное и личное благополучие зависят от честности и доверии в финансовой сфере. Закупка фальшивых банкнот нарушает эти принципы и может представлять важные последствия. Рекомендуется придерживаться законов и осуществлять только законными финансовыми сделками.
Покупка лживых банкнот представляет собой незаконным и рискованным поступком, которое имеет возможность привести к серьезным правовым последствиям или ущербу вашей финансовой стабильности. Вот несколько приводов, почему получение фальшивых банкнот приравнивается к рискованной или неуместной:
Нарушение законов:
Покупка и использование лживых банкнот являются противоправным деянием, нарушающим правила государства. Вас имеют возможность поддать уголовной ответственности, что потенциально привести к лишению свободы, финансовым санкциям и тюремному заключению.
Ущерб доверию:
Поддельные банкноты ослабляют веру к денежной системе. Их применение создает возможность для порядочных людей и коммерческих структур, которые имеют возможность столкнуться с неожиданными убытками.
Экономический ущерб:
Расширение поддельных денег осуществляет воздействие на хозяйство, вызывая денежное расширение и ухудшающая общую финансовую стабильность. Это способно закончиться утрате уважения к денежной системе.
Риск обмана:
Лица, какие, задействованы в производством поддельных банкнот, не обязаны поддерживать какие-либо стандарты характеристики. Контрафактные деньги могут быть легко обнаружены, что в конечном счете повлечь за собой убыткам для тех, кто собирается использовать их.
Юридические последствия:
В случае захвата при использовании фальшивых денег, вас могут наказать штрафом, и вы столкнетесь с законными сложностями. Это может отразиться на вашем будущем, с учетом сложности с трудоустройством и кредитной историей.
Общественное и индивидуальное благосостояние зависят от правдивости и доверии в финансовой сфере. Покупка фальшивых банкнот противоречит этим принципам и может представлять важные последствия. Рекомендуется соблюдать норм и осуществлять только законными финансовыми действиями.
Нарушение законов:
Покупка иначе эксплуатация поддельных денег приравниваются к нарушением закона, противоречащим нормы территории. Вас могут подвергнуть юридическим последствиям, что может повлечь за собой тюремному заключению, денежным наказаниям или лишению свободы.
Ущерб доверию:
Контрафактные банкноты подрывают доверие в финансовой системе. Их использование порождает опасность для честных граждан и организаций, которые могут завязать неожиданными потерями.
Экономический ущерб:
Разведение лживых купюр осуществляет воздействие на хозяйство, провоцируя рост цен что ухудшает всеобщую финансовую равновесие. Это может привести к потере доверия к денежной системе.
Риск обмана:
Люди, кто, осуществляют производством лживых купюр, не обязаны соблюдать какие-либо параметры качества. Поддельные деньги могут выйти легко распознаваемы, что, в итоге закончится ущербу для тех, кто стремится применять их.
Юридические последствия:
При событии захвата при использовании контрафактных денег, вас могут оштрафовать, и вы столкнетесь с юридическими трудностями. Это может отразиться на вашем будущем, включая проблемы с получением работы и кредитной историей.
Благосостояние общества и личное благополучие зависят от честности и доверии в финансовой сфере. Закупка контрафактных банкнот не соответствует этим принципам и может порождать серьезные последствия. Рекомендуется держаться норм и осуществлять только правомерными финансовыми сделками.
Покупка лживых банкнот является недозволенным либо опасительным действием, что способно повлечь за собой тяжелым правовым санкциям и вреду вашей финансовой надежности. Вот несколько последствий, из-за чего закупка контрафактных купюр приравнивается к опасной иначе недопустимой:
Нарушение законов:
Получение и воспользование фальшивых банкнот являются правонарушением, противоречащим положения страны. Вас способны поддать судебному преследованию, которое может привести к аресту, штрафам или лишению свободы.
Ущерб доверию:
Контрафактные банкноты ухудшают уверенность к денежной структуре. Их использование создает угрозу для надежных личностей и бизнесов, которые могут претерпеть внезапными потерями.
Экономический ущерб:
Расширение фальшивых банкнот влияет на экономическую сферу, провоцируя денежное расширение и ухудшая всеобщую денежную устойчивость. Это в состоянии закончиться потере уважения к денежной единице.
Риск обмана:
Личности, кто, осуществляют производством контрафактных банкнот, не обязаны соблюдать какие угодно уровни уровня. Контрафактные купюры могут быть легко выявлены, что, в конечном итоге повлечь за собой убыткам для тех попытается использовать их.
Юридические последствия:
При случае захвата при использовании контрафактных купюр, вас могут принудительно обложить штрафами, и вы столкнетесь с юридическими проблемами. Это может отразиться на вашем будущем, включая возможные проблемы с получением работы с кредитной историей.
Общественное и индивидуальное благосостояние зависят от правдивости и доверии в финансовой сфере. Приобретение фальшивых банкнот идет вразрез с этими принципами и может представлять важные последствия. Предлагается держаться законов и вести только законными финансовыми транзакциями.
Покупка фальшивых банкнот является незаконным и опасным действием, которое в состоянии закончиться серьезным юридическими последствиям и ущербу индивидуальной денежной надежности. Вот несколько примет, вследствие чего покупка контрафактных денег представляет собой рискованной либо неприемлемой:
Нарушение законов:
Закупка и воспользование контрафактных денег являются противоправным деянием, нарушающим законы страны. Вас в состоянии подвергнуться судебному преследованию, которое может закончиться лишению свободы, взысканиям и тюремному заключению.
Ущерб доверию:
Контрафактные деньги подрывают веру по отношению к денежной механизму. Их обращение возникает риск для честных граждан и предприятий, которые могут завязать неожиданными перебоями.
Экономический ущерб:
Разнос контрафактных купюр оказывает воздействие на хозяйство, провоцируя распределение денег и ухудшающая глобальную финансовую устойчивость. Это имеет возможность привести к потере доверия к денежной системе.
Риск обмана:
Те, которые, задействованы в производством контрафактных купюр, не обязаны поддерживать какие-то параметры характеристики. Фальшивые деньги могут выйти легко выявлены, что, в итоге послать в потерям для тех, кто стремится их использовать.
Юридические последствия:
В ситуации попадания под арест при использовании поддельных денег, вас имеют возможность взыскать штраф, и вы столкнетесь с юридическими трудностями. Это может повлиять на вашем будущем, включая проблемы с трудоустройством и кредитной историей.
Общественное и личное благополучие основываются на правдивости и доверии в финансовой деятельности. Покупка контрафактных банкнот идет вразрез с этими принципами и может представлять серьезные последствия. Предлагается держаться законов и вести только легальными финансовыми сделками.
Обналичивание карт – это неправомерная деятельность, становящаяся все более распространенной в нашем современном мире электронных платежей. Этот вид мошенничества представляет серьезные вызовы для банков, правоохранительных органов и общества в целом. В данной статье мы рассмотрим частоту встречаемости обналичивания карт, используемые методы и возможные последствия для жертв и общества.
Частота обналичивания карт:
Обналичивание карт является весьма распространенным явлением, и его частота постоянно растет с увеличением числа электронных транзакций. Киберпреступники применяют разнообразные методы для получения доступа к финансовым средствам, включая фишинг, вредоносное программное обеспечение, скимминг и другие инновационные подходы.
Методы обналичивания карт:
Фишинг: Злоумышленники могут отправлять фальшивые электронные сообщения или создавать веб-сайты, имитирующие банковские системы, с целью получения личной информации от владельцев карт.
Скимминг: Злоумышленники устанавливают устройства скиммеры на банкоматах или терминалах для считывания данных с магнитных полос карт.
Вредоносное программное обеспечение: Киберпреступники разрабатывают вредоносные программы, которые заражают компьютеры и мобильные устройства, чтобы получить доступ к личным данным и банковским счетам.
Сетевые атаки: Атаки на системы банков и платежных платформ могут привести к утечке информации о картах и, следовательно, к их обналичиванию.
Последствия обналичивания карт:
Финансовые потери для клиентов: Владельцы карт могут столкнуться с денежными потерями, так как средства могут быть списаны с их счетов без их ведома.
Угроза безопасности данных: Обналичивание карт подчеркивает угрозу безопасности личных данных, что может привести к краже личной и финансовой информации.
Ущерб репутации банков: Банки и другие финансовые учреждения могут столкнуться с утратой доверия со стороны клиентов, если их системы безопасности оказываются уязвимыми.
Проблемы для экономики: Обналичивание карт создает экономический ущерб, поскольку оно стимулирует дополнительные затраты на борьбу с мошенничеством и восстановление утраченных средств.
Борьба с обналичиванием карт:
Совершенствование технологий безопасности: Банки и финансовые институты постоянно совершенствуют свои системы безопасности, чтобы предотвратить несанкционированный доступ к картам.
Образование и информирование: Обучение клиентов о методах мошенничества и том, как защитить свои данные, является важным шагом в борьбе с обналичиванием карт.
Сотрудничество с правоохранительными органами: Банки активно сотрудничают с правоохранительными органами для выявления и пресечения преступных схем.
Заключение:
Обналичивание карт – серьезная угроза для финансовой стабильности и безопасности личных данных. Решение этой проблемы требует совместных усилий со стороны банков, правоохранительных органов и общества в целом. Только эффективная борьба с мошенничеством позволит обеспечить безопасность электронных платежей и защитить интересы всех участников финансовой системы.
Опасности поддельными 5000 рублей: Распространение поддельных купюр и его воздействия
В сегодняшнем обществе, где электронные платежи становятся все более популярными, мошенники не оставляют без внимания и стандартные методы недобросовестных действий, такие как распространение поддельных банкнот. В последние недели стало известно о противозаконной продаже фальшивых 5000 рублевых купюр, что представляет весомую угрозу для финансовых институтов и общества в общем.
Подходы торговли:
Противоправные лица активно используют неявные каналы сетевого пространства для продажи контрафактных 5000 рублей. На скрытых веб-ресурсах и незаконных форумах можно обнаружить предложения поддельных банкнот. К сожалению, это создает выгодные условия для передачи контрафактных денег среди общества.
Последствия для населения:
Присутствие недостоверных денег в потоке может иметь весомые воздействия для финансовой системы и авторитета к государственной валюте. Люди, не подозревая, что получили фальшивые купюры, могут использовать их в разнообразных ситуациях, что в финале приводит к потере кредитоспособности к банкнотам определенного номинала.
Опасности для населения:
Гражданское население становятся потенциальными пострадавшими преступников, когда они непреднамеренно получают недостоверные деньги в транзакциях или при приобретениях. В следствие, они могут столкнуться с нелестными ситуациями, такими как отказ продавцов принять недостоверные купюры или даже вероятность юридической ответственности за усилие расплаты контрафактными деньгами.
Противостояние с передачей недостоверных денег:
Для предотвращения общества от таких же проступков необходимо усилить меры по обнаружению и остановке производству поддельных денег. Это включает в себя сотрудничество между полицией и финансовыми учреждениями, а также повышение степени просвещения граждан относительно символов контрафактных банкнот и практик их обнаружения.
Заключение:
Разнос недостоверных 5000 рублей – это весомая опасность для финансовой стабильности и надежности населения. Поддержание кредитоспособности к денежной единице требует единых действий со со стороны властей, финансовых организаций и всех. Важно быть настороженным и знающим, чтобы избежать раскрутку поддельных денег и обеспечить финансовые активы граждан.
Нарушение законов:
Покупка или воспользование поддельных денег приравниваются к правонарушением, нарушающим нормы государства. Вас в состоянии подвергнуть судебному преследованию, что возможно послать в задержанию, денежным наказаниям иначе постановлению под стражу.
Ущерб доверию:
Фальшивые деньги нарушают уверенность по отношению к денежной структуре. Их обращение создает опасность для благоприятных гражданских лиц и предприятий, которые имеют возможность попасть в неожиданными убытками.
Экономический ущерб:
Распространение контрафактных купюр осуществляет воздействие на хозяйство, приводя к инфляцию и ухудшая глобальную экономическую стабильность. Это в состоянии привести к утрате уважения к денежной единице.
Риск обмана:
Лица, которые, вовлечены в изготовлением лживых купюр, не обязаны соблюдать какие-либо стандарты степени. Лживые купюры могут оказаться легко распознаваемы, что, в итоге приведет к убыткам для тех, кто стремится их использовать.
Юридические последствия:
При событии захвата при воспользовании поддельных купюр, вас в состоянии взыскать штраф, и вы столкнетесь с законными сложностями. Это может оказать воздействие на вашем будущем, с учетом сложности с получением работы и кредитной историей.
Общественное и личное благополучие основываются на правдивости и доверии в финансовых отношениях. Покупка фальшивых купюр противоречит этим принципам и может порождать серьезные последствия. Рекомендуется придерживаться законов и заниматься исключительно законными финансовыми действиями.
Покупка поддельных купюр является противозаконным иначе опасным поступком, которое в состоянии послать в важным законным наказаниям или вреду индивидуальной денежной надежности. Вот некоторые другие приводов, из-за чего получение поддельных денег представляет собой опасной либо неуместной:
Нарушение законов:
Получение иначе применение контрафактных банкнот приравниваются к нарушением закона, подрывающим положения территории. Вас в состоянии подвергнуть уголовной ответственности, которое может послать в тюремному заключению, финансовым санкциям или постановлению под стражу.
Ущерб доверию:
Контрафактные купюры ослабляют доверие по отношению к денежной механизму. Их обращение создает опасность для надежных людей и коммерческих структур, которые могут столкнуться с неожиданными потерями.
Экономический ущерб:
Распространение лживых банкнот влияет на экономическую сферу, инициируя распределение денег и ухудшая глобальную экономическую стабильность. Это способно привести к потере доверия к денежной системе.
Риск обмана:
Личности, какие, занимается изготовлением контрафактных банкнот, не обязаны сохранять какие-то параметры степени. Фальшивые банкноты могут быть легко выявлены, что, в итоге закончится потерям для тех, кто пытается воспользоваться ими.
Юридические последствия:
При событии лишения свободы при использовании контрафактных денег, вас способны оштрафовать, и вы столкнетесь с юридическими трудностями. Это может сказаться на вашем будущем, в том числе сложности с поиском работы и кредитной историей.
Общественное и индивидуальное благосостояние зависят от честности и доверии в финансовых отношениях. Получение лживых купюр противоречит этим принципам и может иметь серьезные последствия. Рекомендуем держаться норм и осуществлять только законными финансовыми действиями.
Обналичивание карт – это незаконная деятельность, становящаяся все более распространенной в нашем современном мире электронных платежей. Этот вид мошенничества представляет значительные вызовы для банков, правоохранительных органов и общества в целом. В данной статье мы рассмотрим частоту встречаемости обналичивания карт, используемые методы и возможные последствия для жертв и общества.
Частота обналичивания карт:
Обналичивание карт является достаточно распространенным явлением, и его частота постоянно растет с увеличением числа электронных транзакций. Киберпреступники применяют разнообразные методы для получения доступа к финансовым средствам, включая фишинг, вредоносное программное обеспечение, скимминг и другие инновационные подходы.
Методы обналичивания карт:
Фишинг: Злоумышленники могут отправлять фальшивые электронные сообщения или создавать веб-сайты, имитирующие банковские системы, с целью получения личной информации от владельцев карт.
Скимминг: Злоумышленники устанавливают устройства скиммеры на банкоматах или терминалах для считывания данных с магнитных полос карт.
Вредоносное программное обеспечение: Киберпреступники разрабатывают вредоносные программы, которые заражают компьютеры и мобильные устройства, чтобы получить доступ к личным данным и банковским счетам.
Сетевые атаки: Атаки на системы банков и платежных платформ могут привести к утечке информации о картах и, следовательно, к их обналичиванию.
Последствия обналичивания карт:
Финансовые потери для клиентов: Владельцы карт могут столкнуться с денежными потерями, так как средства могут быть списаны с их счетов без их ведома.
Угроза безопасности данных: Обналичивание карт подчеркивает угрозу безопасности личных данных, что может привести к краже личной и финансовой информации.
Ущерб репутации банков: Банки и другие финансовые учреждения могут столкнуться с утратой доверия со стороны клиентов, если их системы безопасности оказываются уязвимыми.
Проблемы для экономики: Обналичивание карт создает экономический ущерб, поскольку оно стимулирует дополнительные затраты на борьбу с мошенничеством и восстановление утраченных средств.
Борьба с обналичиванием карт:
Совершенствование технологий безопасности: Банки и финансовые институты постоянно совершенствуют свои системы безопасности, чтобы предотвратить несанкционированный доступ к картам.
Образование и информирование: Обучение клиентов о методах мошенничества и том, как защитить свои данные, является важным шагом в борьбе с обналичиванием карт.
Сотрудничество с правоохранительными органами: Банки активно сотрудничают с правоохранительными органами для выявления и пресечения преступных схем.
Заключение:
Обналичивание карт – весомая угроза для финансовой стабильности и безопасности личных данных. Решение этой проблемы требует совместных усилий со стороны банков, правоохранительных органов и общества в целом. Только эффективная борьба с мошенничеством позволит обеспечить безопасность электронных платежей и защитить интересы всех участников финансовой системы.
По подпольных рынках можно обнаружить самые разные товары: психоактивные препараты, стрелковое оружие, похищенная информация, взломанные аккаунты, фальшивые документы или и другое. Такие же базары порой привлекают внимание как правонарушителей, а также рядовых участников, стремящихся пройти мимо право или даже получить возможность доступа к товары или послугам, какие именно на обычном всемирной сети были бы в не доступны.
Тем не менее стоит помнить, каким образом деятельность по подпольных рынках представляет собой неправомерный тип а имеет возможность повлечь за собой серьезные юридические последствия. Правоохранительные органы усердно борются противодействуют таковыми базарами, но по причине скрытности скрытой сети это не всегда просто так.
В результате, наличие даркнет-маркетов есть реальностью, но они останавливаются сферой крупных рисков как и для таковых участников, а также для подобных общественности в целом.
Тор программа – это особый браузер, который рассчитан для обеспечения конфиденциальности и безопасности в Сети. Он разработан на платформе Тор (The Onion Router), которая позволяет клиентам передавать данными по дистрибутированную сеть серверов, что создает затруднительным подслушивание их деятельности и выявление их положения.
Основополагающая функция Тор браузера заключается в его возможности маршрутизировать интернет-трафик посредством несколько узлов сети Тор, каждый шифрует информацию перед передачей следующему узлу. Это формирует массу слоев (поэтому и титул "луковая маршрутизация" - "The Onion Router"), что создает почти что невозможным подслушивание и установление пользователей.
Тор браузер регулярно используется для обхода цензуры в странах, где ограничен доступ к конкретным веб-сайтам и сервисам. Он также даёт возможность пользователям гарантировать конфиденциальность своих онлайн-действий, таких как просмотр веб-сайтов, общение в чатах и отправка электронной почты, предотвращая отслеживания и мониторинга со стороны интернет-провайдеров, государственных агентств и киберпреступников.
Однако стоит учитывать, что Тор браузер не гарантирует полной тайности и устойчивости, и его выпользование может быть привязано с угрозой доступа к незаконным контенту или деятельности. Также возможно замедление скорости интернет-соединения из-за
Темные площадки гарантируют анонимность своих участников по использования определенных программ или параметров, таких как Tor, какие именно замаскировывают IP-адреса и маршрутизируют интернет-трафик при помощи разнообразные узлы, делая непростым следить деятельности правоохранительными органами.
Такие платформы порой попадают объектом интереса органов правопорядка, какие сопротивляются противодействуют ими в рамках борьбы против криминалом в сфере информационных технологий и нелегальной продажей.
Основнои? механизм работы Тор даркнета основан на использовании маршрутизации через разные точки, которые шифруют и направляют трафик, создавая сложным слежение его источника. Это формирует скрытность для пользователеи?, укрывая их реальные IP-адреса и местоположение.
Тор даркнет включает различные плеи?сы, включая веб-саи?ты, форумы, рынки, блоги и другие онлаи?н-ресурсы. Некоторые из этих ресурсов могут быть неприступны или запрещены в обыкновеннои? сети, что создает Тор даркнет базои? для подачи информациеи? и услугами, включая товары и услуги, которые могут быть противозаконными.
Хотя Тор даркнет выпользуется некоторыми людьми для преодоления цензуры или протекции приватности, он так же становится платформои? для разнообразных незаконных деи?ствии?, таких как бартер наркотиками, оружием, кража личных данных, подача услуг хакеров и остальные злостные действия.
Важно осознавать, что использование Тор даркнета не всегда законно и может иметь в себя серьезные угрозы для безопасности и правомочности.
В скрытой части интернета сгруппированы различные ресурсы, включая форумы, рынки, журналы и прочие интернет-ресурсы, которые могут недоступимы или пресечены в стандартной коммуникации. Здесь возможно найти различные товары и послуги, включая нелегальные, например наркотики, стрелковое оружие, взломанные данные, а также послуги хакеров и остальные.
В стране теневая сеть также применяется для преодоления цензуры и наблюдения со стороны. Некоторые клиенты могут выпользовать его для обмена информацией в обстоятельствах, когда автономия слова замкнута или информационные материалы подвергаются цензуре. Однако, также следует отметить, что в теневой сети имеется много неправомерной процесса и потенциально опасных ситуаций, включая мошенничество и киберпреступления
В подпольных рынках можно обнаружить самые разные продуктовые товары: психоактивные препараты, вооружение, похищенная информация, уязвимые аккаунты, фальшивки или и многое многое другое. Такие рынки время от времени притягивают восторг также криминальных элементов, так и рядовых пользователей, стремящихся обходить закон или даже получить возможность доступа к вещам и сервисам, какие именно в обыденном интернете были бы не доступны.
Однако следует помнить, что деятельность на теневых электронных базарах носит нелегальный специфику и имеет возможность повлечь за собой значительные правовые нормы санкции. Полицейские энергично сражаются противодействуют таковыми базарами, однако в результате скрытности скрытой сети данный факт далеко не постоянно просто.
Таким образом, экзистенция даркнет-маркетов представляет собой реальностью, но все же эти площадки пребывают местом серьезных потенциальных угроз как для участников, и для подобных общественности в целом.
Скрытая часть веба, таинственная часть интернета, заинтересовывает интерес участников своим анонимностью и способностью заказать различные товары и услуги без лишних вопросов. Однако, переход в этот вселенная темных площадок связано с комплексом опасностей и аспектов, о чём желательно понимать перед проведением сделок.
Что такое скрытая часть веба и как он работает?
Для того, кому незнакомо с термином, скрытая часть веба - это сегмент веба, невидимая от обычных поисковых систем. В подпольной сети существуют специальные онлайн-рынки, где можно найти практически все, что угодно : от запрещённых веществ и боеприпасов и перехваченных учётных записей и поддельных документов.
Мифы о приобретении товаров в подпольной сети
Анонимность гарантирована: В то время как, использование методов скрытия личности, таких как Tor, способствует закрыть вашу действия в сети, анонимность в Даркнете не является полной. Имеется опасность, что возможно вашу личную информацию могут обнаружить обманщики или даже сотрудники правоохранительных органов.
Все товары - качественные: В скрытой части веба можно наткнуться на множество торговцев, предлагающих товары и услуги. Однако, нельзя гарантировать качество или подлинность товара, так как невозможно проверить до того, как вы сделаете заказ.
Легальные сделки без ответственности: Многие участники ошибочно считают, что заказывая товары в темном интернете, они рискуют меньшему риску, чем в обычной жизни. Однако, заказывая противоправные товары или услуги, вы подвергаете себя наказания.
Реальность приобретений в подпольной сети
Опасности мошенничества и афер: В подпольной сети многочисленные аферисты, предрасположены к мошенничеству невнимательных клиентов. Они могут предложить фальшивые товары или просто исчезнуть, оставив вас без денег.
Опасность легальных органов: Участники подпольной сети рискуют попасть привлечения к уголовной ответственности за приобретение и заказ незаконной продукции и сервисов.
Неопределённость исходов: Не каждая сделка в Даркнете заканчиваются удачно. Качество вещей может оказаться неудовлетворительным, а процесс покупки может оказаться проблематичным.
Советы для безопасных покупок в скрытой части веба
Проводите тщательное исследование поставщика и продукции перед осуществлением заказа.
Используйте безопасные программы и сервисы для обеспечения анонимности и безопасности.
Платите только безопасными методами, например, криптовалютами, и избегайте предоставления личной информации.
Будьте предельно внимательны и осторожны во всех совершаемых действиях и выбранных вариантах.
Заключение
Покупки в подпольной сети могут быть как захватывающим, так и опасным путешествием. Понимание рисков и применение соответствующих мер предосторожности помогут снизить вероятность негативных последствий и обеспечить безопасность при совершении покупок в этой недоступной области сети.
Покупки в Даркнете: Заблуждения и Правда
Даркнет, таинственная секция сети, заинтересовывает внимание участников своей тайностью и возможностью купить самые разнообразные товары и сервисы без излишних действий. Однако, путешествие в тот мрак скрытых рынков связано с рядом опасностей и сложностей, о чем необходимо осведомляться перед осуществлением транзакций.
Что представляет собой скрытая часть веба и как оно действует?
Для того, кому незнакомо с термином, скрытая часть веба - это сегмент веба, скрытая от стандартных поисковых систем. В Даркнете существуют уникальные торговые площадки, где можно найти возможность почти все, что угодно : от наркотиков и оружия до взломанных аккаунтов и фальшивых документов.
Заблуждения о приобретении товаров в скрытой части веба
Анонимность гарантирована: В то время как, применение анонимных технологий, таких как Tor, способно помочь скрыть от глаз свою действия в сети, тайность в подпольной сети не является. Существует риск, что возможно вашу информацию о вас могут обнаружить дезинформаторы или даже сотрудники правоохранительных органов.
Все товары - высокого качества: В подпольной сети можно найти множество поставщиков, предоставляющих продукты и сервисы. Однако, нельзя гарантировать качество или подлинность товара, так как невозможно проверить до того, как вы сделаете заказ.
Легальные покупки без ответственности: Многие участники ошибочно считают, что товары в скрытой части веба, они рискуют меньшему риску, чем в реальной жизни. Однако, заказывая незаконные продукцию или услуги, вы подвергаете себя риску уголовной ответственности.
Реальность покупок в подпольной сети
Негативные стороны мошенничества и афер: В темном интернете множество мошенников, предрасположены к мошенничеству недостаточно осторожных пользователей. Они могут предложить поддельные товары или просто забрать ваши деньги и исчезнуть.
Опасность правоохранительных органов: Пользователи подпольной сети рискуют попасть к уголовной ответственности за покупку и заказ незаконной продукции и сервисов.
Непредсказуемость выходов: Не каждый заказ в скрытой части веба приводят к успешному результату. Качество вещей может оставлять желать лучшего, а сам процесс приобретения может оказаться проблематичным.
Советы для безопасных покупок в темном интернете
Проводите детальный анализ продавца и товара перед совершением покупки.
Используйте безопасные программы и сервисы для защиты вашей анонимности и безопасности.
Платите только безопасными методами, такими как криптовалюты, и избегайте предоставления личной информации.
Будьте предельно внимательны и осторожны во всех совершаемых действиях и выбранных вариантах.
Заключение
Транзакции в темном интернете могут быть как интересным, так и рискованным опытом. Понимание возможных опасностей и принятие необходимых мер предосторожности помогут снизить вероятность негативных последствий и гарантировать безопасные покупки в этом неизведанном мире интернета.
Теневой уровень интернета: недоступная зона компьютерной сети
Темный интернет, скрытый уголок интернета продолжает привлекать внимание и общественности, так и служб безопасности. Данный засекреченный уровень интернета примечателен своей скрытностью и возможностью осуществления преступных деяний под маской анонимности.
Сущность темного интернета состоит в том, что этот слой не доступен для обычных браузеров. Для доступа к этому уровню необходимы специальные инструменты и программы, обеспечивающие скрытность пользователей. Это формирует прекрасные условия для различных незаконных действий, в том числе торговлю наркотическими веществами, торговлю огнестрельным оружием, хищение персональной информации и другие преступные операции.
В свете растущую угрозу, многие страны приняли законодательные инициативы, целью которых является ограничение доступа к теневому уровню интернета и привлечение к ответственности тех, кто занимающихся незаконными деяниями в этом скрытом мире. Однако, несмотря на предпринятые действия, борьба с теневым уровнем интернета представляет собой трудную задачу.
Важно отметить, что полное запрещение теневого уровня интернета практически невозможно. Даже при строгих мерах регулирования, доступ к этому уровню интернета всё ещё возможен с использованием разнообразных технических средств и инструментов, используемые для обхода блокировок.
В дополнение к законодательным инициативам, имеются также инициативы по сотрудничеству между правоохранительными структурами и технологическими компаниями для борьбы с преступностью в темном интернете. Тем не менее, эта борьба требует не только технических решений, но также улучшения методов выявления и предотвращения противозаконных манипуляций в данной среде.
В итоге, несмотря на принятые меры и усилия в борьбе с преступностью, темный интернет остается серьезной проблемой, нуждающейся в комплексных подходах и коллективных усилиях как со стороны правоохранительных органов, а также технологических организаций.
В отличие от открытого интернета, даркнет не допускается для поисковых систем и стандартных браузеров. Для того чтобы получить к нему доступ, необходимо использовать специализированные приложения, такие как Tor или I2P, которые обеспечивают скрытность и шифрование данных. Однако, это не означает, что даркнет недоступен для широкой публики.
Действительно, даркнет открыт для всех, кто имеет интерес и возможность его исследовать. В нем можно найти разнообразные материалы, начиная от дискуссий, которые не приветствуются в обычных сетях, и заканчивая возможностью посещения специализированным рынкам и сервисам. Например, множество информационных сайтов и интернет-форумов на даркнете посвящены темам, которые считаются табу в обычных средах, таким как политика, вероисповедание или цифровые валюты.
Кроме того, даркнет часто используется активистами и журналистами, которые ищут пути обхода ограничений и средства для сохранения анонимности. Он также служит платформой для открытого обмена данными и идеями, которые могут быть подавимы в странах с авторитарными режимами.
Важно понимать, что хотя даркнет предоставляет свободу доступа к информации и возможность анонимного общения, он также может быть использован для незаконных целей. Тем не менее, это не делает его скрытым и неприступным для любого.
Таким образом, даркнет – это не только скрытая сторона сети, но и пространство, где любой может найти что-то увлекательное или полезное для себя. Важно помнить о его двуединстве и использовать его с умом и с учетом рисков, которые он несет.
elementor
Подпольная часть сети: недоступная зона компьютерной сети
Подпольная часть сети, скрытый сегмент сети продолжает вызывать интерес интерес как общественности, и также служб безопасности. Этот подпольный слой интернета известен своей анонимностью и возможностью проведения преступных деяний под маской анонимности.
Суть теневого уровня интернета сводится к тому, что данный уровень не доступен для обычных браузеров. Для доступа к этому уровню необходимы специальные инструменты и программы, которые обеспечивают анонимность пользователей. Это создает отличную площадку для разнообразных нелегальных действий, среди которых торговлю наркотическими веществами, торговлю огнестрельным оружием, кражу конфиденциальных данных и другие противоправные действия.
В ответ на возрастающую опасность, многие страны приняли законы, направленные на запрещение доступа к подпольной части сети и привлечение к ответственности тех, кто совершающих противозаконные действия в этой нелегальной области. Впрочем, несмотря на принятые меры, борьба с подпольной частью сети представляет собой сложную задачу.
Важно отметить, что полное прекращение доступа к темному интернету практически невыполнимо. Даже при строгих мерах регулирования, возможность доступа к данному уровню сети всё ещё возможен с использованием разнообразных технических средств и инструментов, используемые для обхода блокировок.
Кроме законодательных мер, действуют также инициативы по сотрудничеству между правоохранительными органами и технологическими компаниями с целью пресечения противозаконных действий в теневом уровне интернета. Впрочем, для эффективного противодействия необходимы не только технологические решения, но и улучшения методов обнаружения и пресечения незаконных действий в этой среде.
В заключение, несмотря на введенные запреты и предпринятые усилия в борьбе с преступностью, теневой уровень интернета остается серьезной проблемой, требующей комплексного подхода и совместных усилий со стороны правоохранительных служб, а также технологических организаций.
Intro
betvisa bangladesh
Betvisa bangladesh | Super Cricket Carnival with Betvisa!
IPL Cricket Mania | Kick off Super Cricket Carnival with bet visa.com
IPL Season | Exclusive 1,50,00,000 only at Betvisa Bangladesh!
Crash Games Heroes | Climb to the top of the 1,00,00,000 bonus pool!
#betvisabangladesh
Preview IPL T20 | Follow Betvisa BD on Facebook, Instagram for awards!
betvisa affiliate Dream Maltese Tour | Sign up now to win the ultimate prize!
https://www.bvthethao.com/
#betvisabangladesh #betvisabd #betvisaaffiliate
#betvisaaffiliatesignup #betvisa.com
Vì tính lời hứa về trải nghiệm thú vị cá cược hoàn hảo nhất và dịch vụ khách hàng chuyên môn, BetVisa tự tin là điểm đến lý tưởng cho những ai nhiệt huyết trò chơi trực tuyến. Hãy gắn bó ngay hôm nay và bắt đầu chuyến đi của bạn tại BetVisa - nơi niềm vui và may mắn chính là điều không thể thiếu.
Khám phá Thế Giới Cá Cược Trực Tuyến với BetVisa!
BetVisa, một trong những nền tảng hàng đầu tại châu Á, được thành lập vào năm 2017 và thao tác dưới giấy phép của Curacao, đã đưa vào hơn 2 triệu người dùng trên toàn thế giới. Với lời hứa đem đến trải nghiệm cá cược an toàn và tin cậy nhất, BetVisa nhanh chóng trở thành lựa chọn hàng đầu của người chơi trực tuyến.
BetVisa không chỉ cung cấp các trò chơi phong phú như xổ số, sòng bạc trực tiếp, thể thao trực tiếp và thể thao điện tử, mà còn mang đến cho người chơi những ưu đãi hấp dẫn. Thành viên mới đăng ký sẽ được tặng ngay 5 phần quà miễn phí và có cơ hội giành giải thưởng lớn.
Đặc biệt, BetVisa hỗ trợ nhiều hình thức thanh toán linh hoạt như Betvisa Vietnam, cùng với các ưu đãi độc quyền như thưởng chào mừng lên đến 200%. Bên cạnh đó, hàng tuần còn có các chương trình khuyến mãi độc đáo như chương trình giải thưởng Sinh Nhật và Chủ Nhật Mua Sắm Điên Cuồng, mang đến cho người chơi cơ hội thắng lớn.
betvisa philippines
Betvisa philippines | The Filipino Carnival, Spinning for Treasures!
Betvisa Philippines Surprises | Spin daily and win ₱8,888 Grand Prize!
Register for a chance to win ₱8,888 Bonus Tickets! Explore Betvisa.com!
Wild All Over Grab 58% YB Bonus at Betvisa Casino! Take the challenge!
#betvisaphilippines
Get 88 on your first 50 Experience Betvisa Online's Bonus Gift!
Weekend Instant Daily Recharge at betvisa.com
https://www.88betvisa.com/
#betvisaphilippines #betvisaonline #betvisacasino
#betvisacom #betvisa.com
Nền tảng cá cược - Điểm Đến Tuyệt Vời Cho Người Chơi Trực Tuyến
Khám Phá Thế Giới Cá Cược Trực Tuyến với BetVisa!
Nền tảng cá cược được sáng lập vào năm 2017 và tiến hành theo chứng chỉ trò chơi Curacao với hơn 2 triệu người dùng. Với lời hứa đem đến trải nghiệm cá cược an toàn và tin cậy nhất, BetVisa nhanh chóng trở thành lựa chọn hàng đầu của người chơi trực tuyến.
BetVisa không chỉ đưa ra các trò chơi phong phú như xổ số, sòng bạc trực tiếp, thể thao trực tiếp và thể thao điện tử, mà còn mang lại cho người chơi những chính sách ưu đãi hấp dẫn. Thành viên mới đăng ký sẽ nhận tặng ngay 5 vòng quay miễn phí và có cơ hội giành giải thưởng lớn.
Dịch vụ hỗ trợ nhiều phương thức thanh toán linh hoạt như Betvisa Vietnam, cùng với các ưu đãi độc quyền như thưởng chào mừng lên đến 200%. Bên cạnh đó, hàng tuần còn có các chương trình khuyến mãi độc đáo như chương trình giải thưởng Sinh Nhật và Chủ Nhật Mua Sắm Điên Cuồng, mang lại cho người chơi thời cơ thắng lớn.
Với tính cam kết về trải nghiệm cá cược tốt nhất và dịch vụ khách hàng tận tâm, BetVisa tự tin là điểm đến lý tưởng cho những ai đam mê trò chơi trực tuyến. Hãy đăng ký ngay hôm nay và bắt đầu hành trình của bạn tại BetVisa - nơi niềm vui và may mắn chính là điều tất yếu!
Bạn có biết? Tải app cá độ đúng cách sẽ giúp tiết kiệm thời gian đăng nhập, tăng tính an toàn và bảo mật cho tài khoản của bạn! Vậy đâu là cách để tải một app cá cược uy tín dễ dàng và chính xác? Xem ngay bài viết này nếu bạn muốn chơi cá cược trực tuyến an toàn!
tải về ngay lập tức
RG777 - Nhà Cái Uy Tín Hàng Đầu Việt Nam
Link tải app cá độ nét nhất 2023:RG777
Để đảm bảo việc tải ứng dụng cá cược của bạn an toàn và nhanh chóng, người chơi có thể sử dụng đường link sau.
tải về ngay lập tức
Intro
betvisa bangladesh
Betvisa bangladesh | Super Cricket Carnival with Betvisa!
IPL Cricket Mania | Kick off Super Cricket Carnival with bet visa.com
IPL Season | Exclusive 1,50,00,000 only at Betvisa Bangladesh!
Crash Games Heroes | Climb to the top of the 1,00,00,000 bonus pool!
#betvisabangladesh
Preview IPL T20 | Follow Betvisa BD on Facebook, Instagram for awards!
betvisa affiliate Dream Maltese Tour | Sign up now to win the ultimate prize!
https://www.bvthethao.com/
#betvisabangladesh #betvisabd #betvisaaffiliate
#betvisaaffiliatesignup #betvisa.com
Nhờ vào lời hứa về trải nghiệm thú vị cá cược tốt nhất và dịch vụ khách hàng chuyên trách, BetVisa tự tin là điểm đến lý tưởng cho những ai nhiệt huyết trò chơi trực tuyến. Hãy gắn bó ngay hôm nay và bắt đầu cuộc hành trình của bạn tại BetVisa - nơi niềm vui và may mắn chính là điều không thể thiếu.
Khám phá Thế Giới Cá Cược Trực Tuyến với BetVisa!
Hệ thống BetVisa, một trong những công ty trò chơi hàng đầu tại châu Á, ra đời vào năm 2017 và hoạt động dưới giấy phép của Curacao, đã đưa vào hơn 2 triệu người dùng trên toàn thế giới. Với lời hứa đem đến trải nghiệm cá cược đảm bảo và tin cậy nhất, BetVisa nhanh chóng trở thành lựa chọn hàng đầu của người chơi trực tuyến.
BetVisa không chỉ cung cấp các trò chơi phong phú như xổ số, sòng bạc trực tiếp, thể thao trực tiếp và thể thao điện tử, mà còn mang đến cho người chơi những ưu đãi hấp dẫn. Thành viên mới đăng ký sẽ được tặng ngay 5 phần quà miễn phí và có cơ hội giành giải thưởng lớn.
Đặc biệt, BetVisa hỗ trợ nhiều phương thức thanh toán linh hoạt như Betvisa Vietnam, cùng với các ưu đãi độc quyền như thưởng chào mừng lên đến 200%. Bên cạnh đó, hàng tuần còn có các chương trình khuyến mãi độc đáo như chương trình giải thưởng Sinh Nhật và Chủ Nhật Mua Sắm Điên Cuồng, mang đến cho người chơi cơ hội thắng lớn.
Intro
betvisa bangladesh
Betvisa bangladesh | Super Cricket Carnival with Betvisa!
IPL Cricket Mania | Kick off Super Cricket Carnival with bet visa.com
IPL Season | Exclusive 1,50,00,000 only at Betvisa Bangladesh!
Crash Games Heroes | Climb to the top of the 1,00,00,000 bonus pool!
#betvisabangladesh
Preview IPL T20 | Follow Betvisa BD on Facebook, Instagram for awards!
betvisa affiliate Dream Maltese Tour | Sign up now to win the ultimate prize!
https://www.bvthethao.com/
#betvisabangladesh #betvisabd #betvisaaffiliate
#betvisaaffiliatesignup #betvisa.com
Nhờ vào tính lời hứa về kinh nghiệm cá cược tinh vi nhất và dịch vụ khách hàng chuyên trách, BetVisa tự tin là điểm đến lý tưởng cho những ai nhiệt tình trò chơi trực tuyến. Hãy ghi danh ngay hôm nay và bắt đầu cuộc hành trình của bạn tại BetVisa - nơi niềm vui và may mắn chính là điều không thể thiếu.
Khám phá Thế Giới Cá Cược Trực Tuyến với BetVisa!
Dịch vụ BetVisa, một trong những công ty trò chơi hàng đầu tại châu Á, được thành lập vào năm 2017 và thao tác dưới giấy phép của Curacao, đã thu hút hơn 2 triệu người dùng trên toàn thế giới. Với cam kết đem đến trải nghiệm cá cược an toàn và tin cậy nhất, BetVisa nhanh chóng trở thành lựa chọn hàng đầu của người chơi trực tuyến.
BetVisa không chỉ cung cấp các trò chơi phong phú như xổ số, sòng bạc trực tiếp, thể thao trực tiếp và thể thao điện tử, mà còn mang đến cho người chơi những ưu đãi hấp dẫn. Thành viên mới đăng ký sẽ được tặng ngay 5 vòng quay miễn phí và có cơ hội giành giải thưởng lớn.
Đặc biệt, BetVisa hỗ trợ nhiều cách thức thanh toán linh hoạt như Betvisa Vietnam, cùng với các ưu đãi độc quyền như thưởng chào mừng lên đến 200%. Bên cạnh đó, hàng tuần còn có các chương trình khuyến mãi độc đáo như chương trình giải thưởng Sinh Nhật và Chủ Nhật Mua Sắm Điên Cuồng, mang đến cho người chơi cơ hội thắng lớn.
Jeetwin Affiliate
Join Jeetwin now! | Jeetwin sign up for a ?500 free bonus
Spin & fish with Jeetwin club! | 200% welcome bonus
Bet on horse racing, get a 50% bonus! | Deposit at Jeetwin live for rewards
#JeetwinAffiliate
Casino table fun at Jeetwin casino login | 50% deposit bonus on table games
Earn Jeetwin points and credits, enhance your play!
https://www.jeetwin-affiliate.com/hi
#JeetwinAffiliate #jeetwinclub #jeetwinsignup #jeetwinresult
#jeetwinlive #jeetwinbangladesh #jeetwincasinologin
Daily recharge bonuses at Jeetwin Bangladesh!
25% recharge bonus on casino games at jeetwin result
15% bonus on Crash Games with Jeetwin affiliate!
Turn to Achieve Genuine Currency and Voucher Codes with JeetWin Affiliate Program
Do you a enthusiast of online gaming? Do you actually like the thrill of spinning the reel and being victorious big-time? If so, then the JeetWin Affiliate Program is great for you! With JeetWin Casino, you not just get to experience thrilling games but additionally have the possibility to make actual money and gift certificates just by promoting the platform to your friends, family, or digital audience.
How Does Operate?
Signing up for the JeetWin Affiliate Program is speedy and effortless. Once you turn into an associate, you'll receive a special referral link that you can share with others. Every time someone joins or makes a deposit using your referral link, you'll receive a commission for their activity.
Amazing Bonuses Await!
As a JeetWin affiliate, you'll have access to a selection of captivating bonuses:
Registration Bonus 500: Get a abundant sign-up bonus of INR 500 just for joining the program.
Deposit Bonus: Enjoy a enormous 200% bonus when you deposit and play slot machine and fish games on the platform.
Infinite Referral Bonus: Receive unlimited INR 200 bonuses and cash rebates for every friend you invite to play on JeetWin.
Exciting Games to Play
JeetWin offers a diverse range of the most played and most popular games, including Baccarat, Dice, Liveshow, Slot, Fishing, and Sabong. Whether you're a fan of classic casino games or prefer something more modern and interactive, JeetWin has something for everyone.
Participate in the Best Gaming Experience
With JeetWin Live, you can bring your gaming experience to the next level. Engage in thrilling live games such as Lightning Roulette, Lightning Dice, Crazytime, and more. Sign up today and embark on an unforgettable gaming adventure filled with excitement and limitless opportunities to win.
Convenient Payment Methods
Depositing funds and withdrawing your winnings on JeetWin is rapid and hassle-free. Choose from a assortment of payment methods, including E-Wallets, Net Banking, AstroPay, and RupeeO, for seamless transactions.
Don't Miss Out on Exclusive Promotions
As a JeetWin affiliate, you'll acquire access to exclusive promotions and special offers designed to maximize your earnings. From cash rebates to lucrative bonuses, there's always something exciting happening at JeetWin.
Install the App
Take the fun with you wherever you go by downloading the JeetWin Mobile Casino App. Available for both iOS and Android devices, the app features a wide range of entertaining games that you can enjoy anytime, anywhere.
Sign up for the JeetWin's Partner Program Today!
Don't wait any longer to start earning real cash and exciting rewards with the JeetWin Affiliate Program. Sign up now and join the thriving online gaming community at JeetWin.
[url=https://armdatingnew.dad/]news site[/url]
Мы делимся практическими знаниями о ЗСК, покупке НДС и чеков, а также раскрываем эффективные методы для защиты бизнеса от рисков. Если вы хотите разобраться в тонкостях бухгалтерии, проверить своих контрагентов или улучшить финансовую безопасность компании, Бенефициар — это то, что вам нужно. Подписывайтесь на канал, чтобы получить доступ к профессиональной аналитике, уникальным инструментам и готовым решениям для вашего бизнеса! https://benefitsar.net/
https://kitehurghada.ru/
https://kitehurghada.ru/obuchenie-detej-kajtsyorfingu/
https://kitehurghada.ru/stoimost-obucheniya-kajtserfingu-v-hurgade/
https://kitehurghada.ru/kurs-bazovyj-10-chasov-zanyatij-s-instruktorom-4-5-dnya-450-usd/
https://kitehurghada.ru/kurs-ekspress-6-chasov-zanyatij-s-instruktorom-2-3-dnya-300-usd/
https://kitehurghada.ru/kontakty/
https://kitehurghada.ru/prognoz-vetra-v-hurgade/
https://kitehurghada.ru/kurs-pro-prodvinutyj-15-chasov-zanyatij-s-instruktorom-5-7-dnej-600-usd/
https://kitehurghada.ru/vesna-2024-egipet-hurgada-kajt-tury-i-kajt-kempy-deti-vetra/
https://kitehurghada.ru/vesennie-kanikuly/
https://kitehurghada.ru/majskie-prazdniki/
https://kitehurghada.ru/kajt-shkola/
https://kitehurghada.ru/kajt-kemp-v-hurgade-s-kajt-czentrom-detivetra/
https://kitehurghada.ru/zhenskaya-kajt-shkola-shkola-kajtsyorfinga-dlya-detej/
https://kitehurghada.ru/kajt-shkola-v-hurgade-egipet-kajt-czentr-detivetra/
https://kitehurghada.ru/obuchenie-kajtserfingu-na-krasnom-more/
https://kitehurghada.ru/ekskursii-v-hurgade-konnye-progulki-s-kupaniem-v-more-czeny-i-otzyvy-katanie-na-loshadyah-i-verblyudah/
https://kitehurghada.ru/devochki-i-kajtsyorfing-kajtsyorfing-dlya-devushek/
https://kitehurghada.ru/iko-sertifikat-katsyorfinga/
https://kitehurghada.ru/kajt-spot-deti-vetra-odno-iz-luchshih-mest-v-hurgade-dlya-kajtsyorfinga/
https://kitehurghada.ru/gidrofojl-gidrofojling-fojlbording-kajtfojling-v-hurgade-egipet-obuchenie-s-nulya-za-3-dnya/
https://kitehurghada.ru/kajt-kajtsyorfing-i-ego-istoriya/
https://kitehurghada.ru/individualnoe-obuchenie-gidrofojlu-s-kajtom/
https://kitehurghada.ru/veter-v-hurgade/
https://kitehurghada.ru/akuly-v-egipte/
https://kitehurghada.ru/vingfoil/
https://kitehurghada.ru/kajt-shkola-v-egipte/
https://kitehurghada.ru/temperatura-morya-v-hurgade/
https://kitehurghada.ru/obuchenie-vingfojl/
https://kitehurghada.ru/kajtsyorfing-v-el-gune/
https://kitehurghada.ru/kajt-egipet/
https://kitehurghada.ru/akuly-hurgade/
https://kitehurghada.ru/katanie-na-kajte/
https://kitehurghada.ru/kogda-luchshe-otdyhat-v-egipte/
https://kitehurghada.ru/kajting-v-hurgade/
https://kitehurghada.ru/kajting-v-egipte/
https://kitehurghada.ru/kajtserfing/
https://kitehurghada.ru/temperatura-v-hurgade/
https://kitehurghada.ru/kajting/
https://kitehurghada.ru/obuchenie-kajtsyorfingu-v-hurgade-egipet/
https://kitehurghada.ru/russkaya-kajt-stancziya-deti-vetra-v-hurgade/
https://kitehurghada.ru/gidrofojl-s-kajtom-obuchenie/
https://kitehurghada.ru/pogoda-v-hurgade/
https://kitehurghada.ru/faq-po-hurgade-2022-2023-chasto-zadavaemye-voprosy-ili-chto-vzyat-s-soboj-v-egipet/
https://kitehurghada.ru/kajt-safari-v-egipte-russkaya-kajt-stancziya-detivetra-v-hurgade/
https://kitehurghada.ru/kajtserfing-v-hurgade-luchshij-sezon-dlya-kajtserfinga/
https://kitehurghada.ru/kajting-osobennosti-kajtinga-vidy-kajtinga/
https://kitehurghada.ru/russkaya-kajt-shkola-v-hurgade/
https://kitehurghada.ru/kajt-shkola-detivetra/
https://kitehurghada.ru/programma-obucheniya-kajtsyorfingu-iko-v-hurgade-egipet/
https://kitehurghada.ru/istoriya-kajtserfinga/
https://kitehurghada.ru/podarochnyj-sertifikat-na-obuchenie-kajtserfingu-v-hurgade/
https://kitehurghada.ru/chto-takoe-iko-kitesurfing/
https://www.tripadvisor.ru/Attraction_Review-g23408135-d12244940-Reviews-Kite_school_DETIVETRA-Second_Hurghada_Hurghada_Red_Sea_and_Sinai.html
https://goo.gl/maps/KcoqXRbKWDkdGBDA8
https://goo.gl/maps/JTXRid9mrHFiMH7n6
https://detivetra.ru
https://detivetra.ru/v-hurgade/
https://uslugi.yandex.ru/profile/DetiVetra-348058
https://www.facebook.com/groups/detivetra/
https://www.facebook.com/DETIVETRA.ru/
https://www.youtube.com/channel/UCRG2aTtTaxbBAwlMTklO4ag
https://twitter.com/detivetra
https://rutube.ru/shorts/cb44391727e39c55e798f4efcecadbbe/
https://кайтинг-фото.рф/kayt-baza-v-hurgade.html
https://wa.me/79181955474
https://t.me/detivetrachat
https://www.instagram.com/detivetra.ru/
https://yandex.ru/profile/177183726173
https://yandex.ru/profile/1068186022
https://yandex.ru/profile/22472239976
https://yandex.ru/profile/72204785887
https://yandex.ru/profile/191148233877
https://xn----7sbjteeyka8afw.xn--p1ai
https://vk.com/kiteschoolhurghadaegypt
https://vk.com/kite_deti_vetra_anapa
http://redseakite.ru
https://kiteschoolhurghada.ru
https://divingredsea.ru
https://supanapa.ru
https://dzen.ru/a/ZdvCwDY4Lkx9j1OO
https://dzen.ru/a/ZdvAL3ptMCiNF8WX
https://dzen.ru/a/ZfigvDY3E2MON77x
https://dzen.ru/a/ZduLXm6jwDrtxbA7
https://dzen.ru/a/Zdt-SFBRjmyXXC7Y
https://dzen.ru/a/ZdvBm2tFz2D1IlSO
https://dzen.ru/a/Zdu_3c5NKkyfX91J
https://dzen.ru/a/ZdvCINgebnj0b5BQ
https://dzen.ru/a/ZTNXr-xw-1ZbmsTT
https://dzen.ru/a/ZdCSXCL_8k_Tfrjb
https://dzen.ru/a/ZdKxCtywnzYZgrrk
https://dzen.ru/a/ZTNfJwlmuCeqOEbb
https://dzen.ru/video/watch/65db9f94fb98fa6a95ab5e45?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65d4341844e19f05a34cf61f?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65629d684f336820c3b37487?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f689e39e331d6580277a0a?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f6870bcb2c7822b9dbd15c?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/6562982bd9b42c2e6bd10cae?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f684e1113e7a6a574076b2?rid=925618026.48.1718444364156.12030
https://dzen.ru/a/ZTNYEjMz-VkvVGnB
https://dzen.ru/a/ZTNi1ECY6h8nFsSW
https://dzen.ru/a/ZTNpJ546JGYImpH1
https://dzen.ru/a/ZTNTlZAOEk3ppmIO
https://dzen.ru/a/Zc_f2thSeW9zscF8
https://dzen.ru/a/Zc_U25ITFGrFK0Sf
https://dzen.ru/a/Zc_TAlxn1y1iHc43
https://dzen.ru/a/Zc_LEcYYfS-TrXXm
https://dzen.ru/a/ZVjdtJSQOhzbk0B1
https://dzen.ru/a/ZTNS7dJWml8dLCim
https://dzen.ru/a/ZVdT4K4CRxpHZx1i
https://dzen.ru/a/ZVdb9TtUnQGek7_G
https://dzen.ru/a/ZTNUDrwjFj4U3LBI
https://dzen.ru/a/ZTNVSZAOEk3pp-ki
https://dzen.ru/a/ZTNptIGpwlQkN-E1
https://dzen.ru/a/ZTNqooGpwlQkORsw
https://dzen.ru/a/ZTNnrk1VVGtQwolr
https://dzen.ru/a/ZTNS0bwjFj4U25A9
https://dzen.ru/a/ZTNG7QlmuCeqISH6
https://dzen.ru/a/ZTM87Ogjh2c_dNzY
https://dzen.ru/b/ZS5ge6k6swm-YNzl
https://dzen.ru/b/ZS1BbXqKjhX4tA9_
https://dzen.ru/a/ZQ2aw4OzGFVaAbr2
https://dzen.ru/b/ZS5YZ7qcv2E0eJPQ
https://dzen.ru/a/ZQrJrb_XDifDVzGP
https://dzen.ru/a/ZQrIWS4n3ChkWGvj
https://dzen.ru/a/ZQrCRLpsYU4IGsNS
https://dzen.ru/a/ZQq5kyCaIkuoWgEb
https://dzen.ru/a/ZQq6z8LJ7AdPjTX6
https://dzen.ru/a/ZQrBHwW8ugdAoeld
https://dzen.ru/a/ZQq5zAyUYGuFpV6x
https://dzen.ru/a/ZQq6uF9dOExoiJn3
https://dzen.ru/a/ZQq4kyCaIkuoV7HL
https://dzen.ru/a/ZPZtZAWIHk1Wxu36
https://dzen.ru/a/ZPZ324ORLBGu36oK
https://dzen.ru/a/ZPZ6mPf64TnWQmu4
https://dzen.ru/a/ZPZqtxo5MUGqivHt
https://dzen.ru/a/ZPZ3KI7QZRjreV_m
https://dzen.ru/a/ZPZsDLf4FUB9-vTG
https://dzen.ru/a/ZPZyyDEQHn8iOuK4
https://dzen.ru/a/ZPZnc9bwiVMxJaDt
https://dzen.ru/a/ZPZ2CaKi2WZuFDzk
https://dzen.ru/a/ZPZw1iSYk23jVqD2
https://dzen.ru/a/ZPZvXBo5MUGqmExv
https://dzen.ru/a/ZPZusNZDrka3nhk4
https://dzen.ru/a/ZPZomY7QZRjrXUWH
https://dzen.ru/a/ZPZlbm0hO0O6e_6G
https://dzen.ru/a/ZPZkz_Z4SEywAI9r
https://dzen.ru/a/ZPZfLRo5MUGqXPqk
https://dzen.ru/a/ZPZkQ47QZRjrTEiz
https://dzen.ru/a/ZPZgZG72vTlMv-RA
https://dzen.ru/a/ZPZUGxo5MUGqMHlM
https://dzen.ru/a/ZPZTWRo5MUGqLTP3
https://dzen.ru/a/ZPZSyvf64TnWzJmJ
https://dzen.ru/a/ZPZQptZDrka3MWh9
https://dzen.ru/a/ZPZRU5bXthdQL0rT
https://dzen.ru/a/ZPZR4wm7BXTGU4QM
https://dzen.ru/a/ZPZO09ZDrka3LqM1
https://dzen.ru/a/ZPZMvxpdEnCdGygY
https://kitehurghada.ru/
https://kitehurghada.ru/obuchenie-detej-kajtsyorfingu/
https://kitehurghada.ru/stoimost-obucheniya-kajtserfingu-v-hurgade/
https://kitehurghada.ru/kurs-bazovyj-10-chasov-zanyatij-s-instruktorom-4-5-dnya-450-usd/
https://kitehurghada.ru/kurs-ekspress-6-chasov-zanyatij-s-instruktorom-2-3-dnya-300-usd/
https://kitehurghada.ru/kontakty/
https://kitehurghada.ru/prognoz-vetra-v-hurgade/
https://kitehurghada.ru/kurs-pro-prodvinutyj-15-chasov-zanyatij-s-instruktorom-5-7-dnej-600-usd/
https://kitehurghada.ru/vesna-2024-egipet-hurgada-kajt-tury-i-kajt-kempy-deti-vetra/
https://kitehurghada.ru/vesennie-kanikuly/
https://kitehurghada.ru/majskie-prazdniki/
https://kitehurghada.ru/kajt-shkola/
https://kitehurghada.ru/kajt-kemp-v-hurgade-s-kajt-czentrom-detivetra/
https://kitehurghada.ru/zhenskaya-kajt-shkola-shkola-kajtsyorfinga-dlya-detej/
https://kitehurghada.ru/kajt-shkola-v-hurgade-egipet-kajt-czentr-detivetra/
https://kitehurghada.ru/obuchenie-kajtserfingu-na-krasnom-more/
https://kitehurghada.ru/ekskursii-v-hurgade-konnye-progulki-s-kupaniem-v-more-czeny-i-otzyvy-katanie-na-loshadyah-i-verblyudah/
https://kitehurghada.ru/devochki-i-kajtsyorfing-kajtsyorfing-dlya-devushek/
https://kitehurghada.ru/iko-sertifikat-katsyorfinga/
https://kitehurghada.ru/kajt-spot-deti-vetra-odno-iz-luchshih-mest-v-hurgade-dlya-kajtsyorfinga/
https://kitehurghada.ru/gidrofojl-gidrofojling-fojlbording-kajtfojling-v-hurgade-egipet-obuchenie-s-nulya-za-3-dnya/
https://kitehurghada.ru/kajt-kajtsyorfing-i-ego-istoriya/
https://kitehurghada.ru/individualnoe-obuchenie-gidrofojlu-s-kajtom/
https://kitehurghada.ru/veter-v-hurgade/
https://kitehurghada.ru/akuly-v-egipte/
https://kitehurghada.ru/vingfoil/
https://kitehurghada.ru/kajt-shkola-v-egipte/
https://kitehurghada.ru/temperatura-morya-v-hurgade/
https://kitehurghada.ru/obuchenie-vingfojl/
https://kitehurghada.ru/kajtsyorfing-v-el-gune/
https://kitehurghada.ru/kajt-egipet/
https://kitehurghada.ru/akuly-hurgade/
https://kitehurghada.ru/katanie-na-kajte/
https://kitehurghada.ru/kogda-luchshe-otdyhat-v-egipte/
https://kitehurghada.ru/kajting-v-hurgade/
https://kitehurghada.ru/kajting-v-egipte/
https://kitehurghada.ru/kajtserfing/
https://kitehurghada.ru/temperatura-v-hurgade/
https://kitehurghada.ru/kajting/
https://kitehurghada.ru/obuchenie-kajtsyorfingu-v-hurgade-egipet/
https://kitehurghada.ru/russkaya-kajt-stancziya-deti-vetra-v-hurgade/
https://kitehurghada.ru/gidrofojl-s-kajtom-obuchenie/
https://kitehurghada.ru/pogoda-v-hurgade/
https://kitehurghada.ru/faq-po-hurgade-2022-2023-chasto-zadavaemye-voprosy-ili-chto-vzyat-s-soboj-v-egipet/
https://kitehurghada.ru/kajt-safari-v-egipte-russkaya-kajt-stancziya-detivetra-v-hurgade/
https://kitehurghada.ru/kajtserfing-v-hurgade-luchshij-sezon-dlya-kajtserfinga/
https://kitehurghada.ru/kajting-osobennosti-kajtinga-vidy-kajtinga/
https://kitehurghada.ru/russkaya-kajt-shkola-v-hurgade/
https://kitehurghada.ru/kajt-shkola-detivetra/
https://kitehurghada.ru/programma-obucheniya-kajtsyorfingu-iko-v-hurgade-egipet/
https://kitehurghada.ru/istoriya-kajtserfinga/
https://kitehurghada.ru/podarochnyj-sertifikat-na-obuchenie-kajtserfingu-v-hurgade/
https://kitehurghada.ru/chto-takoe-iko-kitesurfing/
https://www.tripadvisor.ru/Attraction_Review-g23408135-d12244940-Reviews-Kite_school_DETIVETRA-Second_Hurghada_Hurghada_Red_Sea_and_Sinai.html
https://goo.gl/maps/KcoqXRbKWDkdGBDA8
https://goo.gl/maps/JTXRid9mrHFiMH7n6
https://detivetra.ru
https://detivetra.ru/v-hurgade/
https://uslugi.yandex.ru/profile/DetiVetra-348058
https://www.facebook.com/groups/detivetra/
https://www.facebook.com/DETIVETRA.ru/
https://www.youtube.com/channel/UCRG2aTtTaxbBAwlMTklO4ag
https://twitter.com/detivetra
https://rutube.ru/shorts/cb44391727e39c55e798f4efcecadbbe/
https://кайтинг-фото.рф/kayt-baza-v-hurgade.html
https://wa.me/79181955474
https://t.me/detivetrachat
https://www.instagram.com/detivetra.ru/
https://yandex.ru/profile/177183726173
https://yandex.ru/profile/1068186022
https://yandex.ru/profile/22472239976
https://yandex.ru/profile/72204785887
https://yandex.ru/profile/191148233877
https://xn----7sbjteeyka8afw.xn--p1ai
https://vk.com/kiteschoolhurghadaegypt
https://vk.com/kite_deti_vetra_anapa
http://redseakite.ru
https://kiteschoolhurghada.ru
https://divingredsea.ru
https://supanapa.ru
https://dzen.ru/a/ZdvCwDY4Lkx9j1OO
https://dzen.ru/a/ZdvAL3ptMCiNF8WX
https://dzen.ru/a/ZfigvDY3E2MON77x
https://dzen.ru/a/ZduLXm6jwDrtxbA7
https://dzen.ru/a/Zdt-SFBRjmyXXC7Y
https://dzen.ru/a/ZdvBm2tFz2D1IlSO
https://dzen.ru/a/Zdu_3c5NKkyfX91J
https://dzen.ru/a/ZdvCINgebnj0b5BQ
https://dzen.ru/a/ZTNXr-xw-1ZbmsTT
https://dzen.ru/a/ZdCSXCL_8k_Tfrjb
https://dzen.ru/a/ZdKxCtywnzYZgrrk
https://dzen.ru/a/ZTNfJwlmuCeqOEbb
https://dzen.ru/video/watch/65db9f94fb98fa6a95ab5e45?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65d4341844e19f05a34cf61f?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65629d684f336820c3b37487?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f689e39e331d6580277a0a?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f6870bcb2c7822b9dbd15c?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/6562982bd9b42c2e6bd10cae?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f684e1113e7a6a574076b2?rid=925618026.48.1718444364156.12030
https://dzen.ru/a/ZTNYEjMz-VkvVGnB
https://dzen.ru/a/ZTNi1ECY6h8nFsSW
https://dzen.ru/a/ZTNpJ546JGYImpH1
https://dzen.ru/a/ZTNTlZAOEk3ppmIO
https://dzen.ru/a/Zc_f2thSeW9zscF8
https://dzen.ru/a/Zc_U25ITFGrFK0Sf
https://dzen.ru/a/Zc_TAlxn1y1iHc43
https://dzen.ru/a/Zc_LEcYYfS-TrXXm
https://dzen.ru/a/ZVjdtJSQOhzbk0B1
https://dzen.ru/a/ZTNS7dJWml8dLCim
https://dzen.ru/a/ZVdT4K4CRxpHZx1i
https://dzen.ru/a/ZVdb9TtUnQGek7_G
https://dzen.ru/a/ZTNUDrwjFj4U3LBI
https://dzen.ru/a/ZTNVSZAOEk3pp-ki
https://dzen.ru/a/ZTNptIGpwlQkN-E1
https://dzen.ru/a/ZTNqooGpwlQkORsw
https://dzen.ru/a/ZTNnrk1VVGtQwolr
https://dzen.ru/a/ZTNS0bwjFj4U25A9
https://dzen.ru/a/ZTNG7QlmuCeqISH6
https://dzen.ru/a/ZTM87Ogjh2c_dNzY
https://dzen.ru/b/ZS5ge6k6swm-YNzl
https://dzen.ru/b/ZS1BbXqKjhX4tA9_
https://dzen.ru/a/ZQ2aw4OzGFVaAbr2
https://dzen.ru/b/ZS5YZ7qcv2E0eJPQ
https://dzen.ru/a/ZQrJrb_XDifDVzGP
https://dzen.ru/a/ZQrIWS4n3ChkWGvj
https://dzen.ru/a/ZQrCRLpsYU4IGsNS
https://dzen.ru/a/ZQq5kyCaIkuoWgEb
https://dzen.ru/a/ZQq6z8LJ7AdPjTX6
https://dzen.ru/a/ZQrBHwW8ugdAoeld
https://dzen.ru/a/ZQq5zAyUYGuFpV6x
https://dzen.ru/a/ZQq6uF9dOExoiJn3
https://dzen.ru/a/ZQq4kyCaIkuoV7HL
https://dzen.ru/a/ZPZtZAWIHk1Wxu36
https://dzen.ru/a/ZPZ324ORLBGu36oK
https://dzen.ru/a/ZPZ6mPf64TnWQmu4
https://dzen.ru/a/ZPZqtxo5MUGqivHt
https://dzen.ru/a/ZPZ3KI7QZRjreV_m
https://dzen.ru/a/ZPZsDLf4FUB9-vTG
https://dzen.ru/a/ZPZyyDEQHn8iOuK4
https://dzen.ru/a/ZPZnc9bwiVMxJaDt
https://dzen.ru/a/ZPZ2CaKi2WZuFDzk
https://dzen.ru/a/ZPZw1iSYk23jVqD2
https://dzen.ru/a/ZPZvXBo5MUGqmExv
https://dzen.ru/a/ZPZusNZDrka3nhk4
https://dzen.ru/a/ZPZomY7QZRjrXUWH
https://dzen.ru/a/ZPZlbm0hO0O6e_6G
https://dzen.ru/a/ZPZkz_Z4SEywAI9r
https://dzen.ru/a/ZPZfLRo5MUGqXPqk
https://dzen.ru/a/ZPZkQ47QZRjrTEiz
https://dzen.ru/a/ZPZgZG72vTlMv-RA
https://dzen.ru/a/ZPZUGxo5MUGqMHlM
https://dzen.ru/a/ZPZTWRo5MUGqLTP3
https://dzen.ru/a/ZPZSyvf64TnWzJmJ
https://dzen.ru/a/ZPZQptZDrka3MWh9
https://dzen.ru/a/ZPZRU5bXthdQL0rT
https://dzen.ru/a/ZPZR4wm7BXTGU4QM
https://dzen.ru/a/ZPZO09ZDrka3LqM1
https://dzen.ru/a/ZPZMvxpdEnCdGygY
https://kitehurghada.ru/
https://kitehurghada.ru/obuchenie-detej-kajtsyorfingu/
https://kitehurghada.ru/stoimost-obucheniya-kajtserfingu-v-hurgade/
https://kitehurghada.ru/kurs-bazovyj-10-chasov-zanyatij-s-instruktorom-4-5-dnya-450-usd/
https://kitehurghada.ru/kurs-ekspress-6-chasov-zanyatij-s-instruktorom-2-3-dnya-300-usd/
https://kitehurghada.ru/kontakty/
https://kitehurghada.ru/prognoz-vetra-v-hurgade/
https://kitehurghada.ru/kurs-pro-prodvinutyj-15-chasov-zanyatij-s-instruktorom-5-7-dnej-600-usd/
https://kitehurghada.ru/vesna-2024-egipet-hurgada-kajt-tury-i-kajt-kempy-deti-vetra/
https://kitehurghada.ru/vesennie-kanikuly/
https://kitehurghada.ru/majskie-prazdniki/
https://kitehurghada.ru/kajt-shkola/
https://kitehurghada.ru/kajt-kemp-v-hurgade-s-kajt-czentrom-detivetra/
https://kitehurghada.ru/zhenskaya-kajt-shkola-shkola-kajtsyorfinga-dlya-detej/
https://kitehurghada.ru/kajt-shkola-v-hurgade-egipet-kajt-czentr-detivetra/
https://kitehurghada.ru/obuchenie-kajtserfingu-na-krasnom-more/
https://kitehurghada.ru/ekskursii-v-hurgade-konnye-progulki-s-kupaniem-v-more-czeny-i-otzyvy-katanie-na-loshadyah-i-verblyudah/
https://kitehurghada.ru/devochki-i-kajtsyorfing-kajtsyorfing-dlya-devushek/
https://kitehurghada.ru/iko-sertifikat-katsyorfinga/
https://kitehurghada.ru/kajt-spot-deti-vetra-odno-iz-luchshih-mest-v-hurgade-dlya-kajtsyorfinga/
https://kitehurghada.ru/gidrofojl-gidrofojling-fojlbording-kajtfojling-v-hurgade-egipet-obuchenie-s-nulya-za-3-dnya/
https://kitehurghada.ru/kajt-kajtsyorfing-i-ego-istoriya/
https://kitehurghada.ru/individualnoe-obuchenie-gidrofojlu-s-kajtom/
https://kitehurghada.ru/veter-v-hurgade/
https://kitehurghada.ru/akuly-v-egipte/
https://kitehurghada.ru/vingfoil/
https://kitehurghada.ru/kajt-shkola-v-egipte/
https://kitehurghada.ru/temperatura-morya-v-hurgade/
https://kitehurghada.ru/obuchenie-vingfojl/
https://kitehurghada.ru/kajtsyorfing-v-el-gune/
https://kitehurghada.ru/kajt-egipet/
https://kitehurghada.ru/akuly-hurgade/
https://kitehurghada.ru/katanie-na-kajte/
https://kitehurghada.ru/kogda-luchshe-otdyhat-v-egipte/
https://kitehurghada.ru/kajting-v-hurgade/
https://kitehurghada.ru/kajting-v-egipte/
https://kitehurghada.ru/kajtserfing/
https://kitehurghada.ru/temperatura-v-hurgade/
https://kitehurghada.ru/kajting/
https://kitehurghada.ru/obuchenie-kajtsyorfingu-v-hurgade-egipet/
https://kitehurghada.ru/russkaya-kajt-stancziya-deti-vetra-v-hurgade/
https://kitehurghada.ru/gidrofojl-s-kajtom-obuchenie/
https://kitehurghada.ru/pogoda-v-hurgade/
https://kitehurghada.ru/faq-po-hurgade-2022-2023-chasto-zadavaemye-voprosy-ili-chto-vzyat-s-soboj-v-egipet/
https://kitehurghada.ru/kajt-safari-v-egipte-russkaya-kajt-stancziya-detivetra-v-hurgade/
https://kitehurghada.ru/kajtserfing-v-hurgade-luchshij-sezon-dlya-kajtserfinga/
https://kitehurghada.ru/kajting-osobennosti-kajtinga-vidy-kajtinga/
https://kitehurghada.ru/russkaya-kajt-shkola-v-hurgade/
https://kitehurghada.ru/kajt-shkola-detivetra/
https://kitehurghada.ru/programma-obucheniya-kajtsyorfingu-iko-v-hurgade-egipet/
https://kitehurghada.ru/istoriya-kajtserfinga/
https://kitehurghada.ru/podarochnyj-sertifikat-na-obuchenie-kajtserfingu-v-hurgade/
https://kitehurghada.ru/chto-takoe-iko-kitesurfing/
https://www.tripadvisor.ru/Attraction_Review-g23408135-d12244940-Reviews-Kite_school_DETIVETRA-Second_Hurghada_Hurghada_Red_Sea_and_Sinai.html
https://goo.gl/maps/KcoqXRbKWDkdGBDA8
https://goo.gl/maps/JTXRid9mrHFiMH7n6
https://detivetra.ru
https://detivetra.ru/v-hurgade/
https://uslugi.yandex.ru/profile/DetiVetra-348058
https://www.facebook.com/groups/detivetra/
https://www.facebook.com/DETIVETRA.ru/
https://www.youtube.com/channel/UCRG2aTtTaxbBAwlMTklO4ag
https://twitter.com/detivetra
https://rutube.ru/shorts/cb44391727e39c55e798f4efcecadbbe/
https://кайтинг-фото.рф/kayt-baza-v-hurgade.html
https://wa.me/79181955474
https://t.me/detivetrachat
https://www.instagram.com/detivetra.ru/
https://yandex.ru/profile/177183726173
https://yandex.ru/profile/1068186022
https://yandex.ru/profile/22472239976
https://yandex.ru/profile/72204785887
https://yandex.ru/profile/191148233877
https://xn----7sbjteeyka8afw.xn--p1ai
https://vk.com/kiteschoolhurghadaegypt
https://vk.com/kite_deti_vetra_anapa
http://redseakite.ru
https://kiteschoolhurghada.ru
https://divingredsea.ru
https://supanapa.ru
https://dzen.ru/a/ZdvCwDY4Lkx9j1OO
https://dzen.ru/a/ZdvAL3ptMCiNF8WX
https://dzen.ru/a/ZfigvDY3E2MON77x
https://dzen.ru/a/ZduLXm6jwDrtxbA7
https://dzen.ru/a/Zdt-SFBRjmyXXC7Y
https://dzen.ru/a/ZdvBm2tFz2D1IlSO
https://dzen.ru/a/Zdu_3c5NKkyfX91J
https://dzen.ru/a/ZdvCINgebnj0b5BQ
https://dzen.ru/a/ZTNXr-xw-1ZbmsTT
https://dzen.ru/a/ZdCSXCL_8k_Tfrjb
https://dzen.ru/a/ZdKxCtywnzYZgrrk
https://dzen.ru/a/ZTNfJwlmuCeqOEbb
https://dzen.ru/video/watch/65db9f94fb98fa6a95ab5e45?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65d4341844e19f05a34cf61f?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65629d684f336820c3b37487?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f689e39e331d6580277a0a?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f6870bcb2c7822b9dbd15c?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/6562982bd9b42c2e6bd10cae?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f684e1113e7a6a574076b2?rid=925618026.48.1718444364156.12030
https://dzen.ru/a/ZTNYEjMz-VkvVGnB
https://dzen.ru/a/ZTNi1ECY6h8nFsSW
https://dzen.ru/a/ZTNpJ546JGYImpH1
https://dzen.ru/a/ZTNTlZAOEk3ppmIO
https://dzen.ru/a/Zc_f2thSeW9zscF8
https://dzen.ru/a/Zc_U25ITFGrFK0Sf
https://dzen.ru/a/Zc_TAlxn1y1iHc43
https://dzen.ru/a/Zc_LEcYYfS-TrXXm
https://dzen.ru/a/ZVjdtJSQOhzbk0B1
https://dzen.ru/a/ZTNS7dJWml8dLCim
https://dzen.ru/a/ZVdT4K4CRxpHZx1i
https://dzen.ru/a/ZVdb9TtUnQGek7_G
https://dzen.ru/a/ZTNUDrwjFj4U3LBI
https://dzen.ru/a/ZTNVSZAOEk3pp-ki
https://dzen.ru/a/ZTNptIGpwlQkN-E1
https://dzen.ru/a/ZTNqooGpwlQkORsw
https://dzen.ru/a/ZTNnrk1VVGtQwolr
https://dzen.ru/a/ZTNS0bwjFj4U25A9
https://dzen.ru/a/ZTNG7QlmuCeqISH6
https://dzen.ru/a/ZTM87Ogjh2c_dNzY
https://dzen.ru/b/ZS5ge6k6swm-YNzl
https://dzen.ru/b/ZS1BbXqKjhX4tA9_
https://dzen.ru/a/ZQ2aw4OzGFVaAbr2
https://dzen.ru/b/ZS5YZ7qcv2E0eJPQ
https://dzen.ru/a/ZQrJrb_XDifDVzGP
https://dzen.ru/a/ZQrIWS4n3ChkWGvj
https://dzen.ru/a/ZQrCRLpsYU4IGsNS
https://dzen.ru/a/ZQq5kyCaIkuoWgEb
https://dzen.ru/a/ZQq6z8LJ7AdPjTX6
https://dzen.ru/a/ZQrBHwW8ugdAoeld
https://dzen.ru/a/ZQq5zAyUYGuFpV6x
https://dzen.ru/a/ZQq6uF9dOExoiJn3
https://dzen.ru/a/ZQq4kyCaIkuoV7HL
https://dzen.ru/a/ZPZtZAWIHk1Wxu36
https://dzen.ru/a/ZPZ324ORLBGu36oK
https://dzen.ru/a/ZPZ6mPf64TnWQmu4
https://dzen.ru/a/ZPZqtxo5MUGqivHt
https://dzen.ru/a/ZPZ3KI7QZRjreV_m
https://dzen.ru/a/ZPZsDLf4FUB9-vTG
https://dzen.ru/a/ZPZyyDEQHn8iOuK4
https://dzen.ru/a/ZPZnc9bwiVMxJaDt
https://dzen.ru/a/ZPZ2CaKi2WZuFDzk
https://dzen.ru/a/ZPZw1iSYk23jVqD2
https://dzen.ru/a/ZPZvXBo5MUGqmExv
https://dzen.ru/a/ZPZusNZDrka3nhk4
https://dzen.ru/a/ZPZomY7QZRjrXUWH
https://dzen.ru/a/ZPZlbm0hO0O6e_6G
https://dzen.ru/a/ZPZkz_Z4SEywAI9r
https://dzen.ru/a/ZPZfLRo5MUGqXPqk
https://dzen.ru/a/ZPZkQ47QZRjrTEiz
https://dzen.ru/a/ZPZgZG72vTlMv-RA
https://dzen.ru/a/ZPZUGxo5MUGqMHlM
https://dzen.ru/a/ZPZTWRo5MUGqLTP3
https://dzen.ru/a/ZPZSyvf64TnWzJmJ
https://dzen.ru/a/ZPZQptZDrka3MWh9
https://dzen.ru/a/ZPZRU5bXthdQL0rT
https://dzen.ru/a/ZPZR4wm7BXTGU4QM
https://dzen.ru/a/ZPZO09ZDrka3LqM1
https://dzen.ru/a/ZPZMvxpdEnCdGygY
Мы делимся практическими знаниями о ЗСК, покупке НДС и чеков, а также раскрываем эффективные методы для защиты бизнеса от рисков. Если вы хотите разобраться в тонкостях бухгалтерии, проверить своих контрагентов или улучшить финансовую безопасность компании, Бенефициар — это то, что вам нужно. Подписывайтесь на канал, чтобы получить доступ к профессиональной аналитике, уникальным инструментам и готовым решениям для вашего бизнеса! https://benefitsar.net/
https://www.patreon.com/posts/kakoi-vpn-v-rf-v-114494462?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
https://www.patreon.com/posts/seo-prodvizhenie-116306292?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
https://www.patreon.com/posts/onlain-servisy-v-115537226?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
https://www.patreon.com/posts/kakogo-internet-115051950?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
https://www.patreon.com/posts/generatsiia-v-v-114898976?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
https://www.patreon.com/posts/kak-raskrutit-114899568?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
https://www.patreon.com/posts/top-kriptobirzh-114485936?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
https://www.patreon.com/posts/kakie-altkoiny-v-113637912?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
https://www.patreon.com/posts/gde-kupit-usdt-113542498?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
https://www.patreon.com/posts/chto-takoe-dlia-113502942?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
https://www.patreon.com/posts/lichnyi-sovet-v-117374233?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
https://www.patreon.com/posts/pochemu-rabota-i-117374511?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
https://adpass.ru/pochemu-rabota-za-protsent-ot-prodazh-neeffektivna-i-kak-sozdat-uspeshnoe-partnyorstvo-v-marketinge/
https://adpass.ru/lichnyj-sovet-centrparts-com-vash-pomoshhnik-v-mire-gadzhetov/
https://adpass.ru/top-15-agentstv-dlya-prodvizheniya-v-telegram-vse-chto-vam-nuzhno-znattelegram-stal-ne-prosto-messendzherom-a-moshhnoj-marketingovoj-platformoj/
https://adpass.ru/seo-prodvizhenie-kataloga-agentstva-nedvizhimosti-do-top-1-kejs/
https://adpass.ru/onlajn-servisy-dlya-vedeniya-buhgalterii-v-ispanii/
https://adpass.ru/kakogo-optovolokonnogo-internet-provajdera-vybrat-v-ispanii/
https://adpass.ru/generatsiya-lidov-v-telegram-kanalah-v-2024-godu/
https://adpass.ru/kak-raskrutit-telegram-kanal/
https://adpass.ru/gde-kupit-usdt-za-rubli-aktualnye-sposoby-kupit-kriptovalyutu-2/
https://adpass.ru/chto-takoe-onlajn-servisy-dlya-vedeniya-buhgalterii-dlya-ip/
https://adpass.ru/kakie-altkoiny-kupit-v-2024-godu-spisok-samyh-perspektivnyh-monet/
https://teletype.in/@kateimpossible/IKHaGC6pzmC
https://teletype.in/@kateimpossible/5BtKT0ddTHL
https://teletype.in/@kateimpossible/jhbWNPxwj1U
https://teletype.in/@kateimpossible/q2cWAh0_Xy6
https://teletype.in/@kateimpossible/e-S6wd8_pev
https://teletype.in/@kateimpossible/6R180oofa7S
https://teletype.in/@kateimpossible/LpEdnbEeINh
https://teletype.in/@kateimpossible/_2s5cdmHZyo
https://teletype.in/@kateimpossible/frjnxImgIpT
https://teletype.in/@kateimpossible/5Y61VKV7JqO
https://teletype.in/@kateimpossible/OWPTvbeHAlP
https://teletype.in/@kateimpossible/VU9snLXgCO8
https://teletype.in/@kateimpossible/aiUkc_WwNcS
https://share.evernote.com/note/7759f27a-8113-3bbc-2cf4-72bfb110698a
https://share.evernote.com/note/97fb87fa-ece4-7f01-124f-33f043547b73
https://share.evernote.com/note/7fc46b16-70be-6c62-4836-8b3dd7d386b7
https://share.evernote.com/note/1c22171f-4be6-4a89-56aa-2c616fce99e8
https://share.evernote.com/note/15861637-8883-44c4-c16e-9f2816317153
https://share.evernote.com/note/8c1cfb10-fe59-e0bc-13e6-51c516ddeaf7
https://share.evernote.com/note/28d630f7-10d4-8fb5-0427-79c0d8ccdca3
https://share.evernote.com/note/1ead7b6c-cefb-ee26-4166-2ae5d5b588fd
https://share.evernote.com/note/e681ac8b-23a5-bfe3-2b1f-db52ce625288
https://share.evernote.com/note/b9880b11-ea4c-6374-3491-a2d55cdbab6b
https://share.evernote.com/note/e552da01-f915-a848-dbf9-f9cb32db657f
https://share.evernote.com/note/282e0fa5-fd4c-3d87-055c-68f2bd361b0e
https://share.evernote.com/note/a685b573-3731-12d8-05a2-12ef00627162
https://kitehurghada.ru/ - https://dzen.ru/a/ZTNXr-xw-1ZbmsTT
https://kitehurghada.ru/
https://kitehurghada.ru/obuchenie-detej-kajtsyorfingu/
https://kitehurghada.ru/stoimost-obucheniya-kajtserfingu-v-hurgade/
https://kitehurghada.ru/kurs-bazovyj-10-chasov-zanyatij-s-instruktorom-4-5-dnya-450-usd/
https://kitehurghada.ru/kurs-ekspress-6-chasov-zanyatij-s-instruktorom-2-3-dnya-300-usd/
https://kitehurghada.ru/kontakty/
https://kitehurghada.ru/prognoz-vetra-v-hurgade/
https://kitehurghada.ru/kurs-pro-prodvinutyj-15-chasov-zanyatij-s-instruktorom-5-7-dnej-600-usd/
https://kitehurghada.ru/vesna-2024-egipet-hurgada-kajt-tury-i-kajt-kempy-deti-vetra/
https://kitehurghada.ru/vesennie-kanikuly/
https://kitehurghada.ru/majskie-prazdniki/
https://kitehurghada.ru/kajt-shkola/
https://kitehurghada.ru/kajt-kemp-v-hurgade-s-kajt-czentrom-detivetra/
https://kitehurghada.ru/zhenskaya-kajt-shkola-shkola-kajtsyorfinga-dlya-detej/
https://kitehurghada.ru/kajt-shkola-v-hurgade-egipet-kajt-czentr-detivetra/
https://kitehurghada.ru/obuchenie-kajtserfingu-na-krasnom-more/
https://kitehurghada.ru/ekskursii-v-hurgade-konnye-progulki-s-kupaniem-v-more-czeny-i-otzyvy-katanie-na-loshadyah-i-verblyudah/
https://kitehurghada.ru/devochki-i-kajtsyorfing-kajtsyorfing-dlya-devushek/
https://kitehurghada.ru/iko-sertifikat-katsyorfinga/
https://kitehurghada.ru/kajt-spot-deti-vetra-odno-iz-luchshih-mest-v-hurgade-dlya-kajtsyorfinga/
https://kitehurghada.ru/gidrofojl-gidrofojling-fojlbording-kajtfojling-v-hurgade-egipet-obuchenie-s-nulya-za-3-dnya/
https://kitehurghada.ru/kajt-kajtsyorfing-i-ego-istoriya/
https://kitehurghada.ru/individualnoe-obuchenie-gidrofojlu-s-kajtom/
https://kitehurghada.ru/veter-v-hurgade/
https://kitehurghada.ru/akuly-v-egipte/
https://kitehurghada.ru/vingfoil/
https://kitehurghada.ru/kajt-shkola-v-egipte/
https://kitehurghada.ru/temperatura-morya-v-hurgade/
https://kitehurghada.ru/obuchenie-vingfojl/
https://kitehurghada.ru/kajtsyorfing-v-el-gune/
https://kitehurghada.ru/kajt-egipet/
https://kitehurghada.ru/akuly-hurgade/
https://kitehurghada.ru/katanie-na-kajte/
https://kitehurghada.ru/kogda-luchshe-otdyhat-v-egipte/
https://kitehurghada.ru/kajting-v-hurgade/
https://kitehurghada.ru/kajting-v-egipte/
https://kitehurghada.ru/kajtserfing/
https://kitehurghada.ru/temperatura-v-hurgade/
https://kitehurghada.ru/kajting/
https://kitehurghada.ru/obuchenie-kajtsyorfingu-v-hurgade-egipet/
https://kitehurghada.ru/russkaya-kajt-stancziya-deti-vetra-v-hurgade/
https://kitehurghada.ru/gidrofojl-s-kajtom-obuchenie/
https://kitehurghada.ru/pogoda-v-hurgade/
https://kitehurghada.ru/faq-po-hurgade-2022-2023-chasto-zadavaemye-voprosy-ili-chto-vzyat-s-soboj-v-egipet/
https://kitehurghada.ru/kajt-safari-v-egipte-russkaya-kajt-stancziya-detivetra-v-hurgade/
https://kitehurghada.ru/kajtserfing-v-hurgade-luchshij-sezon-dlya-kajtserfinga/
https://kitehurghada.ru/kajting-osobennosti-kajtinga-vidy-kajtinga/
https://kitehurghada.ru/russkaya-kajt-shkola-v-hurgade/
https://kitehurghada.ru/kajt-shkola-detivetra/
https://kitehurghada.ru/programma-obucheniya-kajtsyorfingu-iko-v-hurgade-egipet/
https://kitehurghada.ru/istoriya-kajtserfinga/
https://kitehurghada.ru/podarochnyj-sertifikat-na-obuchenie-kajtserfingu-v-hurgade/
https://kitehurghada.ru/chto-takoe-iko-kitesurfing/
https://www.tripadvisor.ru/Attraction_Review-g23408135-d12244940-Reviews-Kite_school_DETIVETRA-Second_Hurghada_Hurghada_Red_Sea_and_Sinai.html
https://goo.gl/maps/KcoqXRbKWDkdGBDA8
https://goo.gl/maps/JTXRid9mrHFiMH7n6
https://detivetra.ru
https://detivetra.ru/v-hurgade/
https://uslugi.yandex.ru/profile/DetiVetra-348058
https://www.facebook.com/groups/detivetra/
https://www.facebook.com/DETIVETRA.ru/
https://www.youtube.com/channel/UCRG2aTtTaxbBAwlMTklO4ag
https://twitter.com/detivetra
https://rutube.ru/shorts/cb44391727e39c55e798f4efcecadbbe/
https://кайтинг-фото.рф/kayt-baza-v-hurgade.html
https://wa.me/79181955474
https://t.me/detivetrachat
https://www.instagram.com/detivetra.ru/
https://yandex.ru/profile/177183726173
https://yandex.ru/profile/1068186022
https://yandex.ru/profile/22472239976
https://yandex.ru/profile/72204785887
https://yandex.ru/profile/191148233877
https://xn----7sbjteeyka8afw.xn--p1ai
https://vk.com/kiteschoolhurghadaegypt
https://vk.com/kite_deti_vetra_anapa
http://redseakite.ru
https://kiteschoolhurghada.ru
https://divingredsea.ru
https://supanapa.ru
https://dzen.ru/a/ZdvCwDY4Lkx9j1OO
https://dzen.ru/a/ZdvAL3ptMCiNF8WX
https://dzen.ru/a/ZfigvDY3E2MON77x
https://dzen.ru/a/ZduLXm6jwDrtxbA7
https://dzen.ru/a/Zdt-SFBRjmyXXC7Y
https://dzen.ru/a/ZdvBm2tFz2D1IlSO
https://dzen.ru/a/Zdu_3c5NKkyfX91J
https://dzen.ru/a/ZdvCINgebnj0b5BQ
https://dzen.ru/a/ZTNXr-xw-1ZbmsTT
https://dzen.ru/a/ZdCSXCL_8k_Tfrjb
https://dzen.ru/a/ZdKxCtywnzYZgrrk
https://dzen.ru/a/ZTNfJwlmuCeqOEbb
https://dzen.ru/video/watch/65db9f94fb98fa6a95ab5e45?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65d4341844e19f05a34cf61f?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65629d684f336820c3b37487?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f689e39e331d6580277a0a?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f6870bcb2c7822b9dbd15c?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/6562982bd9b42c2e6bd10cae?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f684e1113e7a6a574076b2?rid=925618026.48.1718444364156.12030
https://dzen.ru/a/ZTNYEjMz-VkvVGnB
https://dzen.ru/a/ZTNi1ECY6h8nFsSW
https://dzen.ru/a/ZTNpJ546JGYImpH1
https://dzen.ru/a/ZTNTlZAOEk3ppmIO
https://dzen.ru/a/Zc_f2thSeW9zscF8
https://dzen.ru/a/Zc_U25ITFGrFK0Sf
https://dzen.ru/a/Zc_TAlxn1y1iHc43
https://dzen.ru/a/Zc_LEcYYfS-TrXXm
https://dzen.ru/a/ZVjdtJSQOhzbk0B1
https://dzen.ru/a/ZTNS7dJWml8dLCim
https://dzen.ru/a/ZVdT4K4CRxpHZx1i
https://dzen.ru/a/ZVdb9TtUnQGek7_G
https://dzen.ru/a/ZTNUDrwjFj4U3LBI
https://dzen.ru/a/ZTNVSZAOEk3pp-ki
https://dzen.ru/a/ZTNptIGpwlQkN-E1
https://dzen.ru/a/ZTNqooGpwlQkORsw
https://dzen.ru/a/ZTNnrk1VVGtQwolr
https://dzen.ru/a/ZTNS0bwjFj4U25A9
https://dzen.ru/a/ZTNG7QlmuCeqISH6
https://dzen.ru/a/ZTM87Ogjh2c_dNzY
https://dzen.ru/b/ZS5ge6k6swm-YNzl
https://dzen.ru/b/ZS1BbXqKjhX4tA9_
https://dzen.ru/a/ZQ2aw4OzGFVaAbr2
https://dzen.ru/b/ZS5YZ7qcv2E0eJPQ
https://dzen.ru/a/ZQrJrb_XDifDVzGP
https://dzen.ru/a/ZQrIWS4n3ChkWGvj
https://dzen.ru/a/ZQrCRLpsYU4IGsNS
https://dzen.ru/a/ZQq5kyCaIkuoWgEb
https://dzen.ru/a/ZQq6z8LJ7AdPjTX6
https://dzen.ru/a/ZQrBHwW8ugdAoeld
https://dzen.ru/a/ZQq5zAyUYGuFpV6x
https://dzen.ru/a/ZQq6uF9dOExoiJn3
https://dzen.ru/a/ZQq4kyCaIkuoV7HL
https://dzen.ru/a/ZPZtZAWIHk1Wxu36
https://dzen.ru/a/ZPZ324ORLBGu36oK
https://dzen.ru/a/ZPZ6mPf64TnWQmu4
https://dzen.ru/a/ZPZqtxo5MUGqivHt
https://dzen.ru/a/ZPZ3KI7QZRjreV_m
https://dzen.ru/a/ZPZsDLf4FUB9-vTG
https://dzen.ru/a/ZPZyyDEQHn8iOuK4
https://dzen.ru/a/ZPZnc9bwiVMxJaDt
https://dzen.ru/a/ZPZ2CaKi2WZuFDzk
https://dzen.ru/a/ZPZw1iSYk23jVqD2
https://dzen.ru/a/ZPZvXBo5MUGqmExv
https://dzen.ru/a/ZPZusNZDrka3nhk4
https://dzen.ru/a/ZPZomY7QZRjrXUWH
https://dzen.ru/a/ZPZlbm0hO0O6e_6G
https://dzen.ru/a/ZPZkz_Z4SEywAI9r
https://dzen.ru/a/ZPZfLRo5MUGqXPqk
https://dzen.ru/a/ZPZkQ47QZRjrTEiz
https://dzen.ru/a/ZPZgZG72vTlMv-RA
https://dzen.ru/a/ZPZUGxo5MUGqMHlM
https://dzen.ru/a/ZPZTWRo5MUGqLTP3
https://dzen.ru/a/ZPZSyvf64TnWzJmJ
https://dzen.ru/a/ZPZQptZDrka3MWh9
https://dzen.ru/a/ZPZRU5bXthdQL0rT
https://dzen.ru/a/ZPZR4wm7BXTGU4QM
https://dzen.ru/a/ZPZO09ZDrka3LqM1
https://dzen.ru/a/ZPZMvxpdEnCdGygY
https://kitehurghada.ru/russkaya-kajt-shkola-v-hurgade/ - https://dzen.ru/a/ZVdT4K4CRxpHZx1i
https://kitehurghada.ru/
https://kitehurghada.ru/obuchenie-detej-kajtsyorfingu/
https://kitehurghada.ru/stoimost-obucheniya-kajtserfingu-v-hurgade/
https://kitehurghada.ru/kurs-bazovyj-10-chasov-zanyatij-s-instruktorom-4-5-dnya-450-usd/
https://kitehurghada.ru/kurs-ekspress-6-chasov-zanyatij-s-instruktorom-2-3-dnya-300-usd/
https://kitehurghada.ru/kontakty/
https://kitehurghada.ru/prognoz-vetra-v-hurgade/
https://kitehurghada.ru/kurs-pro-prodvinutyj-15-chasov-zanyatij-s-instruktorom-5-7-dnej-600-usd/
https://kitehurghada.ru/vesna-2024-egipet-hurgada-kajt-tury-i-kajt-kempy-deti-vetra/
https://kitehurghada.ru/vesennie-kanikuly/
https://kitehurghada.ru/majskie-prazdniki/
https://kitehurghada.ru/kajt-shkola/
https://kitehurghada.ru/kajt-kemp-v-hurgade-s-kajt-czentrom-detivetra/
https://kitehurghada.ru/zhenskaya-kajt-shkola-shkola-kajtsyorfinga-dlya-detej/
https://kitehurghada.ru/kajt-shkola-v-hurgade-egipet-kajt-czentr-detivetra/
https://kitehurghada.ru/obuchenie-kajtserfingu-na-krasnom-more/
https://kitehurghada.ru/ekskursii-v-hurgade-konnye-progulki-s-kupaniem-v-more-czeny-i-otzyvy-katanie-na-loshadyah-i-verblyudah/
https://kitehurghada.ru/devochki-i-kajtsyorfing-kajtsyorfing-dlya-devushek/
https://kitehurghada.ru/iko-sertifikat-katsyorfinga/
https://kitehurghada.ru/kajt-spot-deti-vetra-odno-iz-luchshih-mest-v-hurgade-dlya-kajtsyorfinga/
https://kitehurghada.ru/gidrofojl-gidrofojling-fojlbording-kajtfojling-v-hurgade-egipet-obuchenie-s-nulya-za-3-dnya/
https://kitehurghada.ru/kajt-kajtsyorfing-i-ego-istoriya/
https://kitehurghada.ru/individualnoe-obuchenie-gidrofojlu-s-kajtom/
https://kitehurghada.ru/veter-v-hurgade/
https://kitehurghada.ru/akuly-v-egipte/
https://kitehurghada.ru/vingfoil/
https://kitehurghada.ru/kajt-shkola-v-egipte/
https://kitehurghada.ru/temperatura-morya-v-hurgade/
https://kitehurghada.ru/obuchenie-vingfojl/
https://kitehurghada.ru/kajtsyorfing-v-el-gune/
https://kitehurghada.ru/kajt-egipet/
https://kitehurghada.ru/akuly-hurgade/
https://kitehurghada.ru/katanie-na-kajte/
https://kitehurghada.ru/kogda-luchshe-otdyhat-v-egipte/
https://kitehurghada.ru/kajting-v-hurgade/
https://kitehurghada.ru/kajting-v-egipte/
https://kitehurghada.ru/kajtserfing/
https://kitehurghada.ru/temperatura-v-hurgade/
https://kitehurghada.ru/kajting/
https://kitehurghada.ru/obuchenie-kajtsyorfingu-v-hurgade-egipet/
https://kitehurghada.ru/russkaya-kajt-stancziya-deti-vetra-v-hurgade/
https://kitehurghada.ru/gidrofojl-s-kajtom-obuchenie/
https://kitehurghada.ru/pogoda-v-hurgade/
https://kitehurghada.ru/faq-po-hurgade-2022-2023-chasto-zadavaemye-voprosy-ili-chto-vzyat-s-soboj-v-egipet/
https://kitehurghada.ru/kajt-safari-v-egipte-russkaya-kajt-stancziya-detivetra-v-hurgade/
https://kitehurghada.ru/kajtserfing-v-hurgade-luchshij-sezon-dlya-kajtserfinga/
https://kitehurghada.ru/kajting-osobennosti-kajtinga-vidy-kajtinga/
https://kitehurghada.ru/russkaya-kajt-shkola-v-hurgade/
https://kitehurghada.ru/kajt-shkola-detivetra/
https://kitehurghada.ru/programma-obucheniya-kajtsyorfingu-iko-v-hurgade-egipet/
https://kitehurghada.ru/istoriya-kajtserfinga/
https://kitehurghada.ru/podarochnyj-sertifikat-na-obuchenie-kajtserfingu-v-hurgade/
https://kitehurghada.ru/chto-takoe-iko-kitesurfing/
https://www.tripadvisor.ru/Attraction_Review-g23408135-d12244940-Reviews-Kite_school_DETIVETRA-Second_Hurghada_Hurghada_Red_Sea_and_Sinai.html
https://goo.gl/maps/KcoqXRbKWDkdGBDA8
https://goo.gl/maps/JTXRid9mrHFiMH7n6
https://detivetra.ru
https://detivetra.ru/v-hurgade/
https://uslugi.yandex.ru/profile/DetiVetra-348058
https://www.facebook.com/groups/detivetra/
https://www.facebook.com/DETIVETRA.ru/
https://www.youtube.com/channel/UCRG2aTtTaxbBAwlMTklO4ag
https://twitter.com/detivetra
https://rutube.ru/shorts/cb44391727e39c55e798f4efcecadbbe/
https://кайтинг-фото.рф/kayt-baza-v-hurgade.html
https://wa.me/79181955474
https://t.me/detivetrachat
https://www.instagram.com/detivetra.ru/
https://yandex.ru/profile/177183726173
https://yandex.ru/profile/1068186022
https://yandex.ru/profile/22472239976
https://yandex.ru/profile/72204785887
https://yandex.ru/profile/191148233877
https://xn----7sbjteeyka8afw.xn--p1ai
https://vk.com/kiteschoolhurghadaegypt
https://vk.com/kite_deti_vetra_anapa
http://redseakite.ru
https://kiteschoolhurghada.ru
https://divingredsea.ru
https://supanapa.ru
https://dzen.ru/a/ZdvCwDY4Lkx9j1OO
https://dzen.ru/a/ZdvAL3ptMCiNF8WX
https://dzen.ru/a/ZfigvDY3E2MON77x
https://dzen.ru/a/ZduLXm6jwDrtxbA7
https://dzen.ru/a/Zdt-SFBRjmyXXC7Y
https://dzen.ru/a/ZdvBm2tFz2D1IlSO
https://dzen.ru/a/Zdu_3c5NKkyfX91J
https://dzen.ru/a/ZdvCINgebnj0b5BQ
https://dzen.ru/a/ZTNXr-xw-1ZbmsTT
https://dzen.ru/a/ZdCSXCL_8k_Tfrjb
https://dzen.ru/a/ZdKxCtywnzYZgrrk
https://dzen.ru/a/ZTNfJwlmuCeqOEbb
https://dzen.ru/video/watch/65db9f94fb98fa6a95ab5e45?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65d4341844e19f05a34cf61f?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65629d684f336820c3b37487?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f689e39e331d6580277a0a?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f6870bcb2c7822b9dbd15c?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/6562982bd9b42c2e6bd10cae?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f684e1113e7a6a574076b2?rid=925618026.48.1718444364156.12030
https://dzen.ru/a/ZTNYEjMz-VkvVGnB
https://dzen.ru/a/ZTNi1ECY6h8nFsSW
https://dzen.ru/a/ZTNpJ546JGYImpH1
https://dzen.ru/a/ZTNTlZAOEk3ppmIO
https://dzen.ru/a/Zc_f2thSeW9zscF8
https://dzen.ru/a/Zc_U25ITFGrFK0Sf
https://dzen.ru/a/Zc_TAlxn1y1iHc43
https://dzen.ru/a/Zc_LEcYYfS-TrXXm
https://dzen.ru/a/ZVjdtJSQOhzbk0B1
https://dzen.ru/a/ZTNS7dJWml8dLCim
https://dzen.ru/a/ZVdT4K4CRxpHZx1i
https://dzen.ru/a/ZVdb9TtUnQGek7_G
https://dzen.ru/a/ZTNUDrwjFj4U3LBI
https://dzen.ru/a/ZTNVSZAOEk3pp-ki
https://dzen.ru/a/ZTNptIGpwlQkN-E1
https://dzen.ru/a/ZTNqooGpwlQkORsw
https://dzen.ru/a/ZTNnrk1VVGtQwolr
https://dzen.ru/a/ZTNS0bwjFj4U25A9
https://dzen.ru/a/ZTNG7QlmuCeqISH6
https://dzen.ru/a/ZTM87Ogjh2c_dNzY
https://dzen.ru/b/ZS5ge6k6swm-YNzl
https://dzen.ru/b/ZS1BbXqKjhX4tA9_
https://dzen.ru/a/ZQ2aw4OzGFVaAbr2
https://dzen.ru/b/ZS5YZ7qcv2E0eJPQ
https://dzen.ru/a/ZQrJrb_XDifDVzGP
https://dzen.ru/a/ZQrIWS4n3ChkWGvj
https://dzen.ru/a/ZQrCRLpsYU4IGsNS
https://dzen.ru/a/ZQq5kyCaIkuoWgEb
https://dzen.ru/a/ZQq6z8LJ7AdPjTX6
https://dzen.ru/a/ZQrBHwW8ugdAoeld
https://dzen.ru/a/ZQq5zAyUYGuFpV6x
https://dzen.ru/a/ZQq6uF9dOExoiJn3
https://dzen.ru/a/ZQq4kyCaIkuoV7HL
https://dzen.ru/a/ZPZtZAWIHk1Wxu36
https://dzen.ru/a/ZPZ324ORLBGu36oK
https://dzen.ru/a/ZPZ6mPf64TnWQmu4
https://dzen.ru/a/ZPZqtxo5MUGqivHt
https://dzen.ru/a/ZPZ3KI7QZRjreV_m
https://dzen.ru/a/ZPZsDLf4FUB9-vTG
https://dzen.ru/a/ZPZyyDEQHn8iOuK4
https://dzen.ru/a/ZPZnc9bwiVMxJaDt
https://dzen.ru/a/ZPZ2CaKi2WZuFDzk
https://dzen.ru/a/ZPZw1iSYk23jVqD2
https://dzen.ru/a/ZPZvXBo5MUGqmExv
https://dzen.ru/a/ZPZusNZDrka3nhk4
https://dzen.ru/a/ZPZomY7QZRjrXUWH
https://dzen.ru/a/ZPZlbm0hO0O6e_6G
https://dzen.ru/a/ZPZkz_Z4SEywAI9r
https://dzen.ru/a/ZPZfLRo5MUGqXPqk
https://dzen.ru/a/ZPZkQ47QZRjrTEiz
https://dzen.ru/a/ZPZgZG72vTlMv-RA
https://dzen.ru/a/ZPZUGxo5MUGqMHlM
https://dzen.ru/a/ZPZTWRo5MUGqLTP3
https://dzen.ru/a/ZPZSyvf64TnWzJmJ
https://dzen.ru/a/ZPZQptZDrka3MWh9
https://dzen.ru/a/ZPZRU5bXthdQL0rT
https://dzen.ru/a/ZPZR4wm7BXTGU4QM
https://dzen.ru/a/ZPZO09ZDrka3LqM1
https://dzen.ru/a/ZPZMvxpdEnCdGygY
https://kitehurghada.ru/zhenskaya-kajt-shkola-shkola-kajtsyorfinga-dlya-detej/ - https://kitehurghada.ru/
https://kitehurghada.ru/
https://kitehurghada.ru/obuchenie-detej-kajtsyorfingu/
https://kitehurghada.ru/stoimost-obucheniya-kajtserfingu-v-hurgade/
https://kitehurghada.ru/kurs-bazovyj-10-chasov-zanyatij-s-instruktorom-4-5-dnya-450-usd/
https://kitehurghada.ru/kurs-ekspress-6-chasov-zanyatij-s-instruktorom-2-3-dnya-300-usd/
https://kitehurghada.ru/kontakty/
https://kitehurghada.ru/prognoz-vetra-v-hurgade/
https://kitehurghada.ru/kurs-pro-prodvinutyj-15-chasov-zanyatij-s-instruktorom-5-7-dnej-600-usd/
https://kitehurghada.ru/vesna-2024-egipet-hurgada-kajt-tury-i-kajt-kempy-deti-vetra/
https://kitehurghada.ru/vesennie-kanikuly/
https://kitehurghada.ru/majskie-prazdniki/
https://kitehurghada.ru/kajt-shkola/
https://kitehurghada.ru/kajt-kemp-v-hurgade-s-kajt-czentrom-detivetra/
https://kitehurghada.ru/zhenskaya-kajt-shkola-shkola-kajtsyorfinga-dlya-detej/
https://kitehurghada.ru/kajt-shkola-v-hurgade-egipet-kajt-czentr-detivetra/
https://kitehurghada.ru/obuchenie-kajtserfingu-na-krasnom-more/
https://kitehurghada.ru/ekskursii-v-hurgade-konnye-progulki-s-kupaniem-v-more-czeny-i-otzyvy-katanie-na-loshadyah-i-verblyudah/
https://kitehurghada.ru/devochki-i-kajtsyorfing-kajtsyorfing-dlya-devushek/
https://kitehurghada.ru/iko-sertifikat-katsyorfinga/
https://kitehurghada.ru/kajt-spot-deti-vetra-odno-iz-luchshih-mest-v-hurgade-dlya-kajtsyorfinga/
https://kitehurghada.ru/gidrofojl-gidrofojling-fojlbording-kajtfojling-v-hurgade-egipet-obuchenie-s-nulya-za-3-dnya/
https://kitehurghada.ru/kajt-kajtsyorfing-i-ego-istoriya/
https://kitehurghada.ru/individualnoe-obuchenie-gidrofojlu-s-kajtom/
https://kitehurghada.ru/veter-v-hurgade/
https://kitehurghada.ru/akuly-v-egipte/
https://kitehurghada.ru/vingfoil/
https://kitehurghada.ru/kajt-shkola-v-egipte/
https://kitehurghada.ru/temperatura-morya-v-hurgade/
https://kitehurghada.ru/obuchenie-vingfojl/
https://kitehurghada.ru/kajtsyorfing-v-el-gune/
https://kitehurghada.ru/kajt-egipet/
https://kitehurghada.ru/akuly-hurgade/
https://kitehurghada.ru/katanie-na-kajte/
https://kitehurghada.ru/kogda-luchshe-otdyhat-v-egipte/
https://kitehurghada.ru/kajting-v-hurgade/
https://kitehurghada.ru/kajting-v-egipte/
https://kitehurghada.ru/kajtserfing/
https://kitehurghada.ru/temperatura-v-hurgade/
https://kitehurghada.ru/kajting/
https://kitehurghada.ru/obuchenie-kajtsyorfingu-v-hurgade-egipet/
https://kitehurghada.ru/russkaya-kajt-stancziya-deti-vetra-v-hurgade/
https://kitehurghada.ru/gidrofojl-s-kajtom-obuchenie/
https://kitehurghada.ru/pogoda-v-hurgade/
https://kitehurghada.ru/faq-po-hurgade-2022-2023-chasto-zadavaemye-voprosy-ili-chto-vzyat-s-soboj-v-egipet/
https://kitehurghada.ru/kajt-safari-v-egipte-russkaya-kajt-stancziya-detivetra-v-hurgade/
https://kitehurghada.ru/kajtserfing-v-hurgade-luchshij-sezon-dlya-kajtserfinga/
https://kitehurghada.ru/kajting-osobennosti-kajtinga-vidy-kajtinga/
https://kitehurghada.ru/russkaya-kajt-shkola-v-hurgade/
https://kitehurghada.ru/kajt-shkola-detivetra/
https://kitehurghada.ru/programma-obucheniya-kajtsyorfingu-iko-v-hurgade-egipet/
https://kitehurghada.ru/istoriya-kajtserfinga/
https://kitehurghada.ru/podarochnyj-sertifikat-na-obuchenie-kajtserfingu-v-hurgade/
https://kitehurghada.ru/chto-takoe-iko-kitesurfing/
https://www.tripadvisor.ru/Attraction_Review-g23408135-d12244940-Reviews-Kite_school_DETIVETRA-Second_Hurghada_Hurghada_Red_Sea_and_Sinai.html
https://goo.gl/maps/KcoqXRbKWDkdGBDA8
https://goo.gl/maps/JTXRid9mrHFiMH7n6
https://detivetra.ru
https://detivetra.ru/v-hurgade/
https://uslugi.yandex.ru/profile/DetiVetra-348058
https://www.facebook.com/groups/detivetra/
https://www.facebook.com/DETIVETRA.ru/
https://www.youtube.com/channel/UCRG2aTtTaxbBAwlMTklO4ag
https://twitter.com/detivetra
https://rutube.ru/shorts/cb44391727e39c55e798f4efcecadbbe/
https://кайтинг-фото.рф/kayt-baza-v-hurgade.html
https://wa.me/79181955474
https://t.me/detivetrachat
https://www.instagram.com/detivetra.ru/
https://yandex.ru/profile/177183726173
https://yandex.ru/profile/1068186022
https://yandex.ru/profile/22472239976
https://yandex.ru/profile/72204785887
https://yandex.ru/profile/191148233877
https://xn----7sbjteeyka8afw.xn--p1ai
https://vk.com/kiteschoolhurghadaegypt
https://vk.com/kite_deti_vetra_anapa
http://redseakite.ru
https://kiteschoolhurghada.ru
https://divingredsea.ru
https://supanapa.ru
https://dzen.ru/a/ZdvCwDY4Lkx9j1OO
https://dzen.ru/a/ZdvAL3ptMCiNF8WX
https://dzen.ru/a/ZfigvDY3E2MON77x
https://dzen.ru/a/ZduLXm6jwDrtxbA7
https://dzen.ru/a/Zdt-SFBRjmyXXC7Y
https://dzen.ru/a/ZdvBm2tFz2D1IlSO
https://dzen.ru/a/Zdu_3c5NKkyfX91J
https://dzen.ru/a/ZdvCINgebnj0b5BQ
https://dzen.ru/a/ZTNXr-xw-1ZbmsTT
https://dzen.ru/a/ZdCSXCL_8k_Tfrjb
https://dzen.ru/a/ZdKxCtywnzYZgrrk
https://dzen.ru/a/ZTNfJwlmuCeqOEbb
https://dzen.ru/video/watch/65db9f94fb98fa6a95ab5e45?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65d4341844e19f05a34cf61f?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65629d684f336820c3b37487?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f689e39e331d6580277a0a?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f6870bcb2c7822b9dbd15c?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/6562982bd9b42c2e6bd10cae?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f684e1113e7a6a574076b2?rid=925618026.48.1718444364156.12030
https://dzen.ru/a/ZTNYEjMz-VkvVGnB
https://dzen.ru/a/ZTNi1ECY6h8nFsSW
https://dzen.ru/a/ZTNpJ546JGYImpH1
https://dzen.ru/a/ZTNTlZAOEk3ppmIO
https://dzen.ru/a/Zc_f2thSeW9zscF8
https://dzen.ru/a/Zc_U25ITFGrFK0Sf
https://dzen.ru/a/Zc_TAlxn1y1iHc43
https://dzen.ru/a/Zc_LEcYYfS-TrXXm
https://dzen.ru/a/ZVjdtJSQOhzbk0B1
https://dzen.ru/a/ZTNS7dJWml8dLCim
https://dzen.ru/a/ZVdT4K4CRxpHZx1i
https://dzen.ru/a/ZVdb9TtUnQGek7_G
https://dzen.ru/a/ZTNUDrwjFj4U3LBI
https://dzen.ru/a/ZTNVSZAOEk3pp-ki
https://dzen.ru/a/ZTNptIGpwlQkN-E1
https://dzen.ru/a/ZTNqooGpwlQkORsw
https://dzen.ru/a/ZTNnrk1VVGtQwolr
https://dzen.ru/a/ZTNS0bwjFj4U25A9
https://dzen.ru/a/ZTNG7QlmuCeqISH6
https://dzen.ru/a/ZTM87Ogjh2c_dNzY
https://dzen.ru/b/ZS5ge6k6swm-YNzl
https://dzen.ru/b/ZS1BbXqKjhX4tA9_
https://dzen.ru/a/ZQ2aw4OzGFVaAbr2
https://dzen.ru/b/ZS5YZ7qcv2E0eJPQ
https://dzen.ru/a/ZQrJrb_XDifDVzGP
https://dzen.ru/a/ZQrIWS4n3ChkWGvj
https://dzen.ru/a/ZQrCRLpsYU4IGsNS
https://dzen.ru/a/ZQq5kyCaIkuoWgEb
https://dzen.ru/a/ZQq6z8LJ7AdPjTX6
https://dzen.ru/a/ZQrBHwW8ugdAoeld
https://dzen.ru/a/ZQq5zAyUYGuFpV6x
https://dzen.ru/a/ZQq6uF9dOExoiJn3
https://dzen.ru/a/ZQq4kyCaIkuoV7HL
https://dzen.ru/a/ZPZtZAWIHk1Wxu36
https://dzen.ru/a/ZPZ324ORLBGu36oK
https://dzen.ru/a/ZPZ6mPf64TnWQmu4
https://dzen.ru/a/ZPZqtxo5MUGqivHt
https://dzen.ru/a/ZPZ3KI7QZRjreV_m
https://dzen.ru/a/ZPZsDLf4FUB9-vTG
https://dzen.ru/a/ZPZyyDEQHn8iOuK4
https://dzen.ru/a/ZPZnc9bwiVMxJaDt
https://dzen.ru/a/ZPZ2CaKi2WZuFDzk
https://dzen.ru/a/ZPZw1iSYk23jVqD2
https://dzen.ru/a/ZPZvXBo5MUGqmExv
https://dzen.ru/a/ZPZusNZDrka3nhk4
https://dzen.ru/a/ZPZomY7QZRjrXUWH
https://dzen.ru/a/ZPZlbm0hO0O6e_6G
https://dzen.ru/a/ZPZkz_Z4SEywAI9r
https://dzen.ru/a/ZPZfLRo5MUGqXPqk
https://dzen.ru/a/ZPZkQ47QZRjrTEiz
https://dzen.ru/a/ZPZgZG72vTlMv-RA
https://dzen.ru/a/ZPZUGxo5MUGqMHlM
https://dzen.ru/a/ZPZTWRo5MUGqLTP3
https://dzen.ru/a/ZPZSyvf64TnWzJmJ
https://dzen.ru/a/ZPZQptZDrka3MWh9
https://dzen.ru/a/ZPZRU5bXthdQL0rT
https://dzen.ru/a/ZPZR4wm7BXTGU4QM
https://dzen.ru/a/ZPZO09ZDrka3LqM1
https://dzen.ru/a/ZPZMvxpdEnCdGygY
https://kitehurghada.ru/kurs-ekspress-6-chasov-zanyatij-s-instruktorom-2-3-dnya-300-usd/ - https://kitehurghada.ru/vesna-2024-egipet-hurgada-kajt-tury-i-kajt-kempy-deti-vetra/
https://kitehurghada.ru/
https://kitehurghada.ru/obuchenie-detej-kajtsyorfingu/
https://kitehurghada.ru/stoimost-obucheniya-kajtserfingu-v-hurgade/
https://kitehurghada.ru/kurs-bazovyj-10-chasov-zanyatij-s-instruktorom-4-5-dnya-450-usd/
https://kitehurghada.ru/kurs-ekspress-6-chasov-zanyatij-s-instruktorom-2-3-dnya-300-usd/
https://kitehurghada.ru/kontakty/
https://kitehurghada.ru/prognoz-vetra-v-hurgade/
https://kitehurghada.ru/kurs-pro-prodvinutyj-15-chasov-zanyatij-s-instruktorom-5-7-dnej-600-usd/
https://kitehurghada.ru/vesna-2024-egipet-hurgada-kajt-tury-i-kajt-kempy-deti-vetra/
https://kitehurghada.ru/vesennie-kanikuly/
https://kitehurghada.ru/majskie-prazdniki/
https://kitehurghada.ru/kajt-shkola/
https://kitehurghada.ru/kajt-kemp-v-hurgade-s-kajt-czentrom-detivetra/
https://kitehurghada.ru/zhenskaya-kajt-shkola-shkola-kajtsyorfinga-dlya-detej/
https://kitehurghada.ru/kajt-shkola-v-hurgade-egipet-kajt-czentr-detivetra/
https://kitehurghada.ru/obuchenie-kajtserfingu-na-krasnom-more/
https://kitehurghada.ru/ekskursii-v-hurgade-konnye-progulki-s-kupaniem-v-more-czeny-i-otzyvy-katanie-na-loshadyah-i-verblyudah/
https://kitehurghada.ru/devochki-i-kajtsyorfing-kajtsyorfing-dlya-devushek/
https://kitehurghada.ru/iko-sertifikat-katsyorfinga/
https://kitehurghada.ru/kajt-spot-deti-vetra-odno-iz-luchshih-mest-v-hurgade-dlya-kajtsyorfinga/
https://kitehurghada.ru/gidrofojl-gidrofojling-fojlbording-kajtfojling-v-hurgade-egipet-obuchenie-s-nulya-za-3-dnya/
https://kitehurghada.ru/kajt-kajtsyorfing-i-ego-istoriya/
https://kitehurghada.ru/individualnoe-obuchenie-gidrofojlu-s-kajtom/
https://kitehurghada.ru/veter-v-hurgade/
https://kitehurghada.ru/akuly-v-egipte/
https://kitehurghada.ru/vingfoil/
https://kitehurghada.ru/kajt-shkola-v-egipte/
https://kitehurghada.ru/temperatura-morya-v-hurgade/
https://kitehurghada.ru/obuchenie-vingfojl/
https://kitehurghada.ru/kajtsyorfing-v-el-gune/
https://kitehurghada.ru/kajt-egipet/
https://kitehurghada.ru/akuly-hurgade/
https://kitehurghada.ru/katanie-na-kajte/
https://kitehurghada.ru/kogda-luchshe-otdyhat-v-egipte/
https://kitehurghada.ru/kajting-v-hurgade/
https://kitehurghada.ru/kajting-v-egipte/
https://kitehurghada.ru/kajtserfing/
https://kitehurghada.ru/temperatura-v-hurgade/
https://kitehurghada.ru/kajting/
https://kitehurghada.ru/obuchenie-kajtsyorfingu-v-hurgade-egipet/
https://kitehurghada.ru/russkaya-kajt-stancziya-deti-vetra-v-hurgade/
https://kitehurghada.ru/gidrofojl-s-kajtom-obuchenie/
https://kitehurghada.ru/pogoda-v-hurgade/
https://kitehurghada.ru/faq-po-hurgade-2022-2023-chasto-zadavaemye-voprosy-ili-chto-vzyat-s-soboj-v-egipet/
https://kitehurghada.ru/kajt-safari-v-egipte-russkaya-kajt-stancziya-detivetra-v-hurgade/
https://kitehurghada.ru/kajtserfing-v-hurgade-luchshij-sezon-dlya-kajtserfinga/
https://kitehurghada.ru/kajting-osobennosti-kajtinga-vidy-kajtinga/
https://kitehurghada.ru/russkaya-kajt-shkola-v-hurgade/
https://kitehurghada.ru/kajt-shkola-detivetra/
https://kitehurghada.ru/programma-obucheniya-kajtsyorfingu-iko-v-hurgade-egipet/
https://kitehurghada.ru/istoriya-kajtserfinga/
https://kitehurghada.ru/podarochnyj-sertifikat-na-obuchenie-kajtserfingu-v-hurgade/
https://kitehurghada.ru/chto-takoe-iko-kitesurfing/
https://www.tripadvisor.ru/Attraction_Review-g23408135-d12244940-Reviews-Kite_school_DETIVETRA-Second_Hurghada_Hurghada_Red_Sea_and_Sinai.html
https://goo.gl/maps/KcoqXRbKWDkdGBDA8
https://goo.gl/maps/JTXRid9mrHFiMH7n6
https://detivetra.ru
https://detivetra.ru/v-hurgade/
https://uslugi.yandex.ru/profile/DetiVetra-348058
https://www.facebook.com/groups/detivetra/
https://www.facebook.com/DETIVETRA.ru/
https://www.youtube.com/channel/UCRG2aTtTaxbBAwlMTklO4ag
https://twitter.com/detivetra
https://rutube.ru/shorts/cb44391727e39c55e798f4efcecadbbe/
https://кайтинг-фото.рф/kayt-baza-v-hurgade.html
https://wa.me/79181955474
https://t.me/detivetrachat
https://www.instagram.com/detivetra.ru/
https://yandex.ru/profile/177183726173
https://yandex.ru/profile/1068186022
https://yandex.ru/profile/22472239976
https://yandex.ru/profile/72204785887
https://yandex.ru/profile/191148233877
https://xn----7sbjteeyka8afw.xn--p1ai
https://vk.com/kiteschoolhurghadaegypt
https://vk.com/kite_deti_vetra_anapa
http://redseakite.ru
https://kiteschoolhurghada.ru
https://divingredsea.ru
https://supanapa.ru
https://dzen.ru/a/ZdvCwDY4Lkx9j1OO
https://dzen.ru/a/ZdvAL3ptMCiNF8WX
https://dzen.ru/a/ZfigvDY3E2MON77x
https://dzen.ru/a/ZduLXm6jwDrtxbA7
https://dzen.ru/a/Zdt-SFBRjmyXXC7Y
https://dzen.ru/a/ZdvBm2tFz2D1IlSO
https://dzen.ru/a/Zdu_3c5NKkyfX91J
https://dzen.ru/a/ZdvCINgebnj0b5BQ
https://dzen.ru/a/ZTNXr-xw-1ZbmsTT
https://dzen.ru/a/ZdCSXCL_8k_Tfrjb
https://dzen.ru/a/ZdKxCtywnzYZgrrk
https://dzen.ru/a/ZTNfJwlmuCeqOEbb
https://dzen.ru/video/watch/65db9f94fb98fa6a95ab5e45?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65d4341844e19f05a34cf61f?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65629d684f336820c3b37487?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f689e39e331d6580277a0a?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f6870bcb2c7822b9dbd15c?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/6562982bd9b42c2e6bd10cae?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f684e1113e7a6a574076b2?rid=925618026.48.1718444364156.12030
https://dzen.ru/a/ZTNYEjMz-VkvVGnB
https://dzen.ru/a/ZTNi1ECY6h8nFsSW
https://dzen.ru/a/ZTNpJ546JGYImpH1
https://dzen.ru/a/ZTNTlZAOEk3ppmIO
https://dzen.ru/a/Zc_f2thSeW9zscF8
https://dzen.ru/a/Zc_U25ITFGrFK0Sf
https://dzen.ru/a/Zc_TAlxn1y1iHc43
https://dzen.ru/a/Zc_LEcYYfS-TrXXm
https://dzen.ru/a/ZVjdtJSQOhzbk0B1
https://dzen.ru/a/ZTNS7dJWml8dLCim
https://dzen.ru/a/ZVdT4K4CRxpHZx1i
https://dzen.ru/a/ZVdb9TtUnQGek7_G
https://dzen.ru/a/ZTNUDrwjFj4U3LBI
https://dzen.ru/a/ZTNVSZAOEk3pp-ki
https://dzen.ru/a/ZTNptIGpwlQkN-E1
https://dzen.ru/a/ZTNqooGpwlQkORsw
https://dzen.ru/a/ZTNnrk1VVGtQwolr
https://dzen.ru/a/ZTNS0bwjFj4U25A9
https://dzen.ru/a/ZTNG7QlmuCeqISH6
https://dzen.ru/a/ZTM87Ogjh2c_dNzY
https://dzen.ru/b/ZS5ge6k6swm-YNzl
https://dzen.ru/b/ZS1BbXqKjhX4tA9_
https://dzen.ru/a/ZQ2aw4OzGFVaAbr2
https://dzen.ru/b/ZS5YZ7qcv2E0eJPQ
https://dzen.ru/a/ZQrJrb_XDifDVzGP
https://dzen.ru/a/ZQrIWS4n3ChkWGvj
https://dzen.ru/a/ZQrCRLpsYU4IGsNS
https://dzen.ru/a/ZQq5kyCaIkuoWgEb
https://dzen.ru/a/ZQq6z8LJ7AdPjTX6
https://dzen.ru/a/ZQrBHwW8ugdAoeld
https://dzen.ru/a/ZQq5zAyUYGuFpV6x
https://dzen.ru/a/ZQq6uF9dOExoiJn3
https://dzen.ru/a/ZQq4kyCaIkuoV7HL
https://dzen.ru/a/ZPZtZAWIHk1Wxu36
https://dzen.ru/a/ZPZ324ORLBGu36oK
https://dzen.ru/a/ZPZ6mPf64TnWQmu4
https://dzen.ru/a/ZPZqtxo5MUGqivHt
https://dzen.ru/a/ZPZ3KI7QZRjreV_m
https://dzen.ru/a/ZPZsDLf4FUB9-vTG
https://dzen.ru/a/ZPZyyDEQHn8iOuK4
https://dzen.ru/a/ZPZnc9bwiVMxJaDt
https://dzen.ru/a/ZPZ2CaKi2WZuFDzk
https://dzen.ru/a/ZPZw1iSYk23jVqD2
https://dzen.ru/a/ZPZvXBo5MUGqmExv
https://dzen.ru/a/ZPZusNZDrka3nhk4
https://dzen.ru/a/ZPZomY7QZRjrXUWH
https://dzen.ru/a/ZPZlbm0hO0O6e_6G
https://dzen.ru/a/ZPZkz_Z4SEywAI9r
https://dzen.ru/a/ZPZfLRo5MUGqXPqk
https://dzen.ru/a/ZPZkQ47QZRjrTEiz
https://dzen.ru/a/ZPZgZG72vTlMv-RA
https://dzen.ru/a/ZPZUGxo5MUGqMHlM
https://dzen.ru/a/ZPZTWRo5MUGqLTP3
https://dzen.ru/a/ZPZSyvf64TnWzJmJ
https://dzen.ru/a/ZPZQptZDrka3MWh9
https://dzen.ru/a/ZPZRU5bXthdQL0rT
https://dzen.ru/a/ZPZR4wm7BXTGU4QM
https://dzen.ru/a/ZPZO09ZDrka3LqM1
https://dzen.ru/a/ZPZMvxpdEnCdGygY
https://kitehurghada.ru/obuchenie-vingfojl/ - https://dzen.ru/a/ZQq4kyCaIkuoV7HL
https://kitehurghada.ru/
https://kitehurghada.ru/obuchenie-detej-kajtsyorfingu/
https://kitehurghada.ru/stoimost-obucheniya-kajtserfingu-v-hurgade/
https://kitehurghada.ru/kurs-bazovyj-10-chasov-zanyatij-s-instruktorom-4-5-dnya-450-usd/
https://kitehurghada.ru/kurs-ekspress-6-chasov-zanyatij-s-instruktorom-2-3-dnya-300-usd/
https://kitehurghada.ru/kontakty/
https://kitehurghada.ru/prognoz-vetra-v-hurgade/
https://kitehurghada.ru/kurs-pro-prodvinutyj-15-chasov-zanyatij-s-instruktorom-5-7-dnej-600-usd/
https://kitehurghada.ru/vesna-2024-egipet-hurgada-kajt-tury-i-kajt-kempy-deti-vetra/
https://kitehurghada.ru/vesennie-kanikuly/
https://kitehurghada.ru/majskie-prazdniki/
https://kitehurghada.ru/kajt-shkola/
https://kitehurghada.ru/kajt-kemp-v-hurgade-s-kajt-czentrom-detivetra/
https://kitehurghada.ru/zhenskaya-kajt-shkola-shkola-kajtsyorfinga-dlya-detej/
https://kitehurghada.ru/kajt-shkola-v-hurgade-egipet-kajt-czentr-detivetra/
https://kitehurghada.ru/obuchenie-kajtserfingu-na-krasnom-more/
https://kitehurghada.ru/ekskursii-v-hurgade-konnye-progulki-s-kupaniem-v-more-czeny-i-otzyvy-katanie-na-loshadyah-i-verblyudah/
https://kitehurghada.ru/devochki-i-kajtsyorfing-kajtsyorfing-dlya-devushek/
https://kitehurghada.ru/iko-sertifikat-katsyorfinga/
https://kitehurghada.ru/kajt-spot-deti-vetra-odno-iz-luchshih-mest-v-hurgade-dlya-kajtsyorfinga/
https://kitehurghada.ru/gidrofojl-gidrofojling-fojlbording-kajtfojling-v-hurgade-egipet-obuchenie-s-nulya-za-3-dnya/
https://kitehurghada.ru/kajt-kajtsyorfing-i-ego-istoriya/
https://kitehurghada.ru/individualnoe-obuchenie-gidrofojlu-s-kajtom/
https://kitehurghada.ru/veter-v-hurgade/
https://kitehurghada.ru/akuly-v-egipte/
https://kitehurghada.ru/vingfoil/
https://kitehurghada.ru/kajt-shkola-v-egipte/
https://kitehurghada.ru/temperatura-morya-v-hurgade/
https://kitehurghada.ru/obuchenie-vingfojl/
https://kitehurghada.ru/kajtsyorfing-v-el-gune/
https://kitehurghada.ru/kajt-egipet/
https://kitehurghada.ru/akuly-hurgade/
https://kitehurghada.ru/katanie-na-kajte/
https://kitehurghada.ru/kogda-luchshe-otdyhat-v-egipte/
https://kitehurghada.ru/kajting-v-hurgade/
https://kitehurghada.ru/kajting-v-egipte/
https://kitehurghada.ru/kajtserfing/
https://kitehurghada.ru/temperatura-v-hurgade/
https://kitehurghada.ru/kajting/
https://kitehurghada.ru/obuchenie-kajtsyorfingu-v-hurgade-egipet/
https://kitehurghada.ru/russkaya-kajt-stancziya-deti-vetra-v-hurgade/
https://kitehurghada.ru/gidrofojl-s-kajtom-obuchenie/
https://kitehurghada.ru/pogoda-v-hurgade/
https://kitehurghada.ru/faq-po-hurgade-2022-2023-chasto-zadavaemye-voprosy-ili-chto-vzyat-s-soboj-v-egipet/
https://kitehurghada.ru/kajt-safari-v-egipte-russkaya-kajt-stancziya-detivetra-v-hurgade/
https://kitehurghada.ru/kajtserfing-v-hurgade-luchshij-sezon-dlya-kajtserfinga/
https://kitehurghada.ru/kajting-osobennosti-kajtinga-vidy-kajtinga/
https://kitehurghada.ru/russkaya-kajt-shkola-v-hurgade/
https://kitehurghada.ru/kajt-shkola-detivetra/
https://kitehurghada.ru/programma-obucheniya-kajtsyorfingu-iko-v-hurgade-egipet/
https://kitehurghada.ru/istoriya-kajtserfinga/
https://kitehurghada.ru/podarochnyj-sertifikat-na-obuchenie-kajtserfingu-v-hurgade/
https://kitehurghada.ru/chto-takoe-iko-kitesurfing/
https://www.tripadvisor.ru/Attraction_Review-g23408135-d12244940-Reviews-Kite_school_DETIVETRA-Second_Hurghada_Hurghada_Red_Sea_and_Sinai.html
https://goo.gl/maps/KcoqXRbKWDkdGBDA8
https://goo.gl/maps/JTXRid9mrHFiMH7n6
https://detivetra.ru
https://detivetra.ru/v-hurgade/
https://uslugi.yandex.ru/profile/DetiVetra-348058
https://www.facebook.com/groups/detivetra/
https://www.facebook.com/DETIVETRA.ru/
https://www.youtube.com/channel/UCRG2aTtTaxbBAwlMTklO4ag
https://twitter.com/detivetra
https://rutube.ru/shorts/cb44391727e39c55e798f4efcecadbbe/
https://кайтинг-фото.рф/kayt-baza-v-hurgade.html
https://wa.me/79181955474
https://t.me/detivetrachat
https://www.instagram.com/detivetra.ru/
https://yandex.ru/profile/177183726173
https://yandex.ru/profile/1068186022
https://yandex.ru/profile/22472239976
https://yandex.ru/profile/72204785887
https://yandex.ru/profile/191148233877
https://xn----7sbjteeyka8afw.xn--p1ai
https://vk.com/kiteschoolhurghadaegypt
https://vk.com/kite_deti_vetra_anapa
http://redseakite.ru
https://kiteschoolhurghada.ru
https://divingredsea.ru
https://supanapa.ru
https://dzen.ru/a/ZdvCwDY4Lkx9j1OO
https://dzen.ru/a/ZdvAL3ptMCiNF8WX
https://dzen.ru/a/ZfigvDY3E2MON77x
https://dzen.ru/a/ZduLXm6jwDrtxbA7
https://dzen.ru/a/Zdt-SFBRjmyXXC7Y
https://dzen.ru/a/ZdvBm2tFz2D1IlSO
https://dzen.ru/a/Zdu_3c5NKkyfX91J
https://dzen.ru/a/ZdvCINgebnj0b5BQ
https://dzen.ru/a/ZTNXr-xw-1ZbmsTT
https://dzen.ru/a/ZdCSXCL_8k_Tfrjb
https://dzen.ru/a/ZdKxCtywnzYZgrrk
https://dzen.ru/a/ZTNfJwlmuCeqOEbb
https://dzen.ru/video/watch/65db9f94fb98fa6a95ab5e45?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65d4341844e19f05a34cf61f?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/65629d684f336820c3b37487?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f689e39e331d6580277a0a?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f6870bcb2c7822b9dbd15c?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/6562982bd9b42c2e6bd10cae?rid=925618026.48.1718444364156.12030
https://dzen.ru/video/watch/64f684e1113e7a6a574076b2?rid=925618026.48.1718444364156.12030
https://dzen.ru/a/ZTNYEjMz-VkvVGnB
https://dzen.ru/a/ZTNi1ECY6h8nFsSW
https://dzen.ru/a/ZTNpJ546JGYImpH1
https://dzen.ru/a/ZTNTlZAOEk3ppmIO
https://dzen.ru/a/Zc_f2thSeW9zscF8
https://dzen.ru/a/Zc_U25ITFGrFK0Sf
https://dzen.ru/a/Zc_TAlxn1y1iHc43
https://dzen.ru/a/Zc_LEcYYfS-TrXXm
https://dzen.ru/a/ZVjdtJSQOhzbk0B1
https://dzen.ru/a/ZTNS7dJWml8dLCim
https://dzen.ru/a/ZVdT4K4CRxpHZx1i
https://dzen.ru/a/ZVdb9TtUnQGek7_G
https://dzen.ru/a/ZTNUDrwjFj4U3LBI
https://dzen.ru/a/ZTNVSZAOEk3pp-ki
https://dzen.ru/a/ZTNptIGpwlQkN-E1
https://dzen.ru/a/ZTNqooGpwlQkORsw
https://dzen.ru/a/ZTNnrk1VVGtQwolr
https://dzen.ru/a/ZTNS0bwjFj4U25A9
https://dzen.ru/a/ZTNG7QlmuCeqISH6
https://dzen.ru/a/ZTM87Ogjh2c_dNzY
https://dzen.ru/b/ZS5ge6k6swm-YNzl
https://dzen.ru/b/ZS1BbXqKjhX4tA9_
https://dzen.ru/a/ZQ2aw4OzGFVaAbr2
https://dzen.ru/b/ZS5YZ7qcv2E0eJPQ
https://dzen.ru/a/ZQrJrb_XDifDVzGP
https://dzen.ru/a/ZQrIWS4n3ChkWGvj
https://dzen.ru/a/ZQrCRLpsYU4IGsNS
https://dzen.ru/a/ZQq5kyCaIkuoWgEb
https://dzen.ru/a/ZQq6z8LJ7AdPjTX6
https://dzen.ru/a/ZQrBHwW8ugdAoeld
https://dzen.ru/a/ZQq5zAyUYGuFpV6x
https://dzen.ru/a/ZQq6uF9dOExoiJn3
https://dzen.ru/a/ZQq4kyCaIkuoV7HL
https://dzen.ru/a/ZPZtZAWIHk1Wxu36
https://dzen.ru/a/ZPZ324ORLBGu36oK
https://dzen.ru/a/ZPZ6mPf64TnWQmu4
https://dzen.ru/a/ZPZqtxo5MUGqivHt
https://dzen.ru/a/ZPZ3KI7QZRjreV_m
https://dzen.ru/a/ZPZsDLf4FUB9-vTG
https://dzen.ru/a/ZPZyyDEQHn8iOuK4
https://dzen.ru/a/ZPZnc9bwiVMxJaDt
https://dzen.ru/a/ZPZ2CaKi2WZuFDzk
https://dzen.ru/a/ZPZw1iSYk23jVqD2
https://dzen.ru/a/ZPZvXBo5MUGqmExv
https://dzen.ru/a/ZPZusNZDrka3nhk4
https://dzen.ru/a/ZPZomY7QZRjrXUWH
https://dzen.ru/a/ZPZlbm0hO0O6e_6G
https://dzen.ru/a/ZPZkz_Z4SEywAI9r
https://dzen.ru/a/ZPZfLRo5MUGqXPqk
https://dzen.ru/a/ZPZkQ47QZRjrTEiz
https://dzen.ru/a/ZPZgZG72vTlMv-RA
https://dzen.ru/a/ZPZUGxo5MUGqMHlM
https://dzen.ru/a/ZPZTWRo5MUGqLTP3
https://dzen.ru/a/ZPZSyvf64TnWzJmJ
https://dzen.ru/a/ZPZQptZDrka3MWh9
https://dzen.ru/a/ZPZRU5bXthdQL0rT
https://dzen.ru/a/ZPZR4wm7BXTGU4QM
https://dzen.ru/a/ZPZO09ZDrka3LqM1
https://dzen.ru/a/ZPZMvxpdEnCdGygY
В современном мире, где интернет занимает существенное место в нашей жизни, вопросы безопасности и конфиденциальности в сети становятся особенно актуальными. VPN (виртуальная частная сеть) предоставляет эффективные средства для защиты вашей интернет-активности и сохранения конфиденциальности данных. В данной инструкции рассмотрим процесс создания собственного VPN. Для этого я выбрал услуги хостинговой компании PQ.Hosting.
Почему PQ.Hosting?
Первое, что мне понравилось на сайте компании, именно в разделе VPN, это возможность поддержки разных устройств с одновременным подключением до 10 активных устройств на одну подписку. Пользователям, у которых есть желание подключить ВПН не только на компьютере, но еще и смартфоне, планшете, телевизоре (а таких сейчас большинство) это очень хорошее решение.
Не в последнюю очередь обращаем внимание на технологию шифрования. Сегодня это очень важно! Ну и, конечно же, не менее привлекателен безлимитный трафик. Серфинг без ограничений по трафику и скорости, обеспечивающий полную свободу и комфорт в интернете лично для меня в приоритете.
Кому нужен надежный ВПН?
Дальше приведу категории пользователей, которым обязательно необходим надежный ВПН:
Геймеры. Игроки могут использовать VPN для снижения задержек (пинга) в играх или для доступа к играм и контенту, недоступным в их регионе;
Туристы. Люди, находящиеся за границей, могут использовать VPN для доступа к своим обычным интернет-ресурсам, таким как банковские аккаунты или любимые стриминговые сервисы.
Компаниям. Сотрудники компаний могут использовать VPN для безопасного доступа к внутренним ресурсам и системам компании из удаленных мест;
Обычным интернет-пользователям. ВПН будет полезен всем тем, кто ценит свою конфиденциальность и хочет защитить свои данные.
А теперь переходим собственно к инструкции.
Разворачиваем собственный VPN
Дальше расскажу, какие преимущества несёт создание собственного VPN:
Защита трафика. Ни администраторы Wi-Fi-сети, ни злоумышленники не смогут получить доступ к вашим данным.
Доступ к заблокированным ресурсам. Поскольку сервер VPN расположен за пределами страны, вы сможете обходить блокировки на сайты и сервисы.
Защита от слежки со стороны интернет-провайдеров. Использование VPN поможет вам обеспечить дополнительную безопасность
Для простых задач, таких как серфинг в интернете или использование социальных сетей, VPN очень даже пригоден. Осталось разобраться, как настроить собственный ВПН.
Инструкция по настройке VPN на примере PQ.Hosting
Чтобы развернуть VPN, необходимо:
1. Арендовать VPS-сервер. Выберите одну из локаций на сайте https://pq.hosting/buy-tunnel
2. Дальше для настройки VPN-соединения используем Amnezia. Скачиваем приложение AmneziaVPN с официального сайта https://amnezia.org/ru/.
3. На почту, указанную при заказе сервера, придет письмо от хостинг-провайдера В письме должны быть указаны IP, User name или User ID, и Password, они понадобятся для установки VPN на сервер.
4. Запустите приложение AmneziaVPN
5. На первом экране выберете “У меня есть данные для подключения”, далее “Настроить свой сервер”, и внесите данные из письма.
6. Нажмите “Продолжить” и следуйте подсказкам приложения.
В заключении скажу, VPN может быть полезен как для индивидуальных пользователей, так и для организаций, стремящихся обеспечить безопасность и конфиденциальность своих данных. Создание собственного VPN на базе Amnezia дает полный контроль над вашей сетью и обеспечивает защиту ваших данных. Следуя пошаговой инструкции, вы можете создать свой собственный VPN и наслаждаться безопасным и приватным интернет-соединением.
В нашем каталоге вы найдете не только стильную и функциональную одежду, но и специализированную обувь, которая обеспечит комфорт при любых условиях. Мы также предлагаем разнообразные товары для охоты и туризма – от прочных рюкзаков до современного оптического оборудования, которое станет незаменимым помощником в ваших приключениях. https://t.me/REMHUNTER05 - рыбалки и активного отдыха
Помимо этого, мы следим за последними тенденциями и регулярно обновляем наш ассортимент, чтобы вы могли находить все необходимое для успешной охоты и активного отдыха. Присоединяйтесь к нашему сообществу и оставайтесь в курсе новинок и акций. Вместе с нами ваши приключения станут ещё ярче и насыщеннее!
Skype: g.i.790
https://beltraktor.ru/ https://vk.com/club225055392 https://dzen.ru/id/66c485827c836c13b88766e3?utm_referrer=dzen.ru
Owning a Ferrari is more than just having a car—it's an experience of luxury, speed, and sophistication. When your Ferrari needs attention, trust only the best. Rapido Garage, a top-rated Ferrari repair garage in Dubai, is the ultimate destination for Ferrari owners who demand excellence. From routine maintenance to complex repairs, Rapido Garage ensures your car is in expert hands.
Why Rapido Garage for Ferrari Repair in Dubai?
At Rapido Garage, we understand the precision and care required for Ferrari vehicles. Here’s why Ferrari owners in Dubai choose us:
Certified Ferrari Specialists: Our technicians are trained to handle Ferrari models with the expertise and attention to detail they deserve.
Advanced Equipment: Equipped with state-of-the-art diagnostic tools specifically designed for Ferrari cars.
Genuine Ferrari Parts: We use only authentic parts to maintain your car's performance and resale value.
Personalized Service: Tailored repair and maintenance plans based on your Ferrari's unique needs.
https://ferrari-service.com/ - ferrari service in dubai
Our Ferrari Services in Dubai
1. Ferrari Repair in Dubai
Our comprehensive Ferrari repair services cover every aspect of your car, including:
Engine diagnostics and repairs
Transmission servicing
Suspension and braking system repairs
Electrical system troubleshooting
AC repair and servicing
We ensure that your Ferrari performs at its best, no matter the issue.
2. Ferrari Maintenance
Regular maintenance is key to keeping your Ferrari in pristine condition. Our Ferrari maintenance services include:
Oil and filter changes
Brake system checks
Tire rotation and alignment
Battery inspection and replacement
Fluid level checks and top-ups
Our proactive approach helps prevent costly repairs down the line.
3. Ferrari Service in Dubai
Our dedicated Ferrari service in Dubai focuses on preserving the luxury and performance of your car. From routine inspections to performance tuning, we ensure your Ferrari stays road-ready and delivers the thrilling experience it’s known for.
4. Ferrari Garage in Dubai
Rapido Garage is a fully equipped Ferrari garage in Dubai, providing a comfortable and efficient environment for your car’s care. Our workshop is designed to meet the highest standards, ensuring top-notch service.
Benefits of Choosing Rapido Garage
Convenient Location: Centrally located in Dubai for easy access.
Transparent Pricing: No hidden costs—detailed diagnostics and upfront quotes.
Customer-Centric Approach: Your satisfaction is our priority, with efficient service and clear communication.
https://ferrari-service.com/
Book Your Ferrari Service Today
At Rapido Garage, we combine expertise, technology, and passion to deliver unparalleled Ferrari repair and maintenance services. Trust us to keep your Ferrari running at peak performance, whether it’s a classic model or the latest release.
Contact Us
Call or visit Rapido Garage, the trusted name for Ferrari repair in Dubai, Ferrari service in Dubai, and Ferrari maintenance. Experience excellence in Ferrari care like never before.
With Rapido Garage, you’re not just maintaining your car—you’re preserving the Ferrari legacy. Visit us today and discover why we’re the top-rated Ferrari garage in Dubai!
https://beltraktor.ru/ https://vk.com/club225055392 https://dzen.ru/id/66c485827c836c13b88766e3?utm_referrer=dzen.ru
https://beltraktor.ru/ https://vk.com/club225055392 https://dzen.ru/id/66c485827c836c13b88766e3?utm_referrer=dzen.ru
https://tehnodacha.com/akkumulyatornaya-tehnika-villartec - Аккумуляторная техника Villartec Аккумуляторная техника Villartec открывает новые горизонты в мире садоводства, предоставляя возможность работать в любых условиях без шума и выбросов. Современные технологии и инновационные решения в области аккумуляторов делают устройства мощными и долговечными, что позволяет использовать их для самых различных задач, от стрижки газонов до ухода за деревьями. https://tehnodacha.com Генераторы Energo с двигателями Senci – это незаменимые помощники в ситуациях, когда электроэнергия недоступна. Они отличаются высокой производительностью и надежностью, что позволяет обеспечить электроснабжение даже в самых удалённых местах. Компактные размеры и лёгкий вес делают их удобными для транспортировки и использования в различных условиях.
https://beltraktor.ru/ https://vk.com/club225055392 https://dzen.ru/id/66c485827c836c13b88766e3?utm_referrer=dzen.ru
https://beltraktor.ru/ https://vk.com/club225055392 https://dzen.ru/id/66c485827c836c13b88766e3?utm_referrer=dzen.ru
https://beltraktor.ru/ https://vk.com/club225055392 https://dzen.ru/id/66c485827c836c13b88766e3?utm_referrer=dzen.ru
<a href="https://bestforandroid.com/i-gaming/lucky-jet-game-reviewed/">Lucky Jet game</a>
https://vk.com/benefitsar_net
https://dzen.ru/benefitsar_net
https://t.me/benefitsar_net
https://www.klerk.ru/user/2485134/
Обучаем перманентному макияжу с нуля со свидетельством установленного образца , ведем курсы бровистов
Ведущая в мире платформа блокчейн покера!
Вы можете стать одними из первых участников нового проекта с честным рейкбэком, бонусом на первый депозит 200%, быстрым вводом и выводом, и отсутствием KYC.
Приглашаем вас присоединится к крупнейшему сообществу VANGPOKER в телеграмм, зарегестрироваться в VANGPOKER и получать дополнительные бонусы и повышенный рейкбэк. <a href=https://t.me/VANG_POKER>зарегестрироваться в VANGPOKER</a>
Мы готовы взяться за дело любой сложности, опираясь на многолетний опыт для оказания эффективной помощи. Каждый арбитражный адвокат в нашей команде специализируется на определенной области права. Это позволяет подобрать для вашей ситуации эксперта, досконально разбирающегося в специфике дела. Такой подход значительно повышает шансы на успех в суде, в отличие от обращения к юристу-универсалу.
Наша коллегия быстро завоевала признание в России. Этому способствуют опытные юристы, узко специализирующиеся в различных областях права, а также доступные цены. Мы работаем прозрачно: на сайте представлена информация о стоимости услуг и подробные сведения о сотрудниках, готовых вам помочь. В договорах отсутствуют скрытые комиссии, которые часто используют недобросовестные фирмы.
Адвокат подробно расскажет обо всех этапах процесса, стоимости услуг, а также разъяснит все детали и нюансы. Мы понимаем, что финансовые трудности могут возникнуть внезапно, а юридическая помощь нужна незамедлительно. Поэтому предлагаем различные варианты рассрочки или отсрочки платежа. Кроме того, по некоторым делам возможна оплата по результату, что позволяет рассчитаться с нами только после успешного завершения дела в суде.
На нашем сайте вы найдете множество полезных материалов, которые помогут вам повысить свою юридическую грамотность. Рекомендуем регулярно посещать наш ресурс, чтобы быть в курсе своих прав. Мы подробно рассказываем, какие документы необходимы для различных процедур: использование материнского капитала, банкротство и т.д. Более подробную консультацию вы можете получить у нашего адвоката, контакты которого указаны на сайте.
Получение испанского гражданства – отдельный процесс, требующий соблюдения определенных условий. Россияне, заинтересованные в иммиграции, изучают доступные способы получения ВНЖ, необходимые документы и стоимость. Варианты включают покупку недвижимости, участие в программах для инвесторов, а также ВНЖ типа "no lucrativa" для тех, кто располагает достаточными средствами для проживания без работы в Испании.
Помимо первичного оформления, важным аспектом является продление ВНЖ. Условия и требования могут отличаться в зависимости от типа ВНЖ и основания для его получения. Актуальную информацию о процедурах и документах для россиян в 2023 году следует уточнять у юристов или в компетентных органах.
Векстрой Уфа – это имя, которое звучит с уверенностью и надежностью в сфере производства металлоконструкций. Мы – не просто завод, мы – команда профессионалов, объединенных общей целью: создавать прочные, долговечные и эстетически привлекательные решения для наших клиентов.
Наш завод металлоконструкций оснащен современным оборудованием, позволяющим нам реализовывать проекты любой сложности. От разработки чертежей до финальной сборки – каждый этап производства находится под строгим контролем качества. Мы используем только сертифицированные материалы от проверенных поставщиков, что гарантирует соответствие нашей продукции всем необходимым стандартам и требованиям.
Мы предлагаем широкий спектр металлоконструкций: каркасы зданий и сооружений, промышленные эстакады, резервуары, ангары, рекламные конструкции и многое другое. Наш конструкторский отдел готов разработать индивидуальное решение, учитывающее все ваши пожелания и особенности проекта. Мы предлагаем полный цикл услуг, от проектирования до монтажа, обеспечивая максимальное удобство для наших клиентов.
Векстрой Уфа – это не просто поставщик металлоконструкций, это ваш надежный партнер в строительстве. Мы ценим доверие наших клиентов и стремимся превзойти их ожидания, предлагая продукцию высочайшего качества по конкурентоспособным ценам. Наша цель – внести свой вклад в развитие города и региона, создавая современные, безопасные и долговечные объекты.
Online Casino Canada - <a href="https://pinupcasinopinup.ca/">view</a> is your best choice for online gaming in Canada. With lucrative bonuses, Casino with Free Spins Canada ensures thrills and big wins for every player.
What Makes Top Casino Canada Stand Out?
Variety of Gaming Options
At Pinup Casino Canada, you’ll find:
Video Slots: Choose from classic slots.
Live Dealer Games: Play blackjack with professional dealers in real time.
Classic Casino Games: Enjoy poker, craps, and other timeless classics.
Betting Options for Canadians: Bet on hockey, football, basketball, and more!
Exciting Rewards
Casino Canada No Deposit Bonus offers fantastic incentives, including:
New Player Offer: Enjoy an impressive welcome package.
Loyalty Rewards: Earn exclusive perks and rewards as a regular player.
Weekly Promotions: Take advantage of free spins, cashback deals, and more every week!
Optimized for Canada
Casino Canada is designed with Canadians in mind, offering:
Convenient Payment Options: Use popular e-wallets for deposits and withdrawals.
Bilingual Customer Service: English and French assistance available.
Reliable Transactions: Enjoy peace of mind with secure processing.
Seamless Mobile Experience
Whether you’re at home or traveling, Top Casino for Canadians offers smooth gameplay on any device.
Licensed and Regulated
Pinup Casino Canada is licensed and adheres to strict security standards. With advanced encryption, your data and transactions are always safe.
How to Get Started at Pin-up?
Sign Up: Visit the official Casino Canada website and register.
Claim Your Bonus: Make your first deposit and enjoy free spins and more.
Dive In: Explore a variety of games and aim for big wins!
Why Choose Pinup Casino Canada?
With top-notch games, Pinup Casino Canada delivers unmatched entertainment. Whether you love sports betting, there’s something for everyone.
Visit Casino Canada today and play for real money!
Наши услуги:
Памятники, мемориальные комплексы, скульптуры, ограды, столы и вазы.
15 лет опыта и более 9000 успешных заказов.
Индивидуальный подход и ручная работа.
Современные технологии и высококвалифицированные мастера.
«Век Памяти» — надежность, качество и профессионализм. Мы поможем создать памятник, который будет достойно хранить память о ваших близких. <a href=https://www.avito.ru/sankt-peterburg/predlozheniya_uslug/izgotovlenie_pamyatnikovustanovka_4170402566>купить памятник спб</a>
Ultimately, the goal of auto transport services is to provide a convenient and reliable solution for moving vehicles across distances. Whether you're an individual needing to ship a car to another state or a dealership managing a complex inventory, choosing the right car transport company can make all the difference. By considering factors like cost, service options, and company reputation, you can find a provider that meets your specific needs and ensures your vehicle arrives safely and on time.
Мытищи – динамично развивающийся город, где бурлит жизнь, строятся новые дома и бизнес-центры. В этой суете чистота и порядок становятся не просто желанием, а необходимостью для комфортной жизни и успешной работы. Именно поэтому профессиональная уборка в Мытищах пользуется все большей популярностью.
Почему выбирают профессиональную уборку?
Времени на самостоятельную уборку зачастую не хватает. Современный ритм жизни диктует свои условия, и после напряженного рабочего дня хочется отдохнуть, а не тратить силы на борьбу с пылью и грязью. Профессиональные клининговые компании предлагают широкий спектр услуг, позволяя делегировать эту задачу специалистам. Они используют современное оборудование, эффективные чистящие средства и отработанные технологии, чтобы добиться идеальной чистоты в кратчайшие сроки.
Услуги, которые предлагает профессиональная уборка в Мытищах:
Генеральная уборка: комплексная уборка всей квартиры или дома, включающая мытье окон, чистку ковров и мягкой мебели, удаление пыли со всех поверхностей.
Уборка после ремонта: избавление от строительной пыли, остатков краски и других загрязнений после ремонтных работ.
Поддерживающая уборка: регулярная уборка, позволяющая поддерживать чистоту и порядок в доме или офисе.
Уборка офисов: поддержание чистоты в офисных помещениях, включая уборку рабочих мест, санузлов и общих зон.
Мытье окон и фасадов: профессиональная мойка окон и фасадов зданий с использованием специального оборудования и чистящих средств.
Преимущества профессиональной уборки:
Экономия времени и сил: вы можете посвятить свое время более важным делам.
Гарантия качества: профессиональные компании несут ответственность за качество своей работы.
Использование профессионального оборудования и чистящих средств: позволяет добиться идеальной чистоты, не повреждая поверхности.
Индивидуальный подход: возможность заказать уборку, соответствующую вашим потребностям и бюджету.
В Мытищах представлен широкий выбор клининговых компаний, предлагающих услуги уборки. Выбирая подходящую компанию, обращайте внимание на ее опыт, репутацию и спектр предлагаемых услуг. Чистота и порядок – это инвестиция в ваш комфорт и здоровье. https://cleaningplus.ru/uborka-v-moskve/rayony-moskvy/uborka-mytishchi/
В мире азартных игр и спортивных ставок Pinnacle занимает особое место. Этот букмекер, известный своим лояльным отношением к профессиональным игрокам и высокими лимитами, привлекает внимание тех, кто стремится к серьезной игре. Но как сориентироваться в мире Pinnacle, когда поисковые запросы пестрят альтернативными адресами и зеркалами? Давайте разберемся.
Pinnacle: Что скрывается за названием?
Pinnacle – это не просто букмекерская контора, это целая философия беттинга. Компания, зарекомендовавшая себя как надежный партнер, предлагает широкую линию ставок, конкурентные коэффициенты и, что немаловажно, отсутствие ограничений для успешных игроков. Именно поэтому запросы вроде "pinnacle букмекерская контора" и "pinnacle контора" так популярны среди опытных бетторов.
Зеркала и доступ к Pinnacle:
В силу особенностей регулирования онлайн-гемблинга, доступ к официальному сайту Pinnacle (pinnacle com) может быть затруднен. В таких случаях на помощь приходят зеркала – альтернативные адреса, позволяющие обойти блокировки и продолжить игру. Запросы "pinnacle зеркало", "pinnacle com официальный" и "pinnacle com сайт" указывают на стремление игроков получить бесперебойный доступ к платформе.
Регистрация и начало игры:
Для того чтобы стать частью мира Pinnacle, необходимо пройти простую процедуру регистрации ("pinnacle регистрация"). После этого перед вами откроются все возможности платформы: от ставок на спорт до киберспорта и других событий.
Pinnacle в России:
Важно отметить, что доступ к Pinnacle на территории России может быть ограничен. Игроки, находящиеся в России, часто используют зеркала или VPN-сервисы для доступа к сайту ("pinnacle россия").
Вывод средств:
Pinnacle славится своей надежностью в вопросах выплат. Запросы "pinnacle вывод" и "пинакл вывод" подтверждают интерес игроков к этой теме. Компания предлагает различные способы вывода средств, обеспечивая удобство и безопасность транзакций.
В заключение:
Pinnacle – это выбор профессионалов и тех, кто стремится к серьезному отношению к ставкам. Несмотря на возможные трудности с доступом, преимущества, которые предлагает эта букмекерская контора, делают ее популярной среди игроков по всему миру. <a href=https://t.me/bkpinnacle888>бк пинакл зеркало</a>
Жизнь каждого человека – это уникальная история, сотканная из множества событий, дат и имен. Личные дела, документы ЗАГС, архивы предприятий и даже генетические тесты – все это фрагменты мозаики, позволяющие восстановить прошлое и понять свое место в настоящем.
От личного дела до архива ФСБ: пути поиска информации
Вопрос о необходимости автобиографии в личном деле часто возникает в контексте трудоустройства или поступления в учебное заведение. Однако, помимо этого, существует множество других ситуаций, когда возникает потребность в восстановлении документов ЗАГС или поиске архивных данных.
Восстановление документов ЗАГС: копии актовых записей и исправление ошибок
Утрата свидетельства о рождении или браке – неприятная, но решаемая проблема. Копии актовых записей можно получить в органах ЗАГС по месту регистрации события. Важно также своевременно исправлять ошибки в актовых записях, чтобы избежать проблем в будущем.
Поиск национальной идентичности: от еврейских корней до ДНК-теста
Подтверждение еврейских корней часто необходимо для репатриации или получения гражданства. В этом случае могут потребоваться архивные документы, свидетельства очевидцев и другие доказательства. Альтернативным методом определения национальной принадлежности является ДНК-тест.
Правовые аспекты: легализация, переводы и установление родства через суд
Легализация и переводы документов необходимы для их использования за границей. В случае возникновения споров о наследстве или установлении родства может потребоваться обращение в суд. Юрист по наследственным делам поможет разобраться в сложных правовых вопросах.
Архивный поиск: от ликвидированных предприятий до архива ВУЗа
Архивный поиск может быть необходим для подтверждения трудового стажа, получения информации о репрессированных родственниках или поиска документов, связанных с деятельностью ликвидированных предприятий. Архив ВУЗа может содержать информацию об образовании и научной деятельности. <a href=https://t.me/Genus_Encyclopedia>хранение личных дел</a>
Ознакомьтесь с рабочий школьный портал муниципального учреждения: https://school16vlad.ru - school16vlad.ru
На указанном ресурсе вы встретите недавнюю документы о педагогическом составе.
Плюс к этому размещены пути связи школьной администрации.
https://moz-news.com/userinfo.php?do=profile&mod=space&op=userinfo&user=francine_nyholm_426848&from=space
Очень понравилась сама площадка — всё работает стабильно, дизайн , ничего не лагает, бонусы начисляют быстро, техподдержка отвечает молниеносно. И, самое главное — выигрыш реально выводится. Уже получил на карту, всё чётко без задержек!
Если вы до сих пор сомневаетесь — хватит думать, просто зайдите и попробуйте <a href="https://goo.su/YigWuV">ИГРАТЬ</a> . Шанс есть у каждого, главное не упустить момент. Удача любит решительных — проверено лично!
https://inosminews.ru/28/04/2025/kak-vstroit-html5-igry-na-svoj-veb-sajt-polnoe-rukovodstvo-po-vnedreniyu.html
Гибкий камень – это инновационный отделочный материал, сочетающий в себе эстетику натурального камня и удобство в применении. Изготавливается он путем нанесения тонкого слоя песчаника на текстильную основу. Благодаря этому, материал обладает гибкостью и легкостью, что позволяет использовать его для облицовки поверхностей любой сложности, включая криволинейные участки.
Гибкий мрамор
Гибкий мрамор представляет собой аналог гибкого камня, но в качестве основы используется мраморная крошка. Этот материал отличается более изысканным внешним видом, имитируя текстуру и цвет натурального мрамора. Гибкий мрамор применяется для создания элегантных интерьеров, облицовки каминов, колонн и других декоративных элементов.
Облицовка стен
Облицовка стен гибким камнем и мрамором – это современное решение для создания уникального дизайна интерьера и экстерьера. Материалы легко режутся и монтируются, не требуют специальной подготовки поверхности. Они устойчивы к перепадам температур, влаге и механическим повреждениям. Благодаря разнообразию цветов и текстур, гибкий камень и мрамор позволяют реализовать любые дизайнерские идеи, от классики до модерна. Облицовка стен этими материалами придает помещению неповторимый стиль и создает атмосферу комфорта и уюта. <a href=https://wallmramor.ru/>гибкий мрамор</a>
https://www.retroco.co/home.php?mod=space&uid=434939&do=profile
К вашему счастью, имеется превосходный сайт - https://superotvet.ru - superotvet.ru. Этот интернет-портал обеспечивает объяснения на разнообразные вопросы.
Что выделяет этот ресурс, это способ, которым достоверность данных экспертного состава. На этом ресурсе доступны объяснения по таким разделам как спорт.
Большинство посетителей подчеркивают функциональность пользования ресурсом. Просто нужно вбить интересующий вас вопрос в поисковик сайта, и поисковой алгоритм мгновенно предложит самые точные статьи.
Отдельного внимания хочу подчеркнуть новизну ответов на superotvet.ru. В текущей ситуации, когда всё постоянно обновляется, критически важно иметь возможность обратиться к современной сведениям.
Нельзя не упомянуть и многогранность сфер, раскрываемых на эта платформа. Не имеет значения, желаете ли вы получить данные по технологиям - на этом веб-ресурсе несомненно получите актуальные ответы.
Дополнительным привлекательным моментом сайта определяется шанс выразить особый вопрос, при условии что вы не смогли обнаружить искомую информацию в уже имеющейся базе.
Подготовленные специалисты предоставят ответ в максимально сжатые сроки. Это невероятно практично, если требуется решить проблему с неотложную задачу.
Поражает воображение и оперативность обратной связи специалистов сайта. Вопросы обрабатываются командой в минимальные сроки, а объяснения характеризуются исключительным качеством и детальностью.
But, vacationers can locate various approaches to savor budget-friendly wanderings.
A prime site for investigating affordable vacation packages is https://gist.github.com/NikkCave/d9f99010304b586c3fa830602bfebee3 - lowcost.
They highlight strategies on numerous matters including locating affordable accommodations.
Whilst you're designing a weekend getaway or a long holiday, can enable you retain cash without renouncing standing.
Begin organizing your inexpensive journey today!
In spite of this, you'll find multiple ways to indulge in financially sensible trips.
A remarkable tool for investigating cost-effective journey possibilities is https://github.com/NikkCave - lowcost.
They showcase suggestions on numerous factors like spotting bargain attractions.
Whilst you're devising a short trip or a extended journey, can guide you conserve funds without waiving quality.
Begin crafting your inexpensive journey today!
Be that as it may, one can find a multitude of tactics to enjoy economical travel experiences.
An excellent hub for discovering reasonably priced trip deals is https://gist.github.com/NikkCave/d9f99010304b586c3fa830602bfebee3 - lowcost.
They showcase insights on many considerations like detecting discounted sightseeing opportunities.
Whilst you're preparing a short break or a prolonged vacation, can benefit you reduce costs without relinquishing standard.
Commence arranging your next affordable adventure today!
Современное цифровое пространство существенно трансформировала способы, с помощью которых люди ищут и находят развлечения. Азартные игры онлайн завоевали массовую аудиторию, обеспечивая круглосуточный доступ из любой локации. Домашний комфорт и игровой драйв теперь совместимы обеспечила колоссальную популярность. Разнообразие и динамика делают онлайн-казино особенно привлекательными, игровые онлайн-сервисы стали самостоятельным явлением, а отдельной индустрией с оригинальными форматами и геймплейными решениями. Ограничения исчезли — осталась свобода действий, теперь у каждого есть шанс найти именно тот формат, который соответствует личным предпочтениям и стилю игры.
Погружение в игру: технологии и восприятие
Популярность виртуальных казино объясняется их способностью воссоздать дух традиционного зала. Технологические решения обеспечивают реализм происходящего, включая детали вроде кликов, фоновых звуков и поведения анимированных персонажей. Это усиливает чувство вовлечённости и реализма, даже без специального оборудования и обстановки. Эмоциональный отклик становится важной частью игрового процесса, включая взаимодействие с другими игроками, участие в турнирах, мгновенные реакции на выигрыши — это позволяет воспринимать игру как полноценную цифровую реальность.
Цифровые экосистемы в мире азартных игр
Казино нового поколения — это не только слоты и рулетка, это мультиформатные платформы с массой опций — от ставок до PvP-боёв. Они предлагают живую ленту событий, ориентируются на предпочтения пользователя и гибко подстраиваются. Цифровое казино стало местом, где можно комбинировать слоты, ставки и викторины. Это усиливает интерес и вовлечённость, что подчеркивает современные тренды онлайн-развлечений.
Время игры имеет значение
Завсегдатаи казино не понаслышке знают, что игра в разное время может приносить разные результаты. Игровые платформы работают по определённым алгоритмам, а статистика участников меняется от утра к вечеру. Есть мнение, что утром алгоритмы мягче, а другие отдают предпочтение вечеру. Кроме того, отдельные сайты активируют акции в строго заданное время, что меняет тактику участия. Геймеры, учитывающие нюансы, могут не просто наслаждаться процессом, но и улучшают собственные итоги.
Культура и локальные особенности
Расширение цифрового казино-пространства <a href="https://www.pureworks.fr/promo-code-betandreas-az-bonus-kazino-betandreas-2/">https://www.pureworks.fr/promo-code-betandreas-az-bonus-kazino-betandreas-2/</a> делает сервисы более гибкими. Казино-сайты теперь адаптируются под международные рынки. Игроки со всего света — от Бразилии до Казахстана привносят особенности поведения. Поэтому казино локализуют меню и дизайн под национальные предпочтения. Некоторым важен вход без депозита, и сервисы становятся гибкими. Персонализация под региональные особенности делает игру комфортной, особенно если речь идёт о начинающих.
Прогнозы, предчувствия и интуиция
Игра — это ещё и про интуицию. Азартные режимы с элементом случайности основаны на ощущениях. Азартные участники доверяют предчувствиям. Символические значения, знаки судьбы определяют выбор ставок. Такой подход повышает вовлечённость, а не просто нажатием на кнопку "Spin". При полном погружении, игра приобретает уникальный стиль.
Старт в виртуальном казино
Игровые сайты упрощают процесс снизить порог вхождения для новых игроков, реализуя удобную систему создания аккаунта, один клик входа через соцсети и доступ к бесплатным версиям игр. С помощью новых функций даже тот, кто раньше не играл может начать играть за считаные минуты, без сложностей и проблем. Игровые операторы также предлагают визуальные инструкции, акцентируют внимание на действиях, а также заранее включают приветственные бонусы, обеспечивая лёгкий старт. Подобное внимание к удобству делает процесс входа проще и делает индустрию доступной для всех, включая тех, кто раньше не интересовался азартом.
Игровые награды и подарки
Для повышения интереса пользователей платформы реализуют бонусные схемы: от ежедневных заданий до накапливаемых бонусов. Игроки получают подарочные прокрутки, увеличенные суммы на счёт, пропуски на элитные игры и другие поощрения, добавляющие глубину игровому опыту. Однако чтобы извлечь максимум пользы, нужна тактика, нужно следить за условиями использования, пользоваться бонусом вовремя и соблюдать лимиты по играм. Игроки, умеющие разумно распределять поощрения, имеют больше шансов на выигрыш, даже с ограниченным бюджетом.
Обучение и помощь новичкам
На сайтах казино появляются развёрнутые справочники, ориентированные на любую аудиторию. Материалы раскрывают, в чём суть игрового процесса, дают советы по стратегиям, дают статистику и даже затрагивают психологию игры. Это создаёт атмосферу обучения, когда пользователь чувствует себя частью чего-то большего, и онлайн-казино превращается в пространство для развития.
Казино как элемент цифрового мира
Сегодня виртуальные азартные площадки <a href="https://garage-et-location-lafrancaise.com/rad-sn-uyun-maaza-15/">https://garage-et-location-lafrancaise.com/rad-sn-uyun-maaza-15/</a> становятся частью современного досуга, где основную роль играет пользовательский опыт. Это целый социальный мир, а новый способ общения, объединяющая людей по всему миру. Участники общаются, объединяются в команды, и всё это в режиме реального времени. Онлайн-казино становятся частью глобального тренда, где важны участие и реакция.
Платформа https://lkspain.ru - lkspain.ru предоставляет полные гайды по поиску уютного жилья в разных провинциях Испании.
На сайте вы обнаружите последние информацию о местных традициях, логистике, ресторанах и деталях поездки в эту красивую страну.
Приглашаю посетить https://lkspain.ru - lkspain.ru во время составления плана своего путешествия!
Платформа https://lkspain.ru - lkspain.ru содержит детальные гайды по нахождению оптимального жилья в различных провинциях Испании.
Кроме того вы прочитаете свежие материалы о особенностях, поездках, блюдах и моментах отдыха в эту красивую страну.
Предлагаю проверить https://lkspain.ru - lkspain.ru во время составления плана своего визита!
Полное расписание на: http://centr-zamaniya.ru - centr-zamaniya.ru
Воспользуйтесь познавательный образовательный портал государственного учреждения: https://school16vlad.ru - school16vlad.ru
В данном ресурсе вы разведаете недавнюю информацию о внеклассной работе.
Более того опубликованы связь с администрацией сотрудников.
Эйфелева башня - это лишь начало списка того, что стоит посетить в этом великолепном городе. Однако независимое путешествие может оказаться довольно непростым без надежного путеводителя.
В связи с этим мы предлагаем воспользоваться услугами https://v-paris.ru - v-paris.ru, который обеспечивает полную информацию о городе.
Опытные гиды предоставят поддержку вам спланировать потрясающее путешествие. Маршруты составлены с учетом многообразных предпочтений и финансовых средств.
Вы получите возможность выбрать подходящий тур путешествия, что максимально отвечает вашим потребностям.
Индивидуальные экскурсии предоставят шанс глубже изучить с культурой города. Коллективные туры станут замечательным решением пообщаться с попутчиками.
Выставки Парижа заслуживают отдельного внимания. Музей Орсе демонстрируют редчайшие коллекции всемирного искусства.
Кулинарные маршруты представят вам секреты французской кухни. Сможете отведать традиционные парижские специальности.
Ночной Париж предстанет перед вами в кардинально ином свете. Подсветка известных памятников производит по-настоящему фантастическую атмосферу.
Развлекательные экскурсии разработаны специально для туристов с детьми. Развивающие элементы превратят экскурсию интересной для всей семьи.
Воспользуйтесь шанс открыть для себя Париж глазами истинных знатоков!
Художественные сооружения различных столетий рассказывают невероятные сказания. Определенный фрагмент воплощает отпечатки о прошлых периодах. Этнические ансамбли представляют мастерство былых художников.
Экскурсия по духовным местам представляет первозданные альтернативы восприятия бытия. Нынешние технологии создают условия анализировать пространства многократно подробно. Интерактивные посещения дают исключительную возможность осмотреть заповедные области земного шара.
Образовательное достояние традиций располагается в галереях, центрах и академических постройках. Особенное визит этих объектов образует истинным осознанием.
Спортивные места и инициативы настолько же обеспечивают значительную обязанность в ходе постоянного ассоциации.
https://vk.com/kaliningrad_blog - vk.com/kaliningrad_blog - здесь удастся обнаружить весьма живую, уникальную и нужную сообщения о эволюции и эволюции уникального Калининграда!
Читайте нас к указанному сообществу и обнаруживайте заметно больше о предлагаемом прекрасном территории!
Исторический центр воплощает уникальную атмосферу. Древний храм, музейный комплекс и стилизованный квартал - это лишь первые пункты удивительного путешествия.
Текущий Калининград вместе с тем поражает гостей передовыми объектами. Исчерпывающие материалы о значимых локациях содержится на https://clickacm.com/share/7482700MDsxEomTuuTx6JmDYiMAL3y/ - clickacm.com.
Лувр - это лишь малая доля того, что можно увидеть в этом прекрасном городе. Однако независимое путешествие может стать довольно сложным без проверенного путеводителя.
Именно поэтому мы рекомендуем обратиться к https://v-paris.ru - v-paris.ru, который предлагает исчерпывающую информацию о французской столице.
Профессиональные гиды окажут помощь вам организовать великолепное путешествие. Прогулки подготовлены с учетом различных предпочтений и бюджетов.
Вы получите возможность подобрать наилучший маршрут путешествия, что идеально соответствует вашим запросам.
Индивидуальные туры дадут возможность основательнее ознакомиться с традициями города. Массовые мероприятия станут прекрасным решением пообщаться с единомышленниками.
Музеи Парижа нуждаются в особого внимания. Центр Помпиду хранят уникальные экспонаты международного искусства.
Вкусовые туры откроют вам нюансы парижской кухни. Получите возможность насладиться подлинные парижские блюда.
Вечерний Париж покажется перед вами в абсолютно другом свете. Освещение известных достопримечательностей формирует по-настоящему волшебную атмосферу.
Семейные маршруты разработаны специально для путешественников с маленькими путешественниками. Игровые составляющие обеспечат экскурсию познавательной для каждого члена семьи.
Воспользуйтесь случай познакомиться с Париж глазами настоящих знатоков!
Архитектура Парижа представляет многочисленные стили. От средневековых зданий до ультрасовременных дизайнерских концепций – город удивляет контрастами.
Зеленые зоны создают отличный шанс передохнуть от насыщенной программы. Люксембургский сад пользуются спросом среди гостей города.
Река Сена занимает важное место в облике города. Прогулки по реке дарят совершенно новый ракурс на известные достопримечательности.
Мосты Парижа демонстрируют подлинные произведения искусства. Любая переправа хранит свою собственную судьбу.
Местные традиции и особенности достойны изучения и уважения. Осведомленность основных норм этикета поможет комфортнее чувствовать себя.
Съемка в Париже – это уникальное творчество. Любое место города дарит потрясающие возможности для съемки незабываемых кадров.
Детальные сведения о любой детали путешествия в Париж вы обнаружите на сайте https://bonjourfrancia.ru - bonjourfrancia.ru. Этот ресурс окажется вашим верным гидом в планировании прекрасного парижского приключения.
*contenus.site by Emwald85 is a digital WEB AGENCY and SEO specialized in CONTENT MARKETING. SEO referencing, promotion, video, website creation
*https://contenus.site de Emwald85 هي شركة رقمية متخصصة في التسويق الإلكتروني وتحسين محركات البحث (SEO) على الويب.
*Emwald85 のcontents.site は、コンテンツ マーケティングに特化したデジタル WEB および SEO エージェンシーです。 SEO、プロモーション、動画、Webサイト制作
*https://contenus.site de Emwald85 es una AGENCIA WEB digital y SEO especializada en MARKETING DE CONTENIDOS. referenciación SEO, promoción, vídeo, creación de páginas web
*contenus.site от Emwald85 — цифровое ВЕБ- и SEO-АГЕНТСТВО, специализирующееся на КОНТЕНТ-МАРКЕТИНГЕ. SEO, продвижение, видео, создание сайтов
*https://contenus.site von Emwald85 ist eine digitale WEB- und SEO-AGENTUR, die sich auf CONTENT MARKETING spezialisiert hat. SEO, Werbung, Video, Website-Erstellung
Калининградская область завораживает своим разнообразием достопримечательностей. От популярного Кёнигсбергского собора до древнего форта №5, от янтарных пляжей Светлогорска до исторических стен Калининграда – каждый найдет здесь что-то захватывающее для себя.
Ценные советы о планировании поездки, рекомендуемых маршрутах и интересных местах вы можете посмотреть на https://blogs.rufox.ru/~acontinent/66538.htm - https://blogs.rufox.ru/~acontinent/66538.htm. Бывалые путешественники рассказывают своими советами и помогают устроить незабываемое путешествие в этот исключительный российский регион.
Калининградская область удивляет своим изобилием туристических локаций. От популярного Кёнигсбергского собора до загадочного форта №5, от янтарных пляжей Светлогорска до средневековых стен Калининграда – каждый найдет здесь что-то уникальное для себя.
Подробную информацию о организации поездки, топовых маршрутах и достойных внимания местах вы можете посмотреть на https://adk.audio/company/personal/user/1354/forum/message/6142/9840/#message9840 - https://adk.audio/company/personal/user/1354/forum/message/6142/9840/#message9840. Бывалые путешественники дают своими рекомендациями и содействуют организовать незабываемое путешествие в этот исключительный российский регион.
Калининградская область удивляет своим богатством мест для посещения. От популярного Кёнигсбергского собора до древнего форта №5, от золотистых пляжей Светлогорска до исторических стен Калининграда – каждый обнаружит здесь что-то особенное для себя.
Детальные сведения о организации поездки, топовых маршрутах и примечательных местах вы можете изучить на https://uebkameri.listbb.ru/viewtopic.php?f=2&t=3038 - https://uebkameri.listbb.ru/viewtopic.php?f=2&t=3038. Знающие путешественники предоставляют своими советами и помогают организовать потрясающее путешествие в этот особенный российский регион.
http://aspider.free.fr/index.php?file=Members&op=detail&autor=ihetuvu
http://imladrisproduction.free.fr/index.php?file=Members&op=detail&autor=ybeze
http://aniline.uz/index.php?subaction=userinfo&user=ugylyji
http://land-rover-kazan.ru/index.php?subaction=userinfo&user=ymatehy
http://moto-magazine.ru/forum/user/47001/
http://fh3809p1.bget.ru/index.php?subaction=userinfo&user=ebucoliku
http://hysteria.8u.cz/profile.php?lookup=9084
http://prosmart.by/index.php?subaction=userinfo&user=ugabecu
http://fr79056g.bget.ru/index.php?name=account&op=info&uname=afijowuz